Радикал целого числа — Википедия

Радикал целого числа — число, равное произведению простых делителей целого числа. Радикал числа n обозначается rad⁡n{\displaystyle \operatorname {rad} n}.

Например, для числа 504 имеем:

504=23⋅32⋅7,{\displaystyle 504=2^{3}\cdot 3^{2}\cdot 7,}

rad⁡(504)=2⋅3⋅7=42.{\displaystyle \operatorname {rad} (504)=2\cdot 3\cdot 7=42.}

В формальной записи определение радикала имеет вид

rad⁡n=∏p∣np∈Pp.{\displaystyle \operatorname {rad} n=\prod _{p\mid n \atop p\in \mathbb {P} }p.}

С помощью радикала целого числа формулируется abc-гипотеза, а с помощью аналога понятия радикала формулируется аналогичное (притом) утверждение в кольце многочленов.

• Радикал является наибольшим бесквадратным делителем числа.
• rad⁡a⩽a.{\displaystyle \operatorname {rad} a\leqslant a.}
• rad⁡(ab)=rad⁡a.{\displaystyle \operatorname {rad} (a^{b})=\operatorname {rad} a.}

• Richard K. Guy. Unsolved Problems in Number Theory. — Springer-Verlag, 2004. — P. 102. — ISBN 0-387-20860-7.

Свободные радикалы — Википедия

Свободные радикалы в химии — частицы, содержащие один или несколько неспаренных электронов на внешней электронной оболочке. Свободные радикалы бывают твёрдыми, жидкими и газообразными веществами и могут существовать от очень короткого (доли секунды) до очень длинного времени (до нескольких лет). Радикалы могут быть не только нейтральными, но и ионными (ион-радикалы), а также иметь более одного неспаренного электрона (как, например, у бирадикалов). Свободные радикалы обладают парамагнитными свойствами и являются очень реакционноспособными частицами^[1].

Существование свободных радикалов постулировалось ещё в XIX веке. В 1849 году английский химик Эдуард Франкленд нагреванием иодэтана с цинком получил бутан, полагая, что это этильный радикал. Подобную ошибку допустил и немецкий химик Герман Кольбе, приняв этан за метильный радикал

[2].

C2H5I+Zn→C4h20+ZnI2{\displaystyle {\mathsf {C_{2}H_{5}I+Zn\rightarrow C_{4}H_{10}+ZnI_{2}}}}

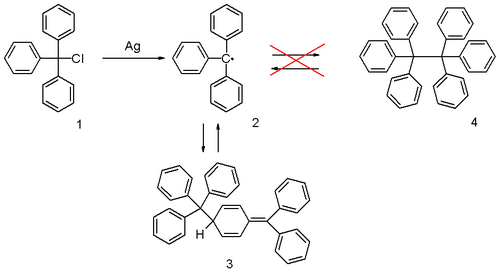Получение трифенилметильного радикала

Впервые свободный радикал в растворе обнаружил американский химик Мозес Гомберг. В 1900 году он открыл трифенилметильный радикал, получив его действием серебра на трифенилметилхлорид. Из-за присутствия этого радикала раствор был окрашен в жёлтый цвет, а затем из раствора выпали белые кристаллы димера этого радикала^[2].

В 1901 году был получен порфирексид, свободный радикал нитроксильной структуры, однако получившие его О. Пилоти и Б. Шверин не идентифицировали его как радикал

[3].

В 1929 году немецкий химик Фридрих Панет идентифицировал метильный и этильный радикалы. В одном из экспериментов он разлагал тетраметилсвинец в токе водорода в термостойкой стеклянной трубке. При этом образовывались метильные радикалы, которые увлекались током водорода дальше по трубке, и металлический свинец, который выпадал на внутреннем диаметре в виде зеркала. Через 30 см от места разложения тетраметилсвинца внутри трубки находилось другое, заранее нанесённое свинцовое зеркало. Пролетающие метильные радикалы реагировали с этим свинцом, снова образуя тетраметилсвинец, который конденсировался в конце установки. Этот же эксперимент позволил благодаря варьированию расстояния между местом разложения и свинцовым зеркалом, а также по скорости тока водорода оценить время жизни радикалов. В условиях опыта (при 1—2 мм рт. ст.) оно составило около 0,0084 секунд^[4].

(Ch4)4Pb→4Ch4⋅+Pb{\displaystyle {\mathsf {(CH_{3})_{4}Pb\rightarrow 4CH_{3}^{\cdot }+Pb}}}

В 1930 году Г. А. Разуваев и В. Н. Ипатьев изучали фотолиз диметилртути в четырёххлористом углероде и установили, что в ходе процесса образуются такие продукты, которые могут образоваться в только в ходе гомолитического распада связи ртуть — углерод. Это послужило доказательством того, что свободные радикалы могут существовать в растворах^[4].

(Ch4)2Hg→Ch4Hg⋅+Ch4⋅{\displaystyle {\mathsf {(CH_{3})_{2}Hg\rightarrow CH_{3}Hg^{\cdot }+CH_{3}^{\cdot }}}}

Ch4⋅+CCl4→Ch4Cl+CCl3⋅{\displaystyle {\mathsf {CH_{3}^{\cdot }+CCl_{4}\rightarrow CH_{3}Cl+CCl_{3}^{\cdot }}}}

Ch4Hg⋅+CCl4→Ch4HgCl+CCl3⋅{\displaystyle {\mathsf {CH_{3}Hg^{\cdot }+CCl_{4}\rightarrow CH_{3}HgCl+CCl_{3}^{\cdot }}}}

CCl3⋅+CCl3⋅→C2Cl6{\displaystyle {\mathsf {CCl_{3}^{\cdot }+CCl_{3}^{\cdot }\rightarrow C_{2}Cl_{6}}}}

Свободные радикалы делят на σ-электронные и π-электронные. У σ-электронных радикалов неспаренный электрон расположен на σ-орбитали. Как следствие, атом с неспаренным электроном сохраняет свою гибридизацию, а радикал имеет практически то же строение, что и исходная молекула. К σ-электронным радикалам относятся фенильный (C₆H₅^•), винильный (CH₂=CH^•) и формильный (HC^•=O) радикалы, а также карбоксильный (CO₂^-•) и пиридильный (C₅H₅N^+•) ион-радикалы. В таких радикалах неспаренный электрон слабо делокализуется. Например, в фенильном радикале спиновая плотность на радикальном центре составляет 0,9918, а существенное взаимодействие наблюдается лишь с орто-протонами^[1][5].

У π-электронных радикалов неспаренный электрон расположен на p-орбитали, вследствие чего радикальный центр имеет sp²-гибридизацию. Окружающие атомы при этом расположены в узловой плоскости этой орбитали, а радикал имеет вид плоского треугольника или низкой пирамиды с очень малым энергетическим барьером инверсии. К π-электронным радикалам относятся, например, алкильные, аллильные и бензильные радикалы. Из них метильный радикал является плоским, а радикалы CF₃^• и C(CH₃)₃^• представляют собой низкие пирамиды. Это подтверждается тем, что, например трифторметильный радикал имеет ненулевой дипольный момент (0,43 Д)^[1].

Стабильность радикалов рассматривают с термодинамических и кинетических позиций, хотя в большинстве случаев оба вида факторов действуют одновременно. Термодинамическая стабильность радикалов связана с тем, насколько эффективно делокализован неспаренный электрон, поскольку делокализация снижает энтальпию образования свободного радикала. Оценить энтальпию образования радикала можно по энергии диссоциации связи, разрыв которой приводит к образованию этого радикала^[6].

Ed(A−B)=ΔfH(A⋅)+ΔfH(B⋅)−ΔfH(A−B){\displaystyle {\mathsf {E_{d}(A\!\!-\!\!B)=\Delta _{f}H(A\cdot )+\Delta _{f}H(B\cdot )-\Delta _{f}H(A\!\!-\!\!B)}}}

Как следствие, в ряду алифатических радикалов термодинамическая стабильность изменяется следующим образом^[6]:

(Ch4)3C⋅>(Ch4)2CH⋅>Ch4Ch3⋅>Ch4⋅.{\displaystyle {\mathsf {(CH_{3})_{3}C\cdot >(CH_{3})_{2}CH\cdot >CH_{3}CH_{2}\cdot >CH_{3}\cdot .}}}

Кинетическая стабильность связана с реакционной способностью радикала по отношению к другим молекулам и радикалам. В первую очередь влияние на кинетическую стабильность оказывает наличие объёмных заместителей около реакционного центра. Если стерические препятствия для подхода реагента к радикалу достаточно велики, то такой радикал может существовать в свободном виде достаточно долгое время. Кинетически стабильные радикалы также называют долгоживущими^[6].

К короткоживущим относятся те свободные радикалы, у которых неспаренный электрон является локализованным, то есть у которых отсутствуют механизмы стабилизации за счёт участия соседних орбиталей или экранирования объёмными заместителями. Короткоживущими являются, например, радикалы NH₂^·, CH₃^·, OH^·, SiH₃^· и др. Такие радикалы приходится стабилизировать либо при помощи сильного охлаждения (жидкими гелием, водородом, азотом или аргоном), либо за счёт эффекта клетки, когда свободные радикалы при низкой температуре находятся в окружении молекул застеклованного растворителя^[1].

Короткоживущие свободные радикалы генерируют, воздействуя на вещество различными физическими или химическими способами. Типичным примером является генерирование метильного радикала при электролизе ацетата натрия в ходе реакции Кольбе^[7].

Ch4COO−→−e−Ch4COO⋅→−CO2Ch4⋅{\displaystyle {\mathsf {CH_{3}COO^{-}{\xrightarrow[{}]{-e^{-}}}CH_{3}COO^{\cdot }{\xrightarrow[{}]{-CO_{2}}}{CH_{3}}^{\cdot }}}}

Также короткоживущие радикалы генерируют фотолизом. При этом энергия кванта, поглощаемого веществом, должна превышать энергию диссоциации одной из его химических связей^[7].

Ph3Hg→hvPh⋅+PhHg⋅{\displaystyle {\mathsf {Ph_{2}Hg{\xrightarrow[{}]{hv}}Ph^{\cdot }+PhHg^{\cdot }}}}

Некоторые органические соединения с низкой энергией диссоциации соответствующей связи дают свободные радикалы при пиролизе. Так, нагревание органических пероксидов (перекиси бензоила, трет-бутилгидропероксида, кумилпероксида, трет-бутилпероксида) приводит к гомолитическому разрыву связи O-O и образованию двух радикалов^[7].

(Ch4)3COOC(Ch4)3→t2(Ch4)3CO⋅{\displaystyle {\mathsf {(CH_{3})_{3}COOC(CH_{3})_{3}{\xrightarrow[{}]{t}}2(CH_{3})_{3}CO^{\cdot }}}}

Долгоживущие свободные радикалы отличаются от короткоживущих тем, что неспаренный электрон в них сильно делокализован, а реакционный центр окружён объёмными заместителями, которые создают пространственные затруднения и понижают реакционную способность этого центра^[7]. Получают их различными химическими реакциями, в том числе реакциями одноэлектронного переноса и реакциями без затрагивания радикального центра^[3].

Типичными представителями этого класса свободных радикалов являются арилметильные радикалы. Некоторые из них являются устойчивыми при комнатной температуре окрашенными кристаллическими или аморфными веществами, содержащими около 6·10²³ спин/моль неспаренных электронов. Например, так называемые инертные радикалы (C₆Cl₅)₂C^•Cl, (C₆Cl₅)₃C^•, (C₆Cl₅)₂C^•C₆H₄OH имеют оранжево-красный цвет и плавятся при высокой температуре^[7].

Димеризация трифенилметильного радикала

В растворах эти радикалы существуют в равновесии с молекулами-димерами. На положение этого равновесия, то есть на соотношение радикала и димера, влияет сольватация, а также электронные и пространственные эффекты^[7]. Первоначально считалось, что димеры имеют структуру гексаарилэтанов, но позже было показано, что они имеют хиноидную структуру^[8].

Степень диссоциации димеров триарилметильных радикалов в бензоле при 25 °С^[7]

Радикал	Степень диссоциации, %	Радикал	Степень диссоциации, %
Ph3C•	2	трет-Bu(п-PhC6H4)2C•	74
(п-PhC6H4)Ph2C•	15	(Ph2C=CH)Ph2C•	80
(β-C10H7)3C•	24	(п-PhC6H4)3C•	100
(α-C10H7)Ph2C•	60	(Ph3C)Ph2C•	100

Ароксильные радикалы также относятся к долгоживущим, хотя они быстро реагируют с кислородом, поэтому работа с ними требует инертной атмосферы или вакуума. Они образуются как промежуточные соединения при окислении фенолов. В чистом виде выделены гальвиноксильный радикал с т. пл. 158 °С и индофеноксильный радикал с т. пл. 136 °С^[7].

Гальвиноксильный радикал

Индофеноксильный радикал

1,3,6,8-Тетра-трет-бутил-9-карбазильный радикал с т. пл. 145 °С

Существует ряд долгоживущих радикалов, у которых радикальный центр находится на атоме азота. Так, аминильные радикалы, устойчивые при 25 °С, получают окислением вторичных аминов. Особенной устойчивостью обладают вердазильные радикалы, являющиеся одними из самых стабильных органических парамагнетиков. Их период полуразложения на воздухе при комнатной температуре может составлять многие годы^[7].

Нитроксильные радикалы по строению схожи с оксидами аминов. Радикальный центр в них находится на атоме кислорода, соединённом с атомом азота. Некоторые нитроксильные радикалы очень устойчивы даже несмотря на то, что неспаренный электрон в них не подвергается делокализации. Известным примером такого устойчивого радикала является тёмно-красный 2,2,6,6-тетраметилпиперидин-1-оксил (TEMPO) с т. пл. 38 °С. Существуют, однако, и иные структуры, где делокализация неспаренного электрона хорошо выражена, а реакционный центр окружён объёмными заместителями^[3].

Иминоксильные радикалы имеют общую формулу RR’C=NO^•. Благодаря наличию двойной связи они могут существовать в виде цис— и транс-изомеров^[3].

Поскольку у свободных радикалов есть неспаренный электрон, они проявляют характерные химические свойства. Так, они вступают в реакции с другими частицами, содержащими неспаренный электрон: со свободными радикалами (в том числе рекомбинируют сами с собой), металлами и молекулярным кислородом^[9].

2R⋅→R−R{\displaystyle {\mathsf {2R\cdot \rightarrow R\!\!-\!\!R}}}

R⋅+R′⋅→R−R′{\displaystyle {\mathsf {R\cdot +R’\cdot \rightarrow R\!\!-\!\!R’}}}

R⋅+Na⋅→R−Na{\displaystyle {\mathsf {R\cdot +Na\cdot \rightarrow R\!\!-\!\!Na}}}

R⋅+⋅O−O⋅→R−O−O⋅{\displaystyle {\mathsf {R\cdot +\cdot O\!\!-\!\!O\cdot \rightarrow R\!\!-\!\!O\!\!-\!\!O\cdot }}}

Также свободные радикалы способны реагировать с соединениями, которые легко диссоциируют на атомы^[9].

2R⋅+I2→2R−I{\displaystyle {\mathsf {2R\cdot +I_{2}\rightarrow 2R\!\!-\!\!I}}}

Один радикал может оторвать атом водорода от другого радикала: при этом происходит диспропорционирование (образуется одно насыщенное и одно ненасыщенное соединение), а общее число радикалов в системе уменьшается^[9].

Ch4Ch3⋅+Ch4Ch3⋅→Ch4Ch4+Ch3=Ch3{\displaystyle {\mathsf {CH_{3}CH_{2}\cdot +CH_{3}CH_{2}\cdot \rightarrow CH_{3}CH_{3}+CH_{2}\!\!=\!\!CH_{2}}}}

Выделяют также реакции с переносом радикального центра, в которых неспаренный электрон в результате отрыва водорода или присоединения радикала по двойной связи оказывается на другой частице^[9].

RH+R′⋅→R⋅+R′H{\displaystyle {\mathsf {RH+R’\cdot \rightarrow R\cdot +R’H}}}

Ch3=Ch3+R⋅→R−Ch3−Ch3⋅{\displaystyle {\mathsf {CH_{2}\!\!=\!\!CH_{2}+R\cdot \rightarrow R\!\!-\!\!CH_{2}\!\!-\!\!CH_{2}\cdot }}}

Существуют и реакции, обратные присоединению, когда радикалы распадаются с разрывом связи в β-положении. Такая фрагментация особенно характерна для алкоксильных радикалов, которые при наличии нескольких путей распада предпочитают тот, при котором образуется более устойчивый алкильный радикал^[9].

RCh3C−O⋅→R⋅+Ch3=O{\displaystyle {\mathsf {RCH_{2}C\!\!-\!\!O\cdot \rightarrow R\cdot +CH_{2}\!\!=\!\!O}}}

Для свободных радикалов характерны реакции перегруппировки, однако в случае радикалов атомы водорода и алкильные группы мигрируют редко (в отличие от перегруппировок карбокатионов). Гораздо чаще встречается миграция фенильной группы или атомов галогена^[9].

Симулированный ЭПР-спектр метильного радикала

Свободные радикалы обнаруживают благодаря их парамагнитным свойствам. Преимущественно для этого используется метод электронного парамагнитного резонанса (ЭПР). Спектры ЭПР позволяют не только обнаружить свободные радикалы, но и получить информацию об их строении и степени делокализации неспаренного электрона. Для этого используют два параметра: g-фактор и константу сверхтонкого расщепления. Первый из них является аналогом химического сдвига в спектроскопии ЯМР^[10].

Сверхтонкое расщепление возникает из-за взаимодействия неспаренного электрона с магнитными ядрами радикала. Если электрон взаимодействует с ядром, имеющим спиновое число I, то в результате расщепления возникает 2I+1 линий. Если таких ядер несколько, например n, то число линий становится равным 2nI+1. У протона спиновое число равно +½, поэтому n эквивалентных протонов расщепляют линию в спектре ЭПР на

n+1 линий. Относительная интенсивность этих линий соответствует биномиальным коэффициентам^[10].

Спектр трифенилметильного радикала ещё более сложен, поскольку там неспаренный электрон взаимодействует с 6 эквивалентными протонами в орто-положении, 6 эквивалентными протонами в мета-положении и 3 эквивалентными протонами в пара-положении. В этом случае число линий от каждой группы эквивалентных протонов нужно перемножать, поэтому суммарное число линий в ЭПР-спектре этого катиона равно 7·7·4 = 196. Спектры сложных радикалов расшифровывают путём расчёта теоретических спектров и сравнения их с экспериментальными^[10].

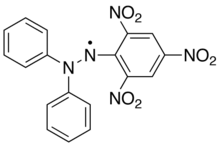Дифенилпикрилгидразильный радикал

Концентрацию свободных радикалов в образце определяют, записывая одновременно спектр эталона и спектр исследуемого образца. Затем интенсивности сигналов сравнивают. В качестве эталона часто используют дифенилпикрилгидразильный радикал Ph

2N-N^•-C₆H₂(NO₂)₃. Этот же радикал, имеющий тёмно-фиолетовую окраску, позволяет следить за образованием и расходованием радикалов в динамике, поскольку при его взаимодействии с другими радикалами окраска изменяется на жёлтую либо исчезает^[10].

Сложные свободные радикалы исследуют методами двойного электрон-ядерного резонанса (ДЭЯР) и химической поляризации ядер. Если концентрация свободного радикала в растворе достаточна, его можно изучить методом ЯМР^[7]

Долгоживущие свободные радикалы находят применение в качестве стабилизаторов, предотвращающих процессы окисления и полимеризации: в частности, ими стабилизируют акрилонитрил, винилацетат, винилиденхлорид, стирол, фурфурол, жиры и масла. В молекулярной биологии они используются в качестве спиновых меток. Их также используют в производстве фотоматериалов, полимерных покрытий, в приборостроении, геофизике и дефектоскопии

[3].

Короткоживущие радикалы встречаются в природе как промежуточные частицы в различных химических реакциях, например радикальном галогенировании^[3].

Свободные радикалы также образуются в организме человека в ходе обычной жизнедеятельности: при биосинтезе простагландинов, в работе митохондрий и фагоцитов. С образованием в организме радикалов связывают процессы старения^[3].

1. ↑ ^{1 2 3 4} Химическая энциклопедия, 1995, с. 154.
2. ↑ ^{1 2} Берберова, 2000, с. 39–40.
3. ↑ ^{1 2 3 4 5 6}
   7 Химическая энциклопедия, 1995, с. 156.
4. ↑ ^{1 2} Берберова, 2000, с. 41.
5. ↑ Днепровский, Темникова, 1991, с. 178–181.
6. ↑ ^{1 2 3} Днепровский, Темникова, 1991, с. 181–183.
7. ↑ ^{1 2 3 4 5 6 7 8 9 10} Химическая энциклопедия, 1995, с. 155.
8. ↑ Днепровский, Темникова, 1991, с. 180.
9. ↑ ^{1 2 3 4 5 6} Днепровский, Темникова, 1991, с. 189–191.
10. ↑ ^{1 2 3 4} Днепровский, Темникова, 1991, с. 175–177.

Сравнение радикалов — АЛГЕБРА — Уроки для 10 классов — конспекты уроков — План урока — Конспект урока — Планы уроков

УРОК 35

Тема. Сравнение радикалов

 

Цель урока. Формирование умений учащихся сравнивать радикалы.

И. Проверка домашнего задания

1. Фронтальная беседа по № 25-37 из «Вопросы и задания для повторения» раздела III.

2. Самостоятельная работа.

Вариант 1

1. Найдите область определения выражения: а) ; б) . (3 балла)

2. Вычислите: а) ; б) 5; в) ·. (3 балла)

3. Упростите: а) ; б) , b > 0. (3 балла)

4. Или подобные радикалы и ? (3 балла)

Вариант 2

1. Найдите область определения выражения: а) ; б) . (3 балла)

2. Вычислите: а) ; б) 4; в) ·. (3 балла)

3. Упростите: а) ; б) , х > 0. (3 балла)

4. Или подобные радикалы и ? (3 балла)

Ответ:

В-1: 1. а) R; б) x 3. 2. а) 3; б) 10; в) 27. 3. а) ; б) . 4. Подобные.

В-2: 1. а) R; б) х 1,5. 2. а) 5; б) 8; в) 8. 3. а) ; б) . 4. Подобные.

 

II. Восприятия и осознания материала о сравнения радикалов

Для сравнения радикалов применяется теорема:

 

Теорема: Если а > b 0, то > , то есть большем положительном підкореневому выражения соответствует и большее значение корня.

Доведение

Проведем доказательство методом от противного. Допустим, . Тогда по свойству степеней с натуральным показателем имеем , т.е. а b. А это противоречит условию а > b.

Пример. Сравним числа и .

Представим и в виде корней с одним и тем же показателем:

= = , а = = . Согласно доказанной теореме, так как 32 > 27, то > , а следовательно, > .

Выполнение упражнений

1. Сравните числа: а) и ; б) и ; в) и ; г) и .

Ответ: а) ; б) 😉 ; г) .

2. Что больше: а) или ; б) или ; в) или г) или ?

Ответ: а) ; б) ; в) ; г) = ?

3. Что меньше: а) или ; б) ли ?

Ответ: а) ; б) .

 

Непосредственно из доказанной теоремы следует:

1) Если а > 1, то > 1 и а.

2) Если 0 а 1, то 0 1 и > а.

3) + > , при условии а > b 0 или b > 0.

Выполнение упражнений

1. Определите знак выражения: а) — 1 ; б) — 1; в) — 5; г) .

Ответ: а) — ; б) + ; в) — ; г) +.

 

2. Расположите в порядке возрастания: а) ; ; ; б) ; ; 😉 ; ; .

 

III. Подведение итогов урока

 

IV. Домашнее задание

Вопросы и задания для повторения раздела III № 13-15, 47. Упражнения № 22, 26, 38.

Что такое радикал как математическое понятие

Это термин, обозначающий символ по извлечению квадратного корня, имеет вид — √. Его можно заменить показателем степени 1/2 т.е. √4 = 4 в степени 1/2.

математ., знак √ извлечения корня

Один из корней двучленного уравнения x в степени n = а называется радикалом

Математический знак √ , которым обозначают действие извлечения корня, а также сами корни уравнения вида x в степени n = а.

Преобразование выражений, содержащих радикалы

Вопросы занятия:

·     ввести понятие «радикал»;

·     рассмотреть примеры, в которых выполняются преобразования выражений с радикалами.

Материал урока

На прошлых уроках мы с вами познакомились с корнем n—ой степени из а, рассмотрели основные свойства корня. На сегодняшнем уроке мы будем решать задачи на преобразование выражений с радикалами, используя все, что мы изучали на предыдущих уроках.

Повторим основные понятия.

Корнем n-ой степени из неотрицательного числа a называют такое неотрицательное число, при возведении которого в степень n получается число а.

Корнем нечётной степени n-ой из отрицательного числа а называют такое отрицательное число, при возведении которого в степень n получается а.

Обозначают:

Число а – это подкоренное число, число n – показатель корня.

Перечислим основные свойства

Прежде чем приступить к решению упражнений, давайте отметим некоторые важные моменты.

Верно ли что:

Нет, так как, например:

Верно ли что:

Нет, так как, например:

В данном случае справедлива формула:

Эта же формула справедлива для любого чётного показателя степени.

Для нечётного показателя степени имеем другую формулу.

Рассмотрим несколько примеров.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Ещё раз хотелось бы обратить ваше внимание, что решая задачи с радикалами, в первую очередь мы должны обратить внимание на то, какой знак может иметь подкоренное выражение. И только после этого приступать к преобразованию выражений.

 

Радикал идеала — Википедия

Материал из Википедии — свободной энциклопедии

В коммутативной алгебре радикал идеала I — это идеал, образованный всеми элементами x такими, что некоторая степень x принадлежит I. Радикальный идеал — это идеал, совпадающий со своим собственным радикалом.

Радикал идеала I в коммутативном кольце R, обозначаемый I{\displaystyle {\sqrt {I}}}, определяется как

I={r∈R∣∃n∈Nrn∈I}{\displaystyle {\sqrt {I}}=\{r\in R\mid \exists n\in \mathbb {N} \,\,\,r^{n}\in I\}}

Интуитивно, для получения радикала идеала нужно взять корни всех возможных степеней из его элементов. Эквивалентное определение радикала идеала I — это прообраз нильрадикала R/I{\displaystyle R/I} при отображении факторизации. Это также доказывает, что I{\displaystyle {\sqrt {I}}} является идеалом.

• В кольце целых чисел радикал главного идеала (a){\displaystyle (a)} — это идеал, порождённый произведением всех простых делителей a{\displaystyle a}.
• Радикал примарного идеала прост. Обратно, если радикал идеала прост, то этот идеал примарен.
• В любом коммутативном кольце Pn=P{\displaystyle {\sqrt {P^{n}}}=P} для простого идеала P{\displaystyle P}^[1]. В частности, каждый простой идеал радикален.

• I=I{\displaystyle {\sqrt {\sqrt {I}}}={\sqrt {I}}}. Более того, I{\displaystyle {\sqrt {I}}} — это наименьший радикальный идеал, содержащий I.
• I{\displaystyle {\sqrt {I}}} — это пересечение всех простых идеалов, содержащих I. В частности, нильрадикал — это пересечение всех простых идеалов.
• Идеал является радикальным тогда и только тогда, когда факторкольцо по нему не содержит нетривиальных нильпотентов.

Основная мотивация для изучения радикалов — это их появление в знаменитой теореме Гильберта о нулях из коммутативной алгебры. Наиболее простая формулировка этой теоремы имеет следующий вид: для любого алгебраически замкнутого поля k{\displaystyle k} и любого конечнопорождённого идеала в кольце многочленов от n{\displaystyle n} переменных над полем k{\displaystyle k} верно следующее равенство:

I⁡(V⁡(J))=J,{\displaystyle \operatorname {I} (\operatorname {V} (J))={\sqrt {J}},}

где

V⁡(J)={x∈kn | f(x)=0 ∀f∈J}{\displaystyle \operatorname {V} (J)=\{x\in k^{n}\ |\ f(x)=0~\forall f\in J\}}

и

I⁡(S)={f∈k[x1,x2,…xn] | f(x)=0 ∀x∈S}.{\displaystyle \operatorname {I} (S)=\{f\in k[x_{1},x_{2},\ldots x_{n}]\ |\ f(x)=0~\forall x\in S\}.}