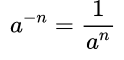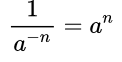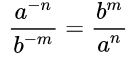Умножение степеней, деление, таблица

Что такое степень числа

Алгебра дает нам такое определение: 

«Степенью n числа а является произведение множителей величиной а n-раз подряд»

• aⁿ — степень, где

a — основание степени

n — показатель степени

Соответственно, aⁿ= a·a·a·a…·a

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число — она решается довольно просто:

2 — основание степени

3 — показатель степени

Действия, конечно, можно выполнять и на калькуляторе — вот несколько подходящих:

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3). Неважно в какой класс перешел ребенок — таблица пригодится всегда.

Число Вторая степень Третья степень 1 1 1 2 4 8 3 9 27 4 16 64 5 25 125 6 36 216 7 49 343 8 64 512 9 81 729 10 100 1000

Свойства степеней: когда складывать, а когда вычитать

Степень в математике с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук и ниже мы их рассмотрим.

Свойство 1: произведение степеней

При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:

aⁿ · a^m = a^m+n

a — основание степени

m, n — показатели степени, любые натуральные числа.

Свойство 2: частное степеней

Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.

 

a — любое число, не равное нулю

m, n — любые натуральные числа такие, что m > n

Свойство 3: возведение степени в квадрат

Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.

(aⁿ)^m = a^{n· m} 

a — основание степени (не равное нулю)

m, n — показатели степени, натуральное число

Свойство 4: степень возведения

При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.

(a · b)ⁿ = aⁿ · bⁿ

a, b — основание степени (не равное нулю)

n — показатели степени, натуральное число

Свойство 5: степень частного

Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.

(a : b)ⁿ = aⁿ : bⁿ

a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0, 

n — показатель степени, натуральное число

Умножение чисел с одинаковыми степенями

Для того, чтобы произвести умножение степеней с одинаковыми показателями, нужно перемножить основания, а показатель степени оставить неизменным:

aⁿ · bⁿ = (a · b)ⁿ , где

a, b — основание степени (не равное нулю)

n — показатели степени, натуральное число

• a⁵ · b⁵ = (a·a·a·a·a) ·(b·b·b·b·b) = (ab)·(ab)·(ab)·(ab)·(ab) = (ab)⁵
• 3⁵ · 4⁵ = (3·4)⁵ = 12⁵ = 248 832
• 16a² = 4²·a² = (4a)²

Умножение степеней с одинаковыми основаниями

Степени с одинаковыми основаниями умножаются путём сложения показателей степеней:

a^m · aⁿ= a^m+n, где

a — основание степени

m, n — показатели степени, любые натуральные числа

• 3⁵ · 3² = 3⁵⁺³ = 3⁸ = 6561
• 2⁸ · 8¹= 2⁸ · 2³ = 2¹¹ = 2048 

Умножение чисел с разными степенями

Если степени разные, но основания одинаковые, то действия производим согласно правилу, описанному выше. А именно:

aⁿ · bⁿ = (a · b)ⁿ

Если же разные и степени, и основания и одно из оснований не преобразуется в число с той же степенью, как у другого числа (как здесь: 2⁸ · 8¹= 2⁸ · 2³ = 2¹¹ = 2048), то производим возведение в степень каждого числа и лишь затем умножаем:

Деление степеней с одинаковыми основаниями

Деление степеней с разными основаниями, но одинаковыми показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.

a — любое число, не равное нулю

m, n — любые натуральные числа такие, что m > n

Деление чисел с одинаковыми степенями

При делении степеней с одинаковыми показателями результат частного этих чисел возводится в степень:

aⁿ : bⁿ = (a : b)ⁿ, где 

a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0, 

n — показатель степени, натуральное число

Деление чисел со степенями

Если степени разные, но основания одинаковые, то действия производим согласно правилу, описанному выше. А именно:

Если же разные и степени, и основания, то возводим в степень каждое число и только потом умножаем:

Подготовиться к сложной контрольной ребенку помогут в детской онлайн-школе Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Запишите вашего ребенка на бесплатный вводный урок математики и начните заниматься ей с удовольствием уже завтра.

Сложение и вычитание степеней ⬅️

Что такое степень числа

В учебниках по математике можно встретить такое определение: 

«Степенью n числа а является произведение множителей величиной а n-раз подряд»

где

a — основание степени

n — показатель степени

Соответственно, aⁿ= a·a·a·a…·a

Читается такое выражение, как a в степени n.

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) на само себя. А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например число 2, то решается она довольно просто:

2 — основание степени

3 — показатель степени

Действия, конечно, можно выполнять и на калькуляторе — вот несколько подходящих:

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).

Число Вторая степень Третья степень 1 1 1 2 4 8 3 9 27 4 16 64 5 25 125 6 36 216 7 49 343 8 64 512 9 81 729 10 100 1000

Свойства степеней: когда складывать, а когда вычитать

Степень в математике с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — давайте их рассмотрим.

Свойство 1: произведение степеней

При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:

a — основание степени

m, n — показатели степени, любые натуральные числа.

Свойство 2: частное степеней

Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.

a — любое число, не равное нулю

m, n — любые натуральные числа такие, что m > n

Свойство 3: возведение степени в квадрат

Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.

a — основание степени (не равное нулю)

m, n — показатели степени, натуральное число

Свойство 4: степень возведения

При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.

a, b — основание степени (не равное нулю)

n — показатели степени, натуральное число

Свойство 5: степень частного

Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.

a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0, 

n — показатель степени, натуральное число

Сложение и вычитание степеней

Как складывать числа со степенями и как вычитать степени — очень просто. Основной принцип такой: выполняется сначала возведение в степень, а уже потом действия сложения и вычитания. Примеры:

• 2³+ 3⁴= 8 + 81= 89
• 6³— 3³= 216 — 27 = 189

И еще несколько правил: при наличии скобок — начинать вычисления нужно внутри них только потом возведение производим в степень затем выполняем остальные действия: сначала умножение и деление после — сложение и вычитание

Сложение степеней с разными показателями

В таком случае действуем согласно общему правилу: сначала выполняем возведение в степень каждого числа, затем — производим сложение.

Сложение степеней с разными основаниями

В целом, это ничем не отличается от предыдущего пункта. Могут быть разные основания, но одинаковые степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим сложение.

• 3⁴+ 5⁴=81 + 625 = 706
• 1⁴+ 7²= 1+ 49 = 50

Как складывать числа с одинаковыми степенями

Точно также, как и в предыдущем примере. Если степени одинаковые, а основания разные, то нельзя сложить основания и затем эту сумму возводить в степень.
Сначала возводим каждое число в степень и затем выполняем сложение.

В уравнениях это будет происходить немного иначе. Если показатель и основание степени одинаковые (тогда это называется переменная, a², например) — их коэффициенты можно складывать. Коэффициент — это число перед переменной a².

2, 3, 5 — коэффициенты

a²  — переменная

Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.

Вычитание степеней с одинаковым основанием

Здесь принцип тот же, что и со сложением: возводим в степень числа и только потом вычитаем их.

Вычитание степеней с разными основаниями

Могут быть разные основания, но одинаковые степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим вычитание.

• 5⁴— 4⁴= 625 — 256 = 369
• 7⁴— 3²= 2401 — 9 = 2392

Вычитание чисел с одинаковыми степенями

Все точно также, как и со сложением. Если степени одинаковые, а основания разные, то нельзя вычесть основания и затем эту разницу возводить в степень. Сначала возводим каждое число в степень и затем выполняем вычитание.

И та же история с коэффициентами: если показатель степени и основание степени одинаковые (тогда это называется переменная, a²) — их коэффициенты можно вычитать. Коэффициент — это число перед переменной a².

6, 3, 2 — коэффициенты

a²  — переменная

Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.

Подготовиться к сложной контрольной ребенку помогут в детской онлайн-школе Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Запишите вашего ребенка на бесплатный вводный урок математики и начните заниматься ей с удовольствием уже завтра.

Свойства степени с целым показателем

Степень с целым показателем Первый урок посвящен понятию обыкновенной степени с целым показателем — это математическая операция, в ходе которой число многократно умножается на само себя. Если некоторое действительное число \(a\) возвести в целую степень \(b\), то это значит, что число \(a\) умножается на само себя \(b\) раз. $$ a^b=\underbrace{a*a*a*…*a}_{b \; раз}, $$ Пример 1 $$ 3^4=\underbrace{3*3*3*3}_{4 \; раза}=81 $$ Часто вы будете сталкиваться с отрицательной степенью. Для того, чтобы ее посчитать, необходимо данное число \(a\) (стоящее под степенью) перевести в обратное и просто возвести в степень. Очень частая ошибка — написание знака минус перед полученным результатом. Знак минус указывает только на отрицательную степень, а сам результат возведнения в степень будет положительным. $$ a^{-b}=\frac{1}{a^b}, $$ Пример 2 $$ 4^{-3}=\frac{1}{4^3}=\frac{1}{64}, $$ Любое число в нулевой степени — равно всегда 1. $$ a^0=1, $$ Также в уроке мы подробно разберем основные свойства степени с целым показателем: степень от произведения и частного двух чисел, степень в степени, произведение и деление двух степеней с одинаковыми основаниями. И на примерах познакомимся с преобразованием сложных степенных уравнений.

Основные свойства степени с целым показателем: $$ 1.\; (a*b)^n=a^n*b^n; $$ Пример 3 $$ (2*5)^3=2^3*5^3=8*125=1000, $$
$$ 2.\; a^n*a^m=a^{n+m}; $$ Пример 4 $$ 2^3*2^4=2^{3+4}=2^7=128, $$
$$ 3.\; \frac{a^n}{a^m}=a^{n-m}; $$ Пример 5 $$ \frac{3^5}{3^3}=3^{5-3}=3^{2}=9, $$
$$ 4.\; (a^n)^m=a^{n*m}; $$ Пример 6 $$ (2^3)^2=2^{3*2}=2^6=64, $$

Разберем несколько примеров заданий, которые иногда встречаются в ЕГЭ и ОГЭ по математике. Как правило, для того, чтобы решить эти задания необходимо хорошо знать все свойства степеней с целым показателем:
Пример 7 $$ \frac{2^4*2^5}{2^7}=\frac{2^9}{2^7}=2^2=4; $$ Здесь мы использовали свойства произведения степеней с одинаковым основанием при умножении и делении – в числителе степени складываются, после этого выполняем операцию деления, степени вычитаются. Формулы №2,№3.

Рассмотрим более сложный пример, когда основания разные:
Пример 8 $$ \frac{3^4*5^3}{15^3}=\frac{3^4*5^3}{(3*5)^3}=\frac{3^4*5^3}{3^3*5^3}=3^{4-3}*5^{3-3}=3^1*5^0=3*1=3; $$ В этом случае необходимо привести все степени к одинаковому основанию. Замечаем, что \(15\) раскладывается, как произведение 3 и 5, получим одинаковые основания и применим формулы №1,№3.

Приложение к уроку «Свойства степени с одинаковыми основаниями».

Инфоурок › Математика ›Презентации›Приложение к уроку «Свойства степени с одинаковыми основаниями».

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ В тетрадях краткий конспект по плану: Символическая запись свойства Пример на применение свойства

2 слайд Описание слайда:

Для любого числа а и любых натуральных чисел n и k справедливо равенство: аn • ak = a n + k Свойство 1: умножение степеней с одинаковыми основаниями

3 слайд Описание слайда:

Доказательство: an = a • a • a •…• a n множителей 2) ak = a • a • a •…• a k множителей 3) an •ak = a • a • a •…• a• a • a • a •…•a= n множителей k множителей = a• a• a•…• a= a n+k n+k множителей Что и требовалось доказать

4 слайд Описание слайда:

Примеры: 23 • 25 = 2 3+5 = 28 = 256 3 •34 = 31 • 34 = 3 1+4 = 35 = 243

5 слайд Описание слайда:

Свойство 2: деление степеней с натуральным показателем Если а – не равное нулю число и n, k – натуральные числа такие, что n > k, то справедливо равенство an : ak = a n-k

6 слайд Описание слайда:

Доказательство: a n-k • a k = a (n-k)+k = a n Итак, a n-k • a k = a n , следовательно, an : ak = a n-k Что и требовалось доказать

7 слайд Описание слайда:

Примеры: 26 : 24 = 2 6-4 = 22 = 4 38 : 35 = 3 8-5 = 33 = 27

8 слайд Описание слайда:

Свойство 3: возведение степени в степень Для любого числа а и любых натуральных чисел n и k справедливо равенство: (а n)k = a n•k

9 слайд Описание слайда:

Примеры (25)2 = 2 2•5 = 2 10 = 1024 (32)3 =36 = 729 ( 23•24)5 = ( 27)5 = 2 35 = 28 = (2•28)3 (29)3 2 27 = 256

10 слайд Описание слайда:

Полезно запомнить! При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются. При возведении степени в степень основание остается прежним, а показатели перемножаются.

11 слайд Описание слайда:

Полезно запомнить! Свойства являются тождествами, их можно применять как слева направо, так и справа налево.

Курс повышения квалификации

Курс повышения квалификации

Курс профессиональной переподготовки

Учитель математики и информатики

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДБ-219997

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Действия со степенями 🐲 СПАДИЛО.РУ

Что такое степень?

Степенью числа a с натуральным показателем n называют произведение n одинаковых множителей, каждый из которых равен а. То есть аⁿ=a×a×a×a …..a (а берется n раз). Число а называют основанием, а число n показателем степени. Показатель показывает, сколько раз берется основание как множитель.

Пример №1.

• 3⁴=3×3×3×3 число 3 берем 4 раза (показатель 4)
• 21³=21×21×21 число 21 берем 3 раза (показатель 3)

Свойства степени (применимы для степеней с одинаковым основанием)

Умножение степеней

При умножении степеней с одинаковым основанием основание оставляют тем же, а показатели складывают:

aⁿ× a^m=a^n+m

Пример №2.

а²×а⁸=а²⁺⁸=а¹⁰

5⁵×5³×5⁴=5⁵⁺³⁺⁴=5¹²

Деление степеней

При делении степеней с одинаковым основанием  основание оставляют тем же, а показатели вычитают:

aⁿ : a^m=a^n—m

Пример №3.

с¹²:с⁵=с^12-5= с⁷

3²³:3²⁰=3^23-20= 3³

Возведение степени в степень

При возведении степени в степень основание оставляют тем же, а показатели умножают:

(aⁿ)^m=a^n×m

Пример №4.

(с¹⁰)²=с²⁰

(6³)⁵=6¹⁵

Степень произведения

При возведении в степень произведения разных множителей необходимо возвести в эту степень каждый множитель:

(a×b×c)^m=a^m×b^m×c^m

Пример №5.

(сmn)⁵=c⁵m⁵n⁵

(3²5⁴)⁶=3¹²5²⁴

Степень дроби  (степень частного)

При возведении в степень обыкновенной дроби необходимо возвести в данную степень числитель и знаменатель дроби:

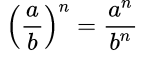
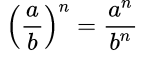
Важные правила для работы со степенями

Запомните!

1. Любое число в нулевой степени равно 1 (а⁰=1).
2. Нуль в любой степени равен нулю (0ⁿ=0).
3. Свойства степени с натуральным показателем применимы для степени с целым отрицательным показателем.

Пример №6.

с^-21 × с^-2=с^-21+(-2)=с^-23

х¹² : х^-2= х^12-(-2)=х¹⁴

(с^-3)⁵=с^-15

Правила для степени с целым отрицательным показателем

1. Степень с целым отрицательным показателем можно представить в виде обыкновенной дроби, числитель которой равен единице, а знаменатель степени с натуральным показателем.
2. Если дана дробь, в знаменателе которой есть степень с целым отрицательным показателем, то ее можно представить в виде степени с натуральным показателем.
3. Если дана дробь, в числителе и знаменателе которой есть степень с целым отрицательным показателем, то можно заменить её дробью, содержащей степень с натуральным показателем, просто поменяв числитель и знаменатель местами.

Правила экспоненты | Законы экспонентов

Правила экспоненты, законы экспоненты и примеры.

Что такое показатель степени

Основание a в степени n равно произведению числа a, n раз:

a ⁿ = а × а × … × а

п раз

a — основание, n — показатель степени.

Примеры

3 ¹ = 3

3 ² = 3 × 3 = 9

3 ³ = 3 × 3 × 3 = 27

3 ⁴ = 3 × 3 × 3 × 3 = 81

3 ⁵ = 3 × 3 × 3 × 3 × 3 = 243

Экспоненты правила и свойства

Название правила	Правило	Пример
Правила продукта	a n ⋅ a m = a n + m	2 3 ⋅ 2 4 = 2 3 + 4 = 128
	a n ⋅ b n = ( a ⋅ b ) n	3 2 ⋅ 4 2 = (3⋅4) 2 = 144
Частные правила	a n / a m = a n — m	2 5 /2 3 = 2 5-3 = 4
	a n / b n = ( a / b ) n	4 3 /2 3 = (4/2) 3 = 8
Правила мощности	( b n ) m = b нм	(2 3 ) 2 = 2 3⋅2 = 64
	b n m = b ( n м )	2 3 2 = 2 (3 2 ) = 512
	м √ ( b n ) = б n / м	2 √ (2 6 ) = 2 6/2 = 8
	b 1/ n = n √ b	8 1/3 = 3 √8 = 2
Отрицательные показатели	b -n = 1/ b n	2 -3 = 1/2 3 = 0.125
Нулевые правила	b 0 = 1	5 0 = 1
	0 n = 0, для n > 0	0 5 = 0
Единые правила	b 1 = b	5 1 = 5
	1 n = 1	1 5 = 1
Минус одно правило		(-1) 5 = -1
Производное правило	( x n ) ‘ = n ⋅ x n -1	( x 3 ) ‘ = 3⋅ x 3-1
Интегральное правило	∫ x n dx = x n +1 / ( n +1) + C	∫ x 2 dx = x 2 + 1 / (2 + 1) + C

Правила произведения экспонентов

Правило продукта с той же базой

a ⁿ ⋅ a ^m = a ^{n + m}

Пример:

2 ³ ⋅ 2 ⁴ = 2 ^{3 + 4} = 2 ⁷ = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128

Правило произведения с таким же показателем

a ⁿ ⋅ b ⁿ = ( a ⋅ b ) ⁿ

Пример:

3 ² ⋅ 4 ² = (3⋅4) ² = 12 ² = 12⋅12 = 144

См .: Показатели умножения

Правила частного экспонента

Правило частных с той же базой

a ⁿ / a ^м = a ^{n — м}

Пример:

2 ⁵ /2 ³ = 2 ^5-3 = 2 ² = 2⋅2 = 4

Правило частных с тем же показателем

a ⁿ / b ⁿ = ( a / b ) ⁿ

Пример:

4 ³ /2 ³ = (4/2) ³ = 2 ³ = 2⋅2⋅2 = 8

См .: Показатели деления

Правила степени экспоненты

Правило мощности I

( a ⁿ ) ^m = a ^n⋅m

Пример:

(2 ³ ) ² = 2 ^3⋅2 = 2 ⁶ = 2⋅2⋅2⋅2⋅2⋅2 = 64

Правило власти II

_a n ^m _{= a} ( n ^m )

Пример:

₂ 3 ² _{= 2} (3 ² ) _{= 2} (3⋅3) _{= 2} 9 _{= 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512}

Силовое правило с радикалами

^м √ ( a ⁿ ) = a ^{n / м}

Пример:

² √ (2 ⁶ ) = 2 ^6/2 = 2 ³ = 2⋅2⋅2 = 8

Правило отрицательных показателей

b ^-n = 1/ b ⁿ

Пример:

2 ^-3 = 1/2 ³ = 1 / (2⋅2⋅2) = 1/8 = 0.125

См .: Отрицательные показатели

Калькулятор экспонент ►

---

См. Также

,

экспонентов: основные правила | Purplemath

Purplemath

Экспоненты — это сокращение для многократного умножения одного и того же самого на себя. Например, сокращение для умножения трех копий числа 5 показано в правой части знака «равно» в (5) (5) (5) = 5 ³ . «Показатель», равный 3 в этом примере, означает, сколько раз умножается значение.То, что умножается (в этом примере 5), называется «базой».

Этот процесс использования экспонент называется «возведением в степень», где показатель — это «степень». Выражение «5 ³ » произносится как «пять в третьей степени» или «пять в третьей степени».

MathHelp.com

Есть две специально названные степени: «до второй степени» обычно произносится как «в квадрате», а «до третьей степени» обычно произносится как «в кубе». Итак, «5 ³ » обычно произносится как «пять кубов».

Когда мы имеем дело с числами, мы обычно просто упрощаем; мы бы предпочли иметь дело с «27», чем с «3 ³ ». Но для переменных нам нужны показатели степени, потому что мы предпочли бы иметь дело с « x ⁶ », чем с « x‍x‍x‍x‍x‍x ».

У экспонентов есть несколько правил, которые мы можем использовать для упрощения выражений.

Чтобы упростить это, я могу думать о том, что означают эти показатели.«До третьего» означает «умножение трех копий», а «до четвертого» означает «умножение четырех копий». Используя этот факт, я могу «расширить» два фактора, а затем вернуться к упрощенной форме. Сначала расширяю:

( x ³ ) ( x ⁴ ) = ( x‍x‍x ) ( x‍x‍x‍x )

Теперь я могу убрать скобки и сложить все множители:

( x‍x‍x ) ( x‍x‍x‍x ) = x‍x‍x‍x‍x‍x‍x

Это семь копий переменной.«Умножение семи копий» означает «в седьмой степени», поэтому это можно переформулировать как:

x‍x‍x‍x‍x‍x‍x = x ⁷

Собираем все вместе, шаги следующие:

( x ³ ) ( x ⁴ ) = ( x‍x‍x ) ( x‍x‍x‍x )

= x‍x‍x‍x‍x‍x‍x

= x ⁷

Тогда упрощенная форма ( x ³ ) ( x ⁴ ) будет:

Обратите внимание, что x ⁷ также равно x ^{(3 + 4)} .Это демонстрирует первое основное правило экспоненты:

Всякий раз, когда вы умножаете два члена с одинаковым основанием, вы можете складывать экспоненты:

( x ^м ) ( x ⁿ ) = x ^{(m + n)}

Однако мы НЕ можем упростить ( x ⁴ ) ( y ³ ), потому что основания разные: ( x ⁴ ) ( y ³ ) = x‍x‍x‍xyyy = ( x ⁴ ) ( y ³ ).Ничего не сочетается.

---

• Упростить ( a ⁵ b ³ ) ( a b ⁷ ).

Теперь, когда я знаю правило (а именно, что я могу добавлять силы к одной и той же базе), я могу начать с перемещения баз, чтобы расположить все одинаковые базы рядом друг с другом:

( a ⁵ b ³ ) ( a b ⁷ ) = ( a ⁵ ) ( a ) ( b ³ ) ( б ⁷ )

Теперь я хочу добавить мощности на a и b .Однако у второго и , похоже, нет мощности. Что мне добавить для этого срока?

Все, что не имеет силы, в техническом смысле «возведено в степень 1». Все, что находится в степени 1, является самим собой, поскольку оно «умножает одну копию» самого себя. Таким образом, приведенное выше выражение можно переписать как:

( a ⁵ ) ( a ) ( b ³ ) ( b ⁷ ) = ( a ⁵ ) ( a ¹ ) ( b ³ ) ( b ⁷ )

Теперь могу комбинировать:

( a ⁵ ) ( a ¹ ) ( b ³ ) ( b ⁷ ) = a ^{5 + 1} b ^{3 + 7} = a ⁶ b ¹⁰

Если сложить все вместе, моя ручная работа будет выглядеть так:

( a ⁵ b ³ ) ( a b ⁷ ) = ( a ⁵ a ¹ ) ( b ³ b ⁷ ) =

---

В следующем примере есть две силы, одна из которых в некотором смысле находится «внутри» другой.

Чтобы сделать упрощение, я могу начать с размышлений о том, что означают показатели степени. «До четвертого» снаружи означает, что я умножаю четыре копии любого основания, указанного в скобках. В этом случае база четвертой степени равна x ² . Умножение четырех копий этой базы дает мне:

Каждый фактор в приведенном выше расширении — это «умножение двух копий» переменной.Это расширяется как:

( x ² ) ( x ² ) ( x ² ) ( x ² ) = ( x‍x ) ( x‍x ) ( x‍x ) ( x‍x )

Убрав скобки, получим:

( x‍x ) ( x‍x ) ( x‍x ) ( x‍x ) = x‍x‍x‍x‍x‍x‍x‍x

Это строка из восьми копий переменной.«Умножение восьми копий» означает «в восьмой степени», поэтому это означает:

x‍x‍x‍x‍x‍x‍x‍x = x ⁸

Собираем все вместе:

( x ² ) ⁴ = ( x ² ) ( x ² ) ( x ² ) ( x ² )

= ( x‍x ) ( x‍x ) ( x‍x ) ( x‍x )

= x‍x‍x‍x‍x‍x‍x‍x

= x ⁸

Обратите внимание, что ( x ² ) ⁴ = x ⁸ , и что 2 × 4 = 8.Это демонстрирует правило второй степени:

Всякий раз, когда у вас есть выражение в степени, которое возведено в степень, вы можете упростить, умножив внешнюю степень на внутреннюю степень:

Если у вас есть продукт в круглых скобках и сила в скобках, то сила идет на каждый элемент внутри. Например:

( xy ² ) ³ = ( xy ² ) ( xy ² ) ( xy ² )

= ( x‍x‍x ) ( y ² y ² y ² )

= ( x‍x‍x ) ( гггггг )

= x ³ y ⁶

= ( x ) ³ ( y ² ) ³

Другой пример:

---

Предупреждение: это правило НЕ работает, если в скобках указана сумма или разница.Экспоненты, в отличие от умножения, НЕ «распределяются» по сложению.

Например, учитывая (3 + 4) ² , НЕ поддавайтесь искушению сказать: « Эй, это равно 3 ² + 4 ² = 9 + 16 = 25 », потому что это неправильно. На самом деле (3 + 4) ² = (7) ² = 49, а не 25.

Если сомневаетесь, запишите выражение в соответствии с определением мощности. Например, учитывая ( x — 2) ² , не пытайтесь делать это в уме.Вместо этого запишите это; «в квадрате» означает «умножение двух копий», поэтому:

( x — 2) ² = ( x — 2) ( x — 2)

= x ( x — 2) — 2 ( x — 2)

= xx — 2 x — 2 x + 4

= x ² — 4 x + 4.

Ошибка ошибочной попытки «распределить» экспоненту чаще всего совершается, когда ученик пытается делать все в уме, вместо того, чтобы показать свою работу.Делайте вещи аккуратно, и вы вряд ли совершите эту ошибку.

---

Теперь, когда я знаю правило о полномочиях на полномочия, я могу провести 4 по каждому из факторов внутри. (Мне нужно помнить, что у c внутри скобок это «в степени 1».)

( a ² ) ⁴ ( b ³ ) ⁴ ( c ¹ ) ⁴

= ( a ^{2 × 4} ) ( b ^{3 × 4} ) ( c ^{1 × 4} )

= a ⁸ b ¹² c ⁴

---

Партнер

---

Есть еще одно правило, которое может или не может быть рассмотрено в вашем классе на данном этапе:

Все, что находится в нулевой степени, равно «1» (пока «что-нибудь» не является нулем само по себе).

Это правило объясняется на следующей странице. Однако на практике это правило означает, что некоторые упражнения могут быть намного проще, чем может показаться на первый взгляд:

• Simplify [(3 x ⁴ y ⁷ z ¹² ) ⁵ (–5 x ⁹ y ³ z ⁴ ) ² ] ⁰

Кого волнует эта фигня в квадратных скобках? Я уверен, что нет, потому что нулевая мощность снаружи означает, что значение всего этого равно 1.Ха!

[(3 x ⁴ y ⁷ z ¹² ) ⁵ (–5 x ⁹ y ³ z ⁴ ) ² ] ⁰ = 1

Между прочим, как только ваш класс охватит «до нуля», вам следует ожидать упражнения, подобного приведенному выше, на следующем тесте.Это распространенный вопрос с подвохом, призванный заставить вас тратить кучу ограниченного времени, но он работает только в том случае, если вы не обращаете внимания.

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении выражений с показателями степени. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок, или просмотрите здесь множество отработанных примеров.)

Щелкните здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.

---

---

URL: https://www.purplemath.com/modules/exponent.htm

,

экспонентов: свойства экспонентов | SparkNotes

Величина с показателем степени состоит из трех компонентов: база, показатель, и коэффициент.

1. В количестве 3 x ⁵ коэффициент равен 3, база равна x , и показатель степени равен 5.
   
2. В количестве 3 (16) ^7x коэффициент равен 3, база равна 16, а показатель степени равен 7 x .
   
3. В количестве 26 (2 y ) ^xy коэффициент равен 26, база равна 2 y , а показатель степени равен xy .
   
4. В количестве r ² , (подразумеваемый) коэффициент равен 1, база равна r , а показатель степени равен 2.

Сложение и вычитание величин с показателями

Мы не можем упростить, сгруппировав два термина вместе, если у них нет та же основа и та же экспонента. Например, мы нельзя объединять термины в таких выражениях, как 5 ² +12 ² или 5 ³ +5 ⁴ . Однако мы можем упростить 4 ⁵ +4 ⁵ и 2 x ² +5 x ² .к сгруппируйте два члена с одинаковым основанием и одинаковой степенью, сложите их коэффициенты. Таким образом, 4 ⁵ +4 ⁵ = 1 (4) ⁵ + 1 (4) ⁵ = (1 + 1) (4) ⁵ = 2 (4) ⁵ и 2 x ² +5 x ² = (2 + 5) x ² = 7 x ² .

Умножение величин на экспоненты

Мы можем умножить две величины на показатели, если у них одинаковые основание.Чтобы умножить две величины с одинаковым основанием, умножьте их коэффициенты и складываем их показатели. Например, 4 (5) ⁵ × 3 (5) ² = (3 × 4) (5) ^{5 + 2} = 12 (5) ⁷ и 5 (2 x ) ² × 6 (2 x ) ^y = (5 × 6) (2 x ) ^{2 + y} = 30 (2 x ) ^{2 + y} .

Разделение величин на экспоненты

Мы можем разделить две величины с показателями, если у них одинаковые основание.Чтобы разделить две величины с одинаковым основанием, разделите их коэффициенты и вычесть их показатели. Например, = (2) ^11-6 = 3 (2) ⁵ и = x ^7-8 = x ^-1 .

Распределительное свойство экспонент

Если показатель степени действует на один член в скобках, мы можем распределите показатель степени по сроку. Например, (2 × 5) ² = (2 ² ) (5 ² ), (3 x ) ⁶ = 3 ⁶ x ⁶ и 3 (4 xy ) ⁵ = 3 (4 ⁵ ) x ⁵ y ⁵ .
Осторожно! Если показатель степени действует на нескольких членах в круглые скобки (т.е. если в скобках стоит знак «+» или «-«), не может распространяться: (5 + 3) ² ≠ 5 ² +3 ² и (4 a + b ) ² ≠ a ² + b ² .

Взять власть над силой

Иногда база будет включать показатель степени, как в выражении (2 ² ) ³ .Если это так, умножьте показатель степени в основании на экспонента, действующая на основание: (2 ² ) ³ = 2 ^{2 × 3} = 2 ⁶ и ( x ⁵ ) ^y = x ^{5 × y} = x ^5y .

,

экспонентов

Показатель числа означает , сколько раз использовать при умножении.

В 8 ² «2» означает использование 8 дважды при умножении,
, поэтому 8 ² = 8 × 8 = 64

Словами: 8 ² можно было бы назвать «8 в степени 2» или «8 во второй степени», или просто «8 в квадрате»

Экспоненты также называются степенями или индексами.

Еще несколько примеров:

Пример: 5 ³ = 5 × 5 × 5 = 125

• Прописью: 5 ³ можно было бы назвать «5 в третьей степени», «5 в степени 3» или просто «5 кубов»

Пример: 2 ⁴ = 2 × 2 × 2 × 2 = 16

• Прописью: 2 ⁴ можно было бы назвать «2 в четвертой степени» или «2 в степени 4» или просто «2–4»

Показатели упрощают запись и использование множества умножений

Пример: 9 ⁶ легче писать и читать, чем 9 × 9 × 9 × 9 × 9 × 9

Вы можете умножить любое число само на себя столько раз , сколько хотите, используя экспоненты.4 = 2 × 2 × 2 × 2 = 16

Отрицательные экспоненты

Отрицательно? Что может быть противоположностью умножения?

Деление!

Отрицательная экспонента означает, сколько раз разделите единицу на число.

Пример: 8 ^-1 = 1 ÷ 8 = 0,125

У вас может быть много делений:

Пример: 5 ^-3 = 1 ÷ 5 ÷ 5 ÷ 5 = 0,008

Но это можно сделать и проще:

5 ^-3 также можно рассчитать как:

1 ÷ (5 × 5 × 5) = 1/5 ³ = 1/125 = 0.008

Отрицательно? Переверните позитив!

Последний пример показал более простой способ работы с отрицательными показателями: Вычислить положительный показатель степени (a n ) Затем возьмите Взаимное (т.е. 1 / a n )

Другие примеры:

Отрицательная экспонента		Взаимное значение положительной экспоненты		Ответ
4 -2	=	1/4 2	=	1/16 = 0.0625
10 -3	=	1/10 3	=	1/1000 = 0,001
(-2) -3	=	1 / (-2) 3	=	1 / (- 8) = -0,125

Что делать, если экспонента равна 1 или 0?

1		Если показатель степени равен 1, то у вас есть только само число (например, 9 1 = 9 )
0		Если показатель степени равен 0, то вы получите 1 (например, 9 0 = 1 )
		А как насчет 0 0 ? Это может быть либо 1, либо 0, поэтому люди говорят, что это «неопределенный» .

Все имеет смысл

Мой любимый метод — начать с «1», а затем умножить или разделить столько раз, сколько говорит показатель степени, тогда вы получите правильный ответ, например:

Пример: Полномочия 5
	.. и т.д ..
5 2	1 × 5 × 5	25
5 1	1 × 5	5
5 0	1	1
5 -1	1 ÷ 5	0.2
5 -2	1 ÷ 5 ÷ 5	0,04
	.. и т.д ..

Если вы посмотрите на эту таблицу, вы увидите, что положительный, нулевой или отрицательный показатель степени на самом деле являются частью одного (довольно простого) паттерна.

Будьте осторожны при группировке

Во избежание путаницы используйте круглые скобки () в таких случаях:

С ():	(-2) 2 = (-2) × (-2) = 4
Без ():	-2 2 = — (2 2 ) = — (2 × 2) = -4

С ():	(ab) 2 = ab × ab
Без ():	ab 2 = a × (b) 2 = a × b × b

,