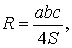Свойства треугольников — интернет энциклопедия для студентов

ОПРЕДЕЛЕНИЕ

Треугольник называется равнобедренным, если его две стороны равны.

Треугольник называется равносторонним, если все три стороны равны.

Основные линии треугольника

Медиана треугольника представляет собой отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектрисом угла треугольника является луч, исходящий из вершины треугольника и делящий его пополам.

Высота треугольника называется перпендикуляром, отбрасываемым от вершины треугольника к противоположной стороне (или ее продолжению).

Средняя линия треугольника — это сегмент, соединяющий середины двух сторон треугольника и параллельный третьей стороне.

Круг может быть вписан в любой треугольник, и круг может быть описан вокруг любого треугольника.

Два треугольника называются равными, если они имеют равные стороны и соответствующие углы.

Знаки равенства треугольников

I знак Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Знак II. Если сторона и углы одного соседнего с ней треугольника равны соответственно стороне и углам соседнего с ней треугольника, то такие треугольники равны.

III. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Треугольники называются подобными, если их стороны пропорциональны.

Признаки сходства треугольников

1. Если два угла одного раневого треугольника находятся в двух углах другого треугольника, то такие треугольники похожи.

2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны, то такие треугольники схожи.

3. Если три стороны одного треугольника пропорциональны двум сторонам другого треугольника, то такие треугольники похожи.

Косинус-теорема. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус дважды произведение этих сторон на косинус угла между ними:

\(\ c^{2}=a^{2}+b^{2}-2 a b \cos (a ; b) \)

Узнайте больше о теореме косинуса по ссылке.

Теорема Синуса. Стороны треугольника пропорциональны синусам противоположных углов. Коэффициент пропорциональности равен диаметру окружности (обобщенная теорема синуса):

\(\ \frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}=2 R \)

Подробнее о связи синуса.

Площадь треугольника можно вычислить по формулам

1. Через высоту и основание

\(\ S=\frac{1}{2} a \cdot h \)

2. С двух сторон и угла между ними.

\(\ S=\frac{1}{2} a \cdot b \sin \alpha \)

3. Согласно формуле Герона

\(\ S=\sqrt{p(p-a)(p-b)(p-c)} \)

где p — полу-периметр треугольника

4. Через радиусы вписанных и описанных кругов

\(\ S=r p \)

где \(\ \mathrm{p} \) — полу периметр треугольника, \(\ \mathrm{r} \) — радиус вписанной окружности;

\(\ S=\frac{a b c}{4 R} \)

\(\ R \) — радиус описанной окружности.

Примеры решения проблем

ПРИМЕР 1

Задача

В треугольнике \(\ A B C \) с \(\ \angle A=45^{\circ} \) высота \(\ \mathrm{BK} \) делит основание на 4 см и 7 см сегментов. Найдите область треугольника \(\ A B C \).

Решение

Высота \(\ \mathrm{BK} \) делит основание на сегменты \(\ A K=4 \mathrm{см} \) и \(\ \mathrm{KC}=7 \mathrm{см} \), следовательно, \(\ \mathrm{AC}=\mathrm{AK}+\mathrm{KC}=11 \mathrm{см} \).

Рассмотрим правый треугольник \(\ \mathrm{ABK} \). Найти \(\ \mathrm{BK} \):

\(\ BK=A K \cdot \operatorname{tg} \angle A=4 \mathrm{см} \)

Площадь треугольника \(\ \mathrm{ABC} \) найдет формулу через основание и высоту:

\(\ S=\frac{1}{2} A C \cdot B K=\frac{1}{2} \cdot 11 \cdot 4=22 \mathrm{см}^{2} \)

Ответ

\(\ S=22 \)

ПРИМЕР 2

Задача

В треугольнике \(\ \mathrm{ABC} \) сторона \(\ A B=4 \mathrm{см} \), \(\ A=8 \mathrm{см} \) и \(\ \angle A=60^{\circ} \) . Найдите все стороны и все углы треугольника.

Решение

Найдите сторону \(\ \mathrm{BC} \). Для этого мы используем теорему косинуса:

\(\ B C^{2}=A B^{2}+A C^{2}-2 A B \cdot A C \cdot \cos \angle A \)

откуда \(\ B C=\sqrt{4^{2}+8^{2}-2 \cdot 4 \cdot 8 \cdot \frac{1}{2}}=\sqrt{48}=4 \sqrt{3} \)

Найдите углы треугольника, используя теорему синуса:

\(\ \frac{A B}{\sin \angle C}=\frac{A C}{\sin \angle B}=\frac{B C}{\sin \angle A} \)

Отсюда

\(\ \ \sin \angle C=\frac{A B}{B C} \sin \angle A=\frac{4}{4 \sqrt{3}} \cdot \frac{\sqrt{3}}{2}=\frac{1}{2} \Rightarrow \angle C=60^{\circ} \)

Далее мы найдем \(\ \angle B \):

\(\ \angle B=180^{\circ}-\angle A-\angle C=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ} \)

Ответ

\(\ B C=4 \sqrt{3} \mathrm{cm} \), \(\ \angle C=60^{\circ} \), \(\ \angle B=90^{\circ} \)

Треугольники. Основные свойства. Признаки равенства. Видеоурок. Геометрия 7 Класс

Геометрических фигур, которые встречаются при решении различных задач, очень много. Изучить свойства всех невозможно.

Поэтому нужно использовать приближенные модели. Одной из таких моделей являются многоугольники – с их помощью можно приближать практически любую геометрическую фигуру с требуемой точностью (см. рис. 1).

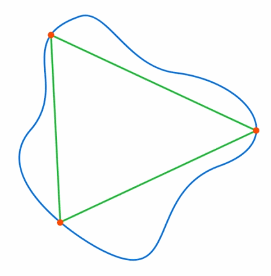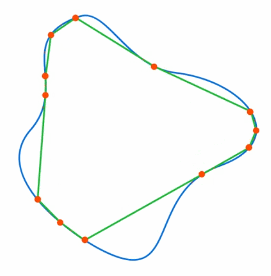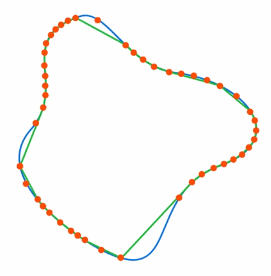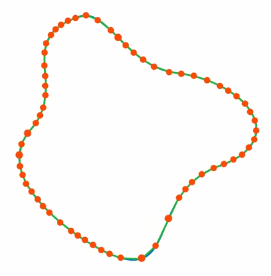
Рис. 1. Приближение фигуры при помощи многоугольника

Самый простой многоугольник – это треугольник (замкнутая ломаная с наименьшим количеством звеньев) (см. рис. 2).

Рис. 2. Произвольный треугольник

Более того, любой многоугольник можно разбить на треугольники (см. рис. 3), значит, изучая свойства треугольников, мы сможем использовать полученные результаты для описания других многоугольников.

Рис. 3. Разбиение многоугольника на треугольники

Простой пример: пусть нам известно, что у всех треугольников сумма углов одинакова и равна . Тогда мы сразу можем ответить на вопрос – чему равна сумма углов четырехугольника: разбиваем его на два треугольника (см. рис. 4) и получаем:

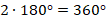
Рис. 4. Разбиение четырехугольника на два треугольника

Попробуйте сами найти сумму углов произвольных пятиугольников и шестиугольников (см. рис. 5).

Рис. 5. Произвольные пятиугольник и шестиугольник

Другой пример применения треугольников – метод триангуляции (от лат. triangulum – «треугольник»): разбиение поверхности на треугольники в геодезии для вычисления расстояний, планировки и строительства крупных инженерных сооружений и городов (см. рис. 6).

Рис. 6. Разбиение поверхности на треугольники в геодезии

Но для того чтобы использовать треугольники для решения различных практических задач, нужно изучить их свойства. Этим мы и займемся.

Как мы уже говорили: треугольник – это минимальная замкнутая ломаная (из двух звеньев замкнутую ломаную не получить, из трех можно, это и будет треугольник). Иначе говоря, это три последовательно соединенных отрезка. Из любых ли трех отрезков можно построить треугольник? Легко убедиться, что нет.

Возьмем самый длинный из отрезков: если два остальных не сойдутся (см. рис. 7), то треугольник из таких отрезков составить не получится.

Рис. 7. Не из любых трех отрезков можно получить треугольник

В некоторых машинах дворники работают следующим образом (см. рис. 8). Чтобы они не мешали друг другу, нужно, чтобы из этих трех отрезков нельзя было составить треугольник.

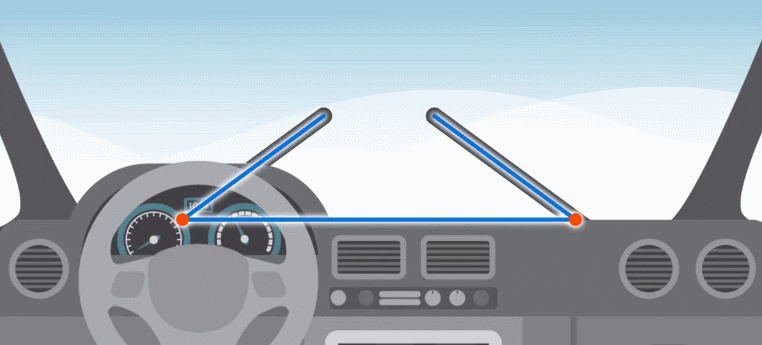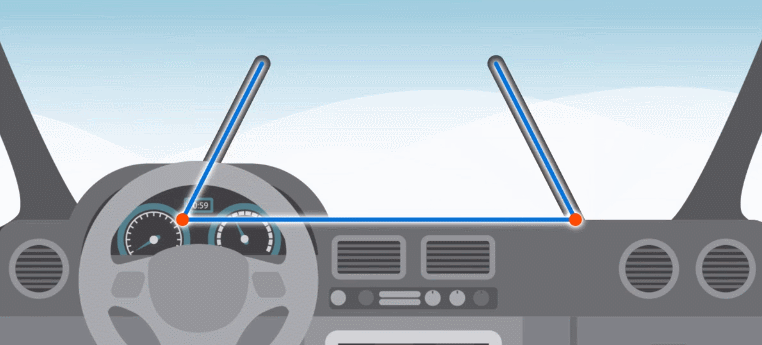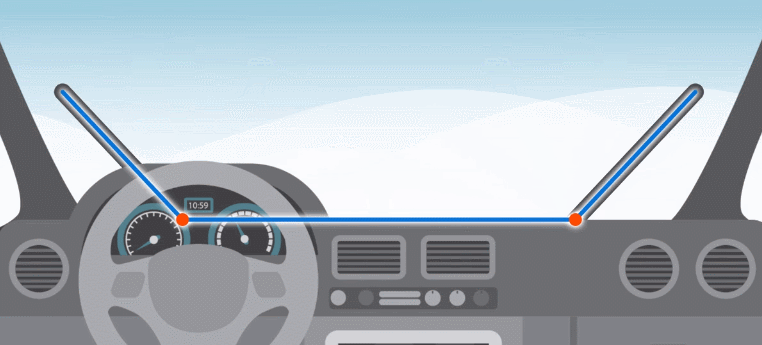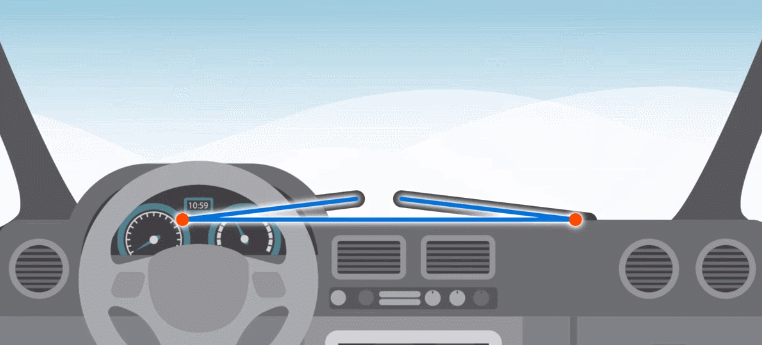
Рис. 8. Работа дворников в машине

Пусть есть ломаная из трех отрезков (см. рис. 9).

Рис. 9. Ломаная из трех отрезков

Зафиксируем один отрезок (см. рис. 10) и попробуем замкнуть ломаную в треугольник (см. рис. 11).

Рис. 10. Фиксация одного из трех отрезков

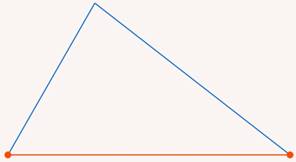
Рис. 11. Замыкание ломаной в треугольник

Понятно, что это возможно лишь в том случае, если сумма длин остальных отрезков больше длины первого (зафиксированного) (см. рис. 12):

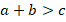
Рис. 12. Неравенство треугольника: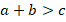

Это утверждение называется неравенством треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон.

Неравенством треугольника нам часто хочется воспользоваться в жизни: вместо того чтобы идти по тротуару, хочется «срезать» и пройти по газону. Потому что так получится короче (быстрее). Поэтому появление табличек с надписями «По газонам не ходить!» частично связано именно с неравенством треугольника.

Неравенство треугольника можно обобщить на случай любого многоугольника (т. е. сформулировать так, чтобы оно было верно не только для треугольника, но и для произвольного многоугольника): длина отрезка, соединяющего концы ломаной, не больше длины самой ломаной (см. рис. 10):

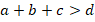
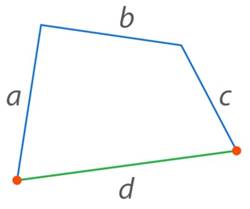
Рис. 10. Обобщенное неравенство треугольника: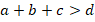

Попробуйте доказать этот факт самостоятельно, используя неравенство треугольника. Ознакомиться с доказательством можно ниже.

---

 

Доказательство обобщенного неравенства треугольника

Доказательство (для произвольного четырехугольника)

Рассмотрим произвольный четырехугольник  (см. рис. 11).

Рис. 11. Произвольный четырехугольник

Докажем, что:

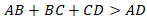
Проведем диагональ  (см. рис. 12).

Рис. 12. В произвольном четырехугольнике  проведена диагональ

В треугольнике

:

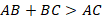
В треугольнике :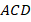

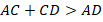
Тогда:

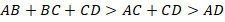
Поскольку такое рассуждение можно повторить для любой из сторон, то получаем, что в любом четырехугольнике любая из сторон меньше суммы трех других.

Доказано.

Доказательство (для произвольного пятиугольника)

Рассмотрим произвольный пятиугольник

 (см. рис. 13).

Рис. 13. Произвольный пятиугольник

Докажем, что:

Проведем диагональ  (см. рис. 14).

Рис. 14. В произвольном пятиугольнике

 проведена диагональ

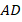
В четырехугольнике 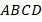 (как мы только что доказали):

В треугольнике :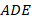

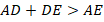
Тогда:

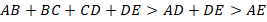
Аналогично получили, что в любом пятиугольнике любая из сторон меньше суммы четырех других.

Доказано.

Доказательство (для произвольного n-угольника).

Рассмотрим произвольный n-угольник 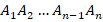 (см. рис. 15).

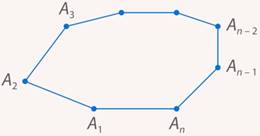
Рис. 15. Произвольный n-угольник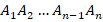

Доказываем его для произвольного -угольника (см. рис. 16), затем проводим в n-угольнике диагональ  (см. рис. 17).

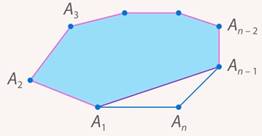
Рис. 16. Произвольный -угольник

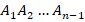
Рис. 17. В произвольном n-угольнике 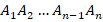 проведена диагональ

Выписываем неравенство для -угольника :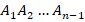

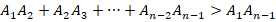
Затем – неравенство для треугольника :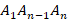

Тогда:

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Серединный перпендикуляр к отрезку

      Определение 1. Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

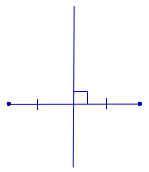
Рис.1

      Теорема 1. Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

      Доказательство. Рассмотрим произвольную точку   D,   лежащую на серединном перпендикуляре к отрезку   AB   (рис.2), и докажем, что треугольники   ADC   и   BDC   равны.

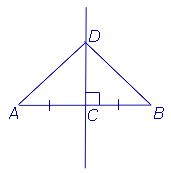
Рис.2

      Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты   AC   и   BC   равны, а катет   DC   является общим. Из равенства треугольников   ADC   и   BDC   вытекает равенство отрезков   AD   и   DB.   Теорема 1 доказана.

      Теорема 2 (Обратная  к теореме 1). Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

      Доказательство. Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка   E   находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки   E   и   A   лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок   EA   пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой   D.

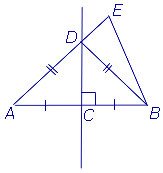
Рис.3

      Докажем, что отрезок   AE   длиннее отрезка   EB.   Действительно,

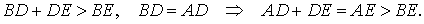
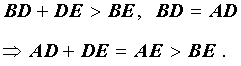
      Таким образом, в случае, когда точки   E   и   A   лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

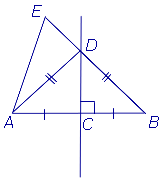
Рис.4

      Теперь рассмотрим случай, когда точки   E   и   A   лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок   EB   длиннее отрезка   AE.   Действительно,

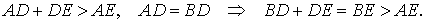
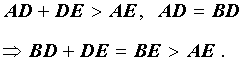
      Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

      Определение 2. Окружностью, описанной около треугольника, называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником.

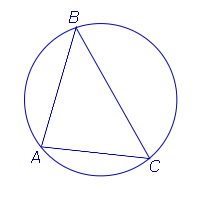
Рис.5

Свойства описанной около треугольника окружности. Теорема синусов

Фигура	Рисунок	Свойство
Серединные перпендикуляры к сторонам треугольника		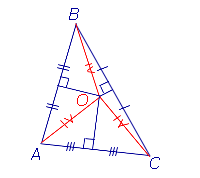Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство
Окружность, описанная около треугольника		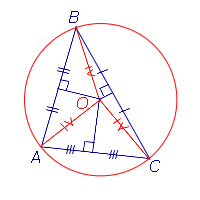Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство
Центр описанной около остроугольного треугольника окружности		Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		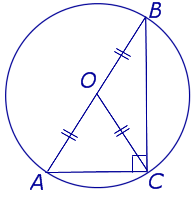Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство
Центр описанной около тупоугольного треугольника окружности		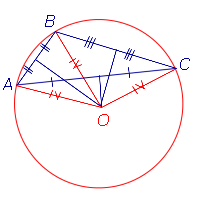Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов		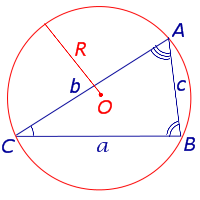Для любого треугольника справедливы равенства (теорема синусов): , где   a , b , c   – стороны треугольника,   A , B , С   – углы треугольника,   R   – радиус описанной окружности. Посмотреть доказательство
Площадь треугольника		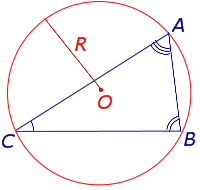Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где   A , B , С   – углы треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности. Посмотреть доказательство
Радиус описанной окружности		Для любого треугольника справедливо равенство: где   a , b , c   – стороны треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности. Посмотреть доказательство

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство

Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов): , где   a , b , c   – стороны треугольника,   A , B , С   – углы треугольника,   R   – радиус описанной окружности. Посмотреть доказательство

Площадь треугольника

Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где   A , B , С   – углы треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности. Посмотреть доказательство

Радиус описанной окружности

Для любого треугольника справедливо равенство: где   a , b , c   – стороны треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности. Посмотреть доказательство

Доказательства теорем о свойствах описанной около треугольника окружности

      Теорема 3. Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

      Доказательство. Рассмотрим два серединных перпендикуляра, проведённых к сторонам   AC   и   AB   треугольника   ABC,   и обозначим точку их пересечения буквой   O   (рис. 6).

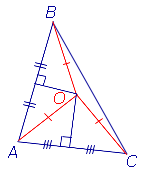
Рис.6

      Поскольку точка   O   лежит на серединном перпендикуляре к отрезку   AC,   то в силу теоремы 1 справедливо равенство:

CO = AO .

      Поскольку точка O лежит на серединном перпендикуляре к отрезку   AB,   то в силу теоремы 1 справедливо равенство:

AO = BO .

      Следовательно, справедливо равенство:

CO = BO ,

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку   BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

      Следствие. Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

      Доказательство. Рассмотрим точку   O,   в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника   ABC   (рис. 6).

      При доказательстве теоремы 3 было получено равенство:

AO = OB = OC ,

из которого вытекает, что окружность с центром в точке   O   и радиусами   OA,   OB,   OC   проходит через все три вершины треугольника   ABC,   что и требовалось доказать.

      Теорема 4 (теорема синусов). Для любого треугольника (рис. 7)

Рис.7

справедливы равенства:

.

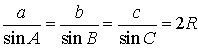      Доказательство. Докажем сначала, что длина хорды окружности радиуса   R хорды окружности радиуса   R,   на которую опирается вписанный угол величины   φ ,   вычисляется по формуле:

      Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

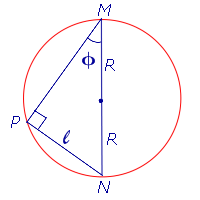
Рис.8

      Угол   MPN,   как угол,опирающийся на диаметр, является прямым угломугол,опирающийся на диаметр, является прямым углом, и равенство (1) вытекает из определения синуса угла прямоугольного треугольника.

      Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

      Формула (1) доказана.

      Из формулы (1) для вписанного треугольника   ABC   получаем (рис.7):

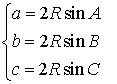
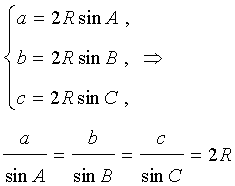
      Теорема синусов доказана.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Персональный сайт — Все о прямоугольных треугольниках

Свойство 2. В прямоугольном треугольнике гипотенуза больше любого из катетов (является самой большой стороной).

Доказательство. Вспомним, что в треугольнике против большего угла лежит большая сторона (и наоборот). Из доказанного выше свойства 1 следует, что сумма углов  и  прямоугольного треугольника равна . Так как угол треугольника не может равняться 0, то каждый из них меньше . Значит,  является самым большим, а, значит, напротив него лежит наибольшая сторона треугольника. Значит, гипотенуза является наибольшей стороной прямоугольного треугольника, то есть: .

 

Свойство 3. В прямоугольном треугольнике гипотенуза меньше суммы катетов.

Доказательство. Это свойство становится очевидным, если вспомнить неравенство треугольника.

Неравенство треугольника

В любом треугольнике сумма любых двух сторон больше третьей стороны.

Из данного неравенства сразу же следует свойство 3.

Примечание: несмотря на то, что каждый из катетов по отдельности меньше гипотенузы, их сумма оказывается больше. В числовом примере это выглядит так: , но .

 

1-й признак (по 2 сторонам и углу между ними): если у треугольников равны две стороны и угол между ними, то такие треугольники равны между собой.

2-й признак (по стороне и двум прилежащим углам): если у треугольников равны сторона и два угла, прилежащие к данной стороне, то такие треугольники равны между собой.Примечание: пользуясь тем, что сумма углов треугольника постоянна и равна , легко доказать, что условие «прилежания» углов не является необходимым, то есть признак будет верен и в такой формулировке: «… равны сторона и два угла, то …».

 3-й признак (по 3 сторонам): если у треугольников равны все три стороны, то такие треугольники равны между собой.

Естественно, все эти признаки остаются верными и для прямоугольных треугольников. Однако у прямоугольных треугольников есть одна существенная особенность – у них всегда есть пара равных прямых углов. Поэтому данные признаки для них упрощаются. Итак, сформулируем признаки равенства прямоугольных треугольников:

1-й признак (по двум катетам): если у прямоугольных треугольников катеты попарно равны, то такие треугольники равны между собой (Рис. 2).

Дано:

Рис. 2. Иллюстрация первого признака равенства прямоугольных треугольников

Доказать: 

Доказательство:  в прямоугольных треугольниках: . Значит, мы можем воспользоваться первым признаком равенства треугольников (по 2 сторонам и углу между ними) и получить: .

 

2-й признак (по катету и углу): если катет и острый угол одного прямоугольного  треугольника равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны между собой (Рис. 3).

Дано:

Рис. 3. Иллюстрация второго признака равенства прямоугольных треугольников

Доказать: 

Доказательство: сразу отметим, что тот факт, что равны углы, прилежащие к равным катетам, не является принципиальным. Действительно, сумма острых углов прямоугольного треугольника (по свойству 1) равна . Значит, если равна одна пара из этих углов, то равна и другая (так как их суммы одинаковы).

Доказательство же данного признака сводится к использованию второго признака равенства треугольников (по 2 углам и стороне). Действительно, по условию равны катеты и пара прилежащих к ним углов. Но вторая пара прилежащих к ним углов состоит из углов . Значит, мы можем воспользоваться вторым признаком равенства треугольников и получить: .

3-й признак (по гипотенузе и углу): если гипотенуза и острый угол одного прямоугольного  треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны между собой (Рис. 4).

Дано:

Рис. 4. Иллюстрация третьего признака равенства прямоугольных треугольников

Доказать: 

Доказательство: для доказательства этого признака можно сразу воспользоваться вторым признаком равенства треугольников – по стороне и двум углам (точнее, следствием, в котором указано, что углы не обязательно должны быть прилежащими к стороне). Действительно, по условию: , , а из свойств прямоугольных треугольников следует, что . Значит, мы можем воспользоваться вторым признаком равенства треугольников, и получить: .

 

4-й признак (по гипотенузе и катету): если гипотенуза и катет одного прямоугольного  треугольника равны соответственно гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны между собой (Рис. 5).

Дано:

Рис. 5. Иллюстрация четвёртого признака равенства прямоугольных треугольников

Доказать: 

Доказательство: для доказательства этого признака воспользуемся признаком равенства треугольников, который мы сформулировали и доказали на прошлом уроке, а именно: если у треугольников равны две стороны и больший угол, то такие треугольники являются равными. Действительно, по условию у нас есть две равных стороны. Кроме того, по свойству прямоугольных треугольников: . Осталось доказать, что прямой угол является наибольшим в треугольнике. Предположим, что это не так, значит, должен быть ещё хотя бы один угол, который больше . Но тогда сумма углов треугольника уже будет больше . Но это невозможно, значит, такого угла в треугольнике быть не может. Значит, прямой угол является наибольшим в прямоугольным треугольнике. А значит, можно воспользоваться сформулированным выше признаком, и получить: .

 

Сформулируем теперь ещё одно свойство, характерное только для прямоугольных треугольников.

Свойство

Катет, лежащий против угла в , в 2 раза меньше гипотенузы (Рис. 6).

Дано:

Рис. 6.

Доказать: AB

Доказательство: выполним дополнительное построение: продлим прямую  за точку  на отрезок, равный . Получим точку . Так как углы  и  – смежные, то их сумма равна . Поскольку , то и угол .

Значит, прямоугольные треугольники  (по двум катетам:  – общий,  – по построению) – первый признак равенства прямоугольных треугольников.

Из равенства треугольников следует равенство всех соответствующих элементов. Значит, . Откуда: . Кроме того,  (из равенства всё тех же треугольников). Значит, треугольник  – равнобедренный (так как у него равны углы при основании), но равнобедренный треугольник, один из углов которого равен , – равносторонний. Из этого следует, в частности, что .

 

Стоит отметить, что верно и обратное утверждение: если в прямоугольном треугольнике гипотенуза в два раза больше одного из катетов, то острый угол, лежащий напротив этого катета, равен .

Примечание: признак означает, что если какое-то утверждение верно, то треугольник является прямоугольным. То есть признак позволяет идентифицировать прямоугольный треугольник.

Важно не путать признак со свойством – то есть, если треугольник прямоугольный, то у него есть такие свойства… Часто признаки и свойства являются взаимно обратными, но далеко не всегда. Например, свойство равностороннего треугольника: в равностороннем треугольнике есть угол . Но это не будет признаком равностороннего треугольника, так как не любой треугольник, у которого есть угол , является равносторонним.

Можно привести и более жизненный пример: свойство слова «хлеб» – в слове «хлеб» 4 буквы. Но наличие 4 букв не является признаком слова «хлеб», так как существует множество слов из 4 букв.

Признак прямоугольного треугольника:

Если в треугольнике медиана равна половине стороны, к которой она проведена, то данный треугольник является прямоугольным, причём медиана проведена из вершины прямого угла.

Примечание: медиана – линия, соединяющая вершину треугольника с серединой противоположной стороны (Рис. 7).

Дано:

Рис. 7.

Доказать: 

Доказательство: поскольку , то  – равнобедренные. Значит, углы при основаниях каждого из этих треугольников равны. То есть, ,  .  Тогда сумма углов треугольника  равна  Значит, . Но: .

 

Теорема Пифагора: .

Решение прямоугольного треугольника:

;

;

.

Теоремы:

• Высота, проведенная из вершины прямого угла, делит гипотенузу на отрезки: . Эти отрезки являются проекциями катетов на гипотенузу.

• Высота, проведенная из вершины прямого угла, равна среднему геометрическому проекций катетов на гипотенузу: .

• Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, делит его на два подобных и подобных исходному треугольнику. Для любых сходственных элементов (медиана, биссектриса, радиусы вписанной и описанной окружностей и т. п.) исходного и полученных треугольников  справедливо соотношение .
• Длина высоты, проведенной из вершины прямого угла, равна отношению произведения длин катетов и гипотенузы: .
• Медиана, проведенная из вершины прямого угла, равна половине гипотенузы. Ее основание является центром описанной около прямоугольного треугольника окружности. Радиус описанной окружности равен этой медиане и равен половине гипотенузы: .

• Радиус вписанной окружности равен половине суммы катетов, уменьшенной на гипотенузы: 

  Веселый календарик

  Календарь

Геронов треугольник — Википедия

Геронов треугольник — треугольник, стороны и площадь которого являются целыми числами^[1][2]. Героновы треугольники названы в честь греческого математика Герона. Термин иногда понимается несколько шире и распространяется на треугольники, имеющие рациональные стороны и площадь^[3].

Все прямоугольные треугольники, стороны которых образуют пифагоровы тройки, являются героновыми, поскольку стороны их по определению целочисленны, а площадь тоже целочисленна, поскольку является половиной произведения катетов, один из которых обязательно имеет чётную длину.

Треугольник со сторонами c, e и b + d, и высотой a.

В качестве примера геронова треугольника, не имеющего прямого угла, можно привести равнобедренный треугольник со сторонами 5, 5 и 6, площадь которого равна 12. Этот треугольник получается путём объединения двух прямоугольных треугольников со сторонами 3, 4 и 5 вдоль стороны длиной 4. Этот подход работает и в общем случае, как показано на рисунке справа. Берётся пифагорова тройка (a, b, c), где c — наибольшая сторона, затем другая тройка (a, d, e), в которой наибольшей стороной будет e, строятся треугольники по заданным длинам сторон и объединяются вдоль стороны с длиной a, получая треугольник со сторонами c, e и b + d и площадью

A=12(b+d)a{\displaystyle A={\frac {1}{2}}(b+d)a} (половина произведения основания на высоту).

Если a чётно, то площадь будет целым числом. Менее очевиден случай, когда a нечётно, но и в этом случае A остаётся целым, поскольку стороны b и d должны быть чётными числами, а следовательно, и b+d будет чётным тоже.

Некоторые героновы треугольники невозможно получить объединением прямоугольных треугольников с целочисленными сторонами методом, описанным выше. Так, например, геронов треугольник со сторонами 5, 29, 30 и площадью 72 нельзя получить из двух пифагоровых треугольников, поскольку ни одна из его высот не является целым числом. Нельзя также построить примитивный пифагоров треугольник из двух меньших пифагоровых треугольников^[4]. Такие героновы треугольники называются неразложимыми^[4]. Однако, если разрешить пифагоровы тройки с рациональными значениями, отказавшись от целочисленности, то разбиение на два прямоугольных треугольника с рациональными сторонами всегда существует^[5], поскольку все высоты геронова треугольника являются рациональными числами (поскольку высота равна удвоенной площади, делённой на основание, и оба эти числа являются целыми). Так, геронов треугольник со сторонами 5, 29, 30 можно получить из рациональных пифагоровых треугольников со сторонами 7/5, 24/5, 5 и 143/5, 24/5, 29. Заметим, что рациональные пифагоровы тройки являются просто версиями целочисленных пифагоровых троек, поделённых на целое число.

Другие свойства героновых треугольников можно найти в статье Целочисленный треугольник#Героновы треугольники.

Точная формула для героновых треугольников[править | править код]

Любой геронов треугольник имеет стороны, пропорциональные значениям^[6]

a=n(m2+k2){\displaystyle a=n(m^{2}+k^{2})}

b=m(n2+k2){\displaystyle b=m(n^{2}+k^{2})}

c=(m+n)(mn−k2){\displaystyle c=(m+n)(mn-k^{2})}

Полупериметр =s=(a+b+c)/2=mn(m+n){\displaystyle =s=(a+b+c)/2=mn(m+n)}

Площадь =mnk(m+n)(mn−k2){\displaystyle =mnk(m+n)(mn-k^{2})}

Радиус вписанной окружности =k(mn−k2){\displaystyle =k(mn-k^{2})}

s−a=n(mn−k2){\displaystyle s-a=n(mn-k^{2})}

s−b=m(mn−k2){\displaystyle s-b=m(mn-k^{2})}

s−c=(m+n)k2{\displaystyle s-c=(m+n)k^{2}}

для целых m, n и k, где

gcd(m,n,k)=1{\displaystyle \gcd {(m,n,k)}=1}

mn>k2≥m2n/(2m+n){\displaystyle mn>k^{2}\geq m^{2}n/(2m+n)}

m≥n≥1{\displaystyle m\geq n\geq 1}.

Коэффициент пропорциональности в общем случае является рациональным числом pq{\displaystyle {\frac {p}{q}}} , где  q=gcd(a,b,c){\displaystyle q=\gcd {(a,b,c)}}  приводит полученный геронов треугольник к примитивному, а  p{\displaystyle p}  растягивает его до требуемых размеров. Например, взяв m = 36, n = 4 и k = 3, получим треугольник со сторонами a = 5220, b = 900 и c = 5400, который подобен геронову треугольнику 5, 29, 30, и коэффициент пропорциональности имеет числитель p = 1 и знаменатель q = 180.

См. также Героновы треугольники с одним углом, вдвое большим другого, Героновы треугольники со сторонами в арифметической прогрессии и Равнобедренные героновы треугольники.

Список примитивных целочисленных героновых треугольников, отсортированный по площади и, в случае равенства площадей, по периметру. «Примитивный» означает, что наибольший общий делитель трёх длин сторон равен 1.

Площадь	Периметр	Длины сторон
6	12	5	4	3
12	16	6	5	5
12	18	8	5	5
24	32	15	13	4
30	30	13	12	5
36	36	17	10	9
36	54	26	25	3
42	42	20	15	7
60	36	13	13	10
60	40	17	15	8
60	50	24	13	13
60	60	29	25	6
66	44	20	13	11
72	64	30	29	5
84	42	15	14	13
84	48	21	17	10
84	56	25	24	7
84	72	35	29	8
90	54	25	17	12
90	108	53	51	4
114	76	37	20	19
120	50	17	17	16
120	64	30	17	17
120	80	39	25	16
126	54	21	20	13
126	84	41	28	15
126	108	52	51	5
132	66	30	25	11
156	78	37	26	15
156	104	51	40	13
168	64	25	25	14
168	84	39	35	10
168	98	48	25	25
180	80	37	30	13
180	90	41	40	9
198	132	65	55	12
204	68	26	25	17
210	70	29	21	20
210	70	28	25	17
210	84	39	28	17
210	84	37	35	12
210	140	68	65	7
210	300	149	148	3
216	162	80	73	9
234	108	52	41	15
240	90	40	37	13
252	84	35	34	15
252	98	45	40	13
252	144	70	65	9
264	96	44	37	15
264	132	65	34	33
270	108	52	29	27
288	162	80	65	17
300	150	74	51	25
300	250	123	122	5
306	108	51	37	20
330	100	44	39	17
330	110	52	33	25
330	132	61	60	11
330	220	109	100	11
336	98	41	40	17
336	112	53	35	24
336	128	61	52	15
336	392	195	193	4
360	90	36	29	25
360	100	41	41	18
360	162	80	41	41
390	156	75	68	13
396	176	87	55	34
396	198	97	90	11
396	242	120	109	13

Фигура называется сравнимой^[en], если площадь равна периметру. Имеется ровно пять сравнимых героновых треугольников — (5,12,13), (6,8,10), (6,25,29), (7,15,20) и (9,10,17)^[7][8]

Почти равносторонние героновы треугольники[править | править код]

Поскольку площадь правильного треугольника с рациональными сторонами является числом иррациональным, никакой равносторонний треугольник не может быть героновым. Однако существует последовательность героновых треугольников, которые «почти правильные», поскольку их стороны имеют вид n − 1, n, n + 1. Несколько первых примеров этих почти равносторонних треугольников перечислены в таблице ниже (последовательность A003500 в OEIS).

Длина стороны			Площадь	Радиус вписанной
n − 1	n	n + 1
3	4	5	6	1
13	14	15	84	4
51	52	53	1170	15
193	194	195	16296	56
723	724	725	226974	209
2701	2702	2703	3161340	780
10083	10084	10085	44031786	2911
37633	37634	37635	613283664	10864

Следующее значение для n можно найти, умножив предыдущее на 4, а затем вычтя значение, ему предшествующее (52 = 4 × 14 − 4, 194 = 4 × 52 − 14, и т. д.). Таким образом,

nt=4nt−1−nt−2{\displaystyle n_{t}=4n_{t-1}-n_{t-2}},

где t означает номер строки в таблице. Эта последовательность является последовательностью Люка. Можно также получить эту последовательность по формуле (2+3)t+(2−3)t{\displaystyle (2+{\sqrt {3}})^{t}+(2-{\sqrt {3}})^{t}} для всех n. Если положить A = площадь, а y = радиус вписанной окружности, то

((n−1)2+n2+(n+1)2)2−2((n−1)4+n4+(n+1)4)=(6ny)2=(4A)2{\displaystyle {\big (}(n-1)^{2}+n^{2}+(n+1)^{2}{\big )}^{2}-2{\big (}(n-1)^{4}+n^{4}+(n+1)^{4}{\big )}=(6ny)^{2}=(4A)^{2}},

где {n, y} являются решениями уравнения n² − 12y² = 4. Небольшая подстановка n = 2x даёт известное уравнение Пелля x² − 3y² = 1, решения которого можно получить из разложения √3 в непрерывную дробь^[9]

Переменная n имеет вид n=2+2k{\displaystyle n={\sqrt {2+2k}}}, где k равно 7, 97, 1351, 18817, …. Числа в этой последовательности имеют свойство, что k последовательных целых имеют целочисленное среднеквадратическое отклонение.^[10]

1. ↑ Carlson, 1970, с. 499—506.
2. ↑ Beauregard, Suryanarayan, 1998, с. 13—17.
3. ↑ Eric W. Weisstein. Heronian Triangle.
4. ↑ ^{1 2} Yiu, 2008, с. 17.
5. ↑ Sierpiński, 2003.
6. ↑ Carmichael, 1959, с. 11—13.
7. ↑ Dickson, 2005, с. 199.
8. ↑ Markowitz, 1981, с. 222—3.
9. ↑ Richardson, 2007.
10. ↑ Online Encyclopedia of Integer Sequences, A011943.

• John R. Carlson. Determination of Heronian Triangles // Fibonacci Quarterly. — 1970. — Т. 8.
• R. D. Carmichael. The Theory of Numbers and Diophantine Analysis. — Dover Publications, Inc., 1959. — С. 1914, Diophantine Analysis.
• Raymond A. Beauregard, E. R. Suryanarayan. The Brahmagupta Triangles. — 1998. — Т. 29, вып. 1 January. — DOI:10.2307/2687630.
• Leonard Eugene Dickson. History of the Theory of Numbers,. — Dover Publications, 2005. — Т. Il: Diophantine Analysis. — ISBN 9780486442334.
• L. Markowitz. Area = Perimeter // The Mathematics Teacher. — 1981. — Т. 74, вып. 3. — С. 222—3.
• William H. Richardson. Super-Heronian Triangles. — 2007.
• Wacław Sierpiński. Pythagorean Triangles. — Переиздание книги 1962 года. — Dover Publications, Inc., 2003. — ISBN 978-0-486-43278-6.
• Paul Yiu. Heron triangles which cannot be decomposed into two integer right triangles. — 41st Meeting of Florida Section of Mathematical Association of America, 2008.
• Online Encyclopedia of Integer Sequences Heronian
• Wm. Fitch Cheney, Jr. Heronian Triangles // Am. Math. Monthly. — 1929. — Т. 36, вып. 1 January. — С. 22—28.
• S. sh. Kozhegel’dinov. On fundamental Heronian triangles // Math. Notes. — 1994. — Т. 55, вып. 2. — С. 151—6. — DOI:10.1007/BF02113294.