Конспект «Алгебра 7 класс. Все формулы и определения»

Алгебра 7 класс. Все формулы и определения.
Краткий курс алгебры за 7 класс.

«Алгебра 7 класс. Все формулы и определения» — это краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского) — М.: Просвещение, 2013.

---

Выражения и их преобразования

☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а:
Степенью числа а с показателем 1 называют само число а:  а¹ = а.
Степень числа а ≠ 0 с показателем 0 равна 1:  а⁰ = 1

.

☑ 2. Свойства степеней с натуральными показателями:

 а^m • аⁿ = а^m+n

При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

а^m : аⁿ = а^m-n, где а ≠ 0, m ≥ n

(а^m)ⁿ = а^mn

При возведении степени в степень основание оставляют прежним, а показатели перемножают.

(ab)ⁿ = аⁿbⁿ

При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.

☑ 3. Одночленами называют произведения чисел, переменных и их степеней, а также сами числа, переменные и их степени. Например, 5а²х, –3а²b³, 4, х, у⁵ — одночлены.

 Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а²b⁴ равна 6.

☑ 4. Многочленом называют сумму одночленов. Например,

3х⁵ – 4х² + 1, 7a³b – ab² + ab + 6—многочлены. Одночлены считают многочленами, состоящими из одного члена.

Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х³у + 3х²у⁵ + ху равна степени одночлена 3х²у⁵, т. е. равна 7.

Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.

☑ 5. При сложении многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,

(3аb + 5с²) + (ab – с²) = 3ab + 5с² + ab – с² = 4аb + 4с²

При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,

(6x² – у) – (2x² – 8у) = 6х² – у – 2х² + 8у = 4х² + 7у

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,

а² (3аb – b³ + 1) = 3а³b – а²b³ + а²

Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,

(5х – 1)(3х + 2) = 15x² – Зx + 10x – 2 = 15x² + 7x – 2

☑ 6. Формулы сокращённого умножения:

(а + b)² = а² + 2аb + b²

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

(а – b)² = а² – 2аb + b²

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

(а + b)³ = а³ + 3а²b + 3ab² + b³

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(а – b)³ = а³ – 3а²b + Заb² – b³

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(а – b)(а + b) = а² – b²

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

а³ + b³ = (а + b)(a² – аb + b²)

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

а³ – b³ = (а – b)(a² + ab + b²)

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.

Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен

5х³ – х²у можно разложить на множители, вынеся за скобки х² : 5х³ – х²у = х² (5х – у). Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:

3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).

Многочлен а⁴ – 25x² можно разложить на множители, используя формулу разности квадратов двух выражений:

а⁴ – 25x² = (а²)² – (5x)² = (а² – 5x)(а² + 5x).

Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.

Уравнения

☑ 8. Корнем уравнения с одной переменной называют значение переменной, при котором уравнение обращается в верное равенство. Например, число 8 — корень уравнения 3x +1 = 5х – 15, так как верно равенство 3•8 + 1= 5•8 – 15.

Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.

☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x² = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.

При решении уравнений с одной переменной используются следующие свойства:

• если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
• если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

☑ 10. Линейным уравнением с одной переменной называют уравнение вида ах = b, где

х — переменная, а и b — числа.

Если а ≠ 0, то уравнение ах = b имеет единственный корень b/a.

Например, уравнение 7х = 2 имеет корень 2/7.

Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.

Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.

☑ 11. Решением уравнения с двумя переменными называют пару значений переменных, обращающую это уравнение в верное равенство. Например, пара чисел х = -1, у = 4 — решение уравнения 5х + 3у = 7

.

Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.

В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.

☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.

☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.

Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.

☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы
так как является верным каждое из равенств   7 + (–1) = 6   и   2 • 7 – (–1) = 15.

Решить систему уравнений — значит найти все её решения или доказать, что решений нет.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.

☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.

При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:

• если прямые совпадают, то система имеет бесконечно много решений, причём координаты любой точки прямой являются решением системы;
• если прямые параллельны, то система не имеет решений; если прямые пересекаются, то система имеет единственное решение, причём координаты точки пересечения прямых являются решением системы.

При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:

• выражают из какого–либо уравнения системы одну переменную через другую;
• подставляют в другое уравнение системы вместо этой переменной полученное выражение;
• решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.

При решении системы двух линейных уравнений с двумя переменными способом сложения

поступают следующим образом:

• умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали в уравнениях противоположными числами;
• складывают почленно левые и правые части уравнений системы; решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.

Функции

☑ 16. Функциональная зависимость, или функция, — это такая зависимость между двумя переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.

Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

☑ 17. Линейной функцией называют функцию, которую можно задать формулой вида у = kx + b, где х — независимая переменная, k и b — числа.

Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.

Если k ≠ 0, то график функции у = kx + b пересекает ось х; если k = 0 и b ≠ 0, то прямая — график функции у = kx + b, параллельна оси х; если k = 0 и b = 0, то график функции совпадает с осью х.

Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.

Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.

 График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k < 0 — во второй и четвёртой координатных четвертях.

☑ 18. График функции у = х² — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.

График функции у = х³ проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.

Статистические характеристики

 ☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.

 Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.

 Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.

Например, медиана ряда чисел  17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел  28, 43, 54, 56, 58, 62 равна 55.

 Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.

Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.

 

---

Вы смотрели Конспект «Алгебра 7 класс. Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:

uchitel.pro

Практика. Линейные уравнения и их системы. Видеоурок. Алгебра 7 Класс

На этом уроке мы потренируемся решать линейные уравнения, системы, а также различные текстовые задачи, которые к ним сводятся.

Пример 1. Решить уравнение: .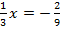

Решение

Вспомним, что деление, по определению, операция, обратная умножению (деление на какое-либо число – это то же самое, что и умножение на обратное к этому числу):

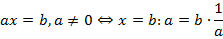
Разделим обе части уравнения на  или умножим на :

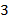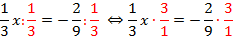
Упростим выражение в левой части уравнения:

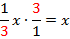
Упростим выражение в правой части уравнения:

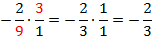
Таким образом, решением уравнения будет: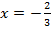

Ответ: .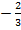

 

Пример 2. Решить уравнение: .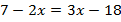

Решение

Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .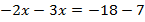

Упростим уравнение – выполним действия в обеих частях уравнения: .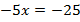

Разделим обе части уравнения на :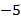

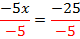
Решением уравнения является .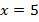

Ответ: .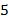

 

Пример 3. Решить уравнение: .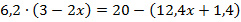

Решение

Раскроем скобки в правой и левой частях уравнения. Для выражения в левой части уравнения используем распределительный закон: .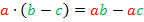

Тогда 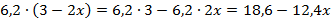. Вспомним, что если перед скобками стоит знак минус, то при раскрытии скобок все знаки всех слагаемых внутри скобок меняются на противоположный: .

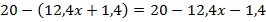Перепишем уравнение после применения преобразований: .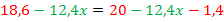

Как и в предыдущем примере, перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .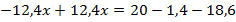

Выполнив действия в обеих частях уравнения, получим тождество: .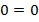

Таким образом, данное равенство верно всегда, при любых значениях переменной.

Ответ: 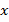 – любое число.

 

Пример 4. Решить уравнение: .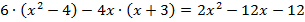

Решение

Раскроем скобки в правой и левой частях уравнения, используя распределительный закон .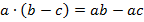

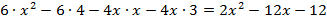
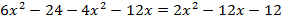
Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .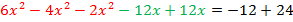

Получаем .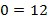

Данное равенство неверно всегда, т.е. оно не выполняется ни при каких значениях переменной.

Ответ: нет решений.

 

Пример 5. Решить уравнение: .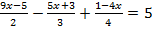

Решение

Избавимся от знаменателей дробей – умножим обе части уравнения на общий знаменатель всех дробей, т.е. число :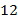

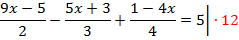
Получим: .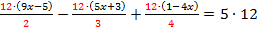

Выполним сокращения и избавимся от знаменателей: .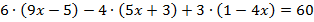

Раскроем скобки:

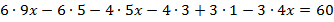
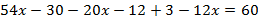
Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .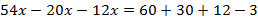

Выполнив действия в обеих частях уравнения, получим следующее уравнение: .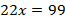

Найдем :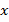

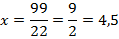
Ответ: .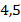

В общем виде системы линейных уравнений выглядят следующим образом: 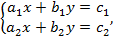 где 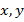 – переменные, 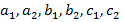– произвольные числа.

Есть несколько методов решения систем уравнений.

1. Метод подстановки.
2. Метод сложения.
3. Графический метод.

Пример 6. Решить систему: .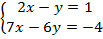

Решение (несколько способов)

1. Метод подстановки – необходимо в уравнении выразить одну переменную через другую и подставить во второе уравнение.

Из первого уравнения выразим 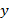, для этого перенесем  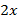из левой части уравнения в правую: .

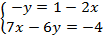Затем умножим обе части первого уравнения на : .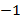

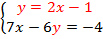Теперь подставим во второе уравнение полученное выражение: .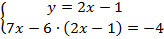

Теперь во втором уравнении только одна переменная 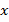, решим его (мы уже умеем это делать – получилось обычное линейное уравнение с одной переменной).

Раскроем скобки во втором уравнении: .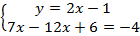

Во втором уравнении перенесем все слагаемые с переменной в левую часть, а без переменной – в правую: .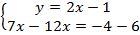

Выполним действия в обеих частях второго уравнения: .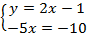

Найдем : .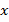

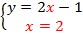Подставим в первое уравнение найденное значение переменной: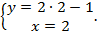

Решением системы будет: .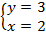

Ответ: .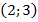

 

2. Метод сложения – нужно преобразовать уравнения так, чтобы при одной переменной в разных уравнениях были противоположные коэффициенты, после этого нужно сложить правые и левые части уравнений.

Избавимся от переменной 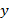. Умножим первое уравнение на : .

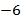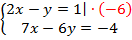Теперь система имеет вид: .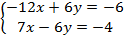

Сложим уравнения системы:

interneturok.ru

Памятка по теме «Решение уравнений» для 7 класса

Памятка для учащихся 7 класса

по теме: «Решение уравнений»

Алгоритм решения:

1. Умножьте обе части уравнения на общий знаменатель дробей (НОК).

2. Запишите дополнительные множители к каждой дроби, которые получаются после сокращения. Не забудьте умножить на общий знаменатель и целую часть уравнения!

3. Умножьте числители на дополнительный множитель.

4. Раскройте скобки, если необходимо.

5. Перенесите неизвестные члены уравнения в левую часть, а известные — в правую.

6. Приведите подобные слагаемые в левой части уравнения и найдите значение правой части.

Получилось линейное уравнение вида ax=b, где x=b:a.

Примеры решения уравнений с дробной частью.

1)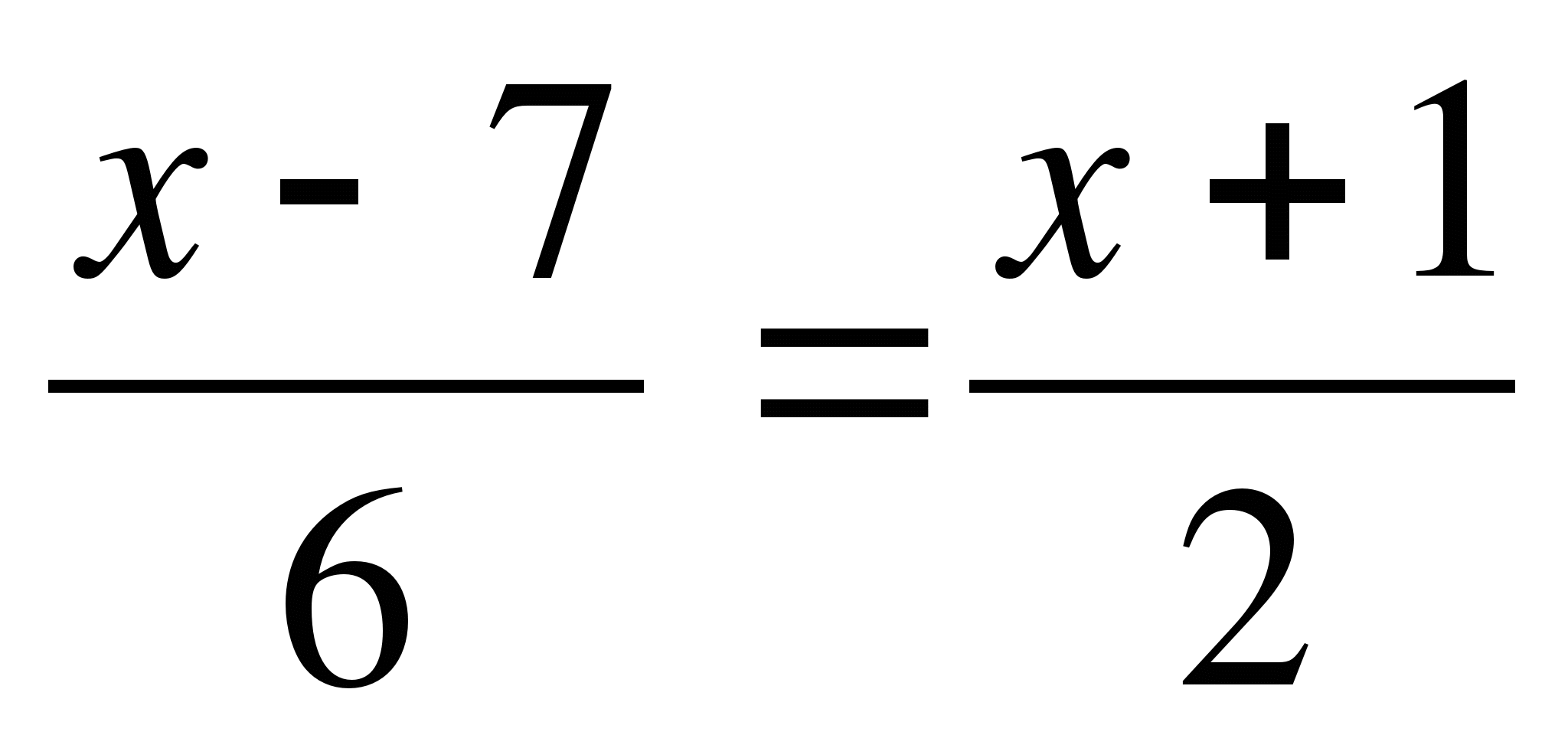 Или:

Решение:

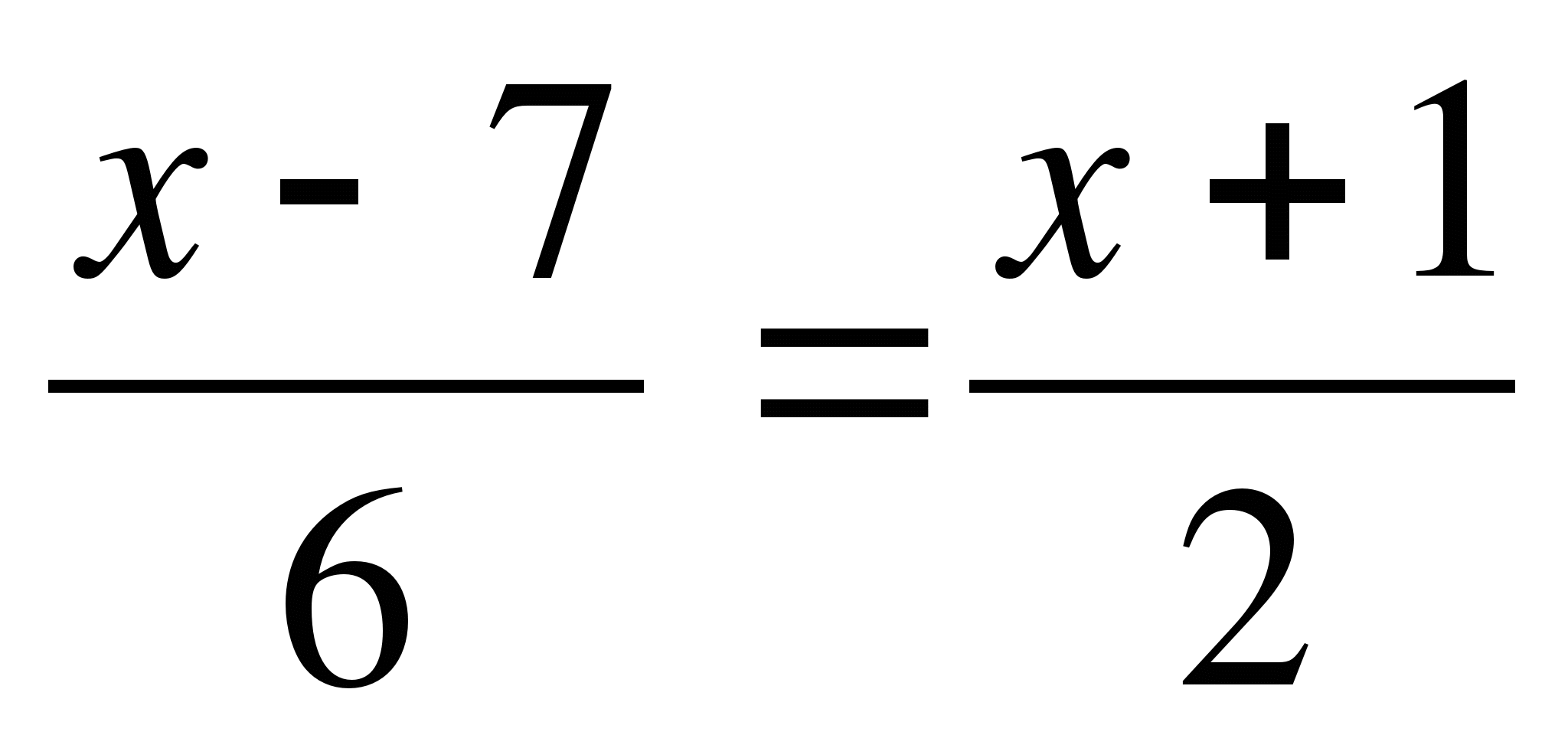— пропорция

Решение:

1 / 3/

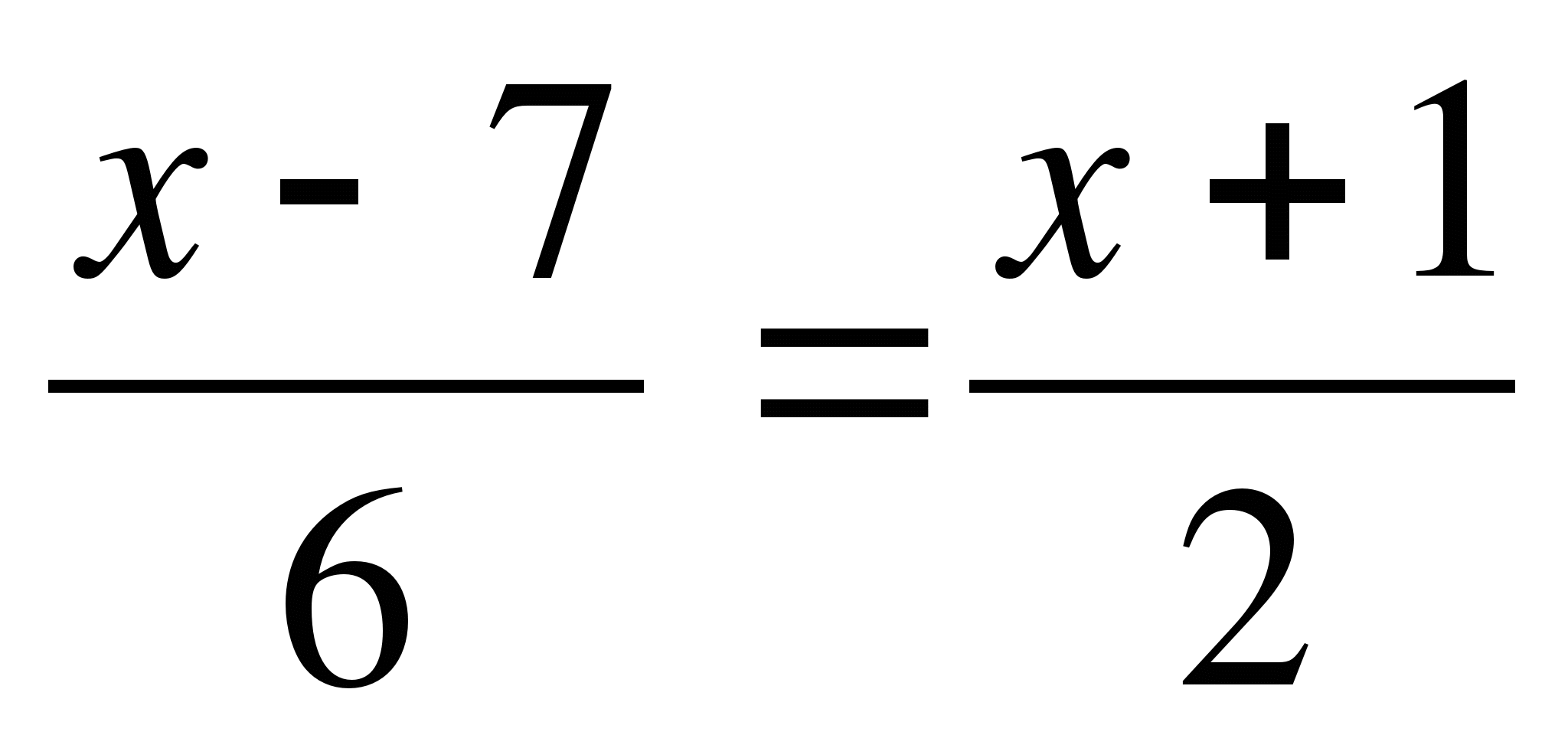|•6

x — 7 = 3(x+1)

x – 7 = 3x + 3

x — 3x = 3+7

-2x = 10

x = 10: (–2)

x = –5

Основное свойство пропорции: произведение крайних членов пропорции

равно произведению ее средних членов.

(x – 7)·2 = 6·(x+1)

2 x – 14 = 6x + 6

2 x –6 x = 6 + 14

-4x = 20

x = 20: (-4)

x = –5

Решение:

8/ 7/ 56/

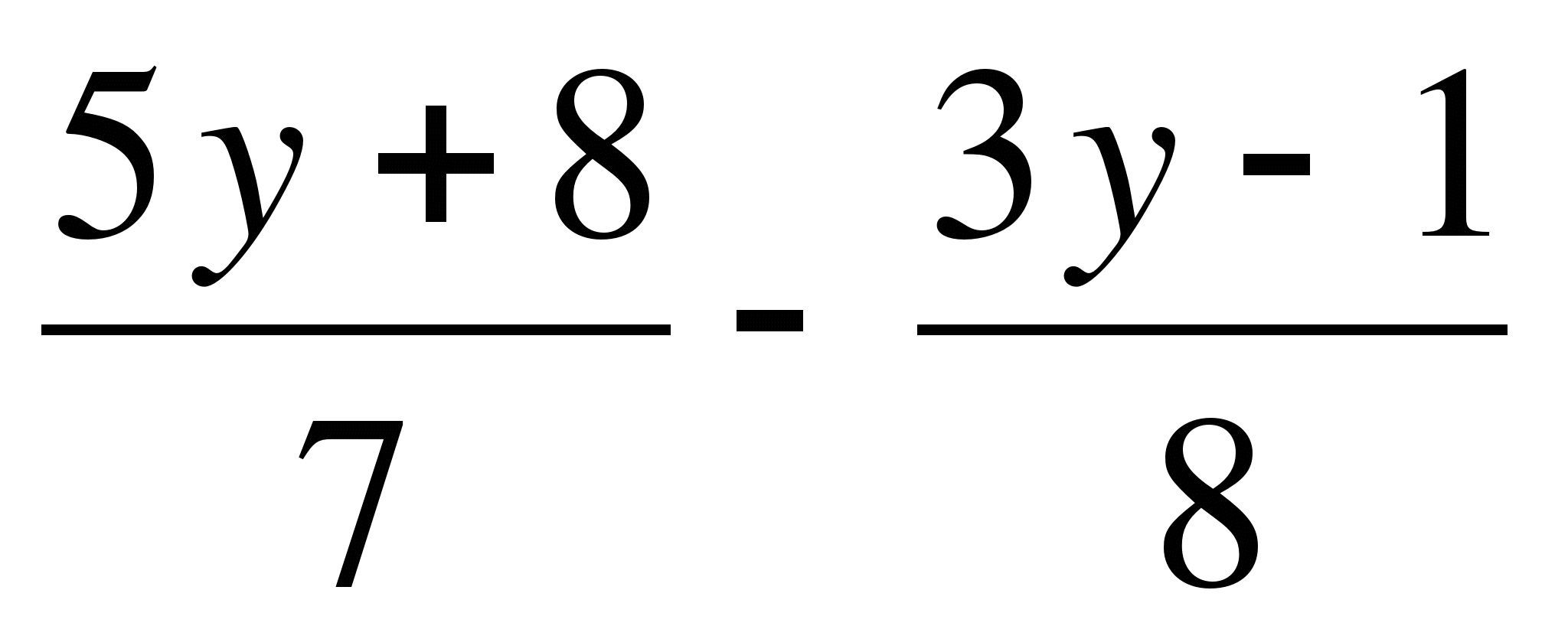= 5 |·56

8(5y + 8) – 7(3y — 1) = 56·5

40y + 64 – 21y +7 = 280

19y = 280 – 64 – 7

19y = 209

y = 209 : 19

y = 11

Решение:

3/ 5/ 15/

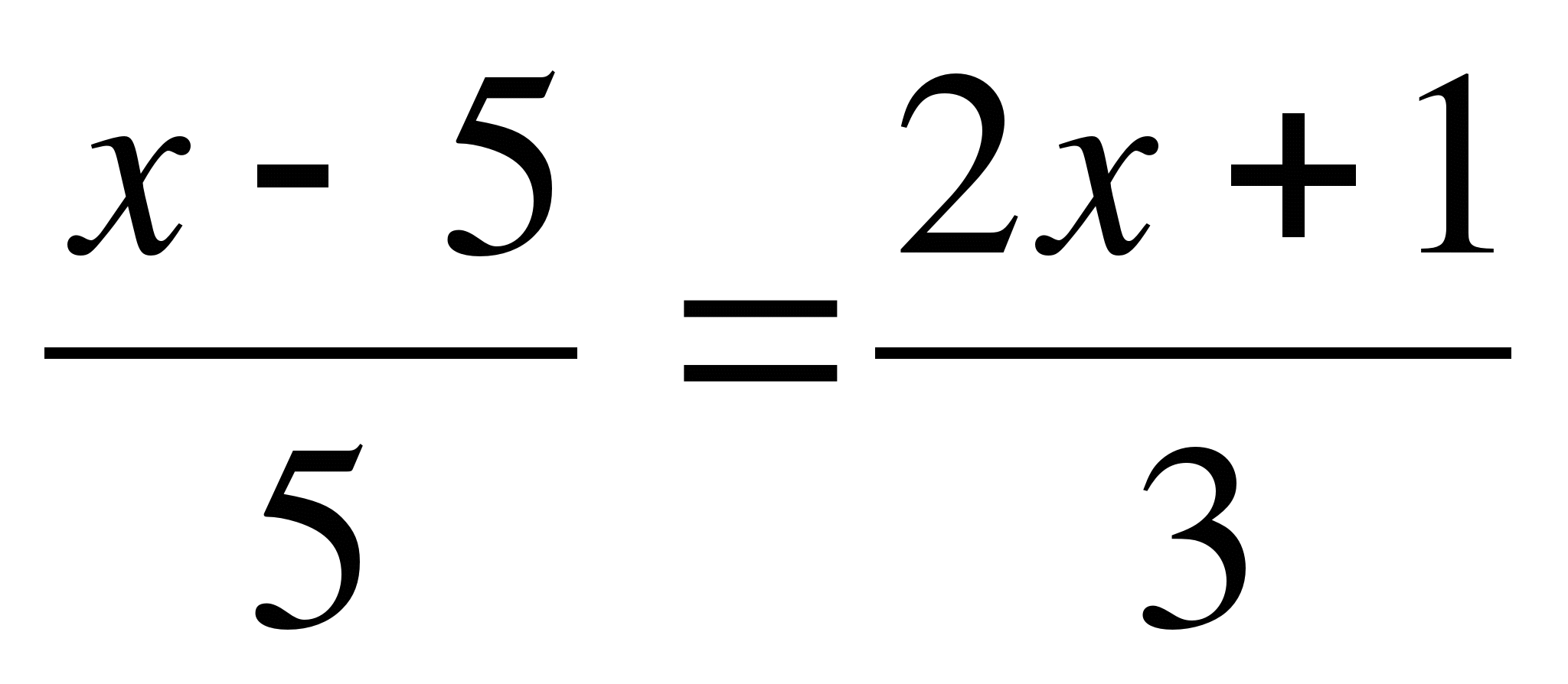— 7 |·15

3(х — 5) = 5(2х + 1) — 15·7

3х – 15 = 10х +5 – 105

3х – 10х = -100 + 15

-7х = -85

х = -85: (-7)

х = 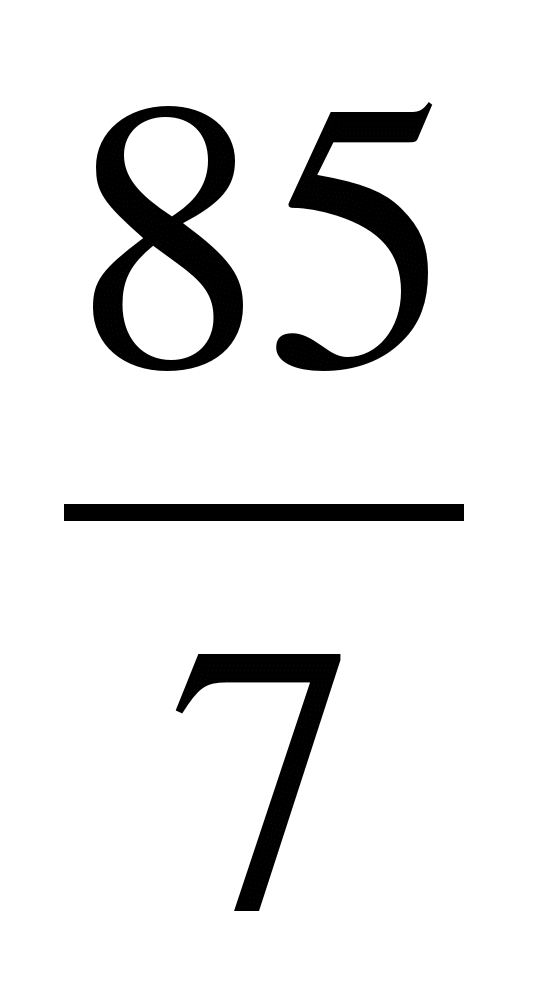= 12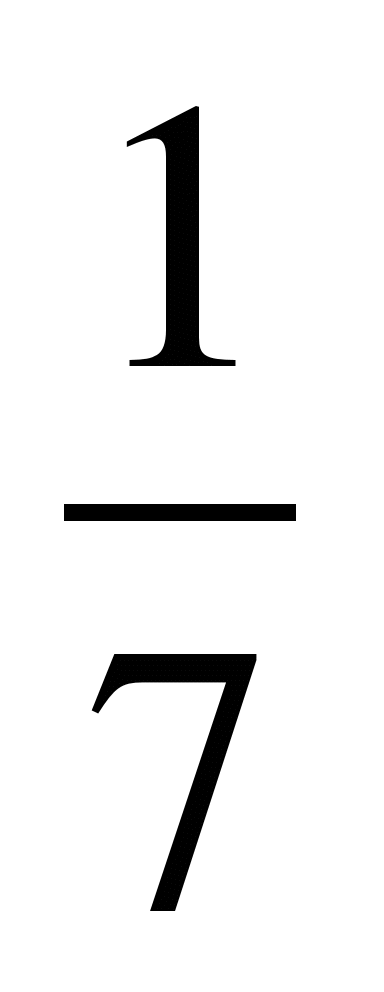

Решение:

3/ 2/ 42/

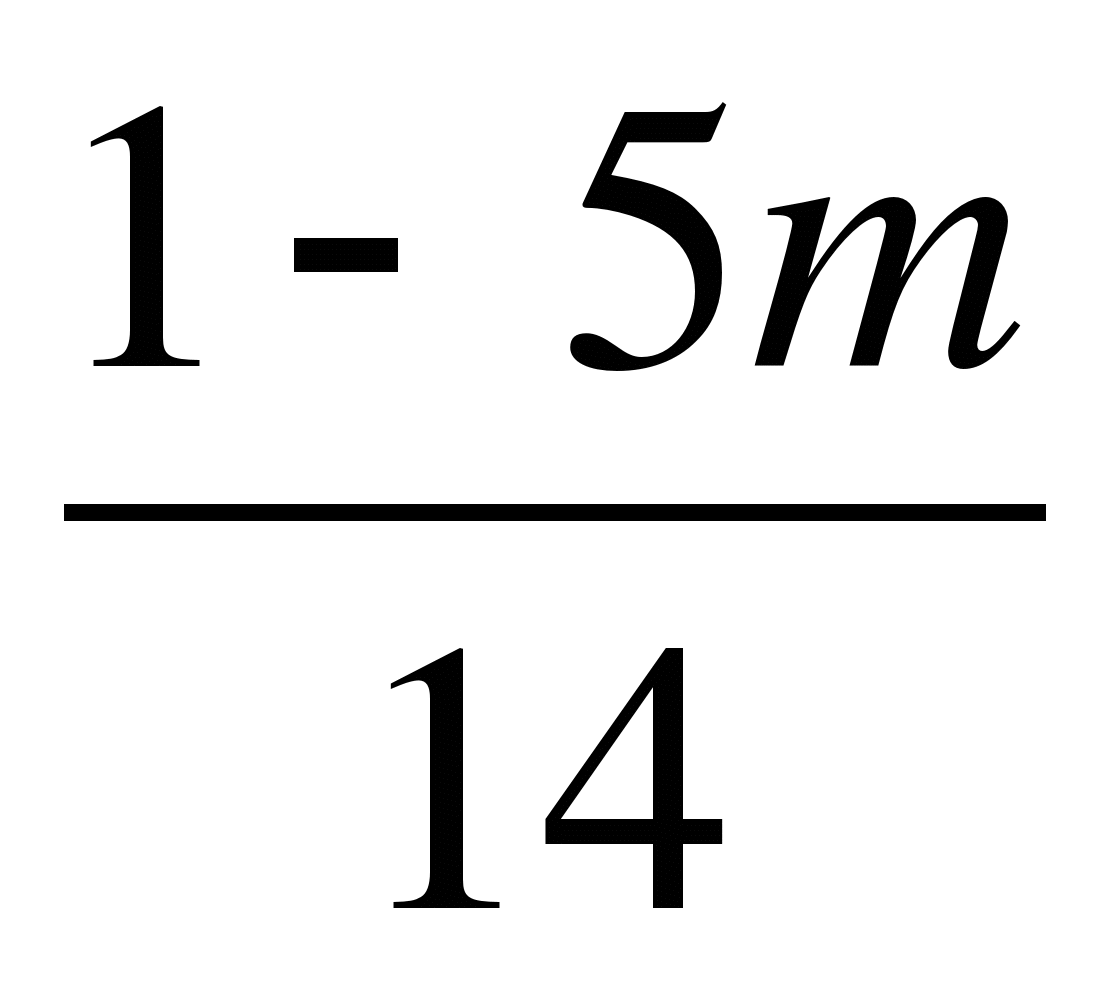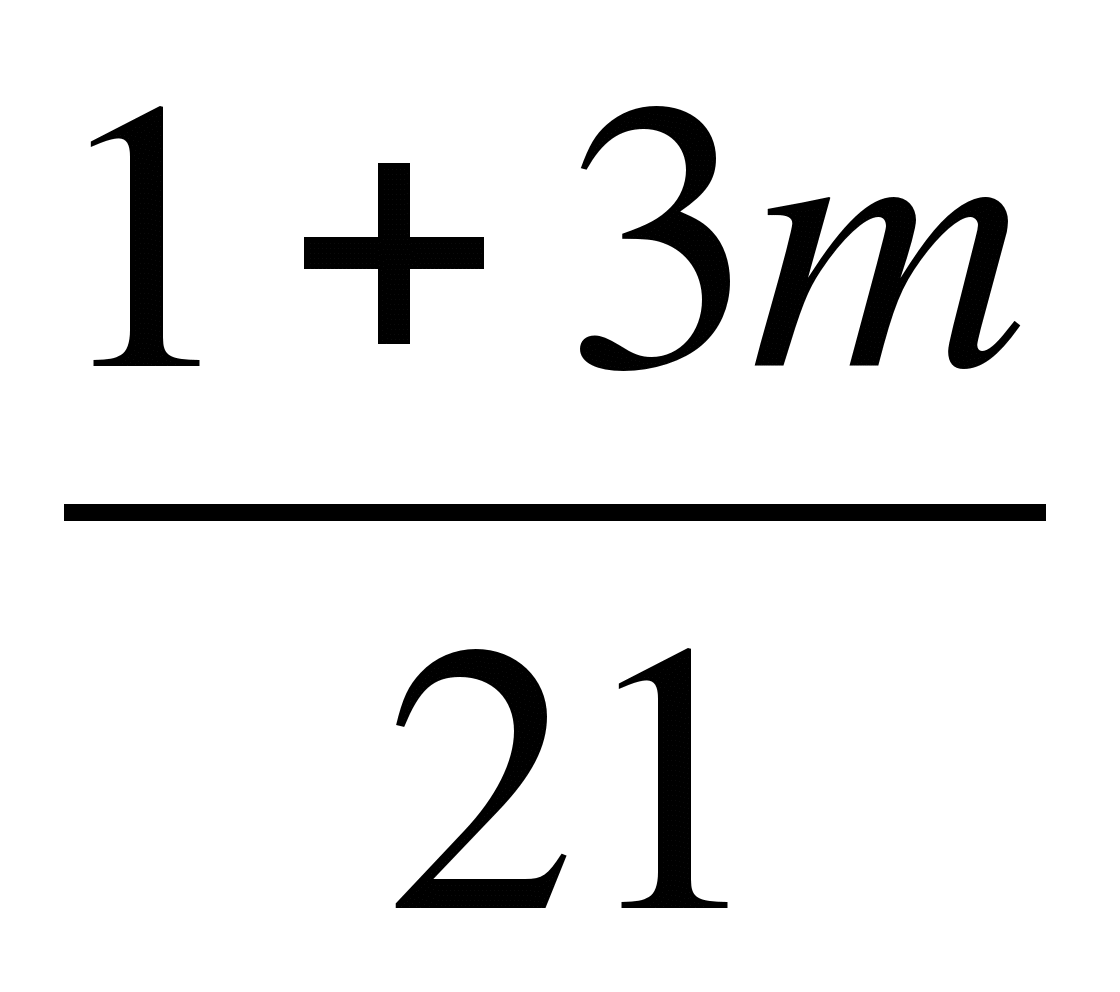– + = 0 |·42

–3(1 – 5m) + 2(1 +3m) = 0

–3 + 15m + 2 + 6m = 0

21m = 0 + 3 – 2

21m = 1

m = 1 : 21

m =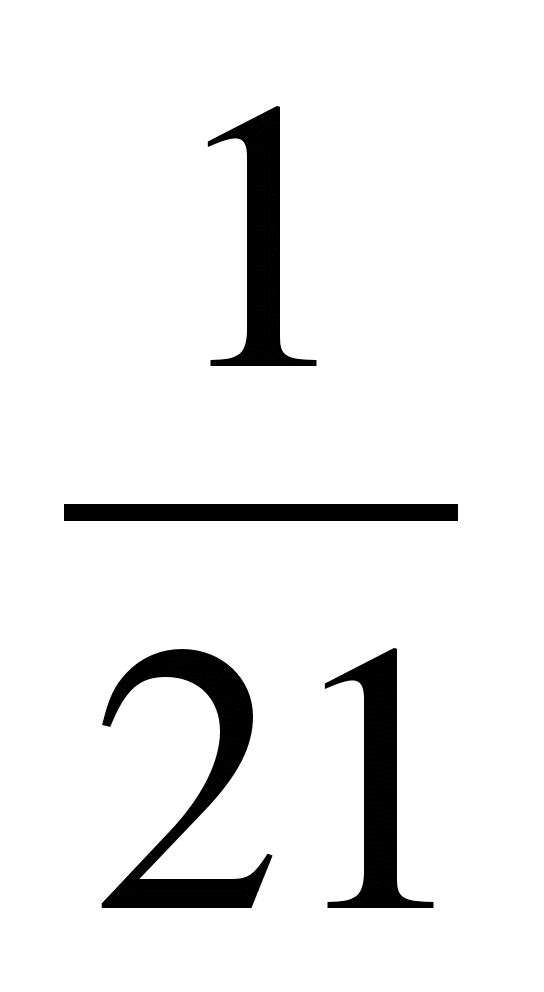

Решение:

6/ 2/ 3/ 6/

2x — 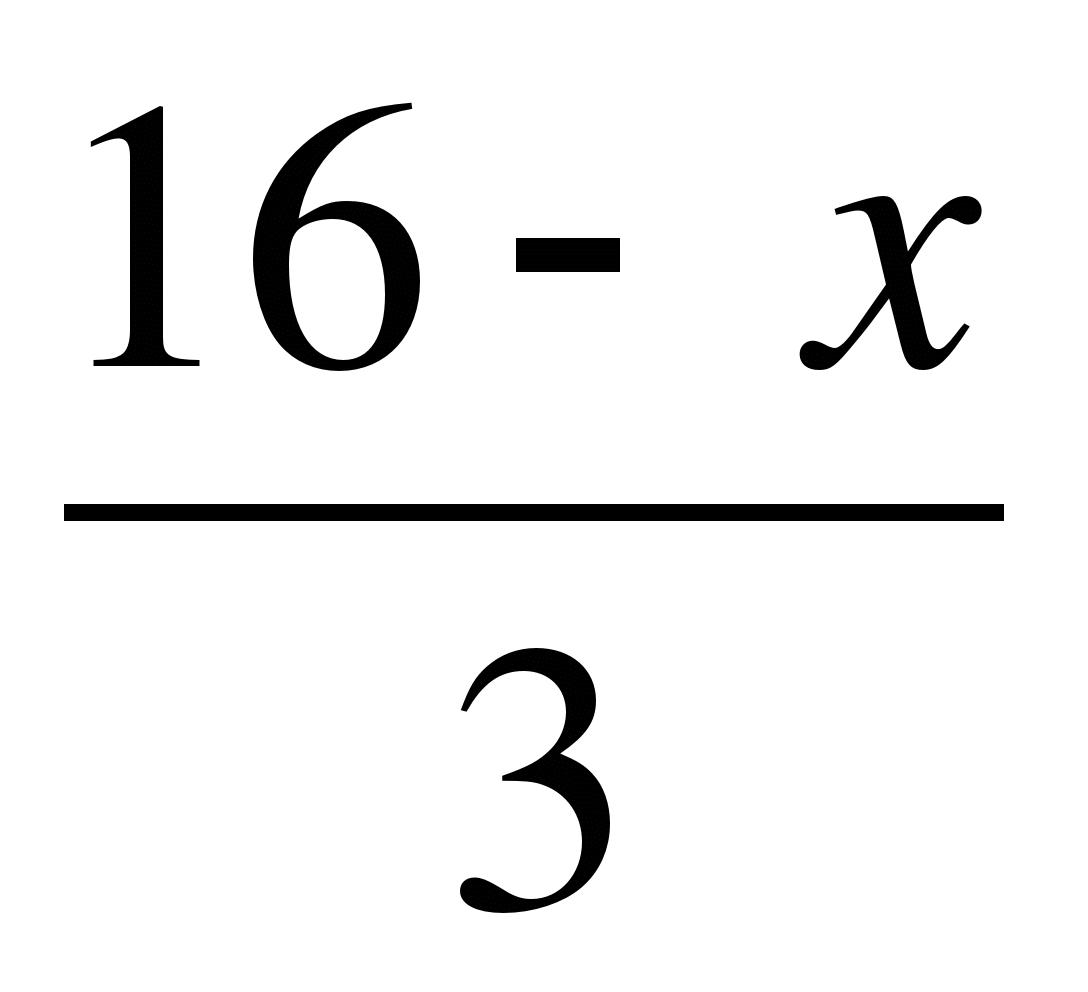= 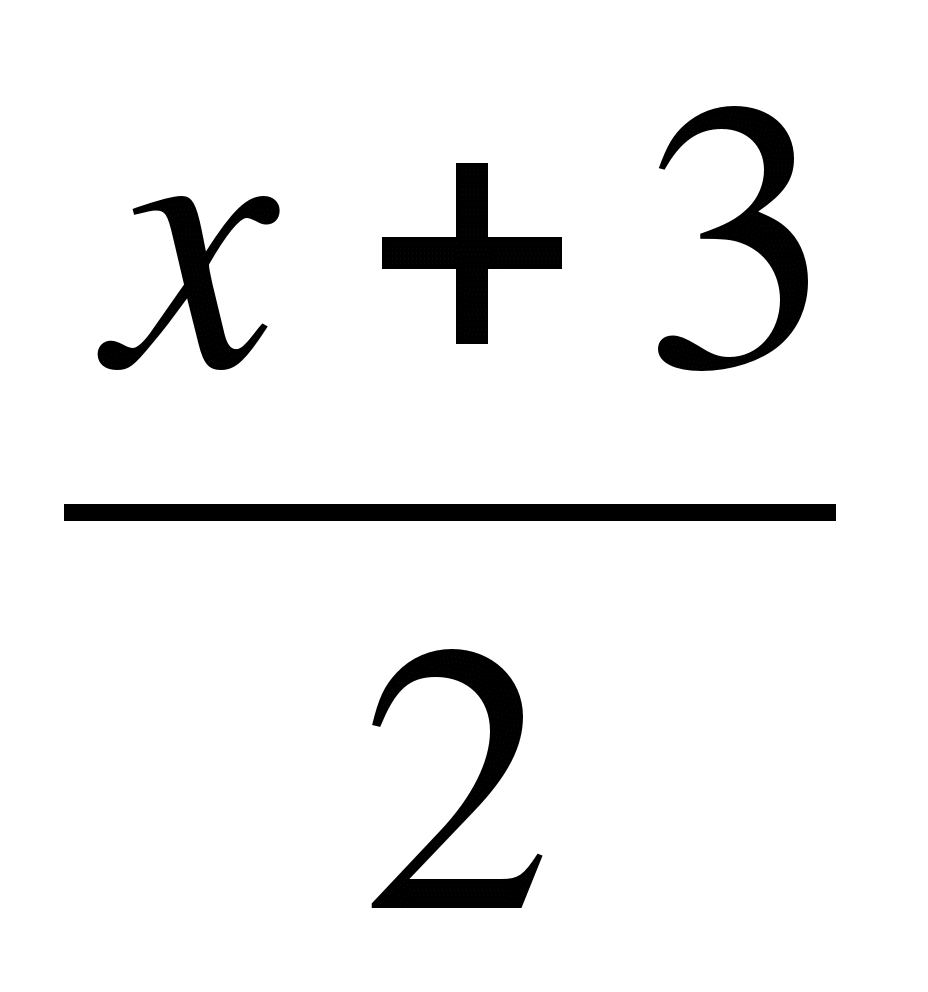+ 6 |·6

6·2x – 2(16 – x) = 3(x +3) +6·6

12x – 32 + 2x = 3x + 9 + 36

14x – 3x = 45 + 32

11x = 77

x= 77 : 11

x = 7

Ответ: 1) —5; 2) 11; 3) 12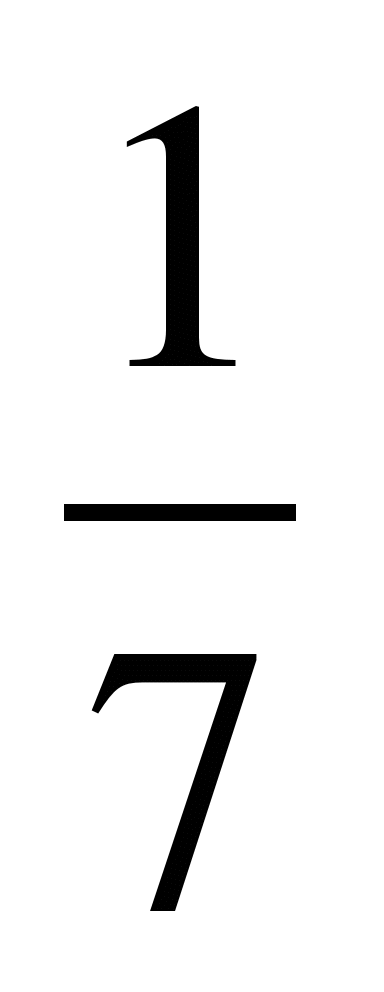; 4) 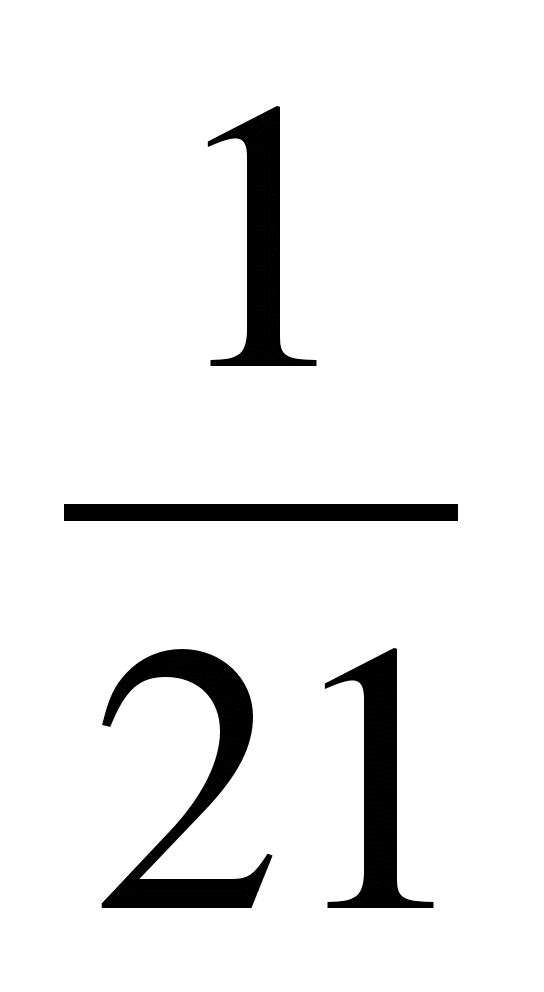; 5) 7.

infourok.ru

Основные понятия — урок. Алгебра, 7 класс.

1. решить систему уравнений:

x+2y−5=0,2x+4y+3=0.

 

Графиком уравнения x&plus;2y−5=0 является прямая.

Найдём две пары значений переменных \(x\) и \(y\), удовлетворяющих этому уравнению.

\(x\)	\(5\)	\(0\)
\(y\)	\(0\)	\(2,5\)

Построим на координатной плоскости \(xОy\) прямую l1, проходящую через эти две точки.

 

Графиком уравнения 2x&plus;4y&plus;3=0 также является прямая.

Найдём две пары значений переменных \(x\) и \(y\), удовлетворяющих этому уравнению.

\(x\)	\(-1,5\)	\(2,5\)
\(y\)	\(0\)	\(-2\)

 

Построим на координатной плоскости \(xОy\) прямую l2, проходящую через эти две точки.

 

 

Прямые l1 и l2 параллельны, значит, система не имеет решений, так как нет точек, удовлетворяющих одновременно и одному, и другому уравнению, т. е. принадлежащих одновременно и одной, и другой из построенных прямых.

Ответ: система не имеет решений.

 

2. Решить систему уравнений:

2x−y−5=0,2x+y−7=0.

 

Построим графики уравнений системы, преобразуя каждое уравнение к виду линейной функции. Получим из первого уравнения \(y=2x-5\) и из второго уравнения \(y=-2x+7\).

 

Графиком уравнения \(y=2x-5\) является прямая.

 

Найдём две пары значений переменных \(x\) и \(y\), удовлетворяющих этому уравнению.

\(x\)	\(0\)	\(3\)
\(y\)	\(-5\)	\(1\)

 

Построим на координатной плоскости \(xОy\) прямую l1, проходящую через эти две точки.

Графиком уравнения \(y=-2x+7\) также является прямая.

 

Найдём две пары значений переменных \(x\) и \(y\), удовлетворяющих этому уравнению.

\(x\)	\(0\)	\(1\)
\(y\)	\(7\)	\(5\)

 

Построим на координатной плоскости \(xОy\) прямую l2, проходящую через эти две точки.

 

Прямые l1 и l2 пересекаются в точке \(A\), координаты которой — единственное решение заданной системы. 

 Ответ: \((3;1)\).

www.yaklass.ru

Конспекты уроков по алгебре на тему «Уравнения и его корни» (7 класс)

Алгебра 7

Урок 13. Глава 1. Выражения, тождества, уравнения (22 часа)

Тема: Решение уравнений, сводящихся к линейным. С/р.

Цель: Проверить знания учащихся по теме «Уравнение и его корни. Решение простейших линейных уравнений».Формировать умение решать по алгоритму уравнения, сводящиеся к линейным.

Ход урока.

1. Организационный момент.

2. Проверка домашнего задания.

3. Актуализация опорных знаний.

1. Что такое уравнение? Что значит решить уравнение? Что называется корнем (решением) уравнения?

2. Какие уравнения называются равносильными? Как проверить являются ли уравнения равносильными?

3. Сформулируйте основные свойства уравнений.

4. Приведите пример уравнения, не имеющего корня.

5. Приведите пример уравнения, имеющего множество корней.

6. Какие уравнения называются линейными?

7. Сколько корней может иметь линейное уравнение?

4. Самостоятельная работа по теме «Уравнение и его корни. Решение простейших линейных уравнений». (15 min)

Вариант 1.

1. Является ли число 5 корнем уравнения 6(х – 4) = 2х + 7?

6(х – 4) = 2х + 7, х = 5, то 6(5 – 4)= 2 ∙ 5 + 7, 6 ≠ 17, значит х = 5, не является корнем уравнения.

2. Сколько корней имеет уравнение (объясните почему?):

а) –2х = 17, т.к. а ≠ 0, то уравнение имеет 1 корень;

б) 0 ∙ х = –6, т.к. а = 0, b ≠ 0, то уравнение не имеет корней;

в) 0 ∙ х = 0, т.к. а = 0, b = 0, то уравн-е имеет бесконечно много корней.

3. Найдите корень уравнения:

а) 26х = –78, б) 0,2х = 28, в) 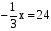, г) ,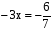

х = –3. х = 140. х = –72. х = .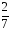

Вариант 2.

1. Является ли число 6 корнем уравнения 7х – 10 = 4(х + 2)?

7х – 10 = 4(х + 2), х = 6, то 7 ∙ 2 – 10 = 4(6 + 2), 32 = 32, значит х = 6, является корнем уравнения.

2. Сколько корней имеет уравнение (объясните почему?):

а) 0 ∙ х = –72, т.к. а = 0, b ≠ 0, то уравнение не имеет корней;

б) 0 ∙ х = 0, т.к. а = 0, b = 0, то уравн-е имеет бесконечно много корней; в) 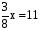, т.к. а ≠ 0, то уравнение имеет 1 корень.

3. Найдите корень уравнения:

а) 21х = 84, б) –1,2х = 0,36; в) 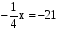; г) .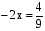

х = 4. х = –0,3. х = -84. х = .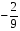

5. Объяснение нового материала.

АЛГОРИТМ № 1

(Решение уравнений вида ax + b = cx + d, где a, b, c, d – некоторые числа)

1. Перенесите слагаемые, содержащие неизвестные, в левую часть урав-нения, а известные – в правую, изменяя их знак на противоположный.

2. Выполните приведение подобных слагаемых.

3. Поделите левую и правую части уравнения на коэффициент при неизвестном, если он не равен нулю.

4. Запишите ответ.

4х + 3х = 28 + 35,

7х = 63,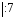

х = 9. Ответ: 9.

АЛГОРИТМ № 2

(Решение уравнений, которые содержат скобки)

1. Раскройте скобки.

2. Перенесите слагаемые, содержащие неизвестные, в левую часть уравнения, а известные – в правую, изменяя их знак на противоположный.

3. Выполните приведение подобных слагаемых.

4. Поделите левую и правую части уравнения на коэффициент при неизвестном, если он не равен нулю.

5. Запишите ответ.

Пример 2. 5(2х – 2,2) = 1 – 4(3,5 – 2х),

10х – 11 = 1 — 14 + 8х,

10х – 8х = 1 – 14 + 11,

2х = – 2,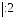

х = –1. Ответ: –1.

АЛГОРИТМ № 3

(Решение уравнений, которые содержат деление на число)

1. Найдите наименьший общий знаменатель для всех дробей, входящих в уравнение.

2. Помножьте каждый член уравнения на наименьший общий знаменатель и сократите дробь.

3. Раскройте скобки, если они есть.

4. Перенесите слагаемые, содержащие неизвестные, в левую часть уравнения, а известные – в правую, изменяя их знак на противоположный.

5. Выполните приведение подобных слагаемых.

6. Поделите левую и правую части уравнения на коэффициент при неизвестном, если он не равен нулю.

7. Запишите ответ.

Пример 3. 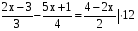, (НОЗ 12)

,

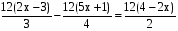4(2х – 3) – 3(5х + 1) = 6(4 – 2х),

8х – 12 – 15х – 3 = 24 – 12х,

8х – 15х + 12х = 24 + 12 + 3,

5х = 39,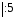

х = 7,8. Ответ: 7,8.

6. Решение уравнений.

Уч.с.30 № 128(а,е). Найдите корень уравнения:

а) 5х – 150 = 0, е) 1,3х = 54 + х,

, ,

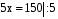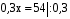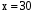. Ответ: 30. 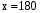. Ответ: 180.

Уч.с.30 № 129(а,г,ж,л). Решите уравнение:

а) 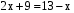, ж) ,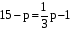

, ,

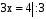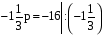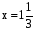. Ответ: 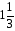. . 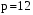Ответ: 12.

г) 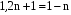, л) ,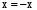

, ,

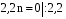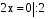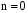. Ответ: 0. 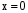. Ответ: 0.

Уч.с.30 № 131(а,б). Найдите корень уравнения:

а) 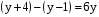, б) ,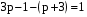

, ,

, ,

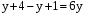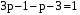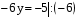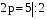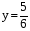. Ответ: 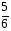. . 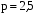Ответ: 2,5.

Уч.с.31 № 134(а). При каком значении переменной значение выражения 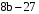равно: а) 5.

а) ,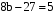

,

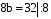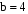. Ответ: 4.

7. Подведение итогов урока.

8. Домашнее задание. п. 7(повторить теорию), № 128(б-д), 129(б,в,д,е), 131(в,г), 134(б).

Алгебра 7. Самостоятельная работа по теме «Уравнение и его корни. Решение простейших линейных уравнений».

Вариант 1.

1. Является ли число 5 корнем уравнения 6(х – 4) = 2х + 7?

2. Сколько корней имеет уравнение (объясните почему?):

а) –2х = 17; б) 0 ∙ х = –6; в) 0 ∙ х = 0.

3. Найдите корень уравнения:

а) 26х = –78; б) 0,2х = 28; в) 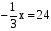; г) .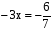

Вариант 2.

1. Является ли число 6 корнем уравнения 7х – 10 = 4(х + 2)?

2. Сколько корней имеет уравнение (объясните почему?):

а) 0 ∙ х = –72; б) 0 ∙ х = 0; в) .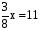

3. Найдите корень уравнения:

а) 21х = 84; б) –1,2х = 0,36; в) 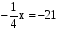; г) .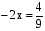

Алгебра 7. Самостоятельная работа по теме «Уравнение и его корни. Решение простейших линейных уравнений».

Вариант 1.

1. Является ли число 5 корнем уравнения 6(х – 4) = 2х + 7?

2. Сколько корней имеет уравнение (объясните почему?):

а) –2х = 17; б) 0 ∙ х = –6; в) 0 ∙ х = 0.

3. Найдите корень уравнения:

а) 26х = –78; б) 0,2х = 28; в) 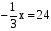; г) .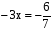

Вариант 2.

1. Является ли число 6 корнем уравнения 7х – 10 = 4(х + 2)?

2. Сколько корней имеет уравнение (объясните почему?):

а) 0 ∙ х = –72; б) 0 ∙ х = 0; в) .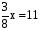

3. Найдите корень уравнения:

а) 21х = 84; б) –1,2х = 0,36; в) 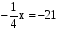; г) .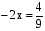

infourok.ru

План-конспект урока по алгебре (7 класс) на тему: Конспект урока по теме «Решение уравнений» 7 класс

Урок алгебры 7 класс

Тема : « Решение линейных уравнений»

разработала учитель математики : Кузнецова Марина Александровна

Тип урока : Закрепление и систематизация знаний ,формирование УН в решении уравнений.

Цели урока:

         Обучающие:

Создать условия :

1. для закрепления навыков решения линейного уравнения и уравнений, которые сводятся к ним,
2. формирование навыка решения уравнения с одним неизвестным сведением его к линейному уравнению с помощью свойств равносильности.

• Развивающие :

Создать условия :

1. для развития мыслительной деятельности учащихся, умения анализировать и делать выводы,
2. для развития умения самоконтроля учащихся,
3. для развития математической речи,
4. для развития внимания и памяти.

          Воспитательные:

Обеспечить условия :

1. для воспитания культуры учебного труда,
2. для самостоятельности и настойчивости а достяжении поставленной цели,
3. для формирования волевых качеств, формирование коммуникабельности, обьективной оценки своих достижений.

Оборудование:Алгебра, учебник для 7 класса под редакцией С.А. Теляковского, интерактивная доска,компьютер, карточки с заданиями для устного счета, рабочая тетрадь, карточки для самостоятельной работы ( тест)

                                                         Ход урока :

1. Организационный момент  — 1мин.

Поприветствовать учащихся, проверить их готовность к уроку.

2. Постановка темы и целей урока. (5-6мин)

а)  « Ум человеческий только тогда понимает обобщение,

                 когда он сам его сделал или проверил»

                                              Л.Н.Толстой.   ( слайд № 1)

• как вы понимаете это выражение ? ( чтобы обладать математическими знаниями нужно самим прорешать , проверить решения различных виды примеров и задач)
• какую тему мы изучали  на прошлых уроках? ( решение линейных уравнений)
• давайте  ответим на вопросы ..

1. Что называется уравнением ……?
2. Корнем уравнения называется……?
3. Решить  уравнение — значит ……?
4. Какие уравнения называются равносильными?
5. Линейные уравнения -это уравнеия……?

3. 6. Какими свойствами мы пользуемся при решении уравнений ?

   -Мы с вами  решали уравнения , применяли свойства  для их решения .

-Как вы думаете ,а какая будет задача  и цели у нас на сегоднешним уроке?

Мы с вами изучили все составляющие этой темы, поэтому сегодня на уроке наша задача повторить и закрепить решение уравнений. закрепить применение всех свойств при решение уравнений.

4. —   Как вы считаете какова тема сегодняшнего урока?

         б) Открываем тетради ,записываем число ,классная работа и тему урока.

           Решение линейных уравнений с одной переменной. (слайд №2)

      3. Проверка домашней работы:  у вас я почти у всех проверила вчера на продленке ( мы все разобрали)

    4. Устная работа : ( 8 -9 мин.)

 а) я вам раздаю карточки ,проставьте туда только ответы. На эту работу вам дается 4 мин.

1	1,5 * (- 2)		8	— 9 – 33
2	17 — ( -24 )		9	— 1\2 х = — 5\12
3	16 — 100		10	— 20 х = 5
4	2,5 \ ( -5 )		11	1\4 х = —  5

давайте сверим ответы (  слайд №3)

1	-3	8	-42
2	41	9	5\6
3	-84	10	-1\4
4	-0,5	11	-20

б)  Давайте найдем на слайде ошибки: (слайд №4)

4х-12=2х+8 4х-2х=8+12

8х+ 54=6х 8х-6х=54 2х=54 х=54\2 х=27

1. Решение линейных уравнений: ( слайд № 5) (10-12 мин )

выполним на доске уравнения с объяснением : ( вызвать 2 учащихся ,ребята решают каждый по 2 уравнения.)

1.      0,5 х +11 = 4 — 3х

2.      ( 2+3х) — ( 4х -7) =10  

3.      0,5 х +7 = 5 ( 0,2 +1,5 х)

4.       4х- 6 =  7+х

                          2         3

1. Самостоятельная работа : (12-13 мин.)

Базовый уровень : 5у= — 5\8   7х -12 = 3х + 4   ( х-7 ) — (2х +9) = -13  4( 3х-2) +х = 12х

Повышенный уровень :   -1,5 х = -9    0,8у +14 = 2 — 1,6у 13- 3( х+1) = 4-5х  0,2 (3х -5 ) — 0,3 ( х-1) = -0,7

дополнительное задание:

При каком  значении у значение выражения   6у -2  в 5 раз меньше выражения  7+2у

   домашняя работа: (« уровень А выполняют:  1,3,5, 7) » ,  « уровень Б выполняют:  2,4, 6,7) »

1.         26х- 0,8 =7  
2.       2\5 х — 1\3  =1\6
3.        -2х = 1,4
4.        3\7х =  — 4\9
5.      3 ( х-1) = 2(х+2)
6.     х+3    =    3х-2  

    2                 7

7.    3(х-5 ) — 2( х+4) = -5х +12

1. Подведение итогов : ( 1 -2 мин.)

-Что мы сегодня отрабатывали на уроке? (Этот материал очень важен ,так как он  встречается во всех экзаменационных работах.)

-Достигли ли вы целей сегодняшнего урока?

-Какие правила применяли при решении уравнений?

2. Разъяснение содержания домашнего задания. (1 мин.) Вложить листок в дневники.
3. Рефлексия:

-вы довольны своей работой на уроке ?

Какой вид деятельности вам понравился больше всего на уроке7

nsportal.ru

Уравнение и его корни

Вопросы занятия:

·  ввести понятия «уравнение с одной переменной», «решение уравнений с одной переменной»;

·  разобрать что значит «решить уравнение»;

· ввести понятие равносильных уравнений.

Материал урока

Рассмотрим следующую задачу.

К заданному числу прибавили 9 и получили в сумме 25. Какое число задумано?

Обозначим букой х задуманное число. Тогда по условию задачи

х + 9 = 25

То есть, чтобы найти неизвестное число, мы составили равенство, которое содержит переменную х. Равенства такого вида называются уравнениями с одной переменной.

Теперь надо найти такое значение переменной х, при подстановке которого в наше уравнение получается верное числовое равенство. Для этого переносим 9 в правую часть равенства и получаем:

х = 25 – 9.

х = 16

 То есть 16 и есть задуманное число.

Найденное значение переменной х называется решением уравнения, или корнем уравнения.

Таким образом, можем сформулировать следующие определения.

Равенство, содержащее одну переменную, называется уравнением с одной переменной, или уравнением с одним неизвестным.

Значение переменной, при котором уравнение превращается в верное числовое равенство, называется корнем (или решением) уравнения.

Рассмотренное выше уравнение имеет один корень.

Но есть уравнения, которые имеют два, три, четыре и более корней или не имеют корней вообще.

Например,

Определение.

Решить уравнение – это значит найти все его корни или доказать, что их нет.

Определение.

Два уравнения называются равносильными, если каждый корень первого уравнения является корнем второго, и наоборот – каждый корень второго уравнения является корнем первого, то есть, оба уравнения имеют одни и те же корни.

Равносильными являются также уравнения, которые не имеют корней.

Например,

 

А теперь сформулируем свойства, которые используются при решении уравнений.

Свойство 1.

Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.

Например,

Свойство 2.

Также, если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнения, равносильное исходному.

Например,

Давайте решим следующие упражнения.

Пример.

Пример.

Пример.

Пример.

videouroki.net