Биссектрисы трапеции

Рассмотрим некоторые задачи, в которых биссектрисы углов трапеции пересекаются.

I. Биссектрисы углов при боковой стороне трапеции пересекаются.

 1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB).

2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам).

3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º.

Вывод:

Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.

Это утверждение, в частности, применяется при решении базовой задачи на трапецию, в которую вписана окружность.

 Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS (доказательство можно посмотреть здесь). Значит, его биссектриса AK является также медианой, то есть точка K — середина BS.

Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD.

Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS.

Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.

Вывод:

Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.

II. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию.

 В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно.

 

 

 Таким образом, BC=BK+KC=AB+CD.

 

 

 

Вывод:

Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции.

В частности, у равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.

III.Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.

 В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно.

 

 

 

 Отсюда AD=AF+FD=AB+CD.

 

 

 

Вывод:

Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции.

У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.

Биссектрисы углов при боковой стороне трапеции

Рассмотрим два полезных свойства, которыми обладают биссектрисы углов при боковой стороне трапеции.

Утверждение 1.

Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.

Дано: ABCD — трапеция, AD ∥ BC,

CO — биссектриса ∠BCD,

DO — биссектриса ∠ADC.

Доказать:∠COD=90º.

Доказательство:

∠ADC+∠BCD=180º (как внутренние односторонние углы при AD ∥ BC  и секущей CD).

Так как CO — биссектриса ∠BCD, то

   

Так как DO — биссектриса ∠ADC,

   

Следовательно,

   

   

По теореме о сумме углов треугольника

   

Отсюда,

   

   

Что и требовалось доказать.

 

Утверждение 2.

Биссектрисы углов при боковых сторонах трапеции пересекаются в точке,  лежащей на средней линии трапеции.

Дано: ABCD — трапеция, AD ∥ BC,

CO — биссектриса ∠BCD,

DO — биссектриса ∠ADC,

MN — средняя линия трапеции.

Доказать: O ∈ MN.

Доказательство:

1) Рассмотрим треугольник COD — прямоугольный (по доказанному утверждению 1).

Проведем из вершины прямого угла COD медиану ON.

По свойству медианы, проведенной к гипотенузе,

   

2) Так как ON=CN, треугольник OCN — равнобедренный с основанием OC.

Следовательно,

   

(как углы при основании равнобедренного треугольника).

Так как CO — биссектриса ∠BCD, 

   

Значит,

   

А так как эти углы — внутренние накрест лежащие при ON и BC и секущей OC, то ON ∥ BC (по признаку параллельности прямых).

Имеем: прямая ON параллельна основанию трапеции BC и проходит через середину боковой стороны CD. Следовательно, эта прямая содержит среднюю линию трапеции. Таким образом, точка O лежит на средней линии трапеции.

Что и требовалось доказать.

Биссектриса — Википедия

Материал из Википедии — свободной энциклопедии

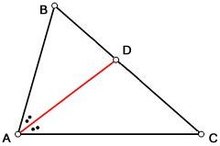Биссектриса AD делит пополам угол A

Биссектри́са (от лат. bi- «двойное», и sectio «разрезание») угла — луч, исходящий из вершины угла и делящий этот угол на два равных угла. Можно также определить биссектрису как геометрическое место точек внутри угла, равноудалённых от сторон этого угла

[1].

Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной. У треугольника существуют три биссектрисы, соответствующие трём его вершинам.

Связанные понятия

• В любом треугольнике ABC{\displaystyle ABC}, кроме внутренней или просто биссектри́сы, можно провести и внешние биссектри́сы, то есть биссектрисы углов, смежных с внутренними углами треугольника. При этом внутренняя и внешняя биссектриса одного и того же угла перпендикулярны.
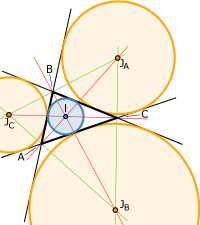
• Проведение в данном треугольнике всех трёх его внешних биссектри́с до их точек пересечения друг с другом в центрах вневписанных окружностей (соответственно JA,JB,JC{\displaystyle J_{A},J_{B},J_{C}}) образует новый треугольник (см. рис.) — треугольник трёх внешних биссектрис. Это — новый треугольник центров вневписанных окружностей с вершинами JA,JB,JC{\displaystyle J_{A},J_{B},J_{C}}, которые касаются соответственно сторон a,b,c{\displaystyle a,b,c} исходного треугольника.
• Центр окружности, проходящей через центры вневписанных окружностей — точка Бевэна.
• Исходный треугольник является ортотреугольником для треугольника ΔJAJBJC{\displaystyle \Delta J_{A}J_{B}J_{C}}
• Точка пересечения симедиан треугольника, образованного центрами его вневписанных окружностей JA,JB,JC{\displaystyle J_{A},J_{B},J_{C}} , является центром эллипса МандАра. Эту точку называют по-английски middlespoint, по-немецки — «Mittelpunkt». Она открыта в 1836-ом году Христианом Генрихом фон Нагелем (Christian Heinrich von Nagel).^[2][3]

Свойства

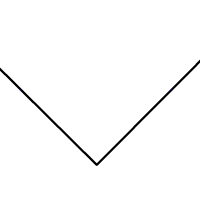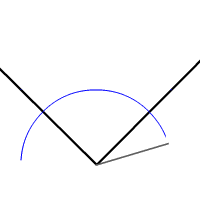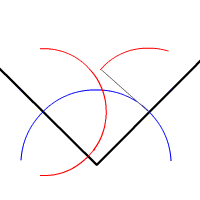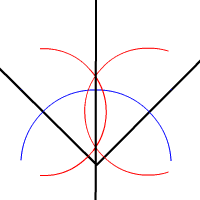
Свойства точек пересечения биссектрис

• Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.
• Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
• Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
• Гипербола Фейербаха — описанная гипербола, проходящая через ортоцентр и центр вписанной окружности (он же — инцентр или точка пресечения внутренних биссектрис треугольника). Её центр лежит в точке Фейербаха. Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через точку Фейербаха.

Свойства, связанные с углами

• Каждая внутренняя (
  внешняя) биссектриса угла треугольника, выходящая из его вершины, делит этот внутренний (внешний) угол треугольника пополам (на две равные половинки).
• Угол между биссектрисами двух смежных углов (между внутренними и внешними биссектрисами углов треугольника при одной вершине) равен 90 градусам.
• Внутренняя биссектриса угла треугольника изогонально сопряжена самой себе.

Свойства биссектрис равнобедренного треугольника

• Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья биссектриса одновременно является медианой и высотой того угла, из которого она выходит.
• Верно и обратное: в равнобедренном треугольнике две биссектрисы равны, и третья биссектриса одновременно является медианой и высотой.
• В равнобедренном треугольнике внутренняя биссектриса угла, противоположного основанию треугольника, является медианой и высотой.
• Одна и только одна биссектриса внешнего угла неравностороннего треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный.
• У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам.
• У равностороннего треугольника все три внутренние биссектрисы равны.

Свойства оснований биссектрис

• Точка пересечения биссектрисы со стороной треугольника называется основанием биссектрисы.

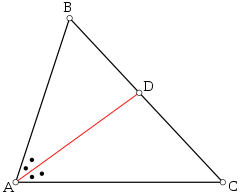BDCD=ABAC{\displaystyle {\frac {BD}{CD}}={\frac {AB}{AC}}} или BDAB=CDAC{\displaystyle {\frac {BD}{AB}}={\frac {CD}{AC}}}.

• Теорема о биссектрисе (см. рис.): Биссектриса внутреннего угла треугольника делит противоположную сторону (то есть делит своим основанием противоположную сторону) в отношении, равном отношению двух прилежащих сторон. То есть BDCD=ABAC{\displaystyle {\frac {BD}{CD}}={\frac {AB}{AC}}} или BDAB=CDAC{\displaystyle {\frac {BD}{AB}}={\frac {CD}{AC}}}.
• Теорема о биссектрисе — частный случай теоремы Штейнера.
• Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника (Одна и только одна биссектриса внешнего угла треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный. У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам. Других возможностей нет).
• Биссектриса внутреннего угла треугольника делит противоположную сторону изотомически по отношению к антибиссектрисе того же угла.
• Окружности, построенные, как на диаметре, на отрезке, соединяющем основания внутренней и внешней биссектрисы , выпущенных из одного угла, проходят через точки Аполлония.
• Через точку Фейербаха проходит окружность, проведённая через основания биссектрис .^[4]

Свойства осей биссектрис

Другие свойства

Длина биссектрис в треугольнике

Для выведения нижеприведённых формул можно воспользоваться теоремой Стюарта.

lc=ab(a+b+c)(a+b−c)a+b=2abp(p−c)a+b{\displaystyle l_{c}={{\sqrt {ab(a+b+c)(a+b-c)}} \over {a+b}}={\frac {2{\sqrt {abp(p-c)}}}{a+b}}}, где p{\displaystyle p} — полупериметр.

lc=ab−albl{\displaystyle l_{c}={\sqrt {ab-a_{l}b_{l}}}}

lc=2abcos⁡γ2a+b{\displaystyle l_{c}={\frac {2ab\cos {\frac {\gamma }{2}}}{a+b}}}

lc=hccos⁡α−β2{\displaystyle l_{c}={\frac {h_{c}}{\cos {\frac {\alpha -\beta }{2}}}}}

Для трёх биссектрис углов A{\displaystyle A}, B{\displaystyle B} и C{\displaystyle C} с длинами соответственно la,lb,{\displaystyle l_{a},l_{b},} и lc{\displaystyle l_{c}}, справедлива формула^[8]

(b+c)2bcla2+(c+a)2calb2+(a+b)2ablc2=(a+b+c)2.{\displaystyle {\frac {(b+c)^{2}}{bc}}l_{a}^{2}+{\frac {(c+a)^{2}}{ca}}l_{b}^{2}+{\frac {(a+b)^{2}}{ab}}l_{c}^{2}=(a+b+c)^{2}.},

wc2=aw⋅bw−ab=CE2=BE⋅AE−ab{\displaystyle w_{c}^{2}=a_{w}\cdot b_{w}-ab=CE^{2}=BE\cdot AE-ab},

где:

• a,b,c{\displaystyle a,b,c} — стороны треугольника против вершин A,B,C{\displaystyle A,B,C} соответственно,
• α,β,γ{\displaystyle \alpha ,\beta ,\gamma } — внутренние углы треугольника при вершинах A,B,C{\displaystyle A,B,C} соответственно,
• hc{\displaystyle h_{c}} — высота треугольника, опущенная на сторону c{\displaystyle c}.
• lc{\displaystyle l_{c}} — длина внутренней биссектрисы, проведённой к стороне c{\displaystyle c},
• al,bl{\displaystyle a_{l},b_{l}} — длины отрезков, на которые внутренняя биссектриса lc{\displaystyle l_{c}} делит сторону c{\displaystyle c},
• wc{\displaystyle w_{c}} — длина внешней биссектрисы, проведённой из вершины C{\displaystyle C} к продолжению стороны AB{\displaystyle AB}.
• aw,bw{\displaystyle a_{w},b_{w}} — длины отрезков, на которые внешняя биссектриса wc{\displaystyle w_{c}} делит сторону c=AB{\displaystyle c=AB} и её продолжение до основания самой биссектрисы.
• Если медиана m{\displaystyle m}, высота h{\displaystyle h} и внутренняя биссектриса t{\displaystyle t} выходят из одной и той же вершины треугольника, около которого описана окружность радиуса R{\displaystyle R}, тогда^{[9]:p.122,#96}

4R2h3(t2−h3)=t4(m2−h3).{\displaystyle 4R^{2}h^{2}(t^{2}-h^{2})=t^{4}(m^{2}-h^{2}).}

Длина частей биссектрис в треугольнике

Уравнения биссектрис

• Если две смежные стороны треугольника записаны уравнениями y1=a1x+b1{\displaystyle y_{1}=a_{1}x+b_{1}} и y2=a2x+b2{\displaystyle y_{2}=a_{2}x+b_{2}}, то в явном виде биссектрисы представимы в виде функций [[1]]:

y=a1a22+1±a2a12+1a22+1±a12+1x+b1a22+1±b2a12+1a22+1±a12+1{\displaystyle y={\frac {a_{1}{\sqrt {a_{2}^{2}+1}}\pm a_{2}{\sqrt {a_{1}^{2}+1}}}{{\sqrt {a_{2}^{2}+1}}\pm {\sqrt {a_{1}^{2}+1}}}}\,x+{\frac {b_{1}{\sqrt {a_{2}^{2}+1}}\pm b_{2}{\sqrt {a_{1}^{2}+1}}}{{\sqrt {a_{2}^{2}+1}}\pm {\sqrt {a_{1}^{2}+1}}}}}

• Биссектриса — это крыса, которая бегает по углам и делит угол пополам.

См. также

Примечания

1. ↑ Иванов А. Б. Биссектриса угла // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия, 1977. — Т. 1. — С. 496. — 576 с. — 150 000 экз.
2. ↑ Kimberling, Clark (1994), «Central Points and Central Lines in the Plane of a Triangle», Mathematics Magazine Т. 67 (3): 163–187, DOI 10.2307/2690608 .
3. ↑ v. Nagel, C. H. (1836), Untersuchungen über die wichtigsten zum Dreiecke gehörenden Kreise, Leipzig .
4. ↑ Акопян А. В., Заславский А. А.. Геометрические свойства кривых второго порядка. — 2-е изд., дополн.. — 2011. — С. 105.
5. ↑ Кто и когда доказал невозможность построения треугольника по трем биссектрисам?. Дистанционный консультационный пункт по математике МЦНМО.
6. ↑ Можно ли построить треугольник по трем биссектрисам, если кроме циркуля и линейки разрешается использовать трисектор. Дистанционный консультационный пункт по математике МЦНМО.
7. ↑ Стариков В. Н. Исследования по геометрии// Сборник публикаций научного журнала Globus по материалам V-й международной научно-практической конференции «Достижения и проблемы современной науки» г. Санкт-Петербург: сборник со статьями (уровень стандарта, академический уровень). С-П.: Научный журнал Globus, 2016. С. 99-100
8. ↑ Simons, Stuart. Mathematical Gazette 93, March 2009, 115—116.
9. ↑ Altshiller-Court, Nathan, College Geometry, Dover Publ., 2007.

Литература

• Коган Б. Ю. Приложение механики к геометрии. — М.: Наука, 1965. — 56 с.
• Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 30-31. — ISBN 5-94057-170-0.

Биссектрисы трапеции

Рассмотрим  задачи, в которых биссектриса угла трапеции делит противоположное основание на отрезки.

Мы уже имели дело с похожей задачей на биссектрису угла параллелограмма, а также рассматривали частный случай для трапеции (когда основание трапеции равно ее боковой стороне, биссектриса трапеции совпадает с ее диагональю).

I. Биссектриса острого угла при большем основании трапеции делит другое основание на отрезки.

 1) ∠BAF=∠DAF (так как AF — биссектриса ∠BAD по условию).

2) ∠DAF=∠BFA (как внутренние накрест лежащие при     AD∥BC и секущей AF).

 

 3) Следовательно, ∠BAF=∠BFA.

4) Следовательно, треугольник ABF — равнобедренный с основанием AF (по признаку равнобедренного треугольника).

5) Следовательно, AB=BF.

 II. Биссектриса тупого угла при меньшем основании трапеции делит другое основание на отрезки.

 Аналогично доказывается, что треугольник ABP — равнобедренный:

1) ∠ABP=∠CBP (так как BP — биссектриса ∠ABC по условию).

 

2) ∠CBP=∠APB (как внутренние накрест лежащие при AD∥BC и секущей BP).

3) Следовательно, ∠ABP=∠APB.

4) Следовательно, треугольник ABP — равнобедренный с основанием BP (по признаку равнобедренного треугольника).

5) Следовательно, AB=AP.

Вывод: в этом случае

биссектриса угла трапеции отсекает от нее равнобедренный треугольник.

Эта задачи — базовые. На их основе существует много других задач.

В следующий раз рассмотрим задачи на пересечение двух биссектрис трапеции.

 

Диагональ трапеции — биссектриса ее угла

Если диагональ трапеции — биссектриса ее угла, что можно сказать о такой трапеции?

Это зависит от того, биссектрисой какого угла является диагональ.

Утверждение 1

Если диагональ трапеции является биссектрисой ее острого угла, то меньшее основание равно боковой стороне трапеции, прилежащей к этому углу.

Дано: ABCD — трапеция,

AD ∥ BC,

AC — биссектриса ∠BAD.

Доказать: BC=AB.

Доказательство:

1) ∠BAC=∠DAC (так как AC — биссектриса ∠BAD по условию)

2) ∠BCA=∠DAC (как внутренние накрест лежащие при AD ∥ BC и секущей AC)

3) Значит, ∠BAC=∠BCA

4) Таким образом, треугольник ABC — равнобедренный с основанием AC (по признаку).

Следовательно, AB=BF.

Что и требовалось доказать.

Утверждение 2

Если диагональ трапеции является биссектрисой ее тупого угла, то большее основание равно боковой стороне трапеции, прилежащей к этому углу.

Дано: ABCD — трапеция,

AD ∥ BC,

BD — биссектриса ∠ABC.

Доказать: AD=AB.

Доказательство:

1) ∠ABD=∠CBD (так как BD — биссектриса ∠ABC по условию).

2) ∠ADB=∠CBD (как внутренние накрест лежащие при AD ∥ BC и секущей BD).

3) Следовательно, ∠ABD=∠ADB.

4) Значит, треугольник ABD — равнобедренный с основанием BD (по признаку).

5) Отсюда, AD=AB.

Что и требовалось доказать.

Утверждение 3

Если диагональ трапеции является биссектрисой ее прямого угла, меньшее основание трапеции равно ее меньшей боковой стороне.

Если AC — биссектриса ∠BAD, то

AB=BC.

Доказательство — аналогично доказательству утверждения 1.

Свойство биссектрисы треугольника | Треугольники

Рассмотрим свойство биссектрисы треугольника с доказательством и задачу на применение свойства.

Теорема (Свойство биссектрисы треугольника)

Биссектриса треугольника делит третью сторону на отрезки, пропорциональные двум другим сторонам:

   

Дано: ∆АВС, АР — биссектриса.

Доказать:

   

 

Доказательство:

I. Если АС=АВ, то биссектриса АР является также медианой, СР=ВР, и

   

II.Если АС≠АВ.

1) Опустим перпендикуляры BN и CF на луч AP.

2) Прямоугольные треугольники ABN и ACF подобны по острому углу (∠BAP=∠CAP, так как AP — биссектриса ∠BAC (по условию)), следовательно,

   

3) Прямоугольные треугольники BNP и CFP  подобны по острому углу (∠BPN=∠CPF (как вертикальные)), следовательно,

   

   

   

Если средние члены пропорции поменять местами, пропорция останется верной, поэтому

   

Что и требовалось доказать.

Задача.

Стороны треугольника равны 10 см, 11 см и 12 см. Найти отрезки, на которые делит биссектриса треугольника среднюю сторону.

Дано: AC=10 см, BC=11 см, AB=12 см, AP = биссектриса.

Найти: CP и BP.

Решение:

По свойству биссектрисы треугольника:

   

   

Пусть CP=x см, тогда BP=11-x см:

   

откуда по основному свойству пропорции

   

   

   

CP=5 см, BP=6 см.

Ответ: 5 см, 6 см.