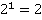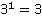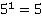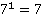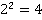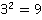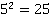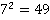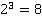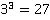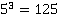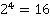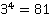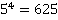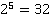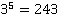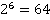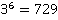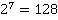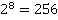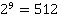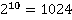Таблица основных степеней. Видеоурок. Алгебра 7 Класс

На этом уроке мы рассмотрим таблицу основных степеней.
Вначале вспомним определение степени. Затем составим таблицу основных степеней чисел от 1 до 10 и решим ряд задач с ее использованием.

Тема: Степень с натуральным показателем и ее свойства

Урок: Таблица основных степеней

Напоминание определения:

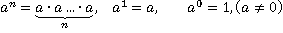
Здесь a — основание степени,

n— показатель степени,

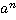— n-ая степень числа.

Из определения степени получаем таблицу основных степеней, где основание – простые числа в пределах 10.

Таблица основных степеней:

Прямая и обратная задачи

1) Вычислить 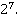 Решение:

По определению степени: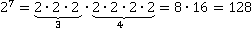

2) Число 729 записать в виде степени.

Решение основано на основной теореме арифметики. Видим, что 729 делится на 3. Разложим число 729 по степеням 3.

729	3
243	3
81	3
27	3
9	3
3	3
1

Получаем, что.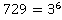

3) Число 256

записать в виде степени.

Разлагаем данное число по степеням двойки по основной теореме арифметики.

256	2
128	2
64	2
32	2
16	2
8	2
4	2
2	2
1

Получаем, что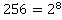

.

Задача: дано 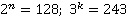. Сравнить n и k.

Решение:

По таблице или по основной теореме арифметики находим:

n = 7, k = 5

Ответ:

Для практических вычислений удобно продолжить таблицу для чисел 1, 0, -1, 10.

Продолжение таблицы для чисел 1; 0; — 1; 10

(сводка правил)

n – натуральное число.

Решим задачи на таблицу (или основную теорему арифметики).

Задача: Найти k, если:

а)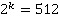

Разлагаем 512 по основной теореме арифметики либо используем таблицу степеней.

512	2
256	2
128	2
64	2
32	2
16	2
8	2
4	2
2	2
1

 

Ответ: .

б)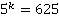

Разлагаем по основной теореме арифметики либо используем таблицу степеней.

625	5
125	5
25	5
5	5
1

 

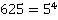
Ответ: .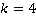

в)

Разлагаем по основной теореме арифметики либо используем таблицу степеней.

343	7
49	7
7	7
1

 

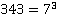
Ответ: .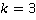

г)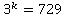

Разлагаем по основной теореме арифметики либо используем таблицу степеней. Видим, что  делится на 3, так как сумма цифр 18 делится на 3.

	3
243	3
81	3
27	3
9	3
3	3
1

 

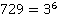
Ответ: .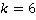

Задача: Вычислить.

а)

б)

Задача: Представить в виде куба некоторого числа.

а) 125.

. Значит, .

Ответ: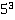

б)

. Значит, .

Ответ:

в)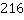

. Значит, .

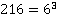Ответ: .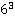

Итак, мы рассмотрели таблицу основных степеней, правило ее формирования и использование в различных типовых задачах.

 

Список рекомендованной литературы

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.

2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ

3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.

 

Рекомендованные ссылки на ресурсы интернет

1. Школьн

Таблица основных степеней — СПИШИ У АНТОШКИ

Таблица степеней

Мы уже знаем с вами таблицу умножения, и постоянно пользуемся при вычислениях. Теперь нам будет полезна таблица степеней простых чисел.

Ниже представлена таблица степеней от 1 до 10.

1n	2n	3n	4n	5n	6n	7n	8n	9n	10n
1	1	2	3	4	5	6	7	8	9	10
3	1	8	27	64	125	216	343	512	729	1000
4	1	16	81	256	625	1296	2401	4096	6561	10000
5	1	32	243	1024	3125	7776	16807	32768	59049	100000
6	1	64	729	4096	15625	46656	117649	262144	531441	1000000
7	1	128	2187	16384	78125	279936	823543	2097152	4782969	10000000
8	1	256	6561	65536	390625	1679616	5764801	16777216	43046721	100000000
9	1	512	19683	262144	1953125	10077696	40353607	134217728	387420489	1000000000
10	1	1024	59049	1048576	9765625	60466176	282475249	1073741824	3486784401	10000000000

Таблица степеней натуральных чисел

Если калькулятора нет под рукой, то воспользуйтесь данной таблицей. Основания степени лежат первой колонке и указаны синим цветом, показатели степени — в заголовках столбцов и указаны красным цветом.

Например, чтобы вычислить четыре в шестой степени, нужно найти строку с числом 4 и на пересечении со столбцом 6 получить результат: 4⁶  = 4096.

Столбец 2, таким образом — это таблица квадратов натуральных чисел, а столбец 3 — таблица кубов натуральных чисел.

Столбцы — показатель степени (красный) Строки — основание степени (синий)	2	3	4	5	6	7	8	9	10
2	4	8	16	32	64	128	256	512	1 024
3	9	27	81	243	729	2 187	6 561	19 683	59 049
4	16	64	256	45  = 1 024	46  = 4 096	16 384	65 536	262 144	1 048 576
5	25	125	625	3 125	15 625	78 125	390 625	1 953 125	9 765 625
6	36	216	1 296	7 776	46 656	279 936	1 679 616	10 077 696	60 466 176
7	49	343	2 401	16 807	117 649	823 543	5 764 801	40 353 607	282 475 249
8	64	512	4 096	32 768	262 144	2 097 152	16 777 216	134 217 728	1 073 741 824
9	81	729	6 561	59 049	531 441	4 782 969	43 046 721	387 420 489	3 486 784 401
10	100	1 000	10 000	100 000	1 000 000	10 000 000	100 000 000	1 000 000 000	10 000 000 000
11	121	1 331	14 641	161 051	1 771 561	19 487 171	214 358 881	2 357 947 691	25 937 424 601
12	144	1 728	20 736	248 832	2 985 984	35 831 808	429 981 696	5 159 780 352	61 917 364 224
13	169	2 197	28 561	371 293	4 826 809	62 748 517	815 730 721	10 604 499 373	137 858 491 849
14	196	2 744	38 416	537 824	7 529 536	105 413 504	1 475 789 056	20 661 046 784	289 254 654 976
15	225	3 375	50 625	759 375	11 390 625	170 859 375	2 562 890 625	38 443 359 375	576 650 390 625
16	256	4 096	65 536	1 048 576	16 777 216	268 435 456	4 294 967 296	68 719 476 736	1 099 511 627 776
17	289	4 913	83 521	1 419 857	24 137 569	410 338 673	6 975 757 441	118 587 876 497	2 015 993 900 449
18	324	5 832	104 976	1 889 568	34 012 224	612 220 032	11 019 960 576	198 359 290 368	3 570 467 226 624
19	361	6 859	130 321	2 476 099	47 045 881	893 871 739	16 983 563 041	322 687 697 779	6 131 066 257 801
20	400	8 000	160 000	3 200 000	64 000 000	1 280 000 000	25 600 000 000	512 000 000 000	10 240 000 000 000
21	441	9 261	194 481	4 084 101	85 766 121	1 801 088 541	37 822 859 361	794 280 046 581	16 679 880 978 201
22	484	10 648	234 256	5 153 632	113 379 904	2 494 357 888	54 875 873 536	1 207 269 217 792	26 559 922 791 424
23	529	12 167	279 841	6 436 343	148 035 889	3 404 825 447	78 310 985 281	1 801 152 661 463	41 426 511 213 649
24	576	13 824	331 776	7 962 624	191 102 976	4 586 471 424	110 075 314 176	2 641 807 540 224	63 403 380 965 376
25	625	15 625	390 625	9 765 625	244 140 625	6 103 515 625	152 587 890 625	3 814 697 265 625	95 367 431 640 625

 Свойства квадратного корня. Властивості квадратного кореня | Описание курса | Показательная функция. Показова функція 

   

Степень с натуральным показателем | Формулы с примерами

Определение степени с натуральным показателем

Определение
где a — действительное число,
n — натурально число.

Читается как: «a в степени n» или
«n-ная степень a»

Калькулятор степени с натуральным показателем

Примеры и свойства

Свойство a в степени 1 равно a.

a¹ = a

Пример 1¹ = 1;     10¹ = 1;      125¹ = 125.

Свойство Нуль в степени n равен нулю.

0ⁿ = 0

Пример 1⁰ = 0;      10⁰ = 0;      432⁰ = 0.

Свойство Если a является положительным числом, то a возведенное в степень
n будет числом положительным.

Если a > 0, то aⁿ > 0

Пример 1²> 0;      12⁴ > 0;      33² > 0.

Свойство Если a является числом отрицательным, и его степень — четное число,
то a в степени n будет число положительное.

Если a и n — четное, то aⁿ > 0

Пример (- 2)⁴ > 0;      (- 33)⁶ > 0;      (- 1,3)⁴⁴ > 0.

Свойство Если a является числом отрицательным, и его степень — нечетное,
то a в степени n будет число отрицательное.

Если a и n — нечетное, то aⁿ

Формулы по алфавиту:

© 2020 Все права защищены
При использовании материалов данного сайта обязательно указывать ссылку на источник

Таблица основных степеней. Алгебра, 7 класс: уроки, тесты, задания.

1.	Квадрат числа (целое число или десятичная дробь) Сложность: лёгкое	2
2.	Куб числа (отрицательное число) Сложность: лёгкое	1
3.	Степень обыкновенной дроби Сложность: лёгкое	1
4.	Степень числа 10 Сложность: лёгкое	1
5.	Степень единицы и десяти Сложность: лёгкое	3
6.	Произведение степеней Сложность: лёгкое	2
7.	Сумма степеней (единица, нуль) Сложность: лёгкое	4
8.	Сумма степеней (десятичные дроби) Сложность: среднее	3
9.	Сумма степеней (обыкновенные дроби) Сложность: среднее	3
10.	Сравнение степени с нулём (целые числа) Сложность: среднее	2
11.	Сравнение степеней (обыкновенные дроби) Сложность: среднее	2
12.	Сравнение выражения с нулём Сложность: среднее	2
13.	Неизвестный показатель степени Сложность: среднее	2
14.	Сумма разрядных слагаемых Сложность: среднее	3
15.	Квадрат единицы, нуля и десяти Сложность: среднее	3
16.	Расположение чисел по возрастанию (убыванию) Сложность: среднее	5
17.	Сумма показателей степеней Сложность: среднее	3
18.	Неизвестный показатель степени, уравнение (произведение) Сложность: сложное	4
19.	Неизвестный показатель степени, уравнение (частное) Сложность: сложное	4
20.	Уравнение, сводимое к линейному Сложность: сложное	5

Конспект+Презентация к уроку алгебры в 7 классе «Свойства степени с натуральным показателем»

Пояснительная записка к уроку

Тема урока: Свойства степени с натуральным показателем.

Цель урока: изучение и первичное восприятие нового учебного материала, осмысление связей и отношений в объектах изучения.

Задачи урока:

• образовательные: самостоятельно изучить свойства степени при работе с учебником, привести полученные знания в систему, применить свойства степени при первичном закреплении знаний.

• воспитательные: формировать у учащихся умение работать в сотрудничестве при работе в группе, воспитывать стремление к личностному росту, формировать адекватную самооценку своей деятельности.

• развивающие: развивать у учащихся умение искать нужную информацию, мыслить, анализировать, делать выводы.

УУД, формируемые на уроке:

• предметные: самостоятельно, по учебнику изучают свойства степени, приводят примеры.

• личностные: применяют правила делового сотрудничества, адекватно оценивают свою учебную деятельность.

• метапредметные:

Регулятивные – работают по составленному плану.

Познавательные – проявляют интерес к основам изучающего, усваивающего и

поискового чтения, передают содержание в сжатом, выборочном виде.

Коммуникативные – умеют организовывать учебное взаимодействие в группе,

строить конструктивные взаимоотношения со сверстниками.

Место урока в изучении темы: третий урок в теме «Степень с натуральным показателем и ее свойства» после уроков изучения понятия степени с натуральным показателем и таблицы основных степеней.

Тип урока: урок изучения и первичного закрепления новых знаний.

Используемое оборудование, наглядность:

• учебник Мордкович А.Г. Алгебра. 7 класс. В 2 частях: учебник, задачник.

• Презентация Microsoft Office PoverPoint.pptx

• интерактивная доска

Технологии:

• технология дифференцированного обучения;

• технология словесной продуктивной и творческой деятельности;

• педагогика сотрудничества;

• Интерактивные технологии.

Формы и методы:

• Индивидуальная работа;

• Фронтальная работа;

• Групповая форма работы;

• Частично-поисковые методы работы;

• Репродуктивный метод;

• Активный метод обучения «Мозаика» (приложение 3)

Рабочие материалы для обучающихся:

1. Карточки 4 цветов для распределения учащихся на группы смешанного состава: сильный, средний, слабый.

2. Дидактические материалы : приложение 1, приложение 2.

Содержательная часть.

Конспект урока

Цель этапа: организационная подготовка к уроку

Приветствие учащихся.

Приветствие учителя.

Подготовка тетрадей к уроку: записывают число, классная работа.

Объявляется основная форма работы на уроке: групповая. Каждой группе учащихся соответствует определенный цвет карточки.

Учащиеся рассаживаются в группы по цвету карточки, которая лежит перед каждым учащимся к началу урока.

Этап 2: Мотивация учебной деятельности ( 1 мин)

Цель этапа: Стимулирование познавательного интереса.

Цель этапа: преобразование обучения в личностно значимое.

Отгадать ребус: (слайд 1)

Отгадывание ребуса, в котором зашифровано слово «степень»

Этап 3: Актуализация опорных знаний (5 мин)

Цель этапа: проверка учителем уровня подготовки учеников

Цель этапа: воспроизведение знаний и умений, необходимых для овладения новым материалом

(слайд 1)

Королевой сегодняшнего урока является степень (щелчок, появляется таблица).

Учащиеся отвечают фронтально, поднимая руку (получают поощрительные жетоны за правильный ответ).

Вопросы учителя к группам:

Ответы учащихся:

1. Дать определение степени

Степенью числа a с натуральным показателем n называют произведение n одинаковых множителей, каждый из которых равен а (щелчок, появляется первый столбец таблицы).

2. Что означает aⁿ, где n=3?

aⁿ, где n=3, означает произведение трех множителей, каждый из которых равен а.

а³ = а·а·а

3. Что означает символ a¹?

Степенью числа а с показателем 1 называют само это число. a¹=а-по щелчку появляется эта надпись в таблице.

4. В записи 7⁹ назовите, что является

степенью, что основанием степени,

что показателем степени?

7⁹ – степень,

7 – основание степени,

9 – показатель степени.

5. Чему равно значение выражения

(-1)²⁰¹⁵, (-1)²⁰¹⁶?

(-1)²⁰¹⁵= -1, т.к. отрицательное число в нечетной степени является числом отрицательным.

(-1)²⁰¹⁶ = 1, т.к. отрицательное число в четной степени является числом положительным. (щелчок, появляется второй столбец таблицы)

6. Сколько нулей содержится в записи числа 10 ²⁰¹?

Число 10 ²⁰¹ содержит 21 нуль.

7. Что больше 0¹⁰⁰⁰ или 1¹⁰?

0¹⁰⁰⁰ меньше 1¹⁰, т.к. 0¹⁰⁰⁰ = 0, 1¹⁰ = 1 (щелчок, появляется надпись 0ⁿ = 0, 1ⁿ = 1).

Этап 4. Изучение нового материала (15 мин)

Цель этапа: знакомство с инструкцией по самостоятельному изучению нового материала.

Цель этапа: знакомство с инструкцией по самостоятельному изучению нового материала.

овладение новыми знаниями и способами действий.

(слайд 2)

Большая часть математических утверждений проходит в своем становлении в три этапа:

• На первом этапе человек в ряде конкретных случаев подмечает некоторую закономерность.

• На втором этапе он пытается сформулировать подмеченную закономерность в общем виде, т.е. предполагает, что эта закономерность действует не только в рассмотренных случаях, но и во всех других аналогичных случаях.

• На третьем этапе он пытается доказать, что закономерность, сформулированная в общем виде, на самом деле верна.

Доказать какое-либо утверждение – это значит объяснить, почему оно верно (объяснить убедительно, а не так: «это верно, потому что это верно»).

При доказательстве можно ссылаться только на уже известные факты.

Давайте попытаемся самостоятельно, с помощью учебника, поддержки учителя и учащихся в группе, пройти все три этапа:

— открыть;

-сформулировать;

-доказать свойства степеней, хорошо известные в математике.

Знакомство с этапами доказательства новых утверждений.

Раздаются задания группам:

1 группа: ξ 17 (стр.87-89, 91) Открытие первое

2 группа: ξ 17 (стр.89-90, 91) Открытие второе

3 группа: ξ 17 (стр.90, 91) Открытие третье

4 группа: ξ 18 (стр.93-95) Открытие четвертое

Учитель оказывает педагогическую поддержку группам и отдельным учащимся (дифференцированный подход)

Работа с учебником.

Каждый ученик группы оформляет полученные знания в таблицу

(приложение 1)

По окончании работы, группы перетасовываются таким образом, чтобы в каждой новой группе оказался хотя бы один ученик из каждой первой группы.

Этап 5: Обмен полученной информацией (7 мин)

Цель этапа: Контроль за обменом полученной информации, оказание педагогической помощи.

Цель этапа: Репродуктивное воспроизведение изученного материала.

Контроль за обменом полученной информации, оказание педагогической помощи. Деятельность учителя минимизирована.

Учащиеся обмениваются полученной информацией.

Представители новых групп систематизируют полученные знания в таблицу ( приложение 2) — 1 таблица на всю группу.

Этап 6: Систематизация полученных знаний (5 мин)

Цель этапа: систематизация и обобщение

Цель этапа: отчет о полученных знаниях

(Слайд 3)

Полученные знания систематизируются в таблицу. По мере получения информации таблица заполняется.

Представители каждой группы доводят до сведения всего класса информацию по схеме:

• Название действия со степенью

• Формулировка свойства (по щелчку появляется запись в таблице)

• Математическая запись свойства

( осуществляется учащимися в интерактивном режиме в графу математическая запись, режим перо)

aⁿ.a ^m = a^n+m

aⁿ:a^m = a^n-m , а≠ 0

(aⁿ)^m = a^nm

Этап 7: Первичная проверка усвоения знаний. Контроль и самопроверка знаний.

(5 мин)

Цель этапа: первичная проверка уровня усвоения и понимания материала

Цель этапа: применить полученные правила действий над степенями при выполнении упражнений на свойства степени.

(Слайд3)

В таблице, в последнем столбце высвечиваются задания на свойства степени:

Учащиеся выполняют задания.

Учащиеся, первыми поднявшие руки по окончании выполнения задания (5 человек) оцениваются учителем.

Затем, осуществляется проверка и самопроверка:

учащиеся фронтально называют ответы, напротив каждого задания в своей тетради ставят «+» или « — », вносят коррективы.

Этап 8: Подведение итогов урока. Рефлексия. (3 мин)

Цель этапа: установление соответствия между поставленными задачами урока и результатами.

Цель этапа: анализ учебной деятельности.

(Слайд 4)

Учащимся предлагается продолжить одно из предложений:

— сегодня на уроке я узнал…

— я приобрел опыт…

— у меня возникли затруднения…

(слайд 4 – по щелчку)

Учащимся предлагается выставить себе оценку за урок по следующим критериям:

Этап 9: Информация о домашнем задании. (2 мин)
Цель этапа: сообщение объема и содержания домашнего задания.	Цель этапа: получение информации о домашнем задании.
ξ 17,18 № 17.15, 17.19, 17.25, 17.28, 18.1, 18.4	Записывают домашнее задание в дневник.
Урок окончен.

Приложения:

Приложение1

Группа 1: открытие первое

действия

Сформулировать свойство

математическая запись

Примеры

Умножение степеней с

одинаковым основанием

Группа 2: открытие второе

действия

Сформулировать свойство

математическая запись

Примеры

Деление степеней

с одинаковым основанием

Группа 3: открытие третье

действия

Сформулировать свойство

математическая запись

Примеры

Возведение

степени в степень

Группа 4: открытие четвертое

действия

Сформулировать свойство

математическая запись

Примеры

Возведение в степень

произведения и частного

Приложение 2

действия

Сформулировать свойство

математическая запись

Примеры

Умножение

степеней с

одинаковым основанием

Деление степеней с

одинаковым основанием

Возведение

степени в степень

Возведение в степень

произведения

и частного

Приложение 3

Содержание активного метода обучения «Мозаика»:

1. Класс делится на 4 группы по 4-5 человек в каждой группе. Группы разноуровнего состава: сильный, средний, слабый.

2. Каждой группе дается задание изучить по учебнику одно из свойств степени,

с которым все учащиеся группы должны разобраться самостоятельно, по учебнику. Каждый ученик включен в самостоятельную работу в группе. Полученную информацию учащиеся вносят в таблицу. На этом этапе осуществляется сотрудничество ученик-ученик. Учитель оказывает педагогическую поддержку нуждающимся в этом учащимся.

3. Группы перетасовываются таким образом, чтобы в каждой новой группе оказался хотя бы один ученик из каждой первой группы. Учащиеся обмениваются полученной информацией. Каждый ученик имеет возможность презентовать свою работу другим. Каждая группа приводит полученные знания в систему (заполняют таблицу).

4. Систематизируются теоретические основы полученных знаний: каждая группа формулирует какое-то свойство и записывает его на математическом языке на интерактивной доске. Другие группы выступают в качестве аппонентов: дополняют, поправляют.

5. Отработка изученных свойств в ходе решения упражнений.