751 — Страна талантов
Частное профессиональное образовательное учреждение «АНАПСКИЙ ИНДУСТРИАЛЬНЫЙ ТЕХНИКУМ»
(ЧПОУ «Анапский индустриальный техникум») Промышленная ул., 2а, город-курорт Анапа, 353454 тел./факс: (86133) 5-81-88; 4-67-10
Преподаватель: Фаренюк Светлана Николаевна
ИНТЕЛЛЕКТУАЛЬНАЯ ИГРА «ХОЧУ ВСЕ ЗНАТЬ» для студентов 2 курсов технических специальностей
ХОД ИНТЕЛЛЕКТУАЛЬНОЙ ИГРЫ «ХОЧУ ВСЕ ЗНАТЬ»
1. Открытие игры. Вступительное слово ведущего игры. 2. Представление команд. 3. КОНКУРС ПО ДИСЦИПЛИНЕ «ИНЖЕНЕРНАЯ ГРАФИКА»
Задание 1 Определить виды
Задание 2 Дан чертѐж проволочной модели. Выполнить ее наглядное изображение.
Задание 3 Выполните наибольшее количество разверток куба
Задание 3 Выполните наибольшее количество разверток куба
Задание 2 Дан чертѐж проволочной модели. Выполнить ее наглядное изображение.
Задание 1 Определить виды
Ответ
4. РАЗМИНОЧНЫЙ КОНКУРС «РЕБУСЫ»
Ответ: Пирамида
Ответ: Треугольник
5. КОНКУРС ПО ДИСЦИПЛИНЕ «ТЕХНИЧЕСКАЯ МЕХАНИКА»
1. Вопрос. Тела 1 и 2 находятся в равновесии. Можно ли убрать действующие системы сил, если тела абсолютно твердые? Что изменится, если тела реальные, деформируемые?
F F F F
Ответ:
— если тела находятся в равновесии и абсолютно твердые, то можно убрать действующие системы сил (согласно 3й аксиоме статики или принципа отбрасывания системы сил эквивалентной нулю).
— если тела реальные, деформируемые, то тело 1 растянется, 2 сожмется.
2. Вопрос. Чем отличается главный вектор от равнодействующей плоской системы произвольно расположенных сил?
Выбрать из предложенных ответов: — величиной; — направлением; — величиной и направлением; — точкой приложения; — ничем.
3. Вопрос. Почему силы притяжения к Земле, действующие на точки тела, можно принять за систему параллельных сил?
Ответ: Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.
4. Вопрос. Что является мерой инертности тела?
Ответ: Масса.
5. Вопрос. Объясните разницу между понятиями «инертность» и «сила инерции».
Ответ: Инертность – способность сохранять свое состояние неизменным, это внутреннее свойство всех материальных сил.
Сила инерции – сила, возникающая при разгоне или торможении тела (материальной точки) и направленная в обратную сторону от ускорения.
6. Вопрос. Вагон массой 1000 кг перемещается по горизонтальному пути на 5 м, коэффициент трения 0,15. Определите работу силы тяжести.
Ответ: 0. Т.к. силы перпендикулярные направлению перемещения, работы не производят.
7. Вопрос. Какими методами определяют внешние и внутренние силы?
Ответ: Внешние – методами теоретической механики. Внутренние – основным методом сопротивления материалов – методом сечений.
8. Вопрос. Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?
Ответ:
N
A
. Значение напряжения (σ) уменьшается в 4 раза.
Комментарий: Численно равнодействующая равна главному вектору системы, но приложена в другой точке, относительно которой главный момент равен 0.
6. КОНКУРС ПО ДИСЦИПЛИНЕ «ЭЛЕКТРОТЕХНИКА»
«Выключатель» Есть 2 комнаты. В одной висит обычная лампочка. Дверь туда закрыта. В другой комнате — 3 выключателя. Из них только один соединѐн с лампочкой. Можно сколько угодно вкл/выкл их. Потом нужно зайти в комнату с лампочкой, сколько угодно и что угодно там делать. А затем сказать, какой выключатель включает лампочку. Решение должно быть честным, т.е. из-за двери ничего не видно и не слышно, выключатели неразборные, не искрят, нельзя использовать какие-либо приборы, помощников, экстрасенсорные способности и пр.
Ответ: решение основано на том, что включенная лампочка нагревается. Нужно включить первый из выключателей, подождать немного и выключить. Затем включить второй и идти в комнату. Если лампочка горит, то тут всѐ ясно -второй выключатель. Если не горит то нужно потрогать лампочку. Если она горячая, то – первый выключатель, иначе — третий.
«Новогодняя ѐлка» Новогодняя ѐлка была украшена гирляндой электрических лампочек, соединенных последовательно. Одна лампочка перегорела. Еѐ выбросили и составили снова цепь. Стала ли гирлянда гореть ярче или наоборот, померкла оттого, что лампочек стало меньше?
Ответ: общее сопротивление гирлянды уменьшилось, а напряжение в сети осталось прежним. Поэтому гирлянда будет гореть ярче.
«Три лампочки» Двухэтажный дом. На втором этаже этого дома находятся три лампочки. На первом этаже расположены три выключателя. Одни выключатель соотвествует одной лампочке. Как можно определить какой выключатель соотвествует какой лампочке, если на второй этаж можно подниматься только один раз. Включать и выключать выключатели можно сколько угодно раз. Ответы типа «выйти на улицу и посмотреть» не являются правильными.
Ответ: включить один выключатель на минут на десять. Выключить его. Включить какой- нибудь из оставшихся двух. Подняться на второй этаж. Одна лампочка теплая, другая горит — дальше все логично.
8.РАЗМИНОЧНЫЙ КОНКУРС «НОВОГОДНИЕ ПРИКЛЮЧЕНИЯ»
Вопрос 1
«Снежная ночь. Елка, гирляндами украшенная, радует очи; чудно кружатся ангелы…» (Достаточно прочитать первые буквы каждого слова в этой фразе). Скажите, кому (или чему) посвящены эти строки?
ответ: Снегурочке . Вопрос 2 У итальянцев есть своеобразный обычай встречать Новый год:
а) сидя на полу; б) стоя на стуле; в) лежа на столе; г) вися на дереве.
ответ: стоя на стуле (и как бы «впрыгивая» в новый год).
Вопрос 3 В Венгрии на новогодний праздничный стол не подают.
ответ: птицу — чтобы счастье в новом году «не улетело» из дома.
Вопрос 4 Новогодним цветком во Вьетнаме считается.
ответ: нарцисс.
ВОПРОС 5 15, 18, 3, 5, 11, 0, 4, 18, 5. Что зашифровано этой цифровой последовательностью?
ответ: «новый год». шифровка очень проста: нечетные буквы (они же согласные) заменены, согласно их положению в русском алфавите, цифрами от 1 до 33, четные (гласные) — от 33 до 1. ноль — пробел.
9. Подведение итогов.
а
1.ПРЕДСТАВЛЕНИЕ КОМАНД (макс.5)
2.ИНЖЕНЕРНАЯ ГРАФИКА оценивается каждое задание (макс.5)
3.РЕБУСЫ (макс.3)
4.ТЕХНИЧЕСКАЯ МЕХАНИКА оценивается каждое задание (макс.5)
5.ГОЛОВОЛОМКИ (макс.3)
6.ЭЛЕКТРОТЕХНИКА оценивается каждое задание (макс.5)
7.НОВОГОДНИЕ ПРИКЛЮЧЕНИЯ (макс.3)
ИТОГО
СВОДНАЯ ВЕДОМОСТЬ РЕЗУЛЬТАТОВ ИГРЫ
Конкурсы
К
о
м
а
н
д
а
К
о
м
а
н
д
а
К
о
м
а
н
д
а
К
о
м
а
н
д
а
К
о
м
а
н
д
а
К
о
м
а
н
д
Тела 1 и ✔ 2 находятся в равновесии, можно ли убрать действующие системы
предмет: язык
категория: сочи (с ответами)
четверть: 3-ья
2. чтение.
2. шокирующая статья д. уитти, угрожающие прогнозы, влияние человека на вымирание видов
3. потому что к концу этого столетия не станет половины всех видов животных. сейчас на грани полного исчезновения находятся каждый четвертый вид млекопитающих, каждый восьмой вид птиц, каждый третий вид амфибий. а значит, каждый день исчезает от 2,7 до 270 видов!
4. «близок тот переломный момент, когда невозможно будет спасти биологическое разнообразие планеты по вине деятельности человека»
5. «страшные прогнозы»
«их нет в будущем»
«одумайтесь, люди! »
6. целевая аудитория текста – все взрослое население земли, так как поднимается актуальная, важнейшая экологическая проблема –исчезновение видов
7. да
1. в тексте конкретные
имена (журналистки и ученого биолога), название университета, в
стенах которого проводились
исследования.
2. статистические данные,
конкретные даты
3. эссе (письмо).
минеральные воды, как известно, используются для лечения и оздоровления. бутылки с такой водой ставят в профилакториях и санаториях, но не все знают, в чем заключаются ее полезные свойства, а также то, какой вред она может принести, если не владеть нужной информацией. (35 слов)
главной особенностью таких вод является то, что их источники находятся под землей. обычная вода из крана не является минеральной, так как отличается от нее по составу, не имеет постоянного состава. даже если водопроводная вода была взята из подземных источников, она все равно не является лечебной, так как перед применением проходит многоуровневую очистку, которая, в свою очередь, меняет ее состав. одним из свойств минеральной воды является то, что ни в одном продукте нет такого набора полезных веществ, как в ней. (112 слов)
употребление минеральной воды является основой лечения во многих оздоровительных и санаторных учреждений, и не просто так: минералка лечит, заряжает энергией, продлевает молодость. однако, нельзя употреблять ее бездумно, ведь все-таки она предназначена для лечения и оздоровления, а не для ежедневного неограниченного использования. (150 слов)
минеральная вода делится на столовую, лечебно-столовую и лечебную. столовая вода может использовать как для приготовления блюд и питья, так и для принятия ванн. ее можно пить в неограниченных количествах, в ней содержится мало соли, и она оказывает благотворное влияние на организм (186 слов
Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.
⇐ ПредыдущаяСтр 2 из 21Следующая ⇒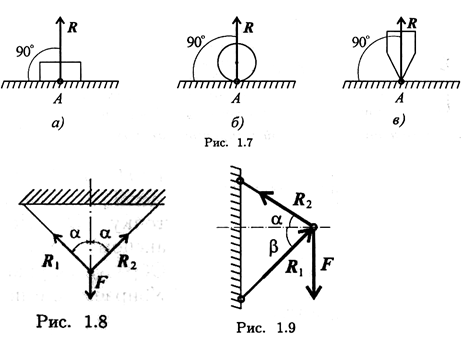 Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Все связи можно разделить на несколько типов.
Связь — гладкая опора (без трения).Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре (рис. 1.7).
Гибкая связь (нить, веревка, трос, цепь). Груз подвешен на двух нитях (рис. 1.8).
Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
Жесткий стержень.
На схемах стержни изображают толстой сплошной линией (рис. 1.9).
Стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня.
Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент наложенными на него связями.
Убираем стержень 1, в этом случае стержень 2 падает вниз. Следовательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2. В этом случае точка А опускается вниз, отодвигаясь от стены. Следовательно, реакция стержня 2 направлена к стене.
Шарнирная опора
 Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
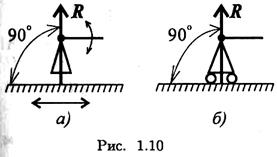
Подвижный шарнир.
Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки) (рис. 1.10).Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, т. к. не допускается только перемещение поперек опорной поверхности.
Неподвижный шарнир. Точка крепления перемещаться не может. Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Её принято изображать ввиде двух составляющих: горизонтальной и вертикальной (Rx, Ry) (рис. 1.11).
Защемление или «заделка». Любые перемещения точки крепления невозможны.
Под действием внешних сил в опоре возникают реактивная сила и реактивный момент МR, препятствующий повороту (рис. 1.12).
Реактивную силу принято представлять в виде двух составляющих вдоль осей координат
R = Rx + Ry
Примеры решения задач
Последовательность решения задач:
- Выбрать тело (точку), равновесие которого следует рассматривать.
- Освободить тело (шарнир) от связей и изобразить действующие на него активные силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира, так как принято предполагать, что стержни растянуты.
- Выбрать оси координат и составить уравнения равновесия, используя условия равновесия системы сходящихся сил на плоскости ∑Xi = 0; ∑Yi = 0. Выбирая оси координат, следует учитывать, что полученные уравнения будут решаться проще, если одну из осей направить перпендикулярно одной из неизвестных сил.
- Определить реакции стержней из решения указанной системы уравнений.
- Проверить правильность полученных результатов, решив уравнения равновесия относительно заново выбранных координат х и у.
Пример 1. Груз подвешен на стержнях и канатах и находится в равновесии (рис. 1.13). Изобразить систему сил, действующих на шарнир А.
Решение
1. Реакции стержней направлены вдоль стержней, реакции гибких связей направлены вдоль нитей в сторону натяжения (рис. 1.13, а).
2. Для определения точного направления усилий в стержнях мысленно убираем последовательно стержни 1 и 2. Анализируем возможные перемещения точки А.
Неподвижный блок с действующими на него силами не рассматриваем.
3. Убираем стержень 1, точка А поднимается и отходит от стены, следовательно, реакция стержня 1 направлена к стене.
4. Убираем стержень 2, точка А поднимается и приближается к стене, следовательно, реакция стержня 2 направлена от стены вниз.
5. Канат тянет вправо.
6. Освобождаемся от связей (рис. 1.13, б).
Пример 2. Шар подвешен на нити и опирается на стену (рис. 1.14а). Определить реакции нити и гладкой опоры (стенки).
Решение
1. Реакция нити — вдоль нити к точке В вверх (рис. 1.14, б).
2. Реакция гладкой опоры (стенки) — по нормали от поверхности опоры.
Пример 3. Представим, что на горизонтально расположенный брус АБ, собственной массой которого пренебрегаем, действует вертикальная нагрузка F, приложенная в точке С бруса (рис. 1.14-1, а). Левый конец бруса А прикреплен к опоре шарниром, а правый В опирается на гладкую наклонную плоскость.
Изобразим брус схематично отрезком АВ, как на рис. 1.14-1, б, и приложим к нему в точке С вертикальную силу F. В точке В со стороны наклонной плоскости к брусу приложена ее реакция RB, направленная перпендикулярно плоскости; линии действия сил F и RBпересекаются в точке О. Кроме этих сил на брус действует еще одна сила — реакция шарнирно-неподвижной опоры. А так как брус находится в равновесии, то линия действия третьей силы также пройдет через точку О, т. е. реакция R шарнир-но-неподвижной опоры направлена вдоль отрезка АО.
Примененный здесь метод рассуждения называется принципом освобождения тела от связей и замены связей их реакциями.
Пример 4. Определить усилие в стержне CD и силу давления груза А на опорную плоскость EF (рис. 1.14-2, а). Массой стержня CD, блока К, каната и трением каната о блок пренебречь.
Натяжение каната во всех его точках одинаково и равно силе тяжести груза В, так как неподвижный блок изменяет только направление силы, действующей на канат.
Рассмотрим равновесие системы: стержень CD и блок К с прилегающим к нему отрезком каната ML. Отбросим связи и заменим их действие соответствующими реакциями (рис. 1.14-2, 6). Для полученной системы сил можно составить только одно уравнение равновесия:
На рис. 1.14-2, в показаны силы, действующие на груз А с прилегающим к нему отрезком каната ОН. REF — реакция опорной плоскости.
Так как груз А находится в равновесии, то
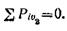
откуда
Rеf = Pa – Рв = 600 – 400 = 200 Н.
Сила давления груза А на опорную плоскость RA показана на рис, 1.14-2, г. Очевидно, RA = REF = 200 H (сила действия равна силе противодействия).
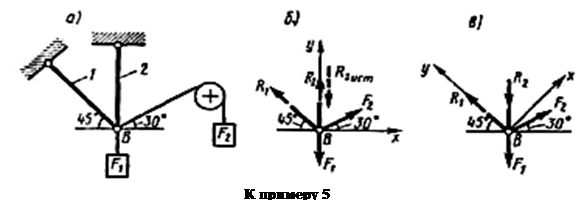
Пример 5.Определить реакции стержней, удерживающих грузы F1 = 70 кН и F2 = 100 кН (рис. а). Массой стержней пренебречь.
 |
Решение
1. Рассматриваем равновесие шарнира В (рис. а).
2. Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей (рис. б).
3. Выбираем систему координат, совместив ось у по направлению С реакцией R2 (рис. б) и составляем уравнения равновесия для системы сил, действующих на шарнир В:
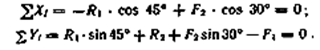
3. Определяем реакции стержней R1 и R2, решая уравнения.
Подставляя найденное значение R1 в уравнение (2), получаем
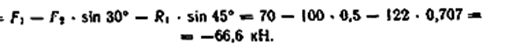
Знак минус перед значением R2 указывает на то, что первоначально выбранное направление реакции неверное — следует направить реакцию R2 в противоположную сторону, т.е. к шарниру В (на рис. б истинное направление реакции R2 показано штриховым вектором).
5. Проверяем правильность полученных результатов, выбрав новое расположение осей координат х и у (рис. а). Относительно этих осей составляем уравнения равновесия:
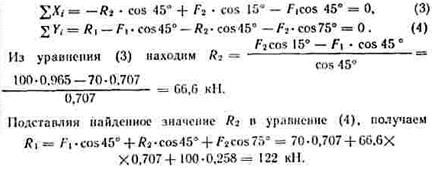
Значения реакций R1 и R2, полученные при решении уравнений (1) и (2), совпадают по величине и направлению со значениями, найденными из уравнений (3) и (4), следовательно, задача решена правильно.
Контрольные вопросы и задания
1. Какая из приведенных систем сил (рис. 1.15) уравновешена?
 |
2. Какие силы системы (рис. 1.16) можно убрать, не нарушая механического состояния тела:
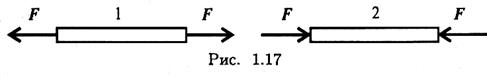 |
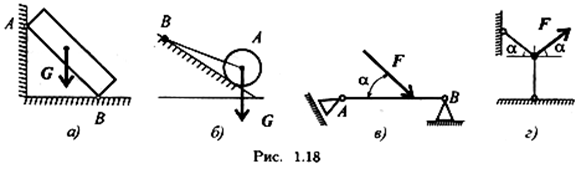
3. Тела 1 и 2 (рис. 1.17) находятся в равновесии. Можно ли убрать действующие системы сил, если тела абсолютно твердые? Что изменится, если тела реальные, деформируемые?
ЛЕКЦИЯ 2
Лекция по дисциплине «Техническая механика» на тему «Основные понятия и аксиомы статики»
Тема: Основные понятия и аксиомы статики
Понятие о силе и системе сил
Сила — это мера механического взаимодействия материальных тел между собой. Взаимодействие характеризуется величиной и направлением, т.е. сила есть величина векторная,1 характеризующаяся точкой приложения (А), направлением (линией действия), величиной (модулем) (рис. 1). Силу измеряют в ньютонах,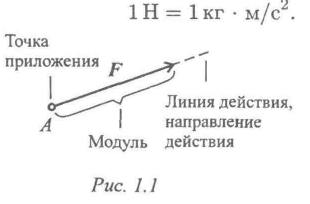
Рисунок 1
Силы, действующие на тело (или систему тел), делятся на внешние и внутренние. Внешние силы бывают активные и реактивные. Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.
Внутренние силы возникают в теле под действием внешних сил.
Совокупность сил, действующих на какое-либо тело, называют системой сил.
Эквивалентная система сил — система сил, действующая так же, как заданная.
Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.
Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.
Аксиомы статики
В результате обобщения человеческого опыта были установлены общие закономерности механического движения, выраженные в виде законов и теорем. Все теоремы и уравнения статики выводятся из нескольких исходных положений. Эти положения называют аксиомами статики».
Первая аксиома
Под действием уравновешенной системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).
Вторая аксиома
Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются (рис. 2).
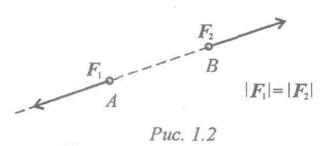
Рисунок 2
Третья аксиома
Не нарушая механического состояния тела, можно добавить или убрать уравновешенную систему сил (принцип отбрасывания системы сил, эквивалентной нулю) (рис. 3).
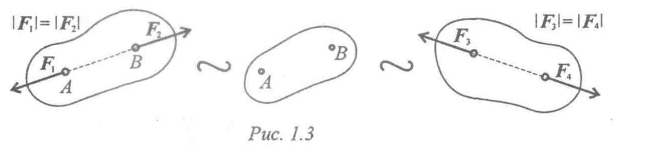
Рисунок 3
Четвертая аксиома (правило параллелограмма сил)
Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке и является диагональю параллелограмма, построенного на этих силах как на сторонах (рис. 4).
Вместо параллелограмма можно построить треугольник сил: силы вычерчивают одну за другой в любом порядке; равнодействующая двух сил соединяет начало первой силы с концом второй.
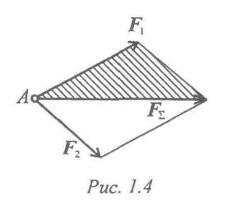
Рисунок 4
Пятая аксиома
При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие (рис. 5).
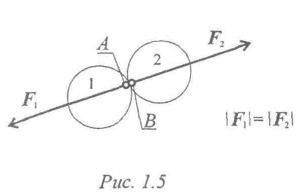
Рисунок.5
Следствие из второй и третьей аксиом
Силу, действующую на твердое тело, можно перемещать вдоль линии ее действия (рис. 6).
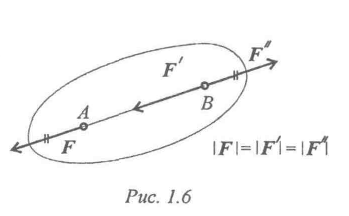
Рисунок 6
Сила F приложена в точке А. Требуется перенести ее в точку В. Используя третью аксиому, добавим в точке В уравновешенную систему сил (F‘;F«). Образуется уравновешенная по второй аксиоме система сил (F;F«). Убираем ее и получим в точке В силу F«, равную заданной F.
Контрольные вопросы и задания
1. Какая из приведенных систем сил (рис. 5) уравновешена?
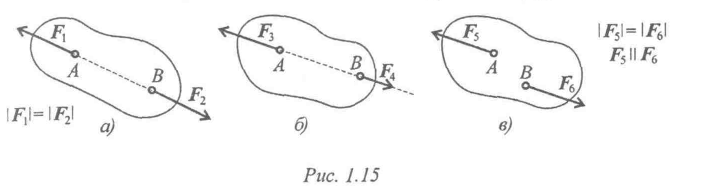
Рисунок 5
2. Какие силы системы (рис. 6 ) можно убрать, не нарушая механического состояния тела?
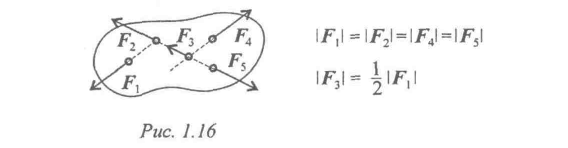
Рисунок 6
3. Тела 1 и 2 (рис. 7) находятся в равновесии. Можно ли убрать действующие системы сил, если тела абсолютно твердые? Что изменится, если тела реальные, деформируемые?

Рисунок 7
1 Векторные величины обозначаются полужирным шрифтом, скалярные величины — обычным.
Сила. Система сил. Равновесие абсолютно твердого тела — Мегаобучалка
СТАТИКА
Глава I. ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМЫ СТАТИКИ
Сила. Система сил. Равновесие абсолютно твердого тела
В теоретической механике изучается движение материальных тел относительно друг друга. Для этого требуется, прежде всего, построить модели объектов и дать определение понятий, с которыми имеет дело механика. В теоретической механике рассматривается простейшая модель «обычного» евклидова трехмерного пространства. Постулируется, что в этом пространстве существует хотя бы одна система координат, в которой справедливы законы Ньютона (инерциальная система). Многочисленные опыты и измерения показывают, что с высокой степенью точности система отсчета с началом в центре Солнечной системы и осями, направленными к «бесконечно удаленным неподвижным» звездам, является инерциальной системой. Если существует хотя бы одна инерциальная система, то их имеется бесчисленное множество. Инерциальная система – это система, в которой действуют законы Ньютона. Инерциальные системы отсчета условно называют неподвижными.
В статике, не внося никаких погрешностей в вычисления, можно считать, что системы координат, жестко связанные с Землей, неподвижны. Условия относительного равновесия в других, неинерциальных системах отсчета, в частности, в системах, движущихся относительно Земли, будут рассмотрены в динамике.
Как для статики, так и для динамики одним из основных является понятие силы. Первичное представление о ней дают наши мускульные ощущения.
В механике под силой понимается мера механического взаимодействия материальных тел, в результате которого взаимодействующие тела могут сообщать друг другу ускорения или деформироваться (изменять свою форму).
Из этого определения сразу вытекают два способа измерения сил:
первый, динамический способ, основан на измерении ускорения тела в инерциальной системе отсчета;
второй, статический способ, основан на измерении деформации упругих тел.
В механике не изучают физическую природу сил. Силы могут возникать при непосредственном контакте тел (например, сила тяги электровоза, передаваемая вагонам, сила трения между поверхностями соприкасающихся тел). Силы возникают и на расстоянии (например, силы притяжения небесных тел, силы взаимодействия электрически заряженных или намагниченных частиц и т.д.).
Сила является векторной величиной – она характеризуется численным значением или модулем, точкой приложения и направлением. Точка приложения силы и ее направление определяют линию действия силы. На рис. 1.1 показана сила F, приложенная к точке А, длина отрезка АВ в соответствующем масштабе равна модулю силы, точка В называется концом силы; у конца силы; у конца силы ставится стрелка, указывающая направление действия силы. Прямая LM называется линией действия силы. Условимся обозначать силу буквой жирного шрифта, например, F, а ее модуль той же буквой обычного шрифта, т.е. F.
Для измерения модуля силы ее сравнивают с некоторой силой, выбранной в качестве единицы. В международной системе единиц измерения физических величин (СИ) за единицу силы принят один ньютон (1 Н), а в технической системе единиц (система МКГСС) – один килограмм силы (1 кГ или 1 кгс – не следует смешивать с единицей массы в системе СИ – 1 кг). Эти единицы связаны соотношениями
1 кГ ≈ 9,81 Н; 1 Н ≈ 0,102 кГ.
Рассматривая действие сил на материальные тела, мы будем отвлекаться не только от физической природы сил, но и от многих свойств самих тел. Так, реальные твердые тела обычно мало изменяют свою форму под действием приложенных к ним сил. Поэтому для решения многих задач механики допустимо вовсе пренебречь малыми деформациями (т.е. малыми изменениями формы) и пользоваться моделью абсолютно твердого тела. Под абсолютно твердым телом понимают тело, в котором расстояния между двумя любыми точками его остаются неизменными независимо от действия тех или иных сил. Для краткости мы будем часто применять выражение «твердое тело» или даже просто «тело», имея в виду только что введенное понятие абсолютно твердого тела.
Совокупность нескольких сил (F1,…, Fn) называется системой сил. Если, не нарушая состояния тела, одну систему сил (F1,…, Fn) можно заменить другой системой (P1,…, Pk) и наоборот, то такие системы называются эквивалентными. Символически это обозначается следующим образом:
(F1,…, Fn) = (P1,…, Pk).
Введенное понятие эквивалентности систем сил не устанавливает условий, при выполнении которых две системы будут эквивалентны. Оно означает только, что эквивалентные системы сил вызывают одинаковое состояние тела (одинаковые ускорения или, если тело не абсолютно твердое, одинаковые деформации).
В том случае, когда система сил (F1,…, Fn) эквивалентна одной силе R, т.е.
(F1,…, Fn) = R,
последняя называется равнодействующей данной системы сил. Это означает, что одна равнодействующая сила может заменить действие всех данных сил. Не всякая система сил имеет равнодействующую.
Как уже отмечалось, в инерциальной системе координат выполняется закон инерции. Это означает, в частности, что тело, находящееся в начальный момент в покое, остается пребывать в этом состоянии, если на него не действуют никакие другие силы.
Если абсолютно твердое тело остается в состоянии покоя при действии на него системы сил (F1,…, Fn), то последняя называется уравновешенной системой сил или системой сил, эквивалентной нулю:
(F1,…, Fn) = 0.
Часто в этом случае говорят, что тело находится в равновесии.
1.2. Аксиомы статики и их следствия
В аксиомах статики формулируются те простейшие и общие законы, которым подчиняются силы, действующие на одно и то же тело, или силы, приложенные к взаимодействующим телам. Эти законы установлены многочисленными непосредственными наблюдениями, а также проверкой следствий (часто далеких и вовсе не очевидных), логически вытекающих из этих аксиом.
Как следует из второго закона Ньютона, тело под действием одной силы приобретает ускорение и, следовательно, оно не может находиться в покое. Это означает, что одна сила не может составлять уравновешенную систему сил. Первая аксиома устанавливает условия, при выполнении которых простейшая система сил будет уравновешена.
Аксиома 1. Две силы, приложенные к абсолютно твердому телу, будут уравновешены (эквивалентны нулю) тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны.
Это означает, что если абсолютно твердое тело находится в покое под действием двух сил, то эти силы равны по модулю, действуют по одной прямой и направлены в противоположные стороны. Обратно, если на абсолютно твердое тепло действуют по одной прямой в противоположные стороны две равные силы и тело в начальный момент находилось в покое, то состояние покоя тела сохранится.
На рис. 1.4 показаны уравновешенные силы, удовлетворяющие соотношениям: (F1, F2) = 0, (P1, P2) = 0.
При решении некоторых задач статики приходится рассматривать силы, приложенные к концам жестких стержней, весом которых можно пренебречь, причем известно, что стержни находятся в равновесии. Из сформулированной аксиомы непосредственно следует, что на такой стержень силы направлены вдоль прямой, проходящей через концы стержня, противоположны по направлению и равны друг другу по модулю. Этот вывод сохраняется и в случае, если ось стержня криволинейная.
Первая аксиома устанавливает необходимые и достаточные условия уравновешивания только двух сил, но, конечно, уравновешенная система сил может состоять и из большего числа сил.
Две следующие аксиомы устанавливают простейшие действия с силами, при которых состояние тела не изменяется.
Аксиома 2. Не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или отбрасывать силы тогда и только тогда, когда они составляют уравновешенную систему, в частности, если эта система состоит из двух сил, равных по модулю, действующих по одной прямой и направленных в противоположные стороны.
Из этой аксиомы вытекает следствие: не нарушая состояния тела, точку приложения силы можно переносить вдоль линии ее действия.
Это следствие показывает, что сила, приложенная к абсолютно твердому телу, представляет собой скользящий вектор.
Обе аксиомы и доказанное следствие нельзя применять к деформируемым телам, в частности, перенос точки приложения силы вдоль линии ее действия меняет напряженно-деформированное состояние тела.
Аксиома 3. Не меняя состояния тела, две силы, приложенные к одной его точке, можно заменить одной равнодействующей силой, приложенной в одной и той же точке и равной их геометрической сумме (аксиома параллелограмма сил).
Эта аксиома устанавливает два обстоятельства:
первое – две силы F1 и F2, приложенные к одной точке, имеют одну равнодействующую, т.е. эквивалентны одной силе
(F1, F2) = R;
второе – аксиома полностью определяет модуль, точку приложения и направление равнодействующей силы
R = F1+F2.
Другими словами, равнодействующую R можно построить как диагональ параллелограмма со сторонами, совпадающими с F1 и F2.
Отметим, что третья аксиома применима к любым, не обязательно абсолютно твердым телам.
Вторая и третья аксиомы статики дают возможность переходить от одной системы сил к другой системе, ей эквивалентной. В частности, они позволяют разложить любую силу Rна две, три и т.д. составляющие, т.е. перейти к другой системе сил, для которой сила Rявляется равнодействующей. Задавая, например два направления, которые лежат с Rв одной плоскости, можно построить параллелограмм, у которого диагональ изображает силу R. Тогда силы, направленные по сторонам параллелограмма, составят систему, для которой R будет равнодействующей. Аналогичное построение можно провести и в пространстве. Для этого достаточно из точки приложения силы R провести три прямые, не лежащие в одной плоскости, и построить на них параллелепипед с диагональю, изображающей силу R, и с ребрами, направленными по этим прямым.
Аксиома 4 (3-й закон Ньютона). Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.
Заметим, что силы взаимодействия двух тел не составляют систему уравновешенных сил, так как они приложены к разным телам.
Если обозначить через Fсилу, с которой Солнце притягивает Землю, то Земля притягивает Солнце с такой же по модулю, но противоположно направленной силой –F.
При движении тела по плоскости к нему будет приложена сила трения Т, направленная в сторону, противоположную движению. Это – сила, с которой неподвижная плоскость действует на тело. На основании аксиомы 4 тело действует на плоскость с такой же силой, но ее направление будет противоположно силе Т.
Аксиома 5. Равновесие деформируемого тела не нарушается, если жестко связать его точки и считать тело абсолютно твердым.
Этой аксиомой (ее иногда называют принципом отвердевания) пользуются в тех случаях, когда речь идет о равновесии тел, которые нельзя считать твердыми. Приложенные к таким телам внешние силы должны удовлетворять условиям равновесия твердого тела, однако для нетвердых тел эти условия являются лишь необходимыми, но не достаточными. Поясним это положение простым примером. Для равновесия абсолютно твердого невесомого стержня необходимо и достаточно, чтобы приложенные к концам стержня силы FиF‘ действовали по прямой, соединяющей его концы, были равны по модулю и направлены в разные стороны. Эти же условия необходимы и для равновесия отрезка невесомой нити, но для нити они недостаточны – необходимо дополнительно потребовать, чтобы силы, действующие на нить, были растягивающими, в то время как для стержня они могут быть и сжимающими.
В заключение рассмотрим случай эквивалентности нулю трех непараллельных сил, приложенных к твердому телу.
Теорема о трех непараллельных силах. Если под действием трех сил тело находится в равновесии и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.
Пусть на тело действует система трех сил F1, F2иF3,причем линии действия сил F1иF2пересекаются в точке А. Согласно следствию из аксиомы 2 силы F1иF2можно перенести в точку А, а по аксиоме 3 их можно заменить одной силой R, причем
R = F1+F2.
Таким образом,
рассматриваемая система сил приведена к двум силам RиF3. По условиям теоремы тело находится в равновесии, следовательно, по аксиоме 1 силы RиF3должны иметь общую линию действия, но тогда линии действия всех трех сил должны пересекаться в одной точке.