7. Движение тел в жидкостях

Сопротивление движению тел в жидкостях. Проведение ряда процессов химической технологии связано с движением твердых тел в капельных жидкостях или газах. К таким процессам относятся, например, осажде­ние твердых частиц из суспензий и пылей под действием сил тяжести и инерционных (например, центробежных) сил, механическое перемеши­вание в жидких средах и др. Как отмечалось, изучение закономерностей этих процессов составляет внешнюю задачу гидродинамики.

При движении тела в жидкости (или при обтекании неподвижного тела движущейся жидкостью) возникают сопротивления, для преодоления которых и обеспечения равномерного движения тела должна быть затра­чена определенная энергия. Возникающее сопротивление зависит главным образом от режима движения и формы обтекаемого тела,

При ламинарном движении, наблюдающемся при небольших скоростях и малых размерах тел или при высокой вязкости среды, тело окружено пограничным слоем жидкости и плавно обтекается потоком (рис. II-20, а). Потеря энергии в таких условиях связана в основном лишь с преодоле­нием сопротивления трения.

С развитием турбулентности потока (например, с увеличением скорости движения тела) все большую роль начинают играть силы инерции. Под действием этих сил пограничный слой отрывается от поверхности тела, что приводит к понижению давления за движущимся телом в непосред­ственной близости от него и к образованию беспорядочных местных зави­хрений в данном пространстве (рис. II-20, б). При этом разность давлений жидкости на переднюю (лобовую) поверхность тела, встречающую обте­кающий поток, и на его заднюю (кормовую) поверхность все больше превы­шает разность давлений, возникающую при ламинарном обтекании тела.

Начиная с некоторых значений критерия Рейнольдса, роль лобового сопротивления становится преобладающей, а сопротивлением трения можно практически пренебречь. В данном случае, как и при движении жидкости по трубам, наступает автомодельный (по отношению к критерию Рей­нольдса) режим.

Сила сопротивления R(н) среды движущемуся в ней телу может быть выражена уравнением закона сопротивления:

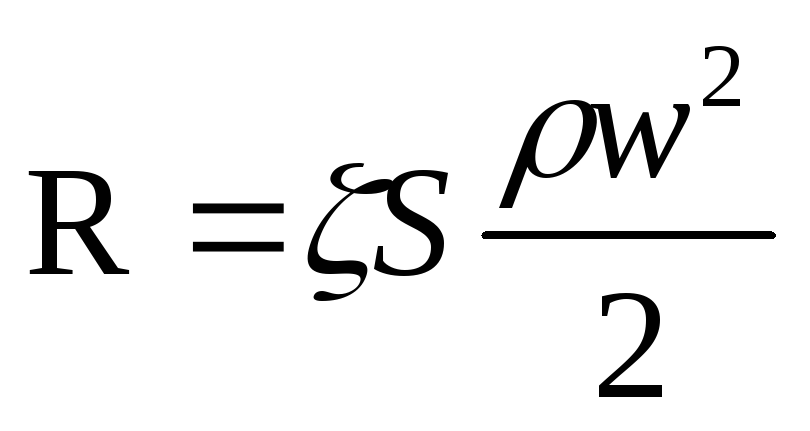(II,62)

где S — площадь проекции тела на плоскость, перпендикулярную направлению его дви­жения, м², w — скорость, м/сек,  — плотность среды, кг/м², —коэффициент сопротивле­ния среды

Отношение R/S представляет собой перепад давлений р (н/м²), пре­одолеваемый движущимся телом. Поэтому, решив уравнение (II, 62) относительно , можно установить, что коэффициент сопротивления  пропорционален критерию Эйлера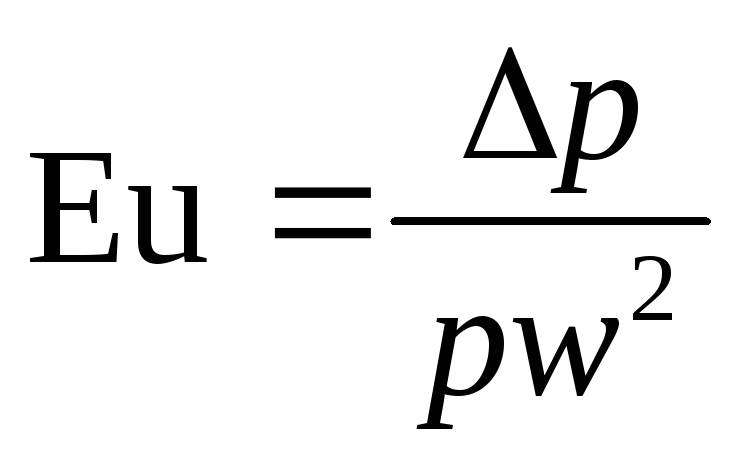

( отличается от Еu лишь множителем 2). Соответственно уравнения для расчета  при различных гидродинамических режимах могут быть получены обработкой опытных данных в виде обобщенных зависимостей между критериями гидродина­мического подобия.

На рис, II-22 представлена зависимость  от критерия Рейнольдса при движении шарообразных частиц диаметром d. Этот диаметр и является определяющим размером в критерии Re. Из графика видно, что сущест­вуют три различных режима движения, каждому из которых соответствует определенный характер зависимости  от Re:

ламинарный режим (область действия закона Стокса) при­близительно при Re < 2

(II,63)

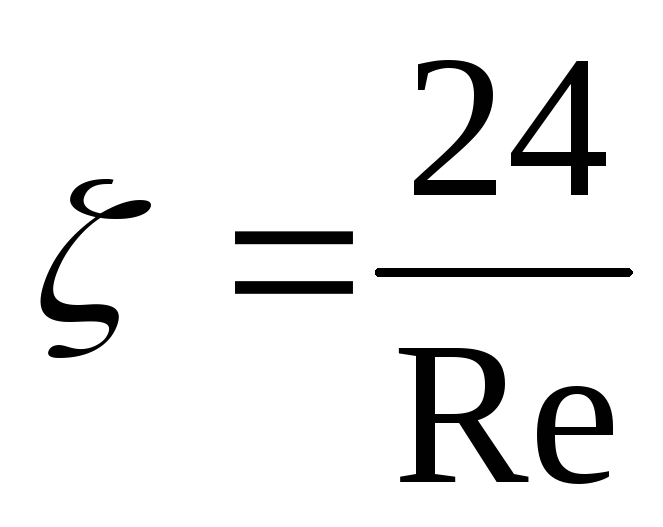
переходный режим при Re = 2-500

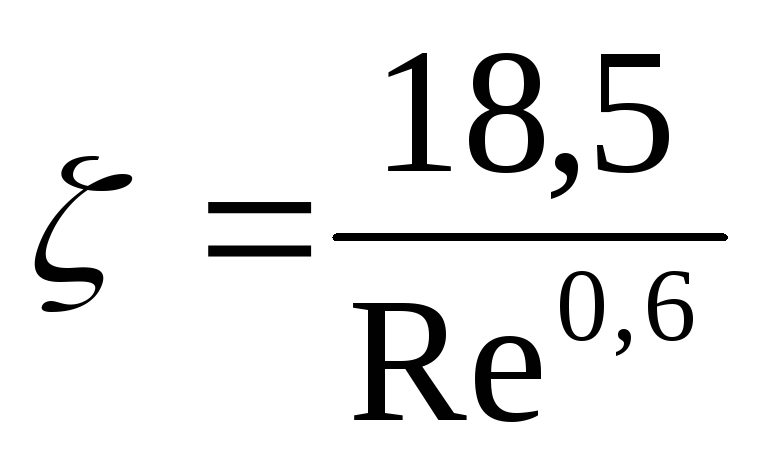(II,63a)

автомодельный режим (область действия квадратичного закона сопротивления Ньютона) при ~2·10⁵ > Re > -500

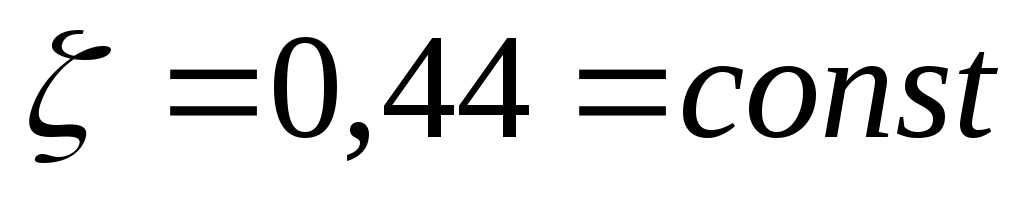(II,63б)

Подстановка в уравнение (II, 62) каждого из приведенных выше урав­нений для  показывает, что при ламинарном режиме сила сопротивления пропорциональна скорости в первой степени, т.е. R ~ w, при переход­ном режиме R ~ w^1,4, а при автомодельном режиме R  w².

При движении тел, отличающихся по форме от шара, значения коэф­фициента сопротивления больше и зависят не только от критерия Re, но и от

фактора формы Ф, т.е.

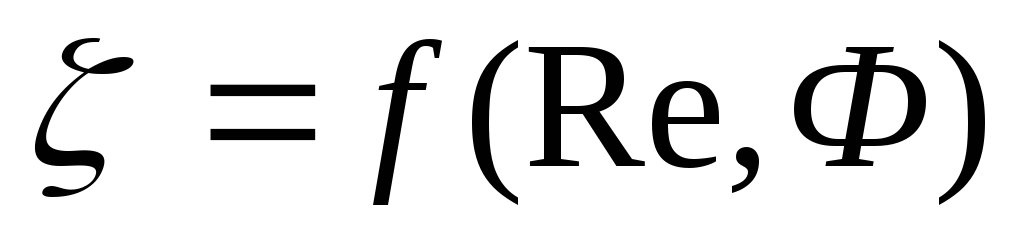(II,64)

Здесь

(II,65)

где F_ш — поверхность шара, имеющего тот же объем, что и рассматривае­мое тело поверхностью F. Например, для куба Ф — 0.806; для цилиндра высотой, в 10 раз превышающей его радиус, Ф = 0.69; для диска, высота которого в 10 раз меньше радиуса, Ф = 0.32. Значения Ф приводятся в справочниках.

Надо заметить, что на самом деле роль фактора формы не всегда может быть сведена лишь к соотношению поверхностей. Поэтому наиболее надежные данные о численных зна­чениях Ф для тел различной формы получаются экспериментально.

Для тел нешарообразной формы определяющим линейным размером в критерии Re служит диаметр эквивалентного шара d, равный диаметру шара, имеющего такой же объем, что и данное тело. Если объем тела V, его масса т, а плотность _т, то значение d может быть най­дено из соотношения

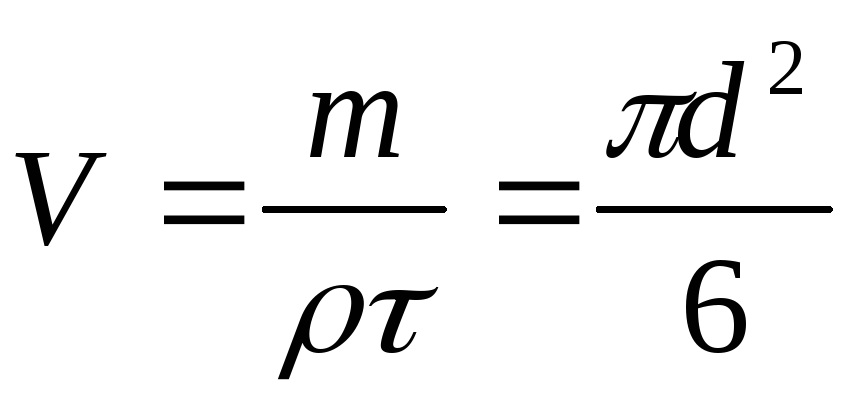
Осаждение частиц под действием силы тяжести. Рассмотрим движение тела в жидкости на примере осаждения твердой частицы в неподвижной среде под действием силы тяжести. Другой пример, связанный с анализом движения в жидкостях механических мешалок, приведен позже.

Если частица массой m (и весом mg) начинает падать под действием силы собственного веса, то скорость ее движения первоначально возрастает со временем. При полном отсутствии сопротивления среды скорость

w менялась бы во времени по известному закону w = g. Однако с увеличением скорости будет расти, согласно уравнению (II,62), сопротивление движению частицы и соответственно уменьшаться ее ускорение. В результате через короткий промежуток времени наступит равновесие: сила тяжести, под действием которой частица движется, станет равна силе деления среды. Начиная с этого момента, ускорение движения будет нулю; и частица станет двигаться равномерно — с постоянной скоростью. Скорость такого равномерного движения частицы в среде назы­вают скоростью осаждения и обозначают символом w_oс.

Сила, движущая шарообразную частицу диаметром d, выражается раз­ностью между ее весом и выталкивающей архимедовой силой, равной весу жидкости (среды) в объеме частицы:

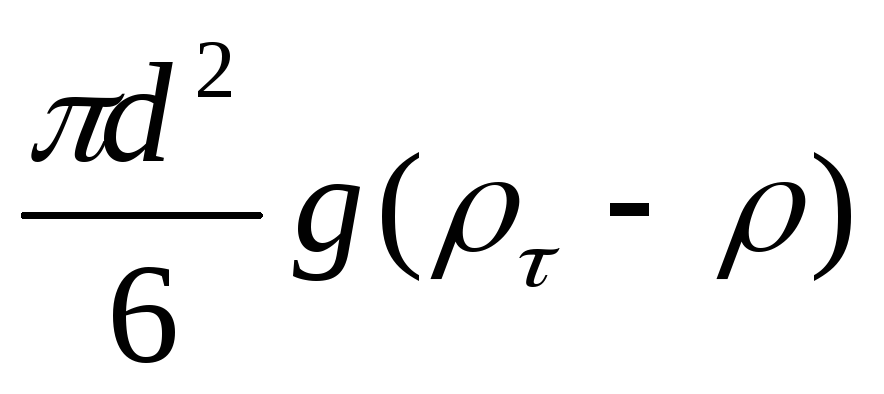
где 

т — плотность твердой частицы;  — плотность среды.

Сила сопротивления среды, в соответствии с уравнением (II,62)

Скорость осаждения w_ос можно найти из условия равенства силы, дви­жущей частицу, и силы сопротивления среды:

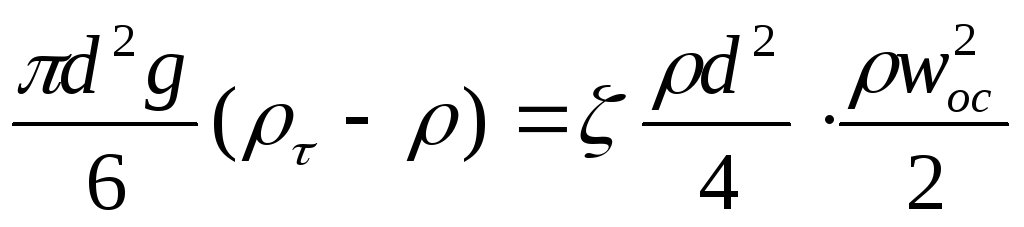
откуда

(II,66)

Значение коэффициента сопротивления  может быть определено по одной из зависимостей — (II,63), (II,63а) или (II,63б). При подстановке в уравнение (II,65) выражения (II,63) для ламинарной области находим формулу

(II,66а)

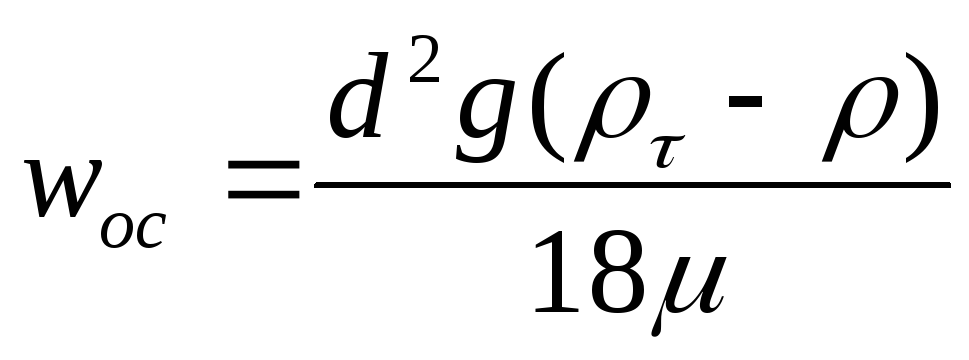
где — вязкость среды.

Это же уравнение можно получить и при использовании выражения закона Стокса, согласно которому сопротивление среды при осаждении в ней мелких частиц выражается зависимостью

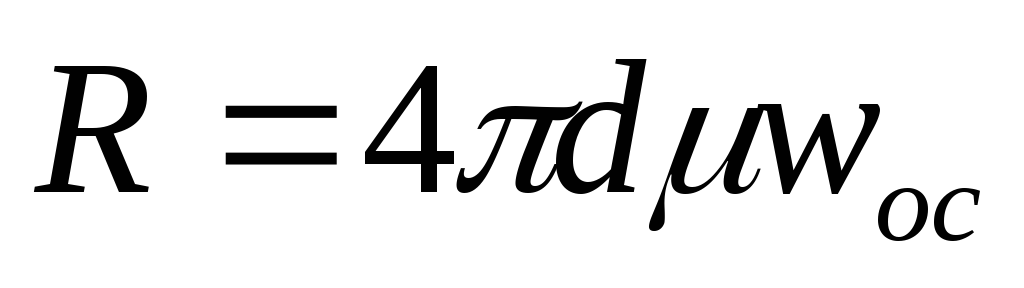(II,67)

Приравниваем действующую силу силе сопротивления середы

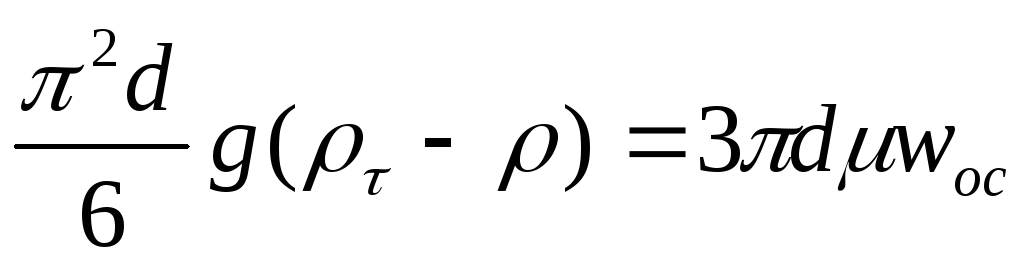
и, определив из этого выражения w_ос, получаем уравнение (II,67).

Максимальный размер частиц, осаждение которых происходит по закону Стокса, можно найти, подставив в уравнение (II,67) вместо скорости осаждения ее выражение через критерии Рейнольдса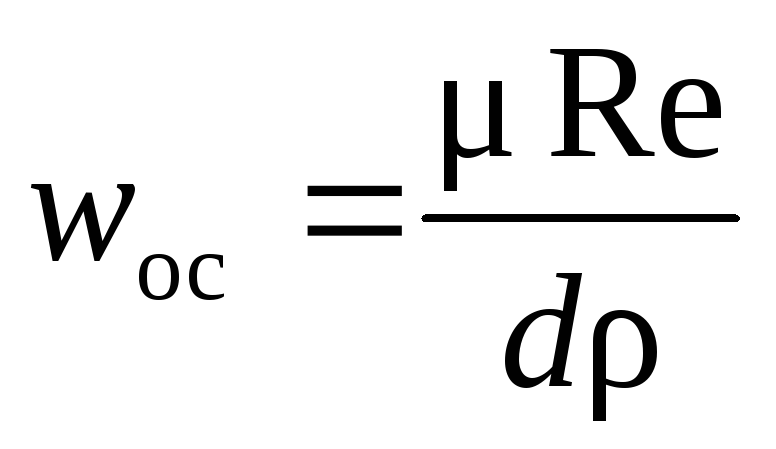

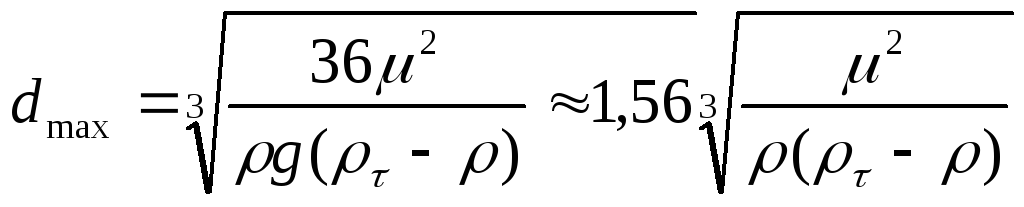и принявRe = 2, т.е. — предельному значению Re для ламинарной об­ласти. Тогда

(II,68)

Существует и минимальный размер частиц, ниже которого наблюдаются отклонения от закона Стокса. Нижний предел применимости закона Стокса соответствует Re  10^-4. При Re  10^-4 на скорость осаждения очень мелких частиц начинает влиять тепловое движение молекул среды. В таких условиях размеры d частиц становятся соизмеримыми со средней длиной  свободного пробега молекул среды. При этом скорость осаждения оказывается ниже рассчитанной по уравнению (II,66). Поэтому вели­чину w_oc, определенную по уравнению (II,66а), следует разделить на поправочный коэффициент

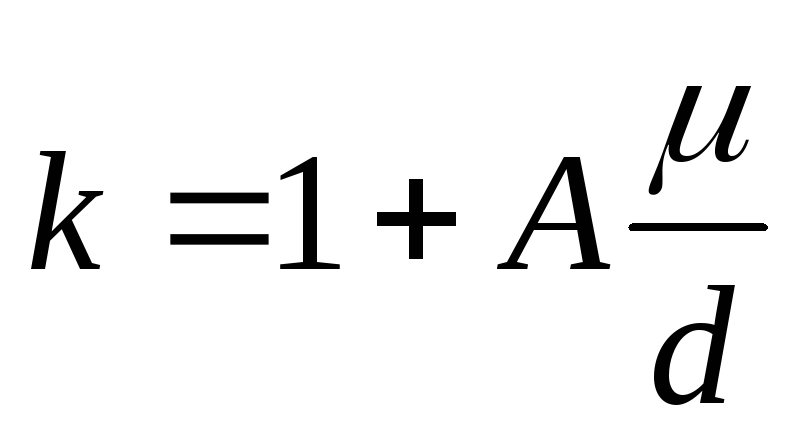(II,69)

причем величина

А меняется в пределах от 1,4 до 20 (для воздуха А = 1.5).

Расчеты показывают, что при осаждении в воздухе частиц пыли раз­мером d > 3 мкм коэффициент k  1. При d  0.1 мкм пыль не осаж­дается, а наблюдается лишь хаотическое броуновское движение ее частиц.

В случае переходной области 2 < Re < 500 после подстановки в уравнение (II,68) выражения (II,62а) для  и некоторых преобразова­ний получим

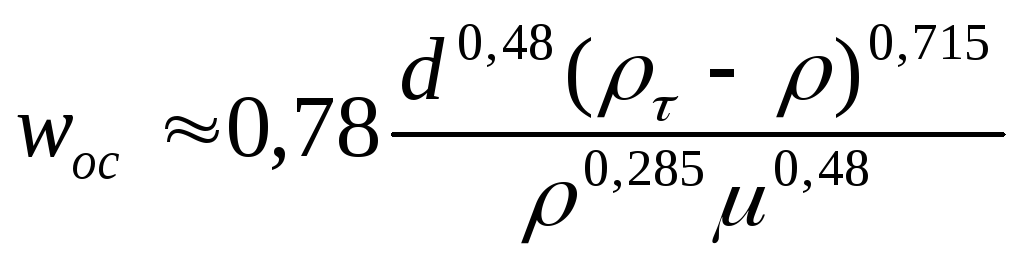(II,70a)

Аналогично для автомодельной области (при Re > 500), согласно вы­ражению (II,62б), подставив  = 0.44 в уравнение (II,65), находим

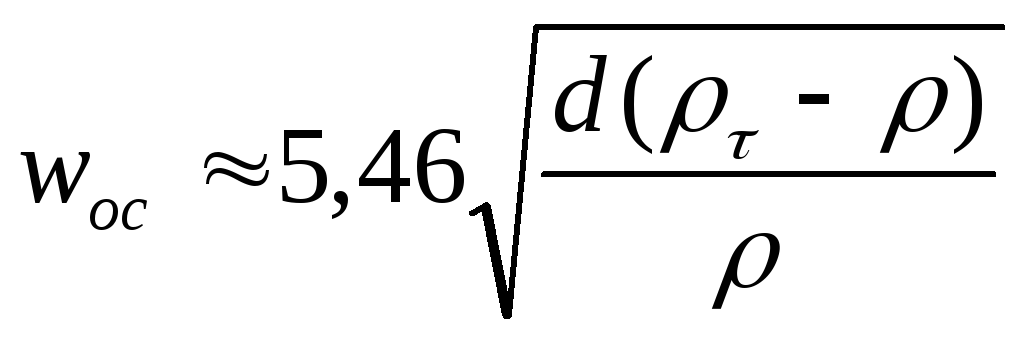(II,70б)

Для того чтобы выбрать расчетное уравнение, соответствующее данной области осаждения, т.е. одно из уравнений (II,70), (II,70а) или (II,70б), необходимо предварительно знать значение критерия Re, в который вхо­дит искомая скорость осаждения w_ос. Поэтому расчет w_оc по приведенным выше уравнениям возможен только методом последовательных прибли­жений. Допуская, что осаждение происходит в определенной области, например ламинарной, рассчитывают по соответствующему уравнению w_ос и по этому значению вычисляют Re. Затем проверяют, лежит ли най­денное значение Re в пределах, отвечающих принятой области осаждения. В случае несовпадения расчет повторяют до получения сходимых резуль­татов.

Вследствие трудоемкости метода последовательных приближений более удобно для определения w_oc пользоваться другим методом, предложен­ным П.В. Лященко. Этот метод основан на преобразовании уравнения (II,64) путем подстановки в него скорости осаждения, выраженной через Re, и возведения обеих частей уравнения в квадрат:

Отсюда

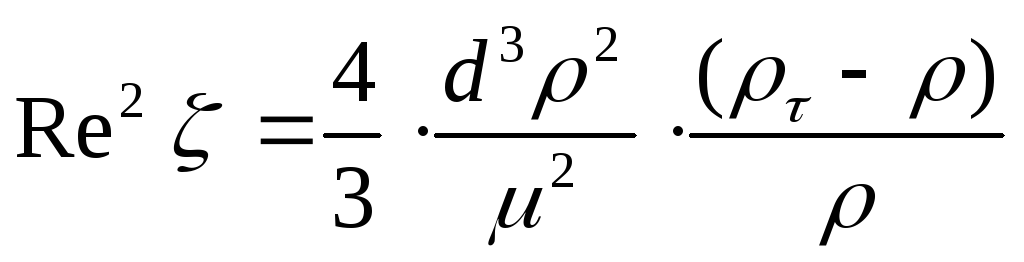(70)

Выражение в правой части этого уравнения принципиально не отли­чается от выражения (II,71) для критерия Аr:

(II,71a)

В данном случае за определяющий линейный размер принят диаметр частицы, а за масштаб разности плотностей частицы и среды — плотность среды, в которой происходит осаждение.

В критерий Архимеда искомая скорость осаждения не входит. Он состоит из величин, которые обычно либо заданы, либо могут быть зара­нее определены.

Таким образом

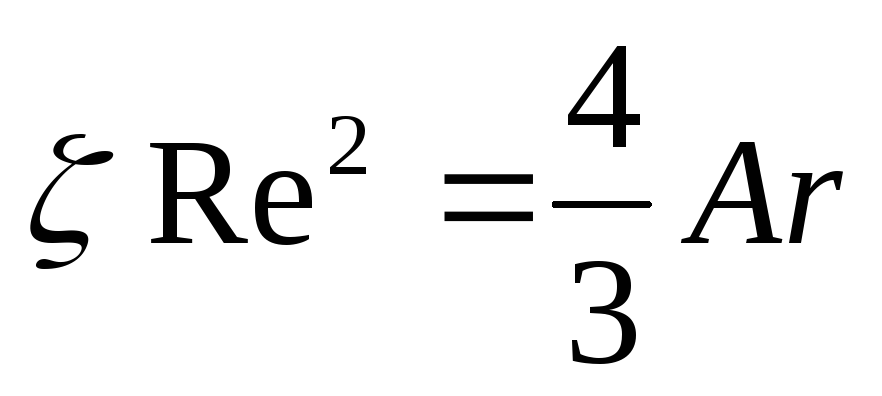(II,72)

Подставив в это обобщенное уравнение критические (граничные) зна­чения критерия Re, отвечающие переходу одной области осаждения в дру­гую, можно найти соответствующие критические значения критерия Аr.

Для области действия закона Стокса (Re < 2) при подстановке выра­жения , согласно зависимости (II,62), в уравнение (II,72) получим

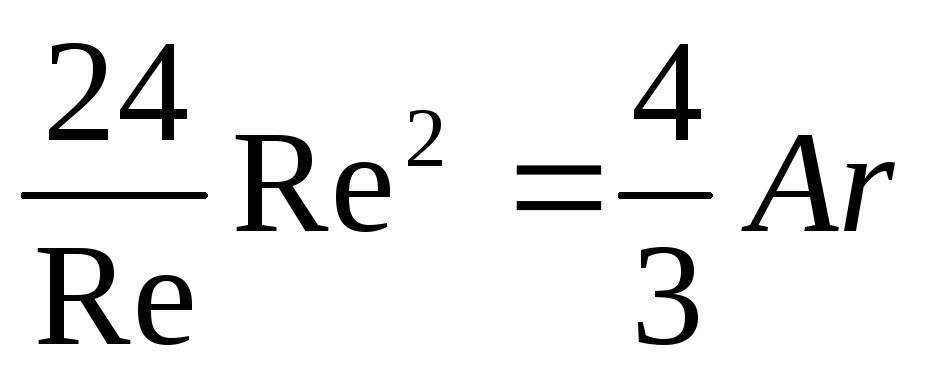
откуда

(II,72a)

Верхнее предельное, или критическое, значение критерия Архимеда для этой области

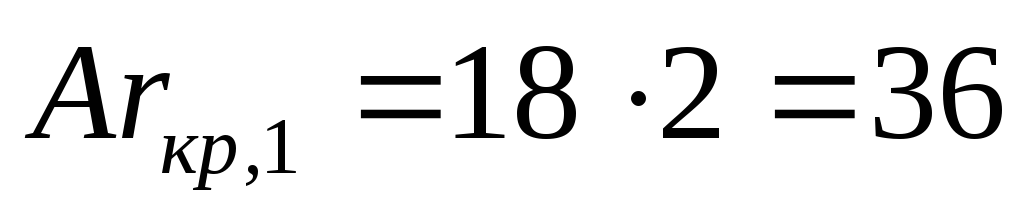
Следовательно, существование ламинарного режима осаждения соот­ветствует условию Ar  36.

Для переходной области, где 2 < Re < 500, подставляем значение , согласно зависимости (II,62а), в уравнение (II,72). Тогда

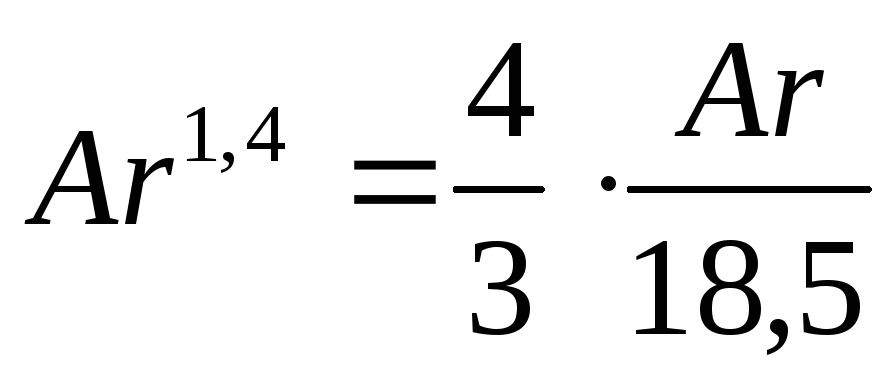
или

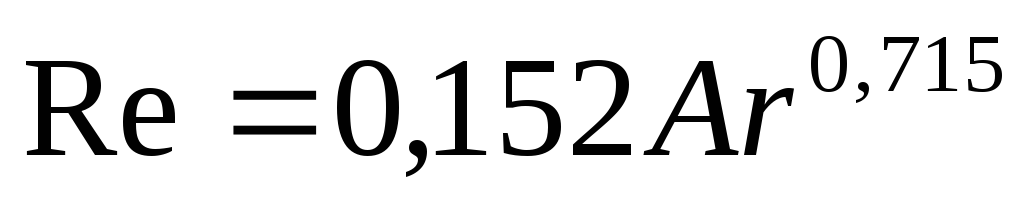(II,72б)

При подстановке в уравнение (II,72б) критического значения Re = 500 находят верхнее предельное значение Ar для переходной области

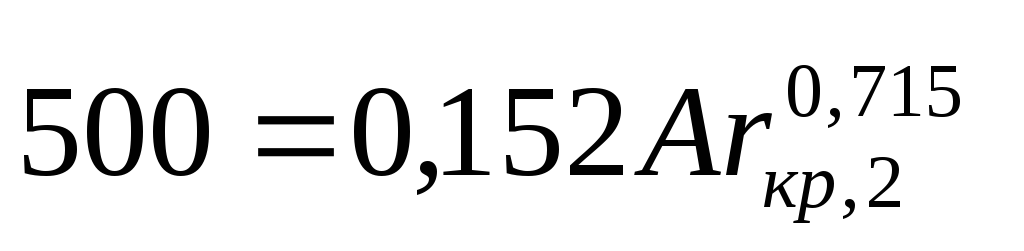
откуда

Аr_кр;2 = 83000

Таким образом, переходная область осаждения соответствует измене­нию критерия Ar в пределах 36 < Ar < 83 000.

Для автомодельной области, где Ar > 83 000, зависимость между Re и Ar можно найти, подставив  = 0.44, в соответствии с выражением (II,72б), в уравнение (II,72а):

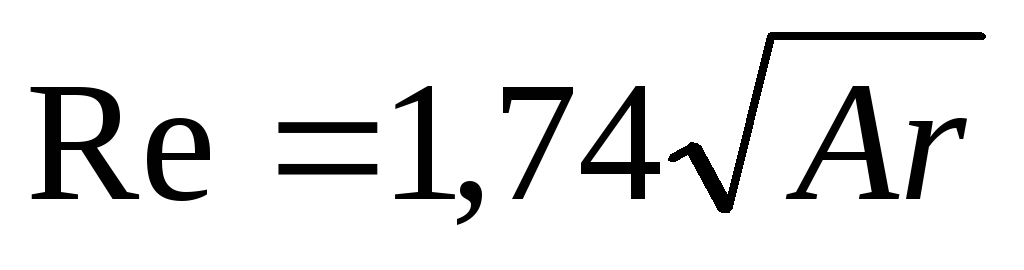(II,72в)

Таким образом, рассчитав критерий Ar, определяют по его значению область, в которой происходит осаждение. Вычисляют, пользуясь одним из уравнений (II,72а), (II,72б) или (II,72в), отвечающим этой области, значение Re и находят по нему скорость осаждения

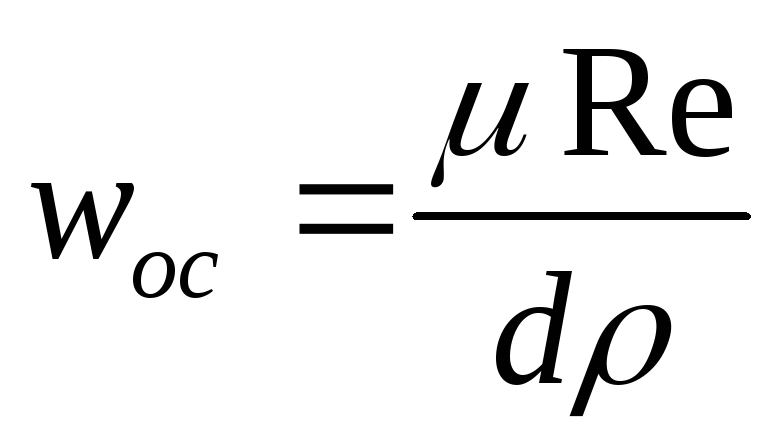(II,73)

Зная область осаждения, можно также рассчитать скорость осаждения по одному из уравнений (II,66), (II,66а) или (II,66б).

Для расчетов может быть использована и единая интерполяционная зависимость, связывающая критерии Re и Ar для всех режимов осаждения:

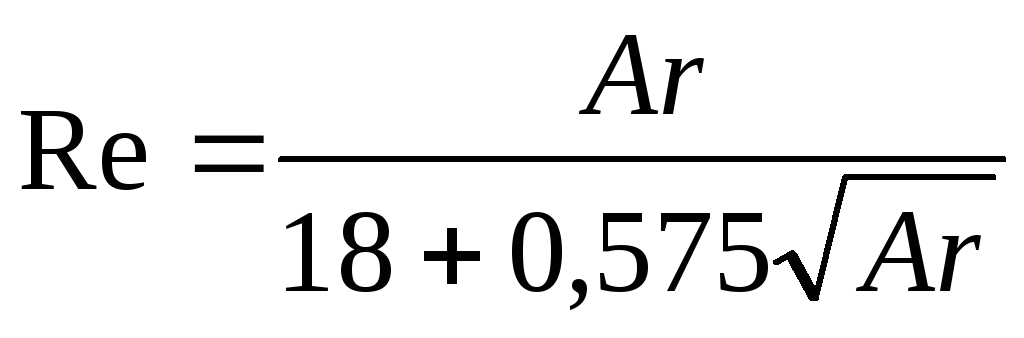(II,73а)

При малых значениях Ar вторым слагаемым в знаменателе можно пренебречь, и уравнение (II,73а) превращается в уравнение (II,120а), соответствующее области действия закона Стокса; при больших же зна­чениях Ar пренебречь можно уже первым слагаемым в знаменателе, и уравнение (II,73) превращается в уравнение (II,72в), отвечающее авто­модельной области.

Скорость осаждения w_ос частиц нешарообразной формы меньше, чем скорость осаждения шарообразных частиц. Чтобы ее рассчитать, значе­ние скорости осаждения w_ос для шарообразных частиц необходимо умно­жить на поправочный коэффициент , называемый коэффициен­том формы

(II,74)

Коэффициент  < 1, и его значения определяют опытным путем. Так, для Частиц округлой формы   0.77, для угловатых частиц   0.66, для продолговатых частиц   0.58 и для пластинчатых частиц   0.43.

Кроме того, при расчете скорости осаждения частиц нешарообразной формы в соответствующие уравнения для определения скорости следует подставлять указанный выше диаметр эквивалентного шара.

Приведенный расчет w_oc и w‘_oc относится к скорости свободного осаждения, при котором осаждающиеся частицы практически не оказывают влияния на движение друг друга. При значительной концен­трации твердых частиц в среде происходит стесненное осажде­ние, скорость которого меньше, чем свободного, вследствие трения и соударений между частицами. Расчет w_ос при стесненном осаждении рас­смотрен позже, посвященной разделению неоднородных смесей.

В случае движения жидких капель в газе или в другой жидкости и пузырьков газа в жидкости уравнения для расчета w_ос усложняются даже для одиночных капель и пузырей вследствие изменения при движе­нии их формы.

studfile.net

1.4. Движение тела в жидкости

Воздействие жидкой или газообразной среды на тело, движущееся в ней с постоянной скоростью v, будет таким же, каким было бы действие на неподвижное тело набегающего на него со скоростью v однородного потока жидкости или газа. Следовательно, при выяснении действующих на тело сил безразлично, что считать движущимся – тело или среду. Удобно предполагать тело неподвижным, а среду движущейся.

Силу F, с которой набегающий поток действует на тело, можно разложить на две составляющие: направленную вдоль скорости v невозмущенного потока силу X, называемую лобовым сопротивлением, и перпендикулярную к v силу Y, называемую подъемной силой. Лобовое сопротивление складывается из сил давления и сил внутреннего трения. Очевидно, что на тело, симметричное относительно направления скорости потока v, может действовать только лобовое сопротивление, подъемная сила в этом случае будет отсутствовать.

Покажем отсутствие лобового сопротивления на примере обтекания идеальной жидкостью очень длинного (бесконечного) цилиндра (Рисунок 2).

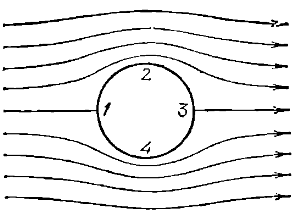
Рис. 2. Обтекание идеальной жидкостью очень длинного (бесконечного) цилиндра

Т.к. идеальная жидкость не обладает вязкостью, то она должна скользить по поверхности цилиндра, полностью обтекая его. Поэтому линии тока должны быть симметричными как относительно прямой, проходящей через точки 1 и 3, так и относительно прямой, проходящей через точки 2 и 4. Теорема Бернулли позволяет по картине линий тока судить о давлении в разных точках потока. Вблизи точек 1 и 3 давление одинаково (больше, чем в невозмущенном потоке, так как скорость вблизи этих точек меньше). Вблизи точек 2 и 4 давление тоже одинаково (меньше, чем в невозмущенном потоке, так как скорость вблизи этих точек больше). Следовательно, результирующая сил давления будет равна нулю. Такой же результат получается для тел любой (в том числе и несимметричной) формы. Этот вывод касается только лобового сопротивления. Подъемная сила, равная нулю для симметричных тел, для несимметричных тел отлична от нуля.

На рисунке 3 показаны линии тока при обтекании идеальной жидкостью полуцилиндра. Вследствие полного обтекания линии тока симметричны относительно прямой, проходящей через точки 2 и 4. Но относительно прямой, проходящей через точки 1 и 3, картина линий тока несимметрична.

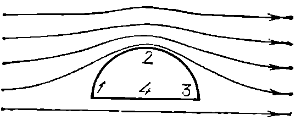
Рис. 3. Линии тока при обтекании идеальной жидкостью полуцилиндра

Вблизи точки 2, где линии гуще, давление меньше, чем вблизи точки 4, в результате чего возникает подъемная сила.

Иначе обстоит дело при движении тела в вязкой жидкости. В этом случае очень тонкий слой жидкости прилипает к поверхности тела и движется с ним как одно целое, увлекая за собой из-за внутреннего трения последующие слои. По мере удаления от поверхности тела скорость слоев становится все меньше и, наконец, на некотором расстоянии от поверхности жидкость будет не возмущенной движением тела. Таким образом, тело оказывается окруженным слоем жидкости с быстро изменяющейся внутри него скоростью. Этот слой называется пограничным. В нем действуют силы вязкого трения, которые, в конечном счете, приложены к телу и приводят к возникновению лобового сопротивления.

Но влияние вязкости не исчерпывается возникновением сил трения. Наличие пограничного слоя изменяет характер обтекания тела жидкостью. Полное обтекание становится невозможным. Действие сил трения в пограничном слое приводит к тому, что поток отрывается от поверхности тела, в результате чего позади тела возникают вихри (Рис. 4).

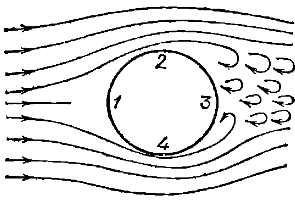
Рис. 4. Появление вихрей

Вихри уносятся потоком и постепенно затухают вследствие трения. При этом энергия вихрей расходуется на нагревание жидкости. Давление, в образующейся за телом вихревой области оказывается пониженным, вследствие чего результирующая сил давления отлична от нуля. Это обуславливает лобовое сопротивление.

Таким образом, лобовое сопротивление складывается из сопротивления трения и сопротивления давления. При данных поперечных размерах тела сопротивление давления сильно зависит от формы тела. Наименьшим сопротивлением давления обладают тела хорошо обтекаемой каплевидной формы.

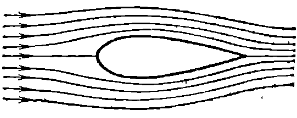
Рис. 5. Обтекание жидкостью тела каплевидной формы

Соотношение между сопротивлением трения и сопротивлением давления определяется значением числа Рейнольдса.

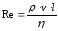_(1.10)

В данном случае v – скорость тела относительно жидкости, l – характерный размер тела (радиус для тела шаровой формы). При малых Re (т.е. при малых v и l) основную роль играет сопротивление трения, так что сопротивлением давления можно пренебречь. С ростом вязкости относительная роль сил трения возрастает. По мере увеличения Re роль сопротивления давления все больше возрастает. При больших значениях Re в лобовом сопротивлении преобладают силы давления.

Число Рейнольдса служит и здесь критерием подобия. Оно определяет характер сил, действующих на тело в потоке жидкости. Это используется в моделировании. Например, модель самолета ведет себя в потоке газа так же, как и её прообраз, если кроме геометрического подобия модели и самолета будет соблюдено равенство для них значений числа Рейнольдса. [4]

Стокс установил, что при небольших скоростях и размерах тел (т.е. при малых Re, когда сопротивление среды обусловлено только силами трения), модуль силы сопротивления определяется формулой

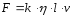. (1.11)

Здесь η – динамическая вязкость среды, v – скорость движения тела, l – характерный размер тела, k – коэффициент пропорциональности, который зависит от формы тела. Для шара, если взять в качестве l его радиус r, коэффициент пропорциональности равен 6π. Следовательно, сила сопротивления движению в жидкостях небольших шариков при малых скоростях равна

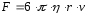(1.12)

Нужно иметь в виду, что формула Стокса справедлива при условии, что расстояние от тела до границ жидкости (до стенок сосуда) намного больше размеров тела. [5]

studfile.net

Ответы@Mail.Ru: Подскажите мне ответы

а) сила сопротивления окружающей среды-жидкости, архимедова сила и, само-собой, сила тяжести. б) сила сопротивления жидкости возрастает прямолинейно скорости по формуле F(сопр. ) = &lt;альфа&gt;*U (альфа — коэффициент) . Шарик будет двигаться равномерно в случае, когда сила сопротивления жидкости будет вызывать ускорение, равное и противоположнонаправленное ускорению свободного падения. То есть, общее ускорение будет равно нулю, поэтому. в) потому что в школьной физике рассматривают идеальные системы отсчета, среды, материальные точки. В такой среде «пренебрегают» сопротивлением воздуха, как это происходит в вакууме. То есть, если подкинуть тело вверх под любым углом с одной скоростью, результирующая конечная скорость перед падением или остановкой на одном уровне над землей будет всегда ниже. Потому что сопротивление среды. Ну, конечно, если тело летит по ветру, это другой случай. д) е) от плотности жидкости, ее вязкости, «влажности» или «сухости» по отношению к веществу из которого изготовлен шарик, скорости движения шарика. ж) мы такого не проходили з) думаю, это связано с турбулентными потоками))) ) логично будет) и) не знаю

Ж. Стокс вывел формулу для силы сопротивления, действующей на шар, движущийся в жидкости поступательно и с постоянной скоростью. Отметим, что формула Стокса справедлива лишь при условии, что при движении шара не возникает турбулентность (завихрение) жидкости. з. и. При турбулентном движении слои жидкости движутся с завихрениями.

touch.otvet.mail.ru

9. Движение тел в жидкостях и газах. Закон Стокса

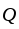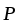При движении тела в жидкости или газе на него действуют две силы: сила , направленная в сторону, противоположную движению тела, а вторая, перпендикулярная к этому направлению. Составляющиеиназываются соответственнолобовым сопротивлением и подъемной силой.

Ясно, что идеальная жидкость не оказывает движению тела никакого сопротивления.

Можно показать, что в несжимаемой идеальной жидкости равномерное движение тела произвольной формы должно было бы происходить без лобового сопротивления. Этот результат называется парадоксом Даламбера.

Учет вязкости жидкости существенно меняет картину взаимодействия тела с потоком. В этом случае очень тонкий слой жидкости прилипает к поверхности тела и движется с ним как одно целое, увлекая за собой из-за трения последующие слои. По мере удаления от поверхности тела скорость слоев становится все меньше и, наконец, на некотором расстоянии от поверхности оказывается практически не возмущенной движением тела. Таким образом, тело оказывается окруженным слоем жидкости, в котором имеется градиент скорости. Этот слой называется пограничным.В нем действуют силы трения, которые и приводят к возникновению лобового сопротивления.

Наличие пограничного слоя существенно меняет характер обтекания тела жидкостью. Полное обтекание тела становится невозможным. Действие сил трения в поверхностном слое приводит к тому, что поток отрывается от поверхности тела, в результате чего позади тела возникают вихри. Вихри уносятся потоком и постепенно затухают вследствие трения. При этом энергия вихрей расходуется на нагревание жидкости. Давление в образующейся за телом вихревой области оказывается пониженным. Поэтому результирующая сил давления будет отлична от нуля. Это давление в свою очередь обуславливает лобовое сопротивление.

Таким образом, лобовое сопротивление складывается из сопротивления трения и сопротивления давления.

При малых числах Рейнольдса сопротивление среды обусловлено практически только силами трения. Стокс установил, что сила сопротивления в этом случае пропорциональна коэффициенту динамической вязкости , скоростидвижения тела относительно жидкости и характерному размеру тела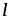: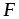~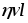. Коэффициент пропорциональности зависит от формы тела. Чаще всего его определяют экспериментальным путем. Вычисления Стокса показали, что для шара коэффициент пропорциональности оказывается равным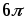. Тогда сила лобового сопротивления для шара радиуса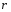при<<1 выражается формулой.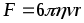

Эта формула известна под названием закона Стокса. Она может быть использована для нахождения вязкости.

При больших числах Рейнольдса влияние вязкости существенно лишь в тонком пограничном слое жидкости, прилегающем к поверхности тела. Как уже было отмечено, это влияние приводит к образованию вихрей сзади тела. Перед телом частицы жидкости в набегающем потоке практически останавливаются, движутся они только за телом. Поэтому, согласно уравнению Бернулли, создается разность давлений, действующих на переднюю 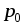и заднююр поверхности тела. Она равна.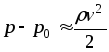

Таким образом, сила лобового сопротивления определяется силой сопротивления давления: .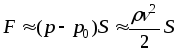

Для тел произвольной формы сила лобового сопротивления представляет вид 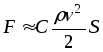, где– наибольшая площадь поперечного сечения тела,С – коэффициент лобового сопротивления.

Величина С зависит от формы тела и числа Рейнольдса. Величина Суменьшается, если уменьшить площадь поперечного сечения тела в том месте, где происходит отрыв потока. Обтекаемые тела испытывают значительно меньшее сопротивление, чем тела с тупой задней частью, так как у первых отрыв потока происходит в задней узкой части тела.

studfile.net

Движение тел в жидкостях и газах — Мегаобучалка

Одной из важнейших задач аэро- и гидродинамики является исследование движе­ния твердых тел в газе и жидкости, в частности изучение тех сил, с которыми среда действует на движущееся тело. а проблема приобрела особенно большое значение в связи с бурным развитием авиации и увеличением скорости движе­ния морских судов.

На тело, движущееся в жидкости или газе, действуют две силы (равнодействующую их обозначим ), одна из которых ( ) направлена в сторону, противопо­ложную движению тела (в сторону по­тока),- лобовое сопротивление,а вторая ( ) перпендикулярна этому направле­нию — подъемная сила(рис.6.9).

Если тело симметрично и его ось сим­метрии совпадает с направлением скоро­сти, то на него действует только лобовое сопротивление, подъемная же сила в этом случае равна нулю. Можно доказать, что в идеальной жидкости равномерное движение происходит без лобового сопро­тивления. Если рассмотреть движение ци­линдра в такой жидкости, то картина линий тока симметрична как от­носительно горизонтального, так и относительно вертикального направлений, т. е. ре­зультирующая сила давления на повер­хность цилиндра будет равна нулю.

Иначе обстоит дело при движении тел в вязкой жидкости (особенно при увеличе­нии скорости обтекания). Вследствие вяз­кости среды в области, прилегающей к по­верхности тела, образуется пограничный слой частиц, движущихся с меньшими ско­ростями. В результате тормозящего дейст­вия этого слоя возникает вращение частиц и движение жидкости в пограничном слое становится вихревым. Если тело не имеет обтекаемой формы (нет плавно утончаю­щейся хвостовой части), то пограничный слой жидкости отрывается от поверхности тела. За телом возникает течение жидко­сти (газа), направленное противоположно набегающему потоку. Оторвавшийся по граничный слой, следуя за этим течением, образует вихри, вращающиеся в противо­положные стороны (рис.6.10).

Лобовое сопротивление зависит от формы тела и его положения относительно потока, что учитывается безразмерным ко­эффициентом сопротивления С_x, определя­емым экспериментально:

R_x = C_x S, (6.15)

где ρ— плотность среды; υ — скорость движения тела; S — наибольшее попере­чное сечение тела.

Составляющую R_xможно значитель­но уменьшить, подобрав тело такой фор­мы, которая не способствует образованию завихрения.

Подъемная сила может быть определе­на формулой, аналогичной (6.15):

R_y = C_y S, (6.16)

где С_у — безразмерный коэффициент подъемной силы.

Основы молекулярной физики и термодинамики

ГЛАВА 7.ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-

КИНЕТИЧЕСКОЙ ТЕОРИИ

Введение

Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.

Идея об атомном строении вещества высказана древнегреческим философом Демокритом Атомистика возрождается в XVII в. и развивается в работах М. В. Ломоносова, взгляды которого на строение вещества и тепловые явления были близки к современным. Строгое развитие молекулярной теории относится к середине XIX в. и связано с работами немецкого физика Р. Клаузиуса, Дж. Максвелла и Л. Больцмана.

Процессы, изучаемые молекулярной физикой, являются результатом совместного действия большого числа молекул. Законы поведения огромного числа молекул изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы определяются свойствами частиц системы, особенностями их движения и усредненнымизначениями динамических характеристик этих частиц (скорости, энергии и т. д.). Например, температура тела определяется скоростью хаотического движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена через среднее значение скорости молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул.

Температура — одно из основных понятий, играющих важную роль не только в термодинамике, но и в физике в целом. Температура – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. Всоответствии с решением XI Генеральной конференции по мерам и весам в настоящее время можно применять только две температурные шкалы — термодинамическую и Международную практическую,градуированные соответственно в кельвинах (К) и в градусах Цельсия (°С). В Международной практической шкалетемпература замерзания и кипения воды при давлении 1,013· 10⁵ Па соответственно 0 и 100°С (реперныеточки).

Термодинамическая шкалаопределяется по одной реперной точке, в качестве которой взята тройная точка воды(температура, при которой лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии). Температура этой точки по термодинамической шкале равна 273,15 К. Градус Цельсия равен кельвину. В термодинамической шкале температура замерзания воды равна 273,15 К (при том же давлении, что и в Международной практической шкале), поэтому термодинамическая температура и температура по Международной практической шкале связаны соотношением

Т=273,15 + t.

Температура T=0 К называется нулем кельвин.Анализ различных процессов показывает, что 0 К недостижим, хотя приближение к нему сколь угодно близко возможно.

В молекулярно-кинетической теории пользуются идеализированной модельюидеального газа,согласно которой считают, что:

1) собственный объем молекул газа мал по сравнению с объемом сосуда;

2) между молекулами газа отсутствуют силы взаимодействия;

3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Модель идеального газа можно использовать при изучении реальных газов, так как они при нормальным условиях, а также при низких давлениях и высоких температурах, близки по своим свойствам к идеальному газу. Кроме того, внеся поправки, учитывающие собственный объем молекул газа и действующие молекулярные силы, можно перейти к теории реальных газов.

megaobuchalka.ru