Теорема косинусов / Соотношения между сторонами и углами треугольника. Скалярное произведение векторов / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
- Теорема косинусов
Теорема
| Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними. |
Доказательство
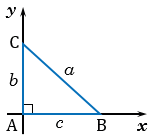
Дано:  АВС, АВ =
АВС, АВ =  , ВС =
, ВС = 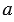 , АС =
, АС = 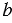
Доказать: . (1)
Доказательство:
Введем прямоугольную систему координат с началом в точке А так, чтобы точка В лежала на положительной полуоси 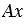 , а точка С имела положительную ординату.
, а точка С имела положительную ординату.
Точка В имеет координаты ( ; 0).
; 0).
Точка С имеет координаты (; 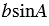 ) (смотри формулы для вычисления координат точки).
) (смотри формулы для вычисления координат точки).
По формуле расстояния между двумя точками получаем:
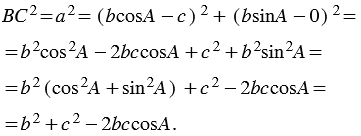
(При выполнении вычислений мы использовали основное тригонометрическое тождество: 
Теорема доказана.
Теорему косинусов еще называют обобщенной теоремой Пифагора. Такое название объясняется тем, что в теореме косинусов содержится как частный случай теорема Пифагора. В самом деле, если в  АВС угол А прямой, то
АВС угол А прямой, то 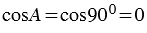 и по формуле (1) получаем , т.е. квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора).
и по формуле (1) получаем , т.е. квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора).
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Синус, косинус, тангенс, котангенс
Основное тригонометрическое тождество. Формулы приведения.
Формулы для вычисления координат точки
Теорема о площади треугольника
Теорема синусов
Решение треугольников
Измерительные работы
Угол между векторами
Скалярное произведение векторов
Скалярное произведение в координатах
Свойства скалярного произведения векторов
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Правило встречается в следующих упражнениях:
7 класс
Задание 1025, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1030, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1031, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1035, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1043, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1070, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1233, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1269, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1274, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
Нахождение длины вектора по теореме косинусов. — КиберПедия
Большинство задач на нахождение длины вектора решаются в координатах. Однако, когда координаты вектора не известны приходится искать другие пути решения.
Пусть известны длины двух векторов , и угол между ними (или косинус угла), а требуется найти длину вектора или . В этом случае можно по теореме косинусов в треугольнике АВС вычислить длину стороны ВС, которая равна искомой длине вектора.
Разберем решение примера для пояснения сказанного.
Пример.
Длины векторов и равны 3 и 7 соответственно, а угол между ними равен . Вычислите длину вектора .
Решение.
Длина вектора равна длине стороны ВС в треугольнике АВС. Из условия нам известны длины сторон АВ и АС этого треугольника (они равны длинам соответствующих векторов), а также угол между ними, поэтому нам достаточно данных для применения теоремы косинусов:
Таким образом, .
Ответ:
.
Итак, для нахождения длины вектора по координатам используем формулы
или ,
по координатам точек начала и конца вектора —
или ,
в некоторых случаях к результату приводит теорема косинусов.
16. Линейно зависимые и линейно независимые системы векторов.
Рассмотрим набор из p n-мерных векторов, обозначим их следующим образом . Составим линейную комбинацию этих векторов и произвольных чисел (действительных или комплексных): . Отталкиваясь от определения операций над n-мерными векторами, а так же свойств операций сложения векторов и умножения вектора на число, можно утверждать, что записанная линейная комбинация представляет собой некоторый
Так мы подошли к определению линейной зависимости системы векторов .
Определение.
Если линейная комбинация может представлять собой нулевой вектор тогда, когда среди чисел есть хотя бы одно, отличное от нуля, то система векторов называется линейно зависимой.
Определение.
Если линейная комбинация представляет собой нулевой вектор только тогда, когда все числа равны нулю, то система векторов называется линейно независимой.
17. Базис пространства R3. Разложение вектора по произвольному базису.
Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.
Приведем некоторые рассуждения, основываясь на этих определениях.
Рассмотрим пространство n-мерных векторов.
Покажем, что размерность этого пространства равна n.
Возьмем систему из n единичных векторов вида
Примем эти векторы в качестве строк матрицы А. В этом случае матрица А будет единичной матрицей размерности n на n. Ранг этой матрицы равен n (при необходимости смотрите статью ранг матрицы: определение, методы нахождения). Следовательно, система векторов линейно независима, причем к этой системе нельзя добавить ни одного вектора, не нарушив ее линейной независимости. Так как число векторов в системе равно n, то размерность пространства n-мерных векторов равна n, а единичные векторы являются базисом этого пространства.
Из последнего утверждения и определения базиса можно сделать вывод, что любая системаn-мерных векторов, число векторов в которой меньше n, не является базисом.
Если переставить местами другие векторы системы , то получим еще один базис.
Если взять линейно независимую систему не единичных векторов, то она также является базисом n-мерного векторного пространства.
Таким образом, векторное пространство размерности n имеет столько базисов, сколько существует линейно независимых систем из n n-мерных векторов.
Если говорить о двумерном векторном пространстве (то есть, о плоскости), то ее базисом являются два любых не коллинеарных вектора. Базисом трехмерного пространства являются три любых некомпланарных вектора.
Рассмотрим несколько примеров.
Пример.
Являются ли векторы базисом трехмерного векторного пространства?
Решение.
Исследуем эту систему векторов на линейную зависимость. Для этого составим матрицу, строками которой будут координаты векторов, и найдем ее ранг:
Таким образом, векторы a, b и c линейно независимы и их количество равно размерности векторного пространства, следовательно, они являются базисом этого пространства.
Ответ:
да, являются.
Пример.
Может ли система векторов быть базисом векторного пространства?
Решение.
Эта система векторов линейно зависима, так как максимальное число линейно независимых трехмерных векторов равно трем. Следовательно, эта система векторов не может быть базисом трехмерного векторного пространства (хотя подсистема исходной системы векторов является базисом).
Ответ:
нет, не может.
Пример.
Убедитесь, что векторы
могут быть базисом четырехмерного векторного пространства.
Решение.
Составим матрицу, приняв ее строками исходные векторы:
Найдем ранг матрицы методом Гаусса:
Таким образом, система векторов a, b, c, d линейно независима и их количество равно размерности векторного пространства, следовательно, a, b, c, d являются его базисом.
Ответ:
исходные векторы действительно являются базисом четырехмерного пространства.
примеры и решения, как найти косинус угла между векторами, вычислите угол между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a→ и b→ , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы OA→=b→ и OB→=b→
Определение 1Углом между векторами a→ и b→ называется угол между лучами ОА и ОВ.
Полученный угол будем обозначать следующим образом: a→,b→^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a→,b→^=0, когда векторы являются сонаправленными и a→,b→^=π , когда векторы противоположнонаправлены.
Определение 2Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π2 радиан.
Если хотя бы один из векторов является нулевым, то угол a→,b→^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a→, b→=a→·b→·cosa→,b→^.
Если заданные векторы a→ и b→ ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cosa→,b→^=a→,b→
Скалярное произведение в координатах. Свойство скалярного произведения
На этом уроке мы выведем формулу, которая позволяет находить скалярное произведение векторов через их координаты, и рассмотрим свойства скалярного произведения.
Вначале сформулируем и докажем формулу для выражения скалярного произведения через координаты для неколлинеарных векторов. Далее рассмотрим скалярное произведение в координатах для коллинеарных векторов – сонаправленных и противоположно направленных. Рассмотрим следствия из полученной формулы в координатах о перпендикулярных векторах и о косинусе угла между ненулевыми векторами. Сформулируем и докажем свойства скалярного произведения: переместительный, распределительный и сочетательный законы и неотрицательность скалярного квадрата.
В конце урока решим несколько задач на использование свойств скалярного произведения и нахождения косинуса угла.
Тема: Соотношения между сторонами и углами треугольника. Раздел 3. Скалярное произведение векторов
Урок: Скалярное произведение векторов в координатах
Тема урока: «Скалярное произведение векторов в координатах. Свойства скалярного произведения». На этом уроке мы выведем формулу вычисления скалярного произведения через координаты векторов, рассмотрим свойства скалярного произведения и решим задачу на использование свойств скалярного произведения векторов.
Сформулируем и докажем центральную теорему урока.
Теорема. Скалярное произведение векторов 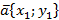 и
и 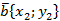 выражается формулой
выражается формулой
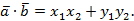

Доказательство.
1. При 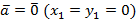 или
или 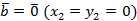 теорема очевидна.
теорема очевидна.
2. Пусть 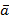 и
и 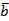 – ненулевые векторы. Тогда по теореме косинусов
– ненулевые векторы. Тогда по теореме косинусов
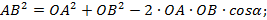
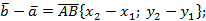
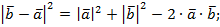
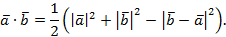
Перейдем в этой формуле к координатам.

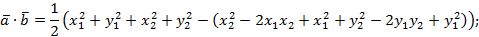
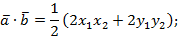
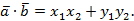
Уточним, что теорема доказана для случая неколлинеарных векторов, в доказательстве был использован треугольник, теорема косинусов, поэтому случай коллинеарных векторов тоже рассмотрим, при этом учтем, что угол между коллинеарными векторами может быть равен 180° или 0°.
3. Пусть 
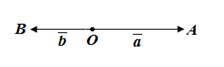
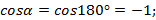

Подгоним это равенство под формулу, полученную при доказательстве теоремы.

Формула та же самая, если записать ее в координатах, то получим
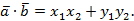
4. Аналогично рассмотрим случай 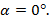



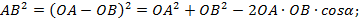
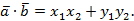
Вывод: 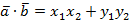 для всех векторов
для всех векторов 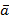 и
и 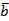 .
.
Сформулируем следствия из доказанной теоремы.
Следствие 1. Ненулевые векторы 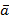 и
и 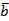 перпендикулярны тогда и только тогда, когда
перпендикулярны тогда и только тогда, когда  .
.
Действительно, 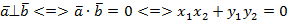 .
.
Следствие 2. Косинус угла между ненулевыми векторами 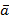 и
и 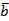 выражается формулой:
выражается формулой:
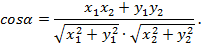
Действительно, 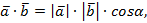

Рассмотрим свойства скалярного произведения векторов.
Для любых векторов 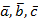 и любого числа k справедливы соотношения:
и любого числа k справедливы соотношения:
1. 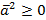 , причем
, причем 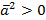 при
при 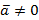 .
.
Доказательство.
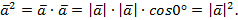
Но  при
при  .
.
2. 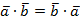 (переместительный закон).
(переместительный закон).
Доказательство (из определения).

3. 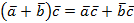 (распределительный закон).
(распределительный закон).
Доказательство.
Для доказательства используем метод координат.
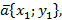
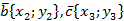 , тогда
, тогда
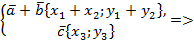
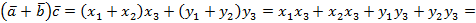
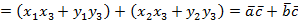 .
.
4. 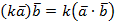 (сочетательный закон).
(сочетательный закон).
Доказательство.
 , значит,
, значит,
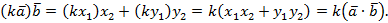
Замечание. Распределительный закон справедлив и в случае нескольких слагаемых, например,
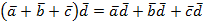 .
.
Задача. Вычислить скалярное произведение векторов  и
и 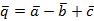 , если
, если 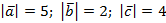 и
и 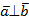 .
.
Решение.
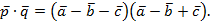
По свойствам скалярного произведения
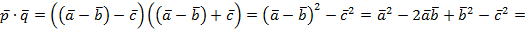
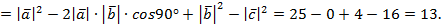
Ответ: 13.
Итак, мы вывели формулу вычисления скалярного произведения векторов через координаты векторов, доказали свойства скалярного произведения и решили задачу на вычисление скалярного произведения с использованием свойств скалярного произведения.
На следующем уроке мы рассмотрим решение задач на вычисление скалярного произведения.
Список литературы
- Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
- Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
- Погорелов А. В. Геометрия. Уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- E-science.ru (Источник).
- Mathematics.ru (Источник).
Домашнее задание
- Атанасян Л. С. и др. Геометрия 7–9 классы. №№1044, 1048.
Теорема косинусов и ее доказательство.
См. также Теорема синусов.
Теорема косинусов является обобщением теоремы Пифагора для произвольного треугольника.
Формулировка теоремы косинусов
Для плоского треугольника со сторонами a,b,c и углом α, противолежащим стороне a, справедливо соотношение:
| Квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними |
Полезные формулы теоремы косинусов:
Как видно из указанного выше, с помощью теоремы косинусов можно найти не только сторону треугольника по двум сторонам и углу между ними, можно, зная размеры всех сторон треугольника, определить косинусы всех углов, а также вычислить величину любого угла треугольника. Вычисление любого угла треугольника по его сторонам является следствием преобразования формулы теоремы косинусов.
Доказательство теоремы косинусов
Рассмотрим произвольный треугольник ABC. Предположим, что нам известна величина стороны AC (она равна некому числу b), величина стороны AB (она равна некому числу c) и угол между этими сторонами, величина которого равна α. Найдем величину стороны BC (обозначив ее длину через переменную a)
Для доказательства теоремы косинусов проведем дополнительные построения. Из вершины C на сторону AB опустим высоту CD.
Найдем длину стороны AB. Как видно из рисунка, в результате дополнительного построения можно сказать, что
AB = AD + BD
Найдем длину отрезка AD. Исходя из того, что треугольник ADC является прямоугольным, нам известны длина его гипотенузы (b) и угол (α) то величину стороны AD можно найти из соотношения его сторон, пользуясь свойствами тригонометрических функций в прямоугольном треугольнике:
AD / AC = cos α
откуда
AD = AC cos α
AD = b cos α
Длину стороны BD найдем как разность AB и AD:
BD = AB — AD
BD = c − b cos α
Теперь запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
для треугольника BDC
CD2 + BD2 = BC2
для треугольника ADC
CD2 + AD2 = AC2
Обратим внимание на то, что оба треугольника имеют общую сторону — CD. Определим ее длину для каждого треугольника — вынесем ее значение в левую часть выражения, а остальное — в правую.
CD2 = BC2 — BD2
CD2 = AC2 — AD2
Поскольку левые части уравнений (квадрат стороны CD) равны, то приравняем правые части уравнений:
BC2 — BD2 = AC2 — AD2
Исходя из сделанных ранее вычислений, мы уже знаем что:
AD = b cos α
BD = c − b cos α
AC = b (по условию)
А значение стороны BC обозначим как a.
BC = a
(Именно его нам и нужно найти)
Получим:
BC2 — BD2 = AC2 — AD2
Заменим буквенные обозначения сторон на результаты наших вычислений
a2 — ( c − b cos α )2 = b2 — ( b cos α )2
перенесем неизвестное значение (а) на левую сторону, а остальные части уравнения — на правую
a2 = ( c − b cos α )2 + b2 — ( b cos α )2
раскроем скобки
a2 = b2 + c 2 — 2c b cos α + ( b cos α )2 — ( b cos α )2
получаем
a2 = b2 + c 2 — 2bc cos α
Теорема косинусов доказана.
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.
Теорема косинусов — Тригонометрия
Формулировка теоремы косинусов:Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними.
Доказательство теоремы косинусов:
Рассмотрим треугольник ABC.
Из вершины C на сторону AB опустим высоту CD.
Исходя из того, что треугольник ADC является прямоугольным, то
величину стороны AD можно найти из соотношения тригонометрических
функций :
AD / AC = cos α
AD = AC
cos α
AD = b cos α
Длину стороны BD найдем как разность AB и AD:
BD = AB — AD
BD = c − b cosα
Теперь запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
CD2 + BD2 = BC2
CD2 + AD2 = AC2
откуда
CD2 = BC2 — BD2
CD2 = AC2 —
AD2
Поскольку левые части уравнений равны, то приравняем правые части уравнений:
BC2 — BD2 =
AC2 —
AD2
a2 — ( c − b cos α )2 = b2 — ( b cos α )2
a2 = ( c − b cos α )2 + b2 — ( b cos α )2
a2 = b2 + c 2 — 2bc cos α + ( b cos α )2 — ( b cos α )2
a2 = b2 + c 2 — 2bc cos α
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), по
Сферические теоремы косинусов — Википедия
Материал из Википедии — свободной энциклопедии
 Сферический треугольник.
Сферический треугольник.Первая и вторая сферические теоремы косинусов устанавливают соотношения между сторонами и противолежащими им углами сферического треугольника.
Теоремы косинусов для сферического треугольника со сторонами a, b, c и углами A, B, C имеют следующий вид:
- cosc=cosacosb+sinasinbcosC,{\displaystyle \cos c=\cos a\cos b+\sin a\sin b\cos C,}
- cosA=−cosBcosC+sinBsinCcosa.{\displaystyle \cos A=-\cos B\cos C+\sin B\sin C\cos a.}
Эти две теоремы двойственны по отношению друг к другу, поскольку углы и стороны всякого сферического треугольника дополняются до развёрнутого угла сторонами и углами соответствующего полярного треугольника. Поэтому достаточно доказать одну из них.
Доказательство
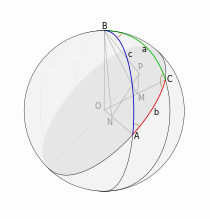 Рисунок к доказательству теоремы косинусов с помощью проекций.
Рисунок к доказательству теоремы косинусов с помощью проекций.Доказательство проведём с помощью проекций[1]. На рисунке показан сферический треугольник ABC на сфере радиуса R с центром в точке O. BP — перпендикуляр к плоскости большого круга, проходящего через сторону b, BM — перпендикуляр к OC, BN — перпендикуляр к OA. По утверждению, обратному теореме о трёх перпендикулярах, PM — перпендикуляр к OC, PN — перпендикуляр к OA. Заметим, что угол PMB равен π — C, кроме того, ON = R cos c и OM = R cos a. Далее, проецируем ломаную OMPN на прямую, содержащую ON.
- pr ON=pr OM+pr MP+pr PN{\displaystyle {\mbox{pr }}ON={\mbox{pr }}OM+{\mbox{pr }}MP+{\mbox{pr }}PN},
- PN⊥OA⇒pr PN=0{\displaystyle PN\perp OA\Rightarrow {\mbox{pr }}PN=0},
- pr OM=OMcosb=Rcosacosb{\displaystyle {\mbox{pr }}OM=OM\cos b=R\cos a\cos b},
- pr MP=PMcos(π−(π2−∠MPN))=PM(−sin∠MPN){\displaystyle {\mbox{pr }}MP=PM\cos(\pi -({\frac {\pi }{2}}-\angle MPN))=PM(-\sin \angle MPN)}
- =BMcos∠PMB(−sinb)=BMcos(π−C)(−sinb)=RsinbsinacosC{\displaystyle =BM\cos \angle PMB(-\sin b)=BM\cos(\pi -C)(-\sin b)=R\sin b\sin a\cos C}.
Подставляем три последних выражения и указанное выше выражение ON = R cos c в первое выражение и получаем:
- cosc=cosacosb+sinasinbcosC{\displaystyle \cos c=\cos a\cos b+\sin a\sin b\cos C}.
Теоремы косинусов для двух других сторон, то есть теорему для cos a и теорему для cos b, получаем аналогично, их также можно получить сразу из формулы для стороны c при помощи круговой перестановки букв:
a→b→c→a,A→B→C→A{\displaystyle a\rightarrow b\rightarrow c\rightarrow a,A\rightarrow B\rightarrow C\rightarrow A}
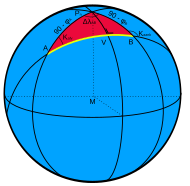 Сферический треугольник для определения кратчайшего расстояния между точками на Земле.
Сферический треугольник для определения кратчайшего расстояния между точками на Земле.Если угол C — прямой, первая теорема косинусов переходит в сферическую теорему Пифагора:
- cosc=cosacosb.{\displaystyle \cos c=\cos a\cos b.}
Хотя для решения косоугольных сферических треугольников обычно используются более удобные формулы, с помощью теоремы косинусов выводится важная для геодезии формула длины ортодромии — кратчайшего расстояния между точками на земной поверхности с известными координатами (в предположении сферичности Земли). Обозначим географические широты двух данных точек φA{\displaystyle \varphi _{A}} и φB{\displaystyle \varphi _{B}}, разность долгот — ΔλAB{\displaystyle \Delta \lambda _{AB}}, кратчайшее расстояние между ними обозначим d, длину дуги в 1 градус — a. Тогда формула длины ортодромии[2]:
- cos(da)=sinφA⋅sinφB+cosφA⋅cosφB⋅cosΔλAB{\displaystyle \cos \left({\frac {d}{a}}\right)=\sin \varphi _{A}\cdot \sin \varphi _{B}+\cos \varphi _{A}\cdot \cos \varphi _{B}\cdot \cos \Delta \lambda _{AB}}
Эта формула сразу получается применением теоремы косинусов к стороне AB сферического треугольника PnAB. Подобная формула справедлива для любой сферической поверхности и поэтому её можно применять также для определения углового расстояния между звёздами по известным их экваториальным координатам[3].
Пример 1: определение углового расстояния между двумя светилами на небесной сфере
Определим угловое расстояние (x) между звездой δ Цефея (экваториальные координаты: α1=22ч 29м, δ1=+58° 25′) и галактикой Туманность Андромеды (α2=0ч 43м, δ2=+41° 16′) на небесной сфере. Выражаем α1 в градусах и долях градуса:
- α1=(22+2960)⋅36024=337∘,25{\displaystyle \alpha _{1}=\left(22+{\frac {29}{60}}\right)\cdot {\frac {360}{24}}=337^{\circ },25}
Аналогично получаем, что α2=10°,75. Выражаем δ1 в градусах и долях градуса:
- δ1=58+2560=58∘,42{\displaystyle \delta _{1}=58+{\frac {25}{60}}=58^{\circ },42}
Аналогично δ2=41°,27. Применяем теорему косинусов[4]:
cosx=cos(90∘−δ1)⋅cos(90∘−δ2)+sin(90∘−δ1)⋅sin(90∘−δ2)⋅cos(α1−α2)=sin58∘,42⋅sin41∘,27+cos58∘,42⋅cos41∘,27⋅cos(337∘,25−10∘,75)=0,89{\displaystyle {\begin{aligned}\cos x&=\cos(90^{\circ }-\delta _{1})\cdot \cos(90^{\circ }-\delta _{2})+\sin(90^{\circ }-\delta _{1})\cdot \sin(90^{\circ }-\delta _{2})\cdot \cos(\alpha _{1}-\alpha _{2})\\&=\sin 58^{\circ },42\cdot \sin 41^{\circ },27+\cos 58^{\circ },42\cdot \cos 41^{\circ },27\cdot \cos(337^{\circ },25-10^{\circ },75)\\&=0,89\end{aligned}}}
Отсюда x=27°,11.
Теорема косинусов в её втором виде (соотношение между тремя углами и стороной) может быть применена для вычисления взаимного наклонения двух орбит при известном наклонении каждой орбиты к какой-то другой плоскости. Например, по этой формуле можно вычислить наклонение орбиты Плутона к орбите Нептуна, используя наклонения их орбит к эклиптике и долготы их восходящих узлов.
Пример 2: определение взаимного наклонения орбит небесных тел
Определим взаимное наклонение (x) орбит Плутона (наклонение орбиты к эклиптике — 17°,14, долгота восходящего узла — 110°,30) и Нептуна (наклонение орбиты к эклиптике — 1°,77, долгота восходящего узла — 131°,79). В соответствующем сферическом треугольнике известны два угла: один равен наклонению орбиты Плутона к эклиптике, другой — дополнению наклонения орбиты Нептуна к эклиптике до 180 градусов. Известна также прилегающая к этим углам сторона, равная разности долгот восходящих узлов Плутона и Нептуна. Осталось применить второй вариант теоремы косинусов — для углов:
cosx=−cos(17∘,14)⋅cos(180∘−1∘,77)+sin(17∘,14)⋅sin(180∘−1∘,77)⋅cos(131∘,79−110∘,30)≈0,9636{\displaystyle {\begin{aligned}\cos x&=-\cos(17^{\circ },14)\cdot \cos(180^{\circ }-1^{\circ },77)+\sin(17^{\circ },14)\cdot \sin(180^{\circ }-1^{\circ },77)\cdot \cos(131^{\circ },79-110^{\circ },30)\\&\approx 0,9636\\\end{aligned}}}
Отсюда x≈15°,51.
Математики средневекового Востока использовали утверждение, равносильное сферической теореме косинусов, при решении конкретных астрономических задач. Эти соотношения, используемые при определении высоты Солнца, встречаются в сочинениях Сабита ибн Корры, ал-Махани, ал-Баттани, Ибн Юниса, ал-Бируни.
Первая явная формулировка теоремы дана в XV веке Региомонтаном, который назвал её «теоремой Альбатегния» (по латинизированному имени ал-Баттани).
- ↑ Приводится по изданию: Степанов Н.Н. Формулы косинуса стороны // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 24—28. — 154 с.
- ↑ Михайлов В.С., Кудрявцев В.Г., Давыдов В.С. 26.2. Основные формулы ортодромии. Способы её задания // Навигация и лоция. — Киев, 2009.
- ↑ Меёс Ж. 9. Угловое расстояние между объектами // Астрономические формулы для калькуляторов. — Мир, 1988. — С. 44—46. — 168 с. — ISBN 5030009361.
- ↑ Lee Kai Ming. PHYS 2021 — The Physical Universe. — 2010. — С. 6. Архивировано 3 декабря 2008 года.
- Вентцель М. К. Сферическая тригонометрия. 2-е изд., ИГКЛ, 1948, 115с.
- Матвиевская Г. П. Очерки истории тригонометрии. Ташкент: Фан, 1990.
- Степанов Н. Н. Сферическая тригонометрия. — Л.-М., 1948.