разные способы доказательства обратной теоремы по геометрии в 8 классе и задачи с примерами решения для этого

Доказательство теоремы Пифагора. Теорема эта известна с давних древних времён. И, справедливости ради, стоит сказать, что не Пифагор открыл, выявил и обнаружил данную геометрическую связь в прямоугольном треугольнике. Это и понятно из простого здравого смысла.

Ещё за долго до рождения Пифагора были построены пирамиды в Египте, и не только там, но и в Китае и многих других местах земли. И, разумеется, сеё факт был известен всем строителям и землемерам древности. Заслуга Пифагора в том, что он её задокументировал и далее передал потомкам.

Доказательство теоремы Пифагора

 

В той статье мы с вами рассмотрим два доказательства: одно из них даётся в школьном курсе математики, другое показывает геометрическое – показывается соответствие площадей квадратов построенных на сторонах треугольника (с ним учеников знакомят далеко не везде). Вы наглядно без лишнего формализма увидите почему квадрат большей стороны прямоугольного треугольника равен сумме квадратов двух других его сторон.

Теорема Пифагора: квадрат гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов.

Доказательство первое.

Представим прямоугольный треугольник следующим образом — построим квадрат, в него впишем (произвольно) ещё один квадрат так что его вершины будут лежать на сторонах первого квадрата.

Получим четыре равных прямоугольных треугольника. Обозначим катеты треугольников соответственно как a и b:

Выразим площадь большего квадрата:

Также она равна сумме четырёх треугольников и квадрата со стороной с:

Можем записать:

Теорема доказана.

Второе доказательство.

Так как «квадрат стороны треугольника» геометрически это квадрат сторона которого равна стороне указанного треугольника, то построим квадраты на катетах и гипотенузе треугольника: Нам нужно показать, что площадь квадрата построенного на гипотенузе равна сумме площадей квадратов построенных на катетах.

Выполним дополнительные построения. Каким образом? Сначала строим квадрат симметричный квадрату построенному на большем катете (он показан серым цветом), а затем остальные элементы:

Определим равные элементы. Для наглядности используем цвета:

*Треугольник «3+8» мы разделили таким образом, что сторона четырёхугольника «8» равна стороне квадрата построенного на малом катете.

Теперь внимание!

«Уложим» квадрат «1» на квадрат построенный на гипотенузе. Площадь квадрата «1» равна площади квадрата «10+9+2». Фигура «2» заняла часть квадрата построенного на гипотенузе. Треугольник «10» равен треугольнику «4» (признак равенства – по гипотенузе и острому углу). Треугольник «9» равен треугольнику «3» (по катету и острому углу).

Итак! Квадрат «1» мы уместили.

Источник: https://matematikalegko.ru/formuli/dokazatelstvo-teoremy-pifagora.html

Теорема Пифагора доказательство

Обращаясь к истории, теорема Пифагора хоть и носит название Пифагора, но открыл ее не он. Так как особые свойства прямоугольного прямоугольника ученые начали изучать намного раньше его. Тем не менее есть два утверждения. Первое гласит о том что Пифагор доказал теорему.

Второе, соответственно что не он. На данным момент не проверить какое из этих мнений верно, но к сожалению, если и было доказательство Пифагора, то оно не дожило до нашего времени. Так же есть мнение что доказательство сделанное Евклидом, было сделано Пифагором, а Евклид его обнародовал.

Несомненно в Египте во времена правления фараонов, возникали вопросы с прямоугольным треугольником. В истории Вавилона он так же участвовал. Из чего можно сделать вывод, что данная теорема, вызывала интерес с древних времен. На сегодняшний день существует 367 различных доказательств.

Чем не может похвастать ни какая другая теорема.

Заметка: Если Вы ищите мебель для лаборатории или просто хотите приобрести вытяжной шкаф (http://www.labmet.ru/shkafy-vytyazhnye.html). Перейдите по данной ссылке и купите все что нужно. Качество гарантированно!

Разберем основные доказательства.

1. Теорема Пифагора доказательство.

Считается что это легкий способ. В нем применяются правильные треугольники.

Если взять равнобедренный прямоугольный треугольник АВС, от гипотенузы АС мы сможем построить квадрат, в котором находятся 4 аналогичных треугольника. С помощью катета АВ и ВС строятся квадраты, содержащие в себе еще по два таких же треугольника.

2. Теорема Пифагора доказательство.

Здесь сочетается как алгебра так и геометрия. Изображаем прямоугольный треугольник abc. И 2 квадрата равных двум длинам катетов а+b. Затем сделаем построение, как на рисунках 2, 3. Вследствие чего получим два квадрата со сторонами а и b.

Второй квадрат содержит 4 треугольника, образуя таким образом квадрат равный гипотенузе c. Интересно что общая площадь квадратов на рис. 2, 3 равная друг другу.
Обобщая все в формулу мы получим. а2+b2 = (а+b)2 — 4 * 1/2 * а * b. Раскрыв скобки получим а2+b2= а2+b2. Площадь рис. 3 вычисляем как S=c2 или а2+b2=с2.ч.т.д.

3. Теорема Пифагора доказательство.

Доказательство найдено в 12 вв, в древней индии.

Построим в квадрате 4 треугольника (прямоугольных). Гипотенузой будет сторона с, катетами в треугольнике а и b. Вычисляем площади квадратов большой- S=c2, и внутренний (а-b)2 2 +4 * 1/2 * а * b. Из чего вывод, что с2= (а-b)2 2+ 4 * 1/2 * а * b, а следовательно, с2= а2+b2.

Источник: https://reshit.ru/Teorema-Pifagora-dokazatelstvo

Теорема Пифагора: формула, доказательство. Обратная теорема

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Если   ∠A = 90°, то   a² + b² = c².

Доказательство:

Возьмём прямоугольный треугольник с катетами a, b и гипотенузой c:

Достроим этот треугольник до квадрата со стороной a + b:

Площадь данного квадрата S будет равна (a + b)²:

S = (a + b)²

С другой стороны, площадь этого квадрата состоит из четырёх одинаковых треугольник, площадь каждого из которых равна половине произведения их катетов (ab : 2), и квадрата со стороной c, поэтому:

S = (a + b)²

или

S = 4 · (	ab	)  + c2 = 2ab + c2
	2

Таким образом:

(a + b)² = 2ab + c²

Так квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

(a + b)² = a² + 2ab + b²,

то для того, чтобы наше равенство было верным  c²  должен быть равен  a² + b².

Таким образом,   (a + b)² = 2ab + c², где   c² = a² + b².

Теорема доказана.

Обратная теорема Пифагора

Обратная теорема Пифагора:

Если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других сторон, то этот треугольник – прямоугольный.

Если   a² +

b² = c², то треугольник ABC – прямоугольный.

Доказательство:

Возьмём треугольник ABC со сторонами  a, b  и  c, у которого  c² = a² + b². Докажем, что  ∠A = 90°:

Рассмотрим прямоугольный треугольник  A₁B₁C₁  с прямым углом  A₁, у которого   A₁B₁ = a   и   A₁C₁ = b:

По теореме Пифагора:

B₁C₁² = A₁B₁² + A₁C₁²

Значит  B₁C₁² = a² + b². Но  a² + b² = c² по условию теоремы. Следовательно  B₁C₁² = c², откуда можно сделать вывод  B₁C₁ = c.

Треугольники  ABC  и  A₁B₁C₁  равны по трём сторонам, поэтому  ∠A = ∠A₁ = 90°, то есть треугольник  ABC  является прямоугольным. Теорема доказана.

Доказательства теоремы Пифагора

Доказательства теоремы Пифагора

 

 

 

Выполнила:

 ученица 11 А класса

Дубицкая Милена

 Руководитель:

учитель математики

Лапко Ирина Валентиновна

 

Содержание

Введение

Основная часть

1. Биография Пифагора

2. Из истории теоремы Пифагора

3. Пять способов доказательства теоремы Пифагора

3.1 Древнекитайское доказательство

3.2. Доказательство простейшее

3.3. Доказательство Хоукинсa

3.4. Доказательство Вальдхейма

3.5. Доказательство Евклида

Заключение

Список литературы

 

Введение

 

    Теорема Пифагора с древнейших лет употребилась в разных спектрах науки, техники и жизни. О ней писали в своих произведениях римский архитектор и инженер Витрувий, греческий писатель-моралист Плутарх, греческий учёный 3 в. Диоген Лаэрций и многие другие. Существует легенда о том, что в честь своего открытия Пифагор принёс в жертву быка или, как рассказывают другие, сто быков. Именно она послужила поводом для юмора в рассказах писателей и в стихах поэтов. Поэт Генрих Гейне(1797-1856), который славился антирелигиозными взглядами и язвительными насмешками над суевериями, в одном из своих произведений высмеивает «учение» о переселении душ следующим образом: «Кто знает! Кто знает! Душа Пифагора поселилась, быть может, бедняку — кандидата, не сумевшего доказать теоремы Пифагора и поэтому провалившегося на экзамене, тогда как в его экзаменаторах обитают души тех самых быков, которых некогда Пифагор принес в жертву бессмертным богам, обрадованный открытием своей теоремы». Возникновение Пифагоровой теоремы начинается задолго до Пифагора. В течение многих лет были сделаны самые разные доказательства теоремы Пифагора.

Цель : узнать историю возникновения доказательства теоремы Пифагора, повысить интерес к точным наукам у учеников. Увидеть сходства и различия между доказательствами.

Задачи :

1) Узнать об учёных ,которые доказали теорему.

2) Узнать об истории доказательства теоремы.

3) Проанализировать другие доказательства.

3) Сделать выводы.

Методы исследования:

1) Изучение и анализ литературы по данной теме.

2) Использование Интернет-ресурсов.

1. Биография Пифагора

   Пифагор Самосский (570—490 гг. до н. э.) — философ, математик, основатель религиозно-философской школы пифагорейцев.

   Родители Пифагора жили на острове Самос. В одних источниках отец ученого был камнерезом, а в других – богатым купцом. Мать Пифагора была из знатного рода Анкея, который являлся основателем греческой колонии Самоса. По преданию рождение ученого предсказала Пифия в Дельфах. Отметим, что имя Пифагор буквально значит «тот, о ком объявила Пифия». Ученый родился в Сидоне Финикийском.

   Античные авторы утверждают, что Пифагор общался со многими известными мудрецами своей эпохи (греками, халдеями, персами, египтянами). В частности, еще в юности он отправился в Египет, где познакомился с местными жрецами. Некоторые авторы утверждают, что он проник в таинства, которые были запретны для чужеземцев.

   Затем Пифагор в числе пленников персидского царя Камбиза попал Вавилон. Здесь он пробыл около 12 лет, пока не вернулся на Самос в 56-летнем возрасте. Античные авторы отмечают, что по возращению на родину соотечественники признали его мудрецом.

   Но существует и другая версия. В частности, по Порфирию, ученый в 40-летнем возрасте покинул родину, потому что был не согласен с тиранической властью Поликрата. Таким образом, неизвестно, посещал ли математик Вавилон и Египет. Хотя современные историки утверждают, что Пифагор мог покинуть Самос не столько из-за разногласий с властью, сколько из желания проповедовать свое учение. Если придерживаться этого мнения, то покинув родину, Пифагор поселился в Кротоне (Южная Италия). Здесь он нашел много последователей, которых привлекала его философия и образ жизни.

   Ученики Пифагора образовали своеобразное братство посвященных, которое состояло из касты отобранных единомышленников, обожествляющих своего учителя. Долгое время он имел огромное влияние в упомянутой греческой колонии. Но из-за в антипифагорейских настроений в Кротоне философ вынужден был перебраться в Метапонт, где и скончался. Так, существует легенда, будто удрученный Пифагор уморил себя голодом.

  Последователи Пифагора пытались изменить законодательство в своих городах. Но большинство населения не разделяло идеалов философа, что вылилось в мятежи в Таренте и Кротоне. Многие пифагорейцы погибли в этих стычка, а другие рассеялись по Греции и Италии. Порфирий отмечает, что и сам Пифагор погиб во время антипифагорейского мятежа в Метапонте.

 

2. Из истории теоремы Пифагора

   На сегодняшний день известно, что эта теорема не была доказана Пифагором. Но некоторые думают, что именно Пифагор полностью доказал её, а другие отрицают этот факт. Многие отдают Пифагору доказательство, которое Евклид приводит в первой книге своих «Начал». Однако, Прокл утверждает, что доказательство в «Началах» принадлежит самому Евклиду.

   Как нам видно, история мало что сохранила о Пифагоре и его математической жизни. Но легенда ведает близкую информацию, сопровождающую открытие теоремы.

   Историю теоремы Пифагора начнем с древнего Китая. Здесь особую роль играет математическая книга Чупей. В этом произведении рассказывается о треугольнике Пифагора со сторонами 3, 4 и 5 следующее:

  «Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4» .

   С лёгкостью можно изобразить способ построения. К верёвке длиною в 12 м. привяжем по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого.

  Прямой угол сосредоточится между сторонами длиной в 3 и 4 метра. В этой книге изображён рисунок, который сопоставляется с одним из чертежей индусской геометрии Басхары.

   Кантор (крупнейший немецкий историк математики) утверждает, что равенство 3 І + 4 І = 5І знали египтяне около 2300 г. до н. э., во времена царя Аменемхета.

  Он был уверен, что «натягиватели веревок» проектировали прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

   Немного больше знали о теореме Пифагора вавилоняне. В некотором рассказе, прилежащем ко времени Хаммураби, т.е. к 2000 году до нашей эры, повествуется приближенное вычисление гипотенузы прямоугольного треугольника; следовательно, в Двуречье могли вычислять прямоугольные треугольниками в несложных случаях.

  У индусов геометрия пересекалась с культом. Из этого следует, что о теореме, о квадрате гипотенузы знали в Индии около 8 века до нашей эры.

   В средние века теорема Пифагора определяла границу, если не наибольших возможных, то, по крайней мере, хороших математических знаний. Весьма узнаваемый чертеж теоремы Пифагора, который и сейчас рисуется учениками, например, в облаченного в мантию профессора или человека в цилиндре, в те времена часто употреблялся как символ математики.

   Приведем иные интерпретации теоремы Пифагора в переводе с греческого, латинского и немецкого языков.

   Теорема Евклида гласит:

«В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол».

   Латинский перевод арабского текста Аннариции (около 900 года до нашей эры), сделанный Герхардом Кремонским (12 век) гласит (в переводе):

   «Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол»

   В Geometry Culmonensis (около 1400года) теорема читается так (в переводе):

“Итак, площадь квадрата, измеренного по длиной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу”

   В русском переводе «Начал» Евклида, теорема Пифагора изображена так: «В прямоугольном треугольнике квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол».

   Можно заметить, во многих странах и многих языках существуют разные варианты трактовки всем известной теоремы. Появившиеся в различное время и в различных языках, они показывают задачи одной математической закономерности, доказательство которой имеет много вариантов.

3. Пять способов доказательства теоремы Пифагора.

3.1. Древнекитайское доказательство.

   На древнекитайском чертеже (приложение 1) четыре равных прямоугольных треугольника с катетами a , b и гипотенузой с расположены так, что их внешний контур образует квадрат со стороной a + b , а внутренний — квадрат со стороной с, построенный на гипотенузе:

a2 + 2ab +b2 = c2 + 2ab

a2 +b2 = c2

3.2. Доказательство простейшее.

   Это доказательство получается в простейшем случае равнобедренного прямоугольного треугольника. Видимо, с него и начиналась теорема.

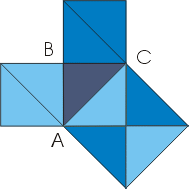
   Оказывается, стоит только посмотреть на сетку равнобедренных прямоугольных треугольников (приложение 2), чтобы убедиться в справедливости теоремы. Например, для треугольника АВС: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, — по два.

Теорема доказана.

3.3. Доказательство Хоукинсa.

   Приведем еще одно доказательство, которое имеет вычислительный характер, однако сильно отличается от всех предыдущих. Оно опубликовано англичанином Хоукинсом в 1909 году; было ли оно известно до этого- трудно сказать. Прямоугольный треугольник ABC с прямым углом C (приложение 3) повернем на 90° так, чтобы он занял положение A’CB’. Продолжим гипотенузу A’В’ за точку A’ до пересечения с линией АВ в точке D. Отрезок В’D будет высотой треугольника В’АВ. Рассмотрим теперь заштрихованный четырехугольник A’АВ’В . Его можно разложить на два равнобедренных треугольника САA’ и СВВ’ (или на два треугольника A’В’А и A’В’В).

SCAA’=b²/2

SCBB’=a²/2

SA’AB’B=(a²+b²)/2

Треугольники A’В’А и A’В’В имеют общее основание с и высоты DA и DB, поэтому :

SA’AB’B=c*DA/2+ c*DB/2=c(DA+DB)/2=c²/2

Сравнивая два полученных выражения для площади, получим:

a²+b²=c²

Теорема доказана.

3.4. Доказательство Вальдхейма.

   Это доказательство также имеет вычислительный характер. Можно использовать рисунки для доказательства основанного на вычислении площадей двумя способами.

Для того чтобы доказать теорему пользуясь рисунком (приложение 4) достаточно только выразить площадь трапеции двумя путями.

Sтрапеции=(a+b)²/2

Sтрапеции=a²b²+c²/2

Приравнивая правые части получим:

a²+b²=c²

Теорема доказана

3.5. Доказательство Евклида

   Как в доказательствах методом разложения, так и при доказательстве евклидового типа можно исходить из любого расположения квадратов. Иногда при этом удается достигнуть упрощений.

   Пусть квадрат, построенный на одном из катетов (на рисунке это квадрат, построенный на большем катете), расположен с той же стороны катета, что и сам треугольник (приложение 5). Тогда продолжение противоположной катету стороны этого квадрата проходит через вершину квадрата, построенного на гипотенузе. Доказательство в этом случае оказывается совсем простым, т. к. здесь достаточно сравнить площади интересующих нас фигур с площадью одного треугольника(он заштрихован) — площадь этого треугольника равна половине площади квадрата и одновременно половине площади прямоугольника.

Заключение

   Теорема Пифагора стала очень известной, что невозможно представить себе человека, который не знает о ней. Я познакомилась с некоторыми историческими и математическими источниками, а также с информацией в Интернете, и обнаружила, что теорема Пифагора уникальна как своей историей, так и она является важным местом в жизни и науке. На это указывают данные мною в этом проекте трактовки текста этой теоремы и пути её доказательств.

   Заметим, теорема Пифагора — одна из основных и, кажется, самая главная теорема геометрии. Её значение состоит в том, что с помощью теоремы можно вывести огромное количество теорем геометрии. Теорема Пифагора интересна тем, что она совсем не очевидна. Например, свойства равнобедренного треугольника можно заметить непосредственно на чертеже. Но как долго не смотри на прямоугольный треугольник, никак незаметно, что между его сторонами есть простое соотношение. Поэтому для её доказательства обычно используют чертежи.

   Заслуга же Пифагора состояла в том, что он дал полноценное научное доказательство этой теоремы.

   Интересна личность самого учёного, память о котором неслучайно сохранила эта теорема. Пифагор — замечательный оратор, учитель и воспитатель, организатор своей школы, ориентированной на гармонию музыки и чисел, добра и справедливости, на знания и здоровый образ жизни. Он вполне может служить примером для нас, далёких потомков.

Приложения

 

Приложение 1

 

Приложение 2 Приложение 3

 

 

Приложение 4 Приложение 5

 

Литература
 

1. Г.И. Глейзер История математики в школе VII — VIII классы, пособие для учителей, — М: Просвещение 1982г.

2. Войтикова Н.В. «Теорема Пифагора» курсовая работа, Анжеро-Судженск, 1999г.

3. В. Литцман .Теорема Пифагора, М. 1960.

4. А.В. Волошинов «Пифагор» М. 1993.

5. Газета «Математика» 17/1996.

6. http://stories-of- success.ru/biografiya_pifagora_zagadochnyi_matematik

Автор материала: М. Дубицкая (11 класс)

Теорема Пифагора

Египет

Древнегреческие авторы писали о существовании в Египте особого метода для построения прямого угла на местности: этому служила кольцевая веревка, на которой были отмечены 12 узелков на равных расстояниях. Если натянуть данную веревку, образовав треугольник со сторонами, пропорциональными 3, 4 и 5, то этот треугольник будет прямоугольным: в самом деле, его стороны удовлетворяют теореме Пифагора (3² + 4² = 5²).

Рис. 1. Египетский треугольник

Прямоугольные треугольники с целочисленными сторонами до сих пор иногда называются египетскими треугольниками. В то же время из сохранившихся древнеегипетских папирусов математического содержания невозможно извлечь никаких свидетельств о знакомстве с теоремой Пифагора, даже в ее частном случае. Вполне возможно, что египтяне знали только об одном целочисленном прямоугольном треугольнике, и знали о нем не раньше середины I тысячелетия до н. э. – времени, к которому относятся первые греческие сведения о египетском методе построения прямого угла.

Вавилон

В отличие от египтян, древние вавилоняне еще в середине II тысячелетия до н. э. хорошо знали, что сумма квадратов катетов равна квадрату гипотенузы. Сохранилась таблица, из которой ясно, что вавилонянам были известны многие «пифагоровы тройки» целых чисел, удовлетворяющих равенству x² + y² = z², в том числе совсем нетривиальные (например, 72, 65, 97 или 3456, 3367, 4825). К сожалению, мы ничего не знаем о том, каким методом были найдены эти числа. Теорема Пифагора использовалась для вычисления диагонали квадрата; радиуса окружности, описанной около равностороннего треугольника; сторон правильных n-угольников. Сохранились и некоторые задачи, при решении которых надо воспользоваться этой теоремой: например, требовалось определить длину шеста, который вначале вертикально прислонен к стене, а затем наклоняется так, что его верхний конец опускается на три локтя, а нижний отходит от стены на 6 локтей.

Рис. 2. Задача о шесте, Вавилон

Можете ли вы решить эту задачу?

Решение

Пусть длина стержня x локтей. Тогда по теореме Пифагора x2 = (x – 3)2 + 62, откуда x2 = x2 – 6x + 9 + 36, 6x = 45, x = 22,5.

Китай

Согласно китайскому «Трактату об измерительном шесте» (II в. до н. э.), теорема Пифагора для частного случая – треугольника со сторонами 3, 4, 5 – была известна в Китае еще в XII в. до н. э., а в общем случае – в VI в. до н. э. В комментариях к этой книге указывается, что доказательство теоремы основывалось на следующем чертеже:

Рис. 3. Геометрическое доказательство теоремы Пифагора, Китай, II в. до н. э.

На этом чертеже видно, что большой квадрат (a + b)² больше, чем квадрат гипотенузы c², на четыре прямоугольных треугольника c катетами a и b, т. е. на 2ab:

(a + b)2 = c2 + 2ab.

Значит, квадрат гипотенузы равен большому квадрату, уменьшенному на два прямоугольника со сторонами a и b, то есть закрашенной фигуре. А эта фигура, в свою очередь, равна сумме квадратов со сторонами a и b:

Рис. 4. Геометрическое доказательство теоремы Пифагора, Китай, II в. до н. э.

На том же чертеже можно увидеть и другое доказательство. Квадрат гипотенузы больше, чем маленький квадрат в центре (a – b)², на те же четыре треугольника, или на два прямоугольника:

c2 = (a – b)2 + 2ab.

Это нас снова приводит к той же закрашенной фигуре, равной сумме квадратов катетов.

В Китае теорема Пифагора называлась правилом «гоу-гу»: термины «гоу» (исходно «крюк») и «гу» («ребро», «связка») обозначали горизонтальный (обычно меньший) и вертикальный (обычно больший) катеты. В классическом китайском трактате «Математика в девяти книгах» (II в. до н. э.) последняя книга называется «Гоу-гу» и посвящена задачам, решаемым с помощью теоремы Пифагора. Вот пример такой задачи.

Имеется водоем со стороной в 1 чжан (10 чи). В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснется его. Спрашивается: какова глубина воды и какова длина камыша?

Рис. 5. Задача о камыше, Китай, II в. до н. э.

В самом трактате «Математика в девяти книгах» решение не дается, приводится только правило, по которому можно вычислить ответ, причем в общем виде: «Половину стороны водоема умножь самое на себя, надводную часть в 1 чи умножь самое на себя, вычти это из первого, остаток раздели на удвоенную надводную часть камыша, получишь глубину воды. Прибавь количество чи надводной части, получишь длину камыша». То есть, в алгебраических обозначениях, если сторона водоема равна 2a (10 чи), а надводная часть b (1 чи), то глубина водоема равна (a² – b²) / 2b, а длина камыша (((a² – b²) / 2b) + b).

Решение

Пусть глубина водоема x чи. Тогда длина камыша (x + b) чи. По теореме Пифагора квадрат этой длины равен сумме квадратов глубины водоема и расстояния от центра до берега, т. е. (x + b)2 = x2 + a2, откуда x2 + 2bx + b2 = x2 + a2, 2bx + b2 = a2, x = (a2 – b2) / 2b, в полном соответствии с ответом, данным в трактате «Математика в девяти книгах». При подстановке конкретных чисел (a = 5, b = 1) получаем x = (25 – 1) / 2 = 12 (чи), а длина камыша, соответственно, x + b = 13 (чи).

Индия

В Индии теорема Пифагора была известна уже в VII–V вв. до н. э., о чем свидетельствует относящийся к этому периоду комментарий к священным книгам – «Ведам», – озаглавленный «Шулва-сутра» (дословно «Правила веревки») и служивший руководством по строительству алтарей и храмов. Такое строительство подчинялось ряду правил: храмы должны были ориентироваться строго по сторонам света, в их основании лежали определенные геометрические фигуры. Теорема Пифагора использовалась для построения прямых углов (как в Египте) и квадратов с площадью, кратной данному квадрату. Для построения квадрата, равновеликого двум данным квадратам, в большом квадрате строили меньший квадрат и соединяли их вершины, находя гипотенузу треугольника, катетами которого служили стороны исходных квадратов.

Рис. 6. Построение квадрата, равновеликого двум данным. Индия, VII–V вв. до н. э.

Доказательство теоремы Пифагора приводится в книге «Венец астрономического учения» индийского математика XII в. Бхаскары. Собственно, все доказательство состоит из чертежа, похожего на вышеприведенный китайский. В качестве пояснения фигурирует лишь слово «Смотри!». В Индии, в отличие от Греции, главным в математическом доказательстве была наглядная убедительность, а не логическая строгость.

Тот же Бхаскара приводит и ряд задач на применение теоремы Пифагора, похожих на задачи «Математики в девяти книгах». Среди них и задача о водоеме – в индийском варианте в ней вместо камыша фигурирует лотос.

Греция

Вполне вероятно, что в Греции теорему Пифагора впервые доказал сам Пифагор или кто-то из пифагорейцев.

Особенностью греческой математики по сравнению с математикой стран Востока было стремление к строгим доказательствам. Первому греческому математику Фалесу последующая традиция приписывает доказательство таких фактов, как равенство полукругов, равенство вертикальных углов, равенство углов при основании равнобедренного треугольника. Если эти сведения верны, то главное новаторство Фалеса заключалось в самой идее математического доказательства утверждений, в общем-то, очевидных, то есть в открытии логической связи между различными математическими фактами. На этом фоне теорема Пифагора выделяется как раз своей неочевидностью, и тот, кто ее доказал, продемонстрировал ценность нового математического подхода, позволяющего доказывать новые результаты.

Неизвестно, как впервые была доказана теорема Пифагора. Рассмотрим доказательство, приведенное в «Началах» Евклида. Российские школьники прошлых времен, изучавшие геометрию по Евклиду, в шутку называли это доказательство «пифагоровы штаны».

Рис. 7. Теорема Пифагора в «Началах» Евклида

Идея доказательства следующая. Квадрат на левом катете – ABFH – равновелик удвоенному треугольнику FBC, потому что у них общее основание FB и общая высота AB = FH. Треугольник FBC равен треугольнику ABD по двум сторонам и углу между ними: FB = AB, BC равно BD, FBC = FBA + ABC = 90° + ABC = CBD + ABC = ABD (фактически, треугольник FBC при повороте вокруг вершины B на 90° перейдет в треугольник ABD). Треугольник ABD равновелик половине прямоугольника BMLD, потому что у них общее основание BD и общая высота BM = LD. Таким образом, квадрат ABFH равновелик прямоугольнику BMLD. Точно так же доказывается, что квадрат на правом катете – CAGK – равновелик прямоугольнику LMCE. Следовательно, оба квадрата на катетах, вместе взятые, равновелики квадрату BCED на гипотенузе.

Модель 1. Теорема Пифагора. Доказательство Евклида

Некоторые авторы, в частности, философ А. Шопенгауэр, критиковали евклидово доказательство как недостаточно наглядное по сравнению с индийским. Однако доказательство Евклида имеет и свои достоинства: в частности, оно демонстрирует, каким именно частям квадрата гипотенузы равновелики квадраты катетов. Кроме того, знакомство с доказательствами Евклида постепенно формирует способность непосредственно усматривать равенство и равновеликость фигур в том числе в не очень очевидных случаях, что бывает полезно при переходе к более сложным задачам.