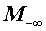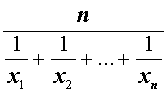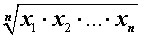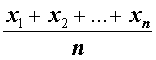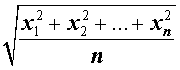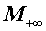Неравенства геометрические: Геометрические неравенства – ГЕОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА В ПЛАНИМЕТРИИ — Детская игровая комната «Волшебный лес»

Posted on 27.02.202120.03.2020 by alexxlab

Содержание

ГЕОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА В ПЛАНИМЕТРИИ

Конькина А.А. 1

Санникова Г.И. 1

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Данная работа посвящена геометрическим неравенствам в планиметрии.

Задачи на геометрические неравенства, т.е. геометрические задачи, в которых требуется сравнить какие-либо величины или доказать неравенство, достаточно редки, но как правило решение их вызывает большой интерес. Такие задачи встречаются в олимпиадных заданиях.

В работе подобраны также задачи на доказательства, где нужно сравнивать какие-либо величины и для построения правильного чертежа.

Выводы, полученные при решении многих из разобранных задач, являются «ключиком» к решению других более сложных геометрических задач.

Основная часть

Неравенство треугольника

В каждом треугольнике любая сторона меньше суммы двух других сторон.

Это простое утверждение называется неравенством треугольника.

Оно даёт ответ на такой вопрос «Всегда ли можно построить треугольник, сторонами которого являются заданные отрезки a, b и c?»

Такой треугольник нельзя построить, если хотя бы один из этих отрезков больше или равен сумме двух других. Чтобы треугольник с заданными длинами сторон существовал, необходимо, чтобы было выполнено три неравенства a < b+c , b < a+c , c < a+b , но необязательно проверять справедливость всех трёх неравенств. Достаточно проверить только одно, остальные будут выполнены автоматически.

Задача №1.

В треугольнике ABC со сторонами AC=a, BC=b высота CN делит сторону AB на части AN=x и BN=y.

Доказать, что если a>b, то a – x < b – y.

Рис.1

Доказательство: Отложим от точки N отрезок KN равный отрезку NB.

По условию a>b (AC>BC), то точка K лежит между AN.

Значит, ∆ CKN= ∆ CBN, CK=CB.

В ∆ ACK, AC=a, CK=CB=b, AK=x – y, согласно неравенству треугольника должно быть выполнено AC∠BDC, BD>BC

Итак, AD>BD, BD>BC, AD>BC, DC>BC, AC=2BC , так как AC=AD+DC

Что и требовалось доказать.

Задача №3. (Олимп. 9 кл.)

Отрезки AB и CD длиной, равной 1, пересекаются в точке O, ∠AOC=60°. Докажите, что AC+BD ≥ 1.

Рис.3

Доказательство: Рассмотрим геометрическое решение.

Пусть ACB1B-параллелограмм.

AC=BB1, AB=CB1, AB║CB1 и ∠AOC=∠DCB1=60° (накрест лежащие углы при секущей OC)

∆ DCB1- равнобедренный, CD = CB1, так как AB=CD=B1C=1

∆ DCB1- равносторонний, то есть DC=B1C=B1D=1,

в ∆ DBB1, BB1+ BD ≥ B1D, но BB1=AC (противоположные стороны параллелограмма) или AC+BD ≥ 1

Что и требовалось доказать.

Задача №4.

Докажите, что сумма медиан треугольника больше полупериметра, но меньше периметра.

Рис.4

Доказательство: Обозначим стороны AB=c, BC=a, AC=b,AL=Ma,

BM=Mb, CK=Mc

Докажем: Ma+Mb+Mc = a+b+c

D принадлежит медиане BM, BM=MD, ABCD – параллелограмм,

(так как DB и AC диагонали), AD║BC, AD=BC=a, AB=CD=c

В ∆ ABC, BC+AB>AC, т.е a+c=2Mb

В ∆ ABC, AC+BC>AB,т.е. a+b=2Mc

В ∆ ABC, AC+AB>BC,т.е. b+c=2Ma

a+c+a+b+b+c>2Mb+2Mc+2Ma, a+b+c>Mb+Mc+Ma

В ∆ ABM, AM+BM>AB, то есть Mb+b:2>с,

В ∆ ALC ma+a:2>b.

В ∆ BKC mc+c:2>a

ma+mb+mc+(a+b+c):2> a+b+c, ma+mb+mc> (a+b+c):2

Что и требовалось доказать.

Задача №5

Пусть точки B и C принадлежат отрезку AD.

Докажите, что, если AB = CD, то для любой произвольной точки P верно неравенство PA+PD ≥ PB+PC.

Рис.6

Доказательство: Если точка P лежит на AD, то неравенство очевидно.

Рассмотрим, если P не принадлежит AD, O-середина AD и BC.

C и B принадлежат отрезку AD. Точка Q симметрична точке P.

CQ ║ PB , а четырёхугольник CPBQ-параллелограмм.

Аналогично в четырёхугольнике APDQ, APDQ-параллелограмм.

Параллелограмм CPBQ находится внутри параллелограмма APDQ

Papdq>Pcpbq, PA+PD ≥ PC+PB.

Что и требовалось доказать.

Соотношение между элементами треугольника

При доказательстве геометрических неравенств часто применяются также теоремы о соотношениях между сторонами и углами в произвольном треугольнике.

«В любом треугольнике напротив большего угла лежит большая сторона и, наоборот – напротив большей стороны лежит больший угол».

Задача№6.

В ∆ ABC серединный перпендикуляр к стороне BC пересекает

Сторону AB в точке D и продолжение стороны AC в точке E.

Докажите, что AD∠AED+∠EAD

Следовательно, ∠ADE >∠AED, так как напротив большего угла лежит

большая сторона, то AE>AD

Что и требовалось доказать.

Задача №7.

На сторонах угла A взяты точки B и C. Через середину отрезка BC проведена прямая, пересекающая стороны угла AB и AC в точках D и E соответственно.

Докажите, что площадь треугольника ADE больше площади треугольника ABC

Рис.7

Доказательство: Рассмотрим отрезки DK и KE.

D лежит между точками A и B.

DKAC+CB.

4.В произвольном выпуклом четырехугольнике найдите точку, сумма расстояний от которого до вершины минимальна.

5.Может ли внутри данного треугольника лежать треугольник с большим периметром, чем данный?

Просмотров работы: 684

Неравенство треугольника. Геометрические неравенства. — Математика

Геометрические неравенства.

При изучении математики ученикам часто приходится сталкиваться с решением неравенств. Одними из наиболее сложных видов неравенств являются геометрические. В школе на их решение отводится не достаточное количество времени, поэтому при работе с подобными неравенствами у учеников возникают трудности. Однако на вступительных экзаменах в ВУЗы и на математических олимпиадах такого рода задания можно встретить достаточно часто. Рассмотрим некоторые из них.

Неравенство треугольника

Теорема (неравенство треугольника):

Каждая сторона треугольника меньше суммы двух других его сторон.

Замечание. Иногда используют также и несколько другую формулировку этой теоремы, подключая попутно и случай вырожденного треугольника:

Длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон.

Заметим, что разница между двумя приведенными формулировками столь незначительна, что нет смысла рассматривать их отдельно. В дальнейшем при решении задач мы будем использовать как первую формулировку теоремы, так и вторую, не оговаривая это отдельно.

Неравенство треугольника возникло, судя по всему, тогда же, когда человек научился ходить и хоть как-то мыслить. Известно, что одну из первых его формализаций приводит Евклид в знаменитых «Началах». Там он доказывает неравенство треугольника следующим образом. Сначала доказывается теорема о том, что внешний угол треугольника больше внутреннего угла, с ним не смежного. Из нее выводится теорема о том, что против большей стороны треугольника лежит больший внутренний угол. Далее, методом от противного доказывается теорема о том, что против большего внутреннего угла треугольника лежит большая сторона. А из этой теоремы выводится неравенство треугольника. Вот такая вот непростая логическая цепочка для доказательства вполне очевидного, казалось бы, неравенства!

Рис. 1

Доказательство теоремы. Рассмотрим треугольник ABC и покажем, что AB AC + BC. При доказательстве воспользуемся одним из видов дополнительных построений – откладыванием равных отрезков (метод спрямления).

В треугольнике ABC (рис. 1) на продолжении стороны

BC отложим отрезок CD, равный AC. В равнобедренном треугольнике ACD

. В треугольнике ABD угол ADB меньше угла BAD, значит, BD AB, или BC + CD AB. Но CD = AC, значит, AC + BC AB.

Замечание. Обратите внимание, что, исходя из формулировки теоремы, следует записать сразу три неравенства:

AB AC + BC;

AC AB + BC;

BC AB + AC.

Нередко, записав одно неравенство, о двух других почему-то забывают. Помните, что это может привести к довольно неприятным ошибкам.

Неравенство треугольника может служить одним из простых критериев принадлежности трех точек одной прямой. Три точки будут принадлежать одной прямой тогда и только тогда, когда в неравенстве треугольника достигается равенство. Естественно, равенство может достигаться лишь в одном из трех неравенств (см. замечание), поскольку одна из точек будет лежать четко между двумя другими.

Докажите, что в треугольнике каждая сторона больше разности двух других сторон.

Приведем в качестве примера использования неравенства треугольника несколько сравнительно несложных геометрических задач.

В треугольнике длины двух сторон равны 5, 27 и 2, 79. Какой может быть длина третьей стороны, если известно, что она является целым числом.
Докажите, что в произвольном четырехугольнике ABCD AB + CD AC + BD.
Докажите, что в треугольнике ABC выполнено неравенство

(a, b, c – стороны треугольника ABC).

Докажите, что медиана AM в произвольном треугольнике ABC по длине меньше, чем .
На плоскости дан квадрат ABCD и точка O. Докажите, что расстояние от точки O до одной из вершин квадрата не превосходит суммы расстояний от O до трех других вершин квадрата.
a, b и c — длины сторон произвольного треугольника. Докажите, что a = y + z, b = x + z и c = x + y, где x, y и z — положительные числа.
Пусть a, b, c – стороны треугольника. Докажите неравенство a³ + b³ + 3abc c³.
a, b и c — длины сторон произвольного треугольника. Докажите, что a² + b² + c² ab + bc + ca).
a, b и c — длины сторон произвольного треугольника. Докажите, что

a(b — c)² + b(c — a)² + c(a — b)² + 4abc a³ + b³ + c³.

a, b и c — длины сторон произвольного треугольника. Докажите, что

+ + 3.

a, b, c – стороны треугольника. Докажите неравенство
a, b, c – длины сторон треугольника. Докажите, что

a, b и c — длины сторон произвольного треугольника. Докажите, что

(a + b — c)(a — b + c)(- a + b + c) abc.

a, b и c — длины сторон произвольного треугольника. Докажите, что

a²b(a — b) + b²c(b — c) + c²a(c — a) 0.

Длины двух сторон треугольника a и b удовлетворяют условию a b, а длины соответствующих им высот равны h_a и h_b.

Доказать неравенство a + h_a ≥ b + h_b и определить, когда достигается равенство.

Докажите, что сумма длин любых двух медиан произвольного треугольника
а) не больше ¾ P, где P – периметр этого треугольника;
б) не меньше ¾ p, где p – полупериметр этого треугольника.

Отрезки AB и CD длины 1 пересекаются в точке O , причем AOC=60^o . Докажите, что AC+BD1 .

Решение

Построим отрезок CB₁ так, что четырехугольник ABB₁C – параллелограмм, тогда AC=BB₁ . Из треугольника BB₁D получаем, что BB₁+BD B₁D и, следовательно, AC+BD B₁D . Остается заметить, что треугольник CB₁D равносторонний ( CD=CB₁=1 , а B₁CD= AOC=60^o ), и, значит, B₁D=1 . Таким образом, получаем AC+BD1 .

Точки C₁, A₁, B₁ взяты на сторонах AB, BC, CA треугольника ABC так, что BA₁ = ^.BC, CB₁ = ^.CA, AC₁ = ^.AB, причем 1/2 P треугольника ABC и периметр P₁ треугольника A₁B₁C₁ связаны неравенствами (2-1)P P₁ P.

Решение

Возьмем на сторонах AB, BC, CA точки C₂, A₂, B₂ так, что A₁B₂| AB, B₁C₂| BC, C₁A₂| CA (рис.). Тогда A₁B₁ A₁B₂ + B₂B₁ = (1 — )AB + (2 — 1)CA. Аналогично B₁C₁ )BC + (2 — 1)AB и C₁A₁ )CA + (2 — 1)BC. Складывая эти неравенства, получаем P₁ P.
Ясно, что A₁B₁ + A₁C B₁C, т. е. A₁B₁ + (1 — )BC ^.CA. Аналогично B₁C₁ + (1 — )CA ^.AB и C₁A₁ + (1 — )AB ^.BC. Складывая эти неравенства, получаем P₁ (2 — 1)P.

Геометрические неравенства. DjVu

СОДЕРЖАНИЕ

Предисловие 4
Список задач, предлагавшихся на математических олимпиадах 12
Задачи 15
1. Задачи смешанного содержания (1 — 42) 15
2. Геометрические неравенства (43 — 64) 23
3. Задачи на отыскание наибольших и наименьших значений геометрических величин (65 — 88) 33
4 Задачи о треугольнике и тетраэдре (89 — 120) 39
Решения 63
Литература 313
Ответы и указания 319

ПРЕДИСЛОВИЕ
Эта книга представляет собой четвертый из сборников вадач, отражающих опыт работы школьного математического кружка при Московском государственном университете и математических олимпиад московских школьниковг). Первый из сборников был посвящен арифметике и алгебре; в него, в частности, был включен раздел, посвященный неравенствам, и значительное место заняли алгебраические и арифметические задачи на отыскание наибольших и наименьших величин. Эта книга имела наиболее счастливую судьбу: она выдержала четыре издания, переводилась на языки национальных республик и на иностранные языки и, видимо, обрела свою читательскую аудиторию. Однако судьба двух последующих книг, посвященных геометрии, была совсем иной.
Вторая книга серии была посвящена планиметрическим задачам. Впервые она вышла в свет в 1952 г. и до 1967 г. не переиздавалась. Подбор нешаблонных задач геометрического содержания, как о том свидетельствует весь опыт работы, школьного математического кружка при МГУ и математических олимпиад, является гораздо более трудным делом, чем составление арифметических, алгебраических, комбинаторных или чисто логических задач, — и ч. 2 книги «Избранные задачи и теоремы…», особенно в ее первом издании 1952 г., была, в очень большой своей части, заполнена довольно стандартными задачами на построение и доказательство, решения которых достаточно далеки от тех приемов и методов, которые встречаются сегодня в математической науке. В 1967 г., в первую очередь благодаря помощи В. П. Паламодова, удалось выпустить новое, полностью переработанное издание этой книги; однако и в своем последнем варианте она в меньшей мере является «олимпиад-ским»х) задачником, чем первая книга серии «Библиотека математического кружка». Третья книга серии, посвященная стереометрии (ее основным составителем является Н. Н. Ченцов), вышла в свет в 1954 г.; она не переиздавалась ни разу, хотя работа над подготовкой нового ее издания ведется уже давно.
Работа над сборниками геометрических задач так затянулась еще и потому, что составители не захотели пойти по простейшему пути. В то время как геометрия в целом переживает в настоящее время определенный кризис, связанный с глубокой перестройкой всей математической науки, один довольно узкий раздел элементарной геометрии бесспорно находится сегодня на подъеме — это учение о так называемых «геометрических экстремальных2) задачах», т. е. о задачах, связанных с отысканием наибольших и наименьших значений геометрических величин и с нахождением численных
*) То есть отличающимся нестандартностью условий задач и методов их решения (составители предлагаемых на математических соревнованиях задач должны стремиться исключить возможность того, что кто-либо из участников соревнования уже раньше встречался со сходной задачей или с рассуждением, близким к рассуждению, приводящему к решению задачи).
2) Математический термин «экстремум» объединяет понятия наибольшего значения, или «максимума», и наименьшего значения, или «минимума»; поэтому «экстремальные задачи» — это задачи на отыскание максимумов и минимумов (т. е. наибольших и наименьших значений).
оценок, ставящих своей целью распознавание’В- каком-либо смысле «выгодных» или «экономичных» геометрических конфигураций. Тематика этого рода породила в послевоенные годы даже целые большие направления, своего рода науки, которую смело можно назвать «элементарной геометрией второй половины XX века». Интерес к геометрическим экстремальным задачам естественно связать с расцветом тех направлений математики, которые относятся к отысканию оптимальных или экономичных режимов работы определенных механизмов или сложных систем. В последние десятилетия оформился целый ряд научных направлений («линейное программирование», «динамическое планирование», «теория игр», «исследование операций», «оптимальное управление», «теория информации» и т. д.), которые специально занимаются задачами такого рода; в некоторых из них находит прямое применение дискретная геометрия.
Таким образом, сборники геометрических задач можно было сделать более яркими и даже, в определенном смысле, более научно актуальными, резко увеличив в них долю «экстремальных» задач. Однако при переработке 2-й части «Избранных задач и теорем» ряд «экстремальных» геометрических задач, содержавшихся в 1-м издании этой книги, был даже исключен из вышедшего в свет в 1967 г. ее 2-го издания2). Это обстоятельство тесно связано с возросшей ролью задач на оценки геометрических величин и геометрические неравенства; нам казалось, что таким задачам уместно посвятить отдельный сборник. Более того, при работе над настоящей книгой мы убедились, что количество заслуживающих внимания геометрических экстремальных задач таково, что их целесообразно разбить на два отдельных сборника, формально совершенно независимых и даже имеющих несколько разный характер: в то время как эта книга ориентирована, в первую очередь, на разбор некоторых «классических» геометрических задач на максимум и минимум (см. цикл задач 3) и непосредственно их продолжающих экстремальных геометрических проблем (цикл задач 4), подготовляемая следующая книга той же серии в значительно большей степени будет порождена теми направлениями геометрии, которые принято именовать «дискретной геометрией» и «комбинаторной геометрией».
Эта книга представляет собой очередной выпуск серии, отражающей долголетний опыт школьного математического кружка при МГУ и московских математических олимпиад — преемственность здесь подчеркивается самим списком ее авторов. Формулировки некоторых задач сборника (например, задач 38 — 42) в какой-то степени навеяны новыми направлениями математики; однако наряду с этим здесь имеется большое число «классических задач на геометрические экстремумы», история которых восходит к XIX веку или является еще более древней (таковы, в частности, многие задачи цикла 3). Но еще важнее то, что решения собранных здесь задач, как правило, следуют традициям, сложившимся в школьной математике в начале этого века и очень сильным в течение того периода работы школьного математического кружка при МГУ, когда самой яркой фигурой кружка был студент механико-математического факультета Додик Шклярский1) — другими словами, «прямым методам» решения экстремальных задач здесь определенно отдается предпочтение перед «косвенными методами». Последнее обстоятельство представляется нам важным; поэтому мы позволим себе остановиться на нем подробнее.
Хорошо известно, что решения «экстремальных» задач, независимо от того, относятся ли они к арифметике, алгебре, геометрии или математическому анализу, могут строиться двумя принципиально различными путями. Прямым называется такое доказательство какого-либо экстремального свойства, в котором, скажем, определенная фигура непосредственно сравнивается с произвольной другой фигурой, удовлетворяющей всем условиям поставленной задачи, и показывается, что первая фигура лучше (или не хуже) каждой другой. Напротив, косвенное доказательство сводится к рассуждению, показывающему, что все фигура, кроме какой-то одной (или нескольких), не могут служить решением задачи, поскольку для каждой такой фигуры можно найтн другую, лучшую? чем она, откуда уже и делается вывод о том, что решением задачи является та единственная фигура, которую мы не можем «улучшить» (или одна или большее число из тех нескольких фигур, которые не могут быть улучшены). Однако рассуждение такого рода содержит существенный пробел, заключающийся в том, что если наша задача вовсе не имеет решения, то полученный этим путем вывод может оказаться ошибочным; доказательство же существования решения задачи требует использования совсем других соображений, которые естественно отнести к топологии — «младшей сестре» геометрии, возникшей в XX веке и сегодня успешно конкурирующей с классической геометрией, из которой она выделилась.
Силу косвенных методов в геометрических экстремальных задачах впервые в полной мере оценил замечательный швейцарский геометр первой половины XIX века Якоб Штейнер; большое место занимали они и в творчестве современника Штейнера, выдающегося немецкого аналиста Лежена Дирихле.
Во второй половине XIX века с резкой критикой Штейнера и Дирихле выступил знаменитый Карл Вейерштрасс; его конструктивная критика и связанные с ней исследования явились тем зерном, из которого впоследствии выросла топология — но одновременно они настолько сильно скомпрометировали косвенные методы решения.экстремальных геометрических проблем, что в первой половине нашего века последние повсеместно считались «ненаучными» (или, во всяком случае, недостаточно строгими). «Необходимо особо остановиться на задачах отыскания наибольшего или наименьшего значения…, — писал в 1947 г. составитель решений к последним изданиям «Элементарной геометрии» знаменитого Жака Адамара проф. Д. И. Перепелкин. — Дело в том, что в более трудных задачах такого рода автор прямо рекомендует решать задачу, исходя из предположения, что существует фигура, для которой имеет место экстремум. Такой путь решения, более или менее естественный в ту эпоху, когда составлялась книга Адамара 1), мы считаем в настоящее Время неприемлемым…» (см. [13], стр. 13 — 14). Однако автор относящейся к следующему историческому периоду книги [21] присопоставлении прямых и косвенных методов решения экстремальных геометрических задач проявляет уже несколько большую умеренность. «Если оставить в стороне соображения эстетического и дидактического порядка, — говорит он, — то косвенный метод представляется более, естественным и, вообще говоря, вероятно, также и более целесообразным. Если иметь в виду лишь определение пока еще неизвестной экстремальной фигуры, то естественно отложить на дальнейшее вопрос о ее существовании; прежде всего следует задаться- вопросом о том, в каких случаях (и каким образом) заданная фигура может быть улучшена. При этом… косвенный метод доказательства не является вполне элементарным и чисто геометрическим…
Обратимся теперь к прямому методу доказательства, который уже в силу того, что он является прямым, представляется более убедительным. Здесь вопросы существования не приходится ставить отдельно, поскольку они автоматически решаются в процессе доказательства. Кроме того, прямое доказательство часто удается свести к самым простым предложениям элементарной геометрии, в то время как в косвенном методе это принципиально невозможно. Но зато прямое доказательство часто требует большего искусства; поэтому исторически такие доказательства находились, как правило, позднее, когда уже были известны менее изящные косвенные решения соответствующих задач» (см. [21], стр. 26 — 27).
Мы столь подробно воспроизвели разные мнения о соотношении прямых и косвенных методов решения задач на максимум и минимум, потому что считаем этот вопрос весьма принципиальным. При этом нам кажется, что если говорить о будущем, то оно бесспорно выскажется в пользу косвенных методов (значение которых в современной прикладной математике во много раз превосходит роль прямых методов). Те соображения эстетического порядка, в которых многие авторы видят дополнительные аргументы в пользу прямых методов, ни в коем случае не следует принимать во внимание: прямые методы «красивее» косвенных лишь в силу своей большей сложности, подобно тому как старинные, весьма изысканные методы нахождения площадей криволинейных фигур кажутся более красивыми, чем вытеснившая их автоматическая процедура решения соответствующих задач с помощью интегрального исчисления. Конечно, сложные методы, требующие отточенного мастерства, кажутся нам красивее простых приемов, связанных с использованием в решении задачи адекватного математического аппарата; однако они неизбежно уступают место этим простым приемам. Также и утверждение о «не-эдементарности» косвенных методов, связанных с необходимостью давать здесь доказательство существования, имеет, быть может, чисто временный характер, поскольку трудно предсказать, как изменится за ближайшие десятилетия элементарная геометрия. Однако сегодня в задачнике для школьников приходится предпочесть прямые методы решения экстремальных задач, поскольку пока мы не имеем доступной литературы, на которую можно было бы сослаться в связи с теоремами существования *). По этой причине и в настоящей книге рассматриваются почти исключительно прямые методы решения задач на максимум и минимум; однако читателю хочется порекомендовать продумать полученные результаты также и с позиций статьи [1] (см. также Дополнение I к книге [30]), резко противоречащей традициям школьного математического кружка при МГУ, но отражающей некоторые важные методологические установки наших дней.
Эта книга содержит 120 задач, разбитых на 4 цикла, причем деление на циклы в значительной степени является условным: легко, например, усмотреть глубокое родство отнесенных к разным циклам задач 46 и 94а), 47 и 94в), 75 и 104а) или 81а) и 1046). Весь текст разбит на три части: «Задачи», «Решения» и напечатанные в конце книги «Ответы и указания» ко всем без исключения задачам. Предполагается, что читатель книги сначала попробует решить задачу самостоятельно; в случае неудачи рекомендуется посмотреть в последней части книги указание (или ответ, который тоже может подсказать решение задачи) и продолжать думать над задачей; решение же следует читать только после продолжительного раздумья над задачей или после того, как ее удалось решить 2). Приложенный к книге список литературы (см. стр. 313 — 318), ни в какой мере не претендующий на полноту и не исчерпывающий все использованные автором источники, обращен более к преподавателю, чем к учащемуся; он может оказаться полезным в случае использования книги в работе (школьного или студенческого) математического кружка.
В работе над этой книгой автору существенно помогли ветераны школьного математического кружка при МГУ В.Г. Болтянский и Л. И. Головина, также как и он являющиеся учениками Д. О. Шклярского: они внимательно прочитали рукопись книги, и их замечания помогли устранить ряд дефектов изложения и улучшить решения некоторых задач. При подготовке книги было использовано первое издание 2-й части «Избранных задач и теорем…», составленное в сотрудничестве с Н. Н. Ченцовым и другими работниками школьного математического кружка при МГУ; в переработке и дополнении материала 2-й части «Избранных задач» большое участие принял В. П. Паламодов. Несколько задач сообщили автору составители геометрического выпуска [14] «Библиотечки физико-математической школы» Н. Б. Васильев (явившийся также основным составителем использованных в настоящей книге обзоров задач последних олимпиад, напечатанных в журнале «Математика в школе» — см. № 3 и 5 за 1965 г., № 5 за 1966 г., № 1 и 5 за 1967 г. и № 4 за 1969 г.) и В. Л. Гу-тенмахер, а также В. Л. Рабинович (Петропавловск-Казах-станский) и Г. А. Тоноян (Ереван). Э. Г. Готман (Арзамас), В. Л. Гутенмахер, В. Л. Рабинович и 3. А. Скопец (Ярославль) поделились с автором своими решениями некоторых задач. И. В. Летников принял значительное участие в подготовке эскизов чертежей; в этой работе ему помогал В. В. Фирсов. Мне приятно выразить здесь всем перечисленным лицам свою искреннюю признательность.
И. М. Яглом

Геометрическая интерпретация неравенств

Геометрическая интерпретация неравенств
Решение неравенств можно показать геометрически на числовой оси. Так, если мы имеем строгое неравенство 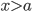, то геометрически это множество изображается в виде той части числовой прямой, которая лежит справа от точки с абсциссой . При этом правее точки наносят штриховку (рис. 1), а саму точку обычно изображают в виде светлого кружка (говорят, что точку «выкалывают»).

Рис. 1

Если имеем нестрогое неравенство $x\leq b$ , то на числовой оси наносят штриховку слева от точки (рис. 2), при этом точку обычно закрашивают в черный цвет, т.е. изображают темной точкой.

Рис. 2

При решении систем линейных неравенств, состоящих из двух неравенств, можно изображать решения с помощью двух числовых осей или с помощью одной оси, с помощью дуг или без дуг, без помощи штриховок или с помощью штриховок , нанося штриховки, имеющие разный угол наклона относительно числовой прямой, снизу и сверху или только сверху (снизу).
Пример 1. Решить систему неравенств, используя геометрическую интерпретацию

$\left\{\begin{matrix} 2x-1<3,\\ 3x+2\geq -7. \end{matrix}\right.$

Решение.
$\left\{\begin{matrix} 2x-1<3,\\ 3x+2\geq -7, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x<1+3,\\ 3x\geq -2-7, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x<4,\\ 3x\geq -9, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x<2,\\ x\geq -3. \end{matrix}\right.$
Дадим четыре варианта геометрической интерпретации примера 1.
1 вариант (с использованием двух числовых осей).
На одной числовой прямой отмечаем все те значения х, при которых выполняется первое неравенство системы, а на второй числовой прямой, расположенной под первой,— все те значения х, при которых выполняется второе неравенство системы (рис. 3). Сравнение этих двух результатов показывает, что оба неравенства одновременно будут выполниться при всех значениях х, заключенных от (-3) до (+2), т.е. $-3\leq x<2\Leftrightarrow x\in [-3;2).$
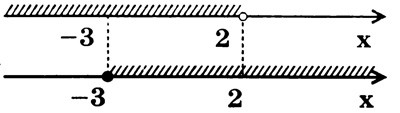
Рис. 3
2 вариант (с использованием одной числовой оси и штриховок снизу и сверху оси). На числовую ось наносим штриховки, расположенные выше и ниже числовой прямой, и находим пересечение решений неравенств, образующих исходную систему.
$\left\{\begin{matrix} 2x-1<3,\\ 3x+2\geq -7, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x<2,\\ x\geq -3. \end{matrix}\right.$
С помощью координатной прямой (рис. 4) находим, что множество решений исходной системы есть полуинтервал [-3;2).
Рис. 4
3 вариант (с использованием одной оси, дуг и штриховок).
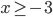$\left\{\begin{matrix} 2x-1<3,\\ 3x+2\geq -7, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x<2,\\ x\geq -3. \end{matrix}\right.$
На числовую ось наносим заданные множества и $x\geq -3$ при помощи дуг и штриховок с разным углом наклона к координатной прямой (рис. 5). Искомое множество изображено двойной штриховкой, при помощи наложения двух штриховок.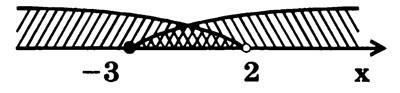
Рис. 5
4 вариант (с использованием одной оси и дуг)
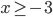$\left\{\begin{matrix} 2x-1<3,\\ 3x+2\geq -7, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x<2,\\ x\geq -3. \end{matrix}\right.$
На числовую ось наносим заданные множества и $x\geq -3$ при помощи только одних дуг, а штриховку наносим только там, где заданные множества пересекаются (рис. 6).
Рис. 6
Ответ: $x\in[-3;2).$
Пример 2. Решить систему неравенств
$\left\{\begin{matrix} 4x+3<7,\\ 2x+1>5. \end{matrix}\right.$

Решение.
$\left\{\begin{matrix} 4x+3<7,\\ 2x+1>5, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4x<7-3,\\ 2x>5-1, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4x<4,\\ 2x>4, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x<1,\\ x>2. \end{matrix}\right.$

Таким образом, любое число, удовлетворяющее обоим неравенствам одновременно, должно быть меньше 1 и больше 2 (рис. 7). Но таких чисел не существует. Поэтому данная система неравенств не выполняется ни при каких значениях 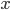, т. е. $x \in$ Ø. О таких системах говорят, что они несовместны (геометрически это означает, что нет наложения штриховок).

Рис. 7
Ответ: $x\in$ Ø.
Пример 3. Решить систему неравенств
$\left\{\begin{matrix} 2x+1\geq 7,\\ 3x-1\leq 8. \end{matrix}\right.$

Решение.
$\left\{\begin{matrix} 2x+1\geq 7,\\ 3x-1\leq 8, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 3,\\ x\leq 3. \end{matrix}\right.$

Изображая данные множества с помощью дуг и штриховок (рис.8), видим, что оба неравенства будут одновременно выполняться только при .
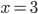Рис. 8
Ответ: {3}.
Пример 4. Решить совокупность неравенств
$\left [ \begin{matrix} 4x+3<7,\\ 2x+1>5. \end{matrix} \right.$

Решение.
$\left [ \begin{matrix} 4x+3<7,\\ 2x+1>5, \end{matrix} \right. \Leftrightarrow \left [ \begin{matrix} x<1,\\ x>2. \end{matrix} \right.$

С помощью числовой прямой (рис.9) находим, что решением заданной совокупности является множество, состоящее из двух полубесконечных интервалов, т. е.
Рис. 9
$\left [ \begin{matrix} x<1,\\ x>2, \end{matrix} \right. \Leftrightarrow x\in(-\propto ;1)\bigcup (2;\propto)$

Oтвет:
$x\in(-\propto ;1)\bigcup (2;\propto)$
.
Пример 5. Решить совокупность неравенств
$\left [ \begin{matrix} 2x+1<7,\\ 3x-1<-1. \end{matrix} \right.$
Решение.
$\left [ \begin{matrix} 2x+1<7,\\ 3x-1<-1. \end{matrix} \right. \Leftrightarrow \left [ \begin{matrix} x<3,\\ x<0. \end{matrix} \right.$
С помощью координатной прямой (рис. 10) находим, что решением исходной совокупности неравенств есть полубесконечный интервал $(-\propto ;3)$ .
Рис. 10
Ответ: $x \in (-\propto ;3).$
Пример 6. Решить совокупность неравенств
$\left [ \begin{matrix} 2x-1<3,\\ 3x+2\geq -7. \end{matrix} \right.$
Решение.
$\left [ \begin{matrix} 2x-1<3,\\ 3x+2\geq -7. \end{matrix} \right. \Leftrightarrow \left [ \begin{matrix} x<2,\\ x\geq -3. \end{matrix} \right.$
С помощью числовой прямой (рис. 11) находим, что решением заданной совокупности неравенств является вся числовая прямая, т. е.
$x\in(-\propto ;\propto ).$

Рис. 11
Ответ: $x\in(-\propto ;\propto ).$
Книга «Геометрические неравенства: Путеводитель в задачах и теоремах» автора Гашков Сергей Борисович
Последние комментарии

Геометрические неравенства: Путеводитель в задачах и теоремах
Автор: Гашков Сергей Борисович Жанр: Математика Год: 2013 Добавил: Admin 17 Май 17 Проверил: Admin 17 Май 17 Формат: DJVU (8731 Kb)

Рейтинг: 0.0/5 (Всего голосов: 0)
Аннотация
Книга содержит более 600 задач и теорем, посвященных геометрическим неравенствам, в основном для выпуклых многоугольников и многогранников. Среди задач есть как легкие, так и трудные; часть задач в разное время предлагались на математических олимпиадах для школьников. К некоторым задачам даны указания, а иногда и полные решения.
Книга предназначена для учащихся, но может быть интересна учителям, студентам и всем, кто интересуется математикой. Содержащиеся в ней задачи могут использоваться в работе математических кружков. Решая их, учащиеся познакомятся с доказательствами интересных геометрических теорем, сильно отличающихся от известных им по школьному курсу, и даже смогут попробовать решить еще никем не решенные задачи.
Объявления
Где купить?

Нравится книга? Поделись с друзьями!
Другие книги автора Гашков Сергей Борисович
Похожие книги
Комментарии к книге «Геометрические неравенства: Путеводитель в задачах и теоремах»

Комментарий не найдено

Чтобы оставить комментарий или поставить оценку книге Вам нужно зайти на сайт или зарегистрироваться

2011 — 2018
10.5. Неравенства и геометрические фигуры
Пусть A₁ (x₁; y₁) и A₂ (x₂; y₂) – точки, координаты которых удовлетворяют исходному неравенству:
ax₁ + by₁ + c > 0; ax₂ + by₂ + c > 0.
По теореме 10.4 координаты (x; y) любой точки отрезка A₁A₂ вычисляются по формулам x = x₁ + λ (x₂ – x₁), y = y₁ + λ (y₂ – y₁), 0 ≤ λ ≤ 1. Рассмотрим
ax + by + c = a (x₁+ λ (x₂ – x₁)) + b (y₁ + λ (y₂ – y₁)) + c = (1 – λ)[ax₁ + by₁ + c] +λ (ax₂ + by₂ + c ) > 0.
Отрезок A₁A₂ не пересекает прямую ax + by + c = 0, следовательно, лежит по одну сторону от нее. Таким образом, множество точек, удовлетворяющих неравенству, лежат в одной полуплоскости.
Покажем, что все точки этой полуплоскости удовлетворяют исходному неравенству. Допустим противное, а именно: существует точка A₀ (x₀; y₀) полуплоскости, координаты которой не удовлетворяют исходному неравенству. Тогда либо ax₀ + by₀+ c = 0, либо ax₀ + by₀ + c < 0. В первом случае точка (x₀; y₀) лежит на прямой, разбивающей плоскость на две полуплоскости, и по определению не принадлежит ни одной из них, и мы приходим к противоречию с предположением. Во втором случае с учетом исходного неравенства ax₁ + by₁ + c > 0 для точки A₁ имеем, во-первых, что (ax₁ + by₁ + c) / (a (x₁ – x₀) + (y₁ – y₀)) < 1, во-вторых, что a (x₀ – x₁) + b (y₀ – y₁) < 0. Рассмотрим отрезок A₀A₁. Точки этого отрезка удовлетворяют равенствам: x = x₁ + λ (x₀ – x₁), y = y₁ + λ (y₀ – y₁). Умножим первое равенство на a, второе – на b, сложим и прибавим к обоим частям c. В результате получим равенство ax + by + c = ax₁ + by₁ + c + λ (a (x₀ – x₁) + b (y₀ – y₁)). Приравняем обе части равенства к нулю. Равенство нулю правой части дает значение λ = (ax₁ + by₁+ c) / (a (x₁ – x₀) + (y₁ – y₀)). C учетом ранее полученных неравенств имеем: 0 < λ < 1. Это значит, что точка (x; y) принадлежит отрезку A₀A₁. С другой стороны, равенство ax + by +c = 0 означает, что точка (x; y) лежит на прямой, разбивающей плоскость на две полуплоскости. То есть отрезок A₀A₁пересекает прямую, разбивающую плоскость на две полуплоскости, следовательно, точки A₀ и A₁ лежат в разных полуплоскостях. Полученное противоречие доказывает теорему.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Неравенства между средними значениями
Для удобства приведем Таблицу из введенных в разделе «Средние значения» определений средних значений для произвольного набора из n положительных действительных чисел
x₁, x₂, … , x_n
Таблица – Средние значения
Минимум
Обозначение:
Формула:
min ( x₁, x₂, … , x_n )
Среднее гармоническое
Обозначение:
M_{– 1}
Формула:
Среднее геометрическое
Обозначение:
M₀
Формула:
Среднее арифметическое
Обозначение:
M₁
Формула:
Среднее квадратичное
Обозначение:
M₂
Формула:
Максимум
Обозначение:
Формула:
max ( x₁, x₂, … , x_n )
Утверждение 1. Пусть p₁ и p₂ – произвольные действительные числа, удовлетворяющие неравенству p₁< p₂ . Тогда для произвольного набора из n положительных действительных чисел
x₁, x₂, … , x_n
справедливо неравенство
,
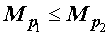причем в этом неравенстве знак равенства выполняется тогда и только тогда, когда все числа
x₁, x₂, … , x_n
равны.
Замечание. Утверждение 1 остается справедливым и в случае, когда 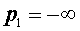, и в случае, когда.
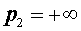Следствие 1. Для произвольного набора из n положительных чисел
x₁, x₂, … , x_n
справедливы следующие неравенства между его средними значениями:
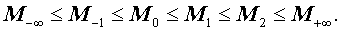
Следствие 2. Для произвольного набора из n положительных чисел
x₁, x₂, … , x_n
любые два из его средних значений
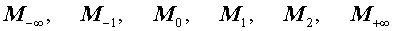
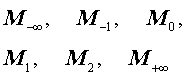
равны между собой тогда и только тогда, когда все числа
x₁, x₂, … , x_n
равны.
Итак, для n произвольных положительных чисел
x₁, x₂, … , x_n
справедлива следующая цепочка неравенств:
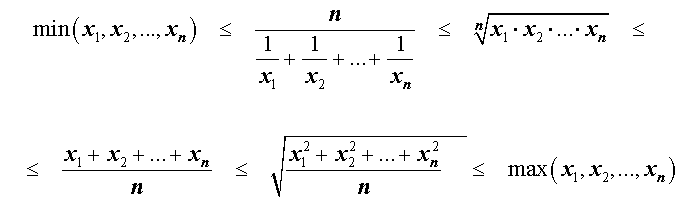
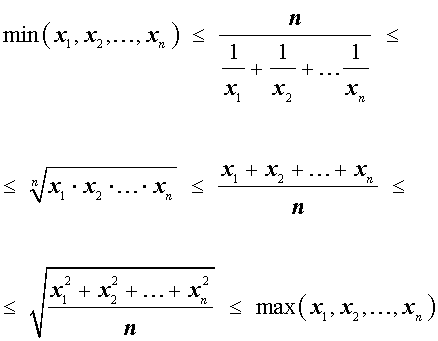
Неравенство Коши о среднем арифметическом и среднем геометрическом
Неравенство
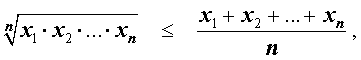
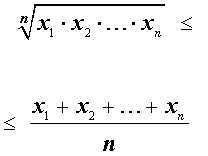
утверждающее, что среднее геометрическое n положительных чисел не превосходит их среднего арифметического, называется неравенством Коши.
В случае, когда n = 2 , неравенство Коши имеет вид
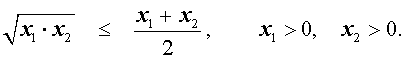
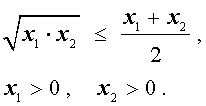
Докажем это неравенство:
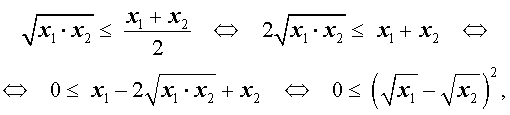
что и требовалось.
Из неравенства Коши с n = 2 , взяв
нетрудно получить очень полезное следствие.
Следствие. Для произвольного положительного числа x выполнено неравенство
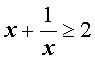
Неравенство о среднем гармоническом и среднем геометрическом
В случае n переменных неравенство о среднем гармоническом и среднем геометрическом имеет вид:
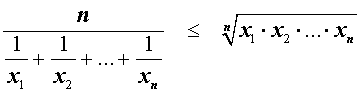
В случае, когда n = 2 , это неравенство имеет вид:
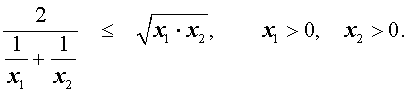
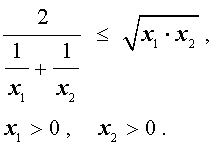
Докажем это неравенство:
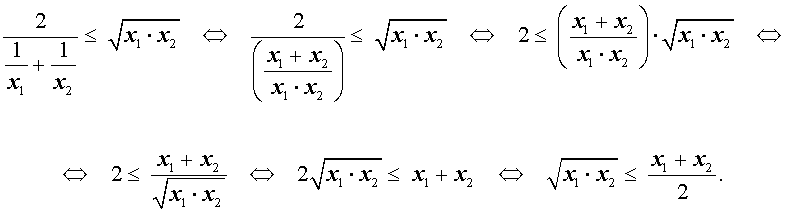
На последнем этапе получилось неравенство Коши, доказанное в предыдущем разделе, следовательно, доказательство неравенства о среднем гармоническом и среднем геометрическом закончено.
Неравенство о среднем квадратичном и среднем арифметическом
В случае n переменных неравенство о среднем квадратичном и среднем арифметическом имеет вид:
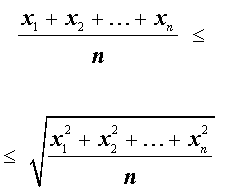
В случае, когда n = 2 , это неравенство имеет вид:
Докажем это неравенство:
что и требовалось.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.