Теорема Пифагора [wiki.eduVdom.com]
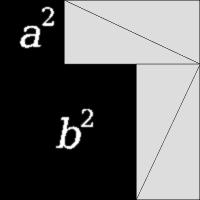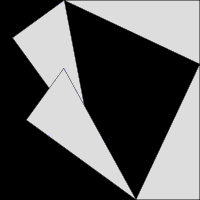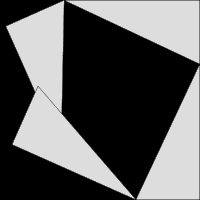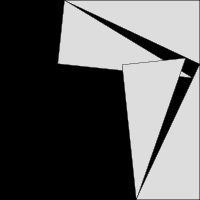
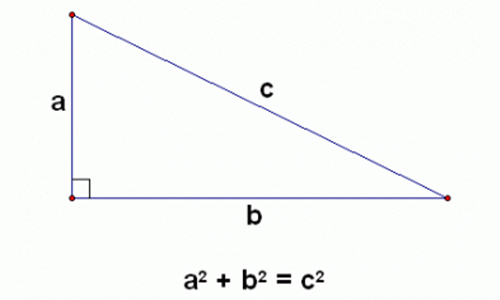
Теорема 1. Теорема Пифагора1). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. AB2 = AC2 + BC2
Рис.1
Доказательство. Пусть ABC — данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С (рис.1).
Получили два прямоугольных треугольника. По определению косинуса угла А запишем:
$$ \cos A = \frac{AD}{AC} = \frac{AC}{AB} $$
Отсюда AB • AD = AC2 .
Аналогично,
$$ \cos B = \frac{BD}{BC} = \frac{BC}{AB} $$
Отсюда АВ • BD = ВС2 .
Складывая полученные равенства почленно и учитывая, что AD + DB = АВ, получим:
АС2 + ВС2 = AB(AD + DB) = АВ2.
Теорема доказана.
Пример 1. В прямоугольнике ACBD (рис.2) стороны равны 5 см и 12 см. Чему равна диагональ АВ?
Рис.2
Решение. Из прямоугольного треугольника АСВ согласно теореме Пифагора имеем: AB2 = AC2 + BC2 или AB2 = 122 + 52 = 169 и, значит, АB = 13 (см).
Пример 2. Диагонали ромба ABCD (рис.3) равны 24 м и 70 м. Найти его сторону.
Рис.3
Решение. Как известно (теорема 1), диагонали ромба взаимно перпендикулярны и делят его углы пополам. Поэтому треугольник АОВ (см. рис.3) прямоугольный с катетами 12 м и 35 м и, значит, по теореме Пифагора $$ АВ = \sqrt{12^2 + 35^2} = \sqrt{144 + 1225} = \sqrt{1369} = \ 37 \ (м). $$
Пример 3. Основание равнобедренного треугольника a, боковая сторона /b. Найти биссектрису, проведенную из вершины, противолежащей основанию.
Решение. Пусть ABC — равнобедренный треугольник с основанием АВ и CD — его биссектриса (рис.4).
Рис.4
Эта биссектриса является одновременно медианой и высотой. Поэтому $AD = \frac{1}{2} \ AB$ и треугольник ADC прямоугольный с прямым углом D. По теореме Пифагора $$ AC^2 = AD^2 + DC^2 \ \ , \ \ b^2 = \left (\frac{a}{2} \right )^2 + DC^2 . $$ Отсюда $$ DC = \sqrt{b^2 — \frac{a^2}{4}} . $$
Пример 4. Мальчик прошёл по направлению от дома 1200 метров, затем повернул на север и прошёл 500 метров. На каком расстоянии (в метрах) от дома оказался мальчик?
Видео-решение.
Пример 5. Высота конуса равна 4 , а длина образующей — 5. Найдите диаметр основания конуса.
Видео-решение.
Пример 6. Найдите диагональ прямоугольника ABCD, если стороны квадратных клеток на рисунке равны 1.
Видео-решение.
Теорема Пифагора — Вики
 Схема, объясняющая доказательство теоремы Пифагора через равнодополняемость[⇨]
Схема, объясняющая доказательство теоремы Пифагора через равнодополняемость[⇨]Теоре́ма Пифаго́ра — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.
Соотношение в том или ином виде предположительно было известно различным древним цивилизациям задолго до нашей эры; первое геометрическое доказательство приписывается Пифагору. Утверждение появляется как Предложение 47 в «Началах» Евклида[⇨].
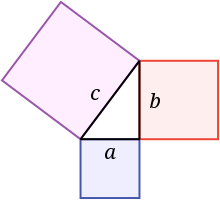
Также может быть выражена как геометрический факт о том, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Верно и обратное утверждение[⇨]: треугольник, сумма квадратов длин двух сторон которого равна квадрату длины третьей стороны, является прямоугольным.
Существует ряд обобщений данной теоремы[⇨] — для произвольных треугольников, для фигур в пространствах высших размерностей. В неевклидовых геометриях теорема не выполняется[⇨].
По мнению историка математики Морица Кантора, в Древнем Египте во времена царя Аменемхета I (около XXIII век до н. э.) было известно о прямоугольном треугольнике со сторонами 3, 4, 5 — его использовали гарпедонапты — «натягиватели верёвок» [1]. В древневавилонском тексте, относимом ко временам Хаммурапи (XX век до н. э.), приведено приближённое вычисление гипотенузы[2]. По мнению Ван-дер-Вардена, очень вероятно, что соотношение в общем виде было известно в Вавилоне уже около XVIII века до н. э.
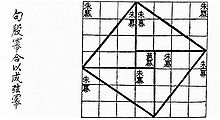
В древнекитайской книге «Чжоу би суань цзин», относимой к периоду V—III веков до н. э., приводится треугольник со сторонами 3, 4 и 5, притом изображение можно трактовать как графическое обоснование соотношения теоремы[3]. В китайском сборнике задач «Математика в девяти книгах» (X—II веков до н. э.) применению теоремы посвящена отдельная книга.
Общепринято, что доказательство соотношения дано древнегреческим философом Пифагором (570—490 до н. э.). Имеется свидетельство Прокла (412—485 н. э.), что Пифагор использовал алгебраические методы, чтобы находить пифагоровы тройки
Приблизительно в 400 году до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Около 300 года до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора
Теорема Пифагора Википедия
 Схема, объясняющая доказательство теоремы Пифагора через равнодополняемость[⇨]
Схема, объясняющая доказательство теоремы Пифагора через равнодополняемость[⇨]Теоре́ма Пифаго́ра — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.
Соотношение в том или ином виде предположительно было известно различным древним цивилизациям задолго до нашей эры; первое геометрическое доказательство приписывается Пифагору. Утверждение появляется как Предложение 47 в «Началах» Евклида[⇨].
Также может быть выражена как геометрический факт о том, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Верно и обратное утверждение[⇨]: треугольник, сумма квадратов длин двух сторон которого равна квадрату длины третьей стороны, является прямоугольным.
Существует ряд обобщений данной теоремы[⇨] — для произвольных треугольников, для фигур в пространствах высших размерностей. В неевклидовых геометриях теорема не выполняется
История
По мнению историка математики Морица Кантора, в Древнем Египте во времена царя Аменемхета I (около XXIII век до н. э.) было известно о прямоугольном треугольнике со сторонами 3, 4, 5 — его использовали гарпедонапты — «натягиватели верёвок»[1]. В древневавилонском тексте, относимом ко временам Хаммурапи (XX век до н. э.), приведено приближённое вычисление гипотенузы[2]. По мнению Ван-дер-Вардена, очень вероятно, что соотношение в общем виде было известно в Вавилоне уже около XVIII века до н. э.

В древнекитайской книге «Чжоу би суань цзин», относимой к периоду V—III веков до н. э., приводится треугольник со сторонами 3, 4 и 5, притом изображение можно трактовать как графическое обоснование соотношения теоремы [3]. В китайском сборнике задач «Математика в девяти книгах» (X—II веков до н. э.) применению теоремы посвящена отдельная книга.
Общепринято, что доказательство соотношения дано древнегреческим философом Пифагором (570—490 до н. э.). Имеется свидетельство Прокла (412—485 н. э.), что Пифагор использовал алгебраические методы, чтобы находить пифагоровы тройки[⇨][4], но при этом в течение пяти веков после смерти Пифагора прямых упоминаний о доказательстве его авторства не находится. Однако когда такие авторы, как
Определение Теорема Пифагора общее значение и понятие. Что это такое Теорема Пифагора
Он известен как теорема к предложению, которая может быть логически продемонстрирована из аксиомы или других теорем, которые уже были соответственно продемонстрированы. В этом контексте важно соблюдать некоторые правила вывода, чтобы прийти к указанной демонстрации.
Пифагор Самосский ( 582 г. до н.э. — 507 г. до н.э.
Пифагор также может сказать, что он считается первым чистым математиком за всю историю и оказал серьезную помощь в развитии научных областей, таких как вышеупомянутая математика, а также геометрия, арифметика, астрономия и музыка. И все благодаря его вышеупомянутой теореме и другим важным открытиям, таким как функциональное значение чисел или несоизмеримость сторон и диагональ того, что такое квадрат.
В частности, можно сказать, что так называемая теорема Пифагора гласит, что квадрат гипотенузы в прямоугольных треугольниках равен сумме квадратов ног
. Чтобы понять это утверждение, мы должны иметь в виду, что треугольник, который идентифицирован как прямоугольник, — это треугольник, который имеет прямой угол (то есть, который измеряет 90º), что гипотенуза состоит из самой длинной стороны указанной фигуры (и противоположной) под прямым углом) и что ноги характеризуются как две меньшие стороны прямоугольного треугольника.Поэтому важность этой теоремы, которая сейчас нас занимает, заключается в том, что она позволяет нам найти меру, основанную на двух конкретных данных. То есть это был важный шаг в математической области, потому что он понял, что, зная длины двух сторон прямоугольного треугольника, мы можем узнать, какова длина третьей стороны.
В 1927 г. математик Е. С. Лумис собрал более 350 доказательств теоремы Пифагора. Лумис разделил эти демонстрации на четыре группы: геометрические демонстрации, которые сделаны на основе сравнения
В случае геометрических демонстраций следует отметить, что многие из них являются авторами или учеными, которые на протяжении всей истории их проводили. Среди них следует выделить, например, великого философа Платона, разработавшего их в своих знаменитых диалогах, или математика Евклида.
Алгебраика также привела к тому, что различные персонажи решили, так или иначе, поднимать, развивать и демонстрировать по-настоящему и ощутимо. Таким образом, в этом случае мы должны упомянуть таких выдающихся фигур, как Леонардо да Винчи, который выполнил построение и демонстрацию этой формы вышеупомянутой теоремы Пифагора.
ТЕОРЕМА ПИФАГОРА это что такое ТЕОРЕМА ПИФАГОРА: определение — История.НЭС
ТЕОРЕМА ПИФАГОРА
Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Даже те, кто в своей жизни далек от математики, продолжают сохранять воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора ясна: это простота — красота — значимость. В самом деле, теорема Пифагора проста, но не очевидна. Противоречие двух начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение. Она применяется в геометрии буквально на каждом шагу. Существует около пятисот различных доказательств этой теоремы, что свидетельствует о гигантском числе ее конкретных реализаций. Исторические исследования датируют появление на свет Пифагора приблизительно 580 годом до нашей эры. Счастливый отец Мнесарх окружает мальчика заботами. Возможности дать сыну хорошее воспитание и образование у него были. Будущий великий математик и философ уже в детстве обнаружил большие способности к наукам. У своего первого учителя Гермодамаса Пифагор получает знания основ музыки и живописи. Для упражнения памяти Гермодамас заставлял его учить песни из «Одиссеи» и «Илиады». Первый учитель прививал юному Пифагору любовь к природе и ее тайнам. Прошло несколько лет, и по совету своего учителя Пифагор решает продолжить образование в Египте. При помощи учителя Пифагору удается покинуть остров Самос. Но пока до Египта далеко. Он живет на острове Лесбос у своего родственника Зоила. Там происходит знакомство Пифагора с философом Ферекидом — другом Фалеса Милетского. У Ферекида Пифагор учится астрологии, предсказанию затмений, тайнам чисел, медицине и другим обязательным для того времени наукам. Затем в Милете он слушает лекции Фалеса и его более молодого коллеги и ученика Анаксимандра, выдающегося географа и астронома. Много важных знаний приобрел Пифагор за время своего пребывания в Милетской школе. Перед Египтом он на некоторое время останавливается в Финикии, где, по преданию, учится у знаменитых сидонских жрецов. Учеба Пифагора в Египте способствует тому, что он сделался одним из самых образованных людей своего времени. Здесь же Пифагор попадает в персидский плен. Согласно старинным легендам, в плену в Вавилоне Пифагор встречался с персидскими магами, приобщился к восточной астрологии и мистике, познакомился с учением халдейских мудрецов. Халдеи познакомили Пифагора со знаниями, накопленными восточными народами в течение многих веков: астрономией и астрологией, медициной и арифметикой. Двенадцать лет пробыл в вавилонском плену Пифагор, пока его не освободил персидский царь Дарий Гистасп, прослышавший о знаменитом греке. Пифагору уже шестьдесят, он решает вернуться на родину, чтобы приобщить к накопленным знаниям свой народ. С тех пор как Пифагор покинул Грецию, там произошли большие изменения. Лучшие умы, спасаясь от персидского ига, перебрались в Южную Италию, которую тогда называли Великой Грецией, и основали там города-колонии Сиракузы, Агригент, Кротон. Здесь и задумывает Пифагор создать собственную философскую школу. Довольно быстро он завоевывает большую популярность среди жителей. Пифагор умело использует знания, полученные в странствиях по свету. Со временем ученый прекращает выступления в храмах и на улицах. Уже в своем доме Пифагор учил медицине, принципам политической деятельности, астрономии, математике, музыке, этике и многому другому. Из его школы вышли выдающиеся политические и государственные деятели, историки, математики и астрономы. Это был не только учитель, но и исследователь. Исследователями становились и его ученики. Пифагор развил теорию музыки и акустики, создав знаменитую «пифагорейскую гамму» и проведя основополагающие эксперименты по изучению музыкальных тонов: найденные соотношения он выразил на языке математики. В Школе Пифагора впервые высказана догадка о шарообразности Земли. Мысль о том, что движение небесных тел подчиняется определенным математическим соотношениям, идеи «гармонии мира» и «музыки сфер», впоследствии приведшие к революции в астрономии, впервые появились именно в Школе Пифагора. Многое сделал ученый и в геометрии. Прокл так оценивал вклад греческого ученого в геометрию: «Пифагор преобразовал геометрию, придав ей форму свободной науки, рассматривая ее принципы чисто абстрактным образом и исследуя теоремы с нематериальной, интеллектуальной точки зрения. Именно он нашел теорию иррациональных количеств и конструкцию космических тел». В школе Пифагора геометрия впервые оформляется в самостоятельную научную дисциплину. Именно Пифагор и его ученики первыми стали изучать геометрию систематически — как теоретическое учение о свойствах абстрактных геометрических фигур, а не как сборник прикладных рецептов по землемерию. Важнейшей научной заслугой Пифагора считается систематическое введение доказательства в математику, и, прежде всего, в геометрию. Строго говоря, только с этого момента математика и начинает существовать как наука, а не как собрание древнеегипетских и древневавилонских практических рецептов. С рождением же математики зарождается и наука вообще, ибо «ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства» (Леонардо да Винчи). Так вот, заслуга Пифагора и состояла в том, что он, по-видимому, первым пришел к следующей мысли: в геометрии, во-первых, должны рассматриваться абстрактные идеальные объекты, и, во-вторых, свойства этих идеальных объектов должны устанавливаться не с помощью измерений на конечном числе объектов, а с помощью
История и определение теоремы Пифагора
Теорему Пифагора, известную геометрическую теорему о том, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы, или в знакомой алгебраической нотации — a2 + b2 = с2, должен знать не только каждый школьник, но и любой уважающий себя образованный человек. В данной статье дано определение теоремы Пифагора. А также кратко описана история ее создания.
История теоремы Пифагора
Определение, ставшее основой математического знания, давно связано с именем греческого математика-философа Пифагора.
По словам сирийского историка Ямблиха (около 250-330 н. э.) свою знаменитую теорему ученый разрабатывал долго. Его ученый путь начался после того, как Пифагор познакомился с математиками Фалесом Милетским и Анаксимандром и стал их учеником. Тогда он отправился в Египет около 535 г. до н. э., чтобы продолжить свое исследование. Он был захвачен во время вторжения в 525 г. до н. э. Камбизом II, царем Персии, и доставлен в Вавилон.
По предположениям некоторых историков, Пифагор даже успел посетить Индию, а затем снова вернулся на побережье Средиземного моря. Ученый вскоре поселился в итальянском Кротоне и создал школу, которую в наше время логичней было бы назвать монастырем. Так зародился пифагореизм — духовно-религиозное учение, все последователи которого придерживались строгих обетов секретности. Все результаты новых математических исследований, проводимых в течение нескольких столетий, были приписаны его имени.

История теоремы Пифагора утверждает, что первое доказательство не принадлежит Пифагору. Вполне вероятно, что вовсе не он доказал теорему, которая тем не менее носит его имя.
Некоторые ученые полагают, что первое доказательство было показано на рисунке. Интересно заметить, что схожие чертежи-доказательства были независимо друг от друга созданы, а позже обнаружены в нескольких разных культурах. Итак, как звучит определение прямоугольного треугольника и теоремы Пифагора? Как выглядит математическая формула последней?
Теорема Пифагора: определение
Для начала разберемся, что такое прямоугольный треугольник. Его отличительной чертой является прямой угол, равный 90 градусам. Собственно, за это его и прозвали прямоугольным!
Визуальная демонстрация теоремы Пифагора полностью подтверждает оригинальное доказательство древнего математического утверждения. Итак, о чем свидетельствует рисунок? Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, которые построены на катетах прямоугольного треугольника. Из этого следует, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Формула: a2 + b2 = c2.
Вывод
Вот уже в течение 4 тысяч лет теорема Пифагора остается базисом математической и геометрической науки. Интересно, что в настоящее время имеется приблизительно 367 различных ее доказательств. В том числе греческого математика Паппа Александрийского (пик деятельности которого пришелся на 320 г. н. э.), арабского врача и математика Табита ибн Курра (жившего около 836-901 г. г.), итальянского художника-изобретателя Леонардо да Винчи (годы жизни: 1452-1519) и даже президента США Джеймса Гарфилда (1831-1881 г. г.).

Тем не менее изначальную историю возникновения и определение теоремы Пифагора должен знать каждый человек, связывающий себя с математикой и научной деятельностью. Ведь, как известно, без знания прошлого нет будущего, а без знания математики невозможно настоящее!
Теорема Піфагора — Вікіпедія
 Теорема Піфагора: a2 + b2 = c2
Теорема Піфагора: a2 + b2 = c2  Анімаційне доведення теореми Піфагора
Анімаційне доведення теореми ПіфагораТеоре́ма Піфаго́ра — одна із засадничих теорем евклідової геометрії, котра встановлює співвідношення між сторонами прямокутного трикутника. Вважається, що вона доведена грецьким математиком Піфагором, на честь котрого вона названа (є й інші версії, зокрема думка, що ця теорема в загальному вигляді була сформульована математиком-піфагорійцем Гіппасом).
Теорема звучить так:
Позначивши довжину гіпотенузи трикутника як c, а довжини катетів як a та b, отримаємо такі формули:
- a2+b2=c2.{\displaystyle a^{2}+b^{2}=c^{2}.\,}
- a2+b2=c.{\displaystyle {\sqrt {a^{2}+b^{2}}}=c.\,}
Отже, теорема Піфагора встановлює співвідношення, яке дає змогу визначити довжину сторони прямокутного трикутника, знаючи довжини двох інших. Відповідно, в алгебраїчній інтерпретації теорему можна сформулювати так:
|
Теорема Піфагора є окремим випадком теореми косинусів, яка визначає співвідношення між сторонами довільного трикутника.
Також доведено зворотне твердження (називають також зворотною до теореми Піфагора):
|
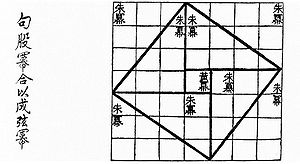 Візуальне доведення для трикутника (3, 4, 5) з книги «Чу Пей» 500—200 до н. е.
Візуальне доведення для трикутника (3, 4, 5) з книги «Чу Пей» 500—200 до н. е.Історію теореми можна розділити на чотири частини: знання про Піфагорові числа, знання про відношення сторін у прямокутному трикутнику, знання про відношення суміжних кутів і доведення теореми.
Мегалітичні споруди близько 2500 до н. е. в Єгипті та Північній Європі містять прямокутні трикутники зі сторонами з цілих чисел.[1]Бартель ван дер Варден висловив гіпотезу, що в ті часи Піфагорові числа були знайдені алгебраїчно.[2]
Написаний між 2000 та 1876 до н. е. папірус часів Середнього Єгипетського царства Berlin 6619 містить задачу, розв’язком якої є числа Піфагора.
Написана під час правління Хамурапі Великого (між 1790 і 1750 до н.е) вавилонська табличка Plimpton 322 містить багато записів, тісно пов’язаних з числами Піфагора.
В сутрах Будхаяни[en], які датуються за різними версіями 8-им чи 2-им століттям до н. е. в Індії, містяться Піфагорові числа, виведені алгебраїчно, формулювання теореми Піфагора та геометричне доведення для рівнобедреного прямокутного трикутника.
В сутрах Апастамби (близько 600 до н. е.) міститься числове доведення теореми Піфагора з використанням обчислення площі. Ван дер Варден вважає, що воно було засноване на традиціях попередників. Згідно з Альбертом Бурком, це оригінальне доведення теореми, і він припускає, що Піфагор відвідав Араконам і скопіював його.
Піфагор, роки життя якого зазвичай приймають за 569 — 475 до н. е., використовує алгебраїчні методи розрахунку піфагорових трійок, згідно з Прокловими коментарями до Евкліда. Прокл, однак, жив між 410 і 485 роками н. е. Згідно з Томасом Гізом, немає ніяких вказівок на авторство теореми протягом п’яти століть після Піфагора. Однак такі автори, як Плутарх або Цицерон, приписали теорему Піфагору у такий спосіб, ніби авторство було широко відоме і безсумнівне.[3]
Близько 400 до н. е. згідно з Проклом, Платон дав метод розрахунку піфагорових трійок, що поєднував алгебру та геометрію. Близько 300 до н. е., в Началах Евкліда маємо найдавніше аксіоматичне доведення, яке збереглося до наших днів.
Написана десь між 500 до н. е. і 200 до н. е., китайська математична книга «Чу Пей» (周髀算经) дає візуальне доведення теореми Піфагора, яка в Китаї називається теорема Гугу (勾股定理), для трикутника із сторонами (3, 4, 5). Під час правління династії Хань, з 202 до н. е. до 220 н. е. Піфагорові трійки з’являються в книзі «Математика в дев’яти книгах» разом із згадкою про прямокутні трикутники.[4]
Вперше зафіксовано використання теореми в Китаї, де вона відома як теорема Гугу (勾股定理), та в Індії, де вона відома як теорема Баскара.
Багато дискутується, чи була теорема Піфагора відкрита один раз чи багато разів. Бойер (1991) вважає, що знання, виявлені в Шульба Сутрах, можуть бути месопотамського походження.[5]
Алгебраїчне доведення[ред. | ред. код]
 Квадрати утворюються з чотирьох прямокутних трикутників.
Квадрати утворюються з чотирьох прямокутних трикутників.Відомо понад сто доведень теореми Піфагора. Тут представлено доведення, засноване на теоремі існування площі фігури:
- Розташуємо чотири однакові прямокутні трикутники так, як це зображено на малюнку.
- Чотирикутник зі сторонами c є квадратом, оскільки сума двох гострих кутів 90∘{\displaystyle 90^{\circ }}, а розгорнутий кут — 180∘{\displaystyle 180^{\circ }}.
- Площа всієї фігури рівна, з одної сторони, площі квадрата зі стороною «a+b», а з іншої — сумі площ чотирьох трикутників і внутрішнього квадрата.
- (a+b)2=4⋅ab2+c2;{\displaystyle (a+b)^{2}=4\cdot {\frac {ab}{2}}+c^{2};}
- a2+2ab+b2=2ab+c2;{\displaystyle a^{2}+2ab+b^{2}=2ab+c^{2};{\frac {}{}}}
- c2=a2+b2;{\displaystyle c^{2}=a^{2}+b^{2};{\frac {}{}}}
Що і необхідно було довести.
За подібністю трикутників[ред. | ред. код]
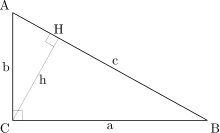 Використання подібних трикутників.
Використання подібних трикутників.Нехай ABC — прямокутний трикутник, в якому кут C прямий, як показано на малюнку. Проведемо висоту з точки C і назвемо H точку перетину зі стороною AB. Утворений трикутник ACH подібний до трикутника ABC, оскільки вони обидва прямокутні (за визначенням висоти) і в них спільний кут A, очевидно, третій кут буде в цих трикутників також однаковий. Аналогічно, трикутник CBH також подібний до трикутника ABC. З подібності трикутників: Якщо
- BC=a,AC=b,AB=c,{\displaystyle BC=a,AC=b,AB=c,\!}
тоді
- ac=HBa та bc=AHb.{\displaystyle {\frac {a}{c}}={\frac {HB}{a}}\ {\text{ та }}\ {\frac {b}{c}}={\frac {AH}{b}}.\,}
Це можна записати у вигляді
- a2=c×HB та b2=c×AH.{\displaystyle a^{2}=c\times HB\ {\text{ та }}\ b^{2}=c\times AH.\,}
Якщо додати ці дві рівності, отримаємо
- a2+b2=c×HB+c×AH=c×(HB+AH)=c2.{\displaystyle a^{2}+b^{2}=c\times HB+c\times AH=c\times (HB+AH)=c^{2}.\,\!}
Іншими словами, Теорема Піфагора:
- a2+b2=c2.{\displaystyle a^{2}+b^{2}=c^{2}.\,\!}
Доведення Евкліда[ред. | ред. код]
Доведення ЕвклідаВ Евклідових «Началах» теорема Піфагора доведена методом паралелограмів. Нехай A, B, C — вершини прямокутного трикутника з прямим кутом A. Опустимо перпендикуляр з точки A на сторону, протилежну до гіпотенузи в квадраті, побудованому на ній. Лінія ділить квадрат на два прямокутники, кожен з яких має таку саму площу, що й квадрати, побудовані на катетах. Головна ідея при доведенні полягає в тому, що верхні квадрати перетворюються на паралелограми такої самої площі, а тоді повертаються і перетворюються на прямокутники в нижньому квадраті і знову при незмінній площі.
Для формального доведення нам необхідні чотири елементарні леми:
- Якщо дві сторони одного трикутника і кут між ними дорівнюють відповідно двом сторонам та куту між ним іншого трикутника, то такі трикутники рівні (сторона-кут-сторона).
- Площа трикутника дорівнює половині площі паралелограма, що має таку саму основу і таку саму висоту.
- Площа прямокутника дорівнює добутку двох суміжних сторін.
- Площа квадрата дорівнює добутку двох його сторін (випливає з третьої леми).
Тоді кожен верхній квадрат пов’язаний з трикутником, конгруентним з іншим трикутником, який пов’язаний поворотом з одним із двох прямокутників, що утворюють нижній квадрат.[6]
Перейдемо до доведення:
- Нехай ACB — прямокутний трикутник з прямим кутом CAB.
- На кожній стороні BC, AB, і CA побудуємо квадрати CBDE, BAGF та ACIH в такому ж порядку. Побудова квадратів тут же вимагає попередньої теореми Евкліда і залежить від постулату паралельності.[7]
- З точки A проводимо пряму, паралельну до BD і CE. Вона перпендикулярно перетне відрізки BC та DE в точках K та L, відповідно.
- Проведемо відрізки CF і AD, отримаємо трикутники BCF і BDA.
- Кути CAB і BAG — прямі; відповідно точки C, A і G — колінеарні. Так само B, A і H.
- Кути CBD і FBA — обидва прямі; тоді кут ABD дорівнює куту FBC, оскільки обидва є сумою прямого кута та кута ABC.
- Трикутники ABD та FBC рівні за двома сторонами та кутом між ними.
- Оскільки точки A, K і L — колінеарні, площа прямокутника BDLK дорівнює двом площам трикутника ABD (BDLK = BAGF = AB2)
- Аналогічно міркуючи, отримаємо CKLE = ACIH = AC2
- З одного боку, площа CBDE дорівнює сумі площ прямокутників BDLK та CKLE, а з іншого боку, це площа квадрата BC2, або AB2 + AC2 = BC2.
«Піфагорові штани» — жартівлива назва цього доказу.
Використовуючи диференціали[ред. | ред. код]
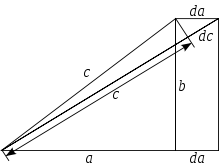 Використання диференціалів.
Використання диференціалів.До теореми Піфагора можна прийти розглядом залежності величини гіпотенузи від приросту сторони (див. малюнок праворуч), застосувавши невелике обчислення.
В результаті приросту сторони a з подібних трикутників для нескінченно малих приростів:
- dadc=ca{\displaystyle {\frac {da}{dc}}={\frac {c}{a}}}
Застосуємо розділення змінних.
- cdc=ada{\displaystyle c\,dc=a\,da}
Інтегруючи, отримаємо:
- c2=a2+const. {\displaystyle c^{2}=a^{2}+\mathrm {const} .\ \,\!}
Якщо a = 0 тоді c = b, отож «константа» — b2. Тоді
- c2=a2+b2.{\displaystyle c^{2}=a^{2}+b^{2}.\,}
Як можна побачити, квадрати отримано завдяки пропорції між приростами та сторонами, тоді як сума є результатом незалежного внеску приростів сторін, що не очевидно з геометричних доведень. В цих рівняннях da і dc, відповідно, — нескінченно малі прирости сторін a і c. Але замість них ми використовуємо Δa і Δc, тоді границя їхнього відношення, якщо вони прямують до нуля, дорівнює da/dc (похідній) і також дорівнює c/a (відношенню довжин сторін трикутників), в результаті чого отримуємо диференціальне рівняння.
Застосування і наслідки теореми[ред. | ред. код]
Піфагорові трійки[ред. | ред. код]
Піфагорові трійки — це три натуральні числа a, b, та c такі, що виконується рівність a2 + b2 = c2. Іншими словами, Піфагорові трійки — це сторони прямокутного трикутника, якщо всі вони є цілими. На мегалітичних спорудах в північній Європі є свідчення, що відомості про такі трійки були відомі до винайдення писемності. Такі трійки зазвичай записують у вигляді (a, b, c). Деякі найвідоміші приклади: (3, 4, 5) та (5, 12, 13).
Примітивними Піфагоровими числами називають такі a, b та c, які є взаємно простими (найбільший спільний дільник a, b та c дорівнює 1)
Нижче наведено перелік примітивних Піфагорових чисел менших від 100:
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97).
- Найкраще запам’ятовуються такі Піфагорові числа (менші від 100):
- (3, 4, 5), (6, 8, 10), (9, 12, 15), (12, 16, 20), (15, 20, 25), (18, 24, 30), (21, 28, 35), (24, 32, 40), (27, 36, 45), (30, 40, 50), (33, 44, 55), (36, 48, 60), (39, 52, 65), (42, 56, 70), (45, 60, 75), (48, 64, 80), (51, 68, 85), (54, 72, 90), (57, 76, 95), (60, 80, 100).
- Ці трійки утворюються множенням першої трійки чисел (3, 4, 5) на числа 2, 3, 4, 5 тощо.
Неспівмірні довжини[ред. | ред. код]
 Побудова відрізків з довжинами, відношення між якими дорівнює квадратному кореню з додатного цілого числа
Побудова відрізків з довжинами, відношення між якими дорівнює квадратному кореню з додатного цілого числаОдним з наслідків теореми Піфагора є те, що відрізки на лінії, довжина яких є неспівмірною (тобто, співвідношення між якими дає ірраціональне число), можуть бути побудовані за допомогою лінійки та циркуля. Теорема Піфагора дає змогу побудувати неспівмірні довжини через те, що гіпотенуза трикутника пов’язана з його сторонам через корінь квадратний.
Малюнок справа демонструє, як побудувати відрізки, довжина яких у співвідношенні дає корінь квадратний будь-якого цілого числа. Кожен трикутник має сторону (позначену «1»), довжина якої є вибрана одиниця вимірювання. На кожному прямокутному трикутнику завдяки теремі Піфагора отримуємо довжину гіпотенузи, виражену у вибраних одиницях. Якщо гіпотенуза пов’язана з одиницею вимірювання через квадратний корінь з додатнім цілим числом, що не є піднесенням до квадрата, тоді ми отримуємо реалізацію неспівмірності для цієї одиниці. Наприклад, √2, √3, √5.
Неспівмірні величини конфліктують з концепцією школи Піфагора про те, що всі числа є цілими. Школа Піфагора давала собі раду з дробами, порівнюючи кратні числа, які мали спільний дільник.[8] Згідно з однією легендою, Гіппаса з Метапонту (близько 470 до н. е.) втопили в морі через те, що він розказував про існування ірраціональних чи неспівмірних величин.[9][10]
Евклідова відстань у різних координатних системах[ред. | ред. код]
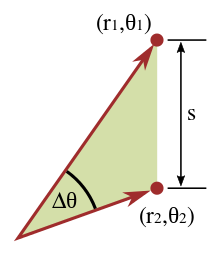
Формулу відстані між точками в декартовій системі координат отримуємо з теореми Піфагора.[11] Якщо маємо точки на площині (x1, y1) і (x2, y2), то відстань між ними, яка також називається Евклідова відстань, можна обчислити так:
- (x1−x2)2+(y1−y2)2.{\displaystyle {\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}.}
Або, узагальнюючи для n-вимірного Евклідового простору, для відстані між двома точками A=(a1,a2,…,an){\displaystyle A\,=\,(a_{1},a_{2},\dots ,a_{n})} та B=(b1,b2,…,bn){\displaystyle B\,=\,(b_{1},b_{2},\dots ,b_{n})} можна сформулювати загальніший випадок теореми Піфагора:
- (a1−b1)2+(a2−b2)2+⋯+(an−bn)2=∑i=1n(ai−bi)2.{\displaystyle {\sqrt {(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}+\cdots +(a_{n}-b_{n})^{2}}}={\sqrt {\sum _{i=1}^{n}(a_{i}-b_{i})^{2}}}.}
Якщо не можна використати Декартові координати, наприклад, у випадку полярних координат, або в загальнішому випадку, якщо треба використати криволінійні координати, формули для розрахунку Евклідової відстані складніші, ніж теорема Піфагора, але можуть бути виведені з її допомогою. Типовий приклад, коли формула відстані між двома точками приведена до криволінійних координат, можна побачити при застосуванні полінома Лежандра у фізиці. Ці формули можна знайти, використовуючи Теорему Піфагора разом із формулами зв’язку криволінійних координат з декартовими. Наприклад, полярні координати (r, θ) можна записати як:
- x=rcosθ, y=rsinθ.{\displaystyle x=r\cos \theta ,\ y=r\sin \theta .\,}
Тоді відстань s між двома точками (r1, θ1) та (r2, θ2) дорівнює:
- s2=(x1−x2)2+(y1−y2)2=(r1cosθ1−r2cosθ2)2+(r1sinθ1−r2sinθ2)2.{\displaystyle s^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}=(r_{1}\cos \theta _{1}-r_{2}\cos \theta _{2})^{2}+(r_{1}\sin \theta _{1}-r_{2}\sin \theta _{2})^{2}.\,}
Якщо піднести до степеня і об’єднати змінні, отримаємо формулу для визначення відстані між точками у полярних координатах:
- s2=r12+r22−2r1r2(cosθ1cosθ2+sinθ1sinθ2)=r12+r22−2r1r2cos(θ1−θ2)=r12+r22−2r1r2cosΔθ ,{\displaystyle {\begin{aligned}s^{2}&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\left(\cos \theta _{1}\cos \theta _{2}+\sin \theta _{1}\sin \theta _{2}\right)\\&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos \left(\theta _{1}-\theta _{2}\right)\\&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos \Delta \theta \end{aligned}}\ ,}
використовуючи формули перетворення добутків функцій. Цю формулу, що є теоремою косинусів, іноді називають узагальненою теоремою Піфагора. [12] Якщо результуючу формулу використати для випадку, коли радіуси знаходяться під прямим кутом, кут між ними дорівнює Δθ = π/2, тоді знову отримаємо теорему Піфагора: s2=r12+r22.{\displaystyle s^{2}=r_{1}^{2}+r_{2}^{2}.\,} Теорема Піфагора справедлива для прямокутних трикутників, проте є частковим випадком загальнішої теореми косинусів, яка справедлива для будь-якого трикутника.
Тригонометрична тотожність Піфагора[ред. | ред. код]
 Подібні прямокутні трикутники показують синус і косинус кута θ
Подібні прямокутні трикутники показують синус і косинус кута θДля прямокутного трикутника із сторонами a, b та гіпотенузою c, запишемо тригонометричні визначення синуса і косинуса кута θ між стороною a та гіпотенузою:
- sinθ=bc,cosθ=ac.{\displaystyle \sin \theta ={\frac {b}{c}},\quad \cos \theta ={\frac {a}{c}}.}
звідси випливає що:
- cos2θ+sin2θ=a2+b2c2=1,{\displaystyle {\cos }^{2}\theta +{\sin }^{2}\theta ={\frac {a^{2}+b^{2}}{c^{2}}}=1,}
де в останньому кроці доведення застосовуємо теорему Піфагора. Цю залежність між синусом і косинусом іноді називають фундаментальною тригонометричною тотожністю Піфагора.[13] В подібних трикутників, співвідношення між сторонами рівне незалежно від розмірів трикутника, а залежить тільки від кутів. Відповідно, на рисунку зображено трикутник з гіпотенузою, яка дорівнює одиниці, сторона протилежна до кута дорівнює sin θ і прилегла сторона — cos θ в одиницях гіпотенузи.
Подібні геометричні фігури на трьох сторонах[ред. | ред. код]
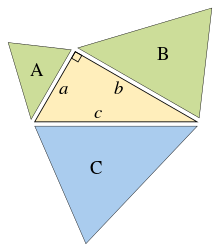 Узагальнення для подібних трикутників, площа зелених фігур A + B = площі синіх C
Узагальнення для подібних трикутників, площа зелених фігур A + B = площі синіх C 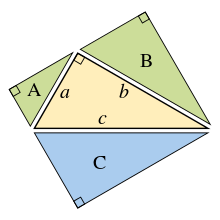 Теорема Піфагора з використанням подібних прямокутних трикутників
Теорема Піфагора з використанням подібних прямокутних трикутниківУзагальнення теореми Піфагора робив Евклід у своїй праці Начала, розширивши площі квадратів на сторонах до площ подібних геометричних фігур:[14]
Якщо побудувати подібні геометричні фігури (див. Евклідова геометрія) на сторонах прямокутного трикутника, тоді сума двох менших фігур буде дорівнювати площі більшої фігури.
Головна ідея цього узагальнення полягає в тому, що площа подібної геометричної фігури пропорційна до квадрату будь-якого свого лінійного розміру і зокрема до квадрату довжини будь-якої сторони. Отже, для подібних фігур з площами A, B і C, що побудовані на сторонах з довжиною a, b і c, маємо:
- Aa2=Bb2=Cc2,{\displaystyle {\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}\,,}
- ⇒A+B=a2c2C+b2c2C.{\displaystyle \Rightarrow A+B={\frac {a^{2}}{c^{2}}}C+{\frac {b^{2}}{c^{2}}}C\,.}
Але, за теоремою Піфагора, a2 + b2 = c2, тоді A + B = C.
І навпаки, якщо ми зможемо довести, що A + B = C для трьох подібних геометричних фігур без використання теореми Піфагора, тоді ми зможемо довести саму теорему, рухаючись у зворотному напрямку. Наприклад, стартовий центральний трикутник може бути повторно використаний як трикутник C на гіпотенузі, і два подібні прямокутні трикутники (A і B), побудовані на двох інших сторонах, які утворюються в результаті поділу центрального трикутника його висотою. Сума площ двох менших трикутників тоді очевидно дорівнює площі третього, таким чином A + B = C і, виконуючи попереднє доведення в зворотному порядку, отримаємо теорему Піфагора a2 + b2 = c2.
Теорема косинусів[ред. | ред. код]
Теорема Піфагора — це окремий випадок загальнішої теореми косинусів, яка пов’язує довжини сторін в довільному трикутнику:[15]
- a2+b2−2abcosθ=c2,{\displaystyle a^{2}+b^{2}-2ab\cos {\theta }=c^{2},\,}
де θ — кут між сторонами a і b.
Якщо θ дорівнює 90 градусів, тоді cosθ = 0 і формула спрощується до звичайної теореми Піфагора.
Довільний трикутник[ред. | ред. код]
Узагальнення теореми Піфагора від Сабіта ібн Курра.[16] Нижній рисунок: відображення трикутника ABD (верхній) з метою утворити трикутник DBA, подібний до трикутника ABC (верхній).Для вибраного кута довільного трикутника із сторонами a, b, c, впишемо рівнобедрений трикутник таким чином, щоб рівні кути при його основі θ дорівнювали вибраному куту. Припустимо, що вибраний кут θ протилежний до сторони позначеної c. В результаті ми отримали трикутник ABD з кутом θ, що протилежний стороні a та стороною r. Другий трикутник утворюється кутом θ, що протилежний до сторони b та стороною з довжиною s, як показано на рисунку. Сабіт ібн Курра[17] стверджував, що сторони в цих трьох трикутниках пов’язані таким чином:[18][19]
- a2+b2=c(r+s) .{\displaystyle a^{2}+b^{2}=c(r+s)\ .}
Коли кут θ наближається до π/2, основа рівнобедреного трикутника зменшується і дві сторони r і s перекривають одна одну все менше і менше. Коли θ = π/2, ADB перетворюється в прямокутний трикутник, r + s = c, і отримуємо початкову теорему Піфагора.
Розглянемо одне з доведень. Трикутник ABC має такі самі кути як і трикутник ABD, але в зворотному порядку. (Два трикутники мають спільний кут у вершині B, обидва мають кут θ і також мають однаковий третій кут, за сумою кутів трикутника) Відповідно, ABC — подібний до відображення ABD трикутника DBA, як зображено на нижньому рисунку. Запишемо співвідношення між сторонами протилежними і прилеглими до кута θ,
- ca=ar .{\displaystyle {\frac {c}{a}}={\frac {a}{r}}\ .}
Так само відображення іншого трикутника,
- cb=bs .{\displaystyle {\frac {c}{b}}={\frac {b}{s}}\ .}
Перемножимо дроби та додамо ці два співвідношення:
- cr+cs=a2+b2 ,{\displaystyle cr+cs=a^{2}+b^{2}\ ,}
що і треба було довести.
Довільні трикутники через паралелограми[ред. | ред. код]
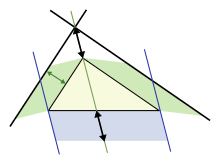 Узагальнення для довільних трикутників,
Узагальнення для довільних трикутників,зелена площа = синій площі
 Побудова доведення для узагальнення паралелограмів
Побудова доведення для узагальнення паралелограмівЗробимо подальше узагальнення для не прямокутних трикутників, використовуючи паралелограми на трьох сторонах замість квадратів.[20] (а квадрати — це звичайно частковий випадок.) Верхній рисунок демонструє, що для гострокутного трикутника, площа паралелограма на довшій стороні дорівнює сумі паралелограмів на двох інших сторонах, за умови що паралелограм на довгій стороні побудовано як зображено на рисунку(розміри відзначені стрілками однакові і визначають сторони нижнього паралелограма). Ця заміна квадратів паралелограмами несе чітку схожість з початковою теоремою Піфагора, вважається, що це сформулював Папп з Александрії в 4 р.н. е.[20]
Нижчий рисунок показує хід доведення. Подивимось на ліву сторону трикутника. Лівий зелений паралелограм має таку саму площу, як ліва частина синього паралелограма, тому що вони мають таку саму основу b і висоту h. Крім того, лівий зелений паралелограм має таку саму площу, як лівий зелений паралелограм на верхньому рисунку, тому що вони мають таку саму основу (верхня ліва сторона трикутника) і таку саму висоту перпендикулярну до цієї сторони трикутника. Аналогічно розмірковуючи для правої сторони три