Урок математики в 5 классе на тему «Решение уравнений»

Достиг ли ты своих целей?

Оцени степень усвоенности:

усвоил полностью

усвоил частично

не усвоил

Продолжи одно из предложений:

“Мне понятно…

“Я запомнил…

“Мне на уроке…

“Я думаю…

3.Знакомство с правилами работы.

Правила работы:

1. Быть внимательным и сообразительным.

2. Не оставлять ни одного вопроса без ответа.

3. На каждое задание затрачивать минимум времени, но максимум усердия.

4. Не подглядывать, не подслушивать, не «проникать» в мысли соседа.

5. Постараться набрать за урок максимальное количество баллов, получив при этом отличные отметки.

4.Устный счёт (самопроверка и оценивание).

слагаемое

15

17

слагаемое

10

10

сумма

40

25

уменьшаемое

37

49

вычитаемое

17

20

разность

35

39

множитель

12

11

множитель

5

15

произведение

30

99

делимое

48

50

делитель

8

7

частное

9

5

Ответы:

25; 30; 8

20; 55; 10

60; 2; 9

6; 63; 10

Критерии оценивания:

12 чисел «5»

11 чисел «4»

10 -7 чисел «3»

6 чисел «2».

5. Цифровой диктант.

1-да, 0-нет.

1. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

2. В записи а+в=с а-множитель.

3. Запись а+в=в+а выражает сочетательное свойство.

4. В записи 12*15+15*13 общий множитель 15.

5. В уравнений х+23=50 неизвестен первый множитель.

6. Решить уравнение-значит найти все его корни (или убедиться. Что уравнение не имеет ни одного корня).

7. Корнем уравнения х*15=45 является число 3.

8. Равенство ( а*в)*с= а*(в*с) означает распределительное свойство.

9. 5 мин=500 сек.

10. Уравнения а*2=120 и х*2=40*3 имеют равные корни.

ОТВЕТЫ: 1 0 0 1 0 1 1 0 0 1

Критерии оценивания:

10+ «5», 9+ «4», 8+»4»,7+»3», 6+»3», 5+ «2».

6.Повторение теоретического материала.

1)Чтобы найти неизвестное слагаемое, надо

А)Из суммы вычесть известное слагаемое

2)Чтобы найти неизвестное уменьшаемое, надо

Б)из уменьшаемого вычесть разность.

3)Чтобы найти неизвестное вычитаемое, надо

В)к разности прибавить вычитаемое.

4)Чтобы найти неизвестный множитель, надо

Г)частное умножить на делитель.

5)Чтобы найти неизвестное делимое, надо

Д)произведение разделить на другой множитель.

6)Чтобы найти неизвестный делитель, надо

Е)делимое разделить на частное.

Ответы: 1 А; 2В; 3Б; 4Д; 5Г; 6Е

Оценивание: 6+ «5», 5+ «4», 4+ «3», 3+ «2».

7.Физкультминутка.

8.Решение уравнений( с последующей проверкой).

Учебник С.А. Козлова, А.Г.Рубин

Стр.131 №6.

Ответы:

А)543 б)900 в)109 г)1100 д)25 е)2160

Ж)40 з)287 и)28

Оценка: 9+ «5»; 8 +»4»; 7+ «4»; 6+ «3»; 5+ «2»

9.Рефлексия.

Достиг ли ты своих целей?

Оцени степень усвоенности:

усвоил полностью

усвоил частично

не усвоил

Продолжи одно из предложений:

“Мне понятно…

“Я запомнил…

“Мне на уроке…

“Я думаю…

10. Итог урока.

11. Домашнее задание.

1) №395, 403 и теория 9повторить)

2) придумать по три примера на каждое правило.

Тест «Уравнение».(индивидуальное задание)

1. Уравнение – это: 

а)равенство, содержащее букву, значение которой надо найти;
б)числовое равенство;
в) буквенное выражение. 

2. Корнем уравнения называется: 

а)любое значение буквы;
б) значение буквы, при котором из уравнения получается верное числовое равенство;
в) значение буквы, при котором из уравнения получается неверное числовое равенство.

3. Решить уравнение, значит: 

а)подставить число в уравнение;
б)заменить букву в уравнении любым числом;
в) найти все его корни (или убедиться, что это уравнение не имеет ни одного корня). 

4. Сделать проверку уравнения, значит: 

а) подставить найденное значение вместо буквы и проверить верность равенства;
б)подставить найденное значение в уравнение;
в) сделать что-то ещё. 

Найди ошибки, если они есть.( на плакате).

1)50+х=600 2) х:17=34 х=34:17 х=2

Х=600+50

100-Х=650

3) 100-а=42 4)37+х=20 х=37-20 х=17

а=100-42

а=58

Индивидуальное задание.(стр.131 №9).

Выписать уравнение с равными корнями.

Памятка для обучающегося «Правила нахождения компонентов при решении уравнений», 5 класс

ПРАВИЛА НАХОЖДЕНИЯ КОМПОНЕНТОВ		ПРАВИЛА НАХОЖДЕНИЯ КОМПОНЕНТОВ
Компоненты при сложении: I слагаемое, II слагаемое. Результат сложения: Сумма. I сл + II сл = Сум I сл = Сум – II сл II сл = Сум – I сл	Компоненты при вычитании: Уменьшаемое, вычитаемое. Результат вычитания: Разность. Ум – Выч = Разн Ум = Разн + Вычит Вычит = Ум – Разн	Компоненты при сложении: I слагаемое, II слагаемое. Результат сложения: Сумма. I сл + II сл = Сум I сл = Сум – II сл II сл = Сум – I сл	Компоненты при вычитании: Уменьшаемое, вычитаемое. Результат вычитания: Разность. Ум – Выч = Разн Ум = Разн + Вычит Вычит = Ум – Разн
Сложение показывает сумму всех слагаемых	Вычитание показывает на сколько уменьшаемое больше вычитаемого	Сложение показывает сумму всех слагаемых	Вычитание показывает на сколько уменьшаемое больше вычитаемого
Компоненты при умножении: I множитель, II множитель. Результат умножения: Произведение. I мн · II мн = Произвед I мн = Произвед : II мн II мн = Произвед : I мн	Компоненты при делении: Делимое, делитель Результат деления: Частное . Делим : делит = Частное Делим = Част · делит делит = Делим : Част	Компоненты при умножении: I множитель, II множитель. Результат умножения: Произведение. I мн · II мн = Произвед I мн = Произвед : II мн II мн = Произвед : I мн	Компоненты при делении: Делимое, делитель Результат деления: Частное . Делим : делит = Частное Делим = Част · делит делит = Делим : Част
Умножение показывает сумму нескольких одинаковых слагаемых	Деление показывает во сколько раз делимое больше делителя	Умножение показывает сумму нескольких одинаковых слагаемых	Деление показывает во сколько раз делимое больше делителя

Компоненты при сложении:

I слагаемое, II слагаемое.

Результат сложения: Сумма.

I сл + II сл = Сум

I сл = Сум – II сл

II сл = Сум – I сл

Компоненты при вычитании:

Уменьшаемое, вычитаемое.

Результат вычитания: Разность.

Ум – Выч = Разн

Ум = Разн + Вычит

Вычит = Ум – Разн

Компоненты при сложении:

I слагаемое, II слагаемое.

Результат сложения: Сумма.

I сл + II сл = Сум

I сл = Сум – II сл

II сл = Сум – I сл

Компоненты при вычитании:

Уменьшаемое, вычитаемое.

Результат вычитания: Разность.

Ум – Выч = Разн

Ум = Разн + Вычит

Вычит = Ум – Разн

Сложение показывает сумму всех слагаемых

Вычитание показывает на сколько уменьшаемое больше вычитаемого

Сложение показывает сумму всех слагаемых

Вычитание показывает на сколько уменьшаемое больше вычитаемого

Компоненты при умножении:

I множитель, II множитель.

Результат умножения:

Произведение.

I мн · II мн = Произвед

I мн = Произвед : II мн

II мн = Произвед : I мн

Компоненты при делении:

Делимое, делитель

Результат деления: Частное .

Делим : делит = Частное

Делим = Част · делит

делит = Делим : Част

Компоненты при умножении:

I множитель, II множитель.

Результат умножения: Произведение.

I мн · II мн = Произвед

I мн = Произвед : II мн

II мн = Произвед : I мн

Компоненты при делении:

Делимое, делитель

Результат деления: Частное .

Делим : делит = Частное

Делим = Част · делит

делит = Делим : Част

Умножение показывает сумму нескольких одинаковых слагаемых

Деление показывает во сколько раз делимое больше делителя

Умножение показывает сумму нескольких одинаковых слагаемых

Деление показывает во сколько раз делимое больше делителя

Разработка урока по математике 5 класс по теме «Решение уравнений»

Технологическая карта урока

Открытия нового знания

Технология построения урока

Системно-деятельностный подход

Тема

«Решение уравнений»

Цель

Создать условия для освоения двух способов решения уравнений, которые раньше не встречались

Основные термины, понятия

Уравнение, корень уравнения

Предметные умения:

формирование навыков устного счета, повторение темы «Упрощение выражений»;

формирование умений решать уравнения, которые раньше не встречались, двумя способами, выбирать наиболее приемлемый способ решения.

Личностные УУД:

формирование способности к самооценке на основе критерия успешной учебной деятельности; воспитание ответственности за общее дело.

Регулятивные УУД:

уметь определять и формулировать цель урока; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действий; планировать свои действия в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать свое предположение.

Познавательные УУД:

уметь отличать новое от уже известного; находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке; уметь осознанно и произвольно строить речевое высказывание; самостоятельно создавать алгоритм деятельности; извлекать из математических текстов необходимую информацию; использовать знаково-символические средства; строить логическую цепочку рассуждений.

Коммуникативные УУД:

уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и следовать им; уметь выражать свои мысли четко, полно и точно.

Фронтальная, работа в парах, индивидуальная.

Книгопечатная продукция

Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд, «Математика 6», М., «Мнемозина», 2014;

тестовые задания, листы самоконтроля.

Технические средства обучения

мультимедиа-проектор, презентация.

Дидактические задачи этапов урока

включение учащихся в учебную деятельность на личностно значимом уровне

2

Актуализация знаний и пробное учебное действие

готовность мышления и осознание потребности к построению нового способа действия

3

Выявление места и причины затруднения

выявление и фиксация места и причины затруднения

4

Построение проекта выхода из затруднения

постановка цели учебной деятельности, выбор способа и средств ее реализации

5

Реализация построенного проекта

построение и фиксация нового знания

6

Первичное закрепление (с комментированием во внешней речи)

применение нового знания в типовых заданиях

7

Самостоятельная работа с самопроверкой по эталону

применение нового знания в типовых заданиях, самопроверка решения

8

Включение в систему знаний и повторение

включение нового знания в систему знаний, повторение и закрепление ранее изученного

9

Рефлексия учебной деятельности на уроке

соотнесение цели урока и его результатов, самооценка работы на уроке, осознание метода построения нового знания.

Технология изучения

Этапы урока

Формируемые умения

Деятельность учителя

Деятельность обучающихся

Мотивация к учебной деятельности

Метапредметные (УУД):

регулятивные:

организация своей учебной деятельности.

коммуникативные:

умение слушать и вступать в диалог, планирование учебного сотрудничества с учителем и сверстниками.

Приветствует учащихся, проверяет готовность к уроку.

«Ну-ка, проверь, дружок,

Ты готов начать урок?

Всё ль на месте,

Всё ль в порядке,

Ручка, книжка и тетрадка?

Все ли правильно сидят?

Все ль внимательно глядят?

Каждый хочет получать

Только лишь оценку «пять»?

Приветствуют учителя. Проверяют готовность к уроку.

Актуализация знаний и пробное учебное действие

Предметные:

формирование навыков устного счета, повторение темы «Упрощение выражений».

Метапредметные (УУД):

познавательные:

структурирование собственных знаний;

регулятивные:

контроль и оценка процесса и результатов деятельности;

коммуникативные:

организация и планирование учебного сотрудничества с учителем и сверстниками.

Вступительное слово учителя:

Ребята, на доске зашифровано слово, которое имеет прямое отношение к теме нашего урока, разгадайте его.

1) 120-20*4

2) 215-(115+97)

3) (549+298)-249

4) 15+420:4

5) (296+157)-146

6) 11+23+27+39+29.

Какое слово получили?

Выполняют задание, участвуют в беседе с учителем, отвечают на поставленные вопросы.

Корень

Выявление места и причины затруднения

Предметные:

проверка знаний определений уравнения, корня уравнения, правил нахождения неизвестного слагаемого, уменьшаемого, вычитаемого; умений решать простые уравнения.

Метапредметные (УУД):

познавательные:

умение осознанно и произвольно строить речевое высказывание в устной форме;

регулятивные:

умение проговаривать последовательность действий на уроке;

коммуникативные:

проявление активности во взаимодействии для решения познавательных задач; умение использовать речь для регуляции своего действия, построение понятных для окружающих высказываний

Какое же отношение корень имеет к нашему сегодняшнему уроку?

У чего есть корни? Нам это не подходит, а еще? Говорят «мои корни отсюда», что это значит? Что предки человека родом из этого края. Но и это к нашему уроку не имеет отношения. В математике понятие «корень» неразрывно связано с понятием уравнения. Давайте вспомним, что же называют уравнением?

Да, действительно уравнение содержит букву, которая обозначает неизвестное, но данное определение неполное. Давайте выполним следующее задание и дадим определение уравнения.

Какое из выражений является уравнением:

1) а-3=45

2) 458-236=222

3) х-34=х-34

4) у-45+7

5) 0*у=9

6) х(х+2)=15

Почему выражения по №2 и 4 не являются уравнениями?

Давайте сформулируем, что такое уравнение.

Что значит решить уравнение?

Что называют корнем уравнения?

Теперь вспомним правила решения уравнений.

Как найти неизвестное слагаемое? Уменьшаемое? Вычитаемое?

У растений.

Корень – это часть слова.

Уравнение – это выражение, содержащее букву.

1, 3, 5, 6

во 2 нет буквы, а в 4 нет знака «=»

Уравнение – это равенство, содержащее букву, значение которой надо найти.

Решить уравнение – значит найти его корни или доказать, что их нет.

Корнем уравнения называют значение буквы, при котором уравнение обращается в верное равенство.

Дают определения

Предлагает решить устно уравнения:

1. 34 + х = 1056

2. 576 – у = 124

3. (х – 15) + 34 = 44

4. с – 195 = 203

5. а + 764 = 764

6. (36 + х) – 16 = 25

Почему при решении 3 и 6 уравнений у вас возникли затруднения?

Мы раньше не встречали такие уравнения и не знаем, как их решать.

Построение проекта выхода из затруднения

Метапредметные (УУД):

познавательные:

умение осознанно и произвольно строить речевое высказывание в устной форме;

регулятивные:

умение определять и формулировать цель урока, планировать свои действия в соответствии с поставленной задачей;

коммуникативные УУД:

уметь оформлять свои мысли в устной форме.

Итак, сформулируйте тему нашего урока.

Какие цели мы может поставить перед собой?

Учитель стимулирует учащихся к высказываниям и подводит их к постановке цели учебной деятельности.

«Решение уравнений»

Предполагаемые ответы:

Решать уравнения.

Знать компоненты при сложении и вычитании.

Знать правила – как найти неизвестные слагаемое, уменьшаемое, вычитаемое.

Реализация построенного проекта

Предметные:

формирование умений решать уравнения, которые раньше не встречались, двумя способами.

Метапредметные (УУД):

регулятивные УУД:

умение работать по коллективно составленному плану, планировать свои действия в соответствии с поставленной задачей;

познавательные УУД:

умение находить ответы на вопросы, используя учебник, осознанно и произвольно строить речевое высказывание; самостоятельно создавать алгоритм деятельности; извлекать из математических текстов необходимую информацию; строить логическую цепочку рассуждений;

коммуникативные УУД:

уметь оформлять свои мысли в устной форме; слушать и понимать речь других.

Предлагает ознакомиться с №375 в учебнике.

Итак, сколько способов решения подобных уравнений существует? В чем особенность каждого способа?

Работа организуется в парах. Несколько учеников озвучивают результат работы, остальные при необходимости уточняют, дополняют.

Первичное закрепление (с комментированием во внешней речи)

Предметные:

формирование умений решать уравнения, которые раньше не встречались, двумя способами, выбирать наиболее приемлемый способ решения.

Метапредметные (УУД):

регулятивные:

умение проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действий; планировать свои действия в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать свое предположение;

познавательные:

выделение и формулирование познавательной цели, рефлексия способов и условий действий,

анализ объектов и синтез;

коммуникативные:

проявление активности во взаимодействии для решения познавательных задач; умение использовать речь для регуляции своего действия, построение понятных для окружающих высказываний.

Комментирует, направляет работу учащихся.

1. Найдите ошибки и решите правильно:

(х – 24)+37 = 49

х – 24 =49 +37,

х – 24 =86,

х = 86 – 24,

х =72.

Предлагает выполнить задание №504 из учебника двумя способами. Комментирует, направляет работу учащихся.

Какой способ удобнее применить для решения данного уравнения?

Вступают в диалог с учителем, предлагают способы решения, выбирают наиболее рациональный способ.

2 учащихся работают у доски с последующими комментариями, остальные в тетрадях.

Самостоятельная работа с самопроверкой по эталону

Предметные:

формирование умений решать уравнения, которые раньше не встречались, двумя способами, выбирать наиболее приемлемый способ решения.

Метапредметные (УУД):

регулятивные УУД:

умение работать по коллективно составленному плану; оценивать правильность выполнения действий; планировать свои действия в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок;

познавательные:

выделение и формулирование познавательной цели, рефлексия способов и условий действия, анализ объектов и синтез.

регулятивные:

планирование своей деятельности для решения поставленной задачи и контроль полученного результата.

Предлагает самостоятельно выполнить тестовые задания. В процессе работы оказывает помощь учащимся по их запросу.

Предлагает осуществить самопроверку. Верные ответы демонстрируются на слайде.

Учащиеся самостоятельно выполняют задания.

Осуществляют самопроверку.

Включение в систему знаний и повторение

Предметные:

формирование умений решать уравнения, которые раньше не встречались, двумя способами, выбирать наиболее приемлемый способ решения.

Метапредметные (УУД):

познавательные:

выделение и формулирование познавательной цели, рефлексия способов и условий действия,

анализ объектов и синтез.

регулятивные:

планирование своей деятельности для решения поставленной задачи и контроль полученного результата.

коммуникативные:

проявление активности во взаимодействии для решения познавательных задач; умение использовать речь для регуляции своего действия, построение понятных для окружающих высказываний.

Предлагает выполнить задание № 447 из учебника, выбрав наиболее приемлемый способ решения. Комментирует, направляет работу учащихся.

Вступают в диалог с учителем, предлагают способы решения, выбирают наиболее рациональный.

2 учащихся работают у доски с последующими комментариями, остальные в тетрадях.

Рефлексия учебной деятельности на уроке

Метапредметные (УУД):

познавательные:

структурирование знаний;

регулятивные:

оценка промежуточных результатов и саморегуляция для повышения мотивации учебной деятельности, оценивание собственной деятельности на уроке;

коммуникативные:

умение анализировать собственные успехи, неудачи, определять пути коррекции.

Вместе с учениками формулирует основные тезисы изученной темы.

Какая же цель стояла перед нами?

Достигли ли мы поставленной цели?

На каком этапе урока вам было легко, а когда трудно? Сможете ли вы сделать домашнее задание?

Предлагает заполнить лист самоконтроля.

Откройте дневники и запишите домашнее задание.

Спасибо за урок, до свидания!

Участвуют в беседе с учителем.

Заполняют лист самоконтроля.

Записывают домашнее задание.

Презентация «Решение уравнений» 5 класс

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Учитель математики МБОУ «Славкинская СШ» Ташина В.А.

2 слайд Описание слайда:

Уравнение — это равенство, содержащее букву, значение которой надо найти. Корень уравнения — это значение буквы, при котором из уравнения получается верное числовое равенство. Решить уравнение — значит найти все его корни или убедиться, что корней нет.

3 слайд Описание слайда:

Решение уравнений на сложение и вычитание Что надо найти Слагаемое x + 9 = 15 Уменьшаемое x — 14 = 2 Вычитаемое 5 — x = 3 Правило Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое. Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое. Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность. Пример решения x + 9 = 15 x = 15 — 9 x = 6 Проверка 6 + 9 = 15 15 = 15 x — 14 = 2 x = 14 + 2 x = 16 Проверка 16 — 2 = 14 14 = 14 5 — x = 3 x = 5 — 3 x = 2 Проверка 5 — 2 = 3 3 = 3

4 слайд Описание слайда:

Решение уравнений на умножение и деление Что надо найти Множитель y • 4 = 12 Делимое y : 7 = 2 Делитель 8 : y = 4 Правило Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. Чтобы найти неизвестное делимое, надо частное умножить на делитель. Чтобы найти неизвестный делитель, надо делимое разделить на частное. Пример решения y • 4 = 12 y = 12 : 4 y = 3 Проверка 3 • 4 = 12 12 = 12 y : 7 = 2 y = 2 • 7 y = 14 Проверка 14 : 7 = 2 2 = 2 8 : y = 4 y = 8 : 4 y = 2 Проверка 8 : 2 = 4 4 = 4

5 слайд Описание слайда:

Решим уравнения Ответ. х=57 Ответ. х=379 Ответ. х=23 Ответ. х=5 Ответ. х=400 Ответ. х=12

6 слайд Описание слайда:

x – 234 = 56 367 + x = 549 369 – x = 23 x + 145 = 189 127 + x = 379 x – 367 = 25 x + 238 = 299 296 – x = 77 I вариант II вариант

7 слайд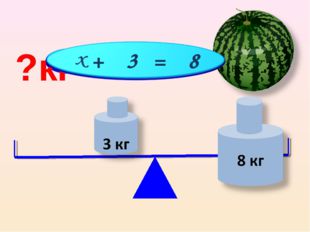 Описание слайда:

?кг + 3 = 8

8 слайд Описание слайда:

Решение задач составить выражение к задаче В одном мешке х кг картофеля, а в другом в 3 раза больше. Сколько кг картофеля в двух мешках? 2Х 3Х 4Х ДРУГОЙ ОТВЕТ

9 слайд Описание слайда:

Решение задач составить выражение к задаче В одном мешке х кг картофеля, а в другом в 3 раза больше. На сколько кг картофеля в первом мешке меньше , чем во втором? Х 2Х 3Х ДРУГОЙ ОТВЕТ

10 слайд Описание слайда:

Решение задач. Составить уравнение к задаче В парке 70 берёз и сосен . Сколько сосен посадили, если берёз в 6 раз больше , чем сосен? Х + 6 = 70 6Х + Х = 70 6Х — Х = 70 ДРУГОЙ ОТВЕТ

11 слайд Описание слайда:

Решение задач. Составить уравнение к задаче В парке посадили берёз на 70 больше , чем сосен . Сколько сосен посадили, если берёз в 6 раз больше , чем сосен? Х + 6 = 70 6Х + Х = 70 6Х — Х = 70 ДРУГОЙ ОТВЕТ

12 слайд Описание слайда:

Решение задач. Составить уравнение к задаче Провод длиной 77 м разрезали на три куска так, что длина второго куска оказалась в 5 раз больше первого, а третий кусок равен второму. Найдите длину каждого куска проволоки. Х + Х + 5Х = 77 Х + 5Х + 5Х = 77 Х + 5Х = 77 ДРУГОЙ ОТВЕТ

13 слайд Описание слайда:

Решение задач. придумать задачу по уравнению m + 5m = 90

14 слайд Описание слайда:

Решение задач. придумать задачу по уравнению 3а + 2а = 75

15 слайд Описание слайда:

Курс профессиональной переподготовки

Учитель математики

Курс повышения квалификации

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДВ-118337

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Урок «Решение уравнений» в 5 классе

МАТЕМАТИКА

5 класс

Тема: «Решение уравнений»

Цель урока: формировать у учащихся понятие уравнения, корня уравнения, умение решать уравнения, способствовать формированию логического мышления, формированию творческой и социальной компетентностей учащихся.

Тип урока: урок усвоения новых знаний.

Оборудование: карточки.

Методы и приемы: взаимопроверка, работа в парах, работа в группах, беседа, самостоятельная работа.

Ожидаемые результаты: после этого урока учащиеся смогут:

— правильно находить решения уравнения;

— проверять правильность решения уравнения;

— сравнивать, обобщать, делать выводы;

— формируется логическое мышление;

— приобретать навыки интерактивной деятельности;

-систематизировать изученный материал.

Во время проведения урока формируются, развиваются творческая и социальная компетентности учащихся.

Ход урока

I. Организационный момент.

а) Этический заряд.

б) Проверка домашнего задания (№ 542 (1,2), 546,548).

1) Взаимопроверка тетрадей (№ 542).

2) № 548 проверить и оценить как творческую работу, учащиеся записывали его на отдельных листах и сдали учителю ( задания повышенной сложности).

II. Актуализация опорных знаний.

Учащиеся получают карточки.

№1. Найдите значение выражения:

2х+3, если х=1, х=10

№2. Вычислите: а) 4×13×25; б) 6а×7в.

III. Изучение нового материала.

1. Учитель называет тему урока «Решение уравнений», цель урока и мотивацию (т.е. существуют задачи, решение которых не обходится без составления уравнений).

Учитель напоминает учащимся, что с понятием «уравнения», «корень уравнения» они встречались уже в младших классах, они понимают, что значит решить уравнение.

Учитель делит класс на несколько групп. Каждой группе предлагается задача.

Задача 1. Масса белого медведя и льва вместе равна 1000 кг, причем масса медведя в три раза больше массы льва. Определите массу медведя и массу льва.

Задача 2. На остановке из трамвая вышло 8 пассажиров, а зашло 12. После этого в трамвае оказалось 42 пассажира. Сколько пассажиров находилось в трамвае до остановки?

Учащиеся коллективно обсуждают и составляют уравнения. Далее учитель вводит определение корня, рассматривает случаи, когда уравнение имеет один корень, несколько корней, бесконечное множество корней и вообще не имеет корней. При этом учащиеся групп принимают активное участие и помогают учителю. Например:

1. 4х+2=10; 2) 0×х=5; 3) х-х=0; 4)(х+5)(х-2)=0;

Учитель обращает внимание учащихся на то, что значит — решить уравнение, а также, учащиеся вспоминают правила нахождения неизвестного слагаемого, неизвестного уменьшаемого, неизвестного вычитаемого.

2. Работа с учебником. Учитель задает вопросы группам, учащиеся обсуждают и отвечают на них.

Вопросы:

1. Что называется корнем уравнения?

2. Что означает – «решите уравнение»?

3. Как найти неизвестное слагаемое?

4. Как найти неизвестное уменьшаемое?

5. Сколько корней может иметь уравнение?

IV. Закрепление знаний. Усвоение знаний.

Основным видом задания, какие должны выполнять учащиеся будут такие:

а) проверка корней уравнения;

б) решение уравнений всех видов;

в) составление уравнения для решения задач.

Учитель предлагает учащимся выполнить устные упражнения:

1. Какое из чисел 3,10,15 является решением уравнения

а) х+17=25; б)4х-5=7;

2. Решите уравнения:

а) х+38=47; б) х-544=218; в)700-у=420; г) 145+х=250;

Далее учащиеся выполняют письменно упражнения № 556 (1,3,5,7,9,11,13) (нечетные), № 558, 566 (1,3,5).

Самостоятельная работа В1, В2.

1. Х+38=64 1) 47+х=81

2. Х-386=495 2) у-296=389

3. (х+86)-72=138 3) (х+92)-64=147

4. 154-(х-110)=86 4) 186-(х-98)=78

V. Подведение итогов. Д/З:

1. §16, № 557 (1,3,5,7), № 569, 574 (1).

2. Творческое задание: составить три уравнения, которые имеют один корень, бесконечное множество корней и вообще не имеют корней.

План-конспект урока по алгебре (5 класс) на тему: Урок математики в 5 классе по теме Решение уравнений.

Урок математики в 5-м классе по теме «Решение уравнений»

Учитель: Миначова Ф.М.

Класс: 5 «А»

Дата проведения урока: 29.10.2013

Учебник: Математика 5 класс, Н.Я.Виленкин, Мнемозина, 2010

Цель: Формирование навыков решения сложных (составных) уравнений двумя способами: с помощью нахождения неизвестного компонента действия; с помощью применения свойств сложения и вычитания для упрощения одной из частей уравнений.

Задачи:

• Обеспечить применение учащимися теоретических знаний об уравнении — понятий: «уравнение», «корень уравнения», «что значит решить уравнение» при выполнении практических заданий.
• Создать условия для формирования умения решать уравнения на основе знаний взаимосвязи компонентов действий (и применяя свойства действий сложения и вычитания).
• Организовать деятельность учащихся по самостоятельному применению знаний в стандартной и изменённой ситуации.
• Создать условия для развития математического кругозора учащихся, мышления, творческой активности, памяти и внимания.
• Создать условия для воспитания культуры общения, аккуратности, организованности.

Оборудование: Проектор, раздаточный материал.

Ход урока

I. Организационный этап

1. Приветствие учителя.
2. Проверка подготовленности учащихся к уроку.
3. Организация внимания учащихся и сообщение темы и целей урока.

Здравствуйте ребята!  Начинаем урок. Проверьте всё ли у вас для этого готово? (учебники, рабочие тетради, раздаточный материал) Сегодня на уроке мы будем  решать уравнения, которые характеризуются как сложные или составные, так как они содержат не одно, а два (а то  и несколько) действий. Но я бы применила другое определение – интересные уравнения. Ведь чем больше действий в арифметическом примере или текстовой задаче, тем интереснее их решать. Не правда ли? ☺ И сегодня наша цель: научиться решать составные уравнения различными способами. А вот девиз урока: «Решай, ищи, твори и мысли»

II. Проверка выполнения домашнего задания.

Но сначала проверим как вы справились с домашним заданием.

№ д.з.	Учитель	Ученик	Ответ
397 (в)	Какое уравнение вы составили для решения данной задачи?	(х+10) – 12 =17	(х+10) – 12 =17
395 (д) 166 = m – 34	Что нужно найти в уравнении?	В уравнении нужно было найти неизвестное уменьшаемое.
	Как найти неизвестное вычитаемое?	Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.	m = 166 + 34
	Какой получили ответ?		200
395 (е) 59 = 81 – k	Что нужно найти в уравнении?	В уравнении нужно было найти неизвестное вычитаемое.
	Как найти неизвестное вычитаемое?	Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.	k = 81 – 59
	Какой получил ответ?		22
397 (б)	Какое уравнение вы составили для решения задачи?	350 + х = 900	350 + х = 900
	Что нужно найти в уравнении?	В уравнении нужно было найти неизвестное слагаемое
	Как найти неизвестное слагаемое?	Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.	х = 900 – 350
	Какой ответ?	550 г сахара добавили в пакет.	550

II. Актуализация знаний.

 Ребята приготовьте карточки №1, которые я раздала вам перед уроком.

	Учитель	Ученик (правильный ответ)
	Что такое уравнение?	Уравнение – это равенство с переменной.
	Что такое корень уравнения?	Корень  уравнения  – это число, при подстановке которого в исходное уравнение последнее обращается в верное равенство.
	Что значит решить уравнение?	Решить уравнение – это значит найти все его корни или доказать, что корней нет.
Карточка № 1	Определите под каким номером записано уравнение?	3, 6, 9
х – 405 = 138	(устно) Найдите корень уравнения по номером 9.	543
х + 357 = 1204	(устно) Найдите корень уравнения по номером 3.	847
1570 – х = 614	(устно) Найдите корень уравнения по номером 6.	956
Карточка № 1	А что записано под остальными номерами?	Под номером 1 записано числовое равенство, под номерами 2, 4, 5, 7, 8 записаны буквенные выражения.
	Что такое буквенное выражение?	Буквенное выражение – это запись чисел и букв, связанных между собой знаками действий.
	Как можно прочитать выражение?	Выражение можно прочитать по последнему действию.
	Что значит упростить выражение?	Упростить выражение – это значит выполнит все возможные действия.
	С помощью чего можно упростить выражение?	Упростить выражение можно с помощью свойств сложения, вычитания, умножения.
Карточка № 1	Используя свойства сложения и вычитания упростите выражения:	(Записи в тетради)
2. х + 4 + 18	Какое свойство можно применить для упрощения  данного выражения?	Можно применить сочетательное свойство сложения                                 х + 4 + 18 = х + (4 + 18) = х + 22
4. 69 – х – 20	Какое свойство можно применить для упрощения  данного выражения?	Можно применить свойство вычитания суммы из числа                 69 – х – 20 = 69 – (х + 20) = 69 – 20 – х = 49 – х
5. 57 + (х + 23)	Какое свойство можно применить для упрощения  данного выражения?	Можно применить сочетательное свойство сложения                                 57 + (х + 23) = 57 + 23 + х = 80 + х
7.(138 + х) – 95	Какое свойство можно применить для упрощения  данного выражения?	Можно применить свойство вычитания числа из суммы               (138 + х) – 95 = 138 – 95 + х = 43 + х
8. 41 –  (х + 23)	Какое свойство можно применить для упрощения  данного выражения?	Можно применить свойство вычитания суммы из числа                 41 –  (х + 23) = 41 – 23 – х = 18 – х

III. Устный счёт.

Раздать учащимся первых парт  карточки для устного счёта. Вычисление цепочкой по рядам «Какой ряд быстрее».

№ парты (пары)	Условие задания	Ответ
1	Наименьшее трёхзначное число уменьшить в 2 раза	50
2	Полученное число уменьшить на 37	13
3	Полученный ответ умножить на 4	52
4	Получившееся число увеличить на 18	70
5	Ответ уменьшить в 10 раз	7
6	Полученное число умножить само на себя	49
7	К полученному произведению прибавить 11	60
8	Проверить все вычисления и поднять руку, если всё правильно. Если есть ошибки, исправить.

IV. Решение уравнений.

А сейчас приступим к решению сложных (составных) уравнений. Рассмотрим два способа  решения следующего уравнения:

(60 + у) – 25  = 72.

I способ. Вопрос учителя: Какое выражение записано в левой части уравнения? Ответ учащегося: В левой части уравнения записана разность. Учитель: Назовите уменьшаемое. Учащийся: (60 + y). Учитель: Назовите вычитаемое. Учащийся: 25. Найдем неизвестное уменьшаемое:

60 + у = 72 + 25,

60 + у = 97, в результате получили простое уравнение, из которого находим  неизвестное слагаемое

у = 97 –  60

у = 37

Проверка: (60 + 37) – 25 = 72

II способ. Сначала упростим выражение, стоящее в левой части уравнения, используя свойства вычитания:

(60 – 25) + у = 72,

35 + у = 72, в результате получили простое уравнение, из которого находим неизвестное слагаемое

у = 72 — 35,

у = 37.

Проверка: (60 + 37) – 25 = 72

Ответ: 37.

Физкультминутка.

Таким образом Составные уравнения можно решить, применяя один из разобранных способов. Вспомним девиз урока: «Решай, ищи, твори и мысли» и выполним из учебника № 376 (а, в, д) (решить уравнения двумя способами).

V. Итог урока.

Этап контроля и самоконтроля.

Исторический экскурс

Ребята, а знаете ли вы, кто и когда придумал первое уравнение? По-видимому, ответить на этот вопрос невозможно. Ещё за 3-4 тысячи лет до нашей эры египтяне и вавилоняне умели решать простейшие уравнения, вид которых и приёмы решения были не похожи на современные. Греки унаследовали знания египтян и пошли дальше. Наибольших успехов в развитии учения об уравнениях достиг греческий учёный Диофант (III век).

В дальнейшем многие математики занимались проблемами уравнений. Одним из них был французский математик, имя которого вы узнаете, если выполните задания, предложенные для самостоятельной работы.

Задания для самостоятельной работы. (карточки №2)

Вариант 1	Вариант 2
Решите уравнение у –  409 = 511. Решите уравнение (24 -х) + 37 = 49. Решите уравнение 23 + х = 50. Решите с помощью уравнения задачу. Если из задуманного числа вычесть 234, то получится 110. Каково задуманное число?	Решите уравнение 700 – х = 605. Решите уравнение (57 – у) +24 = 49. Решите уравнение х + 47 = 60. Решите с помощью уравнения задачу. Катя задумала число. Если вычесть его из числа 348, то получится 185. Какое число задумала Катя?

 

73   Л   217	32   Т   12	27   И   13
163   Е    344	95   В   920	495   А   107

Франсуа Виет жил в 16 веке. Он внёс большой вклад в изучение различных проблем математики и астрономии. Более подробно о некоторых его работах мы поговорим в 8 классе.

Рефлексия. (карточка № 3). Учащиеся заполняют таблицу и дают оценку своей работе на уроке.

План-конспект урока по алгебре (5 класс) на тему: открытый урок «Уравнение» 5 кл

РАЗРАБОТКА УРОКА ПО МАТЕМАТИКЕ

в 5 классе по ФГОС

«Уравнение»

(урок открытия новых знаний).

                         Разработала учитель математики

МКОУ»Кокоринская СОШ»

Сванкулова Алена Анатольевна.

2017 г.

Тема урока: « Уравнение».

Тип урока: урок открытия новых знаний

Класс: 5

Цели по содержанию:

• Обучающие:  формировать навыки нахождения неизвестного в уравнении, тренировать способность к его практическому использованию.
• Развивающие: развитие умения анализировать, сравнивать, обобщать, проводить аналогию, делать выводы, развивать внимание.
• Воспитывающие: воспитание культуры устной и письменной речи, внимательности, аккуратности, культуры своего родного края, воспитание профессионального интереса

Планируемые результаты учебного занятия:

Предметные: построить алгоритм нахождения неизвестного в уравнении, тренировать способность к его практическому применению, объяснять содержательный смысл уравнения, что значит решить уравнение.

Метапредметные:

• Регулятивные: понимать учебную задачу урока, осуществлять решение учебной задачи под руководством учителя, определять цель учебного задания, контролировать свои действия в процессе его выполнения, обнаруживать и исправлять ошибки, отвечать на итоговые вопросы и оценивать свои достижения.
• Коммуникативные: воспитывать любовь к математике, родному краю, коллективизм, уважение друг к другу, умение слушать, дисциплинированность, самостоятельность мышления.
• Познавательные: уметь ориентироваться в своей системе знаний, добывать новые знания, уметь осознанно и произвольно строить речевое высказывание, строить логическую цепочку рассуждений.

Личностные: формировать учебную мотивацию, адекватную самооценку, необходимость приобретения новых знаний.

Используемые технологии: здоровьесбережения, проблемного обучения, дифференцируемый подход в обучении.

Ход урока:

1. ОРГАНИЗАЦИОННЫЙ ЭТАП:

Здравствуйте, ребята! Я рада приветствовать вас на уроке математики.

Урок хочу начать со стихотворения

Встречай гостей, к тебе мы едем

Вновь нам захотелось, посмотреть твою степную красоту

Посмотреть долину, где стоишь ты ,ее мы не проедем

И дома твои, озера, речки, водопады на горах, тайгу

Кош-Агач в стране все знают, он известен,

Расположен в Чуйской он степи, в средине гор!

Виталий Букач

На сегодняшнем уроке мы с вами немного освежим знания о родном крае.

И приступим все к работе.

2. ПОСТАНОВКА ЦЕЛИ И ЗАДАЧ УРОКА. МОТИВАЦИЯ К УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ:

 Тему урока сейчас вы сформулируете сами, для этого прослушайте математическую сказку:

— Жил в избушке на лесной опушке дед по прозвищу Равняло. Любил он с числами подшучивать. Возьмёт дед, выстроит по обе стороны от себя числа, соединит их знаками, а самые резвые в скобки возьмёт, но следит, чтобы одна часть равнялась другой. А потом какое-нибудь число спрячет под маской «икс» и попросит своего внучка, маленького Равнялку, найти его. Равнялка хоть и мал, но дело своё знает: быстро перегонит числа, кроме «икса», в другую сторону. А числа слушаются его, выполняют все действия по приказу, и вот уже известен «икс». Дед смотрит на внучка и радуется: хорошая смена ему растёт.

— Ребята,  о чём шла речь в этой сказке?

-Попробуйте сформулировать тему сегодняшнего урока. (Уравнения.)

-Ребята, почему и для чего нужно изучать эту тему?

— Запишите тему урока в тетрадь.

-Посмотрите на доску и скажите в каких заданиях записано то, что сегодня мы будем изучать.

Задания на доске
№1	№2	№3	№4	№5	№6
2 + х	33-х=15	х +27=43	35-8=27	х -39=45	45 — х

-Как называются эти выражения?(Уравнения)

-Что неизвестно в этих уравнениях?(В №2 — вычитаемое, в №3 — первое слагаемое, в №5 – уменьшаемое)

-Что нужно сделать для нахождения неизвестного?(В №2 – для нахождения вычитаемого нужно из уменьшаемого вычесть разность, в №3 – для нахождения первого слагаемого нужно из суммы вычесть второе слагаемое, в №5 для нахождения уменьшаемого нужно к разности прибавить вычитаемое).

-Какова основная учебная задача на этом уроке?(Узнать, что называется уравнением и корнем уравнения. Вывести алгоритм нахождения неизвестного и научиться его применять при решении уравнений).

Обучающиеся пробуют поставить цель урока и обсуждают пути её достижения, определяют средства достижения цели.  Учитель(если нужно) корректирует и обобщает высказывания обучающихся, а затем формулирует что такое уравнение, корень уравнения и алгоритм нахождения неизвестного.

-Для того, чтобы успешно изучать новую темы, что мы с вами должны хорошо уметь?(Правильно складывать и вычитать).

-Поэтому, что сейчас мы должны провести?(Устный счёт).

На интерактивной доске  показать примеры устного счёта:

Но под каждым примером записаны буквы. Нужно составить 2 слова

36+45	66-48	77+66	213-55	37+48	52-38	55+84	121-46	34+67	84-37	39+66	134-55
С	я	а	к	т	й	Е	у	С	п	ь	ч

1.Найди значение выражения

Правильно Чуйская степь.

Чуйская степь – крупнейшая на Алтае межгорная котловина занимает немалую территорию Кош-Агачского района. Это место одно из самых сухих и холодных в России.

2.Найдите неизвестные

а)457 — у =237;           б) 123+ к =444;       в)  о — 456 = 121;  г)  к +234=500;

Плоскогорье Укок, расположенное на высоте около 2,5 тыс.м над уровнем моря на юге Горного Алтая, лежит на стыке четырех государств: России, Казахстана, Монголии и Китая. Уникальное сочетание факторов природного значения позволило придать плоскогорью Укок статус объекта Всемирного природного наследия ЮНЕСКО.

3.Найдите ошибку:

А)34 +45 = 79

В)38 +67 =106

Г) 91- 54 =47

73 -47 =26

3. АКТУАЛИЗАЦИЯ ЗНАНИЙ И ФИКСАЦИЯ ЗАТРУДНЕНИЯ В ПРОБНОМ ДЕЙСТВИИ:

— Молодцы!  Вы хорошо поработали устно.

-А зачем  мы выполнили эти задания?

-Каким действием проверяется правильность их выполнения?

-Зачем они нужны при изучении темы сегодняшнего урока?(Мы повторили действия сложения и вычитания, повторили нахождение неизвестного, выяснили правильно ли решены примеры. Показали умения считать устно, быстро и правильно. Эти знаниянам  будут необходимы сегодня на уроке.

Класс разбивается на три группы.

Задание для работы в группе. Обучающимся предлагается решить три уравнения за пять минут, при этом должно быть проведено обсуждение решения в группах. Корни уравнения  связаны с некоторыми данными природными объектами Кош-Агачского района:

1)х+56=376;           2)345-х=113;       3)х-190=678.

1)х=320(р. Чуя)

2)х=232(р. Аргут)

3)х=868(Красная горка)

В конце работы предоставляется возможность одному из групп показать своё решение всему классу и рассказать о реках Чуя,Аргут и о Красной горке. Остальные внимательно слушают, при необходимости поправляют и дополняют ответ выступающих.

4. ВЫЯВЛЕНИЕ МЕСТА И ПРИЧИНЫ ЗАТРУДНЕНИЯ:

— Почему у всех вас не получились одинаковые ответы?

— Что вызвало затруднение? (Некоторые не знают алгоритм нахождения неизвестного.)

-Почему некоторые допустили ошибки при решении первого уравнения?(Незнание правила нахождения неизвестного слагаемого).

-Какая ошибка была допущена при решении второго уравнения?(Незнание правила вычитаемого).

-В третьем уравнении какое правило было не правильно использовано?(Правило нахождения вычитаемого)

5. ПОСТРОЕНИЕ ПРОЕКТА ВЫХОДА ИЗ ЗАТРУДНЕНИЯ:

— Тогда какова цель вашей деятельности?( — Узнать алгоритм решений уравнений для нахождения неизвестного слагаемого, вычитаемого и уменьшаемого).

— Скажите, а смысл какого действия поможет нам вывести алгоритм нахождения неизвестного слагаемого?

(По смыслу вычитания, неизвестное слагаемое равно разности суммы и другого слагаемого).

— Как вы будете им пользоваться? (Для того, чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

-А теперь выведите алгоритм решения 2 уравнения, опираясь на только что полученные знания

-Попытайтесь сформулировать правило решения 2 уравнения, используя названия компонентов действия вычитания.(Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность).

-Теперь выведите алгоритм решения 3 уравнения, опираясь на своё решение

-Сформулируйте  правило решения 3 уравнения(Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность).

6. РЕАЛИЗАЦИЯ ПОСТРОЕННОГО ПРОЕКТА:

Задание парам:

— Дополнить известный алгоритм для нахождения неизвестного в уравнении со скобками: ( 45 – х) + 56 =100  .

Обучающиеся работают в парах 5 минут, обсуждаются итоги работы пар. Обучающиеся пытаются сформулировать алгоритмнахождения неизвестного в уравнении со скобками. Учитель может организовать подводящий диалог.

— Вернемся к нашему уравнению и найдем его корень, используя полученный алгоритм.

— Будьте внимательны при оформлении задания!

Кто-то из детей проговаривает и записывает у доски (учитель помогает правильно оформить задание).

— Сравните полученный алгоритм с эталоном в учебнике. Обратите внимание на оформление решения в учебнике двумя способами.

Дети читают решение про себя, затем один ученик вслух.

— Справились с затруднением? – Молодцы!

— Какие задания вы теперь можете выполнять? (Мы теперь можем решать уравнения на нахождение неизвестного).

7.ФИЗКУЛЬТМИНУТКА:

Дружно с вами мы решали и про числа рассуждали,

А теперь мы дружно встали, свои косточки размяли.

На счет раз кулак сожмем, на счет два в локтях сожмем.

На счет три — прижмем к плечам, на 4 — к небесам

Хорошо прогнулись, и друг другу улыбнулись

Про пятерку не забудем — добрыми всегда мы будем.

На счет шесть прошу всех сесть.

     Числа, я и вы, друзья, вместе дружная семья.

8. ПЕРВИЧНОЕ ЗАКРЕПЛЕНИЕ С ПРОГОВАРИВАНИЕМ ВО ВНЕШНЕЙ РЕЧИ:

— Что теперь необходимо сделать?  (Надо научиться применять эталон  для решения уравнений на нахождение неизвестного слагаемого, вычитаемого, уменьшаемого.)

1. Решите уравнения, записанные на доске, проговаривая свои действия по алгоритму. (По одному ученику комментируют решение по алгоритму.)

Задания на доске.

Вычислите:                                            

   а)х +456 =747   (х = 291)                                                               

б)683 – х=352       (х =331)

в)х – 512 =123  (х =635)

2. – Предлагаю теперь поработать самостоятельно

Самостоятельная работа на закрепление для обучающихся с низким уровнем знаний

Карточка
Х+ 435=567	Х – 234 =34	569 – Х =123

Самостоятельная работа на закрепление для обучающихся со среднем уровнем знаний

Карточка
Х+ 435=567	Х – 234 =34	(569 – Х) + 245=353

Самостоятельная работа на закрепление для обучающихся с высоким уровнем знаний

Карточка
Х+ 435=567	(Х – 234) + 111 =534	(569 – Х) + 245=353

Работа проверяется по образцу.

— Повторите еще раз алгоритм нахождения неизвестного в уравнении.

9. САМОКОНТРОЛЬ С САМОПРОВЕРКОЙ ПО ЭТАЛОНУ:

— Выполните задание самостоятельно.

Обучающиеся выполняют задание, после чего учитель открывает на доске или раздаёт эталон для самопроверки.

— Пожалуйста сверьтесь с эталоном.

— Кто действовал так же и получил тот же результат – поставьте «+». – Вы, молодцы!

— У кого получился другой ответ – поставьте «-», найдите по шагам место, где допущена ошибка, обведите её. – Обратите внимание на это место. Ещё раз проговорите алгоритм нахождения неизвестного про себя.

 – Молодцы в том, что сумели найти место, в котором допущена ошибка. – Поставьте рядом «+».

10. РЕФЛЕКСИЯ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ НА УРОКЕ:

— Что нового узнали на уроке?

— Были удачи на уроке? Какие? (Справились с затруднением, узнали, что называется уравнением, корнем уравнения.Научились находить неизвестное в уравнении.)

— Что нам помогло справиться с затруднением?

— Достигли цели урока? (..)

Вспомнили о некоторых достопримечательностей Кош-Агачского района

Фамилия, имя	Нужное  обвести
Я знаю, что называется уравнением	Да                   нет                не уверен
Я знаю, что такое корень уравнения	Да                   нет                не уверен
Я разобрался с правилом, нахождения неизвестного слагаемого в уравнении.	Да                   нет                не уверен
Я разобрался с правилом, нахождения вычитаемого в уравнении.	Да                   нет                не уверен
Я разобрался с правилом, нахождения уменьшаемого в уравнении.	Да                   нет                не уверен
Тема урока мне показалась интересной.	Да                   нет                не уверен
Я выполнил  правильно    …. уравнения  в самостоятельной работе	1                        2                            3

11 . ДОМАШНЕЕ ЗАДАНИЕ:

Учить алгоритм нахождения неизвестного,

Решить карточки на оценку «3», «4», «5».

Спасибо всем за урок!