Пространственная теорема Пифагора Все плоские углы тетраэдра

Пространственная теорема Пифагора

Все плоские углы тетраэдра ОABC при вершине О — прямые. Докажите, что квадрат площади треугольника ABC равен сумме квадратов площадей остальных граней (пространственная теорема Пифагора).

Три формулировки теоремы Пифагора: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов; Квадрат длины диагонали прямоугольника равен сумме квадратов длин двух его взаимно перпендикулярных сторон; Квадрат длины любого отрезка равен сумме квадратов длин его проекций на любые две взаимно перпендикулярные прямые.

(1. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов B BC 2=AB 2+AC 2 A С

2. Квадрат длины диагонали прямоугольника равен B 1 сумме квадратов длин двух его взаимно перпендикулярных сторон B C O 2 O A O O 1 A 1 2=OA 2+OB 2 OC OA=O 1 A 1 OB=O 2 B 1

3. Квадрат длины любого отрезка равен сумме квадратов длин его проекций на любые три взаимно перпендикулярные прямые A c B q B 2 B 1 a A 1 B 1 Доказательство: C p A 1 A 2 1) Отрезки A 1 B 1 и AC – это проекции отрезка АВ на две взаимно перпендиb кулярные прямые к плоскости Y. По теореме Y Пифагора (3 формул. ) AB 2=A 1 B 12+AC 2 ;

2) Спроектируем отрезок A 1 B 1 на прямую а в отрезок А 1 В 1 и на прямую b в отрезок А 2 В 2. По теореме Пифагора 2 A 1 B 1 =A 1 B 12+A 2 B 22; 3) По теореме о проекциях отрезки А 1 В 1 A c A 3 и А 2 В 2 – это проекции отрезка АВ на B прямые a и b. А 3 В 3 АС. q C А 3 В 3=АС; B 3 B 2 A 2 4) Заменяя длины АС и А 1 В 1 B 1 длинами проекций А 1 В 1, b p B 1 А 2 В 2, А 3 В 3, получаем A 1 а равенство: A 1 AB 2=A 1 B 12+A 2 B 22+A 3 B 32

Всегда хочется быть выше перед страхом казаться неумелым… Будь уверен в себе все получится!!!

Теорема Пифагора доказательство

Обращаясь к истории, теорема Пифагора хоть и носит название Пифагора, но открыл ее не он. Так как особые свойства прямоугольного прямоугольника ученые начали изучать намного раньше его. Тем не менее есть два утверждения. Первое гласит о том что Пифагор доказал теорему. Второе, соответственно что не он. На данным момент не проверить какое из этих мнений верно, но к сожалению, если и было доказательство Пифагора, то оно не дожило до нашего времени. Так же есть мнение что доказательство сделанное Евклидом, было сделано Пифагором, а Евклид его обнародовал.

Несомненно в Египте во времена правления фараонов, возникали вопросы с прямоугольным треугольником. В истории Вавилона он так же участвовал. Из чего можно сделать вывод, что данная теорема, вызывала интерес с древних времен. На сегодняшний день существует 367 различных доказательств. Чем не может похвастать ни какая другая теорема.

Заметка: Если Вы ищите мебель для лаборатории или просто хотите приобрести вытяжной шкаф (http://www.labmet.ru/shkafy-vytyazhnye.html). Перейдите по данной ссылке и купите все что нужно. Качество гарантированно!

Разберем основные доказательства.

1 Теорема Пифагора доказательство.

Считается что это легкий способ. В нем применяются правильные треугольники.

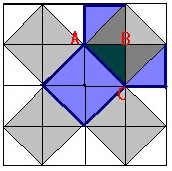
если взять равнобедренный прямоугольный треугольник АВС, от гипотенузы АС мы сможем построить квадрат, в котором находятся 4 аналогичных треугольника. С помощью катета АВ и ВС строятся квадраты, содержащие в себе еще по два таких же треугольника.

2 Теорема Пифагора доказательство.

Здесь сочетается как алгебра так и геометрия. Изображаем прямоугольный треугольник abc. И 2 квадрата равных двум длинам катетов а+b. Затем сделаем построение, как на рисунках 2, 3. Вследствие чего получим два квадрата со сторонами а и b. Второй квадрат содержит 4 треугольника, образуя таким образом квадрат равный гипотенузе c. Интересно что общая площадь квадратов на рис. 2, 3 равная друг другу.

Обобщая все в формулу мы получим. а²+b² = (а+b)² — 4 * 1/2 * а * b. Раскрыв скобки получим а²+b²= а²+b². Площадь рис.3 вычисляем как S=c² или а²+b²=с².ч.т.д.

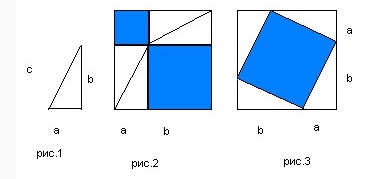
3 Теорема Пифагора доказательство.

Доказательство найдено в 12 вв, в древней индии.

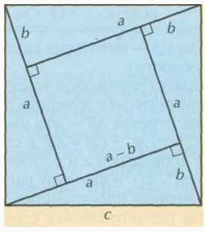
Построим в квадрате 4 треугольника (прямоугольных). Гипотенузой будет сторона с, катетами в треугольнике а и b. Вычисляем площади квадратов большой- S=c

2, и внутренний
(а-b)² 2 +4 * 1/2 * а * b. Из чего вывод, что с²= (а-b)² 2+ 4 * 1/2 * а * b, а следовательно, с²= а²+b².

4 Теорема Пифагора доказательство.

Основано на геометрии, носит название Метод Гарфилда. Построением прямоугольного треугольника ABC найдем доказательство тому , что BC2=AC2+AB2.Продолжим катет AC, создав прямую СD равную катету AB. Соединяя прямую и угол E перпендикулярно АD получаем ED. Прямые AC и ЕD равные между собой.

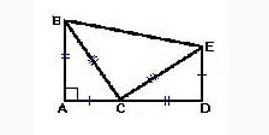
Для доказательства данного действия, воспользуемся так же двумя методами, приравнивая этим выражения.
Находим площадь многоугольника АВЕD. Так как АВ=СD, АС=ЕD, ВС=СЕ, значит S_АВED= 2*1/2 (АВ*АС)+ 1/2 ВС².
Мы видим что АВСD трапеция. А значит S _АВСD = (DE+AB)*1/2AD.
Представим эти методы вместе приравнивая их:
AB*AC+ 1/2 BC²= (DE+AB)*1/2(АС+CD).
Упростим АВ*АС +1/2ВС²= 1/2(АВ+АС)².
Раскрыв скобки получаем : АВ*АС+1/2ВС²=1/2АС+2*1/2(АВ*АС)+1/2АВ².
Итог: ВС²=АС²+АВ². ч.т.д.

Это далеко не все способы доказательства теоремы Пифагора, но основные из них.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

math-public:teorema_pifagora [Президентский ФМЛ №239]

Теорема Пифагора

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Доказательство

Рассмотрим треугольник $\triangle ABC$ с прямым углом $C$.

Пусть $AB=c, AC=b, BC=a$.

Докажем, что $a^2+b^2=c^2$.

Достроим треугольник $ABC$ до квадрата $CDFH$ со стороной $(a+b)$ так, как это показано на рисунке.

Треугольники $\triangle ABC$, $\triangle BDE$, $\triangle EFG$ и $\triangle GHA$ равны по двум катетам.

Тогда у них равны гипотенузы, следовательно $EGAB$ – ромб.

Кроме того из равенства этих треугольников следует, что $\angle 1=\angle 3$, а так как $\angle 1+\angle 2=90^\circ$, то $\angle 2+\angle 3=90^\circ$, следовательно, $\angle ABE=90^\circ$, то есть $BEGA$ – ромб с прямым углом, то есть квадрат.

Квадрат $CDFH$ – составлен из четырех равных треугольников и квадрата со стороной $c$.

Тогда с одной стороны $S_{CDFH}=(a+b)^2$, а с другой $S_{CDFH}=4S_{ABC}+c^2$.

Следовательно, $(a+b)^2=4\cdot\dfrac{ab}{2}+c^2$, откуда $a^2+b^2=c^2$.

Обратная теорема Пифагора

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный.

Доказательство

Пусть в треугольнике $\triangle ABC$ выполняется равенство $AB^2=AC^2+BC^2$.

Докажем, что $\angle C=90^\circ$.

Рассмотрим прямоугольный треугольник $A_1B_1C_1$ с прямым углом $\angle C_1$, у которого $A_1C_1=AC$ и $B_1C_1=BC$.

По теореме Пифагора $A_1B_1^2=A_1C_1^2+B_1C_1^2$, и, значит, $A_1B_1^2=AC^2+BC^2=AB^2$, то есть $A_1B_1=AB$.

Тогда треугольники $ABC$ и $A_1B_1C_1$ равны по третьему признаку равенства, следовательно, $\angle C=\angle C_1=90^\circ.$

Формула Герона

Площадь треугольника со сторонами $a,b$ и $c$ и полупериметром $p$ вычисляется по формуле $S=\sqrt{p(p-a)(p-b)(p-c)}$.

Доказательство

Рассмотрим треугольник $ABC$, в котором $AB=c, BC=a, AC=b$.

В любом треугольнике по крайней мере два угла острые.

Пусть $\angle A$ и $\angle B$ – острые углы треугольника $\triangle ABC$.

Тогда основание $H$ высоты $CH$ треугольника лежит на стороне $AB$.

Пусть $CH=h, AH=y, HB=x$.

По теореме Пифагора $a^2-x^2=h^2=b^2-y^2$, откуда $y^2-x^2=b^2-a^2$, или $(y-x)(y+x)=b^2-a^2$.

Так как $y+x=c$, то $y-x=\dfrac{b^2-a^2}{c}$.

Сложив два последних равенства и разделив на 2, получим: $y=\dfrac{b^2+c^2-a^2}{2c}$.

Поэтому

$h^2=b^2-y^2=(b+y)(b-y)=\left(b+\dfrac{b^2+c^2-a^2}{2c}\right)\left(b-\dfrac{b^2+c^2-a^2}{2c}\right)=\dfrac{(b+c)^2-a^2}{2c}\cdot\dfrac{a^2-(b-c)^2}{2c}=\dfrac{(b+c+a)(b+c-a)(a-b+c)(a+b-c)}{4c^2}=\dfrac{2p(2p-2a)(2p-2b)(2p-2c)}{4c^2}=\dfrac{4p(p-a)(p-b)(p-c)}{c^2}.$

Следовательно, $h=\dfrac{2\sqrt{p(p-a)(p-b)(p-c)}}{c}$.

Но $S_{ABC}=\dfrac{1}{2}hc=\sqrt{p(p-a)(p-b)(p-c)}$.

math-public/teorema_pifagora.txt · Последние изменения: 2016/04/14 00:30 — labreslav