Теорема Виета. Видеоурок. Алгебра 8 Класс

На этом уроке учащиеся смогут узнать об одной из основных теорем в алгебре многочленов – теореме Виета. Мы узнаем ее определение, рассмотрим, как ее можно применять для решения различных задач.

Французский математик Франсуа Виет, изучая квадратные уравнения, обнаружил изящную связь между корнями уравнения и его коэффициентами. Теорема Виета – цель нашего урока.

Вспомним.

Квадратным называется уравнение вида: 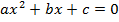, где .

Уравнение можно почленно разделить на :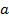

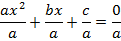
Цель – получить приведенное квадратное уравнение:

; ,

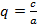
Вспомним формулу корней квадратного уравнения:

;

Теорему Виета сформулируем для приведенного квадратного уравнения:

Числа 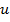,  являются корнями уравнения

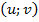 тогда и только тогда, когда пара  является решением системы: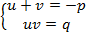

Теорема Виета утверждает, что квадратное уравнение и система одновременно разрешимы или неразрешимы.

Корни уравнения дают все решения системы 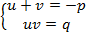. И наоборот, все решения системы дают корни уравнения.

Система симметрическая относительно 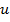 и

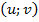, т. е. если пара  является решением, то пара  тоже является решением. Потому что система не изменится, если в системе  и 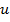 мы поменяем местами, а значит, в формулировке теоремы мы можем заменить пару  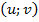на пару .

Докажем теорему Виета.

Дано: 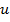,  – корни уравнения .

Доказать: .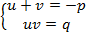

Доказательство

Итак, мы знаем формулу корней квадратного уравнения:

,

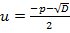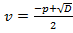
Сложим их:

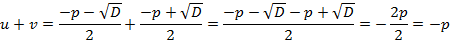
Первое равенство системы доказано.

Есл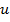и  и  удовлетворяют уравнению, то их сумма равняется .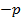

Перемножим 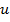 и

:

Числитель мы сократили по формуле разности квадратов.

Вспомним, что такое дискриминант.

Подставим:

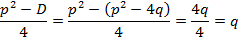
Что и требовалось доказать.

Итак, первая часть теоремы Виета доказана. Есл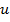и  и  – корни квадратного приведенного уравнения, то они удовлетворяют системе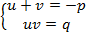

.

Продолжим доказательство.

Дано: 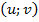 – решение системы .

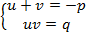Доказать: 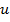,  – корни уравнения .

Доказательство

Мы имеем:

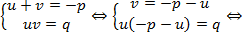
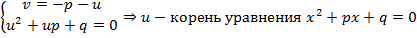
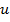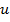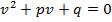Итак, мы доказали, что если выполняются требования системы, то  – корень квадратного уравнения, но так как наша система симметрична, то можно  заменить на  и наоборот. Значит: , т. е.

 тоже корень уравнения .

Итак, в обратную сторону теорема доказана.

А именно, доказано, что если числа 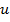 и  образуют пару, которая удовлетворяет системе 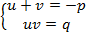, то эти числа являются корнями квадратного уравнения. Теорема Виета для приведенного квадратного уравнения доказана полностью.

Вспомним, что

, .

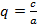Числа 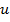,  являются корнями уравнения 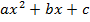 тогда и только тогда, когда пара  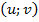является решением системы:

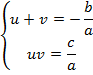
Рассмотрим эти соотношения.

Нарисуем оси координат. Предположим, что

, т. е. ветви параболы направлены вверх. Предположим, что дискриминант , имеются два корня,  и , и есть ось симметрии у параболы. Вспомним, что  или 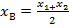 (если есть корни). В терминах 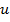, это записывается так: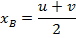

То есть первое уравнение  отражает симметрию параболы относительно прямой 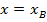 (см. Рис. 1).

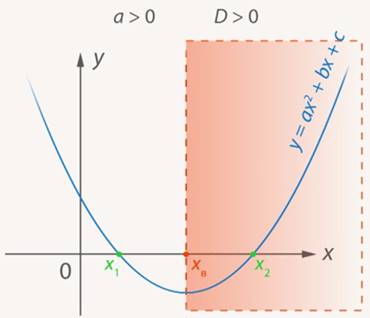
Рис. 1. Симметрия параболы

Что показывает второе уравнение ?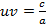

Оно показывает, каковы знаки у корней.

Если 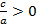, то корни одного знака.

Если 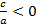, то корни разных знаков.

Мы доказали теорему Виета. Но чем же она хороша?

Во-первых, она иногда позволяет относительно просто решить само уравнение.

Решите уравнение .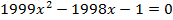

Решение

Это уравнение можно решить через дискриминант, но это довольно утомительно.

Подметим особенность этого уравнения. Если 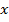 мы опустим, то получим .

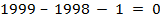Значит, 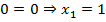 – это очевидный корень уравнения.

Но если мы знаем один корень, то легко найдем и второй корень.

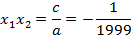
Но так как первый корень нам уже известен, то:

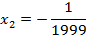
Ответ: , .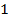

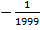Итак, мы нашли корни уравнения по теореме Виета.

Давайте посмотрим, что нам надо было бы сделать, если бы мы захотели решить эту задачу через дискриминант:

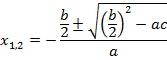
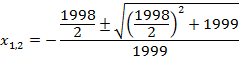
Разница в удобстве решения очевидна.

Рассмотрим еще один пример.

Решите уравнение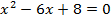

interneturok.ru

§4. Теорема Виета. Приведённое квадратное уравнение

2010-2011 уч. год., № 5, 8 кл. Математика. Квадратные уравнения

2x +1	+	x +1	=	5x + 4
x −1					.
		2x +1		(x −1)(2x +1)

Общий знаменатель дробей, входящих в данное уравнение, равен
(x −1)(2x +1). Умноживобечастиуравненияна (x −1)(2x +1), получим
(2x +1)2 +(x +1)(x −1)=5x +4, 4×2 +4x +1+ x2 −1 =5x +4,
5×2 − x −4 = 0.
Найдём корни полученного квадратного уравнения
x = 1 ± 1 +80 =	1 ±9 , т.е. x =1,		x = −4 .
10	10	1	2	5
При x =1 не определены обе части уравнения,				следовательно, это
число не является корнем уравнения. При x = −			4	общий знаменатель
			5

в нуль не обращается, следовательно, это число является решением данного уравнения.

Пример 3. Решите уравнение

x2 + 2x +7 = 4 + 2x + x2. x2 + 2x +3

Введём новую переменную x2 + 2x +3 = t, тогда для нахождения t

получим уравнение t +t 4 = t +1. Умножим обе части этого уравнения

на t, получим: t + 4 = t2 +t, t2 = 4, t1 = 2, t2 = −2. Решаем уравнение:

x2 + 2x +3 = 2, x2 + 2x +1 = 0,

оно имеет единственное решение x = −1. Уравнение x2 + 2x +3 = −2,

т.е. x2 + 2x +5 = 0, решений не имеет. Следовательно, исходное урав-

нение имеет одно решение x = −1. Пример 4. Решите уравнение

(x + 2)2 + x2 24+ 4x =18.

Введём новую переменную t = (x + 2)2.

© 2011, ФЗФТШ при МФТИ. Составитель: Яковлева Тамара Харитоновна

studfile.net

Обратная теорема Виета

Мы с вами уже знаем теорему Виета. Вспомним её формулировку: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Справедлива также теорема обратная теореме Виета. Запишем её формулировку. Если числа  и  таковы, что их , а , то эти числа являются корнями квадратного уравнения .

С помощью обратной теоремы Виета удобно проверять, правильно ли найдены корни квадратного уравнения, а также по указанным корням составлять уравнения.

Задание: найдите корни уравнения и выполните проверку по теореме, обратной теореме Виета.

И выполним обратное задание: составьте квадратное уравнение по его корням.

Задание: один из корней уравнения  равен четырем. Найдите другой корень и коэффициент .

Решение:

Задание: один из корней уравнения  равен минус пяти. Найдите другой корень и коэффициент .

Итоги:

Сегодня на уроке мы познакомились с обратной теоремой Виета, которая имеет следующую формулировку: если числа  и  таковы, что их сумма равна , а произведение равно , то эти числа являются корнями квадратного уравнения .

videouroki.net

Решение квадратных уравнений с применением теоремы Виета

Цель: Применение теоремы Виета и ей обратной теоремы при нахождении коэффициентов в квадратных уравнениях, при решении заданий из вариантов ЕГЭ.

Воспитательные задачи: Способствовать формированию умений, применять приемы сравнений, обобщения, выделения главного, переноса знаний в новую ситуацию, развитию творческих способностей. Побуждать учащихся к самоконтролю и взаимоконтролю, самоанализу своей учебной деятельности.

Оборудование: плакаты, компьютер, экран, видеопроектор.

Ход урока

I. Вводная беседа. Устные упражнения (5 мин.)

Сегодня на уроке мы с вами вместе подведем итог, как важно применение теоремы Виета. В каких упражнениях применяется теорема и как важно ее знать и применять. (Учитель показывает презентацию, в которой сформулированы цели, задачи, структура урока). <Приложение 1>

Учащиеся формулируют теорему Виета и ей обратную теорему. У доски два ученика записывают формулы теоремы Виета для приведенного и полного квадратных уравнений:

– формулы для полного квадратного уравнения;

– формулы для приведенного квадратного уравнения;

Трое учащихся решают на дополнительных досках индивидуальные задания.

Решите уравнения и выполните проверку по теореме, обратной теореме Виета:

II. Устные упражнения (5 мин.)

Затем с учащимися решаем устные упражнения:

Найдите корни уравнения:

3. Если в квадратном уравнении сумма коэффициентов a + b + c = 0,

То Используя это свойство, решите уравнения:

4. Теорема Виета применяется при нахождении суммы и произведения корней. Покажите, как это выглядит. Перед вами уравнения:

У какого из данных уравнений:

1. Сумма корней равна 6, а произведение – 16?
2. Корни равны?
3. Один из корней уравнения равен 6?
4. Каждый из корней на 2 больше, чем корни уравнения ? Ответ обосновать.

III. Лабораторная работа (3 мин.)

Учащимся предлагается выполнить лабораторную работу.

Составьте квадратные уравнения, которые:

• не имеют корней;
• имеет один из корней, равный 0;
• имеет два корня, равных по модулю, но противоположных по знаку;
• имело бы один корень;
• сумма коэффициентов уравнения равна 0.

Учащиеся выполняют это задание по группам (4–5 учащихся в группе).

Пример лабораторной работы:

IV. Работа с таблицей (3 мин.)

Выполнив лабораторную работу, три группы озвучивают свою лабораторную работу, а остальные группы сдают лабораторные работы на плакатах на проверку (2 мин.).

Один из учащихся (Евсеев А.) заранее готовит презентацию об исследовании знаков в приведенных квадратных уравнениях. <Приложение 2>

Все учащиеся работают с таблицей и отвечают на вопросы о знаках в квадратных уравнениях:

1. Когда корни квадратного уравнения имеют одинаковые знаки?
2. Когда оба корня положительные, отрицательные?
3. Когда корни имеют разные знаки?
4. Когда больший по модулю корень отрицателен?
5. Когда больший по модулю корень положителен?

Сформулируйте выводы о знаках корней квадратных уравнений.

V. Тренировочные упражнения. Работа у доски (23 мин.)

Следующий этап урока: двое учащихся решают у доски задания о нахождении неизвестных коэффициентов в квадратных уравнениях.

1. В уравнении один из корней равен 7. Найдите другой корень и коэффициент р. Ответ:

2. Один из корней уравнения равен 12,5. Найдите другой корень уравнения и коэффициент с. Ответ:

Такого вида уравнения часто встречаются на экзаменах. Поэтому сейчас Слинько В. предлагает просмотреть презентацию о нахождении коэффициентов в квадратных уравнениях. <Приложение 3>

А после просмотра презентации учащимся предлагается решить 2 уравнения самостоятельно с последующей проверкой.

1. Разность корней квадратного уравнения равна 2. Найдите с.

Ответ: c = 35.

2. Разность корней квадратного уравнения равна 6. Найдите с.

Ответ: c = –8,75.

Использование теоремы Виета дает возможность решать более сложные задания.

Трое учащихся решают задания у доски, комментируя и объясняя ход решения:

1. Один из корней уравнения равен 8. Найдите другой корень и коэффициент в.

Ответ: .

2. Один из корней уравнения равен 5,3. Найдите другой корень и коэффициент с.

Ответ: .

3. В уравнении квадратов корней равна . Найдите с. Ответ: с = 9.

VI. Заключение (6 мин.)

В заключение урока подводим итоги. Учащиеся формулируют применение теоремы Виета.

Теорема Виета применяется:

• при нахождении суммы и произведения корней квадратных уравнений;
• при составлении квадратных уравнений;
• при решении уравнений методом подбора;
• при нахождении коэффициентов в уравнении, свободного члена;
• при сравнении знаков коэффициентов в квадратном уравнении.

Один из учащихся рассказывает стихотворение.

По праву достойна в стихах быть воспета
О свойстве корней теорема Виета.
Что проще скажи постоянства такого?
Умножишь ты корни и дробь уж готова!
В числителе с, в знаменателе а,
А сумма корней тоже дроби равна.
Хоть с минусом дробь эта – что за беда?!
В числителе в, в знаменателе а.

Домашнее задание: № 645, № 667, № 671 из учебника «Алгебра 8», автор Макарычев Ю. Н.

Учитель выставляет оценки за урок, благодарит учащихся за работу на уроке.

Также предлагается посмотреть презентацию о решении квадратных уравнений с параметром, в которой рассматриваются задания повышенной сложности, применяемые на экзаменах и малом ЕГЭ. <Приложение 4>

urok.1sept.ru