Урок геометрии в 8 классе «Теорема Виета»
Кезеңдері
Мұғалім әрекеті
Оқушы әрекеті
бағалау
ресурстар
Ұйымдастыру кезеңі
Сыныпта ынтымақтастық атмосферасын қалыптастыру мақсатында оқушыларға «Достар » психологиялық тренингін өткізеді
Оқушыларды топқа бөледі
Оқушылар сызбаға үш досының есімін жазады. Мұғалімнің нұсқауымен бірінші досымен құшақтасады, екінші досының ең жақсы қасиетін айтады, үшіншісіне бір жақсы тілек айтады.
Жазылған үлестірме материалдағы теңдеулердің түрлері бойынша топтарға бөлінеді: «Квадрат теңдеу», «Толымсыз теңдеу» әр топ теңдеуге анықтама береді
үлестірме материалдар
Қызығушылықты ояту
«Сендер қандай сабақта отырсыңдар?»
Алгебра сабағында біз немен айналысамыз?
«Алгебра сабағында»
Есеп шығарамыз
Сабаққа мақсат қою
Бағалау критерийлері құрылып,әрбір оқушыға бағалау парақшаларын таратады сол арқылы оқушылар бағаланады.
Сыни тұрғыдан ойлауды дамыту үшін логикалық есеп шыгару.
Сабақтың эпиграфы ретінде Конфуцийдің сөздері алынады:
Білімге жетелейтін үш жол бар,
Еліктеу жолы-ең жеңіл жол,
Ойлау жолы-ең игілікті жол,
Тәжірибе жолы-ең қиын жол.
Жұптық бағалау
бағалау парақшалары
Мағынаны ашу
Тақырыбымызды ашу үшін сабақты сөзжүмбақ шешуден бастайық
Сөзжүмбақтың шешуі «ВИЕТ»
Жаңа тақырып
Франсуа Виет туралы тарихи мәліметтерге тоқталайық Жаңа тақырыпты өздігінен танысуды ұсынады
Оқулықтағы мысалдарды талдайды, «Жигсо» әдісін қолданып әрбір оқушы өз жолдасына тақырыпты түсіндіреді, мұғалім қол шалалақтаған сайын келесі жұпқа көшеді
Тақырыпты меңгергендерін тақтаға көрсетеді Виет теоремасын тұжырымдайды
алгебра оқулығы
Алған білімдерін бекіту
Деңгейлік есептер таратады
1.Алгоритмдік деңгей
2. Эвристикалық деңгей
1.Квадрат теңдеудің түбірін тауып, Виет теоремасы бойынша тексеру, мақал-мәтел құру.
2.мақал-мәтелдің ішіндегі екі сан есім қвадрат теңдеудің түбірлері болатындай,яғни Виет т. кері теореме б/ша квадрат теңдеу құру
Топтық бағалау
үлестірме материалдар
дәптер
Шығармашылық деңгей
«Квадрат теңдеу» тақырыбында
Синквейн(Бес жол өлең стратегиясы)
Зат есім:Не?
Сын есім:Қандай?
Етістік.Не істеді?
Синоним:
Топтық бағалау
маркер фломастер стикер
Қызығушылықты ояту
Тарихи мәліметтер
ұсынады: квадрат теңдеудің шығу тарихы
Рефлексия
Бүгінгі сабаққа көзқарасының?
Дәстүрлі сабақтан айырмашылығы?
Не ұнады? Не ұнамады?
Білім ағашына стикермен жауаптарын іледі
Өзін-өзі бағалайды
үлестірме материалдар
Бағалау
Оқушылардың бағалау парақшаларындағы формативті бағалары бойынша
жиынтық баға шығарады
«бағдаршам» әдісін пайдаланып тақырыпты түсінуін бағалайды
Өзін-өзі бағалайды
түрлі-түсті кеспе қағаздар
infourok.ru
Система с параметром. Теорема Виета.
При решении этой задачи была использована теорема Виета, и это очень облегчило решение и сделало его прозрачным. Заметить, что именно этот путь надо выбрать, может помочь опыт решения подобных задач.
Задача. При каких значениях параметра  система имеет больше двух решений?
система имеет больше двух решений?
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{y^2-2xy+4y-x^4-2x^3+4x^2=0}\\{y -ax+3a-1=0}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-77cbb99a6fa4fba2e47d15a815d12a07_l3.png)
Рассмотрим первое уравнение системы. Его можно рассматривать как квадратное относительно  :
:
![Rendered by QuickLaTeX.com \[y^2-(2x-4)y-x^2(x^2+2x-4)=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c357048a1ff93645d54811e1efb559e3_l3.png)
Теперь, когда уравнение записано в такой форме, хорошо видно, что удобно применить теорему Виета. Тогда сумма корней –  , а произведение –
, а произведение –  .
.
Тогда получили систему:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{\begin{bmatrix}{y=-x^2}\\{y= x^2+2x-4}}\end{matrix}\\{y =a(x-3)+1}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4dfda2662709c44aea7cd01fa5ecb3c8_l3.png)
Получили две параболы и прямую, которая меняет свой угол наклона, или еще говорят – пучок прямых. Центр нашего пучка находится в точке (3; 1).

Пучок прямых
Теперь предстоит исследовать эту систему, вращая нашу прямую. Начнем с положения прямой, показанного на рисунке.

Рисунок 1.
При таком положении прямой имеем касание и 2 пересечения, то есть три решения. Определим положение прямой в такой ситуации.
![Rendered by QuickLaTeX.com \[-x^2= a(x-3)+1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e46b8fe931acb395b8ceba3a194718c9_l3.png)
При касании такое уравнение должно иметь один корень, то есть  :
:
![Rendered by QuickLaTeX.com \[x^2+ ax-3a+1=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5c873f092950775fad5eac894ba75ff7_l3.png)
![Rendered by QuickLaTeX.com \[D=a^2-4(1-3a)=a^2+12a-4=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f76f67a5b4f6317cc228007a8ee8da57_l3.png)
В свою очередь, дискриминант этого уравнения:
![Rendered by QuickLaTeX.com \[D=144+16=160\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-040a832091bb5045bf919698dd357cb7_l3.png)
![Rendered by QuickLaTeX.com \[a=\frac{-12 \pm \sqrt{160}}{2}=-6 \pm 2\sqrt{10}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e37677f1072408186127be930801f83c_l3.png)
Корень  соответствует рисунку, когда касание происходит вблизи вершины. Если начнем увеличивать коэффициент наклона из этого положения, то скоро придем к положению прямой, показанному на рисунке 2.
соответствует рисунку, когда касание происходит вблизи вершины. Если начнем увеличивать коэффициент наклона из этого положения, то скоро придем к положению прямой, показанному на рисунке 2.

Рисунок 2.
При этом  , и прямая пересекает систему двух парабол ровно в двух точках, то есть нас устраивают значения параметра
, и прямая пересекает систему двух парабол ровно в двух точках, то есть нас устраивают значения параметра  .
.
Увеличивая далее коэффициент наклона, будем все время иметь три корня, до положения, когда прямая будет касаться параболы  .
.

Рисунок 3.
Определим значение параметра при касании:
![Rendered by QuickLaTeX.com \[x^2+2x-4= a(x-3)+1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-cf913de666a27ba13479b0f8dd205dd9_l3.png)
![Rendered by QuickLaTeX.com \[x^2+2x-4- a(x-3)-1=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-dea4fe49be61277285019c01b2dfa31e_l3.png)
![Rendered by QuickLaTeX.com \[x^2+x(2-a)+3a-5=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d660bade10229036c97931cc6c95ea4d_l3.png)
При касании такое уравнение должно иметь один корень, то есть  :
:
![Rendered by QuickLaTeX.com \[D=(2-a)^2-4\cdot(3a-5)=4-4a+a^2-12a+20=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3ac22e0ab97c4a38ce4d48de61c9bb76_l3.png)
![Rendered by QuickLaTeX.com \[a^2-16a+24=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-098356670e44a0bfa7766e3032be463f_l3.png)
![Rendered by QuickLaTeX.com \[D=256-4\cdot24=160\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b7d9410d790332227af0ae44f2eb9c18_l3.png)
![Rendered by QuickLaTeX.com \[a=\frac{16 \pm \sqrt{160}}{2}=8 \pm 2\sqrt{10}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-910151f4ddd4b46464505d5552229680_l3.png)
Итак, второй промежуток устраивающих нас положений прямой, и, следовательно, значений параметра – ![Rendered by QuickLaTeX.com a \in (1; 8 - 2\sqrt{10}]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-51f4d7e05337a9b66310eaa14aedcac3_l3.png) .
.
Вращаем прямую дальше, и видим, что решений два вплоть до момента, когда наша прямая коснется правой ветви параболы  вверху. После этого касания, которому соответствует значение параметра
вверху. После этого касания, которому соответствует значение параметра  , снова будем иметь три решения:
, снова будем иметь три решения:  .
.
Из положения прямой, когда  , «перешагнем» к положению
, «перешагнем» к положению  . Такое значение параметра нас устраивает вплоть до
. Такое значение параметра нас устраивает вплоть до  , когда прямая коснется параболы
, когда прямая коснется параболы  справа. Тогда еще один интервал, который мы возьмем в решение –
справа. Тогда еще один интервал, который мы возьмем в решение – ![Rendered by QuickLaTeX.com a \in (-\infty; -6 - 2\sqrt{10}]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8a475a0ffa215f5e35b9072ba1a9c87d_l3.png) .
.
Записываем ответ: ![Rendered by QuickLaTeX.com a \in (-\infty; -6 - 2\sqrt{10}] \cup [-6 + 2\sqrt{10};1) \cup (1; 8 - 2\sqrt{10}] \cup [8 + 2\sqrt{10};+\infty)](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-67404adacd8bed255bcf2fbad4370b17_l3.png) .
.
easy-physic.ru
Проект «Теорема Виета «
Муниципальное казенное образовательное учреждение
«Очкуровская средняя общеобразовательная школа»
Николаевского муниципального района Волгоградской области
Теорема Виета
Выполнила: Оноприенко Кристина,
обучающаяся 8 класса
МКОУ «Очкуровская СОШ»
Николаевского района
Руководитель: Е.А.Бульба
с. Очкуровка
2015
Оглавление
Введение……………………………………………………………………… ……3
Основная часть
1.Историческая справка……………………………………………………….4
2.Докозательство теоремы Виета……………………………………………..6
3.Состаление блока уравнений решаемых по теореме Виета……………….8
4.Составлеие тренажера………………………………………………………10
Заключение
Практическая значимость проекта………………………………………12
Выводы…………………………………………………………………….13
Список источников информации…………………….…………………………14
Приложение……………………………………………………………………..15
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты корни — дробь уж готова!
В числителе с, в знаменателе а.
А сумма корней тоже дроби ровна.
Хоть с минусом дробь, что за беда!
В числителе b, в знаменателе а.
Введение
Актуальность темы проекта: Применение теоремы Виета является уникальным приемом для решения квадратных уравнений устно. В учебнике очень мало квадратных уравнений, решаемых по теореме Виета. Я и мои одноклассники допускаем ошибки.
Объектом исследования является теорема Виета , как неотъемлемая часть решения квадратных уравнений на уроках алгебры .
Предмет исследования – теорема Виета и составление блока уравнений для закрепления навыка решения квадратных уравнений.
Гипотеза: я предположила, что научиться безошибочно решать уравнения по теореме Виета можно, для этого нужен применяя тренажер.
Цель проекта: составить тренажер уравнений, решаемых по теореме Виета.
Задачи:
узнать историю открытия теоремы Виета;
провести исследование зависимости коэффициентов квадратного
уравнения и произведения и суммы его корней.
научиться доказывать теорему Виета;
самостоятельно составить уравнения, решаемые по теореме Виета
оформить блок уравнений на бумажном носителе и составить тренажер в электронном виде
предложить одноклассникам тренажер для решения уравнений по теореме Виета
Методы:
сравнение результатов самостоятельной работы до проекта и после тренировки решение квадратных уравнений применяя теорему Виета
изучение и анализ электронных источников и литературы
самостоятельная работа по составлению блока уравнений и тренажера

1.Исторические сведения
Франсуа Виет родился в 1540 году на юге Франции в небольшом городке Фантене-ле-Конт.
Отец Виета был прокурором. Сын выбрал профессию отца и стал юристом, окончив университет в Пуату. В 1560 году двадцатилетний адвокат начал свою карьеру в родном городе, но через три года перешел на службу в знатную гугенотскую семью де Партене. Он стал секретарем хозяина дома и учителем его дочери двенадцатилетней Екатерины. Именно преподавание пробудило в молодом юристе интерес к математике.
Когда ученица выросла и вышла замуж, Виет не расстался с ее семьей и переехал с нею в Париж, где ему было легче узнать о достижениях ведущих математиков Европы. Он общался с видным профессором Сорбонны Рамусом, с крупнейшим математиком Италии Рафаэлем Бомбелли вел дружескую переписку.
В 1571 году Виет перешел на государственную службу, став советником парламента, а затем советником короля Франции Генриха III.
В 1580 году Генрих III назначил Виета на важный государственный пост рекетмейстера, который давал право контролировать выполнение распоряжений в стране и приостанавливать приказы крупных феодалов.
В 1584 году по настоянию Гизов Виета отстранили от должности и выслали из Парижа. Обретя покой и отдых, ученый поставил своей целью создание всеобъемлющей математики, позволяющей решать любые задачи.
Виет изложил программу своих исследований и перечислил трактаты, объединенные общим замыслом и написанные на математическом языке новой буквенной алгебры, в изданном в 1591 году знаменитом «Введение в аналитическое искусство». Основу своего подхода Виет называл видовой логистикой, он четко разграничивал числа, величины и отношения, собрав их в некую систему «видов». В эту систему входили, например, переменные, их корни, квадраты, кубы, квадрато-квадраты и т. д. Для этих видов Виет дал специальную символику, обозначив их прописными буквами латинского алфавита. Для неизвестных величин применялись гласные буквы, для переменных — согласные.
Виет показал, что, оперируя с символами, можно получить результат, который применим к любым соответствующим величинам, т. е. решить задачу в общем виде. Это положило начало коренному перелому в развитии алгебры: стало возможным буквенное исчисление.
Знаменитая теорема, устанавливающая связь коэффициентов многочлена с его корнями, была обнародована в 1591 году. Теперь она носит имя Виета, а сам автор формулировал ее так: «Если В+D, умноженное на А, минус А в квадрате равно ВD, то А равно В и равно D».
В трактате «Дополнения к геометрии» он стремился создать некую геометрическую алгебру, используя геометрические методы для решения уравнений третьей и четвертой степеней. Любое уравнение третьей и четвертой степени, утверждал Виет, можно решить геометрическим методом трисекции угла или построением двух средних пропорциональных.
Математиков столетиями интересовал вопрос решения треугольников, так как он диктовался нуждами астрономии, архитектуры, геодезии. Виет первым явно сформулировал в словесной форме теорему косинусов, хотя положения, эквивалентные ей, эпизодически применялись с первого века до нашей эры. Известный ранее своей трудностью случай решения треугольника по двум данным сторонам и одному из противолежащих им углов получил у Виета исчерпывающий разбор. Глубокое знание алгебры давало Виету большие преимущества. Причем интерес его к алгебре первоначально был вызван приложениями к тригонометрии и астрономии. Не только каждое новое применение алгебры давало импульс новым исследованиям по тригонометрии, но и полученные тригонометрические результаты являлись источником важных успехов алгебры. Виету, в частности, принадлежит вывод выражений для синусов (или хорд) и косинусов кратных дуг.
В мемуарах некоторых придворных Франции есть указание, что Виет был женат, что у него была дочь, единственная наследница имения, по которому Виет звался сеньор де ла Биготье. В придворных новостях маркиз Летуаль писал: «…14 февраля 1603 г. господин Виет, рекетмейстер, человек большого ума и рассуждения и один из самых ученых математиков века умер… в Париже. Ему было более шестидесяти лет».
2 .Доказательство теоремы Виета





3.Составление блока уравнений и электронного тренажера
х2 + 17х — 38 = 0,
х2 — 16х + 4 = 0,
3х2 + 8х — 15 = 0,
7х2 + 23х + 5 = 0,
х2 + 2х — 3 = 0,
х2 + 12х + 32 = 0,
х2 — 7х + 10 = 0,
- х2 — 2х — 3= 0,
х2 + 12х + 32 = 0,
2х2 — 11х + 15 = 0,
3х2 + 3х — 18 = 0,
2х2 — 7х + 3 = 0,
х2 + 17х — 18 = 0,
х2 — 17х — 18 = 0,
х2 — 11х + 18 = 0,
х2 + 7х — 38 = 0,
х2 — 9х + 18 = 0,
х2 — 13х + 36 = 0,
х2 — 15х + 36 = 0,
х2 — 5х — 36 = 0.
х2 + х – 2 = 0
х2 + 2х – 3 =0
х2 — 3х + 2 =0
х2 — 2х – 3 = 0
х2 — 3х – 4 = 0
x2 +17x -18=0
x2 + 23x – 24=0
x2 – 39x-40=0
x2 – 37x – 38=0
x2 – 3x – 10 = 0
x2 – 5x + 3 = 0
x2 + 8x – 11 = 0
x2 + 6х + 5 = 0
x2 – x – 12 = 0
x2 + 5x + 6 = 0
x2 + 3x – 10 = 0
x2 – 8x– 9 = 0
х 2 + х – 56 = 0
х 2 – 19х + 88 = 0
х 2 – 4х – 4 = 0
x 2 -15х+14=0
x 2 +8х+7=0
x2+9х+20=0
x2 +18х -11 = 0
x2 +27х – 24 = 0
5х2 +10х – 3 = 0
3х2 — 16х +9 = 0
x2 +18х -11 = 0
x2 +27х – 24 = 0
 -4х-21=0
-4х-21=0 -4х-21=0
-4х-21=0x2-15х+56=0
x2-4х-60=0
x2+5х+6=0
 +2х-3=0
+2х-3=0x2+18х+81=0
 -х-20=0
-х-20=0x2+4х+21=0
x2-10х-24=0
x2+х-56=0
x2-х-56=0
x2+3х+2=0
x2+5х-6=0
x2-18х+81=0
x2-9х+20=0
x2 -5х+6=0
x2-4х-21=0
-x2 -7х+6=0
x2-15х+56=0
х2 – 3х + 2 = 0
х2 – 4х + 3 = 0
х2 – 2х + 4 = 0
х2 – 2х + 5 = 0
х2 – 2х + 6 = 0
х2 – 11х + 24 = 0
х2 + 11х – 30 = 0
х2 + х – 12 = 0
x2 – 6х + 8 = 0
х2 – 15х + 14 = 0
x2 – 15x + 14 = 0
x2+ 4 х -21 =0
х2+ х – 42 =0
х2 – х – 20 =0
х2+ 4 х -32=0
х2— 2х – 35 =0
х2+ х — 20 =0
х2+ 7 х + 10 =0
х2— х — 6=0
х2+ 2 х +0=0
х2+ 6 х+0 =0
х2+ 3х — 18=0
х2+ 5 х -24=0
х2— 2 х — 24=0
х2 – 15х + 14 = 0
х2 + 8х + 7 =0
х2+ 9х – 20=0
х2 – 6х — 7 = 0
х2 + 3х — 10 = 0
х2 – х — 12 = 0
3.Тренажер
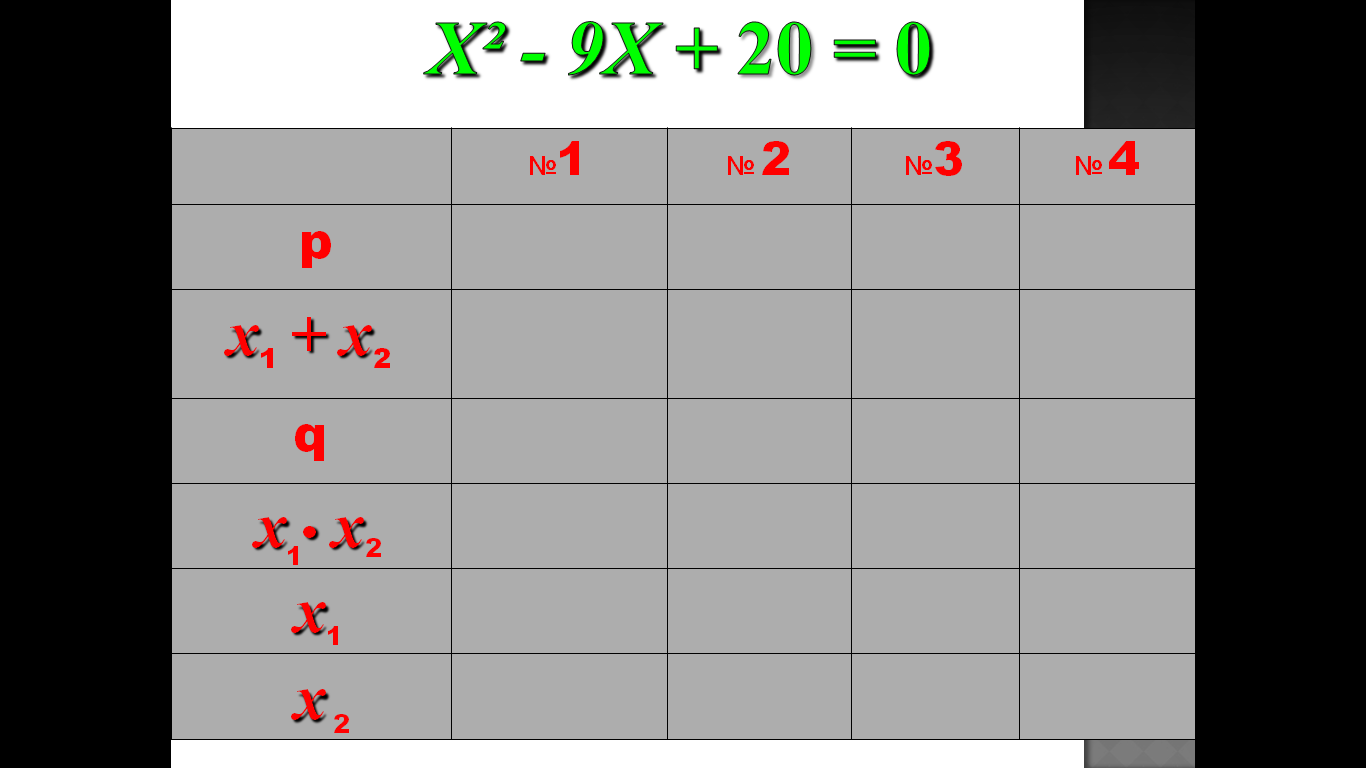
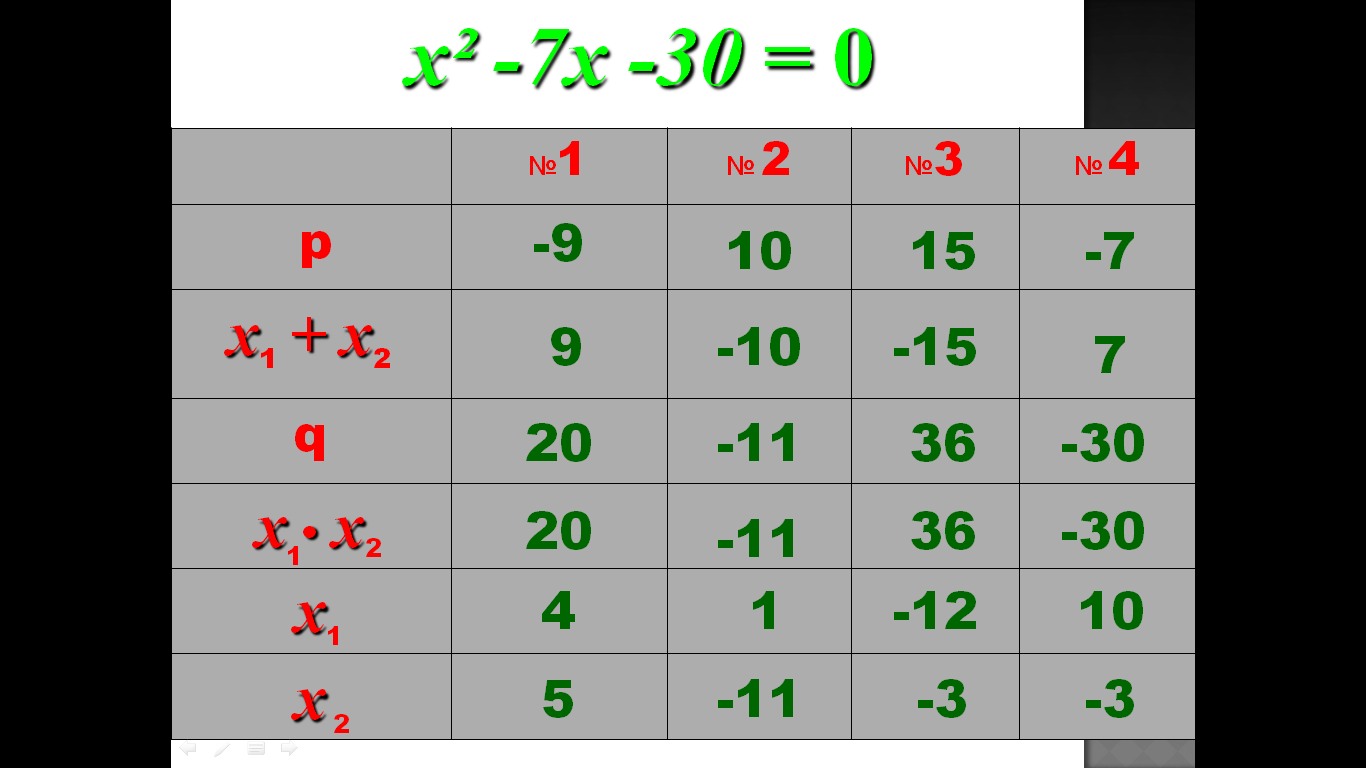
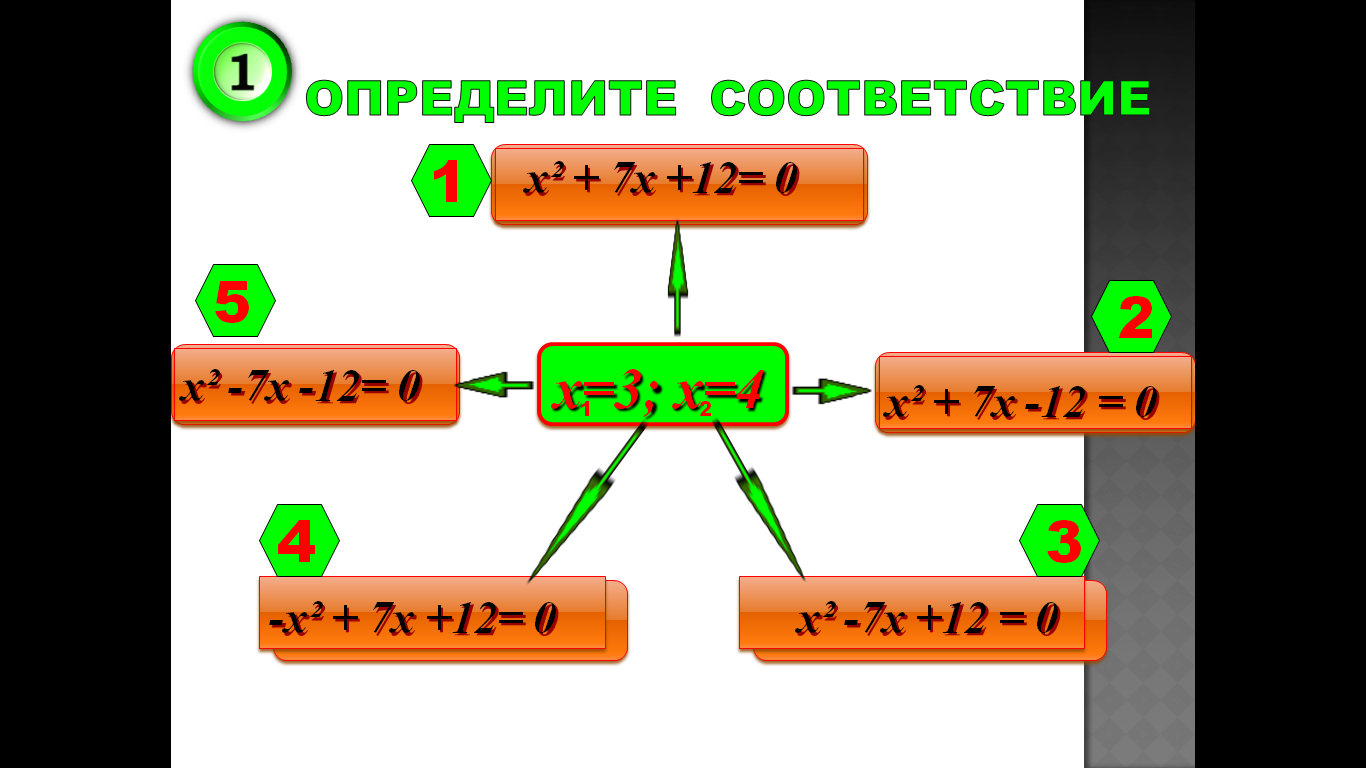
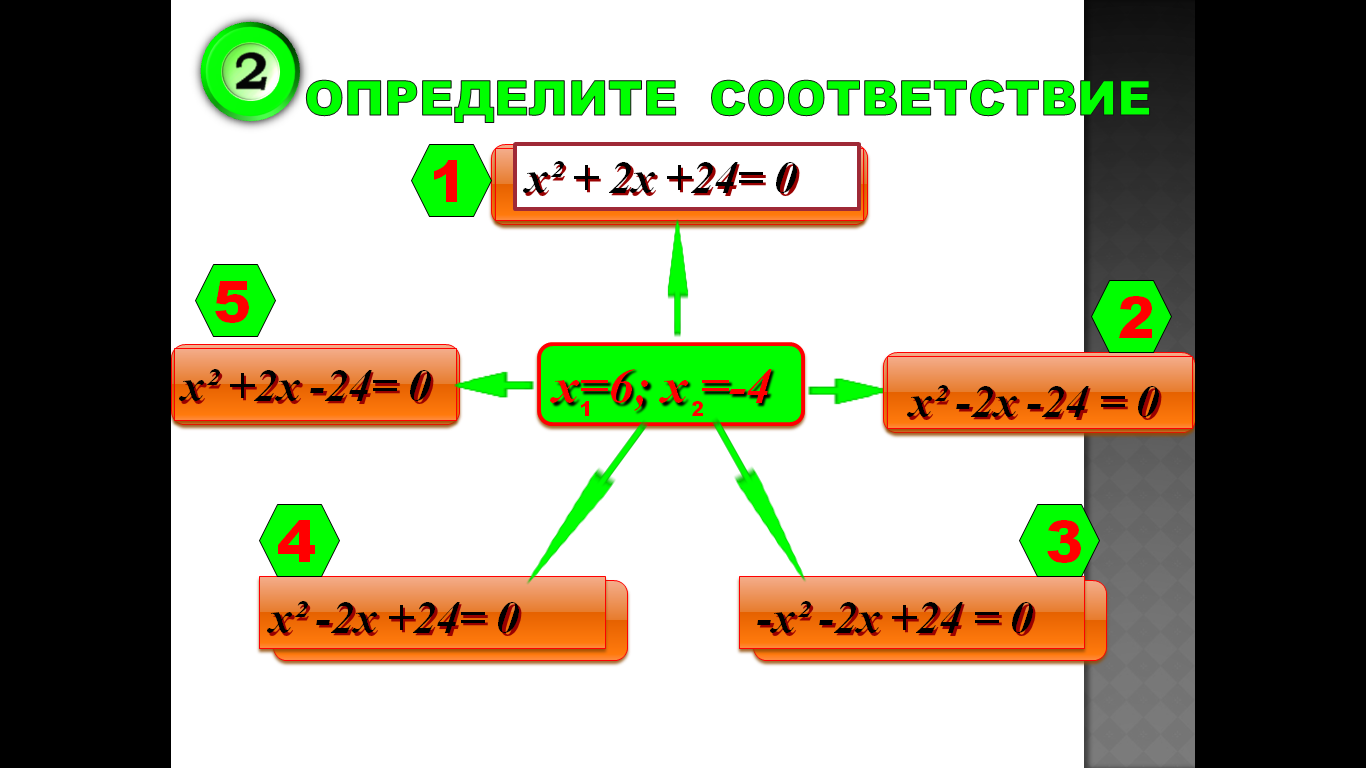
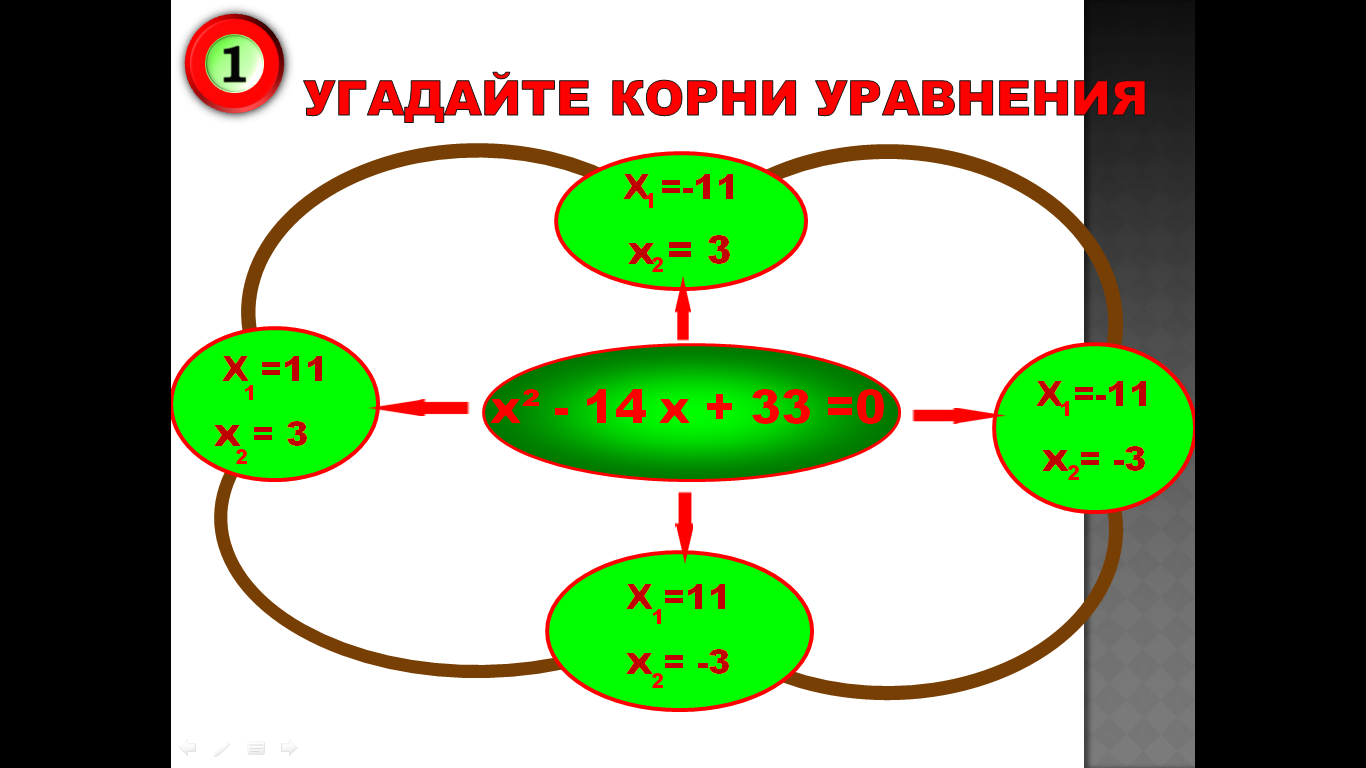
4.Практическая значимость проекта
Применение, а уроках алгебры 8 класса и при итоговом повторении ОГЭ
Выводы:
Результат моего труда – создан блок квадратных уравнений решаемых по теореме Виета.
Я увлеклась работой, проще всего было составить квадратные уравнения, в которых свободный член находится по таблице умножения. Теперь я не только безошибочно нахожу корни уравнения по теореме Виета, но и применяю ее при проверке решения любого квадратного уравнения.
Используя тренажер, я и мои одноклассники научилась решать квадратные уравнения, применяя теорему Виета.
Список источников информации:
Список литературы
Алгебра 8 класс: учебник для общеобразовательных учреждений. Г.В.Дорофеев, С.Б.Суворова
Дидактические материалы по алгебре для 8 класса. В.И.Жохов, Ю.Н.Макарычев, Н.Г.Миндюк. М.: Просвещение, 2000.
Математика. 8 класс: дидактические материалы к учебнику «Математика 8. Алгебра» / под ред. Г. В. Дорофеева. – М. : Дрофа, 2012г.\
Государственная итоговая аттестация. 9 класс. Математика. Тематические тестовые задания./Л.Д. Лаппо, М.А. Попов/-М.: Издательство « Экзамен », 2011
Интернет ресурсы
2.2 http://fcior.edu.ru/card/3726/kvadratnoe-uravnenie.html
2.3 http://kopilkaurokov.ru/matematika/uroki/107955
2.4 http://nsportal.ru/shkola/algebra/library/2012/12/10/razrabotki-urokov-po- teme-teorema-vieta
2.5 http://gigabaza.ru/doc/40685.html
Приложение
Этапы реализации проекта
Этапы
Методы исследования
Содержание работы
Планируемый результат
1.Информационный
Сбор информации, ее анализ
Изучение литературы
Материал для теоретической части проекта
2.Организационный
Анализ, обобщение
Разработка блока уравнений
Материал для работы
3. Технологический этап
Подбор уравнений
Составление тренажера
Тренажер
4. Заключительный
Обобщение опыта
Выводы о проделанной работе, оформление проекта
Проект. Оформление коллекции. Мастер-класс. Участие в конкурсе.
infourok.ru
Теорема Виета и задачи с параметром
О теореме Виета читайте здесь.
В этой статье мы рассмотрим решение задач с параметром, в которых используется теорема Виета.
Задача 1. При каких значениях  корни
корни  уравнения
уравнения  удовлетворяют условию
удовлетворяют условию  .
.
Решение.
показать
Заметим, что в этой задаче не требуется найти значения корней уравнения, но нужно найти, при каком значении параметра корни удовлетворяют заданному соотношению. Поэтому воспользуемся теоремой Виета.
Запишем, каким соотношениям удовлетворяют корни уравнения.
По теореме Виета:

По условию:

Внимание! Не забываем условие того, что корни уравнения — различны и являются действительными числами: дискриминант должен быть больше нуля



Запишем эти условия в систему:

Выразим  и
и  через
через  :
:




Подставим во второе уравнение:






Проверим, удовлетворяет ли найденное значение  последнему условию:
последнему условию:  — верно.
— верно.
Ответ: -4
Задача 2. При каком значении параметра  сумма квадратов корней уравнения
сумма квадратов корней уравнения  наименьшая?
наименьшая?
Решение.
показать
Запишем теорему Виета для этого уравнения:

Условие того, что корни уравнения — действительные числа:  :
:

 — верно при любом значении
— верно при любом значении  .
.
Выразим сумму квадратов корней через сумму и произведение корней:

Перед нами квадратный трехчлен с положительным старшим коэффициентом. Он принимает наименьшее значение в вершине параболы  :
: 
Ответ: 1
Задача 3. Известно, что корни уравнения  на 1 меньше корней уравнения
на 1 меньше корней уравнения  . Найдите
. Найдите  и корни каждого из уравнений.
и корни каждого из уравнений.
Решение.
показать
И.В. Фельдман, репетитор по математике.
ege-ok.ru
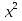 -4х-21=0
-4х-21=0