Методическая разработка урока геометрии в 8-м классе по теме «Теорема Пифагора»
Задачи урока:
1. Образовательные:
- доказать важнейшую теорему геометрии – теорему Пифагора;
- создать условия для формирования умений применения теоремы Пифагора к решению задач.
2. Развивающие:
- развивать внимание, логическое мышление, наблюдательность.
3. Воспитательные:
- воспитывать самостоятельность, нравственные качества;
- стимулировать интерес к предмету.
Тип урока: изучение нового материала.
Оборудование:
- компьютер;
- кодоскоп;
- портрет Пифагора;
- раздаточный материал.
Ход урока
I. Организационно — психологический момент.
Настрой на продуктивную работу.
(слайд 1)
Вступительное слово учителя.
Сегодня на уроке я предлагаю изучить: теорему Невесты, теорему Нимфы, теорему бабочки, теорему 100 быков, рассмотреть “бегство убогих”. (Показ слайдов 2 — 6).
Вопрос: Почему так много вопросов на один урок?
Совершенно верно: эти названия относятся к одной и той же теореме – теореме Пифагора. Названной именем древне-греческого учёного Пифагора, жившего в VI в. до н.э. (портрет). Более 25 веков она известна людям, существует более ста способов её доказательства. Сегодня мы познакомимся с одним из них.
Теорема Пифагора – это символ математики. Великий Гаусс предлагал её использовать в качестве первого сообщения внеземным цивилизациям о существовании на Земле разумной жизни, проведя в лесах России огромные вырубки в форме “пифагоровых штанов”, чтобы этот чертёж был виден из космоса.
Старинная формулировка теоремы Пифагора (слайд 7)
Чертёж к теореме через кодоскоп.
II. Изучение нового материала.
1) Сегодня на уроке пользуясь свойствами площадей многоугольников, установим замечательное соотношение между гипотенузой и катетами прямоугольного треугольника.
Современная формулировка теоремы Пифагора.
| В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. |
Доказательство теоремы проводит учитель на доске. Чертёж и доказательство теоремы учащиеся записывают в тетрадь.
Задание:
Дано:
Дано: ∆АВС – прямоугольный,
a, b – катеты, с – гипотенуза.
Доказать: с2 = а2 + b2.
Доказательство: Достроим треугольник
до квадрата со стороной (a + b) так, как
показано на рисунке. Площадь этого квадрата
Вопрос: Объясните, почему четырёхугольник со стороной с является квадратом?
Тогда S = 4 * 1/2ab + c2 = 2 ab + c2
Таким образом, (a + b)2 = 2ab + c2, откуда с2 = a2+ b2.
Найдите формулировку теоремы в учебнике (с.130).
Многие известные и неизвестные мыслители и писатели прошлого обращались к этой замечательной теореме и посвящали ей свои строки. Теорему Пифагора можно запомнить и с помощью вот такого стихотворения. (Подарок для каждого ученика).
Теорема Пифагора.
Если дан нам треугольник,
То квадрат гипотенузы
Да ещё с прямым углом,
Мы всегда легко найдём
Катеты в квадрат возводим,
Сумму степеней находим
И таким простым путём
К результату мы придём.
2) Применение теоремы Пифагора к решению задач.
С помощью теоремы Пифагора можно решать два вида задач:
- Найти гипотенузу прямоугольного треугольника, если известны катеты.
- Найти катет, если известна гипотенуза и другой катет.
(Виды задач через кодоскоп)
|
|
III. Закрепление.
- Двое учащихся решают задачи из учебника на доске (№483 (б), №484(б)), остальные решение записывают в тетрадь.
- Дидактическая игра (работа в группах). Для устного решения (короткие записи на черновиках) каждому ряду предлагаются соответственно задачи- рисунки, найти х. Ответы к рисункам подаются на стол учителя в письменном виде. По истечении определённого времени происходит обмен рисунками. Выигрывает тот ряд, у которого больше правильных ответов.
Задачи рисунки.
IV. Итог урока.
Вопросы.
- Как называется теорема, которую мы сегодня изучили?
- Почему у неё есть ещё несколько названий?
(Рассказ ученицы, подготовленный заранее. Историческая справка. Приложение 1).
Всем известна теорема Пифагора, но мало кто знает, что существуют жизненные правила Пифагора. они были опубликованы в 1806 году на страницах петербургского журнала “Любители словесности” ( Показ слайдов 8 — 14)
V. Рефлексия.
Учащиеся заполняют таблицу “Фотография урока”. (Приложение 2.)
Литература.
- Геометрия, 7 — 9. Учебник для общеобразовательных учреждений. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. М. Просвещение, 2002.
- Газета “Первое сентября”, №21. 2006.
- Дидактические игры на уроках математики. В.Г. Коваленко. М. Просвещение, 1990.
Проект по математике на тему «Теорему Пифагора» 8 класс
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 1
ИССЛЕДОВАТЕЛЬСКИЙ ПРОЕКТ ПО ГЕОМЕТРИИ НА ТЕМУ:
«ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА»
Автор проекта: Малкова Татьяна 8 «б» класс
Руководитель проекта: Филатникова М.В
учитель геометрии
р. п Чунский
2018 года
Идея моего проекта возникла на уроке геометрии. Когда мы начали изучать теорему Пифагора мне показалось, что на уроке слишком мало времени было уделено ученому, который ее создал, истории создания, применению в обыкновенной жизни. Мне стало интересно, а много ли материала имеется на эту тему и оказалось, что очень много. Поэтому я решила изучить всю эту информацию и представить в виде презентации, которую можно будет использовать на уроках геометрии.
Цель работы
Изучение истории появления и развития теоремы Пифагора.
Изучение исторических сведений по использованию теоремы Пифагора.
Рассмотрение различных видов доказательств теоремы Пифагора.
Создание учебной презентации на тему «Теорема Пифагора».
Задачи работы
Собрать материал по истории появления и развития теоремы Пифагора.
Собрать материал по использованию теоремы Пифагора в Древние века.
Собрать материал по различным видам доказательств теоремы Пифагора.
Проанализировать и обработать собранную информацию.
Систематизировать изученную информацию в презентацию Microsoft Power Point.
В VI веке до нашей эры средоточием греческой науки и искусства стала Иония — группа островов Эгейского моря, расположенных у берегов Малой Азии. Там в семье золотых дел мастера, резчика печатей и гравера Мнесарха родился сын. По преданию, в Дельфах, куда приехали Мнесарх с женой Парфенисой, — то ли по делам, то ли в свадебное путешествие — оракул предрек им рождение сына, который прославится в веках своей мудростью, делами и красотой. Бог Аполлон, устами оракула, советует им плыть в Сирию. Пророчество чудесным образом сбывается — в Сидоне Парфениса родила мальчика. И тогда по древней традиции Парфениса принимает имя Пифиада, в честь Аполлона Пифийского, а сына нарекает Пифагором, то есть предсказанным пифией.
В легенде ничего не говорится о годе рождения Пифагора. Исторические исследования датируют его появление на свет приблизительно 580 годом до нашей эры. Вернувшись из путешествия, счастливый отец воздвигает алтарь Аполлону и окружает юного Пифагора заботами, которые могли бы способствовать исполнению божественного пророчества. Возможности дать сыну хорошее воспитание и образование у Мнесарха были. Как всякий отец, Мнесарх мечтал, что сын будет продолжать его дело — ремесло золотых дел мастера. Жизнь рассудила иначе. Будущий великий математик и философ уже в детстве обнаружил большие способности к наукам. У своего первого учителя Гермодамаса Пифагор получает знания основ музыки и живописи. Для упражнения памяти Гермодамас заставлял его учить песни из «Одиссеи» и «Илиады». Первый учитель прививал юному Пифагору любовь к природе и ее тайнам. «Есть еще другая Школа, — говорил Гермодамас, — твои чувствования происходят от Природы, да будет она первым и главным предметом твоего учения».
Прошло несколько лет, и по совету своего учителя Пифагор решает продолжить образование в Египте, у жрецов. Попасть в Египет в то время было трудно, потому что страну фактически закрыли для греков. Да и властитель Самоса тиран Поликрат тоже не поощрял подобные поездки. При помощи учителя Пифагору удается покинуть остров Самос. Но пока до Египта далеко. Он живет на острове Лесбос у своего родственника Зоила. Там происходит знакомство Пифагора с философом Ферекидом — другом Фалеса Милетского. У Ферекида Пифагор учится астрологии, предсказанию затмений, тайнам чисел, медицине и другим обязательным для того времени наукам. Пифагор прожил на Лесбосе несколько лет. Оттуда путь Пифагора лежит в Милет — к знаменитому Фалесу, основателю первой в истории философской школы. От него принято вести историю греческой философии. Пифагор внимательно слушает в Милете лекции Фалеса, тогда уже восьмидесятилетнего старца, и его более молодого коллегу и ученика Анаксимандра, выдающегося географа и астронома. Много важных знаний приобрел Пифагор за время своего пребывания в Милетской школе. Но Фалес тоже советует ему поехать в Египет, чтобы продолжить образование. И Пифагор отправляется в путь. Перед Египтом Пифагор на некоторое время останавливается в Финикии, где, по преданию, учится у знаменитых сидонских жрецов. Пока он живет в Финикии, его друзья добиваются того, что Поликрат — властитель Самоса, не только прощает беглеца, но даже посылает ему рекомендательное письмо для Амазиса — фараона Египта.
В Египте благодаря покровительству Амазиса Пифагор знакомится с мемфисскими жрецами. Ему удается проникнуть в «святая святых» — египетские храмы, куда чужестранцы не допускались. Чтобы приобщиться к тайнам египетских храмов, Пифагор, следуя традиции, принимает посвящение в сан жреца. Учеба Пифагора в Египте способствует тому, что он сделался одним из самых образованных людей своего времени. К этому периоду относится событие, изменившее его дальнейшую жизнь. Скончался фараон Амазис, а его преемник по трону не выплатил ежегодную дань Камбизу, персидскому Царю, что послужило достаточным поводом для войны. Персы не пощадили даже священные храмы. Подверглись гонениям и жрецы, их убивали или брали в плен. Так попал в персидский плен и Пифагор.
Согласно старинным легендам, в плену в Вавилоне Пифагор встречался с персидскими магами, приобщился к восточной астрологии и мистике, познакомился с учением халдейских мудрецов. Халдеи познакомили Пифагора со знаниями, накопленными восточными народами в течение многих веков: астрономией и астрологией, медициной и арифметикой. Эти науки у халдеев в значительной степени опирались на представления о магических и сверхъестественных силах, они придали определенное мистическое звучаний философии и математике Пифагора… Двенадцать лет пробыл в вавилонском плену Пифагор, пока его не освободил персидский царь Дарий Гистасп, прослышавший о знаменитом греке.
Пифагору уже шестьдесят, он решает вернуться на родину, чтобы приобщить к накопленным знаниям свой народ. С тех пор как Пифагор покинул Грецию, там произошли большие изменения. Лучшие умы, спасаясь от персидского ига, перебрались в Южную Италию, которую тогда называли Великой Грецией, и основали там города-колонии Сиракузы, Агригент, Кротон. Здесь и задумывает Пифагор создать собственную философскую школу.

Довольно быстро он завоевывает большую популярность среди жителей. Энтузиазм населения так велик, что даже девушки и женщины нарушали закон, запрещавший им присутствовать на собраниях. Одна из таких нарушительниц, девушка по имени Теано, становится вскоре женой Пифагора. В это время в Кротоне и других городах Великой Греции растет общественное неравенство, вошедшая в легенды роскошь сибаритов (жителей города Сибариса) бок о бок соседствует с бедностью, усиливается социальная угнетенность, заметно падает нравственность. Вот в такой обстановке Пифагор выступает с развернутой проповедью нравственного совершенствования и познания.
Жители Кротона единодушно избирают мудрого старца цензором нравов, своеобразным духовным отцом города. Пифагор умело использует знания, полученные в странствиях по свету. Он объединяет лучшее из разных религий и верований, создает свою собственную систему, определяющим тезисом которой стало убеждение в нерасторжимой взаимосвязи всего сущего (природы, человека, космоса) и в равенстве всех людей перед лицом вечности и природы. В совершенстве владея методами египетских жрецов, Пифагор «очищал души своих слушателей, изгонял пороки из сердца и наполнял умы светлой истиной».
В Золотых стихах Пифагор выразил те нравственные правила, строгое исполнение которых приводит души заблудших к совершенству. Вот некоторые из них: не делай никогда того, чего ты не знаешь, но научись всему, что следует знать, и тогда ты будешь вести спокойную жизнь; переноси кротко свой жребий, каков он есть, и не ропщи на него; приучайся жить без роскоши.
Со временем Пифагор прекращает выступления в храмах и на улицах, а учит уже в своем доме. Система обучения была сложной, многолетней. Желающие приобщиться к знанию должны пройти испытательный срок от трех до пяти лет. Все это время ученики обязаны хранить молчание и только слушать Учителя, не задавая никаких вопросов. В этот период проверялись их терпение, скромность. Пифагор учил медицине, принципам политической деятельности, астрономии, математике, музыке, этике и многому другому. Из его школы вышли выдающиеся политические и государственные деятели, историки, математики и астрономы. Это был не только учитель, но и исследователь. Исследователями становились и его ученики.
Пифагор развил теорию музыки и акустики, создав знаменитую «пифагорейскую гамму» и проведя основополагающие эксперименты по изучению музыкальных тонов: найденные соотношения он выразил на языке математики. В Школе Пифагора впервые высказана догадка о шарообразности Земли. Мысль о том, что движение небесных тел подчиняется определенным математическим соотношениям, идеи «гармонии мира» и «музыки сфер», впоследствии приведшие к революции в астрономии, впервые появились именно в Школе Пифагора.
Многое сделал ученый и в геометрии. Доказанная Пифагором знаменитая теорема носит его имя. Достаточно глубоко исследовал Пифагор и математические отношения, закладывая тем самым основы теории пропорций. Особенное внимание он уделял числам и их свойствам, стремясь познать смысл и природу вещей. Посредством чисел он пытался даже осмыслить такие вечные категории бытия, как справедливость, смерть, постоянство, мужчина, женщина и прочее. Пифагор и его последователи своими работами заложили основу очень важной области математики — теории чисел.
Попытку Пифагора и его школы связать реальный мир с числовыми отношениями нельзя считать неудачной, поскольку в процессе изучения природы пифагорейцы наряду с робкими, наивными и порой фантастическими представлениями выдвинули и рациональные способы познания тайн Вселенной. Сведение астрономии и музыки к числу дало возможность более поздним поколениям ученых понять мир еще глубже.
После смерти ученого в Метапонте (Южная Италия), куда Пифагор бежал по окончании восстания в Кротоне, его ученики обосновались в разных городах Великой Греции и организовали там пифагорейские общества.

Теорема Пифагора имеет богатую историю. За 8 веков до нашей эры эта теорема была хорошо известна индийцам под названием «правила веревки», использовалась ими для построения алтарей, которые по священному предписанию должны иметь строгую геометрическую форму, ориентированную относительно четырех сторон горизонта. О том, что треугольник со сторонами 3, 4 и 5 есть прямоугольный, знали за 2000 лет до н.э. египтяне, которые использовали этот факт в определении прямых углов при строительстве зданий.
Теорема Пифагора- самая известная из всех геометрических теорем. О ней писали в своих произведениях римский архитектор и инженер Ветрувий, греческий писатель-моралист Плутарх, греческий ученый III века Диаген, Лаэрций, математик V века Прокл и многие другие. Прокл в своих комментариях к «Началам» Евклида пишет относительно предложения о том, что квадрат гипотенузы равен сумме квадратов катетов, следующее: «Если слушать тех, кто любит повторять древние легенды, то придется сказать, что эта теорема восходит к Пифагору. Рассказывают, что в честь этого открытия он принес в жертву быка». Другие говорят, 100 быков. Это послужило поводом для юмора в рассказах писателей и в стихах поэтов. Так, например, немецкий писатель А.Шамиссо написал следующие стихи:
Пребудет вечной истина, как скоро
Её познает каждый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За свет луча, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, её почуя, вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
Долгое время считали, что до Пифагора эта теорема не была известна и поэтому её назвали «теоремой Пифагора». Доказательство теоремы самого Пифагора до нас не дошло.
Во времена Пифагора формулировка теоремы звучала так:
площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
Насчитывается более пятисот доказательств теоремы. Благодаря такому количеству доказательств теорема Пифагора попала в Книгу рекордов Гиннеса как теорема с наибольшим количеством доказательств. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора послужила источником для множества обобщений и плодородных идей. Глубина этой древней истины, по-видимому, далеко не исчерпана. С глубокой древности математики находят все новые и новые доказательства теоремы Пифагора, все новые и новые замыслы ее доказательств. Таких доказательств – более или менее строгих, более или менее наглядных – известно более пятисот, но стремление к преумножению их числа сохранилось.
 Дано: ABC — прямоугольный треугольник с прямым углом С; С∈EF; PO||EF; MN||EF; CD⊥EF.
Дано: ABC — прямоугольный треугольник с прямым углом С; С∈EF; PO||EF; MN||EF; CD⊥EF.
Доказать: квадрат на гипотенузе равен сумме квадратов, построенных на катетах
Доказательство.
Треугольники 1 совпадают при повороте друг друга на 90° ⇒ они равны.
Треугольники 2 совпадают при осевом отображении относительно оси EF и параллельном переносе, т.е. они тоже равны.
При параллельных переносах и поворотах совпадают и все остальные треугольники, т.е. они тоже равны между собой.
Из всего этого следует, что квадрат на гипотенузе равен сумме квадратов, построенных на катетах.
Дополнительные построения:
Построим треугольник АВС с прямым углом С.
Построим ВF=CВ, ВF^ СВ.
Построим ВЕ=АВ, ВЕ^ АВ.
Построим АД=АС, АД^АС.
Точки F, С, Д принадлежат одной прямой
Доказательство: 1. Четырёхугольники АДВF и АВСЕ равновелики,
т.к. треугольники АВF и ЕСВ равны.
2.Треугольники АДF и АСЕ равновелики.
3. Отнимем от обоих равновеликих четырёхугольников
общий для них треугольник АВС, получим:
0,5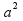 +0,5
+0,5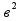 =
=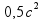 .
.
Соответственно :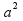 +
+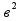 =
=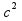 ,
,
что и требовалось доказать.
1. Площадь данного треугольника с одной стороны равна 0,5ab,
с другой 0,5pr, где
p – полупериметр треугольника,
r – радиус вписанной в него окружности (r=0,5(a+b-c)).
2. Имеем: 0,5ab=0,5pr=0,5(a+b+c)·0,5(a+b-c)
0,5ab=0,5(a+b+c)·0,5(a+b-c)
аb=0,5(а2 + ab – ac + ab + b2 – bc + ca + cb — с2)
аb=0,5(а2 + b2— с2 +2ab)/·2
2аb=а2 + b2— с2 +2ab
а2 + b2— с2 =0
3. Отсюда следует, что с2= а2+b2
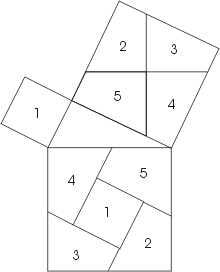
В учебниках нередко встречается разложение указанное на рисунке (так называемое «колесо с лопастями»; это доказательство нашел Перигаль). Через центр квадрата, построенного на большем катете, проводим прямые, параллельную и перпендикулярную гипотенузе. Соответствие частей фигуры хорошо видно из чертежа.
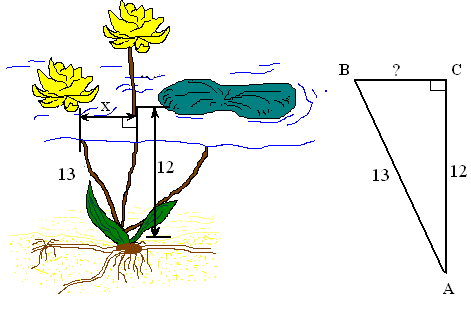
У египтян была известна задача о лотосе:
«На глубине 12 футов растет лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну.»
Попробуйте сами решить эту задачу. Естественно, при решении использовалась теорема Пифагора.
Исторические задачи очень часто представляли в стихах.
Задача Бхаскари:
«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»

Решение.
Пусть CD – высота ствола.
BD = АВ
По теореме Пифагора имеем АВ = 5 .
CD = CB + BD,
CD = 3 + 5 =8.
Ответ: 8 футов.
Задача арабского математика XI века.
На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?


Итак, в треугольнике АDВ: АВ2 =ВD2 +АD2
АВ2=302 +Х2
АВ2=900+Х2;
в треугольнике АЕС: АС2= СЕ2+АЕ2
АС2=202+(50 – Х)2
АС2=400+2500 – 100Х+Х2
АС2=2900 – 100Х+Х2.
Но АВ=АС, так как обе птицы пролетели эти расстояния за одинаковое время.
Поэтому АВ2 =АС2 ,
900+Х2 =2900 – 100Х+Х2,
100Х=2000,
Х=20,
АD=20.
Значит, рыба была на расстоянии 20 локтей от большой пальмы.
Ответ: 20 локтей.
Задача из учебника «Арифметика» Леонтия Магницкого:
«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать». 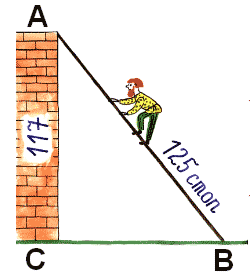
Многие при имени Пифагор вспоминают его теорему. Но неужели мы можем встречать эту теорему только в геометрии? Нет, конечно, нет! Теорема Пифагора встречается в разных областях наук. Например: в физике, астрономии, архитектуре и в других. Но так же Пифагор и его теорема воспеты в литературе.
В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов качественного и количественного исследования, которые позволяют решать задачи, выдвигаемые практикой. Рассмотрим несколько элементарных примеров таких задач, в которых при решении применяется теорема Пифагора.
Строительство.
Окно: в зданиях готического и ромaнского стиля верхние части окон

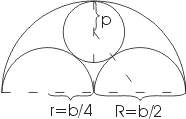
расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг и половине ширины (b/2), для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг. Так как она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления; покажем, как применяется в таких задачах теорема Пифагора.
В романской архитектуре часто встречается мотив, представленный на рисунке. Если bпо-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p.
По теореме Пифагора имеем:
(b/4+p)=(b/4)+(b/4-p)
или
b/16+b*p/2+p=b/16+b/4-b*p+p,
откуда
b*p/2=b/4-b*p.
Разделив на b и приводя подобные члены, получим:
(3/2)*p=b/4, p=b/6.
Крыша: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м, и AB=BF.
Решение:
Треугольник ADC — равнобедренный AB=BC=4 м, BF=4 м. Если предположить, чтоFD=1,5 м, тогда:
А) Из треугольника DBC: DB=2,5м
DC=
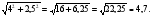
Б) Из треугольника ABF:
AF=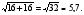
Молниеотвод: защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты.
Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
Решение:
По теореме Пифагора h2 ≥ a2+b2, значит h ≥ (a2+b2)½.
Ответ: h ≥ (a2+b2)½
Астрономия.
Пусть световой луч проходит путь от точки A к точке B. Какой путь проходит луч? Поскольку свет идет туда и обратно одинаковый путь, возникает вопрос: чему равна половина пути, который проходит луч? Если обозначить отрезок АВ символом /, половину времени как t, а также обозначив скорость движения света буквой с, то уравнение примет вид:
с X t = I . Это произведение затраченного времени на скорость.
Попробуем взглянуть на то же явление из другой системы отсчета, например, из космического корабля, пролетающего мимо бегающего луча со скоростью v. При таком наблюдении скорости всех тел изменятся, причем неподвижные тела станут двигаться со скоростью v в противоположную сторону. Предположим, что корабль движется влево. Тогда две точки, между которыми бегает зайчик, станут двигаться вправо с той же скоростью. Причем, в то время, пока зайчик пробегает свой путь, исходная точка А смещается и луч возвращается уже в новую точку С.
Вопрос: на сколько успеет сместиться точка, чтобы превратиться в точку С, пока путешествует световой луч, то есть спросим о половине данного смещения. Если обозначить половину времени путешествия луча буквой t’, а половину расстояния АСбуквой d, то получим наше уравнение в виде: v* t’ = d .Буквой v обозначена скорость движения космического корабля.
Другой вопрос: какой путь при этом пройдет луч света? Чему равна половина этого пути? Чему равно расстояние до неизвестного объекта? Если обозначить половину длины пути света буквой s, получим уравнение:c*t‘=s.
Здесь с — это скорость света, at’ — это тоже время, которое было рассмотрено формулой выше. Теперь рассмотрим треугольник ABC. Это равнобедренный треугольник, высота которого равна /, которое было введено при рассмотрении процесса с неподвижной точки зрения. Поскольку движение происходит перпендикулярно /, то оно не могло повлиять не нее. Треугольник ABC составлен из двух половинок — одинаковых прямоугольных треугольников, гипотенузы которыхАВ и ВС должны быть связаны с катетами по теореме Пифагора. Один из катетов — это d, который был рассчитан только что, а второй катет — это s, который проходит свет, и который тоже рассчитали. Получаем уравнение: s*s =l*l + d*d..
Мобильная связь.
В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу:какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например, радиусе R=200 км, если известно, что радиус Земли равен 6380 км).
Решение:
Пусть АВ=х, BC=R=200 км, ОС=r=6380 км. ОВ=ОА+АВ, следовательно: ОВ=r+х.
Используя теорему Пифагора, получим ответ 2,3 км.
В наши дни теорема Пифагора очень важна и актуальна. И несущественно то, что она была известна за много веков до Пифагора, важно то, что Пифагор выделил её, дополнив собственными исследованиями, повысив значимость в мире математических открытий. Из неё или с её помощью можно вывести большинство теорем геометрии. Теорема Пифагора продолжает оставаться живительным источником красоты, совершенства и творчества для новых и новых поколений. Несмотря на то что, суть теоремы проста и изящна, но было бы ошибкой думать, что в плане её содержания не осталось места для каких-то новых исследований. Результатом одного из таких исследований являются Пифагоровы тройки — наборы из трёх натуральных чисел, из которых сумма квадратов двух чисел равна квадрату третьего числа…
1. Балк М.Б, Балк Г.Д. Математика после уроков: Пособие для учителей. — М.: Просвещение, 1971.
2. Л.С. Атанасян, В.Ф.Бутузов и др. Геометрия, 7-9кл.: Учебник для общеобразовательных учреждений — 19-е изд. – М.: Просвещение, 2009.
3. Г.И. Глейзер. История математики в школе. 7-8кл.: Пособие для учителей, — М.: Просвещение, 1982.
4. Гусев В. А. и др. Математ. словарь для школьников: Сдай экзамены на пять! — Ростов н/Д: Феникс, 2004
5. Ресурсы удаленного доступа [электронный ресурс; рисунки] — Режим доступа: http://festival.1september.ru
Открытый урок по геометрии в 8-м классе на тему «Теорема Пифагора»
Цели урока:
Образовательные:
установить связь между сторонами прямоугольного треугольника (теорема Пифагора). Познакомить с другим способом нахождения гипотенузы прямоугольного треугольника;
Развивающая:
1.развивать мыслительные процессы, способствующие нахождению правильного решения;
2. развивать практические навыки применения данной теоремы;
Воспитательная:
воспитание ответственного отношения к учебному труду, научить преодолевать трудности, настраиваться на успех в любом деле; формировать навыки сотрудничества.
Оборудование:
- Интерактивная доска, мультимедийный проектор, ноутбук, программа МS Office 2003.
- Портрет Пифагора.
- Пифагорова головоломка.
Ожидаемый результат:
1-й уровень:
каждый ученик должен знать зависимость между сторонами прямоугольного треугольника, уметь применять теорему Пифагора для решения задач.
2-й уровень:
каждый ученик должен знать зависимость между сторонами прямоугольного треугольника, уметь доказывать теорему Пифагора, уметь применять теорему Пифагора для решения задач.
3-й уровень:
каждый ученик должен знать зависимость между сторонами прямоугольного треугольника, уметь доказывать теорему Пифагора, уметь применять теорему Пифагора для решения нестандартных задач.
Типология урока: урок усвоения новых знаний.
Основные этапы урока:
- Организационный момент.
- Вступительное слово учителя.
- Актуализация знаний.
- Создание проблемной ситуации.
- Работа над теоремой.
- Решение задач с применением теоремы.
- Домашнее задание.
- Подведение итогов урока (рефлексия по методу неоконченных предложений).
- Весёлая минутка.
ХОД УРОКА
1. Организационный момент.
Учитель:
Ребята, я рада видеть вас на нашем уроке и предлагаю вам перенестись в Древнюю Грецию и стать учениками пифагорейской школы. Мне хотелось бы узнать с каким настроением, вы отправляетесь в путешествие. Помогут выяснить его такие жесты. (хорошее, очень хорошее, параллельно, плохое и очень плохое). Мне приятно, что в основном у вас хорошее или отличное настроение, я обещаю, что к концу урока оно не испортится.
Презентация
II. Вступительное слово учителя.
Слайд 1.
Во время путешествия мы изучим одну из важнейших теорем геометрии – теорему Пифагора. Ведь она является основой решения множества геометрических задач и базой изучения теоретического материала в дальнейшем. Выясним, какое отношение имеет греческий математик Пифагор к «ослиному мосту»
Слайд 2.
Теперь послушаем рассказ о математике, именем которого она названа.
Учитель: А, может, кто –то из вас может мне помочь в рассказе о нём?
ПИФАГОР САМОССКИЙ (ок.580 – ок. 500г. до н.э.)
О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море, поэтому его называют Пифагором Самосским.
В молодости Пифагор был учеником Фалеса, побывал в Египте, где учился у жрецов.
Слайд 3.
В 530 г.до н.э. Пифагор основал так называемую пифагорейскую школу. Около сорока лет учёный посвятил себя, созданной им школе. Учеников школы называли пифагорейцами. Они занимались не только математикой, но и философией, естественными науками.
Известно также, что кроме духовного и нравственного развития учеников Пифагора заботило их физическое развитие. Он не только сам участвовал в Олимпийских играх и два раза побеждал в кулачных боях, но и воспитал плеяду великих олимпийцев.
Слайд 4.
Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда «ослиный мост» или «бегство убогих», так как некоторые ученики, не имевшие серьезной математической подготовки, бежали от геометрии.
Пифагор сделал много важных открытий, но наибольшую славу учёному принесла доказанная им теорема, которая сейчас носит его имя.
III. Актуализация знаний.
Учитель:
Ребята, перед вами лежат листочки с заданиями, подпишите их пожалуйста, и выберете правильный ответ.
Учитель:
Теперь давайте проверять и выставлять себе оценки.
Устная работа по готовым чертежам.
Слайд 5 – прямоугольный треугольник.
Слайд 6 – косинус угла, нахождение гипотенузы.
Слайд 7 – площадь квадрата.
IV. Создание проблемной ситуации.
Слайд 8 — задача «Установи елку».
Откройте тетради, запишите дату и тему урока «Теорема Пифагора».
V. Работа над теоремой.
Слайд 9 — подготовительный треугольник к теореме.
«В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». с2 = а2 +в2.
Словесная формулировка теоремы. Это один из ста способов доказательства теоремы.
Слайд 10 — теорема Пифагора (в стихах).
Слайд 11 — шаржы на теорему Пифагора.
VI. Решение задач
Учитель:
Теорема Пифагора — одна из главных теорем геометрии, с её помощью можно доказывать много других теорем и решить множество задач.
Решим несколько задач.
Слайд 12 — задача № 2.
Слайд 13 — задача №3.
Слайд 14 — закрепление нового материала.
Слайд 15 — разноуровневое домашнее задание.
«5» -задача № 6.
«4» — задача № 7.
«3» — задача № 2(в), 3(в).
К следующему уроку вы должны выучить теорему Пифагора с доказательством, так как вы будете применять её для решения более сложных задач.
Слайд 16 — рефлексия
«Сегодня на уроке я повторил…»
«Сегодня на уроке я узнал…»
«Сегодня на уроке я научился…»
Слайд 17 – Веселая минутка.
( с вопросом для внимательных и наблюдательных – где ошибка?)
Учитель:
Мне хотелось бы узнать какое у вас настроение в конце урока. (с помощью жестов).
А на память о себе я хочу вам подарить часть моего сердца (подарить сердечки)
СПАСИБО ЗА УРОК.
МАТЕМАТИЧЕСКИЙ ДИКТАНТ.
Работу выполнил учащийся 8 «Г» класса _______________________(Ф.И)
Выбери правильный вариант ответа.
1. Закончи предложение: «Треугольник, у которого один угол прямой называется…..»
а) остроугольный; б) равнобедренный; в) равносторонний; г) прямоугольный;
2. Отметь прямоугольный треугольник:
3. Как называются стороны в прямоугольном треугольнике?
а) боковые стороны; б) основания; в) катеты и гипотенуза.
4. У какого треугольника правильно отмечены стороны.
5. Закончи предложение «Косинусом острого угла называется отношение…..»
а) противолежащего катета к гипотенузе;
б) прилежащего катета к гипотенузе;
в) прилежащего катета к противолежащему катету;
г) противолежащего катета к прилежащему катету.
Выбрать формулу площади квадрата:
Конец диктанта.
Оценка «5» — все верные ответы.
Оценка «4» — 5 верных ответов.
Оценка «3» — 4 верных ответа.
«Надо ещё повторить» — 3 и менее верных ответа.
Приложение 2
Презентация к уроку (алгебра, 5 класс) на тему: Можно ли изучать теорему Пифагора в 5 классе
Слайд 1
«Теорема Пифагора для пятиклассников » Авторы работы: Евстратов Максим Рафальский Никита Фотеев Алексей ученики 5 класса школы № 54 Руководитель: Шляхта Ольга Николаевна у читель математикиСлайд 2
Цель проекта: доказать, что теорему Пифагора можно изучать в 5 классе.
Слайд 3
Задачи учебно-исследовательской работы: 1.изучить научную литературу; 2.познакомиться с геометрическими способами доказательствами теоремы; 3.составить презентацию для показа пятиклассникам с целью развития познавательного интереса.
Слайд 4
А МОЖНО ЛИ ТЕОРЕМУ ПИФОГОРА ИЗУЧАТЬ В 5 КЛАССЕ ?
Слайд 5
Докажем, что из двух квадратов определённой площади можно составить третий квадрат, определенной площади. Рассмотрим сначала более простые задачи. Составить из двух квадратов со стороной 1, квадрат со стороной 2.
Слайд 6
Разделим квадраты со стороной 1 по диагонали Способ 1
Слайд 7
Второй квадрат разделим по диагоналям Способ 2: Один квадрат оставим без изменения
Слайд 8
к первому квадрату приставим треугольники , получившиеся в результате деления второго квадрата
Слайд 9
Составить из двух квадратов со стороной 1 и 2 третий квадрат.
Слайд 10
Второй квадрат разделим следующим образам Один квадрат оставим без изменения
Слайд 11
к первому квадрату приставим треугольники , получившиеся в результате деления второго квадрата
Слайд 12
Разделим квадрат двумя способами: a a a a a a a a b b b b b b b b с с с с с с
Слайд 13
Если убрать из каждого квадрата по четыре равных зеленых треугольника, то площади оставшихся частей квадратов будут равны . с с с с a a a a b b b b = Значит, c = a + b . 2 2 2
Слайд 14
Применение теоремы Пифагора Рассмотрим задачу. Найти площадь квадрата и сторону этого квадрата. Задача №1 16 9 ?
Слайд 15
Задача №2 ? 25 169
Слайд 16
Пифагоровы тройки чисел 3 2 +4 2 =5 2 6 2 +8 2 =10 2 5 2 +12 2 =13 2 9 2 +12 2 =15 2 8 2 +15 2 =17 2 12 2 +16 2 =20 2
Слайд 17
Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты. В наш век эта фигура Пифагора выросла в целое дерево .
Слайд 18
Теорему Пифагора изучать в 5-м классе можно! Доказано.
Проектная работа по теме Теорема Пифагора
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ
,,СРЕДНЯЯ ШКОЛА №8”
ПРОЕКТНАЯ РАБОТА
,,ПИФАГОР И ЕГО ТЕОРЕМА”
Выполнил:
Щепин Алексей Артёмович 9а класс
Ямало-Ненецкий автономный округ
г. Новый Уренгой
Руководитель:
Баяринова Елена Алексеевна
Учитель математики
2017г.
ОГЛАВЛЕНИЕ
1.Титульный лист…………………………………..1стр.
2. Оглавление……………………………………… 2стр.
3.Актуальность теоремы……………………..…… 3стр.
4. Цель и задачи……………………………………. 3стр.
5. Введение……………………………..…………4стр.
6. Основная часть…………………………………. 5-7стр.
7. Заключение………………………………………8стр.
8. Вывод……………………………………… …… 9стр.
9. Библиографический список…………………….. 10стр.
Актуальность теоремы Пифагора.
Теорема Пифагора в геометрии важна не меньше, чем таблица умножения в арифметике. Решение многих геометрических задач (как в планиметрии, так и в стереометрии), сводится к рассмотрению прямоугольных треугольников и применению этой замечательной теоремы. Так же большинство задач по нахождению сторон прямоугольных треугольников сводится к использованию этой теоремы. Я решил, что этот материал будет интересен учащимся 8-9 классов, при изучении темы. Помимо исторических сведений в проект вошли доказательства теоремы Пифагора.
Цель работы
Изучение истории появления и развития теоремы Пифагора.
Изучение исторических сведений по использованию теоремы Пифагора.
Рассмотрение различных видов доказательств теоремы Пифагора.
Задачи:
1)Собрать материал о Пифагоре Самосском.
2)Узнать интересный факт о теореме Пифагора.
3) Собрать материал по различным видам доказательств теоремы Пифагора.
4) Проанализировать и обработать собранную информацию.
5) Сделать презентацию.
6)Оформить материал.
Введение:
Основная часть.
Биография Пифагора Самосского
Жизнь Пифагора трудно отличить от легенд. Он родился 570г – 495г до н. э. Пифагор — древний математик и философ-идеалист. Пифагор жил в шестом веке до нашей эры, имел красивую внешность, носил длинную бороду, а на голове золотую диадему. Пифагор — это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор — «убеждающий речью».) Своими речами приобрёл 2000 учеников, которые вместе со своими семьями образовали школу-государство, где действовали законы и правила Пифагора. Родился на острове Самос в Греции . Он получил хорошее образование. Что бы ознакомиться с мудростью ученых востока, уехал в Египет и жил там 22 года.Хорошо изучив науку египтян,а так же математикой,он переехал в Вавилон,где прожил 12 лет. Так же,если верить преданиям,посещал Индию. Пытался организовать свою философскую школу на Самосе,но позже покидает его,переезжая в Кротон. Там его школа действовала около 30 лет. Часто занимался пропорциями и прогрессиями,и вероятно,подобием фигур,так как ему принадлежит решение задачи « По данным двум фигурам построить третью, равновеликую одной из данных и подобную второй». Арифметика его не интересовала. Так же Пифагор, одним из первых считал, что Земля-это шар и центр вселенной.
Факты о Пифагоре:
1)Пифагор – автор рычага.
2)Давно известно имя «отца» демократии. Это Платон. Но в основу своего учения им положены идеи Пифагора, можно сказать, дедушки.
3)Он участвовал в Олимпийских играх и даже выходил победителем в кулачном бою.
4)По мнению Пифагора, все в мире отражается в цифрах. Любимым его числом было 10.
5)Ни в одном из свидетельств раннего времени нет упоминаний о заслугах Пифагора как величайшего космолога, математика древности. А он таковым считается сегодня.
6)Двести лет прошло со дня смерти великого мудреца, прежде чем появились первые документы с упоминанием об этом великом человеке. О нем сообщают самые разные, даже невероятные вещи.
Но на самом деле истинные факты почти невозможно отделить от легенд. Никто не скажет, это реально полубог и чудотворец и совершеннейший мудрец, или таким его сделала молва.
Факт о теореме Пифагора:
В настоящее время никому неизвестно доказательство теоремы самим Пифагором. Факты о доказательствах математика сегодня не известны никому. Считается,что доказательство чертежей Евклидом — это и есть доказательство Пифагора. Однако некоторые ученые спорят с этим утверждением: многие считают, что Евклид самостоятельно доказал теорему, без помощи создателя гипотезы.
Основной способ доказательства теоремы Пифагора.
Доказательство №1.
Рассмотрим прямоугольный треугольник с катетами а, в и гипотенузой с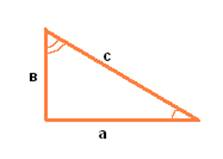
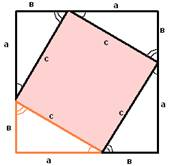
Докажем, что с²=а²+в².
Доказательство:
Достроим треугольник до квадрата со стороной а + в так, как показано на рис. 1, б. Площадь S этого квадрата равна (а + в)² . С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна ½ав , и квадрата со стороной с, поэтому S= 4 * ½ав + с² =2ав + с².
Таким образом,
(а + в)² = 2ав + с²,
откуда
с²=а²+в².
Теорема доказана.
Доказательство №2.
Рассмотрим прямоугольный треугольник с прямым углом С, СD– высота .
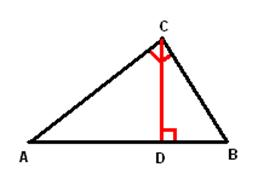
Докажем, что ас² +св² = ав².
Доказательство:
На основании утверждения о катете прямоугольного треугольника:
АС = 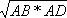 , СВ =
, СВ = 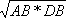 .
.
Возведем в квадрат и сложим полученные равенства:
АС² = АВ * АD, СВ² = АВ * DВ;
АС² + СВ² = АВ * ( АD + DВ), где АD+DB=AB, тогда
АС² + СВ² = АВ * АВ,
АС² + СВ² = АВ².
Теорема доказана.
Доказательство №3.
К доказательству теоремы Пифагора можно применить определение косинуса острого угла прямоугольного треугольника.
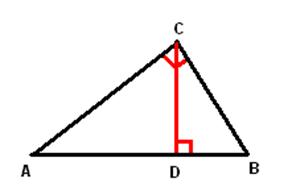
Пусть АВС – данный прямоугольный треугольник с прямым углом С. Проведем высоту СD из вершины прямого угла С.
По определению косинуса угла:
cos А = АD/АС = АС/АВ. Отсюда АВ * АD = АС²
Аналогично,
cos В = ВD/ВС = ВС/АВ.
Отсюда АВ * ВD = ВС² .
Складывая полученные равенства почленно и замечая, что АD + DВ = АВ, получим:АС² + ВС² = АВ (АD + DВ) = АВ²
Доказательство закончено.
Доказательство №4
Изучив тему «Соотношения между сторонами и углами прямоугольного треугольника», можно доказать ещё одним способом.
Рассмотрим прямоугольный треугольник с катетами а, в и гипотенузой с.
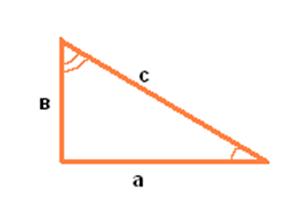
Докажем, что с²=а²+в².
Доказательство.
sinВ= в/с ; cosВ= a/с, то, возведя в квадрат полученные равенства, получим:sin²В= в²/с²; cos²В= а²/с².
Сложив их, получим:
sin²В + cos²В= в²/с²+ а²/с², где sin²В + cos²В=1,
1= (в²+ а²) / с², следовательно,
с²= а² + в².
Доказательство закончено.
Доказательство №5
Так же можно доказать теорему Пифагора с помощью прямоугольной трапеции.
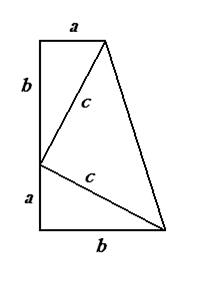
Расположим два равных прямоугольных треугольника так, чтобы катет одного из них был продолжением другого.
Площадь рассматриваемой трапеции находится как произведение полусуммы оснований на высоту
S = 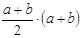
C другой стороны, площадь трапеции равна сумме площадей полученных треугольников:
S = 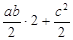
Приравнивая данные выражения, получаем:
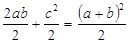 или с2 = a 2 + b 2.
или с2 = a 2 + b 2.
Доказательство закончено.
Заключение:
Ну вот и подошла к концу моя работа!
Итак. Мы узнали новое о теореме Пифагора и о самом Пифагоре в частности. Мы узнали ну или напомнили себе о доказательствах теоремы Пифагора.
Сначала мы узнали о его биографии. Потом о его знаменитой теореме и её важности. Далее мы узнали факты о Пифагоре и о его теореме. Далее повторили или узнали 5 основных доказательств. Мы успешно выполнили все задачи и основную цель. Я доволен своей работой, так как теорема Пифагора одна из самых популярных и делать проектную работу по ней очень интересно. Лично для себя я узнал много нового и интересного.
Вывод:
Мы узнали много нового об этой замечательной теореме и узнали 5 основных способов её доказательства. Главная цель работы выполнена.
Изучить теорему Пифагора и научиться её применять в задачах.
1)Узнать биографию Пифагора Самосского.
Узнали много нового о Пифагоре, как о человеке.
2)Узнать о важности теоремы Пифагора.
Узнали о важности теоремы и о их доказательствах.
3)Узнать факты из жизни Пифагора.
Узнали факты из насыщенной жизни Пифагора.
4)Узнать интересный факт о теореме Пифагора.
Узнали очень интересный факт о теореме Пифагора.
5)Научиться применять теорему Пифагора в 5 способах.
Научились применять теорему Пифагора в решении задач и узнали 5 способов её доказательствах.
Данная работа может быть использована учителем, преподающим геометрию в 8-11 классах, с целью расширения исторических знаний (слайды подачи учебного материала и проверки знаний учащихся по данной теме.
Библиографический список:
https://ru.wikipedia.org/wiki/Теорема_Пифагора
https://www.tutoronline.ru/blog/teorema-pifagora
http://scientificrussia.ru/articles/10-faktov-o-teoreme-pifagora
http://kartinkinaden.ru/nauka/890-interesnye-fakty-o-teoreme-pifagora.html
http://vivareit.ru/samye-interesnye-fakty-o-pifagore/
https://infourok.ru/tema-raznie-sposobi-dokazatelstva-teoremi-pifagora-519374.html
http://www.bestreferat.ru/referat-395917.html
http://moypifagor.narod.ru/
http://psihdocs.ru/metodika-vipolneniya-tvorcheskih-proektov-po-tehnologii.html
https://refdb.ru/look/2770226.html
А так же много других книг и справочников.
Изучение теоремы Пифагора
Геометрия обладает двумя великими сокровищами.
Первое – это теорема Пифагора, которую можно сравнить с мерой золота…
И. Кеплер
Урок № 1. “Знакомство с теоремой Пифагора, её практическое применение”.
Тип урока: урок изучения нового материала.
Урок-практическая работа.
Учащиеся выполняют практическую работу по трем видам прямоугольных треугольников, а именно: измеряют длины катетов и гипотенузы, проверяют выполнение свойства сторон, формулируют теорему Пифагора, учатся применять ее при решении опорных задач, знакомятся с египетским треугольником. На дом получают задание отыскать различные способы доказательства (хотя бы один), интересные исторические сведения по теме.
Урок № 2. “Доказательство теоремы Пифагора”.
Тип урока: урок закрепления и развития знаний, умений, навыков.
Урок-семинар.
Урок № 3. “Применение прямой и обратной теоремы при решении задач”.
Тип урока: урок применения знаний, умений, навыков.
Урок-практикум.
На этом уроке прослушиваются различные способы доказательства теоремы, выбранные по желанию и изучается обратная теорема, отрабатываются знания, умения, навыки при решении различных задач по теме.
Урок № 4. “ Теорема Пифагора”.
Тип урока: урок проверки знаний.
Урок-зачет.
Первую часть урока продолжается отработка навыков по применению теоремы,
Во второй части – зачетная работа.
Образовательные цели:
- Повторить свойства сторон и углов прямоугольного треугольника, нахождение его площади.
- Сформировать умение доказывать теорему.
Развивающие цели:
- Развивать и совершенствовать умение применять имеющиеся знания в измененной ситуации
- Способствовать развитию умения делать выводы и обобщения
Воспитательные цели:
- Способствовать выработке потребности применения изучаемых фактов
- Воспитывать самостоятельность и творчество
Оборудование: портрет ученого, эпиграф к уроку, модели прямоугольных треугольников, модели чертежей к различным способам доказательства теоремы, искусственная елочка.
После сообщения темы и целей урока 4 ученика подготавливают на доске различные способы доказательства теоремы:
Первый ученик предлагает доказательство, известное задолго до жизни Пифагора:
Прямоугольный треугольник достраивается до квадрата со cтороной (а + b). Площадь этого
квадрата равна (а + b)2. С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна ?аb, и квадрата со стороной с, поэтому
S = 4 * 1/2 ab + c2 = 2ab + c2.
Таким образом,
(а + b)2 = 2ab + c2, откуда
c2 = a2 + b2
Второй ученик предлагает доказательство Гарфилда.
Сущность его метода состоит в достраивании прямоугольного треугольника до трапеции. Поэтому площадь полученной фигуры можно находить как площадь прямоугольной трапеции, либо как сумму площадей трех треугольников.
Площадь трапеции равна 1/2 (а + b) (а + b), а сумма площадей треугольников 1/2 a b +1/2a b +1/2с2.
Приравнивая эти выражения, получаем теорему Пифагора.
Третий ученик предлагает доказательство методом разложения квадрата на равные части, называемое “колесом с лопастями”.
Здесь О – центр квадрата, построенного на большем катете, пунктирные линии, проходящие через точку О, перпендикулярны или параллельны гипотенузе.
Четвертый ученик показывает оригинальное доказательство Гофмана, предложенное в 1821 г.
Здесь четырехугольники ADFB и ACBE равновелики, отнимаем от обоих равновеликих четырехугольников общий для них треугольник АВС, получим 1/2а2 + 1/2b2 = 1/2с2, откуда получаем теорему Пифагора.
Класс повторяет определение прямоугольного треугольника, свойства его сторон и углов, формулы площадей треугольника и трапеции, понятие равновеликих фигур, решает задачи.
Задача 1. На площади устанавливают елку высотой 8 метров. Для этого нужны растяжки из проволоки исходящие от вершины и находящиеся на расстоянии 6 м от основания ёлки. Сколько метров проволоки понадобится на одну растяжку?
Задача 2. Один из катетов равен, а другой в 5 раз больше. Найти второй катет, гипотенузу, площадь треугольника, высоту, проведенную к гипотенузе.
Прослушиваются доказательства теоремы, каждый ученик выбирает понятное ему и конспектирует.
Ученица сообщает историческую справку о теореме Пифагора и о количестве способов её доказательства.
Учитель знакомит учащихся с дополнительной литературой по теме и предлагает познакомиться с другими способами доказательства, имеющимися в Интернете.
Итоги урока.
1. Вопросы классу:
- для каких треугольников верна теорема Пифагора
- какой способ доказательства наиболее интересен
2. Выставление оценок
3. Домашнее задание
План-конспект урока «Теорема Пифагора»
ПЛАН-КОНСПЕКТ УРОКА
Предмет: математика
Класс: 8
Тема: «Теорема Пифагора»
Цели:
Развивающие:
Продолжить овладение системой геометрических знаний и умений, необходимых для продолжения обучения.
Воспитательные:
Воспитывать познавательный интерес к геометрии, как к части общечеловеческой культуры.
Образовательные:
Изучить теорему Пифагора, рассмотреть решение задач с её применением.
Тип урока: Урок изучения нового материала.
Методы обучения: Проблемное обучение, эвристическая беседа.
Планируемые результаты:
Знать зависимость между сторонами прямоугольного треугольника.
Уметь доказывать теорему Пифагора.
Уметь применять теорему Пифагора для решения задач
Оборудование: Компьютер, проектор, экран, доска, мел
Структура урока:
Организационный момент (1 мин.)
Актуализация знаний (5 мин.)
Мотивационный этап (3 мин.)
Открытие теоремы (4 мин.)
Формулировка теоремы. Работа над формулировкой (2 мин.)
Доказательство теоремы (6 мин.)
Формирование умений применять теорему (6 мин)
Подведение итогов. Рефлексия (2 мин.)
Постановка домашнего задания (1 мин.)
Ход урока:
Организационный момент.
— Здравствуйте ребята! Все ли готово к уроку? Все ли есть для урока? Садитесь!
Актуализация знаний.
— Прежде чем приступать к изучению новой темы, давайте вспомним некоторые факты, которые мы уже знаем. Эти знания нам необходимы для сегодняшнего урока.
— Дайте определение квадрата? (это прямоугольник, у которого все стороны равны)
слайд 1
— Как найти площадь квадрата? (любую его сторону возвести во вторую степень)
слайд 2
— Как найти площадь квадрата со стороной равной 4, с, a + b (S = 42 = 16;
S = с2 ; S = (a + b)2)
слайд 2
— Какой треугольник называется прямоугольным? (треугольник, у которого один из углов равен 900, т.е. прямой)
слайд 3
— Как называются стороны прямоугольного треугольника? (сторона, которая лежит против прямого угла – гипотенуза, а две другие стороны катеты)
— Как найти площадь прямоугольного треугольника с катетами а и b, и гипотенузой с? ()
слайд 4
— Найдите площадь прямоугольного треугольника с катетами равными 3 и 4. ()
слайд 4
Мотивационный этап.
— А теперь давайте попробуем решить интересную задачу.
слайд 5
Рассматривается рисунок, формулируется задача, которую вроде бы возможно решить, т.к. лестница должна быть вполне определенной длины.
— Но как найти эту длину? (учащиеся испытывают затруднения)
— Оказывается не надо непосредственно измерять длину лестницы. Достаточно знать, в каком соотношении находятся катеты и гипотенуза в прямоугольном треугольнике.
Ставится проблема: найти эту зависимость.
— И сегодня мы узнаем ещё одну, очень важную теорему, связанную с прямоугольным треугольником. Существует замечательное соотношение между гипотенузой и катетами прямоугольного треугольника, справедливость которого была доказана древнегреческим философом и математиком Пифагором. Эта теорема является основой решения множества геометрических задач и базой изучения теоретического материала в дальнейшем, она применяется в геометрии буквально на каждом шагу. Вы и сами в этом скоро убедитесь!
— Откройте тетради, запишите число и тему урока «Теорема Пифагора».
Слайд 6
— Эпиграфом сегодняшнего урока возьмем слова Кеплера: «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора».
— Как вы думаете, какая цель будет у нашего сегодняшнего урока? (Изучить теорему Пифагора, рассмотреть решение задач с её применением)
Слайд 6
Открытие теоремы.
— А сейчас давайте попробуем открыть теорему, т.е. увидеть на примере это замечательное соотношение сторон прямоугольного треугольника! Также, возможно, это соотношение открыли и в древности.
— Так как речь идет о прямоугольном треугольнике, то давайте возьмем такой треугольник с сторонами 3, 4 и 5, и построим на каждой стороне этого треугольника квадраты, со сторонами равными сторонам треугольника.
слайд 7
— Вычислите площади получившихся квадратов. (25, 16, 9)
слайд 7
-Что вы увидели? (сумма площадей квадратов построенных на катетах равна площади квадрата построенного на гипотенузе)
— Действительно это так! 25 = 16 + 9
слайд 7
— Во времена Пифагора теорема так и звучала: «Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах»
слайд 7
— Т.е. сейчас мы все вместе уже открыли формулировку теоремы! Но не нужно думать, что мы уже ее и доказали, ведь мы рассмотрели лишь пример с конкретными длинами катетов и гипотенузы.
Формулировка теоремы. Работа над формулировкой
— Не зря выделены именно эти слова в формулировке теоремы времен Пифагора. В современной формулировке она звучит более коротко. «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов»
слайд 8
— Давайте поработаем над формулировкой.
— Смотря на формулировку, что мы можем записать в дано? (прямоугольный треугольник АВС)
слайд 8
— Что нужно доказать? (АВ2 = АС2 + BC2)
слайд 8
Доказательство теоремы
— На данный момент существует более трехсот способов доказательства этой теоремы. Выберем один.
— Давайте для удобства обозначим длины сторон треугольника a, b и с.
слайд 9
— Так как речь идет о квадрате, построенном на гипотенузе, давайте его построим.
слайд 9
— Чему будет равна каждая сторона этого квадрата? (с)
— Выполним еще дополнительное построение. На каждой стороне этого квадрата построим еще по прямоугольному треугольнику, равному данному.
слайд 9
— Что у нас получилось? (еще один квадрат)
— Обозначьте стороны всех прямоугольных треугольников.
слайд 10
— Чему равна сторона этого квадрата? (a + b)
слайд 11
— Тогда чему будет равна площадь этого квадрата? (S = (a + b)2)
слайд 11
— Как еще можно найти площадь этого квадрата? (нужно найти площади всех фигур из которых он состоит, то есть найти площади четырех прямоугольных треугольников и площадь квадрата. Найти их сумму.)
— Чему равняется площадь квадрата? (с2)
— Чему равняется площадь каждого треугольника? ()
— Тогда чему равняется площадь всего квадрата?
слайд 12
— Тогда исходя из этих двух равенств, докажите теорему Пифагора. (Некоторые дети догадываются приравнять правые части равенств, так как левые равны. И далее останется только упростить)
слайд 12
— Мы доказали теорему? (Да, так как возвращаясь к старому обозначению, получается то что требовалось доказать АВ2 = АС2 + BC2)
— Итак, давайте рассмотрим основные этапы доказательства теоремы. Что мы делали в первую очередь? (ввели новые обозначения)
— На втором этапе? (выполнили дополнительные построения)
— На третьем этапе? (нашли различными способами площадь полученного квадрата)
— И на последнем этапе? (приравняли полученные равенства, упростили, и получили искомое равенство)
7. Формирование умений применять теорему
— А теперь давайте немного отдохнем, прочтя следующее стихотворение, посвященное теореме Пифагора.
слайд 13
— Итак, давайте попробуем решить следующую задачу. «В прямоугольном треугольнике АВС катеты равны 5 и 12. Найдите гипотенузу АВ»
слайд 14
-Что дано? Что нужно найти? Запишите в тетрадь.
слайд 14
— Как решить эту задачу? (используя теорему Пифагора: АВ2 = АС2 + BC2)
— Хорошо. Чему будет равняться АВ?
Используя слайд вместе с учащимися решается задача. В ходе решения ребята убеждаются, в том как легко находится гипотенуза, используя теорему Пифагора.
слайд 14
— Давайте вернемся к задаче, которая была у нас в начале урока.
— Можно в этой задаче применить теорему Пифагора? (да можно, так как стена, расстояние до основания лестницы и сама лестница образуют прямоугольный треугольник, в котором известны катеты)
слайд 15
— Какой длины потребуется лестница? (10 м)
Вместе с учащимися решается задача, применяя теорему Пифагора.
8. Подведение итогов. Рефлексия
— Давайте подведем итог нашего урока. (ученики отвечают на вопросы со слайда)
слайд 16
— А теперь, каждому я раздам карточку, в которой стрелочкой вы укажите, чего вы достигли на уроке для самих себя. Сдайте их пожалуйста в конце урока.
слайд 17
— И после этого запишите домашнее задание.
слайд 18
— Всем спасибо за урок! До свидания!