Конспект урока по геометрии «Трапеция. Средняя линия трапеции. Теорема Фалеса» (8 класс)
Конспект урока по геометрии 8 класс
Тема: Трапеция. Средняя линия трапеции. Теорема Фалеса.
Цели: Систематизировать и обобщить знания по теме «Трапеция. Средняя линия трапеции. Теорема Фалеса», Формировать умения и навыки применять теоремы для решения задач, умения анализировать и структурировать полученные знания и навыки.
Ход урока
Мотивация учебной деятельности.
Вступительное слово учителя: Наш урок посвящен трапеции. Сформулируйте, пожалуйста, определение трапеции.
Существует особенная речь, которая понятна каждому человеку, каким бы языком он не владел. Это – рисунок. Сегодня на уроке мы будем постоянно обращаться к рисункам. Вы продемонстрируете умения применять и знания при решении задач на трапеции.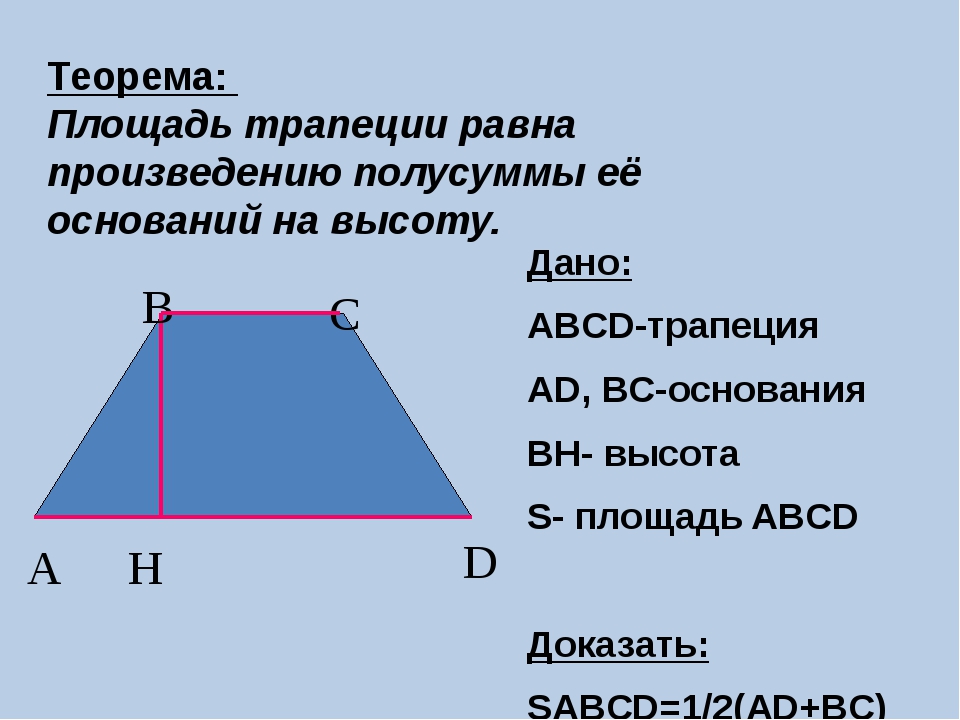
Историческая справка. (Сообщение учащегося).
По Евклиду, любой четырехугольник, который не является параллелограммом, — трапеция. В переводе с древнегреческого слово «трапеция» обозначает «стол», «обеденный стол». Кстати, теперь понятны слова «трапеза» — еда, «трапезная» — место, где едят. То есть они тоже связаны со словом «стол».
Только в ХVII столетии понятие «трапеция» получает современный смысл.
Актуализация опорных знаний.
«Ассоциативный куст»
Ключевым словом «Ассоциативного куста» является трапеция. Обучающиеся по очереди на ветвях «куста» записывают слова, фразы, которые связаны с ключевым словом. Далее ученики раскрывают содержание каждой ветви.
Учитель. Мы вспомнили с вами определения, теоремы, а сейчас вам предстоит показать умения применять эти теоретические знания при решении задач по готовым рисункам. Одновременно попробуем ответить на вопросы, которые возникли при заполнении «куста».
Мы вспомнили с вами определения, теоремы, а сейчас вам предстоит показать умения применять эти теоретические знания при решении задач по готовым рисункам. Одновременно попробуем ответить на вопросы, которые возникли при заполнении «куста».
Устное решение задач.
№1.
Задания для учащихся:1.Чем является отрезок MN?
2.Дайте определение средней линии треугольника.
3.Назовите свойства средней линии треугольника.
4.Чему равна сторона АС?
5.На какие фигуры делит треугольник АВС отрезок MN?
6.Что можно сказать об углах треугольников ВMN и ВАС?
7. Чему равен , если ?

№2.
Задания для учащихся:Чем является отрезок MN в трапеции АВСД? Почему?
Какая существует связь между MN и АД и ВС?
Найдите MN.
Методический комментарий. Изучая формулы координат середины отрезка, как среднее арифметическое координат концов, учащиеся еще раз встретятся с нахождением одного конца отрезка по координатам другого и их среднего арифметического.
№3.
АВСД- равнобедренная трапеция. Докажите, что МР=КД
Указание: Соедините точки М и Р.
Задания для учащихся:
1.Какова длина отрезка МК в прямоугольном треугольнике АВК?
2. Какой вид треугольника АМК?
3. Продолжите цепочку …=…
4. Какой вывод можно сделать по четырехугольнику КМРД? Почему?
Методический комментарий.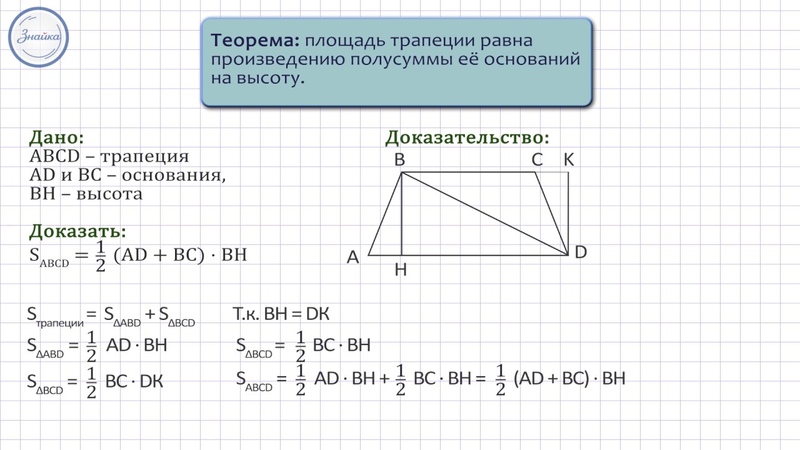 При решении задач на равнобедренную трапецию очень часто применяется этот факт. Поэтому для его лучшего усвоения уместно предложить учащимся еще раз доказать этот факт дома, но другим способом.
При решении задач на равнобедренную трапецию очень часто применяется этот факт. Поэтому для его лучшего усвоения уместно предложить учащимся еще раз доказать этот факт дома, но другим способом.
№4
АС- биссектриса угла А равнобедренной трапеции АВСД.
АВ=4, АД=8. Найти периметр АВСД.
Задания для учащихся:
Продолжите цепочку:
=…
(как односторонние при параллельных прямых ВС и АД) следовательно значит ВС=… и
Методический комментарий. Тот факт, что биссектриса угла трапеции (параллелограмма, прямоугольника)образуют равнобедренный треугольник является опорным фактом, который учащиеся должны знать.
Систематизация и обобщение знаний, умений.
Письменное решение задач.
Класс делится на пять групп. Каждая группа выполняет свое задание, на выполнение которого отводится 8 мин. После завершения работы представитель от каждой группы решает свою задачу на доске.
Задание для 1 группы.
В равнобедренной трапеции высота, проведенная из вершины тупого угла, делит большее основание на отрезки 4см и 20см. Найдите среднюю линию трапеции.
Три стороны трапеции равны 7см каждая. Углы при большем основании равны 60°. Найдите периметр трапеции.
Задание для 2 группы.
Меньшее основание равнобедренной трапеции равно боковой стороне, а диагональ перпендикулярна к боковой стороне. Найдите углы трапеции.
Задание для 3 группы.
BN=NE=AE, NM II EK II AC. Найдите ЕК, АС.Боковая сторона равнобедренной трапеции равна 10см. Биссектриса острого угла трапеции проходит через середину меньшего основания.
 Найдите длину меньшего основания.
Найдите длину меньшего основания.
Задание для 4 группы.
В трапецию АВСД (ВС II AD) вписана окружность с центром в точке О. Найдите угол СОД.
Задание для 5 группы.
В равнобедренную трапецию АВСД с боковой стороной АВ, которая равна 8см, вписана окружность. Найдите среднюю линию трапеции.
Применение умений и навыков.
Выполнение практических заданий.
Учитель. Представьте себе, что вы строители. Как найти длину забора (то есть периметр трапеции АВХС), которым ограждена детская площадка, если вершина Х недоступна и кучей песка частично присыпаны стороны ВХ и ХС?
Эту задачу вы будете решать в парах.
Решение.
1-й способ
Дополнительное построение. ВУ II XC, то УВХС – параллелограмм, а значит, ВУ = ХС.
АВ+ВХ+ХС+АС=АВ+УС+ВУ+АС.
2-й способ
Разделим сторону АВ на три равные части и проведем прямые КН, МД параллельные АС.Измерим ДС, тогда ХС=3ДС.
Измерим АС, МД и найдем ВХ.
Около доски ученики защищают проект. Подводятся итоги. Анализируются положительные и отрицательные стороны проектов.
Итог урока
Домашнее задание. Решите задачу: Докажите, что средняя линия равнобедренной трапеции равна КД (см. рис.).
Средняя линия треугольника. Средняя линия трапеции 8 класс онлайн-подготовка на Ростелеком Лицей
Средняя линии треугольника. Средняя линия трапеции.
Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника.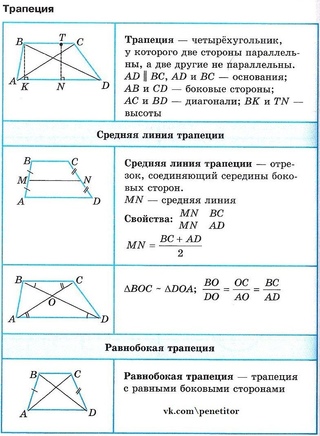
На рисунке средней линией является отрезок DE.
Доказательство. Рассмотрим треугольники ABC и DBE. Они подобны, так как имеют две пары пропорциональных сторон (AB = 2BD, BC = 2BE) и общий угол B. Значит, все углы в этих треугольниках равны. ∠BDE = ∠BAC, следовательно, DE||AC по признаку параллельности: соответствующие углы равны. Коэффициент подобия равен 2, значит, AC = 2DE.
Следствие. Три средних линии делят треугольник на 4 равных треугольника ADF, DBE, ECF, DEF.
Каждый из четырёх треугольников ADF, DBE, ECF, DEF подобен треугольнику ABC с коэффициентом подобия 0,5.
Напомним, что трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции.
Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции.
На рисунке средней линией трапеции является отрезок EF.
Теорема. Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.
Дано: ABCD – трапеция, E – середина AB, F – середина CD.
Доказать: EF||BC||AD, EF = (BC+AD):2.
Доказательство. Проведем через вершину B и середину боковой стороны F трапеции прямую линию. Обозначим точку пересечения прямых BF и AD буквой G.
Рассмотрим треугольники BCF и FDG. В них CF = FD (по условию), ∠BFC = ∠DFG (вертикальные углы), ∠BCF = ∠GDF (накрест лежащие при параллельных прямых). Следовательно, треугольники равны по второму признаку.
Из равенства треугольников следует BF = FG и DG = BC. Значит, отрезок EF является средней линией треугольника ABG.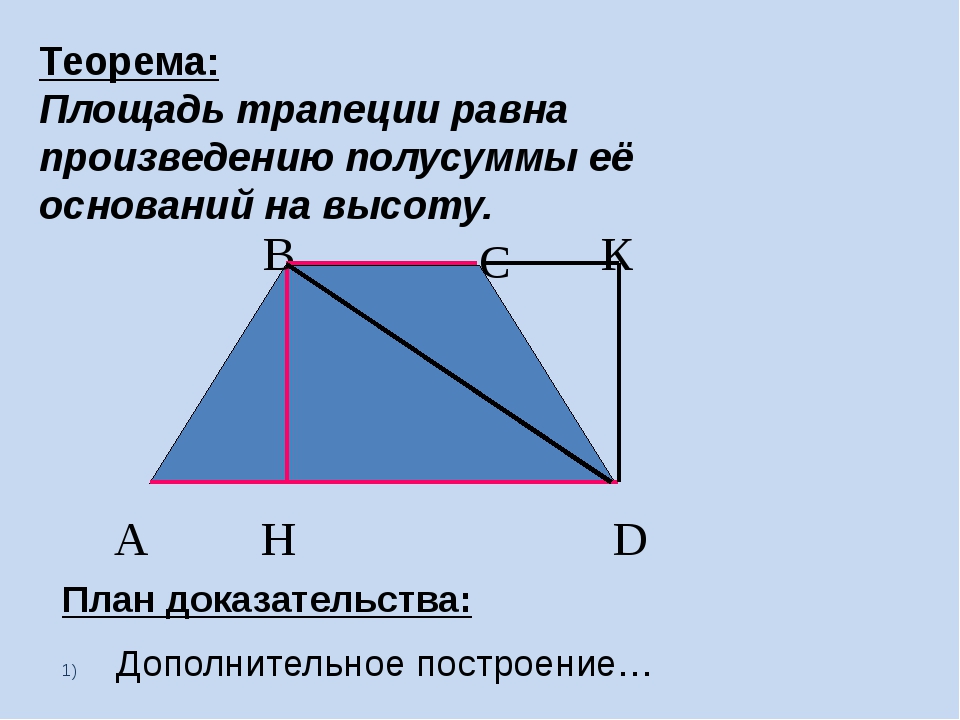
Найдем длину EF. По теореме о средней линии треугольника EF = AG:2 = (AD+DG):2 = (AD+BC):2, что и требовалось доказать.
Конспект урока по геометрии «Площадь трапеции» (8 класс)
презентация к уроку
PPTX / 1.45 Мб
Мамутова Нияра Диляверовна
учитель математики высшей категории
МБОУ «Трудовская школа» Симферопольского района Республики Крым
Республика Крым, Симферопольский район
Конспект урока по геометрии «Площадь трапеции» (8 класс)
Цель:
— вывести формулу площади трапеции, формировать навыки и умения пользоваться ей при решении задач;
— развить у детей умения обобщать, логически мыслить, применять аналогию, наблюдательность, рационально использовать свои знания;
— воспитать интерес к предмету, познакомить учеников с историческими фактами, связанными с данной темой.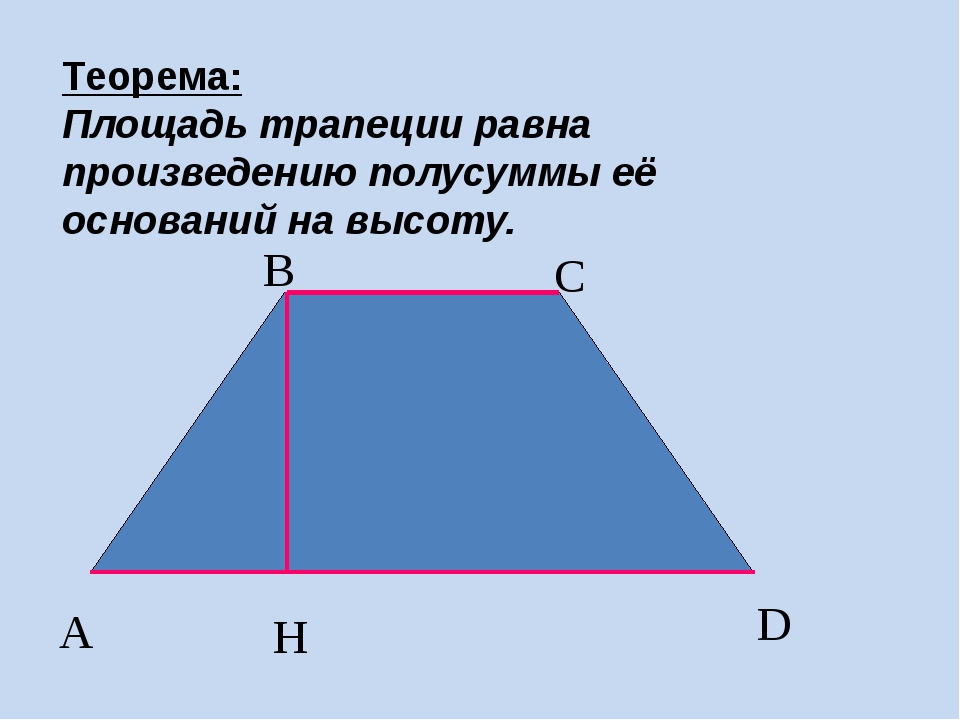
Тип урока: комбинированный урок.
Оборудования: конспект урока, учебник, раздаточный материал, компьютерная презентация, проектор.
Структура урока:
1. Организационный этап. Проверка готовности учеников к уроку.
2. Проверка домашнего задания. Актуализация и коррекция опорных знаний.
3. Объявление темы, целей и задач урока.
4. Восприятие и первичное усвоение нового материала, осмысление связей и отношений в объектах изучения.
5. Обобщение и систематизация знаний.
6. Подведение итогов, объявление домашнего задания.
Ход урока
1. Организационный этап. Проверка готовности учащихся к уроку.
Учитель. Всем доброе утро!
Учащиеся (все вместе). Доброе утро!
2. Проверка домашнего задания.
Актуализация и коррекция опорных знаний.
Проверим домашнее задание. Задачу решает один ученик у доски, все остальные работают устно, отвечая на вопросы.
Устный опрос
1. Чему равна площадь квадрата? Прямоугольника? Параллелограмма? Ромба? Треугольника? Прямоугольного треугольника?
(Площадь квадрата со стороной а равна а2. Площадь прямоугольника равна произведению двух его соседних сторон. Площадь параллелограмма равна произведению его стороны и высоты, которая проведена к этой стороне. Площадь ромба равна половине произведения его стороны и высоты, которая проведена к ней. Площадь прямоугольного треугольника равна половине произведения его катетов.).
2. Стороны прямоугольника равны 5 см и 3 см. Какова площадь прямоугольника? (S = 5 * 3 = 15 (см2)).
3. Сторона квадрата 11 см, какова его площадь? (S = 112=121 (см2)).
4. Площадь квадрата 64 см2, какой длины его сторона? (а=8 см).
Площадь квадрата 64 см2, какой длины его сторона? (а=8 см).
5. Диагонали ромба равны 10 см и 6 см, чему равна его площадь?
6. Площадь прямоугольника 48 см2, одна из его сторон равна 8 см. Вычислите другую его сторону. (b = 48:8=6(см)).
7. Катеты прямоугольного треугольника 10 см и 18 см. Найдите его площадь.
Откройте свои тетради, проверьте письменную домашнюю работу.
Дано: треугольник АВС
АМ перпендикулярно ВС
АВ = 10√2 см
АС = 26 см
Угол В равен 450
Найдите площадь треугольника АВС.
Решение
Рассмотрим
угол В равен 450, тогда треугольник АВМ – равнобедренный с основанием АВ, АМ=ВМ.
Рассмотрим треугольник АМС, угол АМС равен 900, по теореме Пифагора:
АС2 = АМ2 + МС2
МС2 = АС2 – АМ2
МС2 = 262-102
МС2 = 676 – 100
МС2 = 576
МС = 24 см
ВС = ВМ + МС = 10 + 24 = 34 (см)
Ответ: 170 см2.
3. Объявление темы, целей и задач урока.
Запишите дату, классная работа в тетради.
Сегодня на уроке покажем, как использовать математику в практической жизни.
Задача. Актовый зал школы имеет форму трапеции с основанием 20 м и 10 м высотой 8 м. Хватит ли 9 кг краски, чтобы покрасить пол актового зала, если расход краски составляет 1 кг/10 м2?
Слайд 1. Задача.
Что необходимо, чтобы решить данную задачу?
Правильно, необходимо найти площадь трапеции.
Мы уже знаем, как находить площадь квадрата, прямоугольника, параллелограмма, треугольника, ромба. А сейчас выведем формулу для вычисления еще одного многоугольника, а именно трапеции. Таким образом, тема нашего урока «Площадь трапеции».
Слайд 2. Тема урока. Площадь трапеции.
Софья Ковалевская сказала: «У математики есть свой язык – это язык формул».
Повторим, что нам известно о трапеции.
Слайд 3. Проверь себя.
— Что называется трапецией? (Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны).
— Как называются стороны трапеции (Параллельные стороны трапеции называются основаниями, а непараллельные – боковыми сторонами).
— Какие виды трапеций вам известны? (Трапеции бывают произвольными, равнобокими и прямоугольными).
— Что известно про углы трапеции, которые прилегают к боковой стороне? (Сумма двух углов прилежащих к боковой стороне равна 1800).
— Что называется средней линией трапеции? (Средней линией трапеции называют отрезок, который соединяет середины боковых сторон).
— Чему равна средняя линия трапеции? (Средняя линия трапеции параллельна основаниям и равна половине их суммы).
— Что называется высотой трапеции? (Высотой трапеции называют перпендикуляр, опущенный с любой точки прямой, которая содержит одну из основ на прямую, которая содержит другую основу).
При выполнении разного рода работ (покрыть крышу, сшить юбку, покрасить стол) необходимо вычислить площадь трапеции.
Слайд 4. Трапеция вокруг нас
4. Восприятие и первичное усвоение нового материала, осмысление связей и отношений в объектах изучения.
Слайд 5. Задание. Постройте трапецию АВСD c основаниями ВС=а, AD=b. Проведите высоту СН = h. Найдите ее площадь.
Проведите диагональ АС и высоту АН1= h2. Отрезки АН1 и СН являются высотами треугольников АВС и АСD соответственно, в свою очередь данные высоты имеют одинаковую длину, поэтому СН=АН1=h. Вам известно как найти площадь треугольника, если известна его сторона и высота, проведенная к ней. Площадь треугольника равна половине произведения его стороны и проведенной к ней высоты.
Вернемся к трапеции. Трапеция состоит из двух данных треугольников. Вам известно, что если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольник, поэтому площадь трапеции равна:
Выделите полученную формулу рамочкой, подпишите ее название, укажите, что означают буквы a,b – основы, h – высота.
Слайд 6. Формулы площади трапеции
Решение к задаче:
S=1/2(20+10)*8=120 (м2)
120:10=12 (кг) краски необходимо для покраски пола актового зала
Ответ. 9 кг краски для покраски пола не хватит.
Чему равна полусумма основ трапеции? (Полусумма основ равна средней линии l=1/2(a+b)).
То есть, площадь трапеции равна произведению ее средней линии на высоту. Про это свидетельствует следствие из теоремы.
Вопрос к учащимся:
Как найти площадь трапеции?
Какие отрезки необходимо иметь для этого?
Практическое задание. (Обменяйтесь тетрадями) Постройте произвольную трапецию, проведите высоту. (Снова обменяйтесь тетрадями). Отмерьте необходимые отрезки, запишите их длины. Найдите площадь трапеции.
5. Обобщение и систематизация знаний.
Дано ABCD – трапеция
SABCD = 96 см2
BH = 3 см
BC: AD = 3:5
Угол В = 450
Найти: ВС, AD.
Решение
Пусть ВС = (3х) см, AD = (5х) см, тогда
SABCD = ½(ВС+AD)*BH
½(3х+5х)*3=96
½*8х*3=96
4х*3=96
12х=96
х=96:12
х=8
Итак, ВС = 3*8=24 (см), AD = 5*8=40 (см).
Ответ. 24 см, 40 см.
Пришла пора немного отдохнуть, приглашаю вас на физкультминутку.
Слайд 7. Физкультминутка.
Глаза отдохнули, продолжаем работать.
А сейчас мы с вами попробуем решить задачи практического содержания. Задачи получим по рядам, в каждом ряду есть ученики-консультанты, которые помогают всем остальным выполнять задание и комментируют его.
1 ряд. Поперечный срез траншеи имеет форму трапеции. Вычислите площадь этого поперечного среза, если глубина траншеи 1,5 м, ширина в земле 0,8 м, на поверхности земли 1,2 м.
S=1/2(1,2+0,8)*1,5 = 1,5 (м2)
2 ряд. Для защиты грунта от эрозии в районе источника спроектируйте дамбу, которая будет представлять собой трапецию, высотой 3 м и шириной сверху и снизу 2 м и 4 м соответственно. Найдите площадь поперечного среза дамбы.
S=1/2(2+4)*3=12 (м2)
3 ряд. Площадь леса имеет форму трапеции. Вычислите сколько деревьев сгорело во время лесного пожара, если известно, что ширина узкой части леса была 3 км, широкой – 5 км, длина леса 2 км, на 1 км2 росло приблизительно 200 деревьев.
S=1/2(3+5)*2=8 (км2)
8*200=1600 (д.) – деревьев сгорело во время лесного пожара.
Слайд 8. Задачи практического содержания.
А сейчас мы с вами познакомимся с формулой Пика.
Слайд 9. Историческая справка. Формула Пика.
Георг Пик – австрийский математик. Родился 10 августа 1859 года в Австрии. Теорема Пика – классический результат в комбинаторной геометрии и геометрии чисел. Формула Пика была открыта Георгом Пиком в 1899 году. По этой формуле площадь многоугольника с числовыми вершинами равна сумме:
Теорема Пика – классический результат в комбинаторной геометрии и геометрии чисел. Формула Пика была открыта Георгом Пиком в 1899 году. По этой формуле площадь многоугольника с числовыми вершинами равна сумме:
S = i+ b/2 – 1,
где i – количество целочисленных точек в середине многоугольника, b – количество целочисленных точек на границе многоугольника.
Точка координатной плоскости называется целочисленной, если обе ее координаты целые числа. В примере на рисунке i=7, b = 8, таким образом площадь равна
S=7+8/2 – 1 = 10 (квадратных единиц).
А сейчас вы попробуйте вычислить площадь трапеции, используя формулу Пика. Задачи выполняем по вариантам и коллективно комментируем.
6. Подведение итогов, объявление домашнего задания.
Слайд 10. Тестовые задания.
Вы получили тестовые задания на листках, подпишите их и отвечайте на вопросы.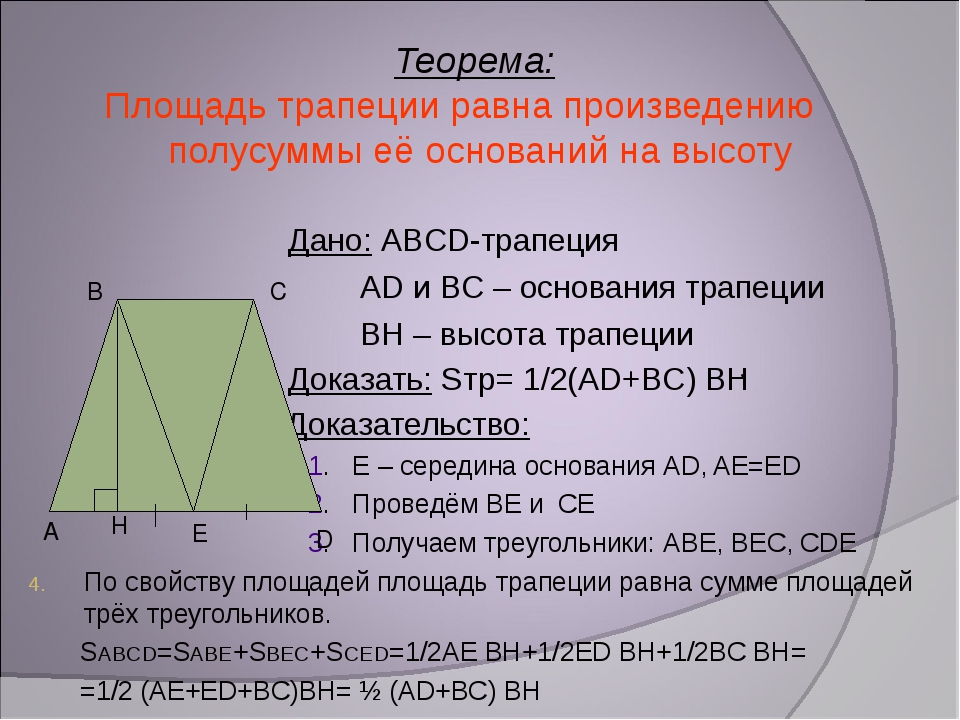
Является ли трапеция жесткой фигурой?
а) да
б) нет
2. В трапецию можно вписать круг, если
а) сумма противоположных углов равна
б) сумма противоположных сторон равна
в) а) и б)
3. Вокруг трапеции можно описать окружность, если:
а) сумма противоположных углов равна
б) сумма противоположных сторон равна
в) а) и б)
4. Запишите формулу для вычисления площади параллелограмма.
5. Запишите формулу для вычисления площади трапеции.
6. Может ли быть диагональ трапеции перпендикулярна к боковой стороне?
а) да
б) нет
7. Площадь квадрата равна 100 дм2. Чему равна сторона квадрата?
а) 20 дм
б) 10дм
в) 50 дм
8. Площадь параллелограмма, сторона которого 20 см, а высота, проведенная к этой стороне – 8 см, равна:
Площадь параллелограмма, сторона которого 20 см, а высота, проведенная к этой стороне – 8 см, равна:
а) 80 см2
б) 160 см2
9. Площадь прямоугольника равна 24 см2, длина – 6 см. Чему равна ширина прямоугольника?
а) 4 см
б) 18 см
в) 12 см
10. Чему равна площадь квадрата, если его периметр равен 40 см?
а) 160 см2
б) 100 см2
Слайд 10-11. Тестовые задания.
Слайд 12. Ответы на тестовые задания.
б)
б)
а)
S = a*h
S = ½(a+b)h
a)
б)
б)
а)
б)
Проверка тестовых заданий (взаимопроверка). Обменяемся с соседом по парте своим тестом и осуществим проверку тестовых заданий. Запишите количество правильных ответов.
Запишите количество правильных ответов.
Дополнительное задание.
Дано: ABCD – трапеция (AB=CD)
AB=CD=20√
Угол А = 600
Найдите: SABCD
Решение
Проведем высоту BH. Рассмотрим треугольник ABH – прямоугольный
(угол AHB=900), угол А равен 600 по условию задачи. По свойству острых углов треугольника, угол ABH равен 900-600=300. По свойству катета, который лежит против угла 300, имеем
АН=1/2AB=1/2*20√3=10√3 (см)
По теореме Пифагора треугольник ABH:
АВ2=АН2+ВН2
ВН2=АВ2 — АН2
ВН2=(20√3)2 — (10√3)2
ВН2= 1200-300
ВН2=900
ВН=30
В трапецию можно вписать круг, поэтому АВ+CD = ВС+AD = 20√3 + 20√3=40√3 (см).
S ABCD = ½(BC+AD)*BH=1/2*40√3*30=600√3 (см2)
Ответ.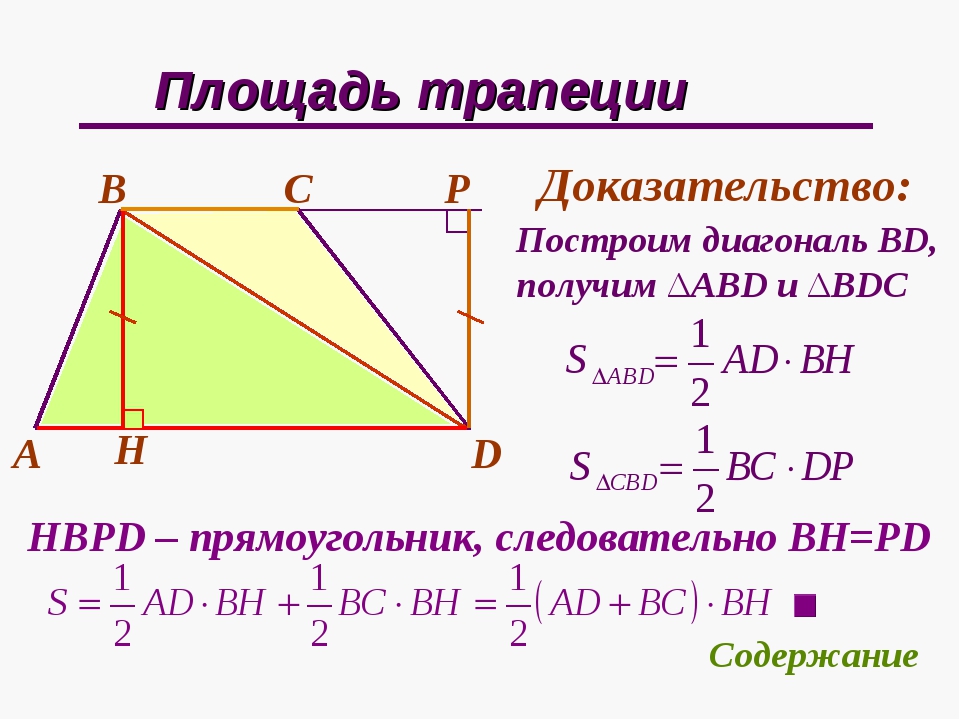 600√3 см2
600√3 см2
Слайд 13. Итог урока
— Что я повторил? (-а?)
— Что нового я изучил? (-а?)
— Где я применю полученные знания?
— Каким образом можно найти площадь трапеции?
Вы с каждым днем убеждаетесь, что окружающий мир – это мир геометрии. А куда в геометрии без формул. «У математики есть свой язык – это язык формул».
Слайд14. Домашнее задание.
Психологический тренинг
У каждого на парте лежит смайлик настроения, подпишите их, возьмите карандаш, закройте глаза и нарисуйте на оборотной стороне смайлика любую геометрическую фигуру. Откройте глаза и посмотрите на доску, с какой из трех предложенных ассоциируется ваша фигура.
Квадрат – ассоциируется с такими чертами характера, как настойчивость, упертость, твердость характера.
Треугольник – настойчивость, уверенность в себе, умение выслушивать другого, прислушиваться к советам и уверенно идти к поставленной цели.
Круг – означает эмоциональность, склонность переживать проблемы других как собственные, сочувствовать, выявлять доброжелательность, открытость.
Список использованной литературы:
Геометрия. 7-9 класс. Учебник / Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. – М., 2014. – 384 с.
чему равна, свойства, доказательство теоремы
Средняя линия трапеции, а особенно ее свойства, очень часто используются в геометрии для решения задач и доказательства тех или иных теорем.
Трапеция – это четырехугольник, у которого только 2 стороны параллельны друг другу. Параллельные стороны называют основаниями (на рисунке 1 — AD и BC), две другие – боковыми (на рисунке AB и CD).
Средняя линия трапеции – это отрезок, соединяющий середины ее боковых сторон (на рисунке 1 — KL).
Свойства средней линии трапеции
- Длина средней линии равна половине суммы длин ее оснований:
- Средняя линия всегда параллельна ее основаниям.

Доказательство теоремы о средней линии трапеции
Доказать, что средняя линия трапеции равна полусумме ее оснований и параллельна этим основаниям.
Дана трапеция ABCD со средней линией KL. Для доказательства рассматриваемых свойств требуется провести прямую через точки B и L. На рисунке 2 это прямая BQ. А также продолжить основание AD до пересечения с прямой BQ.
Рассмотрим полученные треугольники LBC и LQD:
- По определению средней линии KL точка L является серединой отрезка CD. Отсюда следует, что отрезки CL и LD равны.
- ∠ BLC = ∠ QLD, так как эти углы вертикальные.
- ∠ BCL = ∠ LDQ, так как эти углы накрест лежащие при параллельных прямых AD и BC и секущей CD.
Из этих 3 равенств следует, что рассмотренные ранее треугольники LBC и LQD равны по 1 стороне и двум прилежащим к ней углам (см. рис. 3). Следовательно, ∠ LBC = ∠ LQD, BC=DQ и самое главное — BL=LQ => KL, являющаяся средней линией трапеции ABCD, также является и средней линией треугольника ABQ. Согласно свойству средней линией треугольника ABQ получаем:
рис. 3). Следовательно, ∠ LBC = ∠ LQD, BC=DQ и самое главное — BL=LQ => KL, являющаяся средней линией трапеции ABCD, также является и средней линией треугольника ABQ. Согласно свойству средней линией треугольника ABQ получаем:
- KL = 1/2AQ = 1/2 (AD+DQ) = 1/2 (AD+BC)
- KL || AD по свойству средней линии треугольника. А так как AD || BC по определению трапеции, то KL || BC.
Для закрепления материала рекомендуем Вам просмотреть видео урок по данной теме:
Понравилась статья, расскажите о ней друзьям:
Скорее всего, Вам будет интересно:
Средняя линия трапеции / Векторы / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Векторы
- Средняя линия трапеции
Средняя линия трапеции — это отрезок, который соединяет середины её боковых сторон.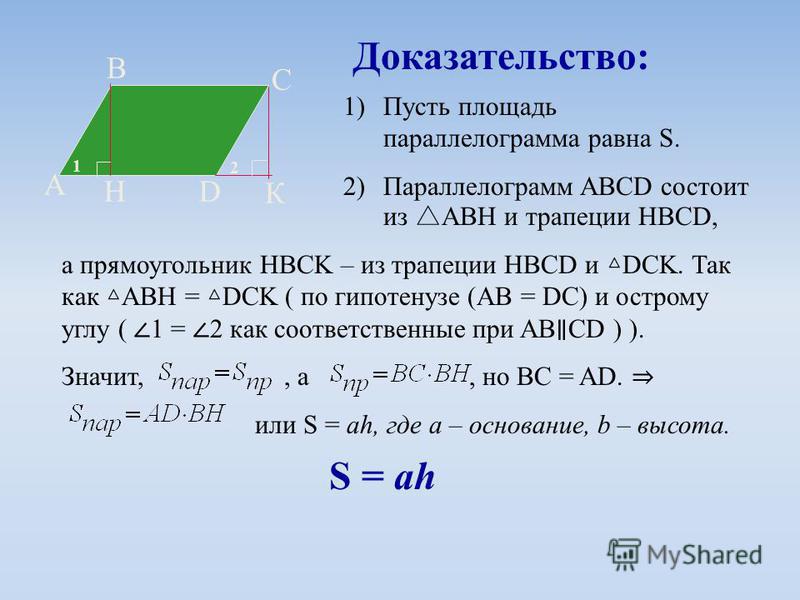
Теорема
Доказательство
Дано: ABCD — трапеция, MN — средняя линия ABCD
Доказать: MN AD,
Доказательство:
По правилу многоугольника = + + и = + + . Сложив эти равенства, получим:
2 = ( + ) + ( + ) + ( + ).
Но M и N — середины сторон АВ и CD, поэтому + = и + = (так как сумму составляют противоположные векторы, а сумма противоположных векторов равна нулевому вектору) . Следовательно, 2 = + , откуда = ( + ).
Так как векторы и сонаправлены, то векторы и также сонаправлены, а длина вектора ( + ) равна AD + ВС. Отсюда следует, что MN AD, . Теорема доказана.
Отсюда следует, что MN AD, . Теорема доказана.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие вектора
Равенство векторов
Откладывание вектора от данной точки
Сумма двух векторов
Законы сложения векторов. Правило параллелограмма
Сумма нескольких векторов
Вычитание векторов
Произведение вектора на число
Применение векторов к решению задач
Векторы
Правило встречается в следующих упражнениях:
7 класс
Задание 793, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 795, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 797, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 810, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 974, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5. com, 2022
com, 2022
Пользовательское соглашение
Copyright
8 класс вопросы к экзамену геометрия
8 класс. Вопросы к экзамену. Геометрия
Нужно знать определения:
Параллелограмма, прямоугольника, ромба, дельтоида, квадрата, трапеции, средней линии, подобных треугольников, коэффициента подобия, ортотреугольника.
формулировки и доказательства (см. учебник)
формул площади квадрата и прямоугольника,
трёх признаков подобия треугольников
Нужно знать формулировки и уметь доказывать следующие утверждения:
3 свойства и 3 признака параллелограмма
Свойства диагоналей ромба и прямоугольника
2 свойства и 2 признака дельтоида
Теорему о средней линии треугольника.
 Средняя
линия треугольника параллельна его
основанию и равна его половине
Средняя
линия треугольника параллельна его
основанию и равна его половинеОбобщение теоремы о средней линии треугольника. Если концы отрезка делят две стороны треугольника в отношении m : n (считая от вершины), то этот отрезок параллелен основанию треугольника а и равен ma/(m+n).
Теорему о средней линии трапеции: средняя линия трапеции параллельна её основаниям и равна их полусумме
Обобщение теоремы о средней линии трапеции. Если концы отрезка делят боковые стороны трапеции в отношении m : n (считая от основания a),то этот отрезок параллелен основаниям трапеции и равен (mb+na)/(m+n).
Теорему Вариньона. Середины сторон четырёхугольника являются вершинами параллелограмма.
2 свойства и 2 признака равнобедренной трапеции
Обобщённую теорему Фалеса.
 Параллельные прямые
высекают на сторонах угла пропорциональные
отрезки.
Параллельные прямые
высекают на сторонах угла пропорциональные
отрезки.Теорему о медианах. Три медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2 : 1, считая от вершины. (Три доказательства – с помощью свойства параллелограмма, площадей, подобия.)
Теорему о биссектрисе. Биссектриса треугольника делит его сторону на отрезки, пропорциональные прилежащим к ним сторонам. (Два доказательства – с помощью площадей и подобия.)
Теорему Пифагора и обратную (два доказательства – с помощью площадей и подобия).
Два свойства и два признака равнобедренной трапеции
Формулы площади параллелограмма S=ah, треугольника S=ah/2, S = Pr/2 и формулу Герона, равностороннего треугольника, трапеции S=(a+b)h/2, ромба, дельтоида.
Теорему об отношении площадей треугольников с равным углом. Площади треугольников с равным углом относятся как произведения сторон, заключающих равные углы.

Сумма расстояний от точки M внутри внутри равностороннего треугольника до его сторон не зависит от положения M.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Свойство ортотреугольника. Высоты исходного треугольника делят углы ортотреугольника пополам.
Замечательное свойство трапеции. В трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.
Надо уметь:
по трём данным сторонам треугольника определять, есть ли в нём тупой угол и находить высоту и и медиану
Находить в прямоугольном или равнобедренном треугольнике, заданном сторонами, высоты, медианы, радиусы окружностей, не пользуясь общими формулами из предыдущего пункта (не стреляя из пушки по воробьям!).
Надо уметь с помощью циркуля и линейки выполнять следующие построения:
Построить параллелограмм по двум сторонам и углу между ними; по двум диагоналям.

Построить трапецию по четырём сторонам.
Восстановить а) треугольник, б) пятиугольник по серединам сторон
Даны отрезки длиной . С помощью циркуля и линейки построить отрезок длиной
а) , б) .
Разделить данный отрезок на n равных частей.
Надо уметь решать задачи:
В трапеции провели диагонали. Площади треугольников, примыкающих к основаниям, равны S1 и S2. Найдите площадь трапеции.
В прямоугольном треугольнике провели высоту к гипотенузе h. а) Найдите h, зная отрезки сa и cb, на которые основание высоты делит гипотенузу. б) Найдите катет a, зная гипотенузу с и отрезок сa.
Конспект урока по математике «Площадь трапеции» 8 класс
Проект урока по геометрии
Тема: «Площадь трапеции»
Класс: 8а
Программа Программы для общеобразовательных учреждений. Геометрия. 7-9 классы. Составитель Бурмистрова Т. А. Москва, Просвещение, 2010.
Геометрия. 7-9 классы. Составитель Бурмистрова Т. А. Москва, Просвещение, 2010.
Учебник Геометрия, 7 – 9: Учеб. для общеобразовательных учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: Просвещение, 2010.
Тип урока: формирование новых знаний с элементами первичного закрепления.
Вид урока: исследовательская работа.
Задачи урока:
Образовательные:
Обобщить формулы нахождения площадей квадрата, прямоугольника, параллелограмма и треугольника.
Повторить приём вывода формул площадей многоугольников (разбиение и достраивание).
Применить обобщённые знания в новых условиях – создать проблемную ситуацию с целью получения формулы площади трапеции.
Доказать формулу площади трапеции.
Научить применять формулу площади трапеции для решения задач.

Развивающие:
Развитие логического и интуитивного мышления, умения работать в проблемной ситуации.
Развитие умения сравнивать математические понятия, находить сходства и различия, выделять главное.
Развитие умения подмечать закономерности, проводить рассуждения по аналогии.
Развитие умения делать выводы, устанавливая причинно- следственные связи.
Развитие математической речи, умения сравнивать, выдвигать гипотезы и вести поисковую деятельность.
Воспитательные:
Воспитывать интерес к предмету через содержания учебного материала.
Воспитывать такие качества характера, как настойчивость в достижение цели, умение работать в коллективе, умение не растеряться в проблемных ситуациях.
Оборудование:
Компьютер для учителя;
Компьютеры для учащихся;
Интерактивная доска;
Набор Электронных учебных модулей (ЭУМ): «Трапеция.
 Средняя линия трапеции. Равнобедренная трапеция» и «Площадь»;
Средняя линия трапеции. Равнобедренная трапеция» и «Площадь»;Чертёжные инструменты.
Методы обучения: проблемно-поисковый.
Формы организации деятельности учащихся: индивидуальная, групповая.
Хронометраж урокаВремя (мин) | |
Организационный момент | 1 |
Подготовительный этап (мотивация изучения нового, выявление целей урока и ориентация учащихся в учебной деятельности на уроке). Постановка учебной задачи. | 3 |
Повторение материала по теме, применение знаний в стандартных ситуациях | 13 |
Этап открытия новых знаний. | 18 |
Этап первичного закрепления новых знаний. | 5 |
Рефлексивно- оценочная часть (Подведение итогов). | 3 |
Сообщение домашнего задания и краткий инструктаж по его выполнению | 2 |
Психолого-педагогическая характеристика класса.
В 8а классе средней школы № 175 г.Н.Новгорода обучаются 26 человек, из них 16 девочек и 10 мальчиков.
В учебной деятельности эти учащиеся имеют высокие общешкольные показатели. Уровень успеваемости тоже высокий. Важнейшим компонентом учебной деятельности является мотив, то есть ради чего деятельность выполняется. Мотивация к учебной деятельности в классе сформирована, у большинства ребят преобладают познавательные мотивы, хорошо развиты способности к изучению предметов математического и практического цикла. Класс заинтересован в успешной учебе. В начальной школе дети обучались по системе Виноградова, что дало им возможность научиться высказывать и отстаивать свою точку зрения. По уровню работоспособности и темпа деятельности в классе преобладают дети со средним темпом деятельности и хорошей работоспособностью, им требуется немного времени на её врабатывание, работоспособность высокая в начале урока и постепенно снижается к концу. Эти ребята обладают умениями сравнивать, анализировать, делать выводы, классифицировать, обобщать, устанавливать причинно-следственные связи. Быстро усваивают учебный материал, при изучении которого предпочтительнее использовать частично-поисковый метод работы, причём могут осуществлять ее самостоятельно или с помощью учителя. Большинство учащихся в классе имеют хорошо развитую речь, умеют задавать и отвечать на вопросы, связно рассказывать.
По уровню работоспособности и темпа деятельности в классе преобладают дети со средним темпом деятельности и хорошей работоспособностью, им требуется немного времени на её врабатывание, работоспособность высокая в начале урока и постепенно снижается к концу. Эти ребята обладают умениями сравнивать, анализировать, делать выводы, классифицировать, обобщать, устанавливать причинно-следственные связи. Быстро усваивают учебный материал, при изучении которого предпочтительнее использовать частично-поисковый метод работы, причём могут осуществлять ее самостоятельно или с помощью учителя. Большинство учащихся в классе имеют хорошо развитую речь, умеют задавать и отвечать на вопросы, связно рассказывать.
Также в классе есть группа детей со слабым типом нервной системы, низкой работоспособностью. Их темп работы быстро снижается и остается на сниженном уровне в течение урока. Эти дети не сразу усваивают учебный материал. Из-за непрочной степени запоминания для них необходимо повторение нужного определения, правила рассуждения, вывода. Операции мышления не сформированы в достаточной степени, им необходима помощь учителя или знающего ученика.
Операции мышления не сформированы в достаточной степени, им необходима помощь учителя или знающего ученика.
Класс отличается особой сплоченностью, в классе сформирована система самоуправления. Командир класса является формальным и неформальным лидером. В любом деле ребята помогают друг другу, поддерживают, поэтому в классе практически никогда не возникает конфликтов ни между учащимися, ни с учителями. Ребята отзывчивы на просьбы педагогов, выполняют общественные поручения. Также у учеников 8а класса налажены дружеские отношения с ребятами из других классов. Дети сложные, у многих подростковый возраст протекает через кризис развития, но в целом дети добрые, отзывчивые, с высокой способностью к эмпатии, ценящие дружбу. В эмоциональном плане дети благополучные, быстро адаптируются, тревожность низкая, психологический фон в классе эмоционально – положительный.
В 8а классе было проведено психодиагностическое исследование, с целью выяснить актуальный уровень развития коммуникативных навыков у детей, психологический климат в классах, трудности во взаимоотношениях у детей, эмоциональное состояние ребят.
Использовались следующие методики:
-социометрия
-методика оценки взаимоотношений в классе
— тест школьной тревожности Филипса
1.Социометрический статус классного коллектива.
Данные исследования статусных позиций детей показали, что большинство детей 8а имеют благоприятное статусное положение в классе. Но также есть дети с низкой статусной позицией. Эти дети требуют повышенного психолого-педагогического внимания. Большинство ребят дружны между собой, поэтому успешно взаимодействуют при групповой работе, причём с разным составом групп. Аутсайдеров нет.
2. Диагностика взаимоотношений в классе.
Исследование показало, в классе преобладает коллективистический тип отношений. Дети воспринимают коллектив как самостоятельную ценность. Ребята заинтересованы как в успехе каждого члена группы, так и класса в целом. Коллектив сформирован, дети заинтересованы в совместной работе, дружны. Анализ индивидуальных анкет детей показал, что у девочек тип взаимоотношений — коллективистический. В классе девочки очень дружны между собой и имеется определённое напряжение во взаимоотношениях с мальчиками. Это связано с подростковым возрастом, когда отношения между полами обостряются. Между мальчиками нет конфликтов. Характер отношений между ними, можно охарактеризовать как деловой — прагматический. Поэтому на уроках необходимо формировать разнополые группы с целью налаживания гендерного взаимодействия между мальчиками и девочками.
Коллектив сформирован, дети заинтересованы в совместной работе, дружны. Анализ индивидуальных анкет детей показал, что у девочек тип взаимоотношений — коллективистический. В классе девочки очень дружны между собой и имеется определённое напряжение во взаимоотношениях с мальчиками. Это связано с подростковым возрастом, когда отношения между полами обостряются. Между мальчиками нет конфликтов. Характер отношений между ними, можно охарактеризовать как деловой — прагматический. Поэтому на уроках необходимо формировать разнополые группы с целью налаживания гендерного взаимодействия между мальчиками и девочками.
3. Тест школьной тревожности Филипса.
Для полной характеристики учащихся, кроме интеллектуальной, была изучена и эмоционально-волевая сфера. Изучение тревожности проходило в два этапа:
первый этап — выявление уровня тревожности, на втором этапе для диагностики эмоционального состояния детей, на фоне которых развиваются социальные контакты в классах, были проведено исследование учащихся по I — VIII факторам теста школьной тревожности Филипса:
I — общая тревожность в школе: общее эмоциональное состояние ребенка, связанное с различными формами его включения в жизнь школы.
II — переживания социального стресса: эмоциональное состояние ребенка, на фоне которого развиваются его социальные контакты, прежде всего — со сверстниками.
III — фрустрация потребности в достижении: неблагоприятный психический фон, не позволяющий ребенку развивать свои потребности в успехе, достижениях высокого результата.
IV — страх самовыражения: негативные эмоциональные переживания ситуаций, сопряженных с необходимостью самораскрытия, предъявления себя другим, демонстрации своих возможностей.
V — страх ситуации проверки знаний: негативное отношение и переживание тревоги в ситуациях проверки, особенно публичной, знаний, достижений, возможностей.
VI — страх не соответствовать ожиданиям окружающих: ориентация на значимых других в оценке своих результатов, поступков и мыслей, тревога по поводу оценок, даваемых окружающим, ожидание негативных оценок.
VII — низкая физиологическая сопротивляемость стрессу: особенности психофизиологической организации, снижающие приспособляемость ребенка к ситуациям стрессогенного характера, повышающие вероятность неадекватного, деструктивного реагирования на тревожный фактор среды.
VIII — проблемы и страхи в отношениях с учителями: общий негативный эмоциональный фон отношений со взрослыми в школе, снижающий успешность обучения ребенка.
Исследование показало, что больше половины детей имеют низкий уровень общей тревожности. Это говорит о том, что большинство учащихся 8б класса не испытывают негативные переживания в ситуациях самораскрытия, демонстрации себя другим и раскрытии своих способностей. Это положительно сказываться на процессе обучения и общения этих детей и позволяет эффективно протекать учебной деятельности.
Анализ результатов детей по факторам, показал низкие значения тревожности по IV (страх самовыражения), V (страх ситуации проверки знаний) и VIII (проблемы и страхи в отношениях с учителем) факторам. Учащиеся не боятся взаимодействовать с учителем, проявлять активность на уроке, демонстрировать себя другим.
Теоретическое обоснование деятельности учителя. | Деятельность ученика. | |
Приветствую учеников. | Создаётся доброжелательный настрой учителя и учеников, класс включается в рабочий ритм. | Ученики концентрируются, настраиваются на работу. |
Сегодня мы продолжаем изучать формулы площадей многоугольников. Актуализация: фронтальный опрос терминов и понятий: Давайте вспомним: Что такое площадь многоугольника? Площади каких многоугольников вы уже умеете находить? Какой приём мы использовали для вывода площадей прямоугольника, параллелограмма и треугольника? В процессе фронтальной беседы с классом на интерактивной доске появляется таблица: | Активизация памяти и мыслительной активности, актуализация знаний необходимых для изучения нового материала. Фронтальная беседа с классом. | Вспоминают определение площади многоугольника, какие многоугольники рассматривались на прошлых уроках. Приём доказательства: разбиение и достраивание многоугольника до фигуры площадь которого уже известна. |
Обобщая, учитель подводит к постановке учебной задачи. Постановка целей и задач урока, что способствует их осознанию, стимулирует заинтересованность в их достижении. Создание «проблемной» ситуации. | Вспоминают, что ими ещё рассматривался четырёхугольник — трапеция. Записать формулу площади трапеции и доказать её. Учащиеся записывают в тетради тему урока. |
С целью качественного усвоения материала теоретические знания проверяются на практике, то есть в решении задач. ЭУМ «Трапеция», который используется на этом этапе урока позволяет учащимся сразу получать информацию от компьютера о правильности решения задачи. Если учащийся затрудняется в решении задачи, то он может посмотреть ответ, где ему будут предложены подсказки. При необходимости имеется возможность возврата к модулю или какой-либо его части. Учитель имеет возможность посмотреть результат в разделе «Статистика». В статистической таблице отражаются успехи учащегося: проверяется правильность ответа, фиксируются использование подсказок, попыток ввода ответа, обращение к решениям, а также время, затраченное учащимся на каждую задачу. | Учащиеся решают задачи и вводят ответ в программу, решение сдают учителю. |
Задача 1.
Задача 2
Задача 3.
Статистика.
ЭОР «Площадь многоугольника» позволяет в наглядной и интерактивной форме повторить материал который необходим для следующего этапа урока. | Один учащийся с помощью компьютера на интерактивной доске выполняет задание, комментируя решение каждой задачи. Решение теста 3 записывается на доске и учащимися в тетради. |
После обсуждения останавливаются на гипотезе, что наверное, через основания и высоту. |
«Открытие» теоремы на основе неполной индукции, выдвижение гипотезы. Создаются условия для развития у учащихся не только логического, но и интуитивного мышления. Этап поиска доказательства теоремы на основе аналогии. Включение учащихся в поисковую деятельность. | После обсуждения устанавливают, что у трапеции два основания, то, наверное, площадь трапеции равна произведению полуссуммы оснований на высоту. Учащиеся предполагают, что трапецию необходимо разбить или достроить до многоугольника, площадь которого уже известна. Это квадрат, прямоугольник, параллелограмм или треугольник. Учащиеся начинают предлагать различные варианты. |
Организация самостоятельной работы на уроке. Создаются условия для самостоятельной мыслительной деятельности учащихся (анализ, синтез, обобщение). Даже если ученику не удаться полностью оформить доказательство, то попробовать найти его он сможет. Дифференциация по степени сложности. Этап оформления доказательства, рассмотрение сразу нескольких способов доказательства теоремы. | Учащиеся записывают доказательства в тетрадь. В результате у них появляется как минимум три доказательства теоремы. | |
5. Этап первичного закрепления новых знаний. А теперь рассмотрим задачи, где необходимо применить формулу площади трапеции. Задачи появляются на доске в виде тестовых заданий. Фронтальная работа с классом. | Специально система задач, для первичного закрепления формулы площади трапеции. Позволяют установить правильности и осознанности усвоения нового учебного материала, ликвидировать типичные ошибки у учащихся. Выполнение этих задач, требует применения знаний в знакомой и измененной ситуации. | Задачи решаются учащимися устно. Для задач 3 и 4 (изменённая ситуация) после правильного ответа, на доске появляется решение, оно проговаривается, чтобы все учащиеся смогли проверить правильность своих рассуждений. |
Даётся анализ и оценка успешности достижения цели и намечается перспектива последующей работы. Адекватность самооценки учащегося оценке учителя. Получение учащимися информации о реальных результатах учения. | Учащиеся ещё раз проговаривают формулу площади трапеции и приём доказательства. | |
Информация о домашнем задании: Найти свой способ разбиения и достраивания трапеции, чтобы получить ещё одно доказательство формулы площади трапеции. Решить задачи из учебника (несложные, для первичного закрепления умения применять формулу) №480 (а, б). Учитель выражает благодарность за урок! | Реализация необходимых и достаточных условий для успешного выполнения домашнего задания всеми учащимися в соответствии с актуальным уровнем их развития. |
Самоанализ урока.
Тема «Площадь трапеции» в структуре курса геометрии 8 класса является заключительной при изучении главы «Площадь». Основной задачей урока является в получение и доказательство формулы площади трапеции. Поэтому был определён тип урока как урок формирования новых знаний с элементами первичного закрепления. На следующих уроках будет происходить дальнейшее закрепление формулы площади трапеции путём решения более сложных задач.
К этому уроку учащиеся уже знакомы с формулами площадей основных многоугольников и умеют их доказывать. Поэтому для этого урока и был выбраны такой вид урока как исследовательская работа и проблемно – поисковый метод изучения нового материала.
Считаю, что все цели: образовательные, развивающие, воспитательные на уроке были достигнуты.
На этапе актуализации была организована фронтальная работа с классом (опрос основных понятий и формул) и индивидуальная работа учащихся по решению задач. Она была организована с использованием интерактивной доски и электронных учебных модулей (работа за компьютером), которые позволили в интерактивной форме без вмешательства учителя проверить знания учащихся по теме «Трапеция» и «Площадь многоугольника». В конце этого этапа учащиеся самостоятельно сформулировали задачу урока.
Для «открытия» теоремы и поиска способа доказательства был использован такой метод научного исследования как аналогия. На этом уроке учитель выполнял роль организатора, а не участника процесса. Результаты работы фиксировались, сравнивались и делались самими детьми. Особый интерес у учащихся вызвал момент урока, где они самостоятельно разбивали и достраивали трапецию. Они увлечённо и заинтересованно предлагали различные варианты решения этой проблемы. Применение методов проблемного обучения на уроке позволило активизировать мыслительную деятельность учащихся в процессе обучения, научить их мыслить логически, научно, творчески, формировать такие чувства, как удовлетворенность от учебной работы, положительное отношение к математике. В результате этой работы учащимися самостоятельно были получены несколько способов доказательства теоремы. На уроке шла работа по созданию ситуации успеха для каждого ребенка, корректировка знаний для детей, испытывающих затруднения.
Применение методов проблемного обучения на уроке позволило активизировать мыслительную деятельность учащихся в процессе обучения, научить их мыслить логически, научно, творчески, формировать такие чувства, как удовлетворенность от учебной работы, положительное отношение к математике. В результате этой работы учащимися самостоятельно были получены несколько способов доказательства теоремы. На уроке шла работа по созданию ситуации успеха для каждого ребенка, корректировка знаний для детей, испытывающих затруднения.
В домашнее задание включены упражнения на закрепление полученных на уроке знаний, а также творческое задание на самостоятельный поиск доказательства теоремы.
Проведённый урок способствовал умственному развитию учащихся во всех его аспектах: получили новую теорему, учитель раскрывал методологию математики (законы и приёмы познания математических закономерностей), развивались интеллектуальные качества ума. А включение учащихся в поисковую деятельность на основе аналогии позволяет формировать у них интуитивное мышление, которое является необходимым компонентом творческого мышления независимо от их будущей профессиональной деятельности.
Равнобедренная трапеция Доказательства Обзор и углы | Что такое Теорема о равнобедренных трапециях? — Видео и стенограмма урока
Углы равнобедренной трапеции
В дополнение к определяющим характеристикам сторон равнобедренной трапеции, которые определены и изображены выше, следует помнить некоторые важные свойства углов равнобедренной трапеции:
- Каждый набор углов основания равнобедренной трапеции равны друг другу.
- Сумма внутренних углов равнобедренной трапеции равна 360 градусов.
- В равнобедренной трапеции углы, противоположные друг другу, являются дополнительными или в сумме составляют 180 градусов.
На диаграмме показана та же самая равнобедренная трапеция ABCD с обозначенными этими новыми угловыми элементами.
Доказательства трапеции
Есть три важных доказательства, связанных с равнобедренными трапециями:
- Как доказать, что диагонали равнобедренной трапеции равны .

- Как доказать, что углы при основании равнобедренной трапеции равны .
- Как доказать, что трапеция является равнобедренной трапецией .
Каждая из этих теорем будет доказана шаг за шагом.
Равнобедренные диагонали
Как доказать, что диагонали равнобедренного треугольника равны?
- Начните с рисования диагоналей.
- Диагонали AC и BD делят трапецию на два треугольника ADC и BCD.
- Эти треугольники имеют пару равных сторон, AD равен BC.
- Треугольники имеют общую сторону DC, которая равна самой себе.
- Треугольники имеют пару равных углов, ADC равно BCD, которые находятся между этими равными сторонами.
- Согласно свойству треугольников Сторона-Угол-Сторона, которое гласит, что если два треугольника имеют две равные стороны и угол между этими сторонами также равен, то сами треугольники конгруэнтны друг другу.
 Итак, треугольники ADC и BCD равны.
Итак, треугольники ADC и BCD равны. - Это означает, что третьи стороны, являющиеся диагоналями AC и BD, также равны.
Углы при основании равнобедренной трапеции
Как доказать, что углы при основании равнобедренной трапеции равны?
- Начните с рисования отрезка CE, параллельного AD. Этот сегмент создает параллелограмм, AECD. Равнобедренная трапеция сама по себе не является параллелограммом, потому что у нее только одна пара параллельных сторон, а у параллелограмма две пары параллельных сторон.
- В параллелограмме противоположные стороны равны. Это означает, что AD равен EC. Уже было известно, что AD равно BC, поэтому теперь можно сказать, что EC равно BC.
- Если EC равно BC, то треугольник BEC является равнобедренной трапецией. Это означает, что углы CBE и CEB равны.
- Помните, что AD параллельна EC, что делает AE секущей парой параллельных прямых.
 При пересечении параллельных прямых секущей смежные внутренние углы являются дополнительными. Итак, углы DAE + AEC = 180.
При пересечении параллельных прямых секущей смежные внутренние углы являются дополнительными. Итак, углы DAE + AEC = 180. - Углы ABC и CBE образуют прямой угол, что делает их дополнительными.
{экв}\угол{DAB}\ +\ \угол{BEC}\ =\ 180 \\ \угол{ABC}\ +\ \угол{CBE}\ =\ 180 \\ \угол{CAB}\ = \ \angle{CBE} {/eq}
- Когда два угла (DAB и ABC) являются дополнительными к равным углам, сами углы равны.
{eq}\angle{DAB}\ =\ \angle{ABC} {/eq}
- Поскольку AECD — параллелограмм, противоположные углы равны.Значит, углы ADC и BEC равны.
- Поскольку AD и DC параллельны, что делает BC секущей, углы EBC и BCD являются параллельными внутренними углами и, следовательно, равны.
- Помните, что углы EBC и CBE равны. Если углы конгруэнтны (равны) конгруэнтным углам, то и сами углы равны. Значит, углы ADC и BCD равны.
{eq}\угол{ADC}\ =\ \angle{CEB} \\ \angle{EBC}\ =\ \angle{BCD} \\ \angle{ADC}\ =\ \angle{BCD} {/ eq}
- Обе пары углов при основании равнобедренной трапеции равны.

{eq}\angle{DAB}\ =\ \angle{ABC} \\ \angle{ADC}\ =\ \angle{BCD} {/eq}
Теорема о равнобедренной трапеции
Как можно доказать, что трапеция является равнобедренной трапецией? Чтобы доказать, что трапеция является равнобедренной трапецией, должны быть верны три вещи:
- Диагонали равны. Это уже доказано.
- Углы при основании равны. Это уже доказано.
- Противоположные углы являются дополнительными.Это доказано ниже.
Как доказать, что противоположные углы трапеции являются дополнительными? Посмотрите на исходную трапецию ABCD.
- Доказано, что углы A и B равны, а углы C и D равны. Также известно, что AB параллельна CD.
- Помните, что последовательные внутренние углы являются дополнительными. Таким образом, углы A и D являются дополнительными, а углы B и C являются дополнительными.

- Подставьте вместо равных углов, и углы A и C являются дополнительными, а углы B и D являются дополнительными. Это пары противоположных углов. Если пары противоположных углов являются дополнительными, это также означает, что сумма углов в трапеции равна 360 градусам.
Все три необходимых критерия подтверждены. Диагонали ABCD равны. Углы при основании ABCD равны. Противоположные углы ABCD смежные.
Следовательно, трапеция ABCD равнобедренная.
Краткий обзор урока
Равнобедренная трапеция — это четырехсторонняя фигура с одной парой параллельных сторон и непараллельными сторонами, которые равны. Чтобы доказать, что трапеция является равнобедренной трапецией, необходимо сначала доказать, что диагоналей трапеции равны друг другу . Это показано путем рисования диагоналей, а затем демонстрации того, как они образуют два конгруэнтных треугольника, используя свойство Сторона-Угол-Сторона.
Доказательство того, что трапеция является равнобедренной трапецией, включает в себя доказательство того, что некоторые факты о ее углах также верны. Нужно доказать, что каждой пары углов при основании трапеции равны друг другу . Добавление двух отрезков, чтобы превратить трапецию в параллелограмм, а затем доказательство равенства углов с использованием этих параллельных линий, помогает показать это свойство. Наконец, нужно доказать, что противоположных угла трапеции являются дополнительными, или в сумме дают 180 градусов . Использование того факта, что последовательные внутренние углы между парой параллельных прямых являются дополнительными, позволяет доказать этот факт.
Нужно доказать, что каждой пары углов при основании трапеции равны друг другу . Добавление двух отрезков, чтобы превратить трапецию в параллелограмм, а затем доказательство равенства углов с использованием этих параллельных линий, помогает показать это свойство. Наконец, нужно доказать, что противоположных угла трапеции являются дополнительными, или в сумме дают 180 градусов . Использование того факта, что последовательные внутренние углы между парой параллельных прямых являются дополнительными, позволяет доказать этот факт.
После подтверждения каждого из этих критериев становится известно, что трапеция является равнобедренной трапецией.
%PDF-1.4 % 197 0 объект > эндообъект внешняя ссылка 197 501 0000000016 00000 н 0000010372 00000 н 0000010600 00000 н 0000010664 00000 н 0000012631 00000 н 0000012884 00000 н 0000012968 00000 н 0000013121 00000 н 0000013184 00000 н 0000013285 00000 н 0000013458 00000 н 0000013526 00000 н 0000013640 00000 н 0000013771 00000 н 0000013839 00000 н 0000013977 00000 н 0000014045 00000 н 0000014189 00000 н 0000014257 00000 н 0000014385 00000 н 0000014453 00000 н 0000014569 00000 н 0000014637 00000 н 0000014704 00000 н 0000014771 00000 н 0000014840 00000 н 0000014911 00000 н 0000014980 00000 н 0000015048 00000 н 0000015139 00000 н 0000015226 00000 н 0000015294 00000 н 0000015411 00000 н 0000015479 00000 н 0000015626 00000 н 0000015687 00000 н 0000015775 00000 н 0000015864 00000 н 0000016010 00000 н 0000016078 00000 н 0000016180 00000 н 0000016316 00000 н 0000016462 00000 н 0000016530 00000 н 0000016650 00000 н 0000016759 00000 н 0000016905 00000 н 0000016973 00000 н 0000017066 00000 н 0000017212 00000 н 0000017280 00000 н 0000017378 00000 н 0000017505 00000 н 0000017650 00000 н 0000017718 00000 н 0000017830 00000 н 0000017931 00000 н 0000018076 00000 н 0000018144 00000 н 0000018248 00000 н 0000018350 00000 н 0000018496 00000 н 0000018564 00000 н 0000018662 00000 н 0000018782 00000 н 0000018927 00000 н 0000018995 00000 н 0000019099 00000 н 0000019201 00000 н 0000019347 00000 н 0000019415 00000 н 0000019517 00000 н 0000019630 00000 н 0000019776 00000 н 0000019844 00000 н 0000019952 00000 н 0000020060 00000 н 0000020205 00000 н 0000020273 00000 н 0000020374 00000 н 0000020476 00000 н 0000020621 00000 н 0000020689 00000 н 0000020794 00000 н 0000020902 00000 н 0000021047 00000 н 0000021115 00000 н 0000021234 00000 н 0000021341 00000 н 0000021486 00000 н 0000021555 00000 н 0000021661 00000 н 0000021761 00000 н 0000021916 00000 н 0000021984 00000 н 0000022087 00000 н 0000022181 00000 н 0000022250 00000 н 0000022368 00000 н 0000022437 00000 н 0000022549 00000 н 0000022617 00000 н 0000022731 00000 н 0000022799 00000 н 0000022925 00000 н 0000022993 00000 н 0000023119 00000 н 0000023187 00000 н 0000023310 00000 н 0000023378 00000 н 0000023483 00000 н 0000023551 00000 н 0000023651 00000 н 0000023719 00000 н 0000023833 00000 н 0000023901 00000 н 0000023959 00000 н 0000024017 00000 н 0000024075 00000 н 0000024133 00000 н 0000024191 00000 н 0000024249 00000 н 0000024307 00000 н 0000024365 00000 н 0000024423 00000 н 0000024481 00000 н 0000024549 00000 н 0000024607 00000 н 0000024665 00000 н 0000024734 00000 н 0000024850 00000 н 0000024919 00000 н 0000025038 00000 н 0000025107 00000 н 0000025238 00000 н 0000025307 00000 н 0000025428 00000 н 0000025497 00000 н 0000025555 00000 н 0000025613 00000 н 0000025671 00000 н 0000025729 00000 н 0000025787 00000 н 0000025856 00000 н 0000025914 00000 н 0000025972 00000 н 0000026040 00000 н 0000026171 00000 н 0000026239 00000 н 0000026359 00000 н 0000026427 00000 н 0000026546 00000 н 0000026614 00000 н 0000026738 00000 н 0000026806 00000 н 0000026931 00000 н 0000026999 00000 н 0000027119 00000 н 0000027187 00000 н 0000027302 00000 н 0000027370 00000 н 0000027428 00000 н 0000027486 00000 н 0000027544 00000 н 0000027602 00000 н 0000027660 00000 н 0000027718 00000 н 0000027776 00000 н 0000027834 00000 н 0000027902 00000 н 0000027960 00000 н 0000028018 00000 н 0000028086 00000 н 0000028202 00000 н 0000028270 00000 н 0000028389 00000 н 0000028457 00000 н 0000028571 00000 н 0000028639 00000 н 0000028765 00000 н 0000028833 00000 н 0000028891 00000 н 0000028949 00000 н 0000029007 00000 н 0000029065 00000 н 0000029123 00000 н 0000029191 00000 н 0000029249 00000 н 0000029307 00000 н 0000029375 00000 н 0000029485 00000 н 0000029553 00000 н 0000029611 00000 н 0000029669 00000 н 0000029737 00000 н 0000029795 00000 н 0000029853 00000 н 0000029922 00000 н 0000030039 00000 н 0000030108 00000 н 0000030224 00000 н 0000030293 00000 н 0000030409 00000 н 0000030478 00000 н 0000030595 00000 н 0000030664 00000 н 0000030780 00000 н 0000030848 00000 н 0000030964 00000 н 0000031033 00000 н 0000031153 00000 н 0000031221 00000 н 0000031338 00000 н 0000031406 00000 н 0000031534 00000 н 0000031602 00000 н 0000031716 00000 н 0000031784 00000 н 0000031901 00000 н 0000031969 00000 н 0000032088 00000 н 0000032156 00000 н 0000032273 00000 н 0000032341 00000 н 0000032466 00000 н 0000032534 00000 н 0000032657 00000 н 0000032725 00000 н 0000032783 00000 н 0000032841 00000 н 0000032899 00000 н 0000032957 00000 н 0000033015 00000 н 0000033073 00000 н 0000033131 00000 н 0000033189 00000 н 0000033247 00000 н 0000033305 00000 н 0000033363 00000 н 0000033421 00000 н 0000033479 00000 н 0000033537 00000 н 0000033595 00000 н 0000033653 00000 н 0000033721 00000 н 0000033779 00000 н 0000033837 00000 н 0000033905 00000 н 0000034022 00000 н 0000034090 00000 н 0000034207 00000 н 0000034274 00000 н 0000034398 00000 н 0000034466 00000 н 0000034590 00000 н 0000034658 00000 н 0000034775 00000 н 0000034843 00000 н 0000034960 00000 н 0000035028 00000 н 0000035145 00000 н 0000035212 00000 н 0000035329 00000 н 0000035397 00000 н 0000035455 00000 н 0000035513 00000 н 0000035571 00000 н 0000035629 00000 н 0000035687 00000 н 0000035745 00000 н 0000035803 00000 н 0000035861 00000 н 0000035919 00000 н 0000035987 00000 н 0000036045 00000 н 0000036103 00000 н 0000036171 00000 н 0000036288 00000 н 0000036356 00000 н 0000036482 00000 н 0000036550 00000 н 0000036675 00000 н 0000036743 00000 н 0000036801 00000 н 0000036859 00000 н 0000036917 00000 н 0000036975 00000 н 0000037043 00000 н 0000037101 00000 н 0000037159 00000 н 0000037228 00000 н 0000037352 00000 н 0000037420 00000 н 0000037532 00000 н 0000037600 00000 н 0000037719 00000 н 0000037787 00000 н 0000037908 00000 н 0000037976 00000 н 0000038135 00000 н 0000038203 00000 н 0000038366 00000 н 0000038434 00000 н 0000038553 00000 н 0000038621 00000 н 0000038746 00000 н 0000038814 00000 н 0000038933 00000 н 0000039001 00000 н 0000039059 00000 н 0000039117 00000 н 0000039175 00000 н 0000039233 00000 н 0000039291 00000 н 0000039349 00000 н 0000039407 00000 н 0000039465 00000 н 0000039523 00000 н 0000039581 00000 н 0000039649 00000 н 0000039707 00000 н 0000039765 00000 н 0000039833 00000 н 0000039950 00000 н 0000040018 00000 н 0000040135 00000 н 0000040203 00000 н 0000040333 00000 н 0000040401 00000 н 0000040520 00000 н 0000040588 00000 н 0000040646 00000 н 0000040704 00000 н 0000040762 00000 н 0000040820 00000 н 0000040878 00000 н 0000040946 00000 н 0000041004 00000 н 0000041062 00000 н 0000041130 00000 н 0000041256 00000 н 0000041324 00000 н 0000041457 00000 н 0000041525 00000 н 0000041650 00000 н 0000041718 00000 н 0000041776 00000 н 0000041834 00000 н 0000041892 00000 н 0000041950 00000 н 0000042018 00000 н 0000042076 00000 н 0000042134 00000 н 0000042203 00000 н 0000042319 00000 н 0000042388 00000 н 0000042519 00000 н 0000042587 00000 н 0000042711 00000 н 0000042779 00000 н 0000042918 00000 н 0000042986 00000 н 0000043123 00000 н 0000043191 00000 н 0000043314 00000 н 0000043382 00000 н 0000043502 00000 н 0000043570 00000 н 0000043628 00000 н 0000043686 00000 н 0000043744 00000 н 0000043802 00000 н 0000043860 00000 н 0000043918 00000 н 0000043976 00000 н 0000044034 00000 н 0000044102 00000 н 0000044160 00000 н 0000044218 00000 н 0000044286 00000 н 0000044344 00000 н 0000044402 00000 н 0000044470 00000 н 0000044592 00000 н 0000044660 00000 н 0000044780 00000 н 0000044848 00000 н 0000044974 00000 н 0000045042 00000 н 0000045100 00000 н 0000045158 00000 н 0000045216 00000 н 0000045274 00000 н 0000045342 00000 н 0000045400 00000 н 0000045458 00000 н 0000045526 00000 н 0000045655 00000 н 0000045722 00000 н 0000045853 00000 н 0000045921 00000 н 0000046043 00000 н 0000046111 00000 н 0000046240 00000 н 0000046308 00000 н 0000046437 00000 н 0000046505 00000 н 0000046636 00000 н 0000046704 00000 н 0000046762 00000 н 0000046820 00000 н 0000046878 00000 н 0000046936 00000 н 0000046994 00000 н 0000047052 00000 н 0000047110 00000 н 0000047178 00000 н 0000047236 00000 н 0000047294 00000 н 0000047354 00000 н 0000047458 00000 н 0000047518 00000 н 0000047622 00000 н 0000047682 00000 н 0000047785 00000 н 0000047845 00000 н 0000047948 00000 н 0000048008 00000 н 0000048111 00000 н 0000048171 00000 н 0000048274 00000 н 0000048334 00000 н 0000048437 00000 н 0000048496 00000 н 0000048599 00000 н 0000048658 00000 н 0000048761 00000 н 0000048822 00000 н 0000048883 00000 н 0000048944 00000 н 0000049005 00000 н 0000049073 00000 н 0000049132 00000 н 0000049191 00000 н 0000049250 00000 н 0000049318 00000 н 0000049385 00000 н 0000049446 00000 н 0000049485 00000 н 0000049827 00000 н 0000050205 00000 н 0000050593 00000 н 0000050615 00000 н 0000050724 00000 н 0000052074 00000 н 0000052096 00000 н 0000052379 00000 н 0000052754 00000 н 0000053137 00000 н 0000053159 00000 н 0000053181 00000 н 0000053368 00000 н 0000053804 00000 н 0000054654 00000 н 0000054960 00000 н 0000055815 00000 н 0000056150 00000 н 0000056947 00000 н 0000057387 00000 н 0000058187 00000 н 0000058209 00000 н 0000059029 00000 н 0000059051 00000 н 0000059661 00000 н 0000059683 00000 н 0000060351 00000 н 0000060373 00000 н 0000061097 00000 н 0000061119 00000 н 0000061804 00000 н 0000061826 00000 н 0000061886 00000 н 0000062241 00000 н 0000063028 00000 н 0000063736 00000 н 0000063758 00000 н 0000064471 00000 н 0000064493 00000 н 0000067128 00000 н 0000072494 00000 н 0000073177 00000 н 0000073293 00000 н 0000073341 00000 н 0000073391 00000 н 0000073816 00000 н 0000078707 00000 н 0000080976 00000 н 0000081536 00000 н 0000083905 00000 н 0000010839 00000 н 0000012608 00000 н трейлер ] >> startxref 0 %%EOF 198 0 объект > эндообъект 199 0 объект > эндообъект 200 0 объект >/Кодировка >>> /DA (/Helv 0 Tf 0 г ) >> эндообъект 696 0 объект > ручей ХУ LSW>ﵯ-Nm` `H`jd0–gq)T?E)s nHli5O2c]6c>tٗ{wϹ=
Добро пожаловать.
 | Департамент образования
| Департамент образованияПредупреждающее сообщение
В вашем поиске использовано слишком много выражений И/ИЛИ. В этот поиск были включены только первые 7 терминов.К сожалению, страница, которую вы ищете, больше не существует, была перемещена или в настоящее время недоступна. Мы выполнили поиск по ключевым словам на основе страницы, которую вы пытаетесь открыть. Соответствующие параметры поиска были предоставлены ниже.
История штата Мэн и онлайн-ресурсы
Мэн История и онлайн-ресурсы … Использование наборов первичных источников (совместно представлено Мэн DOE , Историческим обществом Мэн , Государственным архивом Мэн , … Мэн Государственные служащие Talking Civics & Gov ‘t с сенатором Ангусом Кингом Говоря гражданское право и …
Государственные чиновники, обществоведение и гражданский дискурс
… Государственные чиновники Talking Civics & Gov ‘t с сенатором Ангусом Кингом Говоря об основах общества и… — iCivics) Презентация Преподавание выборов 2020 с iCivics (во главе с Эммой Хамфрис — руководитель… NewsHour) Презентация PBS NewsHour Mid- Технический центр штата Мэн / Веб-страница Дэйва Бордмана …
Гражданско-активные студенты и студенческий голос
… Час новостей) Презентация PBS NewsHour Mid- Технический центр штата Мэн / Веб-страница Дэйва Бордмана … Сенатор Маргарет Чейз Смит: Гендер и политика на президентских выборах 1964 (под руководством Джона Тейлора — MCS … с государственными должностными лицами Мэн Talking Civics & Gov ‘t с сенатором Ангусом Кингом Говоря гражданское право и …
Летняя программа общественного питания (SFSP)
… по этой ссылке и следуйте инструкциям http://www.
 fns.usda. gov /summerfoodrocks Служба летнего питания … для всех детей 18 лет и младше в утвержденных SFSP местах в районах со значительной концентрацией малообеспеченных … Перейти на веб-страницы)
Обучение правильному питанию — Университет штата Мэн, Совместное расширение: Ресурсы EFNEP
…
fns.usda. gov /summerfoodrocks Служба летнего питания … для всех детей 18 лет и младше в утвержденных SFSP местах в районах со значительной концентрацией малообеспеченных … Перейти на веб-страницы)
Обучение правильному питанию — Университет штата Мэн, Совместное расширение: Ресурсы EFNEP
…Учитель на пенсии
… перечисление взносов работодателя Пожалуйста, ознакомьтесь с Законами о пенсионной системе штата Мэн : Раздел 5 – … и услуги; Часть 20: Государственная пенсионная система; Глава 421 . Общие положения; Подглава I, Определения … https://www. мэн . gov / doe / сайты / maine . правительство . doe / файлы /inline- файлы /FY20_RFL_prelimED279_Presented27Feb2019.
 pdf …
pdf …Ежемесячный информационный бюллетень ESEA
… Часы вторник, августа 24 Свяжитесь с Cheryl.Lang @ maine . gov или вашему региональному координатору программы для получения ссылки. … здесь: https://www. мэн . gov / doe / сайты / maine . правительство . doe / файлы /inline- файлы /Grants4ME%20Access%20v4. pdf . За …
Ежемесячный информационный бюллетень ESEA
… 9 ноября, 9:00 Свяжитесь с Cheryl.Lang @ maine . gov или вашему региональному координатору программы для получения ссылки.) … здесь: https://www. мэн . gov / doe / сайты / maine .
 правительство . doe / файлы /inline- файлы / Grants4ME %20Access%20v4. pdf . За …
правительство . doe / файлы /inline- файлы / Grants4ME %20Access%20v4. pdf . За …Ежемесячный информационный бюллетень ESEA
… (Свяжитесь с вашим региональным координатором программы или Cheryl.Lang@ maine . gov для ссылки.) Общие и специальные обновления… здесь: https://www. мэн . gov / doe / сайты / maine . правительство . doe / файлы /inline- файлы / Grants4ME %20Access%20v4. pdf . За …
Годовая финансовая отчетность на конец года
… Требования Загрузите следующие файлов в NEO Financial до 30 августа.
 Фактические … представления в статусе переноса считаются полученными по адресу Maine DOE .
Фактические … представления в статусе переноса считаются полученными по адресу Maine DOE .Годовая финансовая отчетность на конец года
… Требования Загрузите следующие файлов в NEO Financial до 23 августа 2019 г. … представления в статусе миграции считаются полученными по адресу Maine DOE .
Трапеции и воздушные змеи
Расширенный поискСодержание:
Язык: AfarAbkhazAvestanAfrikaansAkanAmharicAragoneseArabicAssameseAsturianuAthabascanAvaricAymaraAzerbaijaniBashkirBelarusianBulgarianBihariBislamaBambaraBengali, BanglaTibetan стандарт, тибетский, CentralBretonBosnianCatalanChechenChamorroCorsicanCreeCzechOld церковнославянский, церковнославянский, Старый BulgarianChuvashWelshDanishGermanDivehi, Мальдивский, MaldivianDzongkhaEweGreek (современный) EnglishEsperantoSpanishEstonianBasquePersian (фарси) Фуле, фулах, пулар, PularFinnishFijianFaroeseFrenchWestern FrisianIrishScottish гэльский, GaelicGalicianGuaraníGujaratiManxHausaHebrew (современный) HindiHiri MotuCroatianHaitian, гаитянский CreoleHungarianArmenianHereroInterlinguaIndonesianInterlingueIgboNuosuInupiaqIdoIcelandicItalianInuktitutJapaneseJavaneseGeorgianKarakalpakKongoKikuyu, GikuyuKwanyama, KuanyamaKazakhKalaallisut , гренландский кхмерский каннада корейский канури кашмирский курдский коми корнуоллский кыргызский латинский люксембургский , летзебургский ганда лимбургский , лимбургский , лимбургский лингала лаосский литовский люба-катанга латышский малагасийский маршалльский мао riMacedonianMalayalamMongolianMarathi (маратхи) MalayMalteseBurmeseNauruanNorwegian BokmålNorthern NdebeleNepaliNdongaDutchNorwegian NynorskNorwegianSouthern NdebeleNavajo, NavahoChichewa, Chewa, NyanjaOccitanOjibwe, OjibwaOromoOriyaOssetian, OsseticEastern пенджаби, Восточная PanjabiPāliPolishPashto, PushtoPortugueseQuechuaRomanshKirundiRomanianRussianKinyarwandaSanskrit (санскрит) SardinianSindhiNorthern SamiSangoSinhalese, SinhalaSlovakSloveneSamoanShonaSomaliAlbanianSerbianSwatiSouthern SothoSundaneseSwedishSwahiliTamilTeluguTajikThaiTigrinyaTurkmenTagalogTswanaTonga (Остров Тонга) TurkishTsongaTatarTwiTahitianUyghurUkrainianUrduUzbekValencianVendaVietnameseVolapükWalloonWolofXhosaYiddishYorubaZhuang, ChuangChineseZulu Предмет:
Класс/уровень: Возраст: 3456789101112131415161718+
Поиск: Все рабочие листыТолько мои подписчикиТолько мои любимые рабочие листыТолько мои собственные рабочие листы
MAT 211: Геометрия
MAT 211: ГеометрияОригинал Сообщение
Отправлено: 04.
 02.2019 17:29
02.2019 17:29 От: Ивет Масулло
Тема: Трапеции тоже параллелограммы?
Я заметил это беспокойство в прошлом году, и вот я снова обеспокоен о консенсусе.
Я заметил, что теперь есть две идеи для трапеций:
- Трапеции имеют одну пару параллельных сторон.
- Трапеции имеют одну или две пары параллельных сторон.
Полагаю, это тривиально, но я зациклился на этом.я хотел бы знать что думают другие.
Итак, все ли трапеции параллелограммы или нет?
Спасибо. Надеюсь, это вызовет разговор.
——————————
Иветт Масулло, HS алгебра и геометрия
New York NY
Ответы
1) Re: Являются ли трапеции параллелограммами?
Залман Усыскин
5 февраля 2019 г. 5:35
5:35
Ваш вопрос поставлен наоборот. Вопрос в том, все ли параллелограммы — это трапеции, а не наоборот.
Ответ зависит от определения «трапеция».
Если «трапеция» определяется как «четырехугольник с ровно одной парой параллельных сторон», то никакие трапеции не являются параллелограммами.
Однако, если «трапеция» определяется как «четырехугольник с по крайней мере одна пара параллельных сторон, то все параллелограммы трапеции.
Первое определение (с точностью) называется «эксклюзивным» определение, потому что тогда трапеции исключают параллограммы.это более распространенное из двух определений в учебниках США. То второе определение (по крайней мере) называется «включающим определение», потому что тогда трапеции включают параллелограммы.
Включающее определение чаще используется геометрами и
других математиков, потому что математики склонны отдавать предпочтение инклюзивным
определения (все целые числа являются рациональными числами, все рациональные числа
действительные числа, все равнобедренные треугольники равнобедренные,
и Т. Д.) и потому, что общие определения большинства типов
четырехугольники имеют тенденцию быть включающими, то есть все квадраты
прямоугольники, все прямоугольники являются параллелограммами и т. д.
Д.) и потому, что общие определения большинства типов
четырехугольники имеют тенденцию быть включающими, то есть все квадраты
прямоугольники, все прямоугольники являются параллелограммами и т. д.
В школьных учебниках по математике Чикагского университета мы используют инклюзивное определение на протяжении десятилетий. И если вы желаете подробного изучения этого предмета, вы, возможно, пожелаете получить книгу, которую я написал, «Классификация четырехугольников — исследование Определение», опубликованном издательством Information Age Publishing.
——————————
Залман Усыскин
Почетный профессор образования
Директор, UCSMP
Чикагский университет
2) Re: Являются ли трапеции параллелограммами?
Джереми Дентон
5 февраля 2019 г. 7:46 | вложение посмотреть вложение
Джереми Дентон
Я говорю нет. Вот почему.
Специальные типы четырехугольников делятся на 3 категории.
- К одной категории относятся те, у которых ровно 2 пары параллельных сторон (параллелограмм, прямоугольник, ромб, квадрат)
- К одной категории относятся те, у которых ровно 1 пара параллельных сторон. (трапеция, равнобедренная трапеция)
- К одной категории относятся те, у которых ровно 0 пар параллельных сторон. (Воздушный змей)
Прикреплен мой Раздаточный материал по семейству четырехугольников. Вид старого документа, но надеюсь это помогает.
3) Re: Являются ли трапеции параллелограммами?
Scott Steketee
5 февраля 2019 г. 7:47
Scott Steketee
Этот вопрос возникает снова и снова, главным образом потому, что
традиционная четырехугольная система классификации использует включающие
определения для каждой категории, кроме трапеции. Есть ряд
способов, которыми мы могли бы определить «прямоугольник», но все они сформулированы таким образом,
в том числе квадраты.Точно так же определяем ли мы «параллелограмм»
с точки зрения параллельных противоположных сторон, конгруэнтных противоположных сторон или
вращательная симметрия, мы не исключаем прямоугольники или ромбы.
Есть ряд
способов, которыми мы могли бы определить «прямоугольник», но все они сформулированы таким образом,
в том числе квадраты.Точно так же определяем ли мы «параллелограмм»
с точки зрения параллельных противоположных сторон, конгруэнтных противоположных сторон или
вращательная симметрия, мы не исключаем прямоугольники или ромбы.
Однако традиционное определение трапеции как четырехугольника с ровно одна пара параллельных сторон, в частности, исключает параллелограммы. Это привело к многочисленным спорам на протяжении многих лет, со многими педагогами и математиками, выступающими за инклюзивность определение трапеции как четырехугольника, имеющего хотя бы одну пару параллельные стороны.Это подход, принятый с википедией статьи о трапеции и Четырехугольник.
Самые сильные аргументы в пользу использования инклюзивного определения в школе
геометрия, как мне кажется, состоит из этих двух: (а) она делает нашу классификацию
система для четырехугольников более последовательная, и (b) это означает, что
любые теоремы о трапециях, которые мы доказываем, или формулы, которые мы разрабатываем, применяются
автоматически в параллелограммы, точно так же, как теоремы о параллелограммах и
формулы автоматически применяются к прямоугольникам, ромбам и квадратам.
—Scott
——————————
Scott Steketee
Старший научный сотрудник
Партнерство 21st Century for STEM Education
Philadelphia PA
4) Re: Являются ли трапеции параллелограммами?
Роберт Нордлинг
5 февраля 2019 г. 8:47
Роберт Нордлинг
Я нашел разъяснения относительно определения трапеции в математике учебный план Вашингтонского университета:
———- учебный план выдержка
Хотите верьте, хотите нет, но нет общего согласия по определению трапеции.
Эксклюзивное определение трапеции
«Четырехугольник, у которого две и только две стороны параллельны, называется
трапеции.»
Однако большинство математиков, вероятно, определили бы это понятие с Инклюзивное определение.
Включающее определение трапеции
«Четырехугольник, у которого по крайней мере две стороны параллельны, называется трапеция.»
Разница в том, что при втором определении параллелограммы
являются трапециями, а под первыми их нет.
Преимущество первого определения в том, что оно позволяет Отличие параллелограмма от других четырехугольников несколько параллельных сторон. Кажется, это было самым важным в более ранние времена. Преимущество инклюзивного определения состоит в том, что любой теорема, доказанная для трапеций, автоматически является теоремой о параллелограммы. Это лучше всего соответствует характеру двадцатого века математика.
Можно прекрасно работать с любым определением.Однако важно договориться на уроке математики о том, определение, используемое в классе.
——————————
[Боб] [Нордлинг]
[Специалист по технологиям в школе]
[Округ Фэрфакс Государственные школы]
[Александрия] [Вирджиния]
5) Re: Являются ли трапеции параллелограммами?
Майкл Хоккей
5 февраля 2019 г. 8:48
Майкл Хоккей
Все ли трапеции p-граммы? Если вы используете определение
трапеция, которая допускает две пары параллельных сторон, тогда ВСЕ p-граммы
являются трапециями, но ТОЛЬКО НЕКОТОРЫЕ трапеции являются p-граммами.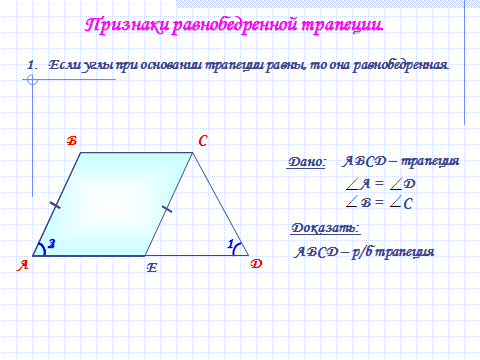 Если ты
используя определение трапеции, которое допускает только 1 пару
стороны параллельны, то никакая фигура не является одновременно трапецией и p-граммом.
Если ты
используя определение трапеции, которое допускает только 1 пару
стороны параллельны, то никакая фигура не является одновременно трапецией и p-граммом.
——————————
Michael Hockey
Gulf Shores High Sch
Orange Beach AL
6) Re : Трапеции тоже параллелограммы?
Шон Ланфир
5 февраля 2019 г. 9:04
Я показываю своим студентам, изучающим геометрию, оба определения, и у нас есть
дискуссия о том, почему математики предпочитают инклюзивное определение
(у трапеции есть хотя бы одна пара параллельных сторон).В виде
другие в этой теме уже сказали, что это определение более
в соответствии с другими определениями четырехугольника. это
также похож на равнобедренный треугольник. Равнобедренный треугольник
имеет по крайней мере две равные стороны, образующие равносторонний треугольник а
тип равнобедренного треугольника. Это полезно, потому что любой
теорема или свойство, которым обладает равнобедренный треугольник, автоматически
наследуется равносторонними треугольниками.
Стоит отметить, что любые теоремы, верные для трапеций справедливы и для параллелограммов.Даже формула площади трапеции работает для параллелограмма.
В моем классе мы расширяем этот разговор до определения летающий змей. В нашем учебнике воздушный змей определяется как четырехугольник с двумя пары последовательных конгруэнтных сторон, но противоположные стороны не конгруэнтный. Это явно исключает ромб из типа воздушного змея, похожего на то, как исключительное определение трапеций явно исключает параллелограмм. Если мы удалим вторую часть определения воздушного змея и разрешить противоположные стороны чтобы быть конгруэнтным, это позволяет ромбу быть воздушным змеем особого типа, давая нам полностью взаимосвязанное генеалогическое древо четырехугольники.Не так уж и шокирующе, теоремы о воздушных змеях случаются верно для ромбов, и обе формулы площади в точности такой же.
Я создал небольшую демонстрацию на Geogebra
(https://www.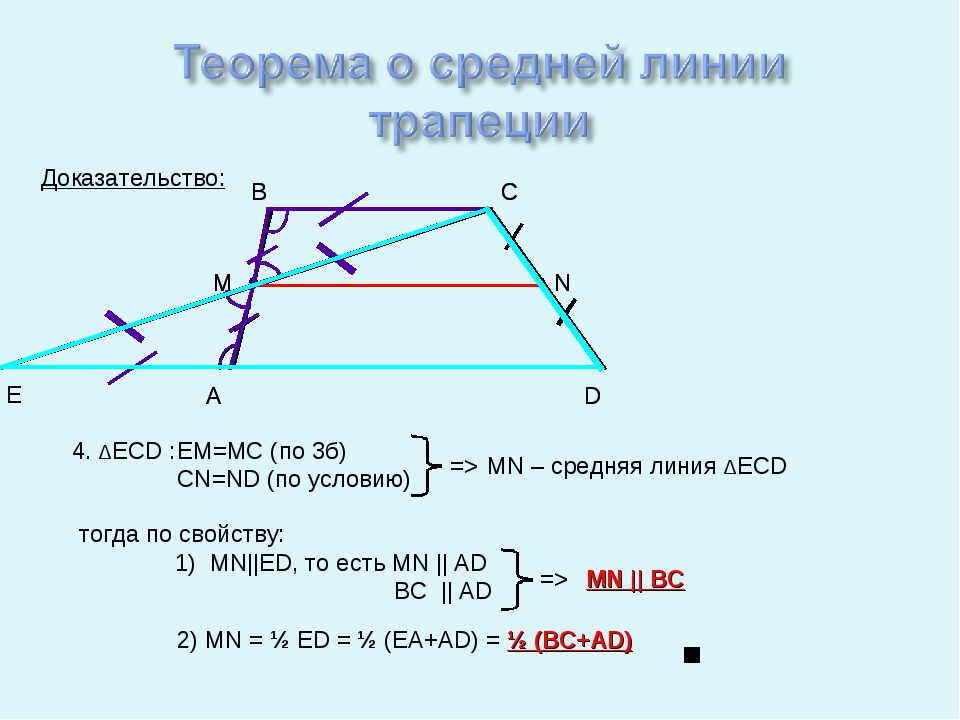 geogebra.org/m/fwxxtx69)
показывает связь между трапециями и параллелограммами.
Я показываю это на своей доске, а затем перетаскиваю точку D вправо, говоря:
«это трапеция, это трапеция, это трапеция…», пока я
попасть в ЕДИНСТВЕННОЕ место (точка (6,3)), где вдруг
не трапеция (по исключительному определению).потом
Я продолжаю перетаскивать его вправо, говоря еще раз: «Это
трапеция, это трапеция, это трапеция…». Я думаю
это достойное изображение странности эксклюзивного определения.
geogebra.org/m/fwxxtx69)
показывает связь между трапециями и параллелограммами.
Я показываю это на своей доске, а затем перетаскиваю точку D вправо, говоря:
«это трапеция, это трапеция, это трапеция…», пока я
попасть в ЕДИНСТВЕННОЕ место (точка (6,3)), где вдруг
не трапеция (по исключительному определению).потом
Я продолжаю перетаскивать его вправо, говоря еще раз: «Это
трапеция, это трапеция, это трапеция…». Я думаю
это достойное изображение странности эксклюзивного определения.
Не буду слишком нравоучительным, но всеобъемлющие определения, на мой взгляд, вид, более соответствующий тому, что такое истинная математика: прекрасный способ представляющих нашу вселенную и показывающих, как все (и все) взаимосвязано.
Шон Ланфеа
Саванна, Джорджия
———————————————
Шон Ланфир
Дневная школа Хэнкока
Саванна, Джорджия
7) Re: Являются ли трапеции параллелограммами?
E Пол Гольденберг
5 февраля 2019 г.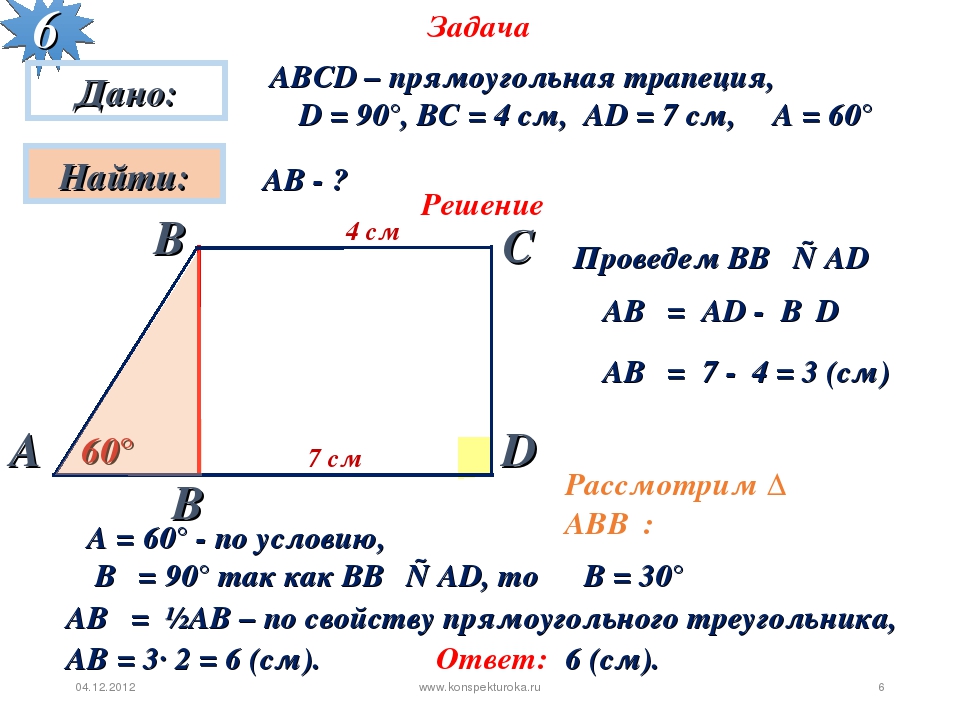 , 10:27 | вложение Посмотреть вложение
, 10:27 | вложение Посмотреть вложение
E Paul Goldenberg
Люди могут найти прикрепленный PDF-файл полезный.Это диаграмма Венна, усложненная тем, что много способов классифицировать/описывать геометрические фигуры. Он использует включительно определение трапеции.
——————————
Paul Goldenberg
EDC (Центр развития образования)
Waltham, MA
8 ) Re: Трапеции тоже параллелограммы?
Элизабет Хенджес
5 февраля 2019 г. 13:27
Элизабет Хенджес
Это определенно НЕ тривиально!
Любое определение приемлемо, но есть разветвления
в зависимости от того, является ли исключительное или инклюзивное определение
используется «трапеция».Если вы используете конкретную учебную программу,
Я предлагаю вам использовать это определение, если вы не категорически против
Это. Будьте осторожны, какой бы выбор вы ни сделали, поскольку в дальнейшем
результаты, возможно, должны быть тщательно сформулированы, чтобы быть верными.
В последнее время, я думаю, большинство людей используют «Трапеция — это четырехугольник». ровно с одной парой параллельных сторон.»
Я использовал каждое определение в зависимости от того, какой учебник был основным книга для данного курса. В HS и выше это стоит обсудить оба определения и то, как выбрать, какое из них использовать. влияет на другие вещи.
Если мы выберем «Трапеция — это четырехугольник с ровно одной парой
параллельных сторон»,
, то параллелограммы не являются трапециями, а значит, и ромбами
ни прямоугольников, а прямоугольник не является равнобедренной трапецией.
Если мы выберем «Трапеция — это четырехугольник, по крайней мере с одной парой
параллельных сторон»,
, то параллелограммы — это трапеции, а значит, ромбы и прямоугольники
равны, а прямоугольник является равнобедренной трапецией.
Мы должны быть осторожны в том, как мы определяем воздушного змея.
ромб — воздушный змей, 90 440, и как мы определяем параллельные линии относительно того, является ли линия прямой или нет. параллельно себе по тем же причинам.
параллельно себе по тем же причинам.
Думаю, почти все определяют равнобедренные треугольники включительно, Например: «Равнобедренный треугольник — это треугольник, в котором хотя бы два конгруэнтные стороны».
———————————————
Beth Hentges
Математический факультет
Century College
White Bear Lake, MN
———————————————
9) Re: Являются ли трапеции параллелограммами?
Джон Пленкнер
Feb 5, 2019 18:08
John Plencner
Из семейства четырехугольников вы получаете три ответвления:
- нет параллельных сторон (разносторонние и воздушные змеи)
-
- два набора параллельных сторон (семейство параллелограммов)
-
- один набор параллельных сторон (семейство трапеций)
Это исключительное определение.
В последние двадцать лет математика движется в направлении
всеобъемлющее определение трапеций, в котором говорится, что «по крайней мере один
набор параллельных сторон».
В «Неформальной геометрии» Прентиса Холла говорится: «ровно один набор параллельными сторонами». То же самое можно сказать и о нескольких текущих текстах, Ларсона «Большие идеи». Я бы пошел с эксклюзивным определением пока, потому что это то, что будет использоваться в тестировании (SAT/ACT/размещение), но предостережение с заявлением, что это является развивающимся определением.
——————————
Джон Пленкнер
Верхнее озеро
.
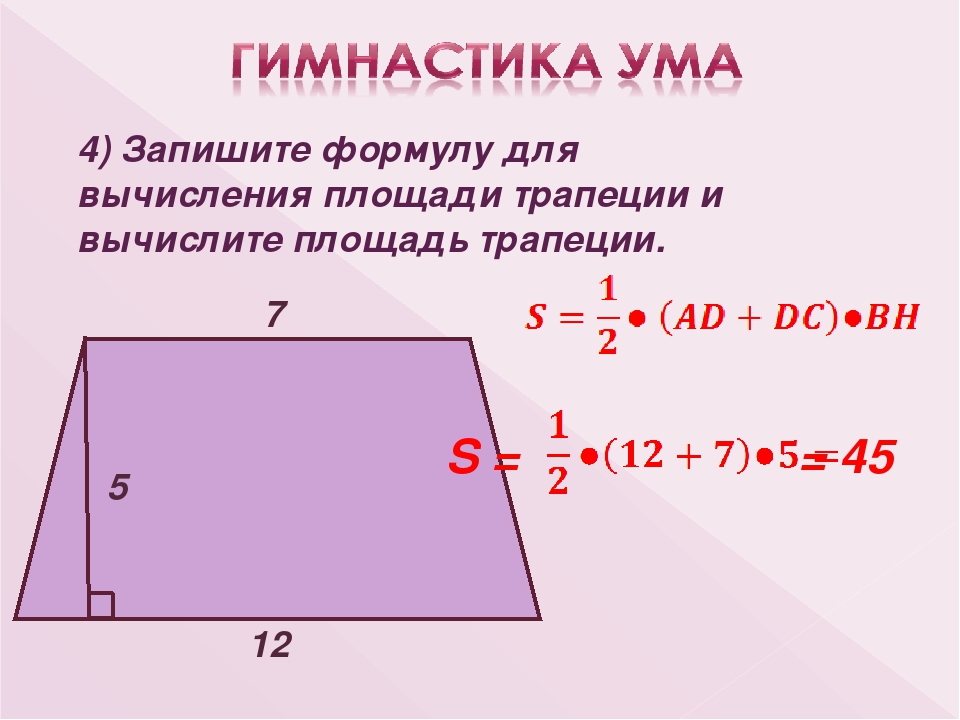
 Найдите длину меньшего основания.
Найдите длину меньшего основания.
 Средняя
линия треугольника параллельна его
основанию и равна его половине
Средняя
линия треугольника параллельна его
основанию и равна его половине Параллельные прямые
высекают на сторонах угла пропорциональные
отрезки.
Параллельные прямые
высекают на сторонах угла пропорциональные
отрезки.

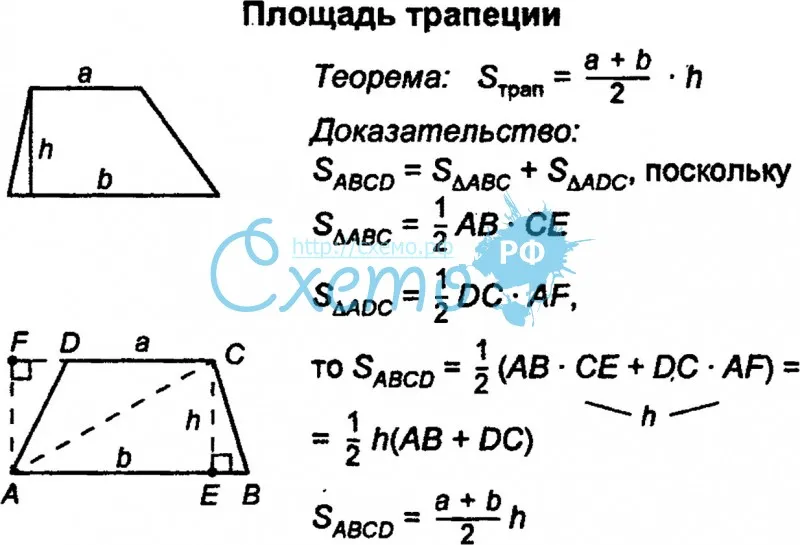
 Средняя линия трапеции. Равнобедренная трапеция» и «Площадь»;
Средняя линия трапеции. Равнобедренная трапеция» и «Площадь»;


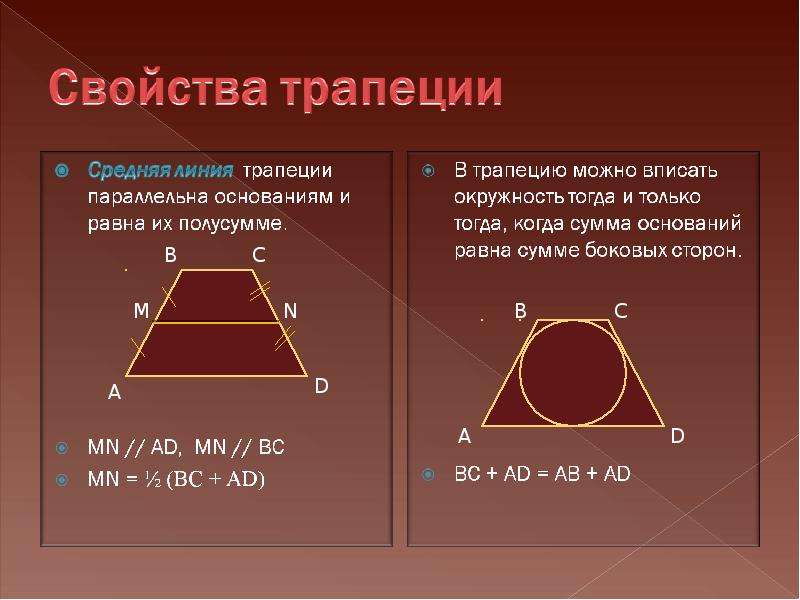
 Статистические таблицы позволяют учителю проанализировать и оценить деятельность учащегося при решении задач и прохождении отдельных тем, экономят время учителя.
Статистические таблицы позволяют учителю проанализировать и оценить деятельность учащегося при решении задач и прохождении отдельных тем, экономят время учителя.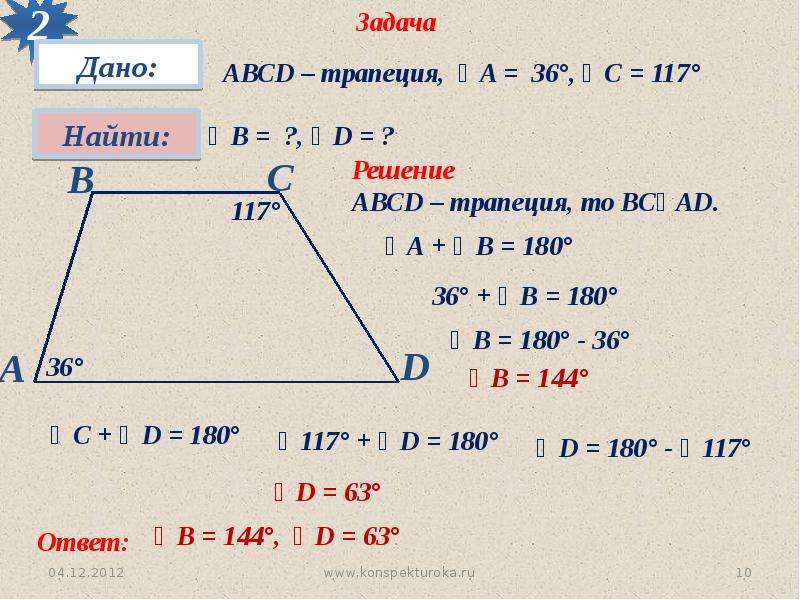
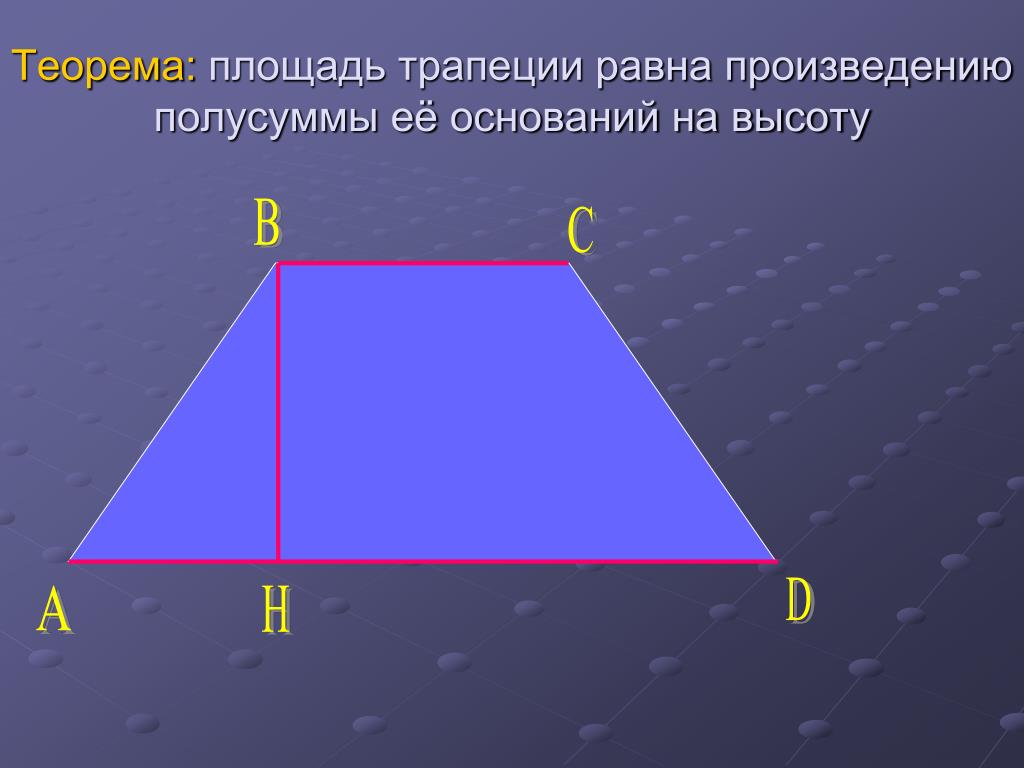 Какой приём можно использовать?
Какой приём можно использовать?

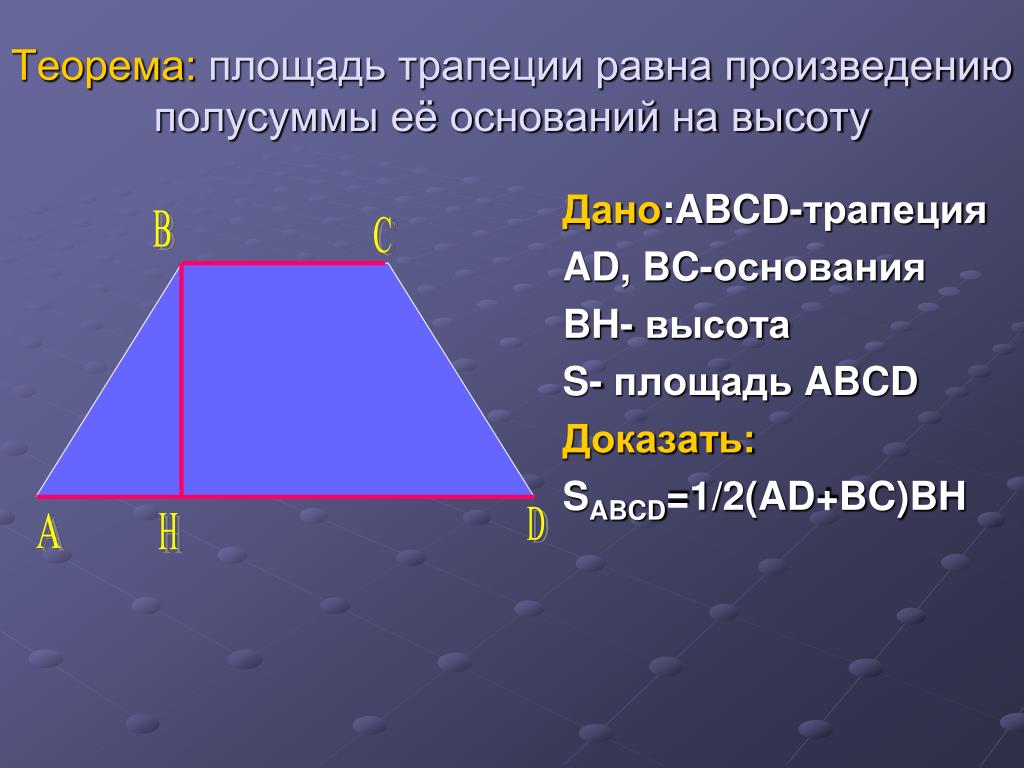

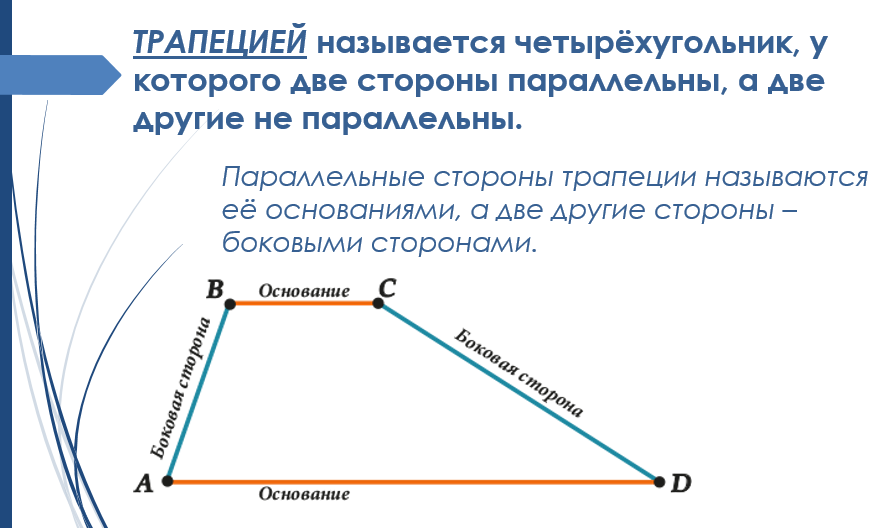
 Итак, треугольники ADC и BCD равны.
Итак, треугольники ADC и BCD равны. При пересечении параллельных прямых секущей смежные внутренние углы являются дополнительными. Итак, углы DAE + AEC = 180.
При пересечении параллельных прямых секущей смежные внутренние углы являются дополнительными. Итак, углы DAE + AEC = 180.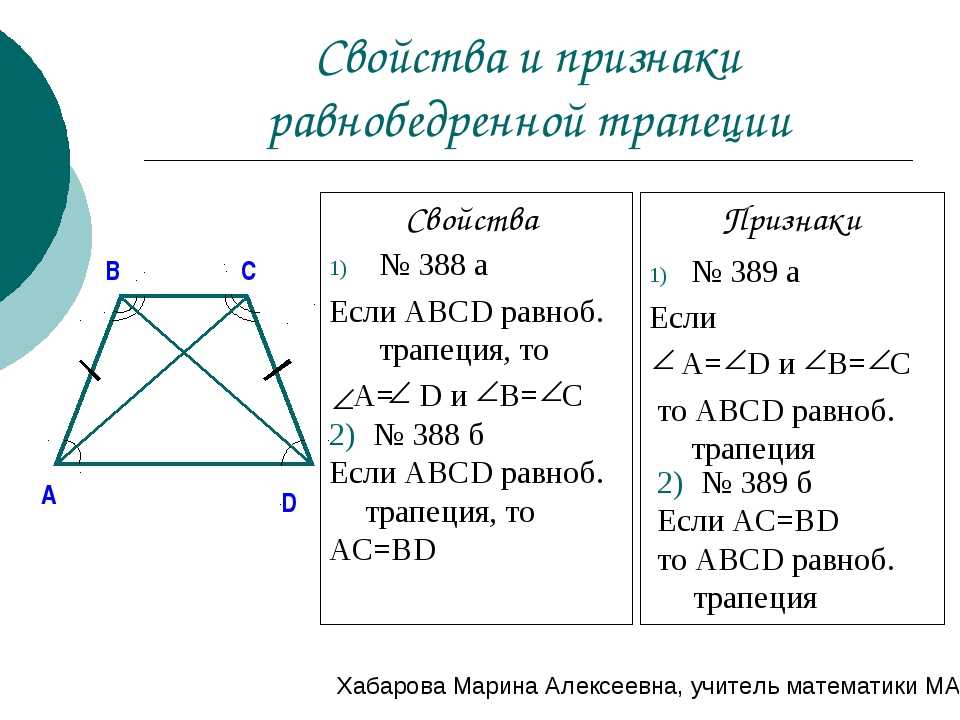

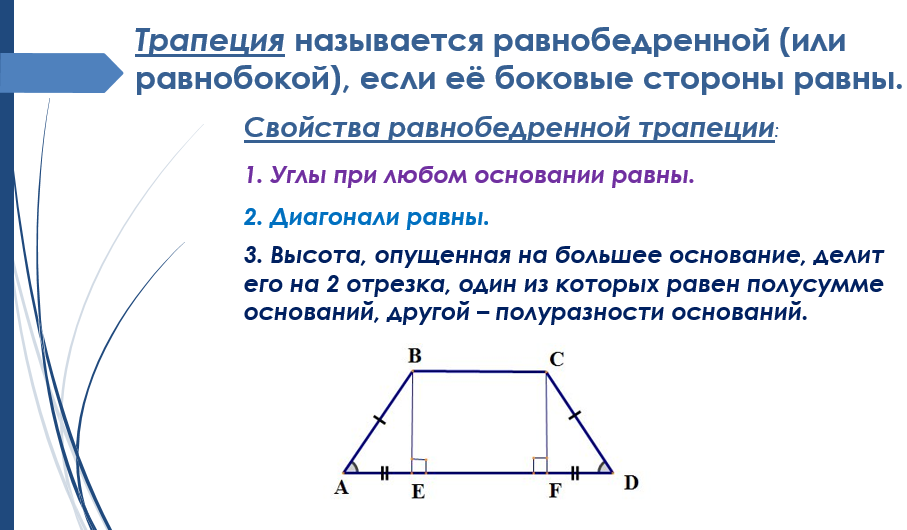 fns.usda. gov /summerfoodrocks Служба летнего питания … для всех детей 18 лет и младше в утвержденных SFSP местах в районах со значительной концентрацией малообеспеченных … Перейти на веб-страницы)
Обучение правильному питанию — Университет штата Мэн, Совместное расширение: Ресурсы EFNEP
…
fns.usda. gov /summerfoodrocks Служба летнего питания … для всех детей 18 лет и младше в утвержденных SFSP местах в районах со значительной концентрацией малообеспеченных … Перейти на веб-страницы)
Обучение правильному питанию — Университет штата Мэн, Совместное расширение: Ресурсы EFNEP
…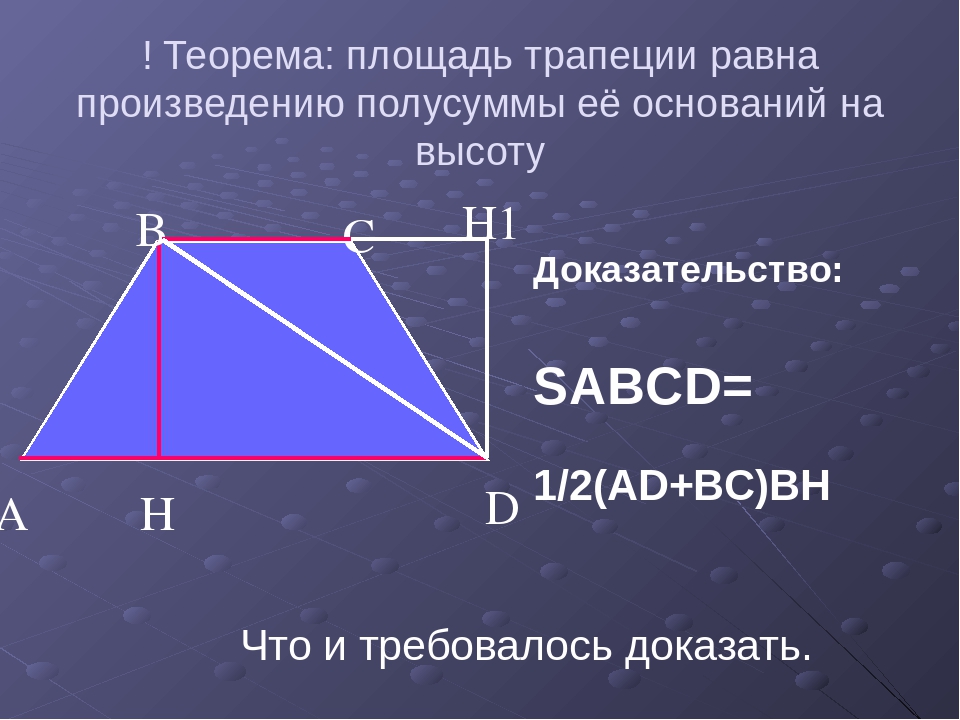 pdf …
pdf … правительство . doe / файлы /inline- файлы / Grants4ME %20Access%20v4. pdf . За …
правительство . doe / файлы /inline- файлы / Grants4ME %20Access%20v4. pdf . За … Фактические … представления в статусе переноса считаются полученными по адресу Maine DOE .
Фактические … представления в статусе переноса считаются полученными по адресу Maine DOE .