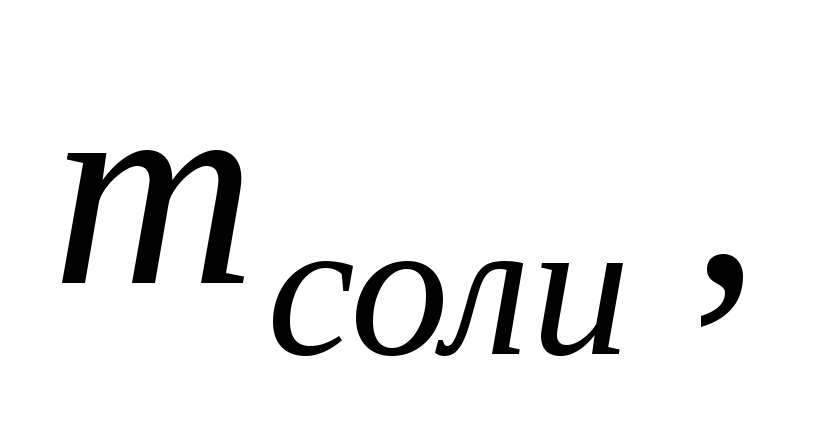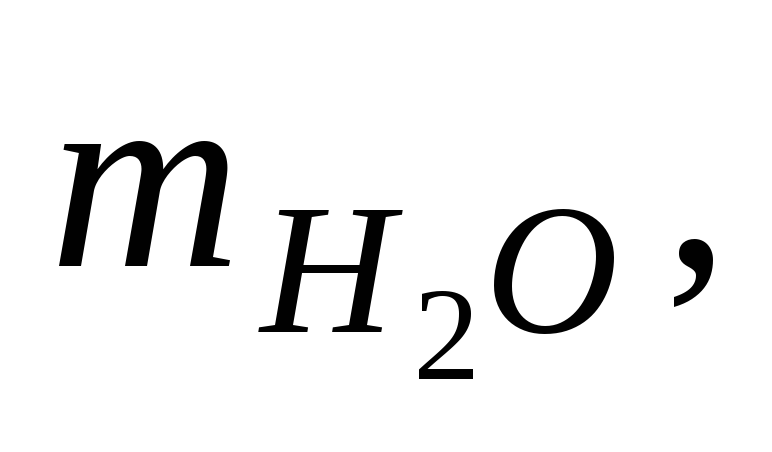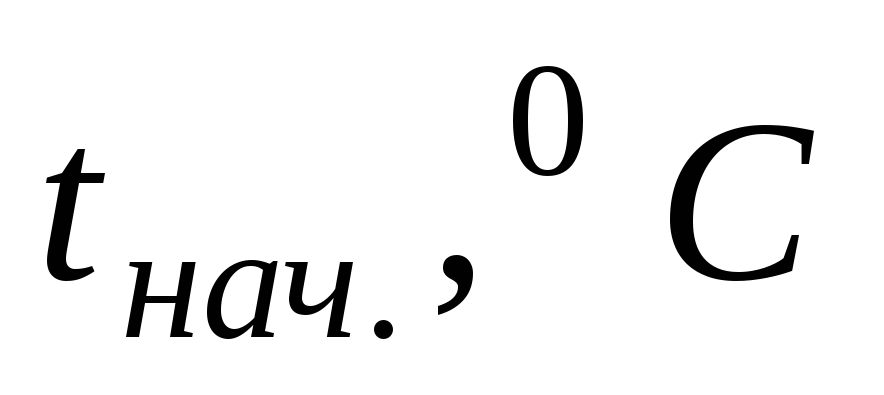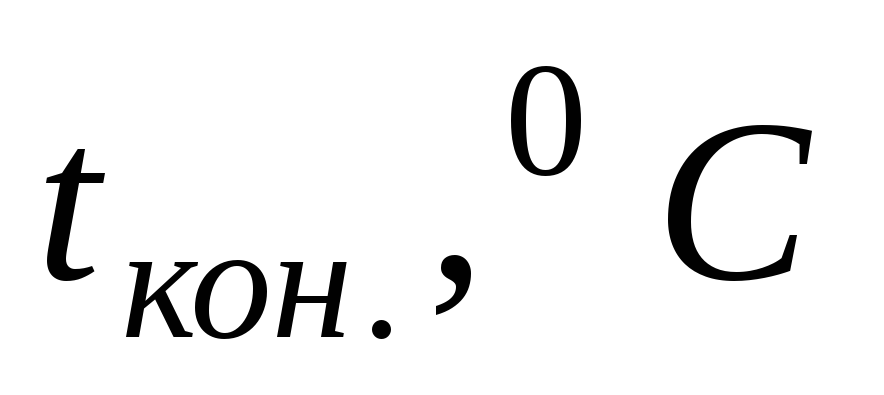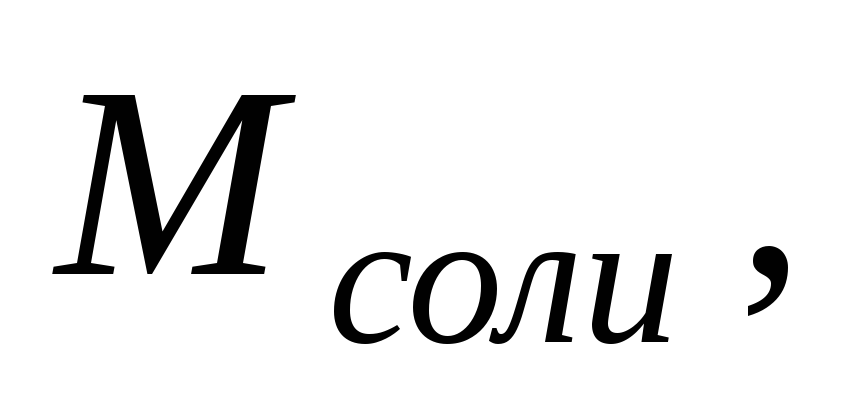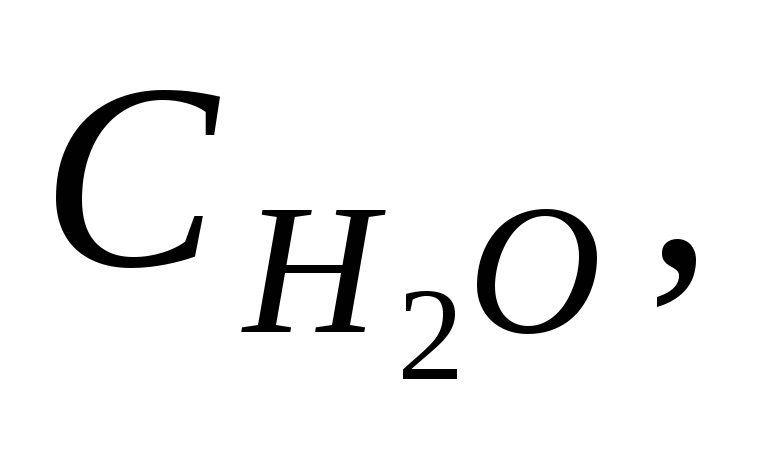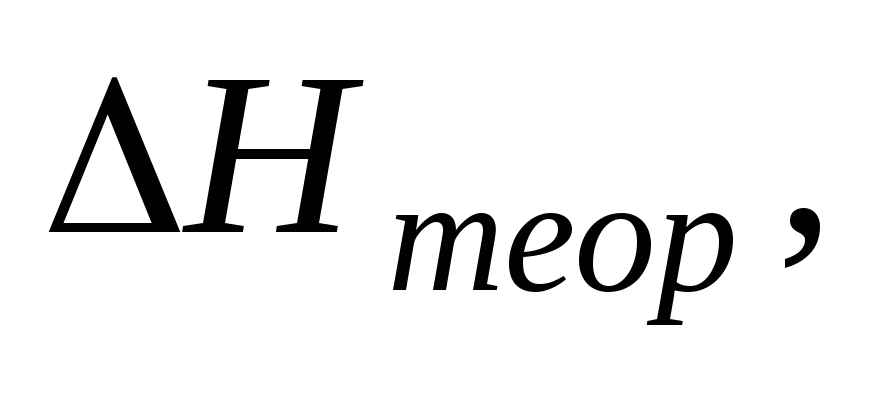Тепловые эффекты химических реакций.

Тепловые эффекты химических реакций изучает раздел термодинамики, называемый термохимией.

Количество выделенного ( или поглощенного ) тепла в химическом процессе называется теплотой реакции.

Из уравнения ( 2 ) следует, что теплота изохорного процесса ( V = const, V = 0 ) равна изменению внутренней энергии системы:

Q_v = U ( 3 ),

теплота изобарного процесса равна изменению энтальпии системы :

Qp = U + pV = ( U + pV ) = H, ( 4 )

где

H = U + pV — энтальпия системы.

Таким образом теплота изохорного или изобарного процессов являются функциями состояния системы.

Уравнения ( 3 ) и ( 4 ) обосновывают экспериментально установленный закон Гесса:

теплота химической реакции ( в изохорном и изобарном процессе ) не зависит от пути протекания реакции, а определяется только исходным и конечным состояниями системы ( т.е. видом и состоянием исходных и конечных веществ ).

Это означает, что теплота реакции равна сумме теплоты всех ее промежуточных стадий. Пользуясь этим, можно вычислить тепловые эффекты процессов, экспериментальное изучение которых по тем или иным причинам невозможно.

ПРИМЕР 1. В реакции нейтрализации слабой уксусной кислоты:

CH₃COOH + NaOH = CH₃COONa + H₂O

( a ) CH₃COOH + OH^ = CH₃COO^ + H₂O, H_a

можно выделить две стадии:

( б ) диссоциация CH₃COOH = CH₃COO^ + H⁺, H_б

( в ) нейтрализация H⁺ + OH^ = H₂O, H_в

Реакция ( а ) представляет собой сумму реакций ( б ) и ( в ), и из закона Гесса следует, что H_а = H_б + H_в.

Диссоциация слабой кислоты ( реакция ( б )) не протекает до конца, поэтому измерить теплоту этой реакции невозможно, однако, определив экспериментально теплоту нейтрализации слабой кислоты ( H_а ) и сильной кислоты ( H_в ), можно рассчитать теплоту реакции диссоциации слабой кислоты: H

б = H_а  H_в.

Величины внутренней энергии, энтальпии и, следовательно, тепловых эффектов реакций зависят от состояния веществ и параметров системы, поэтому для возможности их сравнения вводятся понятия стандартного состояния вещества и стандартных условий.

Стандартным состоянием называется состояние индивидуального вещества в наиболее устойчивой его форме при давлении р = 101325 Па ( 1 атм ), для растворенного вещества — при его концентрации в растворе, равной 1 моль/л.

Стандартными условиями считаются нормальное атмосферное давление р=101325 Па и температура Т = 298,15 К ( 25 С ).

Стандартной теплотой ( энтальпией ) образования химического соединения называют тепловой эффект реакции образования одного моля этого соединения из простых веществ в стандартном состоянии. Обозначается Н

f^_,298( ), единицы измерения  кДж/моль .

Из этого определения следует, что стандартная энтальпия образования простых веществ равна нулю. Стандартные энтальпии образования соединений приводятся в термодинамических таблицах ( см. приложение ).

Из закона Гесса следует, что

теплота реакции равна сумме энтальпий образования продуктов реакции минус сумма энтальпий образования исходных веществ.

Для химической реакции в общем виде:

a₁A₁ + a₂A₂ +  = b₁B₁ + b₂B₂ + 

стандартная теплота рассчитывается по уравнению:

Н^_х.р. =  b_i  Н_f^_,298( B_i )   a_j  Н_f^_,298( A_j ), ( 5 )

прод исх

где а_j и b_i — стехиометрические коэффициенты исходных веществ

и продуктов реакции соответственно;

Н_f^_,298( A_j ) и Н_f^_,298( B_i ) — стандартные энтальпии образования

исходных веществ и продуктов реакции.

ПРИМЕР 2. Рассчитайте стандартную теплоту реакции:

2 ZnS(т) + 3 O₂(г)

= 2 ZnO(т) + 2 SO₂(г)

Для расчета воспользуемся уравнением ( 5 ):

Н^_х.р. = 2 Н_f^_,298( ZnO ) + 2 Н_f^_,298( SO₂ ) — 2 Н_f^_,298( ZnS ) — 3 Н_f^_,298( O₂ )

Значения энтальпий образования веществ выписываем из термодинамической таблицы

( см. приложение ).

Тогда Н^_х.р. = 2 ( -349.0 ) + 2 ( -296.9 ) — 2 ( -201.0 ) — 3( 0 ) = -889.8 кДж

Н^_х.р  0 — реакция экзотермическая.

Экспериментальная часть.

ОПЫТ 1. Определение теплоты реакции нейтрализации.

Определяются тепловые эффекты следующих реакций:

HCl (р) + NaOH(р) = NaCl(р) + H

2O(ж)

CH₃COOH(р) + NaOH(р) = CH₃COONa(р) + H₂O(ж)

Проводимые реакции различаются силой участвующих в них кислот — соляная кислота является сильной и в растворе полностью диссоциирована на ионы, уксусная кислота слабая и диссоциирует лишь частично. Поэтому химическая сущность изучаемых процессов выражается следующими ионно-молекулярными уравнениями:

H⁺(р) + OH^—(р) = H₂O(р)

CH₃COOH(р) + OH^(р) = CH₃COO^(р) + H₂O(ж)

При нейтрализации уксусной кислоты связыванию ионов водорода и гидроксила предшествует процесс диссоциации: CH₃COOH = CH₃COO^ + H⁺. Теплота диссоциации рассчитывается по закону Гесса ( см. пример 1 ).

Получите у преподавателя задание к опыту и запишите исходные данные:

объемы растворов (мл) V_HCl = V_CHCOOH = V_NaOH =

концентрации (моль/л) C_HCl = C_CHCOOH = C_NaOH =

Мерным цилиндром отмерьте заданное количество соляной кислоты и перелейте ее в калориметрический сосуд. Соберите калориметр. Наблюдайте за показаниями термометра. При достижении постоянства температуры отметьте ее значение и запишите в таблицу ( Тн ).

Мерным цилиндром отмерьте необходимое количество раствора щелочи и осторожно, но быстро прилейте щелочь к раствору кислоты в калориметре. Приведите калориметр в рабочее состояние и наблюдайте за показаниями термометра. Зафиксируйте и отметьте в таблице максимальное

значение температуры ( Тк ).

В аналогичной последовательности проведите опыт с уксусной кислотой и занесите результаты опыта в таблицу.

Уравнение реакции	Тн, С	Тк, С	Т=Тк -Тн	Нэк, кДж	Нтеор, кДж
H+(р) + OH—(р) = H2O(р)
CH3COOH(р) + OH(р) = CH3COO(р) + H 2O(ж)

Теплота реакции рассчитывается по формуле:

Т

Нэк = — [( m_к + m_щ ) C + K ] [Дж] ( 6 )

Vк Cк

Где m_к и m_щ — массы растворов кислоты и щелочи соответственно — принимаются равными объемам V_HCl и V_NaOH в миллилитрах,

С = 4.18 Дж/г К — удельная теплоемкость реакционной смеси,

К = — постоянная (теплоемкость) калориметра,

Т = Тк — Тн — изменение температуры в результате реакции,

V_к и C_к — объем кислоты ( в литрах ) и ее концентрация (моль/л) соответственно.

1) По полученным экспериментальным данным рассчитайте теплоту нейтрализации каждой кислоты. Результаты отметьте в таблице.

2) Рассчитайте теоретическое значение стандартной теплоты нейтрализации каждой кислоты, используя следствие из закона Гесса ( ур. 5 ). Результаты отметьте в таблице.

3) К какому типу ( экзо- или эндотермическому ) относятся данные реакции?

4) Рассчитайте относительную ошибку каждого опыта по уравнению:

О.о. = (Нэк — Нтеор) / Нтеор 100 [ % ]

5) Напишите уравнение реакции диссоциации уксусной кислоты:

6) Пользуясь законом Гесса, рассчитайте теоретическое значение теплоты диссоциации уксусной кислоты ( см. пример 1 ):

7) Рассчитайте теплоту диссоциации уксусной кислоты по полученным экспериментальным данным. Сопоставьте полученные результаты.

4. Термохимия. Закон гесса. Определение тепловых эффектов химических реакций, теплотворной способности кормов. Определение энтропии реакции.

Область науки, изучающей отношение между теплотой и работой, получила название термодинамики. Термодинамика изучает законы превращения энергии, законы перехода одного вида энергии в другой. Превращения энергии подчиняются первому, второму и третьему началам (законам) термодинамики. Причем, если первое начало формирует законы взаимного перехода, то второе и третье определяет направленность превращения энергии.

Первое начало термодинамики представляет собой всеобщий закон природы – закон сохранения энергии, открытый М.В. Ломоносовым в 1758 году. Затем он нашел свое развитие в трудах таких ученых как Г.И. Гесс, Д.Джоуль, Р. Майер, Г. Гельмгольц. Наиболее общей формулировкой закона сохранения энергии является следующая:

Общая сумма энергии материальной системы остается постоянной независимо от изменений, происходящих в ней.

Математически этот закон выражается уравнением:

 Е = const,

где Е – энергия,  — сумма, const – сокращенное constans – постоянный, неизменный.

Из этого закона следует, что энергия данной системы не исчезает и не появляется вновь, а только переходит из одной формы в другую в строго эквивалентных количествах. Это и есть современная формулировка первого начала термодинамики.

Первое начало термодинамики устанавливает связь между количеством энергии, полученной или выделенной системой в каком-либо процессе в виде теплоты Q, количеством произведенной или полученной работы W и изменением внутренней энергии системы U:

U = W ± Q,

Внутренняя энергия (U) является полной энергией системы и представляет собой сумму потенциальной и кинетической энергий всех составляющих частей системы (молекул, атомов, ионов и пр.) за исключением потенциальной и кинетической энергии самой системы, как материального тела. Данное уравнение является математическим выражением первого начала термодинамики.

Если процесс изохорный, т.е. если он совершается при постоянном объеме (V = const), то работа не совершается, поскольку при V = const, V = 0 и, следовательно:

W = -P V = 0

Знак минус в этом уравнении указывает на то, что система работает против сил внешней среды. В этом случае:

U = Q_,

где Q_v — количество энергии (Дж/моль или кал/моль), выделенной или поглощенной системой в виде теплоты в ходе процесса при постоянном объеме. Теплота процесса равна изменению внутренней энергии системы и зависит только от конечного и начального состояния системы, т.е.

U₂ – U₁ = U = Q_

В реальной жизни часто встречаются изобарные процессы, протекающие при постоянном давлении (Р = const), например, химические реакции, идущие при атмосферном давлении. Изменение внутренней энергии систе­мы в этом случае будет равно

U = U₂ – U₁ = W + Q_p

где Q_p — количество энергии (Дж/моль или кал/моль), выделенной или поглощенной системой в виде теплоты в ходе процесса при постоянном давлении. Поскольку в ходе процессов, идущих при Р = const объем системы изменяется, то работа в таких процессах будет равна величине

W = -P (V₂ — V₁)

Отсюда:

U₂ – U₁ = Q_p – P(V₂ — V₁).

В результате тепловой эффект процесса, протекающего при Р = const будет равен Q_p = U₂ – U₁ + P (V₂ — V₁)

Q_p = (U₂ + PV₂) – (U₁ + PV₁).

Величина (U + PV) обозначается буквой Н и называется энтальпией. Энтальпия, также как внутренняя энергия, является функцией состояния, т.е. изменение энтальпии (Н = H₂ – Н₁) при переходе системы из состоя­ния 1 в состояние 2 при постоянном давлении не зависит от пути пере­хода, а зависит только от величин энтальпии в конечном (2) и началь­ном (1) состояниях. Таким образом, тепловой эффект процесса, идущего при постоянном давлении будет равен:

Q_p = H₂ – Н₁ = Н

Следует отметить, что физико-химический смысл функций “внутренняя энергия” и “энтальпия” одинаков. Термин “внутренняя энергия” используется для энергетической характеристики процессов, идущих при V = const, а “энтальпия” – для процессов, идущих при P = const. При этом для конденсированных систем Н = U, для газов Н ≠ U.

Первое начало термодинамики дает только энергетическую оценку процессов, протекающих при постоянном объеме или постоянном давлении, но не дает никаких указаний о направлении процесса и предела, до которого изучаемый процесс может идти самопроизвольно. На эти вопросы отвечает второе начало термодинамики посредством новой термодинамической функции, которая называется энтропия и обоз­начается буквой S.

Наблюдения и опыт показывают, что процессы, происходящие в природе, идут в определенном направлении. Жидкость течет от высокого уровня к низкому, вещество диффундирует из области большей концентрации к меньшей, теплота переходит от тела с более высокой температурой к телу с менее высокой и т.д. Все эти процессы происходят самопроизвольно. Второе начало термодинамики гласит:

Каждая материальная система сама по себе стремится к состоянию термодинамического равновесия.

Таким образом, второй закон термодинамики ограничивает превращение энергии в материальной системе. Клаузиус, подобно Ломоносову, так формулирует второе начало термодинамики: теплота не может сама собой перейти от тела менее нагретому к телу более нагретому.

В современной трактовке второе начало термодинамики звучит таким образом:

Энергия самопроизвольно перемещается от системы с более высоким потенциалом к системе с более низким потенциалом энергии того же вида, до тех пор, пока не наступит термодинамическое равновесие.

Изменение энтропии равно тепловому эффекту про­цесса, деленному на абсолютную температуру, при которой он происхо­дит, и измеряется в 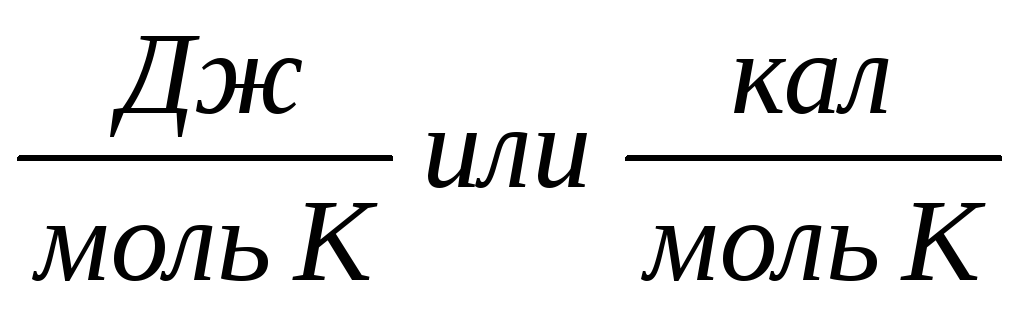. Для обратимых изотермических превращений изменение энтропии равно

∆ S = ,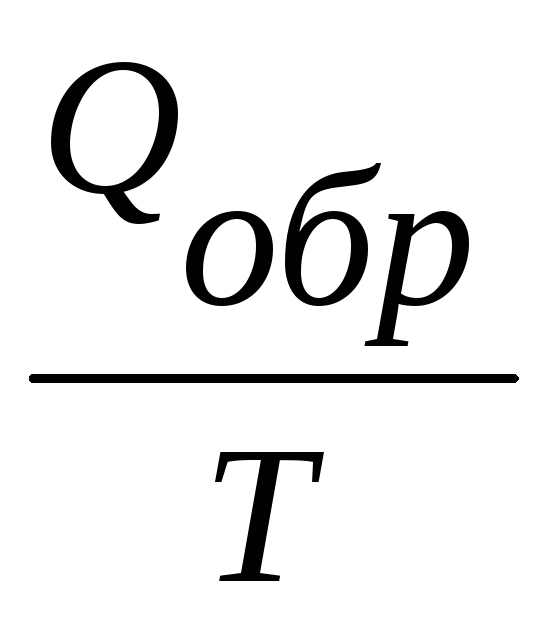

где Q_обр – часть общего количества энергии, выделенной системой в виде тепла. Таким образом, если S = 0, то процесс обратимый. Данное уравнение является математическим выражением второго начала термодинамики для обратимых процессов, происходящих в изолированной системе.

Для необратимых химических процессов, протекающих в изолированной системе, второе начало термодинамики имеет следующий вид:

∆ S >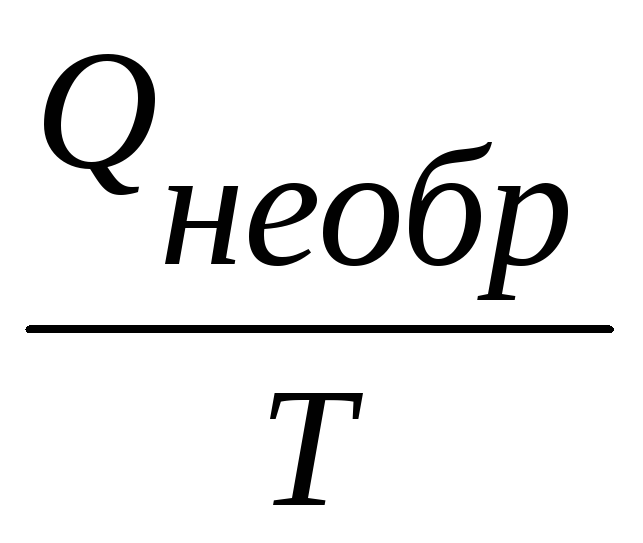

Таким образом, если в изолированной системе протекает самопроизвольный (необратимый) процесс, то S > 0.

Процессы, для которых

∆ S <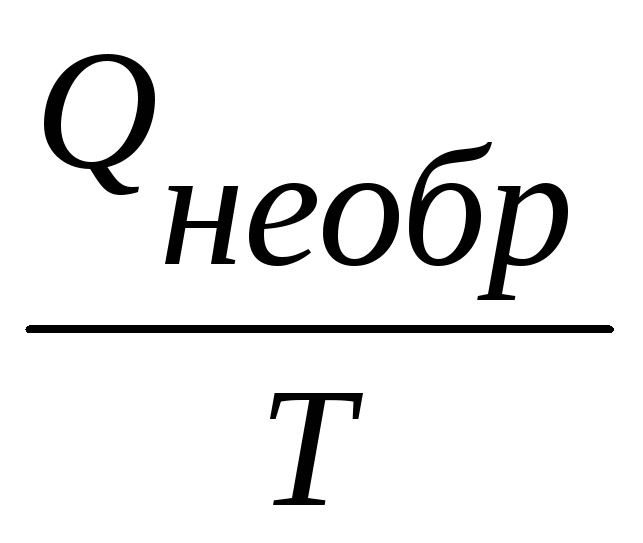

самопроизвольно осуществляться в изолированной системе при постоянной температуре не будут. Энтропия как критерий направленности самопроизвольных (необратимых) процессов может быть использована только для характеристики процессов в изолированных системах.

Физический смысл энтропии сводится к характеристике меры хаоса (беспорядка) в системе. Чем больше изменение энтропии в системе, тем меньше полезной работы может совершить данная система.

Изолированная система является идеальным случаем, т.е. такая система не взаимодействует с окружающей средой ни путем обмена энергией, ни путем обмена веществом. Реальные термодинамические системы являются либо закрытыми (могут обмениваться с окружающей средой энергией), либо открытыми (могут обмениваться с окружающей средой и энергией, и веществом). Для указания на направленность самопроизвольного процесса в таких системах используется другая термодинамическая функция — свободная энергия Гиббса (G).

Термодинамическая функция G = H — TS называется свободной энергией Гиббса, или изобарно-изотермическим потенциалом, или полезной работой. Используется для характеристики системы с точки зрения совершения полезной работы, а также для указания на направленность самопроизвольных процессов, идущих при Р = const и Т = const. В случае самопроизвольных (необратимых) процессов G < 0, Если в ре­зультате процесса G увеличивается (G > 0), то такой процесс идет самопроизвольно в обратном направлении. В обратимых процессах в момент достижения равновесия G = 0.

Термохимия — это раздел термодинамики, в котором изучаются химические реакции с точки зрения их тепловых эффектов. Рассмотрим закрытую термодинамическую систему, в которой происходит химическая реакция

аА + вВ = сС + dD.

В начальном состоянии такая система имеет запас внутренней энергии U₁, (а) молей реагента А и (в) молей реагента В. В конечном состоянии, т.е. после прохождения реакции, система будет иметь запас внутренней энергии U₂, (с) молей продукта С и (d) молей продукте D. Тепловым эффектом реакции будет называться количество энергии, которая выделяется либо поглощается в форме тепла при взаимодейст­вии реагентов А и В с образованием продуктов С и D с учетом стехиометрических коэффициентов реакции. В зависимости от условий, в которых будет протекать химическая реакция (либо V = const, либо Р = сonst), тепловым эффектом реакции будет либо Q_v = U, либо Q_p= Н.

Чтобы сравнить между собой тепловые эффекты разных реакций, необходимо указать точные условия, при которых они протекают. В термодинамике и термохимии за стандартные условия приняты Р = 1 атм и

Т = 298ºК, при этом вещество в этих условиях должно находиться в наиболее устойчивом агрегатном состоянии. Для реакций, проходящих в стандартных условиях, изменение энтальпии обозначается символом Н⁰_298K.

Для реакций, протекающих в газовой фазе, было установлено соотношение между Q_p и Q_:

Q_p = Q_v+ nRT.

Это соотношение устанавливает связь между теплотой реакции при постоянном давлении (Q_p или Н) и теплотой реакции при постоянном объеме (Q_vили U), является следствием из закона Джоуля. В данном уравнении n — разность между числом молей образовавшихся газообразных продуктов и числом молей газообразных реагентов, т.е. n = n_{газовых продуктов} – n_{газовых реагентов}. Для реакций в конденсированных фазах (твердых и жидких), объем которых в ходе реакции практически не изменяется, т.е. n = 0, Н практи­чески не отличается от U. В этих случаях справедливы равенства

Q_p = Q_v и H = U

Реакции, в результате которых вещество получается из элементов, называются реакциями образования. Изменение энтальпии в ходе таких реакций называется энтальпией образования данного соединения. Не все реакции образования можно реализовать практически. Например, реакция

2С + 3H₂ + 1/2O₂ = C₂H₅OH

теоретически является реакцией образования, но практически самопро­извольно не идет. Реакция

С + О₂ = СО₂

тоже является реакцией образования, но в отличие от первой, она достаточно легко может быть проведена практически.

Стандартной энтальпией образования химического соединения называется изменение энтальпии в ходе реакции образования 1 моль данного соединения из элементов в стандартных условиях и обозначается сим­волом .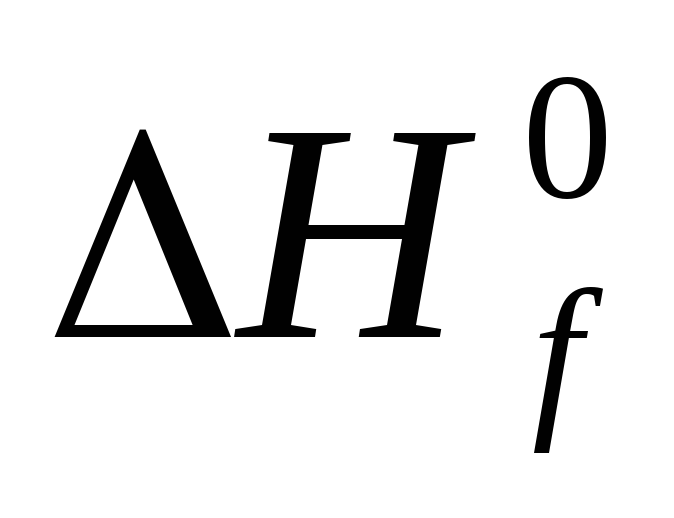

В ходе реакций образования тепловой эффект представляет собой именно стандартную энтальпию образования соединений, потому что стандартная энтальпия образования самих элементов принята рав­ной нулю (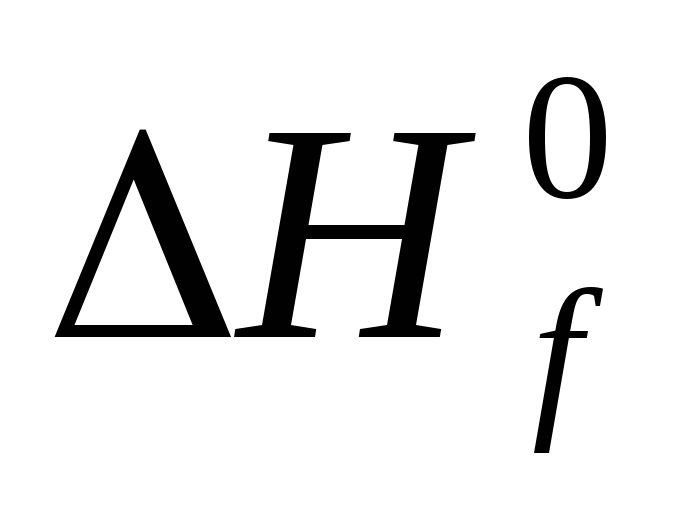_{(элементов)} = 0).

Знание стандартных энтальпий образования позволяет рассчитать тепловой эффект любой химической реакции (Q_p= H) не прибегая к экспериментальным измерениям. Из элементов можно: 1) получить непо­средственно продукты. Соответствующее изменение энтальпии этой реакции будет равно 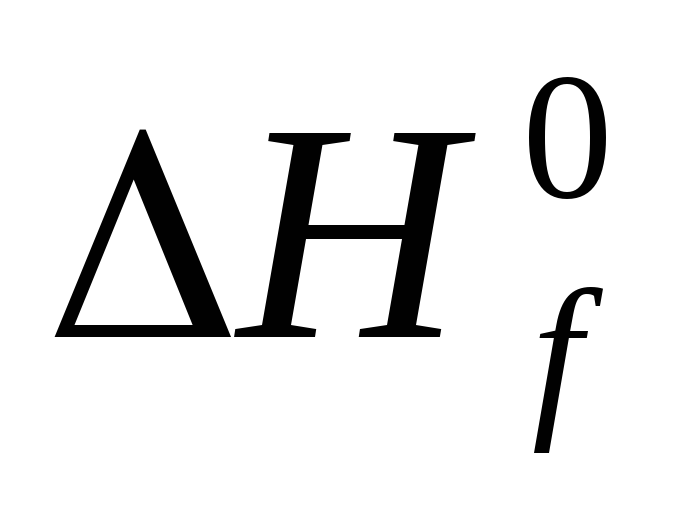_{(продуктов)}. Из элементов можно: 2) получить реагенты. Эта реакция сопровождается изменением энтальпии 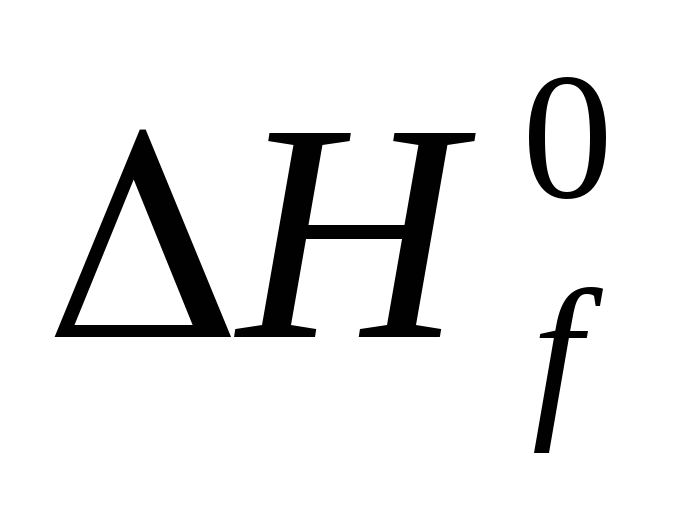_{(реагентов)}. И, наконец, 3) из реагентов можно получить продукты. Изменение энтальпии в ходе этой реакции будет равно Н. Если эти три процесса проходили в стандартных условиях, то термоди­намический баланс этих реакций будет равен:

Н⁰_298K = 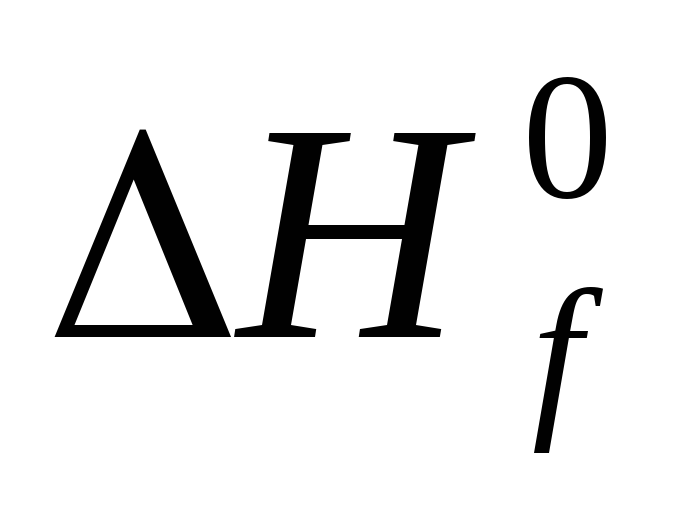_{298К (продукты)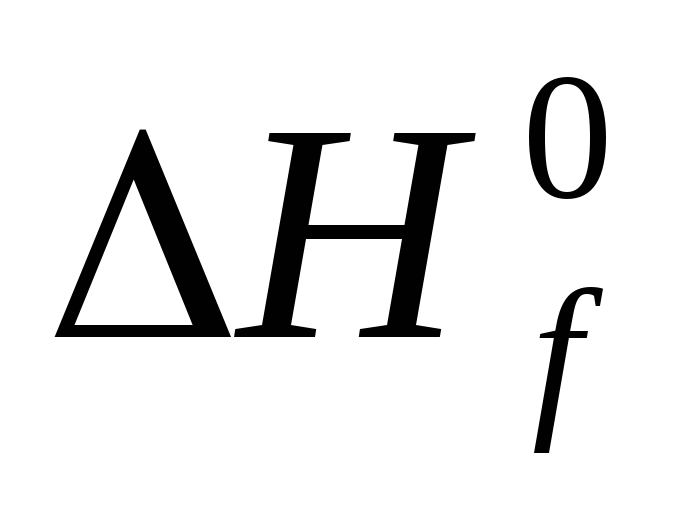} — _{298К (реагенты)}

Таким образом, стандартная энтальпия химической реакции равна разности сумм стандартных энтальпий образования всех продуктов и всех реаген­тов. Так записывается математически закон Гесса.

Если из данных исходных реагентов можно различными путями полу­чить одни и те же конечные продукты, то, независимо от путей получе­ния продуктов, т.е. от вида и количества промежуточных реакций, суммарный тепловой эффект для всех путей будет одним и тем же. Иначе говоря, тепловой эффект химической реакции не зависит от пути перехода «реагенты — продукты», т.е. от промежуточных реакций, а зависит только от вида и состояния продуктов и реагентов. Это положение было постулировано русским ученым Г.И. Гессом в 1840 году и известно как закон Гесса, являющийся основ­ным законом термохимии.

Следствия из закона Гесса:

1. Закон Лавуазье-Лапласа. Тепловой эффект реакции разложения точно равен и противоположен по знаку тепловому эффекту реакции соединения.

Пример:

Са + 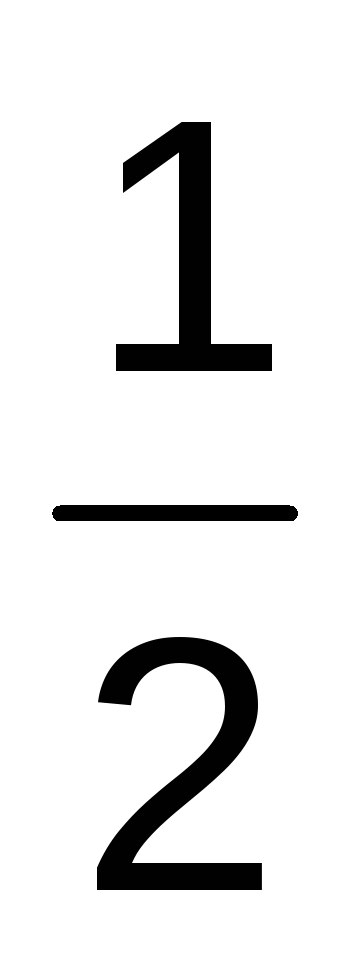О₂ = СаО + 634,71 кДж

СаО = Са + 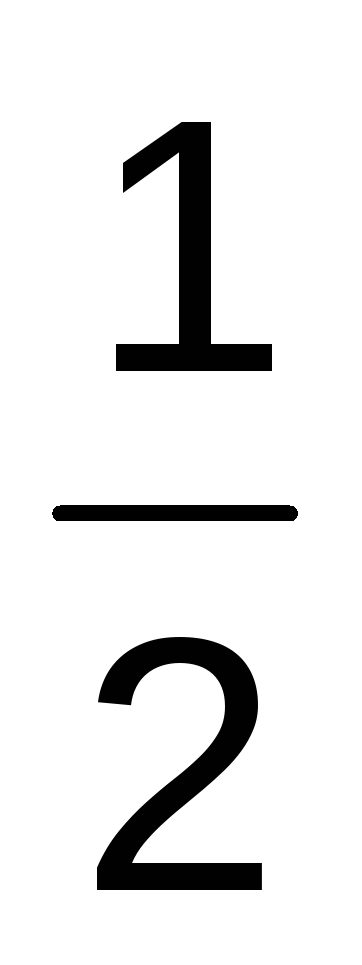О₂ — 634,71 кДж

Q_разл + (-Q_соед ) = 0.

2. Если совершаются две реакции, приводящие из различных начальных состояний к одинаковым конечным, то разница между тепловыми эффектами представляет тепловой эффект перехода из одного начального состояния в другое.

Пример:

С + О₂ = СО₂ + 409,20 кДж (1)

СО + ½ О₂ = СО₂ + 284,93 кДж (2)

Вычитая из (1) уравнение (2), можно вычислит тепловой эффект реакции сжигания углерода до окиси углерода:

С + ½ О₂ = СО+ 124,27 кДж

Таким образом, можно определять тепловые эффекты таких реакций, которые или нереализуемы, или не могут быть проведены чисто и до конца.

3. Если совершаются две реакции, приводящие из одинаковых начальных состояний к различным конечным, то разница между тепловыми эффектами представляет тепловой эффект перехода из одного конечного состояния в другое.

Пример:

С_уг + О₂ = СО₂ + 409,20 кДж

С_гр + О₂ = СО₂ + 393,51 кДж

Таким образом, можно рассчитать тепловой эффект перехода от угля к графиту, который будет равен 409,00 – 393,51=15,69 кДж/моль.

Лекция 2. Химическая энергетика. Тепловые эффекты химических реакций.

Технико-экономический уровень химического производства определяется совокупностью технико-экономических показателей, среди них особенно важны такие как выход готового продукта и степень превращения сырья, селективность и скорость химического процесса, протекающего в реакторе.

Под химическим процессом в реакторе понимают химическую реакцию и сопутствующие ей явления массо- и теплопереноса. В химическом реакторе можно условно выделить три зоны: зону подвода реагирующих веществ в зону химических реакций, зону химических реакций и зону отвода продуктов из зоны химических реакций. В первой и третьей зонах реактора протекают физические процессы подвода и отвода веществ, подчиняющиеся общим законам массопередачи. Во второй зоне химического реактора протекает ряд химических реакций, каждая из которых характеризуется скоростью (кинетический фактор) и состоянием равновесия в системе (термодинамический фактор). Следовательно, для оценки протекающих в этой зоне явлений необходимо исследовать влияние различных факторов на скорость химической реакции и полноту протекания ее, т. е. состояние равновесия в системе.

Основные технологические показатели 1 и 3 третьей зоны химико-технологического процесса. Выход готового продукта определяется как отношение массы полученного продукта к массе сырья, затраченного на его производство. Для одностадийного процесса, протекающего по схеме АВ выход равен 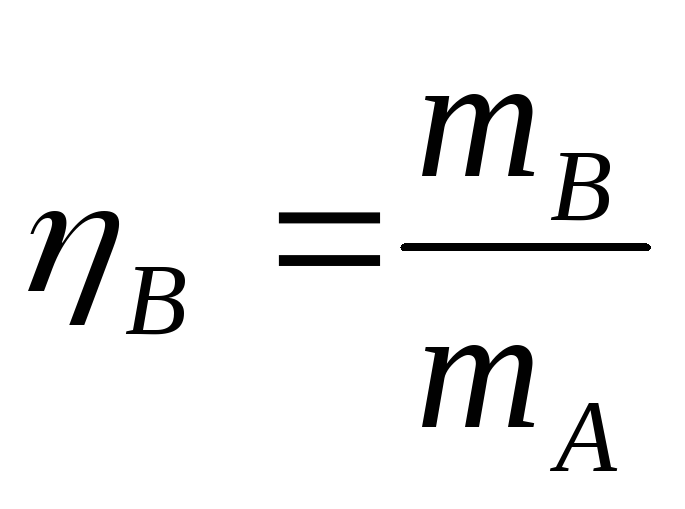(1)

Если в основе процесса лежит химическая реакция, описываемая конкретным уравнением, то для необратимых реакций выход определяется как отношение массы, полученной на практике m_В(пр) к массе, теоретически возможной по стехиометрическому уравнению m_В(теор).

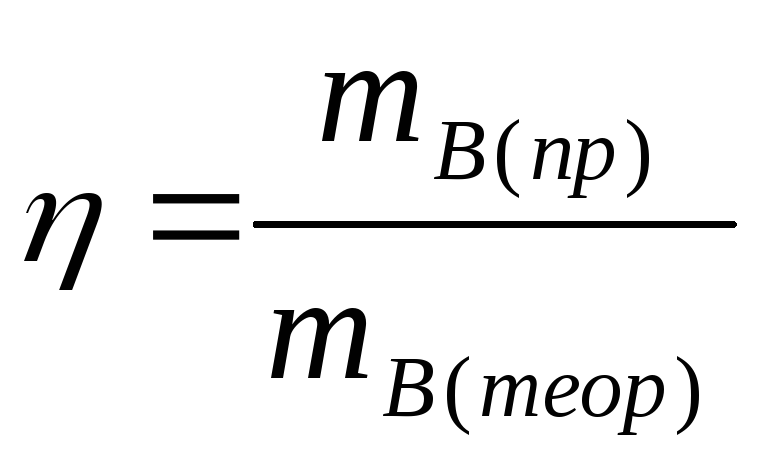(2)

Выход для обратимой реакции определяется как отношение практически полученной массы продукта к максимально возможной массе его, которая может быть получена в данных условиях производства.

Степенью превращения сырья называется отношение массы сырья, вступившего в химическое превращение за время , к исходной массе его (m_ао).

(3)

где m_a— количество сырья, не вступившего в реакцию превращения за время .

Выход продукта и степень превращения выражаются в долях единицы или процентах. Для оценки состояния равновесия в реакторе обычно используют равновесную степень превращения (равновесный выход продукта), который определяется из равновесного закона действующих масс.

Одной из важнейших характеристик всякого технологического процесса является его энергетика. Основным признаком любой химической реакции является выделение или поглощение теплоты, происходящее при химических превращениях одних веществ в другие. Реакции, протекающие с выделением теплоты, носят название экзотермических реакций, а сопровождающиеся поглощением теплоты — эндотермических. К первым относятся, как правило, все реакции соединения, а типичными реакциями второго типа являются реакции разложения.

Количество теплоты, выделяющейся или поглощающейся при химической реакции, называют тепловым эффектом реакции. Обычно его выражают в килоджоулях (кДж).

Строго говоря, теплота, выделяемая или поглощаемая в результате химического превращения, является своеобразным «участником» химической реакции. Поэтому для соблюдения закона сохранения и превращения энергии количество теплоты, сопровождающее химическую реакцию, должно быть включено в ее уравнение. Уравнения химических реакций, в которых приводятся значения тепловых эффектов, называют термохимическими.

Знак «+» перед значением теплового эффекта в правой части уравнения означает, что теплота выделяется, в то время как для эндотермических реакций тепловой эффект должен быть взят со знаком «-», если он указан в правой части уравнения.

Следует отметить, что значение теплового эффекта в термохимическом уравнении строго соответствует количествам реагентов и продуктов, определяемым стехиометрическими коэффициентами. Наиболее часто встречающейся формой записи термохимических уравнений является такая, согласно которой образуется один моль продукта реакции. Например, тепловой эффект реакции взаимодействия водорода с кислородом

Н₂ + 1/2О₂ = Н₂О_(г) + 242 кДж

должен быть удвоен для реакции, в которой используются удвоенные коэффициенты:

2Н₂ + О₂ = 2Н₂О_(г) + 484 кДж

В чем же причина поглощения или выделения теплоты при химических превращениях? Каждое тело обладает определенным запасом внутренней энергии. Внутренняя энергия включает все виды энергии, характеризующие тело: энергию движения молекул относительно друг друга, энергию движения электронов и атомов в молекуле и т. д. Запас внутренней энергии каждого тела зависит от природы тела, его массы и от условий, в которых оно находится.

Суммарная внутренняя энергия продуктов реакции в общем случае отличается от суммарной внутренней энергии реагентов, так как в процессе реакции происходит изменение молекулярного состава вещества, а, следовательно, и изменение межатомных расстояний в продуктах реакции по сравнению с исходными реагентами. Одновременно происходит и перестройка электронных оболочек атомов взаимодействующих молекул. Эта суммарная разница как раз и соответствует тепловому эффекту реакции. Очевидно, что он, подобно внутренней энергии, должен зависеть от условий, в которых находятся реагенты и продукты.

Чтобы иметь возможность сравнивать различные химические реакции и производить термохимические расчеты, необходимо относить значения тепловых эффектов к одному и тому же состоянию исходных продуктов и реагентов. В качестве такого состояния, называемого стандартным, обычно выбирают температуру 298К (25°С) и давление 10⁵Па (а также концентрацию 1 моль/л для растворов).

Термохимические законы. Рассмотрим основные законы термохимии, которые являются частными проявлениями закона сохранения и превращения энергии. Первый закон термохимии обычно формулируют следующим образом: Тепловой эффект прямой реакции равен по абсолютному значению и противоположен по знаку тепловому эффекту обратной реакции. Иначе говоря, осуществив в системе какой-либо химический процесс, а затем ему противоположный, мы возвращаем систему в первоначальное состояние с той же внутренней энергией, какую она имела.

При термохимических расчетах особенно важным является один из видов тепловых эффектов — теплота образования.

Теплотой образования называют тепловой эффект реакции образования одного моля химического соединения из простых веществ, устойчивых при данных условиях.

Например, теплота образования силиката кальция есть тепловой эффект реакции, равный 1635 кДж на 1 моль продукта:

Са + Si + ³/₂О₂ = СаSiO₃ + 1635 кДж/моль

Будем в дальнейшем тепловой эффект реакции образования при стандартных условиях обозначать символом Q₂₉₈

Однако нужно понимать, что в термохимии и термодинамике приняты разные исходные положения для учета изменения энергии при химических реакциях. Термохимия, как было указано ранее, рассматривает, сколько энергии приобрела (или отдала) окружающая среда, в которой происходит химическая реакция. Термодинамика, напротив, учитывает изменения энергии, происходящие в самой реакции, т.е. при переходе исходных реагентов в продукты реакции. При этом в термодинамике тепловой эффект реакции образования, проводимой при постоянном давлении, обозначают символом Н₂₉₈ (энтальпия), который численно равен, но противоположен по знаку величине Q₂₉₈. Следовательно, эндотермическим процессам (-Q₂₉₈) соответствуют положительные значения Н₂₉₈, а экзотермическим (+Q₂₉₈) — отрицательные, т.е. — Н₂₉₈. Например, эндотермическая реакция паров воды с углем с учетом теплового эффекта может быть выражена двумя способами:

Н₂О_(г) + С_тв = СО_(г) + Н_2(г) — 132 кДж/моль

Н₂О_(г) + С_тв = СО_(г) + Н_2(г) (Н =132кДж/моль)

Оба способа записи термохимического уравнения химической реакции эквивалентны и показывают, что при взаимодействии паров воды с углем происходит поглощение теплоты.

Второй термохимический закон, открытый в 1840 г. известным русским химиком Гессом, является важнейшим и формулируется следующим образом: тепловой эффект химической реакции не зависит от пути ее протекания и определяется только начальным и конечным состоянием системы.

Например, силикат кальция можно получить двумя путями:

1) из простых веществ, сжигая эквимолярные количества кальция и кремния совместно в кислороде:

Са + Si + ³/₂О₂ = СаSiO₃ (Н₁)

2) из простых веществ, предварительно превращенных в оксиды:

Са + ¹/₂О₂ = СаО (Н₂)

Si + O₂ = SiO₂ (Н₃)

с последующим взаимодействием оксидов:

СаО + SiO₂ = СаSiO₃ (Н₄)

В соответствии с законом Гесса получается:

Н₁ = Н₂ + Н₃ + Н₄

Закон Гесса часто используют для определения тепловых эффектов, которые трудно или невозможно измерить непосредственно.

Важным следствием закона Гесса является правило, согласно которому тепловой эффект реакции равен разности суммы теплот образования продуктов реакции и суммы теплот образования исходных веществ.

Н_x.p. = Н_обр (продуктов) — Н_обр (реагентов) (4)

Суммирование следует производить с учетом количества вещества, участвующего в реакции, т.е. с учетом стехиометрических коэффициентов в уравнении, например:

Fе₂О₃ + 3СО = 2Fе + 3СО₂ (Н)

Н = 3Н_CO2 – Н_Fe2O3 – 3Н_CO

Теплота образования всех простых веществ принята равной нулю.

Знание теплот образования веществ и тепловых эффектов реакций позволяет делать приближенные, но очень важные выводы.

Во-первых, чем больше по абсолютному значению экзотермический эффект образования соединения, тем оно термически устойчивее.

Во-вторых, эндотермические и слабоэкзотермические соединения являются, как правило, химически малоустойчивыми и обладают более высокой реакционной способностью, чем сильно экзотермические вещества.

Наконец, необходимо подчеркнуть, что значения тепловых эффектов реакций образования химических соединений, как и другие их свойства, находятся в периодической зависимости от атомных номеров элементов, образующих эти химические соединения.

Направление протекания химических реакций. Из анализа энергетики химических взаимодействий непосредственно следует еще более важный вывод о принципиальной возможности прогнозирования многих химических реакций. Свыше 100 лет назад основой для таких прогнозов служил принцип Бертло-Томсена, согласно которому химический процесс осуществляется лишь в том случае, если он сопровождается выделением теплоты, т.е. является экзотермическим. Однако на практике оказалось, что многие эндотермические реакции довольно легко осуществляются при повышенных температурах.

Теперь известно, что, помимо стремления к минимуму энергии, в физико-химических системах существует еще одна тенденция — стремление к увеличению беспорядка.

Стремление к переходу в наиболее вероятное состояние характерно для всех систем. Количественной мерой беспорядка системы (неупорядоченности состояния системы) является величина S, называемая энтропией. Таким образом, с учетом вышесказанного энтропия увеличивается при расширении, плавлении веществ и т.д. Кроме того, энтропия возрастает при переходе вещества из кристаллического состояния в газообразное (S_г>>S_ж>S_тв). Величина энтропии, аналогично энтальпии, не зависит от пути протекания реакции и определяется только начальным и конечным состоянием системы, т.е. является функцией состояния системы. Более того, для расчета изменения энтропии при химической реакции также применимы соотношения, аналогичные законам Гесса и следствиям из них:

S_x.p. = S_{обр(продуктов)} — S_{обр (реагентов)} (5)

Важной характеристикой состояния системы является общая энергия системы, называемая энергией Гиббса (свободной энергией системы) и определяемая соотношением:

G = H – TS (6)

Являясь функцией состояния системы, также как энтальпия и энтропия, энергия Гиббса при протекании химической реакции определяется следующим образом:

G_x.p. = Н_x.p. – ТS_x.p. = G_{обр(продуктов)} — G_{обр(реагентов)} (7)

Важным свойством энергии Гиббса является ее способность определять направление протекания химического процесса.

Если изменение энергии Гиббса химической реакции меньше нуля (G<0), то при отсутствии внешних воздействий в нормальных условиях процесс протекает в сторону образования продуктов реакции.

Если же это изменение является положительной величиной (G>0), то процесс может протекать в сторону образования исходных веществ.

Из условия G=0 (состояние равновесия) можно рассчитать равновесные количества веществ, находящихся в равновесном состоянии.

5.3. Энтальпия системы. Тепловые эффекты химических реакций

Теплота Q и работа A функциями состояния не являются, ибо они служат формами передачи энергии и связаны с процессом, а не с состоянием системы. При химических реакциях А — это работа против внешнего давления, т.е. в первом приближении

А = рV,

где V — изменение объема системы (V₂ – V₁).

Так как большинство химических реакций проходит при постоянном давлении, то для изобарно-изотермического процесса (р = const, Т= const) теплота Q_p будет равна:

Qp = ∆U + p∆V,

Qp= (U₂ – U₁) + p(V₂ – V₁)

Qp = (U₂ + pV₂) – (U₁ + pV₁)

Сумму U+ pV обозначим через Н, тогда

Qp = H₂ – H₁ = ∆H

Величину Н называют энтальпией. Таким образом, теплота при р=const и Т=const приобретает свойство функции состояния и не зависит от пути, по которому протекает процесс. Отсюда теплота реакции Q_p в изобарно-изотермическом процессе равна изменению энтальпии системы Н (если единственным видом работы является работа расширения):

Qp = ∆H

Энтальпия, как и внутренняя энергия, является функцией состояния: ее изменение (H) определяется только начальным и конечным состояниями системы и не зависит от пути перехода. Нетрудно видеть, что теплота реакции в изохорно-изотермическом процессе (V= const; Т = const), при котором V=0, равна изменению внутренней энергии системы:

Qv = ∆U

Теплоты химических процессов, протекающих при р, Т=const и V, Т=const, называют тепловыми эффектами.

При экзотермических реакциях энтальпия системы умень­шается и Н < 0 (Н₂ < H₁), а при эндотермических энтальпия системы увеличивается и Н > 0 (Н₂ > Н₁). В дальнейшем теп­ловые эффекты всюду выражаются через H.

5.4. Термохимические расчеты

Термохимические расчеты основаны на законе Гесса, позволяющее рассчитать энтальпию химической реакции: тепловой эффект реакции зависит только от природы и физического состояния исходных веществ и конечных продуктов, но не зависит от пути перехода.

Часто в термохимических расчетах применяют следствие из закона Гесса: тепловой эффект реакции (Н_x.p.) равен сумме теплот образования Н_обр продуктов реакции за вычетом суммы теплот образования исходных веществ с учетом коэффициентов перед формулами этих веществ в уравнении реакции:

∆Hx.p. = ∑∆H_обр^прод — ∑∆H_обр^исх (1) Пример 1. При взаимодействии кристаллов хлорида фосфора (V) с парами воды образуется жидкий РОС1₃ и хлороводород. Реакция сопровождается выделением 111,4 кДж теплоты. Напи­шите термохимическое уравнение этой реакции.

Решение. Уравнения реакций, в которых около символов химических соединений указываются их агрегатные состояния или кристаллическая модификация, а также числовое значение тепло­вых эффектов, называют термохимическими. В термохимических уравнениях, если это специально не оговорено, указываются значения тепловых эффектов при постоянном давлении Qp, равные изменению энтальпии системы Н. Значение Н приводят обычно в правой части уравнения, отделяя его запятой или точкой с запятой. Приняты следующие сокращенные обозначения агрегат­ного состояния вещества: г — газообразное, ж — жидкое, к — крис­таллическое. Эти символы опускаются, если агрегатное состояние веществ очевидно.

Если в результате реакции выделяется теплота, то Н < 0.Учитывая сказанное, составляем термохимическое уравнение данной в примере реакции:

PCl₅(к) + H₂O(г) = POCl₃(ж) + 2HCl(г)

∆Hx.p.= -111,4 кДж

Пример 2. Реакция горения этана выражается уравнением:

С₂Н₆(г) + 3¹/₂О₂= 2СО₂(г)+3Н₂О(ж)

∆Hх.р.= -1559,87 кДж

Вычислите теплоту образования этана, если известны теплоты образования СO₂(г) и Н₂O(ж) (см. табл. 15).

1.3. Тепловые эффекты физико-химических процессов. Термохимические законы

11

Первый закон термодинамики имеет большое значение, так как позволяет решать различные практические задачи: опреде- лять тепловые эффекты физико-химических процессов, работу расширения или сжатия идеального газа и т. д.

В результате протекания физико-химических процессов мо- жет выделяться или поглощаться тепло, что обусловлено пере- стройкой энергетических уровней атомов или молекул участ- вующих и образующихся в ходе процесса веществ.

Теплота, выделяемая или поглощаемая при протекании физико- химических процессов при условии, что процесс протекает непре- рывно при постоянном объёме или давлении и единственным ви- дом работы является работа против внешнего давления, называется тепловым эффектом. Соотношения (1.5) и (1.8) позволяют определять тепловые эффекты: при постоянном объёме он равен изменению внутрен- ней энергии (∆U), при постоянном давлении — изменению энтальпии (∆Н).

Процессы, протекающие с выделением теплоты называются экзотермическими ∆Н (∆U) < 0, а с поглощением теплоты — эн- дотермическими ∆Н (∆U) > 0.

Тепловой эффект процесса определяется как экспериментально (кало- риметрическим способом), так и с помощью термохимических расчетов. Его можно рассчитать, если известны теплоты образования исходных ве- ществ и продуктов, образующихся в результате протекания реакции. Изо- барной теплотой образования сложного вещества (∆НОБР) называется коли- чество энергии, выделяемое, реже поглощаемое, при образовании 1 моль сложного вещества из простых. Если исходные вещества и продукты ре- акции находятся в стандартных условиях (Т = 298 К и Р = 101,3 кПа), то теплота образования 1 моля соединения называется стандартной теплотой образования (∆H0ОБР ). Для большинства сложных веществ стандартные те-

плоты образования приведены в справочных таблицах; для простых ве- ществ (Н2, О2, N2 и др.) — условно приняты равными нулю.

Расчеты тепловых эффектов основаны на двух законах:

•Закон Лавуазье-Лапласа — теплота образования сложного вещества равна по абсолютной величине и обратно по знаку теплоте его разложения.

•Закон Гесса — тепловой эффект процесса не зависит от пути его протекания и числа стадий, а зависит от начального и конечного со- стояния системы или суммарный тепловой эффект многостадийного процесса (∆НСУМ) равен алгебраической сумме тепловых эффектов от- дельных стадий (∆Нi), т. е.

12

∆HСУМ = ∑∆Нi .

Из закона Гесса следует, что суммарный тепловой эффект химиче- ской реакции при стандартных условиях равен разности между суммой теплот образования продуктов реакции (∆H0прод ) и суммой теплот образо-

вания исходных веществ (∆H0исх ) с учётом стехиометрических коэффи- циентов, стоящих в уравнении реакции, т. е.

∆H0Х.Р. = ∑n’ ∆Н0КОН − ∑n» ∆Н0ИСХ ,

где n’ и n» — стехиометрические коэффициенты, стоящие в уравнении реакции.

Численное значение теплового эффекта зависит:

• от природы веществ и их агрегатного состояния. Например, процесс образования воды из водорода и кислорода в зависимости от ее агре- гатного состояния характеризуется различными величинами.

H		+	1	О		= Н О		∆Н0 = −241,8 кДж		,
	2(Г)		2		2(Г)	2	(Г)		моль
Н		+	1	О		= Н О		∆H0 − 285,8	кДж .
	2(Г)		2		2(Г)	2	(Ж)		моль

Буквы в круглых скобках у химических формул указывают на агрегат- ное состояние веществ: кристаллическое (кр), жидкое (ж), газообразное (г).

• от числа молей участвующих в реакции веществ. Например:

1 N		2(Г)		+	3	Н	2(Г)	= NH	3(Г)	∆Н0 = −46,2кДж,
2					2
N	2(Г)		+ 3Н				= 2NH			∆Н0	= −92,4кДж .
					2(Г)			3(Г)

Закон Гесса позволяет рассчитать тепловые эффекты химических ре- акций, фазовых и модификационных превращений, термического раз- ложения веществ и др. физико-химических процессов.

1.4. Зависимость теплового эффекта от температуры. Уравнение Кирхгофа

Так как внутренняя энергия веществ является функцией объёма, давле- ния и температуры, то, очевидно, и тепловые эффекты реакций зависят от условий, при которых эти реакции протекают. Практически наибольшие

13

значение имеет влияние температуры на тепловые эффекты процессов. Термохимические опыты показывают наличие хотя и небольшого, но

вполне определенного изменения теплового эффекта реакции с темпера- турой. Чтобы его найти необходимо знать характер зависимости тепло- вого эффекта от температуры. Исследуя эту зависимость Кирхгоф ис- пользовал температурный коэффициент теплового эффекта, равный от- ношению приращения теплового эффекта d(∆H) (для Р = const) и d(∆U) (для V = const) к изменению температуры dT.

Установлено, что температурный коэффициент теплового эффек- та определяется изменением мольной теплоемкости продуктов реак- ции и исходных веществ.

d(∆H)	= ∆CP ,	(P = const),	(1.13)
dT
где ∆СP — изменение изобарной теплоемкости.
d(∆U)	= ∆CV ,	(V = const),	(1.14)
dT

где ∆СV — изменение изохорной теплоемкости.

Уравнения (1.13) и (1.14) выражают закон Кирхгофа: температур-

ный коэффициент теплового эффекта равен изменению теплоем- кости системы, обусловленному протеканием данного процесса.

Следует отметить, что для газообразных систем справедливо соотно- шение, называемое уравнением Майера:

СP – СV = R,
где R — газовая постоянная, равная	8,31 Дж моль К.
При этом для одноатомного газа	СV =	3	R	и	5	R	для двух-
		2			2

атомного газа.

При исследовании температурной зависимости тепловых эффектов чаще используется уравнение (1.13), так как большинство процессов про-

текает при Р = const. Если ∆СР > 0, то d(dT∆H) > 0, следовательно с повыше-

нием температуры тепловой эффект будет увеличиваться. Если же ∆СР < 0,

то d(dT∆H) < 0 — с ростом температуры тепловой эффект уменьшается.

Для получения расчетной формулы уравнение Кирхгофа (1.13) необ- ходимо проинтегрировать

14

T∫2 d(∆H) = T∫2 ∆CP dT

T1 T1

Для небольшого температурного интервала можно пренебречь изме- нением теплоемкости и считать СP постоянной, не зависящей от темпе- ратуры величиной. Тогда

∆HT	= ∆HT + ∆CP (T2 − T1), СP ≠ f(T).	(1.15)
2	1
Если принять Т1 = 298К, то выражение (1.15) имеет вид:
	∆HT = ∆h3980 + ∆CP (T − 298).	(1.16)

Изменение теплоемкости ∆СР определяется разностью суммарных тепло- емкостей продуктов реакции (CРКОН ) и исходных веществ (СP ИСХ ), взятых с

учётом стехиометрических коэффициентов (n’ и n») в уравнении реакции

∆CP = ∑n’CР0КОН − ∑n»СР0ИСХ .

(1.17)

1.5. Работа идеального газа

Для большинства физико-химических процессов единственным ви- дом работы является работа против внешнего давления. Многие газы при достаточно низких давлениях и высоких температурах подчиняются законам идеальных газов. Первый закон термодинамики позволяет вы- вести математические соотношения для вычисления работы идеального газа в различных термодинамических процессах. Как уже указывали, работа против внешнего давления выражается А = Р ∆V или для конеч- ного изменения объёма от V1 до V2

V2
A = ∫P dV .	(1.18)
V1
Изохорный процесс отвечает условию постоянства	объёма
(V = const), работа расширения равна нулю: А = 0.

В изобарном процессе (P = const) интегрирование выражения

(1.18) приводит к соотношению
А = Р (V2 – V1).	(1.19)
Пользуясь выражением Р V = R T для 1 моля, можно	в выраже-

15

нии (1.19) заменить Р V1, на R T1 и Р V2 на R T2, тогда

А = R (T2 – T1),

а для n молей

А = n R (T2 – T1),

т. е. работа расширения совершается за счет повышения температуры. Для вычисления работы газов в изотермическом процессе (Т = const)

в уравнение (1.18) подставим P = RTV (из уравнения Менделеева-

Клапейрона (1.10) для 1 моля), получим выражение:

A = V∫2 RT dV ,

V1 V

которое после интегрирования имеет вид:

A = RT ln V2 ,

V1

а для n молей

A = nRT ln V2 .

V1

Зная, что при постоянной температуре давление обратно пропор- ционально объёму (Р V = const), то работу можно выразить и через отношение давлений Р1 и Р2.

A = nRT ln P1 . P2

В адиабатическом процессе (Q = 0) работа совершается за счет убыли внутренней энергии (выражение (1.12)). Но так как dU = СV dT после ин- тегрирования соотношения (1.12) получим:

А = СV (Т1 – Т2),

а для n молей

А = n СV (T1 – T2).

Определение тепловых эффектов химических реакций

Цель работы: определить опытным путем тепловые эффекты процессов растворения из полученных данных, пользуясь законом Гесса, рассчитать теплоты гидратации солей.

Теоретическая часть.

Все химические реакции сопровождаются выделением или поглощением энергии, чаще всего в виде тепла Количество последней может быть измерено и выражено в единицах энергии (Дж, кал и т.д.)

Разница первоначального и конечного уровней энергии системы представляет собой энергетический эффект или изменение энтальпии реакции, который обозначается ΔН_r.

При экзотермических реакциях система с большим запасом энергии переходит в состояние с меньшим запасом энергии. Такие реакции сопровождаются выделением тепла, и их тепловой эффект считается отрицательным (ΔН_r <0).

При эндотермических реакциях, наоборот, система с меньшим запасом энергии переходит в состояние с более высоким запасом энергии. Такие реакции сопровождаются поглощением тепла, и их тепловой эффект принято считать положительным (ΔН_r >0).

Для термохимических расчетов большое значение имеют величины энтальпий образования веществ.

Под энтальпией образования вещества понимается изменение энтальпии реакции образования одного моля сложного вещества из простых веществ, например:

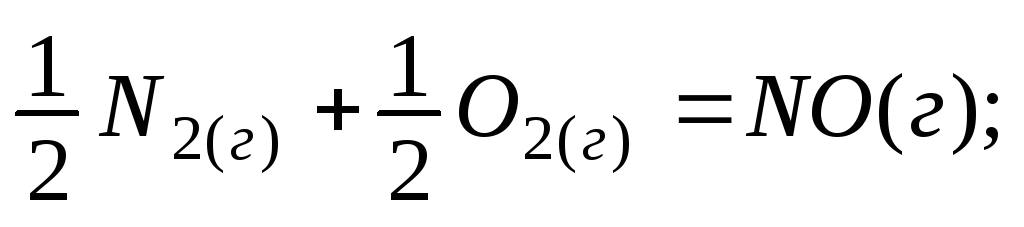
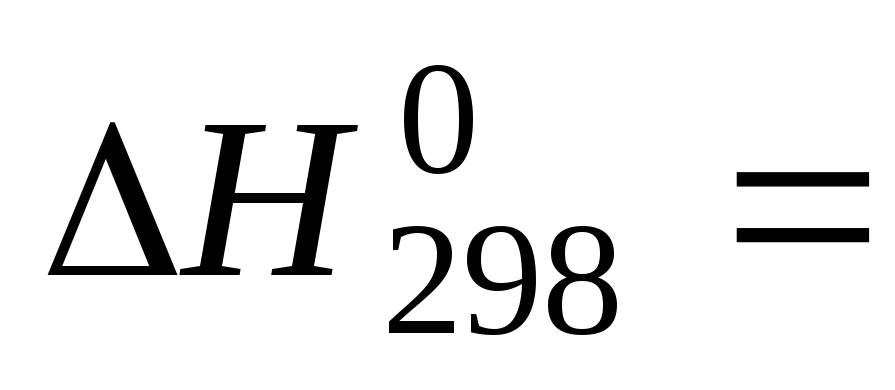+90,4 кДж/моль;

Верхний и нижний индексы при ΔН указывают на то, что энтальпия образования приведена к стандартным условиям (давление 101325 Па или 1 атм и температура 298 К или 25⁰ С).

Значения энтальпий образования веществ приведены в таблицах термодинамических потенциалов.

Термохимические расчеты основаны на использовании закона Гесса и вытекающих из него следствий:

1. Тепловой эффект химического процесса равен сумме тепловых эффектов всех промежуточных стадий процесса.

Например, процесс получения двуокиси углерода из угля и кислорода может быть проведен в одну стадию:

С(т) + О₂(г) = СО₂(г) ΔН_r = -94 ккал

Но этот же процесс можно провести в две стадии:

С(т) + 1/2 О₂(г) -= СО(г) ΔН_r = -26,4 ккал

CO(г) + 1/2O₂(г) = CO₂(г) ΔН_r =-67,6 ккал

Согласно закону Гесса, сумма тепловых эффектов двух последних реакций должна равняться тепловому эффекту первой реакции, что и наблюдается в действительности: {-26,4-67,6 = -94 (ккал)}.

2. Тепловой эффект химической реакции равен разности теплот образования конечных и исходных участников реакции, умноженных на их стехиометрические коэффициенты (т.e. коэффициенты перед формулами данных веществ в уравнении реакции).

Например, реакция горения пропана протекает по схеме:

С₃Н₈(г) + 5О_г(г) = ЗСО₂(г) + 4Н₂О(г)

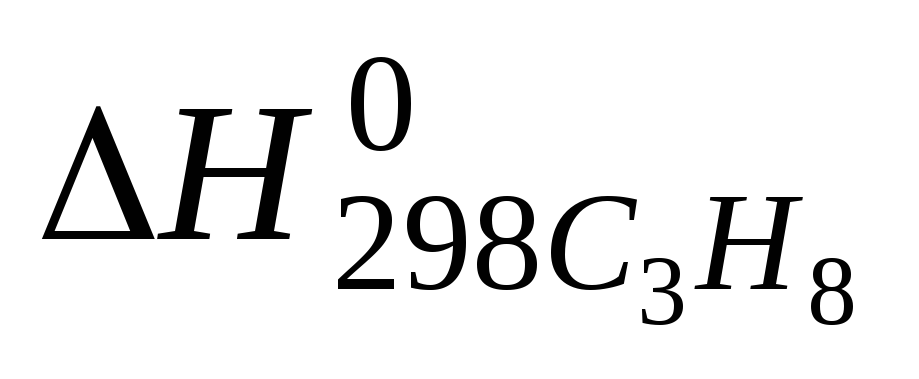
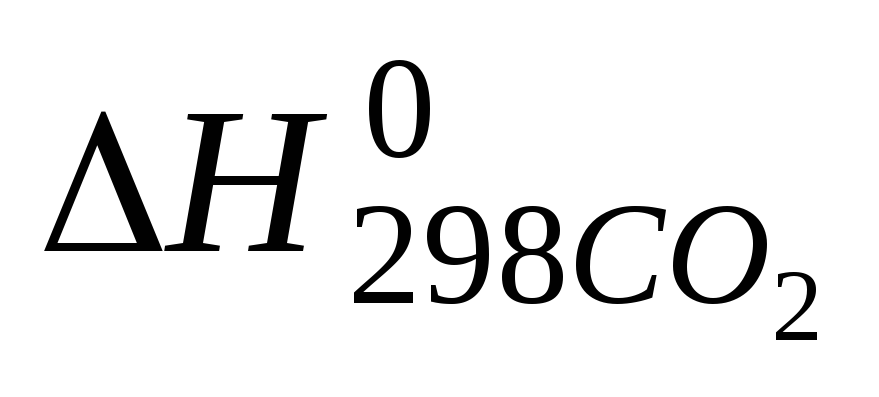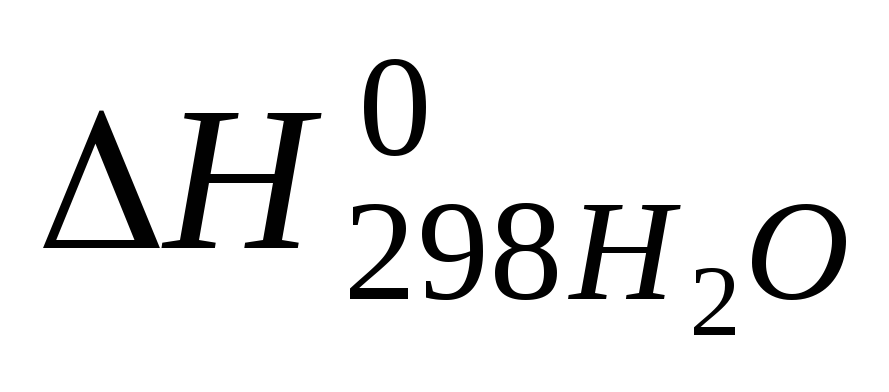Теплоты образования исоответственно равны -103,8; -393,6 и-241,9 кДж/моль.

Тепловой эффект реакции горения С₃Н₈(г) рассчитывается по формуле:

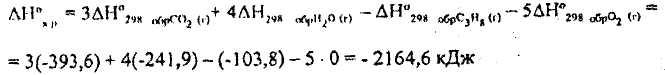
Практическая часть

Методика проведения опытов:

Для определения тепловых эффектов процессов, протекающих в водных растворах, используют простейший калориметр, приведенный на рис 2.1.

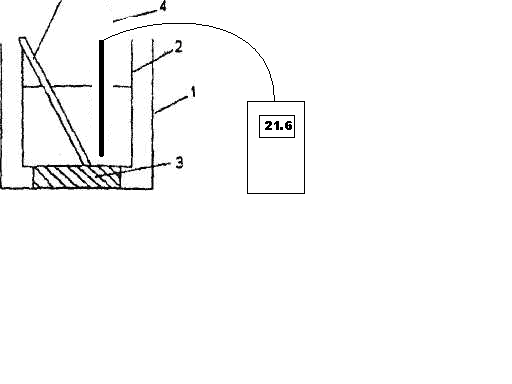
Рис.2.1. Схема калориметра:

1 — внешний стакан калориметра; 2 -внутренний стакан калориметра, 3 — теплоизолирующая прокладка; 4-термометр; 5 — мешалка.

Так как слой воздуха, находящийся между стенками внешнего и внутреннего стаканов калориметра, является хорошим теплоизолятором, то все тепло, выделяющееся (или поглощающееся) в результате протекания реакции, идет на нагревание (или охлаждение) реакционной смеси и внутреннего стакана калориметра. Экспериментально определяется изменение температуры реакционной смеси, сопровождающее данный процесс. Для этого во внутренний стакан калориметра отмеривают с помощью мерного цилиндра 25 — 30 мл воды и измеряют начальную температуру t_нач. с помощью термометра, который помещают непосредственно в жидкость, следя, чтобы он не касался дна и стенок внутреннего стакана (см. рис.1).

Не вынимая термометра из жидкости, во внутренний стакан засыпают сухую соль. Раствор перемешивают мешалкой до полного растворения, следя одновременно за показаниями термометра. Температура в ходе процесса может повышаться или понижаться. Конечную температуру t_кон. фиксируют в тот момент, когда столбик термометра останавливается.

Все данные, необходимые для расчетов, сводят в таблицу (форма таблицы дана в описании опытов).

Тепловой эффект процесса, протекающего в калориметре, рассчитывается по формуле:

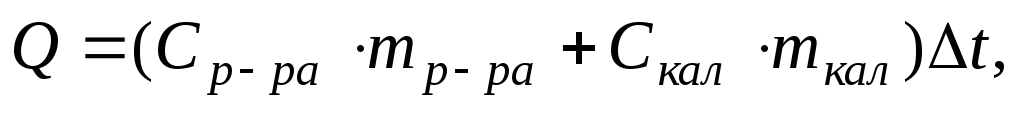
где С_р._ра — удельная теплоемкость раствора, находящегося во внутреннем стакане калориметра, которую можно принять равной удельной теплоемкости воды С_н0 — 4,18 Дж/г град;

т_р-ра — масса раствора во внутреннем стакане калориметра, г;

С_кал — удельная теплоемкость внутреннего стакана калориметра;

т_кал — масса калориметра;

Δt — изменение температуры в ходе опыта, град С.

Учитывая, что удельная теплоёмкость стекла, из которого сделан внутренний стакан калориметра, мала, вторым слагаемым можно пренебречь, тогда формула для расчета теплового эффекта примет вид:

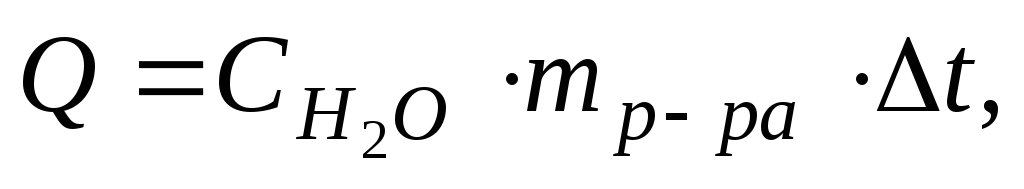
Опыт №1. Определение мольной теплоты растворения соли.

Опыт проводят согласно описанию с выданной преподавателем навеской соли. Химическая формула соли и ее масса указаны на обертке навески. Данные, необходимые для расчета, сводят в таблицу 2.1.

Таблица 2.1. Параметры для расчета мольной теплоты растворения соли.

Химическаяформула соли	г	г				г/моль	Дж/г·град	кДж/моль
1.							4,18
2.							4,18

Мольную теплоту растворения, то есть теплоту, выделяющуюся или поглощающуюся при растворении в воде 1 моля соли, рассчитывают по формуле:

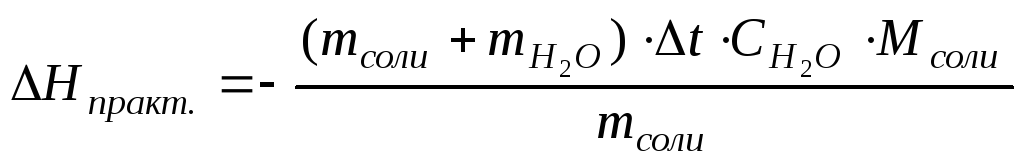
Пользуясь приведенной в конце работы таблицей, в которой приведены теоретические значения мольных теплот растворения некоторых солей, рассчитайте относительную погрешность определения:

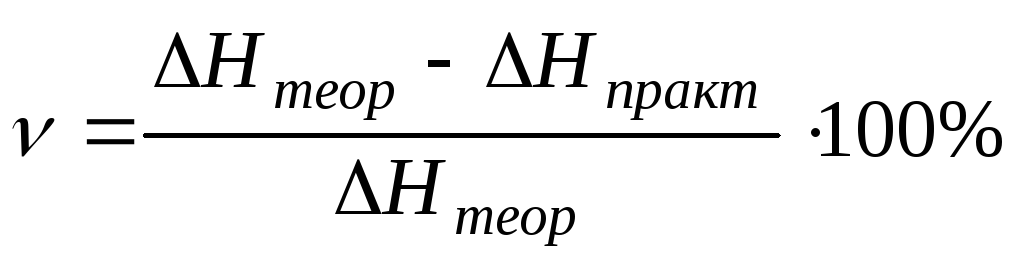
Опыт №2. Определены мольной теплоты гидратации соли.

Гидратацией называют процесс присоединения к соли определенного количества молекул воды с образованием кристаллогидрата данной соли, например:

Na₂СO₃ + l0H₂O = Na₂CO₃ · 10Н₂О.

Для определения мольной теплоты гидратации в воде растворяют сначала навеску

безводной соли:

Na₂СO₃ + пH₂O = Na₂CO₃ · пН₂О; ΔНрастворения безв.соли

а затем навеску кристаллогидрата данной соли

Na₂CO₃ · 10Н₂О + (п-10)H₂O = Na₂CO₃ · пН₂О; ΔНрастворения кристаллогидрата

Оба процесса проводят согласно описанию, данному в практической части, и данные вносят в таблицу 2.1.

Пользуясь формулой для расчета мольной теплоты растворения, приведенной в 1-ом опыте, рассчитывают ΔН растворения безводной соли и кристаллогидрата.

Теплоту гидратации вычисляют, пользуясь законом Гесса:

ΔНрастворения безв.соли = ΔНгидратации + ΔНрастворения кристаллогидрата

Относительную погрешность определения рассчитывают исходя из данных табл.2.

Таблица 2.2. Мольные теплоты растворения и гидратации для некоторых солей и кристаллогидратов

Формула соли или кристаллогидрата	ΔНгидратации, кДж/моль	ΔНрастворения, кДж/моль
CuSO4 · 5Н2О	77,8	+10,50
ZnSO4 · 7H2O	-95,0	+18,87
K2Cr207		+70,0
Na2CO3 безв.		-25.0
MgSO4		-84,8
СаС12		-72,8
Na2SO4·10H2O	80,5
NH4NO3		+26,8
Na2S2O3		+27,6

Выводы:

в выводах каждого опыта должно быть указано, какой тип реакций — экзо- или эндотермическая — наблюдается для данной соли и на основании чего можно сделать такое заключение.

Лабораторная работа №3

1.4.2. Тепловой эффект химической реакции. Термохимические уравнения.

Любые химические реакции всегда сопровождаются теми или иными энергетическими эффектами, выделением или поглощением тепла, совершением электрической или механической работы.

Изучением энергетических эффектов химических и физико-химических явлений занимается наука, называемая химической термодинамикой.

Количество выделившейся или поглотившейся теплоты в химической реакции называется тепловым эффектом.

Химические реакции, в которых указан тепловой эффект реакции при Р,Т=const называются термохимическими.

Так как тепловой эффект зависит от агрегатного состояния вещества, его обозначают нижними индексами справа у химических формул

(к – кристаллическое, г – газообразное, ж ‑ жидкое).

Н_2(г) + Сl_2(г) = 2НСl_(г) + 185 кДж

Независимость теплового эффекта химической реакции от пути процесса при Р,Т = const была установлена в 1836 г русским ученым Гессом Германом Ивановичем. Закон Гесса гласит.

Тепловой эффект химической реакции не зависит от пути ее протекания, а зависит лишь от природы и агрегатного состояния исходных веществ и продуктов реакции.

1.4.3. Скорость реакции, ее зависимость от различных факторов.

Если рассмотреть две реакции: горения водорода 1. 2Н₂ + О₂ = 2Н₂О_(ж) и реакцию нейтрализации 2. Н⁺ + ОН^– = Н₂О_(ж), то с точки зрения химической термодинамики вероятность протекания первой реакции почти в 3 раза превышает вероятность протекания второй. Однако, скорость первой реакции очень мала:

при 25 С она прореагирует наполовину за 500 млрд лет;

при 300 С прореагирует наполовину за 300 млн лет;

при 600 С прореагирует наполовину за доли секунды.

В то же время реакция нейтрализации с образованием воды, протекающая в растворах, вероятность протекания которой значительно меньше по сравнению с первой реакцией, идет практически мгновенно.

Представление о скоростях химических реакций и факторах, влияющих на скорость, исключительно важно для управления химическими процессами.

Область химии, изучающая молекулярный механизм химических реакций и скорость их протекания, называется ХИМИЧЕСКОЙ КИНЕТИКОЙ.

В зависимости от типа химической реакции, их скорость может определяться по-разному, поэтому необходима классификация химических реакций.

На данном этапе мы ограничимся изучением только гомогенных реакций.

Гомогенные реакции – протекающие в однородной среде без каких-либо границ раздела между реагирующими веществами (газ, раствор). В этом случае молекулы всех реагирующих веществ находятся в одинаковых условиях.

В результате химической реакции происходит изменение количества исходных веществ и образование новых. Поэтому для гомогенных реакций скорость химической реакции измеряется изменением концентрации реагирующих веществ в единицу времени:

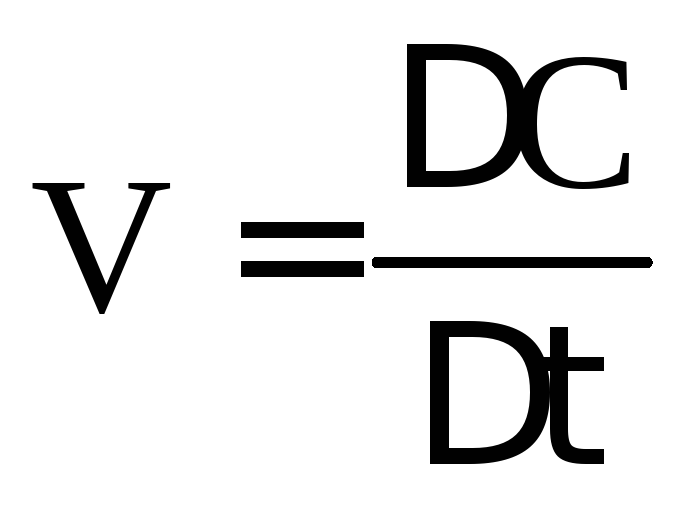‑средняя скорость реакции за промежуток времени Dτ.

Скорость химической реакции – величина переменная по времени, т.к. концентрации веществ непрерывно изменяются, поэтому часто используют истинную (мгновенную) скорость реакции.

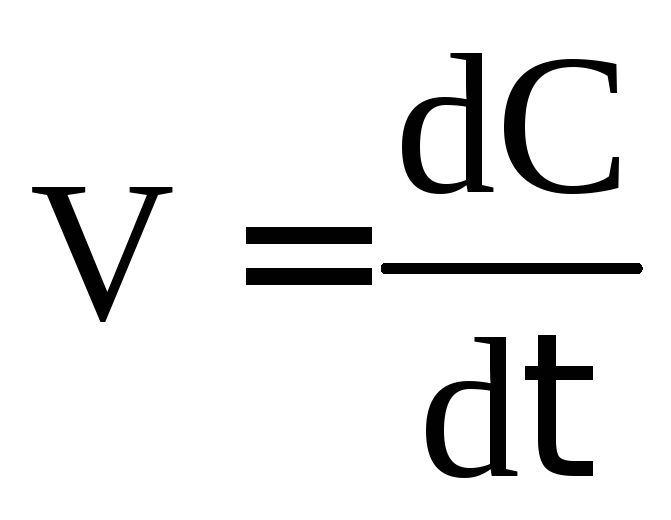при Dτ ® 0.

Скорость реакции можно измерять, зная изменение концентрации хотя бы одного участника реакции. Например, для реакции:

аА + вВ = сС + dD

ее скорость можно определить по любому участнику реакции с учетом стехиометрических коэффициентов (минус для реагентов, т.к. их концентрация в процессе реакции уменьшается, плюс для продуктов, т.к. их концентрация увеличивается):

V = .

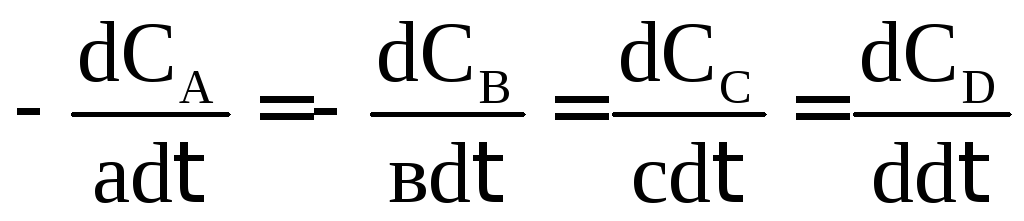Зависимость скорости реакции от концентрации реагирующих веществ.

Необходимым условием для осуществления акта химического взаимодействия между молекулами должно быть их столкновение, необходимое для разрушения старых и образования новых связей. Столкновение молекул в некотором реакционном пространстве при заданной температуре происходит тем чаще, тем больше этих молекул. Поэтому скорость реакции зависит от концентрации реагирующих веществ.

С этой точки зрения интересно рассмотреть такую задачу.

Пример. Какая реакция протекает с наибольшей скоростью при комнатной температуре?

1. Zn  и  HCl (1% р-р)

2. Zn  и  HCl (30% р-р)

3. Zn  и  HCl (10% р-р)

4. ZnCl₂ (р-р)   и  AgNO₃ (р-р).

В растворе некоторые вещества (сильные электролиты) подвергаются электролитической диссоциации на ионы. Таким образом, в растворах первую задачу – разрушение старых связей – осуществляет полярный растворитель (в водных растворах – вода). Напишем молекулярные и ионные уравнения этих реакций (для 1-3 реакций они будут одинаковы).

Zn  +  2HCl = ZnCl₂ + Н₂; Zn  +  2H⁺ + 2Cl^— = Zn²⁺ + 2Cl^— + Н₂

4. ZnCl₂ + 2AgNO₃ = 2AgCl + Zn(NO₃)₂;

Zn²⁺ + 2Cl^— + 2Ag⁺ + 2NO₃^— = 2AgCl + Zn²⁺ + 2NO₃^—.

Видно, что для первых трех реакций, чтобы прошла реакция необходимо превратить цинк в ион. На это надо затратить определенную энергию, поэтому скорость этих реакций будет меньше, чем в реакции №4, где эту работу: образование ионов хлора и серебра сделал полярный растворитель – вода.

Реакции, проходящие в растворах без изменения степеней окисления, называются ионообменными и они протекают практически мгновенно.

Если мы рассматриваем скорости 1-3 реакций, то наибольшая среди них будет реакция №2, так как концентрация соляной кислоты больше.

Основным законом химической кинетики является открытый в 1864-1867 г.г. Гульдбергом и Вааге закон действующих масс для скорости химической реакции (ЗДМ).

Скорость элементарной (простой) реакции пропорциональна произведению концентрации реагирующих веществ в степенях, равных стехиометрическим коэффициентам в уравнении реакции.

Для условно простой реакции аА +bВ = продукты математическая запись ЗДМ будет иметь вид (обращаю Ваше внимание, что концентрации веществ, входящие в это уравнение неравновесные). Чем дальше от состояния равновесия, тем скорость больше, а в состоянии равновесия скорость реакции равна нулю. Равновесные концентрации обозначаются в квадратных скобках, поэтому запись этого закона в таком виде V=k^.[A]^a.[B]^b не имеет смысла, так как V=0 в состоянии равновесия.

.

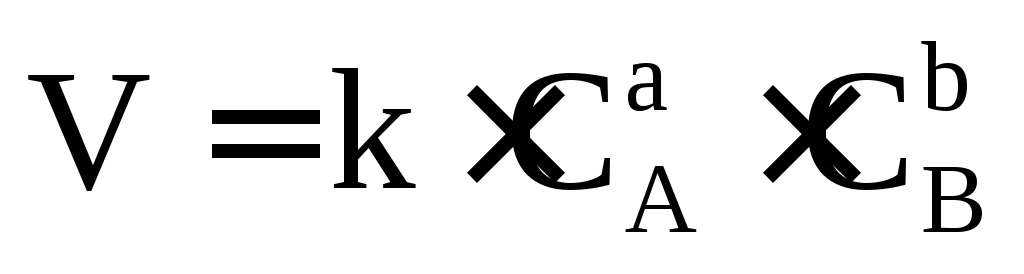ЗДМ справедлив только для наиболее простых по своему механизму взаимодействий, протекающих в газах или разбавленных растворах, поэтому все химические реакции делятся на простые (элементарные) и сложные.

Простые реакции идут в одну стадию без образования промежуточных соединений. Они характеризуются молекулярностью реакции. Она определяется числом молекул, одновременным взаимодействием которых осуществляется акт химического взаимодействия. В зависимости от этого простые реакции бывают:

мономолекулярные – I₂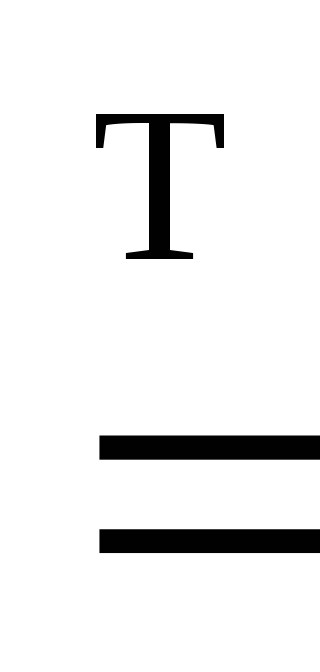2I;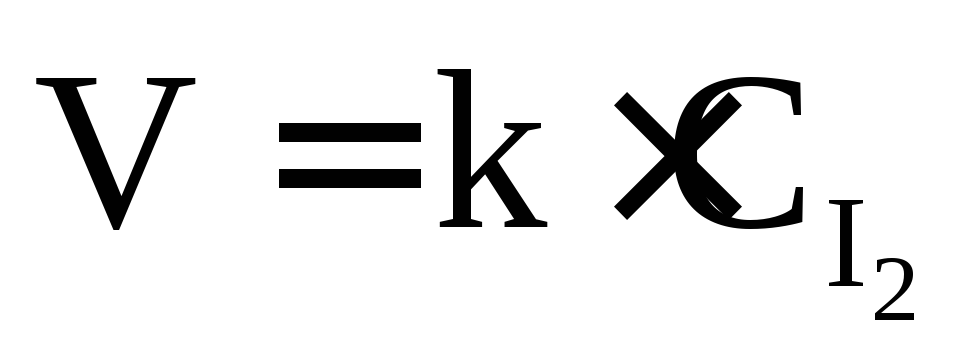; реакция первого порядка;

бимолекулярные – Н₂ + I₂ = 2HI; 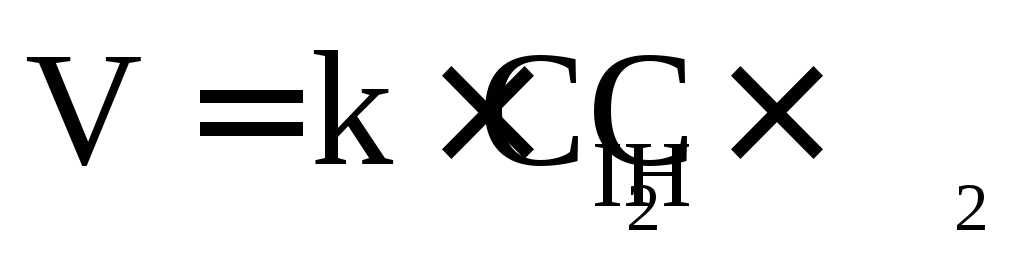; реакция второго порядка;

тримолекулярные – 2NO + H₂ = N₂O + H₂O; 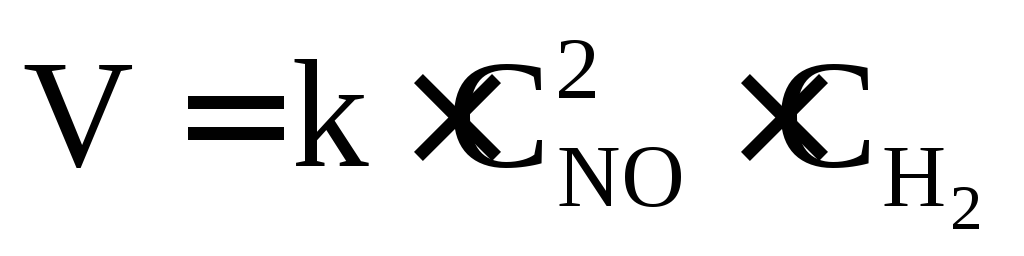; реакция третьего порядка. Тримолекулярных реакций известно очень мало.

Мы ограничились рассмотрением только гомогенных простых реакций, но большинство реакций сложные и гетерогенные, которые протекают на границе раздела фаз. Математическое выражение для закона действующих масс в этом случае получило название кинетического уравнения.

Интересно рассмотреть задачу, подобные которой встречаются в тестах ЕГЭ.

Пример. От чего зависит скорость химической реакции между медью и азотной кислотой?

Гетерогенными называются реакции, протекающие в среде, разделенной на отдельные части физическими границами раздела, на которых и происходит химическое взаимодействие.

Для гетерогенной реакции ее скорость зависит от величины поверхности раздела между взаимодействующими фазами. Если в реакции участвует твердое тело, то его концентрация не входит в кинетическое уравнение, т.к. она практически не меняется. Роль твердого тела отражается введением его поверхности, на которой протекает данная реакция.

Кинетическое уравнение для нашей реакции: Cu + HNO₃ = продукты выглядит так.

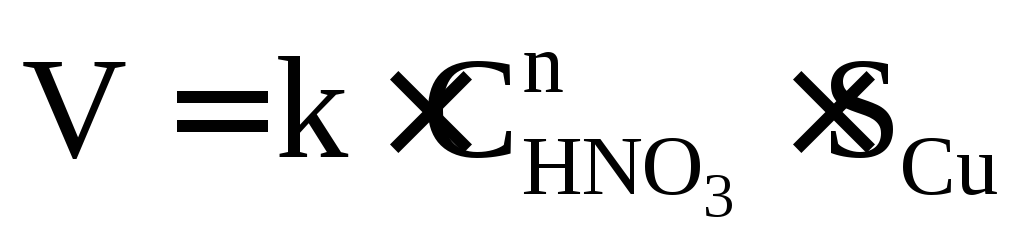
Согласно нашему кинетическому уравнению скорость реакции зависит только от концентрации азотной кислоты, но не зависит от объема колбы, в которой проходит реакция; от объема кислоты и практически не зависит от массы меди, так как поверхность раздела при этом изменяется незначительно. Больший эффект увеличения скорости будет, если применять мелко раздробленную медь, но основным фактором все же остается изменение концентрации кислоты.

Зависимость скорости реакции от температуры

Скорость подавляющего большинства химических реакций при повышении температуры возрастает, причем она очень чувствительна к изменению температуры. Зависимость скорости реакции от температуры старались установить многие ученые. Так в 1884 г. голландский ученый Якоб Вант Гофф, изучив примерно 50 различных реакций, пришел к выводу, что при повышении температуры на каждые 10 градусов скорость гомогенной реакции увеличивается в 2-4 раза. (Правило Вант-Гоффа).

Однако, это чисто эмпирически выведенное правило Вант-Гоффа справедливо не для всех реакций, но оно удобно для примерной оценки изменения скорости химической реакции от температуры, если температурный коэффициент определен.

Химическое взаимодействие между двумя частицами происходит при их столкновении, которое необходимо для разрыва старых и образования новых связей. Однако если бы каждое столкновение частиц приводило к их взаимодействию, то все реакции протекали бы мгновенно. На самом деле не каждое столкновение приводит к взаимодействию, а только такое, при котором энергия сталкивающихся частиц достаточна для возбуждения их связей.

Энергия, необходимая для приведения одного моль реагирующих молекул в реакционноспособное состояние, называется энергией активации. Е_а (кДж/моль)

То есть скорость химической реакции носит пороговый характер. Столкновение частиц с Е>Е_а приводит к реакции. Энергия активации реакции зависит от природы частиц и пути (механизма) реакции. Энергия активации, наряду с порядком реакции, очень важная кинетическая характеристика химической реакции. В дальнейшем на основе данных молекулярно-кинетической теории с учетом энергии активации Аррениусом было выведено уравнение, связывающее скорость химической реакции с температурой.

Рассмотрение этого материала Вам предстоит уже в ВУЗе.