Проверочный тест по алгебре по теме «Решение линейных уравнений», (7 класс)
Проверочный тест по теме
«Решение линейных уравнений» (7 класс)
I вариант:
Обязательная часть.
А1. Найдите корень уравнения 2х – 1 = 7.
Варианты ответов:
а) 4
б) 3
в) -4
г) -3
А2. Решите уравнение -3у = 27.
Варианты ответов:
а) 9
б) -9
в) 81
г) -81
А3. Решите уравнение 4х + 4 = -6х – 5.
Варианты ответов:
а) -0,9
б) 4,5
в) -4,5
г) 0,9
А4. Какое из чисел является корнем уравнения 4(х + 6) = х.
Варианты ответов:
а) 8
б) -8
в) 6
г) -6
Дополнительная часть.
В1. Решите уравнение 4 – 2(5 + 4х) –х + 1.
Решение: ______________________________________________________________________________________________________________________________________________________
Ответ:
В2. Решите уравнение -2х + 1 -3(х – 4) = 4(3 – х) + 4.
Решение: ______________________________________________________________________________________________________________________________________________________
II вариант:
Обязательная часть.
А1. Найдите корень уравнения 2х – 10 = — 4.
Варианты ответов:
а) 7
б) 3
в) -7
г) -3
А2. Решите уравнение 4у = -36.
Варианты ответов:
а) 9
б) -9
в) 144
г) -144
А3. Решите уравнение 3х + 3 = -2 — 7х .
Варианты ответов:
а) -0,5
б) 0,25
в) -0,25
г) 0,5
А4. Какое из чисел является корнем уравнения 9(х + 7) = -х.
Варианты ответов:
а) 2
б) -2
в) 6,3
г) -6,3
Дополнительная часть.
В1. Решите уравнение 10 – 3(1 — 7х) –4х — 8.
Решение: ______________________________________________________________________________________________________________________________________________________
Ответ:
В2. Решите уравнение -2х + 1 +5(х – 2) = -4(3 – х) + 1.
Решение: __________________________________________________________________________________________________________________________________
xn--j1ahfl.xn--p1ai
б | в | |
б | в | |
б | в | |
3 | 1 | 2 | б | в |
3 | 2 | 4 |
doc4web.ru
Тест по алгебре (7 класс) на тему: Тест по теме: «Системы линейных уравнений»
Тест 7
«Системы линейных уравнений»
Вариант 1
А1. Какая из пар чисел является решением линейного уравнения .
1) 2) 3) 4)
А2. Для какого уравнения пара чисел является решением?
1) 2) 3) 4)
А3. Решите систему уравнений
1) 2) 3) 4)
А4. Пусть — решение системы линейных уравнений
Найдите . 1) 2) 3) 4)
А5. Пусть — решение системы линейных уравнений
Найдите . 1) 2) 3) 4)
А6. Пусть — решение системы линейных уравнений
Найдите . 1) 2) 3) 4)
А7. На каком из рисунков изображено графическое решение системы линейных уравнений
1) | 2) | 3) | 4) | |||
А8. Найдите координаты точки пересечения графиков уравнений и .
1) 2) 3) 4)
А9. Сколько точек пересечения имеют графики уравнений и ?
1) 1 2) 2 3) бесчисленное количество 4) ни одной
А10. Сколько решений имеет система уравнений
1) 1 2) 2 3) бесчисленное количество 4) ни одного
Тест 7
«Системы линейных уравнений»
Вариант 2
А1. Какая из пар чисел является решением линейного уравнения ?
1) 2) 3) 4)
А2. Для какого уравнения пара чисел является решением?
1) 2) 3) 4)
А3. Решите систему уравнений
1) 2) 3) 4)
А4. Пусть — решение системы линейных уравнений
Найдите . 1) 2) 3) 4)
А5. Пусть — решение системы линейных уравнений
Найдите . 1) 2) 3) 4)
А6. Пусть — решение системы линейных уравнений
Найдите . 1) 2) 3) 4)
А7. На каком из рисунков изображено графическое решение системы линейных уравнений
1) | 2) | 3) | 4) | |||
А8. Найдите координаты точки пересечения графиков уравнений и .
1) 2) 3) 4)
А9. Сколько точек пересечения имеют графики уравнений и ?
1) 1 2) 2 3) бесчисленное количество 4) ни одной
А10. Сколько решений имеет система уравнений
1) 1 2) 2 3) бесчисленное количество 4) ни одного
Ответы:
Вариант | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 |
1 | 1 | 4 | 2 | 2 | 1 | 3 | 2 | 4 | 3 | 4 |
2 | 4 | 4 | 3 | 3 | 4 | 2 | 1 | 2 | 4 | 3 |
nsportal.ru
Тест по алгебре в 7 классе «Системы линейных уравнений»
ТЕСТ «Системы линейных уравнений» 7класс
Вариант1
Часть А
А1. Даны уравнения с двумя переменными. Линейным является
1) 5x2+3y=7 2) x+y=10 3) 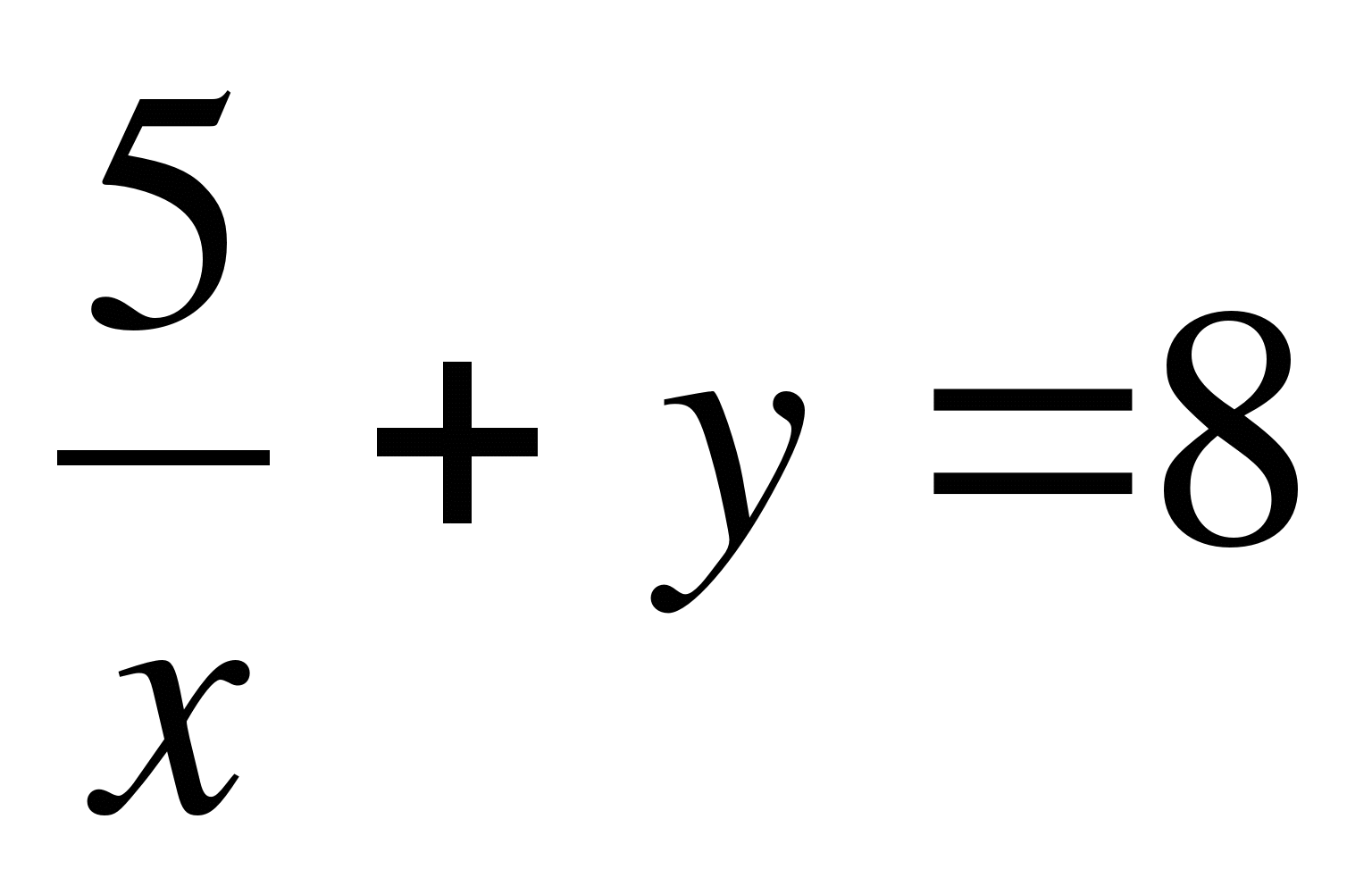 4) 7xy+x=5
4) 7xy+x=5
А2. Решением уравнения x – 2y= -4 является пара чисел
1) (2;0) 2) (0; -4) 3) (-4;0) 4) (1;-2)
А3. Выразите из уравнения 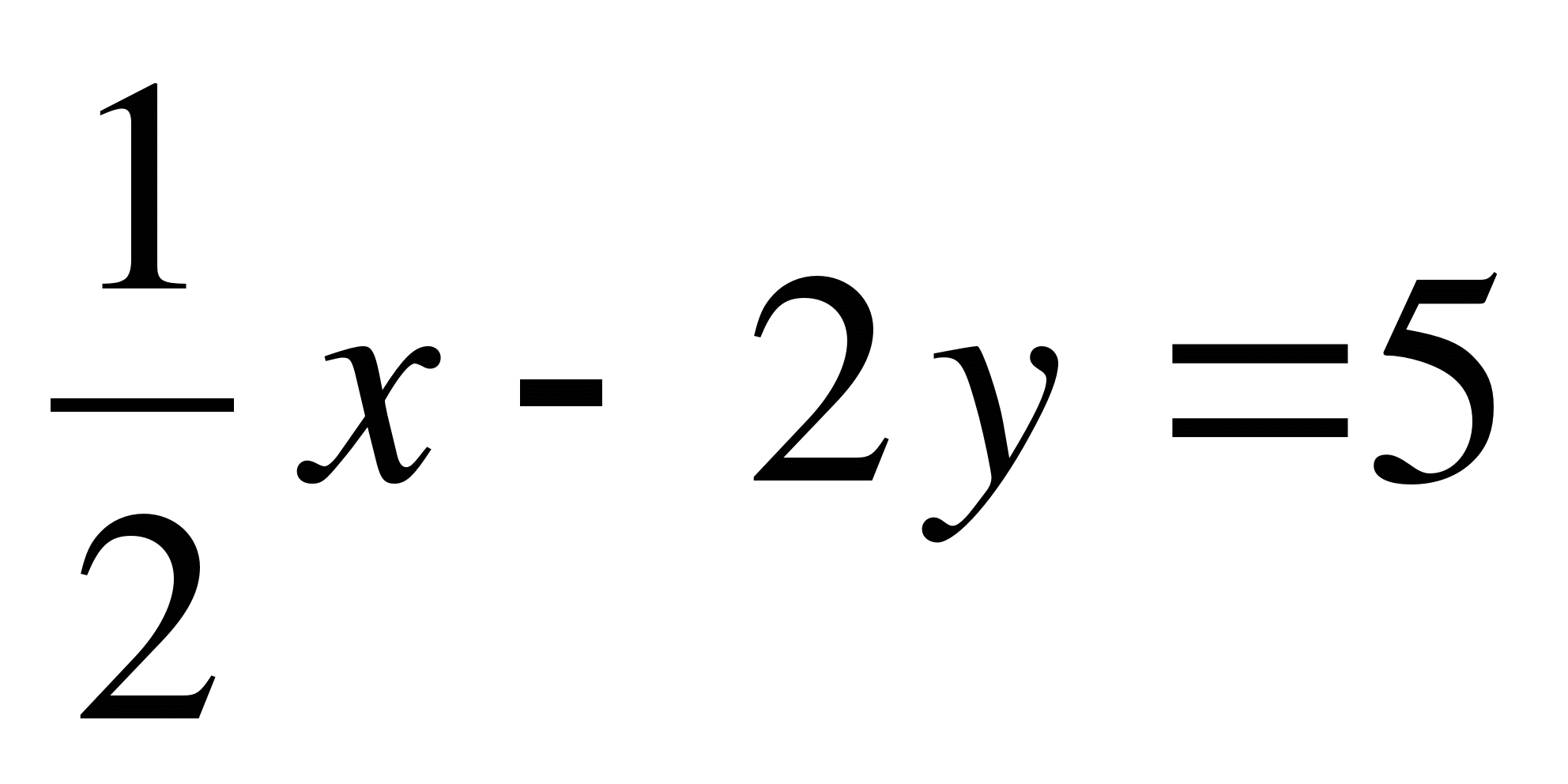 x через y
x через y
1) 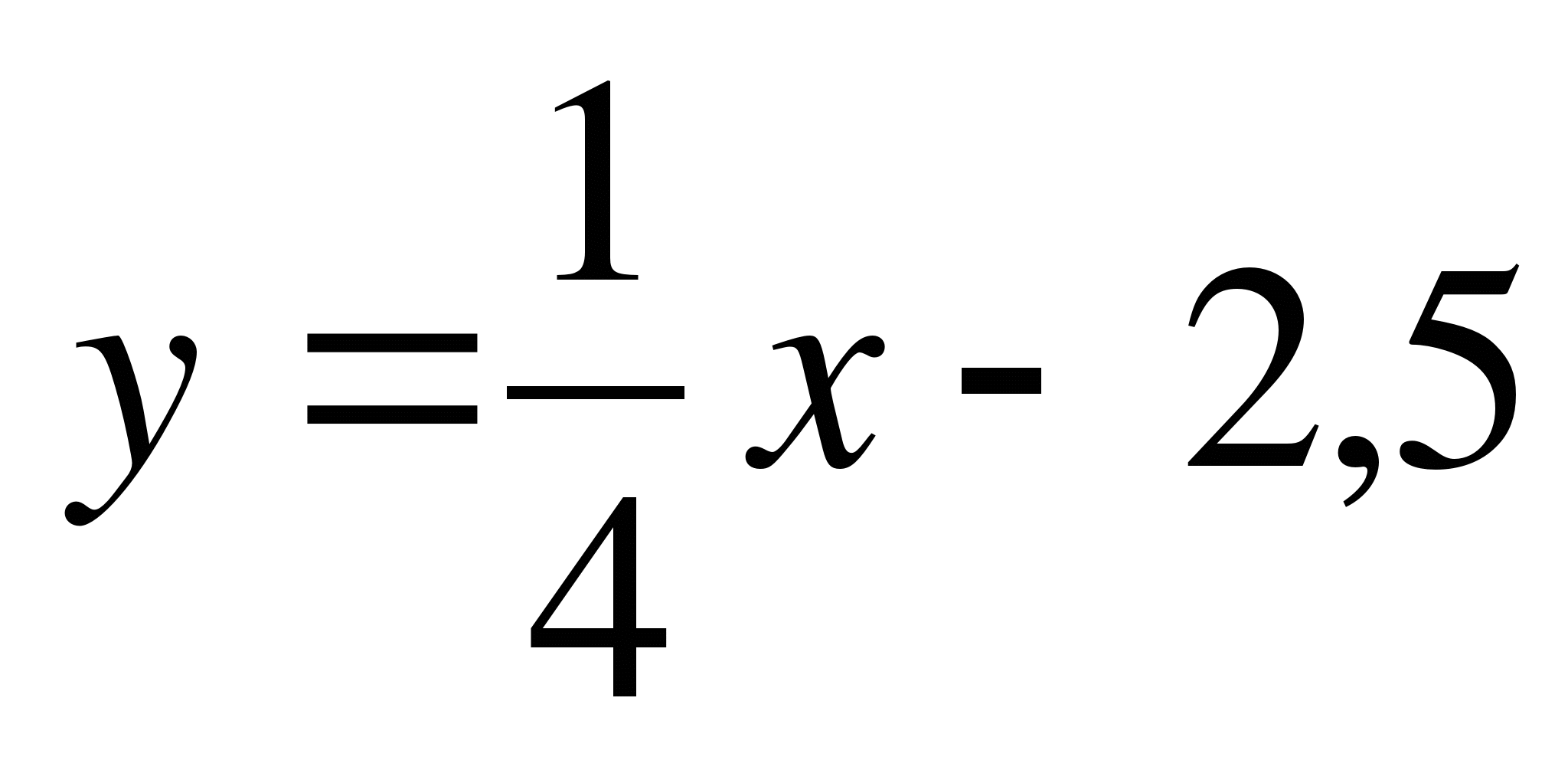 ; 2) y=x – 2,5; 3) x=y+2,5; 4) x
; 2) y=x – 2,5; 3) x=y+2,5; 4) x
А4. График уравнения х+2=0 изображен на рисунке
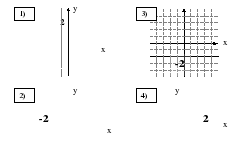








у
А5 Решением системы уравнений 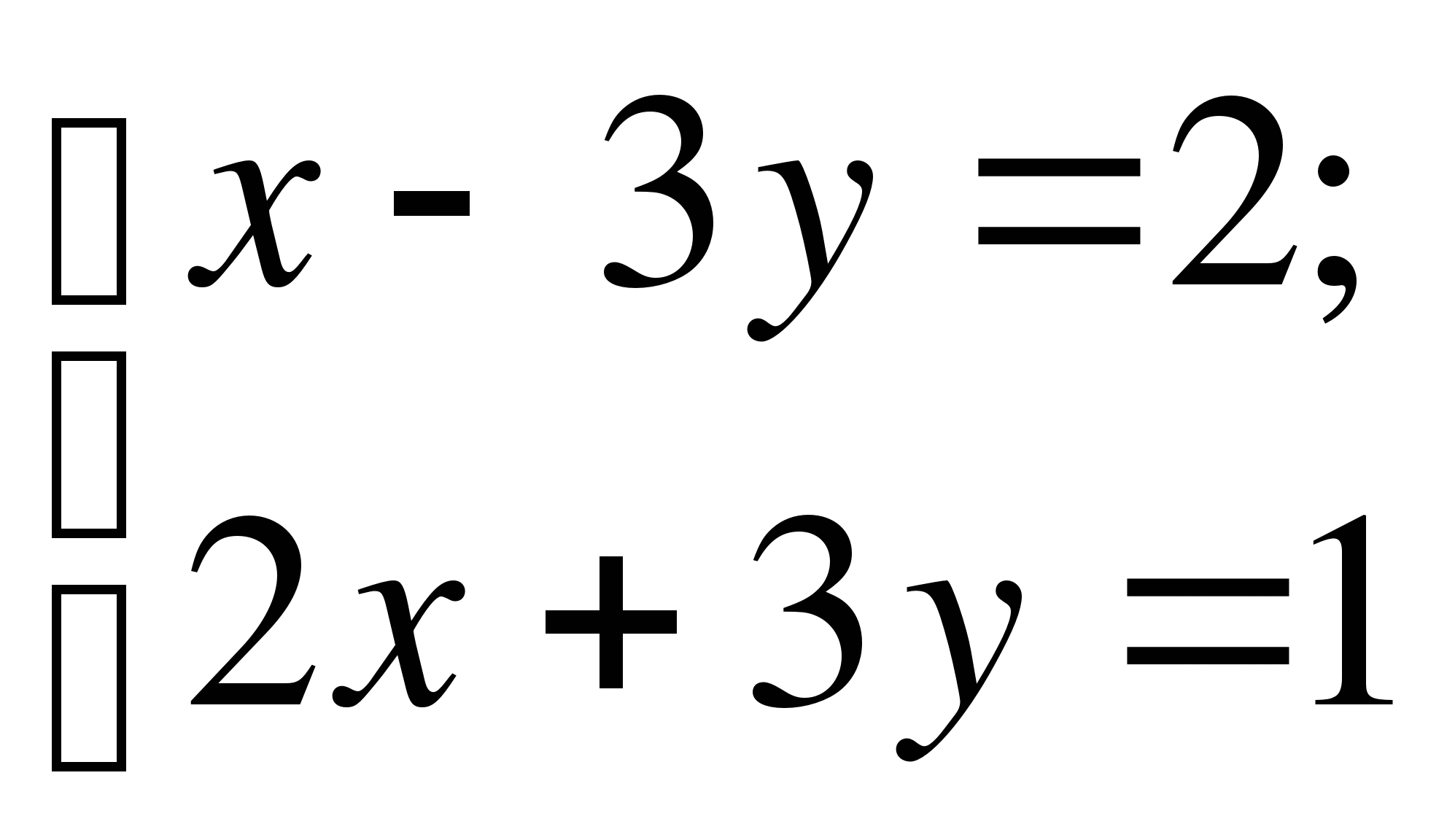 является пара чисел
является пара чисел
1) (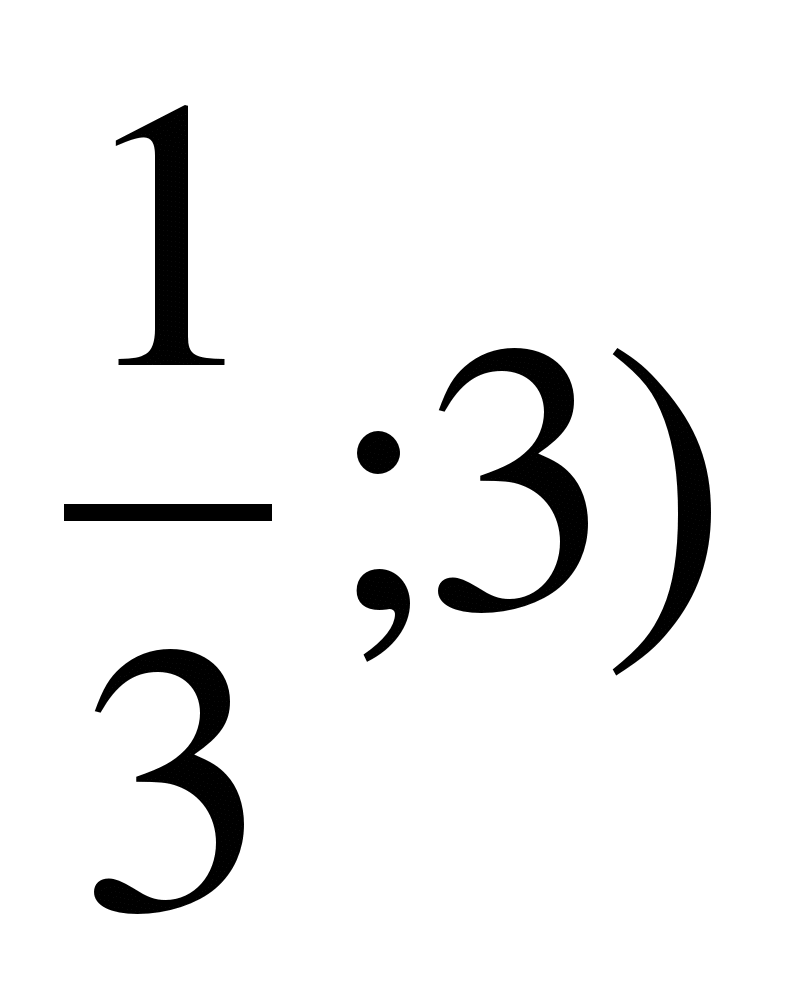 2) (
2) (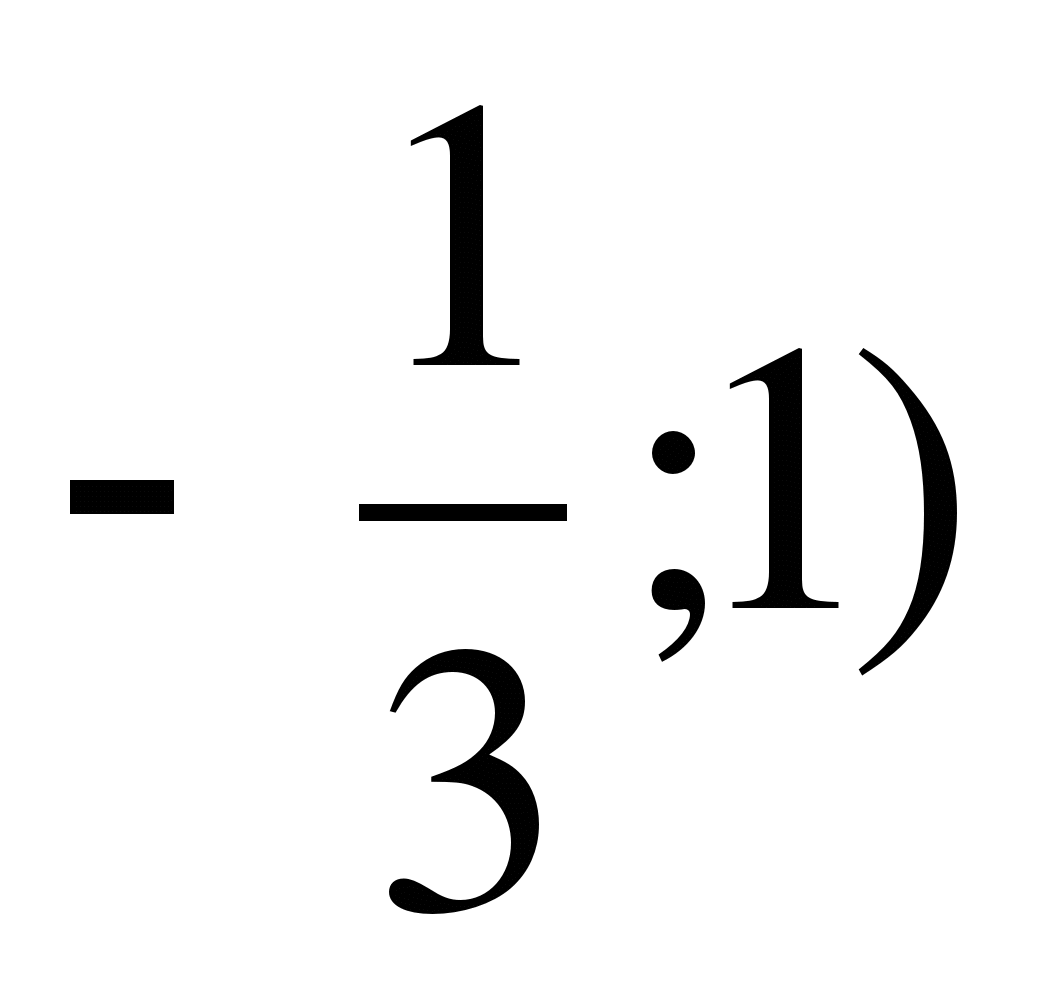 3)
3) 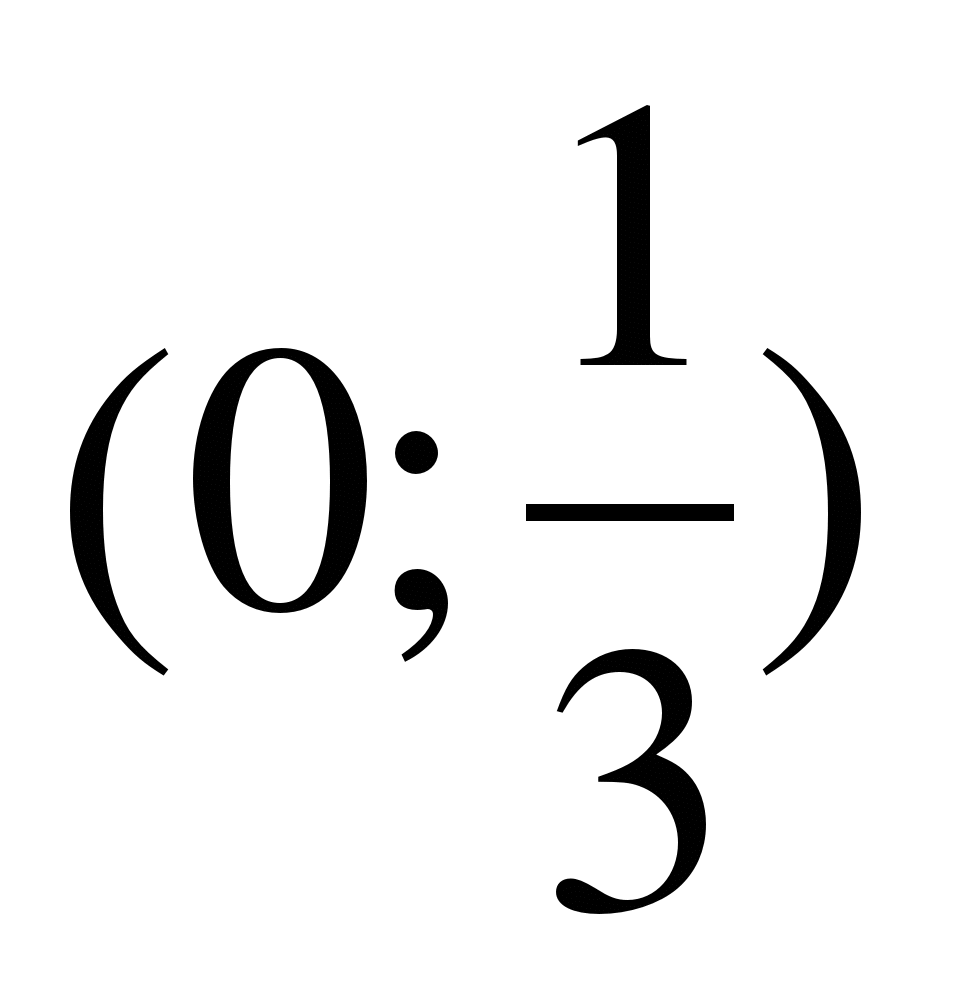
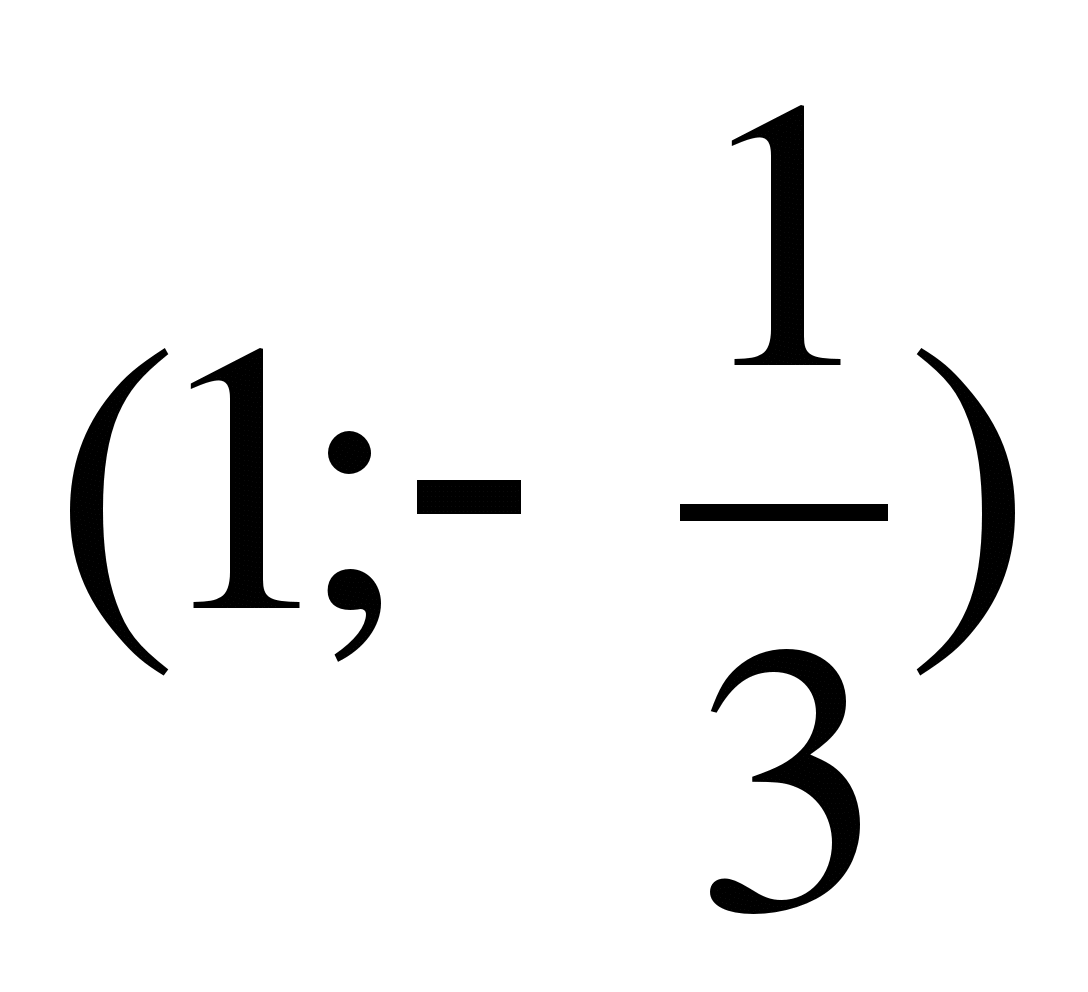
А6. Система двух линейных уравнений с двумя неизвестными может иметь
1) Одно решение 2) Два решения 3) Три решения 4) Четыре решения
А7. Система имеет единственное решение. Если первое её уравнение имеет вид 3х – 2у=1, то вторым уравнением будет
1) 6х – 4у=2; 2) 9х – 6у=4; 3) 3х+2у=1; 4) -3х+2у=1
А8. Система 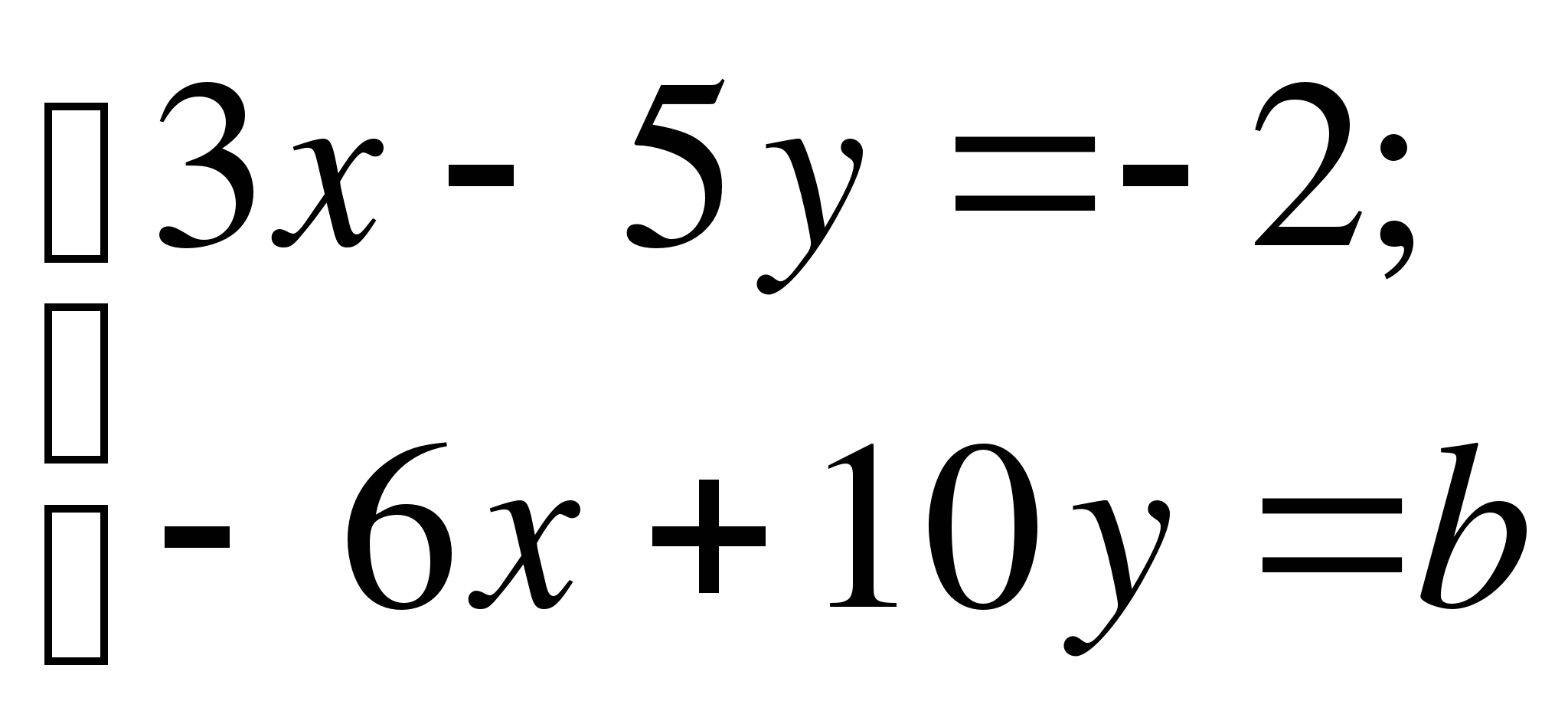 имеет бесконечно много решений, если b равно
имеет бесконечно много решений, если b равно
1) 4 2) -4 3) 1 4) 0
А9. Геометрическая иллюстрация решения системы, не имеющей решения, изображена на рисунке
1) 2) 3) 4)
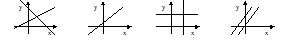
А


у
10. На рисунке изображено графическое решение системы 1
1
1
)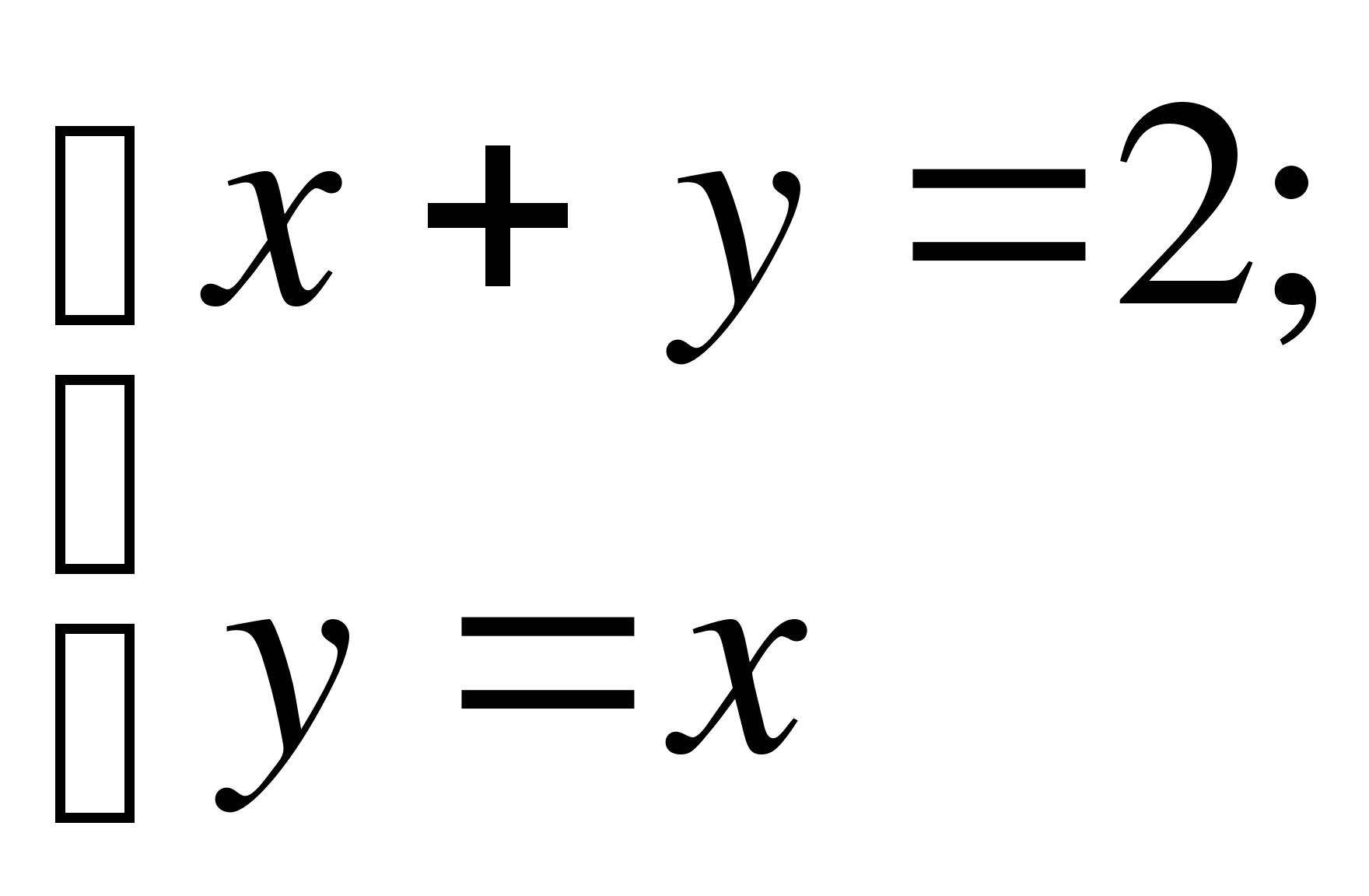 2)
2) 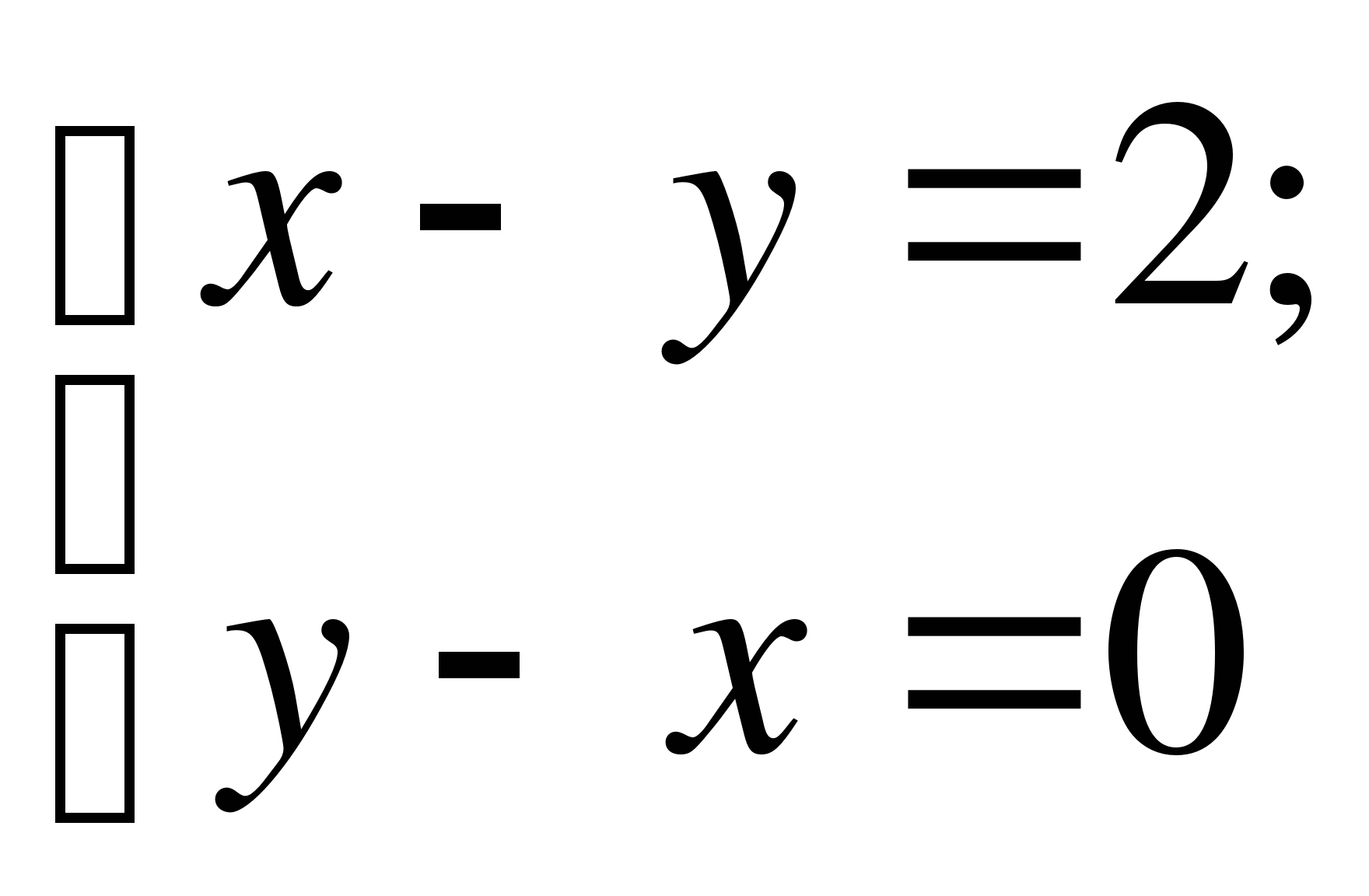
3
х
)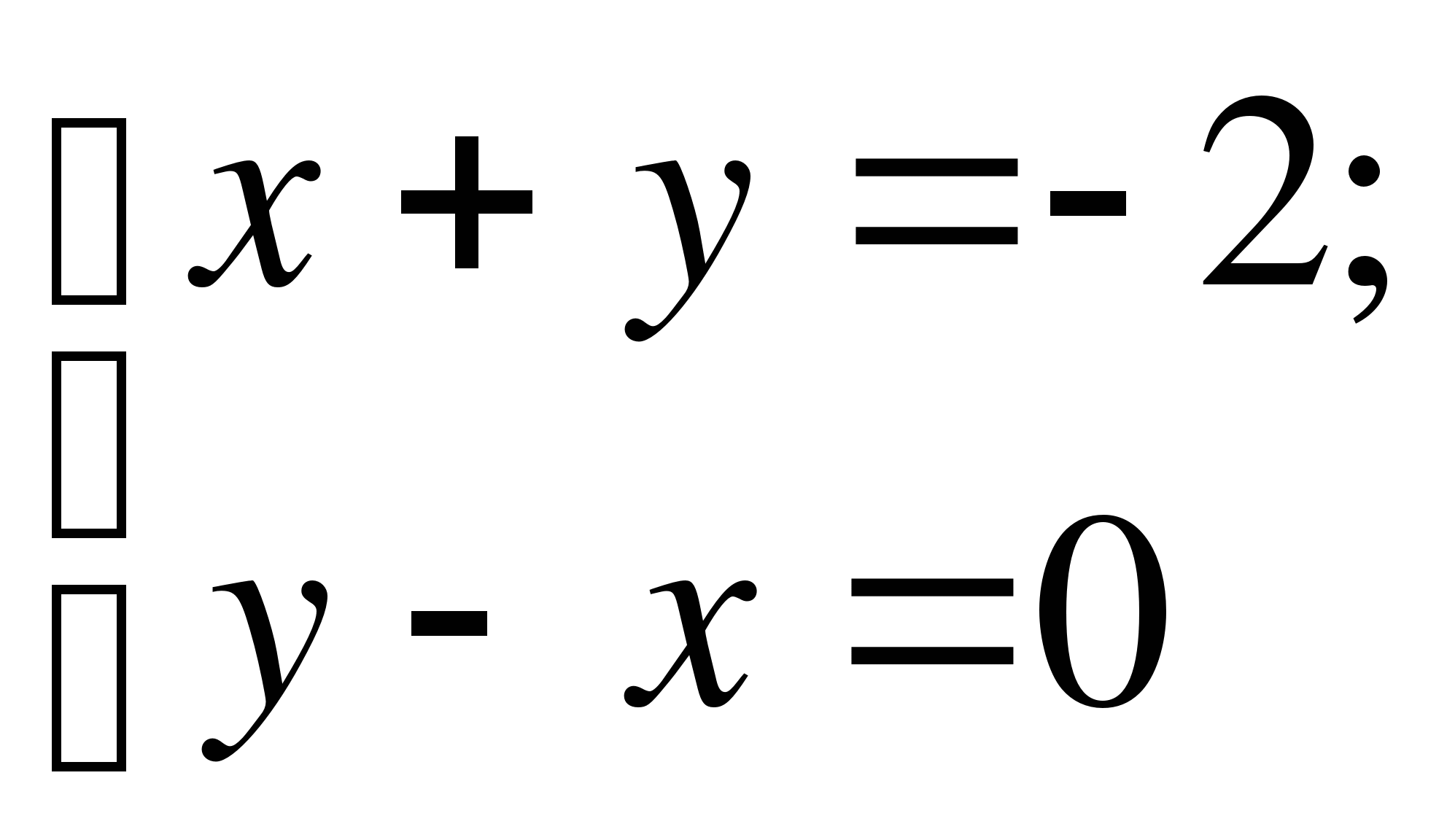 4)
4) 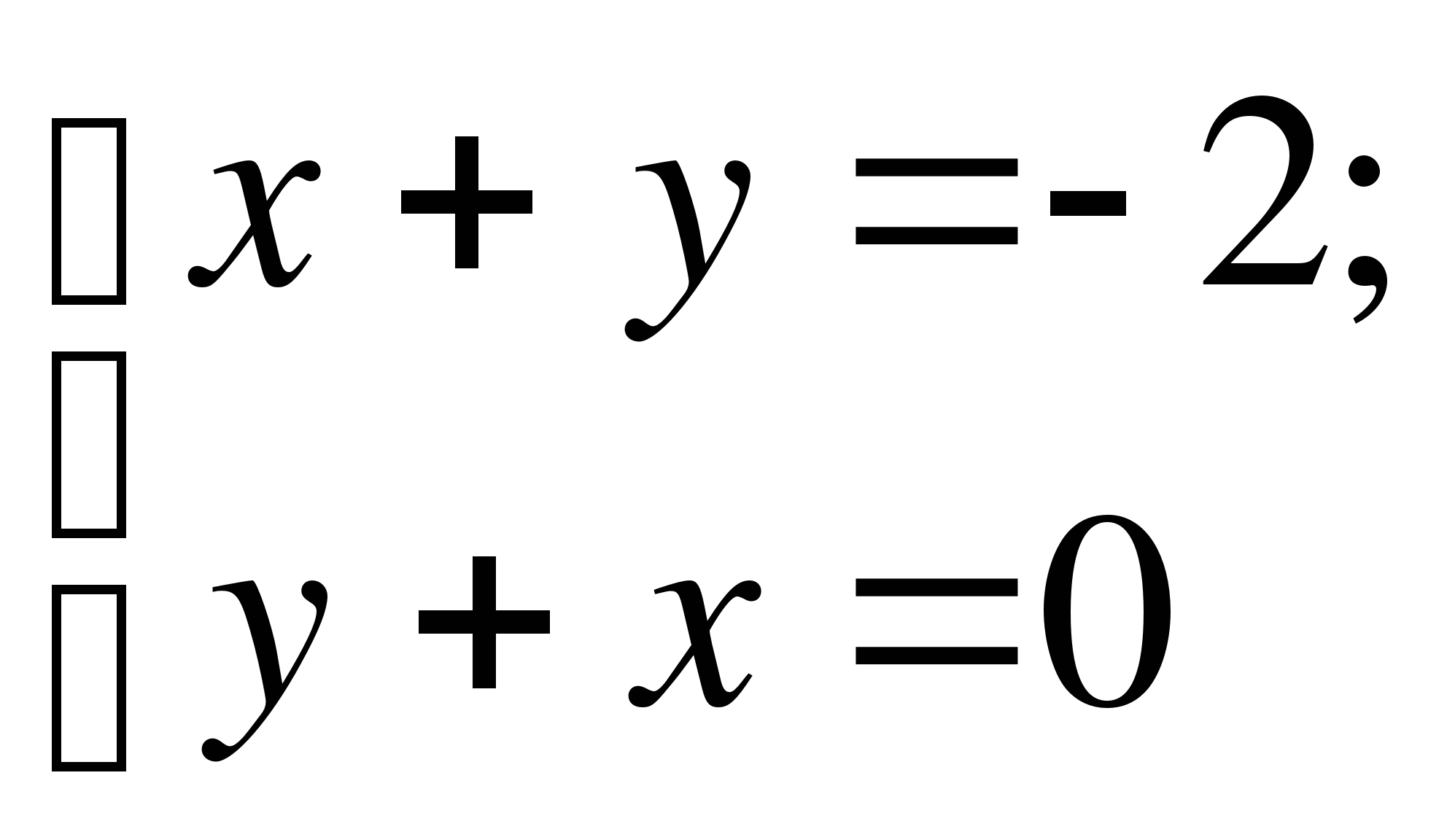
А11. Графики линейных уравнений х + у = -5 и 2х – у = -4 пересекаются в точке, расположенной в координатной четверти
1) I 2) II 3) III 4) IV
А12. Сумма двух чисел равна 48. Первое число больше второго в 2 раза. Найдите эти числа. Если х – первое число, а у – второе, тогда по условию задачи получим систему
1) 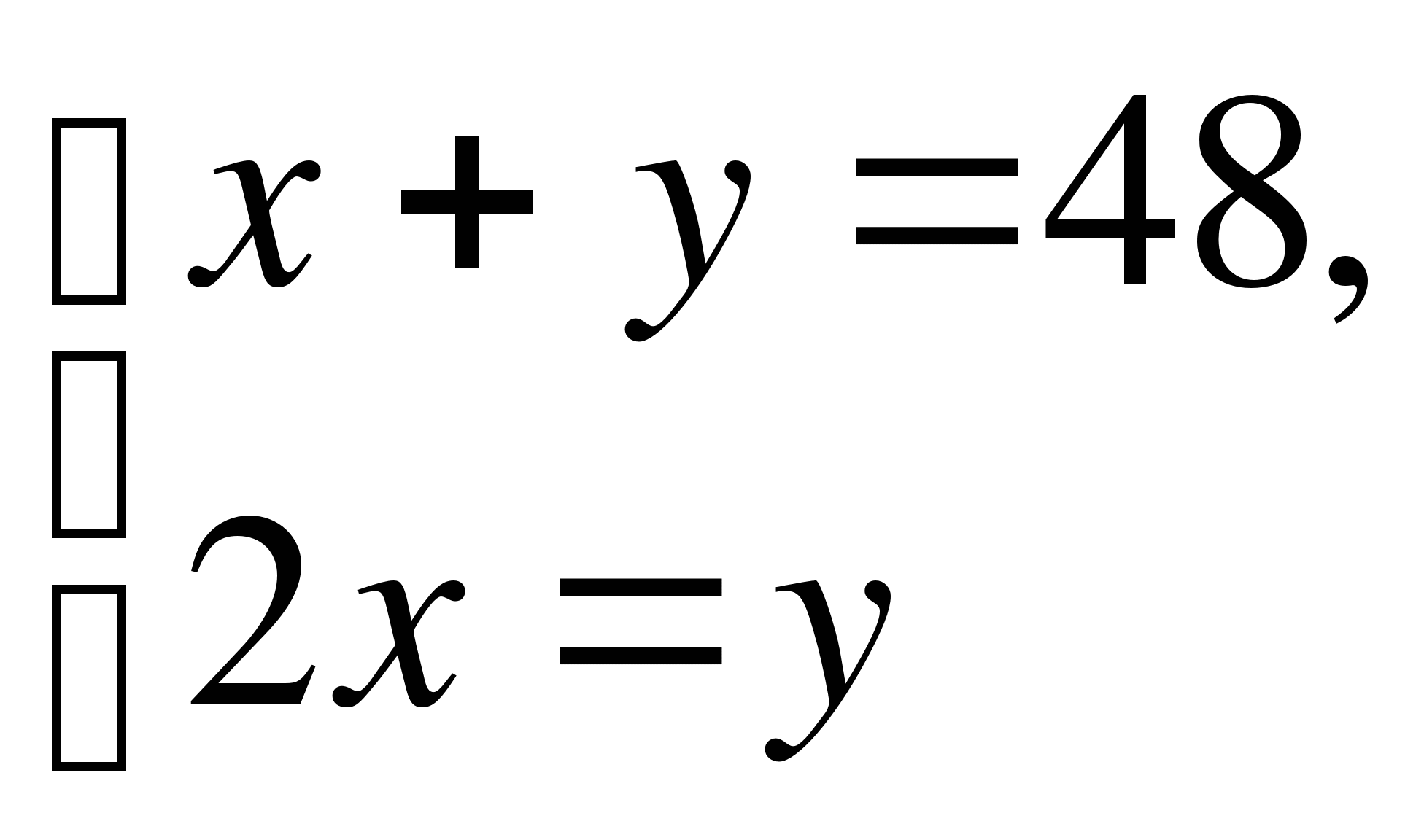 2)
2) 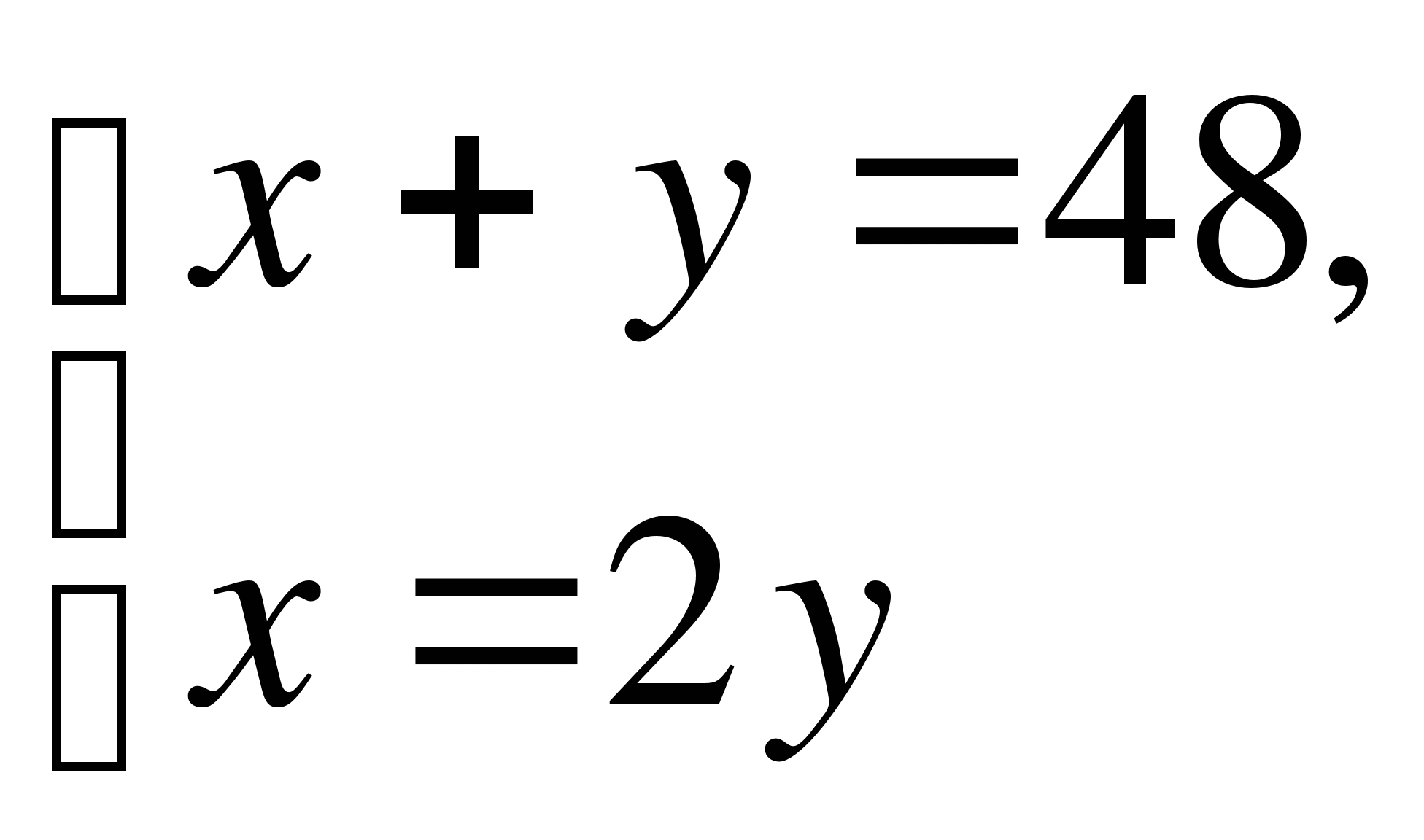 3)
3) 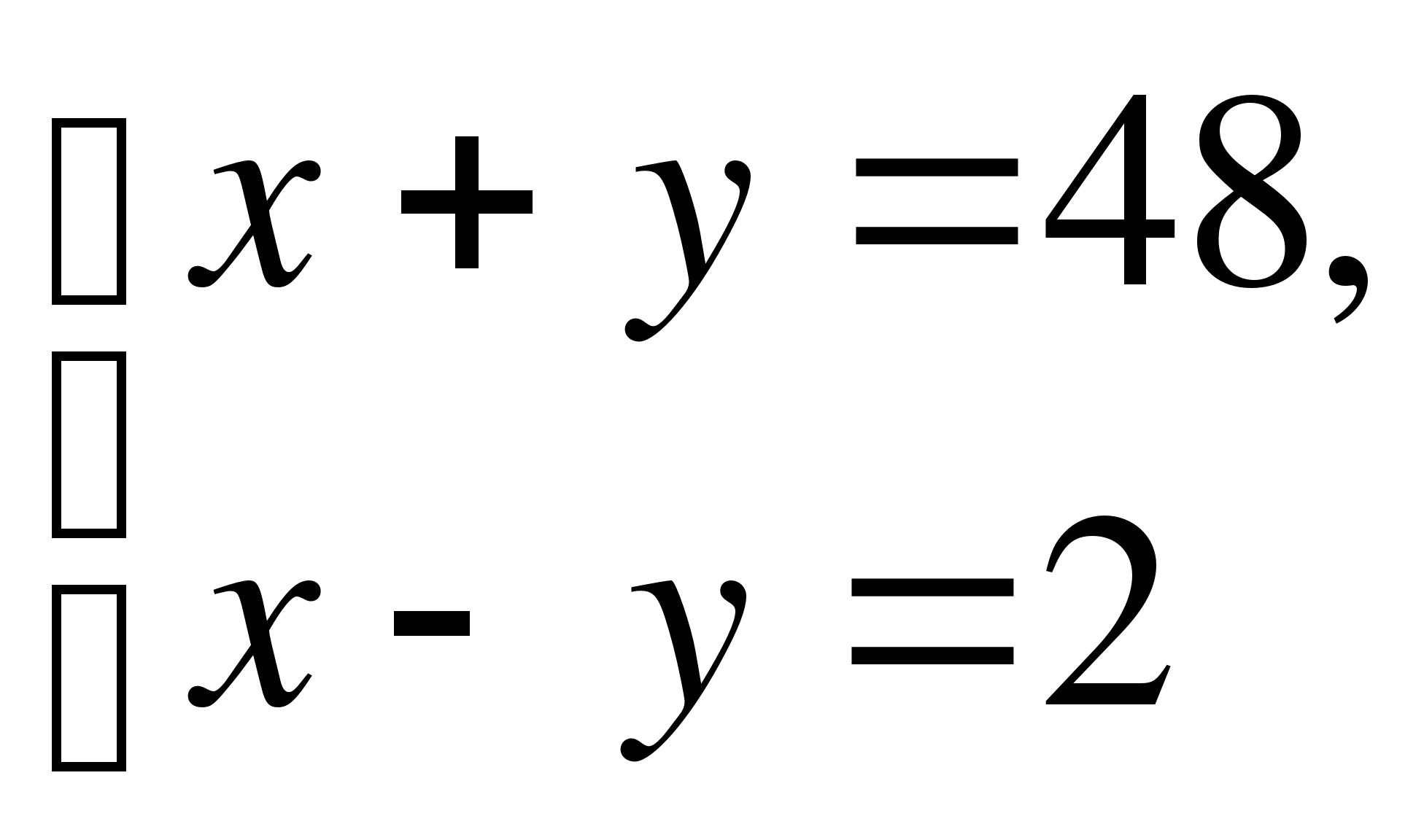
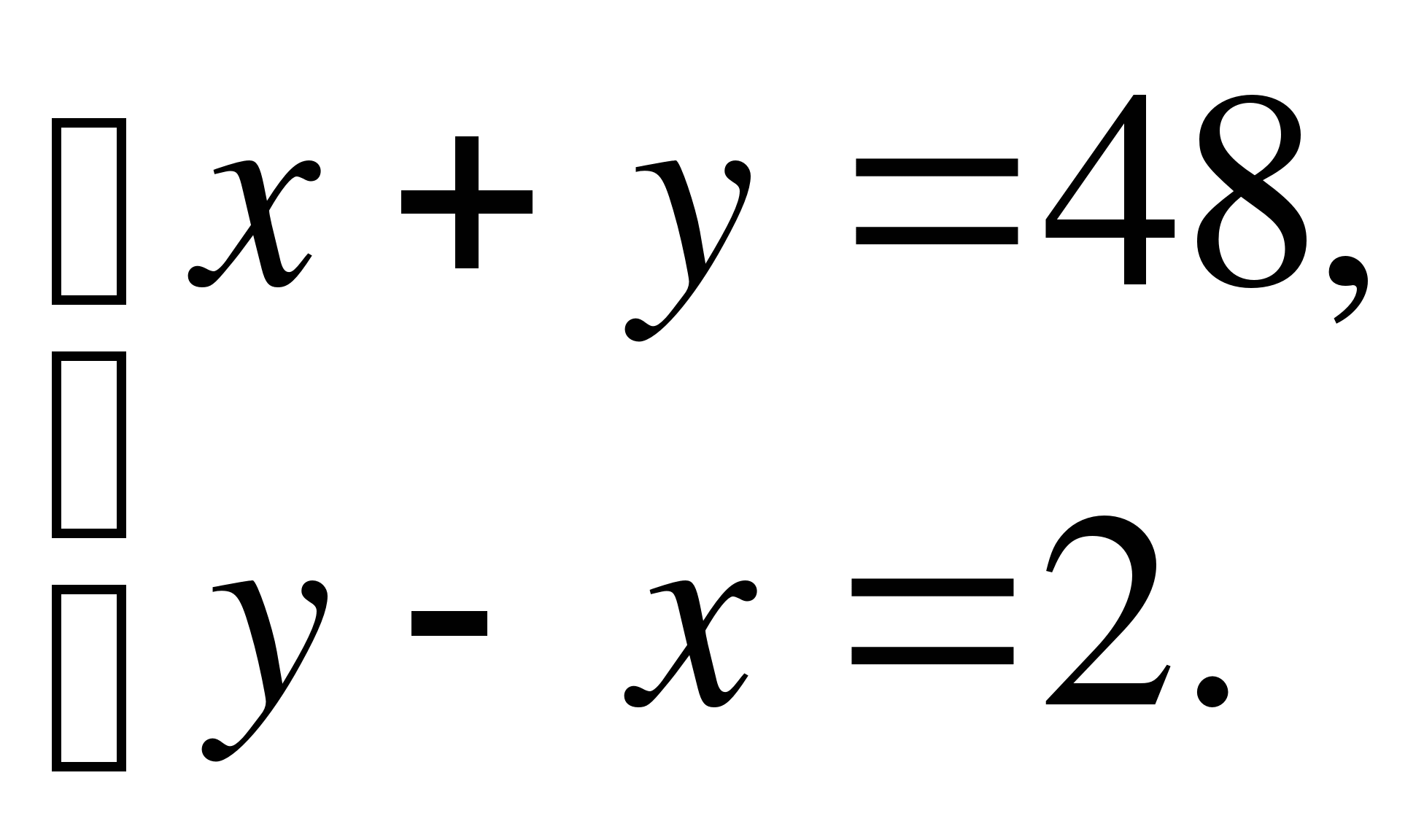
Часть В
В1. Пусть (х;у) – решение системы 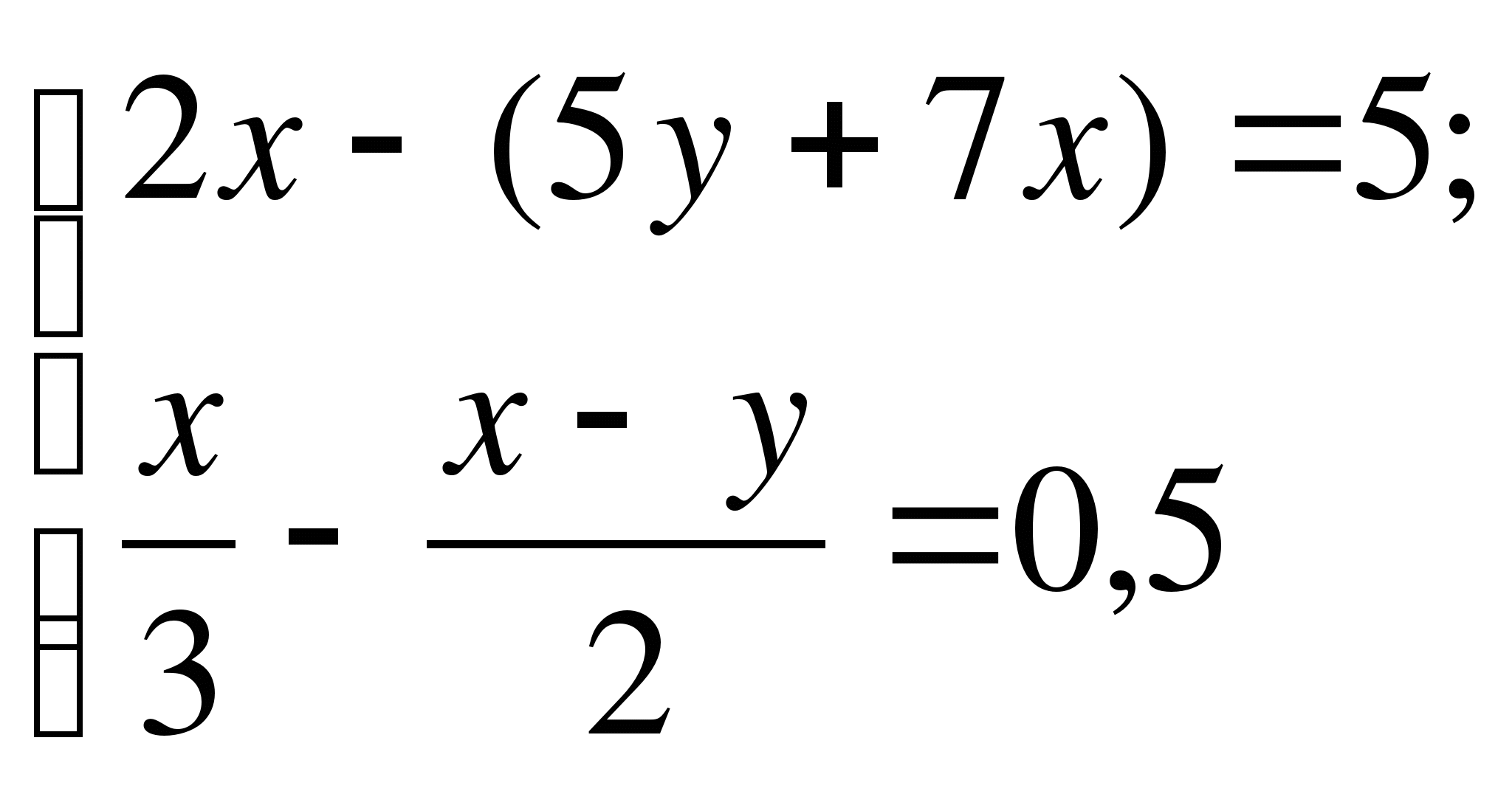 . Найдите х+3у.
. Найдите х+3у.
В2. Пусть (х;у) – решение системы 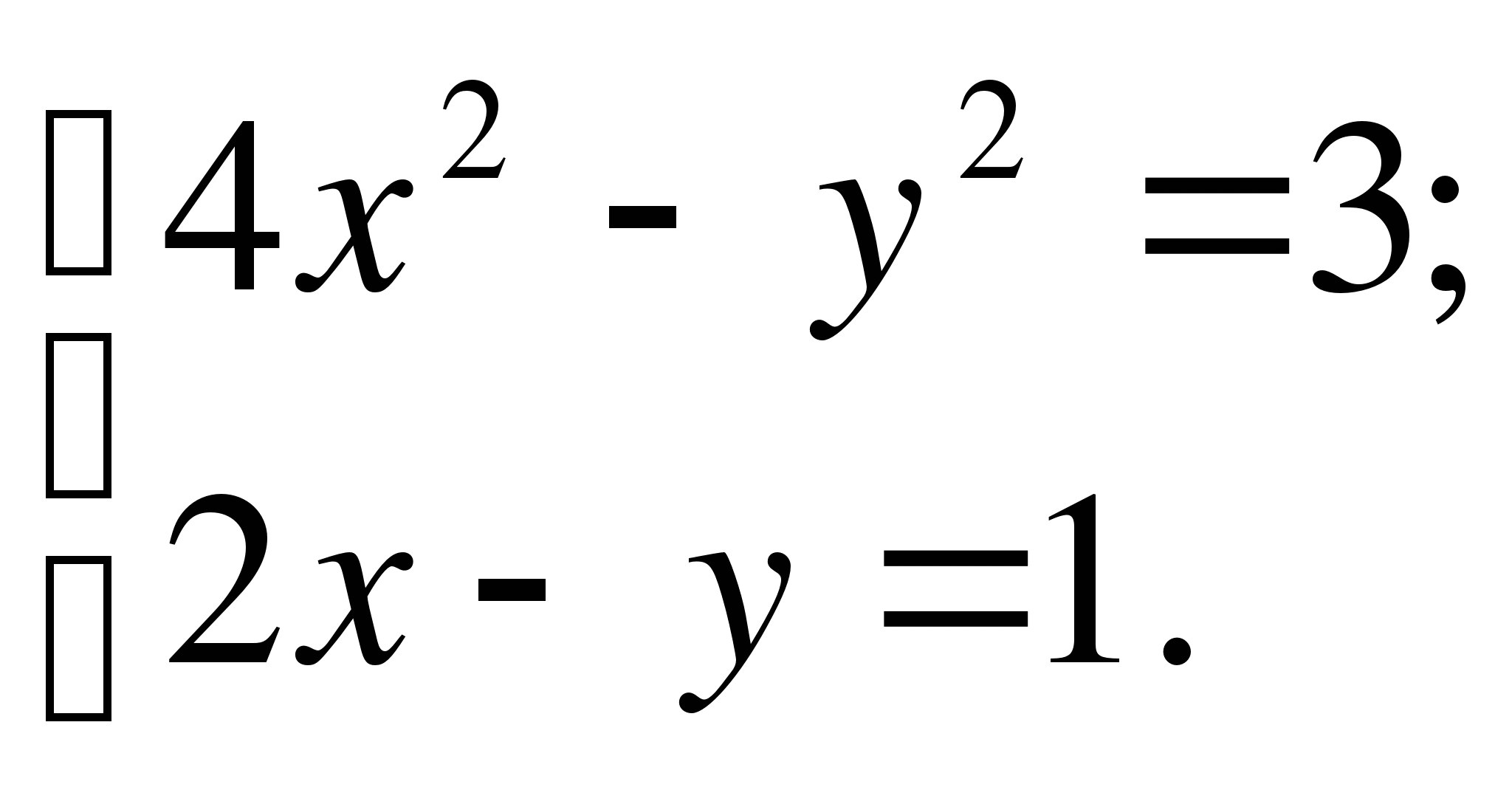 .
. Найдите у.
Найдите у.
ТЕСТ «Системы линейных уравнений» 7класс
Вариант2
Часть А
А1. Даны уравнения с двумя переменными. Линейным является
1) 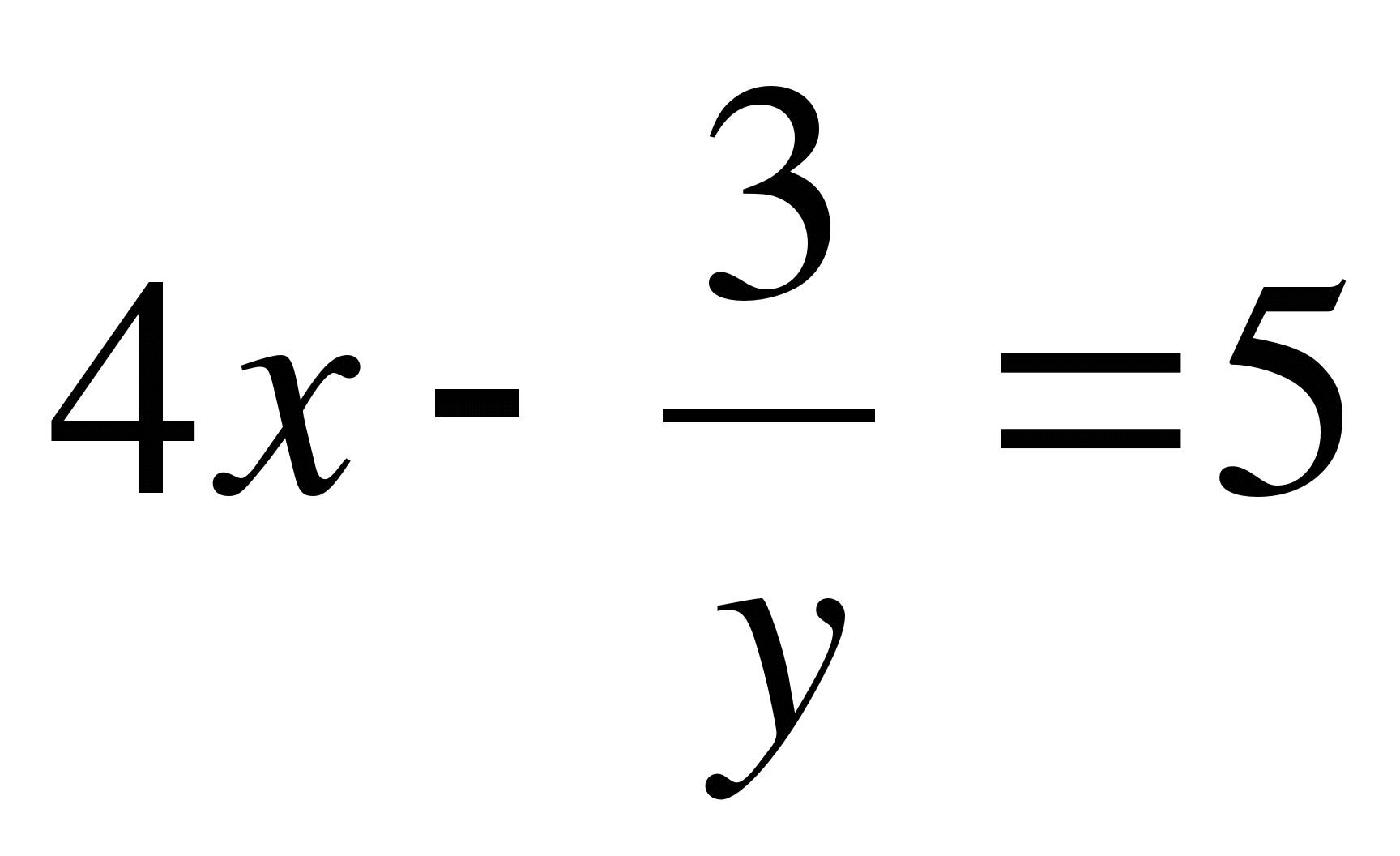 2) 3x2+5y=7 3)
2) 3x2+5y=7 3) 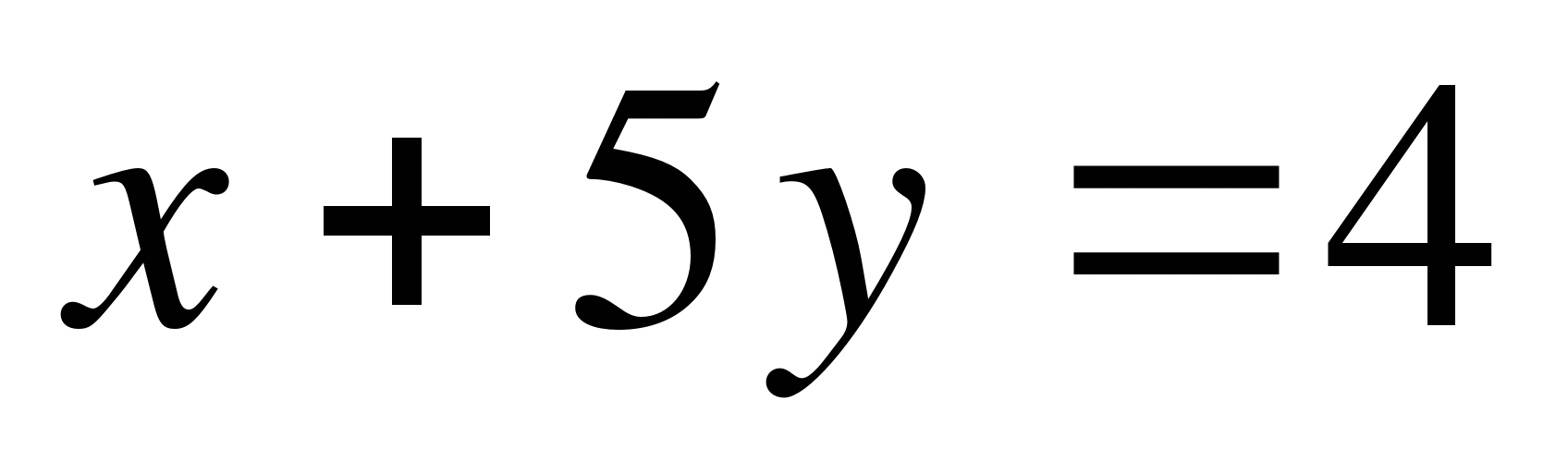 4) 3xy+5y=4
4) 3xy+5y=4
А2. Решением уравнения x – 3y= -6 является пара чисел
1) (0;-6) 2) (0; 2) 3) (3;1) 4) (1;-3)
А3. Выразите из уравнения 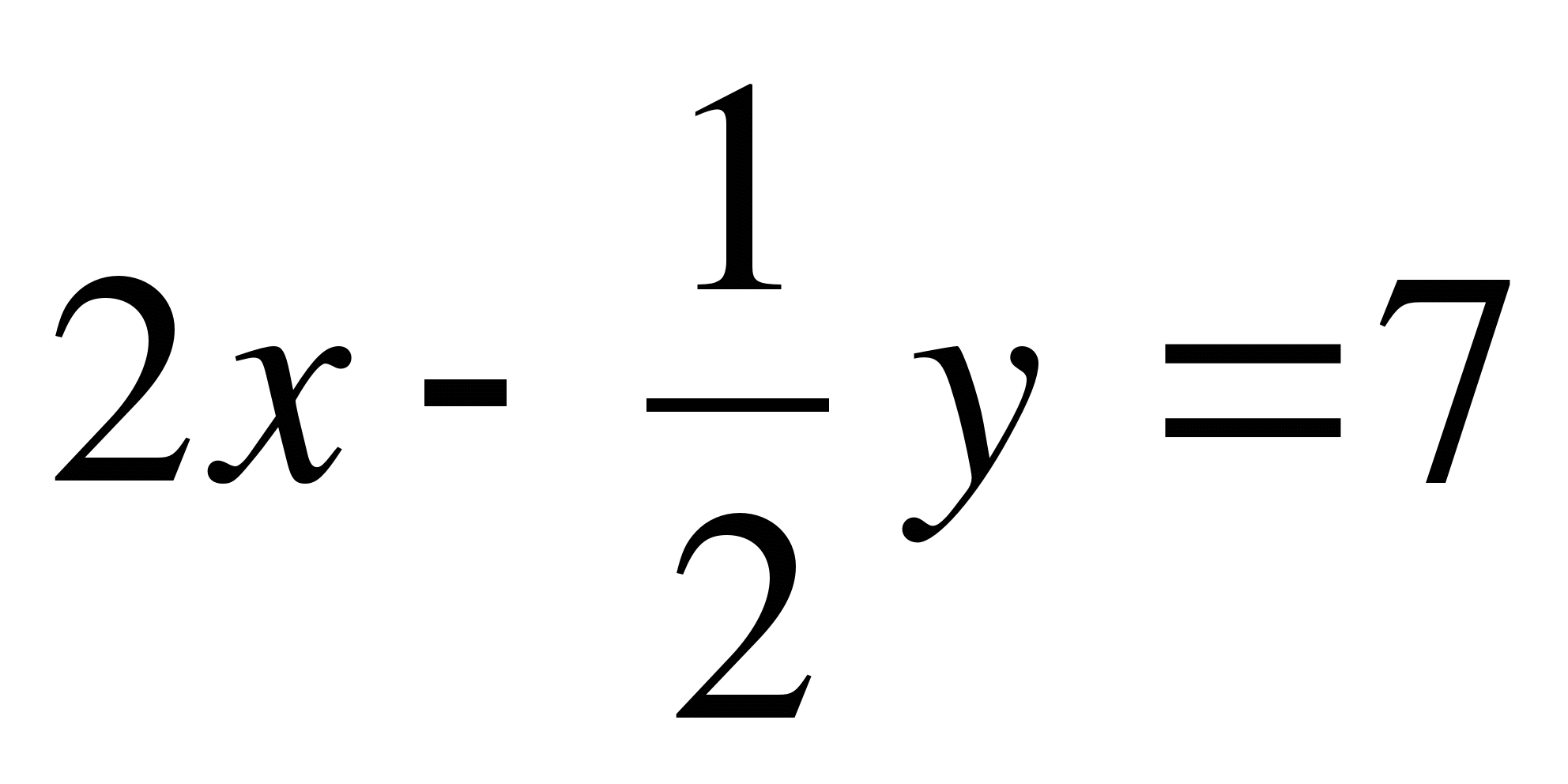 y через x
y через x
1) 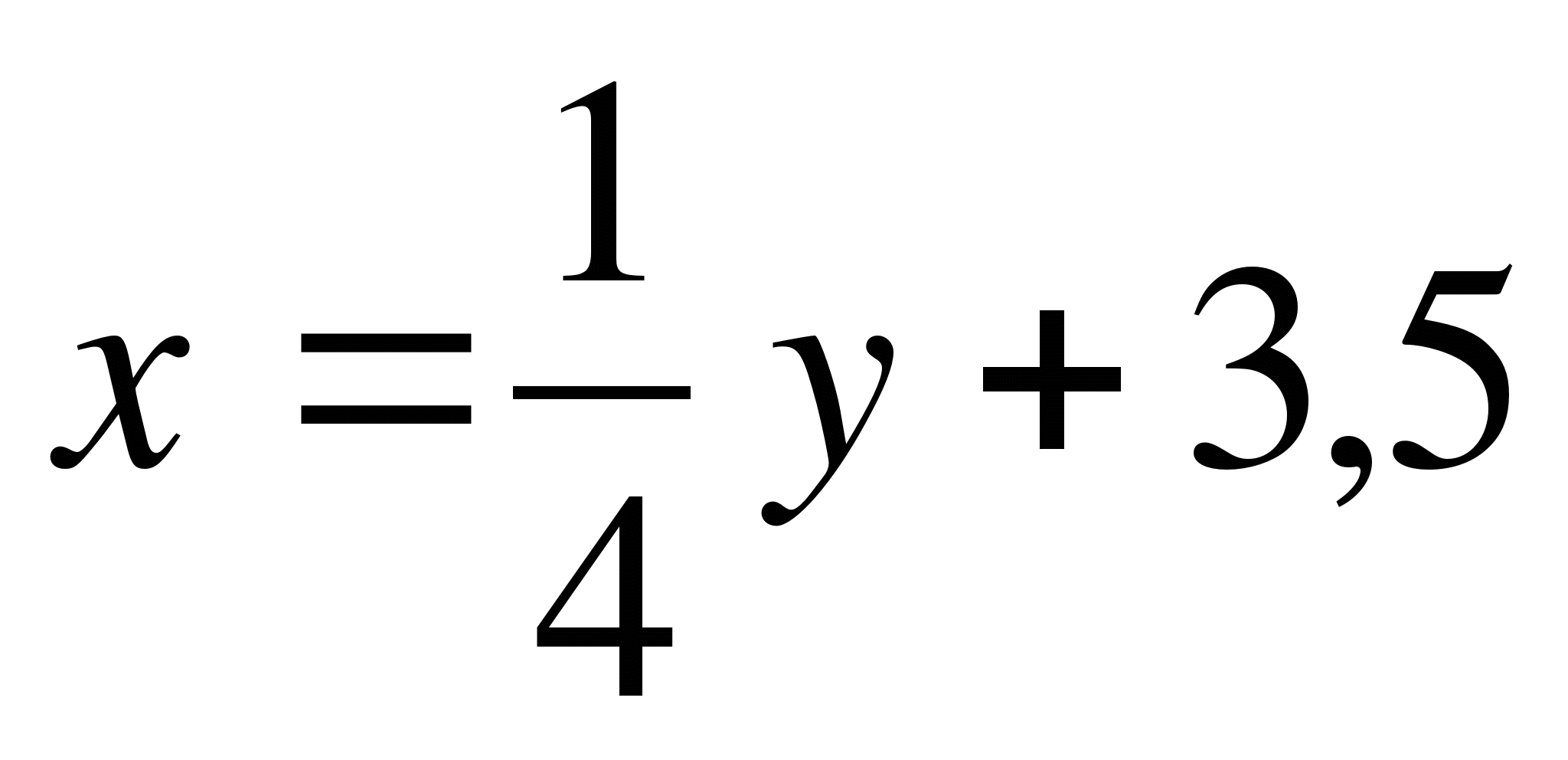 ; 2) x=y+3,5; 3) y=x+3,5; 4) y=4x-14
; 2) x=y+3,5; 3) y=x+3,5; 4) y=4x-14
А4. График уравнения x – 3 = 0 изображен на рисунке
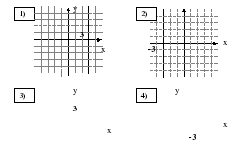





у
А5 Решением системы уравнений 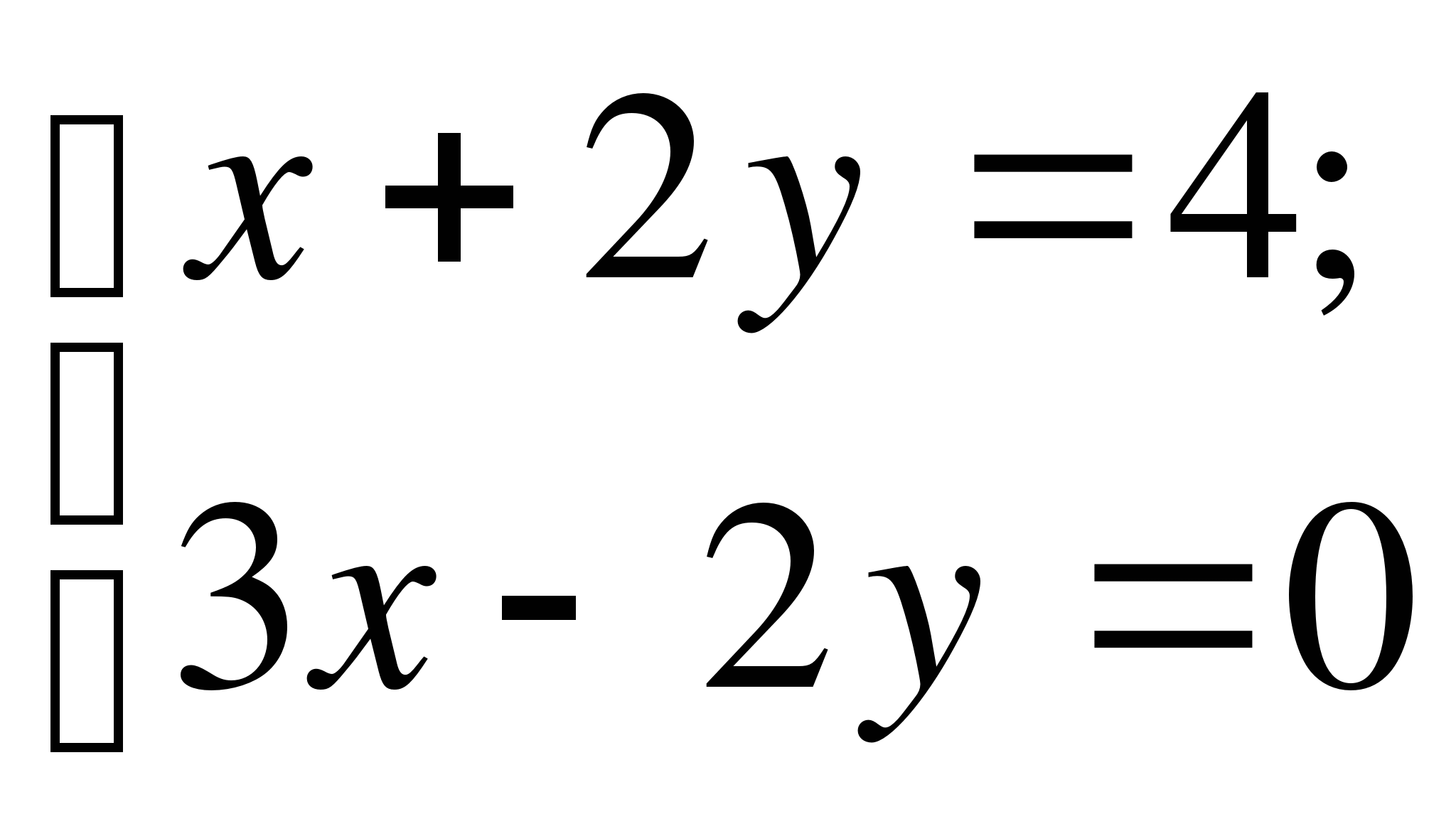
1) (1; 2) 2) (1; 1,5) 3) (1,5; 1) 4) (0; 0)
А6. Система двух линейных уравнений с двумя неизвестными может иметь
1) два решения 2) три решения 3) бесконечно много решений 4) семь решений
А7. Система имеет единственное решение. Если первое её уравнение имеет вид 4х+3у = -2, то вторым уравнением будет
1) 8х+6у = — 4 ; 2) 3х+4у = — 2; 3) – 4х – 3у = 2; 4) 2х+1,5у = -1
А8. Система 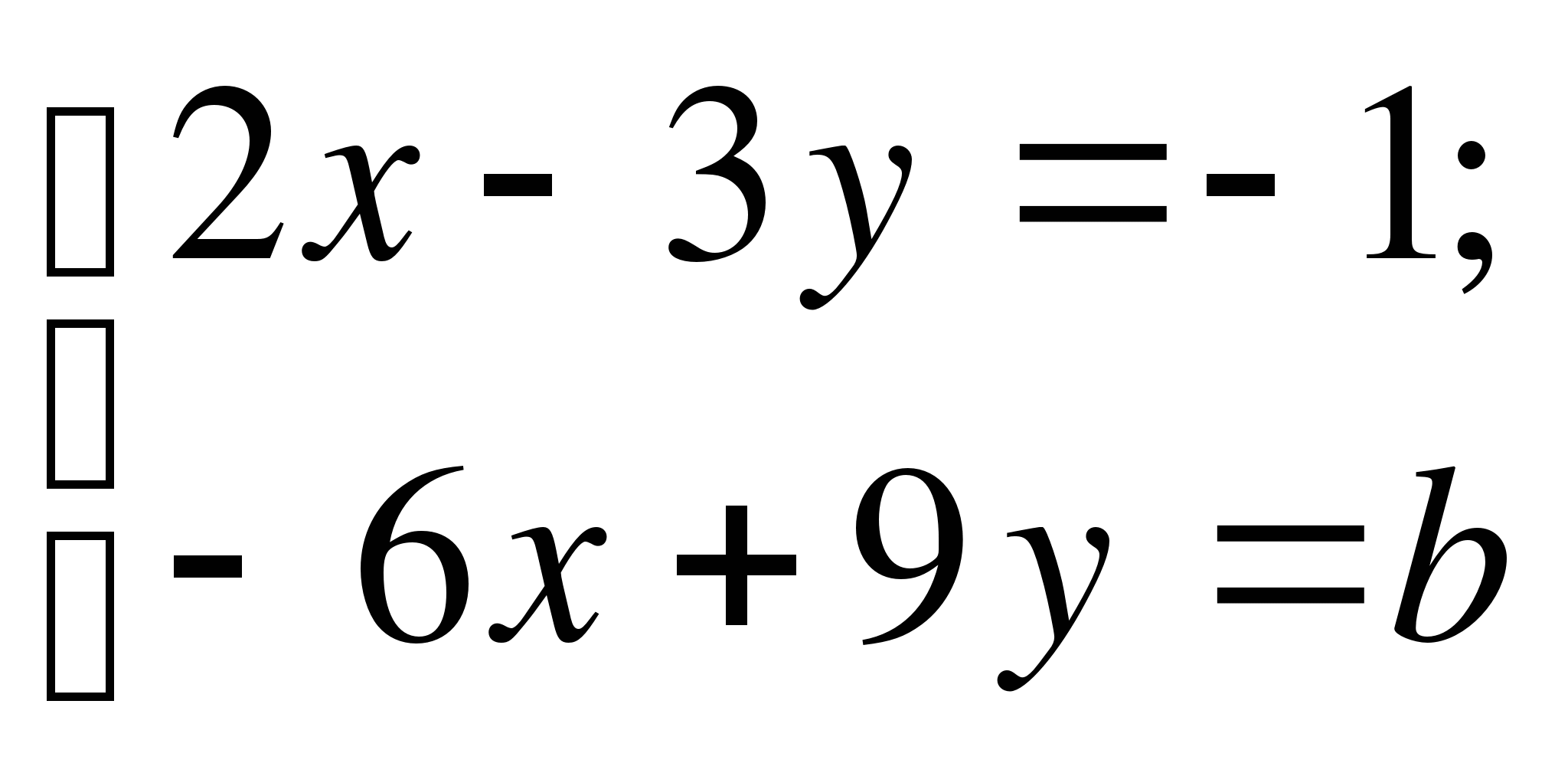 имеет бесконечно много решений, если b равно
имеет бесконечно много решений, если b равно
1)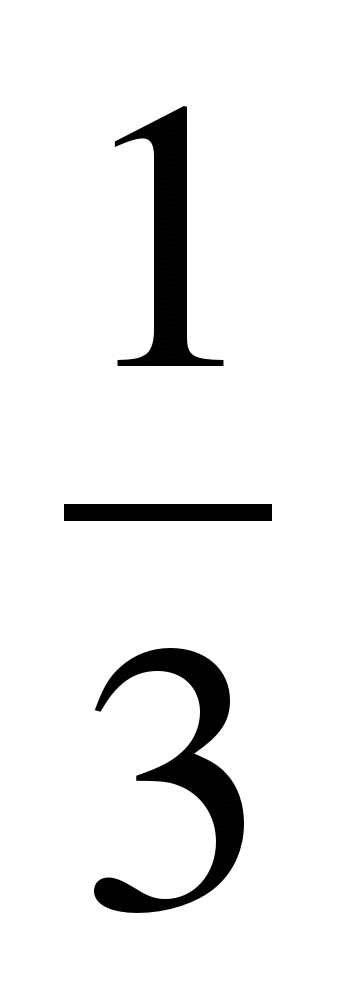 2)
2)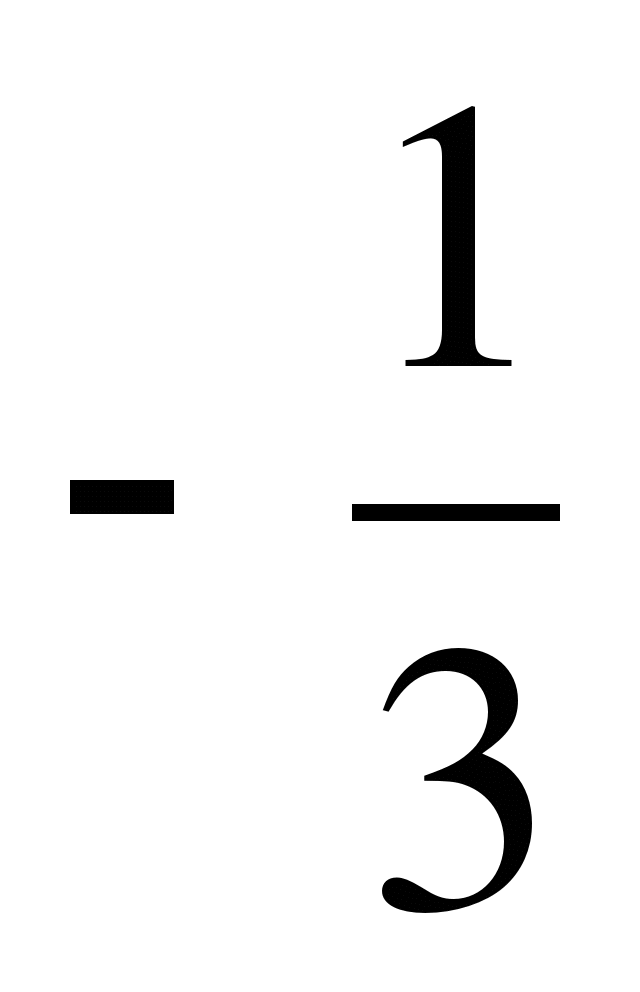
А9. Геометрическая иллюстрация решения системы, не имеющей решения, изображена на рисунке
у
1) 2) 3) 4)у
у
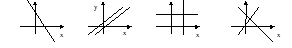
А


у
10. На рисунке изображено графическое решение системы 1
1
1

 2)
2) 
3
х
) 4)
4) 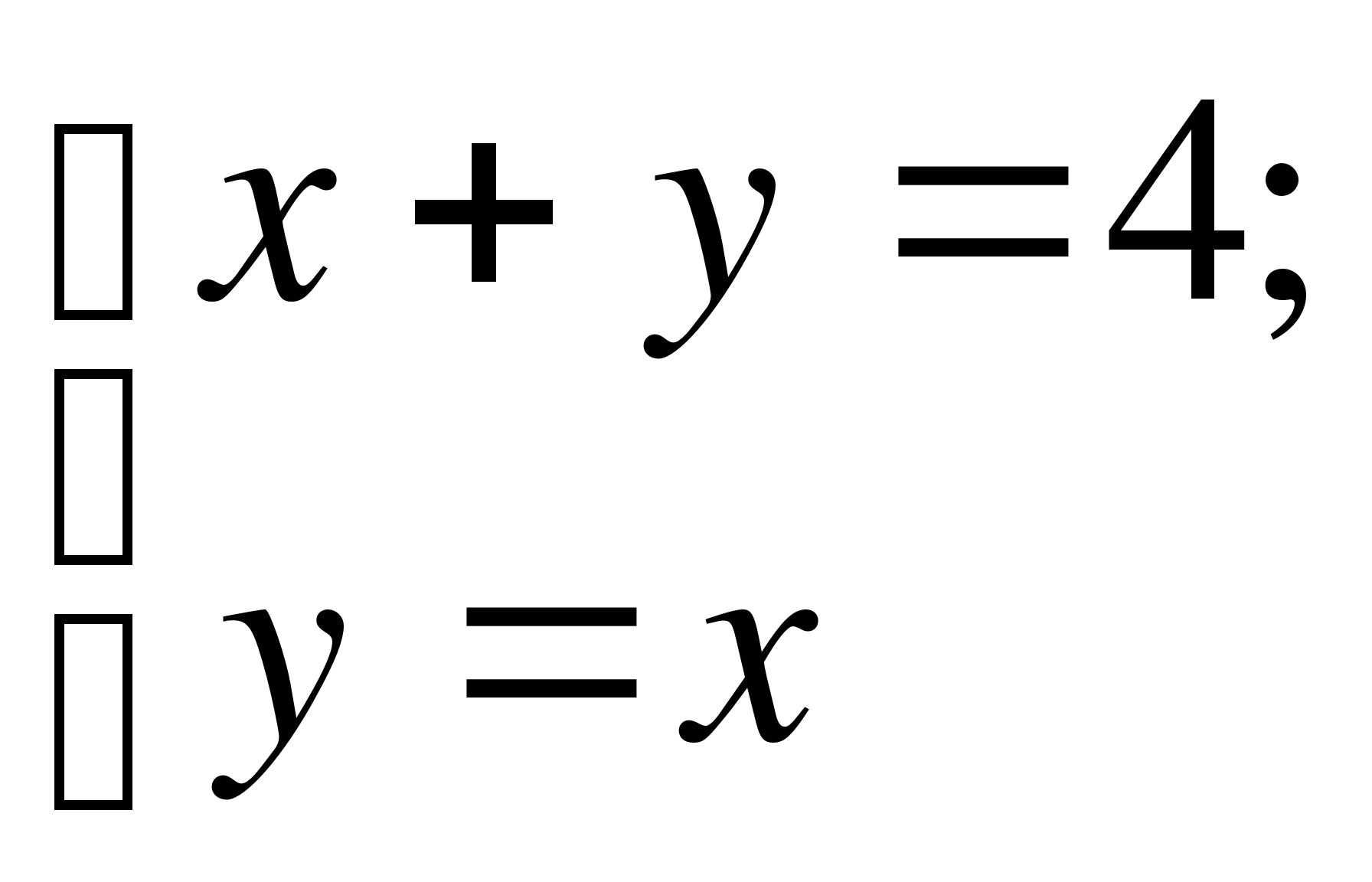
А11. Графики линейных уравнений 3x – y = 1 и 2х + у = -6 пересекаются в точке, расположенной в координатной четверти
1) I 2) II 3) III 4) IV
А12. Сумма двух чисел равна 36. Первое число меньше второго в 3 раза. Найдите эти числа. Если х – первое число, а у – второе, тогда по условию задачи получим систему
1) 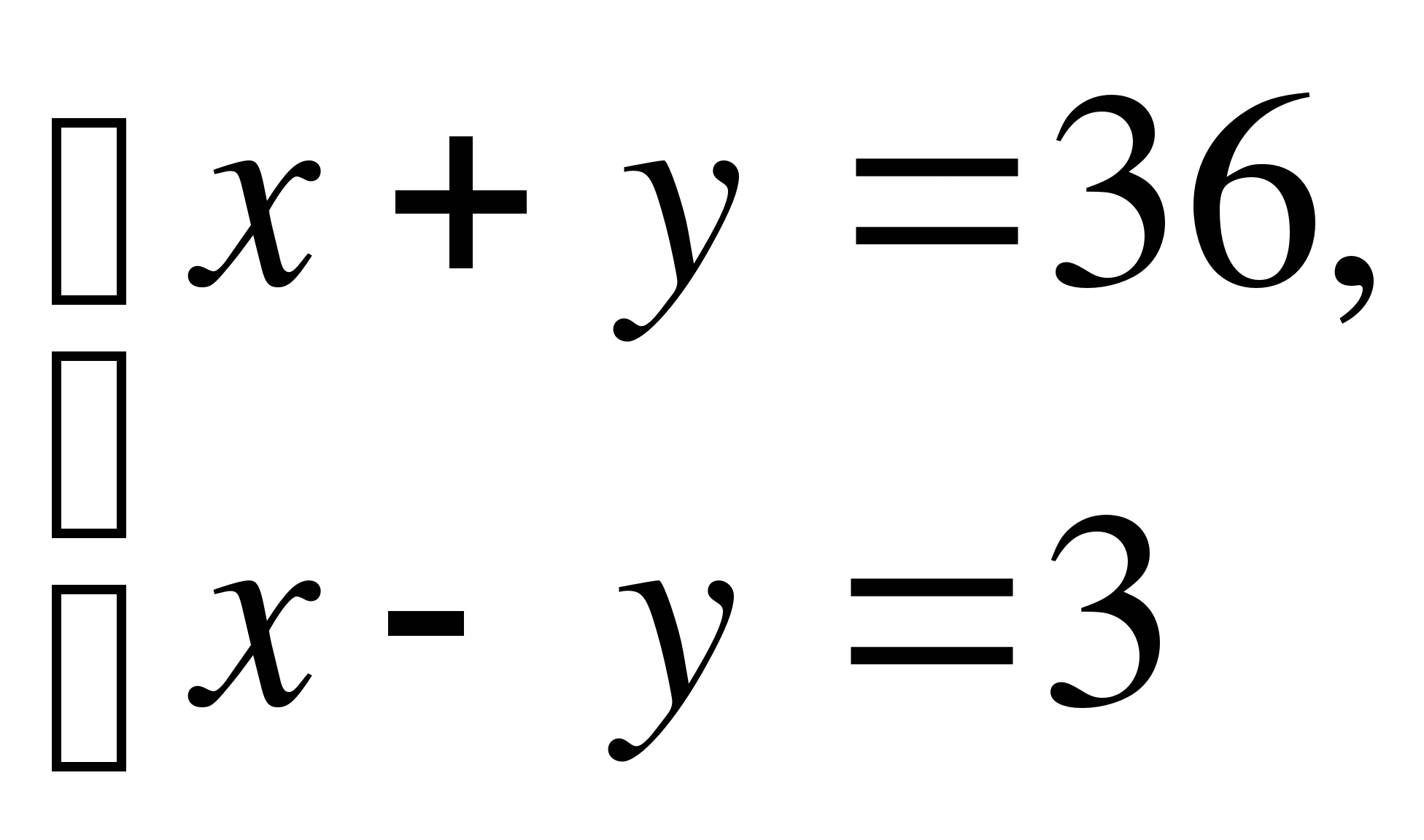 2)
2) 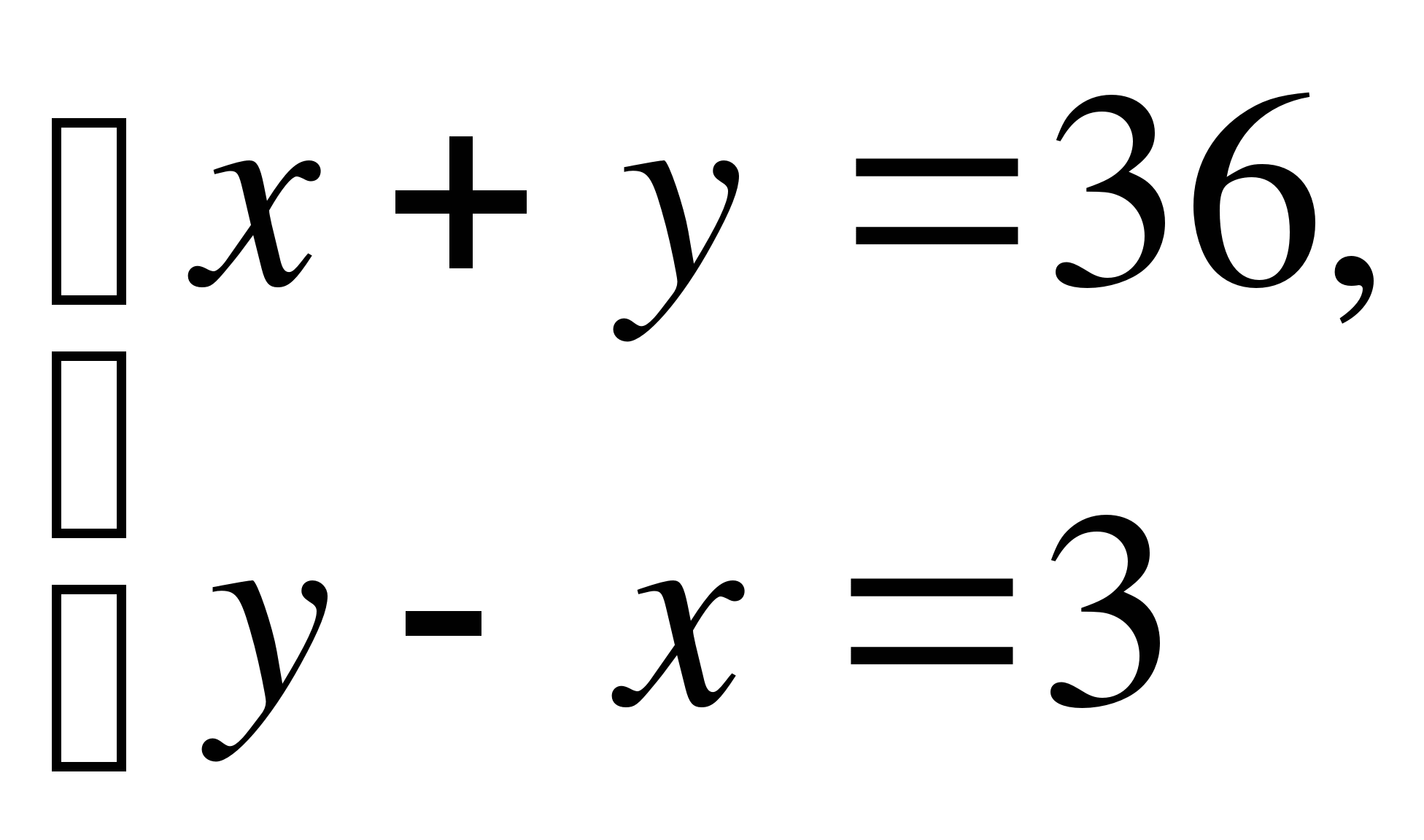 3)
3) 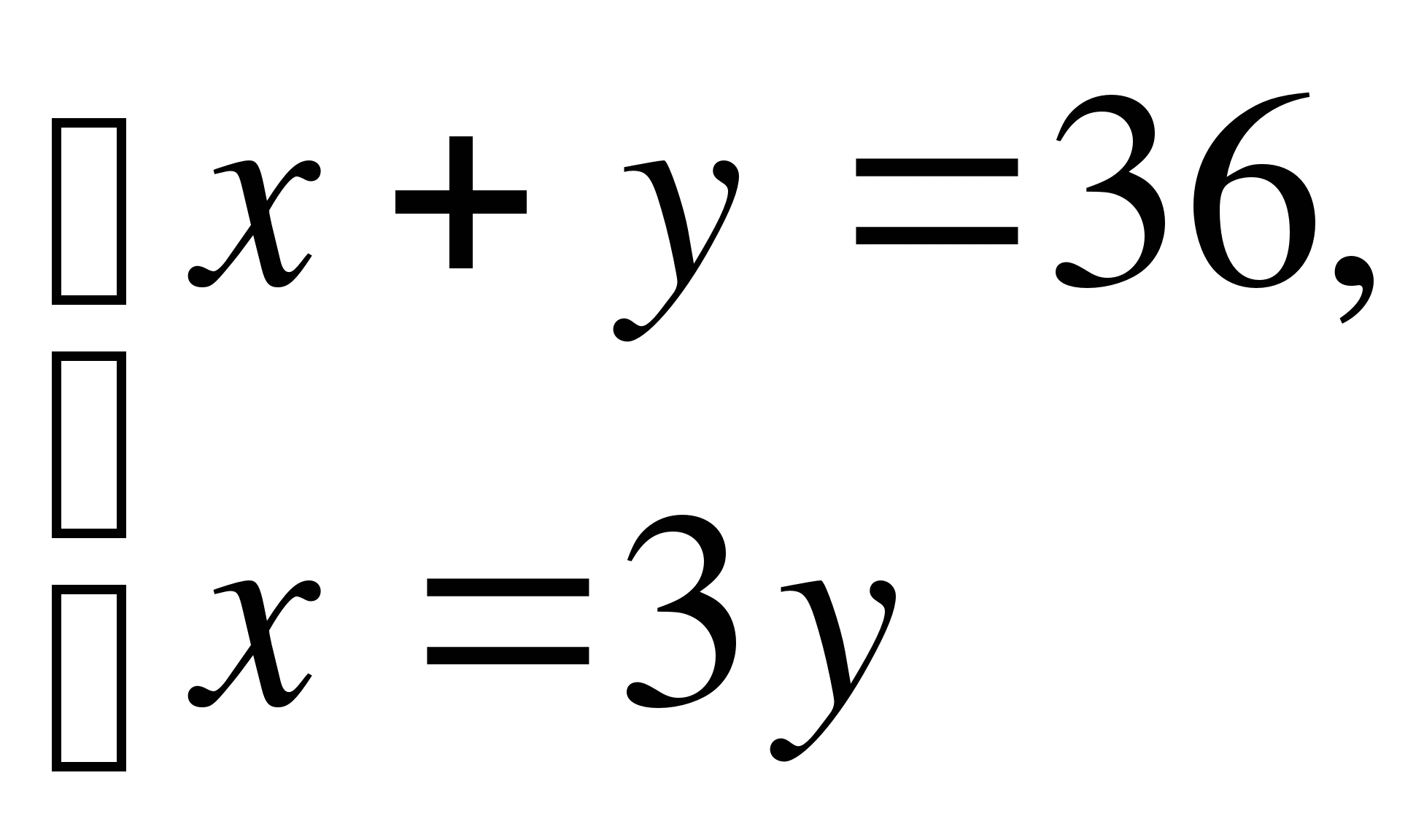 4)
4) 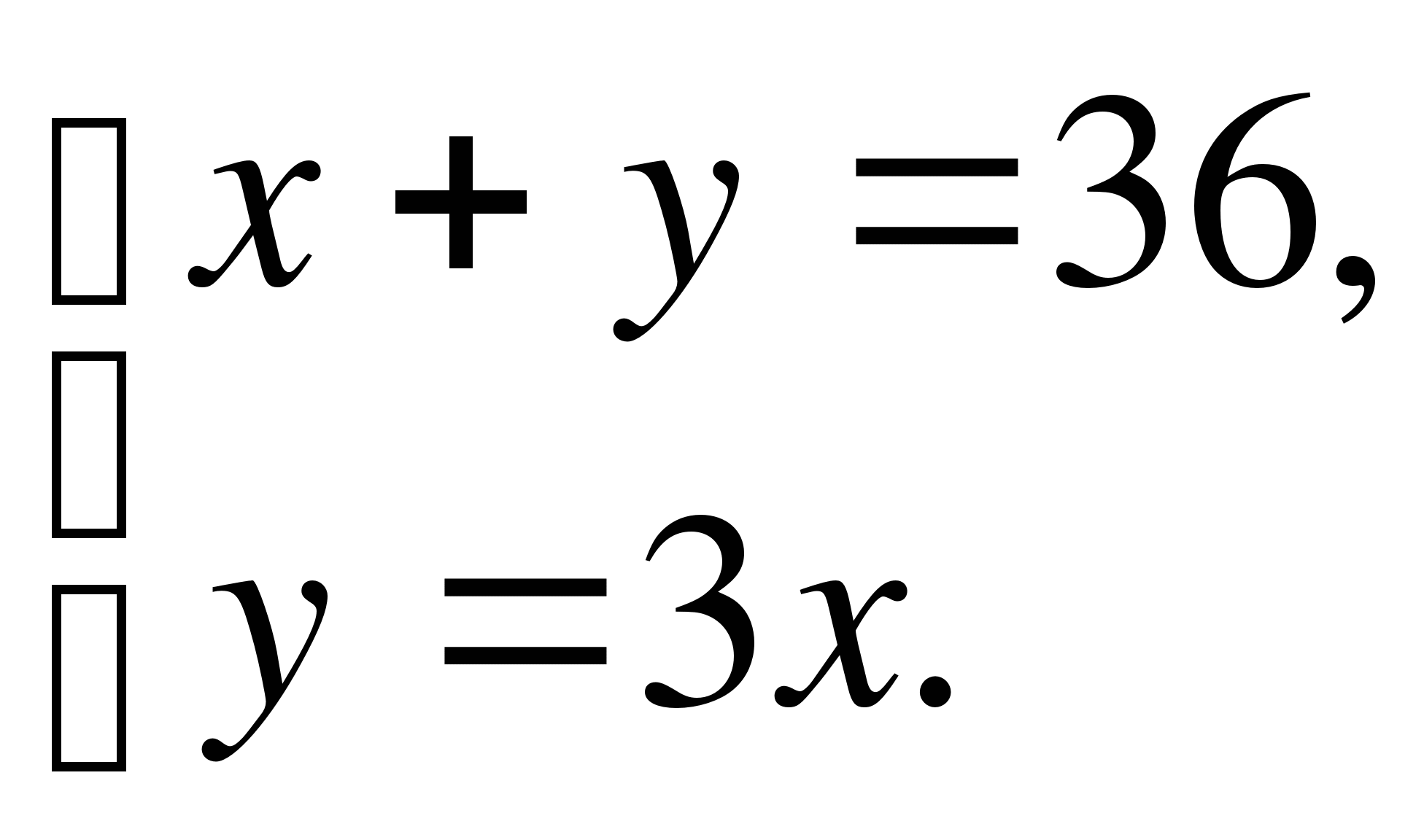
Часть В
В1. Пусть (х;у) – решение системы 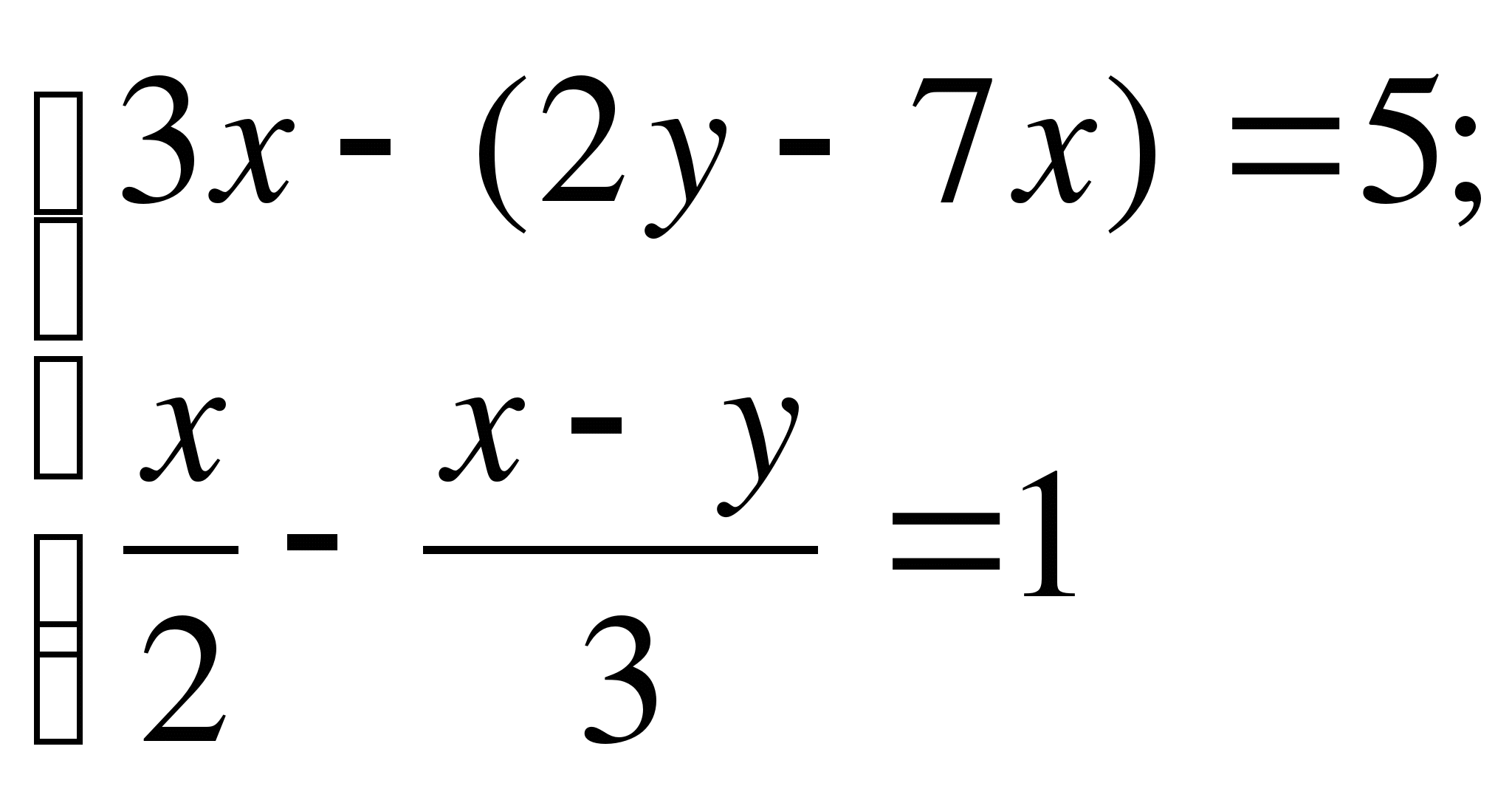 . Найдите х – 4у.
. Найдите х – 4у.
В2. Пусть (х;у) – решение системы 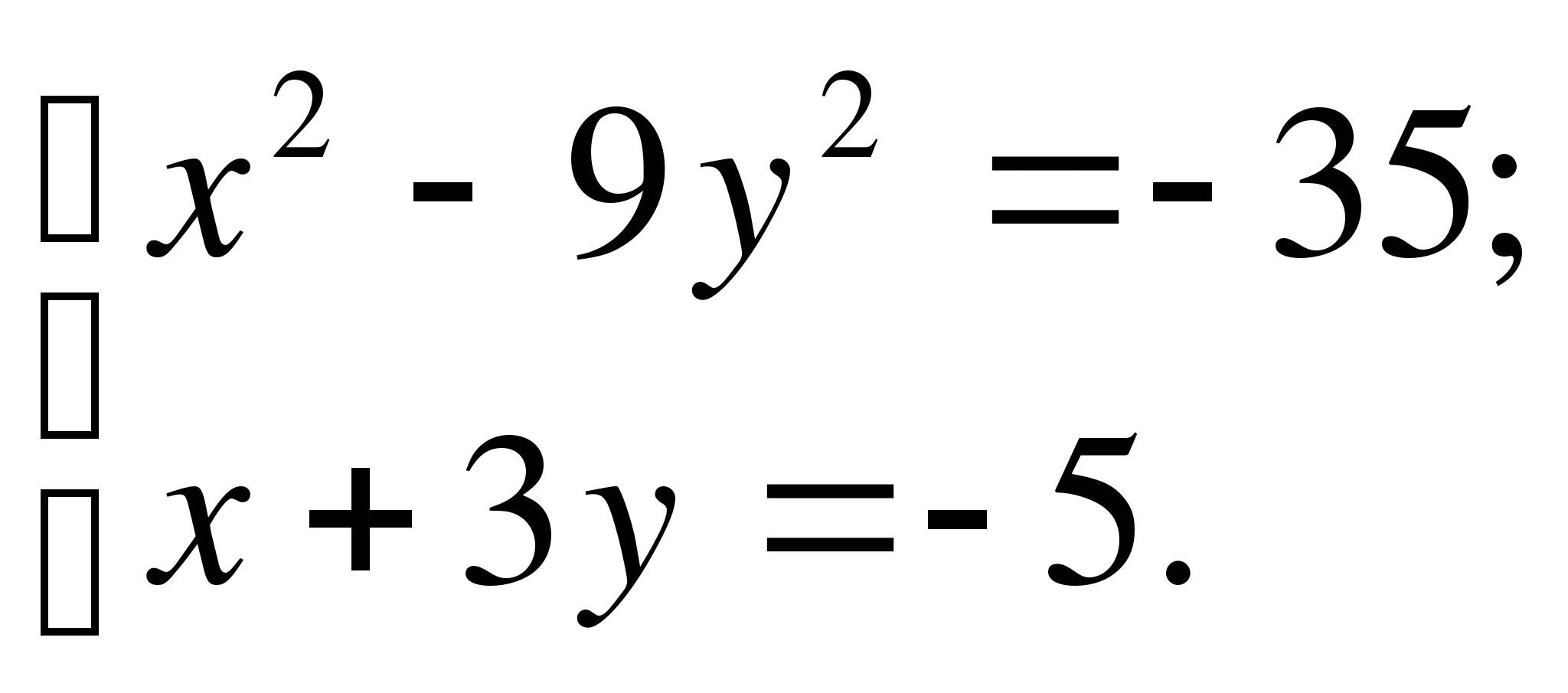 .
. Найдите у.
Найдите у.
infourok.ru
Тест по алгебре (7 класс) на тему: Тест по теме «Системы линейных уравнений»
Тест по теме «Системы линейных уравнений с двумя переменными» (алгебра, 7класс).
1 вариант
А1. Выберите линейное уравнение с двумя переменными:
а) 2х+4у2 = 20 б) ху+6 = 26 в) (х+4)(у-3) = 5 г) 3х-у = 18
А2.Найдите решение уравнения 2х+3у =2:
а) (-5;-4) б) (5;-4) в) (-5;4) г) (5;4)
А3. Выразите переменную х через переменную у из уравнения 5у -2х = -15:
а) х = -15-5у б) х = 2,5у+7,5 в) х = -2,5у+7,5 г) х = 2,5у-7,5
А4. Абсцисса точки, принадлежащей графику уравнения 2х-3у =-7, равна 4. Найдите ординату этой точки.
а)5 б) -5 в) 4 г) 0
А5. Пара чисел (-4;-1) является решением уравнения ах+3у-5= 0, если а равно:
а) 2 б) 0,5 в) -2 г) 0
А6. Решением системы служит пара:
а)(-4;3) б)(4; -3) в)(-3; 4) г)(3;-4)
В1. Координаты точки пересечения графика уравнения -5х+3у = 9 и оси абсцисс являются решением системы:
а) б) в) г)
В2. Выясните, сколько решений имеет система:
а) единственное б) бесконечно много в) ни одного г) два
В3. Подберите к данному уравнению 2х + 3у = -11 такое уравнение, чтобы решением получившейся системы была пара (2; -5)
а) 3х – у = 14 б) у – 5х = -20 в) 7х+4у = 6 г) –х – 4у = 18
С1. Система имеет бесконечно много решений при а равном:
а)0 б)1 в)12 г)
Тест по теме «Системы линейных уравнений с двумя переменными» (алгебра, 7класс).
2 вариант
А1. Выберите линейное уравнение с двумя переменными:
а) 2х2-4у = 20 б) 3ху = 18 в) х-4у = 26 г) (5х-4)(у+8) = 5
А2. Найдите решение уравнения: 4х-3у = 5
а) (1;2) б) (-2;1) в) (-1;2) г) (2;1)
А3. Выразите переменную х через переменную у из уравнения -6у +3х = 24
а) х = 8-3у б) х = 3у+8 в) х = 2у+8 г) х =-4-2у
А4. Ордината точки, принадлежащей графику уравнения 6х+2у = 2, равна 4. Найдите абсциссу этой точки.
а)-11 б) 1 в)-1 г) 11
А5.Пара чисел (-4;-1) является решением уравнения 4х+ау+5 = 0, если а равно:
а) 11 б) 21 в) -21 г) -11
А6. Решением системы служит пара:
а)(-4;2) б)(4; 2) в)(-2; 4) г)(2;-4)
В1.Координаты точки пересечения графика уравнения -5х+3у = 9 и оси ординат являются решением системы:
а) б) в) г)
В2. Выясните, сколько решений имеет система:
а) единственное б) бесконечно много в) ни одного г) два
В3. . Подберите к данному уравнению 4х –2у = -18 такое уравнение, чтобы решением получившейся системы была пара (-2; 5)
а) 2х + у = 14 б) 2х – 3у = -19 в) у – 4х = 24 г) –х +3у = 18
С1. Система имеет бесконечно много решений при а равном:
а)0 б)1 в)15 г)
Ключи к тестам:
А1 | А2 | А3 | А4 | А5 | А6 | В1 | В2 | В3 | С1 | |
I | г | в | б | а | в | в | в | б | г | в |
в | г | в | в | г | б | б | а | б | в |
ФИО Шишкова Елена Николаевна
Должность учитель математики
Место работы МБОУ СОШ №29 г. Владимир
Почтовый адрес 600033, г. Владимир
ул. Доватора, дом №19
nsportal.ru
Тест «Линейные уравнения и линейные неравенства»
Математика 6 класс
Вариант 1
1. Найти корень уравнения: -8х = -24
а) -3; б) корней нет; в) 3; г) множество решений
2. Найти корень уравнения: 3у – (5-у) = 11
а) -4; б) корней нет; в) 4; г) множество решений
3. Найти корень уравнения: 4(х -2) = 4х +13
а) -4; б) корней нет; в) 4; г) множество решений
4. Найти корень уравнения: (7х + 1) – ( 6х + 3) = 5
а) 7; б) корней нет; в) -7; г) множество решений
5. Найти корень уравнения: 8х + 40 = 8(х + 2) + 24
а) 0; б) корней нет; в) 4; г) множество решений
6. Найти корень уравнения: 0,8 – у = 3,2+ у
а) 0,8; б) корней нет; в) – 1,2; г) множество решений.
7. Найти корень уравнения: 2х – 0,7х = 0
а) 0; б) корней нет; в) 1,3; г) множество решений
8. Как называется промежуток: (3;7)
а) отрезок; б) интервал; в) луч; г) полуинтервал
9. Как называется промежуток: [2;7]
а) отрезок; б) интервал; в) луч; г) полуинтервал
10. Как называется промежуток: (-14;-7]
а) отрезок; б) интервал; в) луч; г) полуинтервал
11. Как называется промежуток: (3;+ ∞)
а) отрезок; б) интервал; в) луч; г) открытый луч
12. Как называется промежуток: (-∞;-2]
а) отрезок; б) интервал; в) луч; г) открытый луч
Запишите в виде промежутка:
13. числовой промежуток от минус бесконечности до 0
а) (-∞;1) б) (0;+ ∞) в)(- ∞;0] г) (- ∞;0)
14. числовой промежуток от -3 до 4, включая -3
а) (-3;4) б) [-3;4) в) [-3;4] г) (-3;4]
15. числовой промежуток от 2 до 5, включая 2 и 5
а) [2;5] б) (2;5] в) [2;5) г) (2;5)
16. числовой промежуток от 0 до плюс бесконечности, включая ноль
а) [0;-∞) б) (0;+∞] в) (0;+∞) г) [0;+∞)
17. числовой промежуток от -1 до плюс бесконечности,
а) [-1;-∞) б) (-1;+∞] в) (-1;+∞) г) [-1;+∞)
Найдите пересечение промежутков:
18. (-8;6] и [-5;8]
а) (-5; 6) б) [-5;6] в) (-8; 8) г)[-5;8]
19. (-4;+ ∞) и (-5;0]
а) (-5; 0) б) [-5;-4] в) (-4; 0] г)[-5;0]
20. [-9;3) и (-∞;0]
а) (-∞; -9) б) [-9;3] в) (-9; 0) г)[-9;0]
Найдите объединение промежутков:
21. [-9;9] и [-1;10]
а) (-∞; -9) б) [-1;9] в) (-9; 10) г)[-9;10]
22. [-4;3] и [1;+ ∞)
а) [-4; +∞) б) [-4;1] в) (-4; +∞] г)[1; +∞)
Решите неравенство:
23. -5х < 25
а) (-5; +∞) б) [-5;1] в) ( -∞;5] г)( -∞;-5)
24. 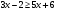
а) (4; +∞) б) [-4;1] в) ( -∞;-4] г)( -∞;-4)
25. 2( х + 3 ) < 3 – х
а) (-1; +∞) б) [-1;1] в) ( -∞;-1] г)( -∞;-1)
Математика 6 класс
Вариант 2
1. Найти корень уравнения: – 2х = -14
а) 7; б) корней нет; в) -7; г) множество решений
2. Найти корень уравнения: 8у – ( 7у – 42) = 51
а) 9; б) корней нет; в) -9; г) множество решений
3. Найти корень уравнения: 7(х + 4) = 7х – 15
а) -3; б) корней нет; в) 3; г) множество решений
4. Найти корень уравнения: (6х + 1) – (3 – 2х) = 14
а) 2; б) корней нет; в) -2; г) множество решений
5. Найти корень уравнения: 9у – 25 = 9(у – 2) -7
а) -3; б) корней нет; в) 3; г) множество решений
6. Найти корень уравнения: 6х-(7х – 12)=101
а) 67; б) корней нет; в) -89; г) множество решений
7. Найти корень уравнения: 3у + ( у-2)= 2(2у -1)
а) 8; б) корней нет; в) -2; г) множество решений
8. Как называется промежуток: (3;7)
а) отрезок; б) интервал; в) луч; г) полуинтервал
9. Как называется промежуток: [-3;7)
а) отрезок; б) интервал; в) луч; г) полуинтервал
10. Как называется промежуток: [1;5]
а) отрезок; б) интервал; в) луч; г) полуинтервал
11. Как называется промежуток: [0;+ ∞)
а) отрезок; б) интервал; в) луч; г) открытый луч
12. Как называется промежуток: (-∞;-7)
а) отрезок; б) интервал; в) луч; г) открытый луч
Запишите в виде промежутка:
13. числовой промежуток от минус бесконечности до 0, включая 0
а) (-∞;1) б) (0;+ ∞) в)(- ∞;0] г) (- ∞;0)
14. числовой промежуток от -3 до 4, включая -3
а) (-3;4) б) [-3;4) в) [-3;4] г) (-3;4]
15. числовой промежуток от 2 до 5, включая 5
а) [2;5] б) (2;5] в) [2;5) г) (2;5)
16. числовой промежуток от 0 до плюс бесконечности,
а) [0;-∞) б) (0;+∞] в) (0;+∞) г) [0;+∞)
17. числовой промежуток от -1 до плюс бесконечности, включая -1
а) [-1;-∞) б) (-1;+∞] в) (-1;+∞) г) [-1;+∞)
Найдите пересечение промежутков:
18. [-8;2] и [1;9]
а) (-8;9) б) [1;2] в) (1; 2) г)[-8;9]
19. [-3;7) и (-8;2]
а) (-8; 7) б) [-3;2] в) (-3; 2) г)[-8;7]
20. [-2;9] и [4;10]
а) (-2; 10) б) [-2;10] в) (4; 9) г)[4;9]
Найдите объединение промежутков:
21. (-∞;9] и [7;+ ∞)
а) (-∞; 9) б) [7;9] в) (-∞; +∞) г)[7;9)
22. (-4;8] и [0;10)
а) (-4; 10) б) [0;8] в) (-∞; +∞) г)[0;8)
Решите неравенство:
23. -9х > -36
а) (-4; +∞) б) [-4; 0] в) ( -∞;4] г)( -∞; 4)
24. 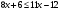
а) (6; +∞) б) [6; +∞) в) ( -∞;6] г)( -∞; 6)
25. 3( х — 2 ) > х – 12
а) (-3; +∞) б) [-3; 3] в) ( -∞;-3] г)( -∞; -3)
infourok.ru
Тест по алгебре (9 класс) на тему: тест по теме «Решение систем линейных уравнений»
По теме: методические разработки, презентации и конспекты
«Решение систем линейных уравнений» Урок обобщающего повторенияУрок разноуровневого обощающего повторения…
Презентация к уроку «Решение систем линейных уравнений» 7 классПрезентация по теме : «Решение систем линейных уравнений» к уроку «Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. На уроке решаются задачи с практичес…
Урок алгебры в 7 классе «Решение задач с помощью систем линейных уравнений»Рекомендации к уроку: учителю математики совместно с классным руководителем необходимо провести заранее анкету о типе личности учащихся по объектам труда (методика Е.А. Климова). На начало урока класс…
Урок ао теме «Решение систем линейных уравнений» 7 классУрок по закреплению умений и навыков по решению систем линейных уравнений с двумя переменными. Содержит групповую работу, карту продуктивности, творческие задания….
 Урок «: Решение задач составлением систем линейных уравнений с двумя переменными»
Урок «: Решение задач составлением систем линейных уравнений с двумя переменными»Цель: развитие познавательного интереса при решении задач.Задачи: образовательная: способствовать совершенствованию полученных знаний по применению и развитию при работе с задачами, обобщить и система…
Использование ИКТ на уроке алгебры «Решение систем линейных уравнений»Разработка урока, создание презентации, УУД….
 Методическая разработка урока алгебры в 7 классе «Различные способы решения систем линейных уравнений» способы решения систем уравнений
Методическая разработка урока алгебры в 7 классе «Различные способы решения систем линейных уравнений» способы решения систем уравненийУрок алгебры в 7 классе направлен на обобщение и систематизацию различных способов решения систем уравнений: метода сравнения, сложения, подстановки, графического метода, метода Крамера, выбора рацион…
nsportal.ru