Связь производной с монотонностью и точками экстремума функции
Функция \(f\) возрастает на множестве \(M\), если для любых двух точек \(x_1 < x_2\) из \(M\) справедливо неравенство \(f(x_1) < f(x_2)\) (чем больше аргумент из \(M\), тем больше значение \(f\)).
Функция \(f\) убывает на множестве \(M\), если для любых двух точек \(x_1 < x_2\) из \(M\) справедливо неравенство \(f(x_1) > f(x_2)\) (чем больше аргумент из \(M\), тем меньше значение \(f\)).
Функция \(f\) неубывает на множестве \(M\), если для любых двух точек \(x_1 < x_2\) из \(M\) справедливо неравенство \(f(x_1) \leq f(x_2)\) (при увеличении аргумента из \(M\), значение \(f\) по крайней мере не уменьшается).
Функция \(f\) невозрастает на множестве \(M\), если для любых двух точек \(x_1 < x_2\) из \(M\) справедливо неравенство \(f(x_1) \geq f(x_2)\) (при увеличении аргумента из \(M\), значение \(f\) по крайней мере не увеличивается).
Замечание
Если функция возрастает на \(M\), то про неё также верно, что она неубывает на \(M\).
Если функция убывает на \(M\), то про неё также верно, что она невозрастает на \(M\).
Стоит также отметить, что фразы “функция неубывает на \(M\)”\(\ \) и “функция не является убывающей на \(M\)”\(\ \)в общем случае значат совсем не одно и тоже.
Теорема
Если дифференцируемая на некотором интервале \(I\) функция неубывает на нём, то её производная не отрицательна на \(I\).
Если производная функции не отрицательна на некотором интервале \(I\), то эта функция неубывает на \(I\).
Если производная функции не отрицательна на некотором интервале \(I\), причём производная равна 0 не более чем в конечном числе точек из \(I\), то эта функция возрастает на \(I\).
Теорема
Если дифференцируемая на некотором интервале \(I\) функция невозрастает на нём, то её производная не положительна на \(I\).
Если производная функции не положительна на некотором интервале \(I\), то эта функция невозрастает на \(I\).
Если производная функции не положительна на некотором интервале \(I\), причём производная равна 0 не более чем в конечном числе точек из \(I\), то эта функция убывает на \(I\).
Определение
Точка \(x_0\) называется точкой строгого локального максимума функции \(f(x)\), если существует некоторый интервал \(I\), содержащий точку \(x_0\), такой что для любой точки \(a\) из \(I\), отличной от \(x_0\), верно \(f(x_0) > f(a)\).
Точка \(x_0\) называется точкой строгого локального минимума функции \(f(x)\), если существует некоторый интервал \(I\), содержащий точку \(x_0\), такой что для любой точки \(a\) из \(I\), отличной от \(x_0\), верно \(f(x_0) < f(a)\).
Точка \(x_0\) называется точкой локального максимума функции \(f(x)\), если существует некоторый интервал \(I\), содержащий точку \(x_0\), такой что для любой точки \(a\) из \(I\) верно \(f(x_0) \geq f(a)\).
Точка \(x_0\) называется точкой локального минимума функции \(f(x)\), если существует некоторый интервал \(I\), содержащий точку \(x_0\), такой что для любой точки \(a\) из \(I\) верно \(f(x_0) \leq f(a)\). Точка \(x_0\) называется точкой локального экстремума функции \(f(x)\), если она является точкой её локального максимума или точкой локального минимума.
Замечание
Всякая точка строгого локального максимума функции \(f\) является также и точкой её локального максимума.
Всякая точка строгого локального минимума функции \(f\) является также и точкой её локального минимума.
Теорема
Если функция имеет экстремум в точке \(x_0\), то её производная в этой точке либо равна \(0\), либо не существует.
Определение
Точка \(x_0\), в которой \(f'(x_0)\) равно нулю или не существует, называется критической точкой функции \(f(x)\).
Таким образом, все точки экстремума функции \(f(x)\) являются и её критическими точками. Обратное, вообще говоря, не верно.
shkolkovo.net
Применение производной для исследования функций на монотонность и экстремумы
Рассмотрим график функции 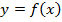 (Рис. 1).
(Рис. 1).
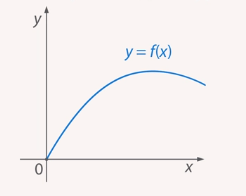
Рис. 1. График функции 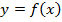
Функция описывает некий реальный процесс, например поход на прогулку,  – это расстояние от дома,
– это расстояние от дома, 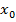
 (Рис. 2).
(Рис. 2).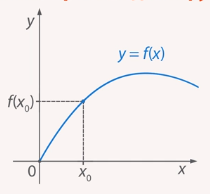
Рис. 2. Значение 
По прошествии времени  – приращение аргумента. Получился момент времени
– приращение аргумента. Получился момент времени 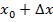 . В этот момент времени расстояние от дома равнялось
. В этот момент времени расстояние от дома равнялось 
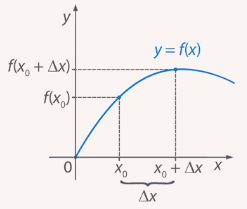
Рис. 3. Приращение аргумента  , значение
, значение 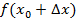
Имеем знаменитый треугольник (Рис. 4). Здесь  – приращение аргумента,
– приращение аргумента,  – приращение функции, а тангенс это отношение
– приращение функции, а тангенс это отношение 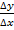
 пройдено расстояние
пройдено расстояние  .
. 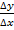 – это средняя скорость, но если
– это средняя скорость, но если 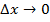 , то и числитель и знаменатель стремятся к нулю. И если эта дробь стремится к некоторому числу, то это число и называется производной данной функции в данной точке. Она обозначается так:
, то и числитель и знаменатель стремятся к нулю. И если эта дробь стремится к некоторому числу, то это число и называется производной данной функции в данной точке. Она обозначается так:
Это определение производной (Рис. 4). Теперь нужно понять, каков смысл производной.
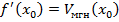 – это мгновенная скорость в данной точке.
– это мгновенная скорость в данной точке.
Если в этой точке провести касательную, которая имеет угол наклона  , то производная в этой точке есть тангенс угла наклона касательной.
, то производная в этой точке есть тангенс угла наклона касательной.  .
.

Рис. 4. Определение производной
Итак, нам надо исследовать функцию, рассмотрим инструменты, имеющиеся у нас.
Из соотношения 
 – это физический и геометрический смысл производной.
– это физический и геометрический смысл производной.
Монотонно возрастающая функция – это функция, у которой большему значению аргумента соответствует большее значение функции.
Монотонно убывающая функция – это функция, у которой большему значению аргумента соответствует меньшее значение функции.
Если 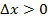 , то знак приращения
, то знак приращения  и знак производной в точке
и знак производной в точке 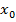
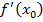 . То есть если производная
. То есть если производная 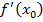 в этой точке больше нуля, то
в этой точке больше нуля, то  и понятно, что функция в окрестности этой точки будет возрастать. А если производная меньше нуля, значит,
и понятно, что функция в окрестности этой точки будет возрастать. А если производная меньше нуля, значит,  и понятно, что в окрестности этой точки функция будет убывать.
и понятно, что в окрестности этой точки функция будет убывать.Далее, производная в точке 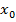 есть тангенс угла наклона касательной (Рис. 5). Касательная описывается линейной функцией. В окрестности точки
есть тангенс угла наклона касательной (Рис. 5). Касательная описывается линейной функцией. В окрестности точки 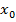
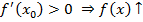
И наоборот, если линейная функция убывает, угол тупой, тангенс – величина отрицательная, значит, линейная функция убывает, а с ней убывает функция 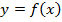 .
.
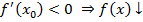

Рис. 5. Угол наклона касательной в точке 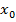
Так события развиваются в окрестностях точки 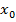 . Эти события подчиняются геометрическому смыслу производной (ее физическому смыслу, соотношению
. Эти события подчиняются геометрическому смыслу производной (ее физическому смыслу, соотношению  ).
).
Рассмотрим функцию и ее поведение на всей ОДЗ (Рис. 6). Предположим, что это график исследуемой функции.
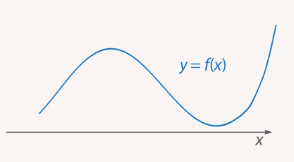
Рис. 6. График функции 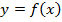
Есть точка 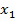 . Касательная наклонена под острым углом
. Касательная наклонена под острым углом 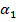 (Рис. 7). Значит, в точке
(Рис. 7). Значит, в точке 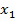 функция возрастает.
функция возрастает.

Рис. 7. Угол наклона касательной в точке 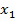
В точке  касательная параллельна оси
касательная параллельна оси  , значит точка
, значит точка  – точка экстремума. Об этом мы поговорим отдельно.
– точка экстремума. Об этом мы поговорим отдельно.
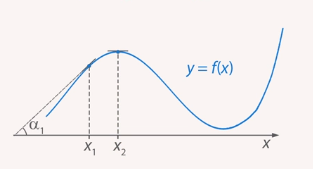
Рис. 8.  – точка экстремума
– точка экстремума
В точке  угол
угол 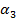 наклона касательной будет тупым, тангенс будет величиной отрицательной, значит, производная отрицательная и функция здесь убывает (Рис. 9).
наклона касательной будет тупым, тангенс будет величиной отрицательной, значит, производная отрицательная и функция здесь убывает (Рис. 9).
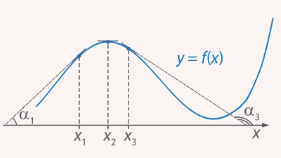
Рис. 9. Угол наклона касательной в точке 
И, наконец, в точке  производная равно нулю и дальше функция возрастает (Рис. 10).
производная равно нулю и дальше функция возрастает (Рис. 10).

Рис. 10. Угол наклона касательной в точке  – точке экстремума
– точке экстремума
Выясняется, что функция возрастает на интервалах, где производная больше нуля:

Если же значение производной отрицательное, то функция убывает:
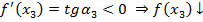
Вся ОДЗ состоит из отдельных точек, значит, надо выделить те интервалы, на которых производная меньше нуля, на которых производная больше нуля, и они определят те участки ОДЗ, на которых функция либо возрастает, либо убывает. Этот же вывод мы получим, рассматривая соотношение  . На тех областях, на которых производная
. На тех областях, на которых производная 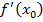 меньше нуля,
меньше нуля,
interneturok.ru
Поиск точек экстремума функции
Точка \(x_0\) называется точкой локального максимума функции \(f(x)\), если существует некоторый интервал \(I\), содержащий точку \(x_0\), такой что для любой точки \(a\) из \(I\) верно \(f(x_0) \geq f(a)\).
Точка \(x_0\) называется точкой локального минимума функции \(f(x)\), если существует некоторый интервал \(I\), содержащий точку \(x_0\), такой что для любой точки \(a\) из \(I\) верно \(f(x_0) \leq f(a)\).
Точка \(x_0\) называется точкой локального экстремума функции \(f(x)\), если она является точкой её локального максимума или точкой локального минимума.
Теорема
Если функция имеет экстремум в точке \(x_0\), то её производная в этой точке либо равна \(0\), либо не существует.
Определение
Точка \(x_0\), в которой производная \(f'(x_0)\) равна нулю или не существует, называется критической точкой функции \(f(x)\).
Таким образом, все точки экстремума функции \(f(x)\) являются и её критическими точками. Обратное, вообще говоря, не верно.
Производные элементарных функций
\[\begin{aligned}
&C’ = 0, где C — \text{число}\\
&(x^n)’ = n\cdot x^{n — 1}, где n — \text{действительное}, x > 0\\
&(\ln x)’ = \dfrac{1}{x}\\
&(a^x)’ = a^x\ln a, где a > 0\\
&(\sin x)’ = \cos x\\
&(\cos x)’ = -\sin x\\
&(\mathrm{tg}\, x)’ = \dfrac{1}{\cos^2x}\\
&(\mathrm{ctg}\, x)’ = -\dfrac{1}{\sin^2x}
\end{aligned}\] \[\begin{aligned}
&(\mathrm{arcsin}\, x)’ = \dfrac{1}{\sqrt{1 — x^2}}\\
&(\mathrm{arccos}\, x)’ = -\dfrac{1}{\sqrt{1 — x^2}}\\
&(\mathrm{arctg}\, x)’ = \dfrac{1}{1 + x^2}\\
&(\mathrm{arcctg}\, x)’ = -\dfrac{1}{1 + x^2}
\end{aligned}\] Производная суммы функций в точке \(x_0\) равна сумме производных этих функций в точке \(x_0\).
Производная функции \(C\cdot f(x)\), где \(C\) – число, равна \(C\cdot f'(x)\).
Производная произведения
Пусть \(f(x)\) и \(g(x)\) имеют производные в точке \(x_0\), тогда
\[(f\cdot g)'(x_0) = f'(x_0)\cdot g(x_0) + f(x_0)\cdot g'(x_0).\]
Пример
\(f(x) = \sin x\), \(g(x) = e^x\), \(x_0 = 0\), тогда \((f\cdot g)'(x_0) = (\sin x)’|_{x_0}\cdot e^{x_0} + \sin x_0\cdot (e^x)’|_{x_0} = \cos x_0\cdot e^{x_0} + \sin x_0\cdot e^{x_0} = \cos 0\cdot e^{0} + \sin 0\cdot e^{0} = 1\). Здесь выражение \(h(x)|_{x_0}\) обозначает значение функции \(h(x)\) в точке \(x_0\).
Производная частного
Пусть \(f(x)\) и \(g(x)\) имеют производные в точке \(x_0\) и \(g(x_0)\neq 0\), тогда
\[\left(\dfrac{f}{g}\right)'(x_0) = \dfrac{f'(x_0)\cdot g(x_0) — f(x_0)\cdot g'(x_0)}{g^2(x_0)}.\]
Пример
\(f(x) = e^x\), \(g(x) = x\), \(x_0 = 1\), тогда \(\left(\dfrac{e^x}{x}\right)'(x_0) = \dfrac{(e^x)’|_{x_0}\cdot x_0 — e^{x_0}\cdot 1|_{x_0}}{{x_0}^2}\), но так как \(1\) – константа, то \(1|_{x_0} = 1\), тогда \(\left(\dfrac{e^x}{x}\right)'(x_0) = \dfrac{e^{x_0}\cdot x_0 — e^{x_0}}{{x_0}^2} = e — e = 0\). Здесь выражение \(h(x)|_{x_0}\) обозначает значение функции \(h(x)\) в точке \(x_0\).
Определение
Сложная функция – функция вида \(f(g(x))\), где \(f(y)\) и \(g(x)\) – функции.
Производная сложной функции
Пусть \(f(y)\) и \(g(x)\) имеют производные в точках \(g(x_0)\) и \(x_0\) соответственно, тогда
\[\big(f(g(x))\big)’|_{x_0} = f'(g(x_0))\cdot g'(x_0).\] Здесь выражение \(h(x)|_{x_0}\) обозначает значение функции \(h(x)\) в точке \(x_0\): \(h(x)|_{x_0} = h(x_0)\).
Пример
\(f(y) = e^y\), \(g(x) = x^2 + 1\), \(x_0 = 0\), тогда \(f(g(x))’|_{x_0} = (e^{y})’|_{{x_0}^2 + 1}\cdot 2x_0 = e^{{x_0}^2 + 1}\cdot 2x_0 = e\cdot 0 = 0\).
shkolkovo.net
Как найти экстремум (точки минимума и максимума) функции
Простой алгоритм нахождения экстремумов. Учимся находить с bugaga.net.ru.- Находим производную функции
- Приравниваем эту производную к нулю
- Находим значения переменной получившегося выражения (значения переменной, при которых производная преобразуется в ноль)
- Разбиваем этими значениями координатную прямую на промежутки (при этом не нужно забывать о точках разрыва, которые также надо наносить на прямую), все эти точки называются точками «подозрительными» на экстремум
- Вычисляем, на каких из этих промежутков производная будет положительной, а на каких – отрицательной. Для этого нужно подставить значение из промежутка в производную.
Из точек, подозрительных на экстремум, надо найти именно экстремумы. Для этого смотрим на наши промежутки на координатной прямой. Если при прохождении через какую-то точку знак производной меняется с плюса на минус, то эта точка будет максимумом, а если с минуса на плюс, то минимумом.
Чтобы найти наибольшее и наименьшее значение функции, нужно вычислить значение функции на концах отрезка и в точках экстремума. Затем выбрать наибольшее и наименьшее значение.
https://bugaga.net.ru/ege/math/ekstremum.html bugaga.net.ru
Рассмотрим примерНаходим производную и приравниваем её к нулю:
Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём -2, тогда производная будет равна -0,24, для второго возьмём 0, тогда производная будет 2 , а для третьего возьмём 2, тогда производная будет -0,24. Проставляем соответствующие знаки.
Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет точка минимума, а при прохождении через 1 – с плюса на минус, соответственно это точка максимума.
Смотрите также:
Еще больше материалов для подготовки к ЕГЭ
bugaga.net.ru
Достаточные условия экстремума функции.
Для нахождения максимумов и минимумов функции можно пользоваться любым из трех признаков экстремума, конечно, если функция удовлетворяет их условиям. Самым распространенным и удобным является первый из них.
Первое достаточное условие экстремума.
Пусть
функция y=f(x) дифференцируема
в 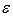 -окрестности
точки
-окрестности
точки 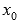 ,
а в самой точке
,
а в самой точке 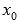 непрерывна.
непрерывна.
Тогда
Другими словами:
если в точке
 функция
непрерывна и в ней производная меняет
знак с плюса на минус, то
функция
непрерывна и в ней производная меняет
знак с плюса на минус, то  —
точка максимума;
—
точка максимума;если в точке
 функция
непрерывна и в ней производная меняет
знак с минуса на плюс, то
функция
непрерывна и в ней производная меняет
знак с минуса на плюс, то  —
точка минимума.
—
точка минимума.
Алгоритм нахождения точек экстремума по первому признаку экстремума функции.
Находим область определения функции.
Находим производную функции на области определения.
Определяем нули числителя, нули знаменателя производной и точки области определения, в которых производная не существует (все перечисленные точки называют точками возможного экстремума, проходя через эти точки, производная как раз может изменять свой знак).
Эти точки разбивают область определения функции на промежутки, в которых производная сохраняет знак. Определяем знаки производной на каждом из интервалов (например, вычисляя значение производной функции в любой точке отдельно взятого интервала).
Выбираем точки, в которых функция непрерывна и, проходя через которые, производная меняет знак — они и являются точками экстремума.
Слишком много слов, рассмотрим лучше несколько примеров нахождения точек экстремума и экстремумов функции с помощью первого достаточного условия экстремума функции.
Пример.
Найти
экстремумы функции 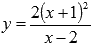 .
.
Решение.
Областью определения функции является все множество действительных чисел, кромеx=2.
Находим
производную: 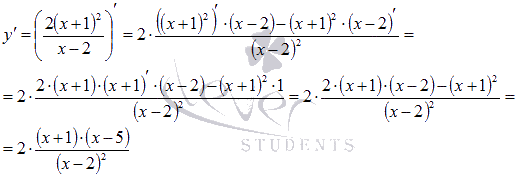
Нулями
числителя являются точки x=-1 и x=5,
знаменатель обращается в ноль при x=2.
Отмечаем эти точки на числовой оси 
Определяем знаки производной на каждом интервале, для этого вычислим значение производной в любой из точек каждого интервала, например, в точках x=-2, x=0, x=3 иx=6.
 ,
следовательно, на интервале
,
следовательно, на интервале  производная
положительна (на рисунке ставим знак
плюс над этим интервалом). Аналогично
производная
положительна (на рисунке ставим знак
плюс над этим интервалом). Аналогично 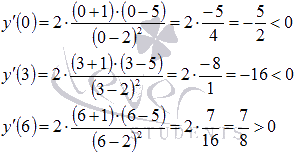
Поэтому над вторым интервалом ставим минус, над третьим – минус, над четвертым – плюс.
Осталось выбрать точки, в которых функция непрерывна и ее производная меняет знак. Это и есть точки экстремума.
В
точке x=-1 функция
непрерывна и производная меняет знак
с плюса на минус, следовательно, по
первому признаку экстремума, x=-1 –
точка максимума, ей соответствуем
максимум функции  .
.
В
точке x=5 функция
непрерывна и производная меняет знак
с минуса на плюс, следовательно, x=-1 –
точка минимума, ей соответствуем минимум
функции  .
.
Графическая иллюстрация.
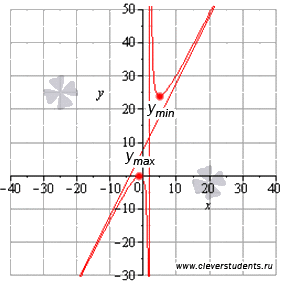
Ответ:
 .
.
ОБРАТИТЕ
ВНИМАНИЕ: первый достаточный признак
экстремума не требует дифференцируемости
функции в самой точке  .
.
Пример.
Найдите
точки экстремума и экстремумы функции  .
.
Решение.
Областью
определения функции является все
множество действительных чисел. Саму
функцию можно записать в виде: 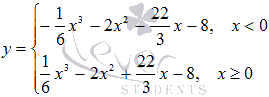
Найдем
производную функции: 
В
точке x=0 производная
не существует, так как значения
односторонних пределов при стремлении
аргумента к нулю не совпадают: 
В
это же время, исходная функция является
непрерывной в точке x=0 (смотрите
разделисследование
функции на непрерывность):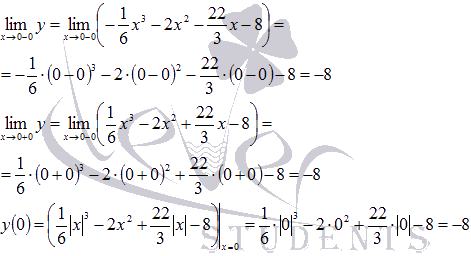
Найдем
значения аргумента, при котором
производная обращается в ноль: 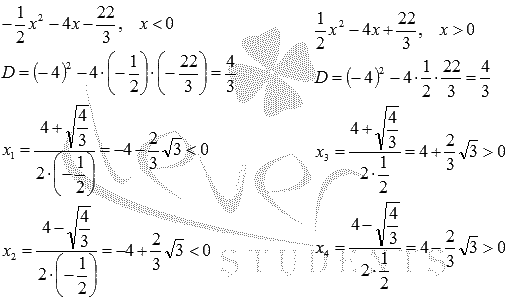
Отметим
все полученные точки на числовой прямой
и определим знак производной на каждом
из интервалов. Для этого вычислим
значения производной в произвольных
точках каждого интервала, к примеру,
при x=-6,
x=-4, x=-1, x=1, x=4, x=6. 
То
есть, 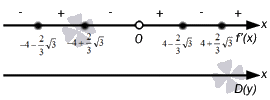
Таким
образом, по первому признаку экстремума,
точками минимума являются 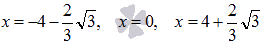 ,
точками максимума являются
,
точками максимума являются  .
.
Вычисляем
соответствующие минимумы функции 
Вычисляем
соответствующие максимумы функции 
Графическая иллюстрация.
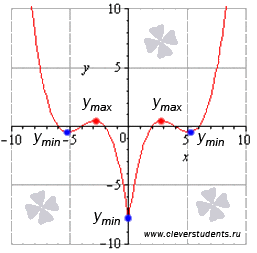
Ответ:
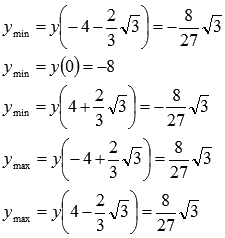 .
.
studfile.net
Возрастание и убывание функций, экстремумы
Экстремумы функции
Определение 1
Точки $x_0$ называются точками экстремума функции, если они являются точками максимума и минимума для функции $f(x)$.
Определение 2
Точка $x_0$ называется точкой максимума функции $f(x)$, если существует такая окрестность данной точки, что для всех $x$ из этой окрестность выполняется неравенство $f(x)\le f(x_0)$.
Определение 3
Точка $x_0$ называется точкой максимума функции $f(x)$, если существует такая окрестность данной точки, что для всех $x$ из этой окрестность выполняется неравенство $f(x)\ge f(x_0)$.
Понятие экстремума функции тесно связано с понятием критической точки функции. Введем её определение.
Определение 4
$x_0$ называется критической точкой функции $f(x)$, если:
1) $x_0$ — внутренняя точка области определения;
2) $f’\left(x_0\right)=0$ или не существует.
Для понятия экстремума можно сформулировать теоремы о достаточных и необходимых условиях его существования.
Теорема 1
Необходимое условие экстремума
Если функция $y=f(x)$ имеет экстремум в точке $x_0$, то либо $f’\left(x_0\right)=0$, либо производная в точке $x_0$ не существует.
Теорема 2
Достаточное условие экстремума
Пусть точка $x_0$ является критической для функции $y=f(x)$ и лежит в интервале $(a,b)$. Пусть на каждом интервале $\left(a,x_0\right)\ и\ (x_0,b)$ производная $f'(x)$ существует и сохраняет постоянный знак. Тогда:
1) Если на интервале $(a,x_0)$ производная $f’\left(x\right)>0$, а на интервале $(x_0,b)$ производная $f’\left(x\right)
2) Если на интервале $(a,x_0)$ производная $f’\left(x\right)0$, то точка $x_0$ — точка минимума для данной функции.
3) Если и на интервале $(a,x_0)$, и на интервале $(x_0,b)$ производная $f’\left(x\right) >0$ или производная $f’\left(x\right)
Данная теорема проиллюстрирована на рисунке 1.

Рисунок 1. Достаточное условие существования экстремумов
Примеры экстремумов (Рис. 2).

Рисунок 2. Примеры точек экстремумов
Правило исследования функции на экстремум
1) Найти область определения функции $f(x)$;
2) Найти производную $f'(x)$;
3) Найти точки, в которых выполняется равенство $f’\left(x\right)=0$;
4) Найти точки, в которых $f'(x)$ не существует;
5) Отметить на координатной прямой все найденные точки и область определения данной функции;
6) Определить знак производной $f'(x)$ на каждом получившемся промежутке;
7) Сделать выводы о наличии максимумов и минимумов на каждом промежутке, используя теорему 2.
Возрастание и убывание функции
Введем, для начала, определения возрастающей и убывающей функций.
Определение 5
Функция $y=f(x)$, определенная на промежутке $X$, называется возрастающей, если для любых точек $x_1,x_2\in X$ при $x_1
Определение 6
Функция $y=f(x)$, определенная на промежутке $X$, называется убывающей, если для любых точек $x_1,x_2\in X$ при $x_1f(x_2)$.
Исследование функции на возрастание и убывание
Исследовать функции на возрастание и убывание можно с помощью производной.
Для того чтобы исследовать функцию на промежутки возрастания и убывания, необходимо сделать следующее:
1) Найти область определения функции $f(x)$;
2) Найти производную $f'(x)$;
3) Найти точки, в которых выполняется равенство $f’\left(x\right)=0$;
4) Найти точки, в которых $f'(x)$ не существует;
5) Отметить на координатной прямой все найденные точки и область определения данной функции;
6) Определить знак производной $f'(x)$ на каждом получившемся промежутке;
7) Сделать вывод: на промежутках, где $f’\left(x\right)0$ функция возрастает.
Примеры задач на исследования функций на возрастание, убывание и наличие точек экстремумов
Пример 1
Исследовать функцию на возрастание и убывание, и наличие точек максимумов и минимумов: $f(x)={2x}^3-15x^2+36x+1$
Так как первые 6 пунктов совпадают, проведем для начала их.
1) Область определения — все действительные числа;
2) $f’\left(x\right)=6x^2-30x+36$;
3) $f’\left(x\right)=0$;
\[6x^2-30x+36=0\] \[x^2-5x+6=0\] \[x=3,\ x=2\]4) $f'(x)$ существует во всех точках области определения;
5) Координатная прямая:

Рисунок 3.
6) Определить знак производной $f'(x)$ на каждом промежутке:
\[f’\left(x\right) >0,\ при\ \left(-\infty ,2\right)\ (3,+\infty )\] \[f’\left(x\right)7) Изобразим все на одном рисунке:
Рисунок 4.
Получаем:
Функция возрастает, при $\left(-\infty ,2\right)\ (3,+\infty )$, функция убывает, при $\left(2,3\right)$.
Точка $x=2$ — точка максимума, точка $x=3$ — точка минимума.
spravochnick.ru
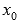 функция
непрерывна и в ней производная меняет
знак с плюса на минус, то
функция
непрерывна и в ней производная меняет
знак с плюса на минус, то  —
точка максимума;
—
точка максимума;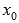 функция
непрерывна и в ней производная меняет
знак с минуса на плюс, то
функция
непрерывна и в ней производная меняет
знак с минуса на плюс, то 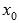 —
точка минимума.
—
точка минимума.