Что такое трапеция: свойства четырёхугольника, теоремы и формулы

В курсе геометрии за 8-й класс подразумевается изучение свойств и признаков выпуклых четырёхугольников. К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.

Определение и виды

В отличие от других четырёхугольников, изучаемых в школьной программе, трапецией принято называть такую фигуру, две противоположные стороны которой параллельны друг другу, а две другие — нет. Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.

Различные виды указаны на рисунке ниже.

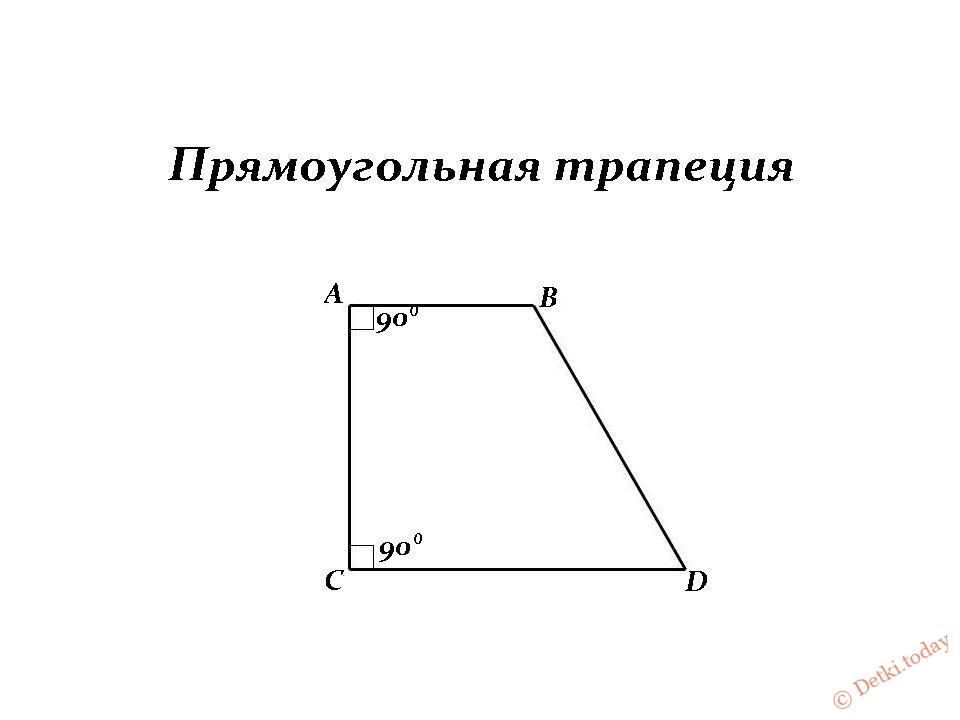
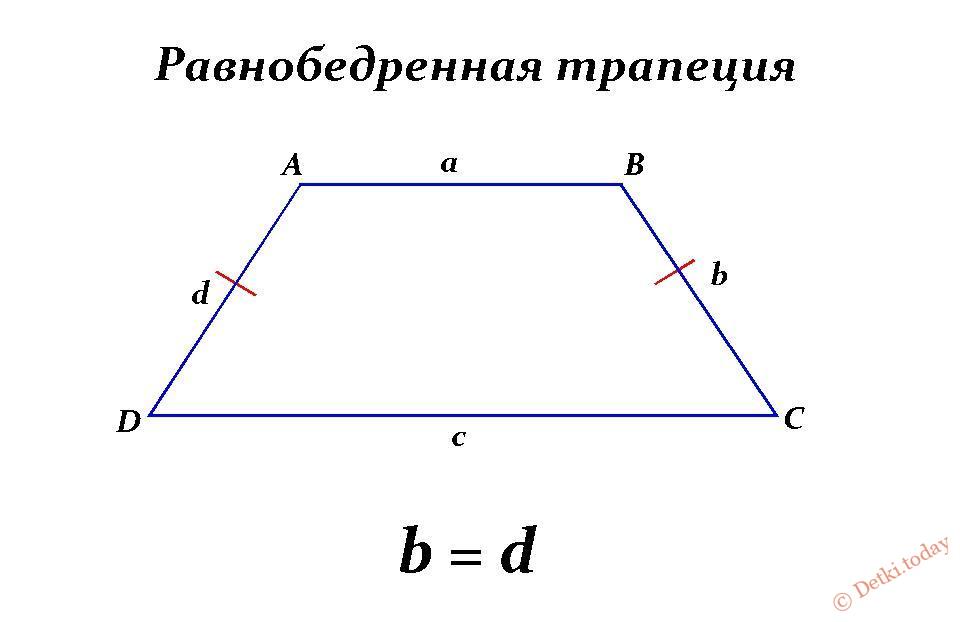
На изображении под номером 1 изображена произвольная трапеция. Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.

Важнейшие свойства и формулы

Для описания свойств четырёхугольника принято выделять определённые элементы. В качестве примера можно рассмотреть произвольную трапецию ABCD.

В её состав входят:

• основания BC и AD — две стороны, параллельные по отношению друг к другу;
• боковые стороны AB и CD — два непараллельных элемента;
• диагонали AC и BD — отрезки, соединяющие противоположные вершины фигуры;
• высота трапеции CH — перпендикулярный основаниям отрезок;
• средняя линия EF — линия, соединяющая середины боковых сторон.

Основные свойства элементов

Чтобы решить задачи по геометрии или доказать какие-либо утверждения, наиболее часто используют свойства, которые связывают различные элементы четырёхугольника. Они формулируются следующим образом:

1. Средняя линия всегда проходит параллельно обоим основаниям фигуры и численно равна их полусумме: EF = (BC + AD)/2.
2. Точка пересечения диагоналей фигуры разделяет их с таким же соотношением длины, с каким относятся основания трапеции: AD : BC = AO : CO = DO : BO.
3. Основание можно вычислить, зная длину второго основания и средней линии: BC = 2 · EF — AD, AD = 2 · EF — BC.
4. Боковые стороны вычисляются, если известна высота фигуры и синус угла при основании: AB = CH / sinA, CD = CH / sinD.
5. Для расчёта высоты необходимо знать, чему равна боковая сторона и прилегающий угол: CH = AB · sinA = CD · sinD.

Кроме того, часто полезно знать и применять следующие утверждения:

1. Биссектриса, проведённая из произвольного угла, отделяет на основании отрезок, длина которого равна боковой стороне фигуры.
2. При проведении диагоналей образуются 4 треугольника; из них 2 треугольника, образованных основаниями и отрезками диагоналей, обладают подобием, а оставшаяся пара имеет одинаковую площадь.
3. Через точку пересечения диагоналей O, середины оснований, а также точку, в которой пересекаются продолжения боковых сторон, можно провести прямую.

Вычисление периметра и площади

Периметр рассчитывается как сумма длин всех четырёх сторон (аналогично любой другой геометрической фигуре):

P = AD + BC + AB + CD.

Есть несколько способов, как можно рассчитать площадь трапеции по формуле. Следует выбрать из них наиболее подходящий вариант, опираясь на то, какие данные известны по условию задачи.

Вписанная и описанная окружность

Окружность возможно описать около трапеции только в том случае, когда боковые стороны четырёхугольника равны.

Чтобы вычислить радиус описанной окружности, необходимо знать длины диагонали, боковой стороны и большего основания. Величина p, используемая в формуле, рассчитывается как полусумма всех вышеперечисленных элементов: p = (a + c + d)/2.

Для вписанной окружности условие будет следующим: сумма оснований должна совпадать с суммой боковых сторон фигуры. Радиус её можно найти через высоту, и он будет равен

r = h/2.

Частные случаи

Рассмотрим часто встречаемый случай — равнобокую (равностороннюю) трапецию. Её признаки — равенство боковых сторон или равенство противолежащих углов. К ней применимы все утверждения, которые характерны для произвольной трапеции. Другие свойства равнобедренной трапеции:

1. Прямая, которая проходит через середины оснований фигуры, пересекает их под углом 90 градусов.
2. Углы, лежащие при любых основаниях, попарно равны.
3. Длины диагоналей совпадают.
4. Высота будет равна средней линии, если диагонали проходят перпендикулярно друг к другу.
5. Высота, опущенная из вершины к основанию, делит его на 2 отрезка, длина большего вычисляется как половина суммы оснований, а длина меньшего — как половина разности.

Прямоугольная трапеция встречается в задачах не так часто. Её признаки — наличие двух смежных углов, равных 90 градусов, и наличие боковой стороны, перпендикулярной основаниям. Высота в таком четырёхугольнике одновременно является одной из его сторон.

Все рассмотренные свойства и формулы обычно используются для решения планиметрических задач. Однако также их приходится применять в некоторых задачах из курса стереометрии, например, при определении площади поверхности усечённой пирамиды, внешне напоминающей объёмную трапецию.

1001student.ru

5.1.3 Трапеция

Видеоурок 1: Параллелограмм и трапеция. Часть 1

Видеоурок 2: Параллелограмм и трапеция. Часть 2

Лекция: Трапеция

Все четырехугольники, которые описывались раньше, можно отнести к параллелограммам, потому что их противолежащие стороны параллельны. Однако, есть четырехугольник, который не имеет данного свойства, он называется трапецией.

Основным отличием трапеции от любого другого произвольного четырехугольника считается то, что она имеет две параллельные стороны, а другие две – нет.

У трапеции есть 4 стороны, две из которых называются основаниями, а другие две – боковыми сторонами.

Любая трапеция имеет меньшее и большее основание. Если бы основания были бы равны, то трапеция стала бы параллелограммом.

Еще одной отличительной особенностью трапеции считается средняя линия – это прямая, которая ограничена серединами боковых сторон трапеции. Средняя линия всегда параллельная основаниям трапеции и равна их полусумме:

Существует три основных типа трапеции:

• Произвольная – которая имеет произвольные длины сторон и углы.

• Прямоугольная – один угол у такой трапеции является прямым.

• Равнобокая – такая трапеция имеет равные боковые стороны.

Диагонали и стороны трапеции:

d₁, d₂ – диагонали, а с, d – боковые стороны.

Формулы для нахождения длин сторон трапеции:

Площади трапеций:

cknow.ru

Площадь трапеции: формулы, примеры, решения задач

Трапеция – четырехугольник у которого две стороны параллельны. Параллельные стороны – это основание, непараллельные стороны – боковые.

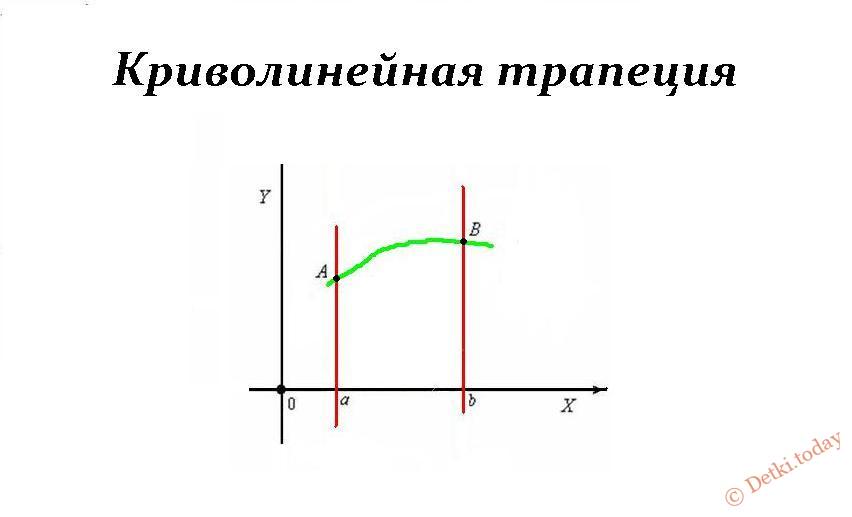
Существует несколько основных видов: криволинейная, равнобедренная, произвольная, прямоугольная. Вычисления площади трапеции по формуле разнятся в зависимости от конкретного типа геометрической фигуры.

Содержание:

Что такое трапеция: типы и отличия

Всего существует четыре типа, отличающихся между собой не только вариативностью углов, но и возможным наличием криволинейных отрезков.

• Произвольная – любой четырехугольник, две стороны которого параллельны, а две другие – расположены произвольно (разные по длине и не под прямым углом относительно параллельных сторон).
• Прямоугольная – трапеция, в которой один угол у основания равен 90⁰.
• Равнобедренная (равнобокая) – фигура, обладающая одинаковыми по длине боковыми сторонами.
  
• Криволинейная трапеция – четырехугольник с парой параллельных сторон и двумя сторонами, ограниченными графиком неотрицательной обязательно непрерывной функции.
  

Площадь произвольной трапеции

Вариативность расчета площади произвольной трапеции невелика. Ее можно вычислить относительно заданных размеров основания и высоты; посчитать через обозначенные четыре стороны фигуры; решить пример, зная длину средней линии и высоты; по указанным диагоналям и углом между ними; высчитать через основания и два угла.

Формула через основания и высоту

Основная формула расчета данного способа: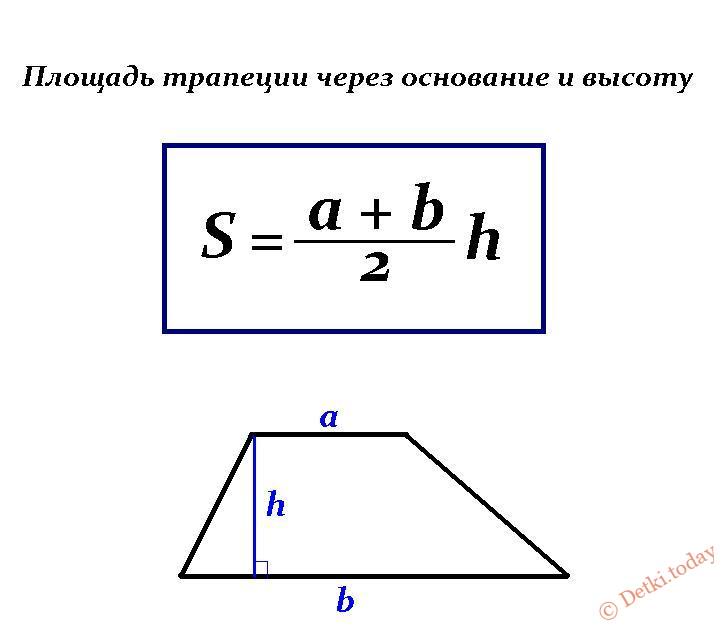

Где а и b – параллельные стороны, а h – высота четырехугольника.

Пример задачи: Дана плоская геометрическая фигура, параллельные стороны которой соответствуют длине 12 и 20 см, а высота равна – 10 см. Как найти площадь?

Решение: Допустимое решение согласно вышеприведенной формуле S = (a + b)/2 x h: S = (12 + 20)/2 x 10 = 160 см².

Формула через высоту и среднюю линию

Зная длину средней линии и высоту плоской фигуры, всегда можно найти площадь трапеции, выполнив буквально одно действие:

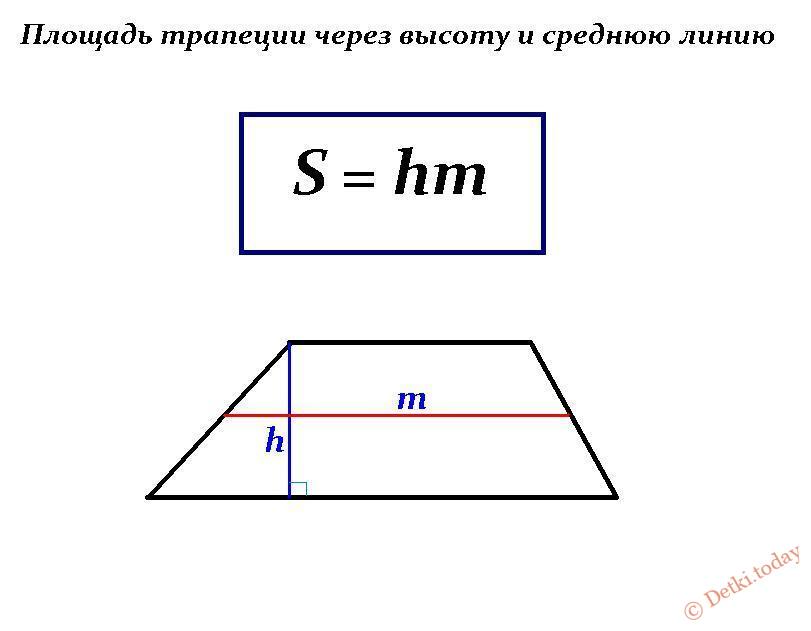
Где h – высота четырехугольника, а m – средняя линия (прямая, соединяющая середины боковых сторон).

Пример решения задачи: Дана трапеция, в которой длина средней линии – 28 см, а высота фигуры – 19 см. Какова площадь плоского четырехугольника?

Решение: Используя формулу S = hm, подставляем вместо букв цифровые значения из условия задачки. Получаем S = 28 х 19 = 532 см².

Формула через четыре стороны

Этот метод не так прост, как предыдущие. Здесь взяты за основу основные теоремы геометрии, а потому принцип расчета площади трапеции выглядит следующим образом:

Где a, b, c, d – четыре стороны фигуры, причем сторона b в обязательном порядке должна быть длинней а.

Пример вычисления: Даны стороны – a = 2 см, b = 4 см, c = 8 см, d = 7 см. Как найти площадь трапеции?

Расчет: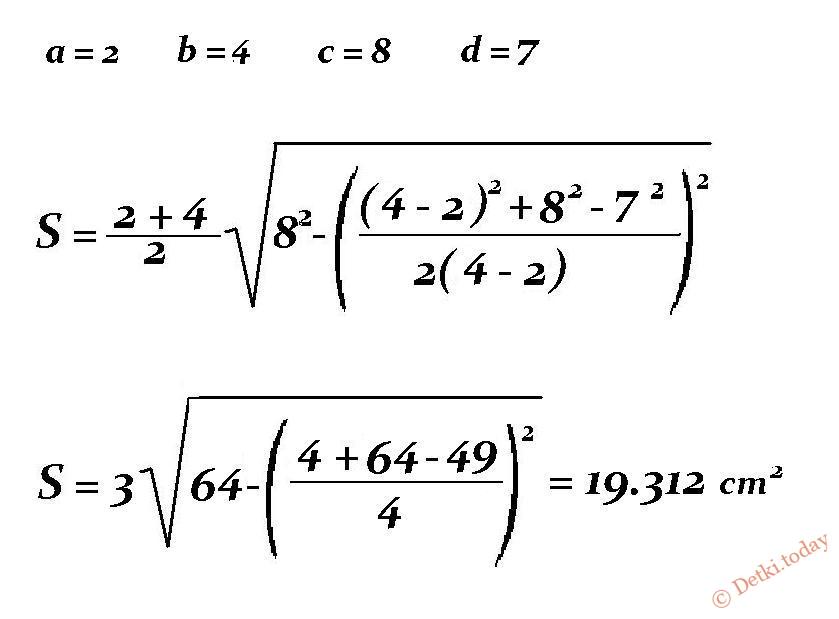

Формула через диагонали и угол между ними

Вычислить площадь трапеции также можно, зная размеры обеих диагоналей и значения угла между ними.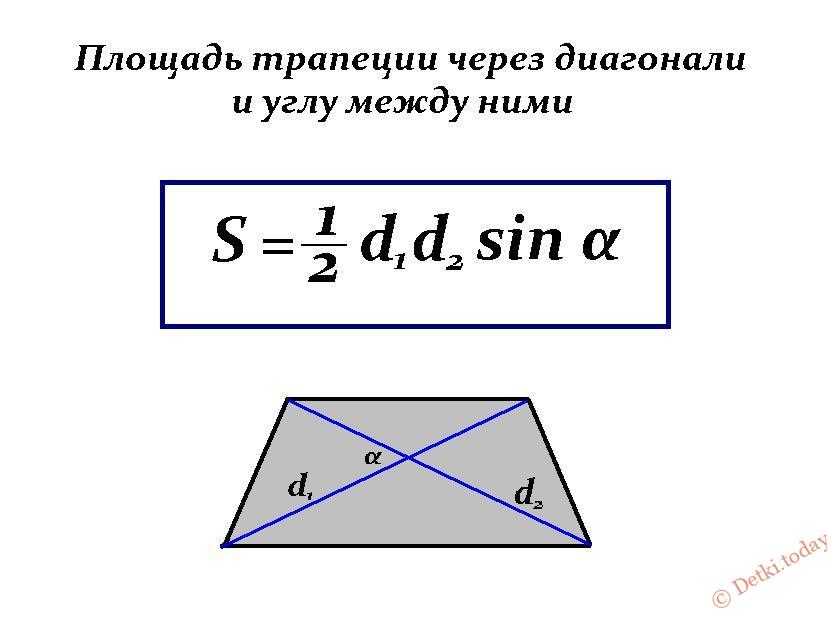

Обозначения: d₁ и d₂ — первая и вторая диагонали, α – угол между диагоналями.

Пример: Вычислить площадь фигуры при следующих известных значениях — d₁ = 17 см, d₂ = 25 см, α = 35⁰.

Верное решение: S = ½ х 17 х 25 х sin35 = 212,5 х 0,57 = 121,125 см².

Формула через основания и два угла

Еще один вариант вычисления, основанный на расчете площади трапеции посредством длин двух оснований и двух углов.

Значения букв: b, a – длины оснований, α и β – углы.

Как посчитать (пример): Пускай угол α будет равен 67⁰, угол β = 106⁰, длина основания а равно 8 см, размер b = 11 см.

Решение: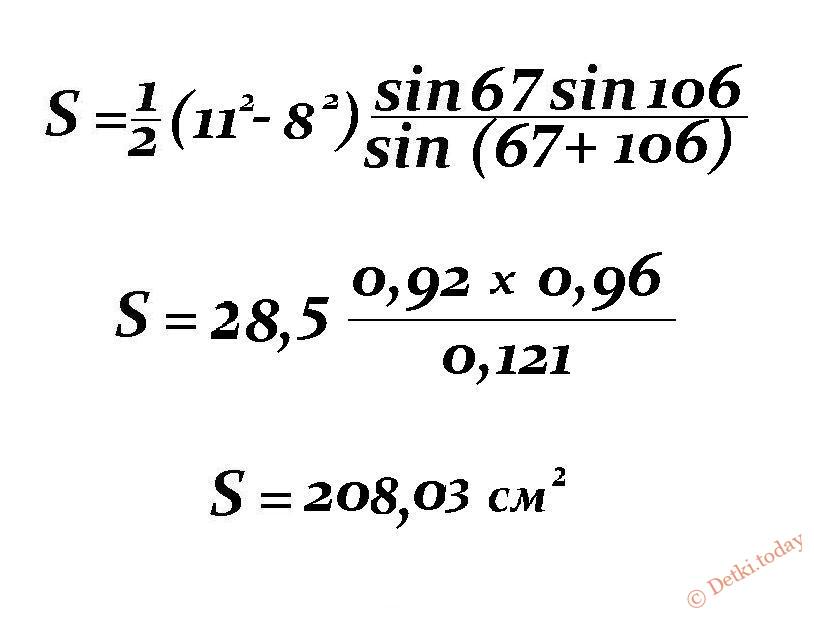

Обучающее видео

Отличным подспорьем в изучении основных типов вычислений площади являются видеоматериалы с доступным, легким языком изложения, подробными объяснениями и примерами решения задач.

Видео «Трапеция: решение задач»

Видео для новичков – доходчиво изложенная информация, содержащая основные формулы вычисления площади трапеции.

Видео «Площадь трапеции»

Видео содержит максимально полную информацию о видах трапеций, правильных буквенных обозначениях и вариантах решений разноплановых задач при помощи всех известных методов и принципов расчета.

Все перечисленные формулы и способы вычисления широко применимы во время изучения геометрии в школах и ВУЗах. Студенту, школьнику и абитуриенту предоставленная информация пригодится в качестве онлайн шпаргалки в период интенсивной подготовки к экзаменам, контрольным работам, написания рефератов, курсовых и подобных работ.

detki.today