Задача 11.

В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 46. Найдите ее среднюю линию.

Решение: + показать

Задача 12.

Найдите среднюю линию трапеции , если стороны квадратных клеток равны .

Решение: + показать

Вы можете пройти тест по теме «Трапеция»

egemaximum.ru

Трапеция — свойства и признаки: площадь, средняя линия прямоугольной, равнобедренной, как найти высоту

С такой формой как трапеция, мы встречаемся в жизни довольно часто. К примеру, любой мост который выполнен из бетонных блоков, является ярким примером. Более наглядным вариантом можно считать рулевое управление каждого транспортного средства и прочее. О свойствах фигуры было известно еще в Древней Греции, которую более детально описал Аристотель в своем научном труде «Начала». И знания, выведенные тысячи лет назад актуальны и по сегодня. Поэтому ознакомимся с ними более детально. …

Основные понятия

Рисунок 1. Классическая форма трапеции.

Трапеция по своей сути является четырехугольником, состоящим из двух отрезков которые параллельны, и двух других, которые не параллельны. Говоря об этой фигуре всегда необходимо помнить о таких понятиях как: основания, высота и средняя линия. Два отрезка четырехугольника которые параллельны друг другу называются основаниями (отрезки AD и BC). Высотой называют отрезок перпендикулярный каждому из оснований (EH), т.е. пересекаются под углом 90° (как это показано на рис.1).

Если сложить все градусные меры внутренних углов, то сумма углов трапеции будет равна 2π (360°), как и у любого четырехугольника. Отрезок, концы которого являются серединами боковин (IF) именуют средней линей. Длина этого отрезка составляет сумму оснований BC и AD деленную на 2.

Существует три вида геометрической фигуры: прямая, обычная и равнобокая. Если хоть один угол при вершинах основания будет прямой (например, если ABD=90°), то такой четырехугольник называют прямой трапецией. Если боковые отрезки равны (AB и CD), то она называется равнобедренной (соответственно углы при основаниях равны).

Как найти площадь

Для того, чтобы найти площадь четырехугольника ABCD пользуются следующей формулой:

Рисунок 2. Решение задачи на поиск площади

Для более наглядного примера решим легкую задачу. К примеру, пускай верхнее и нижнее основания равны по 16 и 44 см соответственно, а боковые стороны – 17 и 25 см. Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что

Пускай DF – будет высотой. Из ΔADE (который будет равнобоким), получим следующее:

Т.е., выражаясь простым языком, мы вначале нашли высоту ΔADE, которая по совместительству является и высотой трапеции. Отсюда вычислим по уже известной формуле площадь четырехугольника ABCD, с уже известным значением высоты DF.

Отсюда, искомая площадь ABCD равна 450 см³. То есть можно с уверенностью сказать, что для того, чтобы вычислить площадь трапеции потребуется только сумма оснований и длина высоты.

Важно! При решении задача не обязательно найти значение длин по отдельности, вполне допускается, если будут применены и другие параметры фигуры, которые при соответствующем доказательстве будут равны сумме оснований.

Виды трапеций

В зависимости от того, какие стороны имеет фигура, какие углы образованы при основаниях, выделяют три вида четырехугольника: прямоугольная, разнобокая и равнобокая.

Разнобокая

Существует две формы: остроугольная и тупоугольная. ABCD остроугольна только в том случае, когда углы при основании (AD) острые, а длины сторон разные. Если величина одного угла число Пи/2 более (градусная мера более 90°), то получим тупоугольную.

Если боковины по длине равны

Рисунок 3. Вид равнобокой трапеции

Если непараллельные стороны равны по длине, тогда ABCD называется равнобокой (правильной). При этом у такого четырехугольника градусная мера углов при основании одинакова, их угол будет всегда меньше прямого. Именно по этой причине равнобедренная никогда не делится на остроугольные и тупоугольные. Четырехугольник такой формы имеет свои специфические отличия, к числу которых относят:

1. Отрезки соединяющие противоположные вершины равны.
2. Острые углы при большем основании составляют 45° (наглядный пример на рисунке 3).
3. Если сложить градусные меры противоположных углов, то в сумме они будут давать 180°.
4. Вокруг любой правильной трапеции можно построить окружность.
5. Если сложить градусную меру противоположных углов, то она равна π.

Более того, в силу своего геометрического расположения точек существуют основные свойства равнобедренной трапеции:

1. Если диагонали пересекаются под углом, то половина суммы оснований будет равна длине высоты.
2. В случае, когда в правильную трапецию построена, или может быть построена, окружность, то квадрат высоты равен произведению величин оснований.
3. Ось симметрии и средняя линия трапеции являются одним и тем же ГМТ.
4. Когда диагонали пересекаются под прямым углом, тогда для вычисления площади потребуется формула: 
5. Окружность вписанная в трапецию, делает величину средней линии равной боковой.

Значение угла при основании 90°

Перпендикулярность боковой стороны основания емкая характеристика понятия «прямоугольная трапеция». Двух боковых сторон с углами при основании быть не может, потому как в противном случае это будет уже прямоугольник. В четырехугольниках такого типа вторая боковая сторона всегда будет образовывать острый угол с большим основанием, а с меньшим тупой. При этом, перпендикулярная сторона также будет являться и высотой.

Это интересно! Чему равна и как найти площадь равностороннего треугольника

Отрезок между серединами боковин

Если соединить середины боковых сторон, и полученный отрезок будет параллельный основаниям, и равен по длине половине их суммы, то образованная прямая будет средней линией. Значение этого расстояния вычисляется по формуле:

Для более наглядного примера рассмотрим задачу с применением средней линии.

Задача. Средняя линия трапеции равна 7 см, известно, что одна из сторон больше другой на 4 см (рис.4). Найти длины оснований.

Рисунок 4. Решение задачи на поиск длин оснований

Решение. Пусть меньшее основание DC будет равно x см, тогда большее основание будет равняться соответственно (x+4) см. Отсюда, используя формулу средней линии трапеции получим:

Получается, что меньшее основание DC равно 5 см, а большее равняется 9 см.

Важно! Понятие средней линии является ключевым при решении многих задач по геометрии. На основании её определения, строятся многие доказательства для других фигур. Используя понятие на практике, возможно более рациональное решение и поиск необходимой величины.

Определение высоты, и способы как её найти

Как уже отмечалось ранее, высота представляет собой отрезок, который пересекает основания под углом 2Пи/4 и является кратчайшим расстоянием между ними. Перед тем как найти высоту трапеции, следует определиться какие даны входные значения. Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.

Рисунок 5. Решение задачи на поиск высоты трапеции

Решение:

Проведем отрезки DF и CH под прямыми углами к основанию AD.Согласно определению, каждый из них будет являться высотой заданной трапеции (рис.5). В таком случае, зная длину каждой боковины, при помощи теоремы Пифагора, найдем чему равна высота в треугольниках AFD и BHC.

Сумма отрезков AF и HB равна разности оснований, т.е.:

Пускай длина AF будет равняться x cм, тогда длина отрезка HB= (20 – x)см. Как было установлено, DF=CH , отсюда .

Тогда получим следующее уравнение:

Получается, что отрезок AF в треугольнике AFD равен 7,2 см, отсюда вычислим по той же теореме Пифагора высоту трапеции DF:

Т.е. высота трапеции ADCB будет равна 9,6 см. Как можно убедиться, что вычисление высоты процесс больше механический, и основывается на вычислениях сторон и углов треугольников. Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.

Важно! В сущности трапецию часто рассматривают как два треугольника, или как комбинацию прямоугольника и треугольника. Для решения 90% всех задач, встречаемых в школьных учебниках, свойства и признаки этих фигур. Большинство формул, для этого ГМТ, выведены полагаясь на «механизмы» для указанных двух типов фигур.

Как быстро вычислить длину основания

Перед тем, как найти основание трапеции необходимо определить какие параметры уже даны, и как их рационально использовать. Практическим подходом является извлечение длины неизвестного основания из формулы средней линии. Для более ясного восприятия картинки покажем на примере задачи, как это можно сделать. Пускай известно, что средняя линия трапеции составляет 7 см, а одно из оснований 10 см. Найти длину второй основы.

Решение: Зная, что средняя линия равна половине суммы основ, можно утверждать, что их сумма равна 14 см.

(14 см = 7 см × 2). Из условия задачи, мы знаем, что одно из равно 10 см, отсюда меньшая сторона трапеции будет равна 4 см (4 см = 14 – 10).

Более того, для более комфортного решения задач подобного плана, рекомендуем хорошо выучить такие формулы из области трапеции как:

• средняя линия,
• площадь,
• высота,
• диагонали.

Зная суть (именно суть) этих вычислений можно без особого труда узнать искомое значение.

Видео: трапеция и ее свойства

Видео: особенности трапеции

Вывод

Из рассмотренных примеров задач можно сделать нехитрый вывод, что трапеция, в плане вычисления задач, является одной из простейших фигур геометрии. Для успешного решения задач прежде всего не стоит определиться с тем, какая информация известна об описываем объекте, в каких формулах их можно применить, и определиться с тем, что требуется найти. Выполняя этот простой алгоритм, ни одна задача с применением этой геометрической фигуры не составит усилий.

tvercult.ru

Все формулы боковых сторон прямоугольной трапеции

1. Формула боковой стороны (с) прямоугольной трапеции через другие стороны и угол при нижнем основании

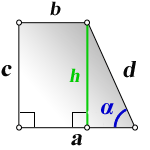
a — нижнее основание

b — верхнее основание

α — угол при нижнем основании

h — высота трапеции

c — боковая сторона под прямым углом к основаниям

Формулы длины боковой стороны (с) :

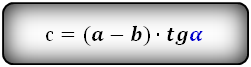
2. Формулы боковой стороны (с) прямоугольной трапеции через диагонали  и угол между ними

a — нижнее основание

b — верхнее основание

d₁ , d₂ — диагонали трапеции

α , β — углы между диагоналями

c — боковая сторона под прямым углом к основаниям

Формулы длины боковой стороны (с):

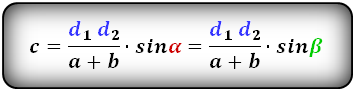
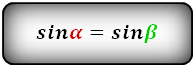
3. Формулы боковой стороны (с) прямоугольной трапеции через площадь

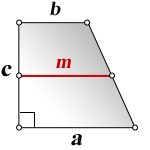
a — нижнее основание

b — верхнее основание

m — средняя линия трапеции

c — боковая сторона под прямым углом к основаниям

Формула длины боковой стороны (с) :

4. Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании

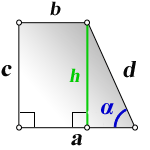
a — нижнее основание

b — верхнее основание

c — боковая сторона под прямым углом к основаниям

α — угол при нижнем основании

h — высота трапеции

d — боковая сторона

Формулы длины боковой стороны (d) :

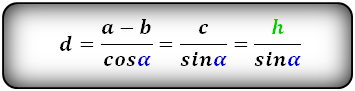
5. Формула боковой стороны (d) прямоугольной трапеции через площадь

a — нижнее основание

b — верхнее основание

m — средняя линия трапеции

α — угол при нижнем основании

d — боковая сторона

Формула длины боковой стороны (d) :

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

www-formula.ru

«Трапеция. Равнобедренная и прямоугольная трапеция»

План урока.

Урок № 37 по математике в 8 классе.

Трапеция. Равнобедренная и прямоугольная трапеция.

Цель урока

Создать условия для формирования понятия «Трапеция», «Равнобедренная трапеция», «Прямоугольная трапеция», элементов и видов трапеций; для рассмотрения решения задач, в которых раскрываются свойства трапеции.

Планируемые образовательные результаты

1. Предметные умения: умеют объяснять, какой многоугольник называется трапецией (равнобедренной и прямоугольной), знать элементы трапеций, знать свойства и признаки равнобедренной трапеции, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологией.

2. формирование у учащихся понятия “трапеция”; умений называть элементы и виды трапеции; умений называть свойства и признаки трапеции и применять эти свойства при решении простейших задач.

Метапреметные:

Познавательные: проводят информационно-смысловой анализ текста и лекции, осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, умением устанавливать причинно — следственные связи.

Регулятивные: принимают и сохраняют учебную задачу.

Коммуникативные: умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач, работать в группе.

Личностные: умеют контролировать процесс и результат математической деятельности.

Основные понятия.

Трапеция, основания трапеции, боковые стороны трапеции, равнобедренная и прямоугольная трапеция.

Трудовые действия учителя

1.Разработка технологической карты урока. 2. Подготовка презентаций к уроку, наглядных пособий, демонстративного материала, раздаточного материала.

Учебно-методическое обеспечение (средства, оборудование)

Для учителя

1. учебник; 2. индивидуальные задания; 3. презентация; 4. компьютер; 5. интерактивная доска.

Для обучающихся

1. учебник;

2. тестовые задания;

3. цветные карточки;

4. листы самооценивания;

Этап (ход) урока, включая демонстрируемые трудовые действия учителя.

Для учителя

Для обучающихся

1. Организационный этап.

Взаимное приветствие. Учитель предлагает определить готовность к уроку. Создает условия для возникновения у обучающихся внутренней потребности включения в учебную деятельность. Знакомит с эпиграфом урока.

Три пути ведут к знанию: путь размышления – это путь благородный, путь подражания – это путь самый легкий; путь опыта – это путь самый горький.(Слайд 1)

Ученики рассаживаются по местам. Проверяются наличие принадлежностей, знакомятся с листами самооценки.

2. Этап актуализация знаний по теме «Четырехугольники»; Подведение учащихся к новой теме.

Предлагает вспомнить ранее изученный материал. 1. Устная работа по готовым чертежам. На слайде изображены различные выпуклые четырёхугольники. Среди них известные ребятам параллелограмм, прямоугольник, квадрат, ромб и новый четырёхугольник (трапеция) (слайд 2) — Вспомните, с какими четырехугольниками и их свойствами вы хорошо знакомы? 2. Геометрическая разминка. — Выберите верные утверждения: (слайд 3,4) 1.Параллелограмм — это четырехугольник, у которого стороны попарно равны? (да) 2. Сумма углов четырехугольника 180⁰? (нет) 3. Противоположные углы параллелограмма равны? (да) 4. Диагонали параллелограмма равны? (нет). 5. Диагонали ромба пересекаются и точкой пересечения делятся пополам? (да) 6. Квадрат является ромбом? (да) 7. Диагонали прямоугольника равны? (да) 8. Диагонали ромба являются биссектрисами его углов? (да)

По ходу работы идет проверка ответов (слайд 5) и выставление баллов в оценочные листы.

Называют четырехугольники.

Выбирают верные утверждения. Работают с сигнальными карточками; зелёные карточки — верно, красные – неверно.

3. Этап целеполагания и планирования.

1. Ответы на вопросы по слайду 6:

— Среди представленных фигур, что вы заметили?

— Что общего у этих фигур?

—Чем отличается выделенный четырехугольник от других?

—А кто знает, как называется этот четырехугольник?

-Эта фигура называется трапецией.

-Как вы думаете какова тема сегодняшнего урока?

— Ребята, подумайте, чему бы вы сегодня хотели научиться и что хотели бы узнать нового на уроке о данном четырехугольнике?

— Как вы считаете, какой будет цель нашего урока?

— Какие нужно поставить задачи для достижения нашей цели?

— Записываем в тетрадь дату и тему сегодняшнего урока: «Трапеция».

Ответ: «Фигура стоящая справа незакрашена». Ответ: «Все фигуры являются четырехугольниками». Ответ: «Не является параллелограммом. У него две стороны параллельные, а две другие нет».) Ученики либо отвечают, либо нет.

Учащиеся формулируют тему урока.

Ученики ставят перед собой цели урока: — Сформировать понятие трапеции. — Научиться определять виды трапеции, находить её элементы. — Научиться изображать трапецию. — Выяснить свойства и признаки равнобедренной трапеции. — Научиться применять полученные знания в процессе решения задач. Формулируют задачи урока.

Записывают дату и тему урока.

3. Поисковая деятельность по открытию новых знаний.

1. Изображение трапеции. Практическая работа.

• Начертите четырехугольник, у которого две стороны параллельны, а две другие – не параллельны (на доске и в тетрадях должен появиться рис.1) — На что похожа эта фигура? —Да, и в правду она похожа на стол и в переводе означает стол. Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только две противолежащие стороны параллельны. 2. Определение трапеции. —Рассмотрим четырехугольник, про который можем сказать, что две противолежащие стороны параллельны, две другие не параллельны. Вниманию учащихся учитель представляет слайд 6 и ставить цель на данный этап урока. – А теперь сравните параллелограмм и трапецию и на основе сравнительного анализа выведите определение трапеции.

— Как он называется? — Сформулируем точное определение.

3. Элементы трапеции. Учитель предлагает по учебнику (п.44, стр. 103) проверить выдвинутую гипотезу, а также по тексту ознакомиться с элементами трапеции. (слайд 8) 4. Работа по готовым чертежам. Предлагает задание для обсуждения в группах: — Определите, какие из предложенных четырехугольников являются трапециями и почему? (слайд 9) 5. Виды трапеции. — Найдите отличия в представленных трапециях и предложите название каждому виду трапеции (слайд 10.)

6. Свойства и признаки равнобедренной трапеции.

Учитель предлагает поделится на группы и провести исследовательскую работу. Задание: исследовать углы и диагонали равнобедренной трапеции, сформулировать свойства и признаки. (слайд 11)

Строят четырехугольник, у которого две стороны параллельны, а две другие – не параллельны.

Ответ: на стол

Идет обсуждение в группах.

Результат работы: учащиеся дают определение трапеции, ключевым моментом в котором должны быть слова «четырехугольник, у которого только одна пара противолежащих сторон параллельна».

Работают по тексту учебника.

Данные слайда учащиеся заносят в конспект.

Каждая группа называет по одной трапеции и объясняет ответ.

Учащиеся обсуждают задание в группах и делают выводы: «что трапеция ABCD содержит прямые углы, а трапеция KLMN имеет равные боковые стороны». Дают предполагаемые названия видов трапеций.

Информация со слайда заносится учащимися в конспект.

Обсуждают в группах и один ученик из группы делает вывод и формулирует свойство равнобедренной трапеции.

Из выясненных свойств ученики составляют признаки равнобедренной трапеции.

4. Физкульминутка.

Используется методика здоровьесберегающей технологий «зрительные метки».

Учитель обращает внимание учащихся на развешанные по периметру класса цветные фигурки четырехугольников и дает задание отыскать среди них трапеции (все фигурки пронумерованы) (слайд 12)

Учащиеся дают в ответ № четырехугольника, который является трапецией.

5. Этап первичного закрепления и применения новых знаний.

1. Решение задач по готовым чертежам. Учитель предлагает обсудив в парах решить задачи: №1 (устно). Один из углов равнобедренной

трапеции равен 68°. Найдите остальные углы трапеции. №2 (письменно). Дана ABCD – трапеция, ВЕ||CD, АВЕ=75, ВАЕ=40. Найти углы трапеции.

2. Вывод.

—Чему равна сумма двух углов при боковых сторонах трапеции?

— Как найдем второй угол, если первый известен?

Учитель предлагает оценить свою работу и проставить баллы в оценочные листы.

Ученики решают задачи и свои ответы обсуждают в парах. Один ученик решает задачу с комментариями у доски.

Решают задачу в тетрадях , записывают ответы и проверяют свои ответы с ответом ученика, решивший задачу у доски. По ходу решения задач ученики выясняют и делают вывод, что сумма двух углов при боковой стороне трапеции равна 180⁰ . В оценочных листах проставляют баллы за правильно решенные задачи.

6. Самоконтроль изученного материала.

1. Тест.

— А теперь проведем самоконтроль изученного материала. Учитель предлагает ответить на вопросы теста по теме «Трапеция» (приложение № 2).

Выполняют тест, ответы заносят в оценочные листы и проставляют баллы за правильные ответы.

7. Подведение итогов. Оценивание.

1. Подведение итогов урока. Фронтальный опрос (слайд 21):

1. Какой четырехугольник называется трапецией?

2. Назовите элементы трапеции и ее виды.

3. Вспомните свойства равнобедренной трапеции.

2. Самооценка.

— Учитель предлагает просуммировать набранные баллы и используя шкалу перевести баллы в оценку за урок.

Отвечают на вопросы, называют основные понятия нового материала.

Заполняют листы самооценки: суммируют полученные баллы за урок и используя шкалу, переводят баллы в оценку.

8. Рефлексия.

Учитель задает вопросы о цели урока, побуждает учащихся к высказыванию мнения, чему они научились на уроке. — Как вы думаете, нам удалось достичь поставленной цели?

Предлагает продолжить предложения. На уроке я узнал…

Мне было интересно, что …

Я разобрался в том, что…

Мне стало понятно ,что…

Мне было увлекательно…

Я познакомился …

Формулируют конечный результат своей работы на уроке. Подводят итог урока.

9. Домашнее задание

Домашнее задание.

1. п. 44, выучить конспект по рабочей тетради.

2. Ответить на контрольные вопросы

3. Решить задачи №386, 387.

4. Творческое задание. Сделать презентацию на тему «Трапеция в жизни человека»

Записывают домашнее задание в дневники.

Приложение №1

Оценочный лист по теме «Трапеция»

ученика 8 класса _____________________________________________ дата __________

Этап урока

Вид задания

Правильные ответы

Количество баллов

Актуализация.

1.____ 2.____ 3.____ 4.____

5.____ 6.____ 7.____ 8.____

3 б. — за 8-7 правильных ответов

2 б. — за 6-5 правильных ответов

1 б. — за 4-3 правильных ответа

Закрепление и применение новых знаний.

Решение задач.

№1. Ответ:_____________________

№2. Ответ:_____________________

Самоконтроль изученного материала.

Тест

1.___ 2.___ 3.___ 4.___ 5.___

Оценка за урок

Критерии выставления оценок:

«5» – 9 -10 баллов,

«4» – 7-8 баллов,

«3» – 5 -6 баллов.

Приложение №2

1. Укажите верное утверждение: трапеция – это…

1) параллелограмм;

2) четырехугольник, у которого две стороны равны;

3) четырехугольник, у которого две стороны параллельны;

4) четырехугольник, у которого только две противоположные стороны параллельны.

2. Продолжите определение: трапеция называется равнобедренной, если…

1) две ее боковые стороны равны;

2) две ее соседние стороны равны;

3) любые две стороны трапеции равны;

4) другой ответ.

3. Укажите верное утверждение:

1) Только в прямоугольной трапеции углы при основании равны;

2) Углы при основании равны в любой трапеции;

3) Если трапеция равнобедренная, то противолежащие углы ее равны;

4) У равнобедренной трапеции углы при основании равны.

4. Укажите верное утверждение:

1) Сумма углов, прилежащих к одной стороне трапеции равна 180 градусов;

2) Сумма углов трапеции зависит от ее вида;

3) Сумма углов, прилежащих к боковой стороне и равна 180 градусов;

4) В трапеции сумма углов равна 180 градусов.

5. Укажите верное утверждение:

1) Трапеция может быть только прямоугольной и равнобедренной;

2) Трапеция может быть прямоугольной, равнобедренной;

3) Любой разносторонний четырехугольник можно назвать трапецией;

4) Четырехугольник с параллельными противолежащими сторонами называется трапецией.

Приложение 3

Ключи к тесту «Трапеция»

ответ

1.

4

2.

1

3.

4

4.

3

5.

4

infourok.ru