Иррациональные выражения. Преобразование иррациональных выражений
Выражения, содержащие корень, который нельзя извлечь, называются иррациональными или радикальными.
Примеры:
 – иррациональные выражения
– иррациональные выражения
Сложение и вычитание
При сложении или вычитании иррациональных выражений их пишут одно за другим с сохранением их знаков.
Примеры:

В некоторых случаях с помощью преобразования можно сделать иррациональные выражения подобными, то есть, имеющими одинаковые показатели корней и подкоренные числа (или выражения), а затем сделать приведение.
Примеры:


Умножение и деление
При умножении иррациональных выражений с одинаковыми показателями корней перемножаются их подкоренные числа или выражения:

При делении иррациональных выражений с одинаковыми показателями корней подкоренное число или выражение делимого делится на подкоренное число или выражение делителя:

Примеры:


Возведение в степень
Чтобы возвести в степень иррациональное выражение, следует возвести в степень подкоренное число или выражение:

Примеры:


При возведении  в n-ю степень знак корня отбрасывается, так как возведение числа (или выражения) в n-ю степень и извлечение из него корня n-ой степени – это взаимно сокращающиеся действия:
в n-ю степень знак корня отбрасывается, так как возведение числа (или выражения) в n-ю степень и извлечение из него корня n-ой степени – это взаимно сокращающиеся действия:

Извлечение корня
Чтобы извлечь корень из иррационального выражения, следует показатели корней перемножить:
 , так как
, так как 
Пример:

С помощью таких преобразований можно упростить извлечение корней 4-й, 6-й, 8-й, 9-й и т. п. степеней из чисел.
Примеры:


Сокращение корней
Величина иррационального выражения не изменится, если показатель корня и подкоренного выражения умножить или разделить на одно и то же число:

так как извлечение корня и возведение в степень – это взаимно сокращающиеся действия, если их показатели равны.
На этом свойстве основано сокращение корней и приведение их к одному показателю.
Сокращение корней – это деление показателей корня и подкоренного числа (или выражения) на одно и то же число, если оно является общим множителем для всех показателей.
Примеры:


Приведение корней к одному показателю
Приведение корней к общему показателю имеет большое сходство с приведением дробей к общему знаменателю. Рассмотрим два способа:
- Показатели корней не имеют общих множителей. В этом случае показатель каждого корня и его подкоренное число (или выражение) умножают на произведение остальных корней.
Рассмотрим три выражения:
 ,
,Так как у данных показателей нет общего множителя, то просто перемножаем все показатели между собой. Полученный результат и станет общим показателем. После приведения к общему показателю выражения будут иметь следующий вид:

- Показатели корней имеют общий множитель. В этом случае надо найти НОК показателей и умножить показатель каждого корня на недостающий множитель.
Рассмотрим два выражения:
 ,
,НОК (4, 6) = 12, значит, для первого выражения дополнительным множителем будет 3, а для второго 2. После приведения к общему показателю выражения будут иметь следующий вид:

При умножении и делении иррациональных выражений с разными показателями их приводят к общему показателю, а затем уже умножают или делят их подкоренные числа или выражения.
Примеры:


Действия с иррациональными выражениями примеры. Преобразование рациональных и иррациональных выражений
Предлагаемые материалы предназначены для учащихся 8 класса и включают в себя теоретические основы тождественных преобразований рациональных и иррациональных выражений, типы задач на преобразование таких выражений и текст контрольной работы .
1. Теоретические основы тождественных преобразований
Выражениями в алгебре называют записи, состоящие из чисел и букв, соединенных знаками действий.
https://pandia.ru/text/80/197/images/image002_92.gif»>.gif»> – алгебраические выражения.
В зависимости от операций различают рациональные и иррациональные выражения.
Алгебраические выражения называют рациональными, если относительно входящих в него букв а , b , с , … не выполняется никаких других операций, кроме операций сложения, умножения, вычитания, деления и возведения в целую степень.
Алгебраические выражения, содержащие операции извлечения корня из переменной или возведения переменной в рациональную степень, не являющуюся целым числом, называются иррациональными относительно этой переменной.
Тождественным преобразованием данного выражения называется замена одного выражения другим, тождественно равным ему на некотором множестве.
В основе тождественных преобразований рациональных и иррациональных выражений лежат следующие теоретические факты.
1. Свойства степеней с целым показателем:
 , n ÎN; а 1=а ;
, n ÎN; а 1=а ;
, n ÎN, а ¹0; а 0=1, а ¹0;

, а ¹0;
, а ¹0;
, а ¹0, b ¹0;
 , а ¹0, b ¹0.
, а ¹0, b ¹0.
2. Формулы сокращенного умножения:
где а , b , с – любые действительные числа;
Где а ¹0, х 1 и х 2 – корни уравнения 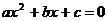 .
.
3. Основное свойство дроби и действия над дробями:
 , где b ¹0, с ¹0;
, где b ¹0, с ¹0;
;  ;
;
4. Определение арифметического корня и его свойства:
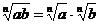 ; , b ¹0; https://pandia.ru/text/80/197/images/image026_24.gif»>; ;
; , b ¹0; https://pandia.ru/text/80/197/images/image026_24.gif»>; ; 
где а , b – неотрицательные числа, n ÎN, n ³2, m ÎN, m ³2.
1. Типы упражнений на преобразование выражений
Существуют различные типы упражнений на тождественные преобразования выражений. Первый тип : явно указано то преобразование, которое необходимо выполнить.
Например.
1. Представьте в виде многочлена .
При выполнении указанного преобразования использовали правила умножения и вычитания многочленов, формулу сокращенного умножения и приведение подобных слагаемых.
2. Разложите на множители: 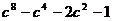 .
.
При выполнении преобразования использовали правило вынесения общего множителя за ско
«Преобразование алгебраических, рациональных, иррациональных, степенных выражений»
ПРАКТИЧЕСКАЯ РАБОТА № 1
Тема: « Преобразование алгебраических, рациональных, иррациональных, степенных выражений».
Цель работы: научиться выполнять преобразование алгебраических, рациональных, иррациональных, степенных выражений с использованием формул сокращенного умножения, основных свойств корней и степеней.
Теоретические сведения.
КОРНИ НАТУРАЛЬНОЙ СТЕПЕНИ ИЗ ЧИСЛА, ИХ СВОЙСТВА.
Корень n – степени: 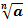 , n — показатель корня, а – подкоренное выражение
, n — показатель корня, а – подкоренное выражение
Если n – нечетное число, то выражение 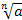 имеет смысл при
имеет смысл при 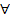 а
а
Если n – четное число, то выражение 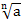 имеет смысл при
имеет смысл при 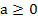
Арифметический корень: 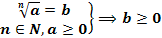
Корень нечетной степени из отрицательного числа: 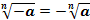
ОСНОВНЫЕ СВОЙСТВА КОРНЕЙ
Правило извлечения корня из произведения:
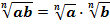
Правило извлечения корня из дроби:

Правило извлечения корня из корня:
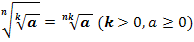
Правило вынесения множителя из под знака корня:
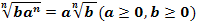
Внесение множителя под знак корня:
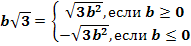 ,
,
Показатель корня и показатель подкоренного выражения можно умножить на одно и тоже число.
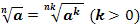
Правило возведения корня в степень.
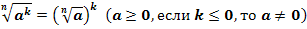
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
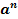 =
=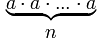 ,a – основание степени, n – показатель степени
,a – основание степени, n – показатель степени
Свойства:
При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным.
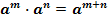
При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным.
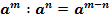
При возведении степени в степень показатели перемножаются.
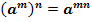
При возведении в степень произведения двух чисел, каждое число возводят в эту степень, а результаты перемножают.
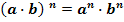
Если в степень возводят частное двух чисел, то в эту степень возводят числитель и знаменатель, а результат делят друг на друга.
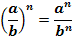
Если

СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ



По определению:

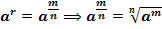
Свойства:





Пусть r рациональное число
 , тогда
, тогда
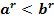 при r>0
при r>0 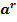 >
>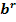 при r<0
при r<0
7 .Для любого рациональных чисел r и s из неравенства 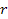 >
>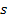 следует
следует
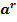 >
>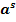 при a>1
при a>1 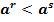 при
при 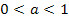
Формулы сокращённого умножения.
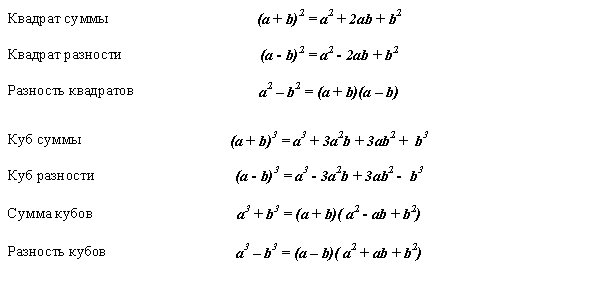
Пример 1. Упростите выражение 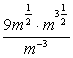 .
.
Решение
Применим свойства степеней (умножение степеней с одинаковым основанием и деление степеней с одинаковым основанием): 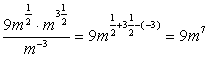 .
.
Ответ: 9m7 .
Пример 2.Сократить дробь: 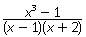
Решение.Так область определения дроби 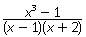 все числа, кроме х ≠ 1 и х ≠ -2.Вместе с тем
все числа, кроме х ≠ 1 и х ≠ -2.Вместе с тем 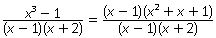 .Сократив дробь, получим
.Сократив дробь, получим 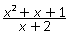 .Область определения полученной дроби: х ≠ -2, т.е. шире, чем область определения первоначальной дроби. Поэтому дроби
.Область определения полученной дроби: х ≠ -2, т.е. шире, чем область определения первоначальной дроби. Поэтому дроби 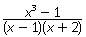 и
и 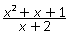 равны при х ≠ 1 и х ≠ -2.
равны при х ≠ 1 и х ≠ -2.
Пример 3.Сократить дробь: 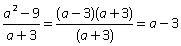
Пример 4.Упростить: 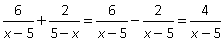
Пример 5.Упростить: 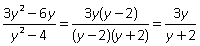
Пример 6. Упростить: 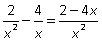
Пример 7. Упростить: 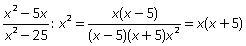
Пример 8.Упростить: 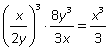
Пример 9. Вычислить: 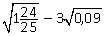 .
.
Решение.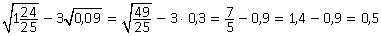
Пример 10.Упростить выражение: 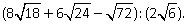
Решение.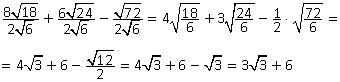
Пример 11.Сократить дробь 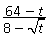 , если
, если 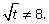
Решение.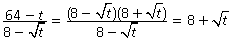 .
.
Пример 12.Освободиться от иррациональности в знаменателе дроби 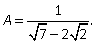
Решение. В знаменателе имеем иррациональность 2-й степени, поэтому помножим и числитель, и знаменатель дроби на сопряженное выражение, то есть сумму чисел 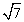 и
и 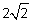 , тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность.
, тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность.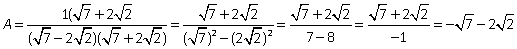
1. Упростите выражение:
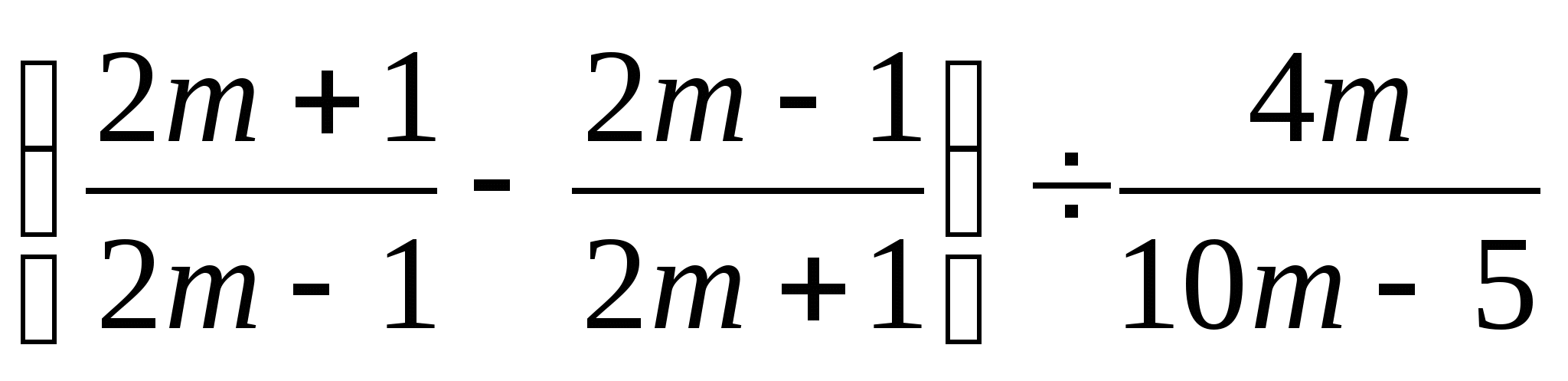
2. Найдите значение выражения:
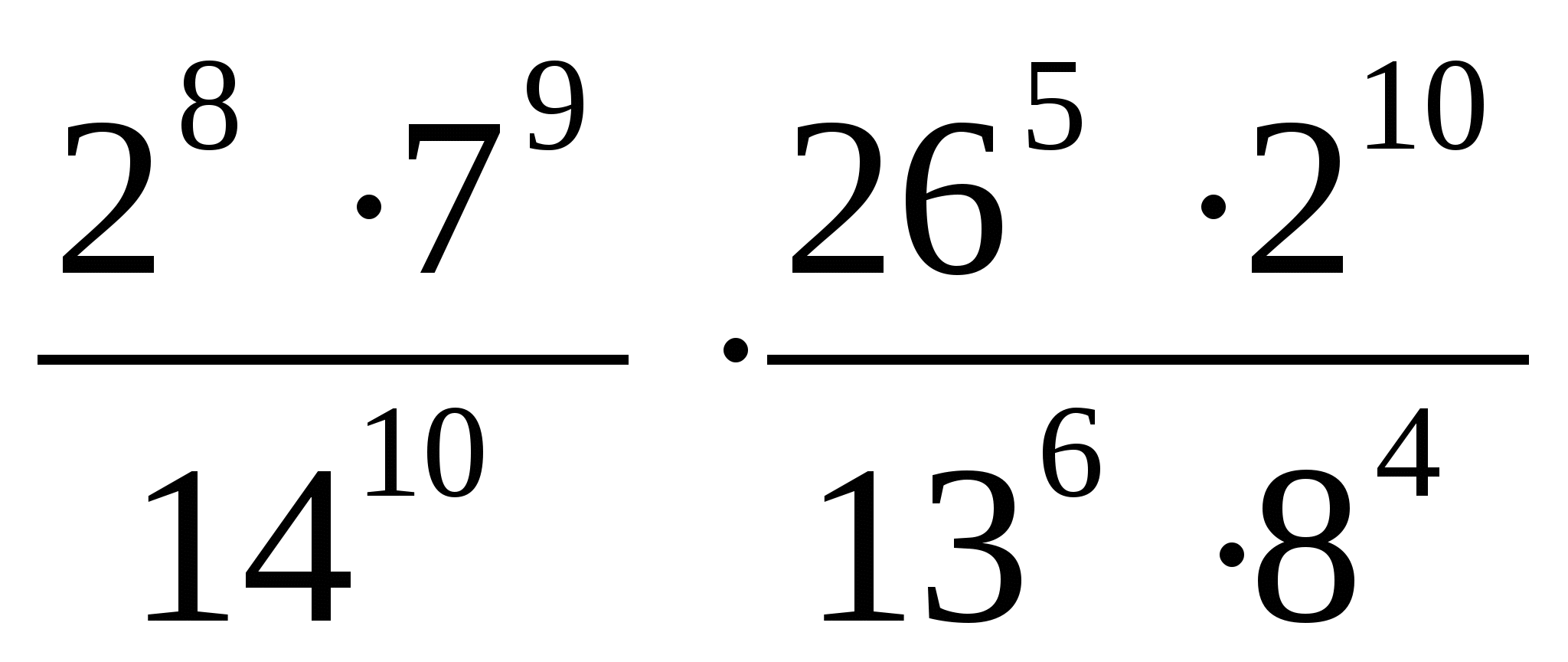
3. Представьте степень с дробным показателем в виде корня
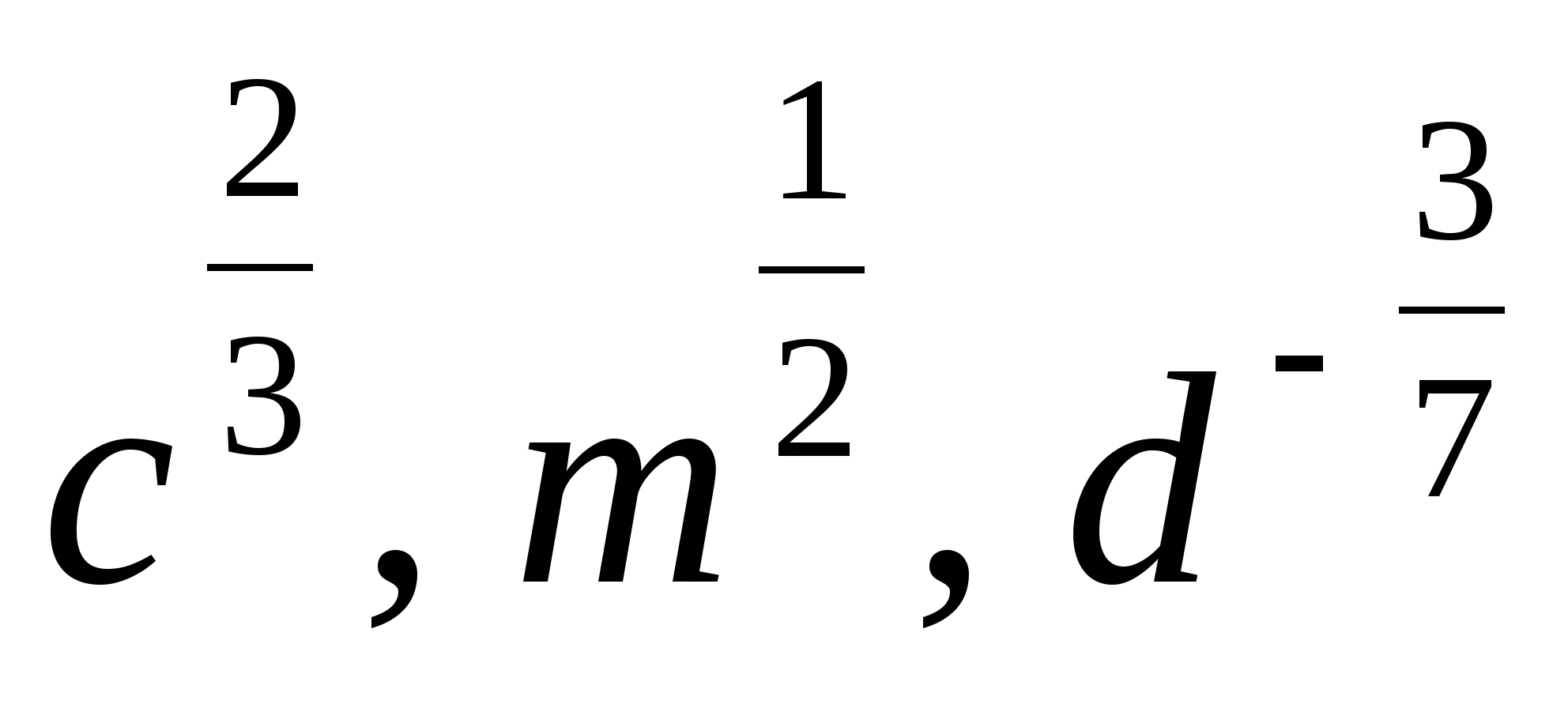
4. Привести указанное выражение к виду 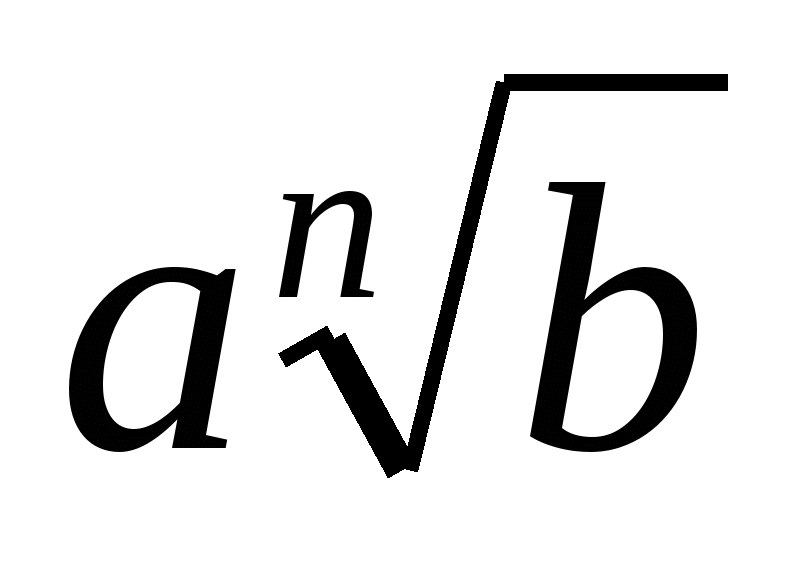 , где а -рациональное число, b – натуральное число
, где а -рациональное число, b – натуральное число
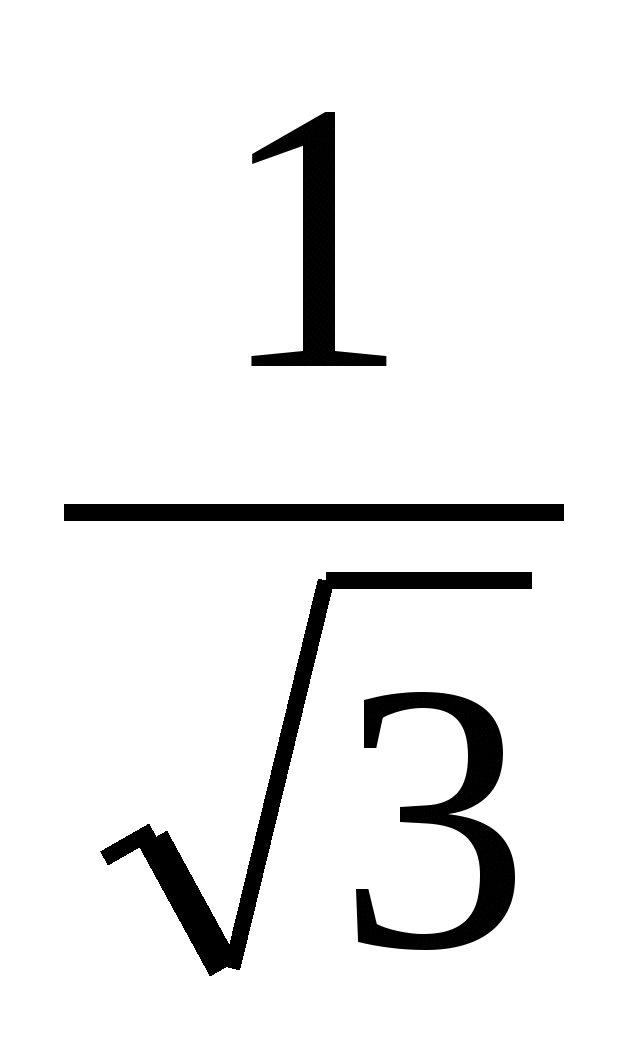 ,
, 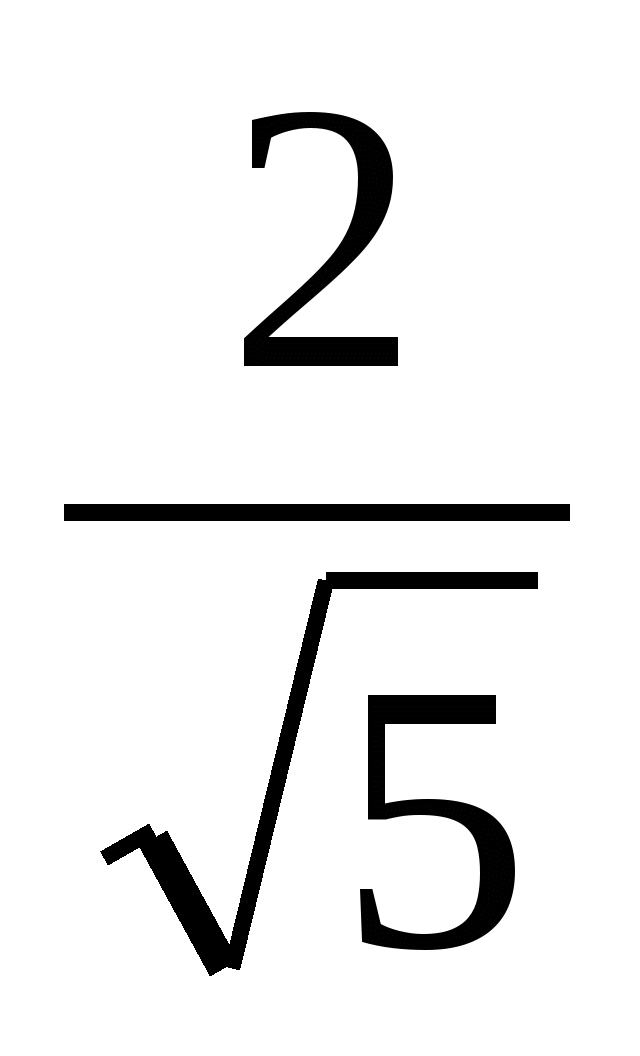
5. Упростить:
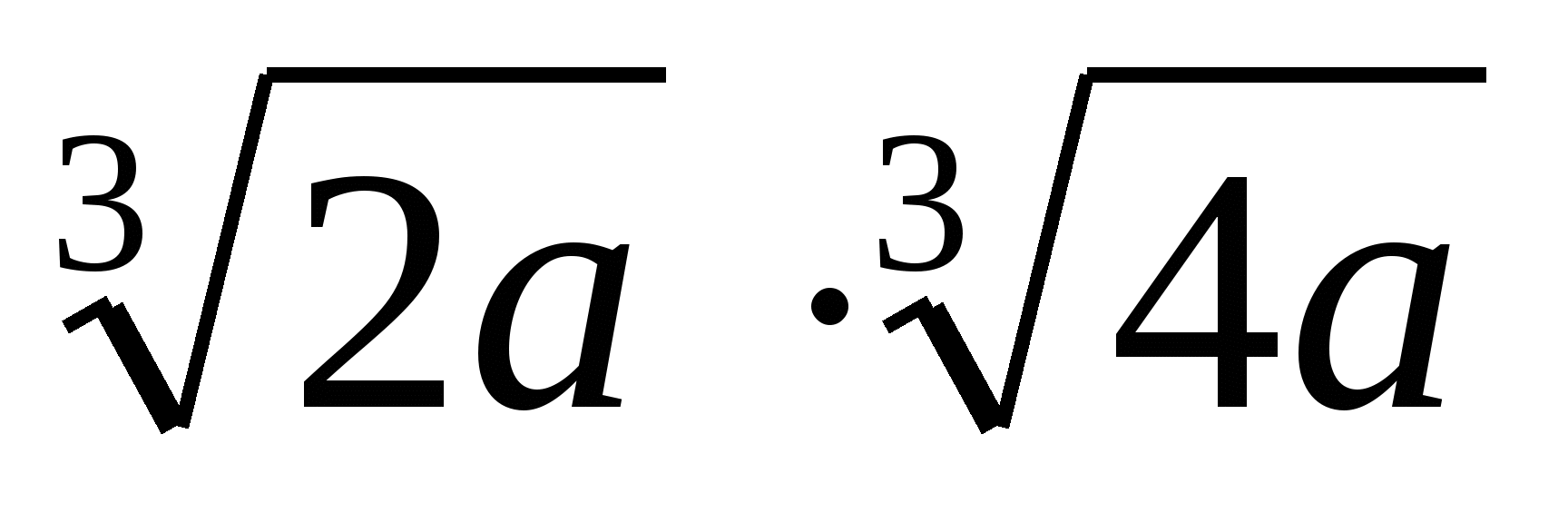 ;
; 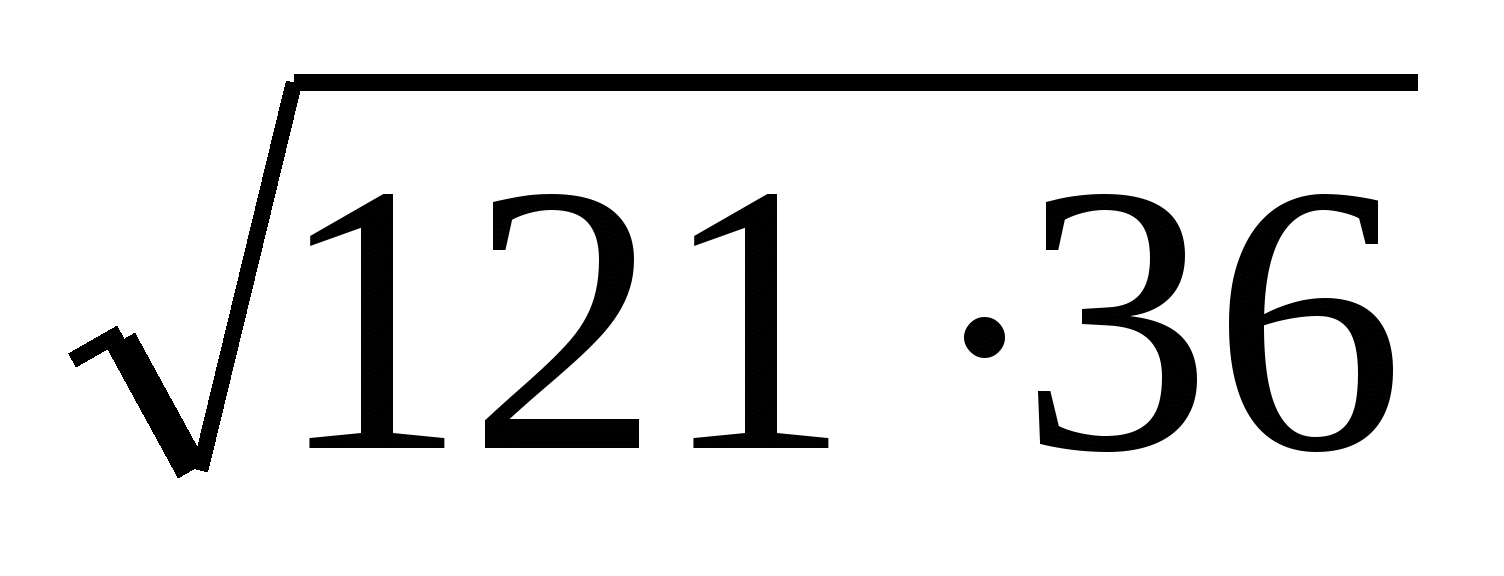
6. Замените арифметические корни степенями с дробным показателем
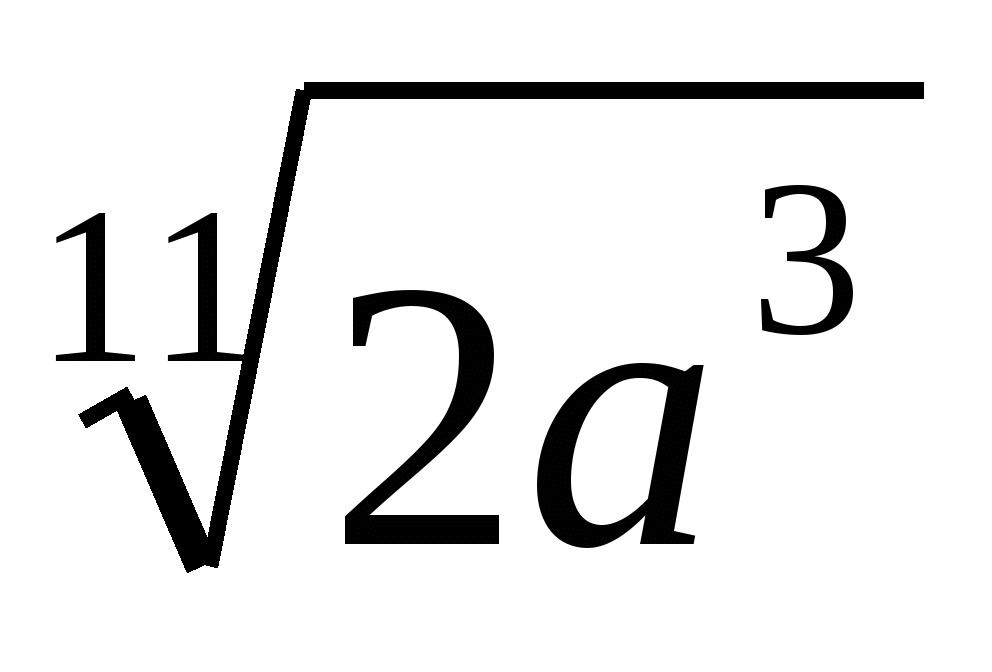 ,
, 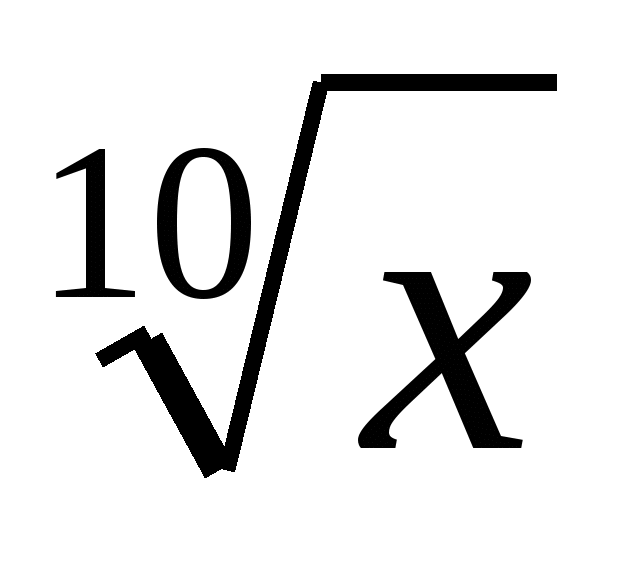 ,
, 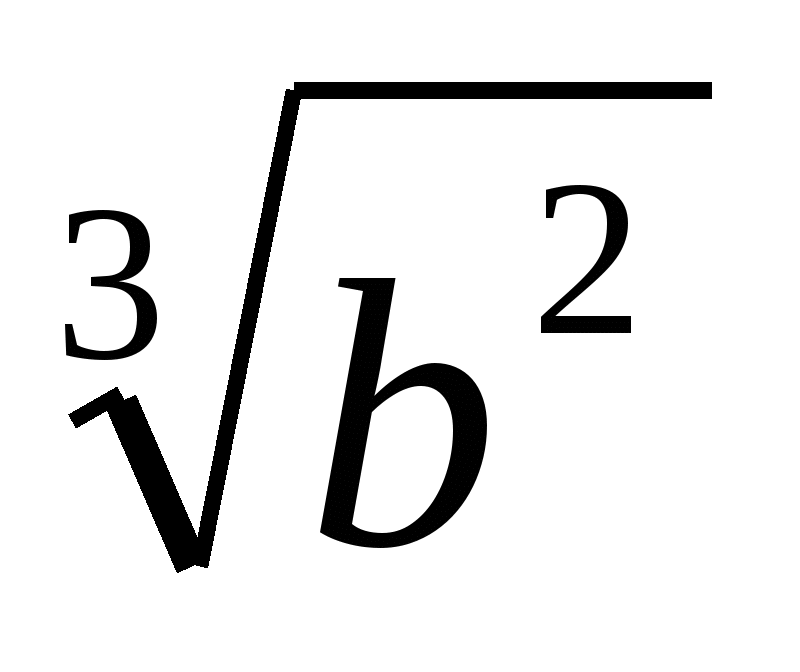
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
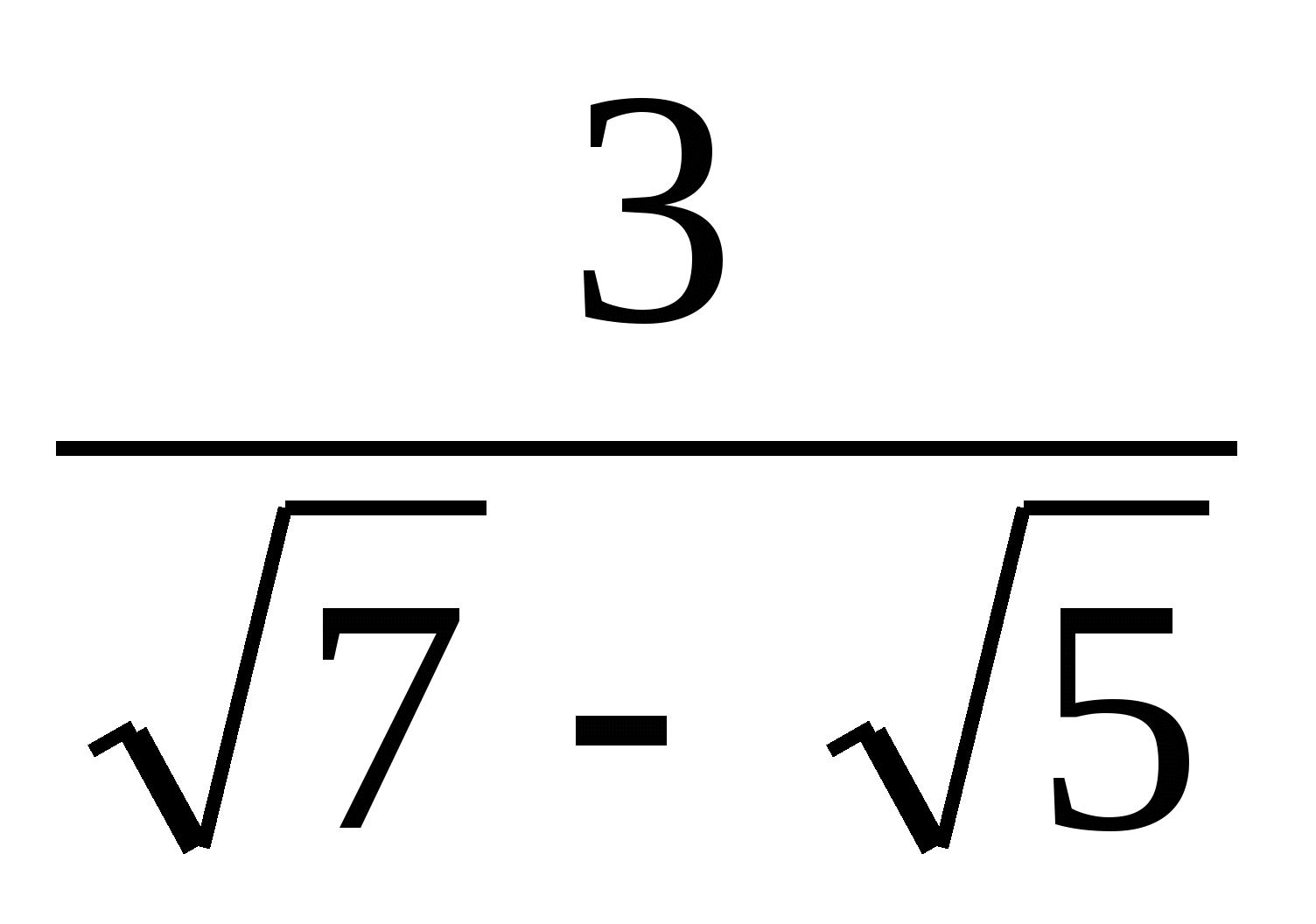 10. Выполните действие:
10. Выполните действие:
8. Сократите дробь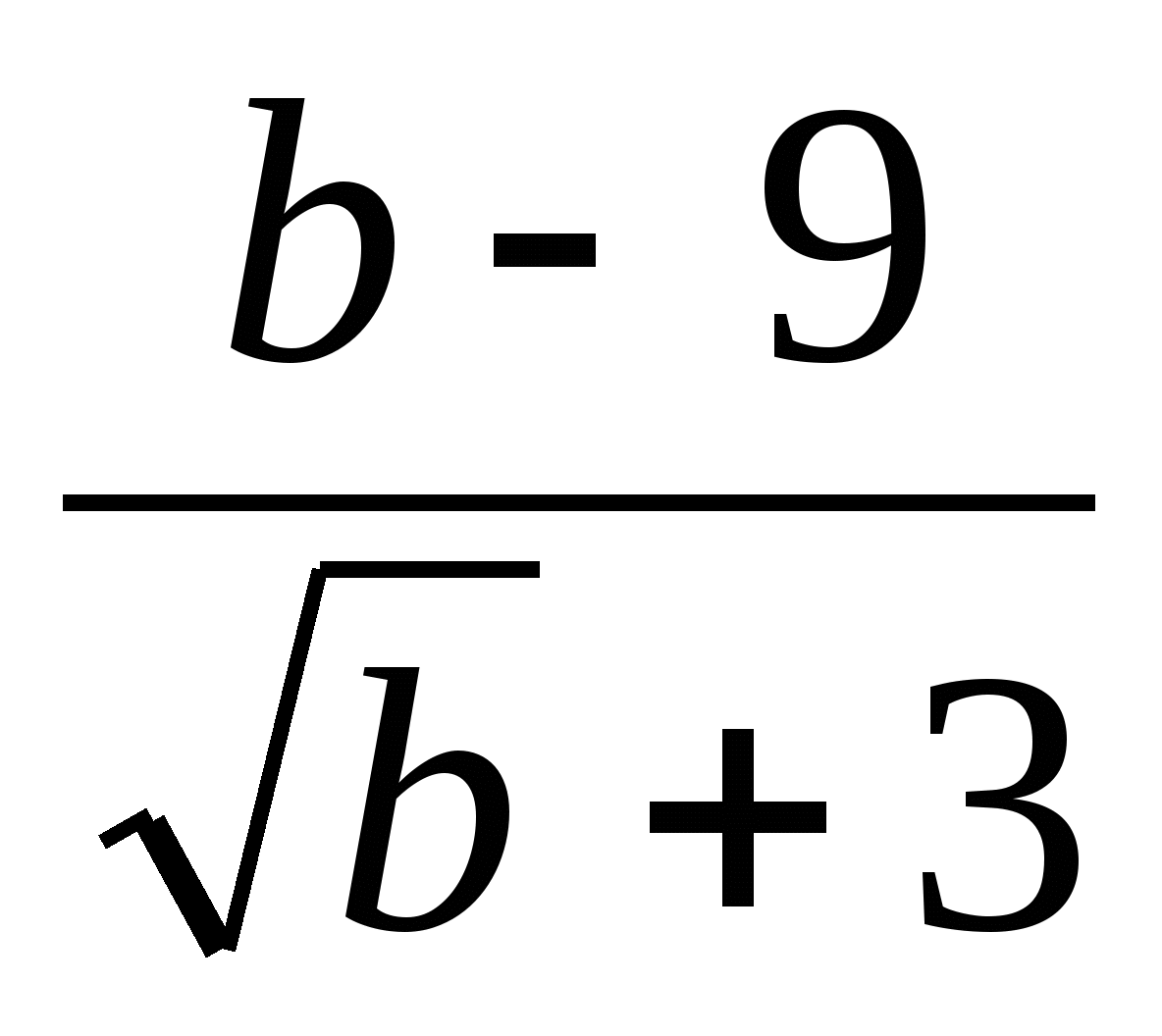
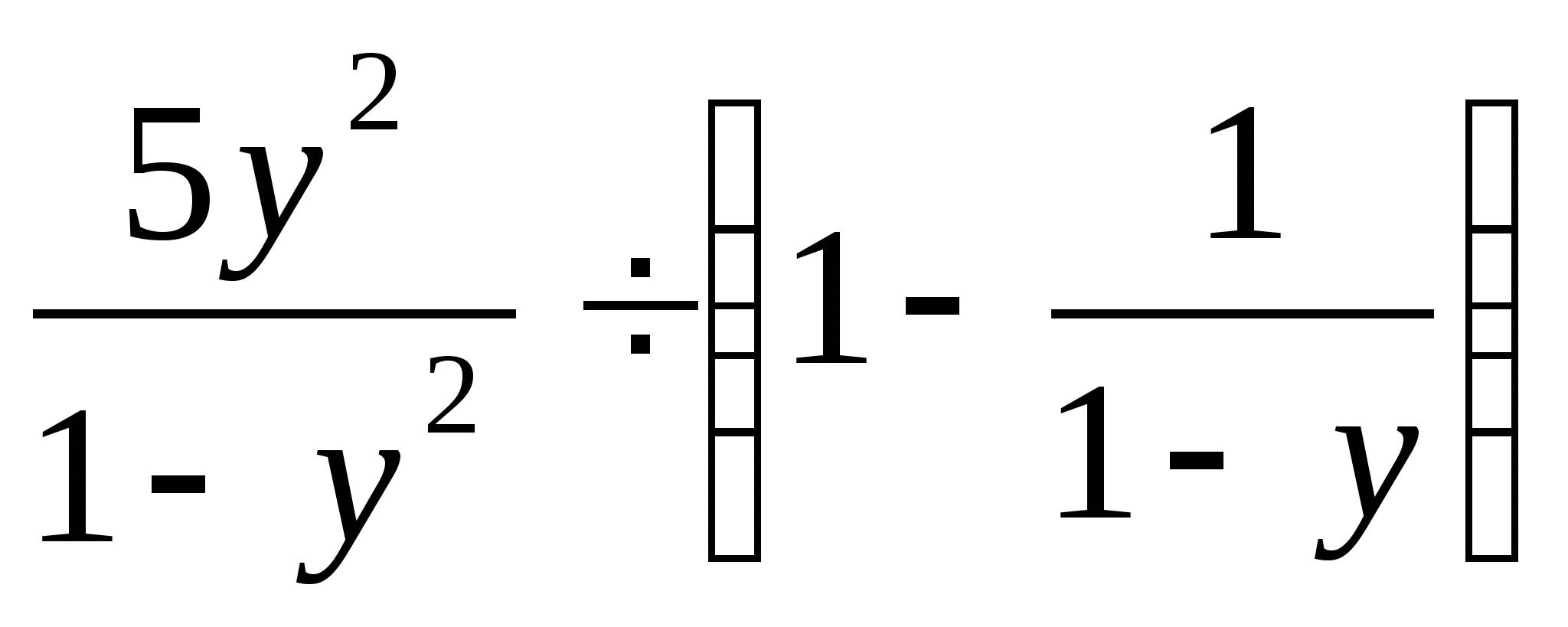
9. Выполните действие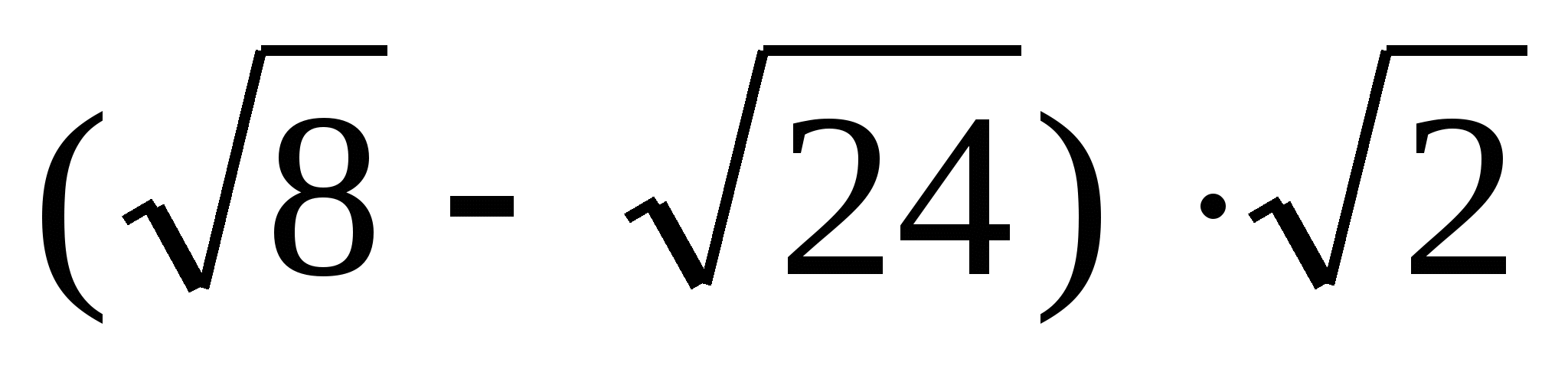
ВАРИАНТ — II
1. Упростите выражение:
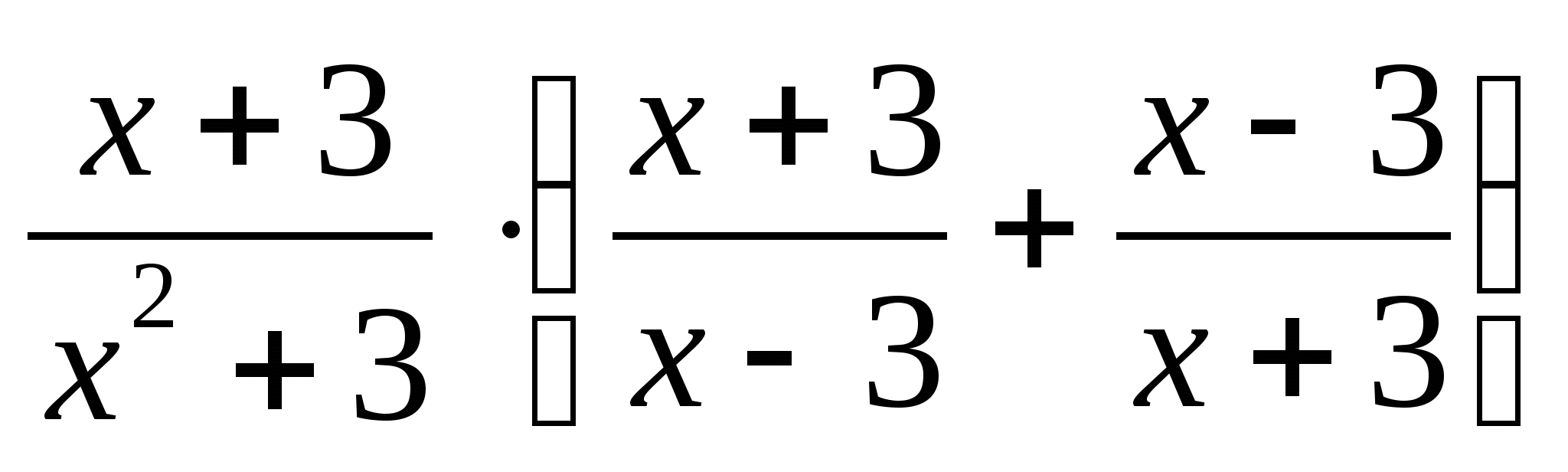
2. Найдите значение выражения:
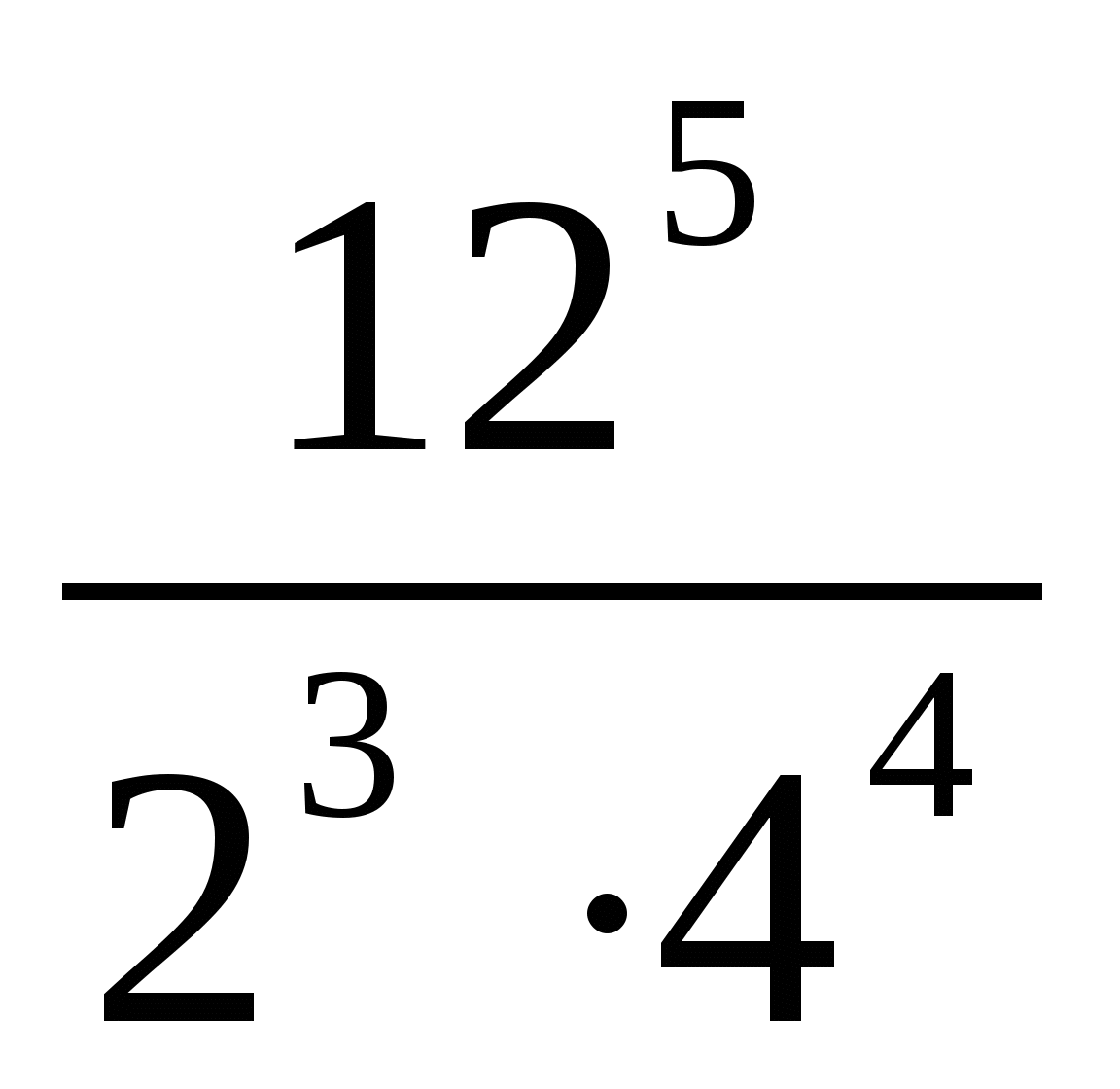
3. Представьте степень с дробным показателем в виде корня
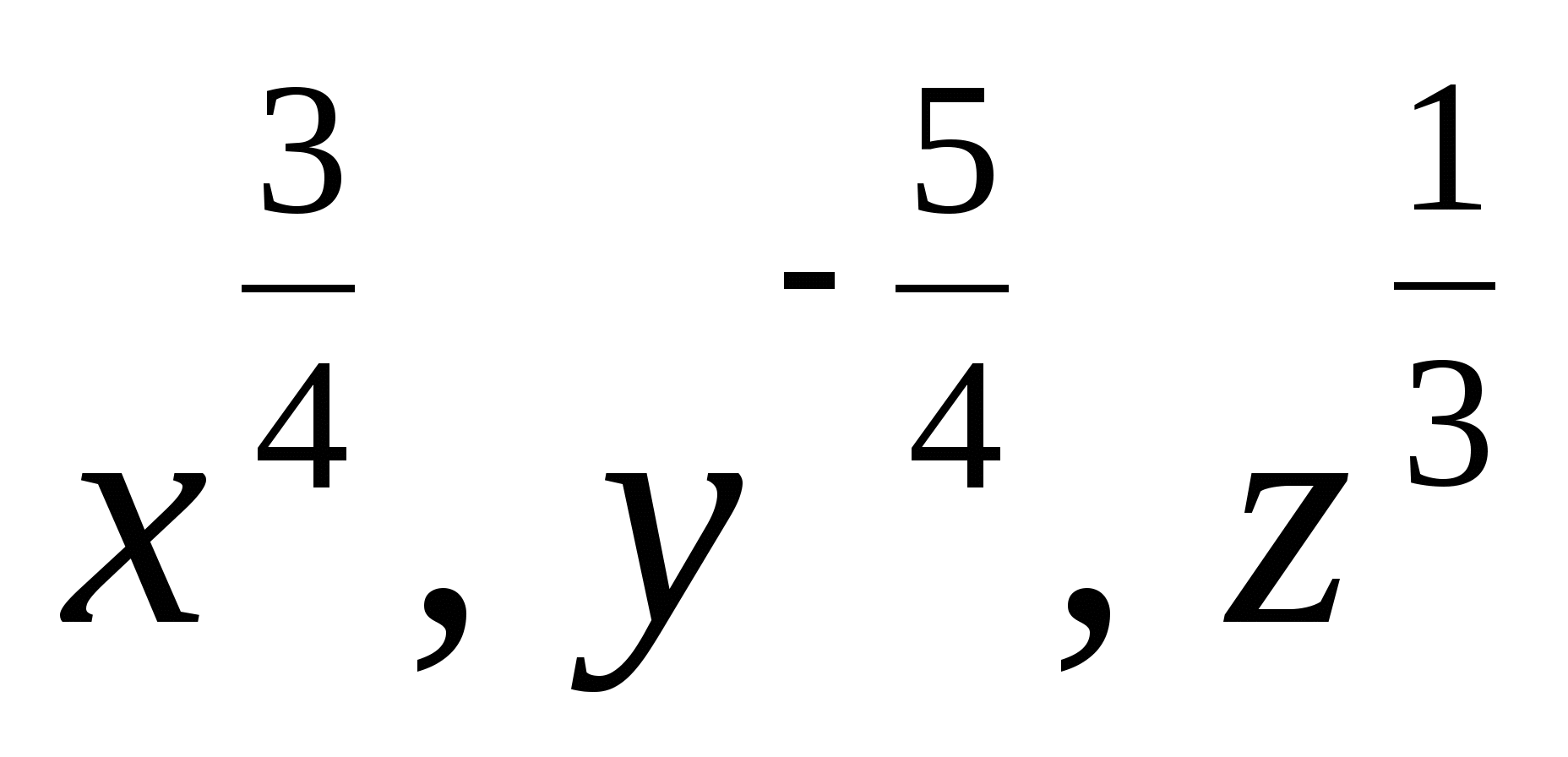
4. Привести указанное выражение к виду 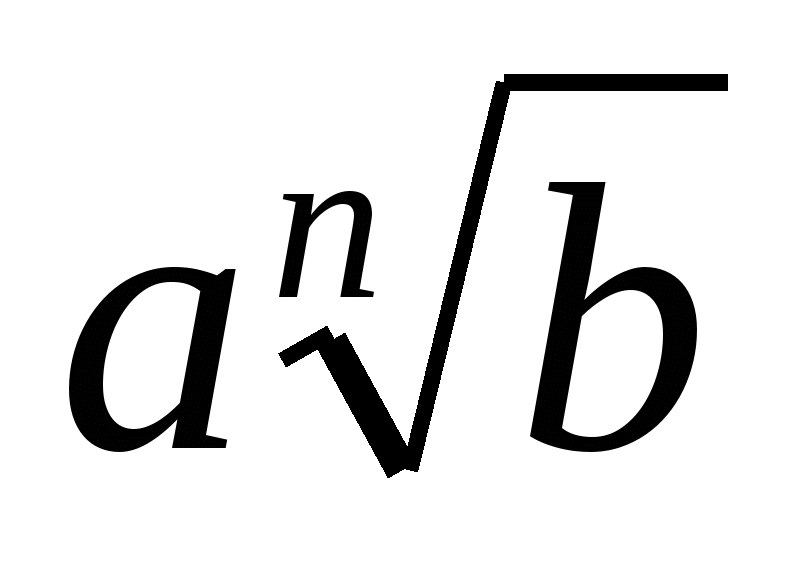 , где а- рациональное число, b – натуральное число
, где а- рациональное число, b – натуральное число
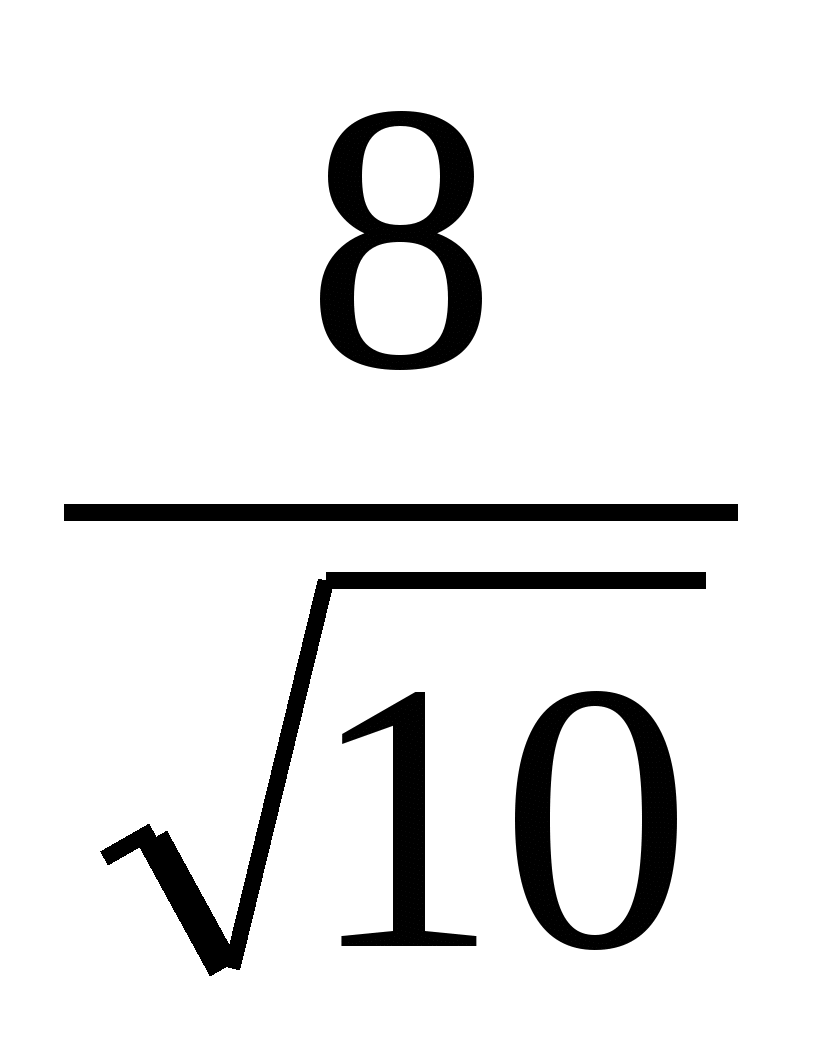 ,
, 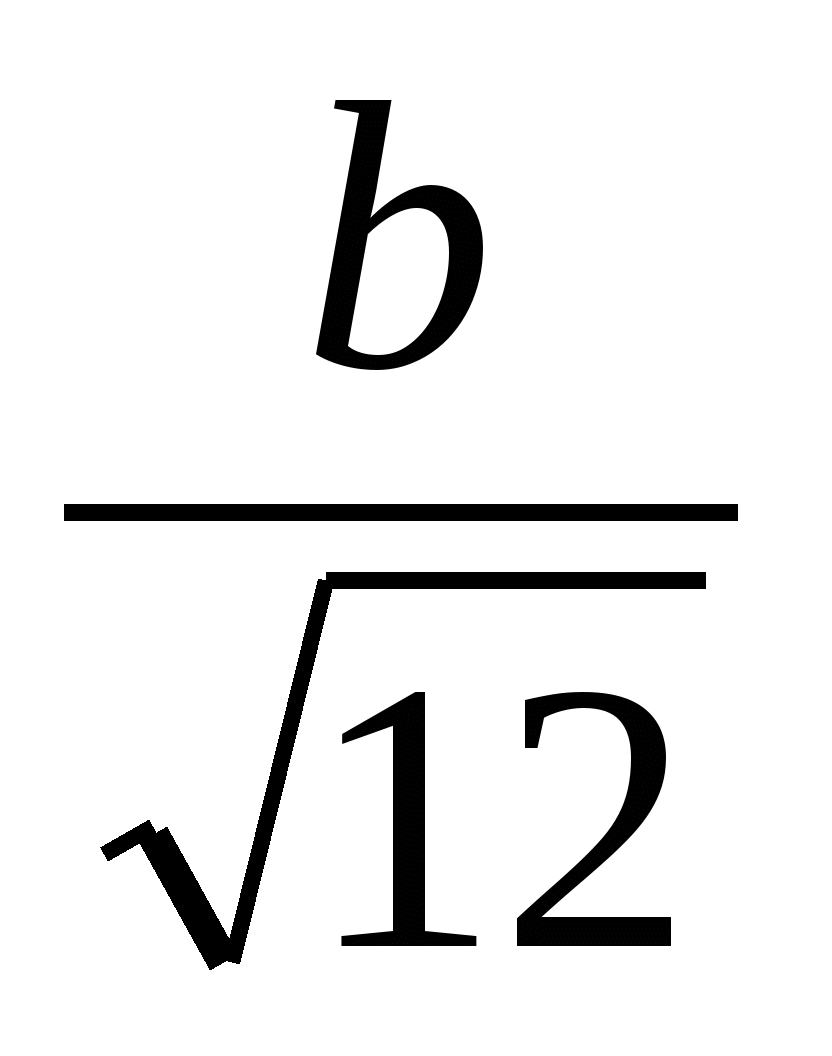
5. Упростить:
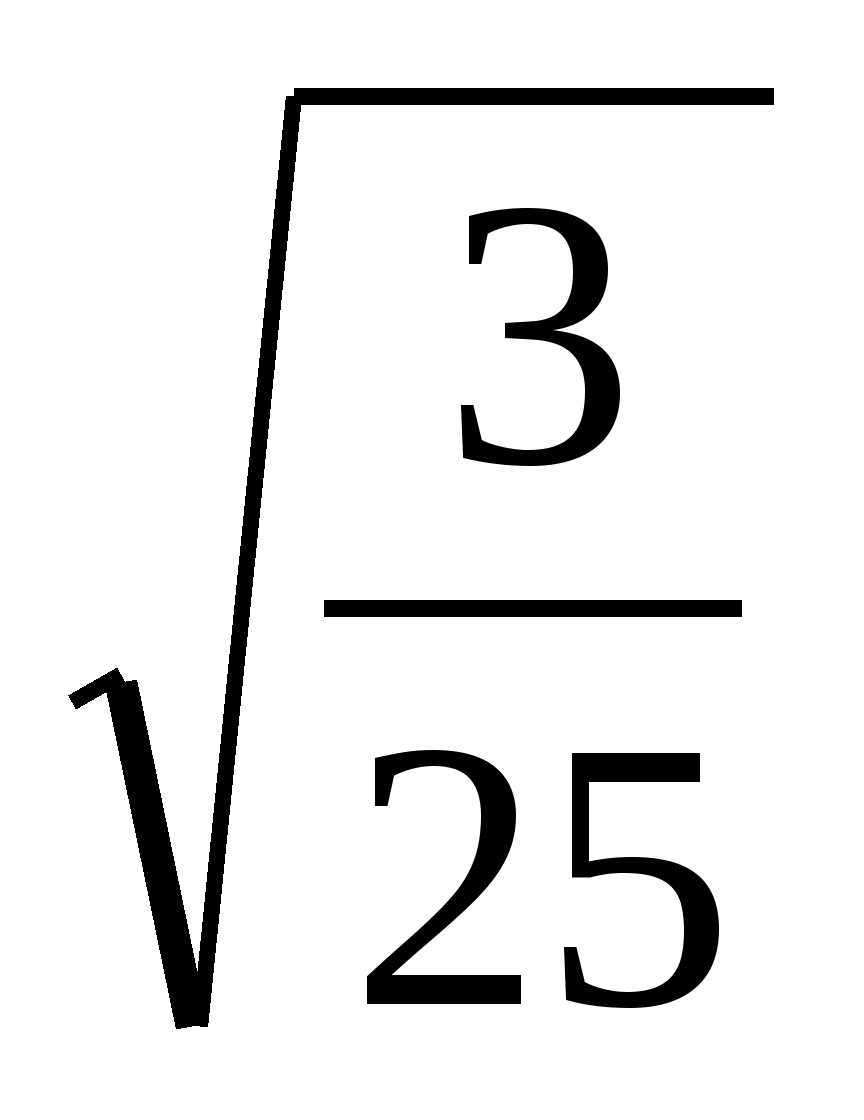 ;
; 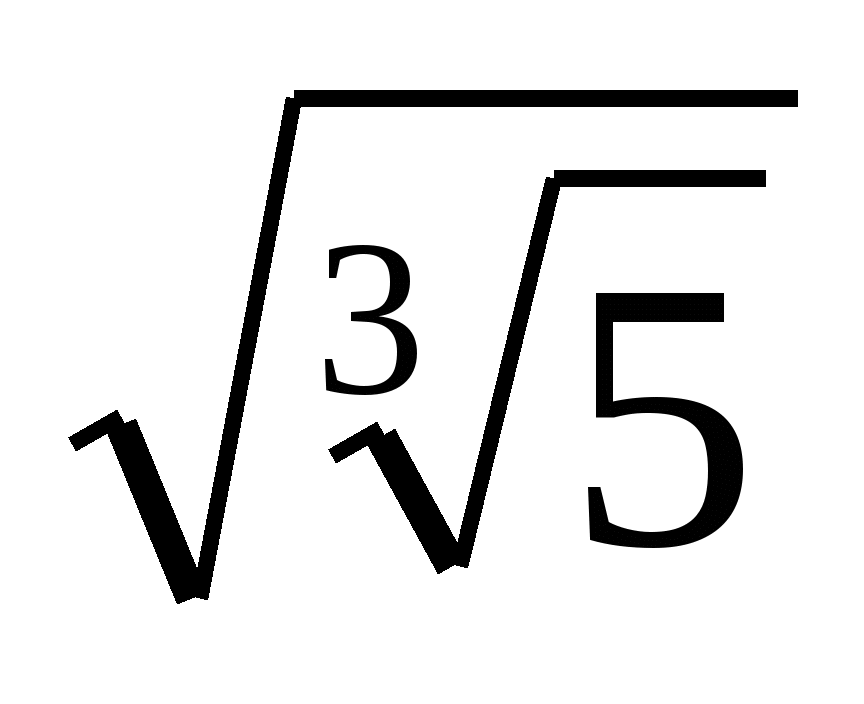
6. Замените арифметические корни степенями с дробным показателем
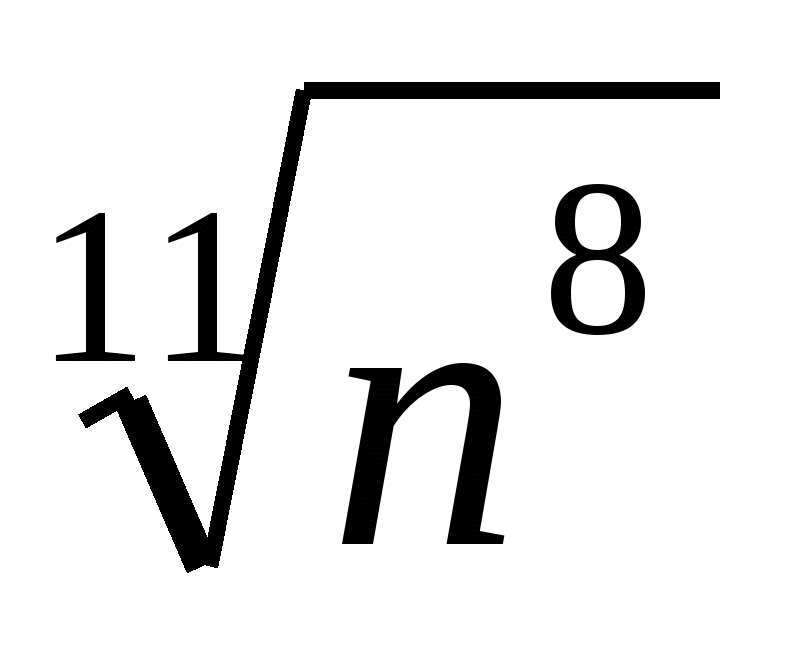 ,
, 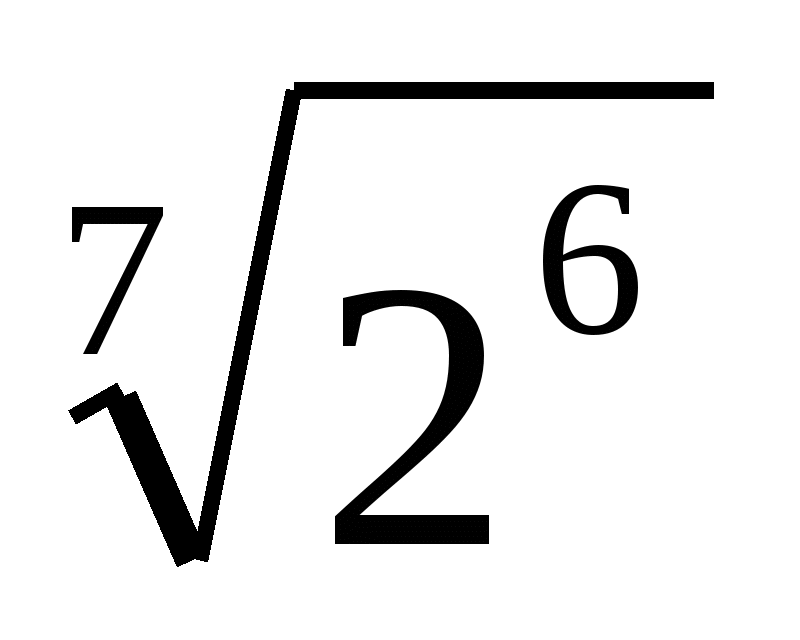 ,
, 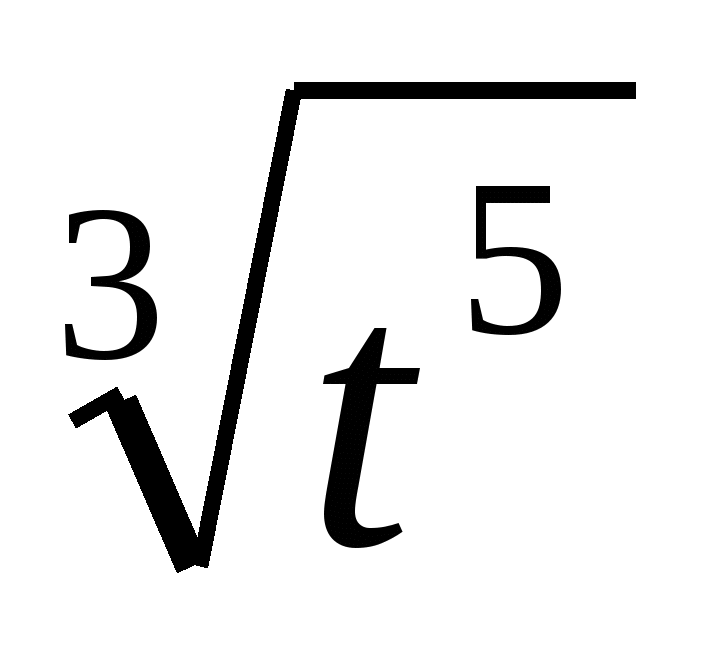
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
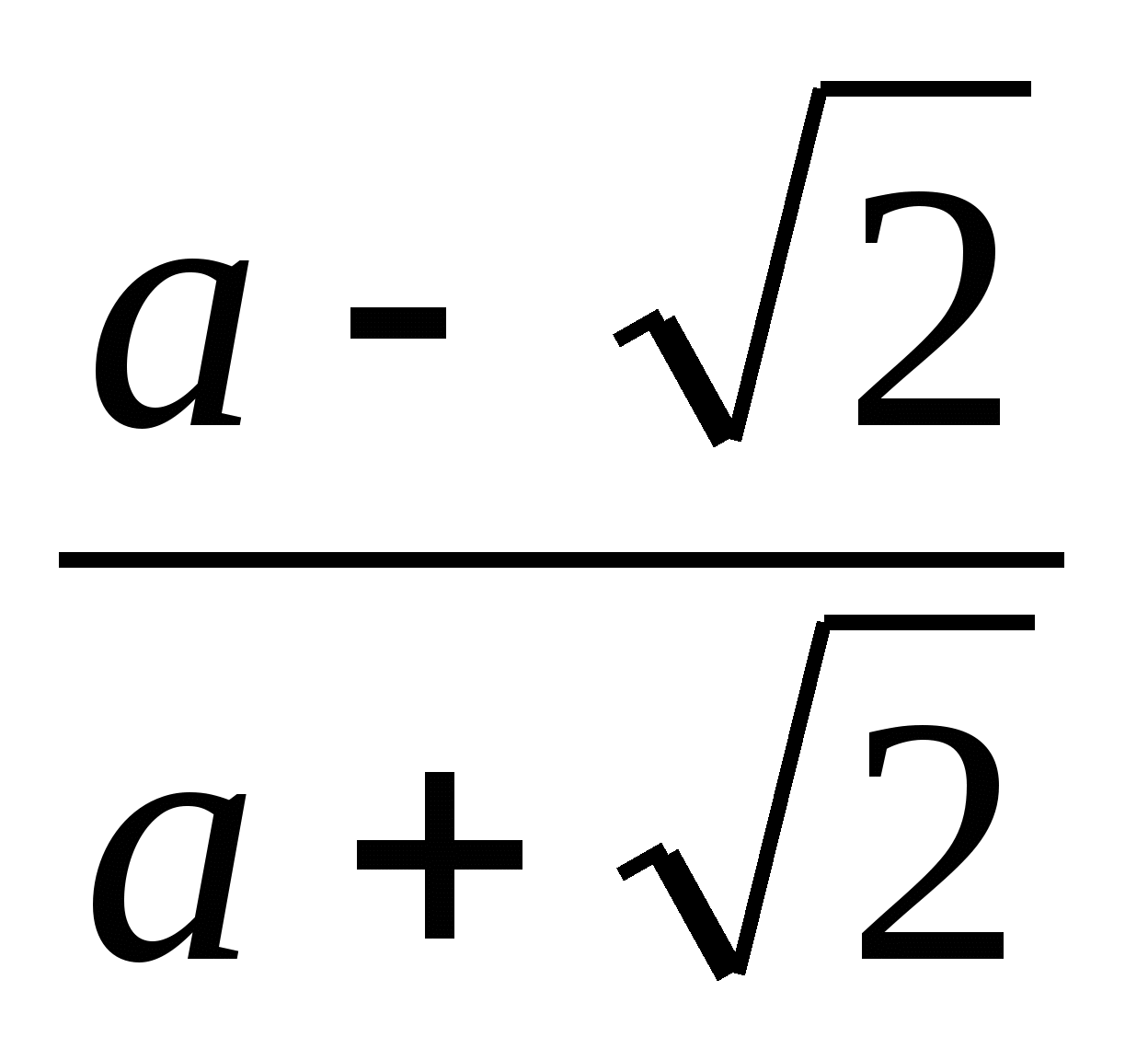 10. Выполните действие:
10. Выполните действие:
8. Сократите дробь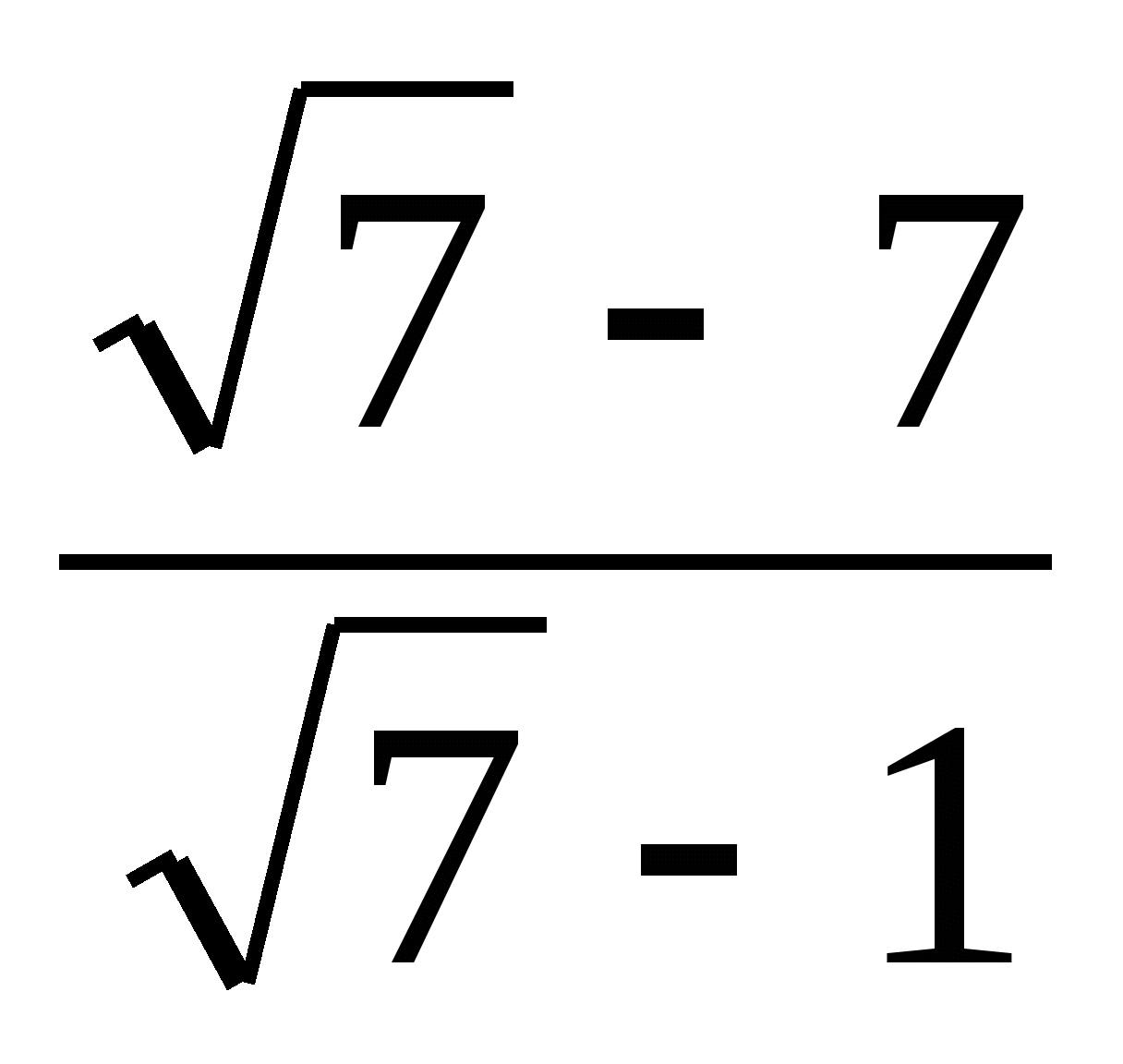
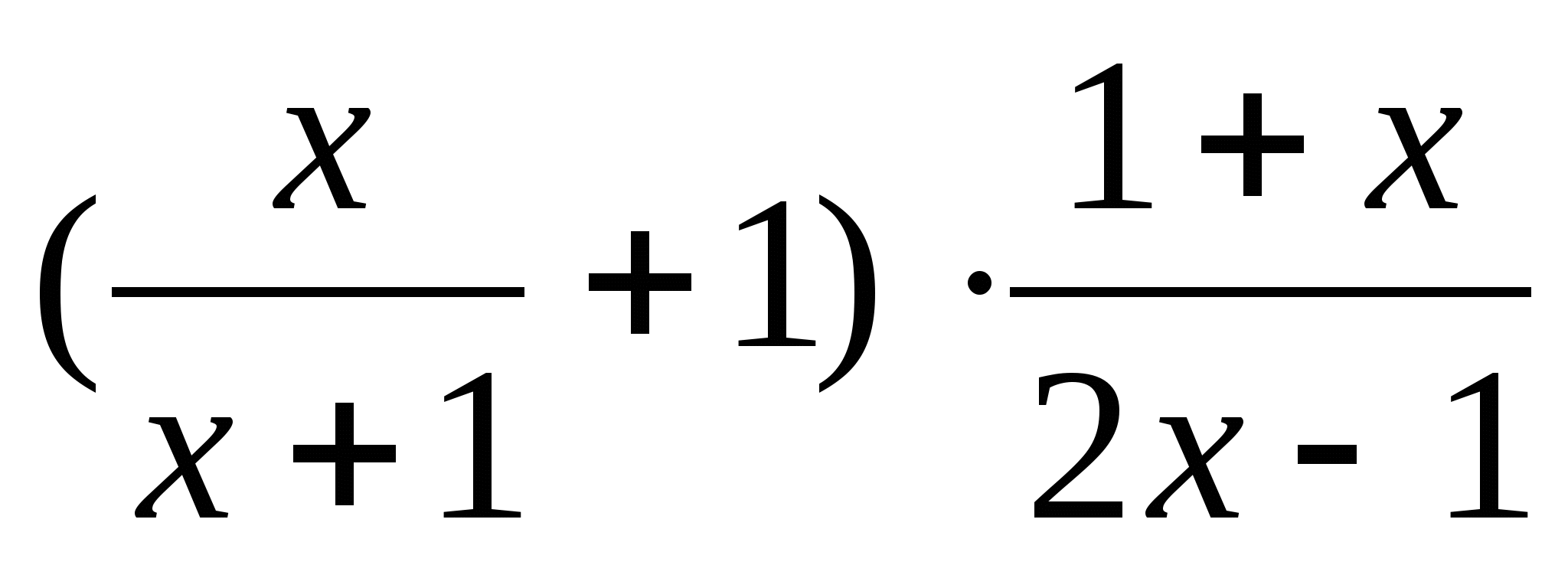
9. Выполните действие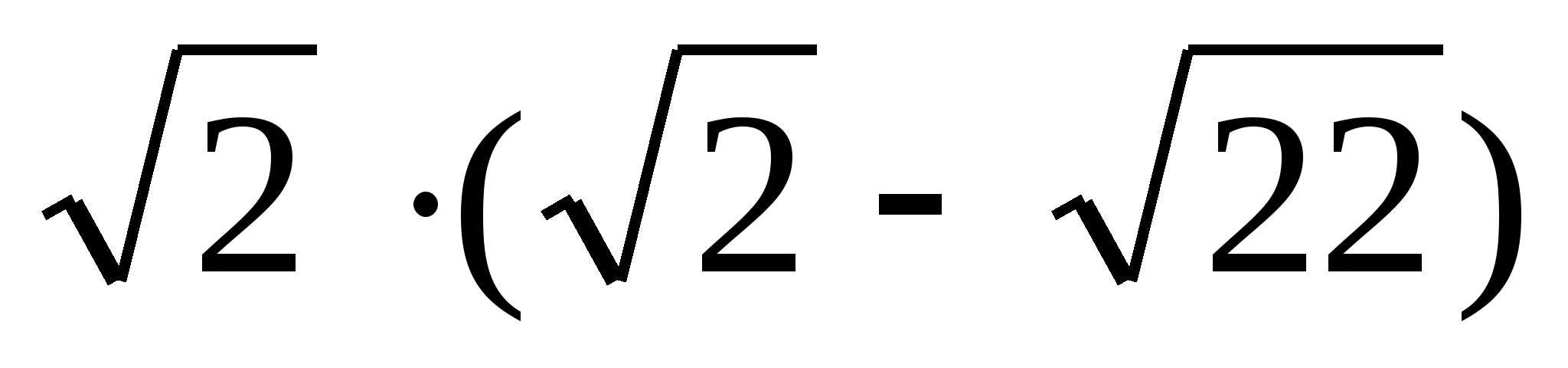
1. Выполните действие:
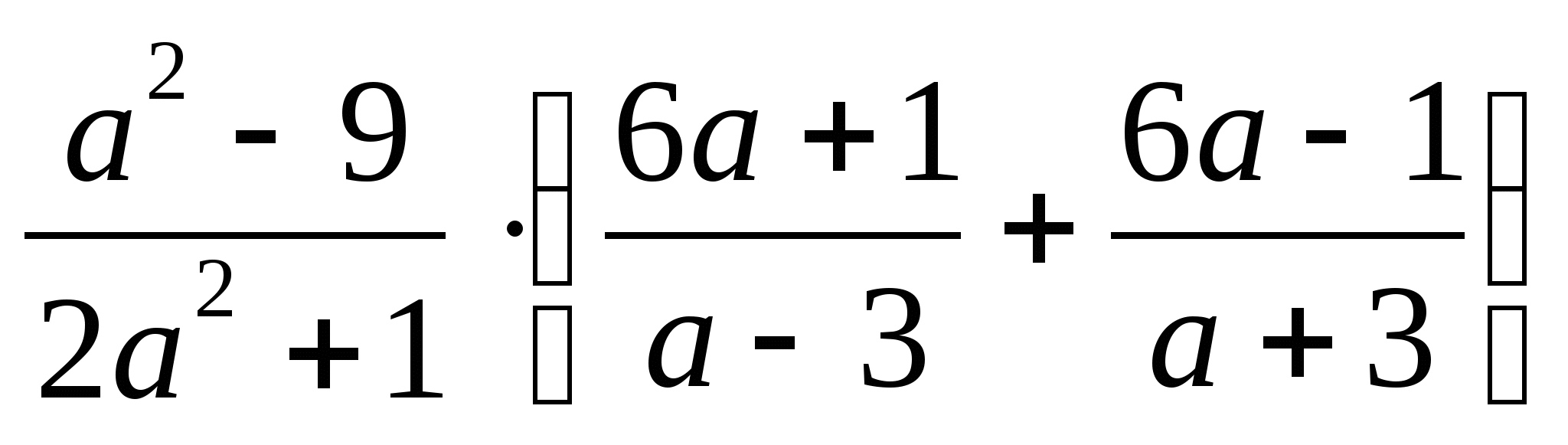
2. Найдите значение выражения:
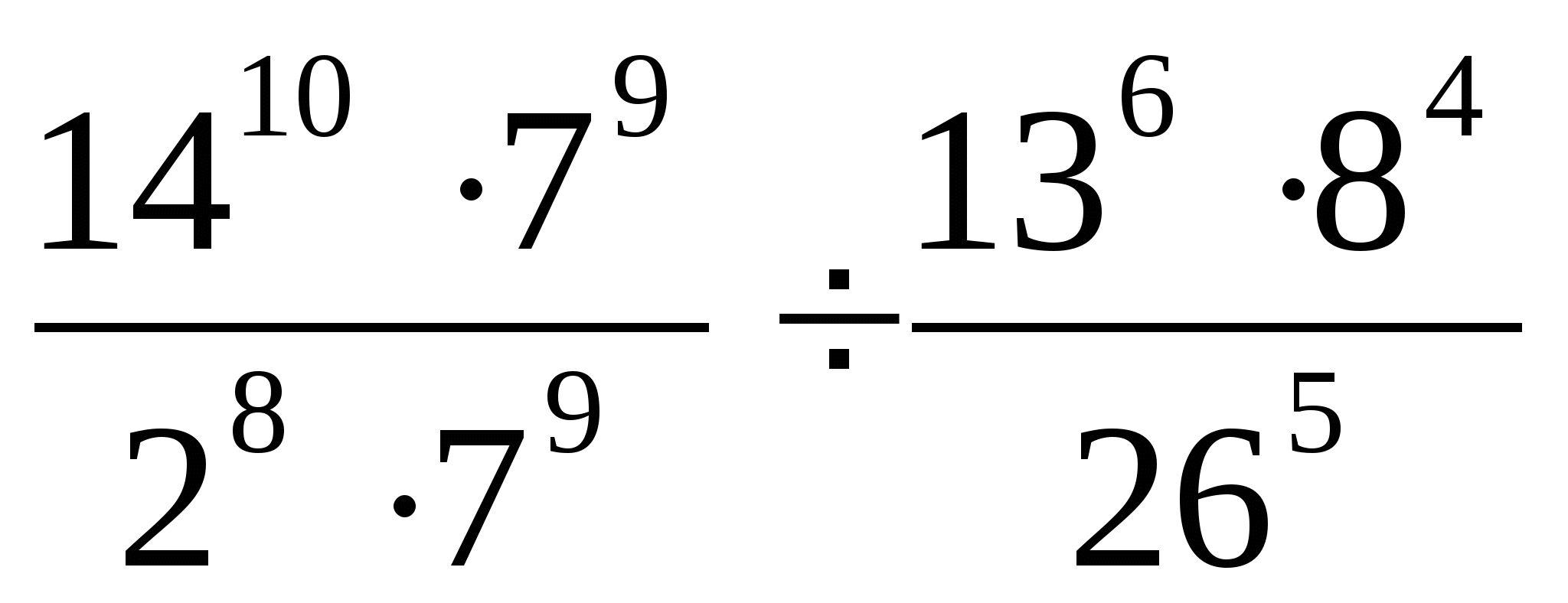
3. Представьте степень с дробным показателем в виде корня
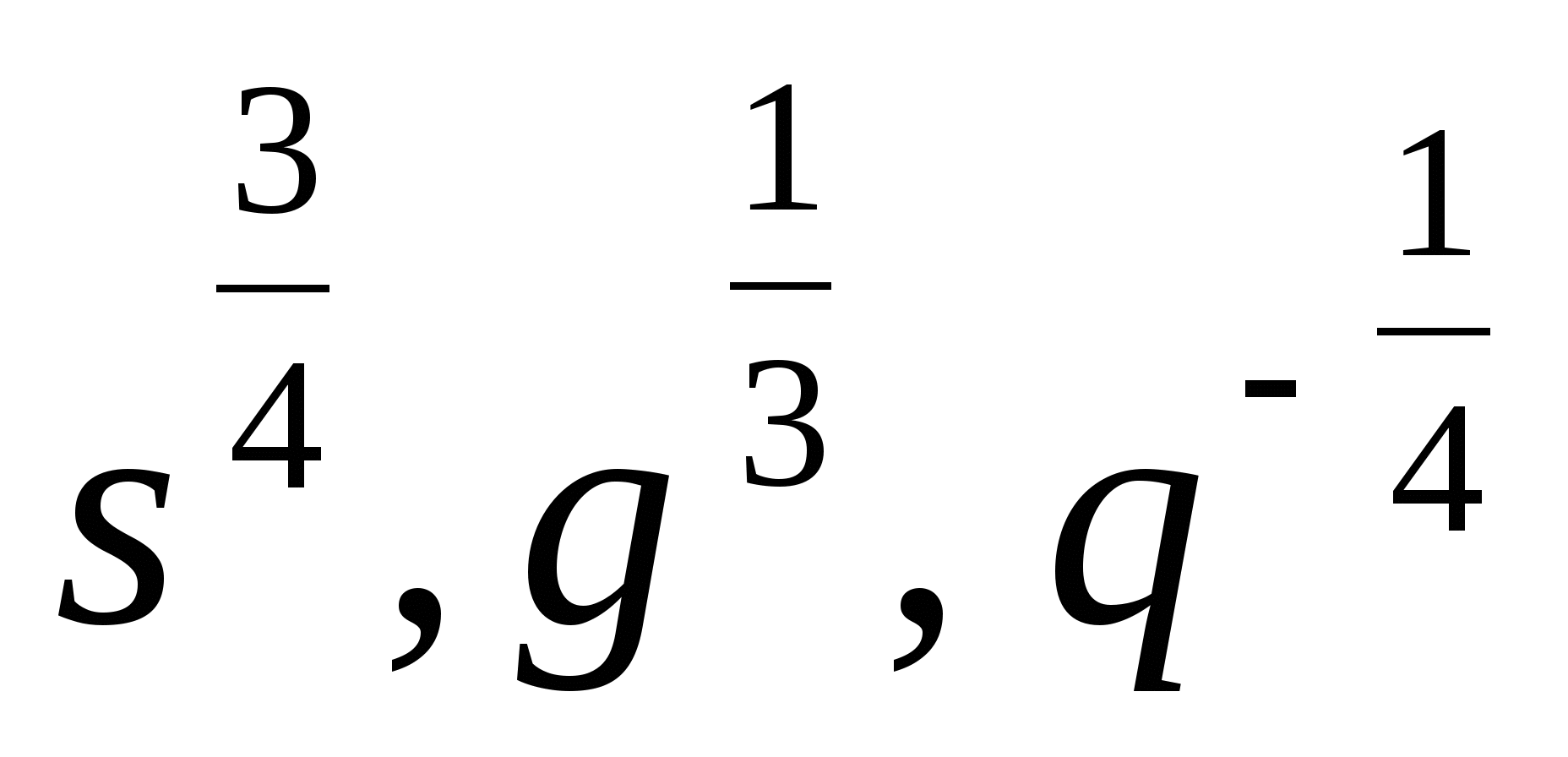
4. Привести указанное выражение к виду 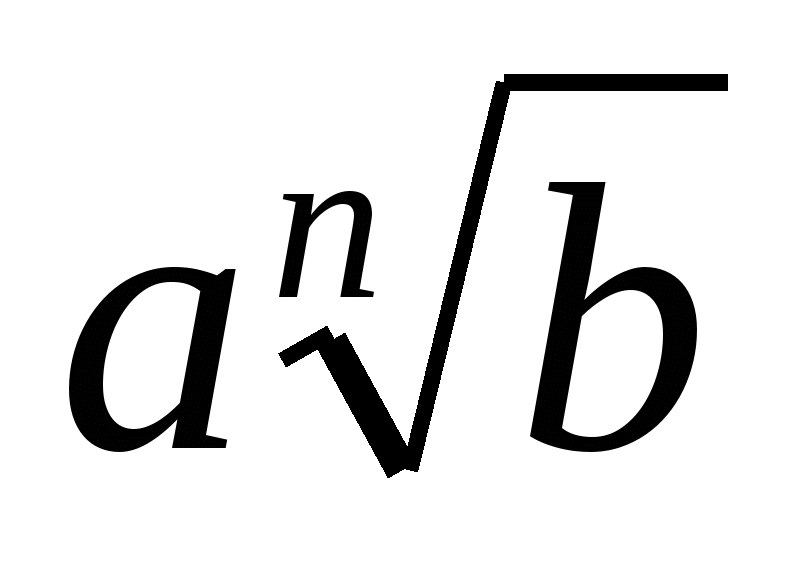 , где а -рациональное число, b – натуральное число
, где а -рациональное число, b – натуральное число
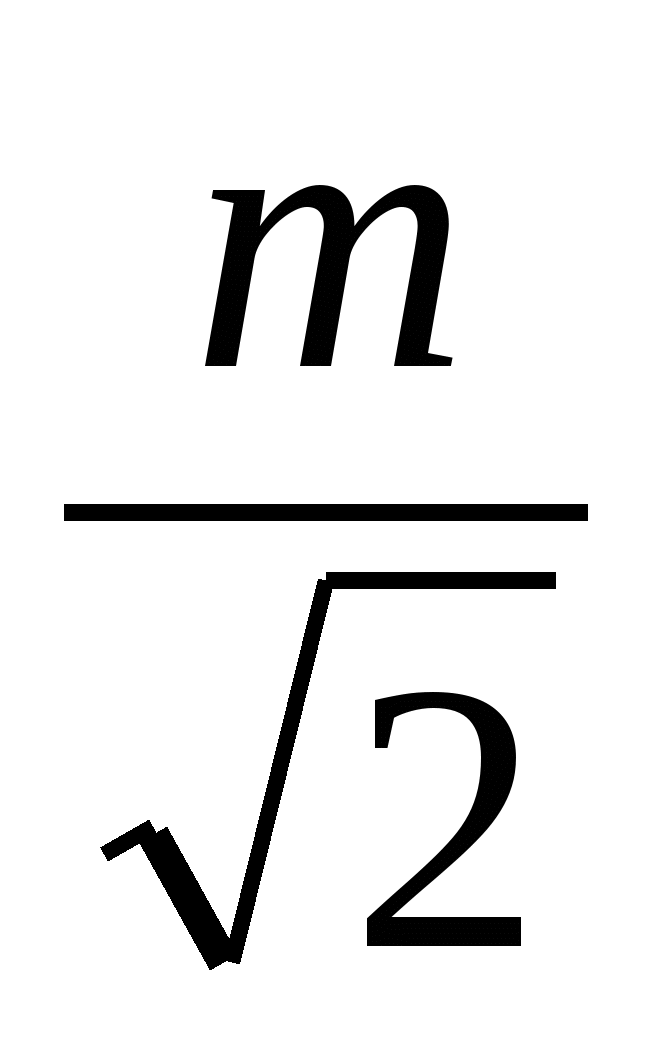 ,
, 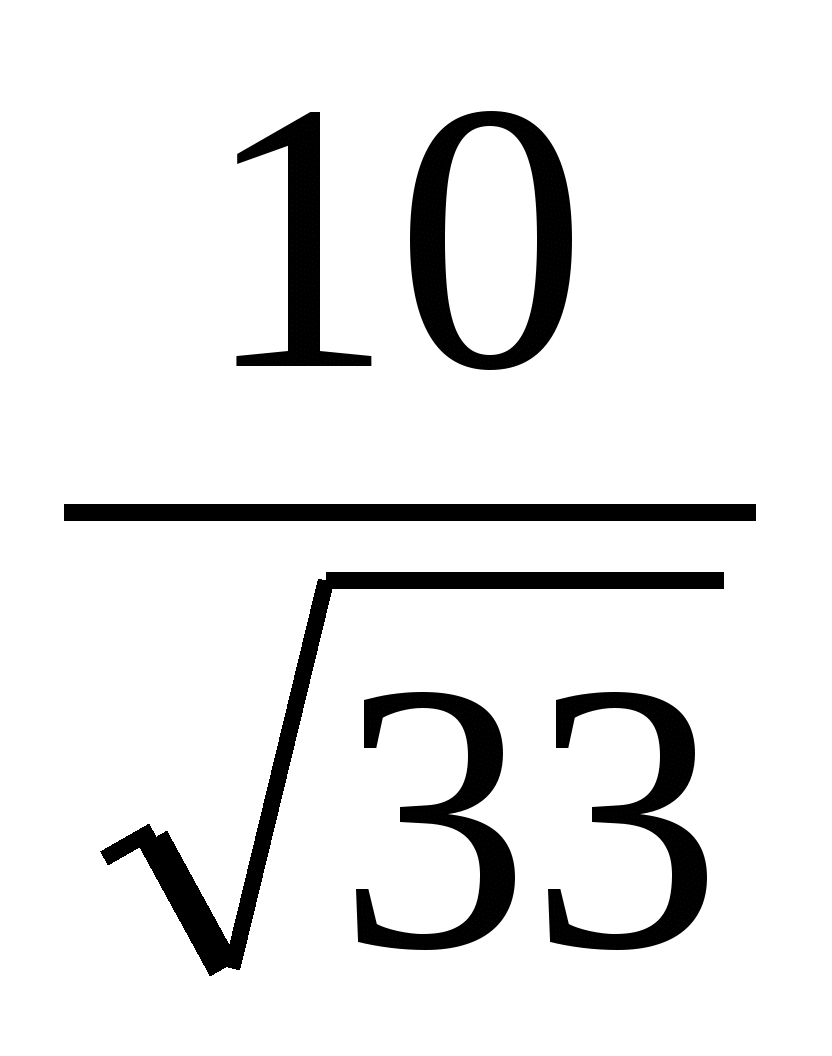
5. Упростить:
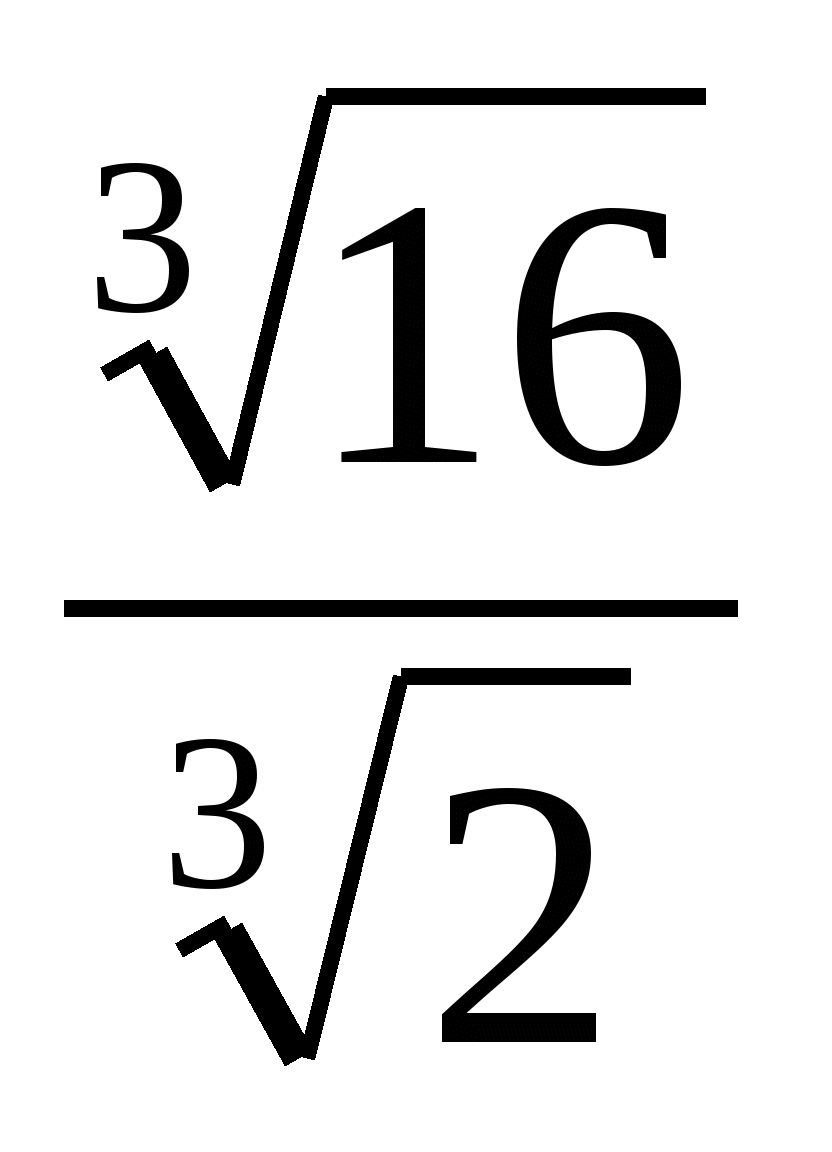 ;
; 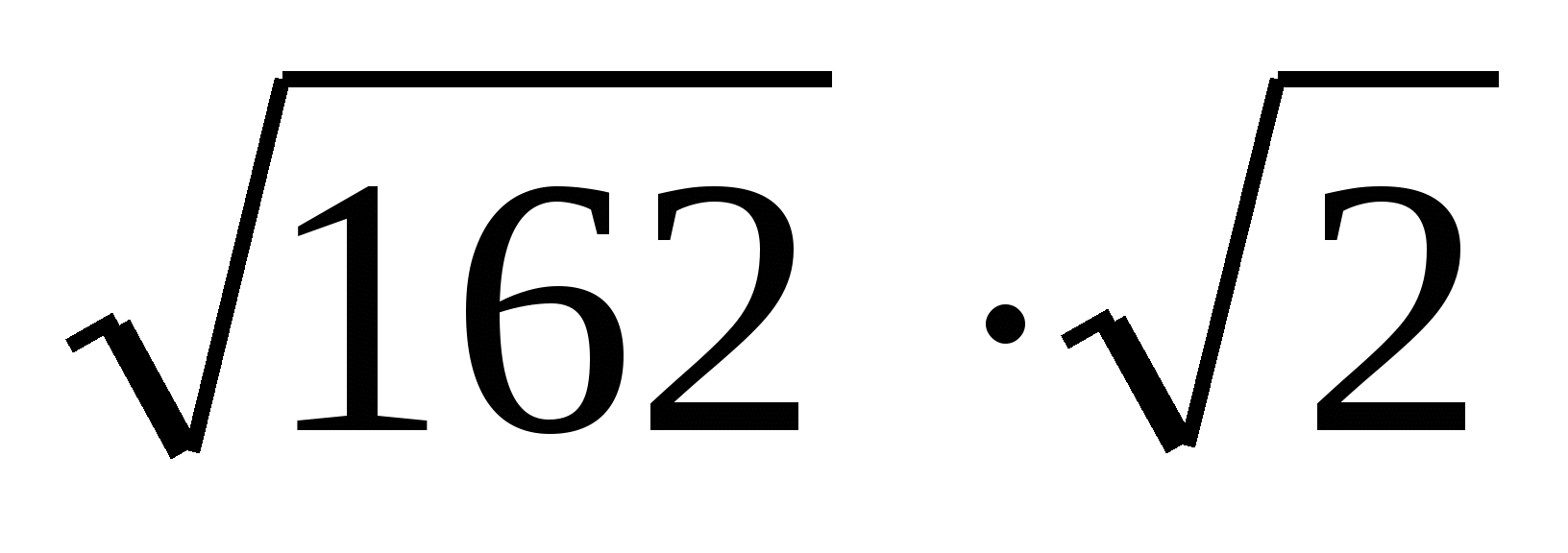
6. Замените арифметические корни степенями с дробным показателем
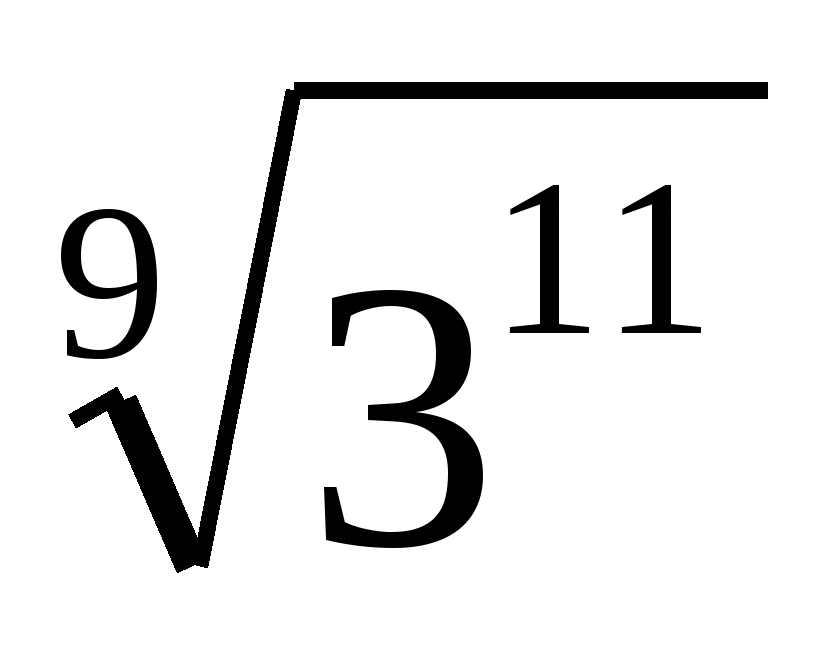 ,
, 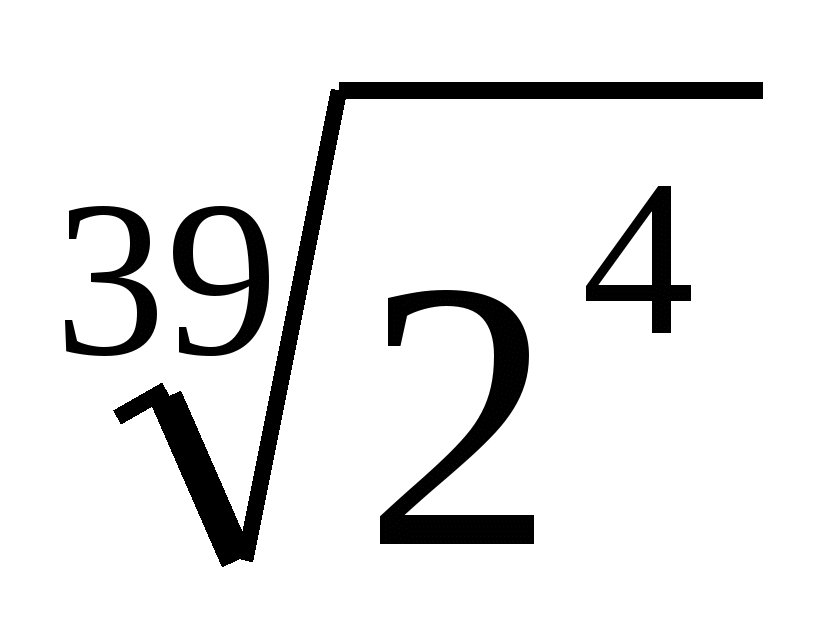 ,
, 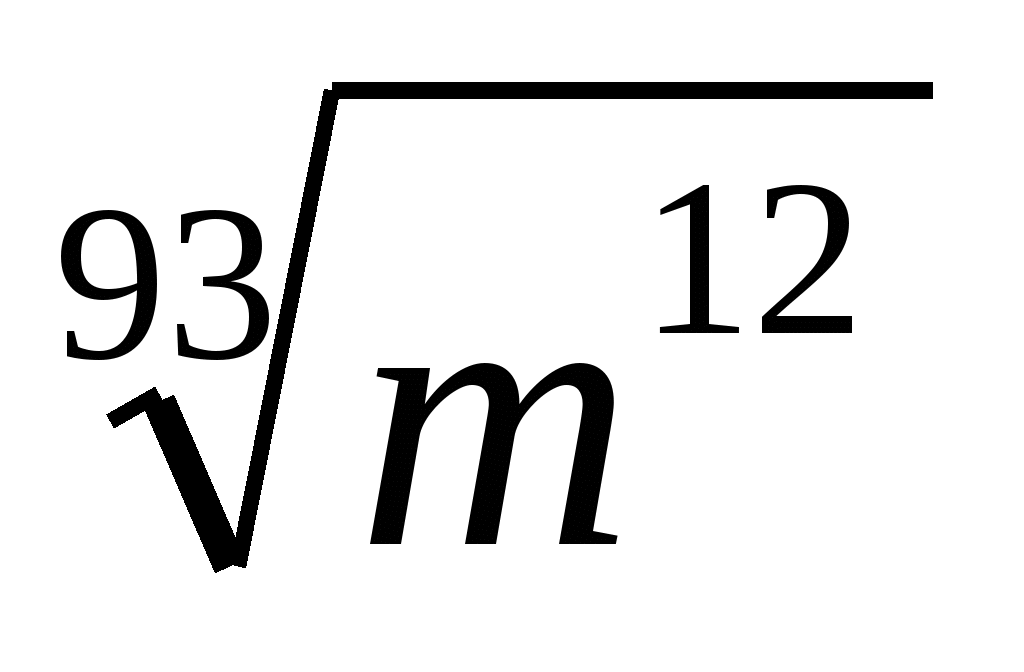
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
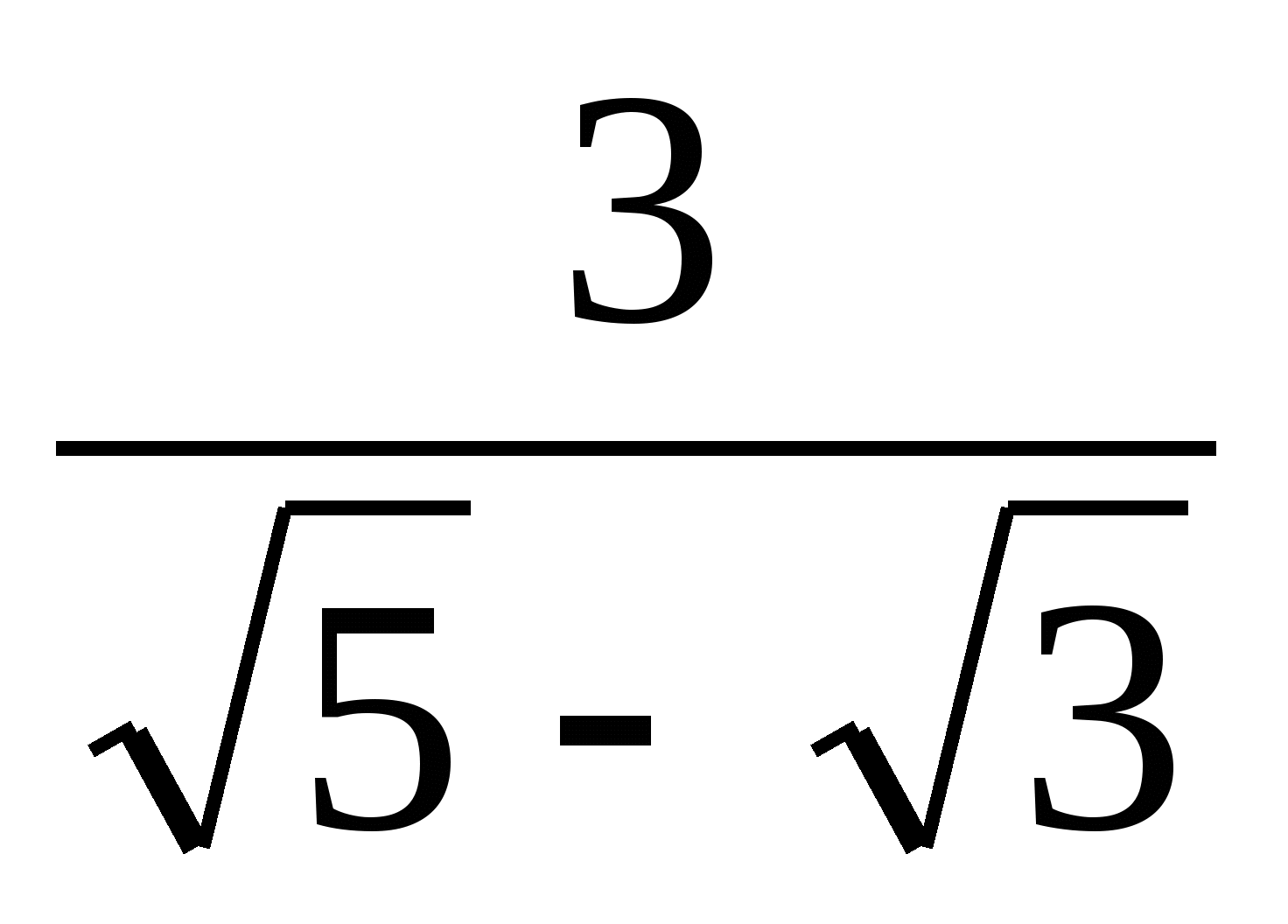 10. Выполните действие:
10. Выполните действие:
8. Сократите дробь 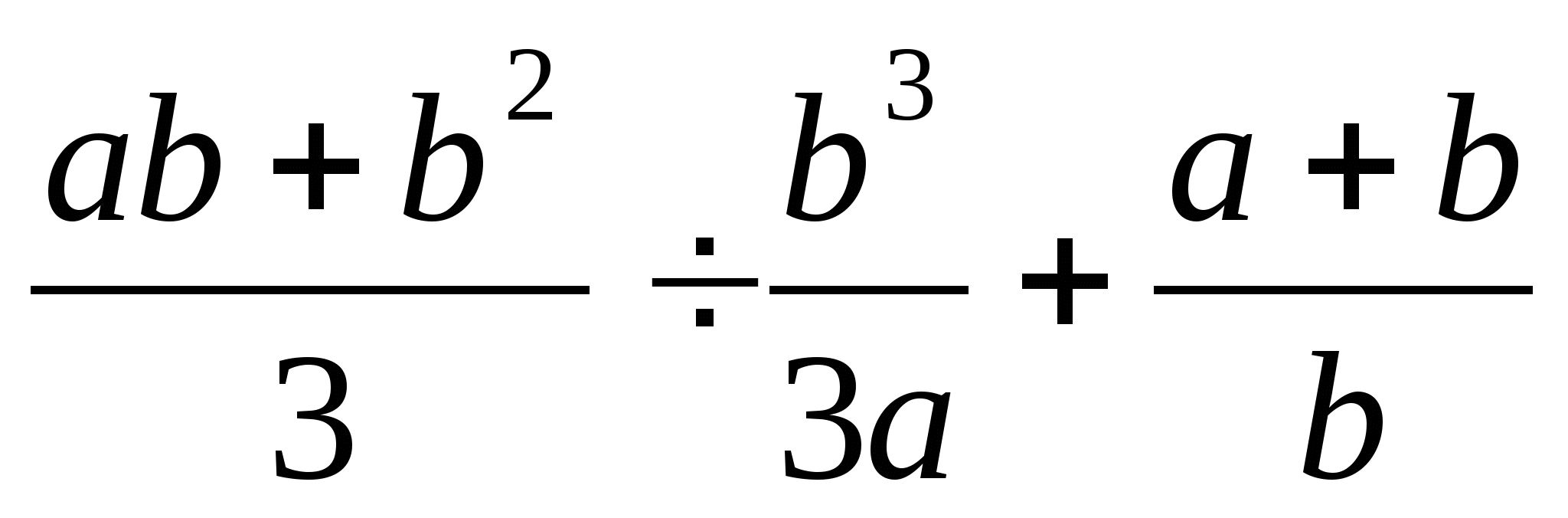
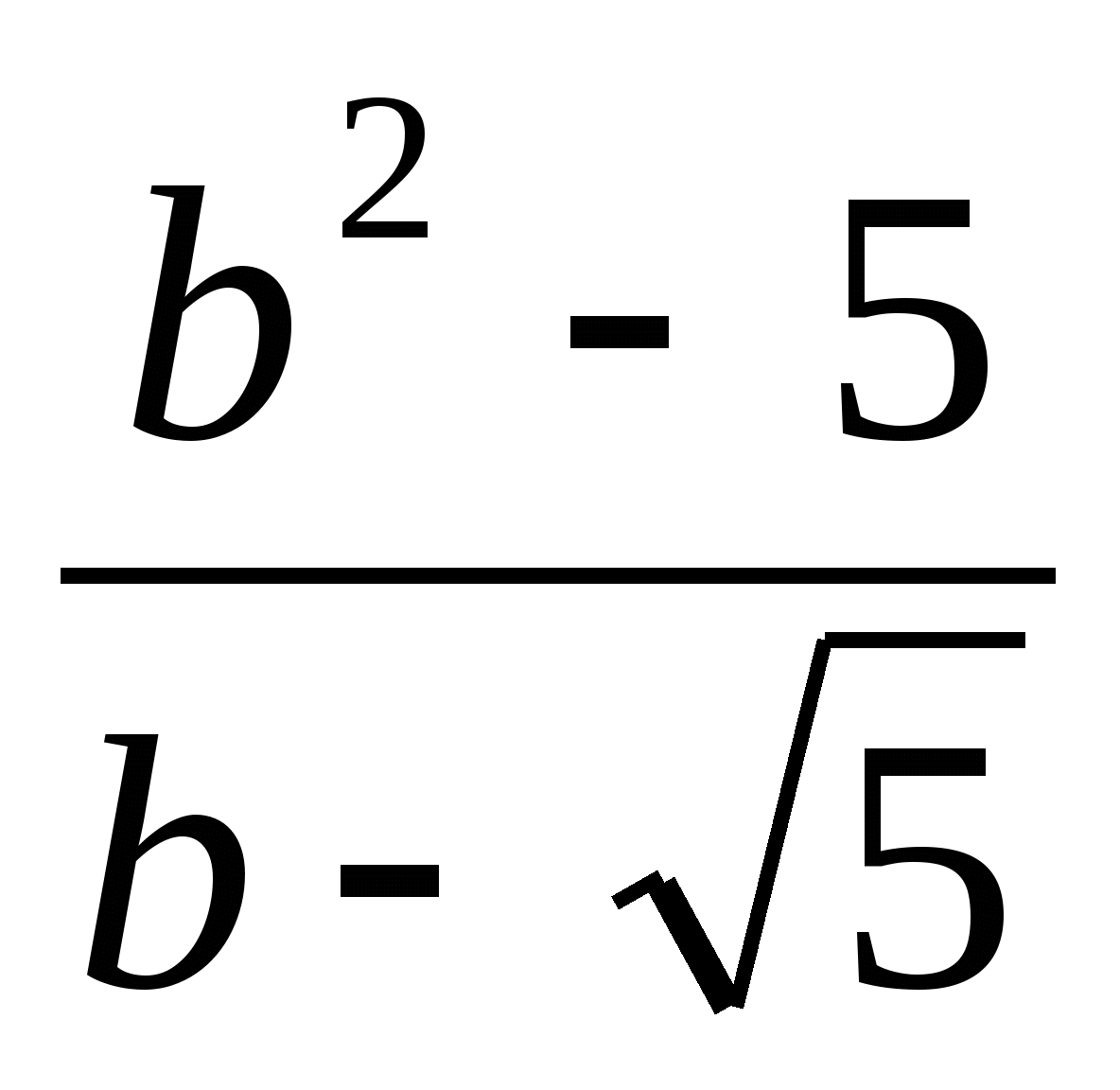
9. Выполните действие
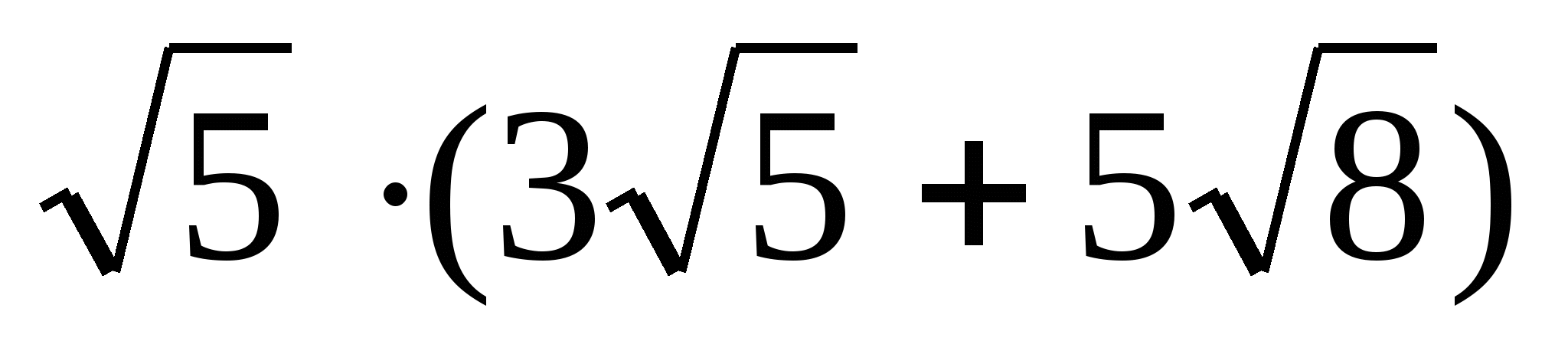
ВАРИАНТ — IV
1. Выполните действие:
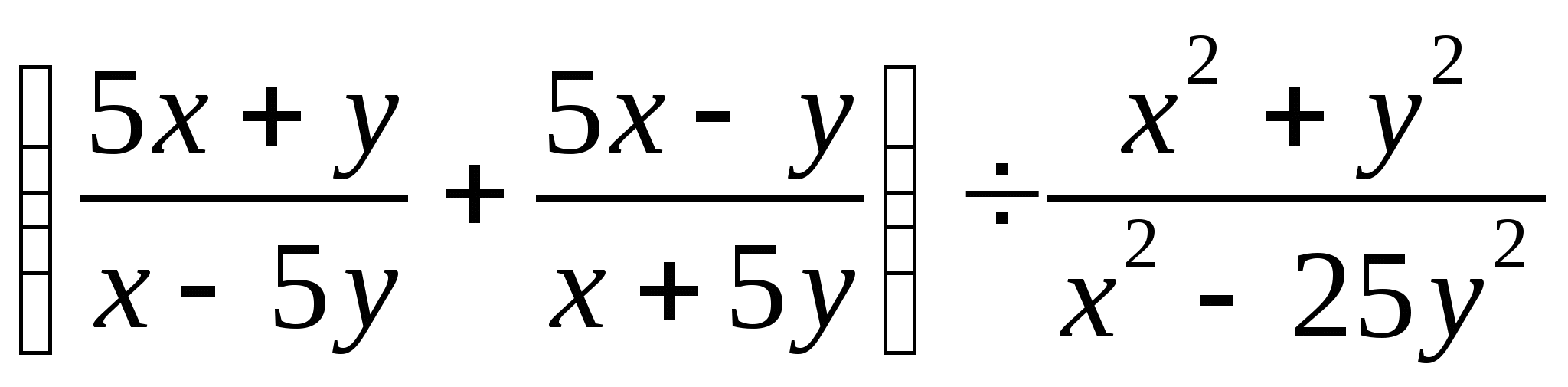
2. Найдите значение выражения:
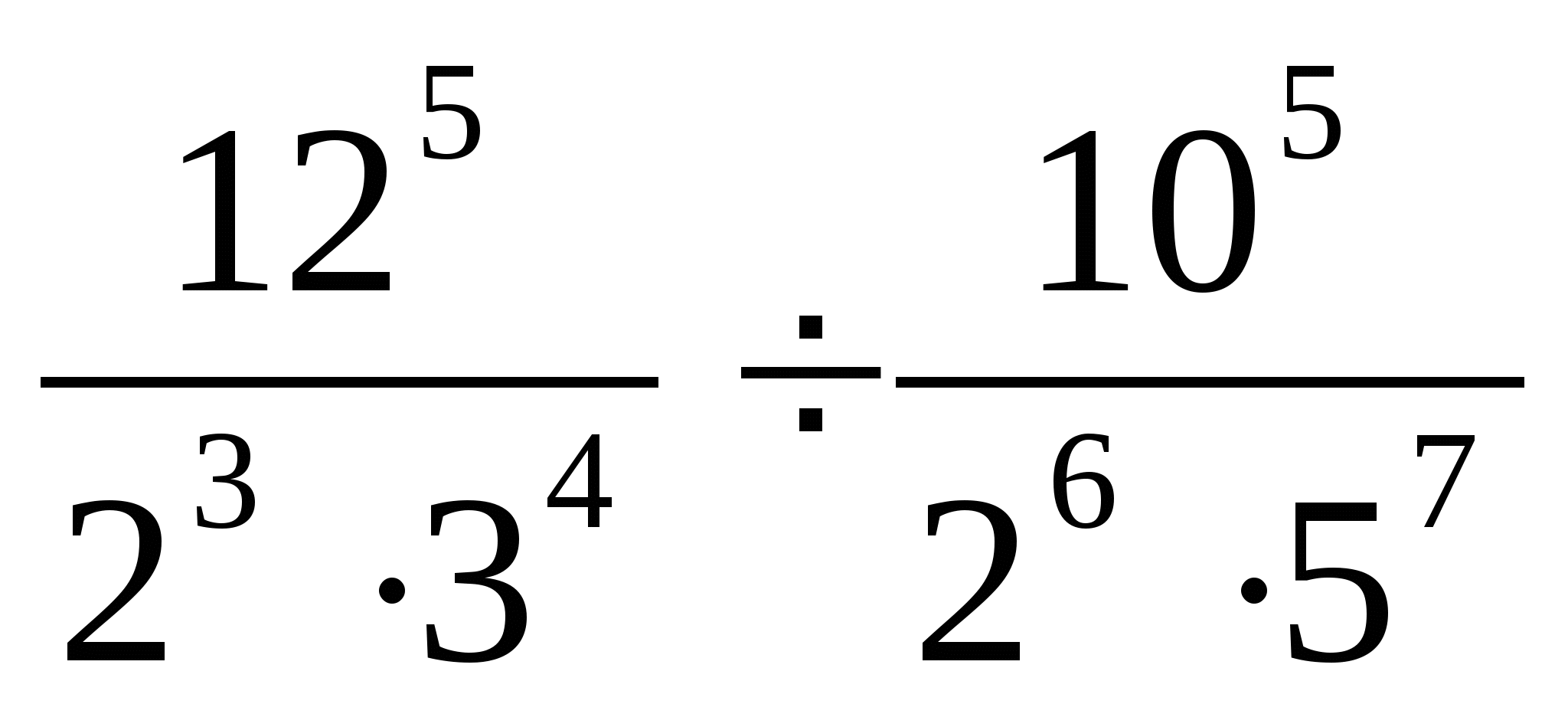
3. Представьте степень с дробным показателем в виде корня

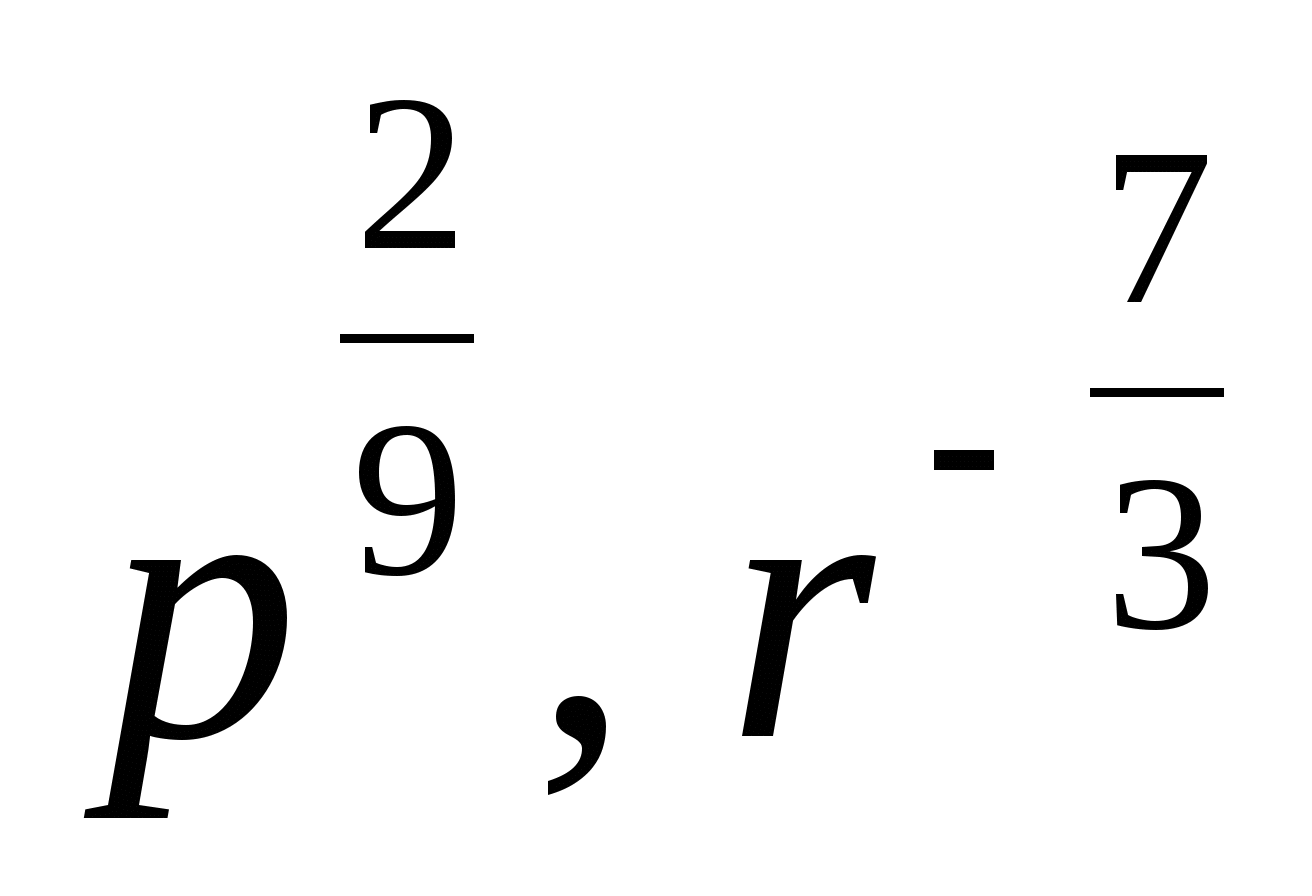 ,
, 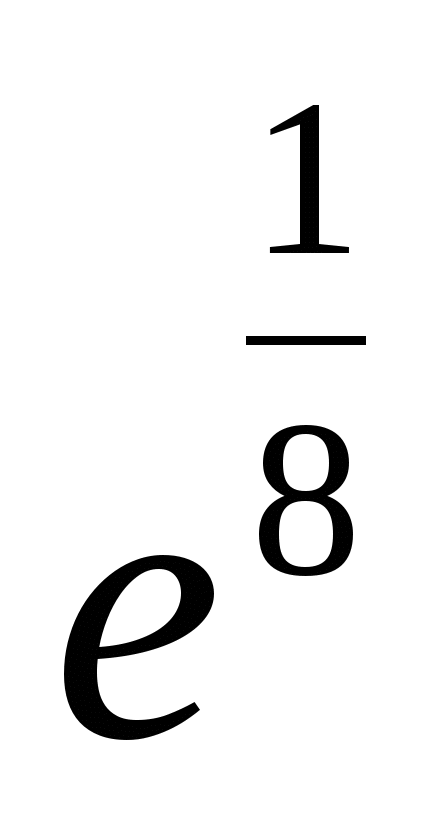
4. Привести указанное выражение к виду 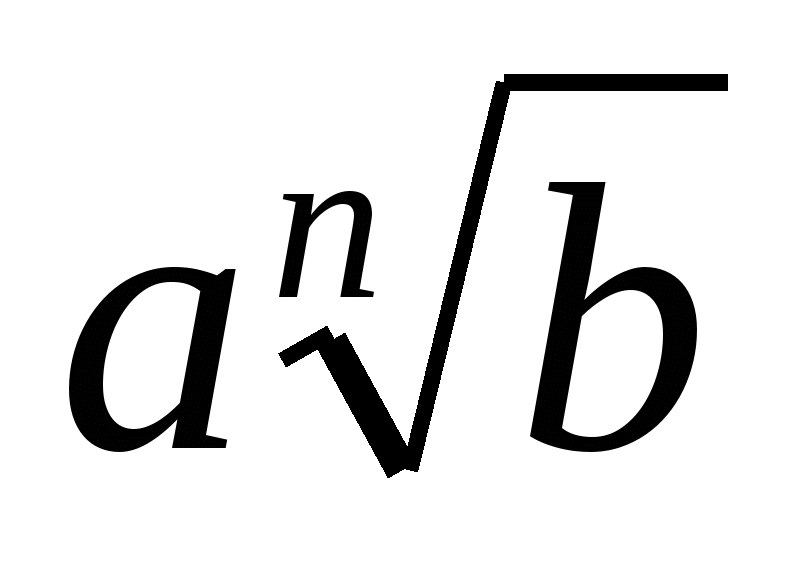 , где а- рациональное число, b – натуральное число
, где а- рациональное число, b – натуральное число
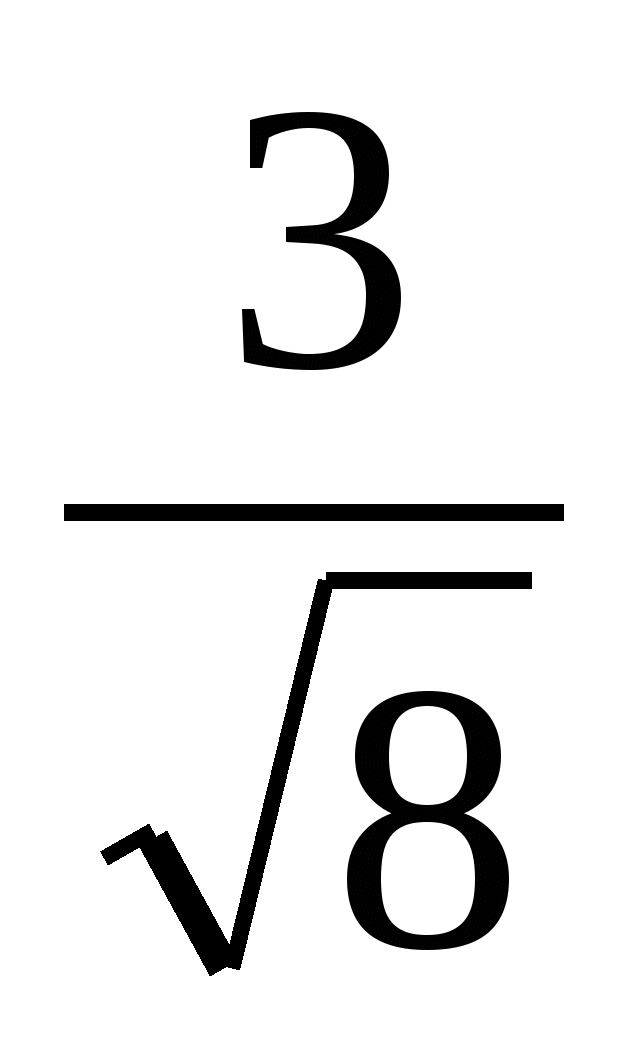 ,
, 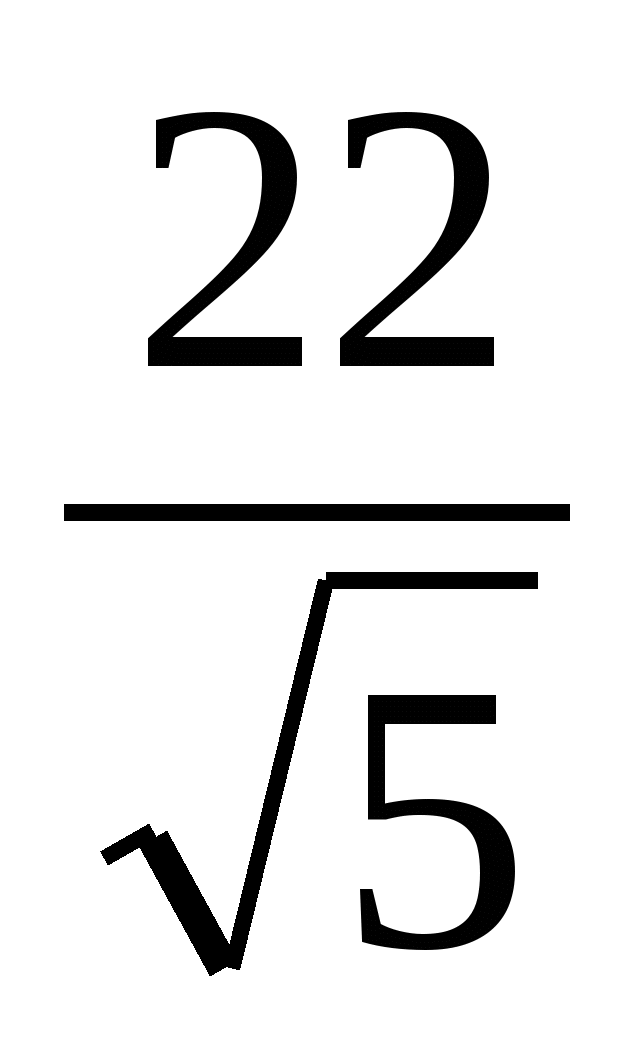
5. Упростить:
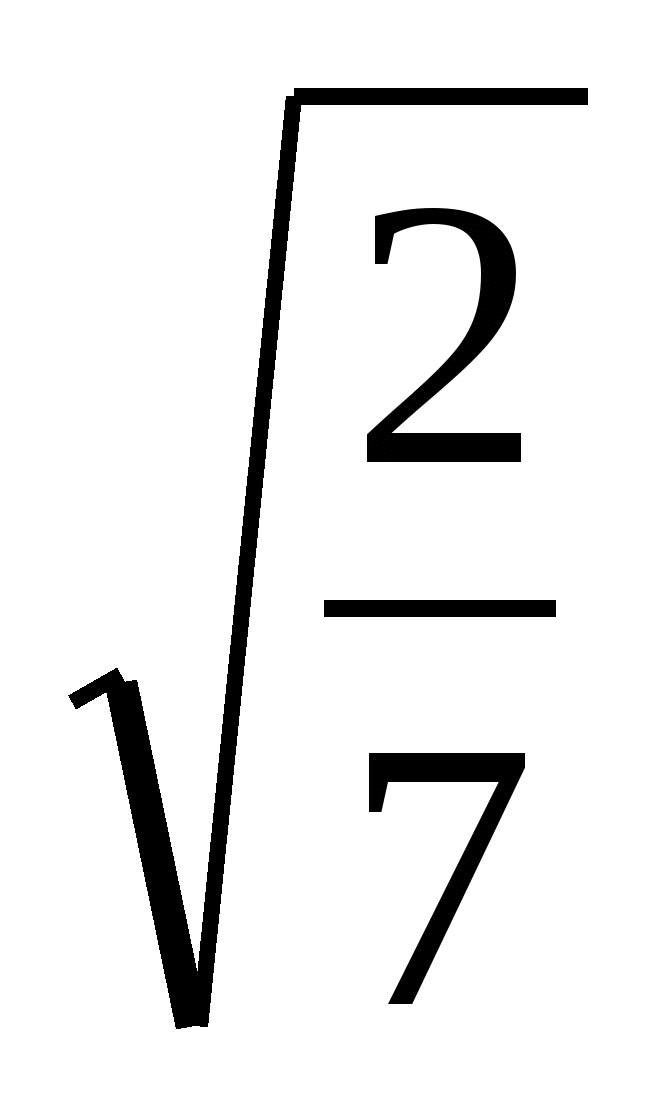 ;
; 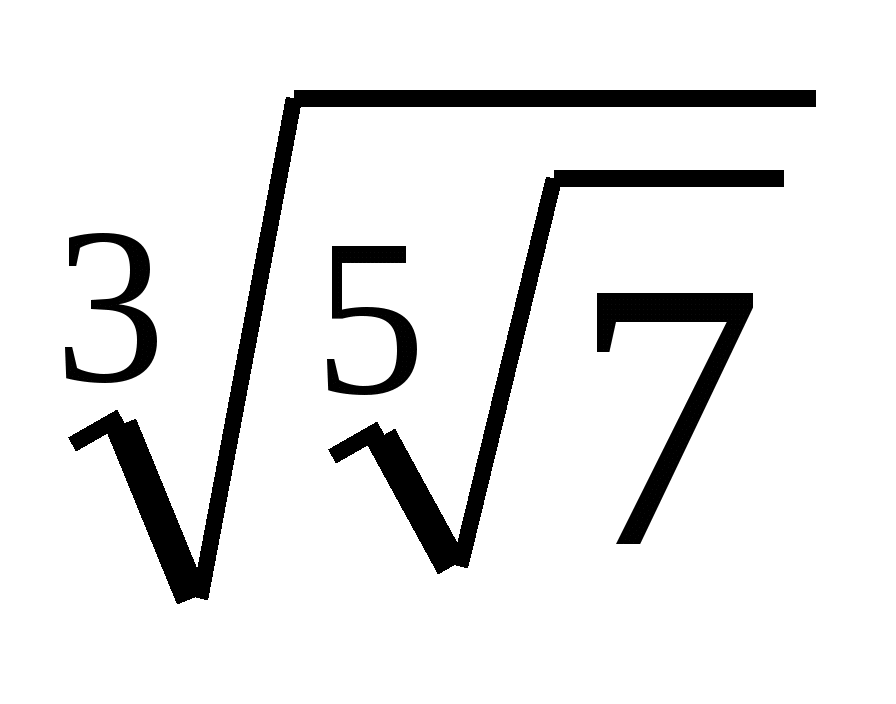
6. Замените арифметические корни степенями с дробным показателем
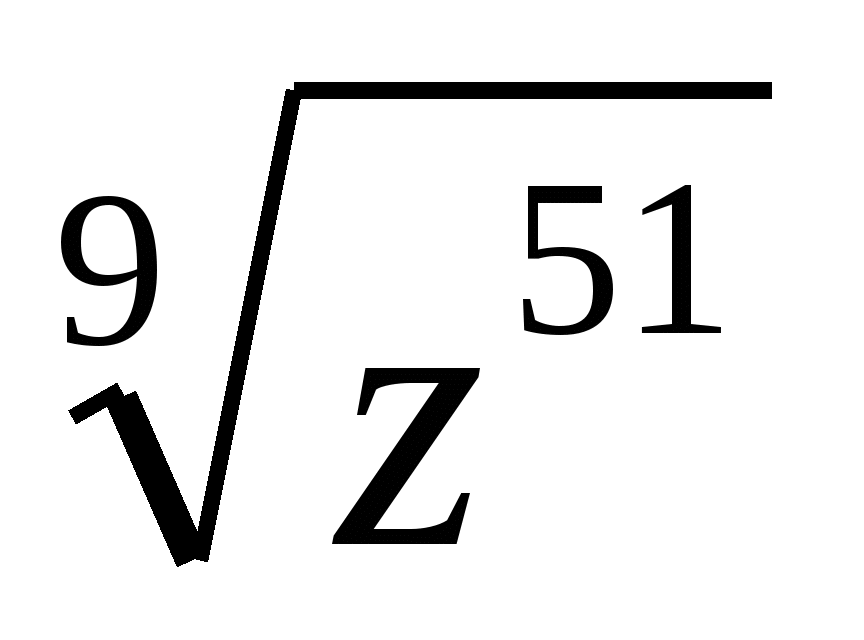 ,
, 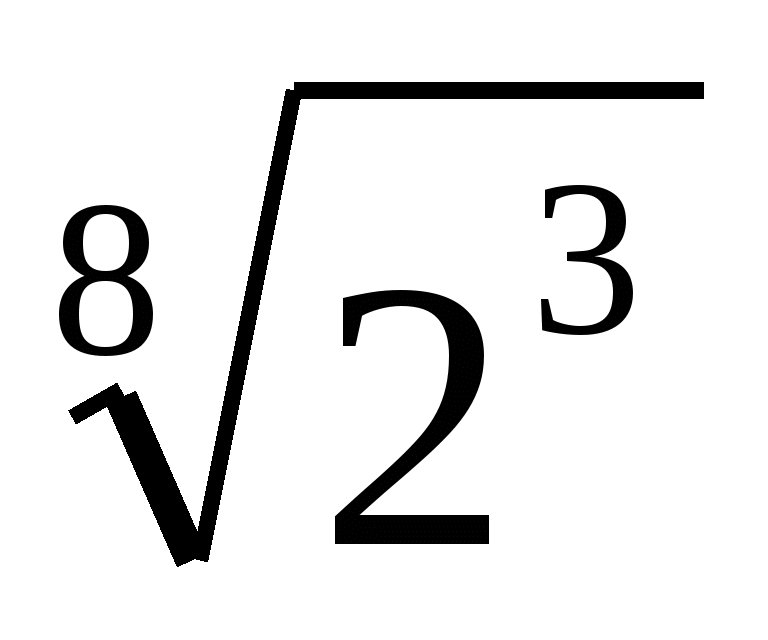 ,
, 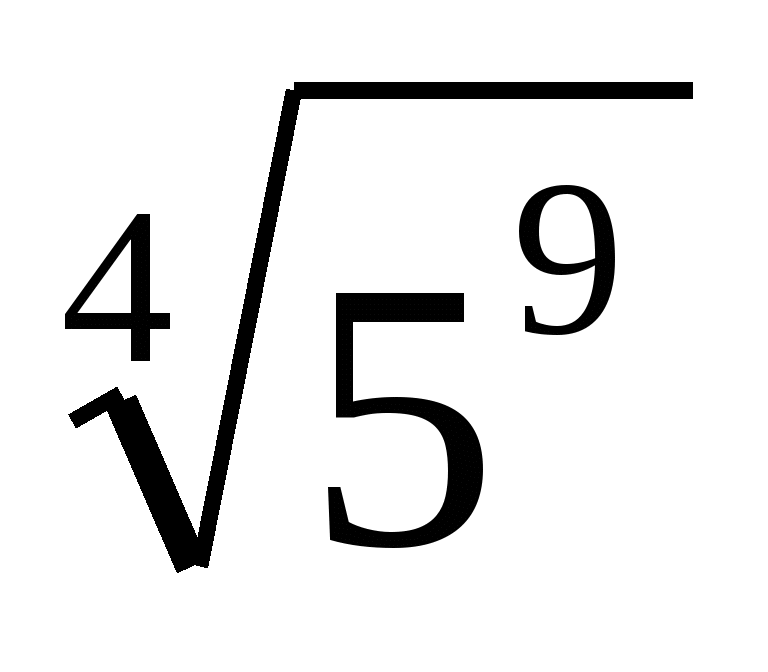
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
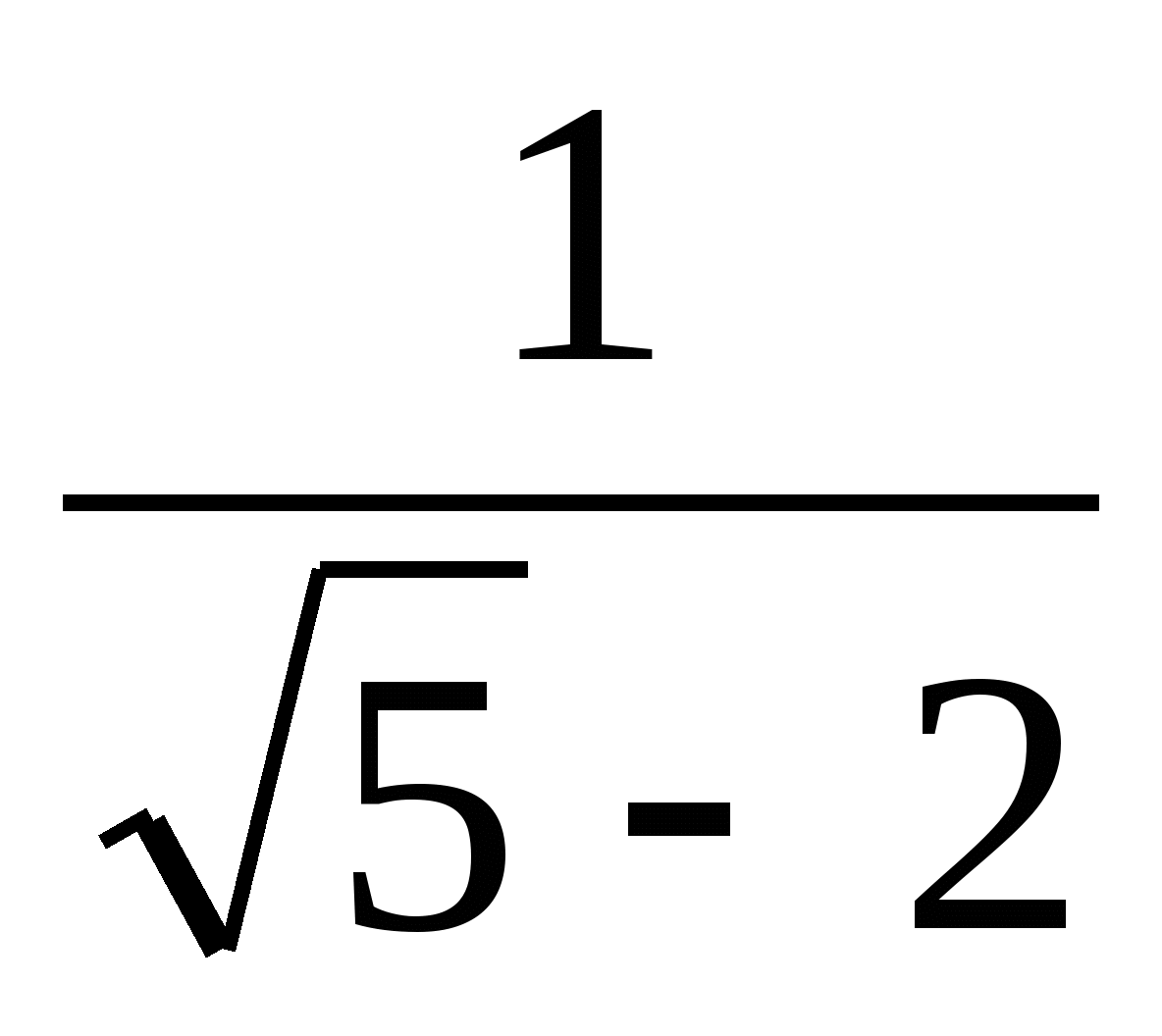 10. Выполните действие:
10. Выполните действие:
8. Сократите дробь 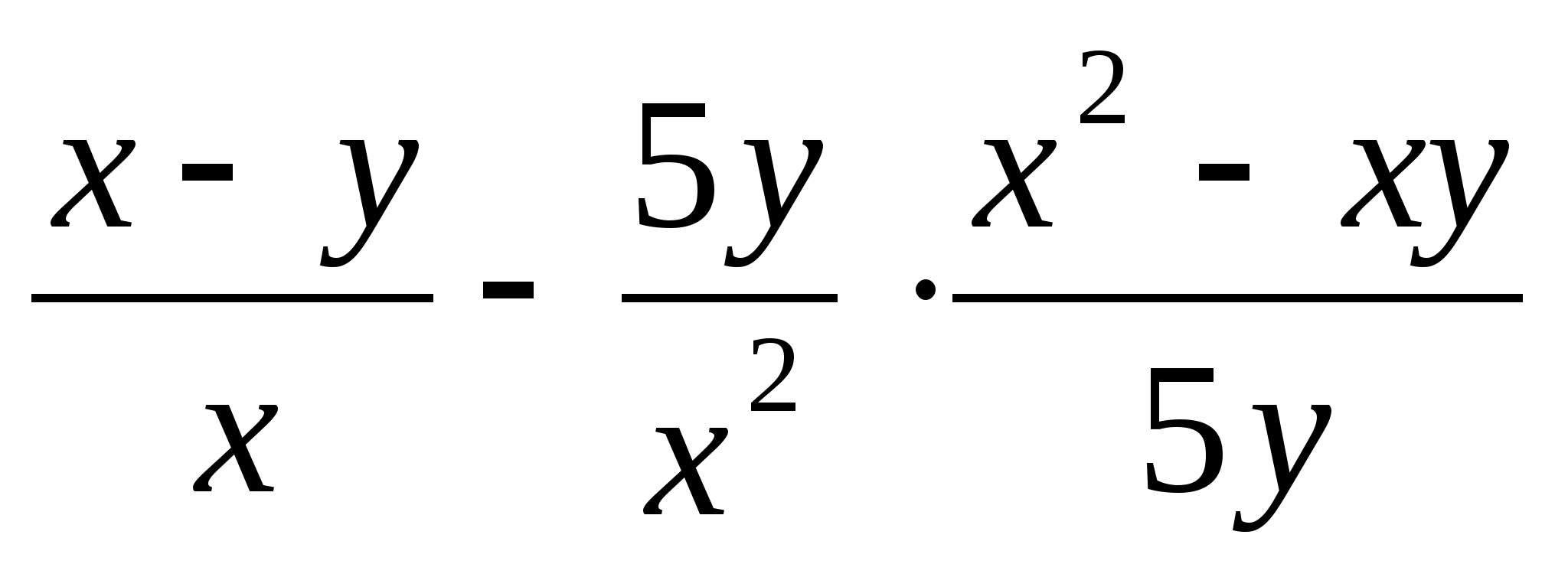
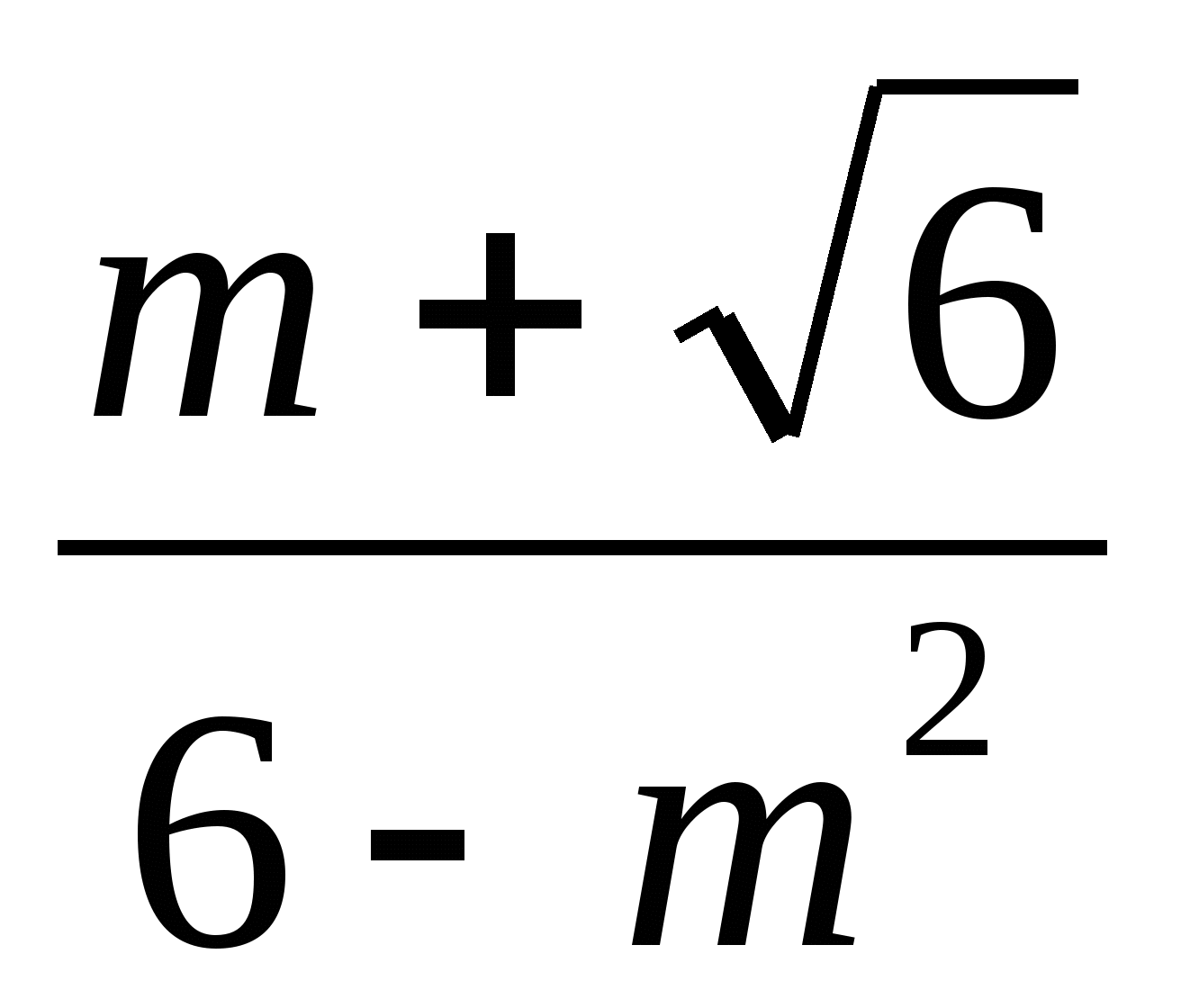
9. Выполните действие
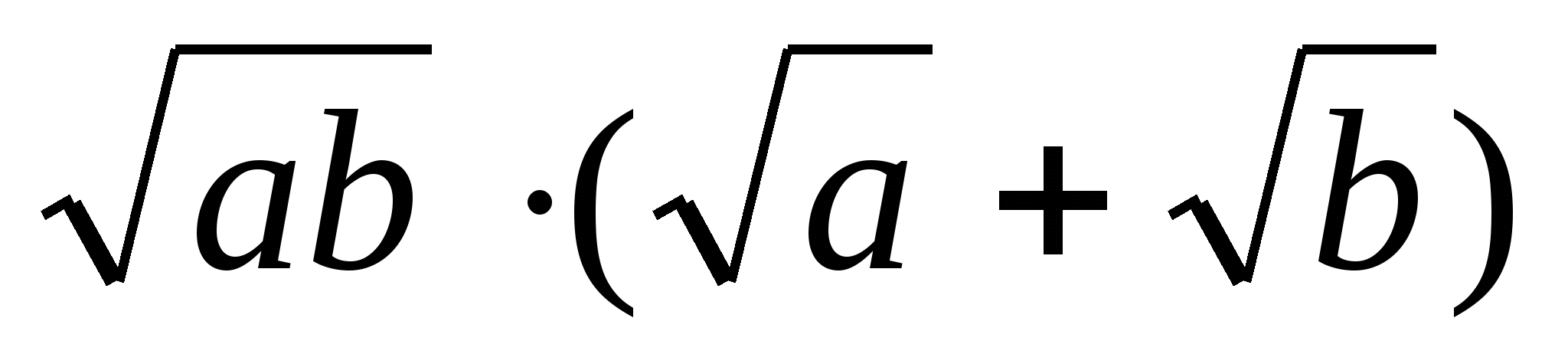
1. Упростите выражение:
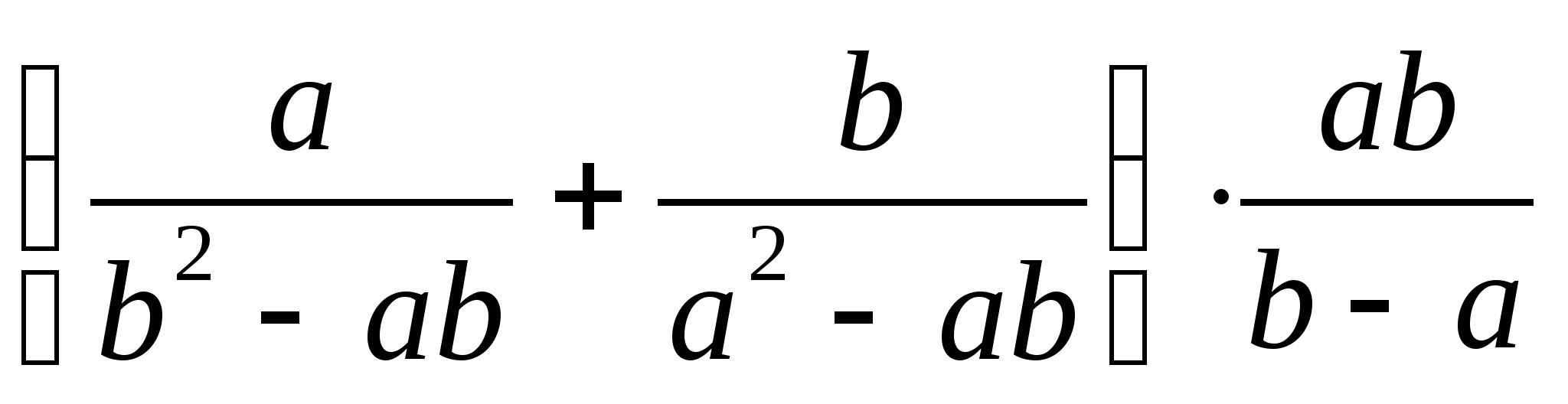
2. Найдите значение выражения:
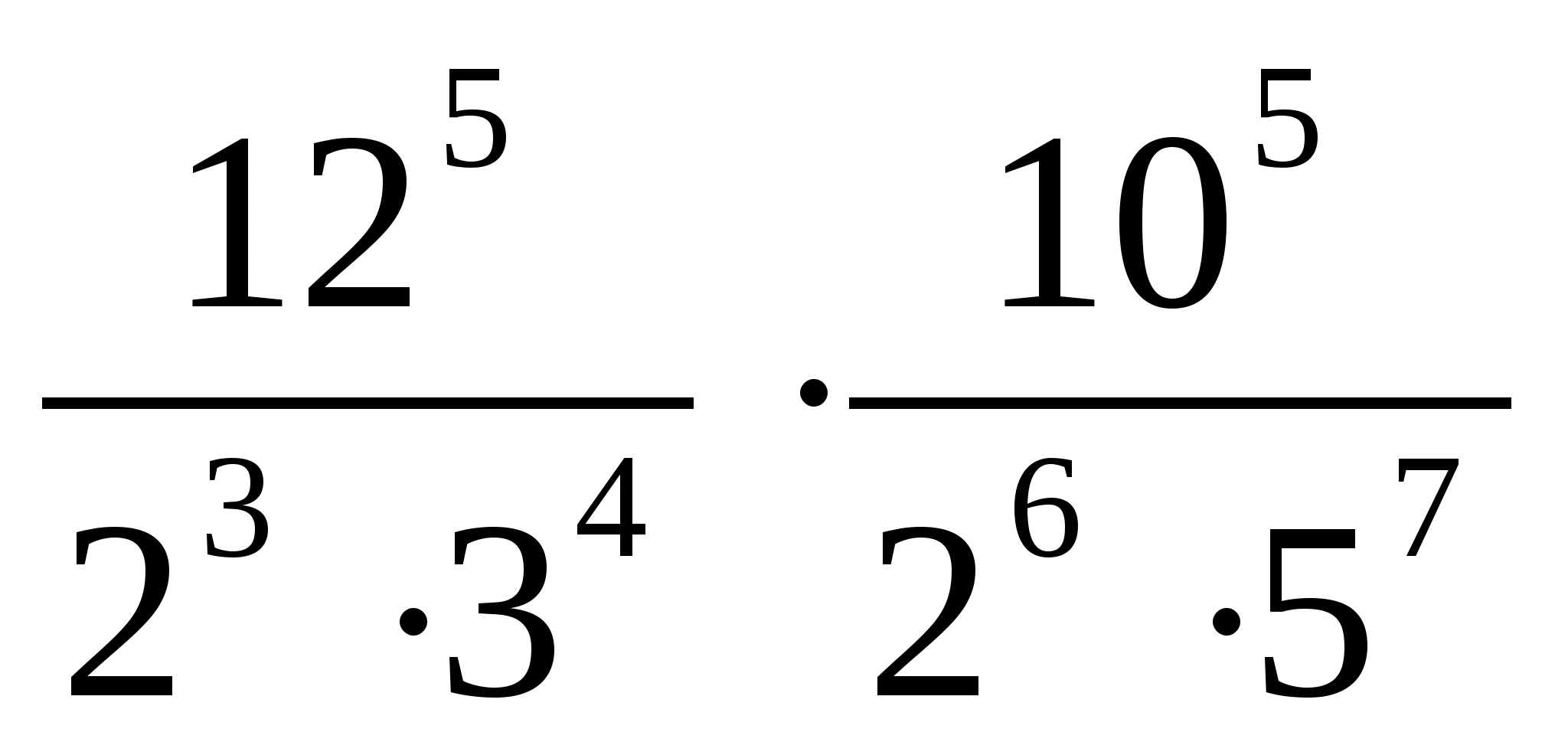
3. Представьте степень с дробным показателем в виде корня

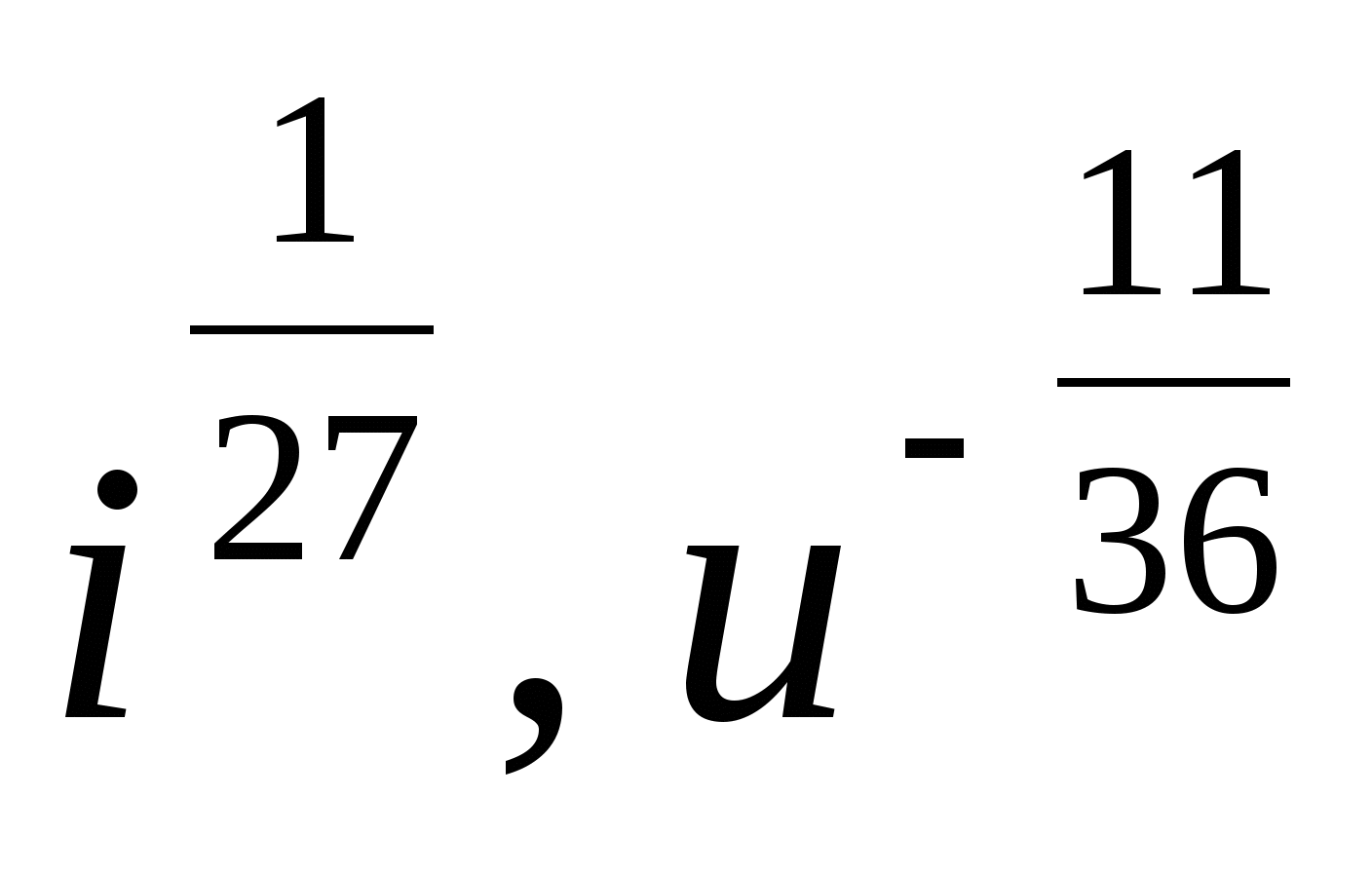 ,
, 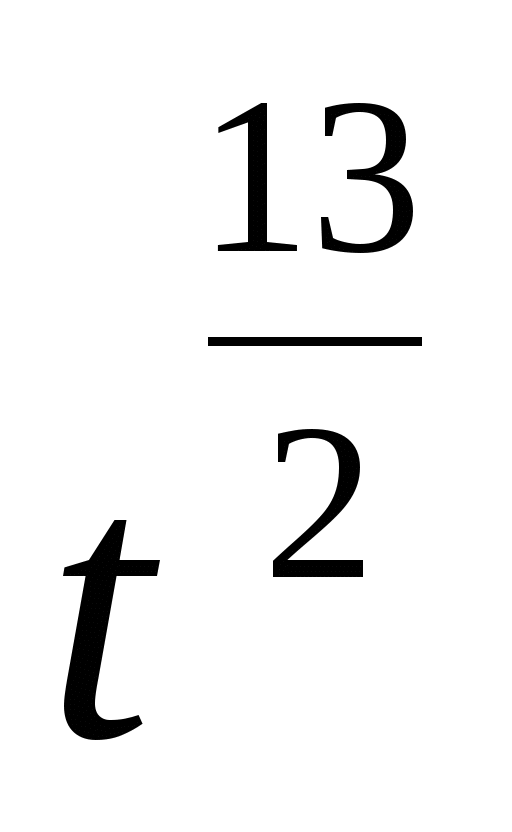
4. Привести указанное выражение к виду 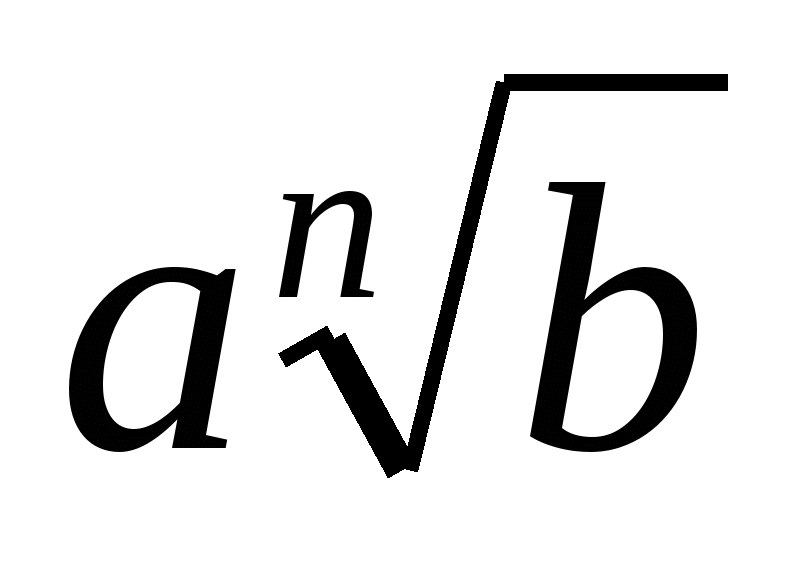 , где а- рациональное число, b – натуральное число
, где а- рациональное число, b – натуральное число
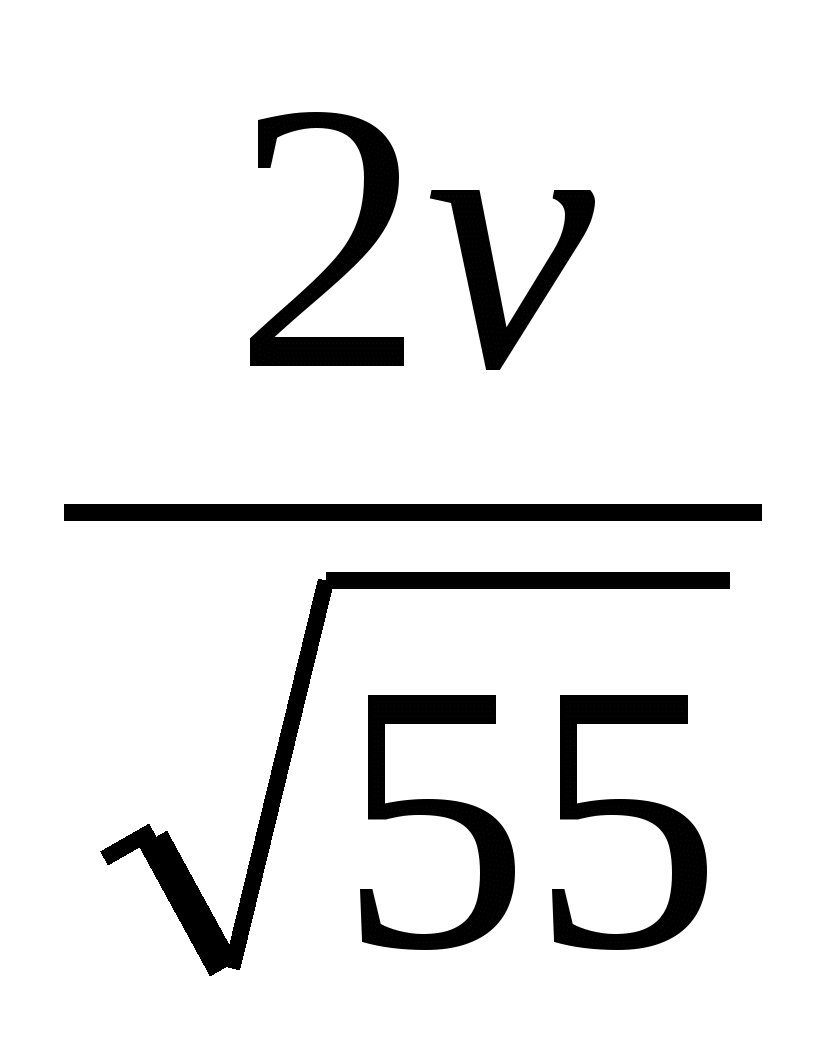 ,
, 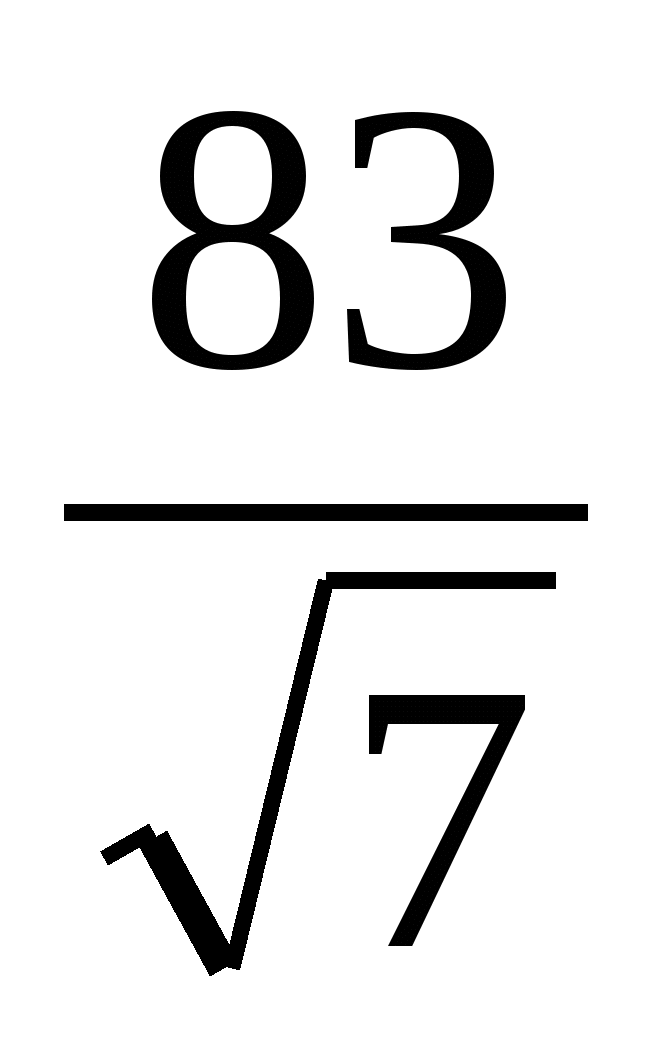
5. Упростить:
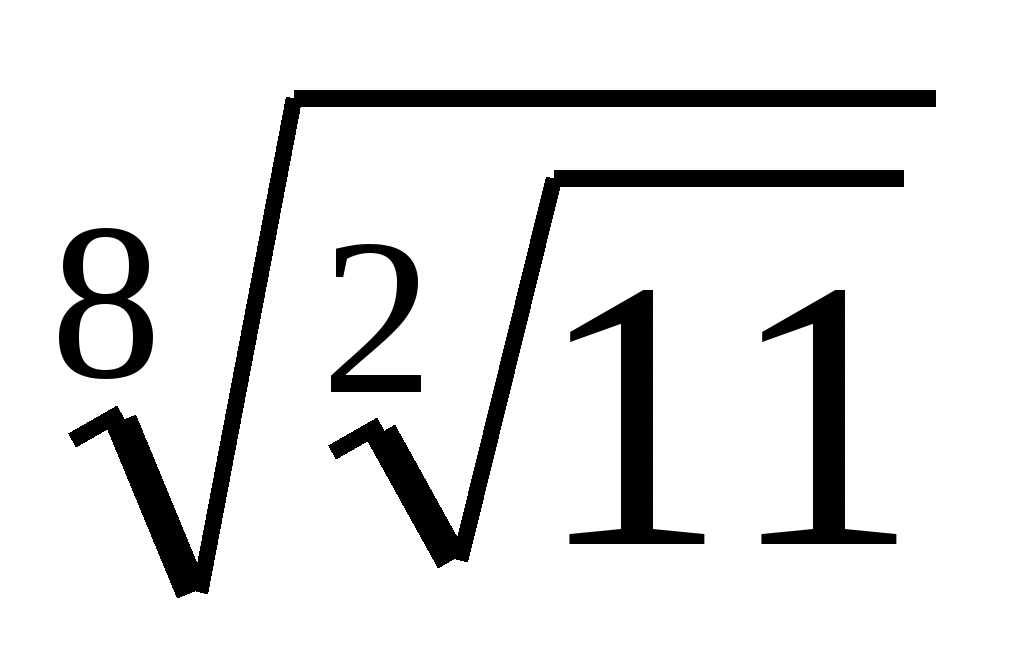 ;
; 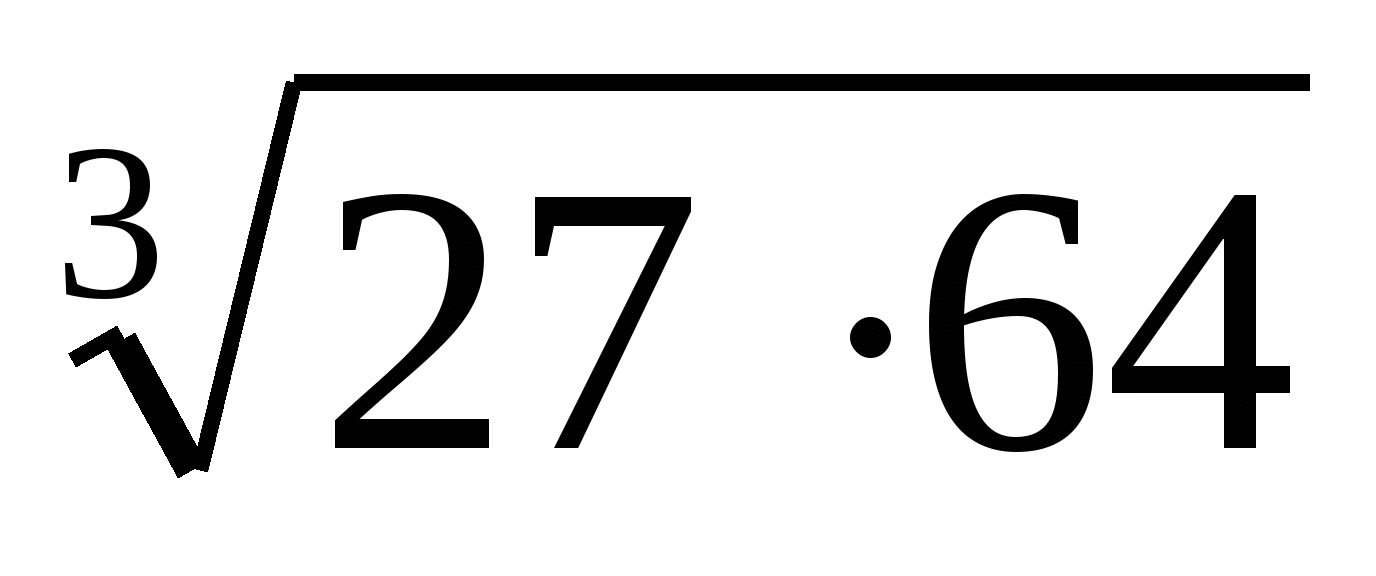
6. Замените арифметические корни степенями с дробным показателем
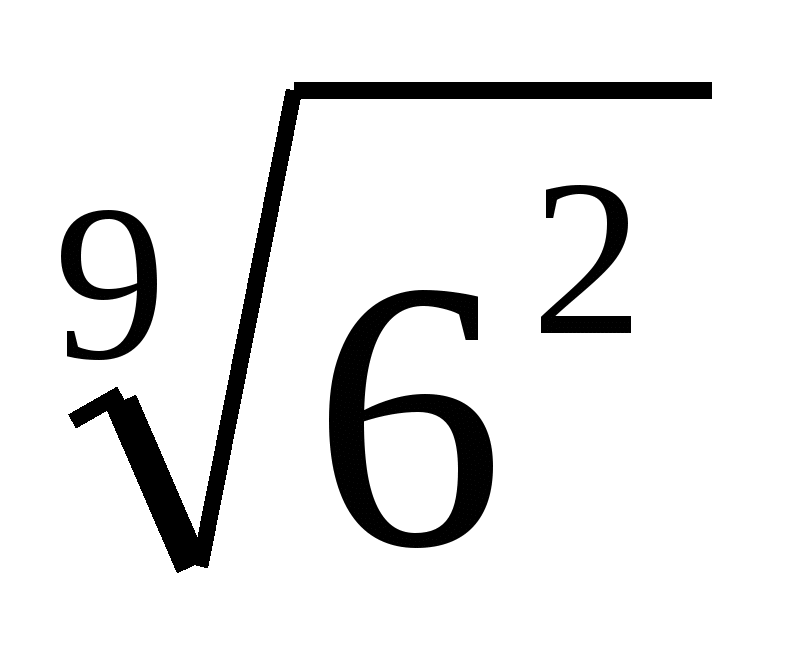 ,
, 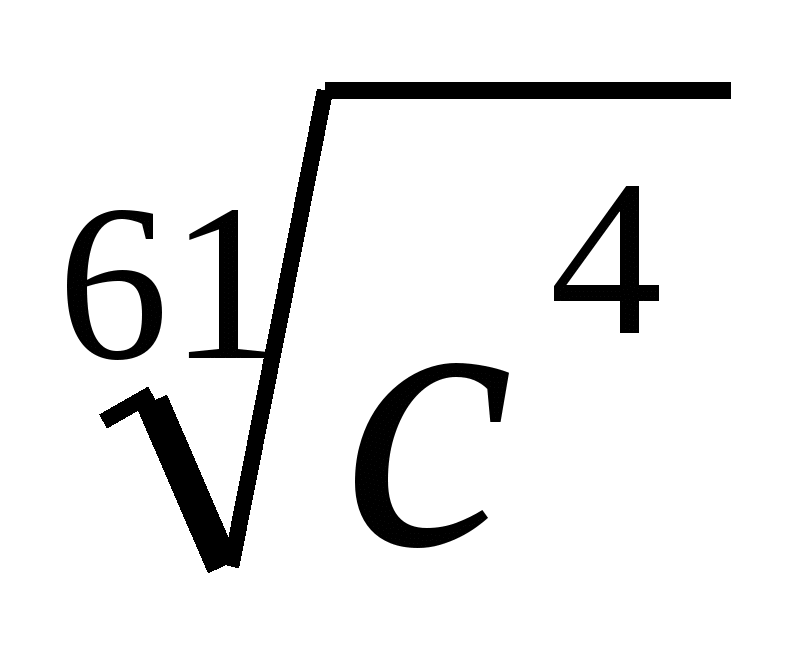 ,
, 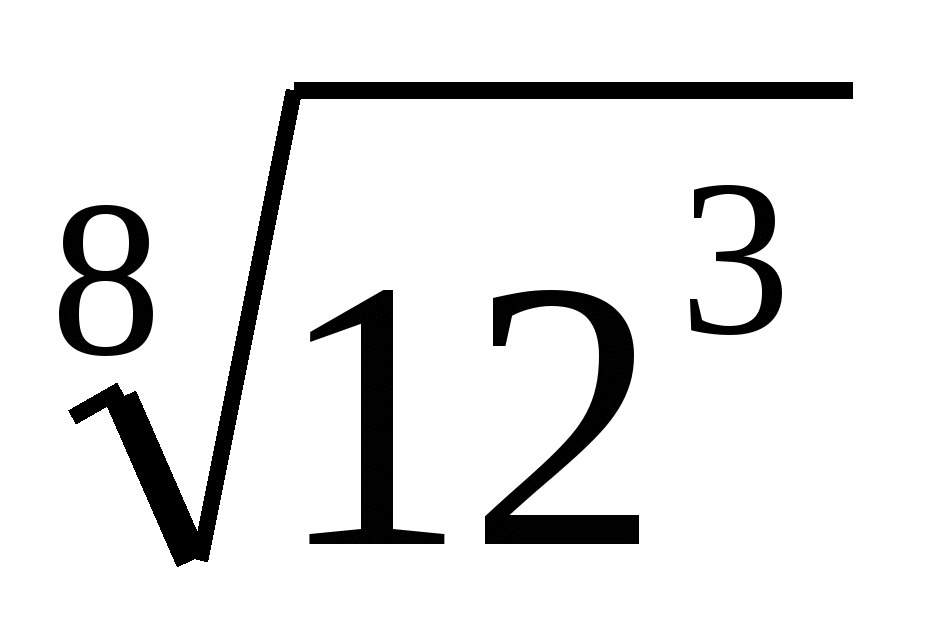
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
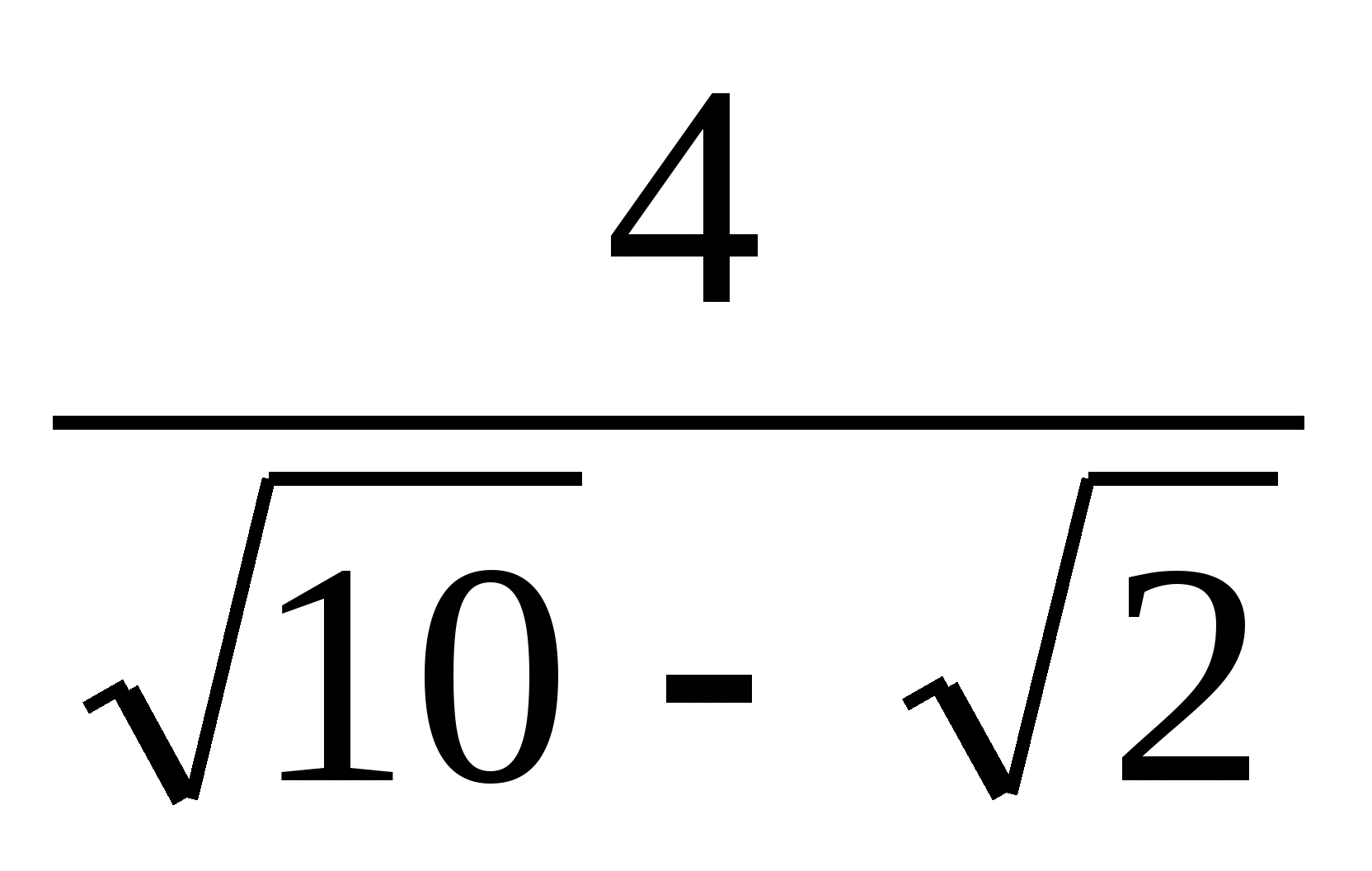 10. Выполните действие:
10. Выполните действие:
8. Сократите дробь 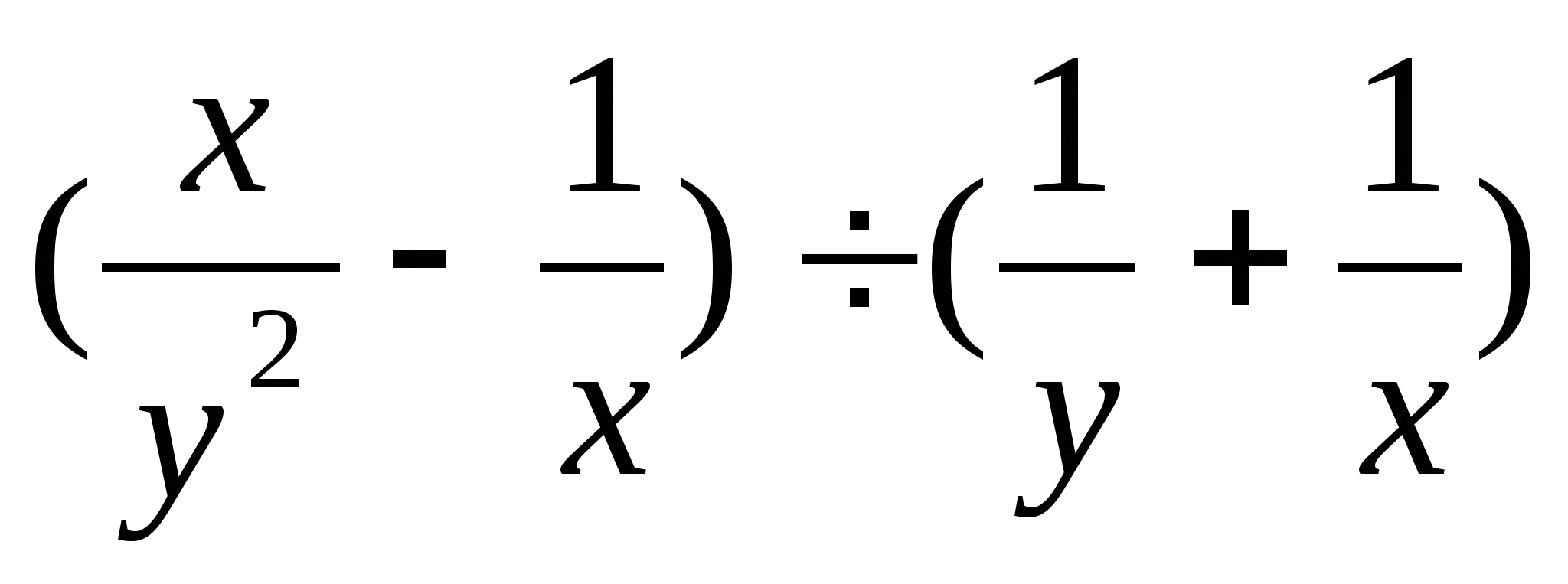
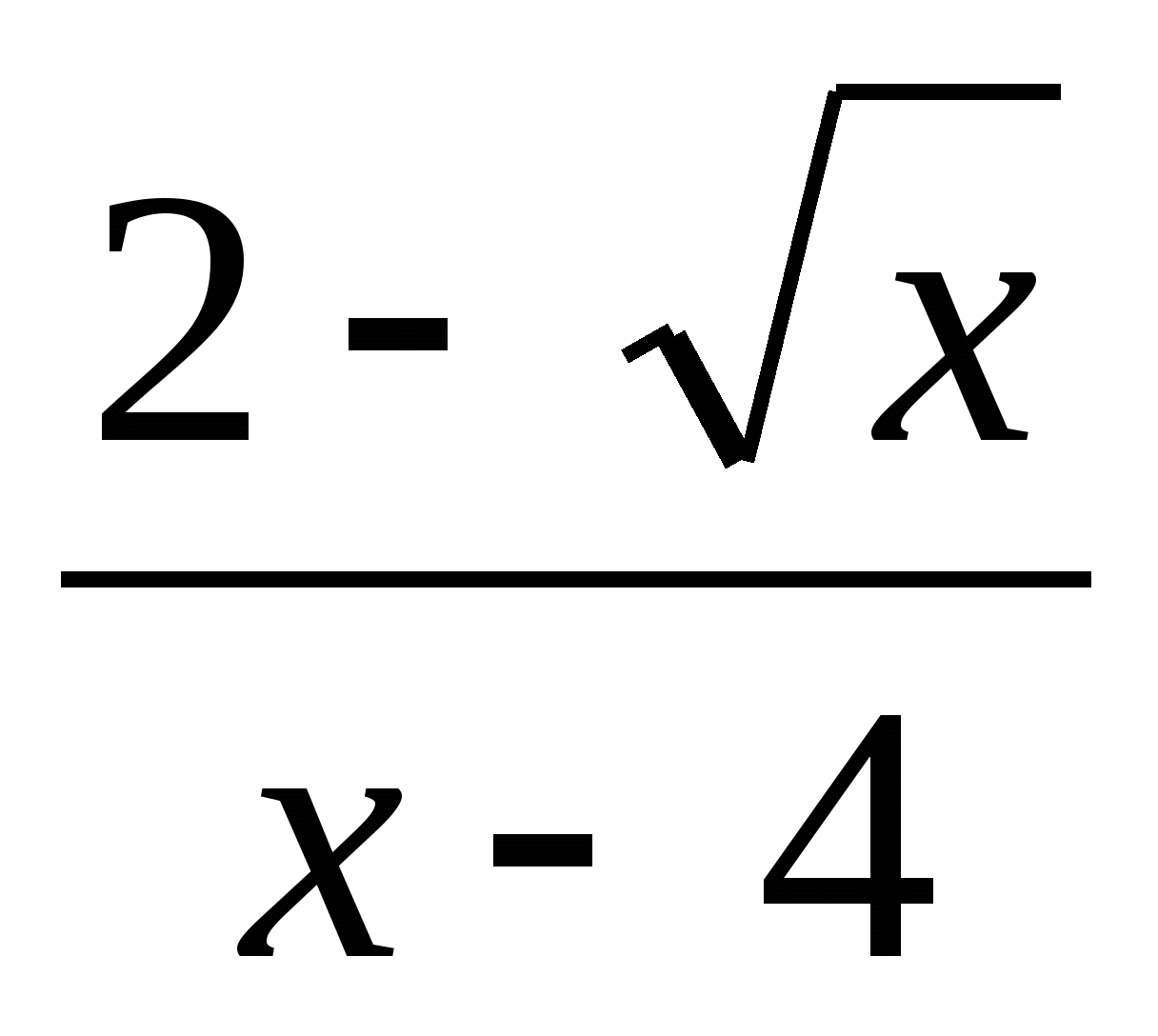
9. Выполните действие
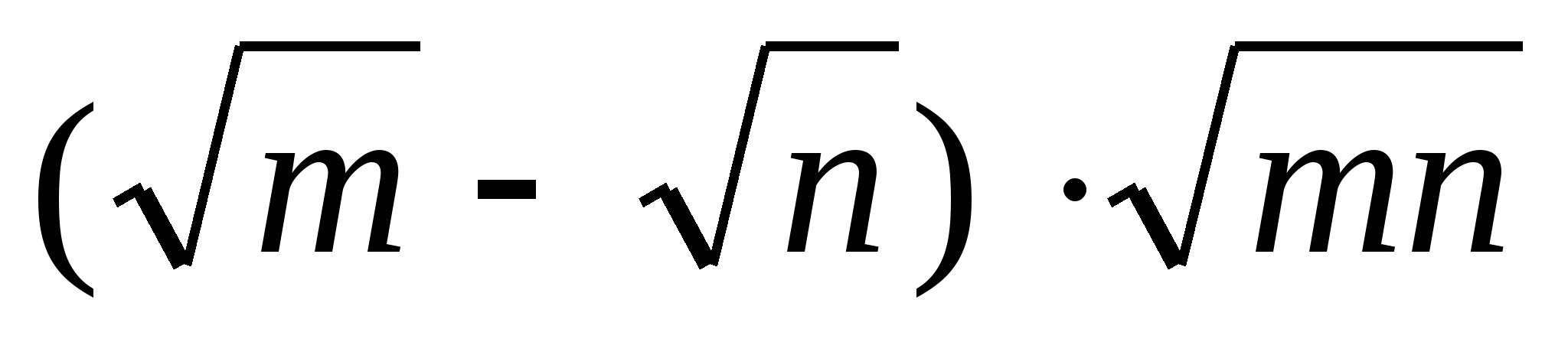
ВАРИАНТ — VI
1. Упростите выражение:
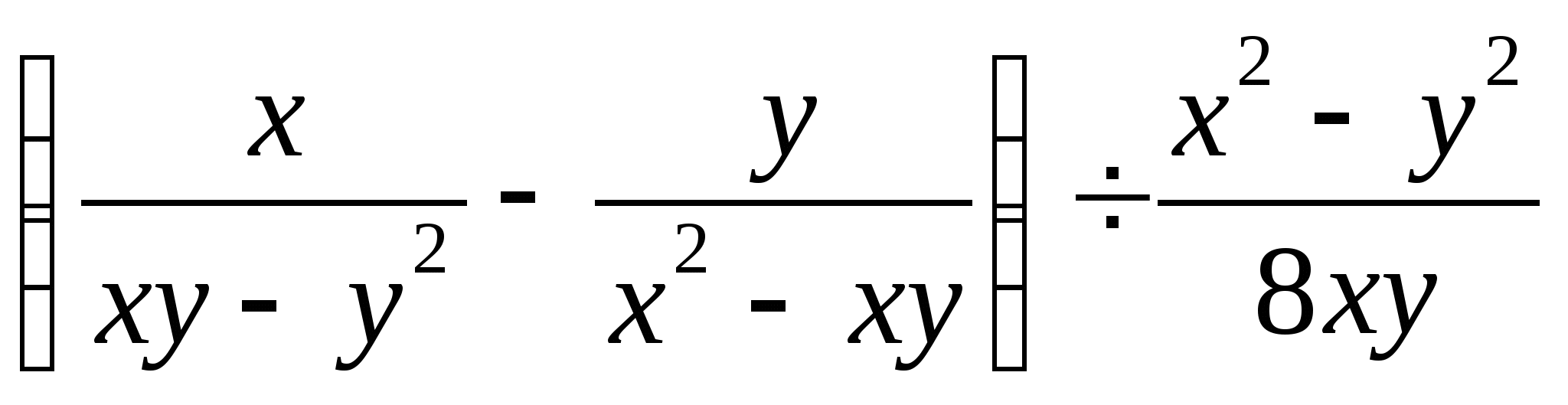
2. Найдите значение выражения:
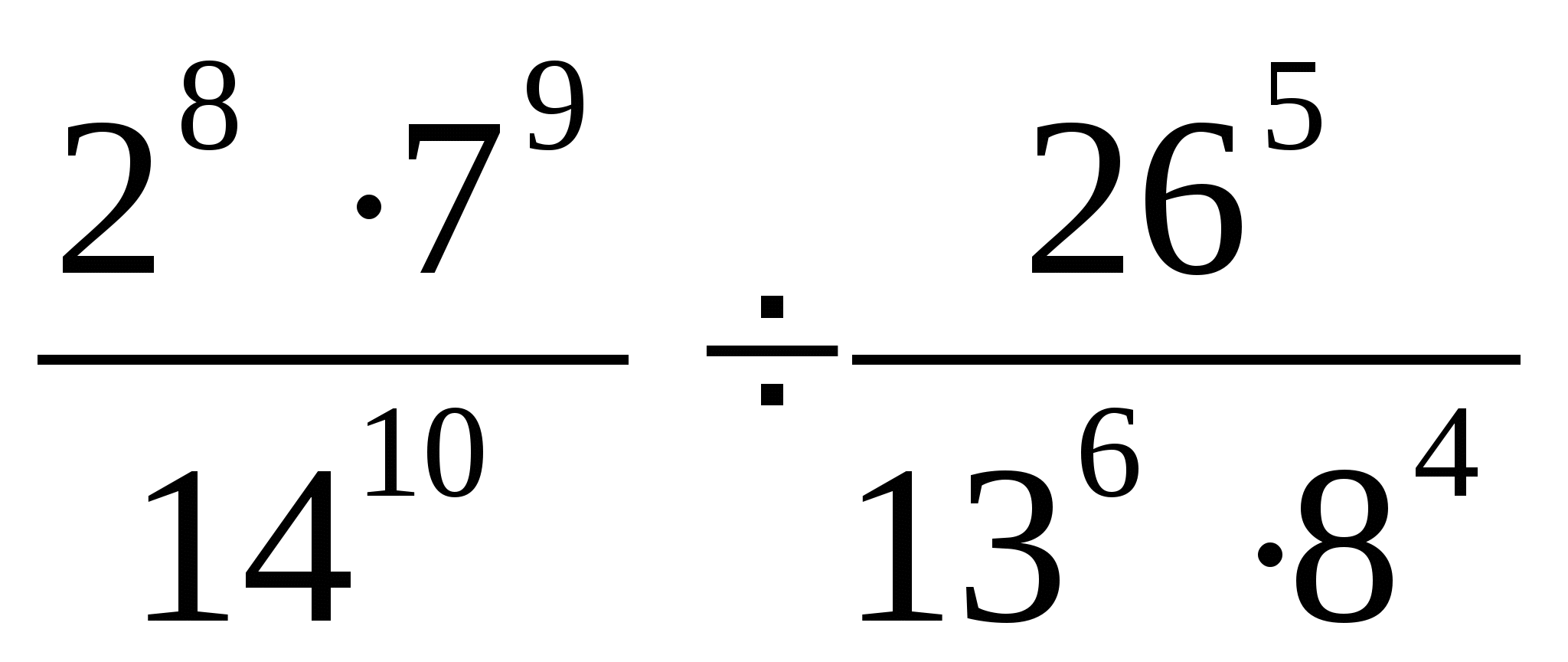
3. Представьте степень с дробным показателем в виде корня

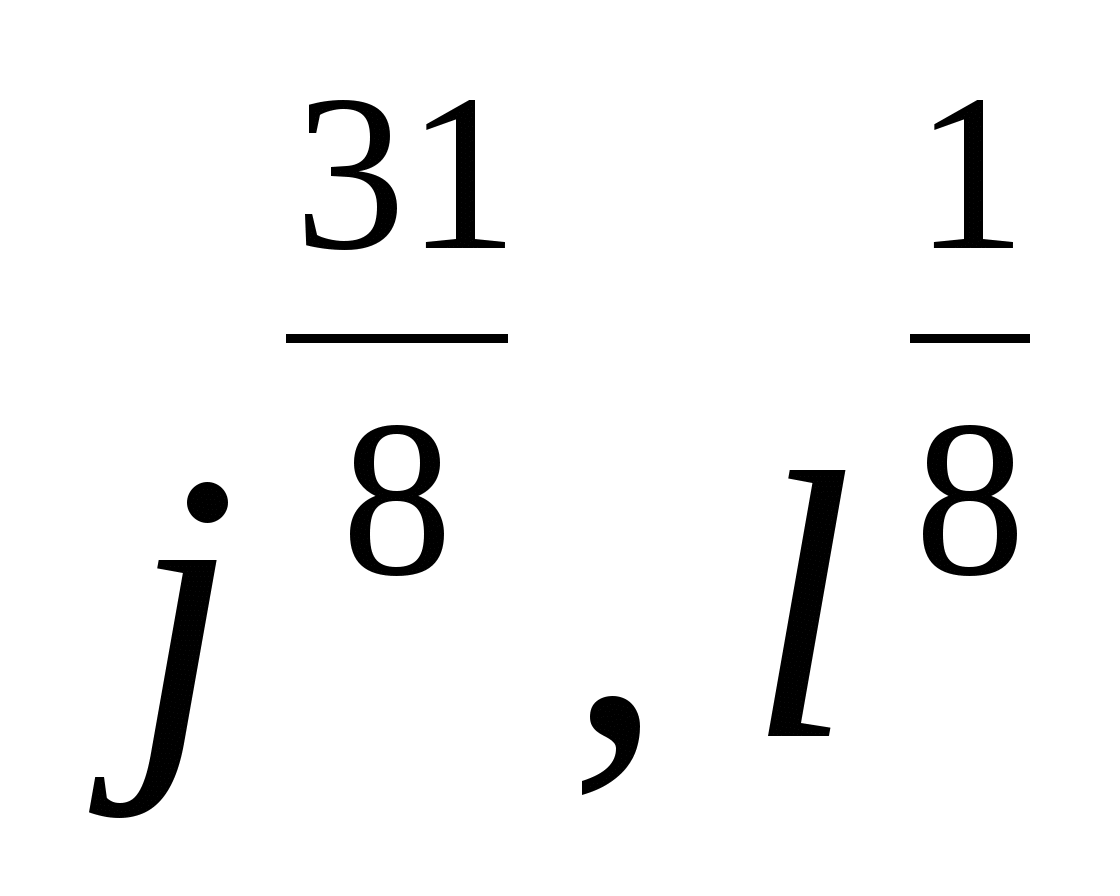 ,
, 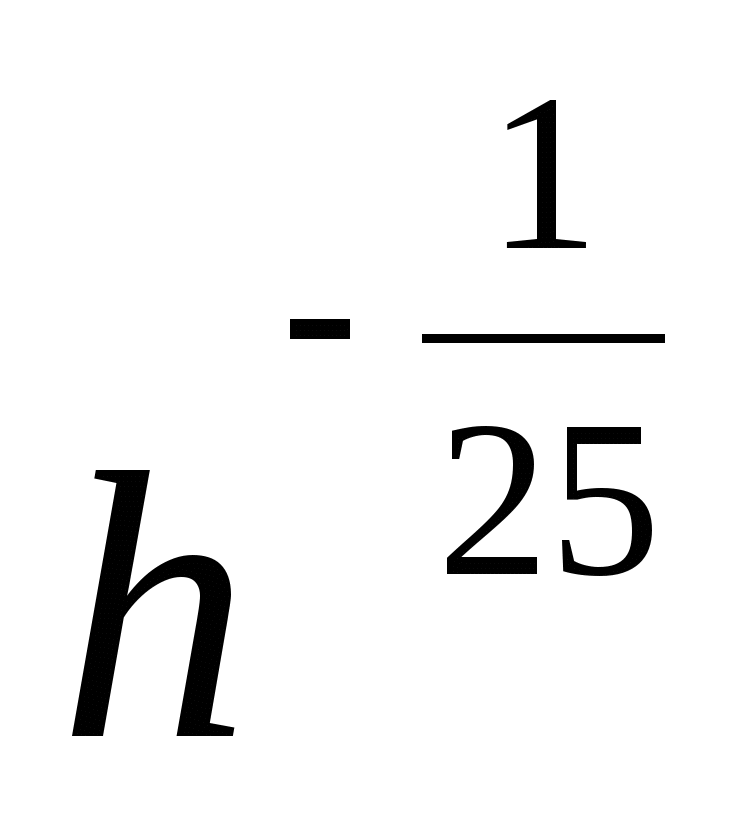
4. Привести указанное выражение к виду 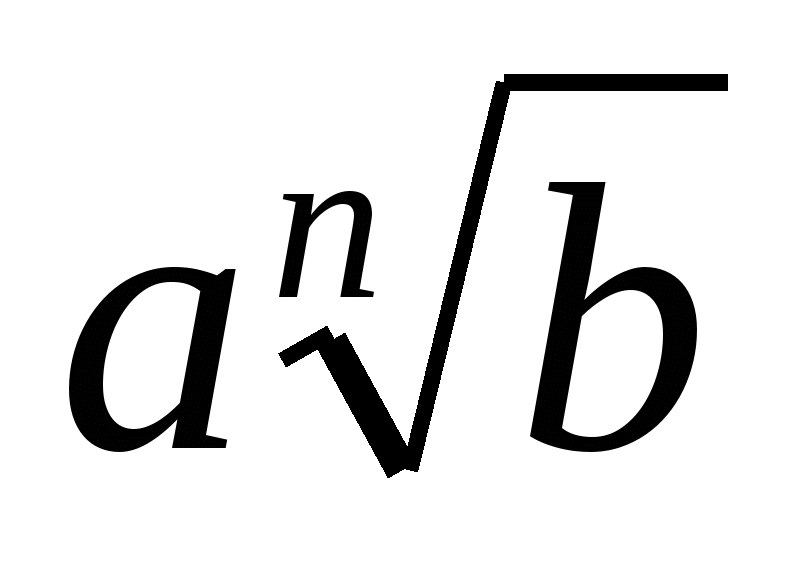 , где -а рациональное число, b – натуральное число
, где -а рациональное число, b – натуральное число
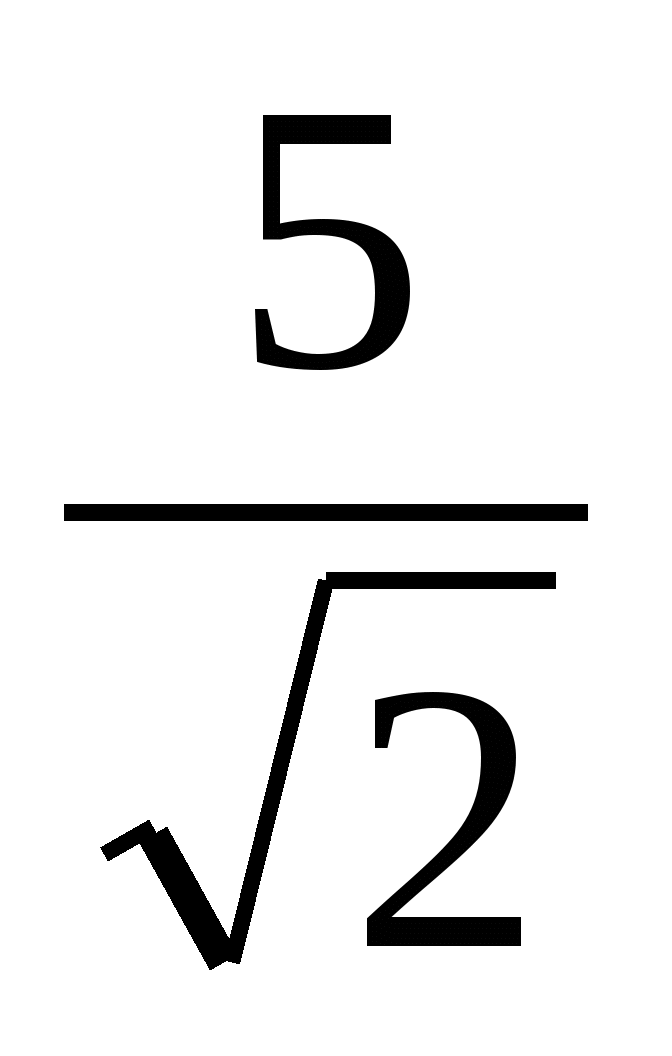 ,
, 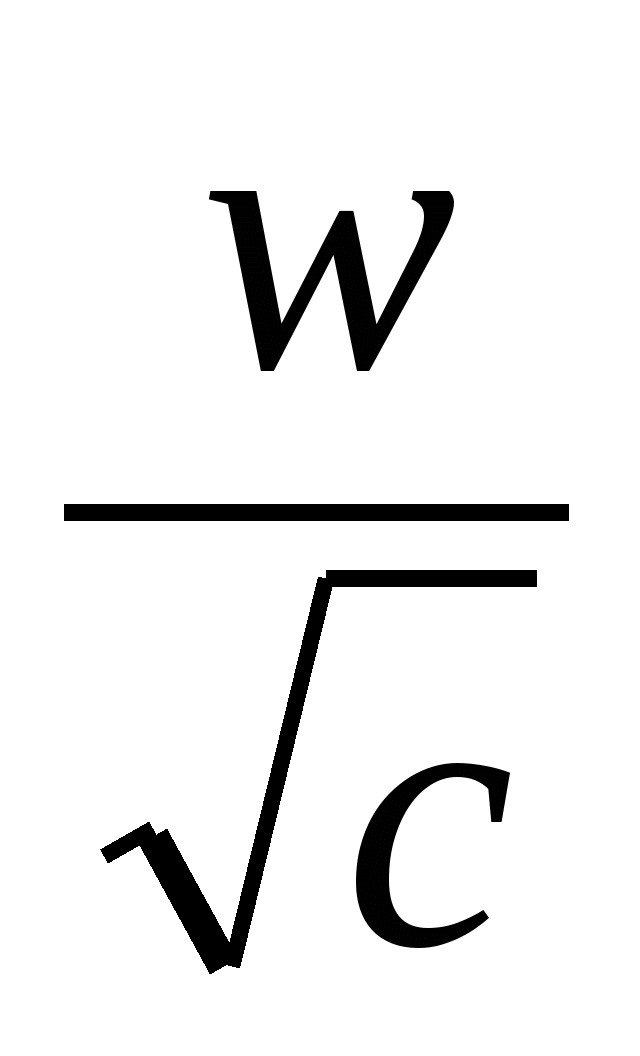
5. Упростить:
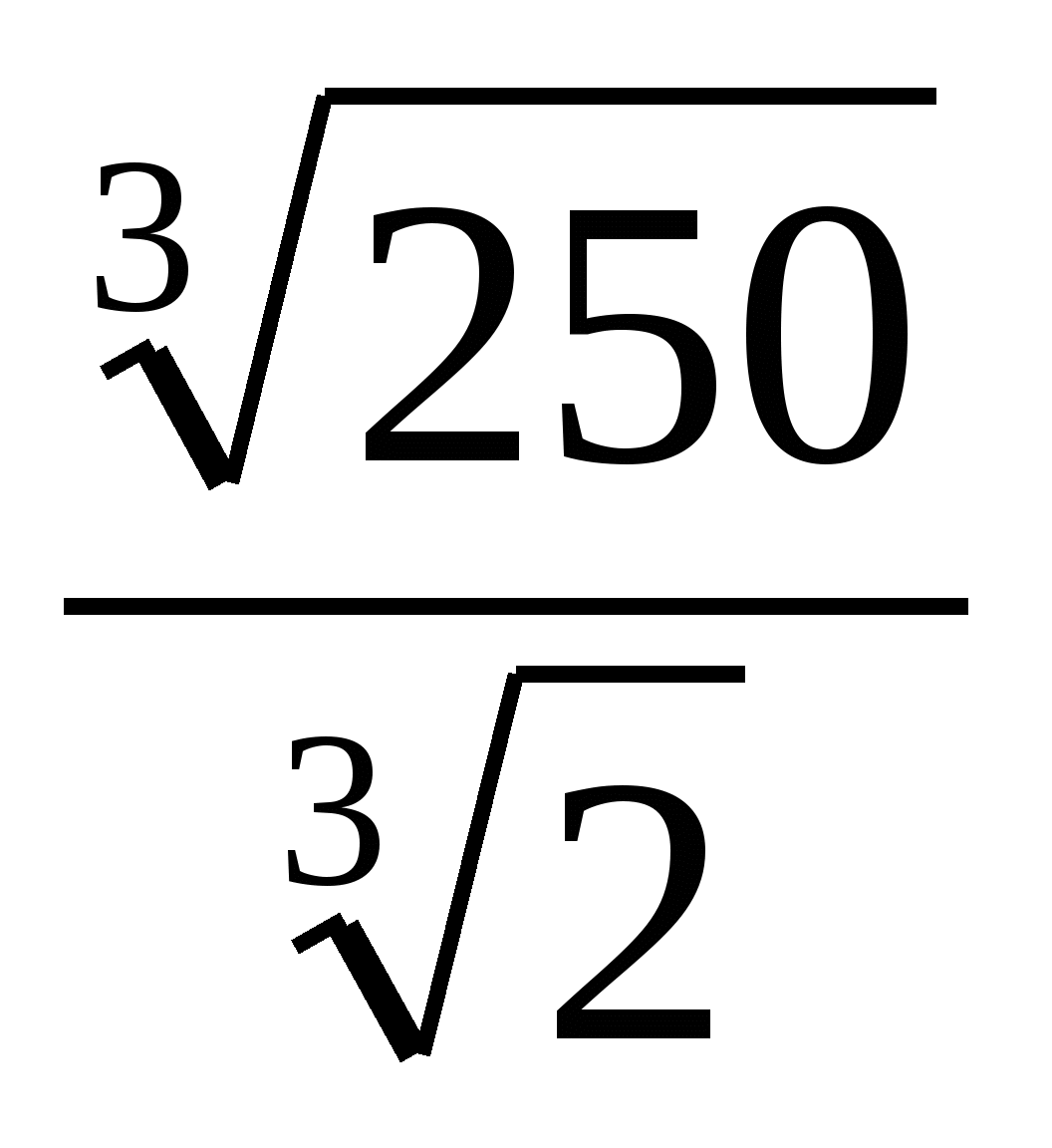 ;
; 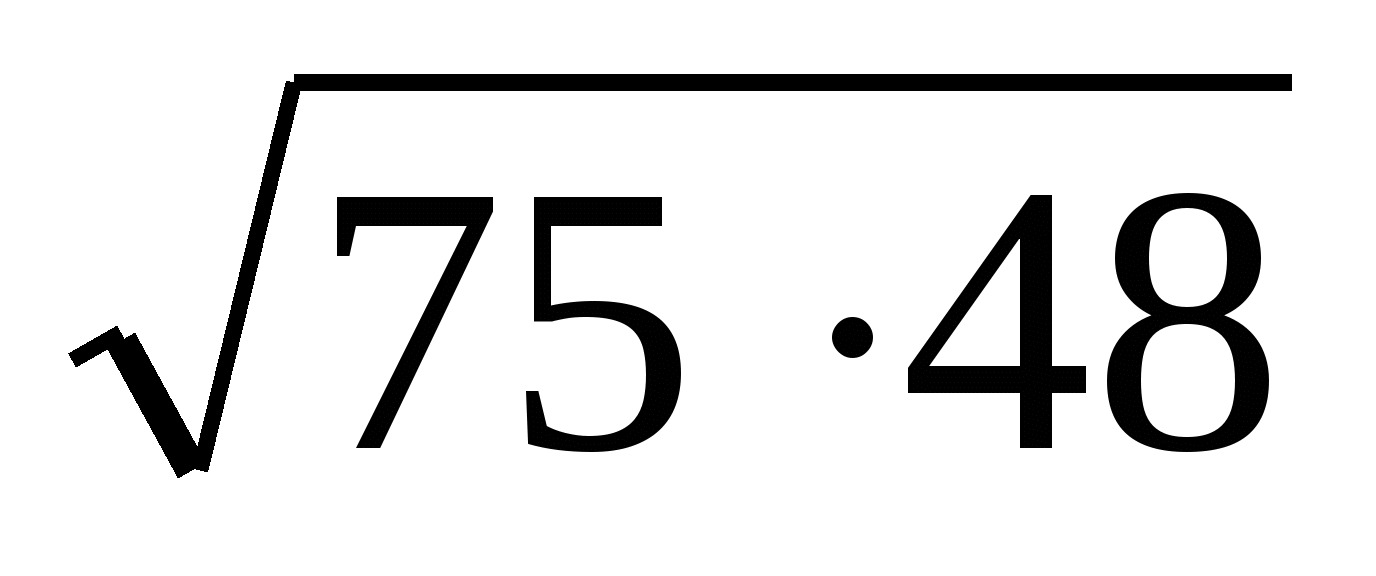
6. Замените арифметические корни степенями с дробным показателем
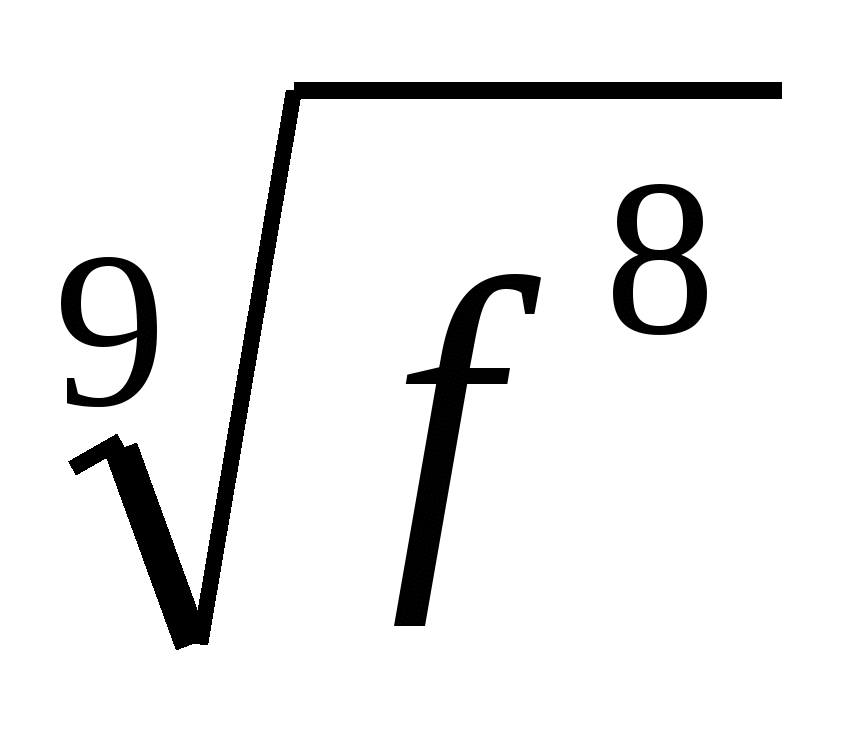 ,
, 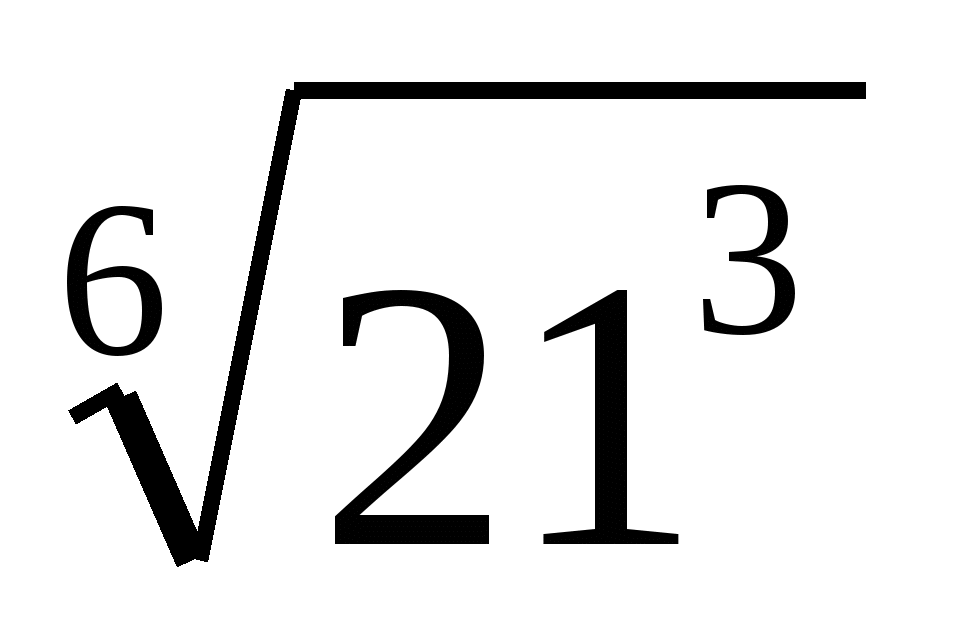 ,
, 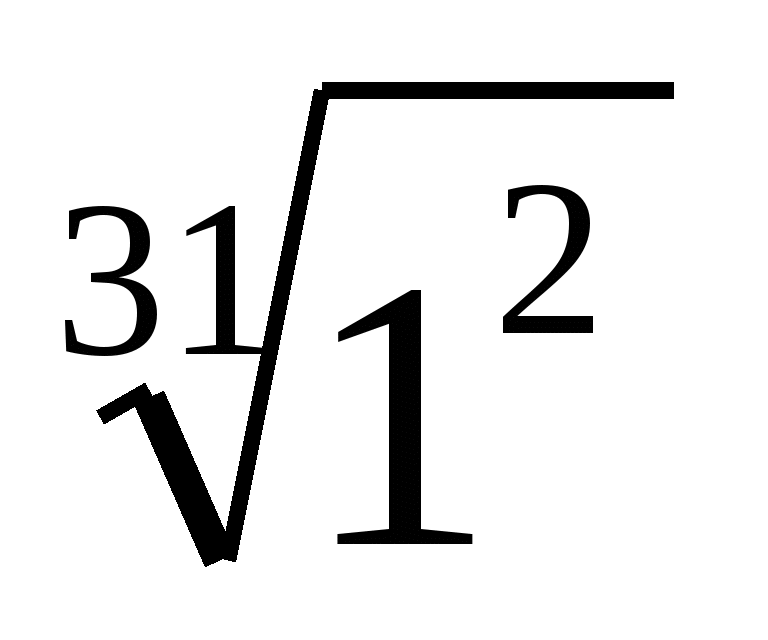
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
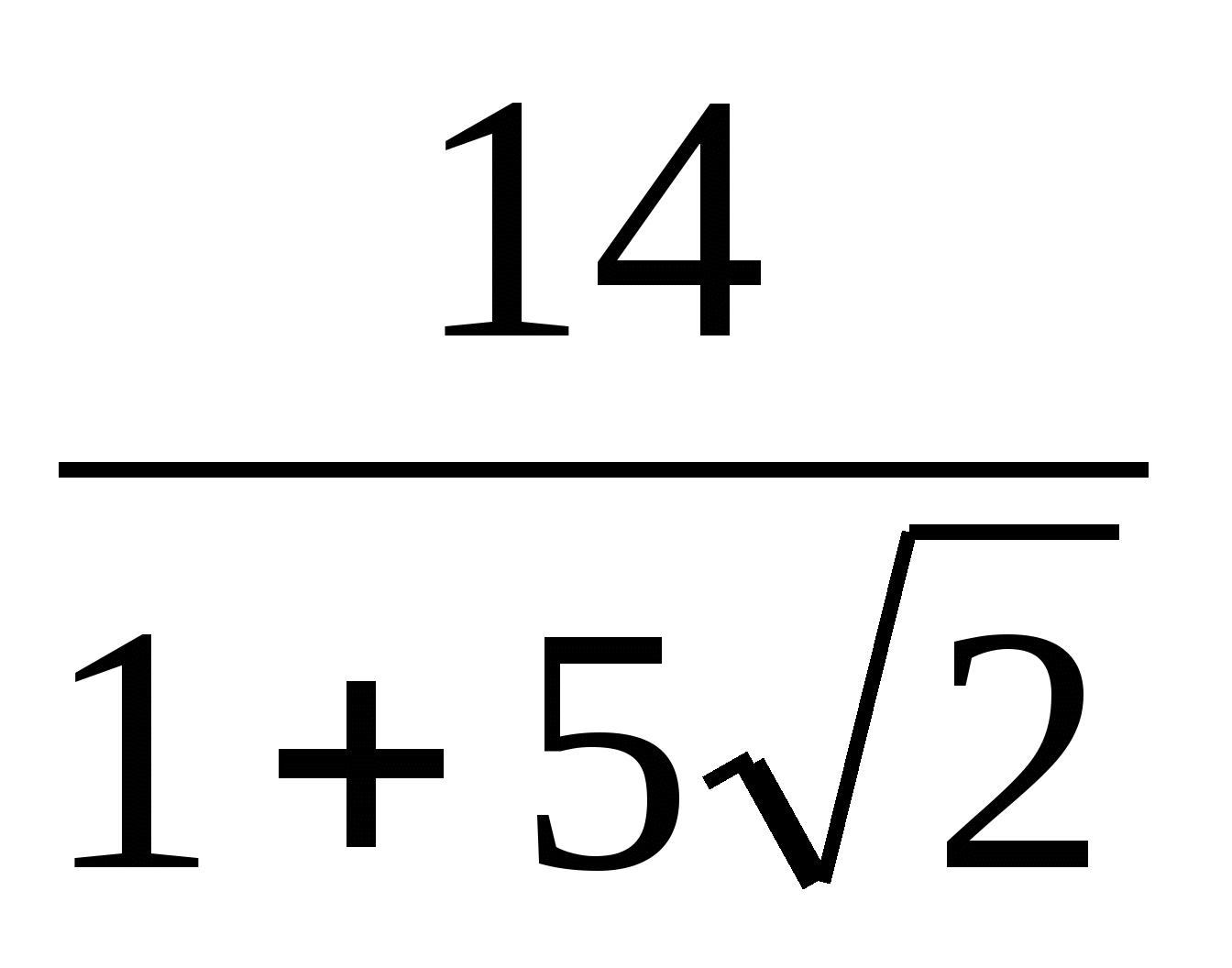 10. Выполните действие
10. Выполните действие
8. Сократите дробь 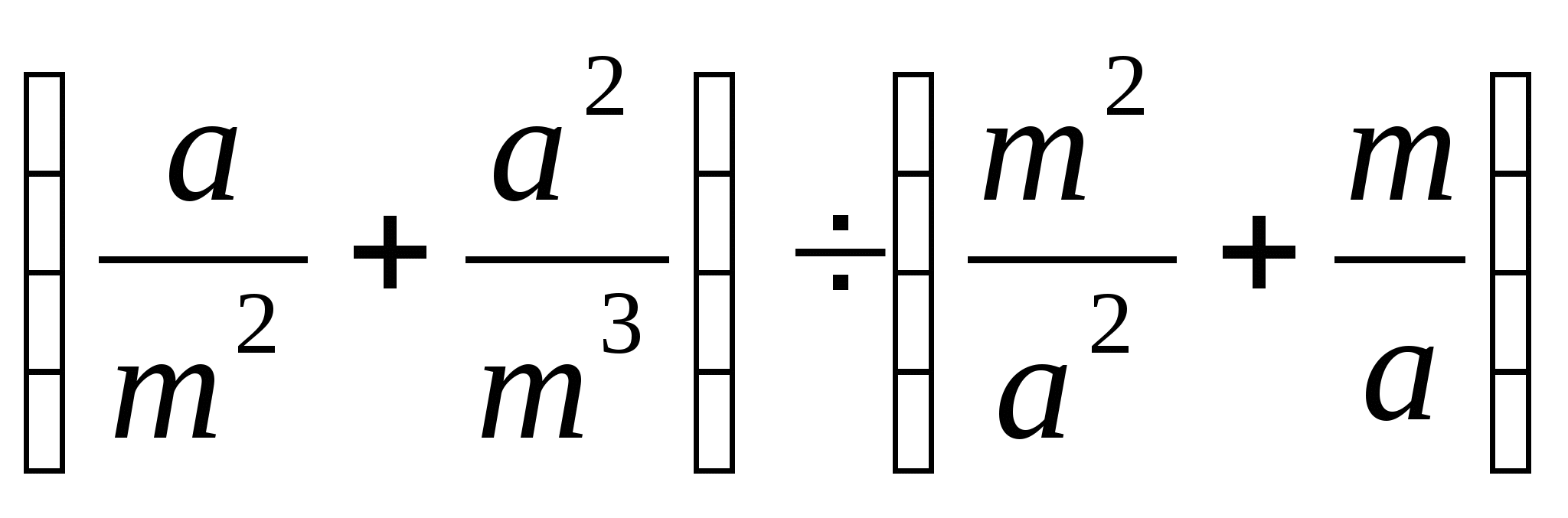
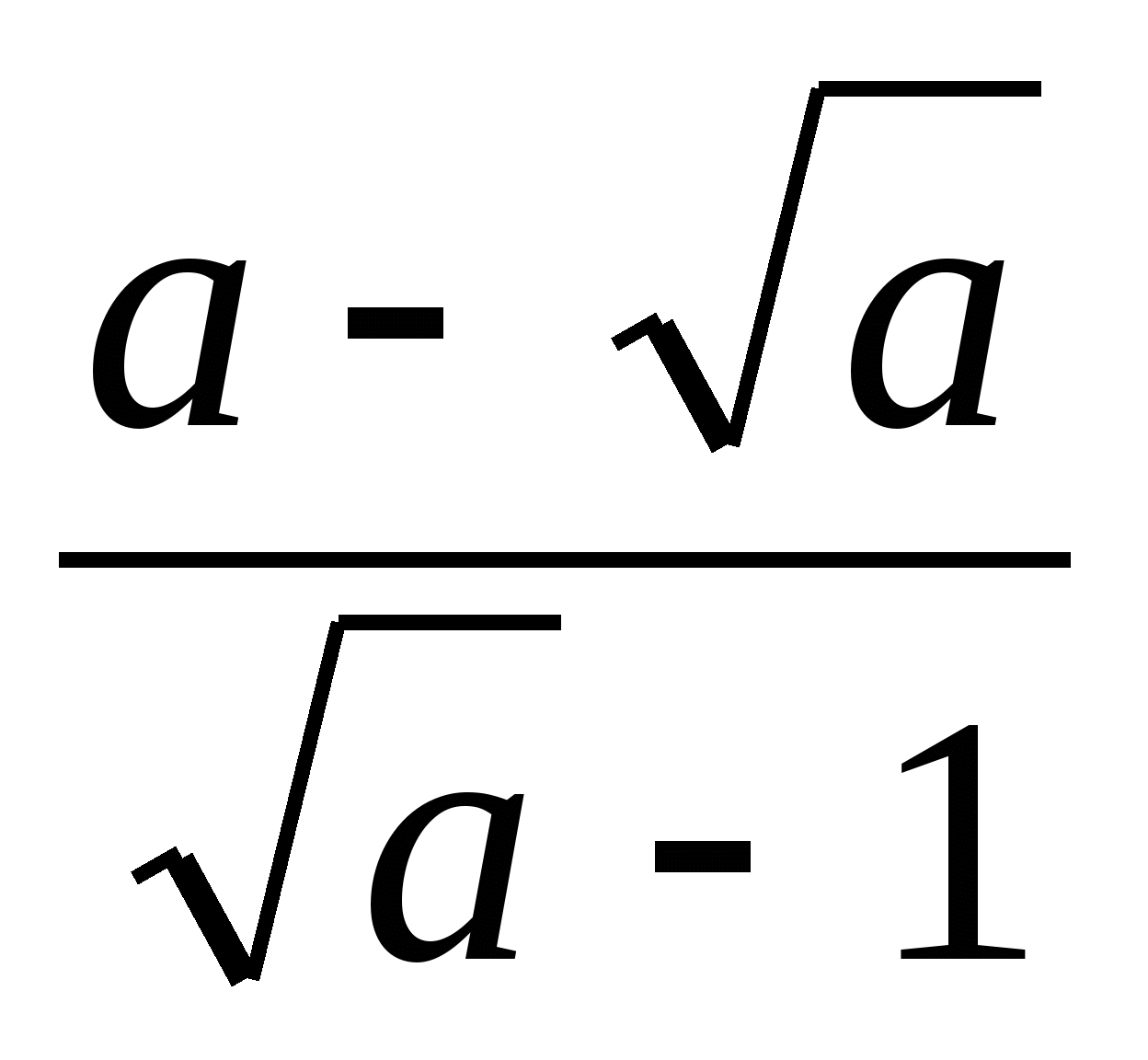
9. Выполните действие
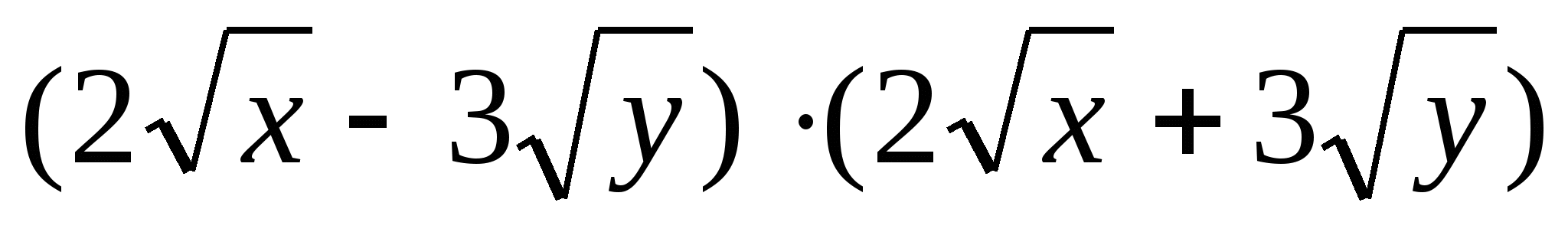
Иррациональные числа и действия над ними.
Иррациональным числом называется число, которое нельзя представить в виде дроби m/n, где m – целое, n – натуральное . Примерами иррациональных чисел могут служить числа ㄫ, e, а так же числа, со знаками радикала n-ой степени, не являющиеся точными n-ми степенями. Рассмотрим более подробно иррациональные числа, содержащие знак радикала (корня) второй степени, не являющиеся точными квадратами. Например, число √2 – иррациональное, так как никакое рациональное число в квадрате не равно 2. Отсюда вытекают два основных свойства квадратного корня:Если вы чувствуете, что число под корнем достаточно большое, однако целиком корень извлечь нельзя, попробуйте вынести множитель из-под знака корня. Для этого разложите подкоренное число на простые множители и если в этом разложении существуют парные множители, из каждой пары вынесите по одному из-под знака корня. Например,
Oднако при внесении и вынесении из-под знака корня множителей, содержащих переменные, будьте особенно внимательны! Почитайте ЗдесьДействия над иррациональными числами.
Это означает, что для умножения и деления можно записать все под одним корнем, например:
√2・√3=√(2・3)=√6
Так же помним, что если перед корнем стоит множитель, а от перестановки множителей произведение не меняется, то5
√2・4√3=5
・√2・4・√3=5
・4・√2・√3=20√6Однако запомните раз и навсегда, что нет такого правила для сложения корней! Складывать (и вычитать) можно только числа с одинаковыми корнями, для этого складываем их рациональную часть, а корень оставляем тот же.
Избавление от иррациональности в знаменателе дроби
Если видите знак корня в знаменателе дроби – избавляйтесь от нее! Для начала напомню вам два правила: Иррациональность бывает двух типов:11. В знаменателе стоит иррациональное число, над которым выполняют действие умножения (или вообще не выполняют никакого действия). 22. В знаменателе стоит число, участвующее в сложении или вычитании. Для избавления от иррациональности в знаменателе в первом случае вам необходимо умножить и числитель и знаменатель дроби (основное свойство дроби) на точно такой же корень:
Во втором случае вам необходимо и числитель и знаменатель дроби умножить на сопряженное выражение (точно такое же выражение, но с другим действием, производимым с числами):
Советую так же изучить статью, которая подскажет вам, как быть, если под знаком корня вы увидите сумму или разность, содержащую иррациональное число.Задания, предложенные в тестах:
В5, РТ-19 (2 этап)
Иррациональные числа — урок. Алгебра, 8 класс.
Термины рациональное число, иррациональное число происходят от латинского слова ratio — разум
(буквальный перевод: «рациональное число — разумное число», «иррациональное число — неразумное число»; впрочем, так говорят и в реальной жизни: «он поступил рационально» — это значит, что он поступил разумно; «так действовать нерационально» — это значит, что так действовать неразумно).
Иррациональным числом называют бесконечную десятичную непериодическую дробь.
Если натуральное число \(n\) не является точным квадратом, т. е. n≠k2, где k∈ℚ, то n — иррациональное число.
Пример:
5=2,23606798…11=3,31662479…
Иррациональные числа встречаются не только при извлечении квадратного корня, но и во многих других случаях, в чём вы не раз убедитесь в старших классах.
Если длину любой окружности разделить на её диаметр, то в частном получится иррациональное число \(3,141592…\) Для этого числа в математике введено специальное обозначение π (буква греческого алфавита «пи»; версия происхождения этого понятия такова: с буквы π начинается греческое слово периферия — окружность). Иррациональность числа π была доказана в \(1766\) г. немецким математиком И. Ламбертом.
Итак,
1. любая арифметическая операция над рациональными числами (кроме деления на \(0\)) приводит в результате к рациональному числу.
2. Арифметическая операция над иррациональными числами может привести в результате как к рациональному, так и к иррациональному числу.
3. Если в арифметической операции участвуют рациональное и иррациональное числа, то в результате получится иррациональное число (кроме умножения и деления на \(0\)).
4. Поскольку операция извлечения квадратного и кубического корня из положительного числа часто приводит к иррациональным числам, условились алгебраическое выражение, в котором присутствует операция извлечения квадратного и кубического корня из переменной, называть иррациональным выражением.
Преобразование алгебраических выражений, рациональных и иррациональных выражений

Преобразование алгебраических выражений, рациональных и иррациональных выражений

Основные арифметические действия
- Сложение
- Вычитание
- Умножение
- деление

Определение:
Алгебраические выражения, составленные из чисел и букв с помощью действий сложения, вычитания, умножения и деления, называют рациональными .

Примеры рациональных выражений

Алгебраические выражения
Иррациональные выражения
Рациональные выражения
(выражения, в котором хотя бы одна переменная содержится под знаком корня)
Целые выражения (не содержат деления на выражение с переменной)
Дробные выражения (содержат деление на выражение с переменной)

Упростите выражение:
Ответ:

Множество всех допустимых значений переменных называют областью определения выражения
Чтобы найти область определения дробного выражения, надо из множества всех действительных чисел исключить те значения, которые обращают в нуль, содержащиеся в выражении делители.

Пример №1
Найти область определения выражения:
Ответ:
и

Пример №2
Найти область определения выражения:
Ответ:
множество пар значений переменных x и y , таких, что x≠y.

Алгебра – это наука и искусство преобразования буквенных выражений. Преобразования выполняются по определенным правилам – алгебраическим законам , которые вводятся на основе свойств арифметических действий.
Если одно рациональное выражение может быть получено из другого с помощью алгебраических преобразований, то такие два рациональных выражения называют тождественно равными (или просто равными).
Математика. Иррациональные выражения. Примеры + решения.
Выражения, содержащие корень, который нельзя извлечь, называются иррациональными или радикальными.
Примеры:
 – иррациональные выражения
– иррациональные выражения
Сложение и вычитание
При сложении или вычитании иррациональных выражений их пишут одно за другим с сохранением их знаков.
Примеры:

В некоторых случаях с помощью преобразования можно сделать иррациональные выражения подобными, то есть имеющими одинаковые показатели корней и подкоренные числа (или выражения), а затем сделать приведение.
Примеры:


Умножение и деление
При умножении иррациональных выражений с одинаковыми показателями корней перемножаются их подкоренные числа или выражения:

При делении иррациональных выражений с одинаковыми показателями корней подкоренное число или выражение делимого делится на подкоренное число или выражение делителя:

Примеры:


Возведение в степень
Чтобы возвести в степень иррациональное выражение, следует возвести в степень подкоренное число или выражение:

Примеры:


При возведении  в n-ю степень знак корня отбрасывается, так как возведение числа (или выражения) в n-ю степень и извлечение из него корня n-ой степени – это взаимно сокращающиеся действия:
в n-ю степень знак корня отбрасывается, так как возведение числа (или выражения) в n-ю степень и извлечение из него корня n-ой степени – это взаимно сокращающиеся действия:

Извлечение корня
Чтобы извлечь корень из иррационального выражения, следует показатели корней перемножить:
 , так как
, так как 
Пример:

С помощью таких преобразований можно упростить извлечение корней 4-й, 6-й, 8-й, 9-й и т. п. степеней из чисел.
Примеры:


Сокращение корней
Величина иррационального выражения не изменится, если показатель корня и подкоренного выражения умножить или разделить на одно и то же число:

так как извлечение корня и возведение в степень – это взаимно сокращающиеся действия, если их показатели равны.
На этом свойстве основано сокращение корней и приведение их к одному показателю.
Сокращение корней – это деление показателей корня и подкоренного числа (или выражения) на одно и то же число, если оно является общим множителем для всех показателей.
Примеры:


Приведение корней к одному показателю
Приведение корней к общему показателю имеет большое сходство с приведением дробей к общему показателю. Рассмотрим два способа:
- Показатели корней не имеют общих множителей. В этом случае показатель каждого корня и его подкоренное число (или выражение) умножают на произведение остальных корней.
Рассмотрим три выражения:
 ,
,так как у данных показателей нет общего множителя, то просто перемножаем все показатели между собой, полученный результат и станет общим показателем. После приведения к общему показателю выражения будут иметь следующий вид:

- Показатели корней имеют общий множитель. В этом случае надо найти НОК показателей и умножить показатель каждого корня на недостающий множитель.
Рассмотрим два выражения:
 ,
,НОК (4, 6) = 12, значит для первого выражения дополнительным множителем будет 3, а для второго 2. После приведения к общему показателю выражения будут иметь следующий вид:

При умножении и делении иррациональных выражений с разными показателями, их приводят к общему показателю, а затем уже умножают или делят их подкоренные числа или выражения.
Примеры:


 ,
,
 ,
,
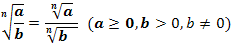
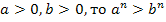
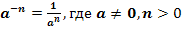
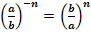
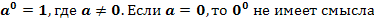
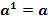
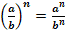
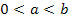 , тогда
, тогда