Площа трапеції. Формули

Задачі на площу трапеції розв’язують в шкільному курсі планіметрії. Розрахунки не надто складні при вивченні цієї теми, однак з плином часу забувається і теоретичний матеріал і формули для обчислення площі трапеції. З даного матеріалу Ви навчитеся знаходити площу трапеції та ознайомитеся з поширеними для обчислень формулами.

Формули площі трапеції

1. Площа трапеції рівна добутку півсуми основ на висоту:

Середня лінія трапеції рівна півсумі основ, тому попередню формулу площі можна записати у вигляді

Нижче на рисунку наведено відповідні формули та позначення

2. Якщо задано діагоналі трапеції та кут між ними (див. рис.),

то площу трапеції знаходять через половину добутку діагоналей трапеції на синус кута між ними.
Варто зазначити, що неважливо чи тупий чи гострий кут підставляємо у формулу.
Значення площі від цього не поміняється.

Дана формула, як і попередня, достатньо проста в обчисленнях.

Наступна формула вимагає більшої кількості розрахунків.

3. Бувають складні приклади на трапецію, коли задано усі чотири її сторони. В таких випадках використовують першу формулу площі трапеції

або другу

При застосуванні формули слід пам’ятати, що між сторонами повинні виконуватися умови b>a і c>d.

4. Якщо в завданні відомо, що трапеція рівнобічна (бічні сторони рівні) то для того, щоб знайти площу трапеції крім вище наведених формул використовують наступні:

• якщо задано основу, бічну сторону та кут між ними
  
  
• якщо відомий радіус вписаного кола та кут при основі
  

Тут r – радіус вписанного кола, alpha – кут при основі, c – бічна сторона рівнобічної трапеції.

Якщо радіуса вписаного кола та потрібного кута не задано в умові прикладу – користуйтеся вище наведеними формулами площі трапеції.

Тепер Ви знаєте як знайти площу трапеції, використовуйте наведені формули на практиці та не майте проблем у навчанні.
Далі розглянемо готові відповіді до прикладів на трапеції та покажемо, як застосовувати формули площі на практиці.

Вас може зацікавити:
1. Трапеція. Знаходження площі,периметра, середньої лінії
2. Площа рівнобічної трапеції
3. Обчислення площі трапеції
4. Ромб. Обчислення площі, висоти, діагоналей

yukhym.com

Все формулы средней линии трапеции

Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции — отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.

---

1. Формула средней линии трапеции через основания

b — верхнее основание

a — нижнее основание

m— средняя линия

 

Формула средней линии, (m ):

 

 

2. Формулы средней линии через основание, высоту и углы при нижнем основании

b — верхнее основание

a — нижнее основание

α, β — углы трапеции

h — высота трапеции

m — средняя линия

 

Формулы средней линии трапеции, (m):

---

 

3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

α, β — углы между диагоналями

d₁ , d₂ — диагонали трапеции

h — высота трапеции

m — средняя линия

 

Формулы средней линии трапеции, (m ):

---

 

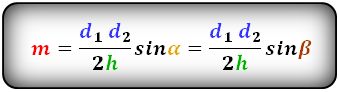
4. Формула средней линии трапеции через площадь и высоту

S — площадь трапеции

h

— высота трапеции

m — средняя линия

 

Формула средней линии трапеции, (m):

---

---

 

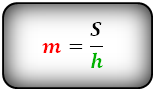
Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

www-formula.ru

Трапеция. Формулы, признаки и свойства трапеции

Определение.

Трапеция — это четыреугольник у котрого две стороны паралельны, а две другие стороны не паралельны.

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четыреугольник у которого одна пара противоположных сторон паралельна и стороны не равны между собой.

Элементы трапеции:

• Основы трапеции — параллельные стороны
• Боковые стороны — две другие строрны
• Средняя линия — отрезок, соединяющий середины боковых сторон.

Виды трапеций:

• Равнобедренная трапеция — трапеция у которой боковые стороны равны
• Прямоугольная трапеция — трапеция у которой одна из боковых сторон перпендикулярна основам

Рис.1		Рис.2

Основные свойства трапеции

1. В трапецию можна вписать окружность если сумма длин оснований равна сумме длин боковых сторон:

AB + CD = BC + AD

2. Средняя линия трапеции разделяет пополам любой отрезок который соединяет основы, так же делит диагонали пополам:

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции паралельна основаниям и равна их полусумме:

4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.

5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины как сотношение между основаниями:

BC : AD = OC : AO = OB : DO

7. Диагонали трапеции d₁ и d₂ связаны со сторонами соотношением:

d₁² + d₂² = 2ab + c² + d²

Сторона трапеции

Формулы определения длин сторон трапеции:

1. Формула длины оснований трапеции через середнюю линию и другую основу:

a = 2m — b

b = 2m — a

2. Формулы длины основ через высоту и углы при нижнем основании:

a = b + h · (ctg α + ctg β)

b = a — h · (ctg α + ctg β)

3. Формулы длины основ через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a — c·cos α — d·cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

с =	h	d =	h
	sin α		sin β

Средняя линия трапеции

Определение.

Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:

Высота трапеции

Формулы определения длины высоты трапеции:

1. Формула высоты через сторону и прилегающий угол при основании:

h = c·sin α = d·sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d1d2	=	sin δ ·	d1d2
		a + b			a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d1d2	=	sin δ ·	d1d2
		2m			2m

4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

1. Формулы диагоналей по теореме косинусов:

d₁ = √a² + d² — 2ad·cos β

d₂ = √a² + c² — 2ac·cos β

2. Формулы диагоналей через четыре стороны:

d1 =	√	d 2 + ab —	a(d 2 — c2)	d2 =	√	c2 + ab —	a(c2 — d 2)
			a — b				a — b

3. Формула длины диагоналей через высоту:

d₁ = √h² + (a — h · ctg β)² = √h² + (b + h · ctg α)²

d₂ = √h² + (a — h · ctg α)² = √h² + (b + h · ctg β)²

4. Формулы длины диагонали через сумму квадратов диагоналей:

d₁ = √c² + d ² + 2ab — d₂²

d₂ = √c² + d ² + 2ab — d₁²

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту: 2. Формула площади через среднюю линию и высоту:

S = m · h

3. Формула площади через через диагонали и угол между ними:

S =	d1d2	· sin γ	=	d1d2	· sin δ
	2			2

4. Формула площади через четыре стороны:

S =	a + b	√	c2 —	(	(a — b)2 + c2 — d 2	)	2
	2				2(a — b)

5. Формула Герона для трапеции

S =	a + b	√(p — a)(p — b)(p — a — c)(p — a — d)
	|a — b|

где

p =	a + b + c + d	— полупериметр трапеции.
	2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

P = a + b + c + d

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d1
	4√p(p — a)(p — c)(p — d1)

где a — большее основание

Окружность вписанная в трапецию

В трапецию можна вписать окружность если сумма длин оснований равна сумме длин боковых сторон:

a + b = c + d

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
	2		2		a + b

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

0oq.ru

Метод трапецій (математика) — Вікіпедія

Матеріал з Вікіпедії — вільної енциклопедії.

Функція f(x) (синій колір) апроксимується лінійною функцією (червоний колір).

В математиці, метод трапецій є методом наближеного обчислення значення визначеного інтегралу

∫abf(x)dx.{\displaystyle \int _{a}^{b}f(x)\,dx.}

Ідея методу трапецій полягає в наближенні області під графіком функції f(x){\displaystyle f(x)} трапецією та обчисленні її площі^[1]. Якщо застосувати цю ідею безпосередньо до інтервалу [a,b]{\displaystyle [a,b]}, то отримаємо

∫abf(x)dx≈f(a)+f(b)2(b−a),(∗){\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {f(a)+f(b)}{2}}(b-a),\quad (*)}

але це незадовільно через велику похибку.

Для точнішого обчислення значення інтегралу, слід попередньо розбити інтервал інтегрування [a,b]{\displaystyle [a,b]} на n{\displaystyle n} підінтервалів [a,x1],[x1,x2],…,[xn−1,b],{\displaystyle [a,x_{1}],[x_{1},x_{2}],\ldots ,[x_{n-1},b],} та застосувати формулу (*) до кожного із них. Таким чином, отримуємо:

∫abf(x)dx=∑i=1n∫xi−1xif(x)dx≈∑i=1nf(xi)+f(xi−1)2Δxi,{\displaystyle \int _{a}^{b}f(x)\,dx=\sum _{i=1}^{n}\int _{x_{i-1}}^{x_{i}}f(x)\,dx\approx \sum _{i=1}^{n}{\frac {f(x_{i})+f(x_{i-1})}{2}}\Delta x_{i},}

де Δxi=xi−xi−1,x0=a,xn=b.{\displaystyle \Delta x_{i}=x_{i}-x_{i-1},x_{0}=a,x_{n}=b.}

У методі трапецій переважно застосується розбиття інтервалу інтегрування на n{\displaystyle n} рівних відрізків довжиною h=Δx=(b−a)/n.{\displaystyle h=\Delta x=(b-a)/n.} Тоді попередня формула перетворюється на таку:

∫abf(x)dx≈(f(a)+f(b)2+∑i=1n−1f(xi))h,{\displaystyle \int _{a}^{b}f(x)\,dx\approx \left({\frac {f(a)+f(b)}{2}}+\sum _{i=1}^{n-1}f(x_{i})\right)h,}

і похибка, так званий залишковий член E(f){\displaystyle E(f)} не перевищує за (b−a)3M12n2,{\displaystyle {\frac {(b-a)^{3}M}{12n^{2}}},} де M=max⁡{|f″(x)|:x∈[a,b]}{\displaystyle M=\operatorname {max} \{|f»(x)|:x\in [a,b]\}} — це максимум другої похідної функції f(x){\displaystyle f(x)} на всьому інтервалі^{[джерело?]}. Відзначимо, що за збільшення числа n{\displaystyle n} інтервалів розбиття, залишковий член зменшується як O(1/n2).{\displaystyle O(1/n^{2}).}

1. ↑ Турчак Л. И. (1987). Основы численных методов. Москва: Наука. 

uk.wikipedia.org