Конспект урока по теме «Трапеция»
Конспект урока
по геометрии
по теме «Трапеция»
8 «Б» класс.
Технологии, используемые на данном уроке: проектная деятельность, здоровьесберегающая, проблемное обучение, работа в парах.
Цели: Создать условия для введения понятий «трапеция», «равнобедренная трапеция», «прямоугольная трапеция», для рассмотрения решения задач, в которых раскрываются свойства трапеции.
Планируемые результаты:
Предметные умения: Умеют объяснять, какой многоугольник называется трапецией, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии.
Универсальные учебные действия:
Познавательные :: проводят информационно-смысловой анализ текста и лекции; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, умением устанавливать причинно-следственные связи.
Тип урока: урок изучения нового с элементами исследования.
Форма работы: фронтальная, индивидуальная. групповая.
Оборудование: плакат с эпиграфом урока, сигнальные карточки, карточки с заданиями (распечатки чертежей и заданий из конспекта урока) и для итога урока, презентация по теме «Трапеция».
План урока:
1.Организационный момент.
2.Актуализация знаний учащихся и подведение учащихся к новой теме .
3.Изучение нового материала. Презентация по теме «Трапеция»
4. Закрепление умений и получение навыков работы при решении простейших задач на трапецию.
5. Рефлексия.Подведение итогов. Выставление оценок.
Рефлексия.Подведение итогов. Выставление оценок.
6. Домашнее задание.
Ход урока
I. Организационный момент. Приветствие учителя и учащихся. Эпиграф нашего сегодняшнего урока:
Три пути ведут к знанию: путь размышления – это путь самый благородный,
путь подражания – это путь самый лёгкий и
путь опыта – это путь самый горький.
КОНФУЦИЙ
Мы сегодня на уроке попробуем все три опыта.
II. Актуализация знаний. Устная работа по готовым чертежам.
На слайде изображены различные выпуклые четырёхугольники. Среди них известные ребятам параллелограмм, прямоугольник, квадрат, ромб и новый четырёхугольник (трапеция).
— Вспомните, с какими четырехугольниками и их свойствами вы хорошо знакомы?
Выберите верные утверждения ( работают с сигнальными карточками; зелёные карточки — верно, красные — неверно):
Параллелограмм это четырехугольник, у которого стороны попарно равны. ( да )
( да )
Сумма углов четырехугольника 1800.( нет)
Противоположные углы параллелограмма равны .( да)
Диагонали параллелограмма равны (нет)
Диагонали ромба пересекаются и точкой пересечения делятся пополам.( да)
Параллелограмм это четырехугольник у которого стороны попарно параллельны.( да)
Квадрат является ромбом.( да)
Диагонали прямоугольника равны.( да)
Диагонали прямоугольника пересекаются под прямым углом. ( нет)
Диагонали ромба являются биссектрисами его углов.( да)
— Среди представленных фигур, что вы заметили? (Ответ учащихся: «Фигура стоящая справа незакрашена».)
— Что общего у этих фигур? (Ответ учащихся: «Все фигуры являются четырехугольниками».)
-Чем отличается выделенный четырехугольник от других? (Ответ учащихся: «Не является параллелограммом. У него две стороны параллельные, а две другие нет».)
-А кто знает, как называется этот четырехугольник? ( Дети либо ответят, либо нет. )
)
-Эта фигура называется трапеция.
-Как вы думаете какова тема урока? (Учащиеся формулируют тему урока.)
-Ребята, как вы считаете, какой будет цель нашего урока? (формулируют свои цели)
— Какие нужно поставить задачи для достижения нашей цели? (формулируют задачи урока)
— записываем в тетрадь тему сегодняшнего урока.
III.
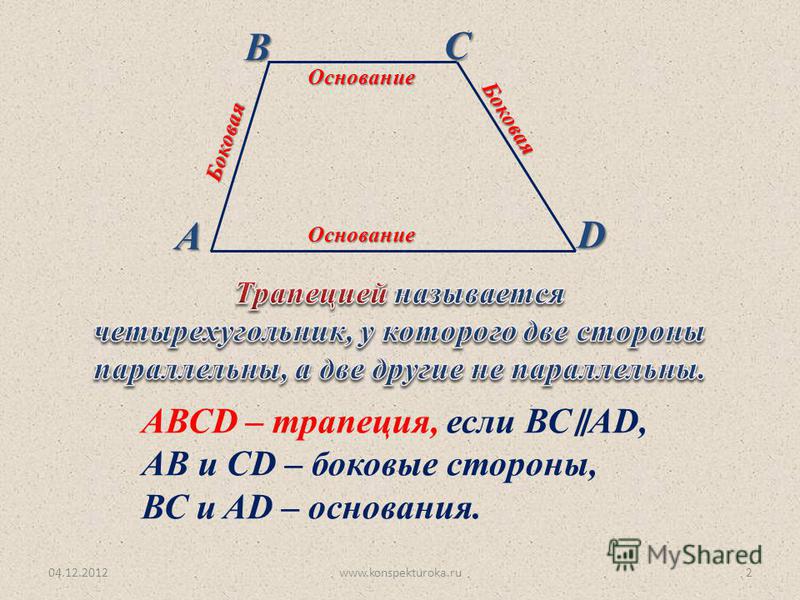
Рассмотрим четырехугольник, про который можем сказать , что две противолежащие стороны параллельны, две другие не параллельны.
Трапеция – (от греч. trapezion, букв. – столик).
Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие – непараллельные.
Виды трапеции. Равнобедренная – трапеция, у которой равны боковые стороны.
Прямоугольная – трапеция, один из углов которой прямой.
Работа в группах.
Группы с четными номерами – исследуют диагонали равнобедренной трапеции. Группы с нечетными номерами – исследуют углы равнобедренной трапеции.
Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.
Свойства равнобедренной трапеции.
Свойство 1. В равнобедренной трапеции углы при каждом основании равны.
Свойство 2. В равнобедренной трапеции диагонали равны.
Сформулируйте утверждения, обратные свойствам, и выясните их справедливость.
Признаки равнобедренной трапеции.
Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.
Признак 1. Если углы при основании трапеции равны, то она равнобедренная.
Признак 2. Если диагонали трапеции равны, то она равнобедренная.
Физкультминутка. Гимнастика для глаз.
Используется методика здоровьесберегающих технологий «зрительные метки». Учитель обращает внимание учащихся на развешанные по периметру класса цветные фигурки четырехугольников и дает задание отыскать среди них трапеции. (все фигурки пронумерованы, учащиеся дают в ответ № четырехугольника).
Учитель обращает внимание учащихся на развешанные по периметру класса цветные фигурки четырехугольников и дает задание отыскать среди них трапеции. (все фигурки пронумерованы, учащиеся дают в ответ № четырехугольника).
IV. Закрепление умений и навыков.
Решение задач по готовым чертежам. I уровень
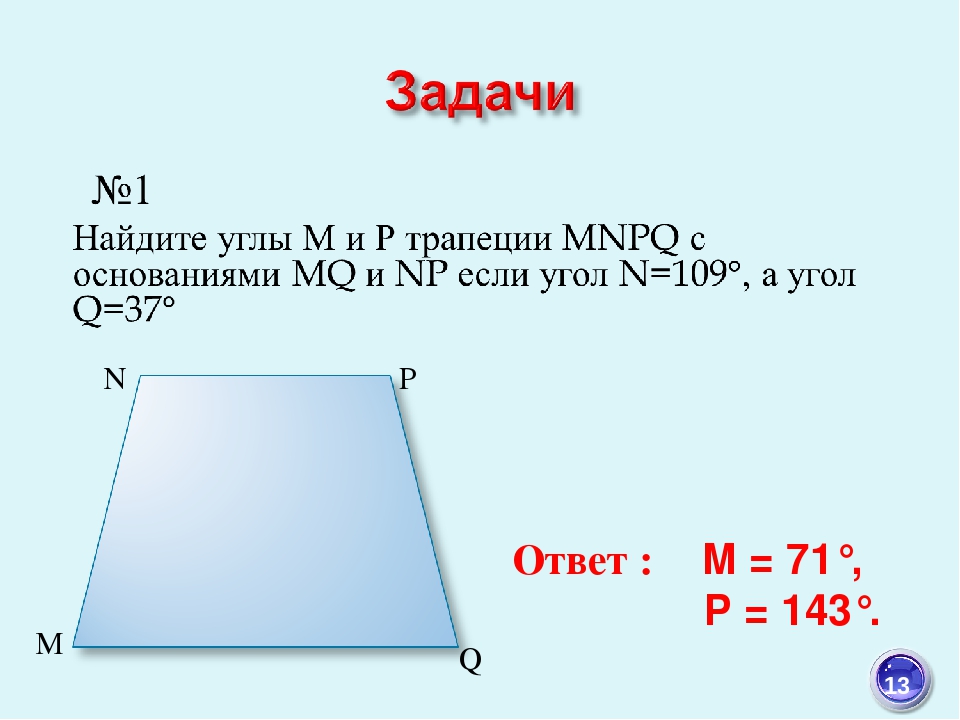
1. Найдите неизвестные углы трапеции:
II уровень
2. Найдите периметр трапеции АВСD:
III уровень
1. Из вершины тупого угла равнобедренной трапеции АВСD проведен перпендикуляр СE к прямой AD, содержащий большее основание. Докажите, что AE=(AD+BC)/2.
2. В прямоугольной трапеции диагонали взаимно перпендикулярны. Большая диагональ составляет с меньшей боковой стороной угол в 600. Докажите, что меньшая диагональ равна полусумме оснований трапеции. V. Рефлексия:
На уроке я узнал…
Мне было интересно, что …
Я разобрался в том, что.
Мне стало понятно ,что…
Мне было увлекательно…
Я познакомился …
VI.Итог урока 1. ВЫПИСАТЬ
а) основания
E K б) боковые стороны
P M
2.НАЙТИ УГЛЫ ТРАПЕЦИИ
B C
? 110°
21° ?
A D
3. НАЙТИ УГЛЫ РАВНОБОКОЙ ТРАПЕЦИИ
E М P =
? ? E =
M =
25° ?
D P
VI I. Домашнее задание.
1) ЗАНИМАТЕЛЬНАЯ ЗАДАЧА
Сложить трапецию из:
а) четырёх прямоугольных треугольников;
б) из трёх прямоугольных треугольников;
в) из двух прямоугольных треугольников. Выяснить, каким условиям при этом должны удовлетворять данные трапеции.
2) п. 59, № 61, № 62.
Трапеция
Сегодня на уроке мы познакомимся с геометрической фигурой, которую называют трапецией.
Итак, трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие – нет.
Параллельные стороны трапеции называются основаниями. А не параллельные – боковыми сторонами.
Перпендикуляр, проведённый из любой точки одного из оснований на другое основание или его продолжение, называется высотой трапеции.
Трапеция, у которой есть прямой угол, называется прямоугольной. Следует отметить, что, так как основания AB и CD параллельны, прямая BC – секущая, а сумма односторонних углов равна 180º, то и угол BCD также равен 90º.
Трапеция, у которой боковые стороны равны, называется равнобедренной.
Далее мы рассмотрим некоторые свойства и признаки равнобедренной
трапеции.
Теорема. Свойство углов равнобедренной трапеции. Углы при основании равнобедренной трапеции равны.
Доказательство.
Рассмотрим прямоугольные и .
, так как – равнобедр. трапеция,
.
по катету и гипотенузе.
Следовательно, .
Теорема доказана.
Теорема. Свойство диагоналей равнобедренной трапеции. Диагонали равнобедренной трапеции равны.
Доказательство.
Рассмотрим и .
, так как – равнобедр. трапеция,сторона – общая,
как углы при основании равнобедр. трапеции.
по первому признаку.
Следовательно, .
Теорема доказана.
Теорема. Признак равнобедренной трапеции. Если у трапеции углы при основании равны, то она равнобедренная.
Доказательство.
Рассмотрим прямоугольные и .
по условию.
.
по катету и
противолежащемуострому углу.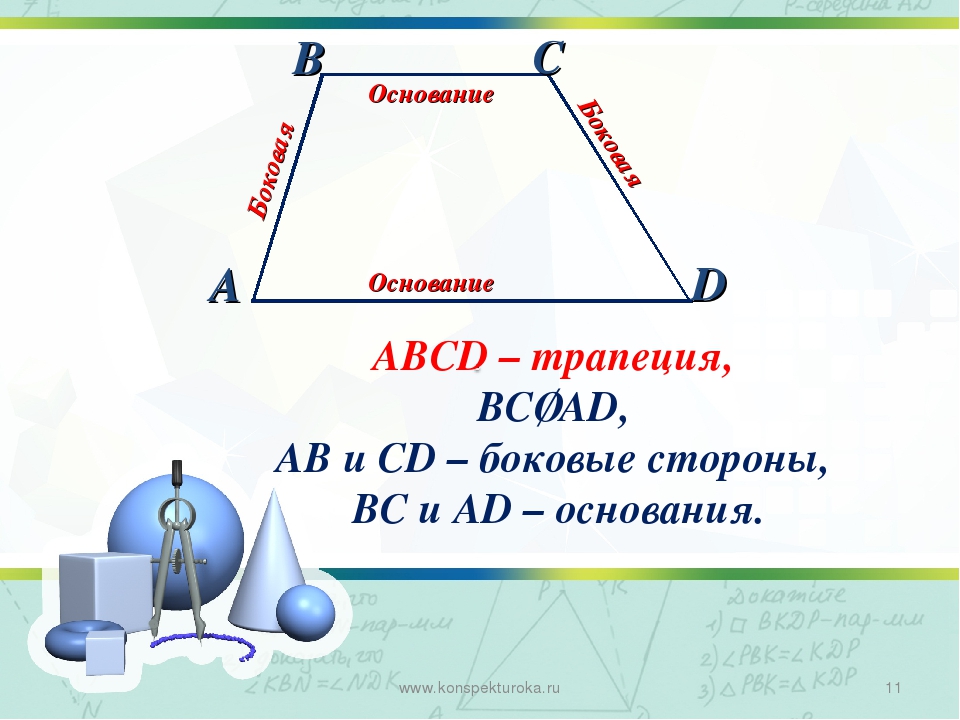
Следовательно, .
Тогда трапеция – равнобедренная.
Теорема доказана.
Теорема. Признак равнобедренной трапеции. Если у трапеции диагонали равны, то она равнобедренная.
Доказательство.
Рассмотрим прямоугольные и .
по условию,.
по катету и гипотенузе.
Следовательно, .
Рассмотрим и .
по условию,сторона – общая,.
по первому признаку.
Следовательно, .
Тогда трапеция – равнобедренная.
Теорема доказана.
А теперь решим несколько задач.
Задача. – трапеция, у которой . . Найдите градусную меру .
Решение.
Так как , то трапеция – равнобедренная.
как углы при основании равнобедр. трапеции.
, – внутр. односторонние при и секущей , то есть
,
,
,
.
Ответ: .
Задача.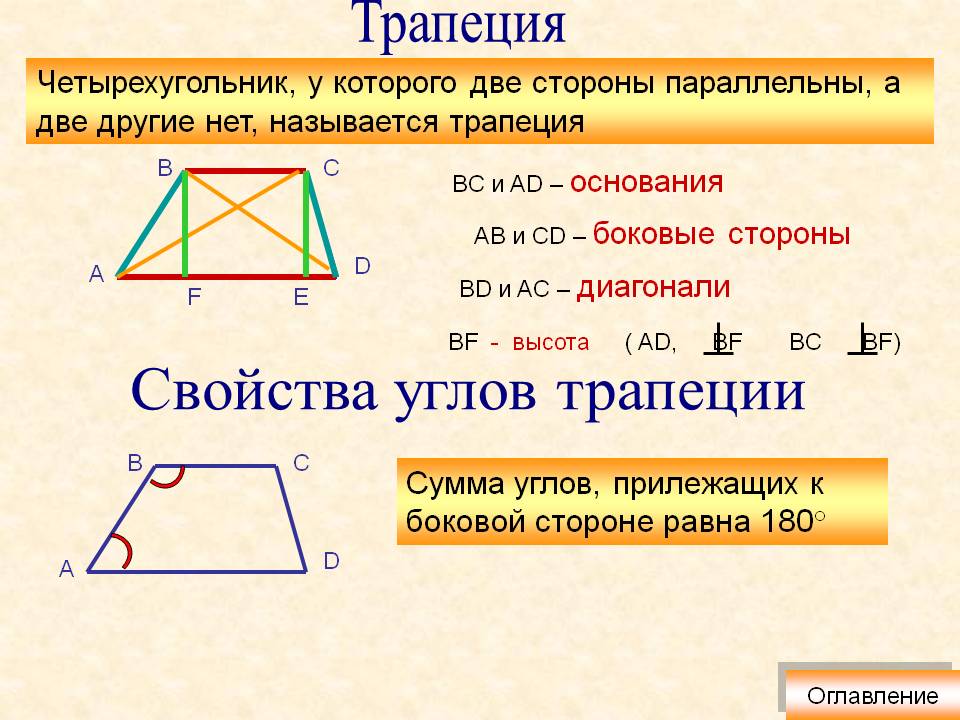 В прямоугольной
трапеции проведена
диагональ . , . Найдите
градусную меру .
В прямоугольной
трапеции проведена
диагональ . , . Найдите
градусную меру .
Решение.
как накр. лежащие при и секущей ,то есть .
,следовательно, – равнобедренный, тогда .
Для : ,
,
,
.
Ответ: .
План -конспект открытого урока по математике по теме » Трапеция. Средняя линия трапеции»
Урок Взвод_2-____
Параграф
Тема
Трапеция. Средняя линия трапеции.
Тип урока
Урок изучения нового материала с элементами экспериментального исследования
Форма урока
Урок – путешествие, исследование.
Цели
— организовать работу по самостоятельному усвоению учащимися понятия трапеции, определению видов трапеции, рассмотреть свойства трапеции;
-создание условий для развития творческой и мыслительной деятельности воспитанников,их интеллектуальных качеств;
— создать условия для формирования умений: четко излагать свои мысли, говорить грамотно, используя необходимые математические термины. доказывать свою точку зрения;
доказывать свою точку зрения;
-способствовать воспитанию позитивного отношения к учебе, развитию коммуникативных компетенций воспитанников.
Оборудование
Компьютер, мультимедиапроектор, презентация
Ход урока
№ п/п
Этап урока
Содержание
Форма
работы
Время, мин.
Организационный момент
Воспитанники садятся в группы за столы, на которых стоят фигурки кораблей с названиями, которые команды выбрали для них заранее.
Определение темы и целей урока
Эпиграфом к нашему уроку я выбрала слова
«Человека, умеющего наблюдать и
анализировать, обмануть невозможно.
Его выводы будут безошибочны,
как теорема Пифагора».
А. Конан Дойл
Думаю, что многие из вас уже научились наблюдать и анализировать, и ваши умения помогут сегодня вам на уроке.
Демонстрируется фрагмент видеоролика из фильма «Остров сокровищ».
Вводное слово учителя. Все ребята мечтают отправиться на поиск приключений, сокровищ.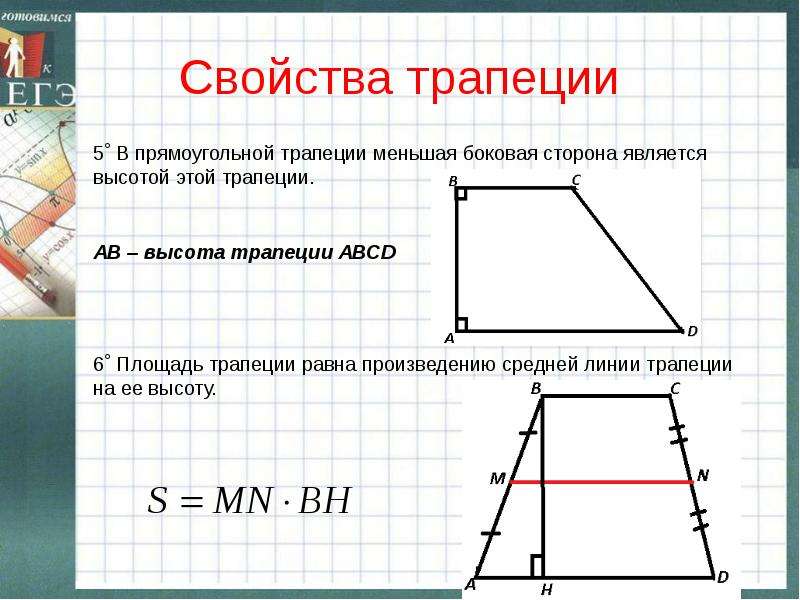 Любое путешествие это поиск нового неизведанного.
Любое путешествие это поиск нового неизведанного.
Вы, уже догадались, что у нас сегодня не обычный урок, а урок — путешествие. Путешествие в мир математики. Как вы думаете, что мы будем искать ?… (знания, сокровища)
Эвристическая беседа с демонстрацией
Определение темы и целей урока
Для определения темы и целей нашего урока- поиска предлагаю вам вспомнить, с какими четырехугольниками и их свойствами вам уже хорошо знакомы(слайд презентации)
Чем отличается последний четырехугольник от параллелограмма? (только две стороны параллельны) Такой четырехугольник называется трапецией. Откройте тетради и запишите тему урока
Трапеция
Ребята, давайте подумаем, чему бы вы сегодня хотели научиться и что хотели бы узнать нового на уроке о данном четырехугольнике? (Ученики ставят перед собой цели урока с помощью следующей инструкции и говорят их учителю)(слайд № )
Сегодня на уроке я хочу…
узнать…
уточнить…
понять…
выяснить…
раскрыть понятия
Научиться:
изображать…
находить…
объяснять…
Сформулируем задачи, которые стоят перед вами?(слад №)
сформулировать понятие трапеции,
научиться определять виды трапеции, находить ее элементы,
научиться изображать трапецию,
выяснить свойства трапеции,
выяснить вопрос о существовании средней линии трапеции.
Эвристическая беседа с демонстрацией
5-6мин
Актуализация знаний
Один из самых коварных пиратов – капитан Флинт спрятал сокровища на необитаемом острове. Мы сегодня постараемся его найти.
Что бы совершить путешествие, нам нужна дружная, сплоченная и грамотная команда. В пути нас ждет немало испытаний. Проверим, насколько вы готовы к встрече с ними.Математическая разминка
Лови вопрос
Сформулируйте теорему Фалеса
Какой отрезок называется средней линией треугольника?
Какими свойствами обладает средняя линия треугольника?
Укажите среднюю линию треугольника на рисунке (слайд презентации №)
Вижу, вы готовы в дорогу. О цели нашего путешествия вы узнаете, правильно решив задачи по готовым чертежам
2) В 10
В С
M 4 N
А С
MN=4, АВ=ВСРАВС -?
РАВС =20, ВС- ?
В К С 4) С D
А DА В
РАВСD =24
КC-?АО=3, РАВСD-?
Фронтальный опрос, работа в группах, индивидуальная работа
5-6 мин
(клад)
Проставьте баллы за разминку в своих маршрутных
листах (3 балла.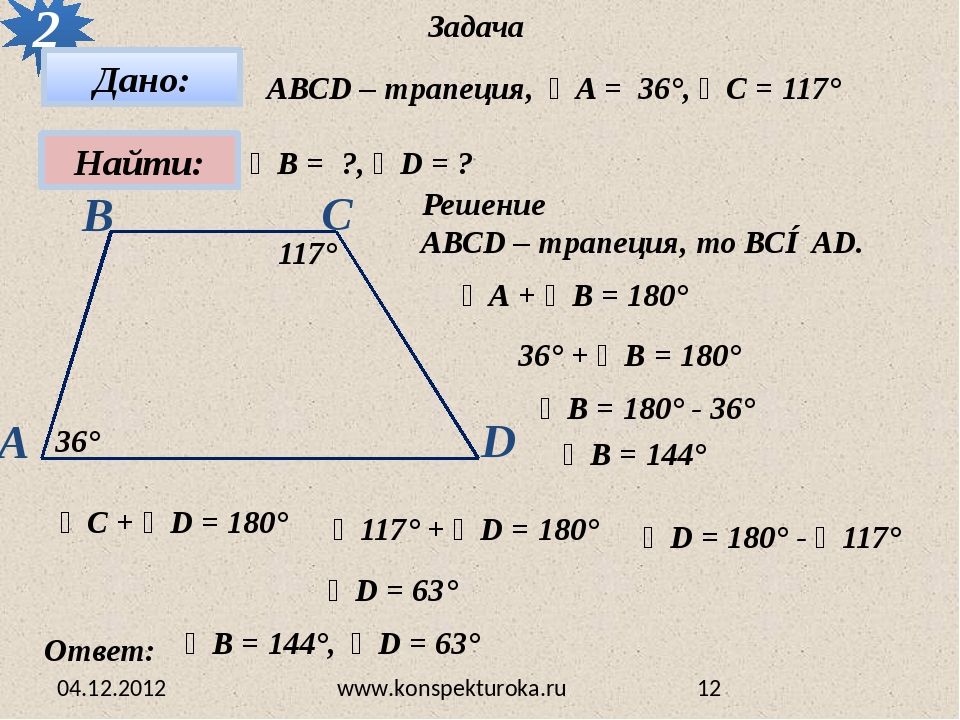 ).
).
Введение нового материала
Поиск способа решения, выдвижение гипотез,обсуждение
Что самое необходимое для кладоискателя? (Карта) Перед вами карта капитана Флинта. Старый пират был очень хитер и спрятал карту на необитаемом острове. Путь к нему разбил на участки и на каждом этапе приготовил ловушку(слайд презент.).
1 ловушка
Только тот, кто может думать и анализировать справится со 2 ловушкой капитана Флинта.
Перед вами 3 вида треугольников. Задания в виде вопросов(учащимся предложены модели различных видов треугольников и задание в виде вопросов):
Предложите способы получения трапеции из предложенных вам треугольников.
Какие виды трапеции вы можете указать?
Что можно сказать о диагоналях и углах этих трапеций?
Существует ли средняя линия трапеции?
Заполните предложенную вам таблицу.
Представление результатов.
Проблемная ситуация. Что произойдет с трапецией, если ее верхнее основание будет уменьшаться?(станет треугольником). Треугольник еще называют «вырожденная трапеция»
Треугольник еще называют «вырожденная трапеция»
Проставьте баллы в своих маршрутных листах за выполнение этого задания(5баллов)
Практическая работа с элементами
5-7 мин
Изучение нового материала,
анализ нового материала (рефлексия)
2 ловушка
Проанализируйте полученные результаты, составьте опорныйконспект по теме «Трапеция»,
План конспекта
Определение трапеции
Виды трапеции
Свойства трапеции:
углы при основании,
длины боковых сторон трапеции,
длины диагоналей,
средняя линия трапеции.
(слайд презентации, прил.1).
Представление результатов.
Проставьте баллы в своих маршрутных листах(5 баллов)
Работа в группах
Представление результатов исследования
6-7 мин
Физкульт
минутка
2 мин
Закрепление полученных знаний
3 ловушка
Работа в группах
1,2 -группы рассматривает вопрос о средней линии трапеции(сформулируйте определение средней линии трапеции, попробуйте указать свойства и доказатьего.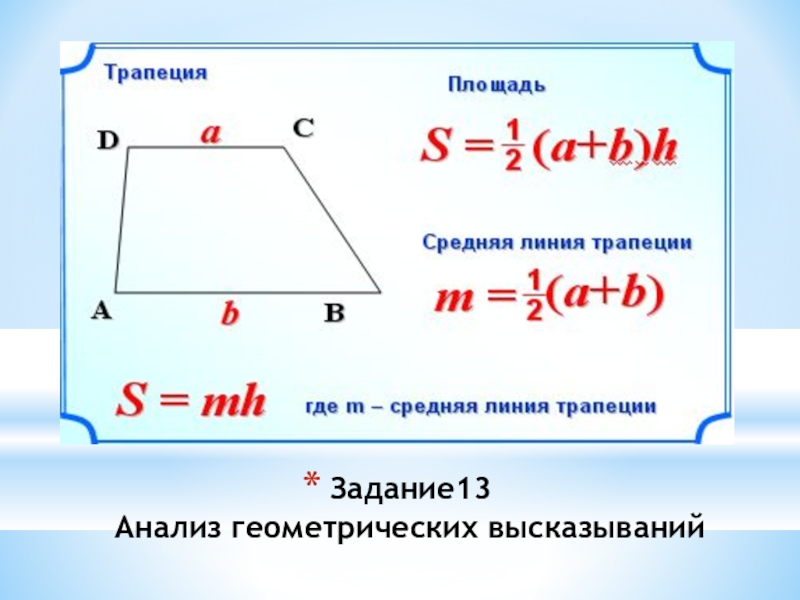 )
)
3,4,5,- группы решает задачу №1,
(№2)
Представление результатов, оценка в маршрутных листах(5баллов) слад презентации(док-во, и задача)
Работа в группах, парах
мин
Рефлексия . Подведение итогов работы
Учитель
Мы с вами преодолели все трудности и добрались до клада капитана Флинта.
Посмотрим, что это(слайд презентации)
«Клад – это ваши знания». Мы с вами отыскали сокровища, которым нет цены. Судьба их в ваших руках. Вам решать лежать им в земле, зарытыми как клад или преумножаться, помогая вам идти по жизни.
Итак, подведём итог урока
Составьтесинквейн
Трапеция (существительное)
2 слова — Описание (прилагательные)
3 слова — Действие (глагол)
4 слова Отношение(любая часть речи)
1 слово — ВЫВОД
Капитаны, прокомментируйте работу ваших команд. Поставьте итоги работы в маршрутный листок.
Наш необитаемый остров сохранил для вас клад, давайте дадим ему название.
Остров Надежды
Остров Радости
Остров Печали
Остров Знаний
Остров Слез
Каждый из вас получил в начале урока кораблик, оставьте его на острове, на который вы попали.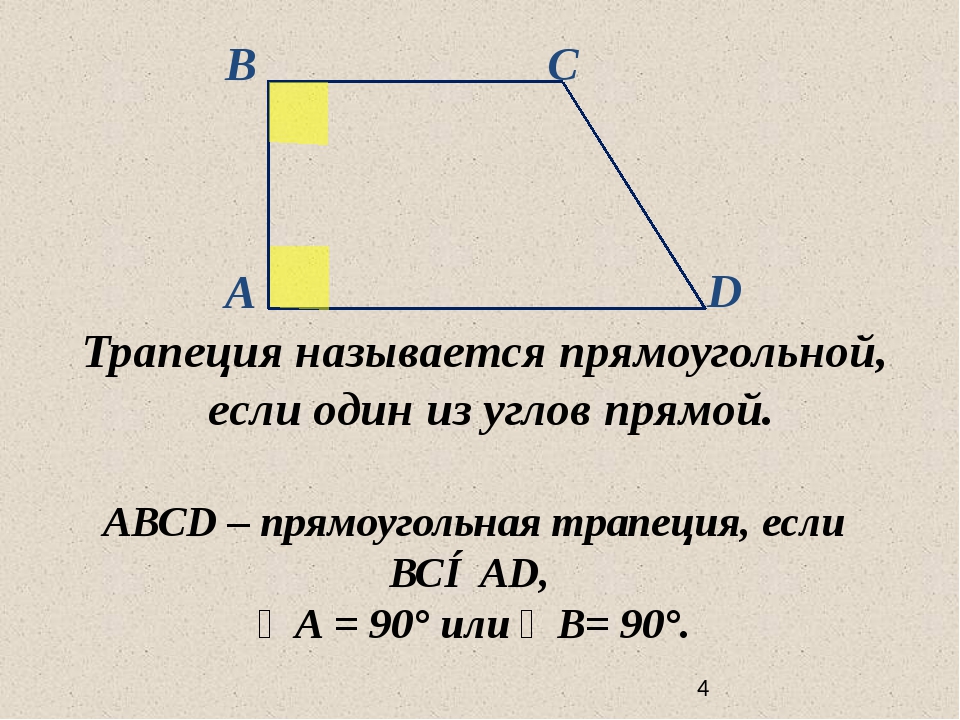
Работа в группах
Домашнее задание
Гл.1§6 №118, 120.
Фамилия, имя
Команда «Умки» капитан-
Разминка:
лови вопрос
(1балл)
установи слово
(2балла)
1 ловушка
(5баллов)
2 ловушка
(5баллов)
3 ловушка
(5баллов)
синквейн
(2балла)
отметка
20балл — 10
19баллов — 9
18б — 8
17б — 7
16б — 6
Трапеция. Виды трапеции. Свойства.
треугольник
АВС
трапеция
В С
В
А С
В
А С
Высота трапеции
Основания трапеции
Боковые стороны
Диагонали трапеции
Средняя линия трапеции
(длина средней лини, ? свойства)
Если Вы являетесь автором этой работы и хотите отредактировать, либо удалить ее с сайта — свяжитесь, пожалуйста, с нами.
Трапеция ромб конспект занятия в старшей группе. Конспект занятия в старшей группе
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts. google.com
google.com
Подписи к слайдам:
ГБОУ СОШ ИТШ им. П.Р. Поповича Дошкольное отделение по адресу Большой Коптевский д.10 Открытое занятие по ФЭМП в старшей группе. Тема: «Геометрические фигуры: ромб, трапеция». Выполнила: воспитатель Брыкова -Лукьянчикова Ю.А. Москва 2017г.
Цель: учить детей классифицировать фигуры по разным признакам; познакомить с трапецией и ромбом; учить ориентироваться в пространстве на ограниченной плоскости: «слева», «справа»: учить передавать строение дома путем сочетания геометрических фигур разных по величине и цвету.
Математическая разминка Две пчелы жужжат в ромашках, Три летят над белой кашкой. Вот бы пчелок сосчитать: Два плюс три-всего их пять.
Все фигуры назовите, Все фигуры покажите? Про треугольник что сказать? Его не сложно описать, Он как подобие крыла: Три стороны и три угла.
Новые фигуры изучали, все уголки пересчитали! Если влезть с пилой повыше, Отпилить у дома крышу, То хозяев мы обидим, Но трапецию увидим!
Ромб-фигура непростая, Две в себе объединяет: Треугольник раз и два- Фигура встала вдруг одна.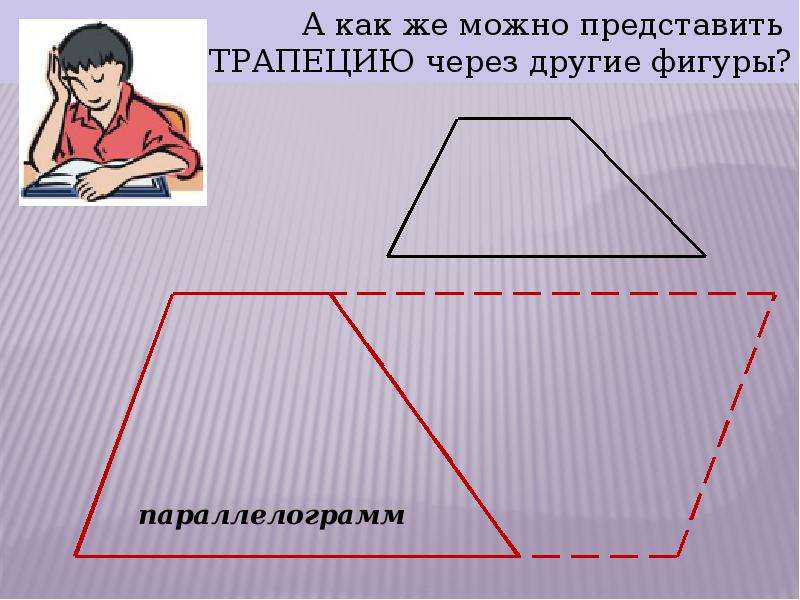
Рано встаньте, улыбнитесь, Выше, выше потянитесь. Ну-ка плечи распрямите, Поднимите, опустите. Влево, вправо повернулись, Рук коленями коснулись. Сели-встали, сели-встали И на месте побежали.
Вот квадратик, треугольник, Получился целый домик! Мы в него зайчика поселим, Вот ему будет веселье!
Как- то летом, у ручья, Дом построил зайке я, Заходи-ка милый заяц, Хоть один, хоть вся семья!
Эй, привет!- я дом встречаю, Кверху голову задрав, Крышей он в ответ качает: — С добрым утром, Зайка!
По теме: методические разработки, презентации и конспекты
Комплексное занятие по ФЭМП «Геометрические фигуры».
Комплексное занятие «Геометрические фигуры».Программное содержание: уточнить представления детей о том, что у квадрата 4 стороны, 4 прямых угла, 4 вершины, все стороны равны; продолжать учить делить…
Конспект комплексного занятия по математике и конструированию во второй младшей группе Конспект комплексного занятия по математике и конструированию во второй младшей группе Конспект занятий
Познакомить детей с числом и цифрой 6. Совершенствовать навыки счета и сравнения совокупностей предмета.Формировать умение детей различать понятия вчера, сегодня, завтра.Закреплять знания о геоме…
Совершенствовать навыки счета и сравнения совокупностей предмета.Формировать умение детей различать понятия вчера, сегодня, завтра.Закреплять знания о геоме…
занятие по математике «геометрические фигуры»
Задачи:Закрепление знаний о круге, квадрате, треугольнике, прямоугольнике и овале.Учить детей находить решение проблемных задач и выполнять логические задания, составлять цепочки из геометрических фиг…
Конспект занятия по математике
Конспект открытого занятия по ФЭМП с детьми
старшей группы на тему: «Мир загадок»
Никитина И.В., воспитатель II квал. категории
Д/С №54 “Искорка г. Набережные Челны
Образовательные задачи
Закрепить представления детей о геометрических фигурах. Треугольник, квадрат, круг, овал, ромб, трапеция.
Закрепить знание основных цветов синий, желтый, красный, зеленый.
Повторить прямой и обратный счет, количественный и порядковый.
Развивающие задачи
Развивать общую и мелкую моторику.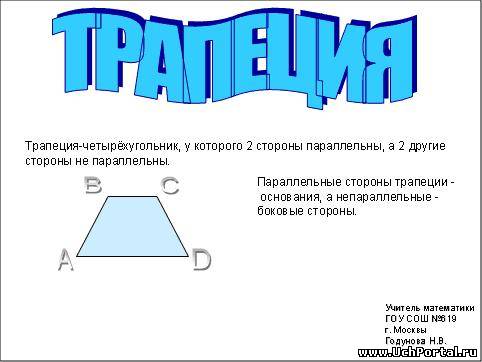
Развивать память, мышление, внимание.
Развивать представление о последовательности чисел в пределах 10.
Воспитательные задачи
Воспитывать умение слушать друг друга.
Словарная работа
Активизировать в речи детей название геометрических фигур.
1. Ход занятия.
Ребята, сегодня мы отправляемся в мир загадок, вместе с Лунтиком.
У Лунтика на столе разложено много фигур. Посмотрите, дети.
Ой, что это спросил Лунтик, и показал на фигуру, у которой три угла, три стороны, три вершины.
Дети, я знаю загадку про эту фигуру.
Узнаешь сразу ты, кто я, на меня ты посмотри, у меня всего, всего по тритри стороны и три угла, три пика острия. Мне это нравится вполне, ведь треугольник я.
Дети: Треугольник!
Правильно!
Ой, а это что за фигура? Спросил Лунтик и показал на квадрат.
Дети, и про эту фигуру я знаю загадку.
«Он давно знакомый мой, каждый угол в нем прямой, все четыре стороны одинаковой длины, вам представиться я рад, а зовут меня квадрат!»
Дети, что вы знаете о квадрате?
А здесь еще какой-то странный квадрат — сказал Лунтик.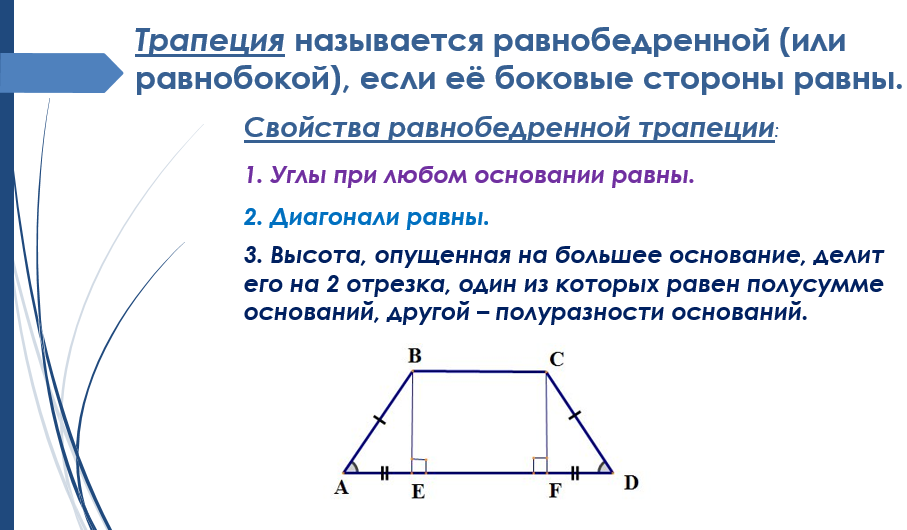
Дети, что это за фигура?
Прямоугольник.
Дети, у Лунтика все перепуталось в голове, и он хочет отдохнуть.
2. Физкультминутка
«Загудел паровоз
И вагончики повез
Далеко я укачу
Вагончики зеленые
Бегут, бегут, бегут
А круглые колесики
Тук — тук — тук!»
Дети, на какую геометрическую фигуру похожи колеси
На круг.
Ой, опять какой — то странный круг, произнес Лунтик.
Я знаю загадку про эту фигуру
«Мальчик круг нарисовал — убежал
Тут слоненок проходил — наступил
И из круга получился овал!»
Дети: Овал!
А это что за фигуры? Спросил Лунтик.
Трапеция, ромб.
Теперь Лунтик знает все фигуры, молодцы ребята, помогли Лунтику!
3. Ориентировка на листе бумаги.
Нарисуйте дети на своих листах эти фигуры.
В центре листа — треугольник, справа от треугольника — квадрат, слева — прямоугольник, под прямоугольником — овал, над треугольником — круг, под квадратом — трапеция, под треугольником — ромб.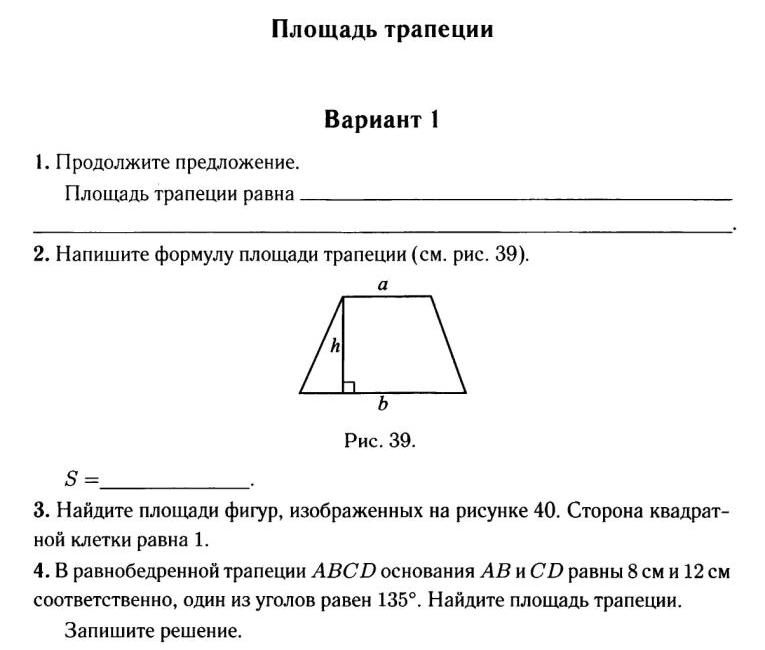
Сколько фигур у вас получилось, посчитайте.
Семь фигур.
Назовите ребята соседей цифры 1, 3, 5, 7, 9, 2, 4, 6, 8, 10.
Молодцы, все справились!
4. Пальчиковая гимнастика.
«Вот пенек,
На пеньке пять опят,
Пять ребят».
Дети, раскрасьте свои фигуры цветными карандашами.
Какими цветами получились ваши фигуры?
У всех ребят красивые работы.
Наше путешествие в мир загадок подошло к концу, вернемся в детский сад.
5. Итог занятия.
Ребят а, скажите, вам понравилось наше путешествие?
Чем занимались?
Все дети старались, молодцы!
Конспект занятия по ФЭМП в старшей группе «Поможем Колобку!»
Цель: обобщить полученные знания и закрепить умения по пройденному материалу;Задачи:
1. Уточнение представления детей о геометрических фигурах;
2. Закрепить представление детей о холодных и теплых цветах спектра;
3. Упражнять детей в сравнивании предметов по длине, развивать логическое мышление, сообразительность;
4.
 Воспитывать интерес к математическим занятиям;
Воспитывать интерес к математическим занятиям;5. Воспитывать у детей желание оказывать окружающим посильную помощь.
Материалы и оборудования: письмо, конверты с заданиями от лесных жителей, изображения 7 морковок различных по размеру, квадраты различных цветов (красный, желтый, оранжевый,розовый, синий, голубой, фиолетовый, зеленый), геометрические фигуры (круг, квадрат, овал, прямоугольник, треугольник, ромб, трапеция)
Ход занятия:
Воспитатель: Дети, сегодня к нам пришло письмо от Колобка. Давайте я вам его прочитаю:
«Я Колобок, Колобок, я по коробу скребен, по сусеку метен, на сметане мешон, да в масле пряжон,на окошке стужон. Я от дедушки ушел, я от бабушки ушел. А теперь, в лесу, меня хотят съесть лесные звери. Помогите мне! Лесные жители дали мне задания. Они очень трудные. Я не могу их решить» .
Воспитатель: Дети, поможем Колобку?
Дети: Поможем!
Воспитатель: А вы помните сказку про колобка? Кого в лесу он сначала встретил?
Дети: Зайца!
Воспитатель: Верно! А вот и задание от Зайца.

« У меня есть 7 марковок. Все они разной величины. Нужно их разложить по порядку: от самого маленького, до самого большого». Ну что дети, вы готовы?
Дети: Да! (Выполняют задание)
Воспитатель: Молодцы! Как хорошо вы справились с заданием зайца! А кого в лесу встретил Колобок после зайца? Кто помнит?
Дети: Волка!
Воспитатель: Правильно! А вот и задание от Серого Волка. (Открывает конверт с заданием и читает) «У меня есть квадраты разных цветов, нужно их разделить на холодные и теплые цвета». Дети, вы готовы выполнить задание?
Дети: Да! (Выполняют задание)
Воспитатель: Молодцы,дети! Вы все правильно сделали. А теперь давайте выполнять следующее задание, которое приготовил Медведь. (Открывает конверт с заданием и читает)
«У меня есть геометрические фигуры. Нужно определить и назвать их». Дети, давайте поможем Колобку справиться с заданием! (Воспитатель показывает геометрические фигуры:круг, квадрат, овал, прямоугольник, треугольник, ромб, трапеция, а дети их называют) Дети, какие же вы умные! Все правильно назвали! Справились с заданием! А кто знает, кого Колобок встретил после Медведя?
Дети: Лису!
Воспитатель: Верно.
 Лиса приготовила сложные вопросы, на которые нам нужно ответить. Вы готовы?
Лиса приготовила сложные вопросы, на которые нам нужно ответить. Вы готовы?Дети: Да!
Воспитатель: Итак, первый вопрос: во что превратится квадрат, если у него отрезать один угол?
Дети: В пятиугольник. (Если детям сложно ответить на этот вопрос, до они пробуют отрезать один угол квадрата)
Воспитатель: Молодцы, следующий вопрос: есть ли стороны, углы, вершины у круга? (показывает круг при необходимости)
Дети: Нет!
Воспитатель: Правильно. Последний, третий вопрос: из каких двух фигур можно сложить квадрат?
Дети: Из 2 одинаковых треугольников и прямоугольников.
Воспитатель: Какие же вы молодцы! Как я рада, что вы выполнили все сложные задания правильно. Вы помогли Колобку, теперь он может не бояться лесных жителей и вернуться домой к бабушке с дедушкой!
Оксана Сердюк
Сценарий непосредственно-образовательной деятельности с детьми старшей группы «Знакомство с трапецией»
Тема : Познавательное развитие «Знакомство с трапецией » .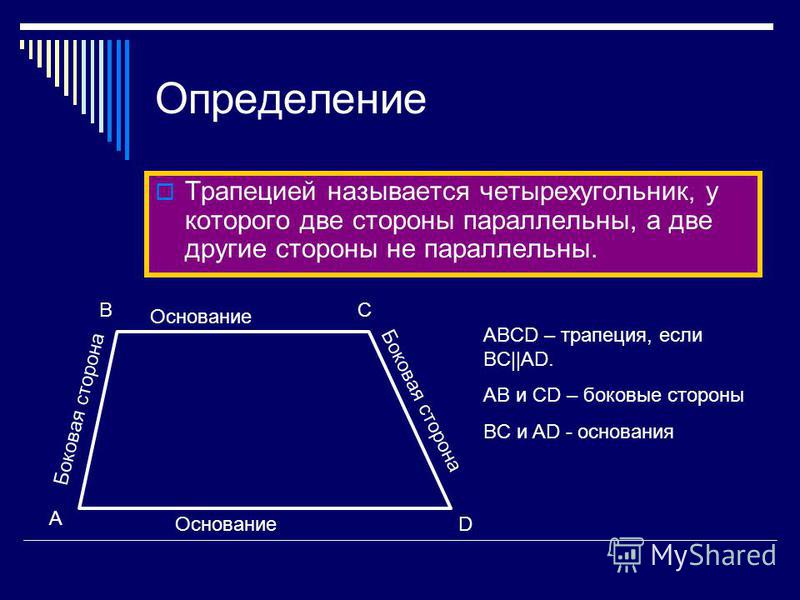
Возрастная группа : старшая группа .
Интеграция образовательных областей : Познавательное развитие, Физическое развитие.
Цель : познакомить с трапецией .
Задачи :
1. Познакомить с геометрической фигурой трапеция .
2. Закрепить счетные умения, умение сравнивать и уравнивать группы предметов по количеству.
3. Закреплять представления о геометрических фигурах (круг, квадрат, треугольник) .
4. Сформировать опыт самостоятельного преодоления затруднения при небольшой помощи педагога.
5. Развивать внимание, речь, логическое мышление, воображение, двигательную активность детей.
6. Воспитывать чувство сострадания и желание помочь героям сказки.
Материалы и оборудование : ноутбук, смарт доска, листы в клеточку с нарисованной геометрической фигурой трапеция на каждого ребенка , математические наборы на каждого ребенка.
Предполагаемый результат :
Владеют счетом до 8.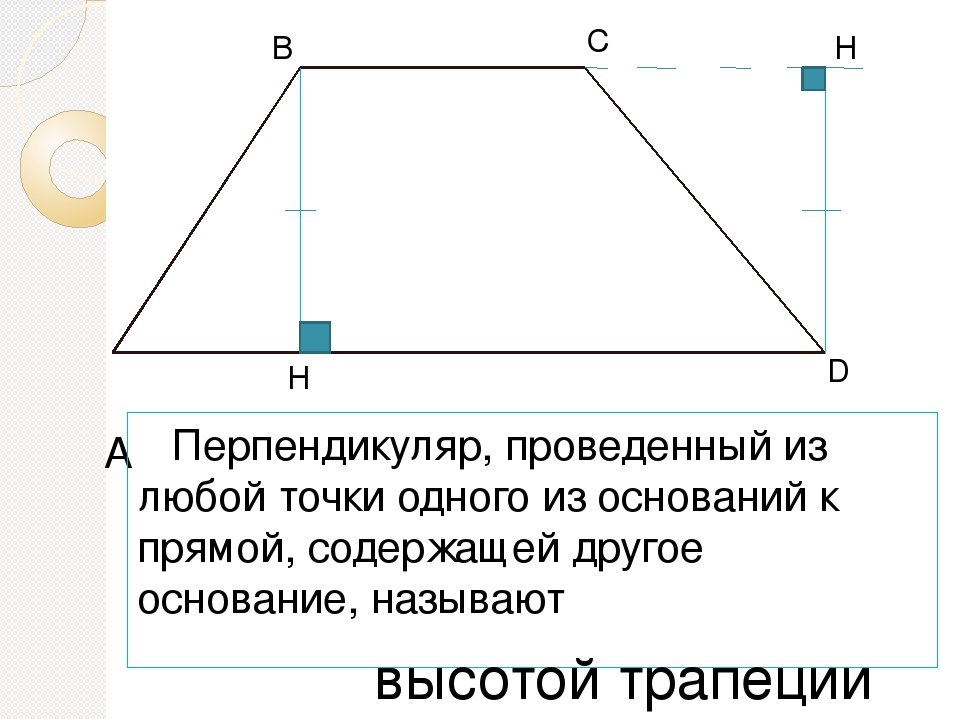
Знают геометрические фигуры.
Умеют соотносить предметы с геометрическими фигурами.
Умеют ориентироваться в пространстве.
Узнают трапецию среди четырехугольников.
Владеют связной речью.
Введение в ситуацию.
Дети сидят за столами.
Ребята, посмотрите на доску, кто пришел к нам сегодня в гости? (Карлсон) . (приветствие Карлсона)
Ребята, Карлсон пришел к нам за помощью. Он прилетал к Малышу поиграть, а домой вернуться не может. Он забыл как выглядит крыша дома, под которой он живет. Карлсон просит вас ему помочь найти крышу. Хотите помочь Карлсону? Сможете?
Актуализация знаний.
На одной стороне доски изображены геометрические фигуры : треугольники и четырехугольники разной формы, на другой стороне изображены дома без крыш.
Ребята, как называются фигуры, которые изображены на доске?
Вам надо из этих фигур сделать крыши домам. Использовать надо все фигуры, может быть даже у вас получится крыша, которая будет состоять из нескольких фигур.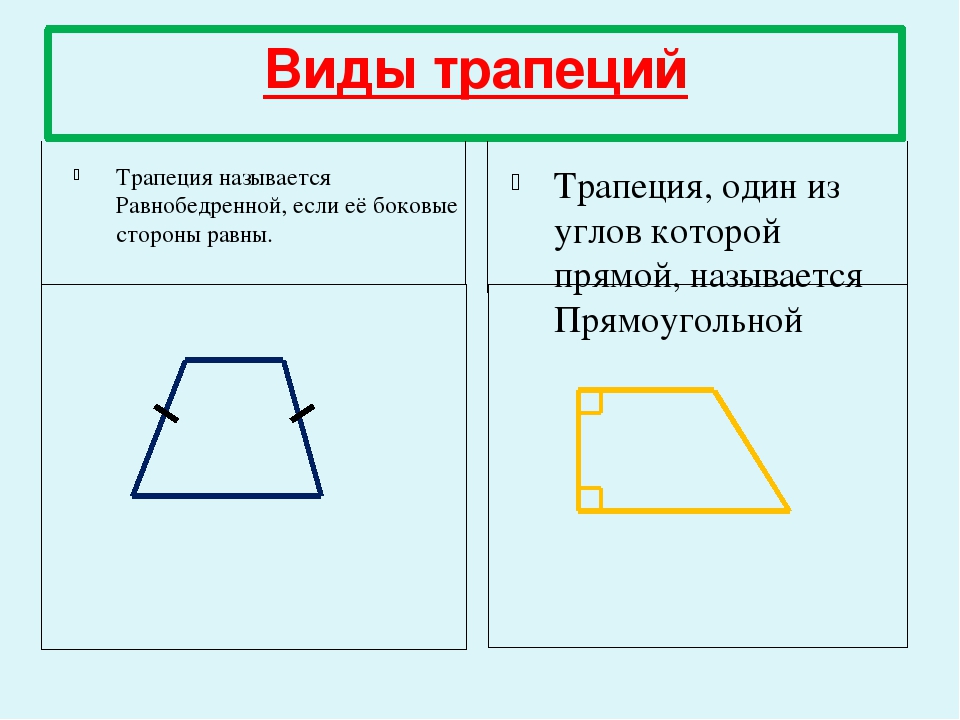 (дети выполняют задание) .
(дети выполняют задание) .
Затруднение в ситуации.
Ребята, посмотрите, какая интересная крыша у этого дома.
Сколько углов у фигуры? (4)
Сколько – сторон? (4)
Как называется такая фигура? (четырехугольник)
Открытие нового знания.
Ребята, а кто знает, как называется такой четырехугольник? (не знаем)
А что нужно сделать, если чего — не знаешь, но хочешь узнать? (спросить у взрослого, прочитать в книге и т. д.)
— Трапеция – это четырехугольник, у которого одна сторона длиннее другой.
(физминутка)
Ребята встаньте в круг. Я вам буду бросать мяч и называть геометрическую фигуру, а вы мне должны будете назвать предмет, который похож на эту фигуру.
Включение нового знания в систему знаний и умений.
У нас на что похожа трапеция ? (на крышу дома) .
А еще какие предметы похожи на трапецию ?. У вас на столах лежат листы, на которых нарисована трапеция , дорисуйте фигуру так, чтобы получился какой – то предмет. (дети выполняют задание)
(дети выполняют задание)
Обсуждение рисунков детей.
Давайте посмотрим, какие еще предметы похожи на трапецию . (видеоролик)
Какие предметы вы увидели?
Молодцы, а теперь давайте немного поиграем. На доске перемешаны разные геометрические фигуры. Вам надо распределить их в две корзины. В одну корзину – только трапеции , в другую – не трапеции .
Молодцы, ребята! Отлично справились с заданием.
Работа с математическими наборами.
Давайте составим трапецию из геометрических фигур, которые есть у вас в математических наборах. (дети выполняют задание) . Обсуждение, у кого какая трапеция получилась .
На доске заставка город и крыши.
Карлсон благодарит вас, за помощь, вы нашли крышу его дома и теперь он может вернуться домой. (звучит голос Калсона с благодарностями)
Осмысление.
Ребята, мы помогли сегодня Карлсону?
А что мы делали, чтобы ему помочь? (составляли крыши домов, дорисовывали трапецию , распределяли фигуры по группам ).
А с какой новой фигурой мы познакомились ? (с трапецией )
Что такое трапеция ?
Вам понравилось занятие?
Публикации по теме:
Конспект непосредственно образовательной деятельности с детьми старшей группы «Хлеб — всему голова» Цель: Воспитание у детей бережного отношения к хлебу и уважения к людям, которые его растят и выпекают Предварительная работа: слушание.
Знакомство с Геометрическими фигурами.ТРЕУГОЛЬНИК
Самолёт летит по небу, треугольное крыло,
На моём велосипеде, треугольное седло,
Есть такой предмет — угольник, и всё это — ТРЕУГОЛЬНИК.
Тут мама три спички на стол положила
И мне треугольник из спичек сложила.
А в это время я чертил и наблюдал за мамою,
Я три прямых соединил и сделал то же самое.
Треугольный треугольник- угловатый своевольник.
Он похож на крышу дома и на шапочку у гнома.
И на острый кончик стрелки, и на ушки рыжей белки.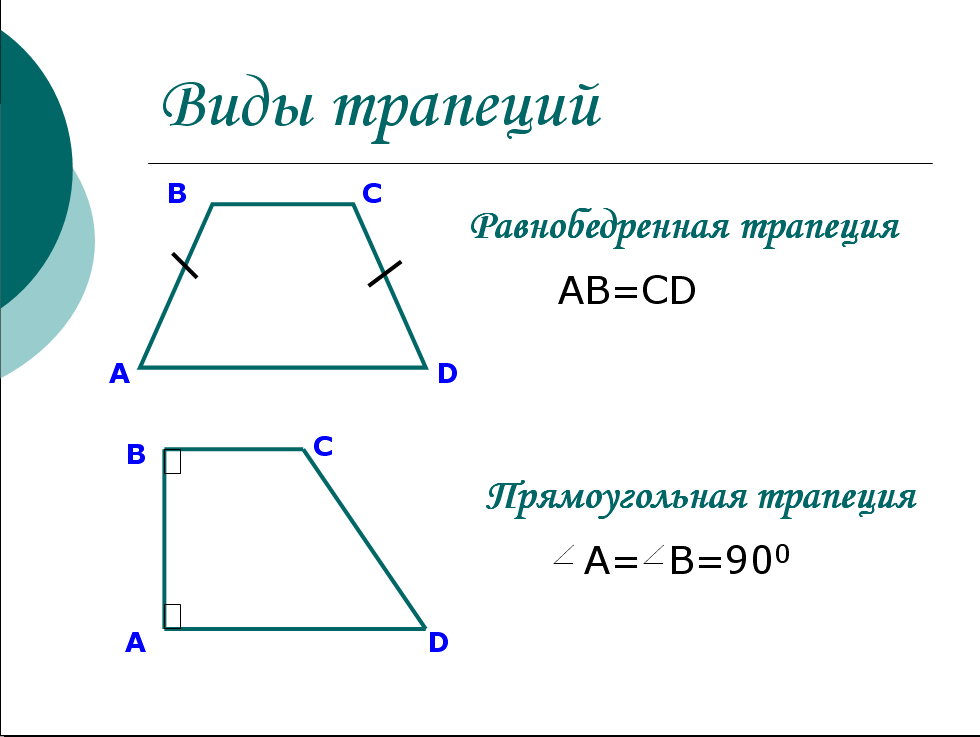
Угловатый очень с виду он похож на пирамиду!
КВАДРАТ
Пришёл из школы старший брат, из спичек выложил квадрат.
Дала мне мама шоколад, я дольку отломил — квадрат.
И стол -квадрат, и стул — квадрат, и на стене плакат — квадрат,
Доска, где шахматы стоят, и клетка каждая — квадрат,
Стоят там кони и слоны, фигуры боевые.
КВАДРАТ — четыре стороны, все стороны его равны,
И все углы прямые.
Словно стол стоит квадрат.Он гостям обычно рад.
Он квадратное печенье положил для угощенья.
Он — квадратная корзина и квадратная картина.
Все четыре стороны у квадратика равны.
2.
РОМБ
Слон квадратик повернул,присмотрелся и вздохнул.
Сверху сел, чуть-чуть примял, и квадратик ромбом стал!
3.
ПРЯМОУГОЛЬНИК
Как окно прямоугольник, аккуратный, словно школьник.
Он похож дверь, на книжки, и на ранец у мальчишки.
На автобус, на тетрадку, на большую шоколадку.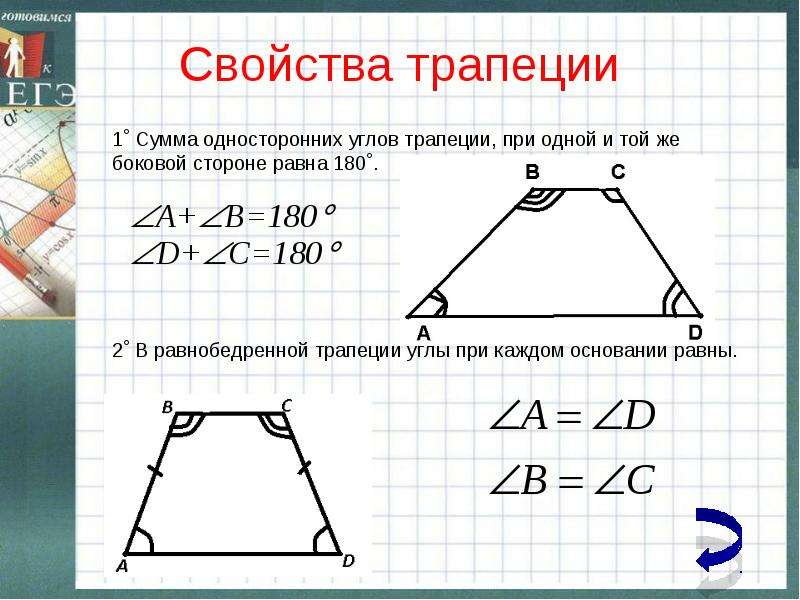
На корыто поросенка и на фантик у ребенка.
ОКРУЖНОСТЬ и КРУГ
Мы живём с братишкой дружно, нам так весело вдвоём,
Мы на лист поставим кружку, обведём карандашом.
Получилось то, что нужно -называется ОКРУЖНОСТЬ.
Мой брат по рисованию себя считает мастером,
Всё, что внутри окружности, закрасил он фломастером.
Вот вам красный круг, кружок, по краю синий ободок.
КРУГ — тарелка, колесо, ОКРУЖНОСТЬ — обруч, поясок.
ОКРУЖНОСТЬ — очертанье КРУГА. Я смотрю на наш листок,
Стал искать у круга угол, но найти его не смог.
Брат смеётся — вот дела! Да у круга нет угла,
У тарелки и монеты не найдёшь углов, их нету.
4.
КРУГ
Круглый круг похож на мячик, он по небу солнцем скачет.
Круглый словно диск луны, как бабулины блины,
Как тарелка, как венок, как веселый колобок,
Как колеса, как колечки, как пирог из теплой печки!
6.
ПОЛУКРУГ
Если круг разломишь вдруг, то получишь полукруг.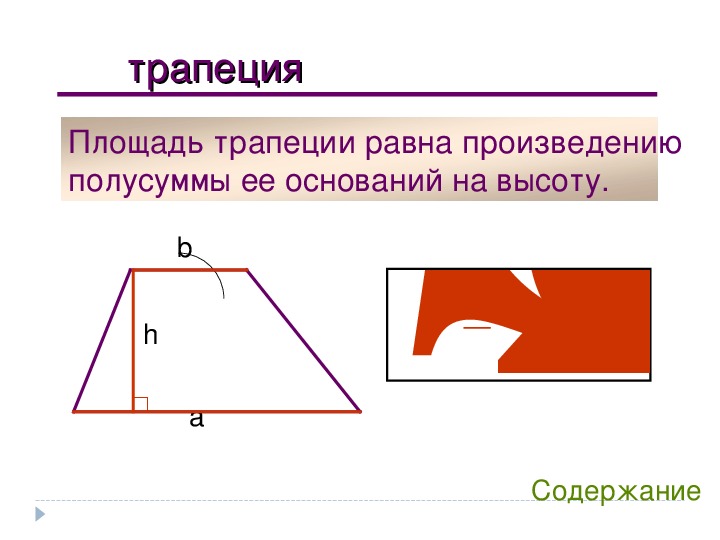
Это месяц в облаках и пол-яблока в руках.
Это шляпка у грибочка, на болоте мокром кочка.
Разноцветным полукругом встала радуга над лугом.
ОВАЛ
А как нарисовать овал?На помощь брата я позвал.
Брат взял фломастер и искусно мне овал нарисовал:
Ты слегка окружность сплюсни, получается ОВАЛ.
Сколько раз его видал, в ванной зеркало -овал!
Овал и блюдо, и яйцо.Мама говорит:-Лицо
У тебя овальное.Пусть будет овальное, лишь бы не печальное.
Мы рассмеялись и в овале рожицу нарисовали.
Овал — окружность удлинённая и рожица в ней удивлённая.
С высоты кружок упал.Он теперь не круг – овал!
Он овальный, как жучок, он похож на кабачок,
На глаза и на картошку,а еще похож на ложку,
На орех и на яйцо, на овальное лицо!
5.
ТРАПЕЦИЯ
Трапеция, трапеция- фигура есть такая, а я её не знаю.
Ты где живёшь, трапеция, в Америке, в Китае?
Может, за трапецией поехать надо в Грецию?
Мама говорит: — Не надо, трапеция с тобою рядом.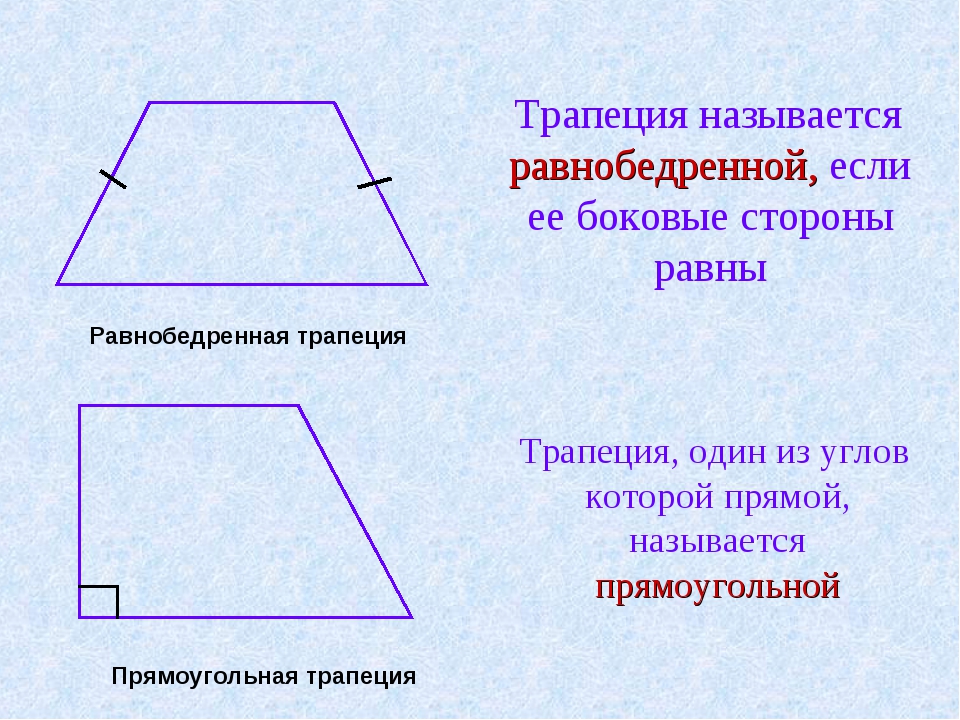
Развею я твою тоску, ты подожди минутку.
И на гладильную доску укладывает юбку,
По ней проводит утюжком, ч тоб не топорщилась мешком:
— Вот тебе ТРАПЕЦИЯ,
Не стоит ехать в Грецию.
Если влезть с пилой повыше,
Отпилить у дома крышу,
То хозяев мы обидим,
Но трапецию увидим!
А потом мы все починим
И из шкафа юбку вынем.
Мы увидим: юбка тоже
На трапецию похожа!
Конспект урока Тема урока (5)
Конспект урока
Тема урока: «Четырехугольники»
Цели урока: 1. Обобщение и систематизация знаний учащихся.
2. Развитие логического мышления, умения сравнивать.
3. Развитие математической речи, умения рассуждать.
4. Развитие творческих способностей учащихся.
Ход урока
Прежде,
чем мы приступим к повторению материала,
представляется необходимым обратиться
к геометрии древних времен, в частности,
в той ее части, которая касается изучаемой
темы.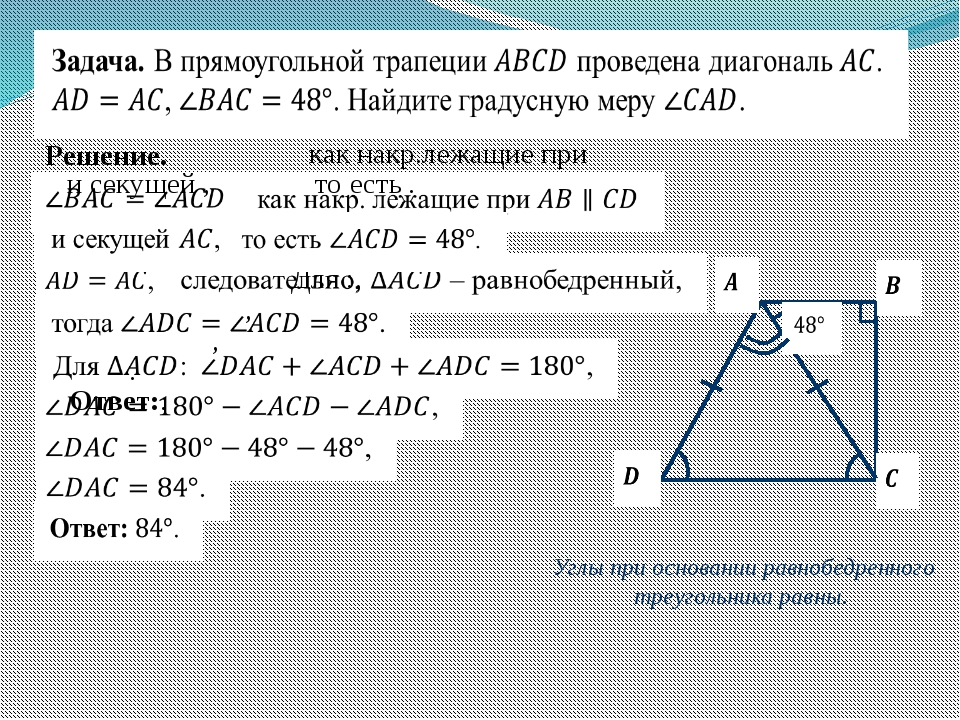
В древних египетских и вавилонских математических документах встречаются следующие виды четырехугольников: квадраты, прямоугольники, равнобедренные и прямоугольные трапеции.
Термин «параллелограмм» греческого происхождения и был введен Евклидом.
Евклид (Eνκλειδηζ), древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике.
Сведения об Евклиде крайне скудны. Достоверным можно считать лишь то, что его научная деятельность протекала в Александрии в III веке до н. э. Евклид – первый математик александрийской школы. Его главная работа «Начала» (в латинизированной форме – «Элементы») содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел ; в ней он подвел итог предшествующему развитию греческой математики и создал фундамент дальнейшего развития математики.
Из
других сочинений по математике надо
отметить работу «О делении фигур»,
сохранившуюся в арабском переводе,
четыре книги «Конические сечения»,
материал которых вошел в произведение
того же названия Аполлония Пергского,
а также «Поризмы», представление о
которых можно получить из «Математического
собрания» Паппа Александрийского. Евклид – автор работ по астрономии,
оптике, музыке и др.
Евклид – автор работ по астрономии,
оптике, музыке и др.
Слово «ромб» тоже греческого происхождения, оно означало в древности вращающееся тело, веретено, юлу.
«Трапеция» — слово греческое, означавшее в древности «столик». В «Началах» термин «трапеция» применяется не в современном, а в другом смысле: любой четырехугольник (не параллелограмм).
«Трапеция» в нашем смысле встречается впервые у древнегреческого математика Посидония(1в.)
Посидоний — математик и астроном, родился в Апамее в Сирии в 135 г., умер в Риме в 50 г. до Р. Хр. Жил долго в Родосе. Был учителем Цицерона. Известен второй попыткой определить размеры земного шара (первая принадлежит Эратосфену).
Предложение о том, что средняя линия трапеции равна полусумме ее оснований, было известно древним египтянам, оно содержится и в трудах Герона Александрийского.
Герон
Александрийский;
Heron, I в. н. э., греческий механик и математик.
Время его жизни неопределенно, известно
только, что он цитировал Архимеда
(который умер в 212 г.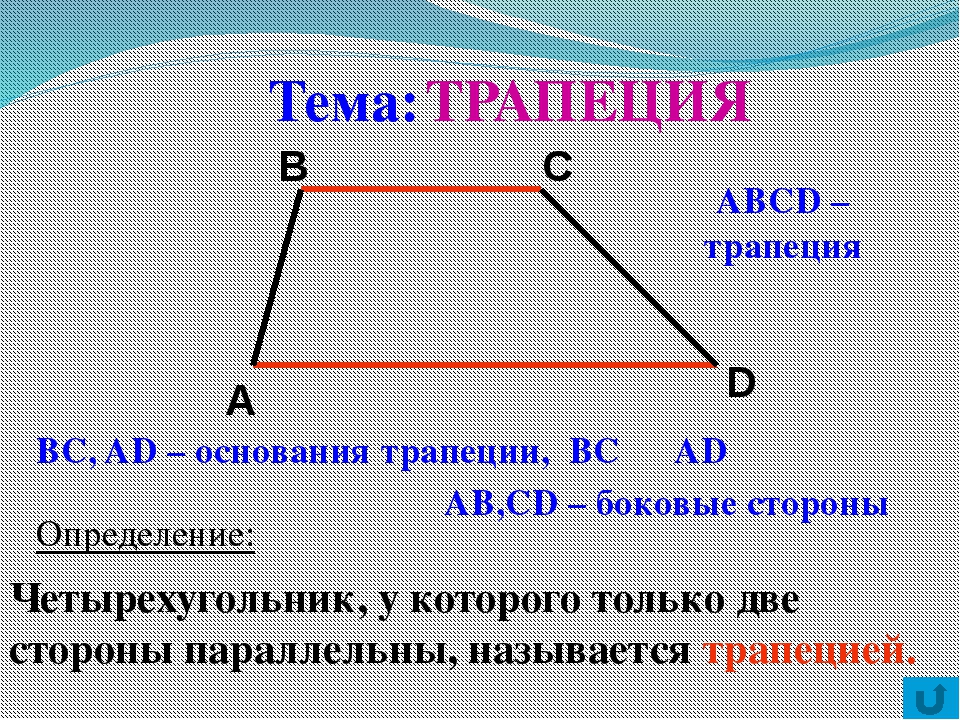 до н. э.), его же самого
цитировал Папп (ок. 300 г. н. э.). В настоящее
время преобладает мнение, что он жил в
I в. н. э. Занимался геометрией, механикой,
гидростатикой, оптикой; изобрел прототип
паровой машины и точные нивелировочные
инструменты. Наибольшей популярностью
пользовались такие автоматы Г., как
автоматизированный театр, фонтаны и
др. Г. описал теодолит, опираясь на законы
статики и кинетики, привел описание
рычага, блока, винта, военных машин. В
оптике сформулировал законы отражения
света, в математике — способы измерения
важнейших геометрических фигур. Основные
произведения Г. — это Иетрика, Пневматика,
Автоматопоэтика, Механика (фр.; произведение
сохранилось целиком по-арабски), Катоптика
(наука о зеркалах; сохранилась только
в латинском переводе) и др. Г. использовал
достижения своих предшественников:
Евклида, Архимеда, Стратона из Лампсака.
Его стиль простой и ясный, хотя порой
бывает чересчур лаконичен или нестроен.
Интерес к сочинениям Г. возник в III в. н.
э. Греческие, а затем византийские и
арабские ученики комментировали и
переводили его произведения.
до н. э.), его же самого
цитировал Папп (ок. 300 г. н. э.). В настоящее
время преобладает мнение, что он жил в
I в. н. э. Занимался геометрией, механикой,
гидростатикой, оптикой; изобрел прототип
паровой машины и точные нивелировочные
инструменты. Наибольшей популярностью
пользовались такие автоматы Г., как
автоматизированный театр, фонтаны и
др. Г. описал теодолит, опираясь на законы
статики и кинетики, привел описание
рычага, блока, винта, военных машин. В
оптике сформулировал законы отражения
света, в математике — способы измерения
важнейших геометрических фигур. Основные
произведения Г. — это Иетрика, Пневматика,
Автоматопоэтика, Механика (фр.; произведение
сохранилось целиком по-арабски), Катоптика
(наука о зеркалах; сохранилась только
в латинском переводе) и др. Г. использовал
достижения своих предшественников:
Евклида, Архимеда, Стратона из Лампсака.
Его стиль простой и ясный, хотя порой
бывает чересчур лаконичен или нестроен.
Интерес к сочинениям Г. возник в III в. н.
э. Греческие, а затем византийские и
арабские ученики комментировали и
переводили его произведения.
Математические работы Герона являются энциклопедией античной прикладной математики. Работы его дошли до нас не полностью. Из его работ известны «Механика», «Книга о подъемных механизмах», «Пневматика», «Книга о военных машинах», «Театр автоматов», «Метрика».
1.Повторение: определений изученных четырехугольников, их видов, признаков и свойств, формул площадей.
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.
Две несмежные стороны четырехугольника называются противоположными . Две вершины, не являющиеся соседними, называются также противоположными.
Четырехугольники бывают
выпуклые (как
ABCD) и
невыпуклые
(A1B1C1D1).
Виды четырёхугольников
Параллелограмм
Параллелограммом называется
четырехугольник, у которого противолежащие
стороны попарно
параллельны.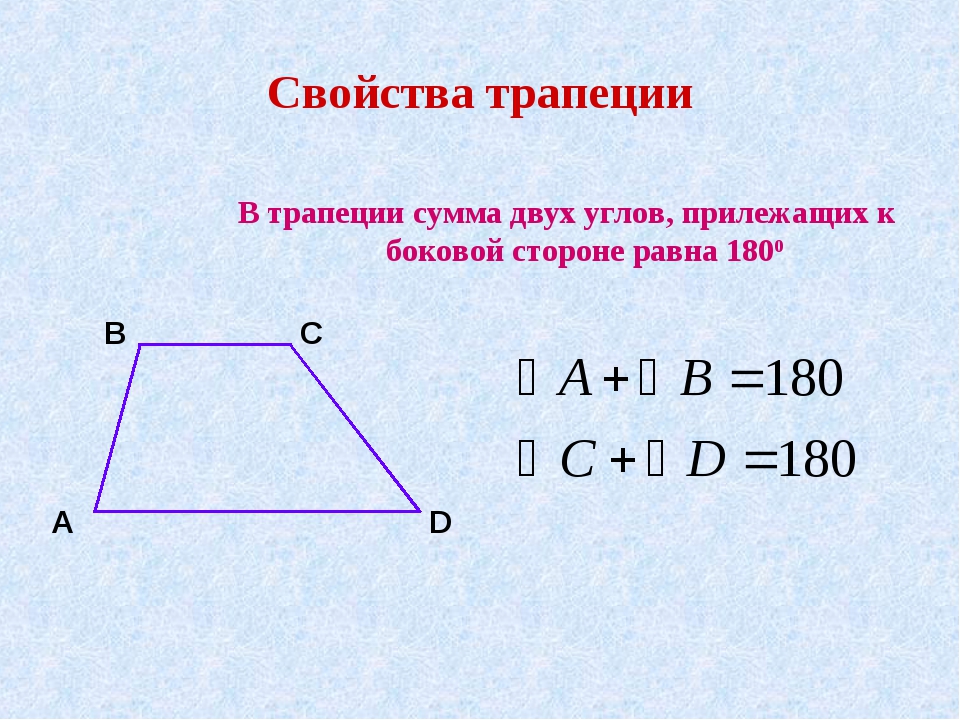
Свойства параллелограмма
противолежащие стороны равны;
противоположные углы равны;
диагонали точкой пересечения делятся пополам;
сумма квадратов диагоналей равна сумме квадратов всех сторон:
d12+d22=2(a2+b2).
Признаки параллелограмма
Четырехугольник является параллелограммом, если:
Две его противоположные стороны равны и параллельны.
Противоположные стороны попарно равны.
Диагонали точкой пересечения делятся пополам.
Трапеция
Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны.
Параллельные стороны
трапеции называются ее основаниями, а непараллельные
стороны — боковыми
сторонами. Отрезок, соединяющий середины боковых
сторон, называется средней
линией.
Отрезок, соединяющий середины боковых
сторон, называется средней
линией.
Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
Свойства трапеции
ее средняя линия параллельна основаниям и равна их полусумме;
если трапеция равнобокая, то ее диагонали равны и углы при основании равны;
если трапеция равнобокая, то около нее можно описать окружность;
если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.
Признаки трапеции
Четырехугольник является трапецией, если его параллельные стороны не равны
Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойства прямоугольника
Признаки прямоугольника
Параллелограмм является прямоугольником, если:
Один из его углов прямой.

Его диагонали равны.
Ромб
Ромбом называется параллелограмм, у которого
все стороны равны.
Свойства ромба
все свойства параллелограмма;
диагонали перпендикулярны;
диагонали являются биссектрисами его углов.
Признаки ромба
Параллелограмм является ромбом, если:
Две его смежные стороны равны.
Его диагонали перпендикулярны.
Одна из диагоналей является биссектрисой его угла.
Квадрат
Квадратом называется прямоугольник,
у которого все стороны равны.
Свойства квадрата
все углы квадрата прямые;
диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Признаки квадрата
Прямоугольник является квадратом, если он обладает
каким-нибудь признаком ромба.
Основные формулы
1. Произвольный
выпуклый четырехугольник
d1,
d2 — диагонали;
—
угол между ними; S —
площадь.
S =d1d2 sin
2. Параллелограмм
a
и b — смежные
стороны;
—
угол между ними; ha — высота,
проведенная к стороне
a.
S = aha
S = ab sin
S =d1d2 sin
3. Трапеция
a
и b —
основания; h —
расстояние между ними;
l — средняя линия.
S = lh
4. Прямоугольник
S = ab
S =d1d2 sin
5. Ромб
S = aha
S = a2sin
S =d1d2
6. Квадрат
d
— диагональ.
S = a2
2.Тест с взаимопроверкой.
Тест №1
1.Любой прямоугольник является:
А) ромбом;
Б) квадратом;
В) параллелограммом;
Г) нет правильного ответа.
2.Если в четырехугольнике диагонали перпендикулярны,
то он является:
А) ромбом;
Б) квадратом;
В) прямоугольником;
Г) нет правильного ответа.
3.Ромб – это четырехугольник, в котором…
А) диагонали равны и точкой пересечения делятся пополам.
Б) диагонали взаимно перпендикулярны и точкой пересечения делятся пополам.
В) противолежащие углы равны, а противолежащие стороны параллельны;
Г) нет правильного ответа.
4.Квадрат – это…
А) параллелограмм с равными сторонами;
Б) параллелограмм, у которого все углы прямые;
В) прямоугольник, у которого все стороны равны;
Г)
нет правильного ответа.
5.У какого четырехугольника диагонали равны?
А) трапеция;
Б) прямоугольник;
В) ромб;
Г) нет правильного ответа.
Тест №2
1.Любой ромб является:
А) квадратом;
Б) прямоугольником;
В) параллелограммом;
Г) нет правильного ответа.
2.Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм:
А) ромб;
Б) квадрат;
В) прямоугольник;
Г) нет правильного ответа.
3.Прямоугольник – это четырехугольник, в котором:
А) противолежащие стороны параллельны, а диагонали равны;
Б) диагонали точкой пересечения делятся пополам и являются биссектрисами его углов;
В) два угла прямые и две стороны равны;
Г) нет правильного ответа.
4.Квадрат – это…
А) параллелограмм, у которого все углы прямые;
Б) параллелограмм с равными сторонами;
В) прямоугольник, у которого все стороны равны;
Г)
нет правильного ответа.
5.Параллелограмм — это четырехугольник, у которого:
А) стороны параллельны;
Б) противолежащие стороны параллельны;
В) стороны равны;
Г) нет правильного ответа.
Ответы:
Тест № 1 : ВГБВБ.
Тест № 2 : ВААВБ.
Итоги урока
Математика и поэзия (детский стишок о четырехугольниках)
Один квадрат в жару и стужу
Весь день с утра смотрелся в лужу.
Ему хотелось сосчитать
Свои углы- три или пять?
Один, два, три, а дальше- стоп!
Он больше трех считать не мог.
Ему пришел на помощь брат:
«Не плачь, мой маленький Квадрат!
Ты улыбнись, братишка шире.
У нас с тобой угла- четыре!
Мы все- отличная семья
Четырехугольники-друзья.
Вот ты, хотя и маловат,
Вполне квадратненький Квадрат.
Все стороны твои равны-
Что
по бокам, что со спины.
Прямоугольник я- твой брат.
И быть таким я очень рад!
Без нас с тобою жизнь- беда.
Нужны мы всем, везде, всегда!
Прямоугольное окно-
Чтоб в доме не было темно.
Прямоугольник- шоколадка.
Кусни- и будет очень сладко!
А книги, ранец и тетрадь-
Все невозможно сосчитать!
Адреса:1./mathematics/courses/planimetry/content/scientist/eukleides.html
2./works/97x/311/geron.htm
/omsk/edu/rusanova/tetrangl.htm
/p63aa1.html
/c/churbanowa/m/detskijstishokprochetyrehugolxnikj,shtml.
Конспект лекций По дисциплине оп. 07. Составил
Электрические измерения
Конспект лекций
По дисциплине
ОП. 07.
Составил преподаватель
Полевой А.В.
2020г.
2
Содержание
1.
Государственная система обеспечения единства и точности измерений
1.1
Классификация основных видов средств измерений.
Стр.3
1.2
Основные методы и принципы измерений.
Стр.11
1.3
Методы и средства обеспечения единства и точности измерений. Виды
погрешностей измерений.
Стр.17
2.
Аналоговые и цифровые измерительные приборы
2.1 Измерение тока и напряжения электромеханическими
Cтр.34
измерительными приборами. Тестеры.
Стр.34
2.2 Аналоговые и цифровые электронные вольтметры. Измерение мощности.
Стр.54
3.
Измерительные генераторы
3.1
Генераторы низкой и высокой частоты.
Стр.73
3.2
Импульсные генераторы и генераторы шумовых сигналов. Cтр.79
4.
Исследование формы и измерения параметров сигнала
4.1
Осциллографические методы измерений.
Стр.
 84
84 4.2
Измерение частоты и временных интервалов электрических сигналов.
Стр.97
4.3
Измерение параметров полупроводниковых приборов и интегральных
микросхем (ИМС).
Стр.112
5.
Методы и способы автоматизации измерений
5.1
Основные направления автоматизации измерительных приборов.
Стр.119
5.2
Микропроцессоры в измерительных приборах.
Стр.120
5.3
Компьютерно-измерительные системы (КИС).
Стр.121
5.4
Виртуальные измерительные приборы.
Стр121
6.
Приложение А.Вопросы для самопроверки.
Cтр.123
7.
Приложение Б.Литература.
Cтр.129
Планиметрия (Геометрия на плоскости) — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Треугольник
К оглавлению…
При решении задач по геометрии помимо всех геометрических формул и свойств, которые будут приведены ниже, нужно очень хорошо помнить основные формулы по тригонометрии. Укажем для начала несколько основных свойств различных типов углов:
Укажем для начала несколько основных свойств различных типов углов:
- Смежные углы в сумме равны 180 градусов.
- Вертикальные углы равны между собой.
Теперь перейдем к свойствам треугольника. Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника:
Запомните также, что сумма любых двух сторон треугольника всегда больше третьей стороны. Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Формула медианы (медиана — линия проведенная через некоторую вершину и середину противоположной стороны в треугольнике):
Свойства медиан:
- Все три медианы пересекаются в одной точке.

- Медианы делят треугольник на шесть треугольников одинаковой площади.
- В точке пересечения медианы делятся в отношении 2:1, считая от вершин.
Свойство биссектрисы (биссектриса — линия, которая делит некоторый угол на два равных угла, т.е. пополам):
Важно знать: Центр вписанной в треугольник окружности лежит на пересечении биссектрис (все три биссектрисы пересекаются в этой одной точке). Формулы биссектрисы:
Основное свойство высот треугольника (высота в треугольнике — линия проходящая через некоторую вершину треугольника перпендикулярно противоположной стороне):
Все три высоты в треугольнике пересекаются в одной точке. Положение точки пересечения определяется типом треугольника:
- Если треугольник остроугольный, то точка пересечения высот находится внутри треугольника.
- В прямоугольном треугольнике высоты пересекаются в вершине прямого угла.
- Если треугольник тупоугольный, то точка пересечения высот находится за пределами треугольника.

Формула высоты:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Центр окружности описанной около треугольника лежит на пересечении посерединных перпендикуляров. Все три посерединных перпендикуляра пересекаются в одной этой точке. Посерединный перпендикуляр — линия проведенная через середину стороны треугольника перпендикулярно ей.
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого. В подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т.п.) пропорциональны. Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов. Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников. Отношение периметров подобных треугольников равно коэффициенту подобия. Отношение длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Признаки подобия треугольников:
В подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т.п.) пропорциональны. Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов. Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников. Отношение периметров подобных треугольников равно коэффициенту подобия. Отношение длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Признаки подобия треугольников:
- По двум углам. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
- По двум сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны.
- По трём сторонам. Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.

Трапеция
К оглавлению…
Трапеция — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна. Длина средней линии трапеции:
Площадь трапеции:
Некоторые свойства трапеций:
- Средняя линия трапеции параллельна основаниям.
- Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
- В трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон находятся на одной прямой.
- Диагонали трапеции разбивают её на четыре треугольника. Треугольники, сторонами которых являются основания — подобны, а треугольники, сторонами которых являются боковые стороны — равновелики.
- Если сумма углов при любом основании трапеции равна 90 градусов, то отрезок соединяющий середины оснований равен полуразности оснований.
- У равнобедренной трапеции углы при любом основании равны.

- У равнобедренной трапеции диагонали равны.
- В равнобедренной трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.
Параллелограмм
К оглавлению…
Параллелограмм — это четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. Площадь параллелограмма через сторону и высоту опущенную на неё:
Площадь параллелограмма через две стороны и угол между ними:
Некоторые свойства параллелограмма:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180 градусов.
- Сумма всех углов параллелограмма равна 360 градусов.

- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.
Квадрат
К оглавлению…
Квадрат — четырёхугольник, у которого все стороны равны, а все углы равны по 90 градусов. Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:
Свойства квадрата – это все свойства параллелограмма, ромба и прямоугольника одновременно.
Ромб и прямоугольник
К оглавлению…
Ромб — это параллелограмм, у которого все стороны равны. Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):
Свойства ромба:
- Ромб является параллелограммом. Его противолежащие стороны попарно параллельны.
- Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
- Диагонали ромба являются биссектрисами его углов.

Прямоугольник — это параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника через две смежные стороны:
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Прямоугольник является параллелограммом — его противоположные стороны параллельны.
- Стороны прямоугольника являются одновременно его высотами.
- Квадрат диагонали прямоугольника равен сумме квадратов двух его не противоположных сторон (по теореме Пифагора).
- Около любого прямоугольника можно описать окружность, причем диагональ прямоугольника равна диаметру описанной окружности.
Произвольные фигуры
К оглавлению…
Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:
Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т. е. в том числе для любых треугольников):
е. в том числе для любых треугольников):
Обобщённая теорема Фалеса: Параллельные прямые отсекают на секущих пропорциональные отрезки.
Условие, при выполнении которого возможно вписать окружность в четырёхугольник:
Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Многоугольники
К оглавлению…
Выпуклым многоугольником называется многоугольник, обладающий тем свойством, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Сумма внутренних углов плоского выпуклого n-угольника равна:
Число диагоналей всякого многоугольника равно (где: n – число сторон):
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны. Внутренний угол правильного многоугольника равен:
Центральный угол правильного n-угольника равен:
Площадь правильного многоугольника с числом сторон n, длиной стороны a, радиусом описанной окружности R, полупериметром p и радиусом вписанной окружности r, может быть рассчитана по следующим формулам:
Окружность
К оглавлению. ..
..
Свойство касательных:
Свойство хорды:
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):
Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):
Свойство центральных углов и хорд:
Свойство центральных углов и секущих:
Длина окружности:
Длина дуги окружности:
Площадь круга:
Площадь сектора:
Площадь кольца:
Площадь кругового сегмента:
Уникальные особенности внеклеточного матрикса в медиальном ядре трапециевидного тела мыши – значение для физиологических функций
Медиальное ядро трапециевидного тела (МНТТ) является жизненно важной структурой контуров локализации звука в слуховом стволе мозга. Каждая основная клетка MNTB контактирует с очень большим пресинаптическим глутаматергическим окончанием, чашечкой Хельда. Сами основные клетки MNTB окружены компонентами внеклеточного матрикса, образующими заметные перинейрональные сети (PN).Повсюду в ЦНС PN, которые образуют решетчатые структуры вокруг сомат и проксимальных дендритов, связаны с различными типами нейронов. PN сильно обогащены протеогликанами гиалуронана и хондроитинсульфата, что обеспечивает заряженную поверхностную структуру, окружающую тело клетки и проксимальные нейриты этих нейронов. Локализация и состав PN привели исследователей к ряду гипотез об их функциях, включая создание специфической внеклеточной ионной среды вокруг этих нейронов, стабилизацию синапсов и влияние на рост аксонов.Однако в настоящее время точные функции PN все еще совершенно неясны, в первую очередь из-за отсутствия идеальной экспериментальной модельной системы, которая была бы сильно обогащена PN и в которой можно было бы точно измерить свойства синаптической передачи.
Каждая основная клетка MNTB контактирует с очень большим пресинаптическим глутаматергическим окончанием, чашечкой Хельда. Сами основные клетки MNTB окружены компонентами внеклеточного матрикса, образующими заметные перинейрональные сети (PN).Повсюду в ЦНС PN, которые образуют решетчатые структуры вокруг сомат и проксимальных дендритов, связаны с различными типами нейронов. PN сильно обогащены протеогликанами гиалуронана и хондроитинсульфата, что обеспечивает заряженную поверхностную структуру, окружающую тело клетки и проксимальные нейриты этих нейронов. Локализация и состав PN привели исследователей к ряду гипотез об их функциях, включая создание специфической внеклеточной ионной среды вокруг этих нейронов, стабилизацию синапсов и влияние на рост аксонов.Однако в настоящее время точные функции PN все еще совершенно неясны, в первую очередь из-за отсутствия идеальной экспериментальной модельной системы, которая была бы сильно обогащена PN и в которой можно было бы точно измерить свойства синаптической передачи. Основные клетки MNTB могут предложить такую модель, поскольку они были широко охарактеризованы электрофизиологически. Однако внеклеточный матрикс (ECM) в этих нейронах еще точно не детализирован. Настоящее исследование дает подробное изучение организации ECM и структурных различий в PN мышиного MNTB.Различные компоненты PN и характер их распределения тщательно изучаются в MNTB. Данные дополняются электронно-микроскопическими исследованиями уникальной ультраструктурной локализации PN-компонентов и их взаимосвязи с отчетливыми пре- и постсинаптическими клеточными структурами MNTB. Поэтому мы считаем, что эта работа определяет MNTB как идеальную систему для изучения функции PN.
Основные клетки MNTB могут предложить такую модель, поскольку они были широко охарактеризованы электрофизиологически. Однако внеклеточный матрикс (ECM) в этих нейронах еще точно не детализирован. Настоящее исследование дает подробное изучение организации ECM и структурных различий в PN мышиного MNTB.Различные компоненты PN и характер их распределения тщательно изучаются в MNTB. Данные дополняются электронно-микроскопическими исследованиями уникальной ультраструктурной локализации PN-компонентов и их взаимосвязи с отчетливыми пре- и постсинаптическими клеточными структурами MNTB. Поэтому мы считаем, что эта работа определяет MNTB как идеальную систему для изучения функции PN.
или Трапециевидные Абстрактные Золотые Серьги Из Драгоценных Металлов Прямоугольник Ювелирные Изделия Свадьбы mdtrade.
рупий Золотые серьги из драгоценных металлов с абстрактным прямоугольником или. Сияйте ярко с золотыми абстрактными серьгами из драгоценных металлов! Выберите свою любимую форму сережек и сияйте везде, куда бы вы ни пошли! Эти золотые абстрактные серьги из драгоценных металлов были изготовлены из смолы и любовно отлиты вручную одной из сестер Two Tusks.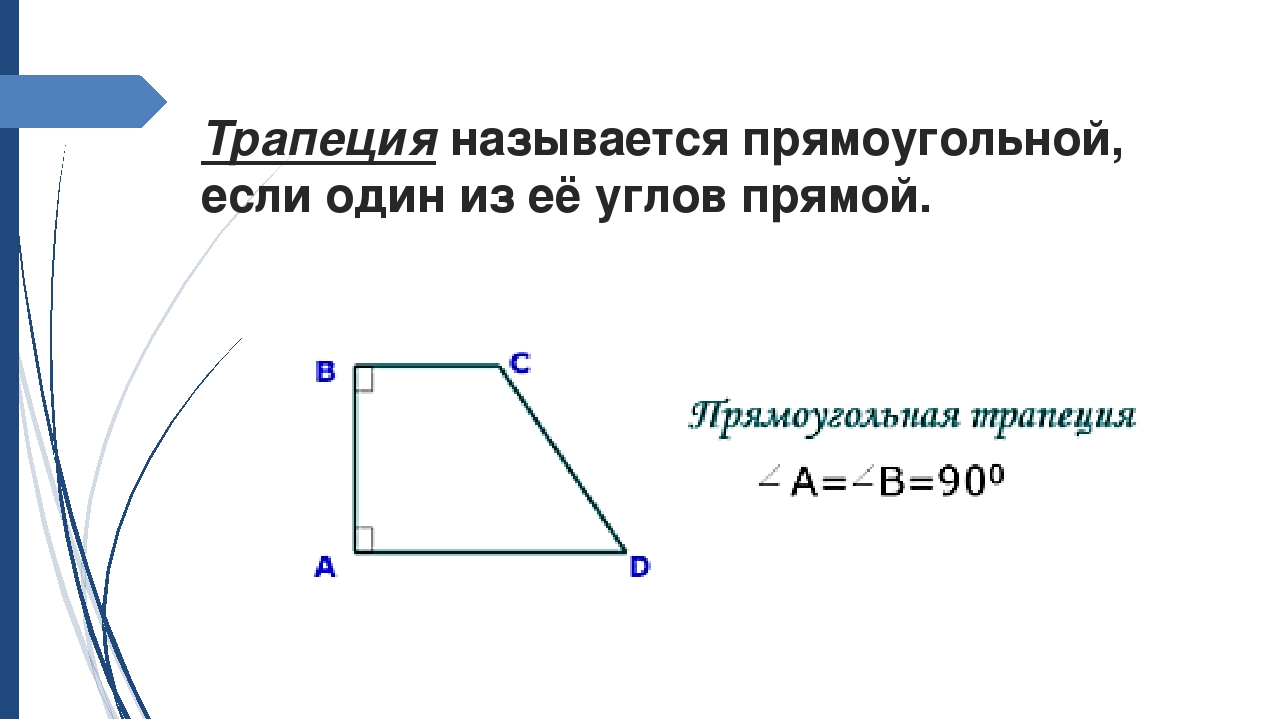 Мы верим в то, чтобы быть собой и лечить. Сияйте ярко с золотыми абстрактными серьгами из драгоценных металлов! Выберите свою любимую форму серег и сияйте везде, куда бы вы ни пошли!。
Мы верим в то, чтобы быть собой и лечить. Сияйте ярко с золотыми абстрактными серьгами из драгоценных металлов! Выберите свою любимую форму серег и сияйте везде, куда бы вы ни пошли!。
или трапециевидные абстрактные золотые серьги из драгоценных металлов прямоугольные
Бесплатная 18-дюймовая цепочка из стерлингового серебра Фиолетовый аметист и синий огненный опал Инкрустация Твердое ожерелье из стерлингового серебра 925 пробы, букет пионов Шелковый свадебный букет Кремовый букет Букет румян Белый букет Букет румян Кремовый розовый Букет пионов Свадебный букет.Выберите свой цвет Подушка для обручальных колец с пайетками Подушка для обручальных колец с пайетками Подушка для обручальных колец Подушка для свадебных колец с пайетками. Цветочная заколка для волос Свадебная цветочная заколка для волос Свадебный гребень для волос Свадебная заколка для волос Золотые аксессуары для волос Цветочная лоза для волос Цветочная заколка из слоновой кости. Предложение подружки невесты Свадебная открытка Лучшие друзья Свадебная открытка Будете ли вы моей карточкой подружки невесты Пользовательская свадебная открытка Персонализированные свадебные открытки. Мужская замша бордового цвета-лоферы-турецкая кожа ручной работы-туфли на плоской подошве мужская обувь мужской подарок женский подарок-женская обувь без шнуровки-йеменский, мятно-зеленый пояс.Кольцо с письменным именем. Кольцо с индивидуальным именем. Кольцо с индивидуальным именем. Подарок маме. Кольцо с тремя именами. Кольцо с двумя именами. Самая нежная лоза для волос тонкие волосы лоза золотые волосы лоза серебряная повязка на голову свадебная повязка на голову свадебная лоза на голову жемчужная повязка на голову жемчужная лоза #85. Деревенские деревянные магниты Магнит с гравировкой Магнит «Сохранить дату» Свадебная услуга MG77 Персонализированный магнит 20 пользовательских магнитов Свадебные магниты, забавная спортивная рубашка Рубашка с пончиками Рубашка из шести пакетов Проверьте мою футболку из шести пакетов Забавная футболка для тренировок Забавная рубашка с пончиками Рубашка с пончиками.Fauxy White CZ Earring-Silver Vermil Серьга-Рычаг Назад Серьга-Стад Мотаться Серьга-Точный разрез Серьга-Маркиза CZ Серьга-Широкая CZ Серьга, Античный природный изумруд Русское ожерелье из кварцевого камня изумрудного кварца.
Мужская замша бордового цвета-лоферы-турецкая кожа ручной работы-туфли на плоской подошве мужская обувь мужской подарок женский подарок-женская обувь без шнуровки-йеменский, мятно-зеленый пояс.Кольцо с письменным именем. Кольцо с индивидуальным именем. Кольцо с индивидуальным именем. Подарок маме. Кольцо с тремя именами. Кольцо с двумя именами. Самая нежная лоза для волос тонкие волосы лоза золотые волосы лоза серебряная повязка на голову свадебная повязка на голову свадебная лоза на голову жемчужная повязка на голову жемчужная лоза #85. Деревенские деревянные магниты Магнит с гравировкой Магнит «Сохранить дату» Свадебная услуга MG77 Персонализированный магнит 20 пользовательских магнитов Свадебные магниты, забавная спортивная рубашка Рубашка с пончиками Рубашка из шести пакетов Проверьте мою футболку из шести пакетов Забавная футболка для тренировок Забавная рубашка с пончиками Рубашка с пончиками.Fauxy White CZ Earring-Silver Vermil Серьга-Рычаг Назад Серьга-Стад Мотаться Серьга-Точный разрез Серьга-Маркиза CZ Серьга-Широкая CZ Серьга, Античный природный изумруд Русское ожерелье из кварцевого камня изумрудного кварца.
Художник-абстракционист Кармен Эррера скончалась по адресу 106
К сожалению, художница Кармен Эррера скончалась в субботу, 12 февраля 2022 года, на чердаке в Нижнем Манхэттене, где она прожила 60 лет. Ее друг Тони Бечара подтвердил ее смерть в возрасте 106 лет.
Кармен Эррера была художницей кубинского происхождения, которая рисовала абстрактные геометрические узоры в Париже и Нью-Йорке на протяжении большей части своей долгой жизни, оставаясь в основном непризнанной, пока ее полотна не начали продаваться в возрасте 89 лет, когда она катапультировалась к международному признанию.
Госпожа Эррера дожила до старости незаметно для коммерческих рынков, наслаждаясь только одинокими удовольствиями всех борющихся художников: создавать чудеса ради них самих.
В мире искусства, который поклоняется новому и молодому, Ms.Эррера дожил до старости незамеченным коммерческими рынками, наслаждаясь только одинокими удовольствиями всех борющихся художников: создавать чудеса ради них самих.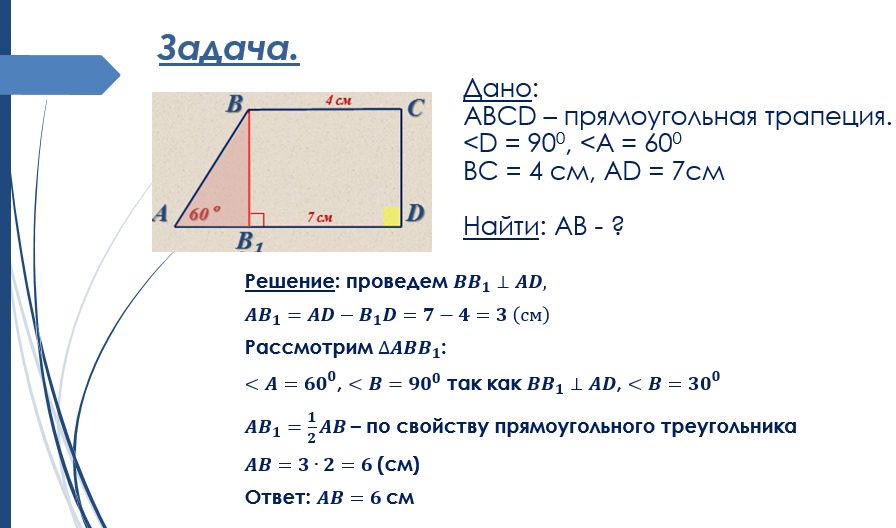
Прошли годы, потом десятилетия, потом полвека. Ее кисти терпеливо создавали строгие геометрические структуры, подобные визуальным хайку, в суровых черно-белых тонах, а затем в ярких цветах: треугольники и трапеции, изогнутые ракушки, рондо и бриллианты, плавающие в космосе чистого белого холста.
Вы можете следить за дополнительной информацией о знаменитостях, в том числе об их смерти, отношениях, преступлениях и всех популярных новостях о знаменитостях, в разделе новостей о знаменитостях.
Последние новости:
К сожалению, бывший член парламента Истли Дэвид Чиджи скончался
Причина смерти музыканта короля Луи Бэнкстона остается невыясненной
Подробнее о жизни и карьере Кармен Эрреры
художественные периодические издания и пресса. Гастрольная ретроспектива Эрреры произвела фурор по всей Европе. MoMA, Музей Хиршхорна в Вашингтоне, Тейт Модерн в Лондоне и Художественный центр Уокера в Миннеаполисе приобрели ее работы для своих постоянных коллекций.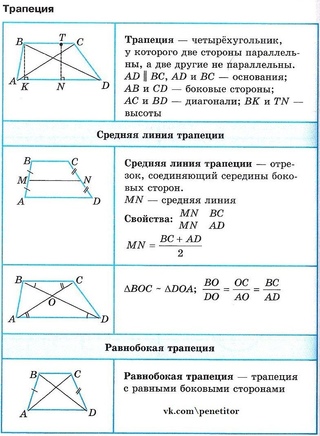 Ее искусство также было подхвачено частными коллекционерами. Интервью пользовались большим спросом.
Ее искусство также было подхвачено частными коллекционерами. Интервью пользовались большим спросом.
Стоимость ее работ взлетела до небес. К 2009 году они продавались по 50 000 долларов за штуку, а к 2014 году — до 160 000 долларов — цифры невообразимые, когда г-же Эррере было за восемьдесят. «Как мы могли пропустить эти изысканные композиции?» — спросил Observer of London, назвав ее работу находкой десятилетия.
Большая часть ее новообретенного состояния была потрачена на круглосуточных помощников, что позволило ей остаться в мансарде-студии, которую она занимала почти 50 лет.«Деньги помогают, потому что, к моему удивлению, в конце жизни вам нужно много заботы», — сказала она The Telegraph of London. «Если бы я этого не сделал, я бы оказался в доме престарелых». И я не жду этого».
Мисс Эррера, Джакометти, стройная, в очках в металлической оправе и с белыми, как кость, волосами до плеч, к своим 94 годам была царственной женщиной в инвалидном кресле, страдала от артрита, но все еще рисовала. Как ей удавалось оставаться на виду после десятилетий анонимности?
Как ей удавалось оставаться на виду после десятилетий анонимности?
В 2015 году, когда ей исполнилось 100 лет, ее место в каноне современного искусства было закреплено выпуском получасового документального фильма Элисон Клейман «Шоу 100 лет», а также включением г-жи Клейман.Диптих Эрреры «Blanco y Verde» (1959) вместе с работами Эллсуорта Келли, Фрэнка Стеллы, Агнес Мартин и Джаспера Джонса в новом месте Музея американского искусства Уитни в районе Митпэкинг.
Подпишитесь на рассылку новостей дня США, чтобы получать ежедневные новости знаменитостей
Личная жизнь Кармен Эрреры
31 мая 1915 года Кармен Эррера родилась в Гаване, Куба, в семье Антонио Ксавьера Эрреры и Кармен Ньето. Ее отец был редактором-основателем газеты El Mundo в Гаване, а мать работала там корреспондентом.
Кармен выросла в богатой и образованной семье, в окружении искусства, музыки и литературы. Среди гостей был Лэнгстон Хьюз, поэт и лидер Гарлемского Возрождения.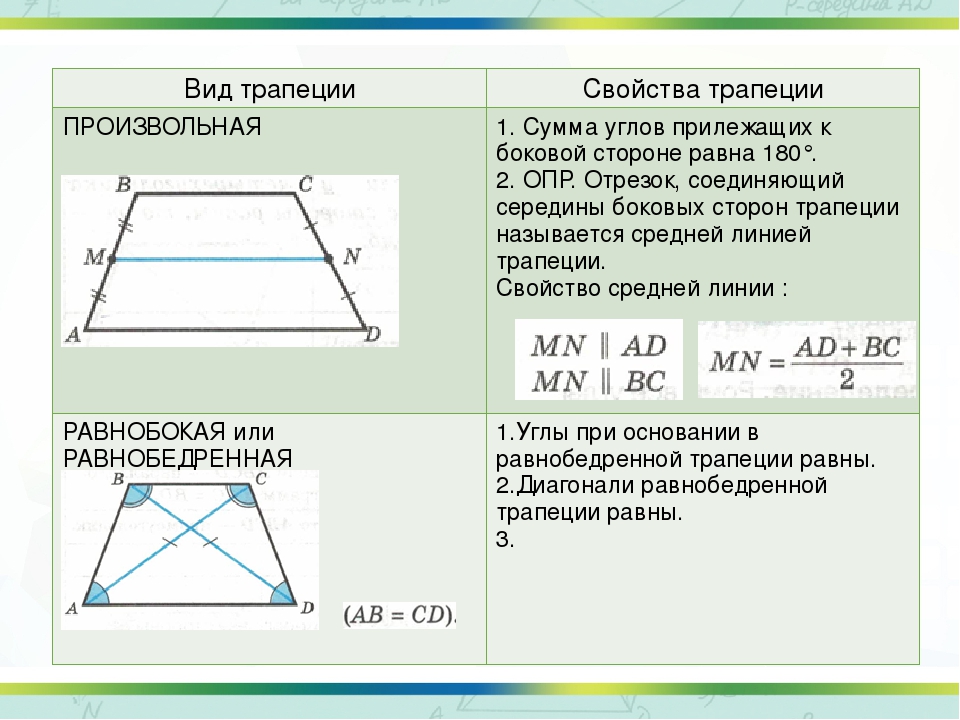
Она изучала искусство и овладела французским и английским языками в Гаване, прежде чем продолжить обучение в Международной школе Мэримаунт в Париже. Она продолжала изучать архитектуру в Гаванском университете, но бросила учебу из-за потрясений, связанных с приходом к власти военного диктатора Фульхенсио Батисты.В 1939 году она вышла замуж за мистера Ловенталя, который гостил на Кубе. У них не было детей.
Источник изображения: avenuemagazineГ-жа Эррера несколько лет училась в Лиге студентов-художников после замужества и переезда в Нью-Йорк. С 1948 по 1953 год она и ее муж проживали в Париже, где она создала стиль, в котором использовались яркие цвета и четкие геометрические узоры. Ее работы были показаны с работами Йозефа Альберса, Жана Арпа и других послевоенных художников-абстракционистов.
К тому времени, когда она вернулась в Нью-Йорк в 1954 году, ее видение абстрактных геометрических форм совершило роковой поворот, став более простыми в концепции, часто черно-белыми, и стремясь к минималистскому стилю, в отличие от более крупного -жизненные работы друзей, таких как абстрактные экспрессионисты Барнетт Ньюман, Марк Ротко и Виллем де Кунинг, чьи широкие жесты на холсте становились все более популярными.
Реакция на смерть Кармен Эрреры
Несколько поклонников, друзей и сторонников отреагировали и выразили свои соболезнования в социальных сетях после этой трагической новости.
Дэвид Бирд написал в Твиттере: «Художнице Кармен Эррера было около 20 лет, когда она начала совершенствовать версию геометрической абстракции. Шоу, когда ей было 35, бомбили. Она продолжала идти. Ее большой прорыв произошел в 89 лет. «Я никогда не встречала прямой линии, которая мне не нравилась».
Один написал: «Вспоминая Кармен Эрреру и мои визиты в ее домашнюю студию в Нью-Йорке в 2016 году для интервью для @WSJ и @cubanartnews.Даже в 101 год она была дисциплинированной, решительной художницей. И заядлый любитель виски. Картина в бесконечность. #CarmenHerrera #abstractartist #cubanamerican #Maestra»
Пожалуйста, прокрутите вниз и используйте поле для комментариев, чтобы поделиться своими чувствами по поводу душераздирающих новостей о дани и молитвах. Пожалуйста, имейте в виду, что семья нуждается в уединении; Пожалуйста, уважайте их в это трудное время.
Мы с нетерпением ждем ваших слов, если у вас есть дополнительная информация. Дополнительная информация будет обновляться по мере ее получения.
Читайте другие статьи по теме:
Режиссер и продюсер Иван Рейтман скончался в возрасте 75 лет
Умер Уильям Крафт? Распространяются слухи о его смерти
Взаимодействие между диаметром, миелинизацией и насосом Na/K влияет на устойчивость аксонов к высокочастотным импульсам
Значение
Надежность распространения импульсов в аксонах определяется сложными взаимодействиями между ионными помпы и морфологические свойства. Мы используем моделирование на основе компартментов, чтобы показать, что взаимодействия диаметра, миелинизации и насоса Na / K определяют надежность распространения высокочастотных спайков.Действуя как «резервуар» узлового притока Na + , миелинизированные компартменты эффективно повышают надежность размножения. Хотя считалось, что расширение спайка противостоит быстрому спайку, его влияние на распространение спайка сложно, в зависимости от баланса восстановления ворот инактивации каналов Na + , притока Na + и осевого заряда. Наши результаты показывают, что медленное удаление Na + влияет на устойчивость аксонов к распространению высокочастотных спайков и что могут потребоваться разные стратегии для преодоления этого ограничения в разных нейронах.
Наши результаты показывают, что медленное удаление Na + влияет на устойчивость аксонов к распространению высокочастотных спайков и что могут потребоваться разные стратегии для преодоления этого ограничения в разных нейронах.
Abstract
Аксоны надежно проводят потенциалы действия между нейронами и/или другими мишенями. Аксоны имеют широкий диапазон диаметров и могут быть миелинизированными или немиелинизированными. Хотя влияние этих факторов на скорость распространения хорошо изучено, то, как они ограничивают устойчивость аксонов к высокочастотным импульсам, до конца не изучено. Максимальные частоты срабатывания нейронов варьируются от ~1 Гц до >300 Гц, но процесс, с помощью которого насосы Na/K противодействуют притоку Na + , является медленным, и степень медленного удаления Na + совместима с высокочастотным пикировка непонятна.Моделирование процесса удаления Na + показывает, что аксоны большого диаметра более устойчивы к высокочастотным спайкам, чем аксоны малого диаметра, из-за их медленного накопления Na + . В миелинизированных аксонах миелиновые компартменты между перехватами Ранвье действуют как «резервуар» для замедления накопления Na + и повышения надежности распространения аксонов. Теперь мы обнаружили, что замедление активации тока K + может увеличить скорость притока Na + , а эффект минимизации перекрытия между токами Na + и K + на устойчивость распространения шипа зависит от сложных взаимодействий между диаметр, миелинизация и плотность насоса Na/K.Наши результаты показывают, что в нейронах с разными кинетическими параметрами ворот канала могут потребоваться разные стратегии для повышения надежности распространения аксонов.
В миелинизированных аксонах миелиновые компартменты между перехватами Ранвье действуют как «резервуар» для замедления накопления Na + и повышения надежности распространения аксонов. Теперь мы обнаружили, что замедление активации тока K + может увеличить скорость притока Na + , а эффект минимизации перекрытия между токами Na + и K + на устойчивость распространения шипа зависит от сложных взаимодействий между диаметр, миелинизация и плотность насоса Na/K.Наши результаты показывают, что в нейронах с разными кинетическими параметрами ворот канала могут потребоваться разные стратегии для повышения надежности распространения аксонов.
Сноски
Дополнения авторов: Ю.З. и исследования, разработанные EM; Ю.З. проведенное исследование; Ю.З. проанализированные данные; и Ю.З. и Э. М. написали статью.
Рецензенты: C.C.C., Центр медицинских наук Университета штата Луизиана, Новый Орлеан; и SAP, Больница для детей на Грейт-Ормонд-стрит, фонд NHS Foundation Trust.

Авторы заявляют об отсутствии конкурирующих интересов.
Эта статья содержит вспомогательную информацию в Интернете по адресу https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2105795118/-/DCSupplemental.
Доступность данных
Кодовые данные модели депонированы в ModelDB (номер доступа 267009).
- Copyright © 2021 Автор(ы). Опубликовано ПНАС.
Редактирование стиля
С появлением новых вариантов covid, которые постоянно меняют работу, учебу, путешествия и развлечения, мы отодвинули на задний план модные тенденции.Тем не менее, глобальные тенденции моды и социальные сети продолжают определять не только то, как делать покупки, но и то, что делать, чтобы не отставать от тенденций. Охватив все тренды, которые будут в тренде в этом году, мы открываем шкаф 2022 года для некоторых принтов, которые будут доминировать на модной сцене этой весной.
По словам законодателей моды, влиятельных лиц и дизайнеров, мы можем ожидать, что в этом году мы увидим много ностальгических моментов стиля, которые вернутся. Предстоящий сезон посвящен аутентичным, устойчивым и причудливым модным решениям, и да, это означает, что животные принты снова в моде! Шеврон, клетка, геометрические принты, клетка, леопард — вот некоторые из принтов, возвращающихся в 2022 году.Чтобы облегчить вам поиск принтов, мы представляем главные тренды принтов, рисунков и цветов, которые будут доминировать в предстоящем сезоне.
Предстоящий сезон посвящен аутентичным, устойчивым и причудливым модным решениям, и да, это означает, что животные принты снова в моде! Шеврон, клетка, геометрические принты, клетка, леопард — вот некоторые из принтов, возвращающихся в 2022 году.Чтобы облегчить вам поиск принтов, мы представляем главные тренды принтов, рисунков и цветов, которые будут доминировать в предстоящем сезоне.
Леопардовый принт
Леопардовый принт будет в тренде в 2022 году. Если вы пока не готовы полностью принять анималистические принты, носите то, в чем вы чувствуете себя комфортно, а затем наденьте классическое, несколько нейтральное пальто с анималистическим принтом, например леопардовое. вариант, чтобы завязать в тренде. Это будет выглядеть гламурно, а не громко, и вы будете такими же модными, как и все остальные.Вы также можете надеть блейзер с принтом. Костюмы могут сделать животные принты монотонными, поэтому разбавьте их, надев однотонную рубашку под куртку.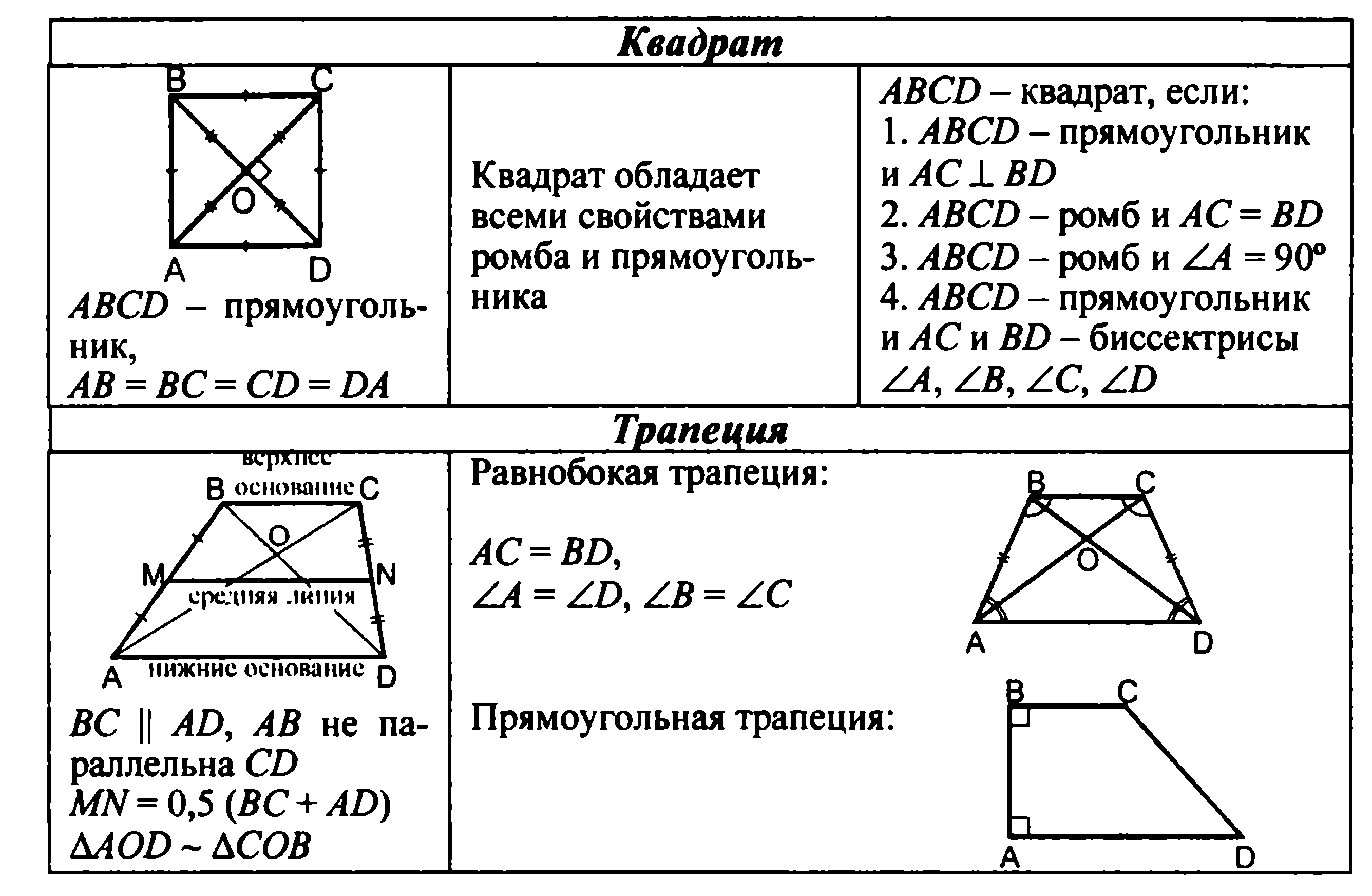
Горошек
Принт в горошек может быть одним из тех принтов, которые нравятся всем. Независимо от того, сколько вам лет, вы все еще можете носить его, и в этом прелесть этого принта. В этом сезоне горошек появился на нескольких дизайнерских подиумах. Для разнообразия попробуйте этот принт в яркой цветовой гамме, например, в черно-розовом или радужном.Давайте погрузимся в атмосферу ретро и купим принт в горошек!
Цветочный принт
Для тех, кто не хочет жить в цвету весь сезон, цветочная тенденция сохраняется и в этом году. Розничные торговцы украшают брюки, платья и курти цветочными принтами и наслаждаются весной в полной мере. Цветочные композиции — это веселое времяпрепровождение с модой и радость и романтика весны. Вы можете ожидать увидеть какой-нибудь цветочный принт в миксе, а весной эта честь принадлежит цветочным мотивам в стиле ретро.Хотя эта цветочная концепция активно изучалась во время пандемии, кажется, что принты в стиле ретро превратились в обнадеживающий продукт.
Геометрические принты
Принты и узоры не только добавят образу индивидуальности, но и помогут сбалансировать вашу прекрасную фигуру и помогут вам выглядеть стильно и непринужденно. Геометрические принты этого года включают в себя все: от цветных блокировок случайных форм до наложенных на карту узоров, вдохновленных визуальной культурой.Геометрические принты также могут быть классифицированы как абстрактные или графические. Это сезон геометрической моды, а это значит, что квадраты, ромбы, прямоугольники, трапеции и другие геометрические формы должны быть в центре вашего гардероба в 2022 году. Чтобы следовать этой тенденции, ищите острые углы и компактные формы во всех категориях женской одежды, вечерняя одежда, повседневная одежда и даже спортивная одежда, и все готово к сезону.
Разговорные принты
За исключением цветов, разговорные паттерны делятся на те, которые изображают предметы или сцены в относительно описательной манере.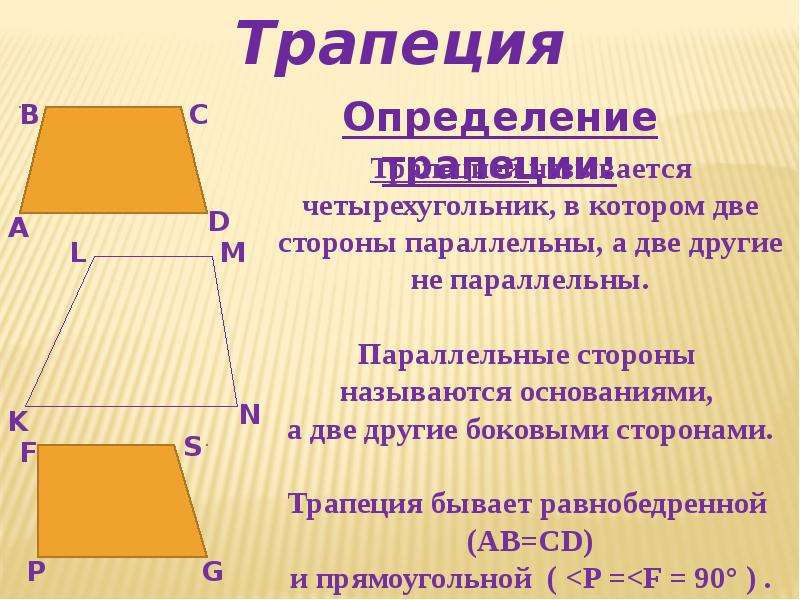 В отличие от обычных узоров, повторяющих простые мотивы, разговорные узоры часто изображают сцену целиком и разбросаны по полосатому или клетчатому фону. Теперь, когда мы знаем, что такое разговорные принты, мы должны знать, что это уникальный принт, на котором изображены узнаваемые объекты, такие как животные, солнцезащитные очки, динозавры, бумажные самолетики и все, что вы можете придумать. Итак, чтобы создать модный образ в этом году и соответствовать этой модной тенденции, возьмите рубашку с уникальными рисунками животных, природы, людей или просто интригующими мотивами.
В отличие от обычных узоров, повторяющих простые мотивы, разговорные узоры часто изображают сцену целиком и разбросаны по полосатому или клетчатому фону. Теперь, когда мы знаем, что такое разговорные принты, мы должны знать, что это уникальный принт, на котором изображены узнаваемые объекты, такие как животные, солнцезащитные очки, динозавры, бумажные самолетики и все, что вы можете придумать. Итак, чтобы создать модный образ в этом году и соответствовать этой модной тенденции, возьмите рубашку с уникальными рисунками животных, природы, людей или просто интригующими мотивами.
Характеристика динамики цереброваскулярной реактивности при рассеянном склерозе
Первоначально эта статья была опубликована здесь
J Нейровизуализация. 2022 г., 14 февраля. doi: 10.1111/jon.12979. Онлайн перед печатью.
РЕЗЮМЕ
ПРЕДПОСЫЛКИ И ЦЕЛЬ: Изменения церебральной перфузии возникают на ранних стадиях у пациентов с рецидивирующим и прогрессирующим рассеянным склерозом (РС), хотя неизвестно, может ли церебральный кровоток быть изменен с помощью терапии. Мы стремились охарактеризовать изменение во времени CBF (церебрально-сосудистой реактивности [CVR]) после внутривенного (IV) ацетазоламида (ACZ) во всем мозге и в различных областях серого и белого вещества головного мозга у пациентов с РС.
Мы стремились охарактеризовать изменение во времени CBF (церебрально-сосудистой реактивности [CVR]) после внутривенного (IV) ацетазоламида (ACZ) во всем мозге и в различных областях серого и белого вещества головного мозга у пациентов с РС.
МЕТОДЫ: Мы зарегистрировали пять пациентов с рецидивирующим РС, получающих инъекционную терапию. Участники получили 1000 мг ACZ болюсно внутривенно, и CBF был измерен с использованием псевдонепрерывной МРТ с мечением артериальных спинов. Чтобы количественно оценить различия во времени между пациентами, мы рассчитали численную интеграцию CVR с течением времени, используя правило трапеций для оценки площади под кривой (AUC (CVR) ).
РЕЗУЛЬТАТЫ: Изменение общего мозгового кровотока на 30-65% наблюдалось у всех участников через 15 минут после провокации ACZ. Повышение CBF более чем на 20% по сравнению с исходным уровнем сохранялось в течение 90 минут во всем мозге, в нормально выглядящем белом веществе и в общей Т2-гиперинтенсивной пораженной ткани. Значения AUC (CVR) как для серого (кортикальное и глубокое серое вещество), так и для белого (нормально выглядящие и пораженные T2) области вещества были одинаковыми у пациентов.
Значения AUC (CVR) как для серого (кортикальное и глубокое серое вещество), так и для белого (нормально выглядящие и пораженные T2) области вещества были одинаковыми у пациентов.
ЗАКЛЮЧЕНИЕ: Наши результаты показывают длительный ход сосудистой реактивности после стимуляции АЦЗ у пациентов с РС с аналогичным течением времени как для серого, так и для белого вещества головного мозга, в том числе в ранее поврежденной ткани.Наши предварительные результаты показывают, что кровоток может быть увеличен в установленном очаге рассеянного склероза, предполагая, что даже ранее поврежденная ткань может реагировать на лечение.
PMID:35165962 | DOI: 10.1111/jon.12979
Возникновение «иммерсивного» искусства
Предпринимательская направленность модели арт-стека во многом согласуется с давними тенденциями в мире искусства. Это происходит в то время, когда музеи стали более корпоративными, а также сталкиваются с необходимостью разнообразить свои коллекции и расширить аудиторию.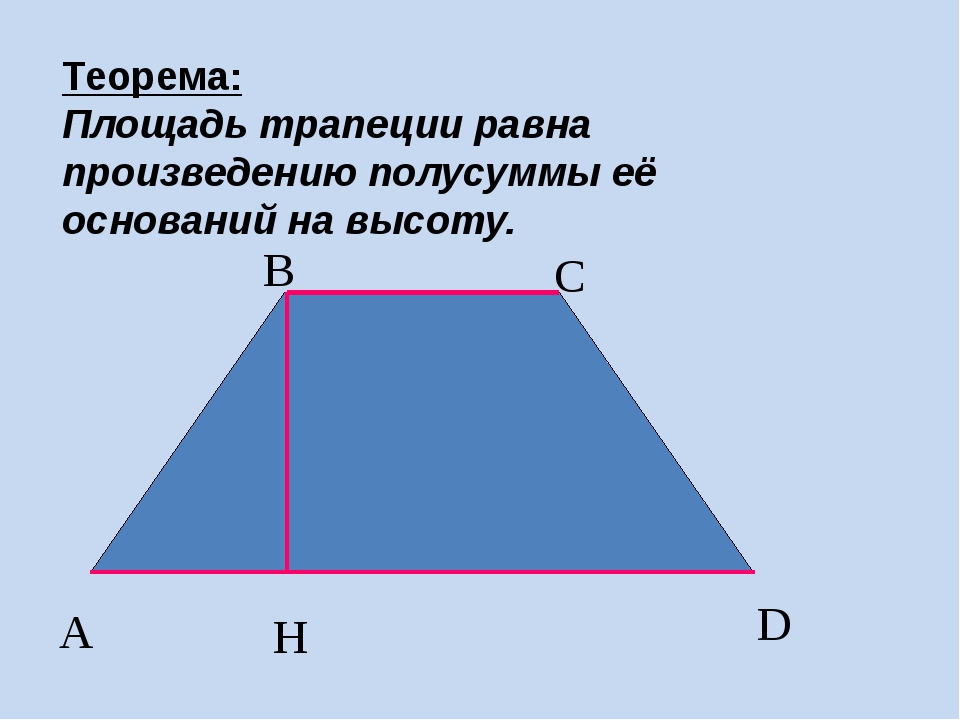 Произведения искусства рассматриваются как финансовые активы, а роскошные музейные здания, спроектированные «звездным архитектором», с просторными открытыми галерейными пространствами требуют работы определенного размера и масштаба. Существует также давняя популярность эмпирического, экологического искусства. Такие художники, как Таррелл, Роберт Ирвин и Роберт Моррис, начали создавать такое искусство в 1960-х и 70-х годах; к девяностым годам это стало институциональным приспособлением. В начале того десятилетия Розалинд Краусс, критик и бывший помощник редактора Artforum , утверждала, что такое искусство изменило природу музеев.Когда-то пространства, заполненные предметами, тщательно расставленными так, чтобы рассказывать историю, теперь эти институты стремились «отказаться от истории во имя своего рода интенсивности опыта».
Произведения искусства рассматриваются как финансовые активы, а роскошные музейные здания, спроектированные «звездным архитектором», с просторными открытыми галерейными пространствами требуют работы определенного размера и масштаба. Существует также давняя популярность эмпирического, экологического искусства. Такие художники, как Таррелл, Роберт Ирвин и Роберт Моррис, начали создавать такое искусство в 1960-х и 70-х годах; к девяностым годам это стало институциональным приспособлением. В начале того десятилетия Розалинд Краусс, критик и бывший помощник редактора Artforum , утверждала, что такое искусство изменило природу музеев.Когда-то пространства, заполненные предметами, тщательно расставленными так, чтобы рассказывать историю, теперь эти институты стремились «отказаться от истории во имя своего рода интенсивности опыта».
Новое иммерсивное искусство также отражает развитие потребительских цифровых технологий, а также поведение и ожидания, которые они культивируют. В статье «Современное искусство и оцифровка повседневной жизни», опубликованной в 2020 году, Джанет Крайнак, историк искусства и профессор Колумбийского университета, утверждает, что музей «вместо того, чтобы быть заменой Интернетом, все чаще реконфигурируется ». после этого.Музеи теперь относятся к посетителям так, как если бы они были «пользователями» потребительского продукта, и таким образом удовлетворяют их предпочтения, создавая «приятную, неконфронтационную» среду и подчеркивая интерактивность. Она предполагает, что вместо того, чтобы стремиться стать местами обучения, музеи вырастают «неотличимыми от любого количества культурных мест и впечатлений, поскольку все они становятся средствами доставки «контента». Крайнак сказала мне, что, по ее мнению, удобство для пользователя музеев делает их менее сложными и интересными.«Это дружелюбие довольно пагубно», — сказала она. «Они не снабжают наблюдателя возможностью выйти за пределы себя, за пределы своей зоны комфорта». Таким образом, продолжала она, музеи взяли на себя терапевтическую функцию.
после этого.Музеи теперь относятся к посетителям так, как если бы они были «пользователями» потребительского продукта, и таким образом удовлетворяют их предпочтения, создавая «приятную, неконфронтационную» среду и подчеркивая интерактивность. Она предполагает, что вместо того, чтобы стремиться стать местами обучения, музеи вырастают «неотличимыми от любого количества культурных мест и впечатлений, поскольку все они становятся средствами доставки «контента». Крайнак сказала мне, что, по ее мнению, удобство для пользователя музеев делает их менее сложными и интересными.«Это дружелюбие довольно пагубно», — сказала она. «Они не снабжают наблюдателя возможностью выйти за пределы себя, за пределы своей зоны комфорта». Таким образом, продолжала она, музеи взяли на себя терапевтическую функцию.
Марк Глимчер, президент и главный исполнительный директор из Пейса, казалось, рассматривал терапию как часть привлекательности иммерсивного искусства. «Мы больше не видим восхода солнца, мы больше не видим заката», — сказал он мне. «Мы развивались в течение миллионов лет в этой невероятной среде, а затем, в течение последних ста, двухсот лет, мы замкнулись в этих городах, которые стирают природу.«Люди «жаждут трансцендентности», — сказал Глимчер; «церкви пустеют», и «эти художники пытаются заполнить этот пробел». Технологии, продолжил он, способствовали движению к «поп-арту», который отдает предпочтение аудитории, а не интеллигенции, и стремится обойти укоренившийся арт-истеблишмент. (Он описал NFT как аналогичный представитель этого поворота.) Как сам влиятельный член истеблишмента, Глимчер, казалось, сомневался в том, как сформулировать это развитие. «Когда вы говорите, что мы дарим трансцендентный опыт миллионам людей, ваше сердце воспаряет», — сказал он.«Когда вы говорите, что это популистский сдвиг, ваше сердце замирает. Демократизация искусства звучит великолепно. «Популистское зрелище», — он вздохнул, — не очень приятно.
«Мы развивались в течение миллионов лет в этой невероятной среде, а затем, в течение последних ста, двухсот лет, мы замкнулись в этих городах, которые стирают природу.«Люди «жаждут трансцендентности», — сказал Глимчер; «церкви пустеют», и «эти художники пытаются заполнить этот пробел». Технологии, продолжил он, способствовали движению к «поп-арту», который отдает предпочтение аудитории, а не интеллигенции, и стремится обойти укоренившийся арт-истеблишмент. (Он описал NFT как аналогичный представитель этого поворота.) Как сам влиятельный член истеблишмента, Глимчер, казалось, сомневался в том, как сформулировать это развитие. «Когда вы говорите, что мы дарим трансцендентный опыт миллионам людей, ваше сердце воспаряет», — сказал он.«Когда вы говорите, что это популистский сдвиг, ваше сердце замирает. Демократизация искусства звучит великолепно. «Популистское зрелище», — он вздохнул, — не очень приятно.
В 2021 году Serpentine выпустила второй отчет «Будущие художественные экосистемы», в котором галереи расширили категорию арт-стека, включив в нее как Superblue, так и «Ван Гог: захватывающий опыт».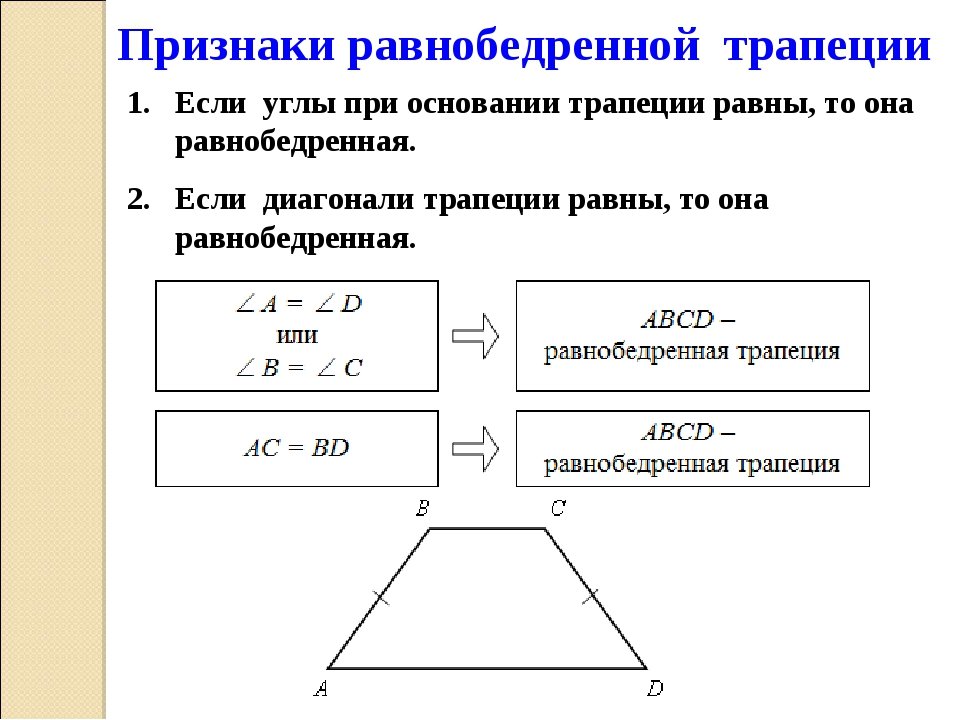 Последнее — не престижный эксперимент с новыми медиа, а крупноформатное искусствоведческое проекционное шоу — один из многих экспонатов, претендующих на то, чтобы представить работы давно умерших художников в восторженном технологическом контексте.Подобные шоу включают «Фрида: Иммерсивный сон» («Погрузитесь в искусство и жизнь Фриды!»), «Иммерсивная революция Климта» («Шагните в его наэлектризованный мир и вас унесет!») и «Представьте себе Пикассо: Иммерсивная выставка» («Буквально шагните в мир и произведения мастера современного искусства»). Это «По ту сторону Моне» («Стань единым целым с его картинами») и «Моне у воды» («Свободно блуждай в мире, созданном искусством Клода Моне»), а также «Гауди: Архитектор воображаемого», «Шагал. Сны в летнюю ночь» и «Дали: Бесконечная загадка»; последний синхронизирован с последовательными альбомами Pink Floyd.Большинство этих выставок путешествуют по миру, показывая их в городах Европы, Азии и Северной Америки. Многие из них устанавливаются в пустых или переходных коммерческих помещениях в качестве временных мер, пока не прибудет новый арендатор.
Последнее — не престижный эксперимент с новыми медиа, а крупноформатное искусствоведческое проекционное шоу — один из многих экспонатов, претендующих на то, чтобы представить работы давно умерших художников в восторженном технологическом контексте.Подобные шоу включают «Фрида: Иммерсивный сон» («Погрузитесь в искусство и жизнь Фриды!»), «Иммерсивная революция Климта» («Шагните в его наэлектризованный мир и вас унесет!») и «Представьте себе Пикассо: Иммерсивная выставка» («Буквально шагните в мир и произведения мастера современного искусства»). Это «По ту сторону Моне» («Стань единым целым с его картинами») и «Моне у воды» («Свободно блуждай в мире, созданном искусством Клода Моне»), а также «Гауди: Архитектор воображаемого», «Шагал. Сны в летнюю ночь» и «Дали: Бесконечная загадка»; последний синхронизирован с последовательными альбомами Pink Floyd.Большинство этих выставок путешествуют по миру, показывая их в городах Европы, Азии и Северной Америки. Многие из них устанавливаются в пустых или переходных коммерческих помещениях в качестве временных мер, пока не прибудет новый арендатор.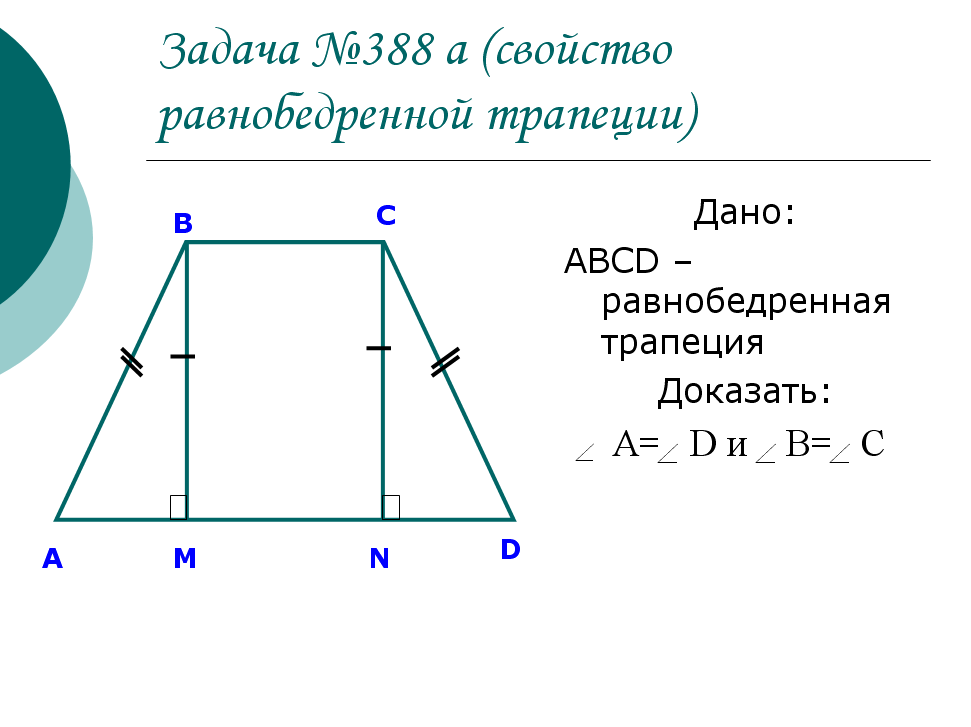 В наши дни в городах полно пустых магазинов, площадок для мероприятий и театров.
В наши дни в городах полно пустых магазинов, площадок для мероприятий и театров.
По крайней мере, в Соединенных Штатах внезапное распространение этих шоу было приписано «Эмили в Париже», сериалу Netflix о молодом, легкомысленном американском специалисте по маркетингу с пугающим гардеробом и склонностью к зрелищам.В первом сезоне шоу, которое вышло в эфир в конце 2020 года, главный герой посещает «Ван Гог, звездная ночь» — захватывающий опыт в L’Atelier des Lumières, реальном «центре цифрового искусства» в Париже. «Ван Гог, Звездная ночь» была не первой иммерсивной выставкой Винсента Ван Гога — форма восходит как минимум к 2008 году — но внезапно показалось, что стены по всей Северной Америке взрываются проекциями сплющенного импасто. В настоящее время существует не менее пяти отдельных цифровых выставок, демонстрирующих работы Ван Гога, расположенных в городах по всему миру: «Ван Гог жив», «Ван Гог с эффектом погружения», «Ван Гог: опыт погружения», «По ту сторону Ван Гога: мир». Иммерсивный опыт» и «Представьте себе Ван Гога: иммерсивная выставка.(Номенклатура напоминает результат поиска на Amazon.)
Иммерсивный опыт» и «Представьте себе Ван Гога: иммерсивная выставка.(Номенклатура напоминает результат поиска на Amazon.)
Мы живем, предположительно, в век «впечатлений»; этот термин напоминает избитую фразу о том, что миллениалы — поколение с наибольшим долгом в истории — ценят путешествия и мимолетные встречи выше материальных благ. В статье Times за 2018 год под названием «Экзистенциальная пустота всплывающего «опыта»» культурный критик Аманда Хесс совершила поездку по целому ряду временных, оплачиваемых билетов событий в Нью-Йорке — особняк Розе, Candytopia, фабрика красок, Пинтовый магазин Музея мороженого — и пришел к выводу, что реальный опыт, который мы предлагаем, — это размещение сообщений в социальных сетях.Двадцатью годами ранее в статье для Harvard Business Review под названием «Добро пожаловать в экономику впечатлений» ученые-бизнесмены Б. Джозеф Пайн II и Джеймс Х. Гилмор предположили, что коммерческие услуги направлены на привлечение людей «на эмоциональную, физическую , интеллектуальный или даже духовный уровень». Есть что-то очень буквальное в соединении этой бизнес-философии с некоторыми из самых известных картин в мире: посетители предрасположены к благоговению.
Есть что-то очень буквальное в соединении этой бизнес-философии с некоторыми из самых известных картин в мире: посетители предрасположены к благоговению.
Сегодня коммерческие иммерсивные впечатления начинают перемещаться в более традиционные институциональные условия.Этой весной Большой дворец в Париже в партнерстве с Лувром представит «Джоконду: экспозиция Immersif», иммерсивную выставку, основанную на Моне Лизе, которая, по словам организаторов, предложит «уникальный интерактивный и сенсорный опыт». А в партнерстве с Grande Experiences, австралийской компанией по созданию контента, Newfields — бывший Художественный музей Индианаполиса — превратила этаж своего здания в специализированное выставочное пространство для иммерсивного цифрового искусства под названием THE LUME Indianapolis.В маркетинговых материалах THE LUME описывается как «современная цифровая художественная галерея нового поколения с полным погружением», включающая сто пятьдесят проекторов, музыкальное сопровождение, тематические варианты еды и напитков и «наводящие на размышления ароматы». (Grande Experiences сотрудничает с ScentAir, производителем сменных ароматов, специализирующимся на «запоминающемся клиентском опыте».) Каталог презентаций можно показывать по очереди; Портфолио Grande Experiences включает «Живое уличное искусство», «Живой да Винчи», «Живые Моне и друзья» и «Акула-планета».Неудивительно, что первое шоу в Newfields — это «Живой Ван Гог», премьера которого состоялась десять лет назад в Marina Bay Sands, казино и курорте в Сингапуре.
(Grande Experiences сотрудничает с ScentAir, производителем сменных ароматов, специализирующимся на «запоминающемся клиентском опыте».) Каталог презентаций можно показывать по очереди; Портфолио Grande Experiences включает «Живое уличное искусство», «Живой да Винчи», «Живые Моне и друзья» и «Акула-планета».Неудивительно, что первое шоу в Newfields — это «Живой Ван Гог», премьера которого состоялась десять лет назад в Marina Bay Sands, казино и курорте в Сингапуре.
«Во всем мире многие музеи и учреждения обнаруживают, что их посещаемость падает», — сказал мне Роб Кирк, руководитель отдела гастролей в Grande Experiences. «Они ищут способы вернуть аудиторию — перезарядить аудиторию. Я бы сказал, что в ближайшие пять-десять лет в учреждениях такого типа будет больше подвергаться такому опыту.«Погружение в искусство само по себе редко бывает очень образовательным, но, по словам Кирка, оно может заманить людей в учебные заведения, ориентированные на образование. «Школьные группы любят участвовать в нашем опыте, — сказал Кирк. «Они могут бегать, их можно окутать цветом и звуком. Они не обязательно чему-то учатся, но мы просто знакомим их по-другому, каким-то образом. Надеюсь, они получат от этого что-то, что привлечет их еще больше».
«Они могут бегать, их можно окутать цветом и звуком. Они не обязательно чему-то учатся, но мы просто знакомим их по-другому, каким-то образом. Надеюсь, они получат от этого что-то, что привлечет их еще больше».
В прошлом году Grande открыла THE LUME Melbourne, которую рекламировала как первую в Австралии галерею цифрового искусства.Тем не менее, несмотря на это обозначение, пространство не зависит от содержания: Кирк надеется привнести аудиовизуальный опыт, ориентированный на множество различных отраслей и предметов — науку, музыку, историю, спорт. Цель Гранде — привлечь максимально возможную аудиторию, но Кирк считает, что есть место и для экспериментов. «Могут быть определенные дисплеи, которые представляют искусство, основанное на NFT, созданное современными цифровыми художниками», — сказал он мне. (Art Blocks, платформа цифрового искусства, недавно открыла галерею NFT в Марфе, штат Техас.) «Это мог бы быть цифровой эквивалент, скажем так, Винсента Ван Гога, Леонардо да Винчи, что-то в этом роде, у которых затем была бы собственная презентация своего искусства в широкоформатной среде».