Площадь прямоугольной трапеции | Треугольники
Площадь прямоугольной трапеции можно найти по любой из формул для площади произвольной трапеции. Некоторые из общих формул могут быть упрощены на основании свойств прямоугольной трапеции.
I. Площадь трапеции равна произведению полусуммы оснований на высоту.
Площадь прямоугольной трапеции ABCD,
AD∥BC,
равна
Так как меньшая боковая сторона прямоугольной трапеции перпендикулярна основаниям, то она равна высоте трапеции, то есть
Если обозначить AD=a, BC=b, CF=AB=h, то формула площади прямоугольной трапеции через основания и высоту (меньшую боковую сторону):
II. Площадь трапеции равна произведению средней линии на высоту.
Если MN — средняя линия прямоугольной трапеции ABCD,
то площадь
Если обозначить среднюю линию MN=m, меньшую боковую сторону AB=h, получим формулу для нахождения площади прямоугольной трапеции через среднюю линию:
III. Площадь трапеции равна половине произведения диагоналей трапеции на синус угла между ними.
Площадь трапеции равна половине произведения диагоналей трапеции на синус угла между ними.
Для прямоугольной
трапеции
ABCD,
AD∥BC,
Так как sin(180º-α)=sin α, то также
Если AC=d1, BD=d2, ∠COD=φ, то
В частности, если диагонали трапеции перпендикулярны, то
VI. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.
Так как в трапецию можно вписать окружность, то
AD+BC=AB+CD=p. Следовательно,
или
Обозначив AD=a, BC=b, CD=c, AB=h=2r, получим формулы площади прямоугольной трапеции через радиус вписанной окружности:
Если в трапецию вписана окружность, площадь трапеции также можно найти как удвоенное произведение радиуса и средней линии. Формула
Если в прямоугольную трапецию вписана окружность, ее площадь равна произведению оснований.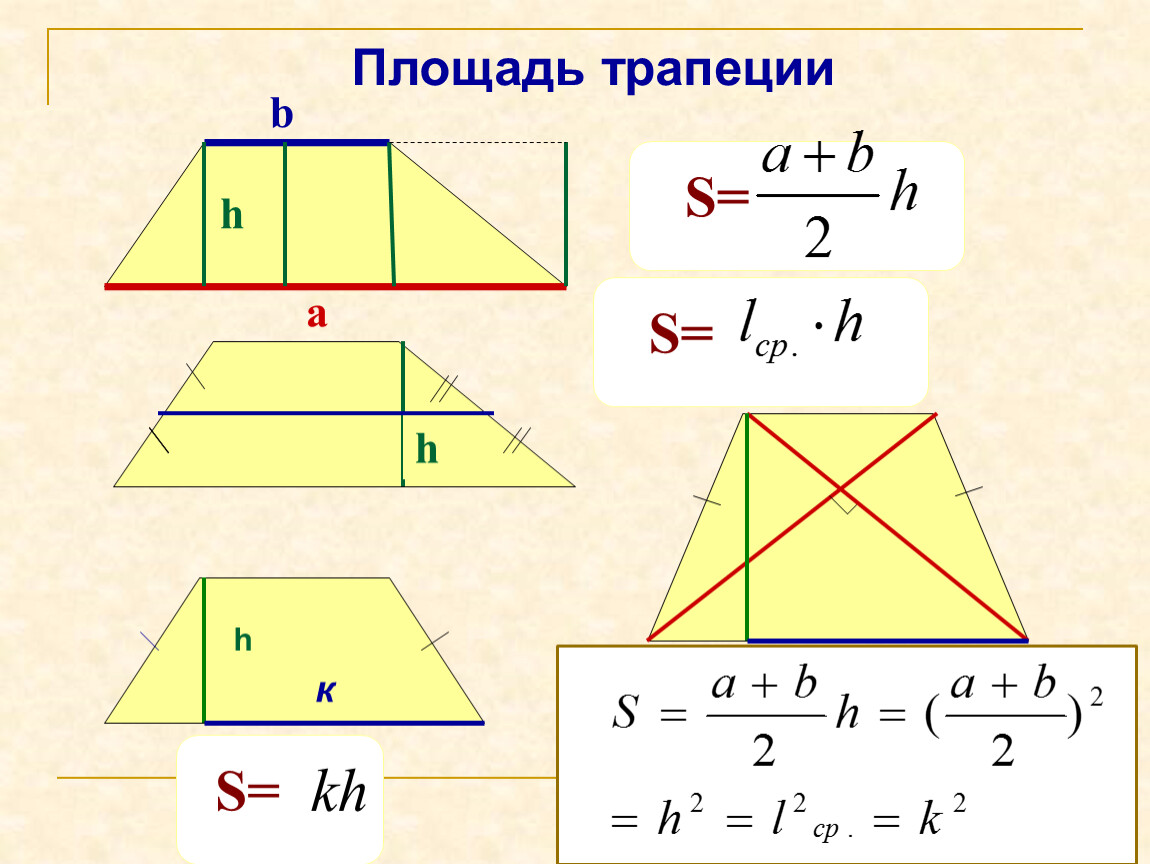
или
Трапеция формулы основания. Трапеция. Свойства трапеции. III. Объяснение нового материала
Трапеция — это четырехугольник, имеющий две параллельные стороны, являющиеся основаниями и две не параллельные стороны, являющиеся боковыми сторонами.
Также встречаются такие названия, как равнобокая или равнобочная .
— это трапеция, у которой углы при боковой стороне прямые.
Элементы трапеции
a, b — основания трапеции (a параллельно b ),
m, n — боковые стороны трапеции,
d 1 , d 2 — диагонали трапеции,
h — высота трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),
MN — средняя линия (отрезок, соединяющий середины боковых сторон).
Площадь трапеции
- Через полусумму оснований a, b и высоту h : S = \frac{a + b}{2}\cdot h
- Через среднюю линию MN и высоту h : S = MN\cdot h
- Через диагонали d 1 , d 2 и угол (\sin \varphi ) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}
Свойства трапеции
Средняя линия трапеции
Средняя линия параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:
MN || a, MN || b, MN = \frac{a + b}{2}
Сумма углов трапеции
Сумма углов трапеции , прилежащих к каждой боковой стороне, равна 180^{\circ} :
\alpha + \beta = 180^{\circ}
\gamma + \delta =180^{\circ}
Равновеликие треугольники трапеции
Равновеликими , то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB
и DOC
, образованные боковыми сторонами. {2}
.
{2}
.
Отношение длин отрезков и оснований
Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:
\frac{OX}{OY} = \frac{BC}{AD}
Это будет являться справедливым и для высоты с самими диагоналями.
ФГКОУ «МКК «Пансион воспитанниц МО РФ»«УТВЕРЖДАЮ»
Руководитель отдельной дисциплины
(математика, информатика и ИКТ)
Ю. В. Крылова _____________
«___» _____________ 2015 г.
«Трапеция и ее свойства »
Методическая разработка
преподавателя математики
Шаталиной Елены Дмитриевны
Рассмотрено и
на заседании ПМО от _______________
Протокол №______
Москва
2015 год
Оглавление
Введение 2
Определения 3
Свойства равнобедренной трапеции 4
Вписанные и описанные окружности 7
Свойства вписанных и описанных трапеций 8
Средние величины в трапеции 12
Свойства произвольной трапеции 15
Признаки трапеции 18
Дополнительные построения в трапеции 20
Площадь трапеции 25
10. Заключение
Заключение
Список используемой литературы
Приложение
Доказательства некоторых свойств трапеции 27
Задачи для самостоятельных работ
Задачи по теме «Трапеция» повышенной сложности
Проверочный тест по теме «Трапеция»
Введение
Данная работа посвящена геометрической фигуре, которая называется трапеция. «Обычная фигура»,- скажете вы, но это не так. Она таит в себе много тайн и загадок, если приглядеться и углубиться в ее изучение, то вы откроете для себя много нового в мире геометрии, задачи, которые раньше не решались, покажутся вам легкими.
Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Трапеция встречается впервые у древнегреческого ученого Посидония (2 век до н.э.). В нашей жизни много разных фигур. В 7 классе мы близко познакомились с треугольником, в 8 классе по школьной программе мы начали изучать трапецию.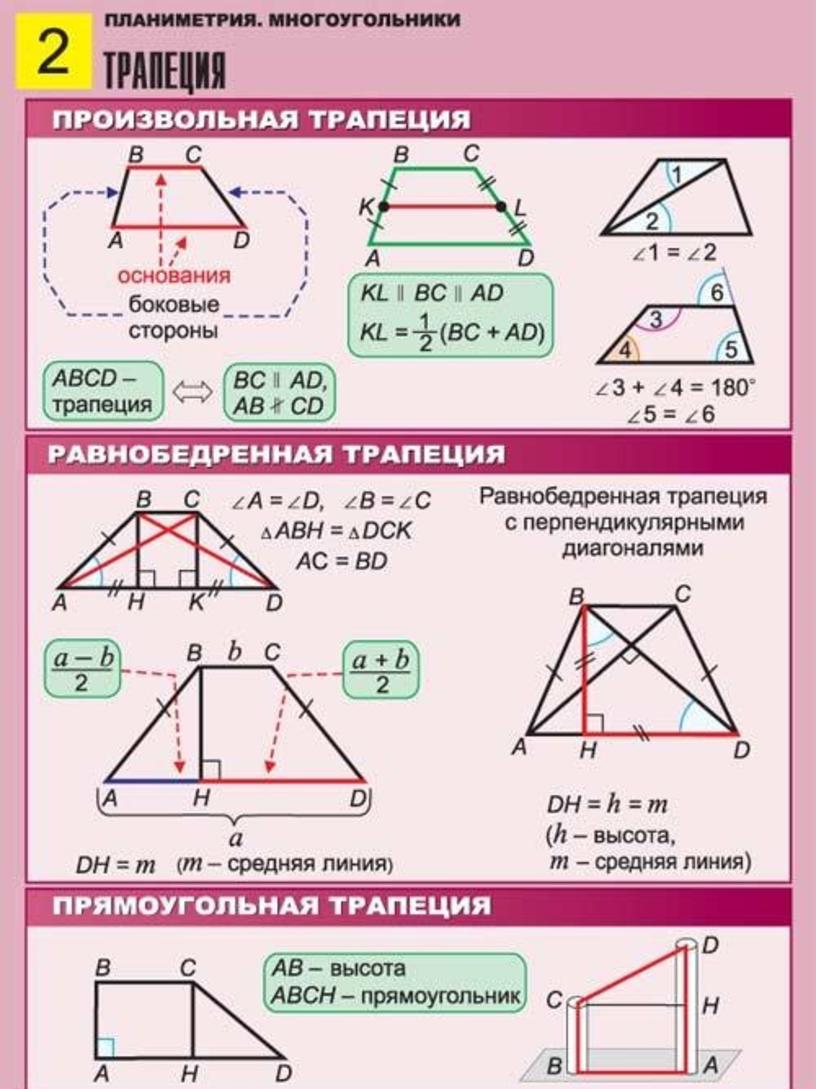 Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.
Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.
В работе рассматриваются свойства знакомые воспитанницам по пройденному материалу в учебнике, но в большей степени неизвестные свойства, которые необходимы для решения сложных задач. Чем больше количество решаемых задач, тем больше вопросов возникает при решении их. Ответом на эти вопросы иногда кажется тайной, узнавая, новые свойства трапеции, необычные приемы решения задач, а также технику дополнительных построений, мы постепенно открываем тайны трапеции. В интернете, если забить в поисковике, о методах решения задач по теме «трапеция» очень мало литературы. В процессе работы над проектом найден большой объем информации, которая поможет воспитанницам в глубоком изучении геометрии.
Трапеция.
Определения
Трапеция
– четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются
основаниями.
Другие две —
боковые стороны
.
Если боковые стороны равны, трапеция называется
равнобедренной
.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Расстояние между основаниями называется высотой трапеции .
2 . Свойства равнобедренной трапеции
3. Диагонали равнобедренной трапеции равны.
4
1
0. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.
3. Вписанная и описанная окружность
Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность.
Е
сли трапеция равнобедренная, то около неё можно описать окружность.
4 . Свойства вписанных и описанных трапеций
2.Если в равнобедренную трапецию можно вписать окружность, то
сумма длин оснований равна сумме длин боковых сторон. Следовательно, длина боковой стороны равна длине средней линии трапеции.
4 . Если в трапецию вписана окружность, то боковые стороны из ее центра видны под углом 90°.
Е сли в трапецию вписана окружность, которая касается одной из боковых сторон, разбивает ее на отрезки m и n, тогда радиус вписанной окружности равен среднему геометрическому этих отрезков.
1
0
. Если окружность построена на меньшем основании трапеции как на диаметре, проходит через середины диагоналей и касается нижнего основания, то углы трапеции 30°, 30°, 150°, 150°.
5. Средние величины в трапеции
Среднее геометрическое
В любой трапеции с основаниями a и b для a > b справедливо неравенство :
b
˂
h
˂
g
˂
m
˂
s
˂
a
6. Свойства произвольной трапеции
Свойства произвольной трапеции
1
. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой.
2. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.
3. Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.
Точка пересечения продолжения боковых сторон произвольной трапеции, точка пересечения ее диагоналей и середин оснований лежат на одной прямой.
5. При пересечении диагоналей произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.
 е. имеют равные площади).
е. имеют равные площади). 6. Сумма квадратов диагоналей произвольной трапеции равна сумме квадратов боковых сторон, сложенной с удвоенным произведением оснований.
d 1 2
7
. В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований d 1 2 — d 2 2 = a 2 – b 2
8 . Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
9. Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам.
7 . Признаки трапеции
8 . Дополнительные построения в трапеции
1. Отрезок, соединяющий середины боковых сторон — средняя линия трапеции.
Отрезок, соединяющий середины боковых сторон — средняя линия трапеции.
2
. Отрезок, параллельный одной из боковых сторон трапеции, один конец которого совпадает с серединой другой боковой стороны, другой принадлежит прямой, содержащей основание.
3
. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции.
4
. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.
5. Высоты трапеции, опущенные из вершин одного основания, высекают на прямой, содержащей другое основание, отрезок, равный первому основанию.
6
. Отрезок, параллельный одной из диагоналей трапеции проводится через вершину – точку, являющуюся концом другой диагонали. В результате получается треугольник с двумя сторонами, равными диагоналям трапеции, и третьей – равной сумме оснований
7
.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции.
8. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, они перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.
9. Биссектриса угла трапеции отсекает равнобедренный треугольник.
1
0. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
1
 Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам. 1
2
. Продолжение боковых сторон трапеции до пересечения дает возможность рассматривать подобные треугольники.
13. Если в равнобедренную трапецию вписана окружность, то проводят высоту трапеции — среднее геометрическое произведения оснований трапеции или удвоенное среднее геометрическое произведения отрезков боковой стороны, на которые она делится точкой касания.
9. Площадь трапеции
1 . Площадь трапеции равна произведению полусуммы оснований на высоту S = ½(a + b ) h или
П
лощадь трапеции равна произведению средней линии трапеции на высоту S = m h .
2. Площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону.
Площадь равнобедренной трапеции с радиусом вписанной окружности равным r и углом при основании α:
10. Заключение
ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ?
Трапеция в спорте: Трапеция — безусловно прогрессивное изобретение человечества. Она предназначена для того, чтобы разгрузить наши руки, сделать хождение на виндсерфере комфортным и легким отдыхом. Хождение на короткой доске вообще не имеет смысла без трапеции, так как без нее невозможно правильно распределить тягу между степсом и ногами и эффективно разогнаться.
Трапеция в моде: Трапеция в одежде была популярна ещё в средние века, в романскую эпоху IX-XI вв. В тот период основу женской одежды составляли туники в пол, к низу туника сильно расширялась, что и создавало эффект трапеции. Возрождение силуэта произошло в 1961-ом году и стало гимном молодости, независимости и утонченности. Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги. Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции.
Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции.
Трапеция в природе: трапеция встречается и в природе. У человека есть трапециевидная мышца, у некоторых людей лицо имеет форму трапеции. Лепестки цветов, созвездия, и конечно же вулкан Килиманджаро тоже имеют форму трапеции.
Трапеция в быту: Трапеция используется и в быту, т.к ее форма практична. Она встречается в таких предметах как: ковш экскаватора, стол, винт, машина.
Трапеция — символ архитектуры инков. Доминирующая стилистическая форма в архитектуре инков проста, но изящна — это трапеция. Она имеет не только функциональное значение, но и строго ограниченное художественное оформление. Трапециевидные дверные проемы, окна, и стенные ниши найдены в постройках всех типов, и в храмах и в менее значительных зданиях более грубых, если можно так выразиться, постройках. Трапеция встречается и в современной архитектуре. Эта форма зданий является необычной, поэтому такие постройки всегда притягивают взгляды прохожих.
Трапеция в технике: Трапеция используется при конструировании деталей в космических технологиях и в авиации. Например, некоторые солнечные батареи космических станций имеют форму трапеции так как имеют большую площадь, значит накапливают больше солнечной эн
В 21 первом веке люди уже практически не задумываются о значении геометрических фигур в их жизни. Их совершенно не волнует какой формы у них стол, очки или телефон. Они просто выбирают ту форму, которая практична. Но именно от формы той или иной вещи может зависеть использование предмета, его предназначение, результат работы. Сегодня мы познакомили вас с одной из величайших достижений человечества- с трапецией. Мы приоткрыли вам дверь в удивительный мир фигур, поведали вам тайны трапеции и показали, что геометрия вокруг нас.
Список используемой литературы
Болотов А.А., Прохоренко В.И., Сафонов В.Ф., Математика Теория и Задачи. Книга 1 Учебное пособие для абитуриентов М.1998 Издательство МЭИ.
Быков А.А, Малышев Г.Ю., ГУВШ факультет довузовской подготовки. Математика. Учебно-методическое пособие 4 часть М2004
Гордин Р.К. Планиметрия. Задачник.
Иванов А.А.,. Иванов А.П, Математика: Пособие для подготовки к ЕГЕ и поступлению в вузы-М: Издательство МФТИ,2003-288с. ISBN 5-89155-188-3
Пиголкина Т.С, Министерство образования и науки РФ федеральное государственное бюджетное образовательное учреждение дополнительного образования детей «ЗФТШ Московского физико-технического института (государственного университета)». Математика. Планиметрия. Задания №2 для 10-ых классов (2012-2013 учебный год).
Пиголкина Т.С., Планиметрия (часть1).Матиматическая Энциклопедия Абитуриента. М., издательство российского открытого университета 1992.
Шарыгин И.Ф.Избранные задачи по геометрии конкурсных экзаменов в ВУЗЫ (1987-1990) Львов Журнал «Квантор» 1991.
Энциклопедия «Аванта плюс», Математика М., Мир энциклопедий Аванта 2009.
Приложение
1. Доказательство некоторых свойств трапеции.
Доказательство некоторых свойств трапеции.
1. Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках K и L . Доказать, что если основания трапеции равны а и b , то длина отрезка KL равна среднему геометрическому оснований трапеции. Доказательство
Пусть О — точка пересечения диагоналей, AD = а, ВС = b . Прямая KL параллельна основанию AD , следовательно, K О ║ AD , треугольники В K О и BAD подобны, поэтому
(1)
(2)
Подставим (2) в (1) , получим KO =
Аналогично LO = Тогда K L = KO + LO =
В о всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжения боковых сторон лежат на одной прямой.
Доказательство: Пусть продолжения боковых сторон пересекаются в точке К. Через точку К и точку О пересечения диагоналей проведём прямую КО.
K
Окажем, что эта прямая делит основания пополам.
Обозначим ВМ = х, МС = у, AN = и, ND = v . Имеем:
∆ ВКМ ~ ∆AKN →
M
x
B
C
Y
∆ MК C ~ ∆NKD → →Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Многоугольник — часть плоскости, ограниченная замкнутой ломаной линией. Углы у многоугольника обозначаются точками вершин ломаной. Вершины углов многоугольника и вершины многоугольника — это совпадающие точки.
Определение. Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны.
Свойства параллелограмма
1. Противолежащие стороны равны.
На рис. 11 AB = CD ; BC = AD .
2. Противолежащие углы равны (два острых и два тупых угла).
На рис. 11 ∠A = ∠C ; ∠B = ∠D .
3 Диагонали (отрезки прямой, соединяющие две противолежащие вершины) пересекаются и точкой пересечения делятся пополам.
На рис. 11 отрезки AO = OC ; BO = OD .
Определение. Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие — нет.
Параллельные стороны называются ее основаниями , а две другие стороны — боковыми сторонами .
Виды трапеций
1. Трапеция , у которой боковые стороны не равны,
называется разносторонней (рис. 12).
2. Трапеция, у которой боковые стороны равны, называется равнобокой (рис. 13).
13).
3. Трапеция, у которой одна боковая сторона составляет прямой угол с основаниями, называется прямоугольной (рис. 14).
Отрезок, соединяющий середины боковых сторон трапеции (рис. 15), называется средней линией трапеции (MN ). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Трапецию можно назвать усеченным треугольником (рис. 17), поэтому и названия трапеций сходны с названиями треугольников (треугольники бывают разносторонние, равнобедренные, прямоугольные).
Площадь параллелограмма и трапеции
Правило. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
В курсе геометрии за 8-й класс подразумевается изучение свойств и признаков выпуклых четырёхугольников. К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.
Определение и виды
В отличие от других четырёхугольников, изучаемых в школьной программе, трапецией принято называть такую фигуру, две противоположные стороны которой параллельны друг другу, а две другие — нет. Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.
Различные виды указаны на рисунке ниже .
На изображении под номером 1 изображена произвольная трапеция. Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.
Важнейшие свойства и формулы
Для описания свойств четырёхугольника принято выделять определённые элементы. В качестве примера можно рассмотреть произвольную трапецию ABCD.
В её состав входят:
- основания BC и AD — две стороны, параллельные по отношению друг к другу;
- боковые стороны AB и CD — два непараллельных элемента;
- диагонали AC и BD — отрезки, соединяющие противоположные вершины фигуры;
- высота трапеции CH — перпендикулярный основаниям отрезок;
- средняя линия EF — линия, соединяющая середины боковых сторон.

Основные свойства элементов
Чтобы решить задачи по геометрии или доказать какие-либо утверждения, наиболее часто используют свойства, которые связывают различные элементы четырёхугольника. Они формулируются следующим образом:
Кроме того, часто полезно знать и применять следующие утверждения:
- Биссектриса, проведённая из произвольного угла, отделяет на основании отрезок, длина которого равна боковой стороне фигуры.
- При проведении диагоналей образуются 4 треугольника; из них 2 треугольника, образованных основаниями и отрезками диагоналей, обладают подобием, а оставшаяся пара имеет одинаковую площадь.
- Через точку пересечения диагоналей O, середины оснований, а также точку, в которой пересекаются продолжения боковых сторон, можно провести прямую.
Вычисление периметра и площади
Периметр рассчитывается как сумма длин всех четырёх сторон (аналогично любой другой геометрической фигуре):
P = AD + BC + AB + CD.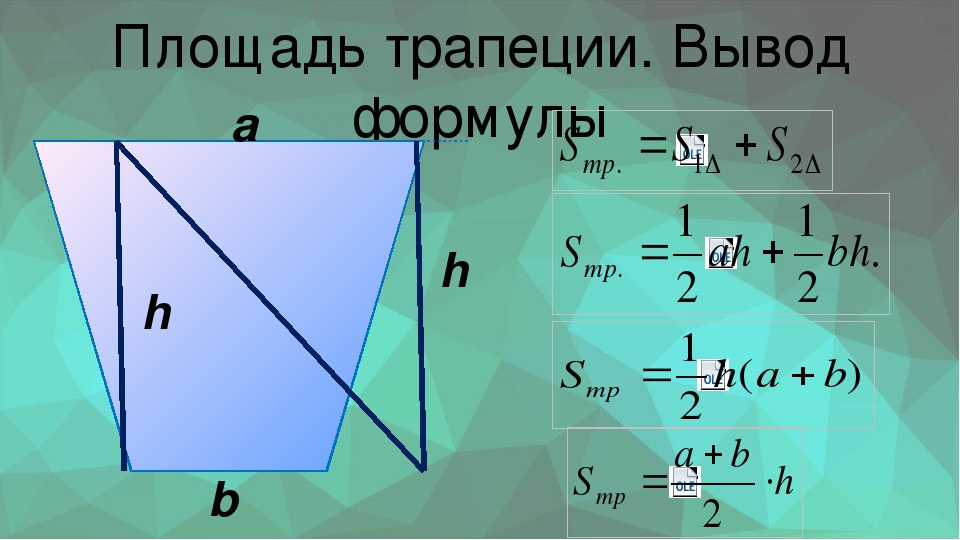
Вписанная и описанная окружность
Окружность возможно описать около трапеции только в том случае, когда боковые стороны четырёхугольника равны.
Чтобы вычислить радиус описанной окружности, необходимо знать длины диагонали, боковой стороны и большего основания. Величина p, используемая в формуле, рассчитывается как полусумма всех вышеперечисленных элементов: p = (a + c + d)/2 .
Для вписанной окружности условие будет следующим: сумма оснований должна совпадать с суммой боковых сторон фигуры. Радиус её можно найти через высоту, и он будет равен r = h/2.
Частные случаи
Рассмотрим часто встречаемый случай — равнобокую (равностороннюю) трапецию. Её признаки — равенство боковых сторон или равенство противолежащих углов. К ней применимы все утверждения , которые характерны для произвольной трапеции. Другие свойства равнобедренной трапеции:
Прямоугольная трапеция встречается в задачах не так часто. Её признаки — наличие двух смежных углов, равных 90 градусов, и наличие боковой стороны, перпендикулярной основаниям.
Высота в таком четырёхугольнике одновременно является одной из его сторон.
Все рассмотренные свойства и формулы обычно используются для решения планиметрических задач. Однако также их приходится применять в некоторых задачах из курса стереометрии, например, при определении площади поверхности усечённой пирамиды, внешне напоминающей объёмную трапецию.
Трапеции Формула — Энциклопедия по машиностроению XXL
Трапеций формула для вычисления определенных интегралов 182 Трапеция — Площадь 106 [c.587]Таким же образом по известным формулам можно вычислить центробежный момент инерции трапеции, моменты инерции сектора, координаты центра масс ГО, его центральные и главные моменты инерции и т. д. [c.46]
Неявный метод Адамса второго порядка точности называют также методом трапеций, ему соответствует формула интегрирования [c.238]
Комбинированные методы и алгоритмы анализа.
 При решении задач анализа в САПР получило достаточно широкое распространение временное комбинирование численных методов. Наиболее известны рассмотренные выше алгоритмы ФНД для численного интегрирования ОДУ, являющиеся алгоритмами комбинирования формул Гира. Другим примером временного комбинирования методов служат циклические алгоритмы неявно-явного интегрирования ОДУ. В этих алгоритмах циклически меняется формула интегрирования — следом за шагом неявного интегрирования следует шаг явного интегрирования. В базовом алгоритме неявно-явного интегрирования используют формулы первого порядка точности — формулы Эйлера. Такой комбинированный алгоритм оказывается реализацией А-устойчивого метода второго порядка точности, повышение точности объясняется взаимной компенсацией локальных методических погрешностей, допущенных на последовательных неявном и явном шагах. Следует отметить, что в качестве результатов интегрирования принимаются только результаты неявных шагов, поэтому в алгоритме комбинированного неявно-явного интегрирования устраняются ложные колебания, присущие наиболее известному методу второго порядка точности — методу трапеций.
При решении задач анализа в САПР получило достаточно широкое распространение временное комбинирование численных методов. Наиболее известны рассмотренные выше алгоритмы ФНД для численного интегрирования ОДУ, являющиеся алгоритмами комбинирования формул Гира. Другим примером временного комбинирования методов служат циклические алгоритмы неявно-явного интегрирования ОДУ. В этих алгоритмах циклически меняется формула интегрирования — следом за шагом неявного интегрирования следует шаг явного интегрирования. В базовом алгоритме неявно-явного интегрирования используют формулы первого порядка точности — формулы Эйлера. Такой комбинированный алгоритм оказывается реализацией А-устойчивого метода второго порядка точности, повышение точности объясняется взаимной компенсацией локальных методических погрешностей, допущенных на последовательных неявном и явном шагах. Следует отметить, что в качестве результатов интегрирования принимаются только результаты неявных шагов, поэтому в алгоритме комбинированного неявно-явного интегрирования устраняются ложные колебания, присущие наиболее известному методу второго порядка точности — методу трапеций.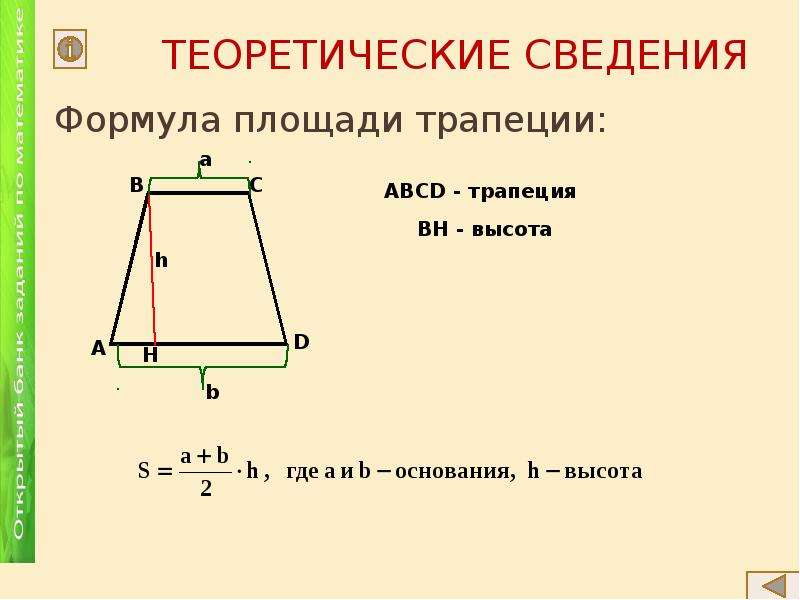 [c.247]
[c.247]Этот же результат можно получить по графику зависимости F от X (рис. 232, б), вычисляя площадь а заштрихованной на чертеже трапеции и учитывая знак работы.) В полученной формуле Xq представляет собой начальное удлинение пружины )io, а Xi — конечное удлинение пружины Xj. Следовательно, [c.212]
Координату центра тяжести площади трапеции определяем по формуле (59.1) [c.144]
На основании этой формулы можно найти следующее правило графического построения центра тяжести площади трапеции иа продолжениях оснований [c.312]
По формуле (6.19) будем иметь для ординаты центра тяжести трапеции [c.139]
Заменив этот интеграл разностным аналогом, например по формуле трапеции, получим для )( -го слоя систему нелинейных алгебраических уравнений [c.62]
Уравнение для поверхностей равного расхода определим из уравнения (2.6.11), для чего вычислим интеграл по формуле трапеций и затем продифференцируем по х
[c. 80]
80]
Продолжая процесс построения этих профилей, получим бесконечную прямолинейную решетку треугольников ). Эта решетка обладает волновым сопротивлением, определяемым по известным формулам для потерь полного давления в системе из двух косых скачков. Заметим, что аналогичным путем можно получить решетку, состоящую из трапеций (рис. 10.61,6), которая имеет большую густоту, чем соответствующая решетка из треугольников. [c.82]
На участке ВС обе эпюры изгибающих моментов линейны. Поэтому интеграл Мора на этом участке можно вычислить по формуле трапеций [c.161]
Конечно, недостаточно привести формулы и дать указания по их применению, необходимы соответствующие упражнения. Применение формулы (8.6) надо показать на, так сказать, классическом примере — определении удлинения бруса постоянного поперечного сечения под действием его собственной силы тяжести. Есть ли смысл требовать от учащихся, как это нередко делается, запоминания окончательного результата Конечно, надо обратить их внимание на то, что удлинение получается вдвое меньшим, чем при действии приложенной к свободному концу бруса сосредоточенной силы, равной его силе тяжести. Если преподаватель имеет склонность к задачам развивающего характера, то целесообразно рассмотреть задачи типа примера 2.9 из учебника [12], либо задачи 1.22, 1.23 из задачника [15]. Конечно, бюджет времени позволит решить только одну задачу указанного типа. Если подобная задача будет задана на дом, то необходимо дать учащимся указание по выбору начала координат (в вершине конуса или в точке пересечения боковых сторон трапеции), иначе они запутаются в интегрировании. Но, повторяем, такие задачи мы отнюдь не относим к числу обязательных.
[c.69]
Есть ли смысл требовать от учащихся, как это нередко делается, запоминания окончательного результата Конечно, надо обратить их внимание на то, что удлинение получается вдвое меньшим, чем при действии приложенной к свободному концу бруса сосредоточенной силы, равной его силе тяжести. Если преподаватель имеет склонность к задачам развивающего характера, то целесообразно рассмотреть задачи типа примера 2.9 из учебника [12], либо задачи 1.22, 1.23 из задачника [15]. Конечно, бюджет времени позволит решить только одну задачу указанного типа. Если подобная задача будет задана на дом, то необходимо дать учащимся указание по выбору начала координат (в вершине конуса или в точке пересечения боковых сторон трапеции), иначе они запутаются в интегрировании. Но, повторяем, такие задачи мы отнюдь не относим к числу обязательных.
[c.69]
По формуле трапеций находим / = 0,09693 и вычисляем производную для сечения с =—0,5932. [c.450]
Применяя формулу трапеций, получаем Су = 1,386-1,149 = 1,592. [c.557]
[c.557]
Производим численное интегрирование, используя формулу трапеций Ух = [c.558]
Для численного интегрирования используем формулу трапеций и находим В == = 0,069. [c.563]
Применяя формулу трапеций, осуществляем численное интегрирование = [c.569]
О -f- 9,238 с шагом Аи = 0,9238. Для численного интегрирования применяем формулу трапеций Ui = 0,1009 =0,1216. По этим данным находим = [c.575]
Формула трапеций. Пусть п=1 тогда Хо=а, Х = Ь, [c.8]
Формула (1.10) называется формулой трапеций (рис. 1.2), На практике эту формулу применяют не ко всему отрезку сразу, а разбивают его на интервалы. Пусть h= Ь—а)1п, Xi = a + ih. Применяя формулу (1.10) к каждому из интервалов Jti+i] и суммируя, получаем ь [c.9]
Уравнения (V.2.14) и (V.2.15) решаются с помощью метода последовательных приближений, при этом интегралы, входящие в эти уравнения, заменяются конечными суммами по формуле численного интегрирования и правилу трапеции с переменным шагом. [c.202]
[c.202]
При заданном значении р (для трапеции) и В/Н (для параболы) используются формулы, связывающие характеристику живого сечения и заданный параметр [например, (16.26) для трапеции]. Найдя по вычисленному значению а соответствующую строку в таблице, принимаем по этой строке все необходимые безразмерные отношения линейных элементов живого сечения к г. и затем находим значения этих элементов Rг. н найдем предварительно). [c.48]
Задача об определении наивыгоднейшего профиля канала может решаться с различных точек зрения. Из различных профилей с заданной площадью поперечного сечения наибольшей пропускной способностью обладает тот, который имеет наименьший смоченный периметр у, так как при этом будет больше гидравлический радиус R, а следовательно, по формуле (61.7) расходная характеристика К. С этой точки зрения наиболее выгодными профилями каналов являются окружность и полуокружность, так как при заданной площади длина окружности короче периметра любого многоугольника той же площади. Однако профили канала в форме круга или полукруга употребляются весьма редко чаще всего профилю придается форма трапеции, причем заложение откосов назначается в зависимости от грунта или способа крепления стенок канала.
[c.238]
Однако профили канала в форме круга или полукруга употребляются весьма редко чаще всего профилю придается форма трапеции, причем заложение откосов назначается в зависимости от грунта или способа крепления стенок канала.
[c.238]
Среди водосливов этого типа особое место занимает водослив, у которого tg а = Д- При этом, как показывают опыты, при Ь >3// компенсируется влияние бокового сжатия, и расход через такой водослив можно рассчитывать по формуле прямоугольного водослива (73.2) с шириной, равной нижнему основанию трапеции. [c.280]
Какой вид имеет формула нормальных напряжений и как расположена нейтральная ось в случае, когда полюс находится на одной из главных центральных осей инерции сечения При каких значениях эксцентриситета продольной силы эпюра нормальных напряжений в поперечном сечении бруса прямоугольного сечения имеет вид прямоугольника, трапеции, треугольника и перекрученной трапеции [c.405]
С помощью формулы (11.
 25) можно перемножать эпюры, имеющие вид перекрученных трапеций при этом произведения ординат, имеющих одинаковые знаки, берутся со знаком плюс, а разные—со знаком минус. В случае, например, показанном на рис. 11.16, в, результат перемножения эпюр в виде перекрученной и обычной трапеций равен (//6) х 2a — 2bd+ad—b ), а в случае, показанном на рис. 11.16, г, равен (1/6) ( — 2ас — — 2bd+ad+b ).
[c.442]
25) можно перемножать эпюры, имеющие вид перекрученных трапеций при этом произведения ординат, имеющих одинаковые знаки, берутся со знаком плюс, а разные—со знаком минус. В случае, например, показанном на рис. 11.16, в, результат перемножения эпюр в виде перекрученной и обычной трапеций равен (//6) х 2a — 2bd+ad—b ), а в случае, показанном на рис. 11.16, г, равен (1/6) ( — 2ас — — 2bd+ad+b ).
[c.442]Формула (11.25) применима и тогда, когда одна или обе перемножаемые эпюры имеют вид треугольника. В этих случаях треугольник рассматривается как трапеция с одной крайней ординатой, равной нулю. [c.442]
Заметим, что методика расчета 7-интеграла вдоль сторон элементов посредством интегрирования по методу трапеций приводит к меньшей точности, чем по формуле (13.15). Для получения же высокой точности интегрирования вдоль сторон необходима методика, обеспечивающая малую погрешность приведения к узлам [c.93]
Подчеркнем, что это первое приближение носит промежуточный характер. Далее для определения окончательного значения вычисляют интеграл (1.45) по формуле трапеций с учетом (1.46)
[c.33]
Далее для определения окончательного значения вычисляют интеграл (1.45) по формуле трапеций с учетом (1.46)
[c.33]
Определим такие границы для погрешностей формул прямоугольников и трапеций, используя разложение функций / (j ) на отрезке [д , в ряд Тейлора около точки Х = (х + Xi+i)/2 и ограничиваясь членами второго порядка [c.61]
Основными параметрами деталей, вычисляемыми при решении метрических задач геометрического моделирования, являются площади, массы, моменты инерции, объемы, центры масс и т. д. Для определения этих параметров исходный геометрический объект (ГО) разбивается иа элементарные геометрические объекты. Например, в плоской с )нгуре выделяются секторы (если в контуре имеются дуги окружности), треугольники и трапеции. Приведем формулы для вычисления метрических параметров некоторых элементарных геометрических объектов. Площадь -го сектора радиуса Г/, [c.45]
Среди неявных методов интегрирования при / = onst применяют методы Эйлера, трапеций, Шихмана.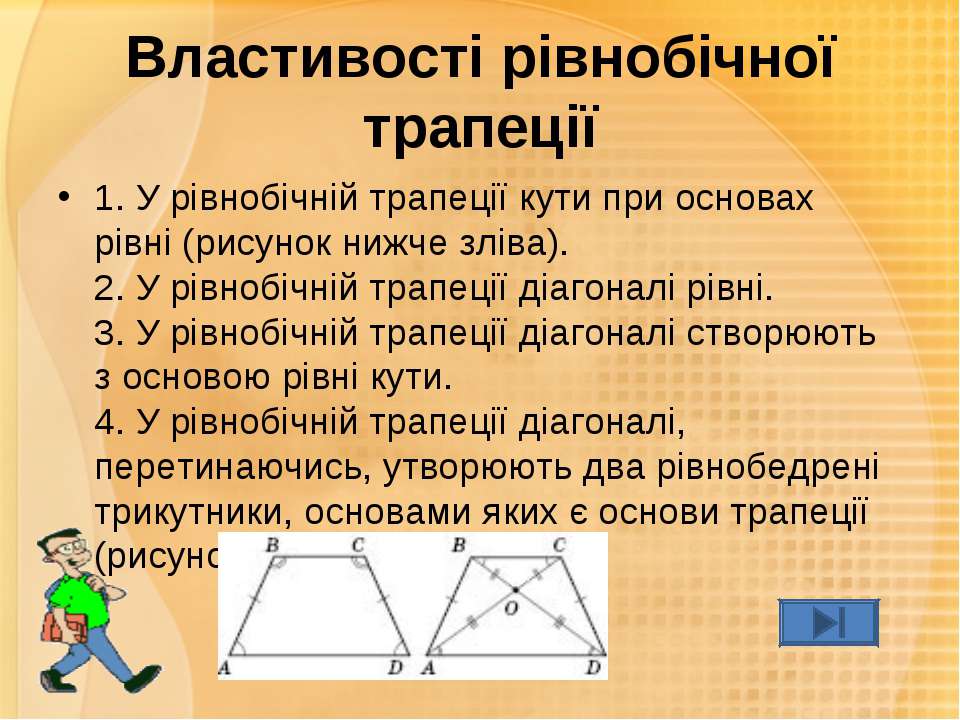 Их положительными особенностями являются А-устойчивость и сравнительно малый объем памяти, требующийся для хранения результатов интегрирования, полученных на предыдущих шагах. Однако метод Эйлера не обеспечивает необходимой точности при анализе переходных процессов в сла-бодемпфированных системах. Метод трапеций в его первоначальном виде (5.9) имеет недостаток, заключающийся в появлении в численном решении ложной колебательной составляющей уже при сравнительно умеренных значениях шагов, поэтому метод трапеций удобен только при принятии мер, устраняющих ложные колебания. Значительное уменьшение ложных колебаний, но при несколько больших погрешностях, дает формула Шихмана.
[c.241]
Их положительными особенностями являются А-устойчивость и сравнительно малый объем памяти, требующийся для хранения результатов интегрирования, полученных на предыдущих шагах. Однако метод Эйлера не обеспечивает необходимой точности при анализе переходных процессов в сла-бодемпфированных системах. Метод трапеций в его первоначальном виде (5.9) имеет недостаток, заключающийся в появлении в численном решении ложной колебательной составляющей уже при сравнительно умеренных значениях шагов, поэтому метод трапеций удобен только при принятии мер, устраняющих ложные колебания. Значительное уменьшение ложных колебаний, но при несколько больших погрешностях, дает формула Шихмана.
[c.241]
Графическое и численное интегрирование. Этот прием применяется в тех случаях, когда функцию нельзя проинтегрировать в аналитической форме или это связано с большим объемом работы. Численное интегрирование ведется по квадратурным формулам Ньюто-на Котеса (правило трапеций, правило Симпсона, правило Уэддля, формула Грегори), формулам Гаусса и Чебышева. [c.111]
[c.111]
В предыдущем параграфе расс.мотрено трение в поступательной паре с плоскими направляющими под действием нагрузки Q, направленной под углом а к нормали. При этом получена формула (7.3) для определения силы трения. Если направляющие ползуна имеют другую форму, нанри.мер трапеции (клина) или цилиндра, то для определения силы трения можно воспользоваться понятием приведенного коэффициента трения / и приведенного угла трения р, которые учитывают форму направляющих. [c.74]
Одно из возможных обобщений наложенной методики состоит в использовании более точных — по сравнению с (5.155) — квадратурных формул, например формулы трапеций (для простоты Aii — Дт = onst) [c.248]
Уравнение для поверхности пленки определим из уравнения (1.5.7), для чего представим интеграл по одной из формул численного интегрирования и затем продифференцируем полученную разностную формулу по х. Если проинтегрировать (1.5.7) по формуле трапеции, то уравнение для определения формы поверхности Гтримет вид
[c. 37]
37]
Этот вывод весьма просто объясняется рис. 3.4. На рисунке дана прямая, характеризующая истинную теплоемкость газа. Требуется найти среднюю теплоемкость в пределах и t . Теплота, расходуемая при нагреве газа от ili до 2. представляется площадью заштрихованной трапеции, а средняя теплоемость в пределах температур и 2 представляет собой среднюю линию трапеции, т. е. полусумму нижнего и верхнего оснований трапеции, что приводит при подсчете к формуле (3.21). [c.37]
Разобьем область, занимаемую телом в плоскости гг в момент времени 1 — кН, квадратной сеткой с шагом А, узловые точки которой обозначим через /А, /А. В следующий момент времени / 4-= (А1) А решение будет получено в узловых точках сетки, смещенной на полшага по г и 2, координаты которой будут (1 + /2)А, (у + /2)А. На такой сетке уравнения (4.13), используя, например, формулу трапеций, можно записать в виде [c.652]
При кручении стержней, имеющих форму равнобедренной трапеции, приближенное значение наибольших касательных напряжений и угла закручивания можно получить, рассчитывая стержень с сечением эквивалентного прямоугольника.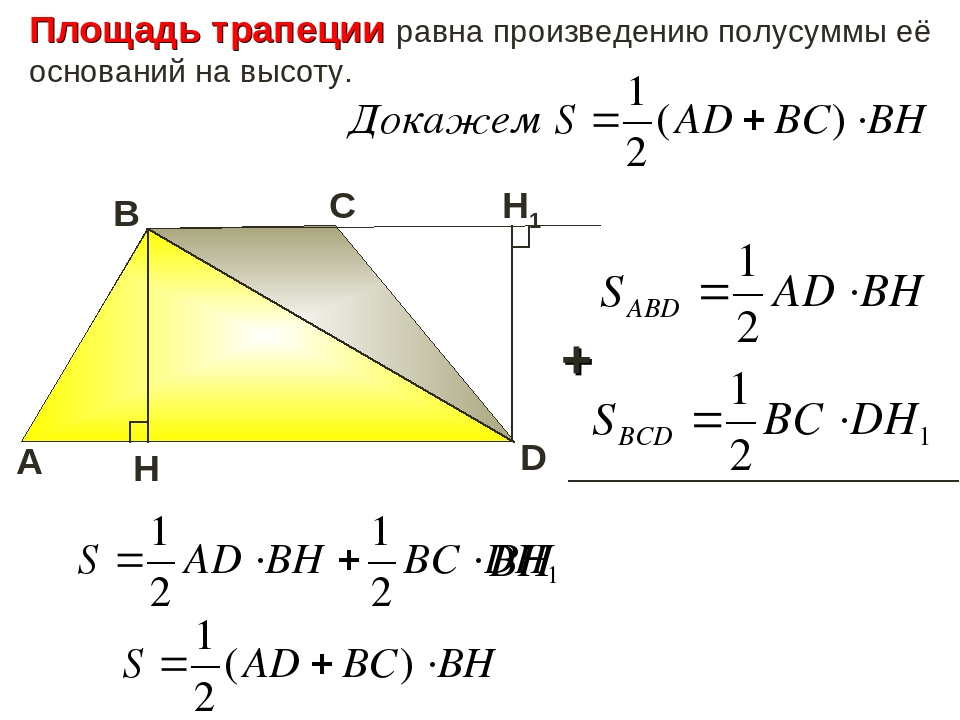 Последний строится следующим образом (рис. 218) из центра тяжести С трапеции опускают перпендикуляры СВ и D на боковые стороны и затем проводят вертикали через точки В w D. Полученный прямоугольник abed и будет тем эквивалентным сечением рассматриваемого трапецеидального стержня, к которому должны быть применены формулы (9.28) — (9.33).
[c.239]
Последний строится следующим образом (рис. 218) из центра тяжести С трапеции опускают перпендикуляры СВ и D на боковые стороны и затем проводят вертикали через точки В w D. Полученный прямоугольник abed и будет тем эквивалентным сечением рассматриваемого трапецеидального стержня, к которому должны быть применены формулы (9.28) — (9.33).
[c.239]
Формула трапеций. При ее получении функция / (х) интерполируется на каждом элементарном отрезке [Xj, Xj+i линейной функцией (рис. 2.10). Тогда [c.60]
Рассчитать площадь трапеции онлайн. Площадь трапеции: формулы и методика вычислений
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними.
 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — отрезок, соединяющий середины боковых сторон.
Данная геометрическая фигура широко распространена в реальной жизни.
Трапеция в реальности
В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
- дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
- ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, основания зданий;
- производство — различные изделия и детали.
При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
P = a + b + c + d,
где a и c – основания фигуры, b и d – ее боковые стороны.
Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.
Примеры из реальной жизни
Платок
Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.
Откосы
К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму.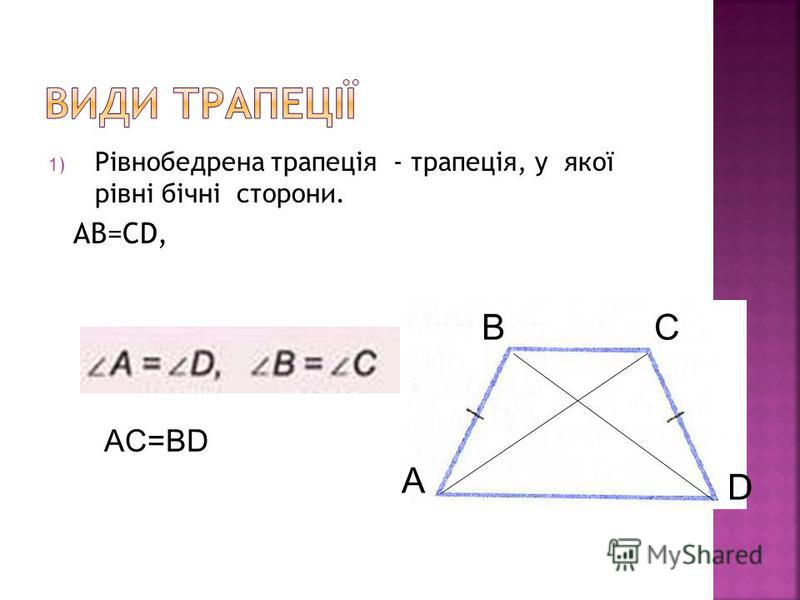 Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.
Заключение
Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
Определяем трапецию
Что это за фигура в целом? Трапецией называют многоугольник из четырех углов с двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под различными углами. Ее параллельные стороны называют основаниями, а для непараллельных сторон применяют наименование «боковые стороны» или «бедра». Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других. Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.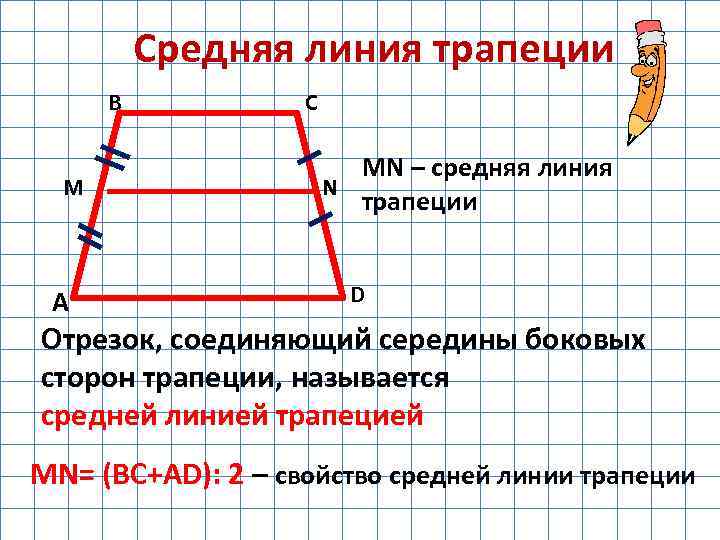
Свойства трапеции
Остановимся коротко на свойствах этой фигуры. Сумма углов, прилегающих к любой боковой стороне, всегда равняется 180°. Надо заметить, что все углы трапеции в сумме составляют 360°. У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком — это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:
Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!
У трапеции всегда можно опустить высоту на основание. Высота — это перпендикуляр, часто обозначаемый символом h, который проведен из любой точки одного основания на другое основание или его продолжение. Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Самые простые формулы площади трапеции
Разберем две самые популярные и простые формулы, с помощью которых находят площадь трапеции. Достаточно умножить высоту на полусумму оснований, чтобы легко найти искомое:
S = h*(a + b)/2.
В этой формуле a, b обозначают основания трапеции, h — высоту. Для удобства восприятия в этой статье знаки умножения отмечены символом (*) в формулах, хотя в официальных справочниках знак умножения обычно опускают.
Рассмотрим пример.
Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?
Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2 = 12. Итак, полусумма равняется 12 см. Теперь полусумму умножаем на высоту: 12*7 = 84. Искомое найдено. Ответ: площадь трапеции равна 84 кв. см.
Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически вытекает из предшествующего понятия средней линии: S=m*h.
Использование диагоналей для вычислений
Другой способ нахождения площади трапеции на самом деле не так уж сложен. Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d 1 d 2) на синус угла между ними:
S = ½ d 1 d 2 sina.
Рассмотрим задачу, которая показывает применение этого способа. Дано: трапеция с длиной диагоналей равной соответственно 8 и 13 см. Угол a между диагоналями равняется 30°. Найти площадь трапеции.
Решение. Используя вышеприведенную формулу, легко вычислить требуемое. Как известно, sin 30° составляет 0,5. Следовательно, S = 8*13*0,5=52. Ответ: площадь равна 52 кв. см.
Ищем площадь равнобокой трапеции
Трапеция может быть равнобокой (равнобедренной). Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок. Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Какие же есть методики вычисления площади такой фигуры? Нижеприведенный способ потребует больших вычислений. Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор. Вот эта формула:
S = c *sin a *(a — c *cos a ),
где с — боковое бедро, a — угол при нижнем основании.
Равнобокая трапеция обладает диагоналями одинаковой длины. Верно и обратное утверждение: если у трапеции диагонали равны, то она является равнобедренной. Отсюда следующая формула, помогающая найти площадь трапеции — полупроизведение квадрата диагоналей на синус угла между ними: S = ½ d 2 sina.
Находим площадь прямоугольной трапеции
Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Применяем смекалку
Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.
Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.
Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Используем формулу Пика
Напоследок приведем еще одну оригинальную формулу, помогающую искать площадь трапеции. Она называется формулой Пика. Ею удобно пользоваться, когда трапеция нарисована на клетчатой бумаге. Подобные задачи часто встречаются в материалах ГИА. Выглядит она следующим образом:
S = M/2 + N — 1,
в этой формуле M — количество узлов, т.е. пересечений линий фигуры с линиями клетки на границах трапеции (оранжевые точки на рисунке), N — количество узлов внутри фигуры (синие точки). Удобнее всего пользоваться ею при нахождении площади неправильного многоугольника. Тем не менее, чем больше арсенал используемых методик, тем меньше ошибок и лучше результаты.
Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.
И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.
- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Формула вычисления высоты трапеции. Площадь трапеции: формулы и методика вычислений
На простой вопрос «Как найти высоту трапеции?» существует несколько ответов, и все потому, что могут быть даны разные исходные величины. Поэтому и формулы будут различаться.
Эти формулы можно запомнить, но они несложно выводятся. Нужно только применять ранее изученные теоремы.
Принятые в формулах обозначения
Во всех приведенных ниже математических записях верны такие прочтения букв.
В исходных данных: все стороны
Для того чтобы найти высоту трапеции в общем случае потребуется воспользоваться такой формулой:
н = √(с 2 — (((а — в) 2 + с 2 — d 2)/(2(а — в))) 2). Номер 1.
Не самая короткая, но и встречается в задачах достаточно редко. Обычно можно воспользоваться другими данными.
Обычно можно воспользоваться другими данными.
Формула, которая подскажет, как найти высоту равнобедренной трапеции в той же ситуации, гораздо короче:
н = √(с 2 — (а — в) 2 /4). Номер 2.
В задаче даны: боковые стороны и углы при нижнем основании
Принимают, что угол α прилежит к боковой стороне с обозначением «с», соответственно угол β к стороне d. Тогда формула для того, как найти высоту трапеции, в общем виде будет такой:
н = с * sin α= d * sin β. Номер 3.
Если фигура равнобедренная, то можно воспользоваться таким вариантом:
н = с * sin α= ((а — в) / 2) * tg α. Номер 4.
Известны: диагонали и углы между ними
Обычно к этим данным присоединяются еще известные величины. Например, основания или средняя линия. Если даны основания, то для ответа на вопрос, как найти высоту трапеции, пригодится такая формула:
н = (d 1 * d 2 * sin γ) / (а + в) или н = (d 1 * d 2 * sin δ) / (а + в). Номер 5.
Это для общего вида фигуры. Если дана равнобедренная, то запись преобразится так:
Если дана равнобедренная, то запись преобразится так:
н = (d 1 2 * sin γ) / (а + в) или н = (d 1 2 * sin δ) / (а + в). Номер 6.
Когда в задаче идет речь о средней линии трапеции, то формулы для поиска ее высоты становятся такими:
н = (d 1 * d 2 * sin γ) / 2m или н = (d 1 * d 2 * sin δ) / 2m. Номер 5а.
н = (d 1 2 * sin γ) / 2m или н = (d 1 2 * sin δ) / 2m. Номер 6а.
Среди известных величин: площадь с основаниями или средней линией
Это, пожалуй, самые короткие и простые формулы того, как найти высоту трапеции. Для произвольной фигуры она будет такой:
н = 2S / (а + в). Номер 7.
Она же, но с известной средней линией:
н = S / m. Номер 7а.
Как ни странно, но для равнобедренной трапеции формулы будут выглядеть так же.
Задачи
№1. На определение углов при нижнем основании трапеции.
Условие. Дана равнобедренная трапеция, боковая сторона которой 5 см. Ее основания равны 6 и 12 см. Требуется найти синус острого угла.
Требуется найти синус острого угла.
Решение. Для удобства следует ввести обозначение. Пусть левая нижняя вершина будет А, все остальные по часовой стрелке: В, С, Д. Таким образом, нижнее основание будет обозначено АД, верхнее — ВС.
Нужно провести высоты из вершин В и С. Точки, которые укажут концы высот будут обозначены Н 1 и Н 2 , соответственно. Поскольку в фигуре ВСН 1 Н 2 все углы прямые, то она является прямоугольником. Это означает, что отрезок Н 1 Н 2 равен 6 см.
Теперь нужно рассмотреть два треугольника. Они равны, так как являются прямоугольными с одинаковыми гипотенузами и вертикальными катетами. Отсюда следует, что и меньшие катеты у них равны. Поэтому их можно определить как частное от разности. Последняя получится от вычитания из нижнего основания верхнего. Делиться оно будет на 2. То есть 12 — 6 нужно поделить на 2. АН 1 = Н 2 Д = 3 (см).
Теперь из теоремы Пифагора нужно найти высоту трапеции. Она необходима для нахождения синуса угла. ВН 1 = √(5 2 — 3 2) = 4 (см).
Воспользовавшись знанием о том, как находится синус острого угла в треугольнике с прямым углом, можно записать такое выражение: sin α= ВН 1 / АВ = 0,8.
Ответ. Искомый синус равен 0,8.
№2. На нахождение высоты трапеции по известному тангенсу.
Условие. У равнобедренной трапеции нужно вычислить высоту. Известно, что ее основания равны 15 и 28 см. Дан тангенс острого угла: 11/13.
Решение. Обозначение вершин такое же, как в предыдущей задаче. Снова нужно провести две высоты из верхних углов. По аналогии с решением первой задачи нужно найти АН 1 = Н 2 Д, которые определятся как разность 28 и 15, деленная на два. После подсчетов получается: 6,5 см.
Поскольку тангенс — это отношение двух катетов, то можно записать такое равенство: tg α= АН 1 / ВН 1 . Причем это отношение равно 11/13 (по условию). Так как АН 1 известен, то можно вычислить высоту: ВН 1 = (11 * 6,5) / 13. Простые расчеты дают результат в 5,5 см.
Ответ. Искомая высота равна 5,5 см.
№3. На вычисление высоты по известным диагоналям.
Условие. О трапеции известно, что ее диагонали равны 13 и 3 см. Нужно узнать ее высоту, если сумма оснований составляет 14 см.
Решение. Пусть обозначение фигуры будет таким же, как раньше. Предположим, что АС — меньшая диагональ. Из вершины С нужно провести искомую высоту и обозначить ее СН.
Теперь потребуется выполнить дополнительное построение. Из угла С нужно провести прямую, параллельную большей диагонали и найти точку ее пересечения с продолжением стороны АД. Это будет Д 1 . Получилась новая трапеция, внутри которой начерчен треугольник АСД 1 . Он-то и нужен для дальнейшего решения задачи.
Искомая высота окажется еще и ей же в треугольнике. Поэтому можно воспользоваться формулами, изученными в другой теме. Высота треугольника определяется как произведение числа 2 и площади, деленное на сторону, к которой она проведена. А сторона оказывается равна сумме оснований исходной трапеции. Это исходит из правила, по которому выполнено дополнительное построение.
В рассматриваемом треугольнике все стороны известны. Для удобства введем обозначения х = 3 см, у = 13 см, z = 14 см.
Теперь можно сосчитать площадь, воспользовавшись теоремой Герона. Полупериметр будет равен р = (х + у + z)/ 2 = (3 + 13 + 14) / 2 = 15 (см). Тогда формула для площади после подстановки значений будет выглядеть так: S = √(15 * (15 — 3) * (15 — 13) * (15 — 14)) = 6 √10 (см 2).
Ответ. Высота равна 6√10 / 7 см.
№4. Для поиска высоты по сторонам.
Условие. Дана трапеция, три стороны которой равны 10 см, а четвертая 24 см. Нужно узнать ее высоту.
Решение. Поскольку фигура равнобедренная, то потребуется формула под номером 2. В нее нужно просто подставить все значения и сосчитать. Это будет выглядеть так:
н = √(10 2 — (10 — 24) 2 /4) = √51 (см).
Ответ. н = √51 см.
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет.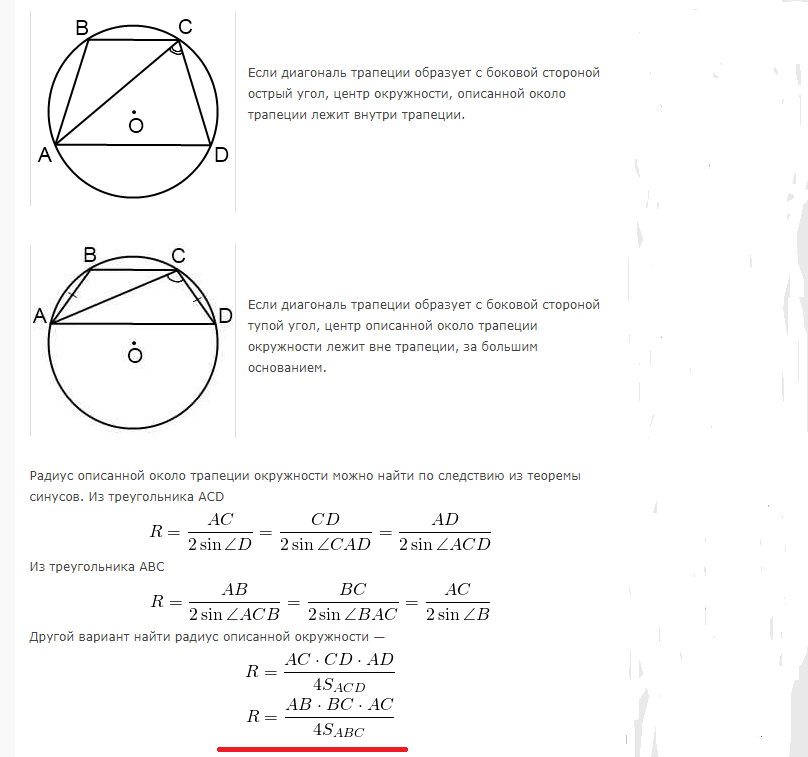 Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними.
 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника .
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда
Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике : Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .
(S) трапеции, начните вычисление высоты (h) с нахождения полусуммы длин параллельных сторон: (a+b)/2. Затем на полученное значение разделите площадь — результат и будет искомой величиной: h = S/((a+b)/2) = 2*S/(a+b).
Зная длину средней линии (m) и площадь (S) можно упростить формулу из предыдущего шага. По определению средняя линия трапеции равна полусумме ее оснований, поэтому для вычисления высоты (h) фигуры просто разделите площадь на длину средней линии: h = S/m.
Можно определить высоту (h) такого и в том случае, если даны только длина одной из боковых сторон (с) и угол (α), образуемый ей и длинным основанием. В этом случае следует рассмотреть , образуемый этой стороной, высотой и коротким отрезком основания, который отсекает опущенная на него высота. Этот треугольник будет прямоугольным, известная сторона будет в нем гипотенузой, а высота — катетом. Отношение длин и гипотенузы равно противолежащего катету угла, поэтому для вычисления высоты трапеции умножьте известную длину стороны на синус известного угла: h = с*sin(α).
Такой же треугольник стоит рассмотреть и если даны длина боковой стороны (с) и величина угла (β) между ней и другим (коротким) основанием. В этом случае величина угла между боковой стороной (гипотенузой) и высотой (катетом) будет на 90° меньше известного из условий угла: β-90°. Так как отношение длин катета и гипотенузы равно косинусу угла между ними, то высоту трапеции вычислите умножением косинуса уменьшенного на 90° угла на длину боковой стороны: h = с*cos(β-90°).
Если вписана окружность известного радиуса (r), вычисления высоты (h) будет очень проста и не потребует никаких других параметров. Такая окружность по определению должна каждого из оснований только одной точкой и эти точки будут лежать на одной линии с центром . Это значит, что расстояние между ними будет равно диаметру (удвоенному радиусу), проведенному перпендикулярно основаниям, то есть совпадающим с высотой трапеции: h=2*r.
Трапецией считается такой четырехугольник, у которого две стороны параллельны, а две другие нет. Высотой трапеции называется отрезок, проведенный перпендикулярно между двумя параллельными прямыми. В зависимости от исходных данных ее можно вычислить по-разному.
Высотой трапеции называется отрезок, проведенный перпендикулярно между двумя параллельными прямыми. В зависимости от исходных данных ее можно вычислить по-разному.
Вам понадобится
- Знание сторон, оснований, средней линии трапеции, а так же, опционально, ее площадь и/или периметр.
Инструкция
Допустим, имеется трапеция с теми же данными, что и на рисунке 1. Проведем 2 высоты, получим , у которого 2 меньшие стороны катетами прямоугольных треугольников. Обозначим меньший катит за x. Он находится
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу.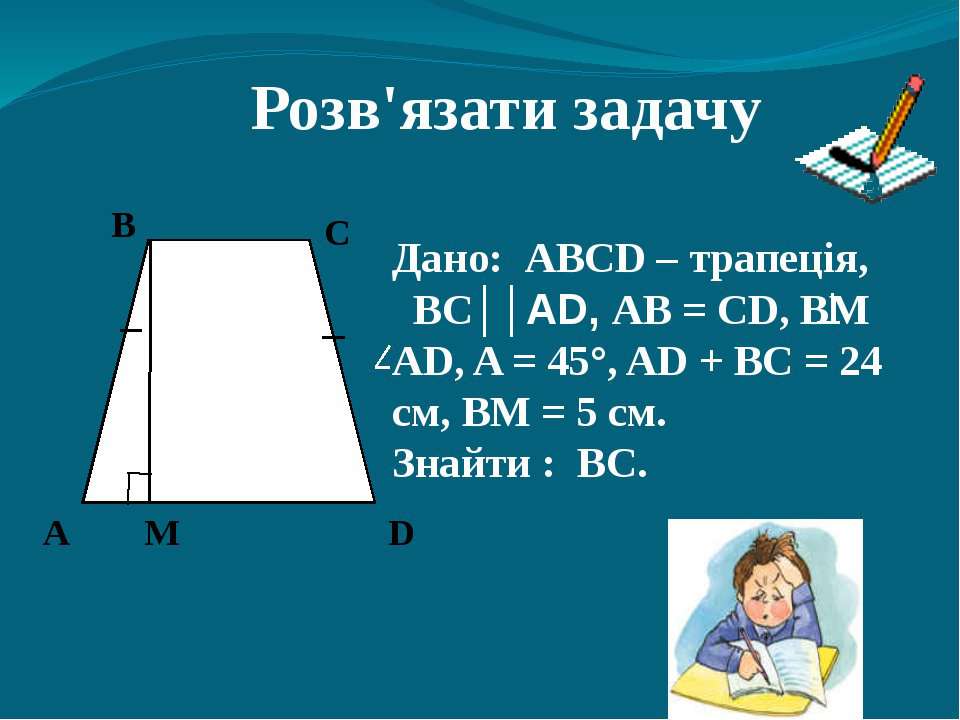 На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Формула итераций метода трапеций и анализ итерационного процесса
В этой статье используются следующие примеры вопросов:
Код Matlab, используемый в этой статье для решения проблемы, выглядит следующим образом:
1. Файл основной функции, имя файла main.m
%% основная функция
% Инициализация
clc;
clear;
h = 0. 02;
n = 5;
init = 1;
for i = 1: (n+1)
x(i) = h * (i-1);
end
% Трапециевидный метод
trapezoid = trapezoidMethod(x, n, h, init);
plot(x, trapezoid,'g');
hold on;
02;
n = 5;
init = 1;
for i = 1: (n+1)
x(i) = h * (i-1);
end
% Трапециевидный метод
trapezoid = trapezoidMethod(x, n, h, init);
plot(x, trapezoid,'g');
hold on;
2. Файл подфункции, имя файла trapezoidMethod.m
%% Трапециевидный метод
function result = trapezoidMethod(x, n, h, init)
% Без поправки к исходному значению
for k = 1: n+1
y(1, k) = init;
end
% Метод Эйлера получает начальное значение первого столбца
for i = 1: n
y(i+1, 1) = y(i) + h * f_xy(x(i), y(i));
end
% Метод трапеции повторяется на основе предыдущего значения столбца
for k = 1: n
for i = 1: n
a = f_xy(x(i), y(i,k));
b = f_xy(x(i+1), y(i+1, k));
y(i+1, k+1) = y(i,k) + (h/2) * (a + b);
end
end
%Последний столбец - это то, что вы хотите
for i = 1: n+1
result(i) = y(i, n+1);
end
end
Анализ решения проблем в этой статье выглядит следующим образом:
В этом эксперименте самая большая проблема заключается в понимании формулы метода трапеции. {(k+1)}
yi+1(k+1)Это должно быть результатом предыдущих k раз, которые были исправлены непрерывной рекурсией, то есть k-е значение не задано напрямую формулой Эйлера (1), чтобы рекурсивно получить значение k + 1 раз, так как в следующей программе Метод расчета является неправильным пониманием этой итерационной формулы:
{(k+1)}
yi+1(k+1)Это должно быть результатом предыдущих k раз, которые были исправлены непрерывной рекурсией, то есть k-е значение не задано напрямую формулой Эйлера (1), чтобы рекурсивно получить значение k + 1 раз, так как в следующей программе Метод расчета является неправильным пониманием этой итерационной формулы:
for i= 1: n
% формула (1) Метод Эйлера дает начальное значение
y(i+1) = y(i) +h*f_xy(x(i),y(i));
% формула (2) Коррекция трапеции
a = f_xy(x(i));
b = f_xy(x(i+1), y(i+1));
y(i+1) = y(i) + (h/2) * (a + b);
end
Для правильной процедуры, пожалуйста, обратитесь к релейно-контактной схеме этой статьи.
Во-вторых, следует отметить еще один момент: в (1) и (2) формулы трапеции есть y i y_i
yiОдин элемент, если он написан в программе Matlab: y (i). Проведите следующие эксперименты (i = 1, 2, 3):
Согласно двумерной матрице из предыдущей статьи, можно узнать, что экспериментальные результаты показывают, что y (i) каждый раз принимает значение из первого столбца. Это не соответствует смыслу формулы трапеции. Вам следует перепишите y (i) как y (i, k).
Это не соответствует смыслу формулы трапеции. Вам следует перепишите y (i) как y (i, k).
Наконец, схема процесса создания матрицы:
Как найти основание трапеции в прямоугольной трапеции: Все формулы основания прямоугольной трапеции — ЭкоДом: Дом своими руками
Все формулы основания прямоугольной трапеции
1. Формула длины оснований прямоугольной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
2. Формулы длины оснований через боковые стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α — угол при нижнем основании
Формулы длины оснований :
3. Формулы длины оснований трапеции через диагонали и угол между ними
Формулы длины оснований трапеции через диагонали и угол между ними
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
Формулы длины оснований :
4.Формулы длины оснований трапеции через площадь
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
h — высота трапеции
Формулы длины оснований :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Все формулы сторон равнобедренной трапеции
1. Формула длины основания равнобедренной трапеции через среднюю линию
Формула длины основания равнобедренной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины основания:
2.Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Все формулы боковых сторон прямоугольной трапеции
1. Формула боковой стороны (с) прямоугольной трапеции через другие стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
d — боковая сторона
α — угол при нижнем основании
h — высота трапеции
c — боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с) :
2. Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
c — боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с):
3. Формулы боковой стороны (с) прямоугольной трапеции через площадь
a — нижнее основание
b — верхнее основание
m — средняя линия трапеции
c — боковая сторона под прямым углом к основаниям
Формула длины боковой стороны (с) :
4.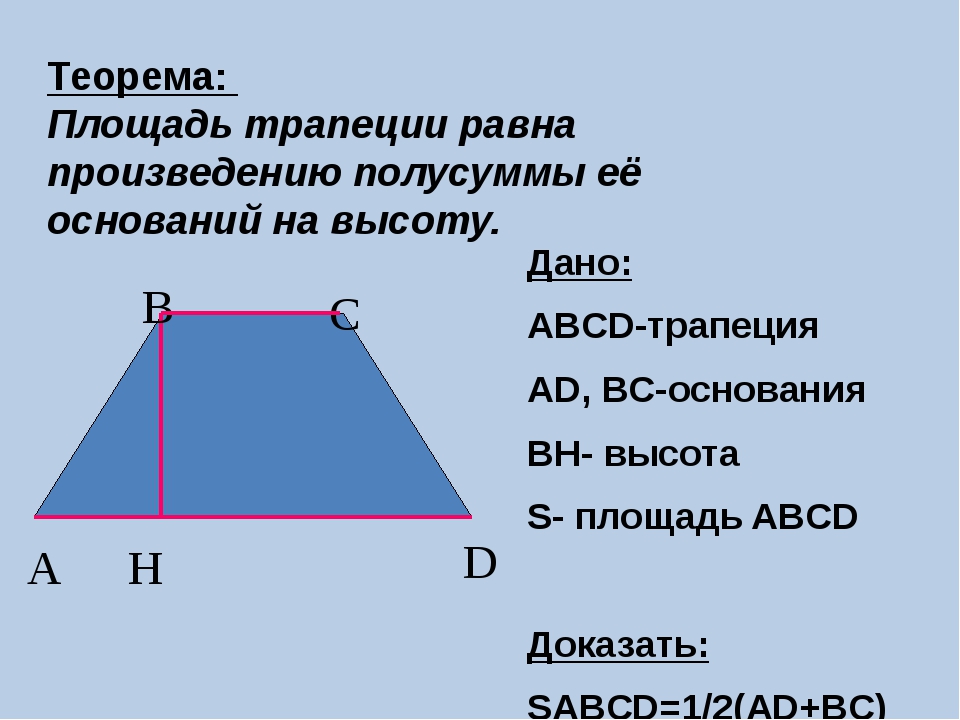 Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
α — угол при нижнем основании
h — высота трапеции
d — боковая сторона
Формулы длины боковой стороны (d) :
5. Формула боковой стороны (d) прямоугольной трапеции через площадь
a — нижнее основание
b — верхнее основание
m — средняя линия трапеции
α — угол при нижнем основании
d — боковая сторона
Формула длины боковой стороны (d) :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Прямоугольная трапеция
См. также: трапеция и ее свойства.
также: трапеция и ее свойства.
Прямоугольная трапеция — это трапеция, у которой хотя бы один из углов прямой (классическое определение)
Примечание. На самом деле, у прямоугольной трапеции, как минимум, два прямых угла (см. ниже — свойства)
Другие определения:
- Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
Формулы для прямоугольной трапеции
Обозначения формул даны на чертеже выше.
Соответственно:
a и b — основания трапеции
с — боковая сторона прямоугольной трапеции, перпендикулярная основаниям
d — боковая сторона трапеции, не являющаяся перпендикулярной основаниям
α — острый угол при большем основании трапеции
m — средняя линия трапеции
Интерпретация формул:
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна высоте трапеции (Формула 1)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна произведению синуса острого угла при большем основании на длину второй боковой стороны. (Треугольник CKD — прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)
(Треугольник CKD — прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)
Боковая сторона, перпендикулярная основаниям, равна произведению разности оснований на тангенс острого угла при большем основании. (Треугольник CKD — прямоугольный. Поскольку трапеция — прямоугольная, то длина KD — это и есть разность оснований, а h/KD=tgα по определению тангенса, а c=h, откуда с/KD=tgα) (Формула 3)
Боковая сторона, которая не перпендикулярна основаниям, равна частному разности оснований к косинусу острого угла при большем основании или частному высоты трапеции и синуса острого угла при большем основании. (разность оснований равна KD. В прямоугольном треугольнике CKD по определению косинуса cos α = KD / d, откуда и проистекает искомая формула) (Формула 4)
Боковая сторона прямоугольной трапеции, которая не перпендикулярна основаниям, равна корню квадратному из разности квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее — следствие из теоремы Пифагора — из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
(Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее — следствие из теоремы Пифагора — из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна корню квадратному из суммы квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, прямоугольный, далее — следствие из теоремы Пифагора — находим сумму квадратов катетов и извлекаем из полученного выражения квадратный корень) (Формула 6)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна частному от деления двойной площади трапеции на сумму ее оснований. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 7)
Боковая сторона прямоугольной трапеции, которая не перпендикулярна основаниям, равна частному от деления двойной площади трапеции на произведение суммы ее оснований и синуса острого угла при основании. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)
(Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)
Так как прямоугольная трапеция — это частный случай трапеции, то остальные формулы и свойства можно посмотреть в разделе «Трапеция».
Свойства прямоугольной трапеции
- У прямоугольной трапеции два угла обязательно прямые
- Оба прямых угла прямоугольной трапеции обязательно принадлежат смежным вершинам
- Оба прямых угла в прямоугольной трапеции обязательно прилежат к одной и той же боковой стороне
- Диагонали прямоугольной трапеции образуют с одной из боковых сторон прямоугольный треугольник
- Длина боковой стороны трапеции, перпендикулярной основаниям равна ее высоте
- У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям
- У прямоугольной трапеции два угла прямые, а два других – острый и тупой
Задача
В прямоугольной трапеции большая боковая сторона равна сумме оснований, высота равна 12 см. Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Решение.
Обозначим трапецию как ABCD. Обозначим длины оснований трапеции как a (большее основание AD) и b (меньшее основание BC). Пусть прямым углом будет
∠A.
Площадь прямоугольника, стороны которого равны основаниям трапеции, будет равна
S = ab
Из вершины C верхнего основания трапеции ABCD опустим на нижнее основание высоту CK. Высота трапеции известна по условию задачи. Тогда, по теореме Пифагора
CK2 + KD
2 = CD2
Поскольку большая боковая сторона трапеции по условию равна сумме оснований, то CD = a + b
Поскольку трапеция прямоугольная, то высота, проведенная из верхнего основания трапеции разбивает нижнее основание на два отрезка
AD = AK + KD. Величина первого отрезка равна меньшему основанию трапеции, так как высота образовала прямоугольник ABCK, то есть BC = AK = b, следовательно, KD будет равен разности длин оснований прямоугольной трапеции KD = a — b.
то есть
122 + (a — b)2 = (a + b)2
откуда
144 + a2 — 2ab + b2 = a2+ 2ab + b2
144 = 4ab
Поскольку площадь прямоугольника S = ab (см. выше), то
144 = 4S
S = 144 / 4 = 36
Ответ: 36 см
2 .
Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции
Определение.
Прямоугольная трапеция — это трапеция у котрой одна из боковых стороны перпендикулярна основам.
Признаки прямоугольной трапеции
Трапеция будет прямоугольной если выполняется одно из этих условий:
1. В тапеции есть два смежных прямых угла:
∠BAD = 90° и ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:
AB ┴ BC, AB ┴ AD
Основные свойства прямоугольной трапеции
1. В трапеции есть два смежных прямых угла:
∠BAD = ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:
Одна боковая сторона перпендикулярна основам:
AB ┴ BC ┴ AD
3. Высота равна меньшей боковой стороне:
h = AB
Стороны прямоугольной трапеции
Формулы длин сторон прямоугольной трапеции:
1. Формулы длины оснований через стороны и угол при нижнем основании:
a = b + d cos α = b + c ctg α = b + √d 2 — c2
b = a — d cos α = a — c ctg α = a — √d 2 — c2
2. Формулы длины оснований через стороны, диагонали и угол между ними:
| a = | d1d2 | · sin γ — b = | d1d2 | · sin δ — b |
| c | c |
| b = | d1d2 | · sin γ — a = | d1d2 | · sin δ — a |
| c | c |
3. Формулы длины оснований трапеции через площадь и другие стороны:
Формулы длины оснований трапеции через площадь и другие стороны:
| a = | 2S | — b b = | 2S | — a |
| c | c |
4. Формула боковой стороны через другие стороны и угол при нижнем основании:
c = √d 2 — (a — b)2 = (a — b) tg α = d sin α
5. Формулы боковой стороны через основы, диагонали и угол между ними:
| c = | d1d2 | · sin γ = | d1d2 | · sin δ |
| a + b | a + b |
6. Формулы боковой стороны через площадь, основы и угол при нижнем основании:
| d = | S | = | 2S |
| m sin α | (a + b) sin α |
7. Формула боковой стороны через другие стороны, высоту и угол при нижнем основании:
| d = | a — b | = | c | = | h | = √c2 + (a — b)2 |
| cos α | sin α | sin α |
Средняя линия прямоугольной трапеции
Формулы длины средней линии прямоугольной трапеции:
1. Формулы средней линии через основание, высоту (она же равна стороне d ) и угол α при нижнем основании:
Формулы средней линии через основание, высоту (она же равна стороне d ) и угол α при нижнем основании:
| m = | a — h · | ctg α | = | b + h · | ctg α |
| 2 | 2 |
2. Формулы средней линии через основания и боковые стороны сторону:
| m = | a — | √d 2 — c2 | = | b + | √d 2 — c2 |
| 2 | 2 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
формулы через стороны, углы, диагонали, площадь
В данной публикации мы рассмотрим различные формулы, с помощью которых можно вычислить высоту прямоугольной трапеции.
Напомним, в прямоугольной трапеции одна из боковых сторон перпендикулярна ее основаниями, и потому одновременно является высотой фигуры.
Нахождение высоты прямоугольной трапеции
Через длины сторон
Зная длины обоих оснований и большей боковой стороны прямоугольной трапеции, можно найти ее высоту (или меньшую боковую сторону):
Данная формула следует из теоремы Пифагора. В данном случае высота h – это неизвестный катет прямоугольного треугольника, гипотенуза которого равняется d, а известный катет – разности оснований, т.е. (a-b).
Через основания и прилежащий угол
Если даны длины оснований и любой из прилежащих к ним острых углов, то вычислить высоту прямоугольной трапеции можно по формуле:
Через боковую сторону и прилежащий угол
Если известна длина боковой стороны прямоугольной трапеции и прилежащий к ней угол (любой), найти высоту фигуры удастся таким образом:
Примечание: с помощью этой формулы можно, в т.ч. , доказать, что меньшая боковая сторона – это и есть высота трапеции:
Через диагонали и угол между ними
При условии, что известны длины оснований прямоугольной трапеции, диагонали и угол между ними, рассчитать высоту фигуры можно так:
Если вместо суммы оснований известна длина средней линии, то формула примет вид:
m – средняя линия, которая равна половине суммы оснований, т. е.m = (a+b)/2.
е.m = (a+b)/2.
Через площадь и основания
Если известна площадь прямоугольной трапеции и длина ее оснований (или средней линии), найти высоту можно таким образом:
онлайн калькулятор, формула расчета, пример вычисления
Ниже вы узнаете, как выглядят формулы для нахождения площади прямоугольной трапеции, а также сможете воспользоваться онлайн-калькуляторами для её расчёта.
Определение 1
Особенность прямоугольной трапеции в том, что её высота равна стороне, расположенной перпендикулярно двум основаниям.
Для того чтобы вычислить площадь прямоугольной трапеции через 3 её стороны, воспользуйтесь нашим онлайн-калькулятором. Для расчёта введите имеющиеся данные в поля для ввода.
Площадь прямоугольной трапеции
Высота прямоугольной трапеции $h$ равна длине стороны $c$, расположенной под прямым углом к двум основаниям трапеции $a$ и $c$.
Следовательно, формула для вычисления площади прямоугольной трапеции имеет вид:
$S = \frac12 \cdot (a + c) \cdot b$, где
$a$ — малое основание;
$с$ — большее основание;
$b$ — перпендикулярная основаниям сторона.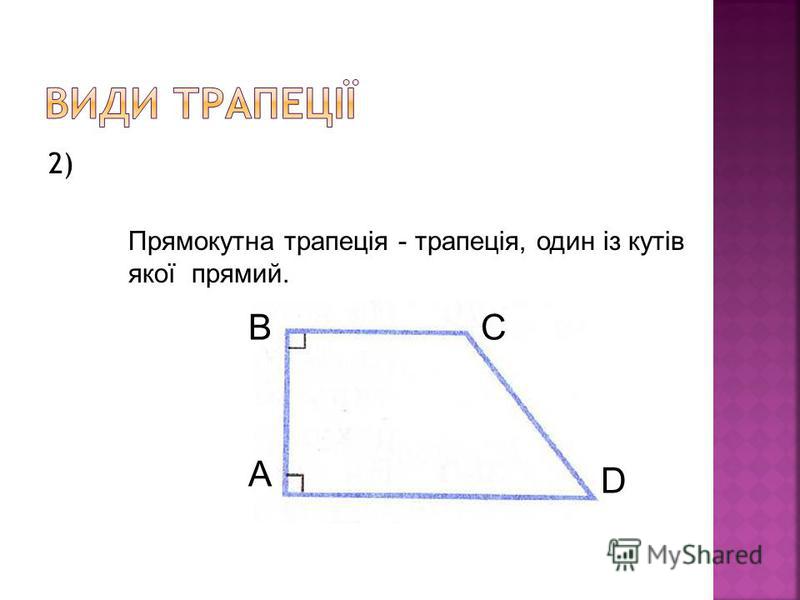
Пример 1
Задача
Дана прямоугольная трапеция, сторона $b$ у которой равна $2.32$ см, сторона $a$ составляет $2. 42$, и сторона $c$ равна $3.94$ см. Чему равна площадь трапеции?
Решение:
Воспользуемся приведённой выше формулой:
$S =\frac{(2.42 + 3.93) \cdot 2.32}{2} = 7.37$ кв. см.
Проверим ответ с помощью онлайн-калькулятора. Значения совпадают, а значит, решение найдено верно.
Также площадь прямоугольной трапеции можно рассчитать и по другим формулам, общим для всех видов трапеций, например, через среднюю линию и высоту. Высоту в формуле также можно заменить на сторону, перпендикулярную основаниям.
Площадь трапеции по высоте и средней линии
Формула нахождения площади трапеции по высоте и средней линии:
$S = m \cdot h$, где
$S$ — площадь трапеции,
$m$ — средняя линия,
$h$ — высота трапеции. 2) \cdot \frac{\sin (α) \cdot \sin (γ)}{\sin (α + γ)}$, где
$S$ — площадь трапеции,
$b$ — большее основание,
$g$ — малое основание,
$α$ — первый угол при основании,
$γ$ — второй угол при основании.
Также площадь прямоугольной трапеции можно найти через диагонали и угол между ними.
Площадь трапеции по диагонали и углу между диагоналями
Формула нахождения площади трапеции по диагонали и углу между диагоналями:
$S =\frac12 \cdot d1 \cdot d2 \cdot \sin (α)$, где
$S$ — площадь трапеции,
$d1$ — первая диагональ,
$d2$ — вторая диагональ,
$α$ — угол между диагоналями.
Рассмотрим пример.
Пример 2
Задача
Дана прямоугольная трапеция с диагоналями $d1$ и $d2$, равными $2. 22$ см и $2.64$ см. Угол между диагоналями $α$ равен $56°$. Чему равна площадь прямоугольной трапеции?
Решение:
Синус заданного угла $α$ равен $0.83$, найти его можно по специальным таблицам, приведённым на нашем сайте. Теперь подставим все известные значения:
$S = \frac{2.22 \cdot 2.64 \cdot 0.83}{2} = 2.43$ кв. см.
Вычисленный ответ совпадает с ответом онлайн-калькулятора, а значит, решение — верное. 2}$, где
2}$, где
$S$ — площадь трапеции,
$a$ — малое основание,
$b$ — большее основание,
$c, d$ — боковые стороны.
Как найти длину стороны трапеции
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
3 калькулятора трапеций Прокрутите вниз для получения инструкций и определений. Площадь трапеции = ((сумма оснований) ÷ 2) • высота Линия, параллельная линиям AD и BC, находится в середине линий AB и DC. Длина медианы = (Линия AD + Линия BC) ÷ 2
|
Как найти периметр и площадь трапеции [видео]
Площадь и периметр трапеции
Привет, и добро пожаловать в это видео о поиске площади и периметра трапеции!
Трапеция — это четырехсторонний многоугольник или «четырехугольник», у которого есть по крайней мере один набор параллельных сторон. У трапеции есть два типа сторон: ножки и основания. У трапеции две ножки и два основания.
У трапеции есть два типа сторон: ножки и основания. У трапеции две ножки и два основания.
Мы можем сказать, какие стороны являются основаниями, потому что они параллельны друг другу. Здесь мы видим, что верх и низ параллельны из-за совпадающих стрелок на этих сторонах. Зная длину ног и оснований, мы можем найти периметр трапеции.
Периметр — это расстояние вокруг объекта. Например, если мы хотим построить забор вокруг двора в форме трапеции, нам нужно знать периметр двора, чтобы знать, сколько ограждений купить.
Для трапеции формула периметра: «Периметр трапеции, P равен измерению основания один плюс размер основания два плюс размер ноги один плюс размер ноги два».
Нам не нужно запоминать эту формулу, потому что, как и в случае с любым другим типом многоугольника, это просто причудливый способ сказать, что складывает все стороны вместе !
Давайте найдем периметр этой трапеции:
Вот и все! Перейдем к области . Вот трапеция на миллиметровой бумаге:
Вот трапеция на миллиметровой бумаге:
Помните, что площадь — это мера того, сколько квадратных единиц уместится внутри фигуры. Сколько квадратов внутри нашей трапеции?
24 полных квадрата плюс восемь половинных квадратов, что означает, что площадь трапеции составляет 28 квадратных единиц. Но что, если у нас нет миллиметровой бумаги или трапеции удобного размера? Вот почему нам нужна формула!
Формула для нахождения площади трапеции: «Площадь трапеции A равна h, высоте трапеции, умноженной на длину основания один плюс длину основания два, деленную на два.”
Обратите внимание, что деление суммы оснований на два — это среднее значение этих длин. Поскольку в нашем примере задача изображена на графике, мы можем видеть, что верхняя база, которую мы назовем базой 1, имеет длину три единицы. Наша нижняя база, база 2, имеет длину 11 единиц. Высота трапеции, то есть расстояние между основаниями, составляет четыре единицы:
Для площади нам не нужны измерения двух ножек, только два основания и высота, которую также можно назвать . высота . Поскольку у нас есть все три, мы можем вставить их в нашу формулу:
высота . Поскольку у нас есть все три, мы можем вставить их в нашу формулу:
Это тот же ответ, который мы получили при подсчете!
Давайте попробуем еще одну:
Хорошо, она выглядит немного иначе, чем трапеция, которую мы только что сделали.Но мы можем сказать, что это трапеция, потому что у нее один набор из параллельных сторон . Мы можем использовать формулу, поэтому теперь нам просто нужно выяснить, какие числа куда идут. Параллельные стороны являются основаниями, поэтому мы можем установить основание 1 равным 6 сантиметрам и основание 2 равным 3 сантиметрам. Внутри трапеции нет пунктирной или цветной линии, соединяющей основания, которые явно соответствовали бы высоте, но нижняя сторона соединяет основания и перпендикулярна им, как мы можем судить по символу прямого угла.Так что 4 сантиметра — это высота, хоть и боком! Давайте подключим все это:
Эта формула также работает для определения площади параллелограммов . Это потому, что все параллелограммы являются трапециями, поскольку у них есть по крайней мере один набор параллельных сторон. Фактически, у всех параллелограммов есть два набора.
Это потому, что все параллелограммы являются трапециями, поскольку у них есть по крайней мере один набор параллельных сторон. Фактически, у всех параллелограммов есть два набора.
Вот и все, что нужно для определения периметра и площади трапеций.
Спасибо за просмотр и удачной учебы!
| 1D линия, круговая дуга, парабола, спираль, кривая Коха 2D Правильные многоугольники: Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, девятиугольник, десятиугольник, шестиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольника Другие многоугольники: 90 064 Круглые формы: 3D Архимедовы тела: Каталонских Сухой остаток: Твердые тела Джонсона: Другие многогранники: 000, большой додекаэдр200064 Круглые формы: 4D | Anzeige Расчеты на правой трапеции (или правой трапеции). Формулы: Длины сторон, диагонали и периметр имеют одинаковые единицы измерения (например,грамм. метр), площадь равна этой единице в квадрате (например, квадратный метр). Доля: © Jumk.de Webprojects Anzeige |
Расчет трапеции
Описание и формулы для расчета трапеций
Определение трапеции
Трапеция — это четырехугольная геометрическая форма со следующими характеристиками:
Трапеции А имеют одну пару параллельных сторон, которые являются основаниями трапеции
Противоположные стороны различаются по длине
Легенда
\ (a \) Длина стороны a
\ (b \) Длина стороны b
\ (c \) Длина стороны c
\ (d \) Длина стороны d
\ (e \) Диагональ e
\ (f \) Диагональ f
\ (h \) Высота
\ (м \) Средний сегмент
\ (A \) Площадь
\ (P \) Периметр
\ (α \) Угол Альфа
\ (β \) Угол Beta
\ (γ \) Угловая гамма
\ (δ \) Угол Дельта
Формулы для расчета трапеции
Расчет длины стороны \ (a \) трапеции
\ (\ Displaystyle а = (A · 2) / ч-с \)
Расчет длины стороны \ (b \) трапеции
\ (\ Displaystyle Ь = час / грех (β) \)
Расчет длины стороны \ (c \) трапеции
\ (\ Displaystyle с = (А · 2 / ч) — а \)
Расчет длины стороны \ (d \) трапеции
\ (\ Displaystyle d = час / грех (α) \)
Расчет диагонали \ (e \) трапеции
\ (\ Displaystyle е = \ sqrt {a ^ 2 + b ^ 2 — 2 · a · b · соз (β)} \)
Расчет диагонали \ (f \) трапеции
\ (\ Displaystyle f = \ sqrt {a ^ 2 + d ^ 2-2 · a · d · cos (α)} \)
Расчет высоты \ (h \) трапеции
\ (\ Displaystyle ч = (2 · а) / (а + с) \)
Вычислить средний сегмент \ (m \) трапеции
\ (\ Displaystyle м = (а + с) / 2 \)
Расчет площади \ (A \) трапеции
\ (\ Displaystyle А = (а + с) / 2 · час \)
Расчет периметра \ (P \) трапеции
\ (\ Displaystyle P = a + b + c + d \)
Вычислить угол альфа \ (α \) трапеции
\ (\ Displaystyle α = asin (ч / д) \)
\ (\ Displaystyle α = 180 — δ \)
Расчет угла бета \ (β \) трапеции
\ (\ Displaystyle β = asin (ч / Ь) \)
\ (\ Displaystyle β = 180 — γ \)
Расчет угловой гаммы \ (γ \) трапеции
\ (\ Displaystyle γ = 180 — β \)
Расчет дельты угла \ (δ \) трапеции
\ (\ Displaystyle δ = 180 — α \)
Видео с вопросом: Определение длины основания в трапеции с учетом длины, высоты и площади другого основания
Стенограмма видео
Трапеция площади 132 и основания 20
имеет высоту 11. Какая длина у другого
Какая длина у другого
база?
Было бы разумно начать это
вопрос, нарисовав диаграмму для моделирования информации. В этом вопросе нам сказано, что мы
есть трапеция. Мы можем помнить, что трапеция — это
четырехугольник, то есть четырехугольник с парой параллельных сторон. Высота 11 единиц. Нам сказали, что одна из баз
20, и нам нужно найти длину другого основания.Когда мы говорим о базах в
трапеции, то есть длины параллельных сторон. Мы не знаем, какая база равна 20, но
запишем это как нижнюю базу.
Для расчета длины
другая база, нам понадобится информация о местности. В некоторых странах слово
трапеция используется для обозначения фигуры с одной парой параллельных сторон. Здесь нам говорят, что этот район
132 кв.И мы можем использовать формулу для
площадь трапеции или трапеции, которая говорит нам, что площадь равна половине
ℎ раз 𝑏 суб-один плюс 𝑏 суб-два. ℎ обозначает высоту
трапеция, и 𝑏 sub one и 𝑏 sub two — это две основы. Итак, взяв эту формулу, мы
Итак, взяв эту формулу, мы
можем заполнить тот факт, что площадь 132, высота 11. И мы не знаем ни одной из баз,
так что давайте оставим это как 𝑏 sub one. А затем добавляем базу 20.
Мы можем переписать это уравнение в виде
найти 𝑏 sub одним несколькими способами. Но давайте начнем с удаления этого
половину, умножив обе части уравнения на два. 132 умноженное на два дает нам
264. А с правой стороны мы
все равно 11 умножить на к югу от единицы плюс 20. Затем мы можем разделить обе части
уравнение на 11. 264, деленное на 11, дает 24. И тогда в правой части
у нас будет единицы плюс 20.Затем мы можем найти 𝑏 sub one с помощью
вычитая 20 из обеих частей уравнения. Итак, наш ответ:
другая база должна была быть длиной в четыре единицы.
Формулы правой трапеции — xGeometry
|
$$ 2p = B + b + S + h $$
Периметр
$$ A = \ frac {\ left (B + b \ right) \ times h} {2} $$
Площадь
$$ B + b = \ frac {2A} {h} $$
Сумма баз
$$ h = \ frac {2A} {B + b} $$
Высота
$$ p_ {1} = B — b $$
Косая боковая проекция
$$ B — b = p_ {1} $$
Разница баз
$$ S = \ sqrt {{p_ {1}} ^ 2 + {h} ^ 2} $$
Сторона (теорема Пифагора)
$$ p_ {1} = \ sqrt {{S} ^ 2 — {h} ^ 2} $$
Косая боковая проекция
$$ h = \ sqrt {{S} ^ 2 — {p_ {1}} ^ 2} $$
Высота
$$ d_ {1} = \ sqrt {{B} ^ 2 + {h} ^ 2} $$
Длинная диагональ (теорема Пифагора)
$$ B = \ sqrt {{d_ {1}} ^ 2 — {h} ^ 2} $$
Более длинная база
$$ h = \ sqrt {{d_ {1}} ^ 2 — {B} ^ 2} $$
Высота
$$ d_ {2} = \ sqrt {{b} ^ 2 + {h} ^ 2} $$
Более короткая диагональ (теорема Пифагора)
$$ b = \ sqrt {{d_ {2}} ^ 2 — {h} ^ 2} $$
Укороченная база
$$ h = \ sqrt {{d_ {2}} ^ 2 — {b} ^ 2} $$
Высота
Определение
Правая трапеция — это трапеция с прямым углом (90 градусов).
Формула трапеции — Что такое формула трапеции? Примеры
Трапеция, также известная как трапеция, представляет собой четырехугольник или четырехугольник. Он имеет один набор противоположных сторон, которые параллельны, и набор непараллельных сторон. Параллельные стороны известны как основания, а непараллельные стороны известны как катеты трапеции.
Существуют различные типы трапеций: равнобедренная трапеция, правильная трапеция и разносторонняя трапеция.
- Трапеция с двумя непараллельными сторонами одинаковой длины называется равнобедренной трапецией.
- Прямой трапецией называется трапеция, имеющая не менее двух прямых углов.
- Прямоугольная равнобедренная трапеция — это трапеция, которая одновременно является прямой и равнобедренной трапецией. В евклидовой геометрии такие трапеции автоматически являются прямоугольниками.
- У разносторонней трапеции нет ни сторон, ни углов равной меры.
Рассмотрим подробнее формулы трапеций.
Что такое формула трапеции?
Мы будем изучать следующую формулу трапеции
- Периметр трапеции
- Площадь трапеции
Формула для вычисления периметра трапеции
Периметр трапеции определяется как сумма всех ее сторон или полная граница трапеции.Рассмотрим трапецию ABCD, как показано ниже, с размерами сторон a, b, c и d. Давайте посмотрим на формулу трапеции
.Формула периметра трапеции вычисляется путем нахождения суммы всех сторон, т. е. AB + BC + CD + DA
Периметр трапеции = сумма всех сторон = a + b + c + d
где a, b, c и d — стороны трапеции.
Формула для вычисления площади трапеции
Площадь определяется как площадь или область, занимаемая трапецией.Это половина произведения суммы его оснований и расстояния между ними. Это трапеция ABCD, как показано ниже.
Площадь трапеции определяется как:
Площадь трапеции = (1/2) × h × (a + b)
где,
- а = короткая база
- b = удлиненная база
- h = высота или расстояние между двумя основаниями
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.
Забронируйте бесплатный пробный урок
Рассмотрим применение формулы трапеций в следующих решенных примерах.
Примеры использования формулы трапеции
Пример 1: Если периметр трапеции равен 60 единицам, а три ее стороны равны 15 единицам, 20 единицам и 16 единицам соответственно, найдите размер четвертой стороны, используя формулу трапеции.
Решение:
Дано: Периметр = 60 единиц, a = 15 единиц, b = 20 единиц, c = 16 единиц, d = ?
Мы знаем, что по формуле трапеции
Периметр трапеции = сумма всех сторон
⇒ а + б + в + г = 60
⇒ 15 + 20 + 16 + д = 60
.⇒ d = 9 единиц
Ответ: Таким образом, четвертая сторона равна 9 единицам.
Пример 2: Используя формулу площади трапеции, найдите площадь трапеции, у которой основания равны 19 единицам и 15 единицам, а высота равна 8 единицам.
Решение:
Дано:
а = 17 шт.
б = 19 шт.
ч = 8 единиц
Мы знаем, что по формуле трапеций
Площадь трапеции = h(a + b) / 2
= 8 (15 + 19) / 2
= 4 × 34
= 136 шт. 2
Ответ: Таким образом, площадь трапеции 136 единиц 2
Пример 3. Если площадь трапеции равна 120 дюймов, а длины оснований равны 12 дюймам и 20 дюймам, найдите высоту трапеции, используя формулу трапеции?
Решение:
Предположим, что основания равны a и b, а высота трапеции равна h.Используя данную информацию, мы должны найти высоту, которая является расстоянием между основаниями. Подставим все эти значения в площадь трапеции по формуле:
Формула площади трапеции, A = [(a + b)/2] × h
120 = [(20 + 12)/2] × ч
120 = 16 × ч
ч = 7,5 дюйма
Следовательно, высота трапеции равна 7,5 дюйма.
Ответ: Высота трапеции 7,5 дюймов.
Часто задаваемые вопросы о формуле трапеции
Что такое периметр формулы трапеции?
Периметр трапеции равен сумме всех сторон.Он выражается как P = a + b + c + d. Где a, b, c и d — стороны трапеции.
Какова площадь формулы трапеции?
Формула площади трапеции выражается как A = (1/2) × h × (a + b). Где «a» – это более короткое основание, «b» – более длинное основание, а h – расстояние между двумя основаниями 90 003
Как рассчитать высоту трапеции, используя формулу трапеции?
Формула площади трапеции, A = [(a + b)/2] × h
Чтобы вычислить высоту трапеции, мы можем вычислить площадь трапеции по формуле
.
h = 2А/(а+b).Где «а» — более короткое основание, «b» — более длинное основание, «h» — расстояние между двумя основаниями, а A — площадь трапеции.
Каковы две основные формулы трапеций ?
Две основные формулы трапеций:
Периметр трапеции равен сумме всех сторон. Выражается как P = a + b + c + d. Где a, b, c и d — стороны трапеции.
Где a, b, c и d — стороны трапеции.
Формула площади трапеции, A = [(a + b)/2] × h.
Формула трапеций | Количественные вопросы GMAT
Автор Dominate the GMAT / 22 февраля 2011 г. / БлогПо какой-то причине трапеции обычно пугают студентов на GMAT.Может быть, это потому, что формула для нахождения площади трапеции «не похожа» на все остальные формулы четырехугольника. Может быть, это потому, что трапеции имеют причудливую форму. Какой бы ни была причина, я хотел бы сделать вашу жизнь намного проще, пока вы продолжаете подготовку к GMAT и работаете над курсом Dominate the GMAT.
В частности, я хотел бы помочь вам осмыслить площадь трапеции таким образом, чтобы это имело для вас смысл. Видите ли, большинство вопросов по решению задач GMAT и достаточности данных, связанных с трапециями, обычно сводятся к вашей способности правильно применять формулу площади трапеции. Однако, как я уже неоднократно говорил, вы оказываете себе медвежью услугу, если пытаетесь втиснуть в голову кучу формул. В день экзамена вы будете просто перегружены умственными способностями и начнете сходить с ума, если не сможете вспомнить конкретную формулу (или, что еще хуже, если спутаете ее с другой, запрятанной глубоко в уголках вашего мозга). К счастью для вас, есть лучший способ.
Однако, как я уже неоднократно говорил, вы оказываете себе медвежью услугу, если пытаетесь втиснуть в голову кучу формул. В день экзамена вы будете просто перегружены умственными способностями и начнете сходить с ума, если не сможете вспомнить конкретную формулу (или, что еще хуже, если спутаете ее с другой, запрятанной глубоко в уголках вашего мозга). К счастью для вас, есть лучший способ.
Обо всем по порядку. Что такое трапеция? Трапеция — это четырехсторонняя геометрическая фигура (то есть четырехугольник ), две стороны которого параллельны, а две — нет (см. рисунок ниже).Две параллельные стороны называются основаниями . Высота трапеции — это просто высоты , как и в случае с треугольниками (см. обучающее видео GMAT Geometry — Triangles). Вам может понадобиться нарисовать высоту, если одна из сторон еще не перпендикулярна основаниям.
Возникает вопрос: какова площадь этой трапеции? Позвольте мне сделать вашу жизнь очень простой. В день экзамена полезно помнить, что площадь четырехугольника равна , всегда оснований, умноженных на высоту. А = Ь*ч. Очень просто.
В день экзамена полезно помнить, что площадь четырехугольника равна , всегда оснований, умноженных на высоту. А = Ь*ч. Очень просто.
Сейчас вы можете сказать: «Но, Бретт, подожди! Это не та формула площади трапеции, которую я видел!» Ну, это и не так. Позволь мне объяснить.
Формула площади трапеции по-прежнему A = b*h. Вопрос в том, какую базу вы используете? Видите ли, проблема трапеций в том, что у них два основания, каждое из которых имеет разную длину. С прямоугольниками, например, все просто — любое выбранное вами основание по определению имеет ту же длину, что и параллельная ему сторона (т.е. другая база). То же и с квадратами. То же и с параллелограммами. Но не так для трапеций.
Посмотрите на эту цифру. Если мы выберем более длинное основание, в данном случае b1, что произойдет, если мы умножим b1 * h? Полученная площадь слишком велика! (обратите внимание, что синие треугольники — это лишняя площадь за пределами самой трапеции).
Итак, мы должны выбрать более короткую базу, верно? Ну, как видите, у нас обратная проблема. Полученная площадь слишком мала на на количество красных треугольников.
Есть очень простое решение. Если более длинное основание дает слишком большую площадь, а меньшее основание дает слишком маленькую площадь, что, если мы просто возьмем среднее значение двух оснований? Конечно же, это именно то, что вы должны делать. Графически вы можете видеть, как усреднение баз дает площадь, которая идеально уравновешивает избыток, создаваемый большими базами (области, заштрихованные синим цветом), и дефицит, создаваемый более короткой базой (области, заштрихованные красным).
Итак, хотя формула площади трапеции могла показаться вам странной, когда вы впервые прочитали ее в учебнике, надеюсь, теперь вы видите, что на самом деле это просто основание, умноженное на высоту, за исключением того, что «основание», которое мы используем, — это среднее два основания [1/2(b1+b2)].
Подводя итог:
Площадь трапеции = 1/2 (b1 + b2) * h
Теперь, когда вы это знаете, вы должны быть в состоянии решать большинство трапециевидных вопросов по решению задач GMAT и вопросам достаточности данных GMAT.В вашем официальном руководстве GMAT Review, 12-е изд., есть отличный пример приложения на стр. 172, № 145. Попробуйте и посмотрите, как вы это сделаете. (Подсказка: вам также нужно будет применить кое-что из того, что вы знаете о прямоугольных треугольниках). Пояснение к ответу на стр.232. Как всегда, не стесняйтесь обращаться ко мне по электронной почте ([email protected]) с вопросами.
Усвойте этот подход, чтобы вы могли выйти и доминировать на GMAT!
Площадь трапеции
|
Эссе № 3 — Некоторые «средние» трапеции
Эссе 3Шеннон Амбергер
Введение
В математике существует множество различных типов средних значений,
все они имеют разные уравнения, которые можно использовать для их нахождения.
Хотя большинство людей могут запомнить эти уравнения и соотношения
среди типов средних большинство никогда не связывают с геометрией.В этом эссе я представляю семь различных типов среднего и
как построить их в трапеции.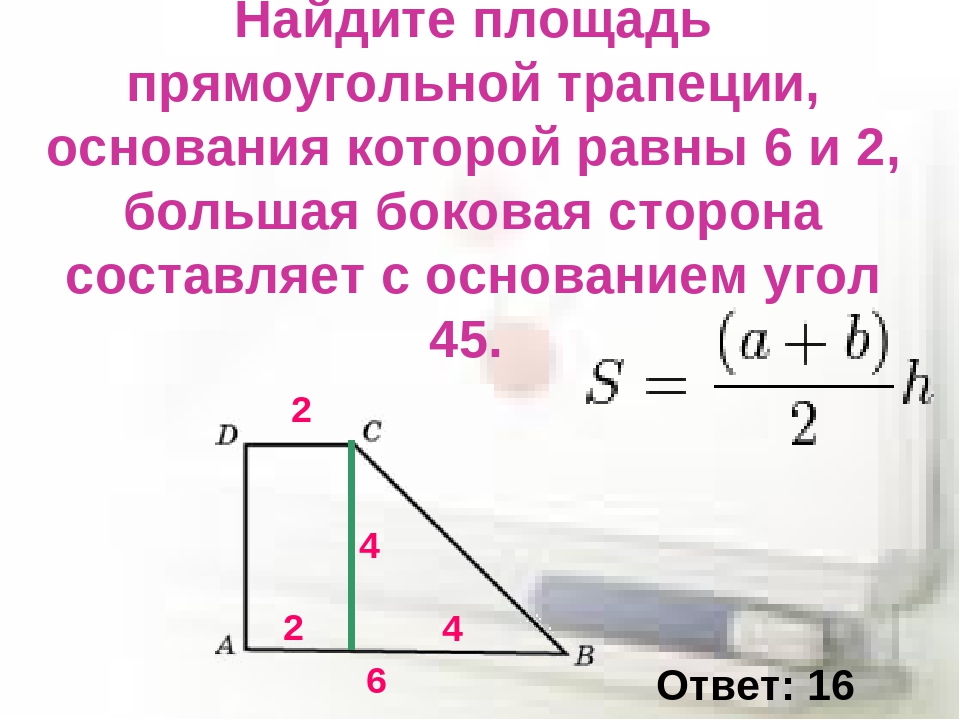 Затем я сравниваю их значения
путем построения всех семи типов средних в одной трапеции.
Затем я сравниваю их значения
путем построения всех семи типов средних в одной трапеции.
Ресурс:
Евы, Ховард (1992). Введение в История математики . Издательство Saunders College: Филадельфия, Пенсильвания.
Арифметика Среднее
Среднее арифметическое «А» любого можно найти два действительных числа «a» и «b» используя следующее уравнение: A = (a + b)/ 2 .
В трапеции с основаниями длины «а» а «b» — среднее арифметическое, «A» — длина отрезка, параллельного основаниям и также делит стороны трапеции пополам.
Нажмите ЗДЕСЬ увидеть пошаговое построение среднего арифметического в трапеция.
Геометрический Среднее
Среднее геометрическое «G» любых двух действительные числа «a» и «b» можно найти с помощью следующее уравнение: G = sqrt(ab) .
В трапеции с основаниями длины «а»
а «b» — среднее геометрическое, «G» — длина
отрезка, параллельного основаниям и делящего
трапецию на две подобные трапеции.
Нажмите ЗДЕСЬ , чтобы см. пошаговое построение среднего геометрического в трапеции.
Гармоника Среднее
Среднее гармоническое «H» любых двух действительные числа «a» и «b» можно найти с помощью следующее уравнение: H = 2ab/(a + b) .
В трапеции с основаниями длины «а» и «b» — среднее гармоническое, «H» — длина отрезка, параллельного основаниям и также проходящего через пересечение диагоналей трапеции.
Нажмите ЗДЕСЬ увидеть пошаговое построение среднего гармонического в трапеции.
Герониан Среднее
Героновское среднее «h» любых двух действительные числа «a» и «b» можно найти с помощью следующее уравнение: h = (a + sqrt(ab) + b)/ 3 .
В трапеции с основаниями длины «а»
а «b» — среднее по Герону, «h» — длина
отрезка, параллельного основаниям и также
1/3 пути от среднего арифметического к среднему геометрическому. 2)/ 3(a +
б) .
2)/ 3(a +
б) .
В трапеции с основаниями длины «а» и «b» центроидальное среднее, «g» длина отрезка, параллельного основаниям и также проходит через центр тяжести площади трапеции.
Нажмите ЗДЕСЬ чтобы увидеть пошаговое построение центроидального среднего в трапеция.
Сравнение Средства
Семь типов средних, представленных выше, имеют следующие отношения, когда «а» и «б» являются действительными числами, и когда «а» не равно «б» :
Н < G < ч < А < г < г < сВот пример трапеции, содержащей все семь средств.Фигура и размеры, кажется, поддерживают вышеуказанные отношения.
Нажмите ЗДЕСЬ чтобы увидеть доказательство того, что вышеуказанные отношения верны.
Так что же происходит, когда a = b?
Нажмите ЗДЕСЬ для эскиза GSP, который позволяет вам анимировать приведенную выше фигуру в
чтобы наблюдать, что происходит со средними сегментами как «а»
приближается к «б».
Возврат на домашнюю страницу Шеннон
Периметр и площадь трапеции Правило формулы
Формула трапециевидной линейки
Четырехугольник с двумя параллельными сторонами называется трапецией.Его также можно назвать Трапецией в большинстве частей мира. Две стороны, которые параллельны в трапеции, известны как основания, а непараллельные стороны известны как боковые стороны. А расстояние между двумя параллелями называется высотой.
Был интересный спор между школами, когда один профессор утверждал, что трапеция имеет только один набор параллельных сторон, в то время как другой профессор утверждал, что у трапеции может быть более одного набора параллельных сторон. На основании второго определения считается, что Трапеция является частным случаем параллелограмма.В то же время первое утверждение не считает параллелограмм трапецией.
Существует ряд свойств, которые помогут вам идентифицировать любой четырехугольник как трапецию. Это –
Это –
- Диагонали и углы при основании трапеции будут равны.
- Если провести медиану на трапеции, то она будет параллельна основанию, а ее высота будет равна средней длине ее оснований.
- Точка пересечения диагоналей коллинеарна серединам противоположных сторон.
Периметр трапеции Формула
Концепция трапеции часто используется в различных физических вычислениях и сложных математических расчетах. Кроме того, это часть учебы в школьные годы и конкурсных экзаменов. Если вы хотите заняться инженерным делом, необходимо глубокое понимание концепции. Здесь мы обсудим, как рассчитать периметр трапеции.
Чтобы вычислить периметр, нужно просуммировать все четыре стороны.Например, если есть одна трапеция, длины сторон которой равны a, b, c и d, то формула для вычисления периметра будет иметь вид –
.\[\большой P=a+b+c+d\]
Где,
a, b, c, d — длины каждой стороны.
Площадь трапеции Формула
Вам должно быть любопытно узнать, как вычислить площадь трапеции по формуле. Что ж. Это легко вычислить, взяв среднее двух оснований и умножив его на высоту. В математике площадь трапеции задается формулой –
Что ж. Это легко вычислить, взяв среднее двух оснований и умножив его на высоту. В математике площадь трапеции задается формулой –
\[\большая площадь\;трапеции\; = \frac{1}{2} \times h \times (a + b)\]
Где:
h = высота ( Примечание – это высота перпендикуляра, а не длина катетов.)
a = короткое основание
b = длинное основание
Центроид трапеции Формула
Как мы уже говорили ранее, трапеция — это четырехугольник с двумя параллельными сторонами. Центроид трапеции находится где-то между двумя основаниями. Центроид формулы трапеции в математике задается как —
\[\НАИБОЛЬШИЙ x = \frac{b+2a}{3(a+b)}h\]
Где
h = высота трапеции
a и b = параллельные стороны,
Формула равнобедренной трапеции
Четырехугольник — это четырехугольник, у которого только одна пара параллельных сторон, а непараллельные стороны равны по длине.Существует два популярных типа трапеций: одна — равнобедренная, а другая — прямоугольная трапеция.



 Высота в таком четырёхугольнике одновременно является одной из его сторон.
Высота в таком четырёхугольнике одновременно является одной из его сторон. В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов: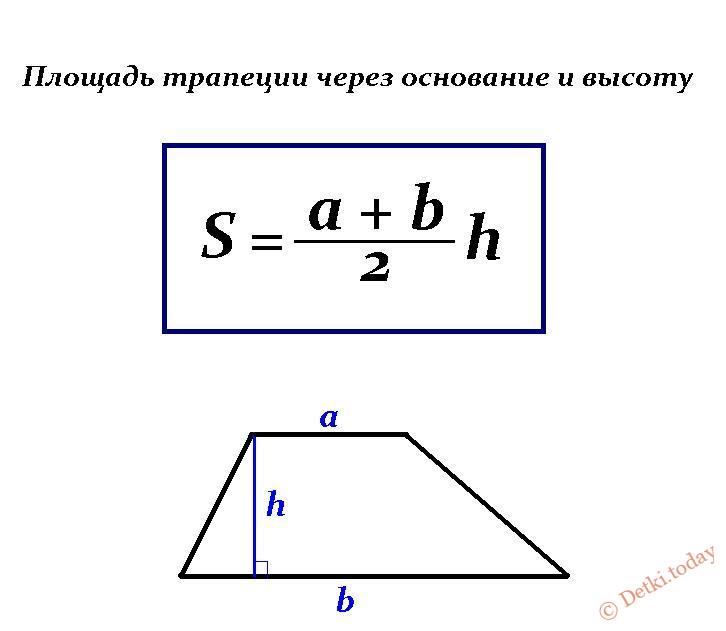
 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов: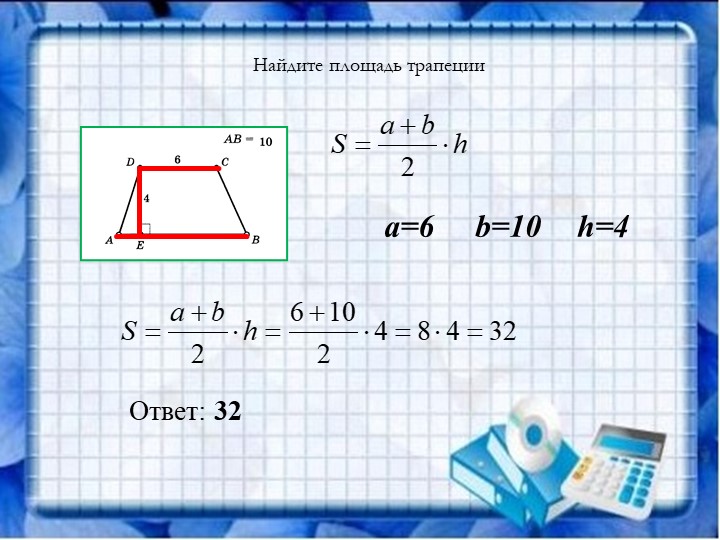
 02;
n = 5;
init = 1;
for i = 1: (n+1)
x(i) = h * (i-1);
end
% Трапециевидный метод
trapezoid = trapezoidMethod(x, n, h, init);
plot(x, trapezoid,'g');
hold on;
02;
n = 5;
init = 1;
for i = 1: (n+1)
x(i) = h * (i-1);
end
% Трапециевидный метод
trapezoid = trapezoidMethod(x, n, h, init);
plot(x, trapezoid,'g');
hold on;



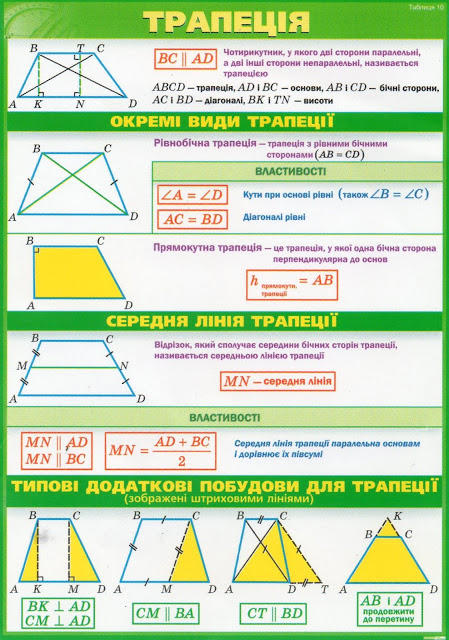 Спираль, Треугольник Рело, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой многоугольник дуги, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник
Спираль, Треугольник Рело, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой многоугольник дуги, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник Это трапеция с двумя смежными прямыми углами. Введите длины двух параллельных сторон a и c, а также основания b или наклонной стороны d. Выберите количество десятичных знаков и нажмите Рассчитать. Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать угловые единицы.
Это трапеция с двумя смежными прямыми углами. Введите длины двух параллельных сторон a и c, а также основания b или наклонной стороны d. Выберите количество десятичных знаков и нажмите Рассчитать. Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать угловые единицы.
