Урок геометрии «Равновеликие фигуры в решении задач»
Цель урока:
- повторение и обобщение ключевых задач о равновеликих фигурах;
- обучение учащихся поиску решения задач в ходе создания проблемно-познавательной ситуации;
- развитие грамотной устной и письменной математической речи учащихся.
Оборудование: доска, с заготовленными чертежами или слайды; раздаточный материал: учебное пособие Атанасян Л.С. и др. Геометрия: дополнительные главы к школьному учебнику 8 класса.
Ход урока
Заканчивая изучение темы «Площади», сегодня мы повторяем и развиваем наши знания о равновеликих фигурах.
1. Чтобы вспомнить понятие «равновеликие фигуры», поиграем в «Да» и «Нет».
Я составила диктант-попурри, выбрав вопросы из ваших диктантов, связанных с этим понятием. Я читаю вопрос, его автор комментирует правильный ответ.
Учащимся к семинару по теме «Площади» было предложено домашнее задание: составить диктант из пяти вопросов по данной теме, ответы на которые предполагали либо «да», либо «нет».
Диктант.
- Верно ли, что фигуры, имеющие равные площади, называются равновеликими?
- Верно ли, что равные многоугольники равновелики?
- Верно ли, что если площади фигур равны, то и фигуры равны?
- Могут ли равновеликие фигуры быть равными?
- Верно ли, что диагонали параллелограмма делят его на четыре равновеликих треугольника?
2. Какие ключевые (базовые) задачи о равновеликих треугольниках мы рассматривали?
№1. Медиана треугольника разделяет его на два равновеликих треугольника.
Обоснуйте это утверждение (открыть заготовленный рис. №1 и по ходу обоснования сделать запись, рисунок не стирать).
№1 и по ходу обоснования сделать запись, рисунок не стирать).
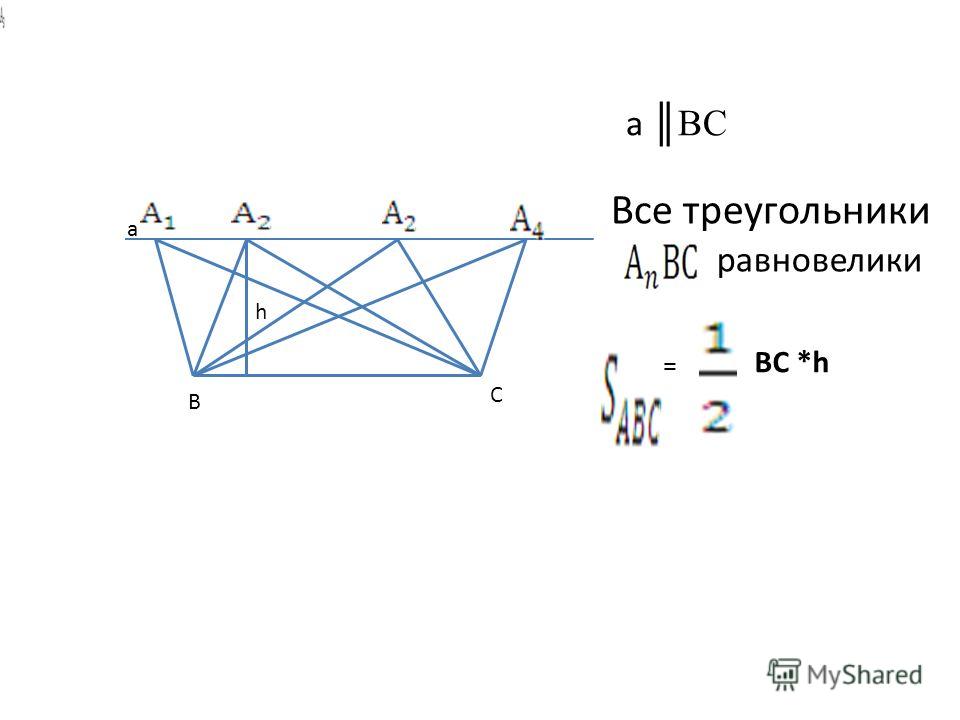
№2. Все треугольники с общим основанием, вершины которых лежат на прямой, параллельной основанию, равновелики.
Обоснуйте это утверждение (открыть рис. №2 и по ходу обоснования сделать запись, рисунок не стирать).
1) На рисунке 3 я начертила ломаную ADB. Сравните площади четырёхугольников ADBС и ADBХ, ответ обоснуйте.
Вывод:
Сколько четырёхугольников равновеликих четырёхугольнику ADBC можно построить на рисунке 3?
Ответ: бесконечно много.
Что для этого надо сделать?
Ответ: отметить точку на прямой
Полученный четырёхугольник будет равновелик четырёхугольнику ADBC.
Какой результат я могла бы получить, если бы дополнила рисунок 3 ломаной из
3-х звеньев? 4-х звеньев?
Ответ: бесконечно много равновеликих пятиугольников, шестиугольников и т. д.
д.
Показать рисунок 4.
2) Начертите выпуклый четырёхугольник ABCD. Проведите диагональ AC. (рис.5)
Как построить четырёхугольник, равновеликий четырёхугольнику ABCD, диагональ которого есть отрезок AC?
Ответ: провести прямую а такую, что а ll АС, и D.
Пусть E, четырёхугольник ABCD равновелик четырёхугольнику ABCE.
Докажите последнее утверждение.
3) Есть ли на Рис. 6 равновеликие треугольники?
Какое утверждение позволяет нам это доказать?
Пусть .
Можно ли выразить площадь четырёхугольника ABCO через и ?
Ответ: да,
Можно ли выразить площадь четырёхугольника ABCO через ?
Ответ: да,
Как связаны ?
Ответ:
4) Решим задачу о разбиении данного выпуклого четырёхугольника на две равновеликие части.
Прочитаем условие задачи № 130 [1]
№ 130. В выпуклом четырёхугольнике ABCD через середину O диагонали BD проведена прямая, параллельная диагонали AC. Она пересекает сторону AD в точке E.
Она пересекает сторону AD в точке E.
Докажите, что .
Сделаем чертёж (рис.7).
На рисунке отметим, что точка О – середина BD и укажем, что EO ll AC. Итак, что мы должны доказать? . Обозначим . Какую часть должна составлять площадь каждой фигуры от S? Проанализируем условие, подумаем: по условию точка О – середина BD, какое утверждение, связанное с равносильностью фигур, мы могли бы использовать?
Ответ: медиана делит треугольник на два равновеликих треугольника.
Что нам надо провести на чертеже, чтобы можно было это утверждение применить?
Ответ: медианы АО и СО.
Решение
- Проведём АО и СО.
- по свойству медианы.
- , по свойству 2 площадей.
Какое условие мы не использовали?
Ответ: EO ll AC.
Можем ли мы сравнить площади четырёхугольников ABCE и ABCO? - т.к. EO ll AC, то , , .
- , , значит, по свойству 2 площадей , ч.
 т.д.
т.д.
Итог урока
Сегодня мы посвятили урок равновеликим многоугольникам. А где это может нам понадобиться, где практически можно применить полученные знания?
Пусть пройдёт какое-то время и кому-то из вас доведётся стать землеустроителем. Всем известно, что земледельцу не важно, какой формы участок, важна его площадь.
Допустим, что надо решить задачу: разделить участок на две части, равные по площади, если участок имеет форму: а) треугольника; б) четырёхугольника, при условии, что граница должна проходить через вершину многоугольника (столб на участке, например, стоит в этой вершине, и никому не хочется иметь его на своей земле).
Как выгоднее проводить границу: в виде ломаной или в виде отрезка прямой?
Ответ: длина отрезка меньше длины ломаной, соединяющей его концы, значит, если граница пройдёт по отрезку, то меньше материала уйдёт на ограждение.
Сформулируйте поставленную задачу на языке геометрии.
Ответ: а) Разделить треугольник на две равновеликие части прямой, проходящей через его вершину.
Как это сделать?
Ответ: Провести медиану из этой вершины.
Ответ: б) Разделить четырёхугольник на две равновеликие части прямой, проходящей через его вершину.
Как это сделать?
Решить задачу №130.
- Провести АС.
- Провести ВD.
- Отметить точку О середину ВD.
- Провести прямую mтакую, чтоm ll AC,
- m пересекает CD в точке М
- АМ – искомая граница.
Как разделить на две равновеликие части участок, имеющий форму пятиугольника?
Я не знаю. А вы?
Литература
- Атанасян Л.С. и др. Геометрия: дополнительные главы к школьному учебнику 8 класса. М.: Просвещение, 1996.
Равновеликие многоугольники | Математика
152. До сих пор мы занимались сравнением отрезков, углов и дуг круга. Теперь обратим внимание на то, что мы умеем строить многоугольники, выделяющие из плоскости ее определенную часть, многоугольники, имеющие площадь. Возникает потребность установить возможность узнавать, когда две площади равны, или когда одна из них больше другой.
Теперь обратим внимание на то, что мы умеем строить многоугольники, выделяющие из плоскости ее определенную часть, многоугольники, имеющие площадь. Возникает потребность установить возможность узнавать, когда две площади равны, или когда одна из них больше другой.
Площадью вообще называется определенная, ограниченная со всех сторон, часть плоскости.
Если две площади совпадают при наложении, то они, подобно отрезкам и углам, признаются нами равными. Если два многоугольника равны (т. е. совпадают при наложении), то и площади их равны.
Мы легко можем составить представление о возможности находить сумму и разность площадей. Пусть имеем два многоугольника (чер. 158) I и II. Мы можем построить многоугольник BCDE, равный II так, чтобы одна его сторона пошла по стороне BF многоугольника ABFGH, который равен многоугольнику I. Тогда получим новый многоугольник ABCDEFGH, площадь которого слагается из площадей I и II многоугольников, то есть
площ. ABCDEFGH = площ. I + площ.
Мы можем выполнить сложение этих же двух площадей иначе и придем. Напр., к многоугольнику A’B’F’G’H’E’D’C’, о котором также имеем:
площ. A’B’F’G’H’E’D’C’ = площ. I + площ. II
Для того, чтобы получилось согласи с привычною для нас мыслью, что сложение ведет лишь к одному результату, мы должны признать, что два полученные результата одинаковы, то есть:
площадь ABCDEFGH = площадь A’B’F’G’H’E’D’C’
Таким образом, является возможность строить многоугольники, не равные между собою (многоугольник A’B’F’G’H’E’D’C’ вообще не равен многоугольнику ABCDEFGH, так как при наложении они, вообще говоря, не могут совпасть: например, может случиться, что у одного из них сторон меньше, чем у другого — на чертеже, напр., ∠C’A’B’ может оказаться выпрямленным), но площади которых мы признаем равными.
Не трудно также установить возможность вычитания площадей; напр., многоугольник ABCDEFA (чер. 159) имеет площадь, равную разности площадей 4-угольника ABCDA и треугольника AFE.
Две площади, ограниченные прямыми линиями, считаются равными не только тогда, когда они при наложении совмещаются, но и тогда, если каждая их них является суммою или разностью двух (или нескольких) площадей, совпадающих попарно при наложении.
Мы рассматриваем только площади, ограниченные прямыми линиями.
Если же одна площадь слагается из частей так, что из них не только можно составить другую площадь, но и остаются лишние части, то первая площадь больше второй.
Два многоугольника, не равные между собою, но имеющие равные площади, называются равновеликими. На чер. 158 мы получили многоугольник A’B’F’G’H’E’D’C’ равновеликий многоугольнику ABCDEFGH.
153. Рассмотрим один пример равновеликих многоугольников, важный для последующего.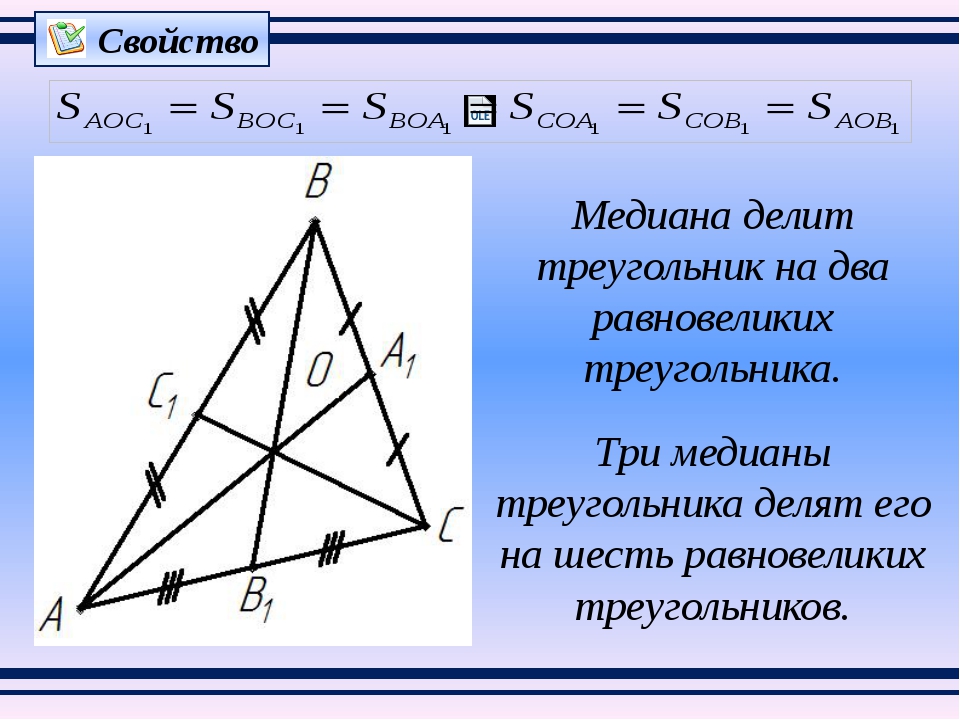
Построим два параллелограмма с одинаковыми основаниями и высотами. Это построение легко выполнить: Строим две параллельных прямых XY и X’Y’ (чер. 160) и на них отрезки AB = A’B’ = DC = D’C’; построив затем отрезки AD, BC, A’D’ и B’C’, получим два параллелограмма ABCD и A’B’C’D’ с равными основаниями (AB = A’B’) и с равными высотами, так как прямые XY и X’Y’ параллельны (п. 55).
Рассмотрим 2 трапеции AA’D’D и BB’C’C. Так как AB = A’B’, то AA’ = BB’ и также DD’ = CC’, т. е. параллельные стороны наших трапеций соответственно равны; непараллельные их стороны также равны: AD = BC и A’D’ = B’C’. Кроме того, не трудно убедиться в равенстве соответствующих углов ∠DAA’ = ∠CBB’, ∠AA’D’ = ∠BB’C’ и т. д., как соответственных при параллельных. Если передвинуть вторую трапецию так, чтобы точка B попала в A и сторона BB’ пошла бы по AA’, то в силу равенства сторон и углов нетрудно убедиться, что наши 2 трапеции равны. Далее мы видим:
площ. ABCD = площ. AA’D’D – площ. BA’D’C
площ. A’B’C’D’ = площ. BB’C’C – площ. BA’D’C,
A’B’C’D’ = площ. BB’C’C – площ. BA’D’C,
т. е. площадь каждого параллелограмма является разностью двух совпадающих при наложении площадей, а поэтому
площ. ABCD = площ. A’B’C’D’.
Более наглядное объяснение: для получения площади параллелограмма ABCD надо от площади трапеции AA’D’D отрезать площадь BA’D’C, а для получения площади параллелограмма A’B’C’D’ надо от площади трапеции BB’C’C отрезать ту же площадь BA’D’C; оба раза от равных площадей отрезать одну и ту же площадь, – поэтому и остатки равны.
Вот другой способ для выяснения равенства площадей параллелограммов, имеющих равные основания и высоты.
Построим два параллелограмма ABCD и A’B’CD (чер. 161 — I) так, чтобы их равные (верхние, например) основания совпали (CD — их общее верхнее основание). Вследствие равенства их высот, противоположные стороны AB и A’B’ располагаются на одной прямой. Тогда видим, что ∆ADA’ = ∆BCB’ (так как AD = BC, A’D = B’C и ∠ADA’ = ∠BCB’) и что
площ. ABCD = площ. A’BCD + площ. AA’D
A’BCD + площ. AA’D
площ. A’B’CD = площ. A’BCD + площ. BCB’.
Слагаемые наших сумм попарно равны, отсюда заключаем, что
площ. ABCD = площ. A’B’CD.
То же самое можно выразить образно: отрезав от площади ABCD площадь ADA’ и приставив отрезанную часть с другой стороны в положение BCB’ (ведь ∆BCB’ = ∆ADA’), получим площадь параллелограмма A’B’CD.
Но иногда одним разрезом обойтись нельзя. На чер. 161 (II) дан более сложный случай, где придется площадь левого параллелограмма разрезать на части a, b, c, d, e и f и перенести их в положения b’, c’, d’, e’ и f’ (a останется на месте), – тогда составится площадь правого параллелограмма. Разрезать площадь одного параллелограмма надо по прямым параллельным сторонам другого параллелограмма (параллелограммы располагаются так, как на чер. II).
Рекомендуется вырезать два параллелограмма с равными основаниями и равными высотами из разноцветной бумаги и разрезать площадь одного на такие куски, чтобы из них составить площадь другого.
Не трудно убедиться, что если основания у двух параллелограммов равны, а высоты нет, то площадь того параллелограмма больше, у которого больше высота.
154. Прямоугольник представляет частный вид параллелограмма. Поэтому:
Параллелограмм равновелик прямоугольнику, имеющему такие же основание и высоту.
Превращение параллелограмма в равновеликий ему прямоугольник можно выполнить так: из вершин D и C параллелограмма ABCD (чер. 162 — I и II) опускаем перпендикуляры DE и CF на сторону AB. Тогда получим прямоугольник DEFC, равновеликий, в силу предыдущего, данному параллелограмму.
Полезно увидать равновеликость параллелограмма прямоугольнику непосредственно, не ссылаясь на предыдущий п.; напр., для случая, данного на чер. II, имеем: после построения DE ⊥ EB к площади ABCD мы приложили еще площадь ∆ADE, после построения CF ⊥ AF мы из площади EBCD вычли площадь ∆BCF, но ∆BCF = ∆ADE, следовательно, полученная после вычитания площадь EDCF равна данной площади ABCD.
155. В виде упражнений разберем следующие случаи равновеликости. Пусть на отрезке a + b (чер. 163) построен квадрат и пусть построены еще прямые, соединяющие точки, где граничат слагаемые отрезки. Тогда видим, что площадь всего квадрата слагается из четырех частей: 1) площади квадрата со стороною a, 2) площади квадрата со стороною b и 3) из площадей двух прямоугольников со сторонами a и b. Поэтому имеем:
Площ. (a + b, a + b) = площ. (a, a) + площ. (b, b) + 2 площ. (a, b).
Здесь обозначения: (a + b, a + b), (a, b) и т. д. Выражают прямоугольники, стороны которого суть в 1-м a + b и a + b, а во 2-м a и b.
Также из чертежа 164 увидим:
Площ. (a – b, a – b) = площ. (a, a) + площ. (b, b) – 2 площ. (a, b).
Из чертежа 165 увидим:
Площ. ABCD = площ. AGKE + площ. GKFB – площ. DEKH – площ. HKFC
или площ. (a + b, a – b) = площ. (a, a) + площ. (a, b) – площ. (a, b) – площ. (b, b)
или площ. (a + b, a – b) = площ. (a, a) – площ. (b, b).
(b, b).
Эти зависимости могут служить иллюстрациями известных алгебраических формул.
156. Если построим диагональ BD параллелограмма ABCD (чер. 166), то получим ∆ABD, имеющий такие же основания и высоту, как и параллелограмм. Кроме того, известно, что ∆ABD = ∆DBC. Поэтому имеем:
Площадь треугольника равна половине площади параллелограмма, имеющего такие же основание и высоту.
Или сокращенно:
Треугольник равновелик половине параллелограмма, имеющего такие же основание и высоту.
Из сравнения только что полученного результата с тем, который мы нашли в п. 153, можем заключить:
Треугольники, имеющие равные основания и равные высоты, равновелики.
Добавим еще: если у двух параллелограммов одинаковые основания, но разные высоты, то площадь того параллелограмма больше, у которого высота больше, – это ясно из того, что параллелограмм с меньшею высотою можно превратить в равновеликий ему, площадь которого занимает лишь часть площади другого параллелограмма. Отсюда заключаем, что если у двух треугольников одинаковые основания, но разные высоты, то площадь того треугольника больше, у которого высота больше.
Отсюда заключаем, что если у двух треугольников одинаковые основания, но разные высоты, то площадь того треугольника больше, у которого высота больше.
Добавление. Любой треугольник можно превратить в равновеликий ему прямоугольник.
Пусть имеем ∆ABC (чер. 166 bis, где даны 2 варианта: слева дан ∆ со всеми острыми углами, а справа ∆ с тупым углом). Если у треугольника все углы острые, то построим любую его высоту BD, а если у треугольника один угол тупой, напр., ∠B (в ∆ABC справа), то построим высоту ВD именно из вершины этого тупого угла (в таком случае всегда высота BD идет внутри треугольника). Разделим затем высоту BD пополам в точке M и построим через M прямую EF || AC, а через точки A и C прямые AE ⊥ AC и CF ⊥ AC. Тогда ясно: 1) ∆KBM = ∆KAE (точка K есть точка пересечения AB и EF), 2) ∆MBL = ∆FCL (точка L есть точка пересечения BC и EF), откуда следует, что площ. AEFC = площ. ∆ABC.
157. Построим геометрическое место вершин равновеликих треугольников, имеющих общее основание.
Пусть имеем ∆ACB (чер. 167). Чтобы другой треугольник с тем же основанием AB имел такую же площадь, надо, согласно предыдущему п., чтобы его высота равнялась высоте данного. Для этого необходимо, чтобы его вершина была расположена на таком же расстоянии от прямой AB, как и точка C. Таких точек бесчисленное множество и все они расположены на прямой MN, параллельной основанию и проходящей чрез точку C. Конечно, возможно на таком же расстоянии построить еще другую параллельную AB, по другую ее сторону.
Итак, геометрическое место вершин треугольников, равновеликих между собою и имеющих общее основание, есть прямая (или две прямых), параллельная основанию.
Иногда то же свойство выражают в такой форме:
От перенесения вершины треугольника по прямой, параллельной основанию, его площадь не изменится.
158. Упражнения.
1. Превратить данный треугольник ABC в равновеликий ему с тем же основанием AB, но чтобы угол при точке A был данный.
2. Превратить данный треугольник ABC в равновеликий ему с тем же основанием AB, но чтобы сторона, выходящая из точки A, была равна данному отрезку.
3. Превратить ∆ABC в равновеликий ему равнобедренный с тем же основанием AB.
Надо воспользоваться геометрическим местом п. 157 и геометрическим местом вершин равнобедренных треугольников, имеющих основание AB, – этим местом является перпендикуляр к AB чрез его середину.
4. Превратить ∆ABC в равнобедренный ему треугольник с другим основанием AD (чер. 168).
Соединив C с D, построив BE || CD и соединив E с D, получим искомый ∆AED (часть ABE осталась неизменною, а ∆BEC равновелик ∆BED).
Мы увеличили основание (было AB, стало AD). Можно также уменьшить его.
5. На диагонали BD параллелограмма ABCD (чер. 169) взята точка M и чрез нее построены прямые EF и KL, параллельные сторонам параллелограмма. Тогда параллелограммы AKME и MFCL равновелики.
6. На сторонах ∆ABC (чер. 170) построены параллелограммы ACED, CEFB и BFDA (сторона BF, если ее продолжить, пройдет внутри отрезка AC). Параллелограмм ACED равновелик сумме параллелограммов ABFD и BCEF.
Параллелограмм ACED равновелик сумме параллелограммов ABFD и BCEF.
7. Превратить данный параллелограмм в равновеликий ему ∆ с тою же высотой.
159. Задача 1. Превратить данный параллелограмм в равновеликий ему с данным основанием.
Пусть дан параллелограмм ABFE (чер. 169) и требуется превратить его в равновеликий ему с основанием, равным отрезку BK. Отложив данное основание BK на основании BA данного параллелограмма, как это сделано на чертеже, построим прямую KML || AE; затем построим прямую BM и продолжим ее до пересечения в точке D с продолжением стороны AE данного параллелограмма. Наконец, построим прямую DC || AB, которая пересекает прямую KML в точке L и продолжение прямой BF в точке C. Тогда параллелограмм KBCL есть искомый.
В самом деле: ∆DML = ∆DME; ∆BDC = ∆BDA; след., площ. BMLC = площ. BMEA; но ∆BMF = ∆BMK; след., площ. BMLC + площ. BMK = площ. BMEA + площ. BMF, или площ. BKLC = площ. BFEA. Совершенно так же решается задача о построении прямоугольника, равновеликого данному и имеющего данное основание.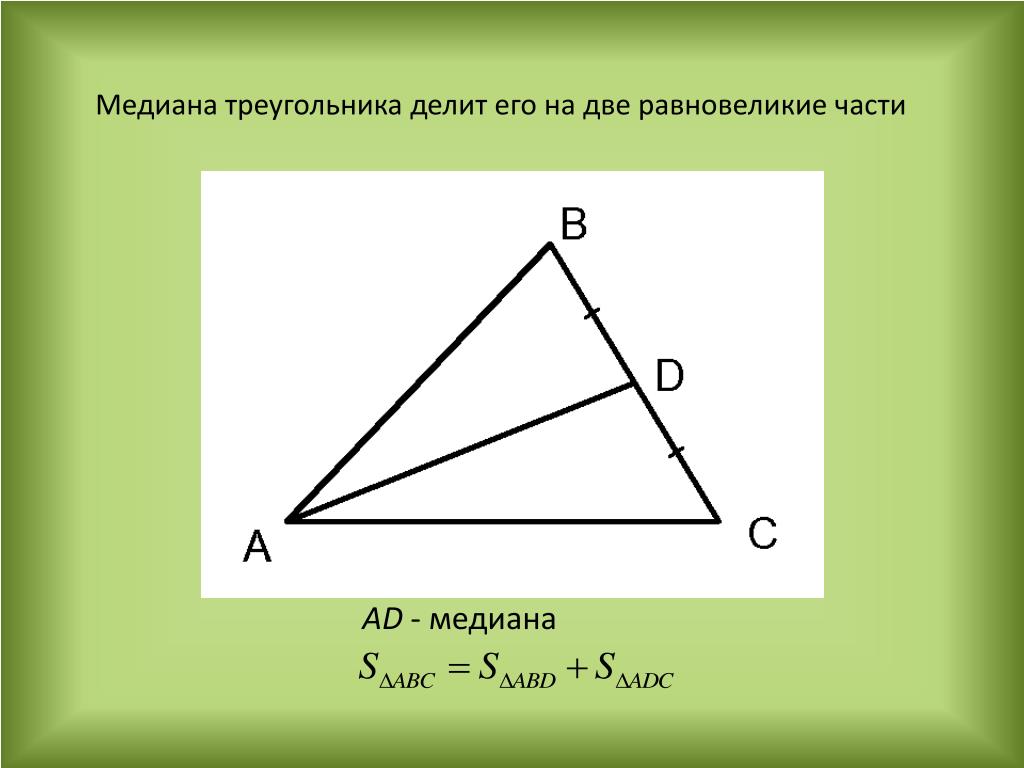
Задача 2. Превратить 4-угольник в равновеликий ему треугольник.
Пусть требуется 4-угольник ABCD (чер. 171) превратить в равновеликий ему треугольник.
Для этого диагональю BD разобьем площадь четырехугольника на две части и один из треугольников, напр. ∆ABD, превратим в равновеликий ему с тем же основанием BD так, чтобы один из углов 4-угольника, напр. ∠B, выпрямился. Для этого надо вершину A перенести по прямой, параллельной основанию BD, в точку K, где эта параллельная пересекается с продолжением стороны BC. Тогда ∆KBD равновелик ∆ABD и, следовательно, ∆DKC равновелик 4-угольнику ABCD.
Пусть теперь имеем 6-угольник ABCDEF (чер. 172). Отсечем диагональю AC сначала ∆ABC и превратим его в равновеликий ему ∆AKC с тем же основанием AC, где вершина K есть точка пересечения прямой BK || AC с продолжением стороны DC. Тогда наш 6-угольник превратился в равновеликий ему 5-угольник AKDEF. Повторяя тот же прием еще раз, превратим полученный 5-угольник в равновеликий ему 4-угольник, затем последний — в равновеликий ему треугольник. Таким образом, всякий многоугольник, имеющий площадь, можно превратить в равновеликий ему треугольник.
Таким образом, всякий многоугольник, имеющий площадь, можно превратить в равновеликий ему треугольник.
Теперь процесс сложения и вычитания площадей (п. 152) упрощается: каждый из данных многоугольников превратим в равновеликий ему треугольник, построим новый многоугольник, площадь которого равна сумме или разности площадей полученных треугольников (приложим один треугольник к другому, или наложим один на другой) и этот многоугольник превратим опять в равновеликий ему треугольник.
160. Упражнения.
1. Превратить невыпуклый 4-угольник (имеющий площадь) в равновеликий ему треугольник.
2. Построить треугольник, равновеликий сумме данного треугольника и невыпуклого 8-угольника (чер. 173).
Построить также треугольник, равновеликий их разности.
3. Построить ∆, площадь которого была бы в 2, 3… раза больше площади данного ∆, а основание осталось бы то же.
4. В треугольнике ABC проведена средняя линия MN, где M и N суть середины сторон AB и BC. Тогда площадь ∆MBN в 4 раза меньше площади ∆ABC.
Тогда площадь ∆MBN в 4 раза меньше площади ∆ABC.
5. Стороны BA и BC треугольника ABC продолжены и увеличены в 2 раза каждая. От соединения концов продолжений получится новый треугольник, площадь которого в 4 раза больше площади данного.
6. Стороны BA и BC треугольника ABC (чер. 174) продолжены так, что BK = 3BA и затем построено KL || AC. Площадь ∆KBL в 9 раз больше площади ∆ABC.
Построим еще MN, где M и N середины отрезков AK и CL, APR и CPQ, где P середина отрезка MN, и, наконец, QM и RN. Тогда MQ || AR || BL и NR || CQ || BK.
Легко теперь увидать, что 1) сторона BL в 3 раза больше стороны BC, 2) сторона KL в 3 раза больше стороны AC и 3) площадь ∆KBL в 9 раз больше площади ∆ABC. Итак, если стороны треугольника увеличить в 3 раза, то площадь его увеличится в 9 раз.
7. Во сколько раз увеличится площадь треугольника, если стороны его увеличить в 4 раза каждую? (Как выполнить построение, необходимое для увеличения каждой стороны в 4 раза?)
161. Выполним следующее построение: 1) Из концов гипотенузы AC (чер. 175) прямоугольного треугольника ABC (∠B = d) построим AE ⊥ AC и CD ⊥ AC, отложим AE = CD = AC и соединим точки D и E, – получим квадрат AEDC, стороны которого = AC (AEDC есть квадрат, построенный на гипотенузе). 2) Продолжим AB по направлению BG (BG ⊥ BC), построим CF ⊥ BC и чрез точку D построим прямую GF, перпендикулярную к BG и к CF (ведь CF || BG). Тогда получим квадрат BCFG, сторона которого = катету BC прямоугольного ∆ABC; в самом деле, ∆CDF = ∆ABC, так как CD = AC (по первому построению), ∠DCF = ∠BCA, потому что оба эти угла дополняются углом BCD до прямого, а этого достаточно для равенства прямоугольных треугольников (углы при B и F прямые), следов., CF = BC = BG = GF (CBGF есть квадрат, построенный на катете BC). 3) Построим BK — продолжение BC, AL ⊥ AB (AL || BK) и чрез точку E построим прямую EL, перпендикулярную к BK и к AL. Тогда получится квадрат ABKL, сторона которого равна катету AB прямоугольного ∆ABC. Доказательство, такое же, как и в предыдущем построении, вытекает из равенства треугольников ALE и ABD; ABKL есть квадрат, построенный на катете AB.
Выполним следующее построение: 1) Из концов гипотенузы AC (чер. 175) прямоугольного треугольника ABC (∠B = d) построим AE ⊥ AC и CD ⊥ AC, отложим AE = CD = AC и соединим точки D и E, – получим квадрат AEDC, стороны которого = AC (AEDC есть квадрат, построенный на гипотенузе). 2) Продолжим AB по направлению BG (BG ⊥ BC), построим CF ⊥ BC и чрез точку D построим прямую GF, перпендикулярную к BG и к CF (ведь CF || BG). Тогда получим квадрат BCFG, сторона которого = катету BC прямоугольного ∆ABC; в самом деле, ∆CDF = ∆ABC, так как CD = AC (по первому построению), ∠DCF = ∠BCA, потому что оба эти угла дополняются углом BCD до прямого, а этого достаточно для равенства прямоугольных треугольников (углы при B и F прямые), следов., CF = BC = BG = GF (CBGF есть квадрат, построенный на катете BC). 3) Построим BK — продолжение BC, AL ⊥ AB (AL || BK) и чрез точку E построим прямую EL, перпендикулярную к BK и к AL. Тогда получится квадрат ABKL, сторона которого равна катету AB прямоугольного ∆ABC. Доказательство, такое же, как и в предыдущем построении, вытекает из равенства треугольников ALE и ABD; ABKL есть квадрат, построенный на катете AB. 4) Продолжим FG и LK до пересечения в точке M.
4) Продолжим FG и LK до пересечения в точке M.
В предыдущем мы нашли, что ∆CDF = ∆ABC и ∆AEL = ∆ABC. Мы можем еще найти треугольники, равные ∆ABC. Прежде всего это ясно для ∆EMD, гипотенуза которого ED равна гипотенузе AC и ∠MED = ∠BAC, как углы с параллельными сторонами. Затем, построив отрезок MB, получим два равных треугольника ∆BMG = ∆BMK (так как MB есть диагональ прямоугольника BKMG). Легко увидать, что KB = AB (стороны квадрата), KM = BG (противоположные стороны прямоугольника) = BC (стороны квадрата). Поэтому ∆BKM = ∆ABC (так как катеты их равны), а следовательно и ∆MGB = ∆ABC.
Итак, имеем:
∆ABC = ∆CFD = ∆AEL = ∆EMD = ∆BKM = ∆MGB.
Рассмотрим площадь ACFMLA. Если от этой площади отрезать куски, занимаемые треугольниками AEL, EMD и CDF, то останется площадь, занимаемая квадратом AEDC, то есть
площ. AEDC = площ. ACFMLA – 3 площ. ∆ABC.
Но такие же три части мы можем отрезать от площади пятиугольника ACFML иным способом, отрезав площади треугольников BMK, BGM и ABC, – эти три треугольника равны, как мы уже нашли, прежним.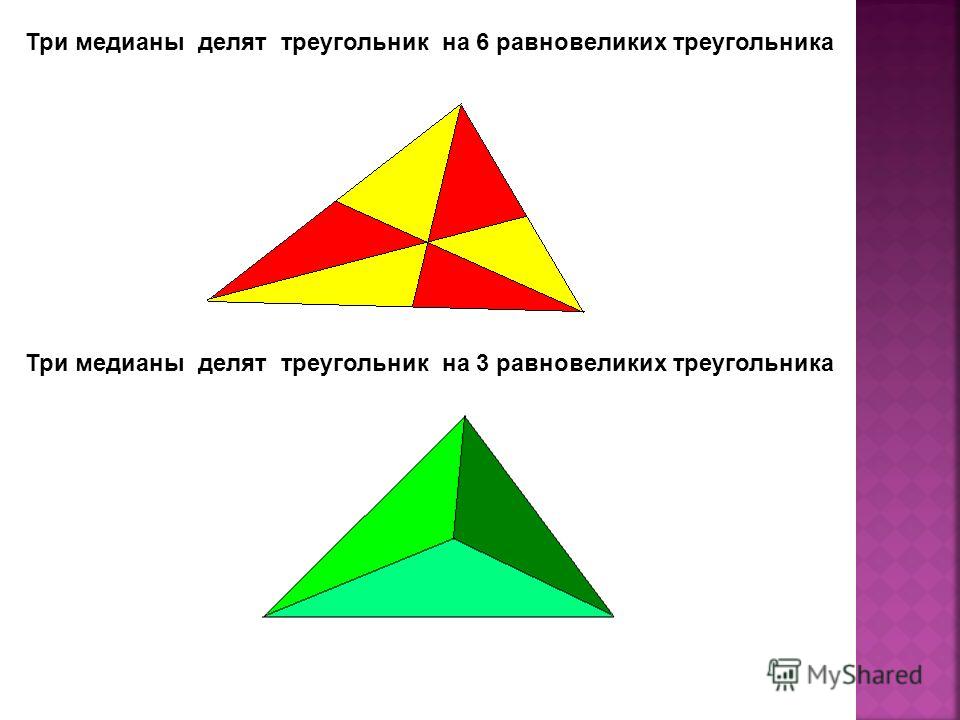 Отняв от площади, занимаемой пятиугольником ACFML, площади треугольников BMK, MBG (или сразу отнять площадь прямоугольника BKMG) и ABC, получим площади, занимаемые квадратами ALKB и BGFC, т. е. площ. ALKB + площ. BGFC = площ. ACFMLA – 3 пл. ∆ABC.
Отняв от площади, занимаемой пятиугольником ACFML, площади треугольников BMK, MBG (или сразу отнять площадь прямоугольника BKMG) и ABC, получим площади, занимаемые квадратами ALKB и BGFC, т. е. площ. ALKB + площ. BGFC = площ. ACFMLA – 3 пл. ∆ABC.
Так как в обоих случаях мы отнимали поровну (утроенную площадь ∆ABC), то остатки должны быть равны, т. е.
площ. AEDC = площ. ALKB + площ. BGFC,
или в словесной форме:
Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.
Это свойство известно под именем теоремы Пифагора.
Можно и иными способами (их много) выяснить то же свойство. Вот еще два из них:
1) Пусть имеем прямоугольный ∆ABC (чер. 176). Обозначим его катеты каждый одною буквою: BC = a и AC = b. Отложим на продолжениях катетов отрезки BL = b и AK = a и построим квадрат CKDL, сторона которого = a + b. Далее построим точки M и N так, чтобы KM = b, MD = a, DN = b и NL = a и соединим A с M, M с N и N с B; тогда получим квадрат AMNB, площадь которого получается, если от площади квадрата CKDL отнять площади 4 равных треугольников ABC, AMK и т. д. Построив затем прямые AA’ || CL и MM’ || KC, получим два квадрата: OMDA’, сторона которого = a и OACM’, сторона которого = b; сумма площадей этих квадратов получается, если от площади квадрата CKDL отнять площади 2 прямоугольников OAKM и OM’LA’, каждый из которых имеет стороны a и b и площадь каждого равна удвоенной площади ∆ABC (ясно видно, например, что площ. OAKM = 2 площ. ∆AMK, но AMK = ∆ABC).
д. Построив затем прямые AA’ || CL и MM’ || KC, получим два квадрата: OMDA’, сторона которого = a и OACM’, сторона которого = b; сумма площадей этих квадратов получается, если от площади квадрата CKDL отнять площади 2 прямоугольников OAKM и OM’LA’, каждый из которых имеет стороны a и b и площадь каждого равна удвоенной площади ∆ABC (ясно видно, например, что площ. OAKM = 2 площ. ∆AMK, но AMK = ∆ABC).
Отсюда вытекает справедливость теоремы Пифагора.
2) Пусть имеем прямоугольный ∆ABC (чер. 177). Построим квадраты AF, AN и BK на его гипотенузе и катетах и продолжим стороны LK и MN до пересечения в точке R. Затем построим прямую BR и продолжим стороны AE и CF до пересечения в S и в Q с прямыми MR и RK. Тогда ∆BLR = ∆ABC, так как у них равные катеты BL = BC, LR = BN = AB; следовательно, BR = AC = AE = CF. Кроме того, ∠RBL = ∠ACB, но ∠BCA = ∠QCK, так как каждый из них дополняется углом BCQ до прямого. Поэтому ∠RBL= ∠QCK и, следовательно, RB || QC || SA и, след., RB = QC = SA.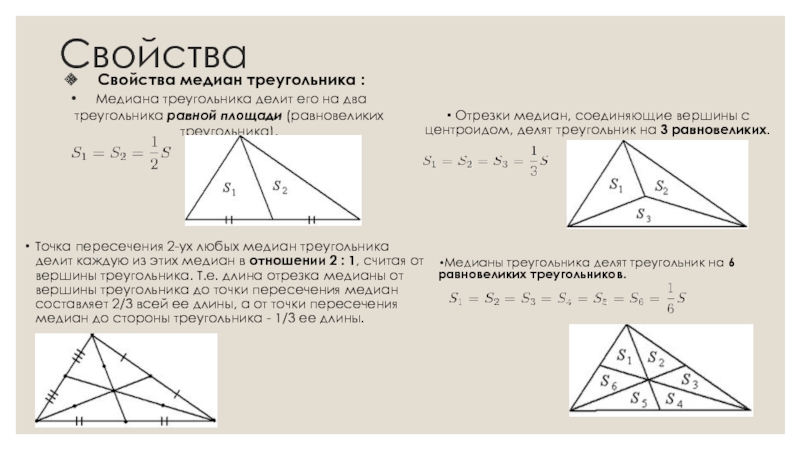 Продолжим RB до пересечения со сторонами квадрата AF в точках D и P; тогда BP ⊥ AC и BP ⊥ EF (ибо RP || SE). Параллелограмм ASRB равновелик прямоугольнику EADP (у них равные основания PD = BR и одинаковые высоты), по тот же параллелограмм ASRB равновелик квадрату AMNB. Также найдем, что прямоугольник PDCF равновелик квадрату CBLK, а, следовательно, квадрат ACFE равновелик сумме квадратов AMNB и BLKC.
Продолжим RB до пересечения со сторонами квадрата AF в точках D и P; тогда BP ⊥ AC и BP ⊥ EF (ибо RP || SE). Параллелограмм ASRB равновелик прямоугольнику EADP (у них равные основания PD = BR и одинаковые высоты), по тот же параллелограмм ASRB равновелик квадрату AMNB. Также найдем, что прямоугольник PDCF равновелик квадрату CBLK, а, следовательно, квадрат ACFE равновелик сумме квадратов AMNB и BLKC.
162. Упражнения.
1. Вершины L и F квадратов, построенных на катетах (чер. 175), расположены на одной прямой с точкой B, вершиной прямого угла треугольника.
2. Построить квадрат равновеликий сумме данных двух квадратов.
3. Построить квадрат равновеликий разности двух данных квадратов.
4. Построим на чер. 177 прямые BE и MC, которые пересекутся пусть в точке X; тогда точки E, A, X и C лежат на одном круге, диаметр которого есть EC. (Выясняется это так: ∆ABE = AMC, откуда ∠AEX = ∠ACX). Отсюда вытекает, что CM ⊥ BE. Далее легко найти, что AR || BE и, следовательно, CM ⊥ AR.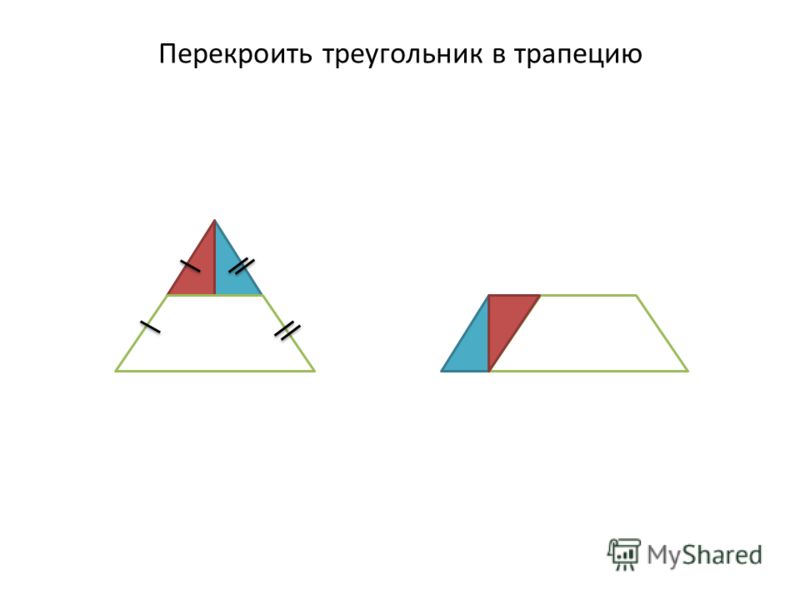
Пользуясь этим, показать:
5. Прямые CM и AK пересекаются на BD (BD ⊥ AC).
163. Превратить трапецию в равновеликий треугольник.
Пусть имеем трапецию ABCD (чер. 178). Найдем середину M одной из ее непараллельных сторон, построим прямую CM и найдем ее точку пересечения K с прямой DA. Тогда ∆AMK = ∆MBC и, следовательно, трапеция ABCD равновелика ∆KCD, у которого та же высота (CH), а основание KD = KA + AD = BC + AD, то есть трапеция равновелика треугольнику, имеющему такую же высоту, а основание которого равно сумме параллельных сторон трапеции.
Площадь. Равновеликие фигуры [Love Soft]
Равновеликие фигуры — плоские фигуры с одинаковыми площадями или геометрические тела с одинаковыми объемами.
Разрезанием на части и перекладыванием их можно любой многоугольник превратить в равновеликий ему квадрат.
Это следствие из теоремы Больяй — Гервина: равносоставленные фигуры являются равновеликими, а равновеликие многоугольники являются равносоставленными.
Понятие равносоставленности лежит в основе «метода разбиения», применяемого для вычисления площадей многоугольников: параллелограмм «разрезанием и перекладыванием» сводят к прямоугольнику, треугольник — к параллелограмму, трапецию — к треугольнику.
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.
Достроим треугольник до прямоугольника. Площадь треугольника равна половине площади прямоугольника.
Проведем через середину боковой стороны трапеции прямую, параллельную второй боковой стороне. Площадь трапеции равна площади полученного параллелограмма.
Перекраивание трапеции в равносоставленный треугольник:
видео — Площадь трапеции. Сведение к площади треугольника
Подробнее
Площадь трапеции с основаниями длин a и b и длиной высоты h равна S=(a+b)/2•h. Убедиться в этом можно воспользовавшись формулой для вычисления площади треугольника. Для этого необходимо разрезать трапецию на такие части, из которых можно составить треугольник.
Убедиться в этом можно воспользовавшись формулой для вычисления площади треугольника. Для этого необходимо разрезать трапецию на такие части, из которых можно составить треугольник.
Разрежем трапецию вдоль линии, соединяющей вершину с серединой противоположной боковой стороны. Повернём отрезанный треугольник до того момента, когда оба основания трапеции окажутся на одной прямой. Убедитесь, что две части боковой стороны при этом лягут на одну прямую, то есть, получится действительно треугольник.
Одна из сторон получившегося треугольника имеет длину, равную сумме длин оснований трапеции, а длина высоты треугольника, проведённой к этой стороне, совпадает с высотой трапеции.
Один из способов подсчёта площади треугольника состоит в нахождении половины произведения длины стороны на длину высоты, опущенную на эту сторону. Применение этого способа и даёт привычную формулу площади трапеции.
Модель можно сделать из доски толщиной около 10 мм. Для удобства демонстрации две части, на которые она разрезается, удобно соединять между собой при помощи магнитов.
Равносоставленность
Равновеликие многогранники не всегда являются равносоставленными. Так, например, куб и равновеликий ему правильный тетраэдр не являются равносоставленными — так называемая теорема Дена.
Вопросы
Квадраты с равными сторонами равновелики?
Равносторонние треугольники с равными сторонами равновелики?
Равносторонние треугольники равновелики?
Задачи
Задача A
Доказать, что всякая прямая, проходящая через точку пересечения диагоналей параллелограмма, делит его на 2 равновеликие части.
Доказательство.
Задача B — Про торт и бесстыдную птичку
Решается на основании задачи A.
У бабушки было два внука, которые должны были приехать на выходные погостить. Она, как любая добропорядочная бабушка, приготовила для них торт. И поставила его на подоконник. Но пока он там стоял, над домом бабушки пролетала бесстыдная птичка. И так получилось, что она справила свою нужду аккурат на краешек торта. Бабушка увидав это не упала духом и решила, что этот кусочек она просто вырежет (см рисунок). Бабушка была очень справедливая, внуков любила одинаково, и к своей работе относилась трепетно. Помогите бабушке разделить весь оставшийся торт на две совершенно одинаковые по площади части.
Она, как любая добропорядочная бабушка, приготовила для них торт. И поставила его на подоконник. Но пока он там стоял, над домом бабушки пролетала бесстыдная птичка. И так получилось, что она справила свою нужду аккурат на краешек торта. Бабушка увидав это не упала духом и решила, что этот кусочек она просто вырежет (см рисунок). Бабушка была очень справедливая, внуков любила одинаково, и к своей работе относилась трепетно. Помогите бабушке разделить весь оставшийся торт на две совершенно одинаковые по площади части.
Бабушка имеет идеальный глазомер, она легко способна находить на глаз середины и пересечения любых отрезков. И у бабушки есть замечательный нож, которым она умеет лихо отрезать куски торта по любой намеченной прямой.
Решение.
Задание
Начертите равновеликие треугольники.
Решение.
Задача
Доказать, что медиана делит треугольник на два равновеликих треугольника.
Решение.
У треугольников одинаковые основания и одна и та же высота. Поэтому треугольники имеют одинаковую площадь.
Следствие. Диагонали параллелограмма разбивают его на четыре равновеликих треугольника.
Задача
Доказать, что медианы треугольника разбивают его на шесть равновеликих треугольников.
Решение.
Рассмотреть попарно эти шесть треугольников. У них одинаковые основания и одна и та же высота. Поэтому попарно треугольники имеют одинаковую площадь. В силу транзитивности все 6 треугольников равновелики.
Задача
Начертите треугольник ABC. Через вершину B проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади.
Решение.
Подсказка: Используйте теорему Фалеса: (разделите АC на 3 равные части).
У треугольников одинаковые основания и одна и та же высота. Поэтому треугольники имеют одинаковую площадь.
Задача
Постройте полукруг, равновеликий данному кругу.
Постройте круг, равновеликий данному полукругу.
Задача
Доказать, что круг на рисунке разбит на 9 равновеликих частей
Решение
Но капитан словно бы и не заметил нашего недоверия. Он положил чертёж на бочку и стал объяснять. — Перед вами круг с двумя взаимно перпендикулярными диаметрами. Каждый диаметр разделён на три равные части, а каждая из этих трёх равных частей, в свою очередь, представляет собой диаметр малого круга. Как видите, таких малых кругов в большом круге пять, и они совершенно одинаковы
Известно, что если диаметр круга уменьшить, допустим, в три раза, то площадь круга уменьшится при этом в трижды три раза.
Отсюда следует, что площадь каждого из пяти малых кругов в девять раз меньше большого. Ведь три в квадрате равно девяти ( 3 * 3 = 9 ) !
Капитан перевёл дух и продолжал:
— Остаётся вычислить, чему равна площадь каждой из четырёх заштрихованных частей, заключённых между малыми кругами.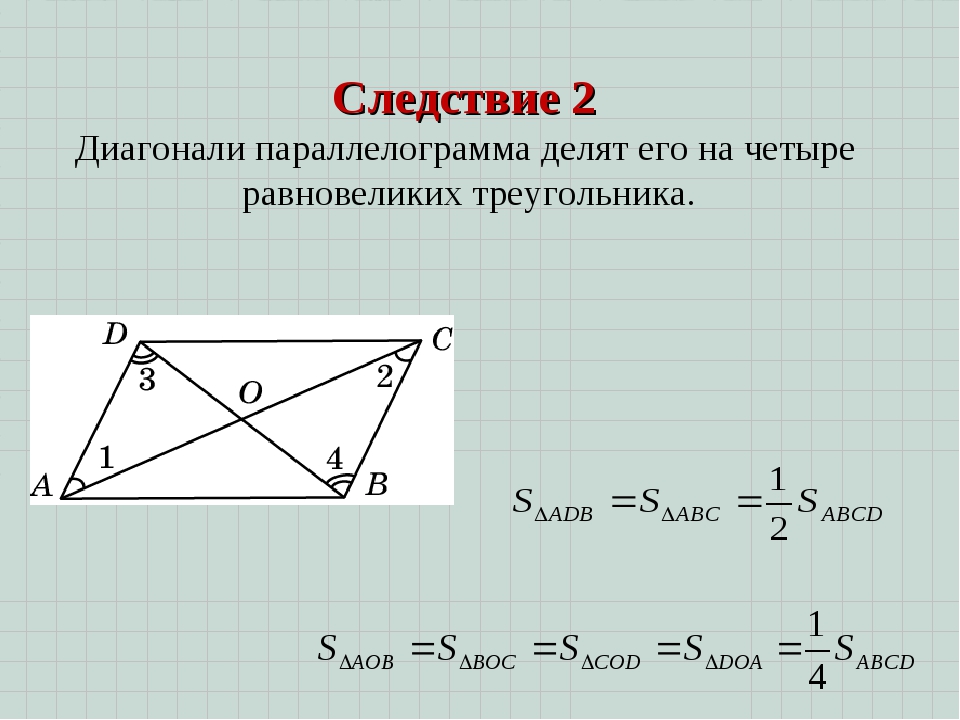
— Ну, это просто! — сейчас же выскочил я.- Если площадь большого круга принять за 9/9, то площадь всех пяти малых кругов составит 5/9, а на оставшиеся четыре части придётся 4/9. И части эти, само собой, тоже конгруэнтны.
— Отсюда ясно,- подытожил Пи,- что площадь каждой из заштрихованных частей также составляет 1/9 часть площади большого круга. Вот и выходит, что площадь большого круга разделена на девять равновеликих частей.
Задача
Найти площадь четвертой части
Решение
Подсказка. Нужно соединить точку внутри четырехугольника с его вершинами.
После этого существующие отрезки станут медианами треугольников. Как известно, медиана делит площадь треугольника пополам.
Отсюда уравнения:
И легко получаем c+d = 32+16-20 = 28
Вывод — квадрат на рисунке можно заменить на любой четырехугольник.
mat/geom/area. txt · Последние изменения: 2016/01/18 00:22 — kc
txt · Последние изменения: 2016/01/18 00:22 — kc
Corel Draw на уроках геометрии
Corel Draw на уроках геометрииРешение задач на разрезание играет важную роль в формировании понятий площади, равновеликости и равносоставленности, развитии геометрических представлений.
Две фигуры называются равносоставленными, если они могут быть разложены на одинаковое число попарно равных фигур.
Из свойств площади следует, что равносоставленные фигуры равновелики. В частности, равносоставленные многоугольники равновелики. Например, изображенные на рисунке правильный шестиугольник и параллелограмм — равносоставленные фигуры, так как обе они составлены из шести равных равносторонних треугольников.
Естественно
поставить обратный вопрос: всякие ли два
равновеликих многоугольника
равносоставлены? Утвердительное его
решение было получено в XIX веке.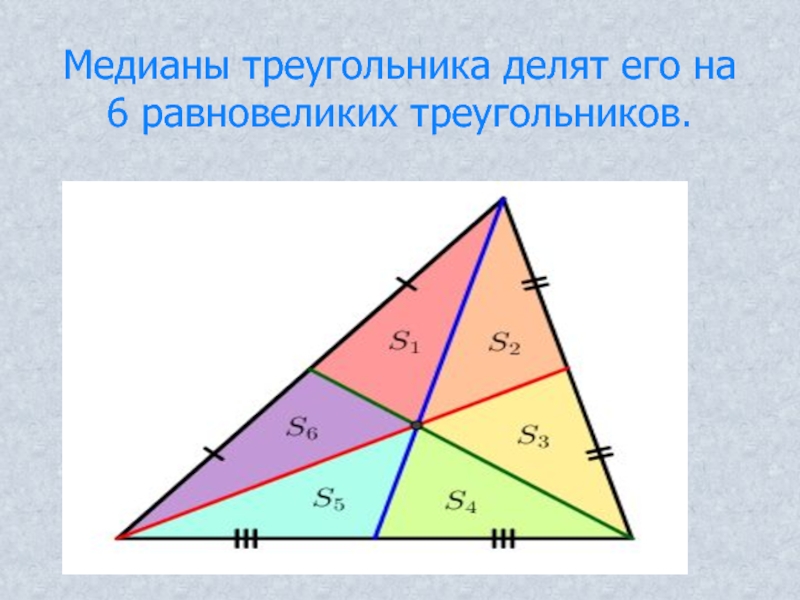
Теорема. Любые два равновеликих многоугольника равносоставлены.
Доказательство этой теоремы будет получено как результат применения нескольких теорем.
Теорема 1. Две фигуры, равносоставленные с одной и той же фигурой, равносоставлены.
Доказательство. Действительно, пусть фигуры Ф’ и Ф» равносоставлены с фигурой Ф. Рассмотрим линии, разбивающие фигуру Ф на части, из которых можно составить фигуру Ф’ и, кроме того, линии, разбивающие фигуру Ф на части, из которых можно составить фигуру Ф». Те и другие линии разбивают фигуру Ф на более мелкие части, из которых можно составить как фигуру Ф’, так и Ф». Таким образом, фигуры Ф’ и Ф» равносоставлены.
Теорема
2. Любые два
равновеликих параллелограмма
равносоставлены.
Любые два
равновеликих параллелограмма
равносоставлены.
Доказательство. Рассмотрим сначала два параллелограмма с равными основаниями . По условию они равновелики, значит, имеют равные высоты. Проведем внутри каждого параллелограмма отрезки, параллельные сторонам другого параллелограмма. Тогда оба параллелограмма разобьются на одинаковое число попарно равных треугольников.
Пусть
теперь параллелограммы не имеют равных
сторон. Построим третий параллелограмм,
имеющий с первым одинаковые основание и
высоту. Поскольку при этом другую сторону
третьего параллелограмма можно выбирать
произвольно, сделаем ее равной одной из
сторон второго параллелограмма. Тогда
третий параллелограмм будет равновелик и с
первым, и со вторым, и с каждым из них имеет
по равной стороне. Следовательно, он
равносоставлен и с первым, и со вторым
параллелограммом. В силу теоремы 1, первый и
второй параллелограммы равносоставлены.
В силу теоремы 1, первый и
второй параллелограммы равносоставлены.
Теорема 3. Любые два равновеликих треугольника равносоставлены.
Доказательство. Каждый треугольник продолжением средней линии преобразуется в равновеликий ему параллелограмм. Поэтому два равновеликих треугольника преобразуются в два равновеликих параллелограмма. В силу теоремы 2 эти параллелограммы равносоставлены и, следовательно, равносоставлены исходные треугольники.
Теорема 4. Всякий многоугольник равносоставлен с некоторым треугольником.
Доказательство.
Рассмотрим
многоугольник и одну из его вершин
перенесем параллельно диагонали на
продолжение одной из сторон.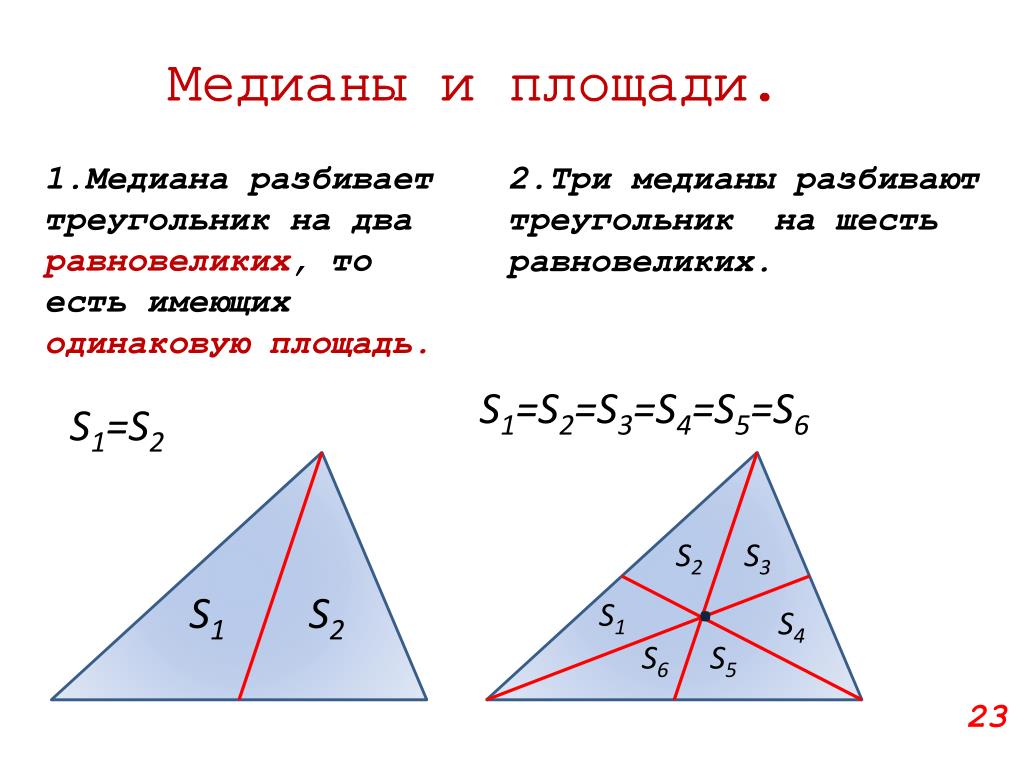 При этом
исходный многоугольник преобразуется в
равновеликий многоугольник с числом сторон,
на единицу меньшим. Имея в виду, что мы
заменили один треугольник другим —
равновеликим, а остальная часть осталась
неизменной, получим, что новый
многоугольник будет равносоставлен с
исходным. Продолжая этот процесс, мы
превратим исходный многоугольник в
равносоставленный с ним треугольник.
При этом
исходный многоугольник преобразуется в
равновеликий многоугольник с числом сторон,
на единицу меньшим. Имея в виду, что мы
заменили один треугольник другим —
равновеликим, а остальная часть осталась
неизменной, получим, что новый
многоугольник будет равносоставлен с
исходным. Продолжая этот процесс, мы
превратим исходный многоугольник в
равносоставленный с ним треугольник.
Приступим теперь к доказательству основной теоремы. Напомним ее формулировку:
Теорема. Любые два равновеликих многоугольника равносоставлены.
Доказательство.
Пусть М’ и М»
— равновеликие многоугольники. Рассмотрим
равносоставленные с ними треугольники Т’ и
Т» соответственно. Эти треугольники
равновелики, а следовательно,
равносоставлены. Значит, равносоставлены и
исходные многоугольники М’ и М».
Высота искомого треугольника, очевидно, будет четвёртой пропорциональной
к данному основанию и к основанию и высоте данного тре-
*) Пользуясь только циркулем и линейкой. Прим. ред. перевода
239 ПОСТРОЕНИЯ.
угольника, так как четыре таких числа, что произведение двух из них
равно произведению двух других, составляют пропорцию. Когда высота
найдена, мы отложим её на каком-либо перпендикуляре к данному
основанию и, таким образом, получим вершину одного из бесчисленного
множества треугольников, который удовлетворяет условиям.
Ясно,, что точно так же можно построить треугольник, имеющий
данную высоту и равновеликий данному треугольнику.
265. Задача. Построить треугольник, равновеликий данному
многоугольнику.
Разложим многоугольник на треугольники и превратим их в треугольники
с общим основанием с помощью предыдущего построения.
Треугольник, имеющий то же основание и высоту, равную сумме
высот всех составляющих треугольников,
будет равновелик сумме этих треугольников,
т.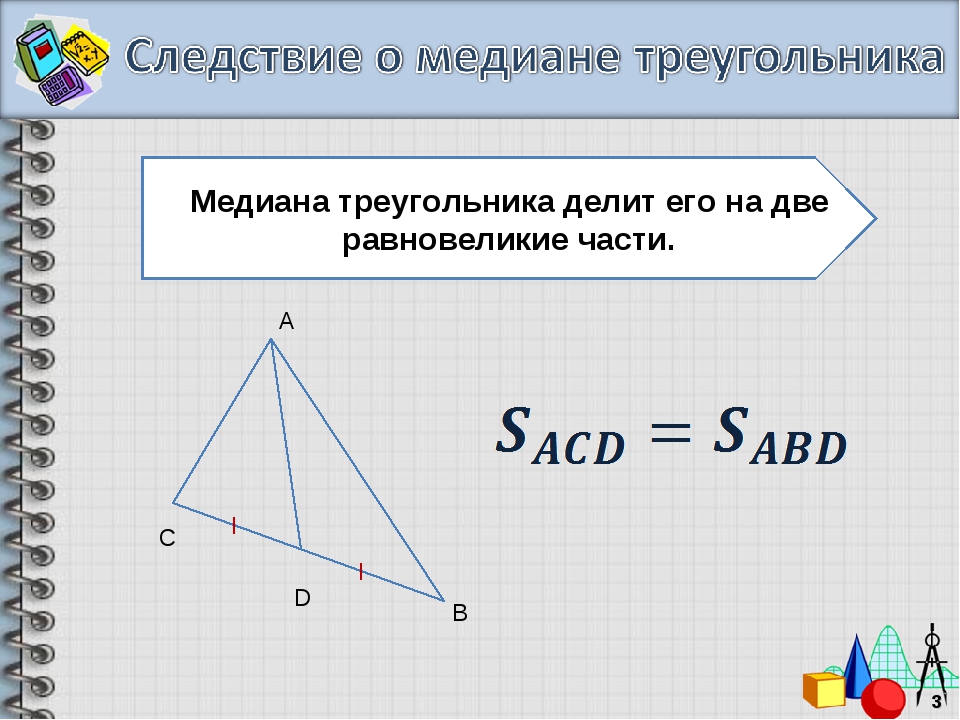 е. данному многоугольнику.
е. данному многоугольнику.
Это построение может быть значительно
сокращено; мы это сейчас пока-
В жем, предполагая для простоты, что
многоугольник выпуклый.
Пусть дан многоугольник ABCDE
(черт. 229). Проведём диагональ СЕ, которая
соединяет две верщины, смежные с
Черт. 229. одной и той же вершиной D, и через эту *
. вершину D проведём параллельно СЕ прямую
DU до пересечения с продолжением стороны АЕ в точке D\
Треугольник CEDT равновелик треугольнику CED (п. 250), а многоугольник
АВСП — соответственно многоугольнику ABCDE; таким
образом, мы заменим данный многоугольник равновеликим ему многоугольником,
имеющим на одну сторону меньше, чем первоначальный. Мы
продолжаем это построение до тех пор, пока не придём к треугольнику.
Задача. Построить квадрат, равновеликий данному многоугольнику.
Сторона искового квадрата будет средним пропорциональным
между основанием и половиной высоты треугольника, полученного
предыдущим построением.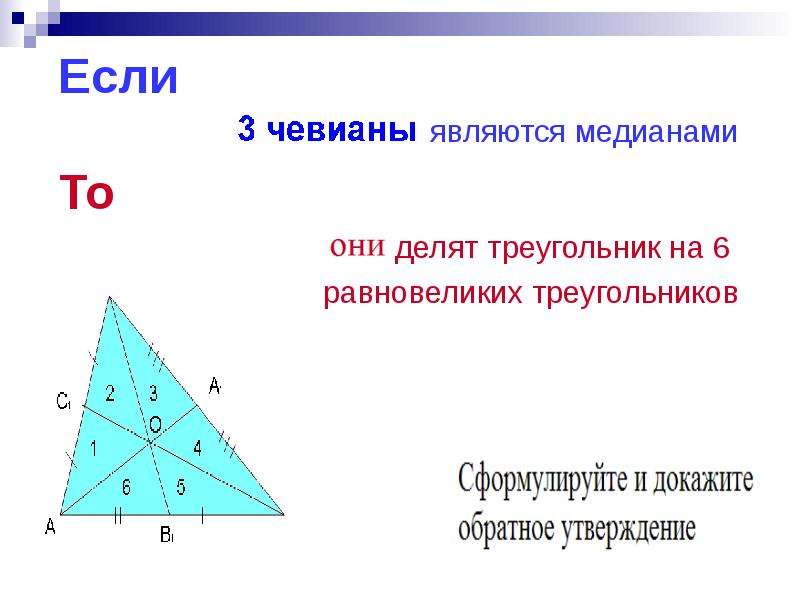
266, Задача. Построить многоугольник, равновеликий данному
многоугольнику и подобный другому данному многоугольнику.
Пусть требуется построить многоугольник Р, подобный данному
многоугольнику F и равновеликий другому данному многоугольнику
Рх. Пусть d — сторона квадрата, равновеликого многоугольнику Р’,
а — сторона квадрата, равновеликого многоугольнику Рх; эти стороны
можно определить тем же путём, как это было указано выше. Отношение
площадей многоугольников Рг и Р%, т. е. отношение площадей
многоугольника Р’ и искомого многоугольника, 6yAej
240 ПОСТРОЕНИЯ.
Следовательно, если A!Bf — какая-нибудь сторона многоугольника
F, то соответствующая сторона АВ искомого многоугольника
определяется из пропорции
а’ АВ’
а АВ ’
поэтому её можно найти построением четвёртой пропорциональной
(п. 151), и задача приведена к построению За, п. 152.
267, Знаменитая задача о квадратуре круга состоит в построении
стороны квадрата, равновеликого данному кругу.
Эта сторона, как видно из выражения для площади круга, есть
средняя пропорциональная между радиусом и длиной полуокружности,
и задача была бы разрешена, если бы была известна последняя.
Обратно, если бы была построена сторона квадрата, равновеликого
данному кругу, то длина полуокружности получилась бы как третья
пропорциональная к радиусу и стороне квадрата. Задача о квадратуре
круга сводится к той задаче, о которой мы говорили в п. 184: Построить
отрезок, равный длине окружности данного радиуса. Как
мы уже говорили, эта задача, а следовательно, и задача о квадратуре
круга не могут быть решены с помощью линейки и циркуля.
УПРАЖНЕНИЯ.
319. Построить прямоугольник, зная его периметр и площадь.
Какой из прямоугольников, имеющих данный периметр, будет имёть
наибольшую площадь?
320. Вписать в круг прямоугольник данной площади.
Какой из прямоугольников, вписанных в данный круг, будет иметь наибольшую
площадь?
321. Разделить треугольник на равновеликие части прямыми данного
Разделить треугольник на равновеликие части прямыми данного
направления.
Та же задача для произвольного многоугольника.
322. Разделить четырёхугольник прямыми, выходящими из одной его
вершины, на данное число равновеликих частей. Показать, что для построения
точек пересечения искомых прямых со сторонами четырёхугольника
достаточно разделить на равные части диагональ, которая не проходит
через данную вершину, и через точки деления провести прямые, параллельные
другой диагонали, до пересечения со сторонами четырёхугольника.
323. Разделить произвольный многоугольник на равновеликие части
прямыми, выходящими из одной и той же вершины.
ЗАДАЧИ К ЧЕТВЁРТОЙ КНИГЕ.
324. Показать, что формулировку предложений упражнения 296 можно
видоизменить так, что они будут верны, каково бы mi было положение
точки О на плоскости, условившись перед числом, выражающим площадь
треугольника, ставить знак + или в зависимости от направления вращения.
325. Если два многоугольника прямо гомотетичны и меньший расположен
внутри большего, то площадь любого многоугольника, описанного около
одного из них и вписанного в другой, будет средней пропорциональной между
площадями данных многоугольников.
241 ПОСТРОЕНИЯ.
326. Найти отношение площади данного треугольника к площади треугольника,
имеющего своими сторонами медианы данного треугольника.
327. Через две вершины треугольника проведены прямые, делящие
противоположные стороны в данных отношениях. Найти отношения, площадей
тех частей, на которые эти прямые делят площадь треугольника.
328. Через три вершины треугольника проведены прямые, делящие
противоположные стороны в данных отношениях. Найти. отношение площади
треугольника, образованного этими прямыми, к площади данного
треугольника. Вывести отсюда теоремы пп. 197 и 198, которые дают условие,
при котором все три прямые проходят через одну и ту же точку.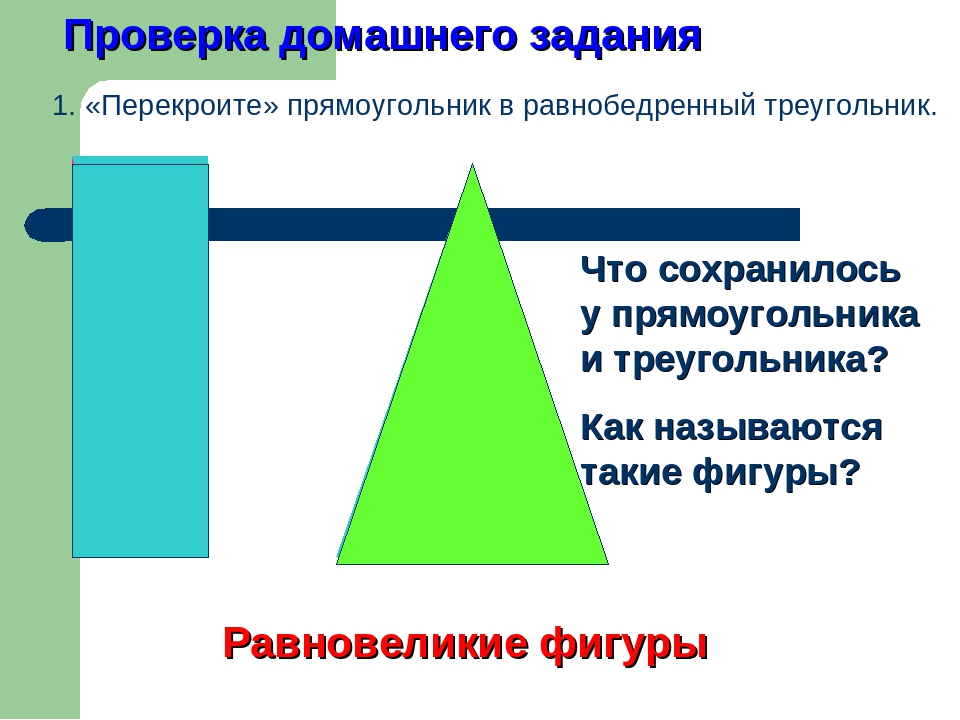
329. Через точку внутри угла провести секущую так, чтобы она образовала
со сторонами угла треугольник данной площади. (Прежде всего
ртроим параллелограмм, имеющий заданную площадь, один из углов которого
совпадает с данным углом и одна из сторон которого проходит через
данную точку. Искомая секущая должна отсекать от этого параллелограмма
треугольник, площадь которого равнялась бы сумме площадей двух
других треугольников, лежащих вне построенного параллелограмма и
образованных этой “секущей, сторонами параллелограма и сторонами данного
угла.)
330. Среди всех прямых, которые проходят через точку, ‘заданную
внутри угла, и пересекают его стороны (но не их продолжения), найти ту,
которая образует со сторонами угла треугольник, имеющий наименьшую
площадь.
331. Среди всех многоугольников с одним и тем же числом сторон и
вписанных в один и тот же круг наибольшую площадь будет иметь правильный
многоугольник *) (доказать).
332. Построить треугольник, зная его сторону, соответствующую высоту
и радиус вписанной окружности.
333. В данный круг вписать трапецию, зная один из её углов и площадь.
334. Треугольник и параллелограмм имеют одно и то же основание,
по равному углу при основании и одну и ту же площадь. Разрезать одну
из этих фигур на такие две части, чтобы они, будучи сложены иначе, давали
бы другую фигуру.
335. Два треугольника имеют одно и то же основание и одну и ту же
высоту. Разрезать один из них на части так, чтобы сложенные иначе они
дали бы другой. (Свести эту задачу к подобному же вопросу о параллелограммах,
пользуясь результатом предыдущей задачи.)
336. Та же задача для каких-либо двух равновеликих треугольников.
337. Та же задача для каких-либо двух равновеликих многоугольников.
338. Пусть даны четыре точки А, В, С, D; произведение площади треугольника
BCD на степень точки А относительно круга, описанного около
этого треугольника, равно каждому из произведений, образованных таким
же образом точкой В и треугольником CAD, или точкой С и треугольником
ABO, или точкой D и треугольником АС В (доказать). лощадь многоугольника увеличим; выполняя эту операцию
лощадь многоугольника увеличим; выполняя эту операцию
столько раз,’ сколько будет необходимо для того, чтобы заменить
данный многоугольник правильным многоугольником, получим искомое
предложение.
242 ПОСТРОЕНИЯ.
Показать, кроме того, что эти равенства можно считать верными как
по величине, так и по знаку, если использовать соглашение, установленное
в задаче 324.
339. Каждое из произведений, рассмотренных в предыдущей задаче,
равно площади треугольника, стороны которого выражаются теми же числами,
что и произведения АВ • СД АС « DB, AD — ВС (доказать; см. п. 218,
упр. 270а).
340. Разрезать треугольник на равнобедренные треугольники. Та же
задача для произвольного многоугольника.
341. Вычислить площадь треугольника, образованного тремя дугами окружности
одного и того же радиуса R, попарно пересекающимися под прямым
углом.
342. Если два треугольника симметричны друг с другом относительно*
центра их общей вписанной окружности, то площади восьми треугольников,
которые образуются их сторонами, дают в произведении шестнадцатую степень
радиуса этой окружности.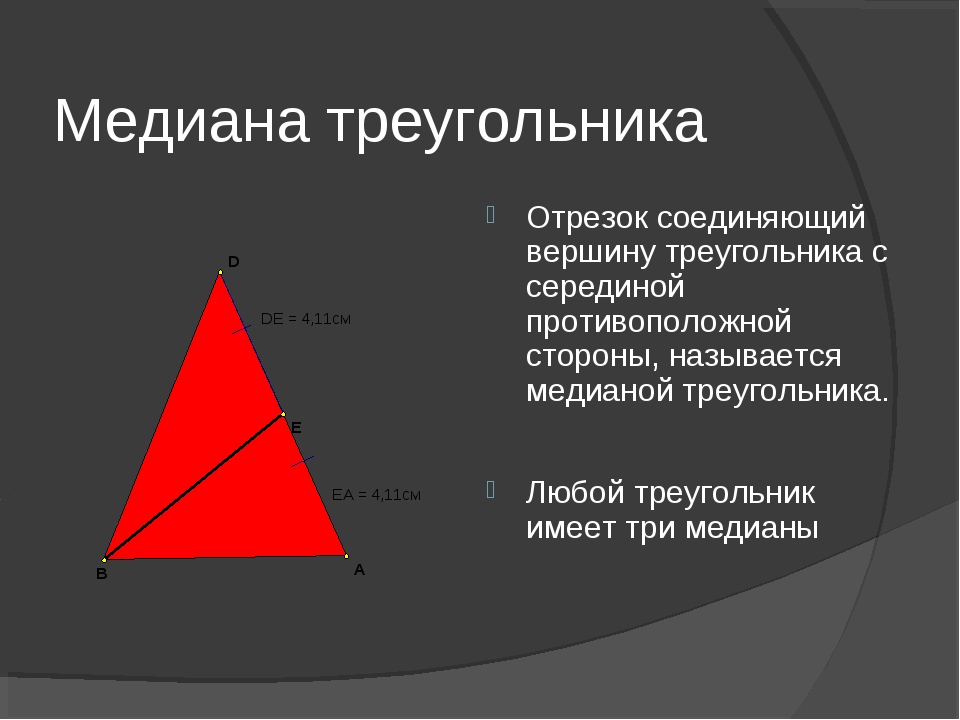
243 ПОСТРОЕНИЯ.
ПОСТРОЕНИЯРавновеликие многоугольники
Два многоугольника называются равновеликими, если их площади равны
Примером равновеликих многоугольников могут служить любые равные многоугольники. Обратное утверждение, конечно, неверно: равновеликие многоугольники могут быть не равными. Также примером равновеликих многоугольников являются равносоставленные многоугольники.
Задача деления площадей фигур с помощью прямых, пересекающих их, и превращения одной фигуры в другую путем разрезания и пересоставления их частей возникла еще в древности из потребностей практики, землемерия и архитектуры. В сохранившемся на арабском языке сочинении Евклида «О делении фигур» рассматривается вопрос о том, как можно с помощью прямой линии, проходящей через данную точку, разделить пополам или в некотором отношении площадь данного многоугольника.
Проблема деления площадей особенно интересовала математиков эпохи Возрождения. Одной из самых простых и удобных для измерения площадей фигур является квадрат. Поэтому издавна появилось стремление превращать любую фигуру в равновеликий квадрат. Евклид, например, ставит и решает задачу о построении квадрата, равновеликого данному многоугольнику.
Поэтому издавна появилось стремление превращать любую фигуру в равновеликий квадрат. Евклид, например, ставит и решает задачу о построении квадрата, равновеликого данному многоугольнику.
Задачи преобразования равновеликих фигур занимали умы ученых 19 века и поныне интересуют математиков.
Рассмотрим несколько типов задач:
Практические задачи (задачи на «разрезание»):
Задача № 1:
Разделить данный треугольник на три равновеликих треугольника прямыми, выходящими из одной вершины.
Решение
Разделим сторону АС на три равных отрезка (AD, DN, NC). Проведем через вершину B три прямые, проходящие через точки D, N. Образуются три треугольника: ABD, DBN, NBC.
Полученные треугольники являются равновеликими, так как имеют общую высоту и равные стороны, к которым эта высота проведена.
Предлагаем задачи для самостоятельного решения.
Задача № 2:
Вырежьте из бумаги два равных прямоугольника, у каждого из которых одна сторона вдвое больше другой.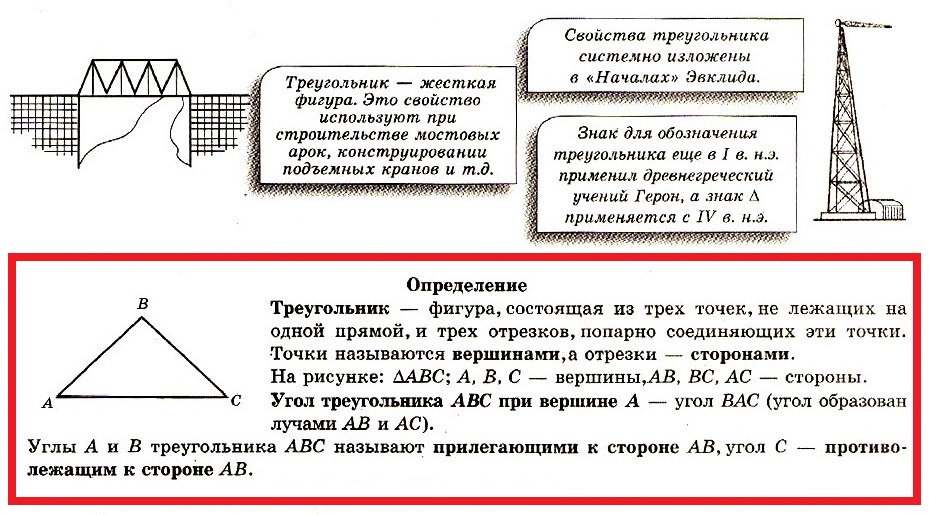 Один из них разрежьте на 2 части так, чтобы из них можно было составить прямоугольный треугольник. Другой разрежьте на 3 части так, чтобы из них можно было составить квадрат.
Один из них разрежьте на 2 части так, чтобы из них можно было составить прямоугольный треугольник. Другой разрежьте на 3 части так, чтобы из них можно было составить квадрат.
Задача № 3:
Постройте прямоугольный треугольник и покажите, как его разрезать на части так, чтобы из них можно было сложить прямоугольник, равновеликий данному треугольнику.
Задача № 4:
Постройте треугольник, не являющийся прямоугольным. Покажите, как его разрезать на три части так, чтобы из них можно было сложить прямоугольник с тем же основанием, равновеликий данному треугольнику.
Задача № 5:
Нарисуйте на клетчатой бумаге два разных прямоугольных треугольника, у которых площади:
1) равны двум клеткам
2) равны трем клеткам
3) равны 4,5 клеткам
Задача № 6:
Нарисуйте на клетчатой бумаге квадрат, площадь которого равна 2, 4, 5, 8, 9, 10, 16, 17, 18, 20, 25, 26 клеткам.
Задача № 7:
Превратить треугольник в равновеликий ему параллелограмм.
Задача № 8:
Превратить параллелограмм в равновеликий ему треугольник.
Задача № 9:
Постройте квадрат, площадь которого в два раза больше пощади данного квадрата.
Задача № 10:
Вырежьте из бумаги два равных прямоугольных треугольника и составьте из них:
1) равнобедренный треугольник
2) прямоугольник
3) параллелограмм, не являющийся прямоугольником
Объясните, почему площади всех полученных фигур равны между собой.
Задача № 11:
Данный прямоугольник разделить на 4 равновеликие части прямыми, выходящими из одной вершины.
Задача № 12:
Данный параллелограмм разделить на 4 равновеликие части прямыми, выходящими из одной вершины.
Задача № 13:
Данный параллелограмм разделить на 3 равновеликие части прямыми, выходящими из одной вершины.
Задачи на построение:
Задача № 1: Дан треугольник ABC. Найдите геометрическое место точек P, для которых треугольники APB и ABC равновелики.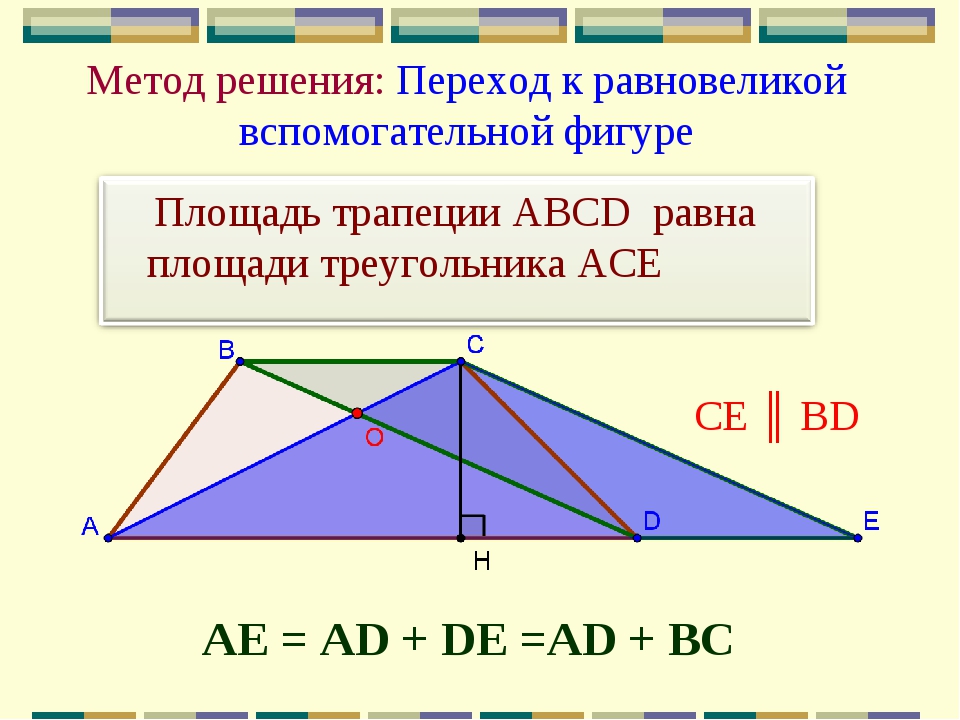
Решение:
Поскольку равновеликие треугольники APB и ABC имеют общее основание AB, то равны их высоты, проведенные из вершин соответственно C и P. Значит, геометрическое место точек Р совпадает с геометрическим местом точек, удаленных от прямой АВ на расстояние, равное высоте CH треугольника АВС, а это, как известно, — две параллельные прямые, удаленные от прямой АВ на расстояние, равное CH.
Предлагаем задачи для самостоятельного решения.
Задача № 2:
Дан треугольник ABC. Найдите геометрическое место точек P, для которых треугольники APB и APC равновелики.
Задача № 3:
Дан треугольник ABC. Найдите геометрическое место точек P, для которых треугольники APB, APC и BPC равновелики.
Подсказка:
Задачи на доказательство:
Задача № 1:
Точка O лежит на прямой, содержащей диагональ AC параллелограмма ABCD. Докажите, что площади треугольников AOB и AOD равны.
Решение
Выполним дополнительное построение: ВМ, DN – высоты. Затем рассмотрим прямоугольные треугольники AND и СМВ. Т. к. сторона AD равна стороне BC (по свойству параллелограмма), а угол DAC равен углу BCA (накрест лежащие углы при параллельных прямых AD ,BC и секущей AC), то треугольник AND будет равен треугольнику СМВ. Из равенства треугольников следует равенство соответствующих сторон BM=DN. Значит, площадь треугольника AOB будет равна площади треугольника AOD, так как эти треугольники имеют общую сторону АО и равные высоты, проведенные к этой стороне.
Затем рассмотрим прямоугольные треугольники AND и СМВ. Т. к. сторона AD равна стороне BC (по свойству параллелограмма), а угол DAC равен углу BCA (накрест лежащие углы при параллельных прямых AD ,BC и секущей AC), то треугольник AND будет равен треугольнику СМВ. Из равенства треугольников следует равенство соответствующих сторон BM=DN. Значит, площадь треугольника AOB будет равна площади треугольника AOD, так как эти треугольники имеют общую сторону АО и равные высоты, проведенные к этой стороне.
Предлагаем задачи для самостоятельного решения.
Задача № 2:
Докажите, что медианы разбивают треугольник на шесть равновеликих треугольников.
Задача № 3:
Отрезок, соединяющий середины двух противоположных сторон выпуклого четырёхугольника, разделил его на два четырёхугольника, имеющих равные площади. Докажите, что эти стороны параллельны.
Задача № 4:
Докажите, что треугольники ABC и DHF равновелики, если угол A равен углу D и AB: DH = DF : AC.
Задача №5:
В треугольнике АВС проведены медианы АМ и ВК, которые пересекаются в точке О. Докажите, что треугольники АОК и ВОМ равновелики. Попробуйте дать два различных доказательства.
Докажите, что треугольники АОК и ВОМ равновелики. Попробуйте дать два различных доказательства.
Задача №6:
Трапеция равновелика треугольнику, образованному продолжениями её боковых сторон и меньшим основанием. Докажите, что отношение длин оснований этой трапеции равно.
Задача №7:
Диагонали трапеции АВСD с основаниями АВ и СD пересекаются в точке О. Докажите, что треугольники АОD и ВОС имеют равные площади.
Фигуры совпадающие при наложении называются. Равные фигуры это
В этой задаче нам нужно разобраться с понятие равенства фигур.
Геометрическая фигура
Разберемся с понятием геометрическая фигура. Для этого введем определение.
Определение: Геометрическая фигура — это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.
Равные фигуры
- Геометрические фигуры будут называться если они имеют одинаковую форму, размеры, их площади и периметры равны;
- Например длина квадрата 4 см.
 2. Площади двух фигур равны. Но сами фигуры равны не будут, потому что у них разная форма;
2. Площади двух фигур равны. Но сами фигуры равны не будут, потому что у них разная форма; - Если взять два круга, очевидно, что их формы равны. Но если у них разные радиусы, но фигуры не будут является равными;
- Равными фигурами будут называться два квадрата с равной стороной, два круга с одинаковым радиусом.
Одним из основных понятий в геометрии является фигура. Под этим термином подразумевается множество точек на плоскости, ограниченное конечным числом линий. Некоторые фигуры могут рассматриваться как равные, что тесно связано с понятием движения. Геометрические фигуры могут рассматриваться не изолированно, а в том или ином соотношении друг с другом – их взаимное расположение, соприкосновение и прилегание, положение «между», «внутри», соотношение, выраженное в понятиях «больше», «меньше», «равно».
Геометрия изучает инвариантные свойства фигур, т.е. те, которые остаются неизменными при тех или иных геометрических преобразованиях. Такое преобразование пространства, при котором остается неизменным расстояние между точками, составляющими ту или иную фигуру, называется движением.
Движение может выступать в разных вариантах: параллельный перенос, тождественное преобразование, поворот вокруг оси, симметрия относительно прямой или плоскости, центральная, поворотная, переносная симметрия.
Движение и равные фигуры
Если возможно такое движение, которое приведет к совмещению одной фигуры с другой, такие фигуры называют равными (конгруэнтными). Две фигуры, равные третьей, равны и между собою – такое утверждение было сформулировано еще Евклидом, основоположником геометрии.Понятие конгруэнтных фигур может быть объяснено и более простым языком: равными называются такие фигуры, которые полностью совпадут при наложении их друг на друга.
Это достаточно легко определить, если фигуры даны в виде неких предметов, которыми можно манипулировать – например, вырезаны из бумаги, поэтому в школе на уроках нередко прибегают к такому способу объяснения данного понятия. Но две фигуры, начерченные на плоскости, нельзя физически наложить друг на друга. В данном случае доказательством равенства фигур выступает доказательство равенства всех элементов, составляющих эти фигуры: длина отрезков, размер углов, диаметр и радиус, если речь идет об окружности.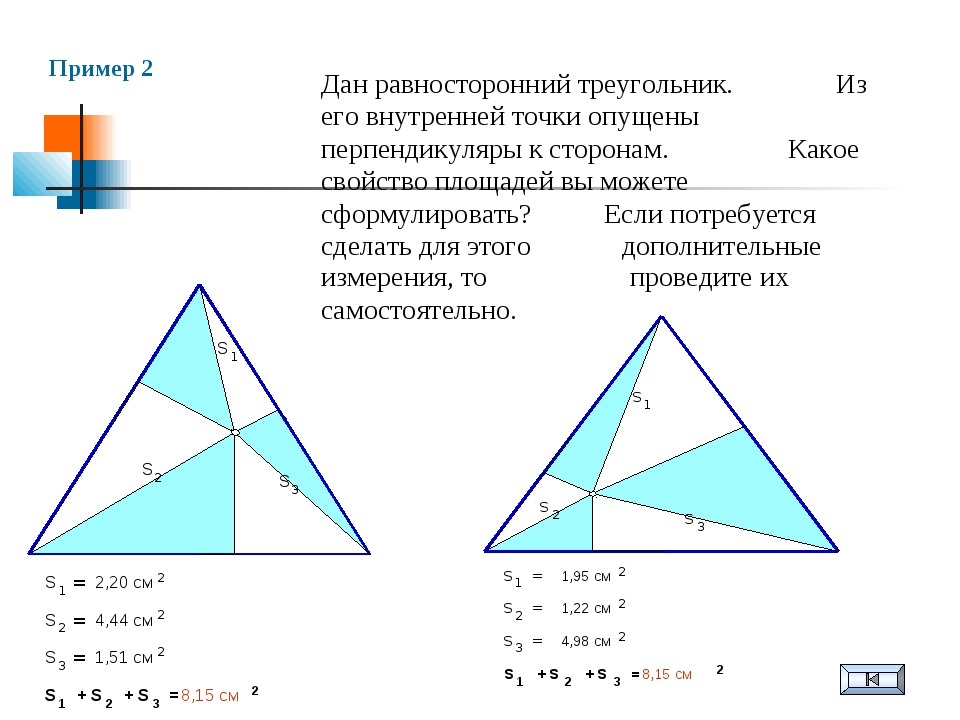
Равновеликие и равносоставленные фигуры
С равными фигурами не следует смешивать равновеликие и равносоставленные фигуры – при всей близости данных понятий.Равновеликими называются такие фигуры, которые имеют равную площадь, если это фигуры на плоскости, или равный объем, если речь идет о трехмерны телах. Совпадение всех элементов, составляющих данные фигуры, не является обязательным. Равные фигуры будут равновеликими всегда, но не всякие равновеликие фигуры можно назвать равными.
Понятие равносоставленности чаще всего применяют к многоугольникам. Оно подразумевает, что многоугольники можно разбить на одинаковое количество соответственно равных фигур. Равносоставленные многоугольники всегда являются равновеликими.
В этой задаче нам нужно разобраться с понятие равенства фигур.
Геометрическая фигура
Разберемся с понятием геометрическая фигура. Для этого введем определение.
Определение: Геометрическая фигура — это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.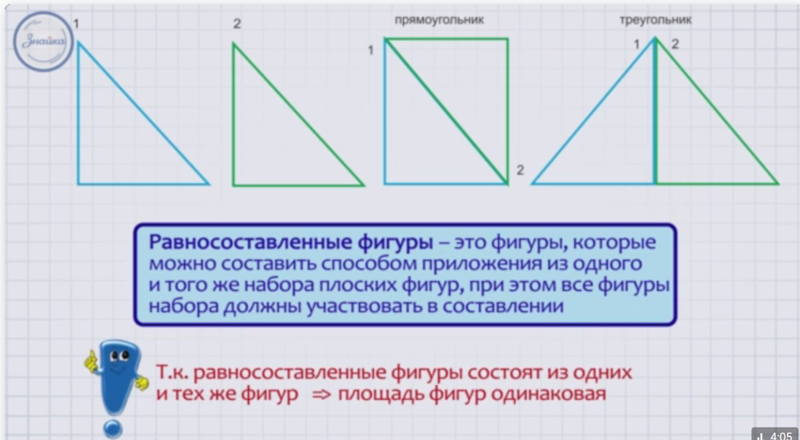 2. Площади двух фигур равны. Но сами фигуры равны не будут, потому что у них разная форма;
2. Площади двух фигур равны. Но сами фигуры равны не будут, потому что у них разная форма;
Какие фигуры называются равными?
Равными называют фигуры , которые совпадают при наложении.
Частой ошибкой на этот вопрос является ответ, в котором упоминаются равные стороны и углы геометрической фигуры. Однако при этом не принимается в учет, что стороны геометрической фигуры не обязательно бывают прямыми. Поэтому только совпадение геометрических фигур при наложении может быть признаком их равенства.
На практике это легко проверить с помощью наложения, они должны совпасть.
Все очень просто и доступно, обычно равные фигуры видно сразу.
Равными называются те фигуры, у которых совпадают параметры геометрии. Эти параметры: длина сторон, величина углов, толщина.
Проще всего понять что фигуры равны можно с помощью наложения. Если величины фигур одинаковы — их называют равными.
Равными называют только те геометрические фигуры, которые имеют абсолютно одинаковые параметры:
1) периметр;
2) площадь;
4) размеры.
То есть, если одну фигуру наложить на другую, то они совпадут.
Ошибочно полагать, что если фигуры имеют одинаковые периметр или площадь, то они равны. На самом деле, геометрические фигуры, у которых равна площадь называются равновеликими.
Фигуры называются равными, если они совпадают при наложении друг на друга.Равные фигуры имеют одинаковые размеры, форму, площадь и периметр. А вот равные по площади фигуры могут быть и не равными между собой.
В геометрии, по правилам, равные фигуры должны иметь одинаковую площадь и периметр, то есть у них должны быть абсолютно одиноковые формы и размеры. И они должны полностью совпадать при их наложении друг на друга. Если же есть какие-то расхождения, то эти фигуры уже нельзя будет назвать равными.
Фигуры можно назвать равными при условии, если они полностью совпадают при наложении друг на друга, т.е. они имеют одинаковые размеры, форму и следовательно площадь и периметр, а также другие характеристики. В противном случае говорить о равности фигур нельзя.
В самом слове равные заложена суть.
Это фигуры которые полностью идентичные друг другу. То есть полностью совпадают. Если фигуру положить одну на одну тогда фигуры будут перекрывать себя со всех сторон.
Они одинаковые то есть равные.
В отличие от равных треугольников (для определения которых достаточно выполнения одного из условий — признаков равенства), равными фигурами называют такие, которые имеют одинаковую не только форму, но и размеры.
Определить, равна ли одна фигура другой, можно методом наложения. При этом фигуры должны совпасть и сторонами и углами. Это и будут равные фигуры.
Равными могут быть только такие фигуры, которые при их наложении полностью совпадут сторонами и углами. На самом деле для всех простейших многоугольников равенство их площади свидетельствует и о равенстве самих фигур. Пример: квадрат со стороной а всегда будет равен другому квадрату с той же стороной а. Тоже касается и прямоугольников и ромбов — если их стороны равны сторонам другого прямоугольника, они равны. Более сложный пример: треугольники будут равными, если у них равны стороны и соответствующие углы. Но это только частные случаи. В более общих случаях, равенство фигур доказывается все-таки наложением, а это наложение в планиметрии высокопарно именуют движением.
На самом деле для всех простейших многоугольников равенство их площади свидетельствует и о равенстве самих фигур. Пример: квадрат со стороной а всегда будет равен другому квадрату с той же стороной а. Тоже касается и прямоугольников и ромбов — если их стороны равны сторонам другого прямоугольника, они равны. Более сложный пример: треугольники будут равными, если у них равны стороны и соответствующие углы. Но это только частные случаи. В более общих случаях, равенство фигур доказывается все-таки наложением, а это наложение в планиметрии высокопарно именуют движением.
Фигуры называют равными, если совпадает их форма и размеры. Из этого определения следует, например, что если заданные прямоугольник и квадрат имеют равные площади, то они всё-равно не становятся равными фигурами, так как это разные фигуры по форме. Или, два круга однозначно имеют одну и туже форму, но если их радиусы различны, то это тоже не равные фигуры, так как не совпадают их размеры. Равными фигурами являются, например, два отрезка одинаковой длины, два круга с одинаковым радиусом, два прямоугольника с попарно равными сторонами (короткая сторона одного прямоугольника равна короткой стороне другого, длинная сторона одного прямоугольника равна длинной стороне другого).
На глаз бывает трудно определить, равны ли фигуры, имеющие одинаковую форму. Поэтому для определения равенства простых фигур их измеряют (с помощью линейки, циркуля). У отрезков длину, у кругов радиус, у прямоугольников длину и ширину, у квадратов только одну любую сторону. Тут следует отметить, что не все фигуры можно сравнивать. Нельзя, например, определить равенство прямых, т. к. любая прямая бесконечна и, следовательно, все прямые, можно сказать, равны между собой. То же самое касается лучей. Хотя у них есть начало, но нет конца.
Если же мы имеем дело со сложными (произвольными) фигурами, то бывает даже сложно определить, имеют ли они одинаковую форму. Ведь фигуры могут быть перевернуты в пространстве. Посмотрите на рисунок ниже. Трудно сказать, одинаковые ли это по форме фигуры или нет.
Таким образом, нужно иметь надежный принцип сравнения фигур. Он таков: равные фигуры при наложении друг на друга совпадают .
Чтобы сравнить две изображенные фигуры наложением, на одну из них накладывают кальку (прозрачную бумагу) и копируют (срисовывают) на нее форму фигуры. Копию на кальке пытаются наложить на вторую фигуру так, чтобы фигуры совпали. Если это удастся, то заданные фигуры равные. Если нет, то фигуры не равные. При наложении кальку можно поворачивать как угодно, а также переворачивать.
Копию на кальке пытаются наложить на вторую фигуру так, чтобы фигуры совпали. Если это удастся, то заданные фигуры равные. Если нет, то фигуры не равные. При наложении кальку можно поворачивать как угодно, а также переворачивать.
Если можно вырезать сами фигуры (или они представляют собой отдельные плоские объекты, а не нарисованы) то калька не нужна.
При изучении геометрических фигур можно заметить множество их особенностей, связанных с равенством их частей. Так, если сложить круг вдоль диаметра, то две его половинки окажутся равными (они совпадут наложением). Если разрезать прямоугольник по диагонали, то получится два прямоугольных треугольника. Если один из них повернуть на 180 градусов по часовой или против часовой стрелки, то он совпадет со вторым. То есть диагональ разбивает прямоугольник на две равные части.
Какой угол называется развернутым? Какие фигуры называются равными? Обьясните как сравнить два отрезка? какая точка называется
серединой отрезка?
Какой луч называется биссектрисой угла?
что такое градусная мера угла?
Какая фигура называется треугольником?Какие треугольники называются равными?Какой отрезок называют медианой треугольника?Какой отрезок называют
биссектрисой треугольника?Какой отрезок называют высотой треугольника?Какой треугольник называется равнобедренным?Какой треугольник называется равносторонним?Что такое окружность? Определение радиуса, диаметра, хорды. Дайте определение параллельных прямых.Какой угол называется внешним углом треугольника?Какой треугольник называется остроугольным, какой треугольник называется тупоугольным, какой прямоугольным. Как называются стороны прямоугольного треугольника?Свойство двух прямых, параллельных третьей.Теорема о прямой, пересекающей одну из параллельных прямых.Свойство двух прямых перпендикулярных к третьей
Дайте определение параллельных прямых.Какой угол называется внешним углом треугольника?Какой треугольник называется остроугольным, какой треугольник называется тупоугольным, какой прямоугольным. Как называются стороны прямоугольного треугольника?Свойство двух прямых, параллельных третьей.Теорема о прямой, пересекающей одну из параллельных прямых.Свойство двух прямых перпендикулярных к третьей
Какая фигура называется ломаной? Что такое звенья вершины и длина ломаной?
Объясните какая ломанная называется многоугольником. Что такое вершины, стороны, периметр и диагонали многоугольника? Какой многоугольник называется выпуклым?
Объясните какие углы называются выпуклыми углами многоугольника. Выведите формулу для вычисления суммы углов выпуклого n-угольника. Докажите, что сумма внешних углов выпуклого многоугольника. ВЗЯТЫХ по одному прикаждой вершине, равна 360 градусов.
Чему равна сумма углов выпукого четырехугольника?
1)Какая фигура называется четырехугольником?
2)Что такое вершины,углы стороны диагонали периметр четырехугольника?
3)Какие углы стороны четырехугольник называется выпуклым?
4)чему равна сумма углов выпуклого четырехугольника?
5)какой четырех угольник называется выпуклым?
6)какой четырех угольник называют параллелограмм?
7)какими свойствами обладает параллелограмм?
8)назовите признаки параллелограмма.
9)сформулируйте свойства прямоугольника.
10)какой четырехугольник называется квадратом?
11)сформулируйте свойства ромба.
12)какой четырехугольник называется ромбом?
13)какой четырехугольник называется прямоугольником?
14)какими свойствами обладает квадрат? ответьте пожалуйста кратко…
Геометрия Атанасян 7,8,9 класс «Вопросы ответы на вопросы для повторения к главе 2 к учебнику геометрии 7-9 класс атанасян Объясните, какая фигура
называется треугольником.
2. Что такое периметр треугольника?
3. Какие треугольники называются равными?
4. Что такое теорема и доказательство теоремы?
5. Объясните, какой отрезок называется перпендикуляром, проведённым из данной точки к данной прямой.
6. Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник?
7. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник?
8. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?
9. Какой треугольник называется равнобедренным?
Какой треугольник называется равнобедренным?
10. Как называются стороны равнобедренного треугольника?
11. Какой треугольник называется равносторонним?
12. Сформулируйте свойство углов при основании равнобедренного треугольника.
13. Сформулируйте теорему о биссектрисе равнобедренного треугольника.
14. Сформулируйте первый признак равенства треугольников.
15. Сформулируйте второй признак равенства треугольников.
16. Сформулируйте третий признак равенства треугольников.
17. Дайте определение окружности.
18. Что такое центр окружности?
19. Что называется радиусом окружности?
20. Что называется диаметром окружности?
21. Что называется хордой окружности?
Назад Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока: Повторить тему «Площадь параллелограмма». Вывести формулу площади треугольник, ввести понятие равновеликих фигур. Решение задач по теме «Площади равновеликих фигур».
Ход урока
I. Повторение.1) Устно по готовому чертежу вывести формулу площади параллелограмма.
2) Какова зависимость между сторонами параллелограмма и высотами, опущенными на них?
(по готовому чертежу)
зависимость обратно пропорциональная.
3) Найти вторую высоту (по готовому чертежу)
4) Найти площадь параллелограмма по готовому чертежу.
Решение:
5) Сравните площади параллелограммов S1, S2, S3 . (Они имеют равные площади, у всех основание a и высота h).
Определение: Фигуры, имеющие равные площади, называются равновеликими.
II. Решение задач.
Решение задач. 1) Доказать, что всякая прямая, проходящая через точку пересечения диагоналей, делит его на 2 равновеликие части.
Решение:
2) В параллелограмме ABCD CF и CE высоты. Доказать, что AD ∙ CF = AB ∙ CE.
3) Дана трапеция с основаниями a и 4a. Можно ли через одну из её вершин провести прямые, разбивающие трапецию на 5 равновеликих треугольников?
Решение: Можно. Все треугольники равновеликие.
4) Доказать, что если на стороне параллелограмма взять точку A и соединить её с вершинами, то площадь получившегося треугольника ABC равна половине площади параллелограмма.
Решение:
5) Торт имеет форму параллелограмма. Малыш и Карлсон делят его так: Малыш указывает на поверхности торта точку, а Карлсон по прямой, проходящей через эту точку, разрезает торт на 2 куска и один из кусков забирает себе. Каждый хочет получить кусок побольше. Где Малыш должен поставить точку?
Где Малыш должен поставить точку?
Решение: В точке пересечения диагоналей.
6) На диагонали прямоугольника выбрали точку и провели через неё прямые, параллельные сторонам прямоугольника. По разные стороны образовались 2 прямоугольника. Сравните их площади.
Решение:
III. Изучение темы «Площадь треугольника»начать с задачи:
«Найти площадь треугольника, у которого основание a, а высота h».
Ребята, используя понятие равновеликих фигур, доказывают теорему.
Достроим треугольник до параллелограмма.
Площадь треугольника равна половине площади параллелограмма.
Задание: Начертите равновеликие треугольники.
Используется модель (из бумаги вырезаны 3 цветных треугольника и склеены у оснований).
Упражнение №474. «Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой».
У треугольников одинаковые основания a и одна и та же высота h. Треугольники имеют одинаковую площадь
Вывод: Фигуры, имеющие равные площади, называются равновеликими.
Вопросы к классу:
- Равновелики ли равные фигуры?
- Сформулируйте обратное утверждение. Верно ли оно?
- Верно ли:
а) Равносторонние треугольники равновелики?
б) Равносторонние треугольники с равными сторонами равновелики?
в) Квадраты с равными сторонами равновелики?
г) Докажите, что параллелограммы, образованные при пересечении двух полос одинаковой ширины под разными углами наклона друг к другу, равновелики. Найдите параллелограмм наименьшей площади, образующийся при пересечении двух полос одинаковой ширины. (Показать на модели: полоски одинаковой ширины)
На доске написаны задания по выбору:
1. «Разрежьте треугольник двумя прямыми линиями так, чтобы можно было из частей сложить прямоугольник».
Решение:
2. «Разрежьте прямоугольник по прямой линии на 2 части, из которых можно сложить прямоугольный треугольник».
Решение:
3) В прямоугольнике проведена диагональ. В одном из получившихся треугольников проведена медиана. Найдите соотношения между площадями фигур .
Решение:
Ответ:
3. Из олимпиадных задач:
«В четырёхугольнике ABCD точка E- середина AB, соединена с вершиной D, а F – середина CD, с вершиной B. Доказать, что площадь четырёхугольника EBFD в 2 раза меньше площади четырёхугольника ABCD.
Решение: провести диагональ BD.
Упражнение №475.
«Начертите треугольник ABC. Через вершину В проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади».
Использовать теорему Фалеса (разделить АC на 3 равные части).
V. Задача дня.Для неё отвела крайнюю правую часть доски, на которой пишу задачу сегодняшнего дня. Ребята могут решать её, а могут и не решать. На уроке данную задачу мы сегодня не решаем. Просто те, кому они интересны, могут списать её, решить её дома или в перемену. Обычно уже в перемену многие ребята начинают решать задачу, если решили, то показывают решение, и я фиксирую это в специальной таблице. На следующем уроке к этой задаче обязательно возвращаемся, уделяя её решению небольшую часть урока (а на доске может быть записана новая задача).
«В параллелограмме вырезан параллелограмм. Разделите оставшуюся часть на 2 равновеликие фигуры».
Решение: Секущая AB проходит через точку пересечения диагоналей параллелограммов O и O1.
Дополнительные задачи (из олимпиадных задач):
1) «В трапеции ABCD (AD || BC) вершины A и B соединены с точкой M – серединой стороны CD. Площадь треугольника ABM равна m. Найти площадь трапеции ABCD».
Решение:
Треугольники ABM и AMK – равновеликие фигуры, т.к. AM – медиана.
S ∆ABK = 2m, ∆BCM = ∆MDK, S ABCD = S ∆ABK = 2m.
Ответ: S ABCD = 2m.
2) «В трапеции ABCD (AD || BC) диагонали пересекаются в точке O. Доказать, что треугольники AOB и COD равновеликие».
Решение:
S ∆BCD = S ∆ABC , т.к. у них общее основание BC и одинаковая высота .
3) Сторона АВ произвольного треугольника АВС продолжена за вершину В так, что ВР = АВ, сторону АС за вершину А так, что АМ = СА, сторону ВС за вершину С так, что КС = ВС. Во сколько раз площадь треугольника РМК больше площади треугольника АВС?
Решение:
В треугольнике МВС : МА = АС, значит, площадь треугольника ВАМ равна площади треугольника АВС. В треугольнике АРМ : ВР = АВ, значит, площадь треугольника ВАМ равна площади треугольника АВР. В треугольнике АРС : АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК : ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК : ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,
Ответ: Площадь треугольника МРК в 7 раз больше площади треугольника АВС.
4) Сцепленные параллелограммы.
2 параллелограмма расположены так, как показано на рисунке: они имеют общую вершину и ещё по одной вершине у каждого из параллелограммов лежит на сторонах другого параллелограмма. Доказать, что площади параллелограммов равны.
Решение:
и , значит,
Список использованной литературы :
- Учебник «Геометрия 7-9» (авторы Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев (Москва, «Просвещение», 2003).
- Олимпиадные задачи разных лет, в частности из учебного пособия «Лучшие задачи математических олимпиад» (составитель А.А. Корзняков, Пермь, «Книжный мир», 1996).
- Подборка задач, накопленных за много лет работы.
Одним из основных понятий в геометрии является фигура. Под этим термином подразумевается множество точек на плоскости, ограниченное конечным числом линий. Некоторые фигуры могут рассматриваться как равные, что тесно связано с понятием движения. Геометрические фигуры могут рассматриваться не изолированно, а в том или ином соотношении друг с другом – их взаимное расположение, соприкосновение и прилегание, положение «между», «внутри», соотношение, выраженное в понятиях «больше», «меньше», «равно».Геометрия изучает инвариантные свойства фигур, т.е. те, которые остаются неизменными при тех или иных геометрических преобразованиях. Такое преобразование пространства, при котором остается неизменным расстояние между точками, составляющими ту или иную фигуру, называется движением.Движение может выступать в разных вариантах: параллельный перенос, тождественное преобразование, поворот вокруг оси, симметрия относительно прямой или плоскости, центральная, поворотная, переносная симметрия.
Движение и равные фигуры
Если возможно такое движение, которое приведет к совмещению одной фигуры с другой, такие фигуры называют равными (конгруэнтными). Две фигуры, равные третьей, равны и между собою – такое утверждение было сформулировано еще Евклидом, основоположником геометрии.Понятие конгруэнтных фигур может быть объяснено и более простым языком: равными называются такие фигуры, которые полностью совпадут при наложении их друг на друга.Это достаточно легко определить, если фигуры даны в виде неких предметов, которыми можно манипулировать – например, вырезаны из бумаги, поэтому в школе на уроках нередко прибегают к такому способу объяснения данного понятия. Но две фигуры, начерченные на плоскости, нельзя физически наложить друг на друга. В данном случае доказательством равенства фигур выступает доказательство равенства всех элементов, составляющих эти фигуры: длина отрезков, размер углов, диаметр и радиус, если речь идет об окружности.Равновеликие и равносоставленные фигуры
С равными фигурами не следует смешивать равновеликие и равносоставленные фигуры – при всей близости данных понятий.Равновеликими называются такие фигуры, которые имеют равную площадь, если это фигуры на плоскости, или равный объем, если речь идет о трехмерны телах. Совпадение всех элементов, составляющих данные фигуры, не является обязательным. Равные фигуры будут равновеликими всегда, но не всякие равновеликие фигуры можно назвать равными.Понятие равносоставленности чаще всего применяют к многоугольникам. Оно подразумевает, что многоугольники можно разбить на одинаковое количество соответственно равных фигур. Равносоставленные многоугольники всегда являются равновеликими.
какие фигуры называются равными? и получил лучший ответ
Ответ от Ирина Печенкина[гуру]
Вот настоящее определение
Ответ от Даниил Зазерин [новичек]
утырские
Ответ от GAMER [новичек]
Фигуры, которые совпадают при наложении называются РАВНЫМИ
Вот настоящее определение
Ответ от Никита Ткачук [новичек]
Ответ от Дмитрий Глебов [новичек]
123
Ответ от Мария Бирюкова [новичек]
Как сравнить два отрезка
Ответ от Ўлия Котельникова [новичек]
Фигуры, которые совпадают при наложении называются РАВНЫМИ
Ответ от Маэстро Донецк [новичек]
Если их приложить то узнаешь они равны или нет
Ответ от Ђащи Елнур [новичек]
спасибо
Ответ от Андрей Экк [новичек]
Фигуры, которые совпадают при наложении называются РАВНЫМИ Вот настоящее определение
Ответ от BaBy [активный]
у которых равны углы
Ответ от Андрей Сидельников [гуру]
Подобные (размер)
Ответ от Ёветка Букина [гуру]
Если бедра, талия и грудь — одинаковы, то фигуры равные. С натяжечкой….
Ответ от Никита Александрович [гуру]
Те, котрые можно совместить наложением! Единственно верное определение
Ответ от Ѐинат Верницкий [гуру]
Определения верны у Иришки, и у Никимты александровича.
Верны но НЕ ТОЧНЫ, покольку неопределеноЮ что такое наложение, это надо определить.
ПОЭТОМУ, если уж быть точным, то фигуры называются равными, ЕСЛИ СУЩЕСТВУЕТ такое преобразование пространства (на котором эти фигуры определены) , сохраняющее расстояния между любыми двумя точками, при котором одна их этих фигур переходит в другую.
ТО есть ЕСЛИ МОЖНО определить какимнибудь способом наложение, совмещающее фигуры — они равны.
Ответ от четкая)) [новичек]
две фигуры называют равными
Ответ от Александра Ставская [новичек]
Фигуры, которые совпадают при наложении называются РАВНЫМИ. Две геометрические фигуры называются равными, если их можно совместить при наложении. Или равны все углы.
треугольников — равносторонние, равнобедренные и чешуйчатые
Треугольник имеет три стороны и три угла | ||
Три угла всегда складываются в 180 ° |
Равносторонний, равнобедренный и чешуйчатый
Треугольникам даны три специальных имени, которые показывают, сколько сторон (или углов) равны.
Может быть 3 , 2 или Нет равных сторон / углов:
Равносторонний треугольник Три равных стороны | |
Равнобедренный треугольник Две равные стороны | |
Скаленовый треугольник Нет равные стороны |
Как запомнить? По алфавиту идут 3, 2, нет:
- Равносторонний : «равный» — боковой (боковой означает сторона), поэтому все стороны имеют равные стороны
- Равнобедренный : означает «равноногие», а у нас две ноги , верно? Также i SOS celes имеет два одинаковых «S ides», соединенных стороной « O dd».
- Скален : означает «неровный» или «нечетный», поэтому нет равных сторон.
Какой тип угла?
Треугольники также могут иметь имена, которые сообщают вам, какой тип угла находится внутри :
Острый треугольникВсе углы меньше 90 ° | |
Прямой треугольникИмеет прямой угол (90 °) | |
Тупой треугольникИмеет угол более 90 ° |
Объединение имен
Иногда у треугольника будет два имени, например:Правый равнобедренный треугольникИмеет прямой угол (90 °), а также два равных угла. Вы можете угадать, каковы равные углы? |
Поиграй с ним…
Попробуйте перетащить точки и составить разные треугольники:
Вы также можете поиграть с Интерактивным треугольником.
Уголки
Три внутренних угла всегда составляют 180 °
Периметр
Периметр — это расстояние по краю треугольника: просто сложите три стороны:
Площадь
Площадь составляет , половина базовой, умноженная на высоту .
- «b» — расстояние по основанию
- «h» — высота (измеренная под прямым углом к основанию)
Площадь = ½ × b × h
Формула работает для всех треугольников.
Примечание: более простой способ записать формулу — bh / 2
Пример: Какова площадь этого треугольника?
(Примечание: 12 — это высота , а не длина левой стороны)
Высота = h = 12
База = b = 20
Площадь = ½ × b × h = ½ × 20 × 12 = 120
Основание может быть любой стороной. Убедитесь, что «высота» измеряется под прямым углом к »основанию». :
(Примечание: вы также можете рассчитать площадь, исходя из длин всех трех сторон, используя формулу Герона.)
Почему область «половина bh»?
Представьте, что вы «удвоили» треугольник (перевернули его вокруг одного из верхних краев), чтобы получилась квадратная форма (параллелограмм), которую можно преобразовать в простой прямоугольник:
ЗАТЕМ вся площадь составляет bh , что соответствует обоим треугольникам, поэтому только один будет ½ × bh .
типов треугольников — объяснения и примеры
В геометрии треугольник является наиболее важной формой , определяемой как замкнутая двумерная диаграмма, содержащая 3 стороны, 3 угла и 3 вершины.Проще говоря, треугольник — это многоугольник с 3 сторонами. Слово «треугольник» происходит от латинского слова «triangulus», что означает треугольник.
В древние времена астрономы создали метод, называемый триангуляцией, для определения расстояний до далеких звезд. Они измеряют расстояние от двух разных мест, затем измеряют угол, образованный сдвигом или параллаксом, образованным движением наблюдателя между двумя точками. Затем они применяли закон синусов для вычисления необходимого расстояния.
Египтяне создали пирамиды около 2900 г. до н. Э. Его форма на самом деле напоминает трехмерную пирамиду с треугольными гранями. Это идеально спроектированная модель, длина и углы которой одинаковы со всех сторон. Милет (624 г. до н.э. — 547 г. до н.э.), греческий математик, перенял геометрию Египта и был доставлен в Грецию.
Аристарх (310 г. до н.э. — 250 г. до н.э.), греческий математик, использовал вышеуказанный метод, чтобы найти расстояние между Землей и Луной. Эратосфен (276 г. до н.э. — 195 г. до н.э.) снова использовал тот же метод для определения расстояния вокруг поверхности Земли (называемого окружностью).
В этой статье обсуждаются значение треугольника , различных типов треугольников и их свойства, а также их применение в реальной жизни.
Что такое треугольник?
Треугольник — это двумерная замкнутая фигура с 3 сторонами. Это многоугольник с тремя углами, тремя вершинами и тремя углами, соединенными вместе, которые образуют замкнутую диаграмму. Мы используем символ ∆ для обозначения треугольника.
Рисунки A и B представляют собой треугольники.
Различные типы треугольников
Типы треугольников классифицируются на основе:
- Длины сторон
- Внутренние углы
Классификация треугольников по величине внутренних углов
Согласно По измерению внутренних углов мы можем разделить треугольники на три категории:
- Острый угол
- Тупоугольный
- Прямоугольный
Острый треугольник
Треугольник с острым углом — это треугольник, в котором все три внутренние углы менее 90 градусов.
Каждый из углов a, b и c меньше 90 градусов.
Тупой треугольник
Тупой треугольник — это треугольник, в котором один из внутренних углов больше 90 градусов.
Угол a более тупой, а углы b и c острые.
Прямой треугольник
Прямоугольный треугольник — это треугольник, в котором один из углов равен точно 90 градусам. Гипотенуза — это сторона прямоугольного треугольника с наибольшей длиной.
На рисунке выше угол a = 90 градусов, а углы b и c — острые углы.
Классификация треугольников по длине их сторон
Мы можем классифицировать треугольники на 3 типа в зависимости от длины их сторон:
- Скален
- Равнобедренный
- Равносторонний
Равнобедренный треугольник
Равнобедренный треугольник треугольник, в котором две стороны и два угла равны. Треугольники одинаковой длины показаны по дуге с каждой стороны.
На диаграмме выше , длина стороны AB = AC и ∠ ABC = ∠ ACB.
Равносторонний треугольник
У равностороннего треугольника все три стороны равны, и все три внутренних угла также равны. В этом случае каждый внутренний угол равностороннего треугольника составляет 60 градусов. Равносторонний треугольник иногда называют равносторонним треугольником, потому что все три угла равны.
В равностороннем треугольнике стороны AB = BC = AC и ∠ ABC = ∠ ACB = ∠ BAC
Обратите внимание, что углы равностороннего треугольника не зависят по длинам сторон.
Масштабный треугольник
Разносторонний треугольник — это треугольник, в котором все стороны имеют разные размеры, и все внутренние углы также разные.
Свойства треугольника
Свойства треугольников широко используются. Многие математики использовали его при решении своих задач. Евклидова геометрия и тригонометрия широко используют свойства треугольников.
Вот несколько основных свойств треугольника:
- Треугольник — это двумерный многоугольник
- Треугольник имеет 3 стороны, 3 угла и 3 вершины.
- Сумма длин любых двух сторон треугольника больше длины оставшейся стороны.
- Сумма длин трех сторон дает периметр треугольников.
- Площадь треугольника равна произведению основания на высоту.
Рабочие примеры на различных типах треугольников
Пример 1
Найдите значение угла x в треугольнике ниже.
Решение
Это равнобедренный треугольник, в котором две стороны равны, а также два угла равны.Следовательно,
x = (180 ° — 70 °) / 2
x = 110 ° / 2
= 55 °
Пример 2
Найдите угол y в прямоугольном треугольнике, показанном ниже.
Решение
Один угол прямоугольного треугольника равен 90 °. Итак, мы;
y + 50 + 90 = 180
y = (180 — 140) °
y = 40 °
Пример 3
Классифицируйте следующий треугольник.
Решение
Это разносторонний треугольник, потому что все стороны и углы имеют разные размеры.Точно так же треугольник также можно классифицировать как тупой треугольник, потому что один угол тупой.
Пример 4
Классифицируйте треугольник, показанный ниже.
Решение
Это равнобедренный треугольник. Две стороны равны, и два угла равны по размеру.
Применение треугольников
Давайте рассмотрим некоторые из реальных приложений треугольников:
- Дорожные знаки. Большинство дорожных знаков отображаются на треугольных структурах.
- Пирамиды Египта: пирамиды — древние памятники, построенные египтянами. Пирамиды имеют треугольную форму.
- Ферма: Фермы крыш или мостов изготавливаются треугольной формы, потому что треугольник считается самой прочной формой.
- Бермудский треугольник: Бермудский треугольник — это треугольная область в Атлантическом океане, где считается, что любое судно или самолет, проходящие через точку, проглатываются. Считается, что 50 кораблей и 20 самолетов загадочным образом исчезли в Бермудском треугольнике.
- Глобальная система позиционирования (GPS) работает с алгоритмами триангуляции для определения долготы и широты объекта.
- Лестница, прислоненная к стене, имеет форму треугольника.
- Эйфелева башня имеет треугольную форму.
- Концепция треугольников рассчитывает высоту или высоту высоких объектов, таких как флагштоки, горы, здания и т. Д.
- Сэндвичи и кусочки пиццы имеют треугольную форму.
Свойства и типы треугольников | GMAT GRE Geometry Tutorial
Щелкните здесь, чтобы посмотреть это содержательное видео.Лучшие университеты мира
В серии статей об основных строительных блоках геометрии, после обзора линий, лучей и сегментов, на этот раз мы рассмотрим типы и свойства треугольников.
Определение: Треугольник — это замкнутая фигура, состоящая из трех отрезков.
Треугольник состоит из трех отрезков прямых и трех углов. На рисунке выше AB, BC, CA — три отрезка прямых, а ∠A, ∠B, ∠C — три угла.
Существует три типа треугольников по сторонам и три по углам.
Виды треугольников по сторонам
Равносторонний треугольник : Треугольник, все три стороны которого равны по длине, является равносторонним треугольником.
Так как все стороны равны, то и все углы равны.
Равнобедренный треугольник : Треугольник, имеющий две стороны равной длины, является равнобедренным треугольником.
Два угла, противоположные равным сторонам, равны.
Разносторонний треугольник: Треугольник, имеющий три стороны разной длины, называется разносторонним треугольником.
Виды треугольников на основе углов
Острый треугольник: Треугольник, все углы которого являются острыми, называется остроугольным или острым треугольником.
Треугольник с тупым углом: Треугольник, у которого один угол тупой, называется треугольником с тупым углом или Тупым треугольником.
Прямоугольный треугольник: Треугольник, один угол которого является прямым, называется прямоугольным или прямоугольным.
На рисунке выше сторона, противоположная прямому углу BC, называется гипотенузой.
Для прямоугольного треугольника ABC,
BC 2 = AB 2 + AC 2
Это называется теоремой Пифагора .
В треугольнике выше 5 2 = 4 2 + 3 2 . Только треугольник, удовлетворяющий этому условию, является прямоугольным.
Следовательно, теорема Пифагора помогает определить, является ли треугольник прямоугольным.
Виды треугольников
Есть разные типы прямоугольных треугольников. На данный момент наше внимание сосредоточено только на специальной паре прямоугольных треугольников.
- 45-45-90 треугольник
- 30-60-90 треугольник
45-45-90 треугольник :
Треугольник 45-45-90, как следует из названия, представляет собой прямоугольный треугольник, в котором два других угла составляют 45 ° каждый.
Это равнобедренный прямоугольный треугольник.
In ∆ DEF, DE = DF и ∠D = 90 °.
Стороны треугольника 45-45-90 имеют соотношение 1: 1: √2.
30-60-90 треугольник :
Треугольник 30-60-90, как следует из названия, представляет собой прямоугольный треугольник, в котором два других угла составляют 30 ° и 60 °.
Это разносторонний прямоугольный треугольник, поскольку ни одна из сторон или углов не равны.
Стороны треугольника 30-60-90 находятся в соотношении 1: √3: 2
Как и любой другой прямоугольный треугольник, эти два треугольника удовлетворяют теореме Пифагора.
Основные свойства треугольников
- Сумма углов в треугольнике составляет 180 °. Это называется свойством суммы углов.
- Сумма длин любых двух сторон треугольника больше длины третьей стороны. Точно так же разница между длинами любых двух сторон треугольника меньше длины третьей стороны.
- Сторона, противоположная наибольшему углу, является самой длинной стороной треугольника, а сторона, противоположная наименьшему углу, является самой короткой стороной треугольника.
На рисунке выше ∠B — наибольший угол, а сторона, противоположная ему (гипотенуза), — наибольшая сторона треугольника.
На рисунке выше ∠A — это наибольший угол, а сторона, противоположная ему, BC, — наибольшая сторона треугольника.
- Внешний угол треугольника равен сумме его внутренних противоположных углов. Это называется свойством внешнего угла треугольника.
Здесь ∠ACD — внешний угол к ∆ABC.
Согласно свойству внешнего угла ∠ACD = ∠CAB + ∠ABC.
Сходство и конгруэнтность в треугольниках
Фигуры одинакового размера и формы являются конгруэнтными фигурами. Если две формы совпадают, они остаются конгруэнтными, даже если их перемещать или вращать. Формы также останутся конгруэнтными, если мы отразим формы, создав зеркальные изображения. Две геометрические формы совпадают, если они точно покрывают друг друга.
Фигуры одинаковой формы, но пропорциональных размеров являются аналогичными фигурами.Они остаются похожими, даже если их перемещать или вращать.
Подобие треугольников
Два треугольника называются подобными, если соответствующие углы двух треугольников совпадают, а длины соответствующих сторон равны пропорционально .
Он записывается как ∆ ABC ∼ ∆ XYZ и обозначается как ∆ ABC ‘подобен’ ∆ XYZ.
Здесь ∠A = ∠X, ∠B = ∠Y и ∠C = ∠Z AND
AB / XY = BC / YZ = CA / ZX
Необходимые и достаточные условия для того, чтобы два треугольника были подобны, следующие:
(1) Боковой-боковой-боковой (SSS) критерий подобия:
Если три стороны треугольника на пропорциональны соответствующим трем сторонам другого треугольника, то говорят, что треугольники подобны.
Здесь ∆ PQR ∼ ∆ DEF как
PQ / DE = QR / EF = RP / FD
(2) Боковой угол-сторона (SAS) критерий сходства :
Если соответствующие две стороны двух треугольников равны , пропорциональны и один включенный угол равен соответствующему включенному углу другого треугольника, то треугольники подобны.
Здесь ∆ LMN ∼ ∆ QRS, в котором
∠L = ∠Q
QS / LN = QR / LM
(3) Угол-угол-угол (AAA) Критерий сходства:
Если три соответствующих угла двух треугольников равны, то два треугольника подобны.
Здесь ∆ TUV ∼ ∆ PQR как
∠T = ∠P, ∠U = ∠Q и ∠V = ∠R
Соответствие треугольников
Два треугольника называются конгруэнтными, если все стороны одного треугольника равны соответствующим сторонам другого треугольника и соответствующие углы равны.
Он записывается как ∆ ABC ≅ ∆ XYZ и говорит, что ∆ ABC ‘конгруэнтно’ ∆ XYZ.
Необходимые и достаточные условия для того, чтобы два треугольника были конгруэнтны, следующие:
(1) Боковой-боковой-боковой (SSS) критерий конгруэнтности :
Если три стороны треугольника равны соответствующим трем сторонам другого треугольника, то треугольники называются конгруэнтными.
Здесь ∆ ABC ≅ ∆ XYZ, так как AB = XY, BC = YZ и AC = XZ.
(2) Боковой угол-боковой (SAS) критерий соответствия :
Если две стороны и угол между двумя сторонами треугольника равны двум соответствующим сторонам и включенному углу другого треугольника, то треугольники конгруэнтны.
Здесь ∆ ABC ≅ ∆ XYZ, поскольку AB = XY, ∠A = ∠X и AC = XZ.
(3) Угол-сторона-угол (ASA) Критерий конгруэнтности : Если два угла и включенная сторона треугольника равны соответствующим двум углам и включенной стороне другого треугольника, то треугольники конгруэнтны.
На рисунке выше ∆ ABD ≅ ∆ CBD, в котором
∠ABD = ∠CBD, AB = CB и ∠ADB = ∠CDB.
(4) Критерий конгруэнтности прямоугольной гипотенузы : Если гипотенуза и одна сторона прямоугольного треугольника равны соответствующей гипотенузе и стороне другого прямоугольного треугольника, то треугольники конгруэнтны.
Здесь ∠B = ∠Y = 90 ° и AB = XY, AC = XZ.
Площадь треугольника:
Площадь треугольника определяется по формуле
Площадь треугольника = (1/2) * Основание * Высота
Чтобы найти площадь треугольника, мы проводим перпендикулярную линию от основания до противоположной вершины, которая дает высоту треугольника.
Итак, площадь ∆ PQR = (1/2) * (PR * QS) = (1/2) * 6 * 4 = 12 кв. Единиц.
Для прямоугольного треугольника легко найти площадь, так как есть сторона, перпендикулярная основанию, поэтому мы можем рассматривать ее как высоту.
Высота ∆ XYZ равна XY, а его площадь составляет (1/2) * XZ * XY кв. Единиц.
Теперь, как нам найти площадь тупого треугольника LMN?
Для тупого треугольника мы удлиняем основание и проводим линию, перпендикулярную от вершины к расширенному основанию, которая становится высотой треугольника.
Следовательно, площадь ∆ LMN = (1/2) * LM * NK кв. Единиц.
Решите следующие
1)
∆ ABC — прямоугольный треугольник, а CD ⊥ AB (⊥ означает «перпендикуляр»).
Найдите i) ∠ACD и ii) ∠ABC.
A. 25, 35
B. 35, 35
C. 25, 25
D. 35, 25
Ответ : C
Пояснение :
Рассмотрим ∆ ACD.
∠ADC + ∠DAC + ∠ACD = 180 ° (так как сумма углов в треугольнике равна 180 °)
90 + 65 + ∠ACD = 180 ° → ∠ACD = 25 °
∠ACD + ∠DCB = 90 ° → 25 + ∠DCB = 90 → ∠DCB = 65 °
In ∆ BCD, ∠DCB + ∠CBD + ∠BDC = 180 ° (опять же, сумма всех углов в треугольнике)
65 + ∠CBD + 90 = 180 → ∠CBD = 25 ° = ∠ABC.
2) Определите, являются ли следующие прямоугольные треугольники
A. Оба являются прямоугольными треугольниками
B. ∆ ABC не является прямоугольным треугольником, ∆ DEF является прямоугольным треугольником
C. ∆ ABC является прямоугольным треугольником, ∆ DEF не является прямоугольным треугольником
D. Оба треугольника не являются прямоугольными
Ответ: B
Пояснение :
Тройка, удовлетворяющая теореме Пифагора, — это набор сторон, образующих прямоугольный треугольник.
3)
Если ∆ ABC = 3 (∆ DEF), что из следующего верно?
А.∠E = ∠F = 40 °, ∠D = 120 ° AND DE = DF = 2 и EF = 3
B. ∠E = ∠F = 40 °, ∠D = 110 ° AND DE = DF = 2 и EF = 3
C. ∠E = ∠F = 40 °, ∠D = 100 ° AND DE = DF = 2 и EF = 3
D. ∠E = F = 40 °, ∠D = 110 ° AND DE = DF = 3 и EF = 3
Ответ: C
Пояснение :
AB и AC равны → противоположные углы равны.
Следовательно, B = ∠C = 40 ° → ∠A = 100 °.
∆ ABC = 3 (∆ DEF) → ∆ ABC и ∆ DEF подобны.
Когда два треугольника подобны, их соответствующие углы равны, а соответствующие стороны пропорциональны.
→ DE = DF = 6/3 = 2 и EF = 3
→ ∠E = ∠F = 40 ° и ∠D = 100 °
Отношения и размеры — Факты о прямоугольном треугольнике
Вы уже встретили прямоугольный треугольник на предыдущем уроке. Подружитесь с ним! Он один из самых популярных существующих полигонов, в основном из-за его решения проблем способности.
прямоугольный треугольник имеет один угол, равный 90 градусам. Прямоугольный треугольник тоже может быть равнобедренным. треугольник — это означает, что у него две стороны, которые равны.Правый равнобедренный треугольник имеет угол 90 градусов и два угла 45 градусов. Это единственный прямоугольный треугольник, который является равнобедренным треугольником. Эта версия прямоугольного треугольника настолько популярны, что их пластиковые модели изготавливают и используют архитекторы, инженеры, плотники и художники-графики в их дизайне и строительстве Работа.
Еще одно интересное Прямой треугольник — это треугольник 30-60-90 градусов. Отношение этого треугольника самая длинная сторона к самой короткой стороне — «два к одному».»То есть самая длинная сторона вдвое длиннее самой короткой стороны. Он тоже изготовлен из пластика и широко используется в приложениях для проектирования, рисования и строительства.
Вы можете найти бесконечное количество примеров прямоугольных треугольников. Один из самых известных — «треугольник 3, 4, 5».
Египтяне использовал этот треугольник для топографической съемки. Некоторые считают, что они тоже его использовали чтобы помочь спроектировать их пирамиды.Независимо от того, сделали они это или нет, треугольник 3-4-5 до сих пор используется геодезистами. Плотники и плотники также используют его для изготовления их углы квадратные.
Пифагор был греческий математик, живший около 2500 лет назад и разработавший самая известная формула в геометрии, возможно, во всей математике! Он доказал что для прямоугольного треугольника сумма квадратов двух сторон, которые соединяются под прямым углом равняется квадрату третьей стороны.Третья сторона — сторона, противоположная прямому углу — называется гипотенузой прямоугольного треугольника. Две более короткие стороны обычно называют «ногами».
Эта формула называется теоремой Пифагора в честь Пифагора. Обычно пишут как показано в приведенном ниже уравнении, где a и b — меры катеты треугольника и c — мера гипотенузы.
Давай попробуйте теорему Пифагора, используя этот прямоугольный треугольник со сторонами 5 и 12 см, а гипотенуза 13 см.Мы можем проверить, что теорема Пифагора верно путем подстановки значений. Квадратный корень из 169 равен 13, что — мера гипотенузы в этом треугольнике.
Теорема Пифагора имеет множество применений. Вы можете использовать его, чтобы проверить, действительно ли треугольник — это прямоугольный треугольник. Или вы можете использовать его, чтобы найти недостающие меры сторон. Воспользуемся теоремой Пифагора, чтобы найти недостающую меру катет прямоугольного треугольника SAM.
Заменить значения в формулу и выполните вычисления, как это. Мы находим, что квадрат гипотенузы или c в квадрате равен 400. Чтобы найти c, мы извлекаем квадратный корень из 400, то есть 20. Это значение, которое мы ищем. для, недостающий размер ноги,
Калькулятор равностороннего треугольника
Калькулятор равностороннего треугольника поможет вам в вычислении параметров правильного треугольника.Если вы ищете площадь равностороннего треугольника, его высоту, периметр, радиус описанной окружности или внутренний радиус, этот отличный инструмент — беспроигрышный вариант. Прокрутите вниз, чтобы узнать больше о полезных формулах и узнать, что такое равносторонний треугольник.
Что такое равносторонний треугольник?
Равносторонний треугольник, также называемый правильным треугольником, представляет собой треугольник, у которого все три стороны равны. Каковы другие важные свойства этой конкретной правильной формы?
- все три внутренних угла совпадают друг с другом и все они равны 60 °;
- : высоты, биссектрисы угла, серединные перпендикуляры и медианы совпадают.
Равносторонний треугольник — это частный случай равнобедренного треугольника, у которого не только две, но и все три стороны равны.
Площадь и высота равностороннего треугольника
Формула для площади правильного треугольника равна квадрату стороны, умноженному на квадратный корень из 3, деленному на 4:
площадь = (a² * √3) / 4
и уравнение высоты равностороннего треугольника выглядит следующим образом:
h = a * √3 / 2 , где a — сторона треугольника.
Но знаете ли вы, откуда берутся формулы? Вы можете найти их как минимум двумя способами: исходя из теоремы Пифагора или используя тригонометрию.
1. Использование теоремы Пифагора
Основная формула для площади треугольника: сторона
на(основание), умноженная на высотуh, деленная на 2:площадь = (а * в) / 2Высота равностороннего треугольника разделяет равносторонний треугольник на два прямоугольных.Один катет этого прямоугольного треугольника равен высоте, другой катет составляет половину стороны, а гипотенуза — это сторона равностороннего треугольника.
(a / 2) ² + h² = a²После несложных преобразований получаем формулу высоты равностороннего треугольника:
h = a * √3 / 2Подставляя
hв первую формулу площади, мы получаем уравнение для площади равностороннего треугольника:площадь = a² * √3 / 4
2.Использование тригонометрии
Начнем с формулы площади тригонометрического треугольника:
area = (1/2) * a * b * sin (γ), гдеγ— угол между сторонамиМы помним, что в равностороннем треугольнике все стороны и все углы равны, поэтому формула упрощается до:
площадь = 0,5 * a * a * sin (60 °)Более того, мы знаем, что синус 60 ° равен √3 / 2, поэтому формула для площади равностороннего треугольника:
площадь = (1/2) * a² * (√3 / 2) = a² * √3 / 4Высота равностороннего элемента происходит от определения синуса:
h / a = sin (60 °), поэтомуh = a * sin (60 °) = a * √3 / 2
Периметр равностороннего треугольника, описанная окружность и радиус вписанной окружности
Вы можете легко найти периметр равностороннего треугольника, сложив стороны всех треугольников вместе.У правильного треугольника все стороны равны, поэтому формула для периметра:
периметр = 3 *
Как найти радиус окружности, описывающей три вершины, и радиус вписанной окружности?
радиус_ описанной окружности = 2 * h / 3 = a * √3 / 3
incircle_radius = h / 3 = a * √3 / 6
Как я могу использовать калькулятор равностороннего треугольника?
Возьмем пример из повседневной жизни: мы хотим найти все параметры знака доходности.
- Введите данное значение в правое поле . Предположим, у нас есть знак с длиной стороны 36.
- Калькулятор равностороннего треугольника мгновенно находит другие значения . Теперь мы знаем, что:
- Высота знака уступки 31,2 дюйма
- его площадь составляет 561 кв. Дюйм
- периметр: 108 дюймов
- : радиус описанной окружности 20,8 дюйма
- радиус вписанной окружности 10,4 дюйма
- Оцените гибкость нашего инструмента .Обновите калькулятор и введите другой параметр, например периметр. Это тоже работает, разве не круто?
Равнобедренный треугольник — определение математического слова
Равнобедренный треугольник — определение математического слова — Math Open Reference Треугольник, две стороны которого равны. Попробуйте это Перетащите оранжевые точки на каждую вершину, чтобы изменить форму треугольника. Обратите внимание, что он всегда остается равнобедренным треугольником, стороны AB и AC всегда равны по длине. Слово равнобедренное произносится как «глаз- sos -ell-easy» с ударением на «sos».Это любой треугольник с двумя сторонами одинаковой длины.Если все три стороны имеют одинаковую длину, это называется равносторонний треугольник. Очевидно, что все равносторонние треугольники также обладают всеми свойствами равнобедренного треугольника.
Недвижимость
- Неравную сторону равнобедренного треугольника обычно называют «основанием» треугольника.
- Углы основания равнобедренного треугольника всегда равны. На рисунке выше углы ∠ABC и ∠ACB всегда одинаковы
- Когда третий угол является прямым, он называется «равнобедренный прямоугольный треугольник».
- Высота — это расстояние по перпендикуляру от основания до самой верхней вершины.
Построение равнобедренного треугольника
Можно построить равнобедренный треугольник заданных размеров, используя только циркуль и линейку. Посмотрите на эти три конструкции:Решение равнобедренного треугольника
Основание, катет или высота равнобедренного треугольника можно найти, если вы знаете два других. А серединный перпендикуляр базы образует высота треугольника, как показано справа.Это образует два совпадающие прямоугольные треугольники это может быть решено с помощью Теорема Пифагора как показано ниже.Нахождение базы
Чтобы найти базу с учетом шага и высоты, используйте формулу: где:L — длина отрезка
A — высота
Нахождение отрезка
Чтобы найти длину ноги с учетом базы и высоты, используйте формулу: где:B — длина основания
A — высота
Высота
Чтобы найти высоту по базе и ноге, используйте формулу: где:L — длина ножки
B — основание
Внутренние углы
Если вам дадут один внутренний угол равнобедренного треугольника можно найти два других.
Например, нам дан угол при вершине, как показано справа от 40 °. Мы знаем, что внутренние углы всех треугольников составляют в сумме 180 °. Таким образом, два базовых угла должны в сумме составлять 180-40 или 140 °. Поскольку два основных угла совпадают (одна и та же мера), каждый из них составляет 70 °.
Если нам дан базовый угол, скажем, 45 °, мы знаем, что базовые углы совпадают (та же мера) а внутренние углы любого треугольника всегда складываются в 180 °. Таким образом, угол при вершине должен составлять 180-45-45 или 90 °.
Другие темы треугольника
Общие
Периметр / Площадь
Типы треугольников
Центры треугольника
Соответствие и сходство
Решение треугольников
Треугольник викторины и упражнения
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Математическая сцена — Треугольники — Урок 1
Правила урока 1 для треугольников
Обычно вершины треугольника обозначаются заглавными буквами. буквы и боковые стороны строчными буквами.
Также принято маркировать сторону, противоположную углу A, знаком малый a, сторона, противоположная углу B, с малым b и сторона, противоположная углу C с маленькой c (см. диаграмму).
Стороны, образующие ответвления угла A, примыкают к A. Сторона, на которой стоит треугольник, называется основанием треугольника.
сумма углов треугольника 180 °. В этом легко убедиться, нарисовав прямую прямая, проходящая через угол B и параллельная стороне b.(см. диаграмму).
Углы, образованные этой линией, равны A, B и C (по правилу
что чередующиеся углы между параллельными линиями равны).
Также A + B + C = 180, так как вместе они составляют прямую линию.
Прямая из угла B, перпендикулярная базовой линии b, называется высота треугольника. Высота обозначена буквой h на диаграмме ниже.
Ранее вы узнали, что площадь треугольника задается формула.
Площадь F = × b × h
Буква G используется здесь для обозначения точки, где высота и базы пересекаются. Эту точку иногда называют перпендикулярной проекцией точку B на прямую b.
Два треугольники называются подобными, если все углы одного треугольника равны все углы другого. Если мы хотим показать, что два треугольника похожи достаточно показать, что два угла равны.Если два угла равны, это Очевидно, что третий угол в каждом должен быть равен.
Треугольники на диаграмме выше
похожи. Отсюда следует, что отношения между соответствующими сторонами равны
одно и тоже.
Другими словами:
| и |
Теперь мы рассмотрим несколько примеров с использованием этих соотношений.
Пример 1Треугольники на схеме похожи на равные углы отмечены таким же образом.Мы хотим рассчитать длину сторон помечены x и y.
Начнем с маркировки треугольников, чтобы мы могли видеть больше. легко, какие стороны соответствуют друг другу.
Мы можем записать следующие соотношения:
к / к = 36/33 = 24 / у = б / ц
Это означает, что y / 24 = 33/36
и, следовательно, y = 24 × 33/36 = 22 см.
Также a / b = х / 36 = 20/24 = а / б
Это дает нам x = 36 × 20/24 = 30 см.Еще одно правило, использующее пропорции в треугольниках можно вывести.
Проводим прямую, разрезающую с двух сторон треугольника и параллельна третьей стороне. Эта линия разделяет треугольник на две части, верхняя часть представляет собой треугольник, похожий на ABC, оригинальный треугольник. Обозначим стороны этого меньшего треугольника значком буквы x, y и z.Следующее сейчас правда:
Проведенная линия разделяет сторону c на две части, x и r, и сторону a на z и t. Подставляя x + r для c и z + t in для a в приведенном выше уравнении, мы получаем следующий результат:
Мы показали, что любая строка через две стороны треугольника и параллельно третьей стороне делит эти два стороны в таком же соотношении.
Пример 2
Две стороны треугольника ABC, AB и BC равны 30 см. длина и третья сторона AC, базовая линия, составляет 42 см.Проводим линию через точку X на AB, параллельную основанию, длиной 14 см. Найдите длину линий BX и AX.
14 / 42 = XB / 30
XB = 30 × 14 / 42 = 10 см
AX = 30 — 10 = 90 430 20 см
В большинстве случаев, если мы хотим узнать размер углов треугольника нам нужно либо нарисовать точную диаграмму, либо Измерьте углы или воспользуйтесь правилами тригонометрии.
Равносторонний. Равнобедренный. Прямоугольный.
В равностороннем В треугольнике все стороны равны, а все углы равны 60.
В равнобедренном треугольнике две стороны одинаковой длины и два угла (углы, образованные основанием линии) равны. Если мы знаем один угол в равнобедренном треугольнике, мы можем найти другие углы. Перпендикуляр от вершины к базовой линии (высоте) в равнобедренный треугольник делит треугольник на два равных прямоугольных треугольники.
Стороны права угловой треугольник ABC удовлетворяет правилу Пифагора, то есть 2 + b 2 = c 2 .
Также обратное правда. Если соблюдается правило Пифагора, треугольник прямоугольный.
Мы можем проверить, что Третий треугольник на приведенной выше диаграмме расположен под прямым углом с использованием правила Пифагора.
5 2 + (53) 2 = 10 2
25 + 75 = 100
Обратите внимание, что длина
гипотенуза (10 см) в этом треугольнике вдвое больше длины кратчайшей стороны (5
см).
В этом случае углы треугольника всегда равны 30,
60 и 90 °.
Найдите площадь равностороннего треугольника со сторонами длиной 20 см.
Начнем с рисования высоты h треугольника. Это разделяет треугольник на два равных прямоугольных треугольника. Используя правило Пифагора, мы можем рассчитать h.
ч 2 + 5 2 = 10 2
ч 2 = 10 2 -5 2 = 100 — 25 = 75 = 5 2 × 3
ч = 53 ≈ 8.7
Площадь A = × 10 × h ≈ × 10 × 8,7 ≈ 43 см 2
Пример 4
Руки равнобедренного треугольника 30 см. в длину, а базовая линия — 42 см. Найдите длину линии, проведенной через две равные стороны, параллельной основание и 10 см от основания.
Сначала делим треугольник на два правых угловые треугольники, нарисовав высоту h от вершины до основания.Сейчас мы используем правило Пифагора для расчета высоты.
ч 2 + 21 2 = 30 2
ч 2 = 30 2 -21 2 = 459
ч ≈ 21,4
y = h — 10 ≈ 21,4 — 10 ≈ 11,4 см
Использование правила отношения для подобных треугольников получаем:
y / h = x / 21
x ≈ 21 × 11.4 / 21,4 ≈ 11 см
Следовательно, длина параллельная линия 22 см .
Нарисуйте прямоугольный треугольник с помощью гипотенуза AB в качестве базовой линии, так что угол при вершине C равен 90. Мы затем нарисуйте высоту от C до AB, как показано на диаграмме:
Эта линия делит угол при вершине на два части (не равны, если треугольник не равнобедренный).Если одна часть — x, тогда другой должен быть 90− x. Легко видеть, что два базовых угла должны составлять 90 — x (на справа) и x (слева) как сумма углов в любом треугольнике всегда равна 180.
Обратите внимание, что все углы в обоих меньших треугольники, а также в исходном треугольнике ABC равны и равны 90, х и 90 — х. Следовательно, эти три треугольника похожи.
Следующее правило выполняется для всех прямоугольных треугольники:
высота, проведенная от вершины до гипотенузы, делит прямоугольный треугольник на два треугольника, которые похожи на исходный треугольник.
Это дает три набора соотношений.
Используя греческие буквы a для стороны, противоположной угол, обозначенные x и b, для стороны, противоположной углу, обозначенному 90− x, как показано на на диаграмме получаем следующее:
Два меньших треугольника похожи, поэтому
Исходный треугольник и треугольник с верхним углом x похожи поэтому
Исходный треугольник и треугольник с верхним углом 90 − x аналогичный
Пример 5
Прямоугольный треугольник обозначен две более короткие стороны длиной 7 см и 10 см.Высота, нарисованная на гопотенузе делит треугольник на два треугольника. Найдите площадь этих двух треугольников.
Сначала воспользуемся Пифагором для вычисления длины гипотенузы, c.
c 2 = 10 2 + 7 2 = 149, Тогда c ≈ 12,2 см
Затем мы используем одно из указанных выше соотношений для вычисления a.
a / c = a / a
a = a 2 / c ≈ 10 2 / 12.2 ≈ 8,2 см
А потом б.
b ≈ 12,2 — 8,2 ≈ 4 см
Теперь нам нужно рассчитать высоту h.
b / c = h / a
h = ab / c ≈ 10 × 7 / 12,2 ≈ 5,7 см
Области теперь легко найти.
Площадь F 1 = × b × h ≈ × 4 × 5,7 ≈ 11,4 см 2
Площадь F 2 = × a × h ≈ × 8.2 × 5,7 ≈ 23,4 см 2
Попробуйте пройти тест № 1 по треугольникам.
Не забудьте использовать контрольный список для следите за своей работой.
. т.д.
т.д.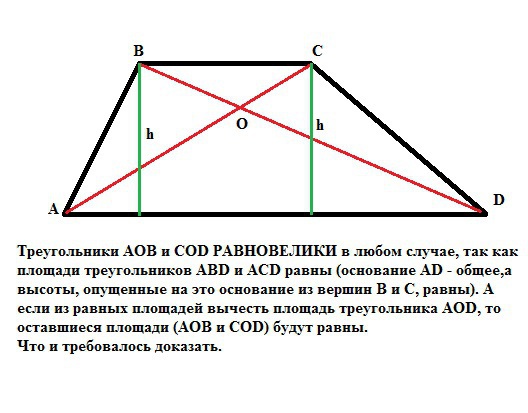 2. Площади двух фигур равны. Но сами фигуры равны не будут, потому что у них разная форма;
2. Площади двух фигур равны. Но сами фигуры равны не будут, потому что у них разная форма;