Равновеликие треугольники | Треугольники
Определение.
Равновеликие треугольники — это треугольники, которые имеют одинаковую площадь.
Равновеликие треугольники могут быть равными (так как равные треугольники имеют равные площади), но также могут иметь разные стороны и разные углы.
Например, треугольники ABC и MKF — равновеликие, так как их площади равны.
По формуле
Можно заметить, что если сторону треугольника увеличить в k раз, а высоту, проведенную к этой стороне, уменьшить в k раз, то получим треугольник, равновеликий данному.
Равновеликие треугольники в треугольнике
Медиана делит треугольник на два равновеликих треугольника.
Равновеликие треугольники в трапеции
При пересечении диагоналей в произвольной трапеции ABCD образуется три пары равновеликих треугольников:
1) ∆ABD и ∆ACD,
2) ∆ABC и ∆BCD,
3) ∆ABO и ∆COD.
Доказательство:
1) Проведём в треугольниках ABD и ACD высоты BH и CF.
BK=CF (как высоты трапеции), следовательно,
2) Аналогично,
и
3)
Так как площади треугольников ABD и ACD равны (по доказанному), то и
Таким образом, треугольники , образованные боковыми сторонами и диагоналями трапеции, имеют равные площади.
Что и требовалось доказать.
www.treugolniki.ru
Равновеликие фигуры | Треугольники
Определение.
Равновеликие фигуры — это фигуры, которые имеют одинаковые площади.
Равновеликие тела — это тела, которые имеют равные объёмы (равновеликие тела часто также называют равновеликими фигурами).Равные фигуры — это фигуры, которые совпадают при наложении (у них соответствующие стороны равны и соответствующие углы равны).
Равные фигуры имеют равные площади, поэтому равные фигуры являются также равновеликими. Обратное, вообще говоря, неверно.
Примеры равновеликих фигур.
рисунок 1
1) Прямоугольник и квадрат, изображенные на рисунке 1, — равновеликие фигуры.
Площадь прямоугольника
a=8, b=2, S=8∙2=16
Площадь квадрата
S=4²=16.
То есть, прямоугольник со сторонами a и b и квадрат со стороной c являются равновеликими, если
рисунок 2
2) Треугольник и квадрат, изображенные на рисунке 2 — равновеликие фигуры, так как имеют равные площади.
Площадь квадрата S=3²=9.
Площадь треугольника
Треугольник со стороной a и проведенной к ней высоте ha и квадрат со стороной c являются равновеликими, если
рисунок 3
3) Треугольник и трапеция, изображенные на рисунке 3 — равновеликие, поскольку их площади равны.
Площадь треугольника
Площадь трапеции
Треугольник со стороной c и проведенной к ней высотой hс и трапеция с основаниями a и b и высотой h являются равновеликими, если
www.treugolniki.ru
Равновеликие фигуры
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока: Повторить тему «Площадь параллелограмма». Вывести формулу площади треугольник, ввести понятие равновеликих фигур. Решение задач по теме «Площади равновеликих фигур».
Ход урока
I. Повторение.
1) Устно по готовому чертежу вывести формулу площади параллелограмма.
2) Какова зависимость между сторонами параллелограмма и высотами, опущенными на них?
(по готовому чертежу)
зависимость обратно пропорциональная.
3) Найти вторую высоту (по готовому чертежу)
4) Найти площадь параллелограмма по готовому чертежу.
Решение:
5) Сравните площади параллелограммов S1, S2, S3. (Они имеют равные площади, у всех основание a и высота h).
Определение: Фигуры, имеющие равные площади, называются равновеликими.
II. Решение задач.
1) Доказать, что всякая прямая, проходящая через точку пересечения диагоналей, делит его на 2 равновеликие части.
Решение:
2) В параллелограмме ABCD CF и CE высоты. Доказать, что AD ∙ CF = AB ∙ CE.
3) Дана трапеция с основаниями a и 4a. Можно ли через одну из её вершин провести прямые, разбивающие трапецию на 5 равновеликих треугольников?
Решение: Можно. Все треугольники равновеликие.
4) Доказать, что если на стороне параллелограмма взять точку A и соединить её с вершинами, то площадь получившегося треугольника ABC равна половине площади параллелограмма.
Решение:
5) Торт имеет форму параллелограмма. Малыш и Карлсон делят его так: Малыш указывает на поверхности торта точку, а Карлсон по прямой, проходящей через эту точку, разрезает торт на 2 куска и один из кусков забирает себе. Каждый хочет получить кусок побольше. Где Малыш должен поставить точку?
Решение: В точке пересечения диагоналей.
6) На диагонали прямоугольника выбрали точку и провели через неё прямые, параллельные сторонам прямоугольника. По разные стороны образовались 2 прямоугольника. Сравните их площади.
Решение:
III. Изучение темы «Площадь треугольника»
начать с задачи:
«Найти площадь треугольника, у которого основание a, а высота h».
Ребята, используя понятие равновеликих фигур, доказывают теорему.
Достроим треугольник до параллелограмма.
Площадь треугольника равна половине площади параллелограмма.
Задание: Начертите равновеликие треугольники.
Используется модель (из бумаги вырезаны 3 цветных треугольника и склеены у оснований).
Упражнение №474. «Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой».
У треугольников одинаковые основания a и одна и та же высота h. Треугольники имеют одинаковую площадь
Вывод: Фигуры, имеющие равные площади, называются равновеликими.
Вопросы к классу:
- Равновелики ли равные фигуры?
- Сформулируйте обратное утверждение. Верно ли оно?
- Верно ли:
а) Равносторонние треугольники равновелики?
б) Равносторонние треугольники с равными сторонами равновелики?
в) Квадраты с равными сторонами равновелики?
г) Докажите, что параллелограммы, образованные при пересечении двух полос одинаковой ширины под разными углами наклона друг к другу, равновелики. Найдите параллелограмм наименьшей площади, образующийся при пересечении двух полос одинаковой ширины. (Показать на модели: полоски одинаковой ширины)
IV. Шаг вперёд!
На доске написаны задания по выбору:
1. «Разрежьте треугольник двумя прямыми линиями так, чтобы можно было из частей сложить прямоугольник».
Решение:
2. «Разрежьте прямоугольник по прямой линии на 2 части, из которых можно сложить прямоугольный треугольник».
Решение:
3) В прямоугольнике проведена диагональ. В одном из получившихся треугольников проведена медиана. Найдите соотношения между площадями фигур .
Решение:
Ответ:
3. Из олимпиадных задач:
«В четырёхугольнике ABCD точка E- середина AB, соединена с вершиной D, а F – середина CD, с вершиной B. Доказать, что площадь четырёхугольника EBFD в 2 раза меньше площади четырёхугольника ABCD.
Решение: провести диагональ BD.
Упражнение №475.
«Начертите треугольник ABC. Через вершину В проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади».
Использовать теорему Фалеса (разделить АC на 3 равные части).
V. Задача дня.
Для неё отвела крайнюю правую часть доски, на которой пишу задачу сегодняшнего дня. Ребята могут решать её, а могут и не решать. На уроке данную задачу мы сегодня не решаем. Просто те, кому они интересны, могут списать её, решить её дома или в перемену. Обычно уже в перемену многие ребята начинают решать задачу, если решили, то показывают решение, и я фиксирую это в специальной таблице. На следующем уроке к этой задаче обязательно возвращаемся, уделяя её решению небольшую часть урока (а на доске может быть записана новая задача).
«В параллелограмме вырезан параллелограмм. Разделите оставшуюся часть на 2 равновеликие фигуры».
Решение: Секущая AB проходит через точку пересечения диагоналей параллелограммов O и O1.
Дополнительные задачи (из олимпиадных задач):
1) «В трапеции ABCD (AD || BC) вершины A и B соединены с точкой M – серединой стороны CD. Площадь треугольника ABM равна m. Найти площадь трапеции ABCD».
Решение:
Треугольники ABM и AMK – равновеликие фигуры, т.к. AM – медиана.
S∆ABK = 2m, ∆BCM = ∆MDK, SABCD = S∆ABK = 2m.
Ответ: SABCD = 2m.
2) «В трапеции ABCD (AD || BC) диагонали пересекаются в точке O. Доказать, что треугольники AOB и COD равновеликие».
Решение:
S∆BCD = S∆ABC, т.к. у них общее основание BC и одинаковая высота.
3) Сторона АВ произвольного треугольника АВС продолжена за вершину В так, что ВР = АВ, сторону АС за вершину А так, что АМ = СА, сторону ВС за вершину С так, что КС = ВС. Во сколько раз площадь треугольника РМК больше площади треугольника АВС?
Решение:
В треугольнике МВС: МА = АС, значит, площадь треугольника ВАМ равна площади треугольника АВС. В треугольнике АРМ: ВР = АВ, значит, площадь треугольника ВАМ равна площади треугольника АВР. В треугольнике АРС: АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК: ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК: ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,
Ответ: Площадь треугольника МРК в 7 раз больше площади треугольника АВС.
4) Сцепленные параллелограммы.
2 параллелограмма расположены так, как показано на рисунке: они имеют общую вершину и ещё по одной вершине у каждого из параллелограммов лежит на сторонах другого параллелограмма. Доказать, что площади параллелограммов равны.
Решение:
и , значит,
Список использованной литературы:
- Учебник «Геометрия 7-9» (авторы Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев (Москва, «Просвещение», 2003).
- Олимпиадные задачи разных лет, в частности из учебного пособия «Лучшие задачи математических олимпиад» (составитель А.А. Корзняков, Пермь, «Книжный мир», 1996).
- Подборка задач, накопленных за много лет работы.
Приложение.
urok.1sept.ru
Треугольник. Формулы и свойства треугольников.
Определение. Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Типы треугольников
По величине углов
 Остроугольный треугольник — все углы треугольника острые.
Остроугольный треугольник — все углы треугольника острые.
 Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
 Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
По числу равных сторон
 Разносторонний треугольник — все три стороны не равны.
Разносторонний треугольник — все три стороны не равны.
 Равнобедренный треугольник — две стороны равны.
Равнобедренный треугольник — две стороны равны.
 Равносторонним треугольник или правильный треугольник — все три стороны равны.
Равносторонним треугольник или правильный треугольник — все три стороны равны.
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
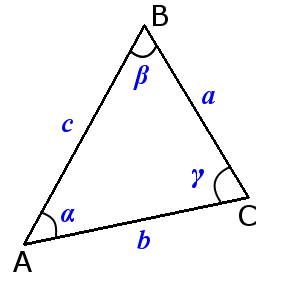
Сумма углов треугольника равна 180°:
α + β + γ = 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β, тогда a > b
если α = β, тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a2 = b2 + c2 — 2bc·cos α
b2 = a2 + c2 — 2ac·cos β
c2 = a2 + b2 — 2ab·cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианыa = 23√2(mb2 + mc2) — ma2
b = 23√2(ma2 + mc2) — mb2
c = 23√2(ma2 + mb2) — mc2
Медианы треугольника
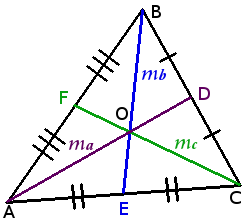
Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
Медианы треугольника пересекаются в одной точке. (Точка пересечения медиан называется центроидом)
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AOOD = BOOE = COOF = 21
Медиана треугольника делит треугольник на две равновеликие части
S∆ABD = S∆ACD
S∆BEA = S∆BEC
S∆CBF = S∆CAF
Треугольник делится тремя медианами на шесть равновеликих треугольников.
S∆AOF = S∆AOE = S∆BOF = S∆BOD = S∆COD = S∆COE
Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 12√2b2+2c2-a2
mb = 12√2a2+2c2-b2
mc = 12√2a2+2b2-c2
Биссектрисы треугольника
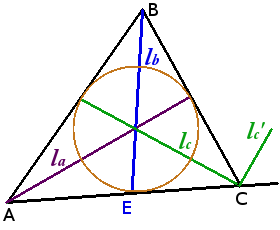
Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника:
Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AEAB = ECBC
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Угол между lc и lc‘ = 90°
Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√bcp(p — a)b + c
lb = 2√acp(p — b)a + c
lc = 2√abp(p — c)a + b
где p = a + b + c2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2bc cos α2b + c
lb = 2ac cos β2a + c
lc = 2ab cos γ2a + b
Высоты треугольника
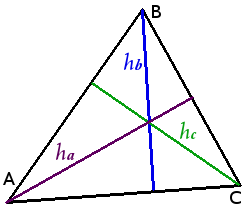
Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Если в треугольнике две высоты равны, то треугольник — равнобедренный.
ha:hb:hc = 1a:1b:1c = (bc):(ac):(ab)
Формулы высот треугольника
Формулы высот треугольника через сторону и угол:ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Формулы высот треугольника через сторону и площадь:ha = 2Sa
hb = 2Sb
hc = 2Sc
Формулы высот треугольника через две стороны и радиус описанной окружности:ha = bc2R
hb = ac2R
hc = ab2R
Окружность вписанная в треугольник
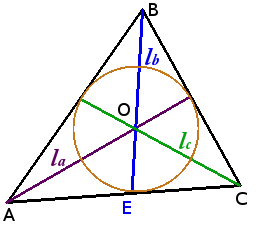
Определение. Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру: Радиус вписанной в треугольник окружности через три стороны:r = (a + b — c)(b + c — a)(c + a — b)4(a + b + c)
Радиус вписанной в треугольник окружности через три высоты:Окружность описанная вокруг треугольника
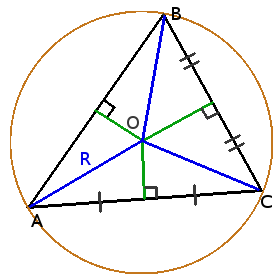
Определение. Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
Центр вписанной в треугольник окружности лежит на пересечении серединных перпендикуляров к уго сторонам.
Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь: Радиус описанной окружности через площадь и три угла:R = S2 sin α sin β sin γ
Радиус описанной окружности через сторону и противоположный угол (теорема синусов):R = a2 sin α = b2 sin β = c2 sin γ
Связь между вписанной и описанной окружностями треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то.rR = 4 sinα2sinβ2sinγ2 = cos α + cos β + cos γ — 1
Средняя линия треугольника
Определение. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
1. Любой треугольник имеет три средних линии
2.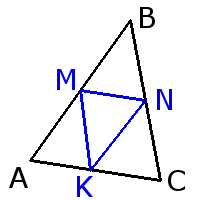 Средняя линия треугольника параллельна основанию и равна его половине.
Средняя линия треугольника параллельна основанию и равна его половине.MN = 12AC KN = 12AB KM = 12BC
MN || AC KN || AB KM || BC
3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольникаS∆MBN = 14 S∆ABC
S∆MAK = 14 S∆ABC
S∆NCK = 14 S∆ABC
4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.∆MBN ∼ ∆ABC
∆AMK ∼ ∆ABC
∆KNC ∼ ∆ABC
∆NKM ∼ ∆ABC
Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника

Периметр треугольника ∆ABC равен сумме длин его сторон
P = a + b + c
Формулы площади треугольника
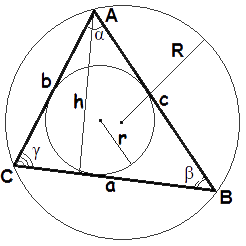
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высотыS = 12a · ha
S = 12b · hb
S = 12c · hc - Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
где p = a + b + c2 — полупериметр треугльника. - Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.S = 12a · b · sin γ
S = 12b · c · sin α
S = 12a · c · sin β - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Равенство треугольников
Определение. Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства. У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)
Признаки равенства треугольников
Теорема 1.
Первый признак равенства треугольников — по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.Теорема 2.
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.Теорема 3.
Третий признак равенства треугольников — по трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.Подобие треугольников
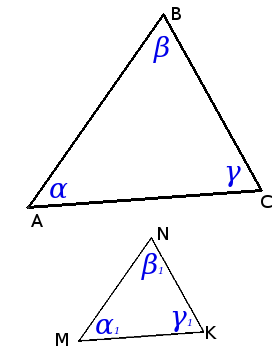 Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.
Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.∆АВС ~ ∆MNK => α = α1, β = β1, γ = γ1 и ABMN = BCNK = ACMK = k,
где k — коэффициент подобияПризнаки подобия треугольников
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.Второй признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.Третий признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны. Свойства. Площади подобных треугольников относятся как квадрат коэффициента подобия:S∆АВСS∆MNK = k2
ru.onlinemschool.com
Урок геометрии «Равновеликие фигуры в решении задач»
Цель урока:
- повторение и обобщение ключевых задач о равновеликих фигурах;
- обучение учащихся поиску решения задач в ходе создания проблемно-познавательной ситуации;
- развитие грамотной устной и письменной математической речи учащихся.
Оборудование: доска, с заготовленными чертежами или слайды; раздаточный материал: учебное пособие Атанасян Л.С. и др. Геометрия: дополнительные главы к школьному учебнику 8 класса.
Ход урока
Заканчивая изучение темы «Площади», сегодня мы повторяем и развиваем наши знания о равновеликих фигурах.
1. Чтобы вспомнить понятие «равновеликие фигуры», поиграем в «Да» и «Нет».
Я составила диктант-попурри, выбрав вопросы из ваших диктантов, связанных с этим понятием. Я читаю вопрос, его автор комментирует правильный ответ.
Учащимся к семинару по теме «Площади» было предложено домашнее задание: составить диктант из пяти вопросов по данной теме, ответы на которые предполагали либо «да», либо «нет». Данную работу можно было выполнять группами по два человека, увеличив количество вопросов. Для быстрой проверки умения оперировать с понятиями при проведении диктантов используются сигнальные карточки: треугольники белого цвета и цветные треугольники, вырезанные из бумаги, при ответе «Да» учащиеся поднимают карточку белого цвета, при ответе «Нет» — цветной треугольник.
Диктант.
- Верно ли, что фигуры, имеющие равные площади, называются равновеликими?
- Верно ли, что равные многоугольники равновелики?
- Верно ли, что если площади фигур равны, то и фигуры равны?
- Могут ли равновеликие фигуры быть равными?
- Верно ли, что диагонали параллелограмма делят его на четыре равновеликих треугольника?
2. Какие ключевые (базовые) задачи о равновеликих треугольниках мы рассматривали?
№1. Медиана треугольника разделяет его на два равновеликих треугольника.
Обоснуйте это утверждение (открыть заготовленный рис. №1 и по ходу обоснования сделать запись, рисунок не стирать).
№2. Все треугольники с общим основанием, вершины которых лежат на прямой, параллельной основанию, равновелики.
Обоснуйте это утверждение (открыть рис. №2 и по ходу обоснования сделать запись, рисунок не стирать).
1) На рисунке 3 я начертила ломаную ADB. Сравните площади четырёхугольников ADBС и ADBХ, ответ обоснуйте.
Вывод:
Сколько четырёхугольников равновеликих четырёхугольнику ADBC можно построить на рисунке 3?
Ответ: бесконечно много.
Что для этого надо сделать?
Ответ: отметить точку на прямойm и соединить её с точками A и B.
Полученный четырёхугольник будет равновелик четырёхугольнику ADBC.
Какой результат я могла бы получить, если бы дополнила рисунок 3 ломаной из
3-х звеньев? 4-х звеньев?
Ответ: бесконечно много равновеликих пятиугольников, шестиугольников и т.д.
Показать рисунок 4.
2) Начертите выпуклый четырёхугольник ABCD. Проведите диагональ AC. (рис.5)
Как построить четырёхугольник, равновеликий четырёхугольнику ABCD, диагональ которого есть отрезок AC?
Ответ: провести прямую а такую, что а ll АС, и D.
Пусть E, четырёхугольник ABCD равновелик четырёхугольнику ABCE.
Докажите последнее утверждение.
3) Есть ли на Рис. 6 равновеликие треугольники?
Какое утверждение позволяет нам это доказать?
Пусть .
Можно ли выразить площадь четырёхугольника ABCO через и ?
Ответ: да,
Можно ли выразить площадь четырёхугольника ABCO через ?
Ответ: да,
Как связаны ?
Ответ:
4) Решим задачу о разбиении данного выпуклого четырёхугольника на две равновеликие части.
Прочитаем условие задачи № 130 [1]
№ 130. В выпуклом четырёхугольнике ABCD через середину O диагонали BD проведена прямая, параллельная диагонали AC. Она пересекает сторону AD в точке E.
Докажите, что .
Сделаем чертёж (рис.7).
На рисунке отметим, что точка О – середина BD и укажем, что EO ll AC. Итак, что мы должны доказать? . Обозначим . Какую часть должна составлять площадь каждой фигуры от S? Проанализируем условие, подумаем: по условию точка О – середина BD, какое утверждение, связанное с равносильностью фигур, мы могли бы использовать?
Ответ: медиана делит треугольник на два равновеликих треугольника.
Что нам надо провести на чертеже, чтобы можно было это утверждение применить?
Ответ: медианы АО и СО.
Решение
- Проведём АО и СО.
- по свойству медианы.
- , по свойству 2 площадей.
Какое условие мы не использовали?
Ответ: EO ll AC.
Можем ли мы сравнить площади четырёхугольников ABCE и ABCO? - т.к. EO ll AC, то , , .
- , , значит, по свойству 2 площадей , ч.т.д.
Итог урока
Сегодня мы посвятили урок равновеликим многоугольникам. А где это может нам понадобиться, где практически можно применить полученные знания?
Пусть пройдёт какое-то время и кому-то из вас доведётся стать землеустроителем. Всем известно, что земледельцу не важно, какой формы участок, важна его площадь.
Допустим, что надо решить задачу: разделить участок на две части, равные по площади, если участок имеет форму: а) треугольника; б) четырёхугольника, при условии, что граница должна проходить через вершину многоугольника (столб на участке, например, стоит в этой вершине, и никому не хочется иметь его на своей земле).
Как выгоднее проводить границу: в виде ломаной или в виде отрезка прямой?
Ответ: длина отрезка меньше длины ломаной, соединяющей его концы, значит, если граница пройдёт по отрезку, то меньше материала уйдёт на ограждение.
Сформулируйте поставленную задачу на языке геометрии.
Ответ: а) Разделить треугольник на две равновеликие части прямой, проходящей через его вершину.
Как это сделать?
Ответ: Провести медиану из этой вершины.
Ответ: б) Разделить четырёхугольник на две равновеликие части прямой, проходящей через его вершину.
Как это сделать?
Решить задачу №130.
- Провести АС.
- Провести ВD.
- Отметить точку О середину ВD.
- Провести прямую mтакую, чтоm ll AC,
- m пересекает CD в точке М
- АМ – искомая граница.
Как разделить на две равновеликие части участок, имеющий форму пятиугольника?
Я не знаю. А вы?
Литература
- Атанасян Л.С. и др. Геометрия: дополнительные главы к школьному учебнику 8 класса. М.: Просвещение, 1996.
urok.1sept.ru
Медиана делит треугольник | Треугольники
Утверждение.
Медиана делит треугольник на два равновеликих треугольника.
Равновеликие треугольники — это треугольники, имеющие равные площади.
То есть медиана делит исходный треугольник на два треугольника с равными площадями (или медиана делит площадь треугольника пополам).
Дано: ABC,
BM — медиана.
Доказать:
Доказательство:
1 способ:
По формуле
∠AMB +∠CMB=180º (как смежные).
Так как sin(180º-α)=sin α, то
sin∠CMB=sin(180º-∠AMB)=sin∠AMB.
CM=AM (так как BM- медиана треугольника ABC).
Следовательно,
Что и требовалось доказать.
2 способ:
Проведём высоту BH.
По формуле
Так как AM=CM, то
Что и требовалось доказать.
Найти площадь треугольникаwww.treugolniki.ru
Конспект «Треугольник. Равенство треугольников» — УчительPRO
«Треугольник. Равенство треугольников»
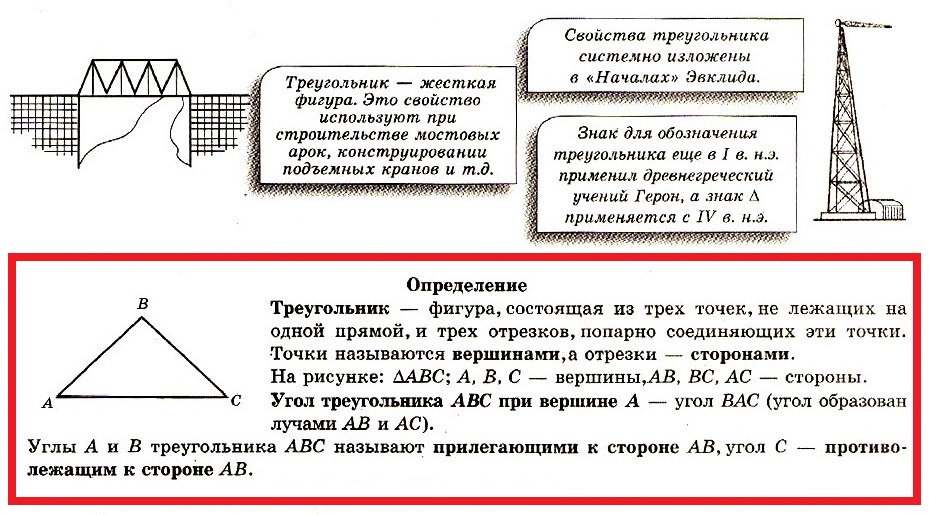
Треугольник — фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами.
Треугoльник — жесткая фигура. Это свойство используют при строительстве мостовых арок, конструировании подъемных кранов и т.д. Свойства треугольника системно изложены в «Началах» Эвклида. Знак для обозначения треугольника еще в I в. н.э. применил древнегреческий учений Герон, а знак Δ применяется с IV в. н.э.

Медиана, биссектриса и высота треугольника

Равные треугольники

Аксиома существования треугольника, равного данному.
Каким бы ни был треугольник, существует треугольник, равный ему в заданном расположении относительно данной полупрямой.
Свойства равных треугольников
1. В равных треугольниках соответствующие стороны равны.
2. В равных треугольниках соответствующие углы равны.
3. Периметры равных треугольников равны.
4. Площади равных треугольников равны.
5. Против равных сторон лежат равные углы.
6. Против равных углов лежат равные стороны.
Признаки равенства треугольников

Дополнительные признаки равенства
• Если две стороны и медиана, проведенная к третьей стороне треугольника, соответственно равны двум сторонам и медиане, проведенной к третьей стороне другого треугольника, такие треугольники равны.
• Если два угла и высота,проведенная к стороне, к которой прилегают эти углы, одного треугольника, соответственно равны двум углам и высоте, проведенной к стороне, к которой прилегают эти углы, другого треугольника, то такие треугольники равны.
• Если сторона, высота и медиана, проведенные к стороне одного треугольника, соответственно равны стороне, высоте и медиане, проведенным к этой стороне другого треугольника, то эти треугольники равны.
• Если медиана и углы, на которые она делит угол, одного треугольника, соответственно равны медиане и углам,на которые она делит угол, другого треугольника, эти треугольники равны.
Это конспект по теме «Треугoльник. Равенство треугольников». Выберите дальнейшие действия:
uchitel.pro
 Остроугольный треугольник — все углы треугольника острые.
Остроугольный треугольник — все углы треугольника острые.
 Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
 Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
 Равнобедренный треугольник — две стороны равны.
Равнобедренный треугольник — две стороны равны.
 Равносторонним треугольник или правильный треугольник — все три стороны равны.
Равносторонним треугольник или правильный треугольник — все три стороны равны.