Формулы тригонометрических уравнений
Для удобной работы все формулы для решения простейших тригонометрических уравнений, включая частные случаи, а также таблицы арксинусов, арккосинусов, арктангенсов и арккотангенсов собраны на одной странице.
I. sin x =a
При │a│>1 это уравнение решений не имеет.
При │a│не превосходящем 1 уравнение имеет бесконечное множество решений:
Таблица арксинусов
II. cos x=a
При │a│>1 это уравнение решений не имеет.
При │a│не превосходящем 1 уравнение имеет бесконечное множество решений:
Таблица арккосинусов
Частные случаи синуса и косинуса:
III. tg x=a
Уравнение имеет бесконечное множество решений при любых значениях a.
Таблица арктангенсов
IV. ctg x = a
Уравнение имеет бесконечное множество решений при любых значениях a.
Таблица арккотангенсов
www.uznateshe.ru
Формулы для решения простейших тригонометрических уравнений
Прежде чем решать тригонометрические уравнения, вы должны хорошо разбираться в тригонометрическом круге.
Все тригонометрические уравнения, какими они не были – простыми или сложными, в итоге сводятся к решению четырех типов простейших тригонометрических уравнений.
Вы просто обязаны уметь решать уравнения вида

Формулы–алгоритмы будут разбросаны по трем статьям,
здесь же они собраны все вместе =>
+ показать

Давайте разбираться. В этой статье мы рассмотрим решение уравнения вида  . Решение остальных типов простейших уравнений смотрим здесь: часть 2 (
. Решение остальных типов простейших уравнений смотрим здесь: часть 2 ( ), часть 3 (
), часть 3 ( ,
, 
Уравнение вида 
Решим уравнение 
Мы должны подобрать такие значения аргумента  , то есть такие значения углов, косинус которых равнялся бы
, то есть такие значения углов, косинус которых равнялся бы  .
.
Смотрим на тригонометрический круг, на оси косинусов находим  :
:

Выстраиваем через эту точку вертикаль, получаем две точки на круге:

Но надо понимать, что за этими точками скрывается бесконечно много других точек, – таких, косинус в которых также равен  . Мы об этом подробно говорили в предыдущей статье, когда знакомились с тригонометрическим кругом.
. Мы об этом подробно говорили в предыдущей статье, когда знакомились с тригонометрическим кругом.
На координатной прямой подходящие нам точки располагаются так:

А с графической точки зрения решение уравнения 

Как все точки взять в ответ?
Нам поможет счетчик  . Возьмем
. Возьмем  , то есть
, то есть 
Решением уравнения 

Возьмите, поперебирайте различные значения  подставьте в вышеуказанную формулу.
подставьте в вышеуказанную формулу.
Вы получите как раз точки  при
при  ,
,

 ,
, при
при  и т.д.
и т.д.
То что нам нужно!
Если бы мы решали, например, уравнение  , то решением бы было
, то решением бы было

 .
.
Я думаю, вы уже увидели общий принцип формирования ответа.
Давайте дадим формулу, которой можно руководствоваться, решая уравнения
 , где
, где  – из
– из ![Rendered by QuickLaTeX.com [-1;\:1]](http://xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
(в противном случае, когда  – не из
– не из ![Rendered by QuickLaTeX.com [-1;\;1]](http://xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) – решений нет)
– решений нет)
Но вам формула будет понятна, если вы уже знакомы с понятием «арккосинус».

Если нам попадается уравнение с нетабличным значением косинуса, вроде этого 

Частные случаи решения уравнения 
1) 

Мы должны бы записать так:

Но можно записать решение иначе (ведь в данном случае между точками расстояние – полкруга, значит нам можно использовать полукруговой счетчик  ):
):

2) 

У нас только одна серия корней:
 то есть
то есть 
3) 

Аналогично решению примера 2, решение такое: 
egemaximum.ru
Тригонометрия — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Некоторые рекомендации к выполнению тригонометрических преобразований
К оглавлению…
При выполнении тригонометрических преобразований следуйте следующим советам:
- Не пытайтесь сразу придумать схему решения примера от начала до конца.
- Не пытайтесь преобразовывать сразу весь пример. Продвигайтесь вперёд маленькими шагами.
- Помните, что кроме тригонометрических формул в тригонометрии можно по-прежнему применять все справедливые алгебраические преобразования (вынесение за скобку, сокращение дробей, формулы сокращённого умножения и так далее).
- Верьте, что всё будет хорошо.
Основные тригонометрические формулы
К оглавлению…
Большинство формул в тригонометрии часто применяется как справа налево, так и слева направо, поэтому учить эти формулы нужно так хорошо, чтобы Вы легко смогли применить некоторую формулу в обоих направлениях. Запишем для начала определения тригонометрических функций. Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:
Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:


Формулы двойного угла. Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:
Котангенс двойного угла:

Дополнительные тригонометрические формулы
К оглавлению…
Тригонометрические формулы сложения. Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:
Тангенс суммы:
Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение. Сумма синусов:
Разность синусов:

Сумма косинусов:

Разность косинусов:
Сумма тангенсов:
Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Тригонометрические формулы преобразования произведения в сумму. Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:

Формулы понижения степени. Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формулы половинного угла. Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
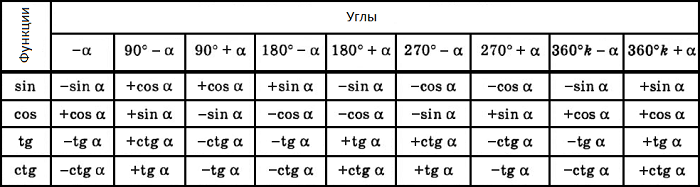
Тригонометрические формулы приведения
К оглавлению…
Функцию косинус называют кофункцией функции синус и наоборот. Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила:
- Если в формуле приведения угол вычитается (прибавляется) из 90 градусов или 270 градусов, то приводимая функция меняется на кофункцию;
- Если же в формуле приведения угол вычитается (прибавляется) из 180 градусов или 360 градусов, то название приводимой функции сохраняется;
- При этом перед приведенной функцией ставится тот знак, который имеет приводимая (т.е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
К оглавлению…
По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения
К оглавлению…
Для решения некоторого тригонометрического уравнения его нужно свести к одному из простейших тригонометрических уравнений, которые будут рассмотрены ниже. Для этого:
- Можно применять тригонометрические формулы приведенные выше. При этом не нужно пытаться преобразовать сразу весь пример, а нужно двигаться вперед маленькими шагами.
- Нужно не забывать о возможности преобразовать некоторое выражение и с помощью алгебраических методов, т.е. например, вынести что-нибудь за скобку или, наоборот, раскрыть скобки, сократить дробь, применить формулу сокращенного умножения, привести дроби к общему знаменателю и так далее.
- При решении тригонометрических уравнений можно применять метод группировки. При этом нужно помнить, что для того чтобы произведение нескольких множителей было равно нолю, достаточно чтобы любой из них был равен нолю, а остальные существовали.
- Применяя метод замены переменной, как обычно, уравнение после введения замены должно стать проще и не содержать первоначальной переменной. Также нужно не забыть выполнить обратную замену.
- Помните, что однородные уравнения часто встречаются и в тригонометрии.
- Раскрывая модули или решая иррациональные уравнения с тригонометрическими функциями нужно помнить и учитывать все тонкости решения соответствующих уравнений с обычными функциями.
- Помните про ОДЗ (в тригонометрических уравнениях ограничения на ОДЗ в основном сводятся к тому, что делить на ноль нельзя, но не забываем и о других ограничениях, особенно о положительности выражений в рациональных степенях и под корнями четных степеней). Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Главное, если не знаете, что делать, делайте хоть что-нибудь, при этом главное правильно использовать тригонометрические формулы. Если то, что Вы при этом получаете становиться все лучше и лучше, значит продолжайте решение, а если становиться хуже, значит вернитесь к началу и попробуйте применить другие формулы, так поступайте пока не наткнетесь на правильный ход решения.
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:

Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:






educon.by
Решение тригонометрических уравнений. Тест — курсы по математике
Тестирование онлайн
Арксинус, арккосинус, арктангенс, арккотангенс
Арксинус
Если есть выражение sinx=a, то x=arcsina. То есть арксинусом числа а называется такое число x , что его синус равен а.
Ограничения:
Арккосинус
Если есть выражение cosx=a, то x=arccosa. То есть арккосинусом числа а называется такое число x , что его косинус равен а.
Ограничения:
Арктангенс
Если есть выражение tgx=a, то x=arctga. То есть арктангенсом числа а называется такое число x , что его тангенс равен а.
Ограничения:
Арккотангенс
Если есть выражение сtgx=a, то x=arсctga. То есть арккотангенсом числа а называется такое число x , что его котангенс равен а.
Ограничения:
Не табличное значение «аркфункций» можно найти пользуясь калькулятором. Для того, чтобы понять почему у функций именно такие ограничения, необходимо изучить их графики.
Решение уравнения sinx=a
Общее решение уравнения
Частные случаи
Решение уравнения cosx=a
Общее решение уравнения
Частные случаи
Решение уравнения tgx=a, ctgx=a
Общее решение уравнения
Частные случаи для tgx=a
Частные случаи для ctgx=a
fizmat.by