градусная и радианная мера угла, интервалы и отрезки, свойства точки
п.1. Понятие тригонометрии
Тригонометрия – это раздел математики, в котором изучаются тригонометрические функции и их использование.
Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.
Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
| Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета, ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным; по часовой стрелке – отрицательным. |
Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
Радианной мерой угла называется отношение длины дуги окружности, заключенной между сторонами угла и центром в вершине угла, к радиусу этой окружности.
Найдем радианную меру прямого угла ∠AOB=90°. {\circ} $$ Таблица соответствия градусных и радианных мер некоторых углов {\circ} $$ Таблица соответствия градусных и радианных мер некоторых углов
п.4. Свойства точки на числовой окружностиПостроим числовую окружность. Обозначим O(0;0), A(1;0)
Каждой точке M(t) на числовой окружности соответствует бесконечное множество действительных чисел t с точностью до полного периода 2π: $$ M(t) = M(t+2\pi k),\ \ k\in\mathbb{Z} $$ Например:
п. {\circ}\\ \frac{17\pi}{6}=\frac{18-1}{6}\pi=3\pi-\frac{\pi}{6}\rightarrow \pi-\frac{\pi}{6}=\frac{5\pi}{6}\\ \frac{27\pi}{4}=\frac{28-1}{4}\pi=7\pi-\frac{\pi}{4}\rightarrow \pi-\frac{\pi}{4}=\frac{3\pi}{4} \end{gather*} {\circ}\\ \frac{17\pi}{6}=\frac{18-1}{6}\pi=3\pi-\frac{\pi}{6}\rightarrow \pi-\frac{\pi}{6}=\frac{5\pi}{6}\\ \frac{27\pi}{4}=\frac{28-1}{4}\pi=7\pi-\frac{\pi}{4}\rightarrow \pi-\frac{\pi}{4}=\frac{3\pi}{4} \end{gather*} |
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
| Сравниваем каждое число с границами четвертей: \begin{gather*} 0,\ \ \frac\pi2\approx\frac{3,14}{2}=1,57,\ \ \pi\approx 3,14\\ 3\pi\ \ 3\cdot 3,14\\ \frac{3\pi}{2}\approx \frac{3\cdot 3,14}{2}=4,71,\ \ 2\pi\approx 6,28 \end{gather*} |
\(\frac\pi2\lt 2\lt \pi \Rightarrow \) угол 2 радиана находится во 2-й четверти
\(\pi\lt 4\lt \frac{3\pi}{2} \Rightarrow \) угол 4 радиана находится в 3-й четверти
\(\frac{3\pi}{2}\lt 5\lt 2\pi \Rightarrow \) угол 5 радиана находится в 4-й четверти
\(7\gt 2\pi\), отнимаем полный оборот: \(0\lt 7-2\pi\lt \frac\pi2\Rightarrow\) угол 7 радиан находится в 1-й четверти.
Пример 5. Изобразите на числовой окружности множество точек \((k\in\mathbb{Z})\), запишите количество полученных базовых точек.
| $$ \frac{\pi k}{2} $$ | $$ -\frac{\pi}{4}+2\pi k $$ |
Четыре базовых точки, через каждые 90° | Две базовых точки, через каждые 180° |
| $$ \frac{\pi}{3}+\frac{2\pi k}{3} $$ | $$ -\frac{\pi k}{5} $$ |
Три базовых точки, через каждые 120° | Пять базовых точек, через каждые 72° |
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
| $$ \left[0;\ \frac{\pi}{3}\right] $$ | $$ \left(-\frac{\pi}{4};\ \pi\right] $$ |
| $$ \left[\frac\pi2;\ \frac{5\pi}{4}\right) $$ | $$ (1;\ 3) $$ |
| \begin{gather*} 1\ \text{рад}=\frac{180^{\circ}}{\pi}\approx 57,3^{\circ}\\ 3\ \text{рад}=\frac{180^{\circ}}{\pi}\cdot 3\approx 171,9^{\circ} \end{gather*} |
Числовая окружность в 10 классе по алгебре, урок и презентация
Дата публикации: .
Урок и презентация на тему: «Числовая окружность: определение, общий вид, длина. Единичная окружность»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать: Числовая окружность (PPTX )
Что будем изучать:
1. Числовая окружность в жизни.
2. Определение числовой окружности.
3. Общий вид и длина числовой окружности.
4. Местонахождение основных точек окружности.
Числовая окружность и жизнь
В реальной жизни часто встречается движение по окружности. Например, соревнования велосипедистов, которые проезжают определенный круг на время или соревнования гоночных автомобилей, которым надо проехать наибольшее количество кругов за отведенное время.
Рассмотрим конкретный пример…
Бегун бежит по кругу длиной 400 метров. Спортсмен стартует в точке А (рис. 1) и движется против часовой стрелки. Где он будет находится через 200 м, 800 м, 1500 м? А где провести финишную черту, если бегуну необходимо пробежать 4195 м?
1) и движется против часовой стрелки. Где он будет находится через 200 м, 800 м, 1500 м? А где провести финишную черту, если бегуну необходимо пробежать 4195 м?
Решение:
Через 200 м бегун будет находиться в точке С. Так как он пробежит ровно половину дистанции.
Пробежав 800 м, бегун сделает ровно два круга и окажется в точке А.
1500м – это 3 круга по 400 м (1200 м) и еще 300 м , то есть $\frac{3}{4}$ от беговой дорожки, финиш этой дистанции в точке D.
Где будет находиться наш бегун пробежав 4195 м? 10 кругов – это 4000 м, останется пробежать 195 м, это на 5 м меньше, чем половина дистанции. Значит финиш будет в точки K, расположенной около точки С.
Определение числовой окружности
Запомните!
Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам. Единичной окружностью называют окружность радиуса 1.
Общий вид числовой окружности
1) Радиус окружности принимается за единицу измерения.

2) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Диаметры АС и BD делят окружность на четыре четверти:
первая четверть – это дуга AB.
вторая четверть – дуга BC.
третья четверть – дуга CD.
четвертая четверть – дуга DA.
3) Начальная точка числовой окружности – точка А.
Отсчет от точки А против часовой стрелки называется положительным направлением. Отсчет от точки А по часовой стрелке называется отрицательным направлением.
Длина числовой окружности
Длина числовой окружности вычисляется по формуле:
$L = 2 π * R = 2 π * 1 = 2 π$.
Так как это единичная окружность, то $R = 1$.
Если взять $π ≈ 3,14$, то длина окружности L может быть выражена числом:
$2 π ≈ 2 * 3,14 = 6,28$.
Длина каждой четверти равна: $\frac{1}{4}*2π=\frac{π}{2}$.
Местонахождение основных точек окружности
Основные точки на окружности и их названия представлены на рисунке:
Каждая из четырёх четвертей числовой окружности разделена на три равные части. Около каждой из полученных двенадцати точек записано число, которому она соответствует.
Около каждой из полученных двенадцати точек записано число, которому она соответствует.
Если точка $М$ числовой окружности соответствует числу $t$ , то она соответствует и числу вида $t+2π *k$, где $k$ – целое число. $М(t) = M(t+2π*k)$.
Рассмотрим пример.
В единичной окружности дуга АВ разделена точкой М на две равные части, а точками К и Р — на три равные части. Чему равна длина дуги: AM, МВ, АК, КР, РB, АР, КМ?
Длина дуги $АВ =\frac{π}{2}$. Разделив ее на две равные части точкой М, получим две дуги, длиной $\frac{π}{4}$ каждая. Значит, $AM =МВ=\frac{π}{4}$.
Дуга АВ разбита на три равные части точками К и Р. Длина каждой полученной части равна $\frac{1}{3}* \frac{π}{2}$, т. е. $\frac{π}{6}$. Значит, $АК = КР = РВ =\frac{π}{6}$.
Дуга АР состоит из двух дуг АК и КР длиной — $\frac{π}{6}$. Значит, $АР = 2 *\frac{π}{6} =\frac{π}{3}$.
Осталось вычислить длину дуги КМ. Эта дуга получается из дуги AM исключением дуги АК. Таким образом, $КМ = AM – АК =\frac{π}{4} — \frac{π}{6} = \frac{π}{12}$.
Таким образом, $КМ = AM – АК =\frac{π}{4} — \frac{π}{6} = \frac{π}{12}$.
Найти на числовой окружности точку, которая соответствует заданному числу:
$2π$, $\frac{7π}{2}$, $\frac{π}{4}$, $-\frac{3π}{2}$.
Решение:
Числу $2π$ соответствует точка А, т.к. пройдя по окружности путь длиной $2π$, т.е. ровно одну окружность, мы опять попадем в точку А.
Числу $\frac{7π}{2}$ соответствует точка D, т.к. $\frac{7π}{2}=2π+\frac{3π}{2}$, т.е. двигаясь в положительном направлении, нужно пройти целую окружность и дополнительно путь длиной $\frac{3π}{2}$, который закончится в точке D.
Числу $\frac{π}{4}$ соответствует точка М, т.к. двигаясь в положительном направлении, нужно пройти путь в половину дуги АВ длиной $\frac{π}{2}$, который закончится в точке M.
Числу $-\frac{3π}{2}$ соответствует точка В, т.к. двигаясь в отрицательном направлении из точки А, нужно пройти путь длиной $\frac{3π}{2}$, который закончится в точке В.
Пример.
Найти на числовой окружности точки:
а) $21\frac{π}{4}$;
б) $-37\frac{π}{6}$.
Решение:
Воспользуемся формулой: $М(t) = M(t+2π*k)$ (8 слайд) получим:
а) $\frac{21π}{4} = (4+\frac{5}{4})*π = 4π +\frac{5π}{4} = 2*2π +\frac{5π}{4}$, значит числу $\frac{21π}{4}$ соответствует такое же число, что и числу $\frac{5}{4π}$ – середина третьей четверти.
б) $-\frac{37π}{6}=-(6+\frac{1}{6})*π =-(6π +\frac{π}{6}) = -3*2π — \frac{π }{6}$. Значит, числу $-\frac{37π}{6}$ соответствует такое же число, что и числу $-\frac{1}{6π}$. Тоже самое, что и $\frac{11π}{6}$.
Пример.
Найти все числа t, которым на числовой окружности соответствуют точки, принадлежащие заданной дуге:
а) ВА;
б) МK.
Решение:
а) Дуга ВА – это дуга с началом в точке В и концом в точке А, при движении по окружности против часовой стрелки. Точка В соответственно равна $\frac{π}{2}$, а точка А равна $2π$. Значит, для точек t имеем: $\frac{π}{2} ≤ t ≤ 2π$. Но согласно формуле на слайде 8, числам $\frac{π}{2}$ и $2π$ соответствуют числа вида $\frac{π}{2}+2π*k$ и $2π+2π*k$ соответственно.
Тогда наше число t принимает значения:
$\frac{π}{2} +2π*k ≤ t ≤ 2π +2π*k$, где $к$ – целое число.
б) Дуга МK – это дуга с началом в точке М и концом в точке К. Точка М соответственно равна $-\frac{3π}{4}$, а точка К равна $\frac{π}{4}$.
Значит для точек t имеем:
$\frac{-3π}{4} ≤ t ≤\frac{π}{4}$.
Согласно формуле на слайде 8 числам $-\frac{3π}{4}$ и $\frac{π}{4}$ соответствуют числа вида: $-\frac{3π}{4}+2π*k$ и $\frac{π}{4}+2π*k$ соответственно.
Тогда наше число t принимает значения:
$-\frac{3π}{4}+2π*k ≤ t ≤ \frac{π}{4} +2π*k$, где $к$ – целое число.
Задачи для самостоятельного решения
1) На единичной окружности дуга ВС разделена точкой Т на две равные части, а точками К и Р на три равные части. Чему равна длина дуги: ВТ, ТС, ВК, КР, РС, ВР, КТ?
2) Найти на числовой окружности точку, которая соответствует заданному числу:
$π$, $\frac{11π}{2}$, $\frac{21π}{4}$, $-\frac{7π}{2}$, $\frac{17π}{6}$.
3) Найти все числа t, которым на числовой окружности соответствуют точки, принадлежащие заданной дуге:
б) АС;
в) PM, где P – середина дуги АВ, а точка М – середина DA.

Математика — Clever Study Club
Математика является универсальным инструментом, позволяющим решать расчетные и аналитические задачи в технических, социально-экономических и даже гуманитарных сферах профессиональной деятельности. Кроме того, математика, как известно, «ум в порядок приводит», то есть развивает логическое и образное мышление, аналитические способности, интуицию и даже эстетическое восприятие.
Для систематизации знаний в рамках школьного курса математики, мы предлагаем изучить следующие разделы и тем:
Модуль «Основы дискретной математики»
Основы математической логики. Основные логические функции: конъюнкция, дизъюнкция, инверсия, строгая дизъюнкция, импликация, эквивалентность.
Основы теории вероятностей и математической статистики. Понятие и виды событий. Операции над событиями. Понятие вероятности. Классическое определение вероятностей и его статистическая интерпретация. Теорема сложение несовместных и совместных событий.
Понятие множества. Операции над множествами. Числовые множества. Арифметические действия с отрицательными числами, обыкновенными и десятичными дробями, арифметическими квадратными корнями.
Числовая последовательность. Понятие числовой последовательности. Арифметическая и геометрическая последовательности. Формулы n-го члена и суммы первых n-х членов арифметической и геометрической прогрессий.
Модуль «Алгебра»
Понятие функции. Определение функции, графика функции. Основные свойства функций.
Линейная функция. Свойства линейной функции. Линейные уравнения. Системы линейных уравнений. Линейные неравенства и системы линейных неравенств.
Обратная пропорциональность. Свойства функции. Дробные уравнения. Дробные неравенства. Метод интервалов.
Показательная функция.
 Свойства показательной функции. Показательные уравнения. Показательные неравенства.
Свойства показательной функции. Показательные уравнения. Показательные неравенства. Логарифмы. Определение логарифма. Свойства логарифма.
Логарифмическая функция. Свойства функции. Логарифмические уравнения. Логарифмические неравенства.
Тригонометрические функции. Числовая окружность. Нахождение тригонометрических функций табличных углов с помощью числовой окружности. Формулы приведения. Тригонометрические функции двойного угла, суммы и разности углов.
Графики тригонометрических функций. Свойства тригонометрических функций.
Обратные тригонометрические функции. Свойства функций.
Понятие производной функции. Производная как скорость изменения функции. Физический смысл производной. Правила дифференцирования. Таблица производных. Нахождение производных функций. Геометрический смысл производной. Производная сложной функции.
Применение производных в исследовании функций. Исследование функций на монотонность и точки экстремума.
 Нахождение наибольших и наименьших значений функций на отрезке. Исследование функций на выпуклость-вогнутость и точки перегиба.
Нахождение наибольших и наименьших значений функций на отрезке. Исследование функций на выпуклость-вогнутость и точки перегиба. Понятие неопределенного и определенного интеграла. Понятие первообразной функции. Неопределенный интеграл как семейство первообразных. Правила интегрирования функций. Понятие определенного интеграла. Геометрический смысл определенного интеграла.
Модуль «Геометрия»
Треугольники. Виды треугольников. Формулы площадей треугольников. Признаки равенства треугольников. Равнобедренный треугольник и его свойства. Равносторонний треугольник и его свойства. Подобные треугольники. Признаки подобия треугольников. Теорема Пифагора.
Тригонометрия. Тригонометрические функции в прямоугольных треугольниках. Теорема синусов. Теорема косинусов.
Четырехугольники. Свойства четырехугольников. Формулы площадей четырех угольников. Многоугольники. Правильные многоугольники и их свойства.
Окружность. Вписанные и центральные углы. Свойства касательных к окружности. Окружности, описанные около и вписанные в треугольники и многоугольники.
Окружности, описанные около и вписанные в треугольники и многоугольники.
Стереометрия. Взаимное расположение в пространстве прямых, прямой и плоскости, плоскостей. Угол между прямыми в пространстве, угол между прямой и плоскостью, угол между плоскостями. Теорема о трех перпендикулярах и обратная ей. Построение сечений.
Многогранники. Свойства: призмы, пирамиды, цилиндра, шара. Формулы площадей поверхности и объемов.
Модуль «Задачи повышенной сложности»
Задачи с параметром. Экономические задачи. Задачи на теорию чисел.
Числовая окружность, тригонометрический круг и единичная окружность
Любая окружность, которую мы соотносим с действительными числами будет числовая. Но на практике (для удобства) используют единичную окружность, т.е. окружность с радиусом = 1 и центром в начале координат.
Ну, и поскольку у каждой точки окружности есть координаты на осях Х и Y, которые являются косинусом и синусом угла β, соответственно круг является тригонометрическим, т. е. связанным с этими самыми функциями из тригонометрии.
е. связанным с этими самыми функциями из тригонометрии.
Большой плюс, что на тригонометрическом круге можно увидеть разные углы (а не только, как в треугольнике). Ведь неважно, где мы поставим точку на круге, мы всегда сможем определить для нее косинус и синус по абсциссе и ординате даже по самому простому и схематичному рисунку.
Важно только помнить, что угол всегда рисуется от оси OX (называется углом поворота) и получается такая схема, где положительные углы всегда отображаются против часовой стрелки, а отрицательные — по часовой.
Вместе с положительными углами движется и отсчет четвертей круга:
0° до 90° — I четверть,
90° до 180° — II четверть,
180° до 270° — III четверть,
270° до 360° — IV четверть
Еще лайфхаки с градусами и кругами
Соответственно, если точно помнить, что целый круг — это 360°, то 50° будет в том же месте, где и -310° (проверьте;)
Если нужны углы более 360°, то делим их на 360, отбрасываем целые части и рисуем обычный угол. Например, угол в 795° = (360° * 2) + 75° — значит, просто рисуем угол в 75° и смотрим его синусы/косинусы.
Например, угол в 795° = (360° * 2) + 75° — значит, просто рисуем угол в 75° и смотрим его синусы/косинусы.
Добавить интересную новость
Тригонометрические функции. Числовая окружность — презентация онлайн
1. Числовая окружность
10 класс. Мордкович А.Г.Тригонометрические функции.
Числовая окружность
Валиева Ю.Ф.
2. Цель урока
• ввести понятие числовой окружности;• формирование умения записывать
множество чисел, соответствующих на
числовой окружности точке;
• формирование умения находить на
числовой окружности точку,
соответствующую данному числу.
3.
 Числовая прямая Прямая, на которой заданы точка отсчета,
Числовая прямая Прямая, на которой заданы точка отсчета,единичный отрезок и положительное
направление, называется числовой прямой.
Определение?
Любому действительному числу можно
сопоставить точку на числовой прямой , и
наоборот.
Свойство?
Нанесите на числовую прямую числа π, 2π, -π, -2π.
Нанесите на числовую прямую промежутки (π; 2π), [-2π; π/2].
-2π
-π
-6
-3
-1 0
1
π
2π
3
6
4. Числовая прямая
Запишите координаты точек :А
B
C
D
5
10
6
3
Запишите промежутки и соответствующие неравенства:
-2π
-π
1
проверка
[DA)
2
проверка
[BC]
D
B
5
6
0
6
5
t
6
2
5
t
6
4
A
2
π
C
5
3
2π
t
5. Числовая окружность
Определение.+
R=1
А(0)
—
Единичную окружность называют числовой окружностью, если между
действительными числами и точками окружности установлено
соответствие:
Числу t = 0 сопоставлена точка А – правый конец горизонтального
диаметра: А(0).

Если t > 0, то, двигаясь из точки А в направлении против часовой
стрелки (положительное направление обхода окружности), опишем по
окружности путь АМ длиной t, тогда М – искомая М(t).
Если t
(отрицательное направление обхода окружности), опишем по
окружности путь АМ длиной |t|, тогда М – искомая М(t).
6. Числовая окружность
π2
2π
3
π
3
3π
4
π
6
+
R
π
0
2π
О
11π
6
7π
6
5π
4
4π
3
3π
2
5π
3
7π
4
5π
3
5π
4
π
4
5π
6
3π
2
4π
3
7π
4
11π
6
7π
6
R
π
2π
О
0
π
6
5π
6
3π
4
2π
3
π
2
π
3
π
4
7. Задание 1.
1. Обозначьте на числовой окружности точку, которая4 4 5
соответствует данному числу:
; ;
;
; ;5 ; 3
8 8 3
3 2
5π
2
4π
Проверка (7)
3
π
8
5π
R=1
— 3π
О
0
π
8
4π
3
5
1
2 2
2
2
2
5 2 2
3 2
2.
 Какое взаимное
Какое взаимноерасположение на
числовой окружности
точек, соответствующих
4
4
и
;
и
.
числам 8
8 3
3
8. Задание 2 (№ 20 — №23).
Какой четверти числовой окружности принадлежит точка,соответствующая числу: 2; 5; -5; -9; -17; 31; -95.
π/2 ≈ 3,14/2 = 1,57
2
π
-17 2
3π/2 ≈ 3*3,14/2 = 4,71
-5
Проверка (7)
9
II
π
I
R=1
95
0
5 = 4,71+0,29
9 = 6,28+2,72
17 = 2*6,28+4,44
-9
III
IV
17 3π
5
2
31
-95
31 = 4*6,28 + 5,88
95 = 15*6,28 +0,8
9. Задание 3 (№17).
-4πЗадание 3 (№17).
Как расположены на координатной прямой и на числовой
окружности точки, соответствующие числам:
π
2
t+2πk
a) t и –t;
t
б) t и t+2πk, k Z;
π
в) t и t+π;
0
О
г) t+π и t-π;
t-π
-t
-2π
t+π
3π
2
-π
-t
t-π
t
0
π
2π
t+π
4π
t
10.
 Задание 4. Постройте геометрическую модель дуги числовой окружности,
Задание 4. Постройте геометрическую модель дуги числовой окружности,все точки которой удовлетворяют неравенству.
π
2
2π
π
3
3
5
3π
4
π
4
t
5π
π
4
4
6
6
R
π
0
2π
О
7π
6
-3π
5π
44
11π
π
6
4π
3
3π
2
5π
3
7π
4
7
t
6
6
3
3
t
4
4
11. Задание 5.
Найдите все числа t, которым на числовой окружностиk Z
соответствуют точки, принадлежащие открытой дуге
3
2 k t
2 k
AB
π
4
4
2
2π
π
3
5
7
3
2 k t
2 k
DC
4
3π
4
4
4
π
5π
А
В
π
2
k
t
2 k
PR
6
6
6
R 6
R=1
π
0
О
P
7π
6
5π
4
С
D
4π
3
3π
2
5π
3
7π
4
11π
6
12.
 Итог урока • Каким вопросам был
Итог урока • Каким вопросам былпосвящен урок?
• Чему научились на уроке?
13. Домашнее задание
§4.№4.54.11(в,г)
14. Источники
• А.Г. Мордкович, «Алгебра и начала анализа», 10 — 11 классы,часть 1, учебник.
• А.Г. Мордкович, «Алгебра и начала анализа», 10 — 11 классы,
часть 2, задачник.
Числовая окружность
ЧИСЛОВАЯ ОКРУЖНОСТЬ
ЧИСЛОВАЯ ОКРУЖНОСТЬ
- Окружность имеет радиус равный 1
- Точка А(0) является началом отсчета
- Длина окружности равна С = 2П
- Против часовой стрелки идет положительное направление обхода окружности, а по часовой — отрицательное
- На окружности точка М соответствует положительному числу t
- На окружности точка N соответствует отрицательному числу s
ЧИСЛОВАЯ ОКРУЖНОСТЬ
ЗАДАЧА №1
Найти на числовой окружности точки, соответствующие
числам
Решение:
1) Так как длина всей окружности 2П, то ее половина будет соответствовать числу П
2) Теперь разделим верхнюю полуокружность на 4 равные части
3) Первая часть от начала отсчета будет соответствовать числу
4) Вторая часть от начала отсчета будет соответствовать числу
5) Третья часть от начала отсчета будет соответствовать числу
ЧИСЛОВАЯ ОКРУЖНОСТЬ
ЗАДАЧА №2
Найти на числовой окружности точки, соответствующие
числам
Решение:
1) Так как по часовой стрелки идет отрицательное направление обхода длины окружности, то будем работать с нижней полуокружностью
2) Разделим нижнюю полуокружность на 4 равные части
3) Первая часть от начала отсчета будет соответствовать числу , вторая часть будет соответствовать числу ,
третья часть будет соответствовать числу
ЧИСЛОВАЯ ОКРУЖНОСТЬ
ЗАДАЧА №3
Найти на числовой окружности точки, соответствующие
числам
Решение:
- Аналогично предыдущим
выполненным заданиям разделяем верхнюю полуокружность на 6 равных частей и нижнюю также на 6 равных частей
- Затем отсчитываем от начала отсчета в противоположном направлении часовой стрелки какая часть будет соответствовать выбранной точки, также как в предыдущих задачах
ЧИСЛОВАЯ ОКРУЖНОСТЬ
ЗАДАЧА №4
Найти на числовой окружности точки, соответствующие
числам
Решение:
- Аналогично предыдущему
выполненному заданию разделяем верхнюю полуокружность на 6 равных частей и нижнюю также на 6 равных частей
- Затем отсчитываем от начала отсчета по направлению часовой стрелки какая часть будет соответствовать выбранной
точки, также как в предыдущих задачах
ЧИСЛОВАЯ ОКРУЖНОСТЬ
ЗАДАЧА №5
Найти на числовой окружности точки, соответствующие
числам 1; 2; 3; 4; 5
Решение:
2
1
Известно, что
Найдем следующие приближенные значения
3
4
5
ЧИСЛОВАЯ ОКРУЖНОСТЬ
Перпендикулярные диаметры окружности разбивают ее на 4 равные части.
Эти части называются четверти
2
1
Нумерация четвертей приведена на рисунке
3
Например,
Число 1 находится в 1 четверти
Числа 2 и 3 во 2 четверти
Число 4 в 3 четверти
Число 5 в 4 четверти
4
5
ЧИСЛОВАЯ ОКРУЖНОСТЬ
Изображение точек на окружности может совпадать
Например, будут совпадать точки
Все совпадающие точки данного вида можно представить в виде формулы
— число на окружности,
n – любое целое число
СПАСИБО ЗА ВНИМАНИЕ!
Урок «числовая окружность на координатной плоскости». Тригонометрическая окружность
Определение 1
. Числовой осью
(числовой прямой, координатной прямой
) Ox
называют прямую линию, на которой точка O
выбрана началом отсчёта (началом координат)
(рис.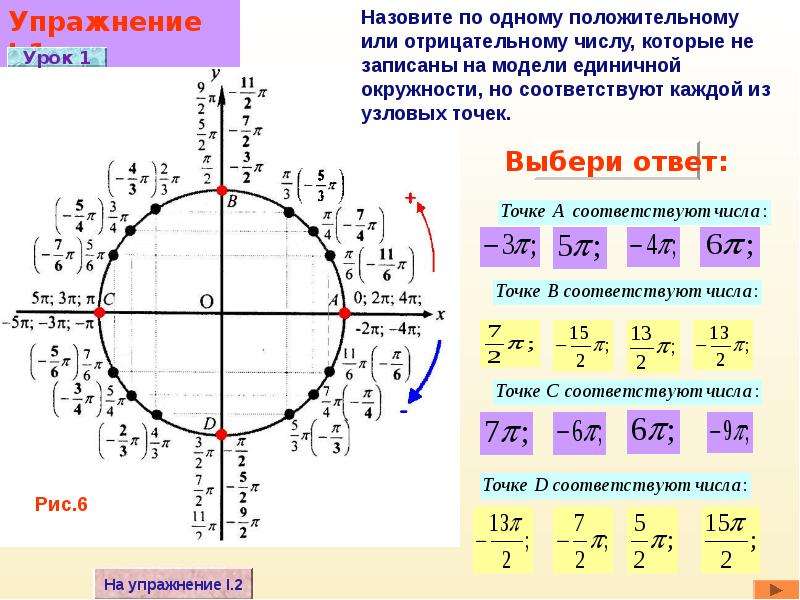 1), направление
1), направление
O → x
указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины .
Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .
Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .
Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
Замечание
. Прямоугольную декартову систему координат Oxy ,
изображённую на рисунке 2, называют правой системой координат
, в отличие от левых систем координат
, в которых поворот луча Ox
на угол 90°
до луча Oy
осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат , не оговаривая этого особо.
Прямоугольную декартову систему координат Oxy ,
изображённую на рисунке 2, называют правой системой координат
, в отличие от левых систем координат
, в которых поворот луча Ox
на угол 90°
до луча Oy
осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат , не оговаривая этого особо.
Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату , которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA 1 и AA 2 на прямые Ox и Oy соответственно (рис.3).
Определение 4 . Абсциссой точки A называют координату точки A 1 на числовой оси Ox , ординатой точки A называют координату точки A 2 на числовой оси Oy .
Обозначение
. Координаты (абсциссу и ординату) точки
A
в прямоугольной декартовой системе координат Oxy
(рис. 4) принято обозначать A (x ; y )
или A = (x ; y ).
4) принято обозначать A (x ; y )
или A = (x ; y ).
Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).
Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти (квадранта ), нумерация которых показана на рисунке 5.
Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .
Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.
Утверждение 1 . Расстояние между двумя точками координатной плоскости
A 1 (x 1 ; y 1) и A 2 (x 2 ; y 2)
вычисляется по формуле
Доказательство
. Рассмотрим рисунок 6.
Рассмотрим рисунок 6.
| Уравнение окружности на координатной плоскости |
| | A 1 A 2 | 2 = = ( x 2 — x 1) 2 + ( y 2 — y 1) 2 . | (1) |
Следовательно,
что и требовалось доказать.
Уравнение окружности на координатной плоскости
Рассмотрим на координатной плоскости Oxy (рис. 7) окружность радиуса R с центром в точке A 0 (x 0 ; y 0) .
Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.
Единичной окружностью называют окружность радиуса 1.
Общий вид числовой окружности.
1) Ее радиус принимается за единицу измерения.
2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.
3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая
точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:
первая четверть – это дуга AB
вторая четверть – дуга BC
третья четверть – дуга CD
четвертая четверть – дуга DA
4) Начальная точка числовой окружности – точка А.
Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против
часовой стрелки называется положительным направлением .
Отсчет от точки А по
часовой стрелке называется отрицательным направлением .
Числовая окружность на координатной плоскости.
Центр радиуса числовой окружности соответствует началу координат (числу 0).
Горизонтальный диаметр соответствует оси x , вертикальный – оси y .
Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).
Значения x и y в четвертях числовой окружности:
Основные величины числовой окружности:
Имена и местонахождение основных точек числовой окружности:
Как запомнить имена числовой окружности.
Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.
Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.
1) Начнем с крайних точек на осях координат.
Начальная точка – это 2π (крайняя правая точка на оси х , равная 1).
Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х , равная -1, называется π.
Крайняя верхняя точка на оси у , равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.
Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у , равной -1. Но если она включает три четверти – значит имя ей 3π/2.
2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у , и относительно центра осей, и относительно оси х . Это нам и поможет знать их значения точек без зубрежки.
Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у , и относительно центра осей, и относительно оси х . Это нам и поможет знать их значения точек без зубрежки.
Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:
— Относительно оси у
в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.
— Относительно центра осей координат
все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей.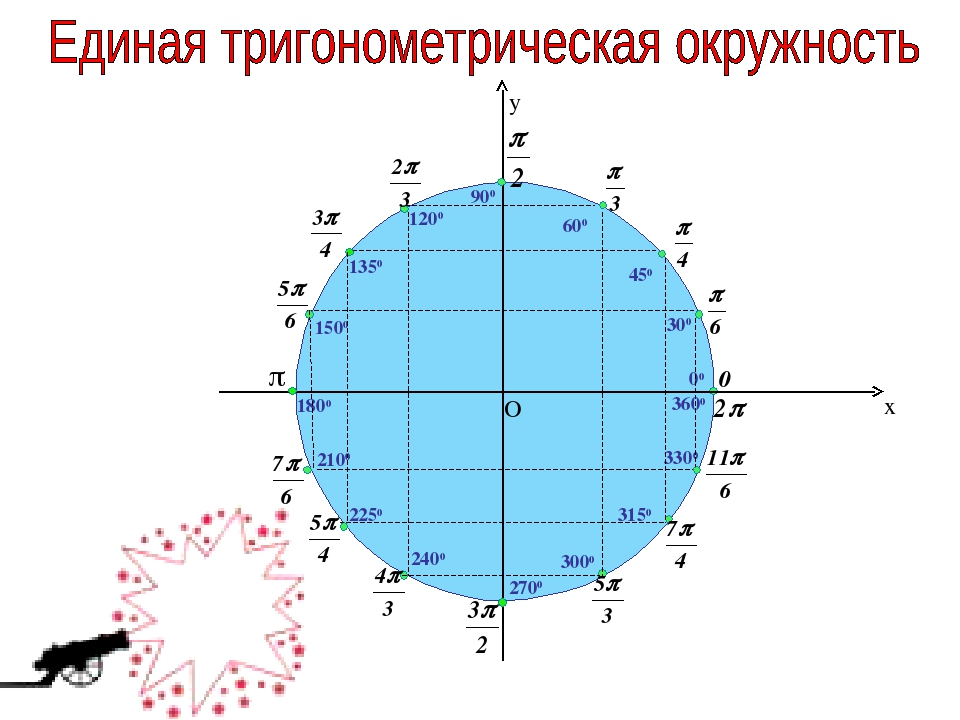 Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.
Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.
Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.
— Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.
Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.
3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.
Особенности числовой окружности. Сравнение с числовой прямой.
Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.
На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:
Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k , то получим новое выражение:
t = t + 2πk .
Отсюда формула:
Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):
Представляем вашему вниманию видеоурок по теме «Числовая окружность». Дается определение, что такое синус, косинус, тангенс, котангенс и функции y = sin x , y = cos x , y = tg x , y = ctg x для любого числового аргумента. Рассматривается стандартные задачи на соответствие между числами и точками в единичной числовой окружности для нахождения каждому числу единственной точки, и, наоборот, на нахождение для каждой точки множество чисел которые ей соответствуют.
Рассматривается стандартные задачи на соответствие между числами и точками в единичной числовой окружности для нахождения каждому числу единственной точки, и, наоборот, на нахождение для каждой точки множество чисел которые ей соответствуют.
Тема: Элементы теории тригонометрических функций
Урок: Числовая окружность
Наша ближайшая цель — определить тригонометрические функции: синус , косинус , тангенс , котангенс-
Числовой аргумент можно откладывать на координатной прямой или на окружности.
Такая окружность называется числовой или единичной, т.к. для удобства берут окружность с
Например, дана точка Отметим ее на координатной прямой
и на числовой окружности .
При работе с числовой окружностью условились, что движение против часовой стрелки — положительное направление, по часовой стрелке — отрицательное.
Типовые задачи — нужно определить координаты заданной точки либо, наоборот, найти точку по ее координатам.
Координатная прямая устанавливает взаимно-однозначное соответствие между точками и числами. Например, числу соответствует точка А с координатой
Каждая точка В с координатой характеризуется только одним числом — расстоянием от 0 до взятым со знаком плюс или минус.
На числовой окружности взаимно-однозначное соответствие работает только в одну сторону.
Например, есть точка В на координатной окружности (рис.2), длина дуги равна 1, т.е. эта точка соответствует 1.
Дана окружность, длина окружности Если то — длина единичной окружности.
Если мы прибавим , получим ту же точку В, еще — тоже попадем в т. В, отнимем — тоже т. В.
Рассмотрим точку B: длина дуги =1, тогда числа характеризуют т. В на числовой окружности.
Таким образом, числу 1 соответствует единственная точка числовой окружности — точка В, а точке В соответствует бесчисленное множество точек вида .
Для числовой окружности верно следующее:
Если т. М числовой окружности соответствует числу то она соответствует и числу вида
Можно делать сколько угодно полных оборотов вокруг числовой окружности в положительном или отрицательном направлении — точка одна и та же. Поэтому тригонометрические уравнения имеют бесчисленное множество решений.
Поэтому тригонометрические уравнения имеют бесчисленное множество решений.
Например, дана точка D. Каковы числа, которым она соответствует?
Измеряем дугу .
множество всех чисел, соответствующих точке D.
Рассмотрим основные точки на числовой окружности.
Длина всей окружности.
Т.е. запись множества координат может быть различной.
Рассмотрим типовые задачи на числовую окружность.
1. Дано: . Найти: точку на числовой окружности.
Выделяем целую часть:
Необходимо найти т. на числовой окружности. , тогда.
В это множество входит и точка .
2. Дано: . Найти: точку на числовой окружности.
Необходимо найти т.
т.также принадлежит этому множеству.
Решая стандартные задачи на соответствие между числами и точками на числовой окружности, мы выяснили, что можно для каждого числа найти единственную точку, и можно для каждой точки найти множество чисел, которые характеризуются данной точкой.
Разделим дугу на три равные части и отметим точки M и N.
Найдем все координаты этих точек.
Итак, наша цель — определение тригонометрических функций. Для этого нам необходимо научиться задавать аргумент функции. Мы рассмотрели точки единичной окружности и решили две типовые задачи — найти точку на числовой окружности и записать все координаты точки единичной окружности.
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. — М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс: учеб.для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
— М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил.
№№ 531; 536; 537; 541; 552.
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Числовая окружность в координатной плоскости
Повторим: Единичная окружность – числовая окружность, радиус которой равен 1. R=1 C=2 π + — у х
R=1 C=2 π + — у х
Если точка М числовой окружности соответст-вует числу t, то она соответствует и числу вида t+2 π k , где k – любое целое число (k ϵ Z) . M(t) = M(t+2 π k), где k ϵ Z
Основные макеты Первый макет 0 π у х Второй макет у х
х у 1 А(1, 0) B (0 , 1) C (- 1, 0) D (0 , -1) 0 x>0 y>0 x 0 x 0 y
Найдем координаты точки М, соответствующей точке. 1) 2) х у М P 45° O A
Координаты основных точек первого макета 0 2 x 1 0 -1 0 1 y 0 1 0 -1 0 0 x 1 0 -1 0 1 y 0 1 0 -1 0 D у х
М P х у O A Найдем координаты точки М, соответствующей точке. 1) 2) 30°
М P Найдем координаты точки М, соответствующей точке. 1) 2) 30° х у O A В
Используя свойство симметрии, найдем координаты точек, кратных у х
Координаты основных точек второго макета x y x y у х
Пример Найти координаты точки числовой окружности. Решение: P у х
Пример Найти на числовой окружности точки с ординатой Решение: у х x y x y
Упражнения: Найти координаты точек числовой окружности: а) , б) . Найти на числовой окружности точки с абсциссой.
Найти на числовой окружности точки с абсциссой.
Координаты основных точек 0 2 x 1 0 -1 0 1 y 0 1 0 -1 0 0 x 1 0 -1 0 1 y 0 1 0 -1 0 Координаты основных точек первого макета x y x y Координаты основных точек второго макета
По теме: методические разработки, презентации и конспекты
Дидактический материал по алгебре и началам анализа в 10 классе (профильный уровень) «Числовая окружность на координатной плоскости»
Вариант 1.1.Найти на числовой окружности точку:А) -2∏/3Б) 72.Како й четверти числовой окружности принадлежит точка 16.3.Найти ко…
Дата: Урок 1
тема: Числовая окружность на координатной прямой
Цели: ввести понятие модели числовой окружности в декартовой и криволинейной системе координат; формировать умение находить декартовы координаты точек числовой окружности и выполнять обратное действие: зная декартовы координаты точки, определять её числовое значение на числовой окружности.
Ход урока
I. Организационный момент.
Организационный момент.
II. Объяснение нового материала.
1. Разместив числовую окружность в декартовой системе координат, подробно разбираем свойства точек числовой окружности, находящихся в различных координатных четвертях.
Для точки М числовой окружности используют запись М (t ), если речь идет о криволинейной координате точки М , или запись М (х ; у ), если речь идет о декартовых координатах точки.
2. Отыскание декартовых координат «хороших» точек числовой окружности. Речь идет о переходе от записи М (t ) к М (х ; у ).
3. Отыскание знаков координат «плохих» точек числовой окружности. Если, например, М (2) = М (х ; у ), то х 0; у 0. (школьники учатся определять знаки тригонометрических функций по четвертям числовой окружности.)
1. № 5.1 (а; б), № 5.2 (а; б), № 5.3 (а; б).
Данная группа заданий направлена на формирование умения отыскивать декартовы координаты «хороших» точек на числовой окружности.
Решение:
№ 5.1 (а).
2. № 5.4 (а; б), № 5.5 (а; б).
Эта группа заданий направлена на формирование умений находить криволинейные координаты точки по её декартовым координатам.
Решение:
№ 5.5 (б).
3. № 5.10 (а; б).
Данное упражнение направлено на формирование умения находить декартовы координаты «плохих» точек.
V. Итоги урока.
Вопросы учащимся:
– Что собой представляет модель – числовая окружность на координатной плоскости?
– Как, зная криволинейные координаты точки на числовой окружности, найти её декартовы координаты и наоборот?
Домашнее задание: № 5.1 (в; г) – 5.5 (в; г), № 5.10 (в; г).
Дата: Урок 2
ТЕМА: Решение задач на модели «числовая окружность на координатной плоскости»
Цели: продолжить формирование умения переходить от криволинейных координат точки на числовой окружности к декартовым координатам; формировать умение отыскивать на числовой окружности точки, координаты которых удовлетворяют заданному уравнению или неравенству.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Назовите криволинейные и декартовы координаты точек на числовой окружности.
2. Сопоставьте дугу на окружности и её аналитическую запись.
III. Объяснение нового материала.
2. Отыскание на числовой окружности точек, координаты которых удовлетворяют заданному уравнению.
Рассматриваем примеры 2 и 3 со с. 41–42 учебника.
Важность этой «игры» очевидна: учащиеся готовятся к решению простейших тригонометрических уравнений вида Для понимания сути дела следует прежде всего научить школьников решать эти уравнения с помощью числовой окружности, не переходя к готовым формулам.
При рассмотрении примера на нахождение точки с абсциссой обращаем внимание учащихся на возможность объединения ддвух серий ответов в одну формулу:
3. Отыскание на числовой окружности точек, координаты которых удовлетворяют заданному неравенству.
Рассматриваем примеры 4–7 со с. 43–44 учебника. Решая подобные задачи, мы готовим учащихся к решению тригонометрических неравенств вида
После рассмотрения примеров учащиеся могут самостоятельно сформулировать алгоритм решения неравенств указанного типа:
1) от аналитической модели переходим к геометрической модели – дуга МР числовой окружности;
2) составляем ядро аналитической записи МР ; для дуги получаем
3) составляем общую запись:
IV. Формирование умений и навыков.
1-я группа. Нахождение точки на числовой окружности с координатой, удовлетворяющей заданному уравнению.
№ 5.6 (а; б) – № 5.9 (а; б).
В процессе работы над этими упражнениями отрабатываем пошаговость выполнения: запись ядра точки, аналитической записи.
2-я группа. Нахождение точек на числовой окружности с координатой, удовлетворяющей заданному неравенству.
№ 5.11 (а; б) – 5.14 (а;б).
Главное умение, которое должны приобрести школьники при выполнении данных упражнений, – это составление ядра аналитической записи дуги.
V. Самостоятельная работа.
Вариант 1
1. Обозначьте на числовой окружности точку, которая соответствует заданному числу, и найдите её декартовы координаты:
2. Найдите на числовой окружности точки с данной абсциссой и запишите, каким числам t они соответствуют.
3. Обозначьте на числовой окружности точки с ординатой, удовлетворяющей неравенству и запишите при помощи двойного неравенства, каким числам t они соответствуют.
Вариант 2
1. Обозначьте на числовой окружности точку, которая соответствует данному числу, и найдите её декартовы координаты:
2. Найдите на числовой окружности точки с данной ординатой у = 0,5 и запишите, каким числам t они соответствуют.
3. Обозначьте на числовой окружности точки с абсциссой, удовлетворяющей неравенству и запишите при помощи двойного неравенства, каким числам t они соответствуют.
VI. Итоги урока.
Вопросы учащимся:
– Как найти на окружности точку, абсцисса которой удовлетворяет заданному уравнению?
– Как найти на окружности точку, ордината которой удовлетворяет заданному уравнению?
– Назовите алгоритм решения неравенств с помощью числовой окружности.
Домашнее задание: № 5.6 (в; г) – № 5.9 (в; г),
№ 5.11 (в; г) – № 5.14 (в; г).
Единичный круг
«Единичный круг» — это круг с радиусом 1.
Будучи настолько простым, это отличный способ узнать и поговорить о длине и углах.
Центр помещен на график в месте пересечения осей x и y, так что мы получаем здесь аккуратное расположение.
Синус, косинус и тангенс
Поскольку радиус равен 1, мы можем напрямую измерить синус, косинус и тангенс.
Что происходит, когда угол θ равен 0 °?
cos 0 ° = 1, sin 0 ° = 0 и tan 0 ° = 0
Что происходит, когда θ составляет 90 °?
cos 90 ° = 0, sin 90 ° = 1 и tan 90 ° не определено
Попробуйте сами!
Попробуй! Перемещайте мышь, чтобы увидеть, как разные углы (в радианах или градусах) влияют на синус, косинус и тангенс
. ./algebra/images/circle-triangle.js
./algebra/images/circle-triangle.js
«Стороны» могут быть положительными или отрицательными в соответствии с правилами декартовых координат.Это также приводит к изменению синуса, косинуса и тангенса между положительными и отрицательными значениями.
Также попробуйте Interactive Unit Circle.
Пифагор
Теорема Пифагора гласит, что для прямоугольного треугольника квадрат длинной стороны равен сумме квадратов двух других сторон:
x 2 + y 2 = 1 2
Но 1 2 равно 1, поэтому:
x 2 + y 2 = 1
уравнение единичной окружности
Кроме того, поскольку x = cos и y = sin, получаем:
(cos (θ)) 2 + (sin (θ)) 2 = 1
полезная «идентичность»
Важные углы: 30
° , 45 ° и 60 ° Вы должны попытаться запомнить sin, cos и tan для углов 30 ° , 45 ° и 60 ° .
Да, да, запоминать вещи — это боль, но это облегчит жизнь, если вы их узнаете не только на экзаменах, но и в других случаях, когда вам нужно сделать быстрые оценки и т. Д.
Это значения, которые вы должны запомнить!
| Уголок | Грех | Cos | Tan = Sin / Cos |
|---|---|---|---|
| 30 ° | 1 2 | √3 2 | 1 √3 знак равно √3 3 |
| 45 ° | √2 2 | √2 2 | 1 |
| 60 ° | √3 2 | 1 2 | √3 |
Как помнить?
Чтобы помочь вам запомнить, sin идет «1,2,3» :
sin (30 ° ) = √ 1 2 = 1 2 (поскольку √1 = 1)
sin (45 ° ) = √ 2 2
sin (60 ° ) = √ 3 2
И cos идет «3,2,1»
cos (30 ° ) = √ 3 2
cos (45 ° ) = √ 2 2
cos (60 ° ) = √ 1 2 = 1 2
Всего 3 числа
На самом деле достаточно знать 3 числа: 1 2 , √2 2 и √3 2
Потому что они работают как для cos , так и для sin :
А как насчет загара?
Ну, tan = sin / cos , поэтому мы можем рассчитать это так:
tan (30 °) = sin (30 °) cos (30 °) = 1/2 √3 / 2 = 1 √3 = √3 3 *
tan (45 °) = sin (45 °) cos (45 °) = √2 / 2 √2 / 2 = 1
tan (60 °) = sin (60 °) cos (60 °) = √3 / 2 1/2 = √3
* Примечание: написание 1 √3 может стоить вам марок (см. Рациональные знаменатели), поэтому вместо этого используйте √3 3
Рациональные знаменатели), поэтому вместо этого используйте √3 3
Быстрый набросок
Еще один способ помочь вам запомнить 30 ° и 60 ° — это сделать быстрый набросок:
| Нарисуйте треугольник со сторонами 2 | ||
Разрезать пополам.Пифагор говорит, что новая сторона — √3 .1 2 + (√3) 2 = 2 2 1 + 3 = 4 | ||
| Затем используйте sohcahtoa для sin, cos или tan |
Пример: sin (30 °)
Синус: soh cahtoa
синус противоположен делению гипотенузы
грех (30 °) = напротив гипотенуза знак равно 1 2
Весь круг
Для всего круга нам нужны значения в каждом квадранте с правильным знаком плюс или минус в соответствии с декартовыми координатами:
Обратите внимание, что cos — первое, а sin — второе, поэтому идет (cos, sin) :
Сохранить как PDF
Пример: Что такое cos (330 °)?
Сделайте такой набросок, и мы увидим, что это «длинное» значение: √3 2
А это тот же единичный круг в радианах .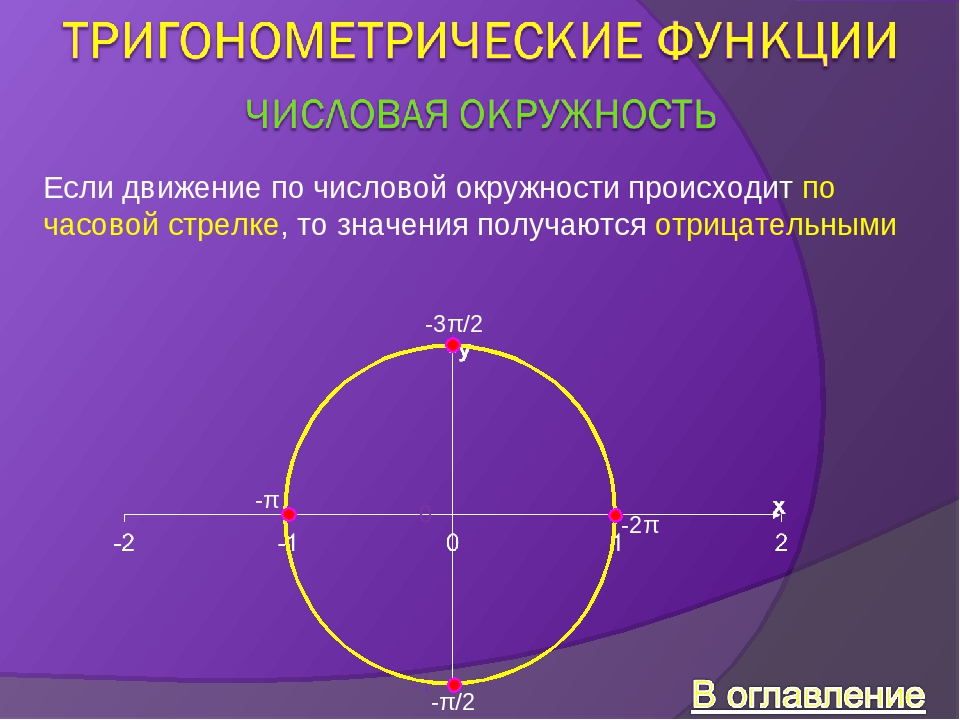
Пример: Что такое грех (7π / 6)?
Подумайте: «7π / 6 = π + π / 6», затем сделайте набросок.
Тогда мы можем видеть, что это отрицательное значение и является «коротким» значением: −½
7708, 7709, 7710, 7711, 8903, 8904, 8906, 8907, 8905, 8908
Сноска: откуда берутся значения?
Мы можем использовать уравнение x 2 + y 2 = 1, чтобы найти длины x и y (которые равны cos и sin при радиусе 1 ):
45 градусов
Для 45 градусов x и y равны, поэтому y = x :
x 2 + x 2 = 1
2x 2 = 1
x 2 = ½
x = y = √ (½)
60 градусов
Возьмите равносторонний треугольник (все стороны равны, а все углы равны 60 °) и разделите его пополам.
Сторона «x» теперь ½ ,
Сторона «y»:
(½) 2 + y 2 = 1
¼ + у 2 = 1
y 2 = 1-¼ = ¾
y = √ (¾)
30 градусов
30 ° — это всего лишь 60 ° с заменой x и y, поэтому x = √ (¾) и y = ½
А:
√1 / 2 = √2 / 4 = √2 √4 = √2 2
Также:
√3 / 4 = √3 √4 = √3 2
И вот результат (такой же, как и раньше):
| Уголок | Грех | Cos | Tan = Sin / Cos |
|---|---|---|---|
| 30 ° | 1 2 | √3 2 | 1 √3 знак равно √3 3 |
| 45 ° | √2 2 | √2 2 | 1 |
| 60 ° | √3 2 | 1 2 | √3 |
Как использовать единичный круг в триггере
Вы, вероятно, имеете интуитивное представление о том, что такое круг: форма баскетбольного кольца, колеса или четверти. Вы, возможно, даже помните из средней школы, что радиус — это любая прямая линия, которая начинается от центра круга и заканчивается по его периметру.
Вы, возможно, даже помните из средней школы, что радиус — это любая прямая линия, которая начинается от центра круга и заканчивается по его периметру.
Единичный круг — это просто круг с радиусом, равным 1. Но часто он сопровождается некоторыми другими особенностями.
Единичная окружность может использоваться для определения отношений прямоугольного треугольника, известных как синус, косинус и тангенс. Эти отношения описывают, как углы и стороны прямоугольного треугольника соотносятся друг с другом.Скажем, например, у нас есть прямоугольный треугольник с углом 30 градусов, а длина самой длинной стороны, или гипотенузы, равна 7. Мы можем использовать наши предопределенные отношения прямоугольного треугольника, чтобы вычислить длины двух оставшихся сторон треугольника. .
Эта ветвь математики, известная как тригонометрия , имеет повседневные практические приложения, такие как строительство, GPS, сантехника, видеоигры, машиностроение, плотник и аэронавигация.
Чтобы запомнить стандартный единичный круг, нам нужно иметь возможность вспомнить три основных компонента:
- Четыре квадранта
- 16 углов
- (x, y) координаты для каждого из 16 углов, где радиус касается круга периметр
В помощь вспомним поездку в Unit Pizza Palace.Выделите несколько минут, чтобы запомнить следующее, пока не сможете повторить его, не глядя:
- 4 кусочка пиццы
- 3 пирога за 6 долларов
- 2 квадратных стола
- 1 , 2, 3
Шаг 1: 4 ломтика пиццы
Представьте себе одну целую пиццу, разрезанную на четыре ровных ломтика. В математике мы бы назвали эти четыре части круга квадрантами .
Мы можем использовать координаты (x, y) для описания любой точки вдоль внешнего края круга.Координата x представляет собой расстояние, пройденное влево или вправо от центра. Координата Y представляет собой пройденное расстояние вверх или вниз. Координата x — это косинус угла, образованного точкой, началом координат и осью x. Координата Y — это синус угла.
Координата x — это косинус угла, образованного точкой, началом координат и осью x. Координата Y — это синус угла.
В единичном круге прямая линия, идущая вправо от центра круга, достигнет края круга в координате (1, 0). Если бы мы вместо этого пошли вверх, влево или вниз, мы коснулись бы периметра в точках (0, 1), (-1, 0) или (0, -1) соответственно.
Все четыре связанных угла (в радианах, а не в градусах) имеют знаменатель 2. (Радиан — это угол, полученный, когда радиус оборачивается вокруг круга . Градус измеряет углы по пройденному расстоянию. Окружность составляет 360 градусов или 2π радиан).
Числители начинаются с 0, начиная с координаты (1,0), и ведут счет против часовой стрелки на 1π. Этот процесс даст 0π / 2, 1π / 2, 2π / 2 и 3π / 2. Упростите эти дроби, чтобы получить 0, π / 2, π и 3π / 2. Quad
Шаг 2: 3 пирога за 6 долларов
Начните с «3 пирога».»Взгляните на ось y. Все радианные углы справа и слева от оси y имеют знаменатель 3. У каждого оставшегося угла есть числитель, который включает математическое значение пи, записанное как π.
У каждого оставшегося угла есть числитель, который включает математическое значение пи, записанное как π.
«3 пирога на 6» используется для вызова оставшихся 12 углов в стандартном единичном круге с тремя углами в каждом квадранте. Каждый из этих углов записывается в виде дроби.
«За 6 долларов» напоминает нам, что в В каждом квадранте оставшиеся знаменатели равны 4, а затем 6.
Самая сложная часть этого шага — заполнение числителя для каждой дроби.
В квадранте 2 (верхняя левая четверть круга) поставьте 2, затем 3, затем 5 перед π.
Ваш первый угол в квадранте 2 будет 2π / 3. Если сложить 2 в числителе и 3 в знаменателе, получится 5. Посмотрите на угол в квадранте 4 (нижняя правая четверть круга). Поместите эту 5 в числитель перед π. Повторите этот процесс для двух других углов в квадрантах 2 и 4.
Мы повторим тот же процесс для квадрантов 1 (вверху справа) и 3 (внизу слева). Помните, что точно так же, как x совпадает с 1x, π совпадает с 1π. Итак, мы добавляем 1 ко всем знаменателям в квадранте 1.
Итак, мы добавляем 1 ко всем знаменателям в квадранте 1.
Процесс перечисления углов в градусах (а не радианах) описан в конце этой статьи.
Шаг 3: 2 квадратных таблицы
Цифра 2 в «2 квадратных таблицах» напоминает нам, что все оставшиеся 12 пар координат имеют знаменатель 2.
«Квадрат» напоминает нам, что числитель каждая координата включает квадратный корень.Мы только начинаем с квадранта 1, чтобы упростить ситуацию. (Подсказка: помните, что квадратный корень из 1 равен 1, поэтому эти дроби можно упростить до 1/2.)
Шаг 4: 1, 2, 3
«1, 2, 3» показывает последовательность чисел под каждым квадратным корнем. Для координат x квадранта 1 мы считаем от 1 до 3, начиная с верхней координаты и идя вниз.
Координаты Y имеют те же числители, но отсчитывают от 1 до 3 в обратном направлении, снизу вверх.
Квадрант 2 имеет те же координаты, что и квадрант 1, но координаты x отрицательны.
Квадрант 3 переключает координаты x и y с квадранта 1. Все координаты x и y также отрицательны.
Все координаты x и y также отрицательны.
Как и квадрант 3, квадрант 4 также переключает координаты x и y из квадранта 1. Но только координаты y отрицательны.
Углы в градусах
Вы можете ссылаться на углы в градусах, а не в радианах. Для этого начните с 0 градусов по координате (1,0).Оттуда мы прибавим 30, 15, 15, а затем 30. В квадранте 1 мы прибавляем 30 к 0, чтобы получить 30, прибавляем 15 к 30, чтобы получить 45, прибавляем 15 к 45, чтобы получить 60, и прибавляем 30 к 60, чтобы получить 90.
Затем мы повторяем процесс для оставшихся квадрантов, добавляя 30, 15, 15 и 30, пока не дойдем до конца круга. Таким образом, квадрант 4 будет иметь углы от 270 до 330 градусов (см. Рисунок 10).
Практическое применение
Ранее в этой статье мы упоминали, что единичная окружность может использоваться для нахождения двух неизвестных сторон прямоугольного треугольника с углом 30 градусов, а самая длинная сторона, или гипотенуза, равна длине 7.Давайте попробуем.
Обратите внимание на 30 ° на единичной окружности. Используйте эту линию и ось x, чтобы создать треугольник следующим образом.
В единичном круге любая линия, которая начинается в центре круга и заканчивается по его периметру, будет иметь длину 1. Таким образом, самая длинная сторона этого треугольника будет иметь длину 1. Самая длинная сторона правой стороны. треугольник также известен как «гипотенуза». Точка, где гипотенуза касается периметра окружности, находится в √3 / 2, 1/2.
Итак, мы знаем, что основание треугольника (по оси x) имеет длину √3 / 2, а высота треугольника равна 1/2.
Еще один способ подумать об этом: основание в √3 / 2 раза больше длины гипотенузы, а высота в 1/2 раза больше длины гипотенузы.
Итак, если длина гипотенузы равна 7, основание нашего треугольника будет 7 x √3 / 2 = 7√3 / 2. Высота треугольника будет равна 7 x 1/2 = 7/2.
Что такое единичный круг | StudyPug
Что такое Unit Circle?
В мире исчисления, предварительного исчисления и тригонометрии вы часто встретите ссылки и проблемы, связанные с «единичной окружностью». «Но, как ни странно, нас редко когда-либо учат, что это такое!
«Но, как ни странно, нас редко когда-либо учат, что это такое!
Проще говоря, единичная окружность — это математический инструмент, упрощающий использование углов и тригонометрических функций. Понимая и запоминая «единичный круг», мы можем легко справляться с трудностями, которые в противном случае требовали бы вычислений, и значительно облегчили нашу жизнь.
Единичный круг, в его простейшей форме, на самом деле именно то, что он звучит: круг на декартовой плоскости с радиусом ровно 1unit1 unit1unit.Как этот пустой кружок ниже:
Пустая единичная окружность с радиусом 1Затем, заполнив этот единичный круг обычно используемыми углами и оценив эти углы с помощью синуса и косинуса, мы получим нечто немного более сложное:
Синус и косинус вычисленные углы единичной окружностиБоишься? Не надо. Этот образ может показаться устрашающим, но когда мы разбиваем его на более последовательные части, начинают появляться закономерности.
Единичный круг со всеми 6 функциями триггера Таблица:
Вместо того, чтобы ссылаться на это устрашающее изображение выше, давайте упростим единичный круг с помощью sincostanseccsc \ sin \ cos \ tan \ sec \ cscsincostanseccsc и cot \ cotcot на красивой маленькой диаграмме:
Схема упрощенной единичной окружности с sin cos tan sec csc и cot В приведенной выше таблице единичного круга приведены все значения единичного круга для всех 4 квадрантов единичного круга. Как видите, здесь указаны градусы единичной окружности и радианы единичной окружности. Вы должны знать и то, и другое, но, скорее всего, вы будете решать проблемы в радианах. Теперь возникает следующий естественный вопрос: как я могу запомнить единичный круг?
Как видите, здесь указаны градусы единичной окружности и радианы единичной окружности. Вы должны знать и то, и другое, но, скорее всего, вы будете решать проблемы в радианах. Теперь возникает следующий естественный вопрос: как я могу запомнить единичный круг?
Как запомнить единичный круг:
Запомнить единичную окружность на самом деле намного проще, чем вы думаете, благодаря нескольким маленьким уловкам:
Уловка 1:
Из-за следующих 4 уравнений нам нужно запомнить только значения единичной окружности для синуса и косинуса.
tanθ = sinθcosθ, cotθ = cosθsinθ, secθ = 1cosθ, cscθ = 1sinθ \ tan \ theta = \ frac {\ sin \ theta} {\ cos \ theta}, \ cot \ theta = \ frac {\ cos \ theta} {\ sin \ theta}, \ sec \ theta = \ frac {1} {\ cos \ theta}, \ csc \ theta = \ frac { 1} {\ sin \ theta} tanθ = cosθsinθ, cotθ = sinθcosθ, secθ = cosθ1, cscθ = sinθ1С этими 4 уравнениями нам даже не нужно запоминать единичную окружность с касательной!
Уловка 2:
Зная, в каких квадрантах x и y положительны, нам нужно только запомнить значения единичного круга для синуса и косинуса в первом квадранте, поскольку значения меняют только свой знак. Чтобы использовать этот трюк, нам нужно сначала понять несколько вещей:
Чтобы использовать этот трюк, нам нужно сначала понять несколько вещей:
i) Первое, что нужно отметить, это то, какие значения синуса и косинуса дают нам на единичной окружности. Благодаря SOHCAHTOA мы знаем это:
sinθ \ sin \ thetasinθ дает нам координату Y, а cosθ \ cos \ thetacosθ дает нам координату Xii) Теперь посмотрим на каждый квадрант:
Квадрант 1 : X положительный, Y положительный
Квадрант 2 : X отрицательный, Y положительный
Квадрант 3 : X отрицательный, Y отрицательный
Квадрант 4 : X положительный, Y отрицательный
iii) Далее, посмотрим, где находится каждый квадрант:
Квадрант 1 : 0 — π2 \ frac {\ pi} {2} 2π
Квадрант 2 : π2 − π \ frac {\ pi} {2} — \ pi2π −π
Квадрант 3 : π \ piπ — 3π2 \ frac {3 \ pi} {2} 23π
Квадрант 4 : 3π2−2π \ frac {3 \ pi} {2} — 2 \ pi23π −2π
iv) Значение синуса и косинуса всегда будет «одинаковым» для одного и того же знаменателя:
sinπ3 = 32andsin4π3 = −32 \ sin \ frac {\ pi} {3} = \ frac {\ sqrt {3}} {2} и \ sin \ frac {4 \ pi} {3} = — \ frac {\ sqrt {3}} {2} sin3π = 23 и sin34π = −23С учетом этих приемов процесс запоминания единичного круга становится намного проще!
Как использовать единичный круг:
Лучший способ освоить единичный круг — это попрактиковаться в единичном круге.
Пример 1:
Найдите sin4π3 \ sin \ frac {4 \ pi} {3} sin34π
Шаг 1. Определите квадрант
Поскольку мы имеем дело с синусом, который мы со временем запомним, все, что нам нужно сделать, это выяснить, в каком квадранте мы находимся, чтобы мы знали, будет ли наш ответ положительным или отрицательным.
Поскольку:
3π2> 4π3> π \ frac {3 \ pi} {2}> \ frac {4 \ pi} {3}> \ pi23π> 34π> πТаким образом, мы находимся в третьем квадранте.Таким образом, поскольку синус дает нам координату y, и мы находимся в третьем квадранте, наш ответ будет отрицательным!
Шаг 2: Решить
Следующий шаг прост — используя то, что мы запомнили, мы можем легко решить эту задачу.
sin4π3 \ sin \ frac {4 \ pi} {3} sin34π = -32 \ frac {\ sqrt {3}} {2} 23Пример 2:
Найдите tanπ \ tan \ pitanπ
Шаг 1. Определите квадрант
Поскольку мы имеем дело с единичным кругом с загаром, нам нужно будет использовать значения, которые мы запомнили из синуса и косинуса, а затем решить. Однако сначала нам нужно выяснить, в каком квадранте мы находимся, чтобы знать, будут ли наши ответы для синуса и косинуса положительными или отрицательными.
Однако сначала нам нужно выяснить, в каком квадранте мы находимся, чтобы знать, будут ли наши ответы для синуса и косинуса положительными или отрицательными.
Поскольку:
3π2> π> π2 \ frac {3 \ pi} {2}> \ pi> \ frac {\ pi} {2} 23π> π> 2πТаким образом, мы находимся между вторым и третьим квадрантами по оси абсцисс. Поскольку синус дает нам координату y, а мы находимся на оси x, наш ответ фактически будет равен нулю! Кроме того, поскольку косинус дает нам координату x, и мы находимся между вторым и третьим квадрантами (где косинус для обоих отрицательный), наш ответ будет отрицательным!
Шаг 2: Решить
Следующий шаг прост — используя то, что мы запомнили, мы можем легко решить эту задачу.Но в этом случае нам понадобится один дополнительный шаг. Мы должны использовать уравнение для касательной, обсуждавшееся ранее в уловке 1 , предполагая, что мы не запомнили значения касательной на единичной окружности.
tanθ = sinθcosθ = 0-1 = 0 \ tan \ theta = \ frac {\ sin \ theta} {\ cos \ theta} = \ frac {0} {- 1} = 0tanθ = cosθsinθ = −10 = 0Пример 3:
Найдите cscπ6 \ csc \ frac {\ pi} {6} csc6π
Шаг 1. Определите квадрант
Определите квадрант
Поскольку мы имеем дело с косекансом, важно понимать, что нам нужно будет использовать значения синуса для решения уравнения для косеканса, описанного ранее в уловке 1 .Однако сначала нам нужно выяснить, в каком квадранте мы находимся, чтобы знать, будет ли наш ответ для синуса положительным или отрицательным.
Поскольку:
π2> π6> 0 \ frac {\ pi} {2}> \ frac {\ pi} {6}> 02π> 6π> 0Таким образом, мы находимся в первом квадранте. Таким образом, поскольку синус дает нам координату y, и мы находимся в первом квадранте, наш ответ будет положительным!
Шаг 2: Решить
Следующий шаг прост — используя то, что мы запомнили, мы можем легко решить эту задачу.Но и в этом случае нам снова нужен один дополнительный шаг. Мы должны использовать уравнение для косеканса, обсуждавшееся ранее в уловке 1 , предполагая, что мы не запомнили значения косеканса на единичной окружности.
cscπ6 = 1sinπ6 = 10,5 = 2 \ csc \ frac {\ pi} {6} = \ frac {1} {\ sin \ frac {\ pi} {6}} = \ frac {1} {0,5} = 2csc6π = sin6π 1 = 0,51 = 2 Теперь, когда мы немного попрактиковались, займемся еще немного самостоятельно! В кратчайшие сроки вы будете готовы к любой предстоящей викторине с единичным кругом.
3 совета эксперта по использованию единичной окружности
Если вы изучаете тригонометрическую систему или математику — или готовитесь к этому — вам нужно будет познакомиться с единичным кругом. Единичная окружность — это , важный инструмент, используемый для нахождения синуса, косинуса и тангенса угла. Но как это работает? И какую информацию нужно знать, чтобы ею пользоваться?
В этой статье мы объясним, что такое единичный круг и почему вы должны его знать. Мы также даем вам три совета, которые помогут вам запомнить, как использовать единичный круг.
Изображение функции: Gustavb / Wikimedia
Единичная окружность: базовое введение
Единичная окружность — это окружность с радиусом 1. Это означает, что для любой прямой линии, проведенной от центральной точки круга до любой точки вдоль края круга, длина этой линии всегда будет равна 1. (Это также означает, что диаметр круга будет равен 2, так как диаметр равен удвоенной длине радиуса. )
)
Как правило, центральная точка единичной окружности находится там, где пересекаются оси x и y, или в координатах (0, 0):
Единичная окружность, или триггерная окружность, как ее еще называют, полезно знать, потому что позволяет нам легко вычислить косинус, синус и тангенс любого угла от 0 ° до 360 ° (или от 0 до 2π радиан).
Как вы можете видеть на приведенной выше диаграмме, вычерчивая радиус под любым углом (отмечен ∝ на изображении), вы создадите прямоугольный треугольник. На этом треугольнике косинус — это горизонтальная линия, а синус — это вертикальная линия. Другими словами, косинус = x-координата, а синус = y-координата. (Самая длинная линия треугольника, или гипотенуза, является радиусом и поэтому равна 1.)
Почему все это так важно? Помните, что вы можете найти длины сторон треугольника, используя теорему Пифагора или $ a ^ 2 + b ^ 2 = c ^ 2 $ (где a и b — длины сторон треугольника, а c — длина гипотенузы). 2θ = 1 $$
2θ = 1 $$
Имейте в виду, что эти значения могут быть отрицательными в зависимости от сформированного угла и в какой квадрант попадают координаты x и y (более подробно я объясню это позже).
Вот обзор всех основных углов в градусах и радианах на единичной окружности:
Единичный круг — градусы
Единичный круг — радианы
А что, если треугольник не образовался? Давайте посмотрим на , что происходит, когда угол равен 0 °, образуя горизонтальную прямую линию вдоль оси x:
В этой строке координата x равна 1, а координата y равна 0.Мы знаем, что косинус равен координате x, а синус равен координате y, , поэтому мы можем записать это:
Что если угол равен 90 ° и образует идеально вертикальную линию вдоль оси y?
Здесь мы видим, что координата x равна 0, а координата y равна 1.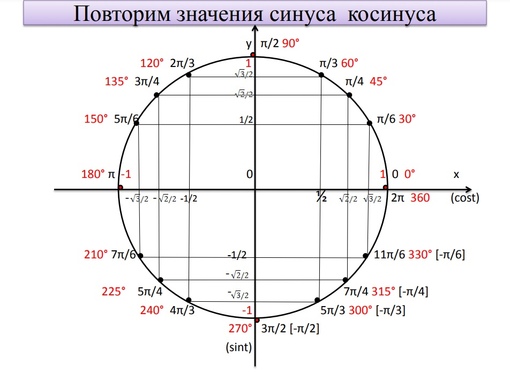 Это дает нам следующие значения для синуса и косинуса:
Это дает нам следующие значения для синуса и косинуса:
- $ \ cos90 ° = 0 $
- $ \ sin90 ° = 1 $
Этот слоган определенно подходит, если вы не любитель математики.
Почему вы должны знать единичную окружность
Как указано выше, единичная окружность полезна, потому что позволяет нам легко найти синус, косинус или тангенс любого градуса или радиана. Особенно полезно знать круговую диаграмму единиц, если вам нужно решить определенные триггерные значения для домашнего задания по математике или если вы готовитесь к изучению математического анализа.
Но как именно знание единичного круга может вам помочь? Допустим, вам задали следующую задачу на тесте по математике, и не разрешено использовать калькулятор для ее решения:
$$ \ sin30 ° $$
С чего начать? Давайте еще раз взглянем на диаграмму единичного круга — на этот раз со всеми основными углами (как в градусах, так и в радианах) и их соответствующими координатами:
Джим. belk / Викимедиа
belk / Викимедиа
Не расстраивайтесь! Помните, все, что вам нужно, это $ \ sin30 ° $. Глядя на этот график, мы видим, что , координата y равна $ 1/2 $ при 30 °. А поскольку координата y равна синусу, наш ответ будет следующим:
$$ \ sin30 ° = 1/2 $$
Но что, если вы столкнетесь с проблемой, в которой вместо градусов используются радианы? Процесс ее решения остался прежним. Скажем, например, у вас возникла проблема, которая выглядит так:
$$ \ cos {{3π} / 4} $$
Опять же, используя диаграмму выше, мы можем видеть, что координата x (или косинус) для $ {3π} / 4 $ (который равен 135 °) составляет $ — {√2} / 2 $.Вот как бы тогда выглядел наш ответ на эту проблему:
$$ \ cos ({3π} / 4) = — {√2} / 2 $$
Все это довольно просто, если у вас есть приведенная выше круговая диаграмма единиц для использования в качестве справочной информации. Но в большинстве случаев (если не всегда) это не так, и вы должны будете отвечать на эти типы математических вопросов, используя только свой мозг.
Так как же можно запомнить единичный круг? Читайте наши главные советы!
Как запомнить единичный круг: 3 основных совета
В этом разделе мы даем вам несколько основных советов по запоминанию триггерного круга, чтобы вы могли с легкостью использовать его для решения любой математической задачи, которая в нем требует.
Я бы не рекомендовал практиковать единичный круг с клейкими наклейками, но, эй, это только начало.
# 1: Запоминание общих углов и координат
Чтобы эффективно использовать единичный круг, вам нужно запомнить наиболее распространенные углы (как в градусах, так и в радианах), а также их соответствующие координаты x и y.
Приведенная выше диаграмма представляет собой полезную диаграмму единичного круга, на которую стоит обратить внимание, поскольку она включает все основные углы в градусах и радианах в дополнение к их соответствующим координатным точкам по осям x и y.
Вот диаграмма, содержащая ту же информацию в виде таблицы:
Угол (градусы) | Угол (радианы) | Координаты точки на окружности |
0 ° / 360 ° | 0 / 2π | (1, 0) |
30 ° | $ π / 6 $ | $ ({√3} / 2, 1/2) $ |
45 ° | $ π / 4 $ | долл. США ({√2} / 2, {√2} / 2) долл. США |
60 ° | $ π / 3 $ | долл. США (1/2, {√3} / 2) долл. США |
90 ° | $ π / 2 $ | (0, 1) |
120 ° | $ {2π} / 3 $ | $ (- 1/2, {√3} / 2) $ |
135 ° | $ {3π} / 4 $ | долл. |
150 ° | $ {5π} / 6 $ | $ (- {√3} / 2, 1/2) $ |
180 ° | π | (-1, 0) |
210 ° | $ {7} / 6 $ | $ (- {√3} / 2, -1/2) $ |
225 ° | $ {5π} / 4 $ | $ (- {√2} / 2, — {√2} / 2) $ |
240 ° | $ {4π} / 3 $ | $ (- 1/2, — {√3} / 2) $ |
270 ° | $ {3π} / 2 $ | (0, -1) |
300 ° | $ {5π} / 3 $ | долл. США (1/2, — {√3} / 2) долл. США |
315 ° | $ {7π} / 4 $ | долл. США ({√2} / 2, — {√2} / 2) долл. США США |
330 ° | $ {11π} / 6 $ | $ ({√3} / 2, -1/2) $ |
Теперь, хотя вы можете попытаться запомнить все эти координаты и углы, это — много вещей, которые нужно запомнить.
К счастью, есть прием, который поможет вам запомнить самые важные части единичного круга.
Посмотрите на координаты выше, и вы заметите четкую закономерность: все точки (за исключением точек под 0 °, 90 °, 270 ° и 360 °) чередуются между тремя значениями (положительными или отрицательными):
- 1/2 доллара
- $ {√2} / 2 $
- $ {√3} / 2 $
Каждому значению соответствует короткая, средняя или длинная линия для косинуса и синуса:
Вот что означают эти длины:
- Короткая горизонтальная или вертикальная линия = 1/2 доллара США
- Средняя горизонтальная или вертикальная линия = $ {√2} / 2 $
- Длинная горизонтальная или вертикальная линия = $ {√3} / 2 $
Например, если вы пытаетесь решить $ \ cos {π / 3} $, вы должны сразу знать, что этот угол (равный 60 °) указывает на короткую горизонтальную линию на единичной окружности. Следовательно, его соответствующая координата x должна равняться $ 1/2 $ (положительное значение, поскольку $ π / 3 $ создает точку в первом квадранте системы координат).
Следовательно, его соответствующая координата x должна равняться $ 1/2 $ (положительное значение, поскольку $ π / 3 $ создает точку в первом квадранте системы координат).
Наконец, хотя полезно запомнить все углы в таблице выше, обратите внимание, что , безусловно, самые важные углы, которые следует запомнить, следующие:
- 30 ° / $ π / 6 $
- 45 ° / $ π / 4 $
- 60 ° / $ π / 3 $
Относитесь к негативам и позитивам, как к кабелям, которые потенциально могут убить вас, если подключите их неправильно.
# 2: Узнай, что отрицательно, а что положительно
Очень важно уметь различать положительные и отрицательные координаты x и y, чтобы вы могли найти правильное значение для триггерной проблемы. Напоминаем, что w , будет ли координата на единичной окружности положительной или отрицательной, зависит от , в какой квадрант (I, II, III или IV) попадает точка:
Вот диаграмма, показывающая, будет ли координата положительной или отрицательной в зависимости от квадранта, в котором находится конкретный угол (в градусах или радианах):
Квадрант | Координата X (косинус) | Координата Y (синус) |
Я | + | + |
II | – | + |
III | – | – |
IV | + | – |
Допустим, вам задали следующую задачу на тесте по математике:
$$ \ cos210 ° $$
Еще до того, как вы попытаетесь ее решить, вы должны быть в состоянии распознать, что ответом будет отрицательное число , поскольку угол 210 ° попадает в квадрант III (где x-координаты всегда отрицательны ).
Теперь, используя уловку, которую мы изучили в совете 1, вы можете вычислить, что угол 210 ° создает длинной горизонтальной линии. Следовательно, наш ответ таков:
$$ \ cos210 ° = — {√3} / 2 $$
# 3: Умейте находить касательную
Наконец, важно знать, как использовать всю эту информацию о триггерной окружности, синусе и косинусе, чтобы иметь возможность найти тангенс угла.
В триггере, чтобы найти тангенс угла θ (в градусах или радианах), вы просто делите синус на косинус:
$$ \ tanθ = {\ sinθ} / {\ cosθ} $$
Например, вы пытаетесь решить эту проблему:
$$ \ tan300 ° $$
Первый шаг — составить уравнение в терминах синуса и косинуса:
$$ \ tan300 ° = {\ sin300 °} / {\ cos300 °} $$
Теперь, чтобы найти касательную, нам нужно найти синус и косинус 300 °.Вы должны быстро распознать, что угол 300 ° попадает в четвертый квадрант, а это означает, что косинус или координата x будет положительным, а синус или координата y — отрицательным.
Вы также должны сразу знать, что угол 300 ° создает короткую горизонтальную линию и длинную вертикальную линию. Следовательно, косинус (горизонтальная линия) будет равен $ 1/2 $, а синус (вертикальная линия) будет равен $ — {√3} / 2 $ (отрицательное значение y, поскольку эта точка находится в квадранте IV. ).
Теперь, чтобы найти касательную, все, что вам нужно сделать, это подключить и решить:
$$ \ tan300 ° = {- {√3} / 2} / {1/2} $$
$$ \ tan300 ° = -√3 $$
Пришло время мурлыкать математические навыки!
Набор практических вопросов «Единичный круг»
Теперь, когда вы знаете, как выглядит единичный круг и как его использовать, давайте проверим, что вы узнали, с помощью нескольких практических задач.
вопросов
- $ \ sin45 ° $
- $ \ cos240 ° $
- $ \ cos {5π} / 3 $
- $ \ tan {2π} / 3 $
ответов
- $ {√2} / 2 $
- $ -1 / 2 $
- $ 1/2
- $ -√3 $
Ответ объяснения
# 1: $ \ sin45 ° $
При этой проблеме есть два фрагмента информации, которые вы должны сразу определить:
- Ответ будет положительным, , поскольку угол 45 ° находится в квадранте I, а синус угла равен координате y
- Угол 45 ° образует вертикальную линию средней длины (для синуса)
Поскольку 45 ° означает положительную линию средней длины, правильный ответ: $ {√2} / 2 $.
Если вы не знаете, как это понять, нарисуйте диаграмму, которая поможет вам определить, будет ли длина линии короткой, средней или длинной.
# 2: $ \ cos240 ° $
Как и проблема №1 выше, есть два элемента информации, которые вы должны быстро понять, решая эту проблему:
- Ответ будет отрицательным, , поскольку угол 240 ° находится в квадранте III, а косинус угла равен координате x
- Угол 240 ° образует короткую горизонтальную линию (для косинуса)
Поскольку 240 ° обозначает короткую отрицательную линию, правильный ответ: $ -1 / 2 $.
# 3: $ \ cos {5π} / 3 $
В отличие от задач, описанных выше, в этой задаче вместо градусов используется радиана, . Хотя это может сделать проблему более сложной для решения, на самом деле здесь используются те же основные шаги, что и для двух других проблем.
Во-первых, вы должны понять, что угол $ {5π} / 3 $ находится в квадранте IV, поэтому координата x или косинус будет положительным числом. Вы также должны уметь сказать, что $ {5π} / 3 $ создает короткую горизонтальную линию.
Вы также должны уметь сказать, что $ {5π} / 3 $ создает короткую горизонтальную линию.
Это дает вам достаточно информации, чтобы определить, что ответ составляет $ 1/2 $.
# 4: $ \ tan {2π} / 3 $
Эта задача касается тангенса, а не синуса или косинуса, а это значит, что с нашей стороны потребуется немного больше математических вычислений. Прежде всего, вспомните основную формулу для нахождения тангенса:
$$ \ tan θ = {\ sin θ} / {\ cos θ} $$
Теперь давайте возьмем полученную степень — $ {2π} / 3 $ — и подставим ее в это уравнение:
$$ \ tan {2π} / 3 = {\ sin {2π} / 3} / {\ cos {2π} / 3} $$
Теперь вы должны быть в состоянии решить для синуса и косинуса отдельно, используя то, что вы запомнили о единичной окружности.Поскольку угол $ {2π} / 3 $ находится в квадранте II, координата x (или косинус) будет отрицательной, а координата y (или синусом) будет положительной.
Затем вы сможете определить на основе одного только угла, что горизонтальная линия — это короткая линия, , а вертикальная линия — это длинная линия. Это означает, что косинус равен $ -1 / 2 $, а синус равен $ {√3} / 2 $.
Теперь, когда мы вычислили эти значения, все, что нам нужно сделать, это вставить их в наше исходное уравнение и найти тангенс:
$$ \ tan {2π} / 3 = {{√3} / 2} / {- 1/2} $$
$$ \ tan {2π} / 3 = -√3 $$
Что дальше?
Если вы в ближайшее время будете сдавать SAT или ACT, вам нужно будет знать некоторые триггеры, чтобы вы могли преуспеть в разделе математики. Взгляните на наши экспертные руководства по тестированию SAT и ACT, чтобы вы могли точно узнать, что вам нужно знать в день теста!
Помимо запоминания единичного круга, неплохо научиться вставлять числа и ответы. Прочтите наши руководства, чтобы узнать все об этих двух полезных стратегиях, которые вы можете использовать в любом тесте по математике, включая SAT и ACT!
Решение окружностей, радианов и длин дуги
Цели
Круги и тригонометрия
Обратите внимание, что соотношение двух сторон в прямоугольном треугольнике меняется при изменении острых углов: Для простоты зафиксируем гипотенузу треугольника на заданной длине: пока мы назовем ее r .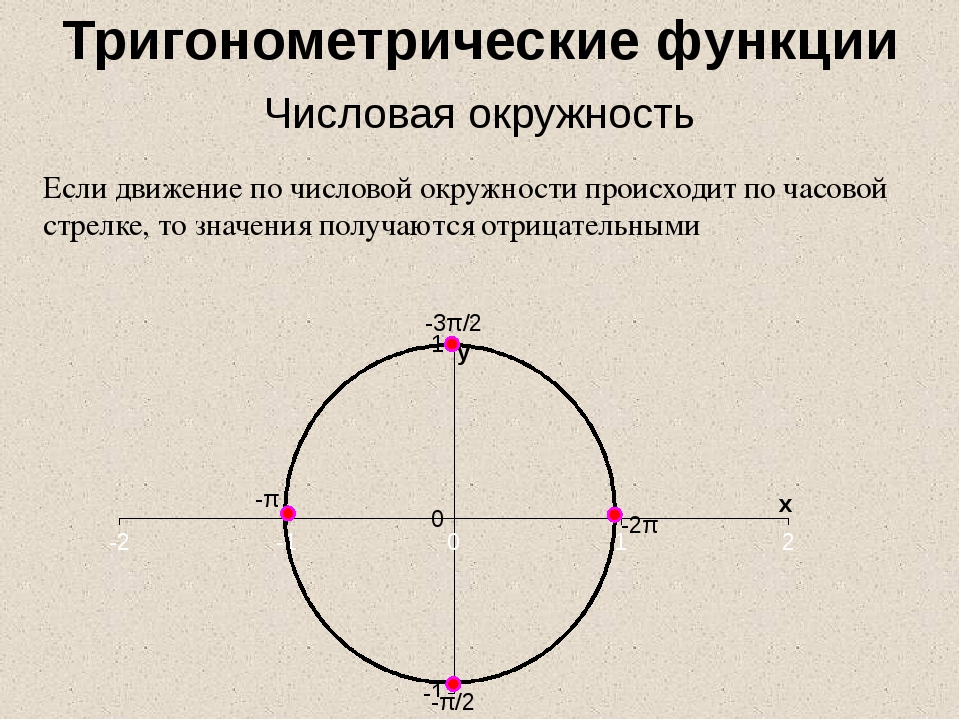 Назовем один из острых углов θ (другой острый угол 90 ° — θ .)
Назовем один из острых углов θ (другой острый угол 90 ° — θ .)
При изменении угла θ, противоположная и соседняя стороны треугольника также изменяются.
Здесь вы можете заметить, что, когда мы «вращаем» гипотенузу длиной r, , мы получаем окружность. Окружность имеет радиус r, , а его центральная точка — вершина, соответствующая углу θ.
Если мы наложим на эту окружность набор осей координат с началом в центре, мы увидим, что смежная сторона прямоугольного треугольника — это расстояние вдоль оси x , а противоположная сторона — расстояние, параллельное оси y — ось. Кроме того, вершина треугольника на окружности должна иметь координаты ( x 1 , y 1 ), где x 1 — длина соседней стороны, а y 1 длина противоположной стороны.
По теореме Пифагора мы знаем следующее соотношение между r, x 1 и y 1 .
Если мы «нормализуем» гипотенузу до длины 1 (то есть установим r равным 1), то мы назовем получившуюся окружность единичной окружностью . В этом случае окружность пересекает оси на y, = ± 1 и x = ± 1.
Итак, что все это значит для нас? Почему нам должно быть до этого дело? Во-первых, обратите внимание, что мы объединили наши концепции координатных графов, кругов и прямоугольных треугольников — они взаимосвязаны. Таким образом, логически мы ожидаем, что тригонометрия сыграет роль в нашем понимании кругов, а также прямоугольных треугольников. Но прежде чем мы углубимся в эту взаимосвязь, мы должны сначала определить некоторые свойства угла θ в этом контексте.
Угловые измерения
До сих пор мы полагались исключительно на градусы как на единицу измерения угла.Еще одна единица измерения, с которой вы должны быть знакомы, — это радиан. Во-первых, обратите внимание, что длина окружности равна 2 πr, , где r — радиус. Если мы отделим радиус от окружности, у нас останется просто 2 π: это в некотором смысле, насколько «далеко» круг проходит вокруг своего центра, независимо от радиуса. Другими словами, 2 π — это угол, заметаемый на радиус окружности.
Во-первых, обратите внимание, что длина окружности равна 2 πr, , где r — радиус. Если мы отделим радиус от окружности, у нас останется просто 2 π: это в некотором смысле, насколько «далеко» круг проходит вокруг своего центра, независимо от радиуса. Другими словами, 2 π — это угол, заметаемый на радиус окружности.
Как вы, наверное, знаете, 2 π также эквивалентно 360 °.Единицей измерения угла в данном случае является радиан. Один радиан определяется как угол, образованный таким образом, что часть круга (или длина дуги ), охватываемая этим углом, равна радиусу круга.
Другой способ взглянуть на это: если мы возьмем отрезок длиной r (радиус) и сформируем его по окружности, то получится угол, образованный радиусами, соединяющими центр окружности с концами дуги. иметь меру 1 радиан.Оказывается, один радиан равен примерно 57,3 °.
Обычно угол θ отсчитывается от оси x- против часовой стрелки. Если используется направление по часовой стрелке, углу просто присваивается отрицательное значение. Так, например, π радиан (180 °) и –π радиан (–180 °) соответствуют одной и той же точке на окружности.
Для наших целей мы в первую очередь будем иметь дело с углами между –2 π и 2 π, включительно (то есть –2 π ≤ θ ≤ 2 π ).Определены углы, большие по величине, чем 2 π , но они перекрываются с меньшими углами, поэтому мы не будем их подробно рассматривать.
Практическая задача: Преобразуйте каждую из следующих угловых мер в радианы. Обязательно используйте точные выражения для своих ответов.
а. 60 ° б. 270 ° с. -90 ° д. 120 °
Решение: Во-первых, обратите внимание, что 360 ° равно 2 π радиан. Мы можем использовать это соотношение для преобразования градусов в радианы. Ниже приведен расчет для части а; остальные части следуют тому же шаблону. Обратите внимание, что отрицательный знак (часть c) переводится напрямую из градусов в радианы.
Мы можем использовать это соотношение для преобразования градусов в радианы. Ниже приведен расчет для части а; остальные части следуют тому же шаблону. Обратите внимание, что отрицательный знак (часть c) переводится напрямую из градусов в радианы.
а. г. 3 Пи / 2 радиана c. -Pi / 2 радиана г.
Практическая задача: Преобразование каждой из следующих угловых мер из радианов в градусы.
а. г. г.
Решение: Здесь просто используйте тот же процесс, что и в предыдущей практической задаче, но используйте обратное соотношение радианов и градусов. Опять же, ниже показан только расчет для части a; остальные похожи.
а.-22,5 ° б. 360 ° с. 36 °
Приложение к тригонометрическим функциям
Теперь мы наконец можем понять, какое отношение окружности имеют к тригонометрии. Давайте снова посмотрим на наш единичный круг.
Давайте снова посмотрим на наш единичный круг.
Каждая точка P на единичной окружности, обозначенная координатами ( x 1 , y 1 ), также может быть выражена через угол θ .Обратите внимание на следующее, где мы применяем то, что мы узнали о триггере прямоугольного треугольника:
Другими словами, точка P имеет координаты (cos θ, sin θ ), где θ — это угол, образованный между осью x- и радиусом к P. Мы также определили две функции:
sin θ = расстояние точки P от оси x
cos θ = расстояние точки P от оси y
Тангенс угла, tan θ, — это просто отношение этих расстояний (в частности, ). При изменении угла θ эти расстояния изменяются; однако мы можем изобразить их графически, чтобы увидеть, как они себя ведут. Ниже представлены функции синуса, косинуса и тангенса, построенные для области θ [-2 π , 2 π ]. Обратите внимание, что для вычисления триггерных функций с использованием радианов вместо градусов, вы должны убедиться, что ваш калькулятор находится в режиме радиан, а не в градусном режиме.
При изменении угла θ эти расстояния изменяются; однако мы можем изобразить их графически, чтобы увидеть, как они себя ведут. Ниже представлены функции синуса, косинуса и тангенса, построенные для области θ [-2 π , 2 π ]. Обратите внимание, что для вычисления триггерных функций с использованием радианов вместо градусов, вы должны убедиться, что ваш калькулятор находится в режиме радиан, а не в градусном режиме.
Практическая задача: Шина имеет радиус (внешний радиус) 10 дюймов.На самом верху шины наносится небольшая отметка, а затем шина слегка накатывается вперед, так что отметка поворачивается на угол пи / 4 радиан. Насколько высоко над землей находится отметка в этой точке?
Решение: Эта проблема требует, чтобы мы применили многое из того, что мы узнали. Сначала нарисуйте «шину» (круг) с радиусом 10 дюймов и нарисуйте точку в верхней части шины, чтобы обозначить отметку.
Сначала нарисуйте «шину» (круг) с радиусом 10 дюймов и нарисуйте точку в верхней части шины, чтобы обозначить отметку.
Теперь давайте «повернем» шину на радиан (также равный 45 °).Мы покажем метку в ее исходном и новом положении. (Мы опускаем «внутренний круг» шины для ясности.)
Мы можем использовать основные факты об углах, чтобы перерисовать эту ситуацию в более знакомой форме.
Теперь мы хотим найти высоту отметки над землей.Используя определения на рисунке ниже, эта высота составляет 10 + y.
Наша задача — вычислить у. Мы можем использовать тригонометрию следующим образом.
Таким образом, оценка около 17. 07 дюймов над землей.
07 дюймов над землей.
Единичный круг — Уравнение единичной окружности
Единичный круг из самого названия определяет круг с единичным радиусом. Круг — это замкнутая геометрическая фигура без сторон и углов. Единичный круг обладает всеми свойствами круга, и его уравнение также выводится из уравнения круга. Кроме того, единичный круг полезен для получения стандартных угловых значений всех тригонометрических соотношений.
Здесь мы изучим уравнение единичной окружности и поймем, как представить каждую из точек на окружности единичной окружности с помощью тригонометрических соотношений cosθ и sinθ.
Что такое единичный круг?
Единичный круг — это круг с радиусом, равным 1 единице. Единичный круг обычно представлен в декартовой координатной плоскости. Единичный круг алгебраически представлен с помощью уравнения второй степени с двумя переменными x и y. Единичная окружность применяется в тригонометрии и помогает находить значения тригонометрических соотношений: синус, косинус и тангенс.
Определение единичного круга
Геометрическое место точки, находящейся на расстоянии одной единицы от фиксированной точки, называется единичной окружностью.
Уравнение единичной окружности
Общее уравнение круга: (x — a) 2 + (y — b) 2 = r 2 , которое представляет собой круг с центром (a, b) и радиусом r. Это уравнение круга упрощено и представляет собой уравнение единичного круга. Единичная окружность образуется с центром в точке (0, 0), которая является началом координатных осей. и радиусом 1 ед. Следовательно, уравнение единичной окружности: (x — 0) 2 + (y — 0) 2 = 1 2 .Это упрощается, чтобы получить уравнение единичной окружности.
Уравнение единичной окружности: x 2 + y 2 = 1
Здесь для единичной окружности центр лежит в точке (0,0), а радиус равен 1 единице. Вышеупомянутое уравнение удовлетворяет всем точкам, лежащим на окружности в четырех квадрантах.
Нахождение тригонометрических функций по единичной окружности
Мы можем вычислить тригонометрические функции синуса, косинуса и тангенса, используя единичную окружность.Давайте применим теорему Пифагора в единичном круге, чтобы понять тригонометрические функции. Рассмотрим прямоугольный треугольник, помещенный в единичный круг в декартовой координатной плоскости. Радиус круга представляет собой гипотенузу прямоугольного треугольника. Радиус-вектор составляет угол θ с положительной осью x, а координаты конечной точки радиус-вектора равны (x, y). Здесь значения x и y — это длина основания и высота прямоугольного треугольника. Теперь у нас есть прямоугольный треугольник со сторонами 1, x, y.Применяя это в тригонометрии, мы можем найти значения тригонометрического отношения следующим образом:
- sinθ = Высота / Гипотеза = y / 1
- cosθ = База / Гипотенуза = x / 1
Теперь у нас sinθ = y, cosθ = x, и, используя это, мы теперь имеем tanθ = y / x. Точно так же мы можем получить значения других тригонометрических соотношений, используя прямоугольный треугольник внутри единичной окружности. Также, изменяя значения θ, мы можем получить главные значения этих тригонометрических соотношений.
Точно так же мы можем получить значения других тригонометрических соотношений, используя прямоугольный треугольник внутри единичной окружности. Также, изменяя значения θ, мы можем получить главные значения этих тригонометрических соотношений.
Единичный круг с Sin Cos и Tan
Любая точка на единичной окружности имеет координаты (x, y), которые равны тригонометрическим тождествам (cosθ, sinθ). Для любых значений θ, образованных линией радиуса с положительной осью x, координаты конечной точки радиуса представляют собой косинус и синус значений θ. Здесь у нас есть cosθ = x и sinθ = y, и эти значения помогают вычислить другие значения тригонометрических соотношений. Применяя это дальше, мы имеем tanθ = sinθ / cosθ или tanθ = y / x.
Еще один важный момент, который следует понять, это то, что значения sinθ и cosθ всегда лежат между 1 и -1, а значение радиуса равно 1, и оно имеет значение -1 на отрицательной оси x. Весь круг представляет собой полный угол в 360º, а четыре квадрантные линии круга составляют углы 90º, 180º, 270º, 360º (0º). При 90º и 270º значение cosθ равно 0, и, следовательно, значения тангенса угла наклона при этих углах не определены.
При 90º и 270º значение cosθ равно 0, и, следовательно, значения тангенса угла наклона при этих углах не определены.
Пример: Найдите значение тангенса угла 45º, используя значения sin и cos из единичной окружности.
Решение:
Мы знаем, что tan 45 ° = sin 45 ° / cos 45 °
Используя круговую диаграмму единиц:
грех 45 ° = 1 / √2
cos 45 ° = 1 / √2
Следовательно, tan 45 ° = sin 45 ° / cos 45 °
= (1 / √2) / (1 / √2)
= 1
Ответ: Следовательно, tan 45 ° = 1
Круговая диаграмма в радианах
Единичный круг представляет собой полный угол в 2π радиан. А единичный круг разделен на четыре квадранта под углами π / 2, π.3π / 2 и 2π соответственно. Далее в пределах первого квадранта под углами 0, π / 6, π / 4, π / 3, π / 2 — стандартные значения, которые применимы к тригонометрическим отношениям. Точки на единичном круге для этих углов представляют стандартные угловые значения отношений косинуса и синуса. При внимательном рассмотрении рисунка ниже значения повторяются в четырех квадрантах, но с изменением знака. Это изменение знака происходит из-за опорных осей x и y, которые положительны с одной стороны и отрицательны с другой стороны от начала координат.Теперь с помощью этого мы можем легко найти значения тригонометрических соотношений стандартных углов в четырех квадрантах единичной окружности.
При внимательном рассмотрении рисунка ниже значения повторяются в четырех квадрантах, но с изменением знака. Это изменение знака происходит из-за опорных осей x и y, которые положительны с одной стороны и отрицательны с другой стороны от начала координат.Теперь с помощью этого мы можем легко найти значения тригонометрических соотношений стандартных углов в четырех квадрантах единичной окружности.
Единичный круг и тригонометрические идентичности
Идентификаторы единичной окружности синуса, косеканса и тангенса могут быть дополнительно использованы для получения других тригонометрических идентификаторов, таких как котангенс, секанс и косеканс. Тождества единичной окружности, такие как косеканс, секанс, котангенс, являются соответствующими обратными величинами синуса, косинуса и тангенса.Кроме того, мы можем получить значение tanθ, разделив sinθ на cosθ, и мы можем получить значение cotθ, разделив cosθ на sinθ.
Для прямоугольного треугольника, помещенного в единичный круг в декартовой координатной плоскости, с гипотенузой, основанием и высотой, измеряющими единицы, x, y соответственно, тождества единичного круга могут быть заданы как,
- sinθ = y / 1
- cosθ = x / 1
- tanθ = sinθ / cosθ = y / x
- с (θ = 1 / x
- csc (θ) = 1 / y
- детская кроватка (θ) = cosθ / sinθ = x / y
Единичный круг Пифагорейские тождества
Три важных пифагоровых тождества тригонометрических соотношений можно легко понять и доказать с помощью единичной окружности. Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Три пифагорова тождества в тригонометрии заключаются в следующем.
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Три пифагорова тождества в тригонометрии заключаются в следующем.
- sin 2 θ + cos 2 θ = 1
- 1 + загар 2 θ = сек 2 θ
- 1 + детская кроватка 2 θ = cosec 2 θ
Здесь мы попытаемся доказать первое тождество с помощью теоремы Пифагора.Возьмем x и y в качестве катетов прямоугольного треугольника с единицей гипотенузы 1. Применяя теорему Пифагора, получаем x 2 + y 2 = 1, что представляет собой уравнение единичной окружности. Также в единичном круге мы имеем x = cosθ и y = sinθ, и применяя это в приведенном выше утверждении теоремы Пифагора, мы имеем, cos 2 θ + sin 2 θ = 1. Таким образом, мы имеем успешно доказал первое тождество с помощью теоремы Пифагора. Далее в пределах единичного круга мы также можем доказать два других тождества Пифагора.
Единичная окружность и тригонометрические значения
Различные тригонометрические тождества и их значения главных углов могут быть вычислены с помощью единичной окружности. В единичном круге косинус является координатой x, а синус — координатой y. Давайте теперь найдем их соответствующие значения для θ = 0 ° и θ = 90º.
Для θ = 0 ° координата x равна 1, а координата y равна 0. Следовательно, мы имеем cos0º = 1 и sin0º = 0.Давайте посмотрим на другой угол 90º. Здесь значение cos90º = 1 и sin90º = 1. Далее, давайте воспользуемся этой единичной окружностью и найдем важные значения тригонометрической функции θ, такие как 30º, 45º, 60º. Кроме того, мы также можем измерить эти значения θ в радианах. Мы знаем, что 360 ° = 2π радиан. Теперь мы можем преобразовать угловые меры в радианы и выразить их в радианах.
Единичный круговой стол:
Таблица единичной окружности используется для перечисления координат точек единичной окружности, соответствующих общим углам, с помощью тригонометрических соотношений.
| Угол θ | Радианы | Sinθ | Cosθ | Tanθ = Sinθ / Cosθ | Координаты |
|---|---|---|---|---|---|
| 0 ° | 0 | 0 | 1 | 0 | (1, 0) |
| 30 ° | π / 6 | 1/2 | √3 / 2 | 1 / √3 | (√3 / 2, 1/2) |
| 45 ° | π / 4 | 1 / √2 | 1 / √2 | 1 | (1 / √2, 1 / √2) |
| 60 ° | π / 3 | √3 / 2 | 1/2 | √3 | (1/2, √3 / 2) |
| 90 ° | π / 2 | 1 | 0 | undefined | (0,1) |
Мы можем найти функции секанса, косеканса и котангенса, используя следующие формулы:
- сек θ = 1 / cosθ
- cosecθ = 1 / sinθ
- cotθ = 1 / tanθ
Мы обсудили единичный круг для первого квадранта. Точно так же мы можем расширить и найти радианы для всех квадрантов единичной окружности. Цифры 1/2, 1 / √2, √3 / 2, 0, 1 повторяются вместе со знаком во всех 4 квадрантах.
Точно так же мы можем расширить и найти радианы для всех квадрантов единичной окружности. Цифры 1/2, 1 / √2, √3 / 2, 0, 1 повторяются вместе со знаком во всех 4 квадрантах.
Единичный круг в сложной плоскости
Единичный круг состоит из всех комплексных чисел, абсолютное значение которых равно 1. Следовательно, оно имеет уравнение | z | = 1. Любое комплексное число z = x + \ (i \) y будет лежать на единичной окружности с уравнением, заданным как x 2 + y 2 = 1.
Единичный круг можно рассматривать как единичные комплексные числа на комплексной плоскости, т.е.е., набор комплексных чисел z, заданный формой,
z = e \ (i \) t = cos t + \ (i \) sin t = cis (t)
Приведенное выше соотношение представляет собой формулу Эйлера.
Часто задаваемые вопросы по Unit Circle
Что такое единичный круг в математике?
Единичный круг — это круг с радиусом в одну единицу. Обычно единичный круг представлен в координатной плоскости с центром в начале координат. Уравнение единичной окружности с радиусом одна единица и центром в точке (0, 0): x 2 + y 2 = 1.Кроме того, единичная окружность применяется в тригонометрии и используется для нахождения главных значений тригонометрических соотношений синуса и косинуса.
Обычно единичный круг представлен в координатной плоскости с центром в начале координат. Уравнение единичной окружности с радиусом одна единица и центром в точке (0, 0): x 2 + y 2 = 1.Кроме того, единичная окружность применяется в тригонометрии и используется для нахождения главных значений тригонометрических соотношений синуса и косинуса.
Как найти грех и разум, используя единичный круг?
Единичный круг можно использовать для определения значений sinθ и Cosθ. В единичном круге радиуса 1 единица и с центром в (0, 0), возьмем радиус, наклоненный к положительной оси x под углом θ, и конечную точку радиуса как (x, y). Нарисуйте перпендикуляр от конца радиуса к оси x, и он образует прямоугольный треугольник с радиусом в качестве гипотенузы.Соседняя сторона этого треугольника — это значение x, противоположная сторона треугольника — значение y, а гипотенуза равна 1 единице. Далее, используя формулу тригонометрического соотношения, имеем sinθ = Opp / Hyp = y / 1 и cosθ = Adj / Hyp = x / 1. Таким образом, sinθ = y и cosθ = x.
Таким образом, sinθ = y и cosθ = x.
Что такое определение триггерных функций с помощью единичной окружности?
Тригонометрическую функцию можно вычислить для главных значений с помощью единичной окружности. Для единичного круга, имеющего центр в начале координат (0, 0), радиус 1 единицу, если радиус наклонен под углом θ и конечная точка радиус-вектора равна (x, y), то cosθ = x и sinθ = y.Кроме того, все остальные тригонометрические отношения могут быть рассчитаны на основе этих двух значений. Кроме того, основные значения можно вычислить, изменив значение θ.
Как найти конечную точку на единичной окружности?
Конечная точка на единичной окружности может быть найдена с помощью уравнения единичной окружности x 2 + y 2 = 1. Если данная точка удовлетворяет этому уравнению, то это точка, лежащая на единичной окружности. . Кроме того, конечную точку на единичном значении можно найти для значения θ, найдя значения cosθ и sinθ.
Что такое уравнение единичной окружности?
Уравнение единичной окружности: x 2 + y 2 = 1. Здесь считается, что единичная окружность имеет центр в начале (0, 0) координатных осей и имеет радиус 1. Блок. Это уравнение единичной окружности было получено с помощью формулы расстояния.
Как вывести уравнение единичной окружности?
Уравнение единичной окружности может быть вычислено с использованием формулы расстояния координатной геометрии.Для круга, имеющего центр в начале координат (0, 0), радиус 1 единицу, любая точка на окружности может быть принята как (x, y). Применяя определение круга и используя формулу расстояния, мы имеем (x — 0) 2 + (y — 0) 2 = 1, что можно упростить как x 2 + y 2 = 1
Когда загар не определен на единичном круге?
Единичный круг, имеющий уравнение x 2 + y 2 = 1, помогает найти тригонометрические отношения sinθ = y и cosθ = x. Используя эти значения, мы можем удобно найти значение tanθ = sinθ / cosθ = y / x. Tanθ будет неопределенным для cosθ = 0, т.е. когда θ равно 90 ° и 270 °.
Используя эти значения, мы можем удобно найти значение tanθ = sinθ / cosθ = y / x. Tanθ будет неопределенным для cosθ = 0, т.е. когда θ равно 90 ° и 270 °.
Какая связь между прямоугольными треугольниками и единичной окружностью?
Правые треугольники и единичный круг связаны однозначно. Любую точку на единичном круге можно визуализировать как прямоугольный треугольник с радиусом как гипотенузу прямоугольного треугольника и координаты точки как две другие стороны прямоугольного треугольника.Уравнение окружности x 2 + y 2 = 1 полностью удовлетворяет теореме Пифагора, относящейся к прямоугольному треугольнику. Кроме того, прямоугольный треугольник внутри единичного круга помогает получить значения тригонометрического отношения.
Для чего используется единичный круг?
Единичный круг особенно полезен в тригонометрии. Для тригонометрических соотношений sinθ, cosθ, tanθ их значения главных углов 0º, 30º, 45º, 60º, 90º могут быть легко вычислены с использованием единичной окружности. Кроме того, единичный круг полезен для представления комплексных чисел на плоскости арганда.
Кроме того, единичный круг полезен для представления комплексных чисел на плоскости арганда.
Каковы квадранты единичного круга?
Единичный круг состоит из четырех квадрантов, аналогичных квадрантам в системе координат. Четыре квадранта имеют равную площадь и составляют одну четвертую площади круга. Каждый из квадрантов образует угол 90 ° или прямой угол в центре круга.
Как описать единичный круг комплексными числами?
Единичный круг состоит из всех комплексных чисел с абсолютным значением как 1, таким образом, любое комплексное число z = x + \ (i \) y будет лежать на единичном круге с уравнением, заданным как x 2 + y 2 = 1 .Следовательно, уравнение единичной окружности можно представить как | z | = 1.
Единичный круг — Рубрики тригонометрии
Темы | Дом
15
Определения
Знаков в каждом квадранте
Углы квадрантные
Единичный круг
АНАЛИТИЧЕСКАЯ ТРИГОНОМЕТРИЯ является расширением тригонометрии прямоугольного треугольника. Это происходит на плоскости x — y . Поскольку тригонометрия фактически используется в исчислении и физике, она не связана с решением треугольников. Он становится математическим описанием вещей, которые вращаются или вибрируют, таких как свет, звук, пути планет вокруг Солнца или спутников вокруг Земли. Следовательно, необходимо иметь углы любого размера и распространять на них значения тригонометрических функций. Мы делаем это сейчас.
Это происходит на плоскости x — y . Поскольку тригонометрия фактически используется в исчислении и физике, она не связана с решением треугольников. Он становится математическим описанием вещей, которые вращаются или вибрируют, таких как свет, звук, пути планет вокруг Солнца или спутников вокруг Земли. Следовательно, необходимо иметь углы любого размера и распространять на них значения тригонометрических функций. Мы делаем это сейчас.
Пусть радиус длиной r охватывает угол θ в стандартном положении, и пусть его конечная точка имеет координаты ( x , y ).Возникает вопрос: как теперь определить шесть тригонометрических функций от θ?
Мы будем брать реплику из первого квадранта. В этом квадранте
радиус r завершится точкой ( x , y ). Эти координаты определяют прямоугольный треугольник. Далее следуют определения шести тригонометрических функций в виде прямоугольного треугольника (тема 2).
| грех θ | = | y r | csc θ | = | r y | |
| cos θ | = | x r | сек θ | = | r x | |
| tan θ | = | y x | детская кроватка θ | = | x y | |
Согласно теореме Пифагора,
Таким образом, мы расширяем значение тригонометрических функций до углов, которые заканчиваются в любом квадранте .Это в единицах координат ( x , y ) конечной точки расстояния r от начала координат.
Но прежде чем мы приведем пример, рассмотрим следующий вопрос:
Будет ли функция θ зависеть от длины r ?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.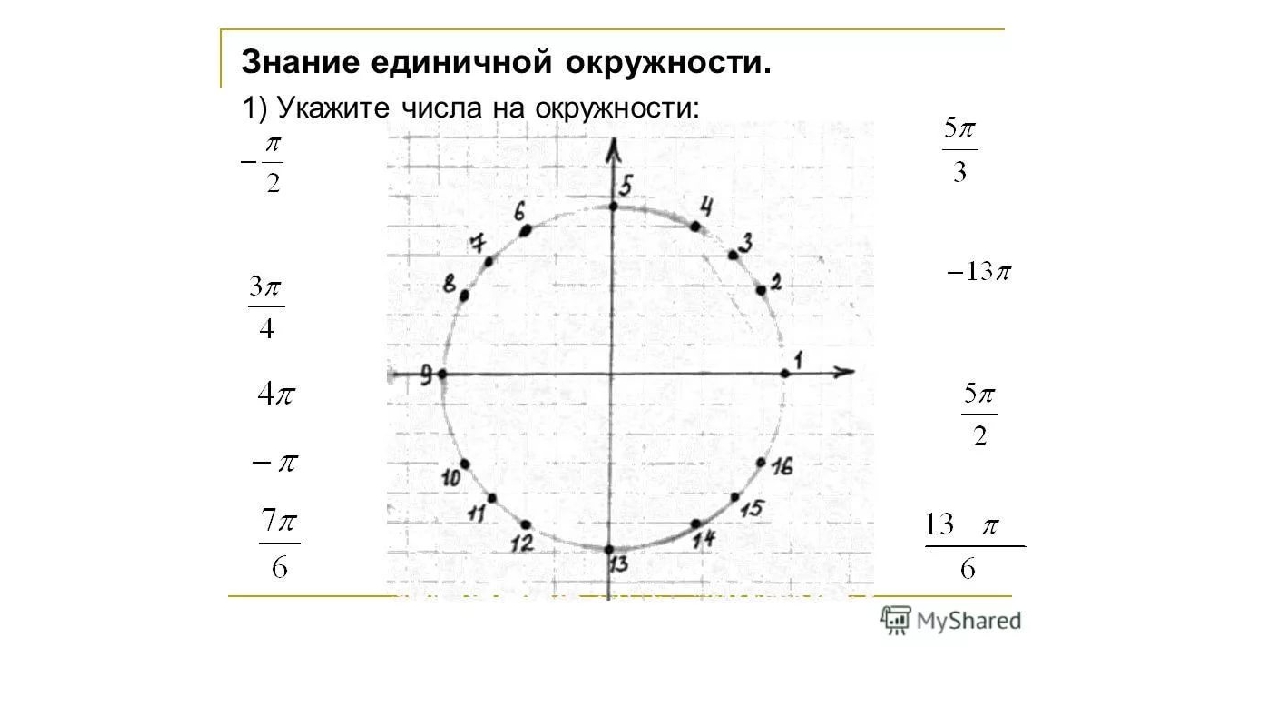
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала ответьте на вопрос сами!
Нет, не будет.Функции определяются как отношения сторон, а не их длины.
Скажем, AB и AC — два разных радиуса. Но треугольники ABD, ACE похожи. (Теорема 15) Пропорционально
DB: BA = EC: CA
sin θ — противоположно гипотенузе — не зависит от длины радиуса. То же самое и с остальными функциями. Поэтому мы можем выбрать любой радиус, какой захотим. Обычно мы берем r = 1.Как мы увидим, это называется единичным кругом.
Фактически, тригонометрические функции зависят только от угла θ — и по этой причине мы говорим, что они являются функциями от θ.
Пример 1. Прямая линия, вставленная в начале координат, заканчивается в точке (3, 2), поскольку она проходит под углом θ в стандартном положении. Оцените все шесть функций θ.
Ответ . x = 3, y = 2. Следовательно, по определениям:
Следовательно, по определениям:
| грех θ | = | y r | = | 2 | csc θ | = | r y | = | 2 | |
| cos θ | = | x r | = | 3 | сек θ | = | r x | = | 3 | |
| tan θ | = | y x | = | 2 3 | детская кроватка θ | = | x y | = | 3 2 | |
Проблема 1. Прямая от начала координат проходит под углом θ и заканчивается в точке (3, −4). Оцените шесть функций θ.
Прямая от начала координат проходит под углом θ и заканчивается в точке (3, −4). Оцените шесть функций θ.
x = 3, y = −4. Следовательно,
| грех θ | = — | 4 5 | csc θ | = — | 5 4 | |
| cos θ | = | 3 5 | сек θ | = | 5 3 | |
| tan θ | = — | 4 3 | детская кроватка θ | = — | 3 4 | |
Проблема 2.Знаки в каждом квадранте.
а) Алгебраический знак греха θ всегда будет знаком
а) координаты? y , потому что sin θ = y / r , а r всегда положителен.
а) Следовательно, в каких квадрантах грех θ — y — будет положительным? I и II.
a) В каких квадрантах sin θ будет отрицательным? III и IV.
b) Алгебраический знак cos θ всегда будет знаком
b) координаты? x , потому что cos θ = x / r , и опять же, r всегда равно
положительный.
a) Следовательно, в каких квадрантах cos θ — x — будет положительным? I и IV.
a) В каких квадрантах cos θ будет отрицательным? II и III.
c) В каких квадрантах алгебраический знак tan θ ( y / x ) будет положительным?
I и III. x и y будут иметь одинаковые знаки.
d) В каких квадрантах алгебраический знак tan θ будет отрицательным?
II и IV. x и y будут иметь противоположные знаки.
e) csc θ будет иметь тот же знак, что и другая функция?
sin θ, потому что они обратны.
е) сек θ будет иметь тот же знак, что и другая функция?
cos θ
г) детская кроватка θ будет иметь тот же знак, что и другая функция?
загар θ
Углы квадрантные
Квадрантный угол — это угол, который заканчивается на оси x или y .
Проблема 3.
а) Каковы углы квадранта в градусах?
0 °, 90 °, 180 °, 270 °; и углы, совпадающие с ними.
б) Каковы углы квадранта в радианах?
| 0, | π 2 | , π, | 3π 2 | ; и углы, совпадающие с ними. |
c) Когда угол заканчивается на оси x , каково значение
c) y -coördinate? 0. По оси x : y = 0.
d) Когда угол заканчивается на оси y , каково значение
c) x -координат? 0. По оси y — x = 0.
То, что не существует числа со знаминателем 0, является арифметическим фактом.
Следовательно, если знаменатель тригонометрической функции — x или y — равен 0, функция не будет существовать под этим квадрантным углом.
Например,
Там, где x = 0, tan θ не существует. Где x = 0? Когда угол заканчивается на оси y .
| tan θ не будет существовать при θ = | π 2 | и θ = | 3π 2 | или у — | π 2 | , что составляет |
терминал.
Эти значения θ будут особенностями tan θ. (Тема 18 Precalculus.)
Задача 4. Для каких квадрантных углов не существуют следующие функции?
| а) детская кроватка θ | детская кроватка θ = | x y | . Следовательно, всякий раз, когда y = 0, то есть на Следовательно, всякий раз, когда y = 0, то есть на |
ось x — детская кроватка θ не существует.cot θ не будет существовать при θ = 0 и θ = π.
б) сек θ
| сек θ = | r x | . Следовательно, sec θ не будет существовать, если x = 0, |
| , который находится на оси y . сек θ не будет существовать при θ = | π 2 |
в) грех θ
| грех θ = | y r | .Но r никогда не равняется 0. Нет угла, для которого |
sin θ не существует.
Единичный круг
Тригонометрические функции являются функциями только угла θ. Поэтому мы можем выбрать любой радиус, который нам нравится, и самый простой — это круг радиуса 1, единичный круг.
На единичном круге функции принимают особенно простую форму. Например,
| грех θ | = | y 1 | = y . |
| cos θ | = | x 1 | = х . |
Значение sin θ составляет координата y конечной точки единичного радиуса. Значение cos θ — координата x
Что касается углов квадранта, единичная окружность показывает следующее:
Если функция существует под квадрантным углом,
она может иметь только значения 0, 1 или -1.
Рассмотрим sin θ для каждого квадрантного угла. Мы только что видели, что значение sin θ составляет , значение y — значение:
.sin θ = y .
Следовательно, для каждого квадрантного угла значение sin θ — y — равно 0, 1 или -1.
| При θ = 0, | грех θ = 0. | |
| При θ = | π 2 | , грех θ = 1. |
| При θ = π, | грех θ = 0. | |
| При θ = | 3π 2 | , грех θ = -1. |
Чтобы оценить функцию под углом квадранта, ученик должен нарисовать единичный круг.
Проблема 5. Оцените следующее. Нет столов
а) cos 0 °
cos 0 ° = 1.cos θ равен x -координату.
б) cos 90 ° = 0 в) cos 180 ° = -1
г) cos 270 ° = 0
д) загар 0 °
tan 0 ° = 0. tan θ равен y / x = 0/1 = 0.
е) загар 90 ° 1/0 не существует.
ж) загар 180 ° = 0
ч) загар 270 ° не существует.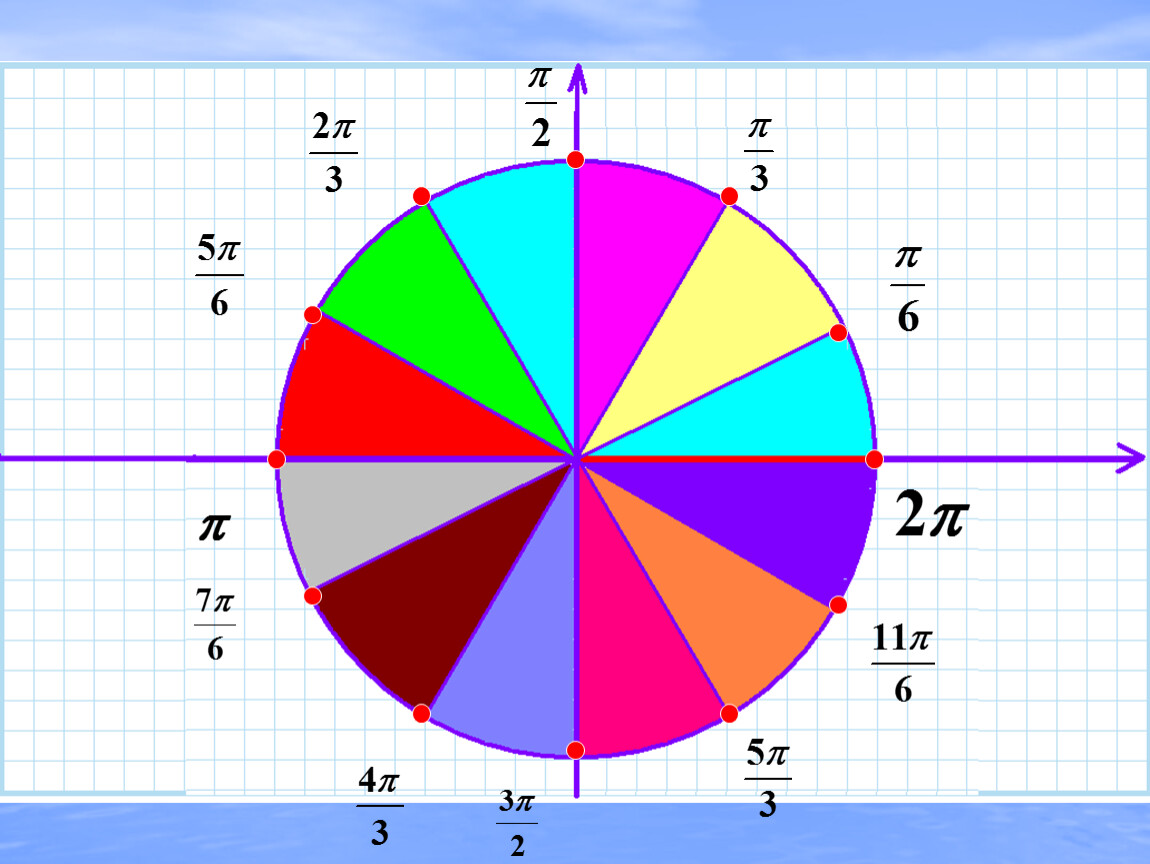
Проблема 6. Оцените следующее — если оно существует. Таблиц нет.
| б) грех | π 2 | = 1 | в) грех | π | = 0 | г) cos | π | = -1 |
| д) детская кроватка 0 | = x / y .Не существует. | е) детская кроватка | π 2 | = 0 |
| г) загар | π 2 | Не существует. | ч) сек 0 | = 1/ x = 1 |
| и) csc (- | π 2 | ) | = -1 | к) грех 2π | = 0 |
| л) грех 3π | = 0 | л) грех 4π | = 0 |
| т) грех (−π) | = 0 | п) cos 2π | = 1 |
| о) cos 3π | = -1 | р) cos 4π | = 1 |
| q) cos 5π | = -1 |
Проблема 7.
 Точка M — искомая.
Точка M — искомая.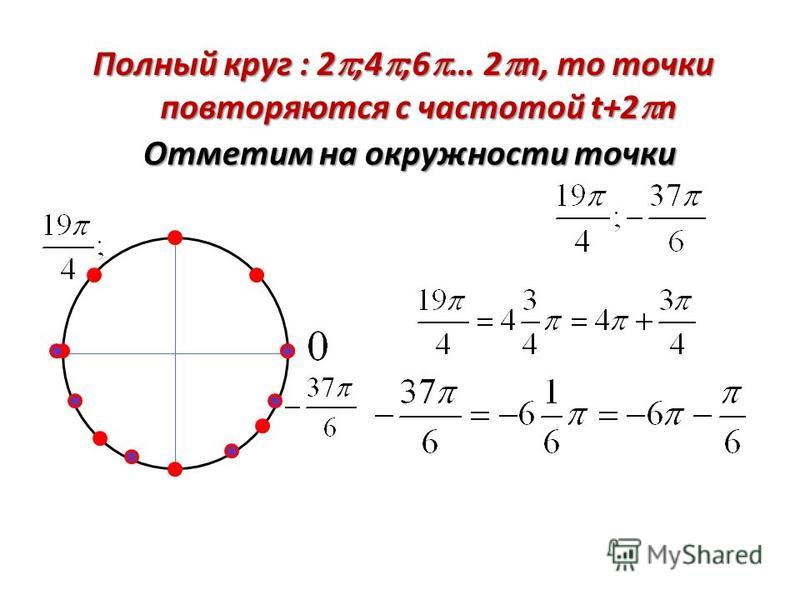 США (- {√2} / 2, {√2} / 2)
США (- {√2} / 2, {√2} / 2)