Как выносить множитель из под корня. Как вынести множитель из-под знака корня: теория, примеры, решения
В данном материале мы продолжим рассказывать о том, как преобразовывать рациональные выражения, а конкретно о том, как правильно выносить множитель из-под знака корня. В первом пункте объясним, зачем нужно такое преобразование, далее покажем, как именно оно делается и сформулируем общее для всех случаев правило. Далее покажем, какие существуют методы, чтобы привести подкоренное выражение к удобному для преобразования виду, и разберем примеры решений задач.
Yandex.RTB R-A-339285-1
Что такое вынесение множителя из-под знака корня
Чтобы лучше понять суть подобного преобразования, нужно сначала сформулировать, что такое вообще вынесение множителя из-под знака корня. Сформулируем определение:
Определение 1
Вынесение множителя из-под знака корня представляет собой замену выражения B n · C n на произведение B · C n с условием, что n – нечетное число, или же на произведение B · C – где n – четное число, а B и C – другие числа и выражения.
Если мы имеем в виду только квадратный корень, то есть число n равно двум, то процесс вынесения множителя можно свести к замене выражения B 2 · C на произведение B · C . Отсюда и название данного преобразования: после того, как оно было проведено, множитель B y оказывается свободным от знака корня.
Приведем примеры, поясняющие данное определение. Так, допустим, у нас есть выражение 2 2 · 3 . Оно аналогично B 2 · C , где B равно двум, а C – трем. Заменив данный корень на произведение 2 · 3 и опустив знаки модулей (это можно сделать, поскольку оба множителя являются положительными числами), мы получим 2 · 3 . Мы вынесли множитель 2 2 из-под знака корня.
Приведем еще один пример подобного преобразования. У нас есть выражение (x 2 — 3 · x · y · z) 2 · x = x 2 — 3 · x · y · z · x . Здесь из-под корня был вынесен не просто числовой множитель, а целое выражение с переменными (x 2 − 3 · x · y · z) 2 .
Оба примера относятся к случаю вынесения множителя из-под квадратного корня. Можно также производить данные преобразования и для корней n -ной степени. Вот пример с кубическим корнем: (3 · a 2) 3 · 2 · a 2 3 = 3 · a 2 · 2 · a 2 3
Можно также производить данные преобразования и для корней n -ной степени. Вот пример с кубическим корнем: (3 · a 2) 3 · 2 · a 2 3 = 3 · a 2 · 2 · a 2 3
Пример с корнем шестой степени: 1 2 · x 2 + y 2 6 · 5 · (x 2 + y 2) 6 можно преобразовать в произведение 1 2 · x 2 + y 2 · 5 · (x 2 · y 2) 6 , которое, в свою очередь, упрощается до 1 2 · (x 2 + y 2) · 5 · (x 2 + y 2) 6 . В данном случае мы выносим множитель 1 2 · x 2 + y 2 6 .
Мы выяснили, что такое вынесение множителя из-под знака корня. Теперь перейдем к доказательствам, т.е. поясним, почему произведение, полученное в итоге данного преобразования, равнозначно исходному выражению.
Почему возможно заменить корень на произведение
В этом пункте мы будем разбираться, как возможна такая замена и почему корень B n · C n равнозначен произведениям B · C n и B · C n . Обратимся к ранее изученным теоретическим положениям.
Когда мы разбирали преобразование иррациональных выражений, у нас получились некоторые важные результаты, которые мы собрали в таблицу. Здесь нам будут нужны только два из них:
Здесь нам будут нужны только два из них:
1. Выражение A · B n при условии нечетности n может быть заменено на A n · B n , а для четных n – A n · B n .
2. Выражение A n n при нечетном значении n может быть преобразовано в A , а при четном – в | A | .
Определение 2
Используя эти результаты и зная основные свойства модуля, мы можем вывести следующее:
- при четном n: B n · C n = B n n · C n = B · C n ;
- при нечетном n: B n · C n = B n n · C n = B n n · C n = B · C n .
Эти выражения лежат в основе преобразований, которые мы проводим, вынося множитель из-под знака корня.
Следовательно, можно вывести две формулы:
Определение 3
С помощью данных формул можно выполнить вынесение из-под корня сразу нескольких множителей.
Основное правило вынесения множителя из-под корня
Когда нам нужно решать примеры с подобными преобразованиями, чаще всего приходится предварительно приводить подкоренное выражение к виду B n · C . С учетом этого момента мы можем записать следующие правила.
С учетом этого момента мы можем записать следующие правила.
Определение 4
Для вынесения множителя из-под корня в выражении A n нужно предварительно привести корень к виду B n · C n и после этого перейти к произведению B · C n (при нечетном показателе) или к B · C n (при четном показателе, при необходимости раскрываем модули).
Таким образом, схема решения подобных задач выглядит следующим образом:
A n → B n · C n → B · C n , е с л и n — н е ч е т н о е B · C n , е с л и n — ч е т н о е
Если нам надо вынести несколько множителей, то действуем так:
A n → B 1 n · B 2 n · . . . · B k n · C n → B 1 · B 2 · . . . · B k · C n , е с л и n — н е ч е т н о е B 1 · B 2 · . . . · B k · C n , е с л и n — ч е т н о е
Теперь можно переходить к решению задач.
Задачи на вынесение множителя из-под знака корня
Пример 1Условие: выполните вынесение множителя за знак корня в трех выражениях: 2 2 · 7 , — 1 2 3 2 · 5 , (- 0 , 4) 7 · 11 7 .
Решение
Мы видим, что подкоренные выражения во всех трех случаях уже имеют нужный нам вид. Поскольку в первых двух примерах показателем корня является четное число, а в третьем – нечетное, записываем следующее:
- Показатель корня равен 2 . Берем правило вынесения множителя для четного показателя и вычисляем: 2 2 · 7 = 2 · 7 = 2 · 7
- Во втором выражении показатель тоже четный, значит, — 1 2 3 2 · 5 = — 1 2 3 · 5 = 1 2 3 · 5
В этом случае мы можем сначала преобразовать выражения, исходя из основных свойств корня:
— 1 2 3 2 · 5 = — 1 2 · 1 2 3 2 · 5 = 1 2 3 2 · 5
А потом уже выносить множитель: 1 2 3 2 · 5 = 1 2 3 · 5 = 1 2 3 · 5 . - Последнее выражение имеет нечетный показатель, поэтому нам понадобится другое правило: (- 0 , 4) 7 · 11 7 = — 0 , 4 · 11 7 .
Возможен и такой вариант расчета:
— 0 , 4 7 · 11 7 = (- 1) 7 · 0 , 4 7 · 11 7 = = — 0 , 4 7 · 11 7 = — 0 , 4 7 · 11 7 = — 0 , 4 · 11 7
Или такой:
— 0 , 4 7 · 11 7 = (- 1) 7 · 0 , 4 7 · 11 7 = = — 0 , 4 7 · 11 7 = 0 , 4 7 · — 11 7 = 0 , 4 · — 11 7 = — 0 , 4 · 11 7
Ответ: 1) 2 · 7 ; 2) 1 2 3 · 5 ; 3) — 0 , 4 · 11 7 .
Пример 2
Условие: преобразуйте выражение (- 2) 4 · (0 , 3) 4 · 7 4 · 11 4 .
Решение:
При помощи схемы, приведенной во втором пункте статьи, мы можем вынести из-под корня сразу три множителя.
(- 2) 4 · (0 , 3) 4 · 7 4 · 11 4 = = — 2 · 0 , 3 · 7 · 11 4 = 4 , 2 · 11 4
Можно сделать преобразование в несколько шагов, вынося множителя по одному, но так будет гораздо дольше.
Есть и другой способ. Преобразуем само выражение, приведя его к виду B n · C . После этого уже будем выносить множители:
(- 2) 4 · (0 , 3) 4 · 7 4 · 11 4 = = (- 2 · 0 , 3 · 7) 4 · 11 4 = (- 4 , 2) 4 · 11 4 = = — 4 , 2 · 11 4 = 4 , 2 · 11 4
Ответ: (- 2) 4 · (0 , 3) 4 · 7 4 · 11 4 = — 4 , 2 · 11 4 = 4 , 2 · 11 4 .
Разберем более подробно тот случай, когда подкоренное выражение требует предварительного преобразования. Здесь есть несколько моментов, которые нужно дополнительно пояснить.
Предварительное преобразование подкоренного выражения
Мы уже отмечали, что выражение под корнем не всегда имеет удобный для нас вид. Часто корень дан как A n , и множитель, который нужно вынести, не представлен в явном виде. Иногда это обозначено в условии, но довольно часто множитель приходится определять самостоятельно. Посмотрим, как надо действовать в этих случаях.
Часто корень дан как A n , и множитель, который нужно вынести, не представлен в явном виде. Иногда это обозначено в условии, но довольно часто множитель приходится определять самостоятельно. Посмотрим, как надо действовать в этих случаях.
Допустим, нам надо вынести заранее определенный множитель B . Естественно, подкоренное выражение должно быть таким, чтобы эта операция была возможна. Тогда для преобразования A n в B n · C n достаточно определить второй множитель, т.е. вычислить значение C из выражения A = B n · C .
Пример 3
Условие: есть выражение 24 · x 3 . Вынесите из-под знака корня множитель 2 3 .
Решение
Здесь мы имеем n = 3 , A = 24 · x , B 3 = 2 3 . Тогда из A = B n · С вычисляем C = A: (B n) = 24 · x: (2 3) = 3 · x .
Значит, 24 · x 3 = 2 3 · 3 · x 3 . Подкоренное выражение имеет нужный нам вид, и мы можем воспользоваться правилом для нечетного показателя и подсчитать: 24 · x 3 = 2 3 · 3 · x 3 = 2 · 3 · x 3 .
Ответ: 24 · x 3 = 2 · 3 · x 3 .
А как быть в случае, если множитель, который нужно вынести, не указан? Тогда у нас есть определенная свобода выбора, и мы можем использовать несколько подходов к решению задачи.
Допустим, нам дано выражение, под корнем у которого стоит степень или произведение нескольких степеней. В таком случае, зная основные свойства степени, мы можем преобразовать выражение в удобный для нас вид с очевидно указанными множителями для вынесения.
Пример 4
Условие : необходимо вынести множитель из-под корня в трех выражениях – 2 4 · 5 4 , 2 7 · 5 4 , 2 22 · 5 4 .
Решение
Преобразование первого выражения не представляет особой сложности, т.к. подобные примеры мы уже разбирали. Сразу вычисляем: 2 4 · 5 4 = 2 · 5 4 = 2 · 5 4 .
Во втором примере легко догадаться, как преобразовать подкоренное выражение: нужно просто представить 2 7 как 2 4 · 2 3 .
2 7 · 5 4 = 2 4 · 2 3 · 5 4 = 2 4 · 40 4 = 2 · 40 4 = 2 · 40 4
В последнем примере также нужно начать с преобразования подкоренного выражения. Сразу отметим, что итоговый вид будет таким:
Сразу отметим, что итоговый вид будет таким:
2 5 4 · 2 2 · 5 4
Теперь покажем, как именно прийти к этому виду. Сначала выполняем деление 22 на 4 , получаем 5 с остатком 2 (если нужно, повторите, как правильно выполнять деление с остатком). Иначе говоря, 22 можно рассматривать как 4 · 5 + 2 . Используя свойства степени, можем записать:
2 22 + 2 5 · 4 + 2 = 2 5 · 4 · 2 2 = (2 5) 4 · 2 2
Таким образом:
2 22 · 5 4 = (2 5) 4 · 2 2 · 5 4 = (2 5) 4 · 20 4 = = 2 5 · 20 4 = 32 · 20 4
Ответ: 1) 2 4 · 5 4 = 2 · 5 4 , 2) 2 7 · 5 4 = 2 · 40 4 , 3) 2 22 · 5 4 = 32 · 20 4 .
Если выражение под корнем не является степенью или произведением степеней, надо попробовать представить его в таком виде. Чаще всего встречаются следующие случаи.
Подкоренное выражение – натуральное составное число. Тогда мы сразу можем увидеть нужные множители, которые надо вынести из-под знака корня, предварительно разложив данное число на простые множители.
Пример 5
Условие : выполните вынесение множителя из-под знака корня в следующих выражениях: 1) 45 ; 2) 135 ; 3) 3456 ; 4) 102 .
- Выполняем разложение 45 на простые множители.
То есть 45 = 3 · 3 · 5 = 3 2 · 5 , а 45 = 3 2 · 5 . В этом выражении видно, что выносить мы будем множитель 3 2 . Вычисляем:
3 2 · 5 = 3 · 5 = 3 · 5
- Теперь представим в нужном виде число 135 и получим: 135 = 3 · 3 · 3 · 5 = 3 3 · 15 . Иначе можно записать, что 3 2 · 3 · 5 = 3 2 · 15 . Следовательно, 135 = 3 2 · 15 . Мы видим, что вынесению из-под знака корня подлежит множитель 3 2 :
3 2 · 15 = 3 · 15 = 3 · 15
- Разложим на простые множители число 3456:
3456 1728 864 432 216 108 54 27 9 3 1 2 2 2 2 2 2 2 3 3 3
У нас получилось, что 3456 = 2 7 · 3 3 , а 3456 = 2 7 · 3 3 . Поскольку 2 7 = 2 3 · 2 + 1 = (2 3) 2 · 2 и 3 3 = 3 2 · 3 , то 2 7 · 3 3 = (2 3) 2 · 2 · 3 2 · 3 = (2 3) 2 · 3 2 · 6 = = 2 3 · 3 · 6 = 24 · 6
- Представим натуральное число 102 как произведение простых множителей и получим 2 · 3 · 17 .
 Видим, что все множители имеют показатель, равный единице, а показатель корня в этом примере равен двум. Следовательно, в данном примере ни один множитель не нужно выносить из-под знака корня, то есть такое действие для 102 нецелесообразно.
Видим, что все множители имеют показатель, равный единице, а показатель корня в этом примере равен двум. Следовательно, в данном примере ни один множитель не нужно выносить из-под знака корня, то есть такое действие для 102 нецелесообразно.
Ответ: 1) 45 = 3 · 5 ; 2) 135 = 3 · 15 ; 3) 3456 = 24 · 6 ; 4) 102 .
Теперь разберем, как решать примеры, у которых подкоренное выражение представлено в виде обыкновенной дроби. В этом случае следует числитель и знаменатель разложить на простые множители и посмотреть, можно ли вынести какие-то из них за знак корня. Если у нас есть десятичная дробь или смешанное число, предварительно заменяем их обыкновенными дробями, после чего переходим от корня отношения к отношению корней.
Пример 6
Условие: выполните вынесение множителя за корень в выражении 200 · 0 , 000189 · x 3 и упростите его.
Решение
Для начала перейдем от десятичной дроби к обыкновенной и разложим ее числитель и знаменатель на простые множители.
0 , 189 = 189 1000000 = 3 3 · 7 2 6 · 5 6
Используя свойства степени, перепишем выражение в следующем виде:
3 2 2 · 5 2 3 · 7
Подставим получившееся выражение в исходное и получим:
200 · 0 , 000189 · x 3 = = 200 · 3 2 2 · 5 2 3 · 7 · x 3 = = 200 · 3 2 2 · 5 2 · 7 · x 3 = 6 · 7 · x 3
К такому же ответу можно прийти и с помощью других преобразований:
200 · 0 , 000189 · x 3 = = 200 · 189 1000000 · x 3 = 200 · 189 1000000 3 · x 3 = = 200 · 189 3 1000000 3 · x 3 = 200 · 3 3 · 7 3 100 3 3 · x 3 = = 200 · 3 · 7 3 100 · x 3 = 6 · 7 3 · x 3 = 6 · 7 · x 3
Ответ: 200 · 0 , 000189 · x 3 = 6 · 7 · x 3 .
Иными словами, для обнаружения множителя, который можно вынести за знак корня, можно преобразовывать подкоренное выражение любыми допустимыми способами.
Пример 7
Условие: выполните упрощение иррационального выражения 2 · (3 + 2 · 2) .
Решение
Мы можем преобразовать выражение в скобках как 2 + 2 · 2 + 1 и далее как 2 2 + 2 · 2 · 1 + 1 2 .
То, что у нас получилось, можно свернуть в квадрат суммы с помощью формулы сокращенного умножения: 2 2 + 2 · 2 · 1 + 1 = 2 + 1 2 .
В итоге: 2 · 3 + 2 · 2 = 2 · 2 + 1 2 . Теперь выносим 2 + 1 2 за знак корня и упрощаем выражение:
2 · 2 + 1 2 = 2 · 2 + 1 = = 2 · 2 + 1 = 2 + 2
Ответ: 2 · 3 + 2 · 2 = 2 + 2 .
Теперь посмотрим, как вынести из-под знака корня выражение, содержащее переменные. В целом можно сказать, что для этого используются те же методы, что и при работе с числами.
Пример 8
Условие: вынесите множитель из-под знака корня в выражениях (x — 5) 5 4 и (x — 5) 6 4 .
Решение
- Выполняем преобразование в первом примере.
(x — 5) 5 4 = (x — 5) 4 · x — 5 4 = x — 5 · x — 5 4
Знак модуля можно опустить. Посмотрим, каким условием определяется область допустимых значений переменной для исходного выражения. Таким условием будет неравенство (x − 5) 5 ≥ 0 . Для его решения выбираем метод интервалов и получаем x ≥ 5 . Если значение x принадлежит области допустимых значений, то значением выражения x — 5 будет неотрицательное число. Значит, можем записать следующее:
Если значение x принадлежит области допустимых значений, то значением выражения x — 5 будет неотрицательное число. Значит, можем записать следующее:
x — 5 · x — 5 4 = x — 5 · x — 5 4
- (x — 5) 6 4 = (x — 5) 4 · x — 5 2 4 = = x — 5 · (x — 5) 2 4 = x — 5 · x — 5 2 4
Выполним сокращение показателей корня и степени на два. Обратимся к таблице результатов из статьи о преобразовании иррациональных выражений, о которой мы говорили выше. Возьмем из нее следующий результат: выражение A m n · m можно заменить на A n при условии, что m и n – натуральные числа. Следовательно,
x — 5 · x — 5 2 4 = x — 5 · x — 5
Нужно ли здесь убирать знак модуля? Посмотрим на область допустимых значений данного выражения: ее составляют все действительные числа, поскольку (x − 5) 6 ≥ 0 для любого x . При этом значения x − 5 могут быть больше 0 , если x > 5 , равными 0 или отрицательными. Значит, оставляем выражение в виде x — 5 · x — 5 или представляем его в виде системы уравнений
(x — 5) · x — 5 , x ≥ 5 (5 — x) · 5 — x , x
Ответ: 1) (x — 5) 5 4 = (x — 5) · x — 5 4 ; 2) (x — 5) 6 4 = x — 5 · x — 5 .
Пример 9
Условие: выполните упрощение выражения x 5 + 2 · x 4 · y + x 3 · y 2 .
Решение
Выносим за скобки x 3 и получаем x 3 · (x 2 + 2 · x · y + y 2) . Выражение в скобках можно представить в виде квадрата суммы: x 3 · (x 2 + 2 · x · y + y 2) = x 3 · (x + y) 2 .
Теперь видим множители, подлежащие вынесению из-под корня: x 3 · (x + y) 2 = x 2 · x · (x + y) 2 = x · x + y · x
Также мы можем убрать знаки модуля, в которых находится x, поскольку область допустимых значений будет определена условием x 5 + 2 · x 4 · y + x 3 · y 2 ≥ 0 . Оно равносильно x 3 · (x + y) 2 ≥ 0 , а из него можно сделать вывод, что x ≥ 0 . У нас получилось, что x · x + y · x .
Ответ: x 5 + 2 · x 4 · y + x 3 · y 2 = x · x + y · x .
Это все, что мы хотели бы вам рассказать о вынесении множителя за знак корня. В следующей статье мы разберем обратное действие – внесение множителя под корень.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Формулы корней.
 Свойства квадратных корней.
Свойства квадратных корней.Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Пусть дано выражение . Мы можем этот корень представить в более простом виде, применив к нему теорему об извлечении корня из произведения (§ 97):
Точно так же
Такое преобразование называется вынесением множителя за знак корня.
В результате применения этого преобразования данное выражение упрощается и часто сокращаются требуемые вычисления. В этом можно убедиться на следующих примерах.
Пр и мер 1. Вычислить с точностью до 0,01 выражение
Вычислим каждый из корней с точностью до 0,01:
Нам пришлось извлечь квадратный корень из трёх чисел, и притом мы не можем быть уверены, что результат действительно даст величину выражения с точностью до 0,01 (для уверенности в этом нужно было бы вычислить корни с точностью большей, чем заданная).
Попробуем упростить данное выражение, вынося за знак радикала те множители, которые возможно:
Итак, после преобразования нам придётся извлечь квадратный корень только из одного числа.
Вычислив его с точностью до 0,01, найдём:
Теперь видно, что в первом вычислении мы сделали ошибку на одну сотую, то есть получили результат не с заданной точностью.
Пример 2. Вычислить выражение
Подставив в данное выражение получим:
Нам придётся извлечь корень из шестизначного числа.
Мы значительно упростим вычисления, если предварительно вынесем за знак корня те множители, которые возможно. Будем иметь:
Подставив теперь легко найдём:
Во всех предыдущих примерах подкоренное выражение мы разлагали на множители, выделяя такие, показатель которых делится на два, и извлекали из них корень. В дальнейшем надо приобрести навык сразу выносить нужные множители за знак корня, не прибегая к предварительному разложению на множители подкоренного выражения.
Как видно из примеров, для вынесения множителей из-под знака квадратного корня достаточно показатель каждого множителя разделить на два и записать перед знаком корня этот множитель с показателем, равным полученному частному, а под знаком корня тот же множитель с показателем, равным полученному остатку.
В предыдущем примере .
2. Внесение множителей под знак квадратного корня.
Иногда бывает полезно, наоборот, подвести под знак корня множители, стоящие перед ним.
Пусть, например, требуется вычислить с точностью до 0,001 выражение Вычислив с точностью до 0,001 и умножив результат на 20, получим:
Заранее можем сказать, что результат не соответствует заданной точности, так как, умножив приближённое число 2,646 на 20, мы увеличили в 20 раз и ошибку.
Чтобы получить ббльшую точность, возьмём с точностью до 0,0001. Получим:
Но мы не можем и теперь быть уверены, что достигли требуемой точности.
Произведём вычисление другим способом. Представим данное выражение в таком виде:
Вычислив с точностью до 0,001, получим:
Такоза действительная величина данного выражения, вычисленная с точностью до 0,001.
Рассмотренное преобразование называется внесением множителя под знак корня.
Приведённый пример показывает целесообразность в некоторых случаях такого преобразования.
Чтобы внести под знсис квадратного корня стоящие перед ним множители, достаточно возвести эти множители в квадрат и подкоренное выражение умножить на полученный результат.
В двух первых примерах сначала множитель, стоящий перед знаком корня, был подведён под знак корня, затем произведено умножение.
В третьем примере обе эти операции были выполнены сразу.
3. Приведение подкоренного выражения к целому виду.
Если подкоренное выражение дробное, то часто бывает целесообразно привести его к целому виду, или, как говорят, освободить подкоренное выражение от знаменателя.
Покажем на примерах, как это делается.
Пр имер 1.
Чтобы из знаменателя подкоренного выражения можно было извлечь корень, умножим числитель и знаменатель этого выражения на а. Получим.
Инструкция
Подберите подкоренному числу такой множитель, вынесение которого из под корня действительно выражение — иначе операция потеряет . Например, если под знаком корня с показателем, равным трем (кубический корень), стоит число 128, то из под знака можно вынести, например, число 5. 3. Результатом будет 125, а это позволяет разбить 250 на множители 125 и 2, а значит вынести из под знака корня число 5, оставив там число 2.
3. Результатом будет 125, а это позволяет разбить 250 на множители 125 и 2, а значит вынести из под знака корня число 5, оставив там число 2.
Источники:
- как вынести из под корня
- Квадратный корень из произведения
Вынести из-под корня один из сомножителей необходимо в ситуациях, когда нужно упростить математическое выражение. Бывают случаи, когда выполнить нужные вычисления с помощью калькулятора невозможно. Например, если вместо чисел используются буквенные обозначения переменных.
Инструкция
Разложите подкоренное выражение на простые сомножители. Посмотрите, какой из сомножителей повторяется столько же раз, указано в показателей корня , или больше. Например, вам нужно извлечь корень из числа а в четвертой степени. В этом случае число можно представить как а*а*а*а = а*(а*а*а)=а*а3. Показателю корня в этом случае будет соответствовать сомножитель а3. Его и нужно вынести за знак .
Извлеките корень получившихся подкоренных в отдельности там, где это возможно. Извлечение корня представляет собой алгебраическое действие, обратное возведению в степень. Извлечение корня произвольной степени из числа найти такое число, которое при возведении его в эту произвольную степень даст в результате данное число. Если извлечение корня произвести нельзя, оставьте подкоренное выражение под знаком корня так, как оно есть. В результате проведения перечисленных действий вы произведете вынесение из-под знака корня .
Извлечение корня представляет собой алгебраическое действие, обратное возведению в степень. Извлечение корня произвольной степени из числа найти такое число, которое при возведении его в эту произвольную степень даст в результате данное число. Если извлечение корня произвести нельзя, оставьте подкоренное выражение под знаком корня так, как оно есть. В результате проведения перечисленных действий вы произведете вынесение из-под знака корня .
Видео по теме
Обратите внимание
Будьте внимательны при записи подкоренного выражения в виде сомножителей – ошибка на этом этапе приведёт к неправильным результатам.
Полезный совет
При извлечении корней удобно пользоваться специальными таблицами или таблицами логарифмических корней – этим вы значительно сократите время на нахождение правильного решения.
Источники:
- знак извлечения корня в 2019
Упрощение алгебраических выражений требуется во многих разделах математики, в том числе при решении уравнений высших степеней, дифференцировании и интегрировании. При этом используется несколько методов, включая разложение на множители. Чтобы применить этот способ, нужно найти и вынести общий множитель за скобки .
При этом используется несколько методов, включая разложение на множители. Чтобы применить этот способ, нужно найти и вынести общий множитель за скобки .
Инструкция
Вынесение общего множителя за скобки – один из самых распространенных способов разложения . Этот прием применяется для упрощения структуры длинных алгебраических выражений, т.е. многочленов. Общим может быть число, одночлен или двучлен, а для его поиска применяется распределительное свойство умножения.
Число.Посмотрите внимательно на коэффициенты при каждом многочлена, можно ли разделить их на одно и то же число. Например, в выражении 12 z³ + 16 z² – 4 очевидным является множитель 4. После преобразования получится 4 (3 z³ + 4 z² — 1). Иными , это число является наименьшим общим целочисленным делителем всех коэффициентов.
Одночлен.Определите, ли одна и та же переменная в каждый из слагаемых многочлена. Предположим, что это так, теперь посмотрите на коэффициенты, как в предыдущем случае. 4 – 2 z³ + z² — 4 z + 4 = 0. Путем простой подстановки найдите z1 = 1 и z2 = 2, значит, за скобки можно вынести двучлены (z — 1) и (z — 2). Для того, чтобы найти оставшееся выражение, воспользуйтесь последовательным делением в столбик.
4 – 2 z³ + z² — 4 z + 4 = 0. Путем простой подстановки найдите z1 = 1 и z2 = 2, значит, за скобки можно вынести двучлены (z — 1) и (z — 2). Для того, чтобы найти оставшееся выражение, воспользуйтесь последовательным делением в столбик.
Сложение корней с числами. Как вынести множитель из-под корня? Почему подкоренные выражения должны быть неотрицательными
Тема про квадратные корни является обязательной в школьной программе курса математики. Без них не обойтись при решении квадратных уравнений. А позже появляется необходимость не только извлекать корни, но и выполнять с ними другие действия. Среди них достаточно сложные: возведение в степень, умножение и деление. Но есть и достаточно простые: вычитание и сложение корней. Кстати, они только на первый взгляд кажутся такими. Выполнить их без ошибок не всегда оказывается просто для того, кто только начинает с ними знакомиться.
Что такое математический корень?
Это действие возникло в противовес возведению в степень. Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.
Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.
Если в степени стоит двойка, то и корень будет квадратным. Он является самым распространенным в школьной математике. У него даже нет указания, что он квадратный, то есть возле него не приписывается цифра 2. Математическая запись этого оператора (радикала) представлена на рисунке.
Из описанного действия плавно вытекает его определение. Чтобы извлечь квадратный корень из некоторого числа, нужно выяснить, какое даст при умножении на себя подкоренное выражение. Это число и будет квадратным корнем. Если записать это математически, то получится следующее: х*х=х 2 =у, значит √у=х.
Какие действия с ними можно выполнять?
По своей сути корень — это дробная степень, у которой в числителе стоит единица. А знаменатель может быть любым. Например, у квадратного корня он равен двум. Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней.
И требования к этим действиям у них одинаковые. Если умножение, деление и возведение в степень не встречают затруднений у учеников, то сложение корней, как и их вычитание, иногда приводит в замешательство. А все потому что хочется выполнить эти операции без оглядки на знак корня. И здесь начинаются ошибки.
По каким правилам выполняется их сложение и вычитание?
Сначала нужно запомнить два категорических «нельзя»:
- нельзя выполнять сложение и вычитание корней, как у простых чисел, то есть невозможно записать подкоренные выражения суммы под один знак и выполнять с ними математические операции;
- нельзя складывать и вычитать корни с разными показателями, например квадратный и кубический.
Наглядный пример первого запрета: √6 + √10 ≠ √16, но √(6 + 10) = √16 .
Во втором случае лучше ограничиться упрощением самих корней. А в ответе оставить их сумму.
Теперь к правилам
- Найти и сгруппировать подобные корни. То есть те, у которых не только стоят одинаковые числа под радикалом, но и они сами с одним показателем.

- Выполнить сложение корней, объединенных в одну группу первым действием. Оно легко осуществимо, потому что нужно только сложить значения, которые стоят перед радикалами.
- Извлечь корни в тех слагаемых, в которых подкоренное выражение образует целый квадрат. Другими словами, не оставлять ничего под знаком радикала.
- Упростить подкоренные выражения. Для этого нужно разложить их на простые множители и посмотреть, не дадут ли они квадрата какого-либо числа. Понятно, что это справедливо, если речь идет о квадратном корне. Когда показатель степени три или четыре, то и простые множители должны давать куб или четвертую степень числа.
- Вынести из-под знака радикала множитель, который дает целую степень.
- Посмотреть, не появилось ли опять подобных слагаемых. Если да, то снова выполнить второе действие.
В ситуации, когда задача не требует точного значения корня, его можно вычислить на калькуляторе. Бесконечную десятичную дробь, которая высветится в его окошке, округлить. Чаще всего это делают до сотых. А потом выполнять все операции для десятичных дробей.
Чаще всего это делают до сотых. А потом выполнять все операции для десятичных дробей.
Это вся информация о том, как выполняется сложение корней. Примеры, расположенные ниже, проиллюстрируют вышесказанное.
Первое задание
Вычислить значение выражений:
а) √2 + 3√32 + ½ √128 — 6√18;
б) √75 — √147 + √48 — 1/5 √300;
в) √275 — 10√11 + 2√99 + √396.
а) Если следовать приведенному выше алгоритму, то видно, что для первых двух действий в этом примере ничего нет. Зато можно упростить некоторые подкоренные выражения.
Например, 32 разложить на два множителя 2 и 16; 18 будет равно произведению 9 и 2; 128 — это 2 на 64. Учитывая это, выражение будет записано так:
√2 + 3√(2 * 16) + ½ √(2 * 64) — 6 √(2 * 9).
Теперь нужно вынести из-под знака радикала те множители, которые дают квадрат числа. Это 16=4 2 , 9=3 2 , 64=8 2 . Выражение примет вид:
√2 + 3 * 4√2 + ½ * 8 √2 — 6 * 3√2.
Нужно немного упростить запись. Для этого производится умножение коэффициентов перед знаками корня:
√2 + 12√2 + 4 √2 — 12√2.
В этом выражении все слагаемые оказались подобными. Поэтому их нужно просто сложить. В ответе получится: 5√2.
б) Подобно предыдущему примеру, сложение корней начинается с их упрощения. Подкоренные выражения 75, 147, 48 и 300 будут представлены такими парами: 5 и 25, 3 и 49, 3 и 16, 3 и 100. В каждой из них имеется число, которое можно вынести из-под знака корня:
5√5 — 7√3 + 4√3 — 1/5 * 10√3.
После упрощения получается ответ: 5√5 — 5√3. Его можно оставить в таком виде, но лучше вынести общий множитель 5 за скобку: 5 (√5 — √3).
в) И снова разложение на множители: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36. После вынесения множителей из-под знака корня имеем:
5√11 — 10√11 + 2 * 3√11 + 6√11. После приведения подобных слагаемых получим результат: 7√11.
Пример с дробными выражениями
√(45/4) — √20 — 5√(1/18) — 1/6 √245 + √(49/2).
На множители нужно будет разложить такие числа: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Аналогично уже рассмотренным, нужно вынести множители из-под знака корня и упростить выражение:
Аналогично уже рассмотренным, нужно вынести множители из-под знака корня и упростить выражение:
3/2 √5 — 2√5 — 5/ 3 √(½) — 7/6 √5 + 7 √(½) = (3/2 — 2 — 7/6) √5 — (5/3 — 7) √(½) = — 5/3 √5 + 16/3 √(½).
Это выражение требует того, чтобы избавиться от иррациональности в знаменателе. Для этого нужно умножить на √2/√2 второе слагаемое:
5/3 √5 + 16/3 √(½) * √2/√2 = — 5/3 √5 + 8/3 √2.
Для полноты действий нужно выделить целую часть у множителей перед корнями. У первого она равна 1, у второго — 2.
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Шаги
Часть 1 из 2: Определение корнейОбозначение корней. Выражение под знаком корня () означает, что из этого выражения необходимо извлечь корень определенной степени.
- Корень обозначают знаком.
- Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: (27)
- Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).
- Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5 (2)
- Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
- Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.
Запомните, какие корни можно складывать, а какие нельзя. Так же, как нельзя складывать разные члены выражения, например, 2а + 2b 4ab, вы не можете складывать разные корни.
 Но вы можете сложить числа, стоящие под одним корнем, например, (2 + 3) = (5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236).
Но вы можете сложить числа, стоящие под одним корнем, например, (2 + 3) = (5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236).Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
2 (3) + (81) + 2 (50) + (32) + 6 (3)
- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
2 (3) + 2 (50) + (32) + 6 (3) + (81) - Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.

2 (50) + (32) + 2 (3) + 6 (3) + (81)
Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
У кубического корня из 3 подобных корней нет.
- Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.
Внимание, только СЕГОДНЯ!
Все интересное
Число, которое находится под знаком корня, часто мешает решению уравнения, с ним неудобно работать. Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из…
Корнем из числа x называется такое число, которое при возведении в степень корня будет равно x. Множителем называется умножаемое число. То есть, в выражении вида x*ª-&radic-y нужно внести x под корень. Инструкция 1Определите степень…
Если подкоренное выражение содержит набор математических действий с переменными, то иногда в результате его упрощения есть возможность получить относительно простое значение, часть которого можно вынести из под корня. 2 = x, x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …
2 = x, x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …
Корень в математике может иметь два значения: это арифметическое действие и каждое из решений уравнения, алгебраического, параметрического, дифференциального или любого другого. Инструкция 1Корень n-ной степени из числа a — это такое число, что…
При выполнении различных арифметических действий с корнями часто бывает необходимо умение преобразовывать подкоренные выражения. Для упрощения расчетов может понадобиться вынести множитель за знак радикала или внести под него. Это действие можно…
Корнем называют значок, обозначающий математическую операцию нахождения такого числа, возведение которого в указанную перед знаком корня степень должно дать число, указанное под этим самым знаком. Часто для решения задач, в которых присутствуют…
Знаком корня в математических науках называется условное обозначение для корней. Число, находящееся под знаком корня, называется подкоренным выражением. n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.…
n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.…
Корень из числа проще всего вычесть с помощью калькулятора. Но, если у вас нет калькулятора, тогда надо знать алгоритм вычисления квадратного корня. Дело в том, что под корнем сидит число в квадрате. Например, 4 в квадрате — это 16. То есть корень квадратный из 16 будет равен четырем. Так же 5 в квадрате — это 25. Поэтому корень из 25 будет 5. И так далее.
Если число небольшое, то его можно легко вычесть устно, к примеру, корень из 25 будет равен 5, а корень из 144-12. Также на калькуляторе можно посчитать, есть специальный значок корня, нужно вбить число и нажать на значок.
Поможет также таблица квадратных корней:
Есть еще способы, которые более сложные, однако очень эффективные:
Корень из какого либо числа можно вычесть с помощью калькулятора, тем более они есть в каждом телефоне на сегодняшний день.
Можно попробовать примерно прикинуть как может получится данное число, умножив одно число само на себя.
Вычислить корень квадратный из числа не сложно, особенно, если есть специальная таблица. Всем хорошо известная таблица еще с уроков алгебры. Такая операция называется извлечение квадратного корня из числа quot;aquot;, другими словами решение уравнения. Почти все калькуляторы, в смартфонах имеют функцию определения квадратного корня.
Результатом извлечения квадратного корня из известного числа будет другое число, которое, при возведении во вторую степень (квадрат), даст то самое число, которое нам известно. Рассмотрим одно из описаний расчтов, которое представляется кратким и понятным:
Вот видео по теме:
Вычеслить корень квадратный из числа можно несколькими способами.
Самым популярным способом — является использование специальной таблицы кореня (смотрите ниже).
Также на каждом калькуляторе есть функция при помощи которой можно узнать корень.
Или при помощи специальной формулы.
Извлечь квадратный корень из числа можно несколькими способами. Один из них — самый быстрый, с помощью калькулятора.
Один из них — самый быстрый, с помощью калькулятора.
Но если нет калькулятора, то можно это сделать вручную.
Результат получится точным.
Принцип практически такой же как деление столбиком:
Попробуем без калькулятора найти значение квадратного корняот числа, к примеру, 190969.
Таким образом, вс предельно просто. В вычислениях главное придерживаться определнных простых правил и логически размышлять.
Для этого нужна таблица квадратов
Вот например, корень из 100 = 10, из 20 = 400 из 43 = 1849
Сейчас практически все калькуляторы, в том числе и на смартфонах умеют высчитывать квадратный корень из числа. НО если калькулятора у вас нет, то можно найти корень из числа несколькими простыми способами:
Разложение на простые множители
Разложите подкоренное число на множители, являющиеся квадратными числами.
В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 это квадратное число. Разделив 400 на 25, вы получите 16, которое также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
Запишите это как: 400 = (25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть (а х b) = a x b .
Воспользовавшись этим правилом, извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
В нашем примере извлеките корень из 25 и из 16.
Если подкоренное число не раскладывается на два квадратных множителя (а это происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
Теперь вы можете оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу.
Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (1 = 1) и 4 (4 = 2). Таким образом, значение 3 расположено между 1 и 2. Та как значение 3, вероятно, ближе к 2, чем к 1, то наша оценка: 3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
Этот метод также работает с большими числами. Например, рассмотрим 35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (25 = 5) и 36 (36 = 6). Таким образом, значение 35 расположено между 5 и 6. Та как значение 35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что 35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Еще один способ разложите подкоренное число на простые множители.
Простые множители числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, 45 = (3 х 3 х 5). 3 можно вынести за знак корня: 45 = 35. Теперь можно оценить 5.
Рассмотрим другой пример: 88.
= (2 х 4 х 11)
= (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
2(2 х 11) = 22 х 11. Теперь можно оценить 2 и 11 и найти приблизительный ответ.
Может быть полезным будет еще это обучающее видео:
Чтобы извлечь корень из числа следует воспользоваться калькулятором, либо если нет подходящего, советую зайти вот на этот сайт и решить задачу с помощью онлайн калькулятора, который за секунды выдаст правильное значение.
Факт 1.
\(\bullet\)
Возьмем некоторое неотрицательное число \(a\)
(то есть \(a\geqslant 0\)
). 2=400\\
\hline \end{array}\]
2=400\\
\hline \end{array}\]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\]
Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\)
, то первоначально вы должны найти значения \(\sqrt{25}\)
и \(\sqrt{49}\)
, а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\)
или \(\sqrt b\)
при сложении \(\sqrt
a+\sqrt b\)
найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt
2+ \sqrt {49}\)
мы можем найти \(\sqrt{49}\)
– это \(7\)
, а вот \(\sqrt
2\)
никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt
2+7\)
. Дальше это выражение, к сожалению, упростить никак нельзя \(\bullet\)
Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad
\sqrt a:\sqrt b=\sqrt{a:b}\]
(при условии, что обе части равенств имеют смысл )
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot
2}=\sqrt{64}=8\)
;
\(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\)
;
\(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}=
5\cdot 8=40\)
. \(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
\(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\)
. Так как \(44100:100=441\)
, то \(44100=100\cdot 441\)
. По признаку делимости число \(441\)
делится на \(9\)
(так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\)
, то есть \(441=9\cdot 49\)
.
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}=
\sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\]
Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}=
\sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{
\dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot
\sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\)
Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\)
(сокращенная запись от выражения \(5\cdot
\sqrt2\)
). Так как \(5=\sqrt{25}\)
, то \
Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\)
,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\)
. 2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\)
и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\)
(число “пи”, приблизительно равное \(3,14\)
), \(e\)
(это число называют числом Эйлера, приблизительно оно равно \(2,7\)
) и т.д.
\(\bullet\)
Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\)
.
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
\(\bullet\)
Модуль вещественного числа \(a\)
– это неотрицательное число \(|a|\)
, равное расстоянию от точки \(a\)
до \(0\)
на вещественной прямой. 2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3
\(\bullet\)
Следует запомнить, что \[\begin{aligned}
&\sqrt 2\approx 1,4\\
&\sqrt 3\approx 1,7 \end{aligned}\]
Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
\(\bullet\)
Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. 2=168\cdot 168=28224\)
.
2=168\cdot 168=28224\)
.
Следовательно, \(\sqrt{28224}=168\)
. Вуаля!
Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор
. Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.

- Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.
В математике любое действие имеет свою пару-противоположность – в сущности, это представляет собою одно из проявлений гегелевского закона диалектики: «единство и борьба противоположностей». Одно из действий в такой «паре» направлено на увеличение числа, а другое, обратное ему – на уменьшение. Например, действие, противоположное сложению – это вычитание, умножению соответствует деление. Имеется и своя диалектическая пара-противоположность и у возведения в степень. Речь идет об извлечении корня.
Извлечь из числа корень такой-то степени – это значит вычислить, какое число необходимо возвести в соответствующую степень, чтобы в итоге получилось данное число. Две степени имеют свои отдельные названия: вторая степень называется «квадратом», а третья – «кубом». Соответствено, корни данных степеней приятно именовать квадратным корнем и кубическим. Действия с кубическими корнями – тема для отдельного разговора, а сейчас поговорим о сложении квадратных корней.
Две степени имеют свои отдельные названия: вторая степень называется «квадратом», а третья – «кубом». Соответствено, корни данных степеней приятно именовать квадратным корнем и кубическим. Действия с кубическими корнями – тема для отдельного разговора, а сейчас поговорим о сложении квадратных корней.
Начнем с того, что в ряде случаев квадратные корни проще сначала извлечь, а потом уже складывать результаты. Предположим, нам необходимо найти значение такого выражения:
Ведь совсем не сложно вычислить, что корень квадратный из 16 равен 4, а из 121 – 11. Следовательно,
√16+√121=4+11=15
Впрочем, это самый простой случай – здесь речь идет о полных квадратах, т.е. о таких числах, которые получаются при возведении в квадрат целых чисел. Но так бывает не всегда. Например, число 24 – это не полный квадрат (не найти такого целого числа, которое при возведении его во вторую степень дало бы в результате 24). То же самое относится к такому числу, как 54… Что делать, если нам необходимо сложить корни квадратные из этих чисел?
В таком случае мы получим в ответе не число, а другое выражение. Максимум, что мы можем тут сделать – это максимально упростить исходное выражение. Для этого придется вынести множители из-под корня квадратного. Посмотрим, как это делается, на примере упомянутым чисел:
Максимум, что мы можем тут сделать – это максимально упростить исходное выражение. Для этого придется вынести множители из-под корня квадратного. Посмотрим, как это делается, на примере упомянутым чисел:
Для начала разложим на множители 24 – таким образом, чтобы из одного из них легко можно было извлечь корень квадратный (т.е., чтобы он был полным квадратом). Такое числи есть – это 4:
Теперь проделаем то же самое с 54. В его составе таким числом будет 9:
Т.о., у нас получается следующее:
√24+√54=√(4*6)+ √(9*6)
Теперь извлечем корни из того, из чего можем их извлечь: 2*√6+3*√6
Здесь есть общий множитель, который мы можем вынести за скобки:
(2+3)* √6=5*√6
Это и будет результатом сложения – больше ничего тут извлечь нельзя.
Правда, можно прибегнуть к помощи калькулятора – правда, результат будет приблизительным и с огромным количеством знаков после запятой:
√6=2,449489742783178
Постепенно округляя его, мы получим приблизительно 2,5. Если нам все-таки хотелось бы довести до логического завершения решение предыдущего примера, мы можем умножить этот результат на 5 – и получится у нас 12,5. Более точного результата при таких исходных данных получить нельзя.
Если нам все-таки хотелось бы довести до логического завершения решение предыдущего примера, мы можем умножить этот результат на 5 – и получится у нас 12,5. Более точного результата при таких исходных данных получить нельзя.
Вынесение множителя за знак корня. 8-й класс
Цель урока. Обучающий аспект. Знать
определение и уметь применять свойства
квадратного корня. Научиться выносить множитель
за знак корня по составленному на уроке
алгоритму. Развивающий аспект. Развитие
математически грамотной речи. Развитие мышления
посредством: анализа и синтеза при работе над
выводом алгоритма; постановки и решения проблемы
(логические умозаключения при возникновении
проблемной ситуации и ее разрешении). Воспитывающий
аспект. Воспитывать соблюдение норм поведения
в коллективе, уважение к мнению окружающих при совместной
деятельности в группах.
Учащиеся знают и умеют |
Учащиеся не знают |
Знают определение квадратного корня и умеют применять его свойства. |
Способ вынесения множителя за знак корня. |
Тип урока. Урок изучения новых знаний.
Этапы урока 1. Подготовка к активной учебно-познавательной деятельности.Образовательные задачи этапа.
Обеспечение мотивации познавательной
деятельности учащихся. Актуализация опорных
знаний и умений. Создание условий для
самостоятельной формулировки учащимися темы и
целей урока. Форма организации обучения –
фронтальная.
Деятельность учителя |
Деятельность учащихся |
Вопрос о темах прошлых уроков. Предлагается дать определение арифметического квадратного корня из числа. Назвать свойства арифметического квадратного корня. Таблички со свойствами и определением вывешиваются на доске после ответов учащихся. Упражнения для устной работы представлены на доске. Вопрос учителя о том, зачем нужно решить эти примеры? При обращении к примеру №3, возникает
проблемная ситуация. Учащиеся не могут выполнить
это задание. Вопрос учителя о сходстве и
различиях в записанных выражениях. |
Предполагаемые ответы. Определение = в, в >= 0, в2 = а. Свойства : = ·; Представленные примеры являются подготовительными для успешной работы на уроке. Задания для устной работы:
= =100; = 9·7; = 50= 25 · 2; 20= 4·5; 27= 9·3; 80= 16·5; 125= 25·5; 98= 49·2. а) , б) и , и Ответ. В первом столбике нет
множителей перед корнями, а во втором – есть
множитель. Можно будет сравнить, если будет
единая запись. Формулировка цели урока. Научиться выносить множитель за знак корня. Запись темы урока в тетрадь. |
Образовательные задачи этапа. Организация деятельности учащихся по выводу алгоритма вынесения множителя за знак корня. Восприятие, осмысление, первичное запоминание способа действий. Форма организации обучения – индивидуальная, групповая. Метод обучения – продуктивный, частично-поисковый.
3. Первичная проверка понимания.Образовательные задачи этапа. Установление правильности и осознанности усвоения
Алгоритма вынесения множителя за знак корня. Форма организации обучения – фронтальная. Метод обучения – репродуктивный.
4. Домашнее задание.Образовательные задачи этапа. Обеспечение
понимания цели, содержания и способов выполнения
домашнего задания. Форма организации обучения –
фронтальная. Метод обучения – репродуктивный.
Обеспечение
понимания цели, содержания и способов выполнения
домашнего задания. Форма организации обучения –
фронтальная. Метод обучения – репродуктивный.
| Деятельность учителя | Деятельность учащихся |
Учитель предлагает выбрать примеры по теме урока и на повторение из учебника (“Алгебра-8” под ред. С. А. Теляковского – М.: Просвещение, 2007), которые учащиеся смогут выполнить самостоятельно дома. |
Предложения учащихся по д.з. обсуждаются № 407(б, г, е, з), 409(а-г), 420(а). Все ученики согласны с таким набором заданий и записывают его в дневник. |
 Подведение итогов урока.
Подведение итогов урока.
Образовательные задачи этапа. Анализ и оценка работы учащихся на уроке. Формулировка учащимися итогов урока: достижение цели, освоение способа вынесения множителя за знак корня.
Форма организации обучения – фронтальная, индивидуальная.
Метод обучения – репродуктивный.
| Деятельность учителя | Деятельность учащихся |
Вопросы о достижении цели урока. Задание по карточке, критерии оценки:
Работы выполняются под копирку, один
экземпляр сдается учителю. Проверка примеров по ответам, алгоритма по записям на доске. Выставление отметок в дневник. |
Вспомнить поставленную цель, озвучивание результата работы на уроке. Формулировка алгоритма. Работа над заданием по карточке, самопроверка, самооценка. Задание Приложение 3 Вынесите множитель за знак корня: а)= 3 б)= 5 в) Запишите алгоритм действий. |
Калькулятор корней онлайн — особенности извлечения корней с подробным объяснением
Калькулятор
Заполните поля для вычисления корня из числа
Онлайн-калькулятор – удобный ресурс, помогающий решать задачи, примеры, в котроых встречаются квадратные или степенные корни. Чтобы правильно извлекать корни уравнения онлайн, важно хорошо знать терминологию, основные математические понятия. Что такое квадратный корень – это процесс, обратный возведению натурального числа в квадрат (перемножению числа или понимаемого под ним математического объекта на самое себя).
Что такое квадратный корень – это процесс, обратный возведению натурального числа в квадрат (перемножению числа или понимаемого под ним математического объекта на самое себя).
Таблица корней от 0 до 99
Извлечение корней
Представить работу калькулятора можно с помощью таблицы квадратов двузначных чисел. По горизонтали в каждом из столбцов указаны единицы от одного до девяти, по вертикали – десятки. Достаточно выяснить, в какой из ячеек находится подкоренное число. Несложно догадаться, что по горизонтали в левой крайней колонке указаны десятки, в верхней строчке таблицы – единицы.
Допустим, под корнем стоит 7056. Находим значение в таблице. Это 8 десятков и 4 единицы, число 84. То есть, 84 это квадратный корень онлайн из 7056. Онлайн-калькулятор находит значения любого подкоренного выражения по подобным таблицам.
При перемножении отрицательных величин получается величина, больше нуля. Извлечение арифметического квадратного корня возможно только из положительного числа (матрицы).
Извлечение арифметического квадратного корня возможно только из положительного числа (матрицы).
Свойства арифметического квадратного корня
Пользоваться онлайн-калькулятором будет проще, если сначала упростить выражение, привести в удобный для вычисления вид. Чтобы преобразовать подкоренное значение, стоит воспользоваться правилами умножения, деления корней, возведение их в степень. Свойства корней стоит вызубрить, их всего три. Каждое рассмотрено ниже отдельно. Решение корней онлайн упрощается после математических преобразований подкоренного значения или выражения. Для этого достаточно знаний арифметики и азов алгебры.
Умножение корней
Если произведение подкоренного выражения можно представить в виде двух множителей, достаточно перемножить корни, извлеченные из этих множителей: допустим, под корнем стоит число 576. Преобразуем его в два множителя: 64 и 9. Затем извлекаем корень из 64, он равен 8, подобную процедуру проводим со вторым из множителей. Квадратный корень из девяти равен 3. Осталось найти результат: 8х3=24. Корень 576 равен 24.
Квадратный корень из девяти равен 3. Осталось найти результат: 8х3=24. Корень 576 равен 24.
Формулой свойство изображается так:
Раскладывая подкоренное значение на множители, можно значительно упростить процесс вычисления квадратных корней.
Деление корней
Следующее свойство удобно для извлечения корней из дробных чисел. Когда подкоренное выражение представлено в виде дроби, следует воспользоваться правилом деления. Проще запомнить это свойство по формуле:
Обратная формула трактуется следующим образом: корень из частного равен частному корней.
Допустим, нужно извлечь квадратный корень из дроби 25/144. Для этого необходимо извлечь корень из 25, это 5. Затем подобную манипуляцию произвести с делителем дроби: корень 144 равен двенадцати. После извлечения корня из 25/144 получаем дробь 5/8. Если корень необходимо вычислить из десятичной дроби, нужно представить ее в виде натуральной. Например, 0,64 это 64/100. В результате получаем 8/10 или 0,8. Все довольно просто. Если из делимого или делителя корень не извлекается, при решении примеров или задач его оставляют под знаком корня.
Например, 0,64 это 64/100. В результате получаем 8/10 или 0,8. Все довольно просто. Если из делимого или делителя корень не извлекается, при решении примеров или задач его оставляют под знаком корня.
Возведение в степень
Последнее свойство корней – это возведение его в степень. Тут все просто: достаточно перенести степень под корень, подставить к подкоренному выражению.
При возведении подкоренного числа в квадрат с последующим извлечением квадратного корня получаем первоначальное подкоренное выражение. На слух выражение воспринимается сложно. Проще усвоить формулу:
Из формулы видно, что этим свойством удобно пользоваться при возведении квадратного корня в четную степень, ее можно сразу делить на два и убирать знак корня. Как всегда, пример: чтобы возвести в шестую степень квадратный корень числа 3, необходимо возвести число 3 в куб, степенной показатель 6 поделить пополам.
Внесение под знак корня
При решении задач и примеров возникает необходимость вносить под корень множитель. Например, чтобы вычислить 4 корня из 4, можно представить выражение в виде двух корней: первым подкоренным выражением будет 42, второе останется неизменным. Финальное выражение нетрудно произвести, воспользовавшись формулами:
Например, чтобы вычислить 4 корня из 4, можно представить выражение в виде двух корней: первым подкоренным выражением будет 42, второе останется неизменным. Финальное выражение нетрудно произвести, воспользовавшись формулами:
Формулу запомнить легко, она может пригодиться на экзамене.
Сравнение корней
Для графического решения уравнений нередко приходится сравнивать корни. Как это сделать быстро при сравнении квадратных корней? Воспользоваться еще одним правилом: чем больше подкоренное выражение, тем больше значение корня. Допустим, нужно сравнить
2√3 и 3√2. Вносим числа в подкоренные выражения. Получаем под знаками корней два выражения: 22х3 и 32х2. Осталось сравнить числа 12 и 18. Второе больше.
Свойства квадратных корней распространяются на другие коренные значения: четные или нечетные. Важно помнить, что в подкоренном выражении с четным показателем не может быть отрицательных чисел. С нечетными числами такое возможно. Результат в этом случае тоже будет отрицательным.
С нечетными числами такое возможно. Результат в этом случае тоже будет отрицательным.
На этом экскурс по свойствам, сравнению корней можно считать исчерпывающим. Зная эти правила обращения с корнями, можно упростить сложное выражение. Пользоваться нашим онлайн-калькулятором с подсказками очень просто.
«Вынесение множителя за знак корня. Внесение множителя под знак корня» 8 класс
МБОУ «Кокрекская средняя общеобразовательная школа»
Хасавюртовский район ,с.Кокрек
Тема: «Вынесение множителя за знак корня.
Внесение множителя под знак корня»
8 класс
Составитель: учитель математики
Шамсудинова Т.Ж.
2019 г.
План-конспект урока
Цель урока: изучение правил преобразований с квадратными корнями (вынесение множителя за знак корня и внесение множителя под знак корня), и умение применять их в простейших случаях.
Задачи:
Образовательные:
· обеспечить в ходе урока усвоение умений выносить множитель из-под знака корня и вносить множитель под знак корня;
· провести диагностику усвоения системы знаний и умений и её применения для выполнения практических заданий стандартного уровня с переходом на более высокий уровень
Развивающие:
· развивать внимание, логическое мышление, память, наблюдательность, сообразительность;
· приёмы сравнения, умение анализировать, делать выводы,
развивать математическую речь,
·
Развить познавательную
активность, положительную мотивацию к предмету.
· Развивать потребности к самообразованию
Воспитательные:
· содействовать формированию коммуникативного опыта; доброжелательности, взаимопомощи, сотрудничества;
· содействовать формированию потребности в познании, интереса к математике как к науке;
· содействовать формированию умения адекватно оценивать собственные достижения;
Планируемые результаты
в направлении личностного развития:
— уметь ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи;
— уметь осознавать и понимать личную ответственность за будущий результат;
в метапредметном направлении:
-уметь использовать математическую терминологию;
— уметь использовать эталон для самопроверки;
— уметь воспринимать устную речь;
в предметном направлении:
— владеть математическими знаниями и умениями, необходимыми для продолжения образования;
— уметь использовать математическую терминологию;
-уметь
применять теоремы о квадратных корнях для вычисления значений выражений,
содержащих квадратные корни.
Тип урока: урок изучения нового материала.
Формы работы с учащимися: фронтальная, индивидуальная, групповая, с использованием ЭОР.
Методы и технологии, используемые на уроке: проблемно-поисковые, ИКТ, дифференцированные, групповые, разноуровневые , игровые
Оборудование: компьютер, проектор.
Дидактические средства: рабочая тетрадь, раздаточный материал (цветные кружки, памятки, карточки).
Базовый учебник: « Алгебра» 8 класс, Макарычев Н.Ю., Миндюк Н.Г. и др., издательство « Просвещение», 2014г.
Ресурсное обеспечение:
1. мультимедийный проектор;
2.экран;
3.компьютер.
Математика сложна-
Это знает каждый.
Только всем она нужна
Её знанье важно.
Если хочешь чтоб успех
Рядом шёл по жизни,
Ты решай не меньше всех,
будет всё отлично!
План урока
1. Организационный момент
Организационный момент
2. Актуализация знаний.
3. Усвоение нового материала.
4. Первичная проверка понимания.
5. Закрепление знаний, отработка умений.
6. Проверка усвоения темы.
7. Домашнее задание
8. Подведение итогов. Рефлексия.
Ход урока
Девиз урока:
Мало иметь хороший ум, главное – хорошо его применять.
Р. Декарт.
I. Организационный момент.
Приветствие учащихся и гостей.
Древнегреческий математик Фалес говорил:
— Что есть больше всего на свете? – Пространство.
— Что быстрее всего? – Ум.
— Что мудрее всего? – Время.
— Что приятнее всего? – Достичь
желаемого.
Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата.
Прежде чем приступить к новой теме урока, давайте вспомним с вами пройденный материал.
2.Подготовка к активной учебно-познавательной деятельности
Образовательные задачи этапа:
— обеспечение мотивации познавательной деятельности учащихся;
— актуализация опорных знаний и умений;
— создание условий для самостоятельной формулировки учащимися темы и целей урока.
Формы организации обучения – фронтальная.
Методы обучения – репродуктивный.
Актуализация знанийУстная работа, с помощью которой ведётся повторение основных фактов, свойств на основе систематизации знаний. Подготовка класса к изучению нового материала.
Вычислить:
— 15 +
«Установи соответствие»
1) Соедини линиями выражения,
соответствующие друг другу.
∙ 20
()²
∙
а
()²
«Найди ошибку»
=8 (верно) =0 (верно) = ( ошибка) = (ошибка) =20 (верно)
=900 (ошибка) = 8 (ошибка) =11а2 (верно)
« Представьте»
1) …числа в виде произведения таких множителей, чтобы один из них являлся квадратом рационального числа.
125; 72; 27; 8; 75
2)…. числа в виде
арифметического корня:
числа в виде
арифметического корня:
3, 11, 4, 15, 2.
« Сравните» ( что больше?):
а) и ; б) и ; в) 7 и ; г) и ;
Сравнить: и
Как можно это сделать?
Решение этой проблемы находим при изучении новой темы.
3.Усвоение нового материала
Образовательные задачи этапа:
организация деятельности учащихся по выводу алгоритма вынесения множителя за знак корня и внесение множителя под знак корня;
восприятие, осмысление, первичное запоминание способа действий.
Формы организации обучения – индивидуальная, групповая.
Методы обучения – продуктивный, частично-поисковый.
Вопрос учителя о
сходстве и различиях в записанных выражениях.
Ответ. В первом столбике нет множителей перед корнями, а во втором — есть множитель. Можно будет сравнить, если будет единая запись.
Учитель подводит детей к формулировке темы урока. Дети формулируют тему урока и записывают в тетрадь. Вместе с учителем ставят задачи урока:
1) Научиться выносить множитель за знак корня и вносить множитель под знак корня.
2)Развивать логическое мышление, вычислительные навыки и
Сообразительность, стремление к познанию нового,
3) Воспитывать ответственность, самостоятельность, культуру речи.
Учитель объясняет, что сегодня ученики узнают два преобразования. Поэтому для удобства надо разделить полстраницы пополам. И оставить строку для названия преобразований.
Учитель: В левом столбце упростите . Каким образом можно представить подкоренное выражение? Ученики работают по условию –«подумай – запиши – обсуди в команде».
В ходе фронтальной беседы
учитель с учениками перебирают возможные варианты разложения числа 72. Обсуждают, какое из разложений удобно. Решают пример, обосновывая каждый шаг.
Обсуждают, какое из разложений удобно. Решают пример, обосновывая каждый шаг.
Появляется запись . Сравнивают подкоренные выражения в начале примера и в конце. Делают вывод, что упростили подкоренное выражение. Повторяют шаги.
Один из учеников у доски пробует таким же образом упростить ? Обсуждают название данного преобразования.
Формулируют алгоритм вынесения множителя из-под корня. В это время алгоритм появляется на экране.
Алгоритм ВЫНЕСЕНИЯ МНОЖИТЕЛЯ ИЗ-ПОД ЗНАКА КОРНЯ:
1) Представим подкоренное выражение в виде произведения таких множителей, чтобы из одного можно было бы извлечь квадратный корень.
2) Применим теорему о корне из произведения.
3) Извлечем корень
Запишем данное преобразование и в буквенном виде:
Если а = a
После
этого переходят ко второй колонке. Определяют, какое там будет преобразование.
Решают пример – представить в виде корня. Обсуждают способ решения.
Применяют этот способ для примера . Формулируют алгоритм, в ходе повторения
шагов. Появляется алгоритм.
Определяют, какое там будет преобразование.
Решают пример – представить в виде корня. Обсуждают способ решения.
Применяют этот способ для примера . Формулируют алгоритм, в ходе повторения
шагов. Появляется алгоритм.
Алгоритм ВНЕСЕНИЕ МНОЖИТЕЛЯ ПОД ЗНАК КОРНЯ
1) Представим число, стоящее перед корнем в виде арифметического квадратного корня.
2) Преобразуем произведение квадратных корней в квадратный корень из произведения подкоренных выражений..
3) Выполним умножение под знаком корня.
Пример.
Запишем данное преобразование в буквенном виде:
Если а.
4.Первичная проверка понимания.
Образовательные задачи этапа: установление правильности и осознанности усвоения алгоритма вынесения множителя за знак корня.
Форма организации обучения – фронтальная.
Метод обучения – репродуктивный.
Учитель раздает листочки, на
которых записаны алгоритмы, и приведены примеры, которые решали. Ученики читают
хором каждый алгоритм. Алгоритм
Ученики читают
хором каждый алгоритм. Алгоритм
Вынести множитель из-под корня | Внести множитель под корень |
1. Разложить подкоренное выражение на множители удобным способом. | 1. Число, стоящее перед корнем, представить в виде корня. |
2. Применить теорему «корень из произведения». 3. Извлечь корень. | 2. Применить теорему «произведение корней». 3. Выполнить умножение под знаком корня. |
5.Закрепление знаний, отработка умений.
(доска, проектор)
Работа в
парах. Сравнение по эталону. (За каждое правильное задание 1 балл)
Сравнение по эталону. (За каждое правильное задание 1 балл)
1) № 407 (г,д,), № 410 (а,в), № 414 (а,в)
2). Расшифруй слово
Найди соответствие и составь слово
Получилось слово — радикал
Немного истории.
• Радикал в переводе Radix- имеет два значения: сторона и корень. Греческие математики вместо «извлечь корень» говорили «найти сторону квадрата по его данной величине (площади)»
• Начиная с XIII века, итальянские и другие европейские математики обозначали корень латинским словом Radix или сокращенно R.
• В XV веке Н.Шюке писал R212 вместо
•
Название «радикал» связано с
термином «корень»: по-латыни корень – radix (он же редис – корнеплод). Также
слово «радикальный» в русском языке является синонимом слова «коренной».
Происхождение же символа связывают с написанием латинской буквы r.
• Радикальные изменения, те. коренные изменения.
3) Попробуйте отгадать, кто из ученых впервые ввел знак
арифметического квадратного корня.
Найди наибольшее числовое значение —
получишь ответ.
Б. Паскаль –
Р. Декарт –
П.Ферма –
Х. Рудольф –
Правильный ответ – Р. Декарт
Рене Декарт французский дворянин, в 1629 г. переселился в Голландию. Воин, математик, философ, физиолог, мыслитель.
Декарт – математик:
ü заложил основы аналитической геометрии.
ü Ввел буквенные обозначения в алгебру x2, y3, a + b и т.д.
ü Ввёл Декартовы координаты, определяющие функцию переменной величины.
ü Ввёл в 1637 г современный знак радикала
ü Разработал общий геометрический способ решения уравнений 3, 4, 5, 6 степеней.
Декарт – физик:
ü Дал понятие импульса силы.
ü Ввел понятие рефлекса (дуга Декарта).
ü Высказал закон сохранения количества движения.
6) Проверка усвоения темы
Разноуровневая самостоятельная работа (на листочках)
1 уровень «3»
— закончите вынесение множителя из-под знака корня
— закончите внесение множителя
2 уровень «4»
— сравните значения выражений
и
и
3 уровень «5»
— расположите в порядке возрастания числа
7.Домашнее задание.
Образовательные задачи этапа: обеспечение понимания цели, содержания и способов выполнения домашнего задания.
Форма организации обучения – фронтальная.
Метод обучения – репродуктивный.
П.18 № 407 (а,в,д,ж), 410(б,д,е), 414 (в,г)
8.Подведение итогов урока
Образовательные задачи этапа:
— анализ и оценка работы учащихся на уроке;
—
формулировка учащимися итогов
урока: достижение цели, освоение способа вынесения множителя за знак корня.
Форма организации обучения – фронтальная, индивидуальная.
Метод обучения – репродуктивный.
Учитель: — С какими преобразованиями вы познакомились на уроке?
Ребята, какую цель вы для себя ставили на урок?
Достигли ли вы её?
. Рефлексия.
Наше занятие подходит концу. Пожалуйста, поделитесь своими мыслями о сегодняшнем занятии (хотите одним предложением).
· Трудным ли для тебя был материал урока?
· На каком из этапов урока было труднее всего, легче всего?
· Что нового ты узнал на уроке? Чему научился?
· Работал ли ты на уроке в полную меру сил?
· Как эмоционально ты чувствовал себя на уроке?
Оцени свою работу на уроке
«Где отсутствует точное знание, там действуют догадки,
а из десяти догадок девять – ошибки.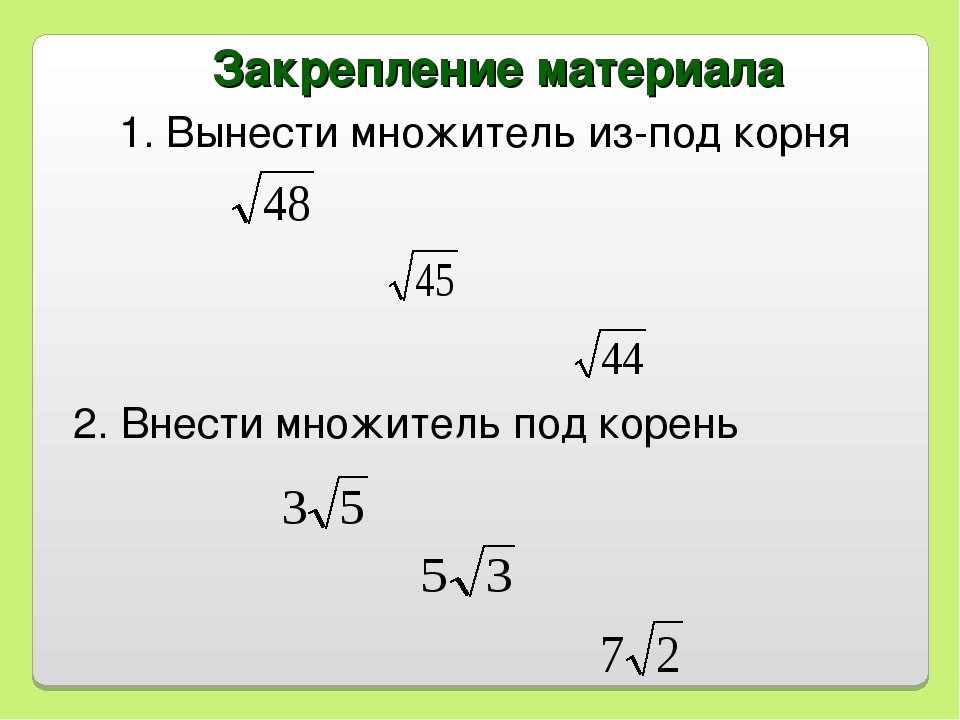 »
»
Думайте и применяйте свои знания!
— Спасибо за урок, желаю вам дальнейших успехов в освоении трудной, но интересной науки под названием математика!
Литеатура
1. Афанасьева Т. Л., Топилина Л. А. Алгебра. 8 класс: поурочные планы по учебнику Макарычева Ю. Н., Миндюк Н. Г., Нешкова К. И., Суворовой С. Б. Волгоград: Издательство «Учитель», 2005
2. Кузнецова Л. В., Суворова С. Б., Бунимович Е. А., Колесникова Т. В., Рослова Л. О. ГИА выпускников 9 классов в новой форме. Математика. 2011/ ФИПИ – М.: Интеллект – центр, 2011
3. Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Под редакцией С. А. Теляковского. Алгебра. Учебник для 8 класса. – М.: Просвещение. 1998.
Вынести множитель из под знака корня онлайн. Формулы корней
Инструкция
Подберите подкоренному числу такой множитель, вынесение которого из под корня действительно выражение — иначе операция потеряет . Например, если под знаком корня с показателем, равным трем (кубический корень), стоит число 128, то из под знака можно вынести, например, число 5. При этом подкоренное число 128 придется разделить на 5 в кубе: ³√128 = 5∗³√(128/5³) = 5∗³√(128/125) = 5∗³√1.024. Если наличие дробного числа под знаком корня не противоречит условиям задачи, то можно в таком виде. Если же нужен более простой вариант, то сначала разбейте подкоренное выражение на такие целочисленные множители, кубический корень одного из которых будет являться целым число м. Например: ³√128 = ³√(64∗2) = ³√(4³∗2) = 4∗³√2.
Например, если под знаком корня с показателем, равным трем (кубический корень), стоит число 128, то из под знака можно вынести, например, число 5. При этом подкоренное число 128 придется разделить на 5 в кубе: ³√128 = 5∗³√(128/5³) = 5∗³√(128/125) = 5∗³√1.024. Если наличие дробного числа под знаком корня не противоречит условиям задачи, то можно в таком виде. Если же нужен более простой вариант, то сначала разбейте подкоренное выражение на такие целочисленные множители, кубический корень одного из которых будет являться целым число м. Например: ³√128 = ³√(64∗2) = ³√(4³∗2) = 4∗³√2.
Используйте для подбора множителей подкоренного числа , если вычислять в уме степени числа не представляется возможным. Особенно это актуально к корня м с показателем степени больше двух. Если есть доступ в интернет, то можно производить вычисления встроенными в поисковые системы Google и Nigma вычислителями. Например, если надо найти наибольший целочисленный множитель, который можно вынести из под знака кубического корня для числа 250, то перейдя на сайт Google введите запрос «6^3», чтобы проверить, нельзя ли вынести из под знака корня шестерку. 3. Результатом будет 125, а это позволяет разбить 250 на множители 125 и 2, а значит вынести из под знака корня число 5, оставив там число 2.
3. Результатом будет 125, а это позволяет разбить 250 на множители 125 и 2, а значит вынести из под знака корня число 5, оставив там число 2.
Источники:
- как вынести из под корня
- Квадратный корень из произведения
Вынести из-под корня один из сомножителей необходимо в ситуациях, когда нужно упростить математическое выражение. Бывают случаи, когда выполнить нужные вычисления с помощью калькулятора невозможно. Например, если вместо чисел используются буквенные обозначения переменных.
Инструкция
Разложите подкоренное выражение на простые сомножители. Посмотрите, какой из сомножителей повторяется столько же раз, указано в показателей корня , или больше. Например, вам нужно извлечь корень из числа а в четвертой степени. В этом случае число можно представить как а*а*а*а = а*(а*а*а)=а*а3. Показателю корня в этом случае будет соответствовать сомножитель а3. Его и нужно вынести за знак .
Извлеките корень получившихся подкоренных в отдельности там, где это возможно. Извлечение корня представляет собой алгебраическое действие, обратное возведению в степень. Извлечение корня произвольной степени из числа найти такое число, которое при возведении его в эту произвольную степень даст в результате данное число. Если извлечение корня произвести нельзя, оставьте подкоренное выражение под знаком корня так, как оно есть. В результате проведения перечисленных действий вы произведете вынесение из-под знака корня .
Извлечение корня представляет собой алгебраическое действие, обратное возведению в степень. Извлечение корня произвольной степени из числа найти такое число, которое при возведении его в эту произвольную степень даст в результате данное число. Если извлечение корня произвести нельзя, оставьте подкоренное выражение под знаком корня так, как оно есть. В результате проведения перечисленных действий вы произведете вынесение из-под знака корня .
Видео по теме
Обратите внимание
Будьте внимательны при записи подкоренного выражения в виде сомножителей – ошибка на этом этапе приведёт к неправильным результатам.
Полезный совет
При извлечении корней удобно пользоваться специальными таблицами или таблицами логарифмических корней – этим вы значительно сократите время на нахождение правильного решения.
Источники:
- знак извлечения корня в 2019
Упрощение алгебраических выражений требуется во многих разделах математики, в том числе при решении уравнений высших степеней, дифференцировании и интегрировании. При этом используется несколько методов, включая разложение на множители. Чтобы применить этот способ, нужно найти и вынести общий множитель за скобки .
При этом используется несколько методов, включая разложение на множители. Чтобы применить этот способ, нужно найти и вынести общий множитель за скобки .
Инструкция
Вынесение общего множителя за скобки – один из самых распространенных способов разложения . Этот прием применяется для упрощения структуры длинных алгебраических выражений, т.е. многочленов. Общим может быть число, одночлен или двучлен, а для его поиска применяется распределительное свойство умножения.
Число.Посмотрите внимательно на коэффициенты при каждом многочлена, можно ли разделить их на одно и то же число. Например, в выражении 12 z³ + 16 z² – 4 очевидным является множитель 4. После преобразования получится 4 (3 z³ + 4 z² — 1). Иными , это число является наименьшим общим целочисленным делителем всех коэффициентов.
Одночлен.Определите, ли одна и та же переменная в каждый из слагаемых многочлена. Предположим, что это так, теперь посмотрите на коэффициенты, как в предыдущем случае. 4 – 2 z³ + z² — 4 z + 4 = 0. Путем простой подстановки найдите z1 = 1 и z2 = 2, значит, за скобки можно вынести двучлены (z — 1) и (z — 2). Для того, чтобы найти оставшееся выражение, воспользуйтесь последовательным делением в столбик.
4 – 2 z³ + z² — 4 z + 4 = 0. Путем простой подстановки найдите z1 = 1 и z2 = 2, значит, за скобки можно вынести двучлены (z — 1) и (z — 2). Для того, чтобы найти оставшееся выражение, воспользуйтесь последовательным делением в столбик.
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Пусть дано выражение . Мы можем этот корень представить в более простом виде, применив к нему теорему об извлечении корня из произведения (§ 97):
Точно так же
Такое преобразование называется вынесением множителя за знак корня.
В результате применения этого преобразования данное выражение упрощается и часто сокращаются требуемые вычисления. В этом можно убедиться на следующих примерах.
Пр и мер 1. Вычислить с точностью до 0,01 выражение
Вычислим каждый из корней с точностью до 0,01:
Нам пришлось извлечь квадратный корень из трёх чисел, и притом мы не можем быть уверены, что результат действительно даст величину выражения с точностью до 0,01 (для уверенности в этом нужно было бы вычислить корни с точностью большей, чем заданная).
Попробуем упростить данное выражение, вынося за знак радикала те множители, которые возможно:
Итак, после преобразования нам придётся извлечь квадратный корень только из одного числа.
Вычислив его с точностью до 0,01, найдём:
Теперь видно, что в первом вычислении мы сделали ошибку на одну сотую, то есть получили результат не с заданной точностью.
Пример 2. Вычислить выражение
Подставив в данное выражение получим:
Нам придётся извлечь корень из шестизначного числа.
Мы значительно упростим вычисления, если предварительно вынесем за знак корня те множители, которые возможно. Будем иметь:
Подставив теперь легко найдём:
Во всех предыдущих примерах подкоренное выражение мы разлагали на множители, выделяя такие, показатель которых делится на два, и извлекали из них корень. В дальнейшем надо приобрести навык сразу выносить нужные множители за знак корня, не прибегая к предварительному разложению на множители подкоренного выражения.
Как видно из примеров, для вынесения множителей из-под знака квадратного корня достаточно показатель каждого множителя разделить на два и записать перед знаком корня этот множитель с показателем, равным полученному частному, а под знаком корня тот же множитель с показателем, равным полученному остатку.
В предыдущем примере .
2. Внесение множителей под знак квадратного корня.
Иногда бывает полезно, наоборот, подвести под знак корня множители, стоящие перед ним.
Пусть, например, требуется вычислить с точностью до 0,001 выражение Вычислив с точностью до 0,001 и умножив результат на 20, получим:
Заранее можем сказать, что результат не соответствует заданной точности, так как, умножив приближённое число 2,646 на 20, мы увеличили в 20 раз и ошибку.
Чтобы получить ббльшую точность, возьмём с точностью до 0,0001. Получим:
Но мы не можем и теперь быть уверены, что достигли требуемой точности.
Произведём вычисление другим способом. Представим данное выражение в таком виде:
Вычислив с точностью до 0,001, получим:
Такоза действительная величина данного выражения, вычисленная с точностью до 0,001.
Рассмотренное преобразование называется внесением множителя под знак корня.
Приведённый пример показывает целесообразность в некоторых случаях такого преобразования.
Чтобы внести под знсис квадратного корня стоящие перед ним множители, достаточно возвести эти множители в квадрат и подкоренное выражение умножить на полученный результат.
В двух первых примерах сначала множитель, стоящий перед знаком корня, был подведён под знак корня, затем произведено умножение.
В третьем примере обе эти операции были выполнены сразу.
3. Приведение подкоренного выражения к целому виду.
Если подкоренное выражение дробное, то часто бывает целесообразно привести его к целому виду, или, как говорят, освободить подкоренное выражение от знаменателя.
Покажем на примерах, как это делается.
Пр имер 1.
Чтобы из знаменателя подкоренного выражения можно было извлечь корень, умножим числитель и знаменатель этого выражения на а. Получим.
В данном материале мы продолжим рассказывать о том, как преобразовывать рациональные выражения, а конкретно о том, как правильно выносить множитель из-под знака корня. В первом пункте объясним, зачем нужно такое преобразование, далее покажем, как именно оно делается и сформулируем общее для всех случаев правило. Далее покажем, какие существуют методы, чтобы привести подкоренное выражение к удобному для преобразования виду, и разберем примеры решений задач.
Далее покажем, какие существуют методы, чтобы привести подкоренное выражение к удобному для преобразования виду, и разберем примеры решений задач.
Yandex.RTB R-A-339285-1
Что такое вынесение множителя из-под знака корня
Чтобы лучше понять суть подобного преобразования, нужно сначала сформулировать, что такое вообще вынесение множителя из-под знака корня. Сформулируем определение:
Определение 1
Вынесение множителя из-под знака корня представляет собой замену выражения B n · C n на произведение B · C n с условием, что n – нечетное число, или же на произведение B · C – где n – четное число, а B и C – другие числа и выражения.
Если мы имеем в виду только квадратный корень, то есть число n равно двум, то процесс вынесения множителя можно свести к замене выражения B 2 · C на произведение B · C . Отсюда и название данного преобразования: после того, как оно было проведено, множитель B y оказывается свободным от знака корня.
Приведем примеры, поясняющие данное определение. Так, допустим, у нас есть выражение 2 2 · 3 . Оно аналогично B 2 · C , где B равно двум, а C – трем. Заменив данный корень на произведение 2 · 3 и опустив знаки модулей (это можно сделать, поскольку оба множителя являются положительными числами), мы получим 2 · 3 . Мы вынесли множитель 2 2 из-под знака корня.
Так, допустим, у нас есть выражение 2 2 · 3 . Оно аналогично B 2 · C , где B равно двум, а C – трем. Заменив данный корень на произведение 2 · 3 и опустив знаки модулей (это можно сделать, поскольку оба множителя являются положительными числами), мы получим 2 · 3 . Мы вынесли множитель 2 2 из-под знака корня.
Приведем еще один пример подобного преобразования. У нас есть выражение (x 2 — 3 · x · y · z) 2 · x = x 2 — 3 · x · y · z · x . Здесь из-под корня был вынесен не просто числовой множитель, а целое выражение с переменными (x 2 − 3 · x · y · z) 2 .
Оба примера относятся к случаю вынесения множителя из-под квадратного корня. Можно также производить данные преобразования и для корней n -ной степени. Вот пример с кубическим корнем: (3 · a 2) 3 · 2 · a 2 3 = 3 · a 2 · 2 · a 2 3
Пример с корнем шестой степени: 1 2 · x 2 + y 2 6 · 5 · (x 2 + y 2) 6 можно преобразовать в произведение 1 2 · x 2 + y 2 · 5 · (x 2 · y 2) 6 , которое, в свою очередь, упрощается до 1 2 · (x 2 + y 2) · 5 · (x 2 + y 2) 6 . В данном случае мы выносим множитель 1 2 · x 2 + y 2 6 .
В данном случае мы выносим множитель 1 2 · x 2 + y 2 6 .
Мы выяснили, что такое вынесение множителя из-под знака корня. Теперь перейдем к доказательствам, т.е. поясним, почему произведение, полученное в итоге данного преобразования, равнозначно исходному выражению.
Почему возможно заменить корень на произведение
В этом пункте мы будем разбираться, как возможна такая замена и почему корень B n · C n равнозначен произведениям B · C n и B · C n . Обратимся к ранее изученным теоретическим положениям.
Когда мы разбирали преобразование иррациональных выражений, у нас получились некоторые важные результаты, которые мы собрали в таблицу. Здесь нам будут нужны только два из них:
1. Выражение A · B n при условии нечетности n может быть заменено на A n · B n , а для четных n – A n · B n .
2. Выражение A n n при нечетном значении n может быть преобразовано в A , а при четном – в | A | .
Определение 2
Используя эти результаты и зная основные свойства модуля, мы можем вывести следующее:
- при четном n: B n · C n = B n n · C n = B · C n ;
- при нечетном n: B n · C n = B n n · C n = B n n · C n = B · C n .

Эти выражения лежат в основе преобразований, которые мы проводим, вынося множитель из-под знака корня.
Следовательно, можно вывести две формулы:
Определение 3
С помощью данных формул можно выполнить вынесение из-под корня сразу нескольких множителей.
Основное правило вынесения множителя из-под корня
Когда нам нужно решать примеры с подобными преобразованиями, чаще всего приходится предварительно приводить подкоренное выражение к виду B n · C . С учетом этого момента мы можем записать следующие правила.
Определение 4
Для вынесения множителя из-под корня в выражении A n нужно предварительно привести корень к виду B n · C n и после этого перейти к произведению B · C n (при нечетном показателе) или к B · C n (при четном показателе, при необходимости раскрываем модули).
Таким образом, схема решения подобных задач выглядит следующим образом:
A n → B n · C n → B · C n , е с л и n — н е ч е т н о е B · C n , е с л и n — ч е т н о е
Если нам надо вынести несколько множителей, то действуем так:
A n → B 1 n · B 2 n · . . . · B k n · C n → B 1 · B 2 · . . . · B k · C n , е с л и n — н е ч е т н о е B 1 · B 2 · . . . · B k · C n , е с л и n — ч е т н о е
. . · B k n · C n → B 1 · B 2 · . . . · B k · C n , е с л и n — н е ч е т н о е B 1 · B 2 · . . . · B k · C n , е с л и n — ч е т н о е
Теперь можно переходить к решению задач.
Задачи на вынесение множителя из-под знака корня
Пример 1Условие: выполните вынесение множителя за знак корня в трех выражениях: 2 2 · 7 , — 1 2 3 2 · 5 , (- 0 , 4) 7 · 11 7 .
Решение
Мы видим, что подкоренные выражения во всех трех случаях уже имеют нужный нам вид. Поскольку в первых двух примерах показателем корня является четное число, а в третьем – нечетное, записываем следующее:
- Показатель корня равен 2 . Берем правило вынесения множителя для четного показателя и вычисляем: 2 2 · 7 = 2 · 7 = 2 · 7
- Во втором выражении показатель тоже четный, значит, — 1 2 3 2 · 5 = — 1 2 3 · 5 = 1 2 3 · 5
В этом случае мы можем сначала преобразовать выражения, исходя из основных свойств корня:
— 1 2 3 2 · 5 = — 1 2 · 1 2 3 2 · 5 = 1 2 3 2 · 5
А потом уже выносить множитель: 1 2 3 2 · 5 = 1 2 3 · 5 = 1 2 3 · 5 .
- Последнее выражение имеет нечетный показатель, поэтому нам понадобится другое правило: (- 0 , 4) 7 · 11 7 = — 0 , 4 · 11 7 .
Возможен и такой вариант расчета:
— 0 , 4 7 · 11 7 = (- 1) 7 · 0 , 4 7 · 11 7 = = — 0 , 4 7 · 11 7 = — 0 , 4 7 · 11 7 = — 0 , 4 · 11 7
Или такой:
— 0 , 4 7 · 11 7 = (- 1) 7 · 0 , 4 7 · 11 7 = = — 0 , 4 7 · 11 7 = 0 , 4 7 · — 11 7 = 0 , 4 · — 11 7 = — 0 , 4 · 11 7
Ответ: 1) 2 · 7 ; 2) 1 2 3 · 5 ; 3) — 0 , 4 · 11 7 .
Пример 2
Условие: преобразуйте выражение (- 2) 4 · (0 , 3) 4 · 7 4 · 11 4 .
Решение:
При помощи схемы, приведенной во втором пункте статьи, мы можем вынести из-под корня сразу три множителя.
(- 2) 4 · (0 , 3) 4 · 7 4 · 11 4 = = — 2 · 0 , 3 · 7 · 11 4 = 4 , 2 · 11 4
Можно сделать преобразование в несколько шагов, вынося множителя по одному, но так будет гораздо дольше.
Есть и другой способ. Преобразуем само выражение, приведя его к виду B n · C . После этого уже будем выносить множители:
После этого уже будем выносить множители:
(- 2) 4 · (0 , 3) 4 · 7 4 · 11 4 = = (- 2 · 0 , 3 · 7) 4 · 11 4 = (- 4 , 2) 4 · 11 4 = = — 4 , 2 · 11 4 = 4 , 2 · 11 4
Ответ: (- 2) 4 · (0 , 3) 4 · 7 4 · 11 4 = — 4 , 2 · 11 4 = 4 , 2 · 11 4 .
Разберем более подробно тот случай, когда подкоренное выражение требует предварительного преобразования. Здесь есть несколько моментов, которые нужно дополнительно пояснить.
Предварительное преобразование подкоренного выражения
Мы уже отмечали, что выражение под корнем не всегда имеет удобный для нас вид. Часто корень дан как A n , и множитель, который нужно вынести, не представлен в явном виде. Иногда это обозначено в условии, но довольно часто множитель приходится определять самостоятельно. Посмотрим, как надо действовать в этих случаях.
Допустим, нам надо вынести заранее определенный множитель B . Естественно, подкоренное выражение должно быть таким, чтобы эта операция была возможна. Тогда для преобразования A n в B n · C n достаточно определить второй множитель, т. е. вычислить значение C из выражения A = B n · C .
е. вычислить значение C из выражения A = B n · C .
Пример 3
Условие: есть выражение 24 · x 3 . Вынесите из-под знака корня множитель 2 3 .
Решение
Здесь мы имеем n = 3 , A = 24 · x , B 3 = 2 3 . Тогда из A = B n · С вычисляем C = A: (B n) = 24 · x: (2 3) = 3 · x .
Значит, 24 · x 3 = 2 3 · 3 · x 3 . Подкоренное выражение имеет нужный нам вид, и мы можем воспользоваться правилом для нечетного показателя и подсчитать: 24 · x 3 = 2 3 · 3 · x 3 = 2 · 3 · x 3 .
Ответ: 24 · x 3 = 2 · 3 · x 3 .
А как быть в случае, если множитель, который нужно вынести, не указан? Тогда у нас есть определенная свобода выбора, и мы можем использовать несколько подходов к решению задачи.
Допустим, нам дано выражение, под корнем у которого стоит степень или произведение нескольких степеней. В таком случае, зная основные свойства степени, мы можем преобразовать выражение в удобный для нас вид с очевидно указанными множителями для вынесения.
Пример 4
Условие : необходимо вынести множитель из-под корня в трех выражениях – 2 4 · 5 4 , 2 7 · 5 4 , 2 22 · 5 4 .
Решение
Преобразование первого выражения не представляет особой сложности, т.к. подобные примеры мы уже разбирали. Сразу вычисляем: 2 4 · 5 4 = 2 · 5 4 = 2 · 5 4 .
Во втором примере легко догадаться, как преобразовать подкоренное выражение: нужно просто представить 2 7 как 2 4 · 2 3 .
2 7 · 5 4 = 2 4 · 2 3 · 5 4 = 2 4 · 40 4 = 2 · 40 4 = 2 · 40 4
В последнем примере также нужно начать с преобразования подкоренного выражения. Сразу отметим, что итоговый вид будет таким:
2 5 4 · 2 2 · 5 4
Теперь покажем, как именно прийти к этому виду. Сначала выполняем деление 22 на 4 , получаем 5 с остатком 2 (если нужно, повторите, как правильно выполнять деление с остатком). Иначе говоря, 22 можно рассматривать как 4 · 5 + 2 . Используя свойства степени, можем записать:
2 22 + 2 5 · 4 + 2 = 2 5 · 4 · 2 2 = (2 5) 4 · 2 2
Таким образом:
2 22 · 5 4 = (2 5) 4 · 2 2 · 5 4 = (2 5) 4 · 20 4 = = 2 5 · 20 4 = 32 · 20 4
Ответ: 1) 2 4 · 5 4 = 2 · 5 4 , 2) 2 7 · 5 4 = 2 · 40 4 , 3) 2 22 · 5 4 = 32 · 20 4 .
Если выражение под корнем не является степенью или произведением степеней, надо попробовать представить его в таком виде. Чаще всего встречаются следующие случаи.
Подкоренное выражение – натуральное составное число. Тогда мы сразу можем увидеть нужные множители, которые надо вынести из-под знака корня, предварительно разложив данное число на простые множители.
Пример 5
Условие : выполните вынесение множителя из-под знака корня в следующих выражениях: 1) 45 ; 2) 135 ; 3) 3456 ; 4) 102 .
- Выполняем разложение 45 на простые множители.
То есть 45 = 3 · 3 · 5 = 3 2 · 5 , а 45 = 3 2 · 5 . В этом выражении видно, что выносить мы будем множитель 3 2 . Вычисляем:
3 2 · 5 = 3 · 5 = 3 · 5
- Теперь представим в нужном виде число 135 и получим: 135 = 3 · 3 · 3 · 5 = 3 3 · 15 . Иначе можно записать, что 3 2 · 3 · 5 = 3 2 · 15 . Следовательно, 135 = 3 2 · 15 . Мы видим, что вынесению из-под знака корня подлежит множитель 3 2 :
3 2 · 15 = 3 · 15 = 3 · 15
- Разложим на простые множители число 3456:
3456 1728 864 432 216 108 54 27 9 3 1 2 2 2 2 2 2 2 3 3 3
У нас получилось, что 3456 = 2 7 · 3 3 , а 3456 = 2 7 · 3 3 . Поскольку 2 7 = 2 3 · 2 + 1 = (2 3) 2 · 2 и 3 3 = 3 2 · 3 , то 2 7 · 3 3 = (2 3) 2 · 2 · 3 2 · 3 = (2 3) 2 · 3 2 · 6 = = 2 3 · 3 · 6 = 24 · 6
Поскольку 2 7 = 2 3 · 2 + 1 = (2 3) 2 · 2 и 3 3 = 3 2 · 3 , то 2 7 · 3 3 = (2 3) 2 · 2 · 3 2 · 3 = (2 3) 2 · 3 2 · 6 = = 2 3 · 3 · 6 = 24 · 6
- Представим натуральное число 102 как произведение простых множителей и получим 2 · 3 · 17 . Видим, что все множители имеют показатель, равный единице, а показатель корня в этом примере равен двум. Следовательно, в данном примере ни один множитель не нужно выносить из-под знака корня, то есть такое действие для 102 нецелесообразно.
Ответ: 1) 45 = 3 · 5 ; 2) 135 = 3 · 15 ; 3) 3456 = 24 · 6 ; 4) 102 .
Теперь разберем, как решать примеры, у которых подкоренное выражение представлено в виде обыкновенной дроби. В этом случае следует числитель и знаменатель разложить на простые множители и посмотреть, можно ли вынести какие-то из них за знак корня. Если у нас есть десятичная дробь или смешанное число, предварительно заменяем их обыкновенными дробями, после чего переходим от корня отношения к отношению корней.
Пример 6
Условие: выполните вынесение множителя за корень в выражении 200 · 0 , 000189 · x 3 и упростите его.
Решение
Для начала перейдем от десятичной дроби к обыкновенной и разложим ее числитель и знаменатель на простые множители.
0 , 189 = 189 1000000 = 3 3 · 7 2 6 · 5 6
Используя свойства степени, перепишем выражение в следующем виде:
3 2 2 · 5 2 3 · 7
Подставим получившееся выражение в исходное и получим:
200 · 0 , 000189 · x 3 = = 200 · 3 2 2 · 5 2 3 · 7 · x 3 = = 200 · 3 2 2 · 5 2 · 7 · x 3 = 6 · 7 · x 3
К такому же ответу можно прийти и с помощью других преобразований:
200 · 0 , 000189 · x 3 = = 200 · 189 1000000 · x 3 = 200 · 189 1000000 3 · x 3 = = 200 · 189 3 1000000 3 · x 3 = 200 · 3 3 · 7 3 100 3 3 · x 3 = = 200 · 3 · 7 3 100 · x 3 = 6 · 7 3 · x 3 = 6 · 7 · x 3
Ответ: 200 · 0 , 000189 · x 3 = 6 · 7 · x 3 .
Иными словами, для обнаружения множителя, который можно вынести за знак корня, можно преобразовывать подкоренное выражение любыми допустимыми способами.
Пример 7
Условие: выполните упрощение иррационального выражения 2 · (3 + 2 · 2) .
Решение
Мы можем преобразовать выражение в скобках как 2 + 2 · 2 + 1 и далее как 2 2 + 2 · 2 · 1 + 1 2 .
То, что у нас получилось, можно свернуть в квадрат суммы с помощью формулы сокращенного умножения: 2 2 + 2 · 2 · 1 + 1 = 2 + 1 2 .
В итоге: 2 · 3 + 2 · 2 = 2 · 2 + 1 2 . Теперь выносим 2 + 1 2 за знак корня и упрощаем выражение:
2 · 2 + 1 2 = 2 · 2 + 1 = = 2 · 2 + 1 = 2 + 2
Ответ: 2 · 3 + 2 · 2 = 2 + 2 .
Теперь посмотрим, как вынести из-под знака корня выражение, содержащее переменные. В целом можно сказать, что для этого используются те же методы, что и при работе с числами.
Пример 8
Условие: вынесите множитель из-под знака корня в выражениях (x — 5) 5 4 и (x — 5) 6 4 .
Решение
- Выполняем преобразование в первом примере.
(x — 5) 5 4 = (x — 5) 4 · x — 5 4 = x — 5 · x — 5 4
Знак модуля можно опустить. Посмотрим, каким условием определяется область допустимых значений переменной для исходного выражения. Таким условием будет неравенство (x − 5) 5 ≥ 0 . Для его решения выбираем метод интервалов и получаем x ≥ 5 . Если значение x принадлежит области допустимых значений, то значением выражения x — 5 будет неотрицательное число. Значит, можем записать следующее:
Посмотрим, каким условием определяется область допустимых значений переменной для исходного выражения. Таким условием будет неравенство (x − 5) 5 ≥ 0 . Для его решения выбираем метод интервалов и получаем x ≥ 5 . Если значение x принадлежит области допустимых значений, то значением выражения x — 5 будет неотрицательное число. Значит, можем записать следующее:
x — 5 · x — 5 4 = x — 5 · x — 5 4
- (x — 5) 6 4 = (x — 5) 4 · x — 5 2 4 = = x — 5 · (x — 5) 2 4 = x — 5 · x — 5 2 4
Выполним сокращение показателей корня и степени на два. Обратимся к таблице результатов из статьи о преобразовании иррациональных выражений, о которой мы говорили выше. Возьмем из нее следующий результат: выражение A m n · m можно заменить на A n при условии, что m и n – натуральные числа. Следовательно,
x — 5 · x — 5 2 4 = x — 5 · x — 5
Нужно ли здесь убирать знак модуля? Посмотрим на область допустимых значений данного выражения: ее составляют все действительные числа, поскольку (x − 5) 6 ≥ 0 для любого x . При этом значения x − 5 могут быть больше 0 , если x > 5 , равными 0 или отрицательными. Значит, оставляем выражение в виде x — 5 · x — 5 или представляем его в виде системы уравнений
При этом значения x − 5 могут быть больше 0 , если x > 5 , равными 0 или отрицательными. Значит, оставляем выражение в виде x — 5 · x — 5 или представляем его в виде системы уравнений
(x — 5) · x — 5 , x ≥ 5 (5 — x) · 5 — x , x
Ответ: 1) (x — 5) 5 4 = (x — 5) · x — 5 4 ; 2) (x — 5) 6 4 = x — 5 · x — 5 .
Пример 9
Условие: выполните упрощение выражения x 5 + 2 · x 4 · y + x 3 · y 2 .
Решение
Выносим за скобки x 3 и получаем x 3 · (x 2 + 2 · x · y + y 2) . Выражение в скобках можно представить в виде квадрата суммы: x 3 · (x 2 + 2 · x · y + y 2) = x 3 · (x + y) 2 .
Теперь видим множители, подлежащие вынесению из-под корня: x 3 · (x + y) 2 = x 2 · x · (x + y) 2 = x · x + y · x
Также мы можем убрать знаки модуля, в которых находится x, поскольку область допустимых значений будет определена условием x 5 + 2 · x 4 · y + x 3 · y 2 ≥ 0 . Оно равносильно x 3 · (x + y) 2 ≥ 0 , а из него можно сделать вывод, что x ≥ 0 . У нас получилось, что x · x + y · x .
У нас получилось, что x · x + y · x .
Ответ: x 5 + 2 · x 4 · y + x 3 · y 2 = x · x + y · x .
Это все, что мы хотели бы вам рассказать о вынесении множителя за знак корня. В следующей статье мы разберем обратное действие – внесение множителя под корень.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Как складывать квадраты. Правило сложения квадратных корней. Пример вычисления приблизительного значения
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Приветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать). Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.
Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)
Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)
Вы ведь тоже ещё не вкурили?
Урок получился довольно большим, поэтому я разделил его на две части:
- Сначала мы разберём правила умножения. Кэп как бы намекает: это когда есть два корня, между ними стоит знак «умножить» — и мы хотим что-то с этим сделать.
- Затем разберём обратную ситуацию: есть один большой корень, а нам приспичило представить его в виде произведения двух корней попроще. С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
Тем, кому не терпится сразу перейти ко второй части — милости прошу. С остальными начнём по порядку.
Основное правило умножения
Начнём с самого простого — классических квадратных корней. Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:
Правило умножения. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:
\[\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\]
Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.
Примеры. Рассмотрим сразу четыре примера с числами:
\[\begin{align} & \sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10; \\ & \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8; \\ & \sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18; \\ & \sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\cdot \frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}. \\ \end{align}\]
Как видите, основной смысл этого правила — упрощение иррациональных выражений. И если в первом примере мы бы и сами извлекли корни из 25 и 4 без всяких новых правил, то дальше начинается жесть: $\sqrt{32}$ и $\sqrt{2}$ сами по себе не считаются, но их произведение оказывается точным квадратом, поэтому корень из него равен рациональному числу .
Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.
Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.
Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.
Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:
\[\begin{align} & \sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6; \\ & \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \\ & =\sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}. \\ \end{align}\]
И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.
Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.
Но это было лирическое отступление. Теперь рассмотрим более общий случай — когда в показателе корня стоит произвольное число $n$, а не только «классическая» двойка.
Случай произвольного показателя
Итак, с квадратными корнями разобрались. А что делать с кубическими? Или вообще с корнями произвольной степени $n$? Да всё то же самое. Правило остаётся прежним:
Чтобы перемножить два корня степени $n$, достаточно перемножить их подкоренные выражения, после чего результат записать под одним радикалом.
В общем, ничего сложного. Разве что объём вычислений может оказаться больше. Разберём парочку примеров:
Примеры. Вычислить произведения:
\[\begin{align} & \sqrt{20}\cdot \sqrt{\frac{125}{4}}=\sqrt{20\cdot \frac{125}{4}}=\sqrt{625}=5; \\ & \sqrt{\frac{16}{625}}\cdot \sqrt{0,16}=\sqrt{\frac{16}{625}\cdot \frac{16}{100}}=\sqrt{\frac{64}{{{25}^{2}}\cdot 25}}= \\ & =\sqrt{\frac{{{4}^{3}}}{{{25}^{3}}}}=\sqrt{{{\left(\frac{4}{25} \right)}^{3}}}=\frac{4}{25}.
{2n}}}=\left| a \right|. \\ \end{align}\]
Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:
Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?
При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)
Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.
Умножение корней с разными показателями
Ну хорошо, теперь мы умеем перемножать корни с одинаковыми показателями. А что, если показатели разные? Скажем, как умножить обычный $\sqrt{2}$ на какую-нибудь хрень типа $\sqrt{23}$? Можно ли вообще это делать?
Да конечно можно. Всё делается вот по этой формуле:
Правило умножения корней.
{2}}}=\sqrt{5}. \\ \end{align}\]
Но тогда получается какая-то хрень:
\[\sqrt{-5}=\sqrt{5}\]
Этого не может быть, потому что $\sqrt{-5} \lt 0$, а $\sqrt{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:
- Убиться об стену констатировать, что математика — это дурацкая наука, где «есть какие-то правила, но это неточно»;
- Ввести дополнительные ограничения, при которых формула станет рабочей на 100%.
В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)
Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.
Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:
Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.
2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
Инструкция
1. Во-первых, при сложении квадратных корней испробуйте извлечь эти корни. Это будет допустимо, если числа под знаком корня являются полными квадратами. Скажем, пускай задано выражение?4 + ?9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: ?4 + ?9 = 2 + 3 = 5.
2. Если под знаком корня нет полных квадратов, то испробуйте перенести из под знака корня множитель числа. Скажем, пускай дано выражение?24 + ?54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, тот, что дозволено перенести из под знака квадратного корня. В числе 54 – множитель 9. Таким образом, получается что: ?24 + ?54 = ?(4 * 6) + ?(9 * 6) = 2 * ?6 + 3 * ?6 = 5 * ?6. В данном примере в итоге выноса множителя из под знака корня получилось упростить заданное выражение.
3. Пускай сумма 2-х квадратных корней является знаменателем дроби, скажем, A / (?a + ?b). И пускай перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда дозволено воспользоваться дальнейшим методом. Умножьте числитель и знаменатель дроби на выражение?a – ?b. Таким образом в знаменателе получится формула сокращенного умножения: (?a + ?b) * (?a – ?b) = a – b. По аналогии, если в знаменателе дана разность корней: ?a – ?b, то числитель и знаменатель дроби нужно умножить на выражение?a + ?b. Для примера, пускай дана дробь 4 / (?3 + ?5) = 4 * (?3 – ?5) / ((?3 + ?5) * (?3 – ?5)) = 4 * (?3 – ?5) / (-2) = 2 * (?5 – ?3).
4. Разглядите больше непростой пример избавления от иррациональности в знаменателе. Пускай дана дробь 12 / (?2 + ?3 + ?5). Нужно умножить числитель и знаменатель дроби на выражение?2 + ?3 – ?5:12 / (?2 + ?3 + ?5) = 12 * (?2 + ?3 – ?5) / ((?2 + ?3 + ?5) * (?2 + ?3 – ?5)) = 12 * (?2 + ?3 – ?5) / (2 * ?6) = ?6 * (?2 + ?3 – ?5) = 2 * ?3 + 3 * ?2 – ?30.
5. И наконец, если вам нужно только примерное значение, то дозволено посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для всего числа и запишите с нужной точностью (скажем, два знака позже запятой). А после этого совершите требуемые арифметические операции, как с обыкновенными числами. Скажем, пускай нужно узнать примерное значение выражения?7 + ?5 ? 2,65 + 2,24 = 4,89.
Видео по теме
Обратите внимание!
Квадратные корни ни в коем случае невозможно складывать как примитивные числа, т.е. ?3 + ?2 ? ?5!!!Полезный совет
Если вы раскладываете число на множители, дабы перенести квадрат из под знака корня, то совершите обратную проверку – перемножьте все получившиеся множители и получите изначальное число.В математике любое действие имеет свою пару-противоположность – в сущности, это представляет собою одно из проявлений гегелевского закона диалектики: «единство и борьба противоположностей».
Одно из действий в такой «паре» направлено на увеличение числа, а другое, обратное ему – на уменьшение. Например, действие, противоположное сложению – это вычитание, умножению соответствует деление. Имеется и своя диалектическая пара-противоположность и у возведения в степень. Речь идет об извлечении корня.
Извлечь из числа корень такой-то степени – это значит вычислить, какое число необходимо возвести в соответствующую степень, чтобы в итоге получилось данное число. Две степени имеют свои отдельные названия: вторая степень называется «квадратом», а третья – «кубом». Соответствено, корни данных степеней приятно именовать квадратным корнем и кубическим. Действия с кубическими корнями – тема для отдельного разговора, а сейчас поговорим о сложении квадратных корней.
Начнем с того, что в ряде случаев квадратные корни проще сначала извлечь, а потом уже складывать результаты. Предположим, нам необходимо найти значение такого выражения:
Ведь совсем не сложно вычислить, что корень квадратный из 16 равен 4, а из 121 – 11.
Следовательно,
√16+√121=4+11=15
Впрочем, это самый простой случай – здесь речь идет о полных квадратах, т.е. о таких числах, которые получаются при возведении в квадрат целых чисел. Но так бывает не всегда. Например, число 24 – это не полный квадрат (не найти такого целого числа, которое при возведении его во вторую степень дало бы в результате 24). То же самое относится к такому числу, как 54… Что делать, если нам необходимо сложить корни квадратные из этих чисел?
В таком случае мы получим в ответе не число, а другое выражение. Максимум, что мы можем тут сделать – это максимально упростить исходное выражение. Для этого придется вынести множители из-под корня квадратного. Посмотрим, как это делается, на примере упомянутым чисел:
Для начала разложим на множители 24 – таким образом, чтобы из одного из них легко можно было извлечь корень квадратный (т.е., чтобы он был полным квадратом). Такое числи есть – это 4:
Теперь проделаем то же самое с 54. В его составе таким числом будет 9:
Т.
о., у нас получается следующее:
√24+√54=√(4*6)+ √(9*6)
Теперь извлечем корни из того, из чего можем их извлечь: 2*√6+3*√6
Здесь есть общий множитель, который мы можем вынести за скобки:
(2+3)* √6=5*√6
Это и будет результатом сложения – больше ничего тут извлечь нельзя.
Правда, можно прибегнуть к помощи калькулятора – правда, результат будет приблизительным и с огромным количеством знаков после запятой:
√6=2,449489742783178
Постепенно округляя его, мы получим приблизительно 2,5. Если нам все-таки хотелось бы довести до логического завершения решение предыдущего примера, мы можем умножить этот результат на 5 – и получится у нас 12,5. Более точного результата при таких исходных данных получить нельзя.
Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение.
Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.Шаг 1. Извлечение квадратных корней
Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9 . Первое число 4 является квадратом числа 2 . Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Все, пример решен. Но так просто бывает далеко не всегда.Шаг 2. Вынесение множителя числа из-под корня
Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .
Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9 .
Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.
Шаг 3. Сокращение знаменателя
Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b) .
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .
Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .Пример сложного сокращения знаменателя
Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.
Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .Получаем:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.
Шаг 4. Вычисление приблизительного значения на калькуляторе
Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней.
Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Пример вычисления приблизительного значения
Необходимо вычислить приблизительное значение данного выражения √7 + √5 .
В итоге получаем:
√7 + √5 ≈ 2,65 + 2,24 = 4,89 .
Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.
Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.
Объясните, пожалуйста, как получить квадратный корень из этого числа без калькулятора? корень квадратный из 256
√256
разделите числа на группы по 2, начиная с правой стороны
какое наибольшее число в квадрате делится на 2?
, это число 1
поставить 1 над 2 и слева от корня
1
_______
1 √2 56
1 * 1 = 1, поэтому поместите 1 под 2
1
________
1 √2 56
1
вычесть и убавить 56 и удвоить 1 в частном
поместите 2 рядом с 1 после вычитания
1
________
1 √2 56
1
_________
2 1 56
выберите наибольшее число, назовите его x, которое можно поставить рядом с 2 и выше 56, так что x * 2x не превышает 156
, это число 6, потому что 6 * 26 = 156
теперь у вас есть ответ 16
другой пример:
√66564
2 5 8
__________
2 √6 65 64
4
__________
45 2 65
2 25
_________
508 40 64
40 64
_______
0
этот метод требует очень много времени, особенно если число очень большое или если вы хотите, чтобы ответ числа, например √7, состоял из нескольких цифр.
, если у вас нет идеального квадрата, вы можете использовать метод проб и ошибок
√7 =?
наибольшее число в квадрате меньше 7 равно 2
попробуйте 2.5 в квадрате, что равно 6,25
попробуйте 2,6 в квадрате, что составляет 6,76
попробуйте 2,7 в квадрате, что составляет 7,29, что слишком велико
, так что у нас пока 2,6
попробуйте 2,65 в квадрате, что составляет 7,0225, что слишком велико
, поэтому мы должны использовать 2,64
попробуйте 2,645 в квадрате, что составляет 6,996025
пока у нас 2,645
попробуйте 2,6459 в квадрате, что составляет 7.0007868
попробуйте 2,6458 в квадрате, что также является большим
попробуйте 2,6457 в квадрате, что равно 6.9997285
продолжайте, пока не наберете нужное количество цифр
кстати, √7 = 2,64575131 …
9.1: Упростить и использовать квадратные корни
Практика ведет к совершенству
Упростить выражения квадратными корнями
Упростите следующие упражнения.
Пример \ (\ PageIndex {34} \)
\ (\ sqrt {36} \)
- Ответ
6
Пример \ (\ PageIndex {35} \)
\ (\ sqrt {4} \)
Пример \ (\ PageIndex {36} \)
\ (\ sqrt {64} \)
- Ответ
8
Пример \ (\ PageIndex {37} \)
\ (\ sqrt {169} \)
Пример \ (\ PageIndex {38} \)
\ (\ sqrt {9} \)
- Ответ
3
Пример \ (\ PageIndex {39} \)
\ (\ sqrt {16} \)
Пример \ (\ PageIndex {40} \)
\ (\ sqrt {100} \)
- Ответ
10
Пример \ (\ PageIndex {41} \)
\ (\ sqrt {144} \)
Пример \ (\ PageIndex {42} \)
\ (- \ sqrt {4} \)
- Ответ
−2
Пример \ (\ PageIndex {43} \)
\ (- \ sqrt {100} \)
Пример \ (\ PageIndex {44} \)
\ (- \ sqrt {1} \)
- Ответ
-1
Пример \ (\ PageIndex {45} \)
\ (- \ sqrt {121} \)
Пример \ (\ PageIndex {46} \)
\ (\ sqrt {−121} \)
- Ответ
ненастоящее число
Пример \ (\ PageIndex {47} \)
\ (\ sqrt {−36} \)
Пример \ (\ PageIndex {48} \)
\ (\ sqrt {−9} \)
- Ответ
ненастоящее число
Пример \ (\ PageIndex {49} \)
\ (\ sqrt {−49} \)
Пример \ (\ PageIndex {50} \)
\ (\ sqrt {9 + 16} \)
- Ответ
5
Пример \ (\ PageIndex {51} \)
\ (\ sqrt {25 + 144} \)
Пример \ (\ PageIndex {52} \)
\ (\ sqrt {9} + \ sqrt {16} \)
- Ответ
7
Пример \ (\ PageIndex {53} \)
\ (\ sqrt {25} + \ sqrt {144} \)
Вычисление квадратного корняВ следующих упражнениях вычислите каждый квадратный корень между двумя последовательными целыми числами.
Пример \ (\ PageIndex {54} \)
\ (\ sqrt {70} \)
- Ответ
\ (8 <\ sqrt {70} <9 \)
Пример \ (\ PageIndex {55} \)
\ (\ sqrt {55} \)
Пример \ (\ PageIndex {56} \)
\ (\ sqrt {200} \)
- Ответ
\ (14 <\ sqrt {200} <15 \)
Пример \ (\ PageIndex {57} \)
\ (\ sqrt {172} \)
Приблизительные квадратные корниВ следующих упражнениях округлите каждый квадратный корень и округлите до двух десятичных знаков.
Пример \ (\ PageIndex {58} \)
\ (\ sqrt {19} \)
- Ответ
4,36
Пример \ (\ PageIndex {59} \)
\ (\ sqrt {21} \)
Пример \ (\ PageIndex {60} \)
\ (\ sqrt {53} \)
- Ответ
7,28
Пример \ (\ PageIndex {61} \)
\ (\ sqrt {47} \)
Упростить выражения переменных квадратными корнями
Упростите следующие упражнения.
{20}} \)
квадратных корней
Как мы их делаем?
Квадратный корень из числа б является решением уравнения Икс 2 знак равно б . Все числа, кроме 0 имеет два квадратных корня, положительный и отрицательный. Положительный квадратный корень — это главный квадратный корень и написано б . Чтобы обозначить отрицательный корень, напишите — б и чтобы указать оба корня, напишите ± б .
Итак, мы звоним 5 «квадратный корень» из 25 и писать 25 знак равно 5 так как 5 2 знак равно 25 . (Подробнее об этом см. Экспоненты.) Поскольку ( — 5 ) 2 также равно 25 это также «квадратный корень» из 25 , но мы пишем — 25 знак равно — 5 потому что это не главный квадратный корень.
Не все целые числа имеют квадратный корень из целого числа. Например 2 знак равно 1,414213562 … (Десятичная дробь продолжается вечно и никогда не повторяет шаблон. Это называется иррациональный номер .)
Как вы можете оценить значение квадратного корня, например 70 ? Что ж, вы могли сначала заметить, что 64 знак равно 8 и 81 год знак равно 9 , поскольку 64 и 81 год оба являются полными квадратами.70 находится посередине 64 и 81 год , так 8 < 70 < 9 . С 70 ближе к 64 чем 81 год , 70 ближе к 8 .
Чтобы найти лучшее приближение, вы можете использовать калькулятор:
70 ≈ 8,3666
Квадратный корень из 169 | Как найти
Что такое квадратный корень из 169?
Квадратный корень из 169 равен 13 — технически это главный квадратный корень из 169.
169 = 13
Как найти квадратный корень из 169
Когда мы подходим к проблеме таким образом, мы находим квадратный корень (sqrt) исходного числа. Квадратный корень из x — это число n, которое удовлетворяет этому уравнению:
Каждое положительное число имеет два квадратных корня , положительный и отрицательный.
Положительный квадратный корень называется главным квадратным корнем , и обычно понимается, что это именно тот корень, который нас интересует.
В данном случае нам нужен положительный квадратный корень из 169.
Нахождение квадратного корня из 169 путем факторизации
Чтобы решить 169, мы можем разложить на множители число под знаком корня. Разложение на простые множители первых нескольких простых чисел поможет нам увидеть, какие из них могут быть множителями целевого числа.
Факторы нахождения 169 Простое число (n) 169 ÷ n Фактор? 2 84. 5
№ 3 56,33 № 5 33,8 № 7 24.14286 № 11 15,36 № 13 13 Да! 17 9,941 № Только одно простое число является делителем 13, и само умножение на него дает наше целевое число 169.
Перепишите исходную задачу, заменив найденный нами коэффициент на исходное число:
169 = 13 * 13 = 132
Нельзя оставлять показатель степени под радикалом. Чтобы удалить показатели из-под знаков корня, разделите четные показатели на 2, затем переместите основание (в данном случае 13) и полученную в результате показатель за знак корня.
Разделите показатель степени 2 на 2:
1322 = 131
Вынесите 131 за пределы знака корня и оставьте 1 под знаком корня (поскольку 169 не может быть равным , ничто )
131 = 1311
1311 — это квадратный корень из 169 в радикальной форме — это простейшая радикальная форма.
Новый результат выглядит сложным, но если вы упростите детали, вы обнаружите, что это не так:
Это дает 13 * 1, что составляет 13.
Главный квадратный корень из 169 равен 13.
Квадратный корень из 169 является рациональным числом, потому что это полный квадрат — в ответе нет десятичных знаков.
Как вычислить квадратный корень из 169?
Другой способ найти квадратный корень из 169 — это оценить, используя известные квадраты.
Вы, наверное, сразу вспомните, что 122 это 144. 169 больше или меньше 144? Это больше, значит, вам нужно большее число.
Попробуем 15.Мы вычисляем 152 = 225, что слишком много.
Теперь мы узнали, что квадратный корень из 169 находится где-то между 12 и 15. Попробуйте два оставшихся целых числа:
142 = 196 — приближаемся!
132 = 169
Квадратный корень из 169 равен 13.
Хотя на практике -13 также является квадратным корнем из 169, мы всегда ищем главный квадратный корень. Если не попросить найти «все» квадратных корней из 169, мы придерживаемся нашего ответа 13.
Вы можете проверить, что у вас есть правильный квадратный корень из числа, умножив число (13) на само (13), чтобы увидеть, равно ли оно целевому числу (169):
13 * 13 = 169
Корень квадратный из 169 методом деления
Деление в столбик — это еще один способ найти квадратный корень из 169 с помощью калькулятора.
Для начала работайте справа налево и разделите действительное число 169 на две пары двузначных чисел.
169 = 01-69-
Теперь вы работаете над каждой парой отдельно.Какой самый большой идеальный квадрат меньше или равен 1? Ответ: 1.
И квадратный корень из 1 тоже 1.
Итак, ставим один сверху и снизу вот так:
1 01-69-1 0-
Теперь вычтите 1 из единицы и перенесите оставшиеся 69 в свой ответ:
1 01-69-1 0-69-
Следующим шагом будет удвоение числа на самом верху, которое равно 1. Итак, 1 × 2 = 2.
Затем вы используете цифру 2 и оставшееся число внизу (69), чтобы создать эту математическую задачу:
2? _ ×? _ ≤ 69
Попробуйте найти, какое число подходит для завершения уравнения.Наибольшее допустимое число — 3. Это означает, что у нас есть:
23_ × 3_ = 69
Теперь вы можете прибавить 3 к вершине вашей задачи о длинном делении и 69 к нижней части; 69 минус 69 равно 0, так что все готово. Верхняя часть — это квадратный корень из 169.
1 301-69-1 0-69-0 69
Ответ: 13.
Корни и радикалы
Квадратные и кубические корни
Напомним, что квадратный корень — это число, которое при умножении само на себя дает исходное число.
числа — это число, которое при умножении само на себя дает исходное число. Например, 5 — это квадратный корень из 25, потому что 52 = 25. Поскольку (−5) 2 = 25, мы можем сказать, что −5 также является квадратным корнем из 25. Каждое положительное действительное число имеет два квадратных корня: положительный и отрицательный. По этой причине мы используем знак корня для обозначения главного (неотрицательного) квадратного корня Положительного квадратного корня из положительного действительного числа, обозначаемого символом. и отрицательный знак перед корнем — для обозначения отрицательного квадратного корня.
25 = 5 Положительный квадратный корень из 25-25 = −5 Отрицательный квадратный корень из 25
Ноль — единственное действительное число с одним квадратным корнем.
0 = 0, потому что 02 = 0
Пример 1
Оценить.
- 121
- −81
Решение:
- 121 = 112 = 11
- −81 = −92 = −9
Если подкоренное выражение Выражение A внутри знака корня, An.
число внутри радикального знака может быть разложено на квадрат другого числа, тогда квадратный корень из числа очевиден. В этом случае мы имеем следующее свойство:
a2 = a, если a≥0
Или, в более общем смысле,
a2 = | a | если a∈ℝ
Абсолютное значение важно, потому что a может быть отрицательным числом, а знак корня обозначает главный квадратный корень. Например,
(−8) 2 = | −8 | = 8
Используйте абсолютное значение, чтобы гарантировать положительный результат.
Пример 2
Упростить: (x − 2) 2.
Решение:
Здесь выражение переменной x − 2 может быть отрицательным, нулевым или положительным. Поскольку знак зависит от неизвестной величины x , мы должны обеспечить получение главного квадратного корня, используя абсолютное значение.
(x − 2) 2 = | x − 2 |
Ответ: | x − 2 |
Важность использования абсолютного значения в предыдущем примере становится очевидной, когда мы оцениваем с использованием значений, которые делают подкоренное выражение отрицательным.
Например, если x = 1,
(x − 2) 2 = | x − 2 | = | 1−2 | = | −1 | = 1
Затем рассмотрим квадратный корень отрицательного числа. Чтобы определить квадратный корень из −25, вы должны найти число, возведение которого в квадрат дает −25:
.−25 =? или (?) 2 = −25
Однако возведение любого действительного числа в квадрат всегда дает положительное число. Квадратный корень отрицательного числа в настоящее время не определен. А пока мы заявим, что -25 не является действительным числом.Следовательно, функция извлечения квадратного корня Функция определяется как f (x) = x. заданный как f (x) = x, не определяется как действительное число, если значения x отрицательны. Наименьшее значение в домене равно нулю. Например, f (0) = 0 = 0 и f (4) = 4 = 2. Напомним график функции извлечения квадратного корня.
Домен и диапазон состоят из действительных чисел, больших или равных нулю: [0, ∞). Чтобы определить область определения функции, содержащей квадратный корень, мы смотрим на подкоренное выражение и находим значения, которые дают неотрицательные результаты.
Пример 3
Определите область определения функции, заданной формулой f (x) = 2x + 3.
Решение:
Здесь подкоренное выражение 2x + 3. Это выражение должно быть нулевым или положительным. Другими словами,
2x + 3≥0
Решите для x .
2x + 3≥02x≥ − 3x≥ − 32
Ответ: Домен: [−32, ∞)
Кубический корень Число, которое при трехкратном использовании в качестве множителя с самим собой дает исходное число, обозначенное символом 3.числа — это число, которое при трехкратном умножении на само себя дает исходное число. Кроме того, мы обозначаем корень куба с помощью символа 3, где 3 называется индексом Положительное целое число n в обозначении n, которое используется для обозначения корня n -й степени .. Например,
643 = 4, потому что 43 = 64
Произведение трех равных множителей будет положительным, если множитель положительный, и отрицательным, если множитель отрицательный.
По этой причине у любого действительного числа будет только один действительный кубический корень.Следовательно, технические детали, связанные с основным корнем, не применяются. Например,
−643 = −4, потому что (−4) 3 = −64
В общем случае для любого действительного числа a мы имеем следующее свойство:
a33 = a, если a∈ℝ
При упрощении кубических корней ищите множители, которые являются идеальными кубами.
Пример 4
Оценить.
- 83
- 03
- 1273
- −13
- −1253
Решение:
- 83 = 233 = 2
- 03 = 033 = 0
- 1273 = (13) 33 = 13
- −13 = (- 1) 33 = −1
- −1253 = (- 5) 33 = −5
Может случиться так, что подкоренное выражение не является полным квадратом или кубом.
3≈2
Поскольку кубические корни могут быть отрицательными, нулевыми или положительными, мы не используем никаких абсолютных значений.
Пример 5
Упростить: (y − 7) 33.
Решение:
Кубический корень из куба количества и есть это количество.
(у-7) 33 = у-7
Ответ: y − 7
Попробуй! Вычислите: −10003.
Ответ: −10
Затем рассмотрим функцию кубического корня Функция, определенная как f (x) = x3 .:
f (x) = x3 Функция кубического корня.
Поскольку кубический корень может быть как отрицательным, так и положительным, мы заключаем, что область состоит из всех действительных чисел. Нарисуйте график, нанеся точки. Выберите несколько положительных и отрицательных значений для x , а также ноль, а затем вычислите соответствующие значения y .
xf (x) = x3 Упорядоченные пары − 8−2f (−8) = — 83 = −2 (−8, −2) −1−1f (−1) = — 13 = −1 (−1, −1) 00f (0) = 03 = 0 (0,0) 11f (1) = 13 = 1 (1,1) 82f (8) = 83 = 2 (8,2)
Постройте точки и нарисуйте график функции кубического корня.
График проходит проверку вертикальной линии и действительно является функцией. Кроме того, диапазон состоит из всех действительных чисел.
Пример 6
Дано g (x) = x + 13 + 2, найти g (−9), g (−2), g (−1) и g (0).Нарисуйте график g.
Решение:
Заменить x заданными значениями.
xg (x) g (x) = x + 13 + 2 Упорядоченные пары − 90g (−9) = — 9 + 13 + 2 = −83 + 2 = −2 + 2 = 0 (−9,0) −21g ( −2) = — 2 + 13 + 2 = −13 + 2 = −1 + 2 = 1 (−2,1) −12g (−1) = — 1 + 13 + 2 = 03 + 2 = 0 + 2 = 2 (-1,2) 03g (0) = 0 + 13 + 2 = 13 + 2 = 1 + 2 = 3 (0,3)
Мы также можем зарисовать график, используя следующие переводы:
y = x3 Базовая функция корня куба y = x + 13 Горизонтальный сдвиг влево 1 единица = x + 13 + 2 Вертикальный сдвиг вверх на 2 единицы
Ответ:
энные корни
Для любого целого числа n≥2 мы определяем корень n -го числа, которое при возведении в степень n -го (n≥2) дает исходное число.
положительного действительного числа как числа, которое при возведении в степень n в -й степени дает исходное число. Для любого неотрицательного действительного числа a мы имеем следующее свойство:
ann = a, если a≥0
Здесь n называется индексом, а an называется подкоренным выражением. Более того, мы можем ссылаться на все выражение An как на радикал. Используется при обращении к выражению формы An .. Когда индекс является целым числом, большим или равным 4, мы говорим «корень четвертой степени», «корень пятой степени» и скоро.Корень n -й степени любого числа очевиден, если мы можем записать подкоренное выражение с показателем, равным индексу.
Пример 7
Упростить.
- 814
- 325
- 17
- 1164
Решение:
- 814 = 344 = 3
- 325 = 255 = 2
- 17 = 177 = 1
- 1164 = (12) 44 = 12
Примечание : Если индекс равен n = 2, то радикал указывает на квадратный корень, и принято писать радикал без индекса; а2 = а.
Мы уже позаботились о том, чтобы определить главный квадратный корень действительного числа. На этом этапе мы расширяем эту идею до n корней -й степени, когда n четные. Например, 3 — это корень четвертой степени из 81, потому что 34 = 81. А поскольку (−3) 4 = 81, мы можем сказать, что −3 также является корнем четвертой степени из 81. Следовательно, мы используем знак корня n для обозначения главного (неотрицательного) корня n -й степени Положительный корень n -й степени, когда n четное. когда n четно.В этом случае для любого действительного числа a мы используем следующее свойство:
ann = | a | Когда n равно
Например,
814 = 344 = | 3 | = 3 814 = (- 3) 44 = | −3 | = 3
Отрицательный корень n -й степени, когда n четный, будет обозначаться отрицательным знаком перед корнем — n.
−814 = −344 = −3
Мы видели, что квадратный корень из отрицательного числа не является действительным, потому что любое действительное число, возведенное в квадрат, даст положительное число.
Фактически, аналогичная проблема возникает для любого четного индекса:
−814 =? или (?) 4 = −81
Мы видим, что корень четвертой степени из −81 не является действительным числом, потому что четвертая степень любого действительного числа всегда положительна.
−4−814−646} Эти радикалы не являются действительными числами.
Предлагаем вам попробовать все это на калькуляторе. Что там написано?
Пример 8
Упростить.
- (-10) 44
- −1044
- (2г + 1) 66
Решение:
Поскольку индексы четные, используйте абсолютные значения, чтобы гарантировать неотрицательные результаты.
- (-10) 44 = | -10 | = 10
- −1044 = −10,0004 не является действительным числом.
- (2y + 1) 66 = | 2y + 1 |
Когда индекс n нечетный, таких проблем не возникает.
Произведение нечетного числа положительных факторов положительно, а произведение нечетного количества отрицательных факторов отрицательно. Следовательно, когда индекс n является нечетным, существует только один действительный корень n -й степени для любого действительного числа a . И вот недвижимость у нас:
ann = a Если n нечетное
Пример 9
Упростить.
- (-10) 55
- −325
- (2 года + 1) 77
Решение:
Поскольку индексы нечетные, абсолютное значение не используется.
- (-10) 55 = -10
- −325 = (- 2) 55 = −2
- (2y + 1) 77 = 2y + 1
Таким образом, для любого действительного числа a у нас есть
ann = | a | Когда n четноann = aКогда n нечетно
Когда n является нечетным , корень n -й степени равен положительным или отрицательным в зависимости от знака подкоренного выражения.
273 = 333 = 3−273 = (- 3) 33 = −3
Когда n равно , корень n -й степени равен положительному или ненастоящему в зависимости от знака подкоренного выражения.
164 = 244 = 2164 = (- 2) 44 = | −2 | = 2−164 Не действительное число
Попробуй! Упростить: −8−325.
Ответ: 16
Упрощение радикалов
Не всегда подкоренное выражение является полной степенью данного индекса. Если это не так, мы используем правило произведения радикалов с заданными действительными числами An и Bn, A⋅Bn = An⋅Bn. и правило частного для радикалов с заданными действительными числами An и Bn, ABn = AnBn, где B ≠ 0.чтобы упростить их. Учитывая действительные числа An и Bn,
Правило продукта для радикалов:
A⋅Bn = An⋅Bn
Правило частного для радикалов:
ABn = AnBn
Радикал — это упрощенный радикал, в котором подкоренное выражение не состоит из каких-либо множителей, которые могут быть записаны как полные степени индекса.
если он не содержит каких-либо факторов, которые могут быть записаны как абсолютные степени индекса.
Пример 10
Упростить: 150.
Решение:
Здесь 150 можно записать как 2⋅3⋅52.
150 = 2⋅3⋅52 Примените правило произведения для радикалов. = 2⋅3⋅52 Упростите. = 6 ⋅ 5 = 56
Можем проверить наш ответ на калькуляторе:
150≈12,25 и 56≈12,25
Также стоит отметить, что
12.252≈150
Ответ: 56
Примечание : 56 — точный ответ, а 12,25 — приблизительный ответ. Мы даем точные ответы, если не указано иное.
Пример 11
Упростить: 1603.
Решение:
Используйте разложение на простые множители 160, чтобы найти наибольший коэффициент идеального куба:
160 = 25⋅5 = 23⋅22⋅5
Замените подкоренное выражение этой факторизацией, а затем примените правило произведения для радикалов.
1603 = 23⋅22⋅53 Примените правило произведения для радикалов. = 233⋅22⋅53 Упростите. = 2⋅203
Мы можем проверить наш ответ на калькуляторе.
1603≈5,43 и 2203≈5,43
Ответ: 2203
Пример 12
Упростить: −3205.
Решение:
Здесь отметим, что индекс нечетный, а подкоренное выражение отрицательное; следовательно, результат будет отрицательным.Мы можем разложить подкоренное выражение на множители следующим образом:
−320 = −1⋅32⋅10 = (- 1) 5⋅ (2) 5⋅10
Затем упростите:
−3205 = (- 1) 5⋅ (2) 5⋅105 Примените правило произведения для радикалов. = (- 1) 55⋅ (2) 55⋅105Simplify. = — 1⋅2⋅105 = −2⋅105
Ответ: −2105
Пример 13
Упростить: -8643.
Решение:
В этом случае рассмотрим эквивалентную дробь с −8 = (- 2) 3 в числителе и 64 = 43 в знаменателе, а затем упростим.
−8643 = −864 3 Примените правило частного для радикалов. = (- 2) 33433Simplify. = — 24 = −12
Ответ: −12
Попробуй! Упростить: 80814
Ответ: 2543
Основные выводы
- Чтобы упростить извлечение квадратного корня, найдите наибольший коэффициент полного квадрата корневого выражения, а затем примените правило произведения или частного для радикалов.
- Чтобы упростить кубический корень, найдите наибольший коэффициент идеального куба подкоренного выражения, а затем примените правило произведения или частного для радикалов.
- При работе с корнями n , n определяет применимое определение. Мы используем ann = a, когда n нечетно и ann = | a | когда n четно.
- Чтобы упростить n корней -й степени, найдите множители, мощность которых равна индексу n , а затем примените правило произведения или частного для радикалов.
Обычно процесс упрощается, если вы работаете с разложением на простые множители подкоренного выражения.
Тематические упражнения
Часть A: квадратные и кубические корни
Упростить.
49
164
183
8273
Определите область определения данной функции.

Оценить по определению функции.
Дано f (x) = x − 1, найти f (1), f (2) и f (5)
Дано f (x) = x + 5, найти f (−5), f (−1) и f (20)
Дано f (x) = x + 3, найти f (0), f (1) и f (16)
Дано f (x) = x − 5, найти f (0), f (1) и f (25)
Дано g (x) = x3, найти g (−1), g (0) и g (1)
Дано g (x) = x3−2, найти g (−1), g (0) и g (8)
Дано g (x) = x + 73, найти g (−15), g (−7) и g (20)
Дано g (x) = x − 13 + 2, найти g (0), g (2) и g (9)
Нарисуйте график данной функции и укажите ее область определения и диапазон.

Часть B:
n -е корни
Упростить.

1325
12435
32516
6169
5271253
732755
−58273
−8625164
Часть C: упрощение радикалов
Упростить.

15049
2009 г.
675121
19281
541253
403433
2242435
5325
−1325
−1646
Упростить.
Дайте точный ответ и примерный ответ с округлением до сотых.
9649
19225
2881253
62583
Перепишем следующее как радикальное выражение с коэффициентом 1.
Каждая сторона квадрата имеет длину, равную квадратному корню из площади квадрата.Если площадь квадрата составляет 72 квадратных единицы, найдите длину каждой из его сторон.
Каждое ребро куба имеет длину, равную кубическому корню из объема куба. Если объем куба составляет 375 кубических единиц, найдите длину каждого из его ребер.
Ток I , измеренный в амперах, определяется формулой I = PR, где P — потребляемая мощность, измеренная в ваттах, а R — сопротивление, измеренное в омах.Если у 100-ваттной лампочки сопротивление 160 Ом, найдите необходимый ток. (Округлить до сотых долей ампера.)
Время в секундах, в течение которого объект находится в свободном падении, определяется формулой t = s4, где s представляет собой расстояние в футах, на которое объект упал. Сколько времени потребуется объекту, чтобы упасть на землю с вершины 8-футовой стремянки? (Округлите до ближайшей десятой секунды.)
Часть D: Обсуждение
Объясните, почему существует два действительных квадратных корня для любого положительного действительного числа и один действительный кубический корень для любого действительного числа.
Что такое квадратный корень из 1 и кубический корень из 1? Объяснить, почему.
Объясните, почему −1 не является действительным числом и почему −13 является действительным числом.
Изучите и обсудите методы, используемые для вычисления квадратных корней, до того, как электронные калькуляторы начнут широко использоваться.
ответов
[−15, ∞)
г (−1) = — 1; г (0) = 0; г (1) = 1
г (−15) = — 2; г (-7) = 0; г (20) = 3
Домен: [−9, ∞); диапазон: [0, ∞)
Домен: [1, ∞); диапазон: [2, ∞)
Домен: ℝ; диапазон: ℝ
Домен: ℝ; диапазон: ℝ
Домен: ℝ; диапазон: ℝ
Домен: ℝ; диапазон: ℝ
567
15311
3235
2753
Умножение квадратных корней: 3 простых метода [с примерами]
Ваши ученики знают, как умножать экспоненты, но теперь пришло время научить их умножению квадратных корней и чудесному миру предалгебры.Но вы опасаетесь, что они могут подумать: «В классе математики мы узнали больше об алгебре, например, X + 10 = Y, но почему меня это должно волновать?»
Вы хотите, чтобы они поняли, что французский математик Жан де Ронд д’Аламбер сказал знаменитую фразу: «алгебра щедра; она часто дает больше, чем от нее просят ».
То, что вы не видите X и Y, не означает, что вы не используете алгебру каждый день. Умение умножать квадратные корни — это один из камней на живописном пути к пониманию актуальности алгебры в реальной жизни.
Преподаватели, подобные вам, знают, что не всегда легко сделать эти абстрактные и сложные концепции интересными и увлекательными.
Этот пост в блоге, разделенный на три части, призван изменить это!
- Что такое квадратные корни
- Как умножить квадратные корни
- Привлечение способов закрепить знания учащихся о квадратном корне
Часть первая: Что такое «квадратный корень»?
Квадратный корень из числа относится к множителю, который можно умножить само на себя, чтобы получить это число.Другими словами, нахождение квадратного корня — это процесс, противоположный возведению числа в квадрат.
Извлечь квадратный корень можно только из неотрицательных чисел — даже тех, которые не дают целых чисел. Это потому, что любое число раз само по себе является положительным или нулевым — вы никогда не получите отрицательный продукт, возведя в квадрат отрицательное число. Как вы видели выше, квадратный корень отменяет возведение в квадрат, поэтому отрицательные числа не могут иметь квадратные корни.
Тем не менее, точные квадратные числа являются наиболее эффективными при обучении студентов умножению квадратных корней.
На рисунке ниже мы видим, что квадратный корень из 16 равен 4, потому что 4 в квадрате, или 42, равняется 16.
В классе математики уравнение такого типа будет выглядеть так:
Учащиеся видят это Впервые наверняка возникнут вопросы: Что это за символ в виде галочки? Почему на нем крошечная цифра?
Бретт Берри, основательница Math Hacks, в своей статье о понимании логарифмов и корней создала ясный и лаконичный образ со всей терминологией root .
Многие вопросы о нахождении квадратных корней не включают корневой индекс. Однако корневые индексы необходимы при вычислении более высоких индексированных корней, таких как кубические, четвертые или пятые корни.
Когда мне когда-нибудь понадобится умножать квадратные корни?Независимо от того, насколько хорошо вы преподаете эти алгебраические концепции, студенты всегда будут задавать этот вопрос. ☝️
И вы должны быть готовы предоставить им законные ответы. Например, умножение квадратного корня может быть важно для:
- Знание площади их будущих домов
- Архитекторов
- Художников
- Плотников
- Строителей
- Дизайнеров
- Инженеров
Есть и другие! В то время как некоторым придется вычислять уравнения каждый день, другие будут использовать эти концепции для составления оценок.Одно можно сказать наверняка: люди этих профессий изучали математику в школе в детстве и используют ее до сих пор!
Часть вторая: 3 простых метода умножения квадратных корней
Умножение квадратных корней без коэффициентов
1. Умножьте каждое подкоренное и так же, как без радикала или символа квадратного корня.
2. Упростите подкоренное выражение, вычленив все полные квадраты. Если в подкоренном выражении нет полных квадратов, значит, оно уже упрощено.В этом случае вы можете упростить √98 до √2, а √49 — до полного квадрата.
3. Извлеките квадратный корень из полного квадрата. В этом примере упростите √49 до 7 и поместите его перед оставшимся выражением √2.
Умножение квадратных корней с коэффициентами
1. Умножение коэффициентов перед знаками корня , если они есть.
2. Умножьте каждое подкоренное выражение так же, как и без радикала или символа квадратного корня.
3. Упростите подкоренное выражение, вычленив все полные квадраты. В этом примере вы можете упростить √40 до √4 и √10.
4. Извлеките квадратный корень из полного квадрата и умножьте его на коэффициент . В этом примере упростите √4 до 2 и умножьте его на 6.
Умножение квадратных корней с переменными
В дополнение к числам радикалы могут содержать другие вещи, такие как переменные и показатели степени.Упрощение радикалов с помощью переменных следует тем же правилам, что и упрощение радикалов с числами.
1. Умножаем подкоренные выражения . Если есть коэффициенты, их тоже умножьте.
Примечание : для умножения радикалов, содержащих переменные,:
- Корневой индекс должен быть таким же
- Значение x — вместе с любыми другими переменными — должно быть больше или равно нулю
2. Найдите множители на простые множители, чтобы определить точные квадратные множители. Для этого вы можете использовать дерево факторов, как на изображении ниже.
Например, 2 и 9 равны 18, а 9 упрощается до 3 и 3. Таким образом, разложение на простые множители и квадратные множители для 18 будут 2, 3 и 3. Разложение на простые множители 30 равно 2, 3 и 5. Вы также можете разбить и переставить переменные экспоненты — вы можете переписать x3 как x2 и x .
Часть третья: Действия по закреплению знаний учащихся о квадратном корне
Создайте радикальные башни чисел
Лиза Тарман, педагог из Пенсильвании, создала сотни учебных материалов.Ее «Лабиринт упрощающих радикалов» — это освежающий и увлекательный подход к традиционным рабочим листам.
Попросите учащихся начать с левого верхнего угла. Им придется упростить радикалы, чтобы добраться до конца лабиринта. Получите доступ к бесплатному рабочему листу Тармана и ответьте на него здесь.
Если вы хотите лабиринт умножающих радикалов, посмотрите этот от Teachers Pay Teachers!
Play Prodigy
Prodigy — бесплатная адаптивная математическая игра, которой пользуются полтора миллиона учителей и более 50 миллионов студентов по всему миру! Он предлагает контент по всем основным математическим темам и охватывает с 1 по 8 класс, в том числе, как:
- Вычислить идеальные корни
- Переписать показатели степени как корни
Использование Prodigy в вашем классе поможет учащимся развить беглость математики и уверенность в себе. будущая средняя школа и курсы математики на уровне колледжа.Ваш класс будет исследовать мир, наполненный захватывающими квестами, которые предоставляют персонализированный, согласованный с учебной программой контент и данные об учениках в режиме реального времени.
Помня об этих методах и упражнениях, вы поймете, что умножение квадратных корней не должно оставаться неуместным или пугающим для вас или ваших учеников.
При эффективном использовании упражнения, подобные приведенным выше, могут помочь укрепить понимание учащимися и повысить уровень вовлеченности учителей, которые редко становятся свидетелями на уроках математики.
Вы педагог? Настройте вопросы по математике, чтобы дополнить учебный материал и дифференцировать инструкции, обращая внимание на проблемные места каждого учащегося.
Prodigy также предлагает мощные инструменты для немедленной подготовки отчетов как для учителей, так и для родителей. От отчетов о прогрессе до отчетов об использовании и т. Д. — используйте данные своего ученика или ребенка, чтобы определить, где они преуспевают или у них проблемы, чтобы вы могли настроить для них контент в игре.
Нажмите здесь или на баннер ниже, чтобы начать работу менее чем за пять минут!
4. Полномочия, корни и радикалы
На этой странице
Связанный раздел
Не пропустите главу «Экспоненты и радикалы», где мы более подробно рассмотрим эти темы.
На этой странице мы продолжим рассмотрение того, как работают числа, прежде чем применять процедуры к алгебре. Все работает так же, за исключением того, что в алгебре мы используем буквы для обозначения чисел.
Индексы
Индексы (или степени , или степени ) очень полезны в математике. Индексы — это удобный способ записи умножения, в котором есть много повторяющихся членов.
Пример индекса
В примере 5 3 мы говорим, что:
5 — это база и
3 — это индекс (или степень , , или показатель степени ).
5 3 означает «умножить 5 на себя 3 раза».
[Или, точнее, «многократно умножить 5 само на себя так, чтобы получилось три 5 в умножении», или даже лучше, «три пятерки, умноженные вместе». См. Обсуждение этого вопроса в разделе «Камни преткновения в математике».]
То есть 5 3 означает
5 3 = 5 × 5 × 5
Примеры целочисленных показателей
Что произойдет, если у нас будет индекс 1, а может, 0 или даже -2?
Давайте создадим шаблон, используя наш пример выше, чтобы мы могли видеть, что означают эти особые случаи.-1 = 1 / 5`
Эти легко испортить, и они могут лишить вас сна без надобности, когда вы позже будете заниматься алгеброй.
Как правило, любое число a (кроме 0) в степени 1 равно a .
a 1 = a
Кроме того, любое число a (кроме 0) в степени 0 равно 1.
a 0 = 1
И любое число a (кроме 0) в степени -1 равно «1 / a».-1 = 1 / а`
Умножение чисел с одинаковым основанием
Нам часто нужно умножить что-то вроде следующего:
4 3 × 4 5
Мы замечаем, что числа имеют одинаковое основание (то есть 4), и мы думаем об этом так:
4 3 × 4 5 `= \ underbrace {(4 xx 4 xx 4)} _ {3″ из них «} xx \ underbrace {(4 xx 4 xx 4 xx 4 xx 4)} _ {5 «из них»} `
Мы получаем 3 четверки из первой скобки и 5 четверок из второй, так что в сумме у нас будет 3 + 5 = 8 четверок, умноженных вместе.
4 3 × 4 5 = 4 3 + 5 = 4 8 (Если кому-то интересно, окончательный ответ — 65 536. 🙂
В целом можно сказать для любого числа a и индексов m и n :
a м × a n = a ( m + n )
Деление чисел с одинаковым основанием
В качестве примера разделим 3 6 на 3 2 :
. 2}` = {(3xx3xx3xx3xx3xx3)} / (3xx3) `= 3 × 3 × 3 × 3 = 3 4 = 81
Мы вычли 2 тройки наверху и 2 тройки внизу дроби, оставив 4 тройки наверху (и цифру 1 на Нижний).(m-n) `
Возведение индексного выражения в индекс
В качестве примера возведем число 4 2 в степень 3:
(4 2 ) 3 = 4 2 × 4 2 × 4 2
Из приведенного выше примера умножения мы видим, что это даст нам 4 6 . Мы могли бы это сделать как:
(4 2 ) 3 = 4 2 × 3 = 4 6
В общем имеем для любой базы a и индексов m и n :
( a m ) n = a mn
Повышение эффективности продукта
Пример числа:
(5 × 2) 3 = 5 3 × 2 3
В данном случае с числами лучше сначала произвести умножение в скобках, а затем возвести наш ответ в степень 3. n, (ane0)`
ПРИМЕЧАНИЕ 1: Эти правила применяются, когда a и b являются положительными и m и n являются целыми числами .7`
, потому что это , в отличие от терминов (буквенная часть возведена в другую степень). (Мы можем разложить это на множители, но не можем каким-либо образом расширить или добавить термины.)
Чтобы узнать, как все это используется в алгебре, перейдите по ссылке:
Корни и радикалы
Мы используем радикальный знак : `sqrt (\ \)`
Означает «квадратный корень». Квадратный корень на самом деле является дробным индексом и эквивалентен возведению числа в мощность 1/2.(1/2) = sqrt (25) = 5`
Так же можно
Кубический корень: `root (3) x` (что эквивалентно возведению в степень 1/3) и
Корень четвертой степени: `root (4) x` (степень 1/4) и так далее.
См. Больше в разделе «Дробные экспоненты».
Основные моменты, на которые следует обратить внимание:
Связанный раздел
Как упоминалось выше, если вам нужна дополнительная информация по этой теме, перейдите по ссылке: Показатели и Радикалы.
Если a ≥ 0 и b ≥ 0, имеем:
`sqrt (axxb) = sqrt (a) xxsqrt (b)`
Однако это работает только для умножения.2) = а`
Это смущает многих студентов. Но это просто означает:
- Начните с числа
- Квадрат
- Найдите квадратный корень из результата
- Закончите с номером, с которого вы начали
Например, начать с 3.
Квадрат, получится 9.
Извлеките квадратный корень и получите 3, то есть с того места, где вы начали.
Почему это важно? Часто нам нужно «отменить» квадрат при решении уравнения, поэтому мы находим квадратный корень из обоих стороны.
 Видим, что все множители имеют показатель, равный единице, а показатель корня в этом примере равен двум. Следовательно, в данном примере ни один множитель не нужно выносить из-под знака корня, то есть такое действие для 102 нецелесообразно.
Видим, что все множители имеют показатель, равный единице, а показатель корня в этом примере равен двум. Следовательно, в данном примере ни один множитель не нужно выносить из-под знака корня, то есть такое действие для 102 нецелесообразно.

 В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители. Воспользовавшись этим правилом, извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
Воспользовавшись этим правилом, извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня. Простые множители числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
Простые множители числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
 Объявление
темы урока.
Объявление
темы урока.




 {2n}}}=\left| a \right|. \\ \end{align}\]
{2n}}}=\left| a \right|. \\ \end{align}\] {2}}}=\sqrt{5}. \\ \end{align}\]
{2}}}=\sqrt{5}. \\ \end{align}\] 2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.

 Одно из действий в такой «паре» направлено на увеличение числа, а другое, обратное ему – на уменьшение. Например, действие, противоположное сложению – это вычитание, умножению соответствует деление. Имеется и своя диалектическая пара-противоположность и у возведения в степень. Речь идет об извлечении корня.
Одно из действий в такой «паре» направлено на увеличение числа, а другое, обратное ему – на уменьшение. Например, действие, противоположное сложению – это вычитание, умножению соответствует деление. Имеется и своя диалектическая пара-противоположность и у возведения в степень. Речь идет об извлечении корня. Следовательно,
Следовательно, о., у нас получается следующее:
о., у нас получается следующее: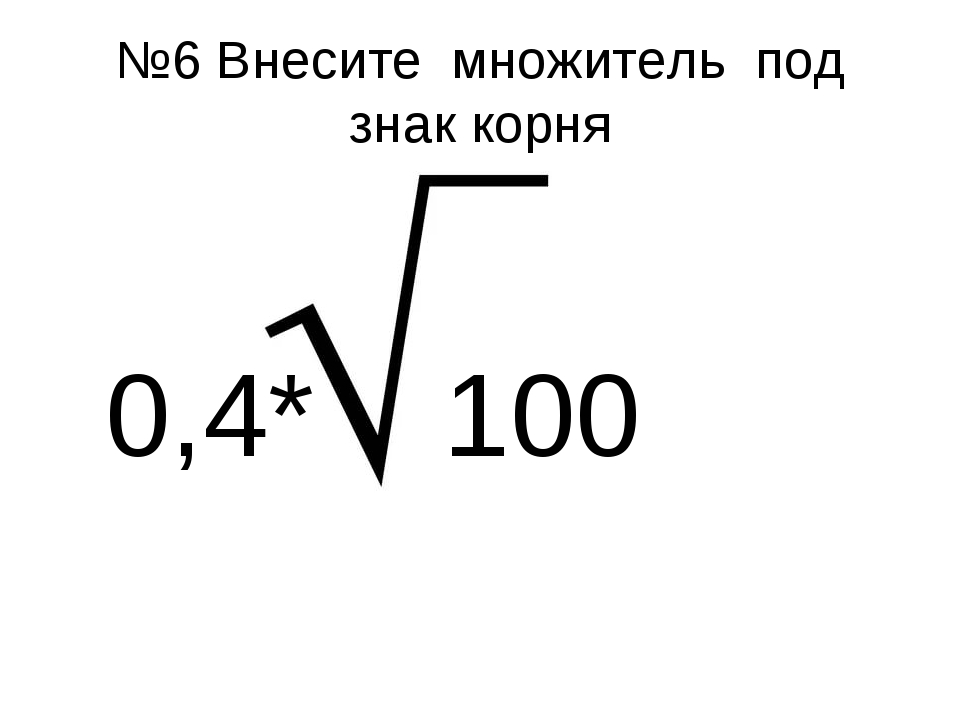 Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ). 

 Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.



 {20}} \)
{20}} \)

 5
5

 И квадратный корень из 1 тоже 1.
И квадратный корень из 1 тоже 1. числа — это число, которое при умножении само на себя дает исходное число. Например, 5 — это квадратный корень из 25, потому что 52 = 25. Поскольку (−5) 2 = 25, мы можем сказать, что −5 также является квадратным корнем из 25. Каждое положительное действительное число имеет два квадратных корня: положительный и отрицательный. По этой причине мы используем знак корня для обозначения главного (неотрицательного) квадратного корня Положительного квадратного корня из положительного действительного числа, обозначаемого символом. и отрицательный знак перед корнем — для обозначения отрицательного квадратного корня.
числа — это число, которое при умножении само на себя дает исходное число. Например, 5 — это квадратный корень из 25, потому что 52 = 25. Поскольку (−5) 2 = 25, мы можем сказать, что −5 также является квадратным корнем из 25. Каждое положительное действительное число имеет два квадратных корня: положительный и отрицательный. По этой причине мы используем знак корня для обозначения главного (неотрицательного) квадратного корня Положительного квадратного корня из положительного действительного числа, обозначаемого символом. и отрицательный знак перед корнем — для обозначения отрицательного квадратного корня. число внутри радикального знака может быть разложено на квадрат другого числа, тогда квадратный корень из числа очевиден. В этом случае мы имеем следующее свойство:
число внутри радикального знака может быть разложено на квадрат другого числа, тогда квадратный корень из числа очевиден. В этом случае мы имеем следующее свойство: Например, если x = 1,
Например, если x = 1,
 По этой причине у любого действительного числа будет только один действительный кубический корень.Следовательно, технические детали, связанные с основным корнем, не применяются. Например,
По этой причине у любого действительного числа будет только один действительный кубический корень.Следовательно, технические детали, связанные с основным корнем, не применяются. Например, 3≈2
3≈2
 положительного действительного числа как числа, которое при возведении в степень n в -й степени дает исходное число. Для любого неотрицательного действительного числа a мы имеем следующее свойство:
положительного действительного числа как числа, которое при возведении в степень n в -й степени дает исходное число. Для любого неотрицательного действительного числа a мы имеем следующее свойство:
 Фактически, аналогичная проблема возникает для любого четного индекса:
Фактически, аналогичная проблема возникает для любого четного индекса: Произведение нечетного числа положительных факторов положительно, а произведение нечетного количества отрицательных факторов отрицательно. Следовательно, когда индекс n является нечетным, существует только один действительный корень n -й степени для любого действительного числа a . И вот недвижимость у нас:
Произведение нечетного числа положительных факторов положительно, а произведение нечетного количества отрицательных факторов отрицательно. Следовательно, когда индекс n является нечетным, существует только один действительный корень n -й степени для любого действительного числа a . И вот недвижимость у нас:
 если он не содержит каких-либо факторов, которые могут быть записаны как абсолютные степени индекса.
если он не содержит каких-либо факторов, которые могут быть записаны как абсолютные степени индекса.

 Обычно процесс упрощается, если вы работаете с разложением на простые множители подкоренного выражения.
Обычно процесс упрощается, если вы работаете с разложением на простые множители подкоренного выражения.




 Дайте точный ответ и примерный ответ с округлением до сотых.
Дайте точный ответ и примерный ответ с округлением до сотых.