Решение задач по теме «Числовая окружность на координатной плоскости»
Мы рассматриваем числовую окружность с центром в начале координат, 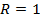 и началом отсчета в точке
и началом отсчета в точке 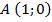 , как показано на рисунке 1.
, как показано на рисунке 1.
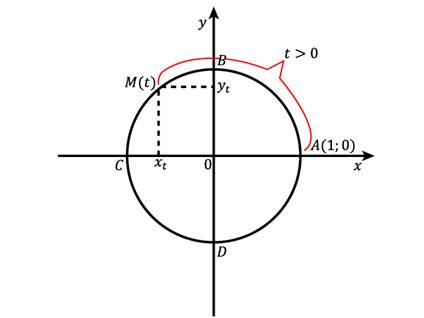
Рис. 1. Числовая окружность
Каждому действительному числу 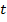 соответствует единственная точка
соответствует единственная точка 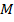 на этой окружности ( рис. 1).
на этой окружности ( рис. 1).
Как получается эта точка 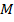 ?
?
Откладываем дугу 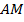 , равную по модулю
, равную по модулю 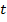 , против часовой стрелки (если
, против часовой стрелки (если 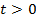 ) и по часовой стрелке (если
) и по часовой стрелке (если 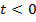 ). Итак, точка
). Итак, точка 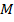
Каждая точка 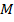 имеет единственную пару декартовых координат: абсциссу
имеет единственную пару декартовых координат: абсциссу 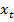 и ординату
и ординату 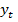 (рис. 1). Имеем действительное число
(рис. 1). Имеем действительное число 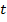 , по нему находим единственную точку на окружности
, по нему находим единственную точку на окружности 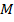
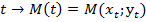 .
.Таким образом, каждому действительному числу 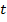 сопоставляется два числа
сопоставляется два числа 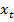 и
и
interneturok.ru
Числовая окружность в координатной плоскости — урок. Алгебра, 10 класс.
Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок.
Начальная точка числовой окружности \(A\) совмещена с точкой \((1;0)\).
Каждая точка числовой окружности имеет в координатной плоскости свои координаты.
Найдём сначала координаты тех точек координатной плоскости, которые получены на макетах числовой окружности.
Точка Mπ4 — середина \(I\) четверти. Опустим перпендикуляр \(MP\) на прямую \(OA\) и рассмотрим треугольник \(OMP\). Так как дуга \(AM\) составляет половину дуги \(AB\), то ∡MOP=45°.
Значит, треугольник \( OMP \) — равнобедренный прямоугольный треугольник и \(OP = MP\), т. е. у точки \(M\) абсцисса и ордината равны: \(x = y\).
Так как координаты точки \(M(x;y)\) удовлетворяют уравнению числовой окружности x2+y2=1, то для их нахождения нужно решить систему уравнений: x2+y2=1x=y |
Подставив \(x\) вместо \(y\) в первое уравнение системы, получим следующее решение:
x2+x2=1;2×2=1;x2=12;x=12=22;y=x=22.
При решении учитываем, что абсцисса точки \(M\) положительна.
Получили, что координаты точки \(M\), соответствующей числу π4, будут Mπ4=M22;22.
Аналогично можно получить координаты и других точек первого макета числовой окружности, учитывая только знаки координат в каждой четверти.
Полученные результаты запишем в таблицу.
Точка окружности |
| \(0\) | π4 | π2 | 3π4 | π | 5π4 | 3π2 | 7π4 | 2π |
Абсцисса \(x\) | \(1\) | 22 | \(0\) | −22 | \(-1\) | −22 | \(0\) | 22 | \(1\) |
Ордината \(y\) | \(0\) | 22 | \(1\) | 22 | \(0\) | −22 | \(-1\) | −22 | \(0\) |
Рассуждаем аналогично для точки \(M\), если теперь она соответствует числу π6.
Треугольник \(MOP\) прямоугольный. Так как дуга \(AM\) составляет третью часть дуги \(AB\), то ∡MOP=30°.
Катет \(MP\) лежит против угла \(30\) градусов в прямоугольном треугольнике, значит, равен половине гипотенузы, т. е. ордината точки \(M\) равна MP=12;y=12 |
Абсциссу \(x\) точки \(M\) найдём, решив уравнение:
x2+y2=1;
x2=1−122=1−14=34;x=32.
При решении учитываем, что абсцисса точки \(M\) положительна.
Получили, что координаты точки \(M\), соответствующей числу π6, будут Mπ6=M32;12.
Аналогично можно получить координаты и других точек второго макета числовой окружности, учитывая только знаки координат в каждой четверти.
Полученные результаты запишем в таблицу.
Точка окружности |
π6 | π3 | 2π3 | 5π6 | 7π6 | 4π3 | 5π3 | 11π6 | |
Абсцисса \(x\) | 32 | 12 | −12 | −32 | −32 | −12 | 12 | 32 |
Ордината \(y\) | 12 | 32 | 32 | 12 | −12 | −32 | −32 | −12 |
www.yaklass.ru
Числовая окружность. Видеоурок. Алгебра 9 Класс
Представляем вашему вниманию видеоурок по теме «Числовая окружность». Дается определение, что такое синус, косинус, тангенс, котангенс и функции y=sin x, y=cos x, y=tg x, y=ctg x для любого числового аргумента. Рассматривается стандартные задачи на соответствие между числами и точками в единичной числовой окружности для нахождения каждому числу единственной точки, и, наоборот, на нахождение для каждой точки множество чисел которые ей соответствуют.
Тема: Элементы теории тригонометрических функций
Урок: Числовая окружность
Наша ближайшая цель – определить тригонометрические функции: синус, косинус, тангенс, котангенс-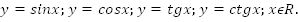
Числовой аргумент можно откладывать на координатной прямой или на окружности.
Такая окружность называется числовой или единичной, т.к. для удобства берут окружность с 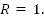
Например, дана точка 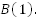 Отметим ее на координатной прямой
Отметим ее на координатной прямой
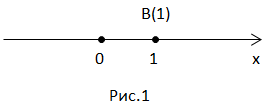
и на числовой окружности.
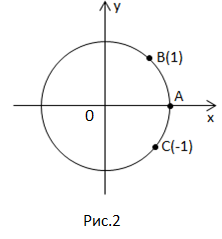
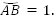
При работе с числовой окружностью условились, что движение против часовой стрелки – положительное направление, по часовой стрелке – отрицательное.
Типовые задачи – нужно определить координаты заданной точки либо, наоборот, найти точку по ее координатам.
Координатная прямая устанавливает взаимно-однозначное соответствие между точками и числами. Например, числу 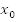 соответствует точка А с координатой
соответствует точка А с координатой 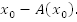
Каждая точка В с координатой 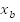 характеризуется только одним числом – расстоянием от 0 до
характеризуется только одним числом – расстоянием от 0 до 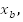
На числовой окружности взаимно-однозначное соответствие работает только в одну сторону.
Например, есть точка В на координатной окружности (рис.2), длина дуги 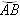 равна 1, т.е. эта точка соответствует 1.
равна 1, т.е. эта точка соответствует 1.
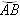 =1.
=1.
Дана окружность, длина окружности 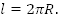 Если
Если 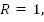 то
то 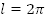
Если мы прибавим 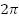 , получим ту же точку В, еще
, получим ту же точку В, еще 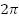 – тоже попадем в т. В, отнимем
– тоже попадем в т. В, отнимем 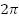 – тоже т. В.
– тоже т. В.
Рассмотрим точку B: длина дуги 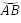 =1, тогда числа
=1, тогда числа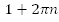
interneturok.ru
| 1. |
Единичная окружность, квадранты
Сложность: среднее |
1 |
| 2. |
Числовая окружность
Сложность: лёгкое |
5 |
| 3. |
Определение чисел, соответствующих точке
Сложность: лёгкое |
1 |
| 4. |
Соответствие точек числовой окружности числам
Сложность: лёгкое |
1 |
| 5. |
Определение координат точек
Сложность: лёгкое |
1 |
| 6. |
Длина дуги на числовой окружности, разделённой точками
Сложность: среднее |
3 |
| 7. |
Длина дуги на числовой окружности
Сложность: среднее |
1 |
| 8. |
Симметрия точек на числовой окружности
Сложность: среднее |
2 |
| 9. |
Принадлежность точек числовой окружности
Сложность: среднее |
1 |
| 10. |
Расположение точек на числовой окружности
Сложность: сложное |
3 |
| 11. |
Сравнение абсциссы и ординаты точки
Сложность: сложное |
3 |
| 12. |
Соответствие между числами и точками числовой окружности
Сложность: сложное |
4 |
www.yaklass.ru
Тригонометрия для чайников. Урок1. Тригонометрия с нуля
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sinα=Противолежащий катетгипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cosα=Прилежащий катетгипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tgα=Противолежащий катетПрилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctgα=Прилежащий катетПротиволежащий катет
Рассмотрим прямоугольный треугольник ABC, угол C равен 90°:
sin∠A=CBAB
cos∠A=ACAB
tg∠A=sin∠Acos∠A=CBAC
ctg∠A=cos∠Asin∠A=ACCB
sin∠B=ACAB
cos∠B=BCAB
tg∠B=sin∠Bcos∠B=ACCB
ctg∠B=cos∠Bsin∠B=CBAC
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках (−1;0) и (1;0), ось y в точках (0;−1) и (0;1)
На данной окружности будет три шкалы отсчета – ось x, ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами (1;0), – то есть от положительного направления оси x, против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A. Рассмотрим ∠SOA, обозначим его за α. Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠SOA=α=∪SA.
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B) и на ось игрек (точка C).
Отрезок OB является проекцией отрезка OA на ось x, отрезок OC является проекцией отрезка OA на ось y.
Рассмотрим прямоугольный треугольник AOB:
cosα=OBOA=OB1=OB
sinα=ABOA=AB1=AB
Поскольку OCAB – прямоугольник, AB=CO.
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90°:
Опускаем из точки A перпендикуляры к осям x и y. Точка B в этом случае будет иметь отрицательную координату по оси x.Косинус тупого угла отрицательный.
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0° до 180°. Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x. (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0°,30°,45°,60°,90°,120°,135°,150°,180°. Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y.
Координата по оси x – косинус угла, координата по оси y – синус угла.
Пример:
cos150°=−32
sin150°=12
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный.
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный.
sin2α+cos2α=1
Данное тождество – теорема Пифагора в прямоугольном треугольнике OAB:
AB2+OB2=OA2
sin2α+cos2α=R2
sin2α+cos2α=1
| 0° | 30° | 45° | 60° | 90° | |
| sinα | 0 | 12 | 22 | 32 | 1 |
| cosα | 1 | 32 | 22 | 12 | 0 |
| tgα | 0 | 33 | 1 | 3 | нет |
| ctgα | нет | 3 | 1 | 33 | 0 |
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin180°=sin(180°−0°)=sin0°
sin150°=sin(180°−30°)=sin30°
sin135°=sin(180°−45°)=sin45°
sin120°=sin(180°−60°)=sin60°
cos180°=cos(180°−0°)=−cos0°
cos150°=cos(180°−30°)=−cos30°
cos135°=cos(180°−45°)=−cos45°
cos120°=cos(180°−60°)=−cos60°
Рассмотрим тупой угол β:
Для произвольного тупого угла β=180°−α всегда будут справедливы следующие равенства:
sin(180°−α)=sinα
cos(180°−α)=−cosα
tg(180°−α)=−tgα
ctg(180°−α)=−ctgα
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
asin∠A=bsin∠B=csin∠C
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
asin∠A=bsin∠B=csin∠C=2R
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a2=b2+c2−2bc⋅cos∠A
b2=a2+c2−2ac⋅cos∠B
c2=a2+b2−2ab⋅cos∠C
Модуль геометрия: задания, связанные с тригонометрией.
Скачать домашнее задание к уроку 1.
epmat.ru
Числовая окружность на координатной плоскости. Синус и косинус
В ходе урока вы сможете самостоятельно изучить тему «Числовая окружность на координатной плоскости. Синус и косинус». В первой части урока рассматривается круг и его составные части. Разбираются примеры задач. Далее дается определения sinα и cosα, рассказывается о том, как вычислять эти значения и находить синусы и косинусы для основных реперных точек окружности
Мы уже знаем, что аргумент можно откладывать на числовой окружности. Рассмотрим круг и его основные части, которые нам будут нужны в дальнейшем.
Определение радиана. Углы могут измеряться разными единицами – градусами и радианами.
Радианом называется такой центральный угол, длина дуги которого равна радиусу (рис.1).
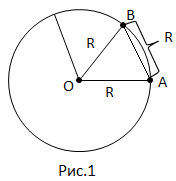
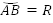 ;
;
Ð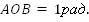
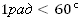 , т.к. длина хорды АВ меньше длины дуги
, т.к. длина хорды АВ меньше длины дуги 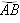 .
.
Связь радиана и градуса.
Окружность разделили на 360 равных частей и угол, равный одной части, приняли за угол в 
А сколько углов в 1рад можно получить в одной окружности?
Длина окружности 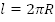 , т.е. в окружности содержится
, т.е. в окружности содержится 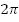 штук радиусов R.
штук радиусов R.
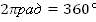 ;
;
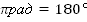 — связь градуса и радиана;
— связь градуса и радиана;
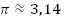 — иррациональное число.
— иррациональное число.
Типовые задачи.
1. Дано: 
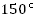 . Перевести в рад.
. Перевести в рад. 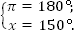
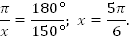
a) Дано:  Перевести в рад.
Перевести в рад. 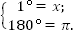
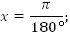
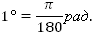
2. Дано: 1рад. Перевести в градусы. 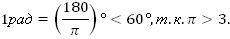
interneturok.ru
Тригонометрический круг ☑️ со всеми значениями, круг синусов и косинусов, линия, ось тангенса на окружности, как пользоваться и находить точки
Общие сведения
Для правильного решения тригонометрических задач следует изучить основные понятия, формулы, а также методы нахождения основных величин. Раздел математики, изучающий функции косинуса, синуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса и арккотангенса, называется тригонометрией. Окружность, которая используется для решения геометрических задач на плоскости, имеет единичный радиус.
Значения функций, которые можно по ней находить, называются тригонометрическими. Однако существует множество способов нахождения их значений, но в некоторых ситуациях при использовании формул приведения решение затянется на продолжительное время, а вычисления будут громоздкими. Чтобы этого избежать, нужно использовать тригонометрический круг со всеми значениями. С его помощью также можно определить, является ли функция четной или нечетной.
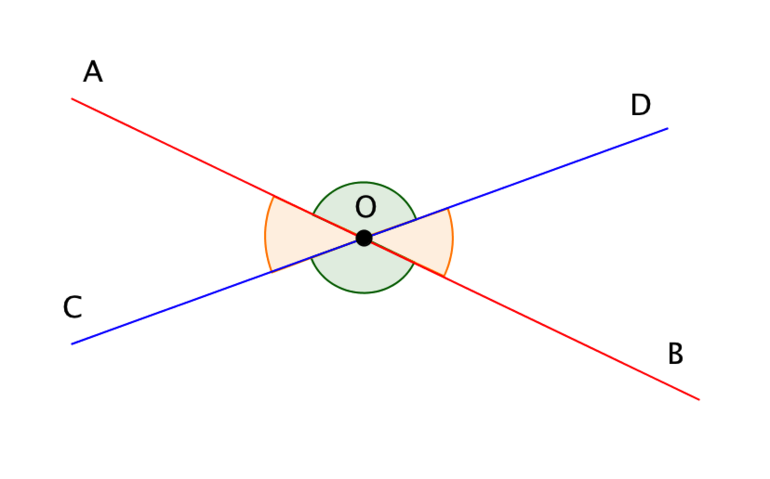
Углы и их классификация
Перед тем как понять основное назначение тригонометрических функций, следует обратить внимание на классификацию углов. Она является важной для вычисления тригонометрических выражений. Углы в математических дисциплинах делятся на следующие типы:
- Острые.
- Прямые.
- Тупые.
- Развернутые.
- Выпуклые.
- Полные.
К первому типу относятся углы любой размерности градусной единицы измерения, которая не превышает 90 (а<90). Если значение соответствует 90, то он является прямым (а=90). Угол считается тупым, при выполнении следующего условия: 90<a<180. Если градусная размерность угла соответствует 180, то он является развернутым (а = 180). Выпуклым считается угол, когда выполняется такое условие: 180 < a < 360. Следует отметить, что он является смежным с острым углом. В случае, когда значение градусной размерности соответствует 360 градусам, то он является полным (а=360).
Однако углы измеряются не только в градусах, но и в радианах. Для решения тригонометрических задач оптимальным выбором градусной меры является радиан. Для соотношения между двумя единицами измерения применяется простая формула: 180 (град) = ПИ (рад). Из соотношения можно вывести формулу для перевода градусов в радианы: Pрад = (а * ПИ) / 180. Переменная «а» — значение величины градусной меры заданного угла. Обратное соотношение принимает следующий вид: а = (Ррад * 180) / ПИ.
Для быстрого перевода единиц измерения применяют такие инструменты: радианная табличка, программное обеспечение и тригонометрическая окружность. Однако для начала следует обратить внимание на тригонометрические функции, которые присутствуют в задачах физико-математического уклона.
Информация о функциях
Тригонометрических функций всего четыре вида: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существует столько же типов обратных функций: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg). Они получили широкое применение не только в математических задачах, но также используются в физике, электронике, электротехнике и других дисциплинах. Основной их особенностью считается возможность представления какого-либо закона.

Например, зависимость амплитуды напряжения переменного тока от времени описывается следующим законом: u = Um * cos (w*t) (графиком является косинусоида). Гармонические звуковые колебания также подчиняются определенному закону, в котором присутствует тригонометрическая функция. Кроме того, можно находить значения корня тригонометрического уравнения.
Синусом угла называется величина, равная отношению противолежащего катета прямоугольного треугольника к его гипотенузе. Следовательно, косинус — отношение прилежащего катета к гипотенузе. Тангенс — отношение величины противолежащего катета к прилежащему. Котангенс является обратной функцией тангенсу, т. е. отношение прилежащего к противолежащему.
Функции arcsin, arccos, arctg, arcctg применяются в том случае, когда нужно найти значение угла в градусах или радианах. Вычисления выполняются по специальным таблицам Брадиса или с помощью программ. Также можно использовать тригонометрическую окружность.
Тригонометрический круг
Чтобы воспользоваться тригонометрической окружностью для решения задач, нужны такие базовые знания: понятие о синусе, косинусе, тангенсе, котангенсе, системе координат и теореме Пифагора. Для построения единичной окружности используется декартовая система координат с двумя осями. Точка «О» — центр пересечения координатных осей, ОХ — ось абсцисс, ОУ — ординат.
Для решения задач различного типа применяется и теорема Пифагора. Она справедлива только для прямоугольного треугольника (один из углов — прямой). Ее формулировка следующая: квадрат гипотенузы в произвольном прямоугольном треугольнике равен сумме квадратов катетов. Следует также знать основные соотношения между функциями острых углов в заданном прямоугольном треугольнике:
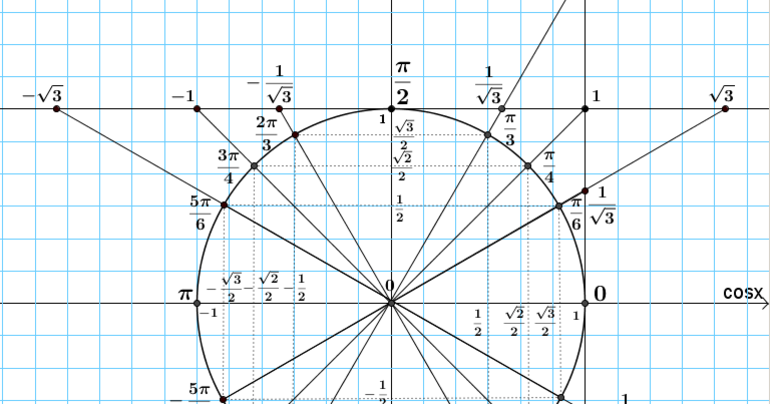
- a + b = 180.
- cos(a) = sin(b).
- cos(b) = sin(a).
- tg(a) = ctg(b).
- tg(b) = ctg(a).
- tg(a) = 1 / ctg(a).
- tg(b) = 1 / ctg(b).
Существуют и другие тригонометрические тождества, но для работы с кругом этого перечня будет достаточно.
Построение «инструмента»
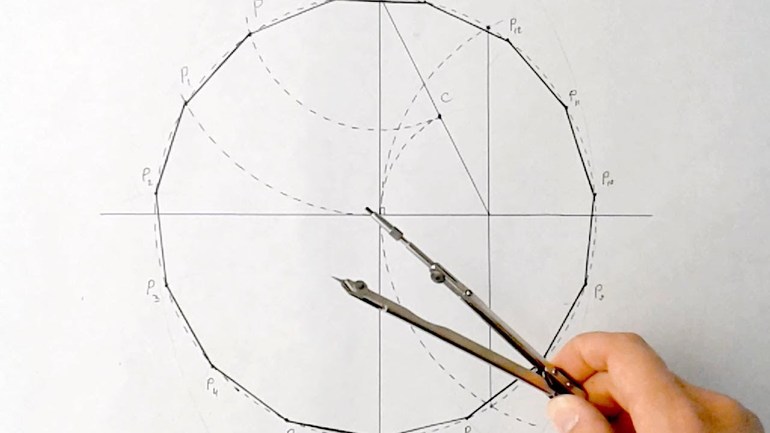
Построить окружность, которая ускорит процесс решения задач, довольно просто. Для этого потребуются бумага, карандаш, резинка и циркуль. Далее необходимо нарисовать любую немаленькую окружность. После этого отметить ее центр карандашом, поставив точку. Пусть она будет называться «О». Через эту точку следует провести две перпендикулярные прямые (угол пересечения равен 90 градусам). Обозначить их следующим образом: «х» (горизонтальная) и «у» (вертикальная).
Окружность является единичной, но не стоит рисовать ее такой, поскольку работать будет неудобно. Этот прием называется масштабированием. Он широко применяется практически во всех сферах человеческой деятельности. Например, инженеры не чертят двигатель космического корабля в натуральную величину, поскольку с таким «рисунком» будет неудобно и невозможно работать. Они используют его макет.
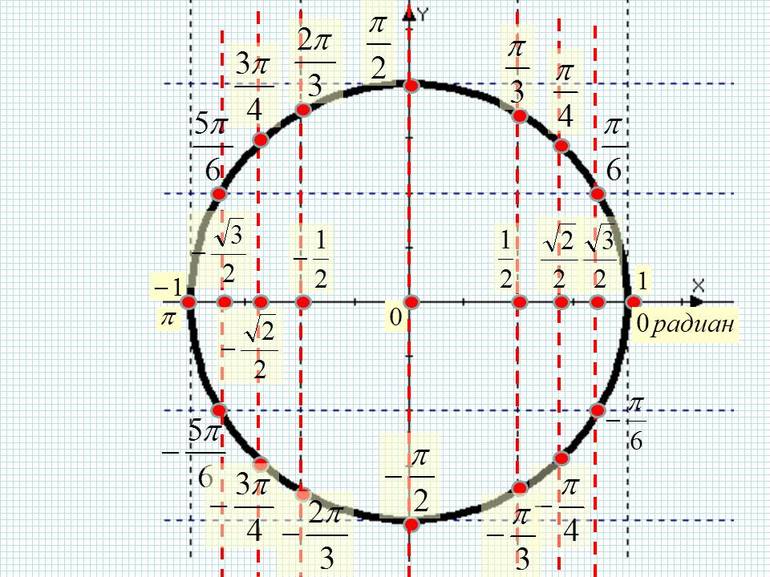
Окружность пересекается с осями декартовой системы координат в 4 точках со следующими координатами: (1;0), (0;1), (-1;0) и (0;-1). Области, которые делят декартовую систему координат на 4 части, называются четвертями. Их четыре:
- Первая состоит из положительных координат по х и у.
- Вторая имеет по х отрицательные и положительные по у.
- Третья — только отрицательные значения.
- Четвертая — положительные значения по х и отрицательные по у.
Исходя из этих особенностей, определяется числовой знак функции, позволяющий определить ее четность и нечетность. Кроме того, на ней следует отметить углы следующим образом: 0 и 2ПИ соответствует точке с координатами (1;0), ПИ/2 — (0;1), ПИ — (-1;0) и 3ПИ/2 — (0;-1).
Готовый макет
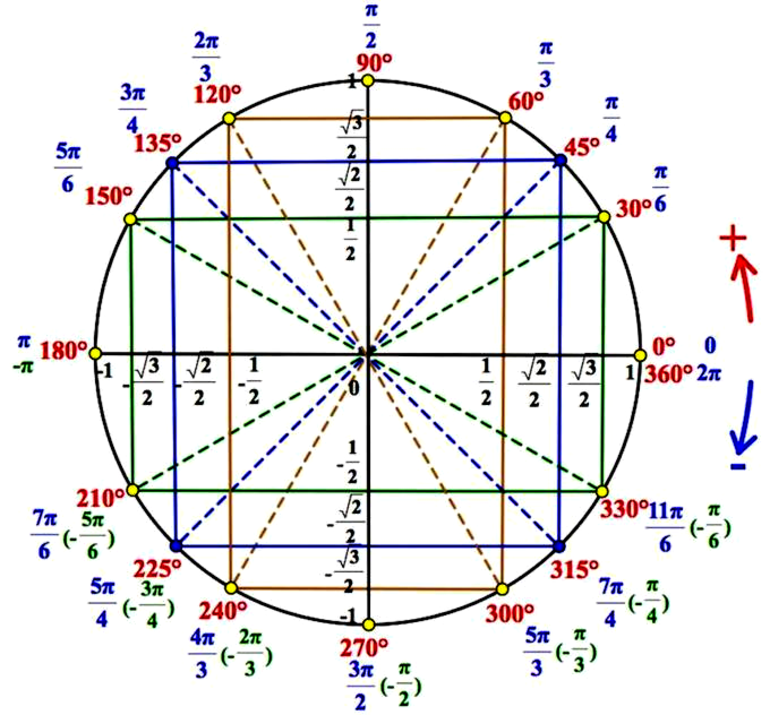
Для решения задач специалисты рекомендуют иметь рабочий и готовый макеты тригонометрических окружностей. Первый применяется для нахождения значений нестандартных углов (например, синуса 185 градусов). Тригонометрическим кругом (рис. 1) удобно пользоваться в том случае, когда значение угла является стандартным (90, 60 и т. д.).
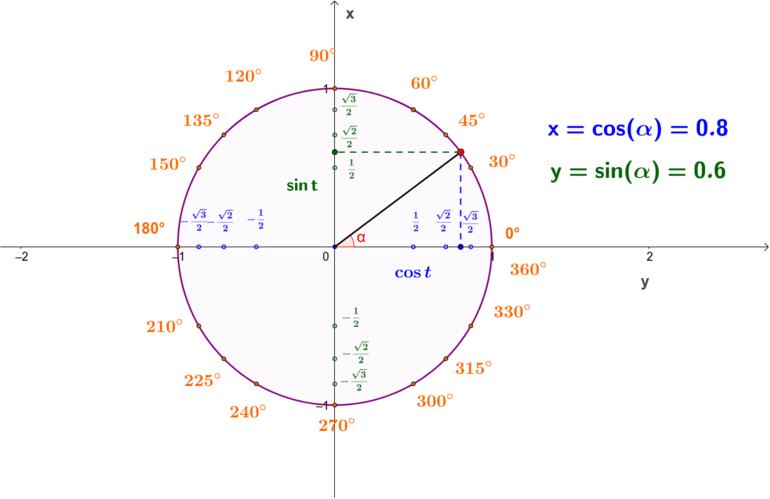
Рисунок 1. Готовый макет тригонометрического круга синусов и косинусов.
Для нахождения необходимых значений объединяют две фигуры — единичную окружность и прямоугольный треугольник. Гипотенуза последнего равна 1 и соответствует радиусу окружности. Ось ОХ — косинусы, ОУ — синусы. С помощью этого «инструмента» определение синусов и косинусов становится намного проще. Для нахождения значения sin(30) необходимо воспользоваться следующим алгоритмом:
- Отметить угол на окружности и достроить его до прямоугольного треугольника.
- Если катет лежит напротив угла в 30 градусов, то он равен 0,5 от длины гипотенузы.
- sin(30) = 1 * 0,5 = 0,5.

Для нахождения косинуса необходимо использовать основное тригонометрическое тождество, которое связывает sin и cos: (sin(a))^2 + (cos(a))^2 = 1. Из равенства величина cos(30) = sqrt[1 — (sin(30))^2]= sqrt[1 — 0,5^2] = sqrt(3) / 2.
Однако после всех вычислений следует выбрать знак функции. В данном случае угол находится в первой четверти. Следовательно, функция имеет положительный знак. Для нахождения тангенса и котангенса можно воспользоваться следующими формулами: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a). Подставив значения синуса и косинуса, можно определить значение tg: tg(30) = 0,5 / (sqrt(3) / 2) = 1 / sqrt(3) = sqrt(3) / 3. Тогда котангенс можно найти двумя способами:
- Через известный тангенс: ctg(30) = 1 / (1 / sqrt(3)) = sqrt(3).
- Использовать основное отношение: ctg(30) = (sqrt(3) / 2) / (1/2) = sqrt(3).
Вычислить значения синуса и косинуса для угла 60 градусов очень просто. Для этого нужно воспользоваться основными тождествами: sin(60) = сos(30) = sqrt(3) / 2, cos(60) = sin(30) = 1/2, tg(30) = ctg(60) = sqrt(3) / 3, tg(60) = ctg(30) = sqrt(3). Значения для 45 градусов определяются следующим образом:
- Прямоугольный треугольник с углом 45 градусов является равносторонним (катеты равны).
- (sin(45))^2 + (cos(45))^2 = 1.
- 2 * (sin(45))^2 = 1.
- sin(45) + cos(45) = sqrt(2) / 2.
Тангенс и котангенс равен 1. Если угол равен 90, то необходимо внимательно посмотреть на рисунок 1. Следовательно, sin(90) = 1, cos(90) = 0, tg(90) = 1 и ctg(90) не существует. Линия тангенса на окружности не отображается. В этом случае нужно пользоваться основными тригонометрическими тождествами.
Правила использования
Инструмент позволяет легко и быстро находить значения тригонометрических функций любых углов. Если при решении задачи требуется найти sin(270), то нужно выполнить простые действия:
- Пройти против часовой стрелки (положительное направление) 180 градусов, а затем еще 90.
- На оси синусов значение составляет -1 (точка лежит на оси).
Существуют задачи, в которых угол представлен отрицательным значением. Например, нужно определить синус, косинус, тангенс и котангенс угла (-7ПИ/6). В некоторых случаях заданное значение следует перевести в градусы: -7ПИ/6 = -210 (градусам). Если в условии отрицательный угол, то движение следует осуществлять по часовой стрелке от нулевого значения (пройти полкруга, а затем еще 30). Можно сделать вывод о том, что значение -210 соответствует 30. Следовательно, синус вычисляется следующим образом: sin(-210) = -(sin(ПИ + 30)) = — 1/2, cos(-210) = sqrt(3)/2, tg(-210) = sqrt(3)/3 и ctg(-210) = sqrt(3).
Пример случая, когда нет необходимости переводить радианы в градусы, является следующим: нужно вычислить значения тригонометрических функций угла 5ПИ/4. Необходимо расписать значение угла таким образом: 5ПИ/4 = ПИ + ПИ/4. Против часовой стрелки следует пройти половину круга (ПИ), а затем его четвертую часть (ПИ/4). Далее нужно спроецировать координаты точки на ось синусов и косинусов. Это соответствует значению sqrt(2)/2. Тангенс и котангенс заданного угла будут равны 1.
Встречаются задачи, в которых значение угла превышает 360 градусов. Например, требуется найти значения тригонометрических функций угла (-25ПИ/6). Для решения необходимо разложить угол следующим образом: (-25ПИ/6) = — (4ПИ + ПИ/6). Можно не делать обороты, поскольку 4ПИ соответствует двойному обороту и возврату в точку (-ПИ/6). Это объясняется периодом функций синуса и косинуса, который равен 2ПИ. Значения функций sin, сos, tg и ctg равны следующим значениям: — 1/2, sqrt(3)/2, sqrt(3)/3 и sqrt(3) соответственно.
Таким образом, тригонометрический круг позволяет оптимизировать вычисления в дисциплинах с физико-математическим уклоном, в которых используются тригонометрические функции. Не имеет смысла устанавливать дополнительное программное обеспечение, пользоваться таблицами, поскольку это занимает некоторое время. При помощи этого «универсального инструмента» можно найти значение любого угла.
nauka.club