Тупые углы: описание и особенности
Треугольник – это геометрическая фигура, имеющая три соединенные между собой линиями точки, которые лежат не на единой прямой в плоскости. Вершины треугольника – точки в основании углов, а линии, соединяющие их, называют сторонами треугольника. Чтобы определить площадь такой фигуры, часто используют внутреннее пространство треугольника.
Классификация
Кроме треугольников, имеющих неодинаковые стороны, существуют равнобедренные, то есть обладающие двумя одинаковыми сторонами. Их называют боковыми, а еще одну сторону – основанием фигуры. Существует еще один вид таких многоугольников – равносторонние. Все три их стороны имеют одинаковую длину.
Для треугольников присуща градусная система измерения. Эти фигуры могут иметь разные углы, поэтому их классифицируют так:
- Прямоугольные – имеющие угол 90 градусов. Две стороны, прилежащие к этому углу, называют катетами, а третью – гипотенузой;
- Остроугольные – это треугольники, обладающие всеми острыми углами, не превышающими 90 градусов;
- Тупоугольные – один угол больше 90 градусов.
Определение и параметры треугольника
Как уже было отмечено, треугольник – это один из видов многоугольников, имеющий три вершины и столько же прямых, их объединяющих. Обозначают линии, как правило, одинаково: углы – маленькими латинскими буквами, а противоположные стороны каждого – соответствующей большой буквой.
Если сложить все углы какого-либо треугольника, получится сумма в 180 градусов. Чтобы узнать внутренний угол, нужно из 180градусов вычесть величину внешнего угла треугольника. Для того чтобы узнать, чему равняется угол, находящийся снаружи, стоит сложить два раздельных от него угла внутри.

В каждом треугольнике, имеет он острые или тупые углы, противоположно большому углу находится наибольшая сторона. Если же прямые между вершинами одинаковы, то, соответственно, и каждый угол равняется 60 градусам.
Тупоугольный треугольник
Тупой угол треугольника всегда больше 90-градусного угла, но меньше развернутого. Таким образом, тупой угол равен от 90 до 180 градусов.
Возникает вопрос: бывает ли более одного тупого угла в такой фигуре? Ответ находится на поверхности: нет, потому что сумма углов должна быть менее 1800. Если два угла будут иметь, например, по 95 градусов, то третьему просто не найдется места.
Два тупоугольных многоугольника равны:
- если равны обе их стороны и угол, находящийся между ними;
- если одна сторона и два угла, находящиеся рядом с ней, равны;
- если три стороны тупоугольных треугольников имеют равенство.
Замечательные линии тупоугольного треугольника
Во всех треугольниках, имеющих тупые углы, есть линии, называемые замечательными. Первая из них – высота. Она представляет собой перпендикуляр из одной из вершин на соответствующую ей сторону. Все высоты сталкиваются в точке, которая именуется как ортоцентр. В треугольнике с тупыми углами он будет находиться за пределами самой фигуры. Что касается острых углов, то центр там находится в самом треугольнике.
Еще одна линия – медиана. Это черта, проведенная от вершины к центру соответствующей стороны. Все медианы сходятся в треугольнике, а место их совмещения – это центр тяжести такого многоугольника.
Биссектриса – линия, делящая пополам как тупые углы, так и остальные. Пересечение трех таких линий всегда бывает только в самой фигуре и определяется как центр круга, вписанного в треугольник.
В свою очередь, центр круга, описанного вокруг фигуры, можно получить из трех срединных перпендикуляров. Это линии, которые были опущены из середин прямых, соединяющих вершины. Место пересечения трех срединных перпендикуляров в треугольнике, имеющем тупые углы, находится снаружи фигуры.
Урок 33. угол. виды углов: прямой, острый, тупой — Математика — 2 класс
Математика, 2 класс
Урок № 33. Угол. Виды углов: прямой, острый, тупой
Перечень вопросов, рассматриваемых в теме:
— Какие бывают углы?
— Как распознавать углы?
Глоссарий по теме:
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
Острый угол – это угол, который меньше прямого.
Тупой угол – это угол, который больше прямого.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. – 5-е изд. – М.: Просвещение, 2014. – с.8-9.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.3.
- Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.16.
Теоретический материал для самостоятельного изучения
Рассмотрите фигуры и выберите лишнюю.

Лишняя фигура под номером 2. Она образована незамкнутой линией.
Она называется угол.
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
Посмотрите на рисунки: по-разному открытый веер, образует разные углы.


У каждого угла есть две стороны и вершина. Углы бывают прямые, острые и тупые. Углы определить можно помощью чертежного угольника.

Прямой угол определяем с помощью чертежного угольника.
Угол, который меньше прямого угла называется острым углом.

Угол, который больше прямого угла называется тупым углом.

Посмотрите, как из обычного листа бумаги можно сделать модель прямого угла. Моделью можно воспользоваться, если у вас нет чертежного угольника. Возьмите лист бумаги и перегните его 2 раза, как показано на рисунках 1 и 2. И получите модель прямого угла.

Разверните лист. Линии сгиба образовали 4 прямых угла.

Чтобы определить, какой угол начерчен, на него накладывают угольник или модель прямого угла.

Вывод: Углы могут быть прямыми и непрямыми. Чтобы определить прямой угол или нет, нужно взять особый инструмент – угольник. Если, приложив угольник к углу, вершиной к вершине, стороны совпадут, то угол – прямой. Не совпадут – непрямой. Непрямые углы делятся на: тупые и острые. Угол, величина которого меньше величины прямого – острый, а, если величина угла больше величины прямого – тупой.
Тренировочные задания.
1.Посмотрите на крыши домов и домиков. Какие углы ты видишь на рисунке? Соотнесите вид угла с изображением домика.

Правильные ответы:

2. Выберите цифры, в записи которых присутствуют только прямые углы.

Правильные ответы:

Определение тупой угол общее значение и понятие. Что это такое тупой угол
Чтобы начать углубленный анализ того, что означает тупой угол, мы должны приступить к полному выяснению этимологического происхождения двух слов, которые его формируют:
-Ангуло, в первую очередь, это термин, который определяется по греческому происхождению. Это происходит от «ankulos» (скрученный), который позже получен в латинском слове «angulus», которое уже имеет значение «угла».
-Обтусо, во-вторых, имеет латинское происхождение. Это происходит от «obtusus», который можно перевести как «неуклюжий», и который является результатом суммы двух четко различимых частей: префикса «ob-», что означает «против», и прилагательного «tusus», который является синонимом. «избили».
Углы — это геометрические фигуры, которые сформированы из двух лучей, которые берут начало в одной и той же вершине, или двух линий, которые находятся на одной поверхности и пересекаются друг с другом. По его характеристикам мы можем различать многочисленные типы углов.
Одним из наиболее распространенных способов определения углов является их амплитуда. В этом кадре мы находим тупые углы : это углы, которые измеряют более 90º и менее 180º . Например : углы 92º, 105º, 136º, 161º и 179º.
Не менее актуальным является определение того, что тупой угол образуется из объединения в вершине двух лучей и что существуют различные способы его измерения. Тем не менее, одним из наиболее распространенных является использование транспортира или прибегнуть к использованию в сочетании скоса и квадрата.
Это означает, что тупые углы имеют большую амплитуду, чем нулевые углы (которые измеряют 0º), острые углы (более 0º и менее 90º) и
Другие классификации обрамляют тупые углы между косыми углами (поскольку они не являются прямыми) и выпуклыми углами (они меньше плоского угла).
Разные геометрические фигуры имеют тупые углы. Примером является тупой треугольник, который имеет тупой угол и два острых угла. Треугольники obtusángulos, в свою очередь, являются наклонными треугольниками, потому что они не имеют прямого угла. В соответствии с этими классификациями тупые треугольники могут быть равнобедренными (тупой угол образован двумя равными сторонами, а третья больше) или разносторонними (эти три стороны имеют разные размеры, даже те, которые составляют тупой угол).
Кроме того, не забывайте, что тупой угол становится фундаментальной опорой математики в целом, а также прямым и острым углом.
Важно знать, что во многих случаях тупые углы часто путают с так называемыми рефлекторными углами. Они имеют особенность в том, что они могут измерять так же, как те, что упоминались ранее, но они отличаются тем, что отражения формируются во внешней части формы.
Определение тупой угол общее значение и понятие. Что это такое тупой угол
Чтобы начать углубленный анализ того, что означает тупой угол, мы должны приступить к полному выяснению этимологического происхождения двух слов, которые его формируют:
-Ангуло, в первую очередь, это термин, который определяется по греческому происхождению. Это происходит от «ankulos» (скрученный), который позже получен в латинском слове «angulus», которое уже имеет значение «угла».
-Обтусо, во-вторых, имеет латинское происхождение. Это происходит от «obtusus», который можно перевести как «неуклюжий», и который является результатом суммы двух четко различимых частей: префикса «ob-», что означает «против», и прилагательного «tusus», который является синонимом «избили».
Углы — это геометрические фигуры, которые сформированы из двух лучей, которые берут начало в одной и той же вершине, или двух линий, которые находятся на одной поверхности и пересекаются друг с другом. По его характеристикам мы можем различать многочисленные типы углов.
Одним из наиболее распространенных способов определения углов является их амплитуда. В этом кадре мы находим тупые углы : это углы, которые измеряют более 90º и менее 180º . Например : углы 92º, 105º, 136º, 161º и 179º.
Не менее актуальным является определение того, что тупой угол образуется из объединения в вершине двух лучей и что существуют различные способы его измерения. Тем не менее, одним из наиболее распространенных является использование транспортира или прибегнуть к использованию в сочетании скоса и квадрата.
Это означает, что тупые углы имеют большую амплитуду, чем нулевые углы (которые измеряют 0º), острые углы (более 0º и менее 90º) и прямые углы (90º). С другой стороны, они имеют меньшую амплитуду относительно плоских углов (180º) и перигональных углов (360º).
Другие классификации обрамляют тупые углы между косыми углами (поскольку они не являются прямыми) и выпуклыми углами (они меньше плоского угла).
Разные геометрические фигуры имеют тупые углы. Примером является тупой треугольник, который имеет тупой угол и два острых угла. Треугольники obtusángulos, в свою очередь, являются наклонными треугольниками, потому что они не имеют прямого угла. В соответствии с этими классификациями тупые треугольники могут быть равнобедренными (тупой угол образован двумя равными сторонами, а третья больше) или разносторонними
Кроме того, не забывайте, что тупой угол становится фундаментальной опорой математики в целом, а также прямым и острым углом.
Важно знать, что во многих случаях тупые углы часто путают с так называемыми рефлекторными углами. Они имеют особенность в том, что они могут измерять так же, как те, что упоминались ранее, но они отличаются тем, что отражения формируются во внешней части формы.
| 1. | Виды углов | 1 вид — рецептивный | лёгкое | 1 Б. | Дано изображение угла. Необходимо определить вид угла. |
| 2. | Прямые, острые и тупые углы | 1 вид — рецептивный | лёгкое | 1 Б. | Дана картинка с тремя угольниками. Необходимо определить вид угла. |
| 3. | Прямые углы вокруг нас | 1 вид — рецептивный | лёгкое | 1 Б. | Необходимо выбрать из списка предметы, которые имеют прямые углы. |
| 4. | Фигура | 2 вид — интерпретация | среднее | 2 Б. | Необходимо выбрать из списка фигуру, у которой имеется тупой угол. |
| 5. | Ломаная линия | 2 вид — интерпретация | среднее | 2 Б. | Дана ломаная линия. Необходимо определить вид углов. Проверяется умение определять вид углов. |
| 6. | Углы | 2 вид — интерпретация | среднее | 2 Б. | Дано изображение с углами. Необходимо ответить на вопрос по поводу количества углов. Проверяется умение определять вид угла. |
| 7. | Часы | 2 вид — интерпретация | среднее | 2 Б. | Даны часы. Необходимо выбрать часы, стрелки которых образуют тупой угол. |
Угол. Виды углов — прямой, острый, тупой
М — Ох, и устали же мы сегодня. Целый день перетаскивали из угла в угол наш волшебный говорящий буфет.
Помните, как выглядит план наших парадных залов? Мы хотели поставить буфет в один из углов золотого зала. Но, сколько не пытались это сделать, у нас толком ничего не получилось. Если мы приставляли его к одной стене, то между буфетом и другой стеной оставалось пространство. Тогда мы попытались поставить буфет в зелёный зал. Там он вообще не входил ни в один из углов.
- Мы так устали. И теперь просто не представляем, что же нам делать, куда можно поставить наш волшебный буфет.
- Плюс, слышишь, наш компьютер включился. Наверное, сейчас нам по скайпу будет звонить царица Математика.
- Ах, мои дорогие Плюс и Минус! Очень обидно, что прежде чем двигать по всему замку буфет, вы не познакомились с темой «Виды углов». Придётся сегодня мне объяснить вам эту тему.
Итак, сегодня мы поговорим о видах углов — прямых, острых и тупых углах.
- Какие странные названия — прямой, острый, тупой.
- Что же такое угол? Если мы поставим точку, а от этой точки проведём прямую, у нас получится прямая, ограниченная с одной стороны точкой. Такая линия называется луч. А если из этой же точки мы проведём ещё один луч, то у нас получится угол. При этом точка, из которой были проведены лучи, называется вершиной угла, а сами лучи в этом случае называются стороны угла.
Посмотрите, какие разнообразные углы можно построить:
Среди них вы можете увидеть и острые, и прямые, и тупые углы.
- А как же мы отличим, какие из углов острые, какие — прямые, а какие — тупые?
- Начнём мы с прямого угла. Посмотрите на этот лист бумаги. Сейчас мы перегнём его вдвое, потом ещё раз вдвое. Только сгибать надо аккуратно. Так, чтобы линии сгиба совместились и не выглядывали одна из-под другой. Наш лист сложен в 4 раза. И вот получился угол. Такой угол, который образуется аккуратным сгибанием листа в четыре раза, называется прямым углом.
А сейчас развернём лист бумаги:
Видите, на нём видны линии сгиба. И у нас видны уже четыре угла с одной общей вершиной. А ещё есть специальная линейка—треугольник. У неё один угол прямой и два острых. Сейчас мы положим такую линейку на наш лист бумаги так, чтобы вершины прямого угла линейки и углов на бумаге совместились. А теперь попытаемся совместить стороны. Получилось?
- Да, стороны прямого угла треугольника точно легли на стороны прямого угла на бумаге.
- Теперь так же положим линейку и на остальные три угла. Как видите, и здесь совмещаются стороны. Значит точно, все эти углы одинаковые. Все они – прямые.
- С прямыми углами понятно. А что же это за углы — острые и тупые.
- Я хочу вам показать один угол. Видите, он такой острый, что его вершиной даже можно слегка уколоться.
А теперь посмотрите, угол развернулся, раскрылся. Его вершиной уже вряд ли можно уколоться. Теперь угол стал тупым:
А теперь давайте вернёмся к тем углам, которые мы нарисовали. Сейчас на первый угол кладём линейку.
Вершина линейки совмещается с вершиной угла. Одна из сторон линейки совместилась со стороной угла, а вот вторая спряталась под треугольником. Значит, угол раскрыт меньше, чем прямой угол треугольника. Такие углы, которые раскрыты меньше прямого угла, называются острыми углами.
Посмотрите на следующий угол. Он раскрыт значительно шире первого, но, когда мы прикладываем к нему линейку:
Видно, что одна из сторон опять спряталась под линейку. Значит, этот угол тоже острый.
Переходим к следующему углу:
Его вершина и стороны точно совместились с вершиной и сторонами прямого угла линейки. Как вы думаете, какой это угол?
- Конечно, прямой!
- Совершенно верно. Этот угол прямой. А вот этот?
- Наверное, острый. Видите, как он наклонился.
- А если приложить линейку? Ну что, какой угол?
- Я ошибся… Этот угол тоже прямой………….
- Ну что же, продолжим. Рассмотрим следующий угол:
Посмотрите, между второй стороной линейки и стороной нарисованного угла как будто ещё один уголок появился. Значит, этот угол раскрыт немного шире, чем прямой. Такие углы, которые раскрыты больше прямого угла, называются тупыми углами.
- Ну, а если посмотреть на последний угол, то здесь даже без линейки-треугольника понятно, что он тупой.
- Да, это очень хорошо видно. Но мы всё-таки приложим линейку и к нему:
Сейчас очень хорошо видно, что этот угол раскрыт намного шире прямого. Конечно, он - тупой.
Ну что, Плюс и Минус, вы поняли, какие бывают углы?
- Да, поняли. А если присмотреться, то в обычных комнатах все углы — прямые.
- А еще прямые углы у учебников и тетрадей.
- У школьных парт и столов.
- И у нашего волшебного буфета тоже все углы прямые.
- Значит, поставить его можно только туда, где стены образуют прямой угол. Посмотрите ещё раз внимательно на план парадных залов.
Ну, где вы можете найти прямой угол?
- По-моему, в золотом зале все углы тупые, в зелёном — все острые. А вот прямой….
- Мне кажется, я вижу два прямых угла в синем зале. Но, всё-таки, проверю-ка я это при помощи линейки:
Урра! Получилось! В синем зале- 2 прямых угла. Вот если бы мы сначала поработали с планом парадных залов, не пришлось бы волшебный буфет таскать по всему дворцу.
- Ну, а теперь повторите, пожалуйста, чему вы сегодня научились.
- Угол образуется двумя лучами, которые выходят из одной точки.
- Прямой угол можно получить аккуратным сгибанием листа бумаги вчетверо. Но лучше воспользоваться специальной линейкой-треугольником.
- Углы, которые раскрыты меньше прямого угла, называются острыми углами.
- Углы, которые раскрыты больше прямого угла, называются тупыми углами.
- Хорошо, урок вы усвоили. А теперь за работу — поставьте волшебный буфет туда, куда его можно поставить — в синий зал.
До свидания.
- До свидания, царица. Спасибо за урок!
- До свидания, ребята. Нам пора за работу.
Что такое тупой угол?
Если градусная мера угла больше 90 и меньше 180 градусов, то такой угол называют тупым (рисунок 1).
Если обозначить угол , то для тупого угла запишем .
Рисунок 1
Тупой угол является большим от прямого и меньшим от развернутого.
Пример.
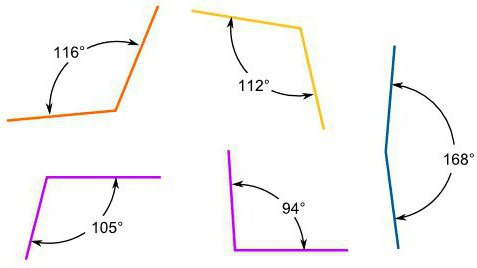
На рисунке 2 изображены углы. Назовите, какие из них острые и какие тупые.
Рисунок 2
Решение.
Назовем тупые углы – ZFG, LKN, NZX, CNK.
Острые углы (градусная мера меньше 90 градусов) – ABM, EOP, BEC, MOD.
Угол YCK – прямой (градусная мера равна 90 градусов, такой угол не является ни острым, ни прямым).
Пример.
Острый угол параллелограмма равен 53 градуса. Найти тупой угол данного параллелограмма.
Решение.
Так как сумма углов параллелограмма, которые прилегают к одной стороне, равна 180 градусов, то тупой угол, который необходимо найти, будет равен:
Ответ:
Пример.
Треугольник имеет два острых и один тупой угол. Острые углы равны 28 и 34 градуса. Найти тупой угол.
Решение. Обозначим искомый тупой угол – х. По теореме о сумме углов треугольника известно, что:
Найдем неизвестное:
Ответ. Тупой угол треугольника равен .