100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА

В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.

— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?

— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.

Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.

Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.

— Расскажите поподробнее?

— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.

— Система оценивания останется прежней?

— Количество предметов остается прежним — три обязательных предмета и два на выбор.

Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.

Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.

— А апелляция?

— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.

— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?

— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.

— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?

— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.

— На сколько процентов будет обновлена база вопросов?

— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты.

Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.

— По вашему мнению система справится с возможными хакерскими атаками, взломами?

— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.

Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.

— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?

— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.

— Сколько человек будет сидеть в одной аудитории?

— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.

— Будут ли ужесточены требования по дисциплине, запрещенным предметам?

— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.

Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.

— А наблюдатели будут присутствовать во время сдачи тестирования?

— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.

— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?

— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.

Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.

— Сколько средств выделено на проведение ЕНТ в этом году?

Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.

— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?

— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.

mordkovitch-gdz-8-2002 (ГДЗ Алгебра 8 класс — Задачник

знаменатель, y 2 − 2 ⋅ y ⋅ + ⎜ ⎟ − ⎜ ⎟ + 1 = 0 ,2 ⎝2⎠ ⎝ 2⎠225 ⎞ ⎛ 21 ⎞⎛⎟ =0,⎜ y − ⎟ − ⎜⎜2 ⎠ ⎝ 2 ⎟⎠⎝5 − 21 2 x + 1 5 + 21,, 4 x + 2 = 10 x − 5 + 2 21x − 21 ,=22x −122 x + 1 5 − 217 − 21,, 4 x + 2 = 10 x − 5 − 2 21x + 21 , x2 =.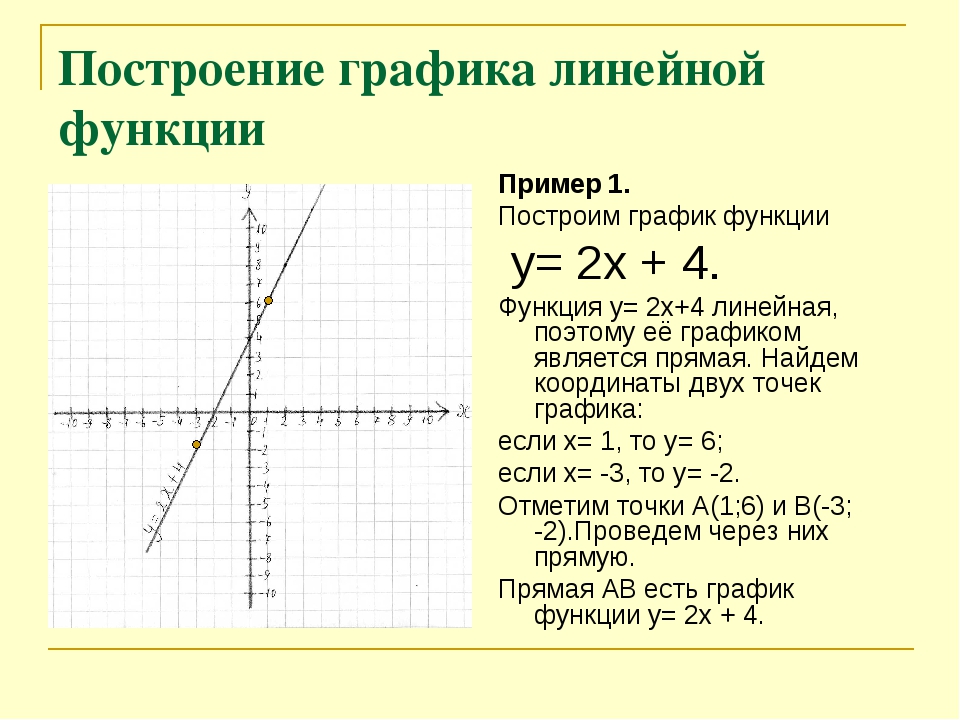 x1 ==26 + 2 21 2 x − 16 − 2 21№ 982. а) x2 − 5 x = 0 , если х ≥ 0, то x = x , имеем х2 – 5х = 0, х(х – 5) = 0,y1 =5 + 21,27 + 21⎛521 ⎞⎛521 ⎞y− +⎜⎜ y − −⎟⎜⎟⎟ = 0 ,⎟⎜2222⎝⎠⎝⎠y2 =х1 = 0, х2 = 5; если х < 0, то x = − x , имеем х2 + 5х = 0,х(х + 5) = 0, х1 = 0, х2 = -5; Ответ: -5; 0; 5;196www.gdz.pochta.ru3х2 + 4х = 0,б) 3x 2 + 4 x = 0 , при х ≥ 0 имеем4⎞44⎛x 2 + x = 0 , x ⎜ x + ⎟ = 0 , х1 = 0, x2 = − ,3⎠33⎝4x = − не удовлетворяет условию х ≥ 0, значит, не является корнем;344⎞4⎛при x < 0 имеем 3х2 – 4х = 0, x2 − x = 0 , x ⎜ x − ⎟ = 0 , х1 = 0, x2 = ,333⎝⎠4x = не удовлетворяет условию х < 0, значит, не является корнем;3Ответ: 0;в) 2 x 2 + x − 3x = 0 , при х ≥ 0 имеем 2х2 + х – 3х = 0,2х2 – 2х = 0, х(х – 1) = 0, х1 = 0, х2 = 1;при х < 0 имеем 2х2 – х – 3х = 0, 2х2 – 4х = 0,х2 – 2х = 0, х(х – 2) = 0, х1 = 0, х2 = 2, х = 2 не удовлетворяет условию x < 0,значит, не является корнем; Ответ: 0; 1;г) 4 x 2 − 3 x + x = 0 , при х ≥ 0 имеем 4х2 – 3х + х = 0,4х2 – 2х = 0, 2х2 – х = 0, х(2х – 1) = 0, х1 = 0, х2 = 0,5;при х < 0 имеем 4х2 + 3х +х = 0, х2 + х = 0, х(х + 1) = 0, х1 = 0, х2 = -1;Ответ: -1; 0; 0,5.№ 983.а) 4 x 2 +xx= 0 , при х ≥ 0 имеем 4 x 2 + = 0 ,xx4х2 + 1 = 0, 4х2 = -1 нет корней;при х < 0 имеем4 x2 +x1= 0 , 4х2 – 1 = 0, x2 = , х1,2 = ±0,5,4−xх = 0,5 – не удовлетворяет условию x < 0, значит, не является корнем;Ответ: — 0,5;б) x2 −3x23x 2=0,= 0 , при х ≥ 0 имеем x2 −xxх2 – 3х = 0, х(х – 3) = 0, х1 = 0, х2 = 3;х = 0 не входит в ОДЗ уравнения;при х < 0 имеем х2 + 3х = 0, х(х + 3) = 0, х1 = 0, х2 = -3; Ответ: ±3;в) x2 −4xx= 0 , при х ≥ 0 имеем x 2 −4x= 0 , х2 – 4 = 0, х = ±2,xх = -2 – не удовлетворяет условию х ≥ 0, значит, не является корнем;при х < 0 имеем х2 + 4 = 0, х2 = -4 нет корней; Ответ: 2;г) 2 x 2 +x2 +x2x= 0 , при х ≥ 0 имеем 2 x 2 + = 0 ,2×21⎞x⎛= 0 , x ⎜ x + ⎟ = 0 , х1 = 0,4⎠4⎝x2 = −1,4197www.gdz.pochta.ruх=0 не корень, т.к.

не входит в ОДЗ, x = −1не удовлетворяет условию х ≥ 0,4значит, не является корнем;при х < 0 имеем x2 −x=x1⎞⎛= 0 , x ⎜ x − ⎟ = 0 , х1 = 0,44⎠⎝x2 =1,41не удовлетворяет условию х < 0, значит, не является корнем;4Ответ: нет корней. §31. Формулы корней квадратного уравнения№ 984. а) х2 + 5х – 6 = 0, a = 1, b = 5, c = -6, D = b2 – 4ac = 25 + 4⋅6 = 49;б) x2 – 1,3x + 2 = 0, a = 1, b = -1,3, c = 2, D = b2 – 4ac = 1,69 — 4⋅2 = -6,31;в) х2 – 2,4х + 1 = 0, а = 1, b = -2,.4, с = 1, D = b2 – 4ac = 5,76 – 4 = 1,76;г) х2 – 7х – 4 = 0, a = 1, b = -7, c = -4, D = b2 – 4ac = 49 + 16 = 65.№ 985. а) 3х2 + 2х – 1 = 0, a = 3, b = 2, c = -1, D = b2 – 4ac = 4 + 4⋅3 = 16;б) -х2 + 4х + 3 = 0, a = -1, b = 4, c = 3, D = b2 – 4ac = 16 + 4⋅3 = 28;в) -2х2 + 5х + 3 = 0, a = -2, b = 5, c = 3, D = b2 – 4ac = 25 + 4⋅2⋅3 = 49;г) 4х2 – 5х – 4 = 0, a = 4, b = -5, c = -4, D = b2 – 4ac = 25 + 4⋅4⋅4 = 89.№ 986.

а) х2 – 8х–84 = 0, D = 64 + 4⋅84 > 0, значит, уравнение имеет 2 корня;б) 36х2 – 12х + 1 = 0, D = 144 — 4⋅36 = 0, значит, уравнение имеет 1 корень;в) х2 – 22х – 23 = 0, D = 222 + 4⋅23 > 0, значит, уравнение имеет 2 корня;г) 16х2 – 8х + 1 = 0, D = 64 — 4⋅16 = 0, значит, уравнение имеет 1 корень.№ 987. а) х2 + 3х – 24 = 0, D = 9 + 4⋅24 > 0, значит, уравнение имеет 2 корня;б) х2 – 16х + 64 = 0, D = 256 — 4⋅64 = 0, значит, уравнение имеет 1 корень;в) х2 – 2х + 5 = 0, D = 4 — 4⋅5 < 0, значит, уравнение не имеет корней;г) х2 + 6х + 9 = 0, D = 36 — 4⋅9 = 0, значит, уравнение имеет 1 корень.№ 988.

а) х2 – 5х + 6 = 0, D = 25 — 4⋅6 = 1 > 0, значит,x1 =−b + D 5 + 1−b − D 5 − 1===2;= 3, x2 =2a22a2б) х2 – 2х – 15 = 0, D = 4 + 4⋅15 = 64 > 0, значит,x1 =−b + D 2 + 8−b − D 2 − 8== −3 ;== 5 , x2 =2a22a2в) х2 + 6х + 8 = 0, D = 36 — 4⋅8 = 4 > 0, значит,x1 =−b + D −6 + 2−b = D −6 − 2== −4 ;== −2 , x2 =2a22a2г) х2 – 3х – 18 = 0, D = 9+4⋅18 = 81 > 0, значитx1 =−b + D 3 + 9−b − D 3 − 9== −3 .== 6 , x2 =2a22a2№ 989. а) х2 + 4х + 4 = 0, D = 16 — 4⋅4 = 0, значит, x = −б) х2 + 8х + 7 = 0, D = 64 — 4⋅7 = 36 > 0, значит,198b4= − = −2 ;2a2www.gdz.pochta.rux1 =−8 + 6−8 − 6= −1 , x2 == −7 ;22в) х2 – 34х + 289 = 0, D = 1156 – 4⋅289 = 0, значит, x =г) х2 + 4х + 5 = 0, D = 16 — 4⋅5 < 0, значит, нет корней.№ 990.

а) 2х2 + 3х + 1 = 0, D = 9 – 4⋅2 = 1 > 0, значит,x1 =34= 17 ;2−3 + 1−3 − 1= −0,5 , x2 == −1 ;44б) 3х2 – 3х + 4 = 0, D = 9 – 4⋅3⋅4 < 0, значит, нет корней;в) 5х2 – 8х + 3 = 0, D = 64 – 4⋅5⋅3 = 4 > 0, значит,x1 =8+ 28−2= 0,6 ;= 1 , x2 =1010г) 14х2 – 5х – 1 = 0, D = 25 + 4⋅14 = 81 > 0, значит,x1 =5+95−91= 0,5 , x2 ==− . 28287№ 991. а) 4х2 + 10х – 6 = 0, 2х2 + 5х – 3 = 0, D = 25 + 4⋅2⋅3 = 49 > 0, значит,x1 =−5 + 7 1−5 − 7= , x2 == −3 ;42410= −0, 2 ;2 ⋅ 258+ 228−2= 1 , x2 ==1;в) 3х2–8х + 5 = 0, D = 64 — 4⋅3⋅5 = 4 > 0, значит, x1 =636б) 25х2 + 10х + 1 = 0, D = 100 — 4⋅25 = 0, значит, x = −г) 4х2 + х + 67 = 0, D = 1 — 4⋅4⋅67 < 0, значит, нет корней.№ 992. а) 3х2 + 32х + 80 = 0, D = 1024 — 4⋅3⋅80 = 64 > 0, значит,x1 =−32 + 8−32 − 8202= −4 , x ==−= −6 ;6633б) 100х2 – 160х + 63 = 0, D = 25600 — 4⋅100⋅63 = 400 > 0, значит,x1 =160 + 20160 − 20= 0,9 , x2 == 0,7 ;200200в) 5х2 + 26х – 24 = 0, D = 676 + 4⋅5⋅24 = 1156 > 0, значит,x1 =−26 + 34−26 − 34= 0,8 , x2 == −6 ;1010г) 4х2 – 12х + 9 = 0, D = 144 — 4⋅4⋅9 = 0, значит, x =12= 1,5 .8№ 993.а) х2 = 2х + 48, х2 – 2х – 48 = 0, D = 4 + 4⋅48 = 196 > 0, значит,x1 =2 + 142 − 14= 8 , x2 == −6 ;22б) 6х2 + 7х = 5, 6х2 + 7х – 5 = 0, D = 49 + 4⋅6⋅5 = 169 > 0, значит,x1 =−7 + 13−7 − 132= 0,5 , x2 == −1 ;12123в) х2 = 4х + 96, х2 – 4х – 96 = 0, D = 16 + 4⋅96 = 400 > 0, значит,199www.gdz.pochta.rux1 =4 + 204 − 20= −8 ;= 12 , x2 =32г) 2х2 – 2 = 3х, 2х2 – 3х – 2 = 0, D = 9 + 4⋅2⋅2 = 25 > 0, значит,x2 =3+ 53−5= −0,5 .= 2 , x2 =44№ 994.

а) -х2 = 5х – 14, х2 + 5х – 14 = 0, D = 25 + 4⋅14 = 81 > 0, значит,x1 =−5 + 9−5 − 9= 2 , x2 == −7 ;22б) -3х2 + 5 = 2х, 3х2 + 2х – 5 = 0, D = 4 + 4⋅3⋅5 = 64 > 0, значит,x1 =−2 + 8−2 − 81= 1 , x2 == −1 ;663в) 25 = 26х – х2, х2 – 26х + 25 = 0, D = 676 — 4⋅25 = 576 > 0, значит,x1 =26 + 2426 − 24= 25 , x2 ==1;22г) -5х2 = 9х – 2, 5х2 + 9х – 2 = 0, D = 81 + 4⋅5⋅2 = 121 > 0, значит,x1 =−9 + 11−9 − 11= 0, 2 , x2 == −2 .1010−7 ± 41;2−3 ± 17;б) 2х2 + 3х – 1 = 0, D = 9 + 4⋅2 = 17 > 0, значит, x1,2 =45 ± 13;в) х2 – 5х + 3 = 0, D = 25 — 4⋅3 = 13 > 0, значит, x1,2 =21 ± 21.г) 5х2 – х – 1 = 0, D = 1 + 4⋅5 = 21 > 0, значит, x1,2 =10№ 995.

а) х2 + 7х + 2 = 0, D = 49 — 4⋅2 = 41 > 0, значит, x1,2 =№ 996. а) х2 + 2х – 7 = 0, D = 4 + 4⋅7 = 32 > 0, значит,x1,2 =−2 ± 32 −2 ± 4 2== −1 ± 2 2 ;22б) 2х2 – 4х – 1 = 0, D = 16 + 4⋅2 = 24 > 0, значит,x1,2 =4 ± 24 4 ± 2 6 2 ± 6==;442в) х2 + 6х + 3 = 0, D = 36 — 4⋅3 = 24 > 0, значит,x1,2 =−6 ± 24 −6 ± 2 6== −3 ± 6 ;22г) 2х2 – 10х + 1 = 0, D = 100 — 4⋅2 = 92 > 0, значит,x1,2 =10 ± 92 10 ± 2 23 5 ± 23==. 442№ 997.а) 0,6х2 + 0,8х – 7,8 = 0, 6х2 + 8х – 78 = 0, 3х2 + 4х – 39 = 0,D = 16 + 4⋅3⋅39 = 484 > 0, значит, x1 =200−4 + 22−4 − 22131= 3 , x2 == − = −4 ;6633www.gdz.pochta.ruб) 0,25х2 – х + 1 = 0, 25х2 – 100х + 100 = 0, х2 – 4х + 4 = 0,D = 16 — 4⋅4 = 0, значит, x =4=2;2в) 0,2х2 – 10х + 125 = 0, 2х2 – 100х + 1250 = 0, х2 – 50х + 625 = 0,D = 2500 — 4⋅625 = 0, значит, x =50= 25 ;2г) 4х2 – 7х – 7,5 = 0, 8х2 – 14х – 15 = 0, D = 106 + 4⋅8⋅15 = 676 > 0, значит,x1 =14 + 2614 − 26= 2,5 , x2 == −0,75 .1616№ 998.

а) 6х(2х + 1) = 5х + 1, 12х2 + 6х –5х – 1 = 0, 12х2 +х – 1 = 0,D = 1 + 4⋅12 = 49 > 0, значит, x1 =−1 + 7−1 − 71=− ;= 0, 25 , x2 =24324б) 2х(х – 8) = -х – 18, 2х2 – 16х + х + 18 = 0, 2х2 – 15х + 18 = 0,D = 225 — 4⋅2⋅18 = 81 > 0, значит, x1 =15 + 915 − 9= 6 , x2 == 1,5 ;44в) 8х(1 + 2х) = -1, 16х2 + 8х + 1 = 0, D = 64 — 4⋅16 = 0, значит, x =−9= −0, 25 ;32г) х(х – 5) = 1 – 4х, х2 – 5х – 1 + 4х = 0, х2 – х – 1 = 0, D = 1 + 4 = 5 > 0, значит,x1,2 =1± 5.2№ 999. а) (х – 2)2 = 3х – 8, х2 – 4х + 4 – 3х + 8 = 0, х2 – 7х + 12 =0,D = 49 — 4⋅12 = 1 > 0, значит, x1 =7 +17 −1= 4 , x2 ==3;22б) (3х – 1)(х + 3) + 1 = х(1 + 6х), 3х2 – х + 9х – 3 + 1 – х – 6х2 = 0,-3х2 + 7х – 2 = 0, 3х2 – 7х + 2 = 0, D = 49 — 4⋅3⋅2 = 25 > 0, значит,x1 =7+57−5 1= ;= 2 , x2 =636в) 5(х + 2)2 = -6х – 44, 5х2 + 20х + 20 + 6х + 44 = 0, 5х2 + 26х + 64 = 0,D = 676 — 4⋅5⋅64 < 0, значит, нет корней;г) (х + 4)(2х – 1) = х(3х + 11), 2х2 + 8х – х – 4 = 3х2 + 11х, х2 + 4х + 4 = 0,42D = 16 — 4⋅4 = 0, значит x = − = −2 .№ 1000.

Уравнение имеет 1 корень, если D = 0:а) х2 – mx + 9 = 0, D = m2 — 4⋅9 = m2 – 36, m2 – 36 = 0, m2 = 36, m1,2 = ±6;б) x2 + 3mx + m = 0, D = 9m2 – 4m, 9m2 – 4m = 0, m(9m – 4) = 0,m1 = 0, m2 =4;9в) x2 + mx + 16 = 0, D = m2 — 4⋅16, m2 – 64 = 0, m2 = 64, m1,2 = ±8;г) x2 – 2mx + 3m = 0, D = 4m2 — 4⋅3m, m2 – 3m = 0, m(m – 3) = 0, m1=0, m2 = 3.№ 1001.3х2 – рх – 2 = 0, D = p2 + 4⋅3⋅2 = p2 + 16,p2 + 16 > 0 для любого р, значит, D > 0 для любого р, значит, уравнениеимеет при любом р 2 корня, что и требовалось доказать. 201www.gdz.pochta.ru№ 1002.I этап: Пустьх – искомое натуральное число, тогда х2 – его квадрат или х + 56.Уравнение: х2 = х + 56.II этап: х2 – х – 56 = 0, D = 1 + 4⋅45 = 225, x1 =1 + 15= 8 , x2 = -7.2III этап: х2 = –7 – не удовлетворяет условию задачи.Так что искомое число 8.

Подготовка к ЕГЭ по теме «Первообразная»

Подготовка к ЕГЭ по теме «Первообразная»

 

Задания уровня В.                                

1. Вычислите площадь фигуры, ограниченной линиями у = ,  у = 0,5х

Ответ:

 

2. Первообразная функции f(х) = 3х² + 2х при х = 1 принимает значение В1. Найдите ее значение при х = -1

Ответ: 79

 

3. Вычислите площадь фигуры, ограниченной линиями у=2, у=3–х,  х = 0

Ответ:

 

4. Первообразная функции f(х) = 4х³+2х при = 1 принимает значение 25. Найдите ее значение при х = 2

Ответ: 43

 

5. Найдите площадь фигуры, ограниченной линиями у = 2х², у = 4х

Ответ: 8/3

 

6. Найдите площадь фигуры, ограниченной линиями у = х², у = -2х

Ответ: 4/3

 

7. Найдите площадь фигуры, ограниченной линиями у= 9х²–6х+1, у = 0, х= 0

Ответ:

 

8. Найдите площадь фигуры, ограниченной линиями у = 4х² + 12х + 9, у = 0, х = 0          

Ответ: 4,5

 

9. найдите площадь фигуры, ограниченной линиями у = 1–х, у = 0 и у=(х+1)², где х ≥ -1

Ответ: 5/6

 

10. Найдите площадь фигуры, ограниченной линиями у = х – 1, у = 0 и у=(х-3)², где х ≤ 3

Ответ: 5/6

 

11. Найдите площадь фигуры, ограниченной графиком функции у = -х²+х-4 и осями координат.

Ответ: 8/3

 

12. Найдите площадь фигуры, ограниченной графиком функции у=х²+6х+9 и осями координат

Ответ: 9

 

13. Вычислите площадь фигуры, ограниченной графиком функции          у=х² -4х-4 и прямой у=-х

Ответ: 125/6

 

14. Найдите площадь фигуры, ограниченной графиком функции у=3-х² и прямой у=2х

Ответ: 32/3

 

15. Найдите площадь фигуры, ограниченной линиями у=х²-4х+4, у=0 и х=0

Ответ: 8/3

 

16. Найдите площадь фигуры, ограниченной линиями у= и у=

Ответ: 4/3

 

17. Найдите площадь фигуры, ограниченной линиями у-х²=0 и у²-х=0

Ответ:

 

18. Найдите площадь фигуры, ограниченной линиями у=(1-х) (х-5), у=4 и х=1

Ответ: 2

 

19. Найдите площадь фигуры, ограниченной линиями у-х²=0 и у²+х=0

Ответ:

 

20. Найти площадь фигуры, ограниченной линиями у=(х+1) (3-х), у=4 и х=3

Ответ: 2

 

21. Найти площадь фигуры, ограниченной графиком функции у=sinх, касательной к графику в его точке с абсциссой х₀=π и прямой х=0,5π

Ответ:-1

 

22. Найдите площадь фигуры, ограниченной графиком функции у=cosх, касательной к нему в его точке с абсциссой х₀=1,5π и прямой х=2π

Ответ: S=-1

 

23. Найдите площадь фигуры, ограниченной графиком функции у=sin х, определенной на отрезке [о;π], и прямой, проходящей через точки М(π/2;1) и N (π; 0)

Ответ: 1 

 

24. Найти площадь фигуры, ограниченной графиком функции у=cosх, определенной на отрезке [-π/2; π/2] и прямой, проходящей через точки А(-π/2; 0) и В (0; 1)

Ответ: 1 

 

25. Найти площадь фигуры, ограниченной графиком функций у=х³/4 и у=

Ответ: 1

 

26. Найти площадь фигуры, ограниченной графиками функций у=х³/9 и у=

Ответ: 3,75

 

27. Найдите площадь фигуры, ограниченной линиями у=, у=6-х, у=0

Ответ: 7

 

28. Найдите площадь фигуры, ограниченной линиями у=, у=х-6, у=0

Ответ: 18

 

Задания уровня С                                                 

1. Составьте уравнение касательной, проведенной к графику функции   f(х)=-х²+4 параллельно прямой у=-2х+6. Вычислите площадь фигуры, ограниченной графиком данной функции, этой касательной и осью ординат.

Ответ: у=5-2х; S=.

 

2. Составьте уравнение касательной, проведенной к графику функции   f(х)=-х²+4х параллельно прямой у=2х+3. Вычислите площадь фигуры, ограниченной графиком данной функции, этой касательной и осью ординат.

Ответ: у=2х+1; S=.

 

3. Вычислите площадь фигуры, ограниченной графиком функции у=- х²+3 и двумя касательными к этому графику, проходящими через точку на оси ОУ и образующими между собой угол 90º

Ответ:

 

4. Вычислите площадь фигуры, ограниченной графиком функции у=х²+2,5 и двумя касательными к этому графику, проходящими через точку на оси ОУ и образующими между собой угол 90º.

Ответ:

 

5. Вычислите площадь фигуры, ограниченной графиком функции у= — х²+1 и касательными, проведенными к этому графику в точках пересечения его с осью абсцесс

Ответ: 4/3

 

6. Вычислите площадь фигуры, ограниченной графиком функции у=-х²+4х и касательными, проведенными к этому графику в точках пересечения его с осью абсцисс

Ответ: 16/3

 

7. Найдите площадь фигуры, ограниченной графиком функции f(х)=2х-2 и графиком ее первообразной F(х), зная, что F(0)=1

Ответ:

 

8. Функция F является первообразной для функции f(х)=2х-4. Найдите площадь фигуры ограниченной графиками функций f и F, зная, что график функции F проходит через точку А(0; 4)

Ответ: 4/3

 

9. Вычислите площадь фигуры, ограниченной параболой у=4х-х2 и прямой, проходящей через точки (4; 0) и (0; 4)

Ответ:

 

10. Вычислите площадь фигуры, ограниченной параболой у=3х²(х≤0), прямой у=0 и прямой, проходящей через точки (-3; 0) и (0; 4,5)

Ответ: 4

 

11. Составьте уравнение касательной к графику функции у=-3х²+6х+1 в точке пересечения этого графика с осью ординат. Вычислите площадь фигуры, ограниченной графиком данной функции, найденной касательной и прямой х=2

Ответ: у=6х+1; 8

 

12. Составьте уравнение касательной к графику функции у=-2х²+4х+1 в точке пересечения этого графика с осью ординат. Вычислите площадь фигуры, ограниченной графиком данной функции, найденной касательной и прямой х=2

Ответ: у=4х+1;

 

13. Найдите площадь фигуры, ограниченной графиком функции                          и прямой у=1,5

Ответ: 4/3

 

14. Найдите площадь фигуры, ограниченной  графиком функции у= S 3t²dt и прямой у=1

Ответ: 0,5

 

15. Найдите площадь фигуры, ограниченной графиком функции у= —  и прямыми у=0, х= — 5, х = -2,5. Не пользуясь микрокалькулятором, сравните полученное значение площади с числом 2

Ответ: S=ln4, S<2

 

16. Найдите площадь фигуры, ограниченной графиком функции у=е^х+1 и прямыми х= -2, х= -1, у=0. Не пользуясь микрокалькулятором, сравните полученное значение площади с числом 0,5

Ответ: S=1-е^-1; S>0,5

 

17. Для каждого а>0 найдите площадь фигуры, ограниченной графиком функции у= -х³+ах² и осью абсцисс. При каких значениях, а эта площадь равна 4/3?

Ответ: S=а⁴/12; S=4/3 при а=2

 

18. Для каждого а<0 найдите площадь фигуры, ограниченной прямыми х=2а, х=а, у=0 и графиком функции у= -3/х. Сравните полученное значение площади с числом 3.

Ответ: S=3ln; S<3

19. В каком отношении делится площадь четырехугольника ОВСД, где 0(0;0), В(1; 2) С(4; 2), Д(4; 0), параболой у=(2-х)²+1

Ответ: 17; 4 (или 4,25; возможен ответ 4; 17)

 

20. Найдите площадь фигуры, ограниченной линиями у= х³, у=3-х, у= -4х

Ответ: 5

 

21. Найдите площадь фигуры, ограниченной линиями у=-  х³, у=х+4, у=5х

Ответ: 7

 

22. Найдите площадь фигуры, ограниченной линиями х · [у]=2, х=1, х=3

Ответ: 4ln 3

 

24. Найдите площадь фигуры, ограниченной линиями х [у]=3, х=1, х=2

Ответ: 6ln 2

 

25. Докажите, что площадь фигуры, ограниченной графиком функции у=2е^2х и прямыми у=0, х= -0,5; х=t (при t< -0,5), меньше 1

 

26. Найдите ту первообразную функции f(х)=2х+4, график которой касается прямой у=6х+3. Вычислите площадь фигуры, ограниченной графиком найденной первообразной и прямыми у=6х+3 и у=0

Ответ: Первообразная у=х²+4х+4, площадь 2,25

 

27. Найдите ту первообразную функции f(х)=2х-2, график которой касается прямой у= -4х. Вычислите площадь фигуры, ограниченной графиком найденной первообразной и прямыми у= -4х, у=0

Ответ: Первообразная у=х²-2х+1, площадь 2/3

 

28. Фигура ограничена линиями у=  х² и у=х. Отрезок наибольшей длины, заключенный внутри этой фигуры и принадлежащий прямой х=а, делит фигуру на две части. Докажите, что площади этих частей равны.

 

29. Фигура ограничена линиями у= х² и у=-3х. Отрезок наибольшей длины, заключённый внутри этой фигуры и принадлежащей прямой х=а, делит фигуру на две части. Докажите, что площади этих частей равны.

 

30. Найдите площадь фигуры, ограниченной графиком функции у=х²-2х+3, касательной к графику в его точке с абсциссой 2 и прямой х=-1.

Ответ: 9

 

31. Найдите площадь фигуры, ограниченной графиком функции у=3+2х-х², касательной к графику в его точке с абсциссой 3 и прямой х=0.

Ответ: 9

 

32. Найдите площадь фигуры, ограниченной линиями у=(х-2)(2х-3) и у=0

Ответ:

 

33. Найдите площадь фигуры, ограниченной линиями у=(3х+2)(х-1) и у=0

Ответ: 125/54

 

34. Найдите площадь фигуры, ограниченной линиями у=  и у= х

Ответ:

 

35. Найдите площадь фигуры, ограниченной линиями у= , у=х и х=е.

Ответ: 0,5(е²-3)

 

36. Найдите площадь фигуры, ограниченной линиями у=  и у=6-х.

 

37. Найдите площадь фигуры, ограниченной параболой у= 4х-х² и прямой, проходящей через вершину параболы и начало координат.

Ответ: 12-5ln5

 

38. Найдите площадь фигуры, ограниченной параболой у=х²-6х и прямой, проходящей через вершину параболы и начало координат.

Ответ: 4/3

 

39. Найдите площадь фигуры, ограниченной графиком функции                  у= -х³-2х²-х+3 и касательной к нему, проведённой в точке графика с абсциссой -1

Ответ:

 

40. Найдите площадь фигуры, ограниченной графиком функции             у=х³-4х²+4х-5 и касательной к нему, проведённой в точке графика с абсциссой 2.

Ответ: 4/3

 

41. Найдите площадь фигуры, ограниченной параболами у-х²-2х и у=  х².

Ответ: 16/3

 

42. Найдите площадь фигуры, ограниченной параболами у-4х-х² и у=  х².

Ответ: 6

 

43. Найдите площадь фигуры, ограниченной графиками функций у=  и   у=3-х

Ответ:

 

44. Найдите площадь фигуры, ограниченной графиками функций у=х² и у=2х-х².

Ответ: 16/3

 

45. Укажите все первообразные функции g(х)=3х²+2х-2, графики которых имеют ровно две общие точки с графиком функции , графики которых имеют ровно две общие точки с графиком функции g(х).

Ответ: G₁(х)=х³+х²-2х-3;  G₂(х)=х³+х²-2х+6

 

46. Укажите все первообразные функции f(х)=5+2х-3х², графики которых имеют с графиком функции f(х) ровно две общие точки.

Ответ: F₁(х)= -х³+х²+5х-13; F₂(х)=-х³+х²+5х+5

 

27. Найдите площадь фигуры, ограниченной линиями у=(3-х)³, у=0,5х, у=0.

Ответ: 1,25

 

28. Найдите площадь фигуры, ограниченной графиком функции у=х²-4х+4 и касательными к этому графику, проходящими через начало координат

Ответ: 16/3

 

29. Найдите площадь фигуры, ограниченной графиком функции у=х²+6х+9 и касательными к этому графику, проходящими через начало координат.

Ответ:18

 

30. Найдите площадь фигуры, ограниченной линиями у= -4(х+3)³,  у+х=0, у=2х.

Ответ: 12

 

31. Найдите площадь фигуры, ограниченной линиями у=3(х-2)³, у+3х=0, у=х

Ответ: 6

32. Фигура ограничена линиями: у=0; у= -х²+2х+3. Найдите отношение площадей фигур, на которые данная фигура делится графиком функции у=(х+1)²

Ответ: 2: 8=  или 3 : 1

 

33. Фигура ограничена линиями у=0 и у=-х²+6х-5. Найдите отношение площадей фигур, на которые данная фигура делится графиком функции у=(х-5)²

Ответ: 3 (или 1/3)

 

34. Найдите площадь  фигуры, ограниченной линиями у=, у=(х+2)³, у=1 и у=0

Ответ: 1

 

35. Найдите площадь фигуры, ограниченной линиями у= у=2-(х+3)³ и у=3

Ответ: 8

 

36. Найдите площадь фигуры, ограниченной линиями у=, у=2+(х-4)³ и у=3

Ответ: 8

 

 

Сложные задания       

1. Вычислите площадь фигуры, ограниченной линиями у =  и у= .

Ответ:  —  ln3

 

2. Вычислите площадь фигуры, ограниченной линиями у=  и у=

Ответ:  —  ln2

 

3. Вычислите площадь фигуры, ограниченной гиперболой у= -1/х, касательной к этой кривой, проведённой в точке с абсциссой х=1, и прямой х=2.

Ответ: ln2-0,5

 

4. Вычислите площадь фигуры, ограниченной графиком функции у=, касательной к этой кривой, проведённой в точке с абсциссой х=1, и прямой х=-1.

Ответ: ln3

 

5. Вычислите площадь фигуры, ограниченной линиями у=, у=3- .

Ответ: 6,5- ln2

 

6. Вычислите площадь фигуры, ограниченной линиями у=  и у=2+4.

Ответ: 32

 

 

7. Вычислите площадь фигуры, ограниченной линиями х=1, у=е, у=-е, х=0, а также отрезком прямой х=1 при -1≤ у ≤ 1.

Ответ: 4

 

8. Вычислите площадь фигуры, ограниченной линиями ху²=1, у= -1, у=1, х=0,  х=0, а также отрезком прямой х=2 при —  ≤ у ≤

Ответ: 2

 

9. Вычислите площадь фигуры, ограниченной линиями у=х²-2х, у= -4х-1 и у=4х-9

Ответ: 16/3

 

10. Вычислите площадь фигуры, ограниченной линиями у=-х²+6х-9, у=2х-5 и у= -2х+7

Ответ: 2/3

 

11. Пользуясь геометрической интерпретацией определённого интеграла, вычислите S dх.

Ответ:  +

 

12. Пользуясь геометрической интерпретацией определённого интеграла, вычислите  dх.

Ответ:  —

13. Найдите все такие точки М графика функции у=х²-4х, что площадь фигуры. Ограниченной этим графиком, касательной к графику, проходящей через точку М, и осью ординат, равна 72

Ответ: (6; 60) и (6; 12)

 

14. Найдите все такие точки М графика функции у=6х-х², что площадь фигуры, ограниченной графиком этой функции, касательной к графику, проходящей через точку №, и осью ординат равна 41

Ответ: (1/5; 5) и (-5; -55)

 

15. Докажите, что при всех к > 0 площадь фигуры, ограниченной графиком функции у=к²х⁵-кх²  и осью абсцисс, не зависит от к.

Ответ: S_ор=  и не зависит от к.

 

16. Докажите, что при всех к > 0 площадь фигуры, ограниченной графиком функции у= х⁴— х⁹ и осью абсцисс, не зависит от к.

Ответ: ; COS???<0

 

17. Докажите, что площади фигур, каждая из которых ограничена графиком функции у=х³-6х²+1  и одной из касательных к этому графику, параллельных оси абсцисс, равны.

Ответ: S_ор=1/10

 

18. Докажите, что площадь фигуры, ограниченной осью ординат, графиком функции у=4х-х²  и касательной к этому графику в точке с абсциссой х₀ ≠ 0, равна площади фигуры, ограниченной графиком той же функции, касательной к графику в точке с абсциссой (-х₀) и осью ординат.

Ответ:

 

19. Вычислите площадь фигуры, ограниченной графиками функций у=0,5х²-2х-1 и у=6,5-1,5×.

Ответ: 25,5

 

20. Вычислите площадь фигуры, ограниченной графиками функций у=-0,5х²+х+7,5 и у=1,5()-1.

Ответ: 25,5

 

21. При каком t площадь фигуры, ограниченной графиком функции у=х⁴+2х², касательной к нему, проведённой в точке графика с абсциссой t, и прямой х=t-1, наименьшая?

Ответ: t=0,25

 

22. Найдите такое р, чтобы площадь фигуры, ограниченной графиком функции у=х-х⁴, касательной к нему, проведённой в точке графика с абсциссой р, и прямой х=р+2, была наименьшей.

Ответ: р=-0,5

 

23. Найдите площадь фигуры, ограниченной линиями у=х+1, у=1- х и у=1-(х-2)³.

Ответ: 2

 

24. Найдите площадь фигуры, ограниченной линиями у=(х+2)³+3, у=-4х и у=-  х.

Ответ: 5

 

25. Найдите площадь фигуры, ограниченной линиями у=4+,            у=-0,6х+2,8 и х=.

Ответ: 12,5

 

26. Найдите площадь фигуры, ограниченной линиями х+=0, у=+4 и у=  х+ .

Ответ: 38/3

 

 

 

 

 

 

 

 

 

Применение производной — Математика — Презентации

МКОУ «Зургановская СОШ»

Решение заданий по материалам открытого банка задач ЕГЭ по математике

Прямая у = 4х + 11 параллельна касательной к графику функции у = х 2 + 8х + 6 .

Найдите абсциссу точки касания.

№ 1

Решение:

Если прямая параллельна касательной к графику функции в какой-то точке (назовем ее х о ), то ее угловой коэффициент (в нашем случае k = 4 из уравнения у = 4х +11 ) равен значению производной функции в точке х о :

k = f ′ (x o ) = 4

Производная функции

f ′ (x) = (х 2 + 8х + 6) ′ = 2x + 8 .

Значит, для нахождения искомой точки касания необходимо, чтобы 2х o + 8 = 4 ,

откуда х о = – 2 .

Ответ: – 2.

Прямая у = 3х + 11 является касательной к графику

функции у = x 3 − 3x 2 − 6x + 6 .

Найдите абсциссу точки касания.

№ 2

Решение:

Заметим, что если прямая является касательной к графику, то ее угловой коэффициент (k = 3) должен быть равен производной функции в точке касания, откуда имеем Зх 2 − 6х − 6 = 3 , то есть Зх 2 − 6х − 9 = 0 или х 2 − 2х − 3 = 0 . Это квадратное уравнение имеет два корня: −1 и 3 . Таким образом есть две точки, в которых касательная к графику функции у = х 3 − Зх 2 − 6х + 6 имеет угловой коэффициент, равный 3 .

Для того чтобы определить, в какой из этих двух точек прямая

у = 3х + 11 касается графика функции, вычислим значения функции в этих точках и проверим, удовлетворяют ли они уравнению касательной.

Значение функции в точке −1 равно у(−1) = −1 − 3 + 6 + 6 = 8 ,

а значение в точке 3 равно у(3) = 27 − 27 − 18 + 6 = −12 . Заметим, что точка с координатами (−1; 8) удовлетворяет уравнению касательной, так как 8 = −3 + 11 . А вот точка (3; −12) уравнению касательной не удовлетворяет, так как −12 ≠ 9 + 11 .

Значит, искомая абсцисса точки касания равна −1 .

Ответ: − 1.

На рисунке изображен график у = f ′(x) – производной функции f(x) , определенной на интервале (–10; 8) . В какой точке отрезка [–8; –4] функция f(x) принимает наименьшее значение.

№ 3

Решение:

Заметим, что на отрезке [–8; –4]

производная функции

отрицательна, значит, сама функция убывает, а значит,

наименьшее значение на этом отрезке она принимает на правом

конце отрезка, то есть в точке –4 .

у = f ′(x)

f(x)

–

Ответ: –4.

На рисунке изображен график у = f ′(x)  – производной функции f(x) , определенной на интервале (–8; 8) . Найдите количество точек экстремума функции f(x) , принадлежащих отрезку [– 6; 6] .

№ 4

Решение:

В точке экстремума производная функции

равна 0 либо не существует.

Видно, что таких точек принадлежащих отрезку [–6; 6] три. При этом в каждой точке производная меняет знак либо с «+» на «–» , либо с «–» на «+» .

у = f ′(x)

+

+

–

–

Ответ: 3.

На рисунке изображен график у = f ′(x)  – производной функции f(x) , определенной на интервале (–8; 10). Найдите точку экстремума функции f(x) на интервале (– 4; 8) .

№ 5

.

Решение:

Заметим, что на интервале (–4; 8) производная в точке

х о = 4 обращается в 0 и при переходе через эту точку меняет знак производной с «–» на «+» , точка 4 и есть искомая точка экстремума функции на заданном интервале.

у = f ′(x)

+

–

Ответ: 4.

На рисунке изображен график у = f ′(x)  – производной функции f(x), определенной на интервале (–8; 8) . Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой у = –2х + 2 или совпадает с ней.

№ 6

Решение:

Если касательная к графику функции f(x) параллельна прямой у = –2x + 2 или совпадает с ней, то ее угловой коэффициент k = –2 , а значит нам нужно найти

количество точек, в которых производная функции

f ′(x) = –2 . Для этого на графике производной проведем прямую у = –2 , и посчитаем количество точек графика производной, лежащих на этой линии. Таких точек 4 .

у = f ′(x)

у = –2

Ответ: 4.

На рисунке изображен график функции у = f(x) , определенной на интервале (–6; 5) . Определите количество целых точек, в которых производная функции отрицательна.

№ 7

у

Решение:

Заметим, что производная функции отрицательна, если сама функция f(x) убывает, а значит, необходимо найти количество целых точек, входящих в промежутки убывания функции.

Таких точек 6 :

х = −4, х = −3, х = − 2,

х = − 1, х = 0, х = 3 .

у = f(x)

х

– 6

– 4

5

– 1

– 2

0

– 3

3

Ответ: 6.

На рисунке изображен график функции у = f(x) , определенной на интервале ( – 6; 6) . Найдите количество точек, в которых касательная к графику функции параллельна прямой у = – 5 .

№ 8

у

Решение:

Прямая у = − 5 горизонтальная, значит, если касательная к графику функции ей параллельна, то она тоже горизонтальна. Следовательно, угловой коэффициент в искомых точках

k = f ′(х) = 0 .

В нашем случае – это точки экстремума.

Таких точек 6 .

1

у = f(x)

х

0

6

– 6

3

5

6

4

2

у = –5

– 5

Ответ: 6.

0 , так как α – острый угол (tg α 0) . Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и ординаты которых − целые числа. Теперь определим модуль углового коэффициента. Для этого построим треугольник ABC. tg α = ВС : АС = 5 : 4 = 1,25 у = f(x) В α 5 х о α С 4 А Ответ: 1,25. «

На рисунке изображен график у = f(x)  – производной функции f(x) , определенной на интервале (–7; 5) и

касательная к нему в точке с абсциссой х о . Найдите значение производной функции f(x) в точке х о .

№ 9

Решение:

Значение производной функции

f ′(х o ) = tg α = k равно угловому коэффициенту касательной,

проведенной к графику этой функции в данной точке.

В нашем случае k 0 , так как

α – острый угол (tg α 0) .

Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и ординаты которых − целые числа.

Теперь определим модуль углового коэффициента. Для этого построим треугольник ABC.

tg α = ВС : АС = 5 : 4 = 1,25

у = f(x)

В

α

5

х о

α

С

4

А

Ответ: 1,25.

На рисунке изображен график функции у = f(x) , определенной на интервале (–10; 2) и

касательная к нему в точке с абсциссой х о .

Найдите значение производной функции f(x) в точке х о .

№ 10

Решение:

Значение производной функции

f ′(х o ) = tg α = k равно угловому коэффициенту касательной,

проведенной к графику этой функции в данной точке.

В нашем случае k , так как

α – тупой угол (tg α .

Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и ординаты которых − целые числа.

Теперь определим модуль углового коэффициента. Для этого построим треугольник ABC.

tg(180°− α ) = ВС : АС = 6 : 8 = 0,75

tg α = − tg (180°− α ) = −0,75

В

у = f(x)

α

6

х о

180° − α

С

А

8

Ответ: −0,75.

На рисунке изображен график производной у = f ′(x)  –функции f(x) , определенной на интервале (–11; 11) .

Найдите количество точек максимума функции f(x) на отрезке [ − 10; 10] .

№ 11

.

Решение:

В точке экстремума производная функции

равна 0 либо не существует . Видно, что таких точек

принадлежащих отрезку [−10; 10] пять.

В точках х 2 и х 4 производная меняет знак с «+» на « − » – это точки максимума.

у

у = f ′(x)

+

+

+

– 10

0

–

–

–

х

10

f(x)

х 3

х 2

х 4

х 5

х 1

max

max

Ответ: 2.

Прямая у = 4х – 4 является касательной к графику функции ах 2 + 34х + 11 . Найдите а .

№ 12

Решение:

Производная функции в точке касания должна совпадать с угловым коэффициентом прямой. Откуда, если за х o принять абсциссу точки касания, имеем: 2ах o + 34 = 4 . То есть ах o = –15 .

Найдем значение исходной функции в точке касания:

ах o 2 + 34х o + 11 = –15x o + 34х o + 11 = 19х o + 11 .

Так как прямая у = 4х – 4 – касательная, имеем:

19х o + 11 = 4х o – 4 , откуда х o = – 1 .

А значит a = 15 .

Ответ: 15.

Прямая у = – 4х – 5 является касательной к графику функции 9х 2 + bх + 20 . Найдите b , учитывая, что абсцисса точки касания больше 0 .

№ 13

Решение.

Если х о – абсцисса точки касания, то 18x o + b = –4 , откуда b = – 4 – 18х о .

Аналогично задаче №12 найдем х о :

9x o 2 + (– 4 – 18х о ) x o + 20 = – 4х o – 5 ,

9x o 2 – 4x o – 18х о 2 + 20 + 4х o + 5 = 0 ,

– 9x o 2 + 25 = 0 ,

х о 2 = 25/9 .

Откуда x o = 5/3 или x o = –5/3 .

Условию задачи соответствует только положительный корень, значит x o = 5/3 , следовательно b = – 4 – 18 ∙ 5/3 , имеем b = –34 .

Ответ: –34.

Прямая у = 2 х – 6 является касательной к графику функции х 2 + 12х + с . Найдите с .

№ 14

Решение.

Аналогично предыдущим задачам обозначим абсциссу точки касания х о и приравняем значение производной функции в точке х о угловому коэффициенту касательной.

2х о + 12 = 2 , откуда x o = –5 .

Значение исходной функции в точке –5 равно:

25 – 60 + с = с – 35 , значит с – 35 = 2 ∙ (–5) – 6 ,

откуда с = 19 .

Ответ: 19.

Материальная точка движется прямолинейно по закону

x(t) = 0,5t 2 – 2t – 6 , где x – расстояние от точки отсчета в метрах,

t – время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6с .

№ 15

Решение.

Так как мгновенная скорость точки в момент времени t o , прямолинейного движения, совершаемого по закону х = х(t) , равна значению производной функции х npu t = t o ,

искомая скорость будет равна

x ′ (t) = 0,5 ∙ 2t – 2 = t – 2 ,

x ′ (6) = 6 – 2 = 4 м/с.

Ответ: 4.

Материальная точка движется прямолинейно по закону

x(t) = 0,5t 2 – 2t – 22 , где x – расстояние от точки отсчета в метрах,  

t – время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 4 м/с ?

№ 16

Решение.

Так как мгновенная скорость точки в момент времени t o , прямолинейного движения, совершаемого по закону х = х(t) , равна значению производной функции х npu t = t o ,

искомая скорость будет равна

x ′ (t o ) = 0,5 ∙ 2t o – 2 = t o – 2 ,

Т.к. по условию, x ′ (t o ) = 4 , то t o – 2 = 4 , откуда

t o = 4 + 2 = 6 м/с.

Ответ: 6.

На рисунке изображен график функции у = f(x) , определенной на интервале (–8; 6) .

Найдите сумму точек экстремума функции f(x) .

№ 17

Решение:

Точки экстремума – это точки минимума и максимума.

Видно, что таких точек принадлежащих промежутку (–8; 6) пять.

Найдем сумму их абсцисс:

-6 + (-4) + (-2) + 2 + 4 = 6 .

у = f ′(x)

Ответ: 6.

На рисунке изображен график производной у = f ′(x)  – функции f(x) , определенной на интервале (–10; 8) .

Найдите промежутки возрастания функции f(x) . В ответе укажите сумму целых точек, входящих в эти промежутки.

Решение:

Заметим, что функция f(x) возрастает, если производная функции положительна; а значит, необходимо найти сумму целых точек, входящих в промежутки возрастания функции.

Таких точек 7 :

х = −3, х = −2, х = 3,

х = 4, х = 5, х = 6, х = 7 .

Их сумма:

− 3+( − 2)+3+4+5+6+7 = 20

у = f ′(x)

+

+

3

5

-3

7

Ответ: 20.

Используемые материалы

• ЕГЭ 2012. Математика. Задача В8. Геометрический смысл производной. Рабочая тетрадь / Под ред. А.Л. Семенова и И.В. Ященко. 3-е изд. стереотип. − М.: МЦНМО, 2012. − 88 с.
• http://mathege.ru/or/ege/Main − Материалы открытого банка заданий по математике 2012 года

Площадь, ограниченная кривой y 4x x2 и Xaxis class 12 maths CBSE

Подсказка : Мы применяем интегралы, чтобы найти площадь данной кривой и оси. Уравнение оси X задается как \ [y = 0 \]. Используя данную кривую и уравнение оси X, находим пределы интегрирования. Решая полученный определенный интеграл, мы получаем искомую площадь данной области.2} \], а ось X — это \ [\ dfrac {{32}} {3} \] sq.unit.
Итак, правильный ответ — «Вариант А».

Примечание : Помните, что уравнение оси X задается как \ [y = 0 \]. Уравнение оси Y задается как \ [x = 0 \]. Используя заданную кривую или любое уравнение, мы находим пределы, а затем решаем их. В определенном интеграле постоянная интегрирования сокращается. Аналогичным образом мы можем найти область, ограниченную кривыми, параболами, окружностями и т. Д.… Во всех случаях метод тот же, что и выше.

РЕШЕНИЕ: (а) Найти наклон касательной к…

Стенограмма видео

Это проблема номер три этого двухчасового исчисления. Восьмое издание Раздел два и семь точек на наклоне касательной к пальцу стопы параппа y равна X минус X в квадрате в точке один три с использованием определения один, а также с использованием уравнения. И для справки. Здесь показано определение 1 для мыла внимания, уравнение для которого также показано здесь, поэтому мы можем начать с определения 1.Наклон равен этому пределу, который мы написали здесь справа. Это взрывоопасная покупка. А в этой проблеме один. Это то, что значение X приближается к функции для X минус X в квадрате. Ах, минус вычисленная функция, а? Если мы оценим, почему Ah в X равняется единице и четырем умноженным на одну минуту одному квадрату. Это три. Хотя я купил X минус, чтобы мы могли продолжить простой поиск числителя. Это квадратичный. Это в форме вопроса. Мы должны иметь возможность учитывать. Здесь X минус один раз по три минуты яйца.Поскольку квадрат X отрицателен, мы имеем здесь отрицательный x. Таким образом, крайнее отношение к X отрицательно. X возведено в квадрат x умноженное на три плюс один два объекта. Это для X. И затем у нас есть отрицательные три из одной минуты, умноженные на три в этой точке, чтобы установить этот предел. Мы не можем отменить этих людей Икс. Сейчас зима, так как X не равен и существует приближается к единице. И то, что мы получаем, взрывается здесь. Три минус одна волшебная пачка на DH. Это использование определения Warner. Давайте также использовать уравнение. Что ж, я допускаю, что здесь, например, эра функции — это X в квадрате.Оценил на плюс h Где один? Итак, четыре умножить на x, где X равно единице плюс h минус количество единица плюс h в квадрате Кейна. Так что это только первый срок. Хватит плюсов у каждого, и этот юридический предмет, связанный с валиумом, получился бы, когда мы знаем, что он четыре умножает на единицу, а этот в квадрате равен № два, три. А новый знаменатель — просто тч. Итак, продолжаем. Он пытается упростить числитель, и это уже сделано. Расширяя термины, мы собираемся в несколько раз расширить процедуру Quantity One, которая дает нам четыре плюс для возраста.Мисс Корн Генетик здесь один плюс возрастная величина в квадрате. Этот биномиальный квадрат становится квадратичным, в частности, один плюс два возраста был возведен в квадрат. О, министерство. Здесь четыре минус один, что равняется трем положительным. Три исключают отрицательный поток, который у нас есть для каждого минус два часа, что тоже упрощает. Четырехкратное возрастание — это слишком ege. И затем мы остаемся с отрицательными, каждый квадрат справа от H. Ну, H и знаменатель советовали с одним агентом друг другу члены в новом Rainer, и мы просто остались с двумя минусами. h оцененный h ноль дает нам ответ пара, что у нас есть определение один.Сколько тоже? Таким образом, подтверждается, что наклон состоит из двух частей. Найдите уравнение вырезки в партии. Поскольку у нас есть точка, которую мы хотим включить в натяжение, если у самцов есть наклон, мы собираемся использовать форму точечного наклона, поэтому я минус y one равно m умноженным на x минус X единица, где x one только одна точка интереса. Нашему белому — три. Наша область действия слишком высока для ее бывшего, и это одно простое решение, объясняющее, почему один равен два X плюс один, поскольку у нас есть естественное значение плюс три. то, что мы сделали, мы были, у нас была вечеринка, которая привела к проблеме, которая здесь, Почему равняется дорогому квадрату и линии натяжения, поэтому равняется два X плюс один как проверочная работа Зуман по направлению к точке один и три до параболы и линия натяжения неразличима s.Итак, мы собираемся пересечь как преобладающую, так и линию напряжения, показанную здесь. Проблема для X-мужчин — это квадратные линии внимания X. Почему следует выражать одно зеленое и оранжевое. И здесь мы видим вероятные зеленые десять миллионов оранжевых. Мы приближаемся к этой точке, которая равна единице к трем, и видим, что начинаем дальше, так как Линия внимания четко отделена от кривой. Но по мере того, как мы приближаемся к Рону, они становятся неразличимыми, все больше и больше времени приближаясь к точке один три, я вижу, что линия натяжения и кривая становятся неразличимыми.

Пример 14 — Докажите, что y2 = 4x, x2 = 4y делит площадь квадрата

Последнее обновление: декабрь.3] = 1/12 × [64−0] = 16/3 ∴ Площадь OAQB = Площадь OBQD — Область OAQP = 32 / 3−16 / 3 = 16/3 Так, Площадь OAQB = Площадь OAQP = Площадь OBRQ = / 𝟑 квадратных единиц Следовательно, доказано.

Показать больше

Графическая викторина наклона

2. Наклон линии B: 3; наклон линии G: 1 3 — Расширение 4.2 Практика 1. A и B; Оба они имеют наклон 3. 2. A и C; Оба они имеют наклон 1. 6 — 3. нет; x = −1 имеет неопределенный наклон, а y = 2 имеет наклон 0.4. да; Обе линии вертикальные и имеют неопределенный наклон. 5. да; Обе линии горизонтальны и имеют наклон 0.

Построение линейных уравнений — Наклон: Основываясь на концепциях из вводного видео выше (таблица x, y и точки пересечения), я строю линию и нахожу ее наклон на основе графика. Затем я рисую линию, используя форму «наклон-пересечение». Я приведу еще три уравнения, чтобы вы попрактиковались в этом.

Здесь наклон в каждой точке перед ai уменьшается на 1. Таким образом, мы помещаем ai в массив наклона, поскольку этот трюк называется «трюком с наклоном», потому что мы рассматриваем общую функцию и анализируем…

Связь между заработанными деньгами и отработанными часами линейна. Джо вычисляет наклон между (4, 30) и (12, 90), затем вычисляет наклон между (4, 30) и (10, 75).

25 марта 2020 г. · Наклон линии показывает, насколько быстро количество случаев удвоится, а крутые линии указывают на короткое время удвоения. Вогнутая кривая показывает, что количество новых случаев увеличивается не по экспоненте. Графики в логарифмической шкале затрудняют различие между медленно увеличивающейся скоростью и уменьшающейся скоростью.

× Close DeltaMath теперь предлагает студентам обзорные курсы с обучающими видео и доступом к более чем 1000 различным навыкам. Отлично подходит для летнего обзора, дополнительной практики для тестов и подготовки к колледжу!

Линейные функции до или после теста LF 2: линейные таблицы из графиков | LF 3: Уклон от двух точек LF 4: Уклон — Подсчет подъема над пробегом на графике LF 5: Написание уравнения пересечения наклона из графика LF 6: Графическое отображение уравнений пересечения наклона LF 7: Создание таблицы из уравнения LF 8 : Построение уравнения пересечения угла наклона с использованием точек пересечения

Увлекательная математическая и научная практика! Улучшите свои навыки с помощью бесплатных задач в «Определение уклона и пересечения Y с заданной формой пересечения склона» и тысяч других практических уроков.