Сколько углов у круга? | UpByte.Net

Учительница математики, прочитав этот вопрос будет возмущена до крайности. Но что поделать — народ интересуется. Кто-то из-за того, что учительница математики так и не ответила на вопрос, а просто начала обзываться нехорошими словами. Кто-то спрашивает, чтобы пошутить так или потролить сеть. Да, есть и те, кто интересуется по личным причинам. Но мы отнесемся к этому вопросу очень серьезно и дадим правильный ответ, который возможно удивит даже гипотетическую учительницу математики. Приготовьтесь.

Давайте начнем издалека и попробуем дать определение круга. Вернее не дать, а найти определение. Википедия думает, что кругом можно назвать следующее:

Круг — геометрическое место точек плоскости (всех таких точек), расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку.

Кажется все понятно? Но, если вы дотошный, то у вас возникнет вопрос — а что такое, простите, геометрическое место точек. Автор этой публикации знал двух друзей-доцентов, которые двадцать лет спорили под пивко: один утверждал что ГМТ (геометрическое место точек) — это просто и понятно, а другой говорил, что это — полная чушь. А вы что думаете по поводу такой формулировки? Вам нравится? Давайте еще раз по слогам: гео-мет-ри-чес-ко-е мес-то то-чек. Чем место геометрическое отличается от обычного места? А что у точек есть размеры? Как точки лепить друг к другу (заполнять область), если у точки нет размеров? А если есть, то какие? Сколько этих самых точек поместится в круг? Все знают, что на отрезке бесконечное число точек? Значит и в круге их будет бесконечное число? Но, когда круг можно считать заполненным, если туда надо накидать бесконечное число точек? Если точек бесконечное число, то и укладывать их туда будем бесконечное число число времени. Ой как все запутано…

Ладно, не мучайте себя размышлениями. И мы тоже вернемся к вопросу — «Сколько углов у круга?». Вы уже осознали, что любое общепринятое определение круга вызывает кучу вопросов. Давайте попробуем дать другое определение. Вот такое:

Круг — это выпуклый правильный \(n\)-многоугольник с числом сторон стремящимся к бесконечности.

Если число сторон стремится к бесконечности, то длина каждой стороны стремится к нулю, а многоугольник приближается кругу. Уяснили? Критикуйте, если сможете. Но, зато теперь мы можем ответить на вопрос — «Сколько углов у круга?». Ответ очевиден — «бесконечное число внутренних углов». При этом величина каждого внутреннего угла стремится к нулю. Так, что, уважаемая гипотетическая учительница, не так уж глупо звучит вопрос вашего «неуча» про количество углов в круге. Или вы не согласны?

P.S. Кстати, можно было бы ответить и так — у круга один внутренний угол величиной в 360 градусов.

Сколько сторон у круга — kak.zydus.su

В Древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении.

В школе изучается много полезных свойств окружности. Одной из самых красивых теорем является следующая: проведем через заданную точку прямую, пересекающую заданную окружность, тогда произведение расстояний от этой точки до точек пересечения окружности с прямой не зависит от того, как именно была проведена прямая. Этой теореме около двух тысяч лет.

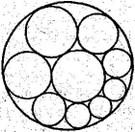
На рис. 2 изображены две окружности и цепочка окружностей, каждая из которых касается этих двух окружностей и двух соседей по цепочке.  Швейцарский геометр Якоб Штейнер около 150 лет назад доказал следующее утверждение: если при некотором выборе третьей окружности цепочка замкнется, то она замкнется и при любом другом выборе третьей окружности. Отсюда следует, что если однажды цепочка не замкнулась, то она не замкнется при любом выборе третьей окружности. Художнику, рисовавшему изображенную цепочку, пришлось бы немало потрудиться, чтобы она получилась, или обратиться к математику для расчета расположения двух первых окружностей, при котором цепочка замыкается.

Вначале мы упомянули о колесе, но еще до колеса люди использовали круглые бревна — катки для перевозки тяжестей.

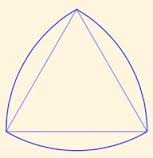А можно ли использовать катки не круглой, а какой-нибудь другой формы? Немецкий инженер Франц Рело обнаружил, что таким же свойством обладают катки, форма которых изображена на рис. 3. Эта фигура получается, если провести дуги окружностей с центрами в вершинах равностороннего треугольника, соединяющие две другие вершины. Если провести к этой фигуре две параллельные касательные, то расстояние между ними будет равно длине стороны исходного равностороннего треугольника, так что такие катки ничем не хуже круглых. В дальнейшем были придуманы и другие фигуры, способные выполнять роль катков.

Энц. «Я познаю мир. Математика», 2006

Источник: geometry-and-art.ru

Читайте также

Сколько углов у круга? Без шуток, я помню, что приблизительно 65000.

Нисколько. Ты путаешь круг с <a rel=»nofollow» href=»http://ru.wikipedia.org/wiki/Правильный_65537-угольник» target=»_blank» >правильным 65537-угольником</a>, который известен тем, что его можно построить циркулем и линейкой.

Тогда уже бесконечность.

360 углов. потому что 360 градусов хотя если подумать то градуся можно перевести в минуты а минуты в секунд и получится 1296000

В градусах =360 или 2 Пи радиан

У круга углов нет. Если мы только сами будем чертить центральнеые и внутренние, то это будет бечсиленное множество.

360 градусов а вобще мне кажется что нет у круга нет углов

У круга нет углов!!!

правильный многоугольник с 65 537 углами и 65 537 сторонами.

Бесконечное множество, т. к. у любой геометрической фигуры можно провести прямую из одного угла в другой и она получится одной длины, а если провести линию из одной точки круга в другую (главное проводить всё через центральную точку так называемую точку »O») и откуда бы ты не провёл линию через центр она будет одной и той же длины.

Круг — это выпуклый правильный n-многоугольник с числом сторон стремящимся к бесконечности. Если число сторон стремится к бесконечности, то длина каждой стороны стремится к нулю, а многоугольник приближается кругу. Уяснили? Критикуйте, если сможете. Но, зато теперь мы можем ответить на вопрос — «Сколько углов у круга?». Ответ очевиден — «бесконечное число внутренних углов». При этом величина каждого внутреннего угла стремится к нулю. Но учительница скажет что вы дебил. P.S. Кстати, можно было бы ответить и так — у круга один внутренний угол величиной в 360 градусов.

Правильный восьмиугольник — Википедия

Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.

Правильный восьмиугольник имеет символ Шлефли {8} ^[1] и может быть построен также как квазиправильный усечённый квадрат, t{4}, в котором перемежаются два типа граней. Усечённый восьмиугольник (t{8}) является шестнадцатиугольником (t{16}).

Построение правильного восьмиугольника

Построение правильного 8-угольника путём складывания листа бумаги

• Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
• Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
• Угол правильного восьмиугольника составляет 135∘{\displaystyle 135^{\circ }}

Формулы расчёта параметров правильного восьмиугольника[править | править код]

Пример:

• t — длина стороны восьмиугольника
• r — радиус вписанной окружности
• R — радиус описанной окружности
• S — площадь восьмиугольника
• k — константа, равная (1+2){\displaystyle (1+{\sqrt {2}})} ≈ 2,414213562373095

Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной kt{\displaystyle kt}, радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:

• Радиус вписанной окружности правильного восьмиугольника:

r=k2t{\displaystyle r={\frac {k}{2}}t}

• Радиус описанной окружности правильного восьмиугольника:

R=tkk−1{\displaystyle R=t{\sqrt {\frac {k}{k-1}}}}

Через сторону восьмиугольника

S=2kt2=2(1+2)t2≃4.828t2.{\displaystyle S=2kt^{2}=2(1+{\sqrt {2}})t^{2}\simeq 4.828\,t^{2}.}

Через радиус описанной окружности

S=4sin⁡π4R2=22R2≃2.828R2.{\displaystyle S=4\sin {\frac {\pi }{4}}R^{2}=2{\sqrt {2}}R^{2}\simeq 2.828\,R^{2}.}

Через апофему (высоту)

A=8tan⁡π8r2=8(2−1)r2≃3.314r2.{\displaystyle A=8\tan {\frac {\pi }{8}}r^{2}=8({\sqrt {2}}-1)r^{2}\simeq 3.314\,r^{2}.}

Площадь можно также вычислить как усечение квадрата

S=A2−a2,{\displaystyle S=A^{2}-a^{2},}

где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.

Если задана сторона a, то длина A равна

A=a2+a+a2=(1+2)a≈2.414a.{\displaystyle A={\frac {a}{\sqrt {2}}}+a+{\frac {a}{\sqrt {2}}}=(1+{\sqrt {2}})a\approx 2.414a.}

Тогда площадь равна:

S=((1+2)a)2−a2=2(1+2)a2≈4.828a2.{\displaystyle S=((1+{\sqrt {2}})a)^{2}-a^{2}=2(1+{\sqrt {2}})a^{2}\approx 4.828a^{2}.}

Площадь через A (ширину восьмиугольника)

S=2(2−1)A2≈0.828A2.{\displaystyle S=2({\sqrt {2}}-1)A^{2}\approx 0.828A^{2}.}

Ещё одна простая формула площади:

 S=2aA.{\displaystyle \ S=2aA.}

Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем

a≈A/2.414.{\displaystyle a\approx A/2.414.}

Два катета углового треугольника можно получить по формуле

e=(A−a)/2.{\displaystyle e=(A-a)/2.}

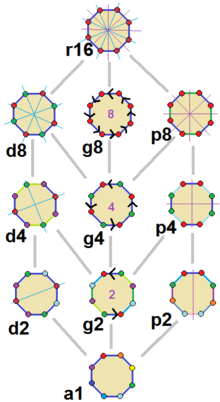11 симметрий правильного восьмиугольника. Линии зеркальных отражений показаны цветом — синие линии проходят через вершины, фиолетовые проходят через середины рёбер, число поворотов указано в центре. Вершины раскрашены согласно симметрии.

Правильный восьмиугольник имеет группу симметрии Dih₈ порядка 16. Имеется 3 диэдральные подгруппы — Dih₄, Dih₂ и Dih₁, а также 4 циклические подгруппы — Z₈, Z₄, Z₂ и Z₁. Последняя подгруппа подразумевает отсутствие симметрии.

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 ^[2]. Диэдральные симметрии делятся на симметрии, проходящие через вершины (обозначены как d — от diagonal), или через рёбра (обозначены как p — от perpendiculars). Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.

На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, равноугольный^[en] восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным^[en] друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Каждая подгруппа симметрии даёт одну или более степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как имеющая ориентированные рёбра.

Разрезание правильного восьмиугольника[править | править код]

Коксетер утверждает, что любой 2m-угольник с параллельными противоположными сторонами можно разрезать на m(m-1)/2 ромбов. Для восьмиугольника m=4 и он разрезается на 6 ромбов, как показано на рисунке ниже. Это разрезание можно рассматривать как 6 из 24 граней проекции многоугольника Петри тессеракта ^[3].

Разрезание правильного восьмиугольника

На 6 ромбов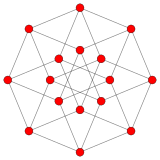

Тессеракт

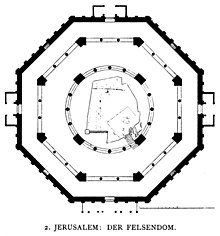Восьмиугольный план Купола Скалы

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и восьмиугольные церкви Норвегии^[en]. Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Другие использования[править | править код]

Связанные многогранники[править | править код]

Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

Восьмиугольник в качестве растянутого квадрата является первым в последовательности растянутых гиперкубов:

• У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986.
• Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — 208 с. — ISBN 9780521098595. books.google  (англ.) Есть перевод на русский Веннинджер, «Модели многогранников», но в ней символы Шлефли не приведены.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — 2008. — С. 275-278. — ISBN 978-1-56881-220-5.

Правильные многоугольники — урок. Геометрия, 9 класс.

Правильными называют многоугольники, у которых равны все стороны и все углы.

На рисунке видны некоторые правильные многоугольники: треугольник, четырёхугольник (квадрат), пятиугольник и шестиугольник.

 

 

Если в правильных выпуклых многоугольниках провести диагонали, то образуются правильные вогнутые многоугольники:

из диагоналей пятиугольника получается пентаграмма, из диагоналей шестиугольника — гексаграмма, а из диагоналей семиугольника — даже две разные гептаграммы.

 

 

Если провести все диагонали из одной вершины, любой \(n\)-угольник можно поделить на \(n-2\) треугольника, таким образом сумма всех внутренних углов определяется по формуле 180°⋅n−2.

 

Так как все углы правильного \(n\)-угольника равны, то величина одного внутреннего угла равна 180°⋅n−2n.

Около любого правильного многоугольника можно описать и вписать в него окружность, при этом совпадают центры обеих окружностей, и эту точку называют центром многоугольника.

 

Вписанная окружность касается всех сторон, описанная окружность проходит через все вершины.

 

 

&angmsd;AOH=360°n;&angmsd;AOK=360°2n=180°n.

 

В треугольнике \(AOK\) связаны сторона \(a\) (половина стороны \(AH\)), радиус описанной окружности \(OA = R\) и радиус вписанной окружности \(OK = r\).

 

a2=R⋅sin180°n;a=2R⋅sin180°n;R=a2sin180°n;a2=r⋅tg180°n;a=2r⋅tg180°n;r=a2tg180°n;r=R⋅cos180°n;R=rcos180°n.

 

Так как \(n\)-угольник состоит из \(n\) треугольников, равных \(AOH\), то

 

Sn−уг.=n⋅SAOH=n⋅AH⋅r2=p⋅r2.

 

Для правильного треугольника и квадрата дополнительно в силе все формулы, которые были рассмотрены в курсе геометрии.