3. Площадь ромба также равна полупроизведению диагоналей, то есть:
\[ S = \dfrac{d_{1} \cdot d_{2} }{2} \]
4. Если известен радиус r окружности, вписанной в ромб , и сторона ромба a, то его площадь вычисляется по формуле:
\[ S = 2 \cdot a \cdot R \]
Свойства ромба
На рисунке выше \( ABCD \) — ромб, \( AC = DB = CD = AD \) . Так как ромб — это параллелограмм, то он обладает всеми свойствами параллелограмма, но так же есть свойства присущие только ромбу.
В любой ромб можно вписать окружность. Центр окружности, вписанной в ромб, является точкой пересечения его диагоналей. Радиус окружности равен половине высоты ромба:
\[ r = \frac{ AH }{2} \]
Свойства ромба
Диагонали ромба перпендикулярны;
Диагонали ромба являются биссектрисами его углов.
Признаки ромба
Параллелограмм, диагонали которого пересекаются под прямым углом, есть ромб;
Параллелограмм, диагонали которого являются биссектрисами его углов, есть ромб.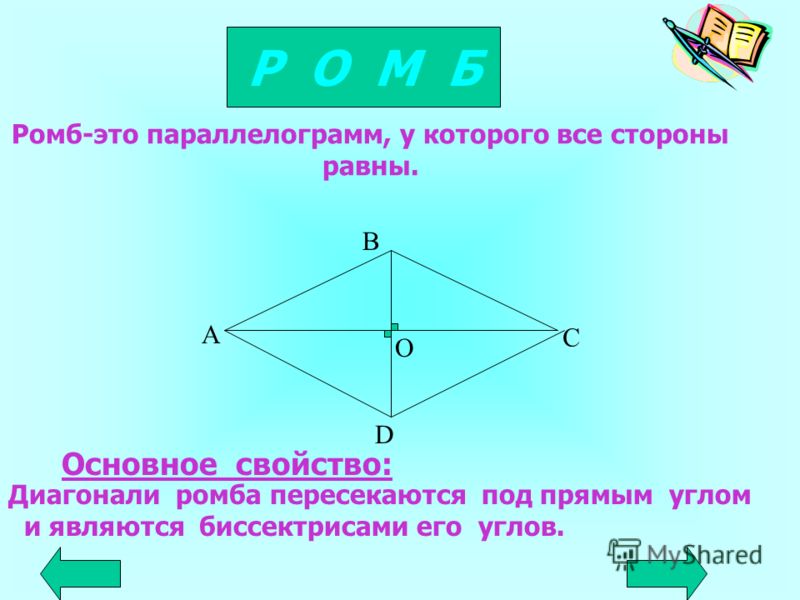
Калькулятор площади ромба
Расчитать площадь фигуры онлайн
Калькулятор: Площадь ромба
Входные данные
Результат
Площадь геометрической фигуры, или площадь фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади фигуры выражается числом заключающихся в него квадратных единиц.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Как найти площадь ромба и углы. Четыре формулы, по которым можно вычислить площадь ромба. Свойства ромба
– это параллелограмм, у которого все стороны равны.Ромб с прямыми углами называется квадратом и считается частным случаем ромба.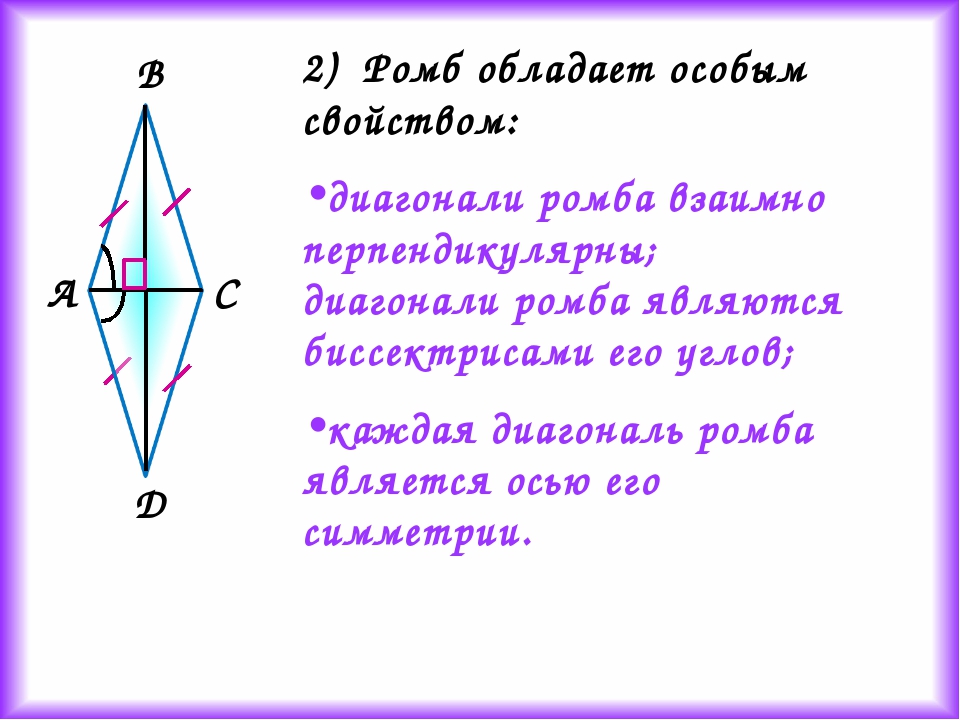 Найти площадь ромба можно различными способами, используя все его элементы – стороны, диагонали, высоту. Классической формулой площади ромба считается расчет значения через высоту.
Найти площадь ромба можно различными способами, используя все его элементы – стороны, диагонали, высоту. Классической формулой площади ромба считается расчет значения через высоту.
Пример расчета площади ромба по этой формуле очень прост. Необходимо только подставить данные и высчитать площадь.
Площадь ромба через диагонали
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
Формула площади ромба через диагонали представляет собой произведение его диагоналей, разделенное на 2.
Рассмотрим пример расчета площади ромба через диагонали. Пусть дан ромб с диагоналями
d1
=5 см и d2
=4. Найдем площадь.
Формула площади ромба через стороны подразумевает и применение других элементов. Если в ромб вписана окружность, то площадь фигуры можно просчитать по сторонам и ее радиусу:
Пример расчета площади ромба через стороны также весьма прост. Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .
Его можно вывести из теоремы Пифагора и по формуле .
Площади ромба через сторону и угол
Формула площади ромба через сторону и угол используется очень часто.
Рассмотрим пример расчета площади ромба через сторону и угол.
Задача: Дан ромб, диагонали которого равны d1
=4 см,d2
=6 см. Острый угол равен α
= 30°. Найдите площадь фигуры через сторону и угол.
Для начала найдем сторону ромба. Используем для этого теорему Пифагора. Мы знаем, что в точке пересечения диагонали делятся пополам и образуют прямой угол. Следовательно:
Подставим значения:
Теперь мы знаем сторону и угол. Найдем площадь:
В школьном курсе в геометрии среди основных задач значительное внимание уделено примерам вычисления площади и периметра ромба. Вспомним что ромб принадлежит к отдельному классу четырехугольников и выделяется среди них равными сторонами. Ромб также является частным случаем параллелограмма если у последнего все стороны равны AB=BC=CD=AD
. Ниже приведен рисунок на котором изображен ромб.
Ниже приведен рисунок на котором изображен ромб.
Поскольку ромб занимает некоторую часть параллелограммов то свойства в них будут похожими.
- Противоположные углы ромба как и параллелограмма равны.
- Сумма углов ромба прилегающих к одной стороне равна 180°.
- Диагонали ромба пересекаются под углом 90 градусов.
- Диагонали ромба являются одновременно биссектрисами его углов.
- Диагонали ромба в точке пересечения делятся пополам.
Признаки ромба
Все признаки ромба вытекают из его свойств и помогают различать его среди четырехугольников, прямоугольников, параллелограммов.
- Параллелограмм у которого диагонали пересекаются под прямым углом является ромбом.
- Параллелограмм у которого диагонали является биссектрисами является ромбом.
- Параллелограмм с равными сторонами является ромбом.
- Четырехугольник у которого все стороны равны является ромбом.
- Четырехугольник у которого диагонали является биссектрисами углов и пересекаются под прямым углом является ромбом.

- Параллелограмм с одинаковыми высотами является ромбом.
Формула периметра ромба
Периметр по определению равен сумме всех сторон. Поскольку в ромба все стороны равны то его периметр вычисляем по формуле
Периметр вычисляется в единицах длины.
Радиус окружности вписанной в ромб
Одними из распространенных задач при изучении ромба является нахождение радиуса или диаметра вписанной окружности. На рисунке изображенном ниже приведены одни из распространенных формул радиуса вписанной окружности в ромб.
Первая формула показывает что радиус окружности вписанной в ромб равен произведению диагоналей разделенному на сумму всех сторон (4а ).
Другая формула показывает что радиус окружности вписанной в ромб равен половине высоты ромба
Вторая формула на рисунке является модификацией первой и применяется при исчислении радиуса окружности вписанной в ромб когда известны диагонали ромба, то есть неизвестные стороны.
Третья формула радиуса вписанной окружности фактически находит половину высоты малого треугольника, который образуется пересечением диагоналей.
Среди менее популярных формул для вычисления радиуса окружности вписанной в ромб можно еще привести такие
здесь D – диагональ ромба, alpha – угол который рассекает диагональ.
Если известна площадь (S)
ромба и величина острого угла (alpha)
то для вычисления радиуса вписанной окружности нужно найти квадратный корень из четверти произведения площади на синус острого угла:
Из приведенных формул Вы без проблем найдете радиус вписанной в ромб окружности, если в условиях примера будут необходимый набор данных.
Формула площади ромба
Формул для вычисления площади приведены на рисунке.
Простейшая выводится как сумма площадей двух треугольников на которые разделяет ромб его диагональ.
Вторая формула площади применяется к задачам в которых известны диагонали ромба. Тогда площадь ромба равна половине произведению диагоналей
Она достаточно проста для того чтобы запомнить, а также — для вычислений.
Третья формула площади имеет смысл когда известен угол между сторонами.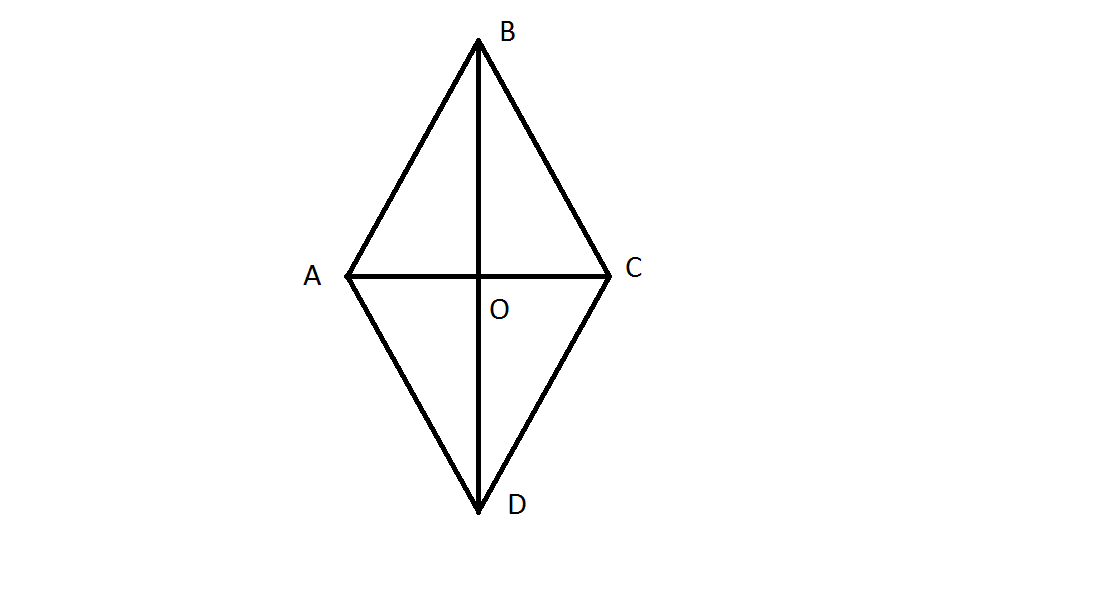 Согласно ей площадь ромба равна произведению квадрата стороны на синус угла. Острый он или нет значения не имеет поскольку синус обоих углов принимает одинаковое значение.
Согласно ей площадь ромба равна произведению квадрата стороны на синус угла. Острый он или нет значения не имеет поскольку синус обоих углов принимает одинаковое значение.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
- Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали. где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
- Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Ромб — это частный случай параллелограмма. Он представляет собой плоскую четырехугольную фигуру, в которой все стороны равны. Данное свойство определяет то, что у ромбов параллельны противоположные стороны и равны противолежащие углы. Диагонали ромба пресекаются под прямым углом, точке их пересечения приходится на середину каждой диагонали, а углы из который они выходят делятся пополам.
1. Если известны обе диагонали ромба AC и BD, то площадь ромба может быть определена как половина произведения диагоналей.
S = ½ ∙ AC ∙ BD
где AC, BD — длина диагоналей ромба.
Чтобы понять почему это так, можно мысленно вписать в ромб прямоугольник таким образом, чтобы стороны последнего были перпендикулярны диагоналям ромба. Становится очевидным, что площадь ромба будет равна половине площади вписанного данным образом в ромб прямоугольника, длина и ширина которого будут соответствовать величине диагоналей ромба.
2. По аналогии с параллелепипедом площадь ромба может быть на найдена как произведение его стороны, на высоту перпендикуляра с опущенного к данной стороне с противолежащей стороны.
S = а ∙ h
где а — сторона ромба;
h — высота перпендикуляра, опущенного на данную сторону.
3. Площадь ромба также равна квадрату его стороны, умноженному на синус угла α
.
S = a 2 ∙ sinα
где, a — сторона ромба;
α
— угол между сторонами.
4. Также площадь ромба может быть найдена через его сторону и радиус вписанной в него окружности.
S = 2 ∙ a ∙ r
где, a — сторона ромба;
r — радиус вписанной в ромб окружности.
Слово ромб произошло от древнегреческого rombus, что в переводе означает «бубен». В те времена бубны действительно имели ромбовидную форму, а не круглую, как мы привыкли видеть их в настоящее время. С тех же времен произошло и название карточной масти «бубны». Очень широко ромбы различных видов используются в геральдике.
Ромб (с древнегреческого ῥόμβος и с латинского rombus «бубен») является параллелограммом, для которого характерно наличие одинаковых по длине сторон. В случае, когда углы составляют 90 градусов (или прямой угол), такую геометрическую фигуру называют квадратом. Ромб — геометрическая фигура, разновидность четырехугольников. Может быть и квадратом, и параллелограммом.
Ромб — геометрическая фигура, разновидность четырехугольников. Может быть и квадратом, и параллелограммом.
Происхождение данного термина
Поговорим немного об истории данной фигуры, что поможет немного раскрыть для себя загадочные тайны древнего мира. Привычное для нас слово, часто встречающееся в школьной литературе, «ромб», берет свое начало от древнегреческого слова «бубен». В Древней Греции эти музыкальные инструменты производились в форме ромба или квадрата (в отличие от современных приспособлений). Наверняка вы заметили, что карточная масть — бубна — обладает ромбической формой. Формирование этой масти восходит к тем временам, когда круглые бубны не использовались в обиходе. Следовательно, ромб — древнейшая историческая фигура, которая была изобретена человечеством задолго до появления колеса.
Впервые такое слово, как «ромб» было употреблено столь известными личностями, как Герон и Папа Александрийский.
Свойства ромба
- Так как стороны ромба противолежат друг другу и являются попарно параллельными, то ромб, несомненно, параллелограмм (АВ || CD, AD || ВС).

- Ромбические диагонали имеют пересечение под прямым углом (AC ⊥ BD), а, значит, перпендикулярны. Следовательно, пересечение делит диагонали пополам.
- Биссектрисами ромбических углов являются диагонали ромба(∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
- Из тождества параллелограммов следует, что сумма всех квадратов диагоналей ромба составляет число квадрата стороны, которое умножили на 4.
Признаки ромба
Ромб в тех случаях является параллелограммом, когда отвечает следующим условиям:
- Все стороны параллелограмма равны.
- Диагонали ромба пересекает прямой угол, то есть они перпендикулярны по отношению друг к другу (AC⊥BD). Это доказывает правило трех сторон (стороны равны и находятся под углом в 90 градусов).
- Диагонали параллелограмма разделяют углы поровну, так как стороны являются равными.
Площадь ромба
- Площадь ромба равна числу, которое является половиной произведения всех его диагоналей.
 2*sinα \)
2*sinα \)
\(α \)- угол между сторонами ромба,
\(a\) — длина стороны ромба,Cторона ромба:
Угол между сторонами в градусах:
Вычислить
Площадь ромба можно найти по двум диагоналям:
\(S=\frac{1}{2}d_1d_2\)
где \(d_1,d_2\) — длины диагоналей.Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Минский государственный лингвистический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-11 классов.
Оставить заявку Я люблю английский язык за его практичность, мелодичность звучания, пластичность и разнообразие слов. Использую игровые методы обучения, диалога, индивидуального подхода.
Я люблю английский язык за его практичность, мелодичность звучания, пластичность и разнообразие слов. Использую игровые методы обучения, диалога, индивидуального подхода.Репетитор по математике
Казанский инженерно- строительный институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 6-9 классов.
Оставить заявку Готовлю к ОГЭ.
Очень интересно и доступно помогу разобраться в изучаемой теме, выполнить домашнюю работу! Математика, это пожалуй одна из самых интересных и захватывающих дисциплин. И если ты полюбишь её и сумеешь понимать, тебе доступны очень многие дисциплины!
Мы вместе будем проходить с тобой этот путь и верю, что тебе всё по силам! Наши уроки будут очень полезными, потому что мы сумеем разобраться в сложных темах, научимся решать задачи и полюбим математику.
Готовлю к ОГЭ.
Очень интересно и доступно помогу разобраться в изучаемой теме, выполнить домашнюю работу! Математика, это пожалуй одна из самых интересных и захватывающих дисциплин. И если ты полюбишь её и сумеешь понимать, тебе доступны очень многие дисциплины!
Мы вместе будем проходить с тобой этот путь и верю, что тебе всё по силам! Наши уроки будут очень полезными, потому что мы сумеем разобраться в сложных темах, научимся решать задачи и полюбим математику.Репетитор по математике
Туркменский государственный университет им.
 Махтумкули
МахтумкулиПроведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-8 классов по математике.
 Как говорил М.В. Ломоносов: «Математику уже затем учить надо, что она ум в порядок приводит». Математика приучает человека логично рассуждать, последовательно мыслить, делать правильные и обоснованные выводы. При изучении тем по математике стараюсь детям объяснять сложное на доступном языке. К каждому ребенку нахожу индивидуальный подход. Помогу подтянуть знания по предмету.
Как говорил М.В. Ломоносов: «Математику уже затем учить надо, что она ум в порядок приводит». Математика приучает человека логично рассуждать, последовательно мыслить, делать правильные и обоснованные выводы. При изучении тем по математике стараюсь детям объяснять сложное на доступном языке. К каждому ребенку нахожу индивидуальный подход. Помогу подтянуть знания по предмету.Решение уравнений
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Записаться на бесплатный урок
Площадь ромба по 2 диагоналям.
 Площадь ромба
Площадь ромбаНесмотря на то, что математика – царица наук, а арифметика – царица математики, самую большую сложность в изучении у школьников вызывает геометрия. Планиметрия – раздел геометрии, который изучает плоские фигуры. Одной из таких фигур является ромб. Большинство задач по решению четырехугольников сводятся к нахождению их площадей. Систематизируем известные формулы и различные способы расчета площади ромба.
Ромб – это параллелограмм, все четыре стороны которого равны. Напомним, что у параллелограмма есть четыре угла и четыре попарно параллельные равные стороны. Как любой четырехугольник, ромб имеет ряд свойств, которые сводятся к следующим: при пересечении диагонали образуют угол, равный 90 градусов (AC ⊥ BD), точка пересечения делит каждую на два равных отрезка. Диагонали ромба также являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.). Отсюда следует, что они делят ромб на четыре равных прямоугольных треугольника. Сумма длин диагоналей, возведенных во вторую степень, равна длине стороны во второй степени, умноженной на 4, т. е. BD 2 + AC 2 = 4AB 2 .
Существует множество методов, используемых в планиметрии для расчета площади ромба, применение которых зависит от исходных данных. Если известны длина стороны и любой угол, можно воспользоваться следующей формулой: площадь ромба равна квадрату стороны, умноженному на синус угла. Из курса тригонометрии известно, что sin (π – α) = sin α, а значит, в расчетах можно использовать синус любого угла – как острого, так и тупого. Частным случаем является ромб, у которого все углы прямые. Это квадрат. Известно, что синус прямого угла равен единице, поэтому площадь квадрата равна длине его стороны, возведенной во вторую степень. Если величина сторон неизвестна, воспользуемся длиной диагоналей. В этом случае площадь ромба равна половине произведения большой и малой диагоналей. При известной длине диагоналей и величине любого угла площадь ромба определяется двумя способами. Первый: площадь – это половина квадрата большей диагонали, умноженная на тангенс половины градусной меры острого угла, т.
е. BD 2 + AC 2 = 4AB 2 .
Существует множество методов, используемых в планиметрии для расчета площади ромба, применение которых зависит от исходных данных. Если известны длина стороны и любой угол, можно воспользоваться следующей формулой: площадь ромба равна квадрату стороны, умноженному на синус угла. Из курса тригонометрии известно, что sin (π – α) = sin α, а значит, в расчетах можно использовать синус любого угла – как острого, так и тупого. Частным случаем является ромб, у которого все углы прямые. Это квадрат. Известно, что синус прямого угла равен единице, поэтому площадь квадрата равна длине его стороны, возведенной во вторую степень. Если величина сторон неизвестна, воспользуемся длиной диагоналей. В этом случае площадь ромба равна половине произведения большой и малой диагоналей. При известной длине диагоналей и величине любого угла площадь ромба определяется двумя способами. Первый: площадь – это половина квадрата большей диагонали, умноженная на тангенс половины градусной меры острого угла, т. е. S = 1/2*D 2 *tg(α/2), где D – большая диагональ, α – острый угол. Если вам известен размер меньшей диагонали, воспользуемся формулой 1/2*d 2 *tg(β/2), где d – меньшая диагональ, β – тупой угол. Напомним, что мера острого угла меньше 90 градусов (меры прямого угла), а тупой угол соответственно – больше 90 0 . Площадь ромба можно отыскать, используя длину стороны (напомним, все стороны у ромба равны) и высоты. Высота – это перпендикуляр, опущенный на противоположную углу сторону или на ее продолжение. Чтобы основание высоты располагалось внутри ромба, ее следует опускать из тупого угла. Иногда в задаче требуется отыскать площадь ромба, исходя из данных, относящихся к вписанной окружности. В этом случае необходимо знать ее радиус. Существуют две формулы, которыми можно воспользоваться для расчета. Итак, чтобы ответить на поставленный вопрос, можно удвоить произведение стороны ромба и радиуса вписанной окружности. Другими словами, необходимо умножить диаметр вписанной окружности на сторону ромба.
е. S = 1/2*D 2 *tg(α/2), где D – большая диагональ, α – острый угол. Если вам известен размер меньшей диагонали, воспользуемся формулой 1/2*d 2 *tg(β/2), где d – меньшая диагональ, β – тупой угол. Напомним, что мера острого угла меньше 90 градусов (меры прямого угла), а тупой угол соответственно – больше 90 0 . Площадь ромба можно отыскать, используя длину стороны (напомним, все стороны у ромба равны) и высоты. Высота – это перпендикуляр, опущенный на противоположную углу сторону или на ее продолжение. Чтобы основание высоты располагалось внутри ромба, ее следует опускать из тупого угла. Иногда в задаче требуется отыскать площадь ромба, исходя из данных, относящихся к вписанной окружности. В этом случае необходимо знать ее радиус. Существуют две формулы, которыми можно воспользоваться для расчета. Итак, чтобы ответить на поставленный вопрос, можно удвоить произведение стороны ромба и радиуса вписанной окружности. Другими словами, необходимо умножить диаметр вписанной окружности на сторону ромба. Если в условии задачи представлена величина угла, то площадь находится через частное между квадратом радиуса, умноженном на четыре, и синусом угла.
Если в условии задачи представлена величина угла, то площадь находится через частное между квадратом радиуса, умноженном на четыре, и синусом угла.Как видите, существует множество способов для нахождения площади ромба. Конечно, чтобы запомнить каждый из них, потребуется терпение, внимательность и, конечно же, время. Но в дальнейшем вы сможете легко выбрать метод, подходящий для вашей задачи, и убедитесь, что геометрия – это несложно.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали. где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
– это параллелограмм, у которого все стороны равны.

Ромб с прямыми углами называется квадратом и считается частным случаем ромба. Найти площадь ромба можно различными способами, используя все его элементы – стороны, диагонали, высоту. Классической формулой площади ромба считается расчет значения через высоту.
Пример расчета площади ромба по этой формуле очень прост. Необходимо только подставить данные и высчитать площадь.
Площадь ромба через диагонали
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.Формула площади ромба через диагонали представляет собой произведение его диагоналей, разделенное на 2.
Рассмотрим пример расчета площади ромба через диагонали. Пусть дан ромб с диагоналями
d1 =5 см и d2 =4. Найдем площадь.Формула площади ромба через стороны подразумевает и применение других элементов. Если в ромб вписана окружность, то площадь фигуры можно просчитать по сторонам и ее радиусу:
Пример расчета площади ромба через стороны также весьма прост.
 Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .
Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .Площади ромба через сторону и угол
Формула площади ромба через сторону и угол используется очень часто.Рассмотрим пример расчета площади ромба через сторону и угол.
Задача: Дан ромб, диагонали которого равны d1 =4 см,d2 =6 см. Острый угол равен α = 30°. Найдите площадь фигуры через сторону и угол.
Для начала найдем сторону ромба. Используем для этого теорему Пифагора. Мы знаем, что в точке пересечения диагонали делятся пополам и образуют прямой угол. Следовательно:
Подставим значения:
Теперь мы знаем сторону и угол. Найдем площадь:– это параллелограмм , у которого все стороны равны, то для него действуют все те же формулы, как и для параллелограмма, включая формулу нахождения площади через произведение высоты и стороны .
Площадь ромба можно найти, также зная его диагонали . Диагонали делят ромб на четыре абсолютно одинаковых прямоугольных треугольника .
 Если мы их рассортируем, так чтобы получить прямоугольник , то его длина и ширина будут равны одной целой диагонали и половине второй диагонали. Поэтому площадь ромба находится умножением диагоналей ромба, сокращенных на два (как площади получившегося прямоугольника).
Если мы их рассортируем, так чтобы получить прямоугольник , то его длина и ширина будут равны одной целой диагонали и половине второй диагонали. Поэтому площадь ромба находится умножением диагоналей ромба, сокращенных на два (как площади получившегося прямоугольника).Если в распоряжении только угол и сторона , то можно вооружиться диагональю в качестве помощника и начертить ее напротив известного угла. Тогда она разделит ромб на два конгруэнтных треугольника, площади которых в сумме дадут нам площадь ромба. Площадь каждого из треугольников будет равна половине произведения квадрата стороны на синус известного угла, как площадь равнобедренного треугольника . Поскольку таких треугольников два, то коэффициенты сокращаются, оставив только сторону во второй степени и синус:
Если внутри ромба вписать окружность , то его радиус будет относиться к стороне под углом 90° , что значит, что удвоенный радиус будет равен высоте ромба . Подставив вместо высоты h=2r в предыдущую формулу, получим площадь S=ha=2ra
Если же вместе с радиусом вписанной окружности, дана не сторона, а угол, то следует сначала найти сторону, проведя высоту таким образом, чтобы получить прямоугольный треугольник с заданным углом.
 Тогда сторона a
может быть найдена из тригонометрических отношений по формуле . Подставляя это выражение в ту же стандартную формулу площади ромба, выходит
Тогда сторона a
может быть найдена из тригонометрических отношений по формуле . Подставляя это выражение в ту же стандартную формулу площади ромба, выходитРомб — это частный случай параллелограмма. Он представляет собой плоскую четырехугольную фигуру, в которой все стороны равны. Данное свойство определяет то, что у ромбов параллельны противоположные стороны и равны противолежащие углы. Диагонали ромба пресекаются под прямым углом, точке их пересечения приходится на середину каждой диагонали, а углы из который они выходят делятся пополам. То есть они диагонали ромба являются биссектрисами углов. Исходя из приведенных определений и перечисленных свойств ромбов их площадь может быть определена различными способами.
1. Если известны обе диагонали ромба AC и BD, то площадь ромба может быть определена как половина произведения диагоналей.
S = ½ ∙ AC ∙ BD
где AC, BD — длина диагоналей ромба.
Чтобы понять почему это так, можно мысленно вписать в ромб прямоугольник таким образом, чтобы стороны последнего были перпендикулярны диагоналям ромба.
 Становится очевидным, что площадь ромба будет равна половине площади вписанного данным образом в ромб прямоугольника, длина и ширина которого будут соответствовать величине диагоналей ромба.
Становится очевидным, что площадь ромба будет равна половине площади вписанного данным образом в ромб прямоугольника, длина и ширина которого будут соответствовать величине диагоналей ромба.2. По аналогии с параллелепипедом площадь ромба может быть на найдена как произведение его стороны, на высоту перпендикуляра с опущенного к данной стороне с противолежащей стороны.
S = а ∙ h
где а — сторона ромба;
h — высота перпендикуляра, опущенного на данную сторону.3. Площадь ромба также равна квадрату его стороны, умноженному на синус угла α .
S = a 2 ∙ sinα
где, a — сторона ромба;
α — угол между сторонами.4. Также площадь ромба может быть найдена через его сторону и радиус вписанной в него окружности.
S = 2 ∙ a ∙ r
где, a — сторона ромба;
Интересные факты
r — радиус вписанной в ромб окружности.
Слово ромб произошло от древнегреческого rombus, что в переводе означает «бубен». В те времена бубны действительно имели ромбовидную форму, а не круглую, как мы привыкли видеть их в настоящее время. С тех же времен произошло и название карточной масти «бубны». Очень широко ромбы различных видов используются в геральдике.
С тех же времен произошло и название карточной масти «бубны». Очень широко ромбы различных видов используются в геральдике.Математика для блондинок: Диагональ, параллелепипед и ромб
Вот такая вот задача. Основанием прямоугольного параллелепипеда является ромб, сторона которого равняется 6 сантиметров, а угол 60 градусов. Высота параллелепипеда равна 8 сантиметров, найдите длину меньшей диагонали параллелепипеда.Начинаем рассуждать. Параллелепипед и ромб в основании — это такая коробочка, которая сверху похожа на ромб. У такого параллелепипеда действительно можно нарисовать две пары диагоналей, длины которых будут разными. Из нижней вершины с острым углом в верхнюю вершину с острым углом можно провести длинную диагональ. А вот тупые вершины (не в смысле, что эти вершины ничего не понимают, а в смысле, что эти вершины прихватизировали тупые углы) будут соединяться короткими диагоналями. Таких диагоналей две, их длина одинаковая. Посмотрим на картинке, как выглядит одна из таких диагоналей.

Диагональ прямоугольного параллелепипеда показана красным цветом, диагонали ромба основания показаны синим цветом. Если очень сильно постараться, напрячь свое воображение и внимательно присмотреться к верхней картинке, то можно увидеть прямоугольный треугольник. Параллелепипед у нас прямоугольный. Значит, боковое ребро расположено под прямым углом к основанию. Диагональ основания (синенькая), диагональ параллелепипеда (красненькая) и ребро (черненькое, мелированое, не успело в парикмахерской перекраситься) образуют этот прямоугольный треугольник. А там, где есть прямоугольный треугольник, там царствует теорема древнего Пифагора. Всегда, не зависимо от того, кого вы в своей стране избрали царём или президентом.В низу, под картинкой, записана эта самая знаменитая теорема применительно к нашему случаю. Не удивляйтесь, если в таком виде вы встречаете теорему Пифагора впервые. Во-первых, не все учились с вами в одном классе и они могут не знать, как именно вас учили правильно записывать теорему Пифагора.
 Во-вторых, в теореме Пифагора главным является не принятая кем-то система закорючек, а смысл — берем две перпендикулярных штучки, возводим в квадрат, складываем в кучку и получаем третью штучку в квадрате. У нас квадрат ребра и квадрат диагонали ромба чудненько складываются в квадрат диагонали параллелепипеда.
Во-вторых, в теореме Пифагора главным является не принятая кем-то система закорючек, а смысл — берем две перпендикулярных штучки, возводим в квадрат, складываем в кучку и получаем третью штучку в квадрате. У нас квадрат ребра и квадрат диагонали ромба чудненько складываются в квадрат диагонали параллелепипеда.Теперь нам необходимо разобраться с диагональю ромба. Берем нашу коробочку в форме прямоугольного параллелепипеда, открываем крышечку и заглядываем внутрь. Почему мы заглядываем внутрь коробочки а не изучаем саму крышечку? Безотказно работает теорема любопытной обезьяны. Попробуйте что-нибудь отрыть и не заглянуть внутрь. А зачем тогда открывали?! Любой, даже безграмотный, математик вам скажет, что теорема требует доказательства. Один момент. Попросите свою маму купить вам что-то в коробочке. Когда она вам её принесет, вы, с закрытыми глазами, откройте крышечку коробочки, а саму коробочку, не глядя, выбросьте в мусор. Не получилось? Всё, теорема доказана.
И так, мы остановились на том, что, встав в позу теоремы Пифагора, мы заглядываем внутрь коробочки.
 Что мы там видим? Если вы верили в Конец Света 2012, тогда там спрятаны припасы на всю оставшуюся жизнь. Вынимайте их из коробки и можете смело доедать (вы ещё долго будете извлекать свои припасы из самых неожиданных мест). Пока вы не придумаете следующую дату Конца Света, вам ничто не угрожает. С пророчеством советую поторопиться. Вокруг очень много жаждущих славы пророков, а ещё больше желающих впихнуть вам партию залежалого товара. Если же вы не верите в Конец Света, то в коробочке были новогодние сладости, которые уже закончились.
Что мы там видим? Если вы верили в Конец Света 2012, тогда там спрятаны припасы на всю оставшуюся жизнь. Вынимайте их из коробки и можете смело доедать (вы ещё долго будете извлекать свои припасы из самых неожиданных мест). Пока вы не придумаете следующую дату Конца Света, вам ничто не угрожает. С пророчеством советую поторопиться. Вокруг очень много жаждущих славы пророков, а ещё больше желающих впихнуть вам партию залежалого товара. Если же вы не верите в Конец Света, то в коробочке были новогодние сладости, которые уже закончились.Всё, наша коробочка пустая и мы можем внимательно изучить донышко. Оно имеет форму ромба, у которого можно провести диагонали. При пересечении, эти диагонали образуют чудненькие треугольнички. Аж четыре штуки. Мы люди не жадные, нам достаточно одного. Что мы знаем об этом треугольничке (на картинке ниже он закрашен в чудный цвет)? Этот треугольник точно не Бермудский и не любовный. А какой? Лезем в Интернет и ищем свойства ромба. Мы их когда-то учили в школе, но это было так давно.
 .. В Интернете полно всякой ерунды, но есть и кое-то интересное нам. Все стороны ромба одинаковые. Диагонали ромба разные. Пересекаются диагонали под прямым углом. Точка пересечения диагоналей делит их на две равные половинки. Каждая диагональ делит угол в вершине поровну (у ромбов и квадратов диагонали не жадные). Кажется, всё. Прочая ерунда о ромбах нас не интересует.
.. В Интернете полно всякой ерунды, но есть и кое-то интересное нам. Все стороны ромба одинаковые. Диагонали ромба разные. Пересекаются диагонали под прямым углом. Точка пересечения диагоналей делит их на две равные половинки. Каждая диагональ делит угол в вершине поровну (у ромбов и квадратов диагонали не жадные). Кажется, всё. Прочая ерунда о ромбах нас не интересует.И так, в результате наших научных исследований мы установили, что наш треугольник является прямоугольным. Гипотенуза у него равна длине стороны ромба, катеты равняются половинкам диагоналей. Снова примеряем деда Пифагора. Длину гипотенузы мы знаем, а вот с двумя катетами проблема. Какой-то лентяй не потрудился измерить диагонали. Зато это чудо умудрилось вымерить величину угла в одной вершине. В традиционном виде теорема Пифагора не катит (это не опечатка, это в смысле «не подходит»). Остается только тригонометрия. Она тоже работает в прямоугольных треугольниках, но придумали её математики исключительно для того, чтобы издеваться над детьми.
 Лично мне так кажется. Думаю, эта идея соберет не маленькую группу Вконтакте. «Я ненавижу тригонометрию» — красивое название для группы, дарю.
Лично мне так кажется. Думаю, эта идея соберет не маленькую группу Вконтакте. «Я ненавижу тригонометрию» — красивое название для группы, дарю.Как сказали бы врачи, показаниями к применению тригонометрии является невозможность применения теоремы Пифагора из-за отсутствия двух размеров треугольника и наличие значения одного из углов. Если бы у нас не было угла, тогда и медицина была бы бессильна. Как применить тригонометрию? Не будем рыскать по Интернету, я покажу вам более надежный инструмент. Назвал я его «портрет тангенса». Приставляем его к вершине треугольника, значение угла в которой нам известно. Горизонтальную палочку располагаем параллельно линии, от которой мы отсчитываем угол (у нас это горизонтальная диагональ). Потом вспоминаем «тангенс — это синус на косинус». Верхняя палочка портрета обозначает синусы, нижняя палочка — косинусы. Нам нужно найти вертикальный катет треугольника. Значит, для этого гипотенузу нужно умножить на синус угла. Если бы нам нужен был горизонтальный катет, мы бы умножали на косинус этого же угла.
 Полная длина вертикальной диагонали ромба (синенькая) получается равной двум длинам катета треугольника.
Полная длина вертикальной диагонали ромба (синенькая) получается равной двум длинам катета треугольника.
Всё. С задачей мы разобрались. Обозначаем диагональ ромба буквой «f«, сторону — буквой «а«, угол — буквой «альфа«. Диагональ параллелепипеда мы обозначим буквой «d«, а его высоту — буквой «h«. Теперь записываем формулы для решения, подставляем в них известные нам значения и получаем результат.
Длина меньшей диагонали получилась равной 10 сантиметров. Можно, конечно, вычислить и длину большей диагонали, но теорема любопытной обезьяны в этом случае наотрез отказывается работать. Она (теорема) точно знает, что ничего вкусненького или интересного в результате вычислений мы не получим.Как найти длину диагонали ромба
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже.
 Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права. Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \ достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем а ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т.
 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
Объяснение урока: Площадь ромба
В этом объяснении мы узнаем, как найти площадь ромба, используя длины его диагоналей.
Напомним, что ромбом называется любой четырехугольник, у которого все четыре стороны равны длина.
 Поскольку ромб также является параллелограммом, его площадь можно вычислить из
длину его основания и высоту перпендикуляра по формуле
площадь=𝑏ℎ.
Поскольку ромб также является параллелограммом, его площадь можно вычислить из
длину его основания и высоту перпендикуляра по формуле
площадь=𝑏ℎ.Альтернативная формула площади ромба, которую мы здесь выводим, вместо этого использует длины его диагоналей. Диагонали любого параллелограмма делят единицу пополам. другое, но дополнительное свойство диагоналей ромба состоит в том, что они перпендикулярны, как показано на рисунке ниже.
Рассмотрим диагональ 𝐵𝐷, которая делит ромб на конгруэнтные треугольники 𝐴𝐵𝐷 и 𝐶𝐵𝐷.Поскольку треугольники равны, каждая их площадь равна половина площади ромба. Эквивалентно, мы можем утверждать, что площадь ромбаплощадьтреугольника𝐴𝐵𝐶𝐷=2×𝐴𝐵𝐷.
Предположим также, что длины диагоналей равны 𝑑 и 𝑑 единиц, как показано на рисунке ниже.
Площадь треугольника 𝐴𝐵𝐷 можно рассчитать по формуле площадьтреугольника=12𝑏ℎ, где 𝑏 представляет основание треугольника и ℎ представляет перпендикулярную высоту.
 Из рисунка мы
определить, что основание этого треугольника равно
𝐵𝐷, длина которого 𝑑
единицы.Перпендикулярная высота этого треугольника равна
𝐴𝐸. Вспоминая еще раз, что диагонали
ромб делит друг друга пополам, мы
известно, что 𝐴𝐸 составляет половину длины
диагональ 𝐴𝐶 и поэтому имеет длину
𝑑2 ед. Следовательно,
площадь треугольниковквадрата единиц𝐴𝐵𝐷=12×𝑑×𝑑2=𝑑𝑑4.
Из рисунка мы
определить, что основание этого треугольника равно
𝐵𝐷, длина которого 𝑑
единицы.Перпендикулярная высота этого треугольника равна
𝐴𝐸. Вспоминая еще раз, что диагонали
ромб делит друг друга пополам, мы
известно, что 𝐴𝐸 составляет половину длины
диагональ 𝐴𝐶 и поэтому имеет длину
𝑑2 ед. Следовательно,
площадь треугольниковквадрата единиц𝐴𝐵𝐷=12×𝑑×𝑑2=𝑑𝑑4.Следовательно, площадь ромба равна площадь ромбаквадратединицы𝐴𝐵𝐶𝐷=2×𝑑𝑑4=𝑑𝑑2.
Формула: Площадь ромба
Площадь ромба равна половине произведения длин его диагонали.Для ромба с диагоналями длины 𝑑 и 𝑑 единиц, площадь ромбаквадрата единиц = 𝑑𝑑2.
В нашем первом примере мы применим эту формулу для вычисления площади ромб, нарисованный внутри прямоугольника.
Пример 1. Нахождение площади ромба внутри прямоугольника
На рисунке показан ромб внутри прямоугольника. Найдите площадь ромба на два десятичных знака.

Ответ
При рассмотрении диаграммы мы видим, что каждая вершина ромба 𝑋𝑇𝑍𝑌 находится в середине одной из сторон прямоугольника.Например, вершина 𝑋 находится на середине стороны 𝐴𝐷. Мы знаем это, потому что 𝐴𝑋 и 𝑋𝐷 есть равной длины. Отсюда можно сделать вывод, что диагональ ромба 𝑋𝑍 параллелен 𝐴𝐵 и 𝐷𝐶, а диагональ 𝑌𝑇 параллелен 𝐴𝐷 и 𝐵𝐶.
Из этого также следует, что 𝑋𝑍=𝐴𝐵=𝐷𝐶 и 𝑌𝑇=𝐴𝐷=𝐵𝐶.
Размеры прямоугольника указаны в вопросе и, следовательно, 𝑋𝑍=15.8 см и 𝑌𝑇=30,3см.
Теперь вспомним, что площадь ромба равна половине произведения длины его диагоналей: площадь ромба=𝑑𝑑2, где 𝑑 и 𝑑 — длины диагонали. В этой задаче длины диагоналей равны 30,3 см и 15,8 см, так что у нас есть площадьсм𝑋𝑇𝑍𝑌=30,3×15,82=478,742=239,37.

Кратко отметим соотношение между ромбом 𝑋𝑇𝑍𝑌 и прямоугольник 𝐴𝐵𝐶𝐷 в предыдущем примере.Площадь любого прямоугольника равна произведению его длины на ширину, или, другими словами, произведение его размеров. В этой задаче длины диагоналей ромба равны размерам прямоугольник, а так как площадь ромба равна половине произведения его диагоналей, это эквивалентно половине произведения размеры прямоугольника. Это свидетельствует о том, что площадь ромб, нарисованный внутри прямоугольника так, что каждая вершина ромба находится в середине одной из сторон прямоугольника, составляет половину площади окружающего его прямоугольника.
Теперь мы рассмотрели один пример того, как вычислить площадь ромба по данному длины двух его диагоналей. Так же возможна работа в др. направление: если нам дана площадь ромба и длина одного из его диагоналей, мы можем вычислить длину другой диагонали, составив и решение уравнения.
 Зная площадь ромба, мы также можем вычислить
длину одной или обеих диагоналей, если мы явно не знаем
длина любого из них, но мы знаем соотношение между их длинами,
как мы увидим в нашем следующем примере.
Зная площадь ромба, мы также можем вычислить
длину одной или обеих диагоналей, если мы явно не знаем
длина любого из них, но мы знаем соотношение между их длинами,
как мы увидим в нашем следующем примере.Пример 2. Расчет длины диагонали ромба по его площади
Одна диагональ ромба в два раза длиннее другой диагонали. Если площадь ромба 81 квадратный миллиметр, какова длина диагоналей?
Ответ
Напомним, что площадь ромба равна половине произведения длин его диагонали 𝑑 и 𝑑: area=𝑑𝑑2.
Пусть длина меньшей диагонали равна 𝑑.Так как другая диагональ в два раза больше первой, имеем 𝑑=2𝑑. Таким образом, мы можем сформировать уравнение, подставив 𝑑=2𝑑 в приведенную выше формулу и установив это выражение, равное известной площади: 𝑑×(2𝑑)2=81.
Упрощение выражения в левой части путем сокращения множителя 2 дает 𝑑=81.
Мы находим 𝑑 путем извлечения квадратного корня из каждой части уравнения, принимая только положительное значение, поскольку 𝑑 представляет длину: 𝑑=√81=9.
 мм
ммМы нашли длину меньшей диагонали 𝑑 быть 9 мм. Вторая диагональ в два раза длиннее, поэтому имеем 𝑑=2𝑑=2×9=18.мм
Длины диагоналей данного ромба равны 9 мм и 18 мм.
В нашем следующем примере мы решим задачу с ромбом и квадратом которые имеют одинаковую площадь. Зная периметр квадрата и длину одной диагонали ромба вычислим длину другая диагональ ромба.
Пример 3. Нахождение длины диагонали ромба по длине другой диагонали и фигуре с одинаковой площадью
Ромб и квадрат имеют одинаковую площадь. Если периметр квадрата 44 и одна из диагоналей ромба равна 10, какой длины другая диагональ, до двух знаков после запятой?
Ответ
Чтобы связать две фигуры, нам нужно найти значение или выражение для каждой из их областей, которые, как нам говорят, равны.Позволять Начнем с рассмотрения квадрата.
Нам дано, что периметр квадрата равен 44 единицам.
 Мы помним, что
периметр фигуры — это расстояние вокруг ее края. В случае
квадрат, у которого четыре равные стороны по 𝑠 единиц длины, периметр равен
равно 4𝑠. Установка этого выражения равным 44 дает уравнение, которое
можно решить, чтобы определить длину стороны квадрата:
4𝑠=44𝑠=11.unit
Мы помним, что
периметр фигуры — это расстояние вокруг ее края. В случае
квадрат, у которого четыре равные стороны по 𝑠 единиц длины, периметр равен
равно 4𝑠. Установка этого выражения равным 44 дает уравнение, которое
можно решить, чтобы определить длину стороны квадрата:
4𝑠=44𝑠=11.unitПлощадь квадрата можно рассчитать по длине его стороны, используя формула площадь квадрата=𝑠.Замена 𝑠=11 дает площадь квадратовквадратных единиц = 11 = 121.
Теперь мы знаем, что площадь ромба также равна 121 кв. Напомним, что площадь одного ромб равен половине произведения длин его диагоналей 𝑑 и 𝑑: площадь ромба=𝑑𝑑2.
Нам дано, что одна диагональ имеет длину 10 единиц, поэтому мы можем составить уравнение: 10×𝑑2=121.
Чтобы решить это уравнение относительно 𝑑, мы сначала упростим в левой части, уменьшив коэффициент 2: 5𝑑=121.

Затем мы делим каждую часть уравнения на 5, чтобы получить 𝑑=1215=24,2.
С точностью до двух знаков после запятой длина другой диагонали ромба равна 24,20 ед.
В предыдущем примере мы использовали наши знания о том, как вычислить площадь квадрат по длине его стороны. Однако квадрат на самом деле является особым типом ромба, у которого две диагонали имеют одинаковую длину. Предположим, что каждая диагональ квадрата имеет длину 𝑑 единиц.Используя формулу площади ромба, площадь квадрата равна половине произведения длин его диагонали, ведущие к areaofsquare=𝑑×𝑑2=𝑑2.
Формула: Площадь квадрата
Площадь квадрата равна половине квадрата длины его диагонали. Для квадрата с диагональю длины 𝑑 единиц, areaofsquasquareunits=𝑑2.
В нашем следующем примере мы рассмотрим, как найти длину диагонали шахматной доске, сначала рассмотрев взаимосвязь между площадью и диагонали меньших квадратов, из которых состоит шахматная доска.

Пример 4. Нахождение длины диагонали квадрата по его площади
Учитывая, что площадь каждого квадрата на шахматной доске равна 81 см 2 , найдите длину диагонали шахматной доски.
Ответ
Шахматная доска состоит из 64 равных квадратов, расположенных в 8 рядов. из 8. Заметим, что длина диагонали шахматной доски, которую мы будет обозначать 𝐷, равно 8-кратной длине диагонали каждого отдельного квадрата, который мы будем обозначать через 𝑑: 𝐷=8𝑑.
Нам известно, что площадь каждой клетки на шахматной доске равна 81 см 2 . Мы вспоминаем и что площадь квадрата можно вычислить по длине его диагональ 𝑑 по формуле areaofsquare=𝑑2.
Следовательно, мы имеем 𝑑2=81.
Чтобы найти 𝑑, мы начнем с умножения каждой стороны этого уравнение на 2, что приводит к 𝑑=162.
Затем извлекаем квадратный корень и упрощаем радикал, что дает 𝑑=√162=√81×2=√81×√2=9√2.
 см
смНаконец, мы можем вычислить длину диагонали шахматную доску (𝐷), вспомнив, что 𝐷=8𝑑. Следовательно, 𝐷=8×9√2=72√2.cm
В предыдущем примере альтернативным подходом было бы
- вычислить длину стороны каждого из меньших квадратов, вспомнив, что areaofsquare=𝑠,
- вычислить длину диагонали каждой из меньших квадраты, применяя теорему Пифагора,
- умножьте это на 8, чтобы получить длину диагонали шахматная доска.
Несмотря на то, что это вполне допустимый метод, он включает такое же количество шагов к методу, который мы представили, поэтому он не более или менее эффективен.
В нашем последнем примере мы найдем разницу между площадями квадрат и ромб, каждый из которых рассчитывается с использованием длин их диагоналей.
Пример 5. Нахождение площадей квадрата и ромба по их диагоналям
Определите разность площадей квадрата с диагональю 10 см и ромб с диагоналями 2см и 12 см.

Ответ
Начнем с вычисления площади каждой фигуры. Площадь квадрата может вычислить по длине его диагонали 𝑑 по формуле areaofsquare=𝑑2.
Следовательно, для квадрата с диагональю 10 см, площадь квадратасм=10×102=50.
Площадь ромба равна половине произведения длин его диагонали 𝑑 и 𝑑: площадь ромба=𝑑𝑑2.
Следовательно, для ромба с диагоналями 2 см и 12 см, площадь ромбасм=2×122=12.
Наконец, мы вычисляем разницу в площади, вычитая площадь меньшего четырехугольника (ромба) из площади большего четырехугольник (квадрат): разность вплощадиквадратаплощадьромбасм=−=50−12=38.
Давайте закончим повторением некоторых ключевых моментов.
Ключевые точки
- Площадь ромба равна половине произведения длин его диагоналей.
- Для ромба с диагоналями длины 𝑑 и
𝑑 единиц,
площадь квадрата ромба = 𝑑𝑑2.

- Площадь квадрата равна половине квадрата длины его диагонали.
- Для квадрата с диагоналями длиной 𝑑 единиц, площадьквадратных квадратов=𝑑2.
Площадь ромба
Ромб – это четырехугольник, все стороны которого имеют неравные диагонали, делящие друг друга пополам.
Примечание : Если с двух противоположных углов сжать квадрат, образуется ромб.
Пусть $$ABCD$$ — ромб, тогда его площадь можно вычислить двумя способами.2}\sin\тета$$.
(2) Если даны две диагонали:
Пусть $$d$$ и $$d’$$ — длины диагоналей $$AC$$ и $$BD$$ соответственно, а так как ромб разбит на четыре равных треугольника, то
Площадь ромба $$ = 4 \times \frac{1}{2} \times \frac{{BD}}{2} \times \frac{{CA}}{2} = 4 \times \frac {{BD \times CA}}{8} = \frac{{BD \times CA}}{2}$$.
Площадь ромба $$ = \frac{{AC \times BD}}{2} = \frac{{d \times d’}}{2}$$.
 \circ = 120 \times 120 \times 0,866 = 12470,4 $$ квадратных см.
\circ = 120 \times 120 \times 0,866 = 12470,4 $$ квадратных см.Пример :
Диагонали ромба равны $$40$$ м и $$30$$ м. Найдите его площадь.
Решение :
Учитывая, что диагонали равны $$d = 40$$ м и $$d’ = 30$$ м,
площадь ромба $$ = \frac{{d \times d’}}{2} = \frac{{40 \times 30}}{2} = 600$$ квадратных метров.
Диагонали параллелограммов, прямоугольников и ромбов [Видео и практика]
Привет и добро пожаловать на это видео о диагоналях! Сегодня мы собираемся исследовать диагонали параллелограммов, прямоугольников, ромбов и квадратов и посмотреть, как эти фигуры соотносятся друг с другом в целом.Давайте начнем!
Все фигуры, которые мы сегодня рассмотрим, являются четырехугольниками , то есть все они четырехсторонние многоугольники. Многоугольник — это фигура с несколькими сторонами.

Типы четырехугольников
Свойства параллелограмма
Параллелограмм — это четырехугольник с двумя наборами параллельных сторон. Синие стрелки обозначают, какие стороны параллельны друг другу. Противоположные стороны параллелограмма, отмеченные зелеными галочками, конгруэнтны, что означает, что они имеют одинаковую меру.
Свойства прямоугольника
Прямоугольник — это форма, которую мы все хорошо знаем, поскольку она так часто встречается в реальном мире. Но одна вещь, о которой мы обычно не задумываемся, это то, что прямоугольники — это просто особый вид параллелограмма. Это означает, что противоположные стороны параллельны и конгруэнтны, как и в нашем первом параллелограмме. Что делает прямоугольник особым параллелограммом , так это то, что его внутренние углы одинаковы. На самом деле все они прямых углов , что означает, что они измеряют 90 градусов.
Свойства ромба
Другой особый параллелограмм — ромб.
 Он обладает всеми свойствами параллелограмма, но все стороны ромба равны. Обратите внимание, что все деления одинаковые, что говорит нам о том, что все стороны имеют одинаковую длину.
Он обладает всеми свойствами параллелограмма, но все стороны ромба равны. Обратите внимание, что все деления одинаковые, что говорит нам о том, что все стороны имеют одинаковую длину.Свойства квадрата
Наш последний специальный параллелограмм является прямоугольником и ромбом одновременно, поэтому он имеет прямые углы прямоугольника и конгруэнтные стороны ромба.Это еще одна форма, которую мы все хорошо знаем: квадрат!
Как видите, противоположные стороны параллельны, все углы прямые и все стороны равны.
Итак, давайте вспомним наши четырехугольники, прежде чем мы начнем исследовать их диагонали:
Здесь мы расположили наши четырехугольники в виде «дерева», начиная с квадрата в качестве ствола. Каждый квадрат — это ромб, а каждый ромб — параллелограмм. Каждый квадрат также является прямоугольником, а каждый прямоугольник является параллелограммом.Вот как это работает, поднимаясь по дереву. Но спуститься не получится. Не каждый параллелограмм является прямоугольником и не каждый ромб является квадратом.

Хорошо, теперь давайте исследуем диагонали этих четырёх четырёхугольников. Диагональ — это отрезок, соединяющий противоположные вершины или углы четырехугольника.
Диагонали параллелограмма
Вот наш обычный неспециальный параллелограмм с показанными диагоналями:
Как видите, диагонали параллелограмма делят друг друга пополам.Другими словами, они разрезают друг друга пополам. Мы могли бы добавить несколько чисел, чтобы лучше проиллюстрировать это…
, или мы могли бы использовать галочки, чтобы показать, что диагонали были разделены пополам:
Поскольку все три специальных четырехугольника, о которых мы говорим, являются параллелограммами, все они будут иметь диагонали, делящие пополам.
Диагонали прямоугольника
Теперь давайте посмотрим на прямоугольник. Вот прямоугольник с его диагоналями:
Диагонали прямоугольника равны, и, опять же, поскольку прямоугольник является параллелограммом, диагонали делят друг друга пополам, делая каждую половину одинаковой длины:
Каждая диагональ прямоугольника также делится прямоугольник на два конгруэнтных прямоугольных треугольника:
Это означает, что, если бы мы захотели, мы могли бы вычислить длину диагонали, используя Теорему Пифагора .

Диагонали ромба
Теперь, когда мы разобрались с прямоугольниками, давайте посмотрим, что произойдет с другим специальным параллелограммом, ромбом:
Еще раз, поскольку каждый ромб является параллелограммом, его диагонали делят друг друга пополам. Однако диагонали НЕ одинакового размера, так что же в этом особенного? Посмотрите на углы, под которыми пересекаются диагонали. Эти углы выглядят так, как будто все они могут быть одинаковыми, а поскольку здесь четыре угла, это должно означать…
Что каждый угол равен 90 градусам! Это означает, что диагонали ромба перпендикулярны друг другу 90 335 в дополнение к тому, что 90 336 делят друг друга пополам.
Диагонали квадрата
Итак, остался только один четырехугольник, квадрат. Помните, что квадрат является параллелограммом, прямоугольником и ромбом, поэтому он должен обладать всеми свойствами этих фигур:
- Диагонали делят друг друга пополам.
- Диагонали будут одинаковой длины.

- Диагонали будут перпендикулярны друг другу.
Посмотрим, правы ли мы:
Мы были правы! Если мы посмотрим внимательно, то также увидим, что две диагонали делят квадрат на четыре конгруэнтных равнобедренных прямоугольных треугольника.
Обзор
Теперь, когда мы рассмотрели наши четыре параллелограмма и их диагонали, давайте закончим обзор, чтобы посмотреть, что вы можете вспомнить.
Какое из следующих утверждений неверно?
- Каждый прямоугольник является параллелограммом.
- Каждый ромб является квадратом.
- Каждый квадрат является прямоугольником.
- Диагонали параллелограмма делят друг друга пополам.
- Диагонали ромба пересекаются под прямым углом.
- Диагональ прямоугольника делит его на два равных прямоугольных треугольника.
- Диагонали прямоугольника имеют одинаковую длину.
- Четырехугольник, диагонали которого делятся пополам, пересекаются под прямым углом и равны, должен быть квадратом.

Помните дерево? Не каждый ромб является квадратом, но каждый квадрат является ромбом.
Спасибо за просмотр и удачной учебы!
Ромб
Ромб – это параллелограмм, у которого все стороны равны. Форма ромба также часто упоминается как ромб, как масть в стандартной колоде карт.
Стороны ромба
Все стороны ромба равны, а его противоположные стороны параллельны.
Углы ромба
Противоположные углы ромба, как и у параллелограмма, равны. Кроме того, смежные углы ромба являются дополнительными, а это означает, что сумма каждой пары смежных углов равна 180°, а сумма всех внутренних углов равна 360°.
Диагонали ромба
Ромб может иметь две диагонали; диагонали являются перпендикулярными биссектрисами друг к другу.
Диагонали AC и BD являются биссектрисами ромба ABCD.
Диагонали ромба делят его углы пополам:
Диагонали AC и BD делят противоположные углы ромба ABCD пополам.

Квадрат
У квадрата четыре равные стороны и четыре прямых угла, что делает его частным случаем ромба. Ромб также является квадратом, если все его углы прямые.
Симметрия в ромбе
Ромб имеет 2 оси симметрии и вращательную симметрию 2-го порядка, что означает, что его можно повернуть таким образом, что он будет выглядеть так же, как исходная форма 2 раза на 360°.
Линия симметрии Вращательная симметрия Обе диагонали являются линиями симметрии Угол поворота 180° вокруг своего центра Площадь ромба
Площадь ромба с диагоналями d 1 и d 2 is,
Пусть AC = d 1 и BD = d 2 для ромба ABCD выше.Ромб ABCD можно разделить на треугольники ABC и ADC диагональю AC. Площадь △ABC = AC×BE, где BE — высота △ABC.
 Площадь △ADC = AC×DE, где DE — высота △ADC. Площадь ромба ABCE равна сумме площадей △ABC и △ADC.
Площадь △ADC = AC×DE, где DE — высота △ADC. Площадь ромба ABCE равна сумме площадей △ABC и △ADC.Если известны длина основания (b) и высота (h) ромба, площадь ромба равна
А = б·ч
Площадь ромба – объяснение и примеры
В статье Полигона мы видели, что ромб представляет собой четырехугольник с четырьмя параллельными сторонами одинаковой длины .Противоположные углы ромба также равны.
Аналогично, диагонали ромба пересекаются под прямым углом, и их длины всегда равны . Квадрат — это разновидность ромба, у которого все 4 угла прямые. Иногда ромб называют ромбом, ромбом или ромбом.
В этой статье вы узнаете, как вычислить площадь ромба, используя формулы трех площадей ромба.
Как вычислить площадь ромба?
Площадь ромба – это область, ограниченная 4 сторонами ромба .
Есть три способа найти площадь ромба.
Один из способов заключается в использовании высоты и стороны ромба.
 Второй метод влечет за собой использование стороны и угла, а последний метод влечет за собой использование диагоналей.
Второй метод влечет за собой использование стороны и угла, а последний метод влечет за собой использование диагоналей.Эти формулы для вычисления площади ромба известны под общим названием формулы площади ромба. Давайте взглянем.
Формула площади ромба
Площадь ромба можно найти несколькими способами.Мы увидим каждый из них один за другим ниже.
Площадь ромба с использованием высоты и основания
Когда высота или высота и длина сторон ромба известны, площадь определяется по формуле;
Площадь ромба = основание × высота
A = b × h
Разберем это на примере: 30 см, а высота 15 см.
Раствор
A = B × H
= (30 x 15) см 2
= 450 см 2
Следовательно, площадь ромба составляет 450 см 2 .
Пример 2
Вычислите площадь ромба, показанного ниже.
Раствор
a = b × h
= (18 x 24) мм 2
Пример 3
Если высота и площадь ромба находятся на 8 см и 72 см.
 2, соответственно, найдите размеры ромба.
2, соответственно, найдите размеры ромба.Раствор
A = B × H
A = B × H
72 см 2 = 8 см x B
Разделите обе стороны на 80118
72 см 2 /8 см = B
B = 9 см.
Следовательно, размеры ромба 9 см на 9 см.
Пример 4
Основание ромба в 3 раза больше высоты плюс на 1 больше. Если площадь ромба 10 м 2 , найдите основание и высоту ромба.
Раствор
Пусть высота Rhombus = x
и базы = 3x + 1
a = b × h
10 м 2 = x (3x + 1)
10 = 3x 2 + x
3x 2 + x – 10 = 0
Решите квадратное уравнение.
⟹ 3x 2 + x – 10 = 3x 2 + 6x – 5x – 10
⟹ 3x (x + 2) – 5(x + 2)
+ ⟹ (3x – 2) (3x – 2) ) = 0
⟹ 3x – 5 = 0
⟹ x = 5/3
⟹ x + 2= 0
x = -2
Теперь подставьте значение x.

Высота = х = 5/3 м
Основание = 3х + 1 = 3(5/3) + 1 = 6 м
Итак, основание ромба 6 м, а высота 5/3 м .
Площадь ромба с использованием диагоналей
Учитывая длины диагоналей, площадь ромба равна половине произведения диагоналей.
A = ½ × d 1 × d 2
Где d 1 и d 2 — диагонали ромба.
Пример 5
Две диагонали ромба равны 12 см и 8 см. Вычислите площадь ромба.
Решение:
Пусть d 1 = 12 см и d 2 = 8 см.
A = ½ × d 1 × d 2
= (½ × 12 × 8) см 2 .
= 48 см 2 .
Пример 6
Вычислите длины сторон, если их площадь 24 см 2 , диагональ 8 см, а высота 3 см.
Раствор
Пусть d 1 = 8 см.
д 2 =?
A = ½ × D 1 × D 2
24 см 2 = ½ × 8 × D 2
24 см 2 = 4D 2 = 4D 2
Разделите обе стороны на 4 чтобы получить,
6 = d 2
Следовательно, другая диагональ равна 6 см.

Теперь вычислите длины сторон ромба.
A = b × h
24 см 2 = 3 см x b
Обе стороны разделить на 3.
8 см = b.
Следовательно, длины сторон ромба равны 8 см.
Пример 7
Найдите диагонали показанного ниже ромба, если его площадь равна 3458 см 2 .
Решение
A = ½ × D 1 × D 2 × D 2 × D 2
3,458 см 2 = ½ * 6x * 8x
3,458 см 2 = 24x 2
Divide с обеих сторон по 24.
3,458/24 = x 2
144 = x 2
Найдите квадратный корень из обеих сторон.
x = -12 или 12.
Длина не может быть отрицательным числом; поэтому подставьте только x = 12 в уравнения диагоналей.
6x = 6 * 12 = 72 см
8x = 8 * 12 = 96 см
Следовательно, длины диагоналей 72 см и 96 см.

Пример 8
Предположим, стоимость полировки пола составляет 4 доллара за квадратный метр.Найдите стоимость полировки пола в форме ромба, каждая из его диагоналей равна 20 м и 12 м.
Раствор
Чтобы узнать стоимость полировки пола, умножьте скорость полировки на площадь ромбовидного пола.
A = ½ × 20 м × 12 м
= 120 м 2
Стоимость покраски = 120 м 2 x 4 $ за м.
= 480 долларов
Площадь ромба с использованием длины сторон и угла между ними.
Площадь ромба равна квадрату длины стороны произведения и синусу угла между двумя сторонами.
Площадь ромба = b 2 × Синус (A)
Где A = угол, образованный между двумя сторонами ромба.
Пример 9
Найдите площадь ромба, сторона которого равна 8 см, а угол между двумя сторонами равен 60 градусам.
Решение
A = b 2 × синус (A)
= 8 2 x синус (60)
= 55,43 см9 2.
Практические вопросы
- Найдите длину диагонали ромба, если длина другой диагонали 5 единиц, а площадь ромба 30 квадратных единиц.
- Воздушный змей имеет более короткую диагональ длиной 16 единиц, более короткую сторону длиной 10 единиц и более длинную сторону длиной 17 см. Какова длина другой диагонали?
- Какая площадь ромба, каждая сторона которого равна 18 см, а одна диагональ равна 20 см?
Свойства ромба – Знать формы, формулы
Свойства ромба: Ромб является частным параллелограммом, поскольку он соответствует определению параллелограмма, который представляет собой четырехугольник с двумя наборами параллельных сторон.Кроме того, у ромба, как и у квадрата, все четыре стороны равны.
 Таким образом, ромб также известен как наклонный квадрат. Ромб считается особым параллелограммом, так как он обладает всеми свойствами параллелограмма. Две диагонали ромба служат его двумя линиями симметрии. Ось симметрии — это линия, которая делит предмет на две равные половины. Он производит зеркальное отражение двух сторон объекта. Ромб имеет симметрию отражения вдоль каждой из его диагоналей. На этой странице мы предоставим вам всю необходимую информацию о свойствах параллелограмма.Читайте дальше, чтобы узнать больше.
Таким образом, ромб также известен как наклонный квадрат. Ромб считается особым параллелограммом, так как он обладает всеми свойствами параллелограмма. Две диагонали ромба служат его двумя линиями симметрии. Ось симметрии — это линия, которая делит предмет на две равные половины. Он производит зеркальное отражение двух сторон объекта. Ромб имеет симметрию отражения вдоль каждой из его диагоналей. На этой странице мы предоставим вам всю необходимую информацию о свойствах параллелограмма.Читайте дальше, чтобы узнать больше.Изучите концепции 10-го экзамена CBSE
Ромб Определение: Характеристики ромба
Прежде чем мы обсудим ромб, давайте поймем что такое четырехугольник . В геометрии четырехугольник определяется как замкнутая двумерная форма с четырьмя прямыми сторонами.
Сумма внутренних углов четырехугольника равна 360°. Есть в основном 6 типов четырехугольника:
- Параллелограмм
- Трапеция
- Квадрат
- Прямоугольник
- Воздушный змей
- Ромб
Ромб — особый тип параллелограмма, у которого все четыре стороны равны.
 Таким образом, его также называют равносторонним параллелограммом .
Таким образом, его также называют равносторонним параллелограммом .В приведенном выше ромбе ABCD стороны AB, BC, CD и AD являются сторонами ромба, а AC и BD — диагоналями. Длина AC и BD равна d1 и d2 соответственно. Две диагонали ромба пересекаются под прямым углом, как вы можете видеть на рисунке.
Некоторые характеристики ромба:
- В ромбе противоположные стороны параллельны и противоположные углы равны.
- Все стороны ромба равны по длине.
- Диагонали ромба делят друг друга пополам под прямым углом.
- Форма множественного числа ромба — ромбы или ромбы.
Другие важные статьи по математике:
Свойства ромба
Понимание свойств ромба для учащегося 9-го класса является одной из наиболее важных тем для учащихся 9-го класса CBSE , поскольку их часто спрашивают на выпускном экзамене. Кроме того, мы включили свойства ромба для 8-го класса, чтобы все учащиеся 8-го класса могли воспользоваться ими.
 Вы можете прочитать свойства здесь или загрузить их в виде PDF-файла, представленного ниже, для автономного доступа.
Вы можете прочитать свойства здесь или загрузить их в виде PDF-файла, представленного ниже, для автономного доступа.Мы перечислили все важные свойства ромба в пунктах ниже:
- Все стороны ромба равны.
- Противоположные стороны ромба параллельны.
- Противоположные углы ромба равны.
- В ромбе диагонали делятся пополам под прямым углом.
- Диагонали делят углы ромба пополам. Это одно из важнейших свойств диагоналей ромба.
- Сумма двух смежных углов равна 180°.
- Две диагонали ромба образуют 4 прямоугольных треугольника, конгруэнтных друг другу.
- Линии симметрии ромба : В ромбе есть только две линии симметрии.
- Вращательная симметрия ромба : Ромб имеет вращательную симметрию 180° (порядок 2).
- Если соединить середины всех 4 сторон ромба, получится прямоугольник. Длина и ширина прямоугольника будут вдвое меньше главной диагонали, так что площадь прямоугольника будет равна половине ромба.

- Вы получите еще один ромб, если соедините середины половины диагонали.
- Для ромба нет описанной окружности.
- Также внутри ромба не может быть вписанной окружности.
- Когда меньшая диагональ равна одной из сторон ромба, образуются два конгруэнтных равносторонних треугольника.
- Вы получите цилиндрическую поверхность, имеющую выпуклый конус на одном конце и вогнутый конус на другом конце, когда ромб вращается вокруг любой стороны как оси вращения.
- Вы получите цилиндрическую поверхность с вогнутыми конусами на обоих концах, когда ромб вращается вокруг линии, соединяющей середины противоположных сторон в качестве оси вращения.
- Вы получите твердое тело с двумя конусами, прикрепленными к их основаниям, когда ромб вращается вокруг более длинной диагонали, являющейся осью вращения. В этом случае максимальный диаметр тела равен меньшей диагонали ромба.
- Вы получите твердое тело с двумя конусами, прикрепленными к их основаниям, когда ромб вращается вокруг более короткой диагонали в качестве оси вращения.
 В этом случае максимальный диаметр тела равен большей диагонали ромба.
В этом случае максимальный диаметр тела равен большей диагонали ромба.
Получите формулы алгебры снизу:
Практика 10-го экзамена CBSE Вопросы
Формулы ромба
Мы представили вам список всех формул ромба. Формулы доступны для площади, периметра, диагонали и стороны. Возьми ромб ABCD:
.Стороны: AB, BC, CD и AD
Длина каждой стороны: a
Диагонали: AC, BD
Длина диагоналей : d1, d2Имеем следующие формулы:
Площадь ромба Площадь, A = (d1.D2) / 2 Периметр Rhombus сторона Rhombus сторона, A = P / 4 Диагональ Rhombus Диагональ , d1 = 2(A/d2)
Диагональ, d2 = 2(A/d1)Решенные задачи на ромбе
Здесь мы предоставили некоторые вопросы с решениями, связанными со свойствами ромба :
Q1: Каков периметр ромба, все стороны которого равны 8 см?
Решение : Сторона ромба = 8 см (Дано)
Поскольку все стороны ромба равны, следовательно,
Периметр = 4 x сторона
P = 4 x 8 см
= 32 см
Следовательно, периметр ромба ромб 32 см.
Q2: Найдите диагональ ромба, если его площадь равна 121 см 2 и длина большей диагонали равна 22 см.
Решение : Площадь ромба = 121 см 2 (Дано)
d 1 = 22 см.
Площадь ромба, A = (d 1 xd 2 )/2, получаем
121 = (22 xd 2 )/2
121 = 11 xd 2 18 или 2 18
Значит, длина другой диагонали 11 см.Q3: Найдите периметр следующего ромба:
Решение : все стороны ромба равны, поэтому HO = ( x + 2). А поскольку диагонали ромба перпендикулярны, треугольник HBO прямоугольный. С помощью Pythagorean Thorem, мы получаем,
( HB ) 2 + ( BO ) 2 = ( HO ) 2
x 2 + (x +1) 2 = ( х + 2) 2
9 + + 9 + 2x + 1 = x 2 + 4х + 4
х 2 – 2х -3 = 0
Решая х по формуле квадрата, получаем:
х = 3 или х = –1. Мы можем отбросить x = –1, так как сторона ромба не может быть отрицательной.
Мы можем отбросить x = –1, так как сторона ромба не может быть отрицательной.
∴ Сторона ромба = х + 2
= 5
Следовательно, периметр ромба HRMO равен 5 х 4 ед. = 20 ед.Q4: Длины двух диагоналей ромба d 1 и d 2 равны 5 см и 14 см соответственно. Найдите его площадь.
Решение : Дано:
Диагональ d 1 = 5 см
Диагональ d 2 = 14 см
Площадь ромба, A = (d 1 квадрат)/209 1 xd2 единиц 5 х 14)/2
А = 70/2
А = 35 см 2
Следовательно, площадь ромба = 35 квадратных единиц.Практические вопросы по свойствам ромба
Здесь мы подготовили для вас несколько практических вопросов, связанных со свойствами ромба.
Q1: Если площадь ромба 48 см 2 и одна из его диагоналей 5 см.  Найдите его высоту.
Найдите его высоту.Q2: ABCD — ромб, в котором высота от D до стороны AB делит AB пополам. Найдите значение угла A и угла B.
Q3: Докажите, что площадь ромба равна половине произведения его диагоналей.
Q4: Диагональ AC параллелограмма ABCD делит пополам угол A.
(a) Делит ли угол A пополам и угол C? Назови причины.
(б) Является ли ABCD ромбом? Назови причины.В5: Если длина каждой стороны ромба равна 8 см, а один из его углов равен 60°, то найдите длину диагоналей ромба.
Q6: Ромбовидный лист с периметром 32 м и длиной одной диагонали 10 м окрашен с обеих сторон по цене 5 ₹ за квадратный метр. Найдите полную стоимость картины?
Q7: Длина диагнолов ромба в соотношении 5:4.Площадь ромба 2250 квадратных см. Найдите сторону ромба.
Q8: ABCD — ромб с точкой пересечения диагоналей O и углом DAO = 45°. Найдите угол DCO.
Q9: Докажите, что диагонали ромба делят друг друга пополам под прямым углом.
Q10: Если ABCD ромб и из D, к AB проведена высота, которая делит AB пополам.
 Найдите углы ромба.
Найдите углы ромба.Пробные тесты 10-го экзамена CBSE
Часто задаваемые вопросы о свойствах ромба
Здесь мы предоставили некоторые из часто задаваемых вопросов:
Q1: Каковы основные свойства ромба?
A: Основные свойства ромба следующие:
(i) Противоположные углы равны.
(ii) Диагонали пересекаются под углом 90 градусов.
(iii) Диагонали делят пополам противоположные внутренние углы.
(iv) Смежные углы являются дополнительными.Q2: Какова формула площади и периметра ромба?
A: Площадь ромба = (d1.d2)/2, где d1 и d2 — длины диагоналей ромба
Периметр ромба = 4 x Сторона ромба Q3: Является ли квадрат ромбом?
A: Да, геометрически квадрат также является ромбом, все внутренние углы которого равны 90 градусов.Однако обратное неверно. Ромб может быть, а может и не быть квадратом.
Ромб может быть, а может и не быть квадратом.Q4: Каковы угловые свойства ромба?
A: Противоположные углы ромба равны друг другу. Кроме того, диагонали ромба делят внутренние углы пополам.Q5: Каковы свойства симметрии ромба?
A: Ромб имеет 2 оси симметрии, которые делят его на две одинаковые части.Обе линии симметрии ромба являются его диагоналями. Кроме того, ромб обладает вращательной симметрией. Ромб имеет вращательную симметрию 180 ° (порядок 2).В6: Сколько осей симметрии у ромба?
A: Ромб имеет 2 оси симметрии. Диагонали ромба являются его линиями симметрии.Теперь у вас есть вся необходимая информация о ромбе и его свойствах.Практикуйте больше вопросов и осваивайте эту концепцию.

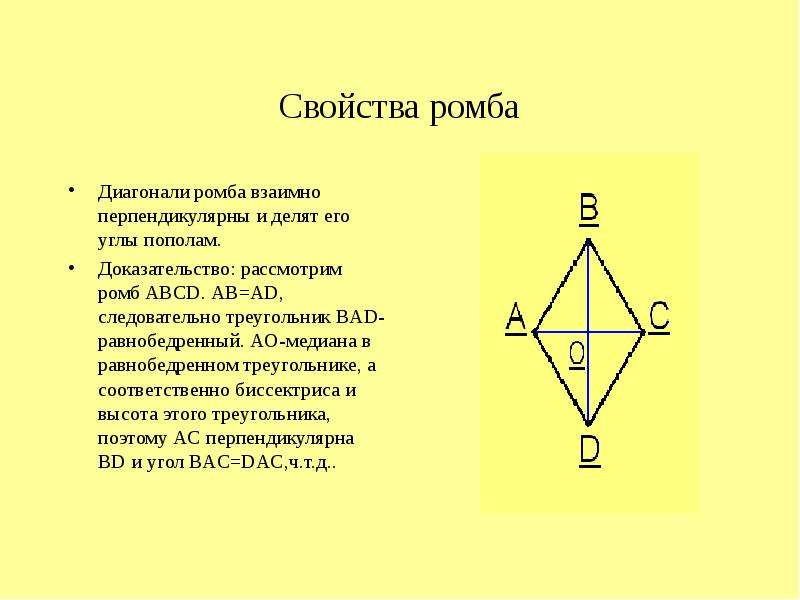
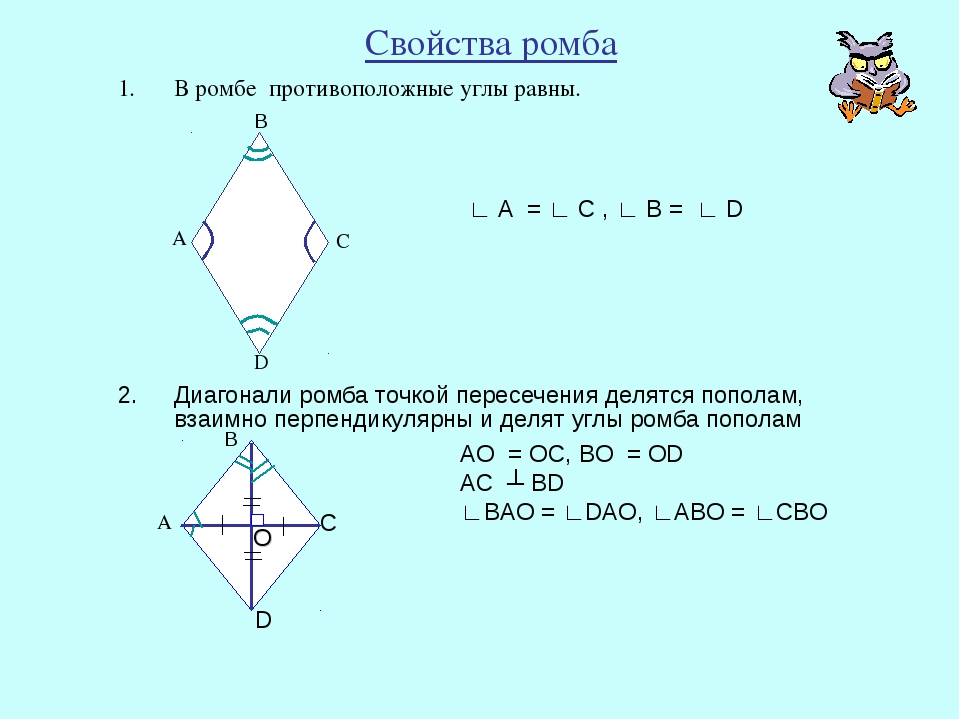

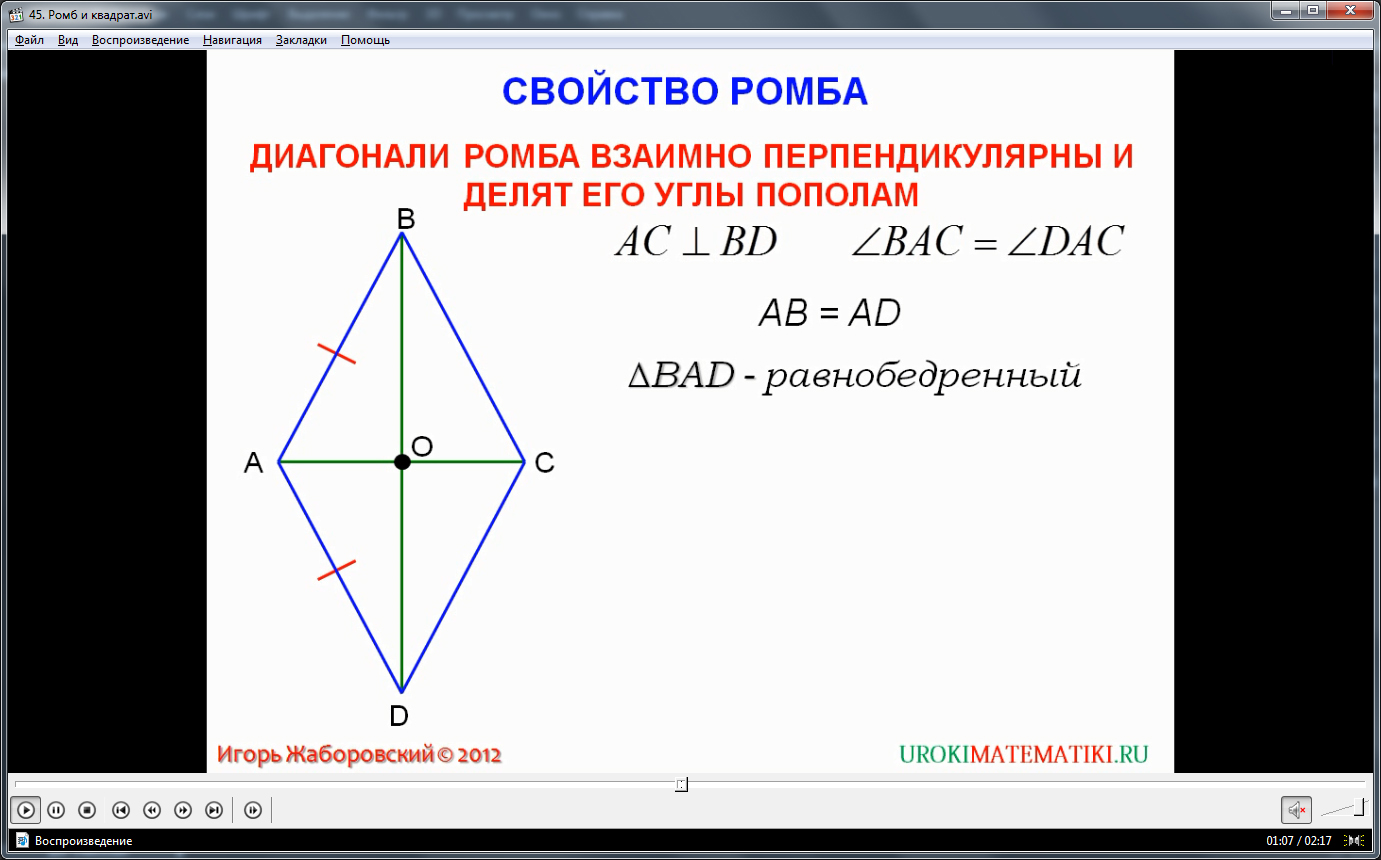
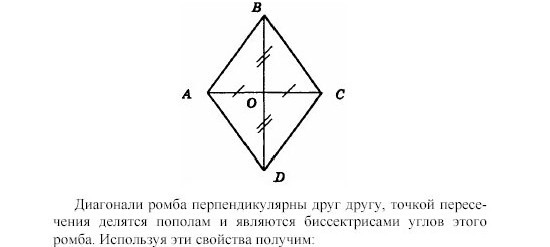 2*sinα \)
2*sinα \) Я люблю английский язык за его практичность, мелодичность звучания, пластичность и разнообразие слов. Использую игровые методы обучения, диалога, индивидуального подхода.
Я люблю английский язык за его практичность, мелодичность звучания, пластичность и разнообразие слов. Использую игровые методы обучения, диалога, индивидуального подхода.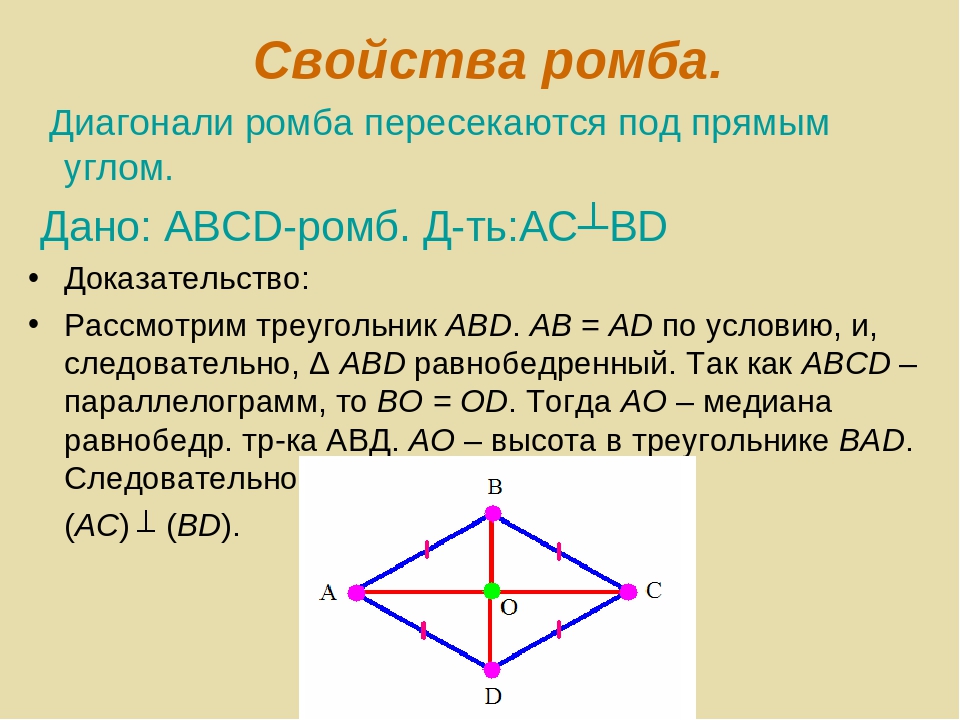 Готовлю к ОГЭ.
Очень интересно и доступно помогу разобраться в изучаемой теме, выполнить домашнюю работу! Математика, это пожалуй одна из самых интересных и захватывающих дисциплин. И если ты полюбишь её и сумеешь понимать, тебе доступны очень многие дисциплины!
Мы вместе будем проходить с тобой этот путь и верю, что тебе всё по силам! Наши уроки будут очень полезными, потому что мы сумеем разобраться в сложных темах, научимся решать задачи и полюбим математику.
Готовлю к ОГЭ.
Очень интересно и доступно помогу разобраться в изучаемой теме, выполнить домашнюю работу! Математика, это пожалуй одна из самых интересных и захватывающих дисциплин. И если ты полюбишь её и сумеешь понимать, тебе доступны очень многие дисциплины!
Мы вместе будем проходить с тобой этот путь и верю, что тебе всё по силам! Наши уроки будут очень полезными, потому что мы сумеем разобраться в сложных темах, научимся решать задачи и полюбим математику. Махтумкули
Махтумкули Как говорил М.В. Ломоносов: «Математику уже затем учить надо, что она ум в порядок приводит». Математика приучает человека логично рассуждать, последовательно мыслить, делать правильные и обоснованные выводы. При изучении тем по математике стараюсь детям объяснять сложное на доступном языке. К каждому ребенку нахожу индивидуальный подход. Помогу подтянуть знания по предмету.
Как говорил М.В. Ломоносов: «Математику уже затем учить надо, что она ум в порядок приводит». Математика приучает человека логично рассуждать, последовательно мыслить, делать правильные и обоснованные выводы. При изучении тем по математике стараюсь детям объяснять сложное на доступном языке. К каждому ребенку нахожу индивидуальный подход. Помогу подтянуть знания по предмету. Площадь ромба
Площадь ромба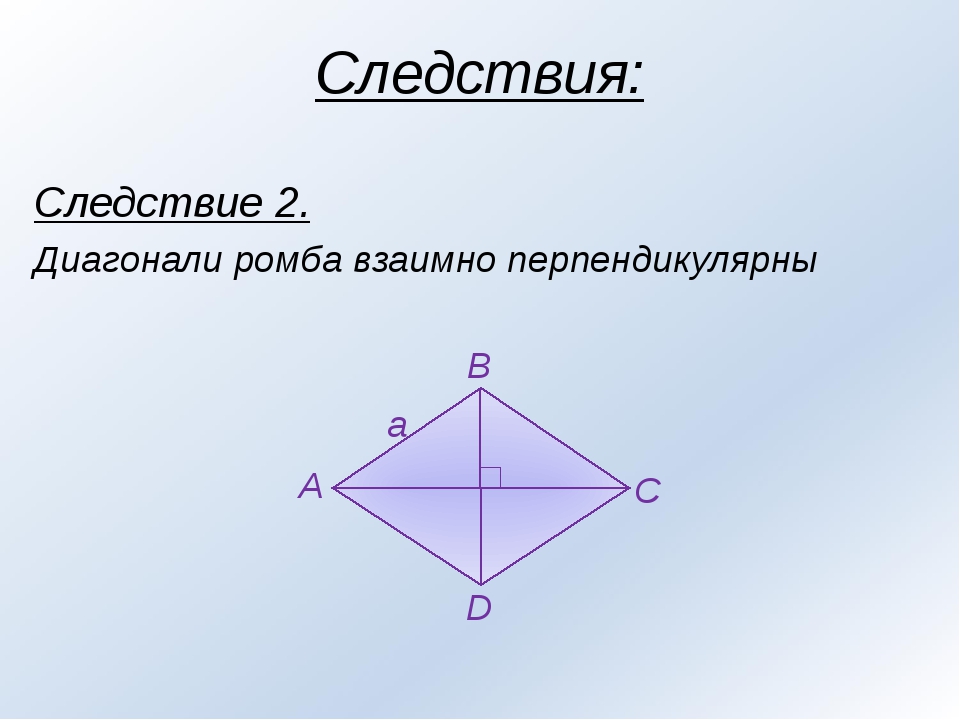 е. BD 2 + AC 2 = 4AB 2 .
Существует множество методов, используемых в планиметрии для расчета площади ромба, применение которых зависит от исходных данных. Если известны длина стороны и любой угол, можно воспользоваться следующей формулой: площадь ромба равна квадрату стороны, умноженному на синус угла. Из курса тригонометрии известно, что sin (π – α) = sin α, а значит, в расчетах можно использовать синус любого угла – как острого, так и тупого. Частным случаем является ромб, у которого все углы прямые. Это квадрат. Известно, что синус прямого угла равен единице, поэтому площадь квадрата равна длине его стороны, возведенной во вторую степень. Если величина сторон неизвестна, воспользуемся длиной диагоналей. В этом случае площадь ромба равна половине произведения большой и малой диагоналей. При известной длине диагоналей и величине любого угла площадь ромба определяется двумя способами. Первый: площадь – это половина квадрата большей диагонали, умноженная на тангенс половины градусной меры острого угла, т.
е. BD 2 + AC 2 = 4AB 2 .
Существует множество методов, используемых в планиметрии для расчета площади ромба, применение которых зависит от исходных данных. Если известны длина стороны и любой угол, можно воспользоваться следующей формулой: площадь ромба равна квадрату стороны, умноженному на синус угла. Из курса тригонометрии известно, что sin (π – α) = sin α, а значит, в расчетах можно использовать синус любого угла – как острого, так и тупого. Частным случаем является ромб, у которого все углы прямые. Это квадрат. Известно, что синус прямого угла равен единице, поэтому площадь квадрата равна длине его стороны, возведенной во вторую степень. Если величина сторон неизвестна, воспользуемся длиной диагоналей. В этом случае площадь ромба равна половине произведения большой и малой диагоналей. При известной длине диагоналей и величине любого угла площадь ромба определяется двумя способами. Первый: площадь – это половина квадрата большей диагонали, умноженная на тангенс половины градусной меры острого угла, т.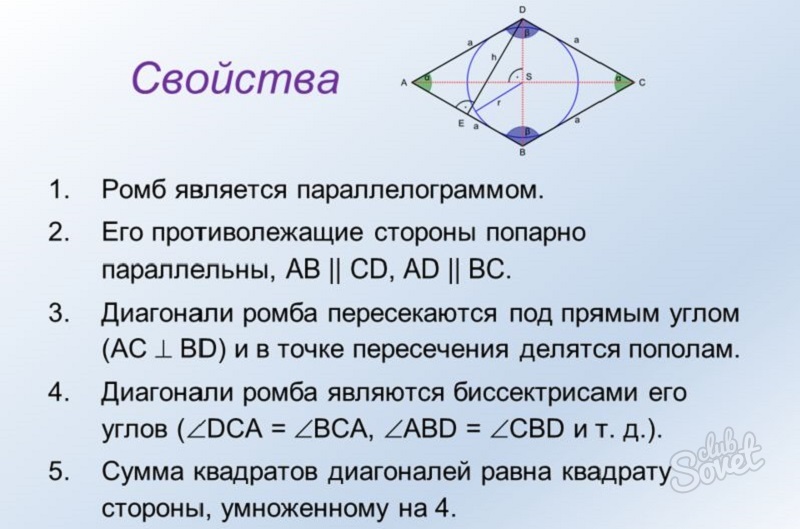 е. S = 1/2*D 2 *tg(α/2), где D – большая диагональ, α – острый угол. Если вам известен размер меньшей диагонали, воспользуемся формулой 1/2*d 2 *tg(β/2), где d – меньшая диагональ, β – тупой угол. Напомним, что мера острого угла меньше 90 градусов (меры прямого угла), а тупой угол соответственно – больше 90 0 . Площадь ромба можно отыскать, используя длину стороны (напомним, все стороны у ромба равны) и высоты. Высота – это перпендикуляр, опущенный на противоположную углу сторону или на ее продолжение. Чтобы основание высоты располагалось внутри ромба, ее следует опускать из тупого угла. Иногда в задаче требуется отыскать площадь ромба, исходя из данных, относящихся к вписанной окружности. В этом случае необходимо знать ее радиус. Существуют две формулы, которыми можно воспользоваться для расчета. Итак, чтобы ответить на поставленный вопрос, можно удвоить произведение стороны ромба и радиуса вписанной окружности. Другими словами, необходимо умножить диаметр вписанной окружности на сторону ромба.
е. S = 1/2*D 2 *tg(α/2), где D – большая диагональ, α – острый угол. Если вам известен размер меньшей диагонали, воспользуемся формулой 1/2*d 2 *tg(β/2), где d – меньшая диагональ, β – тупой угол. Напомним, что мера острого угла меньше 90 градусов (меры прямого угла), а тупой угол соответственно – больше 90 0 . Площадь ромба можно отыскать, используя длину стороны (напомним, все стороны у ромба равны) и высоты. Высота – это перпендикуляр, опущенный на противоположную углу сторону или на ее продолжение. Чтобы основание высоты располагалось внутри ромба, ее следует опускать из тупого угла. Иногда в задаче требуется отыскать площадь ромба, исходя из данных, относящихся к вписанной окружности. В этом случае необходимо знать ее радиус. Существуют две формулы, которыми можно воспользоваться для расчета. Итак, чтобы ответить на поставленный вопрос, можно удвоить произведение стороны ромба и радиуса вписанной окружности. Другими словами, необходимо умножить диаметр вписанной окружности на сторону ромба. Если в условии задачи представлена величина угла, то площадь находится через частное между квадратом радиуса, умноженном на четыре, и синусом угла.
Если в условии задачи представлена величина угла, то площадь находится через частное между квадратом радиуса, умноженном на четыре, и синусом угла.


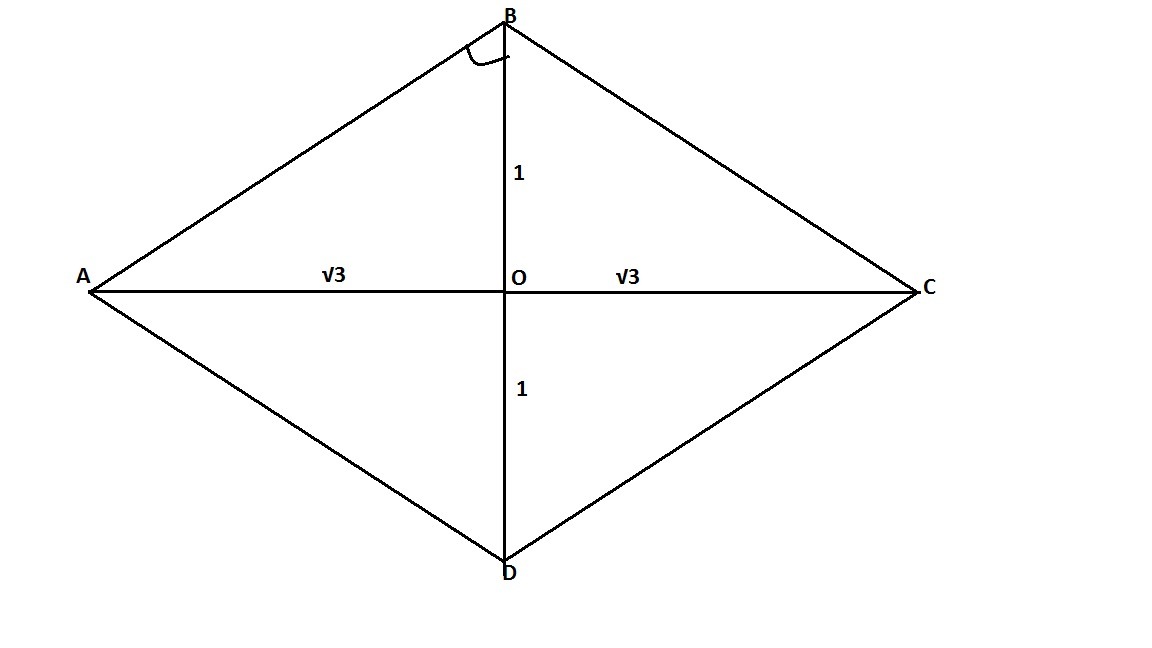 Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .
Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .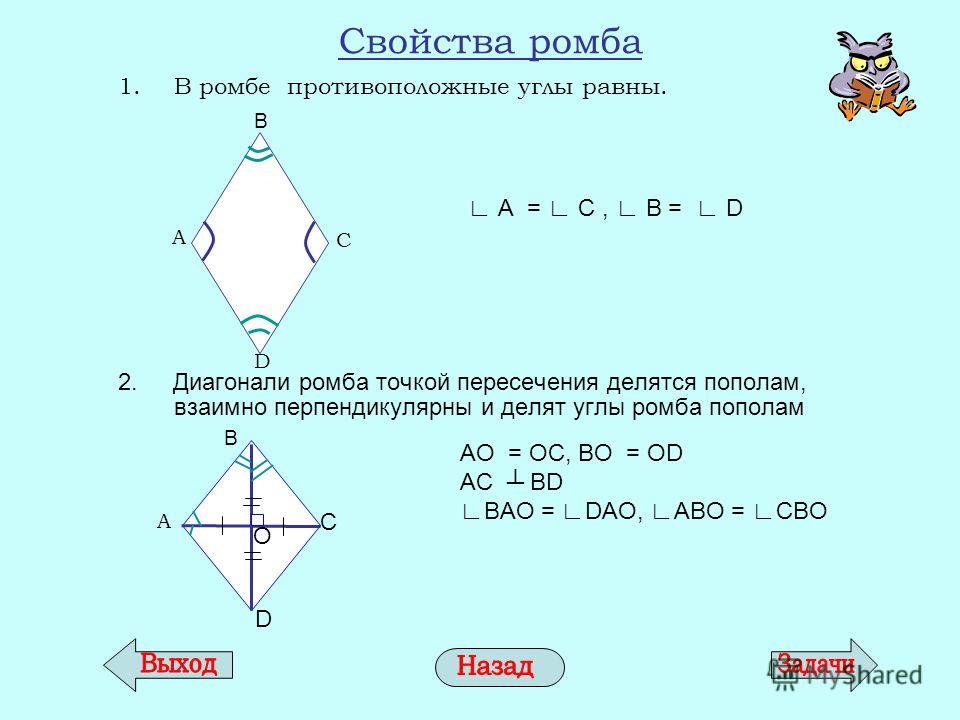 Если мы их рассортируем, так чтобы получить прямоугольник , то его длина и ширина будут равны одной целой диагонали и половине второй диагонали. Поэтому площадь ромба находится умножением диагоналей ромба, сокращенных на два (как площади получившегося прямоугольника).
Если мы их рассортируем, так чтобы получить прямоугольник , то его длина и ширина будут равны одной целой диагонали и половине второй диагонали. Поэтому площадь ромба находится умножением диагоналей ромба, сокращенных на два (как площади получившегося прямоугольника).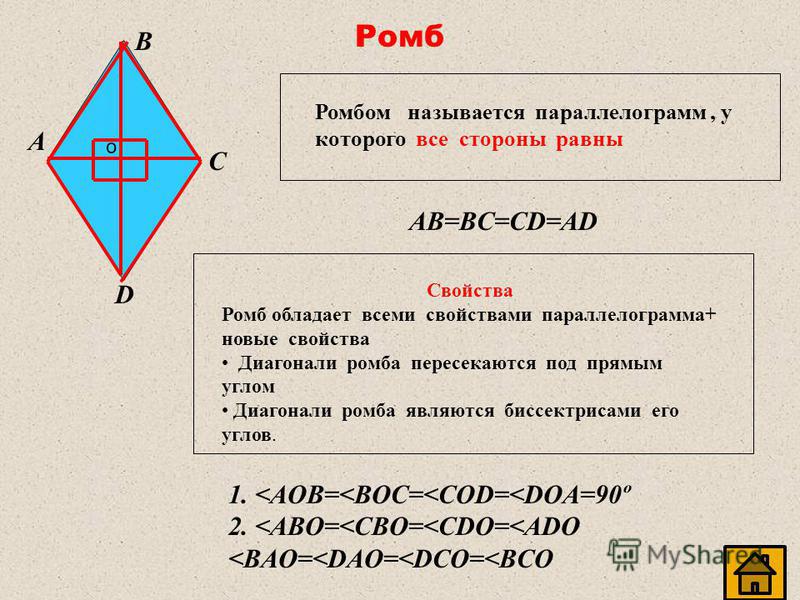 Тогда сторона a
может быть найдена из тригонометрических отношений по формуле . Подставляя это выражение в ту же стандартную формулу площади ромба, выходит
Тогда сторона a
может быть найдена из тригонометрических отношений по формуле . Подставляя это выражение в ту же стандартную формулу площади ромба, выходит Становится очевидным, что площадь ромба будет равна половине площади вписанного данным образом в ромб прямоугольника, длина и ширина которого будут соответствовать величине диагоналей ромба.
Становится очевидным, что площадь ромба будет равна половине площади вписанного данным образом в ромб прямоугольника, длина и ширина которого будут соответствовать величине диагоналей ромба.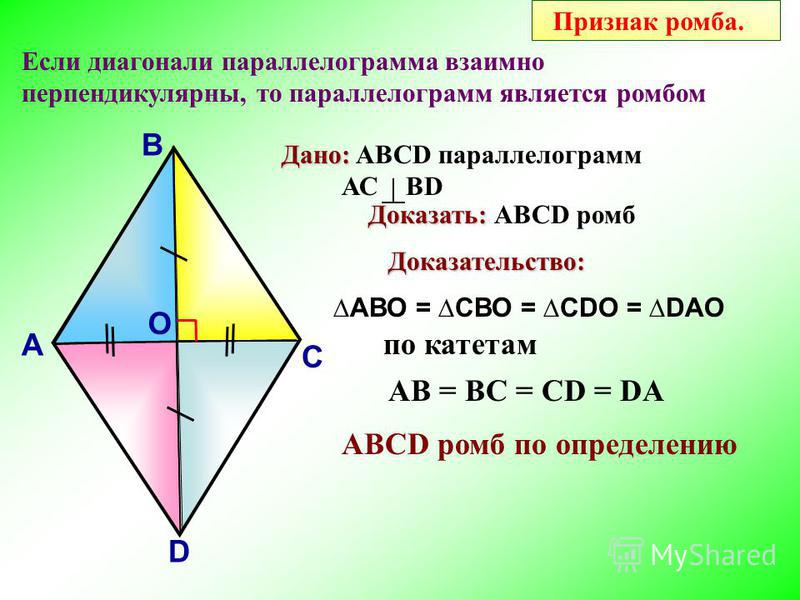 С тех же времен произошло и название карточной масти «бубны». Очень широко ромбы различных видов используются в геральдике.
С тех же времен произошло и название карточной масти «бубны». Очень широко ромбы различных видов используются в геральдике.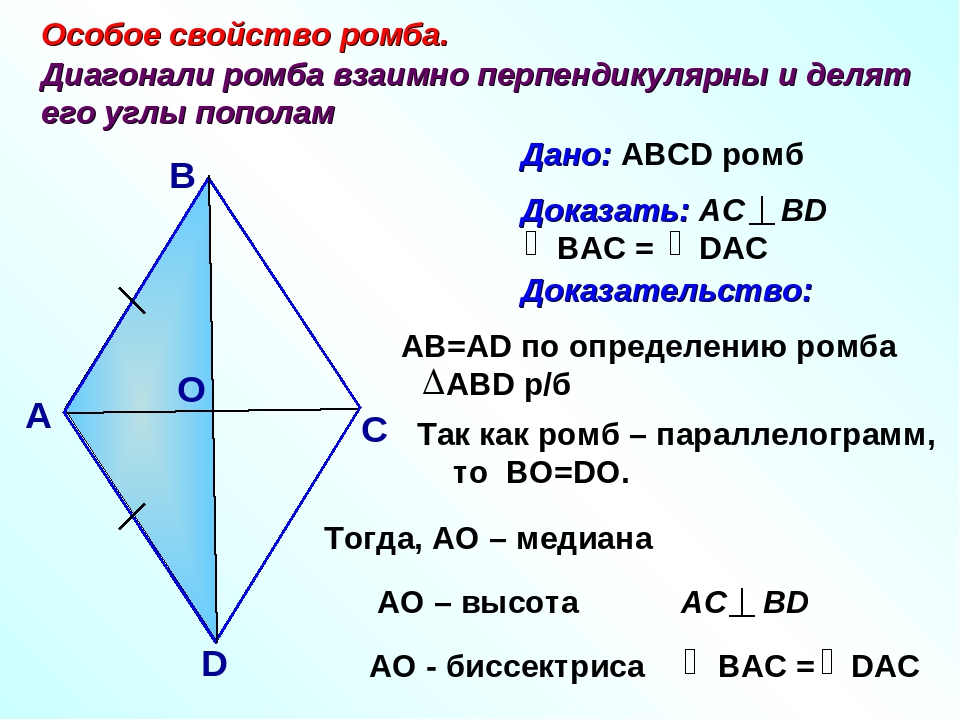
 Во-вторых, в теореме Пифагора главным является не принятая кем-то система закорючек, а смысл — берем две перпендикулярных штучки, возводим в квадрат, складываем в кучку и получаем третью штучку в квадрате. У нас квадрат ребра и квадрат диагонали ромба чудненько складываются в квадрат диагонали параллелепипеда.
Во-вторых, в теореме Пифагора главным является не принятая кем-то система закорючек, а смысл — берем две перпендикулярных штучки, возводим в квадрат, складываем в кучку и получаем третью штучку в квадрате. У нас квадрат ребра и квадрат диагонали ромба чудненько складываются в квадрат диагонали параллелепипеда. Что мы там видим? Если вы верили в Конец Света 2012, тогда там спрятаны припасы на всю оставшуюся жизнь. Вынимайте их из коробки и можете смело доедать (вы ещё долго будете извлекать свои припасы из самых неожиданных мест). Пока вы не придумаете следующую дату Конца Света, вам ничто не угрожает. С пророчеством советую поторопиться. Вокруг очень много жаждущих славы пророков, а ещё больше желающих впихнуть вам партию залежалого товара. Если же вы не верите в Конец Света, то в коробочке были новогодние сладости, которые уже закончились.
Что мы там видим? Если вы верили в Конец Света 2012, тогда там спрятаны припасы на всю оставшуюся жизнь. Вынимайте их из коробки и можете смело доедать (вы ещё долго будете извлекать свои припасы из самых неожиданных мест). Пока вы не придумаете следующую дату Конца Света, вам ничто не угрожает. С пророчеством советую поторопиться. Вокруг очень много жаждущих славы пророков, а ещё больше желающих впихнуть вам партию залежалого товара. Если же вы не верите в Конец Света, то в коробочке были новогодние сладости, которые уже закончились. .. В Интернете полно всякой ерунды, но есть и кое-то интересное нам. Все стороны ромба одинаковые. Диагонали ромба разные. Пересекаются диагонали под прямым углом. Точка пересечения диагоналей делит их на две равные половинки. Каждая диагональ делит угол в вершине поровну (у ромбов и квадратов диагонали не жадные). Кажется, всё. Прочая ерунда о ромбах нас не интересует.
.. В Интернете полно всякой ерунды, но есть и кое-то интересное нам. Все стороны ромба одинаковые. Диагонали ромба разные. Пересекаются диагонали под прямым углом. Точка пересечения диагоналей делит их на две равные половинки. Каждая диагональ делит угол в вершине поровну (у ромбов и квадратов диагонали не жадные). Кажется, всё. Прочая ерунда о ромбах нас не интересует.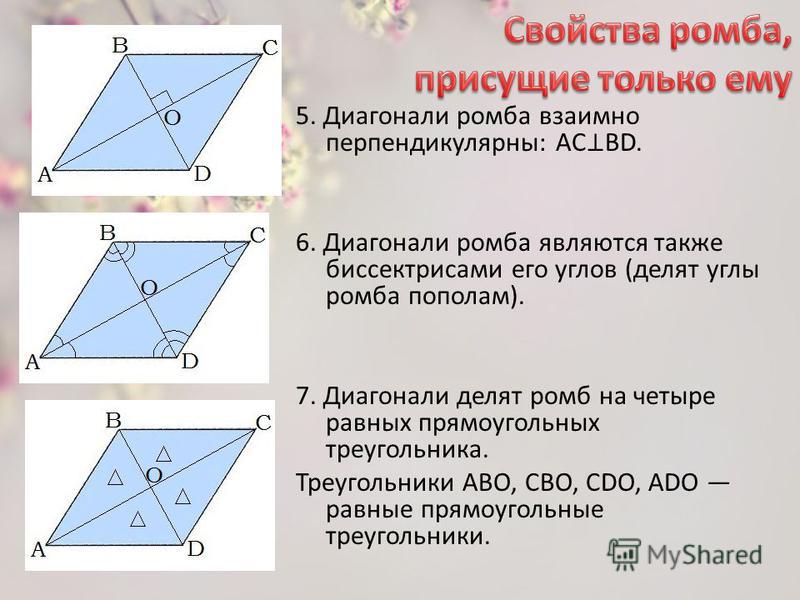 Лично мне так кажется. Думаю, эта идея соберет не маленькую группу Вконтакте. «Я ненавижу тригонометрию» — красивое название для группы, дарю.
Лично мне так кажется. Думаю, эта идея соберет не маленькую группу Вконтакте. «Я ненавижу тригонометрию» — красивое название для группы, дарю. Полная длина вертикальной диагонали ромба (синенькая) получается равной двум длинам катета треугольника.
Полная длина вертикальной диагонали ромба (синенькая) получается равной двум длинам катета треугольника.  Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени. Поскольку ромб также является параллелограммом, его площадь можно вычислить из
длину его основания и высоту перпендикуляра по формуле
площадь=𝑏ℎ.
Поскольку ромб также является параллелограммом, его площадь можно вычислить из
длину его основания и высоту перпендикуляра по формуле
площадь=𝑏ℎ. Из рисунка мы
определить, что основание этого треугольника равно
𝐵𝐷, длина которого 𝑑
единицы.Перпендикулярная высота этого треугольника равна
𝐴𝐸. Вспоминая еще раз, что диагонали
ромб делит друг друга пополам, мы
известно, что 𝐴𝐸 составляет половину длины
диагональ 𝐴𝐶 и поэтому имеет длину
𝑑2 ед. Следовательно,
площадь треугольниковквадрата единиц𝐴𝐵𝐷=12×𝑑×𝑑2=𝑑𝑑4.
Из рисунка мы
определить, что основание этого треугольника равно
𝐵𝐷, длина которого 𝑑
единицы.Перпендикулярная высота этого треугольника равна
𝐴𝐸. Вспоминая еще раз, что диагонали
ромб делит друг друга пополам, мы
известно, что 𝐴𝐸 составляет половину длины
диагональ 𝐴𝐶 и поэтому имеет длину
𝑑2 ед. Следовательно,
площадь треугольниковквадрата единиц𝐴𝐵𝐷=12×𝑑×𝑑2=𝑑𝑑4.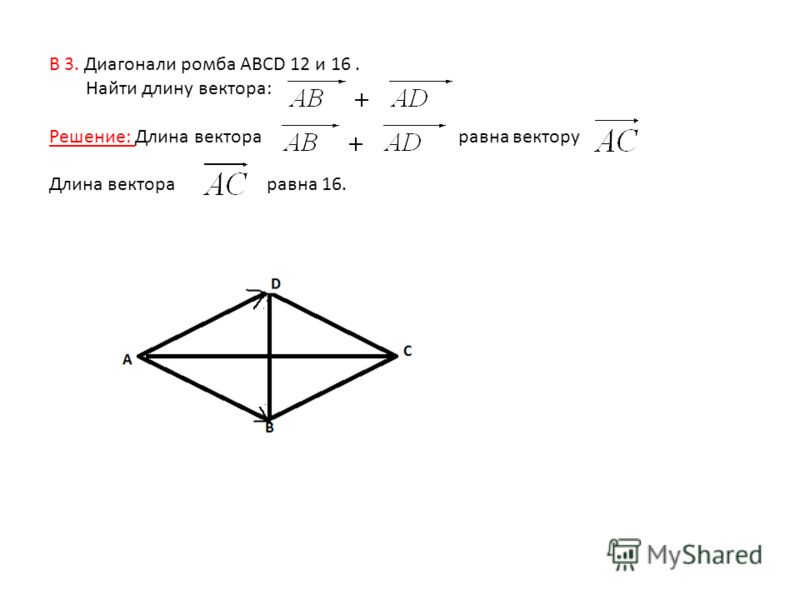
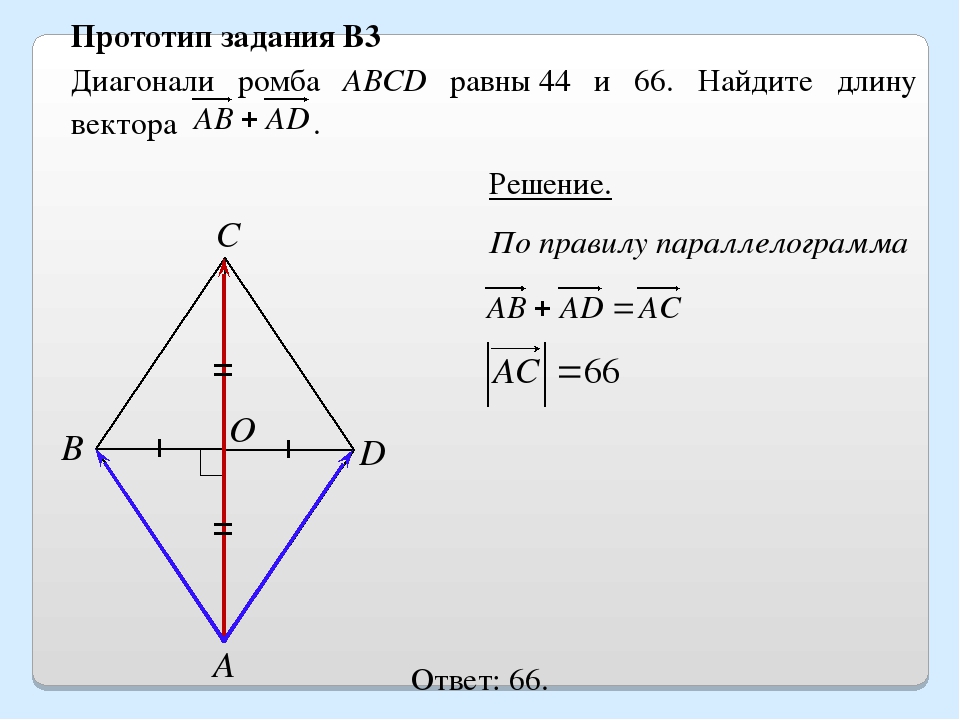
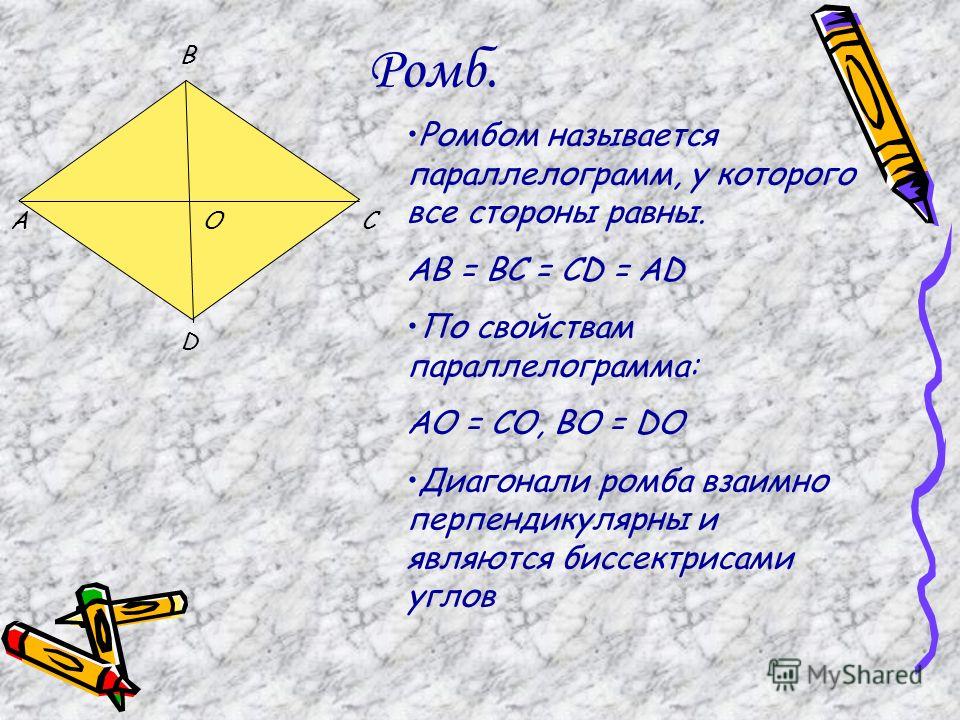 Зная площадь ромба, мы также можем вычислить
длину одной или обеих диагоналей, если мы явно не знаем
длина любого из них, но мы знаем соотношение между их длинами,
как мы увидим в нашем следующем примере.
Зная площадь ромба, мы также можем вычислить
длину одной или обеих диагоналей, если мы явно не знаем
длина любого из них, но мы знаем соотношение между их длинами,
как мы увидим в нашем следующем примере.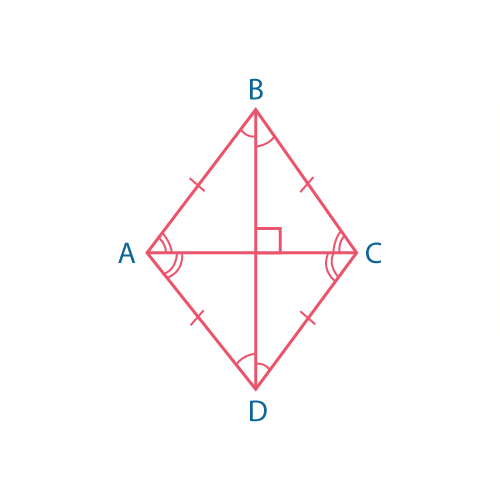 мм
мм Мы помним, что
периметр фигуры — это расстояние вокруг ее края. В случае
квадрат, у которого четыре равные стороны по 𝑠 единиц длины, периметр равен
равно 4𝑠. Установка этого выражения равным 44 дает уравнение, которое
можно решить, чтобы определить длину стороны квадрата:
4𝑠=44𝑠=11.unit
Мы помним, что
периметр фигуры — это расстояние вокруг ее края. В случае
квадрат, у которого четыре равные стороны по 𝑠 единиц длины, периметр равен
равно 4𝑠. Установка этого выражения равным 44 дает уравнение, которое
можно решить, чтобы определить длину стороны квадрата:
4𝑠=44𝑠=11.unit
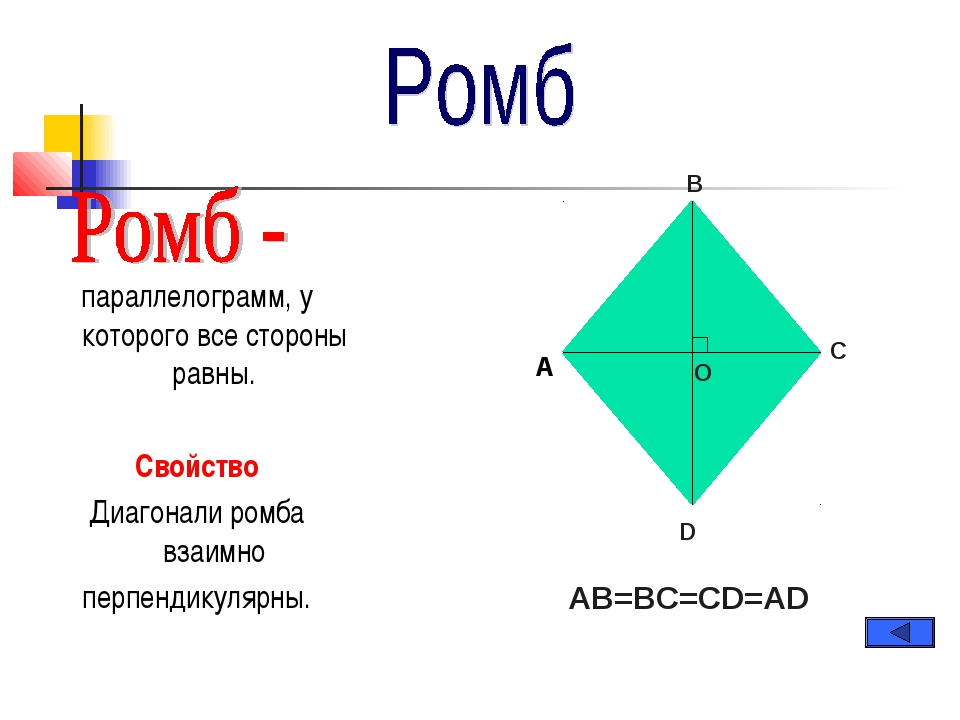
 см
см
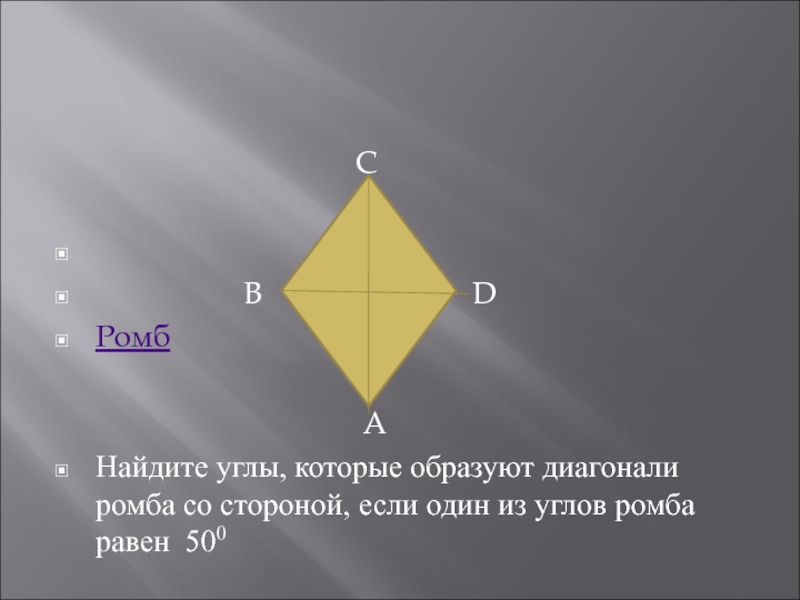
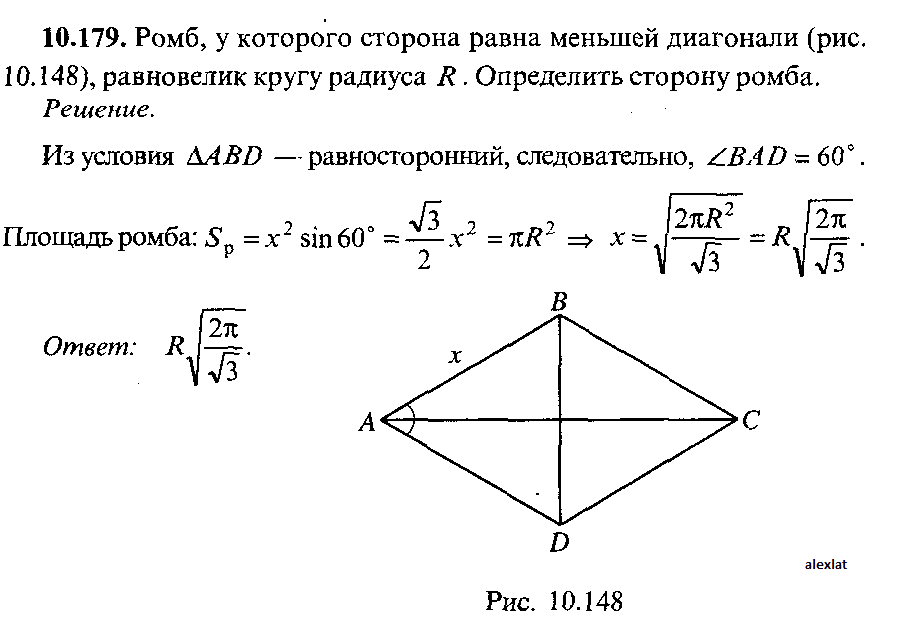 \circ = 120 \times 120 \times 0,866 = 12470,4 $$ квадратных см.
\circ = 120 \times 120 \times 0,866 = 12470,4 $$ квадратных см.
 Он обладает всеми свойствами параллелограмма, но все стороны ромба равны. Обратите внимание, что все деления одинаковые, что говорит нам о том, что все стороны имеют одинаковую длину.
Он обладает всеми свойствами параллелограмма, но все стороны ромба равны. Обратите внимание, что все деления одинаковые, что говорит нам о том, что все стороны имеют одинаковую длину.

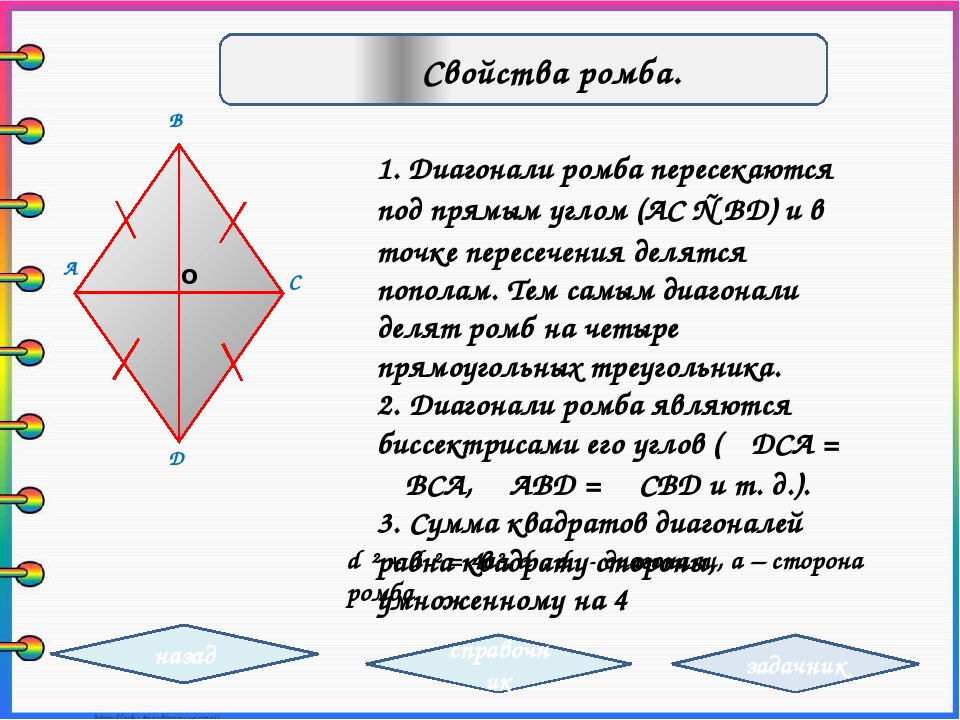
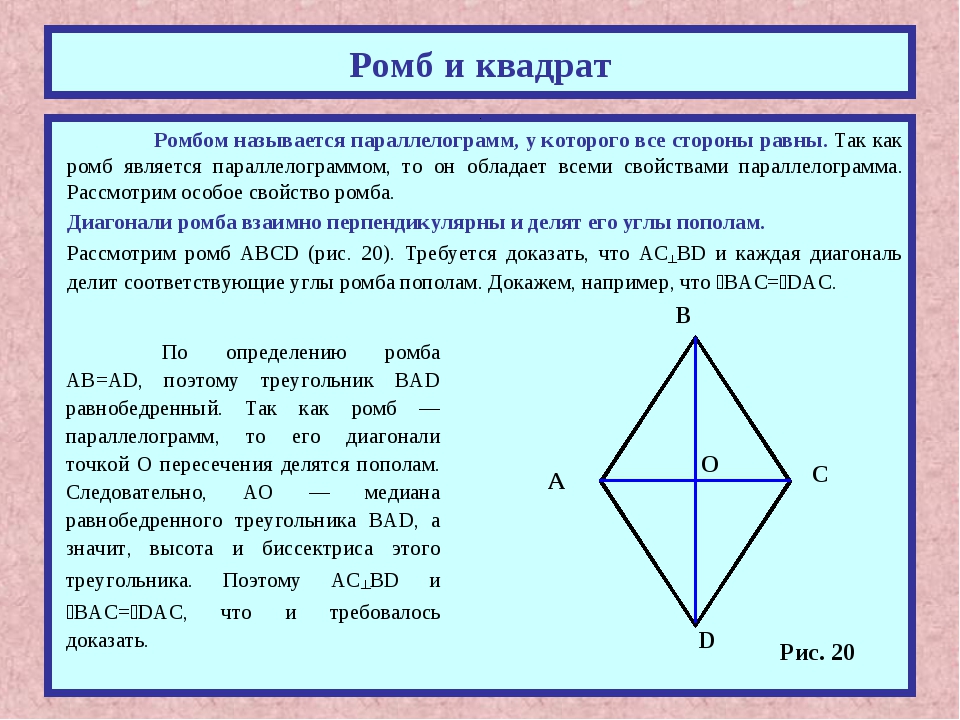
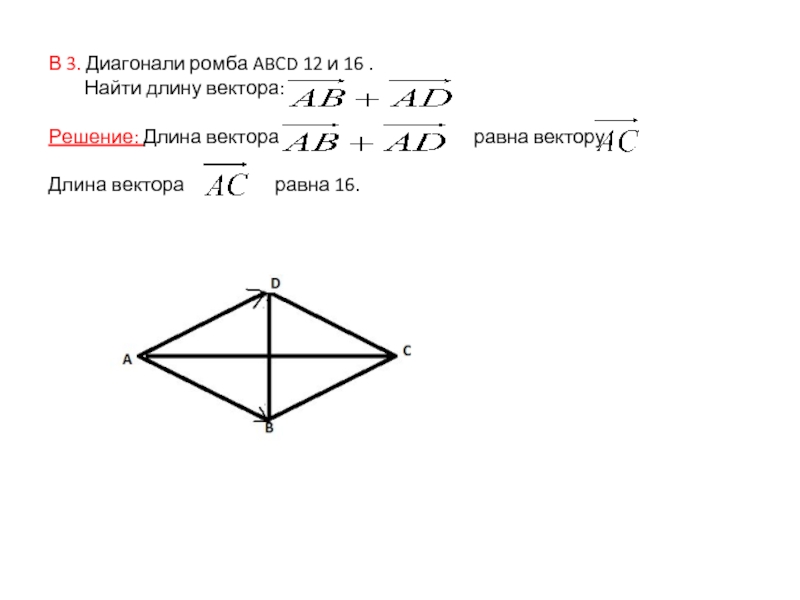
 Площадь △ADC = AC×DE, где DE — высота △ADC. Площадь ромба ABCE равна сумме площадей △ABC и △ADC.
Площадь △ADC = AC×DE, где DE — высота △ADC. Площадь ромба ABCE равна сумме площадей △ABC и △ADC. Второй метод влечет за собой использование стороны и угла, а последний метод влечет за собой использование диагоналей.
Второй метод влечет за собой использование стороны и угла, а последний метод влечет за собой использование диагоналей. 2, соответственно, найдите размеры ромба.
2, соответственно, найдите размеры ромба.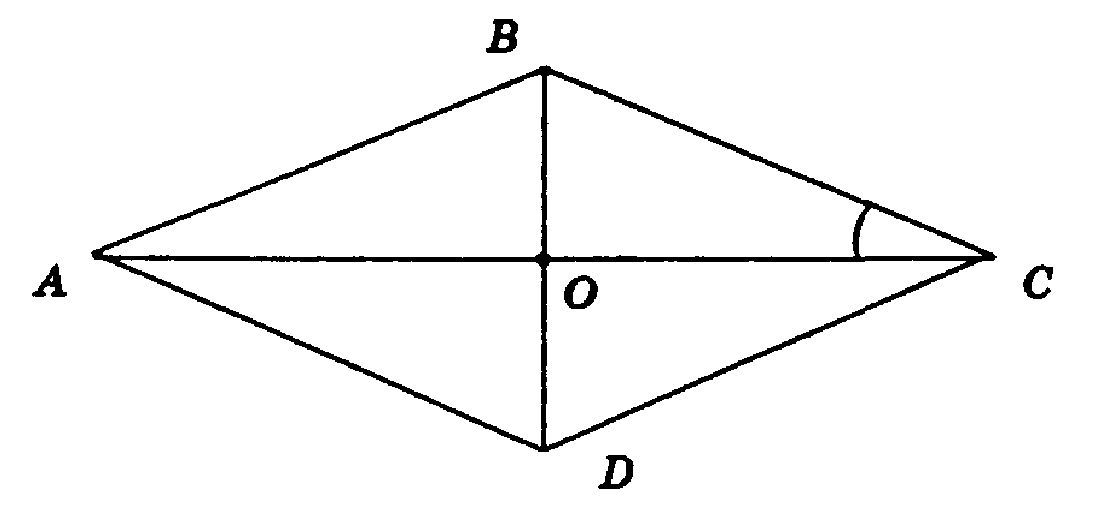



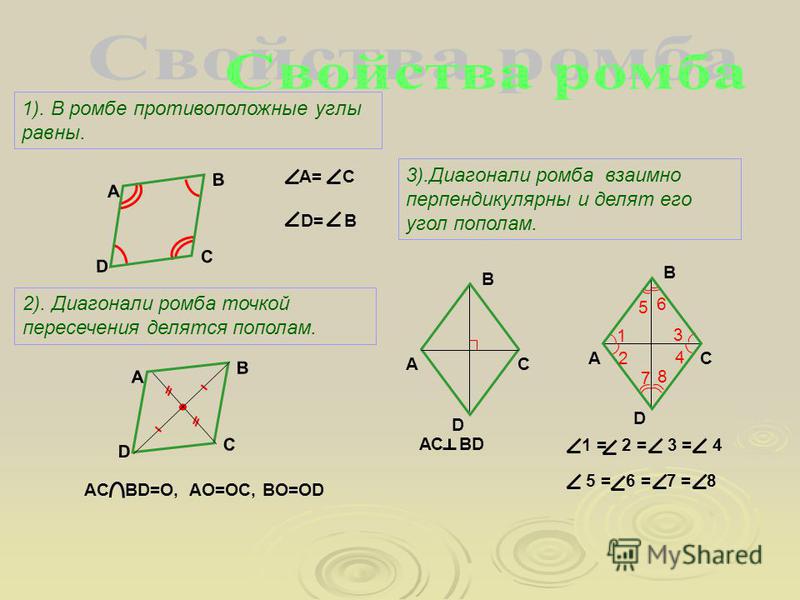 Таким образом, ромб также известен как наклонный квадрат. Ромб считается особым параллелограммом, так как он обладает всеми свойствами параллелограмма. Две диагонали ромба служат его двумя линиями симметрии. Ось симметрии — это линия, которая делит предмет на две равные половины. Он производит зеркальное отражение двух сторон объекта. Ромб имеет симметрию отражения вдоль каждой из его диагоналей. На этой странице мы предоставим вам всю необходимую информацию о свойствах параллелограмма.Читайте дальше, чтобы узнать больше.
Таким образом, ромб также известен как наклонный квадрат. Ромб считается особым параллелограммом, так как он обладает всеми свойствами параллелограмма. Две диагонали ромба служат его двумя линиями симметрии. Ось симметрии — это линия, которая делит предмет на две равные половины. Он производит зеркальное отражение двух сторон объекта. Ромб имеет симметрию отражения вдоль каждой из его диагоналей. На этой странице мы предоставим вам всю необходимую информацию о свойствах параллелограмма.Читайте дальше, чтобы узнать больше. Таким образом, его также называют равносторонним параллелограммом .
Таким образом, его также называют равносторонним параллелограммом .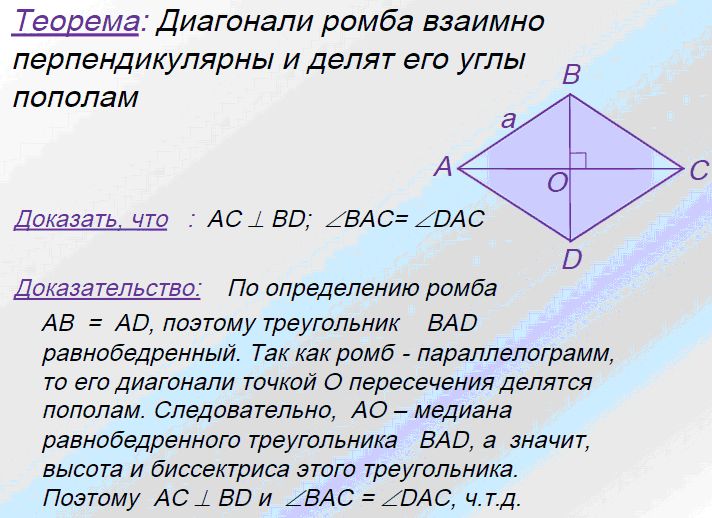 Вы можете прочитать свойства здесь или загрузить их в виде PDF-файла, представленного ниже, для автономного доступа.
Вы можете прочитать свойства здесь или загрузить их в виде PDF-файла, представленного ниже, для автономного доступа.
 В этом случае максимальный диаметр тела равен большей диагонали ромба.
В этом случае максимальный диаметр тела равен большей диагонали ромба.
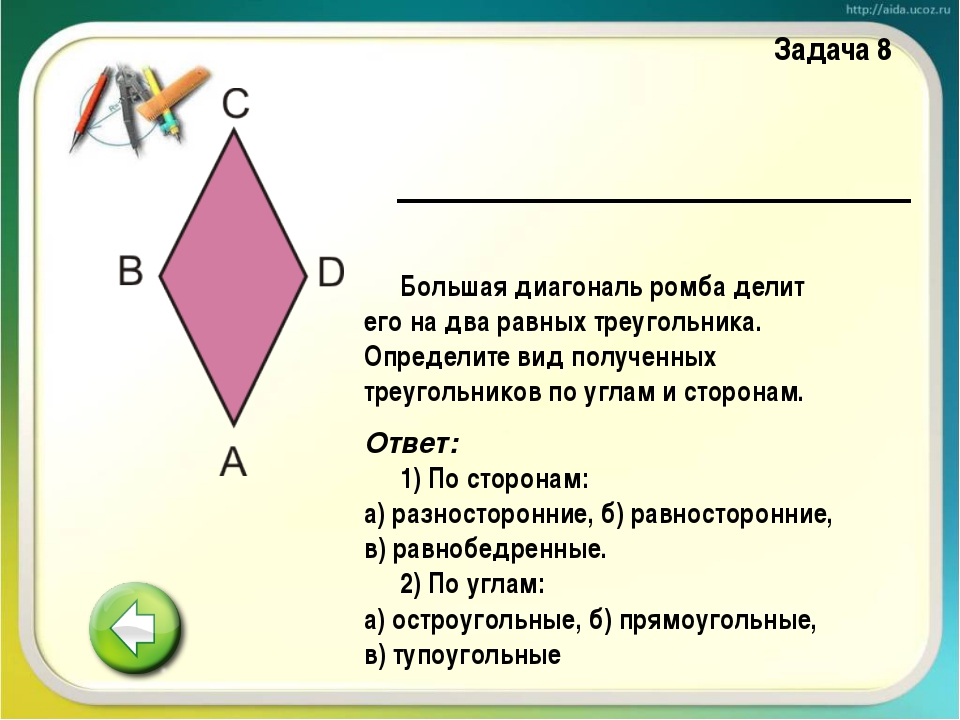 Мы можем отбросить x = –1, так как сторона ромба не может быть отрицательной.
Мы можем отбросить x = –1, так как сторона ромба не может быть отрицательной. 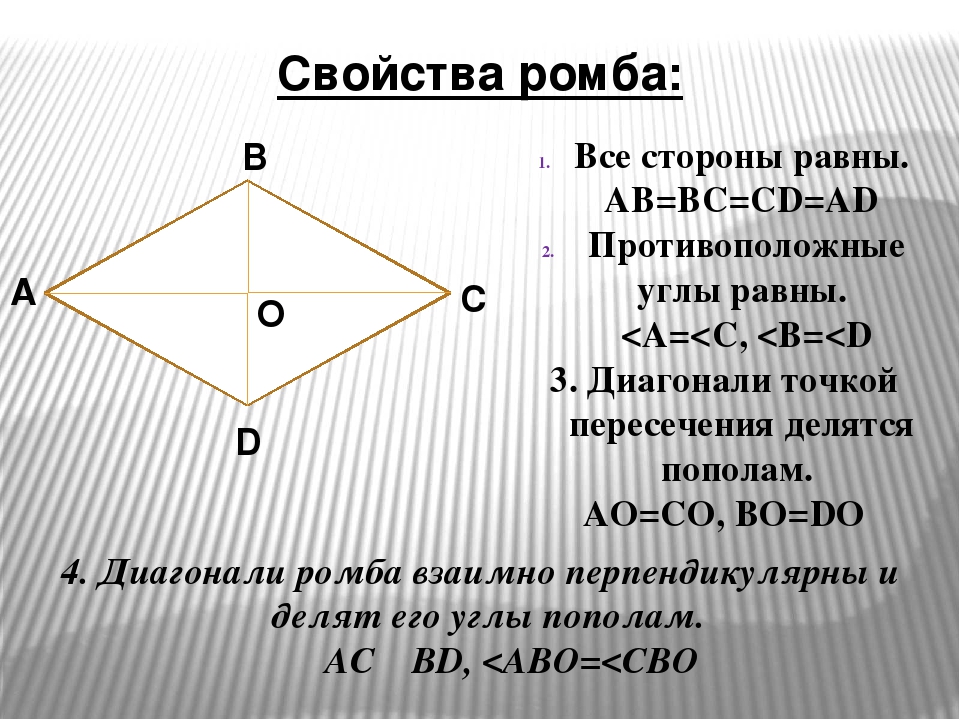 Найдите его высоту.
Найдите его высоту.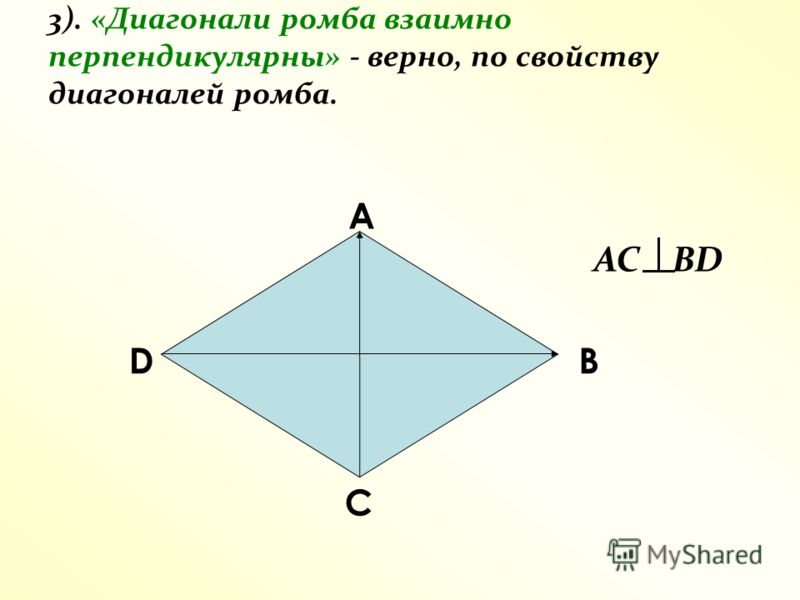 Найдите углы ромба.
Найдите углы ромба.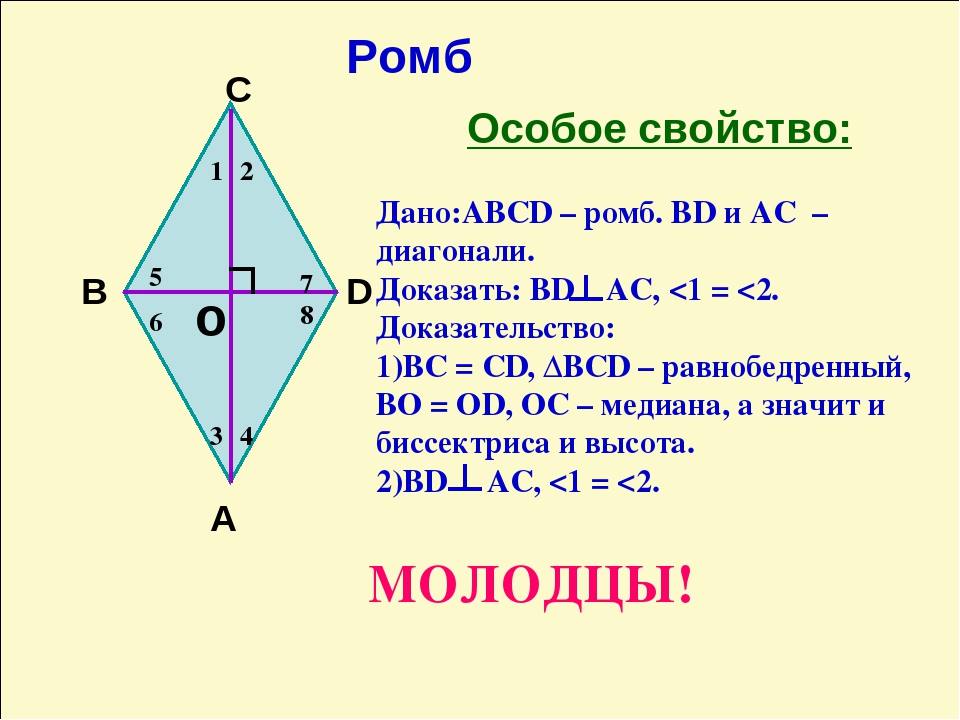 Ромб может быть, а может и не быть квадратом.
Ромб может быть, а может и не быть квадратом.