Диагонали ромба являются биссектрисами его углов.

Дано:

ABCD — ромб,

AC и BD — диагонали.

Доказать:

AC и BD — биссектрисы углов ромба.

Доказательство:

Рассмотрим треугольник ABC.

AB=BC (по определению ромба).

Следовательно, треугольник ABC — равнобедренный с основанием AC (по определению равнобедренного треугольника).

Так как диагонали ромба в точке пересечения делятся пополам, то AO=OC.

Значит, BO — медиана треугольника ABC (по определению медианы).

Следовательно, BO — высота и биссектриса треугольника ABC (по свойству равнобедренного треугольника).

То есть,

BD — биссектриса углов ABC (и ADC).

Из треугольника ABD аналогично доказывается, что AC — биссектриса углов BAD и BCD.

Что и требовалось доказать.

Диагонали ромба | Онлайн калькулятор

Ромб — это четырехугольник, который является параллелограммом, сохраняет все его свойства, но кроме этого он еще и равносторонний. Так как все стороны ромба равны, а из свойств параллелограмма его противоположные углы также равны между собой, диагонали ромба не просто пересекаются в точке, которая делит их на две равные части каждую, а они всегда будут перпендикулярны по отношению друг к другу.

Когда в ромбе проводятся диагонали, они делят его на четыре конгруэнтных прямоугольных треугольника, катетами которого являются половины диагоналей. В любом из полученных прямоугольных треугольников можно, зная гипотенузу (сторона ромба), вычислить оба катета. Для этих целей используются тригонометрические отношения синуса и косинуса в прямоугольном треугольнике — так как оба катета, примем их временно за a и b, неизвестны, для вычислений понадобится один из острых углов в треугольнике.

Чтобы перевести эти формулы в параметры ромба, необходимо связать стороны треугольника со сторонами и диагоналями ромба, а также острый угол треугольника с углами ромба.

Сторона ромба, как было оговорено, становится гипотенузой треугольника, а половины диагоналей берут на себя роль катетов. Тогда в обратном порядке, чтобы найти полноценные диагонали, нужно будет каждый вычисленный катет увеличить в два раза.

Угол, используемый в синусе и косинусе для нахождения катетов и затем диагоналей ромба, является ничем иным как половинным углом самого ромба, так как диагонали ромба являются биссектрисами его углов. То есть будет справедливо следующее равенство:

Теперь для выведения общей формулы диагоналей ромба через сторону ромба и его угол (кстати, выбор острого или тупого угла не сказывается на результате расчетов) выписанные замены должны быть подставлены в исходные формулы треугольника, с которых начинался алгоритм вычислений.

Произведя вычисления обратным ходом, можно также найти сторону ромба через диагонали или угол между сторонами ромба.

allcalc.ru

Диагональ ромба

Свойства ромба:

1. Ромб — частный случай параллелограмма

2. Противоположные стороны — параллельны

3. Все четыре стороны — равны

4. Диагонали пересекаются под прямым углом (90°)

5. Диагонали являются биссектрисами

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

β — тупой угол

Формулы диагоналей через сторону и угол, ( D, d):

Формулы диагоналей через сторону и половинный угол, ( D, d):

Формулы диагоналей через сторону и другую диагональ, ( D, d):

Формулы диагоналей через угол и другую диагональ, ( D, d):

Формулы диагоналей через площадь ( S ) и другую диагональ, ( D, d):

Формулы площади ромба

Формула периметра ромба

Все формулы по геометрии

Все формулы длины стороны ромба

Свойства ромба:

1. Ромб — частный случай параллелограмма

2. Противоположные стороны — параллельны

3. Все четыре стороны — равны

4. Диагонали пересекаются под прямым углом (90°)

5. Диагонали являются биссектрисами

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

β — тупой угол

Формула стороны через диагонали, ( a ):

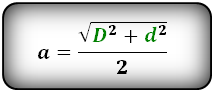
Формулы стороны через диагональ и угол, (

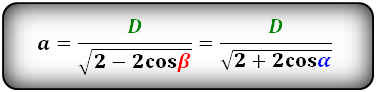
Формулы стороны через диагональ и половинный угол, ( a ):

Формулы стороны через диагонали и угол, ( a ):

Формулы стороны через площадь ромба ( S ) и угол, ( a ):

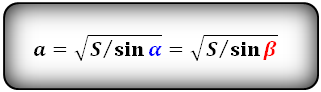
Формулы стороны через периметр ромба ( P ) и угол, ( a ):

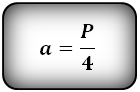
Формулы площади ромба

Формула периметра ромба

Все формулы по геометрии

Подробности

Автор: Administrator

Опубликовано: 27 ноября 2011

Обновлено: 27 сентября 2017

www-formula.ru

Как найти сторону ромба по диагоналям

Как найти сторону ромба по его диагоналям? Это можно сделать разными способами.

Дано:

ABCD — ромб,

Найти:

AB.

Решение:

I способ

По свойствам ромба, его диагонали пересекаются под прямым углом и в точке пересечения делятся пополам.

Поэтому треугольник AOB — прямоугольный,

По теореме Пифагора,

Таким образом, сторона ромба равна половине квадратного корня из суммы квадратов его диагоналей:

II способ.

Сумма квадратов диагоналей ромба равна сумме квадратов его сторон. Так как все стороны ромба равны, то