Трапеция. Свойства, признаки трапеции | Подготовка к ЕГЭ по математике
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
Урок 4. трапеция — Геометрия — 8 класс
Четырёхугольник, две стороны которого параллельны, а две другие не параллельны, называется трапецией. Параллельные стороны называются основаниями трапеции, непараллельные стороны – боковыми сторонами.
Если один из углов трапеции прямой, то она называется прямоугольной. Если боковые стороны трапеции равны, то она называется равнобедренной трапецией (равнобокой).
Сформулируем и докажем свойства равнобедренной трапеции:
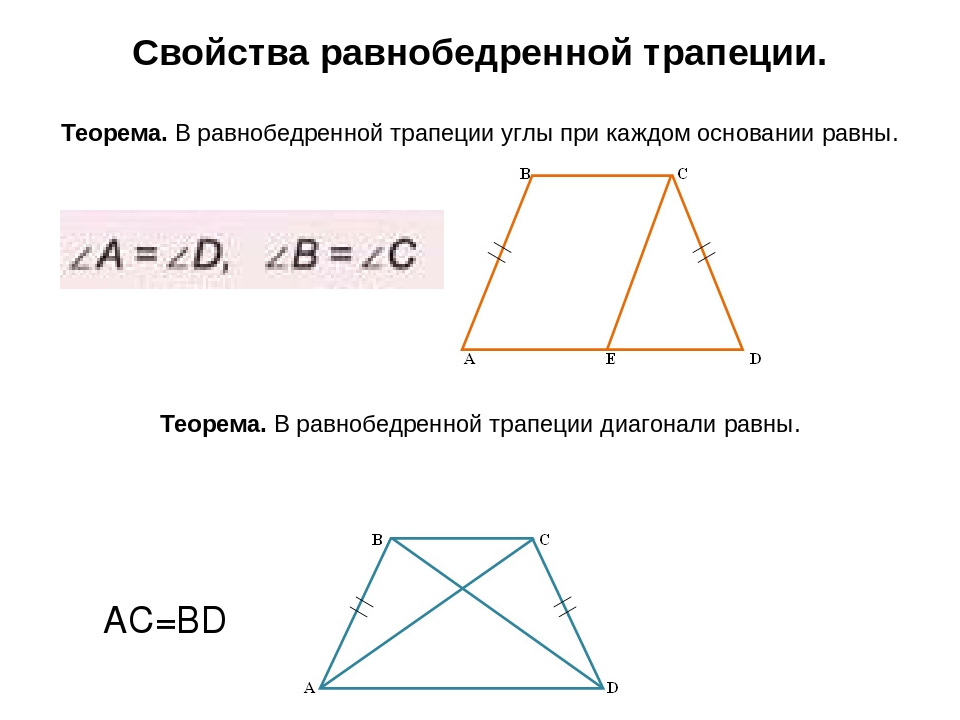
Свойство первое: в равнобедренной трапеции углы при каждом основании равны.
Для доказательства проведём отрезок CK, параллельный AB.
CK || AB, ABCK – параллелограмм (стороны попарно параллельны), значит AB = CK, но AB = CD (трапеция равнобедренная), значит CK = CD, треугольник KCD – равнобедренный,
По свойству равнобедренного треугольника ∠1 = ∠2.
∠2 = ∠3 (соответственные при секущей AD и параллельных AB и CK). Следовательно, ∠1 = ∠3.
ABC = 180° − ∠3 = 180° − ∠1 = ∠BCD.
Дано: ABCD – равнобедренная трапеция, BC || AD
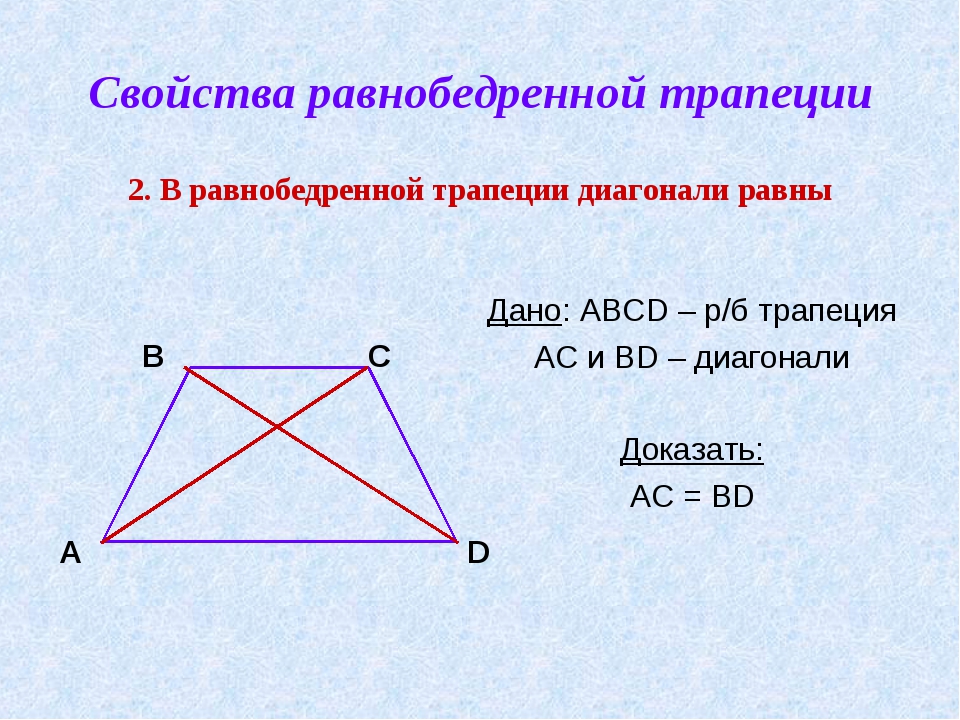
Доказать: AC = BD.

Для доказательства рассмотрим треугольники ABC и DCB. Треугольники ABC и DCB равны (AB = CD, BC – общая сторона, ∠ABC = ∠DCA). Следовательно, AC = BD.
Теоремы, обратные свойствам равнобедренной трапеции, также верны. Это признаки равнобедренной трапеции.
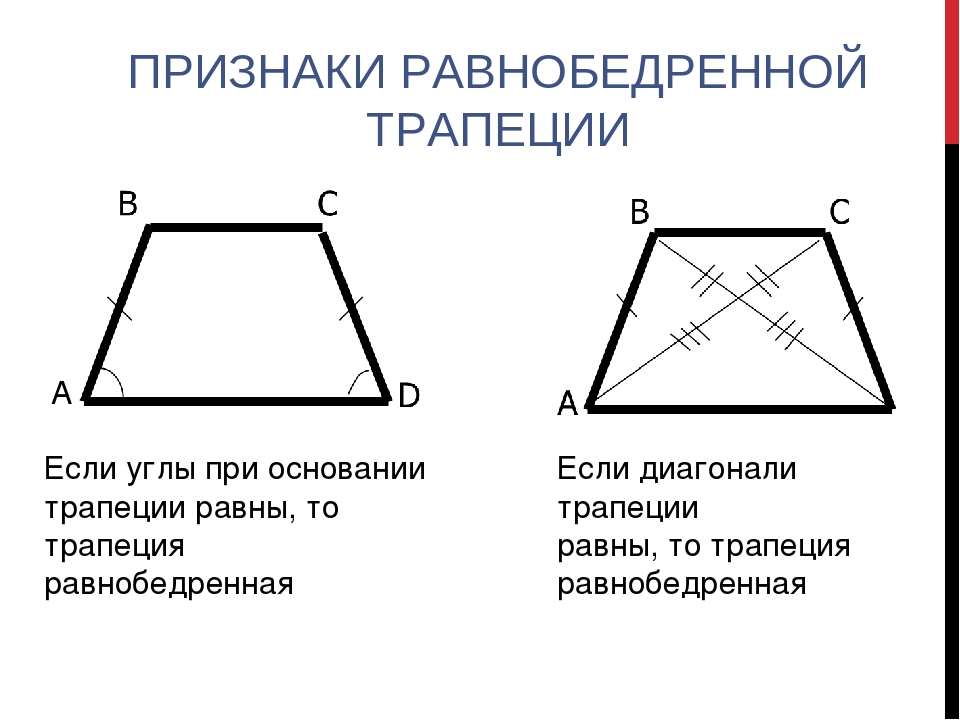
Признак первый: если углы при основании трапеции равны, то трапеция является равнобедренной.
Дано: ABCD – трапеция, BC || AD
∠BAC = ∠CDA
Доказать: ABCD – равнобедренная трапеция
Для доказательства проведем отрезок CK, параллельный AB.
Доказательство:
CK ||
Получится равнобедренный треугольник CKD (∠A = ∠CKD и ∠A = ∠CDA), поэтому
CK = CD и AB = CK = CD. Следовательно, ABCD – равнобедренная трапеция.

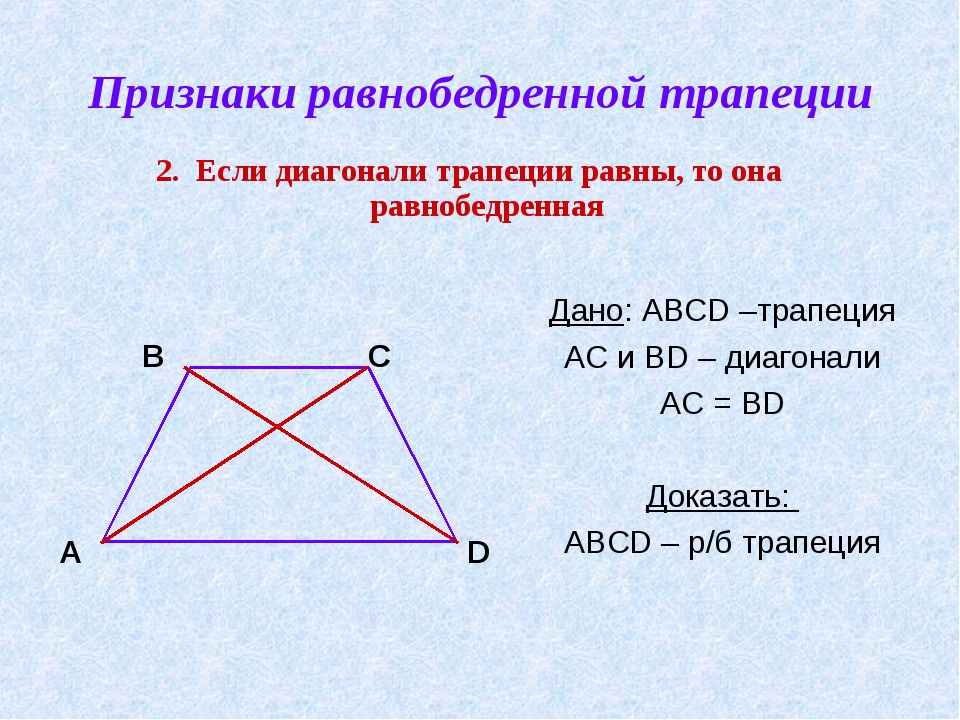
Второй признак: если диагонали трапеции равны, то трапеция равнобедренная.
Дано: ABCD –трапеция, BC || AD
AC = BD
Доказать: ABCD – равнобедренная трапеция
Составим план доказательства второго признака, опираясь на который можно провести доказательство самостоятельно.
Проведем отрезок CK, параллельный BD.
План доказательства
- CK || BD
- Доказать, что BCKD – параллелограмм.
- Доказать, что треугольник ACK – равнобедренный.
- Найти равные углы.
- Доказать равенство треугольников ABD и DCA.
- Доказать равенство сторон AB и CD.
- Сделать вывод.
«Трапеция». 8-й класс
Цель:
- Ввести понятие трапеции, её элементов, виды трапеций.
- Рассмотреть некоторые свойства трапеции.
- Применение знаний при решении задач.

Ход урока
I. Организационный момент.
II. Актуализация знаний.
Кроссворд.
Ключевое слово кроссворда – является темой нашего урока.
- Любой многоугольник разделяет плоскость на две части, одна из которых называется …
- Четырехугольник, у которого противоположные стороны попарно параллельны.
- Отрезок, соединяющий любые две не соседние вершины многоугольника.
- Сумма длин всех сторон многоугольника.
- Две вершины многоугольника, принадлежащие одной стороне, называются…
- В конце урока каждый ученик ждет хорошую …
- Две несмежные стороны четырехугольника называются …
- Любой многоугольник разделяет плоскость на две части, одна из которых внутренняя, а другая
Ответы:
III. Новый материал.
Трапеция – (от греч. trapezion, букв.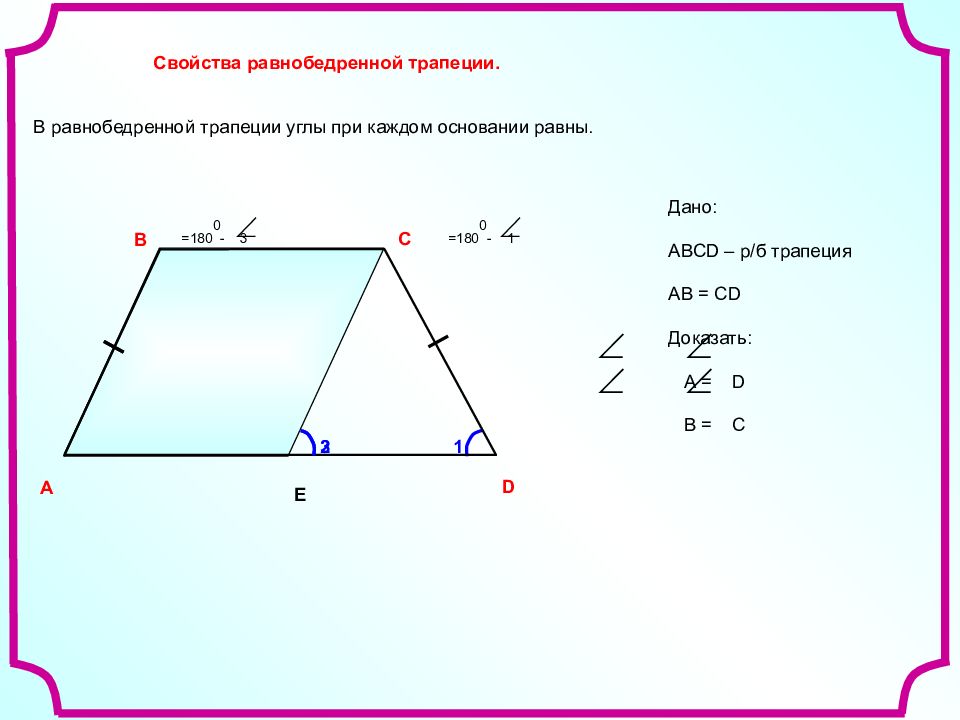 – столик).
– столик).
Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие – непараллельные. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Виды трапеции.
Равнобедренная – трапеция, у которой равны боковые стороны.
Прямоугольная
– трапеция, один из углов которой прямой.Средняя линия трапеции.
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Работа в группах.
Группы с четными номерами – исследуют диагонали равнобедренной трапеции. Группы с нечетными номерами – исследуют углы равнобедренной трапеции.
Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.
Свойства равнобедренной трапеции.
Теорема. В равнобедренной трапеции углы при каждом основании равны.
Доказательство.
Проведем СЕ АВ.
ABCD – параллелограмм (АВ СЕ, ВС AD).
CD = AB = CE, СDE – равнобедренный, СDЕ = СЕD.
АВ СЕ, тогда СЕD = ВАЕ, СDЕ = СЕD = ВАЕ.
ABC = 180° – СDЕ = 180° – ВАЕ = BCD.
Теорема. В равнобедренной трапеции диагонали равны.
Доказательство.
ABC = DСВ (АВ = С, ВС – общая сторона, АВС = ВСD) тогда АС = ВD.
Сформулируйте утверждения, обратные свойствам, и выясните их справедливость.
Признаки равнобедренной трапеции.
Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.
1. Если углы при основании трапеции равны, то она равнобедренная.
Доказательство.
Проведем ЕС АВ.
ABCЕ – параллелограмм, тогда АВ
СЕ,
А =
СЕD,
СЕD –
равнобедренный (D =
СЕD), тогда СЕ = СD.
АВ = СЕ = СD, тогда АВСD – равнобедренная трапеция.
2. Если диагонали трапеции равны, то она равнобедренная.
Доказательство.
Проведем СК ВD.
ВСКD – параллелограмм (т.к. СК ВD, ВС АК).
АСК – равнобедренный, т.к. АС = ВD = СК, САD = СDА.
СК ВD, ВDА = СКD, тогда САD = СКD.
АВD = DСА, т.к. АС=ВD, АD – общая сторона, САD = СКD, тогда АВ = СD, т.е. АВСD – равнобедренная трапеция.
IV. Закрепление.
Решение задач по готовым чертежам.
V. Итог урока:
VI. Домашнее задание.
Параграф 44, вопросы: 10-11, №386, №388.
Основание трапеции равно боковой стороне
Если в условии задачи сказано, что основание трапеции равно ее боковой стороне, то отсюда следует, что диагональ трапеции является биссектрисой ее угла.
1) Если меньшее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне острого угла.
Рассмотрим трапецию ABCD, в которой боковая сторона AB равна меньшему основанию BC.
1) Так как AB=BC, треугольник ABC — равнобедренный с основанием AC. Значит, у него углы при основании равны:∠BAC=∠BCA.
2)∠BCA=∠∠CAD (как внутренние накрест лежащие при AD ∥ BC и секущей AC).
3) Отсюда следует, что ∠BAC=∠CAD, а значит, AC — биссектриса угла BAD.
2) Если большее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне тупого угла.
Рассмотрим трапецию ABCD, в которой большее основание AD равно ее боковой стороне AB.
1) Так как треугольник ABD — равнобедренный с основанием BD, то его углы при основании равны: ∠ABD=∠ADB.
2) ∠CBD=∠ADB (как внутренние накрест лежащие при AD ∥ BC и секущей BD).
3) Отсюда ∠CBD=∠ABD, следовательно, BD — биссектриса угла ABC.
Аналогично доказываются утверждения для прямоугольной и равнобедренной трапеции.
3) Если большее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к меньшему основанию.
4) Если меньшее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к большему основанию.
5) Если меньшее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне острого угла.
6) Если большее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне тупого угла.
7) Если меньшее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой острого угла трапеции.
8) Если большее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой тупого угла трапеции.
В частности, так как сумма противолежащих углов равнобедренной трапеции равна 180º, соответственно, ∠ACD+3∠BCA=180º и ∠BAC+3∠CAD=180º.
Найти углы трапеции равнобедренной трапеции: Углы равнобедренной трапеции — ЭкоДом: Дом своими руками
Углы равнобедренной трапеции
Углы равнобедренной трапеции. Здравствуйте! В этой статье речь пойдёт о решении задач с трапецией. Данная группа заданий входит в состав экзамена, задачки простые. Будем вычислять углы трапеции, основания и высоты. Решение ряда задач сводится к решению прямоугольного треугольника, как говориться: куда мы без теоремы Пифагора, синуса и косинуса?
Работать будем с равнобедренной трапецией. У неё равны боковые стороны и углы при основаниях. О трапеции есть статья на блоге, посмотрите.
Отметим небольшой и важный нюанс, который в процессе решения самих заданий подробно расписывать не будем. Посмотрите, если у нас дано два основания, то большее основание высотами, опущенными к нему, разбивается на три отрезка – один равен меньшему основанию (это противолежащие стороны прямоугольника), два других равны друг другу (это катеты равных прямоугольных треугольников):
Простой пример: дано два основания равнобедренной трапеции 25 и 65. Большее основание разбивается на отрезки следующим образом:
Большее основание разбивается на отрезки следующим образом:
*И ещё! В задачах не введены буквенные обозначения. Это сделано умышленно, чтобы не перегружать решение алгебраическими изысками. Согласен, что это математически неграмотно, но цель донести суть. А обозначения вершин и прочих элементов вы всегда можете сделать сами и записать математически корректное решение.
Рассмотрим задачи:
27439. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
Для того чтобы найти угол необходимо построить высоты. На эскизе обозначим данные в условии величины. Нижнее основание равно 65, высотами оно разбивается на отрезки 7, 51 и 7:
В прямоугольном треугольнике нам известна гипотенуза и катет, можем найти второй катет (высоту трапеции) и далее уже вычислить синус угла.
По теореме Пифагора указанный катет равен:
Таким образом:
Ответ: 0,96
27440. Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 5/7. Найдите боковую сторону.
Косинус острого угла трапеции равен 5/7. Найдите боковую сторону.
Построим высоты и отметим данные в условии величины, нижнее основание разбивается на отрезки 15, 43 и 15:
Ответ: 21
27441. Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен (2√10)/7. Найдите меньшее основание.
Построим высоты. Для того чтобы найти меньшее основание нам необходимо найти чему равен отрезок являющийся катетом в прямоугольном треугольнике (обозначен синим):
Можем вычислить высоту трапеции, а затем найти катет:
По теореме Пифагора вычисляем катет:
Таким образом, меньшее основание равно:
Ответ: 22
27442. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11. Найдите высоту трапеции.
Построим высоты и отметим данные в условии величины. Нижнее основание разбивается на отрезки:
Что делать? Выражаем тангенс известного нам угла при основании в прямоугольном треугольнике:
Ответ: 10
27443. Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен 13/8. Найдите большее основание.
Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен 13/8. Найдите большее основание.
Строим высоты и вычисляем чему равен катет:
Таким образом большее основание будет равно:
Ответ: 71
27444. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.
Строим высоты и отмечаем известные величины на эскизе. Нижнее основание разбивается на отрезки 35, 17, 35:
По определению тангенса:
Ответ: 0,4
77152. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
Построим эскиз, построим высоты и отметим известные величины, большее основание разбивается на отрезки 3, 6 и 3:
Выразим гипотенузу обозначенную как х через косинус:
Из основного тригонометрического тождества найдём cosα
Таким образом:
Ответ: 5
27818. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 500? Ответ дайте в градусах.
Из курса геометрии нам известно, что если имеем две параллельные прямые и секущую, что сумма внутренних односторонних углов равна 1800. В нашем случае это
C условии сказано, что разность противолежащих углов равна 500, то есть
Так как у равнобедренной трапеции углы при основании равны, то есть угол А равен углу В, то можем записать
Имеем два уравнения с двумя неизвестными, можем решить систему:
*Конечно, эту задачу можно было легко решить просто перебирая пары углов )
27833. В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 600. Найдите меньшее основание.
Построим высоты DE и CF:
Меньшее основание равно отрезку EF, так как DC и EF это противолежащие стороны прямоугольника. Отрезок EF мы можем найти если вычислим АЕ. Выразим этот катет прямоугольного треугольника ADE через функцию косинуса:
Так как AE=FB=5, то EF=25–5–5=15. Следовательно и DC=15.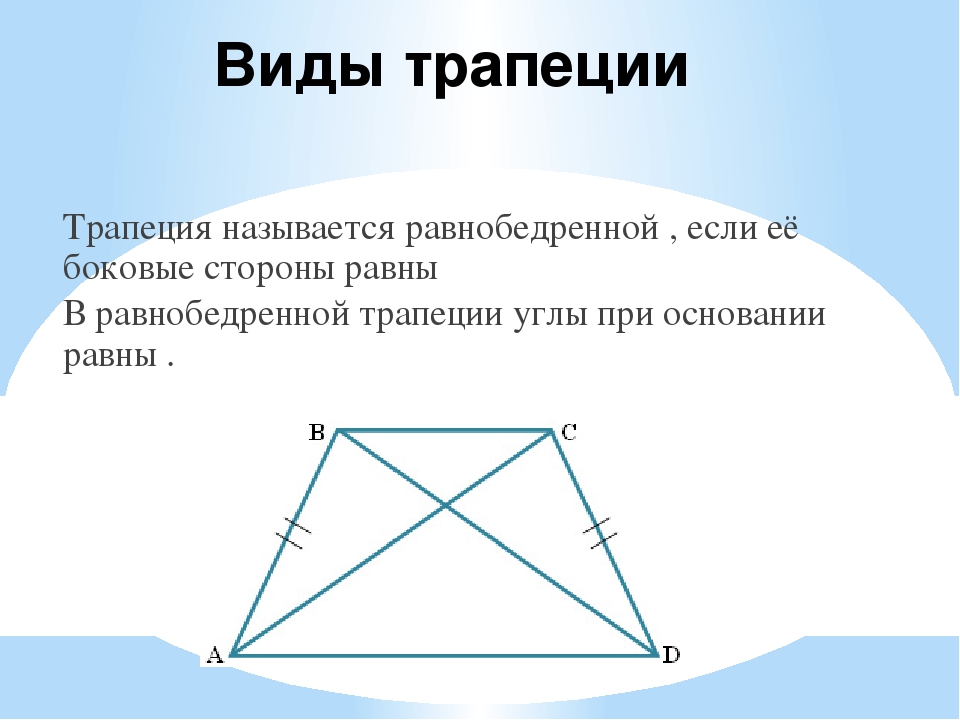
Ответ: 15
27837. Основания равнобедренной трапеции равны 15 и 9, один из углов равен 450. Найдите высоту трапеции.
Из точек D и C опустим две высоты:
Как уже сказано выше они разбивают большее основание на три отрезка: один равен меньшему основанию, два других равны друг другу.
В данном случае они равны 3, 9 и 3 (в сумме 15). Кроме того, отметим что высотами отсекаются прямоугольные треугольники, причём они являются равнобедренными, так как углы при основании равны по 450. Отсюда следует, что высота трапеции будет равна 3.
Ответ: 3
На этом всё! Успеха вам!
С уважением, Александр.
P.S: Расскажите о сайте в социальных сетях!
найдите углы трапеции.
нужно хотя бы 5 заданий!
помогите пожалуйста((
1. Сумма углов, прилежащих к боковой стороне трапеции, равна 180°, следовательно
∠В = 180° — 70° = 110°
∠С = 180° — 50° = 130°
2. Трапеция равнобедренная, значит углы при основаниях равны:
∠М = ∠F = 100°
∠E = ∠N = 180° — 100° = 80°
3. Сумма углов, прилежащих к боковой стороне трапеции, равна 180°, следовательно
Сумма углов, прилежащих к боковой стороне трапеции, равна 180°, следовательно
∠Р = 180° — 75° = 105°
∠S = 180° — 100° = 80°
4. Трапеция прямоугольная, значит
∠F = ∠E = 90°
∠M = 180° — 65° = 115°
5. ∠KLN = ∠MNL = 30° как накрест лежащие при пересечении параллельных KL и MN секущей NL,
ΔNKL равнобедренный, значит углы при основании равны:
∠KNL = ∠KLN = 30°, ⇒ в трапеции
∠N = 60°, ∠M = ∠N = 60°как углы при основании равнобедренной трапеции,
∠K = ∠L = 180° — 60° = 120° (прилежащие к боковой стороне, см. 1)
6. ΔFMK: ∠M = 90°, ∠F = 35°, ⇒∠K = 90° — 35° = 55°
Трапеция равнобедренная, значит в ней:
∠F = ∠K = 55°
∠R = ∠M = 180° — 55° = 125°
7. ΔACD: ∠C = 90°, ∠B = 60°, ⇒ ∠A = 30°
∠BCA = ∠DAC = 30° как накрест лежащие при пересечении параллельных BC и AD секущей AC,
ΔBCA равнобедренный, ⇒
∠ВАС = ∠ВСА = 30°.
Значит ∠BAD = 30° · 2 = 60°. ⇒ трапеция равнобедренная.
В трапеции ∠В = ∠С = 180° — 60° = 120°
8. Трапеция прямоугольная,
∠S = ∠M = 90°.
ΔMRK — равнобедренный, ∠RMK = ∠RKM = (180° — 50°)/2 = 65°
В трапеции ∠К = 65°, тогда
∠R = 180° — 65° = 115° как прилежащие к боковой стороне.
9. Трапеция прямоугольная,
∠Р = ∠Т = 90°.
Из треугольника LPT ∠Т = 90° — 55° = 35°, тогда
∠LTO = ∠LOT = 90° — 35° = 55°
В трапеции ∠L = 180° — 55° = 125°
10. ΔNEM = ΔMFN по гипотенузе и катету (MN — общая, EN = FM), ⇒
∠FNM = ∠EMN и ΔOMN — равнобедренный. {\circ};\)
\(ABCD\) – трапеция \(\Rightarrow \, \angle{CAD}=\angle{ACB}, \, \angle{BDA}=\angle{DBC};\)
\(ABCD\) – трапеция, \(AC \cap BD=O\) \(\Rightarrow \, \triangle{AOD} \backsim \triangle{COB};\)
\(ABCD\) – трапеция, \(AB \cap CD=E\) \(\Rightarrow \, \triangle{AED} \backsim \triangle{BEC}\)
Средняя линия трапеции
Определение. Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.
\( AD||BC, \, M\) – середина \(AB, \, N\) – середина \(CD \, \Rightarrow \) $$ MN||AD, \, MN||BC, \, MN=\frac{1}{2}(AD+BC)$$
Свойства равнобедренной трапеции
1. В равнобедренной трапеции углы при каждом основании равны.
2. Диагонали равнобедренной трапеции равны.
3. Ранобедренную трапецию можно вписать в окружность.
\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, \angle{ABC}=\angle{DCB}, \, \angle{BAD}=\angle{CDA}; \)
\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, AC=BD; \)
\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, ABCD\) вписанная
Признаки равнобедренной трапеции
1. Если углы при некотором основании трапеции равны, то эта трапеция равнобедренная.
2. Если диагонали трапеции равны, то эта трапеция равнобедренная.
3. Если трапецию можно вписать в окружность, то эта трапеция равнобедренная.
\( AD||BC, \, M\) – середина \(AB, \, N\) – середина \(CD \, \Rightarrow \) $$ MN||AD, \, MN||BC, \, MN=\frac{1}{2}(AD+BC)$$
Площадь трапеции
1. Площадь трапеции равна половине произведения суммы её оснований на высоту трапеции.
2. Площадь трапеции равна половине произведения её диагоналей на синус угла между ними.
$$ S=\frac{1}{2}(a+b)h$$ | $$ S=\frac{1}{2} d_1d_2\sin{\varphi}$$ |
Как найти углы равнобедренной трапеции
Трапеция — это плоская четырехугольная геометрическая фигура, отличительной особенностью которой является обязательная параллельность одной пары несоприкасающихся сторон. Эти стороны называются ее основаниями, а две непараллельные составляющие — боковыми сторонами. Разновидность трапеции, у которой длины боковых сторон одинаковы, называется равнобокой или равнобедренной. Формулы нахождения углов такой трапеции легко вывести из свойств прямоугольного треугольника.
Разновидность трапеции, у которой длины боковых сторон одинаковы, называется равнобокой или равнобедренной. Формулы нахождения углов такой трапеции легко вывести из свойств прямоугольного треугольника.
Если известны длины обоих оснований (b и c) и одинаковых по определению боковых сторон (a) равнобедренной трапеции, то для вычисления величины одного из ее острых углов (γ) можно использовать свойства прямоугольного треугольника. Для этого опустите высоту из любого прилегающего к короткому основанию угла. Прямоугольный треугольник будет образован высотой (катет), боковой стороной (гипотенуза) и отрезком длинного основания между высотой и ближней боковой стороной (второй катет). Длину этого отрезка можно найти, отняв от длины большего основания длину меньшего и поделив результат пополам: (c-b)/2.
Получив значения длин двух смежных сторон прямоугольного треугольника, переходите к вычислению угла между ними. Отношение длины гипотенузы (a) к длине катета ((c-b)/2) дает значение косинуса этого угла (cos(γ)), а функция арккосинус поможет преобразовать его в величину угла в градусах: γ=arccos(2*a/(c-b)). Так вы получите величину одного из острых углов трапеции, а поскольку она равнобедренна, то и второй острый угол будет иметь такую же величину. Сумма всех углов четырехугольника должна составлять 360°, а это значит, что сумма двух тупых углов будет равна разности между этим числом и удвоенной величиной острого угла. Поскольку оба тупых угла тоже будут одинаковы, то для нахождения величины каждого из них (α) эту разность надо поделить пополам: α = (360°-2*γ)/2 = 180°-arccos(2*a/(c-b)). Теперь у вас есть формулы вычисления всех углов равнобедренной трапеции по известным длинам ее сторон.
Так вы получите величину одного из острых углов трапеции, а поскольку она равнобедренна, то и второй острый угол будет иметь такую же величину. Сумма всех углов четырехугольника должна составлять 360°, а это значит, что сумма двух тупых углов будет равна разности между этим числом и удвоенной величиной острого угла. Поскольку оба тупых угла тоже будут одинаковы, то для нахождения величины каждого из них (α) эту разность надо поделить пополам: α = (360°-2*γ)/2 = 180°-arccos(2*a/(c-b)). Теперь у вас есть формулы вычисления всех углов равнобедренной трапеции по известным длинам ее сторон.
Если длины боковых сторон фигуры неизвестны, но дана ее высота (h), то действовать нужно по такой же схеме. В этом случае в прямоугольном треугольнике, составленном из высоты, боковой стороны и короткого отрезка длинного основания, вам будут известны длины двух катетов. Их соотношение определяет тангенс нужного вам угла, а эта тригонометрическая функция тоже имеет своего антипода, преобразующего значение тангенса в величину угла — арктангенс. Полученные в предыдущем шаге формулы острого и тупого углов трансформируйте соответствующим образом: γ=arctg(2*h/(c-b)) и α = 180°-arctg(2*h/(c-b)).
Полученные в предыдущем шаге формулы острого и тупого углов трансформируйте соответствующим образом: γ=arctg(2*h/(c-b)) и α = 180°-arctg(2*h/(c-b)).
Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.
1. Формулы длины диагонали равнобедренной трапеции через ее стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагональ трапеции
Формула диагонали трапеции (d ):
2. Формулы длины диагонали равнобедренной трапеции по теореме косинусов
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α, β — углы трапеции
d — диагональ трапеции
Формулы диагонали трапеции (d ):
3. Формула длины диагонали равнобедренной трапеции
Формула длины диагонали равнобедренной трапеции
a — нижнее основание
b — верхнее основание
α, β — углы между диагоналями
h — высота трапеции
m — средняя линия трапеции
S — площадь трапеции
d — диагональ трапеции
Формулы диагонали трапеции (d ):
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через высоту и стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
h — высота трапеции
α — угол при нижнем основании
d — диагональ трапеции
Формулы диагонали трапеции (d ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Найти длину диагонали трапеции
зная все четыре стороны
или две стороны и угол
или высоту, сторону и угол
или площадь, другую диагональ и угол
и еще много других формул.
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции по теореме косинусов:
Формулы диагоналей трапеции через четыре стороны:
2. Формула длины диагоналей трапеции через высоту
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции через высоту:
3. Формула длины диагонали трапеции через другую диагональ
Формула длины диагонали трапеции через другую диагональ
a — нижнее основание
b — верхнее основание
α, β — углы между диагоналями
h — высота трапеции
m — средняя линия трапеции
S — площадь трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции :
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
d1 , d2 — диагонали трапеции
Формула суммы квадратов диагоналей :
Формулы диагоналей трапеции :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула средней линии трапеции через основания (для всех видов трапеции)
Формула средней линии трапеции через основания (для всех видов трапеции)
a — нижнее основание
b — верхнее основание
m — средняя линия
Формула средней линии, (m ):
2. Формулы средней линии через основания, высоту и угол при нижнем основании
a, b — основания трапеции
c — боковая сторона под прямым углом к основаниям
d — боковая сторона
α — угол при основании
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
3.Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
4. Формула средней линии трапеции через площадь и высоту (для всех видов трапеции)
Формула средней линии трапеции через площадь и высоту (для всех видов трапеции)
S — площадь трапеции
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1.Формула боковой стороны (с) прямоугольной трапеции через другие стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
d — боковая сторона
α — угол при нижнем основании
h — высота трапеции
c — боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с) :
2. Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
c — боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с):
3.Формулы боковой стороны (с) прямоугольной трапеции через площадь
a — нижнее основание
b — верхнее основание
m — средняя линия трапеции
c — боковая сторона под прямым углом к основаниям
Формула длины боковой стороны (с) :
4. Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
α — угол при нижнем основании
h — высота трапеции
d — боковая сторона
Формулы длины боковой стороны (d) :
5.Формула боковой стороны (d) прямоугольной трапеции через площадь
a — нижнее основание
b — верхнее основание
m — средняя линия трапеции
α — угол при нижнем основании
d — боковая сторона
Формула длины боковой стороны (d) :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула длины оснований прямоугольной трапеции через среднюю линию
Формула длины оснований прямоугольной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
2.Формулы длины оснований через боковые стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α — угол при нижнем основании
Формулы длины оснований :
3. Формулы длины оснований трапеции через диагонали и угол между ними
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
Формулы длины оснований :
4. Формулы длины оснований трапеции через площадь
Формулы длины оснований трапеции через площадь
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
h — высота трапеции
Формулы длины оснований :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула средней линии равнобедренной трапеции через основания
a — нижнее основание
b — верхнее основание
m — средняя линия
Формула средней линии, (m ):
2.Формулы средней линии через основание, высоту и углы при нижнем основании
a — нижнее основание
b — верхнее основание
c — боковая сторона
α — угол при нижнем осровании
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
d — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m ):
4.Формула средней линии трапеции через площадь и высоту
S — площадь трапеции
h — высота трапеции
α — угол при нижнем осровании
m — средняя линия
Формула средней линии трапеции, (m ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула высоты равнобедренной трапеции через стороны и углы при основании
Формула высоты равнобедренной трапеции через стороны и углы при основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при нижнем основании
h — высота трапеции
Формулы длины высоты, (h ):
2.Формула высоты равнобедренной трапеции через диагонали и углы между ними
d — диагонали трапеции
α , β — углы между диагоналями
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
3. Формула высоты равнобедренной трапеции через площадь
Формула высоты равнобедренной трапеции через площадь
S — площадь трапеции
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1.Формула длины основания равнобедренной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины основания:
2. Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4.Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.
1. Формула высоты трапеции через стороны и углы при основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы длины высоты, (h ):
2. Формула высоты трапеции через диагонали и углы между ними
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
3. Формула высоты трапеции через площадь
Формула высоты трапеции через площадь
S — площадь трапеции
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции — отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.
1. Формула средней линии трапеции через основания
b — верхнее основание
a — нижнее основание
m— средняя линия
Формула средней линии, (m ):
2. Формулы средней линии через основание, высоту и углы при нижнем основании
Формулы средней линии через основание, высоту и углы при нижнем основании
b — верхнее основание
a — нижнее основание
α, β — углы трапеции
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
α, β — углы между диагоналями
d1 , d2 — диагонали трапеции
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
4.Формула средней линии трапеции через площадь и высоту
S — площадь трапеции
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула длины основания трапеции через среднюю линию
Формула длины основания трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
2. Формулы длины сторон через высоту и углы при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
3.Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Как найти углы трапеции?
Трапеция – это геометрическая фигура, четырехугольник, который имеет две параллельные линии. Иные две линии параллельными быть не могут, в таком случае это был бы параллелограмм.
Иные две линии параллельными быть не могут, в таком случае это был бы параллелограмм.
Виды трапеций
Трапеции бывают трех видов: прямоугольная, когда два угла трапеции составляют по 90 градусов; равносторонняя, в которой две боковые линии равные; разносторонняя, где боковые линии разной длинны.
Работая с трапециями, можно научиться вычислять их площадь, высоту, размер линий, а также разобраться в том, как находить углы трапеции.
Прямоугольная трапеция
Прямоугольная трапеция имеет два угла по 90 градусов. Сумма остальных двух углов равняется 180 градусам. Поэтому есть способ, как найти углы прямоугольной трапеции, зная размер одного из углов. Пусть он составляет, например, 26 градусов. Всего лишь необходимо из общей суммы углов трапеции – 360 градусов — вычесть сумму известных углов. 360-(90+90+26) = 154. Искомый угол будет составлять 154 градуса. Можно считать проще: так как два угла — прямые, то в сумме они будут составлять 180 градусов, то есть половину 360; сумма непрямых углов также будет равна 180, поэтому можно сосчитать проще и быстрее 180 -26 =154.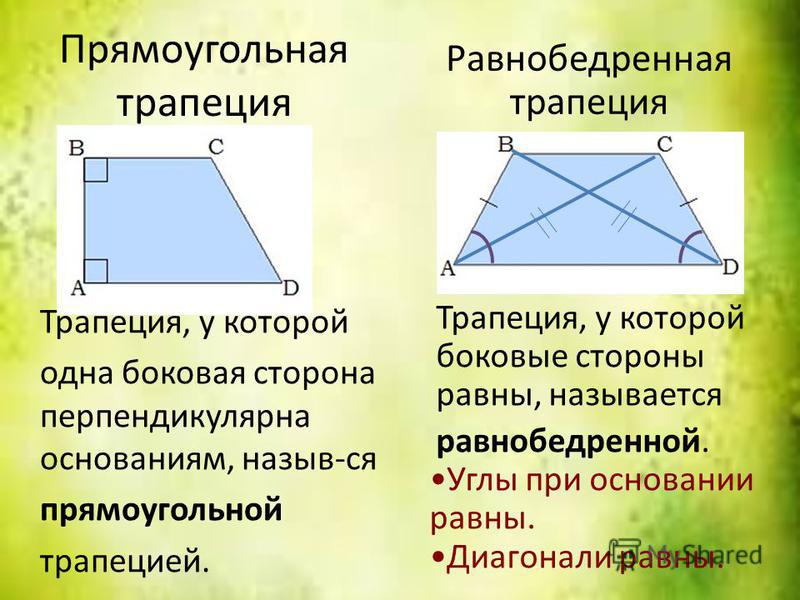
Равнобедренная трапеция
Равнобедренная трапеция имеет две равные стороны, которые не являются основаниями. Есть формулы, которые разъясняют, как найти углы равнобедренной трапеции.
Расчет 1, если даны размеры сторон трапеции
Они обозначаются буквами A, В и C: A – размеры боковых сторон, В и C – размеры основания, меньшего и большего соответственно. Трапецию необходимо также назвать АВСD. Для вычислений необходимо провести высоту Н из угла В. Образовался прямоугольный треугольник ВНА, где АН и ВН – катеты, АВ – гипотенуза. Теперь можно вычислить размер катета АН. Для этого необходимо от большей основы трапеции вычесть меньшую, и разделить пополам, т.е. (с-b)/2.
Чтобы найти острый угол треугольника, необходимо использовать функциюcos. Cos искомого угла (β) будет равен а / ((с-b)/2). Чтобы узнать размер угла β, необходимо воспользоваться функцией arcos. β = arcos 2а/с-b. Т.к. два угла равносторонней трапеции равны, то они будут составлять: угол ВАD = углу СDА = arcos 2а/с-b.
Далее необходимо разобраться, как найти углы трапеции, которые остались. Сделать это достаточно легко. Угол АВС = углу ВСD = 360 – 2х(arcos 2а/с-b) = 180 — arcos 2а/с-b.
Расчет 2. Если даны размеры оснований трапеции.
Имея значения оснований трапеции – а и b, можно воспользоваться тем же методом, что и в предыдущем решении. Из угла b необходимо опустить высоту h. Имея размеры двух катетов только что созданного треугольника, можно воспользоваться похожей тригонометрической функцией, только в этом случае это буде tg. Чтобы преобразовать угол и получить его значение, необходимо воспользоваться функцией arctg. Исходя из формул, получаем размеры искомых углов:
β = arctg 2h/с-b, а угол α = 180 — arctg 2h/с-b/
Обычная разносторонняя трапеция
Есть способ, как найти больший угол трапеции. Для этого необходимо знать размеры обоих острых углов. Зная их, и зная, что сумма углов при любом основании трапеции составляет 180 градусов, делаем вывод, что искомый тупой угол будет состоять из разницы 180 – размер острого угла.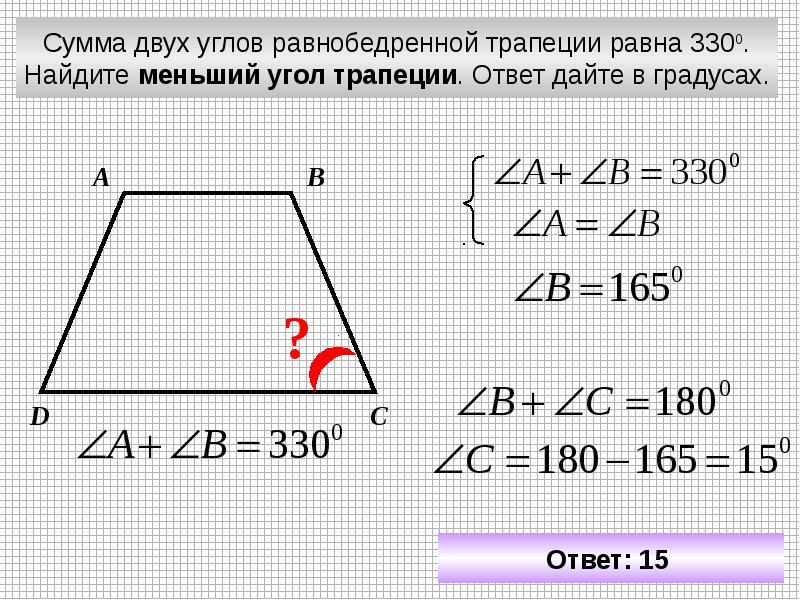 Также можно найти и другой тупой угол трапеции.
Также можно найти и другой тупой угол трапеции.
Трапеция. Свойства, признаки трапеции | Подготовка к ЕГЭ по математике
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
Как найти угол в трапеции
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Равнобедренные трапеции, углы, стороны, диагонали и другие свойства. Объясняется фотографиями и практическими задачами
- Углы основания
- Диагонали
Отличительной чертой этого особого типа трапеции является то, что две непараллельные стороны (XW и YZ ниже) совпадают.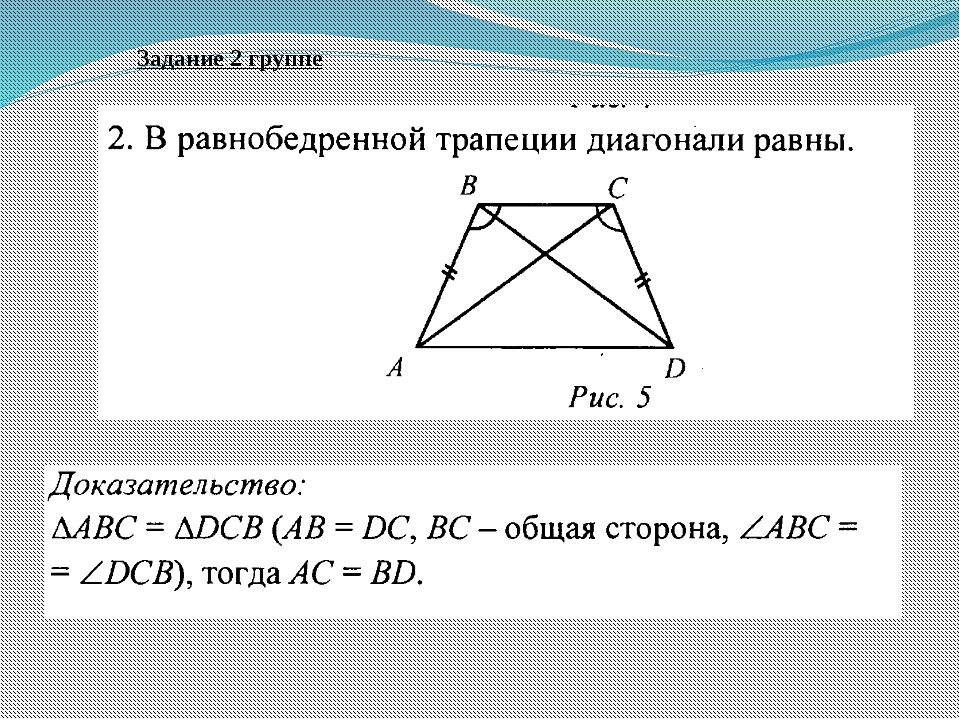
Углы основания
Углы основания равнобедренной трапеции совпадают.
Проблема 1
Если вы знаете, что угол BAD равен 44 °, какова мера $$ \ angle ADC $$?
Покажи ответ
Угол $$ \ angle ADC = 44 ° $$, так как базовые углы совпадают
Проблема 2
$$ \ angle ABC = 130 $$, какой еще угол составляет 130 градусов?
Покажи ответ
Single $$ \ angle ADC = 4 ° $$, так как базовые углы совпадают
Проблема 3
Какое значение j в равнобедренной трапеции ниже?
Покажи ответ
Дж = 5
- Углы основания
- Диагонали
Диагонали равнобедренной трапеции
Проблема 3
Диагонали равнобедренной трапеции совпадают. Какое значение x ниже? (используйте свои знания о диагоналях!)
Покажи ответ
Х = 9
назад к четырехугольникам
рядом с пареллограммами
Реклама
Свойства трапеции — Задача 1
Равнобедренная трапеция имеет две совпадающие ножки и одну пару параллельных сторон.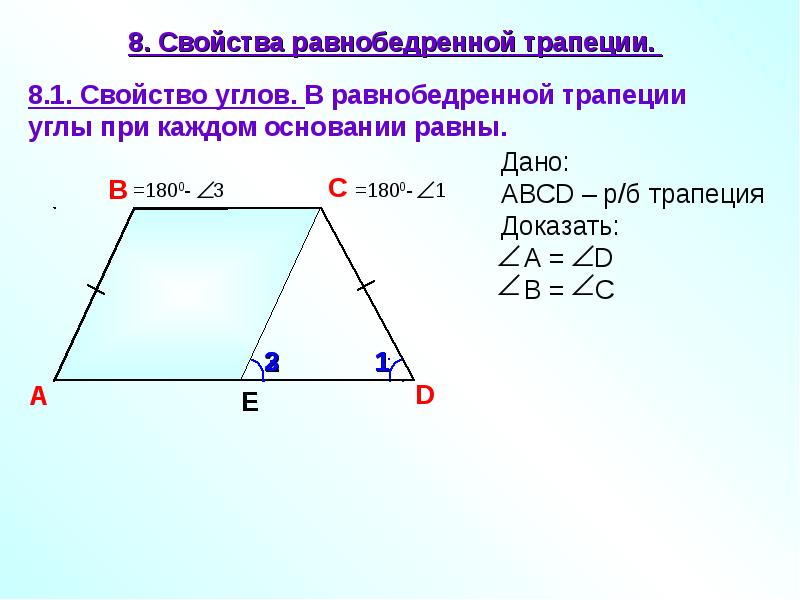 Базовые углы совпадают друг с другом, и при одинаковых боковых внутренних углах верхние углы дополняют соответствующие базовые углы, что означает, что они оба равны 180 ° (мера базового угла).
Базовые углы совпадают друг с другом, и при одинаковых боковых внутренних углах верхние углы дополняют соответствующие базовые углы, что означает, что они оба равны 180 ° (мера базового угла).
Итак, если дана мера одного из верхних углов, вы знаете, что его базовый угол является дополнительным к нему, поэтому вычтите его значение из 180 °, чтобы найти меру базового угла. Затем вспомните, что у равнобедренной трапеции углы основания совпадают. Другой верхний угол является дополнительным к его базовому углу, поэтому он соответствует верхнему углу.Таким образом, только по одному углу равнобедренной трапеции можно найти размеры других углов.
В этой задаче у нас есть равнобедренная трапеция, что означает, что у нас есть две конгруэнтные ноги, когда у нас есть пара параллельных сторон. Итак, давайте посмотрим, что мы знаем о равнобедренных трапециях.
Итак, мы видим, что базовые углы, поэтому, если я смотрю на два базовых угла, они будут конгруэнтны друг другу. Мы также знаем, что те же боковые внутренние углы здесь, поэтому я смотрю на эти треугольники прямо здесь, будут дополнительными, что является определением того же бокового внутреннего угла.
Итак, вернемся к нашей проблеме. Если я посмотрю на единственное, что мы знаем об этой трапеции, это угол B, который равен 110 градусам, я могу начать с нахождения угла C. Я знаю, что эти два должны быть дополнительными, потому что они находятся на одной стороне этой поперечной BC. . Итак, если B равно 110 C, что должно быть? 180 минус 110, что 70 градусов.Итак, я собираюсь написать здесь, что C должно быть 70 градусов.
Теперь вам просто нужно помнить, что ваши базовые углы конгруэнтны друг другу. Итак, я напишу, что D должно быть 70 градусов, а A должно быть 110 градусов. Итак, мы сказали, что А — 110, а D — 70 градусов. Ключевым моментом здесь было помнить, что одни и те же боковые внутренние углы являются дополнительными и что базовые углы в равнобедренной трапеции всегда совпадают.
Равнобедренная трапеция — Калькулятор геометрии
| 1D линия, круговая дуга, парабола, спираль, кривая Коха 2D Правильные многоугольники: Равносторонний треугольник, Квадрат, Пентагон, Шестиугольник, Семиугольник, Восьмиугольник, Нонагон, Десятиугольник, Хендекагон, Додекагон, Шестиугольник, N-угольник, Кольцо многоугольника Другие многоугольники: 90 077 Круглые формы: 3D Архимедовы тела: Каталонских Сухой остаток: Твердые тела Джонсона: Другие многогранники: 000, большой додекаэдр 000 Круглые формы: 4D | Anzeige Расчеты на равнобедренной трапеции (или равнобедренной трапеции). Формулы: Длина стороны, диагональ, высота, радиус и периметр имеют одинаковые единицы измерения (например,грамм. метр), площадь имеет эту единицу в квадрате (например, квадратный метр). Anzeige Серединные перпендикуляры пересекаются в центре описанной окружности. Серединный перпендикуляр к двум параллельным сторонам является осью симметрии равнобедренной трапеции. биссектриса перпендикулярно и описанная окружность © Jumk. Anzeige |
Как найти углы в трапеции
В геометрии трапеция — это четырехугольник (четырехсторонняя фигура), в котором только одна пара противоположных сторон параллельна.Трапеции также известны как трапеции. Параллельные стороны трапеции называются основаниями. Непараллельные стороны называются ножками. Трапеция, как и круг, имеет 360 градусов. Поскольку у трапеции четыре стороны, у нее четыре угла. Трапеции названы по их четырем углам или вершинам, например, «ABCD».
Определите, является ли трапеция равнобедренной. Равнобедренные трапеции имеют линию симметрии, разделяющую каждую половину. Ноги трапеции равны по длине, как и диагонали.В равнобедренной трапеции углы, имеющие общее основание, имеют одинаковую меру. Дополнительные углы, которые представляют собой углы, примыкающие к противоположным основаниям, имеют в сумме 180 градусов. Эти правила можно использовать для расчета угла.
Перечислить данные измерения. Вам может быть дано измерение угла или основания. Или вам может быть дано измерение среднего сегмента, который параллелен обоим основаниям и имеет длину, равную среднему значению двух оснований. Используйте данные измерения, чтобы определить, какие измерения, если не угол, можно рассчитать.Эти рассчитанные измерения затем можно использовать для расчета угла.
Вам может быть дано измерение угла или основания. Или вам может быть дано измерение среднего сегмента, который параллелен обоим основаниям и имеет длину, равную среднему значению двух оснований. Используйте данные измерения, чтобы определить, какие измерения, если не угол, можно рассчитать.Эти рассчитанные измерения затем можно использовать для расчета угла.
Напомним соответствующие теоремы и формулы для решения измерений оснований, опор и диагоналей. Например, теорема 53 утверждает, что базовые углы равнобедренной трапеции равны. Теорема 54 утверждает, что диагонали равнобедренной трапеции равны. Площадь трапеции (независимо от того, является ли она равнобедренной) равна половине длины параллельных сторон, умноженной на высоту, которая представляет собой перпендикулярное расстояние между сторонами.Площадь трапеции также равна произведению среднего сегмента и высоты.
При необходимости нарисуйте прямоугольный треугольник внутри трапеции. Высота трапеции образует прямоугольный треугольник, который подразумевает угол трапеции. Используйте измерения, такие как площадь трапеции, чтобы вычислить высоту, опору или основание, которые разделяет треугольник. Затем найдите угол, используя правила измерения углов, применимые к треугольникам.
Используйте измерения, такие как площадь трапеции, чтобы вычислить высоту, опору или основание, которые разделяет треугольник. Затем найдите угол, используя правила измерения углов, применимые к треугольникам.
Видео с вопросом: Определение угла в равнобедренной трапеции с использованием ее свойств
Стенограмма видео
Показанный динамик представляет собой равнобедренную трапецию.Если угол 𝐹𝐽𝐻 равен 82 градусам, найдите угол 𝐹𝐺𝐻.
Выделим эту трапециевидную форму и включим тот факт, что угол 𝐹𝐽𝐻 составляет 82 градуса. Напомним, что трапеция или трапеция — это четырехугольник с одной парой параллельных сторон. Далее нам говорят, что этот динамик представляет собой равнобедренную трапецию. Это означает, что непараллельные стороны этого четырехугольника совпадают. Итак, здесь сторона 𝐹𝐽 будет равна длине стороны.
Чтобы найти этот неизвестный угол 𝐹𝐺𝐻, нам нужно использовать свойства равнобедренных трапеций. Поскольку у нас есть две конгруэнтные ветви, мы можем сказать, что нижние углы основания совпадают, а верхние углы основания совпадают. Таким образом, угол 𝐹𝐽𝐻 будет таким же, как угол 𝐺𝐻𝐽. И верхние углы основания совпадают. Итак, угол 𝐺𝐹𝐽 конгруэнтен углу. Мы могли бы найти меру угла 𝐹𝐺𝐻, используя ряд различных методов. Однако, пожалуй, самый быстрый способ — использовать это окончательное свойство равнобедренной трапеции.
Таким образом, угол 𝐹𝐽𝐻 будет таким же, как угол 𝐺𝐻𝐽. И верхние углы основания совпадают. Итак, угол 𝐺𝐹𝐽 конгруэнтен углу. Мы могли бы найти меру угла 𝐹𝐺𝐻, используя ряд различных методов. Однако, пожалуй, самый быстрый способ — использовать это окончательное свойство равнобедренной трапеции.
Любой нижний базовый угол является дополнительным к любому верхнему базовому углу.Это означает, что они прибавятся к 180 градусам. Мы знаем, что это правда, потому что у нас есть пара параллельных сторон. Следовательно, угол нижнего основания и угол верхнего основания составляют в сумме 180 градусов. Таким образом, мы можем составить уравнение, согласно которому этот верхний базовый угол, который мы хотим определить, угол 𝐹𝐺𝐻, плюс этот нижний базовый угол должен быть равен 180 градусам. Мы можем вставить информацию, что угол 𝐹𝐽𝐻 равен 82 градусам. А затем вычитая 82 градуса из обеих частей уравнения, мы получим, что угол 𝐹𝐺𝐻 равен 98 градусам.
Мы могли бы, конечно, также ответить на этот вопрос по-другому, вспомнив, что углы в четырехугольнике складываются в 360 градусов и, учитывая нижние углы основания, совпадают, а верхние углы основания совпадают.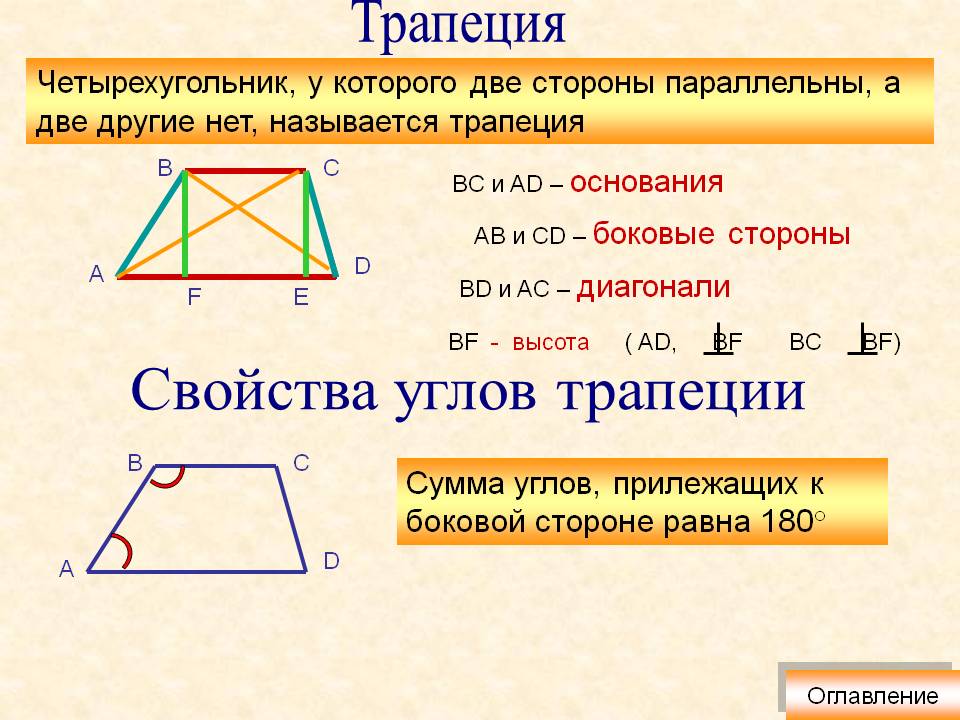 Определив наши неизвестные верхние базовые углы как букву, мы могли бы составить альтернативное уравнение. Решив это, мы обнаружим, что каждый из верхних углов основания равен 98 градусам, что также подтверждает наш первоначальный ответ о том, что мера угла 𝐹𝐺𝐻 равна 98 градусам.
Определив наши неизвестные верхние базовые углы как букву, мы могли бы составить альтернативное уравнение. Решив это, мы обнаружим, что каждый из верхних углов основания равен 98 градусам, что также подтверждает наш первоначальный ответ о том, что мера угла 𝐹𝐺𝐻 равна 98 градусам.
доказательств для равнобедренных трапеций — видео и стенограмма урока
Базовые углы
Углы, образованные между непараллельными сторонами и параллельными сторонами, называемые базовыми углами , равны в равнобедренной трапеции.В трапеции газона Ирен ABCD углы C и D равны.
Чтобы доказать эту теорему, давайте проведем линию CE , параллельную AD , так что ADCE станет параллелограммом.
В этом параллелограмме мы знаем, что линия AD = линия CE .Мы также знаем, что строка AD = строка BC , поэтому мы также знаем, что строка BC = строка CE .
Теперь, поскольку линия BC и линия CE равны, треугольник BCE становится равнобедренным. Следовательно, углы CBE и CEB равны.
Мы понимаем, что линия AD и линия CE параллельны, а линия AE является поперечной.Таким образом, сумма внутренних углов на одной стороне, угла DAE и угла CEA составляет 180 градусов.
Итак,
Следовательно, углы DAB и CBA равны.
Далее мы знаем, что ADCE — параллелограмм, поэтому противоположные углы будут равны.
Теперь углы CBE и BCD будут равны, потому что они являются альтернативными внутренними углами для параллельных прямых AE и CD .
Мы уже знаем, что углы CEB и CEB равны. Следовательно,
Таким образом, доказано, что углы основания равнобедренной трапеции равны.
Диагонали
Диагонали равнобедренной трапеции равны по длине. Итак, в равнобедренной трапеции ABCD Ирен диагонали AC и BD равны.
Итак, в равнобедренной трапеции ABCD Ирен диагонали AC и BD равны.
Чтобы доказать эту теорему, давайте сосредоточимся на двух образованных треугольниках: DAC и CBD . Здесь мы знаем, что линия AD = BC , углы ADC и BCD равны, а сторона CD общая.Ирен вспоминает свойство сторона-угол-сторона треугольников: если в двух треугольниках две стороны и их угол первого треугольника совпадают с двумя сторонами и их углом второго, то два треугольника конгруэнтны. .
Следовательно, треугольники DAC и CBD совпадают.
Следовательно, остальные соответствующие стороны равны, AC = BD .Таким образом, диагонали равны.
Противоположные углы
Сумма противоположных углов равнобедренной трапеции Ирен составляет 180 градусов.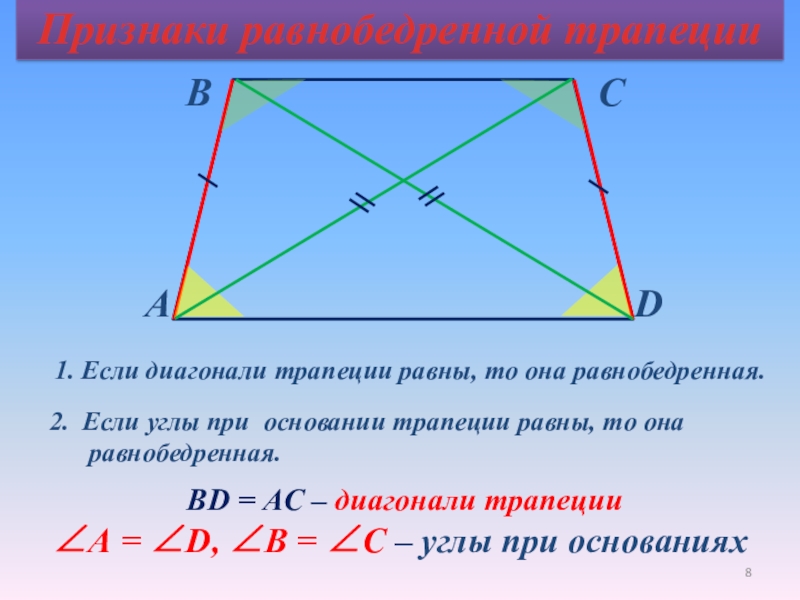 Она может доказать это, зная, что угол A равен углу B , а угол C равен углу D .
Она может доказать это, зная, что угол A равен углу B , а угол C равен углу D .
Она также знает, что AB параллельна CD , что делает пары углов A и D и B и C внутренними углами на одной стороне поперечной. Это означает, что эти пары составляют дополнительных или их сумма равна 180 градусам.
Теперь, заменяя равные углы,
Таким образом, она доказывает, что противоположные углы являются дополнительными в равнобедренной трапеции.
Основываясь на углах основания, диагоналях и сумме противоположных углов, она может посадить свой сад и быть уверенной, что его форма действительно представляет собой равнобедренную трапецию.
Резюме урока
На этом уроке вы узнали, что трапеция с равными, непараллельными сторонами — это равнобедренная трапеция . Затем мы рассмотрели важные теоремы, связанные с ними, и подробно доказали их.
- Базовые углы (углы, образованные между непараллельными сторонами и параллельными сторонами) равны равнобедренной трапеции.

- Диагонали равнобедренной трапеции равны по длине.
Доказательства для равнобедренных трапеций — Видео и стенограмма урока
Углы при основании
Углы, образованные между непараллельными сторонами и параллельными сторонами, называемые углами при основании , равны в равнобедренной трапеции. В газонной трапеции Ирины ABCD углы C и D равны.
Чтобы доказать эту теорему, проведем прямую CE , параллельную AD , так, чтобы ADCE стала параллелограммом.
В этом параллелограмме мы знаем, что линия AD = линия CE . Мы также знаем, что строка AD = строка BC , поэтому мы также знаем, что строка BC = строка CE .
Теперь, поскольку линия BC и линия CE равны, треугольник BCE становится равнобедренным. Следовательно, углы CBE и CEB равны.
Следовательно, углы CBE и CEB равны.
Мы понимаем, что линия AD и линия CE параллельны, а линия AE является поперечной. Итак, сумма внутренних углов на одной стороне, угол DAE и угол CEA составляет 180 градусов.
Итак,
Следовательно, углы DAB и CBA равны.
Далее, мы знаем, что ADCE является параллелограммом, поэтому противоположные углы будут равны.
Теперь углы CBE и BCD будут равны, потому что они являются альтернативными внутренними углами для параллельных прямых AE и CD .
Мы уже знаем, что углы CEB и CEB равны. Следовательно,
Следовательно,
Таким образом, доказано, что углы при основании равнобедренной трапеции равны.
Диагонали
Диагонали равнобедренной трапеции равны по длине. Итак, в равнобедренной трапеции Ирины ABCD диагонали AC и BD равны.
Чтобы доказать эту теорему, давайте сосредоточимся на двух сформированных треугольниках: DAC и CBD .Здесь мы знаем, что прямая AD = BC , углы ADC и BCD равны, а сторона CD общая. Ирэн вспоминает о свойстве треугольников сторона-угол-сторона : если в двух треугольниках две стороны и их угол первого треугольника конгруэнтны двум сторонам и их углу второго треугольника, то эти два треугольника конгруэнтны. .
Следовательно, треугольники DAC и CBD равны.
Следовательно, остальные соответствующие стороны равны, AC = BD .Таким образом, диагонали равны.
Противоположные углы
Сумма противоположных углов равнобедренной трапеции Ирины равна 180 градусам. Она может доказать это, зная, что угол A равен углу B , а угол C равен углу D .
Она также знает, что AB параллельна CD , что делает пары углов A и D и B и C внутренними углами на внутренних углахЭто означает, что эти пары являются дополнительными или их сумма равна 180 градусам.
Теперь, заменив равные углы,
Таким образом, она доказывает, что в равнобедренной трапеции противоположные углы являются дополнительными.
Основываясь на углах основания, диагоналях и сумме противоположных углов, она может посадить свой сад и быть уверенной, что его форма действительно является равнобедренной трапецией.
Подведение итогов
В этом уроке вы узнали, что трапеция с равными непараллельными сторонами является равнобедренной трапецией . Затем мы рассмотрели важные теоремы, связанные с ними, и подробно доказали их.
- В равнобедренной трапеции углы при основании (углы, образованные между непараллельными сторонами и параллельными сторонами) равны.
- Диагонали равнобедренной трапеции равны по длине.
- Сумма противоположных углов равнобедренной трапеции равна 180 градусов.
Свойства трапеции — Задача 1
Равнобедренная трапеция имеет два конгруэнтных катета и одну пару параллельных сторон. Углы при основании конгруэнтны друг другу, и из-за внутренних углов одной и той же стороны верхние углы являются дополнительными к соответствующим углам при основании, что означает, что они оба равны 180 ° — (мера угла при основании).
Итак, если дана мера одного из верхних углов, вы знаете, что его угол при основании является дополнительным к нему, поэтому вычтите его значение из 180°, чтобы найти величину угла при основании.Затем вспомним, что в равнобедренной трапеции углы при основании равны. Другой верхний угол является дополнительным к его основанию, поэтому он равен верхнему углу. Таким образом, по одному углу равнобедренной трапеции можно найти размеры других углов.
В этой задаче у нас есть равнобедренная трапеция, что означает, что у нас есть два конгруэнтных катета, когда у нас есть пара параллельных сторон.Итак, давайте перейдем и посмотрим, что мы знаем о равнобедренных трапециях.
Итак, мы видим, что углы при основании, поэтому, если я смотрю на два угла при основании, они будут конгруэнтны друг другу. Мы также знаем, что внутренние углы одной и той же стороны здесь, поэтому я смотрю на эти треугольники прямо здесь, будут дополнительными, что является определением внутренней стороны одной и той же стороны.
Вернемся к нашей проблеме. Если я взгляну на единственное, что мы знаем об этой трапеции, а именно на угол B, равный 110 градусам, я мог бы начать с нахождения угла C.Ну, я знаю, что эти два должны быть дополнительными, потому что они находятся на одной стороне этой поперечной ВС. Итак, если B равно 110, C должен быть каким? 180 минус 110, что 70 градусов. Поэтому я собираюсь написать здесь, что C должно быть 70 градусов.
Теперь вам просто нужно помнить, что ваши углы при основании конгруэнтны друг другу. Итак, я напишу, что D должно быть 70 градусов, а A должно быть 110 градусов. Таким образом, мы сказали, что A было 110, а D мы сказали, что это 70 градусов. Ключевым моментом здесь было помнить, что внутренние углы одних и тех же сторон являются дополнительными и что углы при основании равнобедренной трапеции всегда равны.
Видео-вопрос: Нахождение меры угла в равнобедренной трапеции с использованием ее свойств
Стенограмма видео
Показанный динамик представляет собой равнобедренную трапецию. Если угол 𝐹𝐽𝐻 равен 82 градусам, найдите угол 𝐹𝐺𝐻.
Если угол 𝐹𝐽𝐻 равен 82 градусам, найдите угол 𝐹𝐺𝐻.
Давайте выделим эту трапециевидную форму и учтем тот факт, что угол 𝐹𝐽𝐻 равен 82 градусам. Можно вспомнить, что трапеция или трапеция – это четырехугольник с одной парой параллельных сторон.Далее нам говорят, что этот динамик представляет собой равнобедренную трапецию. Это означает, что непараллельные стороны в этом четырехугольнике равны. Значит, здесь длина стороны 𝐹𝐽 будет равна стороне 𝐺𝐻.
Чтобы найти этот неизвестный угол 𝐹𝐺𝐻, нам нужно использовать свойства равнобедренных трапеций. Поскольку у нас есть два конгруэнтных катета, мы можем сказать, что нижние углы при основании равны, а верхние углы при основании равны. Таким образом, угол 𝐹𝐽𝐻 будет таким же, как угол 𝐺𝐻𝐽.И углы при основании равны. Значит, угол 𝐺𝐹𝐽 равен углу 𝐹𝐺𝐻. Мы могли бы найти меру угла 𝐹𝐺𝐻, используя ряд различных методов. Однако, пожалуй, самый быстрый способ — использовать это свойство конечной равнобедренной трапеции.
Любой нижний угол основания является дополнительным к любому верхнему углу основания. Это означает, что они добавят 180 градусов. Мы знаем, что это правда, потому что у нас есть пара параллельных сторон. Следовательно, угол нижнего основания и угол верхнего основания в сумме составляют 180 градусов.Таким образом, мы можем составить уравнение, согласно которому этот верхний угол при основании, который мы хотим найти, угол 𝐹𝐺𝐻, плюс этот нижний угол при основании 𝐹𝐽𝐻 должны быть равны 180 градусам. Мы можем подставить информацию о том, что угол 𝐹𝐽𝐻 равен 82 градусам. А затем вычитание 82 градусов из обеих частей уравнения даст нам, что угол 𝐹𝐺𝐻 равен 98 градусам.
Это означает, что они добавят 180 градусов. Мы знаем, что это правда, потому что у нас есть пара параллельных сторон. Следовательно, угол нижнего основания и угол верхнего основания в сумме составляют 180 градусов.Таким образом, мы можем составить уравнение, согласно которому этот верхний угол при основании, который мы хотим найти, угол 𝐹𝐺𝐻, плюс этот нижний угол при основании 𝐹𝐽𝐻 должны быть равны 180 градусам. Мы можем подставить информацию о том, что угол 𝐹𝐽𝐻 равен 82 градусам. А затем вычитание 82 градусов из обеих частей уравнения даст нам, что угол 𝐹𝐺𝐻 равен 98 градусам.
Мы могли бы, конечно, ответить и по-другому, помня, что углы в четырехугольнике в сумме составляют 360 градусов и при условии, что нижние углы при основании равны, а верхние углы при основании равны.Определив наши неизвестные углы при верхнем основании как букву 𝑥, мы могли бы составить альтернативное уравнение. Решив это, мы обнаружим, что каждый из углов при верхнем основании равен 98 градусам, что также подтверждает наш первоначальный ответ о том, что угол 𝐹𝐺𝐻 равен 98 градусам.
Угол равнобедренной трапеции: 2
Введение для угла равнобедренной трапеции:
Трапеция — четырехугольник с парой непараллельных поверхностей и дополнительными двумя параллельными поверхностями.Основание – параллельная сторона трапеции. Если две стороны, не параллельные друг другу, содержат равные длины, то трапеция называется равнобедренной трапецией. Углы при основании этой трапеции равны по размерности.
Угол равнобедренной трапеции
Углы равнобедренной трапеции:
угол равнобедренной трапецииc
Пусть PQRS — трапеция с параллельными сторонами PQ, а RS называется равнобедренной трапецией, если это строгая трапеция с QR = SP. Заметим, что если PQRS — параллелограмм, то это (нестрогая) трапеция с QR = SP.
Сумма внутренних углов любого многоугольника = (n – 2) * 180°.
Здесь равнобедренная трапеция имеет четыре стороны
Итак, внутренний угол = (4 – 2)*180 градусов = 360°.
Внешний угол любого четырехугольника равен 360°
Значит, внешний угол равнобедренной трапеции равен 360°.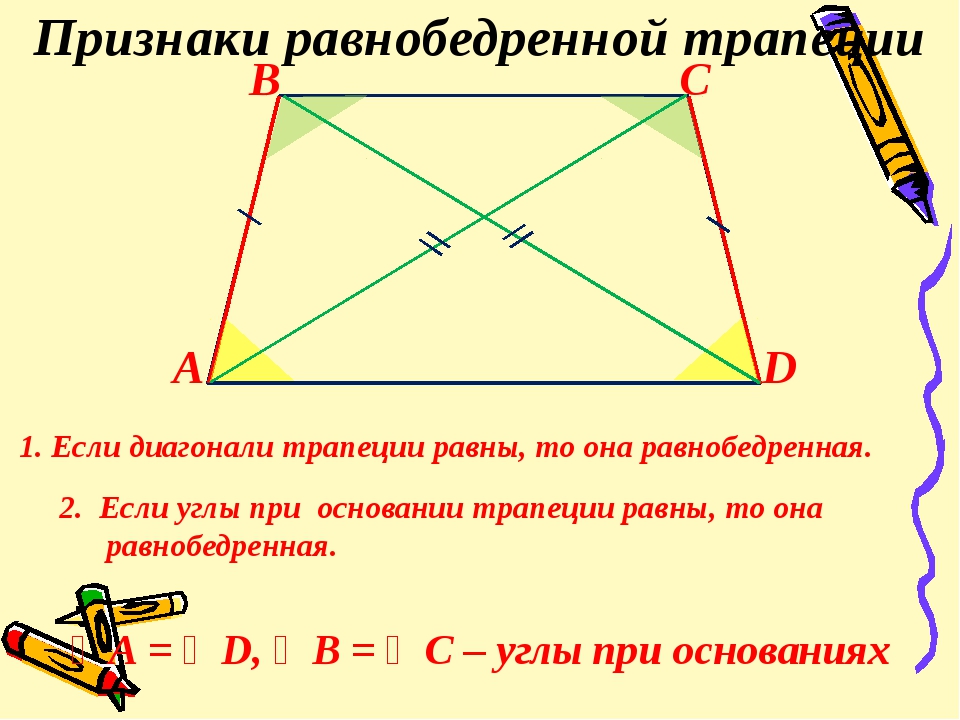
Базовые углы:
Угол равнобедренной трапецииx
У равнобедренной трапеции углы при основании равны.
`/_`QPS = `/_`RSP
`/_`PQR= `/_`SRQ
Линия симметрии равнобедренной трапеции:
Угол равнобедренной трапеции1
Одна линия симметрии равнобедренной трапеции, потому что эти углы равны.
Характеристика равнобедренных трапеций
Углы при основании равнобедренной трапеции равны.
Диагонали равнобедренной трапеции равны
Противолежащие углы вспомогательные.
Сложение двух смежных углов равно 180°
Равнобедренная трапеция с определенным углом и диагональю.
Сумма всех внутренних углов равна 360°
Центр трапеции — отрезок, соединяющий середины непараллельной поверхности.
Имеет аналогичные базы. Его протяженность равна половине сложения длин оснований.
Углы на любой поверхности оснований одинаковой величины/меры (конгруэнтны).
Пример задач для угла равнобедренной трапеции:
Пример 1:
Какова мера `/_`PSR , если `/_`QPS составляет 45 °,?
Решение:
Угол равнобедренной трапецииz
`/_` PSR равен 45°, так как углы при основании равны
Мой предстоящий пост посвящен тому, как найти площадь трапеции на примере, и эта тема Объем трапециевидной призмы даст вам больше понимания об алгебре
Пример 2:
Какой еще угол равен 120°, если `/_`PQR = 120°?
Решение:
угол равнобедренной трапецииb
Смежный угол для `/_`PQR равен `/_`QRS
Итак, `/_`QRS измеряет 120°.
Нравится:
Нравится Загрузка…
РодственныеДиагонали равнобедренной трапеции
Это было за день до теста на полигонах, и я подумал, что было бы полезно написать доказательство, а затем дать отзыв о доказательстве другой команды.
Студенты несколько минут работали в одиночку, размышляя над тем, что было дано и что могло подразумеваться. Затем они работали со своей командой, чтобы обсудить свои идеи и приступить к планированию доказательства.
У некоторых было хорошее начало.
Некоторые, очевидно, занимались поиском и использованием структуры .
Некоторые застряли.
Я поговорил с несколькими группами, выслушал их план, задал несколько вопросов, чтобы расшевелить их.
И тут у меня достала цветная бумага, на которой нужно написать доказательство команды.
Часы тикали, но я думал, что они наверняка смогут обменяться доказательствами с другой командой для обратной связи в течение нескольких минут.
Я разговаривал с другой группой. Они отражали ∆ABC относительно линии AC.
Каким будет изображение ∆ABC относительно линии AC?
Ответ? ∆ACD.
Конечно, это неправильно. Кажется настолько очевидным, что ∆ABC не конгруэнтно ∆ACD. И мне также интересно, как это поможет нам доказать, что AC=BD, поскольку BD не находится ни в одном из этих треугольников. Но вот где эта команда студентов. Теперь у меня есть возможность поддержать их продуктивную борьбу , или я могу остановить продуктивную борьбу, дав им свое объяснение.
Мой выбор? Ножницы. и бумага. И еще время.
Что произойдет, если отразить ∆ABD относительно линии AC?
О! Треугольники не равны.
Итак, существуют ли конгруэнтные треугольники, которые могут привести нас к диагоналям?
∆ABC конгруэнтно ∆BAD.
Откуда ты знаешь?
Отражение.
О чем?
Этот карандаш!
Так что же важного в линии, которую проводит карандаш?
Это линия симметрии трапеции.
Проходит через средние точки.
(Один из членов команды использовал программное обеспечение для динамической геометрии, чтобы отразить ∆ABC в разгар нашего разговора, но у меня нет фотографий ее работы.)
План состоял в том, чтобы команда написала свои доказательства на цветной бумаге, а затем обменялась с другими командами для получения отзывов. Отличная идея, правда? Итак, как поступить, когда осталось 15 минут? Действовать в соответствии с планом и позволить им давать обратную связь без обсуждения всем классом? Или устроить обсуждение всего класса, чтобы соединить студенческую работу? Потому что, как оказалось, нет двух команд, доказывающих конгруэнтность диагоналей одинаково.Я выбрал последнее.
Я попросил первую команду поделиться своей работой.
Их доказательство нуждается в доработке. Но у них есть хорошая идея.
Они доказали, что ∆AMD≅∆BMC, что делает соответствующие стороны конгруэнтными, поэтому с помощью подстановки и постулата сложения отрезков мы можем показать, что диагонали конгруэнтны.
Затем я попросил команду поделиться тем, кто доказал ∆ABC≅∆BAD, используя размышления о линии, содержащей середины оснований.Их письменное доказательство тоже нуждается в доработке. Но у них была хорошая идея.
Другая команда доказала ∆ACD≅∆BDC.
Другая команда построила биссектрисы оснований. Так как основания параллельны, то прямая, перпендикулярная одному из них, будет перпендикулярна и другому. Я не уверен, что они нашли причину, по которой серединные перпендикуляры должны быть параллельными. Они могли бы использовать ∆AZD≅∆BZC, чтобы показать это. Вместо этого они использовали точку Z на обеих серединных перпендикулярах (они знают, что любая точка на серединном перпендикуляре отрезка равноудалена от концов отрезка), чтобы сделать вывод, что ∆AZB и ∆DZC равнобедренные, а затем использовали сложение отрезков. Постулат и замена, чтобы показать, что диагонали конгруэнтны.Не идеально. Но хорошее начало.
Обсуждение Принципов действий NCTM по поддерживает продуктивную борьбу в изучении математики говорит: «Учителя иногда воспринимают разочарование учеников или отсутствие немедленных успехов как индикаторы того, что они каким-то образом подвели своих учеников. В результате они спешат «спасти» учеников, разбивая задачу и шаг за шагом помогая ученикам преодолевать трудности. Несмотря на благие намерения, такое «спасение» подрывает усилия учащихся, снижает когнитивную потребность в задаче и лишает учащихся возможности полностью погрузиться в осмысление математики.
Итак, хотя я и не спас своих учеников, мы так и не смогли получить образцовое доказательство того, что диагонали равнобедренной трапеции конгруэнтны. Узнали ли они что-то о , поняли проблемы и настойчиво решили их ? Конечно. Этого достаточно?
Было бы полезно начать урок следующего года с этой студенческой работы? Или это отменяет продуктивную борьбу ?
Просто надо найти баланс между продуктивной борьбой и образцовой работой, которая на одних уроках дается легче, чем на других? Если да, то на этом уроке я не справился с этим балансом. Тем не менее, путешествие продолжается…
Тем не менее, путешествие продолжается…
Нравится:
Нравится Загрузка…
Родственные
Как найти внутренние углы равнобедренной трапеции? — Ответы на все
Как найти внутренние углы равнобедренной трапеции?
Пояснение: Сумма углов любого четырехугольника равна 360°. Обратите внимание, как можно составить два треугольника с вершинами также на трапеции.Сумма внутренних углов каждого треугольника равна 180˚, поэтому, поскольку можно создать два треугольника, сумма внутренних углов равна 180˚×2=360˚.
Чему равна сумма углов равнобедренной трапеции?
Сумма противоположных углов равнобедренной трапеции равна 180 градусов.
Чему равны внутренние углы равнобедренного треугольника?
Равнобедренных треугольника всегда имеют два эквивалентных внутренних угла, и все три внутренних угла любого треугольника всегда имеют сумму градусов.Так как это остроугольный равнобедренный треугольник, то все внутренние углы должны быть острыми.
Дополнительны ли внутренние углы одинаковых сторон равнобедренной трапеции?
Круто! Теперь, если трапеция равнобедренная, то стороны конгруэнтны, и каждая пара углов основания конгруэнтна. Другими словами, нижние углы при основании равны, и верхние углы при основании также равны. Точно так же из-за односторонних внутренних углов нижний угол основания является дополнительным к любому верхнему углу основания.
Сумма углов трапеции равна 360?
Пояснение: Сумма углов любого четырехугольника равна 360°, а свойства равнобедренной трапеции диктуют, что наборы углов, соединенные параллельными прямыми (в данном случае нижний набор и верхний набор углов), равны.
Какие углы трапеции являются дополнительными?
Найдите угол в трапеции: пример Вопрос № 5 Не может быть определен на основе данной информации. Объяснение: В трапеции углы на одном катете (называемые смежными углами) являются дополнительными, то есть их сумма составляет градусы. а градусы измерения угла — это смежные углы, которые являются дополнительными.
а градусы измерения угла — это смежные углы, которые являются дополнительными.
Все ли углы равнобедренной трапеции равны?
Равнобедренная трапеция имеет одну пару параллельных сторон и другую пару конгруэнтных сторон (означает, что они равны по длине). В равнобедренной трапеции длины диагоналей равны, и по конгруэнтности SSS докажем, что углы при основании равны.
Равны ли противоположные углы равнобедренной трапеции?
Противоположные стороны равнобедренной трапеции имеют одинаковую длину (конгруэнтны).Углы по обе стороны от оснований имеют одинаковую величину/меру (конгруэнтность). Диагонали (здесь не показаны) равны.
Какие углы в треугольнике?
В евклидовом пространстве сумма мер этих трех углов любого треугольника неизменно равна прямому углу, также выражаемому как 180°, π радианам, двум прямым углам или полуобороту….
- СУММА УГЛОВ ТРЕУГОЛЬНИКА ВСЕГДА 180.
- ВНЕШНИЙ УГОЛ РАВЕН СУММЕ ДВУХ ВНУТРЕННИХ ПРОТИВОПОЛОЖНЫХ УГЛОВ.

Какие прямые на трапеции параллельны?
Трапеция – это четырехугольник, у которого ровно одна пара параллельных сторон. Параллельные стороны называются основаниями, а две другие стороны – катетами. А поскольку основания параллельны, мы знаем, что если секущей пересекают две параллельные прямые, то последовательные внутренние углы являются дополнительными.
Имеет ли равнобедренная трапеция дополнительные углы?
Равнобедренные трапеции имеют две противоположные и параллельные стороны.Углы, прилежащие к каждой непараллельной стороне, являются дополнительными. Углы, прилежащие к каждой параллельной стороне, равны.
Имеют ли трапеции дополнительные внутренние углы с одинаковыми сторонами?
Трапеция – это четырехугольник, у которого ровно одна пара параллельных сторон. Параллельные стороны называются основаниями, а две другие стороны – катетами. Точно так же из-за односторонних внутренних углов нижний угол основания является дополнительным к любому верхнему углу основания.
Смежны ли противоположные углы трапеции?
Да, противоположные углы трапеции являются дополнительными.Дополнительные углы трапеции определяются как сумма двух противоположных углов 180…
Каковы наилучшие углы равнобедренной трапеции?
Найдите угол в трапеции : Пример Вопрос № 4 Пояснение: Сумма внутренних углов всех четырехугольников равна 360°. У равнобедренных трапеций два верхних угла равны друг другу. Точно так же равны друг другу и два нижних угла.
Четырехугольники — Трапеции | Shmoop
Трапеции
Последнее семейство четырехугольников — изгои.Они отличаются от остальных четырехугольников, вроде неуклюжего гостя на вечеринке четырехугольника.
В то время как остальные имеют конгруэнтные стороны и углы, о которых можно поболтать, эти четырехугольники просто висят возле закусочной. Время от времени они могут завязать разговор с одиноким многоугольником, который случайно забредет к ним, но это никогда не длится долго, и они просто снова смущенно смотрят себе под ноги.
Трапеция представляет собой четырехугольник с только одним набором параллельных сторон.Они абсолютно не могут иметь два набора параллельных сторон. Поэтому, когда трапеции начинают свою вечеринку после того, как их выгнали из четырехугольника, мы можем быть уверены, что прямоугольников, квадратов и параллелограммов точно не будет в списке гостей. Возьмите это, лохи.
Пример задачи
Является ли этот четырехугольник трапецией?
Сколько пар параллельных прямых вы видите? Верх и низ параллельны друг другу, как и две стороны.Поскольку здесь две пары параллельных прямых, а у трапеции должна быть только одна , это не трапеция. Извини, приятель.
Как и у воздушных змеев с их особыми диагоналями, у трапеций также есть части со специальными именами (хотя и не такими странными, как имена, которые мы имеем для наших частей). Трапеция имеет два основания, каждое из которых является одной из параллельных сторон. Две другие стороны, которые не параллельны друг другу, называются катетами трапеции.
Две другие стороны, которые не параллельны друг другу, называются катетами трапеции.
Поскольку параллельны только основания, а катеты — нет, мы можем рассматривать этот сценарий как две непараллельные секущие, пересекающие пару параллельных прямых.
Глядя на ∠1 и ∠2, мы видим, что они являются последовательными внутренними углами. То же самое касается ∠3 и ∠4. Мы уже знаем (благодаря нашему обширному опыту работы с параллельными прямыми), что последовательные внутренние углы являются дополнительными, поэтому мы доказали, что последовательные углы в трапеции, имеющие один и тот же катет, являются дополнительными.
Когда обе стороны трапеции имеют одинаковую длину, мы имеем особый тип четырехугольника, называемый равнобедренной трапецией .
Как и следовало ожидать, у равнобедренных трапеций конгруэнтные катеты, а также конгруэнтные последовательные углы, общие у основания. Конечно, в то время как у равнобедренных треугольников есть только одно «основание», с которым можно работать, у равнобедренных трапеций их два. Удвойте удовольствие, как мы говорим.
Удвойте удовольствие, как мы говорим.
Пример задачи
Если трапеция JANE равнобедренная и один из ее углов при основании равен 73°, то каковы градусы остальных трех углов?
Существует множество различных способов определения размеров ∠1, ∠2 и ∠3, но мы начнем с того факта, что в равнобедренной трапеции оба угла, имеющие общее основание, равны.Поскольку угол 73° и ∠3 имеют общее основание JE , они конгруэнтны. Другими словами, m∠3 = 73°.
Мы также знаем, что поскольку ∠2 и ∠3 являются последовательными внутренними углами, они являются дополнительными. Мы знаем меру ∠3, поэтому давайте найдем меру ∠2.
м∠2 + м∠3 = 180°
м∠2 + 73° = 180°
м∠2 = 180° – 73°
м∠2 = 107°
А как насчет ∠1? Поскольку у него общее основание с ∠2, эти два угла конгруэнтны друг другу. Это также означает, что m∠1 = 107°.
Мы можем перепроверить это, вспомнив, что все четырехугольники имеют внутренние углы, сумма которых равна 360°. Если мы возьмем сумму этих четырех углов, это число мы должны получить.
Если мы возьмем сумму этих четырех углов, это число мы должны получить.
73° + 73° + 107° + 107° ≟ 360°
360° = 360°
Да. Вот такие углы у нас получились. Насчет этого сомнений нет.
У каждого четырехугольника есть свои VIP, или очень важные многоугольники. И без того эксклюзивная трапециевидная клюшка не исключение. ВИПами семейства трапеций являются равнобедренные трапеции. Если они не славятся своими конгруэнтными углами основания и ногами, то их диагонали говорят сами за себя.Да, верно: у равнобедренных трапеций диагонали равны. Не верите нам? Мы дадим вам подсказку: это связано с чем-то, что называется SAS. (Нет, не «дерзко».)
Другой тип VIP в области трапеций — это прямая трапеция , которая имеет один прямой угол. Конечно, где бы ни находился этот прямой угол, за ним будет следовать еще один, потому что основания параллельны друг другу.
Хотя не все трапеции созданы одинаковыми, нам нужно что-то, чтобы объединить все трапеции, чтобы у них не было гражданской войны или чего-то в этом роде.

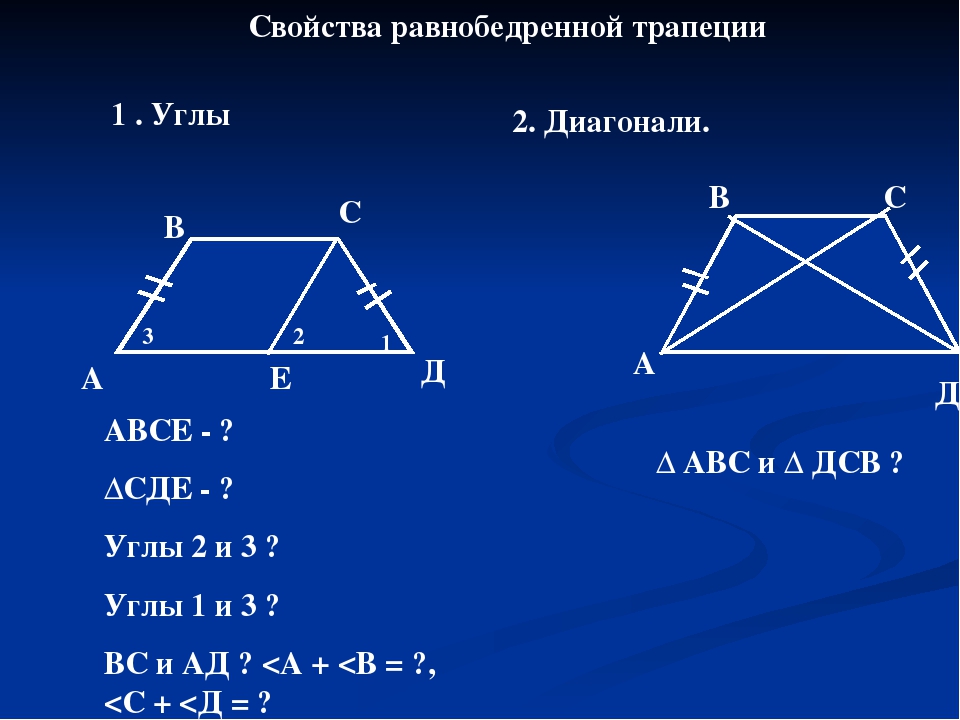 Спираль, Треугольник Рило, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межрасовый треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой дуговый многоугольник, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник
Спираль, Треугольник Рило, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межрасовый треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой дуговый многоугольник, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник Это трапеция с двумя противоположными ногами равной длины. Введите длину трех сторон, выберите количество десятичных знаков и нажмите «Рассчитать». Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать угловые единицы.
Это трапеция с двумя противоположными ногами равной длины. Введите длину трех сторон, выберите количество десятичных знаков и нажмите «Рассчитать». Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать угловые единицы.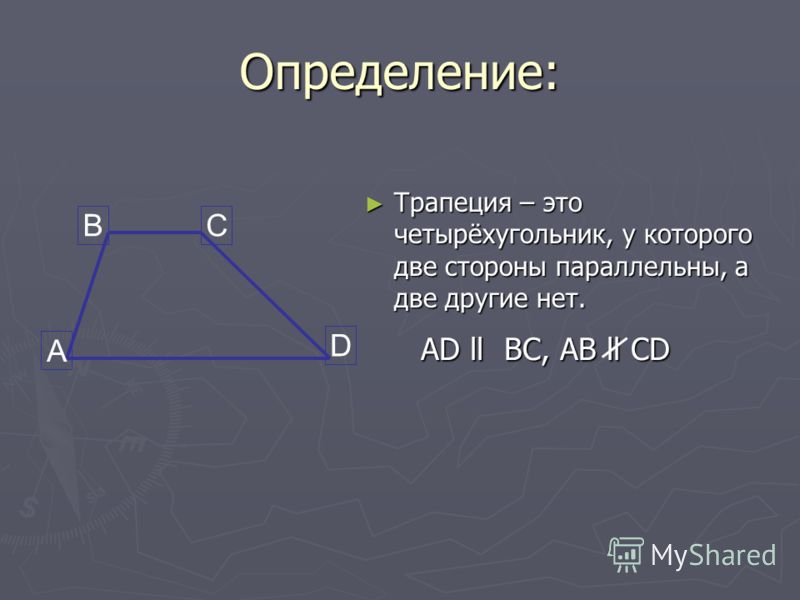 de Webprojects
de Webprojects