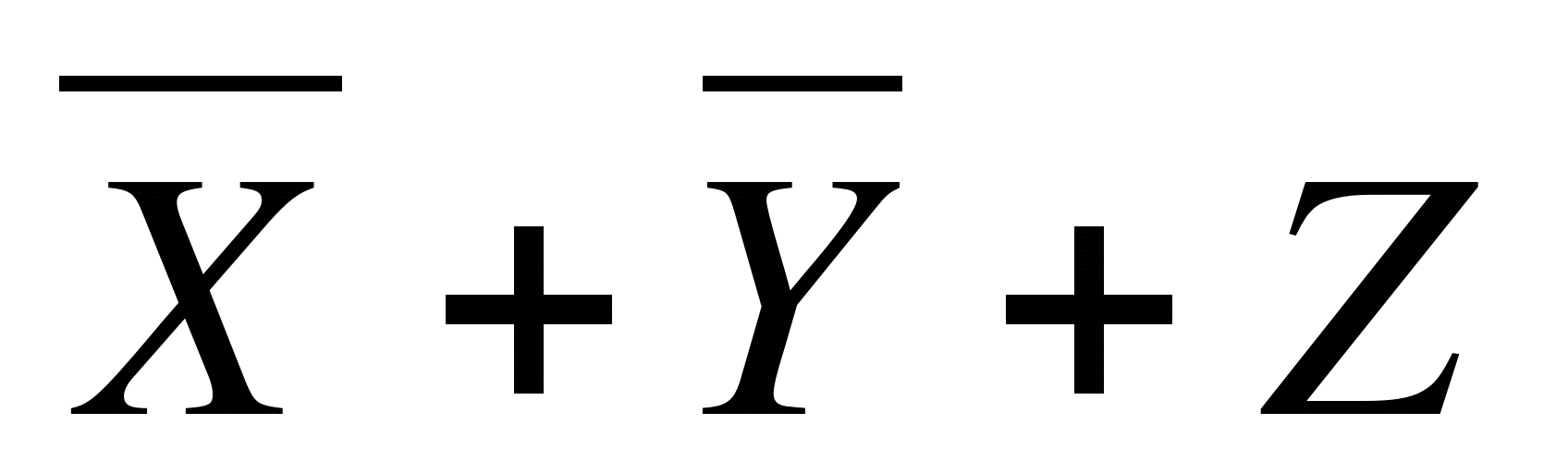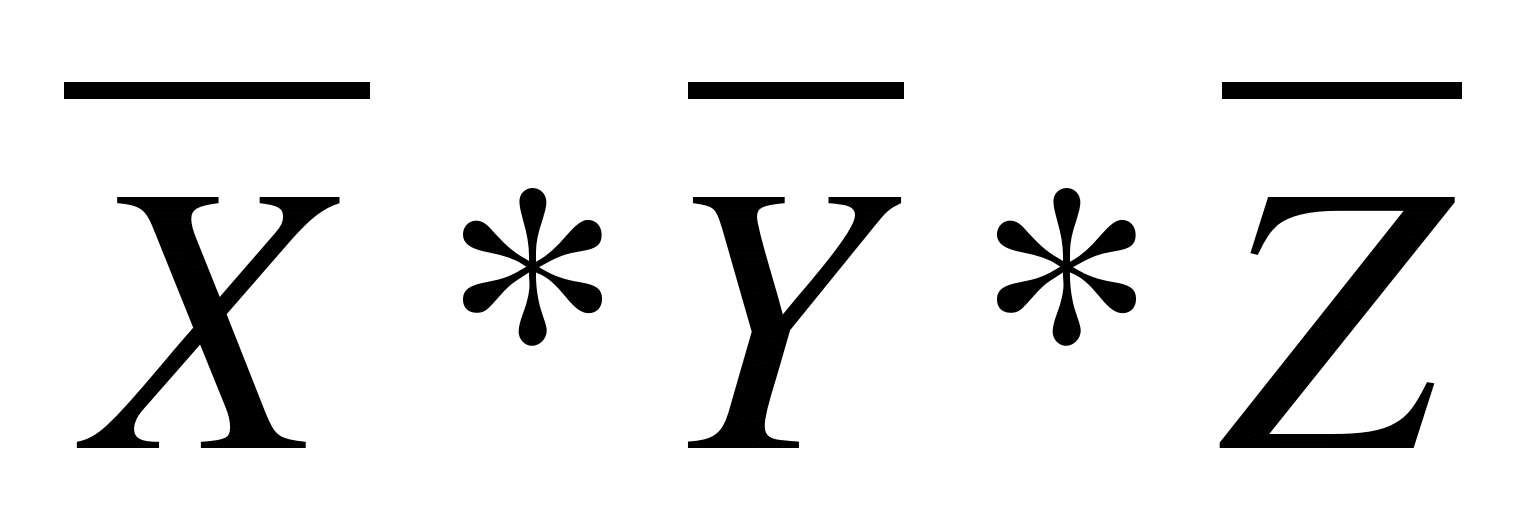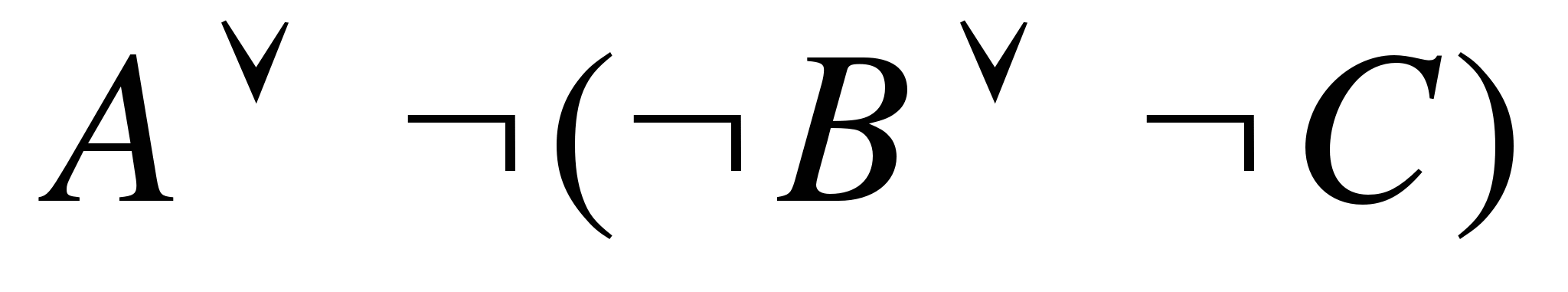3.3. Преобразование алгебраических выражений

Определение 3.8. Алгебраическим выражением называется выражение, составленное из чисел и переменных, знаков действия над ними (сложения, вычитания, умножения, деления, возведения в степень с рациональным показателем, извлечения арифметического корня) и скобок.

Два выражения называют тождественно равными, если при всех допустимых для них значениях переменных соответственные значения этих выражений равны. Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием выражения.

Различают целые рациональные, дробные рациональные и иррациональные выражения. К целым рациональным выражениям относят одночлены и многочлены. Способы их преобразования были рассмотрены в пункте 3.2.

При тождественных преобразованиях дробных рациональных выражений (то есть содержащих деление на выражение с переменной) используются следующие основные приемы.

1. Сокращение дробей, основанное на свойстве дроби: 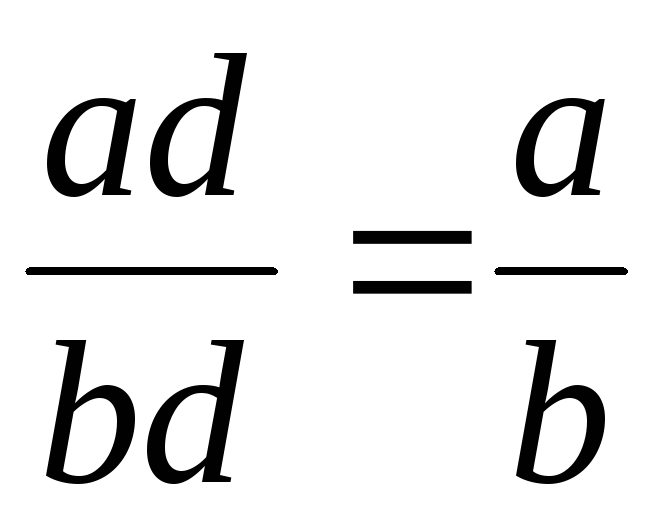. Например,

, ().

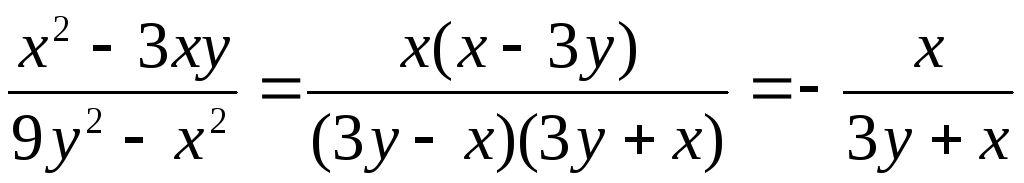2. Приведение к общему знаменателю – для этого необходимо:

1) разложить знаменатель каждой дроби на множители;

2) составить наименьший общий знаменатель;

3) домножив числитель и знаменатель каждой дроби на дополнительные множители, привести их к общему знаменателю.

Напомним, что действия над алгебраическими дробями осуществляются следующим образом

, ,.

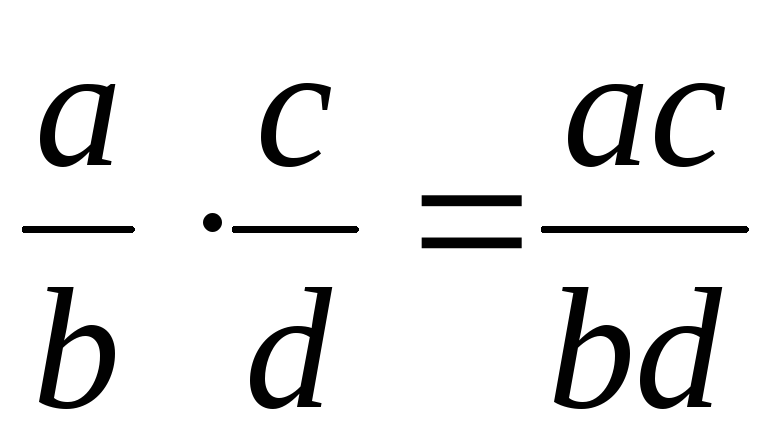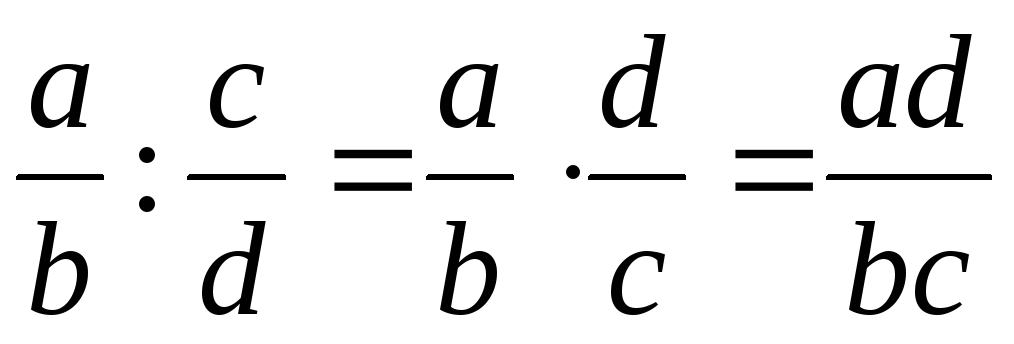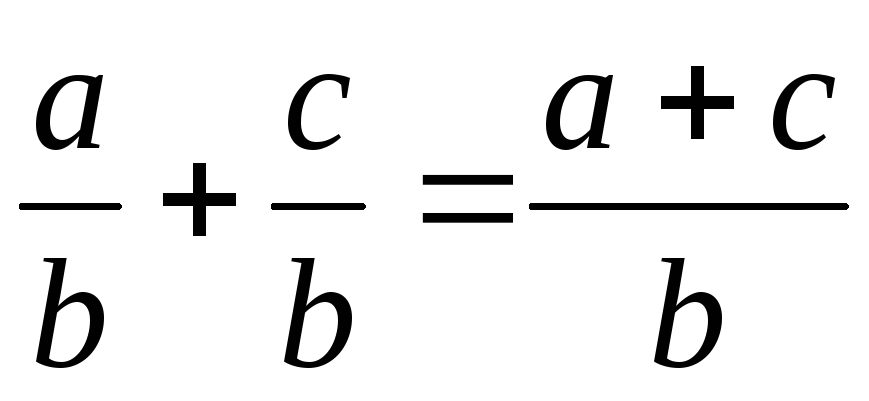Пример 3.12. Упростить выражение

.

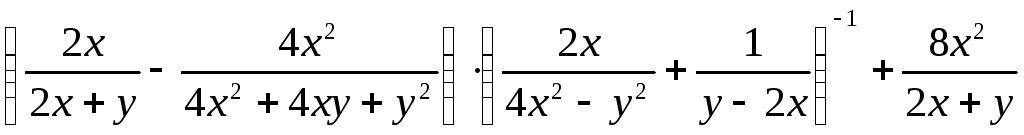Решение.

, ().

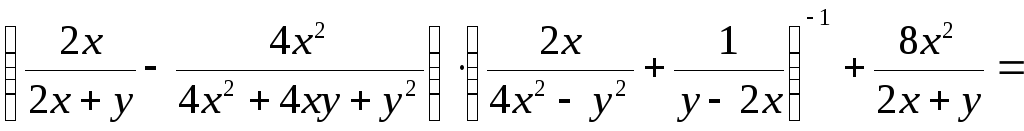
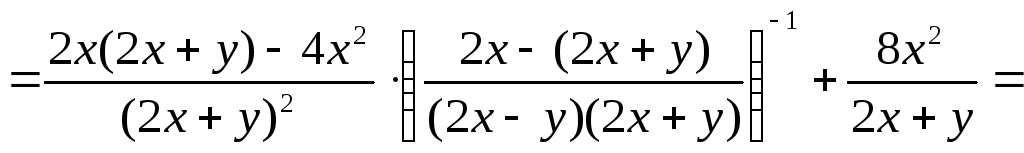
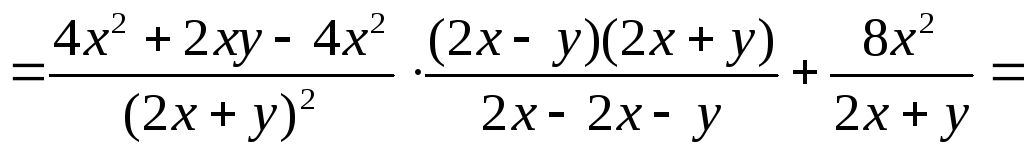
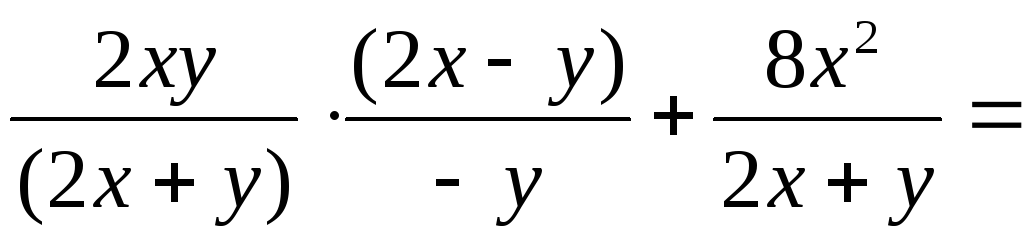
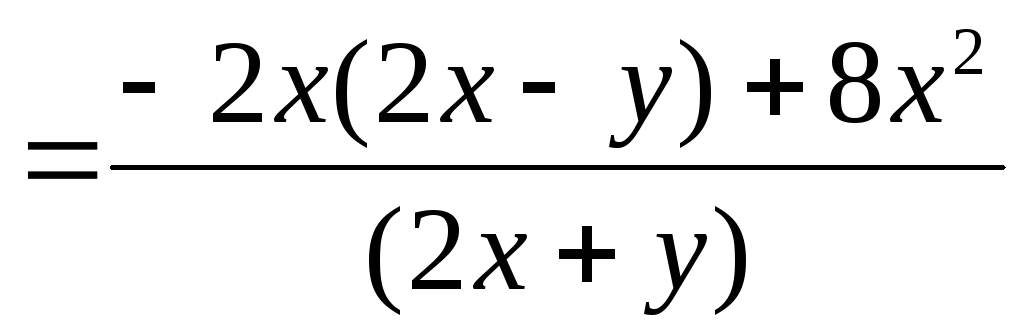
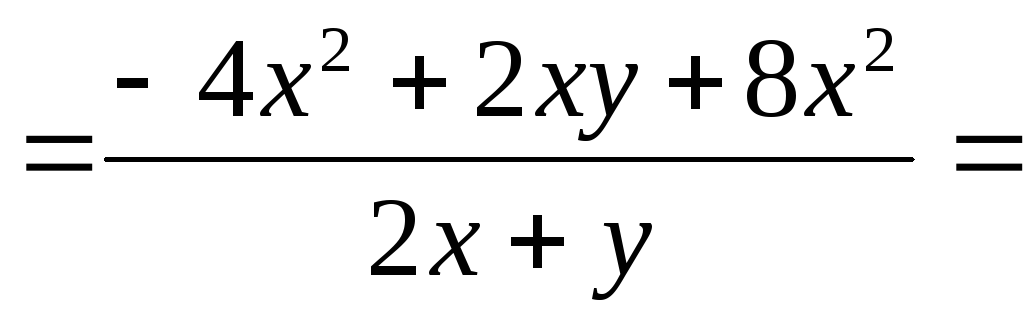
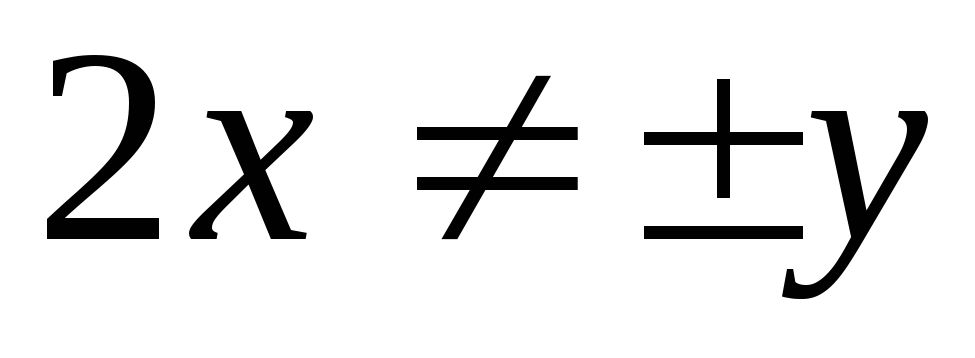Ответ: , ().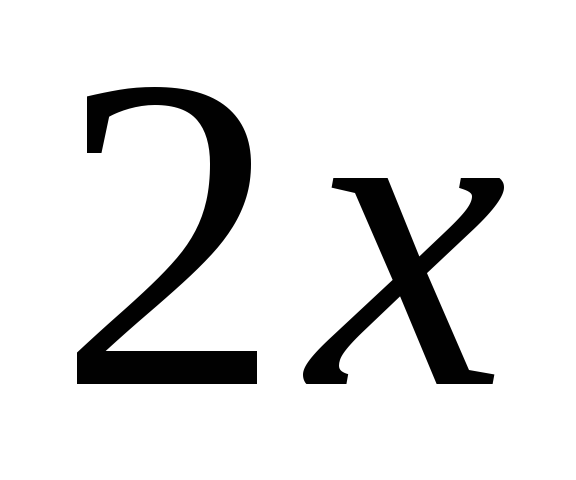

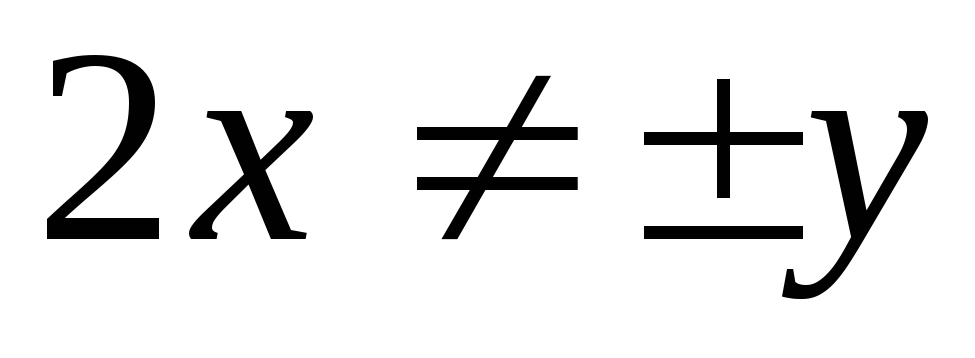Пример 3.13. Упростить выражение

.

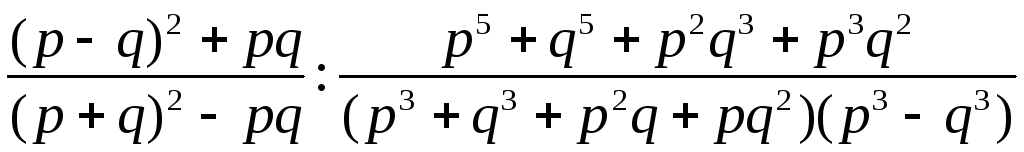Решение.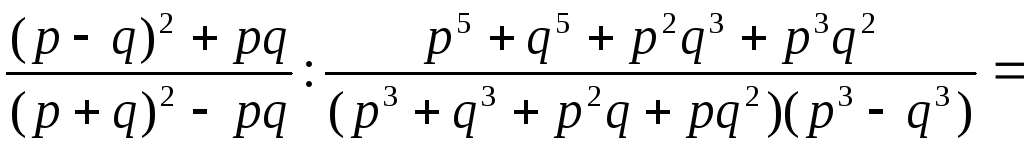

, (,).

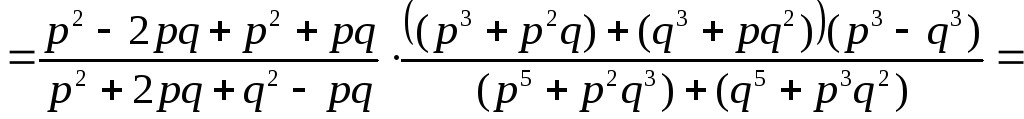
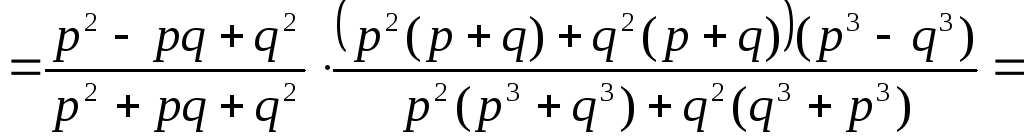
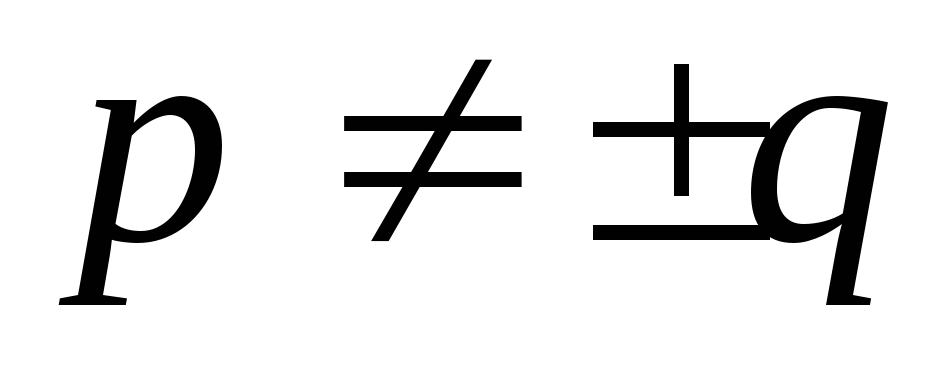Ответ: , (,).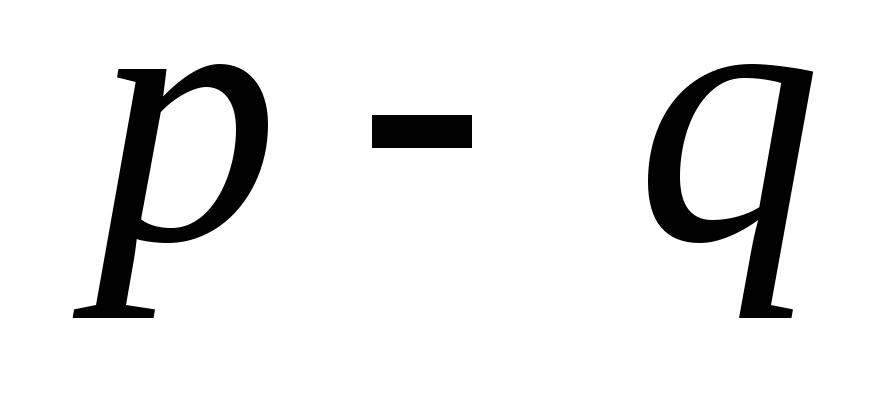

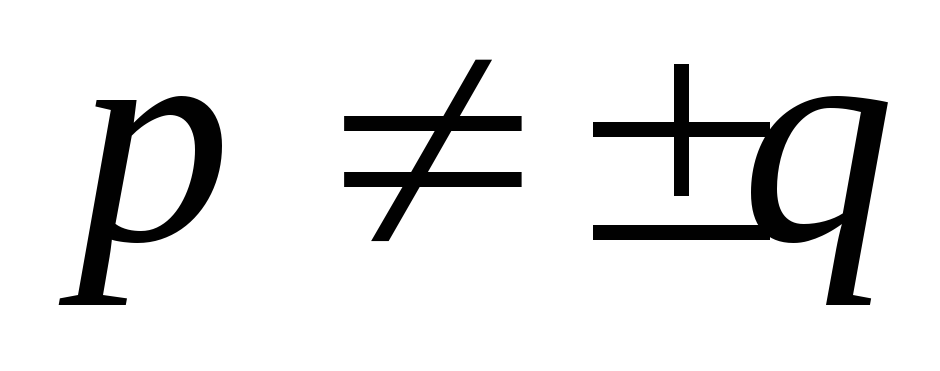Рассмотрим далее преобразование иррациональных выражений. Выражение называется иррациональным

, если оно содержит извлечение корня из переменной или возведение переменной в дробную степень. Как правило, тождественные преобразования выполняются на множестве неотрицательных чисел. При решении примеров мы будем это подразумевать и специально не оговаривать.

Пример 3.14. Упростить выражение .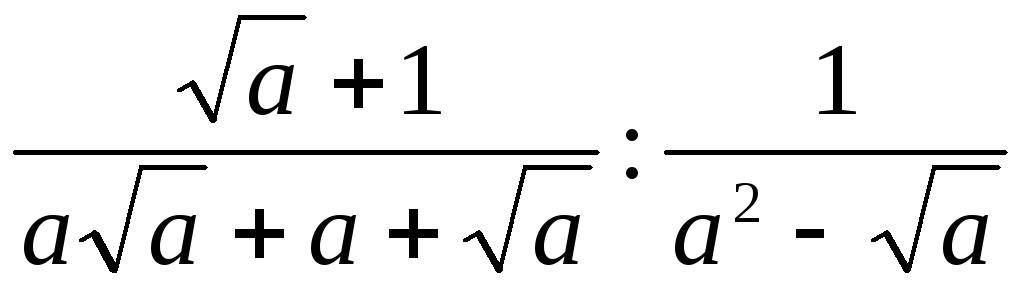

Решение.

.

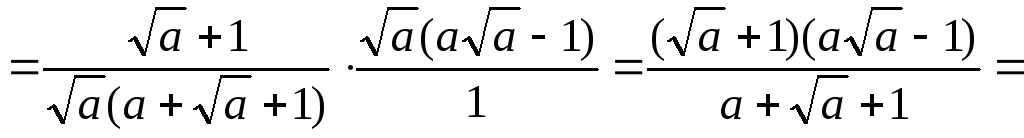
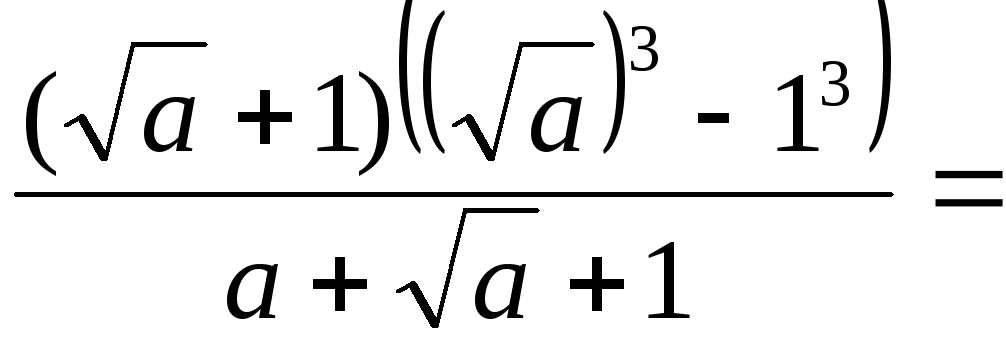
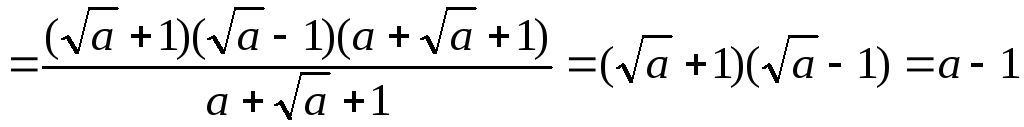Ответ:

.

Пример 3.15. Упростить выражение .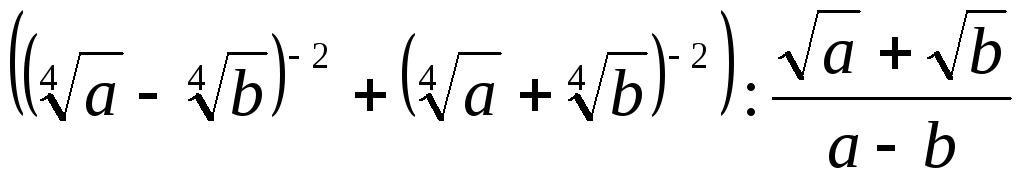

Решение.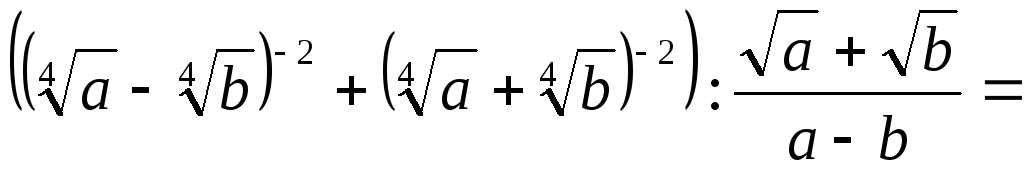

.

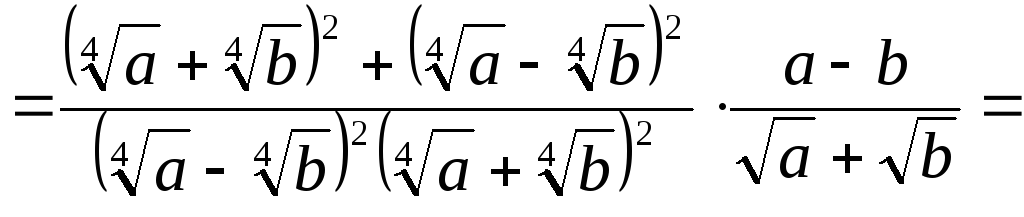
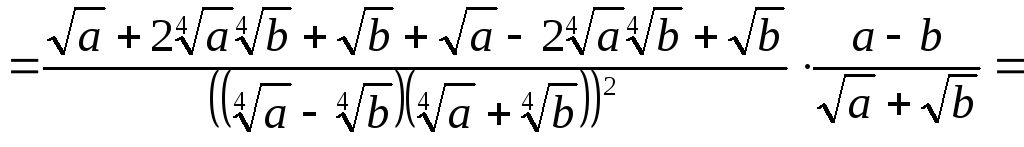
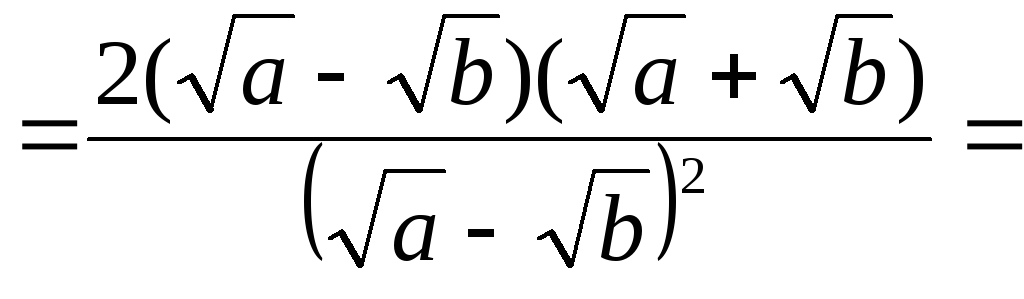
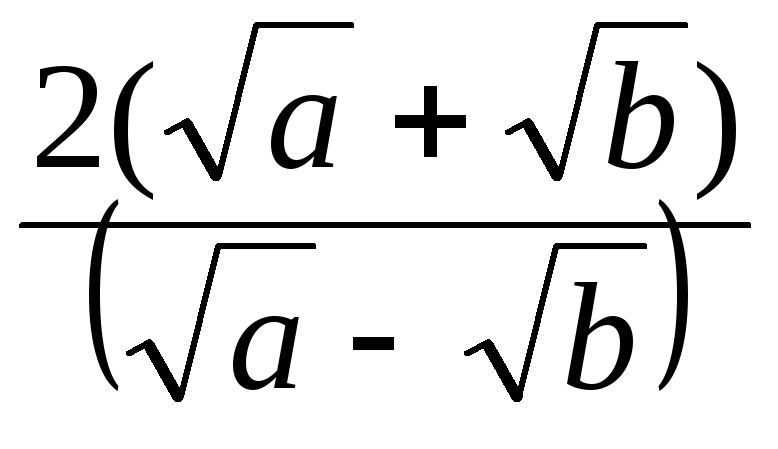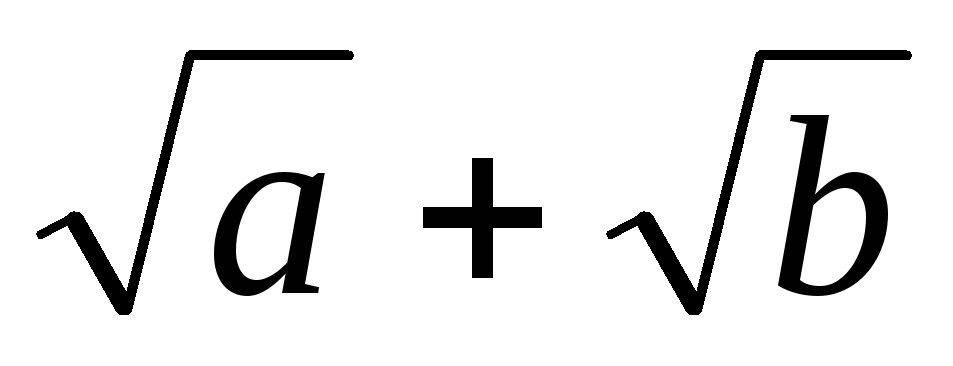Избавимся от иррациональности в знаменателе. Для этого домножим числитель и знаменатель на выражение, сопряженной к знаменателю, то есть на сумму . Получим

.

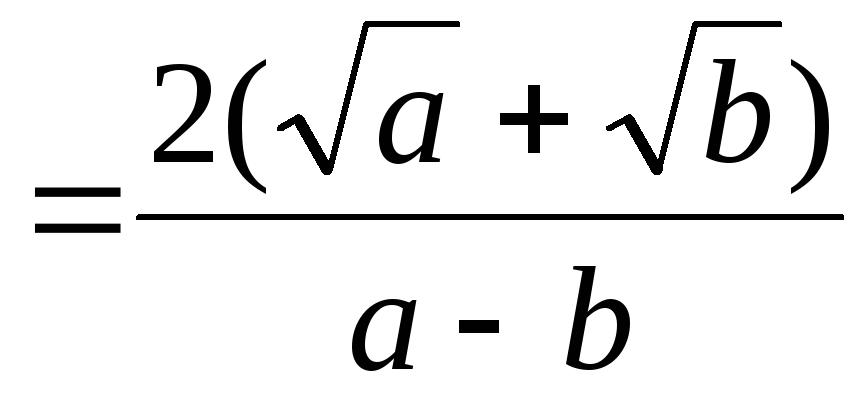Ответ: .

Пример 3.16. Упростить выражение

.

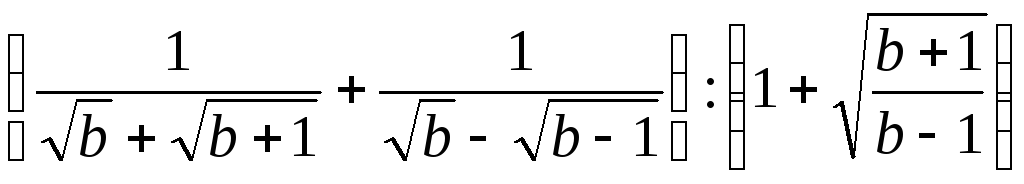Решение. Избавимся от иррациональности в знаменателе каждой из дробей в первой скобке:

,

.

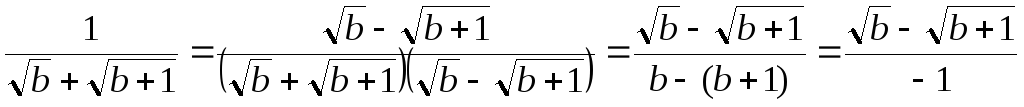
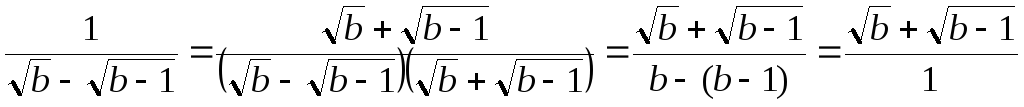Подстановка полученных выражений дает

.

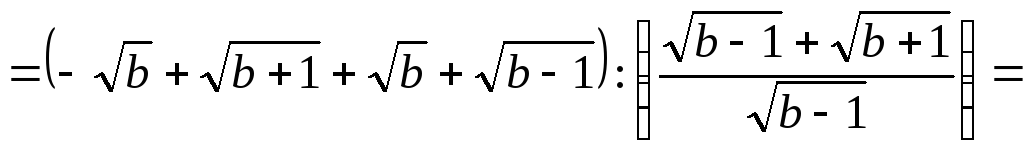
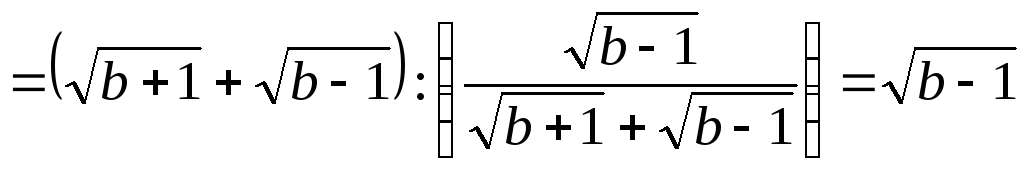Ответ: .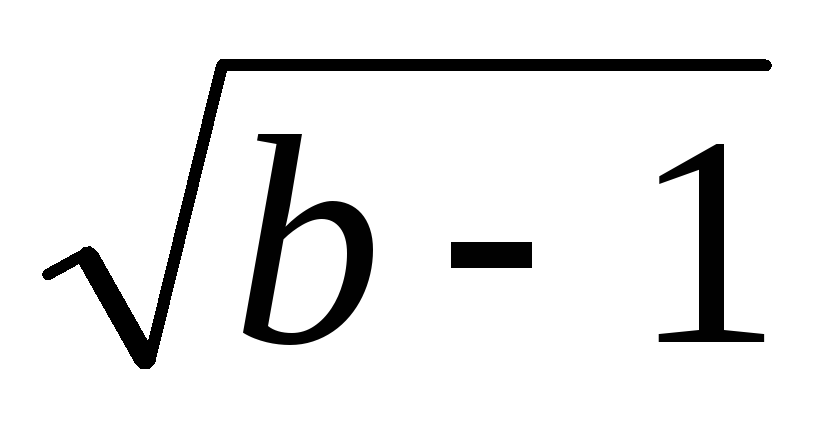

Пример 3.17. Упростить выражение

.

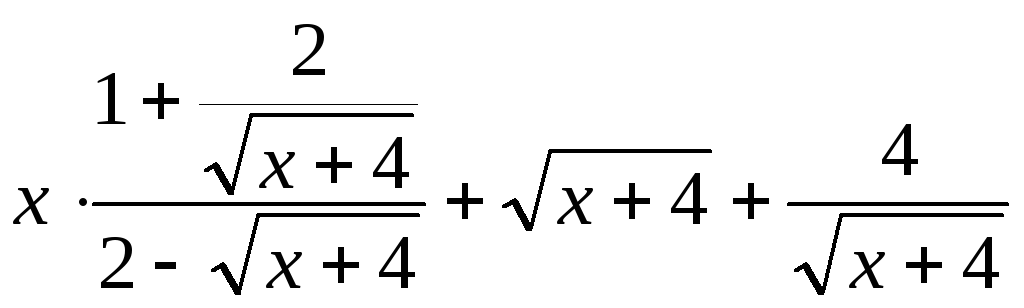Решение. Сделаем замену переменной 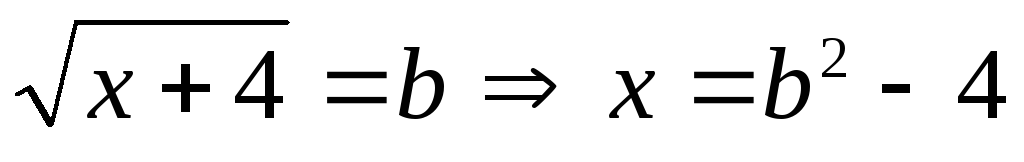. Тогда исходное выражение примет вид

.

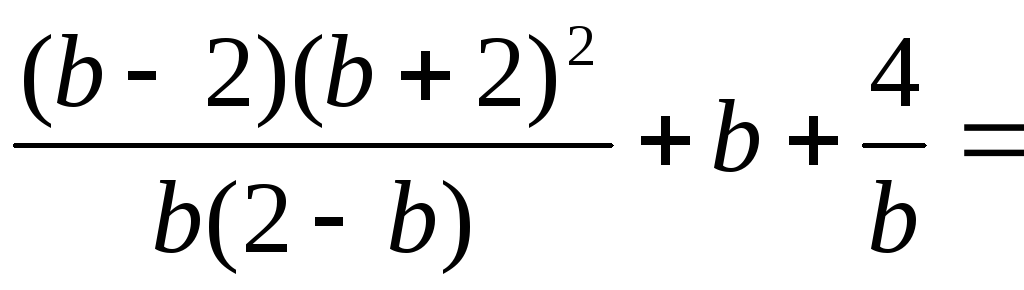
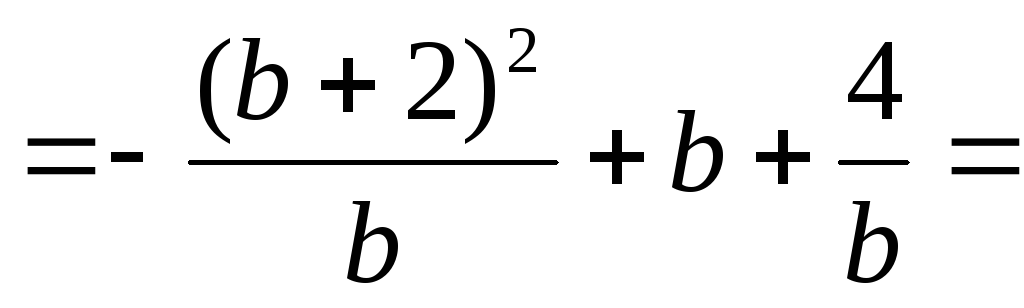
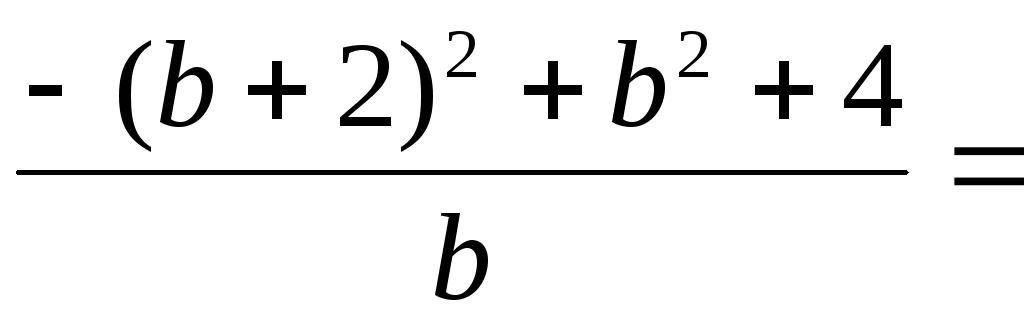
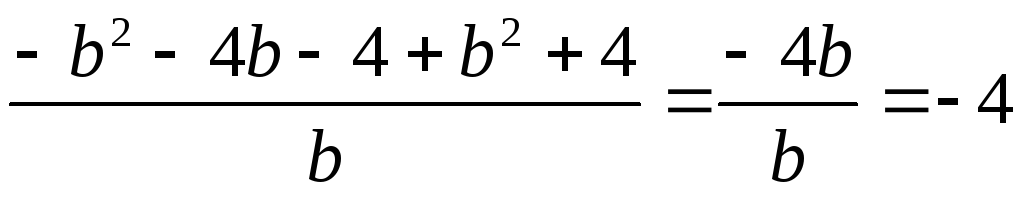Рассмотрим далее пример, содержащий произведение корней с различными показателями.

Ответ: .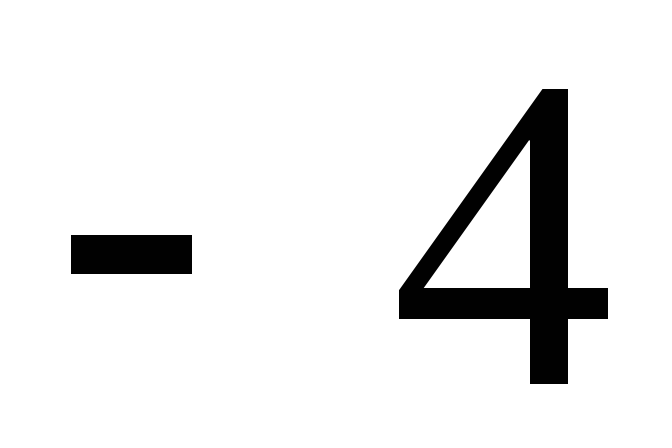

Пример 3.18. Упростить выражение .

Решение.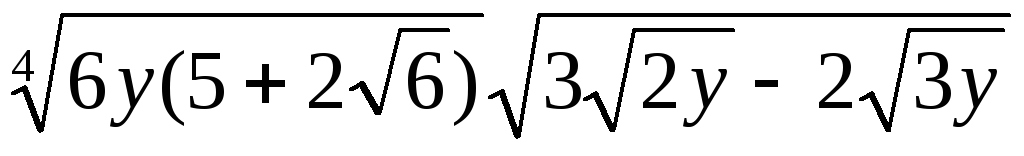

.

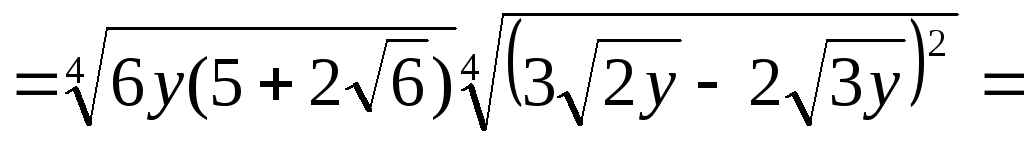
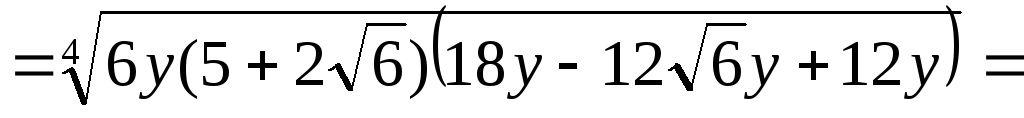
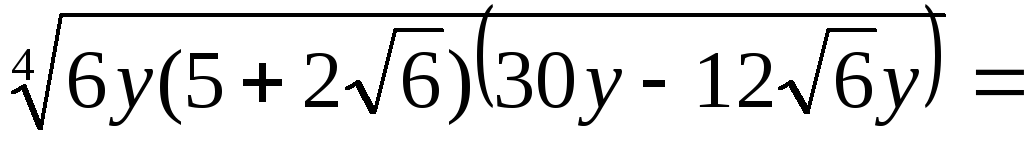
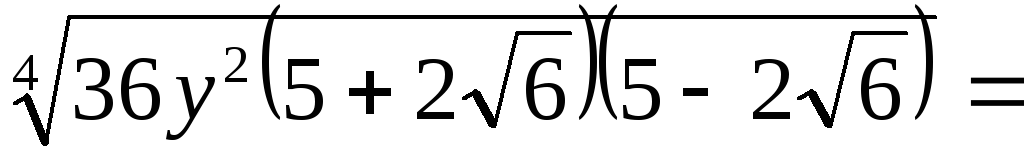
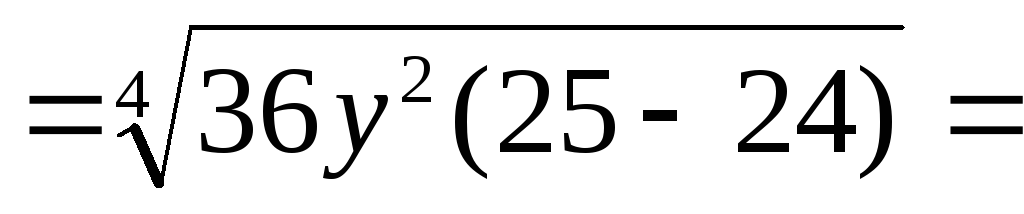
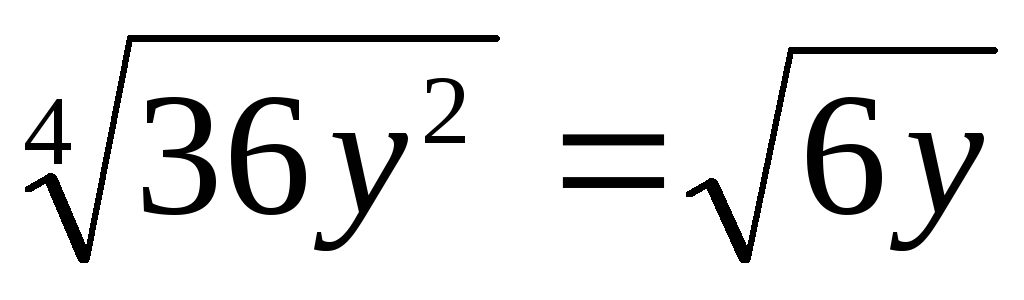Ответ: .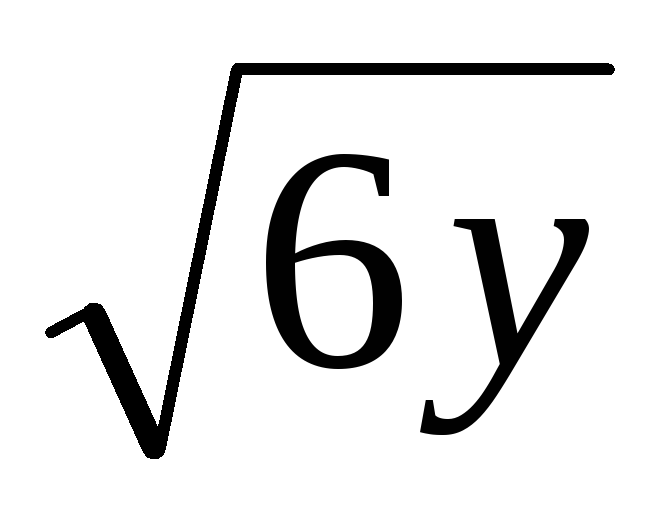

Пример 3.19. Вычислить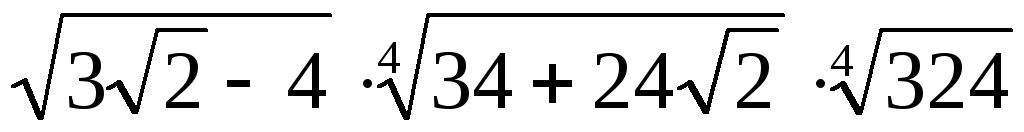

.

Решение. Заметим, что

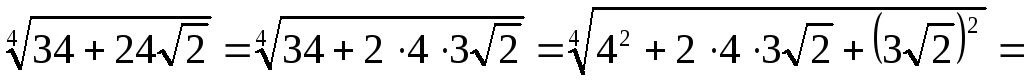
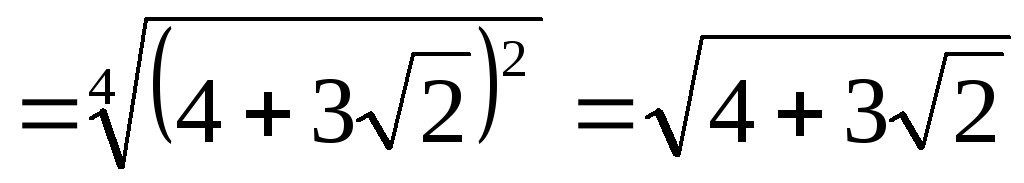, тогда

=.

Ответ: 6.

Пример 3.20. Вычислить .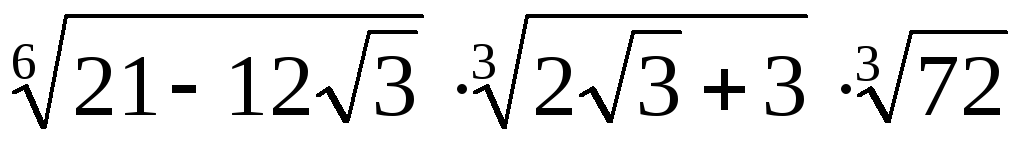

Решение. Так как 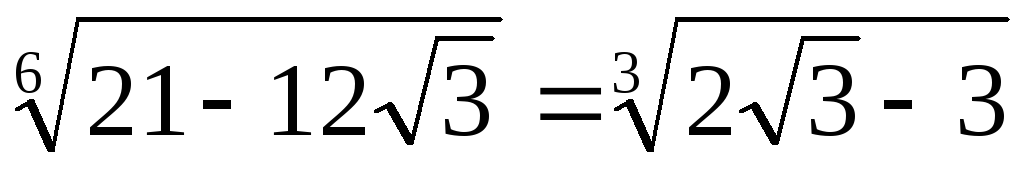, то

=.

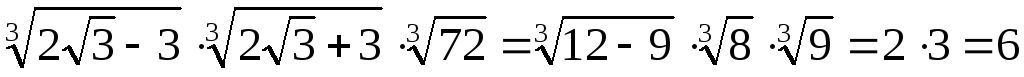Ответ: 6.

Пример 3.21. Вычислить .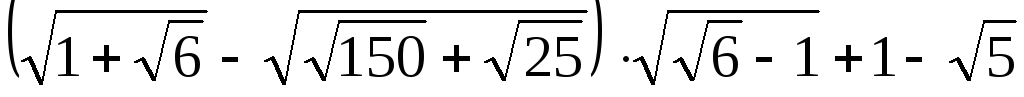

Решение.

.

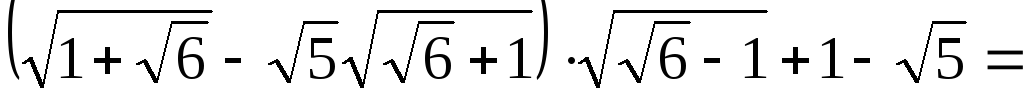
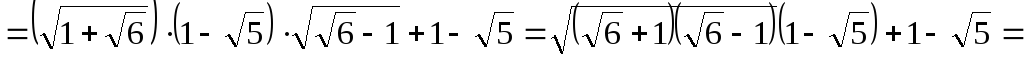
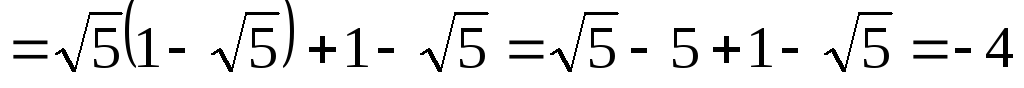Ответ: .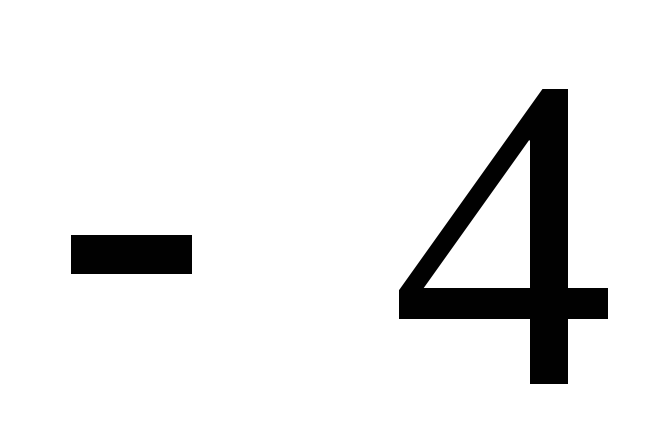

Пример 3.22. Найти значение выражения 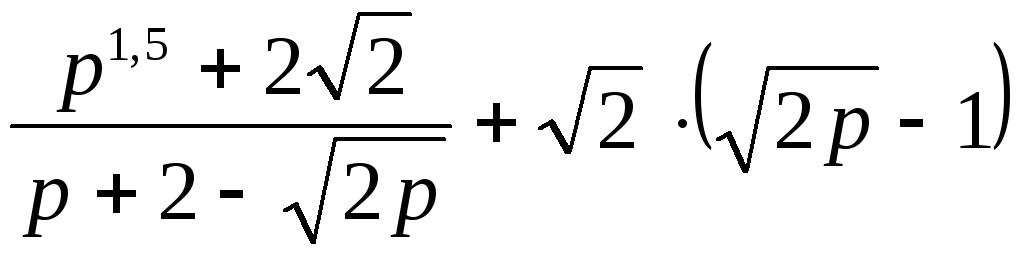при .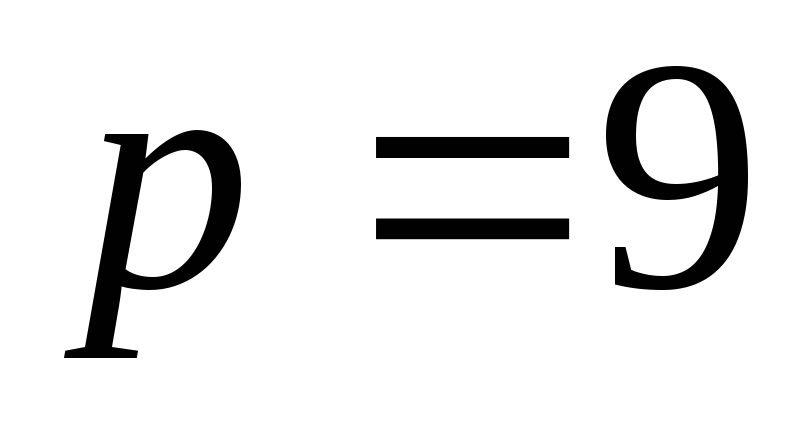

Решение. Упростим предварительно заданное выражение

,

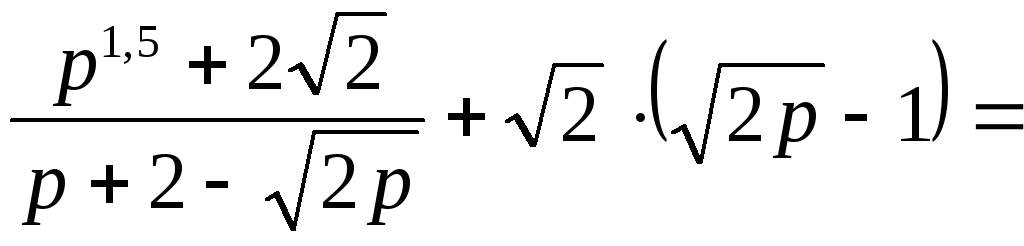
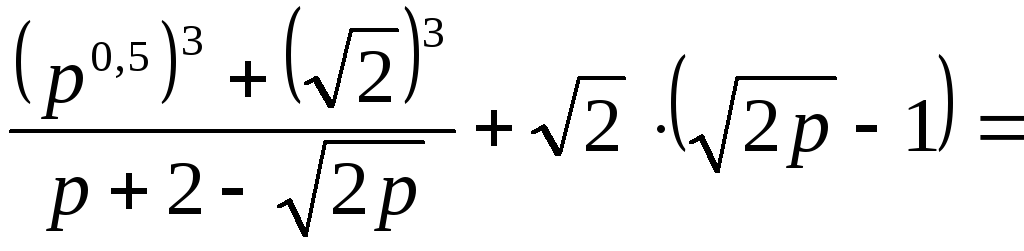
тогда при 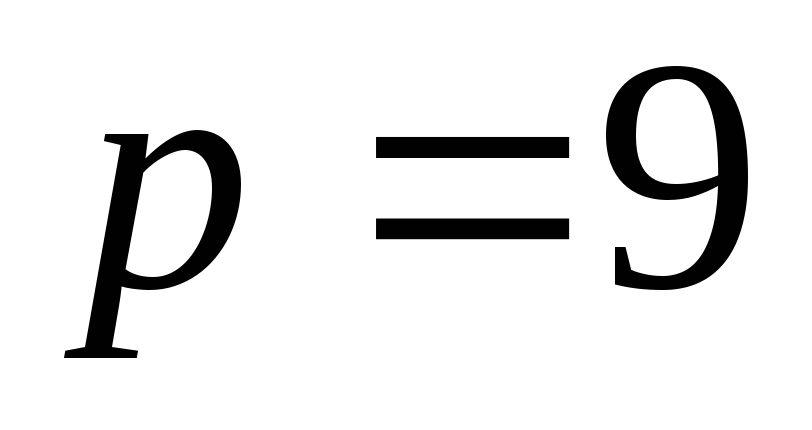получим .

Ответ: 9.

Пример 3.22. Найти значение выражения a) ,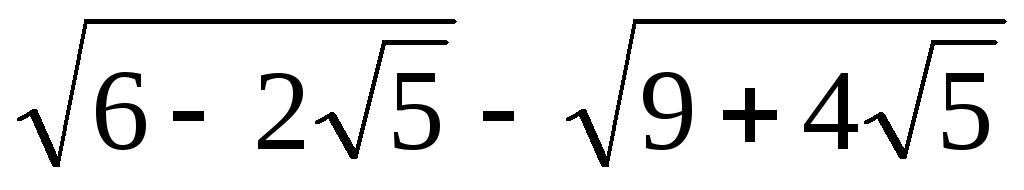

б) , в) .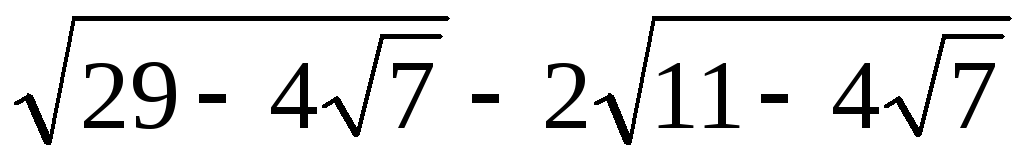

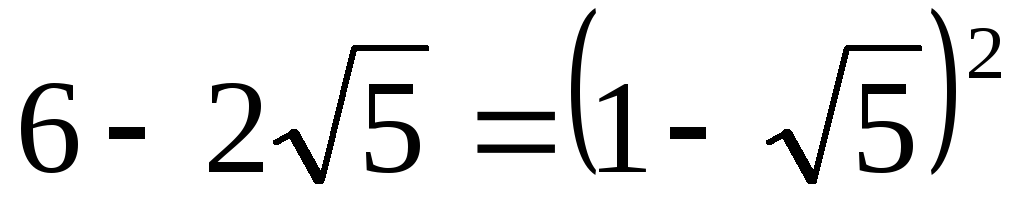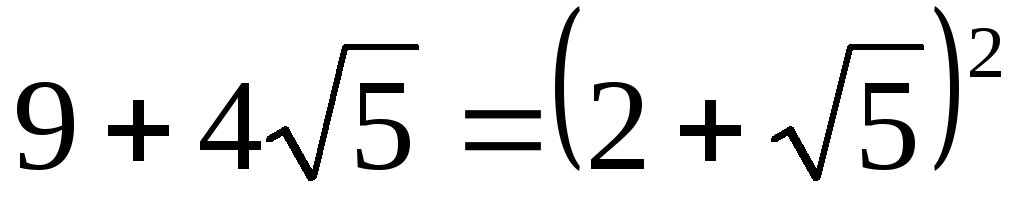Решение. а) Представим оба подкоренных выражения в виде полных квадратов: и , тогда

.

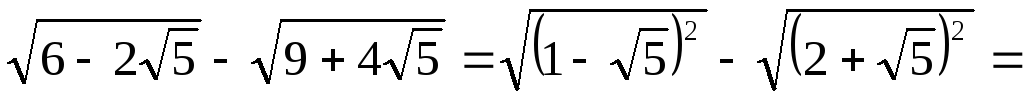
б) Действуя аналогично пункту а), получаем

=

.

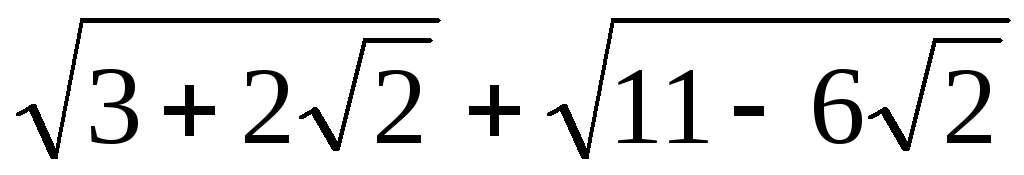в) .

Ответ: a) ; б) 4; в) 3.

Пример 3.23. Упростить выражение

Решение. Проведем преобразования в ОДЗ

().

Ответ: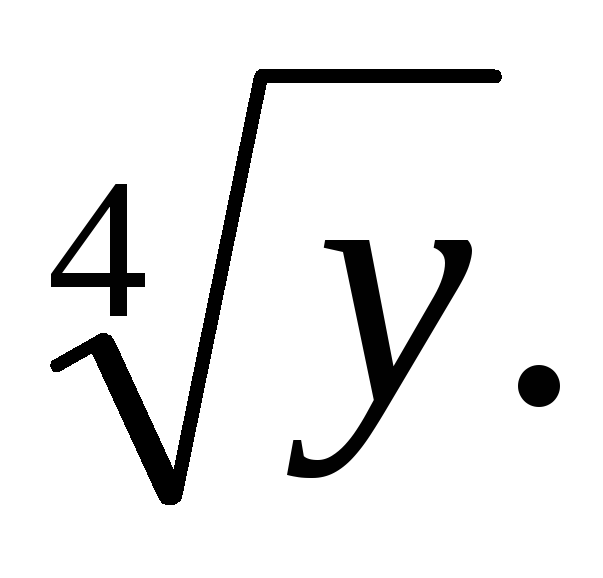

Пример 3.24. Упростить выражение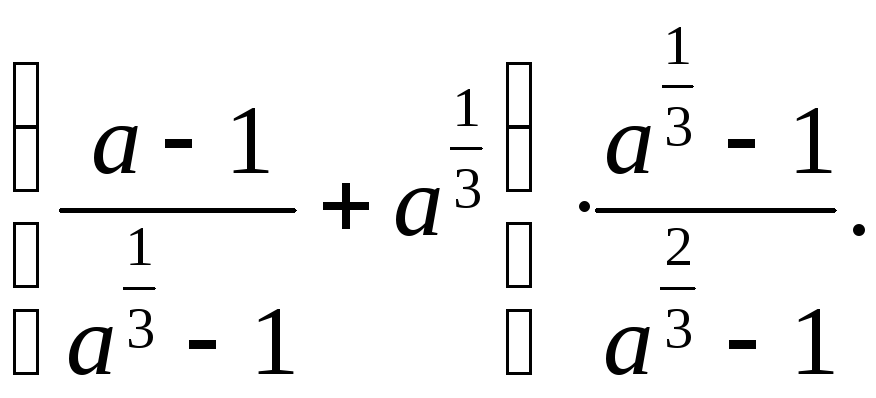

Решение. Проведем преобразования в ОДЗ ().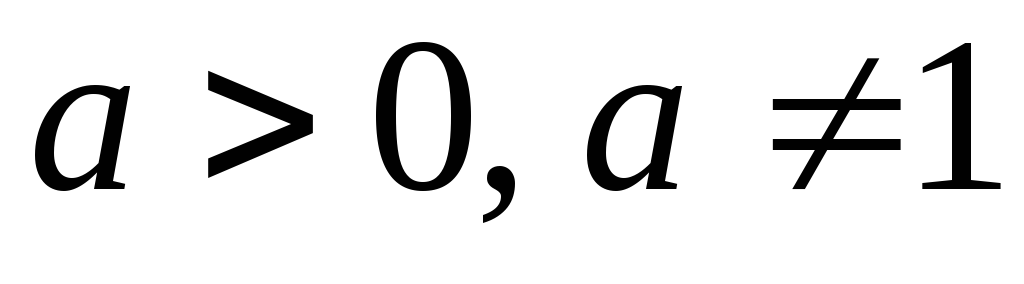

.

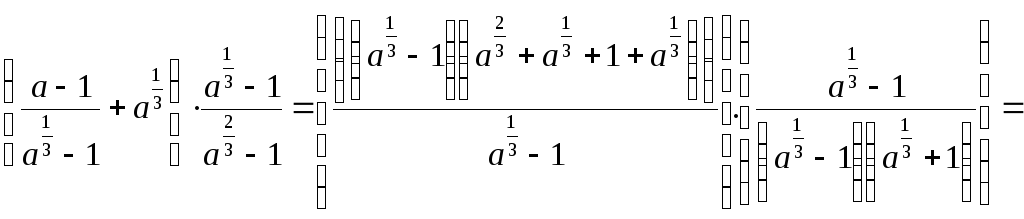
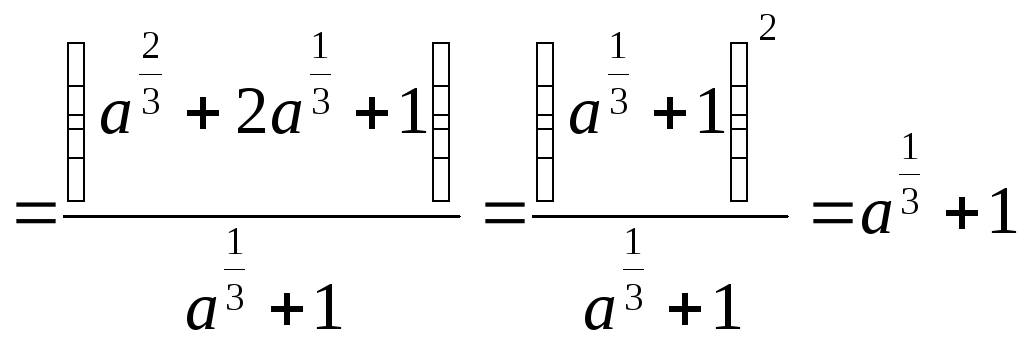Ответ: , .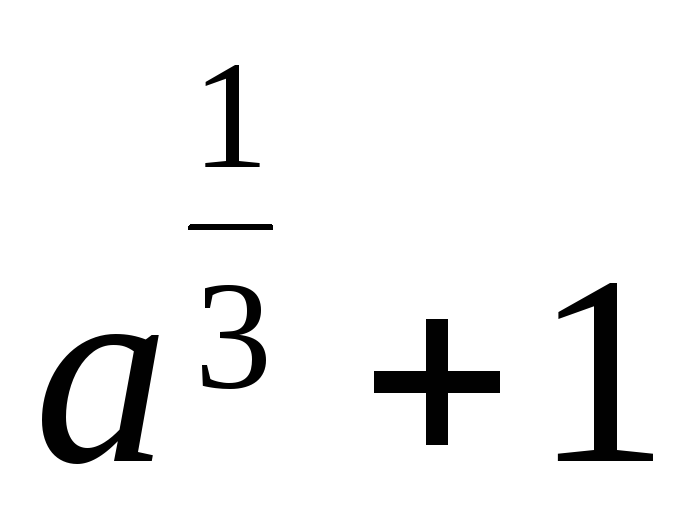

Пример 3.25. Упростить выражение

.

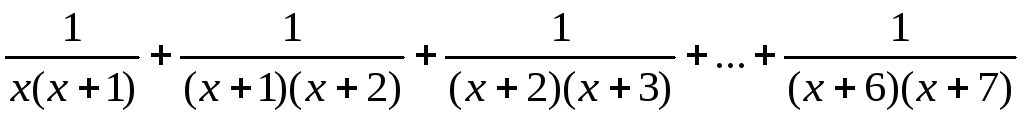Решение. Воспользуемся равенством:

.

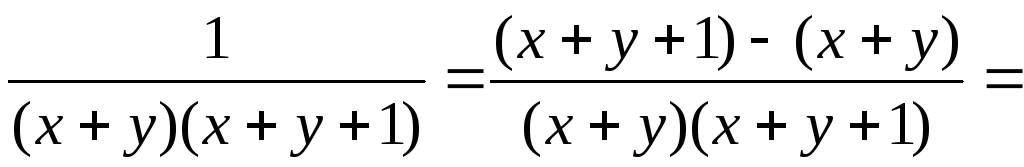
Тогда

.

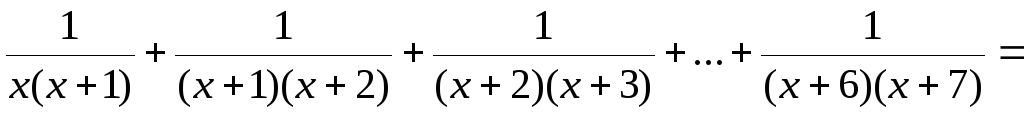
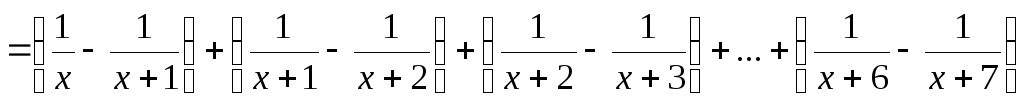Раскрывая скобки и приведя подобные, получаем

.

Ответ: .

studfile.net

Упрощение логических выражений

Основная образовательная задача урока – научить учащихся умению упрощать логические выражения, правильно определять порядок выполнения операций в логическом выражении, устанавливать связи между различными частями сложных логических выражений, умение выбирать лучший вариант решения.

Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.

Обозначим: X – логическое высказывание,  – инверсия, & – конъюнкция,  – дизъюнкция,  – импликация,  – эквиваленция.

Применение основных законов логики для упрощения логических выражений.

Представленные примеры демонстрируют основные приемы упрощения логических выражений.

Упростить логическое выражение:

1)

Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций:

 

Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией.

Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией, затем операцией с константами.

Таким образом,

2)

Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных дизъюнкцией. Сначала преобразуем выражения в скобках.

 

В первой скобке воспользуемся распределительным законом, во второй скобке – раскроем инверсию по правилу де Моргана и избавимся от инверсии по закону двойного отрицания.

Воспользуемся операцией переменной с ее инверсией.

Таким образом,

3)

Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных конъюнкцией. Сначала преобразуем выражения в скобках.

Раскроем инверсию по правилу де Моргана, избавимся от инверсии по закону двойного отрицания.

Воспользуемся переместительным законом и поменяем порядок логических сомножителей.

Применим закон склеивания

Воспользуемся распределительным законом, затем операцией переменной с ее инверсией, затем операцией с константами.

Таким образом,

4)

Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.

В выражении присутствует импликация. Сначала преобразуем импликацию .

Воспользуемся правилом де Моргана, затем законом двойного отрицания, затем раскроем скобки.

Применим закон идемпотенции и перегруппируем логические слагаемые.

Воспользуемся распределительным законом и вынесем за скобки общий логический множитель.

Воспользуемся операцией с константами.

Таким образом,

5)

Рассмотрим 3 способа упрощения этого логического выражения.

1 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.

Воспользуемся распределительным законом и раскроем скобки, затем операцией переменной с ее инверсией и законом идемпотенции.

Воспользуемся распределительным законом и раскроем скобки, затем операцией переменной с ее инверсией.

Воспользуемся законом идемпотенции.

Таким образом,

2 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.

Воспользуемся законом склеивания

Воспользуемся операцией переменной с ее инверсией.

Таким образом,

3 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.

Повторим второй сомножитель , что разрешено законом идемпотенции.

Сгруппируем два первых и два последних сомножителя.

Воспользуемся законом склеивания

Таким образом,

6)

Рассмотрим 2 способа упрощения этого логического выражения.

1 способ. Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.

Воспользуемся распределительным законом и вынесем общий логический множитель за скобки.

2 способ. Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.

Введем вспомогательный логический сомножитель

Сгруппируем 1 и 4, 2 и 3 логические слагаемые. Вынесем общие логические множители за скобки.

Воспользуемся операцией с константами и операцией переменной с ее инверсией.

Таким образом,

Получили два логических выражения:

Теперь построим таблицы истинности и посмотрим, правильно ли упрощено логическое выражение

X	Y	Z
0	0	0	0	0	0	0
0	0	1	0	0	0	0
0	1	0	0	0	0	0
0	1	1	0	1	0	1
1	0	0	1	0	0	1
1	0	1	1	0	1	1
1	1	0	0	0	0	0
1	1	1	0	0	1	1

X	Y	Z
0	0	0	1	0	0	0
0	0	1	1	0	0	0
0	1	0	0	0	0	0
0	1	1	1	0	1	1
1	0	0	1	1	0	1
1	0	1	1	1	0	1
1	1	0	0	0	0	0
1	1	1	1	1	0	1

X	Y	Z
0	0	0	0	0	0
0	0	1	0	0	0
0	1	0	0	0	0
0	1	1	0	1	1
1	0	0	1	0	1
1	0	1	1	0	1
1	1	0	0	0	0
1	1	1	0	1	1

X	Y	Z
0	0	0	0	0	0
0	0	1	0	0	0
0	1	0	0	0	0
0	1	1	1	1	1
1	0	0	1	1	1
1	0	1	1	1	1
1	1	0	0	0	0
1	1	1	1	1	1

Как видно из сравнения таблиц истинности формулы являются равносильными.

urok.1sept.ru

Действия с числовыми и алгебраическими выражениями. Часть 2. Упрощение числовых и алгебраических выражений

Мы уже сталкивались с эквивалентными выражениями, когда приводили дроби к общему знаменателю. Мы записывали цепочки эквивалентных дробей и выбирали из них те, у которых одинаковый знаменатель:

 и  

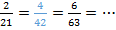
Например, в данном случае это будут дроби: .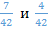

Эквивалентные выражения можно заменять друг другом, от этого смысл и значение записи не изменится.

Например, пусть есть выражение 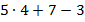. Можно выполнить умножение и получить выражение 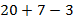. Оба эти числовых выражения равны, эквивалентны.

Если же выполнить все действия в каком-то числовом выражении, то получится его значение: , т.е.  – значение числового выражения . Выполнив все действия, мы упростили числовое выражение.

Алгебраические выражения могут быть записаны по-разному, но означать одно и то же, например: 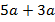 и .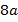

Можно ли сказать, что выражение упрощено? Обычно под упрощением подразумевают эквивалентную запись в таком виде, чтобы для вычисления значения выражения нужно было выполнить как можно меньше действий.

 

Например, чтобы вычислить значение выражения 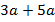 при заданном значении переменной необходимо выполнить 3 действия, а для выражения  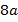– одно действие. Конечно, разница в 2 действия невелика, но, если бы такую операцию нужно было бы проделать 50 раз, тогда разница была бы уже в целых 100 действий.

 

Задача 2. Докажите, что выражение 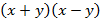 эквивалентно выражению .

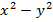Доказательство

Дважды воспользуемся распределительным законом :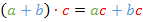

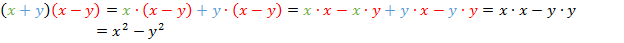
Задача 3. Упростите выражение: .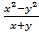

Решение. Воспользуемся формулой разности квадратов :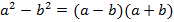

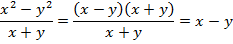
Ответ: .

 

Сравним количество действий, которое необходимо сделать, чтобы вычислит

interneturok.ru

Упрощение тригонометрических выражений

При упрощении тригонометрических выражений используются свойства тригонометрических функций и тригонометрические формулы.

Основные тригонометрические формулы

Соотношения между тригонометрическими функциями одного аргумента

Тригонометрические функции суммы и разности углов

Тригонометрические функции двойного и тройного аргументов

Формулы понижения степени

Тригонометрические функции половинного аргумента

Формулы преобразования произведения тригонометрических функций в сумму

Формулы преобразования суммы тригонометрических функций в произведение

Формулы, выражающие через

Формулы приведения

Примеры решения задач

ПРИМЕР 3

Задание	Упростить тригонометрическое выражение
Решение	Используя формулы тригонометрических функций двойного аргумента, второе слагаемое данного выражение запишется следующим образом     Подставляя это в исходное выражение, получим     Далее, учитывая периодичность синуса     исходное выражение примет вид     Воспользовавшись формулами приведения, окончательно получим:
Ответ

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Урок №5 Упрощение логических выражений (10 класс)

Тема урока: Упрощение логических выражений с использованием законов логики.

Образовательная – изучение способов решения разнообразных заданий по упрощению логических выражений с использованием законов логики;

Развивающая — создать условия для развития познавательного интереса учащихся, способствовать развитию памяти, внимания, логического мышления;

Воспитательная: способствовать воспитанию умения выслушивать мнение других, воспитание воли и настойчивости для достижения конечных результатов.

Тип урока: комбинированный урок

Оборудование: компьютер, мультимедийный проектор, презентация 5.

Ход урока

1. Повторение и актуализацию опорных знаний. Проверка домашнего задания (15 минут)

На предыдущих уроках мы познакомились с основными законами алгебры логики, научились использовать эти законы для упрощения логических выражений.

Выполним проверку домашнего задания по упрощению логических выражений:

а)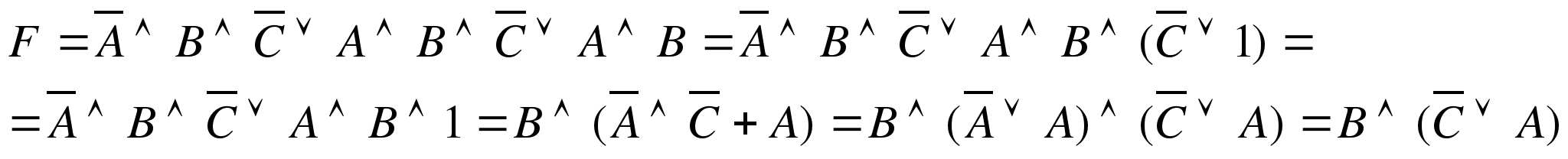

б)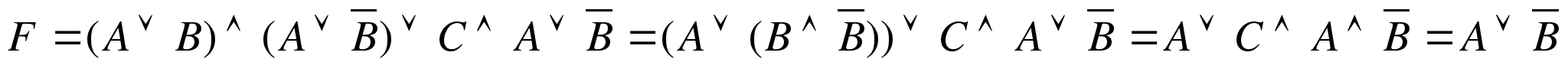

Самостоятельная работа

1 вариант

Упростить следующее логическое выражение:

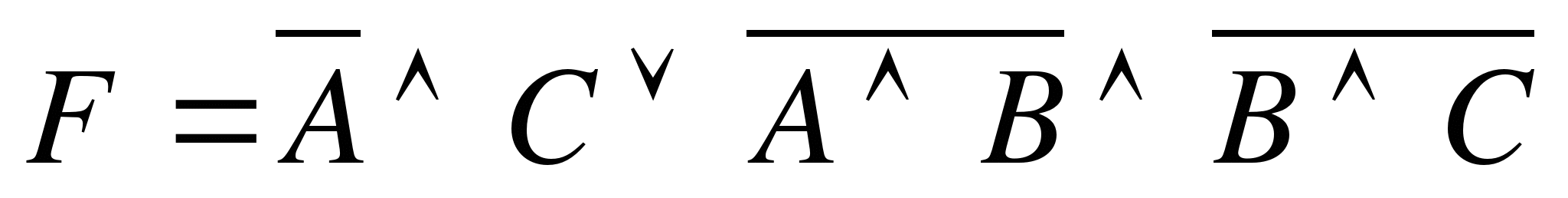
Решение:

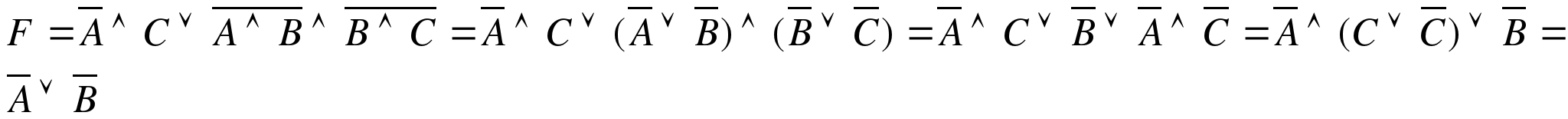
2 вариант

Упростить следующее логическое выражение:

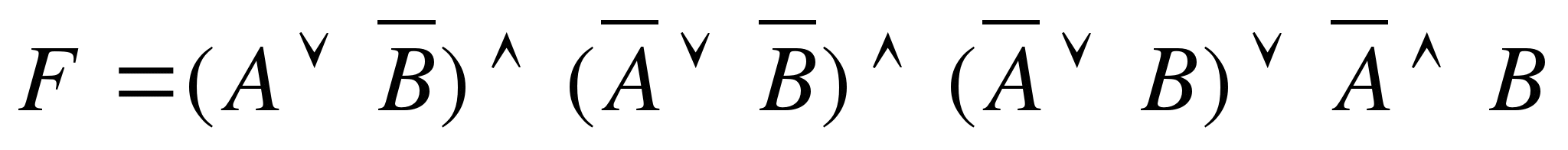
Решение:

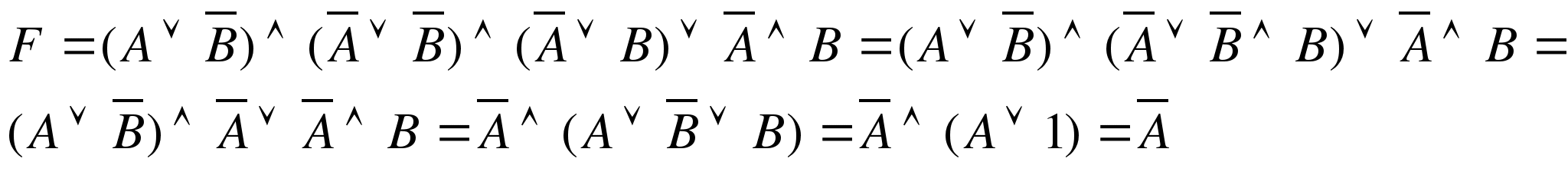
2. Ознакомление с темой урока. Изложение нового материала (30 мин).

Мы продолжаем изучать основы логики и тема нашего сегодняшнего урока «Упрощение логических выражений с использованием законов логики». Изучив данную тему, вы узнаете способы решения разнообразных заданий, содержащихся в ЕГЭ, по упрощению логических выражений с использованием законов логики.

1. Каково наименьшее натуральное число X, при котором высказывание ¬(X·X < 9) → (X >(X + 2)) будет ложным?

Решение: Преобразуем исходное выражение, используя законы логики

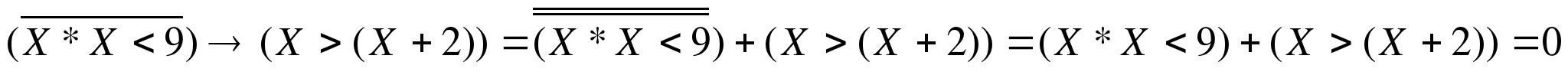
Выражение будет ложным когда обе его части будут ложными:

(Х>(X+2)) – ложь, тогда (X*X<9) – ложь. Следовательно (Х*Х>=9) – истина.

Наименьшее значение Х, при котором верно это неравенство 3.

Ответ: 3.

2). Укажите значения переменных K, L, M, N, при которых логическое выражение

(¬K  M) → (¬L  M  N) ложно.

Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.

Решение:

Преобразуем выражение (¬K  M) → (¬L  M  N), используя законы логики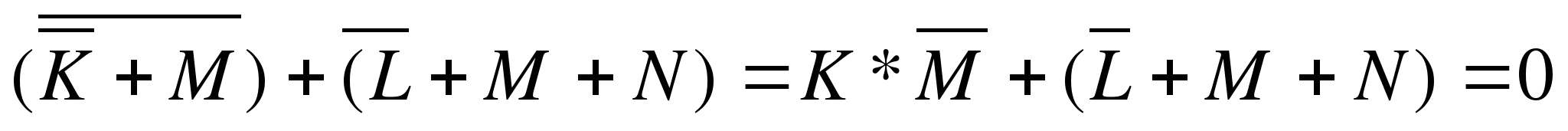

Выражение ложно, когда оба слагаемые ложны. Второе слагаемое равно 0, если M=0, N=0, L=1. В первом слагаемом K=0, так как М=0, а .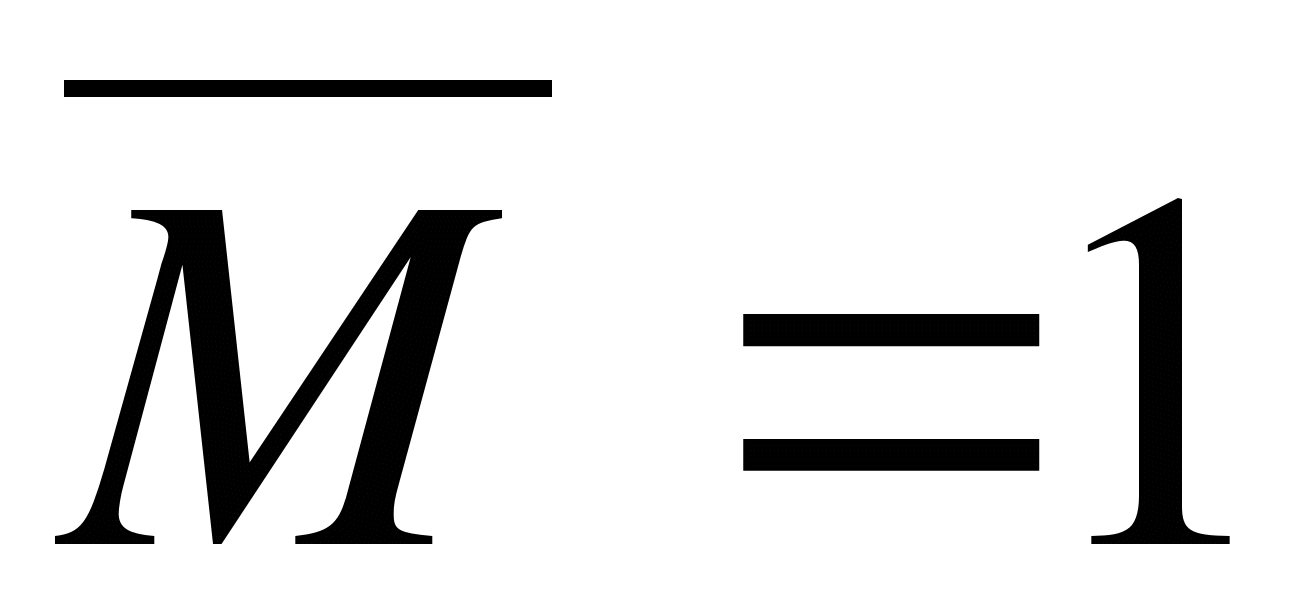

Ответ: 0100

3). Для какого из указанных значений числа Х истинно выражение

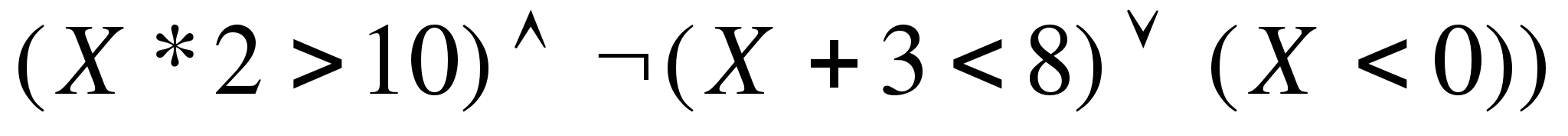
1) 0 2) 2 3) 4 4) 7

Решение: преобразуем выражение

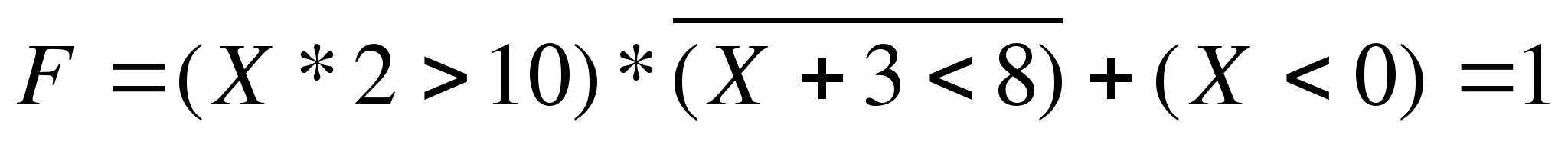
Будем поочередно подставлять значения числа Х в данное выражение и определять значение выражения. Можно решение записать в виде следующей таблицы:

4. Дан фрагмент таблицы истинности выражения F:

Каким выражением может быть F?

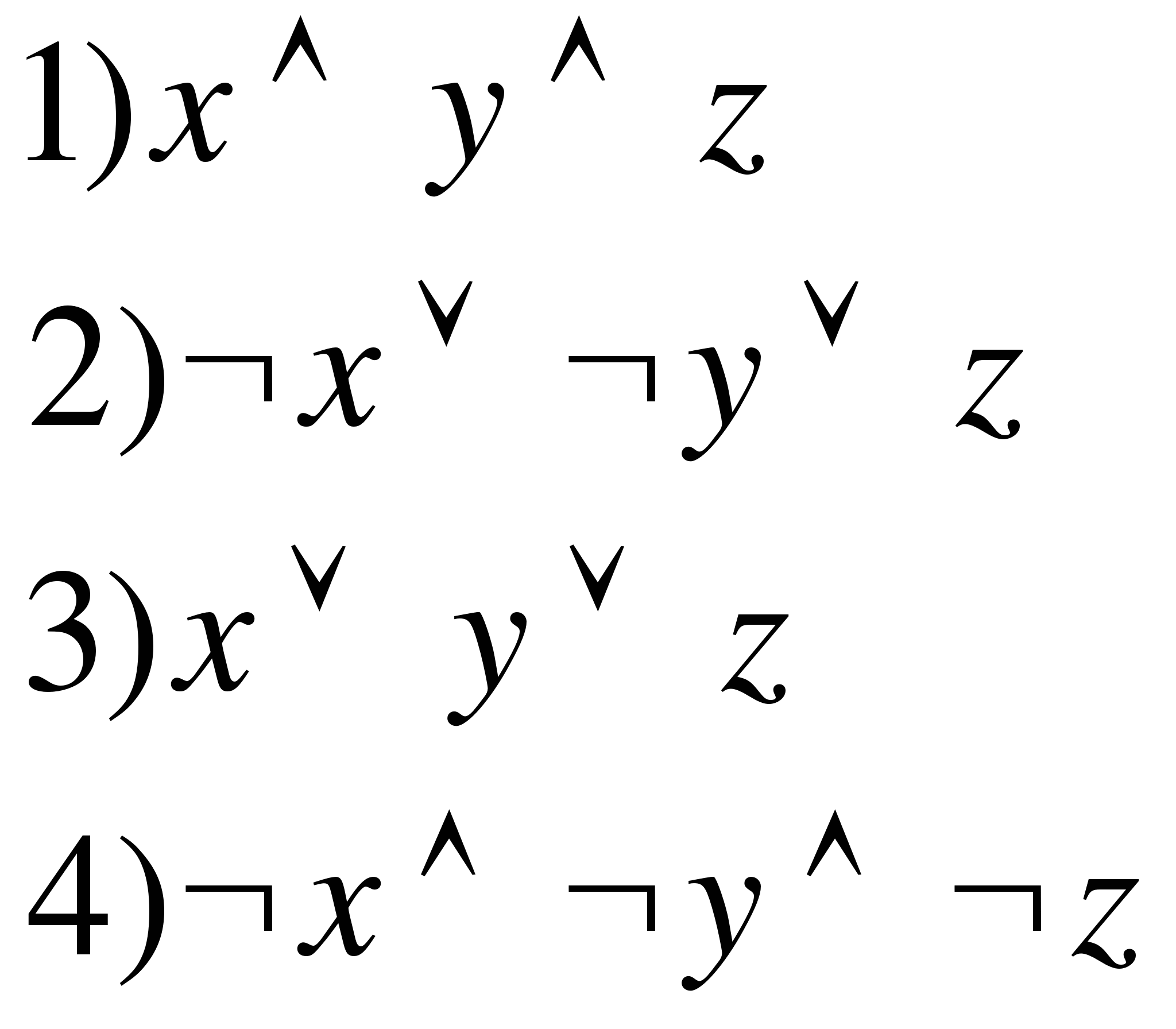
Решение:

Преобразуем логические выражения и определим значения этих выражений при указанных значениях аргументов:

1. Х*Y*Z

2. 

3. X+Y+Z

4. 

Ответ: 1

4. Укажите, какое логическое выражение равносильно выражению

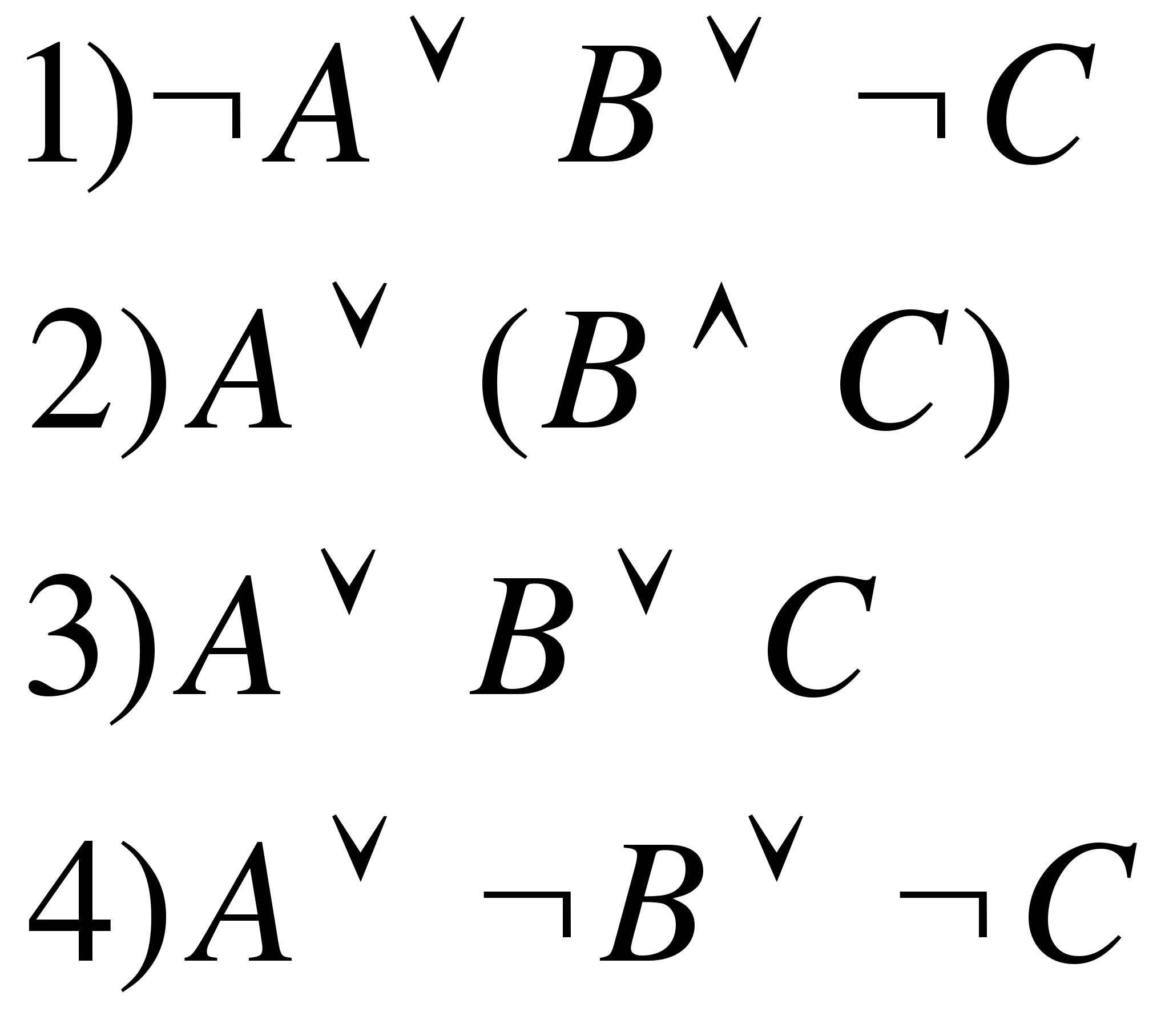
Решение:

Преобразуем запись исходного выражения и предложенных вариантов, используя законы логики:

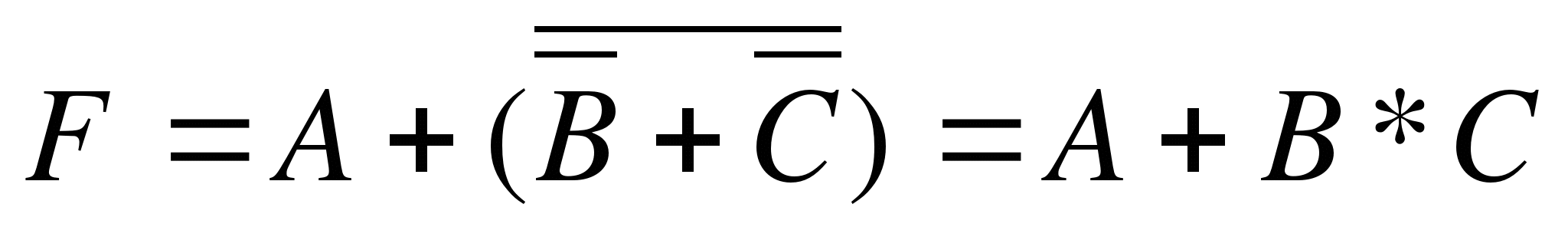
1)

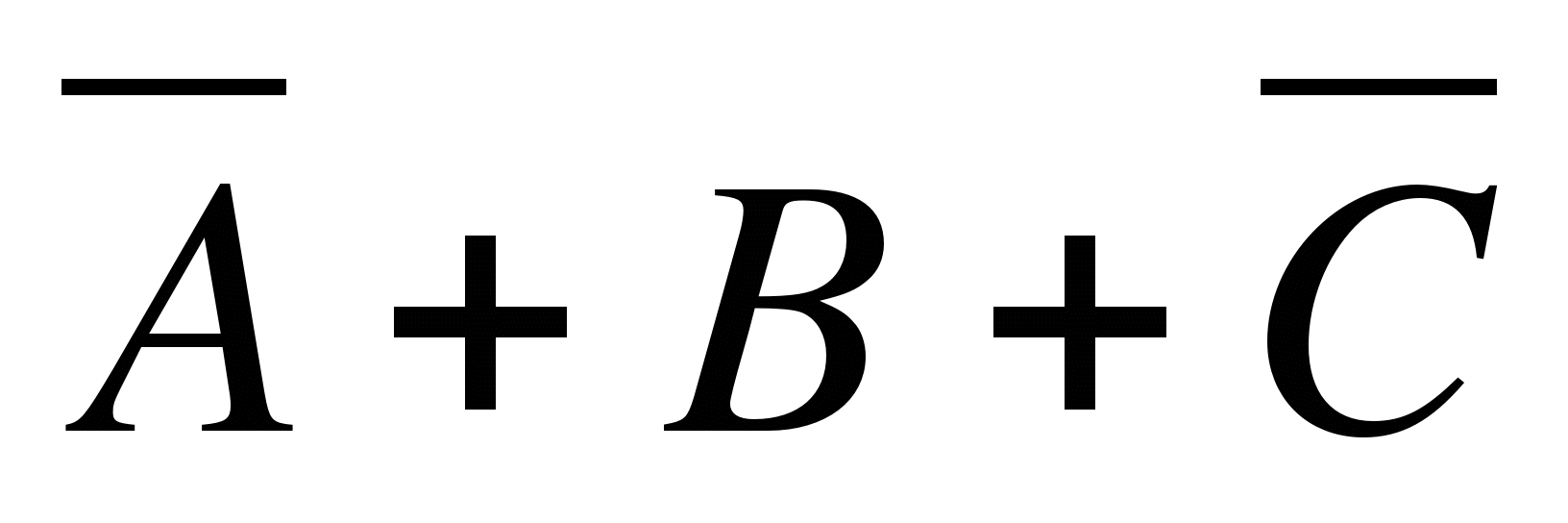
2) A+(B*C)

3) A+B+C

4)

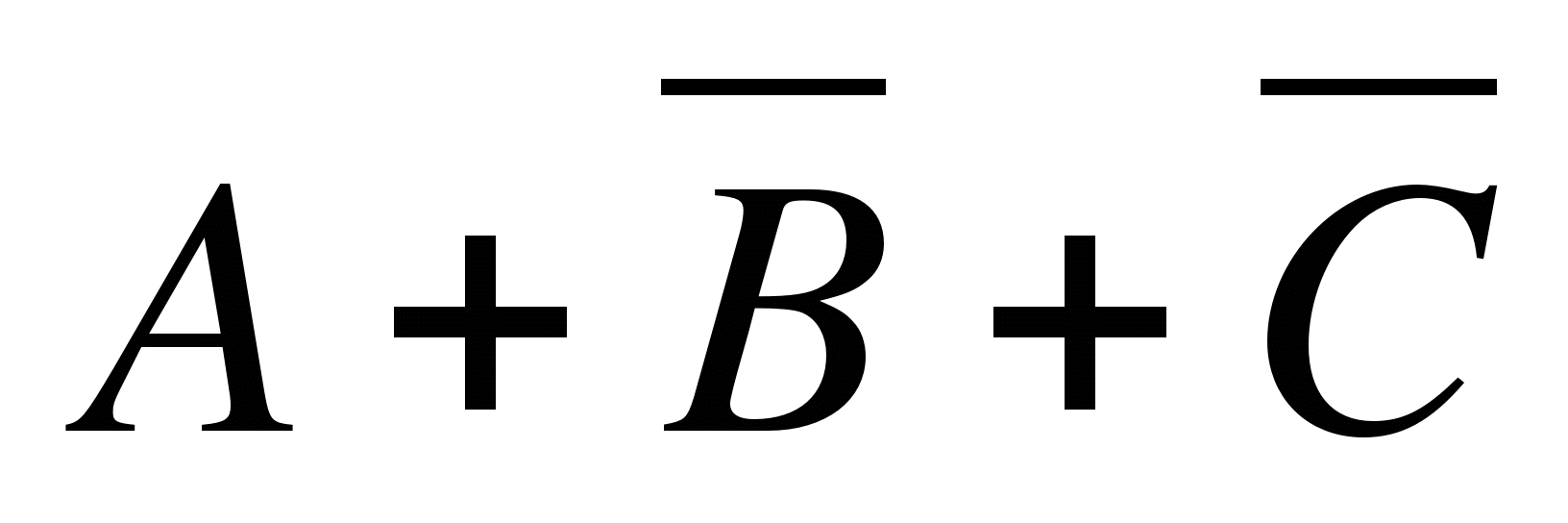
Ответ: 2

6). Какое из приведенных имен удовлетворяет логическому условию:

(первая буква согласнаявторая буква согласная)(предпоследняя буква гласнаяпоследняя буква гласная)?

1) КРИСТИНА 2) МАКСИМ 3) СТЕПАН 4) МАРИЯ

Решение:

Преобразуем исходное выражение, используя законы логики:

(первая буква гласная или вторая буква согласная) и (предпоследняя буква согласная или последняя буква гласная)=1

Результаты анализа представим в виде таблицы:

3. Задание на дом

1. Какое из приведенных слов удовлетворяет логическому условию:

(первая буква согласная→вторая буква согласная) ٨ (последняя буква гласная → предпоследняя буква гласная)?

Если таких слов несколько, укажите наименьшее из них.

1) АННА 2) МАРИЯ 3) ОЛЕГ 4) СТЕПАН

2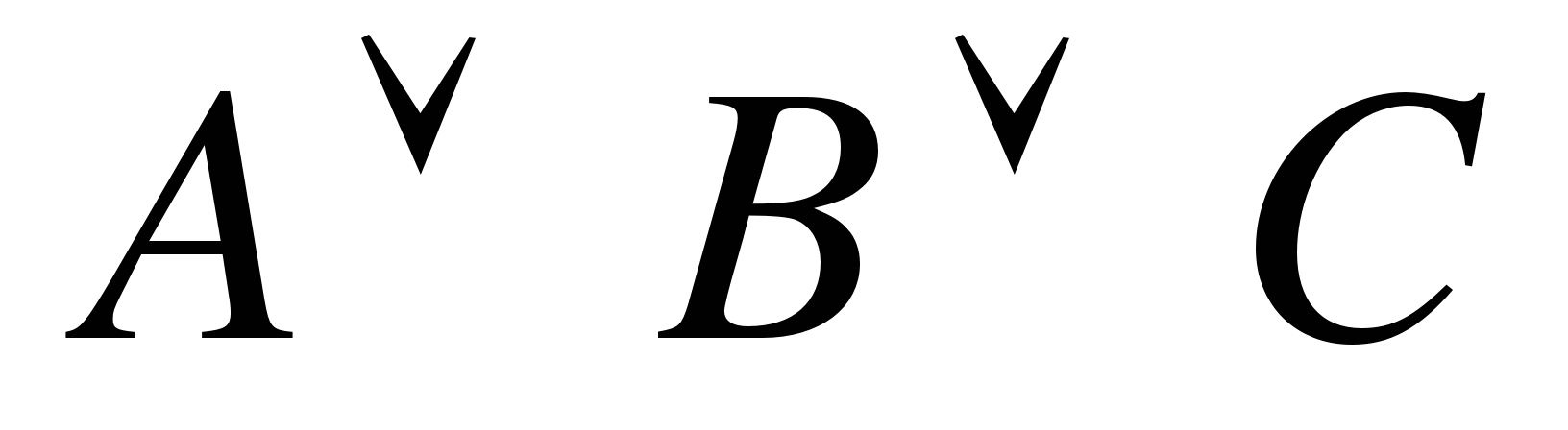. Укажите, какое логическое выражение равносильно выражению

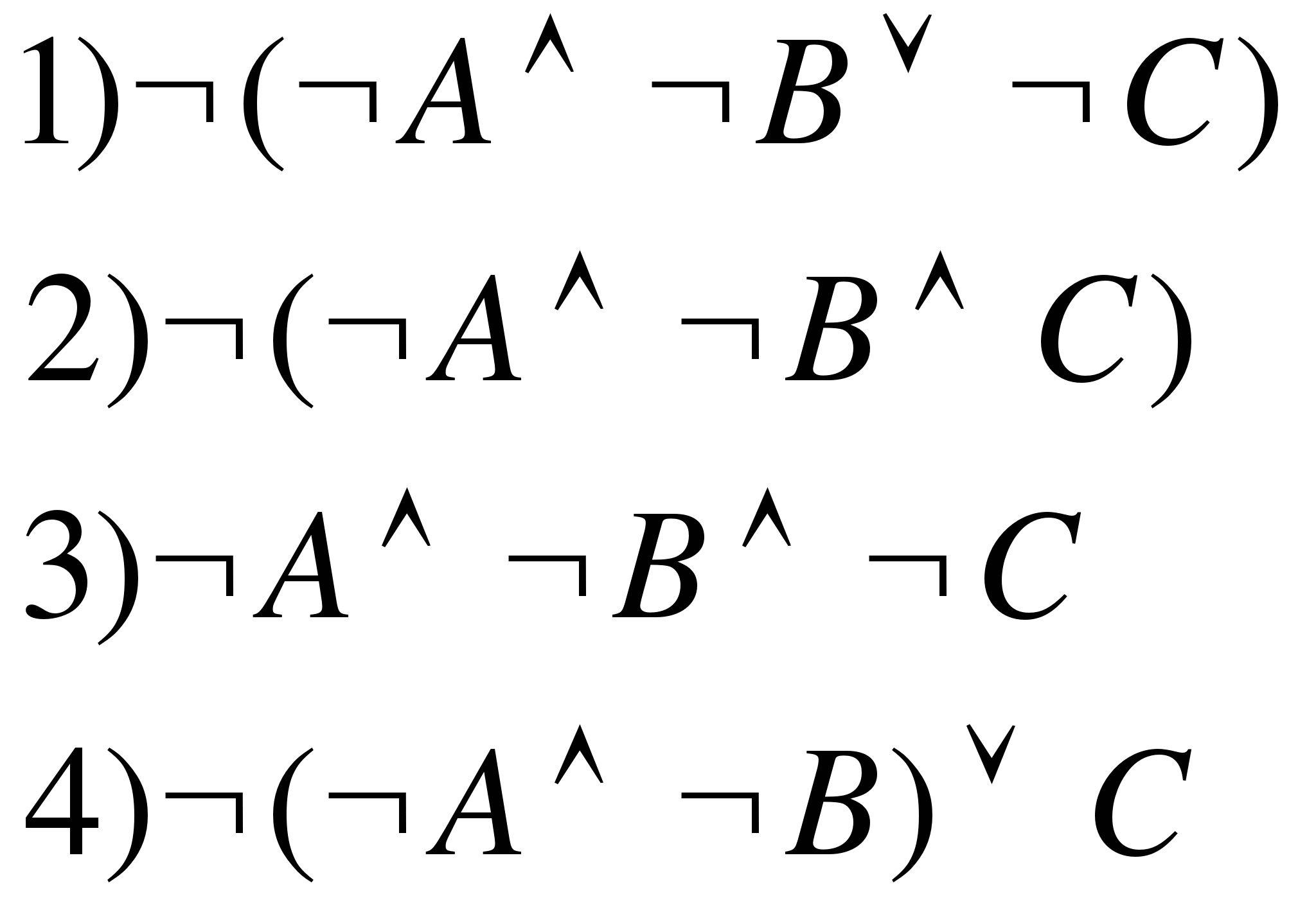
3. Дан фрагмент таблицы истинности выражения F:

0

Какое выражение соответствует F?

infourok.ru

Упрощение выражений — примеры решений

Упростите выражение y=(((x-4)(sqrtx-2))/(sqrtx+2))+4sqrtx и вычислите его значение при х=7.

#721

Упростите выражение (6/(a-1))-(10/(a-1)^2):(10/(a^2-1))-(2a+2)/(a-1).

#709

Найдите значение выражения (9ab/(a+9b))*((a/9b)-(9b/a)) при а=9sqrt8+4, b=sqrt8-4.

#703

Найдите значение выражения при а=81, с=82.

#665

Упростите выражение: sin(a+b)+sin(a-b).

#639

Найдите значение выражения ((xy+y^2)/(15x))*((3x)/(x+y)).

#623

Найдите значение выражения 9b+(5a-9b^2)/b при a = 9, b = 36.

#506

Упростить выражения: а) (3a+b)(2a-5b)-6(a-b)^2; б) (-2a^3*b)^3*(-5a^2*b)^2; в) 4x^4*(-2x^2 )^3; г) (3x-1)(3x+1)+(3x+1)^2.

#442

Найдите значение выражения (a-b)/2:(a^2-b^2)/4 при а=-1,2 и b=2,2.

#113

Упростить выражение u^2-(u-1)^2-2u.

#112

Найдите значение выражения ((a^2-b^2)/2ab):(1/a-1/b) при а=1,1 и b=2,9.

#111

Найдите значение выражения sqrt(x^2-2x+1) при х=2016.

#110

Найдите значение выражения sqrt(a^2-4a+4)+sqrt(a^2-10a+25) при

#109

Найдите значение выражения ((a^3-b^3)/3):(a-b) при а=6 и b=3.

#108

Упростите выражение a^3-(a+1)^3+3a^2 и найдите его значение при a=-1/3.

#107

xn--80aaasqmjacq0cd6n.xn--p1ai

Алгебраические выражения — Математика — 10 класс

Просмотр содержимого документа
«Алгебраические выражения»

Урок 1.Алгебраические выражения

Повторение

курса алгебры 7-9 классов

Реши самостоятельно!

Алгебраическая сумма

Алгебраическая сумма – это запись, состоящая из нескольких алгебраических выражений, соединенных знаком «+» или «-»

Например:

2х+3у;

-0,87а 3 в 4 -0,445ху+56 и т.д.

Алгебраическая сумма может содержать скобки.

№ 1. Раскрыть скобки:

• a+(b-(c+d-5))
• a-(b+(c-d+5))
• a+(-b+(d-c-8))

Степень с натуральным показателем

Степень числа а с натуральным показателем n, большим 1, — это произведение n множителей, каждый из которых равен а.

Степень с натуральным показателем

При этом: а 1 =а, 1 n = 1 и если а  0, то а 0 =1

Степень с целым показателем

Степень с целым показателем

№ 2. Упростить:

Одночлены и многочлены

Одночлен – произведение числовых и буквенных множителей, являющихся степенями с натуральными показателями.

Например: -2ав 2 с 3 ; а; 0,4; ав ∙56 и т.п.

Коэффициент одночлена – числовой множитель одночлена.

Одночлен стандартного вида — это одночлен, в котором на первом месте стоит коэффициент.

Многочлен – сумма одночленов: -2ав 2 с 3 + 5,6 – а

Многочлен стандартного вида – многочлен, в котором все одночлены стандартного вида и среди них нет подобных.

№ 3. Привести одночлен к стандартному виду и найти коэффициент одночлена

а) 7х∙ 8х 2 у

б)-0,3 х 4 ∙5х 2 у 8

в) -7х 3 у 2 ∙ 0,8ху

№ 4. Записать в виде многочлена стандартного вида

а) (а-0,5)(2а 2 -4а+3)

б) (1,5-а)(3а 2 -2а+8)

Формулы сокращенного умножения

№ 5. Разложите на множители:

а) 4а 6 -в 2 с 6

б) 4а 3 -а

№ 10(2,3)

Алгебраические дроби

Алгебраическая дробь – это дробь, числитель и знаменатель которой являются многочленами.

№ 6. Упростите выражение:

Домашнее задание

• П.1. Повторить определения и формулы
• Письменно №1-18(1)
• Принести 2 тетради в клетку для контрольных работ

multiurok.ru