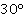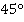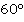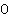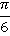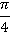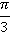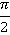Практика. Тригонометрические выражения. Профильный уровень
Тригонометрические функции имеют широкое применение.
Во-первых, они помогают решать геометрические задачи – рассчитывать треугольники и более сложные фигуры. Кроме того, их можно использовать и в быту, например чтобы понять, пролезет ли кровать в дверной проем или нет (до того, как совершить покупку). Или для того, чтобы оценить высоту дома или дерева, ширину реки.
Но чаще тригонометрические функции применяют для решения технических задач: построения чертежей деталей, зданий, расчета нагрузок на составные части механизма, просчета траектории движения и прочее.
Наконец, с помощью тригонометрических функций можно описывать колебания и волны. Об этих понятиях вы уже знаете из курса физики (урок «Механические колебания», урок «Механические волны. Звук»). Именно с помощью синусов и косинусов можно создать математическую модель различных колебаний: от механических до электромагнитных (урок «Электромагнитные волны и свет»).
Это основные сферы применения тригонометрических функций. Те же, кто собрался посвятить свою жизнь технической профессии, увидят и другие применения этого математического инструмента.
Вы уже знаете различные соотношения для тригонометрических функций, с помощью которых можно вычислить их значения и упростить выражение, которое содержит такие функции. На этом уроке мы займемся отработкой навыков упрощения и вычисления.
Прежде чем начать, вспомним, что для углов существуют две основные единицы измерения: градусы и радианы. Все вычисления вы должны уметь делать как в одних, так и в других единицах измерения. Основное соотношение:  радиан. Соответственно, в два раза больший угол:
радиан. Соответственно, в два раза больший угол: 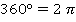 радиан; а в два раза меньший –
радиан; а в два раза меньший – 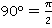

Задание 1.
Известно, что:
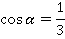
Определить значения синуса, тангенса и котангенса 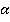 , если
, если 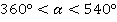 .
.
Решение
Зная значение одной тригонометрической функции, всегда можно найти значение всех остальных с точностью до знака. Для этого понадобится основное тригонометрическое тождество:
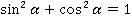
А также определения тангенса и котангенса для произвольного угла:
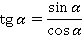
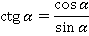
Используем эти инструменты. Подставим значение косинуса в основное тригонометрическое тождество:
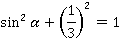
Упростив, получим:
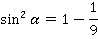
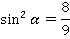
Тогда:
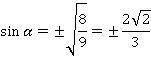
Мы получили два возможных значения синуса: положительное и отрицательное. Зная дополнительную информацию 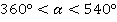 , мы можем однозначно выбрать знак. Отмечаем на окружности точки, соответствующие углам
, мы можем однозначно выбрать знак. Отмечаем на окружности точки, соответствующие углам 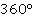 и
и 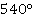 . Угол
. Угол 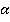 находится между ними, т. е. ему соответствуют точки верхней полуокружности (см. рис. 1).
находится между ними, т. е. ему соответствуют точки верхней полуокружности (см. рис. 1).
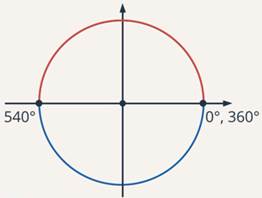
Рис. 1. Иллюстрация к заданию 1
Ординаты всех этих точек положительны, значит, и 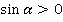 . Еще говорят так: «угол
. Еще говорят так: «угол 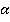 лежит в первой или второй четверти. В этих четвертях синус положительный»:
лежит в первой или второй четверти. В этих четвертях синус положительный»:
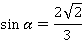
Осталось найти тангенс и котангенс по определению:
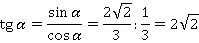
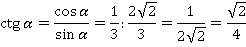
Ответ: 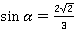 ;
; 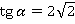 ;
; 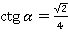 .
.
Задание 2. Найти значение выражения:
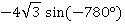
Решение
Идея решения подобных заданий следующая: преобразовать выражение так, чтобы получить острый угол. А затем найти значение функции по таблице:
|
Градусы |
|
|
|
|
|
|
Радианы |
|
|
|
|
|
|
cos |
|
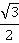
|
|
|
|
|
sin |
|
|
|
|
|
Для преобразования понадобятся формулы приведения:
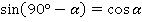
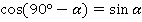
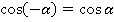

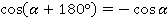
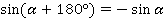
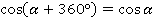
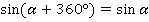
В задании угол отрицательный 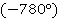 , поэтому начинаем с формул для
, поэтому начинаем с формул для  :
:
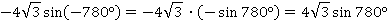
Теперь убираем из аргумента периоды (добавление и вычитание целого числа периодов не меняет значение функции):
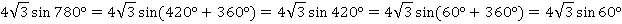
По таблице находим:
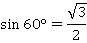
Подставляем в выражение:
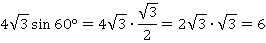
Ответ: 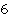 .
.
Отметим, что период 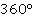 (или
(или 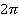 ) для синусов и косинусов мы можем выделять не один раз. Поэтому для больших значений угла удобно его сразу представить в виде
) для синусов и косинусов мы можем выделять не один раз. Поэтому для больших значений угла удобно его сразу представить в виде 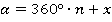 (или
(или 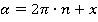 в радианах), где
в радианах), где 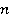 – некоторое целое число. А для этого следует разделить с остатком значение угла на
– некоторое целое число. А для этого следует разделить с остатком значение угла на 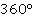 .
.
Например, найдем 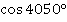 . Делим с остатком
. Делим с остатком 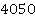 на
на 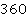 :
:
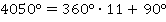
Получаем:
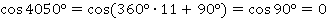
У тангенсов и котангенсов период равен 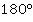 (или
(или 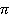 ). Соответственно, угол представляем в виде
). Соответственно, угол представляем в виде 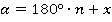 (или
(или 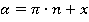 в радианах).
в радианах).
Например, вычислим 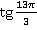 :
:
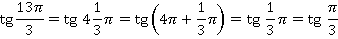
Для этого угла можем уже воспользоваться таблицей:
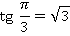
Если в задании с тригонометрическими функциями вам встретились тангенс или котангенс, то лучше сразу расписать их по определению. Это сведет вашу задачу к работе только с синусами и косинусами.
Задание 3. Найти значение выражения:
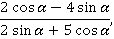
если 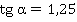 .
.
Решение
По определению:
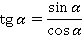
То есть:
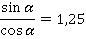
Теперь остались только синусы и косинусы. Из полученного соотношения выразим синус:
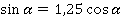
Теперь подставим это в искомое выражение:
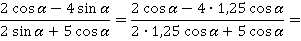
Осталось упростить выражение и получить ответ:
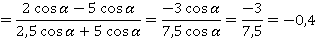
Ответ: 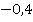 .
.
Другой способ решения
Уменьшить количество различных видов функций в таком выражении можно и другим способом. Если все слагаемые содержат синус и косинус в одинаковой степени, то можно разделить числитель и знаменатель на синус или косинус в этой степени, в данном случае – в первой. Посмотрим, к чему это приведет.
Сразу оговоримся, почему такое деление можно делать. Так как нам дано значение тангенса угла, то косинус этого угла не может равняться 0 (иначе тангенс был бы не определен), а так как тангенс не равен 0, то и синус угла не может равняться 0 (иначе бы тангенс, как отношение синуса и косинуса, тоже был бы равен 0). Поэтому можем смело делить на любую из функций.
Разделим на 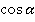 и числитель, и знаменатель:
и числитель, и знаменатель:

Мы получили выражение, которое содержит только тангенс. Осталось подставить его значение из условия:
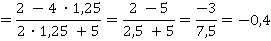
Задание 4. Упростить выражение:
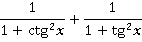
Решение
Видим тангенс и котангенс – выражаем их через синус и косинус:
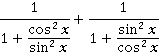
Получились многоэтажные дроби. Лучше избавиться от них, заменив черту дроби знаком деления:
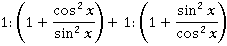
Теперь вспоминаем принципы работы с дробями. Сначала приводим к общему знаменателю:
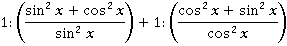
Можно продолжить выполнять операции с дробями. А можно отметить, что в числителях дробей мы видим формулу основного тригонометрического тождества. Можем заменить 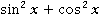 на
на 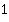 – это существенно упростит наше выражение:
– это существенно упростит наше выражение:
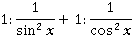
Выполняем деление:
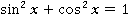
Ответ: 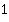 .
.
Кроме основного тригонометрического тождества и определений тангенса и котангенса, вы знаете еще множество формул для работы с тригонометрическими функциями. С их помощью также можно упрощать выражения. Главное – понять, какую формулу нужно использовать. Чем больше практики будет, тем легче вам будет выбрать нужную формулу. Но поначалу не страшно, если выбранный способ решения окажется длинным или не приведет к нужному результату. Тогда нужно вернуться и попробовать использовать другую формулу.
Задание 5. Упростить выражение:
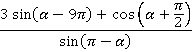
Решение
Упростим каждую из функций по отдельности.
1) 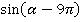 . Для начала выделим период
. Для начала выделим период 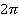 . Его можно выделить
. Его можно выделить 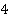 раза:
раза:
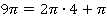
Тогда:

У нас есть формула для 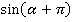 , а тут
, а тут 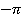 . Что делать? Прибавим период; значение функции при этом не изменится:
. Что делать? Прибавим период; значение функции при этом не изменится:
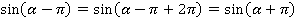
Теперь уже можно использовать формулу приведения:
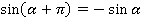
2) 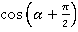 . У нас есть формула для
. У нас есть формула для 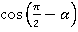 . В ней вычитается угол, а в нашем выражении – сложение. Поэтому, чтобы использовать эту формулу, превратим сложение в вычитание:
. В ней вычитается угол, а в нашем выражении – сложение. Поэтому, чтобы использовать эту формулу, превратим сложение в вычитание:
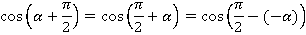
Формулы приведения справедливы для любых углов. Поэтому можем применить ее и для угла  . Получим:
. Получим:
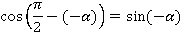
Использовав еще одну формулу приведения, получим:
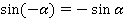
3) 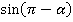 . Перепишем это как
. Перепишем это как 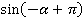 . К углу
. К углу  прибавляется
прибавляется 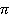 , можем использовать соответствующую формулу приведения:
, можем использовать соответствующую формулу приведения:
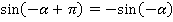
Используя еще одну формулу приведения, получим:
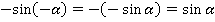
Подставим упрощенные выражения в исходное:
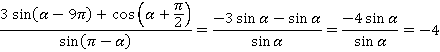
Ответ: 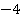 .
.
Другой способ решения
Все три тригонометрические функции содержат аргумент в виде, к которому можно применить правило «головы лошади»:
1. 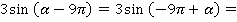
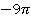 находится там же, где
находится там же, где 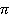 , плюс альфа, третья четверть, синус отрицательный (см. рис. 2). Диаметр гориз
, плюс альфа, третья четверть, синус отрицательный (см. рис. 2). Диаметр гориз
interneturok.ru
Урок 40. преобразование тригонометрических выражений — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №40. Преобразование тригонометрических выражений.
Перечень вопросов, рассматриваемых в теме
- различные приёмы преобразования тригонометрических выражений.
- различные тригонометрические формулами и их использование при преобразовании тригонометрических выражений.
Глоссарий по теме
Преобразование тригонометрических выражений – это упрощение выражений, которое выполняется с помощью тригонометрических формул.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
- Преобразование тригонометрических выражений – это их упрощение, которое выполняется с помощью тригонометрических формул.
Вот некоторые правила, которые помогут нам преобразовывать тригонометрические выражения.
- Если в тригонометрических выражениях разные меры угла, то их следует привести к единой, применяя правила:
1) )
)
Например: 
2)
Например:  .
.
- Если синусы, косинусы, тангенсы и котангенсы содержат разные аргументы, (углы),стараемся привести к одному аргументу (углу).
Например, с помощью формул двойного аргумента(угла)  заменяем на
заменяем на  по формуле
по формуле  .
.
- Если в тригонометрическом выражении необходимо поменять синус на косинус, тангенс на котангенс, то применяем формулы приведения.
Например:  , так как
, так как  , синус меняется на косинус.
, синус меняется на косинус.
 , так как
, так как  , тангенс меняется на котангенс, угол в четвёртой четверти, здесь тангенс отрицательный.
, тангенс меняется на котангенс, угол в четвёртой четверти, здесь тангенс отрицательный.
- Если тригонометрические выражения содержат большое количество тригонометрических функций, то необходимо привести к минимальному количеству видов функций. Для этого используем формулы приведения, основное тригонометрическое тождество или другие формулы.
Например:
вычислить  .
.
Заметим, что  ,
,  ,
,  .
.
Тогда данное выражение примет вид:  ;
;
в скобках формула косинуса двойного угла, т.е.  , значит
, значит

- Если в тригонометрическом выражении нужно понизить степень входящих в него компонентов, применяем формулу понижения степени или формулу половинного аргумента. Только помните: степень понижается, аргумент удваивается.
 ,
, ,
,  ,
, 
Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.
Например: упростите выражение  .
.
Применяем формулу понижения степени для косинуса и получаем:
 .
.
Чтобы определить рациональность значения тригонометрического выражения, мы должны знать, что из всех углов, содержащих рациональное число, лишь углы вида  ;
;  ;
;  , где k целое число, имеют рациональный косинус.
, где k целое число, имеют рациональный косинус.
Например,  число рациональное, так как
число рациональное, так как  .
.
Углы вида  ;
;  ;
;  , где k целое число, имеют рациональный синус.
, где k целое число, имеют рациональный синус.
Углы вида  ;
;  , где k целое число, имеют рациональный тангенс.
, где k целое число, имеют рациональный тангенс.
Примеры и разбор решения заданий тренировочного модуля:
Рассмотрим примеры преобразований тригонометрических выражений.
Пример 1.Вычислите:  .
.
Заметим, что в знаменателе данной дроби у синусов разные углы  и
и  . Используем формулу приведения:
. Используем формулу приведения:  и тогда наше выражение примет вид:
и тогда наше выражение примет вид:  , в знаменателе тригонометрическое тождество, равное 1. Нам осталось 24 разделить на 1, получаем 24.
, в знаменателе тригонометрическое тождество, равное 1. Нам осталось 24 разделить на 1, получаем 24.
Пример 2. Найдите  , если
, если  .
.
Так как  , то разделив числитель и знаменатель данной дроби на
, то разделив числитель и знаменатель данной дроби на  . Получаем:
. Получаем:
 , сократим и заменим
, сократим и заменим  на
на .
.
 , по условию
, по условию  =3, подставим это число в наше выражение:
=3, подставим это число в наше выражение:  .
.
resh.edu.ru
Тригонометрические выражения

Тригонометрические выражения. Друзья! Для вас очередная статья с примерами на вычисление тригонометрических выражений. Примеры довольно простые, большинство из них, при определённом навыке, можно решить устно. Если вы основательно изучили тригонометрию и уяснили все важные и необходимые основы, то с решением не будет никаких трудностей.
Что используется в ходе решения данных выражений: формулы приведения, свойства периодичности тригонометрических функций, свойство чётности нечётности, формулы – синуса и косинуса двойного аргумента и, конечно же, основное тригонометрическое тождество.
Рекомендации:
— если в выражении видите, что один угол больше другого в два раза, то смело используйте соответствующую тригонометрическую формулу двойного аргумента;
— если вы видите, что сумма данных углов (или их разность) составляет 90, 180, 270, 360 градусов, то применяйте формулы приведения.
Последнюю статью с выражениями можно посмотреть здесь (там также использовались формулы функций двойного аргумента).
Формулы периодичности, чётности-нечётности здесь.
Основное тригонометрическое тождество здесь.
Рассмотрим задачи:

17289. Найдите значение выражения

Используем формулу синуса двойного аргумента:

Выражение в числителе «сворачиваем»:

*Второй путь: можно было использовать эту же формулу преобразовав знаменатель.

Ответ: 18

63139. Найдите значение выражения

Для решения этого примера достаточно знать формулу косинуса двойного аргумента:

Преобразуем знаменатель:

Ответ: –22

63229. Найдите значение выражения

В данном случае 63 градуса представляем как разность 900 – 270

Ответ: 33

63763. Найдите значение выражения

Представим 1000 как разность 3600 – 2600, применим свойство периодичности нечётности синуса:

Ответ: –34

63819. Найдите значение выражения

Используем формулу приведения косинуса. Представим 1530 как разность 1800 – 270:

Ответ: –38

63875. Найдите значение выражения

Используем формулу приведения для тангенса. Представим 1480 как разность 1800 – 320:

Ответ: 22

63929. Найдите значение выражения

Представим 3730 как сумму 3600 + 130, используем свойство периодичности:

Ответ: –20

63985. Найдите значение выражения

Используем формулы приведения:

*Применили формулу тригонометрии:

Ответ: –5

97369. Найдите значение выражения

Применяем формулу синуса двойного аргумента в числителе, и формулу приведения в знаменателе:

Ответ: –40

97967. Найдите значение выражения

Применяем формулу синуса двойного аргумента:

Ответ: –7

64097. Найдите значение выражения

Используем формулы приведения и основное тригонометрическое тождество:

Ответ: 37

64149. Найдите значение выражения

Используем формулы приведения и основное тригонометрическое тождество:

*Подробнее:

Ответ: –30

64205. Найдите значение выражения

Используем формулу приведения и основное тригонометрическое тождество:

Ответ: 21

63519. Найдите значение выражения

Косинус функция чётная, то есть

Её период равен 2Пn, то есть

Значит

Используем формулу приведения для косинуса:

Ответ: 6

63587. Найдите значение выражения

Период тангенса равен 180 градусам (Пи радиан), функция тангенса нечётная:

Ответ: 132

63651. Найдите значение выражения

Применяем свойство нечётности синуса, выделяем период и используем формулу приведения:

Ответ: 6

26755. Найдите значение выражения

Посмотреть решение
26756. Найдите значение выражения

Посмотреть решение
26757. Найдите значение выражения

Посмотреть решение
26765. Найдите значение выражения

Посмотреть решение
26766. Найдите значение выражения

Посмотреть решение
26767. Найдите значение выражения

Посмотреть решение
27769. Найдите значение выражения

Посмотреть решение
26770. Найдите значение выражения

Посмотреть решение
77412. Найдите значение выражения

Посмотреть решение
77414. Найдите значение выражения

Посмотреть решение
26772. Найдите значение выражения

Посмотреть решение
26773. Найдите значение выражения

Посмотреть решение
26774. Найдите значение выражения

Посмотреть решение
26761. Найдите значение выражения

Посмотреть решение
26762. Найдите значение выражения

Посмотреть решение
26763. Найдите значение выражения

Посмотреть решение
На этом всё! Успеха Вам!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Преобразование произведений тригонометрических функций в сумму (продолжение)
На уроке продолжают изучаться формулы преобразования произведений тригонометрических функций в сумму, вспоминаются формулы для произведений тригонометрических функций, решаются несколько примеров на вычисление, упрощение, доказательство тождества и уравнения с использованием этих формул.
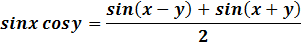
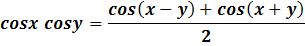
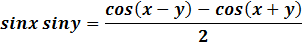
1. Доказать тождество:
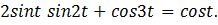
Доказательство:

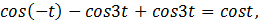
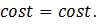
Все преобразования можно сделать в обратном порядке.
2. Вычислить:
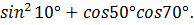
Решение: воспользуемся формулами:
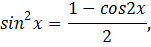
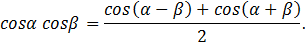
Получим:
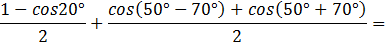
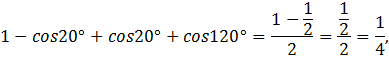
где
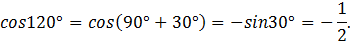
Ответ: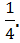
3. Вычислить:
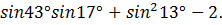
Решение: воспользуемся формулами:
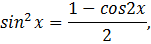
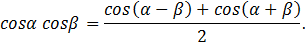
Получим:
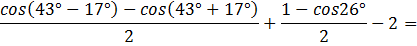
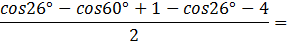
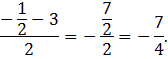
Ответ: 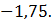
Рекомендации: произведение тригонометрических функций целесообразно преобразовывать в сумму для дальнейшего приведения подобных слагаемых.
4. Решить уравнение:
1) 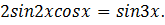
Решение:(1-й способ) используя формулу произведения синуса на косинус 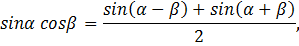
получим:
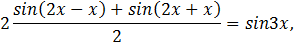
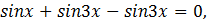
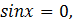

Ответ: 
Решение: (2-й способ) используя формулу
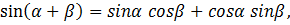
получается:
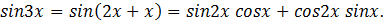
Тогда:
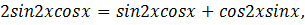
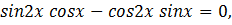
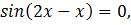
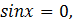

Ответ: 
2) 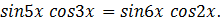
Решение: используя формулу

получается:
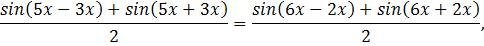
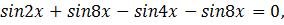
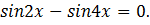
Рассмотрим отдельно полученное уравнение.
3) 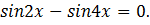
Решение: используя формулу
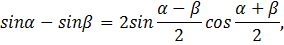
получается:
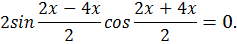
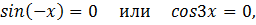
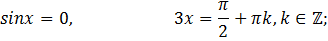
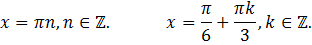
Ответ: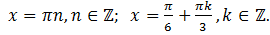
Для возможности объединения полученных множеств изобразим их на единичной окружности 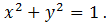

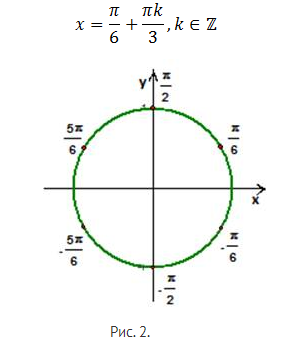
Объединить нельзя (см. рис.1-2.)
На уроке рассматривались и использовались формулы преобразования произведений тригонометрических функций в сумму.
На следующем уроке будет рассмотрено преобразование выражения вида 
Список рекомендованной литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.
8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983
Дополнительные веб-ресурсы
1. Интернет-портал Mathematics.ru (Источник).
2. Портал Естественных Наук (Источник).
3. Интернет-портал exponenta.ru (Источник).
Сделай дома
№№ 23.10(а), 23.6(а), 23.2 (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)
interneturok.ru
Пособие по теме Преобразование тригонометрических выражений
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»
МЕТОДИЧЕСКОЕ ПОСОБИЕ
Для самостоятельной работы студентов
По дисциплине: МАТЕМАТИКА: алгебра и начало математического анализа; геометрия
Тема: «ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ»
Специальность: 34.02.01 Сестринское дело Курс: 1
(базовой подготовки)
Купино
2019
Рассмотрено на заседании предметной цикловой
Методической комиссии по общеобразовательным дисциплинам,
общему гуманитарному и социально-экономическому, математическому и
естественно-научному циклу
Протокол № _____ от «_____» _________20____г.
Автор – составитель: преподаватель математики высшей категории Тюменцева О.Н.
Купино
2019 г
Пояснительная записка к методическому пособию
Методическое пособие предназначено для повторения теоретических и практических знаний по теме.
Цель пособия – повторить понятия: тригонометрических функций, радианной меры углов, таблицы значений тригонометрических функций, формулы перевода градусов в радианы и наоборот, основные тригонометрические тождества и подготовится к занятию по теме «Преобразование простейших тригонометрических выражений».
Данное пособие рекомендовано для студентов первого курса специальности 34.02.01 Сестринское дело. Пособие содержит определения, свойства и формулы по теме: Преобразование простейших тригонометрических выражений, тест для самоконтроля и ключи к тесту.
Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.
Преобразование простейших тригонометрических выражений Под преобразованием тригонометрических выражений понимают упрощение, выполняемое с помощью формул из тригонометрии.
Существуют основные правила, которых следует придерживаться во время преобразования выражений:
1. Во время преобразования выражений, содержащих большое количество тригонометрических функций, необходимо привести его к минимальному количеству видов функций. Для этого следует воспользоваться основными тригонометрическими тождествами, формулами приведения и другими формулами.
2. Если выражение содержит функции с разными аргументами, постарайтесь привести их к одному аргументу.
3. Если для упрощения выражений необходимо получить кофункцию, воспользуйтесь формулами приведения.
4. Если в выражении имеются функции высоких степеней, то можно воспользоваться основным тригонометрическим тождеством или же формулами понижения степеней:
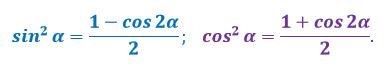
5. Для преобразования некоторых выражений Вам могут помочь дополнительные формулы, которые не рассматривались в предыдущих вопросах:
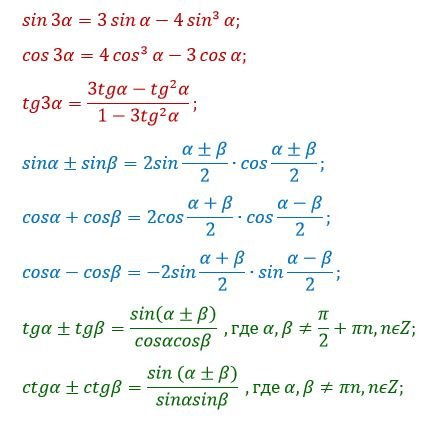
С помощью следующих формул можно избавиться от произведения функций, перейдя к сумме:
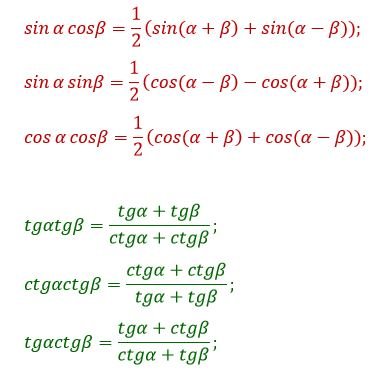
Переход к половинным углам:
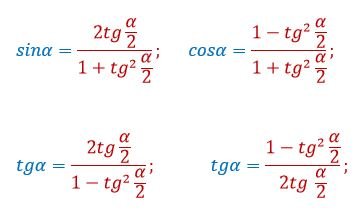
В тождественных преобразованиях тригонометрических выражений могут быть использованы следующие алгебраические приемы: добавление и вычитание одинаковых слагаемых; вынесение общего множителя за скобки; умножение и деление на одну и ту же величину; применение формул сокращенного умножения; выделение полного квадрата; разложение квадратного трехчлена на множители; введение новых переменных с целью упрощения преобразований.
При преобразованиях тригонометрических выражений, содержащих дроби, можно использовать свойства пропорции, сокращение дробей или приведение дробей к общему знаменателю. Кроме того, можно пользоваться выделением целой части дроби, умножением числителя и знаменателя дроби на одинаковую величину, а так же по возможности учитывать однородность числителя или знаменателя. При необходимости можно представлять дробь в виде суммы или разности нескольких более простых дробей.
Кроме того, применяя все необходимые методы преобразования тригонометрических выражений, необходимо постоянно учитывать облась допустимых значений преобразуемых выражений.
Рассмотрим несколько примеров.
Пример 1.
Вычислить А = (sin (2x – π) · cos (3π – x) + sin (2x – 9π/2) · cos (x + π/2))2+ (cos (x – π/2) · cos (2x – 7π/2) + sin (3π/2 – x) · sin (2x – 5π/2))2
Решение.
Из формул приведения следует:
sin (2x – π) = -sin 2x; cos (3π – x) = -cos x;
sin (2x – 9π/2) = -cos 2x; cos (x + π/2) = -sin x;
cos (x – π/2) = sin x; cos (2x – 7π/2) = -sin 2x;
sin (3π/2 – x) = -cos x; sin (2x – 5π/2) = -cos 2x.
Откуда в силу формул сложения аргументов и основного тригонометрического тождества получаем
А = (sin 2x · cos x + cos 2x · sin x)2 + (-sin x · sin 2x + cos x · cos 2x)2 = sin2 (2x + x) + cos2 (x + 2x) = sin2 3x + cos2 3x = 1
Ответ: 1.
Пример 2.
Преобразовать в произведение выражение М = cos α + cos (α + β) · cos γ + cos β – sin (α + β) · sin γ + cos γ.
Решение.
Из формул сложения аргументов и формул преобразования суммы тригонометрических функций в произведение после соответствующей группировки имеем
М = (cos (α + β) · cos γ – sin (α + β) · sin γ) + cos α + (cos β + cos γ) =
= 2cos ((β + γ)/2) · cos ((β – γ)/2) + (cos α + cos (α + β + γ)) =
= 2cos ((β + γ)/2) · cos ((β – γ)/2) + 2cos (α + (β + γ)/2) · cos ((β + γ)/2)) =
= 2cos ((β + γ)/2) (cos ((β – γ)/2) + cos (α + (β + γ)/2)) =
= 2cos ((β + γ)/2) · 2cos ((β – γ)/2 + α + (β + γ)/2)/2) · cos ((β – γ)/2) – (α + (β + γ)/2)/2) = 4cos ((β + γ)/2) · cos ((α +β)/2) · cos ((α + γ)/2).
Ответ: М = 4cos ((α + β)/2) · cos ((α + γ)/2) · cos ((β + γ)/2).
Пример 3.
Показать, что выражение А = cos2 (x + π/6) – cos (x + π/6) · cos (x – π/6) + cos2 (x – π/6) принимает для всех х из R одно и то же значение. Найти это значение.
Решение.
Приведем два способа решения этой задачи. Применяя первый способ, путем выделения полного квадрата и пользуясь соответствующими основными тригонометрическими формулами, получим
А = (cos (x + π/6) – cos (x – π/6))2 + cos (x – π/6) · cos (x – π/6) =
= 4sin2 x · sin2 π/6 + 1/2(cos 2x + cos π/3) =
= sin2 x + 1/2 · cos 2x + 1/4 = 1/2 · (1 – cos 2x) + 1/2 · cos 2x + 1/4 = 3/4.
Решая задачу вторым способом, рассмотрим А как функцию от х из R и вычислим ее производную. После преобразований получим
А´ = -2cos (x + π/6) · sin (x + π/6) + (sin (x + π/6) · cos (x – π/6) + cos (x + π/6) · sin (x + π/6)) – 2cos (x – π/6) · sin (x – π/6) =
= -sin 2(x + π/6) + sin ((x + π/6) + (x – π/6)) – sin 2(x – π/6) =
= sin 2x – (sin (2x + π/3) + sin (2x – π/3)) =
= sin 2x – 2sin 2x · cos π/3 = sin 2x – sin 2x ≡ 0.
Отсюда в силу критерия постоянства дифференцируемой на промежутке функции заключаем, что
А(х) ≡ (0) = cos2 π/6 — cos2 π/6 + cos2 π/6 = (√3/2)2 = 3/4, x € R.
Ответ: А = 3/4 для x € R.
Основными приемами доказательства тригонометрических тождеств являются:
а) сведение левой части тождества к правой путем соответствующих преобразований;
б) сведение правой части тождества к левой;
в) сведение правой и левой частей тождества к одному и тому же виду;
г) сведение к нулю разности левой и правой частей доказываемого тождества.
Пример 4.
Проверить, что cos 3x = -4cos x · cos (x + π/3) · cos (x + 2π/3).
Решение.
Преобразуя правую часть этого тождества по соответствующим тригонометрическим формулам, имеем
-4cos x · cos (x + π/3) · cos (x + 2π/3) = -2cos x · (cos ((x + π/3) + (x + 2π/3)) + cos ((x + π/3) – (x + 2π/3))) = -2cos x · (cos (2x + π) + cos π/3) =
= 2cos x · cos 2x — cos x = (cos 3x + cos x) – cos x = cos 3x.
Правая часть тождества сведена к левой.
Пример 5.
Доказать, что sin2 α + sin2 β + sin2 γ – 2cos α · cos β · cos γ = 2, если α, β, γ – внутренние углы некоторого треугольника.
Решение.
Учитывая, что α, β, γ – внутренние углы некоторого треугольника, получаем, что α + β + γ = π и, значит, γ = π – α – β.
Получим
sin2 α + sin2 β + sin2 γ – 2cos α · cos β · cos γ =
= sin2 α + sin2 β + sin2 (π – α – β) – 2cos α · cos β · cos (π – α – β) =
= sin2 α + sin2 β + sin2 (α + β) + (cos (α + β) + cos (α – β) · (cos (α + β) =
= sin2 α + sin2 β + (sin2 (α + β) + cos2 (α + β)) + cos (α – β) · (cos (α + β) =
= 1/2 · (1 – сos 2α) + ½ · (1 – cos 2β) + 1 + 1/2 · (cos 2α + cos 2β) = 2.
Исходное равенство доказано.
Пример 6
Преобразовать в произведение: 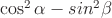 .
.
Применив формулы понижения степени, получим:
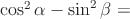
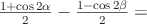

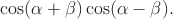
Пример 7
Преобразовать в произведение: 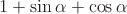 .
.
 заменим через
заменим через 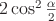 . Чтобы и в
. Чтобы и в  перейти к аргументу
перейти к аргументу  , применим формулу синуса двойного угла:
, применим формулу синуса двойного угла:
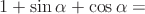
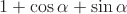
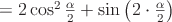
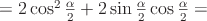
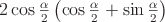
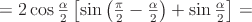
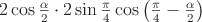
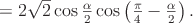
Тест по теме Преобразование простейших тригонометрических выражений
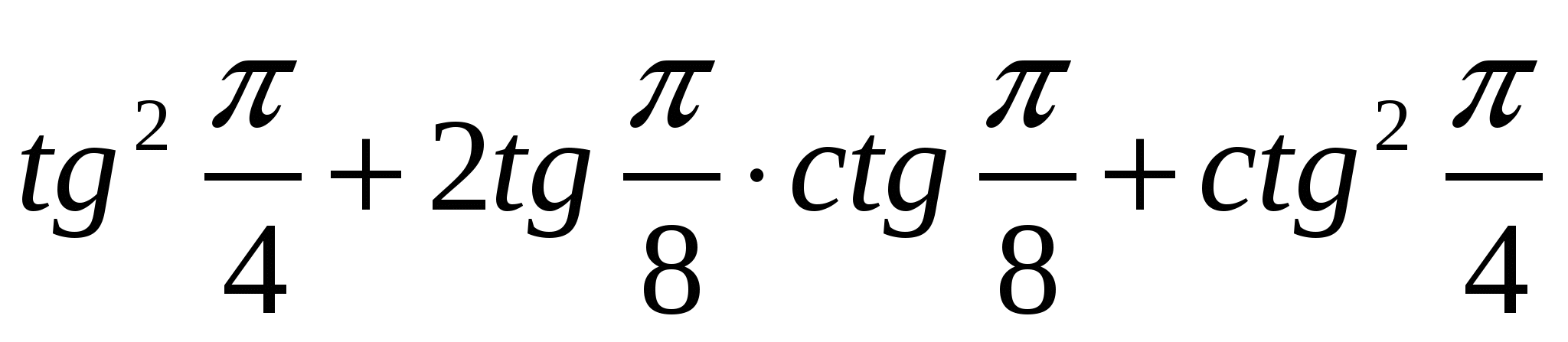
1) 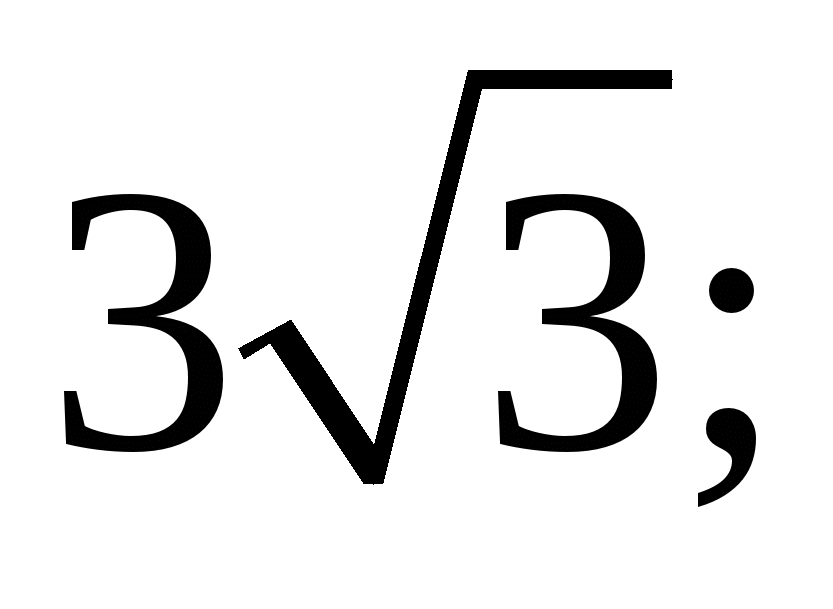 2)
2) 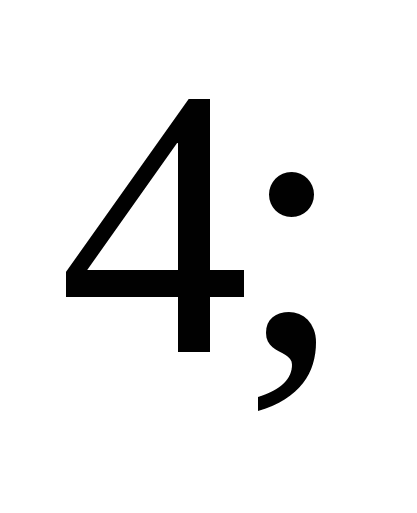 3)
3) 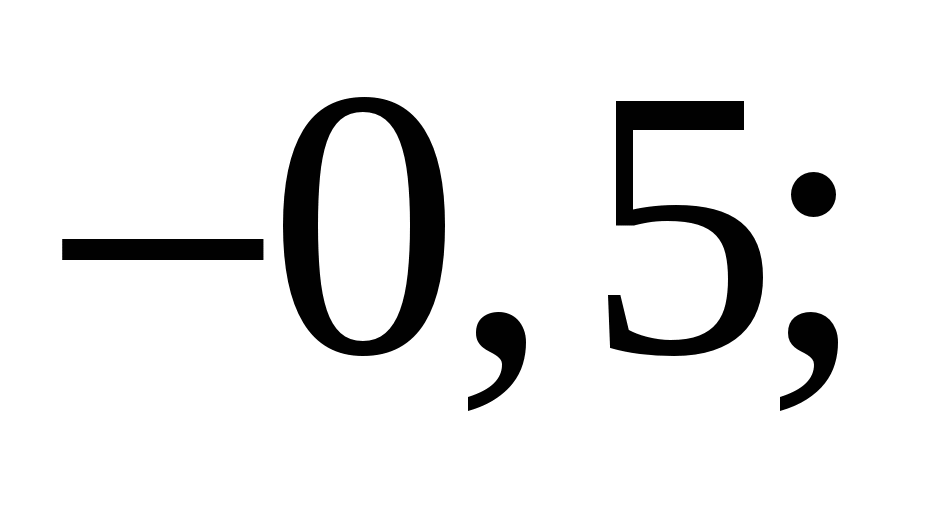 4)
4)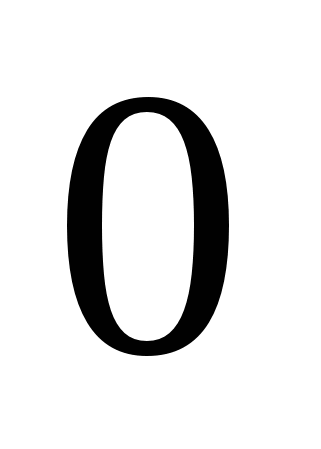
А2
Найдите 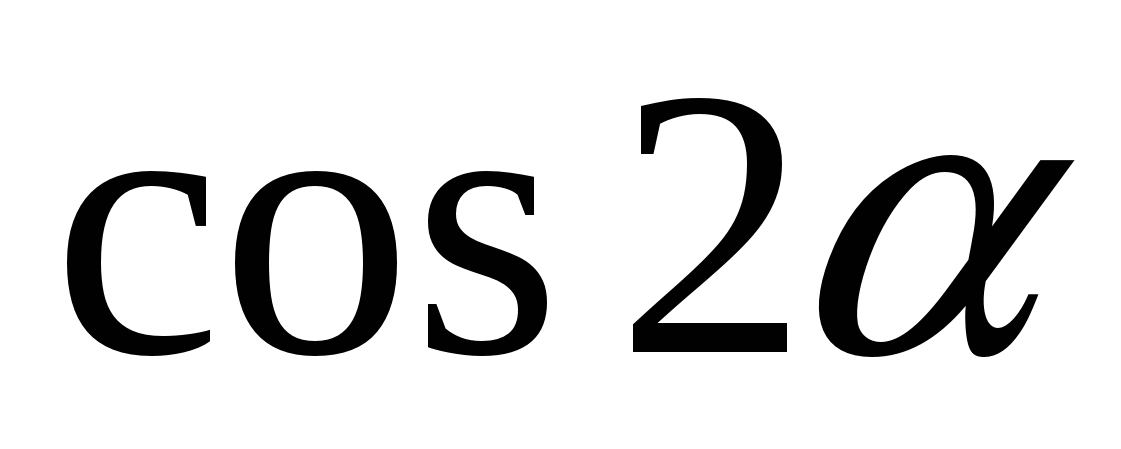 , если
, если 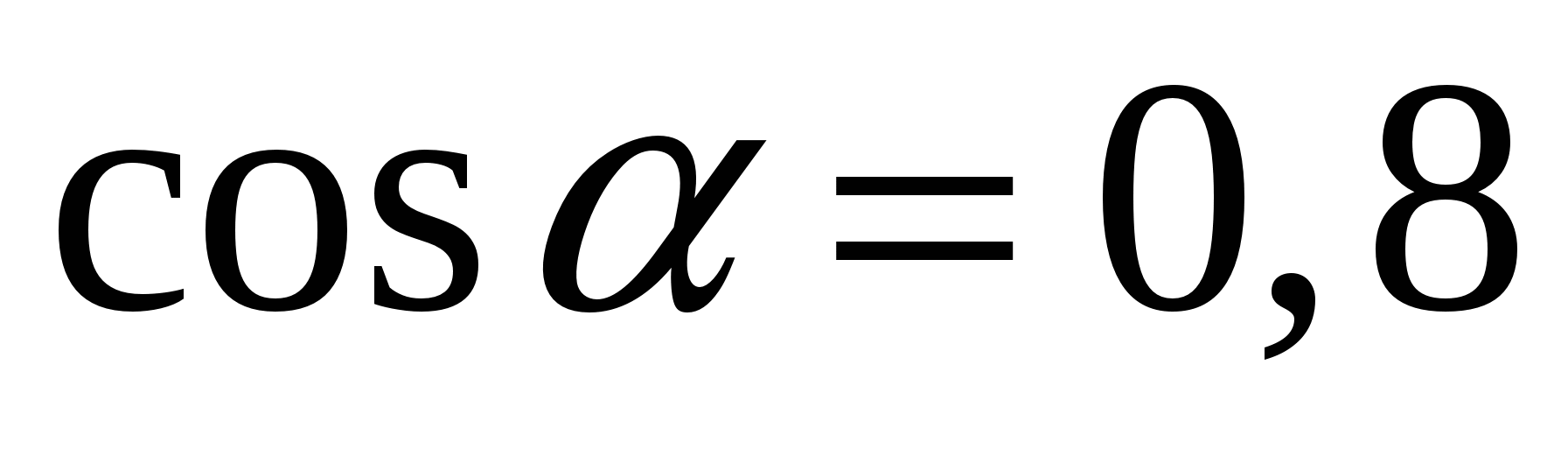
1) 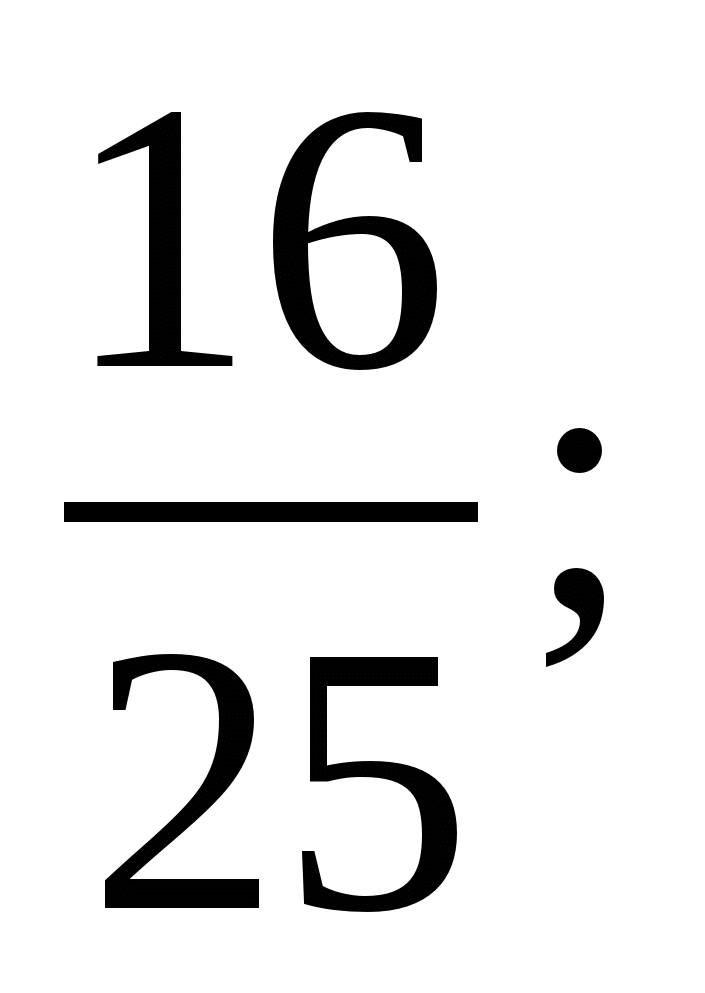 2)
2) 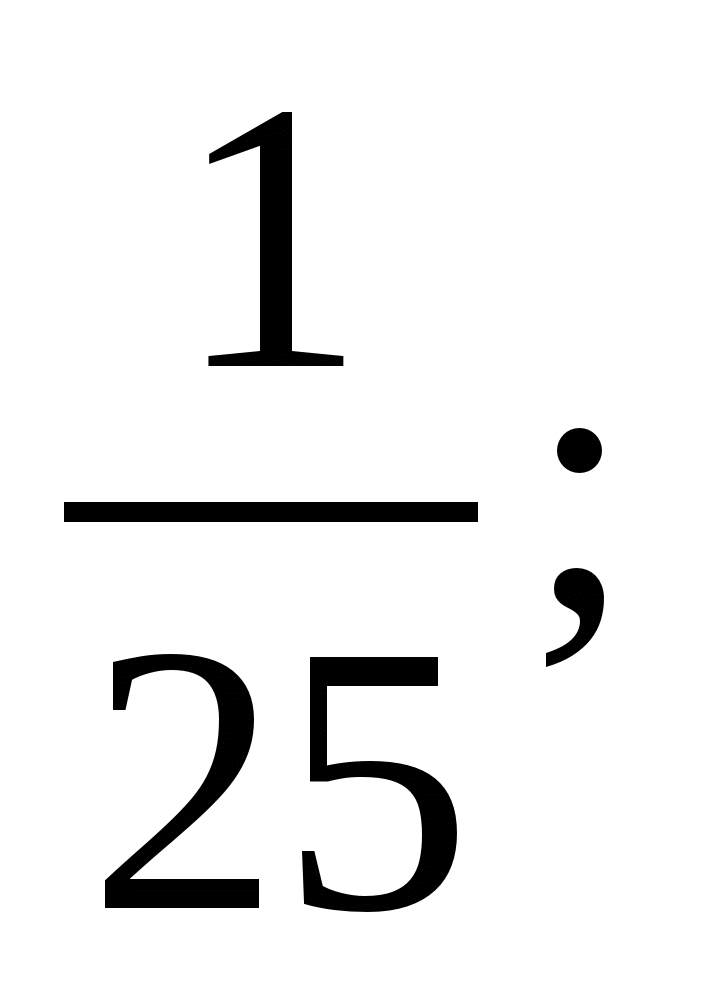 3)
3) 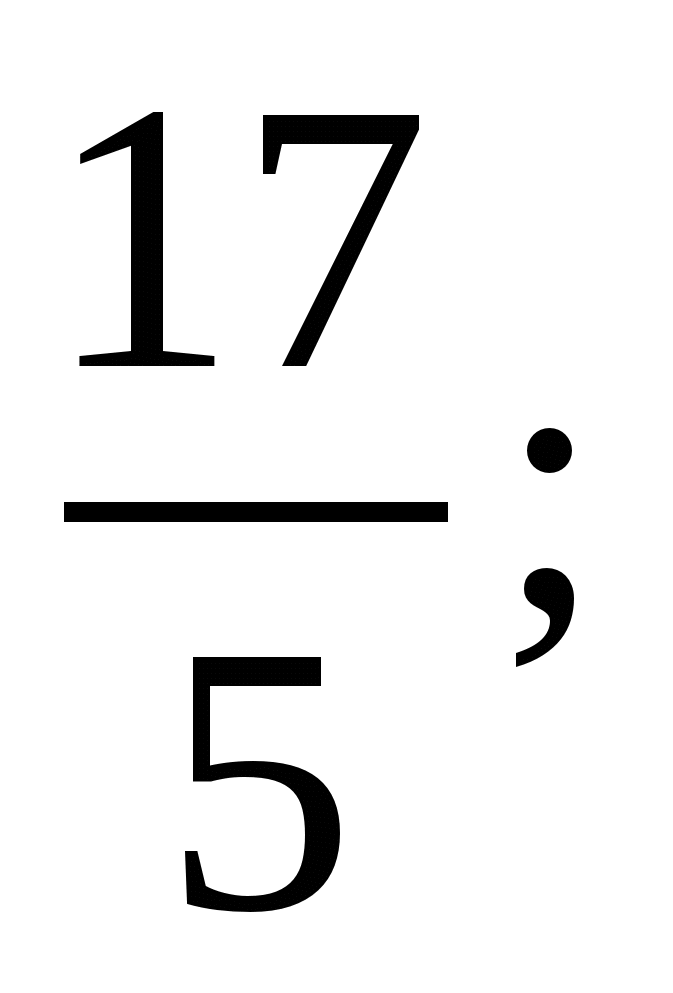 4)
4)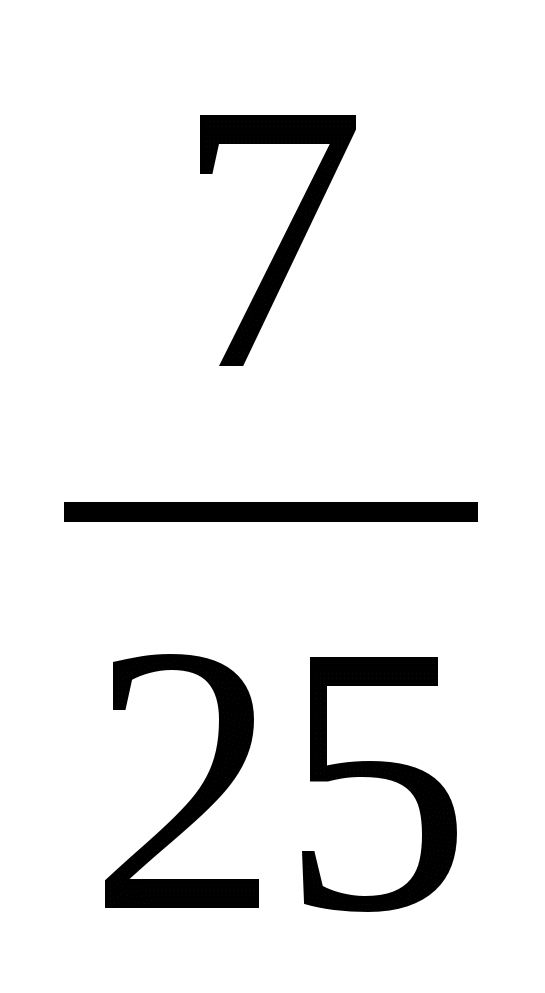
А3
Упростите выражение: 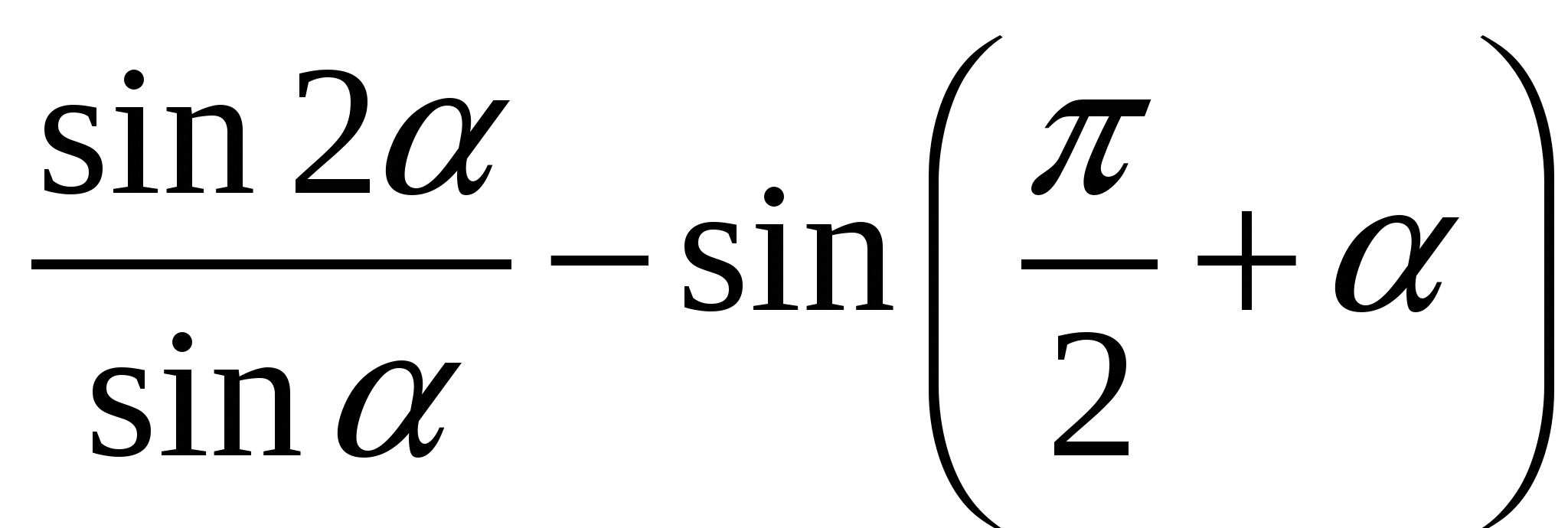
1) 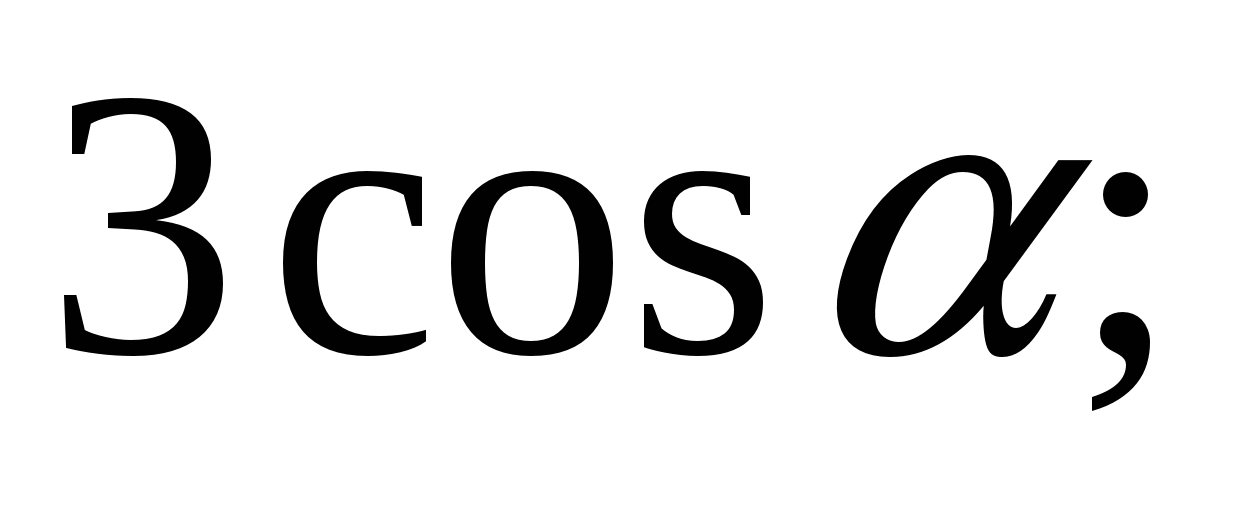 2)
2) 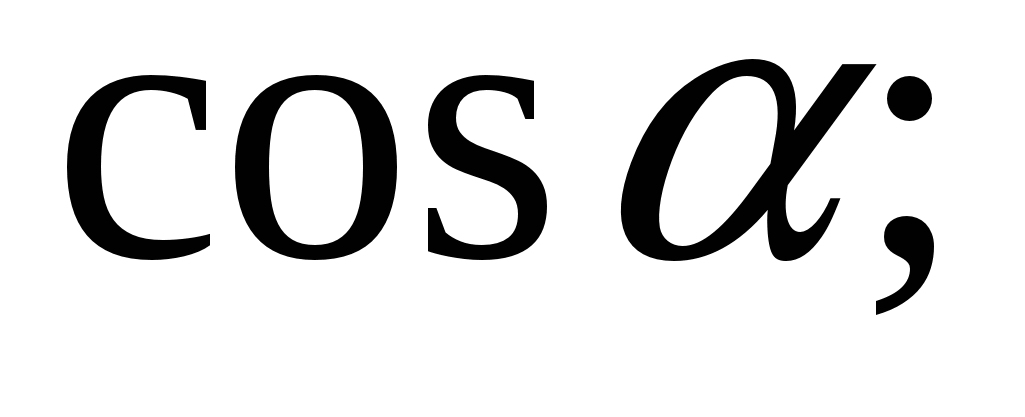 3) 0; 4)
3) 0; 4)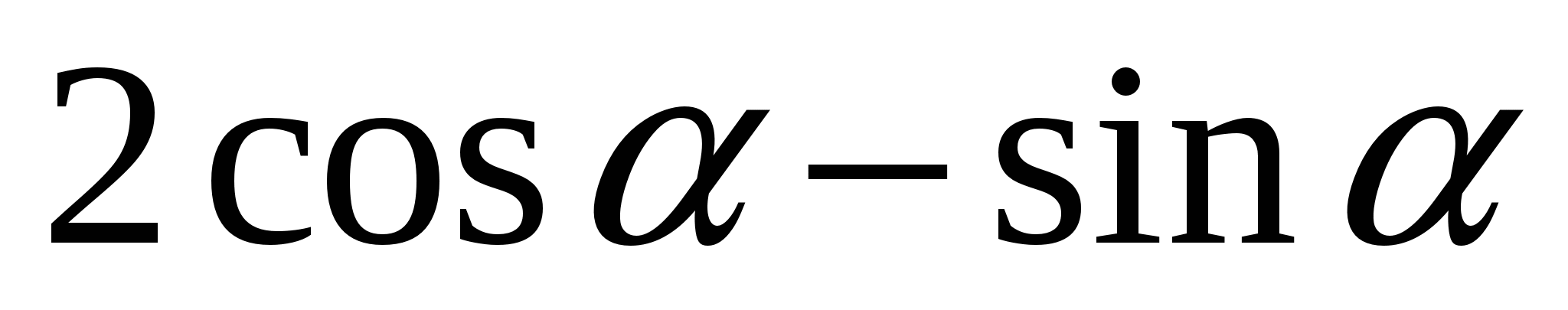
А4
Найдите значение выражения 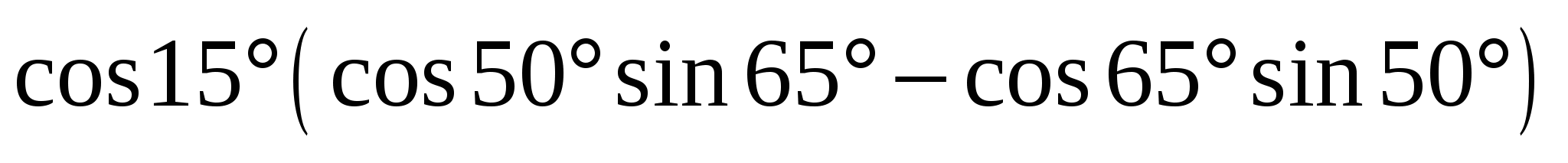
1) 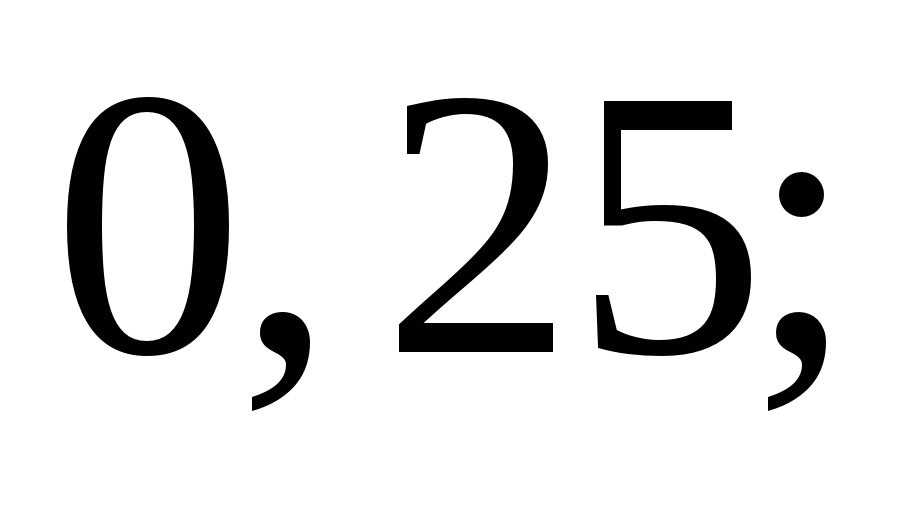 2)
2) 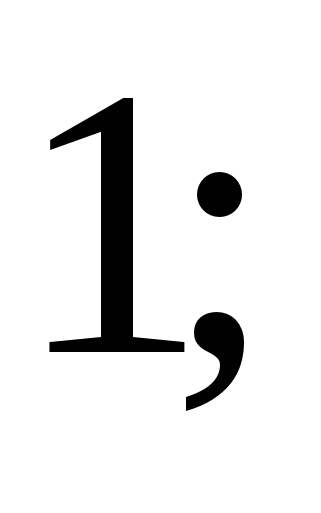 3)
3) 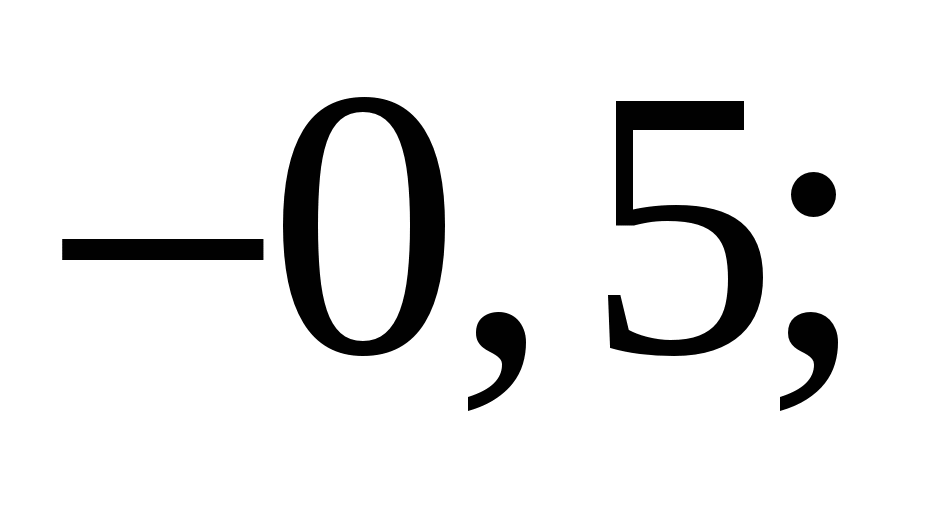 4)
4)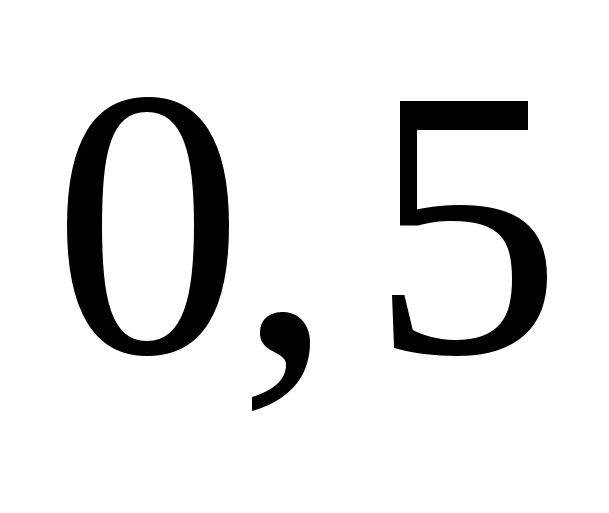
А5
Упростите выражение: 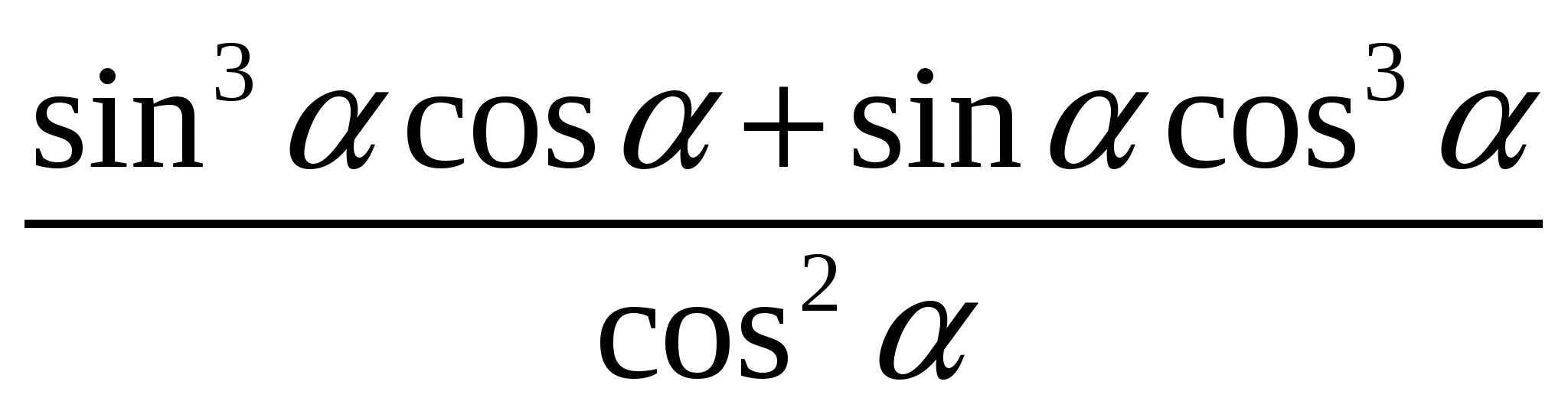
1) 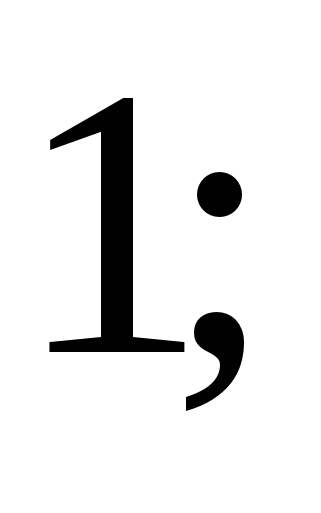 2)
2) 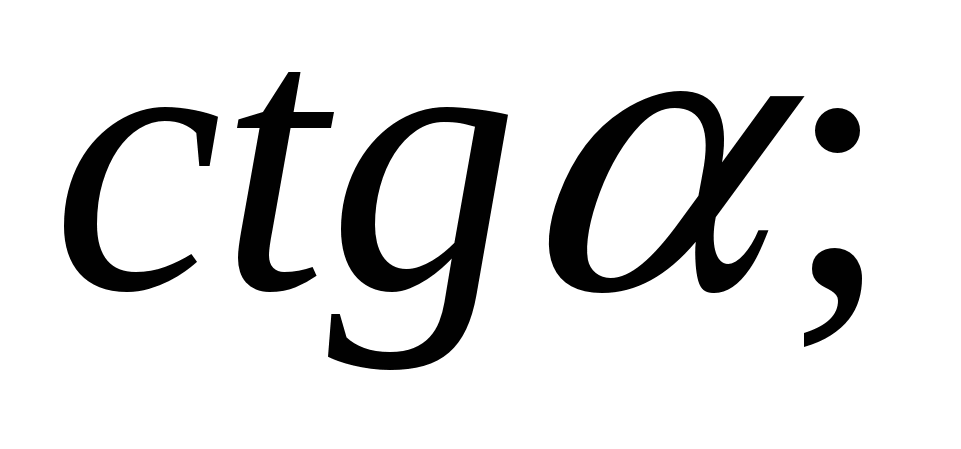 3)
3) 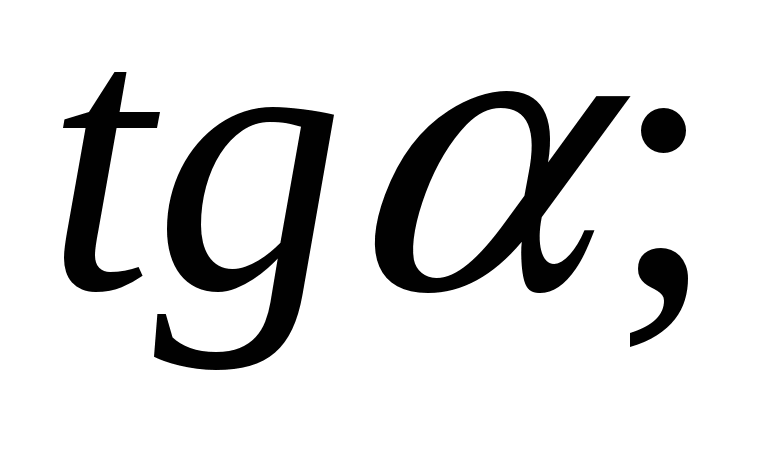 4)
4)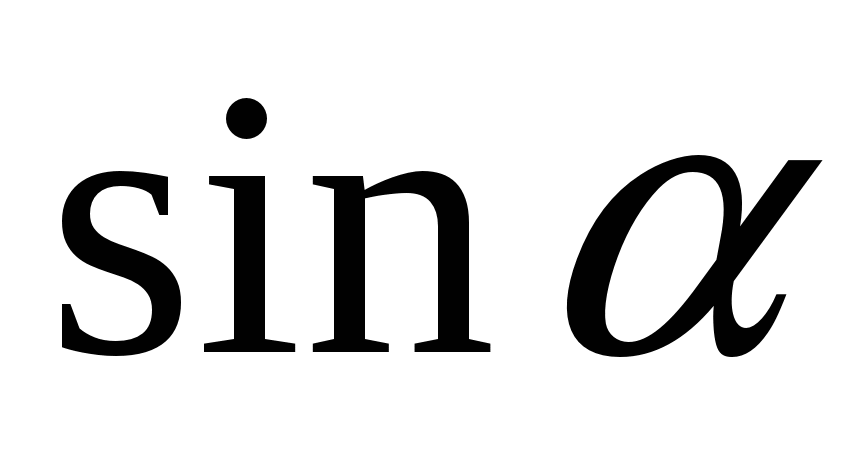
В) Напишите правильный ответ
В1
Вычислите: 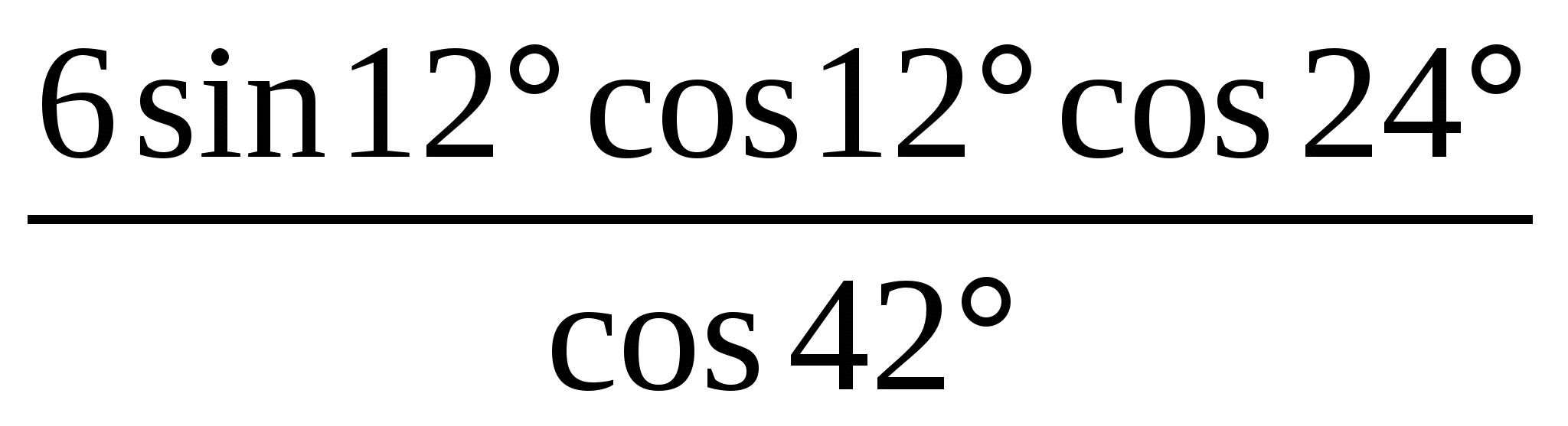
В2
Определите наибольшее значение выражения 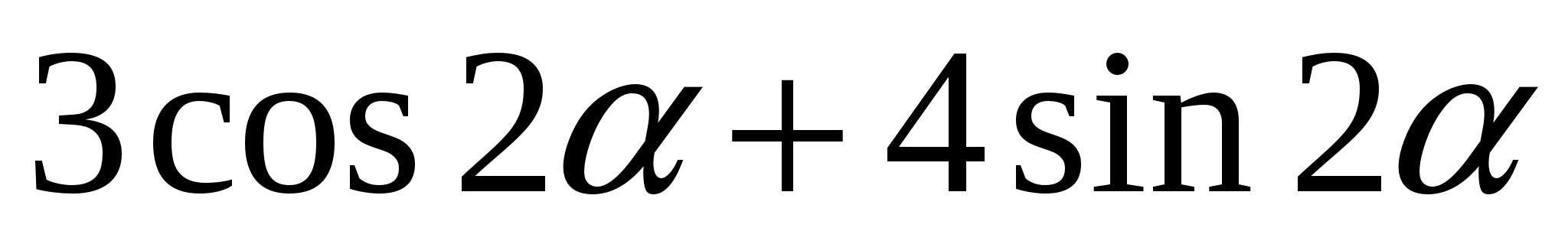
С) Приведите подробное решение данного задания.
С
Вычислите 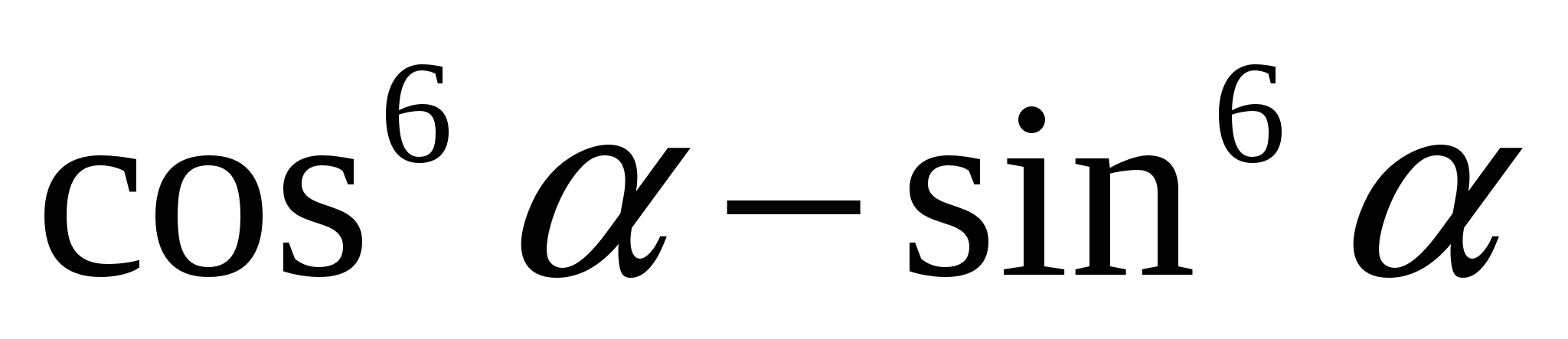 , если
, если 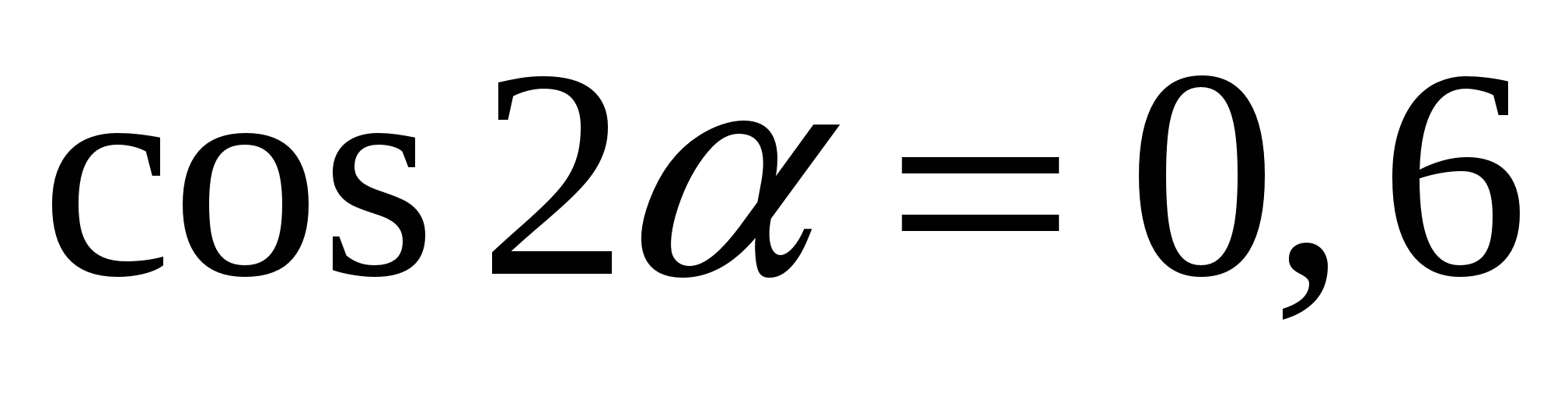 .
.
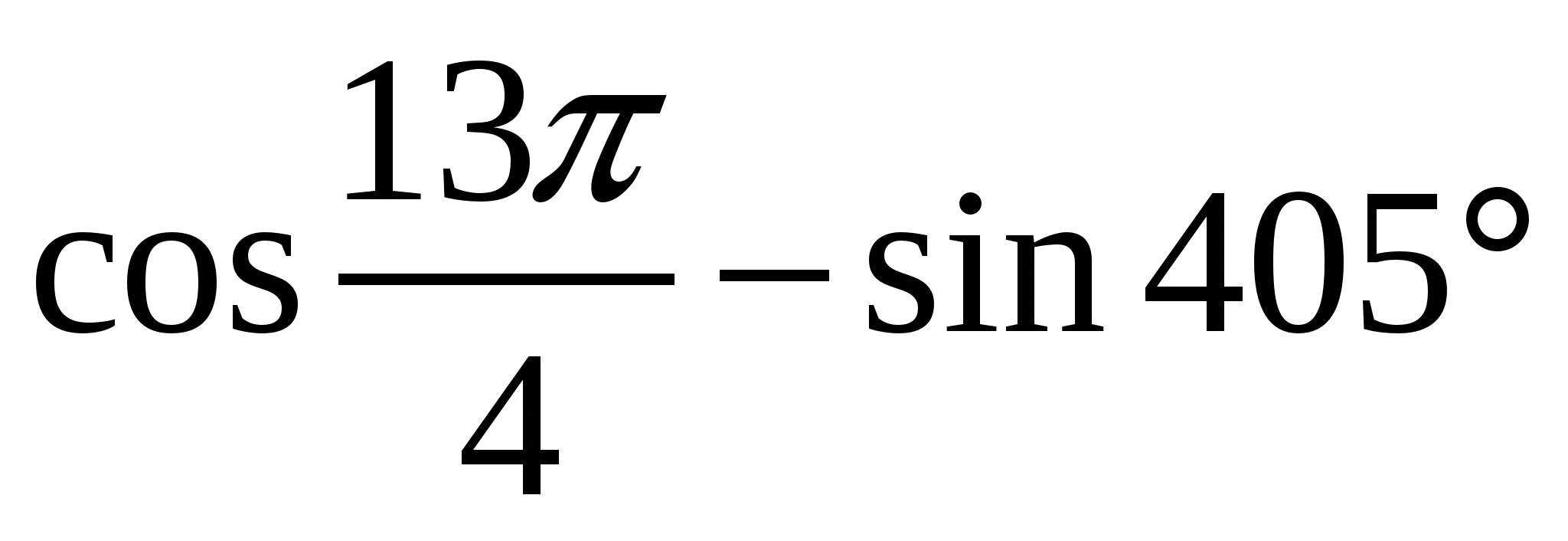
1) 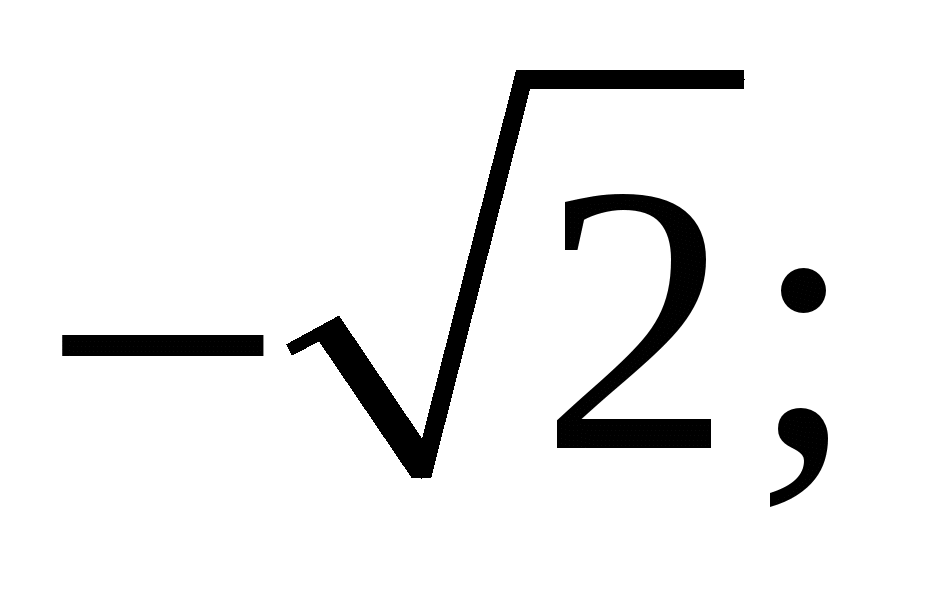 2)
2) 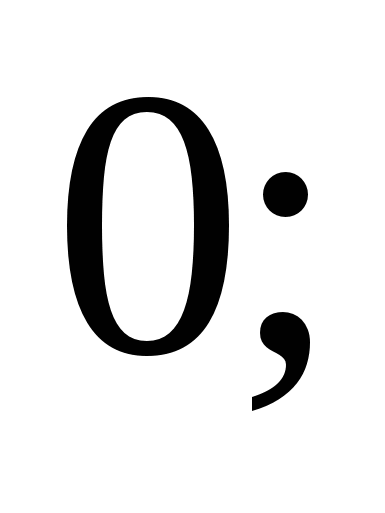 3)
3) 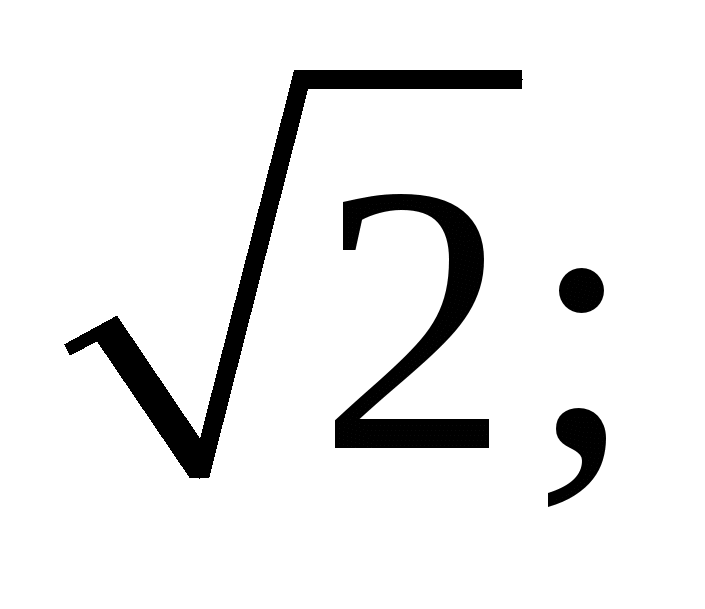 4)
4)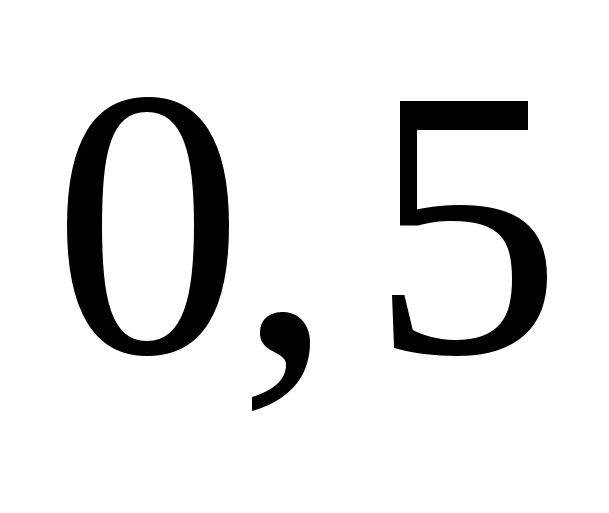
А2
Найдите 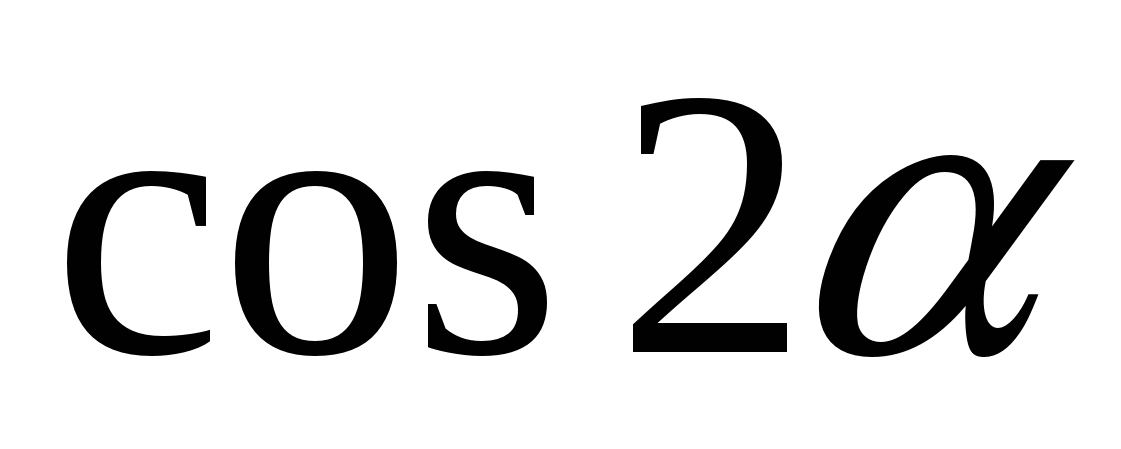 , если
, если 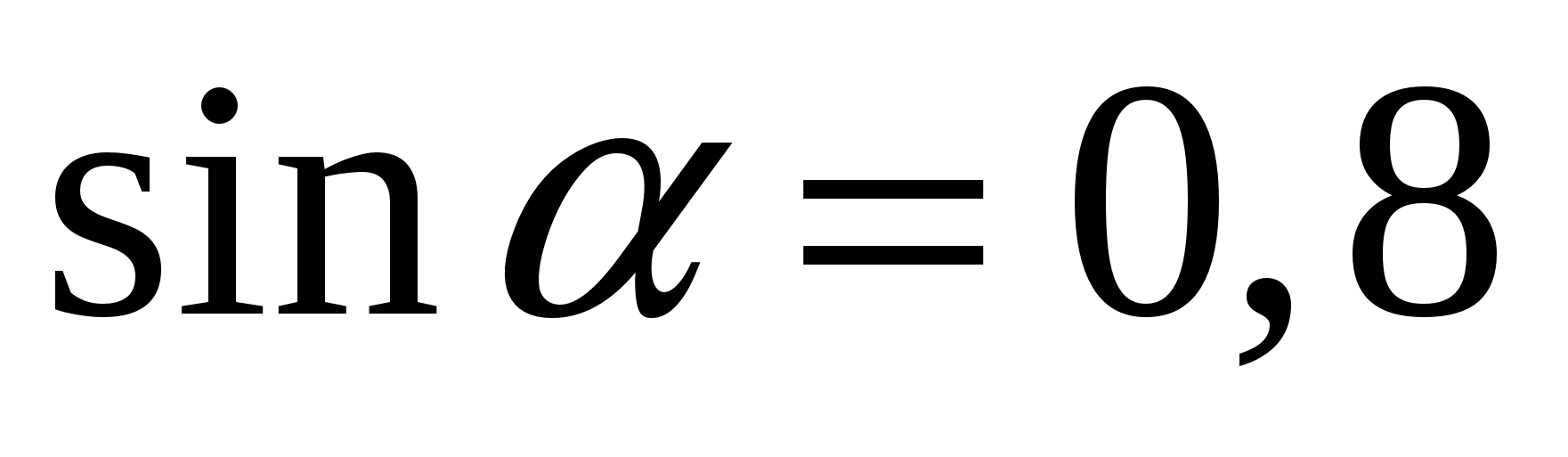
1) 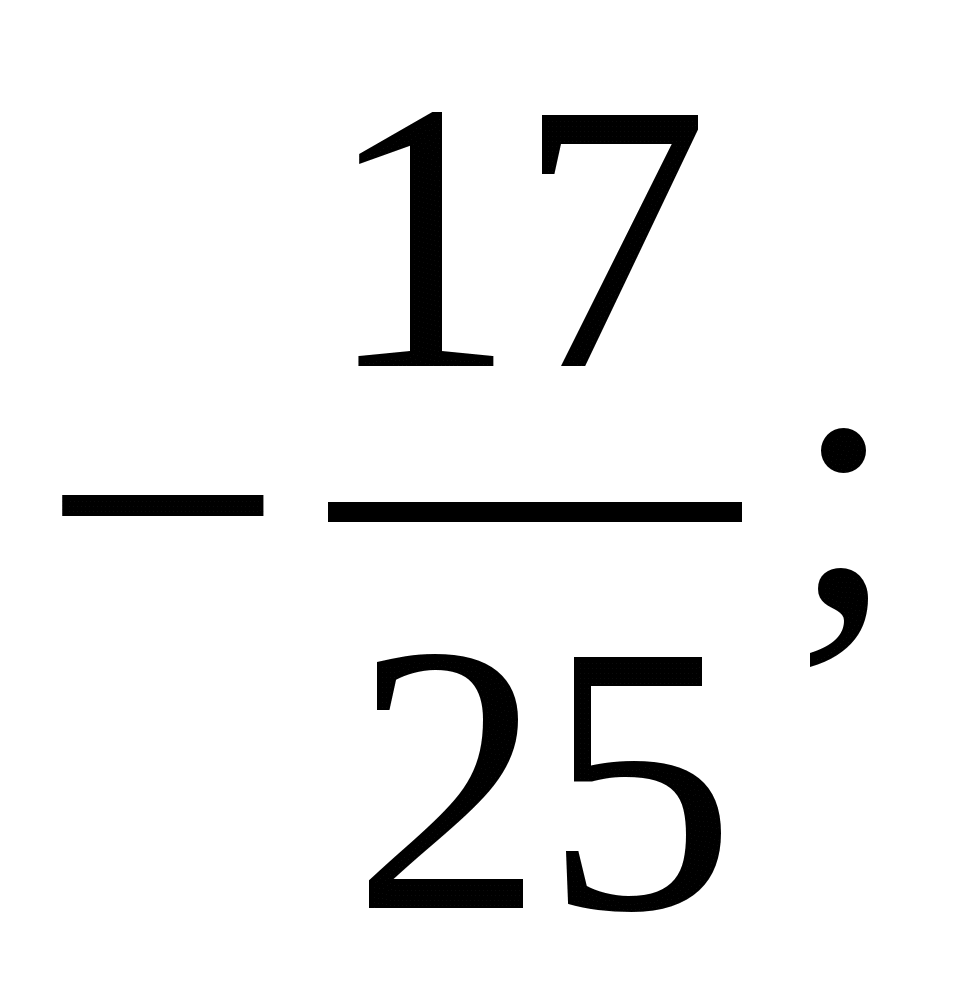 2)
2) 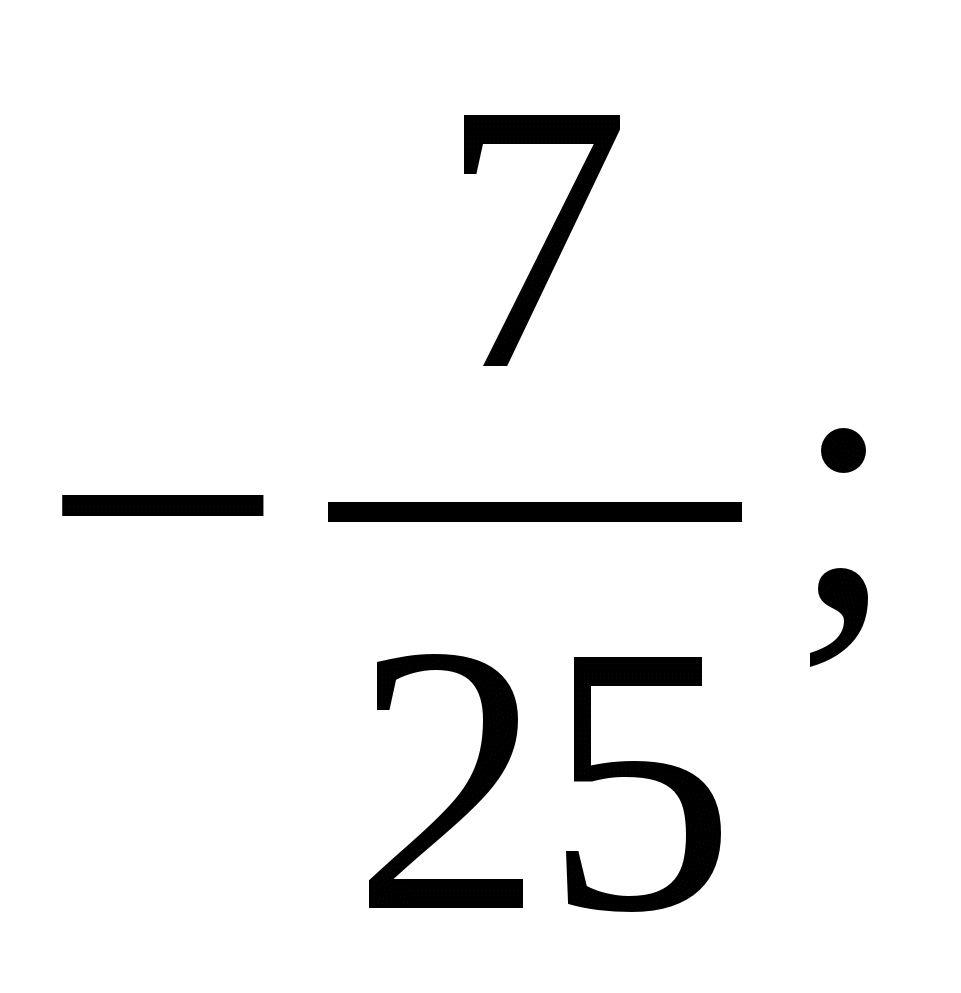 3)
3) 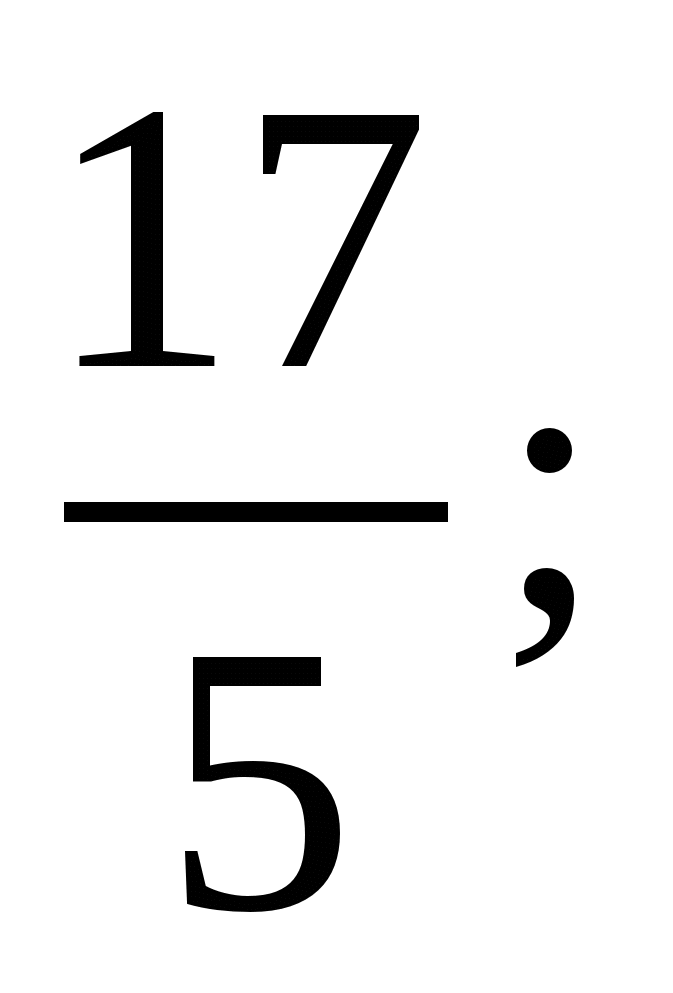 4)
4)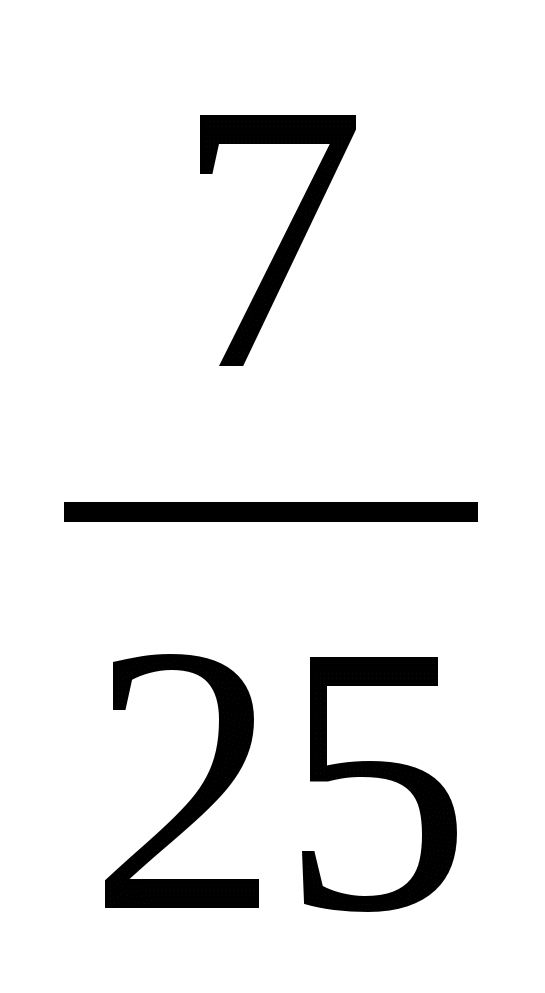
А3
Упростите выражение: 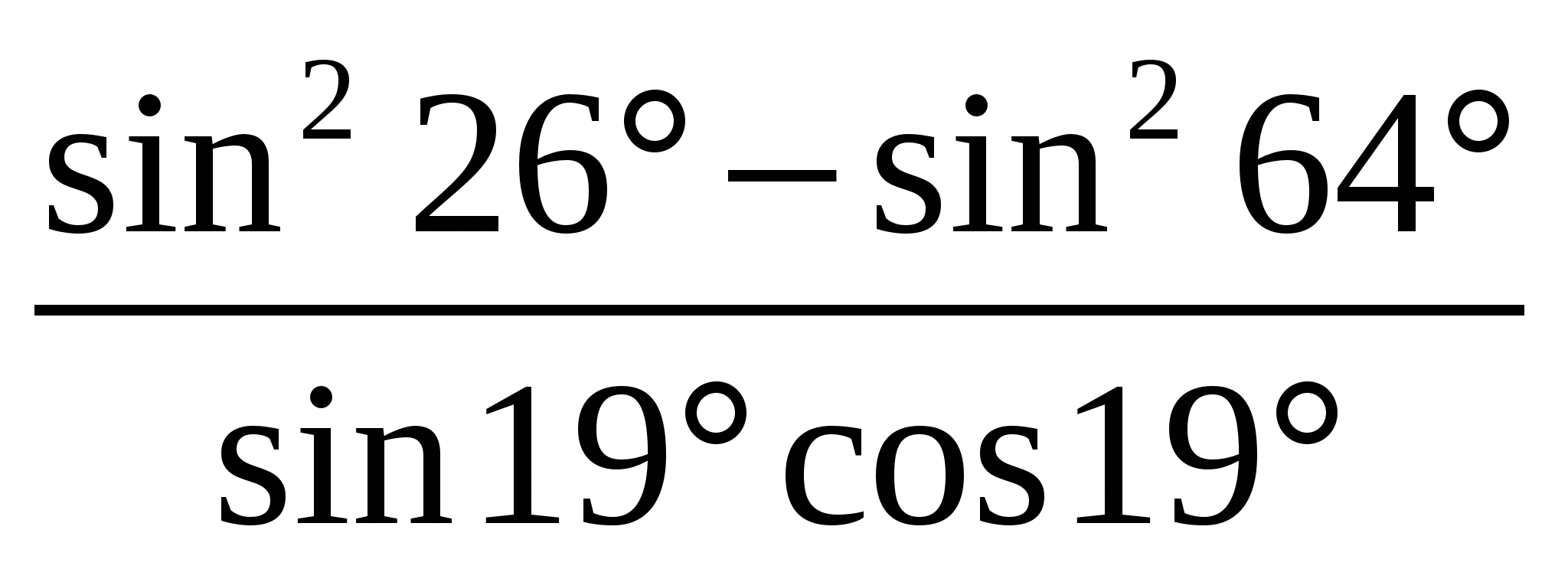
1) 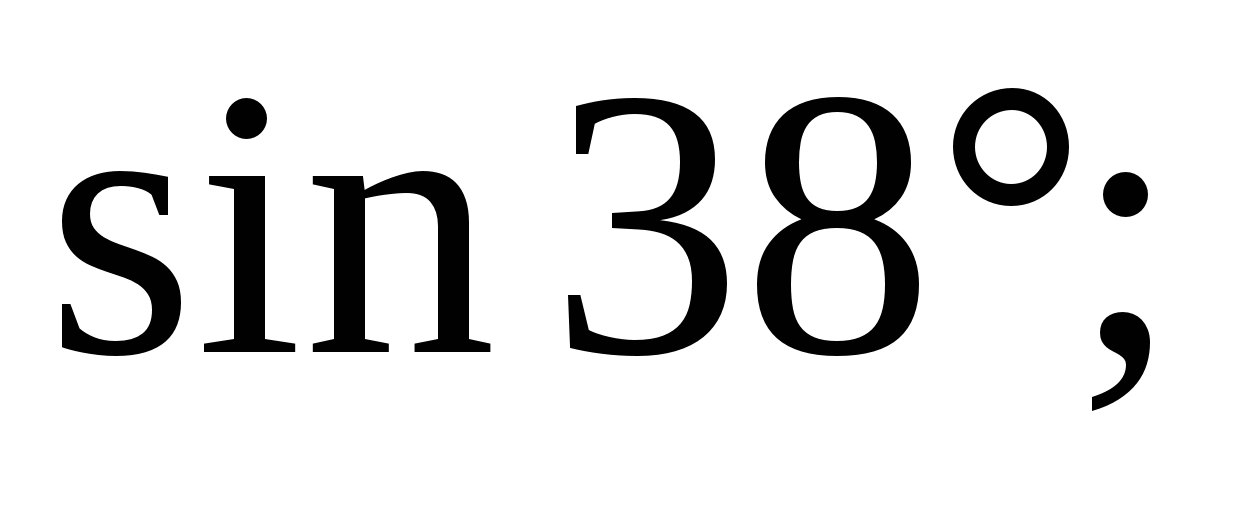 2)
2) 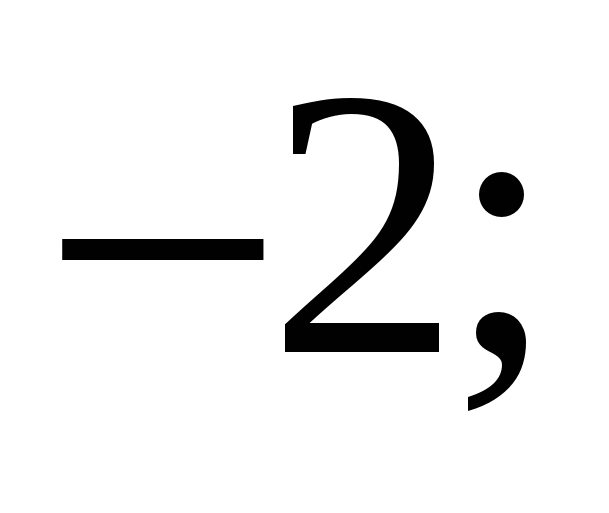 3) 0; 4)
3) 0; 4)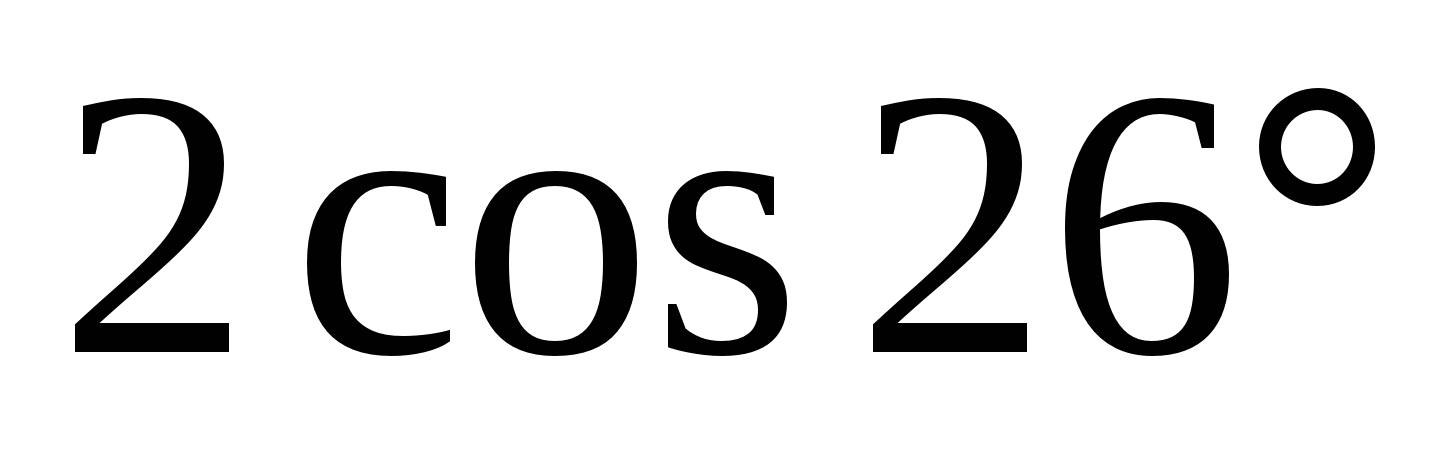
А4
Найдите значение выражения 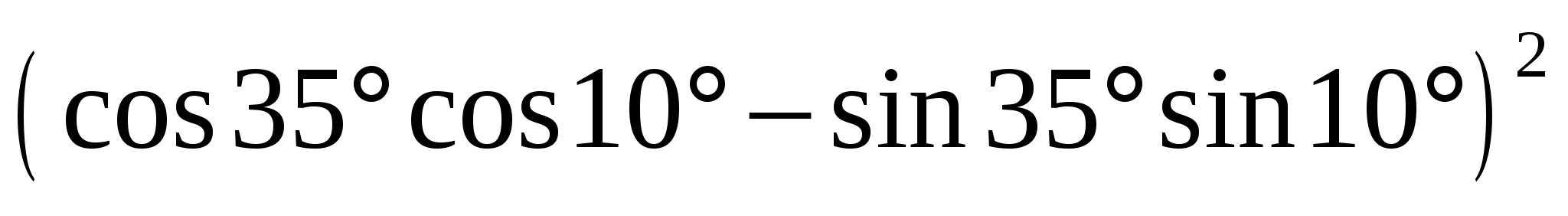
1) 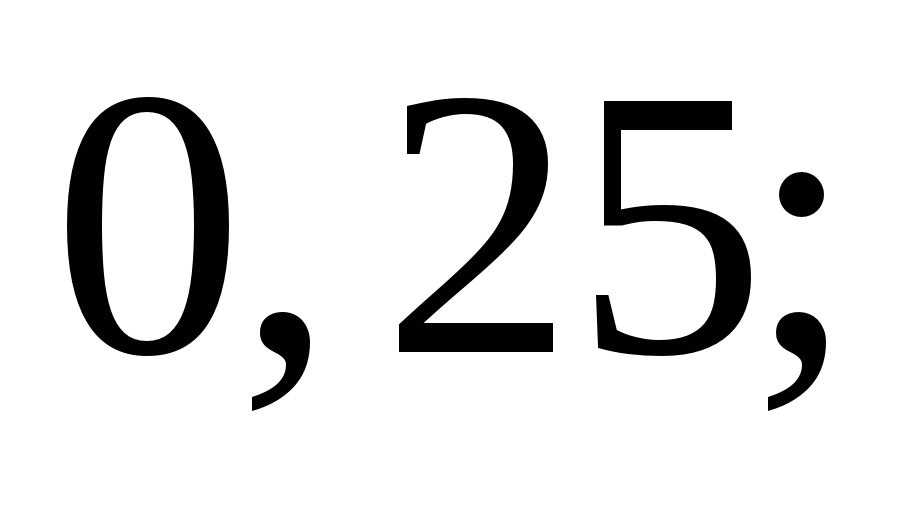 2)
2) 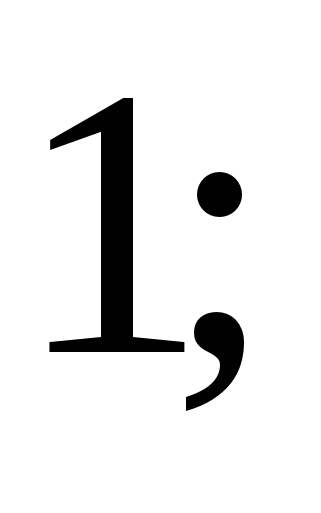 3)
3) 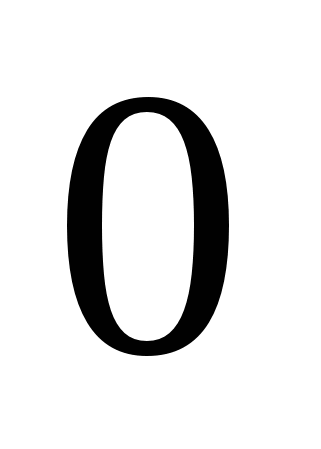 4)
4)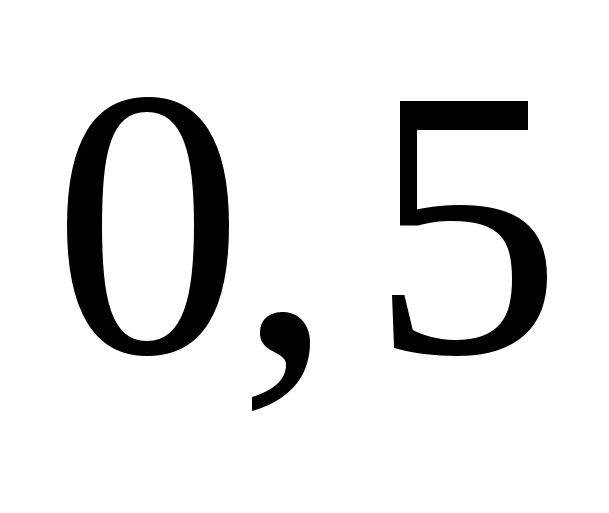
А5
Упростите выражение: 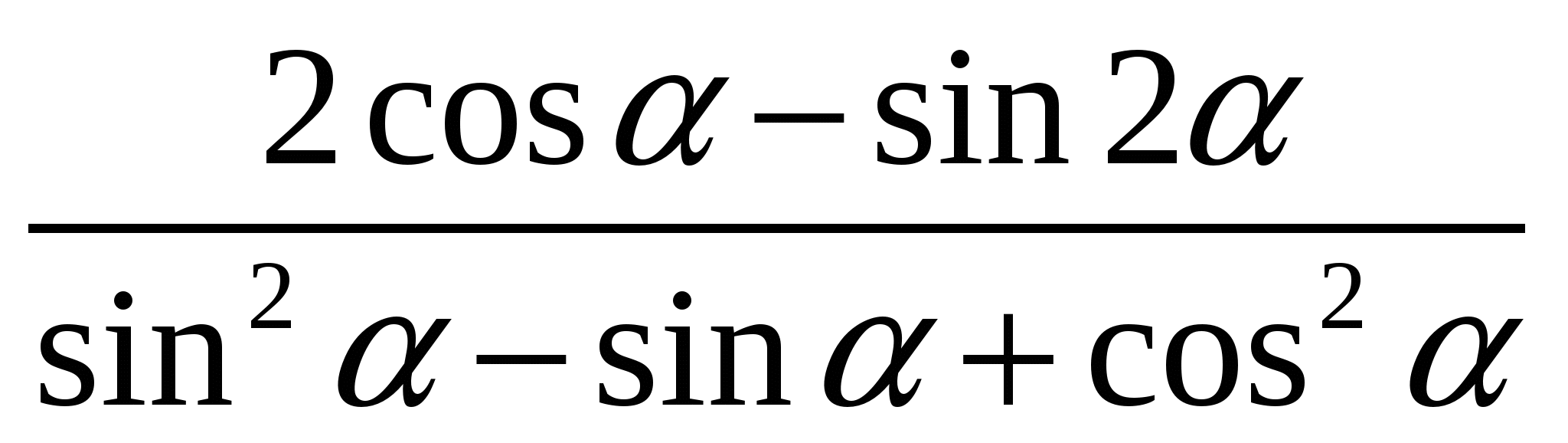
1) 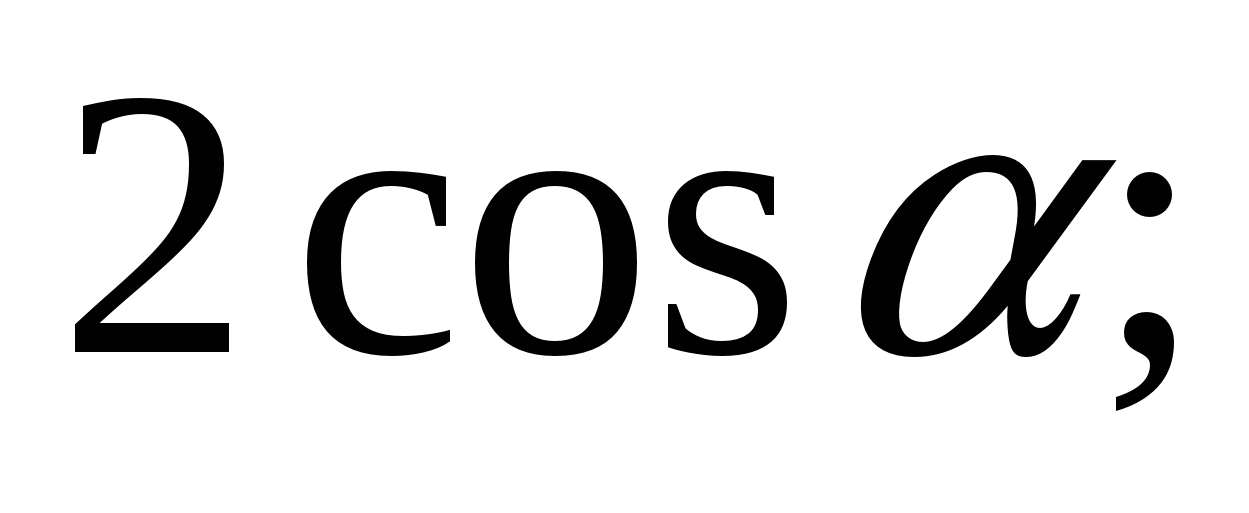 2)
2) 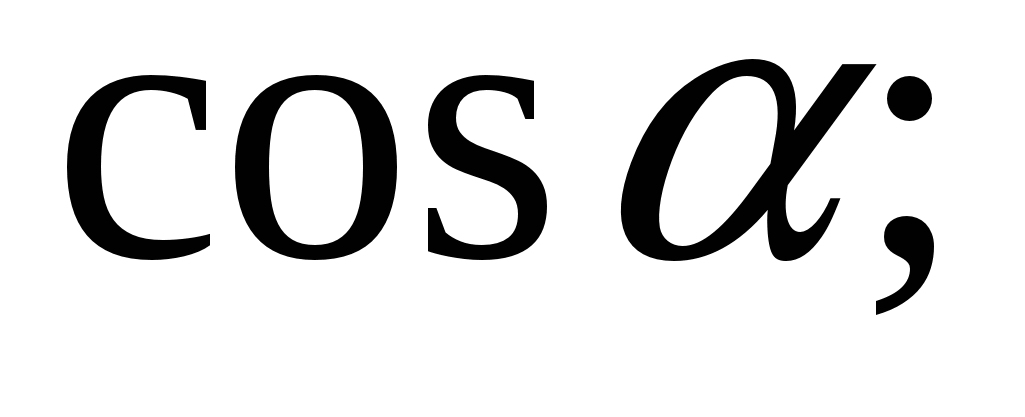 3)
3) 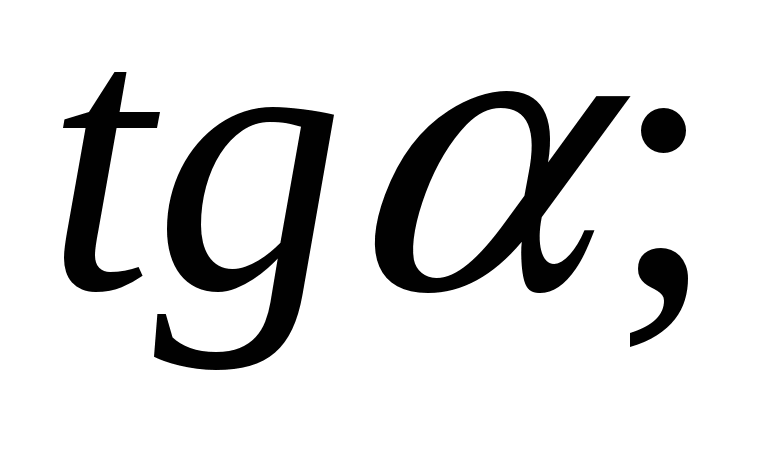 4)
4)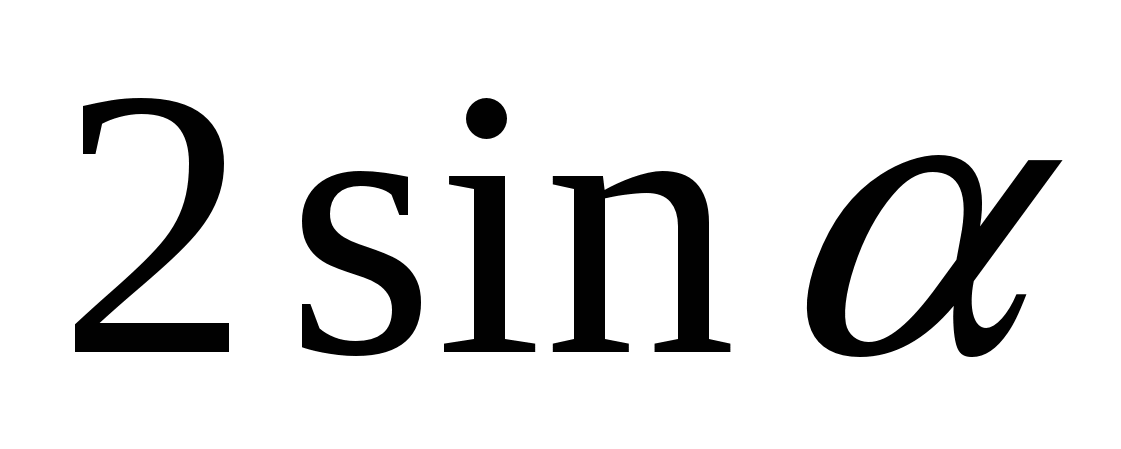
В) Напишите правильный ответ
В1
Вычислите: 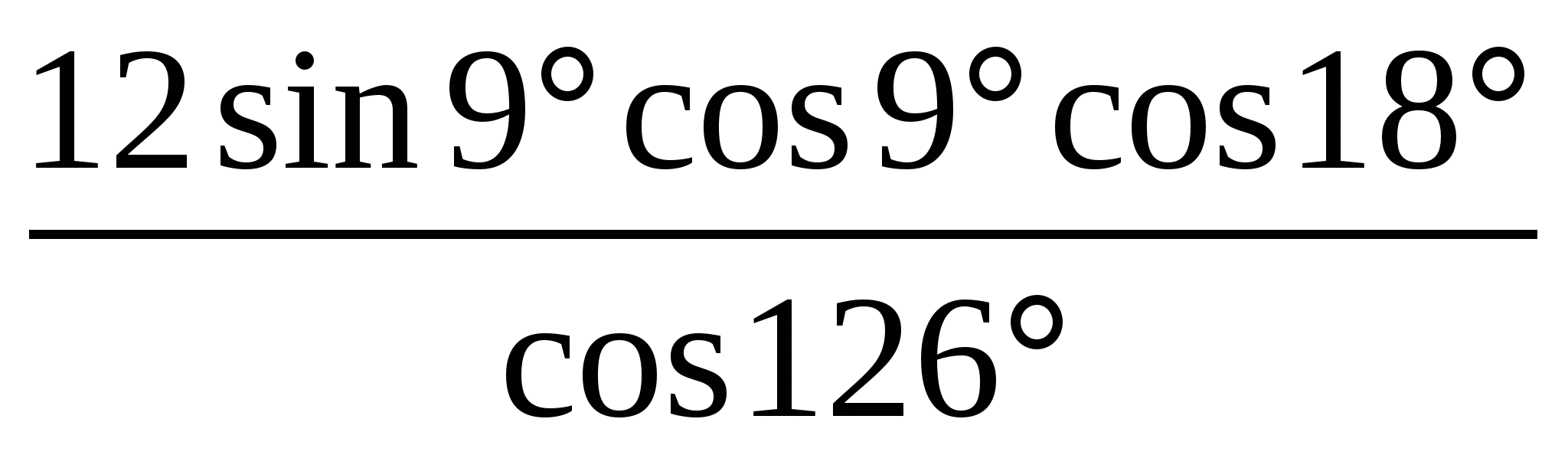
В2
Определите наименьшее значение выражения 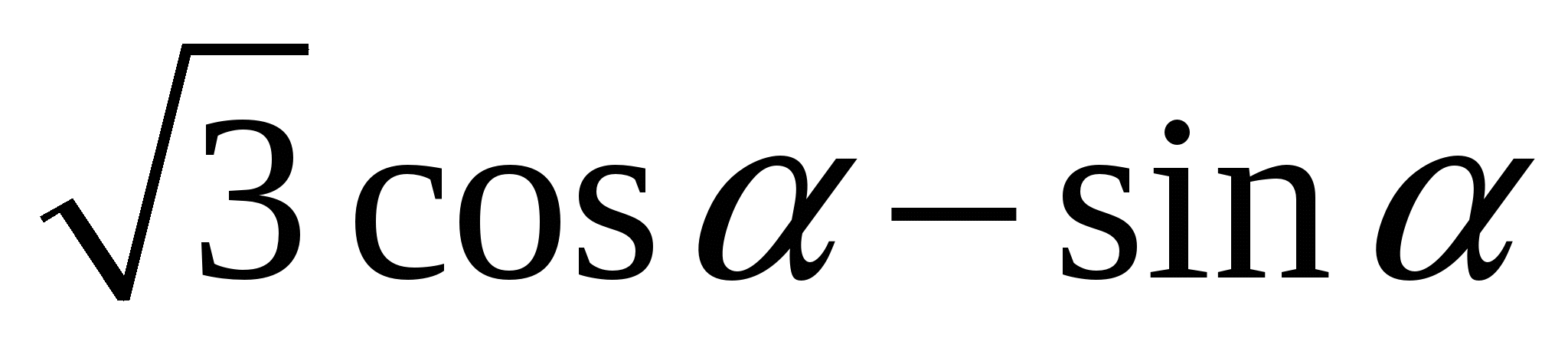
С) Приведите подробное решение данного задания.
С
Вычислите 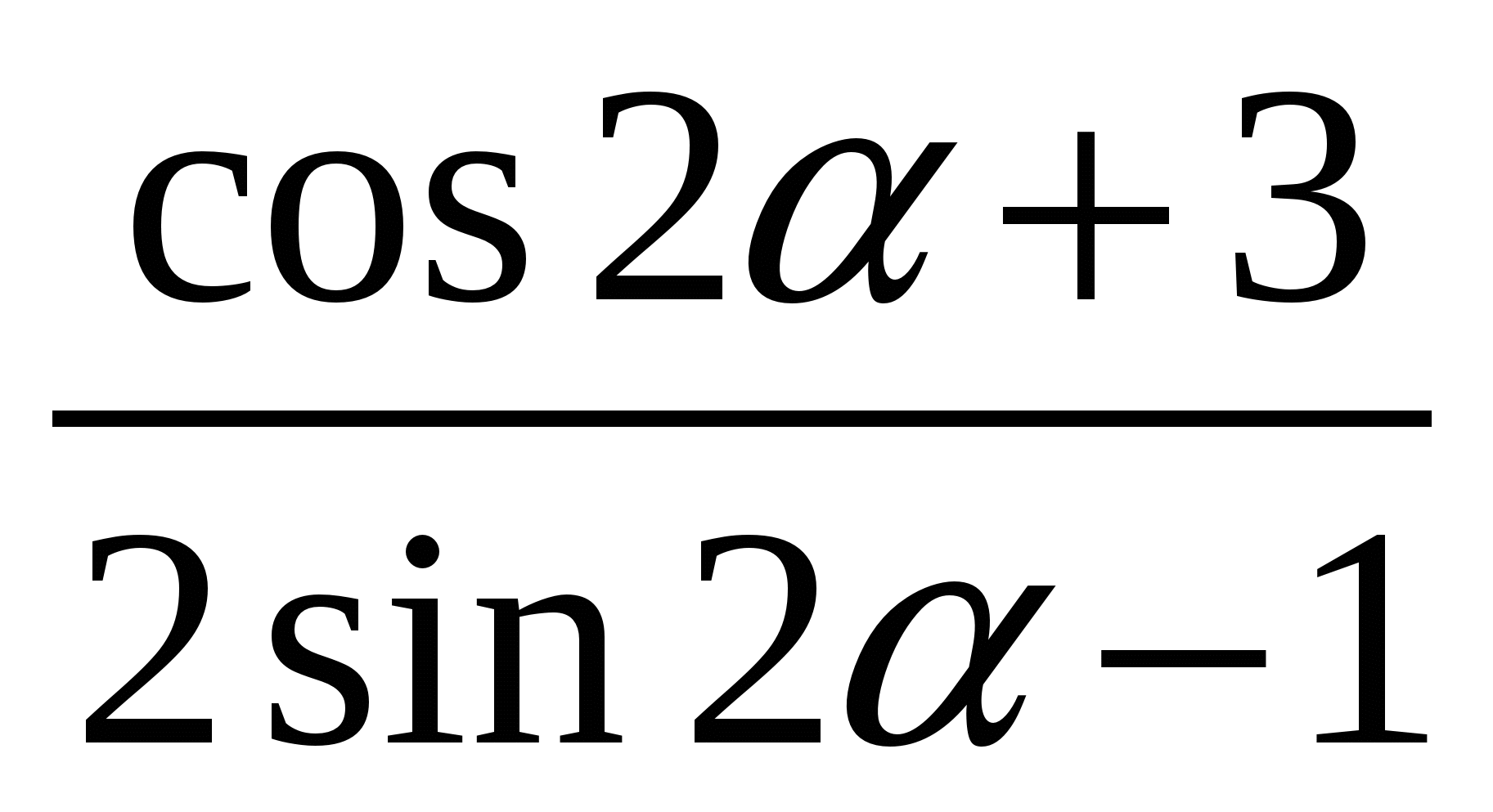 , если
, если 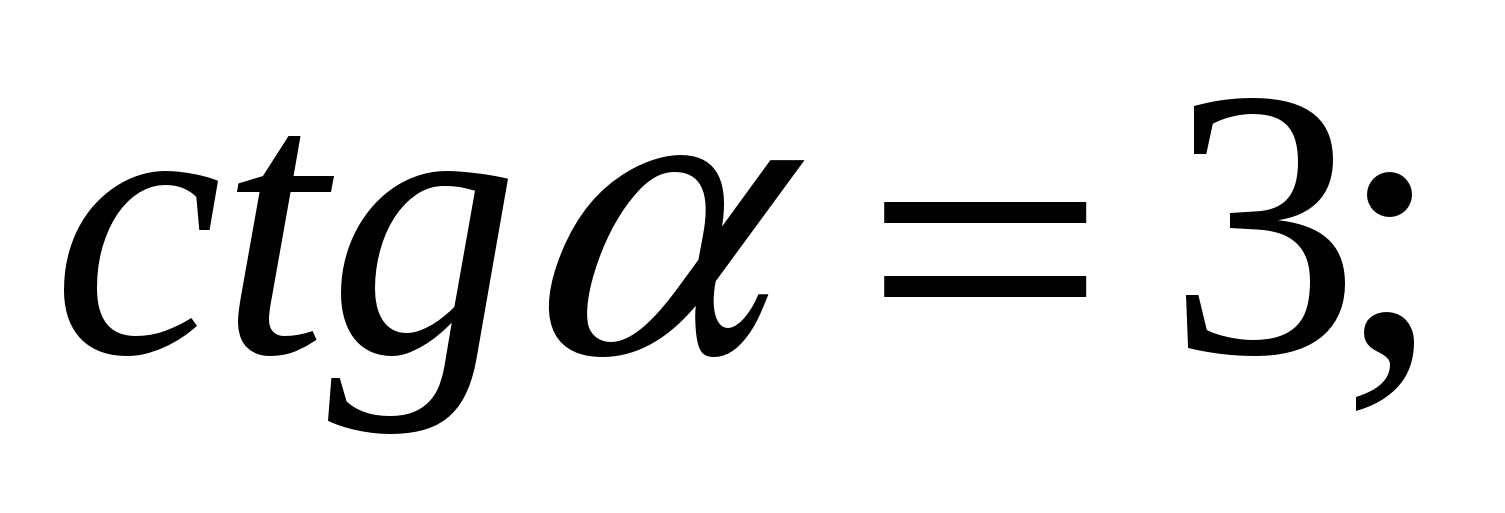
Ключ к тесту по теме Преобразование простейших тригонометрических выражений
Критерии оценивания тестовых заданий
8 вопросов 5 (отлично) (8 ответов)
8 вопросов 4 (хорошо) (7 ответов)
8 вопросов 3 (удов) (6 ответов)
Литература
Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М.: 2018
Башмаков М.И. Сборник задач: учеб. пособие (базовый уровень). 11 кл. – М.: 2012
Интернет-ресурсы
http://school-collection.edu.ru – Электронный учебник «Математика в
школе, XXI век».
http://fcior.edu.ru — информационные, тренировочные и контрольные материалы.
www.school-collection.edu.ru – Единая коллекции Цифровых образовательных ресурсов
infourok.ru
Математика: Тождественные преобразования тригонометрических выражений
2.
Тождественные преобразования тригонометрических выражений
Комментарий. Цель данного раздела — проработать выполнение заданий на тождественные преобразования тригонометрических выражений, поскольку они встречаются в ЕГЭ как в качестве отдельных заданий, так и используются для решения тригонометрический уравнений и неравенств, а так же комбинированных заданий. Для решения задач на упрощение тригонометрических выражений требуется достаточно хорошо знать правила преобразования алгебраических выражений и тригонометрические формулы (уметь применять их как по одной, так и в комплексе).
Основные формулы тригонометрии
Перевод градусной меры угла в радианную и обратно.
Пусть α — градусная мера угла, β — радианная, тогда справедливы формулы:
Формулы зависимости между функциями одного и того же аргумента:
Формулы сложения.
Формулы двойных и половинных углов.
Формулы преобразования суммы в произведение:
Формулы преобразования произведения в сумму:
Формулы приведения:
| sin φ | — sin α |
cos α |
cos α |
sin α |
— sin α |
— cos α |
— cos α |
— sin α |
sin α |
cos φ |
cos α |
sin α |
— sin α |
— cos α |
— cos α |
— sin α |
sin α |
cos α |
cos α |
tg φ |
— tg α |
ctg α |
— ctg α |
— tg α |
tg α |
ctg α |
— ctg α |
— tg α |
tg α |
ctg φ |
— ctg α |
tg α |
— tg α |
— ctg α |
ctg α |
tg α |
— tg α |
— ctg α |
ctg α |
Рассмотрим сначала достаточно простые задания на применение формул тригонометрии.
Пример 2.1.
Вычислить значение sin α, если cos α = 0,3, α — угол в первой четверти.
Решение
Применим основное тригонометрическое тождество, связывающее тригонометрические функции .
Так как по условию задачи cos α = 0,3, то cos2α = 0,09. Значит, sin2α + 0,09 = 1, sin2α = 1 – 0,09 = 0,91. Решая уравнение sin2α = 0,91, получаем два случая (), из которых, обращая внимание на то, какой четверти принадлежит искомый угол, следует выбрать один. Вспомним, что в первой четверти все тригонометрические функции имеют знак «+». Следовательно, .
Ответ: .
Пример 2.2.
Вычислите значение tg α, если ctg α = 0,2.
Решение
Воспользуемся формулой, связывающей тригонометрические функции y = tg α, y = ctg α : tg α ∙ ctg α = 1. Подставляя заданное в условии значение 0,2, получаем, что tg α ∙ 0,2 = 1, откуда tg α = 5.
Ответ: 5.
Пример 2.3.
Упростите выражения;
1) ;
2) ;
3) ;
4) ;
5) ;
6) ;
Решение
Данные задания — на применение формул сложения.
Ответ:
Пример 2.4.
Вычислите:
Решение
Ответ:
Отдельную группу заданий этого типа составляют задания на вычисление одних тригонометрических функций по известным другим.
Пример 2.5.
Известно, что sin α – cos α = 0,3. Найти:
1) sin2α ;
2) sin4α + cos4α ;
3) sin6α + cos6α .
Решение
1) Возведем в квадрат обе части заданного в условии примера равенства и используем формулу «квадрат разности», получаем, что:
sin2α — 2sinα cosα + cos2α = 0,09.
Вспомним основное тригонометрическое тождество и применим формулу синуса двойного угла:
1 — sin2α = 0,09, откуда:
sin2α = 1 — 0,09 = 0,91.
2) Воспользуемся полученным результатом для ответа на вопрос 2.
Для этого сумму sin4α + cos4α представим в специальном виде:
sin4α + cos4α = (sin4α + 2sin2α cos2α + cos4α ) — 2sin2α cos2α = (sin2α + cos2α )2 — 1/2 ∙ sin22α = 1 — 1/2 ∙ 0,91 = 0,545.
Комментарий. Специальный вид, использованный при решении данного примера, позволяет применить формулу «квадрат суммы» и использовать результат, полученный в пункте 1. При последующих преобразованиях использована формула синуса двойного угла.
3) Обратим внимание, что для вычисления значения выражение sin6α + cos6α можно представить в виде суммы кубов.
sin6α + cos6α = (sin2α )3 + (cos2α )3 = (sin2α + cos2α )(sin4α — sin2α cos2α + cos4α ) = 1 ∙ (0,545 – 1/4 ∙ 0,91) = 0,3175.
Ответ:
1) 0,91;
2) 0,545;
3) 0,3175.
Пример 2.6.
Найти tgα, если
Решение
Проверкой можно убедиться, что при cos α = 0 приведенное равенство неверно. Поэтому следует разделить числитель и знаменатель дроби на cos α (на основании основного свойства дроби):
, следовательно, тогда:
раскрывая скобки, приведем далее подобные слагаемые:
3tgα + 4 = 5tgα — 10, 2tgα = 14, получаем, что tgα = 7.
Ответ: 7.
Пример 2.7.
Вычислить cos α, если cos2α = 3/4 и
Решение
Как известно, . Выясним, в каких пределах лежит угол α и какой знак при этом имеет его косинус. Преобразуем заданное в условии задачи двойное неравенство. Разделив одновременно все три части двойного неравенства на 2, получим:
, то есть угол α располагается во второй четверти и, следовательно, cos α < 0.
В приведенной выше формуле выберем знак «минус»:
Ответ:
Комментарий. Следующая группа заданий — вычисление значений различных тригонометрических выражений с использованием тригонометрических формул.
Пример 2.8.
Найти значение выражения: .
Выполним упрощение каждой дроби по отдельности.
С целью сокращения дроби воспользуемся формулой «разность кубов» и получим:
.
Рассмотрим далее выражение . Нужно заметить, что первое третье слагаемые в сумме дают единицу в силу основного тригонометрического тождества. Таким образом:
.
Обратимся далее к преобразованию второй дроби. Применим одну из формул приведения: . Поэтому:
Тогда .
Окончательно получаем:
Ответ: 1.
Пример 2.9.
Вычислить sin10° sin30° sin50° sin70°.
Используем формулу преобразования произведения тригонометрических функций в сумму: sin10° sin50° = 1/2 (cos40° — cos60°) = 1/2 cos 40° — 1/4. Подставим в первоначальное произведение это выражение и учтем, что sin30° = 1/2, получаем:
Ответ:
Комментарий. Для выполнения аналогичных заданий необходимо знание не только тригонометрических формул, но и табличных значений тригонометрических функций.
Рассмотрим далее примеры упрощения тригонометрических выражений с произвольным аргументом.
Пример 2.10.
Упростить выражение: .
Так как числитель заданной дроби имеем достаточно простой вид, начнем с упрощения знаменателя. Для этого применим представление :
.
Приведем полученную разность дробей к общему знаменателю:
.
Следовательно,
Ответ:
Пример 2.11.
Доказать тождество при
Комментарий. Задания на доказательство тождеств вполне можно воспринимать как задания на упрощение выражений, причем с готовым ответом в виде более простой и компактной части равенства.
Решение
В частности, в данном примере попробуем упростить левую часть, чтобы получить такое же выражение, как справа. Для этого помножим числитель и знаменатель подкоренного выражения на 1 + sin α:
.
Вспомнив, что , получаем
Исследуем далее знак числителя и знаменателя подмодульного выражения:
sin α ≥ -1, тогда 1 + sin α ≥ 0 поэтому ;
при следовательно,
Таким образом:
Аналогичным образом преобразуем второе слагаемое левой части:
Тогда ,
что и требовалось доказать.
Пример 2.12.
Найти значение следующих тригонометрических выражений: sin 2α, cos 2α, tg 2α, если .
Решение
Выпишем формулы для вычисления искомых функций:
.
Из основного тригонометрического тождества вычислим:
Далее найдем значения искомых выражений:
Ответ:
Пример 2.13.
Доказать тождество .
Решение
Приведем левую часть к 1:
.
Тождество доказано.
Пример 2.14.
Вычислить значение выражения:
.
Решение
Обратим вниманием, что
Далее, используя формулы приведения, получим:
Воспользуемся табличными значениями и свойствами тригонометрических функций:
Итак, значение выражения равно 0.
Ответ: 0.
Комментарий. Для выполнения заданий, связанных с обратными тригонометрическими функциями, нужно, во-первых, четко помнить определения этих понятий:
Удобно при решении таких задач сделать замену (например, α = arcsin x) и работать с более привычным объектом — углом α, лежащем в первой или четвертой четверти тригонометрического круга, синус которого равен х. При этом выясняется, что задача намного проще, чем казалось вначале.
Пример 2.15.
Вычислить cos(4arctg 5).
Решение
Пусть α = arctg5, тогда tg α = 5. Требуется найти cos4α. Вычислим вначале cos2α, используя универсальную подстановку:
Тогда получаем, что:
Ответ:
Пример 2.16.
Выразить через все обратные функции
Решение
Пусть . Угол α лежит в четвертой четверти, следовательно, cos α > 0.
Найдем все тригонометрические функции угла:
В четвертой четверти находятся арктангенсы отрицательных чисел, поэтому можно утверждать, что .
Но , так как арккосинусы положительных чисел принадлежат первой четверти. В силу четности косинуса cos (-α) = cos α, при этом , то есть , тогда .
Арккотангенсы отрицательных чисел расположены во второй четверти. Например, , следовательно, . Таким образом, угол α выражен через все обратные функции.
Ответ:
Пример 2.17.
Найти arcsin (sin 12).
Решение
По условию задачи требуется найти угол, синус которого равен синусу угла в 12 радиан и который принадлежит промежутку . Заметим, что , поэтому .
Поскольку , угол 12 — 4π является искомым углом: его синус равен sin 12, и он находится в области возможных значений арксинуса.
Ответ: arcsin (sin12) = 12 — 4π.
Пример 2.18.
Вычислить
Решение
Введем два угла: Оба они лежат в первой четверти, значит, все их тригонометрические функции положительны. Мы знаем, что . Требуется найти синус суммы этих углов, а для этого нужно знать их синусы и косинусы.
Во-первых,
Во-вторых, .
Следовательно,
Ответ:
www.e-biblio.ru
Задания В11. Числовые тригонометрические выражения
Воспользуемся формулами приведения, для чего прежде представим иначе 
Решение: + показать Воспользуемся формулами приведения, для чего прежде представим иначе Отбрасываем согласно формулам приведения (При необходимости пользуемся тригонометрическим кругом). Ответ: -16.  :
:
 на круге располагаются здесь:
на круге располагаются здесь:
 , название функции не меняем, знак ставим «–», так как косинус угла III четверти отрицателен:
, название функции не меняем, знак ставим «–», так как косинус угла III четверти отрицателен:

Задача 2.
Найдите значение выражения  .
.
Решение: + показать
Задача 3.
Найдите значение выражения 
Решение: + показать
Задача 4.
Найдите значение выражения 
Решение: + показать
Задача 5.
Найдите значение выражения 
Решение: + показать
Задача 6.
Найдите значение выражения 
Решение: + показать
Задача 7.
Найдите значение выражения 
Решение: + показать
В силу нечетности функции  , получаем:
, получаем:

Далее применяем формулы приведения:


Ответ: -13.
Задача 8.
Найдите значение выражения 
Решение: + показать

Ответ: -8.
Задача 9.
Найдите значение выражения 
Решение: + показать
Задача 10.
Найдите значение выражения 
Решение: + показать
Если мы в формуле двойного угла для косинуса  выразим синус через косинус (
выразим синус через косинус ( ), то получим:
), то получим:

Тогда


Далее, так как  , то, применяя формулы приведения, получаем:
, то, применяя формулы приведения, получаем:

Ответ: 7,5.
Задача 11.
Найдите значение выражения 
Решение: + показать
Если мы в формуле двойного угла для косинуса  выразим косинус через синус (
выразим косинус через синус ( ), то получим:
), то получим:

Тогда


Ответ: 4.
Задача 12.
Найдите  , если
, если  .
.
Решение: + показать
Воспользуемся следующей формулой двойного угла для косинуса:


Ответ: 22.
Задача 13.
Найдите значение выражения 
Решение: + показать

Домножим и числитель и знаменатель на 2, чтобы явно увидеть в знаменателе формулу двойного угла для синуса:

Ответ: 12.
Задача 14.
Найдите значение выражения 
Решение: + показать

Ответ: 80.
🙂 Отдохните немного… –> + показать


Вы можете пройти тест по теме «Задания №9. Числовые тригонометрические выражения».
egemaximum.ru