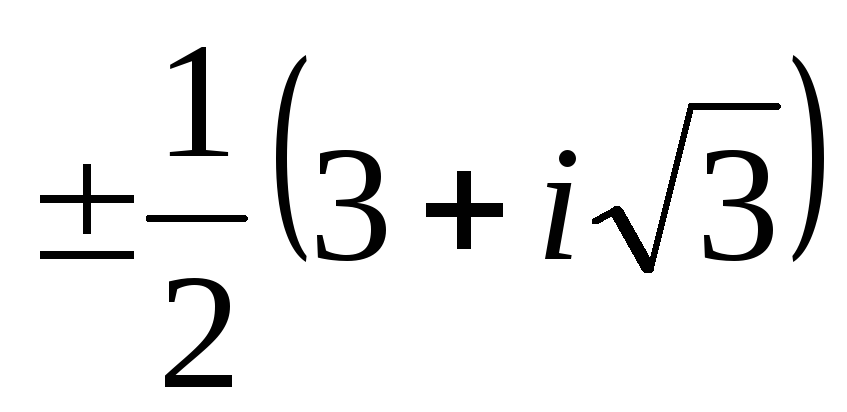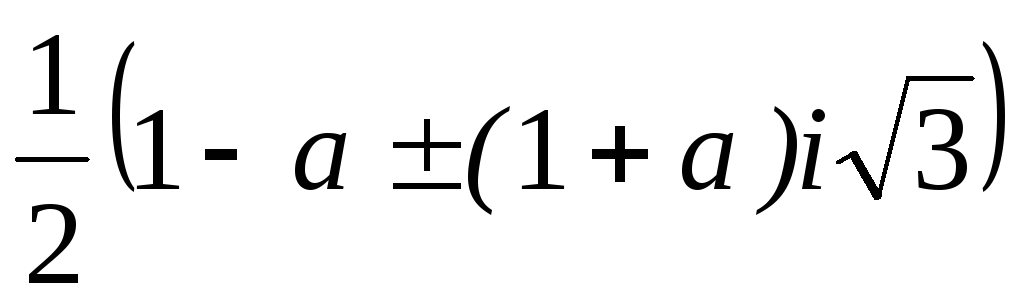Кубическое уравнение — Википедия
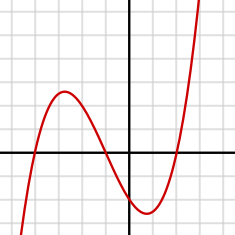 График кубической функции y=(x3+3×2−6x−8)/4{\displaystyle y=(x^{3}+3x^{2}-6x-8)/4}, у которой 3 действительных корня (в месте пересечения горизонтальной оси, где у = 0). Имеются 2 критические точки
Уравнение 8×3+7×2−4x+1{\displaystyle 8x^{3}+7x^{2}-4x+1} имеет один действительный и два мнимых корня.
График кубической функции y=(x3+3×2−6x−8)/4{\displaystyle y=(x^{3}+3x^{2}-6x-8)/4}, у которой 3 действительных корня (в месте пересечения горизонтальной оси, где у = 0). Имеются 2 критические точки
Уравнение 8×3+7×2−4x+1{\displaystyle 8x^{3}+7x^{2}-4x+1} имеет один действительный и два мнимых корня.Куби́ческое уравне́ние — алгебраическое уравнение третьей степени, общий вид которого следующий:
- ax3+bx2+cx+d=0,a≠0.{\displaystyle ax^{3}+bx^{2}+cx+d=0,\;a\neq 0.}
Для графического анализа кубического уравнения в декартовой системе координат используется кубическая парабола.
Кубическое уравнение общего вида может быть приведено к каноническому виду путём деления на a{\displaystyle a} и замены переменной x=y−b3a,{\displaystyle x=y-{\tfrac {b}{3a}},} приводящей уравнение к виду:
- y3+py+q=0,{\displaystyle y^{3}+py+q=0,}
где
- q=2b327a3−bc3a2+da=2b3−9abc+27a2d27a3,{\displaystyle q={\frac {2b^{3}}{27a^{3}}}-{\frac {bc}{3a^{2}}}+{\frac {d}{a}}={\frac {2b^{3}-9abc+27a^{2}d}{27a^{3}}},}
- p=ca−b23a2=3ac−b23a2.{\displaystyle p={\frac {c}{a}}-{\frac {b^{2}}{3a^{2}}}={\frac {3ac-b^{2}}{3a^{2}}}.}
Кубические уравнения были известны ещё в древнем Вавилоне, древним грекам, китайцам, индийцам и египтянам[1][2][3]. Были найдены клинописные таблички Старовавилонского периода (20—16 век до нашей эры), содержащие таблицы вычисления кубов и кубических корней[4][5]. Вавилоняне могли использовать эти таблицы для решения кубических уравнений, но не существует никаких свидетельств, что они это делали[6].
Задача удвоения куба использует простейшее и наиболее старое из кубических уравнений, и древние египтяне не верили, что решение его существует[7]. В пятом веке до нашей эры Гиппократ свёл эту задачу к нахождению двух средних пропорциональных между одним отрезком и другим, вдвое большим его, но не смог решить её с помощью циркуля и линейки[8], что, как теперь известно, невозможно сделать.
В III веке нашей эры древнегреческий математик Диофант нашёл целые и рациональные решения для некоторых кубических уравнений с двумя неизвестными (диофантовых уравнений)
Методы решения кубических уравнений появляются в китайском математическом тексте Математика в девяти книгах, составленном около второго столетия до нашей эры и прокомментированном китайским математиком Лю Хуэем в третьем столетии[2].
В VII веке во времена династии Тан астроном и математик Ван Сяотун в своём математическом трактате, озаглавленном
Цзигу Суаньцзин, изложил и решил 25 кубических уравнений вида x3+px2+qx=N{\displaystyle x^{3}+px^{2}+qx=N}, в 23 из которых p,q≠0{\displaystyle p,q\neq 0}, и в двух уравнениях q=0{\displaystyle q=0}[11].В XI веке персидский поэт и математик Омар Хайям (1048—1131) сделал существенный прогресс в теории кубических уравнений. В ранних работах, посвящённых кубическим уравнениям, он обнаружил, что кубическое уравнение может иметь более одного решения, и утверждал, что уравнение не может быть решено с помощью циркуля и линейки. Он также нашёл геометрическое решение[12][13]. В его более позднем труде, Трактат о демонстрации задач алгебры, он описал полную классификацию кубических уравнений с их общими геометрическими решениями, использующими пересечения конических сечений[14][15].
В двенадцатом столетии индийский математик Бхаскара II пытался решать кубические уравнения без особых успехов. Однако он привёл один пример решения кубического уравнения[16]:
- x3+12x=6×2+35.{\displaystyle x^{3}+12x=6x^{2}+35.}
В том же столетии другой, персидский, математик, Шараф ад-Дин (1135—1213), написал Al-Mu’adalat (Трактат об уравнениях), в котором говорится о восьми типах кубических уравнений с положительными решениями и о пяти типах, не имеющих положительных решений. Он использовал подход, который позднее стал известен как метод «Руффини — Горнера» для численной аппроксимации корня кубического уравнения. Он разработал также концепцию производной функции и экстремумов кривой для решения кубических уравнений, которые могут не иметь положительных значений[17]. Он понял важность дискриминанта кубического уравнения для нахождения алгебраического решения некоторых специальных видов кубических уравнений[18].
Леонардо Пизанский, известный также как Фибоначчи (1170—1250), умел находить положительные решения кубического уравнения x3 + 2x2 + 10x = 20 с помощью вавилонских цифр. Он указал решение 1,22,7,42,33,4,40 (что эквивалентно 1 + 22/60 + 7/602 + 42/603 + 33/604 + 4/605 + 40/606)[19], что отличается от точного решения только на три триллионных.
В начале XVI века итальянский математик Сципион дель Ферро (1465—1526) нашёл общий метод решения важного класса кубических уравнений, а именно, уравнений вида x3+mx=n{\displaystyle x^{3}+mx=n} с неотрицательными n и m. Фактически все кубические уравнения можно свести к такому виду, если допустить возможность для m{\displaystyle m} и n{\displaystyle n} быть отрицательными, но отрицательные числа в то время ещё не были известны. Дель Ферро держал своё открытие в секрете, пока не рассказал о нём перед своей смертью своему ученику Антонио Фиоре (Antonio Fiore).
Никколо Фонтана Тарталья.В 1530 Никколо Тарталья (1500—1557) получил две задачи в виде кубических уравнений от Дзуанне да Кои (Zuanne da Coi) и объявил, что он их может решить. Он вскоре получил вызов от Фиоре на математическое соревнование, которое после его завершения стало знаменитым. Каждый из них должен был предложить определённое число задач сопернику для решения. Оказалось, что все задачи, полученные Тартальей, сводились к кубическим уравнениям типа x3+mx=n{\displaystyle x^{3}+mx=n}. Незадолго до истечения срока Тарталье удалось разработать общий метод решения кубических уравнений этого типа (переоткрыв метод дель Ферро), а также обобщить его на два других типа (x3=mx+n{\displaystyle x^{3}=mx+n} и x3+n=mx{\displaystyle x^{3}+n=mx}). После этого он быстро решил все предложенные ему задачи. Фиоре же получил от Тартальи задачи из различных разделов математики, многие из которых оказались ему не под силу; в результате Тарталья выиграл соревнование.
Позднее Джероламо Кардано (1501—1576) неоднократно пытался убедить Тарталья раскрыть секрет решения кубических уравнений. В 1539 году ему это удалось: Тарталья сообщил свой метод, но при условии, что Кардано никому его не откроет до выхода книги самого Тартальи о кубических уравнениях, над которой он работал и где собирался опубликовать метод. Спустя шесть лет Тарталья так и не опубликовал свою книгу, а Кардано, узнав к тому времени о работах Ферро, счёл возможным опубликовать метод дель Ферро (с упоминанием имени Тартальи, как независимо его открывшего) в своей книге Ars Magna[en] в 1545 году. Кардано оправдывался тем, что обещал не сообщать никому результаты Тартальи, а не дель Ферро. Тем не менее, Тарталья считал, что Кардано нарушил обещание и послал тому вызов на соревнование, который Кардано не принял. Вызов, в конце концов, принял ученик Кардано Лодовико Феррари (1522—1565), и оказался победителем[20].
Кардано заметил, что метод Тарталья иногда (а именно — при наличии трех действительных корней) требует извлечения квадратного корня из отрицательного числа. Он даже включил вычисления с этими комплексными числами в Ars Magna, но, на самом деле, до конца проблему не понял. Рафаэль Бомбелли изучал эту проблему детально, а потому считается первооткрывателем комплексных чисел.
Франсуа Виет (1540—1603) независимо вывел решение кубического уравнения с тремя действительными корнями. Его решение было основано на тригонометрической формуле
- (2⋅cosϕ)3−3⋅(2⋅cosϕ)=2⋅cos(3⋅ϕ).{\displaystyle (2{\cdot }\cos \phi )^{3}-3{\cdot }(2{\cdot }\cos \phi )=2{\cdot }\cos(3{\cdot }\phi ).}
В частности, подстановка x=2⋅a⋅cosϕ{\displaystyle x=2{\cdot }a{\cdot }\cos \phi } приводит уравнение
- x3−3⋅a2⋅x=a2⋅b.{\displaystyle x^{3}-3{\cdot }a^{2}{\cdot }x=a^{2}\cdot b.}
к виду
- 2⋅a⋅cos(3⋅ϕ)=b.{\displaystyle 2{\cdot }a{\cdot }\cos(3{\cdot }\phi )=b.}
Позднее Рене Декарт (1596—1650) углубил работу Виета [21].
Число x{\displaystyle x}, обращающее уравнение в тождество, называется корнем или решением уравнения. Оно является также корнем многочлена третьей степени, стоящего в левой части канонической записи.
Над полем комплексных чисел, согласно основной теореме алгебры, кубическое уравнение
- ax3+bx2+cx+d=0{\displaystyle ax^{3}+bx^{2}+cx+d=0}
всегда имеет 3 корня x1,x2,x3{\displaystyle x_{1},x_{2},x_{3}} (с учётом кратности).
Так как каждый вещественный многочлен нечётной степени имеет хотя бы один вещественный корень, все возможные случаи состава корней кубического уравнения исчерпываются тремя, описанными ниже. Эти случаи легко различаются с помощью дискриминанта
- Δ=a4⋅(x1−x2)2⋅(x1−x3)2⋅(x2−x3)2=−4⋅b3⋅d+b2⋅c2−4⋅a⋅c3+18⋅a⋅b⋅c⋅d−27⋅a2⋅d2.{\displaystyle \Delta =a^{4}{\cdot }(x_{1}-x_{2})^{2}{\cdot }(x_{1}-x_{3})^{2}{\cdot }(x_{2}-x_{3})^{2}=-4{\cdot }b^{3}\cdot d+b^{2}{\cdot }c^{2}-4{\cdot }a{\cdot }c^{3}+18{\cdot }a{\cdot }b{\cdot }c{\cdot }d-27{\cdot }a^{2}{\cdot }d^{2}.}
Итак, возможны только три случая:
- Если Δ > 0, тогда уравнение имеет три различных вещественных корня.
- Если Δ < 0, то уравнение имеет один вещественный и пару комплексно сопряжённых корней.
- Если Δ = 0, тогда хотя бы два корня совпадают. Это может быть, когда уравнение имеет двойной вещественный корень и ещё один отличный от них вещественный корень; либо все три корня совпадают, образуя корень кратности 3. Разделить эти два случая помогает результант кубического уравнения и его второй производной: у многочлена есть корень кратности 3 тогда и только тогда, когда указанный результант также равен нулю.
По теореме Виета корни кубического уравнения x1,x2,x3{\displaystyle x_{1},\,x_{2},\,x_{3}} связаны с коэффициентами a,b,c,d{\displaystyle a,\,b,\,c,\,d} следующими соотношениями[22]:
- x1+x2+x3=−ba,{\displaystyle x_{1}+x_{2}+x_{3}=-{\frac {b}{a}},}
- x1x2+x2x3+x1x3=ca,{\displaystyle x_{1}x_{2}+x_{2}x_{3}+x_{1}x_{3}={\frac {c}{a}},}
- x1x2x3=−da.{\displaystyle x_{1}\,x_{2}\,x_{3}=-{\frac {d}{a}}.}
Делением указанных тождеств друг на друга можно получить ещё несколько справедливых соотношений:
- 1×1+1×2+1×3=−cd,d≠0{\displaystyle {\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+{\frac {1}{x_{3}}}=-{\frac {c}{d}},\quad d\neq 0},
- 1x1x2+1x2x3+1x1x3=bd,d≠0{\displaystyle {\frac {1}{x_{1}x_{2}}}+{\frac {1}{x_{2}x_{3}}}+{\frac {1}{x_{1}x_{3}}}={\frac {b}{d}},\quad d\neq 0},
- 1x1x2x3=−ad,d≠0{\displaystyle {\frac {1}{x_{1}x_{2}x_{3}}}=-{\frac {a}{d}},\quad d\neq 0}.
Общие точные методы решения:
Для некоторых особых типов кубических уравнений существуют специальные методы решения. См., например:
Также можно применять численные методы решения уравнений.
Подстановка Виета[править | править код]
Геометрическое решение Омара Хайяма кубического уравнения для случая a=2,b=16{\displaystyle a=2,b=16}, дающее корень 2{\displaystyle 2}. То, что вертикальная прямая пересекает ось x{\displaystyle x} в центре круга, — специфично для данного конкретного примера.Как указывалось выше, любое кубическое уравнение можно привести к виду:
- t3+pt+q=0,{\displaystyle t^{3}+pt+q=0,}
Сделаем подстановку, известную как подстановка Виета:
- t=w−p3w{\displaystyle t=w-{\frac {p}{3w}}}
В результате получим уравнение:
- w3+q−p327w3=0.{\displaystyle w^{3}+q-{\frac {p^{3}}{27w^{3}}}=0.}
Умножив на w3{\displaystyle w^{3}}, получим уравнение шестой степени от w{\displaystyle w}, которое, на самом деле, является квадратным уравнением от w3{\displaystyle w^{3}}:
- w6+qw3−p327=0{\displaystyle w^{6}+qw^{3}-{\frac {p^{3}}{27}}=0}
Решая это уравнение, получим w3{\displaystyle w^{3}}. Если w1{\displaystyle w_{1}}, w2{\displaystyle w_{2}} и w3{\displaystyle w_{3}} являются тремя кубическими корнями w3{\displaystyle w^{3}}, то корни исходного уравнения можно получить по формулам
- t1=w1−p3w1,t2=w2−p3w2{\displaystyle t_{1}=w_{1}-{\frac {p}{3w_{1}}},\quad t_{2}=w_{2}-{\frac {p}{3w_{2}}}\quad } и t3=w3−p3w3.{\displaystyle \quad t_{3}=w_{3}-{\frac {p}{3w_{3}}}.}
Решение Омара Хайяма[править | править код]
Как показано на графике, для решения уравнения третьей степени x3+a2x=b{\displaystyle x^{3}+a^{2}x=b}, где b>0,{\displaystyle b>0,} Омар Хайям построил параболу y=x2a,{\displaystyle y={\frac {x^{2}}{a}},} окружность, диаметром которой является отрезок [0,ba2]{\displaystyle \left[0,{\frac {b}{a^{2}}}\right]} положительной полуоси x{\displaystyle x}, и вертикальную прямую, проходящую через пересечение параболы и окружности. Решение определяется длиной горизонтального отрезка от начала координат до пересечения вертикальной прямой с осью x{\displaystyle x}.
Простое современное доказательство построения: умножаем на x{\displaystyle x} уравнение и группируем члены
- x4a2=x(ba2−x).{\displaystyle {\frac {x^{4}}{a^{2}}}=x\,\left({\frac {b}{a^{2}}}-x\right)\,.}
Левая часть — это значение y2{\displaystyle y^{2}} на параболе. Уравнение окружности, y2+x(x−ba2)=0,{\displaystyle y^{2}+x\,\left(x-{\frac {b}{a^{2}}}\right)=0,} совпадает с правой частью уравнения и даёт значение y2{\displaystyle y^{2}} на окружности.
- ↑ Британский музей BM 85200
- ↑ 1 2 John Crossley, Anthony W.-C. Lun. The Nine Chapters on the Mathematical Art: Companion and Commentary. — Oxford University Press, 1999. — С. 176. — ISBN 978-0-19-853936-0.
- ↑ 1 2 Van der Waerden. Geometry and Algebra of Ancient Civilizations. — Zurich, 1983. — С. chapter 4. — ISBN 0-387-12159-5.
- ↑ Roger Cooke. The History of Mathematics. — John Wiley & Sons, 2012. — P. 63. — ISBN 978-1-118-46029-0.
- ↑ Karen Rhea Nemet-Nejat. Daily Life in Ancient Mesopotamia. — Greenwood Publishing Group, 1998. — P. 306. — ISBN 978-0-313-29497-6.
- ↑ Roger Cooke. Classical Algebra: Its Nature, Origins, and Uses. — John Wiley & Sons, 2008. — P. 64. — ISBN 978-0-470-27797-3.
- ↑ Guilbeau, 1930 утверждает, что «египтяне полагали, что решение невозможно, но греки подошли к решению ближе.»
- ↑ 1 2 Guilbeau, 1930
- ↑ Thomas L. Heath. Diophantus of Alexandria: A Study in the History of Greek Algebra. — Martino Pub, 2009. — ISBN 978-1578987542.
- ↑ Archimedes (translation by T. L. Heath). The works of Archimedes. — Rough Draft Printing, 2007. — ISBN 978-1603860512.
- ↑ Yoshio Mikami. The Development of Mathematics in China and Japan. — 2nd ed. — New York: Chelsea Publishing Co., 1974. — С. 53—56. — ISBN 978-0-8284-0149-4.
- ↑ Работа Омара Хайама, Scripta Math. 26 (1963), стр. 323—337
- ↑ в книге О’Коннора и Робертсона «Omar Khayyam», MacTutor History of Mathematics archive, University of St Andrews, можно прочитать Эта задача привела Хайама к кубическому уравнению x3 + 200x = 20x2 + 2000 и он нашёл положительный корень этого уравнения как пересечение равнобочной гиперболы и окружности. Приближённое численное решение было затем найдено путём интерполяции тригонометрических таблиц.
- ↑ J. J. O’Connor и E. F. Robertson (1999), Omar Khayyam, в архиве истории математики MacTutor[en], утверждают, «Хайям, похоже, был первым, кто задумался об общей теории кубических уравнений.»
- ↑ Guilbeau, 1930 утверждает, «Омар Аль Хей Хорасан около 1079 года сделал много по пути продвижения методов решения алгебраических уравнений с помощью пересекающихся конических сечений.»
- ↑ Datta, Singh. History of Hindu Mathematics. — Delhi, India, 2004. — С. 76,. — ISBN 81-86050-86-8. стр. 76, Equation of Higher Degree; Bharattya Kala Prakashan
- ↑ O’Connor, John J.; Robertson, Edmund F., «Sharaf al-Din al-Muzaffar al-Tusi», MacTutor History of Mathematics archive, University of St Andrews.
- ↑ J. L. Berggren. Innovation and Tradition in Sharaf al-Din al-Tusi’s Muadalat // Journal of the American Oriental Society. — 1990. — Vol. 110. — Вып. 2. — P. 304—309. — DOI:10.2307/604533.
- ↑ R. N. Knott and the Plus Team. The life and numbers of Fibonacci // Plus Magazine. — 2013.
- ↑ Victor Katz. A History of Mathematics. — Boston: Addison Wesley, 2004. — С. 220. — ISBN 9780321016188.
- ↑ R. W. D. Nickalls. Viète, Descartes and the cubic equation // Mathematical Gazette. — July 2006. — Т. 90. — P. 203—208.
- ↑ Бронштейн И. Н., Семендяев К. А. Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 139.
Формула Кардано — Википедия
Материал из Википедии — свободной энциклопедии
Фо́рмула Карда́но — формула для нахождения корней канонической формы кубического уравнения
- y3+py+q=0{\displaystyle y^{3}+py+q=0}
над полем комплексных чисел. Названа в честь итальянского математика Джероламо Кардано.
Любое кубическое уравнение общего вида
- ax3+bx2+cx+d=0{\displaystyle ax^{3}+bx^{2}+cx+d=0}
при помощи замены переменной
- x=y−b3a{\displaystyle x=y-{\frac {b}{3a}}}
может быть приведено к указанной выше канонической форме с коэффициентами
- p=ca−b23a2=3ac−b23a2,{\displaystyle p={\frac {c}{a}}-{\frac {b^{2}}{3a^{2}}}={\frac {3ac-b^{2}}{3a^{2}}},}
- q=2b327a3−bc3a2+da=2b3−9abc+27a2d27a3.{\displaystyle q={\frac {2b^{3}}{27a^{3}}}-{\frac {bc}{3a^{2}}}+{\frac {d}{a}}={\frac {2b^{3}-9abc+27a^{2}d}{27a^{3}}}.}
Определим величину[1]:
Q=(p3)3+(q2)2.{\displaystyle Q=\left({\frac {p}{3}}\right)^{3}+\left({\frac {q}{2}}\right)^{2}.}
Если все коэффициенты кубического уравнения вещественны, то и Q вещественно, и по его знаку можно определить тип корней[1]:
- Q > 0 — один вещественный корень и два сопряжённых комплексных корня.
- Q = 0 — один однократный вещественный корень и один двукратный, или, если p = q = 0, то один трёхкратный вещественный корень.
- Q < 0 — три вещественных корня. Это так называемый «неприводимый» случай, и именно при анализе этой ситуации впервые исторически возникло понятие комплексного числа, потому что вещественный результат получается по формуле с помощью комплексных чисел[1].
По формуле Кардано, корни кубического уравнения в канонической форме равны:
y1=α+β,{\displaystyle y_{1}=\alpha +\beta ,}
y2,3=−α+β2±iα−β23,{\displaystyle y_{2,3}=-{\frac {\alpha +\beta }{2}}\pm i{\frac {\alpha -\beta }{2}}{\sqrt {3}},}
где
- α=−q2+Q3,{\displaystyle \alpha ={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {Q}}}},}
- β=−q2−Q3,{\displaystyle \beta ={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {Q}}}},}
Дискриминант многочлена y3+py+q{\displaystyle y^{3}+py+q} при этом равен Δ=−108Q{\displaystyle \Delta =-108Q}.
Применяя данные формулы, для каждого из трёх значений α{\displaystyle \alpha } необходимо брать такое β{\displaystyle \beta }, для которого выполняется условие αβ=−p/3{\displaystyle \alpha \beta =-p/3} (такое значение β{\displaystyle \beta } всегда существует).
Если кубическое уравнение вещественное, то рекомендуется по возможности выбирать вещественные значения α,β{\displaystyle \alpha ,\beta }.
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Кубическим уравнением называется уравнение вида
- ax3 + bx2 + cx +d = 0 , (1)
- где a, b,c ,d — постоянные коэффициенты, а х — переменная.
Мы рассмотрим случай, когда коэффициенты являются веществеными числами.
Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.
Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.
Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:
Δ= -4b3d + b2c2 — 4ac3 + 18abcd — 27a2d2 (Да, это дискриминант кубического уравнения)
Итак, возможны только 3 следующих случая:
- Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
- Δ < 0 — уравнение имеет лишь 1 корень. (1 вещественный и пару комплексно сопряженных корней)
- Δ = 0 — хотя бы 2 корня уравнения совпадают. Т.е. мы имеем дело либо с уравнением с 2умя совпадающими корнями, и еще 1ним отличным от них, либо с уравнением с 3емя совпадающими корнями. (В любом случае все корни вещественные. И уравнение имеет 3 совпадающих корня, тогда и только тогда, когда результант его и его второй производной равен нулю)
На практике часто , решение кубических уравнений упирается в разложении их на множители. Т.е. алгоритм приблизительно следующий: угадываем один корень, пусть это будет корень α. Затем делим многочлен на (х- α), (если α корень, то он должен поделиться без остатка). Ну а дальше мы имеем дело с обычным квадратным уравнением. Но угадать можно только рациональный корень, и то, если коэффициенты подобраны удачным образом, так что этот корень просто угадывается. Мы же рассмотрим универсальные методы решения кубичесих уравнений.
Формула Кардано решения кубических уравнений (нахождения корней).
Это формула для нахождения корней канонической формы кубического уравнения. (Над полем комлексных чисел).
Канонической формой кубического уравнения называется уравнение вида
y3 + py + q = 0 (2)
К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:
- x= y — b/3a (3)
- p= — b2/3a2 + c/a
- q= 2b3/27a3 — bc/3a2 + d/a
Итак, приступим к вычислению корней. Найдем следующие величины:
- Q=(p/3)3 + (q/2)2
- α = (-q/2 + Q1/2)1/3
- β = (-q/2 — Q1/2)1/3
Дискриминант уравнения (2) в этом случае равен
Δ = — 108Q
Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражают
§7. Уравнения третьей степени.
Уравнение третьей
степени x3+ax2+bx+c=0 (1)
подстановкойx=y–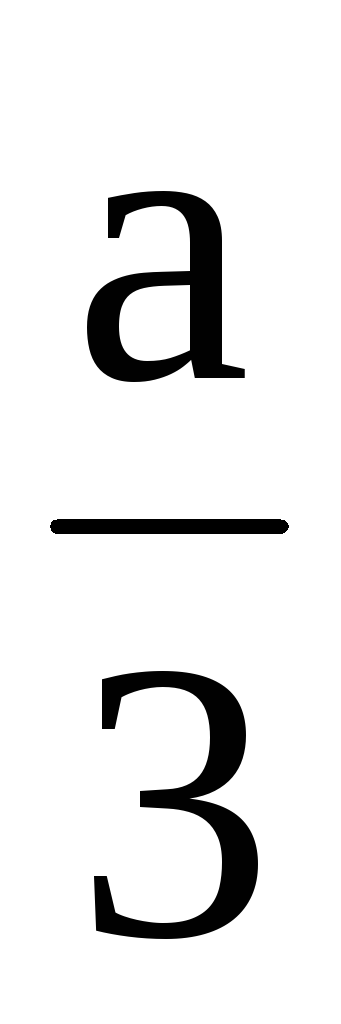 приводится кприведенному кубическому
уравнению y3+py+q=0. (2)
Корни
такого уравнения можно найти по формулам
Кардано:y=u+v=
приводится кприведенному кубическому
уравнению y3+py+q=0. (2)
Корни
такого уравнения можно найти по формулам
Кардано:y=u+v=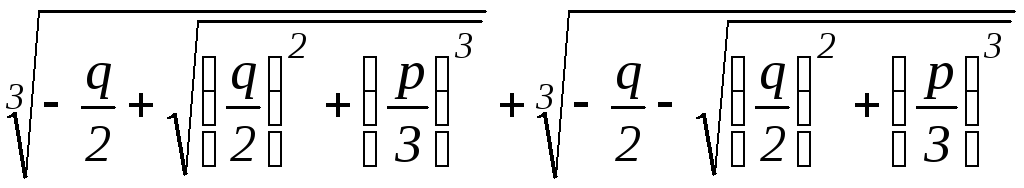 , (3)
гдеu=
, (3)
гдеu=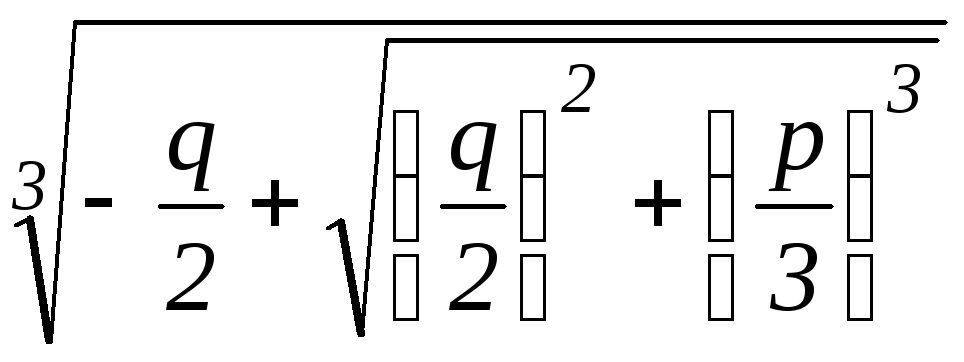 ,v=
,v=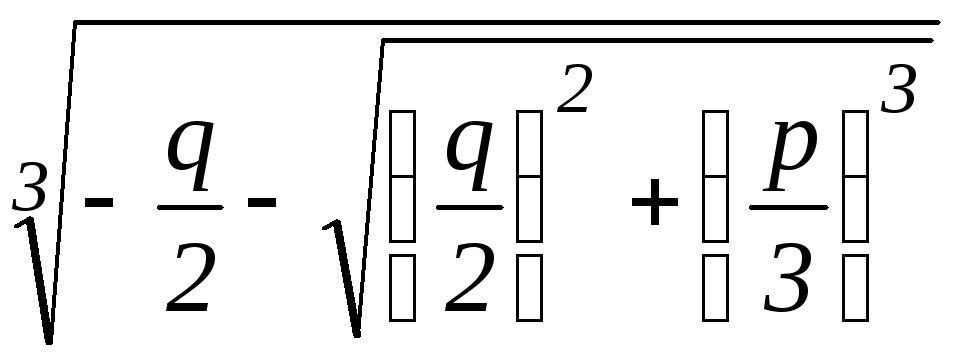 и
они связаны соотношениемuv=
и
они связаны соотношениемuv=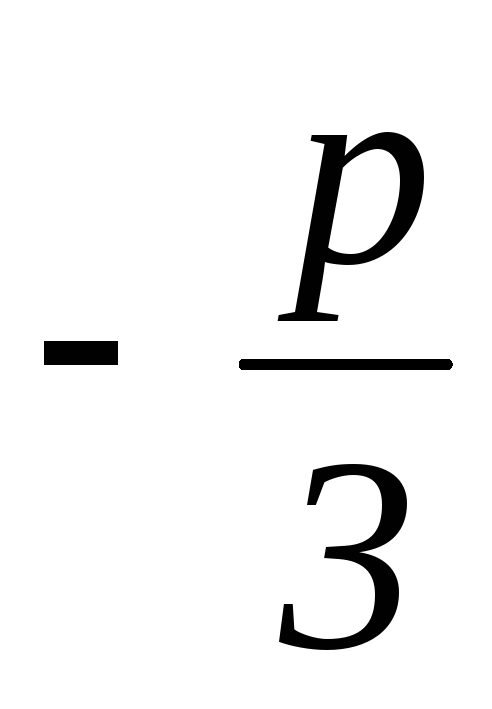
 ,
гдеu=
,
гдеu=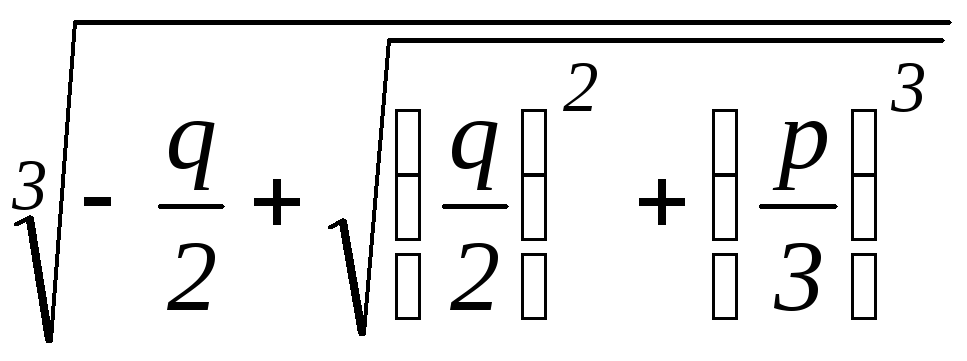 . (5)
Здесь
можно брать любое (одно из двух) значение
квадратного корня; три значения
кубического корня дают три корня
приведенного уравнения (2). Заметим, чтоu0,
еслиp0;
еслиp=0, то никакая
специальная формула не нужна (имеемдвучленное уравнение).
. (5)
Здесь
можно брать любое (одно из двух) значение
квадратного корня; три значения
кубического корня дают три корня
приведенного уравнения (2). Заметим, чтоu0,
еслиp0;
еслиp=0, то никакая
специальная формула не нужна (имеемдвучленное уравнение).Чтобы не запоминать формулу, можно пользоваться методом решения, по сути повторяющим вывод формул Кардано. Чтобы найти корни уравнения (2) (считаем р0), пологаяy=u+v, подставляем его в уравнение: (u+v)3+p(u+v)+q=0. Раскрыв скобки, и перегруппировав члены, получим: (
u3+v3+q)+( 3uv+p)(u+v)=0. Для уничтожения второго слагаемого подберёмu, vтак, чтобы 3uv+p=0 илиuv=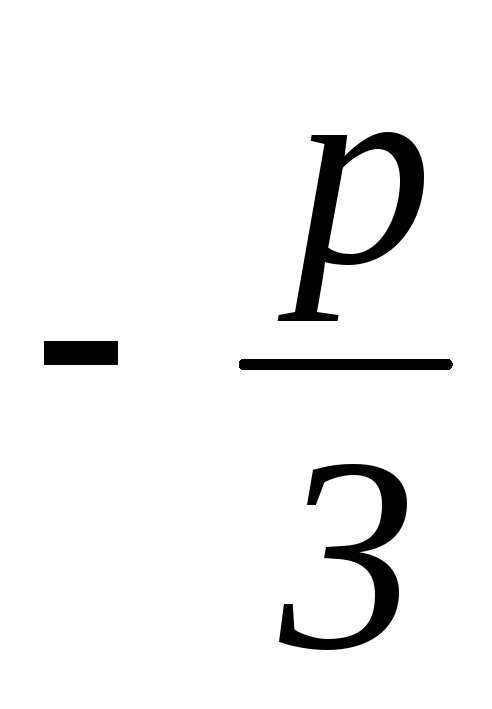 .
Тогда уравнение (2) приводится к системе
уравнений:
.
Тогда уравнение (2) приводится к системе
уравнений:

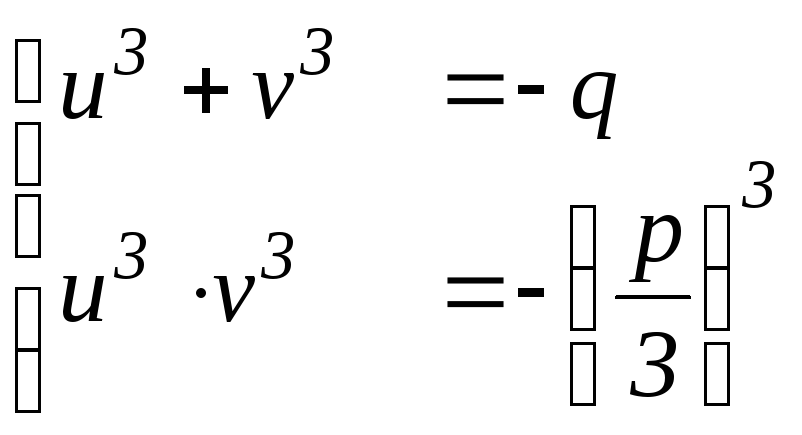 Замечаем,
чтоu3,v3– корни квадратного уравненияz2+qz
Замечаем,
чтоu3,v3– корни квадратного уравненияz2+qz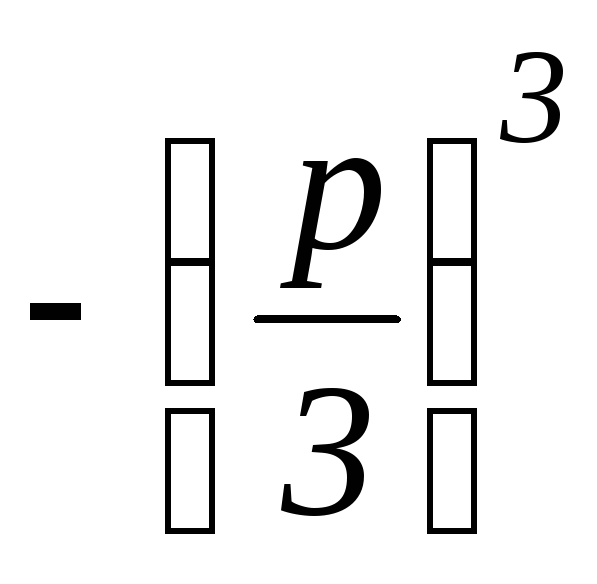 =0.
=0.Затем, выбираем один (любой) корень z1этого квадратного уравнения. Берём в качестве
 ,y1=u1+v1,x1=y1–
,y1=u1+v1,x1=y1–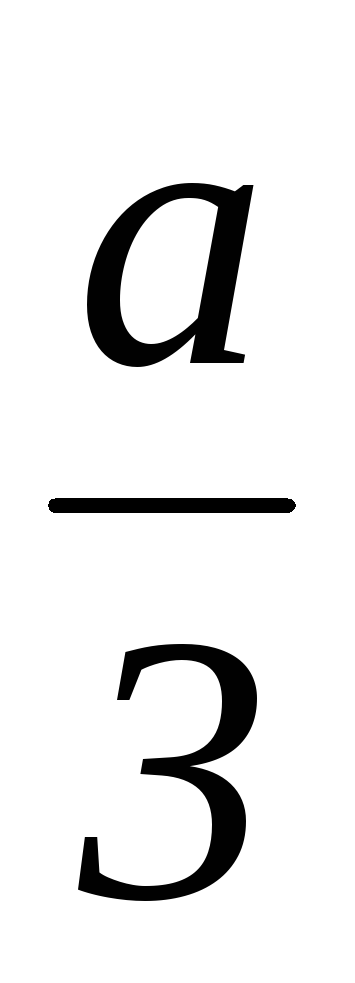 ;u2= u11, v2= v12,y2=u2+v2,x2=y2–;u3= u1 2, v3= v11,y3=u3+v3,x3=y3–
;u2= u11, v2= v12,y2=u2+v2,x2=y2–;u3= u1 2, v3= v11,y3=u3+v3,x3=y3–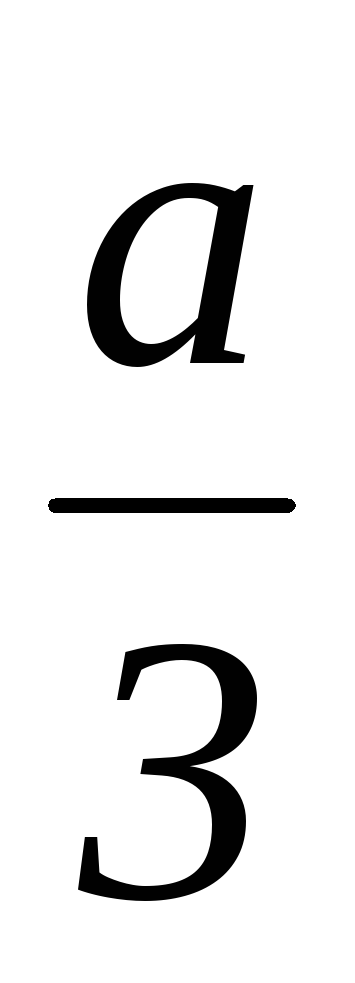 ;
где1,2=
;
где1,2=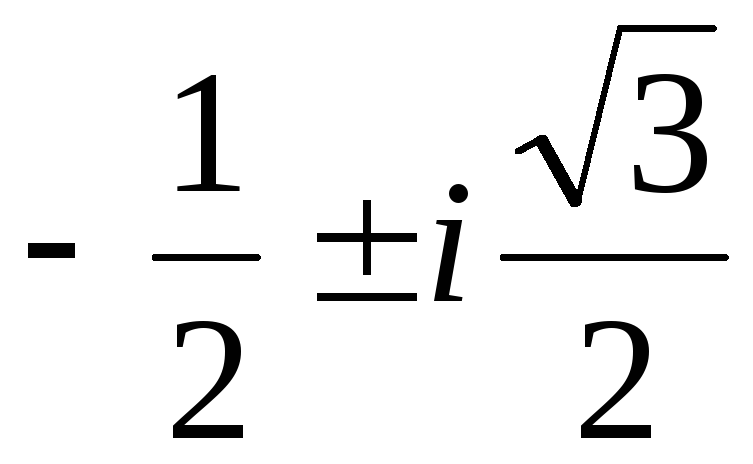 невещественные кубические корни из
единицы. Заметим, что2=(1)2=
невещественные кубические корни из
единицы. Заметим, что2=(1)2= и1=(2)2=
и1=(2)2=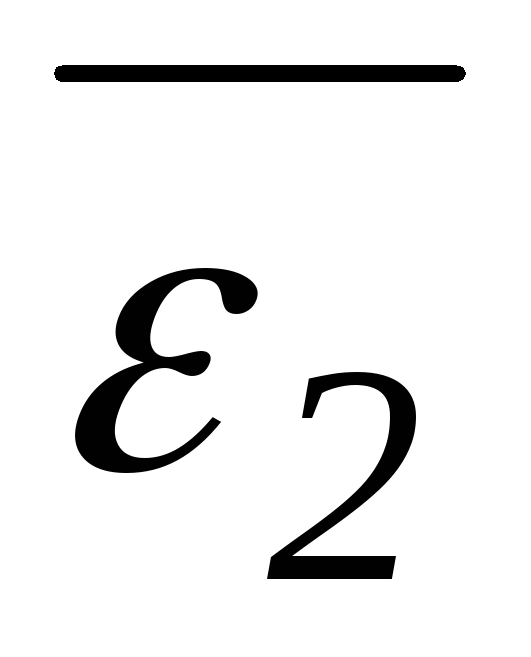 ,
это позволяет варьировать нахождение
,
это позволяет варьировать нахождениеПри исследовании уравнений третьей степени используют теорему:
Теорема. Пустьx3+px+q=0
неполное кубическое уравнение с
действительными коэффициентами.
Обозначим
∆=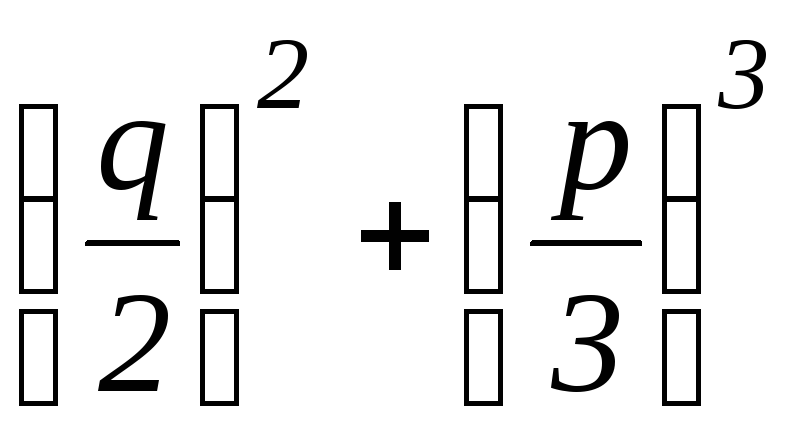 .
.
Если ∆>0, то уравнение имеет один действительный и два мнимых сопряжённых корня.
Если ∆=0, то корни уравнения действительны и хотя бы один из них кратный.
Если ∆<0, то все корни действительны и различны.
Если не все коэффициенты уравнения (2) действительны, то для упрощения вычислений можно вычислить ∆. Если ∆=0 (p0,q0), тогда уравнение (2) имеет два равных корняy2=y3
, и в этом случае корни уравнения (2) можно найти, не прибегая к извлечению корней второй и третьей степени, а именноy1=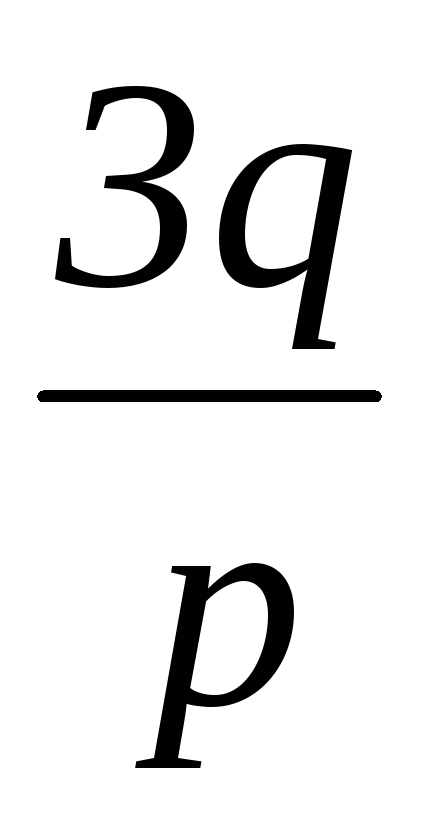 ; y2=y3=
; y2=y3= . (6)
Если
же ∆0, то уравнение
(2) имеет три различных корня, для
нахождения которых, используют один
из вышеописанных способов.
. (6)
Если
же ∆0, то уравнение
(2) имеет три различных корня, для
нахождения которых, используют один
из вышеописанных способов. Пример 1. Решить уравнение:
x3–6x+9=0.
Решение.Уравнение
приведенное (отсутствует член сx2).
Используем модифицированную формулу
Кардано (5):
∆=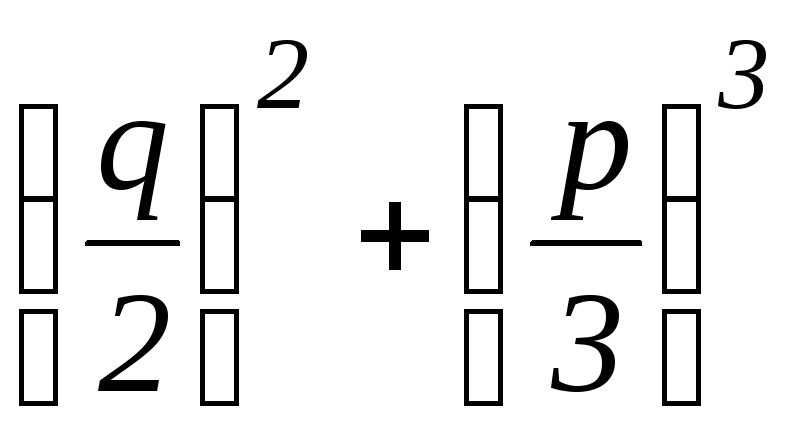 =
=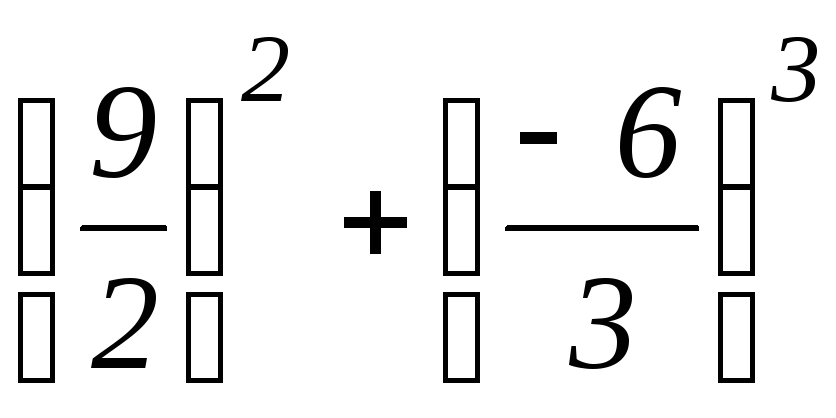 =
=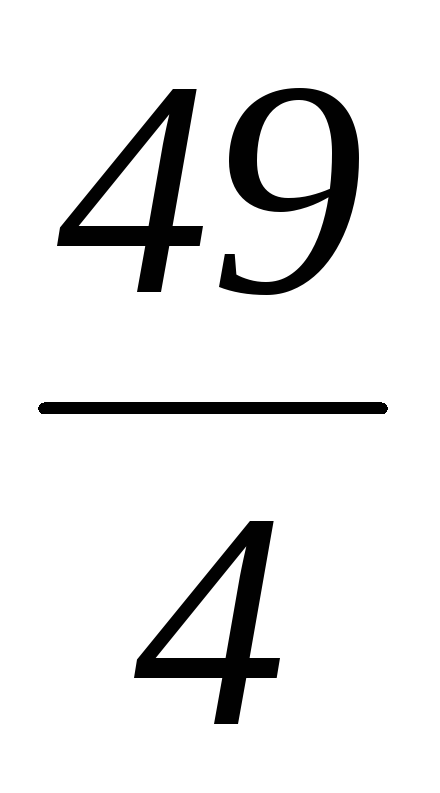
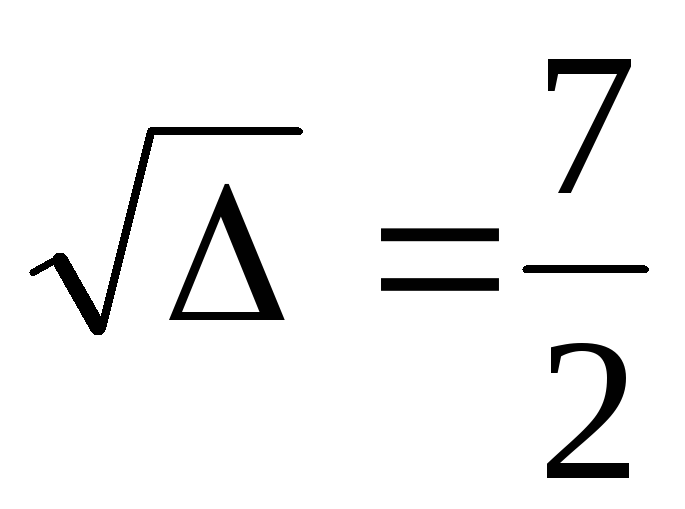 (берём
только одно значение квадратного
корня). Тогдаu=
(берём
только одно значение квадратного
корня). Тогдаu=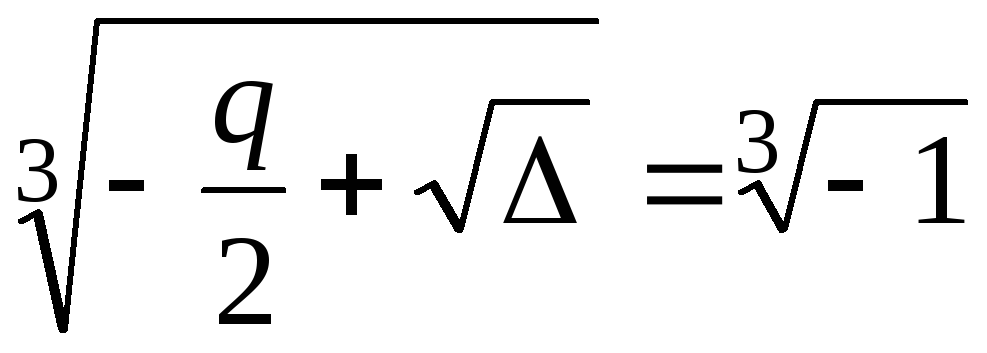 .
Одно
из значений
.
Одно
из значений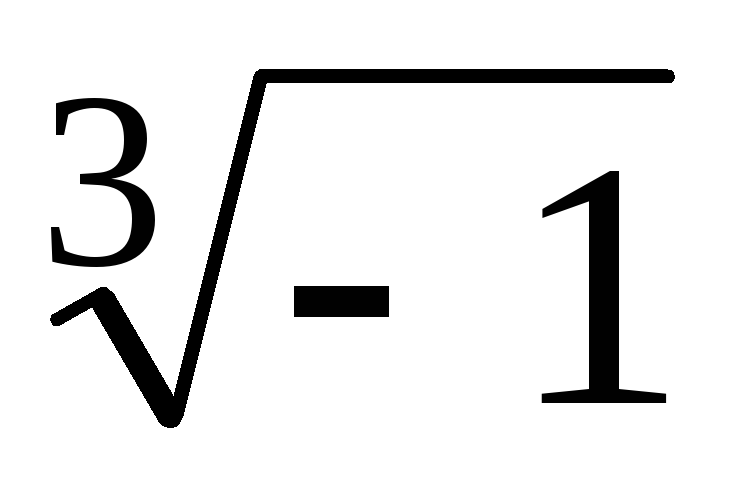 естьu1=–1, ещё
два значения получим, умножаяu1на1,2 – кубические корни из единицы. Итак, u1=–1
, x1=
u1–
естьu1=–1, ещё
два значения получим, умножаяu1на1,2 – кубические корни из единицы. Итак, u1=–1
, x1=
u1–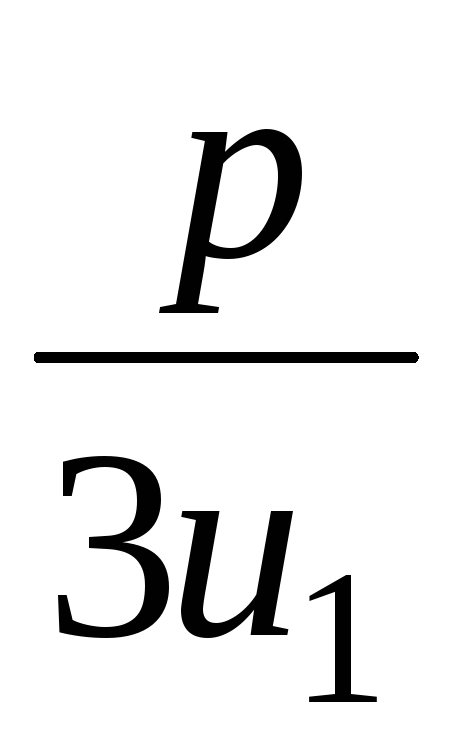 =–1–
=–1–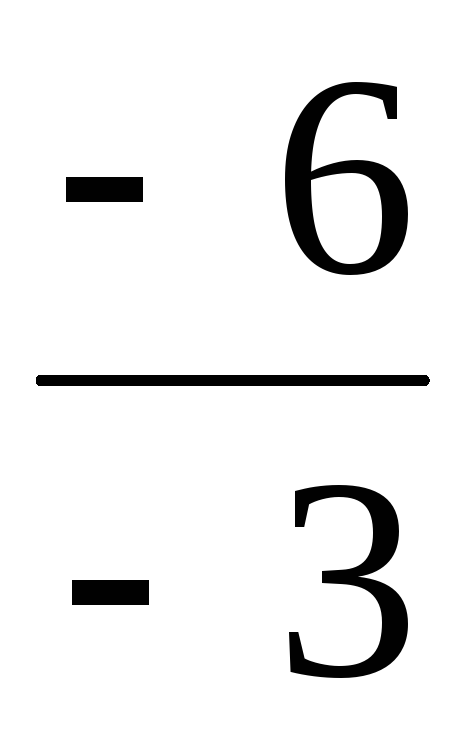 =–3; u2= u11=–1, x2=
u2–
=–3; u2= u11=–1, x2=
u2–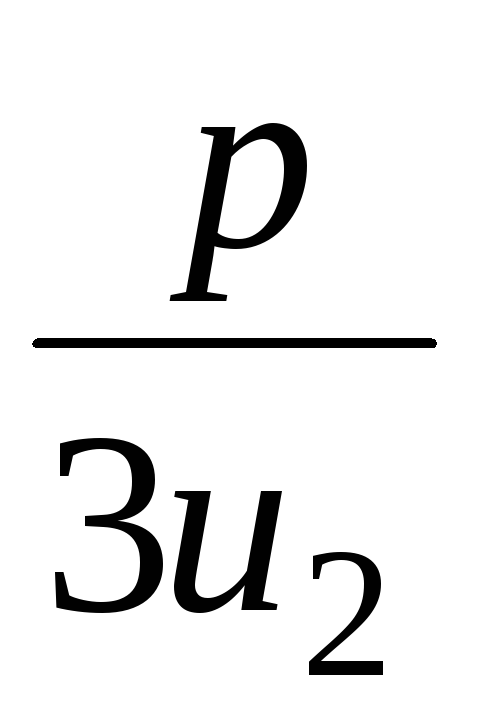 =–1+
=–1+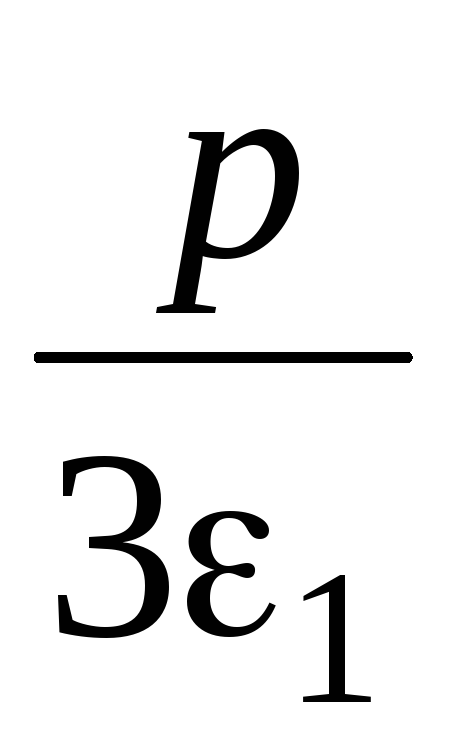 =–1–2/1= =–1–22=
=–1–2/1= =–1–22=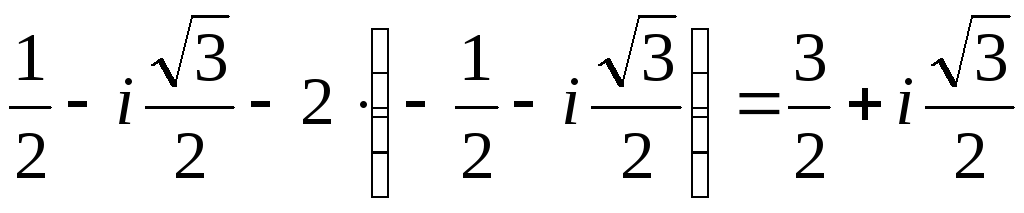 .
Так
как коэффициенты данного уравнения
действительны и ∆>0, тоx3=
.
Так
как коэффициенты данного уравнения
действительны и ∆>0, тоx3=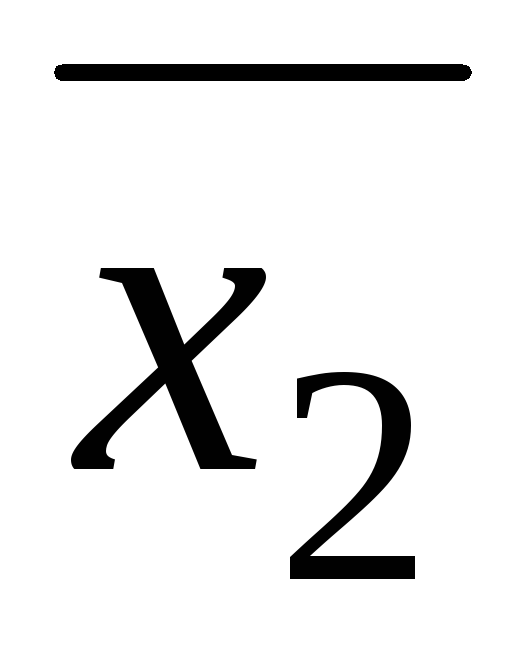 (x3не нужно
вычислять по формуле).
(x3не нужно
вычислять по формуле). Ответ:x1=–3, x2,3= .
.
Пример 2. Решить уравнение:x3+9x2+18x+28=0.
Решение.
Сделаем подстановкуx=y–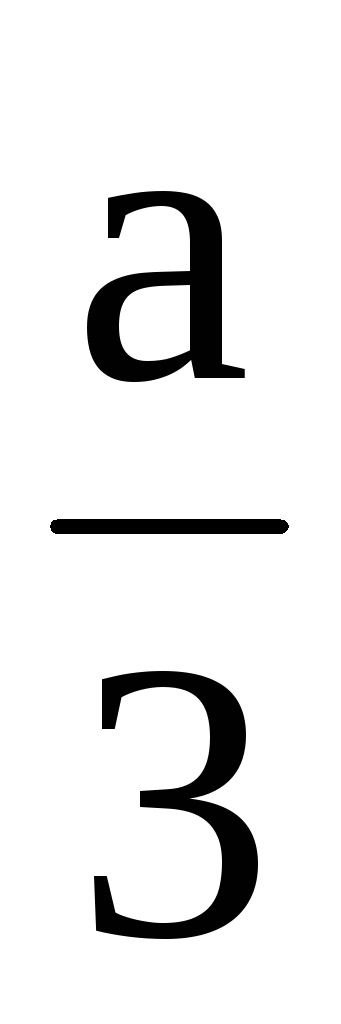 =y–3.
Получим уравнениеy3–9y+28=0.
Полагаемy=u+v: (u+v)3–9(u+v)+28=0, (u3+v3+28)+(3uv–9)(u+v)=0.
Откуда
=y–3.
Получим уравнениеy3–9y+28=0.
Полагаемy=u+v: (u+v)3–9(u+v)+28=0, (u3+v3+28)+(3uv–9)(u+v)=0.
Откуда ,
или
,
или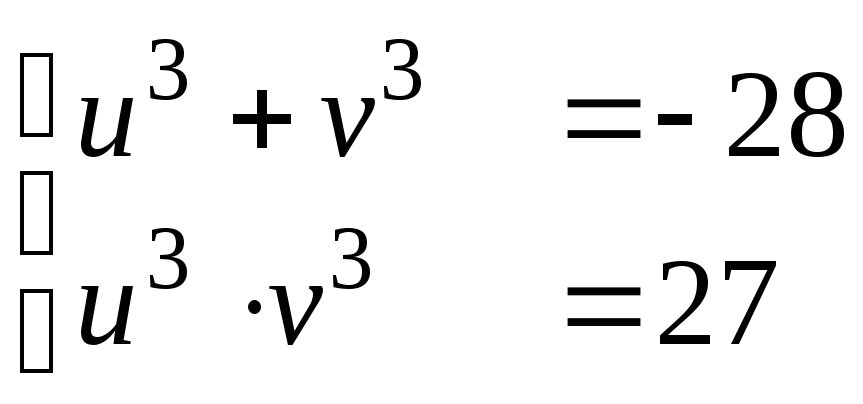 ,
гдеu3,v3– корни квадратного уравненияz2+28z+27=0.
,
гдеu3,v3– корни квадратного уравненияz2+28z+27=0.
Один из корней
последнего уравнения z1=–1,
тогдаu1=–1, v1=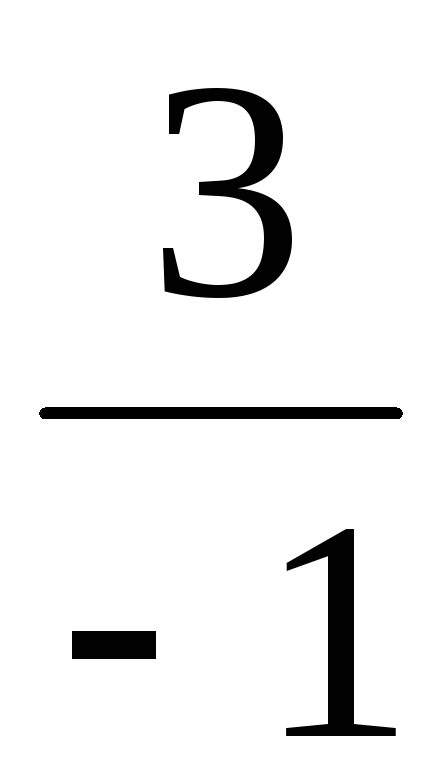 =–3,y1=–4,x1=–7;u2= u11=
=–3,y1=–4,x1=–7;u2= u11=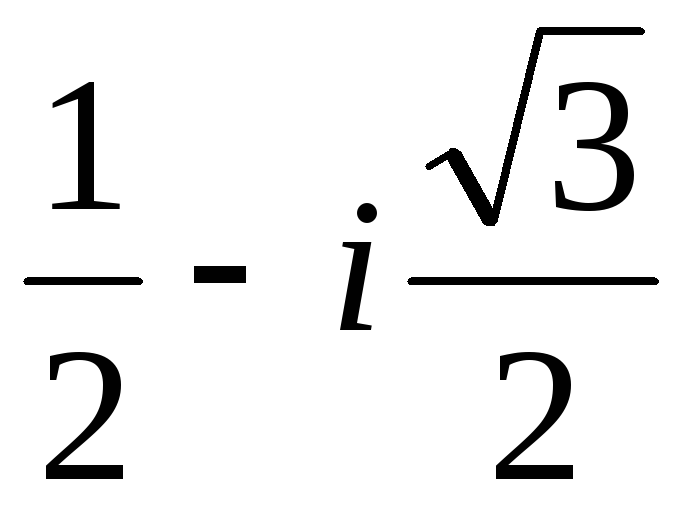 ,v2= v12=
,v2= v12=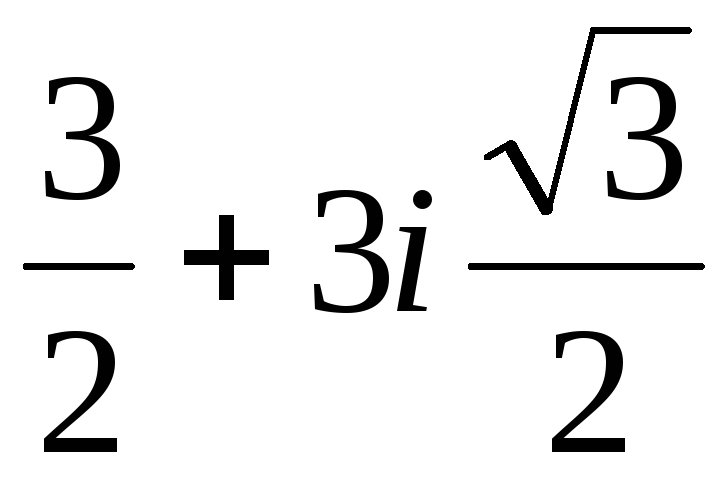 ,y2=
,y2=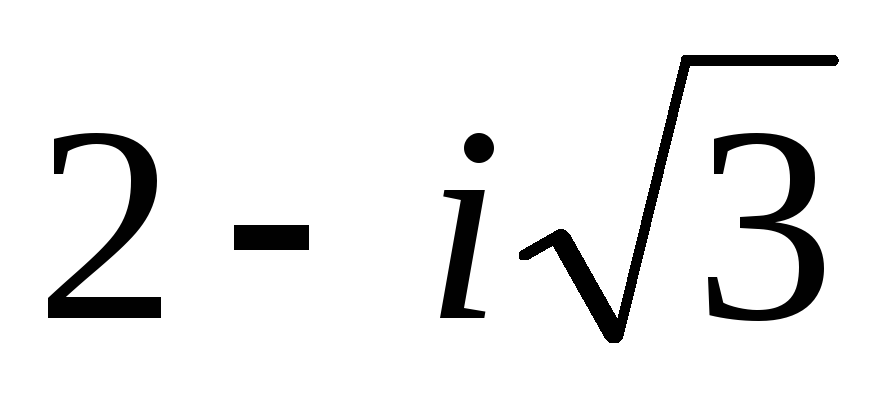 ,x2=
,x2=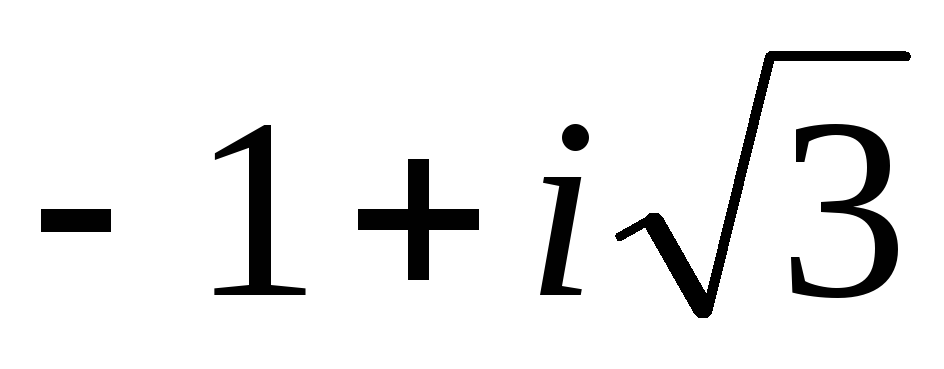 ; Поскольку коэффициенты уравнения
действительны и ∆>0, тоx3=
; Поскольку коэффициенты уравнения
действительны и ∆>0, тоx3=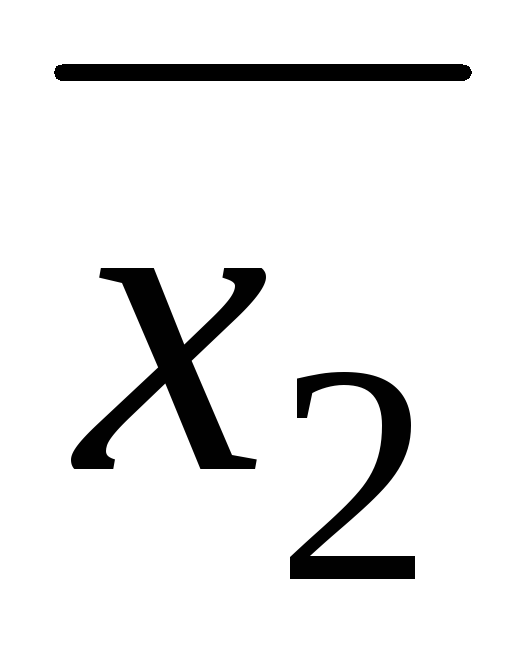 .
.
Ответ: x1=–7, x2,3=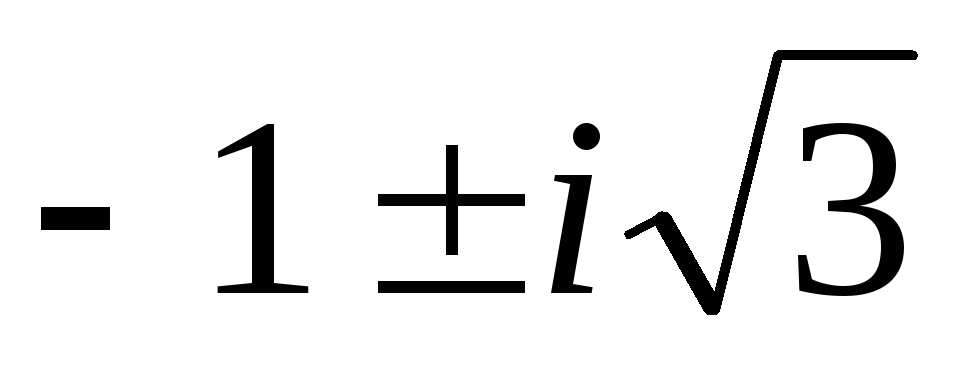 .
.
Пример 3. Решить уравнение:x3+3x–2i=0.
Решение. Данное
уравнение приведенное, и не все его
коэффициенты действительны, поэтому
вычислим ∆.
∆=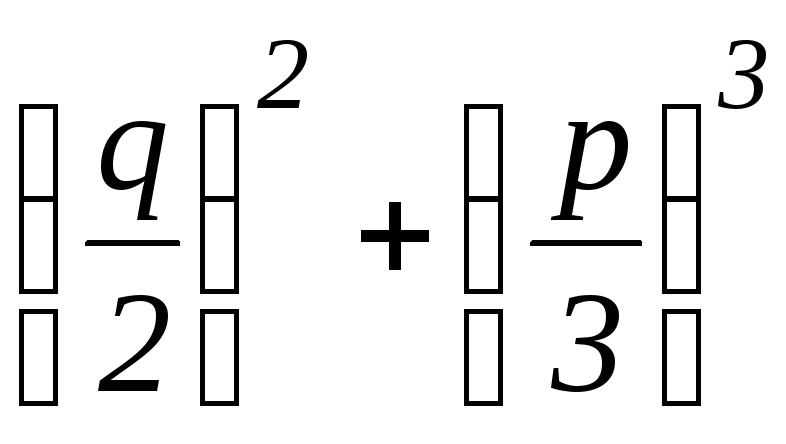 =
=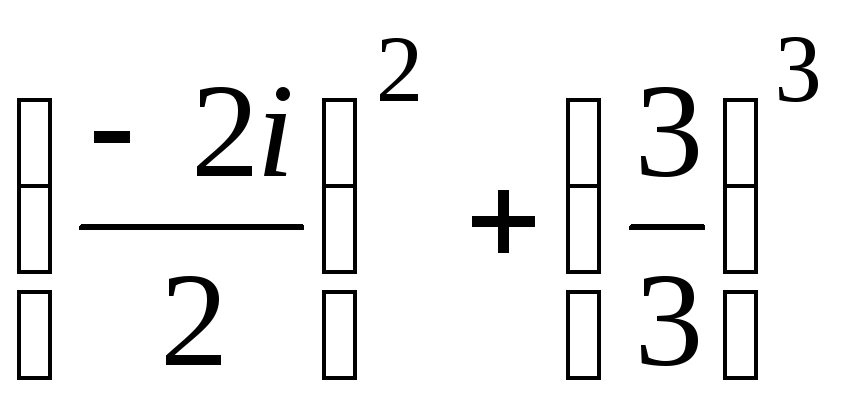 =–1+1=0
Таким
образом корни уравнения можно вычислить
по формулам (6).x1=
=–1+1=0
Таким
образом корни уравнения можно вычислить
по формулам (6).x1= =
=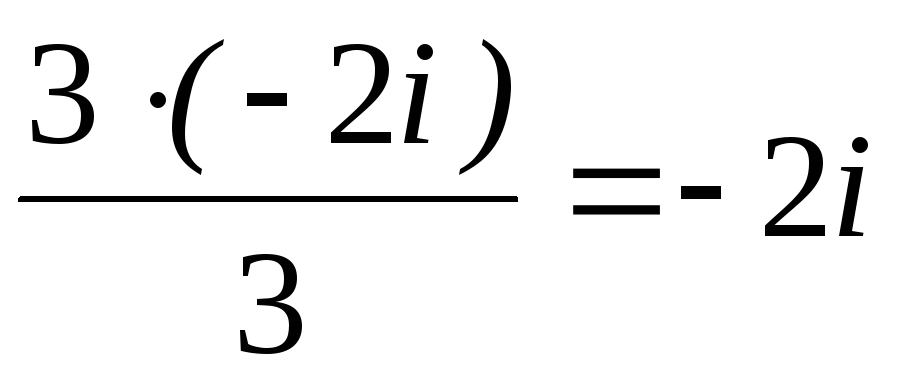 ; x2=x3=
; x2=x3= =
=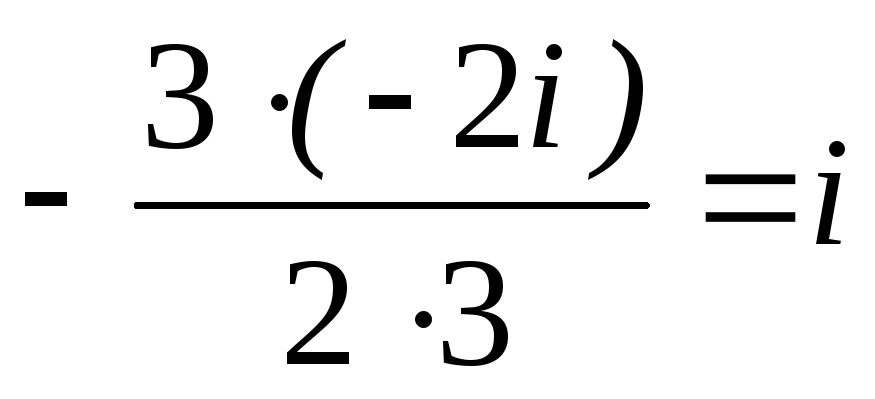 .
.
Ответ: x1=–2i, x2,3=i.
Пример 4. Решить уравнение:x3–3abx+ a3+b3=0
Решение.
Пологаяx=u+v,
получим
(u+v)3–3ab(u+v)+
a3+b3=0
или (u3+v3+ a3+b3)+(3uv–3ab)(u+v)=0.
Откуда Одно
из решений последней системы
Одно
из решений последней системы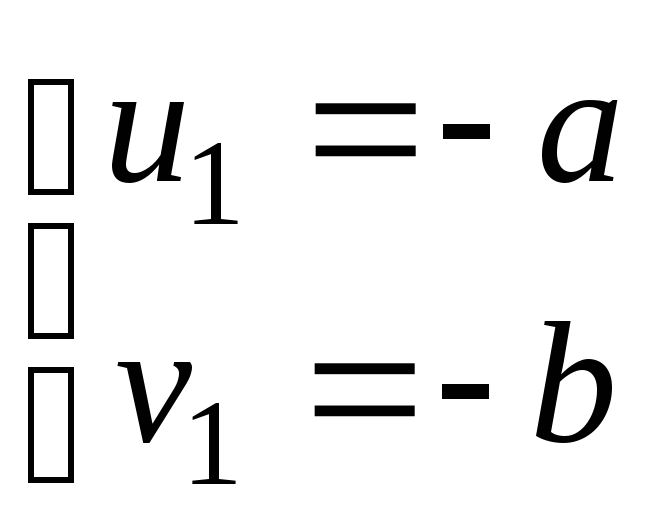
Тогда u1=–a, v1=–b, x1=–a–b; u2= u11=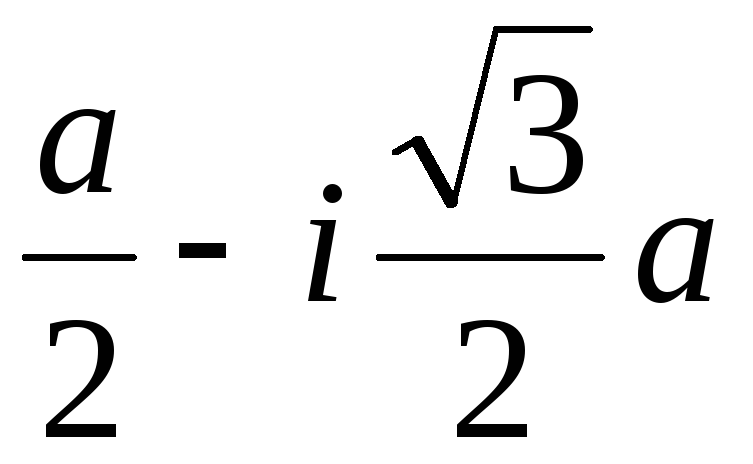 , v2= v12=
, v2= v12=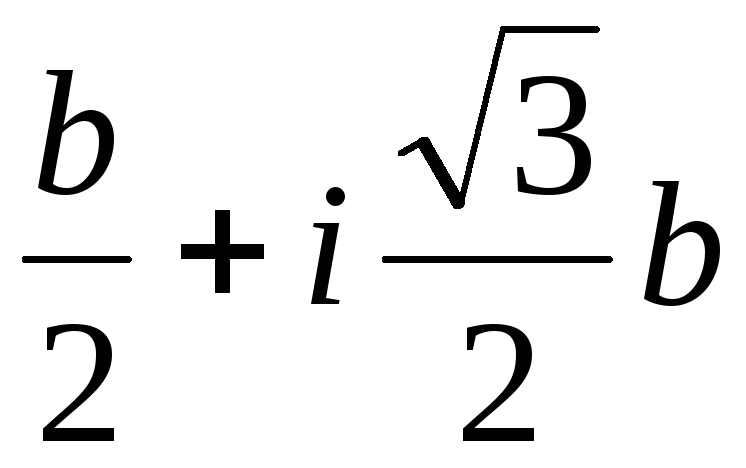 , x2=
, x2=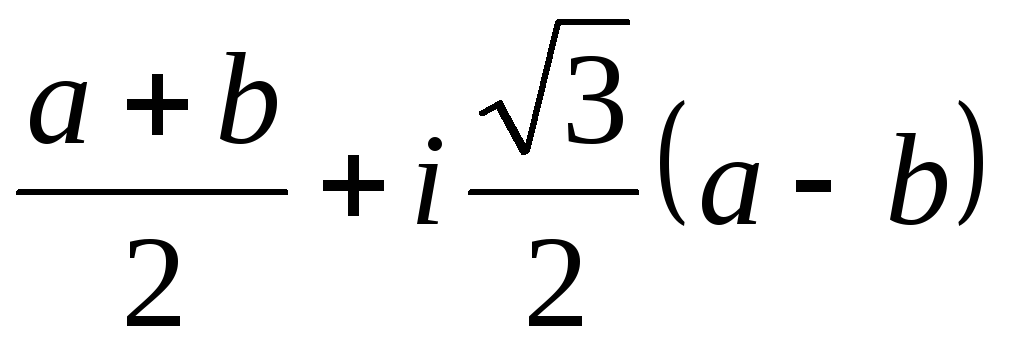 .
.
Ответ: x1=–a–b, x2,3=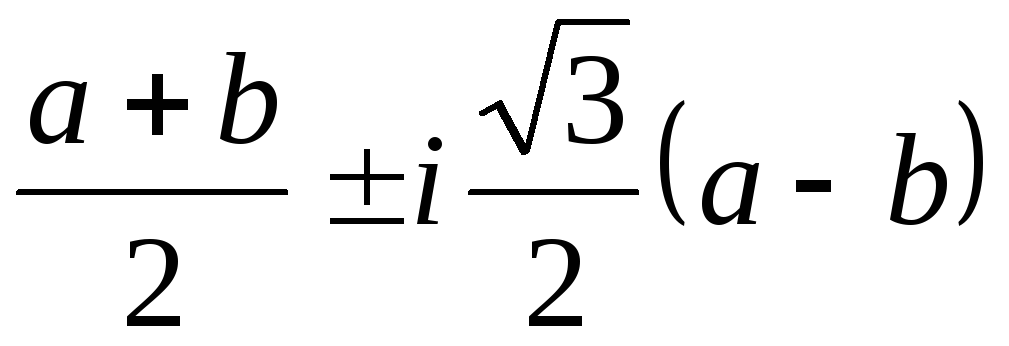 .
.
Замечание: При выписывании ответа воспользовались тем, что при вещественныхa,bне надо вычислять x3. Но если выписанное значениеx3есть корень уравнения при (любых) вещественныхa иb, то ясно, чтоx3 будет корнем при любыхa,b.
Для самостоятельного решения.
Решить уравнения:
x3+6x2–12x+32=0
x3+9x2–18x+44=0
x3–3x2–6x+36=0
x3–12x2+24x–40=0
x3–6ix+4(1–i)=0
x3+(3–3i
 )x–9=0
)x–9=0x3+3ax+1–a3=0
Ответы:
(–8;
 )
)(–11;
 )
)(–3;
 )
)(10;
 )
)(2+2i; –1–i; –1–i)
(i
 ;
; 

(a–1;

Теорема Абеля о неразрешимости уравнений в радикалах — Википедия
Материал из Википедии — свободной энциклопедии
Теорема Абеля — Руффини утверждает, что общее уравнение степени n{\displaystyle n} при n⩾5{\displaystyle n\geqslant 5} неразрешимо в радикалах.
Теория Галуа описывает группу перестановок корней многочленов. Современное доказательство теоремы основано на двух фактах.
Легко видеть, что значительная часть доказательства «спрятана» в теорию Галуа.
Теорема Абеля — Руффини не заявляет о том, что общее уравнение n{\displaystyle n}-й степени при n⩾5{\displaystyle n\geqslant 5} не имеет решения. Если мы допускаем комплексные решения, то основная теорема алгебры гарантирует наличие решений. Суть теоремы Абеля — Руффини сводится к тому, что для произвольных уравнений степени больше четвертой невозможно указать явную формулу для решений, то есть формулу, содержащую только арифметические операции и корни произвольной степени.
Решения таких уравнений можно получить с любой желаемой точностью, используя численные методы, например метод Ньютона.
Кроме того, корни некоторых уравнений высших степеней можно выразить в радикалах. Например, уравнение x5−5×4−10×3−10×2−5x−1=0{\displaystyle x^{5}-5x^{4}-10x^{3}-10x^{2}-5x-1=0} имеет корень x=1+25+45+85+165{\displaystyle x=1+{\sqrt[{5}]{2}}+{\sqrt[{5}]{4}}+{\sqrt[{5}]{8}}+{\sqrt[{5}]{16}}}.
Хотя уравнение пятой степени неразрешимо в радикалах, для его корней существуют формулы с использованием тета-функций.
Явные формулы для степеней меньше пятой[править | править код]
Для уравнений со степенью меньше, чем пятая, можно указать явную формулу решения. Это можно рассматривать как «вторую часть» или как «обратную» теорему Абеля — Руффини. Хотя это утверждение не следует из теоремы Абеля — Руффини, оно верно: см. формулы Кардано (для уравнений третьей степени) и Феррари (для четвёртой).
Первое доказательство теоремы было опубликовано в 1799 году Руффини. В доказательстве было несколько неточностей. В 1824 году полное доказательство было опубликовано Абелем.
Их доказательства основывалось на идеях Лагранжа, связанных с перестановками корней уравнения. Позже эти идеи были развиты в теории Галуа, она позволила сформулировать современное изложение доказательств и послужила отправной точкой в развитии абстрактной алгебры.
Хотя теорема утверждает, что уравнения не имеют общей формулы для решения, некоторые типы уравнений высоких степеней допускают точные решения. Среди них:
Уравнение четвёртой степени — Википедия
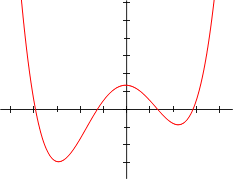
Уравнение четвёртой степени — в математике алгебраическое уравнение вида:
- f(x)=ax4+bx3+cx2+dx+e=0,a≠0.{\displaystyle f(x)=ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a\neq 0.}
Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любом значении коэффициентов).
Так как f(x){\displaystyle f(x)} является многочленом чётной степени, она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если a>0{\displaystyle a>0}, то функция возрастает до плюс бесконечности с обеих сторон, таким образом, функция имеет глобальный минимум. Аналогично, если a<0{\displaystyle a<0}, то функция убывает до минус бесконечности с обеих сторон, таким образом, функция имеет глобальный максимум.
Теорема Виета для уравнения четвёртой степени[править | править код]
Корни уравнения четвёртой степени x1,x2,x3,x4{\displaystyle x_{1},\,x_{2},\,x_{3},\,x_{4}} связаны с коэффициентами a,b,c,d,e{\displaystyle a,\,b,\,c,\,d,\,e} следующим образом:
- x1+x2+x3+x4=−ba,{\displaystyle x_{1}+x_{2}+x_{3}+x_{4}=-{\frac {b}{a}},}
- x1x2+x1x3+x1x4+x2x3+x2x4+x3x4=ca,{\displaystyle x_{1}\,x_{2}+x_{1}\,x_{3}+x_{1}\,x_{4}+x_{2}\,x_{3}+x_{2}\,x_{4}+x_{3}\,x_{4}={\frac {c}{a}},}
- x1x2x3+x1x2x4+x1x3x4+x2x3x4=−da,{\displaystyle x_{1}\,x_{2}\,x_{3}+x_{1}\,x_{2}\,x_{4}+x_{1}\,x_{3}\,x_{4}+x_{2}\,x_{3}\,x_{4}=-{\frac {d}{a}},}
- x1x2x3x4=ea.{\displaystyle x_{1}\,x_{2}\,x_{3}\,x_{4}={\frac {e}{a}}.}
Уравнения четвёртой степени впервые были рассмотрены древнеиндийскими математиками между IV в. до н. э. и II в. н. э.
Лодовико Феррари приписывается получение решения уравнения четвёртой степени в 1540 году, но его работа опиралась на решение кубического уравнения, которого у него не было, поэтому сразу это решение не было опубликовано,[1] а было опубликовано только в 1545 вместе с решением кубического уравнения наставника Феррари — Джероламо Кардано в книге «Великое искусство»[2].
То, что это наибольшая степень уравнения, для которого можно указать общую формулу решения, было доказано в теореме Абеля — Руффини в 1824. Записки, оставленные Галуа, позже привели к элегантной теории корней многочленов, одним из результатов которой была эта теорема.[3]
Через резольвенту[править | править код]
Решение уравнения четвёртой степени
- x4+px2+qx+r=0{\displaystyle x^{4}+px^{2}+qx+r=0}
сводится к решению кубической резольвенты
- y3−2py2+(p2−4r)y+q2=0{\displaystyle y^{3}-2py^{2}+(p^{2}-4r)y+q^{2}=0}
Корни резольвенты y1,y2,y3{\displaystyle y_{1},y_{2},y_{3}} связаны с корнями исходного уравнения x1,x2,x3,x4{\displaystyle x_{1},x_{2},x_{3},x_{4}} (которые и нужно найти) следующими соотношениями:
- y1=(x1+x2)(x3+x4){\displaystyle y_{1}=(x_{1}+x_{2})(x_{3}+x_{4})}
- y2=(x1+x3)(x2+x4){\displaystyle y_{2}=(x_{1}+x_{3})(x_{2}+x_{4})}
- y3=(x1+x4)(x2+x3){\displaystyle y_{3}=(x_{1}+x_{4})(x_{2}+x_{3})}
Корни резольвенты могут быть решены по формуле Кардано. Три формулы соотношений между yi{\displaystyle y_{i}} и xi{\displaystyle x_{i}} вместе с исходным уравнением дают систему из 4 алгебраических уравнений с 4 неизвестными, которая легко решается.
Решение Декарта — Эйлера[править | править код]
В уравнении четвёртой степени
- ax4+bx3+cx2+dx+e=0,a≠0{\displaystyle ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a\neq 0}
сделаем подстановку x=y−b4a{\displaystyle x=y-{\frac {b}{4a}}}, получим уравнение в следующем виде (оно называется «неполным»):
- y4+py2+qy+r=0,{\displaystyle y^{4}+py^{2}+qy+r=0,}
где
- p=8ac−3b28a2,{\displaystyle p={\frac {8ac-3b^{2}}{8a^{2}}},}
- q=8a2d+b3−4abc8a3,{\displaystyle q={\frac {8a^{2}d+b^{3}-4abc}{8a^{3}}},}
- r=16ab2c−64a2bd−3b4+256a3e256a4.{\displaystyle r={\frac {16ab^{2}c-64a^{2}bd-3b^{4}+256a^{3}e}{256a^{4}}}.}
Корни y1,y2,y3,y4{\displaystyle y_{1},\,y_{2},\,y_{3},\,y_{4}} такого уравнения равны одному из следующих выражений:
- ±z1{\displaystyle \pm {\sqrt {z_{1}}}} ±z2{\displaystyle \pm {\sqrt {z_{2}}}} ±z3,{\displaystyle \pm {\sqrt {z_{3}}},}
в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:
- (±z1)(±z2)(±z3)=−q8,{\displaystyle (\pm {\sqrt {z_{1}}})(\pm {\sqrt {z_{2}}})(\pm {\sqrt {z_{3}}})=-{\frac {q}{8}},}
причём z1,z2,z3{\displaystyle z_{1},\,z_{2},\,z_{3}} — это корни кубического уравнения
- z3+p2z2+p2−4r16z−q264=0.{\displaystyle z^{3}+{\frac {p}{2}}z^{2}+{\frac {p^{2}-4r}{16}}z-{\frac {q^{2}}{64}}=0.}
Решение Феррари[править | править код]
Решение уравнения четвёртой степени вида x4+ax3+bx2+cx+d=0{\displaystyle x^{4}+ax^{3}+bx^{2}+cx+d=0} может быть найдено по методу Феррари. Если y1{\displaystyle y_{1}} — произвольный корень кубического уравнения
| y3−by2+(ac−4d)y−a2d+4bd−c2=0,{\displaystyle y^{3}-by^{2}+(ac-4d)y-a^{2}d+4bd-c^{2}=0,} | (2) |
(резольвенты основного уравнения), то четыре корня исходного уравнения находятся как корни двух квадратных уравнений
- x2+a2x+y12=±(a24−b+y1)x2+(a2y1−c)x+y124−d{\displaystyle x^{2}+{\frac {a}{2}}x+{\frac {y_{1}}{2}}=\pm {\sqrt {\left({\frac {a^{2}}{4}}-b+y_{1}\right)x^{2}+\left({\frac {a}{2}}y_{1}-c\right)x+{\frac {y_{1}^{2}}{4}}-d}}}
где подкоренное выражение в правой части является полным квадратом.
Биквадратное уравнение[4] — уравнение четвёртой степени вида ax4+bx2+c=0{\displaystyle ax^{4}+bx^{2}+c=0}, где a,b,c{\displaystyle a,b,c} — заданные комплексные числа и a≠0{\displaystyle a\not =0}. Подстановкой y=x2;y⩾0{\displaystyle y=x^{2};y\geqslant 0} оно сводится к квадратному уравнению относительно y{\displaystyle y}.
Четыре его корня находятся по формуле
- x1,2,3,4=±−b±b2−4ac2a.{\displaystyle x_{1,2,3,4}=\pm {\sqrt {\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}.}
Возвратные уравнения четвёртой степени[править | править код]
Возвратное уравнение четвёртой степени является также относительно легко решаемым: для ax4+bx3+cx2+bx+a=0{\displaystyle ax^{4}+bx^{3}+cx^{2}+bx+a=0} такого, что a≠0{\displaystyle a\neq 0}, решение находится приведением к виду:
- a(x2+1×2)+b(x+1x)+c=0{\displaystyle a\left(x^{2}+{1 \over x^{2}}\right)+b\left(x+{1 \over x}\right)+c=0},
После замены t=x+1x{\displaystyle t={x+{1 \over x}}} ищется решение квадратного уравнения at2+bt+c−2a=0{\displaystyle at^{2}+bt+c-2a=0}, а затем — квадратного уравнения x2−tx+1=0{\displaystyle x^{2}-tx+1=0}.
- ↑ Ferrari biography
- ↑ «Великое искусство» (Ars magna, 1545)
- ↑ Стюарт, Ян. Теория Галуа, издание третье (Chapman & Hall/CRC Mathematics, 2004) (англ.)
- ↑ В литературе до середины XX века биквадратным также могли называть уравнение четвёртой степени общего вида
Кубическое уравнение
Кубическим уравнением является полиномиальное уравнение третьей степени. Общий вид ax3+bx2+cx+d=0, где a ≠ 0.
Кубическое уравнение имеет вид ax3 + bx2 + сх + d = 0. В уравнение должно присутствовать х3, в противном случае уравнение не будет кубическим, но некоторые или все из В, С и D могут быть равны нулю. Бесплатный онлайн калькулятор для расчета уравнения третьей степени, используется для нахождения корней кубического уравнения.
Например, Введите a=1, b=8, c=163 + bx2 + cx + d = 0
Формула кубического уравнения:
discriminant(Δ) = q3 + r2- q = (3c- b2)/9
- r = -27d + b(9c-2b2)
- s = r + √(discriminant)
- t = r — √(discriminant)
- term1 = √(3.0)*((-t + s)/2)
- r13= 2 * √(q)
- x1=(- term1 + r13*cos(q3/3) )
- x2=(- term1 + r13*cos(q3+(2*∏)/3) )
- x3=(- term1 + r13*cos(q3+(4*∏)/3) )
Кубическое уравнение:
ax3 + bx2 + cx + d = 0,
где,
- a = коэффициент x3
- b = коэффициент x2
- c = коэффициент x
- d = constant.
Формула:
x1 = -term1 + r13 * cos(q3 / 3)
x2 = -term1 + r13 * cos(q3 + (2 * ∏) / 3)
x3 = -term1 + r13 * cos(q3 + (4 * ∏) / 3)
term1 и r13 формула:
q = (3c — b2) / 9
r = (-27d + b(9c — 2b2)) / 54
discriminant(Δ) = q3 + r2
r13 = 2 * √ (q)
Если discriminant(Δ) > 0 term1 = (b/3.0)
еще
- s = r + √ discriminant(Δ)
- t = r — √ discriminant(Δ)
- term1 = √ (3.0) * ((-t + s) / 2)
Пример:
Вычислить корни (x1, x2, x3) уравнения третьей степени, x 3 — 4x2 — 9x + 36 = 0
Шаг 1:
Из приведенного выше уравнения, значение a = 1, b = — 4, c = — 9 и d = 36.
Шаг 2:
Найдем значения q и r
q = ((3*-9) — (-4)2) / 9 = -4.77778
r = (-27*36+(-4)*(9*(-9)-2*(-4)2))/54 = -9.62963
Шаг 3:
Найдем значение дискриминанта, обозначается как знак дельта (Δ)
discriminant(Δ)= q3 + r2
discriminant(Δ) = (-4.77778)3 + (-9.62963)2 = -16.3333
Значение дискриминанта меньше 0
Шаг 4:
Найдем term1 и r13
Если Δ< 0, term1 = (b/3.0) = -4 / 3 = -1.33333
term1 = -1.33333
r13 = 2 * √(q)
где, q = -q = 4.77778
r13 = 2 * √ 4.77778 = 4.371626
Шаг 5:
Подставляем значения term1 и r13 в формулу кубического уравнения
x1 = -term1 + r13 * cos(q3 / 3)
x1 = 1.33333 + 4.371626 x cos(4.777783 / 3) = 4
x2 = -term1 + r13 * cos(q3 + (2 * ∏) / 3)
x2 = 1.33333 + 4.371626 x cos(4.777783 + (2 * ∏)/ 3) = -3
x3 = -term1 + r13 * cos(q3 + (4 * ∏) / 3)
x3 = 1.33333 + 4.371626 x cos(4.777783 + (4 * ∏)/ 3) = -3
Шаг 6:
Мы получили корни уравнения, x1 = 4, x2 = -3 и x3 = -3.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
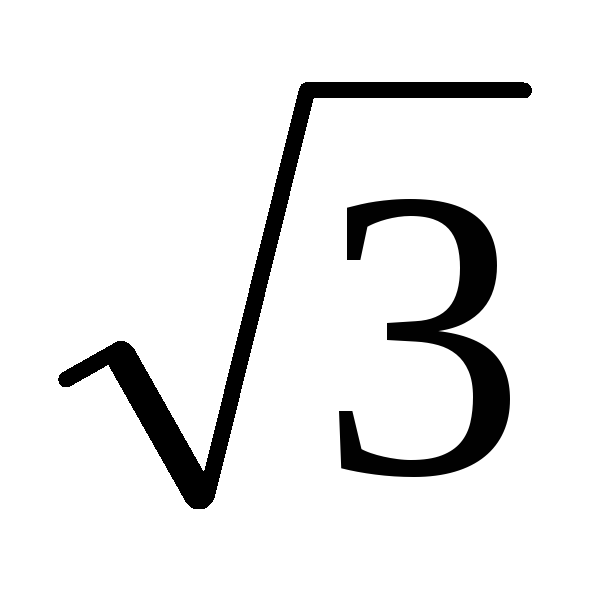 )x–9=0
)x–9=0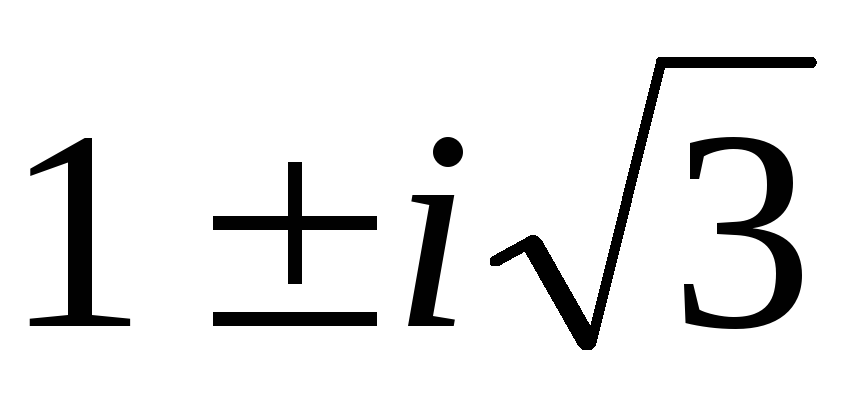 )
)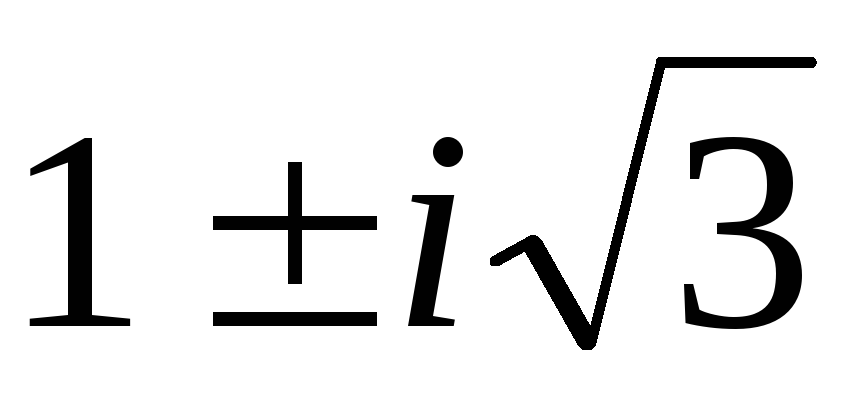 )
) )
)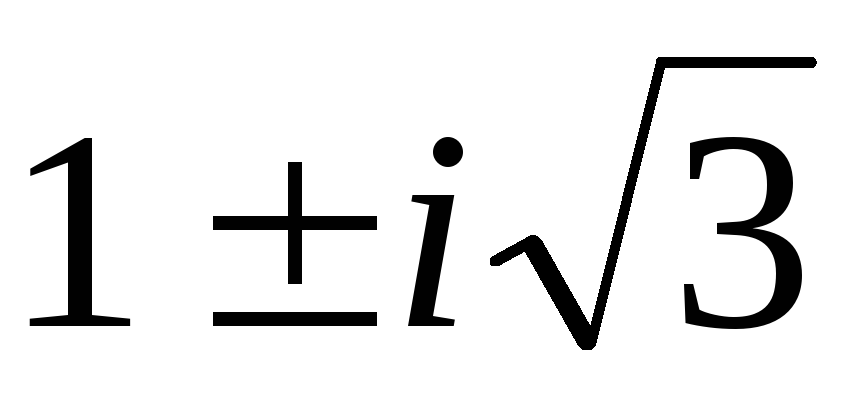 )
)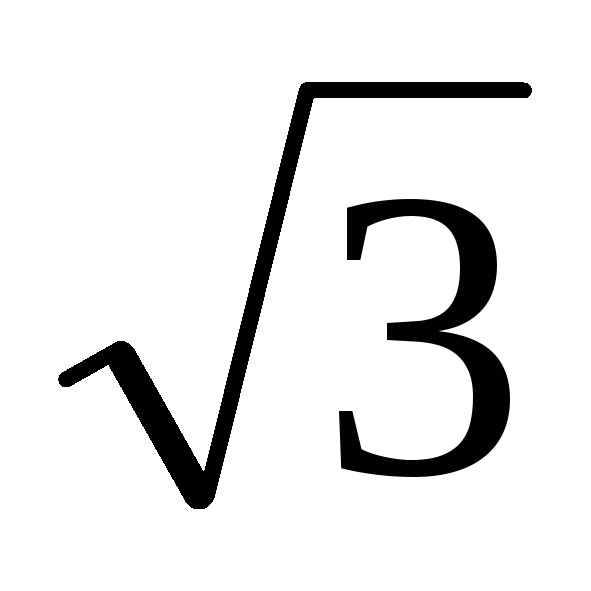 ;
;