Уравнение дискриминант: Как найти Дискриминант? 🤔 Формулы, Примеры решений.

Posted on by alexxlab

Содержание

Как найти Дискриминант? 🤔 Формулы, Примеры решений.

Понятие квадратного уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 8 + 4 = 12. При вычислении левой части получается верное числовое равенство, то есть 12 = 12.

Уравнением можно назвать выражение 8 + x = 12, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени, значит, такое уравнение является квадратным.

Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Есть три вида квадратных уравнений:

  • не имеют корней;
  • имеют один корень;
  • имеют два различных корня.

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, которое находится под корнем в формуле нахождения корней квадратного уравнения. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.


Чаще всего для поиска дискриминанта используют формулу:

В этом ключе универсальная формула для поиска корней квадратного уравнения выглядит так:


Эта формула подходит даже для неполных квадратных уравнений.

Но есть и другие формулы — все зависит от вида уравнения. Чтобы в них не запутаться, сохраняйте табличку или распечатайте ее и храните в учебнике.


Как решать квадратные уравнения через дискриминант

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения.

Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный. Только после этого вычисляем значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax2 + bx + c = 0:

  • как найти дискрининант: D = b2 − 4ac;
  • если дискриминант отрицательный — зафиксировать, что действительных корней нет;
  • если дискриминант равен нулю — вычислить единственный корень уравнения по формуле х = — b2/2a;
  • если дискриминант положительный — найти два действительных корня квадратного уравнения по формуле корней

А вот и еще одна табличка: в ней вы найдете формулы для поиска корней квадратных уравнений при помощи дискриминанта:


Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, важно практиковаться. Вперед!

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x2 — 4x + 2 = 0.

Как решаем:

  1. Определим коэффициенты: a = 3, b = -4, c = 2.

  2. Найдем дискриминант: D = b2 — 4ac = (-4)2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D < 0, корней нет.

Пример 2. Решить уравнение: x2 — 6x + 9 = 0.

Как решаем:

  1. Определим коэффициенты: a = 1, b = -6, c = 9.

  2. Найдем дискриминант: D = b2 — 4ac = (-6)2 — 4 * 1 * 9 = 36 — 36 = 0.

  3. D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x2 — 4x — 5 = 0.

Как решаем:

  1. Определим коэффициенты: a = 1, b = -4, c = -5.

  2. Найдем дискриминант: D = b2 — 4ac = (-4)2 — 4 * 1 * (-5) = 16 + 20 = 36.

  3. D > 0, значит уравнение имеет два корня:

     

x1 = (4 + 6) : 2 = 5,

x2 = (4 — 6) : 2 = -1.

Ответ: два корня x1 = 5, x2 = -1.

Не желаешь повторить формулы сокращенного умножения?

Дискриминант квадратного уравнения. Формулы дискриминанта

Дискриминант квадратного уравнения — это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой  D.

Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:

Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:

  1. Если дискриминант больше нуля, то уравнение имеет два корня.
  2. Если дискриминант равен нулю, то уравнение имеет один корень.
  3. Если дискриминант меньше нуля, то уравнение не имеет корней.

Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:

D = b2 — 4ac,

так как она относится к формуле:

,

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.

Решение квадратных уравнений через дискриминант

Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.

Пример 1. Решить уравнение:

3x2 — 4x + 2 = 0.

Определим, чему равны коэффициенты:

a = 3,  b = -4,  c = 2.

Найдём дискриминант:

D = b2 — 4ac = (-4)2 — 4 · 3 · 2 = 16 — 24 = -8,

D < 0.

Ответ: корней нет.

Пример 2.

x2 — 6x + 9 = 0.

Определим, чему равны коэффициенты:

a = 1,  b = -6,  c = 9.

Найдём дискриминант:

D = b2 — 4ac = (-6)2 — 4 · 1 · 9 = 36 — 36 = 0,

D = 0.

Уравнение имеет всего один корень:

Ответ:  3.

Пример 3.

x2 — 4x — 5 = 0.

Определим, чему равны коэффициенты:

a = 1,  b = -4,  c

= -5

Найдём дискриминант:

D = b2 — 4ac = (-4)2 — 4 · 1 · (-5) = 16 + 20 = 36,

D > 0.

Уравнение имеет два корня:

x1 = (4 + 6) : 2 = 5,

x2 = (4 — 6) : 2 = -1.

Ответ:  5,  -1.

Решение квадратных уравнений

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

  1. Не имеют корней;
  2. Имеют ровно один корень;
  3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

  1. Если D < 0, корней нет;
  2. Если D = 0, есть ровно один корень;
  3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

  1. x2 − 8x + 12 = 0;
  2. 5x2 + 3x + 7 = 0;
  3. x2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.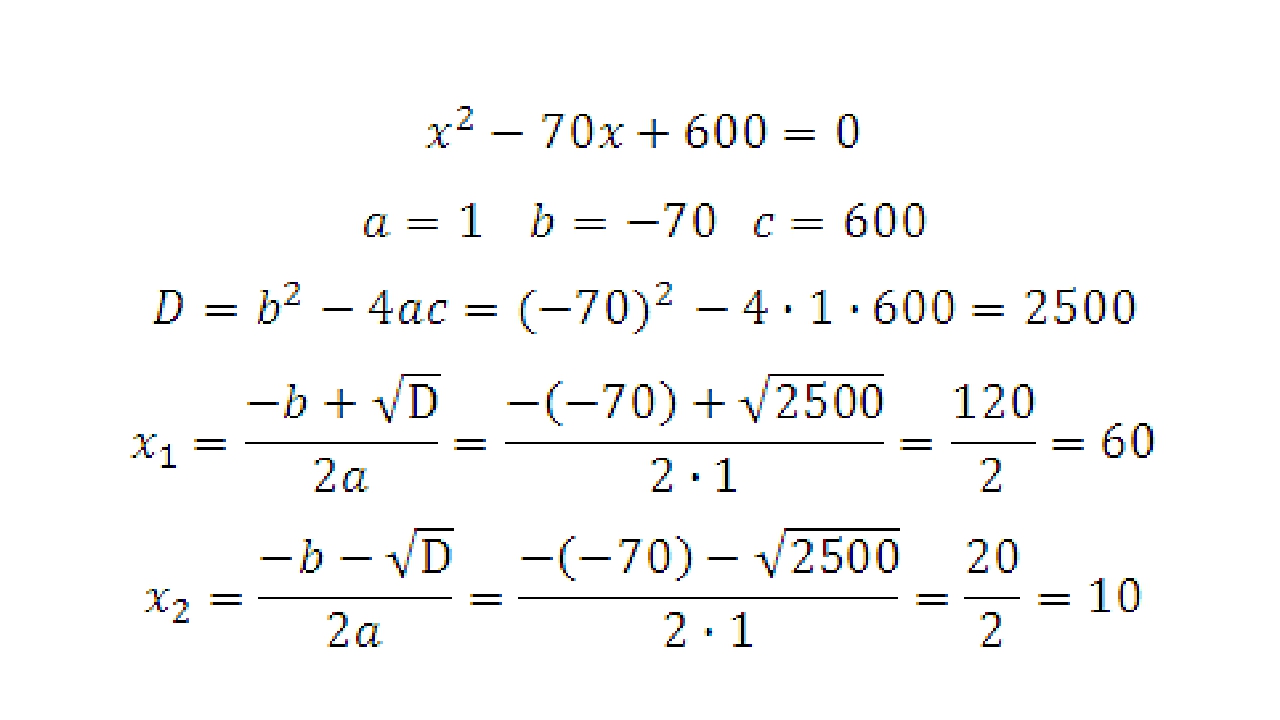

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.

Задача. Решить квадратные уравнения:

  1. x2 − 2x − 3 = 0;
  2. 15 − 2x − x2 = 0;
  3. x2 + 12x + 36 = 0.

Первое уравнение:
x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left( -1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left( -1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 122 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

\[x=\frac{-12+\sqrt{0}}{2\cdot 1}=-6\]

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

  1. x2 + 9x = 0;
  2. x2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax2 + c = 0. Немного преобразуем его:

Решение неполного квадратного уравнения

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:

  1. Если в неполном квадратном уравнении вида ax2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
  2. Если же (−c/a) < 0, корней нет.

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

  1. x2 − 7x = 0;
  2. 5x2 + 30 = 0;
  3. 4x2 − 9 = 0.

x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.

5x2 + 30 = 0 ⇒ 5x2 = −30 ⇒ x2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x2 − 9 = 0 ⇒ 4x2 = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.

Смотрите также:

  1. Теорема Виета
  2. Следствия из теоремы Виета
  3. Тест на тему «Значащая часть числа»
  4. Правила комбинаторики в задаче B6
  5. Как представить обычную дробь в виде десятичной
  6. Задача B15: частный случай при работе с квадратичной функцией

Решение (корни) квадратного уравнения

Квадратным уравнением называется уравнение вида ax² + bx + c = 0, где x — переменная, которая в уравнении присутствует в квадрате, a, b, c — некоторые числа, причём a ≠ 0.

Например, квадратным является уравнение

2x² — 3x + 1 = 0,

в котором a = 2, b = — 3, c = 1.

В квадратном уравнении ax² + bx + c = 0 коэффициент a называют первым коэффициентом, b — вторым коэффициентом, c — свободным членом.

Уравнения вида ax² + bx = 0,

где c =0,

ax² + c = 0,

где b =0, и

ax² = 0,

где a =0 и b =0,

называются неполными квадратными уравнениями.

Найти корни квадратного уравнения значит решить квадратное уравнение.

Для вычисления корней квадратного уравния служит выражение b² — 4ac, которое называется дискриминантом квадратного уравнения и обозначается буквой D.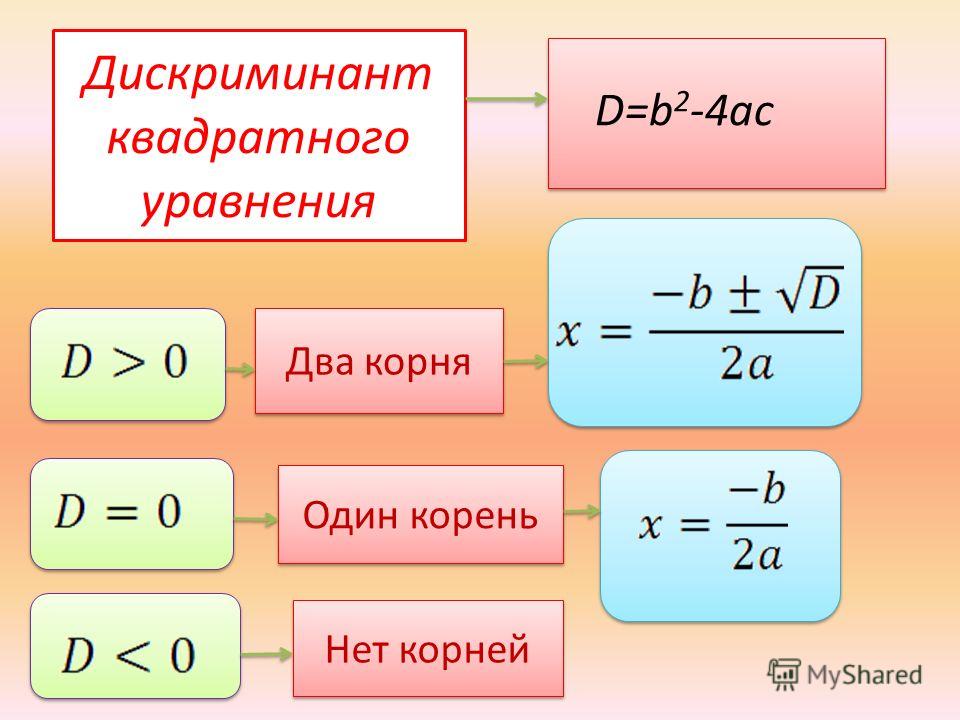

Корни квадратного уравнения имеют следующие сферы применения:

— для разложении квадратного трёхлена на множители, что, в свою очередь, является приёмом упрощения выражений (например, сокращения дробей, вынесение за скобки общего знаменателя и т.д.) в частности, при нахождении пределов, производных и интегралов;

— для решения задач на соотношения параметров меняющегося объекта (корни квадратного уравнения, чаще всего один, являются обычно конечным решением).

График квадратичного трёхлена ax² + bx + c — левой части квадратного уравнения — представляет собой параболу, ось симметрии которой параллельна оси 0y. Число точек пересечения параболы с осью 0x определяет число корней квадратного уравнения. Если точек пересечения две, то квадратное уравнение имеет два действительных корня, если точка пересечения одна, то квадратное уравнение имеет один действительный корень, если парабола не пересекает ось 0x, то квадратное уравнение не имеет действительных корней. На рисунке ниже изображены три упомянутых случая.

Как видно на рисунке, красная парабола пересекает ось 0x в двух точках, зелёная — в одной точке, а жёлтая парабола не имеет точек пересечения с осью 0x.

1. Если дискриминант больше нуля (), то квадратное уравнение имеет два различных действительных корня.

Они вычисляются по формулам:

и

.

Часто пишется так: .

2. Если дискриминант равен нулю (), то квадратное уравнение имеет только один действительный корень, или, что то же самое — два равных действительных корня, которые равны .

3. Если дискриминант меньше нуля (), то квадратное уравнение не имеет действительных корней, а имеет комплексные корни, но нахождение комплексных корней в этой статье рассматривать не будем. В общем случае правильным решением является констатация того, что квадратное уравнение не имеет действительных корней.

Пример 1. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант больше нуля, следовательно, квадратное уравнение имеет два действительных корня.

Путём преобразования в квадратное уравнение следует решать и дробные уравнения, в которых хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное, например, . О том, как это делается — в материале Решение дробных уравнений с преобразованием в квадратное уравнение.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 2. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант равен нулю, следовательно, квадратное уравнение имеет один действительный корень.

Пример 3. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант меньше нуля, следовательно, квадратное уравнение не имеет действительных корней.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Находить корни квадратного уравнения требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.

Пример 4. Найти корни квадратного уравнения:

.

В примере 1 нашли дискриминант этого уравнения:

,

Решение квадратного уравнения найдём по формуле для корней:

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Корни приведённого квадратного уравнения

Формула корней приведённого уравнения имеет вид:

.

Существуют формулы, связывающие корни квадратного уравнения с его коэффициентами. Они впервые были получены французским математиком Ф.Виетом.

Теорема Виета. Если квадратное уравнение ax² + bx + c = 0 имеет действительные корни, то их сумма равна — b/a, а произведение равно с/a:

Следствие. Если приведённое квадратное уравнение x² + px + q = 0 имеет действительные корни и , то

Пояснение формул: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Следовательно, теорему Виета можно применять и для поиска корней приведённого квадратного уравнения.

Если известны корни квадратного уравнения, то трёхчлен, представляющий собой левую часть уравнения, можно разложить на множители по следующей формуле:

.

Этот приём часто используется для упрощения выражений, особенно сокращения дробей.

Пример 9. Упростить выражение:

.

Решение. Числитель данной дроби можем рассматривать как квадратный трёхчлен в отношении x и разложить его на множители, предварительно найдя его корни. Найдём дискриминант квадратного уравнения:

.

Корни квадратного уравнения будут следующими:

.

Разложим квадратный многочлен на множители:

.

Упростили выражение, проще не бывает:

.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 10. Упростить выражение:

.

Решение. И числитель, и знаменатель — квадратные трёхчлены. Значит, их можно разложить на множители, предварительно найдя корни соответствующих квадратных уравнений. Находим дискриминант первого квадратного уравнения:

.

Корни первого квадратного уравнения будут следующими:

.

Находим дискриминант второго квадратного уравнения:

.

Так как дискриминант равен нулю, второе квадратное уравнение имеет два совпадающих корня:

.

Подставим корни квадратных уравнений, разложим числитель и знаменатель на множители и получим:

.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Упрощать выражения путём решения квадратных уравнений требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.

Разумеется, квадратного трёхчлена может может и не быть в выражении в первоначальном виде, он может быть получен в процессе предварительных преобразований выражения.

Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших до наших дней выводов этой формулы принажлежит индийскому математику Брахмагупте (около 598 г.). Среднеазиатский учёный аль-Хорезми (IX в.) получил эту формулу методом выделения полного квадрата с помощью геометрической иллюстрации. Суть его рассуждений видна из рисунка ниже (он рассматривает уравнение x² + 10x = 39).

Площадь большого квадрата равна (x + 5)². Она складывается из площади x² + 10x заштрихованной фигуры, равной левой части рассматриваемого уравнения, и площади четырёх квадратов со стороной 5/2, равной 25. Получается следующее уравнение и его решение:

Пример 11. Отрезок ткани стоит 180 у.ед. Если бы ткани в отрезке было на 2,5 м больше и цена отрезка оставалась бы прежней, то цена 1 м ткани была бы на 1 у.ед. меньше. Сколько ткани в отрезке?

Решение. Примем количество ткани в отрезке за x и получим уравнение:

Приведём обе части уравнения к общему знаменателю:

Произведём дальнейшие преобразования:

Получили квадратное уравнение, которое и решим:

Ясно, что количество ткани не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь один корень — положительный.

Ответ: в отрезке 20 м ткани.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 12. Товар, количество которого 187,5 кг, взвешивают в одинаковых ящиках. Если в каждом ящике количество товара уменьшить на 2 кг, то следовало бы использовать на 2 ящика больше и при этом 2 кг товара остались бы невзвешенными. Сколько кг товара взвешивают в каждом ящике?

Решение. Примем за x количество товара, взвешиваемого в одном ящике. Тогда получим уравнение:

Приведём обе части уравнения к общему знаменателю, произведём дальнейшие преобразования и получим квадратное уравнение. Процесс записывается так:

Найдём дискриминант:

Найдём корни квадратного уравнения:

Количество товара не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь положительный корень.

Ответ: в одном ящике взвешивают 12,5 кг ткани.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Другие темы в блоке «Школьная математика»

Решение квадратных уравнений. Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа.

Квадратным уравнением называется уравнение вида

                 ,

где

x — переменная,

a,b,c — постоянные (числовые) коэффициенты.

В общем случае решение квадратных уравнений сводится к нахождению дискриминанта: 

Формула дискриминанта: .

       О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :

  • D>0 — уравнение имеет 2 различных вещественных корня
  • D=0 — уравнение имеет 2 совпадающих вещественных корня
  • D<0 — уравнение имеет 2 мнимых корня (для непродвинутых пользователей — корней не имеет)

В общем случае корни уравнения равны:

                 .

Очевидно, в случае с нулевым дискриминантом, оба корня равны

                 .

Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:

                

В таком случае корни уравнения вычисляются по формуле:

                

Теорема Виета.

Приведенным квадратным уравнением называется уравнение вида

                ,

то есть квадратное уравнение с единичным коэффициентом при старшем члене.

В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:

                 .

Следует заметить, что любое квадратное уравнение может стать приведенным, если его поделить на коэффициент при старшем члене, то есть при х2.

Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа.





 Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы.  / / Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа.

Поделиться:   

Квадратное уравнение. Решение квадратных уравнений.

Дискриминант. Формула дискриминанта. Теорема Виета.     Версия для печати.
Квадратным уравнением называется уравнение вида:

                 ,

  • где
    • x — переменная,
    • a,b,c — постоянные (числовые) коэффициенты.

В общем случае решение квадратных уравнений сводится к нахождению

дискриминанта
Формула дискриминанта: .
О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :
  • D>0 — уравнение имеет 2 различных вещественных корня
  • D=0 — уравнение имеет 2 совпадающих вещественных корня
  • D<0 — уравнение имеет 2 мнимых корня (для непродвинутых пользователей — корней не имеет)

В общем случае корни уравнения равны:

                 .

Очевидно, в случае с нулевым дискриминантом, оба корня равны

                 .

Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:

                

В таком случае корни уравнения вычисляются по формуле:

                

Теорема Виета о корнях квадратного уранения.

Приведенным квадратным уравнением называется уравнение вида

                ,

то есть квадратное уравнение с единичным коэффициентом при старшем члене.

В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:

                 .

Следует заметить, что любое квадратное уравнение может стать приведенным, если его поделить на коэффициент при старшем члене, то есть при х2
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers

Консультации и техническая
поддержка сайта: Zavarka Team

 Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Квадратное уравнение. Решение квадратных уравнений.

Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа.

Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Теорема Виета.

Квадратным уравнением называется уравнение вида:

                 ,

где
x — переменная,
a,b,c — постоянные (числовые) коэффициенты.

В общем случае решение квадратных уравнений сводится к нахождению дискриминанта

Формула дискриминанта: .
О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :
  • D>0 — уравнение имеет 2 различных вещественных корня
  • D=0 — уравнение имеет 2 совпадающих вещественных корня
  • D<0 — уравнение имеет 2 мнимых корня (для непродвинутых пользователей — корней не имеет)

В общем случае корни уравнения равны:

                 .

Очевидно, в случае с нулевым дискриминантом, оба корня равны

                 .

Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:

                

В таком случае корни уравнения вычисляются по формуле:

                

Теорема Виета.

Приведенным квадратным уравнением называется уравнение вида

                ,

то есть квадратное уравнение с единичным коэффициентом при старшем члене.

В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:

                 .

Следует заметить, что любое квадратное уравнение может стать приведенным, если его поделить на коэффициент при старшем члене, то есть при х2

Найти корни квадратного уравнения с помощью дискриминанта

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Дискриминантное определение, примеры и решения

Содержание


Мы в Cuemath считаем, что математика — это жизненный навык. 2-4ac \\ [0.2 + bx + c = 0 \) — значения \ (x \), которые удовлетворяют уравнению.

Их можно найти по формуле корней квадратного уравнения:

\ (x = \ dfrac {-b \ pm \ sqrt {D}} {2 a} \)

Хотя мы не можем найти корни, просто используя дискриминант, мы можем определить природу корней следующим образом:

  • Если \ (D> 0 \), квадратное уравнение имеет два разных действительных корня:
    \ [\ dfrac {-b \ pm \ sqrt {\ text {Положительное число}}} {2 a} \]
    дает два корня
  • Если \ (D = 0 \), квадратное уравнение имеет только один действительный корень:
    \ [\ dfrac {-b \ pm \ sqrt {0}} {2 a} = \ dfrac {-b} {2 a} \]
    это единственный корень
  • Если \ (D <0 \), квадратное уравнение не имеет действительных корней. то есть имеет два комплексных корня:
    \ [\ dfrac {-b \ pm \ sqrt {\ text {Отрицательное число}}} {2 a} \]
    дает два сложных корня.

Это потому, что квадратный корень отрицательного числа дает мнимое число. т.е. \ (\ sqrt {-1} = i \)

Корень — это не что иное, как координата x точки пересечения с x.

График квадратного уравнения в каждом из этих трех случаев может быть следующим.

Калькулятор дискриминанта (с графиком)

Вот «Дискриминантный калькулятор».2-4ac \)

  • Квадратное уравнение имеет:
    (i) два неравных действительных корня, когда \ (D> 0 \)
    (ii) только один действительный корень, когда \ (D = 0 \)
    (iii) нет действительных корней или два комплексных корня, когда \ (D <0 \)

    • Помогите своему ребенку набрать больше баллов с помощью запатентованного БЕСПЛАТНОГО диагностического теста Cuemath. Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Попытайтесь проверить сейчас.

    Решенные примеры

    Вот несколько примеров дискриминантов и их решения. 2 + Bx + C = 0 \),

    \ [\ begin {align} A & = 9 \\ [0.4} \)

    CLUEless по математике? Узнайте, как учителя CUEMATH объяснят вашему ребенку Дискриминант , используя интерактивные симуляции и рабочие листы, чтобы им больше никогда не приходилось запоминать что-либо по математике!

    Изучите интерактивные и персонализированные онлайн-классы Cuemath, которые сделают вашего ребенка экспертом по математике. Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня!

    Практические вопросы

    Вот несколько занятий для вас.{2} -24 x + 2 = 0} \) имеет только одно действительное решение.

    Образцы материалов олимпиады по математике

    IMO (Международная олимпиада по математике) — это конкурсный экзамен по математике, который ежегодно проводится для школьников. Он побуждает детей развивать свои навыки решения математических задач с точки зрения соревнований.

    Вы можете БЕСПЛАТНО скачать образцы работ по оценкам ниже:

    Чтобы узнать больше об олимпиаде по математике, вы можете нажать здесь

    Часто задаваемые вопросы (FAQ)

    1.2–4 (\ sqrt {3}) (10 \ sqrt {3}) \\ [0,2 см] & = 121-120 \\ [0,2 см] & = 1 \ end {выровнено} \]

    Таким образом, дискриминант данного уравнения равен:

    \ (\ mathbf {D} \) или \ (\ mathbf {\ Delta = 1} \)

    3. Как пользоваться дискриминантной формулой?

    Мы можем использовать дискриминант, чтобы определить природу корней.

    Квадратное уравнение имеет:
    (i) два неравных действительных корня, когда \ (D> 0 \)
    (ii) только один действительный корень, когда \ (D = 0 \)
    (iii) нет действительных корней или два комплексных корня, когда \ (D <0 \)

    Дискриминант | Промежуточная алгебра

    Результат обучения

    • Определите дискриминант и используйте его для классификации решений квадратных уравнений

    Дискриминант

    Квадратичная формула не только генерирует решения квадратного уравнения, но также сообщает нам о природе решений. {2} -4ac <0 [/ latex], тогда число под радикалом будет отрицательным. Поскольку вы не можете найти квадратный корень из отрицательного числа, используя действительные числа, реальных решений не существует. Однако вы можете использовать и мнимые числа. Тогда у вас будет два сложных решения: одно путем сложения мнимого квадратного корня, а другое - путем его вычитания.

    В таблице ниже приведены взаимосвязи между значением дискриминанта и решениями квадратного уравнения.

    {2} -4ac [/ latex].{2} -4 \ left (1 \ right) \ left (10 \ right) = 16-40 = -24 \ end {array} [/ latex]

    Результат — отрицательное число. Дискриминант отрицательный, поэтому квадратное уравнение имеет два комплексных решения.

    В последнем примере мы проведем корреляцию между количеством и типом решений квадратного уравнения и графиком соответствующей функции.

    Пример

    Используйте следующие графики квадратичных функций, чтобы определить, сколько и какого типа решения будет у соответствующего квадратного уравнения [latex] f (x) = 0 [/ latex].{2}} — 4ac [/ латекс]. Он определяет количество и тип решений квадратного уравнения. Если дискриминант положительный, существуют [latex] 2 [/ latex] вещественные решения. Если это [latex] 0 [/ latex], существует [latex] 1 [/ latex] реальное повторяющееся решение. Если дискриминант отрицательный, существуют [latex] 2 [/ latex] комплексные решения (но нет реальных решений).

    Дискриминант также может рассказать нам о поведении графика квадратичной функции.

    Дискриминант в квадратных уравнениях — наглядное пособие с примерами, практическими задачами и бесплатным PDF-файлом для печати

    Чтобы понять, что делает дискриминант, важно хорошо понимать:

    Предварительное требование 2: Какое решение квадратное уравнение:
    Отвечать

    Решение можно представить двумя разными способами.2 + \ blue bx + \ color {green} c $$.

  • Графически, поскольку y = 0 — ось x, решение находится там, где парабола пересекает ось x. (работает только для реальных решений) .

    • На рисунке ниже левая парабола имеет 2 реальных решения (красные точки), средняя парабола имеет 1 реальное решение (красная точка), а самая правая парабола не имеет реальных решений (да, у нее есть мнимые решения).

    Как выглядит дискриминант?
    Отвечать

    Похоже на . .. число.

    5, 2, 0, -1 — каждое из этих чисел является дискриминантом для 4 различных квадратных уравнений.

    Что такое дискриминант?
    Отвечать

    Дискриминант — это число , которое можно вычислить из любого квадратного уравнения.2-4 \ cdot \ красный 3 \ cdot \ color {зеленый} 5 \\ \ text {Дискриминант} = \ в коробке {6} $

    Что говорит нам эта формула?
    Отвечать

    Дискриминант сообщает нам следующую информацию о квадратном уравнении:

    • Если решение — действительное число или мнимое число.
    • Если решение рациональное или иррациональное.2 + 2x + 1 $$.

      Практика 1

      Вычислите дискриминант, чтобы определить количество и характер решений следующего квадратного уравнения: $$ y = x² — 2x + 1 $$. 2-4 \ cdot \ красный 1 \ cdot \ color {зеленый} 1 \\ & = \ в коробке {0} \ end {выровнен} $$

      Поскольку дискриминант равен нулю, мы должны ожидать 1 реальное решение, которое вы можете увидеть на графике ниже.

      Практика 2

      Воспользуйтесь дискриминантом, чтобы узнать природу и количество решений: $$ y = x² — x — 2 $$.2-4 \ cdot \ red 1 \ cdot \ color {green} {-2} \\ & = 1 — -8 \\ & = 1 + 8 = \ 9 в штучной упаковке \ end {выровнен} $$

      Поскольку дискриминант положительный и рациональный, у этого уравнения должно быть 2 реальных рациональных решения. Как вы можете видеть ниже, если вы используете квадратичную формулу для поиска фактических решений, вы действительно получите 2 реальных рациональных решения.

      Практика 3

      Вычислите дискриминант, чтобы определить характер и количество решений: y = x² — 1.2} — 4 \ color {Magenta} {(1)} \ color {Blue} {(- 1)} = 4 $$

      Поскольку дискриминант положительный и представляет собой полный квадрат, у нас есть два вещественных решения, которые являются рациональными.

      Опять же, если вы хотите увидеть реальные решения и график, просто посмотрите ниже:

      Практика 4

      Вычислите дискриминант, чтобы определить характер и количество решений: y = x² + 4x — 5. 2} — 4 \ color {Magenta} {(1)} \ color {Blue} {(- 5)} \\ 16-4 (-5) = 16 +20 \\ = 36 $$

      Поскольку дискриминант этого квадратного уравнения является положительным и представляет собой полный квадрат, существуют два рациональных решения.

      Практика 5

      Вычислите дискриминант, чтобы определить характер и количество решений: y = x² — 4x + 5.

      Покажи ответ

      В этом квадратном уравнении y = x² — 4x + 5. 2} — 4 \ color {Magenta} {(1)} \ color {Blue} {(5)} \\ = 16-20 = -4 $$

      Поскольку дискриминант отрицательный, у этого квадратного уравнения нет реальных решений. Единственные решения мнимые.

      Ниже приведено изображение этого квадратичного графика.

      Практика 6

      Найдите дискриминант, чтобы определить природу и количество решений: y = x² + 4. 2} — 4 \ color {Magenta} {(1)} \ color {Blue} {(4)} = -16 $$

      Поскольку дискриминант отрицательный, у этого квадратного уравнения есть два мнимых решения.

      Решения: 2i и -2i.

      Ниже приведено изображение этого графика уравнений.

      Практика 7

      Найдите дискриминант, чтобы определить природу и количество решений: y = x² + 25.2} — 4 \ color {Magenta} {(1)} \ color {Blue} {(25)} = -100 $$

      Поскольку дискриминант отрицательный, у этого квадратного уравнения есть два мнимых решения.

      Решения 5i и -5i.

      Квадратичная формула: решения и дискриминант

      Purplemath

      Приведем еще несколько примеров.

      • Решите
        x ( x — 2) = 4. Округлите ответ до двух десятичных знаков.

      Я не только не могу применить квадратичную формулу на данном этапе, но и не могу использовать множители. Почему? Потому что это уравнение пока что в правильном виде.

      И я, , разумеется, не могу с невозмутимым видом утверждать, что « x = 4, x — 2 = 4», потому что это , а не , как работает «решение с факторингом».

      Независимо от того, какой метод решения я собираюсь использовать — факторизую ли я на множители или использую квадратичную формулу для поиска ответов — я должен сначала преобразовать уравнение в форму «(квадратичный) = 0».

      MathHelp.com

      Первое, что я сделаю здесь, это умножу на левую часть, а затем переместу 4 из правой части в левую:

      x ( x — 2) = 4

      x 2 — 2 x = 4

      x 2 — 2 x — 4 = 0

      Поскольку нет множителей при (1) (- 4) = –4, которые в сумме дают –2, то эта квадратичная величина не множится.(Другими словами, невозможно, чтобы решение с искусственным факторингом « x = 4, x — 2 = 4» могло быть хоть немного правильным.)

      Значит, факторинг не сработает, но я могу использовать квадратичную формулу; в этом случае я вставлю значения a = 1, b = –2 и c = –4:

      Тогда ответ:

      x = –1.24, x = 3,24 с округлением до двух десятичных знаков.

      Для справки, вот как выглядит график соответствующей квадратичной, y = x 2 — 2 x — 4, выглядит так:

      Как видите, решения из квадратичной формулы совпадают с интерцепциями x . Точки пересечения графика с осью x дают значения, которые решают исходное уравнение.

      Существует еще одна связь между решениями из квадратичной формулы и графиком параболы: вы можете определить, сколько интервалов x вы получите, исходя из значения внутри квадратного корня. Аргумент (то есть содержание) квадратного корня, являющийся выражением b 2 — 4 ac , называется «дискриминантом», потому что, используя его значение, вы можете «различать» (что уметь различать) различные типы решений.

      В данном случае значение дискриминанта b 2 -4 ac было 20; в частности, значение было , а не ноль, и было , а не отрицательным. Поскольку значение не было отрицательным, уравнение должно было иметь по крайней мере одно (действительное) решение; поскольку значение не было нулевым, два решения должны были быть разными (то есть они должны были отличаться друг от друга).

      • Решить 9
        x 2 + 12 x + 4 = 0.Оставьте свой ответ в точной форме.

      Используя a = 9, b = 12 и c = 4, квадратичная формула дает мне:

      Тогда ответ:

      В первом примере на этой странице я получил два решения, потому что значение дискриминанта (то есть значение внутри квадратного корня) было ненулевым и положительным.В результате часть формулы «плюс-минус» дала мне два различных значения; один для «плюсовой» части числителя и другой для «минусовой» части. Однако в этом случае квадратный корень уменьшился до нуля, поэтому плюс-минус ни для чего не учитывался.

      Такое решение, при котором вы получаете только одно значение, потому что «плюс-минус ноль» ничего не меняет, называется «повторяющимся» корнем, потому что x равно

      –2 / 3 , но оно равно этому значению как бы вдвое: –2 / 3 + 0 и –2 / 3 — 0.

      Вы можете лучше увидеть это повторение, если разложите квадратичный множитель (и, поскольку решения были хорошими точными дробями, квадратичный должен разложить ): 9 x 2 + 12 x + 4 = (3 x + 2) (3 x + 2) = 0, поэтому первый множитель дает нам 3 x + 2 = 0, поэтому

      x = –2 / 3 , и (из второго, идентичный коэффициент) 3 x + 2 = 0, поэтому x = –2 / 3 снова.

      Каждый раз, когда вы получаете ноль внутри квадратного корня квадратной формулы, вы получаете только одно решение уравнения в смысле получения одного числа, которое решает уравнение. Но вы получите два решения в том смысле, что одно значение будет подсчитано дважды. Другими словами, дискриминант (то есть выражение b 2 — 4 ac ) с нулевым значением означает, что вы получите одно «повторяющееся» значение решения.

      Ниже показан график связанной функции, y = 9 x 2 + 12 x + 4, выглядит так:

      Парабола только касается оси x при

      x = –2 / 3 ; это на самом деле не пересекается.Это соотношение всегда верно: если у вас есть корень, который встречается ровно дважды (или, что то же самое, если вы получаете ноль внутри квадратного корня), то график будет «целовать» ось в значении решения, но он не пройдет через ось.

      Поскольку нет множителей при (3) (2) = 6, которые в сумме дают 4, эта квадратичная величина не множится. Но квадратичная формула работает всегда; в этом случае я вставлю значения a = 3, b = 4 и c = 2:

      На данный момент у меня есть отрицательное число внутри квадратного корня.Если вы еще не узнали о комплексных числах, вам придется остановиться на этом, и ответ будет «нет решения»; если вы знаете комплексные числа, то можете продолжить вычисления:

      Таким образом, в зависимости от вашего уровня обучения, ваш ответ будет одним из следующих:

      решения в виде вещественных чисел: нет решения

      комплексно-числовых решений:

      Партнер

      Но знаете ли вы о комплексах или нет, вы знаете, что вы не можете изобразить свой ответ, потому что вы не можете изобразить квадратный корень отрицательного числа на правильном декартовом месте.На оси x таких значений нет. Поскольку вы не можете найти графическое решение квадратичной функции, то разумно не должно быть никаких перехватов x (потому что вы можете построить график с перехватом x ).

      Вот график связанной функции, y = 3 x 2 + 4 x + 2:

      Как видите, график не пересекает и даже не касается оси x .Это соотношение всегда верно: если вы получите отрицательное значение внутри квадратного корня, тогда не будет решения для действительного числа и, следовательно, не будет перехватов x . Другими словами, если дискриминант (являющийся выражением b 2 — 4 ac ) имеет отрицательное значение, то у вас не будет графических нулей .

      (взаимосвязь между дискриминантом (являющимся значением внутри квадратного корня), типом решений (два различных решения, одно повторяющееся решение или отсутствие графифицируемых решений) и числом x -перехватываний на графике (два , один или нет) сведены в диаграмму на следующей странице.)

      URL: https://www.purplemath.com/modules/quadform2.htm

      Дискриминант: определение и объяснение | Study.com

    Это формула для нахождения дискриминанта.

    Использование дискриминанта

    Дискриминант сообщает вам, сколько возможных решений имеет конкретное квадратное уравнение.Однако, прежде чем мы сможем использовать квадратное уравнение, мы сначала должны изменить его на стандартную форму . Стандартная форма — это когда все переменные и константы находятся на одной стороне уравнения, а другая сторона равна нулю. Выглядит это так:

    Это квадратное уравнение в стандартной форме.

    Когда у вас есть квадратное уравнение в стандартной форме, вы можете пометить числа соответствующими буквами и вставить значения в формулу для поиска дискриминанта.Результат вашего дискриминанта говорит вам, сколько решений имеет ваша квадратичная.

    Примеры

    Давайте посмотрим на пример:

    Пример 1

    В нашем примере квадратное уравнение дает нам 1 для буквы a , 5 для буквы b и 4 для буквы c . Мы берем эти значения и вставляем их в соответствующие места в формуле дискриминанта, и мы обнаруживаем, что наш дискриминант равен 9, положительному числу.Это говорит нам о том, что у нашего квадратного уравнения есть два возможных вещественных решения. Реальные решения — это решения, которые можно вычислить по формуле корней квадратного уравнения. Когда вы построите график этого квадратного уравнения, вы увидите, что кривая пересекает ось x в двух местах, именно там, где находятся ваши решения.

    Хотя дискриминант сообщает нам количество возможных решений, он не говорит нам, что это за решения. Но это дает нам представление о том, сколько решений нам нужно искать.

    Помните, что если перед переменными нет чисел, предполагается, что перед ними стоит 1. Мы не пишем 1, потому что это математическое соглашение и потому что это выглядит аккуратнее, особенно когда у вас много букв, с которыми нужно работать.

    Рассмотрим другой пример:

    Пример 2

    Мы присвоили нашим буквам соответствующие значения. Подставив соответствующие значения в нашу дискриминантную формулу, мы обнаруживаем, что наш дискриминант равен -31, то есть отрицательное число.Хм … что это могло значить? Когда дискриминант отрицательный, это означает, что реальных решений нет. Это означает, что при построении графика уравнения вы увидите, что оно никогда не пересекает ось x и, следовательно, не имеет реальных решений.

    Есть еще одна возможная ситуация — когда дискриминант равен 0. Когда вы видите это, это означает, что существует только одно возможное реальное решение. На графике уравнение касается оси x только в одной точке.

    Вот таблица, которая поможет вам запомнить возможные дискриминантные ситуации и их значение:

    Дискриминант Количество решений
    > 0 Два реальных решения
    = 0 Одно реальное решение
    <0 Реальных решений нет

    Резюме урока

    Подводя итог, дискриминант помогает вам, сообщая вам, сколько возможных решений имеет квадратное уравнение.Формулу можно найти, посмотрев на квадратный корень в формуле квадратного корня. Возможны три сценария. Если дискриминант положительное число, то есть два реальных решения. Если дискриминант равен 0, то существует только одно реальное решение. Если дискриминант отрицательное число, то реальных решений нет.

    Результаты обучения

    После этого урока вы сможете:

    • Определить дискриминант и вспомнить его назначение
    • Объясните, как найти дискриминант
    • Опишите возможные сценарии использования дискриминанта

    Дискриминант кубического уравнения

    Дискриминант квадратного уравнения

    a x ² + bx + c = 0

    это

    Δ = b ² — 4 ac .

    Если дискриминант Δ равен нулю, уравнение имеет двойной корень, то есть существует уникальный x , который делает уравнение нулевым, и он дважды считается корнем. Если дискриминант не равен нулю, есть два различных корня.

    Кубические уравнения также имеют дискриминант. Для кубического уравнения

    a x ³ + bx ² + cx + d = 0

    дискриминант равен

    Δ = 18 abcd — 4 b ³ d + b ²c² — 4 ac³ — 27 a ² d ².

    Если Δ = 0, уравнение имеет кратный корень, но в противном случае оно имеет три различных корня.

    Замена переменной может свести общее кубическое уравнение к так называемому «вдавленному» кубическому уравнению вида

    x ³ + пикселей + q = 0

    , в этом случае дискриминант упрощается до

    Δ = — 4 p³ — 27 q ².

    Вот пара интересных связей. Идея сведения кубического уравнения к кубическому с углублением восходит к Кардано (1501–1576).То, что в этом контексте называется углубленной кубикой, известно как форма Вейерштрасса (1815–1897) в контексте эллиптических кривых. То есть эллиптическая кривая вида

    y ² = x ³ + ax + b

    Считается, что

    находится в форме Вейерштрасса. Другими словами, эллиптическая кривая имеет форму Вейерштрасса, если правая часть представляет собой углубленную кубику.

    Кроме того, эллиптическая кривая должна быть невырожденной, что означает, что она должна удовлетворять требованиям

    4 a³ + 27 b ² ≠ 0.

    Другими словами, дискриминант правой части отличен от нуля. В контексте эллиптических кривых дискриминант определяется как

    Δ = -16 (4 a³ + 27 b ²)

    , который совпадает с дискриминантом выше, за исключением коэффициента 16, который упрощает некоторые вычисления с эллиптическими кривыми.

    Примечание по полям

    В контексте решения квадратных и кубических уравнений мы обычно неявно работаем с действительными или комплексными числами.Предположим, что все коэффициенты квадратного уравнения действительны. Если дискриминант положительный, есть два различных действительных корня. Если дискриминант отрицательный, есть два различных комплексных корня, и эти корни являются комплексно сопряженными друг другу.

    Аналогичные замечания справедливы для кубических уравнений, когда все коэффициенты действительны. Если дискриминант положительный, существует три различных действительных корня. Если дискриминант отрицательный, имеется один действительный корень и комплексно сопряженная пара комплексных корней.

    В первом разделе я рассмотрел только, был ли дискриминант нулевым, и поэтому утверждения не зависят от поля, из которого берутся коэффициенты.

    Для эллиптических кривых можно работать с множеством полей. Может быть, действительные или комплексные числа, но также и конечные поля. В большинстве сообщений блога, которые я писал об эллиптических кривых, поле представляет собой целые числа по модулю большого простого числа.

    Больше сообщений, связанных с кубическими уравнениями

    .

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *