Линейные уравнения и неравенства (стр. 1 из 3)

Романишина Дина Соломоновна, учитель математики гимназии №2 г. Хабаровска

1. Уравнения с одной переменной.

Равенство, содержащее переменную, называют уравнением с одной переменной, или уравнением с одним неизвестным. Например, уравнением с одной переменной является равенство 3(2х+7)=4х-1.

Корнем или решением уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство. Например, число 1 является решением уравнения 2х+5=8х-1. Уравнение х2+1=0 не имеет решения, т.к. левая часть уравнения всегда больше нуля. Уравнение (х+3)(х-4) =0 имеет два корня: х1= -3, х2=4.

Решить уравнение — значит найти все его корни или доказать, что корней нет.

Уравнения называются равносильными, если все корни первого уравнения являются корнями второго уравнения и наоборот, все корни второго уравнения являются корнями первого уравнения или, если оба уравнения не имеют корней. Например, уравнения х-8=2 и х+10=20 равносильны, т.к. корень первого уравнения х=10 является корнем и второго уравнения, и оба уравнения имеют по одному корню.

При решении уравнений используются следующие свойства:

Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получите уравнение, равносильные данному.

Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Уравнение ах=b, где х – переменная, а и b – некоторые числа, называется линейным уравнением с одной переменной.

Если а¹0, то уравнение имеет единственное решение

.

Если а=0, b=0, то уравнению удовлетворяет любое значение х.

Если а=0, b¹0, то уравнение не имеет решений, т.к. 0х=b не выполняется ни при одном значении переменной.

Пример 1. Решить уравнение: -8(11-2х)+40=3(5х-4)

Раскроем скобки в обеих частях уравнения, перенесем все слагаемые с х в левую часть уравнения, а слагаемые, не содержащие х, в правую часть, получим:

16х-15х=88-40-12

х=36

Ответ: 36.

Пример 2. Решить уравнения:

3х2-5х=0;

х3-2х2-98х+18=0;

х2+7х+12=0.

Эти уравнения не являются линейными, но покажем, как можно решать такие уравнения.

3х2-5х=0; х(3х-5)=0. Произведение равно нулю, если один из множителей равен нулю, получаем х1=0; х2=

.

Ответ: 0;

.

Разложить на множители левую часть уравнения:

х2(х-2)-9(х-2)=(х-2)(х2-9)=(х-2)(х-3)(х-3), т.е. (х-2)(х-3)(х+3)=0. Отсюда видно, что решениями этого уравнения являются числа х1=2, х2=3, х3=-3.

с) Представим 7х, как 3х+4х, тогда имеем: х2+3х+4х+12=0, х(х+3)+4(х+3)=0, (х+3)(х+4)=0, отсюда х1=-3, х2=- 4.

Ответ: -3; — 4.

Пример 3. Решить уравнение: ½х+1ç+½х-1ç=3.

Напомним определение модуля числа:

Например: ½3½=3, ½0½=0, ½- 4½= 4.

В данном уравнении под знаком модуля стоят числа х-1 и х+1. Если х меньше, чем –1, то число х+1 отрицательное, тогда ½х+1½=-х-1. А если х>-1, то ½х+1½=х+1. При х=-1 ½х+1½=0.

Таким образом,

Аналогично

а) Рассмотрим данное уравнение½х+1½+½х-1½=3 при х£-1, оно равносильно уравнению -х-1-х+1=3, -2х=3, х=

, это число принадлежит множеству х£-1.

b) Пусть -1 < х £ 1, тогда данное уравнение равносильно уравнению х+1-х+1=3, 2¹3 уравнение не имеет решения на данном множестве.

с) Рассмотрим случай х>1.

х+1+х-1=3, 2х=3, х=

. Это число принадлежит множеству х>1.

Ответ: х1=-1,5; х2=1,5.

Пример 4. Решить уравнение:½х+2½+3½х½=2½х-1½.

Покажем краткую запись решения уравнения, раскрывая знак модуля «по промежуткам».

-2 0 1 х

х £-2, -(х+2)-3х=-2(х-1), — 4х=4, х=-2Î(-¥; -2]

–2<х£0, х+2-3х=-2(х-1), 0=0, хÎ(-2; 0]

0<х£1, х+2+3х=-2(х-1), 6х=0, х=0Ï(0; 1]

х>1, х+2+3х=2(х-1), 2х=- 4, х=-2Ï(1; +¥)

Ответ: [-2; 0]

Пример 5. Решить уравнение: (а-1)(а+1)х=(а-1)(а+2), при всех значениях параметра а.

В этом уравнении на самом деле две переменных, но считают х–неизвестным, а а–параметром. Требуется решить уравнение относительно переменной х при любом значении параметра а.

Если а=1, то уравнение имеет вид 0×х=0, этому уравнению удовлетворяет любое число.

Если а=-1, то уравнение имеет вид 0×х=-2, этому уравнению не удовлетворяет ни одно число.

Если а¹1, а¹-1, тогда уравнение имеет единственное решение

.

Ответ: если а=1, то х – любое число;

если а=-1, то нет решений;

если а¹±1, то

.

2. Системы уравнений с двумя переменными.

Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Решить систему — значит найти все ее решения или доказать, что их нет. Две системы уравнений называются равносильными, если каждое решение первой системы является решением второй системы и каждое решение второй системы является решением первой системы или они обе не имеют решений.

При решении линейных систем используют метод подстановки и метод сложения.

Пример 1. Решить систему уравнений:

Для решения этой системы применим метод подстановки. Выразим из первого уравнения х и подставим это значение

во второе уравнение системы, получим ,

Ответ: (2; 3).

Пример 2. Решить систему уравнений:

Для решения этой системы применим метод сложения уравнений. 8х=16, х=2. Подставим значение х=2 в первое уравнение, получим 10-у=9, у=1.

Ответ: (2; 1).

Пример 3. Решить систему уравнений:

Эта система равносильна одному уравнению 2х+у=5, т.к. второе уравнение получается из первого умножением на 3. Следовательно, ей удовлетворяет любая пара чисел (х; 5-2х). Система имеет бесконечное множество решений.

Ответ: (х; 5-2х), х–любое.

Пример 4. Решить систему уравнений:

Умножим первое уравнение на –2 и сложим со вторым уравнением, получим 0×х+0×у=-6. Этому уравнению не удовлетворяет ни одна пара чисел. Следовательно, эта система не имеет решений.

Ответ: система не имеет решений.

Пример 5. Решить систему:

Из второго уравнения выражаем х=у+2а+1 и подставляем это значение х в первое уравнение системы, получаем

. При а=-2 уравнение не а=-2 имеет решения, если а¹-2, то .

Ответ: при a=-2система не имеет решения,

при а¹-2 система имеет решение

.

Пример 6. Решить систему уравнений:

Нам дана система из трех уравнений с тремя неизвестными. Применим метод Гаусса, который состоит в том, что равносильными преобразованиями приводят данную систему к треугольной форме. Прибавим к первому уравнению второе, умноженное на –2.

2х+у+3z=13

+ -2х-2у-2z=-12

-у+z=1 или у-z=-1.

Далее к третьему уравнению системы прибавим второе, умноженное на –3,

3х+у+z=8

+ -3х-3у-3z=-18

-2y-2z=-10,

наконец прибавим к этому уравнению уравнение у-z=-1, умноженное на 2, получим — 4z=-12, z=3. Итак получаем систему уравнений:

х+у+z=6

у-z=-1

z=3, которая равносильна данной.

Система такого вида называется треугольной.

Ответ: (1; 2; 3).

3. Решение задач с помощью уравнений и систем уравнений.

Покажем на примерах, как можно решать задачи с помощью уравнений и систем уравнений.

Пример 1. Сплав олова и меди массой 32 кг содержит 55% олова. Сколько чистого олова надо добавить в сплав, чтобы в новом сплаве щсодержалось 60% олова?

Решение. Пусть масса олова, добавленная к исходному сплаву, составляет х кг. Тогда сплав массой (32+х)кг будет содержать 60% олова и 40% меди. Исходный сплав содержал 55% олова и 45% меди, т.е. меди в нем было 32·0,45 кг. Так как масса меди в исходном и новом сплавах одна и та же, то получим уравнение 0,45·32=0,4(32+х).

Решив его, находим х=4, т.е. в сплав надо добавить 4 кг олова.

Пример 2. Задумано двузначное число, у которого цифра десятков на 2 меньше цифры единиц. Если это число разделить на сумму его цифр, то в частном получится 4 и в остатке 6. Какое число задумано?

Решение. Пусть цифра единиц есть х, тогда цифра десятков равна х-2 (х>2), задуманное число имеет вид 10(х-2)+х=11х-20. Сумма цифр числа х-2+х=2х-2. Следовательно, разделив 11х-20 на 2х-2, получим в частном 4 и в остатке 6. Составляем уравнение: 11х-20=4(2х-2)+6, т.к. делимое равно делителю, умноженному на частное, плюс остаток. Решив это уравнение, получим х=6. Итак, было задумано число 46.

mirznanii.com

Методы решения уравнений, неравенств и их систем

Введение

Материал, связанный с уравнениями и неравенствами, составляет значительную часть школьного курса математики. Однако решению всех видов уравнений и неравенств уделяется недостаточно внимания. Актуальность рассмотрения данной темы обусловлена противоречием между тем, что задания, связанные с уравнениями и неравенствами и их системами регулярно встречаются в материалах ЕГЭ и ОГЭ и тем, что их решение, вызывают у учащихся значительные трудности.

Целью данной работы является: Рассмотреть методические основы профильного и углубленного обучения теме «Уравнения, неравенства и их системы».

Из данной цели вытекают задачи:

1. Выделить методы решения уравнений, неравенств и их систем.

2. Выполнить логико-дидактический анализ темы «Уравнения, неравенства и их системы» по школьным учебникам «Алгебра» Ю.Н. Макарычева за 7-9 класс и «Алгебра» А.Г. Мордковича 10-11 класс.

3. Разработать конспект урока по теме «Уравнения, неравенства и их системы» для 8 класса.

Данные практические разработки могут быть использованы в школе.

Данная работа состоит из трех параграфов:

§1. Методы решения уравнений, неравенств и их систем.

§2. Логико-дидактический анализ по теме «Уравнения, неравенства и их системы» по школьным учебникам «Алгебра» Ю.Н. Макарычева за 7-9 класс и «Алгебра» А.Г. Мордковича 10-11 класс.

§3. Конспект урока по теме «Уравнения, неравенства и их системы» для 8 класса.

§1. Методы решения уравнений, неравенств и их систем

Методы решения целых уравнений первой степени.

1. Раскрытие скобок (умножаем многочлен на многочлен). Пример: (2x+1)(3x-2)-6

   x(x+4)=67-2x

2. Домножение на НОК знаменателей дробей обеих частей уравнения. Пример: —

Способы решения целых уравнений.

1. Разложение многочлена на множители. Пример: +3=0

2. С помощью теоремы о корне многочлена. Пример:

3. Введение новой переменной. Пример:

4. Метод неопределенных коэффициентов. Пример:

1. Графический способ. Пример:

2. С помощью алгоритма решения квадратных уравнений:

Алгоритмы и способы решения дробно-рациональных уравнений.

1. а) Умножаем обе части уравнения на общий знаменатель дробей, входящих в уравнение.

б) Решаем полученное целое уравнение.

в) Исключаем из его корней те, которые обращают в нуль общий знаменатель дробей.

Пример:

1. Используя нестандартные преобразования. Пример:

2. Введение новой переменной. Пример:

3. Введение вспомогательной переменной. Пример:

4. Графический способ решения. Пример:

Способы решения целых неравенств с одной переменной.

1.Используя свойства дискриминанта квадратного уравнения и свойств графика квадратичной функции. Пример:

2. Метод интервалов. Пример:

3. Используя свойства графика квадратной функции. Пример:

Способы решения дробно-рациональных неравенств с одной переменной.

1. Разложение на множители числителя и знаменателя. Пример:

2. Используя систему. Примеры:

Способы решения уравнений с переменной под знаком модуля.

1. Замена на систему уравнений. Пример:

2. Замена совокупность из двух систем. Пример:

3. Графический способ с дальнейшей заменой на совокупность из трех систем уравнений. Пример:

Способы решения неравенств с переменной под знаком модуля.

1. Замена на систему неравенств. Пример:

2. Используя свойство модуля. Пример:

3. Графический способ с дальнейшей заменой на совокупность из трех систем неравенств. Пример:

Способы решения уравнений с параметром.

1. Вынесение многочлена за скобку. Пример: ax-2x=a²+a-6

2. Используя дискриминант. Пример:

Способы решения дробно-рациональных уравнений с параметром.

Домножение на общий знаменатель. Пример:

Методы решения систем уравнений с двумя переменными

Метод подставновки:

1. Выражаем из какого-либо уравнения системы одну переменную через другую.

2. Подставляем вместо этой переменной полученное выражение во второе уравнение.

3. Решаем получившееся уравнение с одной переменной.

4. Находим соответствующие значения второй переменной.

Метод сложения:

1. Умножаем левые и правые части уравнений.

2. Складываем почленно левые и правые части уравнений.

3. Решаем получившееся при сложении уравнение с одной переменной.

4. Находим соответствующие значения второй переменной.

б) Разложение на линейные множители.

Пример:

Способы решения линейных неравенств с двумя переменными.

Графический. Пример: 4x-5y20

Способы решения неравенств с двумя переменными выше первой.

Графический. Пример:

Способы решения системы неравенств с двумя переменными.

Графический Пример:

Способы решения неравенств с двумя переменными, содержащие знак модуля.

Графический. Пример:

Методы решения уравнений высших степеней.

1. Метод замены переменной. Пример: x(x-1)(x-2)(x-3)=24

2. Используя делители свободного члена уравнения. Пример: x³+2x²-7x-12=0

3. Деления обеих частей уравнения на x². Пример: 3x⁴-2x³-9x²-4x+12=0

4. Метод замены двух переменных. Пример: 2(x²+x+1)-7(x-1)²=13(x³-1)

5. Графический метод. Пример: x⁵+5x-42=0

6. Используя производную функции. Пример:

   x⁴-8x+63=0

Методы решения показательных уравнений.

1. Функционально-графический метод.

2. Метод введения новой переменной. Пример: 4^x+2^x+1-24=0

Методы решения показательных неравенств.

1. Метод уравнивания показателей. Пример:

2. Метод введения новой переменной. Пример:

3. Деления обеих частей уравнения на число с наибольшим показателем в степени. (однородные уравнения второй степени) Пример: 8^x+18^x2∙27^x

4. Используя свойство дискриминанта. Пример: (x²+x+1)^x≤1

Методы решения логарифмических уравнений.

1. Метод потенцирования. Пример: log₃(x²-3

   x-5)=log₃(7-2x)

2. Используя ОДЗ. Пример: log_x+4(x²-1)= log_x+4(5-x)

3. Используя свойства логарифма. Пример: log₂(x+4)+log₂(2x+3)=log₂(1-2x)

4. Введение новой переменной. Пример: lg²x+lg x+1=

Методы решения логарифмических неравенств.

1. Метод потенцирования. Пример: log₃(2x-4)log₃(14-x)

2. Представление обеих частей неравенства в виде логарифмов с одинаковым основанием. Пример: (16+4x—x²)≤-4

3. Введение новой переменной. Пример:

4. Используя ОДЗ. Пример: log_x-2(2x-3) log

   x_-2(24-6x)

Методы решения уравнений и неравенств с модулем.

1. Раскрытие модуля по определению. Пример:

2. Графический способ. Пример:

3. Используя совокупность уравнений (неравенств). Пример:

Методы решения иррациональных уравнений.

1. Возведение обеих частей уравнения в одну и ту же степень. Пример:

2. Введение новой переменной. Пример:

3. Уединение корня и возведение обеих частей уравнения в степень. Пример:

1. Введение двух новых переменных. Пример:

2. Умножение обеих частей уравнения на выражение сопряженное данному. Пример:

Методы решения иррациональных неравенств.

1. Используя совокупность неравенств. Пример:

2. Введение новой переменной. Пример:

Методы решения систем уравнений.

1. Перемножением правых и левых частей уравнения. Пример:

2. Введение новой переменной. Пример:

3. Метод деления. Пример:

multiurok.ru

Равносильность уравнений и неравенств. Основные приемы решений.

Два уравнения ( неравенства) называются равносильными, если совпадают множества всех их решений или они оба не имеют решений. Из определения равносильности следует, что вместо того, чтобы решать данное уравнение (неравенство), можно решать уравнение (неравенство), ему равносильное.

Пример 1.

Уравнение x=1 равносильно уравнению Öx=1, так как число 1 является корнем каждого уравнения, а других корней ни одно из этих уравнений не имеет.

Уравнения x(x-1)=0 и x(x-1)(x-2)=0 не являются равносильными, т.к. число x=2 — корень второго уравнения, но не корень первого.

В определении равносильности не сказано об ОДЗ уравнений, т.е. равносильные уравнения могут иметь различные области допустимых значений.

При решении уравнений вместо понятия равносильности проще использовать понятие равносильности на множестве: два уравнения (неравенства) называются равносильными на множестве А, если совпадают множества всех их решений, принадлежащих множеству А, или они оба не имеют решений на множестве А.

Уравнения (неравенства) могут быть равносильными на некотором множестве, но не быть равносильными. Например: уравнения x=1 и |x|=1 равносильны на множестве всех неотрицательных чисел, но не равносильны.

Уравнение (неравенство) равносильно данной совокупности уравнений (неравенств, систем) на множестве А, если множество всех корней уравнений (неравенств), принадлежащих А, совпадает со множеством всех решений совокупности уравнений (неравенств, систем), принадлежащих множеству А.

Пример 2.

Уравнение (x²+x+1)(3x+4)(-7x+2)(2x-5)(-12x-16)=0 равносильно совокупности уравнений: 3x+4=0, -7x+2=0, 2x-5=0, 12x+16=0 на множестве всех действительных чисел: т.к. x²+x+1>0 при любом x, то данное уравнений равносильно уравнению (3x+4)(-7x+2)(2x-5)(-12x-16)=0. Любой корень этого уравнения обращает в нуль хотя бы один из входящих в него многочленов, т.е. является корнем хотя бы одного из уравнений данной совокупности. Наоборот, проверкой убеждаемся, что любой корень совокупности удовлетворяет данному уравнению. Поэтому уравнение и данная совокупность уравнений равносильны.

Если для данной пары уравнений любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют следствием первого. Если заменить уравнение его следствием, то множество решений второго уравнения будет содержать все корни исходного уравнения и помимо них может содержать еще некоторые числа, называемые посторонними корнями данного уравнения.

Утверждения о равносильности [6].

1. Уравнения f(x)=g(x) и f(x)-g(x)=0 равносильны.

2. Уравнения f(x)=g(x) и f(x)+a=g(x)+a равносильны для любого числа a.

3. Уравнения f(x)=g(x) и af(x)=ag(x) равносильны для любого числа a 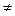0.

4. Уравнения a^f(x) =a^g(x) и f(x)=g(x) равносильны для любого числа a>0, a 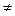1.

5. Если функции y=f(x) и y=g(x) неотрицательны на некотором множестве А. Тогда

уравнения f(x)=g(x) и fⁿ(x)=gⁿ(x) равносильны на этом множестве.

6. Если функции y=f(x) и y=g(x) положительны на некотором множестве А. Тогда

уравнения f(x)=g(x) и log_af(x)=log_ag(x) равносильны на этом множестве.

7. Пусть функция y=j(x) определена и не обращается в ноль ни в одной точке множества А, содержащемся в ОДЗ уравнения f(x)=g(x). Тогда на множестве А уравнения f(x)=g(x) и f(x)j(x)=g(x)j(x) равносильны на этом множестве. Множество А может совпадать с ОДЗ исходного уравнения.

 

Утверждения о равносильности неравенств [6].

 

1. Неравенства f(x)<g(x) и g(x)<f(x) равносильны.

2. Неравенства f(x)<g(x) и f(x)-g(x)<0 равносильны.

3. Неравенства f(x)<g(x) и f(x)+a(x)<g(x)+a(x) равносильны если функция a(x) определена на ОДЗ неравенства f(x)<g(x).

4. Неравенства f(x)<g(x) и a(x)f(x)<a(x)g(x) равносильны, если a(x)> 0 при всех x из ОДЗ неравенства f(x)<g(x). Неравенства f(x)<g(x) и a(x)f(x)>a(x)g(x) равносильны, если a(x)< 0 при всех x из ОДЗ неравенства f(x)<g(x).

5. Неравенства и f(x)g(x)>0 равносильны.

6. Неравенства и f(x)>g(x) равносильны для любого фиксированного числа a из промежутка (1; ).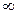

7. Неравенства и f(x)<g(x) равносильны для любого фиксированного числа a из промежутка (0;1).

8. Если функции f(x) и g(x) неотрицательны на множестве A. Тогда неравенства f(x)<g(x) и (f(x))ⁿ<(g(x))ⁿ равносильны на этом множестве (n — натуральное число).

9. Неравенства и f(x)<g(x) равносильны (n — натуральное).

10. Неравенства f²ⁿ(x)<g²ⁿ(x) и |f(x)|<|g(x)| (n — натуральное) равносильны.

11. Пусть a — фиксированное число из промежутка (1; 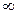) и функции f(x) и g(x) положительны на некотором множестве A, тогда на этом множестве равносильны неравенства f(x)<g(x) и log_af(x)<log_ag(x). Если a — фиксированное число из промежутка (0;1) и функции f(x) и g(x) положительны на некотором множестве A, тогда на этом множестве равносильны неравенства f(x)<g(x) и log_af(x)>log_ag(x).

 



infopedia.su

Линейные уравнения и неравенства | LAMPA

Линейное уравнение

Уравнение вида kx+b=0kx+b=0kx+b=0, где k≠0k\neq 0k≠0, называется линейным уравнением.

Уравнение такого вида имеет одно решение: x=−bkx=-\frac{b}{k}x=−kb​.

2x+3=0⇔x=−32.2 x+ 3=0 \,\,\,\,\Leftrightarrow \,\,\,\, x=-\frac{3}{2}{.}2x+3=0⇔x=−23​.

Решим линейное уравнение 7x+9=5x+137x+9=5x+137x+9=5x+13.
Чтобы решить это уравнение, надо перенести все слагаемые с xxx в одну часть уравнения (например, в левую часть), а все слагаемые без xxx в другую часть уравнения (например, в правую часть): 7x−5x=13−9.7x-5x=13-9{.}7x−5x=13−9.
При переносе слагаемого в другую часть уравнения знак слагаемого меняется. Это происходит, потому что при переносе слагаемого в другую часть уравнения вы как будто вычитаете это слагаемое (в данном случае 5x5x5x) из обеих частей уравнения. В этом смысле уравнение похоже на весы с двумя чашами: если вы сняли гирю определенного веса с одной чаши, то для сохранения равновесия вам надо снять гирю того же веса и с другой чаши.
Упростим левую и правую части уравнения:7x−5x=13−9⇔2x=4.7x-5x=13-9\Leftrightarrow 2x=4{.}7x−5x=13−9⇔2x=4.
Для того чтобы найти xxx, осталось разделить число в правой части уравнения на коэффициент при xxx: 2x=4⇔x=42⇔x=2.2x=4\Leftrightarrow x=\frac{4}{2}\Leftrightarrow x=2{.}2x=4⇔x=24​⇔x=2.

Теперь решим похожее уравнение с другими знаками: 7x−9=13−5x7x-9=13-5x7x−9=13−5x.
Сгруппируем слагаемые с xxx в левой части уравнения, а слагаемые без xxx — в правой части: 7x+5x=13+9.7x+5x=13+9{.}7x+5x=13+9.Обратите внимание на то, что при переносе слагаемых в другую часть уравнения их знак поменялся.
Упростим левую и правую части уравнения:7x+5x=13+9⇔12x=22.7x+5x=13+9\Leftrightarrow 12x=22{.}7x+5x=13+9⇔12x=22.
Для того чтобы найти xxx, осталось разделить число в правой части уравнения на коэффициент при xxx: 12x=22⇔x=2212⇔x=116⇔x=156.12x=22\Leftrightarrow x=\frac{22}{12}\Leftrightarrow x=\frac{11}{6}\Leftrightarrow x=1\frac{5}{6}{.}12x=22⇔x=1222​⇔x=611​⇔x=165​.

Линейное неравенство

Линейное неравенство – это неравенство, которое можно привести к виду kx+b≤0kx+b\le 0kx+b≤0 или к виду kx+b<0kx+b\lt 0kx+b<0, где k≠0k\neq 0k≠0.

Решение неравенства kx+b≤0kx+b\le 0kx+b≤0 зависит от знака при kkk:

• Если k>0k\gt 0k>0, то x≤−bkx\le -\frac{b}{k}x≤−kb​ (знак неравенства сохраняется).
• Если k<0k\lt 0k<0, то x≥−bkx\ge -\frac{b}{k}x≥−kb​ (знак неравенства меняется при делении обеих частей неравенства на отрицательное число).

1)2x+3≥0⇔x≥−32.1) \,\,\,\,\,\,\,2 x+ 3\ge 0 \,\,\,\,\Leftrightarrow \,\,\,\, x\ge -\frac{3}{2}.1)2x+3≥0⇔x≥−23​.
2)−2x+3≥0⇔x≤32.2) -2 x+ 3\ge 0 \,\,\,\,\Leftrightarrow \,\,\,\, x\le \frac{3}{2}.2)−2x+3≥0⇔x≤23​.

lampa.io