Уравнение с двумя переменными и его график
Цель:
· уравнения с двумя переменными;
· решения уравнения с двумя переменными;
· степень уравнения с двумя переменными;
· график уравнения с двумя переменными.
Перед вами записаны уравнения:
Все они являются уравнениями с двумя переменными, так как в каждом из них есть две переменные. Возьмём, например, первое уравнение и подставим в него x=3 и y=5:
Получили неверное равенство. А если подставим x=3 и y=3, то получим верное числовое равенство.
Определение:
Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное числовое равенство.
Пара
чисел (3; 3) является решением данного уравнения. Но это не единственное
решение.
Для определения степени уравнения с двумя переменными, нужно преобразовать его так, чтобы в левой части стоял многочлен стандартного вида, а справа ноль. Тогда степень уравнения считают равной степени данного многочлена.
Чтобы определить степень многочлена с двумя переменными, нужно определить степень каждого одночлена, входящего в состав многочлена, и выбрать из них наибольшую. Степень данного уравнения равна 1.
Пример.
Определить степени уравнений и найти любых два решения.
1. Рассмотрим уравнение:
Преобразуем его:
Степень данного уравнения равна 2.
Найдём два любых решения:
Решением данного уравнения будут пары чисел (0; 2) и (0; -2).
2. Решить уравнение:
Степень уравнения равна 2.
Найдём два решения уравнения:
Получили
две пары чисел: (-1; -6) и (3; 2).
3. Решить уравнение:
Преобразуем его:
Степень данного уравнения равна 3.
Найдём любые два решения:
Получили две пары: (1; 2) и (1; -2).
В ходе выполнения заданий стало понятно, что уравнения с двумя переменными имеют много решений. И указать все решения достаточно сложно. Если решением является пара значений, то его можно изобразить на координатной плоскости в виде точки. Так все решения и образуют график уравнения с двумя переменными.
Определение:
Графиком уравнения с двумя переменными является множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.
Пример.
Так как произведение равно нулю, то каждый из множителей также равен нулю. Решим каждое из полученных уравнений:
Изобразим график данного уравнения:
Решением
являются две прямые: х=7 и у=-3.
2. Построить график уравнения:
Так как произведение равно нулю, то каждый из множителей также равен нулю. Решим каждое из полученных уравнений:
Изобразим график данного уравнения:
Решением являются две прямые: х=-5 и х=2.
Пример.
Составить уравнения, графиками которых являются пары прямых, изображённых на рисунках.
Посмотрим на первый рисунок:
Получили, что прямые являются графиком уравнения.
Обратимся ко второму случаю:
Получили, что эти прямые являются графиком уравнения.
Рассмотрим уравнение:
Графиком уравнения является окружность с центром в точке начала координат и радиусом r.
Например, графиком уравнения:
является окружность с r=4.
Пример.
Записать
уравнение окружности с центром в точке начала координат и r=6.
Получим уравнение окружности:
Если центром окружности не является точка начала координат, то уравнение окружности будет выглядеть так:
Центр окружности имеет координаты (a; b).
Например,
Выполним обратное действие. Но для записи уравнения окружности уже не достаточно только координат центра, необходимо знать и радиус. Например:
Линейное уравнение с двумя переменными
1) 2х=5Линейное уравнение с одной переменной
2) 3х-5у=9
27.08.2020
1
2. Линейное уравнение с двумя переменными
3. Линейное уравнение с двумя переменными
Цель: дать определение линейного уравнения с двумяпеременными и его решения.
27.08.2020
3
27.08.2020
4
5. Линейное уравнение с двумя переменными
Повторение материала.Продолжите фразу:
1. Линейным уравнением с одной переменной
называется уравнение вида .
 ..
..2. Решить уравнение это значит найти …
3.Корнем уравнения называется…
27.08.2020
5
6. Линейное уравнение с двумя переменными
Повторение материала:1. Линейным уравнением с одной переменной
называется уравнение вида ах = в, где х –
переменная, а и в – некоторые числа
2. Решить уравнение это значит найти все его корни или
доказать , что корней нет
3. Корнем уравнения называется значение переменной
при котором уравнение обращается в верное
равенство.
27.08.2020
6
Из данных уравнений выбрать и записать в столбик
линейные уравнения с одной переменной
2х=4, 3х-4=5х, 4х-2=у, 2х=3у, 3в-24,
5х-12=4, х2 –у=5, х+у=1, ху+2=1, 2а+7
2х=4
3х-4=5х
5х-12=4
27.08.2020
4х-2=у
2х=3у
х2 –у=5
х+у=1
ху+2=1
3в-24
2а+7
7
8. Линейное уравнение с двумя переменными
Равенство, содержащее две переменные, называетсяуравнением с двумя переменными.

Линейным уравнением с двумя переменными
называется уравнение вида ах + bу = с , где х и у –
переменные, а, b, с – некоторые числа.
27.08.2020
8
Проверь себя
Из данных уравнений назовите линейные уравнения с
двумя переменными.
1)7-х=у; 2)5х-у=4; 3)2ху+5=х;4)2х-0,4у+7=6; 5)х=ху+8; 6)у- 4х+2у=7
ДА
10. Линейное уравнение с двумя переменными
Решением линейного уравнения с двумя переменныминазывается
пара значений переменных (х; у),
равенство.
27.08.2020
10
Метод подбора.
Для уравнения 2х+у=5 подберем пару чисел,
которая обратит уравнение в верное равенство
Если х = 1, то у=3,
2х1+3=5
Если х = 2, то у = 1,
2х2+1=5
Если х= 3, то у = -1
2 х 3 + (-1) = 5
Так как при подстановки этих значений переменных получается верное
равенство, то пара чисел (1; 3) , (2; 1), (3; -1) является решением
уравнения 2х + у = 5
27.
 08.2020
08.202011
Попробуем
в уравнении 2х + у = 5 выразить одну переменную
через другую
выразим у через х
у = 5 -2х ,
выразим х через у 2х= 5-у , х =
5 у
2
Если х = 1 , то у = 5 — 2 х 1 = 5 – 2= 3,
у = 3 или
Если у = 3, то х = (5 – 3) : 2 = 1 ,
х=1
27.08.2020
12
Попробуй выразить
Уравнение У через Х Х через У
у – 2х = 4
5х + у = 7
27.08.2020
13
Попробуй выразить
Уравнение
у — 2х = 4
5х + у = 7
27.08.2020
У через Х
Х через У
у = 4 + 2х
4 у
х=
2
у = 7 – 5х
7 у
5
х=
14
15. Физкультминутка
Много ль надо нам, ребята, Для умелых нашихрук? Нарисуем два квадрата, А на них огромный
круг, А потом еще кружочек, Треугольный
колпачок. Вот и вышел очень, очень Развеселый
чудачек. (Дети рисуют в воздухе геометрические
фигуры.)
27.08.2020
15
Составим алгоритм решения
линейного уравнения с двумя переменными
х + 4у = 7
1) Выразим одну переменную через другую;
х=7–4у
2) Зададим значение одной переменной;
Если у = 1
3) Вычислим значение другой переменной;
то х = 7 – 4 * 1= 3
4) Запишем ответ
Ответ: ( 3; 1)
х
27.
 08.2020
08.2020у
Домашнее задание:
п.40, стр. 199, п.40, стр 199,
№ 1025 (а,б) № 1025 (а.б)
№ 1030
№ 1030
№ 1032 (а)
27.08.2020
п.40, стр. 199
№ 1030
№ 1032 (а)
Придумать уравнение
и найти две пары
решений
17
Знаем определение линейного уравнения с двумя
переменными.
Понимаем, что значит решить линейное уравнение с
двумя переменными.
Умеем выражать одну переменную через другую.
Умеем находить пары решений.
27.08.2020
18
27.08.2020
19
Вопрос: Как решать уравнение с переменными (неизвестными) в обеих частях уравнения? — Образование и коммуникации
Содержание статьи:
Выражение одной переменной через другую в линейном уравнении с двумя переменными
Видео взято с канала: Математика. В помощь учащимся
Уравнения первой степени с двумя неизвестными. Системы уравнений.
Видео взято с канала: Учимся вместе
Линейные уравнения с переменными с обеих сторон
Видео взято с канала: KhanAcademyRussian
Решение уравнений в несколько действий.
 Как объяснить ребенку решение уравнений? Показать описание
Как объяснить ребенку решение уравнений? Показать описаниеПроверить, как решили уравнения, вы можете здесь: https://go-gl.com/CRMptYc4uW.
=
☝ Кстати, приготовила для вас еще несколько видео по этой теме. Посмотрите их, я очень хочу, чтобы вы лучшее ее усвоили .
=
Здравствуйте, друзья! мы продолжаем тему про решение простых уравнений. В этом видео мы разберем Решение уравнений в несколько действий, а именно мы будем решать Уравнения в 2 3 действия. Также напомню, что мы разбираем только решение уравнений в начальных классах. В этом видео мы разберем решение уравнений в 2 действия. И Вы узнаете, как решать уравнения с двумя действиями. Уравнение в 2 действия решаются довольно просто, если понять логику решения. Мы подробно разберем решение уравнений по действиям. Поэтому если вы затрудняетесь, как как объяснить ребенку решение уравнений, то смотрите это видео до конца.
 После просмотра этого видео вы поймете, как объяснить решение уравнений! А также разберем Решение уравнений в 3 действия. Это видео будет полезно для тех, кому нужно понять Решение уравнений 3 класс, разобрать Решение уравнений 4 класс, и Решение уравнений 5 класс тоже найдете пользу от просмотра. Ставьте лайк, если видео вам понравилось. И делитесь видео в родительских чатах!
После просмотра этого видео вы поймете, как объяснить решение уравнений! А также разберем Решение уравнений в 3 действия. Это видео будет полезно для тех, кому нужно понять Решение уравнений 3 класс, разобрать Решение уравнений 4 класс, и Решение уравнений 5 класс тоже найдете пользу от просмотра. Ставьте лайк, если видео вам понравилось. И делитесь видео в родительских чатах! Видео было полезным?
✅ Тогда жмите на ссылочку и подписывайтесь на канал, чтобы получать новые видео — https://vk.cc/awuYlZ.
Поставьте лайк этому видео. Так я буду знать, что интересно именно вам и с удовольствием раскрою больше секретов ☀.
Мои хорошие, поделитесь этим видео со своими друзьями. Давайте вместе сделаем этот мир счастливее. .
=
Подписывайтесь на меня в социальных сетях. Там будет новый материал, которого нет на канале. Пишите мне комментарии, я буду рада ответить на ваши вопросы .
Будьте со мной Вконтакте — https://vk.cc/awuYZ1.
Рада видеть вас на Facebook — https://vk.
 cc/awuYTQ
cc/awuYTQВидео взято с канала: Просто о сложном. Начальная школа
Как решать уравнения с двумя переменными в целых числах! Лёгкий способ!
Видео взято с канала: mathematical genius
Линейное уравнение с двумя переменными.
Видео взято с канала: из МАТЕМАТИКИ в АЛГЕБРУ 6,7,8 КЛАСС
Алгебра 7 Линейное уравнение с одной переменной
Показать описание✓ Наши репетиторы https://znaika.ru/teachers.
✓ Официальный сайт http://znaika.ru/.
Стас Давыдов Школьник, надевайте рейтузы! https://youtu.be/WpYmKBig0bw.
Кто обидел Соболева? https://youtu.be/CDhbRQiUHsY.
★ПОДПИСАТЬСЯ НА КАНАЛ★.
➜ https://www.youtube.com/channel/UCWmEVmo5Wf-z9x8fQTvWnuw?sub_confirmation=1.
Znaika TV Образовательно-развлекательный канал для школьников. Знайка ТВ Учись интересно!.
Образовательно-развлекательный канал для школьников. Онлайн школа будущего. Видео-уроки, профессии будущего, подготовка к олимпиадам и ЕГЭ, интересные опыты и эксперименты, любопытные факты, школьные лайфхаки, интервью со “звездами” и популярными блогерами, DIY, мастер-классы, челленджи, конкурсы, ответы на вопросы — все самое полезное и интересное о школе, школьной программе и школьной жизни!
▰▰▰▰▰▰▰▰▰▰ ПОПУЛЯРНОЕ ВИДЕО ▰▰▰▰▰▰▰▰▰▰.
Истории | School Life ➜ https://goo.gl/hLHt65.
Большая перемена | Fun ➜ https://goo.gl/3GYbRo.
Раздевалка | School fashion ➜ https://goo.gl/8on1R1.
Каникулы | Adventure ➜ https://goo.gl/NDofCa.
Мастер-классы | DIY ➜ https://goo.gl/xfdjyK.
Полезные советы | School Lifehacks ➜ https://goo.gl/xqWh5T.
Звездолет | Stars ➜ https://goo.gl/SK6r8e.
Олимпиады, ЕГЭ | Сompetition ➜ https://goo.gl/h9GAKq.
Неизведанное | Experiments&Discoveries ➜ https://goo.gl/G777DK.
Будущее | Generation Z ➜ https://goo.gl/WnXJtH.
Видеоуроки | School library ➜ https://goo.gl/HqThC2.
▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰▰.
★МЫ В СОЦИАЛЬНЫХ СЕТЯХ★.
►ВКонтакте: https://vk.com/znaika_ru.
►Facebook: https://www.facebook.com/znaika.tv.
►Instagram: https://www.instagram.com/znaika.ru/.
►Одноклассники: https://ok.ru/znaika.club.
►Twitter: https://twitter.com/znaika_tv.
Библиотека видеоуроков на сайте: https://goo.gl/q3LQsG
Видео взято с канала: Образование. Обучение Znaika TV. Знайка.ру
Обучение Znaika TV. Знайка.ру
Внеклассный урок — Система уравнений с двумя переменными. Системы уравнений с двумя переменными. Способы решения.
Система уравнений с двумя переменными. Уравнения первой степени. Способы решенияУравнение может содержать не одну, а две переменных. Понятно, что такие уравнения называются уравнениями с двумя переменными.
Система уравнений – это два и более уравнений, которыми можно манипулировать для нахождения общих решений. Система из двух уравнений вкючает в себя две переменных, значения которых являются общими для обоих уравнений. С помощью одного уравнения системы решается другое, а в итоге решаются оба уравнения системы.
Способы решения системы уравнений первой степени.
1. Решение методом подстановки.
Суть в том, что в системе уравнений выбираете наиболее простое, в котором одну переменную выражаете через другую. Результат подставляете во второе уравнение, благодаря чему преобразуете его в более простое уравнение с одной переменной. Вычисляете это уравнение и получаете значение одной из переменных. Подставляется его в первое уравнение и получаете значение второй переменной. Так вы решаете всю систему уравнений.
Результат подставляете во второе уравнение, благодаря чему преобразуете его в более простое уравнение с одной переменной. Вычисляете это уравнение и получаете значение одной из переменных. Подставляется его в первое уравнение и получаете значение второй переменной. Так вы решаете всю систему уравнений.
Пример: Решим систему уравнений
│x + y = 1
│2x – y = 2
Решение:
Первое уравнение системы проще второго – его и используем.
Выразим в нем x через у:
x = 1 – y
Подставляем это значение x в наше второе уравнение и находим значение y:
2(1 – y) – y = 2
2 – 2y – y = 2
2 – 3y = 2
3y = 2 – 2
3y = 0
y = 0.
Мы получили значение y. Подставляем его в наше первое уравнение и находим теперь уже значение x:
x + 0 = 1
x = 1
Мы нашли значения обеих переменных.
Ответ:
│x = 1
│y = 0
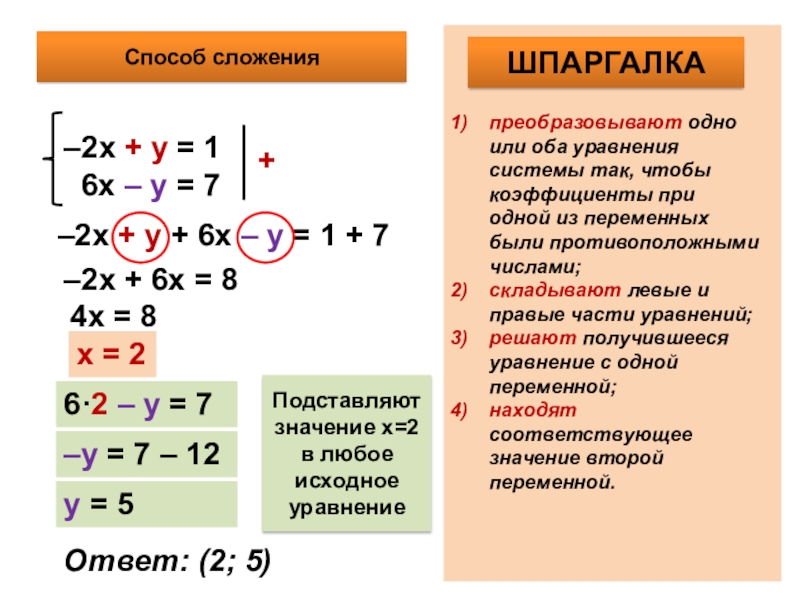
2. Решение методом сложения.
Этот метод целесообразно применять, если при сложении одно из неизвестных пропадает.
Пример 1: Решим систему уравнений
│x + y = 5
│x – y = 1
Решение.
Сложим (вычтем) почленно оба уравнения системы:
│(x + y) + (x – y) = 5 + 1
│(x + y) – (x – y) = 5 – 1
Раскрываем скобки в обоих уравнениях и сводим подобные члены. В результате в первом уравнении пропадает у, во втором х. Мы получаем уравнения с одной переменной, которые проще решать:
│ x + y + x – y = 6
│ x + y – x + y = 4
↓
│2x = 6
│2y = 4
↓
│x = 6 : 2
│y = 4 : 2
↓
│x = 3
│y = 2
Пример решен.
Необязательно производить взаимное сложение и вычитание двух уравнений системы. Часто достаточно бывает произвести одно из двух действий, чтобы вычислить значение одной из двух переменных. А зная одну переменную, мы уже легко сможем найти и вторую.
Пример 2. Решить систему уравнений
│2х + 4у = 26
│8х + 4у = 44
В обоих уравнениях есть число 4у. Значит, можем применить метод сложения. При этом произвести не взаимное сложение, а совершить лишь одно действие: вычесть из первого уравнения второе, чтобы 4у исчезло и чтобы в результате мы получили уравнение с одной переменной:
При этом произвести не взаимное сложение, а совершить лишь одно действие: вычесть из первого уравнения второе, чтобы 4у исчезло и чтобы в результате мы получили уравнение с одной переменной:
2х + 4у – 8х – 4у = 26 – 44.
-6х = -18
х = -18 : (-6)
х = 3
Теперь можем найти и значение у, подставив значение х в любое из двух уравнений системы:
2 · 3 + 4у = 26
6 + 4у = 26
4у = 20
у = 20 : 4
у = 5
Ответ: х = 3, у = 5.
Однако рассмотрим еще один пример.
Пример 3: Решим систему уравнений
│3х + 5у = 21
│8х – 3у = 7
Здесь нет переменных с одинаковыми коэффициентами, чтобы при вычитании они исчезли. Что делать в этом случае? Для таких случаев придумано оригинальное решение: умножим почленно первое уравнение на 3, а второе на 5. От этого истина не пострадает, потому что мы просто получим равносильные уравнения. Зато благодаря этому приему у нас появятся одинаковые переменные 15у:
│(3х + 5у = 21) · 3
│(8х – 3у = 7) · 5
↓
│3 · 3х + 3 · 5у = 3 · 21
│5 · 8х – 5 · 3у = 5 · 7
↓
│9х + 15у = 63
│40х – 15у = 35
Итак, у нас появились одинаковые переменные и мы можем сложить два уравнения, чтобы прийти к уравнению с одной переменной:
9х + 15у + 40х – 15у = 63 + 35
49х = 98
х = 2
Осталось найти значение второй переменной, подставив значение х, например, в первое уравнение системы:
3 · 2 + 5у = 21
6 + 5у = 21
5у = 21 – 6
5у = 15
у = 3.
Ответ: х = 2; у = 3.
Опять же не всегда нужно преобразовывать оба уравнения системы так, как было в предыдущем примере. Бывает и так, что достаточно изменить лишь одно из уравнений.
Пример 4. Решим систему уравнений:
│3х – 4у = 7
│х + 3у = 11
Здесь достаточно второе уравнение умножить на –3. Тогда мы получим число –3х, а при сложении двух уравнений придем к уравнению с одной переменной.
Итак, умножаем второе уравнение на –3:
(х + 3у = 11) · (–3)
–3х – 9у = –33
Теперь складываем два уравнения, приходим к уравнению с одной переменной у и решаем его:
3х – 4у –3х – 9у = 7 – 33
–13у = –26
у = 2.
И находим значение х. Это проще сделать во втором уравнении:
х + 3 · 2 = 11
х + 6 = 11
х = 5.
Ответ: х = 5; у = 2.
3. Решение методом введения новой переменной.
Пример. Решить систему уравнений
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 8 9
│———— – ———— = 1
│ х – 3у 2х + у
Перед нами система сложных уравнений, осложненных дробными числами. Наша задача – упростить их, чтобы потом решить. Если применить какой-нибудь из первых двух методов, получатся еще более сложные уравнения. Зато хорошо подходит метод введения новой переменной, благодаря которому мы целую дробь можем заменить одной переменной. Как это сделать?
Наша задача – упростить их, чтобы потом решить. Если применить какой-нибудь из первых двух методов, получатся еще более сложные уравнения. Зато хорошо подходит метод введения новой переменной, благодаря которому мы целую дробь можем заменить одной переменной. Как это сделать?
Обратите внимание: у первых чисел обоих уравнений одинаковые знаменатели х – 3у, при этом их числители делятся на 2. У вторых чисел тоже одинаковые знаменатели 2х + у, а их числители делятся на 3. Этим и воспользуемся.
1) Выпишем снова нашу систему уравнений, разложив на множители числители второго уравнения и вынеся их за дробь:
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 2 3
│4 · ———— – 3 · ———— = 1
│ х – 3у 2х + у
Теперь в обоих уравнениях у нас абсолютно одинаковые первые дроби и абсолютно одинаковые вторые дроби.
2) Заменим эти дроби новыми переменными a и b следующим образом:
2 3
———— = а, ———— = b.
х – 3у 2х + у
Так мы существенно упрощаем уравнения, которые обретают совсем иной вид:
│ а + b = 2
│4а – 3b = 1
3) Применяем уже известный нам метод подстановки.
Первое уравнение проще, поэтому сначала выражаем в нем а через b:
а = 2 – b.
Подставляем полученное значение а во второе уравнение, раскрываем скобки, приводим подобные члены и вычисляем численное значение b:
4 · (2 – b) – 3b = 1
8 – 4b – 3b = 1
8 – 7b = 1
7b = 8 – 1
7b = 7
b = 1
Раз нам известно численное значение b, то мы легко можем найти и численное значение а. Это проще сделать с помощью первого уравнения:
а + b = 2
а + 1 = 2
а = 2 – 1
а = 1.
Итак:
а = 1, b = 1.
Вписываем в дроби эти значения а и b:
│ 2
│———— = 1
│ х – 3у
│
│ 3
│———— = 1
│ 2х + у
4) Преобразуем эти уравнения по известному вам правилу: неизвестные влево, известные вправо:
│ х – 3у = 2 : 1
│2х + у = 3 : 1
↓
│ х – 3у = 2
│2х + у = 3
5) Решаем эту систему уравнений снова с помощью метода подстановки. Для этого в первом уравнении х выражаем через у:
х = 2 + 3у.
Подставляем во второе уравнение и находим у:
2 · (2 + 3у) + у = 3
4 + 6у + у = 3
7у = 3 – 4
7у = –1
у = –1/7
И с помощью первого уравнения находим х:
х – 3у = 2
х – 3 · (–1/7) = 2
х + 3/17 = 2
х = 2 – 3/7
х = 11/7.
Мы нашли значения х и у в нашей исходной системе уравнений – а значит, решили ее.
Ответ: х = 11/7, у = –1/7
ПРИМЕЧАНИЕ.
Как видно из этого примера, нередки случаи, когда при решении системы уравнений надо последовательно применить сразу несколько методов. 2≥0$. Это означает, что левая часть равенства всегда больше или равна нулю, и равна нулю только, когда оба выражения равны нулю. Значит решением уравнения будет пара чисел (2;1).
2≥0$. Это означает, что левая часть равенства всегда больше или равна нулю, и равна нулю только, когда оба выражения равны нулю. Значит решением уравнения будет пара чисел (2;1).
Ответ: (2;1).
г) Найти все целые решения уравнения: $x-y=12$.
Решение: Пусть x= z, тогда $y=z-12$, z – любое целое число. Тогда решением будет пара чисел (z;z-12), где z – целое число.
д) Найти целочисленные решения уравнения: $4х+7y=29$.
Решение: Выразим х через y: $x=\frac{29-7y}{4}=\frac{28+1-7y}{4}=7+\frac{1-7y}{4}=7-\frac{7y-1}{4}$.
x будет целым, если $7y-1$ делится на 4 без остатка. Давайте посмотрим возможные варианты нашего деления:
1) y – кратно 4. Тогда $y=4n$. $7y-1=7*4n-1=28n-1$ – не делится на 4, значит не подходит.
2) y – при делении на 4 остаток равен 1. $y=4n+1$. $7y-1=28n+7-1=28n+6$ – не делится на 4, значит не подходит.
3) y – при делении на 4 остаток равен 2. $y=4n+2$. $7y-1=28n+14-1=28n+13$ – не делится на 4, значит не подходит.
4) y – при делении на 4 остаток равен 3. $y=4n+3$. $7y-1=28n+21-1=28n+20$ – делится на 4, значит подходит.
$y=4n+3$. $7y-1=28n+21-1=28n+20$ – делится на 4, значит подходит.
Получили $y=4n+3$, найдем х.
$x=7-\frac{7y-1}{4}=7-\frac{28n+20}{4}=7-7n+5=2-7n$
Ответ: ($2-7n;4n+3$).
Два рациональных уравнения называются равносильными, если они имеют одинаковые решения.
Равносильными преобразованиями уравнения называют:
а) Перенос членов уравнения из одной части уравнения в другую, со сменой знака.Пример : $-3x+5y=2x+7y$ равносильно $-3x-2x=7y-5y$
б) Умножение или деление обоих частей уравнений на число, которое не равно нулю.
Пример: $2х-0,5y=0,2xy$ равносильно $20х-5y=2xy$. (Умножили обе части уравнения на 10).
График уравнения с двумя переменными
Пусть дано уравнение u(x;y)= 0. Множество точек (x;y) на координатной плоскости, которые являются решением уравнения u(x;y)= 0, называются графиком функции.
Если уравнение u(x;y)= 0 можно преобразовать к виду y=f(x), то оно считается одновременно графиком уравнения.
Построить график уравнения:а) $y+2x=2$,
b) $yx=5$.
 2+6y=0$.
2+6y=0$.«Линейное уравнение с двумя переменными и его график».
Тема: «Линейное уравнение с двумя переменными и его график».
Тип урока: изучение нового материала.
Вид урока: урок-полилог.
Цель: 1. Получить понятие линейного уравнения с двумя переменными, решения уравнения с двумя переменными; познакомиться со свойствами уравнений с двумя переменными; его графиком.
2. Развивать речь, мышление.
3. Воспитывать самостоятельность мышления, любовь к математике.
(Цели учителя: формировать у учащихся способы и средства по освоению понятий и содержания темы. Мотивировать изучение алгебры, как науки, создающей математические модели окружающей действительности.
Помочь учащимся обогатить свой опыт, взглянув на знакомые понятия с различных точек зрения.
Формирование активной, неравнодушной личности. )
)
Оборудование урока:
Техническое: компьютер, мультимедиапроектор.
Демонстрационное: презентация Microsoft PowerPoint, 3 сосуда. Четыре сосуда: два пустых, два с содержимым и с наклейками «3%» и «30%».
Раздаточное: теоретический справочник, тесты, бланки для построения уравнений.
Ход урока.
1. Организационный момент. — Добрый день. Меня зовут Елена Евгеньевна. Следующие тридцать минут нам суждено с вами прожить вместе.
2. Вступительное слово учителя: — Какой же язык будет помогать нам в общении на сегодняшнем уроке? (язык математики)
— Мне бы хотелось, чтобы у нас сегодня состоялся разговор, ибо как сказал Вовенарг: «Непринужденная беседа — лучшая школа для ума». Хочется еще, чтобы вы помнили слова российского историка Ключевского: «Есть люди, которые умеют говорить, но не умеют ничего сказать. Это ветряные мельницы, которые вечно машут крыльями, но никогда не летают». Надеюсь, что нам сегодня удастся взлететь на вершину новых знаний алгебры.
Надеюсь, что нам сегодня удастся взлететь на вершину новых знаний алгебры.
— Как вы думаете, может ли алгебра понадобиться, например, в парикмахерской? Оказывается, что такие случаи бывают. Послушаем разговор, который там (довольно давно) однажды состоялся. (Звучит запись разговора):
— Ой, здравствуйте, здравствуйте. Мы слышали, что вы математикой увлекаетесь? — обратился к посетителю один из мастеров. — Не поможете ли нам разрешить задачу, с которой мы никак не справимся?
— Уж сколько раствора испортили для этого! – добавил другой.
— В чем задача? – осведомился посетитель.
— У нас имеется два раствора перекиси водорода: 30-процентный и 3-процентный. Нужно их смешать так, чтобы составился 12-процентный раствор. Не можем подыскать правильной пропорции…
Учитель: — А вы смогли бы помочь эти мастерам?
Задачу можно решить и арифметически. Но язык алгебры приводит здесь к успеху проще и быстрее
Переведем эту задачу с родного языка на язык алгебры:
Возьмем 30-процентный раствор перекиси водорода | x граммов |
Возьмем 3-процентный раствор перекиси водорода | y граммов |
В первой порции содержится чистой перекиси водорода | 0,3x |
Во второй порции содержится чистой перекиси водорода | 0,03y |
Всего в двух порциях содержится чистой перекиси водорода | 0,3x + 0,03y |
Смешаем обе порции | (x + y) граммов |
В смеси должно содержаться чистой перекиси водорода | 0,12(x + y) |
0,3x + 0,03y = 0,12(x + y)
Что же это за алгебраический объект у нас получился? Попробуем дать ему название.
(уравнение) (с двумя переменными)
3. Формулирование темы и целей урока.
Это линейное уравнение с двумя переменными.
Сформулируем тему урока. (Линейное уравнение с двумя переменными)
Чтобы вам хотелось узнать сегодня на уроке?
(Что называется линейным уравнением,
Что называется решением уравнения с двумя переменными,
Свойства линейного уравнения)
4. Актуализация базовых знаний с совместным постижением нового материала Нам ведь уже знакомы похожие объекты? Что это за объекты? (линейные уравнения с одной переменной)
Давайте придумаем какое-нибудь линейное уравнение с одной переменной. Пожалуйста, к доске (вызвать 3-4 желающих)
-Посмотрите на доску, перед нами действительно линейные уравнения с одной переменной. Вспомним общий вид линейного уравнения с одной переменной. (ax=b, где a и b –некоторые числа, а x-переменная).
Вспомним общий вид линейного уравнения с одной переменной. (ax=b, где a и b –некоторые числа, а x-переменная).
Выпишите номера тех уравнений, которые бы вы отнесли к линейным уравнениям с двумя переменными? (1,4,6) (со слайда презентации)
1. 3у+2х=0.
2. 5у – 6 =0.
3. 0,2х2 – у +3=0.
4. х+у=15.
5. 4х – 17 = 0.
6. 5х+2у=12
Выпишите номера тех уравнений, которые бы вы отнесли к линейным уравнениям с двумя переменными? (1,4,6)
Определим вид линейного уравнения с двумя переменными: (ax+by=c, где a,b,c некоторые числа, x, y переменные.)
Попробуйте сформулировать определение:
(Линейным уравнением с двумя переменными называется уравнение вида ax+by=c, где a,b,c некоторые числа, x, y переменные)
Откройте теоретический справочник. Прочитайте определение про себя. Не ошиблись ли мы в определении. Есть ли различия?
Прочитайте определение про себя. Не ошиблись ли мы в определении. Есть ли различия?
Придумайте и запишите в этом справочнике свое линейное уравнение с двумя переменными.
Вернемся к линейным уравнениям с одной переменной. Давайте вспомним, как они решаются, и решим какое-нибудь из придуманных уравнений с объяснением, например:
2х+6=10
(Перенесем слагаемое без х в правую часть уравнения, изменив при этом его
знак на противоположный: 2х=10-6 , вычислим результат 2х=4. Разделим обе
части уравнения на 2, получим х=2).
— Ребята , такие уравнения вы хорошо умеете решать.
— А какие свойства применяли при решении этих уравнений? (Если в уравнении слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.)
— А какое еще свойство вы применяли? (Если разделить или умножить обе части уравнения на одно и тоже отличное от нуля число, то получится уравнение равносильное данному.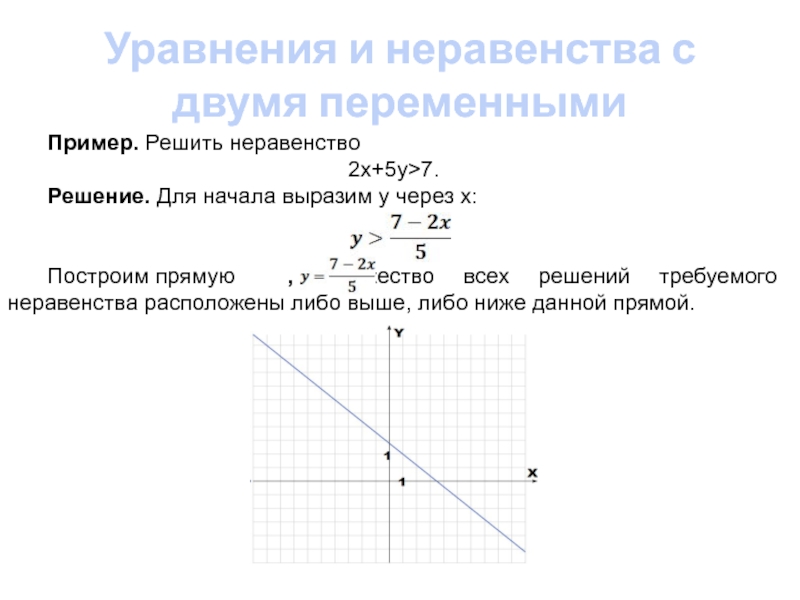 )
)
Линейные уравнения с двумя переменными обладают такими же свойствами.
Применяя эти свойства, будем получать равносильные уравнения. Напомните, пожалуйста, какие уравнения называются равносильными? (Уравнения, имеющие одни и те же решения, называют равносильными. Уравнения, не имеющие решений, также считают равносильными.) Для уравнений с двумя переменными все остается в силе.
Загляните опять в справочник.
Ребята, ведь мы забыли про мастеров из парикмахерской. Это не хорошо. Надо им помочь. Давайте вернемся к той ситуации. Применим свойства уравнений с двумя переменными к полученному нами уравнению, и сведем его к виду, указанному в определении.
0,3x + 0,03y = 0,12(x + y)
0,3x + 0,03y = 0,12x + 0,12y
0,3x – 0,12x = 0,12y – 0,03y
0,18x — 0,09y =0
18x — 9y=0
2x-y=0
При каких значениях x и y наше уравнение обратится в верное равенство?
при х=1, у=2 (записываю на доске) (2∙1=2)
Что же является решением линейных уравнений с двумя переменными? (Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство. )
)
Прочитайте это определение на странице про себя. Не ошиблись ли мы, давая определение?
А какие еще пары чисел будут являться решениями уравнения 2x-y=0?
х=2, у=4
х=3, у=6
х=4, у=8
Правильно решениями этого уравнения будут являться числа, одно из которых в два раза больше другого.
Т.е 3-процентного раствора надо взять вдвое больше, чем 30-процентного. Как же смешать? (дети показывают на практике) мерить будем мерным стаканчиком.
Продолжим знакомство с линейными уравнениями.
Присмотритесь, пожалуйста, к этим парам. Может есть у кого предложение, как записать это решение короче, пользуясь символическим языком математики?
( (2, 4), (3,6), (4, 8) и т.д.)
-При такой записи необходимо знать, значение какой из переменных стоит на первом месте, а какой – на втором. В записи решений уравнения с переменными х и у на первом месте записывают значения х, а на втором – значение у.
В записи решений уравнения с переменными х и у на первом месте записывают значения х, а на втором – значение у.
Где-то нам уже встречалась такая запись! Правильно, это координаты точек на координатной плоскости.
Отметим на координатной плоскости найденные пары решений.
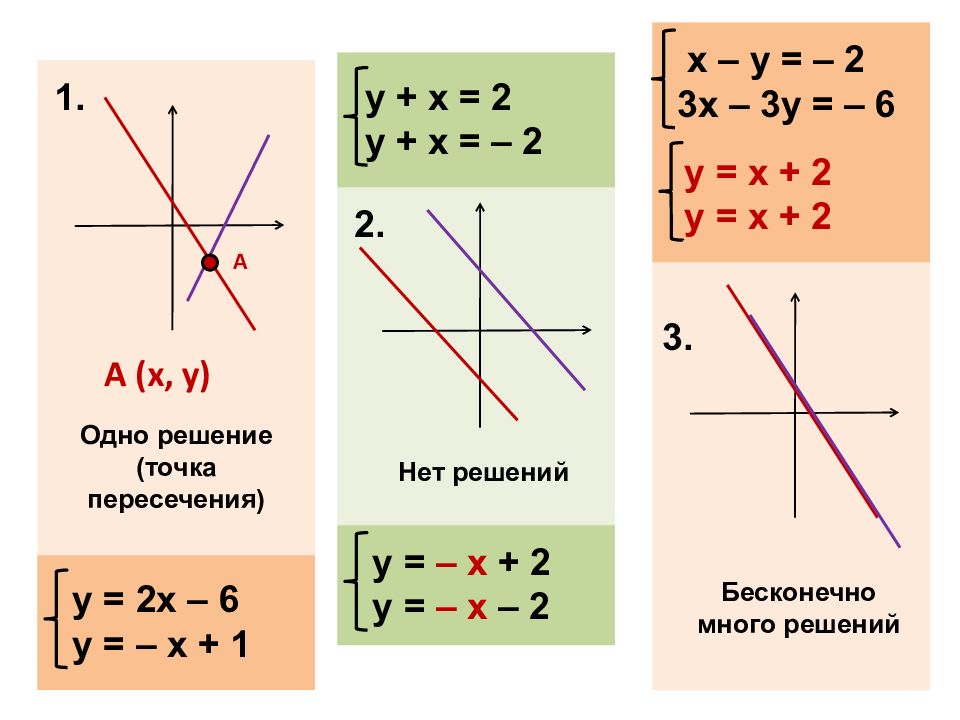
Есть ли еще у нашего уравнения решения? Сколько же у него решений? (бесконечно много)
Можем ли мы все его решения нанести на координатную плоскость? (да, они образуют прямую) Все ли решения будут пригодны для ситуации в парикмахерской?
Сделаем вывод о количестве решений линейного уравнения с двумя переменными (множество решений уравнения с двумя неизвестными, как правило, бесконечно и его изображение на координатной плоскости — прямая линия, а также может быть и пустым)
Всегда ли именно прямая линия?
-Рассмотрим уравнения 5х+2у=12.
-Для удобства нахождения решений уравнения, воспользовавшись свойствами уравнений, выразим из этого уравнения одну
переменную через другую, например у, через х. Для этого перенесем
Для этого перенесем
слагаемое 5х в правую часть уравнения изменив его знак.
2у= -5х+12.
-Разделим обе части этого уравнения на 2:
у= -2,5х+6
Уравнения 5х+2у=12 и
у= -2,5х+6 – равносильны.
-Пользуясь формулой у=-2,5х+6, можно найти сколько угодно решений уравнения
5х+2у=12. Для этого достаточно взять произвольное х и вычислить
соответствующее ему значение у.
Например: если х=2 , то у= -2,5.2+6=1.
если х=0,4 то у= -2,5*0,4+4=5.
Пары чисел (2; 1), (0,4; 5) – решение уравнения 5х+2у=12.
Это уравнение имеет бесконечно много решений.
Этот способ удобен и тогда, когда надо найти не все, а только несколько решений уравнения, причем каждый раз можно выбирать, какую переменную выражать через другую.
Рассмотрим уравнение
2x+0y=13
Построим его график: x=6,5
Рассмотрим уравнение
0x+3y=15
Построим его график:
y=5
5. Подведение итогов. Спасибо вам за общение. Мне понравился полет ваших мыслей. Понятен ли вам язык алгебры?
-Какой вид имеет линейное уравнение с двумя переменными ? (ах+ву=с).
-Что называется решением линейного уравнения с двумя переменными ?
-Приведите примеры таких уравнений.
-Какими свойствами обладают уравнения с двумя переменными?
Презентация «Линейные уравнения с двумя переменными»; 7 класс — К уроку — Математика, алгебра, геометрия
Пояснительная записка
Урок алгебры в
7 классе «Будем знакомы»- это урок
знакомства с новым понятием линейным
уравнением с двумя переменными.
Урок проводиться в нетрадиционной форме. На каждом этапе уроке учитель предлагает обратить внимание на то или иное понятие. Это повышает интерес к новому изучаемому материалу, даёт возможность ученику самостоятельно закрепить новые понятия, проверить себя после выполнения заданий.
Подготовительная работа. Вспомнить с учащимися стандартный вид линейного уравнения с одной переменной, свойства решения уравнений с одной переменной.
Тема урока: Линейные уравнения с двумя переменными.
Цель урока: Дать определение линейного уравнения с двумя переменными; выяснить, что значит решить уравнение с двумя переменными; рассмотреть свойства уравнений.
Ход урока.
На доске записаны уравнения. Предлагаю учащимся поделить эти уравнения на две группы. 2х=4; 0,3х-12=4; 2х=3у; 4х+2=у; 0,2х-4=5х; х+у=1.
2х=4; 0,2х-4=5х; 0,3х-12=4; | х+у=1;
4х+2=у; 2х=3у. |
Предлагаю ребятам самим придумать примеры уравнений второго вида. После примеров пробуем дать определение линейного уравнения с двумя переменными.
Определение. Линейным уравнением с двумя переменными называется уравнение вида ах+ву=с, где а,в,с- некоторые числа, х и у- переменные.
Предлагаю из предложенных уравнений выбрать те, которые подходят под определение уравнения с двумя переменными: 1)7-х=у; 2)5х-у=4; 3)2ху+5=х; 4)2х-0,4у+7=0; 5)х=ху+8; 6)у-4х+2у=7. Объяснить выбор.
Предлагаю подобрать для уравнения 2х+у=5 такие значения переменным, чтобы они обратили данное уравнение в верное равенство. Выясняем, что таких пар чисел можно подобрать много. Например: если х=1, то у=3
если х=2, то у=1
если х=0, то у=5
Но способом подбора
находить пары чисел, которые являются
решением данного уравнения не очень
удобно.
Предлагаю выразить одну переменную через другую.
2х+у=5 1)у=5-2х или 2) . Проверим подобранные пары чисел, выполнив подстановку в уравнения 1) и 2). Убеждаемся в верности найденных решений.
Предлагаю установить порядок нахождения таких пар чисел, которые являются решением линейного уравнений с двумя переменными.
Выразить одну переменную через другую
Придать значение одой переменной
Вычислить значение другой переменной
Предлагаю самостоятельно найти решение линейных уравнений с двумя переменными: у=2х+4; 2х-у=5; 0,5х+2у=8. а)выразить у через х; б)выразить х через у.
Работая с уравнениями, мы пользуемся свойствами:
Переносим слагаемые из одной части в другую, изменив при этом знак на противоположный;
Обе части уравнения
делим на одно и то же число, не равное
нулю.
Предлагаю проверить себя: Найдите пары чисел, которые являются решением данных уравнений при х=0.
1)х-у=5; 20х+у=8; 3)у-6х=1.
Предлагаю найти пары чисел, которые являются решением данного уравнения
2х+у=5; Предлагаю пары чисел.
х
-5
-4
-3
-1
0
4
5
у
0
3
4
-3
-5
-3
0
В конце урока
подвести итог.
Что же мы знаем?
Знаем уравнение линейного уравнения с двумя переменными
Умеем выражать одну переменную через другую
Умеем находить пары чисел, которые являются решением линейных уравнений с двумя переменными.
Линейные уравнения с двумя переменными
Линейные уравнения с двумя переменными — это система уравнений с единственным решением, без решений или с бесконечным числом решений. Линейная система уравнений может иметь n переменных. При решении линейных уравнений с числом переменных n важно помнить, что для решения и определения значений переменных должно быть n уравнений. Множество решений, полученных при решении этих линейных уравнений, представляет собой прямую линию.Линейные уравнения с двумя переменными — это алгебраические уравнения, которые имеют вид y = mx + b, где m — наклон, а b — точка пересечения с y. Это уравнения первого порядка. Например, y = 2x + 3 и 2y = 4x + 9 — линейные уравнения с двумя переменными.
Что такое линейные уравнения с двумя переменными?
Линейные уравнения с двумя переменными имеют порядок высшей экспоненты, равный единице, и имеют одно, нулевое или бесконечно много решений. Стандартная форма линейного уравнения с двумя переменными — ax + by + c = 0, где x и y — две переменные.Решения также можно записывать в упорядоченных парах. Графическое представление линейных уравнений с двумя переменными включает две прямые линии, которые могут быть пересекающимися линиями, параллельными линиями или совпадающими линиями.
Формы линейных уравнений с двумя переменными
Линейное уравнение с двумя переменными может быть в разных формах, таких как стандартная форма, форма пересечения и форма точечного уклона. Например, одно и то же уравнение 2x + 3y = 9 может быть представлено в каждой из форм, таких как 2x + 3y-9 = 0 (стандартная форма), y = (-2/3) x + 3 (форма с угловым пересечением), и y — 5/3 = -2/3 (x + (-2)) (форма точечного наклона). Посмотрите на приведенное ниже изображение, на котором показаны все эти три формы представления линейных уравнений с двумя переменными с примерами.
Посмотрите на приведенное ниже изображение, на котором показаны все эти три формы представления линейных уравнений с двумя переменными с примерами.
Система уравнений означает совокупность уравнений. Мы научимся решать линейные уравнения с двумя переменными разными методами.
Методы решения линейных уравнений с двумя переменными
Существует пять методов решения системы линейных уравнений с двумя переменными. Эти методы описаны ниже:
- Графический метод
- Метод замещения
- Метод перекрестного умножения
- Метод исключения
- Метод определения
Графический метод решения линейных уравнений с двумя переменными
Шаги для графического решения линейных уравнений с двумя переменными приведены ниже:
- Шаг 1: Чтобы решить систему двух уравнений с двумя переменными графически, мы построим графическое изображение каждого уравнения.
- Шаг 2: Чтобы построить уравнение вручную, сначала преобразуйте его в форму y = mx + b, решив уравнение для y.

- Шаг 3: Начните вводить значения x как 0, 1, 2 и так далее и найдите соответствующие значения y или наоборот.
- Шаг 4: Определите точку, где встречаются обе линии.
- Шаг 5: Точка пересечения — это решение данной системы.
Пример: Найдите решение следующей системы уравнений графически.
-x + 2y-3 = 0
3x + 4y-11 = 0
Решение: Мы построим их график и посмотрим, пересекаются ли они в какой-то точке. Как вы можете видеть ниже, обе линии пересекаются в точках (1, 2). Таким образом, решение данной системы линейных уравнений есть x = 1 и y = 2.
Но обе линии не всегда могут пересекаться. Иногда они могут быть параллельны. В этом случае система линейных уравнений с двумя переменными не имеет решения. В некоторых других случаях обе линии совпадают.В этом случае каждая точка на этой прямой является решением данной системы, и, следовательно, данная система имеет бесконечное количество решений. Если у системы есть решение, оно называется непротиворечивым; в противном случае говорят, что это непоследовательно.
Если у системы есть решение, оно называется непротиворечивым; в противном случае говорят, что это непоследовательно.
Рассмотрим систему двух линейных уравнений: \ (a_ {1} \) x + \ (b_ {1} \) y + \ (c_ {1} \) = 0 и \ (a_ {2} \) x + \ (b_ {2} \) y + \ (c_ {2} \) = 0.
Метод замены
Чтобы решить систему двух линейных уравнений с двумя переменными с использованием метода подстановки, мы должны использовать шаги, указанные ниже:
- Шаг 1. Решите одно из уравнений для одной переменной.
- Шаг 2: Подставьте это в другое уравнение, чтобы получить уравнение в терминах одной переменной.
- Шаг 3: Решите его для переменной.
- Шаг 4: Подставьте его в любое из уравнений, чтобы получить значение другой переменной.
Пример: Решите следующую систему уравнений, используя метод подстановки.
х + 2у-7 = 0
2х-5лет + 13 = 0
Решение: Решим уравнение, x + 2y-7 = 0 для y:
х + 2у-7 = 0
⇒2y = 7-x
⇒ у = (7-х) / 2
Подставьте это в уравнение, 2x-5y + 13 = 0:
2x-5y + 13 = 0
⇒ 2x-5 ((7-x) / 2) + 13 = 0
⇒ 2x- (35/2) + (5x / 2) + 13 = 0
⇒ 2x + (5x / 2) = 35/2 — 13
⇒ 9x / 2 = 9/2
⇒ х = 1
Подставьте x = 1 в уравнение y = (7-x) / 2:
у = (7-1) / 2 = 3
Следовательно, решение данной системы x = 1 и y = 3.
Метод перекрестного умножения
Рассмотрим систему линейных уравнений: \ (a_ {1} \) x + \ (b_ {1} \) y + \ (c_ {1} \) = 0 и \ (a_ {2} \) x + \ (b_ {2} \) y + \ (c_ {2} \) = 0.
Чтобы решить эту проблему с помощью метода перекрестного умножения, мы сначала запишем коэффициенты каждого из x и y и константы следующим образом:
Здесь стрелки указывают, что эти коэффициенты необходимо умножить. Теперь мы запишем следующее уравнение, перемножив и вычитая произведения.
\ (\ dfrac {x} {b_ {1} c_ {2} -b_ {2} c_ {1}} = \ dfrac {y} {c_ {1} a_ {2} -c_ {2} a_ {1}) } = \ dfrac {1} {a_ {1} b_ {2} -a_ {2} b_ {1}} \)
Из этого уравнения получаем два уравнения:
\ (\ begin {align}
\ dfrac {x} {b_ {1} c_ {2} -b_ {2} c_ {1}} & = \ dfrac {1} {a_ {1} b_ {2} -a_ {2} b_ {1}} \\ [0,2 см] \ dfrac {y} {c_ {1} a_ {2} -c_ {2} a_ {1}} & = \ dfrac {1} {a_ {1} b_ {2} -a_ {2 } b_ {1}}
\ end {align} \)
Решая каждый из них относительно x и y, решение данной системы:
\ (\ begin {align}
x & = \ frac {b_ {1} c_ {2} -b_ {2} c_ {1}} {a_ {1} b_ {2} -a_ {2} b_ {1}} \\ [0. 2 см] y & = \ frac {c_ {1} a_ {2} -c_ {2} a_ {1}} {a_ {1} b_ {2} -a_ {2} b_ {1}}
2 см] y & = \ frac {c_ {1} a_ {2} -c_ {2} a_ {1}} {a_ {1} b_ {2} -a_ {2} b_ {1}}
\ end {align} \)
Метод исключения
Чтобы решить систему линейных уравнений с двумя переменными с использованием метода исключения, мы будем использовать шаги, указанные ниже:
- Шаг 1. Расположите уравнения в стандартной форме: ax + by + c = 0 или ax + by = c.
- Шаг 2: Проверьте, приведет ли добавление или вычитание уравнений к отмене переменной.
- Шаг 3: Если нет, умножьте одно или оба уравнения на коэффициент при x или y так, чтобы их сложение или вычитание привело к отмене любой из переменных.
- Шаг 4. Решите полученное уравнение с одной переменной.
- Шаг 5: Подставьте его в любое из уравнений, чтобы получить значение другой переменной.
Пример: Решите следующую систему уравнений, используя метод исключения.
2х + 3у-11 = 0
3х + 2у-9 = 0
Сложение или вычитание этих двух уравнений не приведет к отмене какой-либо переменной. Давайте стремимся к сокращению x. Коэффициенты при x в обоих уравнениях равны 2 и 3.Их НОК равно 6. Мы сделаем коэффициенты при x в обоих уравнениях 6 и -6 такими, чтобы члены x отменялись, когда мы добавляем уравнения.
Давайте стремимся к сокращению x. Коэффициенты при x в обоих уравнениях равны 2 и 3.Их НОК равно 6. Мы сделаем коэффициенты при x в обоих уравнениях 6 и -6 такими, чтобы члены x отменялись, когда мы добавляем уравнения.
3 × (2x + 3y-11 = 0)
⇒ 6x + 9y-33 = 0
-2 × (3x + 2y-9 = 0)
⇒ -6x-4y + 18 = 0
Теперь мы добавим эти два уравнения:
6x + 9y-33 = 0
-6x-4y + 18 = 0
Сложив оба приведенных выше уравнения, мы получим
⇒ 5лет-15 = 0
⇒ 5лет = 15
⇒ y = 3
Подставьте это в одно из двух приведенных уравнений и решите полученную переменную относительно x.
2х + 3у-11 = 0
⇒ 2x + 3 (3) -11 = 0
⇒ 2x + 9-11 = 0
⇒ 2x = 2
⇒ х = 1
Следовательно, решение данной системы уравнений есть x = 1 и y = 3.
Метод определения
Определитель матрицы 2 × 2 получается перекрестным умножением элементов, начиная с левого верхнего угла, и вычитанием произведений.
Рассмотрим систему линейных уравнений с двумя переменными: \ (a_ {1} \) x + \ (b_ {1} \) y = \ (c_ {1} \) и \ (a_ {2} \) x + \ (b_ {2} \) y = \ (c_ {2} \). Чтобы решить их с помощью метода определителей (который также известен как правило Краммера), выполните следующие действия:
Чтобы решить их с помощью метода определителей (который также известен как правило Краммера), выполните следующие действия:
- Сначала мы находим определитель, образованный коэффициентами при x и y, и обозначаем его Δ.
Δ = \ [\ left | \ begin {array} {ll} a_1 & b_1 \\ a_2 & b_2 \ end {array} \ right | = a_1 b_2 — a_2b_1 \] - Затем мы находим определитель \ (\ Delta_x \), который получается заменой первого столбца Δ константами.
\ (Δ_ {x} \) = \ [\ left | \ begin {array} {ll} c_1 & b_1 \\ c_2 & b_2 \ end {array} \ right | = c_1 b_2 — c_2b_1 \] - Затем мы находим определитель \ (\ Delta_y \), который получается заменой второго столбца Δ константами.
\ (Δ_ {y} \) = \ [\ left | \ begin {array} {ll} a_1 & c_1 \\ a_2 & c_2 \ end {array} \ right | = a_1 c_2 — a_2c_1 \]
Теперь решение данной системы линейных уравнений находится по формулам:
х = \ (Δ_ {x} \) / Δ
у = \ (Δ_ {y} \) / Δ
Полезные советы
При решении уравнений либо методом подстановки, либо методом исключения:
- Если мы получим истинное уравнение (т.
 е.е., что-то вроде 0 = 0, -1 = -1 и т. д.), то это означает, что система имеет бесконечное количество решений.
е.е., что-то вроде 0 = 0, -1 = -1 и т. д.), то это означает, что система имеет бесконечное количество решений. - Если мы получаем ложное уравнение (т.е. что-то вроде 0 = 2, 3 = -1 и т. Д.), Это означает, что система не имеет решения.
Темы, связанные с линейными уравнениями с двумя переменными
Проверьте эти статьи, связанные с концепцией линейных уравнений с двумя переменными в математике.
Часто задаваемые вопросы о линейных уравнениях с двумя переменными
Что такое линейные уравнения с двумя переменными?
Линейное уравнение — это уравнение со степенью 1.Линейное уравнение с двумя переменными — это тип линейного уравнения, в котором присутствуют две переменные. Например, 2x — y = 45, x + y = 35, a-b = 45 и т. Д.
Как определить линейные уравнения с двумя переменными?
Мы можем идентифицировать линейное уравнение с двумя переменными, если оно выражается в форме ax + by + c = 0, состоящей из двух переменных x и y, а наивысшая степень данного уравнения равна 1.
Можете ли вы решить линейное уравнение с двумя переменными?
Да, мы можем решить уравнение с двумя переменными, используя разные методы и убедившись, что в данной системе уравнений присутствуют два уравнения, чтобы получить значения переменных.Если есть одно решение, это означает, что данные прямые пересекаются, если нет решения, то это означает, что данные уравнения являются параллельными линиями. Если возможных решений бесконечно много, это означает, что данные уравнения образуют совпадающие линии.
Как графически представить линейные уравнения с двумя переменными?
Мы можем представить линейные уравнения с двумя переменными графически, используя шаги, указанные ниже:
- Шаг 1: Систему двух уравнений с двумя переменными можно решить графически, построив график каждого уравнения, преобразовав его в форму y = mx + b, решив уравнение относительно y.
- Шаг 2: Идентифицируются точки пересечения обеих линий.
- Шаг 3: Точка пересечения — это решение данной системы линейных уравнений с двумя переменными.

Как решить систему линейных уравнений с двумя переменными?
У нас есть разные методы решения системы линейных уравнений:
- Графический метод
- Метод замещения
- Метод перекрестного умножения
- Метод исключения
- Определитель или матричный метод
Сколько решений есть у линейного уравнения с двумя переменными?
Предположим, что у нас есть \ (a_ {1} \) x + \ (b_ {1} \) y + \ (c_ {1} \) = 0 и \ (a_ {2} \) x + \ (b_ {2 } \) у + \ (c_ {2} \) = 0.Решения линейного уравнения с двумя переменными:
- Один и уникальный if \ (a_ {1} \) / \ (a_ {2} \) ≠ \ (b_ {1} \) / \ (b_ {2} \)
- Нет, если \ (a_ {1} \) / \ (a_ {2} \) = \ (b_ {1} \) / \ (b_ {2} \) ≠ \ (c_ {1} \) / \ (c_ {2} \)
- Бесконечно много, если \ (a_ {1} \) / \ (a_ {2} \) = \ (b_ {1} \) / \ (b_ {2} \) = \ (c_ {1} \) / \ (c_ {2} \)
Чем линейное неравенство двух переменных похоже на линейное уравнение двух переменных?
Линейное неравенство с двумя переменными и линейное уравнение с двумя переменными имеют следующие общие черты:
- Степень линейного уравнения и линейного неравенства всегда равна 1.

- Оба они решаются графически.
- Способ решения линейного неравенства такой же, как и для линейных уравнений, за исключением того, что он разделен символом неравенства.
Как создавать уравнения с двумя переменными и неравенства
Пример 1
Чтобы ответить на вопрос, когда у вас и вашего друга будет одинаковая сумма денег и сколько денег у вас будет, мы должны сначала определить наши переменные. Поскольку я знаю, что мы собираемся изобразить их на координатной плоскости, я буду использовать x и y , но подойдет любая буква.
Чтобы выбрать, какая переменная является x , а какая y , нам нужно определить, какая из них зависит от другой. В задаче ищу количество денег и количество недель. Зависит ли количество недель от того, сколько у вас денег, или количество денег, которое у вас есть, зависит от количества недель?
Поскольку имеющаяся у вас сумма денег зависит от количества недель, сумма денег является зависимой переменной, y , а количество недель — независимой переменной, x .
Теперь, когда мы определили наши переменные, мы собираемся создать два уравнения. Одно уравнение будет представлять ваши деньги, а второе уравнение — деньги вашего друга. Общая сумма денег, которая у вас есть, и равна тому, сколько у вас есть в настоящее время, 5 долларов, плюс то, сколько вы откладываете каждую неделю, 5 долларов в неделю. Это переводится как y = 5 x +5.
Общая сумма денег, которая есть у вашего друга, на , равна тому, сколько у него сейчас есть, 11 долларов, плюс то, сколько он откладывает каждую неделю, 2 доллара в неделю.Это переводится как y = 2 x +11.
Чтобы решить эту систему уравнений, мы собираемся изобразить оба уравнения на одной и той же координатной плоскости. Когда мы строим график линейных уравнений, нам нужна отправная точка и наклон. Отправной точкой является имеющаяся у вас сумма денег, 5 долларов, которая также является точкой пересечения оси Y в уравнении. Наклон — это сумма, которую вы откладываете, 5 долларов в неделю. Если мы сделаем наклон дробным, это будет 5/1 , что означает, что мы поднимемся на 5 и вправо на 1 от начальной точки по оси Y.
Если мы сделаем наклон дробным, это будет 5/1 , что означает, что мы поднимемся на 5 и вправо на 1 от начальной точки по оси Y.
Затем построим график второго уравнения. Стартовая сумма здесь составляет 11 долларов, а наклон — 2 доллара в неделю. Мы начинаем с 11 по оси Y, затем поднимаемся на 2 и более 1.
Чтобы найти решение этой системы уравнений, мы находим точку пересечения двух прямых. Они пересекаются в точке (2, 15). Это означает, что x = 2 и y = 15. Таким образом, через 2 недели и у вас, и у вашего друга будет по 15 долларов.
Пример 2
Сьюзен и Карлос пошли на карнавал, где им пришлось заплатить за вход и каждый билет на поездку. Сьюзан заплатила за четыре билета на поездку и входной билет, и это обошлось ей в 9 долларов. Карлос заплатил за вход и два билета на поездку, и это обошлось ему в 7 долларов. Сколько стоит входной билет? Сколько стоил каждый билет на поездку?
Сколько стоит входной билет? Сколько стоил каждый билет на поездку?
Поскольку мы пытаемся найти стоимость входа и стоимость билета на поездку, нам нужно определить наши переменные. В данном случае не имеет значения, какое из них мы используем как x и y , потому что эти два события не зависят друг от друга.Допустим, стоимость входа будет нашими y , а стоимость каждого билета будет x .
Теперь мы составим два уравнения, одно для Сьюзен, а другое для Карлоса. Сьюзан купила 4 билета, поэтому нам нужно умножить стоимость одного билета, x , на 4. Она также заплатила за вход, y , поэтому мы должны добавить это к 4 ( x ), и это равняется 9 долларам. она провела. Таким образом, уравнение для Сьюзен: y + 4 x = 9.
Карлос заплатил за 2 билета на поездку, поэтому мы должны умножить стоимость одного билета на поездку, x , на 2.Затем он также заплатил за вход, поэтому мы должны добавить y к 2 (x) , и это равняется 7 долларам, которые он потратил. Уравнение для Карлоса: y + 2 x = 7.
Уравнение для Карлоса: y + 2 x = 7.
Чтобы изобразить эти уравнения на координатной плоскости, мы должны решить их для y .
Для уравнения Сьюзен мы должны вычесть 4 x .
Теперь мы можем посмотреть на уравнение и найти наклон и точку пересечения по оси Y.Наклон равен -4/1, а точка пересечения оси Y равна 9. Итак, мы начинаем с 9 по оси Y, а затем спускаемся на 4, потому что он отрицательный и правый 1.
Для уравнения Карлоса мы должны вычесть 2x с обеих сторон, чтобы найти y .
Теперь, когда у нас есть уравнение в форме пересечения наклона, мы можем видеть, что наклон равен -2/1, а точка пересечения по оси Y равна 7. В этом случае мы начнем с 7 по оси Y и затем идите вниз 2 и вправо 1.
Решение — это точка пересечения этих двух графиков (1, 5). Это означает, что стоимость каждого билета на поездку составляет 1 доллар, а стоимость входного билета — 5 долларов.
Это означает, что стоимость каждого билета на поездку составляет 1 доллар, а стоимость входного билета — 5 долларов.
Краткое содержание урока
Чтобы написать систему уравнений из задачи со словами, нужно выполнить шесть шагов.
- Определите свои переменные. Обязательно определите, что вы ищете, и решите, какая переменная будет представлять какое неизвестное.
- Напишите два уравнения с двумя переменными.
- Представьте свои уравнения в форме пересечения наклона , y = mx + b
- Изобразите уравнения, используя наклон и точку пересечения по оси Y.
- Найдите решение, посмотрев на точку пересечения линий.
- Напишите, что это означает с точки зрения проблемы.
Графические линейные уравнения с двумя переменными — Промежуточная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Построить точки в прямоугольной системе координат
- Постройте линейное уравнение, нанеся точки
- График вертикальных и горизонтальных линий
- Найдите точки пересечения по оси X и Y
- Постройте линию, используя точки пересечения
Прежде чем начать, пройдите тест на готовность.
- Оценить, когда
Если вы пропустили эту проблему, просмотрите (рисунок).
- Оценить, когда
Если вы пропустили эту проблему, просмотрите (рисунок).
- Решите относительно y :
Если вы пропустили эту проблему, просмотрите (рисунок).
Точки графика в прямоугольной системе координат
Подобно тому, как карты используют систему сеток для определения местоположений, система сеток используется в алгебре, чтобы показать взаимосвязь между двумя переменными в прямоугольной системе координат.Прямоугольная система координат также называется плоскостью xy или «координатной плоскостью».
Прямоугольная система координат образована двумя пересекающимися числовыми линиями, горизонтальной и вертикальной. Горизонтальная числовая линия называется осью x . Вертикальная числовая линия называется осью y . Эти оси делят плоскость на четыре области, называемые квадрантами. Квадранты обозначаются римскими цифрами, начиная с верхнего правого угла и продолжаясь против часовой стрелки.См. (Рисунок).
Эти оси делят плоскость на четыре области, называемые квадрантами. Квадранты обозначаются римскими цифрами, начиная с верхнего правого угла и продолжаясь против часовой стрелки.См. (Рисунок).
В прямоугольной системе координат каждая точка представлена упорядоченной парой. Первое число в упорядоченной паре — это координата точки x , а второе число — координата точки y . Фраза «упорядоченная пара» означает, что порядок важен.
Заказанная пара
Упорядоченная пара дает координаты точки в прямоугольной системе координат. Первое число — это координата x .Второе число — координата y .
Какова упорядоченная пара точек пересечения осей? В этой точке обе координаты равны нулю, поэтому ее упорядоченная пара — Точка имеет особое имя. Это называется происхождение.
Происхождение
Точка называется исходной точкой . Это точка пересечения осей x и y .
Это точка пересечения осей x и y .
Мы используем координаты, чтобы найти точку на плоскости xy .Приведем точку в качестве примера. Сначала найдите 1 на оси x и слегка нарисуйте вертикальную линию. Затем найдите 3 на оси y и нарисуйте горизонтальную линию. Теперь найдите точку, в которой эти две линии пересекаются — это точка с координатами См. (рисунок).
Обратите внимание, что сквозная вертикальная линия и сквозная горизонтальная линия не являются частью графика. Мы просто использовали их, чтобы найти точку
.Когда одна из координат равна нулю, точка лежит на одной из осей.На (Рисунок) точка находится на оси y , а точка — на оси x .
Очки по топорам
Точки с координатой y , равной 0, находятся на оси x и имеют координаты
.
Точки с координатой x , равной 0, находятся на оси y и имеют координаты
.Знаки координаты x и координаты y влияют на расположение точек.Вы могли заметить некоторые закономерности, когда рисовали точки в предыдущем примере. Мы можем суммировать знаковые паттерны секторов следующим образом:
Квадранты
До сих пор все решаемые вами уравнения были уравнениями с одной переменной. Почти в каждом случае, когда вы решали уравнение, вы получали ровно одно решение. Но уравнения могут иметь более одной переменной. Уравнения с двумя переменными могут иметь вид. Уравнение такой формы называется линейным уравнением с двумя переменными.
Линейное уравнение
Уравнение формы, где A и B не равны нулю, называется линейным уравнением с двумя переменными.
Вот пример линейного уравнения с двумя переменными, x и y .
Уравнение также является линейным уравнением. Но это не похоже на форму. Мы можем использовать свойство сложения равенства и переписать его по форме.
Переписав, так как мы можем легко увидеть, что это линейное уравнение с двумя переменными, потому что оно имеет форму Когда уравнение находится в форме, мы говорим, что это стандартная форма линейного уравнения.
Стандартная форма линейного уравнения
Линейное уравнение в стандартной форме , когда оно записано
Большинство людей предпочитают, чтобы A , B и C были целыми числами и при написании линейного уравнения в стандартной форме, хотя это не является строго необходимым.
Линейные уравнения имеют бесконечно много решений. Каждому числу, заменяющему x , соответствует значение y .Эта пара значений является решением линейного уравнения и представлена упорядоченной парой. Когда мы подставляем эти значения x и y в уравнение, результатом будет истинное утверждение, потому что значение слева равно равно значению справа.
Каждому числу, заменяющему x , соответствует значение y .Эта пара значений является решением линейного уравнения и представлена упорядоченной парой. Когда мы подставляем эти значения x и y в уравнение, результатом будет истинное утверждение, потому что значение слева равно равно значению справа.
Решение линейного уравнения с двумя переменными
Упорядоченная пара — это решение линейного уравнения, если уравнение является истинным утверждением, когда в уравнение подставляются значения x и y упорядоченной пары.
Линейные уравнения имеют бесконечно много решений. Мы можем построить эти решения в прямоугольной системе координат. Точки будут идеально выровнены по прямой линии. Соединяем точки прямой линией, чтобы получился график уравнения. Мы помещаем стрелки на концах каждой стороны линии, чтобы указать, что линия продолжается в обоих направлениях.
Мы помещаем стрелки на концах каждой стороны линии, чтобы указать, что линия продолжается в обоих направлениях.
График — это визуальное представление всех решений уравнения. Это пример поговорки: «Картинка стоит тысячи слов.Линия показывает вам всех решений этого уравнения. Каждая точка на линии — это решение уравнения. И каждое решение этого уравнения находится на этой линии. Эта линия называется графиком уравнения. Пункты , а не на линии, не являются решениями!
График линейного уравнения
График линейного уравнения представляет собой прямую линию.
- Каждая точка на линии является решением уравнения.
- Каждое решение этого уравнения представляет собой точку на этой прямой.
Показан график.
Для каждой заказанной пары определите:
ⓐ Является ли упорядоченная пара решением уравнения?
ⓑ Находится ли точка на линии?
А: В: С: D:
Подставьте значения x и y в уравнение, чтобы проверить, является ли упорядоченная пара решением уравнения.
ⓐ
ⓑ Нанесите точки и
Точки и находятся на линии, а точка не находится на линии.
Точки, которые являются решениями, находятся на линии, но точка, которая не является решением, не находится на линии.
Использовать график Для каждой упорядоченной пары определите:
ⓐ Является ли упорядоченная пара решением уравнения?
ⓑ Находится ли точка на линии?
А Б
ⓐ да, да ⓑ да, да
Использовать график Для каждой упорядоченной пары определите:
ⓐ Является ли упорядоченная пара решением уравнения?
ⓑ Находится ли точка на линии?
А Б
Построение линейного уравнения по точкам
Есть несколько методов, которые можно использовать для построения графика линейного уравнения.Первый метод, который мы будем использовать, называется построением точек или методом точечного построения. Мы находим три точки, координаты которых являются решениями уравнения, и затем строим их в прямоугольной системе координат. Соединив эти точки в линию, мы получим график линейного уравнения.
Соединив эти точки в линию, мы получим график линейного уравнения.
Как построить график линейного уравнения по точкам
Постройте уравнение, нанеся точки.
Изобразите уравнение, нанеся точки:
Изобразите уравнение, нанеся точки:
Шаги, которые необходимо предпринять при построении линейного уравнения путем нанесения точек, кратко описаны здесь.
Постройте линейное уравнение путем нанесения точек.
- Найдите три точки, координаты которых являются решениями уравнения. Разложите их в виде таблицы.
- Постройте точки в прямоугольной системе координат. Убедитесь, что точки совпадают. Если нет, внимательно проверьте свою работу.
- Проведите линию через три точки. Вытяните линию, чтобы заполнить сетку, и поместите стрелки на обоих концах линии.
Это правда, что для определения линии нужны только две точки, но использование трех точек — хорошая привычка. Если вы нанесете только две точки, и одна из них неверна, вы все равно можете нарисовать линию, но она не будет представлять решения уравнения. Это будет неправильная линия.
Если вы нанесете только две точки, и одна из них неверна, вы все равно можете нарисовать линию, но она не будет представлять решения уравнения. Это будет неправильная линия.
Если вы используете три точки, а одна неверна, точки не выровняются. Это говорит о том, что что-то не так, и вам нужно проверить свою работу. Посмотрите на разницу между этими иллюстрациями.
Когда уравнение включает дробь в качестве коэффициента, мы все равно можем заменить x любыми числами.Но арифметика будет проще, если мы сделаем «хороший» выбор для значений x . Таким образом мы избежим дробных ответов, которые сложно изобразить точно.
Изобразите уравнение:
Найдите три точки, которые являются решениями уравнения. Поскольку это уравнение имеет дробь в виде коэффициента x , мы будем тщательно выбирать значения x . Мы будем использовать ноль в качестве одного варианта и кратное 2 для других вариантов. Почему значение, кратное двум, является хорошим выбором для значений x ? При выборе числа, кратного 2, умножение на упрощается до целого числа
Почему значение, кратное двум, является хорошим выбором для значений x ? При выборе числа, кратного 2, умножение на упрощается до целого числа
Точки показаны на (Рисунок).
Постройте точки, убедитесь, что они совпадают, и проведите линию.
Изобразите уравнение:
Изобразите уравнение:
Вертикальные и горизонтальные линии графика
Некоторые линейные уравнения имеют только одну переменную. У них может быть только x и не y , или только y без x . Это меняет то, как мы составляем таблицу значений, чтобы получить точки для построения.
Давайте рассмотрим уравнение. Это уравнение имеет только одну переменную, x . Уравнение говорит, что x — это , всегда равное , поэтому его значение не зависит от y . Независимо от того, какое значение имеет значение y , значение x всегда равно
Независимо от того, какое значение имеет значение y , значение x всегда равно
Итак, чтобы составить таблицу значений, запишите все значения x . Затем выберите любые значения для y . Поскольку x не зависит от y , вы можете выбирать любые числа, которые вам нравятся.Но чтобы уместить точки на нашем координатном графике, мы будем использовать 1, 2 и 3 для координат y . См. (Рисунок).
Постройте точки из таблицы и соедините их прямой линией. Обратите внимание, что мы нарисовали вертикальную линию.
Что делать, если в уравнении y , но нет x ? Давайте изобразим уравнение на графике. На этот раз значение y- является константой, поэтому в этом уравнении y не зависит от x . Заполните 4 для всех y (рисунок), а затем выберите любые значения для x .Мы будем использовать 0, 2 и 4 для координат x .
Заполните 4 для всех y (рисунок), а затем выберите любые значения для x .Мы будем использовать 0, 2 и 4 для координат x .
На этом рисунке мы изобразили горизонтальную линию, проходящую через ось и в точке 4.
График: ⓐ ⓑ
ⓐ Уравнение имеет только одну переменную, x , а x всегда равно 2. Мы создаем таблицу, где x всегда равно 2, а затем вводим любые значения для y . График представляет собой вертикальную линию, проходящую через ось x в точке 2.
ⓑ Точно так же уравнение имеет только одну переменную, y . Значение y постоянно. Все упорядоченные пары в следующей таблице имеют одинаковую координату y . График представляет собой горизонтальную линию, проходящую через ось и в точке
График представляет собой горизонтальную линию, проходящую через ось и в точке
Изобразите уравнения: ⓐ ⓑ
ⓐ
ⓑ
Изобразите уравнения: ⓐ ⓑ
ⓐ
ⓑ
В чем разница между уравнениями и
Уравнение имеет x и y .Значение y зависит от значения x , поэтому координата y изменяется в соответствии со значением x . Уравнение имеет только одну переменную. Значение y постоянно, оно не зависит от значения x , поэтому координата y всегда равна 4.
Обратите внимание: на графике уравнение дает наклонную линию, а дает горизонтальную линию.
График и в той же прямоугольной системе координат.
Мы замечаем, что первое уравнение имеет переменную x , а второе — нет. Мы составляем таблицу точек для каждого уравнения, а затем наносим на график линии. Показаны два графика.
Изобразите уравнения в той же прямоугольной системе координат: и
Изобразите уравнения в той же прямоугольной системе координат: и
Найти
x — и y — перехватитьКаждое линейное уравнение может быть представлено уникальной линией, которая показывает все решения уравнения.Мы видели, что при построении линии с помощью точек вы можете использовать любые три решения для построения графика. Это означает, что два человека, рисующие линию, могут использовать разные наборы из трех точек.
На первый взгляд, их две линии могут показаться не одинаковыми, поскольку на них будут обозначены разные точки. Но если вся работа была проделана правильно, линии должны быть точно такими же. Один из способов узнать, что это действительно одна и та же линия, — это посмотреть, где линия пересекает ось x и ось y .Эти точки называются пересечениями линии.
Но если вся работа была проделана правильно, линии должны быть точно такими же. Один из способов узнать, что это действительно одна и та же линия, — это посмотреть, где линия пересекает ось x и ось y .Эти точки называются пересечениями линии.
Перехват линии
Точки, где линия пересекает ось x и ось y , называются пересечением линии .
Давайте посмотрим на графики линий.
Во-первых, обратите внимание, где каждая из этих линий пересекает ось x . См. (Рисунок).
Теперь давайте посмотрим на точки, где эти линии пересекают ось y .
ось x в точке: Заказанная пара
для этой точки Линия пересекает
ось y- в точке: Упорядоченная пара
для этой точки Рисунок (a) 36 Рисунок (b) 4 Рисунок (c ) 5 Рисунок (d) 00 Общий рисунок a b
Вы видите закономерность?
Для каждой линии координата y точки, в которой линия пересекает ось x , равна нулю. Точка, в которой линия пересекает ось x , имеет форму и называется точкой пересечения x линии.Перехват x происходит, когда y равно нулю.
Точка, в которой линия пересекает ось x , имеет форму и называется точкой пересечения x линии.Перехват x происходит, когда y равно нулю.
В каждой строке координата x — точки, в которой линия пересекает ось y , равна нулю. Точка, где линия пересекает ось y , имеет форму и называется пересечением оси y линии. Перехват y происходит, когда x равно нулю.
x — перехват и y — перехват строки
Пересечение x — это точка, в которой линия пересекает ось x .
Пересечение y — это точка, в которой линия пересекает ось y .
Найдите точки пересечения x и y на каждом показанном графике.
ⓐ График пересекает ось x в точке Пересечение x- составляет
График пересекает ось y в точке Пересечение y составляет
ⓑ График пересекает ось x в точке. Пересечение x составляет
.График пересекает ось y в точке Пересечение y составляет
ⓒ График пересекает ось x в точке. Пересечение x составляет
.График пересекает ось y в точке Пересечение y составляет
Найдите точки пересечения x и y на графике.
x -перехват:
y -перехват:
Найдите точки пересечения x и y на графике.
x -перехват:
y -перехват:
Признание того, что пересечение x происходит, когда y равно нулю, и что пересечение y происходит, когда x равно нулю, дает нам метод для поиска пересечений линии из ее уравнения.Чтобы найти перехват x , позвольте и решите для x . Чтобы найти перехват y , позвольте и решите относительно y .
Найдите точки пересечения x и y из уравнения прямой
Используйте уравнение линии. Чтобы найти:
Чтобы найти:
- пересечение линии x , позвольте и решить для x .
- y — перехват линии, позвольте и решить для y .
Найдите перехватчик
Давайте найдем перехват x , а найдем перехват y .Мы заполним таблицу, которая напоминает нам о том, что нам нужно найти.
Перехваты — это точки, как показано в таблице.
| x | y |
| 4 | 0 |
| 0 | 8 |
Найдите точки перехвата:
x -перехват:
y -перехват:
Найдите точки перехвата:
x -перехват:
y -перехват:
Построение линии с помощью точек пересечения
Чтобы построить линейное уравнение с помощью точек, необходимо найти три точки, координаты которых являются решениями уравнения. Вы можете использовать точки пересечения x- и y- как две из трех точек. Найдите точки пересечения, а затем найдите третью точку, чтобы обеспечить точность. Убедитесь, что точки совпадают — затем проведите линию. Этот метод часто является самым быстрым способом построить линию.
Вы можете использовать точки пересечения x- и y- как две из трех точек. Найдите точки пересечения, а затем найдите третью точку, чтобы обеспечить точность. Убедитесь, что точки совпадают — затем проведите линию. Этот метод часто является самым быстрым способом построить линию.
Как построить линию с помощью точек пересечения
График с использованием пересечений.
График с пересечениями:
График с пересечениями:
Шаги построения графика линейного уравнения с использованием точек пересечения приведены здесь.
Постройте линейное уравнение, используя точки пересечения.
- Найдите точки пересечения линии x и y .
- Позвольте и решить для x .
- Позвольте и решить для y .

- Найдите третье решение уравнения.
- Постройте три точки и убедитесь, что они совпадают.
- Проведите линию.
График с использованием пересечений.
Найдите точки пересечения и третью точку.
Перечислим точки в таблице и покажем график.
График с пересечениями:
График с пересечениями:
Когда линия проходит через начало координат, точка пересечения x и точка пересечения y являются одной и той же точкой.
График с использованием пересечений.
Эта линия имеет только одну точку пересечения. Это точка
Для обеспечения точности нам нужно нанести три точки.Поскольку точки пересечения x и y — это одна и та же точка, нам нужно еще на две точек, чтобы построить линию.
Полученные три балла сведены в таблицу.
Постройте три точки, убедитесь, что они совпадают, и проведите линию.
График с пересечениями:
График пересечений:
Практика ведет к совершенству
Графические точки в прямоугольной системе координат
В следующих упражнениях нанесите каждую точку в прямоугольную систему координат и определите квадрант, в котором расположена точка.
В следующих упражнениях для каждой упорядоченной пары решите
ⓐ является ли упорядоченная пара решением уравнения? Ⓑ это точка на линии?
ⓐ A: да, B: нет, C: да, D: да ⓑ A: да, B: нет, C: да, D: да
ⓐ A: да, B: да, C: да, D: нет ⓑ A: да, B: да, C: да, D: нет
Построение линейного уравнения по точкам
В следующих упражнениях построите график путем нанесения точек.
График Вертикальные и горизонтальные линии
В следующих упражнениях нанесите на график каждое уравнение.
ⓐⓑ
ⓐⓑ
В следующих упражнениях нарисуйте каждую пару уравнений в одной прямоугольной системе координат.
и
и
Найти x- и y- Перехваты
В следующих упражнениях найдите точки пересечения x и y на каждом графике.
В следующих упражнениях найдите точки пересечения для каждого уравнения.
Построение линии с помощью точек пересечения
В следующих упражнениях построите график с использованием точек пересечения.
Смешанная практика
В следующих упражнениях нанесите на график каждое уравнение.
Письменные упражнения
Объясните, как выбрать три значения x , чтобы составить таблицу для построения графика линии
В чем разница между уравнениями вертикальной и горизонтальной линии?
Вы предпочитаете использовать метод построения точек или метод пересечения точек для построения графика уравнения. Почему?
Почему?
Вы предпочитаете использовать метод построения точек или метод пересечения точек для построения графика уравнения. Почему?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Если бы большинство ваших чеков было:
Уверенно. Поздравляю! Вы достигли целей в этом разделе. Поразмышляйте над своими учебными навыками, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы стать уверенным в своих силах? Быть конкретными.
С некоторой помощью. Это нужно решать быстро, потому что темы, которые вы не осваиваете, становятся ухабами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе. Прежде чем двигаться дальше, важно убедиться, что у вас есть прочный фундамент.К кому обратиться за помощью? Ваши одноклассники и инструктор — хорошие ресурсы. Есть ли в кампусе место, где есть репетиторы по математике? Можно ли улучшить свои учебные навыки?
Нет, не понимаю. Это предупреждающий знак, и вы должны его устранить. Вам следует немедленно обратиться за помощью, иначе вы быстро не справитесь. Как можно скорее обратитесь к своему инструктору, чтобы обсудить вашу ситуацию. Вместе вы сможете составить план оказания вам необходимой помощи.
Это предупреждающий знак, и вы должны его устранить. Вам следует немедленно обратиться за помощью, иначе вы быстро не справитесь. Как можно скорее обратитесь к своему инструктору, чтобы обсудить вашу ситуацию. Вместе вы сможете составить план оказания вам необходимой помощи.
Урок в девятом классе Больше о решении двух уравнений с переменными
Когда мы начнем работу над расследованием, я попрошу учащихся провести «Подумайте-попарно-поделитесь» и перечислите как можно больше важных идей, которые они могут придумать для решения двух уравнений с переменными на основе о том, что они видели до сих пор (см. «Сотрудничество: построение коммуникации и заинтересованности учащихся», где показан пример того, как это работает в моем классе).Студенты, вероятно, предложат много идей, но они попадут в следующие категории:
- Уравнения с двумя переменными имеют много решений.
- Решения могут быть представлены координатами на линии (или кривой) в координатной плоскости.

- Все упорядоченные пары, составляющие линию (или кривую), должны быть решениями уравнения.
Я объясняю своим ученикам, что они собираются продолжить исследование этих идей, исследуя еще несколько линейных функций, которые не обязательно имеют контекст (то есть их область применения — это все действительные числа).Я даю студентам около 10-15 минут на то, чтобы завершить расследование. Мы можем подвести итоги всему классу, или я могу позволить группам поделиться тем, что они обнаружили. В любом случае, вот некоторые моменты этого расследования:
1c) Я посмотрю, найдут ли студенты организованный способ перечисления упорядоченных пар. Например, начните с значения y, а затем найдите соответствующее значение x. Выберите значения y в некотором логическом порядке (y = 1, y = 2, y = 3 …). Затем ученики поймут, что они могут выбрать любое значение y и найти соответствующее значение x.
1e) Проведенная линия (со стрелками на обоих концах) иллюстрирует тот факт, что нам не нужно (и мы не можем) перечислять все решения, мы можем использовать линию, чтобы показать, что существует бесконечное число, и узор из координатных пар на линии.
2b) Существует только одно значение x, которое сделает это уравнение истинным, а именно x = -2. Поскольку мы строим график решения в координатной плоскости, мы можем использовать любое значение y, пока значение x остается x = -2.
2a / 2c) Попросите учащихся обсудить значения, которые они выбрали для x и y.Студенты заметят, что некоторые варианты выбора упрощают вычисления, и нет ничего плохого в том, чтобы время от времени упрощать себе жизнь! Например, в 2a выбор y = 1 или y = -1 приводит к целочисленным ответам для x, а y = 0 — нет. Поскольку учащиеся пытаются изобразить свои решения в виде графика (1, -2), построить график легче, чем (0, -3/2).
Уравнения с более чем одной переменной
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Решите одновременный набор двух линейных уравнений
Быстрый! Мне нужна помощь с:
Выберите пункт справки по математике. ..Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, AreaConversion, VolumeConversion, FindConversion, Massage анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, целые числа, наибольшие общие факторы, наименьшие общие фракции, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, The Equation from slope and y-intLines, The Equation from two pointsLodsottery Практика полиномов Математика, Практика основ , Факторинг разности квадратов, многочленов, факторинга трехчленов, многочленов, факторинга с GCF, многочленов, умножения многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Упрощение, Пример Правые треугольники, Ветер, рисунок
..Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, AreaConversion, VolumeConversion, FindConversion, Massage анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, целые числа, наибольшие общие факторы, наименьшие общие фракции, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, The Equation from slope and y-intLines, The Equation from two pointsLodsottery Практика полиномов Математика, Практика основ , Факторинг разности квадратов, многочленов, факторинга трехчленов, многочленов, факторинга с GCF, многочленов, умножения многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Упрощение, Пример Правые треугольники, Ветер, рисунок
Искусство решения проблем
Система уравнений — это набор уравнений, которые используют одни и те же переменные. Ниже приведен пример системы уравнений.
Ниже приведен пример системы уравнений.
Содержание
- 1 Решите 2 уравнения с переменными менее чем за 5 секунд !!!
- 2 Решение линейных систем
- 2.1 Исключение по Гауссу
- 2.1.1 Проблема
- 2.1.2 Решение
- 2.2 Замена
- 2.2.1 Проблема
- 2.2.2 Решение
- 2.3 Графики
- 2.3.1 Проблема
- 2.3.2 Решение
- 2.4 Расширенные методы
- 2.1 Исключение по Гауссу
- 3 удобные системы
- 3.1 Симметрия
- 3.2 Умная замена
- 4 Проблемы
- 4.1 Вводный
- 4,2 Промежуточное
- 5 См. Также
Решите 2 уравнения с переменными менее чем за 5 секунд !!!
Ссылка на видео: https://youtu.be/pSYT95hSH6M
Решение линейных систем
Система линейных уравнений — это система, в которой все переменные находятся в степени 1. Существует три элементарных способа решения системы линейных уравнений.
Существует три элементарных способа решения системы линейных уравнений.
Исключение по Гауссу
Исключение Гаусса включает удаление переменных из системы путем сложения постоянных кратных двух или более уравнений. Давайте посмотрим на пример:
Проблема
Найдите заказанную пару, для которой
Решение
Мы можем исключить, добавив дважды второе уравнение к первому:
Таким образом.Затем мы можем подключиться к любому из уравнений:
Итак, решение системы есть.
Замена
Второй метод, подстановка, требует решения переменной и последующего включения этой переменной в другое уравнение, что сокращает количество переменных. Мы покажем, как решить ту же задачу из раздела исключения с помощью подстановки.
Проблема
Найдите заказанную пару, для которой
Решение
Первое уравнение можно решить для:
Подставляя это во второе уравнение, получаем
Таким образом. Подключаем это к любому из уравнений и решаем для получения урожайности.
Подключаем это к любому из уравнений и решаем для получения урожайности.
Графики
Третий метод решения системы линейных уравнений состоит в том, чтобы изобразить их на плоскости и наблюдать, где они пересекаются. Мы вернемся к нашему примеру, чтобы проиллюстрировать это.
Проблема
Найдите заказанную пару, для которой
Решение
Изобразим две линии следующим образом:
Из графика видно, что решение системы есть.
Расширенные методы
Матрицы также могут использоваться для решения систем линейных уравнений. Фактически, они дают возможность сделать гораздо более широкие утверждения о системах линейных уравнений.
Существует целая область математики, посвященная изучению линейных уравнений, которая называется линейной алгеброй.
Удобные системы
Некоторые системы можно решить, используя определенные формы. Однако сначала может показаться, что такие системы сложно решить.
Симметрия
Рассмотрим систему ниже.
Ключевым моментом здесь является использование симметрии. Если мы сложим все 5 уравнений, мы получим в общей сложности 4 каждой переменной на LHS. На RHS у нас будет. Таким образом,
Таким образом, вычитание из этого первого уравнения оставляет на левой и правой стороне. Вычитание этого уравнения из второго уравнения оставляет на левой и правой сторонах. И таким образом мы продолжаем таким образом, чтобы найти, что
Умная замена
Рассмотрим систему ниже.
Мы можем позволить и получить двухвариантную линейную систему, представленную ниже.
Решение системы дает и. Подстановка этого обратно приводит к и. Мы можем сделать другую замену, позволив и подставив получить. Переставляем результаты в так. Наконец, подставив обратно, мы получим. Обратное подключение удовлетворяет систему.
Проблемы
Вводный
- 2002 AMC 8 Проблемы / Проблема 17
- 2007 iTest Проблемы / Проблема 2
Средний
- 1989 AIME Проблемы / Проблема 8
- 1993 AIME Проблемы / Проблема 3
См.



 е.е., что-то вроде 0 = 0, -1 = -1 и т. д.), то это означает, что система имеет бесконечное количество решений.
е.е., что-то вроде 0 = 0, -1 = -1 и т. д.), то это означает, что система имеет бесконечное количество решений.