ГДЗ. Математика 5 класс Тарасенкова. Уравнения.
Категория: —>> Математика 5 класс Тарасенкова.
Задание: —>> 553 — 569 570 — 586
наверх
|
|
Задание 553.
Какое из чисел 4. 5, 8 и 10 является корнем уравнения:
Решение:
| 1) 5; | 2) 10; | 3) 4. |
Задание 554.
Решите уравнение устно:
Решение:
| 1) 15 + x: = 55, x = 40; | 3) 60 — y = 45, y = 15; | 5) 88 : x = 8, x = 11; |
| 2) х — 22 = 42, x = 64; | 4) у * 12 = 12, y = 1; | 6) у : 10 = 40, y = 400. |
Задание 555.
Можно ли решить уравнение:
| 1) 8x = 0; | 2) 0 : y = 25; | 3) 5х = 5 | 4) 12 : y = 0? |
Решение:
1) x = 0; 2) Не имеет решений; 3) x = 1; 4) Не имеет решений;
Задание 556.
Решите уравнение:
Решение:
1)28 + (45 + х) = 100;
| 11) 121 : (х — 45) = 11;
|
Задание 557.
Решите уравнение:
Решение:
1) 65 + (х + 23) = 105;
| 6) 9х + 50 = 86;
|
Задание 558.
Составьте уравнение, корнем которого является число:
| а) 8; | б) 14. |
Решение:
| а) 2y = 16; | б) x + 7 = 21. |
Задание 559.
Составьте уравнение, корнем которого является число.
| а) 5; | б) 9. |
Решение:
| а) 25 : x = 5; | б) 5x = 45. |
Задание 560.
Некоторое число увеличили на 67 и получили число 109. Найдите это число.
Решение:
- Некоторое число — x.
- x + 67 = 109;
- x = 109 — 67;
- x = 42.
- Ответ: число 42.
Задание 561.
К некоторому числу прибавили 38 и получили число 245. Найдите это число.
Решение:
- x + 38 = 245;
- x = 245 — 38;
- x = 207.
- Ответ: 207.
Задание 562.
Некоторое число увеличили в 24 раза и получили число 1968. Найдите это число.
Решение:
- 24x = 1968;
- x = 1968 : 24;
- x = 82.
- Ответ: 82.
Задание 563.
Некоторое число уменьшили в 18 раз и получили число 378. Найдите это число.
Решение:
- x : 18 = 378;
- x = 378 * 18;
- x = 6804.
- Ответ: 6408.
Задание 564.
Решение:
- x — 22 = 105;
- x = 105 + 22;
- x = 127.
- Ответ: 127.
Задание 565.
Из числа 128 вычли некоторое число и получили 79. Найдите это число.
Решение:
- 128 — x = 79;
- x = 128 — 79;
- x = 49.
- Ответ: 49.
Задание 566.
Составьте и решите уравнение:
- 1) сумма удвоенного числа х и числа 39 равна 81;
- 2) разность чисел 32 и y в 2 раза меньше числа 64;
- 3) частное суммы чисел х и 12 и числа 2 равно 40;
- 4) сумма чисел х и 12 в 3 раза больше числа 15;
- 5) частное разности чисел у и 12 и числа 6 равно 18;
- 6) утроенная разность чисел у и 17 равна 63.
Решение:
- 1) 2x + 39 = 81
- 2x = 81 — 39;
- 2x = 42;
- x = 42 : 2;
- x = 21;
- 2) (32 — y) * 2 = 64
- 32 — y = 64 : 2;
- 32 — y = 32;
- y = 32 — 32;
- y = 0;
- 3) (x + 12) : 2 = 40
- x + 12 = 40 * 2;
- x + 12 = 80;
- x = 80 — 12;
- x = 68;
- 4) (x + 12) : 3 = 15
- x + 12 = 15 * 3;
- x + 12 = 45;
- x = 45 — 12;
- x = 33;
- 5) (y — 12) : 6 = 18
- y — 12 = 18 * 6;
- y — 12 = 108;
- y = 108 + 12;
- y = 120;
- 6) (y — 17) * 3 = 63
- y — 17 = 63 : 3;
- y — 17 = 21;
- y = 21 + 17;
- y = 38;
Задание 567.
Составьте и решите уравнение:
- 1) разность утроенного числа у и числа 41 равна 64;
- 2) сумма чисел 9 и х в 5 раз меньше числа 80;
- 3) частное суммы чисел у и 10 и числа 4 равно 16;
- 4) разность утроенного числа х и числа 17 равна 10.
Решение:
- 1) 3y — 41 = 64
- 3y = 64 + 41;
- 3y = 105;
- y = 105 : 3;
- y = 15;
- 2) (9 + x) * 5 = 80
- 9 + x = 80 : 5;
- 9 + x = 16;
- x = 16 — 9;
- x = 7;
- 3) (y + 10) : 4 = 16
- y + 10 = 16 * 4;
- y + 10 = 64;
- y = 64 — 10;
- y = 54;
- 4) 3x — 17 = 10
- 3x = 10 + 17;
- 3x = 27;
- x = 27 : 3;
- x = 9;
Задание 568.
Некоторое число увеличили на 5 и полученное число удвоили. В результате получили число 22. Найдите неизвестное число.
Решение:
- (x + 5) * 2 = 22;
- x + 5 = 22 : 2;
- x + 5 = 11;
- x = 11 — 5;
- x = 6;
Задание 569.
Некоторое число увеличили в 7 раз и полученное число уменьшили на 54. В результате получили число 100. Найдите неизвестное число.
Решение:
- 7x — 54 = 100;
- 7x = 100 + 54;
- 7x = 154;
- x = 154 : 7;
- x = 22;
Задание: —>> 553 — 569 570 — 586
reshebniki-uchebniki.ru
В контексте тем: | Традиции и фольклор | ||||||
Раздел 3С | Числовые и буквенные выражения. Уравнения. Задачи | ||||||
Школа: осш №23 им.А.Бокейханова | |||||||
Дата: « 26 » 02 2019 г . | ФИО учителя: Кочкурова Ирина Викторовн | ||||||
Класс: 2 «А» класс. | Количество присутствующих: отсутствующих: | ||||||
Лексическая тема: | Народные музыкальные инструменты | ||||||
Тема урока: | Уравнения на умножение и деление | ||||||
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу): | |||||||
2.2.2.2. Решать простейшие уравнения на умножение и деление; | |||||||
Критерии успеха (Предполагаемый результат): | Все учащиеся будут: решать простейшие уравнения на умножение и деление. Многие учащиеся будут: объяснять, как найти неизвестный компонент умножения и деления. Некоторые учащиеся будут: самостоятельно составлять простейшие уравнения на умножение и деление. | ||||||
Языковая цель | Учащиеся могут: объяснить, как найти неизвестный компонент при делении и умножении. Предметная лексика и терминология: Уравнение, корень уравнения, названия компонентов действий умножения и деления. Серия полезных фраз для диалога/письма Обсуждение: Как найти неизвестный компонент действия? Как связаны действия умножения и деления? Как связаны действия сложения и вычитания? Письмо: Запись уравнений. Решение уравнений. | ||||||
Привитие ценностей | Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество.. | ||||||
Навыки использования ИКТ | ИКТ — просмотр видеоролика, презентация урока. | ||||||
Предварительные знания | Уравнения, взаимосвязь умножения и деления, названия компонентов действий. | ||||||
Ход урока | |||||||
Этапы урока, t | Запланированная деятельность на уроке | Ресурсы | |||||
Начало урока 0-3 | Мотивация. На уроке будь старательным, Будь спокойным и внимательным. Все пиши, не отставая, Слушай, не перебивая. Говорите четко, внятно, Чтобы было все понятно. Если друг стал отвечать, Не спеши перебивать. Деление на группы. (Карточки) | Карточки с изображениями музыкальных инструментов. | |||||
4-6 Критерии успеха | Актуализация. – Чем вы любите заниматься в свободное время? – Любите ли вы слушать музыку, играть на инструментах? — Сегодня у нас необычный урок, к нам в гости спешат сказочные герои, которые помогут нам узнать много нового, и повторить ранее изученные темы. (На доске изображения сказочных героев) — Кто это? — Правильно, это Алдар-Косе, Емеля и Тостик. — Где встречали мы этих героев? (В народных сказках) — К какому разделу относятся народные сказки? (Традиции и фольклор) — Наши сказочные герои приготовили для вас задания, преодолев которые вы узнаете много нового и интересного. — С чего мы начнем наш урок? (Составим план работы на уроке) На доске таблица 1:
— Первое задание мы выполним и узнаем, на каких музыкальных инструментах любят играть наши герои, а еще мы повторим таблицу умножения и деления. ( выполнение №2 с 61) – Как проверить умножение? – Как проверить деление? — На музыкальных инструментах записаны значения выражений, послушайте, что наши герои расскажут о них. | Презентация. Карточки с выражениями. Презентация Слайд 1 Слайд 2 Слайд 3,4,5,6,7 | |||||
Учащиеся решают примеры, составляют равенства и неравенства. | |||||||
Середина урока 7-11 | Постановка цели (проблемная ситуация). Игра: «Я беру тебя с собой». – Угадайте, по какому признаку я собираю объекты. Для этого предлагайте мне математические записи, чем-то похожие на то, что я выбрала, а я буду говорить, могу ли я взять их с собой. Итак, я беру с собой выражение х + 14 = 45. А что у вас? Д: Я беру с собой выражение 25 + у. У: Я не беру тебя с собой. Д: Я беру уравнение х : 6 = 3. У: Я беру тебя с собой. Д: Я беру выражение х · 3 = 12 У: Я беру тебя с собой. Д: Вы берете с собой уравнения? У: Да! Итак, по какому признаку мы собирали объекты? Это уравнения. Рассмотрите пары уравнений в каждом столбике. В чем сходство и отличие? 2 + х = 18 15 – у = 3 2 · х = 18 15 : у = 3 – Какого вида уравнения мы будем учиться решать на этом уроке? (Уравнения на умножение и деление) | Карточки с выражениями. Наборное полотно. | |||||
Критерии успеха | Учащиеся формулируют цель урока при помощи учителя. | ||||||
12-22 | Работа по учебнику. Открытие нового Предлагает выполнить задание №1 в учебнике.(Устно) Рассмотрите рисунки и записи уравнений. – Какой компонент неизвестен? – Как его можно найти? Дети формулируют правило и сверяют с правилом в учебнике. Первичное закрепление с проговариванием. Детям предлагает работать с комментированием по плану: 1. Какой компонент неизвестен? 2. Как найти неизвестный множитель (делимое, делитель)? 3. Запись уравнения. 4. Решение уравнения. 5. Проверка решения. Применение нового. Самостоятельная работа. Предлагает выполнить задание №4 в рабочей тетради с критериями оценивания. ФО (самооценивание) Педагог определяет, кто из детей усвоил материал и на каком уровне. Дети, которые не справились с заданием, возвращаются к №1 в учебнике и повторяют, как найти неизвестный компонент в уравнениях на умножение и деление. | Учебник. Слайд 9 Рабочая тетрадь. | |||||
Критерии успеха | Учащиеся формулируют цель урока при помощи учителя. | ||||||
23-24 | Физминутка | ||||||
24-38 | Работа в группах. Планируем работу: выделим этапы работы над задачей. 1. Прочитаем задачу. 2. Выделим условие, вопрос. 3. Решим задачу. 4. Напишем ответ. Выполнение №3 (а) в учебнике и тетради с проверкой по образцу. Взаимопроверка ФО (Критерии оценивания на доске) Работа над ранее изученным1 Решение задач №5. Работа в парах. Дети записывают выражения по задачам. Обсуждают о числовых данных, которые можно использовать, записывают решения задач и выполняют взаимопроверку. (ФО) Взаимооценивание. (звездочка, квадратик, треугольник) -Скажем спасибо нашим героям за их интересные задания! — И давайте скажем, что нового мы узнали на уроке? | Тетрадь, учебник. Слайд 10 Слайд 12 Слайд 13 | |||||
Критерии успеха | Учащиеся самостоятельно решают задачи на умножение. | ||||||
39-40 | Рефлексия. – Понравился ли вам урок? – Какие задания вы выполнили с удовольствием? – А есть ли задания, при выполнении которых вы испытывали трудности? — Кого бы вы похвалили за работу на уроке? Предлагает оценить свою работу при помощи «Дерева знаний» | Дерево знаний Слайд 14 | |||||
Критерии успеха | Учащиеся оценивают себя при помощи «Дерева знаний». | ||||||
Дифференциация | Оценивание | Здоровье и соблюдение ТБ | |||||
Способные учащиеся строят свои высказывания самостоятельно, а менее способным учитель оказывает поддержку, задавая наводящие вопросы. | Учитель проводит формативное оценивание выполненной работы. | Физкультминутка Под музыку выполняем движения. | |||||
infourok.ru
Умножение и деление целых чисел
При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.
При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть какое правило применять. Также, необходимо изучить несколько законов умножения и деления. Изучение этих правил позволяет избежать некоторые досадные ошибки в будущем.
Законы умножения
Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов, и разумнее будет изучать их последовательно по мере необходимости.
Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.
Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.
Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.
Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.
Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:
Таким образом, если число 3 повторить два раза подряд, получится число 6.
Переместительный закон умножения
Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:
От перестановки мест сомножителей произведение не меняется.
Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.
3 × 5 = 15
Теперь поменяем местами сомножители:
5 × 3 = 15
В обоих случаях, мы получаем ответ 15, значит между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:
3 × 5 = 5 × 3
15 = 15
А с помощью переменных переместительный закон умножения можно записать так:
a × b = b × a
где a и b — сомножители
Сочетательный закон умножения
Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
К примеру выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(3 × 2) × 4 = 3 × (2 × 4)
24 = 24
а с помощью переменных сочетательный закон умножения можно записать так:
a × b × c = (a × b) × c = a × (b × c)
где вместо a, b, c могут стоять любые числа.
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Например, найдём значение выражения (2 + 3) × 5
Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Значит значение выражения (2 + 3) × 5 равно 25.
С помощью переменных распределительный закон умножения записывается так:
(a + b) × c = a × c + b × c
где вместо a, b, c могут стоять любые числа.
Закон умножения на ноль
Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Например, выражение 0 × 2 равно нулю
0 × 2 = 0
В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Ответ — никак.
Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».
И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:
0 × 2 = 2 × 0
0 = 0
Примеры применения закона умножения на ноль:
5 × 0 = 0
5 × 5 × 5 × 0 = 0
2 × 5 × 0 × 9 × 1 = 0
В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.
Мы рассмотрели основные законы умножения. Далее рассмотрим умножение целых чисел.
Умножение целых чисел
Пример 1. Найти значение выражения −5 × 2
Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. Для таких случаев нужно применять следующее правило:
Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.
−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10
Обычно записывают короче: −5 × 2 = −10
Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.
2 × 3 = 6
Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить двойку. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:
То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы
А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.
Пример 2. Найти значение выражения 12 × (−5)
Это умножение чисел с разными знаками. 12 – положительное число, (−5) – отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:
12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60
Обычно решение записывают покороче:
12 × (−5) = −60
Пример 3. Найти значение выражения 10 × (−4) × 2
Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:
Первое действие:
10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40
Второе действие:
−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80
Значит значение выражения 10 × (−4) × 2 равно −80
Запишем решение покороче:
10 × (−4) × 2 = −40 × 2 = −80
Пример 4. Найти значение выражения (−4) × (−2)
Это умножение отрицательных чисел. В таких случаях нужно применять следующее правило:
Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8
Плюс по традиции не записываем, поэтому просто записываем ответ 8.
Запишем решение покороче (−4) × (−2) = 8
Возникает вопрос почему при умножении отрицательных чисел вдруг получается положительное число. Давайте попробуем доказать, что (−4) × (−2) равно 8 и ни чему другому.
Сначала запишем следующее выражение:
4 × (−2)
Заключим его в скобки:
( 4 × (−2) )
Прибавим к этому выражению наше выражение (−4) × (−2). Его тоже заключим в скобки:
( 4 × (−2) ) + ( (−4) × (−2) )
Всё это приравняем к нулю:
(4 × (−2)) + ((−4) × (−2)) = 0
Теперь начинается самое интересное. Суть в том, что мы должны вычислить левую часть этого выражения, и в результате получить 0.
Итак, первое произведение (4 × (−2)) равно −8. Запишем в нашем выражении число −8 вместо произведения (4 × (−2))
−8 + ((−4) × (−2)) = 0
Теперь вместо второго произведения временно поставим многоточие
−8 + … = 0
Теперь внимательно посмотрим на выражение −8 + … = 0. Какое число должно стоять вместо многоточия, чтобы соблюдалось равенство? Ответ напрашивается сам. Вместо многоточия должно стоять положительное число 8 и никакое другое. Только так будет соблюдаться равенство. Ведь −8 + 8 равно 0.
Возвращаемся к выражению −8 + ((−4) × (−2)) = 0 и вместо произведения ((−4) × (−2)) записываем число 8
−8 + 8 = 0
Пример 5. Найти значение выражения −2 × (6 + 4)
Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4)
−2 × (6 + 4) = −2 × 6 + (−2) × 4
Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение
Первое действие:
−2 × 6 = −12
Второе действие:
−2 × 4 = −8
Третье действие:
−12 + (−8) = −20
Значит значение выражения −2 × (6 + 4) равно −20
Запишем решение покороче:
−2 × (6 + 4) = (−12) + (−8) = −20
Пример 6. Найти значение выражения (−2) × (−3) × (−4)
Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
(−2) × (−3) = 6
Второе действие:
6 × (−4) = −(6 × 4) = −24
Значит значение выражения (−2) × (−3) × (−4) равно −24
Запишем решение покороче:
(−2) × (−3) × (−4) = 6 × (−4) = −24
Законы деления
Прежде чем делить целые числа, необходимо изучить два закона деления.
В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное.
Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.
Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.
Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.
Далее рассмотрим законы деления.
На ноль делить нельзя
Любое число запрещено делить на ноль.
Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10 : 5 = 2
Точно так же можно поступать и с другими выражениями. Если к примеру, 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6
12 : 6 = 2
Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю
5 × 0 = 0
Если записать это выражение в обратном порядке, то получим:
0 : 0 = 5
Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно.
В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0
0 : 0 = 2
В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.
Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8
… × 2 = 8
Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:
8 : 2 = 4
Получили число 4. Запишем его вместо многоточия:
4 × 2 = 8
Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5
… × 0 = 5
Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.
Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.
А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.
С помощью переменных данный закон записывается следующим образом:
, при b ≠ 0
Это выражение можно прочитать так:
Число a можно разделить на число b, при условии, что b не равно нулю.
Свойство частного
Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.
Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3
12 : 4 = 3
Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3
(12 × 4) : (4 × 4)
(12 × 4) : (4 × 4) = 48 : 16 = 3
Получили ответ 3.
Теперь попробуем не умножить, а разделить делимое и делитель на число 4
(12 : 4) : (4 : 4)
(12 : 4) : (4 : 4) = 3 : 1 = 3
Получили ответ 3.
Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.
Мы рассмотрели два закона деления. Далее рассмотрим деление целых чисел.
Деление целых чисел
Пример 1. Найти значение выражения 12 : (−2)
Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.
12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6
Обычно записывают покороче:
12 : (−2) = −6
Пример 2. Найти значение выражения −24 : 6
Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.
−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4
Запишем решение покороче:
−24 : 6 = −4
Пример 3. Найти значение выражения −45 : (−5)
Это деление отрицательных чисел. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
−45 : (−5) = |−45| : |−5| = 45 : 5 = 9
Запишем решение покороче:
−45 : (−5) = 9
Пример 4. Найти значение выражения −36 : (−4) : (−3)
Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.
Разделим −36 на (−4), и полученное число разделим на −3
Первое действие:
−36 : (−4) = |−36| : |−4| = 36 : 4 = 9
Второе действие:
9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3
Запишем решение покороче:
−36 : (−4) : (−3) = 9 : (−3) = −3
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
spacemath.xyz
Этапы урока | Деятельность учителя | Деятельность учащихся |
I.Мотивационно-целевой этап 12 мин. | ||
1.Мотивация к учебной деятельности | Ребята, сегодня у нас на уроке гости. Как поступают воспитанные люди? Давайте и мы поприветствуем наших гостей. -Мы начинаем урок математики. Ребята, повернитесь друг к другу, возьмитесь за руки и пожелайте удачи. Мы работаем под девизом: «У нас всё получится!» | Дети приветствуют гостей урока. Дети берутся за руки с соседом и желают удачи |
2.Актуализация знаний и фиксация индивидуального затруднения в пробном действии | Найдите лишнее равенство. 30 + х = 54 48 – 25 = 23 Х ● 5 = 40 36 : х = 9 -Докажите. — Что такое уравнение. Вставьте пропущенные слова Уравнение – это ___________, в котором есть ______________ число. -Сегодня на уроке мы будем решать уравнения. — Прежде чем приступить к новой теме, что мы должны сначала сделать? (вспомнить, что мы знали ранее). 1) Найти неизвестную величину (на доске). х 5 см 6 дм 14м² 2м 15 см² х х 2дм -Что неизвестно? Как найти сторону прямоугольника. -Что неизвестно? Как найти площадь? -Покажите, чему равна сторона, площадь? (7, 3, 12) 2) Решите уравнения на сложение и вычитание, отметив в них части и целое (на листочках и на доске под прямоугольниками) Х + 2=14 15 — х = 5 х — 6 = 2 Х=14 – 2 х = 15 – 5 х =6+2 Х= 12 х = 10 х = 8 -Какую закономерность увидели? Продолжите на 3 числа. (Ответы проверяют по образцу) — С помощью каких правил вы решали уравнения на сложение и вычитание? -Оценим результат при помощи сигнальных карточек (+ и ?). | 48-25=23 – пример, а все остальные равенства – уравнения. Называют пропущенные слова (равенство, неизвестное) Сторона. Чтобы найти сторону прямоугольника, можно площадь разделить на другую сторону. Площадь. Чтобы найти площадь прямоугольника, можно стороны перемножить. У детей на столах цифровой веер. Ответы показывают с помощью веера. Находят неизвестную часть и целое. 12, 10, 8 (6, 4,2) Правила о нахождении целого и части. Оценивают результат при помощи сигнальных карточек. |
3.Побуждение познавательного интереса к новой теме (проблемная ситуация) 3.Выявление причины затруднения. | 3)Решите ещё уравнения. (записываю уравнения между прямоугольниками и уравнениями на сложение и вычитание) Х ● 2 = 14 15 : х = 5 х : 6 = 2 (Дети решают уравнения на листочках самостоятельно в течении 2-3 минут ) — Поднимите руку те, у кого нет ответов. -Какое у вас затруднение? -У кого есть ответы? Какие получились у вас ответы? Как вы это нашли? -Можете ли вы обосновать, что ваше решение уравнений правильное? Вы молодцы, поняли в чём заключается ваша трудность. -Какой следующий шаг? -Чем похожи и чем отличаются новые уравнения от тех, которые уже решали? -Мы изучали такие уравнения? -Почему же возникло затруднение? -Сформулируйте тему урока . | Высказывают причину сложности решения данных уравнений, формулируют затруднение: « Мы не смогли решить эти уравнения (или уравнения со знаками «:» и «●».) Дети показывают на веерах ответы к уравнениям. Подбором и т.д. Формулируют своё затруднение: « Мы не можем обосновать, что правильно решили данные уравнения» Необходимо выяснить, почему эта трудность возникла, определить причину затруднения. Одинаковые числа, но в новых уравнениях вместо сложения и вычитания действия умножения и деления. Нет. Формулируют проблему: « Мы не знаем, как решать уравнения со знаками «:» и «●». Уравнения на умножение и деление. |
4.Формулирование цели урока | -Сформулируйте цель урока. | Формулируют цель своей деятельности: «Узнать, как решать уравнения с действиями умножения и деления» |
II. Ориентировочный этап 3 мин | ||
1.Организация планирования | Какой следующий шаг нашего урока? -Составим план и запишем его на доске: План: 1.Изучить с помощью учебника, как решать уравнения с действиями умножения и деления. 2.Составить алгоритм решения уравнений. 3.Потренироваться в решении таких уравнений. 4.Выполнить самостоятельную работу и сравнить свой результат с образцом. | «Составление плана». Называют предполагаемую последовательность действий по решению проблемы, проговаривая вслух. |
III. Поисково-исследовательский этап 10 мин. | ||
1.Организация осмысленного восприятия информации | -Предлагаю обратиться к нашему помощнику – учебнику, при помощи которого вы самостоятельно изучите, как решать уравнения с действиями умножения и деления, а затем в парах попробуете решить уравнения. -Откроем учебник – урок 40 с.95 Всё ли вам было понятно? Какая тема вам поможет в решении уравнений? — У вас на партах на листочках (1 листок на двоих) записаны уравнения. Х ● 2 = 14 15 : х = 5 х : 6 = 2 Х= Х= Х= Х= Х= Х= -Какие ответы получили? Кто расскажет, как решали данные уравнения? — Какие шаги вы выполняли? (Составление алгоритма, шаги записаны в хаотичном порядке). Записываю: 1.Найти компоненты, соответствующие сторонам и площади прямоугольника 1.2.Если неизвестна сторона, то Применить правило: чтобы найти сторону, надо площадь разделить на другую сторону. 1.3. Если неизвестна площадь, то Применить правило: чтобы найти площадь, надо стороны перемножить. -Для более упрощенного способа предлагаю следующие эталоны.
| Читают учебник, проводят наблюдения, анализируют факты. Нахождение площади и сторон прямоугольника. Представители нескольких пар сообщают результаты поиска, один защищает своё решение у доски Дети располагают шаги алгоритма в нужной последовательности на доске |
Физкультминутка 2 мин. | ||
IV. Практический этап 14 мин. | ||
1.Обеспечение осмысленного усвоения и закрепления знаний 7.Самостоятельная работа с самопроверкой. 8.Включение в систему знаний. | Какой следующий шаг урока? -№4 решение у доски с проговариванием вслух 1)учитель 2,3) ученики у доски -№6 (1,2)(устно) на местах – работа в парах. -Проверим, проговаривая (Образец) Чья пара справилась? -Готовы работать самостоятельно? Следующий шаг. Ещё раз проговорим алгоритм решения уравнений на деление и умножение. -Рабочая тетрадь – урок 40 №4. -Проверим ответы по образцу. -Поднимите руку, у кого были ошибки в работе? Какие? -О чём говорят ваши ошибки? -Оценим свои результаты при помощи сигнальных карточек. -№7.Блиц-турнир Разбор задач (помощь — опорные схемы на нахождение целого и части) а) предлагаю несколько вариантов решения 1) a-b 2) а + b 3) (а-b) +а 4) а + (а-b) -Вы должны выбрать и обосновать правильное решение. б) коллективно, в, г) по уровням обучения самостоятельно (Решение каждой задачи обсуждается фронтально. При проверке используются заполненные схемы к задачам) -Оценим свои результаты при помощи сигнальных карточек | «Тренировка в решении уравнений» Решают уравнения В тетрадях у детей уже записаны уравнения с прямоугольником. 21 : х = 3 х: 8 = 3 х ● 2 = 16 Х= Х= Х= Х= Х= Х= «Самостоятельная работа» Решают самостоятельно, проверяют по образцу на доске. Оценивают результат при помощи сигнальных карточек. Подходят 3 и 4 выражения, так как для ответа на вопрос задачи надо объединить всех рыбок. В 1 аквариуме их а, а во 2 – на b меньше, то есть а – b.Значит, всего в двух аквариумах (а-b) +а или а + (а-b) рыбок (от перестановки слагаемых сумма не изменяется) в, г) Сильные ученики — решают без помощи схем Средние – решают задачи, дополняя схемы Слабые – решают задачи, используя заполненную схему Дети отмечают у себя в тетради, какие задачи решены ими верно, исправляют допущенные ошибки. a ? b с ? (m + n) – a d — b – с или d — ( b + с) Оценивают результат при помощи сигнальных карточек. |
V. Рефлексивно-оценочный этап 4 мин. | ||
1.Беседа по вопросам рефлексивного характера | Наш урок подходит к концу. -Какая тема урока была сегодня? -Какую цель вы ставили на уроке? -Как вы считаете, вы достигли поставленной цели? Почему вы считаете, что добились поставленной цели? -С помощью чего зафиксирован результат урока? -Какое важное открытие вы сделали сегодня на уроке? | Анализируют свою работу на уроке, определяют границу между знанием и незнанием, отвечают на вопросы Уравнения на умножение и деление. Узнать, как решать уравнения на умножение и деление. Да. С помощью эталона. Мы узнали как решать уравнения с действиями деления и умножения. |
2.Самооценка результатов | -Оценим свою работу на уроке при помощи «Лесенки успеха» 4 ступень-все понял(а), могу рассказать, нет ошибок 3 ступень — понял(а), 1 ошибка 2 ступень – понял(а), есть вопросы, есть ошибки 1 ступень – не понял(а), есть ошибки | Осуществляют процедуры самооценки собственной учебной деятельности |
3.Домашнее задание | Запишем домашнее задание: урок 40 №5, №7 дорешать, № 13*,14* (по желанию) | Записывают домашнее задание. |
infourok.ru
Урок математики по теме «Деление дробей в уравнениях»
Форма урока: объяснение нового материала.
Цели урока:
- Обучающая: выработать навыки учащихся умножать и делить обыкновенные дроби, решать и оформлять задачи на уравнения.
- Воспитательная: воспитывать самостоятельность, аккуратность
- Развивающая: развивать внимание, математическую речь, вычислительные навыки учащихся, интерес к математике.
Ожидаемые результаты: дети научаться решать задачи и уравнения на дроби.
Этапы урока |
Время (мин) | Слайды |
| Организационный момент. | 2 | Слайд 1 |
| Устная работа и повторение ранее изученного | 8 | Слайды 2, 3, 4, 5,6 |
| Формирование новых знаний и умений | 10 | Слайды 7, 8 |
| Физкультминутка | 2 | Слайды 9, 10 |
| Закрепление нового материала | 5 | Слайд 11 |
| Проверка знаний (с/р) | 10 | Слайд 12 |
| Постановка домашнего задания | 1 | Слайд 13 |
| Подведение итогов урока | 2 |
ХОД УРОКА
I. Организационный этап
– Здравствуйте, мы проведем сегодня урок по
теме «Деление дробей в уравнених». Откройте
тетради, запишите число, классная работа и тему
урока.
Целью нашего урока является закрепление и
проверка умений умножать и делить обыкновенные
дроби, а также повторить навыки решения задач и
уравнений.
II. Устный опрос учащихся
Чтобы умным в жизни стать
Надо дроби изучать
1) Переведите смешанную дробь в неправильную (Приложение 1, слайд 3)
2) Выделите целую часть (Приложение 1, слайд 4)
3) Умножьте дроби (Приложение 1, слайд 5)
– Повторим правило умножения двух дробей: Чтобы умножить дробь на дробь нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе знаменателем.
4) Выполните деление (в тетрадях с последующей взаимопроверкой, сосед у соседа) (Приложение 1, слайд 6)
– Повторим правило деления двух дробей: Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.
III. Формирование новых знаний и умений
– При изучении темы деление большое значение имеет умение решать уравнения. Рассмотрим пример и запишем его в тетрадь. (Приложение 1, слайд 7)
– Чтобы решить уравнение необходимо
определить какой компонент в уравнении является
неизвестным.
– Какой?
– 1 множитель
– Правильно! Чтобы найти неизвестный множитель,
что нужно сделать?
– Чтобы найти неизвестный множитель необходимо
произведение разделить на известный множитель.
– Находим корень уравнения, выполняя деление.
Выполним проверку и запишем ответ.
– А теперь давайте проверим ваше умение решать задачи.
№ 597 (Приложение 1, слайд 7)
– Сколько всего прошел лыжник ? (26 км)
– Сколько километров прошел в первый день?
(неизвестно)
– Сколько километров прошел во второй день?
(неизвестно)
– Какую величину, с какой сравнивают?
– Что возьмем за х?
– Как найти дробь от числа?
– Сколько километров прошел за два дня?
– Как найти?
– Составим уравнение.
– 14 км лыжник прошел во второй день
26 – 14 = 12 км лыжник прошел в первый день.
№ 598 (Приложение 1, слайд 8)
– Вспомним что такое 1% (одна сотая)
– Какой дробью запишем 75% (75/100 = 3/4)
– Сколько грибов собрала белка? (неизвестно)
– Сколько грибов собрал бельчонок? (неизвестно)
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе белка и бельчонок?
– Составим уравнение.
200 грибов собрала белка
350 – 200 = 150 грибов собрал бельчонок
IV. Физкультминутка
– Встаем и выполняем несколько упражнений.
А теперь, ребята, встали,
Быстро руки вверх подняли,
В стороны, вперёд, назад
Повернулись вправо, влево,
Тихо сели, вновь за дело.
V. Закрепление нового материала
№ 594
– Сколько собрал Митя?
– Сколько собрал Коля?
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе мальчики?
28 грибов собрал Митя
64 – 28 = 36 грибов собрал Коля
VI. «Математический выбор»
Уравнения, оцениваемые в 3 балла: Уравнения, оцениваемые в 5 баллов:
1) 1)
2) 2)
3) 3)
4) 4)
Уравнения, оцениваемые в 6 баллов:
1)
2)
3)
4)
Оценки: 5 – 12 баллов; 4 – 9 баллов; 3 – 6 баллов.
Каждый выбирает себе уравнения по «плечу».
Учитель во время работы оценивает учеников.
VII. Итог урока
– С каким настроением вы сегодня работали на
уроке?
– Какая задача для вас была самой интересной?
– Ребята чему мы научились на сегодняшнем уроке?
– Как найти часть от числа?
– Как найти неизвестный множитель?
Оценки за урок.
VIII. Домашнее задание
– С листов решить любые три уравнения, из тех которые не решали в классе.
urok.1sept.ru
Урок математики в 5 классе по теме «Деление. Решение уравнений» (конспект+презентация)
Повторение по теме «Деление. Решение уравнений»
Цели урока:
— совершенствовать навыки деления чисел;
— развитие умений решать текстовые задачи, уравнения;
— развивать внимание, память, познавательную активность, грамотность математической речи;
— воспитывать дисциплинированность, ответственность, интерес к предмету, самостоятельность.
Ход урока
I. Организационный этап
Проверяется готовность класса к уроку, сообщаются тема и цели урока.
II. Устная работа
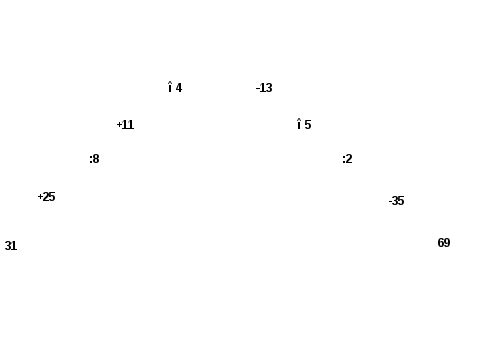
III. Актуализация знаний. Законы деления.
Слайды 3-5
IV. Решение заданий на уроке. Слайды 6-7
V. Физкультминутка.
Гимнастика для глаз
VI. Задача. Слайд 8.
VII. Самостоятельная работа. Слайд 9.
VIII. Решение уравнений Слайды 10-14
IX. Итоги урока и рефлексия
Что мы сегодня вспомнили, чему научились?
Оцените степень усвоения материала.

Ура! Мне все понятно. Небольшие недочеты, Были неудачи, но
есть над чем работать. я все преодолею.
X.Задания на дом.








а)
125х = 1000
х = 8
д) х:71 = 0
х = 71
б) х:16 = 4
х = 4
е) 47х = 0
х = 0
в)75:х = 3
х = 25
ж) 84:х = 6
х = 12
г) х•9 = 81
х = 9
з) х•29 = 58
х = 2
Математический диктант.
— Запишите, как называется:
Число, на которое делят.
Число сто в выражении 23•100
Число, которое получается в результате деления чисел.
Число, на которое умножают.
Число сто в равенстве 300:3 = 100.
Число, которое получается в результате вычитания чисел.
Число, которое делят.
Число сто в выражении 800:100.
—————————————————————————————————-
Математический диктант.
— Запишите, как называется:
Число, на которое делят.
Число сто в выражении 23•100
Число, которое получается в результате деления чисел.
Число, на которое умножают.
Число сто в равенстве 300:3 = 100.
Число, которое получается в результате вычитания чисел.
Число, которое делят.
Число сто в выражении 800:100.
—————————————————————————————————-
Математический диктант.
— Запишите, как называется:
Число, на которое делят.
Число сто в выражении 23•100
Число, которое получается в результате деления чисел.
Число, на которое умножают.
Число сто в равенстве 300:3 = 100.
Число, которое получается в результате вычитания чисел.
Число, которое делят.
Число сто в выражении 800:100.
infourok.ru
Уравнения на умножение и деление
Урок 91. Уравнения на умножение и деление Тема: Народные музыкальные инструменты Дата:22.02.2018. Класс:2 Цель обучения Предполагаемый результат Языковая цель Предшествующие знания Школа: «Минская средняя» Ф.И.О. педагога:Хандусь Н.А. Количество присутствующих: Количество отсутствующих: 2.2.2.2. Решать простейшие уравнения на умножение и деление; уравнения сложной структуры вида: х + (25 – 6) = 38; (24 –3) – х = 8; а + 6 = 7 + 80 Все учащиеся будут: решать простейшие уравнения на умножение и деление. Многие учащиеся будут: объяснять, как найти неизвестный компонент умножения и деления. Некоторые учащиеся будут: самостоятельно составлять простейшие уравнения на умножение и деление. Учащиеся могут: объяснить, как найти неизвестный компонент при делении и умножении. Предметная лексика и терминология: Уравнение, корень уравнения, названия компонентов действий умножения и деления. Серия полезных фраз для диалога/письма Обсуждение: Как найти неизвестный компонент действия? Как связаны действия умножения и деления? Как связаны действия сложения и вычитания? Письмо: Запись уравнений. Решение уравнений. Уравнения, взаимосвязь умножения и деления, названия компонентов действий. План Планируемое Запланированная деятельность Ресурсы время
03 Мотивация
46 711 1слайд 2слайд 3слайд Карточки с выражениями. Наборное полотно. На уроке будь старательным, Будь спокойным и внимательным. Все пиши, не отставая, Слушай, не перебивая. Говорите четко, внятно, Чтобы было все понятно. Если друг стал отвечать, Не спеши перебивать. (деление на группы) Актуализация Математическая разминка 1.5*3=15 2.9*3=27 3.16:4=4 4.48:6=8 5.32:4=8 6.4*7=28 (взаимопроверка) – Чем вы любите заниматься в свободное время? – Любите ли вы слушать музыку, играть на инструментах? На карточках с изображением музыкальных инструментов (доске, наборном полотне) записаны выражения: 2 6 = 12 : 2 = 12 : 6 = – Как связаны между собой выражения? Прочитайте их по разному. – Как проверить умножение? – Как проверить деление? Постановка цели (проблемная ситуация) Игра «Я беру тебя с собой». – Угадайте, по какому признаку я собираю объекты. Для этого предлагайте мне математические записи, чемто похожие на то, что я выбрала, а я буду говорить, могу ли я взять их с собой. Итак, я беру с собой выражение х + 14 = 45. А что у вас? Д: Я беру с собой выражение 25 + у. У: Я не беру тебя с собой. Д: Я беру уравнение 64 + у = 89. У: Я беру тебя с собой. Д: Я беру выражение (12 – 9) + а = 31 . У: Я беру тебя с собой. Д: Вы берете с собой уравнения? У: Да! Итак, по какому признаку мы собирали объекты? Это уравнения. Рассмотрите пары уравнений в каждом столбике. В чем сходство и отличие? 2 + х = 18 2 ∙ х = 18 – Какого вида уравнения мы будем учиться решать на этом 15 – у = 3 15 : у = 3
уроке? (Уравнения на умножение и деление)работа в паре. Открытие нового 1229 самооценивание Учебник. Предлагает выполнить задание №1 в учебнике. Рассмотрите рисунки и записи уравнений. – Какой компонент неизвестен? – Как его можно найти? Дети формулируют правило и сверяют с правилом в учебнике. Первичное закрепление с проговариванием Педагог может предложить работу в парах. Дети получают карточки, на которых записаны уравнения вида: 5 х = 10 х :7 = 2(работа в группе) Детям предлагает работать с комментированием по плану: 1. Какой компонент неизвестен? 2. Как найти неизвестный множитель (делимое, делитель)? 3. Запись уравнения. 4. Решение уравнения. 5. Проверка решения. Самостоятельная работа Предлагает выполнить задание №1 в тетради с критериями оценивания. Педагог определяет, кто из детей усвоил материал и на каком уровне. Дети, которые не справились с заданием, возвращаются к №1 в учебнике и повторяют, как найти неизвестный компонент в уравнениях на умножение и деление. Применение нового Самостоятельное выполнение №4 в учебнике и тетради с проверкой по образцу. Работа над ранее изученным Работу над задачами педагог проводит дифференцировано. Это может быть работа в парах. Дети записывают выражения по задачам. Обсуждают о числовых данных, которые можно использовать, записывают решения задач и выполняют взаимопроверку. Правило на слайде Тетрадь. Учебник, тетрадь. 3040 4145 Рефлексия Педагог предлагает детям оценить, могут ли они:
решать простейшие уравнения на умножение и деление; объяснить, как найти неизвестный компонент умножения и деления; самостоятельно составить и решить уравнения на умножение и деление. Предлагает оценить свою работу при помощи линейки успеха. Линейка успеха. Оценочный лист Название работы Математический диктант Решение уравнений в паре Решение уравнений в прописи самостоятельно Решение задач в
группе Начертание квадрата и деление его на 2 треугольника
znanio.ru


 m+n d
m+n d