Уравнение четвёртой степени — Википедия

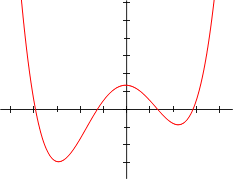
Уравнение четвёртой степени — в математике алгебраическое уравнение вида:

f(x)=ax4+bx3+cx2+dx+e=0,a≠0.{\displaystyle f(x)=ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a\neq 0.}

Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любом значении коэффициентов).

Так как f(x){\displaystyle f(x)} является многочленом чётной степени, она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если a>0{\displaystyle a>0}, то функция возрастает до плюс бесконечности с обеих сторон, таким образом, функция имеет глобальный минимум. Аналогично, если a<0{\displaystyle a<0}, то функция убывает до минус бесконечности с обеих сторон, таким образом, функция имеет глобальный максимум

Теорема Виета для уравнения четвёртой степени

Корни уравнения четвёртой степени x1,x2,x3,x4{\displaystyle x_{1},\,x_{2},\,x_{3},\,x_{4}} связаны с коэффициентами a,b,c,d,e{\displaystyle a,\,b,\,c,\,d,\,e} следующим образом:

x1+x2+x3+x4=−ba,{\displaystyle x_{1}+x_{2}+x_{3}+x_{4}=-{\frac {b}{a}},}

x1x2+x1x3+x1x4+x2x3+x2x4+x3x4=ca,{\displaystyle x_{1}\,x_{2}+x_{1}\,x_{3}+x_{1}\,x_{4}+x_{2}\,x_{3}+x_{2}\,x_{4}+x_{3}\,x_{4}={\frac {c}{a}},}

x1x2x3+x1x2x4+x1x3x4+x2x3x4=−da,{\displaystyle x_{1}\,x_{2}\,x_{3}+x_{1}\,x_{2}\,x_{4}+x_{1}\,x_{3}\,x_{4}+x_{2}\,x_{3}\,x_{4}=-{\frac {d}{a}},}

x1x2x3x4=ea.{\displaystyle x_{1}\,x_{2}\,x_{3}\,x_{4}={\frac {e}{a}}.}

Видео по теме

История

Уравнения четвёртой степени впервые были рассмотрены древнеиндийскими математиками между IV в. до н. э. и II в. н. э.

Лодовико Феррари приписывается получение решения уравнения четвёртой степени в 1540 году, но его работа опиралась на решение кубического уравнения, которого у него не было, поэтому сразу это решение не было опубликовано,^[1] а было опубликовано только в 1545 вместе с решением кубического уравнения наставника Феррари — Джероламо Кардано в книге «Великое искусство»^[2].

То, что это наибольшая степень уравнения, для которого можно указать общую формулу решения, было доказано в теореме Абеля — Руффини в 1824. Записки, оставленные Галуа, позже привели к элегантной теории корней многочленов, одним из результатов которой была эта теорема.

[3]

Решения

Через резольвенту

Решение уравнения четвёртой степени

x4+px2+qx+r=0{\displaystyle x^{4}+px^{2}+qx+r=0}

сводится к решению кубической резольвенты

y3−2py2+(p2−4r)y+q2=0{\displaystyle y^{3}-2py^{2}+(p^{2}-4r)y+q^{2}=0}

Корни резольвенты y1,y2,y3{\displaystyle y_{1},y_{2},y_{3}} связаны с корнями исходного уравнения x1,x2,x3,x4{\displaystyle x_{1},x_{2},x_{3},x_{4}} (которые и нужно найти) следующими соотношениями:

y1=(x1+x2)(x3+x4){\displaystyle y_{1}=(x_{1}+x_{2})(x_{3}+x_{4})}

y2=(x1+x3)(x2+x4){\displaystyle y_{2}=(x_{1}+x_{3})(x_{2}+x_{4})}

y3=(x1+x4)(x2+x3){\displaystyle y_{3}=(x_{1}+x_{4})(x_{2}+x_{3})}

Корни резольвенты могут быть решены по формуле Кардано. Три формулы соотношений между yi{\displaystyle y_{i}} и xi{\displaystyle x_{i}} вместе с исходным уравнением дают систему из 4 алгебраических уравнений с 4 неизвестными, которая легко решается.

Решение Декарта — Эйлера

В уравнении четвёртой степени

ax4+bx3+cx2+dx+e=0,a≠0{\displaystyle ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a\neq 0}

сделаем подстановку x=y−b4a{\displaystyle x=y-{\frac {b}{4a}}}, получим уравнение в следующем виде (оно называется «неполным»):

y4+py2+qy+r=0,{\displaystyle y^{4}+py^{2}+qy+r=0,}

где

p=8ac−3b28a2,{\displaystyle p={\frac {8ac-3b^{2}}{8a^{2}}},}

q=8a2d+b3−4abc8a3,{\displaystyle q={\frac {8a^{2}d+b^{3}-4abc}{8a^{3}}},}

r=16ab2c−64a2bd−3b4+256a3e256a4.{\displaystyle r={\frac {16ab^{2}c-64a^{2}bd-3b^{4}+256a^{3}e}{256a^{4}}}.}

Корни y1,y2,y3,y4{\displaystyle y_{1},\,y_{2},\,y_{3},\,y_{4}} такого уравнения равны одному из следующих выражений:

±z1{\displaystyle \pm {\sqrt {z_{1}}}} ±z2{\displaystyle \pm {\sqrt {z_{2}}}} ±z3,{\displaystyle \pm {\sqrt {z_{3}}},}

в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:

(±z1)(±z2)(±z3)=−q8,{\displaystyle (\pm {\sqrt {z_{1}}})(\pm {\sqrt {z_{2}}})(\pm {\sqrt {z_{3}}})=-{\frac {q}{8}},}

причём z1,z2,z3{\displaystyle z_{1},\,z_{2},\,z_{3}} — это корни кубического уравнения

z3+p2z2+p2−4r16z−q264=0.{\displaystyle z^{3}+{\frac {p}{2}}z^{2}+{\frac {p^{2}-4r}{16}}z-{\frac {q^{2}}{64}}=0.}

Решение Феррари

Решение уравнения четвёртой степени вида x4+ax3+bx2+cx+d=0{\displaystyle x^{4}+ax^{3}+bx^{2}+cx+d=0} может быть найдено по методу Феррари. Если y1{\displaystyle y_{1}} — произвольный корень кубического уравнения

y3−by2+(ac−4d)y−a2d+4bd−c2=0,{\displaystyle y^{3}-by^{2}+(ac-4d)y-a^{2}d+4bd-c^{2}=0,}

(2)

(резольвенты основного уравнения), то четыре корня исходного уравнения находятся как корни двух квадратных уравнений

x2+a2x+y12=±(a24−b+y1)x2+(a2y1−c)x+y124−d{\displaystyle x^{2}+{\frac {a}{2}}x+{\frac {y_{1}}{2}}=\pm {\sqrt {\left({\frac {a^{2}}{4}}-b+y_{1}\right)x^{2}+\left({\frac {a}{2}}y_{1}-c\right)x+{\frac {y_{1}^{2}}{4}}-d}}}

где подкоренное выражение в правой части является полным квадратом.

Биквадратное уравнение

Биквадратное уравнение^[4] — уравнение четвёртой степени вида ax4+bx2+c=0{\displaystyle ax^{4}+bx^{2}+c=0}, где a,b,c{\displaystyle a,b,c} — заданные комплексные числа и a≠0{\displaystyle a\not =0}. Подстановкой y=x2;y⩾0{\displaystyle y=x^{2};y\geqslant 0} оно сводится к квадратному уравнению относительно y{\displaystyle y}.

Четыре его корня находятся по формуле

x1,2,3,4=±−b±b2−4ac2a.{\displaystyle x_{1,2,3,4}=\pm {\sqrt {\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}.}

Возвратные уравнения четвёртой степени

Возвратное уравнение четвёртой степени является также относительно легко решаемым: для ax4+bx3+cx2+bx+a=0{\displaystyle ax^{4}+bx^{3}+cx^{2}+bx+a=0} такого, что a≠0{\displaystyle a\neq 0}, решение находится приведением к виду:

a(x2+1×2)+b(x+1x)+c=0{\displaystyle a\left(x^{2}+{1 \over x^{2}}\right)+b\left(x+{1 \over x}\right)+c=0},

После замены t=x+1x{\displaystyle t={x+{1 \over x}}} ищется решение квадратного уравнения at2+bt+c−2a=0{\displaystyle at^{2}+bt+c-2a=0}, а затем — квадратного уравнения x2−tx+1=0{\displaystyle x^{2}-tx+1=0}.

Примечания

1. ↑ Ferrari biography
2. ↑ «Великое искусство» (Ars magna, 1545)
3. ↑ Стюарт, Ян. Теория Галуа, издание третье (Chapman & Hall/CRC Mathematics, 2004) (англ.)
4. ↑ В литературе до середины XX века биквадратным также могли называть уравнение четвёртой степени общего вида

Литература

Ссылки

Уравнение четвёртой степени — Википедия

Уравнение четвёртой степени — в математике алгебраическое уравнение вида:

f(x)=ax4+bx3+cx2+dx+e=0,a≠0.{\displaystyle f(x)=ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a\neq 0.}

Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любом значении коэффициентов).

Так как f(x){\displaystyle f(x)} является многочленом чётной степени, она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если a>0{\displaystyle a>0}, то функция возрастает до плюс бесконечности с обеих сторон, таким образом, функция имеет глобальный минимум. Аналогично, если a<0{\displaystyle a<0}, то функция убывает до минус бесконечности с обеих сторон, таким образом, функция имеет глобальный максимум

Теорема Виета для уравнения четвёртой степени

Корни уравнения четвёртой степени x1,x2,x3,x4{\displaystyle x_{1},\,x_{2},\,x_{3},\,x_{4}} связаны с коэффициентами a,b,c,d,e{\displaystyle a,\,b,\,c,\,d,\,e} следующим образом:

x1+x2+x3+x4=−ba,{\displaystyle x_{1}+x_{2}+x_{3}+x_{4}=-{\frac {b}{a}},}

x1x2+x1x3+x1x4+x2x3+x2x4+x3x4=ca,{\displaystyle x_{1}\,x_{2}+x_{1}\,x_{3}+x_{1}\,x_{4}+x_{2}\,x_{3}+x_{2}\,x_{4}+x_{3}\,x_{4}={\frac {c}{a}},}

x1x2x3+x1x2x4+x1x3x4+x2x3x4=−da,{\displaystyle x_{1}\,x_{2}\,x_{3}+x_{1}\,x_{2}\,x_{4}+x_{1}\,x_{3}\,x_{4}+x_{2}\,x_{3}\,x_{4}=-{\frac {d}{a}},}

x1x2x3x4=ea.{\displaystyle x_{1}\,x_{2}\,x_{3}\,x_{4}={\frac {e}{a}}.}

История

Уравнения четвёртой степени впервые были рассмотрены древнеиндийскими математиками между IV в. до н. э. и II в. н. э.

Лодовико Феррари приписывается получение решения уравнения четвёртой степени в 1540 году, но его работа опиралась на решение кубического уравнения, которого у него не было, поэтому сразу это решение не было опубликовано,^[1] а было опубликовано только в 1545 вместе с решением кубического уравнения наставника Феррари — Джероламо Кардано в книге «Великое искусство»^[2].

То, что это наибольшая степень уравнения, для которого можно указать общую формулу решения, было доказано в теореме Абеля — Руффини в 1824. Записки, оставленные Галуа, позже привели к элегантной теории корней многочленов, одним из результатов которой была эта теорема.^[3]

Решения

Через резольвенту

Решение уравнения четвёртой степени

x4+px2+qx+r=0{\displaystyle x^{4}+px^{2}+qx+r=0}

сводится к решению кубической резольвенты

y3−2py2+(p2−4r)y+q2=0{\displaystyle y^{3}-2py^{2}+(p^{2}-4r)y+q^{2}=0}

Корни резольвенты y1,y2,y3{\displaystyle y_{1},y_{2},y_{3}} связаны с корнями исходного уравнения x1,x2,x3,x4{\displaystyle x_{1},x_{2},x_{3},x_{4}} (которые и нужно найти) следующими соотношениями:

y1=(x1+x2)(x3+x4){\displaystyle y_{1}=(x_{1}+x_{2})(x_{3}+x_{4})}

y2=(x1+x3)(x2+x4){\displaystyle y_{2}=(x_{1}+x_{3})(x_{2}+x_{4})}

y3=(x1+x4)(x2+x3){\displaystyle y_{3}=(x_{1}+x_{4})(x_{2}+x_{3})}

Корни резольвенты могут быть решены по формуле Кардано. Три формулы соотношений между yi{\displaystyle y_{i}} и xi{\displaystyle x_{i}} вместе с исходным уравнением дают систему из 4 алгебраических уравнений с 4 неизвестными, которая легко решается.

Решение Декарта — Эйлера

В уравнении четвёртой степени

ax4+bx3+cx2+dx+e=0,a≠0{\displaystyle ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a\neq 0}

сделаем подстановку x=y−b4a{\displaystyle x=y-{\frac {b}{4a}}}, получим уравнение в следующем виде (оно называется «неполным»):

y4+py2+qy+r=0,{\displaystyle y^{4}+py^{2}+qy+r=0,}

где

p=8ac−3b28a2,{\displaystyle p={\frac {8ac-3b^{2}}{8a^{2}}},}

q=8a2d+b3−4abc8a3,{\displaystyle q={\frac {8a^{2}d+b^{3}-4abc}{8a^{3}}},}

r=16ab2c−64a2bd−3b4+256a3e256a4.{\displaystyle r={\frac {16ab^{2}c-64a^{2}bd-3b^{4}+256a^{3}e}{256a^{4}}}.}

Корни y1,y2,y3,y4{\displaystyle y_{1},\,y_{2},\,y_{3},\,y_{4}} такого уравнения равны одному из следующих выражений:

±z1{\displaystyle \pm {\sqrt {z_{1}}}} ±z2{\displaystyle \pm {\sqrt {z_{2}}}} ±z3,{\displaystyle \pm {\sqrt {z_{3}}},}

в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:

(±z1)(±z2)(±z3)=−q8,{\displaystyle (\pm {\sqrt {z_{1}}})(\pm {\sqrt {z_{2}}})(\pm {\sqrt {z_{3}}})=-{\frac {q}{8}},}

причём z1,z2,z3{\displaystyle z_{1},\,z_{2},\,z_{3}} — это корни кубического уравнения

z3+p2z2+p2−4r16z−q264=0.{\displaystyle z^{3}+{\frac {p}{2}}z^{2}+{\frac {p^{2}-4r}{16}}z-{\frac {q^{2}}{64}}=0.}

Решение Феррари

Решение уравнения четвёртой степени вида x4+ax3+bx2+cx+d=0{\displaystyle x^{4}+ax^{3}+bx^{2}+cx+d=0} может быть найдено по методу Феррари. Если y1{\displaystyle y_{1}} — произвольный корень кубического уравнения

y3−by2+(ac−4d)y−a2d+4bd−c2=0,{\displaystyle y^{3}-by^{2}+(ac-4d)y-a^{2}d+4bd-c^{2}=0,}

(2)

(резольвенты основного уравнения), то четыре корня исходного уравнения находятся как корни двух квадратных уравнений

x2+a2x+y12=±(a24−b+y1)x2+(a2y1−c)x+y124−d{\displaystyle x^{2}+{\frac {a}{2}}x+{\frac {y_{1}}{2}}=\pm {\sqrt {\left({\frac {a^{2}}{4}}-b+y_{1}\right)x^{2}+\left({\frac {a}{2}}y_{1}-c\right)x+{\frac {y_{1}^{2}}{4}}-d}}}

где подкоренное выражение в правой части является полным квадратом.

Биквадратное уравнение

Биквадратное уравнение^[4] — уравнение четвёртой степени вида ax4+bx2+c=0{\displaystyle ax^{4}+bx^{2}+c=0}, где a,b,c{\displaystyle a,b,c} — заданные комплексные числа и a≠0{\displaystyle a\not =0}. Подстановкой y=x2;y⩾0{\displaystyle y=x^{2};y\geqslant 0} оно сводится к квадратному уравнению относительно y{\displaystyle y}.

Четыре его корня находятся по формуле

x1,2,3,4=±−b±b2−4ac2a.{\displaystyle x_{1,2,3,4}=\pm {\sqrt {\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}.}

Возвратные уравнения четвёртой степени

Возвратное уравнение четвёртой степени является также относительно легко решаемым: для ax4+bx3+cx2+bx+a=0{\displaystyle ax^{4}+bx^{3}+cx^{2}+bx+a=0} такого, что a≠0{\displaystyle a\neq 0}, решение находится приведением к виду:

a(x2+1×2)+b(x+1x)+c=0{\displaystyle a\left(x^{2}+{1 \over x^{2}}\right)+b\left(x+{1 \over x}\right)+c=0},

После замены t=x+1x{\displaystyle t={x+{1 \over x}}} ищется решение квадратного уравнения at2+bt+c−2a=0{\displaystyle at^{2}+bt+c-2a=0}, а затем — квадратного уравнения x2−tx+1=0{\displaystyle x^{2}-tx+1=0}.

Примечания

1. ↑ Ferrari biography
2. ↑ «Великое искусство» (Ars magna, 1545)
3. ↑ Стюарт, Ян. Теория Галуа, издание третье (Chapman & Hall/CRC Mathematics, 2004) (англ.)
4. ↑ В литературе до середины XX века биквадратным также могли называть уравнение четвёртой степени общего вида

Литература

Ссылки

Уравнение четвёртой степени — это… Что такое Уравнение четвёртой степени?

Уравнение четвёртой степени — в математике алгебраическое уравнение вида:

Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любом значении коэффициентов).

Так как является многочленом чётной степени, она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если , то функция возрастает до плюс бесконечности с обеих сторон, таким образом, функция имеет глобальный минимум. Аналогично, если , то функция убывает до минус бесконечности с обеих сторон, таким образом, функция имеет глобальный максимум

Теорема Виета для уравнения четвертой степени

Корни уравнения четвертой степени связаны с коэффициентами следующим образом:

История

Уравнения четвёртой степени впервые были рассмотрены древнеиндийскими математиками между IV в. до н. э. и II в. н. э.

Лодовико Феррари приписывается получение решения уравнения четвёртой степени в 1540, но его работа опиралась на решение кубического уравнения, которого у него не было, поэтому сразу это решение не было опубликовано,^[1] а было опубликовано только в 1545 вместе с решением кубического уравнения наставника Феррари — Джероламо Кардано в книге «Великое искусство»^[2].

То, что это наибольшая степень уравнения, для которого можно указать общую формулу решения было доказано в теореме Абеля — Руффини в 1824. Записки, оставленные Галуа до смерти на дуэли, позже привели к элегантной теории корней многочленов, одним из результатов которой была эта теорема.^[3]

Решения

Решение Декарта — Эйлера

В уравнение четвёртой степени:

Сделаем подстановку , получим уравнение в следующем виде (оно называется «неполным»):

где

Корни такого уравнения равны одному из следующих выражений:

в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:

причём  — это корни кубического уравнения

Решение Феррари

Если уравнение 4-й степени вида , то решение может быть найдено по методу Феррари. Если  — произвольный корень кубического уравнения

(2)

(резольвенты основного уравнения), то четыре корня исходного уравнения находятся как корни двух квадратных уравнений

где подкоренное выражение в правой части является полным квадратом.

См. также

Примечания

Литература

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — Наука, 2003. — 832 с. — 5000 экз. — ISBN 5-8114-0485-9

Ссылки

42

42. РЕШЕНИЕ УРАВНЕНИЯ 4-ой СТЕПЕНИ

Тип игры:                             граф

Класс:                                   8, 9

Тема:                                     Уравнения, приводящиеся к квадратным

Комментарий. Эта игра интересна тем, что важными и полезными являются различные пути получения результата. Это как раз пример на воплощение дидактической идеи – процесс важнее результата.

Кроме обычной организации игры с разбивкой учащихся на группы, идущие различными путями, можно предложить и фронтальный вариант, в котором учитель показывает и комментирует различные этапы решения. Разумеется, при этом ослабляется игровой характер задания, не появляется возможность в деятельностной форме ознакомить учащихся с несколькими важными алгебраическими идеями.

Тип игры: граф (выбор пути решения).

Дано уравнение x(x + 1)(x + 2)(x + 3) = 360.

Шаг 1

Выберите один из возможных способов преобразования уравнения.

1. Перемножить сомножители в левой части.

2. Сгруппировать сомножители по два.

3. Использовать симметрию множителей и сделать замену .

4. Воспользоваться известным тождеством для преобразования произведения четырех подряд идущих целых чисел.

 

Реакция на выбор способа преобразования

1. Этот способ самый прямой, однако не ясно, приведет ли он к цели. Тем не менее, попробуйте перемножить и получить уравнение 4-ой степени вида x⁴ + ax³ + bx² + cx + d = 0.

Закончив вычисления, перейдите к шагу 2.

Сверьте свои вычисления с правильным ответом.

Шаг 2

x⁴ + 6x³ + 11x² + 6x – 360 = 0

Выберите один из двух известных вам типов решения уравнения 4-ой степени.

1.1. Приведение к биквадратному уравнению с помощью удачной замены неизвестного.

1.2. Приведение к возвратному уравнению, используя симметрию коэффициентов.

 

Реакция на второй шаг

1.1. Это хороший путь. Чтобы подобрать замену, советуем выделить полный квадрат, используя первые два слагаемых.

Предлагайте выкладки, подберите необходимую замену и сверьте с ответом.

 

Шаг 3

1.1.1. У вас должно получиться следующее уравнение:

(x² + 3x)² + 2(x² + 3x) –360 = 0.

Теперь замена ясна. Обозначьте новое неизвестное через

y и сверьте ответ.

 

Шаг 4

y² + 2y – 360 = 0

Решите это квадратное уравнение и запишите два его корня: y₁ = (–20), y₂ = (18).

Реакция: верно – неверно.

Для каждого найденного значения y решите уравнение x² + 3x = y. До записи ответа укажите число корней.

 

Шаг 5

Уравнение имеет (2) корня.

Запишите ответ.

 

Шаг 6

x₁ = (–6), x₂ = (3)

 

1.2. Этот путь хороший, но нелегкий. Мешает свободный член – 360. Советуем продолжить путь обычным образом – поделить на x² и заменить . Не пугайтесь того, то x не исчезнет – останется слагаемое вида .

Сверьте с правильным ответом.

 

Шаг 2

Слева и справа стоят полные квадраты. Воспользуйтесь этим, извлеките корни из обеих частей и перейдите к следующему шагу.

 

Шаг 3

Проверьте себя, что вы не забыли извлечь корень с двумя знаками и получить два уравнения:  и .

Вернитесь к неизвестному x и получите два квадратных уравнения.

 

Шаг 4

x² + 3x + 20 = 0

x² + 3x – 18 = 0

До записи ответа укажите число корней исходного уравнения.

Шаги 5 и 6 совпадают с этими шагами в пути 1.1.

 

2. Этот путь самый естественный. Решите, какие пары множителей вы будете объединять.

Шаг 2

Первый и второй		Неудачно, попробуйте другой способ
Третий и четвертый
Первый и третий
Второй и четвертый

 

Первый и четвертый		Это удачный способ, подсказанный соображениями симметрии. Сверьте ответ
Второй и третий

 

Шаг 3

(x² + 3x)(x² + 3x + 2) = 360

Сделайте замену.

2.1. y = (x² + 3x)

2.2. y = (x² + 3x + 1)

2.1. Эта замена естественная, хотя и не самая лучшая. Лучше было бы заменить x² + 3x + 1 = y. Продолжите свой способ и получите квадратное уравнение относительно y.

 

Шаг 4

Совпадает с шагом 4 в 1.1 и дальше до конца.

 

2.2. Это очень толково. Сразу замечаете симметрию. Сверьте уравнение.

 

Шаг 4

y² – 1 = 360; y² = 361

До записи окончательного ответа укажите число корней исходного уравнения.

 

Шаг 5

как в 1.1

 

3. Это способ наиболее короткий. Сверьте запись получающегося биквадратного уравнения.

 

Шаг 2

Запишите квадратное уравнение относительно z² = y.

 

Шаг 3

Решите это квадратное уравнение. Сверьте корни.

 

Шаг 4

,

Вспомните, что y = z².

До записи ответа найдите число корней исходного уравнения.

 

Шаг 5 и далее – тот же, что и в 1.1

 

4. Этот способ хорош, если вы действительно помните тождество x(x + 1)(x + 2)(x + 3) + 1 = (x² + ___x + ___)²

Сверьте ответ.

 

Шаг 2

x(x + 1)(x + 2)(x + 3) + 1 = (x

² + 3x + 1)²

Извлеките корень и перейдите к двум уравнениям относительно x.

Сверьте ответ.

 

Шаг 3

x² + 3x + 1 = –19

x² + 3x + 1 = +19

До записи окончательного ответа укажите число корней исходного уравнения.

 

Шаг 4 = Шаг 5 в 1.1

 

________________________

 

Граф

 

 

Уравнение шестой степени — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 марта 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 марта 2019; проверки требует 1 правка.

Уравне́ние шесто́й сте́пени — алгебраическое уравнение, имеющее максимальную степень 6. В общем виде может быть записано следующим образом:

ax6+bx5+cx4+dx3+ex2+fx+g=0,a≠0.{\displaystyle ax^{6}+bx^{5}+cx^{4}+dx^{3}+ex^{2}+fx+g=0,\quad a\neq 0.}

Несмотря на то, что некоторые частные формы этого уравнения, например, триквадратное или бикубическое, можно решить графически или методом разложения на множители, общее аналитическое решение этого уравнения неизвестно. Из теоремы Абеля — Руффини следует, что в общем виде уравнение 6-й степени не может быть разрешено в радикалах.

Попытка построения общей теории решения уравнения шестой степени впервые была предпринята в 1886 году Фрэнком Коулом^[1]. За восемь лет до этого были предложены алгоритмы решения уравнений пятой степени, и работа Коула пыталась обобщить развитые методы и на уравнение шестой степени.

В основе теории уравнений степени ниже пятой лежат определённые группы линейных преобразований одной переменной, соответствующих группам Галуа исходного уравнения. Такая группа преобразований для уравнения пятой степени соответствует 60 операциям знакопеременной группы A5{\displaystyle A_{5}}. Для уравнения шестой степени такая группа преобразований должна соответствовать уже 360 операциям знакопеременной группы A6{\displaystyle A_{6}}, которые могут быть представлены в виде следующего уравнения:

z′=αz+βγz+δ{\displaystyle z’={\frac {\alpha z+\beta }{\gamma z+\delta }}}

здесь z — это целое число, конгруэнтное 0, 1, 2, 3, 4, 5 или ∞ mod 6{\displaystyle \infty \ \mathrm {mod} \ 6}. При определённом выборе параметров α, β, γ, δ число z’ также будет целым. Можно показать, что существует ровно 360 таких наборов параметров. Феликс Клейн показал, что конечных групп линейных трансформаций одной переменной, удовлетворяющих вышеприведённым условиям, не существует. Число переменных должно быть не меньше трёх в общем случае и не меньше четырёх, если линейные преобразования записаны в однородной форме. Эти особенности приводят к тому, что на практике использование алгоритмов нахождения решения уравнения шестой степени нецелесообразно^[2].

Триквадратное уравнение[править | править код]

Триквадратное уравнение — это алгебраическое уравнение вида

x6+ax3+b=0{\displaystyle x^{6}+ax^{3}+b=0}

Заменой t=x3{\displaystyle t=x^{3}} оно сводится к квадратному уравнению

t2+at+b=0{\displaystyle t^{2}+at+b=0}

Бикубическое уравнение[править | править код]

Бикубическое уравнение — это алгебраическое уравнение вида

x6+ax4+bx2+c=0{\displaystyle x^{6}+ax^{4}+bx^{2}+c=0}

Заменой t=x2{\displaystyle t=x^{2}} оно сводится к кубическому уравнению

t3+at2+bt+c=0{\displaystyle t^{3}+at^{2}+bt+c=0}