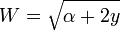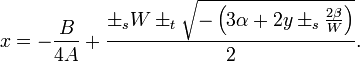5. Уравнения третьей и четвёртой степени
Заадача№1
Решить уравнение третьей степени по формуле Кардано:
x3-3x2-3x-1=0.
Решение :Приведём уравнение к виду , не содержащему второй степени неизвестного. Для этого воспользуемся формулой
x
= y
– ,
где а коэффициент при x2.
,
где а коэффициент при x2.
Имеем : x=y+1.
(y+1)3-3(y+1)2-3(y+1)-1=0.
Раскрыв скобки и приведя подобные члены ,получим:
y3— 6y-6=0.
Для корней кубического уравнения y 3+py+q=0 имеется формула Кардано:
yi= (i=1,2,3,),где
(i=1,2,3,),где 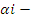
 ,
, =
= .
.
Пусть α1 –одно /любое/ значение радикала α. Тогда два других значения находятся следующим образом:
α2=
α1ε1
, α3=
α1ε2, где ε1= 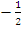 + i
+ i ,
ε2=
,
ε2=  – i
– i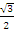 — корень третьей степени из единицы.
— корень третьей степени из единицы.
Если
положить β1=
–  ,
то получим β2=
β1ε2, β3=
β1ε1
,
то получим β2=
β1ε2, β3=
β1ε1
Подставляя полученные значение в формулу yi = αi+βi,найдём корни уравнения
yi+py+q =0:
y1= α1+β1,
y2=
-1/2(α1+β1)
+ i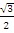 (
α1-β1),
(
α1-β1),
y3=
-1/2(α1+β1)
– i (
α1-β1),
(
α1-β1),
В нашем случае p = -6, q= — 6.
α= 

Одно
из значений этого радикала равно  .
Поэтому положим α1=
.
Поэтому положим α1= .
Тогда β1=
–
.
Тогда β1=
–  = –
= –  =
= ,
,
y1= ,
,
y2= ) + i
) + i ),
),
y2= ) – i
) – i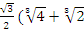 ).
).
Наконец, находим значение x по формуле x = y+1.
x1=
x2= ) + i
) + i ) + 1,
) + 1,
x3= 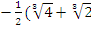 ) – i
) – i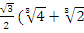
Задача№2
Решить способом Феррари уравнение четвёртой степени :
x4-4x3+2x2-4x+1=0.
Решение: Перенесём три последних члена в правую часть и оставшиеся два члена дополним до полного квадрата .
x4-4x3=-2x2+4x-1,
x4-4x3+4x2=4x2-2x2+4x-1,
(x2-2x)2=2x2+4x-1.
Введём новое неизвестное следующим образом:
(x2-2x+ )2=2x2+4x-1+(x2-2x)y+
)2=2x2+4x-1+(x2-2x)y+ ,
,
(x2-2x+ )2=(2+y)x2+(4-2y)x+(
)2=(2+y)x2+(4-2y)x+(  )
/1/.
)
/1/.
Подберём
y
так, чтобы и правая часть равенства была
полным квадратом .Это будет тогда ,когда
B2-4AC=0,
где A=2+y,
B=4-2y,
C= 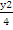 -1.
-1.
Имеем:B2-4AC=16-16y+4y2-y3-2y2+4y+8=0
Или y3-2y2+12y-24=0.
Мы получили кубическую резольвенту ,одним из корней которой является y=2. Подставим полученное значение y=2 в /1/,
Получим (x2-2x+1)2=4x2.Откуда (x2-2x+1)2-(2x)2=0 или (x2-2x+1-2x) (x2-2x+1+2x)=0.
Мы получим два квадратных уравнения:
x2-4x+1=0 и x2+1=0.
Решая их, находим корни первоначального уравнения:
x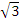 ,
x2=2+,
x3=-I,
x4=i.
,
x2=2+,
x3=-I,
x4=i.
6.Рациональные корни многочлена
Задача№1
Найти рациональные корни многочлена
f(x)=8x5-14x4-77x3+128×2+45x-18.
Решение :Для того, чтобы найти рациональные корни многочлена ,пользуемся следующими теоремами.
Теорема
1. Если
несократимая дробь  является
корнем многочлена f(x)
с целыми коэффициентами ,то p
есть делитель свободного члена, а q-
делитель старшего коэффициента многочлена
f(x).
является
корнем многочлена f(x)
с целыми коэффициентами ,то p
есть делитель свободного члена, а q-
делитель старшего коэффициента многочлена
f(x).
Замечание: Теорема
1 даёт необходимое условие для того,
чтобы рациональное число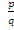 . Было корнем многочлена ,но этого условия
недостаточно , т.е. условие теоремы 1
может выполняться и для такой дроби
. Было корнем многочлена ,но этого условия
недостаточно , т.е. условие теоремы 1
может выполняться и для такой дроби  ,
которая не является корнем многочлена.
,
которая не является корнем многочлена.
Теорема
2: Если
несократимая дробь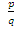 является корнем многочлена f(x)
с целыми коэффициентами, то при любом
целом m
,отличном от
является корнем многочлена f(x)
с целыми коэффициентами, то при любом
целом m
,отличном от  ,
число f(m)
делится на число p-qm,
т.е
,
число f(m)
делится на число p-qm,
т.е  целое число.
целое число.
В частности полагая m=1, а затем m=-1, получим:
если  корень многочлена, не равный ±1,то f(x)
корень многочлена, не равный ±1,то f(x) 
 —
целые числа.
—
целые числа. Замечание: Теорема
2 даёт ещё одно необходимое условие для
рациональных корней многочлена. Это
условие удобно тем, что оно легко
проверяется практически. Находим сначала
f(1)
и f(-1),
а затем для каждой испытываемой дроби
проверяем указанное условие. Если хотя
бы одно из чисел  дробное, то
дробное, то  корнем многочлена f(x)
не является.
корнем многочлена f(x)
не является.
Решение: По теореме 1 корни данного многочлена
следует искать среди несократимых
дробей, числители которых являются
делителями 18, а знаменателями 8.
Следовательно, если несократимая дробь  есть корень f(x),
то p
равно одному из чисел : ±1, ±2, ±3, ±6, ±9,
±18; q
равно одному из чисел
есть корень f(x),
то p
равно одному из чисел : ±1, ±2, ±3, ±6, ±9,
±18; q
равно одному из чисел
±1, ±2,±4, ±8.
Учитывая,
что  =
=  ,
, 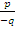 =
=  ,
знаменатели дробей будем брать лишь
положительными.
,
знаменатели дробей будем брать лишь
положительными.
Итак,
рациональными корнями данного многочлена
могут быть следующие числа: ±1, ±2, ±3, ±6,
±9, ±18, ± ,
±
,
±
 ,
±
,
± ,
±
,
± ,
±
,
± ,
±
,
± ,
±
,
± ,
±
,
± .
.
Воспользуемся вторым необходимым.
Так
как f(1)=72,
f(-1)=120,отсюда
в частности следует, что 1 и -1 не являются
корнями f(x).
Теперь для каждой возможной дроби  будем проверять условия теоремы 2 при
m=1
и m=-1,
т. е. будем устанавливать, целыми или
дробными являются числа :
будем проверять условия теоремы 2 при
m=1
и m=-1,
т. е. будем устанавливать, целыми или
дробными являются числа : 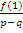 =
=  и
и 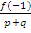 =
= 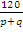
Результаты
сведём в таблицу, где буквы”ц” и “д”
означают соответственно, целым или
дробным является число  или
или 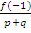
P | 2 | -2 | 3 | -3 | 6 | -6 | 9 | -9 | 18 | -18 | 1 | -1 | 3 | -3 | 9 | -9 | 1 | -1 | 3 | -3 | 9 | -9 | 1 | -1 | 3 | -3 | 9 | -9 |
Q | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 4 | 4 | 4 | 4 | 4 | 4 | 8 | 8 | 8 | 8 | 8 | 8 |
| ц | ц | ц | ц | д | д | ц | д | д | д | ц | ц | ц | д | д | д | ц | д | ц | д | д | д | д | ц | д | д | ц | д |
| ц | ц | ц | ц | ц | ц | ц | ц | ц | д | д | д |
Из
полученной таблицы видно, что  и
и  являются целыми лишь в тех случаях,
когда
являются целыми лишь в тех случаях,
когда равно одному из чисел: 2, -2, 3, -3,
равно одному из чисел: 2, -2, 3, -3,  ,
,  ,
,  ,
,  .
.
По
следствию из теоремы Безу число α- корень
f(x)
тогда и только тогда, когда f(x)  (x-α).
Следовательно, для проверки оставшихся
девяти целых чисел можно применить
схему Горнера деление многочлена на
двучлен.
(x-α).
Следовательно, для проверки оставшихся
девяти целых чисел можно применить
схему Горнера деление многочлена на
двучлен.
8 | -14 | -77 | 128 | 45 | -18 | |
2 | 8 | 2 | -73 | -18 | 9 | 0 |
2 | 8 | 18 | -37 | -92 | -172≠0 |
2 – корень.
Отсюда имеем : x=2 – простой корень f(x). Остальные корни данного многочлена совпадают с корнями многочлена.
F1(x) = 8x4+2x3-73x2-18x+9.
Аналогично проверим остальные числа.
8 | 2 | -73 | -18 | 9 | |
-2 | 6 | -14 | -45 | 72 | -139≠0 |
3 | 8 | 26 | 5 | -3 | 0 |
3 | 8 | 50 | 155 | 462≠0 | |
-3 | 8 | 2 | -1 | 0 | |
-3 | 8 | -22 | 65≠0 | ||
9 | 8 | 74 | 665≠0 | ||
½ | 8 | 6 | 2≠0 | ||
-1/2 | 8 | -2 | 0 | ||
-1/2 | 8 | 6≠0 | |||
3/2 | 8 | 10≠0 | |||
1/4 | 8 | 0 |
-2 – не корень, 3 – корень, -3 –корень, 9 – не корень, ½ — не корень , -1/2 –корень, 3/2 – не корень, ¼ — корень.
Итак, многочлен f(x)= 8x5-14x4-77x3+128x2+45x-18 имеет пять рациональных корней:{2, 3, -3, -1/2, ¼}.
studfile.net
§ 22. Решение уравнений третьей и четвертой степени
Проблема решения уравнений третьей и четвертой степени в радикалах не вызывалась особой практической необходимостью. Ее появление косвенным образом свидетельствовало о постепенном переходе математики к более высокому уровню ее развития, когда математическая наука развивается не только под влиянием запросов практики, но и в силу своей внутренней логики. После решения квадратных уравнений естественно было перейти к решению кубических уравнений.
Уравнения третьей и четвертой степени были решены в Италии в XVI в.
Итальянские математики рассматривали три вида кубических уравнений:
Рассмотрение
трех видов кубических уравнений вместо
одного 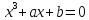 связано с тем, что, хотя математикиXVI
в. были знакомы с отрицательными числами,
но они еще долго не считались настоящими
числами, и ученые стремились записывать
уравнения только с положительными
коэффициентами.
связано с тем, что, хотя математикиXVI
в. были знакомы с отрицательными числами,
но они еще долго не считались настоящими
числами, и ученые стремились записывать
уравнения только с положительными
коэффициентами.
Исторически сложилось так, что сначала алгебраисты занялись уравнением первого типа
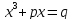 .
(1)
.
(1)
Первоначально его решил профессор Болонского университета Сципион дель Ферро, но полученное решение не опубликовал, а сообщил его своему ученику Фиоре. С помощью секрета решения этого уравнения Фиоре победил на нескольких математических турнирах. Тогда такие турниры были распространены в Италии. Заключались они в том, что два противника в присутствии нотариуса обменивались заранее обусловленным числом задач и договаривались о сроке для их решения. Победитель получал известность и нередко выгодную должность. В 1535 г. Фиоре вызвал на такой поединок любого, кто хочет с ним сразиться. Вызов принял Тарталья.
Никколо Тарталья (1500-1557) рано остался сиротой и вырос в бедности, не получив никакого образования. Тем не менее он был хорошо знаком с математикой того времени и зарабатывал себе на жизнь частными уроками математики. Незадолго до поединка с Фиоре он сумел самостоятельно решить уравнение (1). Поэтому когда противники встретились, Тарталья смог за несколько часов решить задачи Фиоре; все они оказались на уравнении (1). Что касается Фиоре, то он и за много дней не решил ни одной из 30 разнообразных задач Тартальи. Победителем турнира был признан Тарталья. Известие о его победе распространилось по всей Италии. Он стал заведовать кафедрой математики в университете города Вероны.
Метод
Тартальи заключался в следующем. Он
полагал в уравнении (1)  ,
гдеu
и v
– новые неизвестные. Получим:
,
гдеu
и v
– новые неизвестные. Получим:

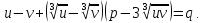
Положим
в последнем уравнении  .
Образуется система уравнений
.
Образуется система уравнений

которая сводится к квадратному уравнению. Из нее находим:
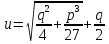 ,
, 
откуда
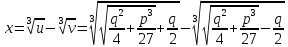 (2)
(2)
Вскоре
после турнира Тарталья легко решил
кубические уравнения второго и третьего
типа. Например, для уравнения второго
типа  он применил подстановку
он применил подстановку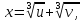 которая привела к формуле
которая привела к формуле
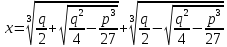 (3)
(3)
Известие об успехи Тартальи дошло до Кардано. Джироламо Кардано (1501-1576) окончил медицинский факультет университета в Павии и был врачом в Милане. Он являлся ученым, не менее талантливым, чем Тарталья, и гораздо более разносторонним: он занимался медициной, математикой, философией и астрологией. Кардано задумал написать книгу энциклопедического характера по алгебре, и она была бы неполна без решения кубических уравнений. Он обратился к Тарталье с просьбой сообщить его способ решения этих уравнений. Тарталья не соглашался, и тогда Кардано поклялся на Евангелии никому не сообщать секрета решения кубических уравнений. По-видимому, Тарталья собирался сам написать книгу по алгебре, включив в нее и свое открытие, но из-за занятости и из-за того, что издание было делом дорогостоящим, откладывал свое намерение. В конце концов в 1545 г. Кардано выпустил свою монографию под названием «Великое искусство», в которую вошло и открытие «моего друга Тартальи». Тарталья был разгневан нарушением клятвы и выступил в печати с разоблачением Кардано. Кончилось тем, что лучший ученик Кардано вызвал Тарталью на публичный поединок. Поединок состоялся в 1548 г. в Милане и закончился, при не вполне ясных обстоятельствах, поражением Тартальи. Формулы корней кубического уравнения получили в истории название формул Кардано, хотя сам Кардано в своей книге и не приводил формул, а излагал алгоритм решения кубического уравнения.
Книга Кардано «Великое искусство» сыграло значительную роль в истории алгебры. В частности, в ней он доказал, что полное уравнение третье степени с помощью подстановки сводится к уравнению без члена с квадратом неизвестного, т.е. к одному из трех видов кубических уравнений, рассмотренных в начале параграфа. Осовременивая изложение, возьмем кубическое уравнение общего вида

с произвольными по знаку коэффициентами вместо тех нескольких типов кубических уравнений, которыми занимался Кардано, и положим в нем

Тогда
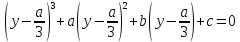 .
.
Нетрудно
проверить, что последнее уравнение не
содержит члена с квадратом неизвестного,
так как сумма членов, содержащих  равна нулю:
равна нулю:
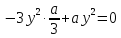 .
.
Аналогично Кардано доказал, что в полном уравнении четвертой степени можно избавиться от члена с кубом неизвестного. Для этого в уравнении четвертой степени общего вида

достаточно
положить 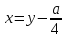 .
.
Позднее
Ф. Виет знакомое нам кубическое уравнение  решил с помощью остроумной подставки
решил с помощью остроумной подставки Будем иметь:
Будем иметь:

 .
.
Положим
в последнем уравнении  .
Из полученного квадратного уравнения
находимt;
затем вычислим
.
Из полученного квадратного уравнения
находимt;
затем вычислим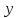 и, наконец,
и, наконец,
Уравнение четвертой степени решил Феррари. Он решал его на примере
 (4)
(4)
(без члена с кубом неизвестного), но вполне общим способом.
Прибавим
к обеим частям уравнения (4)  ,
с тем, чтобы дополнить левую часть до
квадрата суммы:
,
с тем, чтобы дополнить левую часть до
квадрата суммы:
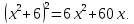
Теперь прибавим к обеим частям последнего уравнения сумму
где t – новое неизвестное:

 (5)
(5)
Так
как левая часть уравнения (5) есть квадрат
суммы, то и правая часть есть квадрат,
а тогда дискриминант квадратного
трехчлена равен нулю: 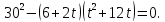 Впрочем, вXVI
в. это уравнение писали в виде
Впрочем, вXVI
в. это уравнение писали в виде
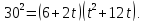 (6)
(6)
Уравнение (6) является кубическим. Найдем из него t уже знакомым способом, подставим это значение t в уравнение (5) и извлечем из обеих частей полученного уравнения квадратный корень. Образуется квадратное уравнение(точнее, два квадратных уравнения).
Приведенный здесь способ решения уравнения четвертой степени вошел в книгу Кардано.
По воззрениям того времени, правило решения кубического уравнения второго типа по формуле (3) нельзя применять в том случае, когда
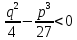 ;
c
современной точки зрения, в этом случае
приходится проводить операции над
мнимыми числами. Например, уравнение
;
c
современной точки зрения, в этом случае
приходится проводить операции над
мнимыми числами. Например, уравнение
 имеет
действительный корень
имеет
действительный корень  ;
кроме того, оно имеет еще два действительных
(иррациональных) корня. Но по формуле
(3) получаем:
;
кроме того, оно имеет еще два действительных
(иррациональных) корня. Но по формуле
(3) получаем:
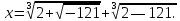
Каким образом из мнимых («воображаемых», как тогда говорили) чисел получается действительное число? Это случай кубического уравнения получил название неприводимого.
Подробно
неприводимый случай разобрал итальянский
математик Рафаэль Бомбелли в книге
«Алгебра», изданной в 1572 г. В формуле
(3) он объяснил эту ситуацию тем, что
первый кубический корень равен  а второй –a-bi
(где a
и b-
действительные числа, t-мнимая
единица), так что их сумма дает
а второй –a-bi
(где a
и b-
действительные числа, t-мнимая
единица), так что их сумма дает
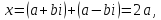
т.е. действительное число.
Бомбелли привел правила действий над комплексными числами.
После выхода книги Бомбелли математикам постепенно становится ясно, что в алгебре без комплексных чисел не обойтись.
studfile.net
РЕШЕНИЕ УРАВНЕНИЙ ЧЕТВЕРТОЙ СТЕПЕНИ СПОСОБОМ ДЕКАРТА-ЭЙЛЕРА
РЕШЕНИЕ УРАВНЕНИЙ ЧЕТВЕРТОЙ СТЕПЕНИ СПОСОБОМ ДЕКАРТА-ЭЙЛЕРА
Фомин Александр Владимирович
студент 2 курса, отделение информационных технологий, Колледж электроники и бизнеса ОГУ, РФ, г. Оренбург
E-mail: f
Нурманова Сабиля Андреевна
научный руководитель, преподаватель I кв. категории предметно-цикловой комиссии физико-математических дисциплин, Колледж электроники и бизнеса ОГУ, РФ, г. Оренбург
Решение уравнений четвертой степени способом Декарта-Эйлера.
Рассмотрим неполное уравнение четвертой степени
х4 + рх2+ qx + r = 0 (1)
с произвольными комплексными коэффициентами р, q, r.
Пусть х1, х2, x3,х4 — его корни. По формулам Виета,
х1 + х2 + x3 + х4 = 0,
х1 х2 + х1 х3 + х1 х4 + х2 х3 + х2 х4 + х3 х4 = p (2)
х2х3х4 + х1х3х4 + х1х2х4 + х1х2х3 = – q,
х1х2х3х4 = r.
Числа х1х2 + х3х4 , х1х3 + х2 х4 и х1х4 + х2х3 являются корнями кубического уравнения
х3 – px2 – 4rx + (4pr – q2) = 0 (3)
Заметим, что
х1х2 + х3х4 = 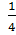 (х1 + х2 – x3 – х4)2 –
(х1 + х2 – x3 – х4)2 –  (х1 + х2 + x3 + х4)2 + (х1х2 + х1 х3 + х1 х4 +
(х1 + х2 + x3 + х4)2 + (х1х2 + х1 х3 + х1 х4 +
+ х2 х3 + х2 х4 + х3 х4) =  (х1 + х2 – x3 – х4)2 + p.
(х1 + х2 – x3 – х4)2 + p.
Аналогично
х1х3 + х2 х4 =  (х1 – х2 + x3 – х4)2 + p,
(х1 – х2 + x3 – х4)2 + p,
х1х4 + х2 х3 =  (х1 – х2 – x3 + х4)2 + p.
(х1 – х2 – x3 + х4)2 + p.
Поэтому, если мы сделаем в уравнении (3) замену х = у + р, то полученное уравнение
у3 + 2 pу2+ (p2— 4r)у — q2 = 0 (4)
будет иметь своими корнями числа
y 1 =  (х1 + х2 – x3 – х4)2,
(х1 + х2 – x3 – х4)2,
y 2 =  (х1 – х2 + x3 – х4)2, (5)
(х1 – х2 + x3 – х4)2, (5)
y 3 =  (х1 – х2 – x3 + х4)2.
(х1 – х2 – x3 + х4)2.
Из формул (5) получаем, что
 (х1 + х2 – x3 – х4)2 = u1,
(х1 + х2 – x3 – х4)2 = u1,
 (х1 – х2 + x3 – х4)2 = u2, (6)
(х1 – х2 + x3 – х4)2 = u2, (6)
 (х1 – х2 – x3 + х4)2 = u3,
(х1 – х2 – x3 + х4)2 = u3,
где u1, u2, u3 — квадратные корни из y1, y2, y3.
Поскольку квадратный корень из комплексного числа имеет два значения, необходимо уточнить, какие значения квадратных корней следует взять в формулах (7).
Пусть дано тождество
(х1 + х2 – x3 – х4) (х1 – х2 + x3 – х4) (х1 – х2 – x3 + х4) = 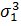 – 4 σ 1 σ 2 + 8 σ 3,
– 4 σ 1 σ 2 + 8 σ 3,
где ơ1, ơ2, ơ3 — элементарные симметрические многочлены от х1, х2, х3, х4. Для корней уравнения (1) имеем, в силу формул (2):
(х1 + х2 – x3 – х4) (х1 – х2 + x3 – х4) (х1 – х2 – x3 + х4) = 8q.
Отсюда следует, что
u1, u2, u3 = – q. (7)
Условие (7) оставляет четыре из восьми вариантов выбора значений квадратных корней из y1, y2, у3. Любой из этих четырех вариантов допустим, так как, перенумеровав подходящим образом х1, х2, х3, х4, можно умножить на (– 1) любые два из выражений х1 + х2 – x3 – х4, х1 – х2 + x3 – х4, х1 – х2 – x3 + х4, не изменив третьего. Например, если поменять номера у х1 и х2 и одновременно у х3 и х4, то выражение х1 + х2 – x3 – х4 не изменится, в то время как остальные два умножатся на (– 1). Складывая равенства (6) и равенство х1 + х2 + x3 + х4 = 0, находим: x1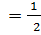 (u1 + u2 – u3).
(u1 + u2 – u3).
Аналогично находим:
x 2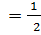 (u1 – u2 – u3),
(u1 – u2 – u3),
x 3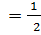 (– u1 + u2 – u3),
(– u1 + u2 – u3),
x 4 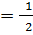 (– u1 – u2 + u3).
(– u1 – u2 + u3).
Эти формулы можно объединить в одну:
x = 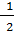 (
(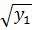 +
+  +
+ 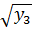 ), (8)
), (8)
которую следует понимать таким образом, что значения квадратных корней выбираются всеми возможными способами, лишь бы их произведение равнялось (– q).
Подставляя полученную формулу в выражения для корней кубического уравнения (3), найденные при помощи формулы Кардано, можно получить явную формулу, выражающую корни уравнения (1) через его коэффициенты, которая, однако, столь громоздка, что выписывать ее не имеет смысла.
Пример. Решите уравнение на множестве действительных чисел
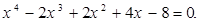
Решение. Поставим задачу привести это уравнение к виду

Для этого воспользуемся подстановкой  получим:
получим:
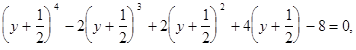
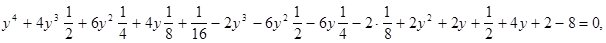

 , откуда находим
, откуда находим 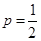 ,
, 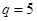 ,
,  .
.
 ,
,
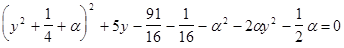
или
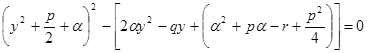
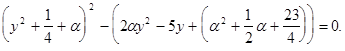
Подберем 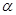 так, чтобы квадратный трехчлен, стоящий в скобках, стал полным квадратом, чтобы затем получить разность квадратов двух выражений.
так, чтобы квадратный трехчлен, стоящий в скобках, стал полным квадратом, чтобы затем получить разность квадратов двух выражений.
Для этого его дискриминант должен быть равен нулю
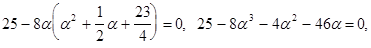

Мы получили кубическое уравнение относительно 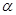 . Решение кубических уравнений по формуле Кардано нам уже известно.
. Решение кубических уравнений по формуле Кардано нам уже известно.
Положим 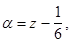 тогда кубическое уравнение примет вид:
тогда кубическое уравнение примет вид:
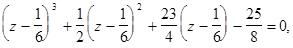
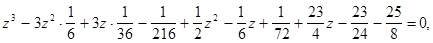
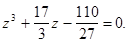

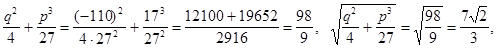
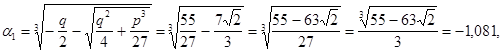


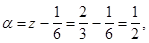
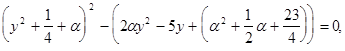
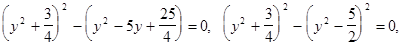
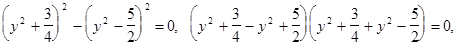
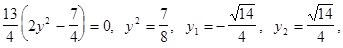
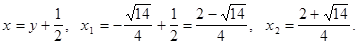
Ответ: 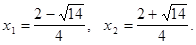
Список литературы:
1.Винберг Э.Б. Алгебра многочленов: учебное пособие для студентов заочников III—IV курсов физико-математических факультетов педагогических институтов. М.: Просвещение, 1980. — 175 с.
2.Курош А.Г. Алгебраические уравнения произвольных степеней. М.: Наука, 1975. — 34 с.
3.Мишина А.П, Проскуряков И.А. Высшая алгебра. Линейная алгебра, многочлены, общая алгебра. М.: Наука, 1980. — 563 с.
4.Сушкевич А.К. Основы высшей алгебры. М.: ОГИЗ, 1941. — 462 с.
5.Туманов С.И. Поиски решения задачи. М.: Просвещение, 1969. — 275 с.
6.Тишин В.И. Математика для учителей и учащихся: рациональные алгебраические уравнения. М.: Комаричи, 2002. — 166 с.
sibac.info
Вывод формул решения алгебраического уравнения четвёртой степени.
Вывод формул решения алгебраического уравнения четвёртой степени.1. Приведение уравнения к каноническому виду.
Сделаем замену переменного по формуле:Получим уравнение:
Раскроем скобки:
Получим уравнение:
Уравнение приведено к каноническому виду:
2. Решение уравнения
Способ №1.
Решение при помощи разложения на два квадратных уравнения
Рассмотрим случай, когда q не равно нулю.Верно тождество:
Поэтому:
Получили уравнение:
Выберем параметр z так, чтобы правая часть этого уравнения была полным квадратом относительно y. Для этого необходимо и достаточно, чтобы дискриминант из коэффициентов трехчлена относительно y, стоящего справа, обращался в нуль:
Мы получили кубическое уравнение.
Вывод формул кубичекого уравнения.
Если z — один из корней кубического уравнения:
то уравнение
запишется в виде:
Отсюда следует:
Необходимо решить два квадратных уравнения:
Получаем четыре корня:
Корни этих квадратных уравнений y1, y2, y3, y4 являются решением исходного уравнения
Рассмотрим случай, когда q=0
Уравнение
имеет четыре корня:
Способ №2.
Решение Декарта-Эйлера.
Обоснование этого способа решения уравнения четвёртой степени находится в стадии разработки.
Эта программа находит четыре корня уравнения четвёртой степени двумя способами
Способ №1.
Решение при помощи разложения на два квадратных уравнения
Если q не равно нулю, то кубическое уравнениевсегда имеет положительный действительный корень, так как при z=0 значение многочлена в левой части уравнения отрицательно: -q^2/8, а при стремлении z к плюс бесконечности значение многочлена в левой части уравнения также стремится к плюс бесконечности, то есть становится положительным при некотором положительном z=M, и так как непрерывная на отрезке [0; M] функция принимает на интервале (0; M) любое промежуточное, в том числе и нулевое, значение, то существует положительный корень этого кубического уравнения. Таким положительным корнем является либо первый корень в программе решения кубического уравнения, где под знаком косинуса стоит аргумент F/3, так как Cos(F/3)≥0 при 0≤F≤3/2*Pi, если кубическое уравнение имеет три различных действительных корня, либо единственный действительный корень этого кубического уравнения.
Если какой-то из действительных корней кубического уравнения принимает нулевое значение, то решается биквадратное уравнение
Способ №2.
Решение Декарта-Эйлера.
После приведения алгебраического уравнения четвёртой степени к каноническому виду программа находит три корня кубического уравненияЕсли это кубическое уравнение имеет три действительных положительных корня, то уравнение четвёртой степени имеет четыре действительных корня.
Если это кубическое уравнение имеет три действительных корня, один положительный и два отрицательных, то уравнение четвёртой степени имеет две пары комплексно-сопряжённых корней.
Если это кубическое уравнение имеет один положительный действительный корень и два комплексно сопряжённые корня, то уравнение четвёртой степени имеет два действительных и два комплексно-сопряжённых корня. Программа на javascript «Решение уравнения четвёртой степени Ax4+Bx3+Cx2+Dx+E=0» Программа «Решение уравнения четвёртой степени Ax4+Bx3+Cx2+Dx+E=0». Код программы «Решение уравнения четвёртой степени Ax4+Bx3+Cx2+Dx+E=0» Вывод корней кубического уравнения. На главную страницу.
ateist.spb.ru
Уравнения 4 степени с помощью решателя онлайн
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Решения данного рода уравнений можно выполнять по общей схеме решения уравнений высших степеней. Данного рода уравнения имеют решения в радикалах благодаря методу Феррари, позволяющему свести решения к кубическому уравнению. Однако в большинстве случаев с помощью разложения многочлена на множители удается быстро найти решение уравнения.

Так же читайте нашу статью «Решить уравнения онлайн по алгебре решателем»
Допустим, дано двучленное уравнение четвертой степени:
\[4x^4 + 1 = 0\]
Выполним разложение \[4x^4+1\] на множители многочлена:
\[4x^4+1=4x^4+4x^2-4x^2+1=(2x^2+1)^2-4x^2=(2x^2-2x+1)(2x^2+2x+1)\]
Определяем корни первого квадратного трехчлена:
\[2x^2-2x+1=0\]
\[D=(-2)^2-4 \cdot2 \cdot1=-4\]
\[x_1= \frac{2+ \sqrt D}{2 \cdot 2}=\frac{1}{2} +i\]
\[x_2=\frac{2- \sqrt D}{2 \cdot 2}=\frac{1}{2} -i\]
Определяем корни второго трехчлена:
\[2x^2+2x+1=0\]
\[D=2^2-4\cdot2\cdot1=-4\]
\[x_3= \frac{-2+ \sqrt D}{2 \cdot 2}=-\frac{1}{2} +i\]
\[x_4= \frac{-2- \sqrt D}{2 \cdot 2}=-\frac{1}{2} -i\]
В результате, исходное уравнение имеет четыре комплексных корня:
\[x=\frac{1}{2}\pm i\]
\[x=-\frac{1}{2}\pm i\]
Где можно решить уравнения 4 степени онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте.А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
www.pocketteacher.ru
Уравнения четвертой степени — Уравнения — Математика — Каталог статей
Уравнения четвертой степени
Метод решения уравнений четвертой степени нашел в XVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется – метод Феррари.
Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени
x4+px³ +qx²+ix+s = 0
можно избавиться от члена px³ подстановкой x = y-p/4 . Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:
. x4ax²+bx+c = 0
Идея Феррари состояла в том, чтобы представить уравнение в виде A² = B² , где левая часть – квадрат выражения A = x² + s, а правая часть – квадрат линейного уравнения B от X, коэффициенты которого зависят от S . После этого останется решить два квадратных уравнения: A= Bи A =-B и . Конечно, такое представление возможно только при специальном выборе параметра s. Удобно взять s в виде a/2+p, тогда уравнение перепишется так:
. (15)
Правая часть этого уравнения – квадратный трехчлен от x. Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е.
, или
b² = 2t(4t² + a² -4c)
Это уравнение называется резольвентным (т.е. «разрешающим»). Относительно t оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень t0. При t = t0 правая часть уравнения (15) принимает вид
,
а само уравнение сводится к двум квадратным:
.
Их корни и дают все решения исходного уравнения.
Решим для примера уравнение
.x4-10x²+8x+5=0
Здесь удобнее будет воспользоваться не готовыми формулами, а самой идеей решения. Перепишем уравнение в виде
x4-10x²+8x-5
и добавим к обеим частям выражение 2sx²+s², чтобы в левой части образовался полный квадрат:
.(x²+s)² = (10+2s)·x²+8x+s²-5
Теперь приравняем к нулю дискриминант правой части уравнения: 16-(10-2s)·(s²-5) =0
или, после упрощения,
.s³+5s²-5s-33=0
Один из корней полученного уравнения можно угадать, перебрав делители свободного члена: s0 = -3. После подстановки этого значения получим уравнение
(x²-3)² = 4x²+8x+4 = 4·(x+1)²,
откуда x²-3 = ±2·(x+1). Корни образовавшихся квадратных уравнений — и . Разумеется, в общем случае могут получиться и комплексные корни.
alexlat.ucoz.ru
Уравнение четвертой степени — это… Что такое Уравнение четвертой степени?
- Уравнение четвертой степени
Уравнение четвёртой степени — в математике алгебраическое уравнение вида:
 .
.Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любом значении коэффициентов).
Решения
Решение Декарта — Эйлера
Сделав подстановку
 , получим уравнение в следующем виде (он называется «неполным»):
, получим уравнение в следующем виде (он называется «неполным»):- y4 + py2 + qy + r = 0.
Корни y1, y2, y3, y4 такого уравнения равны одному из следующих выражений:
в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:
 ,
,
причём z1, z2 и z3 — это корни кубического уравнения
Решение Феррари
Основная статья: Метод Феррари
Представим уравнение четвёртой степени в виде:
- Ax4 + Bx3 + Cx2 + Dx + E = 0,
Его решение может быть найдено из следующих выражений:



- если β = 0, решив u4 + αu2 + γ = 0 и, сделав подстановку
 , найдём корни:
, найдём корни: .
.
- если β = 0, решив u4 + αu2 + γ = 0 и, сделав подстановку


 , (любой знак квадратного корня подойдёт)
, (любой знак квадратного корня подойдёт)![U = \sqrt[3]{R}](//xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) , (три комплексных корня, один из которых подойдёт)
, (три комплексных корня, один из которых подойдёт)![y = - {5 \over 6} \alpha +U + \begin{cases}U=0 &\to -\sqrt[3]{Q}\\U\ne 0 &\to -{P\over 3U}\end{cases},](//xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)


- Два ±s должны иметь одинаковый знак, ±t — независимы. Для того, чтобы найти все корни, надо найти x для знаковых комбинаций ±s,±t = +,+ для +,− для −,+ для −,−. Двойные корни появятся два раза, тройные корни — три раза и корни четвёртого порядка — четыре раза. Порядок корней зависит от того, какой из кубических корней U выбран.
См. также
Литература
- Корн Г., Корн Т. (1974) Справочник по математике.
Ссылки
Wikimedia Foundation. 2010.
- Уравнение состояния газа Ван-дер-Ваальса
- Уравнение третьей степени
Смотреть что такое «Уравнение четвертой степени» в других словарях:
уравнение четвертой степени — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN quartic equation … Справочник технического переводчика
Уравнение четвёртой степени — График многочлена 4 ой степени с четырьмя корнями и тремя критическими точками. Уравнение четвёртой степени в математике алгебраическое уравнение вида: Четвёртая степень для алгебраических уравнений является наивысшей, при которой… … Википедия
Возвратное уравнение четвёртой степени — Уравнение вида: anxn + an − 1xn − 1 + … + a1x + a0 = 0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, то есть если an − k = ak, при k = 0, 1, …, n. Содержание 1 Уравнение четвёртой степени … Википедия
БИКВАДРАТНОЕ УРАВНЕНИЕ — в котором неизвестный член в четвертой степени. Полный словарь иностранных слов, вошедших в употребление в русском языке. Попов М., 1907. БИКВАДРАТНОЕ УРАВНЕНИЕ от лат. bis, дважды, и quadratum, квадрат. Уравнение, в котором наибольшая степень… … Словарь иностранных слов русского языка
Алгебра — вместе с арифметикой есть наука о числах и через посредство чисел о величинах вообще. Не занимаясь изучением свойств каких нибудь определенных, конкретных величин, обе эти науки исследуют свойства отвлеченных величин как таковых, независимо от… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ПОЛЕТА ТЕОРИЯ И ПРАКТИКА — совокупность прикладных знаний, позволяющих авиационным инженерам на занятий в области аэродинамики, проблем прочности, двигателестроения и динамики полета летательных аппаратов (т.е. теории) создать новый летательный аппарат или улучшить… … Энциклопедия Кольера
МАТЕМАТИКИ ИСТОРИЯ — Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом… … Энциклопедия Кольера
Важнейшие открытия в физике — История технологий По периодам и регионам: Неолитическая революция Древние технологии Египта Наука и технологии древней Индии Наука и технологии древнего Китая Технологии Древней Греции Технологии Древнего Рима Технологии исламского мира… … Википедия
УРАВНЕНИЯ — Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений. Если равенство справедливо для любых допустимых значений входящих в него неизвестных, то оно называется тождеством; например, соотношение вида… … Энциклопедия Кольера
Теорема Абеля — Теорема Абеля Руффини утверждает, что общее уравнение степени при неразрешимо в радикалах. Содержание 1 Подробности … Википедия
dic.academic.ru

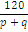

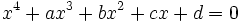 .
.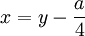 , получим уравнение в следующем виде (он называется «неполным»):
, получим уравнение в следующем виде (он называется «неполным»):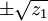
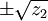
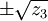
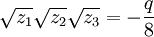 ,
,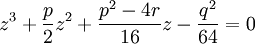
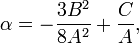
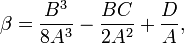
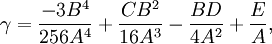
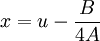 , найдём корни:
, найдём корни: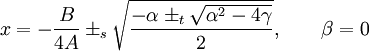 .
.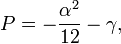
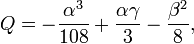
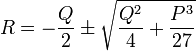 , (любой знак квадратного корня подойдёт)
, (любой знак квадратного корня подойдёт)![U = \sqrt[3]{R}](/800/600/https/dic.academic.ru/pictures/wiki/files/57/90034f31688ee818ff7c9ef96f161e26.png) , (три комплексных корня, один из которых подойдёт)
, (три комплексных корня, один из которых подойдёт)![y = - {5 \over 6} \alpha +U + \begin{cases}U=0 &\to -\sqrt[3]{Q}\\U\ne 0 &\to -{P\over 3U}\end{cases},](/800/600/https/dic.academic.ru/pictures/wiki/files/56/8c1e98c3bde7ff50520640bff29eb7c3.png)