| 1. |
Биквадратное уравнение
Сложность: лёгкое |
1 |
| 2. |
Дробное уравнение
Сложность: лёгкое |
1 |
3.
|
Дробное рациональное уравнение
Сложность: лёгкое |
1 |
| 4. |
Дробное уравнение, основное свойство пропорции
Сложность: среднее |
3 |
5.
|
Дробное уравнение, приведение к общему знаменателю
Сложность: среднее |
3 |
| 6. |
Дробное рациональное уравнение, область определения
Сложность: среднее |
3 |
7.
|
Введение новой переменной
Сложность: сложное |
3 |
| 8. |
Решение уравнения
Сложность: сложное |
3 |
9.
|
Произведение корней уравнения Сложность: сложное | 3 |
Конспект урока математики в 8 классе «Решение уравнений»
Рожкова Е.И.
Предмет: алгебра. 8 класс
Тема урока: «Решение задач с помощью квадратных уравнений»
Урок №1-3
Урок № 1
Тема урока: «Решение задач с помощью квадратных уравнений».
Цель урока:
— научиться решать задачи с помощью квадратных уравнений;
— закреплять навыки решения квадратных уравнений;
— развивать логическое мышление учащихся.
Задачи урока: Научить составлять уравнение по условию задачи, определять тип текстовой задачи, знать особенности алгоритма её решения.
Тип урока: Урок изучения нового материала.
Формы работы учащихся на уроке: Фронтальная, индивидуальная, парная.
Описание необходимого технического оборудования для проведения урока: Компьютер учителя,
интерактивная доска.
Структура и ход проведения урока:
1.Сообщение темы и цели урока.
2.Повторение и закрепление пройденного материала.
3.Изучение нового материала.
4.Задание на уроке.
5.Задание на дом.
6.Подведение итогов.
Ход урока:
1.Сообщение темы и цели урока.
Оргмомент: Приветствие, проверка готовности учеников к уроку.
На уроках математики вы действительно учитесь решать задачи, в том числе и при помощи составления уравнения. Уравнения у вас могут получиться самые разные, поэтому так важно умение решать любые уравнения.
В начале урока ученики устно отвечают на вопросы учителя:
— Вспомним, что мы изучили на предыдущих уроках алгебры? Какую тему? Чему научились?
(Ответы: Квадратные уравнения, научились их решать)
— Зачем нам нужно уметь решать уравнения? В чем нам эти знания могут пригодиться?
(Ответ: при решении задач)
— Как вы думаете, какой же будет тема сегодняшнего урока?
(Ответ: «Решение задач с помощью квадратных уравнений»).
Запишите сегодняшнее число и тему урока в тетради!
И так, тема нашего урока «Решение задач с помощью квадратных уравнений». Всякая хорошо решенная математическая задача доставляет умственное наслаждение. Эти слова Г. Гессе станут эпиграфом нашего урока. Надеюсь, что вы действительно получите удовольствие от результатов вашего труда на уроке.
2.Повторение и закрепление пройденного материала.
Сначала проверим, как вы усвоили пройденный материал.
Фронтальный опрос.
Вопросы задает учитель:
— Дать определение «Квадратного уравнения». Название его коэффициентов. Привести пример.
— Как решать квадратные уравнения? (по формуле корней квадратного уравнения)
— Что такое «Дискриминант» квадратного уравнения?
— Как он обозначается? Что означает это слово в переводе с латыни? (Д, «различитель»)
— Что же он различает? (Количество корней квадратного уравнения).
— Сформулируйте правило определения количества корней в квадратных уравнениях.
(Д>0, Д=0, Д<0).
— Напишите формулу корней квадратного уравнения! (На доске) (формула I)
— Напишите частный случай общей формулы. (формула II)
— Сделайте вывод: чем хороша каждая из этих формул?
Итак, мы повторили, как можно решить квадратное уравнение.
Сейчас я хотела бы проверить, как вы усвоили эти формулы и определения.
Ученики получают карточки с заданиями. Заполняют пропущенные слова в карточках.
1.Вариант
1.Уравнение вида , где a, b, c — заданные числа, a0, x — переменная,
называется…
2. Полное квадратное уравнение не имеет корней, если D . ..
..
3. Уравнение вида называется…
4. Квадратное уравнение имеет два корня, если…
5. Дано уравнение . D =…
2.Вариант
1. Если квадратное уравнение, то a… коэффициент, с…
2. Уравнение x² = a, где a < 0, не имеет…
3. Полное квадратное уравнение имеет единственный корень, если …
4. Уравнение вида ax² + c = 0, где a 0, c 0, называют … квадратным уравнением.
5. Дано уравнение x²- 6x + 8 = 0. D =…
Проводится взаимопроверка. Ответы показываем через интерактивную доску.
Важно отметить наиболее активных и успешно справившихся с заданием учеников.
3.Изучение нового материала.
Ребята! У меня возникла проблема. Я надеюсь, вы мне поможете. Мне необходимо обнести изгородью огородный участок, он имеет прямоугольную форму. Одна из сторон на 10 метров больше другой, площадь всего участка 1200. Сколько необходимо мне закупить материала? Возможно ли, решить задачу с помощью квадратного уравнения?
Решение задачи:
Выбираем наименьшую из сторон, обозначаем ее – х метров. Тогда большая сторона (х+10) метров. Знаем, что площадь всего участка 1200. Получаем уравнение:
х(х+10)=1200,
Раскроем скобки.
+10х=1200,
+10х-1200=0,
D=100+4800=4900,
==-40, ==30.
Корень уравнения равный -40 –не подходит, так как длина не может быть отрицательной величиной; =30 м – это длина наименьшей стороны изгороди. Значит х+30=40 м – наибольшая сторона изгороди, а длина всей изгороди, т.е. периметр участка, будет равен Р=2×(30+40)=140 метров. Следовательно, мне необходимо купить 140 метров материала для обнесения огородного участка изгородью.
Значит х+30=40 м – наибольшая сторона изгороди, а длина всей изгороди, т.е. периметр участка, будет равен Р=2×(30+40)=140 метров. Следовательно, мне необходимо купить 140 метров материала для обнесения огородного участка изгородью.
Ответ: 140 м.
С чего же нужно начинать решать задачи? Отвечают дети с помощью учителя.
1.Выбрать неизвестно.
2.Затем составить уравнение.
3.Решить его.
4. Сделать вывод о корнях.
5. Выполнить дополнительные действия.
Разбор (по учебнику) задачи №1 и №2.
4.Задание на уроке.
Задача № 559
Произведение двух натуральных чисел, одно из которых на 6 больше другого, равно 187. Найдите эти числа.
Решение: Пусть меньшее число х, тогда большее х+6. По условию произведение этих чисел равно 187.
По условию произведение этих чисел равно 187.
Получаем уравнение:
х(х+6)=187,
+6х=187,
+6х-187=0,
D=36+748=784,
==-17, ==11.
Корень =-17 –не подходит, поскольку не натуральное число. =11 – это наименьшее число, тогда х+6=11+6=17 – наибольшее число.
Ответ: 11,17
Задача № 563
Найдите катеты прямоугольного треугольника, если известно, что сумма равна 23 см, а площадь данного треугольника равна 60.
Решение: Пусть катеты треугольника равны, а см и б см. Сумма катетов по условию равна 23 см. т.е. а+б=23. Площадь треугольника равна 60. т.е. аб=60.
Получаем систему уравнений:
Решаем второе уравнение через дискриминант.
-23б+120=0,
D=529-480=49,
==8, ==15.
Один из катетов треугольника равен 15 см
Значит, второй катет равен а=23-б=23-15=8см.
Ответ: 8см, 15см.
5.Задание на дом.
Пункт 23, №560, №564, на повторение №576.
6.Подведение итогов.
Отметить работу каждого ученика; ещё раз повторить алгоритм решения задач с помощью квадратных уравнений.
Спасибо за урок!
Решение квадратных уравнений 8 класс
Методическая разработка урока алгебры
«Решение квадратных уравнений» 8 класс
Тип урока: урок обобщения и систематизации знаний
Форма урока: урок-путешествие.
Цель: обобщение и систематизация знаний по теме квадратные уравнения.
УМК: Алгебра: 8 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – М.: Вентана-Граф, 2013. – 256 с.
Алгебра: дидактические материалы: 8 класс: пособие для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович и др. – М.: Вентана-Граф, 2015. – 96 с.
Задачи:
1) повторить и обобщить полученные знания по теме
2) выявить и восполнить пробелы знаний в теме
3) при необходимости составить план индивидуализированной работы по коррекции учебных затруднений
Планируемый результат:
1) личностные результаты:
идентификация себя, как полноправного субъекта общения;
формирование умения структурированно выражать свои мысли;
формирование способности применять свои знания и умения к решению новых проблем;
2) метапредметные результаты:
освоение способов познавательной деятельности;
определение адекватных способов решения учебной задачи на основании заданных алгоритмов;
самостоятельное выполнение творческой работы;
развитие умений анализировать, аргументировать сделанный выбор;
отражение в устной и письменной форме результатов своей деятельности;
оценивание своих учебных достижений;
работа в группах и индивидуально;
владение навыками само- и взаимоконтроля;
умение
ставить личностные цели и оценивать степень их достижения.
3) предметные результаты:
решение различными способами квадратных уравнений, а также уравнений и задач сводящихся к ним;
определение количества корней квадратных уравнений по дискриминанту и их знаков по коэффициентам;
расширение знаний учащихся по теме.
Форма работы: фронтальная, индивидуальная, групповая.
Ресурсы: учебник, раздаточный материал.
План урока:
Организационный момент — 1 мин
Постановка темы и целей урока, мотивация деятельности – 3 мин
Актуализация знаний — 5 мин
Основной этап:
История квадратных уравнений — 5 мин.
Повторение материала, применение знаний на практике – 24 мин.
Рефлексия — 5 мин
Подведение итогов — 2 мин
Организационный момент. Приветствие учащихся. Определение отсутствующих. Проверка готовности учащихся к уроку. Организация внимания.
Постановка
темы и целей урока, мотивация деятельности осуществляется при помощи технологии
развития критического мышления.
Стадия вызова
Ребята, какой раздел мы с вами изучали на протяжении нескольких занятий?
Учащийся: Квадратные уравнения.
Верно!
Включается видеофрагмент из сериала “Доктор Кто”.
Ребята слышите этот звук? Что это такое?
Учащиеся вместе с учителем просматривают видеоролик, где знакомятся со средством передвижения во времени и пространстве — тардис.
Как вы думаете, зачем нам этот летательный аппарат?
Учащийся: Мы отправимся в путешествие?
Правильно, мы отправимся в путешествие во времени, познакомимся с учеными, сделавшими вклад в развитие математики, обогатим наши знания о науке и способах решения квадратных уравнений, а также применим все полученные знания на практике.
Ребята, посмотрите на таблицу, давайте ее заполним:
Знаю | Хочу узнать | Узнал |
Что вам уже известно о квадратных уравнениях? (учащиеся называют, а учитель фиксирует ответы в таблице) | Что бы вы еще хотели узнать на уроке? (учащиеся называют, а учитель фиксирует ответы в таблице) | Заполняем в конце урока (подведение итогов урока) |
Учитель перечисляет озвученные учащимися ответы:
Знаю:
Что такое квадратное уравнение
Что такое корень уравнения
Как найти корни квадратного уравнения
Что такое дискриминант
Что такое теорема Виета и как ее применять и т. д.
д.
Хочу узнать:
Когда было первое упоминание о квадратных уравнениях
Как решали уравнения в древности
Кто вывел правила решения квадратных уравнений, которыми мы пользуемся сейчас
Как применять различные алгоритмы решения уравнений
Как решать задачи, сводящиеся к решению квадратных уравнений и т.д.
А чему мы с вами будем продолжать учиться на уроке?
Учащиеся: Решать уравнения, отвечать аргументировано на вопросы, использовать различные алгоритмы решения квадратных уравнений, использовать теорему Виета при решении квадратных уравнений.
Сегодня у нас урок закрепления полученных знаний по теме квадратные уравнения.
Вы многому научились, а сейчас, благодаря тардис у нас есть возможность еще раз переместиться в другую эпоху и вспомнить историю возникновения и становления квадратных уравнений.
Что мы могли бы предложить в качестве оплаты за путешествие?
Учащийся 1: Деньги.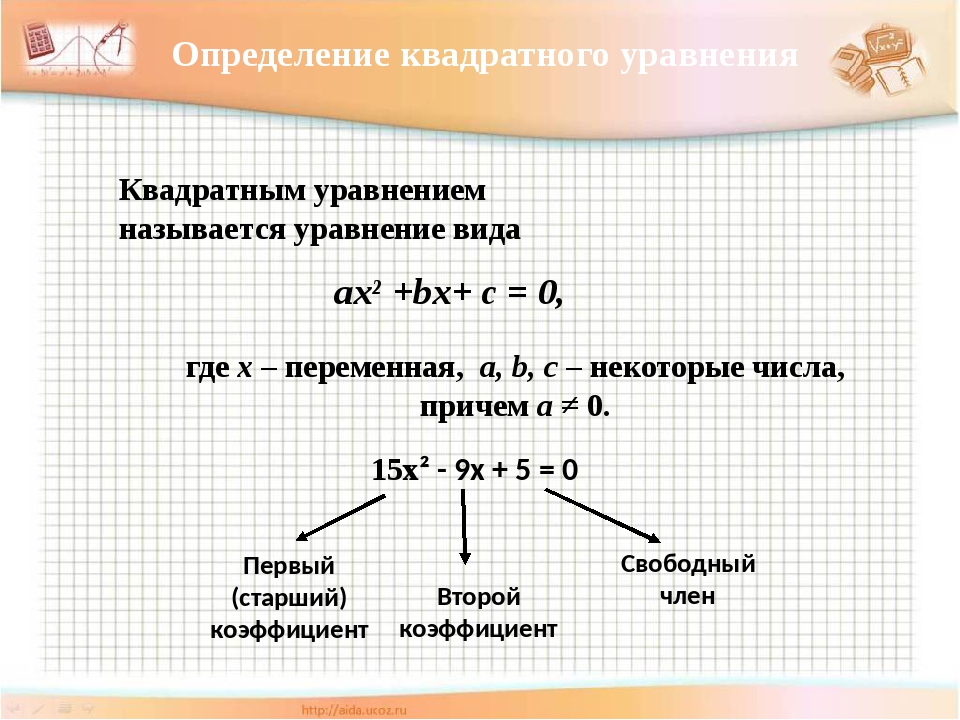
Учащийся 2: Знания.
Хорошая идея, расплачиваться с тардис мы будем нашими знаниями и правильными ответами.
Актуализация знаний
Итак, чтобы отправиться в Древний Вавилон давайте вспомним, что мы знаем о квадратных уравнениях.
Какие виды квадратных уравнений вы знаете?
Учащиеся: Полные и неполные, приведенные и неприведенные.
Каков общий вид квадратных уравнений?
Учащиеся: .
Назовите коэффициенты этого уравнения (учащиеся выполняют прямую задачу).
Учащиеся:
Составьте полное квадратное уравнение, если (учащиеся выполняют обратную задачу).
Учащиеся:
Составьте квадратное уравнение с коэффициентом . Каков вид данного уравнения?
Учащиеся: Неполное квадратное уравнение .
Какой прием мы используем для решения этого уравнения?
Учащиеся: Необходимо вынести общий множитель за скобки,
затем использовать равенство 0 произведения множителей.
Назовите вид уравнения, в котором отсутствует коэффициент b, объясните, как решать это уравнение.
Учащиеся: Неполное квадратное уравнение . Есть два способа решения. Первый: перенести свободный член за знак равенства, тогда корни имеют значения , при этом . Второй: если возможно, используем формулу разности квадратов.
Какие уравнения мы называем линейными?
Учащиеся: Уравнения первой степени, общий вид
Что значит решить уравнение?
Учащиеся: Найти значение переменной, которое при подстановке в исходное уравнение дает верное числовое равенство
Как называется данное значение переменной?
Учащиеся: Корень
От чего зависит количество корней квадратного уравнения?
Учащиеся: От значения дискриминанта
Что такое дискриминант?
Учащиеся: Термин образован от лат. discriminar, что в переводе — «разбирать», «различать».
Сколько корней имеет квадратное уравнение, если дискриминант больше 0?
Учащиеся: Два
Сколько корней имеет квадратное уравнение, если дискриминант меньше 0?
Учащиеся: Ни одного.
А что мы можем сказать про значение дискриминанта, если квадратное уравнение имеет всего один корень?
Учащиеся: Дискриминант равен нулю.
Отлично, мы вспомнили некоторые из положений пройденного материала, тардис заправлена и мы можем отправляться в путь.
Кто из вас знает, где и когда были обнаружены первые упоминания о квадратных уравнениях?
Учащийся 1: В Древнем Вавилоне.
Учащийся 2:До нашей эры.
Отправляемся в Древний Вавилон!
Включается видеофрагмент из сериала “Доктор Кто” (видеофрагмент перемещения во времени).
Основной этап
История развития квадратных уравнений
Квадратные уравнения в Древнем Вавилоне
В древности одними из наиболее часто возникающих перед людьми задач были задачи, связанные с разделением земли. То есть необходимо было находить площади земельных участков.
Квадратные
уравнения умели решать около 2000 лет до н. э. вавилоняне. В то время еще не
было алгебраической записи уравнения, большинство трудов имело именно
описательный характер, т.е. всё записывалось с помощью слов.
э. вавилоняне. В то время еще не
было алгебраической записи уравнения, большинство трудов имело именно
описательный характер, т.е. всё записывалось с помощью слов.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Видеофрагмент перемещения во времени и на слайде изображение древней Индии.
Какую страну мы сейчас посетим?
Учащийся: Древнюю Индию.
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже в астрономическом трактате в 499 г. Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную форму, некоторые из них сводились к решению квадратных уравнений.
Видеофрагмент перемещения во времени и на слайде
изображение древней Индии.
Квадратные уравнения у Аль-Хорезми
Аль-Хорезми арабский учёный, который в 825 г. написал книгу «Книга о восстановлении и противопоставлении». Это был первый в мире учебник алгебры. Он также дал шесть видов квадратных уравнений и для каждого из шести уравнений в словесной форме сформулировал особое правило его решения:
Вы видите, что теорией решения квадратных уравнений занимались величайшие умы древности и их изыскания лежат в основе современных методов решения квадратных уравнений.
Видеофрагмент перемещения во времени.
Квадратные уравнения в Европе XIII — XVII вв
Методы решения квадратных уравнений принимают знакомый нам вид уже в XIII-XVII вв в Европе.
Формулы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду:
при
всевозможных комбинациях знаков коэффициентов b, сбыло сформулировано в Европе
лишь в 1544 г. М. Штифелем.
М. Штифелем.
Одним из методов решения квадратного уравнения было выделение полного квадрата. Скажите, на чем основан данный метод?
Учащийся: На использовании формул сокращенного умножения.
Верно, давайте рассмотрим следующие примеры
1.
Кто расскажет, как решить данное уравнение?
Учащийся: Применим формулу квадрата разности и получим уравнение . Данное уравнение имеет один корень .
Хорошо, следующее задание, немного сложнее.
2.
Учащийся: Прибавим и отнимем 4 к левой части
уравнения, чтобы использовать формулу квадрата суммы двух чисел. Получим . Затем . Свернем по формуле . Теперь воспользуемся
формулой разность квадратов . (Здесь, учащиеся могут
предложить другой способ решения: перенести свободный член за знак равенств,
после чего использовать двойственность корней квадратного уравнения. ) Приведем подобные,
получим . Если произведение
множителей равно нулю, значит, хотя бы один из множителей равен нулю.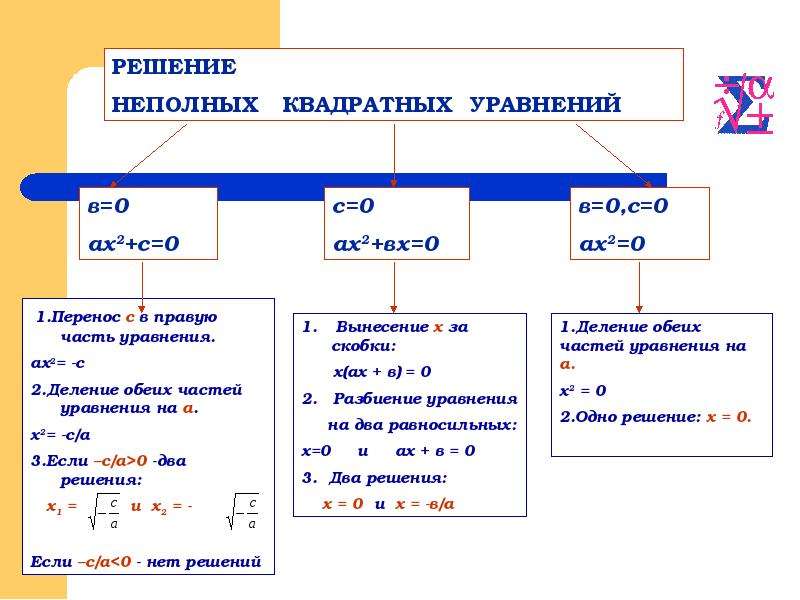 Следовательно, корнями уравнения являются следующие числа:
Следовательно, корнями уравнения являются следующие числа:
Дискриминант облегчил решение квадратных уравнений, т.к. корни уравнений можно найти по формулам.
Ребята, назовите, пожалуйста, формулу нахождения дискриминанта.
Учащийся:
Верно, а как, зная дискриминант, мы находим корни уравнения?
Учащийся:
Задание №656 выполнить в тетрадях.
Учащиеся выполняют задание.
А теперь ребята поменяйтесь тетрадями с соседом по парте для взаимопроверки.
Учащиеся проверяют работы друг друга.
А теперь карандашиком на полях поставьте оценку своему однокласснику:
· Если задания выполнены верно, ставьте 5
· Если есть одна ошибка/ несколько исправлений, ставьте 4
· Если допущено две ошибки, ставьте 3
· Если верно сделано менее половины заданий, ставьте 2
Вывод
формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет
признавал только положительные корни. Вы помните, что Франсуа Виет –
французский математик, основоположник символической алгебры. Он облегчил
решение квадратных уравнений.
Вы помните, что Франсуа Виет –
французский математик, основоположник символической алгебры. Он облегчил
решение квадратных уравнений.
Ребята, давайте вспомним теорему Виета.
Учащийся: Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Верно. А что же такое приведенное квадратное уравнение?
Учащийся: Это уравнение, у которого первый коэффициент равен единице, а=1.
Правильно, кто назовет мне общий вид приведенного квадратного уравнения?
Учащийся:
Скажите, как зависят знаки корней уравнения от его свободного члена?
Учащийся: Если q<0, корни имеют разные знаки, если q>0, корни одного знака.
Согласно теореме Виета, каким свойством обладают корни квадратного уравнения?
Учащийся: Их сумма равна второму коэффициенту, взятому
с противоположным знаком, а произведение равно свободному члену.
Рассмотрим пример . Ребята решите данный пример с помощью теоремы Виета.
Учащийся: Согласно теореме Легко видеть, что данным равенствам удовлетворяют .
Повторим и обратную теорему. Составьте уравнение, корнями которого являются числа .
Учащийся: Искомое уравнение имеет вид . Согласно теореме, коэффициенты и корни связаны следующими соотношениями:Следовательно, искомое уравнение:
Мы рассмотрели теорему Виета для приведенного квадратного уравнения, а какова формула для полного квадратного уравнения?
Учащийся:
Поскольку мы уже затронули связь коэффициентов и корней, расскажите мне о способе решения квадратного уравнения, основанном на свойстве коэффициентов.
Учащийся 1: Если , то
Учащийся 2: Если , то
Молодцы! Найдите корни, не производя письменных расчетов.
1.
Учащийся: Поскольку сумма коэффициентов равна нулю, значит
2.
Учащийся: Поскольку сумма коэффициентов, когда b взято с противоположным знаком, равна нулю, значит
Вспомните, пожалуйста, что такое биквадратное уравнение или, как его еще называют, двуквадратное?
Учащийся: Биквадратным называют уравнение вида
Каким образом мы можем решить такое уравнение?
Учащийся: С помощью замены переменной
Посмотрите на данный пример:
С помощью замены переменной сведем данное уравнение к виду
Отсюда . Вернемся к замене переменной, . Из первого уравнения получим . Из второго понимаем, что корней нет, поскольку квадрат числа не может быть числом отрицательным.
Посмотрите на следующий пример: . Какую здесь замену будем проводить?
Учащийся: Замена
Верно!
Зная, как решаются квадратные уравнения, вам не составит большого труда решить задачу. Рассмотрим задание №802 учебника.
Каким способом воспользуемся для облегчения решения?
Учащийся: Можно воспользоваться табличным способом. Движение происходит условно на двух участках.. Составим таблицу, обозначив скорость
на первом участке за х .
Движение происходит условно на двух участках.. Составим таблицу, обозначив скорость
на первом участке за х .
| S | v | T |
Первый участок | 150км | х | |
Второй участок | 240км | х+5 |
Составим уравнение, зная, что на весь путь было потрачено 5ч.
Итак,
пора возвращаться домой, ребята. Но чтобы вернуться, нам необходимо хорошо
выполнить маленькую самостоятельную работу и показать, как вы умеете работать в
команде.
Учитель раздает учащимся задания:
1 группа решает полное квадратное уравнение
2 группа решает неполное квадратное уравнение
3группа решает приведенное квадратное уравнение с помощью теоремы Виета
4 группа решает неприведенное квадратное уравнение с помощью теоремы Виета
5 группа решает биквадратное уравнение
6 группа решает уравнение с помощью замены переменной
7 группа составляет уравнение для решения задачи. Моторная лодка прошла 35 км по озеру, а затем 34 км по реке, впадающей в это озеро, за 2 ч. Найдите собственную скорость лодки, если скорость течения реки составляет 1 км/ч.
Учитель собирает тетради для проверки и выставления оценок, говорит, что пора возвращаться, тардис готова.
Видеофрагмент перемещения во времени.
Мы успешно приземлились. Спасибо вам за работу на уроке.
Понравилось вам наше путешествие? (ответы учащихся)
Сейчас
мы вернемся к таблице, которую заполняли в начале урока и заполним последний
столбец. (Учащиеся заполняют таблицу)
(Учащиеся заполняют таблицу)
Итак, мы с вами узнали:
• Когда было первое упоминание о квадратных уравнениях
• Историю квадратных уравнений
• Как применять методы решения квадратных уравнений т.д.
А сейчас давайте определим степень вашей готовности к контрольной работе.
Учитель раздает карточки каждому учащемуся для заполнения:
Я знаю |
|
Я умею |
|
Я затрудняюсь в решении |
|
Я хочу получить знания/научиться |
|
Учитель
собирает заполненные карточки для диагностики готовности к контрольной работе
по теме и определения дальнейшей индивидуальной работы с учащимися.
Учитель дает оценку работы учащихся, ставит отметки в журнал.
Домашнее задание: №918 (1, 3, 5, 7), №919 (2), №920 (1)
Квадратные уравнения. Разработка раздела образовательной программы алгебры 8 класса
1. Разработка раздела образовательной программы алгебры 8 класса
•Квадратное уравнение и его корни.•Неполные квадратные уравнения.
•Метод выделения полного квадрата.
•Решение квадратных уравнений.
•Приведенное квадратное уравнение. Теорема Виета.
•Уравнения, сводящиеся к квадратным.
•Решение задач с помощью квадратных уравнений.
•Решение простейших систем, содержащих уравнения
второй степени.
3. Пояснительная записка
показать один из способов обобщения исистематизации знаний по теме «Квадратные
уравнения» в курсе алгебры 8 класса.
Проанализировать формирование умения решать
квадратные уравнения до изучения данного модуля и
определить роль и место данного модуля в курсе
алгебры 8 класса.

Предложить конкретное тематическое планирование
по данному модулю.
Предложить разработку одного урока из данного
модуля с описанием технологий.
4. Актуальность темы
«Квадратные уравнения» — главная тема цикла«Квадратные уравнения – квадратичная функция –
квадратные неравенства»
Навык решения квадратных уравнений необходим
каждому ученику для итоговой аттестации за курс
основной и старшей школы
Умение решать квадратные уравнения является
одним из базовых умений для приобретения новых
знаний (решения сюжетных задач, исследования
функций элементарными средствами)
Прикладное значение квадратных уравнений
(физика-давление в жидкости и газе, работа,
мощность; химия-расчеты в лабораторных работах;
вопросы экономики)
Освоение темы поднимает учащихся на качественно
новую ступень овладения содержанием школьной
математики
5. Используемые педагогические технологии
Технология развивающего обучения снаправленностью на развитие творческих
качеств личности (каждая личность
воспринимается непризнанным гением)
Технология проблемного обучения
(создание под руководством учителя
проблемной ситуации, активная
самостоятельная деятельность учащихся по
её разрешению, в результате чего происходит
творческое овладение знаниями и развитие
мыслительных способностей).

Технология коллективного способа
обучения (общение учащихся в мини-группах
по 3-4 человека, когда каждый учит каждого)
Технология уровневой дифференциации
(обучение каждого учащегося на уровне его
возможностей и способностей)
Компьютерные технологии (использование
ИКТ, подготовка презентаций)
Фронтальная, индивидуальная, групповая, коллективная
1. Словесные методы: рассказ, беседа, объяснение, работа с
литературой, описание
2. Практические: задачи, упражнения
3. Наглядные: демонстрация слайдов, плакаты с формулами
4. Исследовательские методы
5. Метод проблемного изучения
1. Самостоятельные работы (с последующей проверкой
и контролирующего характера)
2. Математические диктанты
3. Тесты
4. Контрольная работа
5. Зачет
8. Требования к знаниям и умениям
квадратное уравнениекорни уравнения
решить уравнение
старший коэффициент, второй коэффициент, свободный член
полное квадратное уравнение
неполное квадратное уравнение
приведенное квадратное уравнение
корень квадратного трехчлена
дискриминант квадратного уравнения
рациональное уравнение
биквадратное уравнение
посторонний корень
равносильные и неравносильные преобразования уравнений
квадратных уравнений(полных, неполных, приведенных)
биквадратных уравнений
рациональных уравнений
• решать текстовые задачи с помощью составления уравнений
10.
 Ожидаемые результаты деятельности Получение прочных знаний о решении квадратных
Ожидаемые результаты деятельности Получение прочных знаний о решении квадратныхуравнений и овладение приемами решения на уровне
навыка.
Развитие познавательных интересов, творческих
способностей учащихся, логической культуры
Приобретение опыта самостоятельного поиска,
анализа при решении задач.
Качественная подготовка к итоговой аттестации по
данной теме.
Готовность учащихся к восприятию материала курса
алгебры и начал анализа на старшей ступени
обучения.
11. Цели изучения темы «Квадратные уравнения»
Образовательные:познакомиться с определением квадратного уравнения,
его видами;
ввести формулы для нахождения корней;
изучить теорему Виета, сформировать навык в её
применении теоремы в нестандартных ситуациях;
Развивающие:
развитие логического и вариативного мышления,
способности самостоятельно решать учебные
задачи и работать с дополнительной литературой;
развитие навыка самоконтроля;
Воспитательные:
воспитание трудолюбия, активности в работе, воли
и настойчивости для достижения конечных
результатов;
воспитание интереса к предмету;
формирование коммуникативных навыков и
волевых качеств личности;
14.
 Задачи, решаемые при изучении темы «Квадратные уравнения» Формирование знаний
Задачи, решаемые при изучении темы «Квадратные уравнения» Формирование знанийучащихся о способах решения
квадратных уравнений,
личностной мотивации к
изучению данной темы.
Развитие навыка
сознательного восприятия
учебного материала,
логического мышления,
способности анализировать,
сравнивать, обобщать.
Развитие навыка творческого подхода к решению
задач и навыка исследовательской работы над
уравнениями.
Развитие внимания, аккуратности, речи, памяти,
инициативы, критического отношения к себе и к
другим.
Развитие черт саморегулирующей личности с
гибкими осознанными знаниями,
самостоятельности, ответственности, активной
жизненной позиции, культуры общения,
интеллигентности.
№
Содержание
материала
Технология
1
Квадратное уравнение
и его корни
Проблемноразвивающий
метод, постановка общей учеб.
задачи, создание
пробл. ситуации
2
Решение простейших Проблемноквадратных уравнений развивающий
Тип урока
Тех.

оснащение
Виды
контроля
Домашне
е задание
§25, №№
403-404(чет),
405(6)
Получение
новых
знаний
Презентация,
плакат
Слайды с
задачами
метод
Закрепление
новых
знаний
Самостоятельная
работа со
взаимопроверкой
§25, №№
408-410(чет),
415(2)
3
Неполные квадратные
уравнения
Проблемноразвивающий
метод
Получение
новых
знаний
Презентация,
слайды с
задачами
Самостоятельная
работа со
взаимопроверкой
§26, №№
419- 421(чет)
4
Метод выделения
полного квадрата
Проблемно
развивающий
метод
Получение
новых
знаний
Презентация,
слайды с
задачами
Самостоятельная
работа со
взаимопроверкой
§27, №№
429 (чет),
430(2)
5
Решение полного
квадратного
уравнения по формуле
корней
Проблемно
развивающий
метод
Получение
новых
знаний
Презентация,
слайды с
задачами
Самостоятельная
работа со
взаимопроверкой
§28, №№
434(6),
435(2),
437(2),
439(2)
6
Проблемно
Решение полных
квадратных уравнений развивающий
метод
со вторым четным
коэффициентом
Комбинирова
нный
Презентация,
слайды с
задачами
Проверочная
работа
§28, №№
444(чет),
436(чет),
437(4),
439(4)
№
Содержание
материала
Технология
Тип урока
Тех.

оснащение
Виды
контроля
Домашнее
задание
7
Урок — практикум по
решению квадратных
уравнений
Дифференцированный
подход
Закрепление
новых знаний
Слайды с
задачами
Математический диктант,
самостоятельная работа
§28, №№
440(2,4), 441(2),
443(2), 439(2)
8
Решение квадратных
уравнений
нестандартными
методами
Проблемно
развивающий
метод
Комбинирова
нный
Слайды с
задачами
9
Приведенные квадратные уравнения.
Теорема Виета
Проблемно
развивающий
метод
Получение
новых знаний
Презентация
Тест
§29, №№
455(чет),
456(чет),
457(6,8)
10
Применение теоремы
Виета
Проблемно
развивающий
метод
Комбинирова
нный
Слайды с
задачами
Самост.работ
а со взаимопроверкой
§29, №№ 458(6),
460(4), 461(4),
462(4)
11
Решение уравнений,
приводимых к виду
квадратного.
 Биквадратное уравнение
Биквадратное уравнениеПроблемно
развивающий
метод
Получение
новых знаний
Презентация,
слайды с
задачами
Тест
§30, №№
468-469(чет),
535(4)
12
Решение рациональных уравнений, приводимых к квадрат.
Проблемно
развивающий
метод
Комбинирова
нный
Тест
§30, №№ 470(6),
471(6), 536(2)
в тетради уравнения, решаемые по сумме
коэфф. и заменой переменной
Технология
Тип урока
Урок-практикум по
решению уравнений,
сводящихся к
квадратным
Уровневая
дифференциа
ция,
групповой
метод
Закрепление
новых знаний
Слайд с
задачами
14
Решение задач с
помощью квадратных
уравнений
Проблемно
развивающий
метод
Получение
новых знаний
Слайды с
задачами
15
Решение задач с
помощью квадратных
уравнений
Проблемно
развивающий
метод
Закрепление
новых знаний
Слайды с
задачами
16
17
Решение задач с
помощью квадратных
уравнений
Проблемно
развивающий
метод
Закрепление
новых знаний
18
Решение простейших
систем, содержащих
уравнение второй
степени
Проблемно
развивающий
метод
Получение
новых знаний
№
Содержание
материала
13
Тех.

оснащение
Виды
контроля
Домашнее
задание
Самостоятель
ная работа по
группам
§30, №№ 474(2),
551(4), 553(2)
§31, №№ 476(2),
480, 529
Самостоятель
ная работа
обучающего
характера
§31, №№ 482(6),
530(чет),
«Проверь себя»,
№3, стр. 148
§31, №№ 486,
546(2), 550(чет)
Слайды с
задачами
§32, №№ 493(4),
494(4), 495(4)
№
Содержание
материала
Технология
Тип урока
19-20
Решение
простейших систем,
содержащих
уравнение второй
степени
Уровневая
дифференциа
ция
Закрепление
новых знаний
21
Урок-зачет по решению квадратных
уравнений
Индивидуаль
но-групповой
метод
22
Обобщающий урок
по теме «Квадратные уравнения»
23
Контрольная работа
по теме «Квадратные уравнения»
Тех.
оснащение
Виды
контроля
Домашнее
задание
Слайды с
задачами
Разноуровневая самостоятельная
работа
§32, №№ 496(4),
500(3), 506(2)
Комбинирова
нный
Слайды с
задачами
Зачет
№№ 735(4),
740(2), 742(6),
745(6)
Дифференцированный
метод
Обобщение
знаний
Презентация,
слайды с
задачами
Домашняя
проверочная
работа
Индивидуаль
ная форма
Урок
контроля
знаний и
умений
Слайд с
текстом
работы
— расширение и углубление представлений учащихся о решении
уравнений; организация поисковой деятельности учащихся при
решении неполных квадратных уравнений;
— развитие умения самостоятельно приобретать новые знания;
использование для достижения поставленной задачи уже полученные
знания; установление закономерности многообразия связей для
достижения уровня системности знаний;
— воспитание навыков самоконтроля; выработка желания и
потребности обобщать полученные факты; развитие
самостоятельности и творчества.

частично-поисковый (эвристический)
метод самопроверки
метод взаимопроверки
мультимедийный проектор
таблица самооценки
таблицы с заданиями
23. Ход урока
I. Мотивационно – ориентировочная часть1.Устная работа.
Разложите на множители и выберите правильный ответ:
Неправильные ответы исчезают. Ученики проверяют правильность
выполнения ими задания. Ставят оценки в свою карту контроля
(самооценка).
Слайд 1
Слайд 2
Решите уравнение.
Сколько корней имеет
уравнение?
Распределите данные
уравнения на четыре
группы и объясните, по
какому признаку вы это
сделали.
1-я группа: имеет три слагаемых;
2-я группа: оба слагаемых содержат
переменную;
3-я группа: одно слагаемое с
переменной, а другое нет;
4-я группа: одночлен с переменной в
квадрате.
Слайд 3
Слайд 4
25. 2. Постановка учебной задачи
1. Как называются все эти уравнения?(квадратные)2.
 Дать определение квадратного уравнения.
Дать определение квадратного уравнения.Запишите уравнение первой группы в общем виде.
Общий вид квадратного уравнения:
Известно, что хорошее начало — половина сделанного. Очень
важно правильно определить в уравнении коэффициенты.
Слайд 5
26. Занесите в таблицу коэффициенты предлагаемых уравнений.
Организация проверки по слайду 6Самооценка.
Слайд 6
27. Восстановите квадратное уравнение
Уравнениеа — старший
коэффициент
b — второй
коэффициент
с — свободный
член
3
-2
1
1
2
0
3
0
4
-4
0
0
9
0
-4
3
-4
0
Организация проверки по слайду7. Самооценка.
Все ли уравнения здесь полные?
В каких случаях квадратные уравнения можно считать
неполными? (Дать характеристику каждой группе)
Каких уравнений записано больше?
Какая задача встает перед нами?
Задача: систематизировать знания по решению неполных
квадратных уравнений (тема записывается в тетрадь)
Слайд 7
28.
 III. Операционно-исполнительская часть I. На доске решить неполное квадратное уравнение.
III. Операционно-исполнительская часть I. На доске решить неполное квадратное уравнение.Записать общее решение каждого
1) х²+2х=0 2) 5х²-3=0 3) 9х²-4=0 4) х²-5=0 5) 3х²+4=0
Проверка решения у доски. Обобщить, сделать выводы и открыть слайд 8.
Общее решение неполных квадратных уравнений:
ах 2 bх 0
а 0, b 0, с 0
х ( ах b) 0
х 0,
ах b 0
х
b
а
ах 2 0, а 0, b 0, с 0
х 0
ах 2 с 0, а 0, b 0, с 0
с
,
а
с
если 0 два корня ;
а
с
0 нет корней
а
с
х ( )
а
х2
х
(
с
)
а
29. 2. Первичное осмысление и применение изученного материала.
Обучающая самостоятельная работаКритерий оценки:
Оценка «5» — 8 баллов
Оценка «4» — 6-7 баллов
Оценка «3» — 3 балла
1. Решить уравнение
а ) 2 х 2 18 0
а) 6 х 2 12 0
б ) 5 х 2 15 х 0
б ) 3 х 2 12 х 0
в) х 2 5 0
в) 7 х 2 0
2. Составить квадратное уравнение имеющее корни:
3 и -3
0и6
3.
 Решить уравнение:
Решить уравнение:( х 1) 2 (1 х) 5 6
( х 4)( х 4) 2 х 16
Организация проверки: взаимопроверка по слайду 9.
30. 3. Прежде чем перейти к последнему этапу урока и получить домашнее задание, решите следующие задачи:
Игровая ситуацияa) При каком значении m уравнение 3 х 2 (m 1) х m 4 0
обращается в неполное квадратное уравнение. Запишите это
уравнение.
Меньшее значение m укажет номер ряда, а большее значение укажет
номер парты, где сидят учащиеся, которые должны будут подготовить
к следующему уроку историческую справку о неполных квадратных
уравнениях (m=1, m=4)
Слайд 10
б) Выписать коэффициенты уравнений
4х2 9 x 0
4х2 2х 0
1 2x 4х2 0
Выписанные коэффициенты уравнений и есть номера заданий в
учебнике для домашней работы.
Слайд 11
8 класс АЛГЕБРА — К урокам математики
19 мая выставлены четвертные оценки в электронном дневнике. Прошу самостоятельно посмотреть. Доступ к таблицам с оценками закрыт.
 Новых заданий до конца четверти не будет.
Новых заданий до конца четверти не будет.Хорошего вам отдыха!!!
14.05.2020
Тема. Повторение. Квадратные корни. Системы уравнений.
Учебник повторить стр.140-142, 147-148, обратить внимание на разобранные задачи.
Решить №721,725,726,727-во всех номерах нечетные задания
Системы уравнений: №545-1,3,5,7 (образцы стр. 200-201). Вспомните, как записать ответ в системе уравнений (х;у) — как координаты.
В пятницу 15.05 (на один день) выложу текст итоговой проверочной работы (вместо геометрии).
Темы. Квадратные уравнения. График квадратичной функции. Квадратные неравенства. Квадратные корни. Системы уравнений и неравенств.
13.05.2020
Тема. Повторение. Решение неравенств и систем неравенств
Повторить стр.39-41 задачи 1-5, свойства, решить №706-1,3,5), 707-1,3)
Повторить стр.55-56 задачи 1-4, стр.48-49, решить №709 весь.
Выполнить тест, ответ записать в виде неравенства (например, х>3 ), нет решений, любое число, номер правильного ответа, в зависимости от задания и решения
Реклама!!!!
Образовательный центр «Сириус» проводит в онлайн-формате олимпиаду. Олимпиада проводится в тестовом режиме, предполагается, что эта Олимпиада сможет заменить или дополнить ВсОШ. Сложность задач соответствует уровню школьного этапа Всероссийской олимпиады.
Олимпиада проводится в тестовом режиме, предполагается, что эта Олимпиада сможет заменить или дополнить ВсОШ. Сложность задач соответствует уровню школьного этапа Всероссийской олимпиады.
Попробовать свои силы в решении нестандартных задач приглашаются школьники 4-10 классов из любого субъекта Российской Федерации.
Для участия школьнику нужно подать заявку на сайте Центра «Сириус» по одному или нескольким предметам на выбор.
По результатам олимпиады школьники получат рекомендации «Сириуса» по своему дальнейшему обучению и развитию, будут приглашены к участию в следующих дистанционных программах и конкурсных отборах на очные программы. Одновременно «Сириус» направит успешные результаты участников в регионы. Подробнее про олимпиаду:
https://sochisirius.ru/news/3519
Расписание Олимпиады:
| Даты туров | Предмет | Классы (на момент участия) |
|---|---|---|
| 20-22 апреля | Биология | 4-6 |
| 21-23 апреля | Биология | 7-8 |
| 22-24 апреля | Биология | 9-10 |
| 26-28 апреля | Астрономия | 4-10 |
| 27-29 апреля | Химия | 7-10 |
| 12-14 мая | Математика | 3-6 |
| 13-15 мая | Математика | 7-8 |
| 14-16 мая | Математика | 9-10 |
| 19-21 мая | Физика | 6-8 |
| 20-22 мая | Физика | 9-10 |
| 26-29 мая | Информатика | 4-10 |
29. 04.2020 Следующие задания после 11.05.2020
04.2020 Следующие задания после 11.05.2020
Тема. Квадратные неравенства.
Повторить три способа решения квадратных неравенств (см. ниже)
1. С помощью систем неравенств
2. Графический способ решения
3. Метод интервалов
Задания.
1. Каждое неравенство решить тремя способами ( если это возможно). Обратите внимание, при решении любым способом сначала надо решить квадратное уравнение. Его решение записываете 1 раз, а дальше три способа решения неравенства, используя корни квадратного уравнения.
1) 2х2+5х-12>0
2) -x2-3x+4≤0
3) x2+4x+5<0 (можно решить только графически, потому что D<0)
2. Решить неравенства: учебник стр.284 ПРОВЕРЬ СЕБЯ №3-а,б), 4
Отчет о проделанной работе выложить в Google Classroom
ВСЕ объяснения, видео и образцы ниже.20-25 апреля
Тема. Метод интервалов
25.04.2020
Все задание. №679-1) — переписать из образца, решить №679-2,3,4)
№679-1) — переписать из образца, решить №679-2,3,4)
№680-1) переписать из образца, решить №680-2)
№685-1) переписать из образца, решить № 684-2), 685-2)
№677-1,3) переписать из образца, решить №677-2,4)
№682-1) переписать из образца, решить №682-2)
Отчет о проделанной работе выложить в Google Classroom, присоединиться по коду kycfb53 до вторника 28.04.2020
ВСЕ объяснения, видео и образцы ниже.Метод интервалов применяется не только для решения квадратных неравенств. Этим способом можно решать дробно-рациональные неравенства, неравенства, в которых в левой части записано произведение нескольких множителей в скобках, и многие другие. Сегодня я разбираю решение еще двух видов неравенств. Опять же, берем самые простые случаи. Это №679, 680, 684, 685, 677, 682, разбираю решения, ниже видео.
Примеры нужно переписать в тетрадь и решить самим аналогичные.
Аналогично решают №684,685. Только для того, чтобы найти значения х,при которых числитель и знаменатель равны нулю, нужно решить квадратные уравнения. В образце 2 (еще ниже) разбираю 685-1) пример, остальные самостоятельно. Красным цветом написаны пояснения, их писать в решении не нужно.
В образце 2 (еще ниже) разбираю 685-1) пример, остальные самостоятельно. Красным цветом написаны пояснения, их писать в решении не нужно.
Остались №677, 682. Принцип решения тот же. Нужно найти значения х, при которых левая часть неравенства равна 0.
Для этого решаем уравнения. Разбираю нечетные примеры, четные решаются аналогично. См. образец 3, красным цветом написаны пояснения, их писать в решении не нужно.
22.04.2020
Метод интервалов является основным методом решения неравенств, и не только квадратных.
Дело в том, что выражение слева от знака равно принимает то положительные, то отрицательные значения, в зависимости от значений х. Ученые обратили на это внимание, вывели и доказали некоторую закономерность. И назвали этот способ решения методом интервалов. Суть его в том, что находятся все значения х, при которых выражение равно 0, и эти точки отмечают на координатной прямой. Они разбивают прямую на промежутки. Например:
Промежутки
Промежутки
Для всех х из одного промежутка выражение принимает значения одного знака — или плюс, или минус.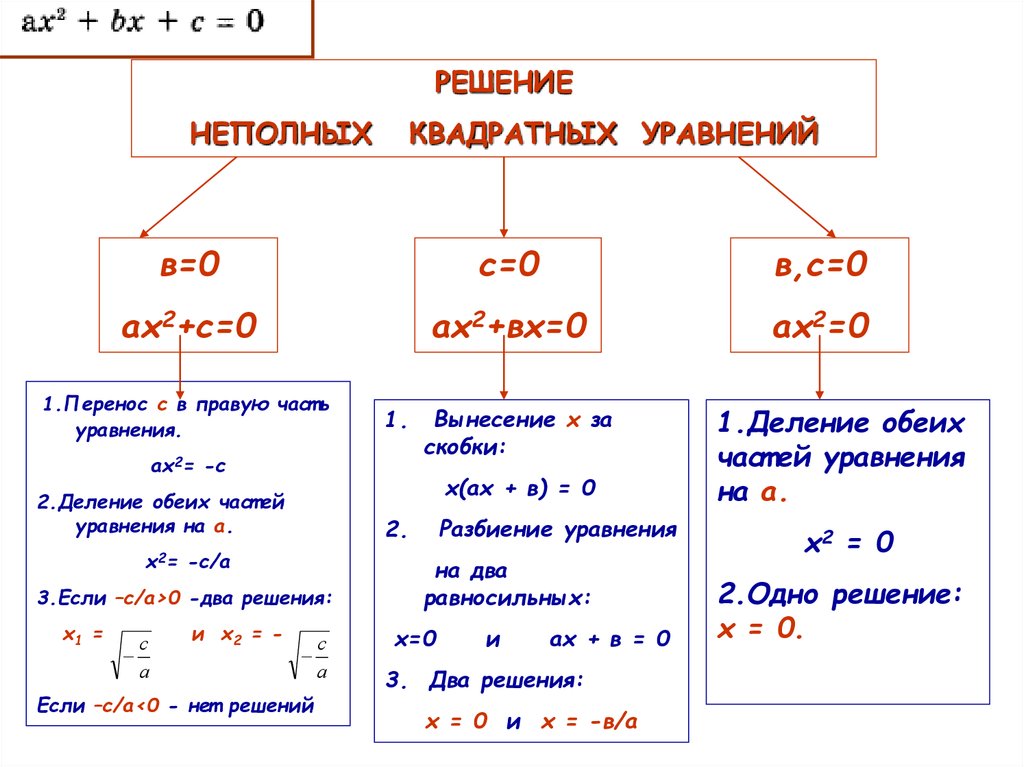 Поэтому выбирают одно значение х, подставляют его в выражение, по ответу определяют этот знак. видео
Поэтому выбирают одно значение х, подставляют его в выражение, по ответу определяют этот знак. видеоОбразец записи решений:
Определив знак на каждом промежутке, выбирают те промежутки, которые являются решением заданного неравенства. Если знак у неравенства > или ≥, то все решения неравенства будут на промежутках, у которых знак плюс, если знак у неравенства < или ≤ , то все решения неравенства будут на промежутках, у которых знак минус. видео2
Образец (еще 2 решения)
Этот метод может применяться только для неравенств, у которых есть корни у соответствующего квадратного уравнения. Если у уравнения нет корней, то такое неравенство решается только графически (нужно строить эскиз графика квадратичной функции).
И если сравнить два способа решения: с помощью систем неравенств и метод интервалов, то второй намного короче. Поэтому его и используют намного чаще!
Разобрать видео, в учебнике стр.276
Задание на два урока
№675 весь, 676-5), 689 -1,2,4,5) Образец выше!, повторение № 690-3,5,6)- решить с помощью эскиза графика квадратичной функции. Выложить в Google Classroom, присоединиться по коду kycfb53 до пятницы 24.04.2020
Выложить в Google Classroom, присоединиться по коду kycfb53 до пятницы 24.04.2020
13-18 апреля
Тема на эту неделю: Решение квадратного неравенства с помощью графика квадратичной функции
Будет три задания, я сохраню сквозную нумерацию, прошу в заголовке письма указывать № задания и предмет, а то вы же сами путаетесь, на какое письмо я отвечаю. Все задания пока сохраняются на этой странице, если вы что-то пропустили, можно посмотреть.
6 задание по алгебре
Проверочная работа.
Решите квадратные неравенства с помощью графика квадратичной функции.Решения отправить [email protected]х2-8х+15>0
3x2+11x-4≤0
4x2-8x+9>0
-4x2+4x-1 ≥0
x2+3x+5<0
Обратите внимание!
Точка касания параболы с осью Ох может быть только если квадратное уравнение имеет 1 корень — это задача 2 в учебнике и мой образец решения.
Если квадратное уравнение не имеет корней, то ни о каких точках касания речи нет, писать, что их нет, не нужно!
Вы пишете, что график лежит выше (или ниже) оси Ох. Это задача 3 в учебнике и таблица ниже для выбора решения. Эта информация и для решения №663 из задания 5.
16.04.2020
5 задание по алгебре
Прочитайте задачу 3 стр. 270. Это образец рассуждений для третьего случая, когда квадратное уравнение не имеет корней. Значит нет точек пересечения с осью Ох,
| значит график лежит выше (a>0), функция всегда положительная у>0, но у=ax2+bx+c Тогда при решение неравенства возможны два варианта 1. ax2+bx+c>0 верно при любых значениях х. Ответ: х-любое число 2. ax2+bx+c<0 неверно при любых значениях х. Ответ: нет решений. Это верно и для нестрогих неравенств(≤) | |
| значит график лежит ниже (a<0), функция всегда отрицательная у<0, но у=ax2+bx+c Тогда при решение неравенства возможны два варианта 1.  ax2+bx+c>0 неверно при любых значениях х. Ответ: нет решений. ax2+bx+c>0 неверно при любых значениях х. Ответ: нет решений.2. ax2+bx+с<0 верно при любых значениях х. Ответ: х-любое число Это верно и для нестрогих неравенств(≤) |
по плану на стр. 270 решить квадратные неравенства с помощью эскиза графика №663-1,3,5), 664-1,3,5,7).
При построении эскиза графика вершину находить не нужно! Оформление по образцу. Вместо точки касания, пишем парабола расположена ниже (выше) оси Ох. И вывод по таблице. Если есть вопросы, пишите.
Отчет о вашей работе отправить на почту. Оценка будет суммироваться по итогам трех заданий и проверочной работы.
4 задание по алгебре 8б на 13.04.2020, 8а, 8в на 15.04.2020
параграф 41 стр.268-270, по плану на стр. 270 решить квадратные неравенства с помощью графика №661-1,3), 662-1,3,5)
Ответ на вопросы: выше образец
Только проблема у вас не в том, что написано в образце, а в понимании, когда у>0 (функция >0) , y<0 (функция <0) по виду графика. Я это объясняла на последней неделе четверти, а многие уже не ходили в школу. Пока внимательно почитайте на стр.269 текст у рисунка. Работы шлем, я проанализирую, пойму, что не ясно.
Я это объясняла на последней неделе четверти, а многие уже не ходили в школу. Пока внимательно почитайте на стр.269 текст у рисунка. Работы шлем, я проанализирую, пойму, что не ясно.
При построении эскиза графика квадратичной функции координаты вершины параболы искать не нужно!
Достаточно найти нули функции — точки пересечения с осью Ох. И нарисовать график приблизительно!
Он нам нужен для понимания, где значения функции (т.е. у) положительны, а где отрицательны, а где равны нулю!
Отчет о вашей работе отправить на почту. Оценка будет суммироваться по итогам двух заданий и проверочной работы.
-Кто не выполнил третье задание (ниже), помните, что оно обязательно.
3 задание по алгебре
11.04.2020 8а, 8б, 8в ( домашняя работа)
Тема. Квадратное неравенство и его решение.
Просмотрите еще раз видео ниже, если забыли, и решим задания №653-1,4).
В №653 чтобы решить неравенство, нужно решить неполное квадратное уравнение, чтобы просто разложить левую часть на множители. НО в первом задании это формула сокращенного умножения — (х-2)(х+2)<0,
НО в первом задании это формула сокращенного умножения — (х-2)(х+2)<0,
а в 4) можно вынести за скобки общий множитель х — х(х-2)>0.
Значит квадратное уравнение можно не решать, если на множители можно разложить другим способом.
После разложения на множители, неравенство решаем по общему плану.
Если >0 , то множители или оба положительные — рассматриваем этот случай, или оба отрицательные, тогда второй случай. При решении каждого неравенства обязательно рассматривают оба случая и записывают общий ответ (это видео1 и видео2, они разделились на 2 части, потому что при записи я случайно выключила запись, должно было быть одно общее видео)
Если <0, то в этом случае знаки у множителей должны быть разные (плюс на минус дает минус при умножении).И опять же, при решении таких неравенств, нужно рассматривать два случая. Первый множитель положительный, второй — отрицательный, и, наоборот, первый -отрицательный, второй — положительный.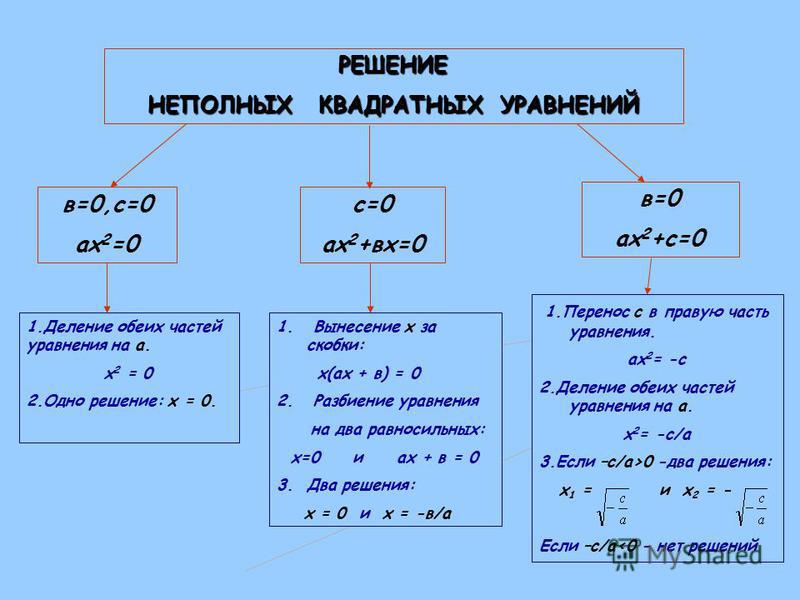 В каждом случае решение и общий ответ.
В каждом случае решение и общий ответ.
Не забывайте графическую иллюстрацию, подписывать ось х.
Смотрите фото решения, перепишите образцы.
Ответы на ваши вопросы по работе, которая ниже1)Во втором задании просто решить неравенство, а потом дополнительно выписать целые числа
2)В задании в) получается отрицательный дискриминант, значит нет корней и разложить на множители мы не можем. Получается, что пока решить такое неравенство вы не можете. Так и пишите
3)Если обе части неравенства разделить или умножить на отрицательное число, то меняется знак неравенства
Например: -3x>9 разделим на (-3) получим x<9:(-3), то есть x<-3
Решения этих заданий отправляем мне на почту (№653 отправлять не нужно).При решении неравенств нужно было соединить ваши знания о решении квадратных уравнений и о способах решения систем. Напишите в письме, пожалуйста, как вы считаете, вы поняли тему, она сложная или нет.
Перед следующим уроком повторите материалы на сайте.
Если у квадратного уравнения нет корней, то нет нулей функции. И нужны дополнительные точки2 задание по алгебре
09.04.2020 8а, 8б, 8в
Новая тема. Квадратное неравенство и его решение.
Для улучшения ситуации с пониманием этой темы, я записала 3 видео. Качество их оставляет желать лучшего, еще и оговорилась пару раз (например, систему неравенств назвала системой уравнений, и где-то знак не тот сказала. Прошу простить эти оплошности.) Я только учусь. Работать на камеру не умею, с камерой тоже. Но других вариантов у нас пока нет. А темы требуют озвучки))
Для решения неравенств требуется вспомнить, как мы решали системы неравенств в начале года, промежутки и запись решения с круглыми и квадратными скобками. Это стр. 55-56 учебника. В процессе занятия мы это повторим.
А теперь новый материал.
В тетради записываем тему, примеры неравенств с фото внизу и выписываем из учебника определения по плану:
Квадратное уравнение можно решать по общей формуле, совсем не обязательно по теореме, обратной теореме Виета. Кто как умеет!!!!
Кто как умеет!!!!
При решении неравенств нужно рассмотреть все возможные знаки множителей, при которых получается верное неравенство.
Если >0 , то множители или оба положительные — рассматриваем этот случай, или оба отрицательные, тогда второй случай. При решении каждого неравенства обязательно рассматривают оба случая и записывают общий ответ (это видео1 и видео2, они разделились на 2 части, потому что при записи я случайно выключила запись, должно было быть одно общее видео)
Если <0, то в этом случае знаки у множителей должны быть разные (плюс на минус дает минус при умножении).И опять же, при решении таких неравенств, нужно рассматривать два случая. Первый множитель положительный, второй — отрицательный, и, наоборот, первый -отрицательный, второй — положительный. В каждом случае решение и общий ответ.(это видео 3)
Множителями в этих неравенствах являются выражения в скобках (х+2)(х-6)
почитайте еще в учебнике на стр.263. Может там понятнее
Может там понятнее
в итоге получаем образец записи решения неравенства, его нужно переписать в тетрадь:
Оттуда переписываем второй образец записи
По этим образцам выполняем задания
№652-1,3), 654-1,3)
По желанию: разобрать задачу 3 стр. 263 в учебнике и решить №654-5)
Все решения высылаем мне в день занятия, т.е. 09.04.2020 на почту
1 задание по алгебре
06.04.2020- 8Б
08.08.2020 — 8А, 8В
Повторяем построение графика квадратичной функции
a>0 – ветви вверх, a<0 – ветви вниз
подставить x0 в формулу, задающую функцию, и найти y0
с Ох: у=0, решить уравнение ах2+bх+с=0 , корни этого уравнения х1 и х2 наз. нули функции – (х1;0) и (х2;0)
с Оу: х=0, у=с – (0;с)
Построить графики трех функций (план есть в тетрадях, кто болел-потерял — чуть позже прикреплю картинку) и выслать мне на почту. Работу подписать на каждой странице.
Работу подписать на каждой странице.
- х2-3х+2=0
- -9х2-6х-1=0
- 2х2+3х-2=0
Извините! Немного расползается текст из-за формул. На телефоне не очень красиво.
Урок по алгебре для 8 класс а «Решение квадратных уравнений» — К уроку — Математика, алгебра, геометрия
Тема урока: «Решение квадратных уравнений»
Класс: 8
Цели урока:
Образовательные: отработка способов решения неполных квадратных уравнений;
формирование навыков решения квадратных уравнений по
формуле.
Развивающие: развитие логического мышления, памяти, внимания;
развитие обще-учебных умений, умения сравнивать и обобщать.
Воспитательные: воспитание трудолюбия, взаимопомощи, математической культуры.
Тип урока: совершенствование знаний, умений и навыков.
Оборудование: интерактивная доска Smartboard, программа Noteebook и PoverPoint.
Ход урока:
Тема нашего урока «Решение квадратных уравнений». На данном уроке мы будем заниматься повторением способов решения квадратных уравнений.
На данном уроке мы будем заниматься повторением способов решения квадратных уравнений.
Сегодня на уроке мы с вами повторим и закрепим знания и умения решения квадратных уравнений. Каждый из вас должен уметь правильно, быстро и рационально решать квадратные уравнения.
Эта тема очень важная в курсе математики, она является первой ступенькой в изучении сложного материала.
Сегодня мы посмотрим, как вы научились решать квадратные уравнения.
I. Актуализация.
1. Какие из данных уравнений являются квадратными?
Какие из данных уравнений являются неполными квадратными уравнениями?
а) х2 + 3х – 19 =0, г) х2-7х+11=0,
б) 4х2+5х=0, д) 2х2-5х+1=0,
в) 8х2=0, е) 3х2-21х=0.
2. Вам представлены уравнения, которые определены по какому-то признаку.
Как вы думаете какое из уравнений этой группы является лишним?
а) 8х2-3х=0, а) х2-5х+1=0,
б) х2-25=0, б) 9х2-6х+10=0,
в) х2+4х-7=0, в) 2х2+8х-7=0,
г) 5х2=0. г) 8х2+12х+10=0.
3. Найдите корни уравнения:
Найдите корни уравнения:
а) (х-6)(х+3)=0, г) 9х2-16=0,
б) х(х+9)=0, д) х2=0.
в) х2-7х=0,
4. Найдите дискриминант и определите число корней:
а) х2-3х+1=0,
б) 5х2-2х+6=0,
в) 3х2-4х+2=0.
5. Решение неполных квадратных уравнений.
На доске написаны, в разном порядке, решения трёх уравнений. Учащимся предлагается выйти и составить правильное решение каждого уравнения.
х2-25=0, х2-3х=0, х2+16=0,
(х-5)(х+5)=0, х(х-3)=0, х2=-16
х-5=0 или х+5=0 х=0 или х-3=0 Ответ: нет решений
х1=5 х2=-5 х=3
Ответ: х1=5, х2=-5. Ответ: х1=0, х2=3.
II. Практическая работа.
Давайте вспомним формулы решения полных квадратных уравнений.
ах2+bх+с=0
если b-четное число если b-нечетное число
k=b:2
D= b2-4ас D=k2-ас
х1= , х1= ,
х2= х2=
• Сколько корней может иметь квадратное уравнение?
• Отчего зависит количество корней квадратного уравнения?
если D>0, то уравнение имеет два корня
если D=0, то уравнение имеет один корень х= или х=
если D<0, то уравнение не имеет решения
1. Учащиеся работают самостоятельно в тетрадях, на каждое уравнение один ученик у доски и заполняет таблицу:
Учащиеся работают самостоятельно в тетрадях, на каждое уравнение один ученик у доски и заполняет таблицу:
Решить уравнение и вставить правильный ответ.
х2-5х=0
3х2= — 96
х2=256
х2-11х+30=0
х2-4х=45
2х2-х+3=0
На доске представлен список ответов к уравнениям
нет решений,
-16, 16
0, 5
нет решений
-5, 9
5,6
2. Решить квадратное уравнение двумя способами(к доске выходят два ученика)
х2+8х+16=0
1 способ 2 способ
х2+8х+16=0, х2+8х+16=0,
(х+4)2=0, а=1, b=8, с=16
х+4=0, k=4
х= -4 D=k2-ac=0
x= = -4
III. Итог урока
На протяжении всего урока мы с вами решали уравнения.
— А что такое уравнение? (уравнение- равенство двух выражений с переменной)
— Что называется корнем уравнения? (корень уравнения- значение переменной, при
котором уравнение обращается в верное
числовое равенство)
— Что значит решить уравнение? (решить уравнение- это значит найти все его корни
или доказать, что корней нет)
История алгебры уходит своими корнями в древние времена.
Задачи, связанные с уравнениями решались ещё в Древнем Египте и Вавилоне. Теория уравнений интересовала и интересует математиков всех времён и народов.
В древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто представлялись в стихотворной форме.
Задача знаменитого индийского математика XII века Бхаскары:
Обезьянок резвых стая
Всласть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась,
А двенадцать по лианам
Стали прыгать, повисая…
Сколько ж было обезьянок.
Ты скажи мне, в этой стае?
Решение:
Всего — х
Забавлялись —
Прыгали – 12
+ 12 = х,
+ 12 = х,
х2 – 64х + 768 = 0,
х1=16, х2=48.
IV. Самостоятельная работа.
1 вариант 2 вариант
1) 2х2+3х-5=0, 1) 3х2+5х-2=0,
2) 3х2-27=0, 2) 18-2х2=0,
3) х2+2х=0, 3) 3х-х2=0,
4) 21х2-5х+1=0, 4) х2+25=0,
5) х2+36=0, 5) 5х2-26х+5=0,
6) 4х2-28х+49=0 6) 2х2-5х+3=0
Учащимся предлагается самостоятельно проверить решение своего варианта и поставить себе оценку за работу на уроке.
Проверь ответы:
1 вариант 2 вариант
-2,5; 1 -2,
-3;3 -3, 3
-2; 0 0; 3
;
нет решений
нет решений ; 5
3,5 1; 1,5
V. Домашнее задание.
Подготовиться к контрольной работе.
На странице приведен фрагмент.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Есть мнение?
Оставьте комментарий
Языковые цели
| Учащиеся будут: аргументированно рассуждать о количестве корней приведённого квадратного уравнения; вести рассуждения о корнях квадратного уравнения, опираясь на теорему Виета ; оперировать
предметной лексикой и терминологией данного раздела. Предметная лексика и терминология: приведённое квадратное уравнение; сумма корней приведённого квадратного уравнения; произведение корней приведённого квадратного уравнения; Серия полезных фраз для диалога/письма: найдём сумму корней приведённого квадратного уравнения…; найдём произведение корней приведённого квадратного уравнения…;корни данного квадратного уравнения одного знака, т.к. … ; корни данного квадратного уравнения разного знака, т.к. … | Привитие ценностей | Умение учиться, добывать самостоятельно информацию, анализировать ситуацию, адаптироваться к новым ситуациям, ставить проблемы и принимать решения, отвечать за качество своей работы и своей группы, умение организовывать свое время, воспитывать уважение к разнообразию культур и мнений на уроке | Середина урока 4-38 мин
| Изучение нового материала: Теорема Виета Учитель: Квадратное уравнение, старший
коэффициент которого равен единице называется приведённым. Рассмотрим несколько приведенных квадратных уравнений. Найдите их корни, а также сумму и произведение этих корней. , , ,; , , ,; , , ,; Какие закономерности вы видите между суммой и произведением корней уравнения и его коэффициентами? Попробуйте их сформулировать. Предполагаемый ответ учащихся: Для каждого из приведенных уравнений сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену. Учитель: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Такое
утверждение называется прямой теоремой Виета и выполняется для любого
приведенного квадратного уравнения, имеющего корни. Докажем эту теорему.
Рассмотрим приведенное квадратное уравнение (где
старший коэффициент равен 1, второй коэффициент обозначен буквой, свободный член -. Пусть , тогда уравнение имеет два различных () или равных корня: и . Найдем сумму и произведение этих корней:: Доказано, что , . Заметим, что и ранее, и сейчас в случае, когда дискриминант квадратного уравнения равнялся нулю, мы говорили, что уравнение имеет два равных (или одинаковых) корня. Тогда теорема Виета выполняется. Если считать, что в этом случае уравнение имеет один корень, то не понятно, как использовать теорему Виета ( что в этом случае считать корнем ). Теорему Виета легко применять к произвольному квадратному уравнению.. Пусть это уравнение имеет корни и . Разделим все части уравнения на старший коэффициент и получим равносильное приведенное квадратное уравнение . Для него (и для исходного уравнения) по доказанной теореме Виета выполняются соотношения: , . 1. Запишите результат деления обеих частей уравнения на первый коэффициент: (4 б). a); b) ; c) ; d). 2.Заполните таблицу: (15 б) 3. Не решая приведённое квадратное уравнение, корни которого и , заполните таблицу: (8 б) 4. Составьте квадратное уравнение по его корням:(проверка по готовым решениям, взаимооценивание), (12 б) a); b); c); d).
5. Решите уравнение и проверьте ответ по теореме Виета:(доп.задание) a); b); c) ; d) . Проверка решения заданий №1-3 проводится по методики «Карусель». № 4 Результаты заносятся в оценочный лист. |
1. Запишите результат деления обеих частей уравнения на первый коэффициент: . a); b) ;
2. Заполните таблицу по образцу: х1+х2= — р х1× х2=с Образец
х1+х2= — 8 -3+(-5)=-8 х1× х2=15 -3×(-5)=15
| Конец урока 39-40 мин
| Учитель демонстрирует задания для домашней работы на экране ноутбука, отвечает на вопросы учащихся и мобилизует их на рефлексию своей работы. Задания для домашней работы: 1. стр 72 № 8.1, 8.6 2. Подготовьте теоретические вопросы по разделу 8.2А «Квадратные уравнения». Рефлексия: Оценочный лист___________________________
0-15 баллов -Надо постараться 16-25 баллов -Есть пробелы в понимании темы (Удовлетворительно) 26-33 балла -Хорошо 34-39 баллов- Отлично
|
|
8 класс | Математика | Iowa Core
В 8-м классе учебное время должно быть сосредоточено на трех важнейших областях: (1) формулировка и объяснение выражений и уравнений, включая моделирование связи двумерных данных с линейным уравнением и решение линейных уравнений и систем линейных уравнений; (2) понимание концепции функции и использование функций для описания количественных отношений; (3) анализ двух- и трехмерного пространства и фигур с использованием расстояния, угла, подобия и конгруэнтности, а также понимание и применение теоремы Пифагора.
- Учащиеся используют линейные уравнения и системы линейных уравнений для представления, анализа и решения различных задач. Учащиеся узнают уравнения пропорций ( y/x = m или y = m x ) как специальные линейные уравнения ( y = m x + b ), понимая, что 90 константа пропорциональности ( м ) — наклон, а графики — линии, проходящие через начало координат. Они понимают, что наклон ( м ) линии представляет собой постоянную скорость изменения, так что если вход или координата x изменяется на величину A , выход или координата y изменяется на величину м · А .Учащиеся также используют линейное уравнение для описания связи между двумя величинами в двумерных данных (например, между размахом рук и ростом учащихся в классе). На этом уровне подгонка модели и оценка ее соответствия данным выполняются неформально. Интерпретация модели в контексте данных требует, чтобы учащиеся выражали отношение между двумя рассматриваемыми величинами и интерпретировали компоненты отношения (такие как наклон и y -пересечение) с точки зрения ситуации.

Учащиеся стратегически выбирают и эффективно реализуют процедуры для решения линейных уравнений с одной переменной, понимая, что при использовании свойств равенства и концепции логической эквивалентности они сохраняют решения исходного уравнения. Учащиеся решают системы двух линейных уравнений с двумя переменными и связывают системы с парами прямых на плоскости; они пересекаются, параллельны или являются одной и той же линией. Учащиеся используют линейные уравнения, системы линейных уравнений, линейные функции и свое понимание наклона линии для анализа ситуаций и решения проблем.
- Учащиеся понимают понятие функции как правило, которое назначает каждому входу ровно один выход. Они понимают, что функции описывают ситуации, когда одна величина определяет другую. Они могут переводиться между представлениями и частичными представлениями функций (отмечая, что табличные и графические представления могут быть частичными представлениями), и они описывают, как аспекты функции отражаются в различных представлениях.

- Учащиеся используют идеи о расстоянии и углах, их поведении при перемещении, вращении, отражении и расширении, а также идеи о конгруэнтности и сходстве для описания и анализа двухмерных фигур и решения задач.Учащиеся показывают, что сумма углов в треугольнике есть угол, образованный прямой линией, и что различные конфигурации линий порождают подобные треугольники из-за углов, образующихся при пересечении параллельных прямых секущей. Учащиеся понимают формулировку теоремы Пифагора и ее обратной формы, а также могут объяснить, почему теорема Пифагора верна, например, путем разложения квадрата двумя разными способами. Они применяют теорему Пифагора для нахождения расстояний между точками на координатной плоскости, для нахождения длин и для анализа многоугольников.Учащиеся завершают свою работу над объемом, решая задачи, связанные с конусами, цилиндрами и сферами.
Wolfram|Alpha Примеры: Common Core Math: 8 класс: выражения и уравнения
Выражения
Работа с эквивалентными выражениями.
Используйте экспоненциальные законы для упрощения выражений (CCSS.Math.Content.8.EE.A.1):
Еще примеры
Уравнения
Представлять и решать задачи с уравнениями.
Решите уравнение (CCSS.Content.Math.8.EE.C.7):
Решите уравнение с показателями (CCSS. Содержание.Математика.8.EE.A.2):
Содержание.Математика.8.EE.A.2):
Найдите уравнение прямой между двумя точками (CCSS.Содержание.Математика.8.EE.B.6):
Решите систему уравнений (CCSS. Содержание.Математика.8.EE.C.8):
Содержание.Математика.8.EE.C.8):
Еще примеры
Научная нотация
Используйте экспоненциальную запись для представления больших и малых чисел.
Преобразование между стандартной и экспоненциальной записью (CCSS.Content.Math.8.EE.A.3):
Сравните числа, выраженные в экспоненциальном представлении (CCSS. Содержание.Математика.8.EE.A.3):
Содержание.Математика.8.EE.A.3):
Выполнение вычислений с экспоненциальной записью (CCSS.Содержание.Математика.8.EE.A.4):
Еще примеры
Общие базовые стандарты для 8-го класса
Ниже приведены общие базовые стандарты для 8-го класса со ссылками на поддерживающие их ресурсы. Мы также поощряем множество упражнений и работу с книгами.
Мы также поощряем множество упражнений и работу с книгами.
8 класс | Система счисления
Знай, что есть нерациональные числа, и аппроксимируй их рациональными числами.
8.NS.A.1Знайте, что числа, не являющиеся рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.2). Например, усекая десятичное разложение квадратного корня из 2, покажите, что квадратный корень из 2 находится между 1 и 2, а затем между 1,4 и 1,5, и объясните, как продолжить, чтобы получить более точные приближения.
Упражнение: Найдите приблизительное значение для Pi, класс 8 | Выражения и уравнения
Работа с радикалами и целыми показателями.
8.EE.A.1 Знать и применять свойства целочисленных показателей степени для создания эквивалентных числовых выражений. 3) = 1/27.9, и определить, что население мира более чем в 20 раз больше.
3) = 1/27.9, и определить, что население мира более чем в 20 раз больше.
8.EE.A.4 Выполнение операций с числами, выраженными в экспоненциальном представлении, включая задачи, в которых используются как десятичные, так и экспоненциальные представления. Используйте научные обозначения и выбирайте единицы соответствующего размера для измерения очень больших или очень малых величин (например, используйте миллиметры в год для распространения по морскому дну). Интерпретировать научную нотацию, созданную технологией.
Обозначение индекса — степени 10Понимать связи между пропорциональными отношениями, линиями и линейными уравнениями.
8.EE.B.5 Нарисуйте пропорциональные отношения, интерпретируя удельную скорость как наклон графика. Сравните два разных пропорциональных отношения, представленных по-разному. Например, сравните график «расстояние-время» с уравнением «расстояние-время», чтобы определить, какой из двух движущихся объектов имеет большую скорость.
8.EE.B.6Используйте подобные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для прямой, проходящей через начало координат, и уравнение y = mx + b для прямой, пересекающей вертикальную ось в точке b.
Анализ и решение линейных уравнений и пар одновременных линейных уравнений.
8.EE.C.7 Решите линейные уравнения с одной переменной.
а. Приведите примеры линейных уравнений от одной переменной с одним решением, бесконечным числом решений или отсутствием решений. Покажите, какая из этих возможностей имеет место, последовательно преобразовывая данное уравнение в более простые формы, пока не получится эквивалентное уравнение вида x = a, a = a или a = b (где a и b — разные числа).
б. Решите линейные уравнения с коэффициентами рациональных чисел, включая уравнения, решения которых требуют расширения выражений с использованием дистрибутивного свойства и сбора подобных членов.
8.EE.C.8 Анализировать и решать пары одновременных линейных уравнений.
а. Поймите, что решения системы двух линейных уравнений с двумя переменными соответствуют точкам пересечения их графиков, потому что точки пересечения удовлетворяют обоим уравнениям одновременно.
б. Решите системы двух линейных уравнений с двумя переменными алгебраически и оцените решения, построив уравнения в виде графика. Решите простые случаи путем проверки. Например, 3x + 2y = 5 и 3x + 2y = 6 не имеют решения, потому что 3x + 2y не может быть одновременно 5 и 6.
c. Решайте реальные и математические задачи, приводящие к двум линейным уравнениям с двумя переменными. Например, зная координаты двух пар точек, определите, пересекает ли прямая, проходящая через первую пару точек, прямую, проходящую через вторую пару.
Класс 8 | Функции
Определение, оценка и сравнение функций.
8.F.A.1 Поймите, что функция — это правило, которое назначает каждому входу ровно один выход. График функции представляет собой набор упорядоченных пар, состоящих из входа и соответствующего выхода. (Обозначение функции не требуется в 8 классе.)
Диапазон доменов и кодовый домен Инъективный Сюръективный и Биективный8.F.A.2 Сравните свойства двух функций, каждая из которых представлена по-разному (алгебраически, графически, численно в таблицах или словесными описаниями).2, дающая площадь квадрата как функцию длины его стороны, нелинейна, потому что ее график содержит точки (1,1), (2,4) и (3,9), которые не лежат на прямой.
График функций и калькуляторИспользуйте функции для моделирования отношений между величинами.
8.F.B.4 Построить функцию для моделирования линейной зависимости между двумя величинами. Определить скорость изменения и начальное значение функции по описанию зависимости или по двум значениям (x, y), в том числе прочитать их из таблицы или из графика. Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений.
Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений.
8.F.B.5 Качественно описать функциональную связь между двумя величинами, анализируя график (например, где функция возрастает или убывает, линейна или нелинейна). Нарисуйте график, демонстрирующий качественные характеристики функции, описанной словесно.
График функций и калькулятор Возрастающие и убывающие функции8 класс | Геометрия
Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для геометрии.
8.G.A.1 Экспериментально проверить свойства вращения, отражения и переноса:
a. Линии превращаются в прямые, а отрезки прямых в отрезки прямой одинаковой длины.
б. Углы принимаются равными углам.
в. Параллельные прямые переводятся в параллельные прямые.
8.G.A.2Понять, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.
8.G.A.3 Описать эффект расширения, перемещения, поворота и отражения двухмерных фигур с использованием координат.
Симметрия — отражение и вращение8.G.A.4Понять, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.
Загадка жонглера Сэма Лойда Симметрия — отражение и вращение8.G.A.5Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образованных при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников. Например, расположите три копии одного и того же треугольника так, чтобы казалось, что три угла образуют линию, и приведите аргумент в терминах секущей, почему это так.
Поймите и примените теорему Пифагора.
8.RUS6 Объясните доказательство теоремы Пифагора и ее обращение.
8.RUS.7 Применение теоремы Пифагора для определения неизвестных длин сторон в прямоугольных треугольниках в реальных и математических задачах в двух и трех измерениях.
8.RUS.8 Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.
Расстояние между 2 точками Упражнение: Прогулка по пустынеРешайте реальные и математические задачи на объем цилиндров, конусов и сфер.
8.G.C.9Знать формулы объемов конусов, цилиндров и сфер и использовать их для решения реальных и математических задач.
Площадь круга Треугольник Квадрат Прямоугольник Параллелограмм Трапеция Эллипс и секторКласс 8 | Статистика и вероятность
Исследование моделей связи в двумерных данных.
8.SP.A.1 Построение и интерпретация диаграмм рассеяния для данных двумерных измерений для изучения закономерностей связи между двумя величинами. Опишите шаблоны, такие как кластеризация, выбросы, положительная или отрицательная связь, линейная связь и нелинейная связь.
8.SP.A.2Знайте, что прямые линии широко используются для моделирования отношений между двумя количественными переменными. Для точечных диаграмм, которые предполагают линейную связь, неформально аппроксимируют прямую линию и неформально оценивают соответствие модели, оценивая близость точек данных к линии.
8.SP.A.3 Использование уравнения линейной модели для решения задач в контексте данных двумерных измерений, интерпретация наклона и точки пересечения. Например, в линейной модели биологического эксперимента интерпретируйте наклон равным 1.5 см/час, что означает, что дополнительный час солнечного света каждый день связан с дополнительными 1,5 см высоты взрослого растения.
8.SP.A.4 Поймите, что закономерности ассоциации также можно увидеть в двумерных категориальных данных, отображая частоты и относительные частоты в двусторонней таблице. Постройте и интерпретируйте двустороннюю таблицу, обобщающую данные по двум категориальным переменным, собранным у одних и тех же субъектов. Используйте относительные частоты, рассчитанные для строк или столбцов, чтобы описать возможную связь между двумя переменными.Например, соберите данные от учеников вашего класса о том, соблюдается ли у них комендантский час по вечерам в школе и есть ли у них работа по дому. Есть ли доказательства того, что те, у кого комендантский час, также, как правило, занимаются домашними делами?
Используйте относительные частоты, рассчитанные для строк или столбцов, чтобы описать возможную связь между двумя переменными.Например, соберите данные от учеников вашего класса о том, соблюдается ли у них комендантский час по вечерам в школе и есть ли у них работа по дому. Есть ли доказательства того, что те, у кого комендантский час, также, как правило, занимаются домашними делами?
CMP3 8 класс — Проект «Подключенная математика»
8-1 Мышление с помощью математических моделей
Понятия и пояснения | Примеры домашних заданий | Математический фон
В задании «Мышление математическими моделями» ваш ребенок будет моделировать отношения с помощью графиков и уравнений.Они будут использовать модели для анализа ситуаций и решения проблем. Исследования в этом разделе помогут им понять следующие идеи.
- Представление данных с помощью графиков, таблиц, словесных описаний и алгебраических выражений.

- Распознавать линейные и нелинейные зависимости в таблицах и графиках.
- Использование уравнений линейной и обратной вариации для моделирования двумерных данных
- Используйте остаточный анализ для измерения соответствия моделей линейной и обратной вариации.
- Анализ, приближение и решение линейных уравнений.
- Используйте линейные и обратные вариационные уравнения для решения задач, прогнозирования и принятия решений
- Используйте диаграммы рассеяния, двусторонние таблицы и коэффициенты корреляции для описания закономерностей ассоциации в парах переменных.
- Используйте стандартное отклонение для измерения изменчивости распределения данных.
Когда ваш ребенок сталкивается с новой проблемой, полезно задать такие вопросы, как:
- Каковы ключевые переменные в этой ситуации?
- Если существует закономерность, связывающая переменные, достаточно ли она сильна, чтобы я мог делать прогнозы?
- Какая закономерность связывает переменные?
- Какое уравнение будет выражать отношения?
- Как я могу использовать уравнение, чтобы ответить на вопросы об отношениях?
8-2 В поисках Пифагора
Понятия и пояснения | Примеры домашних заданий | Математический фон
В В поисках Пифагора ваш ребенок изучит важное соотношение между длинами сторон прямоугольного треугольника. Они научатся:
Они научатся:
- Разработка стратегий для нахождения расстояния между двумя точками на координатной сетке
- Объясните доказательство теоремы Пифагора
- Понимать и использовать теорему Пифагора для решения повседневных задач
- Записывайте дроби как повторяющиеся или заканчивающиеся десятичные дроби
- Запись десятичных дробей в виде дробей
- Распознавать рациональные и иррациональные числа
- Найдите иррациональные числа в числовой строке
- Соотнесите площадь квадрата с длиной его стороны, а объем куба с длиной его стороны
- Оценка квадратных и кубических корней
Когда ваш ученик сталкивается с новой проблемой, полезно задать такие вопросы, как:
- Какие величины в этой задаче?
- Является ли Теорема Пифагора полезной и уместной в этой ситуации?
- Откуда я знаю?
- Нужно ли мне найти расстояние между двумя точками?
- Как связаны длина стороны и площадь квадрата?
- Как вычислить квадратный или кубический корень числа?
8-3 Рост, Рост, Рост
Понятия и пояснения | Примеры домашних заданий | Математический фон
В игре Растет, растет, растет ваш ребенок будет изучать экспоненциальные функции, один из наиболее важных типов нелинейных отношений. Исследования в этом подразделении помогут им научиться:
Исследования в этом подразделении помогут им научиться:
- Определение ситуаций, в которых количество растет или уменьшается экспоненциально
- Распознавать связи между моделями роста в таблицах, графиках и уравнениях, которые представляют экспоненциальные функции
- Построение уравнений для выражения отношения между переменными в экспоненциальной функции в таблицах данных, графиках и проблемных ситуациях
- Сравнение экспоненциальной и линейной функций
- Разработать и использовать правила работы с показателями степени, включая экспоненту, для записи и интерпретации эквивалентных выражений
- Решайте задачи об экспоненциальном росте и спаде из различных областей, включая науку и бизнес
Пока ваш ребенок работает над задачами в этом разделе, задавайте вопросы о ситуациях, связанных с нелинейными отношениями, например:
- Как узнать, является ли отношение между переменными экспоненциальной функцией?
- Что такое фактор роста или распада?
- Какое уравнение моделирует данные таблицы, графика или проблемной ситуации?
- Что я могу узнать об этой ситуации, изучая таблицу или график экспоненциальной функции?
- Как я могу ответить на вопросы о проблемной ситуации, изучая таблицу, график или уравнение, представляющее показательную функцию?
8-4 Лягушки, блохи и окрашенные кубики
Понятия и пояснения | Примеры домашних заданий | Математический фон
В наборе «Лягушки, блохи и раскрашенные кубики» ваш ребенок изучит квадратичные функции, важный тип нелинейных функций. Они научатся
Они научатся
- Распознавание закономерностей изменения квадратичных отношений
- Напишите уравнения для квадратичных функций, представленных в виде таблиц, графиков и проблемных ситуаций
- Соедините квадратные уравнения с закономерностями в таблицах и графиках квадратичных функций
- Использование квадратного уравнения для определения максимального или минимального значения, точек пересечения по осям x и y, линии симметрии и других важных особенностей графика квадратичной функции
- Распознавать эквивалентные квадратные выражения
- Использовать Распределительное Свойство для записи эквивалентных квадратных выражений в факторизованной и расширенной форме
- Используйте таблицы, графики и уравнения квадратичных функций для решения задач в различных ситуациях из геометрии, науки и бизнеса
- Сравните свойства квадратичных, линейных и экспоненциальных функций
Когда ваш ребенок сталкивается с новой проблемой, полезно задать такие вопросы, как:
- Что такое независимые и зависимые переменные?
- Как узнать, являются ли отношения между переменными квадратичными?
- Какое уравнение моделирует квадратичную функцию, заданную в виде таблицы, графика или задачи?
- Как я могу ответить на вопросы о проблемной ситуации, изучая таблицу, график или уравнение, представляющее квадратичную функцию?
8-5 Бабочки, вертушки и обои
Понятия и пояснения | Примеры домашних заданий | Математический фон
В наборе «Бабочки, вертушки и обои» ваш ребенок научится:
- Определите фигуры, которые имеют различные виды симметрии
- Описывать типы симметрии, используя отражения, повороты и переносы
- Используйте преобразования симметрии, чтобы сравнить размер и форму фигур, чтобы увидеть, являются ли они конгруэнтными или похожими
- Эффективно определять конгруэнтные и подобные треугольники и четырехугольники
- Использование свойств конгруэнтных и подобных треугольников для решения задач о формах и измерениях
Когда ваш ученик сталкивается с новой проблемой, полезно задать такие вопросы, как:
- Как я могу использовать симметрию для описания формы и свойств фигур в проекте или задаче?
- Какие фигуры в узоре конгруэнтны?
- Какие части конгруэнтных фигур будут сопоставлены преобразованием конгруэнтности?
- Какие фигуры в задаче подобны?
8-6 Скажи это символами
Концепции и пояснения Примеры домашних заданий | Математический фон
Алгебра предоставляет идеи и символы для выражения информации о количественных переменных и отношениях. В Say It With Symbols ваш ребенок будет решать задачи, предназначенные для развития его понимания и навыков использования символических выражений и уравнений в алгебре. Они научатся:
В Say It With Symbols ваш ребенок будет решать задачи, предназначенные для развития его понимания и навыков использования символических выражений и уравнений в алгебре. Они научатся:
- Представление паттернов и взаимосвязей в символических формах
- Определить, когда различные символьные выражения математически эквивалентны
- Напишите алгебраические выражения в удобных эквивалентных формах
- Объедините символьные выражения, используя алгебраические операции, чтобы сформировать новые выражения
- Анализ выражений или уравнений для определения моделей изменений в таблицах и графиках, которые представляет выражение или уравнение
- Решите линейные и квадратные уравнения, используя символьные рассуждения
- Использовать алгебраические рассуждения для проверки обобщений и предположений
Когда ваш ребенок сталкивается с новой проблемой, полезно задать такие вопросы, как:
- Какое выражение или уравнение представляет закономерность или взаимосвязь в контексте?
- Можете ли вы написать эквивалентное выражение для данного выражения, чтобы предоставить новую информацию об отношениях?
- Какие операции могут преобразовать данное уравнение или выражение в эквивалентную форму, которую можно использовать для ответа на вопрос?
- Как символическое рассуждение может помочь подтвердить гипотезу?
8-7 Это в системе
Понятия и пояснения | Примеры домашних заданий | Математический фон
В этом модуле ваш ребенок будет писать и решать системы линейных уравнений и неравенств, которые моделируют реальные ситуации. Методы решения этих алгебраических систем сочетают в себе графические и алгебраические рассуждения из более ранних модулей Connected Mathematics. Вы узнаете, как
Методы решения этих алгебраических систем сочетают в себе графические и алгебраические рассуждения из более ранних модулей Connected Mathematics. Вы узнаете, как
- Решение линейных уравнений и систем линейных уравнений с двумя переменными
- Решение линейных неравенств и систем неравенств с двумя переменными
- Использовать системы линейных уравнений и неравенств для решения задач
Когда ваш ребенок сталкивается с новой проблемой, полезно задать такие вопросы, как:
- Какие переменные в этой задаче?
- Требует ли задача решения системы уравнений или неравенств, связывающих эти переменные?
- Какая стратегия будет наиболее эффективной при решении системы?
8-8 Функциональный разветвитель
Понятия и пояснения | Примеры домашних заданий | Математический фон
Функции были основной темой на протяжении всей работы вашего ребенка с алгеброй.В Function Junction ваш ребенок более подробно рассмотрит функции и изучит новые функции. Исследования в этом подразделении помогут им научиться:
Исследования в этом подразделении помогут им научиться:
- Определение области определения и диапазона функций и обозначение f (x) для выражения функций
- Проверить числовые и графические свойства ступенчатых и кусочно заданных функций
- Исследование свойств и использования обратных функций
- Изучение свойств и приложений арифметических и геометрических последовательностей
- Исследуйте отношения между функциями с графиками, связанными преобразованиями, такими как переводы и расширения
- Выражайте квадратичные функции в эквивалентной вершинной форме и используйте эту новую форму для решения уравнений и графических набросков
- Разработайте формулу для решения любого квадратного уравнения
- Изучение значения комплексных чисел и операций с ними
- Используйте полиномиальные выражения и функции для моделирования и ответов на вопросы о шаблонах данных и графиках, которые не могут быть представлены линейными, квадратичными, обратными или экспоненциальными функциями
По мере того, как они решают проблемы этого подразделения, будет полезно продолжать задавать такие вопросы, как:
- Какие переменные в ситуации и как они связаны?
- Какой знакомый тип функции можно использовать для моделирования взаимосвязи переменных или требуется что-то новое?
- Как алгебраические выражения и графики отношений между переменными связаны друг с другом?
- Как можно записать алгебраическое выражение для функции в форме, облегчающей набросок или анализ графика или решение уравнения?
Шаблон для занятия по системам уравнений, 8 класс
Одной из самых сложных тем по математике для 8 класса являются системы уравнений. Уроки, основанные на деятельности, — это один из способов, когда вы пытаетесь учить студентов; Я также люблю использовать онлайн-видео. Но самое полезное, чем я могу поделиться с вами из своего опыта, — это шаблон, который я разработал, чтобы помочь учащимся решить систему уравнений, используя метод подстановки.
Уроки, основанные на деятельности, — это один из способов, когда вы пытаетесь учить студентов; Я также люблю использовать онлайн-видео. Но самое полезное, чем я могу поделиться с вами из своего опыта, — это шаблон, который я разработал, чтобы помочь учащимся решить систему уравнений, используя метод подстановки.
Обучение системам уравнений
Я не помню, чтобы мне приходилось решать системы уравнений, пока я не учился в старшей школе. Тем не менее, в Единых основных государственных стандартах это является частью учебной программы для каждого учащегося средней школы.Фактически, это вершина алгебраической части учебного плана 8 класса. Учащиеся объединяют идеи о решении уравнений, построении графика линейной функции с использованием наклонов и точек пересечения, уравнений со многими решениями и без них, а также о переводе текстовых задач в алгебраические модели. Решение систем уравнений – это большой труд для юного ума!
Мне нравится последовательность, используемая в моем нынешнем учебнике для обучения студентов этим навыкам, которая заключается в том, чтобы сначала решать системы уравнений с помощью графика, затем заменять, затем исключать, а затем следуют уравнения со многими решениями и без них. Сначала используя графическую систему уравнений, учащиеся могут визуально подойти к тому, что представляет собой решение системы. После этого с помощью метода подстановки углубимся в алгебраические манипуляции (именно здесь и появляется загружаемый шаблон). Мне нравится его размещение здесь, потому что таким образом у меня все еще есть остальная часть модуля, чтобы помочь студентам, которые борются с длительностью процесса или самой алгеброй.
Сначала используя графическую систему уравнений, учащиеся могут визуально подойти к тому, что представляет собой решение системы. После этого с помощью метода подстановки углубимся в алгебраические манипуляции (именно здесь и появляется загружаемый шаблон). Мне нравится его размещение здесь, потому что таким образом у меня все еще есть остальная часть модуля, чтобы помочь студентам, которые борются с длительностью процесса или самой алгеброй.
Когда учащиеся сталкиваются с третьей фазой модуля, решая систему методом исключения, это как глоток свежего воздуха.Студенты иногда говорят: «Почему вы не научили нас этому раньше?» Мой типичный ответ таков: «Вы бы никогда не работали над изучением замещения, если бы я сначала научил вас исключению!» Окончание с системами без решений или со многими решениями полезно, поскольку позволяет учащимся сравнивать и противопоставлять различные методы, выбирая тот, который основан на структуре первоначально заявленной системы уравнений деятельности. В этой кульминационной части модуля мы можем провести содержательные дискуссии о том, почему учащиеся выбирают замену, а не замену.устранение.
В этой кульминационной части модуля мы можем провести содержательные дискуссии о том, почему учащиеся выбирают замену, а не замену.устранение.
Шаблон, помогающий учащимся решать системы уравнений
Итак, вернемся к шаблону. Поскольку учащимся очень трудно справиться со многими этапами любых систем уравнений, я использую этот шаблон, чтобы помочь в этом процессе. Некоторые учащиеся воспользуются шаблоном пару раз, а затем отложат его в сторону, потому что хорошо понимают этапы. Другие, кто склонен немного больше бороться с простым решением уравнений с одной переменной, могут использовать шаблон в качестве руководства для процесса.
В каждом блоке они фокусируются на одном аспекте процесса, затем стрелка показывает им, есть ли следующий блок для следующего шага. Они могут спокойно сосредоточиться на задаче по алгебре в каждой ячейке (решение y , замена, упрощение, нахождение х , когда y известно, проверка решений), а затем сделать шаг назад, чтобы посмотреть, что будет дальше в таблице.


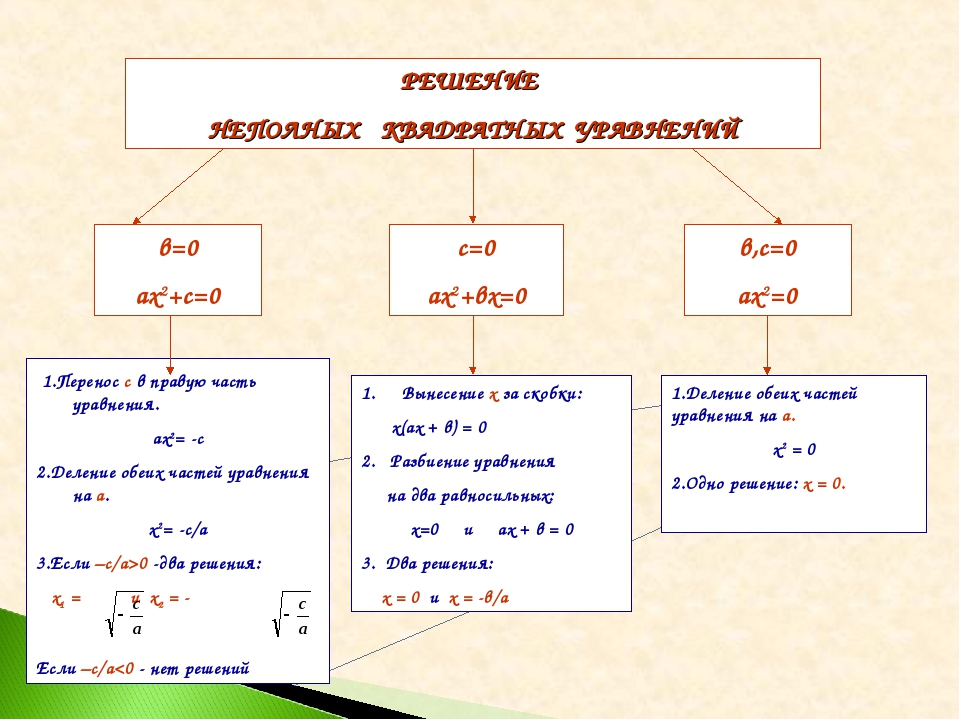 Найдем его дискриминант: .
Найдем его дискриминант: .
 х2 +
х2 +

