Как найти уравнение нормали к графику функции в заданной точке?
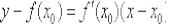
На данном уроке мы узнаем, как найти уравнение нормали к графику функции 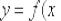 в точке
в точке 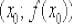 и разберём многочисленные
и разберём многочисленные
примеры, которые касаются этой задачи. Для качественного усвоения материала нужно понимать геометрический смысл производной и
уметь их находить хотя бы на уровне следующих статей:
Как найти производную? Производная сложной функции
и
Простейшие задачи с производными.
Перечисленные уроки позволят «чайникам» быстро сориентироваться в теме и поднять свои навыки дифференцирования практически с полного нуля. По существу, сейчас последует развёрнутое продолжение параграфа об уравнении касательной 3-й статьи из вышеприведенного списка. Почему продолжение? Уравнение нормали тесно связано с уравнением касательной. Помимо прочего я рассмотрю задачи о том, как построить уравнения этих линий в ситуациях, когда функция задана неявно либо параметрически.
Но сначала освежим воспоминания: если функция  дифференцируема в точке
дифференцируема в точке  (т.е. если существует конечная производная
(т.е. если существует конечная производная 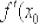 ), то уравнение касательной к графику функции в точке
), то уравнение касательной к графику функции в точке 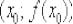 можно найти по следующей формуле:
можно найти по следующей формуле:

Это самый распространенный случай, с которым мы уже столкнулись на уроке Простейшие задачи с производными. Однако дело этим не
ограничивается: если в точке 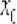 существует бесконечная производная:
существует бесконечная производная: 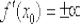 , то касательная будет параллельна оси
, то касательная будет параллельна оси  и её уравнение примет вид
и её уравнение примет вид 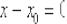 . Дежурный пример: функция
. Дежурный пример: функция 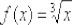 с
с
производной 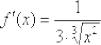
вблизи критической точки 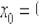 . Соответствующая касательная выразится уравнением:
. Соответствующая касательная выразится уравнением:
(ось ординат).
Если же производной 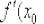 не существует (например, производной от
не существует (например, производной от 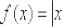 в точке
в точке 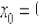 ), то, разумеется, не существует и общей касательной.
), то, разумеется, не существует и общей касательной.
Как различать последние два случая, я расскажу чуть позже, а пока что вернёмся в основное русло сегодняшнего урока:
Что такое нормаль? Нормалью к графику функции 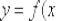 в точке
в точке 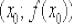
(понятно, что касательная должна существовать). Если совсем коротко, нормаль – это перпендикулярная к касательной прямая, проходящая через точку касания.
Как найти уравнение нормали? Из курса аналитической геометрии напрашивается очень простой алгоритм: находим
уравнение касательной и представляем его в общем виде
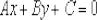 . Далее «снимаем» нормальный вектор
. Далее «снимаем» нормальный вектор  и составляем уравнение нормали по точке
и составляем уравнение нормали по точке 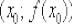 и направляющему вектору
и направляющему вектору 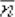
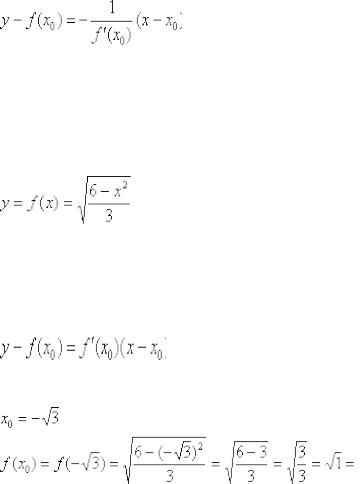
Этот способ применять можно, но в математическом анализе принято пользоваться готовой формулой, основанной на взаимосвязи угловых коэффициентов перпендикулярных прямых. Если
существует конечная и отличная от нуля производная  , то уравнение нормали к графику функции
, то уравнение нормали к графику функции  в точке
в точке 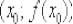 выражается следующим уравнением:
выражается следующим уравнением:
Особые случаи, когда 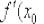 равна нулю либо бесконечности мы обязательно рассмотрим, но сначала «обычные» примеры:
равна нулю либо бесконечности мы обязательно рассмотрим, но сначала «обычные» примеры:
Пример 1 Составить уравнения касательной и нормали к графику кривой
в точке, абсцисса которой равна 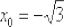 .
.
В практических заданиях часто требуется найти и касательную тоже. Впрочем, это очень только нА руку – лучше будет «набита рука» =)
Решение: Первая часть задания хорошо знакома, уравнение касательной составим по формуле:
В данном случае:
Найдём производную:
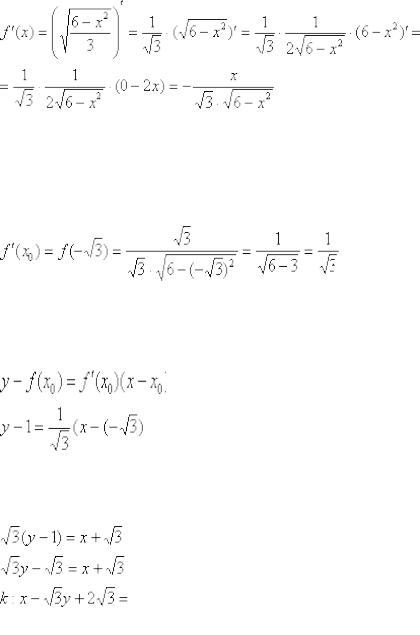
Здесь на первом шаге вынесли константу за знак производной, на втором – использовали правило дифференцирования сложной функции.
Теперь вычислим производную в точке 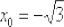 :
:
Получено конечное число и это радует. Подставим 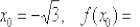
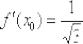 в формулу
в формулу:
Перебросим 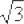 наверх левой части, раскроем скобки и представим уравнение касательной в общем виде:
наверх левой части, раскроем скобки и представим уравнение касательной в общем виде:
Вторая часть задания ничуть не сложнее. Уравнение нормали составим по формуле:
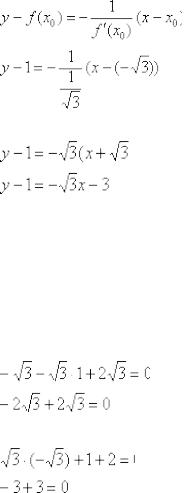
Избавляемся от трёхэтажности дроби и доводим уравнение до ума:
 – искомое уравнение.
– искомое уравнение.
Ответ: 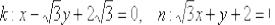
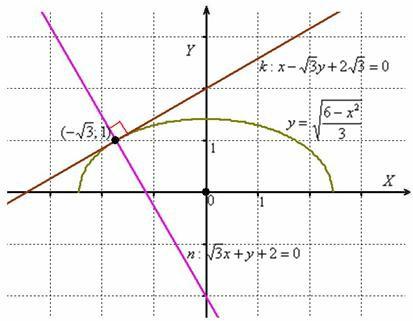
Здесь можно выполнить частичную проверку. Во-первых, координаты точки 
 – верное равенство.
– верное равенство.
 – верное равенство.
– верное равенство.
И, во-вторых, векторы нормали 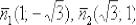 должны быть
должны быть
ортогональны. Это элементарно проверяется с помощью скалярного произведения:
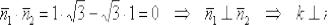 , что и требовалось проверить.
, что и требовалось проверить.
Как вариант, вместо нормальных векторов можно использовать
направляющие векторы прямых.
! Данная проверка оказывается бесполезной, если неверно найдена производная 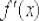
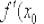 . Это «слабое звено» задания – будьте предельно внимательны!
. Это «слабое звено» задания – будьте предельно внимательны!Чертежа по условию не требовалось, но полноты картины ради:
Забавно, но фактически получилась и полная проверка, поскольку чертёж выполнен достаточно точно =) Кстати, функция
 задаёт верхнюю дугу эллипса. Следующая задача для самостоятельного решения:
задаёт верхнюю дугу эллипса. Следующая задача для самостоятельного решения:
Пример 2 Составить уравнения касательной и нормали к графику функции
В данном случае 
Казалось бы, расчёты пустяковые, а в знаках запутаться более чем реально:
Таким образом:
Поскольку касательная параллельна оси  (Случай №1), то нормаль, проходящая через ту же точку
(Случай №1), то нормаль, проходящая через ту же точку 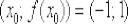 , будет параллельна оси ординат:
, будет параллельна оси ординат:
Чертёж – это, конечно же, дополнительные хлопоты, но зато добротная проверка аналитического решения:
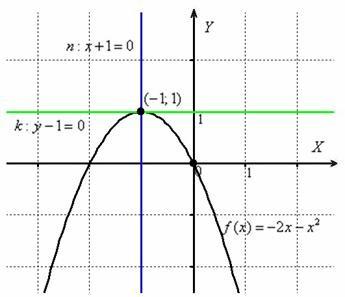
Ответ: 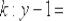 ,
, 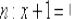
В школьном курсе математики распространено упрощённое определение касательной, которое формулируется примерно так:
«Касательная к графику функции – это прямая, имеющая с данным графиком единственную общую точку». Как видите, в общем случае это утверждение некорректно. Согласно геометрическому смыслу производной, касательной является именно зелёная, а не синяя прямая.
Следующий пример посвящён тому же Случаю №1, когда  : Пример 4
: Пример 4
Написать уравнение касательной и нормали к кривой 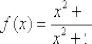 в точке
в точке 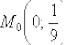 .
.
Краткое решение и ответ в конце урока

существует общая вертикальная касательная:
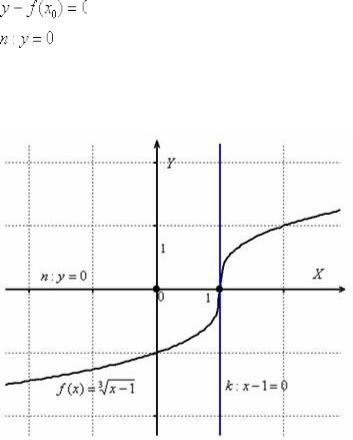
Ну, и очевидно, что нормалью является ось абсцисс. Формально по формуле:
Для лучшего понимания задачи приведу чертёж:
Ответ: 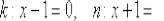
Я рад, что вы не ушли бороздить просторы Интернета, потому что всё самое интересное только начинается! Чтобы осилить материал следующего параграфа, нужно уметь находить производную от неявно заданной функции:
studfile.net
11.3. Уравнение касательной
и нормали. Физический смысл производной
Производная функции 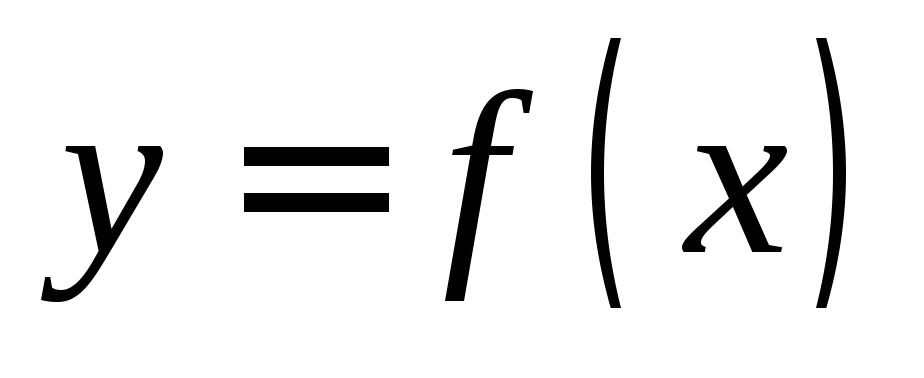 в точке
в точке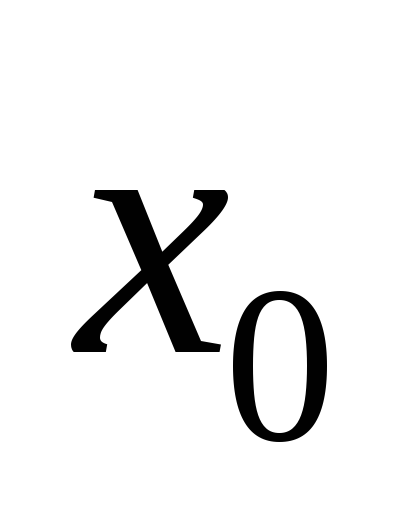 представляет собой угловой коэффициент
касательной, проведенной к графику
функции в точке
представляет собой угловой коэффициент
касательной, проведенной к графику
функции в точке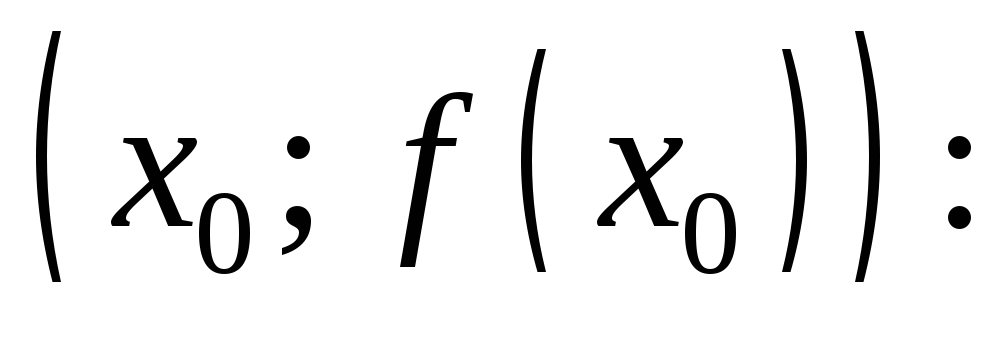
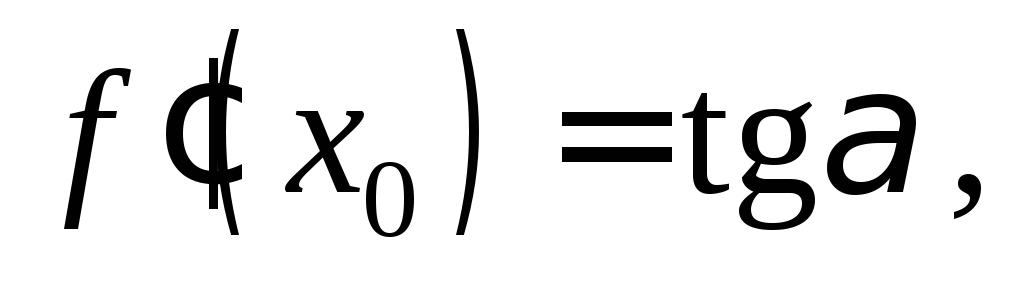
где  – угол наклона касательной к осиOx.
В этом состоит геометрический смысл производной.
– угол наклона касательной к осиOx.
В этом состоит геометрический смысл производной.
Уравнение
касательной, проведенной к графику
функции в точке 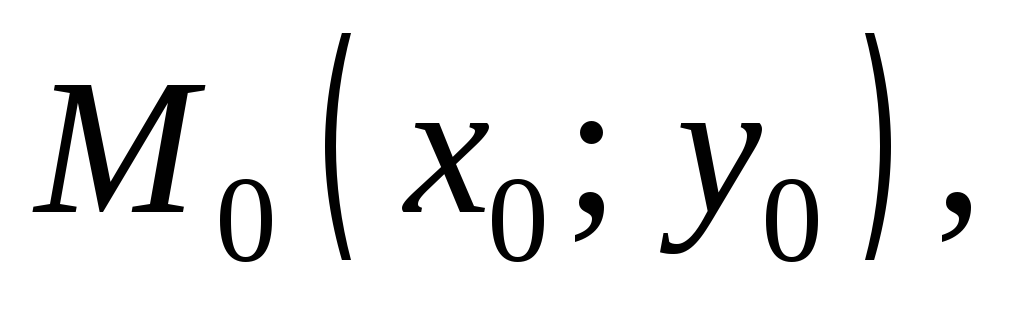 где
где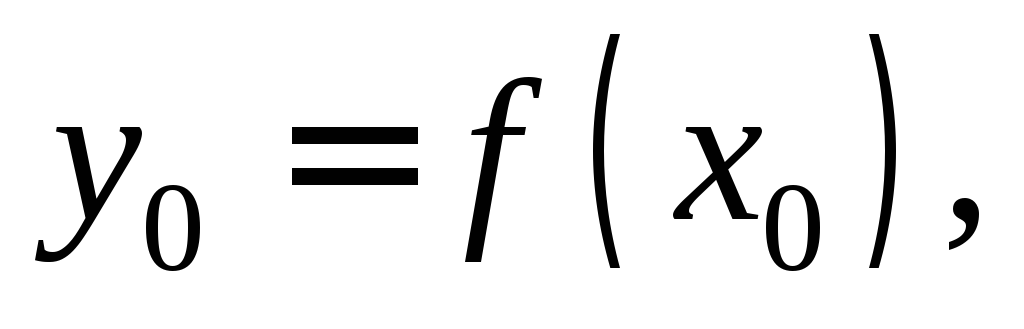 имеет вид:
имеет вид:
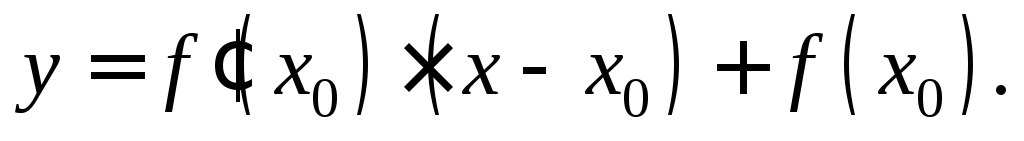 (11.9)
(11.9)
Прямая, проходящая
через точку 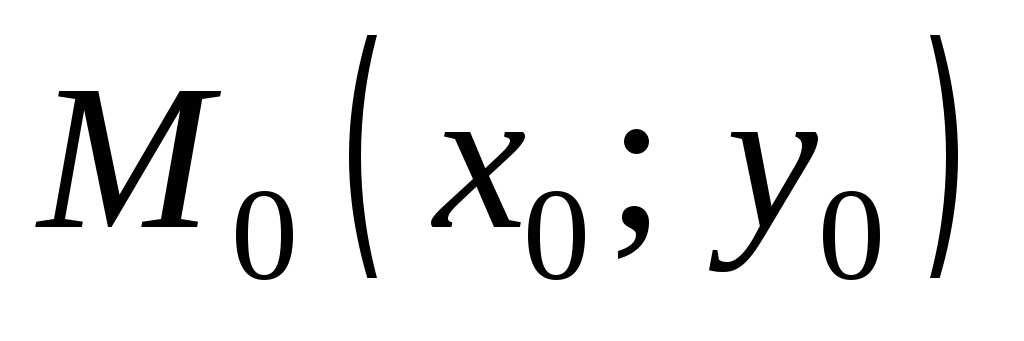 графика функции
графика функции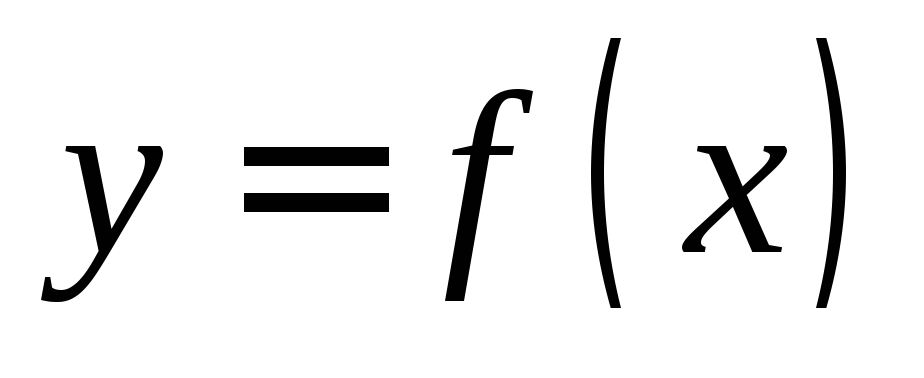 перпендикулярно касательной, проведенной
в этой точке, называетсянормалью к графику функции
перпендикулярно касательной, проведенной
в этой точке, называетсянормалью к графику функции 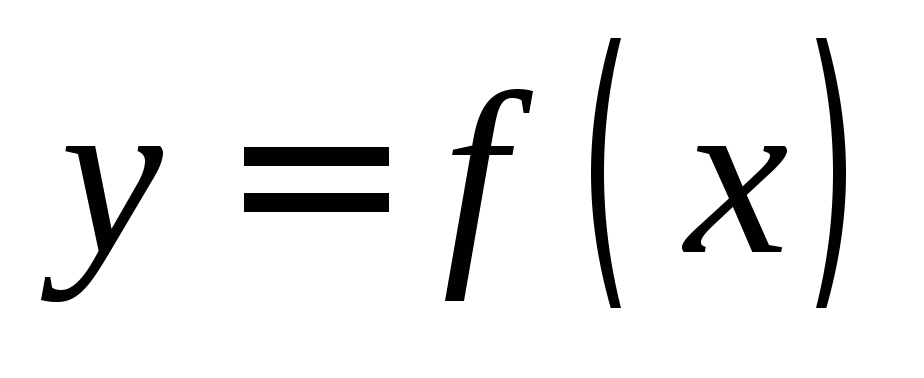 в точке
в точке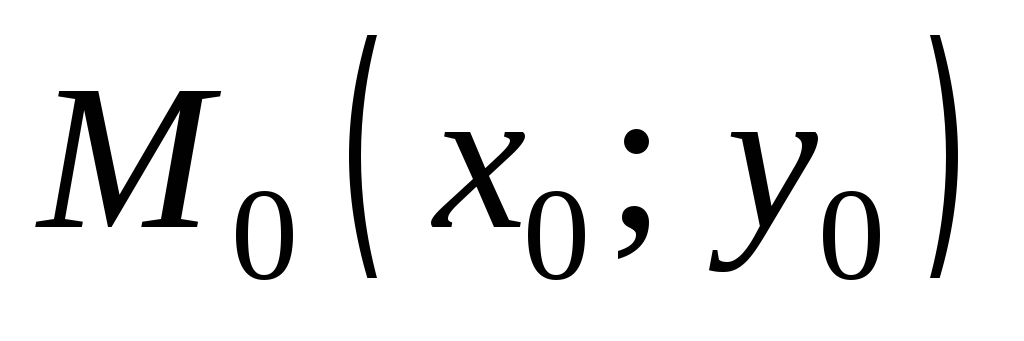 (рис. 11.1). Уравнение нормали имеет вид:
(рис. 11.1). Уравнение нормали имеет вид:
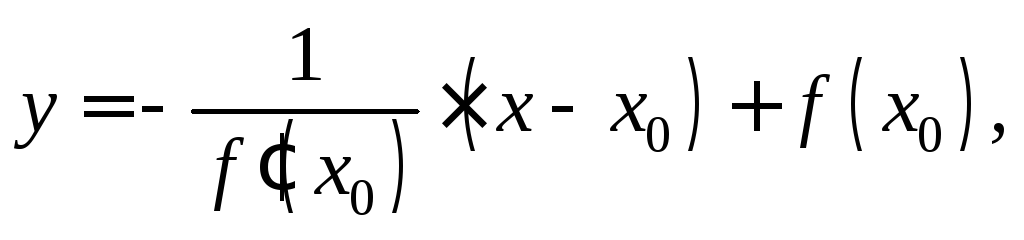 (11.10)
(11.10)
где 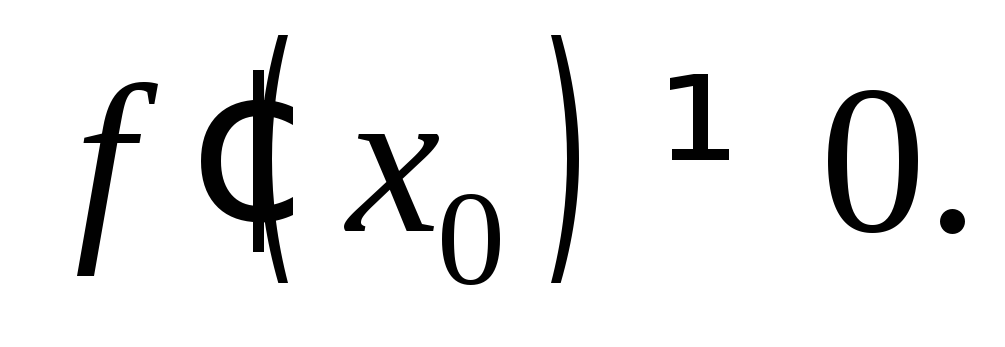

Рис. 11.1
Физические приложения производной
1. Если материальная
точка M движется неравномерно по пути, заданному
функцией 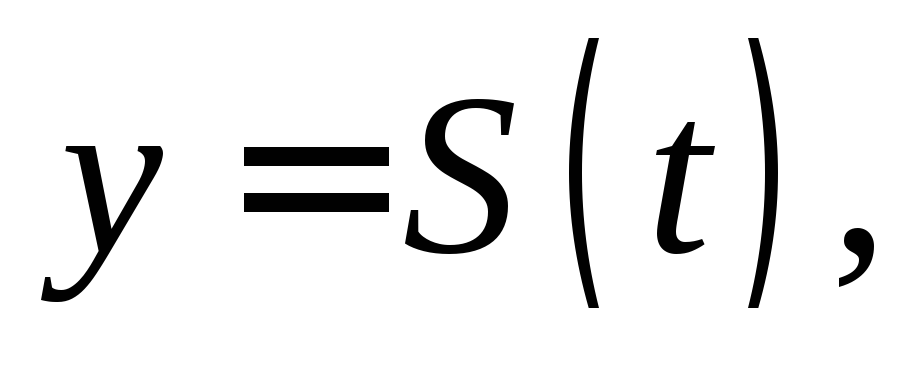 томгновенная
скорость движения в момент времени
томгновенная
скорость движения в момент времени 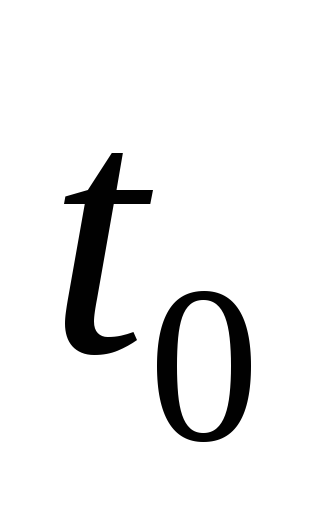 есть производная от путиS по времени t:
есть производная от путиS по времени t:
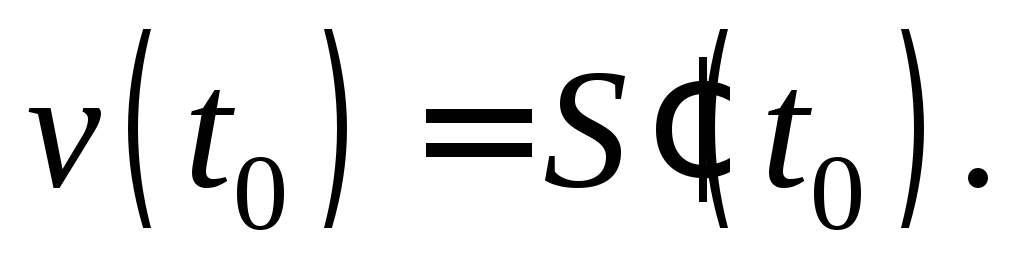 (11.11)
(11.11)
2. Если функцией 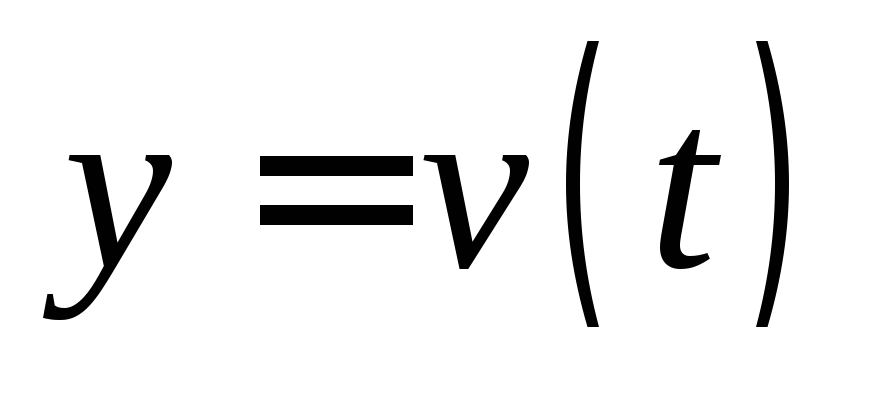 описывается процесс изменения скорости
неравномерного движения в зависимости
от времени, то мгновенное ускорение материальной точки в момент времени
описывается процесс изменения скорости
неравномерного движения в зависимости
от времени, то мгновенное ускорение материальной точки в момент времени  есть производная от скоростиv по времени t:
есть производная от скоростиv по времени t:
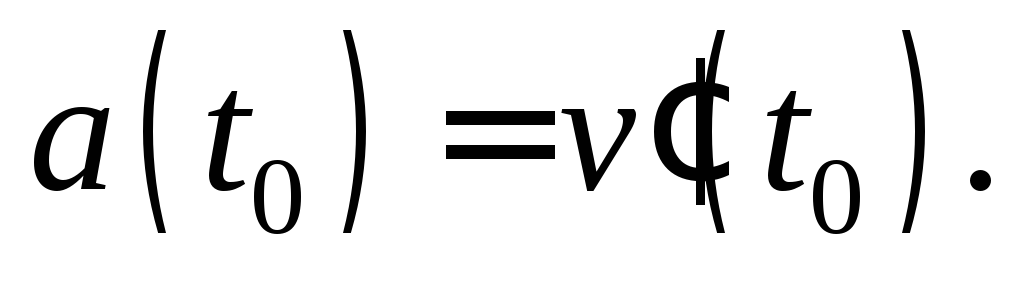 (11.12)
(11.12)
3. Если 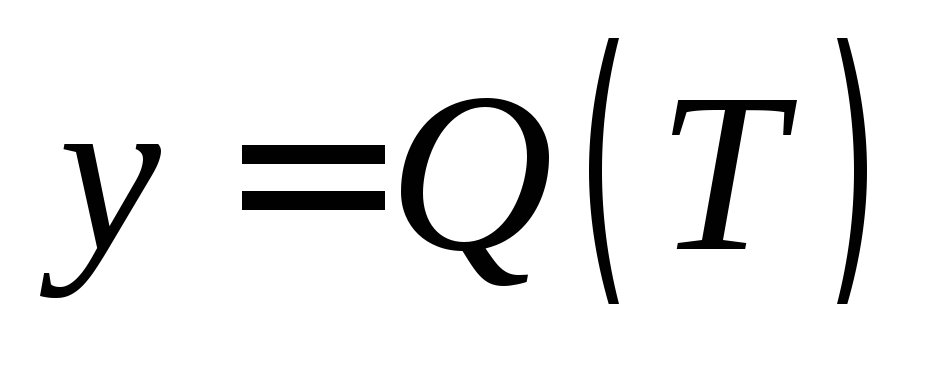 – функция, описывающая процесс изменения
количества теплоты, сообщаемой телу
при нагревании его до температурыT,
то теплоемкость
тела есть
производная от количества теплоты Q по температуре T:
– функция, описывающая процесс изменения
количества теплоты, сообщаемой телу
при нагревании его до температурыT,
то теплоемкость
тела есть
производная от количества теплоты Q по температуре T:
4. Линейная
плотность неоднородного тонкого стержня в точке 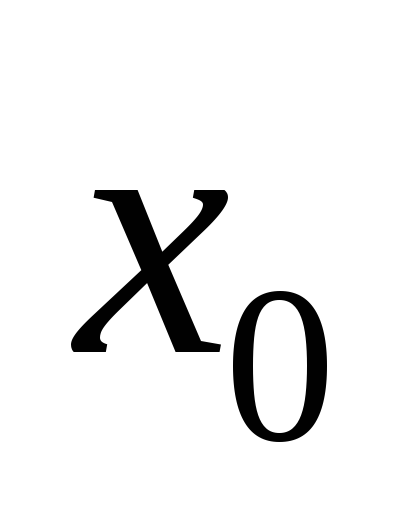 есть производная от массыm по длине l:
есть производная от массыm по длине l:
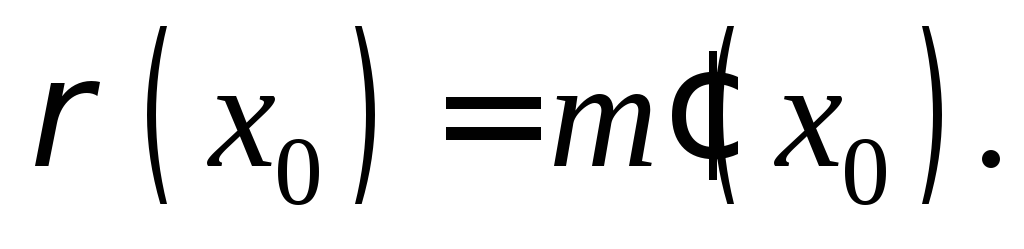
5. Мгновенное значение электродвижущей силы индукции равно скорости изменения магнитного потока, т. е. производной от магнитного потока по времени t:
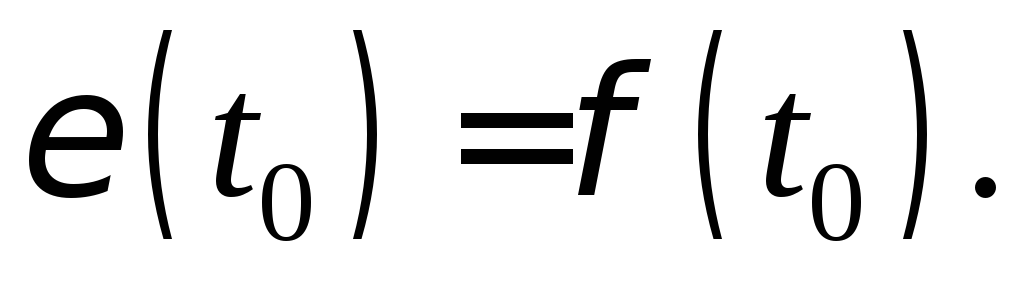
6. Сила тока в колебательном контуре в момент времени t0 равна производной заряда q по времени t:
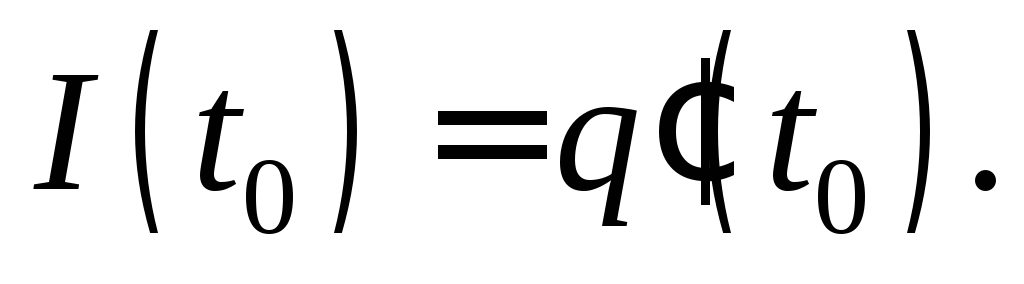
Пример 1. Написать уравнение касательной и
нормали, проведенной к графику функции 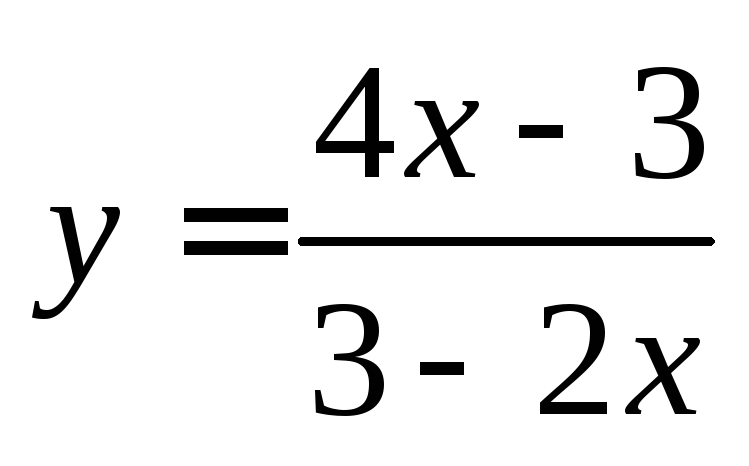 в точке с абсциссойx = 2.
в точке с абсциссойx = 2.
Решение. Для нахождения уравнения касательной
воспользуемся формулой (11.9). Сначала
найдем ординату точки касания 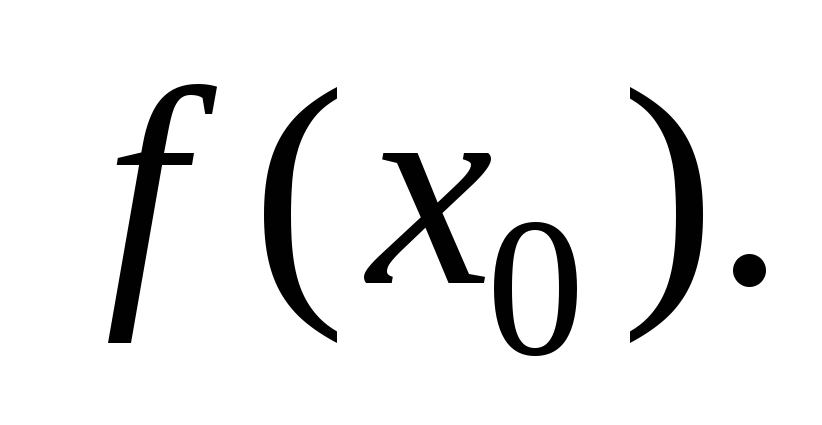 Для этого значение
Для этого значение подставим в уравнение функции:
подставим в уравнение функции:
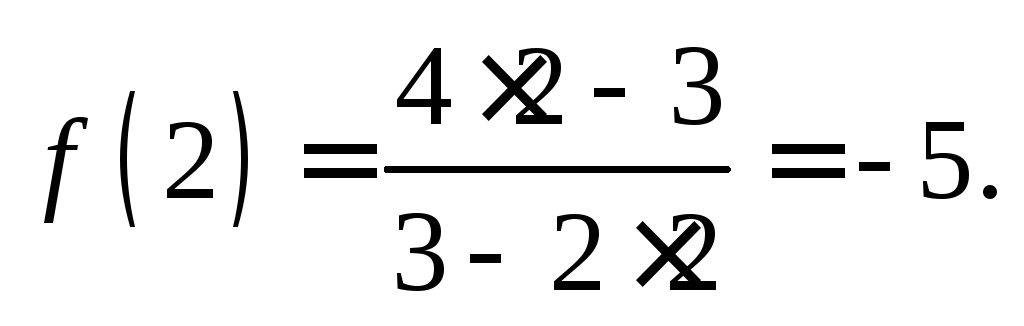
Для нахождения
углового коэффициента найдем производную 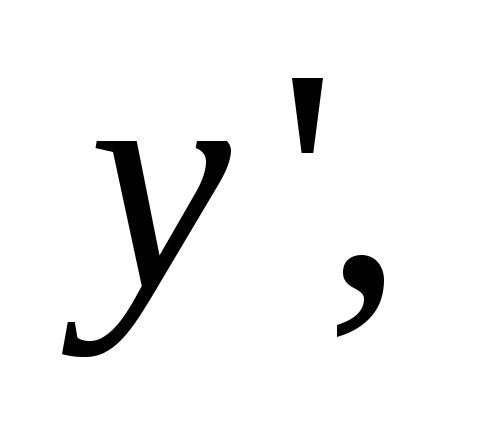 используя формулу дифференцирования
дроби:
используя формулу дифференцирования
дроби:
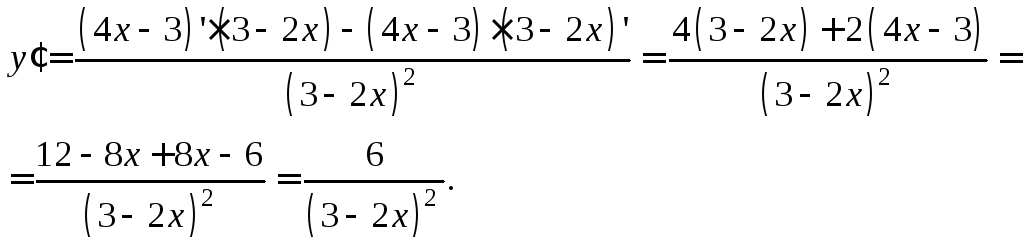
Найдем значение
производной при 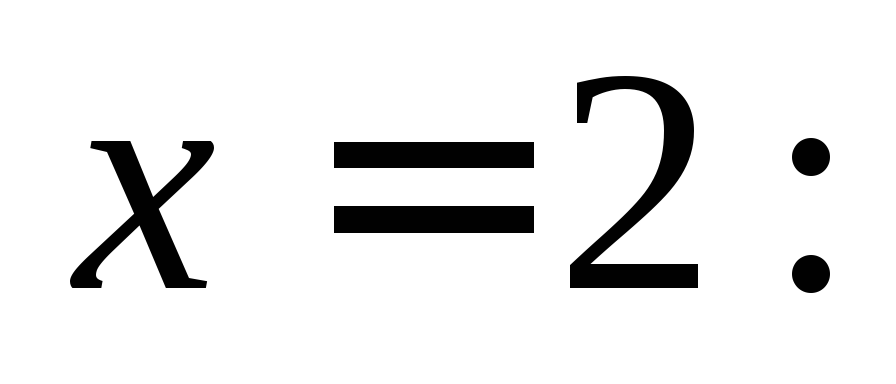
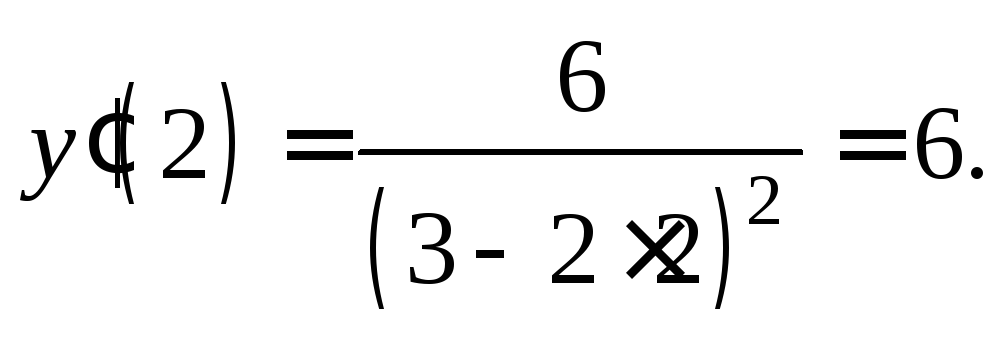
Подставив найденные значения в формулу (11.9), получаем уравнение касательной:
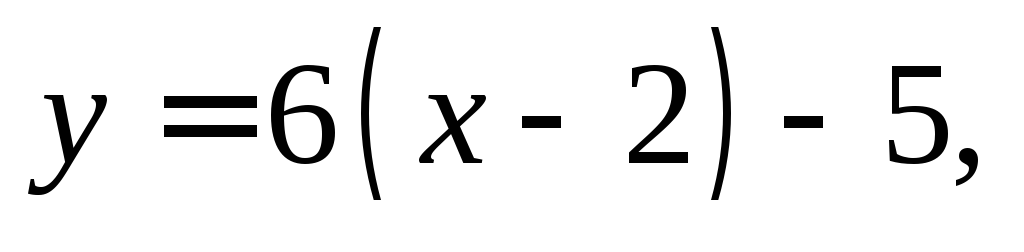 т. е.
т. е. 
Чтобы написать уравнение нормали, воспользуемся формулой (11.10):

Получим, что
уравнение нормали, проведенной к заданной
кривой в заданной точке, имеет вид 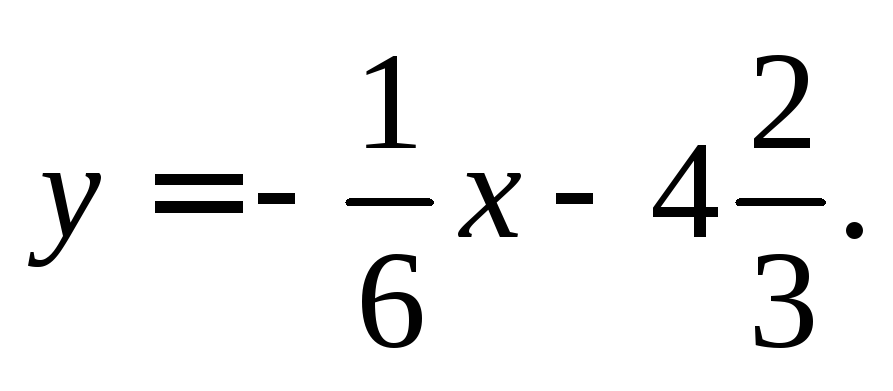
Пример 2. Определить, в какой точке кривой касательная наклонена к оси абсцисс под углом 45.
Решение. Так как тангенс угла наклона касательной к оси абсцисс равен значению производной в точке касания, найдем производную функции:
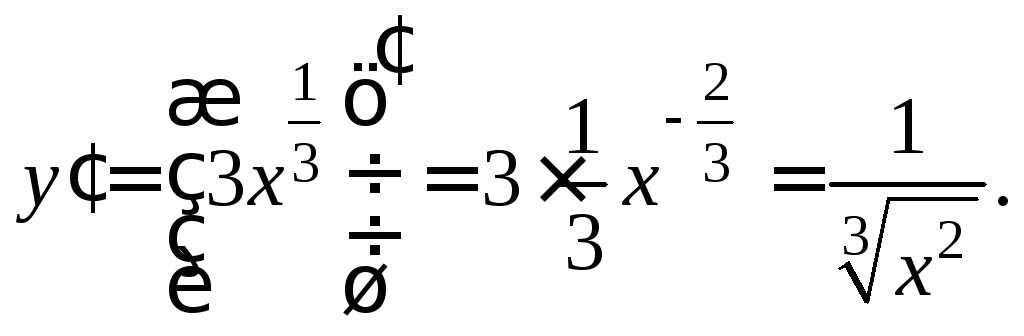
По условию 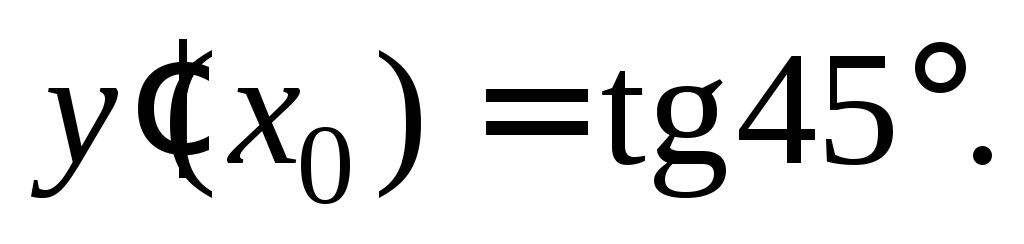 Следовательно,
Следовательно,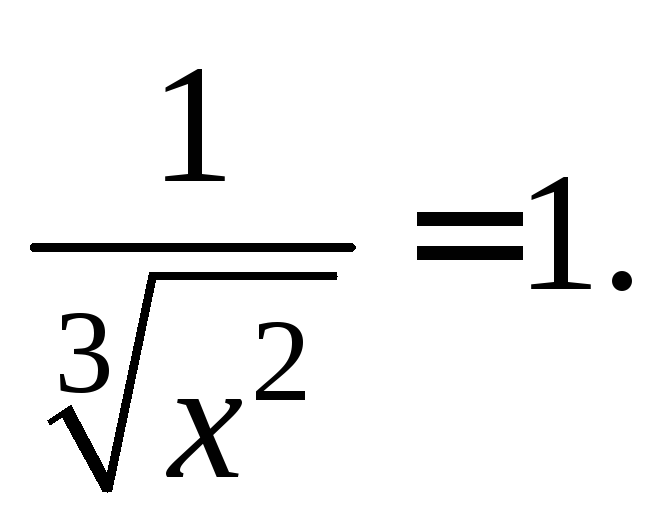
Отсюда:
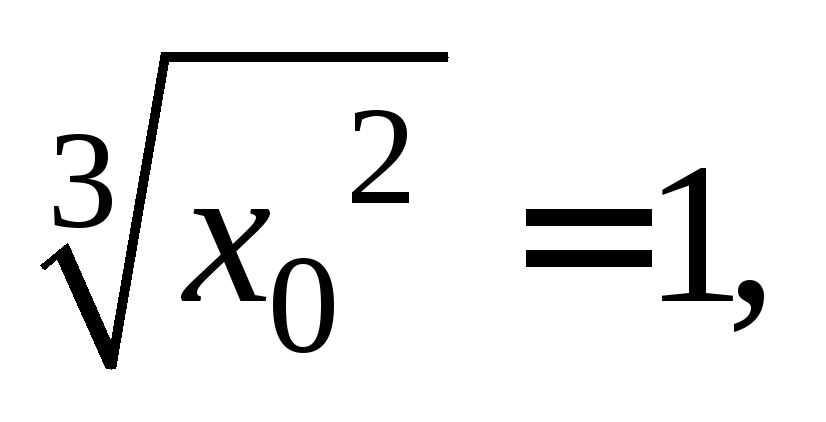
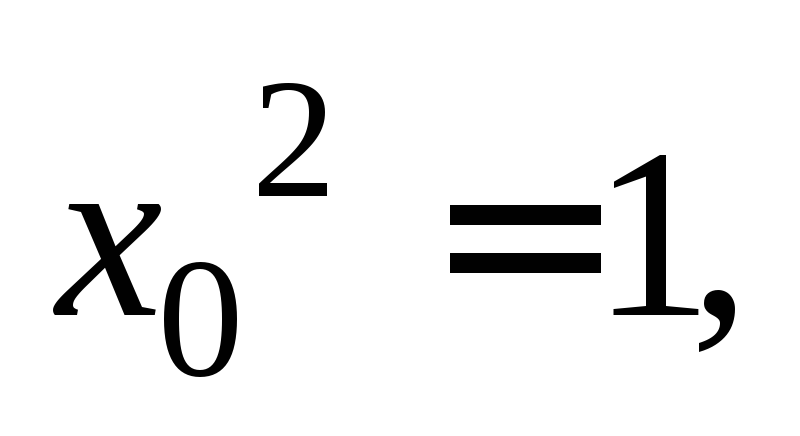
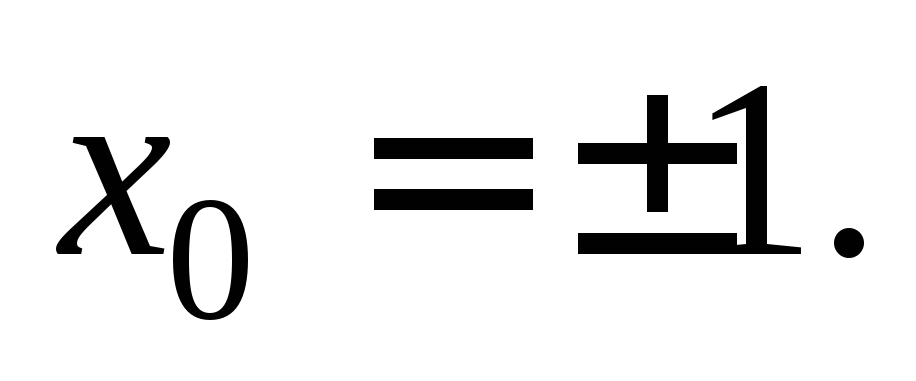
Получили два значения абсциссы точки касания:
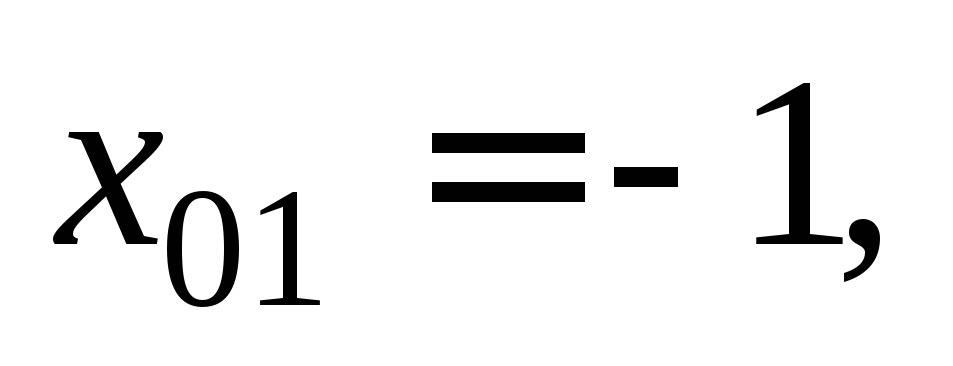
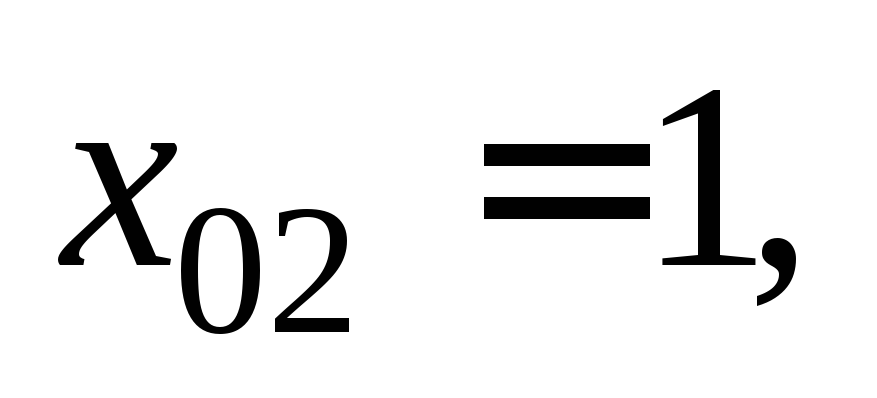
т. е. существуют две точки касания, в которых касательная образует угол 45 с осью Ох.
Найдем соответствующие
ординаты точек касания, подставляя
значения 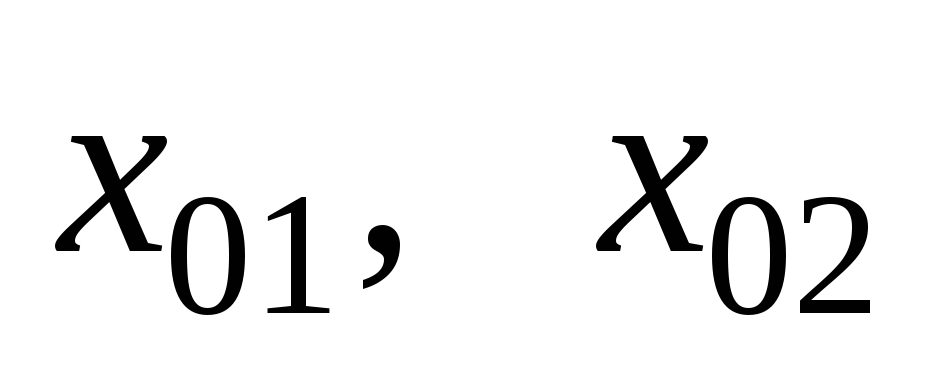 в формулу функции:
в формулу функции:
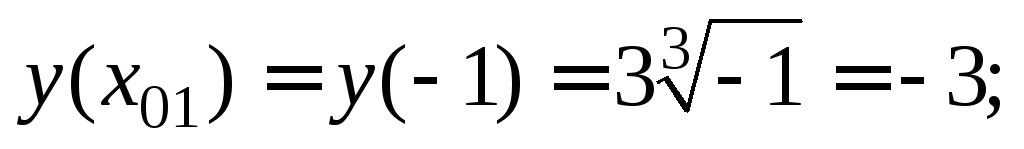
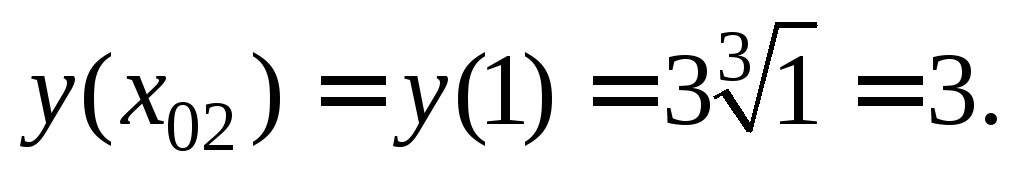
Приходим к ответу:
в точках 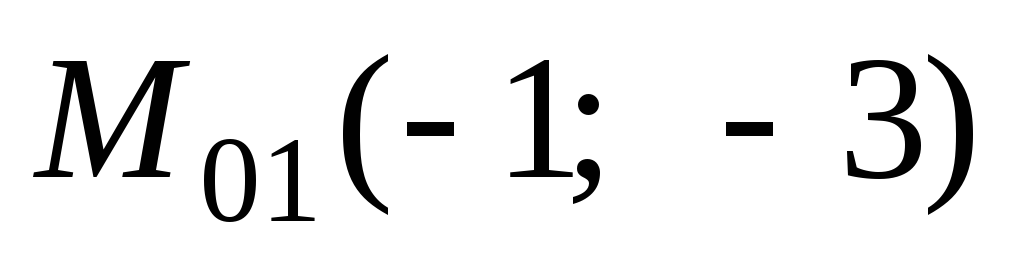 и
и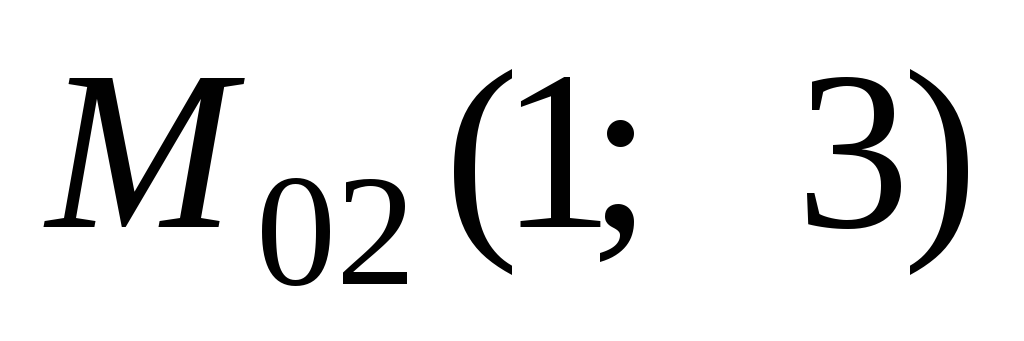 касательная к заданной кривой образует
с осьюОх угол 45.
касательная к заданной кривой образует
с осьюОх угол 45.
Пример 3. Найти острый угол между параболами 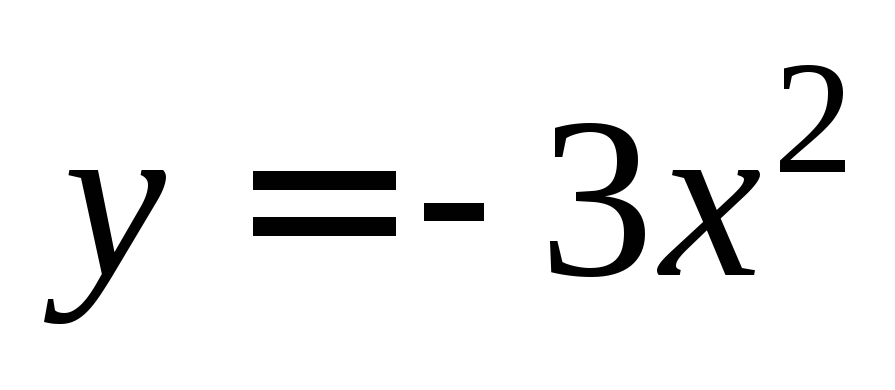 и
и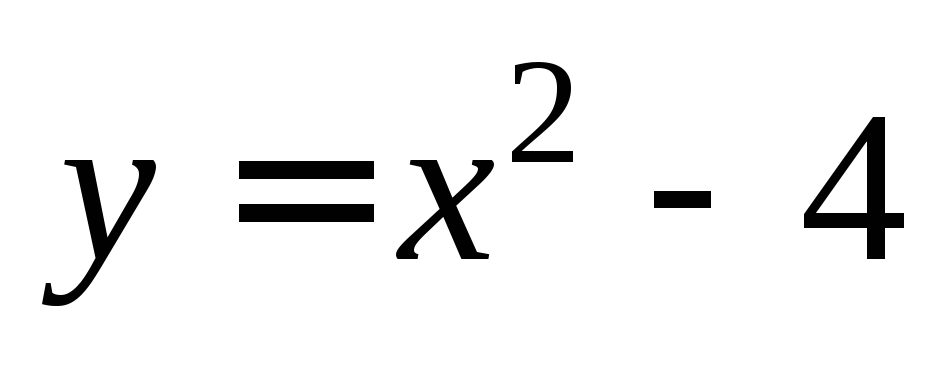 в точке их пересечения, имеющей
отрицательную абсциссу.
в точке их пересечения, имеющей
отрицательную абсциссу.
Решение. Угол между двумя кривыми в точке их пересечения – это угол между касательными к этим кривым, проведенными в точке их пересечения. Тангенс этого угла вычислим по формуле
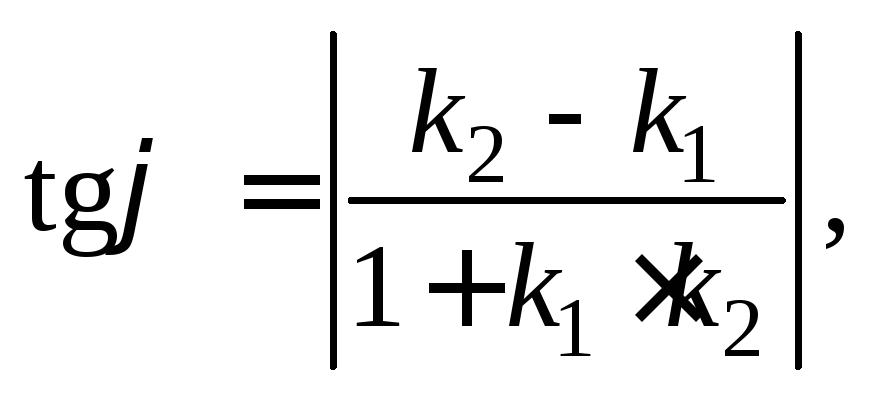 (11.13)
(11.13)
где k1 и k2 – угловые коэффициенты касательных, проведенных к параболам в заданной точке.
Найдем точку пересечения этих парабол. Для этого решим систему:

Отсюда 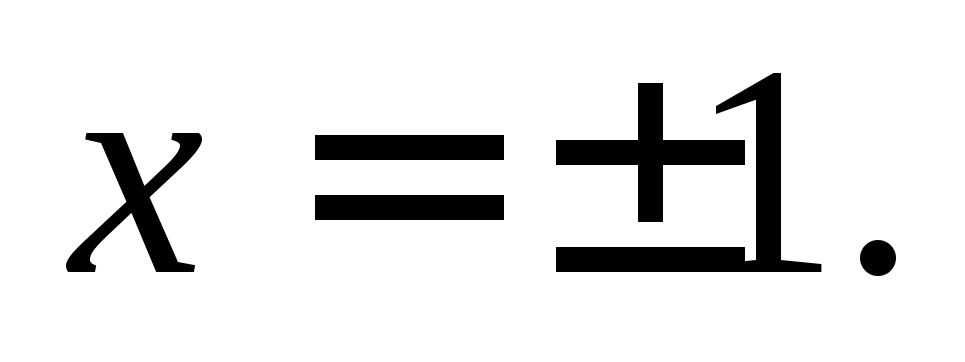 Условию задачи удовлетворяет точка
Условию задачи удовлетворяет точка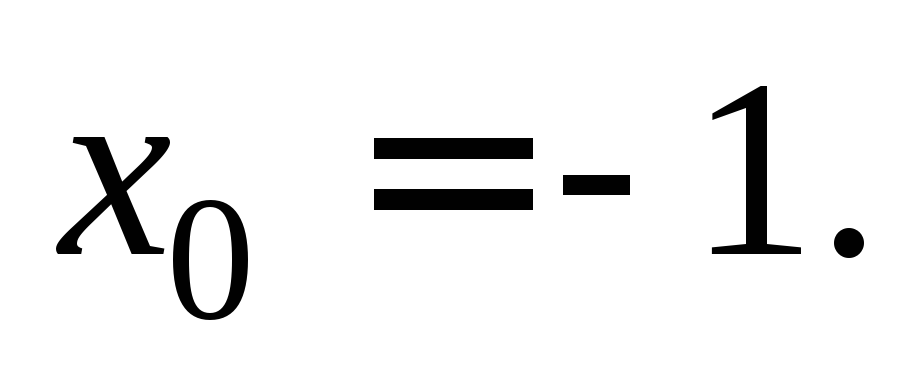 Найдем коэффициентk1:
Найдем коэффициентk1:
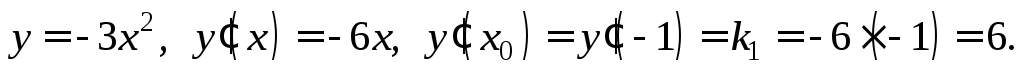
Аналогично найдем k2:

Воспользуемся формулой (11.13) и получим:
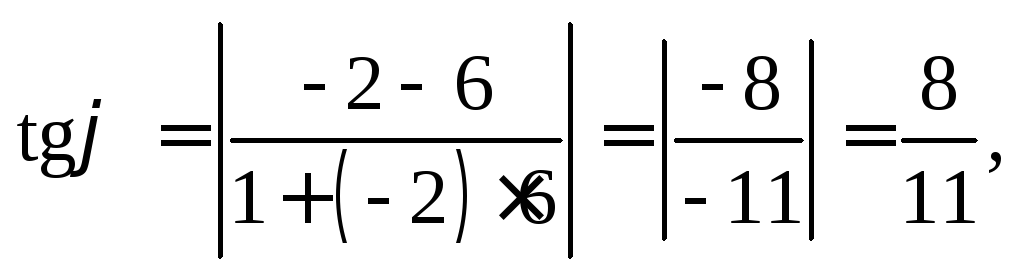
откуда 
Пример 4. Тело движется прямолинейно по закону

Найти скорость движения тела в тот момент, когда ускорение равно нулю.
Решение. Согласно формуле (11.11), скорость есть производная функции S(t), а, согласно формуле (11.12), ускорение а(t) есть производная скорости v(t).
Последовательно вычислим производные:
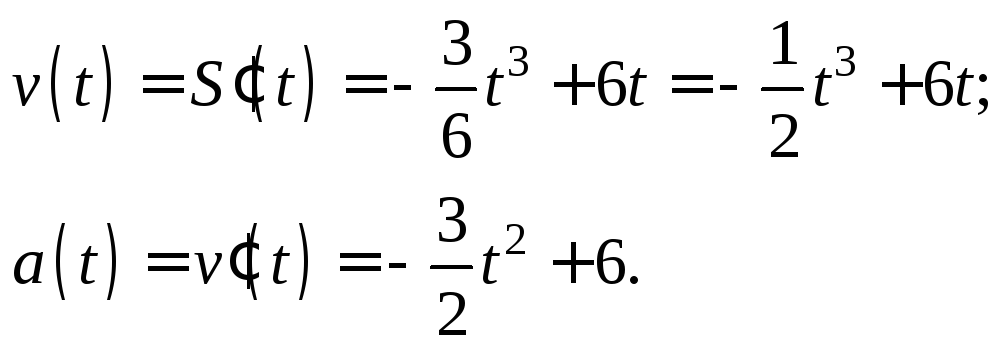
Найдем момент времени, когда ускорение равно нулю:

Вычислим скорость
движения тела в момент времени 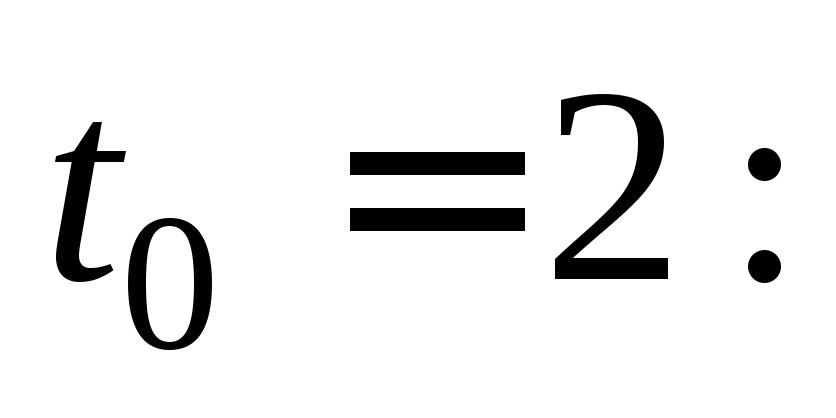
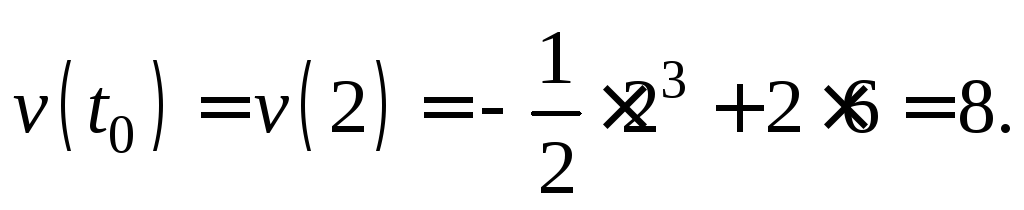
Задания
studfile.net
5. Уравнение касательной плоскости и нормали к поверхности
Если поверхность  задана уравнением
задана уравнением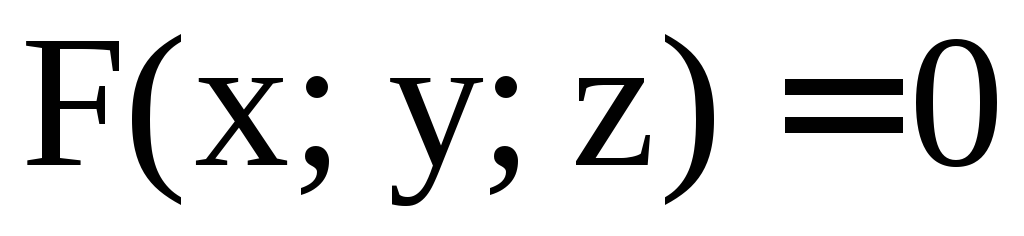 и
и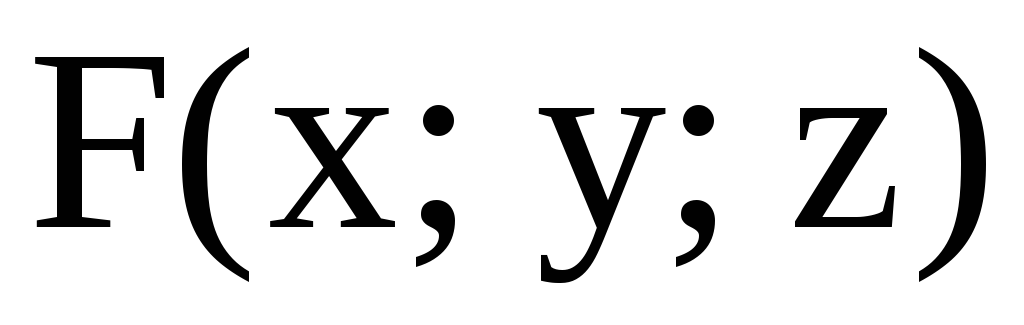 – дифференцируемая функция, то уравнение
касательной плоскости, проведённой к
поверхности (
– дифференцируемая функция, то уравнение
касательной плоскости, проведённой к
поверхности ( )
в точке
)
в точке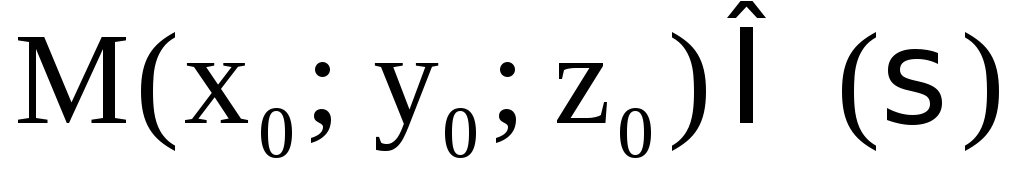 ,
имеет вид
,
имеет вид
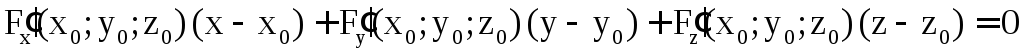 .
.
Уравнение нормали к этой поверхности в той же точке имеет вид
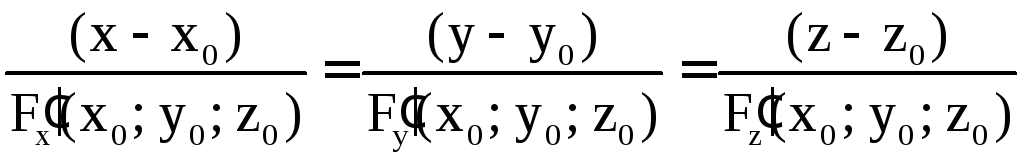 .
.
В частности, если
уравнение поверхности задано в явной
форме 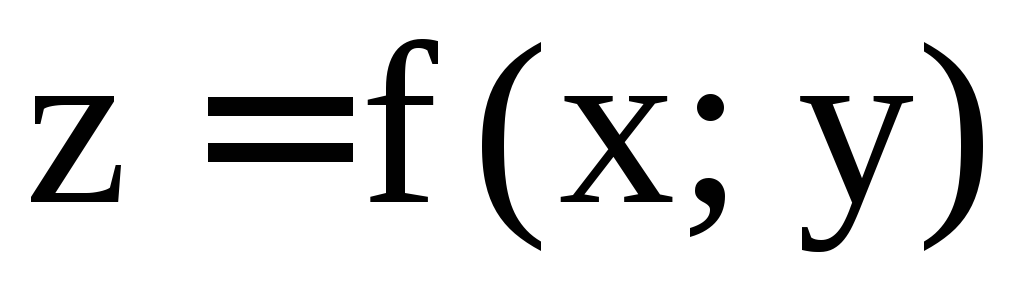 ,
то уравнение касательной плоскости к
поверхности в точке
,
то уравнение касательной плоскости к
поверхности в точке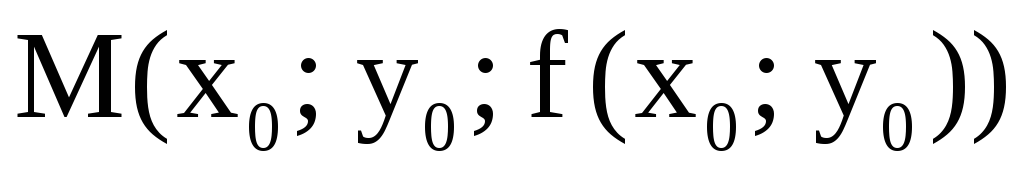 может быть задано в виде
может быть задано в виде
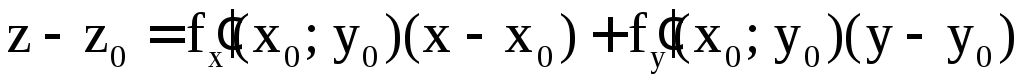 ,
,
а уравнения нормали –
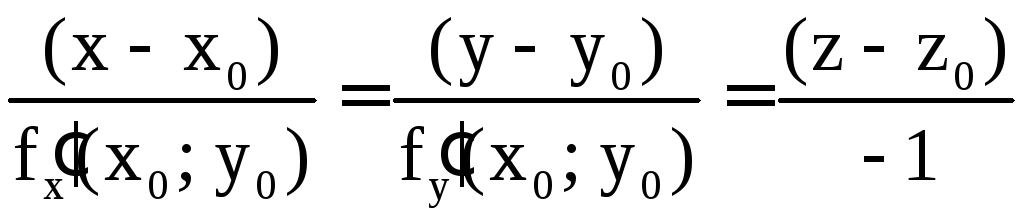 .
.
Пример 7. Составить
уравнения касательной плоскости и
нормали к поверхности 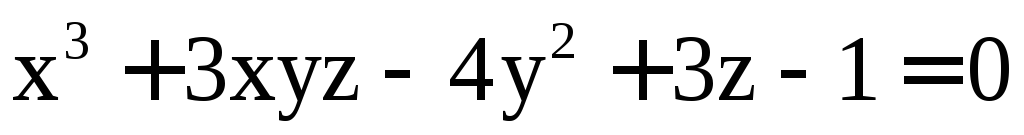 в точке M(2; –1; 1).
в точке M(2; –1; 1).
Решение. Обозначим 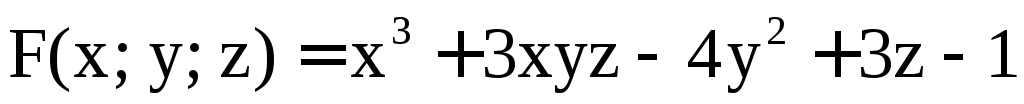 .
Имеем
.
Имеем
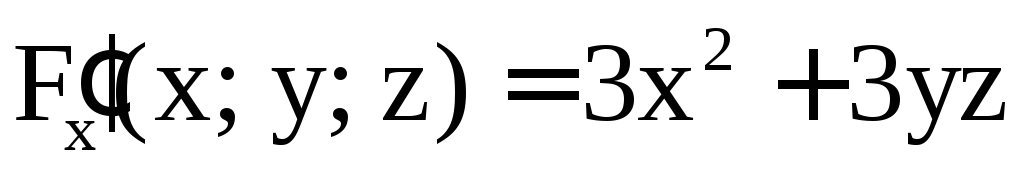 ,
, 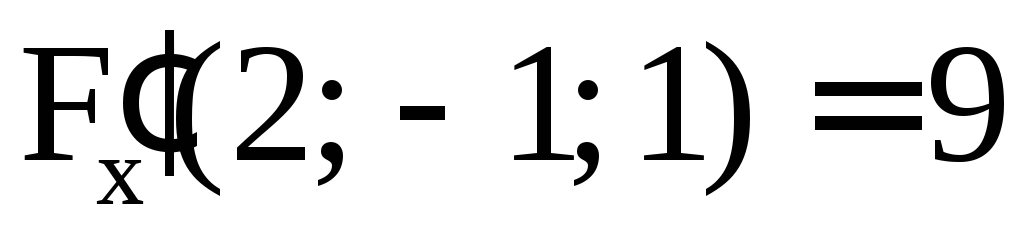 ,
,
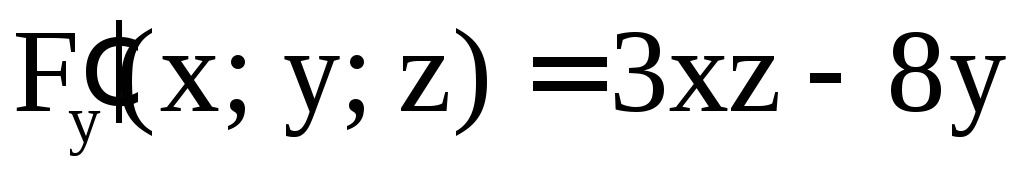 ,
, 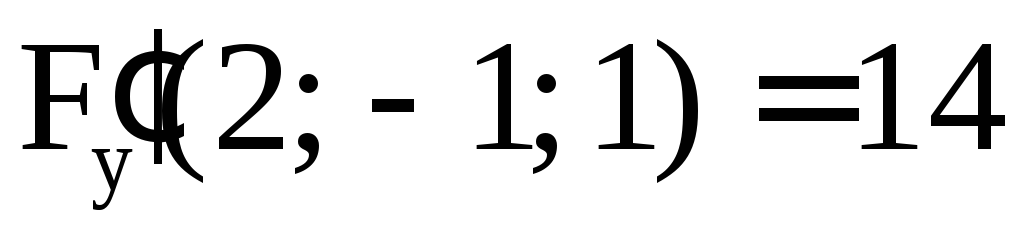 ,
,
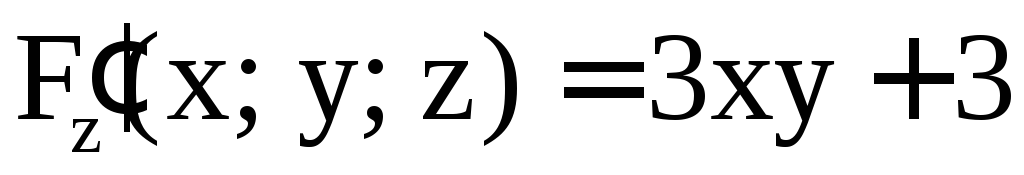 ,
, 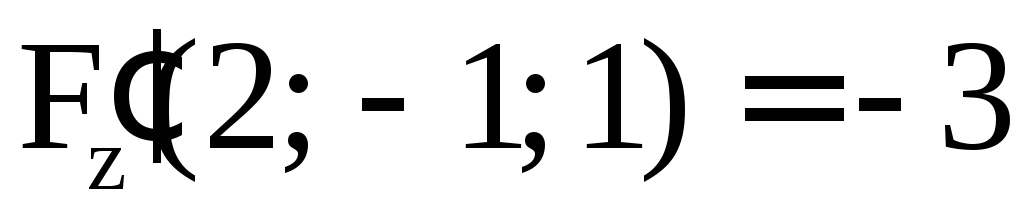 .
.
Отсюда находим уравнение касательной плоскости
9(x – 2) + 14(y + 1) – 3(z – 1) = 0
или
9x + 14y – 3z–1 = 0
и уравнения нормали
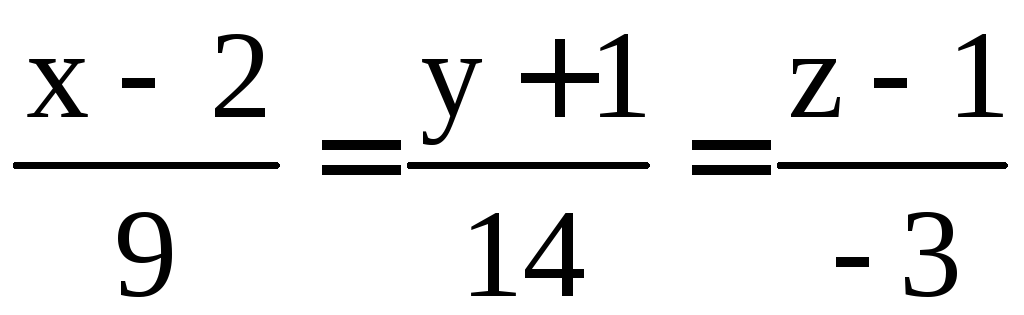 .
.
6. Дифференцирование сложной функции
Пусть 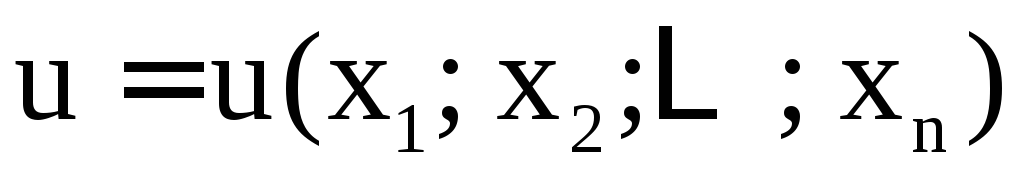 – дифференцируемая
функция отn
переменных
– дифференцируемая
функция отn
переменных  и пусть переменные
и пусть переменные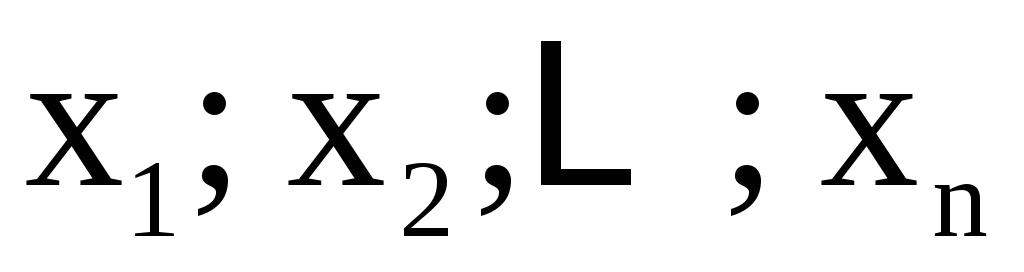 ,
в свою очередь, являются дифференцируемыми
функциями от переменных
,
в свою очередь, являются дифференцируемыми
функциями от переменных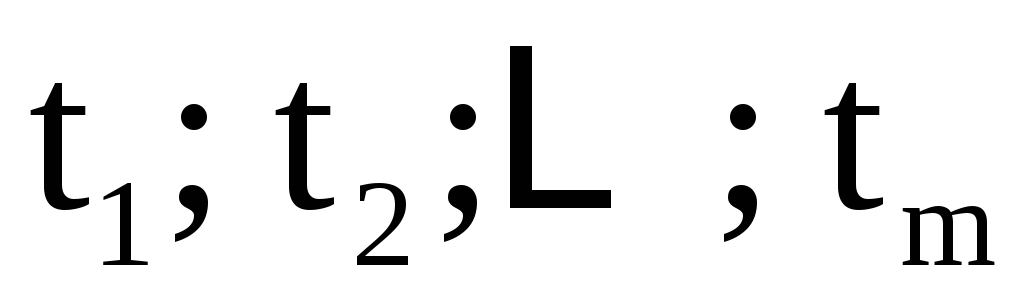 :
:
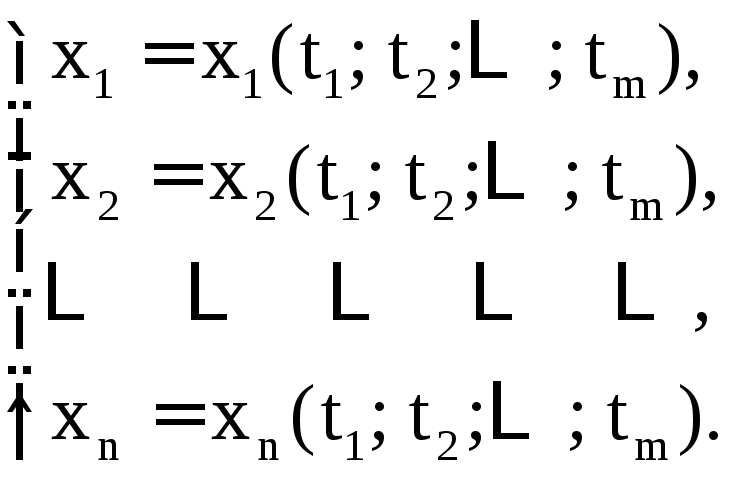
Тогда 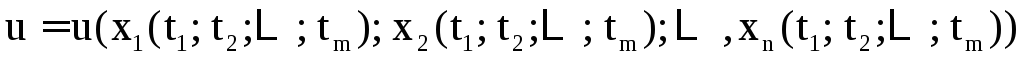 становится дифференцируемой функцией
от переменных
становится дифференцируемой функцией
от переменных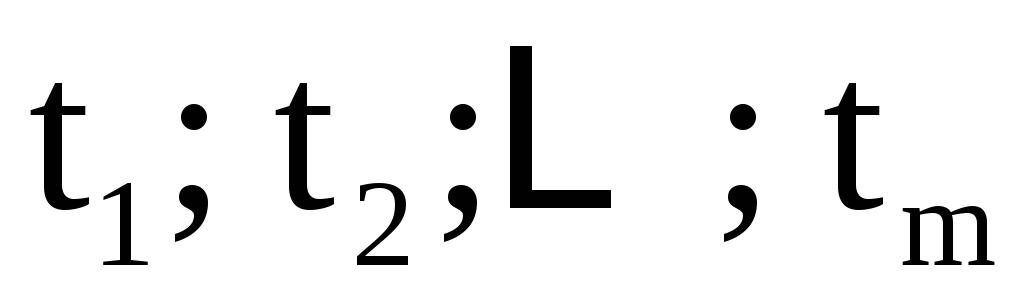 и при этом
и при этом

В частности, если 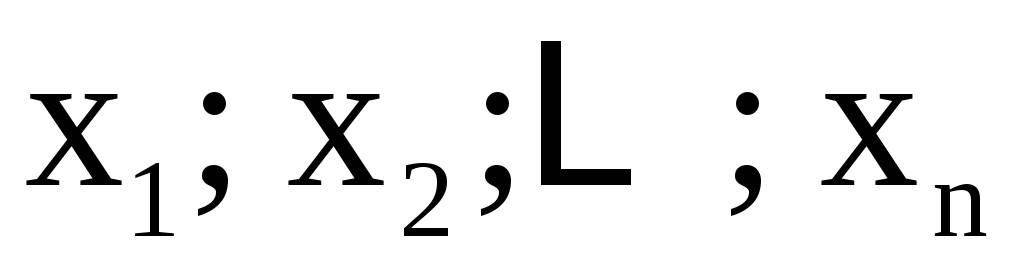 зависят от одного переменного t , то u
становится функцией от одного переменного
t и
зависят от одного переменного t , то u
становится функцией от одного переменного
t и
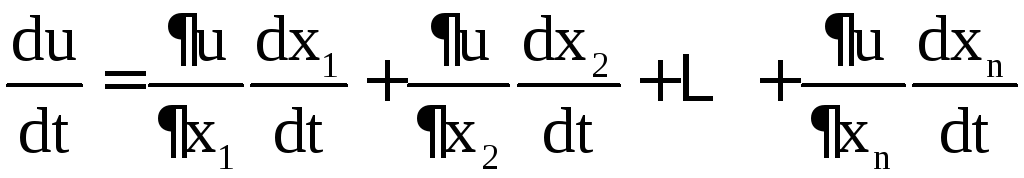 .
.
Пример 8. Найти 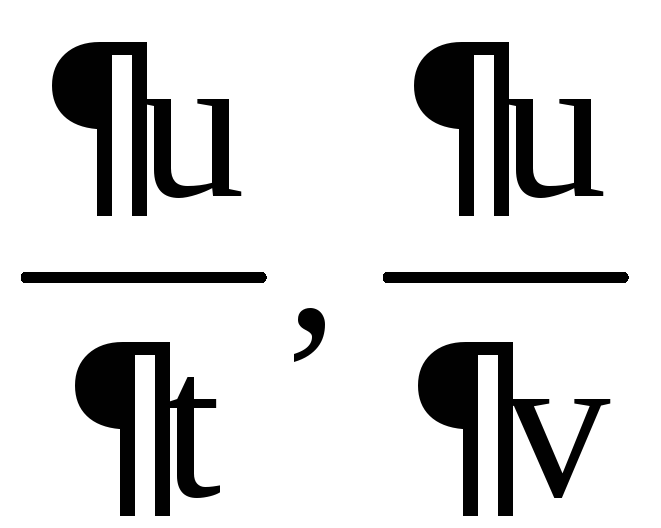 ,
если
,
если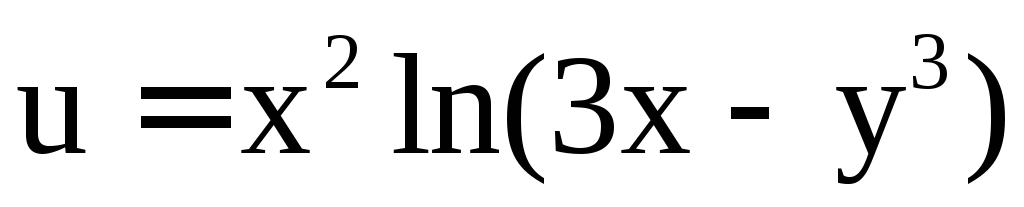 ,
,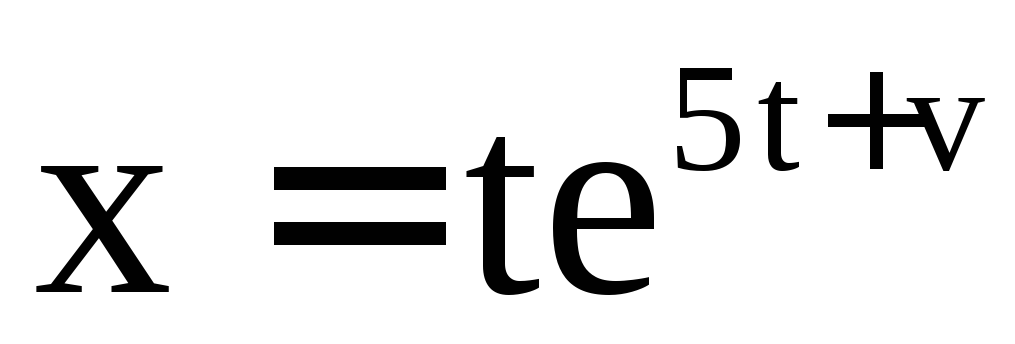 ,
,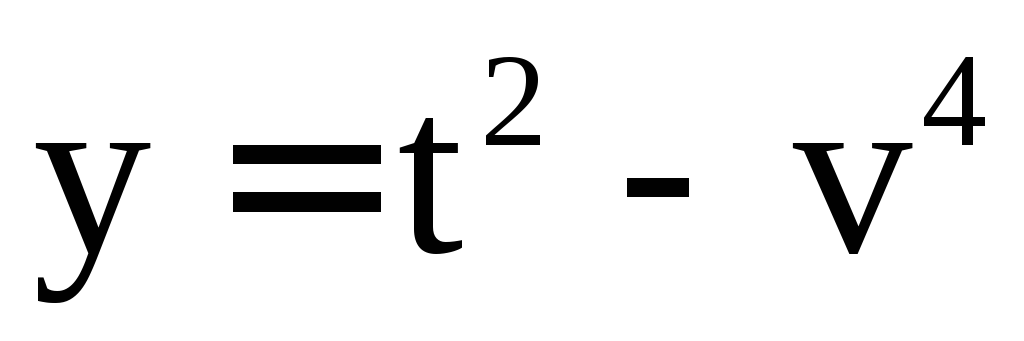 .
.
Решение. Имеем
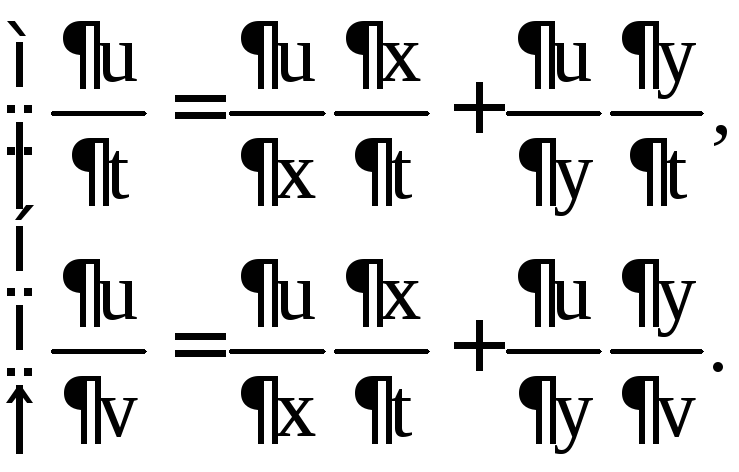
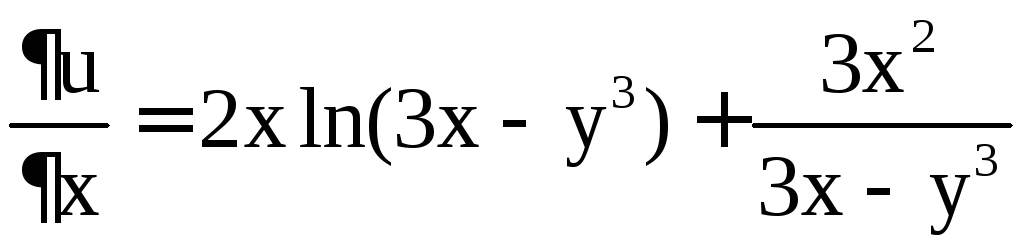 ,
, 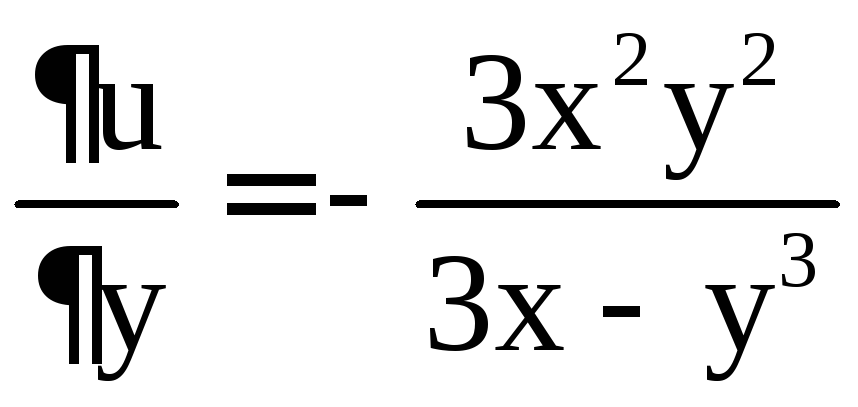 ,
,
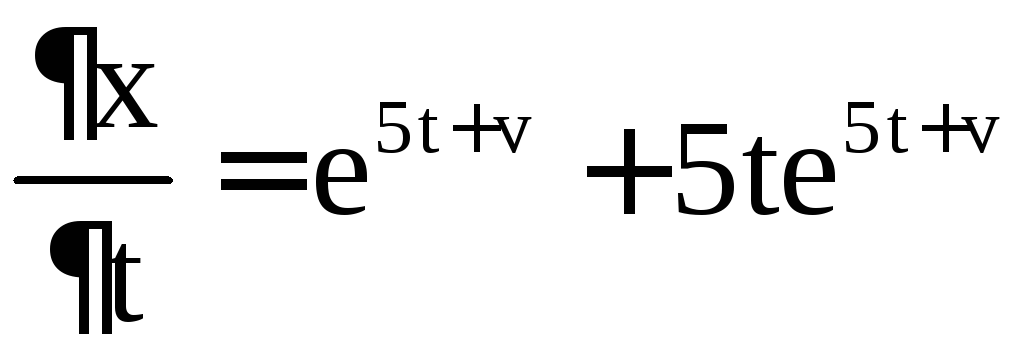 ,
, 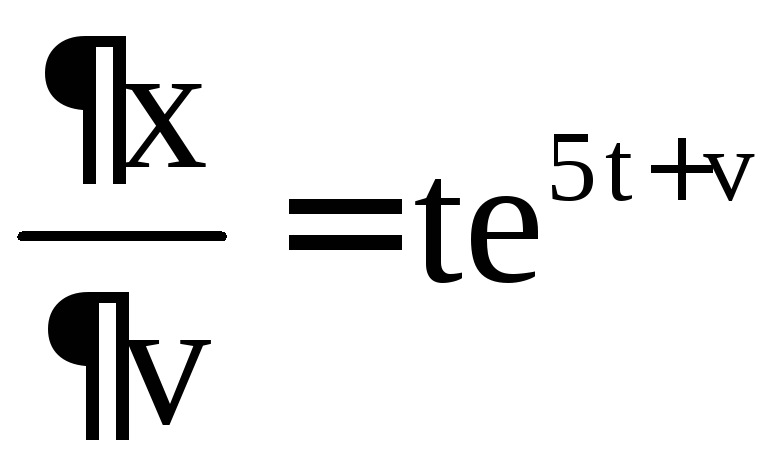 ,
,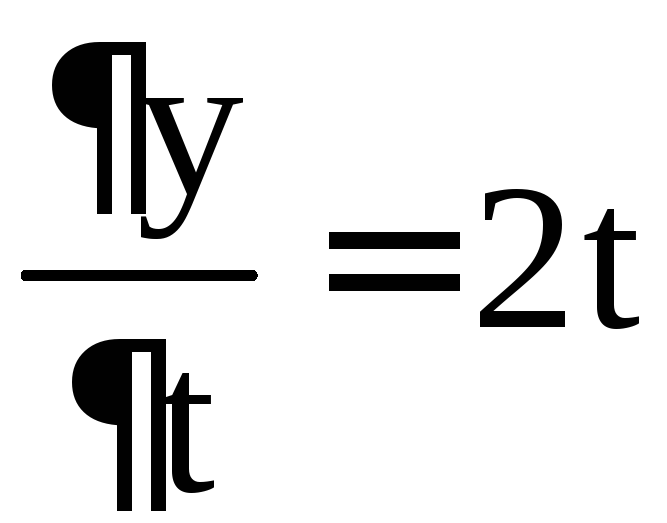 ,
,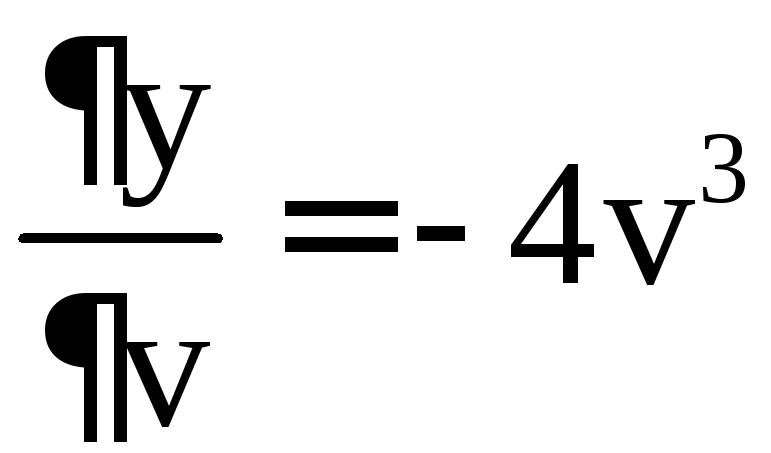 .
.
Отсюда получаем
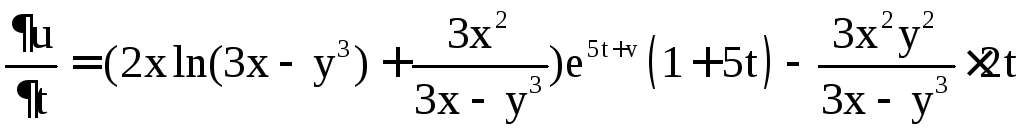 ,
,
 .
.
7. Дифференцирование неявно заданной функции
Пусть функция F(x; y) определена в области (D) и (a; b), (c, d) – проекции (D) на оси 0x и 0y соответственно. Говорят, что уравнение
F(x; y) = 0 (2)
в области (D) задаёт
неявную функцию y = f(x) , если для любого 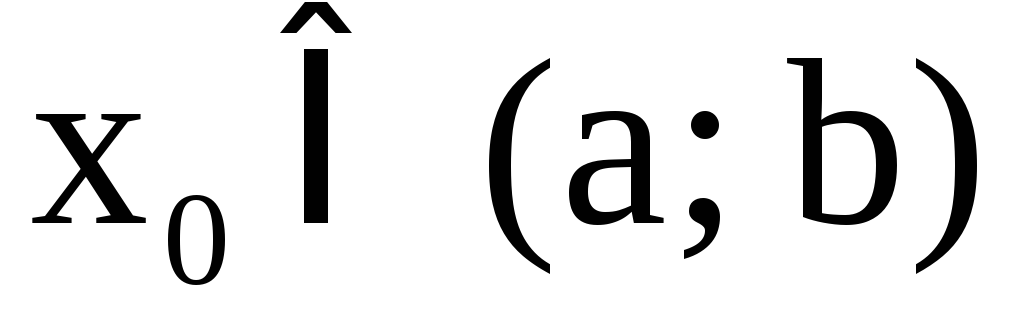 уравнение
уравнение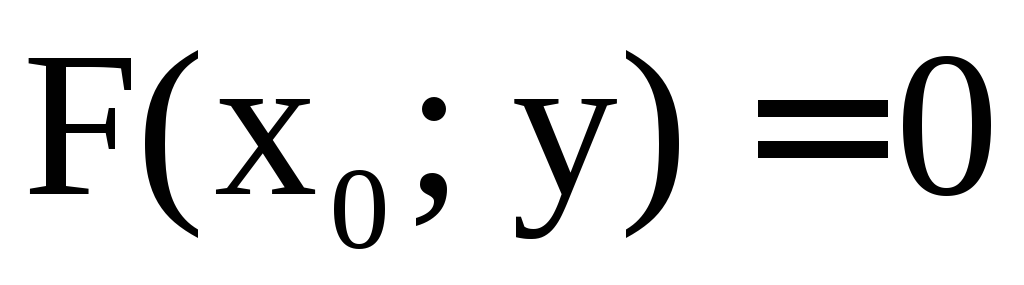 имеет единственное решение
имеет единственное решение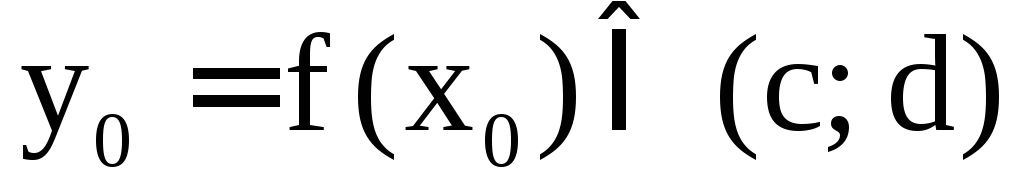 (это решение и является правилом задания
функции: каждому
(это решение и является правилом задания
функции: каждому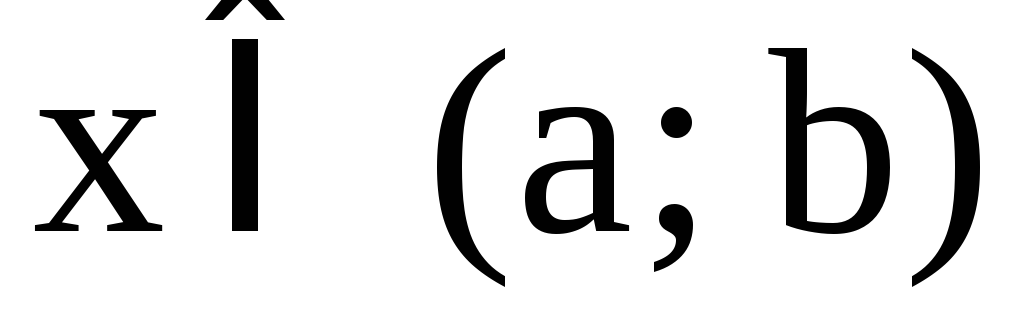 ставится в соответствие решение уравнения
F(x; y) = =0 ).
ставится в соответствие решение уравнения
F(x; y) = =0 ).
Если уравнение
(2) в (D) задаёт неявную функцию  ,
,
F(x; y) дифференцируема
в (D) и 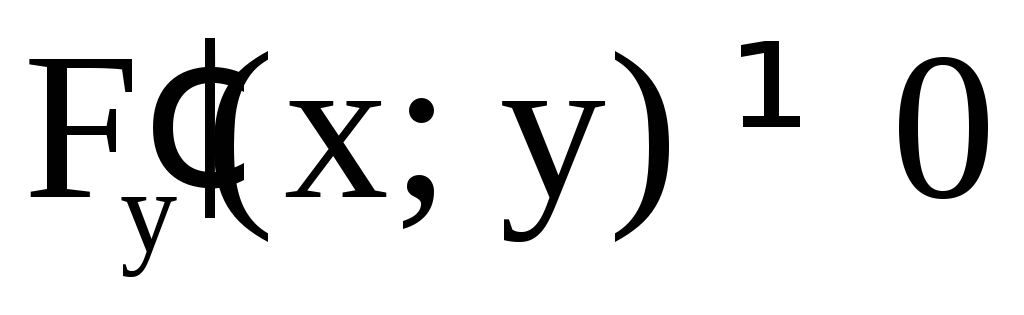 ,
то
,
то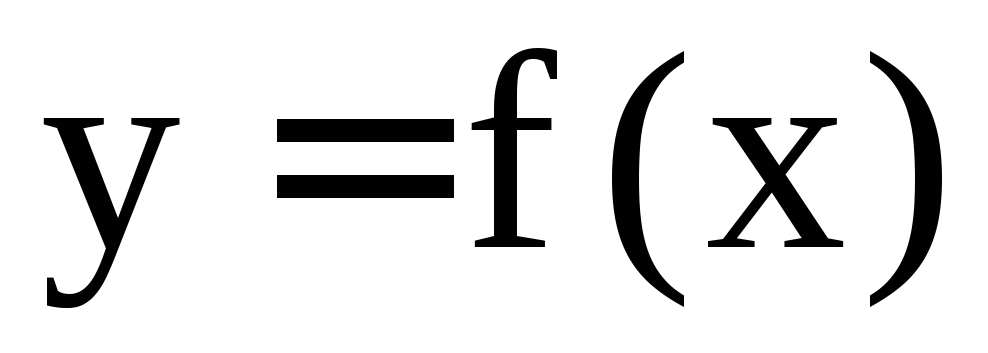 дифференцируема и
дифференцируема и
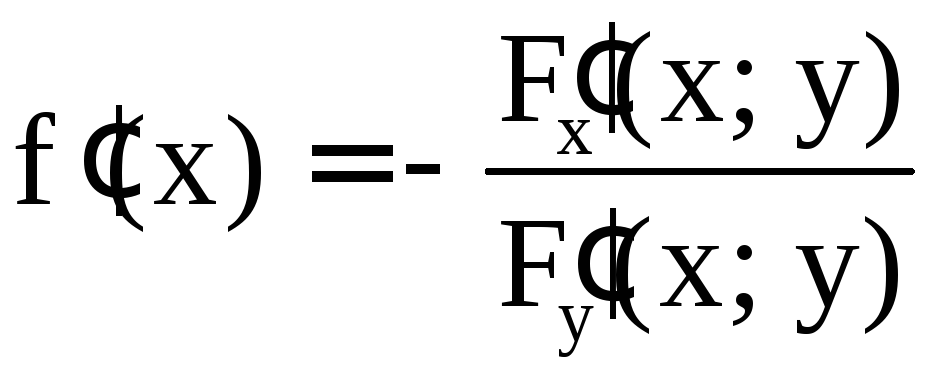 .
.
Вторая производная  находится повторным дифференцированием
последнего равенства.
находится повторным дифференцированием
последнего равенства.
Пример 9. Найти  ,
если
,
если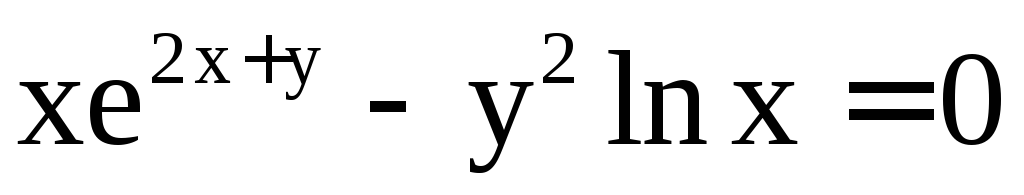 .
.
Решение. Обозначим левую часть уравнения через F(x; y). Тогда
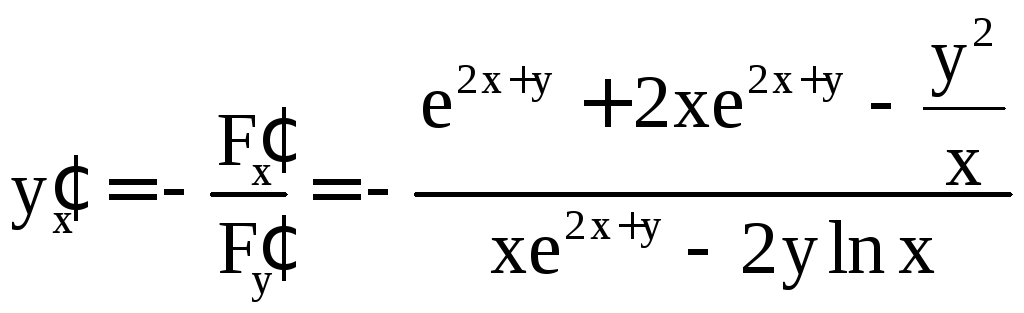 .
.
Аналогично
определяется неявная функция многих
переменных. Пусть функция 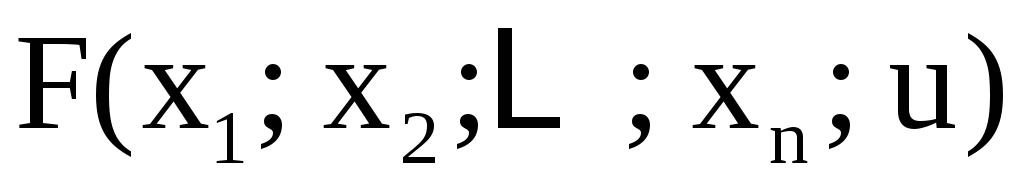 определена в области
определена в области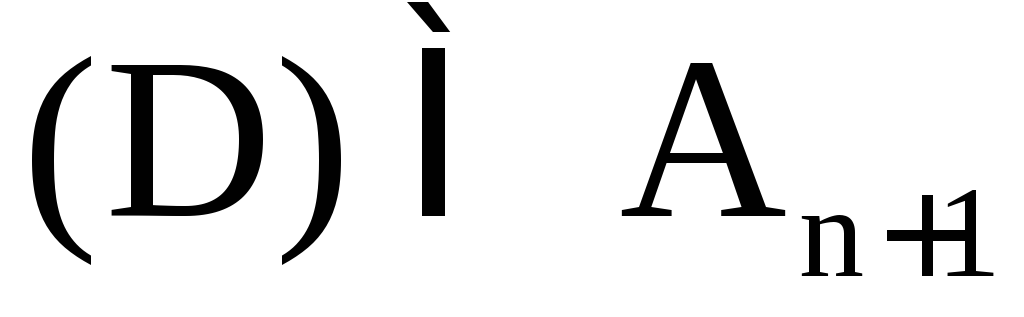 и
и – проекции (D) на n-мерную координатную
плоскость
– проекции (D) на n-мерную координатную
плоскость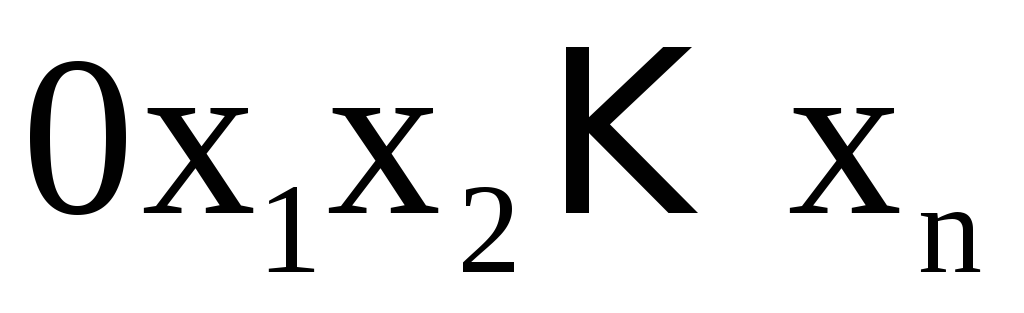 и на ось 0u соответственно. Говорят, что
уравнение
и на ось 0u соответственно. Говорят, что
уравнение
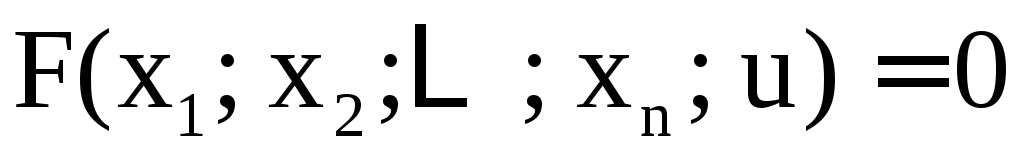 (3)
(3)
задаёт в (D) неявную
функцию 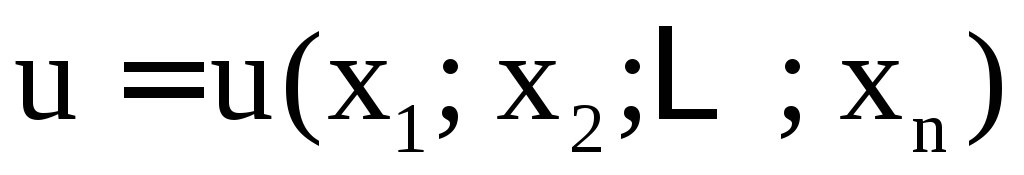 ,
если для любой точки
,
если для любой точки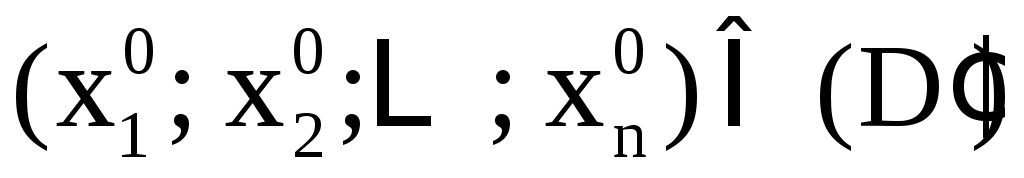 уравнение
уравнение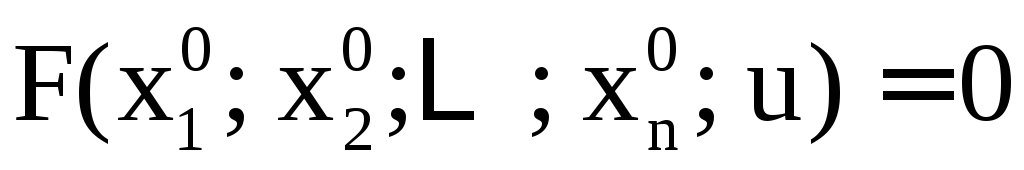 имеет единственное решение
имеет единственное решение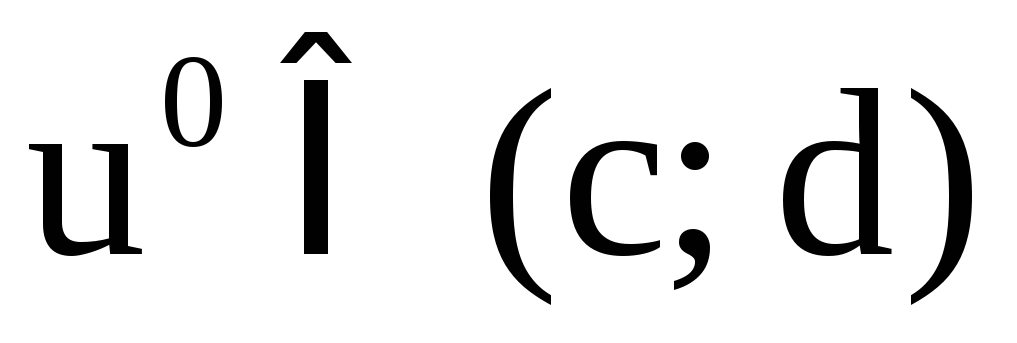 .
Если уравнение (2) в области (D) задаёт
неявную функцию
.
Если уравнение (2) в области (D) задаёт
неявную функцию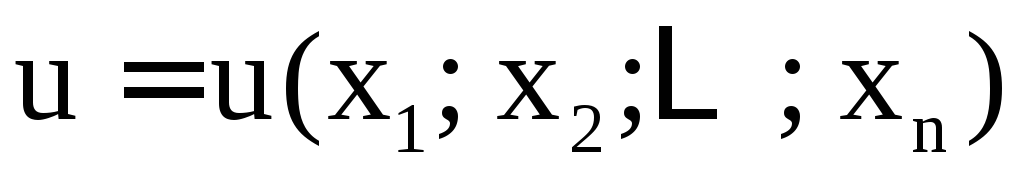 ,
,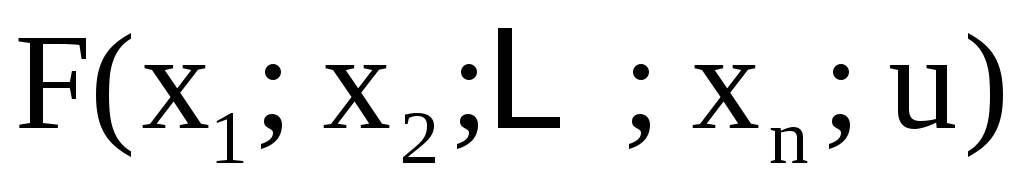 дифференцируема в (D) и
дифференцируема в (D) и всюду в (D), то функция
всюду в (D), то функция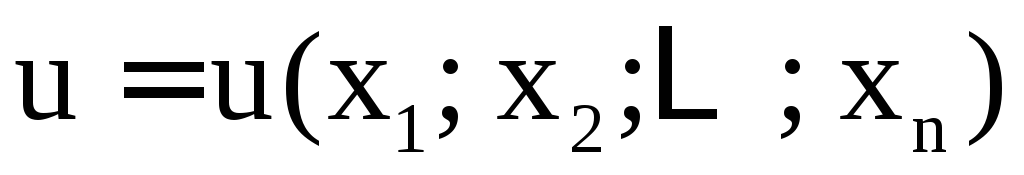 является дифференцируемой и
является дифференцируемой и
 .
.
Пример 10. Найти 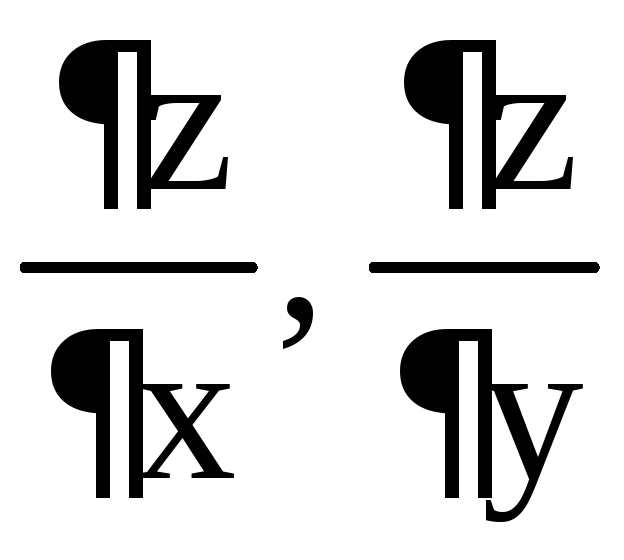 ,
если
,
если
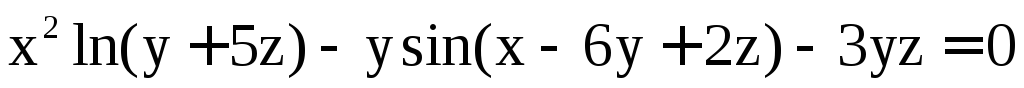 .
.
Решение. Обозначим через F(x; y; z) левую часть уравнения. Имеем
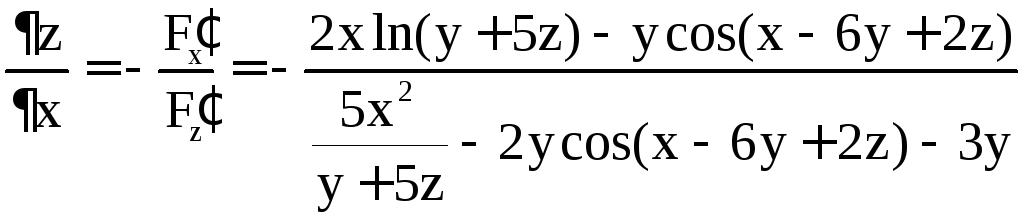 ,
,
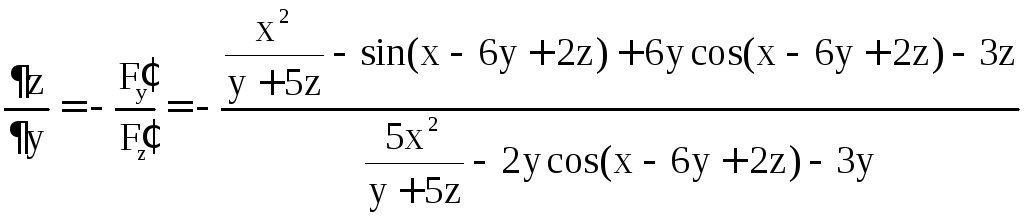 .
.
Подобным образом определяются системы неявных функций. Пусть дана система из m уравнений с (n + m) переменными
 (4)
(4)
и функции 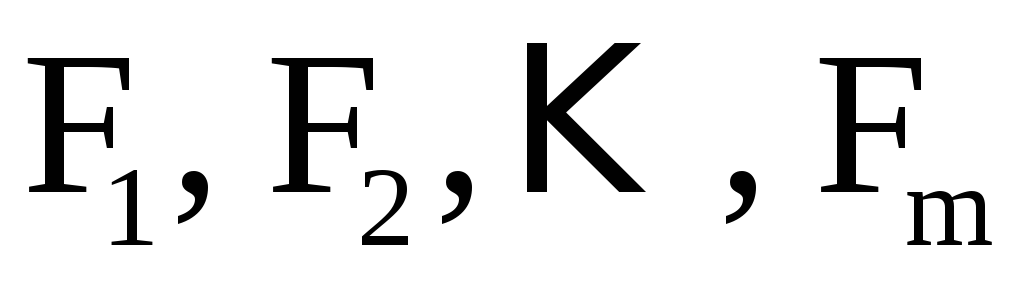 определены в области (D)
определены в области (D)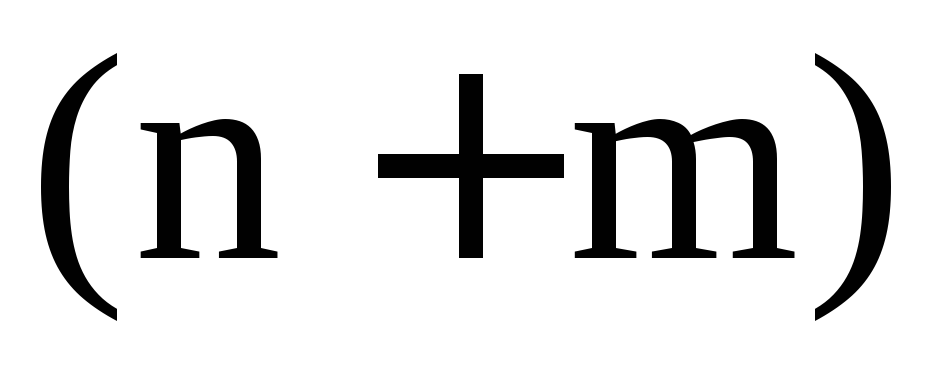 -мерного
пространства. Пусть
-мерного
пространства. Пусть –
проекция (D) на координатную плоскость
–
проекция (D) на координатную плоскость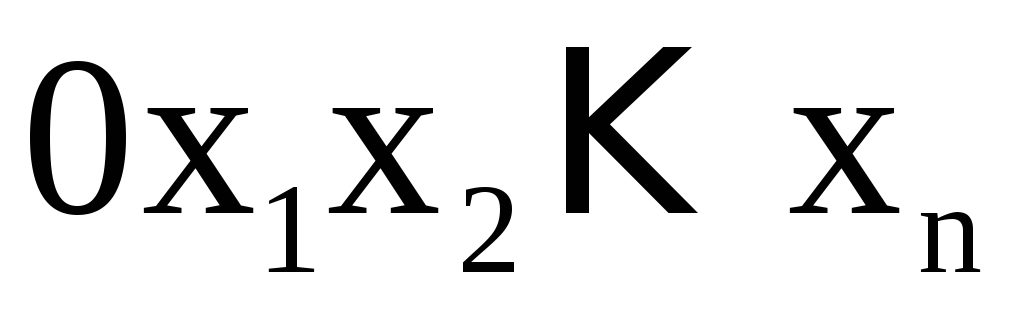 ,
(
,
( )
– проекция (D) на координатную плоскость
)
– проекция (D) на координатную плоскость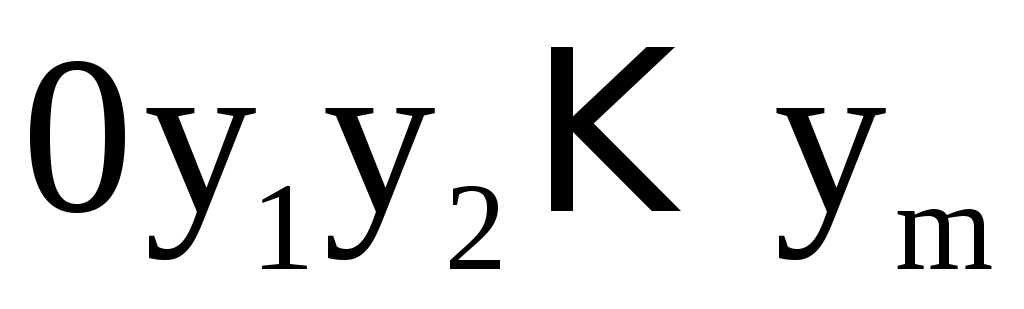 .
Если для любой точки
.
Если для любой точки система уравнений
система уравнений

имеет
единственное решение 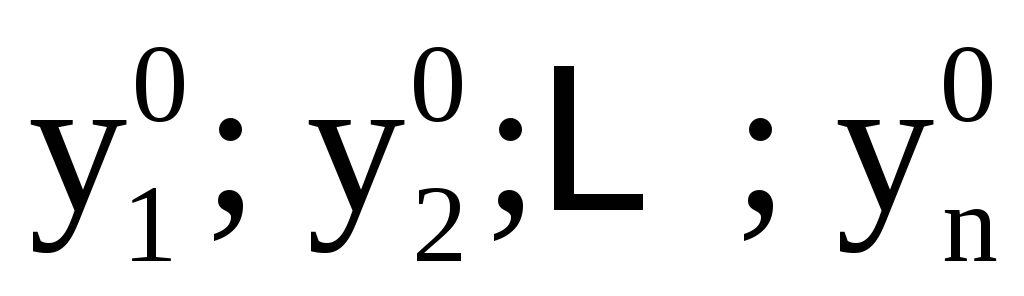 ,
такое что
,
такое что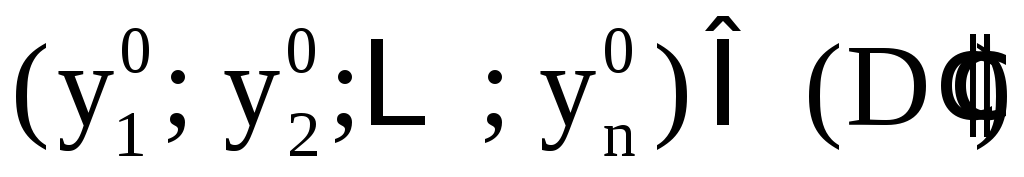 ,
то говорят, что система (4) задаёт неявные
функции
,
то говорят, что система (4) задаёт неявные
функции
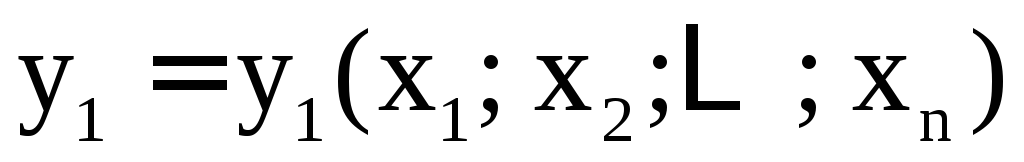 ,
, 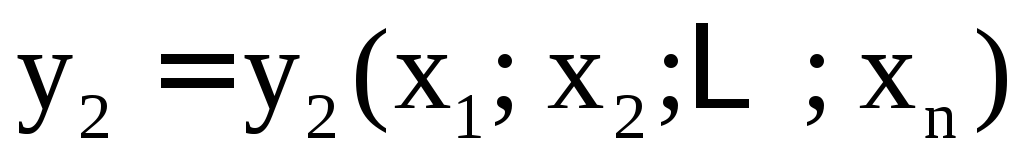 ,
…
,
…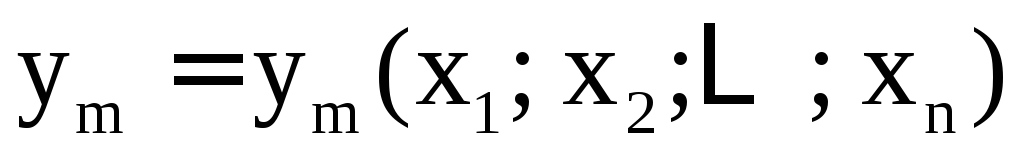 .
.
Решение системы
(4) относительно 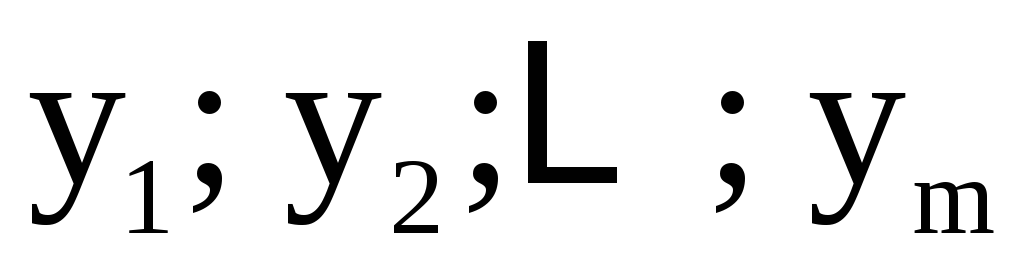 и является правилом задания функции:
каждому
и является правилом задания функции:
каждому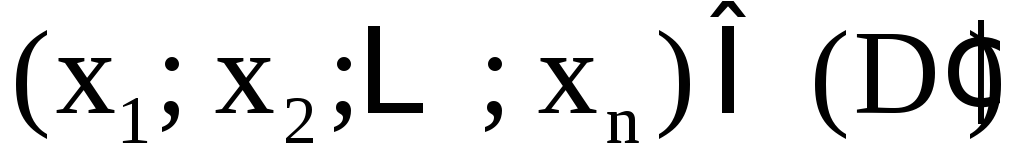 ставится в соответствие решение
ставится в соответствие решение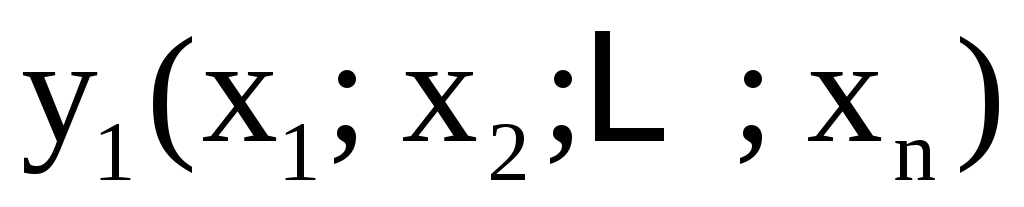 ,
,  ,…,
,…, 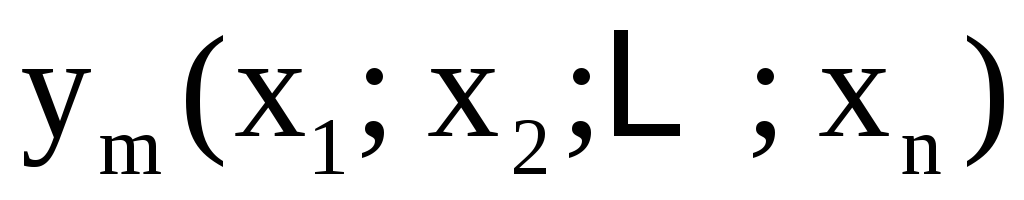 системы (4).
системы (4).
8. Экстремум функции многих переменных
Пусть функция  определена
в некоторой окрестности точки
определена
в некоторой окрестности точки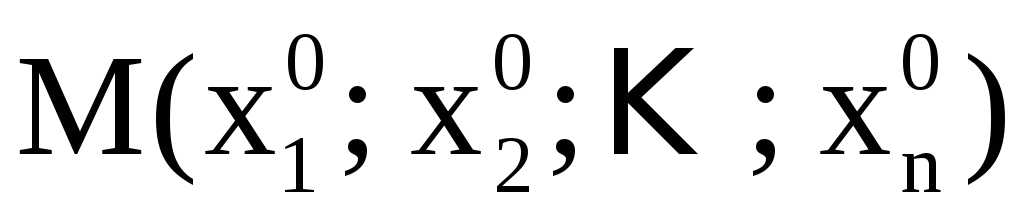 .
Говорят, что точка М является точкой
максимума (минимума) функции
.
Говорят, что точка М является точкой
максимума (минимума) функции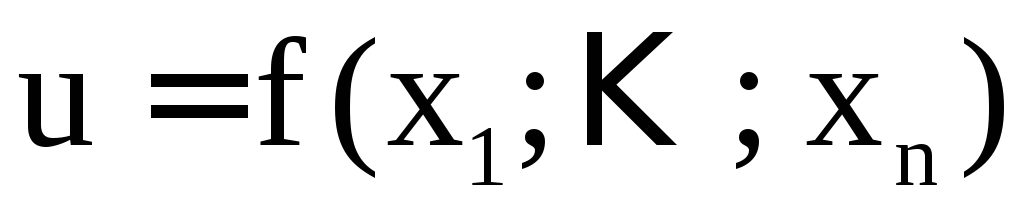 ,
если существует окрестность V точки М,
такая что для любой точки N из этой
окрестности V, отличной от точки М,
справедливо неравенство f(N) < f(M) (f(N) >
f(M)). Точки максимума и точки минимума
функции называют точками экстремума
функции, а значения функции в этих точках
– экстремумами функции.
,
если существует окрестность V точки М,
такая что для любой точки N из этой
окрестности V, отличной от точки М,
справедливо неравенство f(N) < f(M) (f(N) >
f(M)). Точки максимума и точки минимума
функции называют точками экстремума
функции, а значения функции в этих точках
– экстремумами функции.
Теорема 3
(необходимое условие экстремума). Если
М – точка экстремума дифференцируемой
функции  ,
то
,
то
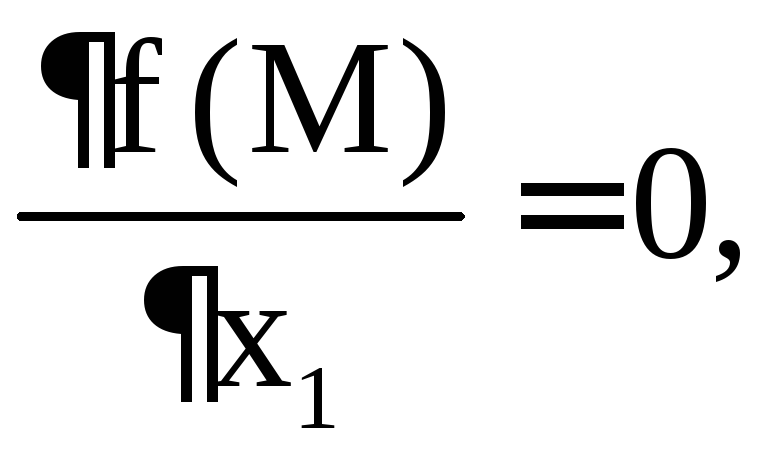
 .
. .
.
. . 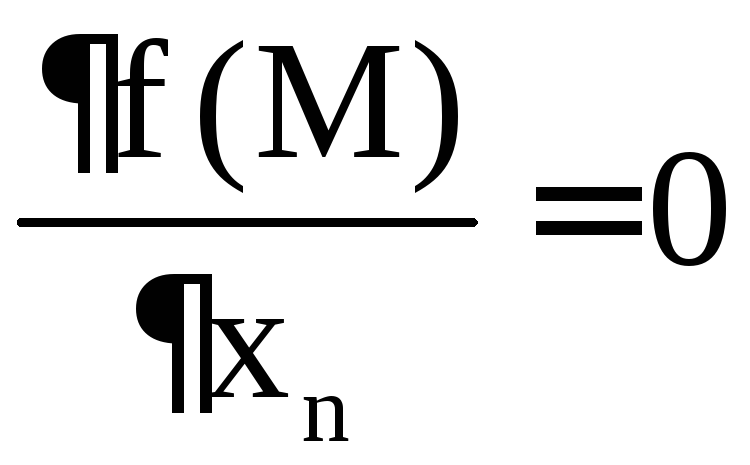 .
(5)
.
(5)
Точка М, в которой выполнены условия (5), называется стационарной точкой. Не любая стационарная точка функции является точкой экстремума. Cледующая ниже теорема даёт достаточное условие для того, чтобы стационарная точка функции двух переменных была точкой экстремума.
Теорема 4 (достаточное
условие экстремума для функции двух
переменных). Пусть 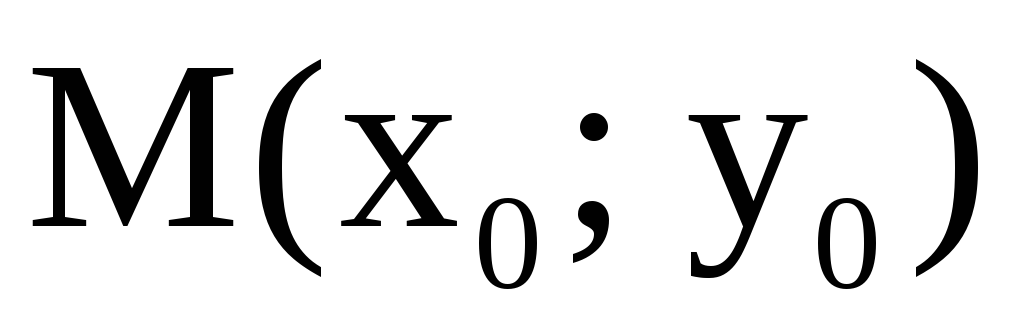 – стационарная точка функции двух
переменных u = f(x; y), дважды непрерывно
дифференцируемой в некоторой окрестности
точки М.
– стационарная точка функции двух
переменных u = f(x; y), дважды непрерывно
дифференцируемой в некоторой окрестности
точки М.
Рассмотрим определитель
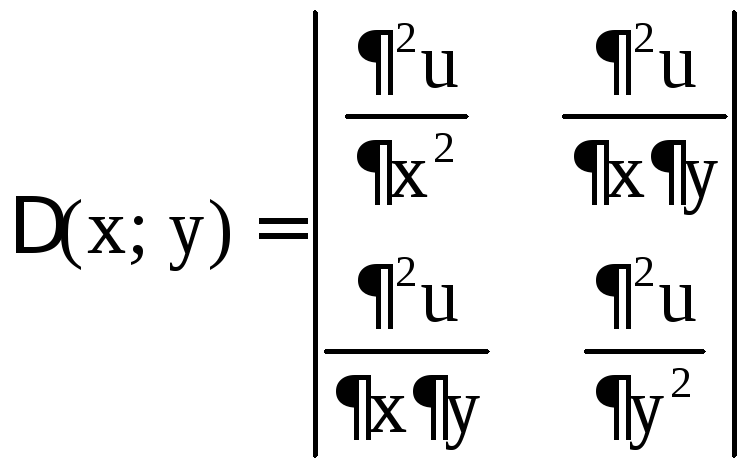 .
.
1) Если 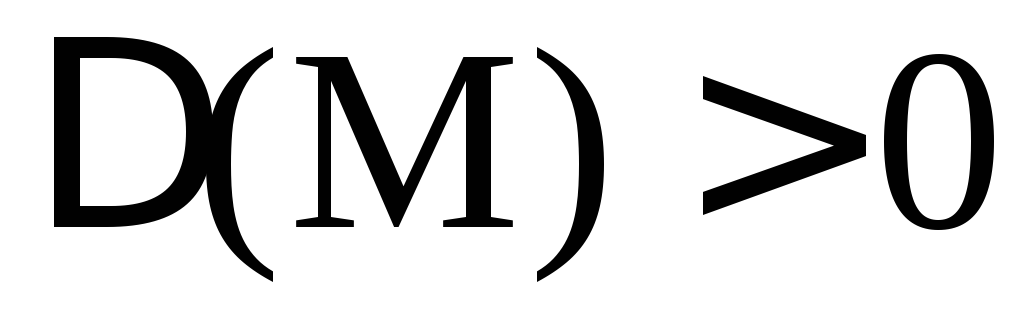 ,
то
,
то является точкой экстремума функции
u(x; y) = f(x; y), а именно: а) если
является точкой экстремума функции
u(x; y) = f(x; y), а именно: а) если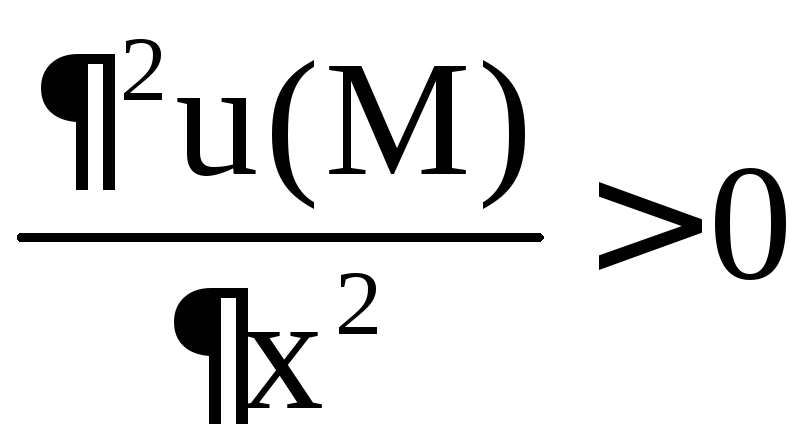 ,
то М – точка минимума; б) если
,
то М – точка минимума; б) если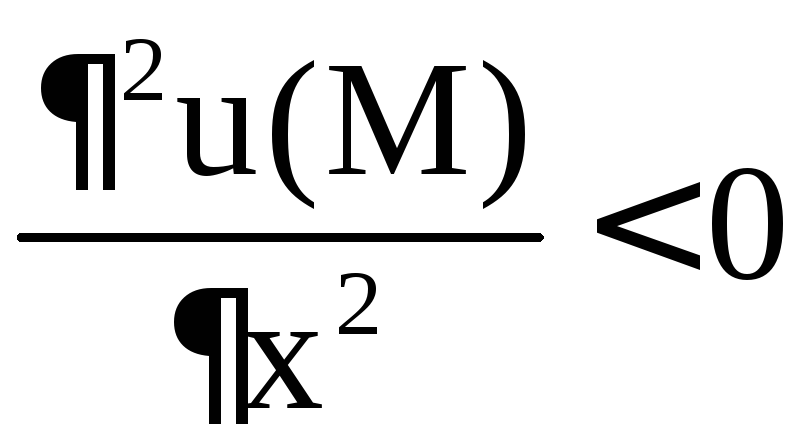 ,
то М – точка максимума.
,
то М – точка максимума.
2) Если 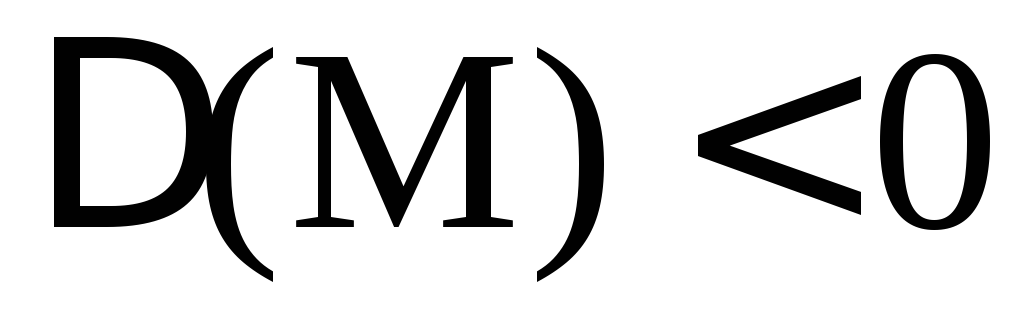 ,
то М не является точкой экстремума.
,
то М не является точкой экстремума.
Пример 11. Найти точки экстремума функции
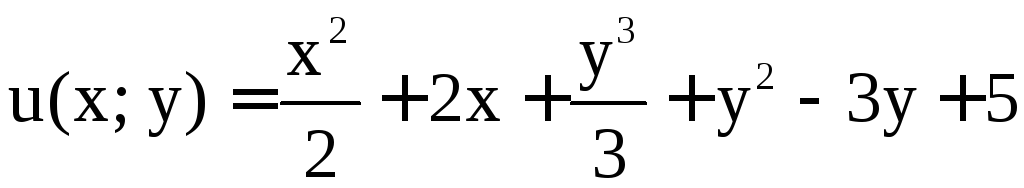 .
.
Решение. Найдём
стационарные точки функции 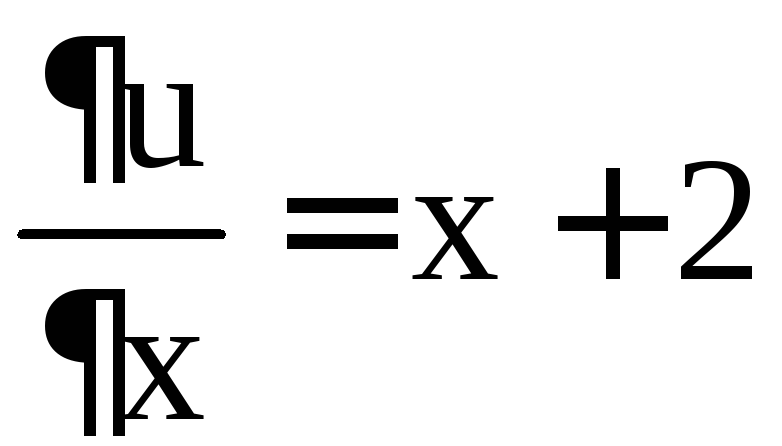 ,
,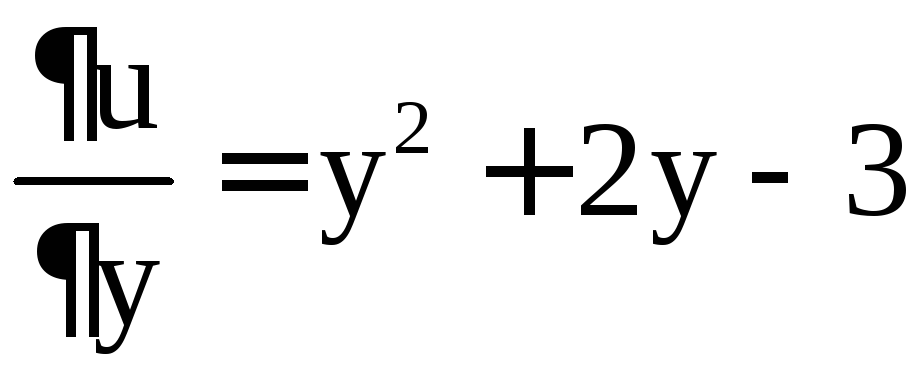 .
Решим систему уравнений
.
Решим систему уравнений

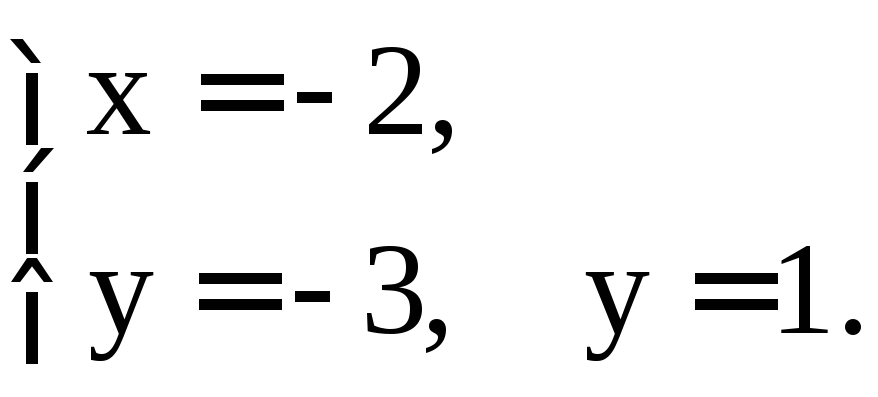
Решением системы являются точки M1(–2; –3), M2(–2; 1). Исследуем эти стационарные точки на экстремум, для чего найдём частные производные второго порядка:
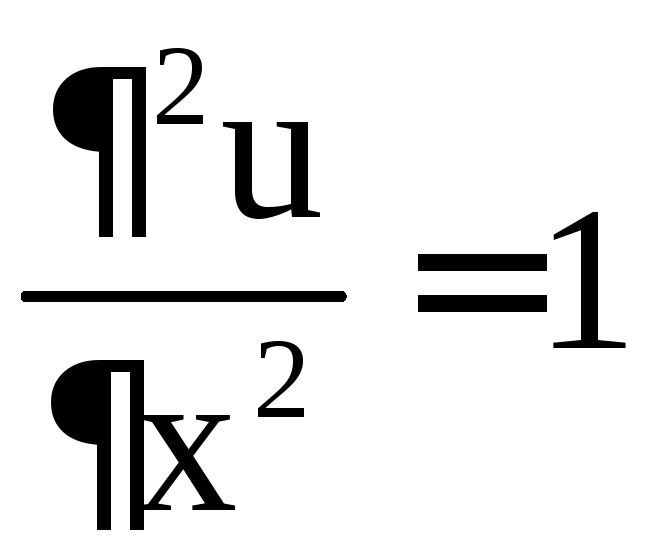 ,
, 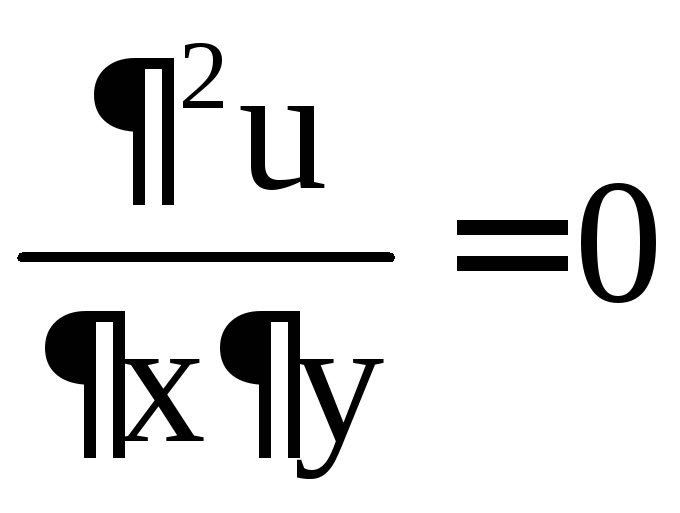 ,
,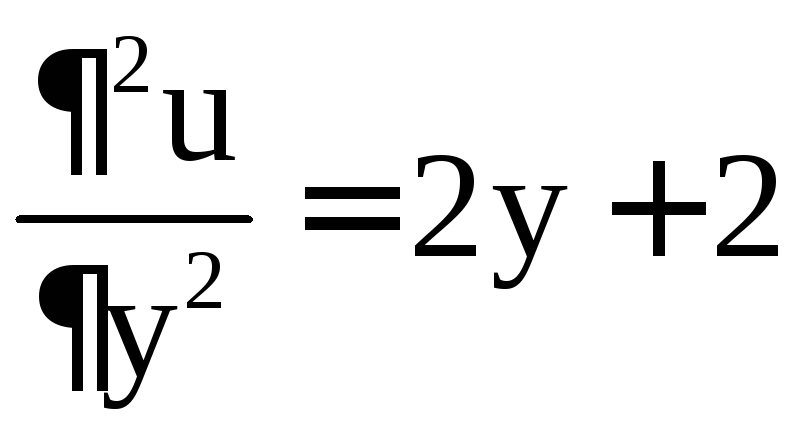 .
.
Имеем
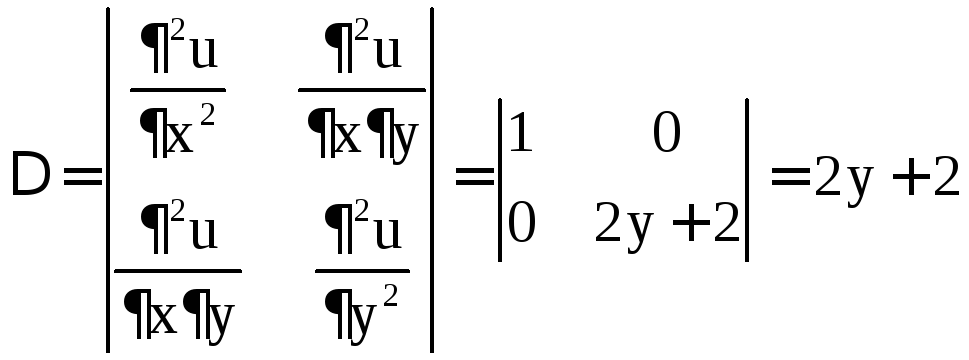 .
.
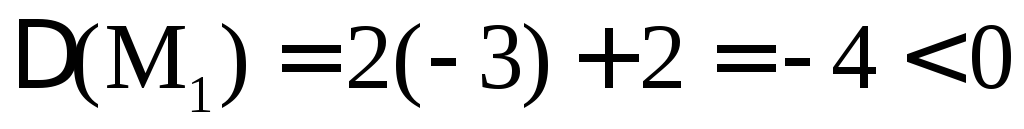 ,
следовательно, M1(–2;
–3) не является точкой экстремума.
,
следовательно, M1(–2;
–3) не является точкой экстремума.
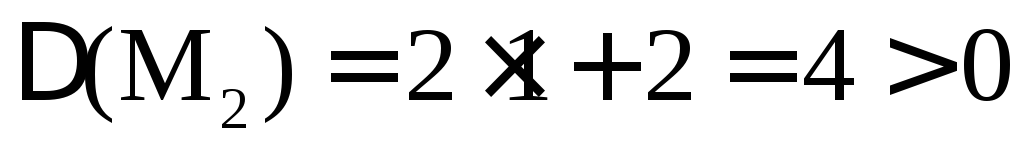 ,
что говорит о том, что M2(–2;
1) является точкой экстремума. А так как
,
что говорит о том, что M2(–2;
1) является точкой экстремума. А так как 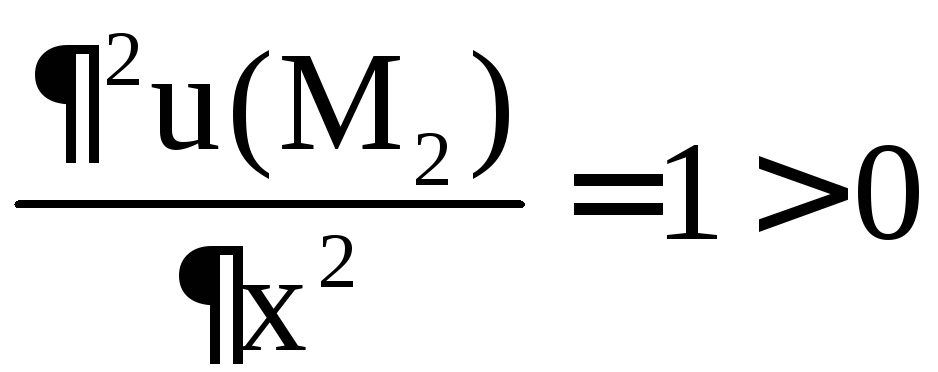 ,
то заключаем, что M2 – точка минимума.
,
то заключаем, что M2 – точка минимума.
Теорема 5
(достаточное условие экстремума для
функции трёх переменных). Пусть 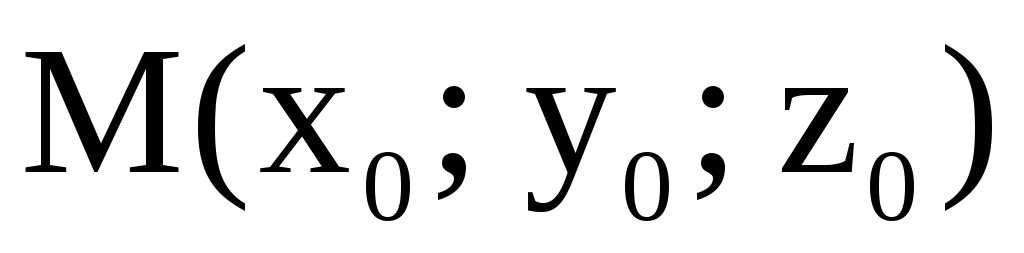 – стационарная точка функции
– стационарная точка функции
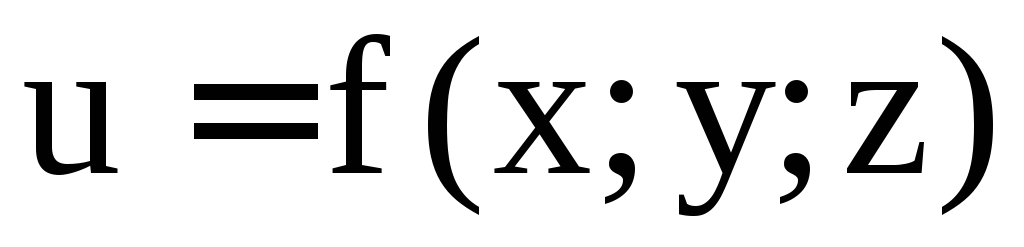 ,
дважды непрерывно дифференцируемой в
некоторой окрестности точки М. Рассмотрим
определители
,
дважды непрерывно дифференцируемой в
некоторой окрестности точки М. Рассмотрим
определители
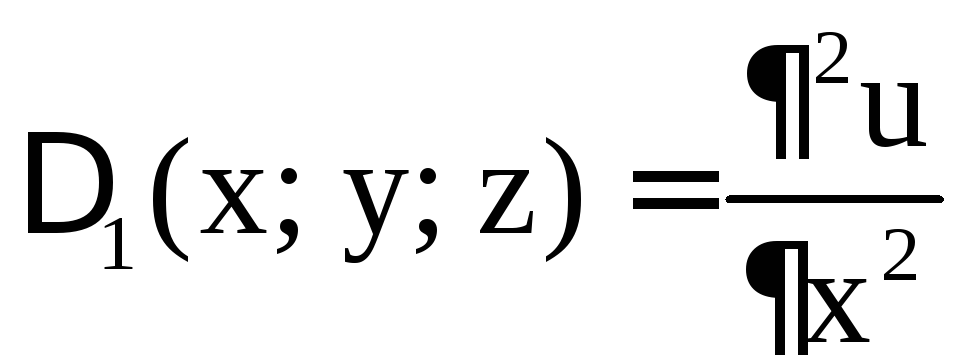 ,
, 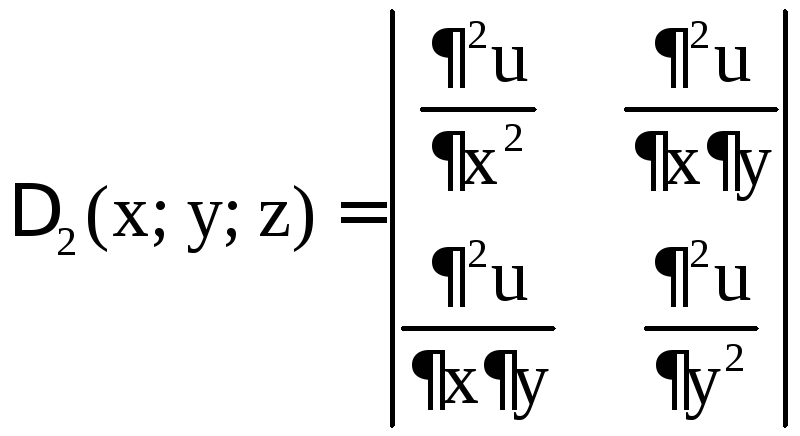 ,
,
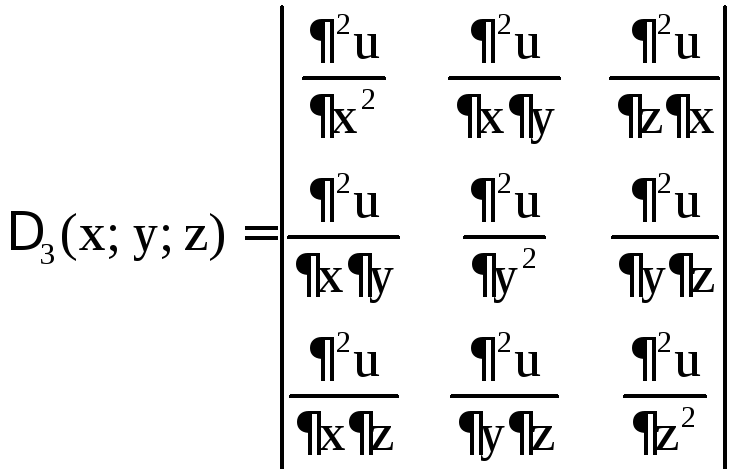 .
.
Пусть 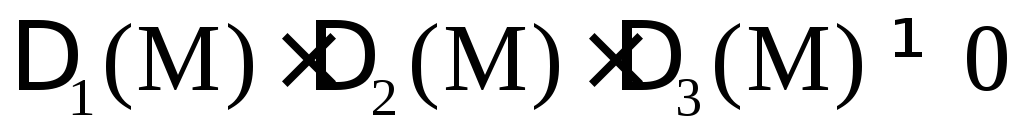 .
Тогда имеем:
.
Тогда имеем:
a) если 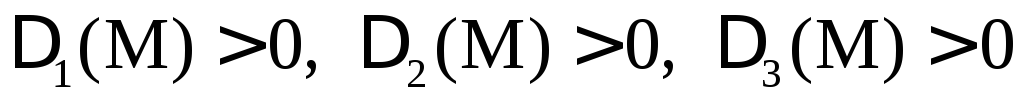 ,
то
,
то – точка минимума;
– точка минимума;
б) если 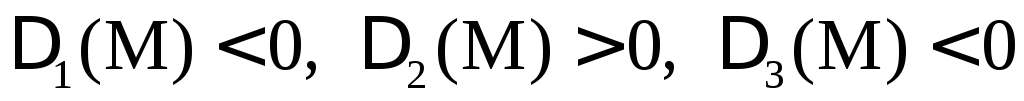 ,
то
,
то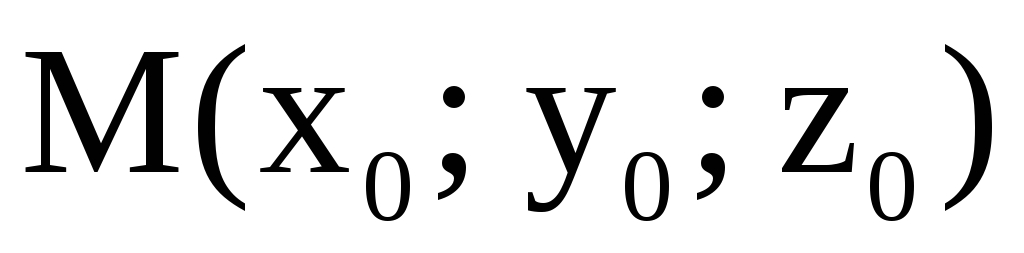 – точка максимума;
– точка максимума;
в) во всех
остальных случаях (при условии 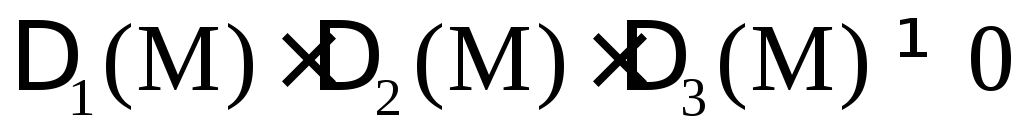 )
М не является точкой экстремума.
)
М не является точкой экстремума.
Пример 12. Найти точки экстремума функции
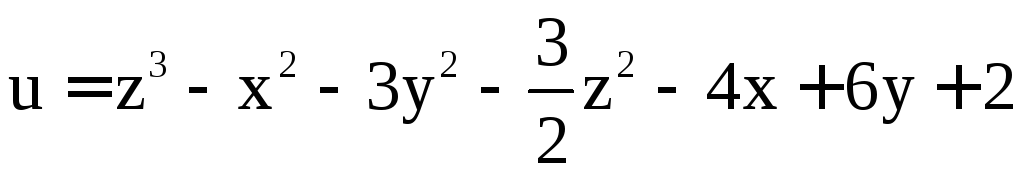 .
.
Решение. Найдём стационарные точки функции 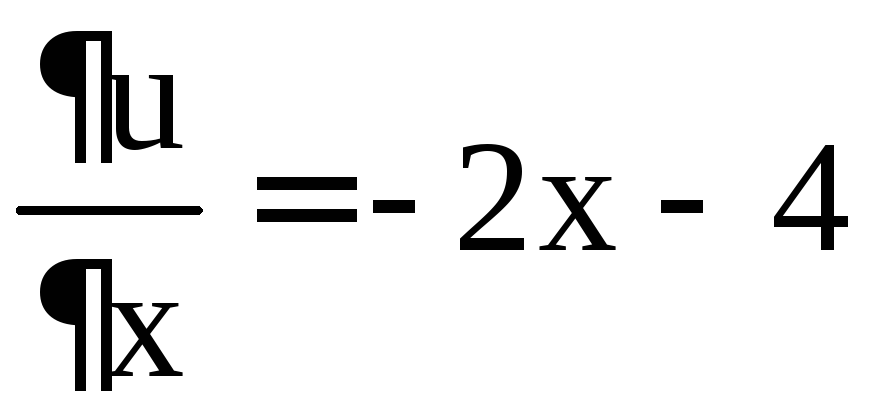 ,
,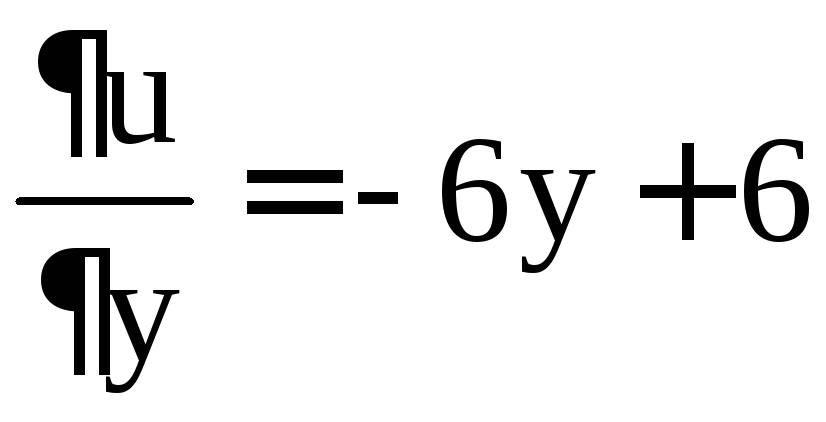 ,
,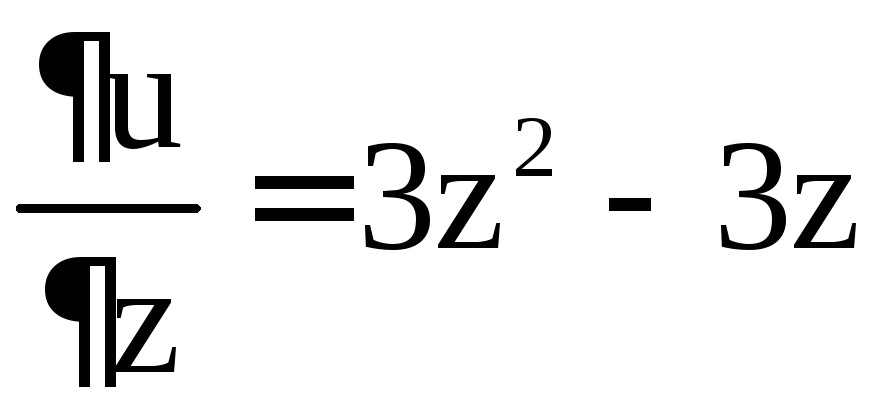 .
Решим систему уравнений
.
Решим систему уравнений
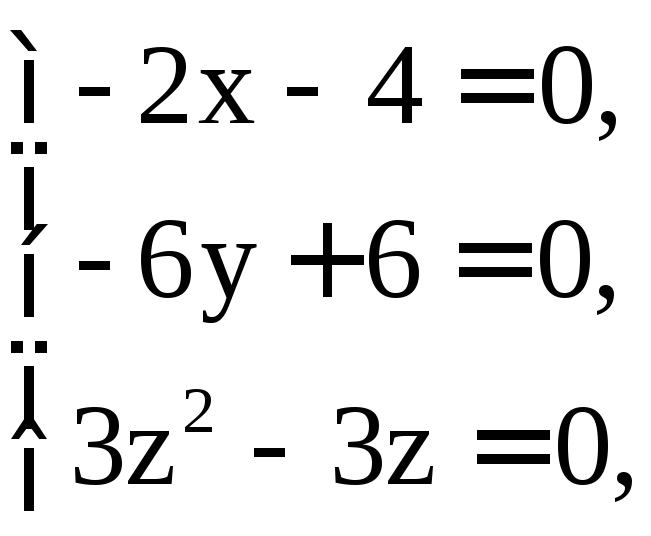

Решение этой системы приводит к двум стационарным точкам
M1(–2; 1; 0) и M2(–2; 1; 1). Проверим, являются ли эти точки точками экстремума.
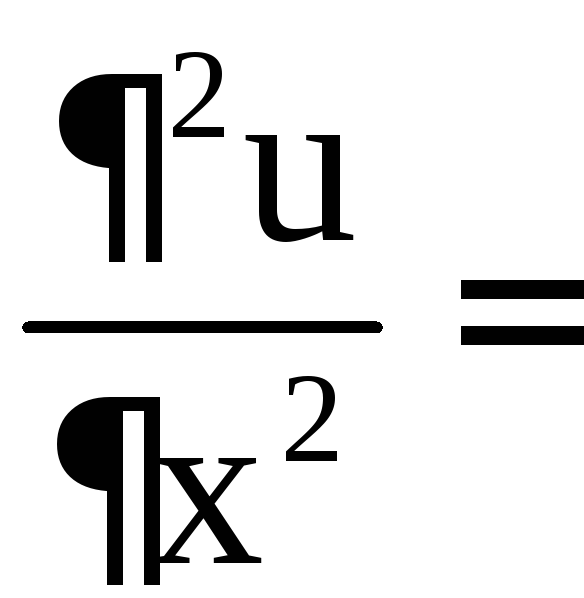 –2,
–2, 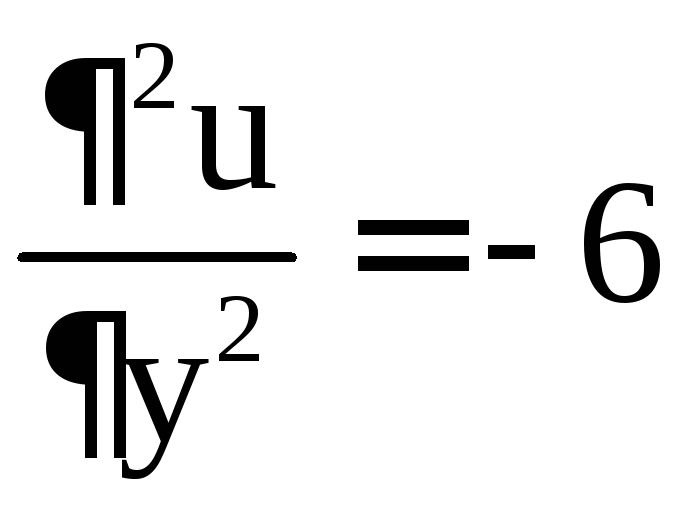 ,
,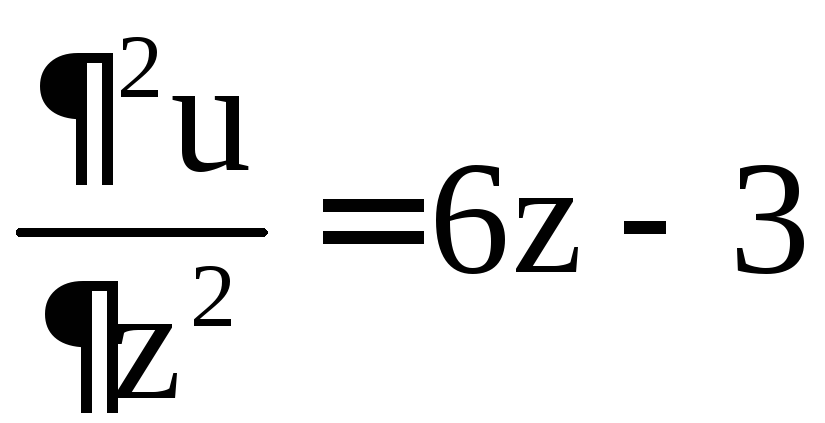 ,
,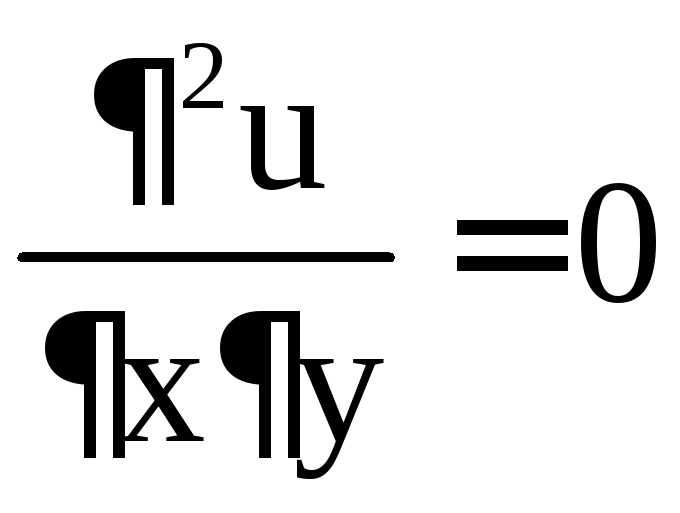 ,
,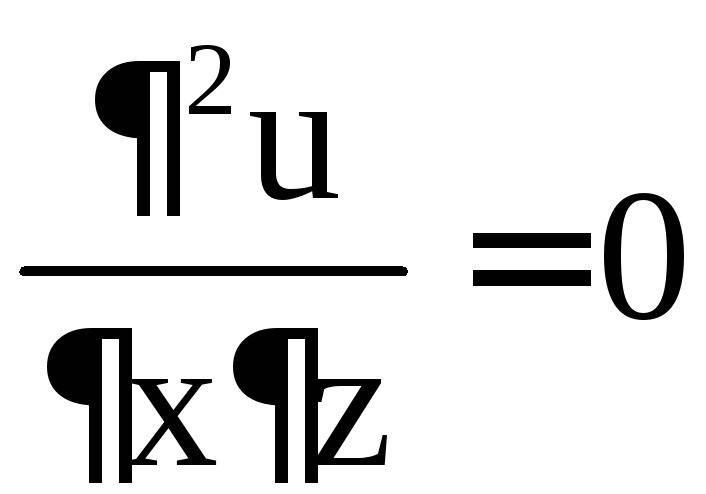 ,
,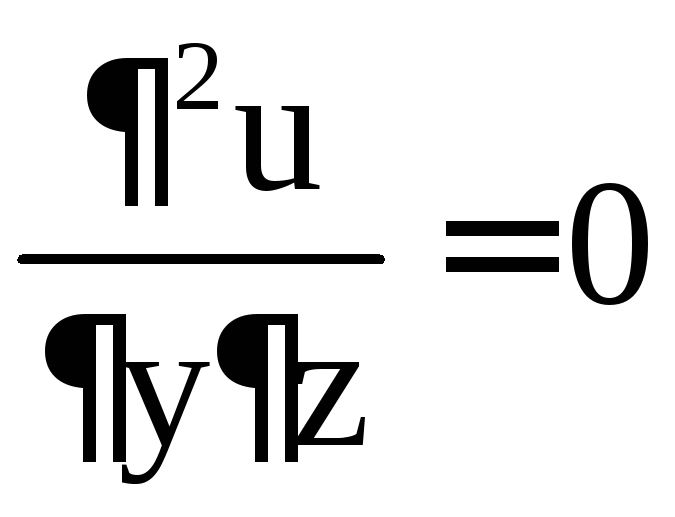 .
.
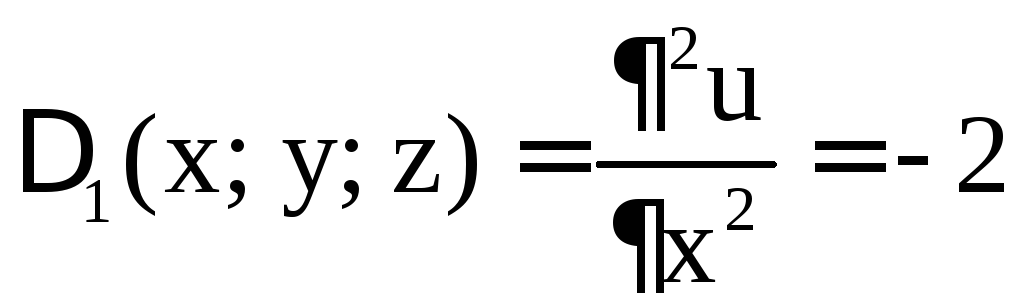 ,
, 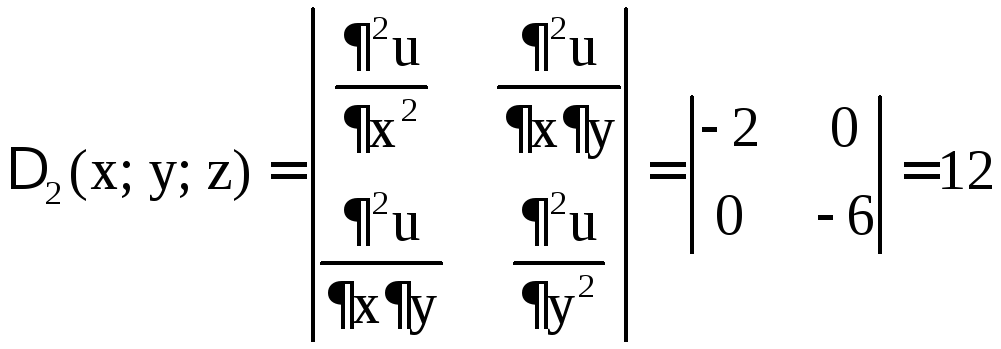 ,
,
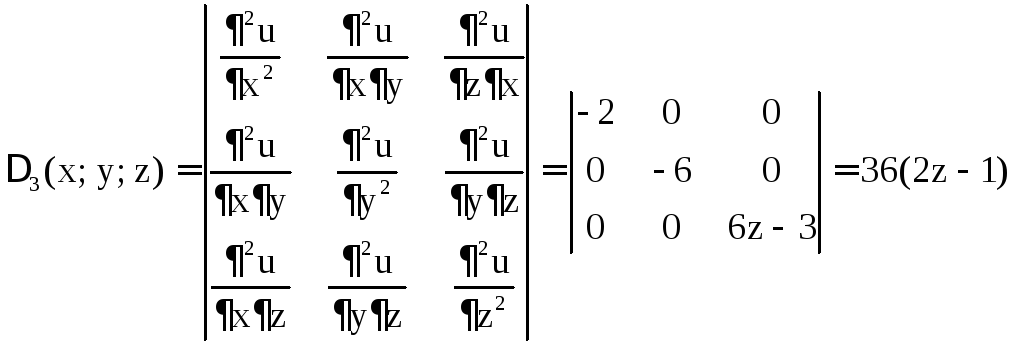 .
.
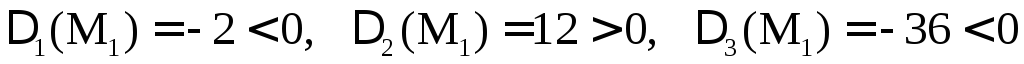 .
.
Следовательно,  является точкой максимума.
является точкой максимума.
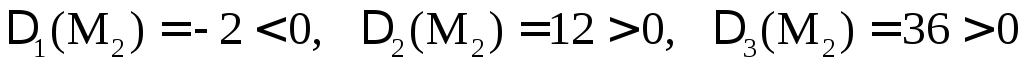 ,
что означает, что
,
что означает, что 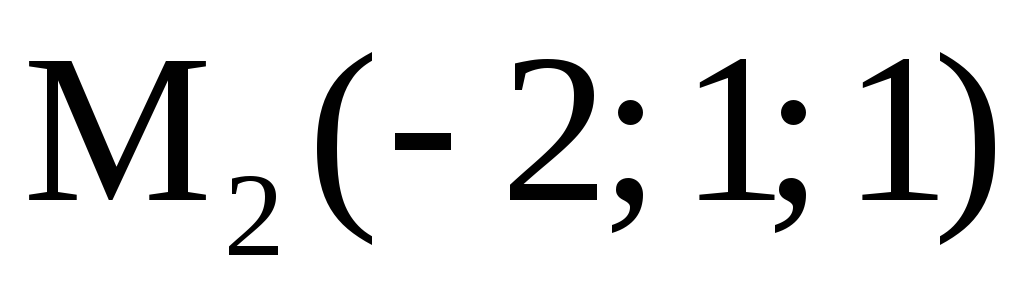 не является точкой экстремума.
не является точкой экстремума.
Аналог теоремы 5 справедлив и для функции u = f(x1; . . .; xn) n переменных, n > 3.
studfile.net